Note: Descriptions are shown in the official language in which they were submitted.
2 ~ 3~ 27371-174
The present invention relatès to a non-recursive half-band
fil-ter. Such fil-ters have become known from the paper titled
"Interpolation, Extrapolationl and Reduction of Computation Speed
in Digital Filters," by Bellanger et al., in IEEE Transactions
on Acoustics, Speech and Signal Processing, Vol. ASSP-22, No. 4,
August, 1974, pp. 231 et. seq.
The known half-band filters process real input signals into
real output signals.
It was the task of the present invention to provide a non-
recursive half-band filter that makes it possible to convert a
real input signal into a complex output signal, or vice versa, in
a less costly manner.
According to a broad aspect of the invention there is pro-
vided a non-recursive half-band filter with complex coefficients
for processing a real value input signal s(kT) by halving the
sampling frequency fA = l/T and for converting this real value
input signal s(kT) into a complex value output signal s(2kT),
wherein its complex coefficients _(l) with 1 = -(N-1)/2 -to (N-1)/2
and the unstraight filter length N, have alternating purely real
and purely imaginary values, therefore no complex values in the
fullest sense; wherein the impulse response of a half-band filter
h(l) with exclusively real values, with the characteristics h(l)
= h(-l) for all ¦11 < (N-1)/2 and h(l) = 0 for 1 = +2, +4, ....
is modulated onto the complex carrier of a frequency of + 1/4 of
the input sampling frequency fA = l/T to give h(l) = h(l) . ei
(_ lfA/4fA) ~ 0) = j_l . ei~ . h(l); and wherein the null
phase ~0 of this complex carrier is an integer multiple m of ~/2
( 0 = m. ~/2 with m = 0,1,2,3,...).
3 ~X~3~3~ 27371~174
According to another broad aspect of the invention there is
provided a non-recursive half-band filter with complex coefficients
for processing a complex value input signal s(2kT) and for doubl-
ing the sampling frequency fA' = 1/2T to fA =2fA' and to convert
this complex value input signal s(2kT) into a real value output
signal s(kT), wherein its complex coefficients h(l) with 1 = -
(N-1)/2 to (N-1)/2 and the unstraight filter length N have alter-
nating purely real and purely imaginary values, therefore no com-
plex values in the fullest sense; wherein the impulse response of
a half-band filter h(l) with exclusively real values, with the
characteristics h(l) = h(-l) for all~ (N-1)/2 and h(l) = 0 for
1 = +2, +4, ... , is modulated onto the complex carrier of a fre-
quency of + 1/4 of the input sampling frequency fA = l/T to give
h(l) = h(l) ej(+ 2~1fA/4fA~ + ~0) j+l e ~ h(l); and
wherein the null phase ~ 0 of this complex carrier is an integer
multiple m of ~/2 (~0 = m .~/2 with m = 0, 1, 2, 3, ...).
The non-recursive half-band filter according to the present
invention permits the conversion of real digital input signals
into complex digital output signals with a simultaneous reduction \
of the sampling frequency by a factor of two, or the conversion
of complex digital input signals into real digital output signals
with a simultaneous increase in the scanning frequency by a fac- /
tor of 2. This relatively inexpensive half-band filter is thus
suitable as a digital pre-filter or post-filter for digital sys-
tems that are used to process complex signals and as a digital
partial filter in a system of antialiasing filters for band lim-
iting whilst complying with the sampling theorem. The advantage
of the half-band filter lies in its linear phase and simultaneously
3a ~ 3~ 27371-174
low cost, whereby in each instance the slnallest possible sampling
frequency required on the basis of the sampling theorem can be
used.
The following description is based on the figures appendad
hereto.
Figure 1 is the block circuit diagram for the digital filter
according to the present invention.
In figures 2a to 2c, several amplitude responses of half-
band filters are plotted over frequency.
Figures 3 and 4 show particularly favourable circuit varia-
tions of the half-band filter.
Figure 5 is the block circuit diagra~ of a half-band filte~
used to process a complex input signal into a real output signal.
Figure 6 is a detailed circuit of the filter shown in figure
5, this circuit having been developed from that in figure 3 by
transposition, i.e., by reversing all the directions indicated
by the arrows and r~placing a branching switch by an adder and
vice versa, and by replacing of a demultiplexer by a multiplexer.
The circuit shown in figure 7 resulted from that in figure
4 in a like manner.
4 1~ 3~'~
In figure 1, the real input signal s(kT) is applied to the
half-band filter DF by halving the sampling rate, which
generates the complex output signal s(2kT).
The amplitude frequency response of a prototype half-band
filter is shown in figure 2a; the pass band of this extends from
-fA/4 + Q f to -~fA/4 - d f, and its stop band is also fA/2 - 2 ~ f
wide. It is also characteristic of the half-band filter that
the transition from the stop-band to the pass-band is constant
and takes place at a width of 2 ~ f. This transmission band is
symmetrical about fA/4. A further characteristic of the half-
band filter is that its ripple in the transmission and the stop
band is squal, i.e., ~1 = v2 = ~. In such a filter there is a
impulse response h(l) with 1 = o to N-l for the unstraight
filter length N, and it follows that each second value is
identically zero, with the exception of the central main value
(see figure 2, p. 233 in the paper by Bellanger et al that is
cited above). Figure 2b shows the frequency range ¦H¦. It can
be seen that this frequency range has been shifted to the right
to a point around the frequency fA/4 relative to the frequency
range of the prototype half~band filter. In addition, in figure
2b the spectrum ¦S¦ of a real input signal s(kT) sampled at the
sampling frequency fA has been inserted; because of the sampling
with fA this repeats periodically in the frequency range
[m.fA, (m+l/2).fA] in the normal position and in the frequency
range [(m+l/2)0fA, (m~l).fA)] in the inverted position with
m = ~ 1, O, +1... 0 The input signal s(kT), applied to the
5 ~ z~3~3~3~
llf-band filter according to the present invention without any
change in the sampling rate, would thus suppress the inverted
position between fA/2 and fA, and naturally with all
repetitions, and also generate a complex signal s~kT). Halving
the sampling rate now results in the dasired spectra, with the
normal position being repeated in each instance in the raster
of fA/2 = fA', thus in the new sampling rate; see figure 2c.
At this point, it should be noted that a complex signal is
obtained at the output of the half-band filter if the frequency
range of the prototype half-band filter according to figure 2a
is shifted by -fA/4 or, aquivalently, by +3fA/~.
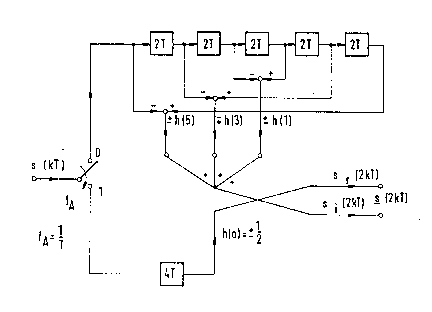
Figure 3 now shows a detailed embodiment of a half-band
filter according to the present invention. First, however, with
reference to figure 2, it should be stated that the halving of
the sampling rate is only carried out after filtering. This
sequence for the process as in figure 2 should to be adhered to
strictly; according to the invention, however, the half-band
filter can be divided into two halves, each of which is supplied
from the start with every second sample of the input signal.
This means nothing else, however, than that the halving of the
sampling rate can take place directly at the filter in pu~, as
is shown in the block schematic diagram in figure 1.
Accordingly, the detailed circuits in figures 3 and 4
incorporate an input-side demultiplexer switch which supplies,
on the one hand, the upper branch, and on the other, the lower
~2B13~3~
~anch with the input signal s(kT), in each instance in time at
the sampling rate fA' = fA/2.
Both figure 3 and figure 4 show, as an example, a
realisation for a filter length of N = 11. Accordingly, the
lower branch incorporates a delay element of the time delay
(N-3).T/2 = 4T, whereas the upper branch incorporates a chain of
five delay elements of time delay 2T. Fi~ure 3 shows two
realisations, namely, for a modulation phase angle ~ O = O and
~o = ~ for m = O and m = 2, respectively.
The output signal of the delay element of the lower ~ranch
is weighted (multiplied) at h(5) = 1/2 (multiplied) and thus
yields the imaginary portion si(2kT) of the output signal. At m
= 2, this is weighted at -1/2. The further processing of the
upper branch now takes place such that (N+~)/4, i.e., three
differential signals are formed:
The first differential signal equals the input signal of the
first, minus the ouput signal of the last delay element;
The second differential signal equals the lnput signal of the
second, minus the output signal of the second last delay
element;
The third differential signal equals the input signal of the
third, minus the output signal of the third last, which is to
say, the middle delay element.
Next, these differential signals are weighted ~multiplied),
and summed and thereby yield the real component of the output
7 ~ 313~3~
c;gnal s(2kT). The weighting is effected according to the
following tables.
Examples for N=ll and ht-l) = h(l) for 1 = o, 1, ...5,
according to the prototype half-band filter according to the
frequency range in figure 2a:
Table 1:
m=O (m=2 with in each instance a changed sign of the complex
coefficients h = Ra(h)+jJm(h))
1 -5 -3 -1 0 1 3 5
Re(h) O O O h(O) 0 0 0
Jm(h) -h(5) h(3) -h(l) h(l) -h(3) h~5)
Table 2:
m=1 (m=3 with in each instance a changed sign of the complex
coefficients)
1 -5 -3 -1 0 1 3 5
Re(h) h(5)-h(3) h(l) -h(l) h(3) -h(5)
... . . ....
Jm(h) O h(O) O O O
The realisation as in figure 4 takes place in the same
manner as in the one shown in figure 3; the sole difference is
in the other null phase value ~0 = m .Tr/~ with m = 1 and 3, the
~ly consequences of which are a diffe~rent welghting and an
exchange of the filter branch outputs.
Figure 5 shows the block schematic diagram for the reversed
use of the half-band filter as in figure 1, namely, for the
generation of a real output signal from a complex input signal.
To this end, there must be a transposition of the circuit shown
above, which results in a reversal of the directions of all the
arrows and the replacement of a branch by an adder, and vice
versa, as well as the replacement of a demultiplexer by a
multiplexer. In a similar manner, the example circuit in
figure 6 is derived from figure 3, and the circuit in figure 7
is derived from that in figure 4.