Note: Descriptions are shown in the official language in which they were submitted.
13~ 3
12~2V
~artial Response Channel Si~nalin~ SYstems
Backqround of the Invention
This invention relates to modulation coding and
s partial response systems
In modulation coding, symbols are encoded as
signals drawn from a constellation in such a way that
only certain seguences of signals are possible.
In recent years, a number of kinds of
tr~llis-type modulation codes have been developed and
applied (e.g., in modems) to realize coding gains of 3
to 6 dB over high-signal-to-noise-ratio, band-limited
channels such as voice grade telephone channels.
Early trallis codes were due to Ungerboeck
(Cjsaka et al., U.S. Patent No. 3,877,768; Ungerboeck,
"Channel Coding with Multilevel/Phase Signals," IEEE
Transactions on Information Theory, Vol. IT-28, pp.
55-67, January, 1982). Ungerboeck's codes for sending n
bits per symbol are based on 4-subset or 8-subset
partitions of one-dimensional (PAM) or two-dimensional
(QAM) 2n+l-point signal constellations, combined with
a rate-l/2 or rate-2~3 linear binary convolutional code
that dQterminQs a sQquence of subsets. A further set of
"uncoded" bits then determines which signal points
25 within the specified subsets are actually sent. The
partition and the code are designed to guarantee a
certain minimum squared distance d2in between
permissible sequences of signal points. Even after
giving effect to the power cost of~an expanded signal
constellation (a factor of four (6 da) in one dimension,
or a factor of two ~3 dB) in two dimensions), the
increase in minimum squared distance yields a coding
:13~6~'~3
2 6041~172
gain that ranges from about a factor of two (3 dB~ for simple
codes up to a factor of four (6 dB) for the most complicated
codes, for values of n that may be as large as desired.
Gallager Canadian Patent Application S.N. 473,150
discussed in Forney et al, "Efficient Modulation for ~and-Limited
Channels," IEEE J. Select. Areas Commun., Vol. SAC-2, ~pp. 632-
647, 1984) devised a multidimensional trellis code based on a 1~-
subset partition of a four--dimensional signal constellation,
combined with a rate-3/4 convolutional code. The four-dimensional
subset is determined by selectiny a pair of two-dimensional
subsets, and the points of the four-dimensional signal
constellation are made up of pairs of points from a two-
dimensional signa7 constellation. With only an 8-state code, a
d2min of four times the uncoded minimum sequence diætance can be
obtained, while the loss due to expanding the signal constellation
can be reduced to about a factor of 21/2 (1.5 dB), yielding a net
coding gain of the order of 4.5 dB. A similar code was designed
by Calderbank and Sloane ("Four-dimensional Modulation With an
Eight-State Trellis Code", AT&T Tech. J., Vol. 64, pp. 1005-1018,
1985 U.S. Patent No. 4,581,601).
Wei Canadian Patent Application S.N. 504,573, now issued
as Canadian Patent No. 1,248,182 devised a number of
multidimensional codes based on partitions of constellations in
four, eight, and sixteen dimensions, combined with rate-(n-1)/n
convolutional codes. His multidimensional constellations again
consist of sequences of points from two-dimensional constituent
constellations. The codes are designed to minimize two-
dimensional constellation expansion, to obtain
pr ~
13~1651~3
performance (coding gain) versus code complexity over a
broad range, and for other advantages such as
transparency t,o phase rotations. Calderbank and Sloane,
"New Trellis Codes", IEEE Trans. Inf. TheorY~ to appear
5 .~arch, 1987, "An Elghc-dimensional Trellis Code," Proc.
IrrE, Vol. 74, pp. 757-759, 19~6 have also devised a
variety of multidimensional trellis codes, generally
with similar performance versus complexity, more
constella~ion expansion, but in some cases fewer states,
lQ All of the above codes are designed for
channels in which the principal impairment (apart from
phase rotations~ is noise, and in particular for
channels with no intersymbol interference. The implicit
assumption is that any intersymbol interference
introduced by the actual channel will be reduced to a
negligible level by transmit and receive filters; or,
more specifically, by an adaptive linear equalizer in
the receiver. Such a system is known to work well if
the actual channel does not have severe attenuation
20 within the transmission bandwidth, but in the case of
severe attenuation ("nulls" or "near nulls") the noise
power may be strongly amplified in the equalizer ("noise
enhancement").
A well-known technique for avoiding such "noise
enhancement" is to design the signaling system for
controlled intersymbol interference rather than no
intersymbol interference. The best-known schemes o
this type are called "partial response" signaling
schemes 5Forney, "Maximum Likelihood Sequence Estimation
of Digital Se~uences in th~ Presence of Intersymbol
Interference," IEEE Trans. Inform. TheorY, Vol. IT-18,
pp. 363 3?~ 1972).
In a typical (one-dimensional) partial response
scheme, the desired output Yk at the receiver is
designed to be the difference of two successive inputs
x~, i.e., y~ = xk - xk_l, rather than Yk =
x~. In sampled-data notation usi~g tAe delay opera.or
D, this means that the ~esired ou~put sequence y~3)
equals x(D)(l-D) rather than x(D); this is t~us called a
~l-D" partial response system. Because the spectrum of
a discrete-tims channel with impulse response l-D has a
null at zero frequency (DC~, the combination of the
transmit and receive filters with the actual channel
likewise must hav~ a DC null to achieve this desired
response, On a channel which has a null or a near null
at DC, a receive equalizer designed for a l-D desired
response will introduce less noise enhancement than one
designed to produce a perfect (no intersymbol
interference) response,
Partial response signaling is also used to
achieve other objectives, such as reducing sens~tivity
to channel impairments near the band ed~e, easing
filtering requirements, allowing for pilot tones at the
band edge, or reducing adjacent-channel interference in
frequency~division multiplexed systems.
Other types of partial response systems include
a l+D system which has a null at the Nyquist band edge,
and a l-D system which has nulls at both DC and the
Nyquist band edge. A quadrature (two-dimensional)
partial responsQ system (QPRS) can be modeled as having
a two-dimensional complex input; the ~complex) response
l+D results in a QPRS-~system which has nulls at both the
upper and lower band edges in a carrier-modulated (QAM)
bandpass system. All of thesQ partial responsQ systems
are closely related to one another, and schemes for one
~3S~5'~3
are easily adapted to another, so one can design a
system for the 1-D response, say, and easily extend it
to the others.
Calderbank, Lee, and Mazo ("Baseband Trellis
Codes ~ith A Spec~ral ~ull at Zero"; submitzed to I~EE
~rans. Inf. Theory) have proposed a scheme to construc~
trellis-coded sequences that hav~ spectral nulls,
particularly at DC, a problem that is related tG the
design of partial response systems, even though its
lo objectives are in general somewhat different.
Calderbank et al. have adapted known multidimensional
trellis codes with multidimensional signal
constellations to produce signal sequences with spectral
nulls by the following technique, The multidimensional
signal constellation has twice as many signal points as
are necessary for the non-partial-response case, and is
divided into two equal size disjoint subsets, one of
multidimensional signal points whose sum of coordinates
is less than or equal to zero, the other whose sum is
2a greater than or equal to zero. A "running digital sum'`
(RDS) of coordinates, initially set to zero, is adjusted
for each selected multidimensional signal point by the
sum of its coordinates. If the current RDS is
nonnegative, then the current signal point is chosen
25 from the signal subset whose coordinate sums are less
than or equal to 2ero; if the RDS is negative, then the
current signal point is chosen from the other subset.
In this way the RDS is kept bounded in a narrow range
near zero, which is known to force the signal sequence
3Q to have a spectral~null at DC. At the same time,
however, the signal points are otherwise chosen from the
subsets in the same way as they would have been in a
non-partial-responsa system: the expanded
1306S43
-- 6 --
multidimensional constellation is divided into a certain
number of subsets with favorable distance properties,
and a rate-(n-l)/n convolutional code determines a
sequence of the subsets such that the minimum squared
5 distance between sequences is ~uaran~eed ~o be at least
dmin. The coding gain is reduced by ~lae
constellation doubling (by a factor of 21/2, or 1.5
da~ in four dimensions, or by a factor of 2 1/4, or
0.75 dB in eight), but otnerwise similar performance is
achieved as in the non-partial response case with
similar code complexity.
Summar~ of the Invention
One general feature of the invention is
generatin~ a sequence of digital signals xk and/or a
sequence of digital signals y~ ~the sequence Yk
being in accord with a given modulation code), k - 1,
2, ..., such that the relationship between the xk
signals and Yk signals is Yk = Xk ~ Xk L' ~
an integer. An encoder selects J signals Yk, J > 1,
~Yk~ Yk+l' Yk+J_l) to be congruent to a
sequence of J coset representatives c~ (modulo M), M
an integer, specified in accordance with the given
modulation code, the J symbols being chosen from one of
a plurality of J-dimensional constellations, the choice
be~ng based on a previous xk " k' ~ k. At least one
of the constellations includes both a point with a
positive sum of coordinates, and another point with a
negative sum of coordinates. The encoder is arranged so
that the signals x~ have finite variance Sx.
Another general feature of the invention is
that the encoder selects the signals xk to be
congruent to a sequence of alternative coset
representatives CX (modulo M), where
~3(~
-- 7 --
Ck = Ck ~ C'k L ~modulo M), in the
case where
Yk Xk + Xk_L,
cl~ = c~ + c'~_~ (modulo M), in the
case where
Yk = Xk ~ ~k-L
Another general feature of the inven~ion is
that the Yk signals fall within an alphabet of
possible Yk signals that are spaced apart within the
alphabet evenly by a spacing ~, and the encoder causes
the sequence Yk to have a variance Sy less than
2So and the sequence xk to have a variance Sx not
much greater than Sy/4(Sy - S0), S0 being
approximately the minimum signal power required to
represent n bits per signal with a ~-spaced alphabet.
Another general feature of the invention is
that the encoder causes the xk and Yk signals to
have any selected variances Sx and Sy within
pxedetermined ranges.
In preferred embodiments, the ranges are
controlled by a parameter ~, Sx is approximately
So/(l _ ~2), and Sy is approximately 2So/~l + ~).
Another general feature of the invention is
apparatu~ for generating a sequence in a given
N-dimenslonal modulation code, by generating a sequence
o~ one-dimensional signals based on coded and uncoded
bits, the modulation code being based on an
N-dimensional constellatîon partitioned into subsets
associated with the code, the subsets each representing
a plurali~y of N-dimensional signals, the apparatu
comprisinq an encoder for deriving, for each
N-dimensional symbol, a set of N, M-valued
one-dimensional coset representatives ck corresponding
to congruence classes of each of the N coordinates
~3~65~3
-- 8 --
(modulo M) of the symbol, each coset representative
designating a subset of one-dimensional values in a
one-dimensional constellation of possible coordinate
values for each of the N dimensions, each
one-dimensional signal in the seq~er.ce ~ei.~ ~elec ed
from the possible coordinate values based on uncoded
bits.
In preferred embodiments, either the xk or
Yk sequence may be delivered as an output; L = l;
Yk = Xk ~ Xk-L; the code may be a trellis code or
a lattice code; M may be 2 or 4 or a multiple of 4 or 2
+ 2i; J may be 1 or the same as the number of dimensions
: in the modulation code; k' = k - l; J is 1 and each
constellation is a one-dimensional range of values
centered on ~xk 1' < B < 1, preferably n, o; there
are a finite set of (e.g., two non-disjoint)
J-dimensional constellations; Yk and xk may be real
valued or complex valued.
Another general feature is a decoder for
decoding a sequence Zk = Yk + nk~ k = 1~2~
into a decoded sequence Yk, where the sequence of
signals Yk is such that ~a) the sequence is from a
given modulation code: (b) the running digital sum
X Y~ + Yk_l + Yk_2 + -- has finite variance
Sx; (c) the signals Yk fall in a predetermined
permissible range dependent on Xk, k' < k; and the
sequence nk represents noise. A range violation
monitor reconstructs the estimated running digital sum
Xk Yx +~Yk-l + - ~ compares the decoded
seque~ce Yk with a predetermined permissibla range
~ased on the estimated running digital sum x~, k' <
k, and generates an indication whenever the Yk is
outside the permissible range.
1306~3
9 ~0412-1723
~ nother general feature of the inventlon 1~ a clecofler
for decoding a sequence Zk ~ Yk ~ nk, k = 1, 2, ..., where the
sequence of signals Yk is such that (a) the sequence is ~rom a
given modulation code, the code bein~ capable of being generated
by an encoder with a finite number Q of states; (b) Yk = Xk ~ Xk
L~ L an in~eger, where the sequence xk has finite variance Sx, and
the sequence nk represents noise, comprisiny a modified ma~irnum
likelihood sequence estimator adapted to find MQ partial decoded
sequences, up to some time K, one sequence for each combination of
the finite number Q of states and each of a finite number M of
integer-spaced values modulo ~1, such that each sequence (a) is in
the code up to the time K; (b) corresponds to the encoder being in
a given state at the time K; ~c) corresponds to a value of xK at
the time K that is congruent to a given one of the values, modulo
M.
~ he invention adapts ~nown modulation codes,
particularly trellis codes, for use in partial response systems
to achleve the same kinds of advantages that trellis codes have in
non-partial response systems -- notably, substantial coding gains
for arbitrarily large numbers n of bits/symbol with reasonable
decoding complexlty. The invention also enables the design of
trellls codes for partial response systems in such a way as to
achieve both a relatively low input signal power Sx and a
relatively low output power Sy, and permits smoothly trading off
these two quantities against each other. Furthermore, higher-
dimensional trellis codes can be adapted for use in partial
response systems which are inherently lower-dimensional.
j:~
! '
~','"'..
~3~)65~3
9a 60~12-1723
According to a broad aspect of the invention there is
provided apparatus for generating a sequence of digital signals xk
and/or a sequence of digital signals Yk, k = 1, 2, ..., such that
the sequence of Yk signals is a partial-response-coded sequence
derived from the sequence of xk signals, said signals Yk being a
sequence in a given mod~la~ion code, sald apparatus comprising
a cose~ selector for generating coset representatives ck in
accordance with said given modulatlon code; and
an encoder for sele~ting J said signals Yk, J ~ Yk,
Yk+1,...~Yk~ 1) to be congruent to a sequence of J coset
representatives ck (modulo AN), AN being an N-dimensional
lattlce, N being a positive integer, said J signals being chosen
from one of a plurality of NJ-dimensional constellatlons, said
choice being based on a previous xk,7k'< k, at least one of said
plurality of NJ-dimensional constellations comprising both a point
with a positive sum of coordinates and another point with a
negative sum of coordinates, said encoder being arranged so that
said signals xk have finite variance Sx.
According to another broad aspect of the invention there
is provided apparatus for generating a sequence of digital signals
Xk, and/or a sequence of digital signals Yk, k = 1, 2, ..., such
that the sequence of Yk signals is a partial-response-coded
sequence derived from the sequence of xk signals, said signals Yk
being a sequence in a given modulation code, said apparatus
comprising
a coset selector for generating coset representatives ck in
accordance with said given modulation code;
~.~
~O~S~3
sb 60412-17~3
a generator of a sequence of alternati~e coset
representatives Ck' chosen so that the sequence of coset
representatives ck i~ a partial-response-coded sequence derived
from the sequence of Ck' signals, and
an encoder for selecting said signals xk to be congruent t~ a
sequence of alternative coset representatives ck" where the
congruence is modulo M if said coset representativès ck are real,
M being an integer, and modulo ~N if said ck signals are N-
dimensional, AN being an N-dimensional lattice, N heing an
integer.
According to another broad aspect of the invention there
is provided apparatus for generating a sequence of digital signals
Xk and~or a sequence of digital signals Yk, k = 1, 2, ..., such
that the sequence of Yk signals is a partial-response-coded
sequence derived ~rom the sequence of xk signals, sald xk and Yk
sequences having variances Sx and Sy, said symbols Yk being a
sequence in a g~ven modulation code, said apparatus comprlsing
means for receiving an input signal; and
an encoder responsive to sald receiving means for generating
said xk and/or Yk signals such that the ratio of variance S to
y
variance Sx is selectable within a predetermined range.
Accordlng to another broad aspect of the invention there
is provided apparatus for generating a sequence of digital signals
Xk and/or a sequence of digital signals Yk, k = 1, 2, ..., capable
of representing n bits per signal, such that the relationship
k Yk is Yk = Xk t xk_L, L an integer, said x and Y
signals having variances Sx and Sy, said Yk signals falling within
,. .
f~ ~ :~
13~6~3
9c 60~ 1723
an alphabet of possible Yk slgnals that are spaced apart within
said alphabet evenly by a spacing ~, said apparatus comprising
means for receiving an input signal having n bits per signal;
and
an encoder responsive to said receiving means for generating
said se~uence Yk and said sequence xk such tha~ said sequence Yk
has a variance Sy less that 2S0 and said sequence xk has a
variance Sx not much greater than Sy2/~(Sy~S0), S0 being
approximately equal to the minimum signal power required to
represent n bits per signal with a ~-spaced alphabet.
According to another broad aspect of the invention there
is provided apparatus for generating a sequence in a given N-
dimensional modulation code by ~enerating a sequence of one-
dimensional signals, N being a positive number, said modulation
code being based on an N-dimensional constellation partltioned
into subsets associated with said code, said subsets each
containing N-dimensional signal points, the choice of said subset
being based on coded bits and uncoded blts of said slgnal points,
said apparatus ~omprising
means for receiving an input signal and generating the coded
blts and the uncoded bits therefrom; and
an encoder for deriving from said coded and uncoded bits, for
each said N-dimensional symbol, a set of N, M-valued one-
dimensional coset representatives ck corresponding to congruence
classes of each of the N coordinates (modulo M~, M being a
positive number, each coset represen~ative designating a subse~ of
one-dimensional values in a one-dimensional constellation of
~,
~L306S~3
9d 6~412-1723
possible coordinate values for each of said N dimenslons,
each said one-dimen~ion signal in said sequence being
selected from said possible coordinate values based on uncoded
bits.
According to another broad aspect of the invention there
is pro~ided in a decoder for decodin~ a sequence Zk ~ Yk + nk~ k =
1, 2, ..., into a decoded sequence Yk, where the sequence of
signals Yk is such that
~a) said sequence is from a given modulation code;
(b) the running diqital sum xk 3 Yk 1 ~ Yk 2 + ~ has
finite variance Sx;
(c) said signals Yk fall in a predetermined permissible
range dependent on Xk', k' < k; and the sequence nk represents
noise,
a range violation monitor comprising:
a means for reconstructing the estimated running digital sum
k Yk + Yk_1 + ..,, and
a means for comparing said decoded sequence Yk with said
predetermined permissible range based on said estlmated running
digital sum Xk,, k' ~ k, and for generating an indication when
said Yk is outside said permissible range.
According to another broad aspect o~ the invention there
is provided a decoder for decoding a sequence xk ~ Yk + nk~ k = 1,
2, ..., where sequence nk represents noise and the sequence of
signals Yk is such that
(a) said sequence is from a given modulation code, said code
being capable of being generated by an encoder with a finite
13~6S ~3
9e 60412-1723
number Q of s~ates;
(b~ Yk ~ Xk i xK_L, L an integer, where said sequence xk has
finite variance Sx, and the sequence nk represents noise,
comprising
a means for receiving the sequence Zk; and
a modifled maximum likelihood sequence estimator responsive
to the receiving means, said estimator being adapted to find MQ
partial decoded sequences up to some time K, where M, Q, and K are
positive finite numbers, one such said sequence for each
combination of said finite number Q of states and each of a finite
number M of integer-spaced values modulo M, such that each said
sequence
la~ is in said code up to said time K;
(b) corresponds to said encoder being in a given said state
at said time K;
(c) corresponds to a value of xk at said time K that is
congruent to a given one of said values, modulo M.
Other advantages and features will become apparent from
the following description of the preferred embodiments, and from
the claims.
B
~3~6~ }3
-- 10 --
Description of the Preferred Embodiments
We first briefly describe the drawinqs.
Dr awinqs
Fiqure 1 is a block diagram of a l-D partial
s response channel~
r igure ~ is a bloc:~ d:iagram o~ an encode~ for
an 8-state Ungerboeck code.
~ igure 3 is a signal constellation for the
Ungerboeck code partitioned into 8 subsets.
Figure 4 is a block diagram of an equivalent
encoder f or the Ungerboeck code.
Figure 5 is a blocX diagram of a generalized
N-dimensional trellis encoder.
Figure 6 is a block diagram of a modified
Figure 5, based on coset representatives.
Figure 7 is a block diagram of an equivalent
one-dimensional encoder.
Figure 8 is a block diagram of a generalized
N-dimensional trellis encoder.
Figure 9 is a block diagram of a generalized
encoder with coset precoding.
Figure 10 is a block diagram combining Figures
8 and 9.
FigurQ 11 is a block diagram of an encoder with
RDS eedback a~d coset pracoding.
Figures 12, 13, 14 are alternative embodiments
of Figure 11.
Figures 15, 16, 17 are block diagrams of three
equivalent filtering arrangements.
3~ Figure lB is a block diagram of a generalized
decoder.
Figures 19, 20, 21 are block diagrams of
alternative encoder~.
13Q65'13
Figure 22 is an alternative signal
constellation.
Figure 23 i5 a block diagram of an encoder for
use with the constellation of Fi~ure 22.
Figures 24, 25, 26 are bl~c~ diagrams of thrae
eguivalent encoders.
Figure 27 is a blocX diagram of an alternative
decoder.
Figure 28 is a schematic diagram of an expanded
signal constQllation,
Figure 29 is a rhombus for use with the
constel].ation of ~igure 23.
Figure 30 is a block diagram of a
twa-dimensional RDS feedback encoder.
Figure 31 is a diagram of the dimensions of a
rhombus for uæe with the constellation of Figure 28.
Figure 32 shows a pair of constellations.
Figure 33 shows two disjoint constellations.
Structure and OPeration
Referring to Figure 1, the invention includes a
technique for generating signal sequences to be used as
inputs for a partial response channel 10, for example a
one-dimensional (real) l-D partial respons~ baseband
system with a null at DC. (Later we shall indicate
briefly how to modify such a design for other types of
partial response systems.) Each output signal Zk f
such a system is given by
Zk Yk + nk'
where the nk sequence (n(D)) represents noise, and the
Yk sequence (y(D)) is a partial-response-coded (PRC)
sequence defined by
Yk Xk - Xk-l'
where the xk seguence (x(D)) is the sequence of
13~6S~3
channel inputs. Because
Xk = X~C_ 1 + Yk '
the xk sequence can be recovered from the PRC sequence
by forming a runnin~ digital sum of the Yx values
S (given an initial value for t;~e ~ sequence), -hus ~e
call the ck sequence tne ~DS sequence. he sampie
variances of the RDS sequence x(D~ and the PRC sequence
y(D) will be denoted as Sx and Sy~ respectively.
The discrete-time partial response l-D
k epresented by block 12) is a composite of the
responses of a chain of transmit filters, an actual
channel, receive filters, equalizers, samplers, etc.,
desiqned in a conventional way to achieve a composite
partial response l-D with the noise power P (of the
noise sequence n(D)) being small relative to the PRC
power Sy~ We shall thus want to send a relatively
large number n of bits per channel input. A detector
(not shown) operates on the noisy PRC sequence z(D~ to
estimate x~D) (or equivalently y(D), since there is a
one-to-one relationship between them). If the detector
is a maximum likelihood sequence estimator, then, to
first order, the objective is to maximize the minimum
squared distance dmin between permissible PRC
seguences y(D).
~n some applications, the design constraint
will simply be to minimize the sample variance Sx of
the RDS (input) sequence. In others. the constraint
will be on Sy~ In still other applications, there
will be an effective power constraint somewhere in the
3a middle of the composite filter chain, so that it will be
desirable to keep both Sx and Sy small, and in fact
to provide for a smooth design tradeoff between them.
13~5'}3
- 13 -
A related problem is the design of sequences
with spectral nulls, e.g., a null at zero frequency
(DC). There the objective may be to design sequences
y(D~ that can represent n bits per sample, that have a
spectral null, that have as small a sample ~ariance Sv
as possible, but that also have a large minimum squared
distance dmin between possible y(D) sequences. A
common auxiliary objective is to keep the variation of
the running digital sum (RDS) of the y(D) sequence
lQ limited as well, for systems reasons. Because the
running digital sum sequence x~D) is, e.g., y(D)/(l-D),
and its sample variance Sx is a measure of its
variation, the present invention may also be applicable
to the design of sequences with spectral nulls.
A number of design principles are useful in
achieving our objectives. The first princip.e is to
design th~ input (RDS) sequence x(D~ so that the output
(PRC) seguence y(D), taken N values at a time, is a
sequence of N-dimensional signal points belonging to
subsets of an N-dimensional constellation determined by
a known N-dimensional trellis code. Then the minimum
squared distance dmin between PRC sequences will be
at least the dmin guaranteed by the trellis code.
Furthermore, a maximum likelihood sequence estimator for
the trelli8 code can be easily adapted for use with this
system, and while perhaps not optimum, it will achieve
the same effective dmin for essentially the same
decoding complexity as for the same trellis code in a
non-partial response system.
An illustrati~e embodiment of the present
invention is based on a known 8-state 2-dimensional
trellis code similar to that of Ungerboeck as described
in the article cited above, which uses a 128-point
two-dimensional constellation to send 6 bits per
13(~6S~3
- 14 -
(two-dimensional) signal. ~This is also similar to the
code used in CCITT Recommendation V.33 for a 14.4 kbps
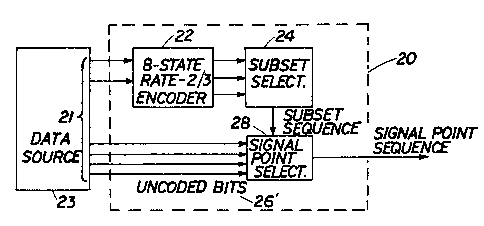
data modem.) Figure 2 sho~s the encoder 20 for this
code. For each six-bit symbol 21 delivered from a data
source 23, 2 o~ the 6 in?ut bits t~ encoder 20 en~er a
rate-2/3, 8-state convolutionaL encoder 22. Ihe 3
output bits of this encoder are used in a subset
selector 24 to select one of 8 subsets of a 128-point
signal constellation, illustrated in Figure 3; there are
16 points in each subset (points in the eight subsets
are labelled A through H respectively) The remaining 4
~'uncoded bits" 26 (Figure 2) are used in a signal point
selector 28 ta select from the chosen subset the
~two-dimensional) signal point to be transmitted. The
code achieves a gain in dmin of a factor of 5 (7
dB) over an uncoded system, but loses about 3 d~ in
using a 128-point rather than a 64-point constellation,
so the net coding gain is about 4 d~.
One-dimensional form of the 2-dimensional Unqerboeck code
The sequence of symbols xk sent over the
channel is one-dim~nsional in a l-D baseband partial
response system. It is helpful (though not essential),
therefore, to transform known trellis codes into
one-dimensional form. There are two aspects to this
transformation: first, to characterize the
two-dimensional subsets as compositions of constituent
one-dimensional subsets, and second, to characterize the
finite two-dimensional constellation as a composition o
constituent one-dimensional constellations. We now show
3Q how this decomposition is done for the illustrative
twa-dimensional Ungerboeck code, and then indicate how
it may be done in the general case of an N-dimensional
trellis cod0.
~306S~3
-- 15 --
The first step is to notice that each of the
eight two-dimensional subsets A, B, ..., can be viewed
as the union of two smaller two-dimensional subsets, say
Ao and A1, Bo and Bl, etc., where each of the 16
smaller subsets can be character~zed as follo-~s Let
the possible values ~f each c~ordir.ate of a signai point
be partitioned into four classes a, b, c, d; then each
of the smaller two-dimensional subsets consists of the
points whose two coordinates are in a specified pair of
classes. A convenient mathematical expression for this
decomposition arises if we scale Figure 3 so that signal
points are ane unit apart in each dimension (and the
coordinates of each point are half-integers); then the
classes a, b, c, d are equivalence classes (modulo 4),
and each of the 16 sets Ao, Al, Bo~ ... are the
points whose two coordinates are congruent to a given
pair (x, y) modulo 4, where x and y may each take on one
of the four values {a, b, c, d~, e.g. {~1/2,
_3/2~. These four values are called
2Q (one-dimensional) 'coset representatives'. The points
of the constellation of Figure 3 have been labeled with
Os and ls to show one possible arrangement of the 16
subsets. For example the Go point 29 has coordinates
x ~ 5/2, y - 9/2, and its coset representatives are
(5/2, 9/2) modulo 4 or (-3/2, 1/2).
We may now modify Figure 2 as follows.
Referring to Figure 4, the three output bits of the
encoder 22 plus one of the uncoded bits 30 are used as
inputs to subsQt selector 32, which selects one of 16
3Q subsets based on the faur input bits, with uncoded ~it
30 selecting between Ao and Al, or 30 and Bl,
etc., accarding to which of the original 8 subsets is
salected by the three convolutionally encoded bits
produced by encoder 22. In effect, encoder 22 and bit
131;~6S'~3
- 16 -
30 represent an 8-state rate-3/4 encoder, with the
output selecting one of 16 subsets, although the set of
possible si~nal point sequences has not changed. Next,
designate each of these 16 smaller subsets by a pair of
one-dimensional coset representatives 34, one ~or eac~
coordinate, ~here each coset represen.ative ck ~.ay
takQ on one of four ~alues. The pair o~ coset
representatives is denoted (clk, c2k).
An aspect of the invention is the observation
that all of the good codes cited above -- i.e., those of
Ungerboeck, Gallager, Wei, and Calderbank and Sloane --
can be transformed in the same way. That is, any of
these ~-dimensional trellis codes can be generated by an
encoder that selects one of 4N subsets, where the
subsets are specified by N 4-valued one-dimensional
coset representatives, corresponding to congruence
classes of each coordinate ~modulo 4). In some cases it
is only necessary to use 2N subsets specified ~y N
2-valued one-dimensional coset representatives (e.g.,
1_1/2}) corresponding to congruence classes of each
coordinate (modulo 2); e.g., for Ungerboeck's 4-state 2D
code, Gallager's 8-state 4D code (and the similar code
of Calderbank and Sloane), Wei's 16-state 4D code and
64-state ~D code, etc. Also, we have observed that many
25 good lattice code8 can be transformed in thiS way; e.g.,
the Schlafli lattice D4 and the Gosset lattice E~
can be represented by seguences of 4 or ~ two-valued
one-dimensional coset representatives (modulo 2); the
~arnes-Wall lattices ~16 and ~32 and the Leech
lattice ~24 can be represented by four-valued
one-dimensional coset representatives (modulo 4).
13(~S~3
- 17 -
A general orm for all of these codes is shown
in Figure 5. The encoder is N-dimensional and operates
once for every N siqnals to be sent over the channel.
In each operation, p bits enter a binary encoder c 33
s and are encoded into p + r coded bits. I'hese coded bi.
select ( in selector 35) one of 2?~r subsets of an
N-dimensional signal constellation (the subsets
corresponding to the 2P~r cosets of a subla~tice ~l
of an N-dimensior.al lattice A, the constellation being
lo a finite set of 2n+r points of a translate of the
lattice ~, such that each subset contains 2n p
points). A further n - p uncoded bits selects ~in
selector 37) a signal point from the selected subset.
Thus the code transmits n bits for every N-dimensional
symbol, using a constellation of 2n+r N-dimensional
signal pointsN The encoder C and the lattice partition
A/~' ensure a certain minimum squared distance
d2in between any two signal point sequences that
belong to a possible subset seguence.
The observation above ~about the
transformability of all good codes) is the result of the
mathematical obse~vation that for all of the good
trellis and lattice codes cited, the lattice 4ZN of
N-tuples of integer multiples of 4 is a sublattice of
thQ lattice ~' (and in some cases 2ZN is). Then,
for somQ integer q, ~' is the union of 2g cosets of
4zN in A', The practical effect of this observation
is that, provided that n ~ g + p, we can take the p + r
coded ~its plus q uncoded bits into a subset selector
that selects one of 2q+p+r cosets of 4ZN in ~, and
further that these cosets can be identified by a
sequence of N 4-valued one-dimensional coset
representatives (clk, c2k, ...~cNk),
Cjk represent integer-spaced equivalence classes
~3~6~
- 18 -
tmodulo 4), Thus already Figure 5 can be modified as
shown in Figure 6. In this modification, we assume that
the 2n+r-point signal constellation divides evenly
into 2q~p+r subsets, each containing the same number
5 of signal points (2n q ?).
~ he illustrative ungereoecX code emDodi~.ent is
an example in which N = 2, ~ = z2, ~,~ = 2RZ2, p
= 2, p + r = 3, ~ = 1, and n = 6.
The second StQp i~ ta decompose the
10 con5tQllation into constituent one-dimensional
constellations. For the constellation of Figure 3, each
coordinate can take on one of 12 values which can be
grouped as 8 'inner points' (e.g., t~l/2, ~3/2,
~S/2, ~7/2}) and 4 'outer points' (e.g., {~9/2,
~11/2~), as suggested by boundary 31 in Figure 3.
There are 2 inner points and 1 oute~ point in each of
the four one-dimensional e~uivalence classes (e.g., the
class whose coset representative is +1/2 contains the
two inner points +1/2 and -7/2, and the outer point 9/2,
because these three points are congruent to +1/2 (modulo
4). Given a coset representative, therefore, it is only
necessary to specify whether a point is an inner point
or an outer point and, i~ an inner point, which of the
two inner points it is, ~his can be done with two bits,
say blk ~' inner or outer) and b2k (a which inner)
(or with one three-valued parameter ak).
WQ may say that the pair (blk, b2k) is a
range identifying parameter ak, which takes on one of
three values, indicating the following three ranges
(a) from 0 to 4 ~inner point, positive);
(b) from -4 to 0 (inner point, negative);
(c) from -6 to -4 and from 4 to 6 (outer
point).
~306S43
-- 19 --
The fact that each range spans a portion of the real
line of total width 4 that contains exactly one point
congruent to any real number (modulo 4) means that the
range-identifyinq parameter a~ plus the coset
representative CX specify a u~ ai~nal ~oi.~-, Cor
any value of Ck.
The signal point selector 36 of Figure 4 can
then be decomposed as follows. Referring to Figure 7,
three uncoded bits ~0 enter a range-identifying
parameter selection element 42 for each pair of
coordinates. One uncoded bit determines whether any
outer point is sent. If so, a second bit then
determines which coordinate will contain the outer
point, and the third bit selects which inner point in
lS the oth~r coordinate. If not, ~oth coordinates are
inner points, and the second and third bits select which
inner point in each coordinate. Thus, in sum, element
42 maps the three uncoded input bits 40 into two pairs
of output bits 44 al = (bll, bl2), 2
2Q (b21~ b22), with each pair of bits used to determine
one coordinate in conjunction with the corresponding
coset representative, cl or c2, generated by coset
representative pair selector 46. Thus the whole encoder
has been reduced to a form in which each coordinate xk
(48) is selected (in a coordinate sQlector 50) by 4
bits, two representing ck and two representing ak '
(blk, b2k).
All constellations commonly used with the
above-cited codes can be decomposed in this way. The
30 principles are similar to those discussed in my U.S. ~j~
Patent 4,597,090 and in Forney et al., "Efficient
Modulation..." cited above, where N-dimensional
constellations were built up from constituent
2-dimensional constellations; a similar buildup from
13Q65~3
- 20 -
2-dimensional constituent constellations ~as used by Wei
in conjunction with trellis codes in his ~h.6-. Pàtent
Application, cited above.
The general form of encoder for N-dimensional
codes is shown in Figure 8. For every ~ c~or~inates, p
bits ,1 enter an encoder ~2 and ~ ~ r coded oi~s ~ are
produ~ed; these plus q uncoded bits 56 enter a selector
58 which selects a sequence of N coset representatives
c~(60)i the remaining n-p-q uncoded bits 62 are
transformed (in a selector 64) into a sequence of
range-identifying parameters ak (66) which together
with the ck determine (in a signal point selector 68)
a sequence of N signal point values xk (70) by a
signal point selection function f(ck, ak) which
operates on a one-dimensional basis. In general, the
range-identifying parameter ak determines a subset of
the real line (one-dimensional constellation) of width
(measure) 4 which contains exactly one element congruent
to any possible ck value (modulo 4), and the function
f(ck, ak) selects that element. For all codes
cited, the coset representative alphabet may be taken as
four integer-spaced values (modulo 4); for some codes,
the coset representative alphabet may be taken as two
integer-spaced valuQs (modulo 2) (in which case the
ranges are of width 2). The sizQ of the ak alphabet
is as large as necQssary to send n bits per N
coordinates. The signal point sequences generated by
this form of encoder are generally the same as those in
the original code, and in particular, are separated by
30 the same minimum squared distance d2in as the ~
original code.
~30~ 3
- 21 -
Cose~ Precodinq
N-dimensional signal point sequences generated
by known good trellis codes, wh~n serialized to
one-dimensional signal points, cannot in general be used
as inputs to the partial response c~a.~nel of Fi~ure 1
without degradation of dmin (Decause of intersy~boi
interference). However, a technique which we call coset
precoding allows the adaptation of these known codes to
partial response systems without increase of Sx or
deg~adation of d2in. The general technique is
illustrated in Figu~e 9.
wo use the same convolutional encoder 52 as
used by the known trellis code, preerably in the form
of Figure 8. The p + r coded output bits 54, rather
than selecting a subset directly, are converted ~as in
Fiqure 8) in a subset selector/serializer 70 into a
sequence ck of N one-dimensional coset representatives
cl, ...~CN, corresponding to the subset that would
be selected in a non-partial response system, These
2Q coset representatives are then 'precoded' (in a precoder
72) into an alternativQ (or 'precoded') coset
representative sequence Ck' (74), where
Ck = Ck-1 + Ck (modulO 4)
(In the cases where it is possible to use modulo 2 coset
representatives, this precoding can be done modulo 2.)
Thus the precoded coset representative sequence 74 is a
running digital sum modulo 4 (or 2) of the ordinary
coset representative sequence. Precoded coset
representatives Ck' can then be grouped N at a time in
grouper 75 to specify tin signal point
selector/serializer 76) an N-dimensional subset; a
signal point can then be selected (based on the uncoded
bits 78) in the usual way; and the resulting signal
1306~3
- 22 -
point can be sent out as a sequence x(D) of N
one-dimensional sîgnals xk over the partial response
channel (in the same order as they were precoded~
Note that if the ck are half-integers, then
tAe Ck' alternate bet~een ~o sets of 4 val~es, o~e
set displaced by l/2 from ~he otAer. ~Ais has on'y a
minor effec~; we can, for example, "dither" alternating
coordinates XX by +l/4 and -1/4 so as to accommodate
this periodicity, Alternatively, -~e may let the ck
alphabet be inte~er-valued, Q . g., {O, l, 2, 3}; then
the Ck' are always from the same alphabet, e.g.,
(~1/2, ~3/2}, These offsets of c~' or CX do
not affect the dmin of the code.
If the encoder is in the form of Figure 8, then
Figure 9 can be put in the form of Figure lo, where the
same hlocks do the same things. In particular, since we
have characterized the function f(ck, ak) as one
that selects the unique element congruent to ck in a
range identified ~y ak, it does not matter if the
precoding changes the ckl alphabet from the ck
alphabet; indeed, the (modulo 4) in the precoder is
unnecessary in principle, though possibly useful in
practice.
With either Figure 9 or Figure lO, it can be
shown that the PRC sequence Yk ' Xk ~ Xk 1 has
elements that are congruent to ck (modulo 4), so they
fall in th~ subsets of the original trellis code, and
therefore have at least the same dmin. The RDS
sequence xk has the same average energy Sx as in the
original trellis code if the Ck' alphabet is the s~e
as the ck alphabQt; sven if not, approximate equality
still holds. (In the illustrative embodiment, the
average energy per coordinate is 10.25, with
~3~65~3
- 23 -
integer-spaced signals.) If the ck are integers, the
Xk are independent, identically distributed random
variables, and thus
(a) Sy = 2Sx;
(b) the spectrum o~ the RDS seq~er.ce
~Xk} is
flat (white) within its Nyquist band;
(c) the spectrum of the PRC sequence
{Yk} is
the same as that of the partial response
channel.
Even if the ck are not integers, these statements are
still approximately true.
Coset precoding can be modified for other kinds
of partial response systems as follows. For a l+D
(one-dimensional) partial response system, use the same
system except with ck_l' subtracted rather than added
in precodQr 72, so that ck = ck ~ cx_l (modulo
4). For a l-D system, replace the delay element D by
a delay element DL, so that Ck' = ck L~ + Ck
For a l+D two-dimensional system, use two l+D precoders
in parallel, with pairs of outputs from the subset
selector~serializer as inputs, and with the two outputs
determining the real and imaginary (in-phase and
quadrature) parts of thQ two-dimensional signal point to
be transmitted.
RDS Feedback
Depending on the application, it may be
desirable to reduce the average energy Sy of the PRC
sequence, at the cost of increasing the average~enerqy
Sx of the RDS sequence. This will also tend to
flatten the PRC spectrum, while raisinq the
low~frequency content of the RDS spectrum. Ju tesen,
"Information Rates and Power Spectra of Digital Codes",
IEEE Trans. Inform. TheorY, Vol, IT-28, pp. 457-472,
13065~}3
- 24 -
1982, has introduced the notion of a "cutoff frequency~'
fO below which the PRC spectrum is small and above
which it tends toward flatness, and has shown tha~ fO
is approximated by fO - (Sy/2SX)f~, where f~J
5 is the Nyquist band edge frequency.)
A general .~ethod of per^orming this tradeo~L
while maintaining the dmin of the trellis code in
the PRC sequences is to augment the encoder of Figures 9
or lo as follows.
The PRC sequence may be computed from the RDS
sequence; for the l-D channel, each PRC signal is just
Yk = Xk ~ Xk 1' Referring to Fig. 11, we may let
the signal point selector 80 base each x~ on xk 1
(by feeding xk back through a delay element 82) as
well as on the current precoded coset representative
Ck' and on the range-identifying parameter ak, in
such a way that large PRC values Yk (calculated in
summer 84) are avoided. As long as the signals xk are
still chosen to be congruent to the Ck' (modulo 4),
the signals Yk will be congruent to the ck ~modulo
4), and therefore will preserve the d2in of the
trellis code. (Note that although the idea is to
precompute the PRC value Yk to keep it small, what is
actually ed back is the previous RDS value xk 1' 50
that we call this RDS feedback.)
For the illustrative embodiment, this could
work as follows. As already noted, the normal selection
function f(ck, ak) of selector 80 can be
characterized by saying that the 8 inner points are the
8 half-integer values lying in the range f ~m -4 to +4,
while the 4 outer points are the 4 half-integer values
lying in the range from -6 to -4 and +4 to +6. We can
vary the inner point range and outer point range as a
function of xk 1' as long as the inner point range
13~6S~3
- 25 -
spans 8 signal points, 2 from each equivalence class,
while the outer point range spans 4 signal points, 1
from each equivalence class.
A general way of doing this is to translate all
ranges by a translation variaDle ~(x~_l) w:~ich is a
function of xk 1 That is, in the illustra~ive
embodiment, the inner point range is modified to be from
-4 + R(x~ 1) to 4 + R(xk_l), and the outer point
range to be from -6 + R(xk l) to -4 + R(xk_l) and
from 4 + R(xk_l) to 6 + R(xk_l).
The function R(xk l) should be generally
increasing with xk l so as to reduce the Yk. We
have been able to show that the optimum choice is
~(Xk l) = ~Xk l~ where n is a parameter in the range
o < n < 1~ When n = O, the RDS feedback through element
82 disappears and Figure ll reduces to coset precoding
as in Figure lO. With this choice, if S0 is the value
of Sx in the ordinary case (B = 0), then it is
approximately true that
(a) Sx ' So/(l - n );
(b) Sy - 2So/( 1 + B);
(c) The spectrum Sx(f) of the RDS sequence is
proportional to 1/(1 - 2ncOS ~ + n ) ~ where ~ =
lrf /fN;
(d) The spectrum Sy(f) of the PRC sequence is
proportional to 2(1 - cos~)/(l - 2n cos~ + B );
the "cutoff frequency" fO is (l-n)fN.
(e) The xk are limited to the range form
-M/2(1+B) to M/2(1-B), and the Yk are limited to the
30 range -M to M, if the range of coordina~es in the
orignal code is from -M/2 to M~2.
As B approaches 1, Sy approaches S0, and
Sy(f) approaches a flat spectrum with a sharp null at
DC. Meanwhile, Sx becomes large and Sx(f)
13~65~3
- 26 --
approaches a l/(l-D) spectrum, except that it remains
finite near DC. We have been able to show that this is
the best possible tradeoff bet~een Sx, Sy~ and S0.
Figures 12, 13, 14 sho~ three equivalent ways
of generating .~ and/or y~ based o~ c,;, a,~, a.~d
~k 1 Figure 12 corresponds most closely ~o ~igure 11.
In Figure 12, the feedback varia~le c'k_l in
coset precoder ~2 is replaced by xk_l, since c'k-l -
Xk 1 tmodulo 4), and only the value of c'k (modulo
4~ is used in selector 80. R~ak) denotes the range
identified by ak, and R(xk 1) represents the range
translation variable introduced by RDS feedback. Since
Yk k Xk-l - c ~ - xk_l (modulo 4) and
C'k ~ Ck + xk_l (modulo 4), Yk ~ Ck
(modulo 4).
Figures 13 and 14 are mathematically equivalent
to Figure 12, in the sense that if they have the same
starting value xk 1 and the same sequence of inputs
(Ck, ak), they will produce the same sets of outputs
(xk~ Yk). In Figure 13, Yk is chosen as the
unique element congruent to ck in the range R(ak) +
R(xk 1) ~ Xk 1~ and xk is determined from Yk as
Yk + Xk 1' so Xk _ c k ~ Ck
+ Xk 1 (modulo 4), and is the unique element in the
range R(ak) + R(xk_l) congruent to c'k (modulo
4). In Figure 14, an innovations variable ik is
chosen as the unique element congruent to cl'K _ ck
+ Xk 1 ~ R~xk_l) (modulo 4) in the range R(ak),
and xk is determined from ik as xk = ik +
R(xk_l), so xk - c k + R(Xk-l) ~ ck~
(modulo 4), and is the unique element in the range
R(ak) + R(xk_l) congruent to c'k (modulo 43.
Figure 12 combines the delay element in the precoder
with the delay element necessary for RDS feedback, and
13(:~65~3
-- 27 --
is most useful if xk is the desired output and the
C'k are always from the same alphabet, e.g. {+1/2,
~3/2~. Figure 13 eliminates the precoder altogether,
and is most useful if Yk is the desired output and the
5 c,~ are always from the same alphabet, e.g {~ 1/2,
+ 3/2~. Figure 1~ takes tAe range transla~ion
variable R(xx 1) outside of the selector, so that the
ik are always chosen from the same range (the union of
all R(ak)); the innovations sequence i(D) is
10 approximately a sequence of independent identically
distributed random variables ik (ignoring the mi~or
variations induced by the c'k congruence constraint)
and this auxiliary sequence can be useful if a white
(spectrally flat) sequence deterministically related to
x~D) or y(D) is desired.
Figures 15, 16, 17 illustrate three equivalent
filtering arrangements for use with the x(D), y(D), and
i(D) seguences of Figures 12, 13, 14. In Figure 15, the
RDS sequence x(D) is filtered in a transmit filter
2Q HT(f) before being transmitted (as signal s(t)) over
the actual channel ~not shown). In Figure 16, the PRC
sequence y(D) is filtered in a transmit filter H'T(f)
whose response is equivalent to that o a cascade of a
l/(l-D) sampled-data filter and HT(f); since y(D) has
a DC null, it does not matter that the response of
l/(l-D) is infinite at DC (particularly if HT(f) also
has a DC null). In Figure 17, the innovations sequence
i(D) is filtered in a transmit filter H"T(f) whose
response is equivalent to that of a cascade of a
l/(l-BD) sampled-data filter an~d HT(f); this is
equivalent to Figures 15, 16 if R(xk 1) = Bxk l;
otherwise, the equivalent sampled-data filter is the
filter corresponding to xk = ik + R(xk 1)' in
13~6S~3
- 28 -
general nonlinear. Any one of these equivalent forms
may be preferable depending on HT(f), R(xk 1)~ and
the implementation technology being used.
Certain modifications of the above RDS feedback
systems may b~ desirable in prac~ ce For examDle,
may ~e desirable to change ~he .~or,~ of tne rar~ges
R(ak) from those used when R(xk 1) = - For
example, in the illustrative embodiment, a simply
implemented form of RDS feedback is as follows: when
xk 1 is positive, let Yk be chosen as usual in the
range from -4 to 4 if ak indicates an inner point, but
if ak indicates an outer point, let Yk be the number
congruent to c~ in the range from -4 to -8; when
Xk 1 is negative, use the range from 4 to 8 for outer
points. Then
(a) the range of the PRC sequence Yk is limited
to -7 1/2 to +7 1/2, rather than -11 to 11 when
there is no RDS feedback;
(b) the PRC variance Sy is reduced to 13.25 from
20.5, a reduction of 1.9 dB, and about 1.1 d~
above S0 ~ 10.25;
(c) thQ mean Of Yk is - 3/2 if xk 1 is
positive, and + 3/2 if xk 1 is negative, so
that the RDS sequence tends to remain in the
neighborhood of zero. While it is difficult to
compute Sx exactly, it follows from the facts
that E[ykxk_l] = Sy/2 and E~Yk Xk-l]
- -(3/2) E[¦xk 1l] that the mean of the
absolute value of xk is Sy/3 = 4.42, so
that the RDS sequepce xk is fairly well
bounded. (With no RDS feedback, the mean of
the absolute value of xk is 2.75);
13065'~3
- 29 -
(d) the variance of the Yk, given xk 1~ is S0
- 11, about 0.3 dB higher than the S0 = 10.25
possible with no RDS feedback. The minimum
possible S.c for s~ = 13 . 25, sO = ll, is
S:c ~ 19.5, correspcndi~ SO n - 0.66
since Sx = Slx¦ 2x
must be greater than (4.42) ~ ls.s, so
with this simple method we achieve less than
the optimal spectral tradeoffi
(e) every possible Yk is associated with a unique
pair (Ck, ak). As we shall discuss in more
detail below, this means that a decoder need
not keep track of an estimated running digital
sum of the estimated PRC sequence, and that
there will be no error propagation in the
decoder.
In summary, this simple method does not achieve
the best power tradeoff between Sx and Sy~ but does
effectively limit not only Sy but also the peak values
of Yk, keeps the RDS sequence xk fairly well
bounded, and avoids error propagation at the receiver.
Thus these methods allow for trading off of
Sx versus Sy (i) from the unconstrained case, where
the x~ sequence is uncorrelated, Sx has the same
energy S0 as is necessary to send n bits per symbol in
the non-partial-response case, and Sy = 2Sx, (ii)
almost to the case where the Yk sequence is
uncorrelated, Sy = S0, and Sx becomes very large.
These tradeoffs are possible for all trellis and lattice
30 codes cited. ~
~3~6S~3
- 30 -
Decodin~The above methods succeed in generating PRC
sequences that belong to a known good code, and
therefore have a d2in at least as great as that of
5 the code.
Referring to rig. 1~, a suitaoie detector for
the noise received PRC sequence z(Dt = y(D) + n(D) is
therefore a maximum likelihood sequence estimator
(Viterbi algorithm) for the known good code, adapted as
follows:
(a) A first step of decoding may be, for each noisy
received PRC value Zk = Yk + nk~ for each
of the four classes of real numbers congruent to
the four one-dimensiQnal coset representatives
Cjk (modulo 4), j = 1,2,3,4, find (block 92)
the closest element Yjk in each class to Zk'
and its 'metric' mjk ~ (Yjk ~ Zk)
(squared distance from z~);
(b) In a cods based on an N-dimensional lattice
partition ~/~', a second step of decoding
may be, for each of the 2P+r cosets of ~' in
~, to find the best (lowest metric) of the
2q cosets of 4ZN whose union is that coset
of ~', by summing the respective metrics of
the constituent one-dimensional metrics mjk
and comparing these sums (block 94);
(c) Decoding can then proceed in the usual manner
(block 96), using as a metric for each coset of
~' the best metric determined in step (b).
The decod~r will ultimately produce an estimate
of the sequence of cosets of A', which can be
mapped to a sequence of estimated coset
representatives Ck, which can be mapped to the
13Q6S'~3
- 31 -
corresponding Yk, from which the original ak
and x~ can be recovered if desired (block
98). These last steps require that the decoder
keep tra~k o~ the running digital sum x,~ l of
~he est imates Yx~
since tne ~RC sequences are i~ ~he Xnown code,
the error probabili~y of this decoder will be at least
as good as that of the known code, in the se~se of
achieving at least the same effective d2in.
However, because the PRC sequences are actually only a
subset of the known code sequences, such a decoder is
not a true maximum likelihood sequence estimator for the
PRC sequences. As a result, it may occasionally decode
to a sequ~nce which is not a legitimate PRC seque~ce.
Legitimate PRC sequences must satisfy the two following
additional conditions:
(a) A legitimate finite PRC sequence y(D) must be
divisible by l-D; i.e., the sum of its
coordinates must be zero;
(b) the range constraints imposed by the signal
paint selector must be satisfied for all Yk
(or equivalently xk or ik), based on the
reconstructed values of the RDS xk 1'
If this decoder makes a normal decoding error,
corre8ponding to a short period of wrong coset QStimates
followed by correct coset estimates, it is possible that
the corresponding finite PRC error sequence will have a
running digital sum other than zero. This will cause a
persistent error in the decoder's estimated running
3a digital sum xk~ which may lead to occasional mapping
errors back to the Yk, ak, and ultimately Xk, even
though the cosets ck are correct, for as long as the
error in the RDS estimate persists.
:~3~6S43
- 32 -
The decoder must therefore continually monitor
(block 99) whether the range constraints in the
reconstructed Yk and xk are satisfied. If they are
not, then it knows that its estimated RDS x,~_l is
incorrect; is should adjus~ by t;~e ~ini.~r~m a.~o~nt
necessary for the range cons~rai,~t to be sa~is'ied,
assuming that the coset sequencQ c~ is correct. With
probability 1, this will eventually result in
resynchronization of the estimated RDS to the correct
value, and normal decoding can resume. However, there
may be a considerable period o~ error propagation.
Avoidance of Error ProPaqation
We now give a general method of avoiding error
propagation at the receiver. The method works best when
the signal constellation consists of all points in ~
within an N-cube, but is not restricted to that case.
It may be regarded as a generalization of the principles
of eaxlier forms of precoding (modulo M) for use with
coded sequences.
The basic idea is that each possible PRC value
Yk should correspond to a unique (Ck, ak) value,
when the code can be formulated in one-dimensional form
as in Figure 7; or, more generally, that each group of N
Yk values should correspond not only to a unique
sequence of N ck values but also to a unique set of
uncoded bits, if a general N-dimensional signal point
selector is used as in Figure 6. Then the inverse map
from decoded Yk to coded and uncoded bits is
independent of the decoder's estimate of the running
3Q digital s~, so that
(a) the decoder need not keep track of the RDS;
(b) error propagation does not occur.
Thus in Figure 18, block 99 can be eliminated.
~3~5'~3
- 33 -
Figure 19 shows how this may be done where the
code can be formulated in one dimensional form, as in
the illustrative embodiment. From ck and a~, a
signal point selector selects a value s~ (cx,
5 a~) as in Figure 8. rn tne illustrative embodiment,
s~ ta~es on one of 12 val~es, ~amely, t.~e
half-integral values in the range from -6 to 6. In
general, Sk will take on one of the values from an
integer-spaced alphabet in a range of width M; we denote
this range by Ro~ Then, as in Figure 13, Yk is
selected as the unique number congruent to Sk ~modulo
M) in the range Ro + R(xk_l) xk_l o
where R(xk 1) is an RDS feedback translation variable,
and xk 1 is the previous RDS signal point. The
current RDS xk is computed as Yk + Xk 1~
Figures 20 and 21 are equivalent methods of
generating xk and/or Yk from the sequence sk such
that Yk ~ Sk (modulo M), analogous to Figures 12
and 14. In Figure 21, an innovations variable ik is
generated which is more or less white and uniformly
distributed OvQr the range Ro~ so that its variance
S0 is approximately M2J12; thus S0 ~ 12 for th0
illustrative embodiment, a penalty of about 0.7 dB over
the value of 80 ~ 10.25 achievable with no RDS
2S feedback. As in Figures 12, 13, 14, all three sequences
xk~ Yk, and ik carry the same information, and as
in Figures 15, 16, 17, any can be used as the input to a
filter which shapes the spectrum for transmission.
The penalty in the innovations variance is
3~ elimi~ted if the original code coordinates are
uniformly distributed over a range Ro; i.e., if the
original constellation is bounded by an N-cube with side
Ro~
~3~ÇiS~3
- 34 -
As an illustrative embodiment with a square
constellation, we use the same two-dimensional 8-state
Ungerboeck encoder as in Figure 2, except with the
12~-point constellation o~ Figure 22 rather than that of
5 Figure 3. The constellation cons~s~s of alternate
~oints from the conventional 2~6-~oint 16 .x 16
constellation; thus the coordinates have the 16
half-integral values { ~ 1/2, ~ 3/2, ..., _
15/2}, but with the restriction that the sum of the
two coordinates must be an even integer (0, modulo 2).
The minimum squared distance between signal points is
thus 2, rather than 1; and the d2in of the code is
lo, rather than 5. The variance of each coordinate is
now 21.25 rather than 10.25, which after scaling by 2 is
a loss of 0.156 dB relative to the Figure 3
constellation, since the cross is more like a circle
than is the square. (In lattice terminology, we are now
using the 8-way lattice partition RZ2/4Z2 rather
than æ /2RZ ).
It will be observed that now each of the eight
subsets corresponds to a uniqua pair of coset
representatives (cl, c2) modulo 4, such that cl +
C2 ~ 0 (modulo 2). Therefore, the three coded bits of
Figure 2 determine a pair of coset representatives
directly in sub8et selector 24, rather than with the aid
of an uncoded bit as in Figure 4. The four uncoded bits
then select one of the 16 points in the selected
subset. In this case, the uncoded bits may simply be
taken two at a time to determine one of the four ranges
3Q -8~to -4, -4 to 0, 0 to 4, or 4 to 8. This is
conveniently expressed by letting the two-bit range
identifying parameters (al, a2) each represent one
of the four values {_2, _6}; then the coordinate
s,election function is simply Sk = f(ck, ak) - ck
~3C~5'~3
- 35 -
+ ak. Note that the possible values for sk are the
16 half-integral values in the range Ro from -8 to 8,
of width M = 16.
Conventional precoding may then be don~ ~odulo
5 16. The entire encoder is illustr2t~d in Fi~re 23.
The RDS value xk is the SUIT sk ~ ~sk-l (m
16). In this case the xk values are essentially
independent identically distributed (white) random
variables, and Yk = Xk - Xk-l ~ Sk (mo
To obtain spectral tradeoffs via RDS feedback
as in Figures 12, 13, 14, let sk continue to represent
the desired congruence class of Yk (modulo 16), and
let R(xk 1) be an RDS feedback variable as in Figures
12, 13, 14, ideally equal to ~xk 1 Then Figures 24,
25, 26 show three equivalent methods of obtaining
qU ces xk and/or Yk = Xk ~ xk_l such that
Yk ~ Sk (modulo 16) and Sx and Sy have the
desired tradeoff, gi~en S0 = 21.25. Here Ro is the
range from -~ to 8.
In this case the innovations variable ik has
variance S0 ~ 162/12 - 21.33, essentially the same
as the variance of each coordinate in Figure 22, so that
there is no penalty beyond the 0.16 dB involved in using
Fig. 22 rather than Fig. 3.
As already noted, the decoder need not keep
track of the RDS, because, given the estimated PRC
sequence Yk, the ck~ ~k~ and ultimately the
original input bit sequence are uniquely determined.
However, if the decoder does keep track of the estimated
3Q ~DS and th~ corresponding ranges that the Yk should
fall into, it can detect that an error has occurred
whenever the decoded Yk falls outside the estimated
S~3
- 36 ~
range. Even if not used for error correction, such
range violation monitoring can yield an estimate of
decoder error rate.
Auqmented Decoders
~ ~rue ~aximum li~elihood sequence estimator
would take into account rhe e~tire state of the encoder
and channel, which in general will include the value of
the RDS xk 1 (~he channel state) as well as the state
of the encoder C. Such a decoder would achieve the true
dmin of th~ PRC sequences, and would be free of
error propagation. However, because xk l in general
takes on a large number of values, in principle possibly
an infinite number with RDS feedback, such a decoder may
not bo practical. In addition, to achieve the true
dmin may require an essentially infinite decoding
delay because the code/channel combination becomes
quasi-catastrophic when n is large, as we shall sxplain
more fully below.
It may be worth considering augmenting the
decoder to at least achieve the true dmin of the
code, however. 3ecause all finite PRC sequences are
divisible by l-D, all finite-weight error sequences must
have even weight. Thus, the true dmin is always
even. In the illustrativQ embodiment, the true
dmin i8 actually 6, not 5.
A general method for achieving the true
dmin in such cases while only doubling the
effective numbQr of states in the decoder is as
follows. LQt the decodQr split each stata of the
encode~ C into two, one corresponding to an even RDS and
one to an odd. During decoding, two sequences then
merge into the same state only if their estimated RDS
has ths same value (modulo 2). Thus, it becomes
imposSible for two sequences differing by an odd-weight
13(36S~
- 37 -
error seguence to merge, so that the effective d2in
is the weight of the minimum even-weight error sequence
in the original code. Further, if there is a decoding
error that res~lts in a persistent estimated RDS error,
as discussed above, that error must ~e at least 2, so it
will tend ~o be detected sooner.
Tha decoder o~ Figure 18 can be used, modified
only as shown in Figure 27. For most codes, each of the
subsets of the signal constellation (cose~s of ~' in
~? will contain points all of which have a sum of
coordinates which is either even or odd. For example,
in Figure 3, four of the eight subsets contain points
whose coordinate sum is O (modulo 2), and 4 contain
points whose coordinate sum is 1 (modulo 2). Thus the
metric of each subset (coset of ~' in ~) can be
determined as before in blocks 92 and 94; the maximum
likelihood sequence estimator 196 is then modified to
find the best sequence of cosets that (a) is in the
code, and ~b) has a running digital sum congruent to
2Q zero (modulo 2). The decoded coset sequence is mapped
back to Yk and xk in block 98 as before, with
adjustment of xk l by block 99 if necessary
(adjustments will now be by multiples of 2).
There is a drawback to this technique, however,
in addition to the doubling of the decoder state space.
Two sequences may differ by an odd-weight error sequence
followed by a long string of zeros (no differences).
The decoder may then ~ollow parallel pairs of states in
the decoder trellis for a very long time, without
3~ re~$olving the ambiguity. This 'quasi-catastrophic'
behavior can ultimately be resolved by th~ maximum
likQlihood sequence estimator only by a range violation
13G6S'~3
- 3~ ~
due to the differing RDS parity on the two paths. Thus,
the decoding delay required to achieve the true
d2in may be very large.
For this ~eason, it Will generally be
preferable simply .o chcse a~. encoder c .~ith ~-~ice the
number of states, and use an unaugmented decoder for c.
For example, there is a 16-state 2-dimensional
Ungerboeck code with d2in = 6; even though it may
have a somewhat larger error coefficient ~han the
8-state code with an augmented 16-state decoder, we
believe that in practice it will be preferable.
It may be worth mentioning that PRC sequences
drawn from the 4-state two-dimensional Ungerboeck code
also have a true d2in of 6, since that code has
dmin ' 4, with the only weight-4 error sequences
being single coordinate errors of magnitude 2, which are
also not divisible by l-D. A 16-state decoder which
keeps track of the RDS modulo 4 can achieve this
dmin. However, in this case not only is the code
quasi-catastrophic, but also the error coefficient is
large, so again it would seem that the ordinary 16-state
2D Ungerboeck code would be preferable.
As mentioned earlier, a complex (or quadrature)
partial response system (QPRS) may be modeled as a 1 + D
sampled-data filter operating on a complex-valued RDS
sequence x(D) to produce a complex-valued PRC sequence
y~D~ - (1 + D) x(D); i-e-~ Yk ' -Xk + X-k-l
used with double-sideband quadrature amplitude
3~} modulation over a bandpass channel, such a system
results in nulls at both band edges, fc ' fN~
where fc is the carrier frequency and fN ~ 1/2T is
the width of a single Nyquist band.
S~-~3
- 39
When N is even and 4ZN is a sublattice of
~', as is the case with all good codes previously
mentioned, then we can adapt a kncwn good code for use
in a QPRS system by using essentially the same
principles as before. .~ coset of 4z~ can be specified
by N/2 complex-valued coset representatives Ck, ~here
coset represQntatives take on on~ of 16 possible values,
corresponding to 4 integer spaced values (modulo 4) for
the real and imaginary parts of Ck, respectively. The
general picture of Figure 8 then holds, except that
coset selector 58 and range-identifying parameter
sQlector 64 select N/2 complex-valued coset
representatives ck and range-identifying parameters
_~, and the signal point selector operates once per
quadrature signal and puts out complex-valued signals
Xk. Coset precoding as in Figure 9 is done by forming
the complex-valued precoded coset c'~ _ ck -
Ck 1' (modulo 4~ onco per quadrature symbol. RDS
feedback as in Figures 11, 12, 13 is done by using a
function R(ak) that identifies a region of complex
space of area 16 that contains exactly one element from
any coset of 4z2, and a complex-valued translation
variable R(xk_~), ideally equal to nxk 1~ In the
cases where 2Z or 2RZ is a sublattice of A',
precoding can be done modulo 2 or 2 + 2i, respectively,
and R(ak) can identify a region of area 4 or a
containing exactly one element from any coset of 2Z~
or 2RZ , respectively.
Hiqher-Dimensional SYstems
We have shown embodiments in which coordinates
of N-dimensional symbols are formed on a
signal-by-signal (one or two-dimensional) basis, with
signal-by-signal feedback of the previous RDS value
Xk 1~ Similar kinds of performance can be obtained by
130~3
- 40 -
systems which select signals on a higher-dimsnsional
basis. In ~uch systems, the precoded coset
representatives must be grouped as in Figure 9 so as to
select subsets in the appropriate dimension, signal
points then selected i.~ that di"ension, and t.~e
coordinates then serialized again for transmission over
the channel. If the order of cosets is maintained, then
such a system retains the property that the PRC
sesuenc~s are from the given code and have the specified
dmin. In such a system it may ~e more natural to
do (RDS) feedback on a higher-dimensional basis rather
than on each signal.
N-Dimensional Codes
Although representation of codes in
one-dimensional form is desirable, it is not essential.
In this section we show how codes may be generated
directly in N dimensions. In certain forms, the
N-dimensional code is entirely equivalent to its
one-dimensional counterpart. In other forms, simplified
2Q emhodiments may be obtained.
Again, we shall use for illustration the
8-state 2-dimensional Ungerboeck-type code of Figure 2,
with the 2-dimensional 128-point constellation of Figure
3. In this constellation, recall that each coordinate
takQs on values from the alphabet of the 12
half-integral values in the range from -6 to 6; the
two-dimensional constellation uses 128 of the 144
possible pairwise combinations of elements of this
alphabet.
As a first step, we expand the signal
constellation to an infinite number of values, as
follows. Let the expanded constellation consist of all
pairs of numbers that are congruent to some point in the
original (Figure 3) constellation (modulo 12). Thus the
13C165'13
- 41 -
points in the expanded constellation consist o~ pairs of
half-integral values. If we regard the original
constellation as a cell bounded by a 12 x 12 square 98,
then the expanded constellation consists of the infinite
repeti~ion of this cell t;~roughout 2-s?ace, as indicated
diagrammatically in Figure 28. No~e that eac;~ cell
contains only 128 of the 144 possible points; there are
4 x 4 'holes' 99 in the expanded constellation.
The key property of this expanded constellation
101 is that if we place a 12 x 12 square anywhere in the
plane (with sides oriented horizontally and vertically),
the square will enclose exactly 128 points, one
congruent to each of the points in the original
constellation. An even more general statement is true:
if we place a rhombus 102 with horizontal width 12 and
vertical height 12 (see Figure 29~ anywhere in the
plane, it too will enclose l2a points, one congruent to
each point in the original constellation.
Referring to Figure 30, we may now implement
RDS feedback on a two-dimensional basis as follows. Let
Xk 1 represent the running digital sum of all Yk
pr~vious to the current (two-dimensional) symbol. Let
R(xk 1) now denote a region of the plane corresponding
to a 12 x 12 rhombus as in Figure 29, with both the
shape and the location of the rhombus possibly depending
k-l et ~Yo,k, Yo,k+l) denote the point in
the original constellation that would be selected (in
selectors 104, 105) by the three coded bits and four
uncoded bits according to the unconstrained code
(Figure 2). Then (in selector 106) select (Yk,
Yk+l) as the unique point in the two-dimensional
expanded constellation that lies within the region
R(xk 1) and is congruent to (Yo~k~ Y0~k+l) (
13~)6~'~3
- 42 -
12); these will be the two coordinates Yk. We can
obtain (xk~ xk+l) from Xk = Yk ~ Xk-l' Xk+
Yk+l + Xk as shown,
we now show that this two-dimensional system
can produce the same outputs as the one-dimensional RDS
feedback system (modulo 12) shown earlier, with the
optimal one-dimensional RDS feedback variable R(xk 1)
= Bxk 1 Referring to Figure 31, in one dimension,
given xk 1' Yk is chosen as the unique value in the
range Ro + Bx~_l - x~_l congruent to Sk
(modulo 12), where we now recognize that Sk is
congruent to YO k. Hence, one coordinate of tho
rhombus used in the two-dimensional system can be taken
to lie in the same width-12 range. Then, given xk 1
and Yk, and thus also Xk = Yk + Xk-l' Yk+l is
chosen as the unique value in the range Ro - (l-B)xk
= Ro - (l-~)Yk ~ B)xk 1 that is congruent to
sk+l ~ Yo k+l (modulo 12). Thus, Yk~l lies in the
range Ro - (l-~)xk_l (same as Yk), shifted by
2Q -(l-~)yk.
Thus, by proper choice of rhombus, we can
emulate the performance of a one-dimensional (modulo 12)
RDS feedback system with a two-dimensional system. It
will thus have the same advantagQs~ including avoidance
of error propagation and near-optimal tradeoff between
Sx, Sy and SO, and the same disadvantages, notably
the increase in SO to 12 over the 10.25 otherwise
possible"
We can choose other two-dimensional RDS
feedback variables (regions) to further simplify
implementation, and achieve other advantages, at the
cost of suboptimal power tradeoffs. For example, a
system almost identical to the simplified
one-dimensional system described earlier results if we
1306~ 3
- 43 -
let R(xk 1) be the square 120 of side 12 centered at
(-2, -2) when xk 1 is positive, and the square 122
centered at (+2, +2) when x~ 1 is negative. Thus ~e
use one of the two constellations 124, 126 shown
schematically in Fi~ure 32
As in the previous one-dimensional system,
inner points are always chosen from the same set
regardless of XX 1~ but outer points are varied so as
to bias Yk in a positive or negative direction. The
ranges of the Yk are strictly limited from -7 1/2 to 7
1/2. rn fact, this system is identical to the earlier
simplified system, except that Yk+l is chosen on the
basis of xk_l, rather than Xk. In practice, all the
measures of performance and spectrum will be very
1~ similar.
Another variant yields a system akin to that o~
the Calderbank, Lee, and Mazo type. A CLM-type system
uses an expanded signal constellation with twice the
ordinary number of signal points, divided into two
disjoint constellations, one to be used when xk 1 is
positive, and the other when xk 1 is negative. Figure
33, for example, shows a 16 x 16 square constellation
divided into two disjoint constellations 110, 112 of 128
points each, æuch that each such constellation divides
evenly into 8 subsets of 16 points each. One
constellation consists of points the sum of whose
coordinates is positive or zero and is used when xk 1
is negative; the other consists of points whose
coordinate sums are negative or zero and is used when
xk_l is positive. In two dimensions, doubling the
constellation size doubles Sy and thus does not yield
a favorable power tradeoff; however, in higher
dimensions the penalty due to the use of two disjoint
constellations is less.
13~65~3
- 4~ -
These ideas can be generalized to N dimensions,
as follows. If there is a one-dimensional formulation
of the code as in Figure 8, using modulus M, then an
N-cube of side M completely surrounds the N-dimensional
constellation, and the resul.ing cell can be replicated
to cover N-space wishout compromising the minimum
squared distance between code sequences that are
congruent to original code sequences modulo M. Then we
may use an N-dimensional RDS feedback function
R(xk 1)' where for all xk_l, R(xk_l) is a reg
of N-space of volume ~ that contains exactly one
point in each equivalence class of N-vectors modulo M,
in an N-dimensional analogue of Figure 30.
Other embodiments are within the following
claims.