Note: Descriptions are shown in the official language in which they were submitted.
~ 202D~94
~BON BIACR PROCE88 CONTROL 8Y8TEN
3~ield of the Inv~ntion
The present invention relates to process controls and,
more particularly, to process controls for controlling
the production of carbon black.
10 Background Information
In the production of carbon black it is desirable to
control certain output variables of the carbon black in
order to produce carbon black of substantially
15 consistent quality. Carbon black output variables that
are often the focus of control are the iodine number and
the DBP. Because the input variables and other physical
parameters of carbon black production processes
frequently change while the carbon black is produced, it
20 has proved difficult to produce carbon black of
substantially consistent quality. Input variables that
frequently fluctuate during the carbon black production
process are, for example, the air humidity and the fuel
quality. Fluctuations in the input variables can have a
25 significant influence on the carbon black output
varia~les, such as iodine number and/or DBP. Likewise,
other unmeasurable physical parameters frequently change
during the carbon black production process, and also
affect the carbon black output variables, such as iodine
202Q594
--2--
number and/or DBP.
In some known carbon black production sy5tems, 6amples
of the carbon black produced are taken at spaced
5 intervals, for example, once every few hours of
operation. - Then, the output variables, such as iodine
number and/or DBP, are measured for each sample. The
operator then adjusts one or more input variables, such
as the feedstock flow rate, after each sample is tested.
10 The operator's adjustment is usually based on his or her
own subjective experience with the particular carbon
black production system, in ordsr to try and bring the
output variables, such as iodine number and/or DBP, back
toward their goal values.
One problem with such known methods of controlling the
production of carbon black is that the carbon black
output variables, such as iodine number and/or DBP, are --~
not controlied during the time intervals between
20 samples. Therefore, if changes in the input variables
or other physical parameters of the carbon black
production system cause the value of the output
variables, such as iodine number and/or DBP, to move
outside of a desirable range of values, the change
25 usually will not be noticed until the next sample is
taken. As a result, a substantial amount of the carbon
black produced may not fall within the customer's
specifications. Yet another problem with such known
methods of controlling the production of carbon black,
3~ is that such methods rely on the subjective analysis of
the operator in order to adjust one or more input
variables, based on the values of the laboratory
measured output variables. As a result, input variable ~ --
adjustments frequently may vary between operators and,
35 therefore, result in an inconsistent quality in the
carb n bla~ k produced.
_3_ 2020~9~
It is an object of the present invention, therefore, to
overcome the problems and disadvantages of known carbon
black production systems.
5 Bummary o~ th~ Invention
The present invention is directed to a method of
controlling the production of carbon black in a carbon
black reactor, and comprises the following steps: (a)
10 measuring at spacsd intervals in time at least one input
variable utilized in the production of carbon black
while the carbon black reactor is operating; (b)
employing at least one algorithm to predict at spaced
intervals at least one output variable of the carbon
black utilizing the at least one input variable measured ~-
during the spaced interval; (c) detPrm;n;n~ at spaced
averaging intervals an average value of the at least one
predicted output variable; and (d) adjusting at spaced
intervals at least one of the input variables ut;1;7;n~
20 the difference between the average value of the at least
one predicted carbon black output variable and a goal
value of that output variable while the reactor is
operating, in order to achieve the goal value of that
output variable to obtain a substantially consistent
25 quality of carbon black.
The method of the present invention preferably further
comprises the following steps: (a) sampling at spaced
intervals in time the carbon black produced while the
30 carbon black reactor is operating; (b) measuring the at
least one output variable from the sampled carbon black
while the carbon black reactor is operating; and (c)
adjusting the at least one algorithm by utilizing the
measured value of the at least one output variable in
35 order to more correctly predict that output variable.
In one embodiment of the present invention, the at least
2~20~9~
--4--
one predicted output variable is the iodine number, and
the input variable adj usted at spaced intervals is the
feedstock flow rate. In another embodiment of the
present invention, the at least one predicted output
5 variable is the DBP, and the input variable adjusted is
the potassium additive solution flow rate.
In another embodiment of the present invention, the at
least one algorithm is adjusted by utilizing a weighted
10 mean of the error variance of the predicted values of
the carbon black output variable during the period the
carbon black sample is taken, and the error variance of
the measured value of that output variable. The at
least one algorithm is preferably adjusted by also
15 employing at least one second algorithm for de~,~rm;n;n~
an optimum estimated output variable. The optimum
estimate of the output variable is based on the weighted
mean of the error variances and the difference between
the measured value of the output variable and the
2 0 average value of the predicted output variable during
the period the sample was taken.
The presen,t invention is also directed to an apparatus
for controlling the production of carbon black in a
25 carbon black reactor. The apparatus comprises metering
means for measuring at spaced intervals in time at least
one input variable utilized in the production of the
carbon black while the carbon black reactor is
operating. Computing means of the apparatus are coupled
3 o to the metering means f or predicting at spaced intervals
at least one carbon black output variable pursuant to at
least one algorithm ~hat utilizes the at least one input
variable measured during the spaced interval. The
computing means further detr~rm; nr~s at spaced averaging
35 intervals an average value of the at least one predicted
output variable over that spaced interval. The
apparatus further comprises adjusting means coupled to
2020~4
--5--
the computing means f or adj usting at spaced intervals
pursuant to an adjusting algorithm the at least one
input variable of the carbon black. The adj ustment is
based on the difference between the average value of the
5 at least one predicted output variable over the spaced
averaging interval and a goal value of that output
variable, to achieve that goal value while the reactor
is operating in order to obtain a substantially
consistent quality of carbon black.
In another embodiment of the present invention, the
apparatus further comprises sampling means for sampling
at spaced intervals the carbon black produced while the
carbon black reactor is operating, so that the at least
15 one output variable can be laboratory measured. The
computing means is responsive to the measured value of -
the at least one output variable for adjusting the at
least one algorithm utilizing the measured value of the
at least one output variable in order to more correctly
2 0 predict that output variable .
Therefore, the method and apparatus of the present
invention compensate for changes in the input variables
and other physical parameters of the carbon black
25 production system while the carbon black reactor is
operating, in order to produce carbon black of
substantially consistent quality. By measuring at
spaced intervals at least one input variable, predicting
at spaced intervals at least one output variable with an
30 algorithm utilizing the at least one input variable,
averaging at spaced averaging intervals the predicted
output variables, and then adjusting at spaced intervals
the at least one input variable by utilizing the average
predicted value of the output variable, the method and
35 apparatus of the present invention produces carbon black
of substantially consistent quality. Likewise, by
sampling the carbon black produced at spaced intervals,
2~20~94
-6-
measuring the at least one output variable from the
sampled carbon black, and adjusting the at least one
algorithm by utilizing that measured value, the
apparatus and method of the present invention can more --
S accurately predict the output variable, and thus further -~
produce carbon black of substantially consistent
quality .
Other advantages and features of the present invention
will become apparent in view of the following detailed
description and drawings taken in connection therewith.
Brici~ Description of thc Dras~ings
Figure 1 illustrates schematically an example of a
furnace carbon black reactor in which the process
control system of the present invention may be employed.
Figure 2 illustrates schematically the hardware
components of the process control system of the present
invention .
Figure 3 is a flow chart that illustrates conceptually
the procedures of the process control system of the
present invention f or controlling the iodine number
and/or the DBP.
Figure 4 is a flow chart that illustrates conceptually
the procedures of the distributed control system of
3 0 Figure 2 in predicting the iodine number and the DBP in
accordance with the present invention.
Figure 5 is a flow chart that illustrates conceptually
the procedures of the distributed control system of
Figure Z for adjusting the feedstock flow rate and the
potassium additive solution flow rate to achieve the
goal iodine number and goal DBP, respectively, in
202a~9~
-7 -
accordance with the present invention.
Figure 6 illustrates schematically a PID algorithm
employed in accordance with the present invention for
5 adjusting the new feedstock flow rate and the new
potassium additive solution flow rate to achieve the
goal iodine number and the goal DBP, respectively.
Figure 7 is a flow chart that illustrates conceptually
lO the procedures of the system controller of Figure 2 for
adj usting the iodine number algorithm and the DBP
algorithm at the end of each carbon black sample period ~ -
in accordance with the present invention.
15 Detailed Descriptio~
The carbon black process control system of the present
invention compensates for variations in the physical
parameters in a carbon black reactor by adjusting one or - =
20 more input variables of the process, in order to control
one or more output variables of the process, and thus
produce carbon black of substantially consistent
quality. The output variables of the carbon black that
are controlled, for example, are iodine number and/or
2 5 DBP .
In Figure 1, an example of a furnace carbon black
reactor, in which the process control system of the
present invention may be employed, is illustrated
3 o schematically . The carbon black reactor shown is a
three-stage reactor, including a burner zone, a
feedstock injection zone, and a reactor zone. It should
be noted, however, that the process control system of
the present invention may be employed with any other ~-
35 type of carbon black reactor or process wherein a
hydrocarbon feedstock is pyrolyzed with hot combustion
gases to produce combustion products containing
.
202~594
--8--
particulate carbon black In the burner zone of the
reactor in Flgure 1, a liquid or gaseous fuel is reacted
with any type of suitable oxidant, preferably air, to
form hot combustion gases. The resulting combustion
5 gases are discharged from the downstream end of the
burner zone and are caused to flow at a high velocity
through the feedstock injection zone. A hydrocarbon
feedstock in either gaseous, vapor or liquid form, which
may be the same or different than the fuel utilized to
10 form the combustion gas stream, is injected into the
combustion gas stream in the feedstock injection zone,
whereupon pyrolysis, or thermal decomposition of the
hydrocarbon feedstock occurs. The reaction mixture of
f eedstocX and combustion gases is then discharged into
15 the reactor zone, where completion of the carbon black
particle formation occurs. The reaction mixture is then
quenched with a suitable fluid, usually water, in the
end of the reactor zone to terminate the carbon black
particle forming reaction. The reaction mixture is then
20 further cooled and the solid carbon black particles are
collected in a manner known to those skilled in the art.
The input variables that are analyzed by the carbon
black process control system of the present invention
25 are also illustrated schematically in Figure l. The
input variables are each measured prior to injection
into the burner zone or feedstock injection zone. The
input variables include the feedstock flow rate, the
fuel flow rate, the air flow rate, the air preheat
30 temperature, the air humidity, the gas or other first
stage fuel quality, the feedstock quality, and/or the -
potassium additive solution flow rate. Usually, only
some of the input variables can be accurately controlled
to control one or more output variables of the carbon
35 black, such as iodine number and/or DBP. Typical
controlled input variables are the feedstock flow rate,
the fuel flow rate, the air flow rate, and/or the
- 20~0$94
g
potassium additive solution flow rate.
In one embodiment of the present invention, the process
control system calculates a predicted iodine number
5 (I2No. ) at spaced intervals, for example, every one to
ten seconds. The predicted iodine numbers are
calculated by an algorithm which is based, in part, on
empirical test results for any given carbon black
reactor geometry in which the process control system is - -
employed. The predicted iodine numbers are then
averaged (I2No.AvG) over spaced intervals, for example,
every two minutes. Based on the average predicted
iodine numbers, a controlled input variable, such as the
feedstock flow rate, is automatically adjusted to
achieYe the goal iodine number (I2No.GOAL). Therefore,
carbon black of substantially consistent quality can be
produced regardless of changes in the measurable input
variables of the carbon black reactor, such as air
humidity and/or changes in the calculated input
variables, such as fuel quality.
In accordance with an example of the pr~sent invention,
the process control system is employed with a three-
stage reactor as illustrated schematically in Figure 1.
The exemplary reactor uses a hydrocarbonaceous oil
feedstock and natural gas fuel. It should be
understood, however, that the process control system of
the present invention may be used equally as well with
any other type of reactor geometry, and any other type
of feedstock and/or fuel. The predicted iodine numbers
( I2No . ) may be calculated in accordance with the
following iodine number algorithm:
( 1 ) I2No . p = KC*OAC + KP*PC + KA*AIR +
- KT*CAT+ KH*AH + XO
The algorithm constants are empirically det~in ~d for
~ 2~20~
--10--
given carbon black reactor geometries. For example, the
algorithm constants for a three-stage reactor, as
illustrated in Figure 1, might have different values
from the algorithm constants for a two-stage reactor
5 (not shown). The algorithm constants are d~f;ne~l as
follows:
KC - overall combustion constant
KP - primary combustion constant
KA - air flow rate constant
KT - air preheat temperature constant
KH - air humidity constant
KO - system intercept constant
15 The feedforward input variables are defined as follows:
OAC - overall combustion [ % ]
PC - primary combustion [96]
AIR - combustion air rate [KSCF~]
zo QT - combustion air preheat temperature [~F]
AH - air absolute humidity [lbs. water/thousand
lbs. dry air]
The feedforward input variables are det~r~; n~rl by
2~ measuring certain input variables of the carbon black
reactor with metering instruments, while the reactor is
operating. Immediately upon measuring the respective
input variables, the feedforward input variables are
calculated based on the following equations:
t2) PC = AIR * loq
GAS * ATBG
wherein:
3~
AIR is the air flow rate [KSCFEI] (standard
cubic feet per hour, in thousands);
20205g~
GAS is the gas flow rate tKSCFH]; and
ATBG is the air to burn gas ratio [SCF air/SCF
gas ], which is the stoichiometric value of the
amount of air required to completely burn the
corresponding volume of gas.
If the carbon black reactor uses a type of fuel other
than gas, for example, a liquid hydrocarbon fuel, then
the flow rate of that fuel would be indicated in
10 equation (2~ in place of the gas flow rate (GAS), and in
the other equations described below where that term also
appears. Likewise, the ATBG would be replaced in the
same equations with the ratio of the stoichiometric
value of the amount of air re~[uired to completely burn
15 the corresponding amount of the type of f~el used.
Similarly, if the carbon black reactor uses any suitable
oxidant other than air, then the flow rate of that
oxidant would be indicated in equation (2) in place of
the air flow rate (AIR), and in the other equations
20 described below where that term also appears.
(3) OAC = AIR * 100
GAS * ATBG + OIL * ATBO
wherein:
AIR is the air flow rate [KSCFH];
GAS is the gas flow rate [KSCFH];
ATBG is the air to burn gas ratio [SCF air/SCF
gas];
OIL is the liquid hydrocarbon feedstock flow
rate [gal./hr. ]; and
ATBO is the air to burn oil ratio tKSCF
air/gal. oil], which is the stoichiometric value of
the amount of air required to completely burn the
corresponding volume of oil (a typical value is
about 1.54 KSCF/gal. oil).
2020~
-12-
If the carbon black reactor uses feedstock other than a
liquid hydrocarbonaceous feedstdck, such as a gaseous
hydrocarbonaceous feedstock, then the flow rate of that
feedstock would be indicated in place of the oil
5 feedstock flow rate (OIL), and in the other equations
described below where that term also appears. Likewise,
the ATBO would be replaced in the same equations with
the ratio of the stoichiometric value of the amount of
air required to completely burn the corresponding amount
10 of the other type of feedstock used.
The air flow rate (AIR) and gas flow rate (GAS) are
measured on-line by known metering instruments before
inj ection into the burner zone of the carbon black
15 reactor. The air and gas meters are preferably
orifice-type meters that compensate for variations in
the flowing pressures and temperatures in generating the
flow rate signals. The ATBG is preferably calculated
based on the input gas composition measured by a gas
20 chromatograph (not shown). The gas chromatograph can
either be employed to determine the gas composition
periodically on-line or periodically off-line. Based on
the updated gas composition, the ATBG value is
correspondingly adjusted. Likewise, the specific
25 gravity measurement of the gas used by the gas meter is
also correspondingly adjusted based on the gas
composition reading of the gas chromatograph. If the
gas chromatograph measures the gas composition on-line,
it ordinarily has the capability to update the ATBG
30 value within the range of at least about every 2 to 10
minutes. The ATBO, on the other hand, ordinarily cannot
be measured and updated on-line. Therefore, the ATBO
value is pre~erably laboratory measured for each
particular grade of feedstock or feedstock blends. The
35 ATBO value might be updated, for e~ample, before a
production run or even once every several months.
202~9g
-13 -
The feedstock flow rate (OIL) is preferably measured by
a Coriolis-type flow meter that measures the mass flow
rate of feedstock, usually in lb5/hr, and the density of
the feedstock, prior to injection into the feedstock
5 injection zone of the reactor. The feedstock flow rate
is preferably converted into a corrected volumetric flow
rate, expressed in gallons per hour (gal./hr. ) . The
combustion air preheat temperature (CAT) is measured by
a thermocouple immediately prior to entry into the
10 burner zone of the reactor. The air absolute humidity
(AH) is measured by a humidity sensor of a type known in
the art, and is expressed in units of lbs. of
water/~hmlc~n~l lbs. dry air. The air absolute humidity
measurements are preferably employed to serve two
15 primary purposes. One purpose is to provide an updated
feedforward input variable (AH) for the iodine number
algorithm. The other purpose is to adjust the air flow
rate (AIR) ~ r ~n~l; n~ on the measured air absolute
humidity (AH) to maintain a 5ubstantially constant dry
2 O air flow rate entering the burner zone of the reactor.
A PID algorithm (proportional, integral, derivative
control algorithm), of a type known in the art, is
preferably employed to adjust the air flow rate =~
r~n~;ng on the updated air absolute humidity readings,
25 in order to compensate for the amount of humidity in the
air and thus maintain a substantially constant dry air
flow rate.
The algorithm constants of t~e iodine number algorithm
30 (equation (1) ) are de~Prm;n~ in accordance with a known
process identification procedure using regression
analysis, and are de~rm;n~d for given types of= carbon
black reactor geometries. Therefore, the values of the
constants will likely be different for substantially
35 different reactor geometries. A known software package,
which includes the following components, "RS/l, "
"RS/Explore, " and "RS/Discover, " sold by BBN Software -
_ _ _ , , ,, , ,, _,
2~20594
-14-
Products Corporation, of Cambridge, Massachusetts, is
preferably employed for performing the regression
analysis procedure. The BBN Software can be used with a
VAX minicomputer, manufactured by the Digital Lquipment
5 Corporation, of Maynard, Massachusetts. The BBN
Software facilitates the implementation of experimental
design procedures, which are known to those skilled in
the art, as well as regression analysis procedures, also
known to those skilled in the art, and is not necessary,
10 but simply provides a convenient means for carrying out
such procedures.
In performing the regression analysis procedure, the
input and output variables in the carbon black
15 production process are identified. The input variables
in relation to the iodine number are, for example, those
illustrated in Figure 1, including the feedstock flow
rate, air flow rate, fuel flow rate, air preheat
temperature and humidity, fuel quality (ATBG), and
20 feedstock quality lATB0). The output variable is the
iodine number (I2No. ) . Based on the input variables and
output variable identified, a series of experiments is
designed to identify the parameters of the algorithm by
employing preferably the BBN Software in a VAX
25 minicomputer. The series of experiments is then run on
a carbon black reactor having the type of reactor
geometry for which the algorithm will be used.
Therefore, the regression analysis procedure will likely
provide constants that have different values for
30 different types of reactor geometries. At different
stages during the experiments, changes are made to the
input variables in a manner prescribed by the designed
experiments. Based on the experiments, a set of input
and corresponding output data is collected. The
35 regression analysis procedure is then performed on the
set of data to identify the empirically ~ rm;ned
constants of the iodine number algorithm (equation (1) ) .
_ _ _ _ _ _ , .. . ....... .... . . .
2~20594
--15--
In accordance with ~ne example of the present invention,
pursuant to the above-described regression analysis
procedure, the following constants were empirically
determined for a three-stage reactor geometry similar to
5 that illustrated schematically in Figure 1:
KC = 12 . 5 KT = 0 . 094
KP = --0 .123 KH - 0 . 238
KA = -0.184 KO = -201 (approximately)
Therefore, in accordance with one embodiment of the
present invention, the input variables nPcPcc~ry to
determine the feedforward input variables of the iQdine
number algorithm (equation (1) ) are measured about once
15 every second. Then, based on those measurements, the
iodine number algorithm is solved about once every
second to generate a new predicted iodine number
(I2No. ). Then, at spaced averaging intervals, for
example, about every two minutes, the predicted iodine
2 0 numbers calculated over that interval are averaged
(I2No.AvG). A controlled input variable, such as the
feedstock flow rate (OIL), is then automatically
adjusted at the end of each averaging interval depending
on the difference between the average predicted iodine ~-
25 number (I2No.AvG) and the iodine number set point or
goal iodine number ( I2No . GOAL), in order to achieve the
goal iodine number. It should be noted, however, that
one or more other input variables, such as the I~IR
and/or GAS can be adjusted instead of the feedstock flow
30 rate (OIL) to achieve the goal iodine number
( I 2N GOAL)
The relationship between the iodine number and the OAC ~
is the primary adjustment relationship. The OAC is a
35 calculated control variable as opposed to a measured
control variable. As will be described below, the
equation defining the OAC includes as its terms the AIR,
2020594
--16--
the GAS, and the OIL. Theref ore, based on the
relationship between the iodine number and the OAC, the
r ~r iate changes in the preferred measured control
variable, OIL, can be derived to achieve the goal iodine
5 number (I2No.GOAL). The feedstock flow rate (OIL) is
the preferred input variable to control, because, for --
one reason, it appears in only one term of the iodine
number algorithm and, therefore, the adjustment
procedure can be relatively simple and straightforward.
The new feedstock flow rate (OILN~W), that is required
to achieve the goal iodine number (I2No.GOAL), is .
estimated based on the f ollowing relationship between
the iodine number and the OAC:
(4) ~I2No. = RC ~t~OAC
wherein:
~I2No. is the I2No.GOAL minus the two
minute average ( or other spaced interval ) o f
the I2 No p ( I 2 No AVG );
~OAC is the new OAC (OACNEW) required to
achieve the I2No. GOAL minus the two minute - -
average of the measured OAC (OACAVG); and
XC is the overall combustion constant . of the --
iodine number algorithm.
Equation (4) is adapted ~rom the partial derivative of
the iodine number algorithm (equation (l) ) with respect
to the OAC. The new feedstock flow rate (OILNEW) is
then detP~; nP~l based on the following equations:
(5) OACNEW = ~I2No. + OACAVG
KC
-17- 2020S94
(6) OACNEW = AIRAVG * 100 _=
GASAVG * ATBG + OILNEW * ~TBO
Equations (5) and (6) are then solved for OILNEW as
5 follows:
(7~ OILNEW = [100 AVG ]
[ATBO* (aI2No./Kc + OACAvG) ]
GASAVG * ATBG
ATBO
Accordingly, OILNEW can then be calculated every two
minutes (or other spaced interval) utilizing the average
15 of the predicted iodine numbers (I2No.AvG) calculated
over that averaging interval, and the feedstock flow
rate (OIL) can then be automatically adjusted in order
to achieve the I2No.GOAL.
20 The carbon black process control system of the present
invention has as an additional feature, an off-line
laboratory measurement procedure. At spaced intervals,
while the carbon black reactor is operating, samples of
the carbon black produced are taken and the iodine
25 number of each sample is measured (I2No. LAB) by known
techniques. The measured iodine number (I2No. LAB) and
its known standard deviation (SDLAB) are de~ ~rm; n.~
along with the average and standard deviation (SDp) of
the predicted iodine numbers (I2No.p) for the period
30 that the sample was taken. Then, depending on the
values oî the measured iodine number (I2No.LAB), its
test standard deviation (SDLAB), and the average and
standard deviation (SDp) of the predicted iodine numbers
(I2No.p), the system intercept constant (KO) of the
35 iodine number algorithm (equation (1) ) is adjusted in
order to calculate a more accurate predicted iodine
number (I2No.p), as will be hereinafter described in
2020594
-18-
further detail. Thus, in accordance with the present
invention, the accuracy of the iodine number control
algorithm (equation (1) ) itself can be systematically
checked against the laboratory measured iodine number
5 (I2No. LAB) and improved while the carbon black reactor
is operating. The off-line sampling feature of the
present invention therefore ~-n~r~nC~tes for unmeasured --
disturbances on the carbon black reactor that are not
currently measured, or cannot be measured, as opposed to
lO the measurable input variables, as described above.
In accordance with the present invention, a filter
algorithm, preferably a Kalman filter algorithm, is
applied to change the system intercept (K0) of the
15 iodine number algorithm. The system intercept (K0) is
changed based on the measured iodine number ( I2No . LAB)
and the predicted iodine riumbers (I2No . ) det~rm; n~d
during the interval that the carbon black sample is
taken, in order to make the iodine number algorithm more
2 0 correctly predict the iodine numbers . The iodine number
of the carbon black sample (I2No.LAB) is measured in a
manner known to those skilled in the art, such as by a
volumetric method of titrating the carbon black sample
with an iodine solution. The iodine number test is -- -
25 preferably performed according to the iodine adsorption
number test given by ASTM Designation: Dl510-85. The
sampling interval when the carbon black sample is taken
is usually within the range of about 2 to 20 minutes.
30 In accordance with the sampling feature of the present
invention, the best estimate o~ the error variance of
the current predicted iodine numbers (VIp), and the
error variance of the laboratory measured iodine number
(VIL) are detPrm; n~. The error variance is the square
35 of the standard deviation of the iodine number.
Therefore, VIL is the square of the standard deviation
(SDLAB) of the laboratory measured iodine number for the
....
2020~94
--19--
sample of carbon black ~I2No.LAB). Because usually only
one laboratory measured iodine number (I2No.LAB) is
taken during each sample period, VIL is essentially a
constant that is de~Prm; n~d by a separate laboratory
5 measured iodine number precision or reproducibility
study, of a type known in the art. VIL, therefore, is
usually updated periodically, for example, once every
several months, or when there is a change in the
procedure for det~rm;n;ng the laboratory measured iodine
10 number (I2No.LAB). VIp is the best estimate of the
error variance of the current predicted iodine number
(I2No. ), as will be described in further detail below.
VIp and VIL are thus each indications of the
uncertainties in the respective iodine number
15 determinations themselves.
Based on the error variances, VIp and VIL, an iodine
number Kalman filter gain (RI), which, as will be
descri~1ed below, i5 then used to update the system
20 intercept (KO) of the iodine number algorithm, is
~1etF~rm;n~ as follows:
( 8 ) KI = VI~
VIp + VIL
The Kalman filter gain (KI), therefore, is essentially a
weighted mean of the error variances (VIp and VIL),
which each reflect the degree of variation in two
ordinarily noisy measurements (I2No.p and I2No.LAB).
30 The I2No. and the I2No.LAB are usually different.
~herefore, the Ralman filter gain (KI) is, in effect, a
weighting coefficient based on statistical information
regarding the reliability o~ the two different
measurements, I2No. and I2No.LAB, that indicates which
35 measurement is more accurate. For e~ample, if KI = l,
then there is a negligible error variance in the
I2No. I,AB and if RI = , then there is a negligible error
.
2~2059~
-20-
variance in the I2No . p .
Based on the Kalman filter gain (KI), a Kalman filter -
algorithm is employed to determine a new optimum
5 estimated iodine number (I2No.FILTER), as follows:
) I2No.FILTER = I2No-AvG + KI (.I2N ~AB
I2No AVG)
10wherein I2No AVG is the average of the predicted
iodine numbers (I2No.p) during the period that the
sample was taken .
Then, based upon the new optimum estimated iodine number . - -
15 rI2No . FILTER), a new system intercept constant (K0NEw)
for the iodine number algorithm is calculated as ~ ~
f ollows:
_.,
(10) KNEW = KOOLD + I2N'FILTER I2No.AvG
It should be noted that a one point change, for example,
in the system intercept constant (Ko) corresponds to a
one point change in the iodine number and, therefore,
the numbers can be directly substituted into equation
25 (10) to solve for KONEW. Therefore, the system
intercept constant (K0) is adjusted, each time the ---
laboratory measured iodine number (I2No LAB) becomes
available, in order to make the iodine number algorithm
(equation (1) ) more correct.
Turning again to the error variances, the best estimate
of the true current error variance of the predicted
iodine number (VIp (k+1) ) at time interval (k+1) and
which, as will be described below, is employed to
35 determine the Kalman filter gain (XI), is det~rmin~d as
follows:
2020594
--21--
(11) VIp(k+l) = VIE(k) + VIM(k+l)
wherein:
VIp(k+1) is the best estimate of the true
current error variance of the current
predicted iodine number (I2No.p) at time
interval ( k+ l );
VIE (k) is the error variance of the previous
optimum iodine number estimate ( I2No ~ FILTEF~)
at time interval (k);
VIM (k+l) is the error variance of the
predicted iodine numbers (I2No.p) at time
interval (k+l) measured over the last sample
perLod .
The new Kalman filter gain (KI (k+1) ) is then determined
from the error variances of the current predicted iodine
numbers ( I2No . ) and the current la~oratory measured
iodine number (I2No.LAB) as follows:
(12) KI(k+1) = VIp(k+l)
[VIp(k+l) + VIL(k+1) ]
VIL(k+1) is the error variance of the current laboratory
measured iodine number (I2No.LAB~ and is defined as
f ollows:
(13) VIL(k+1) = [ PSDLAB/100] I2No.GOAL
PSDLAB is the percent standard deviation of the iodine
number test as det~rm;n~l by a precision or
35 reproducibility study, known in the art. Therefore, the
new optimum Ralman filter gain (RI (k+1) ) is sukstitut~ed
into equation (9) above to solve for the new optimum
2~20~9~
--22--
predicted iodine number (I2No.FILTER). The I2N FILTER
is then substituted into equation (10~ above to solve
for the new system intercept constant (KONEW) to make
the iodine number algorithm more correctly predict the
iodine number.
The error variance of the new optimum estimated iodine
number (VIE(k+l)) to be used in detPrm;n;n~ VIp(k+l) at
the end of the next sample period (VIE (k) in equation
(11) above) is then detPrm;n~d as follows:
(14) VIE(k+l) = _Ir(k+l) * VIL(k+l)
[VIp(k+l) + VIL(k+l) ]
In accordance with another embodiment of the present
invention, the process control system is employed to
control the structure of the carbon black. The
structure of the carbon black is usually laboratory
measured by a Dibutyl Phthalate Absorption Number
("DBP") given by ASTM Designation: D2~14-86. The DBP
value therefore is an indication of the structure of the
carbon black. There are, however, other suitable
measures of carbon black structure that can equally be
controlled by the process control system of the present
invention. One way of controlling the DBP is by
inj ecting a potassium additive solution (X S ), known in
the art, preferably into the feedstock prior to
injecting the feedstock into the feedstock injection
zone of the reactor. The potassium additive solution
(K S) is then dispersed in the reaction mixture in the
reactor zone, and thus has an ionic charge effect on the
particles of carbon black formed. Therefore, usually,
if a higher concentration of potassium additive solution
(K S) is injected into the feedstock, then there will
tend to be less aggregation among the particles of
carbon black formed.
2020~94
--23--
In accordance with the present invention, predicted DBP
values (DBP ) are calculated at spaced intervals, for
example, every one to ten seconds. The predicted DBP
values (DBPp) are calculated by a DBP algorithm which is
5 based, in part, on empirical test results for any given
carbon blacX reactor geometry in which the process
control system is employed. The predicted DBP values
are then averaged over spaced intervals, for e~ample,
every two minutes ~ DBPAVG) . Based on the average
10 predicted DBP values (DBPAVG), a controlled input
variable, such as the potassium additive solution flow
rate (K S) is automatically adjusted to achieve the goal
DBP value ( DBPGOAL) .
15 The predicted DBP values (DBPp) may be calculated in
accordance with the following DBP algorithm:
(15) DBPp = (164.9 -- 17.3 * X)*F for O < X < 1 ~ _
2 0 and
(16) DBPp = (147.6 - 17.3 ~ ln(X))*F for X >1
wherein:
X is the concentration of the potassium ion (K ) in
the feedstock [gm K /100 gal. oil]; and
F is a scale factor calculated to adjust the
algorithm for unmeasured disturbances in the carbon
black reactor or for differences between reactors
(F is usually within the range of about o . 7 to
about 1. 2 ) .
The constants in the DBP algorithm are empirically
determined in accordance with a known process
identification procedure using regression analysis, for
-
~ -24- 2~2~94
any given carbon black reactor geometry, in the same
manner as described above for det~rm;n;n~ the algorithm
constants for the iodine number algorithm. Therefore,
the values of the constants will likely be different for
5 different types of reactor geometries. The measured
input variables in relation to the DBP are preferably
the potassium additive solution flow rate and the
feedstock flow rate. The output variable is DBP or some
other suitable measure of carbon black structure. As
10 described above for the iodine number algorithm, a
series of experiments is then carried out on a carbon
black reactor having the type of reactor q~ ~Ly for
which the algorithm will be used. Based on the
experiments, a set of input and coLL~,~onding output
15 data is collected. The regression analysis procedure is
then performed on the set of data to identify the
constants of the DBP algorithm. The constants in the
DBP algorithm as defined in equations (15) and (16) were
empirically aetermined pursuant to the above-described
20 regression analysis procedure for a three-stage reactor
geometry similar to that illustrated schematically in
P'igure 1.
The DBP algorithm, equations (151 and (16), is employed
25 to predict the ~BP values (DBPp) at spaced intervals,
for example, once every second. Then, the predicted DBP
values are averaged over spaced averaging intervals
(DBPAVG), for example, once every two minutes. Each
average DBP value (DBPAVG) is then employed to calculate
3 o a new potassium additive solution flow rate set point
(R SNEw) using a DBP ad~ust algorithm, defined as
f ollows:
(17) K SNEw [lb/hr] = RATI0 [lb K S/gal. oil] *
OILNEW [gal/hr]
2~20~9~
--25--
wherein:
18) RATI0 = XNEw [gm K /100 qal. oil]
lO0* KMIX [gm K /lb K S]
The XNEw i5 derived from the partial derivative of the
DBP algorithm (equations (15) and (16) ) with respect to
the concentration of the potassium ion in the feedstock
(X), and is defined as follows:
(19) XNEW = (DBPGOAL DBPAvG) + XAVG
17.3 * F
-- AVG --
15 (20) XNEW = (DBPGOAL ~ DBPAVG~ XAvG + XAvG
17.3 * F
AVG 1
and
(21) XAVG = --AVG-- * 100
AVG
KMIX is the mixture strength of the potassium additive
25 solution K S, which is the grams of potassium ion (K )
per pound of potassium additive solution (K S). XNEw is
the new concentration of the potassium ion (K+) in the
feedstock required to achieve DBPGoAL~ K SAvG is the
average potassium additive solution flow rate during the
3 o two-minute interval, and OILAVG is the average f eedstock
flow rate during the two-minute interval. OILNEW is the
current flow rate set point for the feedstock, which is ---
preferably ad]usted in accordance with the iodine number
algorithm, as described above. Therefore, by utilizing
35 the average predicted DBP values (DBPAVG) over the two-
minute interval, the new potassium additive solution
flow rate (K SNEw) can ~e det~rm;n~l in accordance with
- - ~
2020594
--26--
equation ( 17 ), in order to achieve the goal DBP value
GOAL)
The process control system of the prasent invention, has
5 an additional feature, an off-line DBP laboratory
measurement procedure. At spaced intervals, while the
carbon black reactor is operating, samples of the carbon
black produced are taken and the DBP value for each
sampie is measured (DBPLAB), in a manner known to those
10 skilled in the art. The sampling interval when the
carbon black sample is taken is usually within the range
of about 2 to 20 minutes. The DBPLAB is preferably
measured in accordance with ASTM Designation: D2414-86,
as mentioned above.
The measured DBP value (DBPLAB) and its known standard
deviation (SDLAB) are ~-ot~rm; ned along with the average
and standard deviation (SDp) of the predicted DBP values
~DBP ) for the period that the sample was taken. Then,
20 ~r~n~in~ on the measured DBP value (DBPLAB), its
standard deviation (SDLAB), and the average and standard :
deviation of the predicted DBP values (DBP ), the scale
factor (F) of the DBP algorithm (equations (15) and
(16) ) is ad~usted in order to calculate more correct DBP
25 values. Thus, in accordance with the present invention,
the accuracy of the DBP algorithm itself can be
systematically checked against the laboratory measured
DBP value (DBPLAB) and improved while the carbon black
reactor is operating.
In accordance with the sampling feature of the present
invention, the best estimate of the error variance of
the predicted DBP values (VDp) and the error variance of
the laboratory measured DBP value (VDL) are determined.
35 VDL is the square of the standard deviation of the
laboratory measured DBP value (DBPLAB). Because
preferably only one laboratory measured DBP value is
2~20594
-27-
taken during aach sample period, VDL is essentially a
constant that is det~P~; nP~ by a separate precision or
reproducibility study of the DBPLaB measurement
procedure, of a type known in the art. Therefore, VDL
5 is usually updated periodically, for example, once very
several months or whenever there is a change in the
procedure for detPrm;n;n~ the DBPLAB. VDp is the best
estimate of the error variance of the current predicted
DBP value (DBP ), as will be described in further detail - -
lO below.
Based on the error variances, VDp and VDL, a filter
algorithm, preferably a Kalman filter algorithm, is
employed to determine a best estimate of the true DBP
15 value during the period that the sample was taken
(DsPFILTER). The DBPFILTER is generated as a weighted
mean between the DBPLAB and the average of the predicted
DBP values during the period the sample was taken
(DBPAVG). The DBP Ralman filter algorithm for the --
20 DBPFILTER is defined as follows:
(22) DBPFILTER = DBPAvG + KD * (DBPLAB DBPAVG)
KD ls the DBP Kalman filter gain, which is essentially a
25 weighted mean of the error variances, VDp and VDL, and
is defined as follows:
(23) KD = Dr ~~
VDp + VDL
Then, based upon the DBPFILTER,the scale factor (F) of
the DBP algorithm, equations (15) and (16), is adjusted
(FNEW) in order to make the DsP algorithm more correctly
predict the DBP, as follows:
(24) FNEw DBPFILTE~ for O c X < l ._~
164 . 9 - 17 . 3 * (XAvG)
, . .
-28- 2020~94
and
(25) FNEw DBPFILTER for X>l
147.6 - 17.3~1n (X
AVG
XAvG i5 the average concentration of potassium additive
solution (K+S) in the feedstock, as defined in equation
(21), during the period the sample was taken. The new
scale factor (FNEW) is then substituted into the DBP
algorithm (equations (15) and (16) ) to replace the
previous scale factor (F) and thus adjust the algorithm
to more accurately predict the DBP.
The best estimate of the true current error variance of
the predicted DBPValue (VDp(k+l) ) at time interval
(k+l), which is used in equation (23) to determine the ~-~
current DBP Kalman filter gain (KD), is defined as
f ollows:
(26) VDp(k+l) = VDE(k) + VDM(k+1)
wherein:
VDp(k+1) is the best estimate of the true
current error variance of the current
predicted DBP value at time interval (k+l);
VDE is the error variance of the previous
optimum DBP estimate (DsPFTLT~R) at time
interval (k); and
VDM(k+l) is the error YarianCe of the
predicted DBP values (DBPp~ at time interval
(k+l) measured over the last sample period.
The new DBP Kalman filter gain (KD(k+l) ) is then
de~P~minp~l as a weighted mean of the error variances of ~-
2~20~9~
-29-
the current predicted DsP values (DBPp) and the cu~Tent ~_
laboratory measured DBP value (DBPLAB~ as follows: -
(27) RD(ktl) = VD~(k+l)
tVDp(k+1) + VDL(k+1) ]
VDL(k+1) is the error variance of the current laboratory
measured DBP value (DBPLAB) and is defined as follows:
10(28) VDL(k+1) = [PsDLAB/loo] DBPGOAL
Here, PSDLAB is the present standard deviation o~ the
laboratory DBP which is dPt~rm; n~ by a precision or : ~~
reproducibility study, known in the art. Therefore, the
15new DBP Kalman filter gain (KD(k+1) ) is substituted into
equation (22) above to solve for the new optimum
FI1TER) he DBPFILTER is then
substituted into- equations (24) or (25) above to solve
for the new scale factor (FNEW) to make the DBP
20algorithm (equations (15) and (16) ) more correctly
predict the DBP.
The error variance of the new optimum estimated DBP
value (VDE(k+l) ) to be used in det~rm;n;n~ VDp(k+l) at
25the end of the ne~ct sample period (VDE (k) in equation
(26) above) is then deto~;n~ as follows:
(29) VDE(k+1) = VDr~k+1) DL(
VDp(k+l) + VDL(k+l)
In accordance with another embodiment of the present
invention, the process control system further
incorporates a CUSUM ("cumulative sums") pLU~e~U~ or
monitoring the values of the output variables
35controlled, such as iodine number and/or DBP. The CUSUM
compensates for trends in either the iodine number or -. -
DsP that might be the result of unmeasured disturbances
2~20~
-30-
on the carbon black reactor not completely compensated
for by the iodine number algorithm, DBP algorithm, or ~
the respective Kalman f ilter algorithms . Therefore, a
CUSU~q monitors the I2No - LAB and a CUSUM monitors the
5 DBPLAB every time each output variable is measured to
determine if there is a shift in the mean of either
value that is sufficient to require a further adjustment
in the process.
10 Each CUSUM employs two cumulative sums, a high side sum
( H ( i) ) and a low side sum (SL(i) ), to test the I2No.LAB =~
and the DBPLAB, respectively, to determine if there is
an undesirable trend. When the CUSUMs are reset, each
cumulative sum (SH(i) and SL(i) ) is set equal to zero.
15 The two sums are ~P~Pl^m;nP~l as follo~s:
(30) SH(i) = Max [O,SH(i_l) + Yi ~ (GOAL + k) ]
(31) SL(~ in [O,SL(i_l) + Yi ~ (GOAL - k) ]
wherein:
SH ( i 1) is a summation of all previous high
side sums since the last CUSUM reset;
SL( . 1) is the summation of all previous low
side sums since the last CUSUM reset;
Yi is the current laboratory measured value of ~ =
the output variable controlled and, therefore, in
accordance with the previous embodiments it may be
I2No.LAB or DBPLAB;
GOAL is the goal value of the output variable
controlled and, therefore, in accordance with the
previous e~bodiments it may be I2No GOAL or
BPGOAL;
202059~
--31--
k is the allowable slack in the controlled
output variable, which is usually in the range of
about one standard deviation or within which about
68% of the laboratory measured values of the
respective controlled output variable (such as
I2No LAB or DBPLAB) will fall.
A decision interval (-h,h) is set for each controlled
output variable, the exact value of which is chosen
based on experience with the particular carbon black
reactor used, but which is usually near the tolerance
limits set for that output variable. For example, a
typical value of h for iodine number or DBP might be 5.
Therefore, the decision interval h would be 5 iodine -
number units or DBP units on either side of the value of
the I2No.GOAL or DBPGoAL~ respectively-
After each sample of carbon black is taken and the
laboratory measured values for iodine number (I2No.LAB)
and/or DBP (DBPLAB) are de~-~m;n~, those values are
each substituted into equations (30) and (31) for (Yi).
The two cumulative sums, SX(i) and SL(i), are then
computed for both the I2No.LAB and the DBPLAB. Then, if
SH(i) > h or, if SL(i) < - h, for either the iodine -
number or DBP, an alarm signal is generated for the
respective output variable. If an alarm signal is
generated, then the operator is notified to increase the
sampling frequency of the carbon black produced, usually
at least by a factor of two. If an alarm signal is
generated for the iodine number and/or DBP,
respectively, then the Kalman gain (RI) for the iodine
number algorithm, and/or the DBP Kalman filter gain (KD)
for the DsP algorithm, are each set equal to one,
~ respectively. If after the next carbon black sample is - -
35 taken, the I2No.LAB or DBPLAB falls within +k of the
I2No.GOAL or DBPGoAL~ respectively, then the CUSU~ is
reset by setting the cumulative sums SH(i-l) and SL(i_
.. . . . .. .
-32- 2020594
to zero for the respective Yariable. However, if an
alarm slgnal continues to be generated, then the Kalman
filter gain (RI or KD) for the respective output
variable is set equal to one until the laboratory
5 measured value falls within +k of the goal value for
that variab~e.
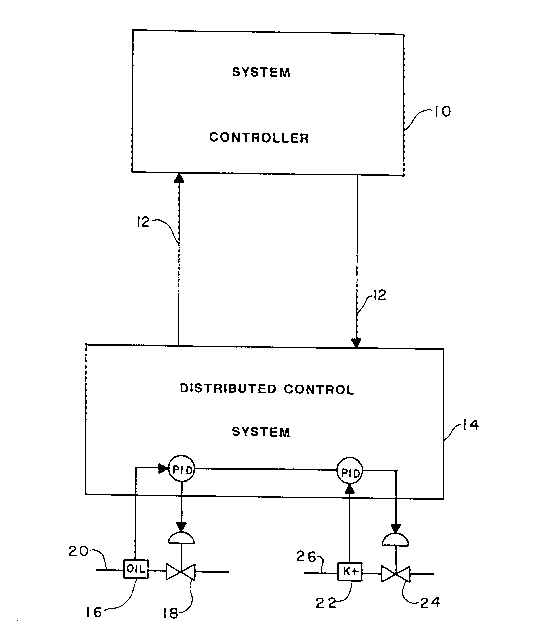
In Figure 2, the hardware components of the process
control system of the present invention are illustrated
10 schematically. The process control system comprises a
system controller indicated generally as 10. The system
controller 10 is a type known to those skilled in the
art, and preferably is a minicomputer, such as a VAX
minicomputer as described above. The system controller
15 10 is coupled through a bus 12 to a distributed control
system 14. The distributed control system 14 is also a
type known to those skilled in the art, such as a Fisher
PRoVOX Instrumentation System, manufactured by Fisher
Controls International , Inc., of ~arshalltown, Iowa.
2 0 The distributed control system 14 is, in turn, coupled
through a PID algorithm (PID) to an oil flow meter 16,
and an automatically adjustable flow valve 18. As
described above, the oil flow meter 16 is preferably a
Coriolis-type flow meter. The oil flow valve 18 is
25 mounted upstream or downstream from the oil flow meter
16 ln a feedstock line 20 of the carbon black reactor.
Therefore, the distributed control system 14 controls
the operation of the valve 18 in order to automatically
adjust the feedstock flow rate (OIIJ~ to achieve the goal
30 iodine number (I2No.GOAL), as will be described in
further detail below. ~he distributed control system 14
is also coupled through a PID algorithm (PID) to a
potassium additive solution flow meter 22, and an
automatically adjustable flow valve 24. The flow meter
35 22 is preferably a Coriolis-type flow meter like the oil
flow meter 16. The flow valve 24 is mounted upstream or
downstream fr_ the flow meter 22 in a potassium
2020594
--33--
additive solution line 26 of the carbon black reactor.
Therefore, the distributed control system 14 also
controls the operation of the valve 22 in order to
automatically adjust the potassium additive solution
5 flow rate (K S) to achieve the goal DBP value (DBPGoAL),
as will be described in further detail belo~.
Turning to Figure 3, a flow chart is illustrated that =~ -:
conceptually describes the procedures of the carbon
lO black process control system of the present invention.
The labels Sl through S12 indicate step 1 through step
12. When the process control system is operating, as
indicated at Sl, the distributed control system 14
generates a predicted iodine number (I2No. ) and a
15 predicted DBP value (DBPp), as indicated at S2 , in
accordance with the iodine number algorithm and DBP
algorithm, respectively, as described above.
Preferably, the iodine number algorithm and, therefore,
the equations for the feedforward input variables are
2 0 embodied as subroutines in the distributed control
system 14. Likewise, the equations of the DBP algorithm
are also preferably carried out by the distributed
control system 14 in subroutines. After each I2No.p and
DBP ~s calculated, they are each then stored in
25 computer memory in the system controller 10. The
distributed control system 14 calculates both the I2No.
and the DBPp about once every second based on the
current input variable readings, as indicated at S3.
Each updated I2No. and DBP is then stored in memory in ~~
30 the system controller lO. Then, as indicated at 54, the
I2No . p and DBPp values stored in the computer memory
over each two-minute interval, are averaged, I2No.AvG
and DBPAVG, by the distributed control system 14, and
stored in the computer memory.
Based upon the I2No.AvG over the two-minute interval,
the new feedstock flo~ rate (OI~EW) is then det~rm; ned
_ _ _ _ ... .. .
2~2~594
--34--
by the distributed control system 14, as indicated at
S5. Likewise, based upon the DBPAVG over the two-minute
interval, the new potassium additive solution flow rate
(K SAvG) is also de~Prm; nPd. Equations (5) through (7),
5 and equations (17) through (21), as described above, are
preferably embodied as subroutines in the distributed
control system 14 for de~Prmin;~ both the new feedstock
flow rate (OILNEW) and the new potassium additive
solution flow rate (K SNEw), respectively. Based on thé
10 new feedstock flow rate (OIL~E~) and the new potassium
additive solution flow rate (K SNEW), the distributed
control system 14 then de~ ; nPc the degree to adjust
the valve 18 and the valve 24 by employing PID
algorithms, as will be described further below. The new
15 feedstock flow rate (OILNEW) and the new potassium
additive solution flow rate (K SNEW~ are then each
updated every two minute5: The valves 18 and 24 are
then, in turn~ adjusted every two minutes based on the
new I2No.AvG and DBPAVG, respectively, to achieve the
20 new flow rates, as indicated at S7.
The first step in the off-line laboratory measurement
features of the present invention is indicated at S8,
which indicates that the system controller 10 computes
25 the average and the standard deviation of both the
I2No. and DBP calculated every second (or other spaced
interval) during the period that the carbon black sample
is taken. ~he carbon black produced is sampled at
spaced intervals, for example, usually within the range
30 of about every one to four hours, and both the iodine
number and the DBP of the sample is measured in a
laboratory (I2No.LAB and DBPLAB), as indicated at Sg.
As mentioned above, the c~rbon black sampling interval
is usually within the range of about 2 to 2 0 minutes .
35 Then, the new system intercept (KO) for the iodine
number algorith~ is updated by the system controller 10,
based on the I2No. LAB and the I2No.AvG calculated during
_ . . .
2~2~9~
--35--
the period that the sample was taken, as lndicated at
S10. Preferably, equations (8) through (14), as
described above, are embodied as subroutines in the
system controller 10. Likewise, the scaling factor (F)
5 is also adjusted based on the DBPLAB and DBPAVG during
the period that the sample was taken. Preferably,
equations ( 2 2 ) through ( 2 9 ), as described above , are
also carried out as subroutines in the distributed
control systems 14. The new system intercept (KONE~) is
10 then used to update the iodine number algorithm for
det~rmin;n~ more accurate predicted iodine numbers
(I2No.p) until the next carbon black sample is taken, as
indicated at S11. Likewise, the new scaling factor
(FNEW) is used to update the DBP algorithm for
15 detPrm;n;n1 more accurate DBP values until the next
carbon black sample is taken, as also indicated at S11.
As indicated at S12, the iodine number algorithm and DBP
algorithm are each updated whenever a carbon black
sample is taken and, therefore, within the range of
2 0 about every 1 to 4 hours .
Turning to Figure 4, a flow chart is illustrated that
describes conceptually the procedures of the distributed
control system 14 in predicting both the iodine number
25 I2No.p in accordance the iodine number algorithm, and
the DBPp in accordance the DBP algorithm, as described
above. The distributed control system 14 first reads
the input data n~,-"c~:~ry to calculate the feedforward
input variables for the iodine number algorithm, and the
30 input variable for the DBP algorithm, as indicated at
S1. The input variables for the iodine number
algorithm, include the feedstock flow rate, gas flow
rate, air flow rate, air preheat temperature, and air
humidity. The A~BG (fuel quality) is a calculated
35 control variable and the ATBO (feedstock quality) is
essentially a constant control variable, as described
above. The input variables for the DsP algorithm are
~ 202~59~
--36--
the potassium additive solution flow rate and the ---
feedstock flow rate.
After reading the input data, the distributed control
5system then compares the input data to a permissible -
range of values for each variable, as indicated at S2.
If any value falls outside of its permissible range
(BAD), then a bad data flag, which is a digital signal,
is set, as indicated at S3. If the bad data flag is
10set, then the I2No. and/or the D8Pp is not calculated
based on that data. If all the data does fall within
the permissible ranges, then both an I2No.p and DBPp are ~ =
calculated based on that set of input data by employing
the iodine nu~ber algorithm and the DBP algorithm,
15respectively, as indicated at S4. Both the I2No. and
DBP are each then compared to a realistic range within
which each output variable should fall, as indicated at
S5. If either the I2No.p or DBPp is not within the
permissible range, then the bad data flag is set and the
20current values for I2No.p and/or DBPp are not used,
~.~r.on~l;ng if one or both falls outside its respective
permissible range. If the I2No. or DBP do fall within
their permissible ranges, then their values are stored
in the computer memory of the system controller 10, as ~--
2S indicated at S6, and are later (at the end of the spaced
interval) each used to update the feedstock flow rate
and the potassium additive solution flow rate,
respectively .
30 Turning to Figure 5, a flow chart is illustrated that
describes conceptually the procedures of the distributed
control system 14 for adjusting both the feedstock flow
rate and the potassium additive solution flow rate. As
indicated at Sl, if the bad data flag was set during the
35 iodine number and/or DBP prediction procedures (BAD), as
illustrated at S3 in Figure 4, then the bad data flag is
cleared and the adj ustment procedures as illustrated in
,, , . _ . . _ . . .
~ 2~20~4
Figure 5 are not implemented for that spaced interval,
for whichever algorithm had the bad input data.
However, if the bad data flag was not set during the
two-minute interval, then the distributed control system
5 14 reads the input data for ti~orm;ning the new
feedstock set point (OILNEW) and/or the potassium
additive solution set point (K SNEw), as indicated at
S2. The input data for OILNEW includes the AIRAvG,
GASAVG, ATBG, ATBO and OACAVG, as defined in equation
10 (7). The input data for the K SNEw includes the K SAvG,
OILAVG, DBPAVG, and XAvG, as defined in equations (17)
through ( 21 ) .
The input data are then compared to a permissible range
15 of values for each term, as indicated at S3. If any of
the values fall outside of their respective permissible
ranges, then the bad data flag is set (BAD).
Accordingly, the feedstock flow rate set point (OILNEW)
and the potassium additive solution set point (K S~Ew)
20 are not adjusted for that spaced interval, if the input
data for one and/or both is bad. If all of the values
fall within their permissible ranges, then the OILNEW
and K SNEw are each updated as described above, as
indicated at S4. Both the OILNEW and K+SNEw are then
25 each compared to a permissible range of values, as
indicated at S5. If either the OILNEW or the K+SNEW
falls outside of its respective permissible range (BAD),
then the procedures end for that respective term and its
flow rate is not ad~usted. If the OILNEW and K SNEw do
30 fall within their permissible ranges, then the values
for OILNEW and K+SNEW are each processed through a PID
algorithm to update the feedstock flow rate and
potassium additive solution flow rate, respectively, as
indicated at S6.
Turning to Figure 6, a typical PID algorithm which is
preferably employed for adjusting the new feedstock flow
~, 2~20~94
--38--
rate (OIL~EW) or for adjusting the new potassium
additive solution flow rate (K~SNEW), i5 illustrated - -
schematically. The flow meter for the feedstock 16 and
the flow meter for the potassium additive solution 22
are each coupled respectively to a flow transmitter -:
(FT)~ Each flow transmitter (FT) i5, in turn, coupled
to the distributed control system 14 and transmits a
signal (Fm) corresponding to the measured flow rate as
sensed by its respective flow meter. The signals for
10 the new flow rate set points for the feedstock and the
potassium additive solution (Fsp) are then each compared
to their respective measured flow rate signals (Fm) as
generated by the flow meters. Based on the respective
comparisons, an error signal (e(t) ), which is e~ual to
15 the respective flow rate set point signal (Fsp) minus
the respective measured flow rate signal (Fm), is
generated for each respective flow rate. Then, based on
the respective error signals (e(t) ), a respective PID
algorithm, which is known to those skilled in the art,
20 generates an output signal (c(t) ) that corresponds to
the adj ustment that should be made to the respective
flow valves 18 or 24 to achieve the flow rate set
points. Each output signal is then sent to a respective =-
current to pneumatic converter (I/P). The current to
25 pneumatic converters (I/P) are each coupled respectively
to the oil flow valve 18 and the potassium additive
solution flow valve 24 for adjusting each respective
valve. The current to pneumatic converters (I/P)
therefore each generate a pressurized output
30 corresponding to the respective PID output signal (c(t) )
that, in turn, adjusts its respective valve to achieve
the flow rate set point. Th~re~ore, each E'ID algorithm
continues to generate changes in the output signal
(c(t) ) until there is no longer an error signal (e(t) ),
35 and thus the flow rate set points are achieved.
Turning to Figure ~, a flow chart is illustrated that
~ 2020~9~
--39--
describes conceptually the procedures of the system
controller 10 for updating the system intercept (RO) of
the iodine number algorithm and/or the scale factor (F)
of the DBP algorithm at the end of each carbon blac3
5 sample period. As indicated at Sl, the system
controller recalls from memory the I2No.p and DBPp
values calculated and stored during the period that the
sample was taken. If the system controller cannot
properly recall the data (Unsuccessful~, then the
10 algorithms are not adjusted. The system controller 10
then reads the values for t~e current I2No LAB and the
DBPLAB and compares them to a permissible range of ~ ~:
values. If either value is out of range, then its :~
respective algorithm is not adjusted. The system
15 controller 10 then employs the CUSUM procedure which
de~r~rminr~c the current sums, SH(i~ and/or SL(i~, for the
current I2No . LAB and DBPLAB values, as indicated at S3 .
If either SX(i) > h or SL(i) < - h for either measured - =
output variable (I2No.LAB or DBPLAB), the 5ystem
2 0 controller generates an alarm signal . If an alarm
signal is generated, then the Kalman filter gain (KI)
for the iodine number algorithm and/or the DBP Kalman
filter gain (KD) for the DBP algorithm are set er~ual to :-
1, depending on whether an alarm signal is generated for ~
25 one or both output variables. Therefore, the new system
intercept (KONEW) for the iodine number algorithm,
and/or the new scale factor (FNEW) for the DBP
algorithm, are both based solely on the laboratory
measured values of I2No. LAB and DBPLAB, respectively .
30 Xowever, if an alarm signal is not generated, then the
system controller r~Ptr~rmin~C the new filtered analytical
properties, I2No.FILTER and DBPFILTER, and, in turn,
adjusts the system intercept constant (KO) and the scale
factor (F) to update the iodine number algorithm and DBP
35 algorithm, respectively, as indicated at 54. Then, as
indicated at 55, the values for the new system intercept
(KONEW) and scale factor (FNEW) are compared to a
j~ 20205~4
--40--
permissible range for each value. If either value i5
out of range, then it is not used to update its
respective algorithm. If the values for KONEW and FNEW
are each within range, then they are each stored in
5 memory, as indicated at S6. Upon storing the values in
memory, the system controller 10 then clears the data
entry flag, as indicated at S7, until the end of the
next s~Dple _i~d.