Note: Descriptions are shown in the official language in which they were submitted.
WO90t13126 PCT/US90/01998
21~a4~
ENERGY/MATTER CONVERSION ME'rHODS AND STRUCTURES
.
. Field of the Invention
This invention relates to methods and apparatus for energy/matter
conversion according to a novei atomic model and the applications derived
05 therefrom including controlled nuclear fusion and the formation of
materials such as superconductors.
~ACKGROUNI;
Toward the end uf the 19th century, many physicists believed that all
of the principles of physics had been discovered. The laws then discussed
10 and accepted, now called "classical physics," included laws relating to
Newton's mechanics, Gibb's thermodynamics, LaGrange and Harnilton's
elasticity ancl hydrodynamics, Maxwell-Boltzmann molecular statistics,
and Maxwell's equations. However, a discrepancy between nature and the
understanding provided by prevaiiing laws was discovered in the case of
- 15 bla~k body radiation, whsrein classical physics predict~d the intensity to
go to infinity as a function of ternperature whila experimentally it goes to
zero. In 1900, Planck made the revolutionary assumption that energy
Ievels were quantized which resulted in a model which was consistent
with experimentation. Models of the atom were developed by Bohr based on
the eoncept of quantized energy ievels. Bohr's model was in agreement
with the observed hydrogen spectrum; however, it failed with the helium
spectrum and could not account for chemical bonds in molecules. It was
reasoned that Bohrls model failed because it was based on the application
of Newtonian rnechanics to a discrete particle, and its limited
applicability was due to the unwarranted condition that the energy levels
be quantized. Quantization occurs in wave m~tion; hence, in 1923 de
Broglie suggested that electrons have a wave aspect analogous to light
with ~ = h/p, where ~ is the wavelength, h is Planck's constant, and p is
the momentum.
In 19~7, Davisson and Gerrner experimentally confirmed de Broglie's
hypothesis by observing diffraction effacts by reflecting electrons from
metals. Schrodinger reasoned further that if electrons have wave
properties, then there must be a wave equation that governs their motion.
In 1926, Schrodinger proposed that the Schrodinger equation, HY' = EY',
.
wo 9o/13126 Pcr/usgo/olggg
2~
was the law which governs the motion of electrons (where ~ is a wave
function, H is a wave operator and E is the energy of the wave). This
equation and its associated postulates provides the basis for the field of
quantum mechanics. Quantum mechanics requires that physics on an
5 atomic scale are quite different from that on a macroscopic scale.
However, it entails postulates which are not proven1 but are ass~med to be
absolute laws of nature. Central to quantum mechanics is that it is
statistical in nature. Knowing the state, a position measurement cannot be
predicted with certainty, and only the probabilities of various possible
10 results can be predicted as reflected in the Heisenberg Uncertainty
Principle: ~p c~x 2 tl which is fundamental to the prevailing view of
quantum mechanics and establishes the lower bound for the uncertainty of
two observables. The Heinsberg Uncertainty Principle states that the
product of the uncertainty in position and the uncertainty in mornentum of
15 an electron must be greater than ~ where ~ is Planck's constant divided by
2~. Prevailing understanding of quantum mechanics does not provide that
an electron is distributed over a larger region of space as a wave is
distributed. Rather, it is believed that the probability patterns (wave
functions) used to describe the eiectron's motion behave like waves and
20 satisfy a wave equation ~Ir(x).
Max Born interpreted ~Ir~(x)~lr(x)dx to be the probability that the
electron is located between x and x ~ dx, where ~ is the complex
conjugate of yr(x), and this interpretation is generally accepted. However,
Born's view results in intangible concepts which conflict with known
25 physical laws. For example, it results in overlap of negative probability
density in molecules, the possibility of an electron instantaneously
traveling from the nucleus to infinity and back which violates
conservation of energy; radial kinetic energy which violates conservation
of energy and angular momentum, and acceleration of a charged particle
3 0 without radiation which violates Maxwell's equations. Schrodinger had a
different interpretation of ~r(x) as a charge density function, but his
interpretation also produces radiation which is contrary to
experimentation as described in Appendix lll.
With respect to the interpretations of Born and Schrodinger, problems
35 have arisen concerning the realiza~ion of kinetic energy, spin, and angular
WO 90/131~6 PCI'/US90/01998
3 2~
momentum of the electron. For instance, there is no time dependence of
the stationary state wave equation; furthermore, the hypothesized
electron-electron repulsions in multiple ~31ectron atoms violates the law
of conservation of energy. Moreover, the Schrodinger equation provides no
5 rational basis for the phenornenon of spin, the Paul Exclusion Principle, or
Hund's Rule. Also, bonding requires exchange of electrons between atoms
which would result in violation of conservation of energy and angular
momentum.
As a result of the forgoing assumptions and incomplete or erroneous
10 models and theories, the numerous resulting conflicting models prevent
the development of useful or functional systems and structures requiring
an accurate understanding of atomic structure and energy transfer. The
Schrodinger equation, for example, does not explain the high transition-
temperature superconductors or "cold" nuclear fusion which comprise the
15 present invention. Thus, advances in materials and energy/matter
conversion is largely limited to laboratory discoveries having limited or
sub-optimal commercial application.
~lIMMARY OF THE 1~1~
The methods and structures according to the present invention provide
20 unique applications of energy/matter conversion according to a novel
mathematical model of the atom consistent wiih Maxwell's equations and
principles of conservation of energy and angular momentum. According to
the present invention, methods and apparatus for the useful generation of
energy are provided wherein fusionable material is selected from a wide
25 range of possible elements wherein the orbital energies of the fusionable
material are determined. The energy of the electrons is selectively
depleted by an energy hole provided by one or more selective materials
- placed in close proximity to the fusionable material. Fusion is permitted
to occur at a rate determined by the relative equality of the orbital
30 energies and the energy hole. According to one embodiment, the rate of
fusion is adjusted by the external control of energies transferred into or
out of the vicinity of the fusionable material and the energy hole to
selectively adjust the equivalence of the energies. The energy produced by
the resulting fusion of the nuclei of the fusionable material is received in
3-5 a surrounding material which serves to energize or propel apparatus for
the generation of power, such as electric power or steam. ~,
WO 90/13126 PCr/US9OtO1998
2054~
A fu~her product according to the pr~3sent invention is the selective
production of matter, including byproducts of the above described fusion,
and matter having special characteristics, such as superconductor
material~ Furthermore, the atomic structure and energy of existing matter
5 is selectively adjustable according to the present invention, such as by
selectively reducing or increasing the electron orbltals by depletion of
energy as described above or selection absorption, such as resonant photon
absorption described according to the present invention. Time and
spherical harmonic angular charge density functions and their energies
10 and angular momenta which describe the electron before and after a
transition are consistent with the laws of conservation of energy and
angular momentum. The radial component of the charge density waves of
the novel atomic model provides that the entire charge density function of
three dimensional space and time does not radiate. The condition for zero
15 radiation is the absence of Fourier components of the space tirne
transform that are synchronous with waves traveling at the speed of light
as described in Appendix I and Appendix ll.
The boundary condition of the radial function which forces the charge
density function to be nonradiative and the result that the moment of
20 inertia of each said function is a function of quantum numbers naturally
give rise to the wavelike nature of the electron. The wavelength is
identical to the de Broglie wavelength, ~ = h/p, for all these functions
that describe the eiectron and its energy in space-time and are hereafter
referred to as Mills orbitals possessing energy, hereafter referred to as
25 the Mills energy. To distinguish the basis of the present invention from
the prior art, the mechanics of the present novel atomic model is
her~inafter referred to as Mills mechanics.
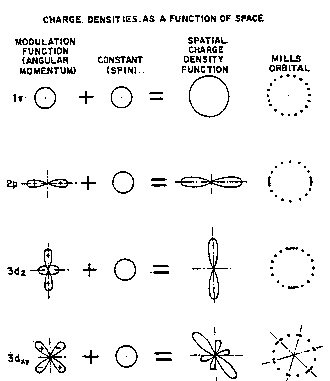
The electron orbitals according to the novel atomic model, referred to
as Mills orbitals, are spherically symmetric charge density functions
3 0 which are the product of a radial delta function, two angular spherical
harmonic functions, and a time harmonic function. Each orbital is the sum
of a constant Mills orbital which rotates with a quantized angular velocity
and a Mills orbital charge density modulation function which also rotates
with a quantized angular velocity to result in a traveling wave of charge
3 5 density on the surface of the sphere. The time harmonic motion of the
former gives rise tQ the phenomenon of magnetic ~ spin of one Bohr
WO 90/13126 PCI/US90/01998
2 0 r~ r~
. .
magneton for the electron. The latter time harmonic traveling naturally
gives rise to orbital angular momentum. The interaction of the
independent time harmonic motions gives rise to spin-orbital coupling,
and the predicted spin, orbital angular momentum, and the associated
5 energies are in exact agreement with experimentation.
The energy of an electron is stored in its electric and magnetic fields.
Orbital energies are approximately equal to ionization energies. The
orbital energies of several one- and two-electron atoms juxtaposed with
their experimentally determined ionization energies appear in Table I and
10 Table I I .
Photon absorption by an electron with a transition to a higher energy
Mills orbital arises naturally where a standing traveling wave of the
photon is formed inside of the Mills orbital. This photon wave is a solution
of Laplace's equation in spherical coordinates; thus, it is a spherical
15 harmonic. The photon wave rotates in bo~h directior~s simultaneously, or it
rotates in the opposite direction of the spin or angular momentum of the
Mills orbital to change the spin or angular momentum by one quantum
which is carried by the photon, thus, the selection rules ~M; ~S = O,+ 1 for
transitions arise naturally from conservation of angular momentum.
20 The electric field of an electron of a Mills orbital in the ground state
is zero inside the orbital and is the field of a point charge at the origin
outside of the orbital; thus, electron-electron repulsions are naturally
eliminated in multi-electron atoms.
The radii of orbitals in atoms are calculated in turn by setting the
25 centripetal force equal to the surn of the coulombic and magnetic forces.
Thus, the result that isolated Mills orbitals are stable where the
couiombic attractive force does not cause the electron to coliapse into
the nucleus arises naturally. For all atoms and ions, there exists a central
coulombic force acting on each orbital that is proportional to the net
30 charge (that is the charge not cancelled by other electrons). A positive
central magnetic spin pairing force exists between two unpaired electrons
which results in pairing in the same shell with spins opposed. Thus, the
Pauli Exclusion Principle arises naturally. A diamagnetic repulsive central
force exists between paired electrons of an inner shell and an unpaired
35 electron of an outer shell. A four body problem does not arise because the
change in the centripetal force of the inner shell electrons affected by the
WO 90/13126 PCI'/US90/01998
2 0 ~
.
outer electron is exactly balanced by the Lorentzian force provided by the
magnetic field of the outer shell electron; thus, it is possible to calculate
the exact radius and exact energy of the Mills orbital of any electron of
any atom. Illustrative examples appear in Table 1 and Table 2.
5 The electric field of a Mills orbital is zero inside the shell, and this
feature naturally gives rise to the chemical bond. Bonding between atoms
occurs because the overlap of Mills orbitals of two atoms reduces the
total energy stored in the electric fields of the participating atoms. The
bond distance of the H2 molecule is determined in accordance with the
10 present invention and shown Appendix V to be the experimentally
confirrned value of .748A.
Mills orbitals are spherical, and the radius increases with the
absorption of electromagnetic energy. When the electron is ionized the
radius of the Mills orbital goes to infinity, and the electron is a plane
15 wave with the de Broglie wavelength. The plane wave nature of an electron
is consistent with the results of prior double slit experiments.
Furthermore, coupling of two such plane waves which are 180 out of
phase as a zero `phonon event provides Cooper pair formation and provides
the basis of a model which provides ~or superconductors Qf high transition
20 temperature which is the present invention. These materials comprise one
or two dimensional lattices that contain atoms whose electrons can be
ionized by an applied electric or rnagnetic field. Moreover, the lattice is of
low symrnetry so that the existence of symmetric phonons is improbable.
Interactions of said phonons and Cooper's pairs causes the pairs to break.
2 5 A representative two-dimensional unit cell is
. .
~ ~11~3, where M is a metal and A, B, C, and D are different atoms or
different oxidation states of the same atorn or atorns.
3û Mills orbitals can resonantly absorb an energy hole, and, as a
consequence, the radius decreases. With sufficient decrease in radius the
electron can annihilate a proton to form a neutron. Thus, K capture arises
naturally from this phenomenon.
Furthermore, outside of the outermost Mills orbital of a neutral atom,
35 the electric field of the nucleus is zero; thus, as the radii of atoms
resonan~ly decrease, atoms can approach more closely before nuclear
WO 90/13126 PCl'/US90/01998
7 2 a ~ J
coulombic repulsive forces occur. And, with sufficient decrease, the
nuclei of atoms, such as deuterium atoms in deuterium molecules, can
approach sufficiently for fusion to occur at relatively low temperature.
This process of providing low temperature fusion according to the present
5 invention is hereafter referred to as Coulombic Annihilation Fusion (CAF).
For deuterium, CA~ requires a source of energy holes of slightly greater
energy than 27 eV (n/2 27.21 eV; n - 2,3,4,...) to cause a resonant radius
reduction of a Mills orbital of the deuterium atom. An iliustration of such
an energy hole system is Pd2+ and Li+ which catalytically removes a
10 quantum of energy during each cycle of a reaction where the oxidation
states increase and decrease by one, respectively, and are regenerated by
the reverse redox reaction. Also, the present invention provides for many
more such energy hole systems.
BRI~.F DESCRIPTIO~LOF~HE [:)RAWINGS
The present invention is further described with respect to the
drawings haYing the following solely exemplary figures, wherein:
Figure 1 is a pictorial illustration of Milis orbitals of the novel atomic
model;
Figure 2 is a pictorial illustration of the magnetic field lines of an
2 0 electron in a Mills orbital in an un-ionized state;
Figure 3 is a pictorial illustration of two approaching hydrogen atoms;
Figure 4 is a pictorial illustration of the two hydrogen molecules as their
Mills orbitals spatially overlap;
Figure 5 is a pictorial illustration of the electric field vectors when the
Mills orbitals of ~wo hydrogen atoms penetrate; and
Figure 6 is a block diagram of a fusion reactor according to one
embodiment of the present invention.
12ET~ILED DE$CRIPTI~QE IHE 1Ny~lllON
J~L!~i~L~S
3 0 Conservation of mass-energy, conservation of linear and angular
momentum, Maxwell's equations, and Newtonian mechanics for sublight
speeds are absolute laws of nature. Thus, a body in equilibrium which is
not acting on or being acted on by another body possesses constant mass-
energy, constant angular momentum, force balance, and is not radiating.
And, a body not at equilibrium exchanges mass-energy and angular
momentum in a conservative manner until the body is again at equilibrium.
WO 90/13126 PCI/US90/01998
2 ~ 7 8
An isolated atom or molecule qualifies as such a body, and a novel model
of the atom and molecules hereafter referred to as Mills mechanics is
derived based solely on these principles, and the charge/mass density
functions which describe the electron are Mills orbitals.
5 Mills Qrbital~
Consider the body of an isolated hydrogen atom at rest in three-
dimensional space. All forces are central and the coordinate system is
spherical. The mass-energy and angular momentum are constant which
necessitates that the equation of motion of the electron of the atom be a
10 time harmonic. Conservation of angular momentum further necessitates
that the electron space-time angular mass density function must be a
solution of a wave equation given in general form as follows:
(v2 + 2 ~; 2) A(~, ~, t) = O
Spherical harmonics are general solutions of this equation. Conservation
15 of momentum and energy in the absence of external forces or energy
exchange determine that ~he angular functions must be separable.
The electron has a charge of 1.6 X 10 -19C and possesses an angular
space-time mass density function which is a spherical and time harmonic.
Charge is conserved and obeys superposition; thus, the mass density
20 function of an electron is equivalent to its charge density function which
depending on the form of its separable radial function will radiate due to
the time harmonic angular acceleration of charge. The condition for
radiation by moving charge is derived from Maxwell's equations in
Appendix 1. To radiate, the space-time Follrier transform of the charge
25 density function must possess components synchronous with waves
traveling at the speed of light. Thus, the product of two spherical
harmonic functions, a time harmonic function, and a radial function must
not possess space-time Fourier components that are synchronous with
waves traveling at the speed of light. The solution of this boundary value 0 problem is the radial function given as foilows:
f( r) = ~(r-rO)
The boundary condition for the product of the said four functions which
results in the absence of radiation is given in Appendix 11. For an angular
frequency of ~ = coo, the space-time Fourier transform is zero when 2~r =
35 n~. This function, with the boundary condition 2~r = n~ is a Mills orbital.
wo 9O/13~26 PCltUS90/01998
2 ~
The boundary condition requires that the electron possess a
wavelength ~. The wavelength of an electron jc, the de Broglie wavelength,
h
;~, a
The exact forms of the angular ,and time harmonic functions can now be
5 solved from the wave equation in spherical coordinates. The form of the
wave equation for the angular and time harmonic functions is as follows:
(v2 ~ 1 ~2 ) A(~ ~ t) 0
( 2 j ~ S~ (sin~ ) r,~ ~ 2 j 2 ~ (~,p~2) r,~ + 2 ~t2 ) A(~, ~, t) = O
The energy, E, of a rotating body is given as follows: E = 1/2 Ic~2,
l O where I is the body's moment of inertia and ~ is its angular velocity. The
angular velocity C3 is related to the frequency ~ as follows:
~ = 2~u
And, the wavelength, ~, can be expressed in terms of the frequency u and
velocity v as follows:
15u~ = v
Substitution of these relationships into the wave equation gives the
result,
2 1 [sin ~ ~ (sin~ 3 ) + Sjn2 ~ p2)] A(9, ~, t) = E A(fl, ~ t)
The time harmonic function K(t) =ei~o is separable and is cancelled
20 yielding the following equation:
2 1 [sln ~ (sin~( ~6 ) + S jn2 ~ ~,p2 ] Y(~, ~) = E Y(~, ~) (6-46)
If we multiply Eq. 6-46 by sin2~ and let
21E
13 ~2
we find the partial differential equation
2~sin~ ~ ( sin~ ~) + ~;~2 + ~ sin2~Y = O (6-48)
To solve this partial differential equation, we use the method of
separation of variabies and let
Y(~, ~) = 9(~) h(~) (6-49)
If we substitute Eq. 6-49 into Eq. 6-48 and then divide by ~ ), we
wo 90/13126 PCI/US90/01998
1 0
2 ~ 9 7
find
9(~) d~ ( sin~ d9 ) ~ ~ Sin2 ~ + 1 d2h (6-50)
Because ~ and ~ are independent variables, we must have that
~(~) d~ ( sin~ d9 ) + ~ sin2 9 = m2 (6-51)
5 and
1 d2h
-- 2= m2 (6-52)
where rn2 is a constant. Note that Eqs. 6-51 and 6-52 add up to Eq. 6-50.
Equation 6-52 is relatively easy to solve, and its solutions are
h(~) = Ameim~and h(~) = A me-im~ (6-53)
10 The requirement that h(~) be continuous is that
h(~ + 2~) = h(~) (6-54)
By substituting Eq. 6-53 into Eq. 6-54, we see that
Ameim(~27~) = Ameim~ ~6-55 )
and that
A me-im(~2~) - A me-im~ (6-56)
Equations 6-55 and 6-56 together imply that
e~i2~1m = 1 (6-57)
In terms of sines and cosines, Eq. 6-57 is
cos(27~m) + i sin (2~m) = 1
20 which implies that m = 0, +1, +2,..., because cos 2J~m = 1 and sin 2J~m = O
for m - 0, ~1, +2,... Thus Eq. 6-53 can be written as one equation
hm(~) = Ameim~ m = 0, +1, +2,...... (6-58)
We can find Am by requiring that the hrn(~) be normalized. The
normalization condition is that
2r~
J d~ h (~)hm(~
m
Using Eq. 6-58 for the hm(~), we have
. 2~1
Aml2 ¦ d~ = 1
o
or
.
WO 90/13126 PCI/US90/01998
~ 1 2 ~ ~ ~L ~ ,-t g
.. . ~ ., ::.
IAml2 2~ = 1
or
Am = (211)-1/2
Thus, the normalized version of Eq . 6-58 is
h,~ ) ~ (2 )1/2 eim~ m = 0, +1, +2,.. (6-59)
The solution to Eq. 6-51 is obtained by the power series method. We shall
not present atl the details for the solution to Eq. 6-51, but when one does
solve Eq. 6-51, it turns out naturally that B in Eq. 6-47 must obey the
condition
B = 1(1+1) 1 = 0, 1, 2,.......... (6-60)
Using the definition of B, Eq. 6-60 is equivalent to
~2
El = 2 1 i(l+ 1 ) I = 0,1,2,..... (6-61 )
A set of discrete energy levels are obtained.
The charge density func~ions of Mills orbitals are given by the solutions to
15 Eq. 6-46. To solve Eq. 6-46, we assumed separation of variables and wrote
Y(~,~) = g(~) h(~) (Eq. 6-49) . The resulting differential equation for h~)
(Eq. 6-52) is r~latively easy to solve, and we showed that its solutions
are ~Eq. 6-59). The differential equation for 9(~)~ (Eq. 6-51), is not easy to
solve. It is conveni~nt to let x = cos ~ and 9(~) = P(x) in Eq. 6-51. Because 0
20 < ~ < ~1, the range of x is -1 < x < +1. Under the change of variable, x - cos ~,
Eq. 6-51 becomes
(I - X2) dx2 - 2xdx + [1(1+1) - 1--x2]P(x) = o (6-69)
In Eq. 6-69 we have used the fact that 13 = 1(1 + I)(Cf. Eq. 6-60). Equation 6-
69 for P(x) is called Legendre~s equation and is a well-known equation in
25 classical physics. It occurs in a variety of problems that are formulated in
spherical coordinates. When the power series method of solution is
applied to Eq. 6-69, the series must bè truncated in order that the
solutions be finite at x = +1. It is this truncation that yields Eq. 6-60. The
soiutions to Eq. 6-69 when m - 0 are called Legendre polynornials and are
30 de.noted by Pl(x). Legendre polynomials arise in a number of physical
problems. The first few Legendre polynomials are given in Table 6-1.
Table 6-1
The First Few Legendre Polynomials, Which Are the Solutions to Eq. 6-69
`' i ;, ' '
Wo 90tl3126 PCltUS90/0199
1 2
2~
with m = O. The Su~script Indexing the Legendre Polynomials Is the Value
of I in Eq. 6-69.
.. . . .
Po (X) = 1
P1 (X) = x
P2 (x) = 1/2 (3x2-1 )
P3 (X) = 1/2 (5X3-3X)
P4 (X) = 1/8 (35x4-30x2+3)
.
10 Notice from Table 6-1 that Pl(x) is an even function if I is even and an odd
function if I is odd. The factors in front of the P1(X) are chosen such that
Pl (1) = 1. In addition, although we shall not prove it, it can be shown
generally that the P1(x) in Table 6-1 are orthogonal or that
JdxPI (x)Pn(x) = O 1- n (~-70)
15 Keep in mind here that the limits on x correspond to the natural, physical
limits on ~(O to J~) in spherical coordinates because x = cos~. The Legendre
polynomials are normalized by the general relation, which we simply
present:
Jdx [Pl (x)]2 = z 2l 1 (6-71 )
2û Fquation 6-71 shows that the normalization constant of ~ (x) is
(21 +1)~2]1 /2
Although the Legendre polynomials arise only in the case m = O, they
are customarily studied first because the solutions for the rn - Ocase,
called associated Legendre functions, are defined in terms of the ordinary
25 Legendre functions. If we denote the associated Legendre polynomials by
Pl l(x), then their defining relation is
Plml(x) = (1-X2)lml/2 ddm Pt(x) (6-72)
wo 90~t3126 pcr/vs9o/o1998
1 3 ~ ?~ 7
Note that only the magnitude of m is relevant here because the defining
differential equation, Eq. 6-69, depends on only m2. The first few
associated Legendre functions are given in Table 6-2.
Before we go on to discuss a few of the properties of the associated
5 Legendre polynomials, let us be sure to realize that it is ~ and not x that
is the variable of physical interest. Table 6-2 also lists the associated
Legendre polynomials in terms of cos ~ and sin ~. Note that the factors
(1 - x2)1/2 in Table 6-2 become sin ~ when the associated Legendre
functions are expressed in the variable ~. Because x = cos ~, Eqs. 6-7û and
10 6-71 are
Jt 2 ~ n
JPI (X~Pn(x)dx = p~ sin~ Pl (Cos6)pn(cos~)=2l+1 (6-73)
-1 0
Because the differential volume element in spherical coordinates is
d~ = r2 sin ~ dr d~ d~, we see that the factor sin ~ d~, in Eq. 6-73, is the "~
part" of d~ in spherical coordinates.
Wo 90/13126 . PCI/US90tO19
1 4
2 ~
Table 6-2
The First Few Associated Legendre Functions Pll l(x)
. .
Po (x) =1
5 P1 (x) = x = cos~
P1 (x) = ~1 - x 2 = sin~
P2(x) = 1/2(3x2 - 1) = 1/2(3 cos
P2(x) = 3X~11 - x2 = 3 cos~ sin~
P2(X) = 3(1 - x2) = 3 sin2 ~
1 0P3(x) = 1/2(5x3 - 3x) = 1/2(5 cos3 ~ - 3 cos ~)
P3(x) = 3/2(5x2 1)(1 - x2)1/2 = 3/2(5 cos2 ~ - 1)sin
P3(x) = 15x(1 - x2) = 15 cos ~ sin
P3(x) = 15(1 - x2)3t2 = 15 sin3 9
.
15 The associated Legendre functions satisfy the relation
Jdx pll l(x) plrt l(x)= Jd~ sin ~ pll l(cos ~) Pln l(cos ~)
-1 0
(21 + 1) (I - Iml)l ~In (6-74)
Equation 6-74 can be used to show that the normalization constant of the
associated Legendre functions is
Nlm = E~ ( I; I m 1~ l] 1 / 2 (6-75)
Returning to the original problem now, Eq. 6-46, the Mills orbitals
WO 90/13126 PCTtUS~0/01998
1 5 2~ r~
functions are pll l(cos ~)hm(~). By referring to Eqs. 6-59 and 6-75, we see
that the functions
ylm(~, ~) = E~ (1 - I ml ) Il] pllm!(cos~) eim~ ~6-76)
are solutions to Eq. 6-46. The Yl (~, ~) form an orthonormal set
27~ r~
k~ Jd9 sin~ ylm(~ ~)* yk( ~6-77)
Note that the Yl (~, ~) are orthonormal with respect to sin~ d~ d~ and do
not just d~ d~. The factor sina d~ d~ has a simple. physical interpretation.
The differential volume element in spherical coordinates is r2 sin~ dr d~
d~ If r is a constant, as it is in the case of a radial delta function, and set
10 equal to unity for convenience, then the spherical coordinate volume
element becomes a surface element, dA = sin~ d~ d~. If this surface
element is integrated over ~ and ~, we obtain 4~, the surface area of a
sphere of unit radius. Thus, sin~ d~ d~ is an area element on the surface of
a sphere of unit radius. According to Eq. 6-77, the Yl (~, ~) are orthonormal
15 over a spherical surface and so are called spherical harmonics. The first
few spherical harmonics are given in Table 6-3.
;,
WO 90/13126 PCI-/US9OtO1998
1 6
C~
Table 6-3
The First Few Spherical Harmonics
yO= ' ' '
O - (4,~)1/2
Y10 = ( 3 ~1 / 2COS ~
y-l ( 3 ~1 / 2 j io
y; 1 ( 3 ~ 1 / 2 -iip
Y2 = (16~1) (3cos2 ~
Y2 = (81~) Sin ~ cos ~ ei~
10 Y21 = (85) sin ~ cos ~ e
Y2 = (32--,~) sin2 ~ e
Y2 = (3125 ) 1 / 2sin2 9 e-2i~
The angular functions of Mills orbitals are spherical harmonics, and
15 the angular kinetic energy is given as
Ek=2~ I(l + 1) 1 = O, 1, 2, ...
The angular kinetio energy Ek is related to the angular momentum, L,
by the following relationship:
L2
Ek - 2 1
20 Thus,L=~1(1+1) 1 = O, 1, 2, ...
Mills orbitals are the product of the angular, radial, and time functions
which are given as follows:
~0 90/13126 PCI/US~0/01998
1 7 2~ 3
M(r, ~, ~, t) = Y(~ (r- rO) ei'l~ot
Y(~,~) is a function of eim~ for l ~ 0. The product ~?im~eic~ot = ei(m~ + ~ot)
is a traveling wave with angular frequency ~,)0.
The angular frequency can be derived from the angular momentum
5 energy as follows:
E=2 1 o~2 = 21 1(1 + 1)
C)2= ~2 1(1 + 1)
11 -
Cl)= I \11(1 + 1 )
In addition to the spherical harmonics of Table 6-3,
10 Y1~2 and Y;l2, with I = 1/2
is also a solution to equation 6-46. A Mills orbital of one of these
functions is a time harmonic spinning charge density function, and it can
be shown that this Mills orbital always possesses a magnetic moment of
one Bohr magneton, B, given as follows:
15~=e~
2~L
where e is the charge and 11 is the mass of the electron and ~ is Planck's
constant divided by 27~. The angular momentum of these functions is
distinguished from that of the former solutions by assigning it the
variable S, the spin angular momentum of the electron which is given as
2 0 fol lows:
S=li~ls(s + 1)
S = 1/2
ms = +1/2
And, the angular momentum, L, is defined as orbital angular momentum.
25 A sum of independent solutions to Eq. 6-46 is a solution, and the same
condition applies to the boundary condition for nonradiation. Thus, the
Mills orbital of the electron is given as the sum of the following
functions:
., ' ' ' . . :,
WO 90/13126 PCT/US90/01998
2~a~
1 8
M(r, ~, ~, t) = Y ~ (r - rO) ei~lt ~ Y ~ (r - rO) ei~t
s
where
C~1 = I '/I(i ~ 1) 1 = O, 1, 2,
'~2= I ~s(s+ 1) s = 1/2
5 Thus, it is apparent that a Mills orbital is a spherical shell of
charge/mass density of zero width where the charge/mass is a base
function defined by Y s to which is added a component of modulation of
s
mass/charge density given by Y ' where the total charge is e, the charge
of an electron, and the total mass is 1l, the mass of the electron.
10 (Diagrams of several representative Milis orbitals are given in Figure1.)
The two components are independent time harmonics which rotate in the
same or opposite directions. The interaction of the two independent
components gives rise to spin-orbital coupling.
It can be demonstrated that the moment of inertia of the orbital
15 angular rnomentum and spin angular momentum are given respectively as
follows:
I spin = ~r2~ s ( S + 1 )
langUlar = llr2~
where ~L is the mass of the electron and r is the radius of the Mills orbital.
20 Substitu~ion of this result into the angular frequency relationships gives:
cq = ~ 1) = r2 ~ r2
11 r ~ I S ( S + 1 ~ ~ -
~S = I ys(s + 1) = ~r2~llS(S + 1 ) 11r2
The linear velocity is obtained from the angular velocity by the following
equation:
WO 90/13~26 PCI/US90/01998
1 9
v = r cl)
Thus, the linear velocity of the spin and orbital Mills orbitals is given as
followS:
tl
v =--
llr
5 To prove this result is consistent with the boundary condition for
nonradiation, the wavelength is derived from this result and the boundary
condition, 2J~r= n~; n =1,2,3,... as follows:
2~
K = ;~ = v = ~.~r2V
h
~ ~ 2~r2~rllv
1 h
~ ~lV
h
~. = p
Pnsition and Ener~ies Q~ s Or~al~
The radius of each Mills orbital can be calculated by equating the
centripetal force with the other central forces. The forces are as follows:
1.) coulombic attractive force of the positively charged nucleus for
the negatively charged Mills orbital;
2.) an attràctive magnetic spin pairing force between two unpaired
electrons which causes them to be at the force balance at
the same radius with vectorially opposed spins; thus, the
magnetic moments cancel;
3.) a repulsive diamagnetic force between two paired electrons and
an unpaired electron where the radius of the former is
unaffected by this force.
Only the coulombic force is involved in the one electron atom. The
coulombic and ~he spin-pairing forces are involved in two electron atoms,
and the coulombic and diamagnetic forces are involved in calculating the
radius of the third electron of a three electron atom, where the previously
calculated radius of the inner shell comprising two spin-paired electrons
is used in the calculation. The orbital energy of any electron can be
3 0 calculated from the calculated radius as the energy stored in its electricand magnetic fields. (The magnetic field of an electron and the energy
,
WO 90/13126 PCI/US90/01998
2 ~
stored in the magnetic field of two electrons is given in Appendix IV. A
magnetic field diagram of an electron is given in Figure 2.) Examples of
one-, two-, and three-electron atoms are given below which demonstrate
the said forces. And, it is further demonstrated, in the case of lithium,
5 that the sum of the orbital energy and the change in orbital energies of the
two remaining inner shell electrons foliowing ionization is equal to the
experimentally determined first ionization energy of lithium.
WO 90/13126 PCr/US9~)/01998
21 2 ~ 7
The One-Electron Atom
~V2
centrlpetal force = r
centripetal electrostatic force = (+Ze)( e)=
4~l0r2 47~EOr2
(obtained by taking the gradient of the electrostatic potential)
5 We can solve for the radius of the electron shell by balancing these forces.
~2
r = 4~l~0r2
The boundary condition is 2J~r = n~ which gives '~ = n r2; v = rc,); thus, v =
tl2
n r When an electron in the ground state absorbs a photon of sufficient
energy to take it to a new non-radiative state, n = 2, 3, 4, ..., force balance
1 û must be maintained. This is possible only if we let Zeff = n and,
therefore,
Vn2 Zeff,,e2
rn 47~0rn2
The reduction of the charge from Ze to Ze/n is caused by trapping a photon
in the orbitsphere cavity--a spherical cavity.
1 5 Therefore,
4~Er n?l2 naO ( 1 )
The energy stored in the electric field of the orbitsphere, Eele ,is
naO naO
27~ 7~ Z 1 27~ 7~ Z
E I = (~ o ¦ ¦ ¦ E2dV = (2) ~ I I J167~2o2nr4
oo
where the electric field,E, is
E=O,r<aO;E=4 e r2 r ~ aO
naO
Eele=8 r n Jr2 dr=- 2=-n2 (2.17714(l0)-l8) J
WO 90/13126 PCr/US90/01998
205~6~ 22
z2
Eele = - n2 (13.583) eV (2)
Equations (1) and (2) can be used for any one-electron atom. The energies
for several one-electron atoms are shown in Table 1.
Table 1 Calculated energies (non-relativistic) and calculated ionization
energies for sorne one-electron atoms (without realtivistic
correction) .
Atom Energy (eV)alonization Energy (eV)
H -13.589 13.595
He+ -54.35 54.587
1 0 Li2+ -122.28 122.45
Be3+ -217.40 217.71
B4+ -339.68 340.22
C5+ 489.14 489.98
N6+ 665.77 667.03
o7+ 869.58 871.39
afrOm equation (2)
Wo 90/13126 PCI`/US90tO1998
2 ~
23
The Two-Electron Atom
~V2
centrlpetal force = r
centripetal electrostatic force = - (Z~
4~l0r2
centripetal magnetic force = ~ Z r3 ~S(S + 1 )
5 ~obtained by taking the gradient of the angular momentum energy)
Consider two indistinguishable electrons where each is subject to an
effective nuclear charge of Z-1 due to cancellation of one nuclear charge
by the other electron. Each electron has a positive spin pairing force for
the other. The balance of force equations is as follows:
10 For n = 1, v2 = r2
r llr3 41~0r2 7 r3 ~IS(S ~ 1 )
and,
r=aO(z t ~ZS(S + 1))
The electrostatic energy is
Eele = (8 ) (4)
The magnetic energy is
- 27~oe2~2
E(magnetic) = 2 3 (5)
(The energy stored in the magnetic field of an electron is derived in
Appendix IV.)
.
` . ~ '
.
.. ..
WO 90/13126 PCI'/US90/0199~
.
2~4~7 24
Table ll The oalculated eiectrostatic and magnetic energies for
some two-electron atoms (without relativistic
corrections) .
5 Atom Atomic R(aO)a Electrostatic Magnetic Total Experimental Number Energyb EnergyC Energylonization
(eV) (eV) (eV)Energy (eV)
He 2 0.567-23.96 -0.63 -24.59 24.587
Li 3 0.356-76.41 -2.54 -78.95 75.638
1 0 Be - 4 0.261-156.08 -6.42 -162.50 153.893
B 5 0.207-262.94 -12.96 -275.90 259.368
G 6 0.171-396.98 -22.83 -419.81 392.077
N 7 0.146-558.20 -36.74 -594.93 552.057
O 8 0.127-746.59 -55.35 -801.95 739.315
1 5 F 9 0.113-962.17 -79.37 -1,041.54953.886
afrOm equation (3)
bfrom equation ~4)
cfrOm equation ~5)
WO 90/1312~ PCI'/US90/01998
2 ~ ;i `'fi~
Three-Electron Atom
(First ionization Energy of Lithium)
From the Li2+ (see Table 2), it was determined that there are two
oppositely spin-paired electrons in a sheil with the radius
r = aO ~2 -- 6
The next electron is added to form a new shell. This is a consequence of a
re~ulsive force that exists between the two spin-paired electrons and the
spin unpaired electron. This repulsive magnetic force arises from the
phenomenon of diamagnetism involving the magnetic field produced by the
10 outer electron and the two paired electrons of the inner shell.
(The following calculation is given by Edward Purcell in Electricity
and Magnetism, p. 370-389. The diamagnetic force of the two paired inner
shell electrons actiny on the outer shell electrons is given as
-mvO~v ~v eB eB
r r = 211 = 4~ vO =--
15 where r, is the radial distance of the first shell from the origin.
~ eB
F= ----
4rl ~
The magnetic flux is that supplied by the constant field inside the shell of
the outer electron and is given by:
~Oe~
B= ~3; therefore,
2 0 F = ~ O
41lr2 r1 llr
~=~s(s+l)
,ur
F=-4 2 ~s(s + 1)
The radius of the orbital for the outer electron of lithium is calculated by
equating the centripetal force to the sum of the coulombic and
2 5 diamagnetic forces as follows:
v2 e2 ~2
r 41~or2 ~ ~ ~ r2 rl ~ls ( S + 1 )
.
'
,
:
. .. ...
WO 90/13126 PCT/US90/0199~
2 ~ 2 6
v = rand r1 = aO ~2 - ~6 , thus,
~2 e2 tl2
r3 47~or2 ~ s(s ~ 1 )
4~lr2aO L2 - 6
a~
r = = 1 '13 /4 - = 2.~6 aO
4 (1 ~¦ 3/4 )
The energy stored in the electric field is calculated as follows:
e2 e2 5 318 V
The field due to the outer shell electron changes the angular velocities
of the inner shell electron; however, the magnetic field of the outer
electron provides a central Lorentzian force which exactly balances the
change in centripetal force due to the change in angular velocity. Thus, the
10 radius of the inner shell is unchanged. Consequently, the electric energy of
the inner shell is unchanged upon ionization. However, the outer field
changes the magnetic moments of the inner shell electrons. The change per
electron is given by Purcell as follows:
Bm =~ B B = 3
1~ where r1 is the radius of the inner shell and r2 is the radius~of the outer
shell .
B e2r12 ~LOe~
411 ~r2
- ~Oe2
r = ~¦s ( s + 1 )
Bm = 4 r22 ~¦s(s + 1 ) ~B = 2
Bm 2~ r1 2 ~fs(S + 1) = 2 r22 ~IS(s ~ 1 )
WO 90/13126 . PCI/US90/01998
:~ 7 ~ 3
- [aO ~1 - ~6 ~ \/ 314
-
4(1 ~3/4 )
Multiply the result by two because there are two electrons.
= ~9~~ 2
= 0.01 67
5 We add one and square to get the fractional change in the magnetic energy
of the inner shell.(because the energy stored in the magnetic field is
proportional to the magnetic field strength squared).
(1.0167)2 1.0338
Thus, the change in magnetic energy of the inner shell is 3.382% which is
1 0 given by: -
2.543 eV (0.3382) = .0860 eV
(Where the magnetic energy of lithium~ appears in Table ll.)
Eionization = .0860 eV + ~.318 eV = 5.4038 eV
The calculated ionization energy without relativistic correction is
15 5.40 eV.
The experimental ionization energy is 5.392 eV.
Energy due to Spin Nuclear Interactions
If the magnetic quantum number of the nucleus is greater than 0, the
nucleus has a magnetic moment and ~he magnetic field of the electron can
2 0 interact with the nuclear rnoment. This interaction is an important
parameter for structural determinations by electron paramagnetic
resonance spectroscopy and Mos~bauer spectroscopy. The energy of
interaction is given as follows:
E = lln- B, where ',~n is the nuclear moment and B is the magnetic flux.
25 In the case of an electron, it can be seen from Figure 2 that the flux of an
electron at the nucleus is uniform and is given in Appendix IV as follows:
B = ~r3 (Ir cos 9 ~ sin ~)
WO 90/13126 PCI'/US90/01998
,2.0~ 7
28
The magnetic moment of a proton is given as follows:
e~
~ lp = 2mp
where, mp is the mass of the proton.
When the nuclear moment is aligned with the electron's field ~ = 0 and the
5 energy is given as follows:
E e~l ~Oe'fl
2mp ~r3
These energies are small. For example the energy of spin-nuclear
interactions for hydrogen are 1.98 ~ 10-5 eV.
The Nature of the Chernical Bond
The driving force of molecular bonding is the decrease in the energy
stored in the electric fields of the participating atoms as a consequence
of overlap of their Mills orbitals. (The magnetic stored energy is involved
but is dominated by the electric stored energy.)
Consider two isolated hydrogen atoms that approach each other along
15 the internuclear axis as shown in Figure 3. The electric field of each atom
is zero for radial distance greater than aO, the radius of the Mills orbital
of the electron. As the Mllls orbitals from one atom penetrates the space
of the other, the electric field components add vectorially. The
components parallel to the internuclear axis cancel, and the perpendicular
20 components add positively. The latter components have a positive
tangential projection onto the angular vectors of the Mills orbitals in the
region of overlap.
The energy stored in the electric fields of the atoms decreases as the
internuclear distance decreases; however, it reaches a minimum then
25 increases rapidly as a function of the internuclear distance. The
trajectory produces the classic potential well, and the internuclear
distance is given the geome~ric calculation in Appendix V as ~12 aO = .748A
which is the exact experimental value. Thus, molecular bonding is
demonstrated to result from interactions of the electric fields of atoms
30 which minimizes the energy. Starting with the case of the hydrogen-
molecule of Appendix V, consider reducing the total char~e of one of the
Mills orbitals. The internuclear distance increases as the charge
decreasès. In the iimit of no charge, the internuclear distance is 2aO. Thls
WO 90/1312S PCI-/US90/019g8
2 ~ 3
29
is apparent from the following argument, the addition of an infinitesimal
amount of charge to the Mills orbital of zero charye produces an
infinitesimal overlap due to an infinitesirnal lowering of the total energy.
Thus, the internuclear distance before the infinitesimal addition was 2aO
5 which is the exact experimentally measured distance for the H2+
molecule.
Furthermore, it can be shown that the diatomic molecule can be
approximated by a harmonic oscillator with quantized energy levels given
as follows:
EVib = (n + 1/2)hl)o n = 0, 1, 2,
t)o =~ ~
where ,u is the reduced mass of ~he atoms, and k is the spring constant
which is proportional to the bond strength; therefore, k is proportional to
the gradient of the function of the bond energy as the internuclear
1 5 distance changes.
It can also be shown that the rotational energies of a diatomic
molecule are given as follows
Erot = hcB(J + 1) J = o, 1, 2,...
Selection Rules
2Q The electrons which are described by Mills orbitals can absorb energy
and achieve an excited state, and they can lose or emit energy and achieve
a lower energy state. In the case electromagnetic radiation, energy flow
is governed by Poynting's theorem
* * *
V S = ~ LH H ~ E E - J E
25 where the parameters are as follows:
S is the power; the first term is the rate of change in the stored magnetic
energy, the second term is the rate of change in the stored electric
energy, and the third term is the dissipated power. For electromagnetic
radiation, the ground state is the lowest energy state. The ground state is
30 given b~ the balance of the centripetal and coulombic forces. For the
hydrogan atom, the radius and energy appear in Table 2 as aO and t3.6 eV,
respectively. The boundary condition for Mills orbitals was given in the
Mills Orbital Section as 2~r= n~ where r = aO for n = 1.
Thus, the absorption or emission of a photon by a hydrogen atom causes
WO 90~13126 PCr~US90/01998
2 0 ~ 7
the radius to change by an integer multiple of aO. The energy of the photon
is the difference in energy of the initial and final orbitals where the
equation for the energies of the orbitals is given in the One Electron Atom
Section. Photon absorption by an electror1 creates a standing wave of the
5 photon's electric and magnetic fields inside of the Mills orbital. These
fields are solutions to Laplace's equations in three dimensions which are
spherical harmonic equations. The photon field exists as a standing wave
where surface currents of the Mills orbital are generated by the said wave
and are boundary conditions for its existence. The angular momentum and
10 spin angular momentum of all Mills orbitals are given by
El = ~ l(l + 1 )
and
-
Es = tl~s(s ~
respectively.
The angular momentum is a vector; thus, it is apparent that the angular
momentum can change by zero or +1 during a photon absorption or
emission event, a transition. Angular momentum must be conserved;
therefore, the quantum of angular momentum is provided by the photon
which carries the exact opposite quantum of angular momentum as that
20 imparted to the Mills orbital. The standing wave of the photon is a
traveling standing wave where the Mills orbital surface currents, induced
by the wave, provide one quantum of angular momentum to the Mills
o!bital in the opposite direction to the angular direction of the traveling
wave. Furthermore, angular momentum is also conserved if the wave does
25 not travel. In this case, the photon wave can be considered as the
superposition of two traveling waves rotating in opposite directions with
the same angular velocity and is analogous to plane polarized light. Thus,
the selection rules for a photon induced transition of ~m, ~s = 0, ~1 arise
naturally (~m is the change in angular momentum, and AS is the change in
30 spin angular momentum) where a change of zero is the nontraveling wave
case and a change of 1 is the traveling wave case This is totally
, c~nsistent with experimentation which. demonstrates these rules to be
correct where the photon carries one or zero quantum of angular
momentum. Consistently, a ~ransition has a rise time and, consequently, a
35 line width, as is the case in electrodynamics.
WO 90/13126 PCr/US90/01998
3 1 2~ 3
The standing photon wave has a nonzero electric field at the Mills
orbital which has a radial component which combined with the induced
surface currents provided by its tangential electric field cause the
centripetal and central coulombic forces to be balanced at an integer
5 multiple of aO. Thus, the standing wave has an effective charge given by
~o~r which reduces the coulombic attraction of the nucleus. Because a
photon can only reduce the coulombic attraction, the ground state, which
contains no photon field, is the smallest radius possible for photon
transitions. It will be shown in the Coulombic Annihilation Fusion Section
10 that the resonant absorption of energy holes can shrink the radius by
quantized fractions of aO.
Effects of External Fields
External magnetic fields align magnetic moments (Bohr magnetons) of
atoms for those with unpaired electrons, or external magnetic fields
15 effect diamagnetic phenomenon in those materials that do not have
unpaired electrons. Neither phenomenon affects the boundary conditions
for nonradiation.
External electric fields cause a redistribution of the charge density of
the Mills orbitals, the charge density functions, to create a dipole moment
20 in the atom or molecuie. This phenomenon is polarization. The orbital
condition 2Jtr= n~ is not Yiolated, so no radiation occurs.
Electrons can absorb photons from magnetic or electric fields to
become ionized. This occurs readily in a conductor or superconductor. Mills
orbitals of electrons are spherically symmetric. As photons are absorbed
25 the radius expands from the ground state with radius r1 to nr1 where n =
2, 3,.... As n goes to infinity the radius r goes to infinity and the Mills
orbital becomes a plane wave. The boundary condition for a Mills orbital
2ntr= n~ still applies; therefore, ~ _ p .The plane wave nature of the
ionized electron is confirmed by double sli~ experiments that demonstrate
3 0 that the resulting interference pattern is consistent with the electron
traveling through both slits simultaneously and possessing a wavelength
h
~ = p.
Metals have electrons as Mills orbitals which indiv :ually absorb
energy in the form of a photon from applied magnetic or electric fields to
WO 90/13126 PCr/US~0/01998
32
2 ~
become ionized to produce individual plane waves which are scattered by
phonons. There exists many electrons which can absorb the electric or
magnetic energy to become ionized and propagate as plane waves through
the material. In the case of superconductors, two electrons are ionized
5 simultaneously and pair 180 out of phase as a zero phonon event to form
Cooper pairs which have a low probability of being scattered as they
propagate. Superconductors are described in detail in the Superconductor
Section .
Superconductors
10 The Mills orbital of an electron is a spherical shell. The shell
annihilates photons during absorption to trap them as standing waves
inside the Mills orbital. The radius of the Mills orbital increases as the
energy stored in the field of the photonic wave increases. Because the
Mills orbital is a sphere, the orbital approaches a plane wave of charge
15 density as the radius goes to infinity. Thus, an electron becomes a plane
wave carrying a plane photon wave when it is ionized. Two electrons ca
be ionized simultaneously to create two traveling waves. If they are
initially oppositely paired in terms of spin and angular momentum, then
the two electrons with their accompanying photonic waves may add
20 destructively. (180 out of phase, as plane waves when they are
simultaneously ionized). This event occurs with no excitation of a phonon
(lattice vibration). That is it must be a zero phonon event because phonons
change the relative phases of the plane waves and exchange energy with
the photonic fields.
25 These paired Mills orbital plane waves, which are 180 out of phase,
carry the supercurrent in superconductors, and are known as Gooper pairs.
They possess a low phonon interaction cross section for dephasing and
breaking in the superconductor. Breaking the pairs requires the
simultaneous absorption by the pair of anti-symmetric phonons. This is
30 the boundary condition because Cooper pair creation was a zero phonon
event; thus, anti-symmetric phonons must simultaneously be absorbed to
break the Cooper pairs to conserve angular and linear momentum of the
entire system-Cooper pair plus phonons (lattice distortions).
Thus, it is apparent that a superconductor with a high transition
3 5 temperature is a material with the following properties:
1.) a large population of atoms with electrons which can
WO 90/13126 PCI'/US90/01998
3 3 ~ ~ ~c~
readily absorb energy from an electric or magnetic ~ield to
become ionized in such a fashion that they can participate
in Cooper pair formation
2.) a low population of phonons at high temperatures
3.) a low population of phonons of sufficient energy to break
Cooper pairs at high ternperatures
4.) a low population or low probability ofopposite symmetry
phonons of energy sufficient to break Cooper pairs.
Materials that contain atoms of transition elements satisfy condition
10 1. Materials which contain one of tWQ dimensional lattices with strong
bond energies satis~y conditions 2 and 3. Ceramics are materials of
condition 2. Materials which contain one or two dimensional lattices with
mixed valency or all different atoms in the unit well satisfy condition 4.
The ideal unit cell is
1~
D_M B, where M is a transition metal and A, B, C, and D are
different atoms or different oxidation states of the same or different
atoms. Perovskite superconductors such as (Ba, Sr, Y) x La2 x CuO4 are 0 examples of materials which contain all of ~he said parameters.
Coulombic Annihilation Fusion
- It was demonstrated in the Selection Rules Section that resonant
photon absorption can only increase the radius of a Mills orbital. For
resonant photon absorption, the ground state has the smallest radius
possible. For the hydrogen, atom the radius of the ground state Mills
orbital is given in Table 1 as aO. This orbital contains no photonic waves,
and the outward centripetal force and the inward coulombic force of the
electron exactiy balance. The relationship is as follows:
~V2 e2
where Y =
aO 4~0aO
3 0 It is apparent from this relationship that the radius would decrease ifthe velocity were somehow decreased To decrease the velocity, energy
must be removed which is equivalent to the absorption of an energy hole
by the electron. When energy is removed the Mills orbital will decrease to
another allowed state where the boundary condition, 2J~r = n~, and the
force balance is met.
; . . '
WO 90/13126 PCI'/US90/01998
2 ~ 9 7
34
Thus, it can be demonstrated, as appears in Appendix Vl, that the
absorption of an energy hole with concomitant shrinkage of the radius of
the Mills orbital is a resonant process with quantum numbers. The
resonance "shrinkage" energy given in Appendix Vl for the hydrogen atom
is n/~ 27.21 eV where n = 2, 3,..., and the radius shrinkage is aO( n1 - n2 )
where n~ is the quantum inte~er of the initial orbital and n2 is the
quantum integer of the final orbital of a radius shrinkage transition.
The electrons in deuterium atoms are described by Mills orbitals which
satisfy the boundary condition 2tlr= n~, and possess no space-time Fourier
10 components synchronous with waves traveling at the speed of light; thus,
they do not radiate. The electric field of the Mills orbital of a deuterium
atom is that of a point charge at the origin for radial distances greater
than the orbital radius. For these distances, the field of the Mills orbital
exactly cancels the field of the proton which is also that of a point charge
15 at the origin. The electric field of a Mills orbital is ~ero inside the
orbital; thus, the electric field inside the orbital of the deuterium atom is
the point charge field of the proton. It was demonstrated in the Nature of
the Chemical Bond Section that ohemical bonding was due to this feature
of electric fields of Mills orbitals where the total energy of the electric
2 0 fields of the participating atoms was minimized when the internuclear
distance is ~2 times the radius of ~he Mills orbital. And, this feature
together with resonant shrinkage of the Mills orbitals is the basis of
"cold fusion" of deuterium, Coulombic Annihilation Fusion, the present
invention. Coulombic repulsions of the nuclei prevent them from
25 approaching sufficiently for the strong nuclear force to dominate and for
fusion to occur. However, outside of the Mills orbital of a deuterium atom
there is no electric field; thus, for each of hNo deuterium atoms, when the
Mills orbital is sufficiently decreased by the resonant absorption by
energy holes, the internuclear distance of two deuterium atoms becomes
3 0 the distance at which the attractive strong nuclear force dominates the
repulsive coulombic force, and fusion of deuterium to helium and tritium
occurs with the release of 931 MeV/amu. The mass change for fusion of
deuterium is 0.03 amu; therefore 28 MeV/atom of energy is.released.
It is demonstrated in Appendix Vl that the radius of the Mills orbital
~ . ,
:
WO 90/13126 PCr/US90/01~98
2 ~ 3 ~
of the deuterium atom will decrease by aO ( n1 ~ n ) when an energy hole
of energy equal to n/2 27.21 eV; n = 2, 3, 4,..., is resonantly absorbed. With
continued resonance shrinkage-absorption of energy holes-by the atom,
the Mills orbital shrinks to small dimensions, and when approximately 100
5 KeV of energy holes have been absorbed the radius is sufficiently small
that the deuterium atom will fuse with another atom of deuterium with a
similar dimension of its Mills orbital.
A catalystic system to produce energy holes of 27.21 eV is a preferred
embodiment of the present invention. For such a system the population of
10 energy holes is not exhausted because they are regenerated.
Palladium 2+ and lithium+ is such a systern. The catalytic cycle which
affects the quantized decrease in the radius of the Mills orbital of the
deuterium atom is as follows:
27.54 eV + Li+ + pd2+ + 2H[ p ] ~ Li + Pd3+ t 2H[(p + I) ] + [(p + 1)2 _ n2] x 13.6 eV
1 5 Li + Pd3~ = Li+ + Pd2+ + 27.54 eV
Overall reaction
2H[a ] _~ 2El[ ( aO l) ] + [(p + 1)2 _p2] x 13-6 eV
where p = 1, 2, 3,....
The Palladium lithium system involves three species. The rate of the
20 resonance shrinkage can be increased by reducing the number of species to
two. Titanium, rubidium, or argon are effective catalysts. The catalytic
reactions are as follows:
27.491 eV + Ti2+ + 2H[~ ~ Ti3+ + e~ + 2H[(p + I) ] + [(p + 1)2 _ p2] x 13.6 eV
Ti3+ + e- ~ Ti2+ + 27.491 eV
2 5 (8.8)
And, the overall reaction is
2H~ p ] ~ 2H (p + l) ] + [(p + 1)2 _p2~ x 13.6 eV
where the ionization energy, Ejon, for Ti2+ is 27.491 eV; p is a integer
27.491 eV+ Rb+ ~ 2H[ p ] ~ Rb2+ + e~ + 2H[(p + ~~ ] + [(p + 1)2 _ p2] X 13.6 eV
Rb2+ +e~ ~ Rb+ + 27.28 eV
Overall reaction
WO 90/13126 PCI/US90/01998
2 ~
3 6
2H[a ~ ~ 2H[( l) ~ + [(p + 1)2 _p2] x 13.6 eV
where the ionization energy, Ejon, ~or Rb+ is 27.28 eV
27 63 eV+ Ar+ + 2H[a0 ] ~ Ar2~ + e~ + 2H[( + l) 1 + ~(P + 1)2 - p2] x 13.6 eV
Ar2+ +e~ ~ Ar~ + 27.63 eV
5 Overall reaction
2H[a0 ] ~ 2H¦ ( aO 1~ 1 + [(p ~1)2 _p2] x 13.6 eV
where the ionization energy, Ejon, for Ar+ is 27.629 eV.
WO 90/13126 PCI'/US90/01998
~3 7 ~ h~ ~J
The present invention comprises a source of energy holes of
approximately 27 eV to resonantly shrink the Mills orbitals of deuterium
atoms, including a source of said holes produced by further
electrochemical reactions or chemical, photochemical, thermal, free
5 radical, sonic, or nuclear reactions or inelastic particles, or photon
scattering reactions. The closer the energy of the hole is to the quantum
of 27.21 eV or the quanta of 2 27.21 eV: n = 2, 3, 4,..., the greater the rate
of reaction because phonons ortranslational or rotational modes do not
have to be simultaneously excited to match the resonant shrinkage energy.
l O Table 3 is a table of ionizatioh energies as given in Chemical Structure
and Bonding, Rodger L. DeKock and Harry P. Gray, the Benjamim Cummings
Publishing Company, Menlo Park, CA, (1980), pp. 76-77 which is
incorporated by reference. Electrochemical couples with ionization energy
differences of approximately 27 eV can catalyze the removal of energy
1~ from the electrons of deuterium and/or tritium atoms and molecules and
catalyze cold fusion of deuterium and/or tritium.
Wo 9~ Pcr/usso/o1998
. 38
Representative electrochemical couples which generate energy holes
of approximately 27 eV appear in Table 4, and some catalytic couples
comprising single elements which are cations, neutral, or anions and
single molecules which are cations, anions, or neutral or combinations of
5 the said species-reactants are also found in Table 4. For n - 2, the
resonance energy is 27.21; for n = 16 the resonance energy is 217.68 eV;
for n = 54, the resonance energy is 734.67 eV.
WO 90/13126 PCI`/lJS90/01998
3 9 2 ~ 7
Table 4. Representative Electrochemical couples that
catalytically produce energy holes of 27 eV to shrink
deuterium atoms.
Electrochemical lonization Energy Hole
Couple Ener~y_ ~ _
Lu3+ 45.19 27.768
F+ 17.422
Pb2+ 32.93 27.~38
Li+ 5.392
Ni2+ 35.17 27.3
Fe+ 7.~
Ag2+ 34.83 27.37
Rh+ -7.46
Zr3+ 34.34 27.241
1 5 Mo+ 7.099
Nb3+ 38.3 27.863
Hg+ 10.437
Cu2+ 36.83 27.605
Au~ 9.225
pb2+ 31.937 27.596
K+ 4.341
Ge2+ 34.22 27.34
Nb+ 6.88
Many others exist and are given in the above referenced Table 3 of
25 ionization energies.
WO 90/13126 PCl`tUS90/01998
r7
Table 4. Some representative single-ions capable of producing
(con~t) energy holes for shrinking deuterium atoms. The number
following the atomic symbol, (n), is the nth ionization
energy of the atom. That is for example, TiZ* + 27.49 eV
= Ti3~ + e-.
Catalytic lon n nth lonization Energy
Al 2+ 3 28.45
Ar 1+ 2 27.63
Ti 2+ 3 27.49
- As 2+ 3 28.35
Rb 1~ 2 27.28
Mo 2+ 3 27.16
Ru 2+ 3 28.47
In 2+ 3 28.03
Te 2+ 3 27.96
Table 4. Some represen~ative two-ion couples capable of
(con't) producing energy holes for shrinking deuterium atoms.
The number following the ion, (n), is the nth iunization
energy of the atom. That is for example, Pd2+ + 32.93 eV
= Pd3+ ~ e- and Li+ + e- = Li + 5.39 eV.
Atom n nth lon- A~om n nth lon-Energy
Oxidiz- ization Redueed izationHole
ed Energy Energy (eV)
(eV~ (eV)
Ne 1 + 2 40.96 H 1 + 1 13.60 27.36
Ar2+ 3 40.74 H 1 + 1 13.60 27.14
Sn3+ 4 40.73 H 1~ 1 13.60 27.14
Pm3 + 4 41.10 H 1 + 1 13.60 27.50
Sm 3 + 4 41.40 H 1 + 1 13.60 27.80
. Dy 3 + 4 41.50 H 1 + 1 13.60 27.90
Kr 3 + 4 52.50 He 1 + 1 24.59 27.91
Rb3+ 4 52.60 He1 + 1 24.59 28.01
K 4+ 5 ~2.66 He2+ 2 54.42 28.24
Zn 4 + 5 82.60 He 2 + 2 54.42 28.18
Se 5 + 6 81.70 He 2 + 2 54.42 27.28
He 1 + 2 54.42 Rb2~ 2 27.28 27.14
WO 90/131~6 PCI/US90/01998
''. ;"
41 ~ ~ ~ J~
Zr 4 + 581.50 He 2 ~ 254.42 27.08
He 1 + 254.42 Mo3+ 327.16 27.26
Si 2 ~ 333.49 Li 1 + 15.39 2B.10
Mn 2+ 333.67 Li 1 + 15.39 28.27
Co 2 + 333.50 Li 1 + 15.39 28.11
Pd 2 + 332.93 Li 1 + 15.39 27.54
1 2 + 333.00 Li 1 + 15.39 27.61
Hf 3 + 433.33 Li 1 + 15.39 27.94
Li 1 + 275.64 C 3 ~ 347.89 27.75
l O Li 1 + 275.64 N 3 + 347.45 28.19
Li 1 + 275.64 Na2+ 247.29 28.35
Li 1 + 275.64 S 4 + 447.30 28.34
Cu 5+ 6103.00 Li 2 + 275.64 27.36
Li 1 + 275.64 Br 4 + 447.30 28.34
Br 6 + 7103.00 Li 2 + 275.64 27.36
V 6 + 7150.17 Li 3 + 3122.45 27.72
Li ~ + 3122.45 Mn6+ 695.00 27.45
Cu 2+ 336.83 Be 1 + 19.32 27.51
Kr 2 + 336.95 Be 1 ~ 19.32 27.63
Cd2+ 337.48 Be 1 + 19.32 - 28.16
Te 3 + 437.41 Be 1 * 19.32 28.09
Ce 3 + 436.76 Be 1 + 19.32 27.44
K 2 + 345.72 Be 2 + 218.21 27.51
V 3 + 446.71 Be ~ ~ 218.21 28.50
Ge 3 + 445.71 Be ~ + 218.21 27.50
Mo3+ 446.40 Be2+ 218.2i 28.19
Bi 3 + 44~.30 Be2+ 218.21 27.09
Be 2 + 3153.89 Ne 5 ~ 5126.21 27.68
Be 2 + 3153.89 Kr 8 + 8126.00 27.89
Be 2 + 3l 53.89 Mo 7 ~ 7126.80 27.09
Be 3 + 4217.71 Al 6 + 6190.47 27.24
Br 2 + 336.00 B 1 + 18.30 27.70
Ce3+ 436.76 B 1 + 18.30 28.46
Cl 3 + 453.46 B 2+ 225.15 28.31
Kr 3 + 452.50 B 2 + 225.15 27.35
Rb 3 + 452.60 B 2 ~ 225.15 27.45
WO 90t13126 PCr/US90/01998
2 ~
42
B 2 + 3 37.93 P 1 + 1 10.49 27.44
P 4 + 5 65.02 B 3 + 3 37.93 27.09
B 2 + 3 37.93 S 1 + 1 10.36 27.57
V 4 + 5 65.23 B 3 + 3 37.93 27.30
5B 2+ 3 37.93 As 1 + 1 9.81 28.12
B 2+ 3 37.93 Se 1 + 1 9.75 28.18
B 2+ 3 37.93 1 1 + 1 10.45 27.48
B 2 + 3 37.93 Ba 2 + 2 10.00 27.93
B 2 + 3 37.93 Ce 2 + 2 10.85 27.08
10B 2 + 3 37.93 Pr 2 + 2 10.55 27.38
B 2 + 3 37.93 Nd 2 + 2 10.73 27.20
B 2 ~ 3 37.93 Pm 2 + 2 10.90 27.03
B 2 + 3 37.93 Hg 1 + 1 10.44 27.49
B 2+ 3 37.93 Rn 1 + 1 10.75 27.18
15B 2 + 3 37.93 Ra 2 + 2 10.15 27.78
Cl 2 + 3 39.61 C 1 ~ 1 11.26 28.35
Zn2+ 3 39.72 C 1 + 1 11.26 23.46
Nb3+ 4 38.30 C 1 ~ 1 11.26 27.04
Pr 3 ~ 4 38.98 C 1 + 1 11.26 27.72
20Kr 3 + 4 52.50 C 2 + 2 24.38 28.12
Rb 3 + 4 52.60 C 2 + 2 24.38 28.22
C 2+ 3 47.89 P 2+ 2 19.73 28.16
Ar 4 + 5 75.02 C 3 ~ 3 47.89 27.13
Fe 4 ~ 5 75.00 C 3 + 3 47.89 27.11
25Ni 4 + 5 75.50 C 3 + 3 47.89 27.61
C 2+ 3 47.89 Cu2+ 2 20.29 27.60
C 2 + 3 47.89 Ga 2 + 220.51 27.38
~ 2~ 3 47.~9 Y 3+ 320.52 27.37
C 2 + 3 47.89 Pd 2 + 219.43 28.46
30C 2+ 3 47.89 Ce3+ 320.20 27.69
C 2 + 3 47.89 Gd 3 + 320.63 27.26
C 2+ 3 47.89 Au 2 + 220.50 27.39
C 2+ 3 47.89 Tl 2 + 220.43 27.46
Sc 4 + 5 91.~6 C 4 + 464.49 27.17
3`5~ - 3 ~ 4 64.49 Cu 3 + 336.83 27.66
C 3 + 4 64.49 Br 3 + 336Ø0 28.4.9
WO 90/13126 PCI'/US90/01998
43 ~3~ )t~!
C 3 + 4 64.49 Kr 3 + 3 36.95 27.54
C 3 + 4 64.49 Cd 3 + 3 37.48 27.01
C 3 + 4 64.49 Te 4 + 4 37.41 27.08
C 3 + 4 64.49 Ce 4 + 4 36.76 27.73
Se3+ 4 42.94 N 1 + 1 14.53 28.41
Eu 3 + 4 42.60 N 1 + 1 14.53 28.07
Ho 3 + 4 42.50 N 1 + 1 14.53 27.97
Er 3 + 4 42.60 N 1 + 1 14.53 28.07
Tm 3 + 4 42.70 N 1 + 1 14.53 28.17
Pb 3 + 4 42.32 N 1 + 1 14.53 27.79
Sr 3 + 4 57.00 N 2 + 2 29.60 27.40
N 2 + 3 47.45 P 2 ~ 2 19.73 27.72
Ar 4 + 5 75.02 N 3 + 3 47.45 27.57
Fe 4 + 5 75.00 N 3 + 3 47.45 27.55
1~ Ni 4 + 5 75.50 N 3 + 3 47.45 28.05
N 2 + 3 47.45 Cu 2 + 2 20.29 27.16
N 2 + 3 47.45 Pd 2 + 2 19.43 28.02
N 2 + 3 47.45 1 2 + 2 19.13 28.32
N 2 + 3 47.45 La 3 + 3 19.18 28.27
N 2 + 3 ~7.45 Ce 3 + 3 20.20 27.25
N 2+ 3 47.45 Tl 2 + 2 20.43 27.02
N 3 + 4 77.47 Cr 4 + 4 49.10 28.37
N 3 + 4 77.47 As 4 + 4 50.13 27.34
N 3 + 4 77.47 La 4 + 4 49.95 27.52
Ne4+ 5 126.21 N ~ 5 97.89 28.32
Fe 6 + 7 1 ~5.00 N 5 + 5 97.89 27.11
Kr 7 + 8 126.00 N 5 + 5 97.89 28.11
Nb6+ 7 125.00 N 5+ 5 97.89 27.11
N 4 + 5 97.89 Te 6 + 6 70.70 27.19
Ne 1 + 2 40.96 O 1 + 1 13.62 27.34
Ar ~ ~ 3 40.74 O 1 + 1 13.62 27.12
Sn 3 + 4 40.73 O 1 + 1 13.62 27.12
Pm 3 + 4 41.10 O 1 + 1 13.62 27.48
Sm 3 + 4 41.~0 O 1 + 1 13.62 27.78
Dy3 ~ 4 41.50 O 1 + 1 13.62 27.88
F ;2+ 3 62.71 O 2+ 2 35.12 27.59
WO 90/13126 P~/US90/01998 .
2 ~ nJ 7
44
Ne2+ 3 63.45 O 2+ 235.12 28.33
O 1 ~ 2 35.12 Mg 1 + 17.65 27.47
O 1 + 2 35.12 Ti 1 + 16.82 28.30
O 1 + 2 35.12 V 1 + 16.74 28.38
O 1 + 2 35.12 Cr 1 + 16.77 28.35
O 1 + 2 35.12 Mn 1 + 17.43 27.68
O 1 + 2 35.12 Fe 1 + 17.87 27.25
O '. + 2 35.12 Co 1 + 17.86 27.26
O 1 + 2 35.12 Ni 1 + 17.64 27.48
O 1 + 2 35.12 Cu 1 + 17.73 27.39
O 1 + 2 35.12 Ge 1 ~ 17.90 27.22
O 1 + 2 35.12 Zr 1 + 16.84 28.28
O 1 + 2 35.12 Nb 1 + 16.88 28.24
O 1 + 2 35.12 Mo 1 + 17.10 28.02
O 1+ 2 35.12 Tc1+ 17.28 27.84
O 1 + 2 35.12 Ru 1 + 17.37 27.75
O 1 + 2 35.12 Rh 1 + 17.46 27.66
O 1 + 2 35.12 Ag 1 + 17.58 27.54
O 1 + 2 35.12 Sn 1 + 17.34 27.77
O 1 + 2 35.12 Ta 1 + 17.89 27.23
O 1 + 2 35.12 W 1 + 17.98 27.14
O 1 + 2 35.12 Re 1 + 17.88 27.24
O 1 + 2 35.12 Pb 1 + 17.42 27.7~
O 1 ~ 2 35.12 Bi 1 + 17.29 27.83
O 2+ 3 ~4.93 Ar 2 + 227.63 27.30
K 4 + 5 82.66 O 3 + 354.93 27.73
O 2+ 3 54.93 Ti 3 + 327.49 27.44
Zn4+ 5 82.60 O 3+ 354.93 27.67
O 2+ 3 54.93 Rb2+ 227.28 27.6~
O 2+ 3 54.93 Mo3 ~ 327.16 27.77
O 3+ 4 77.41 Cr4+ 449.10 28.31
O 3 + 4 77.4 As 4 + 450.13 27.28
O 3+ 4 77.41 La4+ 449.95 27.46
Mg 4 + 5 141.26 O 5 + 5113.90 27.36
O 5+ 6138.12 Sc6+ 6111.10 27.02
Cu 7 ~ 8166.00 O 6 + 6138.12 27.88
WO ~0/131~6 PCT/US90/01998
O 5+ 6138.12 Kr 7 + 7111.00 27.12
S; 3 + 4 45.14 F 1 + 117.42 27.72
K 2+ 3 45.72 F 1 + 117.42 28.30
Ge3+ 4 45.71 F 1 + 117.42 28.29
LU 3 + 4 45.19 F 1 + 117.42 27.77
B; 3 + 4 45.30 F 1 + 117.42 27.88
F 2+ 3 62.71 F 2+ 234.97 27.74
Ne 2 + 3 63.45 F 2 + 234.97 28.48
F 1 + 2 34.97 Mg 1 + 1 7.65 27.32
F 1 ~ 2 34.97 SC 1 + 1 6.54 28.43
F 1 + 2 34.97 T; 1 ~ 1 6.82 28.15
F 1 + 2 34.97 V 1 + 1 6.74 28.23
F 1 + 2 34.97 Cr 1 + 1 6.77 28.20
F 1 + 2 34.97 Mn 1 + 1 7.43 27.54
F 1 + 2 34.97 Fe 1 + 1 7.87 27.10
F 1 + 2 34.97 CO 1 + 1 7.86 27.11
F 1 + 2 34.97 N; 1 + 1 7.64 27.34
F 1 + 2 34.97 CU 1 + 1 7.73 27.24
F 1 + 2 34.97 Ge 1 + 1 7.90 27.07
F 1 ~ 2 34.97 Zr 1 ~ - 1 6.84 28.13
F 1 + 2 34.97 Nb 1 + ~ 16.88 28.09
F 1 + 2 34.97 MQ 1 + 1 7.10 27.87
F 1 + 2 34.97 TC 1 + 1 7.28 27.69
F 1 + 2 34.97 RU 1 I 1 7.37 27.60
F 1 + 2 34.97 Rh 1 + 1 7.46 27.51
F 1 + 2 34.97 A91 + -1 7.58 27.39
F 1 + 2 34.97 Sn 1 1 7.34 27.63
F 1 + 2 34.97 Hf 1 + 1 6.60 28.37
F 1 + 2 34.97 Ta 1 + 1 7.89 27.08
F 1+ 2 34.97 Re1+ 1 7.88 27.09
F 1 ~ 2 34.97 Pb 1 + 1 7.42 27.55
F 1 + 234.97 B; 1 + 1 7.29 27.68
F 2 + 362.71 F 2 + 234.97 27.74
F 2 + 362.71 S 3 + 334.83 27.88
Ar 5 + 691.01 F 3 ~ 362.71 28.30
Cr 5 + 690.56 F 3 + 362.71 -~7.85
'
,
'
.
WO 90/13126 PCl/US90/01998
.
46
2 ~
F 2+ 3 62.71 Ni 3 + 3 35.17 27.54
F 2+ 3 62.71 Ge3+ 3 34.22 28.49
Sr ~ + 6 90.80 F 3 + 3 62.71 28.09
F 2 + 3 62.71 Zr 4 + 4 34.34 28.37
F 2 ~ 3 62.71 Ag 3 + 8 34.83 27.88
F 4+ 5114.24 F 4+ 4 87.14 27.10
Cl 6 + 7114.19 F 4 + 4 87.14 27.06
F 3 + 4 87.14 Ar 4 + 4 59.81 27.33
F 3 + 4 87.14 Zn 4 + 4 59.40 Z7.74
F 3 + 4 87.14 Br 5 + 5 ~9.70 27.44
F 3 + 4 87.14 Te 5 + 5 58.75 23.3g
F 4+ 5114.24 F 4+ 4 87.14 27.10
Mg 4 + 5141.26 F 5 + 5114.24 27.02
F 6+ 7185.18 F 6+ 6157.16 28.02
Cr 7 ~ 8184.70 F 6 + 6157.16 27.54
F 5~ 6157.16 Co7~ 7129.00 28.16
F 5+ 6157.16 Y 8+ 8129.00 28.16
F 6+ 7185.18 F 6 + 6157.16 28.02
F 6+ 7185.18 Ne6+ 6157.93 27.25
F 6+ 7185.18 Co8+ 8157.00 28.18
Cr3 + 4 49.10 Ne 1 + 1 21.56 27.54
La3 + 4 49.95 Ne 1 + 1 21.56 28.39
Ne 1 + 2 40.96 Cl 1 + 1 12.97 28.00
Ne 1 + 2 40.96 Sc 2 + 2 12.80 28.16
Ne 1 + 2 40.96 Ti 2 + 2 13.58 27.38
Cr 4 + 5 69.30 Ne 2 + 2 40.96 28.34
Se 4 + 5 68.30 Ne 2 ~ 2 40.96 27.34
Ne 1 + 2 40.96 Zr 2 + 213.13 27.83
Mo 5 + 6 68.00 Ne 2 + 240.96 27.04
Ne 1 + 2 40.96 Lu 2 + 213.90 27.06
Pb 4 + 5 68.80 Ne 2 + 240.96 27.84
Ar 5 + 6 91.01 Ne3+ 363.45 27.~6
Sc 4 + 5 91.66 Ne 3 ~ 363.45 28.21
Cr 5 + 6 90.56 Ne 3 + 363.45 27.11
3~ Ne2~ 3 63.45 Ni 3 + 335.17 28.28
Ne2+ 3 63.45 Br 3 + 336.00 27.45
, ~
WO 90/13126 PCrtUS90/01998
47
. .
Sr 5 + 690.80 Ne 3+ 363.45 27.35
Ar 6 + 7124.32 Ne 4 + 497.11 27.21
Ne 3 + 497.11 Cr 5 + 569.30 27.81
Fe 6 + 7125.00 Ne 4 ~ 497.11 27.8g
Nb6+ 7125.00 Ne4+ 497.11 27.89
Ne 3 + 497.11 Pb 5 + 568.~0 28.31
Ne 4 + 5126.21 Na 4 + 498.91 27.30
Al 4 + 5153.71 Ne5+ 5126.21 27.50
Ne 4 + 5126.21 Fe 6 + 699.00 27.21
Ne 4 + 5126.21 Rb 7 ~ 799.20 27.01
Si 2 + 333.49 Na 1 + 15.14 28.35
Co 7+ 333.50 Na1 + 15.14 28.36
Pd2+ 332.93 Na 1 ~ 15.14 27.79
1 2 + 333.00 Na 1 + 15.14 27.86
Hf3+ 433.33 Na1+ 15.14 28.19
Na 1 + 247.29 Al 2 + 2~8.83 28.46
Na 1 + 247.29 P 2 + 219.73 27.56
Ar 4 + 575.02 Na 2 ~ 247.29 27.73
Fe 4 + 575.00 Na 2 + 247.29 27.71
Ni 4 + ~75.50 Na 2 + 247.29 28.21
Na 1 + 247.29 Pd 2 + 219.43 27.86
Na 1 + 247.29 In 2 + 218.87 28.42
Na 1 + 247.29 1 2 ~ 21g.13 28.15
Na1 + 247.29 La3+ 319.18 28.11
Na 1 + 247.29 Ce 3 + 320.20 27.09
Na 3 + 498.91 Na 3 + 371.64 27.27
K 5 + 6100.00 Na 3 + 3 71.64 28.36
Na2+ 371.64 Ti 4 + 4 43.27 28.37
Ti 4 + 599.22 Na3+ 371.64 27.58
Fe 5 + 699.00 Na 3 + 3 71.64 27.36
Rb 6 ~ 799.20 Na 3 + 3 71.64 27.56
Na 2 + 371.64 Sr 3 + 3 43.60 28.04
Na 2 + 371.64 Sb 4 + 4 44.20 27.44
Na 2 + 371.64 Gd 4 ~ 4 44.00 27.64
Na 2 + 371.64 ~b 4 + 4 43.70 27.94
Na 3 + 498.91 Na 3 + 3 71.64 27.27
.
wo 9o/13126 PCr/US90/01998
20~69 1
48
Kr 7 + 8 126.00 Na 4 + 4 98.91 27.09
Na 3 + 4 98.91 Rb 5 + 5 71.00 27.91
Na 3 + 4 98.91 Sr 5 + 5 71.60 27.31
Mo 6 + 7 126.80 Na 4 + 4 98.91 27.89
Na 3 + 4 98.91 Te 6 + 6 70.70 28.21
Si 4 + 5 166.77 Na5+ 5 138.39 28.38
Na4+ 5138.39 Sc6+ 6111.10 27.29
Cu 7 + 8 166.00 Na 5 + 5 138.39 27.61
Na 4 + 5 138.39 Kr 7 + 7 111.00 27.39
S 2~ 3- 34.83 Mg1+ 17.65 27.18
Ni 2 + 3 35.17 Mg 1 + 1 7.65 27.52
Br 2 + 3 36.00 Mg 1 + 1 7.65 `28.35
Ag 2 + 3 34.83 Mg 1 + 1 7.65 27.18
Ti 3 + 4 43.27 Mg 2+ 2 15.03 28.23
Se 3 + 4 42.94 Mg 2 + 1 ~.03 27.91
Eu 3 + 4 42.60 Mg 2 + 2 15.03 27.56
Ho 3 + 4 42.50 Mg 2 + 2 15.03 27.47
Er 3 + 4 42.60 Mg 2 + 2 1 ~.03 27.56
Tm 3 + 4 42.70 Mg 2 + 2 15.03 27.67
Pb 3 + 4 42.32 Mg 2 + 2 15.03 27.28
Ni 5 + 6 108.00 Mg 3 ~ 3 80.14 27.86
~n 5 + 6 108.00 Mg 3 + 3 80.14 27.86
Mg 2+ 3 80.14 Kr 4 + 4 52.50 27.64
Mg 2 + 3 80.14 Rb 4 + 4 52.60 27.54
Sb 5 + 6 108.00 Mg 3 + 3 80.14 27.86
Mg 3 + 4 109.24 Se 6 + 6 81.70 27.54
Mg 3 + 4 109.24 Zr 5 + 5 81.50 27.74
Te 6 + 7 137.00 Mg 4 + 4 109.24 27.76
Mg 4 + 5 141.26 Cl 7 + 7 114.19 27.07
Ti 7 + 8 168.50 Mg5+ 5 141.26 27.24
Mg 5 + 6 186.50 Sc 8 + 8 158.70 27.80
Mg 6 + 7 224.94 Mn 8 + 8 196.46 28.48
Si 2 + 3 33.49 Al 1 + 1 5.99 27.51
Mn2+ 3 33.67 Al 1 ~ 15.99 27.68
Co 2 + 3 33.50 Al 1 + 1 5.99 27.51
Ge2+ 334~22 Al 1 + 1 5.~9 .28.23
WO 90/13126 PCI-/US90/01998
49
Zr 3 + 4 34.34 Al 1 + 15.99 28.35
1 2 + 3 33.00 Al 1 + 15.99 27.01
Hf 3 + 4 33.33 Al l + 15.99 27.34
Hg 2+ 3 34.20 Al 1 + 15.99 28.21
S 3+ 4 47.30 Al 2 + 218.83 28.47
V 3 + 4 46.71 Al 2 + 218.83 27.88
Br 3 + 4 47.30 Al 2 + 218.83 28.47
Mo 3+ 4 46.40 Al 2 + 218.83 27.57
Sb4 + 5 56.00 Al 3 + 328.45 27.55
Bi 4 + 5 56.00 Al 3 + 328.45 27.55
Ca7+ 8 147.24 Al 4 + 4119.99 27.25
Al 3 + 4 119.99 Sc 5 + 591.66 28.33
Al 4 + 5 153.71 Kr 8 + 8126.00 27.71
Al 5 + 6 190.47 Ni 8 + 8162.00 28.47
Ni 2~ 3 35.17 Si 1 + 18.15 27.02
~r 2 + 3 36.00 Si 1 + 18.15 27.85
Sr 2 + 3 43.60 Si 2 ~ 216.34 27.25
Sb 3 ~ 4 44.20 Si 2 + 216.34 27.86
Gd3~ 4 44.00 Si 2 ~ 216.34 27.66
~0 Yb3+ 4 43.70 Si 2 ~ 216.34 27.36
K 3 + 4 60.91 Si 3 + 333.49 27.42
Si 2 + 3 33.49 Ca 1 ~ 16.11 27.38
Si 2 + 3 33.49 Ga1 + 16.00 27.49
Si 2 + 3 33.49 Sr 1 + 15.70 27.80
Si 2 + 3 33.49 Y 1 ~ 16.38 27.11
Y 3 + 3 61.80 Si 3 + 333.49 28.31
Mo4+ 5 61.20 Si 3 ~ 333.49 27.71
Si 2 + 3 33.49 In 1 + 15.79 27.71
Si 2 + 3 33.49 Ba 1 ~ 15.21 28.28
Si 2 + 3 33.49 La 1 + 15.58 27.92
Si 2 + 3 33.49 Ce 1 + 15.47 28.02
Si 2 + 3 33.49 Pr 1 + 15.42 28.07
Si 2 + 3 33.49 Nd 1 -~ 15.49 28.00
Si 2 + 3 33.49 Pm 1 f 15.~5 27.94
Si 2 + 3 33.49 Sm 1 + 15.63 27.86
Si 2 + 3 33.. 49 Eu 1 + 1 5.67 27.83
WO 90/13126 PCI'/US90/01998
2 ~ 9 ~
Si 2 + 3 33.49 Gd 1 + 16.14 27.3~
Si 2 + 3 33.49 Tb 1 + 15.85 27.64
Si 2 + 3 33.49 Dy 1 + 15.93 27.57
Si 2 + 3 33.49 Ho l + 16.02 27.47
Si 2 + 3 33.49 Er 1 + 16.10 27.39
Si 2 + 3 33.49 Tm 1 + 16.18 27.31
Si 2 + 3 33.49 Yb 1 + 16.25 27.24
Si 2 + 3 33.49 Lu 1 ~ 15.43 28.07
Si 2 + 3 33.49 Tl 1 + 16.11 27.38
Si 2 + 3 33.49 Ra 1 + 15.28 28.21
Si 2 + 3 33.49 Ac 1 + 15.20 28.29
Si 2 + 3 33.49 Th 1 + 16.10 27.39
Si 2 + 3 33.49 Pa 1 + 15.90 27.59
Si 2 + 3 33.49 U 1 + 16.05 27.44
Si 2 t 3 33.49 Np 1 + 16.20 27.29
Si 2 + 3 33.49 Pu 1 + 16.06 27.43
Si 2 + 3 33.49 Am 1 + 15.99 27.50
Si 2 + 3 33.49 Cm 1 ~ 16.02 27.47
Si 2 + 3 33.49 Bk 1 + 16.23 27.~6
Si 2 + 3 33.49 Cf 1 + 16.30 27.19
Si 2 + 3 33.49 Es 1 + 16.42 27.07
S 4+ 5 72.68 Si 4 + 445.14 27.54
Sc 3 + 4 73.47 Si 4 + 445.14 28.33
Mn4+ 5 72.40 Si 4 + 445.14 27.26
Si 3 + 4 45.14 Co2~ 217.06 28.08
Si3+ 4 45.14 Zn2+ 217.96 27.18
Si 3 + 4 45.14 Ru2+ 216.76 28.38
Si 3 + 4 45.14 Rh2+ 218.08 27.06
Si 3 + 4 45.14 Cd 2 + 216.91 28.23
Sn 4 + 5 72.28 Si 4 + 445.14 27.14
Si 3 + 4 45.14 Bi 2 + 216.69 2B.45
Si 4 + 5166.77 Cu 7 ~ 7139.00 27.~7
Nb3+ 4 38.30 P 1 + 110.49 27.8t
Pr 3 + 438.98 P 1 + 110.49 28.49
S 3+ 447.30 P 2~ 219.73 27.57
Br 3 + 447.30 P 2 + 219.73 27.57
WO 90/13126 PCl`/US91)/01998
51
P 3 + 451.37 S 2 + 223.33 28.04
P 3 + 451.37 Cl 2 + 223.81 27.56
Co 4 + ~79.50 P 4 + 451.37 28.13
P 3+ 45t.37 Kr 2 + 224.36 27.01
5Kr 5 + 678.50 P 4 + 451.37 27.13
P 3 + 451.37 Zr 3 + 322.99 28.38
P 3+ 451.37 Sm 3 + 323.40 27.97
P 3+ 451.37 Tm 3 + 323.68 27.69
P 3 + 4~1.37 Hf 3 + 323.30 28.07
10P 4+ 565.02 Cu3+ 336.83 28.19
Ge 4 + 593.50 P 5 + 565.02 28.48
P 4+ 565.02 Kr 3 + 336.95 28.07
Y 5+ 693.00 P 5+ 565.02 27.98
P 4 + 565.02 Cd 3 + 337.48 27.54
15P 4 ~ 565.02 Te 4 + 437.41 27.61
P 4+ 56~.02 C~4+ 436.76 28.27
P 5 ~ 6220.43 Br B + 8192.80 27.63
P 7+ 8309.41 S 7+ 7280.93 28.48
Nb3+ 438.30 S 1 ~ 110.36 27.94
20Cd2+ 337.48 S 1 + 110.36 27.12
Te 3 + 437.41 S 1 + 110.36 27.05
Ca 2 + 350.91 S 2 + 223.33 27.58
Mn 3 + 4~ .20 S 2 + 223.33 27.87
Co 3 + 4~1.30 S 2 + 223.33 27.97
25Nb4+ 550 55 S 2+ 223.33 27.22
S 2+ 334.83 Sc 1 ~ 16.54 28.29
S 2+ 334.83 Ti 1 + 16.82 28.01
S 2+ 334.83 V 1 + 16.74 28.09
S 2+ 334.83 Cr 1 + 16.77 28.06
30S 2~ 334.83 Mn 1 ~ 17.43 27.40
S 2 + 334.83 Ni 1 + 17.64 27.20
S 2 + 334.83 Cu 1 + 17.73 27.10
S 2 + 334.83 Y 1 + 16.38 28.45
S 2+ 334.83 Zr 1 + 16.84 27.9g
35S 2 ~ 334.83 Nb 1 + 16.88 27.g5
S 2 + 334.83 Mo 1 + 17.10 27.73
WO 90/13126 PCl/US90/01998
2 ~
52
S 2+ 3 34.83 Tc 1 + 17.28 27.55
S 2 + 3 34.83 Ru 1 + 17.37 27.46
S 2 + 3 34.83 Rh 1 + 17.46 27.37
S 2 + 3 34.83 Ag 1 ~ 17.58 27.25
5S 2 + 3 34.83 Sn 1 + 17.34 27.49
S 2 + 3 34.B3 Hf 1 + 16.60 28.23
S 2 + 3 34.83 Pb 1 + 17.42 27.41
S 2 + 3 34.83 Bi 1 + 17.29 27.54
S 2+ 3 34.83 Es 1 ~ 16.42 28.41
10Ar 4 + 5 75.02 S 4 + 447.30 27.72
Fe 4 + 5 75.00 S 4 + 447.30 27.70
Ni 4 + 5 75.50 S 4 + 447.30 28.20
S 3 + 4 47.30 Cu 2 + 220.29 27.01
S 3 + 4 47.30 Pd 2 + 219.43 27.87
15S 3 + 4 47.30 In 2 + 218.87 28.43
S 3 + 4 47.30 i 2 + 219.13 28.17
S 3 + 4 47.30 La 3 + 319.18 28.12
S 3 + 4 47.30 Ce 3 ~ 320.20 27.10
K 5 + 6100.00 S 5 + 572.68 27.32
20S 4 + 5 72.68 Sb 4 + 444.20 28.48
-S 4 + 5 72.68 Lu 4 + 445.19 27.49
S 4+ 5 7~.68 Bi 4 + 445.30 27.38
S 5+ 6 88.05 Ar 4 + 459.81 28.24
S 5 + 6 88.05 K 4 + 460.91 27.14
25S 5 + 6 88.05 Br 5 + 559.70 28.35
Y 6 + 7116.00 S 6 + 688.05 27.95
Ar 2 + 3 40.74 Cl 1 + 112.97 27.77
Rb2~ 3 40.00 C11 + 112.97 27.03
Sn 3 ~ 4 40.73 Cl l + 112.97 27.77
30Nd3+ 4 40.41 Cl l + 112.97 27.44
Pm3 + 4 41.10 Cl 1 ~ 112.97 28.13
Sm 3 + 4 41.40 Cl l + 112.97 28.43
Ca2+ 3 50.91 Cl 2 + 223.81 27.10
Mn 3 + 4 51.20 Cl 2 ~ 223.81 27.39
35Co 3 + 4 51.30 Cl 2 ~ 223.81 27.49
~1.4+ 5 ~7.80 ~13 + 33~.61 28.19
. :
. ;
WO 90/13126 PCI/US90/019g8
r;~
53
Cl 2 + 3 39.61 Ca2+ 211.87 27.74
Ca3 ~ 4 67.10 Cl 3 + 339.61 27.49
Cl 2 + 3 39.81 Br 1 + 111.81 27.80
Cl 2 + 3 39.61 Y 2 + 212.24 27.37
Mo 5+ 6 68.00 Cl 3 + 339.61 28.39
Cl 2 + 3 39.61 Xe 1 + 112.13 27.48
Cl 2 + 3 39.61 Eu 2 + 211.24 28.37
Cl 2 + 3 39.61 Gd2+ 212.09 27.52
Cl 2 + 3 39.61 Tb 2 + 211.52 28.09
Cl 2 + 3 39.61 Dy 2 + 211.67 27.94
Cl 2 + 3 39.61 Ho 2 + 211.80 27.81
Cl 2 + 3 39.61 Er 2 + 211.93 27.68
Cl 2 + 3 39.61 Tm 2 + 212.05 27.56
Cl 2 + 3 39.61 Yb 2 + 212.18 27.43
Se 5 + 6 81.70 C14 + 453.46 28.24
Zr 4 + 5 81.50 Cl 4 + 453.46 28.04
Ct 3 + 4 53.46 Nb3 + 325.04 28.42
Cl 3 + 4 53.46 Sb 3 + 325.30 28.16
Cl 3 + 4 53.46 Cs 2 + 225.10 28.36
Cl 3 + 4 53.46 Yb 3 + 325.03 28.43
Cl 3 + 4 53.46 Bi 3 + 325.56 27.90
Cl ~ + 5 67.~0 C13 + 339.61 28.19
Cl 4 + 5 67.80 Ar 3 + 340.74 27.06
Mn 5 + 6 95.00 Cl 5 + 567.80 27.20
C14 + 5 67.80 7n 3 + 339.72 28.08
Cl 4 + 5 67.80 Rb3 + 340.00 27.80
Cl 4 + ~ 67.80 Sn 4 ~ 440.73 27.07
Cl 4 + 5 67.80 Nd 4 + 4- 40.41 27.39
Cl 4 + 567.80 Tb 4 + 439.80 28.00
Ar 6 + 7124.32 Cl 6 + 697.03 27.29
Cl 5 + 697.03 Cr 5 + 569.30 27.73
Fe 6 + 7125.00 C16 + 697.03 27.97
Nb6+ 7125.00 Cl 6 + 697.03 27.97
Cl 5 ~ 697.03 Pb 5 + 568.80 28.23
Ti 3 + 443.27 Ar 1 + 115.76 27.51
~e3+ 442.94 Ar 1 + 115.76 27.19
wo go/13126 Pcr/us~O/01998
2~ 54
Sr 2 + 343.60 Ar 1 + 115.76 27.84
Sb3 ~ 444.20 Ar 1 + 115.76 28.44
Gd3+ 444.00 Ar 1 ~ 115.76 28.24
Yb3~ 443.70 Ar 1 + 115.76 27.94
5 Fe 3 + 454.80 Ar 2 + 227.63 27.17
Ni 3 + 454.90 Ar 2 + 227.63 27.27
Cu 3+ 455.20 Ar 2 + 227.63 27.57
Sb4+ 556.00 Ar 2 + 227.63 28.37
Bi 4 + 556.00 Ar 2 ~ 227.63 28.37
1 0Ar 2 + 340.74 Sc 2 + 212.80 27.94
Ar 2 + 340.74 Ti 2 + 213.58 27.16
Se4 + 568.30 Ar 3 + 340.74 27.56
Ar 2 + 340.74 Zr 2 + 213.13 27.61
Mo5+ 668.00 Ar 3 + 340.74 27.26
15 Pb4+ 568.80 Ar 3 + 340.74 28.06
Ar 3 + 459.81 K 2 + 231.63 28.19
Ar 3 + 459.81 Xe3+ 332.10 27.71
Ar 3 ~ 459.81 Pb 3 + 331.94 27.87
Bi 5 + 688.30 Ar 4 + 459.81 28.49
20Ar 4 + 575.02 V 4 + 446.71 28.31
Cu ~ + 6103.~0 Ar 5 + 575.02 27.98
Ar 4 + 575.02 Br 4 ~ 447.30 27.72
Br 6 + 7103.00 Ar 5 + 575.02 77.98
Nb5+ 6102.60 Ar 5 + 575.02 27.58
25Ti 5 + 6119.36 Ar 6 + 691.01 28.35
Mn 6 ~ 7119.27 Ar 6 + 691.01 28.26
Ar 5 + 691.01 Ga4+ 464.00 27.01
Ar 5 + 691.01 As 5 + 563.63 27.38
Ar 7 + 8143.46 Y 7 + 7116.00 27.46
30 K 1 + 231.63 K 1 ~ 14.34 27.28
Xe2+ 332.10 K 1 + 14.34 27.76
Pb 2 + 331.94 K 1 * 14.34 27.60
K 1 + 231.63 K 1 ~ 14.34 27.28
Zn 3 + 459.40 K 2 ~ 231.63 27.78
35Br 4 + 559.70 K 2 + 231.63 28.08
K 1 + 231.63 Rb 1 + 14.18 27.45
WO 90/13126 PCI/US90/01998
Z~;@~
Te 4 + 5 ~8.75 K 2 + 231.63 27.13
K 1 + 2 31.63 Cs 1 + 13.89 27.73
Sc 3 + 4 73.47 K 3 + 345.72 27.75
K 2+ 3 45.72 Ni 2 + 218.17 27.55
K 2 + 3 45.72 Zn ~ + 217!96 27.76
K 2+ 3 45.72 As 2 + 218.63 27.09
K 2 + 3 4S.72 Rh 2 + 2i 8.08 27.64
K 2 + 3 45.72 Te 2 + 218.60 27.12
K 2+ 3 45.72 Pt 2 + 218.56 27.16
K 3 + 4 60.91 Mn 3 + 333.67 27.24
K 3 + 4 60.91 Co 3 + 333.50 27.41
Br 5 + 6 88.60 K 4 + 4 60.91 27.69
K 3+ 4 60.91 Pd 3 + 332.93 27.98
K 3+ 4 60.91 1 3 + 333.00 27.91
K 3 + 4 60.91 Hf 4 + 433.33 27.58
Bi 5 + 6 88.30 K 4 ~ 4 60.91 27.39
Sc 5 + 6 111.10 K 5 + 5 82.66 28.44
K 4+ 5 82.66 Fe4+ 454.80 27.86
K 4+ 5 8~.66 Ni 4 + 454.90 27.76
K 4 + 5 82.66 Cu 4 + 455.20 27.46
Kr 6 + 7 111.00 K 5 + 5 82.66 28.34
Ca 6 + 7 127.70 K 6 + 6 100.00 27.70
V 5+ 6128.12 K 6+ 6100.00 28.12
K 5 + 6100.00 Mn 5 + 572.40 27.60
As 5 + 6 t27.60 K 6 + 6 100.00 27.60
K 5 + 6tO0.00 Sr 5 + 571.60 28.40
K 5 + 6100.00 Sn 5 + 572.28 27.72
K 7 + 8l 54.86 Ca 7 + 7127.70 27.16
K 7 + 8l 54.86 As 6 + 6127.60 27.26
K 7 + 8l 54.86 Mo 7 + 7126.80 28.06
Mn 2+ 333.67 Ca 1 + 16.11 27.55
Co2 333.50 Ca 1 + 16.11 27.39
Ge2+ 334.22 Cal + 16.11 28.11
Zr 3 + 4 34.34 Ca 1 + 1 6.11 28.23
Hf 3 + 4 33.33 Ca 1 + 1 6.11 27.22
Hg2+ 334.20 Ga 1 + 16.11 28.Q9
.. . . ... .
- ;
.~
wo go/13126 PCI-/US90/01998
2 ~
56
Zn 2 + 3 39.72 Ca 2 + 211.87 27.85
Rb2+ 3 40.00 Ca2+ 211.87 28.13
Pr 3 + 4 38.98 Ca2+ 211.87 27.11 ~s
Tb 3 + 4 39.80 Ca 2 + 211.87 27.93
Kr 5 + 6 78.50 Ca 3 + 350.91 27.~9
Ca2+ 3 50.91 Zr 3 + 322.99 27.92
Ca 2 + 3 50.91 Sm 3 + 323.40 27.51
Ca2+ 3 50.91 Dy3+ 322.80 28.11
Ca 2 + 3 50.91 Ho 3 + 322.84 28.07
Ca2+ 3 -50.91 Er 3 + 322.74 28.17
Ca2+ 3 50.91 Tm 3 + 323.68 27.23
Ca2+ 3 50.91 Hf 3 + 323.30 27.61
Mn5+ 6 95.00 Ca4+ 467.10 27.90
Ca3+ 4 67.10 ?n3+ 339.72 27.38
~a3+ 4 67.10 Rb3+ 340.00 27.10
Ca 3 + 4 67.10 Pr 4 + 43B.98 28.12
Ca3+ 4 67.10 Tb4+ 439.~0 27.30
Ca 4 + 5 84.41 Sr 4 + 457.00 27.41
Ca 4 + 5 84.41 Sb 5 + ~56.00 28.41
Ca4+ ~ 84.41 Bi 5 + 556.00 28.41
Ca 5 + 6 108.78 Se 6 + 681.70 27.08
Rb 7 + 8 136.00 Ca 6 + 6108.78 27.22
Ca5+ 6 108.78 Zr 5 + 581.50 27.28
Te 6 + 7 137.00 Ca 6 + 6108.78 28.22
Ca6+ 7 127.70 Ti 5 ~ 599.22 28.48
Se 6 + 7 155.40 Ca 7 + 7127.70 27.70
Ca7+ 8 147.24 Ti 6 + 6119.36 27.88
Ca7+ 8 147.24 Mn7+ 7119.27 27.97
Mn2+ 3 33.67 Sc1~ 16.54 i27.13
Ge2+ 3 34.22 Sc 1 + 16.54 27.68
Zr 3 + 4 34.34 Sc 1 + 16.54 27.80
Ag 2 + 3 34.83 Sc l ~ 16.54 28.29
119 2+ 3 34.20 Sc 1 + 16.54 27.66
Rb 2 + 3 40.00 Sc 2 + 212.80 27.20
Sn3+ 4 40.73 Sc2~ 212.80 27.93
Nd 3 ~ 4 40.41 .Sc 2 + 212,80 .27.~61
. . . .
WO 90/13126 PCr/lUS90/01~98
57 2 ~ 9 1
Pm 3 + 4 41.10 Sc 2 + 2 12.80 28.30
Kr 3 + 4 52.50 Sc3 + 324.76 27.74
Rb 3 + 4 52.60 Sc 3 + 3 24.76 27.84
Sc 3 + 4 73.47 Ge 4 + 4 45.71 27.76
Sc 3 + 4 73.47 Mo 4 + 4 46.40 27.07
Sc 3 + 4 73.47 Lu 4 + 4 45.19 28.28
Sc 3 + 4 73.47 Bi 4 + 4 45.30 28.17
Ti 5 + 6 119.36Sc 5 + 5 91.66 27.70
Mn 6 + 7 119.27Sc 5 + 5 91.66 27.61
Sc 4 + 5 91.66 Ga 4 + 4 64.00 2~.66
Sc 4 + 5 91.66 As 5 + 5 63.63 28.03
Cu6+ 7139.00 Sc6~ 6111.10 27.90
Cu 7 + 8 166.00Sc 7 + 7 138.00 28.00
Ni 2 + 3 35.17 Ti 1 + 1 6.82 28.35
Ge2+ 3 34.22 Ti 1 + 1 6.82 27.40
Zr 3 + 4 34.34 Ti 1 + 1 6.82 27.52
Ag 2 + 3 34.83 Ti 1 + 1 6.82 28.01
Hg 2+ 3 34.20 Ti 1 + 1 6.82 27.38
Sn 3 + 4 40.73 Ti 2 ~ 2 13.53 27.15
Pm 3 + 4 41.10 Ti 2 + 2 13.58 27.52
Sm 3 + 4 41.40 Ti 2 + 2 13.58 27.82
Dy3+ 4 41.50 Ti 2 + 2 13058 27.92
Fe3 + 4 54.80 Ti 3 + 3 27.49 27.31
Ni 3 + 4 54.90 Ti 3 + 3 27.49 27.41
Cu 3 + 4 55.20 Ti 3 ~ 3 27.49 27.71
Ti 3 + 4 43.27 Mn2+ 2 15.64 27.63
Ti 3 + 4 43.27 F~ 2 + 2 16.18 27.09
Ti 3 + 4 43.27 Ge2+ 2 15.93 27.33
Rb 4+ 5 71.00 Ti 4 + 4 43.27 27.73
Sr 4 + 5 71.60 Ti 4 + 4 43.27 28.33
Ti 3 + 4 43.27 Mo 2+ 2 16.15 27.12
Ti 3 + 4 43.27 Tc 2 + 2 15.26 28.01
Te 5 + 6 70.70 Ti 4 + ~ 43.27 27.43
Ti 3 + 4 43.27 Hf 2 + 2 14.90 28.37
Ti 3 ~ 4 43.27 Pb 2 + 2 15.03 28.23
As 5 ~ 6 127.60 Ti 5 + 5 99.22 28.38
WO 90/13126 PCI/US90tO199B
2~ 58
Ti 4 ~ 599.22 Rb 5+ ~71.00 28.22
Ti 4 + 599.22 Sr 5 + 571.60 27.62
Mo 6+ 7126.80 Ti 5 + 599.22 27.58
Ti 7 + 8168.50 Ti 7 + 7140.80 27.70
5Ti 7 + 8163.50 Ti 7 + 7140.80 27.70
Mn7+ 8196.46 Ti 8 + 8 168.50 27.96
Ni 2 + 335.17 V 1 + 16.74 28.43
Ge2+ 334.22 V 1 + 16.74 27.48
Zr 3 + 434.34 V 1 + 16.74 27.60
10Ag 2 + 334.83 V 1 + 16.74 28.09
Hg 2 + 334.20 V 1 + 16.74 27.46
Se 3 + 442.94 V 2 + 214.65 28.29
Eu 3 + 442.60 V 2 + 214.65 27.95
Ho 3 + 442.50 V 2 + 214.65 27.85
15Er 3 + 442.60 V 2 + 214.65 27.95
Tm 3 + 442.70 V 2 + 214.65 28.05
Pb 3 + 442.32 V 2 + 214.65 27.67
Sr 3 ~ 457.00 V 3 + 329.31 27.69
Fe 4 + 575.00 V 4 + 446.71 28.29
20V 3 + 446.71 As 2 + 218.63 28.07
V 3 + 446.71 Pd 2 + 2 19.43 27.28
V 3 + 446.71 In 2 + 2 18.87 27.84
V 3 + 446.71 Te 2 + 2 18.60 28.11
V 3 + 446.71 1 2 ~ 219.13 27.58
25V 3 + 446.71 La 3 + 3 lg.18 27.53
V 3 + 446.71 Pt 2 + 2 18.56 28.14
V 3 + 446.71 Hg 2 + 2 18.76 27.95
V 4+ ~65.23 Cu3+ 336.83 28.40
Ge 4 + 593.50 V 5 + 565.23 28.27
30V 4+ 565.23 Kr 3 + 3 36.95 28.28
Y 5+ 693.00 V 5+ 56~.23 27.77
V 4 + 565.23 Cd 3 + 3 37.48 27.75
V 4+ 565.23 Te 4 + 4 37.41 27.82
V 4 ~ 565.23 Ce 4 + 4 36.76 28.47
35Se 6+ 7155.40 V 6 + 612812 27.28
V 6+ 7150.17 Sr 8 + 8 122.30 27.87
,
.
WO 90/13126 PCI'/US90/01998
59 2 ~ ~r~ J ~ 7qJ
Ni 2 + 3 35.17 Cr 1 + 16.7728.40
Ge2+ 3 34.22 Cr 1 + 16.7727.45
Zr 3 + 4 34.34 Cr 1 + 16.7727.57
Ag 2 + 3 34.83 Cr 1 + 16.7728.06
Hg 2+ 3 34.20 Cr 1 + 16.7727.43
Sr2+ 3 43.60 Cr2~ 216.5û27.10
Sb 3 + 4 44.20 Cr 2 + 2 16.50 27.70
Gd 3 + 4 44.00 Cr 2 + 2 16.50 27.50
Yb 3 + 4 43.70 Cr 2 + 2 16.50 27.20
Zn3+ 4 59.40 Cr3 ~ 330.9628.44
Te 4 + 5 58.75 Cr3 + 3 30.96 27.79
Cr 2 + 3 30.96 Cs 1 ~ 1 3.89 27.07
Cr 3 + 4 49.10 Se 2 + 2 21.19 27.91
Cr 3 + 4 49.10 Br 2 + 2 21.80 27.30
1 5 Y 4 + 5 77.00 Cr 4 + 449.1027.90
Cr 3 + 4 49.10 Ag 2 + 2 21.49 27.61
Cr3 + 4 49.10 Xe2+ 221.2127.89
Cr 3 + 4 49.10 Pr 3 + 3 21.62 27.48
Cr3+ 4 49.10 (3d3~ 320.6328.47
Cr 3 + 4 49.10 Tb 3 + 3 21.91 27.19
Cr 3 + 4 49.10 Lu 3 + 3 20.96 28.14
Cr 4 + 5 69.30 Pm 4 + 4 41.10 28.20
Cr4 + 5 69.30 Sm4 + 441.4027.90
Cr 4 + 5 69.30 Dy 4 + 4 41.~0 27.80
Cr 6 + 7 161.10 Ni 7 + 7 133.00 28.10
Cr6+ 7161.10 Zn7+ 7134.0027.10
Cr 7 + 8 184.70 Co 8 + 8 157.00 27.70
Ni 2 + 3 35.17 Mn 1 + 1 7.43 27.73
Ag 2 + 3 34.83 Mn 1 + 1 7.43 27.40
Se3+ 4 42.94 Mn2+ 215.6427.30
Sr 2 + 3 43.60 Mn 2+ 2 15.64 27.96
Gd 3 + 4 44.00 Mn 2 + 2 15.64 28.36
Tm 3 + 4 42.70 Mn 2 + 2 15.64 27.06
Yb 3 + 4 43.70 Mn 2 + 2 15.64 28.06
Mn2~ 3 33.67 Ga1 + 16.0027.67
Mn 2 + 3 33.67 Sr 1 + 1 5.70 27.97
w~ 90/13126 P~T/US90/01998
2 Q ~ 60
Mn2~ 3 33.67 Y 1 + 16.38 27.29
Y 3 + 4 61.80 Mn 3 + 333.67 28.13
Mo 4 + 5 61 .2n Mn 3 + 333.67 27.53
Mn 2+ 3 33.67 In 1 + 15.79 27.88
5Mn 2 + 3 33.67 Ba 1 + 15.21 28.45
Mn 2 + 3 33.67 La 1 + 15.58 28.09
Mn2+ 3 33.67 Ce1 + 15.47 28.20
Mn 2+ 3 33.67 Pr 1 + 15.42 28.24
Mn2+ 3 33.67 Nd1 + 15.49 28.18
10Mn 2+ 3 - 33.67 Pm 1 + l5.55 28.11
Mn 2+ 3 33.67 Sm 1 + 15.63 28.04
Mn2+ 3 33.67 Eu 1 + 15.67 28.00
Mn 2 + 3 33.67 Gd 1 + 16.14 27.53
Mn 2 + 3 33.67 Tb 1 + 15.85 27.82
15Mn 2+ 3 33.67 Dy 1 + 15.93 27.74
Mn2+ 3 33.67 Ho ~ + 16.02 27.65
Mn 2+ 3 33.67 Er 1 + 1 6.10 27.57
Mn2+ 3 33.67 Tm 1 + 16.18 27.48
Mn 2+ 3 33.67 Ybl + 16.25 27.41
20Mn 2+ 3 33.67 Lu 1 + 1 5.43 28.24
Mn 2+ 3 33.67 Hf 1 + 1 6.60 27.07
Mn2+ 3 33.67 TI 1 + 1 6.11 27.56
Mn2+ 3 33.67 Ra 1 + 1 5.28 28.39
Mn 2 + 3 33.67 Ac 1 + 1 5.20 28.47
25Mn2+ 3 33.67 Th 1 + 1 6.10 27.57
Mn 2+ 3 33.67 Pa 1 + 1 5.90 27.77
Mn 2+ 3 33.67 U 1 + 16.05 27.62
Mn2+ 3 33.67 Np 1 + 1 6.20 27.47
Mn2+ 3 33.67 Pu 1 + 1 6.06 27.61
30Mn 2+ 3 33.67 Am 1 + 1 5.99 27.68
Mrl 2+ 3 33.67 Cm 1 + 1 6.02 27.65
Mn 2 + 3 33.67 Bk 1 + 1 6.23 27.44
Mn 2+ 3 33.67 Cf 1 + 1 6.30 27.37
Mn 2+ 3 33.67 Es 1 + 1 6.42 27.25
3 5 Co 4 + 5 79.50 Mn 4 + 451.20 28.30
Kr 5 + 6 78.50 Mn 4 + 451.20 27.30
WO 90/13126 PCI/US90/~1998
.
61 2 ~ 3 ~
Mn3+ 4 51.20 Zr 3 ~ 322.99 28.21
Mn 3+ 4 51.20 Sm 3 + 323.40 27.80
Mn3+ 4 51.20 Dy 3~ 322.80 28.40
Mn 3 + 4 51.20 Ho 3 + 322.84 28.36
Mn 3 + 4 51.20 Er 3 + 322.74 28.46
Mn 3+ 4 51.20 Tm 3 ~ 323.68 27.52
Mn3+ 4 51.20 Hf 3 + 323.30 27.90
Mn 4 ~ 5 72.40 Sb 4 + 444.20 28.20
Mn 4 + 5 72.40 Gd 4 + 444.00 28.40
Mn 4 + 5 72.40 1 u 4 + 445.19 27.21
Mn4+ 5 72.40 Bi 4 + 445.30 27.10
Sr 7 + 8122.30 Mn 6 + 695.00 27.30
Mn 6 + 7119.27 Sr 6 + 690.80 28.47
Ni 2 + 3 35.17 Fe 1 + 17.87 27.30
Br 2 + 3 36.00 Fe 1 ~ 17.87 28.13
Sr 2 + 3 43.60 Fe 2 ~ 216.18 27.42
Sb 3 + 4 44.20 Fe 2 + 216.18 28.02
Gd 3 + 4 44.00 Fe 2 ~ 216.18 27.82
Yb 3 + 4 43.70 Fe 2 + 216.18 27.52
-Te 4 + 5 58.75 Fe 3 + 330.65 28.10
Zn 4 + 5 82.60 Fe 4 + 454.80 27.80
Fe 3 + 4 S4.80 Rb 2 ~ 227.28 27.52
Fe 3 + 4 54.80 Mo 3 + 327.16 27.64
Cu 5 + 6103.00 Fe 5 + 575.00 28.00
Fe~+ 5 75.00 Br 4 + 447.30 27.70
Br 6 ~ 7103.00 Fe 5 + 575.0028.00
Nb 5 + 6102.60 Fe 5 + 575.0027.60
Fe 5 + 699.00 Rb 5 + 571.0028.00
. Fe5+ 699.00 Sr 5 + 571.6027.40
Mo 6 + 7l 26.80 Fe 6 + 699.0027.80
Fe5~ 699.00 Te 6 ~ 670.7028.30
Mo 7 + 8153.00 Fe 7 + 7125.0028.00
Ni 2 + 335.17 Co 1 + 17.86 27.31
Br 2 + 336.00 Co 1 + 17.86 28.14
Sb3+ 444.20 Co2+ 217.0627.14
Lu 3 + 445.19 Co.2 + 217.0628.13
Wo 90/~3126 PCT/US90/û1998
2 0~ 62
Bi 3 + 4 45.30 Co 2+ 217.06 28.24
Co2+ 3 33.50 Ga1 ~ 16.00 27.50
Co 2 + 3 33.50 Sr 1 + 15.70 27.81
Co2+ 3 33.50 Y 1 + 16.38 27.12
5 Y 3 + 4 61.80 Co 3 + 333.50 28.30
Mo 4 + 5 61.20 Co 3 + 333.50 27.70
Co2+ 3 33.50 In 1 + 15.79 27.71
Co2+ 3 33.50 Ba 1 + 15.21 28.29
Co 2+ 3 33.50 La 1 + ~5.58 27.92
10Co 2 + 3 33.50 Ce 1 + 15.47 28.03
Co 2+ 3 33.50 Pr 1 + 15.42 28.08
Co 2 + 3 33.50 Nd 1 + 15.49 28.01
Co2+ 3 33.50 Pm 1 + 15.55 27.95
Co 2 + 3 33.50 Sm 1 + 15.63 27.87
15Co 2+ 3 33.50 Eu 1 + 15.67 27.83
Co 2+ 3 33.50 Gd 1 + 16.14 27.36
Co 2 + 3 33.50 Tb 1 + 15.85 27.65
Co 2 + 3 33.50 Dy 1 ~ 15.93 27.57
Co 2 + 3 33.50 Ho l + 16.02 27.48
20Co 2+ 3 33.50 Er 1 + 1 6.10 27.40
Co2+ 3 33.50 Tm 1 ~ 16.18 27.32
Co 2 + 3 33.50 Yb 1 + 16.25 27.25
Co 2 + 3 33.50 Lu 1 + 1 5.43 28.07
Co2+ 3 33.50 Tl 1 + 1 6.11 27.39
2~Co2+ 3 33.50 Ra1 + 15.28 ~8.22
Co 2+ 3 33.50 Ac 1 + 1 5.20 28.30
Co 2+ 3 33.50 Th 1 + 1 6.10 27.40
Co2+ 3 33.50 Pa 1 + 1 5.90 27.60
Co 2+ 3 33.50 U 1 ~ 16.05 27.45
30Co2 + 3 33.50 Np 1 + 1 6.20 27.30
Co 2 + 3 33.50 Pu 1 + 1 6.06 27.44
Co2+ 3 33.50 Am 1 + t 5.99 27.51
Co 2+ 3 33.50 Cm 1 + 1 6.02 27.48
Co2+ 3 33.50 Bk 1 + 1 6.23 27.27
35Co2+ 3 33.50 Cf 1 + 1 6.30 27.20
Co 2+ 3 33.50 Es 1 + 1 6.42 27.08
:,
.
WO 90/13126 PCI'/US90/01998
6 3 ~ r~
CO 4 + 579.50 CO 4 ~ 451.30 28.20
Kr 5 + 678.50 Co 4 + 451.30 27.20
~o 3 + 451.30 Zr 3 + 322.99 28.31
Co 3 + 4~1.30 Sm 3 ~ 323.40 27.90
Co 3 + 4 51.30 Ho 3 + 3 22.84 28.46
Co3+ 451.30 Tm 3 -~ 323.68 27.62
Co 3 + 4 51.30 Hf 3 + 3 23.30 28.00
Co 4 + 5 79.50 Co 4 + 4 51.30 2~.~0
Co 7 + 8 157.00 Co 7 + 7 129.00 28.00
Co 7 + 8 157.00 Co 7 + 7 129.00 28.00
Co 7 + 8 157.00 Y 8 + 8 129.00 28.00
Ni 2 + 3 35.17 Ni 1 + 1 7.64 27.53
Br 2 + 3 36.00 Ni 1 + 1 7.64 28.36
Ag 2 + 3 34.83 Ni 1 + 1 7.64 27.20
Ge 3 + 4 45.71 Ni 2 ~ 2 18.17 27.54
Mo3+ 446.40 Ni 2 + 218.17 28.23
Lu3+ 445.19 Ni2+ 218.17 27.02
Bi 3 + 4 45.30 Ni 2 + 2 18.17 27.13
Ni 2 ~ 3 35.17 Ni 1 + 1 7.64 27.53
Ni2+ 335.17 Cu1+ 17.73 27.44
Ni2+ 335.17 Ge1~ 17.90 27.27
As 4 + 5 63.63 Ni 3 + 3 35.17 28.46
Ni 2 + 3 35.17 Zr 1 + 1 6.84 28.33
Ni 2 + 3 35.17 Nb 1 + 1 6.88 28.29
Ni 2 + 3 35.17 Mo 1 + 1 7.10 28.07
Ni2~ 335.17 Tc1 + 17.28 27.89
Ni 2 + 3 35.17 ~u 1 + 1 7.37 27.80
Ni 2 + 3 35.17 Rh 1 ~ 1 7.46 27.71
Ni 2 + 3 35.17 Ag 1 ~ 1 7.58 27.59
Ni 2+ 335.17 Sn 1 + 1 7.34 27.83
Ni 2 ~ 3 35.17 Ta 1 + 1 7.8g 27.28
Ni 2 + 3 35.17 W 1 + 1 7.98 27.19
Ni 2 + 3 35.17 Re 1 + 1 7.88 27.29
Ni 2 + 3 35.17 Pb 1 + 1 7.42 27.75
Ni 2+ 335.17 Bi 1 + 1 7.29 27.88
Zn 4 + 5 82.60 Ni 4 + 4 54.90 27.70
.
WO 90/ 1 31 26 Pcr/ US90/0 1 998
~4~
64
Ni 3 + 4 54.90 Rb 2 + 227.28 27.62
Ni 3 4 54.90 Mo3+ 327.16 27.74
Cu 5 + 6103.00 Ni 5 + 575.50 27.50
Ni 4 + ~ 75.50 Br 4 + 447.30 28.20
5Br 6 + 7103.00 Ni 5 + 575.50 27.50
Nb 5 + 6102.60 Ni 5 + 575.50 27.10
Ni 5 + 6108.00 Cu 5 + 579.90 28.10
Rb 7 + 8136.00 Ni 6 + 6108.00 28.00
Ni 7 + 8162.00 Zn 7 + 7134.00 28.00
10Br 2 + 3 36.00 Cu 1 + 17.73 28.27
Ag 2 + 3 34.83 Cu 1 + 17.73 27.10
Br 3 + 4 47.30 Cu 2 + 220.29 27.01
Cu 2+ 3 36.83 Zn 1 + 19.39 27.44
~a 3 + 4 64.00 Cu 3 + 336.83 27.17
15Cu 2+ 3 36.83 As 1 + 19.81 27.02
Cu2+ 3 36.83 Se 1 + 19.75 27.08
Kr 4 ~ 5 64.70 Cu 3 + 336.83 27.87
Cu 2 + 3 36.83 Pd 1 + 18.34 28.49
Cu 2 + 3 36.83 Cd 1 + 18.99 27.84
20Cu2+ 3 36.83 Sbl + 18.64 28.19
Cu 2 + 3 36.83 Te 1 + 19.01 27.82
Cu 2+ 3 36.83 Os 1 + 18.70 28.13
Cu2+ 3 36.83 Ir 1 + 19.10 27.73
Cu 2 + 3 36.83 Pt 1 + 19.00 27.83
25Cu 2+ 3 36.83 Au 1 + 19.23 27.61
Cu 2 + 336.83 Po 1 + 18.42 28.41
Zn 4 + 582.60 Cu 4 + 455.20 27.40
Cu 3 + 455.20 Rb 2 + 227.28 27.92
Cu 3 + 455.20 Mo 3 + 327.16 28.04
30Cu 3 + 455.20 In 3 + 328.03 27.17
Cu 3 + 455.20 Te 3 + 327.96 27.24
-Zn 5 + 6108.00 Cu 5 + 579.90 28.10
Cu 4 + 579.90 Kr 4 ~ 452.50 27.40
Cu 4 + 579.90 Rb 4 + 452.60 27.30
35Sb5+ 6108.00 Cu5+ 579.90 2R.10
Cu 6 + 7139.00 Kr 7 + 7111.00 ~8.00
WO 90/13126 PCI-/US90/01998
6 5 2 ~
Kr 2 + 3 36.95 Zn 1 + 1 9.39 27.56
Cd2+ 3 37.48 Zn 1 + 19.39 28.09
Te 3 + 4 37.41 Zn 1 + 1 9.39 28.02
Ce 3 ~ 4 36.76 Zn 1 + 1 9.39 27.36
Ge 3 + 4 45.71 Zn 2 + 2 17.96 27.75
Mo 3 + 4 46.40 Zn 2 + 2 17.96 28.44
Lu 3 + 4 45.19 Zn 2 ~ 2 17.96 27.23
Bi 3 + 4 45.30 Zn 2+ 2 17.96 27.34
Zn 2+ 3 39.72 Br 1 + 111.81 27.91
1 0 Zn 2 + 3 39.72 Y 2 + 2 12.24 27.48
Mo 5 + 6 68.00 Zn 3 + 3 39.72 28.28
Zn2+ 3 39.72 Xe 1 + 112.13 27.59
Zn 2+ 3 39.72 Eu2+ 211.24 28.48
Zn 2 + 3 39.72 Gd 2 + 2 12.09 27.63
1 5 Zn 2 + 3 39.72 Tb 2 + 2 11.52 28.20
Zn 2 + 3 39.72 Dy 2 + 2 11.67 28.05
Zn 2 + 3 39.72 Ho 2 + 2 11.80 27.92
Zn 2 + 3 39.72 Er 2 + 2 11.93 27.79
Zn 2 + 3 39.72 Tm 2 + 2 12.05 27.67
Zn ? ~ 3 39.72 Yb 2 + 2 12.18 27.54
Zn 3 + 4 59.40 Rh 3 + 3 31.06 28.34
Zn 3 + 4 59.40 X~ 3 ~ 3 32.1û 27.30
Zn 3 + 4 59.40 Pb 3 + 3 31.94 27.46
Kr 6 + 7 111.00 Zn 5+ 5 82.60 28.40
Rb7+ 8136.00 Zn 6+ 6108.00 28.00
Zn 6 + 7 134.00 Sr 7 ~ 7 106.00 28.00
Ge2+ 3 34.22 Gal + 16.00 28.22
Zr 3 + 4 34.34 t3al + 1 6.00 28.34
1 2 + 333.00 Ga1 + 16.00 27.00
Hf 3 + 4 33.33 Ga 1 + 1 6.00 27.33
Hg 2+ 334.20 Ga1 + 16.00 28.20
Te 4 + 5 58.75 ~;a 3 + 3 30.71 28.04
Ga3+ 464.00 Br 3 ~ 336.00 28.00
~;a 3 + 4 64.00 Kr 3 ~ 3 36.95 27.05
Ga 3 + 464.00 Ge 4 + ~36.76 27.24
Br 2 + 336.00 Ge 1 + 17.90 28.10
WO 90tl3126 PCI-/US90/019
2~ 6~ ~;6
Se 3 + 4 42.94 Ge 2 + 215.93 27.01
Sr 2 + 3 43.60 Ge 2 + 2t5.93 27.67
Sb 3 + 4 44.20 Ge 2 ~ 215.93 28.27
Gd 3 + 4 44.00 Ge 2 + 215.93 28.07
Yb 3 + 4 43.70 Ge 2 + 215.93 27.77
Ge2+ 3 34.22 Y 1 + 16.38 27.84
Y 3+ 4 61.80 Ge3+ 334.22 27.58
- Ge2+ 3 34.22 Zr1 + 16.84 27.38
Ge 2 + 3 34.22 Nb 1 + 1 6.88 27.34
1 0 Ge2+ 3 34.22 Mo 1 + 17.10 27.12
Ge2+ 3 34.22 In 1 + 15.79 28.43
Ge 2 ~ 3 34.22 Gd 1 + 1 6.14 28.08
Ge2+ 3 34.22 Tb 1 + 15.85 28.37
Ge2+ 3 34.22 Dy 1 ~ 15.93 2~.29
t 5 Ge 2 + 3 34.22 Ho l + 1 6.02 28.20
Ge2+ 3 34.22 Erl + 16.10 28.12
Ge2+ 3 34.22 Tm 1 + 16.18 28.04
Ge2+ 3 34.22 Yb 1 + 16.25 27.97
Ge2+ 3 34.22 Hf 1 + 1 6.60 27.62
Ge2+ 3 34.22 Tl 1 + 16.11 28.11
Ge2+ 3 34.~2 Th 1 + 1 6.10 28.12
Ge2+ 3 34.22 Pa 1 + 1 5.90 28.32
Ge2+ 3 34.22 U 1 + 16.0~ 28.17
Ge2+ 3 34.22 Np 1 + 1 6.20 28.02
Ge2+ 3 34.22 Pu 1 + 1 6.06 28.16
Ge2+ 3 34.22 Am 1 + 1 5.99 28.23
Ge2+ 3 34.22 Cm 1 + 1 6.02 28.20
Ge2+ 3 34.22 Bk 1 + 1 6.23 27.99
Ge2+ 3 34.22 Cf1 + 16.30 27.92
Ge2+ 3 34.22 Es 1 ~ 1 6.42 27.80
Ge3+ 4 45.71 As 2 + 2 18.63 27.08
Ge 3 + 4 45.71 Rh 2 + 2 18.08 27.63
Ge 3 + 4 45.71 Te 2 + 2 18.60 27.11
Ge3~ 4 45.71 Pt 2 + 2 t8.~6 27.15
Kr 2 + 3 36.95 As 1 + 1 9.81 27.14
Nb3 + 4 38.30 As 1 ~ 1 9.81 28.~9
WO 90/13126 PCI/US90/01998
67 Q ~ r~
Cd 2 ~ 3 37.48 AS 1 + 1 9.81 27.67
Te 3 + 4 37.41 As 1 + 19.81 27.60
Mo3+ 4 46.40 As 2 + 218.63 27.77
Sb4 + 5 56.00 As 3 + 328.35 27.65
Bi 4 ~ 5 56.00 As 3 + 3 28.35 27.65
As 3 + 4 50.13 Br 2 + 2 21.80 28.33
Kr 5 + 6 78.50 As 4 + 4 50.13 28.37
As 3 + 4 50.13 Zr 3 + 3 22.99 27.14
As 3 + 4 50.13 Nd3~ 3 22.10 28.03
As 3 ~ 4 50.13 Pm 3 + 3 22.30 27.83
As 3 + 4 50.13 Tb 3 + 3 21.91 28.22
As 3 + 4 50.13 Dy 3 + 3 22.80 27.33
As 3 ~ 4 50.13 Ho 3 + 3 22.84 27 29
As 3 + 4 50.13 Er 3 + 3 22.74 27.39
As 4 + 5 63.63 Br3 + 3 36.00 27.63
Sr 5 + 6 90.80 As 5 + 5 63.63 27.17
Se 6 + 7 155.40 As 6 + 6 127.60 27.80
As 5 + 6 127.60 Rb 7 + 7 99.20 28.40
Kr 2 + 3 36.95 Se 1 + 1 9.75 27.20
Cd2+ 3 37.48 Se 1 + 19.75 27.73
Te 3 + 4 37.41 Se 1 + 1 9.75 27.66
C~3 + 4 36.76 Se 1 + 1 9.75 27.01
Te4 + 5 58.75 Se3+ 330.82 27.93
Rb 4 + 5 71.00 Se 4 + 4 42.94 28.06
Se 3 + 4 42.94 Tc 2 + 2 15.26 27.68
Se 3 + 4 42.94 Sn 2 + 2 14.63 28.31
Te 5 + 6 70.70 Se 4 + 4 42.94 27.76
Se 3 + 4 42.94 Hf 2 + 2 14.90 28.04
Se3+ 4 42.~4 Pb2+ 21~.03 27.91
Se 4 + 5 68.30 Rb 3 + 3 40.00 28.30
Se 4 + 5 68.30 Sn 4 + 4 40.73 27.57
Se 4 + 5 68.30 Nd 4 + 4 40.41 27.89
Se 4 + 5 68.30 Pm 4 + 4 41.10 27.20
Se5+ 681.70 In 4 + 4 54.00 27.70
Rb2+ 340.00 Br 1 + 1 11.81 28.19
Pr 3 ~ 4 38.98 Br 1 + 1 11.81 27.17
WO 90/13126 PCI'/US90/01998
~5`~ 68
Tb 3 ~ 4 39.80 Br 1 + 1 11.81 27.99
La 3 + 4 49.95 Br 2 + 2 21.80 28.15
Br 2 + 3 36.00 Pd 1 + 1 8.34 27.66
Br 2 ~ 3 36.00 Ag 1 + 1 7.58 28.42
Br 2 + 3 36.00 Cd 1 + 1 8.99 27.01
Br 2 + 3 36.00 Sb 1 + 1 8.64 27.36
Br 2 + 3 36.00 Ta t + 1 7.89 28.11
Br 2 + 3 36.00 W 1 + 1 7.98 28.02
Br 2 + 3 36.00 Re 1 + 1 7.88 28.12
1 0 Br 2 + 3 36.00 Os 1 + 1 8.70 27.30
Br 2 + 3 36.00 Po 1 + 1 8.42 27.58
Br 3 + 4 47.30 Pd 2 + 2 19.43 27.87
Br 3 + 4 47.30 In 2 + 2 18.87 28.43
Br3 ~ 4 47.30 1 2+ 2 19.13 28.17
1 5 Br 3 + 4 47.30 La 3 + 3 19.18 28.12
Br 3 + 4 47.30 Ce 3 + 3 20.20 27.10
Br 4 ~ 5 59.70 Xe 3 + 3 32.1 G 27.60
Br 4 ~ 5 59.70 Pb 3 + 3 31.94 27.76
Y 6+ 7116.00 Br 6 ~ 688.60 27.40
Br 5 + 6 83.60 Mo 5 + 5 61.20 27.40
Pm3+ 4 41.10 Kr 1 + 1 14.00 27.10
Sm 3 + 4 41.40 Kr 1 + 1 14.00 27.40
Dy3 + 4 41.50 Kr 1 + 1 14.00 27.50
Pb3 + 4 42.32 Kr 1 + 1 14.00 28.32
Kr 3 + 4 52.50 Kr 2 + 2 24.36 28.14
Rb3+ 4 52.60 Kr 2 + 2 24.36 28.24
Kr4 + 5 64.70 Kr 3 + 3 38.95 27.75
Kr 2 + 3 36.95 Cd 1 + 1 8.99 27.96
Kr 2 + 3 36.95 Sb 1 + 1 8.64 28.31
Kr 2 + 3 36.95 Te 1 + 1 9.01 27.94
Kr 2 + 3 36.95 Os 1 + 1 8.70 28.25
Kr 2 + 3 36.95 Ir 1 + 1 9.10 27.85
Kr 2 + 3 36.95 Pt 1 + 1 9.00 27.95
Kr 2 + 3 36.95 Au 1 + 1 9.2~ 27.73
Kr 3 + 4 52.50 Kr 2 + 2 24.36 28.14
Kr 3 + 4 52.50 ~Ib 3 + 3 25.04 27.46
.
. . .
WO 90/13126 PCT/US90/019g8
69 ~A~7
Kr 3 + 452.50 Sb3+ 325.30 27.20
Kr 3 + 452.50 Cs 2 + 225.10 27.40
Kr 3 + 4~2.50 Eu 3 + 324.90 27.60
Kr 3 + 452.50 Yb3 + 325.03 27.47
5Kr 4 + 564.70 Kr 3 + 336.95 27.75
Y 5+ 693.00 Kr~ ~64.70 28.30
Kr 4 + 564.70 Cd3+ 337.48 27.22
Kr 4 + 564.70 Te 4 + 437.41 27.29
Kr 4 + 564.70 Ce4+ 436.76 27.94
10Sr 6 ~ 7106.00 Kr 6 + 678.50 27.50
Kr 5 + 678.50 Nb5+ 550.55 27.95
Xe2~ 332.10 Rb1 + 14.18 27.92
Pb 2 + 331.94 Rb 1 + 14.18 27.76
`Rb 2 + 340.00 Y 2 + 212.24 27.76
Mo 5 + 668.00 Rb 3 + 340.00 28.00
Rb2~ 340.00 Xe1 ~ 112.13 27.87
Rb 2 + 340.00 Gd 2 ~ 212.~9 27.91
Rb 2 + 340.00 Tb 2 ~ 211.52 28.48
Rb 2 + 34Q.00 Dy 2 + 211.67 28.33
Rb 2 + 340.00 Ho 2 + 211.80 28.20
Rb 2 + 340.00 Er 2 ~ 211.93 28.07
Rb 2 + 340.00 Tm 2 + 212.05 27.95
Rb2+ 340.00 Yb21 212.18 27.82
Rb 3 + 452.~0 Nb 3 + 325.04 27.56
Rb 3 + 452.60 Sb 3 + 325.30 27.30 -
Rb 3 + 452.60 Cs 2 + 225.10 27.50
Rb 3 + 452.60 Eu 3 + 324.90 27.70
Rb 3 + 452.60 Yb 3 + 325.03 27.57
Rb3+ 452.60 Bi 3 + 325.56 27.04
Rb 6 + 799.20 Rb 5 + 571.00 28.20
Rb4 + 571.00 Sr 3 + 343.60 27.40
Rb 4 + 571.00 Eu 4 + 442.60 28.40
Rb 4 + 571.00 Er 4 + 442.60 28.40
Rb4+ 571.00 Tm 4 ~ 442.70 .28.30
Rb 4 + 5-71.00 Yb 4 + 443.70 27.30
Rb5+ 684.40 Sr 4 + 457.00 27.40
'~ ' " ' ' .
WO 90/13~26 PCll/US90/01998
~5~6~
Rb 5 + 6 84.40 Sb 5 ~ 556.00 28.40
Rb5+ 6 84.40 Bi 5 + 556.00. 28.40
Rb 6 + 7 99.20 Rb 5 ~ 571.00 28.~0
Rb 6 + 7 99.20 Sr 5 + 571.60 27.60
Mo 6 + 7126.80 Rb 7 + 799.20 27.60
Rb 7 + 8136.00 Sb 6 ~ 6108.00 28.00
Pd 2 + 3 32.93 Sr 1 + 15.70 27.24
i 2 + 3 33.00 Sr 1 + 15.70 27.31
Hf 3 + 4 33.33 Sr 1 + 15.70 27.64
Nb3 + 4 38.30 Sr 2 + 211.03 27.27
Pr 3 + 4 38.98 Sr 2 + 211.03 27.95
Sr 4 + 5 71.60 Sr 3 + 343.60 28.00
Sr2+ 3 43.60 Mo2+ 216.15 27.45
Sr 2 + 3 43.60 Tc 2 + 215.26 28.34
Sr 2 + 3 43.60 Sb 2 ~ 216.53 27.07
Te 5 + 6 70.70 Sr 3 + 343.60 27.10
Sr 3 + 4 57.00 Tc 3 + 329.54 27.46
Sr 3 + 4 57.00 Tl 3 + 329.83 27.17
Sr 4 + 5 71.60 Sr 3 + 343.60 28.00
Sr 4 + 5 71.60 Sb4+ 444.20 27.40
Sr 4 + 5 71.60 Gd 4 + 444.00 27.60
Sr 4 + 5 71.60 Yb 4 + 443.70 27.90
Zr 3 + 4 34.34 Y 1 + 16.38 27.96
Ag 2 + 3 34.83 Y 1 + 16.38 28.45
Hg 2 + 3 34.20 Y 1 + 16.38 27.82
Sn3+ 4 40.73 Y 2+ 212.24 28.49
Nd 3 ~ 4 40.41 Y 2 + 212.24 28.17
Tb 3 + 4 39.80 Y 2 + 212.24 27.56
Y 3+ 4 61.80 Zr 4 + 434.34 27.4.6
Y 3+ 4 61.80 Hf4+ 433.33 28.47
Y 3 + 4 61.80 Hg 3 + 334.20 27.60
Y 4+ 577.00 La4+ 449.95 27.05
Y 6~ 7t16.00 Bi 6 + 688.30 27.70
Zr 3 + 434.34 Zr 1 + 16.84 - 27.50
Ag2+ 334.83 Zr1 + 16.84 27.99
Hg 2+ 334.20 Zr 1 + 16.84 27.36
WO 90/13126 PCT/US90/01998
71 2~3~ ~7
Srl 3 + 4 40.73 Zr 2 ~ 2 13.13 27.60
Nd 3 + 4 40.41 Zr 2 + 2 13.13 27.28
Pm 3 + 4 41.10 Zr 2 + 2 13.13 27.97
Sm 3 + 4 41.40 Zr 2 + 2 13.13 28.27
Dy 3 + 4 41.50 Zr 2 + 2 13.13 28.37
Nb4+ 5 50.55 Zr 3 + 3 22.99 27.56
7r 3 + 4 34.34 Zr 1 + 1 6.84 27.50
Zr 3 + 4 34.34 Nb 1 + 1 6.88 27.46
Zr 3 + 4 34.34 Mo 1 + 1 7.10 27.24
10 Zr 3 + 4 34.34 Tc 1 + 1 7.28 27.06
Zr 3 + 4 34.34 Gd 1 + 1 6.14 28.20
Zr 3 + 4 34.34 Tb 1 + 1 5.85 28.49
Zr 3 + 4 34.34 Dy 1 + 1 5.93 28.41
Zr 3 + 4 34.34 Ho t + 1 6.02 28.32
15 Zr 3 + 4 34.34 Er 1 + 1 6.10 28.24
Zr 3 + 4 34.34 Tm 1 + 1 6.18 28.16
Zr 3 + 4 34.34 Yb 1 + 1 6.25 28.09
Zr 3 + 4 34.34 Hf 1 ~ 1 6.60 27.74
7r 3 + 4 34.34 Tl 1 + 1 6.11 28.23
20 Zr 3 ~ 4 34.34 Bi 1 + 1 7.29 27.05
7r 3 + 4 34.34 Th 1 + 1 6.10 28.24
Zr 3 + 4 34.34 Pa 1 + 1 5.90 28.44
Zr 3 + 4 34.34 U 1 + 16.0528.29
Zr 3 + 4 34.34 Np 1 + 1 6.20 28.14
25 Zr 3 + 4 34.34 Pu 1 + 1 6.06 28.28
~r 3 + 4 34.34 Am 1 + 1 5.99 28.35
Zr 3 + 4 34.34 Cm 1 + 1 8.02 28.32
Zr 3 + 4 34.34 Bk 1 + 1 6.23 28.11
Zr 3 + 4 34.34 Cf 1 + 1 6.30 28.04
30 Zr 3 ~ 4 34.34 Es 1 + 1 6.42 27.92
Zr 4 + 5 81.50 In 4 + 4 54.00 27.50
Ag 2 + 3 34.83 Nb 1 + 1 6.88 27.95
Hg 2 + 3 34.20 Nb 1 + 1 6.88 27.32
Sm 3 ~ 4 41.40 Nb 2 + 2 14.32 27.08
35 Eu 3 + 4 42.60 Nb 2 + 2 14.32 28.28
Dy3+ 4 41.50 Nb2+ 214.3227.18
WO 90/13126 PCI-/US90/01998
2 ~ 3~ 7 7 2
Ho 3 + 4 42.50 Nb 2 + 2 14.32 28.18
Er 3 + 4 42.60 Nb 2 ~ 2 14.32 28.28
Tm 3 + 4 42.70 Nb 2 + 2 14.32 28.38
Pb 3 + 4 42.32 Nb 2 + 2 14.32 28.00
Nb3+ 4 38.30 1 1 ~ 110.45 27.85
Nb 3 + 4 38.30 Ba 2 + 2 10.00 28.30
Nb 3 + 4 38.30 La 2 + 2 11.06 27.24
Nb 3 + 4 38.30 Ce 2 + 2 10.85 27.45
Nb 3 + 4 38.30 Pr 2 + 2 10.55 27.75
1û Nb 3 + 4 - 38.30 Nd 2 + 2 10.73 27.57
Nb 3 + 4 38.30 Pm 2 + 2 lO.90 27.40
Nb3+ 4 38.30 Sm 2 + 211.07 27.23
Nb3+ 4 38.30 Eu2+ 211.24 27.06
Nb 3 + 4 38.30 Hg 1 + 1 10.44 27.86
1 5 Nb3+ 4 38.30 Rn 1 + 110.75 27.55
Nb3+ 4 38.30 Ra2+ 210.15 28.15
Nb 4 ~ 5 50.55 Nd 3 + 3 22.10 28.45
Nb 4 + 5 50.55 Pm 3 + 3 22.30 28.25
Nb4+ 5 50.55 Sm 3 + 3 23.40 27.15
Nb 4 + 5 50.55 Dy 3 + 3 22.80 27.75
Nb4+ 5 50.55 Ho 3+ 322.84 27.71
Nb 4 + 5 50.55 Er 3 + 3 22.74 27.81
Nb4+ 5 50.55 Hf 3 + 3 23.30 27.25
Mo 7 + 8 153.00 Nb 7 + 7 125.00 28.00
Ag 2 + 3 34.83 Mo 1 + 1 7.10 27.73
Hg 2+ 3 34.20 Mo 1 + 1 7.10 27.10
Sb 3 + 4 44.20 Mo 2 + 2 16.15 28.05
Gd3+ 4 44.00 Mo2~ 216.15 27.85
Yb3+ 4 43.70 Mo2+ 216.15 27.55
Mo 3 ~ 4 46.40 Rh 2 + 2 18.08 28.32
Mo 3 + 4 46.40 In 2 + 2 18.87 27.53
Mo 3 + 4 46.40 Te 2 + 2 18.60 27.80
Mo 3 + 4 46.40 1 2 + 2 19.13 27.27
Mo 3 + 4 46.40 La 3 + 3 19.18 27.22
Mo 3 ~ 4 46.40 Pt 2 + 2 18.56 27.84
Mo 3 + 4 46.40 Hg 2 + 2 18.76 27.64
..
WO 90/13126 PCI-/US"0/0199
2 ~ 3
73
Mo 4 + 5 61.20 Pd 3 ~ 332.93 28.27
Mo 4~ 5 61.20 1 3 + 333.00 28.20
Mo4+ 5 61.20 Hf 4 + 433.33 27.87
Bi 5 + 6 88.30 Mo5+ 561.20 27.10
Mo 5 + 6 68.00 Sn 4 + 440.73 27.27
Mo 5 + 6 68.00 Nd 4 + 440.41 27.59
Mo 5 + 6 68.00 Tb 4 + 439.80 28.20
Ag 2 + 3 34.83 Tc 1 + 17.28 27.55
Eu 3+ 4 42.60 Tc 2 + 215.26 27.34
1 0 Ho 3 + 4 42.50 Tc 2 + 215.26 27.24
Er 3 + 4 42.60 Tc 2 + 215.26 27.34
Tm 3 + 4 42.70 Tc 2 + 215.26 27.44
Yb3~ 4 43.70 Tc 2 + 215.26 28.44
Pb 3 + 4 42.32 Tc 2 + 215.26 27.06
Ag 2 + 3 34.83 Ru 1 + 17.37 27.46
Sb 3 + 4 44.20 Ru 2 + 216.76 27.44
Gd 3 + 4 44.00 Ru 2 + 216.76 27.24
Lu 3 + 4 45.19 Ru 2 + 216;76 28.43
Sb 4 + 5 56.00 Ru 3 + 328.47 27.53
Bi 4 + 5 56.00 Ru 3+ 328.47 27.53
As 2 + 3 34.83 Rh 1 + 17.46 27.37
Lu3+ 4 45.19 Rh2+ 218.38 27.11
Bi 3 + 4 45.30 Rh 2+ 218.08 27.22
Te 4 + 5 58.75 Rh 3 + 331.06 27.69
Rh 2+ 3 31.06 Cs 1 ~ 13.B9 27.17
Ce3+ 4 36.76 Pd 1 + 18.34 28.42
Pd2+ 3 32.93 In 1 + 15.79 27.14
Pd2 + 3 32.93 Ba 1 ~ 15.21 27.72
Pd 2 + 3 32.93 La 1 + 15.58 27.35
Pd2 + 3 32.93 Ce 1 + 15.47 27.46
Pd 2 + 3 32.93 Pr 1 ~ 15.42 27.51
Pd 2 + 3 32.93 Nd 1 + 15.49 27.44
Pd 2 ~ 3 32.93 Pm 1 + l5.55 27.38
Pd 2 + 3 32.93 Sm 1 + 15.63 27.30
Pd 2 + 3 32.93 Eu 1 + 15.67 27.26
Pd 2 + 3 32.93 Tb 1 ~ 15.85 27.08
.
WO 90/13126 PCT/US90/01998
': `
74
2 ~ 7
Pd 2 + 3 32.93 Dy 1 + 15.93 27.00
Pd 2 + 3 32.93 Lu 1 + 15.43 27.50
Pd 2 + 3 32.93 Ra 1 + 15.28 27.65
Pd 2 + 3 32.93 Ac 1 + 15.20 27.73
Pd 2 + 3 32.93 Pa 1 + 15.90 27.03
Ag 2 + 3 34.83 Ag 1 + 17.58 27.25
La3 + 4 49.95 Ag 2 + 221.49 28.46
Ag 2 + 3 34.83 Ag 1 + 17.58 27.25
Ag 2 + 3 34.83 Sn 1 + 17.34 27.49
Ag 2 + 3 34.83 Hf 1 + 16.60 28.23
Ag 2 + 3 34.83 Pb 1 ~ 17.42 27.41
Ag 2 + 3 34.83 Bi 1 + 17.29 27.54
Ag 2 + 3 34.83 Es 1 + 16.42 28.41
Cd 2 + 3 37.48 Cd 1 ~ 18.99 28.49
Te 3 + 4 37.~1 Cd 1 + 18.99 28.42
Ce3+ 4 36.76 Cd 1 + 18.99 27.76
Sb 3 + 4 44.20 Cd 2 + 216.91 27.29
Gd 3 + 4 44.00 Cd 2 + 216.91 27.09
Lu 3 + 4 45.19 Cd 2 + 216.91 28.28
Bi 3 + 4 45.30 Cd 2 + 216.91 28.39
Cd 2 + 3 37.48 Cd 1 + 18.99 28.49
Cd2+ 3 37.48 Te l + 19.01 28.47
Cd 2 + 3 37.48 1 1 + 110.45 27.03
Cd 2 + 3 37.48 Ba 2 + 210.00 27.48
Cd2+ 3 37.48 Ir 1 + 19.10 28.38
Cd2+ 3 37.48 Pt 1 + 19.00 28.48
Cd2+ 3 37.48 Au 1 ~ 19.23 28.25
Cd2+ 3 37.48 Hg 1 + 110.44 27.04
Cd 2 + 3 37.48 Ra 2 + 210.15 27.33
It'2;+ 3 33.00 In 1 + 15.79 27.21
Hf 3 + 4 33.33 In 1 + 1~.79 27.54
Hg2~ 3 34.20 In 1 + 15.79 28.41
Sb 4 + 5 s6.do in 3 + 328.03 27.97
Bi 4 + ~ 56.00 In 3 + 328.03 27.97
In 3 + 4 54.00 Bi 3 + 325.56 28.44
Eu3+ 4 42.60 Sn 2+ 214.63 27.97
YVO 90/131t6 PCI'IUS90/01998
~ ~ 3 L~ 7
. :~
Ho 3 + 4 42.50 Sn 2 ~ 214.63 27.87
Er 3 + 4 42.60 Sn 2 + 214.63 27.97
Tm 3 + 4 42.70 Sn 2 + 214.63 28.07
Pb 3 + 4 42.32 Sn 2 + 214.63 27.69
Te 4 + 5 58.75 Sn 3 + 330.50 28.25
Pb 4 + 5 68.80 Sn 4 + 440.73 28.07
Sn4 + 5 72.28 Sb4+ 444.20 28.08
Sn 4 + 5 72.28 Gd 4 + 444.00 28.28
Sn 4+ 5 72.28 Lu 4 + 445 19 27.09
1 0 Ce 3 + 4 36.76 Sb 1 + 18.64 28.12
Sb 3 + 4 44.20 Sb 2 + 216.53 27.67
Gd 3 + 4 44.00 Sb 2 + 216.53 27.47
Yb 3 + 4 43.70 Sb 2 + 216.53 27.17
Sb 3 + 4 44.20 Sb 2 + 216.53 27.67
1 5 Sb 3 + 4 44.20 Bi 2 ~ 216.69 27.51
Sb 4 + 5 56.~0 Te 3 + 327.96 28.04
Te 3 + 4 37.41 Te 1 + 19.01 28.40
Ce3+ 4 36.76 Te 1 + 19.01 27.75
Bi 4 + 5 56.00 Te 3 + 327.96 28.04
Te 3 + 4 37.41 Te 1 + 19.01 28.40
Te 3 + 4 37.41 Ba 2 + 210.00 27.41
Te 3 + 4 37.41 Ir 1 + 19.10 28.31
Te 3 + 4 37.41 Pt 1 + 19.00 28.41
Te 3 + 4 37.41 Au 1 + 19.23 28.18
Te 3 + 4 37.41 Ra 2 + 210.15 27.26
Te 5 + 6 70.70 Eu 4 + 442.60 28.10
Te 5 + 6 70;70 Ho 4+ 442.50 28.20
Te 5 + 6 70.70 Er 4 + 442.60 28.10
Te 5 + 6 70.70 Tm 4 + 442.70 28.00
Te 5 + 6 70.70 Pb 4 + 442.32 28.38
1 2 + 3 33.00 Ba 1 + 15.21 27.79
1 2 + 3 33.00 La l + l5.58 27.42
1 2 + 3 33.00 Ce 1 ~ 1~.47 27.53
1 2 ~ 3 33.00 Pr 1 ~ 15.42 27.58
1 2 + 3 33.00 Nd 1 + 15.49 27.51
1 2 + 3 33.00 Pm 1 + 15.55 27.45
.
.
:.
WO 90/l3l2~6~ ~ rt PCI/US90/019!~8
76
I 2 + 3 33.00 Sm 1 t- 15.63 27.37
I 2 + 3 33.00 Eu 1 + 15.67 27.33
I 2 + 3 33.00 Tb 1 + 15.85 27.15
I 2 + 3 33.00 Dy 1 + 15.93 27.07
I 2 ~ 3 33.00 Lu 1 + 15.43 27.57
I 2 + 3 33.00 Ra 1 + 15.28 27.72
I 2 + 3 33.00 Ac l + 15.20 27.80
I 2 + 3 33.00 Pa 1 ~ 15.90 27.10
I 2 + 3 33.00 Am 1 + 15.99 27.01
Nd3+ 4 40.41 Xel + 112.13 28.28
Tb 3 + 4 39.80 Xe 1 + 112.13 27.67
Xe2+ 3 32.10 Cs 1 + 13!89 28.21
Pb 2 + 3 31.94 Cs 1 + 13.89 28.04
Hf 3 + 4 33.33 Ba 1 + ~5.21 28.12
Hf 3 + 4 33.33 La ~ + 15.58 27.75
Pr 3 + 4 38.98 La 2+ 211.06 27.92
La 3 + 4 49.95 Pr 3 + 321.62 28.33
La 3 + 4 49.95 Nd 3 + 322.10 27.~5
La3 + 4 49.95 Pm 3 + 322.30 27.65
La3 + 4 49.9~ Tb 3 + 321.91 28.04
La 3 + 4 49.95 Dy 3 + 322.80 27.15
La 3 + 4 49.95 Ho 3 + 322.84 27.11
La3 + 4 49.9~ Er 3 + 322.74 27.21
Hf 3 + 4 33.33 Ce 1 + 15.47 27.86
Pr 3 + 4 38.. ~8 Ce2+2 10.85 28.13
Ce 3 + 4 36.76 Os 1 ~ 18.70 28.06
Ce3+ 4 36.76 Ir 1 + 19.10 27.66
Ce3+ 4 36.76 Pt 1 + 19.00 27.76
Ce 3 + 4 36.76 Au 1 + 19.23 27.53
Ce3+ 4 36.76 Po l ~ 18.42 28.34
Hf 3 + 4 33.33 Pr 1 + 15.42 27.91
Pr 3 + 4 38.98 Pr 2 + 210.55 28.43
Pr 3 + 4 38.98 Pr ~ + 210.55 28.43
Pr 3 + 4 38.98 Nd 2 + 210.73 28.25
Pr 3 + 4 38.98 Pm 2 + 210.90 28.08
Pr 3 + 4 38.98 Sm 2 + 211.07 27.91
WO gO/13126 PCr/USgO/01998
77 2~
Pr 3 + 4 38.98 Eu 2 + 211.24 27.74
Pr 3 + 4 38.98 Tb 2 + 211.52 27.46
Pr 3 + 4 38.98 Dy 2 + 211.67 27.31
Pr 3 + 4 38.98 Ho 2 + 211.80 27.18
Pr 3 + 4 38.98 Er 2 + 211.93 27.05
Pr 3 + 4 38.98 Rn 1 + 110.75 28.23
Hf 3 + 4 33.33 Nd 1 ~ 15.49 27.84
Nd 3 + 4 40.41 Gd 2 + 212.09 28.32
Nd3+ 4 40.41 Er2 + 21t.93 28.48
Nd 3 + 4 40.41 Tm 2 + 212.05 28.36
Nd 3 + 4 40.41 Yb 2 + 212.18 28.23
Pb 4 + ~ 68.80 Nd 4 + 440.41 28.39
Hf 3 + 4 33.33 Pm 1 + 15.55 27.78
Pm 3 + 4 41.10 Lu 2 + 213.90 27.20
Pb4+ 5 68.80 Pm4~ 441.10 27.70
Hf 3 + 4 33.33 Sm 1 + 15.63 27.70
Sm 3 + 4 41.40 Lu 2 ~ 213.90 27.50
Pb4 + 5 68.80 Sm 4 + 441.40 27.40
Hf 3 + 4 33.33 Eu 1 ~ 15.67 27.66
Eu3 + 4 42.60 Hf 2 + 214.90 27.70
Eu 3 + 4 42.60 Pb 2 + 215.03 27.57
Hf 3 + 4 33.33 Gd 1 + 16.14 27.19
Hg 2+ 3 34.20 Gd 1 ~ 16.14 28.06
Tb 3 + 4 39.80 Gd 2 + 212.09 27.71
Gd3+ 4 44.00 Bi 2 ~ 216.69 27.31
Hf 3 + 4 33.33 Tb 1 + 15.85 27.48
Hg 2 + 3 34.20 Tb 1 + 15.85 28.35
Tb 3 + 4 39.80 Tb 2 + 211.52 28.28
Tb 3 + 4 39.80 Tb 2 ~ 211.52 28.28
Tb3+ 4 39.80 Dy2-~ 211.67 28.13
Tb 3 + 4 39.80 Ho 2 + 211.80 28.00
Tb 3 + 4 39.80 Er 2 + 211.93 27.87
Tb 3 + 4 39.80 Tm 2 + 212.05 27.75
Tb 3 + 4 39.80 Yb 2 + 212.13 27.62
Hf 3 + 4 33.33 Dy 1 + 15.93 27.40
Hg 2 + 3 34.20 Dy 1 + 15.93 28.27
WO 90/13126 PCI'/lJS90/01998
2~ 9~
78
Dy3 ~ 4 41.50 Lu 2 + 213.90 27.60
Pb 4 + 5 68.80 Dy 4 + 441.50 27.30
Hf 3 + 4 33.33 Ho 1 + 16.02 27.31
Hg2+ 3 34.20 Ho1+ 16.02 28.18
Ho3+ 4 42.50 Hf 2 + 214.90 27.60
Ho 3 + 4 42.50 Pb 2 ~ 215.03 27.47
Hf 3 + 4 33.33 Er 1 + 16.10 27.23
Hg2+ 3 34.20 Erl + 16.10 28.10
Er3 + 4 42.60 Hf 2 + 214.90 27.70
Er 3 + 4 42.60 Pb 2 + 215.03 27.57
Hf 3 ~ 4 33.33 Tm 1 + 16.18 27.15
Hg2+ 3 34.20 Tm 1 + 16.18 28.02
Tm 3 + 4 42.70 Hf 2 + 214.90 27.80
Tm 3 + 4 42.70 Pb2+ 215.03 27.67
Hf 3 + 4 33.33 Yb 1 ~ 16.25 27.08
H92+ 3 34.20 Ybl + 16.25 27.95
Yb3+ 4 43.70 Bi 2 + 216.69 27.01
Hf 3 + 4 33.33 Lu 1 + 15.43 27.90
Pb 3 + 4 42.32 Lu 2 + 213.90 28.42
Lu 3 + 4 45.19 Bi 2 + 216.69 28.50
Hg2+ 3 34.20 Hf 1 + 16.6û 27.60
Pb3 + 4 42.32 Hf 2 + 214.90 27.42
Hf 3 + 4 33.33 Tl 1 + 16.11 27.22
Hf 3 + 4 33.33 Ra 1 + 15.28 28.û5
Hf 3 + 4 33.33 Ac 1 + 15.20 28.13
Hf 3 + 4 33.33 Th 1 + 16.10 27.23
Hf 3 + 4 33.33 Pa 1 + 15.90 27.43
Hf 3 + 4 33.33 U 1 + 16.05 27.28
Hf 3 + 4 33.33 Np 1 + 16.20 27.13
Hf 3 + 4 33.33 Pu 1 + 16.06 27.~7
Hf 3 + 4 33.33 Am 1 + 1~.99 27.34
Hf 3 + 4 33.33 Cm 1 + 16.02 27.31
Hf-3 + 4 3~.33 Bk 1 + 16.~3 27.10
Hf 3 + 4 33.33 Cf 1 ~ 16.30 27.03
3~ !Ig2+ 3 34.20 Tl 1 + 16.11 28.09
Hg2+ 3 34.20 Th 1 + 16.10 28.10
WO 90/13126 PCI'/US90/0199~
79 2 0 ~
Hg 2 + 3 34.20 Pa 1 + 1 5.90 23.30
Hg2+ 3 34.20 U 1 + 16.05 28.15
Hg 2 + 3 34.20 Np 1 + 1 6.20 28.00
H~2+ 3 34.20 Pu 1 + 16.06 28.14
Hg2~ 3 34.20 Am 1 + 15.99 28.21
Hg 2 + 3 34.20 Cm 1 + 1 6.02 28.18
Hg 2 + 3 34.20 Bk 1 + 1 6.23 27.97
Hg 2 + 3 34.20 Cf 1 + 1 6.30 27.90
Hg 2 + 3 34.20 Es 1 + 1 6.42 27.78
1 0 Pb 3 + 4 42.32 Pb 2 ~ 2 15.03 27.29
Pb 3 + 4 42.32 Pb 2+ 2 15.03 27.29
n = 16 (resonance shrinkage energy is given by 2 27.21 eV; with n = 16, the
resonance shrinkage energy is 217.68)
Atom nnth lon- Atom nnth lon- Energy
1 5 Oxidiz- ization Reduced ization Hole
ed Energy Energy (eV)
(eV) (eV)
Ne 7 + 8239.09 He 1 + 124.59 214.50
Al 6 + 7241.43 He 1 + 124.59 216.84
Mg6+ 7224.94 Li 1 + 15.39 219.55
P 5+ 6220.43 Li 1 + 15.39 215.04
B 4 + 5340.22 Li 3 + 3122.45 217.77
Mg 6+ 7224.94 Be 1 + 19.32 215.62
Ne 7 + 8239.09 Be 2 + 218.21 220.88
Mg6+ 7224.94 B 1 ~ 18.30 216.64
Al 6 + 7241.43 B 2 + 225.15 216.28
B 3 1 4259.37 Ne2+ 240.96 218.41
B 3 + 4259.37 Si 4 ~ 445.14 214.23
B 3 + 4259.37 C! 3 + 339.61 219.76
B 3 + 4259.37 Ar 3 + 340.74 218.63
B 3 + 4259.37 Ti 4 + 443.27 216.10
B 3 + 4259.37 Zn 3 + 339.72 219.65
B 3 + 4259.37 Se 4 ~ 442.94 216.42
B 3 + 4259.37 Rb 3 + 340.00 219.37
B 3 + 4259.37 Sr 3 ~ 343.60 215.77
.~ ~
WO 90/13126 PCl/US9~/01~98
- 2~ 6~7 80
B 3 + 4 259.37 Sn 4 + 4 40.73 218.63
B 3 + 4 259.37 Sb 4 ~ 4 44.20 215.17
B 3+ 4 259.37 Pr 4 ~ 4 38.98 220.39
B 3 + 4 259.37 Nd 4 + 4 40.41 218.96
B 3 + 4 259.37 Pm 4 ~ 4 41.10 218.27
B 3 + 4 259.37 Sm 4 + 4 41.40 217.97
B 3 + 4 2~9.37 Eu 4 + 4 42.60 216.77
B 3 + 4 259.37 Gd 4 + 4 44.00 215.37
B 3 + 4 259.37 Tb 4 ~ 4 39.80 219.57
B 3 + 4 259.37 Dy 4 + 4 41.50 217.87
B 3 + 4 259.37 Ho 4 -~ 4 42.50 216.87
B 3 + 4 259.37 Er 4 + 4 42.60 216.77
B 3 + 4 259.37 Tm 4 + 4 42.70 216.67
B 3 + 4 259.37 Yb 4 + 4 43.70 215.67
B 3 + 4 259.37 Lu 4 + 4 45.19 214.18
~ 3 + 4 259.37 Pb 4 + 4 42.32 217.05
B 3 + 4 259.37 Bi 4 + 4 45.30 214.07
B 4 + 5 340.22 Ne 5 + 5 126.21 214.01
B 4+ 5 340.22 Al 4 + 4 119.99 220.23
B 4+ 5 340.22 Ar 7 + 7 1~4.32 215.90
B 4 + 5 340.22 Ti 6 + 6 119.36 220.86
B 4 + 5 340.22 Mn 7 + 7 119.27 220.95
B 4 + 5 340.22 Fe 7 + 7 125.00 215.22
B 4 + 5 340.22 Kr 8 + 8 126.00 214.22
B 4 + 5 340.22 Sr 8 + 8 122.30 217.92
B 4 + 5 340.22 Nb 7 + 7 125.00 215.22
Ne 7 + 8 239.09 C 2 + 2 24.38 214.71
Al 6 + 7 241.43 C 2+ 2 24.38 217.05
Na 7 ~ 8 264.18 G 3 + 3 47.89 216.29
Mg 7 + 8 265.90 C 3 + 3 47.89 218.01
P 6 + 7 263.22 C 3 + 3 47.89 215.33
Al 7 + 8 284.59 C 4+ 4 64.49 220.10
S 6+ ~7 2~0.93 C~ 4+ 4 64.49 216.44
C 4+ 5 392.08 Na6+ 6 172.15 219.93
C 4+ 5 392.08 V 8 + 8 173.70 218.38
C 4 + 5 392.08 Zn 8 + 8 174.00 218.08
.
,
.
, ~
WO 90/13126 PCI'/~JS90/01998
81 2 ~ 3 ~
Si 6 + 7 246.52 N 2+ 2 29.60 216.92
Na 7 + 8 264.18 N 3 + 3 47.45 2~6.73
M9 7 + 8 ?65.90 N 3 + 3 47.45 218.45
P 6 + 7 263.22 N 3 + 3 47.45 215.77
S 7 + 8 328.23 O 5 + 5113.90 214.33
F 7 + 8 953.89 O 7 ~ 7739.32 214.57
S 6 + 7 280.93 F 3 + 3 62.71 218.22
Si 7 + 8 303.17 F 4~ 4 87.14 216.03
Ne 7 + 8 239.09 Ne 1 + 1 21.56 217 53
1 0 Al 6 + 7 2~1.43 Ne 1 ~ 1 21.56 219.87
S 6 + 7 280.93 Ne 3 + 3 63.45 217.48
Ne7+ 8 239.09 Ne1 + 1 21.56 217.53
Ne7+ 8 239.09 Al 2 + 2 18.83 ?20 26
Ne 7 ~ 8 23g.09 P 2 + 2 19.73 219.36
1~ Ne 7 + 8 239.09 S 2 + 2 23.33 215.76
Ne 7 + 8 239.09 Cl 2 ~ 2 23.81 215.28
Ne 7 + 8 239.09 Sc 3 ~ 3 24.76 214.33
Ne7+ 8 239.09 Ni2 + 2 18.17 220.92
Ne 7 + 8 239.09 Cu 2 + 2 20.29 218.80
Ne 7 + 8 239.09 Ga 2 + 2 20.51 218.58
Ne 7 + 8 239.0g As ~ + 2 18.63 220.46
Ne 7 + 8 239.09 Se 2 + 2 21.19 217.90
Ne 7 + 8 23g.09 Br 2 + 2 21.80 217.29
Ne 7 + 8 239.09 Kr 2 + 2 24.36- 214.73
Ne7+ 8 239.09 Y 3+ 3 20.52 218.57
Ne 7 + 8 239.09 7r 3 + 3 22.99 216.10
Ne 7 + 8 239.09 Nb 3 + 3 25.04 214.05
Ne 7 + 8 239.09 Pd 2 + 219.43 219.66
Ne 7 + 8 239.09 Ag 2 + 221.49 217.60
Ne7+ 8 239.09 In 2 + 218.87 220.22
Ne 7 + 8 239.09 Te 2 + 218.60 220.49
Ne7+ 8 239.09 1 2 + 219.13 219.9~
Ne 7 + 8 239.09 Xe 2 ~ 221.21 217.88
Ne 7 + 8 239.09 La 3 + 319.18 219.91
Ne 7 + 8 239.09 Ce 3 + 32û.20 218.89
Ne 7 1 8 239.09 Pr 3 + 321.62 217.47
WO 90/13126 PCT/US90/l)l998
r 82
2 ~ $ ~ I
Ne 7 + 8 239.09 Nd 3-~ 322.10 216.99
Ne 7 + 8 239.09 Pm 3 + 322.30 216.79
Ne 7 + 8 239.û9 Sm 3 + 323.40 215.69
Ne 7 + 8 239.09 Eu 3~- 324.90 214.19
Ne 7 + 8 239.09 Gd 3 + 320.63 218.46
Ne7+ 8 239.09 Tb3+ 321.91 217.18
Ne 7 + 8 239.09 Dy 3 + 322.80 216.29
Ne 7 + 8 239.09 Ho 3 + 322.84 216.25
Ne 7 + 8 239.09 Er 3 + 322.74 216.35
1 0Ne 7 + 8 239.09 Tm 3 + 323.68 215.41
Ne 7 + 8 239.09 Yb 3 + 325.03 214.06
Ne 7 + 8 239.09 Lu 3 + 320.96 218.13
Ne7+ 8 239.09 Hf 3 + 323.30 215.79
Ne 7 + 8 239.09 Pt 2 + 218.56 220.53
1 5Ne 7 + 8 239.09 Au 2 + 220.50 218.59
Ne 7 + 8 239.09 Hg 2 + 218.76 220.33
Ne7+ 8 239.09 Tl 2 + 220.43 218.66
Mg 6~ 7 224.94 Na 1 + 15.14 219.80
P 5 ~ 6 220.43 Na 1 ~ 15.14 215.29
Na7+ 8 264.18 Na2~ 247.29 216.89
Mg 7 ~ 8 265.90 Na 2 + 247.29 218.61
P 6 ~ 7 263.22 Na 2 + 247.29 215.93
Na 7 + 8 264.1 8 Na 2 + 247.29 216.89
Na7+ 8 264.18 Si4 ~ 445.14 219.04
25 Na 7 + 8 264.18 S 4 + 447.30 216.88
Na 7 + 8 264.1 8 K 3 ~ 345.72 218.46
Na7+ 8 264.18 Ti 4 + 443.27 220.91
Na7+ 8 264.18 V 4 ~ 446.71 217.47
Na 7 + 8 264.1 8 Cr4 ~ 449.10 215.08
Na7+ 8 264.18 Ge4+ 445.71 218.~7
Na7+ 8 264.18 As 4 ~ 450.13 214.05
Na 7 + 8 264.1 8 Br4 ~ 447.30 216.88
Na 7 + 8 264.18 Sr3 + 343.60 220.58
Na 7 + 8 264.1 8 Mo 4 + 446.40 217.78
Na7+ 8 264.18 Sb4+ 444.20 219.98
Na 7 + 8 264.18 La 4 ~ 449.95 214.23
: ,
WO 90/13126 PCr/US90/01998
8 3 2 Q ~
Na7+ 8 264.18 Gd4+ 4 44.00 220.18
Na7+ 8 264.18 Yb4+ 4 43.70 220.48
Na7+ 8 264.18 Lu4+ 4 45.19 218.99
Na7+ 8 264.18 Bi4+ 4 45.30 218.88
Mg6+ 7 224.94 Mg1~ 17.65 217.29
S 7 + 8 328.23 Mg4 t- 4109.24 218.99
Mg6+ 7 224.94 Mg1~ 17.65 217.29
Mg6+ 7 224.94 Al1+ 15.99 218.95
Mg6+ 7 224.94 Si1+ 18.15 216.79
Mg6+ 7 224.94 P1+ 110.49 214.45
Mg6+ 7 224.94 S1+ 110.36 214.58
Mg6+ 7 224.94 K1+ 14.34 220.60
Mg6+ 7 224.94 Ca1+ 16.11 218.83
Mg6+ 7 224.94 Scl+ 16.54 218.40
Mg6+ 7 224.94 Til+ 16.82 218.12
Mg6+ 7 224.94 V 1~ 16.74 218.20
Mg6+ 7 224.94 Cr1+ 16.77 218.17
Mg6+ 7 224.94 Mnl+ 17.43 217.51
Mg6+ 7 224.94 Fel+ 17.87 217.07
Mg6+ 7 224.94 Co1+ 17.86 217.08
Mg6+ 7 224.94 Ni1+ 17.64 217.31
Mg6+ 7 224.94 Cu1+ 17.73 217.21
Mg6+ 7 224.94 Zn1+ 19.39 215.55
Mg6+ 7 224.94 Ga1+ 16.00 218.94
Mg6+ 7 224.94 Ge1+ 17.90 217.04
Mg6+ 7 224.94 Asl+ 19.81 215.13
Mg6+ 7 224.94 Se1+ 19.75 215.19
Mg6+ 7 224.94 Rb1+ 14.18 220.76
Mg6+ 7 224.94 Sr1+ 15.70 219.24
Mg6+ 7 224.94 ~ 16,38 218.56
Mg6+ 7 224.94 Zr1+ 16.84 218.10
Mg6+ 7 224.94 Nb1+ 16.88 218.06
Mg6+ 7 224.94 Mo1+ 17.1~ 217.84
Mg6+ 7 224.94 Tc1+ 17.28 217.66
Mg6+ 7 224.94 Ru1+ 17.37 217.57
Mg6+ 7 224.94 Rh1+ 17.46 217.48
WO go/13126 P~/VS90/01998
~8S~ 84
Mg 6 + 7 224.94Pd 1 ~ 18.34 216.60
Mg6+ 7 ~24.94Ag 1 + 17.58 217.36
Mg 6+ 7 224.94Cd 1 + 18.9g 215.95
Mg6+ 7 224.94In 1 -~ 15.79 219.15
5Mg6+ 7 224.94Sn 1 + 17.34 217.60
Mg 6 ~ 7 224.94Sb 1 + 18.64 216.30
Mg 6+ 7 224.94Te ~ + 19.01 215.93
Mg 6 + 7 224.941 1 + 110.45 214.49
Mg 6+ 7 224.94Ba 1 + 15.21 219.73
10Mg 6 + 7 224.94Ba 2 + ~10.00 214.94
Mg 6+ 7 224.94La 1 + 15.58 ~19.36
- Mg 6+ 7 224.94Ce 1 + 15.47 219.47
Mg 6 + 7 224.94Ce 2 + 210.85 214.09
Mg6+ 7 224.94Pr1 + 15.42 219.52
15Mg 6 + 7 224.94Pr 2 + 210.55 214.39
Mg6+ 7 224.94Nd 1 + 15.49 219.45
Mg 6 + 7 224.94Nd 2 + 210.73 214.21
Mg ~+ ~ 224.94Pm 1 + 15.55 219.39
Mg 6 + 7 224.94Pm 2 + 210.90 214.04
20Mg6+ 7 224.94Sm 1 + 15.63 219.31
Mg 6+ 7 224.94Eu 1 + 15.67 219.27
Mg 6 + 7 224.94Gd 1 + 16.14 218.80
Mg6+ 7 224.94Tb 1 ~ 15.85 219.09
Mg 6+ 7 224.94Dy 1 + 15.93 219.01
25Mg 6+ 7 224.94Ho l ~ 16.02 218.92
Mg6+ 7 224.94Er1 + 16.10 218.84
Mg 6+ 7 224.94Tm 1 + 16.18 218.76
Mg6+ 7 224.94Yb 1 + 16.25 218.69
-- Mg 6 + 7 224.94Lu 1 + 15.43 219.51
30Mg6+ 7 224.94Hf 1 + 16.60 218.34
Mg 6 + 7 224.94Ta 1 + 17.89 217.05
Mg 6+ 7 224.94W 1 + 17.98 216.96
Mg6 + 7 224.94R~ 1 + 17~88 217.06
Mg 6~ 7 224.94Os 1 ~ 18.70 216.24
35M~ 6+ 7 224.94Ir 1 + 19.10 215.84
Mg 6 + 7 224.94- Pt 1 ~ 19.00 215.94
WO 90/13126 P~/US90/01998
2a~l~$~
B5
Mg 6+ 7 224.94 Au 1 + 19.23 215.71
Mg6+ 7 224.94 Hg1 + 110.44 214.50
Mg6+ 7 224.94 Tl 1 + 16.11 218.83
Mg 6+ 7 224.94 Pb 1 + 17.42 217.52
5Mg6+ 7 224.94 Bi 1 + 17.29 217.65
Mg 6 + 7 224.94 Po 1 + 18.42 216.52
Mg6+ 7 224.94 Rn1+ 110.75 214.19
Mg 6 + 7 224.94 Ra 1 + 15.28 219.66
Mg 6 + 7 224.94 Ra 2 + 210.15 214.79
10Mg 6 + 7 224.94 Ac 1 + 15.20 219.74
Mg 6+ 7 224.94 Th 1 + 16.10 218.84
Mg 6+ 7 224.94 Pa 1 + 15.90 219.04
Mg 6 + 7 224.94 U 1 + 16.05 218.89
Mg 6+ 7 224.94 Np 1 + 16.20 218.74
15Mg 6 + 7 224.94 Pu 1 + 16.06 218.88
Mg 6 + 7 224.94 Am 1 + 15.99 218.95
Mg6+ 7 224.94 Cm 1 + 16.02 218.92
Mg 6~ 7 224.94 Bk 1 + 16.23 218.71
M9 6+ 7 2?4.94 Cf 1 + 16.30 218.64
20Mg6+ 7 224.94 Es1 + 16.42 218.52
Mg7+ 8 265.90 Si 4 + 445.14 220.76
Mg 7 + 8 265.90 P 4 ~ 451.37 214.53
Mg 7 + 8 265.90 S 4 + 447.30 218.60
Mg 7 + 8 265.90 K 3 + 345.72 220.18
25Mg 7 + 8 265.90 Ca 3 + 350.91 214.99
Mg 7 + 8 265.90 V 4 + 446.71 219.19
Mg 7 + 8 265.90 Cr 4 + 449.10 216.80
Mg 7 ~ 8 265.90 Mn 4 ~ 451.20 214.70
Mg 7 + 8 265.90 Co 4 + 451.30 214.60
30Mg 7 + 8 265.90 Ge 4 + 445.71 220.19
Mg 7 + 8 265.90 As 4 + 450.13 215.77
Mg 7 + 8 265.90 Br 4 + 447.30 218.60
Mg 7 + 8 265.90 Nb 5 + 550.55 215.35
Mg 7 + 8 265.90 Mo 4 + 446.40 219.50
35Mg 7 + 8 265.90 La 4 ~ 449.95 215.95
Mg 7 + 8 265.90 Lu 4 ~ 445.19 220.71
WO 90/13126 P~/USgO/01998
20~69~
86
Mg 7+ 8 265.90 Bi 4 ~ 445.30 220.60
P 5+ 6 220.43 Al l + 15.99 214.44
Si 6 + 7 246.52 Al 3 ~- 328.45 218.07
Al 6 + 7 241.43 S 2+ 223.33 218.10
Al 6 + 7 241.43 Cl 2 t 223.81 217.62
Al 6 + 7 241.43 Sc 3 + 324.76 216.67
Al 6 + 7 241.43 Ga2~ 220.51 220.92
Al 6 + 7 241.43 Se 2+ 221.19 220.24
Al 6 + 7 241.43 Br 2 + 221.80 219.63
Al 6 + 7 241.43 Kr 2 + 224.36 217.07
Al 6 + 7 241.43 Rb 2 + 227.28 214.15
Al 6 + 7 241.43 Y 3 + 320.52 220.91
Al 6 + 7 241.43 Zr 3 + 322.99 218.44
Al 6 + 7 241.43 Nb3 + 325.04 216.39
Al 6 + 7 241.43 Mo 3+ 327.16 214.27
Al 6 + 7 241.43 A3 2 + 221.49 219.94
Ai 6 + 7 241.43 Sb 3 + 325.30 216.13
Al 6 + 7 241.43 Xe2+ 221.21 220.22
Al 6 + 7 241.43 Cs 2+ 225.10 216.33
20 . Al 6 + 7 241.43 Pr 3 + 321.62 219.81
Al 6 + 7 241.43 Nd3+ 322.10 219.33
Al 6 + 7 241.43 Pm 3 + 322.30 219.13
Al 6 + 7 241.43 Sm 3 + 323.40 218.03
Al 6 + 7 241.43 Eu 3 ~ 324.90 216.53
Al 6 + 7 241.43 Gd3+ 320.63 220.80
Al 6 + 7 241.43 Tb 3 + 321.91 219.52
Al 6 + 7 24i .43 Dy 3 + 322.80 218.63
Al 6 + 7 241.43 Ho 3 + 322.84 218.59
Al 6 + 7 241.43 Er 3 + 322.74 218.69
Al 6 + 7 241.43 Tm 3 ~ 323.68 217.75
Al 6 + 7 241.43 Yb3+ 325.03 216.40
Al 6 + 7 241.43 Lu 3 + 320.96 220.47
~16 ~ 7 241.43' Hf 3 + 323.3b 218.13
Al 6 + 7 241.43 Au 2 + 220.50 220.93
Al 6 + 7 241.43 Bi 3 ~ 325.56 215.87
Al 7 + 8 284.59 P 5 + 565.02 219.57
WO 90/1312~ PCT/US90/01998
87 ~ r~ ~J
Al 7 + 8 284.59 Cl 5 t 5 67.80 216.79
Al 7 + 8 284.59 Ca4-~ 4 67.10 217.49
Al 7 + 8 284.59 V 5 t- 5 65.23 219.36
Al 7 ~ 8 284.59 Cr 5 ~- ~ 69.30 215.29
Al 7 + 8 2~4.59 ~a4-~ 4 64.00 220.59
Al 7 + 8 284.59 As 5-~ 5 63.63 220.96
Al 7 + 8 284.59 Se 5-~ 5 68.30 216.29
Al 7 + 8 284.59 Kr 5 + 5 64.70 219.89
Al 7 + 8 284.59 Mo 6+ 6 68.00 216.59
Al 7 + 8 284.59 Pb 5 + 5 68.80 215.79
P 6+ 7 263.22 Si 4 + 4 45.14 218.08
Si 6 + 7 246.52 P 3 + 3 30.18 216.34
Si 6 + 7 246.52 Ar 2 + 2 27.63 218.89
Si 6 + 7 246.52 K 2 + 2 31.63 214.90
Si 6 + 7 246.5~ Ti 3 + 3 27.49 219.03
Si 6 + 7 246.52 V 3 + 3 29.31 217.21
Si 6 + 7 246.52 Cr 3 + 3 30.96 215.56
Si 6 + 7 246.52 Fe 3 + 3 30.65 215.87
Si 6 + 7 2~6.52 Ga 3 + ` 3 30.71 215.81
Si 6 + 7 246.52 As 3 + 3 28.35 218.17
Si 6 + 7 246.52 Se 3 + 3 30.82 215.70
Si 6 + 7 246.52 Rb 2 + 2 27.28 219.24
Si 6 + 7 246.52 Mo 3 + 3 27.16 219.36
Si 6 + 7 246.52 Tc 3 + 3 29.54 216.98
Si 6 + 7 246.52 Ru 3 + 3 28.47 218.05
Si 6 + 7 246.52 Rh 3 ~ 3 31.06 215.46
Si 6 + 7 246.52 In 3 + 3 28.03 218.4g
Si 6 + 7 246.52 Sn 3+ 3 30.50 216.02
Si 6 + 7 246.52 Te 3 + 3 27.96 218.56
Si 6 + 7 246.~2 Xe3+ 3 32.10 214.~2
Si 6 + 7 246.52 Tl 3 + 3 29.83 216.69
Si 6 + 7 246.52 Pb 3 + 3 31.94 214.58
Si 6 + 7 ?46.52 Bi 3 + 3 25.56 220.96
Si 7 + 8 303.17 S 6 + 6 88.05 215.12
Si 7 + 8 303.17 K 5 + 5 82.66 220.51
Si 7 + 8 303.17 Ca5+ 5 84.41 218.76
WO 90/13126 PCr/US90/01998
2 ~
Si 7 ~ 8 303.17 Zn 5 + 5 82.60 220.57
Si 7 + 8 303.17 Br 6 + 6 88.60 214.57
Si 7 + 8 303.17 Rb 6 + 6 84.40 218.77
Si 7 + 8 303.17 Bi 6 ~ 6 88.30 214.87
S 6+ 7 280.93 P 5 ~ 565.02 215.91
P 5 + 6 220.43 K 1 -~ 14.34 216.09
P 5 + 6 220.43 Ca 1 + 16.11 214.32
P 5 + 6 220.43 Ga 1 + 16.00 214.43
P 5 ~ 6 220.43 Rb 1 + 14.18 216.25
P 5 + 6 220.43 Sr 1 + 15.70 214.73
P 5+ 6 220.43 Y 1 ~ 16.38 214.05
P 5+ 6 220.43 In 1 + 15.79 214.64
P 5 + 6 220.43 Cs 1 + 13.89 216.54
P 5~ 6 220.43 Ba 1 + 15.21 215.22
P 5 + 6 220.43 La 1 + 15.58 214.85
P 5~ 6 220.43 Ce 1 ~ 15.47 214.96
P 5+ 6 220.43 Pr 1 + 15.42 215.01
P 5 + 6 220.43 Nd 1 + 1 5.49 214.94
P 5+ 6 220.43 Pm t + 15.55 214.88
P 5+ 6 220.43 Sm 1 + 15.63 214.80
P 5 + 6 220.43 Eu 1 + 1 5.67 214.76
P 5 + 6 220.43 Gd 1 + 1 6.14 214.29
P 5 + 6 220.43 Tb 1 + i 5.85 214.58
P 5 + 6 220.43 Dy 1 + 1 5.93 214.50
P 5 + 6 220.43 Ho 1 + 1 6.02 214.41
P 5+ 6 220.43 Er 1 ~ 1 6.10 214.33
P 5+ 6 220.43 Tm 1 ~ 16.18 214.25
P 5+ 6 220.43 Yb 1 + 1 6.25 214.18
P 5+ 6 220.43 Lu 1 ~ 1 5.43 215.00
P 5+ 6 220.43 Tl 1 + 1 6.11 214.32
P 5+ 5 220.43 Ra 1 + 1 5.28 215.15
P 5 + 6 220.43 Ac l + 1 5.20 215.23
P 5+ 6 220.43 Th 1 + 1 6.10 214.33
P ~ + 6 220.43 Pa 1 ~ 1 5.90 214.53
P 5+ 6 220.43 U 1 + 16.05 214.38
P 5 + 6 220.43 Np l + 1 6.20 214.23
WO ~0/13~6 PCI'/US90/01998
8 9 2 ~
. . , ` .
P 5 + 6 220.43 Pu 1 + 16.06 214.37
P 5+ 6 220.43 Am 1 ~ 15.99 214.44
P 5+ 6 220.43 Cm 1 ~ 16.02 214.41
P 5 + 6 220.43 Bk 1 + 16.23 214.Z0
P 5+ 6 220.43 Cf 1 + 16.30 214.13
P 5+ 6 220.43 Es1 + 16.42 214.01
P 6 + 7 263.22 S 4 ~ 447.30 215.92
P 6 + 7 263.22 K 3 + 345.72 217.50
P 6+ 7 263.22 Ti 4 + 443.27 219.95
P 6 + 7 263.22 V 4 + 446.71 216.51
P 6 + 7 263.22 Cr 4 + 449.10 214.12
P 6 + 7 263.22 Ge 4 + 445.71 217.51
P 6 + 7 263.22 Se 4 + 442.94 220.28
P 6 + 7 263.22 Br 4 + 447.30 215.92
P 6 + 7 263.22 Sr 3 + 343.60 219.62
P 6 + 7 263.22 Mo 4 + 446.40 216.82
P 6 + 7 263.22 Sb 4 + 444.20 219.02
P 6 + 7 263.22 Eu4+ 442.60 220.62
P 6 + 7 263.22 Gd 4 ~ 444.00 219.22
P 6 + 7 Z63.22 Ho 4 + 442.50 220.72
P 6 + 7 263.22 Er 4 + 442.60 220.62
P 6~ 7 263.22 Tm 4 + 442.70 220.52
P 6 + 7 263.22 Yb 4 + 443.70 219.52
P 6 + 7 263.22 Lu 4 + 445.19 218.03
P 6 + 7 263.22 Pb 4 + 442.32 220.90
P 6 + 7 263.22 Bi 4 + 445.30 217.92
P 7 + 8 309.41 Ar 6 + 691.01 218.40
P 7 ~ 8 309.41 Sc 5 + 591.66 217.75
P 7 + 8 309.41 Cr 6 + 690.56 218.85
P 7 + 8 309.41 Mn 6 + 695.00 214.41
P 7 + 8 309.41 Ge 5 ~ 593.50 215.91
P 7+ 8 309.41 Br 6 ~ 688.60 220.81
P 7 + 8 309.41 Sr 6 ~ 690.80 218.61
P 7 + 8 309.41 Y 6 + 693.00 216.41
S 6 + 7 280.93 K 4 + 460.91 220.02
S 6 + 7 280.93 V 5 + 565.23 215.70
WO 90/13126 PCI'/US90/01998
2 ~ 9 ~ g o
S 6 + 7 280.93 Ga 4 + 464,00 216.93
S 6 + 7 280.93 As 5 + 563.63 217.30
S 6 + 7 280.93 Kr 5 + 564.70 216.23
S 6+ 7 280.93 Y 4+ 461.80 219.13
S 6 + 7 280.93 Mo 5 + 561.20 219.73
S 7 + 8 328.23 Cl 7 + 7114.19 214.04
S 7 + 8 328.23 Ca 6 + 6108.78 219.45
S 7 + 8 328.23 Sc 6 + 6111.10 217.13
S 7 + 8 328.23 Ni 6 + 6108.00 220.23
S 7 + 8 328.23 Zn 6 + 6108.00 220.23
S 7 + 8 328.23 Kr 7 + 7111.00 217.23
S 7 + 8 328.23 Sb 6 + 6108.00 220.23
Cl 7 ~ 8 348.28 Ca 7 + 7127.70 220.58
Cl 7 + 8 348.28 V 6 + 6128.12 220.16
C17 + 8 348.28 Co7+ 7129.00 219.28
Cl 7 ~ 8 343.28 Ni 7 + 7133.00 215.28
Cl 7 + 8 348.28 Zn 7 + 7134.00 214.28
Cl 7 + 8 348.28 As 6 + 6127.60 220.68
Cl 7 + 8 348.28 Y 8 + 8129.00 219.28
20 n = 54 (resonance shrinkage energy is given by 2 27.21 eV; with n = 54, the
resonance shrinkage energy is 734.67)
Atom n nth lon- Atom nnth lon- Energy
Oxidiz- ization Reduced ization Hole
ed Energy Energy (eV)
(eV) (eV)
O 6+ 7 739.32 Li 1 + 15.39 733.92
F 7 + 8 953.89 Be 4 + 4217.71 736.17
O 6+ 7 739.32 B 1 + 18.30 731.02
0 7+ 8871.39 0.6+ 6138.12 733.27
O 6+ 7 739.32 Na l + 15.14 734.18
0 6+ 7739.32 Mg 1 + 17.65 731.67
O 6+ 7739.32 Al 1 + 15.99 733.33
O 6+ 7739.32 Si 1 + 18.15 731.16
O 6+ 7739.32 K 1 ~ 14.34 734.97
0 6+ i739.32 Ca 1 + 16.11 733.20
WO 90/13126 PCl-/US90/01998
2 ~
91
O 6+ 7 739.32 Sc l + 1 6.54 732.78
O 6+ 7 739.32 Ti 1 ~ 1 6.82 732.49
O 6+ 7 739.32 V 1 + 1 6.74 732.58
O 6+ 7 739.32 Cr 1 ~ 1 6.77 732.55
5O 6+ 7 739.32 Mn 1 + 1 7.43 731.88
O 6+ 7 739.32 Fe 1 + 1 7.87 731.45
O 6 + 7 739.32 Co 1 + 1 7.86 731.46
O 6+ 7 739.32 Ni 1 + 1 7.64 731.68
O 6~ 7 739.32 Cu 1 + 1 7.73 731.59
10O 6+ 7 739.32 Ga1 + 1 6.00 733.32
O 6+ 7 739.32 Ge 1 + 1 7.90 731.42
O 6+ 7 739.32 Rb 1 + 1 4.18 735.14
O 6+ 7 739.32 Sr 1 + 1 5.70 733.62
O 6+ 7 739.32 Y 1 ~ 1 6.38 732.93
15O 6+ 7 739.32 Zr 1 + 1 6.84 732.47
O 6+ 7 739.32 Nb 1 + 1 6.88 732.43
O 6+ 7 739.32 Mo 1 + 1 7.10 732.22
O 6+ 7 739.32 Tc 1 + 1 7.28 732.03
O 6~ 7 739.32 Ru 1 ~ 1 7.37 731.95
20O 6+ 7 739.32 Rh 1 + 1 7.46 731.85
O 6+ 7 739.32 Pd 1 + 1 8.34 730.97
O 6+ 7 739.32 Ag 1 + 1 7.58 731.74
O 8 + 7 739.32 Cd 1 + 1 8.99 730.32
O 6+ 7 739.32 In 1 + 1 5.79 733.53
25O 6+ 7 739.32 Sn 1 + 1 7.34 731.97
O 6 + 7 739.32 Sb 1 + 1 8.64 730.67
O 6~ 7 739.32 Te 1 + 1 9.01 730.31
O 6 + 7 739.32 Cs 1 + 1 3.89 735.42
O 6+ 7 739;32 Ba 1 + 1 5.21 734.10
30O 6+ 7 739.32 La 1 + 1 5.58 733.74
O 6 + 7 739.32 Ce 1 + 1 5.47 733.85
O 6+ 7 739.32 Pr 1 ~ 1 5.42 733.89
O 6+ 7 739.32 Nd 1 ~ 1 5.49 733.83
O 6+ 7 739.32 Pm 1 ~ 1 5.55 733.76
35O 6~ 7 739.32 Sm 1 ~ 1 5.63 733.68
O 6 + 7 739.32 Eu l ~ 1 5.67 733.65
w~ so/13126 PCT/uS9o/01998
2 Q ~ 92
O 6+ 7 739.32 Gd 1 -~ 1 6.14 733.17
O 6+ 7 739.32 Tb 1 -~ 1 5.85 733.47
O 6+ 7 739.32 Dy 1 -~ 1 5.93 733.39
O 6 + 7 739.32 Ho 1 -~ 1 6.02 733.29
O 6+ 7 739.32 Er 1 ~ 1 6.10 733.22
O 6+ 7 739.32 Tm 1 + 1 6.18 733.13
V 6~ 7 739.32 Yb 1 + 1 6.25 733.06
O 6+ 7 739.32 Lu 1 + 1 5.43 733.89
O 6+ 7 739.32 Hf 1 + 1 6.60 732.72
l OO 6+ 7 739.32 Ta 1 + 1 7.89 731.42
O 6+ 7 739.32 W 1 + 1 7.98 731.34
O 6+ 7 739.32 Re 1 + 1 7.88 731.43
O 6+ 7 739.32 Os l + 1 8.7~ 730.61
O 6+ 7 739.32 Ir 1 + 1 9.iO 730.22
15 O 6+ 7 739.32 . Pt 1 + 1 9.00 730.32
O 6+ 7 739.32 Au 1 + 1 9.23 730.09
O 6+ 7 739.32 Tl 1 + 1 6.11 733.21
O 6+ 7 739.32 Pb 1 + 1 7.42 731.90
O 6~ 7 739.32 Bi 1 + 1 7.29 732.03
20 O 6+ 7 739.32 Po 1 + 1 8.42 730.90
O 6+ 7 739.32 Ra1 + 1 5.28 734.04
O 6+ 7 739.32 Ac 1 + 1 5.20 734.11
O 6+ 7 739.32 Th 1 + 1 6.10 733.22
O 6 + 7 739.32 Pa 1 + 1 5.90 733.41
25 - O 6+ 7 739.32 U 1 + 16.05 733.27
O 6+ 7 739.32 Np 1 + 16.20 733.11
O 6+ 7 739.32 Pu 1 + 16.06 733.26
O 6+ 7 73g.32 Am 1 + 15.99 733.33
O 6 + 7 739.32 Cm 1 + 16.02 733.29
30- O 6+ 7 739.32 Bk 1 + 16.23 733.0g
O 6+ 7 739.32 Cf 1 + 16.30 733.02
O 6 + 7 739.32 Es 1 ~ 16.42 732.gO
O 7+ 8 871.39 O 6+ 6138.12 733.27
O 7+ 8 871.39 Na5+ 5138.39 733.00
O 7+ 8 871.39 Mg 5+ 5141.26 730.13
O 7+ 8 871.39 Sc 7 + 7138.00 733.39
WO 90/13126 PCI/US90/01998
2 ~
93
O 7+ 8871.39 Ti 7 ~ 7140.80 730.59
O 7 + 8871.39 Cu 7 + 7139.00 732.39
O 7+ 8871.39 Zn7~ 7134.00 737.39
O 7 + 887t .39 Rb 8 + 8136.00 735.39
O 7+ 8871.39 Te7+ 7137.00 734.39
F 7 + 8953.89 P 6 + 6220.43 733.46
Two-ion couples capable of producing energy holes for shrinking
deuterium atoms involving cations and anions. The number in the column
following the ion, (n), is the nth ionization energy of ~he atom. For
10 example, Ga2+ + 30.71 eV = Ga3+ ~ e- and H ~ e- - H- + 3.08 eV.
Ato m nnth lon- Ato m n nth lon- Energy
Oxidiz- ization Reduced ization Hole
ed Energy Energy (eV)
(eV~ (eV)
1 5 As 2 + 3 28.35 H - 10.80 27.55
Ru 2+ 3 28.47 H - 10.80 27.67
In 2 + 3 28.03 H - 10.80 27.23
Te2+ 3 27.96 H -10.80 27.16
Al 2 + 3 28.45 H - 10.80 27.65
Ar 1 + 2 27.63 H - 10.80 26.83
As 2 + 3 28.35 Li - 10.61 27.74
Ru 2 + 3 28.47 Li - 10.61 27.86
In 2 + 3 28.03 Li - 10.61 27.42
Te 2 ~ 3 27.96 Li - 10.61 27.35
Al 2 ~ 3 28.45 Li - 10.61 27.84
Ar 1 + 2 27.63 Li - 10.61 27.02
Ti 2 + 3 27.49 Li - 10.61 26.88
As 2 + 3 28.35 B - 10.30 28.05
Rb 1 + 2 27.28 B - 10.30 26.98
Mo2+ 3 27.16 B -1 0.30 26.86
Ru 2 + 3 28.47 B - 1 0.30 28.17
In 2 + 3 28.03 B - 1 0.30 27.73
Te2 + 327.96 B - 1 0.30 27.66
Al 2 ~ 328.45 B - 1 û.30 28.15
Ar 1 ~ 227.63 B - 1 0.30 27.33
Ti 2 ~ 327.49 B - 1 0.30 27.19
WO 90/13126 PCI-/US90/01998
` .2~S ~
9~
As 2 ~ 3 28.35 C - 1 1.12 27.23
Tc 2 + 3 29.54 C - 1 1.12 28.42
Ru 2 + 3 28.47 C - 1 1.12 27.35
In 2 + 3 28.03 C - 1 1.12 26.91
Te 2 + 3 27.96 C - 1 1.12 26.84
N 1 + 2 29.60 C - 1 1.12 28.48
AI 2 + 3 28.45 C - 1 1.12 27.33
V 2 + 3 29.31 C - 1 1.12 28.19
As 2 + 3 28.35 O - 1 1.47 26.89
Tc 2 + 3 29.54 O - 1 1.47 28.07-
Ru 2+ 3 28.47 O - 1 1.47 27.00
TI 2 + 3 29.83 O - 1 1.47 28.36
N 1 + 2 29.60 O - 1 1.47 28.14
AI 2 + 3 28.45 O - 1 1.47 26.98
V 2 + 3 29.31 O - 1 1.47 27.84
Ga 2 + 3 30.71 F - 1 3.~5 27.26
Se2 + 3 30.82 F - 1 3.45 27.37
Rh 2 + 3 31.06 F - 1 3.45 27.61
Sn 2+ 3 30.50 F - 1 3.45 27.05
Pb 2 + 3 31.94 F - 1 3.45 28.49
K 1+ 2 31.63 F -1 3.45 28.18
Cr 2 + -3 30.96 F - 1 3.45 27.51
Fe2 3 30.65 F - 1 3.45 27.20
As 2 + 3 28.35 Na - 1 0.52 27.83
Ru 2 + 3 28.47 Na - 1 0.52 27.95
In 2 ~ 3 28.03 Na - 1 0.52 27.51
Te 2 + 3 27.96 Na - 1 0.52 27.44
AI 2 + 3 28.45 Na - 1 0.52 27.93
Ar 1 + 2 27.63 Na - 1 0.52 27.11
Ti 2 + 3 27.49 Na - 1 0.52 26.97
As 2 + 3 28.35 AI ~ 1 0.52 27.83
Ru 2+ 3 28.47 AI - 1 0.52 27.95
ln 2 + 3 28;03 AI -1 0.52 27.51
Te 2 + 3 27.96 A I - 1 0.52 27.44
AI 2 + 3 28.45 AI - 1 0.52 27.93
Ar 1 ~ 2 27.63 AI - 1 0.52 27.11
WO 90tl3126 PCr/lJS90/01998
2~3~7
Ti 2 ~ 3 27.49 Al - 1 0.52 26.97
As 2 + 3 28.35 Si - 1 1.39 26.96
Tc 2 + 3 29.54 Si - 1 1.39 28.15
Ru 2 + 3 28.47 Si - 1 1.39 27.08
Tl 2 + 3 29.83 Si - 1 1.39 28.44
N 1 + 2 29.60 Si - 1 1.39 28.21
Al 2 + 3 28.45 Si - 1 1.39 27.06
V 2 + 3 29.31 Si - l 1.39 27.92
As 2 + 3 28.35 P - 1 0.78 27.57
Ru 2 + 3 28.47 p - 1 0.78 27.69
In 2 + 3 28.03 P - 1 0.78 27.25
Te 2 + 3 27.96 P - 1 0.78 27.18
Al 2 + 3 28.45 P - 1 0.78 27.67
Ar 1 + 2 27.63 P - 1 0.78 26.85
Tc 2 + 3 29.54 S - 1 2.07 27.47
Sn 2 + 3 30.50 S - 1 2.07 28.43
T12 + 3 29.83 S - 1 2.07 27.76
N 1 + 2 29.60 S - 1 2.07 27.53
P 2 + 3 30.18 S - 1 2.07 28.11
V 2 + 3 29.31 S - 1 2.07 27.24
Ga2+ 3 30.71 Cl - 1 3.61 27.10
Se 2 + 3 30.82 Cl - 1 3.61 27.21
Rh 2+ 3 31.06 Cl - 1 3.61 27.45
Sn 2 ~ 3 30.50 Cl - 1 3.61 26.89
Xe2+ 3 32.10 Cl - 1 3.61 28.49
Pb 2 + 3 31.94 Cl - 1 3.61 28.32
K 1 ~ 2 31.63 Cl - 1 3.61 28.01
Cr 2 + 3 30.96 Cl - 1 3.61 27.35
Fe 2 + 3 30.65 Cl - 1 3.61 27.04
A~ 2 + 3 2B.35 ~ - 1 0.69 27.66
Ru 2+ 3 28.47 K - 1 0.69 27.78
In 2 + 3 28.03 K - 1 0.69 27.3~
Te2+ 3 27.96 K - 1 0.69 27.27
Al 2 + 3 28.45 K - 1 0.69 27.75
Ar 1 + 2 27.63 K - 1 Q69 26.93
As 2 + 3 28.35 Fe - 1 0.56 27.79
WO 90/13126 PCl-tUS90/01998
' 6
2 ~ 3 ~J ~
Ru 2 + 3 28.47 Fe - 1 0.56 27.91
In 2 + 3 28.03 Fe - 1 0.~6 27.47
Te 2 + 3 27.96 Fe - 1 0.56 27.40
Al 2 + 3 28.45 Fe - 1 0.56 27.89
Ar 1 + 2 27.63 Fe - 1 0.56 27.07
Ti 2 + 3 27.49 Fe - 1 0.56 26.93
As 2 + 3 28.35 Co - 1 0.95 27.40
Ru 2 + 3 28.47 Co - 1 0.95 27.52
In 2 + 3 28.03 Co - 1 0.95 27.08
Te 2 + 3 27.96 Co - 1 0.95 27.01
Al 2 + 3 28.45 Co - 1 0.95 27.49
V 2 + 3 29.31 Co - 1 0.95 28.36
Tc 2 + 3 29.54 Cu - 1 1.82 27.72
Tl 2 + 3 29.83 Cu - 1 1.82 28.01
N 1 + 2 29.60 Cu - 1 1.82 27.78
P 2 + 3 30.18 Cu - 1 1.82 28.36
V 2 ~ 3 29.31 Cu - 1 1.82 27.49
Ga 2 + 3 30.71 Br - 1 3.36 27.35
Se 2 + 3 30.82 Br - 1 3.36 27.46
Rh 2 + 3 31.06 Br - 1 3.36 27.70
Sn 2 + 3 30.50 Br - 1 3.36 27.14
P 2 + 3 30.18 Br - 1 3.36 26.82
K 1 + 2 31.63 Br - 1 3.36 28.26
Cr 2 + 3 30.96 Br - 1 3.36 27.60
Fe 2 + 3 30.6~ Br - 1 3.36 27.29
As 2 + 3 28.35 Rb - 1 0.30 28.05
Rb 1 ~ 2 27.28 Rb - 1 0.30 26.98
Mo 2 + 3 27.16 Rb - 1 0.30 26.86
Ru 2 + 3 28.47 Rb - 1 0.30 28.17
In 2 + 3 28.03 Rb - 1 0.30 27.73
Te 2 + 3 27.96 Rb - 1 0.30 27.66
Al 2 + 3 28.45 Rb - 1 0.30 28.15
Ar 1 ~ 2 27.63 Rb - 1 0.30 27.33
Ti 2 + 3 27.49 Rb - 1 0.30 27.19
Ga 2 + 3 30.71 1 - 1 3.06 27.65
Se2+ 3 30.82 I - 1 3.06 27.76
WO 90/13126 PCr/US90/01~98
9 7 2 ~ ~ f.~ 3
Rh 2 + 3 31.06 1 - 1 3.06 28.00
Sn 2 + 3 30.50 I - 1 3.06 27.44
P 2 + 3 30.18 1 - 1 3.0627.12
Cr2 + 3 30.96 1 - 1 3.0627.90
Fe 2+ 3 30.65 1 - 1 3.0627.59
As 2 + 3 28.35 Cs - 1 0.30 28.05
Rb 1 + 2 27.28 Cs - 1 0.30 26.98
Mo 2 + 3 27.16 Cs - 1 0.30 26.86
Ru 2 + 3 28.47 Cs - 1 0.30 28.17
In 2 + 3 28.03 Cs 1 0.30 27.73
Te 2 + 3 27.96 Cs - 1 0.30 27.66
Al 2 + 3 28.45 Cs - 1 0.30 28.15
Ar 1 + 2 27.63 Cs - 1 0.30 27.33
Ti 2 + 3 27.49 Cs - 1 0.30 27.19
Tc 2 + 3 29.54 Se - 1 1.70 27.84
Tl 2 + 3 29.83 Se - 1 1.70 28.13
N 1 + 2 29.60 Se- 1 1.7027.90
P 2 + 3 30.18 Se- 1 1.7028.48
V 2 + 3 29.31 Se- 1 1.7027.61
Tc 2 + 3 29.54 Te - 1 2.20 27.34
Sn2+ 3 30.50 Te- 1 2.2028.30
Tl 2 + 3 29.83 Te - 1 2.20 27.63
N 1 + 2 29.60 Te- 1 2.2027.40
P 2 + 3 30.18 Te- 1 2.2027.98
V 2 + 3 29.31 Te- 1 2.2027.11
Fe 2+ 3 30.65 Te- 1 2.2028.45
As 2 + 3 28.35 As- 1 0.60 27.75
Ru 2+ 3 28.47 As- 1 0.60 27.87
In 2 + 3 28.03 As- 1 0.60 27.43
Te 2 ~ 3 27.96 As- 1 0.60 27.36
Al 2 + 3 28.45 A~- 1 0.60 27.85
Ar 1 + 2 27.63 As- 1 0.60 27.03
Ti 2 + 3 27.49 As - 1 0.60 26.89
Tc 2 ~ 3 29.54 Sb - 1 2.00 27.54
Tl 2 + 3 29.83 Sb - 1 2.00 27.83
N 1 + 2 29.60 Sb -1 2.00 27.60
, . . .
,
WO 90/13126 PCT/US90/01998
2 ~ 7 9 8
P 2 + 3 30.18 Sb - 1 2.00 28.18
V 2 + 3 29.31 Sb - 1 2.00 27.31
As 2 ~ 3 23.35 Bi - 1 0.70 27.65
Ru 2 + 3 28.47 Bi - 1 0.70 27.77
In 2 + 3 28.03 Bi - 1 0.70 27.33
Te 2 + 3 27.96 Bi - 1 0.70 27.26
Al 2 + 3 28.45 Bi - 1 0.70 27.75
Ar 1 + 2 27.63 Bi - 1 0.70 26.93
Tc 2 + 3 29.54 Tl - 1 2.10 27.44
l O Sn 2 + 3 30.50 Tl - 1 2.10 28.40
Tl 2 + 3 29.83 Tl - l 2.10 27.73
N 1 + 2 29.60 Tl - 1 2.10 27.50
P 2 + 3 30.18 Tl - 1 2.10 28.08
V 2+ 3 29.31 Tl - I 2.10 27.21
Tc 2 + 3 29.54 Au - 1 2.10 27.44
Sn 2 + 3 30.50 Au - 1 2.10 28.40
Tl 2 + 3 29.83 Au - 1 2.10 27.73
N 1 + 2 29.60 Au - 1 2.10 27.50
P 2 + 3 30.18 Au - 1 2.10 28.08
V 2 + 3 29.31 Au - 1 2.10 27.21
As 2 + 3 28.35 Hb - 1 1.54 26.81
Tc 2 + 3 29.54 Hb - 1 1.54 28.00
Ru 2 + 3 28.47 Hg - 1 1.54 26.93
Tl 2 + 3 29.83 Hb - 1 1.54 28.29
N 1 + 2 29.60 Hg - 1 1.54 28.06
Al 2 + 3 ~8.45 Hb - 1 1.54 26.91
V 2 + 3 29.31 Hb - 1 1.54 27.77
As 2 + 3 28.35 As - 1 0.60 27.75
Ru 2+ 3 23.47 As - 1 0.60 27.87
In 2 ~ 3 28.03 As - 1 0.60 27.43
Te 2 + 3 27.96 As - 1 0.60 27.36
Al 2 ~ 3 28.45 As - 1 0.60 27.85
Ar 1 + 2 27.63 As - 1 0.60 27.03
Ti 2 + 3 27.49 As - 1 0.60 26.89
A~- 2 + 3 28.35 Ce - 1 1.20 27.15
Tc 2 + 3 29.54 Ce - 1 1.20 28.34
. .
WO 90/13126 PC~/US90/01998
9 9 2 0 ~ J
Ru 2+ 3 28.47 Ce - 1 1.20 27.27
In 2 + 3 28.03 Ce -1 1.20 26.83
N 1 + 2 29.60 Ce - 1 1.20 28.40
Al 2 + 3 28.45 Ce - 1 1.20 27.25
V 2 ~ 3 29.31 Ce - 1 1.20 28.11
As 2 + 3 28.35 Fr - 1 0.46 27.89
Rb 1 ~ 2 27.28 Fr -1 0.46 26.82
Ru 2 + 3 28.47 Fr - 1 0.46 28.01
In 2 + 3 28.03 Fr - 1 0.46 27.57
Te 2 + 3 27.96 Fr - 1 0.46 27.50
Al 2 + 3 28.45 Fr - 1 0.46 27.99
Ar 1 + 2 27.63 Fr - 1 0.46 27.17
Ti 2 + 3 27.49 Fr - 1 0.46 27.03
As 2 + 3 28.35 Ge - 1 1.20 27.15
Tc 2 + 3 29.54 G~ - 1 1.20 28.34
Ru 2+ 3 28.47 G~ - 1 1.20 27.27
In 2 + 3 28.03 G~ - 1 1.20 26.83
N 1 + 2 29.60 Ge - 1 1.20 28.40
Al 2 + 3 28.45 Ge - 1 1.20 27.25
V 2 + 3 29.31 G~ - 1 1.20 28.11
As 2 + 3 28.35 Sn - 1 1.25 27.10
Tc 2 + 3 29.54 Sn - 1 1.25 28.29
Ru 2+ 3 28.47 Sn - 1 1.25 27.22
N 1 + 2 29.60 Sn - 1 1.25 28.35
Al 2 + 3 28.45 Sn - 1 1.25 27.20
V 2 + 3 29.31 Sn - 1 1.25 28.06
As 2 + 3 28.35 Pb - 1 1.05 27.30
Tc 2 + 3 29.54 Pb - 1 1.05 28.49
Ru 2+ 3 28.47 Pb - l 1.05 27.42
In 2 + 3 28.03 Pb - 1 1.05 26.98
Te 2 + 3 27.96 Pb - 1 1.05 26.91
Al 2 + 3 28.45 Pb - 1 1.0S 27.40
V 2 + 3 29.31 Pb - 1 1.05 28.26
Tc 2 + 3 29.54 Po - 1 1.80 27.74
Tl 2 + 3 29.83 Po ~1 1.80 28.03
N 1 + 2 29.60 Po - 1 1.80 27.80
WO 90/13126 PCI/US90/01~8
: :: 100
2 ~
P 2+ 3 30.18 Po - 1 1.80 28.38
V 2 + 3 29.31 Po - 1 1.80 27.51
Ga2+ 3 30.71 At - 1 ~.80 27.91
Se 2 ~ 3 30.82 At - l 2.80 28.02
Rh 2~ 3 31.06 At - 1 2.80 28.26
Sn 2 + 3 30.50 A t - 1 2.80 27.70
Tl 2 + 3 29.83 At - 1 2.80 27.03
N 1 + 2 29.60 At - 1 2.80 26.80
P 2+ 3 30.18 At -1 2.80 27 38
Cr 2 + 3 30.96 At - 1 2.80 28.16
Fe 2 + 3 30.65 At - 1 2.80 27.85
As 2 ~ 3 28.35 G~ - 1 1.20 27.15
Tc 2 + 3 29.54 G~ - 1 1.20 28.34
Ru 2 + 3 28.47 Ge ~ 1 1.20 27.27
In 2 + 3 28.03 G~ - 1 1.20 26.83
N 1 + 2 29.60 G~ - 1 1.20 28.40
Al 2 + 3 28.45 G~ - 1 1.20 27.25
V 2 + 3 29.31 G~ - 1 1.20 28.11
As 2 + 3 28.3~ Q~ - 1 0.37 27.98
Rb 1 + 2 27.28 Ga - 1 0.37 26.91
Ru 2 + 3 28.47 Ga - 1 0.37 28.10
In 2 ~ 3 28.03 Ga 1 0.37 27.66
Te 2 + 3 27.96 G~ - 1 0.37 27.59
- Al 2 ~ 3 28.45 Ga - 1 0.37 28.08
Ar 1 + 2 27.63 ~a - 1 0.37 27.26
Ti 2 + 3 27.49 G~ - 1 0.37 27.12
As 2 + 3 28.35 In - 1 0.35 28.00
Rb 1 + 2 27.28 In - 1 0.35 26.93
Mo 2 ~ 3 27.16 In - 1 0.35 26.81
Ru 2 + 3 28.~7 I n - 1 0.35 28.12
In 2 + 3 28.03 In - 1 0.35 27.68
Te 2 + 3 27.96 In - 1 0.35 27.61
Al 2 + 3 28.45 In - 1 0.35 28.10
Ar ~ + 2 27.63 In - 1 0.35 27.28
Ti 2 + 3 27.49 In - 1 0.35 27.14
As 2 + 3 28.35 Ag - 1 1.30 27.05
WO 90/13126 P~T/US90/019~8
101 2Q~ J~
Tc 2 + 3 29.54 Ag - 1 1.30 28.24
Ru 2 + 3 28.47 Ag - 1 1.30 27.1 7
N 1 + 2 29.60 Ag - 1 1.30 28.30
Al 2 + 3 28.45 Ag - 1 1.30 27.15
V 2 + 3 29.31 Ag - 1 1.30 28.01
Cations and anions with n - 16 (resonance shrinkage energy is given by
2 27.21; with n = 16, the resonance shrinkage energy is 217.68)
Atom nnth lon- Atom n nth lon-Energy
Oxidiz- ization Reduced izationHole
ed Energy Energy (eV)
(eV) (eV)
Be 3 + 4217.71 H - 1 0.8021 6.91
Be3+ 4217.71 Li -1 0.61217.10
Be 3 + 4217.71 R - 1 0.30?17 41
1 5 Be 3 + 4217.71 C - 1 1.12216.59
Be 3 + 4217.71 O - 1 1.4721 6.25
P 5 ~ 6220.43 O - 1 1.4721 8.96
P ~ + 6220.43 F r 1 3.45216.98
Be3+ 4217.71 Nb -1 0.52217.19
Be 3 + 4217.71 Al - 1 0.52217.19
Be 3 + 4217.71 Si - 1 1.39216.32
Be 3 + 4217.71 P - 1 0.78216.94
Be 3 + 4217.71 S - 1 2.0721 5.64
P 5 + 6220.43 S - 1 2.07218.36
P~5 + 6220.4~ Cl - 1 3.61216.82
Be 3 + 4217.71 K . - 1 0.6921 7.02
Be 3 + 4217.71 Fe - 1 0.5621 7.1 5
Be 3 + 421 7.71 Co - 1 0.9521 6.76
Be 3 + 4217.71 Cu - 1 1.8221 5.89
P 5 + 6220.43 CU -1 1.8221 8.61
P 5 + 6220.43 E3r -1 3.36217.07
Be 3 + 4217.71 Rb - 1 0.30217.41
P 5 + 6220.43 1 - 1 3.0621 7.37
Be 3 + 4217.71 Cs - 1 0.30217.41
Be 3 ~ 4217.71 Se - 1 1.70216.01
WO 90/13126 PC'r/US90/0199~
2 ~ 9 '~
- 102
P 5 + 6 220.43 Se - 11.70 218.73
P 5 ~ 6 220.43 Te - 12.20 218.23
Be 3 + 4 217.71 As - 10.60 217.11
P 5 + 6 220.43 As - 10.60 219.83
5 P 5 + 6 220.43 Sb - 12.00 218.43
Be 3 + 4 217.71 Bi - 10.70 217.01
P 5 ~ 6 220.43 Bi - 10.70 219.73
P 5 + 6 220.43 Tl - 12.10 218.33
- P 5 + 6 220.43 Au - 12.10 218.33
1 0 Be 3 + 4 217.71 Hg - 11.54 216.17
P 5 + 6 220.43 Hg - 11.54 218.39
Be3+ 4 217.71 As -1 0.60 217.11
P 5 + 6 220.43 As - 10.60 219.83
Be 3 + 4 217.71 Ce - 11.20 216.51
1 5 P 5 + 6 220.43 Ce - 11.20 219.23
Be 3 + 4 217.71 Fr - 10.46 217.25
P 5+ 6 220.43 Fr - 10.46 219.97
Be 3 + ~ 217.71 G9 - 11.20 216.51
P 5 + 6 220.43 G~ - 11.20 219.23
Be 3 ~ 4 217.71 Sn - 11.25 216.46
P 5 + 6 220.43 Sn - 11.25 219.18
Be 3 + 4 217.71 Pb - 11.05 216.66
P 5 + 6 220.43 Pb - 11.05 219.38
P 5 + 6 220.43 Po - 11.80 218.63
P 5+ 6 220.43 At - 12.80 217.63
Be 3 + 4 217.71 Ge - 11.20 216.51
P 5 + 6 220.43 Ge - 11.~0 219.23
Be 3 + 4 217.71 (~ - 10.37 217.34
Be 3 ~ 4 217.71 In - 10.35 217.36
Be 3 ~ 4 217.71 Ag - 11.30 216.41
P 5 + 6 220.43 Ag - 11.30 219.13
Cations and anions with n = 54 (resonance shrinkage energy is giYen by
27.21; with n = 54, the resonance shrinkage energy is 734.67)
Atom n nth lon- A~om n nth lon- Energy
Oxidiz- ization Reduced ization Hole
WO 90/13126 PCI/USgO/01998
103 20~9~
ed Energy Energy (eV)
(eV) (eV)
O 6 + 7739.32 H - 10.80 738.52
O 6 + 7739.32 L i - 10.61 738.70
O 6 + 7739.32 C - 11.12 738.20
O 6+ 7739.32 O - 11.47 737.85
O 6+ 7739.32 F - 13.45 735.87
0 6~ 7739.32 Na - 10.52 738.80
O 6~ 7739.32 Al - 10.52 738.80
O 6+ 7739.32 Si - 11.39 737.93
O 6+ 7739.32 P - 10.78 738.54
O 6+ 7739.32 S - 12.07 737.24
O 6+ 7739.32 Cl - 13.61 735.70
O 6 + 7739.32 K - 10.69 738.62
O 6 + 7739.32 Fe - 10.56 738.76
0 6+ 7739.32 Co - 10.95 738.36
O 6+ 7739.32 Cu - 11.82 737.49
O 6+ 7739.32 Br -13.36 735.95
O 6+ 7739.32 i - 13.06 736.25
O 6 + 7739.32 Se - 11.70 737.61
O 6+ 7739.32 Te - 12.20 737.11
O 6+ 7739.32 As - 10.60 738.72
O 6+ 7739.32 Sb - 12.00 737.32
O 6 ~ 7739.32 Bi - 10.70 738.61
O 6+ 7739.32 Tl - 12.10 737.22
O 6+ 7739.32 Au - 12.10 737.22
0 6~ 7739.32 Hb - 11.54 737.78
O 6+ 7739.32 As - 10.60 738.72
0 6~ 7739.32 Ce - 11.20 738.11
O 6+ 7739.32 Fr -10.46 738.85
0 6+ 7739.32 Gb - 11.20 738.11
O 6+ 7739.32 Sn - 11.25 738.07
O 6+ 7739.32 Pb - 1 1.05 738.27
O 6+ 7739.32 Po - 1 1.80 737.52
O 6 + 7739.32 At - 1 2.80 736.52
0 6 + 7739.32 G~ - 1 1.20 738.11
..,,:
.
.
WO 90t13126 PCI'/US90/01998
. :~ . 104
0 6+ 7739.32 Ga - 10.37 738.95
O 6+ 7739.32 In -1 0.35 738.97
O 6+ 7739.32 Ag - 11.30 738.02
Some representative couples comprising a c~tion and a molecule capable
5 of producing energy holes for shrinking deuterium atoms where the
molecule is reduced. The number in the column following the ion or
molecule, (n), is the nth ionization energy of the atom or molecule. For
exampie, Ga2~ + 30.71 eV = Ga3+ + e- and BF3 + e- = BF3 + 2.65 eV.
Atom nnth lon- Atom n nth lon- Energy
1 0 Oxidiz- ization Reduced ization Hole
ed Energy Energy (eV)
(eV3 ~eV)
Ga2+ 330.71 BF3 - 12.65 28.06
Se 2 + ~30.82 BF3 - 12.65 28.17
1 5 Tc 2 + 329.54 BF3 - 12.65 26.89
Rh 2 + 331.06 BF3 - 12.65 28.41
Sn 2 + 330.50 BF3 - 12.65 27.85
Tl 2 + 329.83 BF3 - 12.65 27.18
N 1 + 229.60 BF3 - 12.65 26.95
P 2 + 330.18 BF3 - 12.65 27.53
Cr2 + 330.96 BF3 - 12.65 28.31
Fe2+ 330.6~ BF3 - 12.65 28.00
Se2 + 330.82 NO2 - 13.91 26.91
Rh 2 + 331.06 NO~ - 13.91 27.15
- Xe2+ 33~.10 NO2 - 13.91 28.19
Pb 2 + 331.94 NO2 - 13.91 28.03
K 1 + 231.63 NO2 - 13.~1 27.72
Cr2 + 330.96 NO~ - 13.91 27.05
As 2 + 328.35 2 - 10.45 27.90
Rb 1 ~ 227.28 2 - 10.45 26.83
Ru2 + 328.47 ~2 - 10.45 28.02
In 2 + 328.03 2 - 10.45 27.58
Te 2 + 327.96 O2 - 10.45 27.51
Al 2 + 328.45 2 - 10.45 28.00
Ar 1 + 227.63 2 - 10.45 27.18
Ti 2 + 327.49 2 - 10.45 27.04
WO 9û/13126 PCl'tUS90tOt998
105 2 ~ 9
As 2 + 3 28.35 SF6 -1 1.43 26.92
Tc 2 + 3 29.54 SF6 - 1 1.43 28.11
Ru 2+ 3 28.47 SF6 - 1 1.43 27.04
Tl 2 + 3 29.83 SF6 - 1 1.43 28.40
N 1 + 2 29.60 SF6 - 1 1.43 28.17
Al 2 + 3 28.45 SF6 - 1 1.43 27.02
V 2 + 3 29.31 SF6 - 1 1.43 27.88
Ga 2 + 3 30.71 WF6 - 1 2.74 27.97
Se 2+ 3 30.82 WF6 - 1 2.74 28.08
Tc 2 ~ 3 29.54 WF6 - 1 2.74 26.80
Rh 2+ 3 31.06 WF6 -1 2.74 28.32
Sn 2 + 3 30.50 WF6 - 1 2.74 27.76
Tl 2 + 3 29.83 WF6 - 1 2.74 27.09
N 1 + 2 29.60 WF6 - 1 2.74 26.86
P 2 + 3 30.18 WF6 - 1 2.74 27.44
Cr 2 + 3 30.96 WF6 - 1 2.74 28.22
Fe 2 + 3 30.65 WF6 - 1 2.74 27.91
Ga 2 + 3 30.71 UF6 - 1 2.91 27.80
Se2 l 3 30.82 UF6 - 1 2.91 27.91
Rh 2 + 3 31.06 UF6 - 1 2.91 28.15
Sn 2 + 3 30.50 UF6 - 1 2.91 27.59
Tl 2 + 3 29.83 UF6 - 1 2.91 26.92
P 2 + 3 30.18 UF6 - 1 2.91 27.27
Cr 2 + 3 30.96 UF6 - 1 2.91 28.05
Fe 2 + 3 30.65 UF6 - 1 2.91 27.74
tc 2 + 3 29.54 CF3 - 1 1.8~ 27.69
Tl 2 + 3 29.83 CF3 - 1 1.85 27.98
N 1 + 2 29.60 CF3 - 1 1.85 27.75
P 2 + 3 30.18 CF3 - 1 1.85 28.33
V 2 + 3 29.31 CF3 - 1 1.85 27.46
As 2 + 3 28.35 CCI3 - 1 1.22 27.13
- Tc 2 + 3 29.54 CCI3 -1 1.22 28.32
Ru 2~ 3 28.47 CCI3 - 1 1.22 27.25
In 2 + 3 28.03 CCI3 - 1 1.22 26.81
N 1 + 2 29.60 CCI3 -1 1.22 28.38
Al 2 + 3 28.45 CCI3 -1 1.22 27.23
.
WO 90/13126 PCI/US90/01998
2 a ~3 L ~3 ~ ~ 1 0 6
V 2 + 3 29.31 CCI3 - 1 1.22 28.09
Ga2+ 3 30 71 SiF3 - 1 3.35 27.36
Se2+ 3 30.82 SiF3 - 1 3.35 27.47
Rh 2 + 3 31.06 SiF3 - 1 3.35 27.71
Sn 2 + 3 30.5C SiF3 - 1 3.35 27.15
P 2 + 3 30.18 SiF3 - 1 3.35 26.83
K 1 + 2 31.63 SiF3 - 1 3.35 28.27
Cr 2 + 3 30.96 SiF3 - 1 3.35 27.61
Fe 2+ 3 30.65 SiF3 - 1 3.35 27.30
1 0 As 2 + 3 28.35 NH2 - 1 1.12 27.23
Tc 2 + 3 29.54 NH2 - 1 1.12 28.42
Ru 2 + 3 28.47 NH2 - 1 1.12 27.35
In 2 + 3 28.03 NH2 - 1 1.12 26.91
Te 2 + 3 27.96 NH2 - 1 1.12 26.84
1 5 N 1 + 2 29.60 NH2 - 1 1.12 28.48
Al 2 + 3 28.45 NH2 - 1 1.12 27.33
V 2 + 3 29.31 NH2 - 1 1.12 28.19
Tc 2 + 3 29.54 PH2 - 1 1.60 27.94
Ru 2+ 3 28.47 PH2 - 1 1.60 - 26.87
Tl 2 + 3 29.83 PH 2 ~ 1 1.60 28.23
N 1 + 2 29.60 Pl 12 - 1 1.60 28.00
Al 2 + 3 28.45 PH 2 - 1 1.60 26.85
V 2 + 3 29.31 PH 2 - 1 1.60 27.71
Tc 2 + 3 29.54 al - 1 1.83 27.71
Tl 2 + 3 29.83 CH - 1 1.83 28.00
N 1 + 2 29.60 a~ - 1 1.83 27.77
P 2 + 3 30.18 ~1 - 1 1.83 - ~ 28.35
V 2 + 3 29.31 a I -1 1.83 27.48
Tc 2 + 3 29.54 S~l - 1 2.19 27.35
Sn 2 + 3 30.50 StJ - 1 2.19 28.31
Tl 2 + 3 29.83 S~l - 1 2.19 27.64
N 1 + 2 29.60 S~l - 1 2.19 27.41
P 2 + 3 30.18 S~J - 1 2.19 27.99
V 2 ~ 3 29.31 S~J - 1 2.19 27.12
Fe 2 ~ 3 30.65 S~l - 1 2.19 28.46
Ga2+ 3 30.71 CN - 1 3.17 27.54
WO 90/13126 PCltUS90/01998
107 . ~2.~ 9 ~
Se 2 + 3 30.82 Cl\t ^ 1 3.17 27.65
Rh 2 + 3 31.06 C~ - 1 3.17 27.89
Sn 2 + 3 30.50 Ci~t - 1 3.17 27.33
P 2 + 3 30.18 CN - 1 3.17 27.01
K 1 + 2 31.63 CN - 1 3.17 28.45
Cr 2 + 3 30.96 CN -1 3.17 27.79
Fe 2 + 3 30.65 CN - 1 3.17 27.48
Tc 2 + 3 29.54 SGN - 1 2.17 27.37
Sn 2 + 3 30.50 SCN - 1 2.17 28.33
1 0 Tl 2 + 3 29.83 SCN - 1 2.17 27.66
N 1 + 2 29.60 SCN - 1 2.17 27.43
P 2 + 3 30.18 SCt~t - 1 2.17 28.01
V 2 + 3 29.31 SCN - 1 2.17 27.14
Fe 2+ 3 30.65 SCN - 1 2.17 28.48
1 5 Ga 2 ~ 3 30.71 SeC~t - 1 2.64 28.07Se 2 ~ 3 30.82 SeCN - 1 2.64 23.18
Tc 2 + 3 29.54 SeCN - 1 2.64 26.90
Rh 2 + 3 31.06 SeCN - 1 2.64 28.42
Sn 2 + 3 30.50 SeCN - 1 2.64 27.86
Tl 2 + 3 29.83 Se~N - 1 2.64 27.19
N 1 + 2 29.60 SeCN ~ 12.64 26.96
P 2 + 3 30.18 SeCN - 1 2.64 27.54
Cr 2 + 3 30.96 SeCN - 1 2.64 28.32
Fe 2 + 3 30.65 SeCN - 1 2.64 28.01
25 Cations and molecular anions with n = 16 (resonance shrinkage energy is
given by 2 27.21 with n = 16, the resonance shrinkage energy is 217.68)
Atom nnth ion- Atom nnth lon- Energy
Oxidiz- i~ation Reduced ization Hote
ed Energy Energy (eV)
(eV) (eV)
P 5 + 6220.43 BF3 - 12.65 217.78
P 5 + 6220.43 NQ2 - 13.91 216.52
Be 3 + 4217.71 2 - 10.45 217.26
P 5 + 6220.43 0~ - 10.45 219.98
Be 3 ~ 4217.71 SF6 - 11.43 216.28
~, .
. .
,
WO 90/13126 PCT/US90/~1998
108
2 ~ 7~
P 5 + 6 220.43 SF6 - l 1.43 219.00
P ~ + 6 220.43 WF6 - 1 2.74 217.69
P 5 + 6 220.43 UF6 - 1 2.91 217.52
P 5+ 6 220.43 CF3 - 1 1.85 218.58
Be 3 + 4 217.71CCI3 - 1 1.22 216.49
P 5 + 6 220.43 CCI3 - 1 1.22 219.21
P 5 ~ 6 220.43 SiF3 - 1 3.35 217.08
Be 3 + 4 217.71 NH2 - 1 1.12 216.59
P 5 + 6 220.43 NH2 - 1 1.12 219.31
Be3+ 4 217.71 PH2 -1 1.60 216.11
P 5 + 6 220.43 PH2 - 1 1.60 218.83
P 5 + 6 220.43 CH - 1 1.83 218.60
P 5 + 6 220.43 SH - 1 2.19 218.24
P 5 + 6 220.43 CN - 1 3.17 217.26
1 5 P 5 + 6 220.43 SCN - 1 2.17 218.26
P 5 + 6 220.43 SeCN - 1 2.64 217.79
Cations and molecular anions with n = 54 (resonance shrinkage energy is
given by 2 27.21 with n = 54, the resonance shrinkage energy is 734.67)
Atom n nth lon- Atomn nth lon- Energy
Oxidiz- ization Reduced ization Hole
ed Energy Energy (eV)
(eV) (eV)
O 6+ 7 739.32 BF3 - 1 2.65 736.66
0 6+ 7 739.32 NC~ - 1 3.91 735.41
O~ 6+ 7 739.32 O2 - 1 0.45 738.86
O 6+ 7 739.32 SF6 - 1 1.43 737.89
O 6~ 7 739.32 WF6 - 1 2.74 738.58
0 6 ~ 7 739.32 UF6 - 1 2.91 736.41
O 6+ 7 739.32 CF3 - 1 1.85 737.47
O 6~ 7 739.32 CCI3 - 1 1.22 738.10
0 6+ 7739.32 SiF3 1 3.35 735 97
0 6+ 7739.32 NH2 - 1 1.12 738.20
0 6+ 7739.32 PH2 - 1 1.60 737.72
0 6+ 7739.32 CH - 1 1.83 737.48
0 6+ 7739.32 SH - 1 2.19 737.13
WO 90/13126 PCT/US90/01998
109 2 ~ 7
0 6 + 7 739.32 CN - 1 3.17 736.15
0 6+ 7 739.32 SCN - 1 2.17 737.15
0 6 + 7 739.32 SeCN -1 2.64 736.67
The fusion of deuterium to 3He releases neutron which can effect the
5 fusion of 6Li to helium. In one embodiment of Coulombic Annihilation
Fusion, 6Li is present in the fusion reaction mixture of deuterium where
fusion of deuterium further drives the fusion of 6Li.
Other atoms in addition to deuterium can be caused to fuse by
Coulombic Annihilation as described for deuterium.
The quantum of energy hole is calculated for the atoms involved and a
reaction or process which removes this much energy and regenerates the
atoms or molecules to be fused is effected until sufficient energy is
removed from the Mills orbitals so that the internuclear distance is
sufficient for the nuclear strong force to dominate the coulombic
15 repulsive force. Fusion then occurs.
Fusion Reactor
The fusion reactor 50, shown in Figure 6 comprises a vessel 52 which
contains the fusion reaction mixture 54, a heat exchanger 60, and a steam
generator 62 where the heat exchanger 60 absorbs heat released by CAF
20 and exchanges it with the steam generator 62 which absorbs heat from the
exchanger 60 and produces steam. The fusion reactor 50 further comprises
a turbine 70 which receives steam from the steam generator 62 and
supplies mechanical power to a power generator 80 which converts the
steam energy into electrical energy, which is received by a load 90 to
25 produce work or for dissipation.
Thè fusion reaction mixture 54 comprises a source of deuterium atoms
56 or a source of molecular deuterium, and a source of energy holes 58
which resonantly remove 2 27.21 eV; n = 2, 3, 4,..., of energy from
deuterium to effect shrinkage to the point of fusion. The source of
3 0 deuterium can be deuterium gas, electrolysis of deuterium oxide,
deuterium from hydrides, or deuterium from metal-deuterium solutions.
A source of ener~y ho!~es com~rises a catalytic energy hole ma~erial
58, typically comprising ol~ctrochernical couples including the catalytic
couples described in the Coulombic Annihilation Fusion Section. Thus, an
3~ exemplary fusion reaction mixture is molecular deuterium a salt of Pd2+
: . . .
WO 90/13126 PCI'/US90/01998
3 L~ rl 11 0
and a lithium+ salt. Palladium absorbs molecular deuterium and the
Pd2+/Li+ catalytic system effect resonant shrinkage of deuterium to the
point of fusion. In one embodiment, the lithium is 8Li in which case the
neutrons released from fusion of deuterium effects the fusion of 6Li to
5 helium.
In other embodiments, the fusionable material is one of any element of
the periodic chart, and the energy of the holes of the said source of energy
holes is resonant with the Mills orbital shrinkage energy which is
calculated using Mills mechanics of the present invention and described
10 for deuterium in Appendix Vl.
In the preferred embodiment, 2H, 3H, or 6Li is used as the fusionable
material .
in all embodiments, the source of energy holes is one or more of an
electrochemical, chemical, photochemical, thermal, free radical, sonic, or
15 nuclear reactions, inelastic photon or particle scattering reactions.
In the latter two cases, the present invention of a fusion reac~or
comprises a particle and/or photon source to supply the said energy holes.
In ail reaction mixtures a selected external energy device 75, such as
an electrode may be used to supply an electrostatic potential or a current
20 to decrease the activation energy of the resonant absorption of an energy
hole.
In another embodiment the fusion mixture 54, further comprises a
surface or material to absorb atoms and/or molecules of the fusionable
material 56. Such surfaces or materials to absorb deuteriurn, or tritium
2 5- comprise transition elements and inner transition elements including iron,
platinum, palladium, zirconium, vanadium, nickel, titanium, Sc, Cr, Mn, Co,
Cu, Zn, Y, Nb, Mo, Tc, Ru, Rh, Ag, Cd, La, Hf, Ta, W, Re, Os, Ir, Au, Hg, Ce, Pr,
Nd, Pm, Sm, Eu, Gd, Tb, Oy, Ho, Er, Tm, Yb, Lu, Th, Pa, and U.
Experimental
30 S. Pons, et al, have demonstrated cold fusion with an electrochemical
cell that electrolyzes deuterium oxide to deuterium at a palladium
electrode with lithium as the counter ion. That excess heat is released and
that some fusion of deuterium is detectabl0 is apparent by the present
invention. Th~ third ionization energy of palladium is 32.93 eV and the
3 5 first ionization energy of lithium is 5.392 eV. This system can
catalytically generate energy holes of
WO 90/13126 PCI'/US90/01998
111 ` 2Q~5~
32.93 eV - 5.392 eV - 27.538 eV
The catalytic reaction is given in the Coulombic Annihilation Fusion
Section. The quantum of energy needed to decrease a Mills orbital by
aO( n1 - n2 ) is 27.21 eV. The energy difference between 27.538 eV and
5 27.21 eV is carried by a phonon or a translational or rotational mode. CAF
occurs at a slower rate when sodium or potassium is used as the
electrolyte because the energy hole produced by the Pd2+/Na~ system is
27.791 eV and the energy hole of the Pd2+/K~ system is 28.589 eV.
The energy holes of the Pd2+/Li+ system are closer to the resonance
10 quantum of 27.21 eV. Thus, it is not surprising that lithium is a superior
counter ion to effect CAF.
That cold fusion at a titanium electrode has been observed by S. E.
Jones et al to proceed a faster rate than with the Pd2+/ Li+ catalytic
system is not surprising in that the catalytic reaction involves only one
1~ atom as the catalyst, and the third ionization energy of titanium is 27.491
eV which is close to the shrinkage quantum of 27.21 eV. The catalytic
reaction appears in the Coulombic Annihilation Fusion Section.
27.21 eV of heat is released during a radius reducing cycle of the Mills
orbital of the deuterium atom in the Pons and Jones systems.
20 Approximately 100 KeV of heat energy is released by the shrinkage
process before the nuclei approach sufficiently for fusion to occur. This
heat is unaccountable by both research groups. Interestingly, this
unaccountable heat was observed in electrochemical cells with pailadium
electrodes, Group I cation electrolytes, and aqueous solutions as long ago
25 as 1924 by Jirsa (Jirsa, F., Z. Physik, Chem., 113, 241 (1924)). Thus, Pons
and Jones' observation of the phenomenon of heat release due to resonant
Mills orbital shrinkage is not the first.
Furthermore, physicist Francesco Scaramuzzi effected cold fusion of
deuterium gas using shavings of titanium; whereas, in 1973, Catlett, et
30 al., (Catlett, D. S., et al., The Journal of Chemical Physics, ~., p. 3432,
~1973)) diffused deuterium gas into palladium and measured no fusion
products by sensitive mass spectroscopy. According to the present model
of-the atom, CAF was catalyzed by Ti2+ in the former experiment, and CAF
was not possible in the latter due to the absence of the second element of
35 a two-element catalytic couple such as Li+ of the Pd2~/Li+ couple.
, . ,
'
,
WO 9û/13126 PCr/US90/01998
2 0 ~ 7
1 1 2
Further Applications
Mills Mechanics, the present invention, is a means to derive a complete
quantitative description of any atom, molecule, or material. The said
descriptions can be used to device novel molecules, materials, and
electronic devices; thus, they can eliminate much experimentation. And,
they can be used to interpret the results of experimentation.
For any atom, the radii of all Mills orbitals are calculated using the
balance of forces as described in the One Electron Section, the Two
Electron Section, and the Three Electron Section. The orbital energies are
10 then calculated as described in the said sections to give the complete
mathematical description of any atom or ion. Thus, with the selection
rules, described in the Section Rules Section, together with the orbital
energies and the principle of conservation of energy, all transitions are
given.
Bonding is calculated by minimizing the total energy stored in the
electric and magnetic fields of the participating atoms as described in the
Nature of the Chemical Bond Section. The resulting minimum for all atoms
describes ~xactly any molecule or material. The physical properties can
then be calculated from the following parameters:
2 0 1.) coordinates of the nuclei and Mills orbitals;
2.) the bond and orbital energies
3.~ the bond energy as a function of said coordinates
- 4.) population of Mills orbitals (e.g., unpaired electron or two spin
paired electrons in a given orbital)
25 Furthermore, Mills mechanics is a means to calculate reaction
coordinates as energy surfaces that describe the intermediates of a
. reaction; thus, reaction mechanisms are given. With this knowledge, novel
syntheses and products can be engineered, catalysts can be developed, and
yields of the desired products increased. Also, phenomenon which occur
30 too rapidly to be observed or have yet to be discovered (recent examples
are cold fusion and high transition temperature superconductors) are
described exactty via Mills mechanics which provides a complete
description of matter on the atomic and molecular level.
WO 90/13126 PCI/US90/01998
2 ~ 3 ~ ~ 9 7
1 1 3
Appenclix I
Proof that the condition for radiation by a charge density function is
that it possesses components of its space-time Fourier Transform which
are synehronous with waves traveling at the speed of light is given.
5 Charge obeys superposition; thus, only a point charge need be considered.
The proof starts with the Fourier components of the current produced by
the moving charge. The electric field is found from the vector wave
equation in Fourier space (k, ~ space). The inverse Fourier transform is
carried over the magnitude of k. The resulting expression demonstrates
10 that ~he radiation field is proportional to Jl(c n ,CI~), where Jl(k,~) is the
space-time Fourier transform of the current perpendicular to k and n ~ Ik
; thus, the necessary condition for radiation by the charge is that its
space-time Fourier transform possesses components which travel at the
speed of light.
15 ` Il. The Source and Its Fourier Transforms
Consider a charged particle of charge q and position rO(t). The charge
density of the particle is described by
p( r, t) = qo[r - r o(t)] (2.1 )
where ~( r - rO ~ is the spatial unit irnpulse function. The current density
20 is
J ( r, tj = qr O(t)o[r - r o(t)] (2.2)
The spatial Fourier trarisform represents the current density as a
superposition of spatial exponentials, exp -j k- r.
r
J( k, t) = ¦ ¦ J d3 kqrO(t)o,[r - rO(t)] exp(-i k r) (2.3)
= qrO(t) exp(-i k- rO)
The full space time Fourier transform is of course,
WO 90/13126 PCl'/US90/01998
2 ~ r~ 1 14
J( k, w) = ¦ ¦ ¦ J dtd3 k J(r,t) exp(-i k r) exp(i~t) (2.4)
The inverse Fourier transform is
J( r,t)= (2 ) ¦d~'~ ¦ ¦ J dk3J(k,cl3) exp(i k r) exp(-ic,~t) (2.5)
Ill. The Electromagnetic Field
The electric field obeys the vector wave equation
V x ~V x E) ~ c2 ~jt2 = ~Il~t (3.1)
The space-time Fourier transform of the vector wave equation is:
k x [ k x E(k,c~) ] + c2 E(k,c~ oJ(k,c~) (3.2)
In the far-field, only the component perpendicular to k is of interest.
10 Concentrating on this component one has
1( l ) k2 C~21C2
with
- k
n Ikl (3.4)
IV. The Inverse Spatial Fourier Transform
15 The inverse space-time Fourier transform involves the integrals
.. ..
J 2--Jt exp(-ic,~t)(2 )3JJJd3kexp(ik-r )
We shall retain the Fourier transform with respect to time and thus
not carry out the integration over ~o. But we shall foous on a spectral
width d~ of the field and thus write down expressions for El(r,~)2 . We
.
.,
WO 90tl3126 PCr/US90/01998
115 2~ 3 ~
! . ' : :;
separate the integrals into an integral over the magnitude of k, and into a
double integral with respect to the angles ~ and ~ of k with respect to r.
E (r ~jdc~) = d~l) ( 1 )3JI d~d~sin~
Jic~ ok2dk k 2[ (2 / 2] e x p ( i k- r ) (4 .1 )
The last integral can be carried out by contour integration. For k r ~ 0,
the contour must be closed into the negative imaginary half plane of k
with the result
d~ 1 2 ~2 Cd ~ d~d~sin~
El(r,~)2~ = (2~) c2 d(c)JJ 41~
~0 cnx[nxJ(c n,~)]exp(iC n-r) (4.2)
ThiS expreSsion may be rewritten in a way that lends itself to an
appealing interpretation. The density of (linearly polarized) modes per
unit volume and unit solid angle, p(cd,Q), is
( Q) d dn 1 (_)2d(C~dn
With this definition, one has
El( r ~C~) 2 = 2 JP(~'Q)dC')dQ~
_ _ C3 -- ~
nx[nxJ(c n,c~)]exp(iC n-r) (4.4)
The field El(r,c,))2 is propsrtional to -J(c n,cl)) namely, the Fourier
component for whiCh k = co/C. Factors of ~D that multiply the Fourier
component Of the Current are due to the density of modes per unit volume
20 and Unit solid angle. An unaccelerated charge does not radiate in free
space, not because it experiences no acceleration, but because it has no
- ,
~ ~ ~ ,.............. . ' '
.
WO 90/13126 PCI/US90/01998
- 116
2~3~3~ ~
Fourier component.
_ ~ _
J(c n,~)
Indeed, from (2.3)
J (k,~) = rdtqv exp(-ik v t + ic,)t)
= 2J~qv~ -v ) (4 5)
The only nonzero Fourier components are for
vcos6 c (4.6)
where ~ is the angle between v and k. The reason for the radiation of
an accelerated charge is that the Fourier decomposition of the current
10 acquires Fourier components that are "synchronous" with the light
velocity, i.e. with the propagation constant Ikl = c . Thus, for example, an
oscillating charge
rO(t) = d sin~Ot (4 7)
has a Fourier spectrum
15 J(k,c~) = 2 Jm(kCos~d){~[Ll~ - (m + 1)cl)o] + ~[c~ - (m - ~ )o]} (4.8)
where the Jm's are Bessel functions of order m. These Fourier components
can, and do, acquire phase velocities that are equal to the light velocity.
For small kd only m = 0 remains and is approximately independent of k,
J( c co`s~d) ~ 1-
V. Integration Over Angles
Starting with (4.2), we note that ~he exponential is a strong function
of ~ whereas the component n x [ n x J] varies much more slowly and thus
can be pulled out from under the integration. We have to integrate an
expression of the form
-
WO 90/131~6 PCI/US90/0199B
1 1 7 2 ~
"
2J~
r7~
1 C"2dC,~ I r d~d~sin~ ) d~
2~ c3 J J 4~ exp(iC cos~-r) = - 2 i c2r 2 exp(iC r)
o o
where the upper limit on ~ is ignored because of the rapid variation of the
exponent. With this result introduced in (4.2) one has
dcl) d~
El(r'~'~)2 = 2 4 '\1 ~0 cr nx[nxJ(C n,~)~ exp(iC- n r) (5.1)
5 Here, n is the direction of the radius vector r.We note now that a factor of
CJ~ appears in front of the current. One may therefore interpret the source
as containing the acceleration where ~ ) represents differentiation with
respect to the time coordinate.
It seems more natural to attribute the factor to the integration over
10 all the modes, in particular because then Cherenkov radiation presents
less of a mystery. Cherenkov radiation is produced by an unaccelerated
particle, but since the velocity of light is less than c, the particle current
can have Fourier components synchronous with c ~here ~ is
the dielectric constant of the medium.
Appendix ll
Space-time Fourier transform of Mills orbitals.
The space-time Fourier transform in three dimensions in polar
coordinates is given as follows:
G(S,~ j ¦ g(r, ~ ), t)es~p (~ srlcos ~ cos
O O
s3n ~3 sin ~3 cos(~ ]) r2 sin ~ dr d~ d~ dt
with circular symmetry,
2 5 ~ ~11
G(S,~ - 2IEJ J g(r, ~3 ) JO 12~1sr sln ~1 sln ~) e~ sr cos
O O
cos ~3) r2 sln ~ dr d~
... . . .
,~, .
. , .
~. ,.
.;
WO 90/13126 PCI'/US90/01998
1 1 8
J
with spherical symmetry.
r~
G(S) - 4~J g(r)slnc (2sr) r~ ~r
O
For separable variables
f(r) 9(~) h(~) k~t) ~ > F(s) 6~)) H(q~) K~)
Mills orbitals are separable into a product of functions of independent
variables, r, ~, ~, and t. The radial functions are delta functions. The time
functions are of the form ei"t~ the angular functions are spherical
15 harmonics, sin or cosine trigonometric functions or sums of these
functions, each raised to various powers. The space-~ime Fourier
transform is derived of the separable variables for the angular space
function of sin ~ and sin a. It follows from the space-time Fourier
transform given below that other possible spherical harmonics angular
20 functions give the same form of result as the transform of sin ~ and sin ~.
The space Fourier transform of f(r) = ~(r-rO) is given as follows: ~
tOO
~(S) ~ 4~1 ~;(r - rl) slnc(2sr) r2dr
J~
` ~(S) - 411rl2 slnc~2srl~
The space Fourier transform of y(~) - sin ~ is given as follows where
there is no dependence on ~:
6(~) - 2J~¦ ¦ sln~3 Jc ~2~sr sin ~3 sin 0) exp (~ sr ~os (~ cos ~)
O o
sin ~ ~2 d~ dr
WO 90~13126 PCI/US90/01998
2 ~
119 :.
G(~ 211~ r2sln~3Jo (2Ttsr sin ~) sln ~3)
O O
cos (2~1sr cos (~) cos ~) d~3 dr
00 (_ 1 )n(~ )2n
J~ (Z) ~ (LZ) ~ nl (~ ~2 ~ 13
z ~ 2~sr slnl~3 sln~3
G~)3 - 2~,1 ¦ r2sln2~ nl ~n ~1)
cos~2~srcos~) cos~3) d~dr
G(~ 2~1 Ir2l ~ r s~ 3 )211 sin~2(n~)
O O n-~ nl (n ~1)
2 0 tos(2~srcos~) cos~3) d~dr
~ 1~ 217~ ~ t-l!n~ r sin(~ )2(n-l) 2n~3
cos~27~srcos~ cos~ dadr
3 0
J~ k) ~ 2 - ~ cos(z cos~ ~sin2~ d~
rll~r~v~ 0
~. ~,," ,.
'. '. ~ ,
WO 90/13126 PCI/US90/01998
.
2~34~7 120
Re (V) > -(l/2)~ Z ~ 271sr cos~)
G(~ 211J r2 ~ r sinE~ )2(~
~ 1 0 l)
r(l)r(~ sr coS~)o
2 2 sin2~3 cos(2TCsrcos~) cos~3) d~3dr
(~r cos~))ur(l )
G(~ 2~ r2 (_1)v I(~rs~n~ )2
~, ._ . ..
1 5 ~ V ~O - l )l
r(2l)rl1~ 2 ) (~Isr cos~3?1) ¦ Sln2V~3 c0S(27~srco~ Cos~3)d~dr
(~sr~s~ ) rll)rO~l)
~ 2
G(~ 2~1 r2 ~ r sln~3 )2(~1)
O ~"g o 1) (1)
~l)r(~
J~(2~sr cos ~3) dr
(~sr cos~
Hankel transform formula:
~-~1/23 (rs)(1~23J~(rS) dr~ S~t/2)
o
Hankel transform relationship:
W0 90/13~26 Pcr/US90/01998
2 ~ 9 3J
121
~0
~(X) <~ == => 9(y; V) ~ y)( ~ /2)J~ y) d~
o
~Im ~ ), m ~- 0, ~, 2.. <~ 9S~ y(l~2~ - O(~)ml ~(mtO-1/2)9(y; m~
r r~(~ (rS)~l/23 J~rs) ~r ~ s(l/2)~0( d )VI SU~O-l112)
1 0 ( ~ ~2)
r1) 5(1/2) Jv(rs) dr ~ ~ ~ (dds)ul s21)
,00 .
J rV s(1/2) J~(rs) dr ~ S(l/2)-2v 21)1 sv, 201 5(1/2)-V
r S~~ 1 /2)s( 1 ~2)Jl~(r~) d~ " 2VI ~-V
oo ~ 00
5(~) - 2~ C sln~3
~ J01~(~- 1)1
r~L,r",~1)
2 2 rl)J~I2~srCos ~3) dr
(~s ~ost~
letr~- r dr... dr'
2~ Cos ~3 2R ~os
oo 00
fi~ 2~ ~ ~ $1n~3 ~a
1~1J l)tO-l~
3 r~1)r~
? . 2 ~) J(sr') dr'
(~s ens~) (2~ cosÇ3)'~
~o
~ 3) 2~ sln~ 3
V'l U (V - l)~
.
~ .
,
WO 90/13126 PCI'/US90/01998
1 2 2
2 ~
r(l~r~
2 2 2~1 S V
111s c os~33Vt2~ tos~3)~ 1 Ol
G(~ 2~t (~ sln~3 3
0~ 1 i3 (V - 1 ) 1 (7't c o s ~3)2l)~ 1 2~ V l
The space Fourier transform of h(~) = sin ~ is given as follows where
10 there is no dependence on ~:
Apply change of variable to the Fourier transform of 9(~) = sin ~.
implies ~- - >~
H(~ sin~ ~2(1)-1~ r(l)rlv~l) S_2
0~1 V (V ~ os~3)Z~ol2Vtl 1)1
The time Fourier transform of K(t)~R~es~P(~ t~) is given as
fo I lows:
f~
J cos~O t expf-K)t) d~ 8 ~ (C4~ 4 ~
The space-time Fourier transform of a Mills orbital is of the ~ollowing
form:
~1(S, ~ F(S3 Gl~) H(~ K(O)
WO 90/13126 PCI/US9~ 1998
~ 0 ~
i~3
oo
~(S, ~4t~rl 2 slnt(2S~ sln~ !
r(l~r(u~l) 2~ 1
2V~ cos~2~
u-~ sin~ 2(0-l~ r(2)r(U 2) ?VI S-2V
0~) (V ~ 2~ cos~
The condit,on for radiation of a charge density function is given in
Appendix 1. The space-time Fourier transform of the charge density
function must not have waves synchronous with waves traveling at the
15 speed of light, that is synchronous with l~)n or synchronous with
c ~where ~ is the dielectric constant of the medium. Given the
angular veiocity, ~ = ~n. the space-time Fourier transform of the Mills
orbital is zero for
20S = ~ when (11.1 )
2~(nrl) = 27~rn = n~ n (11.2)
where n = 1
2~ n=2,3,4,
n = 2 3
is the allowed wavelength for n = 1
r1 is the allowed radius for n = 1
30 Thus, space-time harmonics of c = k or c ~= k do not exist.
Thus, radiation due to charge motion does not occur in any medium when
this boundary condition is met.
WO 90/13126 PCI/US90/01998
':
2~ ~ fi97 124
Appendix lll
The solution to the Schrodinger equation is a wave function ~ (x). An
interpretation of ~y (x) is required. Schrodinger postulated that ~ (x)
represents the amplitude of the particle in some sense, and because the
5 intensity of a wave is the square of the amplitude the ~intensity of the
partic!e~ is proportional to ~ (x) ~Ir (x) [~y t(x) is the complex conjugate of
(x)]. A controversy arose over the meaning of intensity. Schrodinger
considered e ~ '(x) ~ (x) to be the charge density or e ~ t(x) ~ (x) to be the
amount of charge between x and x + dx. Thus, he presumed the electron to
10 be spread all over the region.
The electron has kinetic energy and angular momentum and energy
must be conserved; thus, the motion of an electron must be time harmonic.
It is demonstrated in Appendix I that emission of electromagnetic
radiation occurs if the space-time Fourier transform possesses waves
15 that are light synchronous with waves traveling at the speed of light. It is
demonstrated below that the Schrodinger wave equations have such
components; thus, they must radiate. That no radiation is observed
demonstrates the invalidity of ~hese equations as an accurate description
of an electron.
20 The angular functions of Schrodinger wave equations are spherical
harmonics and their space-time Fourier transform is given in Appendix ll
as the transforms of 9(~), h(~), and k(t). The radial solutions are of the
form of a r raised to a power times a negative exponential of r. The space-
time Fourier transform of the radial function f(r) = re~r/~O follows:
~ OO
re~~r~o3 sinc(2sr) r2dr
Jo
,~0
¦ r3e-(r/~0) s!n 2~(2sr) dr
Jû ~C2sr
,0~ .
(r2¢~(r/~o))/(2 Jls) sin 4~sr dr
j.
.
,
WO 90/13126 PCI/US90/01998
2 0 ~
i25
Let r ~ r'/4~, dr' ~ (1/4J~ dr
1¦ r' 2 es~p ( ~~ ) 5In r's d~
4~ 0 ~ 2~s (4~)~o
1 0
~ne-a~ sln (xy) d~ ~ n~ ( 2 )n~l
O C~, ~ y2
1 5
2 n ~ 2m 4
% ~ )m ( 2~ aJ
m~0
Let x - r, S - y, a ~ 1 /4~aO ~ n ~ 2
00 '
1/4~1 - !? ~-(r/4Jl:~) sin rs dr ~ 1 _
O (4~r~)22~s (4~ 211s
(21)(. (~.~4~o3 )3
~/4~)2 ~ ~2
~ . .
m2'0 ( 2m ~ /47~O)
.
WO 90/13126 PCl'/US90/01998
~Q~4~
Thus, the complete space-time Fourier transform of a Schrodinger
5 wave equation is given as follows:
W(S ~ (21)(_(~/4~0~ )3~ )m
1 0 (47~)3 2~s (1/4~uo~2 ~ s2 m-~O
3 ) ( - ~ )2m
2m ~ 1 1 /4~nO
2~ cOs~3)2o~ ! 5-2t
~t(~sln~3 )2~ ) r~2~r~L,
_ _ _ __ _ 2 2 0 ~
~u ~ cos~3)2U~l2~ 3
25 This transform has components c" = k which are not zero and are
synchronous with waves traveling at the speed of light. Thus, a charge
density function given by the Schrodinger wave equation must radiate in
accordance with Maxwell's Equations.
. ~
WO 90~13126 P{~/US90/01998
1 2 7 ~ Q ~
Appendix IV
Derivation of the Orbital Energy Stored in the Magnetic Fields of Two
Paired Electrons
Derivation of the Magnetic Field
Consider Figure 2; the magnetic fielcl must satisfy the following
relationships:
V- H = 0 in free space (IV.1)
n x (Ha - Hb ) = ~ (IV.2)
n (Ha - Hb ) = (IV.3)
H = - V ~ (IV.4)
2 Il.r 3 sin~ (IV.5)
Ha~ - Hb~ = 2 ~r 3 sin~ (IV.6)
To obtain H~ ,the derivative of Y' with respect to a must be taken, and
this suggests that the ~ dependence of ~ be taken as cos ~ .The field is
15 finite at the origin and is zero at infinity; so, solutions of Laplace's
equation in spherical coordinates are selected because they are consistent
with these conditions.
~=C[r] Cs~; r<rn (IV.7)
~ r 1
Y' = A --~ 3 cos~; r > rn (IV.8)
2 0 The negative gradient of these potentials is
H = r ~Ircos~ sin~) for r < rn (IV.g)
H = rn [r--]3 (Ir 2 cos~ sin~) for r > rn (IV.10)
The continuity conditions of Equations (IV.3), (IV.5), and (IV.6) and are
applied to obtain the following relationships among the variables
2 5 -- = r ~ I V . 1 1 )
rn n
rn rn = 2 ~rn3 (IV.12)
Solving the variables algebraically gives the magnetic fields of an
.
. .
WO 90/13126 PCr/US90/019~8
.
~ 128
2 ~
eiectron:
H = ~r 3 (~r cosl3 - l~ sin~) for r < rn (IV.13)
H = 2~r3 (Ir 2 cos~ -13 sin~) for r > rn (IV.14)
Derivation of the Energy
5 The energy stored in the magnetic field of two electrons is
2 ~
Emag =2 2 ~lo J J JH2r2sin~drd~d~ (IV.15)
o o O
Emag,totai = Emag,externai + Emag.internai (IV.16)
¦ ~ oJ[ llrl3] ~ (IV. 17)
4~ 0e2~2
3IL2r13 (IV.18)
1 o J i [ 2~r3 ] (4cos~ + sin2~) r2sin~drd~d~
2~ oe2~2
3ll2r13 (IV.20)
'4~,o~2~2 2~ oe2~2
Emag.total = 3~L2r13 + 31,l2r13 (IV.21 )
2J~IlOe2fl2
Emag,total = ~2 r13 ( I V . 22)
WO 90/13126 PCT/IJS90/01998
129 20~97
Appendix V
The Hydrogen Molecule
It can be shown easily that the internuclear distance for the dihydrogen,
H2, is 0.748 A. Consider two hydrogen atoms, A and B, approaching each
5 other along the x-axis as shown in Figure 3. The radius of each Mills
orbital is aO. The electrostatic energy is
Einteraction= 2x 2 ~O J~2dv (v 1~
We define this energy as EjnteraCtjon Recall that the electric field is zero
for r > aO. Until the orbitsphere penetrate the energy of interaction,
10 Einteraction, is zero.
As the atoms move closer, the Mills orbitals begin to penetrate. When the
penetration is small, as shown in Figure 4, Ei~teraction decreaseS (is
negative) because most of the electric field vectors from nucleus A in the
overlap region are pointed in direct opposition to the B electric field
15 vectors from nucleus B.
As the atoms move closer and the overlap increases, the Einteraction will
continue to decrease (become more negative). However, the decrease per
unit volume will be smaller because a lower fraction of the A-vectors
will be in direct opposition to the B-vectors. Figure ~ shows the two
20 radial vectors and the net electric field vector (EAg) for the point of
intersection of the Mills orbitals.
We see that
K
EA = E~ = ~a )2 (V.2)
A A (aO)4 (V.3)
2 5 EXB a EXA (V.4)
EAB = EyA + EyB = 2 EyA ~V.5)
From the angle ~,
y _~ EyA ~V.6)
EyA = (a )3 (V.7)
yK
EAB -- 2 (aO)3 (V.8)
'.' .,
WO 90/13126 PCr/US90/01998
2 0 3 ~ ~ ~ 7 1 3 0
Therefore, (EAg)2 will be less than [(EA)2 + (EB)2] when
4y2 K2 2K2
(aO)6 ' (aO)4 (V.9)
y2 < (a2) or y < ~ (V.10)
Thus, for y = O to y ~ aO/~r Ejnteractjon de~reases- For y > aO/~ Einteraction
5 Increases. And for y = aO/~, Ejnte~aCtjon is a minimum. When y = aJ~
RAB = xB = 2x ~ = ~ aO = 0.748A (V.11)
- The experimental internuclear bond distance is 0.746 A
. .
,
.
WO 90/13126 PCrlUS90/01998
131 20~9 7
Appendix Vl
Calculation of the Resonant Energy Hoie to Effect Shrinkage of the
Radius of the Mills Orbital of the Deuteriurn Atom.
For the deuterium atom, the force relationship is given as follows:
llv2 ~2
r = 4~0r2
The boundary condition for nonradiative Mills orbitals derived in
Appendix ll, 21lr= n~, gives:
v=--.
~lr
Consider the case where the electron in the ground state losses kinetic
10 energy, 112 mv2, due to an inelastic collision for example, then the radius
of the Mills orbital will shrink until the boundary condition is satisfied.
The amount of energy which must be carried away (i.e., the magnitude of
the energy hole absorbed) is calculated as follows:
Let r1 = initial radius.
Let r2 = final radius.
The force balance is:
r = 4~0r2
Vo is introduced as a perturbation of the velocity and the magnitude of the
velocity change of the electron from the initial to final Mills orbital is
2 0 calculated as follows:
r~ Lr - Vo)2 = ~2
r2( ~2r12 ,ur1 + ) 4~eor22
Vo2 2tl Vo + t~2 e2
~Lr1 ~L2r1 2 47tEor2
V llrt ~ 2 l2r1 2 IL4~eOr22
Vo= tl ~
~r1 ~l4,l0r2
WO 90/13126 PCI/US90/01~98
2~5~ ~J~
- ; 1 32
e2 ~2
4~1~o ilao
Vo= ~+~
ILr1 ~2aOr2
For the ground state, the radius of the Mills orbital was determined in
the One Electron Atom Section to be aO. Thus, the boundary condition is
5 given as follows.
27~aO = ~
From the boundary condition, 21lr = n~, with r c aO, the radius of any
shrunken state is an integer fraction of the radius of the ground state.
Thus, for the first shrunken state
aO
r2= 2 ~ and in general
- aO
r2-
Substituting r1 = aO and r2= n into the relationship for Vo gives
. .. .
Vo = tl +,~ i h2n
,uaO ~ ~2aO2
Vo =--~ ~--
~aO~ ~aO
1 5 n=2,3,4
The angular velocity of the electron in ground state is a and the angular
velocity in the first shrunken state is--.
~aO
Consider the velocity of the centripetal force equation:
r2 ( Il.r1 - Vo)2 = Fc
2 0 and the relationship resulting from the perturbation:
Vo = 11 i ~ ~ n=2,3,4
~aO ~aO
In order to satisfy the boundary conditions, the first term of Vo, ~,
WO 90/13126 PCI-/US90/0~998
133 20~97
must be negative so that it adds to the initial velocity a to give the
final velocity a ~ and the kinetic energy due to the velocity component
~a must be removed to effect the shrinkage transition.
Ths magnitude of the energy hole which arises from this term is
5 calculated as follows:
E = 2 ~ V2 =
~2
E = 2 ILn 2 2
n=2,3,4.....
Thus, the absorbed energy hole which effects shrinkage is quantized.
10 For the shrinkage transition n = 1 to n = 2, the resonant energy loss to
shrink a Mills orbital by aO ( n1 - n2 ) where n1 is the quantum number of
the initial orbital and n2 is the quantum number of the final orbital is
given as follows:
tl2
E=2n a2;n=2
1~ E ~2 (1.05459 X 10-34)2
~LaO2 (9.109~3 X 10-3~)(5.29177 X 1o-11)2
E = 4.3598285 X 1 o-1 8J = 27.211 682eV
n
Thus, shrinkage requires the electron to lose a resonance energy of 2
27.21 eV where n - 2, 3, 4,.....
Notice that absorption of an energy hole reduces the radius; whereas,
20 absorption of energy as a photon increases the radius. The former
increases the coulombic force by the rnultiple of n; the latter decreases
the coulombic force by the multiple of n where n is the integer of the
transition; thus, the force balance,`and the boundary conditions for
nonradiation are satisfied.
wo 90~13126 PC-/US90/01998
2 ~ ~3 ~ J 1 3 4
Appendix Vll
Detailed Description of Figure 1. Mills Orbitals
Mills orbitals are obtained by adding a constant sphere which is
normalized to a spherical harmonic which is normalized. This function is
5 the charge density on the surface of the spherical delta function that
comprises the Mills orbital. The former can be consider the base charge
density whose current gives rise to ma~netic spin, and the latter can be
considered a charge density function which creates modulation of the
former and whose traveling wave of current gives rise to orbital angular
10 momentum. The total charge of the Mills orbital for an electron is e and
the total mass is ~L.
The application entitled ENERGY/ MATTER CONVERSION METHODS AND
STRUCTURES filed April 21, 1989 is herein incorporated by reference.
These and further methods and embodiments arising from substitution
15 and modifications made by one of ordinary skill in the art are considered
within the scope of the present invention. For instance, in the case of
energy release through fusion according to the present invention, the
fusion material may include more than one element or molecule, where
corresponding energy holes are provided for each fusion element.
20 Therefore, the present invention is not limited except by the claims which
follow.