Note: Descriptions are shown in the official language in which they were submitted.
Cette inveIltion se rapporte aux machines actionnées par
Ull pedalier
Bien que l'application de l'invention ne soit pas limi~ée
à un -type préciC de pedalier, le péclalier circulaire habituel
sera utiLisé aux fins de la presen-~e description, avec un type
particulier de cadre de bicyclette. Cette invention comporte
3 modes différents d~utilisation~ avec une grande varieté de
colutions pour cllacun de ces modes; en plus, il est possible
de combiner entre eux ces 3 modes d t utilisation. Il est prati-
10 quement impossible de donner une description genérale de toutcela sans se référer tout de suite aux dessins; donc, la pré-
sentatioll des différentes figures constituallt les dessins sera
incluse a l'intérieur de l'exposé détaillé.
~uelques définitions:
Déf. 1 : Phase descendante du cycle de pédalape.
- La fig. 1 est Ull cadre de bicyclette avec le pédalier cir-
culaire. La phase descendante s'effectue dans la portion de
1~0 degrés du cycle indiquée par les flèches, c'est-à-dire
quand le pied passe de la position la plus élevée du sol à la
20 position la plus près du sol, en appuyant vers l'avant avec le
;~ pied sur la pédale.
Def. 2 : Phase ascendante du cycle de pédalage.
;La fig. 2 est un cadre de bicyclette avec le pédalier cir-
; culaire. La phase asce~dante s'effectue dans la portion de 1~0
2~ degres du cycle indiquée par les flèches, c'est-à-dire quand
le pied passe de la position la plus près du sol à la position
la plus élevée du sol, quand le pied remonte vers l'arrière.
C'est la phase non motrice du cycle de pédalage ~ue la présen-
te invention va rendre motrice, Il est à noter qu'il est pos-
'
~ 3
2sible d~obtenlr une légere tlaction pendant cette phase grâ-
ce à l'eMploi de cales ou cales-pieds avec ou sans chaussures
specialec, mais ces articles sont très peu efficaces com~e
instrumen~s de traction à cause`des muscles utilisés; au~si,
llS sont pdrIols douloureux e~ même dangereux: en efet, le
pied n'est pas vraiment libre. ~e but premier de ces articles
est de garder le pied en position correcte sur la pedale.
L'invention actuelle repose sur des principes forts diffe-
rents; le pied ll'est pas attaché ~'aucune manière à la pédale
10 et d'autres muscles plus puissants sont utilisés pour rendre
motrice la phase ascendallte du cycle de pëdalage.
Déf. 3 : Les pièces motrices principales ( désignées par
PMP tout au lon~ de la description ).
La fig. 3 illustre ces P~IP, une pour chaque cuisse. Ces
15 P~ sont illustrées dans la position qu'elles occupent sur le
dessus des cuisses ( fig. 4 ). Ces pièces ne sont pas atta~
chées aux cuisses Sur la fig 4, les mécanismes qui relient
ces pièces à la structure de la bicyclette ne sollt pas illus-
trés pour le moment. ~haqu~ DI~ est confortable pour la cuis~
~0 se, de dimension et de forme convenable, conçue pour slappuy-
er sur une portion li~itée de la surface de la cuisse située
près du genou ( la dite surface étank celle la plus éloignée
du sol quand la cuisse est en position hori70ntale par rapport
au sol ). Chaque Pl~ ést lleLément sur lequel se situe le
point d'application de la force que l'on peut exercer par pres-
sion vers le haut sur chaque P~ de la portion de la cuisse en
contact avec la dite PMP quand le pied correspondant passe de
la position la plus près du sol à la position la plus élevée
du sol, danc la portion ascendante du cycle de pedalage (def2).
Chaque PlIP est dotée d'un axe de rotation horizontal par
rapport au sol et perpendiculaire a la cuisse ( désigné par
oo' C~ur les fig. 3 et 4 ). ~UppOSOIlS pour le moment que les
Pl~ sont attachtes à la cuisce de façon à ce qu'elles resteIlt
dans la position indiquée par la fi~. ~ pendant le cycle com-
plet de 360 degrés de pédala,e. Il nous faut conl~aître la tra-
; jectoire décrite dans l'espace par l'axe de rotation de chaque
PIV¢ penàant le cycle complet de 360 degrés de pédalage ( phase
descendante et phase asceridante )~ La fig. 5 montre la jambe
10 gauche vu de profil; OII voit les os de la cuisse et de la han-
che. Le point j est le point central de rotation, situé ~ ltin-
tersection de llos de la cuisse et l'os de la hanche. Il est
évident que la courbe décrite dans l'espace par l'axe de rota-
tiOIl OO ~ de la Pl~P(2) est Ull arc de cercle dont le cer.tre du
15 cercle ( de rayon r ) défini par le dit arc de cercle se si
tue à la jonction de l'os de la cuisse et de la hanche (point
j ), la dite trajectoire étant décrite dans la directicn des-
cendaJte ( fig, 6, 7, ~ ) lors de la phase descendante (def.l)
et la même trajectoire én arc de cercle étant décrite dans la
20 direction ascendante ( fig. 9, 10, 11 ) lors de la phase ascen-
- dante (def.2) du cycle de pédalage. Le symbole pour cet arc de
cercle est C; dans cette description, ce C revient souvent.
Dans ce cas-cij la dé~onstration a été faite avec un pédalier
circulaire; Il est a noter que quel que soit le type de péda-
25 lier utilisé ( verkical, elliptique, etc. ?, la courbe décrite
dans l'espace pa~ l'axe de rotation de la PMP ect toujours ce
même arc de cercle C qu'on vient de définir. Puisqu'on pédale
avec 2 jambes, il existe 2 arc de cercle C, deux points j
( jonction de l'os de la cuisse et de la hanche ).
4 ~ ~ ~ r3 i',J ''-'~
Ces points j se situent en quelque sorte au dessus de la
selle et à peu près sur les bords de cette dernière (voir fig.
12). A quoi servent ces pièces motrices principales (P~) ?
Il existe 3 méthodes pour les u~iliser ; il est possible de
combiner ces méthodes entre el]es ( nous n'étudierons pas ces
- oombinaisons puisqu'elles sont évidentes ) . Nous essaierons
de parler de technique le moins possible pour nous en tenir
aux principes de cette inveIItio~
P~EMIE~E MET~ODE
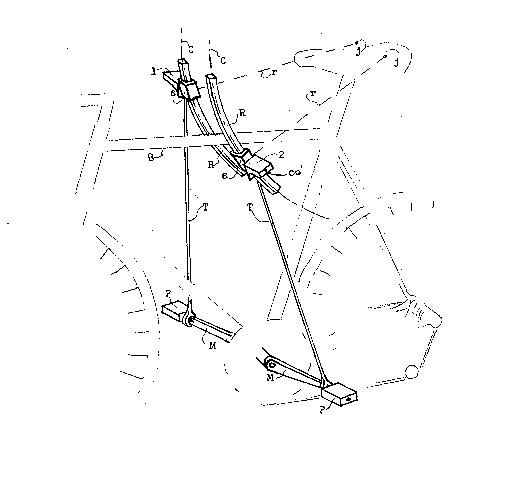
La fig 12 illustre la conception technique la plus simple
que l'on peut imaginer pour cette première méthodeO
Your chaque jambe, imaginons que nous a~ons une tige rigi-
de T reliée par une extrémité à l'axe de rotation de la péda~
le P (entre la manivelle M et la pédale P ) et reliée par 1'-
15 autre extrémité à l'axe de rotation oo' de la P~ (1 et 2)entre la PI~iP et la pièce coulissante désignée par la lettre s~
Cette tige T est un exemple de la revendiquation no. ~ a,b.
Pour chaque jambe, imaginons une pièce rigide courbée R
attachée à la barre centrale B du cadre ( la façon de l'atta-
2~ cher n'a pas été illustrée pour ne pas charger inutilementle dessin; en plus, il stagit de technique, ce qui nta rien a
voir avec les principes de cette invention ). Le rayon de
courbure r de cette pièce courbée R est le m8me que le rayon
de courbure r défini précédemment (fig 6 à ll~i. Donc, la cour-
2~ bure de la pièce R (désignée par C) est identique à l'arc decercle C des ~ig. 6 à 11. Chaque pièce courbée R est dotée d'-
une pièce coulissante s qui monte et descend le long de la
pièce ~ Il est évident que, lorsque la pièce coulissante s
monte ou de.scend le long de R, la Pl~P suit la même trajectoire
puisque l'axe de rotatioIl oo' de la P~IP est relié à la pièce
coulissante s et à l'extrémité supérieure de la tige T. Il
est évident que, lorsque la pièce coulissante s (et, par COII-
séquent la PMP) pour une jambe clonnée se d_place en montant
5 (phase ascendante def. 2), alors la pièce coulissante s (et,
par conséquent la FI~ ) de l'autre jambe se déplace en descen-
dant (phase descendante def. 1), et vice versa. La longueur
de la tige T est telle que, quand le pied est en position cor-
recte sur la pédale, la PMP est en contact avec la cuisse à
10 l'endroit approprié (~ig. 4) pendant le cycle complet ~ie 360
- degrés de pédalage, A noter que la conception technique élé-
mentaire de la fig. 12 perrnet de retirer les jambes ~acile-
ment et de les replacer tout aussi facilement puisque les
PMP (1 et 2) sont toujours exactement à l'endroit approprié
15 en tout point du cycle complet de pédalage. Les pièces R et s
ainsi que le mécanisme les attachant à la barre B constituent
un exemple de la revendiquation ~ ~i. Le fonctionnement de la
premi~re méthode de l'utilisation de l'invention se précise:
Considérons la phase ascendante (def 2) pour la jambe gauche
20 seulement; les ~ig. 13 et 14 permettent de visualiser le fonc-
tionnement. Pour rendre motrice la phase ascendante de la jam,
be gauche, il suffit de pousser vers le haut sur la PMP avec
la portion de la cuisse en contact avec la dite PMP, La PMP(2)
se déplace vers le haut le long de la pièce courbée ~ grâce a
25 la pièce coulissante s. Comme la tige T est attachée à ltaxe
de rotation de la pédale P, cette poussée vers le haut se
transforme en traction sur l'axe de rotation de 1~ pédale. Le
resultat est que le pédalier est actionné pendant la phase as-
cendante de la jambe gauche E~ M~M~ T~M~S que le pied de la
.
p ~
6 ..
jambe droite pousse la pédale droite vers le bas pendant la
phase descenda~te de la jambe droite: les deux jambes tra-
vaillent en même temps, d'où le double effet, Ensuite, le mê~
me processus se répète pour la jambe droite. Le mécanisme de
la fig. 12 est un exernple de la re~endiquation no 2 O ~ no~
ter ~ue les muscles utilisés par l~inventioIl dans la phase
ascendante ne sont pas les mêmes que ceux ~ui sont utilisés
pendant la phase descendante du cycle de pédalage, L'usage
de l~invention est polyvalent, en ce sens que le cycliste a
3 choixO Il n'est pas obligé d'utiliser l'invention dans la
: phase ascendante; dans ce cas il pédale normalement comme
s'il n'y avait pas d~invention. Il peut aussi util1ser la
phase ascendante seulement; dans ce cas, il n'appuie pas sur
les pédales dans la phase descendante. Il peut aussi utili~ .
: 15 ser la " pleine puissance "; il utilise alors les deux pha-
ses simultanément comme expliqué précédeT~ment. Le cycliste
change continuellement son usage de l'invention selon les
hasards de la route (montée, descente, vent, etc.), selon
la fatigue de certains muscles par rapport à d'autres. L'uti-
lisation simultanée de la phase descendante et ascendaIIte
permet. de garder le bassin plus stable sur la selle (une
cuisse pousse vers le bas et l'autre cuisse pousse vers le
haut) et permet dlaider à maintenir la bicyclette dans un
plan vertical plus ~table (il y a moins d'oscillations à
gauche et à droite). L'invention proposée peut permettre Ull
~ developpement musculaire plus harmonieux en ce sens qu'e].le
; permets une meilleure répartition de l'effort entre les dif-
férents muscles ou groupes de muscles. Il peut en résulter
moins de "gros mollets", moins de "grosses cuisses"O.....
.
~ vant de continuer avec la description de dlautres méca-
nismes selon la première methode d'utilisation de cette in-
vention, il convient de faire une mise au point. Les eléments
suivants peuvent varier:
- la longueur de cuisse ( la variable r ),
- la longueur de jambe ( la variable T ),
- la position de la selle ( ce qui fait varier j ).
Ces 3 éléments sont dépendants du cycliste lui-même. En
plus, il y a les éléments dépendants de la bicyclette elle-
10 même: longueur de la manivelle M, forme et dimensions du ca-
dre~,, Il est évident que les différentes conceptions techni-
ques devront tenir compte de ces éléments. Comme ici notre
but est de parler de principes inventifs et non de technique~
nous nous contenterons d'étudier brièvement l'effet sur la
15 position de l'arc de cercle C d'une variation dans chacun des
3 éléments dépendant~du cycliste lui-même, indépendamment les
uns des autres, c'est-à-dire que nous étudierons les effets
sur C d'une ~ariation dans un élément domlé en supposant que
les 2 autres éléments ne varient pas. Quand on~en aura termi-
20 né avec la 3 ième methode d'utilisation de ~'invention,nous reviendrons sur ce sujet en faisant la description dlun
MODELE MATHE~ATIQUE qui permettra une approche généraliséeO
-La fig. 15 montre lljeffet sur C d'une élévation de la selle
( j devient j t ), r et T ne variaIIt pasO C devient C~.
25 -La fig. 16 montre l'eflet sur C d'un~cuisse plu5 courte
( r devient r' ), j et T ne variant pas. C devient C'O
-Les fig. 17 et 1~ montrent l'ef`fet sur C d'une jambe plus
courte ( T devient T' ), r et j ne variant pas. C devient C'
NOUS SUPPOS~RONS QUE T, r et j N~ VA~I~NT PI~S~
. . .. ~
c3~ ~ r 3
Une autre mise au poi.nt est nécessaire. Voir la fig~ 19
Imaginons un véhicule a pédalier où le c~cliste est presque
couché Dans ce cas, il est évidellt que la portion du cycle
de pëdalage où le cycliste peut employer eff`icacement la PMP
est la portion ~ ~; or, si l'~n considère une bicyclette
conventionllelle (fig. 9, 10, 11), la portion clu même cycle
qui est efficace pour utiliser l'invention corresponds à la
phase ascendante (de~. 2). Cette def. 2 n'est pas valide dans
le cas du véhicule de la fig. 19 puisque pendant l'angle ~ le
10 pied se RAPPROCHE~du 501 et il s'en éloigne pendank l'angle ~O
Donc, pour que l~invention soit universelle, c'est à dire s'-
appliquer à n'importe quel type de pédalier et de machine, il
nous faut 2 nouvelles dérinitions pour remplacer les déf. 1 et
2, ces dernières n'étant valides que dans le cas du pédalage
15 absolument vertical PAR RAPPORT AU SO~, Pour ce faire, il ~aut
éliminer le ''SOLI' comme point de repère; la seule référence
valide est la colonne vertebrale et sa position par rapport à
la cuisse. ~n effet, la P~ peut être utilisée seulement quand
llos de la cuisse se replie VERS la colonne vertébrale, la co-
~0 loIme étant présumée en position FIXE par rapport au pédalier.
Voir les fig~ 6 à 11. Soit ~ l'angle iormé entre les deuxdroites imaginaires suivantes:
-Une droite allant de l'axe de rotation oo' de la PI~P (2)
jusqu'au point j, ~
2j -Une droite de réference (désignée par j~) partant du point
j et symbolisant 1'axe de la colomle vertébrale. Evidemment, la
colonne n'est pas droite: il suffit de la symboliser par une
droite choisie arbitrairement et de toujours utiliser cette
même droite pour nos dèfiIlitions, sans changer sa position.
9 'J i~ ? ,1
Soit~ l'angle que llOU5 veIloll~ tout juste de définir,
Voici les deux nouvelles définitions, la déf. 4 généralisant
la déf. 1, et la déf. 5 gélléralisant la déf. 2.
Déf. ~,: Phase d'EXT~NSIC~ D~3 LA C~IISSE du cycle de p~dala-
ge. Il y a ex~ension de la cuisse quand l'angle ~ VA ~NAUGI~NTA~T. Cela coI~respoIIds aux figures 6, 7 et ~.
Déf. 5: Phase de FLEXION DE LA CUI~S~ du cycle de pédalage.
Il y a flexion de la cuisse quand l'an~le ~ ~A ~ DII'iINUANT.
Cela correspollds aux figures 9, 10 e-t llo
10 Nous pouvons maintenant généraliser et dire ceci:
Si la colonIle vertébrale ne change pas de position relati-
ve par rapport au pédalier pendant UII cycle complet de pédala-
ge, alors, pour une jambe donnée, c'est pendant la FL~XION de
la cuisse correspondante que l'invention peut être utilisée,
15 quel que soit le type de pédalier et le dispositif qu'actionne
ce même pédalier. (On entends ici par "cycle complet de pédala-
ge" le chemin parcouru par l'axe de rotation de la pédale entre
son départ d'une pOSitiOIl donnée et son retour ~ 1~ même posi-
tion). Dans le cas particulier de l'engin de la figD 19, la
20 phase "flexion"(déf. 5) corresponds à l'angle ~t~, c'est ~ dire
le chemin parcouru par l'axe de rotation de la pédale du point
~au point ~ dans le SeDS des flèches~ l'angle ~ va en diminu-
ant). La jambe et la cuisse sont illustrés pendant l-a phase
.. ..
d'extensioll (défc 4); ltex-tension se fait du point ~vers le
25 point ~dans le sens des flèches~ l'angle~ va en augmentant~.
; Pour plus de précision ellcore, disons que pour déterminer
le point exact du cycle de pédalage où la flexion débute et le
point exact où la flexion se termine,?il faut utiliser le
MODELE I~ATh~I~ATI~UE proposé plus loin dans cette description~
.
10 ,~ ,p3 ;
a cause du grand nombre de variab]e dont il faut tenir
compte. La fig. 20 propose une méthode graphique approx-
imative pour trouver ces deux points. A noter que la po-
sition du sol n'entre pas en ligne de compte. Le pOiIlt x
est le point de début de flexion et le pOiIIt y est le point
de rin de flexion (donc de début d'ex-tension) : ce sont ces
deux points qu'il faut trouver. Les preuves géométriques ne
seront pas données~ ce serait trop long; seulement la fa~on
de le faire le sera. A noter que dans le cas particulier de
10 fig. 20, la pl~ase ~lexion couvre plus de 1~0 degrés, i.e la
flexion est plus longue que l'extension: résultat qui semble
bizarre mais bierl réel. r et r' sont les CuiSSeE en début et
en fin de flexioll respectivement (on remarque tout de suite
que l'anl-,le avec la colonIIe diminue, pass2nt de~
15 T et T' sont les jambes en début et en fin de flexion respec-
tivement; même chose pour les manivelles M et M'. x et y sont
évidemment des points de début et fin de flexion situés sur la
trajectoire~décrite par l'axe de rotation de la pédale.
Pour trouver x, il faut dessiner un cercle de rayon T qui
20 réponds à deux conditions:
-le centre (~oint a) de ce cercle doit se situer sur la cir-
conférence du cercle de rayon r et de centre j O
-la circonference de ce cercle de rayon T doit être tangente
AU P01~T x à la circoIIférence du cercle de rayon M.
25 Pour trouver y, la méthode est similaire, sauf que le centre
(point b) doit permettre de décrire une circonférence tangente
PAP, L'E~TERI~R (au point y) à la circonférence du ce~cle de
rayon M, Evidemment, les points a et b sont les pOiIItS limites
de l'arc de cercle C dont on parle depuis le débutO
De re~our ~ la PR~IEFl~ I~THOD~ (page ~). Cette méthode
est caractérisée par Ull mécanisme reliant chacune des PI~P
avec l'axe ~e ro-tation de la pédale correspondante, mécanis-
me C031ÇU de fa~on à permettre au pied d'avoir un contact adé-
quat a~ec la pédale quand ladite P~ est en contact avec laportion appropriée de la cuisce à tout instant ]ors du pédala-
ge, ce qui permets d'exercer une force de traction sur l'axe
de rotation de la pédale quand OII exerce une force de pression
sur la PI~ avec la cuisse pendaIlt la flexion de cette dernière,
10 Cela corresponds à la revendication no ~ IJn premier exemple
est celui de la tige T de la fig~ 12. La fig. 21 est une COIl-
ception teclmique élémeIltaire de ce mécanisme, montrant les
pièces constituantes non-assemblées; la tige T pourrait être
composéCde deux tubes vissant l'un dans l'autre pour être de
15 longueur ajustable et portant un roulement à bille~ au bas qui
s'insère sur l'essieu de la ~3édale: on reComlaît la ;pedale P,
la maliivelle M, la FMP en haut. Ces pièces SOIIt po~r le coté
droit du pédalier. La fig. 22 montre les mêmes pièces assem-
blées. ~uant à la fig. 23, une tige rigide de courbure permet-
~O tant le retrait facile de la jambe (désignée par TR) a été ajou-
tée pour une plus grande solidité ( a noter la courbure spéciale
du bas permettant le retrait aisé du pied ). Ces structures mé-
caniques correspondeD~ à la re~endication no ~; il est possible
d'en concevoir d'autres.
Toujours dans le cadre de la PIl~MI~'~E M~THOD~, llOUS allons
décrire plusieurs sortes de mécanismes qui remplissent tous la
même fonc~ion~ soit de permettre aux PMP de ~écrire la tra,jec-
toire en arc-de-cercle (fig. 6 à 11) ~ désignée par la lettre C;
Lesdits mécanismes sont cevx des re~endications ~ à ~ nclus.
12 ~ ,"~
Exemple de l~EVE~DICATION 3.
~ ur la fig. 2~, le côté ab du parallélogramme régulier
est orienté en direction du point j et demeure dans cette
position pendant tout le cycle de pédalage. La distance entre
b et j est egale à la distance eIltre d et l'axe de rotation
de la ~MP. a, b, c, et d sont les points de rotation. Ies
fig. 25 et 26 permetten-t de visualiser le fonctionnement pen-
dant la flexion de la jambe gauche. Pour éviter d'avoir à
f`ournir des preuves geométriques, des preuves graphiques seu-
10 lement seront fournies, avec les conditiollc de forlctiolll;ement.Tout con0le on évitera de parler de technique pour s'en tenir
aux principes de base, on évitera également de parler mathé-
matiques pour limiter l'étendue de la présente d~scription;
le but est d'éviter de mentionner les fa.its qui sont ~iORI~L~-
15 L~ ri EVID~ pour Ime personne normalement compétente.Les remarques précédentes s appliquent à -toute la description.
Sur toutes les figures (de fig. 24 à fig. 2~ inclus) OII a:
ac=acl,bd=bdL r, la aistance entre le poin~ j et l'axe de ro-
tation de la PMP étant égale à r ( longueur de cuisse). Sur
20 les ~ig. 27 et 2~ ) indique la pOsitioII initiale du
parallélogramme et (- - -) la position après le déplacement:
c se déplace en c', d se déplace en d' et PMP en PMP', le
long de la trajectoire C, r est de même longueur pour les
fig. 27 et 2~. La fig. 2~ prouve que pour un même r, on peut
25 varier la longueur du segment bj (ou la distance entre d et
l'axe de rotation de la PM~) et varier l'angle d'~rientation
vers le point j du Seg~ G ab: la PMP décrit LE M~M~ arc.de
cercle C (en passant de PMP à PMP') que sur la fig. 27, à
condition que les règles énumérées précé~.emmentlsoient suivies.
.
13
~xemples de H~V~NDIChTION ~.
Fig. 29: une tige rigide t reli~e par une extrémité à
l'axe de rotation de la Pl~ et reliée par l'autre extrémité
à Uli curseur s qui glis~e le 10ng d'une T.~artie de la circon-
férence d'un cercle ~e rayon ..rA dont le centre est J; évi-
demmen~, s glisse sur la pièce courb~e R dont le rayon de
courbure est rA . Deux points imprtants:
-la tige t est en quelque sorte "soudée" au curseur s de telle
fa~on que l'angle c~forrlle~ entre la tige t et la tangente à
lO'la pièce en arc de cercle ~demeure ~ONSTANT pendant tout le
cycle de petlala2e, r
-une i'ois l'angle ~J déterminé (on a en eff'et le choix de la
valeur num~rique de cet angle, ce qui détermine la position
de la pièce R sur la ciconférence CA du cercle de rayon rA),
15 la longueur de t est calculée de façon ~ ce que l'autre extré-
mité de t (qui est reliée à l'axe de rotation de la P~ se
situe sur l'arc de cercle C de rayon r et de centre j. Puisque
nous parlons de la PR~MI~ M~THGD~, nous retrouvons évidemment
la tige T qui relie l'axe de rotation de la PMP ~ la pédale.
20 Les fig. 30 et 31 permettent de visualiser le fonctionnement,
~ fig. 35 représente schématiquement en 2 dimer.sionc les élé-
ments de la fig. 29, pour un côté donné du pédalier mais sans
inclure T, P, et M. ~près le déplacement, t devient t' et rA
devient rAI et ~ v~ .
~'ig. 32: il s'agit essentiellement des mêmes principes que
ceux du mécanisme de la fig. 29, ~AUF ~ le rayon rB de l'arc
de cercle ~.est PLU~ G~lA~D que le rayon r de l'arc de cercle C
le long duquel se déplace la P~P,~U devient ~ et
La fig. 36 reprends les éléments de la fi~, 32.
.
~JJ~ 3 i
11~
Dans le cas de la fig. ~9~ ou si l'on veut la fig. 35), le
rayon rA de l'arc de cercle CA est PLUS P~TIT que le rayon
r de l'arc de cercle C le lor.g duquel se déplace ].a P~P.
La FIG. 1~ est Ull CAS PA~TICU~IER de la revendication
dans lequel rA~r~r ~T la l.ongueur de t égale 0 ; autrement
dit, l;'élément courb~ li (porteur du curseur s) es~ si-~ué SUI~
et la ~I~P est rattachée directement SUR le curseur s,
~MPL~ de REVENDICATION 5.
I1 s'agit toujours de la PR~ R;. methode puisqu'une tige
10 T relie l'axe de rotation de la pédale à la P~,
Fig. 37: La tige T peut glisser de haut en bas et de bas en
haut à l'interieur du curseur sl; ce curseur sl est fixé
au.curseur s2 et peut tov.rner sur lui-même; le curseur s2 peut
se déplacer danc les 2 sens le long de la tige yy' qui e~Qt
15 située sur l'axe 00'. Le chois de la pOSitiOII pour l'axe 00'
dépends de considérations techniques qui sont hors contexte.
La came cml est déca.lée de 1~0 degrés par rapport à la came
cm2 de l'autre jambe et sont en poC~ition fixe l'une par rap-
port à l'autre, étant reliée entre elles par un axe de rota-
20 tion XXt; la vitesse ang~llaire de rotation de cet ensemble dedeux cames est exactement la meme que la vitesse angulaire de
rotation du pédalier (sur la fig 37, cela a été symbolisé par
une chalne de traIIsmission reliée à deux roues dentées de
même diarnètre et même''nombre de dents, une roue étant fixée
25 à l'axe xxi des cames et l'autre roue étarlt Yixee à l'axe du
pédalier. ~haque came porte une feIIte guide à l'intérieur de
: laquelle glisse une tige ~; la rotation de la came , grâce à
cette X fait bouger le curseur s2 le long de la tige guide yy',
ce qui en retour guide le déplacement de la tige T avec sl.
'
~J~ 3
~ videmmeI;t~ la forme des rainures Ha dan les cames
doivent être calculées de fe~on à ce que le résultat final
soit le àeplacemeIlt exact dec Pl~ le long des courbes en
arc-de-cercle C.
Les fig. 3~ et 39 permette}lt de visualiser le fonctioIlllement
pour la jambe gauche,
La fig. 40 explique le processus à suivre pour des;iner la
came. La première étape conicte à choisir UII axe de refé-
rence GG'. La positior, de cet axe 00' va déterminer la forme
10 de la rainure de la came. ~a fig l~0 il:lustre 4 positions de
manivelle:
-Position 1, manivelle Ml, tige Tl allant de 1 à 1', le point
1' étant situé au bas de C ( début de la flexion).
Le point la est le pOiIIt d~irltersection avec l'axe 00'
15 Symbole:
-Position 2, manivelle ~2, tige T2 allant cle 2 à 2', le point
2' étant situé aussi sur C.
Le point 2a est le point d'intersection avec l'axe 00'
Symbole: - - -
20 -Position 3, manivelle M3, tige T3 allant de 3 à 3', le point
3' étant situé sur C.
Le point 3a e~t le point d'intersection avec l'axe 00
Symbole: - ~ ;l ~~~~~
-Position 4, manivelle r~r, tige T4 allant de 4 à 4', le point
25 4' étant situé sur C. Symbole: ...................
Le point 4a ect le point d'intercection avec l'axe GC'.
L~S POINTS la, 2a, 3a, 4a permettent de dessiner la cameO
~J ~J~ ~i 3 ~ i X.~ ~ ~
16
FIG 41: indique~e sens du déplacement du curseur s2
ainsi que la longueur dudit déplacement.
Quand la pédale passe de la position 1 ~ la posltion 2,
la tige T passe de la ~ 2a (symbolis~ par xl--~ ).Ce mou~e-
ment e-t auesi illustre par la fig. ~3
Quand la pédale passe de ]a position 2 à la position 3
la tige T passe de 2a à 3a (symtolisé par x2~---). Ce mouve-
ment est il]ustré par la fig. 44
Quand la pédale passe de la position 3 à la position L~,
10 la tige T passe de 3a à 4a (symbolisé par x3 ~ ~ ). Ce
mouvemeIIt est illustré par la fig 45
Quand la pédale passe de la position 4 et revient à ~a posi-
tion 1, la tige T passe de 4a à la (symbolisé par x4 ~)
Ce mouvement est illustré par la fig. 46.
15 On obtient finaleme~t: ~
(xl+x42 x2~x3~, ce qui perrnets de dessiner la orr1e
de la rainure de la came. Le résultat final sera celui dési-
ré, c'est-à~ dire que les PI~IP se déplaceront exactement sur
les arc-de cercle C. La fig. 42 indique comrnent dessiner la
20 came,
EXEMPL~ de ~EVENDICATI0N 6.
La fig 47 est encore un exerr.ple de la Pl~EI~IE!~E METH0DE
puisqu'il y a une tige T qui relie la pédale à la P,~JP.
Dans ce cas ci, la came (cm) est en position fixe et porte
25 une rainure(ra) à l'intérieur de laquelle glisse une tige(t)
qui est soudée à un endroit fixe choisi le long de la tige T;
l'endroit que l'on choisi le long de T pour souder t déter-
mine la forlrle de la rainure (ra) de la came. En p~dalant t
glisse à l'intérieur de ra et la PhiP suit exactement la cour_
17 ~Çj~ ?
bure de l'arc-de-cercle C dont on parle depuis le début.
~ncore une Iois~ OII parle de technique le moins possible
pour s'en tenir uniquement aux principeC de l'invention
Les fig ~ et ~9 permet~ent de visualiser le fonctionnement
pendant la flexion de la jambe gauche. La fig. 50 est une
mëthode graphique permettant de dessiner la came cm. Dans
le cas de la fig 50, le point où la petite tige t (qui s1in-
sère dans la rainure) est soudée à T a eté choisi arbitrai-
rement au centre de la tige T. -,
10 ~uatres poC~itions de manivelle sont illustrées: !
-Position Ml; pl est au centre de Tl; symbole~
-Yocition M2; p2 est au centre de T2; symbole:
-Position M3; p3 est au centre de T3; symbole~
-Position M4; p4 est au centre de T4; symbole~
15 On retrouve les ~oints pl, p2, p3, p4 sur la fig, 47
~EMPLE de REVENDICATION 7.
La fig 51 est encore un exemple de la PREMI~RE ~IETHODE
puisqu'il y a une tige T qui relie la pédale à la Pi~YP,
Danc ce cas particulier, la tige t2 est reliée à la tige T
20 au centre, ce qui fait que la courbe décrite dans l'espace
par le point de contact r2 est identique à la courbe de la
fig. 50 (définie par les points plj p2, p3, p4~, La pièce G
porte une fente guide pour l'extrémité rl de la tige tl,
rl, r2, r3, rx sont des points de rotation. Ce mécanisme a
25 toutefois une particularité: les tiges tl et t2 sont en po-
sition fixe l'une par rapport à l'autre comme l'illustre la
fig 52: en réalité, c'est la tige t3 qui tourne autour de
l'axe rx. Les fig. 53, 54, 55 et 56 permettent de voir le
ifonctionnement. Résultat: les Pl~ décrivent les arc C,
h~,,,f.,~,,,
1~
Suffisar~nent d'lnformations ont été données pour comprendre
les principes de fonctionnemellt de cette méthode; les détails
techniques évidell~s po~lr une pelsolllle normcll].emenl; compétente
ont e~é olni , dan~ le ~l~t de limi.ter l'étendue de la descrip-
tiOII.
~X~''~L~ d~ ~V~NDICATION ~.
C'est encore Ull exemple (mais cette fois le dernier) DE Lh
PR~I~iIEi~ THOD~ d'utilisation de l'invention puisqu'une tige
relie la pédale à la pièce motrice principale.
10 FIG 57: de chaque côté du pédalier, un polygone irrégulier
de 7 tiges articulées (dont 4 de ces 7 tiges formellt un par-
rallélogramme régulier) relie l'axe de rotation de la Pl~ à
la structure portant le pédalier (une bicyclette dans ce .
cas ci). Cet ensem~le de tiges se déplace dans un (ou des)
15 plan(s) parallèle(s~ au plan du cercle dont le centre est j
et le rayon est r(en effet, les Pl~ doivent suivre les cour-
~es en arc-de-cercle C). ~n tenant compte de certaines consi-
dérations techniques, on choisit un axe d'orientation X X
CONTINI~LL~ NT ORIENl`~ vers le point j; la tige ~ se situe
20 sur cet axe X X et est la seule des 7 tiges qui ne bouge
pas lors du cycle de pédalage; lors du pédalage, les 6 autres
tiges se déplacent d'une manière symétrique par rapport à la
tige af, respectivement d'un côté et de l'autre de celle-ci~
de fa~on a ce que les Pl~ suivent les courbes C; évidemment,
25 comme les ~anivelles sont décalées de lgO l'une par rapport à
l'autre, les 2 polygones de 7 tiges chacu~ sont toujours in-
versés symétriquement par rapport aux tiges ~. La fig. 5~
est Ull agrandissement du polygone de 7 tiges qui s'attache à
la PP]P gauche au point c.
19
Il est à noter que, similairement à la fig, 52, les tiges
~e et ex sont en positi.on fixe une par rapport à l'autre;
c'est plutôt la tige be qui tourlle autour du poi.nt de rota-
tion e; cela devient évident quand on examine les 3 positions
du polygone illustrées danc les fig. ~0, 61 et 62. On re~arque
que le point c ( où se sikue 1 t axe de rotation de la P~P) se
déplace exactement sur la courbe en arc de cercle C dont le
centre est j, point d'intercection de l'os de la cuisese e~ de
l'os de la hanche. I.a fig. 59 explique, sans donner les preu-
10 ves matllématiques, comment construire un tel polygone, Lafig 5~ montre de quelle fac,on il faut supperposer les 7 ti-
ges le6 unes par dessus les autre~ de fa~on à ce que ces tiges
puissent facilement glisser les unes par dessus les autres pour
paseer d'un côté de l'axe ~ ~ à l'autre côté de ce même axe,
15 Revenons à la ~ig 59:
Il faut:. lbc--~)= ~ de facoII à ce que le point c se con-
fonde avec le point d quand les tiges bc et ab sonk repliées
sur elles-mêmes et alignées sur l'axe imaginaire ~ ~ (ce der-
nier étant toujours orienté vers le point j),
20 Il faut: Pour déterminer où se situe le poin~ x, tracer un
cercle de centre f et de rayon df; à partir du point c, tra-
cer une droite parallèle à ~; à partir du point b, tracer une
droite parallèle à af (ou ~ ~L~); sur la droite ~, tracer une
tangente au cercle de'rayon ~ et de centre ~, Le pOillt x
~5 que 110II cherche se situe au centre du segmenk cy (désigné
par D), Ainsl, quand la ~ige x se repliera sur la tige xe
(ou xf) , le point c se déplacera toujours sur l'arc-de cercle
. Fournir les preuves geoMetriques seralt ~rop long.(~
I~I SE TEiiMINE Lh PRE~lIEE~ f~TH0DE D'~TILISATI0N de l'invention,
D~UXI~ I~1HOD~ D'UTII.I~ATION de l'invention.
Voir ~IG . ~3; on remarque irnmédiatement qu'aucv.ne tige rigide
ne relie l'axe de rotat.ion de la pedale à l'axe de rot~tion
de la PilP correc~pondante (ce qui était la caractt~ri3tiqli~ de
la Pl~ .H~ I~THOD~). Danc. l'exemple de la fig. 6,, il s'a~it
de T ~A~i;`G~ la force F~ qulon exerce svr la PI;lP de la cuic-
se gauche lors de la flexion de cette dernière DII~CTE~'~NT en
uIle force ~ DE ~N~ OPPO~E sur la P~i~' de la cuisse droite
lors de l'extension de cette dernière (évidemment, lors de
10 l'autre pl~ase de 1~0 degrés du cycle de pédalage, c'esk
de la cuisse droite qui est transformée en une ~ eur la
cuisse gauche); la force ~ ainsi exercée S îl~JOUT~ à la force
de pression déj~ exercee par le pied sur la pédale (désignée
par ~ sur la fig. 63 ); tel est le but visé par la 2e m~thodeO
15 Il s'agit donc de concevoir Ull mécanisme qui remplira les
fonctioIls suivantes: réuIir les deux PMP entre el.les de fa~on
à ce que le déplacement d'une des PMY danc: une direction don-
née le long de la trajectoire C entralIle le déplacement de
l'autre PMP dans la direction opl~osée la long de C (pour cette
20 PMP) et permettre de transformer la force q~e l'on peut exer-
cer par pression DE la cuisse SUR une PMP donI~ée pendaIIt la
flexion dc ladite cuisse en une force de pression DE l'autre
Pr~P ~UR la cuisse corlespondante pendant l'extencion de cette
derIlière~ pendaIlt le cycle de pédalage, dan6 le but d'action-
25 ner le pédalier. Tel est l'esseI;ce de la reveIldicatioll 90EX~MP~E de IU3VENDICATION 9
~e mécanisme de.la fi~.67 a été imaginé uniquemeIlt pour dé-
montrer uII principe inventif~ prouver qu'il pe~t êtYe possi-
ble d'accomplir ce que la revendication 9 indique.
21
Le mécanisme de la fi~ 67 est cel.ui de la fig 57 SAUF ~,U~
-les tiges T reliant les pédales aux PMP(s) sont inexistan-
tes (ces tiges concernaient la PE~jlIE.~E M~TH0DE).
-les deux polygones irréguliers (qui SOI;t essentiellement les
mêmes que ceux définis par les fig 5~ à 62 inclusivement)
sont reliés entre el~x par une sorte de ''diflc;i~eI;tiel''(disi-
gI;e par le symbole Dif sur les fig 64 à 6~ inclusivement );
ce différentiel (Dif) est composé de 4 roues d'engrenage(les
no. 1, 2, 3 et ~) de ~a~on c`l ce que ~ roues paral.Leles entre
10 elles tourneIIt en sens contraire l'une de l'autre(fig 6L~,65),
~ne caractéristique importarlte de ce rnecqnisme est illucitrée
par ].a fig 6~; c'est la tige fe du côté gauche du pédalier
qui est soudée directement à la roue d'engrenage no.l, c'est-
à-dire que la rotation de la tige ~ autour du pOiIlt f fait
15 tourner la roue ~'engreIlage no.l. De même, c'est la tige fe
du côt~:i droit du pédaiier ~ui fait tourIler la rol.le d'engre-
lla~e I;0.3. Les deux tiges af sont en pOsitioII fixe par rapport
au différcilltiel(Di~ ET SONT T0UJ0URS 01~IE~T~ES EN DIHECTI0N
des deux P0I~T~S J. Donc, la rota~io~ dans un sens donné d'une
: 20 dec deux tiges fe,fait automatiquemeIit tourner l'autre tige
fe dans le serls oppocië~ ce qui implique que le déplacement
dans Ull sens donIié d'uIle des deux FI~ (le long de ''iOli propre
arc-de-cercle C) entraine ~e déplacernent de l'autre P~ (le
- long de SOli propre aI~c-cle-cercle C) dans la direction opposée;
~5 c'est là l'objectif visé par la DEUXIEM~ TH0I)E d'utilisation.
A nok~l~ qu'il est possible kh~ioriquement de combiner ensemble
, -, . . . . . ~ ... . .. ..
la première ET la deuxième methode d'utilisation de l'inven-
tiOII: par exemple, dans le cas de la fig. 67, il est possi~le
D'AJ0UTER les deux tiges T reliant les pédales aux PMP(s).
~o~,Ç3~ ,J
22
TROISIE~ k~THODE D'UTILIS~TION de l'invention.
Comme dans le cas de la DEUXI¢M~ METHCDE, un seul exernple
de mécallisme sera donne; le but vis6 n'est pas la concep-
tion technique ideale: au contraire, il s'agit de simpli-
fier la technique au maximum pour s'en tenir aux principesinveIltifs. Esselltiellement, cette 3ieme méthode permets
d'~CCU~ J~il l'énergie develonpée (soit er. ,totalité, coit en
partie) par la force de pression DE la cuisse SUE~ une PIqP
donnée pendant la flexion de ladite cuisse, et permets de
10 LIB~ER l~énergie ainsi accumulée en une force de pression
de LA M~i~ pièce motrice principale SUR LA ~;IY~ cuisse ~en-
dant la phase dlex~tension de cette dernière~ dans le but
d~actionner le pédalier
La fig. 69 est un exemple de dispositif selon la reven-
15 dication no. 10. UIle mise au pOiIlt est nécessaire: en théorie~
la 3ième méthode pourrait être utilisée indépe}idamment des
deux autres méthodes pour actionner un pédalier. IL EST POS-
SIBLh' D:'EFFECTUER DIVERSEg COMBINAISONS ENTRE LES 3 METHODES o
P~r exemple, la fig 69 combine ensemble la lère méthode et la
20 3ième méthode; en effet, des tiges T relient les pédales aux
manivelles correspondantes¦uIIe partie seulement de lténergie
est accumulée dans les ressorts RS). La fig 69 est identique
à la fig 24(1ère méthf~de) sauf que des ressorts (un ressort
de chaque côté) relient les pOiIlts c et b. Ces ressorts (RS)
25 SYMBOLISENT la 3ième méthode. La fig 70 indiqu~ ce qui se pas-
se pendant la flexion: le ressort RB devient sous tension
(donc accumule de l~énergie) pendaIIt la flexion car la dis-
tance cb est plus petite que la distance c~b; le ressort re-
tourne cette énergie en se detendant pendant l'extension.
2~
MODELE I~AT~EMATIQUE
! Y
~Z~
~P~I~ /
P(_,~) \ T / ~ / P(~
\ M
x
P(o,o).~ J
P(~ P(~,--)
I
Voir page 7 de la description.
Imaginons un système de coordonllées cartésiennes P(x,y) où
le point P(O,O) est situé au centre de rotation du pédal erO
On recom-aît la manivelle M, la tige T (ou la longueur do la
jambe, le rayon r (ou la longueur de la cuisse~ de l'arc de-
cercle C et l'intersection de l'os de la cuisse et de la
hanche (point j). Soit~J ltangle entre la manivelle M et la
coordonnée horizontale xO Sur le dessin suivant, le ca~]re de
la bicyclette a été ~nlevé pour simplifier le dessin. Les
10 longueursPJet Q-permettent de tenir compte d'un déplacement
du pOillt j (par exemple un changement dans la position de la
selle, une variation dans les dimensiolls du cadre, etc~). Il
s'agit d'exprimer les coordonnées P(x,y) d'un point de la tige
T choisi le long de celle-ci à une distance ~ de l'axe de ro-
15 tation de la pédale. Avec llaide d'un ordinateur, on peut~
:
C j ~i.J t.~
21~grâce à ces équations qui donnent automatiq~ement les
coordonnées x et y d'un pOillt qurlconque sur T, tenir
compte de l'eff'et d~une variatioll de n'importe quelle
facteur (r, M, T, a, b, Di) sur la position ou la cour-
bure de llarc-de-cercle ~, de la came de la I'ig. 50, de
celle de la I'ig 37, etc; dans le cas particulier de l'arc-
de-cercle C, il faut ~ --r; à l'autre limite, dans le cas où
, les équations de ~ et~a ~n fonction de ~J vont nous
donner automatiquement les coordonr.ées circulaires ~-
et ~ ~du cercle décrit par 11axe de rotation de la pé-
dale dorit le rayon est M (longueur de la manivell.e), Voici
donc les équations donIIant les coordonnées ~ et ~ d'un
point P(x,y) choisi sur T (la démonstration mathémati~ue a
été omlse): a et b sont les coordonnées du point ;
en fonction de W
en fonction deUJ
~r ~
~. .
~p (,, ~ ~"P'~ ~ ?
A~
~ t ~ .~ ( + ~ -r + ~ L)
F ~!