Note: Descriptions are shown in the official language in which they were submitted.
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
- 1 -
SIGNAL PROCESSING APPARATUS
This invention relates to apparatus and for and a
method of processing signals.
Signal sampling techniques are used in a number of
fields of technology. A signal is sampled and the
information contained in the samples is utilised to make use
of information contained in the signal.
Sampling make take place in the time domain. For
example, a continuous signal may be sampled at regular
instants of time. As long as the sampling occurs at a rate
greater than the Nyquist rate, all information about the
original signal is retained.
Sampling may also take place in space.
Figure 1 shows a prior art antenna arrangement
comprising an array of spaced-apart antenna elements 1-5.
The elements are coupled via lines 6 to a signal processing
arrangement 7 which is coupled to further circuitry via line
8. The elements are spaced at a constant pitch d. Signals
are applied to, or obtained from, each of the antenna
.............................
....................
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
2 -
elements 1-5 via lines 6 such that a defined phase and/or
amplitude relationship exists between the respective signals
supplied to or obtained from, each element. In this way the
directivity and direction of the antenna beam can be
predetermined or adjusted. The signals received by each of
the individual elements can be considered to comprise
samples of a radiated signal taken at different points in
space.
In general, sampling is performed at regular, equally
spaced intervals. Sampling in the time domain is done at
regular intervals of time under control of a clock. In an
antenna array, such as a binomial array antenna, the
individual elements are all spaced at a uniform pitch.
Uniform intervals are generally employed because the
parameters of such systems are easier to determine on the
basis of uniform intervals. As a consequence the properties
of arrangements based on uniform intervals are well
understood and arrangements based on uniform sampling
intervals are almost universally employed.
While it has been suggested that, in theory, it would
be possible to provide arrangements in which the sampling
intervals are not uniform, it has also been acknowledged
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
- 3 -
that such arrangements would be difficult to design. The
provision of a non-uniform sampling interval would require
the provision of a dedicated signal processing arrangement
to process signals produced by such an arrangement. In
general, a uniform sampling interval arrangement is
perfectly satisfactory and so there has been no need to
attempt to construct an arrangement having a non-uniform
sampling interval because of the very great difficulties
involved in designing such an arrangement.
However, in certain appl'ications it would be
advantageous to be able to use non-uniform sampling
intervals. For example, in installing a phased array
antenna it would be a great advantage to be able to site
individual antenna elements according to site geography
(e.g. to avoid roads or building etc) rather than having to
space the elements apart by a constant pitch determined by
electrical requirements. It would also be desirable in such
a case to be able to use, for signal processing,
conventional signal processing arrangements designed to
operate on data obtained from an array of elements having a
fixed pitch. While it might be possible to design a
dedicated signal processing arrangement for use with a
particular arrangement of non-uniformly distributed
elements, this would obviously entail a great deal of extra
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
- 4 -
expense and design complexity.
Similarly, in radar or sonar applications, it would be
advantageous not to have to transmit pulses at a constant
rate, yet be able to use conventional signal processing
arrangements designed for use with pulses emitted at a
constant rate.
Certain types of signal processing arrangement can
only give a meaningful output if the correct number of
signals are presented to it. If one of the signals is not
present then no output can be obtained until such time as
the correct number of signals are received. Thus if a
single signal of a time-sequence of samples is missing, or
if an antenna element of an array becomes faulty, then it is
not possible to make use of the information contained in the
remaining samples of data or the signal produced by the
remaining elements. It would be advantageous to be able to
provide an output based on such information as is available.
The present invention provides signal processing
arrangement which allows signal processing arrangements
intended for use with uniform sampling intervals to be used
in conjunction with non-uniform sampling intervals.
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
In accordance with the invention, signal processing
apparatus comprises: means for obtaining a first set of
samples of a signal at a first set of non-uniformly-spaced
sampling intervals; means for reconstructing the signal from
the first set of samples; and means for generating, from the
reconstructed signal, a second set of samples of the signal
at a second set of sampling intervals different from the
first.
The second set of sampling intervals may comprise
equally-spaced intervals.
This allows subsequent signal processing to be carried
out with conventional signal processing apparatus designed
to accept samples taken at regularly-spaced intervals.
The number of samples in the first set may be the same
as the number of samples in the second set.
The samples may comprise samples taken at different
instants of time. For example, a continuous signal may be
sampled periodically, or respective echos from a train of
pulses may be sampled in consecutive time frames in a fixed
time relationship to the time of transmission of the
transmitted pulses.
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
6 -
The samples may comprise samples taken at different
locations in space. For example the individual elements of
an antenna array can be considered to sample a radiated
signal at different points in space. These samples are then
suitably processed to produce the desired antenna response.
In a further aspect of the invention, radar apparatus
comprises means to transmit a sequence of non-uniformly
spaced pulses; means to received a sequence of signals
comprising reflections of the `sequence of pulses, the
sequence of signals comprising said first set of samples;
and means to convert the first set of samples into a second
set of samples, said second set of samples representing the
sequence of signals which would have been produced in
response to uniformly-spaced transmitted pulses.
In this way the radar apparatus is not restricted to
the use of pulses transmitted at equally-spaced intervals.
Pulses having an arbitrary transmission interval can be
employed, yet the information conveyed by the reflected
pulses can be processed using conventional data processing
apparatus which requires the transmission of
regularly-spaced pulses.
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
7 -
In another aspect of the invention, antenna apparatus
comprises a plurality of non-uniformly spaced elements,
means for coupling received signals received by individual
ones of said elements to signal processing apparatus to
produce a further set of signals, the further set of signals
corresponding to signals which would have been produced had
the elements been spaced uniformly.
In this way it is possible to receive signals
employing an antenna array being a non-uniform antenna
element spacing, in conjunction with a conventional signal
processing arrangement designed for use with an antenna
array having uniformly spaced elements.
In another aspect of the invention signal processing
apparatus comprises; means for obtaining a first set of
samples of a signal at a first set of uniformly-spaced
sampling intervals; means for reconstructing the signal from
the first set of samples; and means for generating, from the
reconstructed signal, a second set of samples at a second
set of non-uniformly-spaced sampling intervals.
In this way signals with a uniform-spaced sampling
interval are converted to corresponding signals which would
have been produced had sampling taken place using
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
- 8 -
non-uniformly-spaced sampling intervals.
According to yet another aspect of the invention, a
method of signal processing comprises the steps of:
sampling a signal at a first plurality of non-uniform
sampling intervals to obtain a first plurality of samples;
using said first plurality of samples to reconstruct the
signal; and sampling the reconstructed signal at a second
plurality of uniform sampling intervals to produce a second
plurality of samples.
The number of samples of the first plurality may be
the same as the number of samples of the second plurality of
samples.
According to yet another aspect of the invention, a
method of signal processing comprise the steps of: sampling
a signal at a first plurality of uniform sampling intervals
to obtain a first plurality of samples; using said first
plurality of samples to reconstruct the signal; and sampling
the reconstructed signal at a second plurality of
non-uniform sampling intervals to produce a second plurality
of samples.
Exemplary embodiments of the invention will now be
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
9 -
described by way of non-limiting example only with reference
to the drawings in which;
Figure 1 shows a prior art antenna array;
Figure 2 shows an antenna array in accordance with the
invention;
Figure 3 shows a known antenna array;
Figure 4 shows an antenna array for use in conjunction
with the invention;
Figure 5 shows how the arrangement of Figure 4 behaves
when used in conjunction with the invention;
Figure 6 shows waveforms produced by a conventional
doppler radar system; and
Figure 7 shows waveforms of radar pulses produced by
an arrangement in accordance with the invention.
Where a site is free from obstruction, a
regularly-spaced antenna array can be employed. However, in
the arrangement shown in Figure 2 the sites for the elements
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
110 -
corresponding to 2, 3 and 4 of Figure 1 (shown in phantom in
Figure 2) are obstructed by a stream 20, house 21 and marshy
ground 22. Therefore the corresponding elements 12, 13 and
14 are sited at convenient locations having regard to the
site conditions and are no longer arranged at a uniform
spacing. A signal processing arrangement 30 accepts signals
from elements 11-15 on lines 24. The signal processing
apparatus 30 is provided with information as to the actual
spacing of the elements 11-15 and the spacing of the
corresponding uniformly-spaced array which it is to
simulate. The signal processing apparatus 30 produces
output signals on lines 60 corresponding to the signals
which would have been produced had the antenna elements
11-15 been spaced uniformly. The signals on line 60 are
then processed by a conventional fast fourier transform
processor 7 to give an output signal 8. The signal
processing arrangement 30 can be considered to take the
original set of samples, reconstruct the signal from those
samples and re-sample the reconstructed signal at a uniform
sampling rate to produce the second set of output signals.
A second embodiment of the invention will now be
described with reference to Figures 3, 4 and 5. Now as is
known to those skilled in the art, the resolution of an
antenna array is, inter alia, a function of its effective
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
11 -
aperture, i.e. the distance between its extreme elements.
Consider an antenna array shown in Figure 3. The
array comprises n equally-spaced elements 1', 2', ... n'
spaced apart by a distance d'. It has an effective aperture
Al. To obtain a higher resolution it would be necessary to
increase the distance Al by providing more elements.
Because of the weighting assigned to each element, it is
feature of such an array that elements contribute
progressively less signal to the arrangement the further
they are from the centre of the"array. Thus while the
extreme elements are necessary to obtain increased
resolution, they contribute relatively little to the gain of
the array, and the extra expense incurred in obtaining a
higher resolution does not produce a corresponding increase
in sensitivity.
In Figure 4, two additional elements 40, 41 have been
added to the array of Figure 3. Elements 40, 41 are spaced
apart from the end elements 1', n' of the original array by
a much greater distance than the pitch d' of the original
array. The effective aperture of the array now becomes
distance A2. Thus it can be seen that the effective
aperture of the array has been more than doubled without
doubling the number of elements. The signals from the array
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
12 -
are processed by signal processing apparatus 30 to produce a
plurality of output signals 60 corresponding to signals
which would have been produced by a uniform array comprising
n+2 elements 1" , 2111, ... n", (n+1) ", (n+2)1- having an
aperture A2. This effective antenna array as seen by signal
processing circuit 3 is shown in Figure 5. Thus it can be
seen that the effective aperture of an array can be
dramatically increased by the addition of only two
additional elements, and that the original signal processing
arrangement 7 can be retained. The signal processing
circuit 30 in accordance with the invention provides an
interface between the antenna array having a non-uniform
element spacing and a circuit 7 which is only capable of
processing signals from an antenna array having a uniform
element spacing.
A further embodiment of the invention will be
described with reference to Figures 6 and 7.
As is known to those skilled in the art, doppler radar
systems utilise trains of pulses transmitted at
regularly-spaced intervals. The receiver looks for echos
arriving in respective range windows a-e, each range window
being defined in terms of a predetermined range of elapsed
times after the transmission of a pulse. Such an
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
13 -
arrangement is shown diagrammatically in Figure 6, in which
transmitted pulses 61 produce echos 62 from a target. As
the target is at a constant range these echos 62 always lie
within the same range window d. Signal processing circuitry
700 compares the phases of the echos 62 arriving in the same
range windows of successive pulses and uses the change of
phase between successive pulses to determine the rate of
acceleration of the target which gave rise to the echo. The
signal processing required for this is extremely complex and
requires the use of pulses transmitted at regularly-spaced
intervals. Unfortunately the transmission of
regularly-spaced pulses means that it is relatively easy to
detect the transmission of such pulses. It is therefore
relatively easy for a target to detect that it is being
observed and for the target to transmit signals synchronised
to the pulses which will give rise to false echos in the
receiver. Further, as the signal processor requires a
continuous pulse train, any missing or corrupt pulses will
severely upset the operation of the arrangement and give
rise to unusable data.
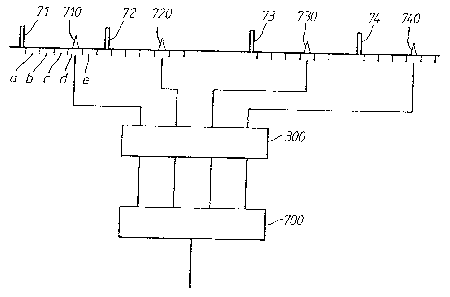
Figure 7 shows an arrangement of pulses transmitted in
an arrangement in accordance with the invention. Pulses
71-74 are transmitted at unequally-spaced intervals. The
echos 710-740 are received in range windows a-e which are
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
14 -
defined at respective constant ranges of times relative to
their associated transmitted pulses but which occur at
correspondingly unequally-spaced times relative to their
adjacent corresponding range windows. The echo signals
received in successive range windows are processed by
processor 300 to extract the phase information so as to
obtain a signal representing the rate of change of velocity
of the target. The signal is then re-sampled so as to
produce a plurality of equally-spaced signals corresponding
to those echos which would have been produced had the
transmitted pulses 71-74 been pulses 61 transmitted at
uniformly spaced time intervals. These equally-spaced
signals can then be processed by a conventional signal
processing arrangement 700.
A number of modifications are possible within the
scope of the invention. For example, it is possible to
compensate for the loss of one a sample channel. A
conventional fast fourier transform circuit requires all
inputs to be present before it can give a meaningful result.
By employing the invention, if one of the antenna elements
of Figure 3 for example had to be taken out of commission or
was otherwise unusable, the circuit 30 could be reprogrammed
to calculate the intermediate signal on the basis of such
information as was received by the remaining antenna
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
elements. It would then convert this information into the
correct number of samples required by the subsequent
processors 30. While some inaccuracy would result from the
absence of this information from the missing antenna, the
information would still be meaningful.
Similarly, instead of calculating the signals which
would have been produced had the antenna elements been
uniformly distributed across aperture A2, the arrangement of
Figure 4 could calculate the signals which would have been
produced by an array having the same pitch d' as Figure 3
but an aperture of A2. While this might produce some
degradation of performance in other respects, the resolution
would be equivalent to an antenna of aperture A2. It would
also be possible to selectively switch out the end elements
40, 41 and revert to operation using only the original n
elements.
In the arrangement of Figure 7, the circuit could be
modified to detect that interference has been received and
to ignore information collected while interference was
present. It would then calculate the acceleration on the
basis of such samples as it has received. The signal
processor would then produce the correct number of samples
at the times required by the subsequent processing
CA 02101177 1993-06-29
P/8802/MRSL/CA/AU
16 -
circuitry. Again, accuracy would be reduced but there would
be no break in the production of meaningful information.
Further, although the operation of signal processing
has been described as a sequence of operations in which a
signal is reconstructed from samples taken at non-uniform
intervals and the reconstructed signal re-sampled at uniform
intervals, the re-sampled signals may be obtained from the
original samples without actually reconstructing the signal
as an intermediate step.
A mathematical analysis relevant to the operation of
the invention will now be given.
Shannon's sampling theorem (Proc. IRE Vol. 37 pp
10-21, Jan 1949) demonstrated that a lowpass bandlimited
signal was "completely determined" by its ordinate sample
values taken at equispaced time intervals. A bandlimited
signal is said to be "completely determined" if (and only
if) the signal may be exactly reconstructed from these
samples.
Proposition 1
An Nth order sampling scheme (denoted saN(t/Tc), where
CA 02101177 1993-06-29
P/8802/MRSL
17 -
TC is the cyclic interval) is the addition of N equispaced
sampling schemes of spacing Tc, each displaced from t=0 by
an amount Uk, where k=0,1,...,N-l. That is
N-1
saN(t/ E E 6(t-n c k) (1)
k=0 n
Proposition 2
An alternative mathematical expression for Nth order
sampling schemes to that given in proposition 1 is
N-l
saN(t/Tc) = E 6(t--&) j * E 6(t-nTc) (2)
k=0 n
where the asterix signifies continous-time convolution.
Proposition 3
A periodic time function gP(t) with periodic interval
NT may be written in the form:
go(t) = g;(t) * E 6(t-nNr) (3)
n
where gp(t) = go(t) for t c (O,Nr) and g'(t) = 0 for t [0,N-r).
CA 02101177 1993-06-29
P/8802/MRSL
18 -
If the periodic time interval Ni- of a periodic time
function is the same as the cyclic period of an Nth order
sampling scheme TC, then the Nth order sampled periodic time
function gpsaw (t/Tc) may be expressed as
tit ~1
g(t) X sa,(t/To= Z gp(k.b(t-,~k) Z b(tn ) (4)
P k-0 n
It can be seen that the finite set of non-equispaced
samples contains all the information about that signal; that
is to say, additional samples over and above those contained
within the periodic interval will reveal no further
information about the signal. Therefore the reconstruction
formula of a sampling theorem-to cater for this case will
ideally be based on only the finite set of samples contained
by the square brackets [-] in (4).
Theorem 1
If the Fourier transform G(f) of a complex-valued
periodic time function gP(t) (periodic over time interval
N-r) contains no frequency components above and including the
Nth harmonic, then gP(t) is completely determined by the
CA 02101177 1993-06-29
P/8802/MRSL
19 -
finite sequence of complex-valued time samples
)go( k) 3kO;
taken at arbitrary but distinct time locations
)idk k=0
within the periodic time interval [0,N-r). The
reconstruction is
N-1 - 7r(~ N-1) N-I jir(N-1) t
g (t) _ NT NT
1k9k)*e
=0 P v=0 sin( (7r/NT)- (Ok v)j (S)
.v/k
Alternatively, if gp(t) is in the form ap(t) +jbp(t) ,
then the real and imaginary components of gp(t) may be
reconstructed independently as;follows:
N-1
a (t) = E a' (~i ) cos((7r(N-1) ). (t- ) )-b (y ) .sin((7r(N-1) ). (t-(P d
P k=0 P k PIT k p k NT k
N-1
x TT sin((ir/Nr)..(t-it i,)) -(6)
v=0 sin ((r/NY). (iP k=iv
v/}c
and
N-1
bp(t) = E aP(ipk).sin((Ir(N-1)).(t-(Pk))+bP(k)-Cos((7[ (N-1)(t_k)
k=0 Nr Nr
N-1
x sin ((-Tr/Nr) . (t-W_) ) (7)
v=0 sin ((it/NT). (cji Div)
k v/k
Note that the real and imaginary samples of gP(.) are
CA 02101177 1993-06-29
P/8802/MRSL
20 -
both required in order to permit reconstruction of either
aP(t) or bp(t) .
Proof
Since gP(t) is periodic over time interval N-T, the
spectrum of gP(t) is a discrete line spectrum consisting of
N harmonics of spectral spacing 1/Nt. That is,
N-1
G(f) = E G(n1Nr).6'(f-rVNr) (8)
n=O
Consequently, gP(t) may be expressed as
j2irt/Nt j2rr2t/Nr j2rr(N _I)t/Nt
gp(t) = G0 + G1.e + G2.e + .,.. + G(N-1).e
N-1 j 2rmt/N-r N-1 j 2IZt/N r n
or g(t) = E Ge = E G e (9)
n= n=0
i.e. gP(t) is a polynomial of degree (N-i).
Suppose we were to evaluate equation (9) at N
arbitrary (but different) values of time
N-i
Vk k =O
CA 02101177 1993-06-29
P/8802/MRSL
21 -
within the periodic time interval (0,N%) such that we
obtained the discrete time sequence
[9p(k)3k=0
that is
NN-1 j (2rr/Nr) ap n
[ 9D (tk)~ Gn. e k (10)
n=O k-0
From equations (9) and (10), let the contents of the
7.
square brackets [-] be denoted as
j (27r/NT) t N-1 j(27r/Nr) Wk N-I
x=e and 1xk]k=0 = e I k_0 respectively.
Using Lagrange's interpolation formula,
N--1 N-1
g (t) = E g' (Tik) ff (x-xv? . (11)
P k=0 P v=0 (xk -xv)
vpk _
'x' and 'xa (where o(, = k or v) may be substituted
-in (11)- to obtain
N-1 N-1 j ( 27r/NT) t j (27r/NT)
9 (t) = E g' (~k) T{ (e - e v (12)
k=0 P v=O v,=k j (2n/Nr) Ykc j (2rr/Nr) Pv
(e - e )
CA 02101177 1993-06-29
P/8802/MRSL
22 -
The contents of the square brackets in [-] in equation
(12) can be written in the form:
j(2ir/Nr)t j(2Jr/N-r)ipv -jrrt/I'T -j(rr/NT)1Pv -j(n/Nr)1yk jrrt/N-r
(e -e ).e .e e e
j (2Tr/Nr) Pik j (27r/Nr) Div - j (Tr/Nr) k (Tr/NT) v
(e -e ).e e
Hence j (7r/Nr) . (t~k)
sin( (Tr/Nt).(t-1 )) e
sin { (Tr/Nr) = k v) )
Substituting back into equation (12) results in:
N-i N-1 j (Tr/Nr) . (t iik)
9 (t) T. g' (iGk T sin{(7r/Nr)=(t--1P._)) .e
P k=0 v=0 sin ((Tr/NT) = (q1k--Vv) )
v/k
or
N-1 n( 1) N_i jTr(N-i) t
Nr
N-r 9 (t) = E g (V~k)_e . TI sin((7r/Nr).(t )). .e
P k=0 p v=0 sin((Tr/Nr).(z v}) (5)
vk
It can be seen that Theorem 1 can be used to create a
'non-equispaced to equispaced transformation' (NESTEST)
process which 'transforms' non-equispaced samples into an
equivalent equispaced set. From then on, conventional
equispaced processing techniques may be applied to the
CA 02101177 1993-06-29
P/8802/MRSL
23
sampled-data set.
The NESTEST process for lowpass bandlimited periodic
time functions (NESTESTt) simply amounts to evaluating
equation (5) at the equispaced time locations in., where
m={0,1,2,...,N-1). Thus, given the non-equispaced sample
set
)9;(Pk) k=0
we can transform this set into an equivalent
equispaced sample set
g' N-1
by means of the following equation:
g(mz) Ian=0
N-1 N
N~1'(~i ).e Nz IT sin( (Tr/N-r). (5~.) ) e
k=0 gPk Ih sin((Tr/N-r). (Wk iv) ) (13)
v,/k J m=o
Therefore, since the Discrete Fourier transform (DFT)
of a finite set of equispaced lowpass bandlimited periodic
time function samples can be obtained from the well-known
equation:
CA 02101177 1993-06-29
P/8802/MRSL
..............
24
N-1 -j 2mnrn
DFrUg (rr)3 J = JG(n/NT)In (1/Nz).E gp(nrr).e N (14)
M=0
Substitution of equation (13) into (14), produces the
DFT of an non-equispaced sample set
gp(k)Ik=--O
as
N-I N-1 jm(N
IG(n/Nr)3n=_0 - (1/Nt)= E Z e NT
rr=0 k=O
N_l -jiun. (2ri--(N-1)) K-1
X
sin((7r/NT) . (n r-qi--)) e N
v~ sin((7r/NT). (ik Div)
v`k f1-o tr 5)
For completeness, inverse cases will now be provided
without proof, since their derivation follows the approach
above in a straightforward manner.
Theorem 2
If the inverse Fourier transform g(t) of a
complex-valued periodic frequency function GP(f) (periodic
over frequency interval 1/-t) contains no temporal components
CA 02101177 1993-06-29
P/8802/MRSL
25 -
above and including the Nth rahmonic, then GP(f) is
completely determined by the finite sequence of
complex-valued frequency samples
LIT-1
taken at arbitrary but distinct frequency locations
N-1
IGn3n=O
within the periodic frequency interval (0,1/.). The
term 'rahmonic' is taken from Cepstral terminology and is
taken to mean 'harmonic in the time domain'. The
reconstruction is
N-1 j7r(N-1)tzp n N-1 -jir(N-l)"rf
G (f) = E G' OP ).e . ff sin 7rr(f-c )) -e
P n=0 P n [v=0 sin ;7rr( in y.) (16)
v/n
Similarly, the 'non-equispaced to equispaced
transformer' NESTESTf is
Gp{zNNr) O
N-1 j7r(N-1) N-1 -j7r(N-1)m -!
E G' OP ).e n. sin 7rr((m/NY)-ry,.)) e N
n=0 P n v=0 sin nr(~Pn v (17)
v/n
m =a
CA 02101177 1993-06-29
P/8802/MRSL
.............
26 -
and the inverse discrete Fourier transform (IDFT) for
a non-equispaced frequency sample set is
g(1cz) IN-1 _
N-1 N-1 j7r(N--1)z-ye N-1 jmn. (2k-(N-1)) N-~
E E G' (0).e n. JJsin itr((m/Nr)--O e N
m~ n=-0 P n v= sin nr(r/i^)
v/-n
k=0
(ts)