Note: Descriptions are shown in the official language in which they were submitted.
2163~61
SPECIFICATION
This invention relates to a modular, combinatorial system, which ensures beams of a multitude of
span ranges through the combinatorial power of one module-type only.
The building structure represents the first technological, aesthetic and economic problem of the
construction.
The construction answers of the society's requirements. The contemporary society could be
described as a high functional variety. This variety enforces the execution of structures of a multitude
of span ranges. The beams are the components, which provide the span variety.
The beams work on flexure. The bending moment depends on the load, dead load plus service load,
10. and on the span. If the load has a constant value, according to the building code, the bending
moment depends on the span only. The bending moment is proportional of the second power of the
span's value. The increase of the span is linear, the magnification of the moment is exponential. If the
span increases, the relevant moment magnifies much more. For example, if the span increases 3
times, the magnification of the bending moment is proportional of 9 times.
The bending resislance of the beam must be relevant to the bending moment's value. When the
span increases the bending resi~lance of the beam must follow the magnification of the bending
moment. The efficiency of the beam's section, in relation to the flexure, must magnify exponentially
too. The bending efficiency of the section is proportional of the value of the section's moment of
inertia.
20. Until now, the problem has been resolved through the following method. In relation to the short
spans, it is in use to make the section of the beam technologically simple. This is the full-web beam,
2163964
usually - rectangular beam. The moment of inertia of this section is weak, on surface unit basis. This
is a bending noneffhcient section. At the same time, the value of the bending moment is weak too, the
technological simplicity of the section compensates the structural nonefficiency of the section and the
beam is utilizable. When the span increases, the rectangular section exhausts quickly its structural
capacity. In this moment the section is out of use. These several spans constitute one range of
spans, the range of shortest spans.
The transition to the following span range requires a transition of the beam section, whose structural
efficiency has to follow the exponential magnihcation of the bending moment. In this way, it is
common to use more sophislicated sections, for example - I-beam bearer. This is also a full-web
10. beam, but through a section more favourable to the resistance - the moment of inertia of this section
is stronger than the such moment of the previous section, on surface unit basis. This section ensures
several spans and exhausts its structural capacity too. This is the following range of spans. This
section is more sophislicdled and the price rises. The price of the span unit of this range is more
expensive than the price of the span unit of the previous range.
The next transition is analogous. The next beam section must be much more erricier,l. This necessity
requires the creation of the open-web beam. For example - the trussed beam. The moment of inertia
of this section is considerably stronger, than the moment of inertia of the previous section, on the
same surface unit basis. The spans provided from this beam-type constitute the next span range.
The section of this type is subsequently more sophi~ led and the price goes higher. The span unit
20. from this range is much more expensive than the span unit from the previous range.
The increase of the span is made always in the same way. The l,ansition to the next span range is
accomplished through a particular solution of the beam's section. Subsequently, there are one or
more types of beams per each span range. Generally, the method is attached to a technologically
'~ 2163g6~
specialized solution and to an exponentially higher price per each span range.
The industrial production is a serial one. If the production of one component type increases, the unit
price decreases and vice-versa. A particular construction has a volume and a number of component
types. In relation to the volume, a higher number of types means a weaker repetition per each type, a
weaker production series. It means a higher technological variety, a higher unit price. The unit price
decreases proportionally to the technological homogeneity of the production.
The general situation in construction could be described as a high technological variety, about its
maximum, of the execution of the beams, a substantial organizational difficulties in the building sites,
an aesthetic noncompatibility among the beams and a high price per constructional volumetric unit.
10. The contemporary situation is so complicated because of the technologically specialized method of
resolution of every problematic span level. Subsequently, the situation could be improved by a
technological universalization of the beam-types' multitude. I have discovered that a
modular-combinatorial method could eliminate the disadvantage, the high technological variety, and
could keep up the advantage, a good bending efficiency over a multitude of span ranges.
Now, every beam-type is specialized to its own span range. The beams of different span ranges are
of different constitutions. That is why, it is not possible to obtain a bigger beam by the superposition
and the juxtaposition of smaller ones. In the majority of cases, the beam is produced on the entire
dimension of the span. The specificity, the technological variety is about its maximum.
A modular method allows for a decomposition of the beam in units smaller than its entire size. The
20. smaller module is respectively more combinatorially flexible. This flexibility permits to endow the
module with combinatorial qualities. Simultaneously, with the dimensions' increase, some
~_ 216346~
combinations among the modules could produce qualitative effects. It is possible, combining the
same modules, to increase the span of the beam and to make it deeper, keeping up the
concentration of the material in the beam section's exl,e",ities. The concentration in the section's
extremities means keeping up a strong moment of inertia in conformity with the span. Otherwise, it
means keeping up a corresponding bending resi~lance in the current of the increasing process. If the
combinatorial power of the modules is sufficient it is possible to obtain a multitude of spans through a
limited number of modules. This is a modular, combinatorial, multispan system.
The fact that the module is smaller than the entire beam allows to penetrate in the intimate
constitution of the beam. The combinatorial operations represent an internal mechanism of
10. constitution. This method allows a double transformation in the current of the magnification. The
process increases the dimensions, a quantitative change, simultaneously, it keeps up a bending
efficient constitution of the beam, a qualitative change. This method surmounts the problem of the
exponential magnification of the bending moment passing over a multitude of spans.
Thanks to the combinatorial power of the system, the process obtains beams of a multitude of spans
combining the same modules. Passing over different span ranges it does not change the
technological bases of the production. The execution of a bigger beam means simply to combine a
bigger number of the same modules. That is why, in this case, the magnification of the price is
quasi-linear proportional to the increase of the span.
The profitableness is proportional to the technological homogeneity of the construction. One modular,
20. combinatorial, multispan system ensures a functional-structural variety by the help of a limited
number of modules, otherwise, keeping up the technological homogeneity about its maximum. In
relation to the volume, the system ensures series of production per type about its maximum and
respectively - a relative price per unit about its minimum.
2163~64
The general situation in construction, based on a modular, combinatorial, multispan system, could be
described as a minimum number of module types and a strong combinatorial power of the modules.
These conditions ensure a high technological homogeneity of the execution of the beams, an
organi,dlional simplicity in the building sites, an aesthetic compatibility among the beams and a low
relative price per constructional volumetric unit.
The relative price means - in comparative with the multitude of traditional technologies, which ensure
the same variety of structural production.
In drawings which illustrate embodiments of the invention,
Figure 01 is a combinatorial module T in two-dimensional projections.
10. Figure 02 is a floor module F in two-dimensional projections.
Figure 03 is basic modules of Multispan Module System in axonometric view: T-HS, F1, F2.
Figure 04 is a staircase module ME, in three projections.
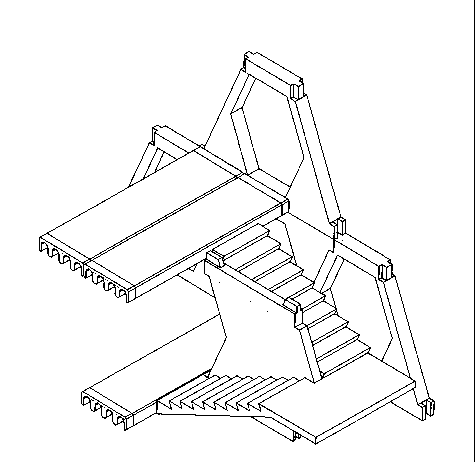
Figure 05 is a staircase module ME, in axonometric view.
Figure 06 is an embodiment of double staircase in three projections.
Figure 07 is an embodiment of double staircase in axonometric view.
Figure 08 is configurations of beams A, B, C; corresponding spans - PA, PB, PC.
Figure 09 is a configuration of a beam D, corresponding span - PD.
Figure 10 is: a circuit configuration - CF8, a three-hinged moment resisting frame based on A beam -
PA3A, a two-hinged moment resisting frame based on A beam - PA2A.
20. Figure 11 is configurations of two particular moment resisting frames based on A beam, PAT - PAS.
Figure 12 is two configurations, a moment resisting frame based on B beam - PB2A and a moment
resisting frame based on C beam - PC2A.
2163~64
Figure 13 is a two-hinged moment resisting frame (halfl, based on D beam - PD2A.
Figure 14 is an exemplary, functionally and structurally variable, configuration - multispan.
Figure 15 is an exemplary high-rise configuration - multispan.
Figure 16 is an exemplary configuration, based on a minimum application of the G beam - multispan.
Figure 17 is an axonometric view of an assembly example of Multispan Module System.
Figure 18 is an assembly detail - K.
Figure 19 is an assembly detail - L.
Figure 20 is an assembly detail - M.
Figure 21 is an assembly detail - N.
10. Figure 22 is an assembly detail - O.
Figure 23 is an assembly detail - P.
Figure 24 is an assembly detail - Q.
Figure 25 is an assembly detail - R.
Figure 26 is assembly details - S1, S2, S3.
Figure 27 is an assembly detail - U.
Figure 28 is a detail of a longitudinal wind bracing for nonseismic geographic zones - V.
Figure 29 is a detail of a longitudinal lateral stiffness for seismic geographic zones - VS.
Figure 30 is an wind bracing example of a three level assembly.
Figure 31 is a post-tensioned beam - W, a parallel possibility.
20. Figure 32 is a detail of bolt's head, which extremity equals the T module's thickness - Y.
Figure 33 is an assembly detail of two T modules, jointed through the big base and the small base -Z.
Figure 34 is a beam cr~ssi"g detail, DC.
The Multispan Module System is constituted basically of two types of modules - T, F, figures 01, 02;
one of which is particular - the T module. This is the combinatorial module constituting beams.
216~64
The T module is trapezium-shaped, figure 01. The static scheme represents a trapezium with
moment resisting angles. The dimension of the trapezium's big base GB represents a multiple of the
small base's PB dimension. The PB dimension represents a multiple of the width LF of the floor
modules F1 and F2, figure 02. In this way, the same floor module is connectible with the big base and
with the small base of the T module. The trapezium's bases have a vertical dimension ET. The ET
dimension may equal the floor F module's tickness EF. The trapezium has a central opening in the
way to ensure the rigidity of the four angles and in particular the rigidity of the big base's two angles.
One exemplary opening represents an irregular hexagon, symmetric about a horizontal axis, HS. The
DV1 dimension is bigger than the ET dimension. Another exemplary opening represents an irregular
10. hexagon, nonsymmetric about a horizontal axis, HNS. The DV2 dimension is similar to the ET
dimension. Another exemplary opening embodies right angles to the big base, ADB. The DV3
dimension is similar to the ET dimension. Another exemplary opening follows the trapezium and
embodies round angles to the big base, OAA. The DV dimension may equal the ET dimension, but it
can not be smaller. The T module's opening may have a multitude types of configurations. Every
opening must be shaped in conformity with the static scheme, it means to ensure four moment
res;aling angles, in particular - the big base's two angles. The T module is executable in different
sizes. The height of the module HT is proportional to the deepness of the beam. The height HT may
equal a fraction of the height of a storey. In this case, the T module's opening is relevant to the
llansition of the mechanical distribution. The height HT may equal the height of a storey too. In this
20. case,the T module's opening is relevant to a door. Except for particular cases - the TAP version,the T
module is transversally p~-ss ~'e. The usual execution of the T module is the open web version, TAV.
Another variant of the T module's execution is the full web version,TAP.The TAP version is aFF' --~'e
on the especially al,t:ssed spots, figures 08, 09, 10, 11, 12, 13, 14, 15. The combinatorial power of
the system is illustrated by the application of the T module's HS-CF8 version, figures 01, 03, 10.
216~64
-
The F module represents a rectangular slab, figure 02. This embodiment is based on the hollow-core
slab. The tickness of the slab EF may equal the ET dimension. The rectangle's extremities,
corresponding to the LF dimension, represent semi-cylindrical cores, which are open at the low site.
These ex~,er".~;os allow to connect the F module on the small cylinders of the big base and on the
small cylinders of the small base of the T module, figure 27. This is the floor module.
The figure 03 illustrates the basic modules of the Multispan Module System on three-dimensional
view. The T module has the niches and the small cylinders, which are relevant to the corresponding
connecting details. The F module is developed in two span versions. The F1 module represents a
floor module of a larger span, GP. The F2 module is the floor module of a shorter span, PP - a
10. recor"mendable dimension for PP is 1/4- 1/3 from the GP span.
The staircase module ME is relevant to one storey and represents a monolithic piece, figure 04. This
is a two flight staircase. The staircase is constituted from a load bearing wall, located in the stairwell.
The two flights and the half space landing are cantilevered on the load bearing wall. All parts of the
staircase are carefully designed in relation with the modular environment, projections - Il, Il-TR. The
projection Il-TR represents the modules as transparent solids. A multi-storey staircase is executab'e
by the superposition of several ME modules. The sl..;.case is precisely modulated and self-
supporting.
The figure 05 illustrates an axonometric view of ME module, located in the middle of the short span.
The staircase modulation allows an execution of a double staircase configuration, figure 06. The
20. double staircase is as precisely modulated as the single staircase is, projection ll.
The figure 07 illustrates an axonometric view of a double staircase, located in the middle of the short
span PP.
216~6q
-
The figure 08 illustrates the first combinatorial position of the system - beam A. A ~ispo~iticn of the T
module, in alternation, the big base - up and down, up and down, ... constitutes a beam, figure 18 -
detail K. The middle-height spots of the trapezium's sides are connected with each other, hgure 19,
detail L. The K, L -type connections pa,lic;pale to the transrnission of the local bending moment. One
wider side co",~'ements a more narrow one from both sides of the joint bctwecn two modules. In this
way, the more rigid angle of the trapezium's big base compliments the less rigid angle of the small
base. This complementarity constitutes an X type vertical parts. These parts ensure the shear
stresses working on local flexure in collaboration with the horizontal parts, the trapezium's bases. The
entire beam works on (general) flexure as a quasi-monolithic one. This is a Virendel-type beam. The
10. deepness of the beam equals the height HT of the T module. Depending on the execution's and
arF'ic-fion's pardn,elers, this beam is able to ensure several spans. This is the first span range - PA.
The figure 08 illustrates the second comb.. ,alorial position - beam B. The big bases of the T module
touch each other, in alternation - up and down, up and down, ... The big bases are directly connected,
figure 20 - detail M. Both extremities of the small base are connected with the middle-height spots of
the adjacent trapeziums' sides, figure 21 - detail N. The O-detail - figure 22, completes the extremities
of the entire beam. Generally, the configuration is triangular. One stress trans",ission between the
connection points of the big bases, points M, is quasi-axial. This quasi-axiallity decreases the local
bending moment of the beam's parts. The value of this local bending moment, quasi-zero, is
considerably smaller, than the value of the local bending moment of the PA-spans beam. This
20. particularity means, that the structural efficiency of the triangular configuration is considerably higher.
The worki"g mode of the B-type beam is similar to the working mode of a truss beam. The deepness
of the B-type beam equals one and a half 1 .5HT of the T-module's height. The bending resistance of
the B-type beam increases by the increase of the height and by the increase of the structural
efficiency. This beam is able to ensure several spans. This is the second range of spans - PB.
2163~6 1
The figure 08, beam C, illustrates the third comt.. ,atorial position. The T modules are connected by
the entire small bases and the exl,~",ities of the big bases. The parts of the beam of this composition
work on local flexure. This is a Virendel-type beam. The deepness of the beam equals two heights
2HT of the T module. The bending resi:,lance of the beam increases by the strong increase of the
height. The spans of this beam-type constitute the third range of spans - PC.
The constitution of the next range beams closes one com~indlorial cycle, figure 09 - beam D. Two
parallel A-type configurations, figure 08, are connected through C-type couple units, figure 08. The
parts of the T module work on flexure to ensure the r~si~lance of the T module's configuration. This is
the micro-local level of flexure. The C-type couples ensure the l~ans"~ission of the shear stresses.
10. The C-couples' ~ispo~ition reflects the distribution of the shear sl,esses. The two A-configurations,
high and low, work on flexure, in collabor~tion with C-couples, to transmit the same shear stresses.
This is the local-level of flexure. At the same time, the two A-configurations transmit two axial
stresses. The A-high configuration works on axial compression. The A-low configuration works on
axial traction. The axial work of the two A-configurations ensure the bending moment of the entire
D-beam. This is the general flexure. This is a Virendel-type beam, which parts work on a thrcc Icvcl
flexure. The three levels of flexure correspond to a double reduction of the D beam's dead load.
The kind of an open web beam means a reduction of the dead load of the beam without penalty to his
bending ,esislance. The openings reduce the beam's dead load. Generally, the D beam is an open
web beam. There are openings among the C-couples. At the same time, the parts of the beam, the C
20. couples and the A configurations, have openings too. The D beam is an open web beam on a macro-
level and on a micro-level. The double reduction represents a loga-ilh",.c, counterversally
exponential, reduction of the D-beam's dead load, in co",parison with the same deepness 4HT beam
without openings.
2163~6il
-
One A configuration is bending resialanl, figure 08 - A. It means, this is an entire beam. On the other
hand, the same A configuration partil~ip~tes in the constitution of a beam, figure 09 - D, as a
component. This particularity means that the T module's combinatorial power provides
beam-combinations of hierarchically different levels. The A beam is reproduced on the D level. This is
a h.erar~h.~-' combinatorial reproduction of beams.
The hie,~rch.c-' reproduction provides an increase of the deepness and, simultaneously, a
loga,ilh",.c decrease of the beam's dead load. The reproduction reproduces an open web beam to
an open web beam. It means, the reproduction keeps up a material concenl,-dlion in the extremities
of the beam's section. The material concer",dtion in the extremities of the section keeps up a
10. maximum value of the section's moment of inertia. The increase of the deepness, the logarithmic
reduction of the dead load and the ~pkeep..,g of maximum moment of inertia compensate the
exponential magnification of the bending mor"enl and ensure a hierarchical reproduction of the
D-beam's bending resislance.
The deepness of the D-beam equals four times 4HT the T-module's height. The spans of the D-type
beams constitute the fourth range of spans - PD.
The combinatorial character of the D-beam introduces a new structural aspect. In case of a multi-
storey construction, the lesialance of the beams is locally treated, for example - per storey. At the
same time, on the base of the D-configuration, it is possible to est-~' sh structural ,~ldtions on the
scale of the entire construction. It is pc~s:~!e to achieve a very powerful all-construction-scale
20. resistance making use of the device, which is utilizable in the scale of the beam unit - the only T-
module and all the rest - this is the T-module's combinatorial power.
The four comt.ndtorial levels A, B, C, D, represent only one combinatorial, hierarchical cycle of the
2163~61
system. Beams of superior levels are also possible. The achievement of these superior levels passes
through combinations similar to those of the transition from A-type level to D-type level. It is possible
to reproduce the D beam on one hierarchically superior level making use of two D beams as
hori~Gnlal components, high and low, of one new G beam and putting in groups of T modules
betv.~ecn the two hori~Gnlal components according to the shear stresses - a second combinatorial,
hierarchical reproduction on a deepness of 16HT, on a logarithmic reduction of the dead load and on
a PG span of the hierarchically next range. Figure 16 illustrates a configuration based on a minimum
G beam. The increase of the deepness, the loga,itl"nic reduction of the dead load and the upkeeping
of a section's maximum moment of inertia reproduce the bending resistance of the G beam on a
10. hierd,~h.-,ally superior level. It is possible too to constitute beams of intermediate deepnesses and
spans between D and G levels, like the first hiera,~;~"c-' reproduction. In cG,nparison with D beam,
these conhgurations are more deep, have longer spans and relevant bending resistance reproduced.
The corn~..,dtorial, hierdr~;h.--' succession is not limited on principle. This is a ~landard"~:petitional
operation of a combinatorial, hi~rdrch-c-' reproduction. The Multispan Module System is
cGl"'-indlorially open.
Although an open hierarchic-' reproductivity, the technological and pra~tical conditions impose
certain limits to the application of the combinatorial development. The beam units of four presented
levels A, B, C, D, are directly ~FP'~ 'e to the construction. The A-type beams, through a relevant
height HT of the T module, are applicable to average scale buildings. The B and C -type beams are
20. apF' --~'e to relatively large buildings. The D-type beams, through a relevant height HT of the T
module, are apF'.c-~'e to megastructures. The beams from levels superior to the level D, as beam
units, exceed the average building scale. These beams are not directly ~p' --~'e to the
contemporary buildings. The beams of level G and over keep theirworth in the sense of structural
rel~tions on the scale of the entire building in the case of large and complex structures, like the D
216~6~
_
beam. In the case of such structures, it is possible to ach.~Ye bending r~s,slance and wind bracing in
the powerful scale of the entire building making use of certain combinations of comb:nalorial levels
superior than D. Such major qualities are accesc;'1le without the arp'ic-~ion of special and expensive
devices. All qualities, average and special, of the system are ~ccescihle on the base of the only T
module, respectively - produced in a very high series. The figures 14, 15 and 16 give a look over this
horizon of possibilities.
The figure 10 illustrates moment resi ,li"9 frame configurations. A particular accomplishment of the T
module allows the constitution of circuit-type configurations, figure 10 - CF8. The figure 10 - PA3A
represents three-hinged moment r~:sialing frame on the base of the A-type beam. The figure 10 -
10. PA2A represents two-hinged moment resisting frame on the base of the same A-type beam.
The figure 11 illustrates more special types of ",o",ent resisting frames. The figure 11 - PAT
represents a macro-trapezium-shaped moment resisting frame on the base of an A-type beam. In the
case of an uniform service load, the trapezium-shaped configuration is very close to the funicular of
forces, the parabola. This particularity means, that the value of the bending moment is downkeeped
to its minimum in relation to given span and service load. Subsequently, the trapezium-shaped
configuration is particularly appropriate to large spans. The figure 11 - PAS illustrates a
free-configuration moment resisting frame on the base of A beam. Such configuration is able to
integrate many functions in the same time. The illustrated configuration i,lleg,dles the functions of a
roof and a stand of a sport hall. If the height of the T module equals the height of a storey, the
20. ho,i~onlal part of a moment resisting frame, or any other configuration, tepresenls a habitable storey.
The figure 12 illustrates the following co",binalorial c~p~ities in the matter of moment res;~li"g
frames. The figure 12 - PB2A represents a moment resisting frame, based on the B-type beam. The
deepness of the frame equals one and a half 1 .5HT heights of the T module. The figure 12 - PC2A
216346~
-
represents a moment resisting frame based on the C-type beam. The respective assembly detail is Z
- figure 33. The deepness equals two 2HT heights of the T module. There are two comb.. ,dlions to
accomplish the direction's change, the moment resisting frame's angle. The illustrated one is the
more rigid combination.
The hgure 13 illustrates a moment resisting frame configuration based on the D-type beam. The
deepness of the "~o",enl resiali"g frame equals four 4HT heights of the T module. There are many
co",t.nations to accol"p';sh the direction's change, the moment resisting frame's angle. The
illustrated combination is the simplest one.
All moment resisting frame configurations are present as examples. The configurations based on
10. A-type beam do not exhaust all combinatorial polenlial in the matter of ",on~enl resisting frames. The
system is cornb nalorially open. At the same time, all possible moment resisting frame configurations,
circuit CF8 included, based on the A-type beam are producible on the base of all other beam-types -
B,C,D,...etc. The Multispan Module System is gradually homogeneous.
The figure 14 illustrates a multifunctional applic~~ion of the system. The general configuration
integrates a multitude of already analysed, beam-configuration units. In the case of a considerably
high-rise configuration a new quality is achievable. The su,uer~,osition of many A-type configurations
produces a structural quality in the vertical direction of the building. Two adjacent T modules
constitute one X-type vertical part, figure 08 - A. The X parts are superposed and constitute pillars,
PX1-PX2 and PX3-PX4 - figure 14. The same parts, with the lr~nsitions through the couples of
20. trapezium's small bases, constitute diagonals - DX1, DX2, DX3, DX4, DX5. The diagonals connect
the pillars. The pillars and the diagonals constitute an entire-building-scale shear-truss. The high-rise
part of the configuration acts as a shear-truss cantilevered out of the ground through the low-rise part.
In the vertical direction, relevant to the wind action, the configuration is bending r~sislanl of a mixed
2163464
type - axial-virendel. The stress l,ansr"ission, in the vertical direction, is quasi-axial through the pillars,
PX1-PX2 and PX3-PX4, and make no problems. In the direction of one diagonal, the stress
I,ansmission through the small-base cour'es provokes a local bending moment. Small-base couples
have a double dimension 2ET, which equals the horizontal dimension of the rigid angle DV1, and
ensure easily, in co"-'~ordtion with the X parts, this local bending moment. Parentl,e~ically, this is a
reason to make the DV dimension bigger than ET dimension. The deepness of the shear-truss
equals the high-rise part's width - PX1 - PX3. Subsequently, the bending resistance or the lateral
stiffness of the shear truss is very powerful and could ensure the wind bracing of a very high-rise
configuration.
10. The figure 15 illustrates another aFp'.--flcn of the system in the matter of high-rise buildings. One
A-type beam can bear floor modules through its low extremity as well as through its high extremity. In
case of such composition one multi-storey configuration needs one A beam on every other floor.
Consequently, every other floor is free from T modules all over the width and the length of the
building. The width of the free space is limited only by the maximum span of the A beams. It is
possible too to make the same configuration through the other beam-types, B, C, ... The functional
advantages of such free spaces are considerable. The vertical l,ansl"ission of the load is
accomplished through the same T modules disposed in the extremities of the configuration's width.
The T modules pillars, CT1, CT2 and CT3-CT4 constitute moment resi~ing macro-angles with the A
beams. In this way, there is one moment resisting frame-effect on every other storey. As a matter of
20. statics, the entire configuration represents a multi-storey moment resisting macro-frame, respectively
- many times statically indeterminate. This moment resisting frame ensures the wind bracing of the
configuration in its plan. The configuration shows possibilities of a double storey height - DHE1 and
DHE2. The possibility of constitution of large simple-span beams is valid in the matter of
hammer-beams too. The configuration shows two large span beams cantilevered out of the both
2163~64
sides of the configuration on the level of the double storey - DHE2.
The figure 16 illustrates a building configuration based on the G beam. The configuration provides a
series of large spaces - among shear parts of the D beams, among shear parts of the G beam and
under the G beam. The configuration is super~ osat'e on itself and may repeat the great space under
the G beam. For exdmFle, it is possible to accommodate Sp~CiQUS television and movie studios at a
high-rise disposHion. Such complex structures could make compatible many urban scale functional
units: high ways, t,dnspo,l stations, shopping malls, theatres, sport arenas, etc., and provide a high
town planning effficiency. The configuration illustrates a minimum development of the G beam. The
maximum G development may achieve a span in the scale of 240 meters (800 feet). The apF' ~ on
10. of the G beam and the maximum span question are a very experir"ental matter. The maximum span
is not limited on principle - the system is coml~ ,~'orially open with bending r~:sialance reproduction.
The limitation is due to technological and practical conditions, which may vary and evolve. The
question of a maximum span remains crcatively and evolutionary open. The G based configuration is
a megastructure. This is a ",ega:jl,ucture in short term and this is an average structure in long term.
The figure 17 illustrates a three-dimensional view of an assembly example of MuHispan Module
System. The large span GP floor module is present as well as the short span PP floor module. There
are, on the both extremities of the short span PP fillet, two superposed staircase modules ME and
three superposed wind bracing details V.
The figure 18 illustrates the assembly detail K of two T modules from the A configuration, figure 08.
20. The slandar~l metal plate PM fills the joint between the pieces. The fixation is made through two bolts
of medium length. The two boHs ensure the transmission of the local bending moment as usual.
The figure 19 illustrates the assembly detail L of A-type beam, figure 08. The metal plate is different
2163~6~
from the standard plate PM. The fixation is made through two longer bolts. This detail ensures,
despite the existence of only one bolt per module, the l,dnsr"ission of the local bending moment.
The figure 20 illustrates the assembly detail M of two T modules of B, C and similar beams, figure 08.
The metal plate equals 2PM. The fixation is made through four bolts of medium length.
The figure 21 illustrates the particular asse,nbly detail N of B-type beam, figure 08. The metal plate is
PM. The fixation is made through two bolts - shorter and longer.
The figure 22 illustrates the assembly detail O of the extremity of B-type beam, figure 08. The
standard metal plate PM is present two times in this detail. The fixation is made through four bolts,
two by two - shorter and medium. The detail is entirely metal.
10. The figure 23 illustrates the assembly detail P of three T modules. The metal plate equals 3PM. The
fixation is made through six bolts of medium length.
The figure 24 illustrates the assembly detail Q of four T modules of a superposition of two A beams,
figure 14. The metal plate equals 2PM. The fixation is made through four bolts of medium length.
The figure 25 illustrates the assembly detail R of four T modules. The metal plate equals 4PM. The
fixation is made through eight bolts of medium length.
The figure 26 illustrates the three assembly details S1, S2, S3 of two T modules, which change the
direction of CF8 and similar configurations, figure 10. The three metal plates are based on the
standard plate PM. The fixation is made through four bolts of medium length, four shorter bolts and
two longer bolts. The l,ans",ission of the local bending moment is normally accomplished. In the case
20. of this assembly, the entire joint is not hinged. We should consider the entire configuration as a
continuous one - the general bending moment is also transmitted.
2163~ 64
The figure 27 illustrates the assembly detail U between T module and F1 or F2 module, figure 17.
The detail is the same on the high extremity and on the low extremity of the T module. The semi-
cylindrical cores of the module's extremity repose on the T module's small cylinders. The extremities
of the cores and the small cylinders have metal hoops. The fixation is made through an welding
among the hoops. As a maner of statics, there is not a moment resisting joint be~cn the T module
and the F module in the transversal direction of the T modules' ~Jisposition. This is a hinged joint.
The figure 28 illustrates the detail of the standard wind bracing, V. The lateral resistance problem has
two directions. The first one is in the plan of the T module's disposition. The second direction is
perpendicular of the first one. One T module configuration is a two-dimensional structure. The
10. configuration is rigid in its plan only. In case of one usual construction, the beams are disposed in the
transversal direction of the building's length, figure 17 - ST. The length of the floor modules F is
d,sposed in the longitudinal direction, figure 17 - SL. The transversal ~li,e~;tion is the direction of the
basic wind bracing problem. The longitudinal direction is the one of the secondary wind bracing
problem ber~use of the bigger building dimension. One T module conhguration is particularly rigid
and ensures the wind bracing in the transversal direction through its proper qualities, figure 14. The V
detail provides the wind bracing in the longitudinal di,~ tion. The system remains two-dimensional
and the wind bracing in the first p,oje~,tion is provided through the floor modules F. The floor module
F has two spans - large F1 and short F2. The large span produces the important functional
sp~ces The short span produces the service spaces: staircases, lifts, corridors, etc.. Functionally, it
20. is possible to d;spose the short span and the large span of the floor module in alternative order. The
short span is appropriate for the application of the wind bracing detail V. The detail represents two
tensile cross-bars. The cross-bars work in collabordlion with the two adjacent floor modules F2, high
and low. The two adjacer,l floor modules F2, the two adjacer,l T modules and the two cross-bars V
constitute a rigid rectangle. In case of wind action the respective T and F2 modules ensure the
2163~64
compression and one of two cross-bars ensures the traction. This way of work ensures the maximum
lightness of the cross-bars. The cross-bars are metal. The cross-bars' extremities are shaped through
the slandar.J plate PM. The fixation on the T modules is a standard fixation, through bolts. The V
detail ensures the secondary wind bracing in terms of the entire building. The tensile cross-bars act
as axial truss members and the V detail has a good performance in nonsei3n,.~ geographic zones.
The figure 29 illustrates the detail of the seismic lateral stiffness, VS. The VS detail is designed for
seismic geographic zones. The detail acts in collaboration with two a.ljacer,l T-modules. The
exl,el".:ies of the T-modules are connected through two moment resisting bars. There are two tensile
cross-bars between the " ,o" ,ent resisting bars. The extremities of the cross-bars do not coincide with
10. the moment resisting bars' extremities. The whole configuration is an eccer,l,ic braced rectangle. In
case of lateral forces, one cross-bar provokes flexure in the moment resi:,li"g bars because of the
eccent,icity. If the lateral forces do not exceed the design forces, the moment resisting bars deflect
and transmit the stresses. In case of excessive earthquake lateral forces, the moment resisling bars
deform up to the stage of noneccenl,icity of the respective diagonal direction, dissipdling the
earthquake's energy. The configuration ~ ~;ssir ~os the energy through a cor,lr "e d deformation and
without structural damages.
The figure 30 illustrates an wind bracing in the case of system's three level assembly example.
The wind bracing of a moment res,iti"g frame, in the transversal direction of the frame's plan, figures
10, 11, 12, 13, is provided in the way of the general wind bracing. The moment ,esijti"g frame has to
20. be built in two identical configurations in juxtaposition of the short span PP. The two moment resisting
frames are connected through the F2 modules and V or VS details, figures 28, 29. This double frame
configuration represents a moment resisling frame unit and has stiffness in the two perpendicular
directions, similar to figure 30 - central part. This method is able to provide lateral stfflness to a heavy
2163~6~
moment resisting frame, for example - a frame based on the D-type beam, figure 13.
The figure 31 illustrates a post-tensioned beam, W. The two trapezium's bases, the big one and the
small one, have three longitudinal cores each. These cores are co-ordinated with the fixation bolts'
cores. In case of necessity, in relation to a beam or an~,lher building part, it is poss~ to pass the
post-tensioning cables through the cores and to apply the respective tension. The figure 31 shows
the anchors of the post-tensioning cables on the extremities of an A-type beam. This assembly
techn.4ue is compatible with the usual one already analysed. In case of a complex construction, it is
possible to apply the usual assembly technique in the majority of cases and to apply a post-
tensioning to certain particular beams and locations. It is a parallel possibility.
10. The figure 32 illustrates a particularity of a medium length assembly bolt, Y. The bolt's extremities,
disposed on the trapezium's big base, are located in niches. The niche's depth approxim~lely equals
the tickness of the bolt's head and nut. In this way the bolts are not an obstacle for the assembly of
the floor modules F1 and F2.
The figure 33 illustrates the assembly detail between two T modules, Z. The detail connects the big
base of one module with the small base of another one. The small base may be located in the middle
of the big base, figure 33, as well as on the extremity of the big base, figure 12.
The figure 34 illustrates a beam crossing detail DC. All T module configurations are two-dimensional.
A parallel disposition of such configurations needs V or VS details to ach ~.c lateral stiffness. The
cross clisposition of T module configurations provides a mutual lateral ~tirr,less and basically such
20. disposition does not need the V or VS details. The system remains two-dimensional and the lateral
stiffness in the first projection is provided through all floor modules F. The system is able to provide a
criss-crossed wall beam configuration through several beam-types - staggered beams. The DC detail
216346~
-
provides a crossing possibility. All beam types A, B, C, D, etc. and respective moment resi:jli, Ig
frames are crossible. The Multispan Module System is crossing homogeneous.
The modules, which illustrate the Multispan Module System, have exemplary dimensions. The
modules, the con,b..,atorial configurations and the details are acco""~'-shed in nominal dimensions.
The T, F and ME modules have not particular ~sl,i~lions in the matter of construction ",aterials. The
concrete is lightly advisable to execute the modules. The three module types T, F and ME are also
executable in construction metals.
Usually, the beams are located in the transversal direction of the building. The floor modules are
located in the longitudinal direction, among the beams. In case of an usual disposition, the floor
10. modules F, of large span GP and short span PP, are located in alternative order. The short span
modules F2 produce service and communicalion spaces. The large span modules F1 produce basic
function spaces. If the height of the T module HT equals the height of the storey, the T module is
transversally pass~le. It is possible to install a door as well as to leave an opening per each T
module. The T modules, it means the solid walls of the building, do not restrict the space
organ;sdlion. If the beams of the storey are A-type beams, figures 08, 14, 15, 16, the structural
elements, which le~ I;.Sh walls, are the T modules. In this case the span equals the length of the
floor modules F1 and F2. The big span GP could be 12 meters (40 feet). In the transversal direction
of the F modules' length, the juxtaposition of such modules is not limited. In case of a high-rise
building, figure 15, the T modules are not needed on each storey. Every other storey is free of such
20. modules. The span equals the span of the A-type beam. This span could be 30 meters (100 feet).
Analogically, the B, C, D-type beams produce i"lerior:~ respectively more spacious, figure 14. The
D-type beam could reach a span of 90 meters (300 feet) and more, figures 09, 14. A complex
configuration, based on several types of beams - G type included, could reach a span of 240 meters
2163~6'1
(800 feet), figure 16 illustrates a minimum appljr~tion of G type. The l\A~I'tisp~n Module System
produces a particularly rich and flexible space gamut.
The space gamut has a functional aspect. The building functions change following the society's
development. The frequency of these changes is increasing. The classic-type buildings have
structures closely related to the function, the function foreseen for the moment of the inauguration of
the building. After the inauguration the full~lional requirements start to change and the classic
buildings become more and more difficult to equip, to adapt to the new requirements. The period of
the functional ~ic;ency is decreasing. On the other hand, the construction materials and the
structures are dcv~l~ping in the opposite direction. The new structures become more and more
10. durable. The entire p~cess of creation dcvclops in double directions, the durability of the structural
effciency increases - the durability of the fun-,1ional effciency decreases. The gap ketwecn the two
durability's devaluates the general efficiency of the building. The improvement of the situation is
possible through the increase of the durability of the fun-;tional efficiency in conformity with the
durability of the structural one.
Multispan Module System holds out big spans and variety of storey heights. The rich space gamut
has very little or has no reldliolls with any functional specificity. These spacious rooms are equipable
and reequipable in different ways and make no obsl~rl~s for any future adapl-~iQn. The lack of
functional specificity means a presence of functional universalism. The stage of Multispan Module
System's universalism is much higher than the one of the exi~lenl construction systems. This is the
20. universalism, which may keep up the functional efficiency's durability on the level of the structural
effciency's durability. This is the stage of the general efr,cier,~;y of the system, which maxi",i~es the
worth of the building. This analysis shows the long term proftableness of Multispan Module System.
One classic structure represents a series of slandar~ internal co",ponents and particular peripheral
2163~64
components. The peripheral components close the entire structure and in this way the volume is
firmly determined. One extension necessity is difficult to execute. The extension requires a partial
destruction of the peripheral components in order to ensure connections with the new components.
A construction through Multispan Module System represents a series of ~landard modules. The
peripheral modules of the construction are idenlical to the internal modules and keep always the
possibility to ensure new connections in the direction of one extension. If the building envelope is not
taken into consideration, the construction is naturally exlensil)le. Multispan Module System is a
structurally open system.
Generally, there are two basic configurations in relation to the seismic behaviour of the structure. The
10. first one is the classic rectangular building frame. Basically, there is not lateral slirr"ess - the
configuration is laterally flexible - maximum flexibility and minimum rigidity. The ach evement of the
stiflness requires the arF'.c~fion of very special devices such as moment r~si~li"g joints, shear walls,
shear trusses etc.. The second one is the trussed building frame (triangular). As a matter of :,lifrl,ess,
this is a very rigid configuration. The members of the structure are prec;sely axially stressed and there
is maximum rigidity and minimum flexibility. At the same time, this kind of structure is not able for
ductile behaviour and for ~lis~ tion of the earthquake's energy. If the earthquake's lateral forces are
larger than the design capacity of the structure, the building is crucially structurally damaged.
The two configurations, the rectangular frame and the trussed frame, are the two structural opposites.
The tMp~ l conhguration provides advantage properties from both structural opposi'es. With the
20. exception of the B-type beam, figure 08, a lldp. --~-' configuration, in its plan, is neither rectangular
nor triangular (trussed). The inclined sides of the trapezium and the double height 2ET of superposed
trapezium's bases allow a quasi-triangular stress transr"ission, figure 14 - DX1, DX2, DX3, DX4, DX5,
which provides considerable stiffness. SimuHaneously, the basic combinatorial position, figure 08 -
216346g
-
beam A, does not e '-'I'sh triangular connections and allows, through the local flexure, more flexible,
ductile behaviour of the structure's components. In the case of earthquake forces, higher than the
design capacity of the structure, the trapezium's bases with the hinges of the web X-parts deflect
considerably and d;~c;l~le the earthquake's energy without structural damages.
The trapezium-shaped structure is a synthesis between both structural oppos~'cs - flexibility and
rigidity.
The structural analyses, present in this specification, have no quantitative character. These analyses
have a qualitative one. In this way, the analyses are valid over a large dimensional and combinatorial
spectrum of concrete exan,F'es.
10. The principle destination of Multispan Module System is the construction. At the same time, the
strong combinatorial power of the system is able to stimulate the space sense and the imagination of
young people. The educational value of the system is considerable and the system is execut-''e as
an educational device. The system is executable too as a model device for all users of the system
and appl.--'le during the pr~cess of a construction projections. In this way, the execution of the
system has no ~t~i~tions in the matter of scales and materials.
Multispan Module System is a combinatorial system. Many combinatorial examples treat the basic
combinatorial power of the system, figures 08, 09, 10, 12, 13. Some e)~an,rles treat the combinatorial
power of the system on a higher levels, figures 11, 14, 15, 16 These examples are chosen in order
to present the character and the stage of the system's comb'. ,~lorial power. The system is
20. CGm~ dlorially open. The all possible combinations are neither countable nor presentable. The
strong cor,lb.. ,dtorial power of the system represents a large creative field for all potenlial users.
24