Note: Descriptions are shown in the official language in which they were submitted.
RD 235981RD 24492
A Method and A~oaratus
For Remotely Calibrating A
Phased Array S, stem
Used For Satellite
Communication
Background of the Invention
Active phased array systems or smart antenna
systems have the capability for performing programmable
changes in the complex gain (amplitude and phase) of the,,
elemental signals that are transmitted and/or received by each
respective element of the phased array.system to accommodate
different beam-forming scenarios. Communications satellites
equipped with phased array systems are desirable since satellites
so equipped have an intrinsic performance advantage over
satellites with conventional reflector antennas. For example, a
communications satellite with a phased array system can offer the
following advantages: reconfigurable beam patterns ranging from
broad-uniform continental coverage down to narrow spot beam
patterns with 3 dB widths of about 1 °; flexibility in varying the
level of effective isotropic radiated power (EIR.P) in multiple
communication channels; and means for providing graceful
system performance degradation to compensate for component
failures. As conditions for the phased array system in the satellite
can change in an unpredictable manner, regularly scheduled
calibration for characteristics of the system, such as phase and
RD 23598/RD 24492
-2-
amplitude characteristics, is generally required to assure optimal
system performance.
In order to obtain meaningful estimates of the
respective complex gains for the elemental signals respectively
formed in each element of the phased array system, the
calibration process must be performed in a time window that is
sufficiently short so that the complex gains for the respective
elemental signals transmitted from each element are substantially
quasi-stationary. For a typical geostationary satellite application,
the relevant time windows are dominated by two temporally
variable effects: changes in the transmitted elemental signals due
to variable atmospheric conditions encountered when such signals
propagate toward a suitable control station located on Earth; and
changes in the relative phase of the transmitted elemental signals
due to thermally induced effects in the satellite, such as phase
offsets in the respective circuit components for each respective
element of the phased array system, and physical warpage of a
panel structure employed for supporting the phased array. The
thermally induced effects are caused primarily by diurnal
variations of the solar icradiance on the phased array panel.
Calibration techniques proposed heretofore are
essentially variations on the theme of individually measuring, one
at a time, the respective complex gain of each single element (SE)
of the phased array system while all the other elements of the
phased array system are turned off. Although these calibration
~"' ~' ~ ~ O ~ ~' RD 235981RD 24492
-3-
techniques (herein referred as SE calibration techniques) are
conceptually simple, these SE calibration techniques unfortunately
have some fundamental problems that make their usefulness
questionable for meeting the calibration requirements of typical
phased array systems for communications satellites. One problem
is the difficulty of implementing a multipole microwave switching
device coupled at the front end of the respective electrical paths
for each elemental signal so as to direct or route suitable test
signals to any single element undergoing calibration. This
multipole switching device is typically necessary in the SE
calibration techniques to measure the complex gain for the
elemental signal respectively formed in any individual element
undergoing calibration at any given time. Another problem of
the SE calibration techniques is their relatively low signal-to-
noise ratio (SNR). This effectively translates into relatively long
measurement integration times. At practical satellite power
levels, the integration times required to extract the calibration
measurements for the SE calibration techniques are often too long
to satisfy the quasi-stationarity time window criteria described
above. In principle, one could increase the effective SNR of the
SE process by increasing the power of the calibration signals
transmitted from each element. However, as each element of the
phased array system is usually designed to operate at near
maximum power, as dictated by the power-handling capacity and
linearity constraints for the circuit components in each element, it
follows that arbitrary additional increases in power levels are
RD 235981RD 24492
-4-
typically not feasible. Thus it is desirable to provide a calibration
method that allows for overcoming the problems associated with
SE calibration techniques.
Summary Of The Invention
Generally speaking, the present invention fulfills the
foregoing needs by providing a method and apparatus for
remotely calibrating a system having a plurality of N elements, N
being a positive integer number. The method includes generating
coherent signals, 'such as a calibration signal and a reference
signal having a predetermined spectral relationship between one
another. The calibration signal which is applied to each
respective one of the plurality of N elements can be orthogonally
encoded based on the entries of a predetermined invertible
encoding matrix, such as a binary Hadamard matrix, to generate
first and second sets of orthogonally encoded signals. The first
and second sets of encoded signals and the reference signal are
transmitted to a remote location. The transmitted first and second
sets of encoded signals are coherently detected at the remote
location. The coherently detected first and second sets of encoded
signals are then decoded using the inverse of the predetermined
invertible encoding matrix to generate a set of decoded signals.
The set of decoded signals is then processed for generating
calibration data for each element of the system.
RD 23598/RD 24492
-5-
Brief Description Of The Drawinec
The features of the invention believed to be novel are
set forth with particularity in the appended claims. The invention
itself, however, both as to organization and method of operation,
together with further objects and advantages thereof, may best be
understood by reference to the following detailed description in
conjunction with the accompanying drawings in which like
numerals represent like parts throughout the drawings, and in
which:
Fig. ~ 1 is a simplified block diagram representation of
a communications satellite using a phased array system that can be
remotely calibrated in accordance with the present invention from
a remote control station;
Fig. 2 is a block diagram representation showing an
exemplary architecture for the phased array system of Fig. l,
and including a coherent signal generator and a controller for
controllably switching respective delay circuits in each element of
the phased array system in accordance with one embodiment for
the present invention;
Figs. 3a and 3b illustrate, respectively, gain
characteristics for a single delay circuit being switched-in, and
for multiple (two) delay circuits being switched-in in any given
one of the elements of the phased array system of Fig. 2;
RD 235981RD 24492
-6-
Fig. 4 shows further details about the coherent signal
generator of Fig. 2;
Fig. 5 is a simplified block diagram for a coherent
detector and a calibration processor situated at the remote control
station of Fig. 1;
Fig. 6 shows further details about the coherent
detector of Fig. 5;
Fig. 7 is a flowchart of an exemplary embodiment
for a calibration method in accordance with the present invention;
- Fig. 8 is a flowchart showing steps used for
orthogonally encoding signals in a coherent system, such as the
phased array system of Fig. 2;
Fig. 9 is a flowchart showing steps used for
measuring in-phase and quadrature components of orthogonally
encoded signals and for decoding the measured in-phase and
quadrature components of the orthogonally encoded signals; and
Fig. 10 is a flowchart showing steps for sequentially
transmitting the orthogonally encoded signals used for calibrating
the phased array system of Fig. 2.
RD 23598/RD 24492
DETAILED DESCRIPTION OF THE
INVENTION
Figure 1 illustrates a communications satellite 10 that
incorporates a phased array system 12 for transmitting and/or
receiving radio frequency (RF) signals 14. If, for example,
phased array system 12 is used in a transmitting mode, then RF
signals 14 can be received at a remote control station 18, such as
an earth-based control station, through a receiving antenna 20.
As will be appreciated by those skilled in the art, a phased array
system operates on the principle that the phase of the RF signals
emitted from the elements of the array can be selectively adjusted
to provide a desired interference pattern at locations that are
spatially remote from each element of the phased array. Consider
an RF transmission from an N-element phased array system at
wavelength ~.. By way of example, choose a coordinate system
with its origin at the center of the phased array. The signals
A(R; ), received at spatial points R; , are the interference sum of N
elemental signals,
A(R;)=K; ~a(n)s(n,R;), (1)
0=1
having waveforms s(n, R; ), such that
w ~ ~ ~ 0 ~ ~ ~. RD 23598IRD 24492
_g_
e;2~~R,-~,Ua
f~ a e-;2n~,.R;/«~R,p (2)
IR; _ rn I IR;
The relative values of the set of coefficients, {a(n)} , give
the relative complex gains associated with respective circuit
components, such as phase shifters 50 (Fig. 2) and power
amplifiers 80 (Fig. 2), for each element of the phased array. It
can be shown that information merely obtained by spatially
sampling any interference pattern transmitted and/or received by
the phased array (but not encoded in accordance with the present
invention) cannot easily extract phase offsets due to the relative
positioning of the elemental horns of the phased array, such as
transmitting horns 90 (Fig. 2). In principle, the value for each
coefficient a(n) could be determined by measuring or sampling
the amplitude and phase of the interference pattern at N distinct
spatial sampling locations {R; } ; i= 1, 2, . . . , N, that are
specifically selected to provide N linearly independent
simultaneous equations. In practice this procedure would be very
difficult to implement as N values of three different parameters
would have to be known to compute a solution. The three
different parameters include the spatial sampling {R; } , the
elemental transmitting horn positions ~,, and the relative values of
the different propagation constants K;.
i~ ~ ~ ~ ~ ~ ~, RD 23598/RD 24492
-9-
In contrast to the above-described spatial sampling
calibration technique, coherent signal encoding of the elemental
signals provides a dramatic simplification as the encoded signals,
which enable to form predetermined time multiplexed beam
patterns, can be received at a single receiver point situated along a
reference direction Ro. Further, as there is only one propagation
constant Ka, its value need not be known to determine the
respective relative values of each complex gain. Also, in the far
field, the parameters of interest can be obtained without
knowledge of the distance to the single receiver point. It is
assumed that the projection angle of reference direction Ro onto
the uniform phase plane of the array is known to a precision
commensurate with the desired calibration accuracy. As will be
appreciated by those skilled in the art, the projection angle can be
measured using readily available attitude measurements from
conventional celestial body sensors, such as Earth, Moon and Sun
sensors.
In the far field, the received signal of any mth coherently
encoded transmission is of the form,
N
A(m,Ro)=Ko a ~~(m~~~a~nle-i2~~ Ro/c~Ro~
°°' '
for m =1, 2, . . . , N.
__ ~~.~00~~
RD 23598IRD 24492
- 10-
If c(m, n) represents the coefficients of a predetermined
invertible, encoding matrix T, such as an unitary, encoding
matrix, then the respective relative values of the product
{a(r)e-~2"' R°%~~~~ cam be obtained directly from the inversion of
matrix T which enables for solving a system of N linearly
independent simultaneous equations. In general, the inverse of a
unitary matrix U is equal to the Hermitian conjugate U' of the
matrix U and thus U-' ._ U'. As will be appreciated by those
skilled in the art, the rows and columns of a unitary matrix, such
as matrix U, form a complete orthonormal set of basis vectors
that span the vector space upon which matrix. U . is defined. In
general, orthogonal transforms are formally defined as the subset
of unitary transformations defined on real vector spaces.
Orthogonal transforms have been used extensively in imaging
applications; see, for example, technical paper by W. K. Pratt, J.
Kane, and H. C. Andrews, "Hadamard Transform Image Coding",
Proc. IEEE 57, No. 1, at 58-68, (January 19b9). As used herein
the matrix T differs from its associated unitary matrix by a
normalization factor ,~N . Accordingly, T is referred as a
renormalized unitary matrix,
T = .,~T, ~ T-' = N T' .
By way of example and not of limitation, it can be shown
that a minimum variance encoding scheme can be achieved when
RD 23598/RD 24492
-11-
using a renormalized unitary matrix where each matrix element
has unit magnitude, i.e., ~c(m, n~ =1. Some notable examples of
equal magnitude renormalized unitary matrices are the classes of
two-dimensional (2D) discrete Fourier transforms (DFT) and
Hadamard matrices.
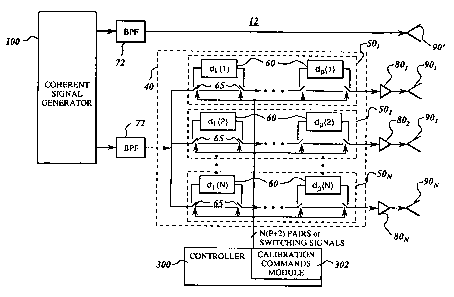
Fig. 2 shows a simplified schematic of an exemplary analog
architecture for an N-element phased array system 12. It will be
appreciated that the present invention need not be limited to
analog architectures being that digital beam-forming architectures
can readily benefit from the teachings of the present invention. It
will be further appreciated that the present invention need not be
limited to a phased array system being that any system that
employs coherent signals, such as coherent electromagnetic
signals employed in radar, lidar, communications systems and the
like; or coherent sound signals employed in sonar, ultrasound
systems and the like, can readily benefit from the teachings of the
present invention.
Phased array system 12 includes a beam-forming matrix 40
made up of N phase shifters 501- SON each having a p-bit beam-
forming capability. Each respective phase shifter for each
element is made up of p independent delay circuits 60 that, by
way of suitable switches 65, can be selectively switched or
actuated into the electrical path for each elemental signal to
provide 2P quantized phase levels corresponding to phase shifts of
2nm/2P for m = 0, 1, . . . ,2P-1. Fig. 2 further shows a coherent
signal generator 100 that supplies a reference tone or signal
RD 23598/RD 24492
- 12-
having a predetermined spectral relationship with respect to a
calibration signal applied to each element of the phased array.
For example, the reference signal can be offset in frequency by a
predetermined factor from the calibration signal. The reference
signal and the calibration signal each passes through respective
bandpass filters 72 having a predetermined passband substantially
centered about the respective frequencies for the reference signal
and the calibration signal. Although in Fig. 2 coherent signal
generator 100 is shown as supplying one reference signal, it will
be appreciated that additional reference signals, if desired, could
be readily obtained from coherent signal generator 100.
As shown in Fig. 2, each phased array element further
includes a respective power amplifier 80 and a respective horn
90. Although Fig. 2 shows that the reference signal is transmitted
from a separate horn 90', the reference signal can, with
equivalent results, be transmitted from any of the phased array
elements as long as the reference signal is injected into the
electrical path after any of the phase shifters 501-50N so that the
reference signal is unaffected by any encoding procedures
performed by the phase shifters. Fig. 2 shows a controller 300
which, during normal operation of the system, can issue switching
commands for forming any desired beam patterns.
In accordance with one preferred embodiment for the
present invention, controller 300 further includes a calibration
commands module 302 for issuing first and second sets of
RD 23598/RD 24492
- 13-
switching signals that allow the delay circuits 60 for encoding
corresponding first and second sets of signals being transmitted
by the N elements of the phased array system to a remote
location, such as control station 18 (Fig. 1).
As suggested above, the controlled switching, i.e., the
encoding, is dictated by the matrix elements or entries of a
predetermined invertible, binary matrix. In particular, a class of
orthogonal matrices, such as binary or bipolar Hadamard
matrices, is optimal in the sense of providing minimal statistical
variance for the estimated calibration parameters. The encoding
matrix can be chosen to have a size NxN if N is an even number
for which a Hadamard matrix can be constructed. If a Hadamard
matrix of order N cannot be constructed, then the next higher
order Hadamard construction can be conveniently used for the
encoding. For example, the next higher order can be
conveniently chosen as K=N+Q where Q is a positive integer
number representing extra transmissions corresponding to non-
existing elements and thus such extra transmissions are effectively
treated as if they were made up of zero value signals. It will be
appreciated by those skilled in the art that this matrix construction
technique is analogous to "zero-filling" techniques used in a Fast
Fourier transform, for example. Henceforth in our discussion
for the sake of simplicity and not by way of limitation we will
only consider Hadamard matrices, represented by H for the
controlled switching (CS) procedure. It will be shown that upon
performing suitable coherent detection and decoding at the
'~ ~ ~ ~ ~ ~ ~ ~ RD 235981RD 24492
- 14-
remote location, the first and second sets of orthogonally encoded
signals allow for determining calibration data indicative of any
changes in the respective complex gains of the delay circuits, and
including the respective signals {s(n) for n=1, 2, . . ., N}
associated with each of the phased array elements when no delay
circuit is switched-in, i.e., each signal associated with a respective
undelayed or "straight-through" electrical path that includes the
respective power amplifier and horn but does not include any
delay circuit in any respective phased array element.
For an analog embodiment, it is assumed that the power
levels for the calibration signal are low enough so that the phase
shifters can be treated as linear microwave devices. For example,
the effect of switching-in or actuating a single delay circuit 60,
such as the ltth delay circuit in any nth phase shifter with a
complex gain d~(n) simply imposes a complex gain as shown in
Fig. 3a to an input signal R(n). The effect of switching-in or
actuating multiple delay circuits 60 and 60' simply generates the
product of the respective complex gains for the multiple circuits
switched-in. For example, as shown in Fig. 3b, if the uth delay
circuit for the nth phase shifter with a complex gain dv(n) is
switched-in together with the ~tth delay circuit, then the complex
gain for the input signal x(n) will be as shown in Fig. 3b.
Fig. 4 shows a simplified schematic for coherent signal
generator 100 used for generating coherent signals, such as the
calibration signal and the reference signal. As used herein the
expression coherent signals refers to signals having a substantially
RD 235981RD 24492
- 15-
constant relative phase relation between one another. As shown
in Fig. 4, a local oscillator 102 supplies an oscillator output signal
having a predetermined frequency fo to respective frequency
multipliers 104, 106 and 108 each respectively multiplying the
frequency of the oscillator output signal by a respective
multiplying factor such as N1, N2 and N3, respectively. As
shown in Fig. 4, the respective output signals of multipliers 108
and 104 is mixed in a first mixer 110 to supply a first mixer
output signal having a frequency f--(N2+N3)fo. Similarly, the
respective output signals of multipliers 106 and 108 are mixed in
a second mixer 112 to supply a second mixer output signal
having a frequency f--(N1+N3)fo. By way of example, the first
mixer output signal can constitute the reference signal and the
second mixer output signal can constitute the calibrated signal
applied to each element of the phased array system.
Fig. 5 shows a simplified block diagram for a coherent
detector 400 and a calibration processor 402 which can be
situated at control station 18 (Fig. 1 ) for detecting and decoding,
respectively, any sequences of encoded coherent signals being
transmitted from the phased array system for determining
calibration data which can then be conveniently "uplinked" to the
satellite to compensate for changes in the various components
which make up each respective element of the phased array
system, such as power amplifiers, horns, and phase shifters.
Fig. 6 shows details about coherent detector 400 and
calibration processor 402. As shown in Fig. 6, the received
RD 235981RD 24492
- 16-
reference signal is supplied to a first mixer 406 and to a phase
shifter 404, which imparts a phase shift of substantially 90~ to the
received coherent reference signal. As further shown in Fig. 6,
each orthogonally encoded signal is supplied to first and second
mixers 406 and 408, respectively. First mixer 406 mixes any
received encoded signal with the reference signal to supply a first
mixer output signal replicating the respective component of any
received encoded signal that is in phase with the reference signal.
Conversely, second mixer 408 mixes any received encoded signal
with the phase shifted reference signal to supply a second mixer
output signal replicating the respective component of any received
encoded signal that is in quadrature (at 90°) with the reference
signal. The in-phase and quadrature components are converted to
digital data by respective analog-to-digital (A/D) converters 409.
As shown in Fig. 6, calibration processor 402 can include register
arrays 4101 and 4102 for storing, respectively, the in-phase
components and the quadrature components supplied by A/D
converters 409. Calibration processor 402 can further include a
memory 412 that can store entries for the inverse matrix H-1
which is used for decoding the respective quadrature components
of the encoded signals. Calibration processor 402 further
includes an arithmetic logic unit (ALU) 412 for performing any
suitable computations used for decoding the respective quadrature
components of the encoded signals. For example, ALU 412 can
be used for computing a difference between each quadrature
component for the first and second sets of orthogonally encoded
CA 02180051 2004-06-25
-17-
RD 235981RD 24492
signal, and computing the product of the resulting difference with the
inverse matrix H-1,.
Fig. 7 shows a flow chart for an exemplary calibration
method in accordance with the present invention. After start of
operations in step 200, step 204 allows for generating coherent
signals, such as the calibration signal and reference signal
generated by coherent signal generator 100 (Figs. 2 and 4). In
accordance with step 204, the calibration signal is applied to each
element of an N-element coherent system, such as the phased
array system of Fig. 2. Step 206 allows for encoding the
calibration signal applied to each element of the coherent system
to generate, for example, first and second sets of encoded signals.
The encoding can be advantageously performed using controlled
switching or toggling of the delay circuits in each element of the
phased array system, that is, no additional or separate encoding
hardware is required being that the encoding is performed based
on the specific delay circuits that are actuated in response to the
switching signals from calibration commands module 110 (Fig. 2).
CA 02180051 2004-06-25
-18-
RD 235981RD 24492
Step 208 allows for transmitting the first and second sets of
encoded signals and the reference signal to a remote location, such
as control station 18 (Fig. 1 ). Step 210 allows for coherently
detecting the transmitted first and second sets of encoded signals
at the remote location. Step 212 allows for decoding the detected
first and second sets of encoded signals to generate a set of
decoded signals which can be conveniently processed in step 214,
prior to end of operations in step 216, for generating calibration
data for each element of the phased array system.
Fig. 8 shows a flow chart, which can be conveniently used
for performing encoding step 206 (Fig. 7) in the phased array
system of Fig. 2. After start of operations in step 222, step 224
allows for generating a first set of switching signals based upon
entries of invertible, binary matrix H. Step 226 allows for
applying the first set of switching signals to actuate respective
ones of the p delay circuits in each element of the phased array
system to generate the first set of encoded signals. In contrast, as
shown in step 228, the second set of switching signals uses -H for
the controlled switching which in turn generates the second set of
encoded signals. Prior to end of operations in step 232, step 230
allows for applying the second set of switching signals to actuate
respective ones of the p delay circuits in each element of the
phased array to generate the second set of encoded signals. This
switching procedure using a Hadamard control matrix effectively
generates an exact unitary (orthogonal) transform encoding of the
RD 235981RD 24492
- 19-
calibration signal applied to each of the phased array elements.
As suggested above, this switching scheme is particularly
advantageous being that the delay circuits themselves provide the
desired encoding, and thus no additional encoding hardware is
required.
Fig. 9 shows a flowchart that can be used for performing,
respectively, detecting step 210 and decoding step 212 (Fig. 7).
After start of operations in step 240, and assuming that the first
and second sets of encoded signals are made up, respectively, of
first and second sets of orthogonally encoded signals, step 242
allows for measuring, with respect to the reference signal,
respective in-phase and quadrature components for the first and
second sets of orthogonally encoded signals which are received at
the remote location. For example, coherent detector 400 (Fig. 6)
allows for measuring both in-phase components and quadrature
components of any received encoded signals. This can further
include measuring, with respect to the reference signal, the phase
and amplitude for each first and second sets of orthogonally
encoded signals which are received at the remote location. It will
be appreciated that absolute measurements are not important since
the calibration data can be effectively obtained from relative
measurements of phase and amplitude, i.e., respective
measurements of variation over time of phase and amplitude for
each received encoded signal relative to the phase of the reference
signal. Step 244 allows for computing a respective difference
between each respective measured in-phase and quadrature
.~. ~ ~ ~ 1 RD 23598/RD 24492
-20-
components for the first and second sets of orthogonally encoded
signals which are received at the remote location. Prior to end of
operations in step 248, step 246 allows for computing the product
of each respective computed difference with the inverse of the
same binary orthogonal matrix, H-' = HT /N used in the controlled
switching encoding. In accordance with another advantage of the
present invention, it will be appreciated that the computation of
inverse matrix H-' is straightforward since the inverse matrix in
this case is simply the transpose of H normalized by the factor
1/N.
Fig. i0 shows a flowchart which provides further details
about transmitting step 208 (Fig. 7) which allows for calibrating
the full set of N(p+1) state variables associated with, for example,
the N elements for the phased array system of Fig. 2. It will be
shown that the controlled switching calibration procedure in
accordance with the present invention generally requires a total of
2N(p+2) individual sequential transmissions, or N(p+2) sequential
transmission pairs, that is, sequentially transmitting N(p+2) pairs
of the first and second sets of orthogonally encoded signals. This
advantageously enables the calibration procedure in accordance
with the present invention to provide information comparable to a
SE calit~ration measurement at a signal-to-noise ratio (SNR)
effectively enhanced by a factor ~p+ 2) 2 N over the SE calibration
measurement with the same maximum elemental signal power for
each transmission.
RD 23598IRD 24492
-21-
After start of operations in step 260, step 262 allows for
sequentially transmitting N pairs of orthogonally encoded signals,
such as corresponding to the first and second sets of orthogonally
encoded signals, wherein each ~tth delay circuit is switched in
accordance with predeterniined encoding rules based upon entries
of matrix H, while each remaining delay circuit in each element
of the phased array system is switched-out. Each sequentially
received transmission pair is conveniently expressed in vector
form as,
Yao = ~YNO ( 1 ), y~o (2)~ . . . ~ Y,~o (N)~T~
Y~ _ ~Y~o ( 1 )~ y~o (2>> . . . , y~o (rrl~T.
(5)
The first subscript index ~t on Y~,o indicates that a
predetermined delay circuit, such as the ~tth delay circuit, is
toggled in accordance with predetermined encoding rules based
upon entries of Hadamard matrix H. The second subscript (zero)
on these vector signals indicates that these are the signals received
when each remaining delay circuit, other than the ~th delay
circuit, is switched-out. For this step of the calibration process,
N transmission pairs of orthogonally encoded signals
corresponding to the N elements of the phased array system are
sequentially transmitted and received at the remote location.
RD 23598IRD 24492
-22-
Any mth sequentially received transmission pair of the first
and second sets of orthogonally encoded signals is, respectively,
represented by,
N N
Y~o(m) _ ~D~{~) s(n). y~o(m) _ ~D~(mn) s(n).
The encoding coefficients D,,(mn), D~(mn) are dictated by
the status of the delay circuits that are switched according to the
following Hadamard encoding rules:
+1 ~th delay circ. of nth element switched out if H(mn) =+1
) d~, (n) ~tth delay circ. of nth element switched in if H(mn) _ -1
- +1 Etth delay circ. of nth element switched out if H{mn) - -1
"( ) d~(n) ~tth delay circ. of nth element switched in if H(mn) _ +1 ~(~)
The differences of the encoding matrices are represented in
component and matrix form as,
D~,(mn) D~ (mn) = H(mn)~1- d~,(n))' D - U' = H(I - d
' ~ ~ N)~ ~8)
As suggested above, decoding can be conveniently
performed at the remote location by computing the difference of
received signal vectors Y~,o, Y~o and multiplying the resulting
vector difference by the inverse of the same Hadamard matrix
that was used in the controlled switching performed onboard the
-- ~ ~, ~ ~ ~ ~ ~ RD 23598/RD 24492
-23-
satellite. In the absence of noise, we obtain a decoded vector
signal Z,,o, such that,
Zr~o -_- H ' (Y,~o - Y o ) = H-' ( D,~ - D,", )S = ~I - d~, ~S.
Step 264 allows for transmitting N(p-1) pairs of
orthogonally encoded signals wherein each ~tth delay circuit is
toggled in accordance with the predetermined encoding rules
while another predetermined delay circuit other than the ~tth
delay circuit, say the with delay circuit, is permanently switched-in
on each of the elements of the phased array. In this case, any mth
received transmission pair of the first and second sets of
orthogonally encoded signals is represented, respectively, by
N N
y~,~(m)=~~D~,(mn)d~(n)s(n), y~y(m)=~D~(rnn)d~(n)s(n). (10)
Here again, the first subscript index It on any component
y,,Y indicates that the ~tth delay circuit is toggled in accordance
with the predetermined encoding rules based upon entries of the
predetermined Hadamard matrix H while the second subscript
index (here the v index) indicates that the with delay circuit is
switched-in on each of the elements of the phased array system.
In this case the resulting set of decoded signals are represented in
vector form by a decoded vector ZNy, such that
RD 235981RD 24492
~.~.~~~~1~
-24-
Z""-H ~(y~" Y~ J H ~~D~ DNl"-(I-dr~~d"S. (11)
The N complex gains, d"(n) are readily computed by
taking the ratio of the decoded vector signal components,
d"(n)=~z~",(n)~z~o(n)~ (12)
The above-described procedure can be repeated using
controlled switching with the predetermined ltth delay circuit and
with each of the other remaining delay circuits singly switched-in
to determine each complex gain, d"(n) for all (p-1) remaining
delay circuits such that v ~ ~c . In this manner, step 264 allows for
transmitting N(p-1 ) pairs of first and second sets of orthogonally
encoded signals wherein the predetermined ~.th delay circuit is
toggled in accordance with the predetermined encoding rules,
while each remaining with delay circuit in each phase-shifting
element of the phased array is sequentially switched-in.
Step 266 allows for transmitting N pairs of first and second
sets of orthogonally encoded signals wherein any delay circuit
other than the ~,th delay circuit, for example the ~th delay circuit
(~ch ~ ~cth), is toggled in accordance with the predetermined
encoding rules, while each remaining delay circuit in each
element of the phased array system is switched out. In this case,
the resulting set of decoded signals are represented in vector form
by decoded vector signal ~o , such that
zoo=y-c~)s.
( 13)
-- '~ ~ ~ ~ ~ 5 ~, RD 23598/RD 24492
-25-
Step 268 allows for transmitting N pairs of first and second
sets of orthogonally encoded signals wherein the ~th delay circuit
is toggled in accordance with the predetermined encoding rules,
while the predetermined ~,th delay circuit in each phase shifter of
the phased array system is switched in. In this case the resulting
set of decoded signals are represented in vector form by decoded
vector signal ~,, such that
Z~,~ _ (I - d~)d,~S.
( 14)
The N complex gains d~ ~ n) are readily computed by taking
the ratio of the decoded vector signal components,
d~(°) = W(n)/z,~o(n)~.
(15)
Once all the respective complex gains dr(n) are determined '
for all y =1, 2, . . . , p; n = I, 2, . . . , N, the "straight-through"
signals
or undelayed signals, f s(n)}, are readily determined from,
s(n) _ ~z~o(n)~1- d~(n)~. ( 16)
Thus the complete calibration data for each respective
complex gain for Nxp delay circuits plus the complex gains for
the N straight-through or undelayed electrical paths are obtained
with N(p+2) transmission pairs that can be conveniently
enumerated as follows:
~r~00~~
ø- RD 235981RD 24482
-26-
\\
Switching Action Measured Result Transmission
Pairs Number
,u th delay unit switched(I _ d~ )S
as per
N
H(mn) entries; all
other delay
units switched-out
~u th delay unit switchedI - d d S
as per
N(p-1 )
H(mn) entries; each
remaining
delay unit with ~ ~tth
being
s uentiall switched-i89-
~ th delay unit (~th (I _ d~~S
~ ~tth) l
N
switched as per H(mn)
entries
;
all other delay units
switched-
out
~ th delay unit switchedI - d d S
as per
N
H(mn) entries; It th
delay unit
switched-in
Mathematics of Hadamard Control Matrices
An Nth order Hadamard matrix 2 is an NxN binary
orthogonal matrix with each entry, [Hjmo = H(~) equal either to
~ 1. An Nth order Hadamard matrix is not unique, as any
permutation of the rows or columns also produces an additional
Nth order Hadamard matrix. Hadamard matrices are orthogonal
matrices with inverses, H-' =HTIN. As an example, we illustrate
the recursive generation of the set of radix 2 natural form
Hadamard matrices. Consider a fundamental matrix of order
N=2.
RD 23598IRD 24492
-27-
+1 +1
Hz= +1 -1.. . (17)
An N=4th order natural form Hadamard matrix can be
constructed as:
+1 +1 +1 +1
HZ Hz +1 -1 +1 -1 1g)
H'= +1 +1 -1 -1 ~ (
HZ _Hz _
+1 -1 -1 +1
The "natural form" Hadamard matrix of order 2N can be
constructed from the Nth order Hadamard matrix using,
H" H" 19)
Hz"=
H" -H~
The orthogonal encoding using a Hadamard control matrix
is based upon the following procedure. Consider a diagonal
matrix d of complex numbers, d --_- diag(d(1),d(2), . . . d(N)).
Construct matrices, D, D", based upon any suitable Hadamard
matrix with their (mn)th matrix elements or entries constructed
according to the following rules:
RD 235981RD 24492
-28-
+1 if H(mn) _ +1 R d(n) if H(mn) _ +1
D(mn) _ ; D (mn) _
d(n) if H(mn) _ -1 +1 if H(mn) _ -1
(20)
Matrices of the differences of D, D" are expressed in
component and matrix form as,
D(m n)- DR(m n) = H(m n)( 1-d(n); D - D" = H(I - d) (21 )
Here I is the identity matrix. Multiplying each side of Eq. (21 ) by
the inverse matrix H-', gives a diagonal matrix,
H''(D-DR)=H-'H(I-d)=I-d. (22)
While only certain features of the invention have been
illustrated and described herein, many modifications,
substitutions, changes, and equivalents will now occur to those
skilled in the art. For example, although the above-described
mathematical background illustrates use of Hadamard matrixes in
their "natural form", it will be understood that the orthogonal
encoding can be performed using all forms of Hadamard matrixes
and thus the present invention is not limited to "natural form"
Hadamard matrixes. It is, therefore, to be understood that the
appended claims are intended to cover all such modifications and
changes as fall within the true spirit of the invention.