Note: Descriptions are shown in the official language in which they were submitted.
~iLE, P~ T~Z'S P~;L~
F~R~N~L~TION ~ ~ 8 ~ 2 ~ ~
APPARATUS AND PROCESS FOR ~RODUCING AN IMAGE SEQUENCE
The motion control is used in the film and video industry
to achieve precise execution and repetition of a camera ' s
movement. The need for such precise movement (which is
programmed through a computer) developed for several
10 reasons. One of these is the automation of cameras in
broadcast studios, i.e., TV news broadcasts. Another, and
until now, the most important use, is in the production of
special effects in multi-composite photography.
15 The current development of computer graphics ~CG) has
created the need for a connection between the worlds of
"real" images photographed by a camera Lens and
"artificial" images generated by computers.
20 An illusion of three-dimensional (3-D) motion in space in a
CG image is a ~-esult of mathematical calculations. Every
element of the image, under consideration of the movement
of the (virtual) "camera" which exists only theoretically,
has to be precisely calculated on the basis of a
25 predetermined program. A CG "camera" is free from all
physical limitations, w~lich strongly affect the motion of a
real camera and the generation of images by it.
An image photographed by a real camera in motion ~real time
30 photography) is influenced by many physical disturbances.
Such disturbances are partly caused by the mass and
corresponding kinetic energy of the camera and by
fluctuations of its path. In the case of multi-composite
photography, the results of these disturbances are improper
35 location and eventually jitter between the different
components of the picture. These disturbances create an
2 21822~
especially significant problem when photographed components
represent different scales. In many cases, there is no
mechanical solution to avoid these oisturbances. If "real
5 time" photography must be used - especially when
photographing living obj ects - then the simplest of motions
must be used (linear travel, smooth side to side pan) for a
short duration. In this context, there is also another
problem. A computer generated image cannot be built on
10 camera position alone. Every component of the CG image has
to have its own locatlon in space (defined by an X-Y-
~coordinates). Existing motion control systems just allow
for the planning and positioning of a camera (according to
the X-Y-~ coordinates of the camera) but do not allow for
15 the planning and positioning of photographed objects. This
is caused by focusing solely on the motion of the camera
and not on the environment the camera is photographing.
The praduction of special effects e(when multi-composite
20 photography has to be applied) is a very complex process.
Few studios in the world can praduce multi-composite
special effects. Also, the production of such effects is
extremely expensive. Irl the past, the studios developed
their own motion control systems without an industry
25 standard. Furthermore, CG software for the production of
computer generated images (which become components of
multi-composite images) is developed without any relation
to e~isting or even standardized motion control system.
30 Therefore, it is necessary to build an integrated hardware
and software system, which can "execute" the same motion in
the above "worlds" and can solve the problem of jitter in
real time photography.
3 218~29~
It is especially an object of the invention to provide an
apparatus and a process for producing film or video
sequences, resp-ectively, the production of which in a
conventional manner re~uires a relatively complicated
s motion of the camera, by means of a simplified and
therefore less j itter-sensitive camera motion.
This object is solved by an apparatus having the features
of claim 1 or a process, respectively, having the features
lo of claim 15
A device, in accordance with the present invention, serves
for simulating photographic images of an obj ect to be
photo-graphed The device has a camera that is movable in
15 an X-Y plane and is rotatable about an axis that extends
through the camera and is substantially perpendicular to
the X-Y plane. The device also includes a rotatable stage
or plat-form. The stage or rotatable platform selectively
rotates an object to be photographed about an object axis
20 which is substantially perpendicular to the X-Y plane. The
camera is provided on a camera mount, which mounts the
camera such that the camera is at least rotatably movable
along a camera axls which is substantially parallel to the
object axis. Furthermore, a drive assembly is provided for
25 reciprocally moving the camera mount along a Y axis toward
and away from the plat-form. A translating means
"translates" a first spatial and angular relationship
between the camera which is movable in an X-Y plane and
rotatable about an axis therethrough, and the object, into
30 a second spatial and angular relationship between the
camera and the object, which supposes that the camera is
movably mounted on the camera mount so as to be rotatable
along the camera axis and movable along the Y axis and the
object is on a rotatable platform, such that a set of the
4 2~
seco~rd relationships will produce substantially the same
photographic images as would be produced by a set of the
first relationships. Controlling means is provided for
5 controlling the drive assembly to regulate movement of the
camera along the Y axis, and for controlling rotational
movement of the platfo rm and the camera according to the
set of second relationships. The camera may also be moved
along the Z-axis, perpe]ldicular to the X-Y plane.
In an advantageous embodiment, the apparatus comprises an
image processing unit for superimpo-sing single images of
plural primary image sequences which in part or completely
have been produced by means of the image taking device or
15 in a synthetic way, especially as computer graphics, for
forming a resulting imc~ge sequence. This superposition of
several images can be carried out uslng means of the film
copying technology or the digital (video) image processing
which are known as such. Herein, the application o~ the
20 technique common be known as Blue-screen technique wherein
during the takes a single-colored screen (Blue-screen) is
provided as background for the take is especially useful.
For facilitating the synchronization between the several
25 image sequences and possibly for creating computer graphics
(especially e.g. "virtual reality~) sequences which are
fitted to the takes of real objects t~1e apparatus in useful
manner, furthermore, comprises a memory means for storing
the control signals which are output to the several
30 components of the apparatus (camera, drive of the camera
mount, rotating stage or turntable, respectively, etc. )
during the taking of a primary image sequence.
%~
Its data input is connected with the output of the
evaluating unit during the taking of at least one primary
image sequence to store the evaluated control signals. The
data output of the memory means optionally during the
5 taking of a further primary image sequence is connectable
with the control inputs of the components or an input of
the evaluating unit or is connectable with an input of the
image processing unit during the production of the
resulting image sequence from plural primary image
10 sequences such that the control signals are directly or
indirectly read out for controlling the further takes
and/or the image processing.
13specially, the evaluating unit comprises an interface for
1~ connecting it with a graphics computer for unidirectionally
or bidirectionally transferrlng controL data for the
apparatus to and/or from this computer for the synchronized
production of phototechnically or videotechnically
generated and of synthetic image sequences.
In a further useful embodiment, the evaluating unit and/or
the image processing unit comprises a scaling unit for
individually adjusting the control signals for the
operation of the apparatus for producing several image
25 sequences with respect to different take conditions -
especlally different scale (object distance, zoom) - and/or
parameters of the several images to be superimposed and
originating from different image sequences. ~ereby e.g. an
adjustment of the relative image size, a rotation of the
30 image plane and/or the adjustment of a corresponding image-
weighing factor for the superposition (mixing) of several
images can be carried out.
` 2~822~0
Furthermore, the image processing unit advantageously
comprises means for the later processing of an image
sequence being formed by superposltion ("matting").
5 A further important embodiment of the apparatus is
characterized in that a controllable, especially rotatable
and~or luminance-controllable lighting means for the
object (s) is provided which lighting means comprises a
control unit being connected to an output of the evaluating
o unit. Hereby, it is ensured that the illumination of each
object is adapted to the special filming technology
according to the invention.
To be able to simply p]-oduce takes in which translational
15 motions of humans, animals, vehicles, etc. shall be shown
in or on the rotating neans further means for translating
or additionally rotating an object with respect to the
rotating means is provided, the means for translating or
additionally rotating comprising a separate drive unit and
20 an input being connected to an output of the evaluating
unit .
For the effective production of image sequences in which
objects with very different size shall be shown at the same
25 time plural rotating means of different size for plural
objects of different size can be provided, which rotating
means are used time-sequentially for taking plural primary
image sequences and comprising a control input which is
connected to an output of the evaluating unit.
The image taking device, i.e. the "camera", especially can
be a film or video camera, and the rotating means can be an
essentially horizontal rotating stage, and the motion
apparatus can comprise a camera ' mount or carriage,
2l8~2~v
respectively, which is guided in a horizontal and a
vertical track, each track being straight.
For medical applications, the image taking device can be a
5 medical imaging device, especially using ultrasound waves,
X-rays or corpuscular rays or nuclear or electron spins for
the image generation . The obj ect is then, of course, a
human being or animal w]~ich is arranged on a rotatable bed.
10 In both latter - as well as in further possible -
applications, the image taking device comprises a support
which is rotatable or pivotable, respectively about three
axes .
15 An advantageous embodiment of the process of the invention
is that single images of plural primary image sequences are
superimposed to a resulting image sequence, wherein the
superposition especially can be carrled out in Blue-screen
manner .
In a useful manner, during the process the drive data being
used during the production of a primary image sequence are
stored and optionally used for the production of a further
primary image sequence and/or for the production of the
25 resulting image sequence from plural primary image
sequences directly or following a transformation for the
image generation.
The drive data for producing different image sequences can,
30 especially for adjusting the relative image size, for
rotating the image plane and/or for adjusting an image-
waiting factor for primary images for producing a resulting
image be scaled and/or weighed.
218~2~
Figure l is a schematic diagram representing the spatial
and angular relationshi.p between a camera location and an
object providing a photograph image according to
conventional photography,
Figure 2 is a schematic diagram representing the spatial
and angular relationship between a camera location and an
obj ect accQrding to an embodiment of the invention which
provides the same photo(~raph image as represented in Figure
10 1,
Figure 3 is a schematic diagram representing the spatial
and angular relationshi]?s between two camera locations and
an object for providing photograph images according to con-
15 ventional photography,
Figures 4a and 4b are schematic diagrams representing thespatial and angular relationships between two camera
locations and an obj ect according to an embodiment of the
20 invention which provide the same photograph images as
represented in Figure 3,
Figure 5 is a schematic diagram representing the spatial
and angular relationships between five camera locations and
25 an obj ect for providing photograph images according to con-
ventional photography.
Figures 6a to 6e are schematic diagrams representing the
spatial and angular relationships between five camera
30 locati.ons and an object according to an embodiment of the
invention which provide the same photograph images as
represènted in Figure 5,
9 21~22~
Figure 7 is a schematic diagram reFresenting the spatial
and angular relationships between five camera locations
curving around an object for providing photograph images
according to conventional photography,
Figures 8a to 8e are schematic diagrams representing the
spatial and angular relationships between five camera
locations and an object accordlng to an embodiment of the
invention which provide the same photograph images as
lo represented in Figure 7,
Figure 9 is a schematic diagram representing the spatial
and angular relationships between five camera locations en-
circling an object and the object for providing photograph
1~ images acco~ding to conventional photography,
Figures lOa to lOe are schematic diagrams representing the
spatial and angular relationships between five camera
locations and an object according to an embodiment of the
20 invention which provide the same photograph images as
represented in Figure 9,
Figure 11 is a schematic diagram representing the spatial
and angular relationships between a camera location and
2~ three obj ects for providing photograph images according to
conventional photography,
Figures 12a to 12c are schematic diagrams representing the
spatial and angular relationships between three camera
30 locations and an obj ect according to the invention which
will provide photograph images which, when combined, will
form the same photograph image as represented in Figure 11,
29~
Figure 13 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three: objects for providing photograph images according to
conventional photography,
Figures 14a to 14c are schematic diagrams representing the
spatial and angular relationships between three camera
locations and an object according to the invention which
will provide photograph images which, when combined, will
10 form the same photograph image as represented in Figure 13,
Figure 15 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three; objects for providing photograph images according to
15 conventional photograph~,
Figures 16a to 16c are schematic diagrams representing the
spatial and angular relationships between three camera
locations and an object according to the invention which
20 will provide photograph images which, when f r~mh; nf~d, will
form the same photograph image as represented in Figure 15,
Figure 17 is a schematic diagram representing the spatial
and angular relationships between a camera location and
25 three sections for providing photograph images according to
conventional photography,
Figures 18, 19 and 20 are each schematic diagrams of a
section illustrating the definition of terms describing the
30 spatial and angular relationship between a Section and a
camera location,
Figures 21a to 21c are schematic diagrams representing
three different spatial and angular relationships between a
211 8~Q
Il
camera locatlon and a section according to an embodiment of
the invention which will provide photograph images which,
when combined, will form the same photograph image as
represented in Figure 17,
Figure 22 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three: sections for providing photograph images according to
conventional photography,
Figures 23a to 23c are schematic diagrams representing
three; different spatial and angular relationships between a
camera location and a section according to an emoodiment of
the invention which wi] l provide photograph images which,
15 when combined, will form the same photograph image as
represented in Figure 22,
Figure 24 is a schematic diagram representing the spatial
and angular relationships between a camera location and
20 three sections for providing photograph images according to
conventional photograph~,
Figures 25a to 25c are schematic diagrams representing
three:different spatial and angular relationships between a
25 camera location and a section according to an embodiment of
the invention which will provide photograph images which,
when combined, will form the same photograph image as
represented in Figure 2g,
30 Figure 26 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three: objects of different sizes for providing photograph
images according to conventional photography,
29~
Figures 27a to 27c are schematic diagrams representing
three different spatial and angular relationships between a
camera location and an object according to an embodiment of
the invention which wi:Ll provide photograph images which,
5 when combined, will form the same photograph image as
represented in Figure 21~,
Figure 28 is a schemat:ic diagram representing the spatial
and angular relationships between a camera location and
o three. objects of different sizes for providing photograph
images acco~ding to conventional photography,
Figures 29a to 29c are schematic diagrams representing
three different spatial and angular relationships between a
15 camera location and an obj ect according to an embodiment of
the invention which will provide photograph images which,
when combined, will form the same photograph image as
represented in Figure 28,
20 Figure 30 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three objects of different sizes for providing photograph
images according to conventional photography,
25 Figures 31a to 31c are schematic diagrams representing
three ;different spatial and angular relationships between a
camera location and an object according to the invention
which will provide photograph images which, when combined,
will form the same ph~tograph image as represented in
30 Figure 30,
Figure: 32 is a schematic diagram representing the spatial
and angular relationships between a camera location and
~82290
three sections for provid~ng photograph images according to
conventional photography,
Figures 33a to 33c are schematic diagrams representing
5 three. different spatial and angular relationships between a
camera location and three sections of different sizes
according to an embodiment of the invention which will
provide photograph images which, when combined, will form
the same photograph image as represented in Figure 32,
Figure 34 is a schematic diagram representing the spatial
and angular relationships between a camera location and
three: sections for providing photograph images according to
conventional photography,
Figures 35a to 35c are schematic ~diagrams representing
three different spatial and angular relationships between a
camera location and three sections of different sizes
according to an embodiment of the invention which will
20 provide photograph images which, when combined, will form
the same photograph image as represented in Figure 34,
Figure 36 is a schematic diagram representing the spatial
and angular relationships between a camera location and
25 three sections for providing photograph images according to
conventional photography,
Figures 37a to 37c are schematic diagrams representing
three different spatial and angular relationships between a
30 camera location and three sections of different sizes
according to an embodiment of the invention which will
provide photograph images which, when combined, will form
the same photograph image as represented in Figure 36,
14 ~i8~2~
Figure 38 i5 a schematic diagram representing the spatial
and angular relationships between an actor "walking" along
a straight line and a following camera at five different
camera-actor spatial relations,
s
Figures 39-43 are schematic diagrams representing the actor
walking around a circular board which is moving along the
straight line AE illustrated in Figure 38, at each of the
locations depicted in Figure 38, respèctively,
Figure 44 is a composite of Figures 39-43,
Figure 45 is a schematic diagram representing five
different spatiai and angular relationships between a
15 camera location and an actor according to an embodiment of
the invention which will provide photograph images
corresponding to the images which can be taken in the
positions represented in Figure 38,
20 Figure 46 is an elevated view of a motion control device
according to an embodiment of the invention,
Figure 47 is an elevated view of a camera portion or camera
mount portion, respectively, of the motion control device
25 according to an embodiment of the invention,
Figure 48 is a schematic (elevated) view of an arrangement
according to the invention including two rotating stages
and lighting for each stage,
Figure 49 is a side elevated view of a motion control
device. modified with respect to Fig. 46, and
X2~
Figurg 50 is a block diagram of an embodiment of the motion
control device.
To better understand the invention, it is preferable to
5 make a differentiation between the movement of a camera in
space and the picture image resulting from this movement.
The actual camera movement (a 3-D movement in reality) will
be called a "physical move".
10 Our experience tells us that a specific picture can be a
result of only one specific "physical move", and existing
motion control systems are based on this assumption.
However, the present invention is based on the observation
that a specific picture can be the result of a different
15 and much simpler "physical move" in space, than our
experience in reality would suggest. The present invention,
the motion simulation control, transforms ~"translates") a
motion of the ca~era in the X-Y plane into motion along the
Y axis (straight travel forward and backward), camera pan
20 (side to side), and rotation of the photographed object on
a rotating stage or turntable.
This is accomplished ~ith the use of three independent
"machines" which each perform one of the simplest
25 mechanical motions, i.e. linear movement or rotation. The
first machine is a linear track system, which moves the
camera back and forth in the Y-direction. The second
machine is a camera head or mount, respectively, which pans
or rotates the camera about an axis which is perpendicular
30 to the X-Y plane. The third machine is the rotatable stage,
which also rotates about an axis which is perpendicular to
the X-Y plane. In operation, the object to be photographed
is placed on the rotatable stage, and the stage, camera
head and linear track system are driven in a coordinated
~ 230
16
manner so that the lnovemerit of these three machines
together simulates the corlventional movement of a camera
relative to an object.
To better understand the invention, it is helpful to
establish a related vocabulary. The Cartesian plot in
Figure 1 represents a bird's eye view of a photographing
situation according to conventional photography. The center
of this plot is the point B.
The camera 10 is located at point C having X and Y
coordinates of x_cam = -2 . 5, y_cam -- -1. 5 . Located in the
middle of the plot, centered at point B, is a round board
12 with its center having X and Y coordinates of x_board =
0, y board = 0. The board has an arrow pointing in the
north direction (i . e., in the direction of the Y axis) . The
north direction will be used as a reference to describe the
values of all the angles of a "physical move". The north
direction has the value 0.
The camera 10 "looks" at target point T, having X and Y
coordinates of x_target = -0.5, y_target = 1.5. The angle
between the north direction and the line between the camera
10 (point C) and point T is called the "camera look" angle
14. In Figure 1, the "camera look" angle 14 has a value of
33.69 (look = 33.69). The distance between the camera 10
(point C) and the center of the board 12 (point B) is
called the "camera travel" distance 16, and has a value of
2.92 graph units (travel = 2.92).
The angle between the direction of the arrow and the line
between the camera 10 (point C) and the center point of
board 12 (point B) is called the "set rotation" angle 18
(s_rot), and has a value of -59.04 (s_rot = -59.04).
. .
17
The angular difference between the angle of the "set
rotation" and the angle of the "camera look" is called the
"camera pan" 20 ~c_pan), and has a value of -25.35 (c_pan
s = -25 . 35 ) .
The values of the "camera travel" 16, the "camera pan" 20
and the "set rotation" 18 are collectively called the
"conditions", and they describe the spatial and angular
lo relationship between the camera 10 and the board 12 in
Figure 1.
Figure 2 is a schematic of the same photographic image
repr-esented in Figure 1, but generated by the motion
IS simulation control of the invention. As shown in Figure 2,
the motion simulation control ircludes a linear track 22,
represented by a straight numbered line, and a round
rotating stage 24 represented by a round circle. As can be
seen from Figure 2, the rotating stage 24 depicts the same
arrow illustrated in Figure 1. The center of the rotating
stage is the reference for the camera position and has a
value of 0 on the track 22. The motion simulation control
also has a camera 26, which moves along the linear track 22
and which pivots or rotates in the same plane as the
rotating stage 24.
Comparing Figure 2 with Figure 1, we see that all of the
"conditions" established in Figure 1 are realized in Figure
2 by the motion simulation control ' s arrangement between
the camera 26 and the rotating stage 24. In Figure 2, the
camera 26 has the same distance from the center of the
rotating stage 24 (i.e., travel = 2.92) as the camera 10 in
Figure 1 from the center of the board 12. Also, in Figure 2
the camera 26 pans to the left from the center of the
. . --
18 ~ 2 ~ ~
rotating stage 24 at the same angle ~c pan = 25.35) as the
camera ln Figure 1 pans to the left from the center of the
board 12. LiXewise, tlle rotating stage 24 in Figure 2
rotates to the same angular position relative to the camera
26 as the board 12 in Figure 1 (s_rot = -59, 04) . The angle
of this rotation in Figure 2 is indicated by the arrow 18
on the rotating stage 24.
In Figure 3, we see a camera lOa corresponding to camera 10
o in Figure 1, and a second camera lOb (point D) which has a
different location in the Cartesian plot as camera lOa, but
which "looks" at the same point in space (point T). New
"conditions" are established for camera lOb in Figure 3.
Figures 4a and 4b illustrate the positions of the camera 26
relative to the stage 24 according to the invention, in
order to "simulate" the camera positions of Figure 3. From
Figure 4a, we can see that the camera 26 and rotating stage
24 of the invention arc rotated to provide an arrangement
between the camera 26 and the rotating stage 24 which
fulfiLls all of the "conditions" for camera lOa established
in Figure 2. similarly, as shown in Figure 4b, the camera
26 and the rotating stage 24 of the invention can be
rotated to provide an arrangement between the camera 26 and
the rotating stage 24 which fulfills all of the
"conditions" for camera lOb established in Figure 3. In
this example, it is not necessary to move the camera along
the linear track 22, because the "travel" distance, i.e.,
the distance from the camera at points C and D to the
center B of the board 12 in Figure 3, is the same for both
camera- locations.
From analyzing Figures 1-4, the conclusion can be drawn
that if the motion simulation control can fulfill all of
21~
l9
the conditions of conventional photography for camera lOa
and camera lOb, the can~eras being located in two different
points of the X-Y plane (at point C and point D), then the
motion simulation control system can fulfill the conditions
5 of any camera located on any point on the X-Y plane used by
conventional photography.
Based on this assumption, it will next be discussed what
happens when a camera travels in the X-Y plane. Figure 5,
10 depicts a physical move of a camera lO along a straight
line according to conventional photography, where the
camera lO travels from point C to point D. As it travels,
the camera lO turns to always observe the same point T. The
5 represented camera locations, lOa, lOb, lOc, lOd, and lOe
15 show 5 phases of the "camera motion". In the drawing, the
conditions for these 5 phases are established. The distance
of the camera travel is 5 graph units (distance = 5. 0) .
Figures 6a-6e depict how the motion simulation control
20 "translates" the straight travel and the camera-to-object
relationship illustrated in Figure 5 into a different kind
of motion or relation, respectively. As can be seen in
Figures 6a-6e, for each position of the camera lO shown in
Figurè 5, the motion simulation control provides an
25 alternate camera position relative to the stage 24 which
creates the same photographic image. For example, Figure 6a
illustrates how the ca~nera 26 and the stage 24 can be
rotated to provide the same conditions as the camera
location lOa in Figure 5. To provide the same conditions as
30 the camera ~ location lOb in Figure 5, the camera 26
embodying the invention is moved closer to the stage 24,
and both the camera 26 and the stage 2~ are rotated
accordingly. A similar procedure is performed to recreate
2 ~ 0
the conditions for the camera locations l0c-lOe, as are
illustrated in Figures 6c-6e.
From this, it will be understood that if the motion
5 simulation control can fulfill the ~conditions established
in Figure 5 for each of the five camera positions which
represent five phases of the travel, then it can fulfill
the conditions for all other phases of the travel. The
conclusion that can be reached is that the camera 26, moved
10 by the motion simulation control, observes the rotating
stage 24 in the same way as the camera lD observes the
board 12.
Observing Figure 5 and Figures 6a-6e, we can see the basic
15 difference between the two kinds of motion, the original
"physical motion" ("PM distance") and the motion effected
or translated by the motion simulation control. The travel
of the camera l0 shown in Figure 5 occurs on the X axis.
The travel executed by the motion simulation control,
20 however, occurs only on the Y axis, along the linear track
22, as shown in Figures 6a-6e. One advantage of using the
motion simulation control in this example is that the total
travel of the camera 26 on the Y axis shown in Figures 6a-
6e (MCS distance -- 2.82 graph units), executed in a forward
25 and backward direction, is much shorter than the travel on
the X axis executed continuously in one direction by the
camera in Figure 5 (PM distance = 5 . 0 graphs units) . The
entire range of movement in the Y-axis direction (i.e., the
travel maximum value minus the travel minimum value will be
30 called the "weg" . In Figure 6a-6e, the weg value is l . 42
(i.e., position at l0a or l0e minus position at l0c, 2.92 -
1.5) . Figures 6a-6e show that the motion on the X axis is
completely eliminated. T1~e difference between travel on the
Y axis (MCS distance) and travel on the X axis (PM
2, ~1822~
distance) shows that the camera moved ~y the motion
simulation control travels much slower than the camera had
to be moved during the original travel. This decrease ln
the speed of the camera travel is very important for the
5 quality of the photographed motion, producing less j itter .
Figure 7 depicts five locations lOa' to lOe' of a camera in
reality, as the camera makes a motion on a curved path
about point T. The various conditions of each camera
10 location can be seen from Figure 7. In Figure 7, the travel
distance is 5 . 55 graph ~InitS .
Figures 8a to 8e illustrate how the same motion is trans-
lated by the motion simulation control according to an
IS embodiment of the invention. Figures 8a-8e depict five
different locations of the camera 26 of the motion
simulation control, eacl ~ Figure corresponding to a position
shown in Figure 7. Each of the camera 26 positions shown in
Figures 8a-8e, along with the relative rotation angles of
20 the camera 26 and the stage 24, provide the same set of
conditions for its corresponding camera position in Figure
7. Accordingly, it will be understood that the camera
positions illustrated in Figures 8a-Se will provide the
same photographic images as the camera positions
25 illustrated in Figure 7. In analyzing these two drawings,
the conclusion is reached that the motion simulation
control "translates" a curved camera motion in the X-Y
plane to a linear, one dimensional camera movement along
the Y axis. Figures 8a-8e demonstrate (as in Figures 6a to
30 6e) that camera motion along the X axis is completely
eliminated by the motion simulation control.
Figure 9 depicts five locations lOa" to lOe" of a camera
representing the points of a circular motion around a board
~ g229~
12 (where travel distarlce = 9.77 graph units). The camera
is "looking" at target point T, (x_target = -0.5, y_target
= 0.5~. As with the previously discussed examples, all
conditions for each camera location- depicted in Figure 9
5 can be fulfilled by the motion simulation control's
arrangement between the camera 26 and the rotating stage
24, as is shown in Figures lOa to lOe. It is interesting to
note that in this example, the "MCS distance" = 0. This
means that the camera 26 of the invention does not travel
10 at all, but instead simply rotates about its axis.
Building upon the basic principles of the invention
discussed above, the operation of the invention wail now
the discussed in more detail. In conventional photography,
15 the camera moves--and photographs the static "world". All
physical work necessary to travel over a distance and to
change the angles of the "look" are solely performed by the
camera. The static "world" photographed by the camera does
not have a clear reference. It exists with an infinite
20 amount of visual elements. This complexity and lack of a
reference in the photographed "world" causes problems in
the production of multicomposite images as well as in the
construction of computer generated images.
25 The present invention is based on the idea that the camera
performs only part of a motion in space and can photograph
only part of the "world" ( i . e . that part which exists on
the rotating stage) . Thi s part of the "world", through its
own rotation, participates in the execution of a motion
30 along with the camera. The "world" is not static and its
infinite amount of visual elements to be photographed are
limited to the visual elements existing on the rotating
stage.- The motion simulation control synthesizes a new
motion in space between the camera and a chosen point in
23 ~18~
the "world". About this point, the (limited) real world
rotates. The center of this rotation becomes a clear
reference for the motion, the location of the photographed
obj ects and the composition of the image .
Referring back to Figure 9, the depicted camera 10 moves in
a circular motion aroun~ the board 12 and remains the same
distance from the center of the board 12 as it travels. The
travel executed by the motion simulation control represents
10 the change in the distance between the center of the board
12 and the camera 10. This is the reason why the camera 26
of the invention represented in Figures lOa-lOe does not
travel at all . The entire distance of the camera ' s travel
in Figure 9 (PM distance = 9.77) is translated into by the
15 rotation of the stage 24 and camera 2~ in Figures lOa-lOe.
The different relationships between the three movements
described as conditions can be produced by forward and
backward travel of the camera, camera pan and rotation of
20 the stage, which can imitate any two-dimensional camera
notion in space. The results are correct images of a chosen
part of the "world" which exists on the rotating stage. The
forward and backward travel of the camera, camera pan and
rotation of the stage form the three basic channels of the
25 motion simulation control. The synchronized work of these
three channels form a virtual "vehicle" which can execute
any motion in space. The motion of the vehicle depends on
the vàrying percëntages of work performed by these three
channels .
The operation of the motion simulation control will now be
explained in greater detail with reference to Figures 11-
25. Here it can be seen that the whole image of the "world"
24 ~ 29~
can be built from separate images of the parts existing on
di f f erent boards .
Figures 11, 13, and 15 schematically show the same linear
5 traveL of camera 10 which was described in Figure 5. To
simplify the description, however, only three phases of the
camera motion are shown (at points C, Ca', and D). In these
Figures there are three boards (12a, 12b, and 12c) located
in different places on the X-Y plane. In each of Figures
11, 13, and 15, conditions are established between the
camera 10, the boards 12a, 12b and 12c, and the target
point T for each camera location.
Figures 12a-12c, 14a~ c and 16a-16C illustrate how the
15 motion simulation control, through different arrangements
between the camera and the rotating stage, can fulfill all
of the conditions established in Figures 11, 13 and 15.
For example, Figures 12a-12c depict three different angular
and spatial relationships between the rotating stage 24 and
20 the camera 26. The first relationship, depicted in Figure
12a, recreates the conditions between the camera 10 and the
board 12a shown in Figure ll. Similarly, the relationship
shown in Figure 12b represents the same conditions that
exist between the camera 10 and the board 12b in Figure 11.
25 Finally, the relationship depicted in Figure 12c
corresponds with the relationship between the camera 10 and
the board 12c in Figure 11.
In a similar fashion, the three different camera-stage
30 relationships shown in Figures 14a-14c correspond to the
relationships between t~le camera 10 and each of the three
boards, labeled 12a, 12b, and 12c depicted in Figure 13.
Additionally, the three different camera-stage
relationships shown in Figures 16a-16c correspond to the
~ 8~29~
relatlonships ~etween the camera lO and each of the three
boards 12a, 12b, and 12c depicted in Figure 15. From these
examples, it will again be understood that by means of the
invention one can recreate the photographic image of each
of three objects by sim]~ly rotating the camera 26 and stage
24 and by moving the camera 26 relative to the stage 24
along a linear track 22
Up until now, the examples of the invention discussed have
only been made with reference to a board with a two-
dimensional arrow. However, as will now be explained, the
present invention can also be used with two- or three-
dimensional objects
Figure 17 illustrates a long arrow-like obj ect 28 (with
points a, d, h, 1, i, e) built from three smaller Sections
28a, 28b, and 28c (formed of points a, b, f, j, i, e,
points b, c, g k j, and f, and points c, d, h, 1, k, and g,
respectively). Each Section rests on a different circular
board 30a, 30b, and 30c, respectively, and each of the
boards includes an arrow pointing i~ the north direction
( i . e ., the Y-axis direction) .
Figures 18, 19 arLd 20 ~pict the section conditions which
can be used to mathematically describe the spatial and
angular rPl~ti~nch;ps between the camera and every corner
of each section. These drawings explain the mathematical
vocabulary used for secti~on conditions ~based on the
"corner b"). For example, Figure 18 illustrates the corner-
to-board distance (cor_board_dist) 32 between the center oi
the board (x board, y_`ooard) and cor=ner b of the object
(x_cor, y_cor), and the corner-board angle (cor-board-
angle) 34 between the direction of the arrow and a line
~18~9~
26
running from the center o~ the board 30b to the corner b oi`
the object.
Figure 19 illustrates the camera pan (c_pan) 36, i.e., the
angle between a line running from the center of the board
30b to the camera 10 and a line runnlng in the direction
that the camera 10 is pointing (i . e ., toward the target
point T) . Figure 19 also shows the corner-to-camera
distance (cor_cam_distance) 38 between the camera lD and
the corner b, and the corner angle (cor_angle) 40 between a
line running from the corner b to the camera 10 and a line
running in the direction that the camera 10 is pointing.
Further, Figure 19 illustrates the set rotation (s_rot) 42,
i.e., the angle between the direction that the camera lO is
pointing and the direction of the arrow.
Lastly, Figure 20: shows how each of the section conditions
has an equivalent when section 28b is placed on the
rotating stage 24 of the invention. The same vocabulary
depicted in Figures 17-19 will be used later for the
discussion of "scale section conditions".
As noted before, Figure 17 shows how three sections, 28a,
28b, and 28c rest on three circlllar boards, 30a, 30b, and
30c to present a conventional photographic image to camera
10 when camera lO is located at point C. In Figures 21a,
21b, and 21c, individual sections 28a, 28b, and 28c are
illustrated resting on the rotating stage 24 of the
invention in the identical position, relative to the camera
26, as these sections on the boards 30a, 30b, and 30c do in
Figure~ 17, respectively. Figure 22 shows the relationship
between the sections 28aJ 28b, and 28c when camera 10 is in
a different location, at point Ca', relative to these
sections. Again, Figures 23a, 23b, and 23c illustrate that,
27 ~22~
when the sections are placed on the rotating stage 24 of
the irvention, and the stage 24 and camera 26 are rotated
and dlstanced appropriately, the sections are in the
identical position, relative to the camera 26, as the
sections depicted in F' gure 22 . Figure 24 illustrates the
relationships between the sections on the boards 30a, 30b,
and 30c and the camera 10 when the camera 10 is in yet a
third location at point D. Figures 25a, 25b, and 25c
illustrate how these relationships can be created by
placing the sections on the rotating stage 24 of the
invention, and then rotating the camera 26 and the stage
24, and moving the camera 26 relative to the stage 24.
The reference for the location of every section in Figures
17, 22, and 24 is the center of every board and the north
direction, which is indicated by the arrow on every board.
As noted before, Figures 21a, 21b, and 21c depict three
separate relationships between the camera 26 and a section
as shown in Figure 17. The first relationship depicted in
Figure 21a, simulates tl1e conditions between the camera 10
and section 28a shown in Figure 17. ~ikewise, the
relationship shown in Figure 21b, simulates the conditions
between the camera 10 and section 28b shown in Figure 17.
Finally, the third relationship shown in Figure 21c,
represents the conditions between the camera 10 and section
28c shown in Figure 17 . From Figuresi 21a-c, 23a-c and 25a-
c, it can be seen that the motion simulation control
through the arrangement between the camera 2 6 and the
rotating stage 24, can fulfill all of the section
conditions depicted in Figures 17, 22 and 24 for three-
dimensional objects. (It will be understood that, since
both the object and the camera view have height, the camera
photographs the nLove in three dimensions. )
28 ~ g ~
rt will be easily understood that if each section on the
rotating stage is photographed separately, the three
resultlng separate images of the sections can be
superimposed onto each other to produce a final image. If
5 the three separate images produced by the relationships
shown in Figures 21a, 21b, and 21c are superimposed on each
other, then the resulting final image will be identical to
the image deplcted in Figure 17. Likewise, if the three
separate re-lationships depicted in Figures 23a, 23b, and
lo 23c are used to produce three separate images, and these
three separate images are combined to produce a final
image, that final image will be identical to the image
described in Figure 22. 1astly, if the three separate
relationships shown in Figures 25a, 25b, and 25c are used
15 to produce three separate images, and these three images
are ~ superimposed onto each other, the final image produced
will be identical to the image resulting from the
relationship depicted in Figure 24. This demonstrates that
separate images of separate sections can be superimposed to
20 form an image of the larger object.
Since three separate images of the sections representing
different locations on the X-Y plane (different parts of
the "world" ) can be connected in one cohesive image of an
25 obj ect, then several conclusions can be drawn.
First, the whole image of the "world" can be built by
superimposing separate images of the small parts of the
"world", which exist on rotating stages. Second, the chosen
30 parts of the "world" can be located in any area of the X-Y
plane. There is no limit to the amount of such chosen partS
whose images can~be superimposed onto each other. Third, an
image of an object, which rests on the rotating stage, is
visually connected (synchronized) with a superimposed image
29 ~1~229~
of another object resting on the surface of a different
rotating stage. Fourth, the dimension of the surface of the
rotating stage theoretically has no limit. In Figures 17,
22, and 2~, the corners of the sections on the boards 30a
5 and 30b extend outside the perimeter of the boards. In
Figures 21a, 21b, 23a, 23b, 25a, and 25b, we see that even
though the corners of the sections extend outside the
perimeter of the rotating stage, all the section conditions
are still fulfilled. The dimensions of the surface of the
o rotating stage are only dictated by the dimensions of the
film studio.
Finally, the construction of existing motion control
systems is based on the assumption that all components of a
15 picture are photographed with the same repetitive motions
(scaled up or scaled down depending on the scale of the
components) and that the camera has to execute a physical
move to attain these motions. The construction of the
present invention is based on a different assumption. All
20 components of the picture are photographed with different
motions. The result is an image identical to that taken
during a conventional physical move, but the conventional
motion is never really executed in space by the camera.
25 The biggest problem in the production of multi-composite
images is the problem of scale. When different components
of an image have different scales (size), it is very
difficult to make them "fit". This problem is caused by two
ma j or f actors .
~he first is that the physical move of the camera has to be
scaled up or scaled do~n depending on the scales of the
components. The scaling up or down of a non-linear physical
move creates different physical conditions (wherein
30 ~i82~D
di~ferent values of kinetic energy are of importance) for
the motors and the construction of the motion control
system. The results are different image "jitters" for the
different components. The second factor is the lack of
clear reference for the location in space of the
photographed components (i.e., where to place an object in
relationship to the camera).
The present invention solves these problems. During a
conventional physical move, the j itter of a picture appears
when the camera is changing its X-Y-Z position in space in
a non-linear manner, since ~itter in camera takes is mainly
caused by centrifugal forces. Jitter does not exist (or is
so minute that it is not detectable in the picture1 when a
physical move ls purely linear in nature. Because the
motion simulation control transforms a non-linear movement
to linear movement, the j itter problem is solved (assuming
that the tracks used irl the motion simulation control are
nearly or perfectly straight).
The full solution to tEle problems caused by scale can be
seen from considering Figures 26, 28 and 30. These Figures
depict three phases of straight travel for camera lO. The
camera travels f~om point A (having coordinates x_cam =
2.5, y_cam = -1.5 in Figure 26) to point Al (having
coordinates x_cam = 2.5, y_cam = 0 in~ Figure 28) to point D
(having coordinates x_cam = 2 . 5, y_cam = l . 5 in Figure 30)
and observes target point T, which is located in the center
of the Cartesian plot. In these Figures, there are three
boards of different si7es, 44, 46, and 48, representing
three ~different scales. Each of these boards has an arrow
pointing in the north direction, which will be used as a
reference again.
2~ g~%~
The refere~ce for the scale i~ the radius of the board. In
the discussed examples, when the radius of the rotating
stage 24 of the invention is l graph unit, the radius of
the board, in scale l: l, has the value of l graph unit
5 ~RADIUS = l . 0), in scale 2: l, has the value of 2 graph
units (RADIUS = 2.0) and in scale 1:2, has the value of 0.5
graph unit (RADIUS = 0.5). The different scales of the
boards only effect the camera's travel according to the
following formula: "scaled travel" = travel ~ RADIUS. In
10 other words, and as can be seen from Figure 26, the actual
or "scaled travel" shown in Figure 26 is converted to
travel for the invention by dividing the "scaled travel" by
the radius. Applylng this formula to the conditions shown
in Figures 26, 28 and 30, "scale conditions" can be
15 established for every phase of the camera lO movement
relative to each of the three boards.
For example, Figures 27a-27c show three relationships
between the camera 26 and the rotating stage 24 according
20 to the invention. The relationship in Figure 27a will
produce the same image as the scale conditions created by
the relationship between the camera lO and board 44 in
Figure 26. That is, the travel between the camera 26 and
the stage 24 in Figure 27a will produce the san e scale as
25 the scaled travel between the camera lO and board 44 in
Fi gure 2 6 .
Similarly, the relationship depicted in Figure 27c will
produce the same image as the scale conditions between the
30 camera lO and board 46 depicted in Figure 26. Likewise, the
relationship depicted in Figure 27c will produce the same
image as the scale conditions between the camera lO and
board 48 in Figure 26.
~ o
2~ ~22~
32
In a similar fashion, tl1e relationships depicted in Figures
29a-29c correspond to the scale conditions depicted in
Figure 28, while the relationships shown in Figures 31a-31c
will produce the same images for each individual board as
the scale conditions depicted in Figure 30. From Figures
27a-27c, 29a-29c, and 3Ia-31c, it can be seen that by
arranging the camera 2 6 and the rotating stage 24, the
motion simulation control can fulfill all of the scale
conditions established from Figures 26, 28 and 30.
The scaling feature of the present invention can be applied
to three-di~nensional objects as well. In Figures 32, 34 and
36, is shown a long arrow-like object 50, which is built
from three smaller sections 50a, 50b, and 50c. Every
section rests on a different board, 52a, 52b, or 52c. It is
important to note that Figures 32, 34 and 36 show the
desired visual result: one object composed from three
sections representing different scales. The dimension of
every section can be established by its relationship to the
radius of every board. In Figure 32, 34 and 36 are
established additional scale section conditions which
describe the relationship between the camera and each
corner of every section.
In Figures 33a-33c, 35a-35c, and 37a-37c, individual
sections 54a, 54b, and 54c are illustrated corresponding to
sections 50a, 50b, and 50c, respectively, resting on the
rotating stage 24 in the identical position relative to the
camera 26 as the sections in Figures 32, 34 and 36. The
reference for the location of every section is the center
of the rotating stage 24 and the direction of the arrow on
the stage 24. The reference for the dimension of every
section is its relationship to the radius of the rotating
stage 24. Figures 33a-33c, 35a-35c, and 37a-37c demonstrate
21~
that the motion simulatlon control, through the arrangement
between the camera 26 and the rotating stage 24, can
fulfill the scale section conditions shown in Figures 32,
34, and 36.
If each section on the rotating stage as depicted in
Figures 33a-33c is photographed separately and the three
images of the sections depicted in each of the Figures are
superimposed onto each other, the final image will be
10 identical to the image described in Figure 32. In the same
fashion, if each section on the rotating stage as depicted
in Figures 35a-35c is photographed separately and the three
images are superimposed onto each other, the final image
will be identical to the image described in Figure 34,
15 while if each section depicted in Figures 37a-37c is
photographed separately and the three images of the
sections depicted in Figure 37a-37c are superimposed onto
each other, the final image will be identical to the image
described in Figure 36. This shows that the superimposed
20 images of sections, which represent different scales, will
form the image of the long arrow-like object.
If three separate imaçres of the sections and different
scales and different locations on the X-Y plane can be
25 corlnected in a cohesive image of one object, then the
following conclusions can be drawn:
First, the whole image of the "world" can be formed by
superimposing separate images of the small parts of the
30 "world" which represent different sca~es. There is no limit
to the amount of the scales which can be applied. Also,
every part of the "world" can be composed from components
representing different scales. The division of the "world"
into small parts allows for the composition of images ad
34 ~1~22~
infinitum. During the travel o~ the camera, "new" parts are
entering and "old" parts are leaving t~le frame (the steady
overlap of the parts). There are no limitations to the
dimensions of the photographed "world".
s
However, a problem could arise with conventional
photography when moving objects have to be transported over
a distance which would exceed the surface of the rotating
stage, i.e., an actor walking in front of a traveling
10 camera The present invention in an embodiment solves this
problem, as will be explained.
Figure 3a is a schematic view of an actor 56 walking from
point A to point E as a camera lO tracks his movement. For
15 clarity, each position of camera lO relative to the actor
56 will be referred to by the point at which the actor is
located for that image. For example, when the actor is at
point A, the actor location and associated camera location
will be identified as 56a and lOa, respectively. The
20 distance between point A and point E is calIed the "walk"
and has the value of 5. ~5 graph units in Figure 38 .
Figure 39 depicts a board 58a whose center is located on
point G. The actor 56 is standing on the board 58a at point
25 A ~the angle GAE = 90~ The distance of the "walk" AE can
be translated to the curved line AE on the board 58a. The
length of the curved line AE is equal to the distance of
the "walk". The curved line ~E is a part of the
circumference of a circle whose radius is equal to the
30 distance between the actor (point A) and the center of the
board ~point G). This radius (in the example) has the value
of 0.82 graph units (walk radius = 0.82).
. ~ --
35 ~2%~
Imagine that the board can "move" on the X-Y plane ~from
point A to point E) in synchronism with the traveling
camera lO, and can rotate clockwise. The actor walks
counter clockwise Qn t~le board 58a (as if the actor were
5 walking on a treadmill) . Figures 39 ~- 44 show five phases
of the "moving" board for points A-E, and "walk conditions"
are established for every phase. During the "walk"
function, the rotation of the board ("final s_rot") is the
sum of two rotations: (l) the rotation from the original
10 conditions (the angle between the center of the board and
the c~mera position, i.e., s_rot); and (2) the rotation of
the board translating the distance of the walk (board-
angle). Fig. 44 is a su~marizing view of the whole motion.
15 Figures 45a-45e show the arrangement accQrding to an
embodiment of the invention between the camera 26, the
rotating stage 24, and the walking actor 56, which fulfills
all of the walk conditions established in Figures 39 - 43,
respectively. The conclusion is drawn that any distance
20 and any direction of t~1e walk can be performed using the
motion simulation control. In the previous description, no
mention was made of the Z axis (height). The elevation of
the camera does not participate in the function of the
"vehicle", thus it can be freely designed. Its only
25 limitation is the level to which the camera 26 of the
invention can be raised above the surface of the rotating
stage. This level is limited by the dimension of the film
studio (ceiling) and the practicality (size) of the
construction of the motion simulation control.
This limitation of height only applies to photographed
components whose images are influenced by the force of
gravity (animate objects, fire, water etc. . . ) . All
components which are not influenced by the force of gravity
~ 29~
(inanimate objects, arc]litectural models, stones, furniture
etc. . . ) can be photographed in different positions
(sideways or upside down). After rotating the camera
sideways, the Z axis exchanges with the X axis. The
5 components which are in the sideways position appear to be
in a normal position. The "vehicle" can now "move" in the
~Y plane. It can "move" up and down along an infinite
length of a vertical wall. After rotating the camera upside
down, obj ects in an upside down position appear normal . The
10 "vehicle" can "move" under an infinite ceiling. The height,
however, like "camera travel" has to be scaled down or
scaled up, depending on the scale of a photographed
component .
15 Figures 46 - 49, are drawings of the construction of the
device of the motion simulation control.
The overall construction, as illustrated in Figure 48,
contains a large rotatir1g stage 24a for photographing human
20 beings and objects in scale 1: l, a small turntable 24b for
photographing models and miniatures in small scales, and a
horizontal linear track 22 which can be set up on the floor
or hung from under the ceiling. Preferably, one end of the
track 22 faces the center of the rotating stage 24a and the
25 other end faces the center of the small turntable 24b. A
tower-like structure 60 travels along this horizontal track
22. The tower 60 is illustrated in more detail in Figure
46. The tower 60 holds a vertical linear track 62. Along
the vertical track travels a carriage 64 which holds a
30 camera head or mount 64, respectively.
Mounted inside the camera head 64 is the camera 26. The
camera head 64 has several motors which can execute the
camera pan, the camera tilt, the camera rotation (sideways
37 ~ 8~
and upside down), zoom, focus, and nodal point ad~ustment.
The camera is mounted in the nodal point position (the
vertex of all angles inside the lens). The nodal point
position has to be steadily adjusted according to the
5 position of the zoom (the nodal point depends on the focal
length of the lens). T]1e X-Y-Z location of the nodal point
represents the X-Y-Z location of the camera position.
The forward and backward motion of the tower 60, along the
10 horizontal linear track 22, executes the "condition" of
camera travel. The reference for the camera travel (travel
= 0) is the center of t~le rotating stage.
The up and down motion of the carriage with the camera head
15 on the vertical linear track 63 executes the height
adjustment of the camera 26. The reference for the height
(level = 0) is the position when the nodal point is on the
same level as the surface of the rotating stage 24a.
20 The side to side motioll of the camera 26 (pan inside the
camera head) executes the "condition" of camera pan. The
reference for the pan (c_pan = 0) is the center of the
rotating stage 24a.
25 The remalning camera functions (zoom, focus, tilt and
rotation) do not participate in the functions of the
"vehicle" and can be freely designed. The tower can be
turned 180 degrees to face the center of the small
turntable 24b. The center and the level of the surface of
30 the turntable 24b become the reference for the camera
travel, pan and rotation (the values = 0). The turntable
24b may be used for photographing miniatures and models.
The separation of the large stage 24a and the small
turntable 24b is for practical reasons. When working with
38 ,~1822~
miniatures and models, different lighting conditions are
needed than when working with actors - what is a
conse~uence of the small depth of focus caused by the
shorter distance between the camera and photographed
5 components.
The rotation of the rotating stage 24a or the small
turntable 24b executes the "condition" of set rotation
(s rot).
The camera support 64 ~ith the camera 26 is shown in Fig.
47 in more detail; herein especially the several motion
possibilities M" (rotation about a vertical axis through
the camera = horizontal camera pan), M~ (rotation about a
15 first horizontal axis which is identical to the optical
axis of the camera), ( rotation about a second horizontal
axis, perpendicular to the optical axis of the camera =
vertical camera pan), Ml~ (vertical shift of the camera) and
MN (nodal point ad]ust) can be recognized.
An additional part o~ the motion control system are
rotating lighting grids 66, 68. These grids hang above the
rotating stage and turntable and rotate in synchronism with
the stage 24a and turntable 24b, respectively. The rotation
25 of the lights produces the same changes of lighting on the
photographed components which occurs in the "world" during
a conventional move.
Fig. 49 shows an embodilrent of the apparatus for moving the
30 camerà 26 which apparatus is modified with respect to the
apparatus shown in Fig. 46 in elevated view. The reference
numerals correspond to those in Figs. 46 to 48 wherein an
" "' has been added to the numerals for differently designed
components .
-- ~18~9~
39
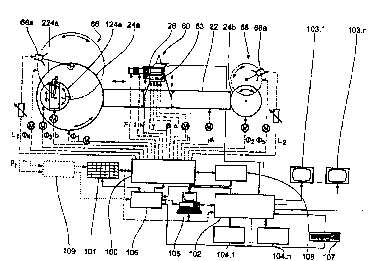
Fig. 50 in the manner of a block diagram shows the:
essential functional units of an embodiment of the motion
control system in more detail, showing the signal
S connections and in detail the several control signals for
the system as well.
The main functional components of the depicted system are a
contral data evaluating unit lO0 with a control data memory
lo 101 being connected to the input as well as to the output
of the former, and an image processing unit 102 at the
output of which plural monitors 103.1 to 103.n and at the
input as well as the output thereof plural video memories
or recorders 104.1 to 104.n, respectively, are arranged
15 (wherein in the Figure two devices of each kind are shown).
The outputs of the control data evaluating unit 100 and the
control data memory 101 are, furthermore, connected to an
input of the image processing unit 1~2 and the input of a
20 computer graphics unit 105, the in- and outputs of the
latter also being connected to the image processing unit
102. Inputs of the control data evaluating unit 100 and the
control data memory 101 are connected to an input unit 10~,
an output of the image processing unit 102 and an output of
25 the computer graphics unit 105 by means of a scaling
processor 106. The control data evaluating unit lO0 and the
computer graphics unit 105 are immediately bidirectionally
connected with one another by means of an interface 108.
30 As shown by means of broken lines bearing a direction arrow
on both ends in the Figures, the control data evaluating
unit lO0 is connected to (not specifically enumerated)
actuators of the components of the motion and lighting
arrangement by means of which the several control steps can
.~ ~t $~9~
be carried out. It both works as an interface for those
components. Preferably, sensors (which are not shown in the
Figure) are connected with the actors, the sensors being
able to sense the actuator positions vice versa. The
5 registration of the current parameters of the apparatus,
however, alternatively can be carrled out such that all
settings ~ including those of the camera mount 64 and the
camera 26 in the case of manual control) are input by means
of the central input unit 107 and the current values of the
10 control signals in their time dependence are immediately
transmitted from the evaluating unit 100 into the control
data memory 101.
Specifically, in 'che Example the fol~owing control signals
15 are used, i . e . input by manual control or evaluated, and
transmitted to the corresponding actuators and optionally
the memory areas of the memory 101:
As can be seen on the left side of the Figure, a control
20 signal Ll for the luminance of the lamp 66a of the lighting
means 66 of the rotating stage 24a is transmitted to a
luminance regulator (e.g. a thyristor control) being
arranged at the input of the lamp 66a, and by means of this
regulator the luminance of the lamp is adjusted. By means
25 of a sensor at the lurninance regulator or a separate photo-
sensor the current luminance can be sensedi however, as
mentioned above; the control signal L1 can immediately be
stored. A control signal (P4 for adjusting the rotational
angle of the lamp 66a above the rotating stage 24a is
30 transmitted to a motor (e.g. step motor) being arranged at
the lighting means 66 and for rotating the lamp 66a. In a
similar manner - as can be seen on the right side of the
Figure - the luminance and the rotational angle of the lamp
68a of the lighting means 68 being provided for the
229~
turntable 24b are cont:~olled by using a luminance control
signal ~2 and a rotatiorl angle control signal ~5.
The rotation of the rotating stage 24a is controlled by a
5 rotating angle control signal ~1 which is transmitted to a
motor driving the rotating stage. A rotation of the
rotating board 124a being arranged on or in the rotating
stage 24a, respectively, is controlled by a rotating angle
control signal ~3 and carried out by a separate motor, and
o a motion of the travelling belt 224a on the rotating board
124a is controlled by a position control signal b and
carried out by means of a separate travelling belt motor.
For each of the rotating stage 24a, the rotating board 124a
and the travelling belt 224a a corresponding sensor for
15 sensing the time dependent position can be provided - for
the above mentioned signals, however, the immediate
transmission from the evaluating unit lO0 into the memory
101 is to be preferred since a control of the components
24a, 24b, 66, 68, 124a and 224a in a manual way just has to
20 be considered for special cases. In analogy to the control
of the rotating stage 2 ~a, the turntable 24b is controlled
by a rotating angle control signal q)2 which is transmitted
to a separate motor being arranged at the turntable 24b.
25 The above mentioned control signals and control functions
are related to the motion, especially rotation, of objects
in relation to the camera 26 and the object lighting which
together form one of the essential elements of the process
for producing an image sequence. The other essential
30 element, namely, (two-dimensional) motion, pans and
adjustments of the camera are carried out in the following
way:
.~ 2~ 82~9~
42
A position controL signal a for predetl~rminin~ the distance
between camera and object is transmitted to a motor (a
conventional electric motor or a linear motor) being
arranged at the rail track 22, and a further position
5 control signal h for predetermining the height of the
camera position above the level of the rotatlng stage 24a
or the turntable 24b, respectively, is transmitted to a
motor~ being provided at the camera tower 60. The signals a
and h (even in the case of manual control) effectively are
10 taken into the memory lOl from the evaluating unit lO0.
Finally, the control of the camera mount 64 and the camera
26 is executed by rotating angle control signals ~, ~ and r
(corresponding to the rotations of the camera mount about
15 three axes referred to as Ma~ M~ and M~ in Fig. 47), the
position control signal N (for the longitudinal adjustment
of the camera position in the camera mount, referred to as
MN in Fig. 47) which are transmitted to corresponding
motors (not shown in the Figures) in the camera mount and
20 the zoom (focus length adjusting) signal f and the
focussing signal F which are transmitted to the camera 26
itself. In the case of a central control of the camera
mount and the camera even those signals can be brought to
the control signal memory lOl immediately from the control
25 unit lO0.
The apparatus is, however, more variably applicable if
sensors for the last-mentioned control or adjustment steps,
respectively, are provided to sense the current position
30 and adjustment of the camera. Those sensors (not shown in
the Figures ) which can be conventional electrical or
photooptical position or angle sensors enable the
registration of the adjustment parameters even in case of a
manual camera control. Such manual control will be
~ ~18~2~
practicised in many pr~ctlcal cases, at least during the
production of one or some image sequence(s), e.g. for the
preparation of an initial control data set which can be
used for later takes or (as explained below) for the image
5 processing.
Position, angle or further adjustment signals - shown in
the left part of the Figure as input signals Pi (without
specifying their origin) - which have been sensed by means
10 of sensors in the apparatus are transmitted to inputs of a
(multi-channel) evaluating unit 109 from where they can be
taken into the memory 101 or transmitted to the scaling
processor 106. The optional character of this embodiment is
expressed by the dotted lines.
The control data evaluating unit 100 specifically can be
embodied as fast microcomputer system in a conventional
manner, the installed software enabling the execution of
the mathematical transformations of the motion coordinates
20 of the motions of camera and object relative to one another
(explained in other parts of the specification) during a
specific camera travel to be shown and a parallel (quasi
multi-channel) processing of a record data set input for
preparing the individual control data for those components
25 of the apparatus which have to be controlled to produce a
specific image sequence. This means that e.g. following to
the input of time dependent path coordinates of a (virtual)
relative motion of camera and object and an (also virtual)
camera pan an evaluatior of a complete control data set for
30 really carrying out the motions of camera, rotating stage
and lighting means will be carried out, and those means are
controlled by this data set completely automatically.
-- ~8~g~
As already mentioned above, furthermore, it is possible to
use this apparatus to produce images under manual control,
to sense the motions or adjustments, respectively, of the
components and to store the corresponding data. Lateron, by
using these data the recording process can be automatically
repeated or optionally the primary data can be scaled
and/or processed in another way, and on the basis of the
thus obtained secondary data a modified motion can be
executed .
Exemplary, a manually controlled take or filming,
respectively, of an object on a rc~tating stage 24a can
deliver the data for automatically producing an exactly
synchronized take of a second (e.g. essentially smaller)
object on the turntable 24b and additionally for the
superposition or mixing, respectively, of both image
sequences with different scales. For this, the control data
first are transformed in accordance with the real sizes of
the object in the scaling processor 106 for controlling the
second taking or filming, and lateron for controlling the
mixing process in the image processing unit 102 a second
scaling data set can be provided. Of course, in this way
plural image sequences - in a completely automatic manner
or partly manually controlled - can be produced, stored in
the video memories 10 ~ .1 to 104 .n and processed under
control using the monitors 103.1 to 103.n.
In a similar manner, by means of the interface 108 a
cooperation of the image producing apparatus with the
computer graphics ~nit 105 can be brought about which
cooperation enables a pre-synchronizing of the image and
computer graphics sequences (or vice versa) and an
essentially perfect mixing of both without perceptible
~8~30
asynchronism or ~ itter. Even in this process a scaling by
means of the scaling processor 106 is possible.
The control data memory 101 is embodied as a random access,
5 multi-channel write-read-memory. In the embodiment
according to Fig. 50 it has a direct connection to the
scaling unit 106 what opens the poss:Lbility to transform a
stored data set independently of the evaluating unit to
other~ geometrical relations and to re-store it in its
10 scaled form.
The image processing unit 102 can be a conventional up-to-
date studio device which has interfaces for connecting the
evaluating unit 100, the computer graphics unit 105 and the
scaling unit 106. The unit 106, furthermore, can comprise
plural stages of "matte" and "ultimatte"-units what
requires that the monitors and recorders or image memories,
respectively, are hierarchically connected.
20 The invention is not limited to the above-mentioned
preferred embodiment. In the contrary, a number of other
embodiments is possible which use the explained solution
even in essentially deviating embodiments . E . g . the above-
explained functional units especially can be integrated
25 into a processor system and/or specific functional units
can be embodied by means of software.
Motion simulation control can be controlled by computer
software. Such software has - in an generalizing view -
30 essentially the following six functions:
1. The design of the "world" (the locations and scales ofthe components );
`~ 2~ 82~3~
46
2. The design of the physical move of the camera
( including the velocity);
3. (possibly) The reception of data from a CG software
about the "world" and "physical move" designed in a CG
5 environment. (Based on the CG data, visual parts of the
"world" can be photographed by the motion control
simulator);
4. The translation of a conventional physical move to the
"vehicle" based on the location of a chosen point of the
10 "world" ( for the mat~1ematics for the conditions, see
attached appendix A);
5. The communication of the "vehicle" data to the motors
of the motion simulation control; and
6. (possibly) The communication of the "world" and
15 "vehicle" data to a CG software (based on the "vehicle"
data, visual parts of the "world" can be generated by a CG
so f tware ) .
In the foregoing description, the problem which exists in
20 the construction of computer generated images was
discussed. These problems are caused by the complexity of
the image of the "world" which comprises an infinite amount
of visual information. The principles of the motion control
simulator should be applied to the construction of the CG
25 image . The subj ect of mathematical calculations should not
be the whole image of the "world". The "world" is divided
into small parts which have different X-Y-Z locations (in
the same way that a CG screen is divided into small
pixels). With the invention, the image of a small part of
30 the "world" is the subj ect for the mathematical
calculation. The principles of the above mentioned
"vehicle" are applied in these calculations. The location
of the CG "camera" in the X axis should be translated to
the Y axis, pan and rotation of the part. Superimposed
~ 8~9~
47
images of the small parts will ~orm the correct and very
complex image of the whole "world".