Note: Descriptions are shown in the official language in which they were submitted.
--w; ~:-:- ~-:~:=.-~. .~ _«:r~ _ _
_... _ .~,..~..,...__r.,~..~__.._~
.~.::.u
.___ _._ ~._~~
--- ~~CA 022261151998-O1-OS
~r'O 97/03417 . ; . . .. . PCT/GB96/01484 ~'-i 's '- v~
AT1VIOSPI-IEI~IC EFFECTS SIMi~L,ATION
The present invention relates to an apparatus and method for simulating the
appearance of atmospheric effects such as snow in a computer generated image.
Simulators are well known which are capable of generating an image on a
screen used by for example a trainee pilot. The image is generated from a
database of
digital information representing for example terrain and buildings as they
appear from
a viewpoint which may move relative to the terrain. The digital data thus
represents a
model of a worldspace and the images are representative of the appearance of
that
worldspace from a particular position. Generally the model will be based on a
series
of planar polygonal objects of known geometry. position. orientation and
surface
attributes_ Examples of such systems are described for example in U.S Patent .
Specification Nos. ~36347~ and ~41?796. The first of these two U.S Patents
describes the basic operation of an image generator in terms of dealing with
the
processing of objects including light points in real time. whereas the second
deals
with the simulation of atmospheric fog.
The simulation of atmospheric effects such as fog and snow is considered to
be of a real significance given the impact that such effects can have on the
ability of a
pilot to monitor aircraft movements by reference to the view from the
aircraft. No
realistic simulations of layered fo~~ were available until an implementation
of the
invention in accordance with U.S Patent X412796 recently become available.
Attempts to provide realistic simulations of snow have to date not been
successful.
.,-r'..-.-w<W:_: -.--,- .' v:.=~:.--~ =,',--.v_~:...-~:;._M-.:.. . .._ _ . _ -
,._a...-:_.,,.~ _~°~.:_ :_ ~.- . ~ ~ ~'.:- .-._.'.c-rT~s.~.,-.gig.;.::-
>=:.:_-~_ _,
CA 02226115 1998-O1-OS w-=
CVO 97/03417: . -. ,.,...,...::.. ,- PCT/GB96/01484 '
r
Whereas fog can be represented as effects having the same characteristics over
a
substantial volume of space, snow by its very nature must be represented as a
series of
discrete elements, and those elements cannot move in a uniform manner if
realism is
to be achieved. Whereas in non-real time systems any required level of detail
can be
produced providing sufficient computing power and time is available. this is
not the
case in real time systems where the computational resources available to
generate a
single image are necessarily limited.
One snow simulator has been displayed which represents the appearance of
snow falling in the vicinity of an aircraft on the ground. Individual flakes
of snow
were represented by light points strings of which were generated in a similar
manner
to that adopted in conventional systems for the simulation of the lights of
moving
vehicles following each other along a road. Effectively the snow was
represented as a
large number of light points moving within a limited volume of worldspace
within
which the simulated aircraft was stationary. Although such a system was
successful
in providing a realistic image in these limited circumstances_ it could not
provide a
realistic simulation in a sufficiently large volume of worldspace to enable
the realistic
simulation of the appearance of snow through which an aircraft is moving.
In an attempt to provide a realistic simulation of snow. the above model
relying upon light points was developed by relying upon repeating modules of
snow.
each module including a set of light strings to simulate snow flakes. and each
module
representing a segment of a three-dimensional torus made up by an array of
modules.
The viewing point was located within a module of the torus, and the torus was
moved
... ., ,,_~_....., ,..,.--'CA 02226115 1998-01-05': -:.-_ . _., .._.;<;..-..,.
.~..:.::.__.r~_..~;~.._~~..,.~,.;_:.--F,.~-~-~-.....,;.~~~ -
WO 97/03417 PCT/GB96/01484
Y
3
in translation with the viewing point. The relative movement between
individual
snow flakes and the viewing point was achieved by rotating the torus about its
centre
such that the viewing point appeared to move through successive modules. This
approach was adopted as it enables relative movement between the torus and the
viewing point to take account of both movement of individual snow flakes in
worldspace and movement of the viewing point relative to that worldspace. In
some
circumstances this arrangement provided satisfactory results, for example when
flying
straight, as in those circumstances a simple rotation of the snow ''torus" was
able to
achieve the correct movement between individual particle of snow and the
viewing
point. Unfortunately. when the aircraft executed a turn, particularly when
moving on
the ground where sharp turns are common_ it was not possible to realistically
represent
movement of snow across the field of view represented on the viewing screen of
the
simulator. The snow model "turned' with the aircraft in a completely
unrealistic
manner. Thus although some systems relying upon the snow torus model described
above were distributed. some users found them unsatisfactory.
It is an object of the present invention to obviate or mitigate the problems
outlined above.
According to the present invention. there is provided a method for simulating
the motion of particles in a computer generated image representing the
appearance
from a predetermined viewing point of a three dimensional worldspace through
which
the particles move. wherein a three dimensional model is defined which is made
up
from a regular array of abutting model portions of predetermined dimensions,
an
_ ...;.--..,::::>._,~_ : . , ~.- ~: :-:.w CA~ 02226115 1998 O1 OS _.. .... _-.
.,_. -,-,:. .,: -. ~:..-:.-::,..;.._..;-.:.,.
WO 97/03417 . .. . . PCTlGB96/01484
Y
4
object is defined the dimensions of which correspond to the dimensions of each
model
portion, the object having characteristics such that it represents the motion
of particles -
through the volume which it occupies, the three dimensional model is
notionally
positioned in worldspace such that the viewing point is located within a
region of the
model selected such that the field of view of particles from the viewing point
is
always within the model, the worldspace model position is translated in steps,
the
magnitude of each step corresponding to the dimensions of the portions, and
the
model being translated in response to movements of the viewing point in
worldspace
so as to maintain the viewing point within the selected region, and an image
of the
worldspace including the model is generated with the object representing the
moving
particles occupying each portion of the model.
The present invention also provides an apparatus for simulating the motion of
particles in a computer generated image representing the appearance from a
predetermined viewing point of a three-dimensional world space through which
the
particles move, comprising means for defining a three-dimensional model which
is
made up from a regular array of abutting model portions of predetermined
dimensions, means for defining an object the dimensions of which correspond to
the
dimensions of each model portion, the object having characteristics such that
it
represents the motion of particles through the volume which it represents,
means for
notionally positioning the three-dimensional model in worldspace such that the
viewing point is located within a region of the model selected such that the
field of
view of particles from the viewing point is always within the model, means
from
.. ..., CA 022261151998-Ofl--Q$'- ... ~..,
:_..~.__,~:~.__:.,...:.:...:.w.::_;::;.~:-,..,.r.__:_~..::,::~=.>.__;.....,
., .. ......._ ... _... ,..,~_~_;,:: :. ., ...
WO 97/03417 PCT/GB96/01484
: Y
translating the worldspace model position in steps the magnitude of each of
which
corresponds to the dimensions of the portions, the translating means being
responsive
to movements of the viewing point in worldspace so as to maintain the viewing
point
within the selected region, and means for generating an image of the
worldspace
including the model with the object representing the moving particles
occupying each
portion of the model.
As the viewing point will always be within the model, and that model will
move in steps without there being any abrupt or discontinuous change in the
particle
distribution in the field of view. a realistic image may be generated.
Individual
regions of the model are self similar. and therefore the fact that the model
might have
moved relative to the viewing point between successive images is not
perceived.
The particles may be snowflakes. raindrops or the like. The model may be
positioned relative to the viewing point such that a notional point on a line
drawn
through the viewing point in a predetermined direction relative to the viewing
point is
always within a predetermined central location of the model. The distance
between
the notional point and the viewing point may be a function of viewing point
speed.
Thus the notional point may be envisaged as a point located at the end of an
imaginary
telescopic pole extending in front of the viewing point. In the case of
simulating the
view from an aircraft, the imaginary pole will extend parallel to the fore and
aft axis
(U-axis) of the simulated aircraft.
The model orientation is fixed in worldspace such that the model does not
rotate with rotations of the viewing point. Individual model portions
preferably will
CA 02226115 2005-10-25
6
be simple cubes within each of which there is a distribution of particles of
predetermined structure. Each cube may be made up from a series of sub-cubes
each
of which has a different distribution of particles from its neighbours.
Although the model portions or cubes are referred to as abutting, and the
model is translated in steps corresponding to the dimension of these abutting
cubes,
the panicle distribution represented by each cube may extend beyond the cube
boundaries so that there is overlap between the particle distributions in
adjacent cubes.
This smoothes out the edges of the cube structure. The visibility of
individual cubes
may be faded out with range to conceal the external boundaries of the model
structure.
The particles may be represented by respective light points, for example
raster
or calligraphic light points. The light points may be in strings such that the
light
points of each string move in unison. Alternatively. the particles may be
represented
by polygons, for examples triangles.
In another aspect, there is provided a method of simulating the motion of
particles
in a computer generated image representing the appearance from a predetermined
viewing point of a three dimensional worldspace through which the particles
move,
wherein a three dimensional model is defined which is made up from a regular
array of
abutting model portions of predetermined dimensions, an object is defined the
dimensions of which correspond to the dimensions of each model portion, the
object
having characteristics such that it represents particles in motion through a
volume which
it occupies, the three dimensional model is notionally positioned in
worldspace such that
the viewing point is located within the model, the field of view from the
viewing point
extends through the model, and a notional point which is in a predetermined
location
relative to the viewing point is within a selected region of the model, the
worldspace
CA 02226115 2005-10-25
6a
model position is translated in steps, the magnitude of each step
corresponding to the
dimensions of the model portions, and the model being translated in response
to
movements of the viewing point in worldspace so as to maintain the notional
point within
the selected region, and an image of the worldspace including the model is
generated
with the object representing the moving particles occupying each portion of
the model.
In another aspect, there is provided an apparatus for simulating the motion of
particles in a computer generated image representing the appearance from a
predetermined viewing point of a three-dimensional world space through which
the
particles move, comprising means for defining a three-dimensional model which
is made
up from a regular array of abutting model portions of predetermined
dimensions, means
for defining an object the dimensions of which correspond to the dimensions of
each
model portion, the object having characteristics such that it represents
particles in motion
through a volume which it represents, means for notionally positioning the
three-
dimensional model in worldspace such that the viewing point is located within
the model,
the field of view from the viewing point extends through the model, and a
notional point
which is in a predetermined location relative to the viewing point is within a
selected
region of the model, means for translating the worldspace model position in
steps the
magnitude of each of which corresponds to the dimensions of the model
portions, the
translating means being responsive to movements of the viewing point in
worldspace so
as to maintain the notional point within the selected region, and means for
generating an
image of the worldspace including the model with the object representing the
moving
particles occupying each portion of the model.
CA 02226115 2005-10-25
6b
Figure 1 is a representation of a snow model made up of an array of cubes. the
mode( being used in one embodiment of the present invention:
Figures 2 and 3 are side and plan views of the model of Finure 1 representing
the notional position relative to the model of an aircraft the view from which
is to be
simulated;
Figure 4 illustrates the movement of the model through worldspace as the
aircraft moves;
Figure 5 is a plan view representing the distribution of sub-cubes in the
model
of Figure 1;
... _,..... .... r.: -__._ . =- CA 02226115 1998 O1 OS=~~-r-=-:~:~ - =.
,.~:.,:~...:.:.~_,~-..~-,>.,~.,.w:..
. ~ . WO 97/03417 PCT/GB96/01484 _
7
Figures 6, 7 and_8 are views in mutually perpendicular directions representing
the positions of simulated snowflakes in one sub-cube; and
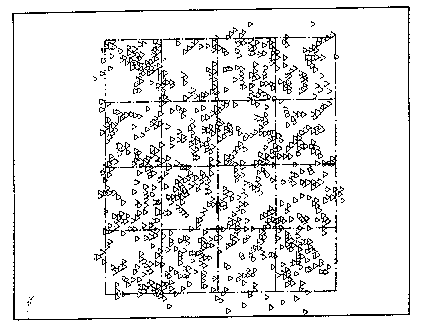
Figure 9 represents the view from above of a layer of sixteen sub-cubes
making up one side of a cube of the model of Figure 1.
Figure I is a three-dimensional representation of a model made up from
seventy four cubes arranged in two layers. The model is used to simulate snow
in a
simulator which generates an image of a worldspace through which an aircraft
flies.
Assuming a worldspace co-ordinate system x, y, z as represented in Figure I ,
the
model will move through worldspace in the directions of each of the three axes
but
will not rotate relative to these axes. Accordingly the edges of each cube
will always
be parallel to one of the three axes. Each cube portion of the model structure
is
occupied by an identical object representing the movement of snow within a
volume
corresponding to the volume of the cube. Typically each cube will have one
hundred
foot sides such that the model structure is two hundred feet high.
Figure 2 is a side view of the model structure of Figure I , and Figure 3 is a
plan view of the model structure of Figure 1. In Figures 2 and 3. a notional
space 1
which is located centrally with respect to the model structure has been
outlined by a
broken line. The space is a notional one hundred foot cube half of which is
located in
the upper layer of cubes and half in the lower layer of cubes.
A representation 2 of an aircraft is also shown in Figures 2 and 3. the broken
line 3 representing the U-axis (fore and aft axis) of the aircraft relative to
the
worldspace within which the model is fixed. A point 4 is located on the line 3
which
a =~. :.-~~-~ .~~,:, =.. z.~ t.,~z-: ~:.- . _ _
... : . , =:.-~ .,..,.;.:; ."--~;. . ~_-~~ ~-. ~r_ _ a - .......,.T:.'.=;" . .
. . . . .~. _.. __. _ ~... , .. r . , -.. =,... ~~x-:<,,~.R . _, , . : ~ ::-<
_Y~.:_.-~ ::-.....,.. . .
-r- ..x., ..t
-- CA 02226115 1998-O1-OS-=-- . --: -
WO 9T/03417 : , ~ ~. ; - . . . .. PCT/GB96/01484' .
8
extends from a viewing point which is within the aircraft 2. The spacing
between the
viewing point and the point 4 is a .function of aircraft speed.
The system operates such that the model is translated through worldspace to
ensure that the point 4 is always located within the region 1. As part of its
normal
processes, the image generator calculates the worldspace coordinates of the
simulated
aircraft, and movements of the model are such as to maintain the require
relationship
between the position of the point 4 and the region 1. The model is translated
in steps
each of which is equal in length to the side dimension of each of the cubes.
This is
illustrated in Figure 4.
Referring to Figure 4. when the point 4 is at position 4a, the model structure
is
positioned with its corners at points ~. 6. 7 and 8. When the point 4 is at
position 4b,
to maintain that point inside the central area I the model has been moved to a
position
such that its corners are at points.9. 10. 1 I and I?. This effectively moves
the central
area of the model structure vertically upward by one hundred feet such that
the point 4
remains within the central region of the structure. When the point 4 has
reached the
position 4c, the model structure has again been moved to maintain the point 4c
within
the central portion of that structure. As a result the model structure is in a
position
such that its corners are at points 13, 14, 15 and 16. Thus is can be seen how
the
model structure follows the aircraft through notional worldspace so as to
always
ensure that the model structure is at an appropriate position around the
viewing point. _,
The spacing between the viewing point and the point 4 is adjusted in
dependence upon aircraft speed in order to provide sufficient time advance to
enable
__.,... _._ _~~ .. . . _.____.__.~_~__~._CA-02226115 1998-~O1-OS ,. __ . .-
....____
CVO 97/03417 PCT/GB96/01484
9
the processing of individual cubes of the structure by the associated image
generator.
When the aircraft is stationary on the ground the viewing point will be
located in the
central region 1, the spacing between the viewing point and the point 4 being
increased to for example two hundred feet when the aircraft is cruising. Thus
the
point 4 is positioned as if it were mounted on the end of a telescopic pole
extending
parallel to the aircraft U-axis. the length of the pole being a function of
aircraft speed.
Therefore the pOIIIL ~ is already dead ahead of the aircraft windshield.
Figure s is a plan view of the structure of Figure I with each of the cubes
being represented by an array of sixteen dots. In fact each cube is made up of
a total
of sixty four sub-cubes. that is four layers of sixteen cubes, with each of
the sub-cubes
defining a different distribution of snow flakes. The dots shown in Figure 5
represent
the centres of individual sub-cubes.
Figures 6. 7 and 8 are views in mutually perpendicular directions of the
distribution of snow flakes in an individual sub-cube. Each triangle in
Figures 6 to 8
represents the position of a single snowflake. The snowflakes are defined as
strings of
light points located on respective straight lines. fW a ofthe triangles being
shaded in
Figures 6 to 8 to represent two strings of snow flakes, one comprising three
flakes and
one comprising two flakes, Located on lines 17 and 18 respectively. The flakes
in
each string move in unison. but the flakes in one string can move in a
different
manner to the flakes in another string. Accordingly complex effects can be
achieved.
Figure 9 is a plan view of the top sixteen sub-cubes of one cube, with the
boundaries of the cubes indicated by lines. It will be seen that there is
overlap
CA 02226115 1998-O1-OS
WO 97/03417 PCT/GB96/01484
between the light points of adjacent sub-cubes, and therefore there will be
overlap
between the light points of adjacent cubes. Typically the light points of any
one
twenty five foot sub cube will be located within a thirty three foot notional
cube.
Therefore although the cubes defining the structure of Figure 1 abut and do
not
overlap, the snowflake distributions represented by the cubes do overlap. This
reduces the possibility of the generated image including "popping" effects.
that is the
sudden appearance of a representation of snow in a region where there was
previously
no snow.
Each cube is broken down into an array of sub-cubes to reduce redundant
processing. Each sub-cube will be allocated a visibility dependent upon its
range
from the viewing point. Accordingly anv sub-cubes more than say three hundred
feet
away from the viewing point will not be processed by the image generator.
The individual snowflakes are represented by techniques familiar to the
designers of image generators which are used for simulating the appearance of
moving strings of lights. A moving li~~ht string is a sequence of points which
continually moves along a defined path. the points appearing at a start point
Ps and
disappearing at an end point Pe. In a typical image generator the following
attributes
may be defined for a light string:
a) Start and end Points in three dimensional space (Ps:Xs. Ys. Zs Pe:Xe.
Ye. Ze)
b) The path of motion (straight or curved) between Ps and Pe
~'~''~'3K'i~~..-. ... J.;~w .~.~..oz',FN~-a...~'.~'>_-rn ~ '~y~:.~ : . . . ~ .
:~~~~.__~a-.~M.-.« ~y. -.
"~~CA~02226115"y1998-O1-OS
~ WO 97/03417 PCT/GB96/01484
c) the speed of motion
d) the spatial separation or temporal interval between points
. e) the intensity, colour, directionality and fade-out range of the points
A typical application is for simulating vehicular traffic along a freeway. In
such an application the lights are modelled white and red so as to present
head-lights
or tail-lights depending upon orientation relative to the viewer eye-point. In
the
present use of snow simulation the lights are used to represent falling
particles (e.g.
snow flakes) that move along a given trajectory. appearing at the ceiling
height of the
cube structure and disappearing at the floor height. Their omni-directional
intensity is
controlled to represent ambient or aircraft landing light illumination.
The image generator maintains a centralised real-time clock "T abs" chat
tracks true elapsed time. All moving strin~~ processing refers back to this
datum such
that multiple copies of a single object will behave in an identical manner.
Furthermore each channel of a multi-channel image generator will have access
to
T abs to guarantee absolute synchronism in strin~~ processing across channels.
The following description covers the simplest case of a single omni-
directional
light on a straight line path. Similar techniques exist for multiple points or
curved
paths.
Attribute data:
Start point Ps (Xs. Ys. Zs) ft
End point Pe (Xe, Ye. Ze) ft
CA 02226115 1998-01-~OS
=WO 97/03417 PGT/GB96/01484
12
Point speed V ft/sec
Deduced data:
Line Length L (computed from Pe - Ps) ft
Point Interval P (computed from L/V ) sec
Variables:
Current string time T string sec
The following calculations are conducted each image generator update frame:
The current T string is computed from the string interval P and T abs.
T string = MOD (T abs.P)
where MOD is the modulus operator that produces the remainder of the
quotient T abs/P (zero results when there is an exact division without a
remainder).
The line ratiometric position r is computed from:
r = T string / P
where r increases linearly from 0.0 (at Ps) to 1.0 (at Pe).
The current position Pp on the line path is given by:
Pp = Ps + r* (Pe - Ps)
i.e. Xp = Xs + r* (Xe - Xs)
.:-=--:~~- _ - . . : ._ .-- .. _.. . _ _.__..-__, _.._. _ ... . ... _ . .- ...
_ _ _._-.,.
... .. - T_ ... CA 02226115 1998-O1-OS '- -_ ._ . , __.. "
. WO 97/03417 PCT/GB96/01484 '
a '
13
Yp = Ys + r* (Ye - Ys)
_ Zp = Zs + r* (Ze - Zs)
- The Pp coordinates then undergo standard graphics perspective divide,
clipping and scaling to create a point in two dimensional screen space. The
fade-range attribute is used to determine when points become too dim to
perceive and may be discarded from the display.
The point may be displayed as a raster light point or a calligraphic light
point depending upon the image generator and display capability. Generally
raster light points will be displayed, as the high quality achievable with
calligraphic light points is not required for the emulation of snow.
A series of light strings each generated as described above is produced for
each sub-cube to produce a distribution such as is illustrated in figures 6 to
8.
The sixty four sub-cubes together define a cube which is repeated in each cube
making up the model structure shown in Figure 1. The image generator
processes each sub-cube within range just as it processes any object within
worldspace to produce the required image information. Thus multiple copies
of each sub-cube are produced, one being used in each cube. These multiple
copies behave in exact synchronism, even across channels of a multi-channel
image generator. This allows the image generator to "jump" into any repeat of
the snow structure without any discontinuities being discernible.
Any convenient approach may be adopted to generate a set of strings
suitable for use in a individual sub-cube. For example, a simple program can
_ -
. . ._.. _.,.... . _.__. .. . .. _ _.. ._ . ._.. -:___. __w _ . .._ , _ . .. .
... ._ _.......-,. .. . .
.. . : ,;...,. ... .;_ _ , :CA 02226115 1998-O1-OS w- ...., ,. :....... ._-
..__..._.~ ::.,.-.-.--._~.;..._.
WO 97/03417_ . . . , PCTiGB96/01484
A r
14
be written to generate a randomised series of strings, the program relying
upon
for example a random seed to ensure differences between successively
generated sub-cubes, ranges for the boundaries of the sub-cube within which
all the sub-cube light points must be located (to provide for variable overlap
between adjacent sub-cubes), a selected number of light points, a range of
acceptable angles of the light strings, a range of intervals between light
points
in individual strings, and range of speeds for the light points. Thus highly
complex and irregular patterns can be readily developed.
The image generator host software stores details of the snow effects
which are to be represented. and performs the necessary computations to
integrate the snow with the other features of the represented scene. The
computational processes are conventional and may for example follow the
procedures such as described in U.S Patent No. ~36347~. Details are given
_ below however of particular computations which are necessary to provide
information specific to the snow simulations.
As is conventional, aircraft space. that is the space in a coordinate
system having its origin at the aircraft centre of gravity. is represented as
(U,V,W)_ Velocities UA, VA and WA represent the motion of a snow particle
relative to the aircraft due to the combined effects of air speed, wind speed
and
turbulence. These velocities are relative to the aircraft axes U. V and Vv and
are with respect to the aircraft centre of gravity. A flight freeze function
may
:.--:.r_°c~r.;uxr.~?k~.r...~,.., .. . . . . , - ~ .. .. _ - .. . -=-
~=:~,.-T.-,;a
.~ ,.-;::,~~;.~..>,.;~.. . . CA 02226115 1998-O1-OS-~
.: .-_ .,:~:.~-:. _: ~ ~ _. ._ . - - , ~- .,, . - ,.,
WO 97/03417 PCT/GB96/01484
be available, and when this is invoked the snow particle motion will be the
result of wind speed and turbulence only.
These snow particle velocity components are multiplied by the frame
period TIME (which may be variable) to create a display screen vector SNPU,
SNPV and SNPW representing the distance moved since the previous image
generation cycle. This displacement vector is rotated from aircraft axes to
worldspace axes to create a delta distance moved in worldspace using a
rotation matrix as follows to create the snow particle position:
Snow particle Northing SNPNG = SNPNG +
(SNPU*BEl 1 + SNPV*BE21 + SNPW*BE31)
Snow particle Fasting SNPEG = SNPEG +
(SNPU*BE12 + SNPV*BE?? + SNPW*BE33)
Snow particle height SNPHD = SNPHD +
(SNPU*BE13 + SNPV*BE23 + SNPW*BE33)
The above rotation matrix is conventional, as is the notation used to
represent that matrix.
The point which is represented as point 4 in Figure 2, 3, and 4 and is
located on a line drawn in the U-axis direction through the eye point is
referred
to hereafter as the centring point. The centring point is projected ahead of
the
- eyepoint at a distance of from zero to two hundred feet in dependence upon
VT which represents the true air speed. At low speeds the centring point is
near the eye point but extends ahead away from the eyepoint with increasing
- _ _ .
_ .~~.~y ,::~ry2.:.~.~'::; _~~ . v; ~~:~_'..,.".'S_
;'::_~. . . ... _ . . -~,.'._ .r-s.
-_....: .~.,~~.. ___..~.~..__-.~~.._.._:~:==_ CA 02226115 1998 O1 05...
WO 97/03417 , PCT/GB96/01484
16
speed until a limiting speed SNVLK is reached. SNVRG is the linear speed
ratio gain, that is the ratio of the true air speed to the limiting speed
limited to
a maximum of unity.
To calculate the height displacement from the aircraft origin of the
centring point the following transformation is performed;
SFPHD = (PEXAC + (SNFPX*SNVRG) )*BE13 +
(PEYAC
)* BE23 +
(PEZAC
)* BE33
SFPHD represents the centring point height displacement in world space
relative to the aircraft. The pilots eye position in aircraft space is
represented by
PEXAC, PEYAC. and PEZAC. The centring point displacement along the aircraft U-
axis is given by (SNFPX *SNVRG). where SNFPX is the maximum distance of the
centring point from the eye and SNVRG is the linear velocity ratio gain. The
rotation
into worldspace is given by BE13, BE23 and BE33. Similar calculations are made
in
respect of Northing and Fasting.
The centring point components are then compared with SNPNG.
SNPEG and SNPHD and the cube repeat dimension (one hundred feet) is
added or subtracted until the central portion of the cube structure is
positioned
over the centring point. Hysteresis is present in this mechanism so as to
prevent potential oscillatory behaviour. This is achieved in respect of the
height dimension as follows;
DO WHILE (SNPHD.GT. (SFPHD+SNRHY))
SNPHD = SNPHD - SNR
END DO
,_..-.~_ :r __..__,.___...___..<.. "....,.~: . __........ .. ... ..CA ,22-
26115 1998-.0_l,-OS .-_.___........_..~_ , ....<.-:::.-.-.;-.-. .._.
.., . : .,. ~;x,~.r~, . _: ... _ . . - - w . ..v . , _ , .
WO 97/0347>,.-~.:~ : PCT/GB96/01484
17
DO WHILE (SNPHD.LT. (SFPHD - SNRHY))
SNPHD = SNPHD + SNR
END DO
In the above, SNR is the dimension of each cube in the structure (one
hundred feet), SNRHY is SNR/2 + 5% to provide the hysteresis to stop
oscillatory switching.
Thus the necessary information required for correctly positioning the
snow structure relative to the viewing point may be readily achieved.
The centring point is close to the eye when performing ground .
handling tasks as this ensures that rapid or large heading changes are
possible
within the cube structure without unnecessary cube jumping. The centring
point is however for examp~e two hundred feet ahead of the eye when cruising.
This provides the image generator with sufficient feed-forward or time
advance to process snow cubes prior to the three hundred foot visibility
range.
It should be noted that the dynamic extension of the distance between the
eyepoint and the centring point only controls the position of the cube
structure
relative to the eyepoint and does not itself impart any perceivable cue.
Because the cube structure has fixed Euler angles and thus does not
rotate relative to worldspace. when the eye rotates about the centre of
gravity
the snow behaves as any other earth aligned model.
.:;._..-,,.. _.. _,.._.,..._._,,. ~ z~._-_,._.~_;.~. . . ~A 02226115 1998-O1-
.OS -. -.,y~ws-~--. _.. ..._._.~=.::_.~i.:.~..,,..,;:.._..:..
WO 97/03417 . ° . _ PCT/GB96/01484
18
Although the foregoing description has implied that the snow is moved
relative to the eye, in fact it '~~ecomes apparent that the snow is largely
stationary relative to worldspace and the aircraft normally is flying though
the
cube structure which jumps one hundred feet as required to maintain
immersion of the eyepoint. In theory the only earth relative motion is
produced by the wind component. which is insignificant at higher air speeds.
Thus a very realistic display can be achieved giving the impression that
the eye point is moving through the simulated snow, enabling wind conditions
to affect the generated image, and maintaining the appropriate cubes with
regards to both translation and rotation.
In summary. the present invention provides the following features:
I . The simulated vehicle appears to move through the model and a seamless
visual flow of particles is perceived.
2. Correct translation axes are obtained for all vehicle motion.
3. Correct rotation axes are obtained for all vehicle motion.
4. Correct axes are obtained for the effects of wind. both steady and gusting.