Note: Descriptions are shown in the official language in which they were submitted.
CA 02253145 1998-10-30
' Doc. No 50344-1 CA Patent
SYSTEM FOR INTERACTIVE VISUALIZATION AND ANALYSIS OF
IMAGING SPECTROMETRY DATASETS OVER A WIDE-AREA NETWORK
Field of the Invention
This invention relates to a lossy data compression system using vector
quantisation, for
reducing data volumes generated by hyper-spectral imaging devices.
Background of the Invention
The next generation of satellite-based remote sensing instruments will produce
an
unprecedented volume of data. Imaging spectrometers, also known as hyper-
spectral imaging
devices, are prime examples. They collect image data in hundreds of spectral
bands
simultaneously from the near ultraviolet through the short wave infrared, and
are capable of
providing direct identification of surface materials.
Hyper-spectral data thus collected are typically in the form of three-
dimensional (3D)
data cube. Each data cube has two dimensions in the spatial domain defining a
rectangular plane
of image pixels, and a third dimension in the spectral domain defining
radiance levels of multiple
spectral bands per each image pixel. The volume and complexity of hyper-
spectral data present a
significant challenge to conventional transmission and image analysis methods.
The raw data
rates for transmitting such data cubes can easily exceed the available
downlink capacity or on-
board storage capacity of existing satellite systems. Often, therefore, a
portion of the data
collected on board is discarded before transmission, by reducing the duty
cycle, reducing the
spatial or spectral resolution, and/or reducing the spatial or spectral range.
Obviously, in such
cases large amounts of information are lost.
For data processing, a similar problem occurs. In computing, a current trend
is toward
desktop computers and Internet based communications. Unfortunately, the data
cubes require a
CA 02253145 2006-O1-16
tremendous amount of storage and, for processing, the storage is preferably
random access
memory (RAM). Current desktop computers often lack sufficient resources for
data processing of
data cubes comprising spectral data.
Recent work related to data compression of mufti-spectral and hyper-spectral
imagery has
been reported in the literature, but most of these studies relate to mufti-
spectral imagery
comprised of only a few spectral bands. These prior art systems for mufti-
spectral imagery yield
small compression ratios, usually smaller than 30:1. There are two reasons for
this:
1 ) the prior art systems do not efficiently remove the correlation in the
spectral domain, and
2) the redundancy of mufti-spectral imagery in the spectral domain is
relatively small
compared to that of hyper-spectral imagery.
One sample prior art system teaches two systems for hyper-spectral imagery.
The first
system uses trellis coded quantization to encode transform coefficients
resulting from the
application of an 8x8x8 discrete cosine transform. The second system uses
differential pulse
code modulation to spectrally decorrelate data, while using a 2D discrete
cosine transform for
spatial decorrelation. These two systems are known to achieve compression
ratios of greater
than 70:1 in some instance; however, it is desirable to have higher
compression ratios with
simpler coding structures than those reported in the literature.
In an article entitled "Lossy Compression of Hyperspectral Data Using Vector
Quantization" by Michael Ryan and John Arnold in the journal Remote Sens.
Environ., Elsevier
Science Inc., New York, N.Y., 1997, Vol. 61, pp. 419-436, an overview of
general vector
quantization techniques as are now known is presented. In particular, the
authors describe
issues such as distortion measures and classification issues arising from
lossy compression of
hyper-spectral data using vector quantization.
Data compression using Vector Quantisation (VQ) has received much attention
because
of its promise of high compression ratio and relatively simple structure.
Unlike scalar
2
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
quantisation, VQ requires segmentation of the source data into vectors.
Commonly, in two-
dimensional (2D) image data compression, a block with nxm (n may be equal to
m) pixels is
taken as a vector, whose length is equal to nxm. Vectors constituted in this
way have no physical
analogue. Because the blocks are segmented according to row and column indices
of an image,
the vectors obtained in this manner change at random as the pixel patterns
change from block to
block. The reconstructed image shows an explicit blocking effect for large
compression ratios.
There are several conventional approaches to constituting vectors in a 3D data
cube of
hyper-spectral imagery. The simplest approach is to treat the 3D data cube as
a set of 2D
monochromatic images, and segment each monochromatic image into vectors
independently as
in the 2D-image case. This approach, however, suffers from not taking
advantage of the high
correlation of data in the spectral domain. There is therefore a need for a
data compression
system that takes advantage of correlation in the spectral domain and the 2D
spatial correlation
between adjacent image pixels.
The VQ procedure is known to have two main steps: codebook generation and
codevector
matching. VQ can be viewed as mapping a large set of vectors into a small
subset of indexed
codevectors forming a codebook. During encoding, a search through a codebook
is performed to
find a best codevector to express each input vector. The index or address of
the selected
codevector in the codebook is stored associated with the input vector or the
input vector location.
Given two systems having a same codebook, transmission of the index to a
decoder over a
communication channel from the first system to the second other system allows
a decoder within
the second other system to retrieve the same codevector from an identical
codebook. This is a
reconstructed approximation of the corresponding input vector. Compression is
thus obtained by
transmitting the index of the codevector rather the codevector itself. Many
existing algorithms
for codebook designs are available, such as the LBG algorithm reported by
Linde, Buzo and
Gray, the tree-structure codebook algorithm reported by Gray, the self
organising feature map
reported by Nasrabadi and Feng. Among these, the LBG algorithm is most widely
used because
of its fidelity. The disadvantages of the LGB algorithm are its complexity and
the time burden
taken to form the codebook. When the input data is a 3D data cube of hyper-
spectral imagery, the
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
processing time can be hundreds of times higher than the normal 2D-image case.
There is
therefore a need for faster codebook generation algorithms with relatively
high fidelity.
It would also be advantageous to provide a method of data compression wherein
data
compressed according to the method is useful for some forms of data
processing, image
generation, and data viewing.
Summary of the Invention
It is an object of the present invention to provide a data compression system
that allows
viewing and analysis of large datastructures without decompression of the
entire datastructure. It
is yet another object of the invention to provide a data compression algorithm
that would allow
relatively fast processing of 3D data cubes in a compressed form.
In accordance with the invention there is provided a method of processing
hyper-spectral image
data defining signal levels of multiple spectral bands in encoded form, the
encoded form
comprising an array of indices and a codebook comprising a plurality of
vectors, the method
comprising the steps of:
for each image pixel,
determining a first band from the multiple spectral bands and an index from
the array of
indices, the index indicative of a vector within the codebook, and
retrieving from the indicated vector within the codebook a value corresponding
to the
first band; and,
displaying an image comprising image pixels, image pixel values based upon the
values retrieved
for each image pixel.
In accordance with the invention there is also provided a method of processing
hyper-spectral
image data defining signal levels of multiple spectral bands per image pixel
in encoded form, the
encoded form comprising an array of indices and a codebook, the method
comprising the step of:
processing spectral vectors within the codebook to produce a processed
codebook, each spectral
vector processed in isolation.
4
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
According to an embodiment the method comprises the further steps of
transmitting the codebook and the array of indices from a first computer to a
second other
computer, the second other computer remote from the first computer,
wherein the step of processing is performed on the second other computer and
includes
determining from the codebook and the array of indices, data within the hyper-
spectral data that
is significant for further analysis;
requesting the data from the first computer;
compressing uncompressed hyper-spectral data associated with the requested
data according to a
known compression algorithm to produce compressed data; and,
transmitting the compressed data to the second computer.
In accordance with the invention there is also provided a method of processing
hyper-spectral
image data defining signal levels of multiple spectral bands per image pixel
in encoded form, the
encoded form comprising an array of indices and a codebook, the method
comprising the step of:
processing spectral vectors within the codebook and data from the index map to
extract
information from the codebook and index map other than pixel values for
display.
In accordance with another aspect of the invention there is provided a system
for processing
hyper-spectral image data defining signal levels of multiple spectral bands in
encoded form, the
encoded form comprising an array of indices and a codebook comprising a
plurality of vectors,
the system comprising:
means for selecting for each image pixel a first band from the multiple
spectral bands and an
index from the array of indices, the index indicative of a vector within the
codebook, and
means for retrieving for each image pixel from the indicated vector within the
codebook a value
corresponding to the first band; and,
means for displaying an image comprising image pixels, image pixel values
based upon the
values retrieved for each image pixel.
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
In accordance with the other aspect of the invention there is also provided a
system for
processing hyper-spectral image data defining signal levels of multiple
spectral bands per image
pixel in encoded form, the encoded form comprising an array of indices and a
codebook, the
system comprising:
means for processing each spectral vector within the codebook in isolation to
produce a
processed codebook.
In accordance with yet another aspect of the present invention there is
provided a system
for processing in a compressed form, hyper-spectral image data defining
radiance levels of
multiple spectral bands per image pixel, said system being initially trained
with image data
defining a predetermined set of training image pixels, said system comprising:
a) vector constitution means having an input for receiving and representing
the image
data as an array of spectrum image vectors XP , said array having a
predetermined dimension h,
each said vector to characterise the spectral bands of an image pixel p, said
vector having a
predetermined dimension of Nn components x~ (~,), ~, having any value between
l and Nb;
b) spectral compressor responsive to the vector constitution means, including
a
compression algorithm for reducing any of said spectrum image vectors to a
binary image vector
XP having a predetermined length L;
c) a codevector generator responsive to the spectral compression means, for
receiving a
predetermined set of training binary image vectors corresponding to the
predetermined set of
training image pixels, said generator having a codevector algorithm for
deriving from said set of
training binary image vectors a finite set of binary codevectors yq and having
means for storing
said set of codevectors;
d) vector matching means responsive to the spectral compressor for receiving
the binary
image vectors and responsive to the codevector generator for reading the
binary codevectors, said
matching means including a distance algorithm for calculating the distance DPN
of any received
6
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
binary imagevector XP to each element yq in the finite set of binary
codevectors, and for
selecting a matched binary codevector having shortest distance from said
received binary image
vector, as a compressed form of the spectrum image vector Xp , said matching
means having an
output for providing an array of said matched binary codevectors as a
compressed form of the
hyper-spectral image data suitable for further image processing;
In an embodiment of the present invention, the compression algorithm used in
spectral
compression, upon receiving a spectral image vector XP performs the steps of:
a) calculating a spectral algebraic mean ~p of the Nn components xp(~,) of the
received
spectrum image vector XP ;
b) generating an amplitude binary vector XP having a length of Nh bits X p
(~,), ~, having
any value between 1 and Nn, where X p (~,) equals a first binary level when xp
(~,) is greater than
or equal to ~P, and XP (~,) equals a second binary level when xP (~,) is
smaller than ~P;
c) generating a slope binary vector XP having a length of Nh-2 bits X p (~,),
~, having a
value between 2 and Nn-1, where Xy (~,) equals a first binary level when
xP(~,+1) is greater than
or equal to xP(~,-1), and X p (~,) equals a second binary level when xp(~,+1)
is smaller than xp(7~-1);
d) calculating a spectral mean deviation MD; as the mean of the absolute
difference
between each of the Nh components xp (~,) of the spectrum image vectors XP and
the spectral
algebraic mean ~~,;
e) generating a mean deviation binary vector X~ having a length of Nb bits X
p'° (~,), 7~
having any value between 1 and Nh, where X~° (7~) equals a first binary
level when the absolute
difference between xP (~.) and ~p is greater than or equal to MDp, and X
p'° (~,) equals a second
binary level when the absolute difference between x~(~,) and ~,P is smaller
than MDp; and
7
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
f) reducing the received spectrum image vectors to a binary image vector XP
having a
length L = 3Nn-2 bits, in the form of a concatenation of the amplitude binary
vector XP , the slope
binary vector Xp and the mean deviation binary vector Xp''°.
In another embodiment of the present invention, the distance algorithm for
determining a
distance such as a Hamming distance, Day, is capable of calculating the
distance between a binary
vector XP and a binary codevector yq as the arithmetic sum of bit-wise
exclusive-OR operations
on all bit pairs (Xp(l), Yy(1)) corresponding to XP and yq ,1 having any value
between 1 and L;
alternatively, a Euclidean distance is calculated between the image vectors Xp
and codevectors
yq .
In accordance with the present invention there is also provided a system for
compressing
hyper-spectral image data defining radiance levels of multiple spectral bands
per each pixel of a
two-dimensional image having N, rows and NC columns of pixels, said system
comprising:
a) vector constitution means for receiving and representing the image data as
a two-
dimensional vector array of N,XN~ spectrum image vectors XP , p having any
value from 1 to
N,XN~ each said vector being positioned at a row co-ordinate i and a column co-
ordinate j of said
vector array, to characterise the spectral bands of an image pixel at similar
i and j co-ordinates
within the two-dimensional image, i having any value from 1 to N, and j having
any value from 1
to N~, said vector having a predetermined dimension of Nn components xp(~,),
7~ having any value
between 1 and Nh;
b) spectral compressor responsive to the vector constitution means for
reducing any of
said spectrum image vectors to a binary image vector XP ;
c) a codevector generator responsive to the spectral compressor for receiving
a
predetermined set of training binary image vectors, deriving therefrom a
finite set of binary
codevectors yq , each codevector identifiable with an index;
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
d) a codebook responsive to the codevector generator for storing, in the form
of a look-up
table, said set of binary codevectors and the set of indices in a one-to-one
mapping relationship
between each binary codevector and its corresponding index;
e) vector matching means responsive to the spectral compressor and the
codebook, for
receiving the binary image vectors, said matching means including a distance
algorithm for
calculating the distance Day of any received binary image vector XP to each
element yq in the
set of binary codevectors in the codebook, and for selecting a matched binary
codevector having
shortest distance from said received binary image vector;
f) a correlation encoder responsive to the vector matching means and the
codebook for
receiving said matched binary codevectors, said encoder comprising
i) means for retrieving from the codebook an index corresponding to each
matched binary
codevector received therein,
ii) means for forming a two-dimensional index array of N, X N~ indices Cp,
each said
index being positioned at a row co-ordinate i and a column co-ordinate j of
said index
array, to correspond to an image pixel at similar i and j co-ordinates within
the two-
dimensional image,
iii) a movable two-dimensional window having W, rows and W~. columns, W, and W
having predetermined values of less than or equal to N, and N~ respectively,
said window
being capable of reading the indices in adjacent index positions within any
cell of W, XW~.
indices from the index array,
iv) a correlation algorithm for moving the window in a predetermined sequence
across
the entire index array, having the window read the indices of one cell at a
time, and
generating a correlation symbol for each cell read by the window, each said
symbol to
refer to no more than once to an index value read within said cell, and to
define a
dissimilarity pattern among index values within said cell.
9
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
This embodiment is intended to reduce the correlation in both spatial and
spectral domain
with the additional benefit of reduced computation complexity.
In accordance yet with another aspect of the present invention there is
provided a system
for compressing, and communicating in a compressed form, hyper-spectral image
data defining
radiance levels of multiple spectral bands per image pixel, said system being
initially trained
with image data defining a predetermined set of training image pixels, said
system comprising:
a) vector constitution means for receiving and representing the image data as
an array of
spectrum image vectors XP , said array having a dimension n, each said vector
to characterise the
spectral bands of an image pixel p, said vector having a predetermined
dimension of Nh
components xp (~,), ~, having any value between l and Nh;
b) spectral compressor responsive to the vector constitution means, including
a
compression algorithm for reducing any of said spectrum image vectors to a
binary image vector
XP~
c) a codevector generator responsive to the spectral compressor and the vector
constitution means, for receiving a predetermined set of training spectrum
image vectors and a
corresponding set of binary image vectors thereto, said generator having a
codevector algorithm
for deriving from said set of spectrum image vectors a finite set of spectrum
codevectors yq , and
for deriving from the corresponding binary image vectors a finite set of
binary codevectors yq ,
and generating a set of indices Cy corresponding to said spectrum codevectors;
d) a codebook responsive to the codevector generator for storing, in the form
of a look-up
table, said finite set of spectrum codevectors yq , together with said finite
set of binary
codevectors yq in a one-to-one mapping relationship to said corresponding
indices Cg;
e) vector matching means responsive to the spectral compressor for receiving
the binary
image vectors, and responsive to the codebook for reading the set of binary
codevectors, said
matching means including a distance algorithm for calculating the distance D~
of any received
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
binary image vector XP to each read codevector yq , and for selecting a
matched binary
codevector having shortest distance from said received binary image vector;
f) an encoder responsive to the vector matching means and the codebook for
receiving
said matched binary codevectors, said encoder comprising means for retrieving
from the
codebook an index to correspond to each matched binary codevector received by
the encoder,
and for forming an array of indices to render a compressed form of the hyper-
spectral image data,
suitable for delivery to a communications or storage medium;
g) a decoder responsive to the communications medium for receiving said
indices,
referring to the codebook to map each received index into a corresponding
spectrum codevector,
and forming an array of reconstructed spectrum codevectors suitable for image
display or further
image processing.
Unlike conventional compression and coding schemes, the vectors constituted by
the
present invention have a physical meaning: each vector is a spectral vector
representative of a
spectrum, and each spectrum is an indicator of the material in a surface such
as the earth's
surface that lies within the field of view. Since the number of materials in
an imaged scene is
usually limited, the number of different encoded spectra can be much smaller
than the total
number of vectors N,xN~.. By taking advantage of this redundancy, the present
invention
expresses all the spectral vectors using a codebook with comparatively few
binary codevectors
and achieves good reconstruction fidelity. This way, the invention makes
better use of the high
correlation often found between bands in the spectral domain and can achieve a
relatively high
compression ratio. Furthermore, encoding the image vectors in a binary form
permits faster
codebook generation and faster codevector matching. In view of the physical
meaning attached
to each encoded binary vector, it would be possible to apply image-processing
operations to the
compressed form of the much shorter and fewer binary vectors than the hyper-
spectral image
data in its raw uncompressed form.
11
CA 02253145 2006-O1-16
Brief Description of the Drawings
Exemplary embodiments of the invention will now be described in conjunction
with the
drawings in which:
Fig. 1 is a perspective view of a hyper-spectral data cube having two
dimensions in the spatial
domain defining a rectangular plane of image pixels, and a third dimension in
the spectral
domain defining radiance levels of multiple spectral bands per each image
pixel;
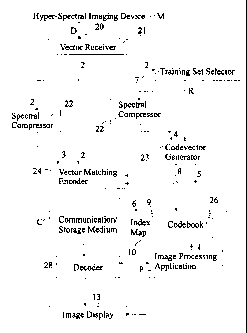
Fig. 2 is a block diagram of a preferred embodiment of a system for
compressing,
communicating and processing in a compressed form, hyper-spectral image data
defining
radiance levels of multiple spectral bands per image pixel, said system being
initially trained
with image data defining a predetermined set of training image pixels;
Fig. 3 illustrates a sequence of signal transformations occurring when the
embodiment of Fig. 2
is in use;
Fig. 4 is a view of a two-dimensional array of NrXN~ indices used for encoding
the array of
encoded image pixels shown in Fig. 3, to illustrate the operation of the
correlation algorithm in
one aspect of the embodiment of Fig. 2.
FIG. 5 is an example of a filtering operation; and
FIG. 6 is a resulting codebook of the example of the filtering operation shown
in FIG. 5
Detailed Description of the Invention
Fig. 2 illustrates in a block diagram, a system 100 for compressing hyper-
spectral image
data D received from a hyper-spectral imaging device M, in accordance with an
embodiment of
the present invention. In general, hyper-spectral data define radiance levels
of multiple spectral
bands per each image pixel. Thus for a planar imaging area, hyper-spectral
data includes a planar
image at each of a plurality of bands. When these images are stacked into a
three-dimensional
array or structure, they form a datacube D. Depending on the characteristics
of the imaging
device M, the image data D produced thereby defines an image of one, two,
three or more
dimensions. An example of a two-dimensional image derived from hyper-spectral
data D is
illustrated in Fil;. I.
Refernng to Fig. 2, vector constitution means, in the form of a vector
receiver 21,
receives at an input port 20 thereof the image data D, and represents the data
D into an array of
12
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
spectrum image vectors 2, herein referred to as XP . The spectrum image
vectors 2 have a same
dimension n as that of the image data D, where n = 1, 2, 3 or more. The
spectrum image vectors
2 are each associated with an image pixel p within the image data D. Each
image vector has a
predetermined dimension of Nn components xn (~,), 7~ having any value between
1 and Nh, where
each component characterises one particular spectral band of an image pixel p.
The array of spectrum image vectors 2 is then transferred to a spectral
compressor 22,
which executes a compression algorithm for reducing any of said spectrum image
vectors 2 to a
binary image vector 3, hereby referred to as XP , which has a predetermined
length L. The
spectral compressor 22 also includes a compression algorithm for use in
training. For clarity, the
spectral compressor 22 is shown twice, once for training and once for
compression functionality,
even though a single spectral compressor 22 commonly exists. The spectral
compressor 22
during execution of the compression algorithm, upon receiving a spectrum image
vector 2
performs the steps of:
a) calculating a spectral algebraic mean p,~ of the Nn components xp(~,) of
the received
spectrum image vector XP ;
b) generating an amplitude binary vector XP having a length of Nn bits X p
(~,), ~, having
any value between 1 and Nn, where XP (~,) equals a first binary level when xp
(~,) is
greater than or equal to p~, and X~ (~.) equals a second binary level when xP
(~,) is smaller
than gyp.
c) generating a slope binary vector XP having a length of Nh-2 bits X p (7~),
~, having a
value between 2 and Nn-1, where X p (~,) equals a first binary level when
xp(~,+1) is
greater than or equal to x~(~,-1 ), and X;, (~,) equals a second binary level
when xP(~,+1 ) is
smaller than xP(~,-1 );
d) calculating a spectral mean deviation MD; as the mean of the absolute
difference
between each of the Nn components x,, (~,) of the spectrum image vectors XP
and the
spectral algebraic mean pp;
13
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
e) generating a mean deviation binary vector XP ° having a length of Nh
bits X p"' (~,), ~,
having any value between 1 and Nh, where X~"(~,) equals a first binary level
when the
absolute difference between x~ (~,) and pp is greater than or equal to MDP,
and X p"' (~,)
equals a second binary level when the absolute difference between x~(7~) and
pp is smaller
than MDp; and
f) reducing the received spectrum image vectors to a binary image vector XP
having a
length L = 3Nh-2 bits, in the form of a concatenation of the amplitude binary
vector Xp ,
the slope binary vector XP and the mean deviation binary vector X~ .
The spectral vectors 2 are also provided to a training set selector 7. A set
of training
vectors R selected from the spectral vectors 2 or selected in another fashion
are provided to a
codevector generator 23. The codevector generator 23 requires training using
the predetermined
set of training vectors R provided in the form of a set of training spectral
vectors R to the spectral
compressor 22, which in turn provides a corresponding set of training binary
vectors 4 to the
codevector generator 23. The codevector generator 23 is used for generating a
finite set of
codevectors such as binary codevectors 5 or other codevectors 8, where
training vectors derived
from the image vectors 2 are mapped onto a particular other codevector 8
and/or binary
codevector 5 for the purpose of vector matching. Of course the codevector
generator 23 is also
capable of determining a set of other codevectors 8 based on the training
image vectors R. This
generator 23 uses a codevector algorithm to derive from the set of training
binary image vectors
4 a finite set of binary codevectors 5, hereby referred to as yq . The
codevector generator 23
includes means for deriving from the received set of training spectrum image
vectors 7, a finite
set of spectrum codevectors 8, hereby referred to as yq , corresponding to the
set of binary
codevectors 5. The codevector generator 23 also comprises memory for storing
the set of other
codevectors 8. Examples of storage means include volatile memory such as RAM,
and non-
volatile memory such as ROM, magnetic storage means such as tape or disk, and
optical storage
14
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
means. Of course, other memory devices may also be employed. Alternatively,
when matching
of binary vectors is not performed, only the codevectors 8 are necessary.
The finite set of binary codevectors 5 are then stored in a codebook 26. The
codebook 26
is in the form of a look-up table, each vector corresponding to an index from
a set of indices 9 in
a one-to-one mapping relationship, the look-up table and a corresponding set
of indices 9 are
herein referred to as Cy.
Binary image vectors 3 generated by the spectral compressor 22 and spectrum
image
vectors 2 are provided to a vector matching system 24, which also receives the
binary
codevectors 5 and/or the other codevectors 8 provided by the codevector
generator 23. The
vector matching system 24 includes means for calculating the distance Dpy
between any received
binary image vector Xp and each element yq in the finite set of binary
codevectors 5 and for
selecting an index associated with a matched codevector 6 having substantially
short distance
from the binary image vector 3. Preferably, the selected index associated with
the matched
codevector 6 has a shortest distance from the binary image vector 3. For
example, the Hamming
distance D~ between a binary image vector XP and a binary codevector yq is
calculated as an
arithmetic sum of bit-wise exclusive-OR operations on all bit pairs (XP(l),
Yy(l)) corresponding to
XP and yq , I having any value between 1 and L. Preferably, a subset of
vectors is identified
using Hamming distance calculations and a vector from the subset is selected
using a more
accurate distance determination such as a determination of Euclidean distance
between other
codevectors and the spectral image data XP . This is achieved as follows. The
vector matching
system 24 comprises means for executing algorithms for reducing a number of
operations
required to calculate the distance Dny between all bit pairs (Xp(l), Yy(l)),
as follows:
i) means for executing a spectral means algorithm for calculating a spectral
algebraic
mean ~; of the Nh components x~(7~) of any of the spectrum image vectors XP
received
from the vector receiver 21, and a spectral algebraic mean p,N of the Nh
components y9(~,)
of any of said set of spectrum codevectors yq ; and
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
ii) means for executing a search acceleration algorithm for identifying a
subset Ty of
binary codevectors y~ corresponding to a subset of spectrum codevector yr
having mean
p., in the vicinity of the mean p,~ of any of the received spectrum image
vectors XP , within
a predetermined difference in magnitude.
A Hamming distance algorithm is used to calculate a distance Dny only for a
smaller subset of
binary codevectors TN. Optionally, a second level of codevector matching is
used which more
accurately selects codevectors based on Euclidean distances.
An index referring to the matched codevector 6 then serves as a compressed
form of the
spectrum image vector XP . The matching system 24 block provides an array of
indices relating to
matched codevectors to serve as a compressed form of the hyper-spectral image
data D, which
would be suitable for further image processing applications P.
The indices 9 indicative of the matched codevectors are then provided to a
communication device and/or a storage device C a in the form of an array of
indices forming a
matched codevector index map 9 to render a compressed data 10 for the hyper-
spectral image
data D, which would be suitable for delivery to a communications or storage
medium C, or for
further image processing applications P.
According to prior art techniques a decoder receives compressed data. The
decoder refers
to a codebook to map each received index into corresponding expanded data, and
forms an
expanded data set suitable for image display or further image processing. This
is used, for
example, in compression and expansion of two-dimensional images.
According to the invention, however, a decoder 28 receives the compressed data
10 from
the communications and/or storage medium. Upon receiving a request for
specific data, the
decoder 28 using the array of indices 9 associating image pixels and
codevectors within a
codebook 26 maps some indices into a corresponding spectrum codevector at a
desired spectral
channel, and forms an array of spectral values suitable for image display or
further image
processing. Therefore, according to the invention, memory requirements are
greatly reduced for
16
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
display, processing, and storage of hyper-spectral data. For example, in order
to extract an image
from compressed data 10 stored in memory reduced memory requirements over
extracting the
datacube result. When spectral vectors are captured having 72 16 bit bands for
2200 lines and
128 pixels across a two-dimensional image of a cross section of the datacube
has 2200x128
pixels (281,600) with a pixel depth of 16 bits, 0.56 megabytes are required to
store each of the
72 single images in each band. When the codebook 26 comprises 4096 codevectors
- an index
value having 12 bits (stored as a 12 bit value), a further 576 kilobytes
(589,824 bytes) is required
to store the codebook and another 412.5 kilobytes, 422,400 bytes, for storing
the array of indices
9 associating image pixels and codevectors within a codebook 26. In this
example, the total
memory requirements for displaying an image - all data stored in RAM - is
about 1 megabyte.
The original datacube has a size of 40.6 megabytes. The resulting compression
ratio is 40.1 when
the codebook and index map sizes are taken into account.
Since 4096 (2'2) codevectors are stored instead of 281,600 codevectors, memory
requirements for navigation through, viewing of, and many forms of processing
are greatly
reduced. Also, processing speed is enhanced significantly. For example, in
order to locate all
locations within an image wherein the associated spectrum comprises a peak in
a predetermined
channel or group of channels requires peak identification on the codevectors
within the codebook
26. According to the prior art, peak identification was required for each
spectrum within the
hyper-spectral data - for 281,600 spectral vectors in the above example. When
4096 codevectors
form a codebook, the speed increase is approximately 70 fold. When 1024
codevectors form a
codebook, the speed increase is near 275 fold. When the datacube is
significantly larger, for
example 1024 x 1024 by 72 bands, the performance increase is 256 for a
codebook of 4096
codevectors and 1024 for a codebook of 1024 vectors. It is apparent to those
of skill in the art
that reduced computation time and memory requirements, allows implementation
of a system for
viewing, navigation, processing and for performing other tasks with compressed
hyper-spectral
data compressed according to the invention on a desktop computer as is
commonly available.
This significantly reduces costs associated with hyper-spectral data analysis
and increases
availability of such analysis to smaller organisations and researchers.
17
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
An alternative embodiment of the invention is disclosed herein, which takes
further
advantage of spatial correlation between adjacent spectral vectors within
datacube D. Here, the
process is similar to that set out above, except for additional inclusion of a
correlation coding
procedure in the vector matching encoder 24 as described below.
18
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Referring again to Fig. 2, in one aspect of the embodiment illustrated, a
cross section of
the datacube represents image data related to a two-dimensional image. There,
a spectrum image
vector representing a pixel (i, j) in the spatial domain is more specifically
defined as
x.., _ ~x~.i ~ 1 )~ x.., ~2)~..., Xi,.l ~Nb) ~T ~i =1 ~2~..., N~ j =1,2,...,
N~) ~ ~ 1 )
as one element within an array 2 having a rectangular spatial domain of N,XN~
pixels and a
spectral domain of Nn spectral bands per pixel. There are a total of N,xN~.
vectors in the array 2
with spatial dimensions N, rows and N~. columns, and the dimension of each
vector is equal to the
number of spectral bands Nn. This is illustrated in Fig. 3, which shows a
sequence of signal
transformations occurring when the embodiment of Fig. 2 is used for
compressing such a three-
dimensional datacube D.
In a similar manner to that described above, these spectrum image vectors 2
are reduced
by the spectral compressor 22 into binary image vectors 3 each formed by
concatenating a set of
3 binary vectors, in a similar manner to what is explained above. The binary
image vectors 3
have a length L = 3 Nn -2 bits which is typically much shorter than the
spectrum image vectors 2.
The spectral compressor 22 first reduces an Nh-band spectrum x;,~ (1) (l =1,
2,..., Nn) into an Nn -
bit amplitude binary vector Xa~ , an (Nn - 2) -bit slope binary vector X;,~
and an Nn -bit mean
deviation binary vector X;,'~° . The amplitude binary vector Xa~ is
constructed from
Xa; = LXa; ~ 1 )~ X; ~2)~..., xa~ (Nb) jT ~i =1 ~2~..., N~ j =1,2,..., N~) ~2)
1 ~xr,i (~.) - ~;,~.~' ~
~'°i (7~) _ ~, =1, 2,..., Nn
~ ~x~,.i(f)-N,r,~~~~
where the scalar quantity ~;~ is defined as the spectral mean of pixel (i j),
19
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Nn
N~~,~=-~xr,.i(f) (t=1,2,...,N, j=1,2,...,N~).
Nn ~=i
It describes the variation in amplitude relative to the mean. The slope binary
vector given
X. ; _ ~X~; ( 1 )~ X.; (2)~..., X; ~ (Nb) JT (i =1,2,..., N~ j =1,2,..., N~) ,
by equation 5 is constructed from
1 ~xr,~(~+1)-x;,~(~-I)J?0
X;(~)= 0 ~x;,,(~+1)-x;,;(~-1)J<0 f -2'3'...,Nn-1. (6)
MD
X~,~ - ~Xi,;'~ ( 1 )~ Xi,;~ (2)s~.., XMD (Nb) jT (i =1 ~2~..., N~ j =1,2,...,
N~)
A mean deviation binary vector X~,"~ is then constructed from
1 ~xr,.i(~)-1~;,;~'MDr,i __
X;,n~°(~)= Q ~x~,i(7,')-~~,i~<MDr,i ~ 1'2'...~Nn (
where MD;~ is defined as spectral mean deviation of pixel (ij),
1 Nn
MD;,~=-~I x~,.~(~)-~~,;~ (1=1.2,...,N, j=1,2,...,N~)
Nn x=~
These three binary vectors Xa~ , ~,~ and XMD are then concatenated to form a
single (3Nn-2)-bit
binary image vector X~,;
A vector matching encoder 24 in the form of a correlation encoder matches
codevectors
2, 3. The encoder 24 determines an index 9 corresponding to each matched
codevector 5, 8
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
received therein. It then forms a two-dimensional array - for a three-
dimensional datacube - of
N,xN~ indices C~, each said index 9 being positioned at a row co-ordinate i
and a column co-
ordinate j of said index array, to correspond to a spectral vector at similar
i and j co-ordinates
within the three-dimensional datacube D. The encoder 24 further comprises a
movable two-
dimensional window having 2 rows and 2 columns, for comparing the spectral
vectors in
adjacent positions within any 2X2 cell of indices 9 from the index array. The
encoder 24 uses a
correlation algorithm for moving the window in a predetermined sequence across
the entire index
array, allowing for reading of the indices of one cell within a window at a
time, and for
generating a correlation symbol for each cell within the window, each said
symbol to refer no
more than once to an index value within said cell, and to define a
dissimilarity pattern among
index values within said cell. The correlation algorithm forms such
correlation symbols by
performing the steps described below with reference to the structure of the
index array as
illustrated in Fig. 4.
Sten I~ Initialise the fiat hln~k
The window is positioned over an initial cell at a corner of the two-
dimensional index
array and the indices therein are used to generate a correlation symbol
referring to values of
dissimilar indices within the initial cell and defining a dissimilarity
pattern among index values
therein. As shown in Fig. 4, the window is located in the upper left corner,
using spectral vectors
at positions A, B, F and G. The spectral vectors at positions B, F and G are
compared with the
codevector associated with the position A. The same procedure is applied for
the vectors F and
G. As shown in the table below, there are 15 possible combinations of the four
indices in Step I,
which are encoded as 15 correlation symbols C; ~ through C;'S . With a
different correlation
symbol, a different number of bits is required to encode the four codevectors
corresponding to
the four indices in the window. Additional 4 bits are used to designate a
particular one of 15
correlation symbols. In all the tables given below, N is the length of a
binary codevector 5.
21
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Correlation SymbolDissimilarity pattern Bits to encode 4
vectors
in the window
Cj>> All 4 indices are different4 loge N +
Cz'~ - C~'~ 2 of the indices are 3 logz N + 4
identical
Ca'~ ' Ci'i 3 of the indices are 2 logz N + 4
identical
2 pairs of indices 2 logz N +
are identical
Cis All 4 indices are identicalloge N + 4
Alternatively, the method is applicable with reasonable modification to a
datacube having
more than three-dimensions.
Sten II~ Process the fiat rwo rows
As shown in Fig. 4, the window is then positioned over a new cell having a
portion overlapping
with the initial cell and the indices within the new cell are used to generate
a correlation symbol
referring to values of indices outside said portion dissimilar to indices
inside said portion, and
defining a dissimilarity pattern among index values inside and outside said
portion. The first two
rows are used but not the first column of the index array since it has been
analysed previously.
The window is then moved over the index array from left to right, for example
over blocks
BCGH, CDHI, DEIJ, etc. In block BCGH, only the indices of codevectors at
position C and H
are produced, because indices at positions B and G are already known from Step
I. There are 10
possible relations between the two new indices and the two known indices. 10
correlation
symbols are used to encode them: C;Z~ through C;;i
22
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
CorrelationDissimilarity pattern Bits to encode
Symbol 2 new vectors
2 new indices are different from 2 known 2 loge N
indices + 4
2 new indices are identical to each other,logz N +
but different from 4
the 2 known indices
C3z~ - 1 new indices is identical to 1 of the loge N +
C61~ 2 known index 4
C~~~ - 2 new indices are identical to 2 known 4
Cio indices
Step III: Process the first two columns
This step is similar to the previous step except the window is moved
vertically. That is,
the window is moved such that it covers the first two columns in a new row of
the index array,
for example, blocks FGKL, KLPQ, PQUV etc. shown in Fig. 4. Coding is performed
as above
excepting the known indices are oriented differently. There are also 10
possible relations
between the two new indices and the two known indices. 10 correlation symbols
are used: C;j~
through C;'o . The coding results are the same as listed in the table under
Step II.
Step IV: Recursivel~process the remaining cells
The window moves to progressively repeat a process of reading the indices of a
new cell
having a portion overlapping a portion of a previously read cell. With each
window location a
correlation symbol is generated referring to values of indices outside said
portion dissimilar to
indices inside said portion, and defining a dissimilarity pattern among index
values inside and
outside said portion, until the entire index array is read. Neither the first
row nor the first column
in the index array is used again, i.e. blocks GHLM, HIMN, LMQR, etc. as these
have been
analysed previously. Only one index in the window needs to be encoded during
this step as the
window is moved to a new location. For example, when the window is located at
block GHLM,
only the index at position M is encoded because the indices at positions G, H
and L are known.
23
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
In Step IV, the new index at position M has only 4 possible relations with the
three known
indices: the same as that at position G or H or L, or different from all of
them. Thus, 4 correlation
symbols C;a~ through Caa~ are used to encode them. If the new index is
identical to one of the
three known indices, 2 bits are sufficient to encode the new index. Only if
the new index is
different from all the three known indices, logz N + 2 bits are required.
Step I occurs only once. The encoder moves the window over the index-map N~ -
2 and
N,-2 times respectively in Step II and III. Step IV is the most frequent
operation. The window
is moved a total of (N, - 2) x (N~. - 2) times to encode an image D with
spatial dimensions N,
rows and N~. columns.
Optionally, the above disclosed correlation procedure uses a window of larger
dimensions
than 2x2 but smaller than that of a N,xN~ index array.
Data analysis viewin~~and decom rn ession
According to an embodiment of the present invention, a codebook comprises a
plurality
of vectors along a single dimension of a data cube or higher order data
structure. In an exemplary
embodiment presented herein, the codevectors are representative of approximate
spectral vectors
and the spatial information is encoded in the index map. There are many
advantages to such a
data structure other than minimising data storage, as is commonly the main
goal of compression.
Some of these advantages and methods of achieving these advantages are set out
herein below.
Often, data processing of hyper-spectral data in the form of datacubes
comprises spectral
processing in the form of filtering, searching, peak identification, spectral
matching and so forth.
According to prior art methods of compression, de-compression (often referred
to as expansion)
is required prior to data processing. Therefore, in order to analyse a data
cube comprising 72
spectral bands and 2200 lines with 128 pixels requires a minimum data storage
of 128*2200*72
information locations. When spectral imaging is performed using a 16 bit
spectrometer, this
results in a requirement for about 40 Mbytes of storage. To optimise
processing time, that
24
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
amount of RAM is required and, even with RAM prices becoming more inexpensive
each day,
the cost of a suitable workstation is considerable. This is more significant
for even larger
datacubes as described earlier.
Using a compression algorithm according to the invention, data processing is
performed
on the codebook directly as described above. For example, peak identification
is easily
performed on each spectrum within a codebook. This is performed using a
smaller amount of
data storage that was necessary according to the prior art. Detecting certain
spectral patterns is
also easily performed on the codebook. By extension, transformations of the
data are often well
suited to being performed directly on the codebook. Of course, when more
accurate processing of
data is desired, further processing may be performed in conjunction with the
codebook
processing step.
An example of a filtering operation is discussed below with reference to Fig.
S. The
codebook shown in Fig. 5 comprises 10 spectral vectors each having 9 bands
therein.
Commonly, a codebook will have many hundreds if not thousands of spectral
vectors in the form
of codevectors. The 10 spectral vectors are very simple merely for exemplary
purposes. A
transform for filtering out spectral vectors that do not have values over 10
in their second through
fifth bands is applied. The transform maps each codevector onto a new
codevector having 10
bands. The first band is a flag indicating transform results. Optionally, the
first band requires a
single bit of information. The results indicate whether or not a spectrum has
been filtered.
Memory optimisation is not performed due to the compact size of the codebook.
Alternatively,
memory optimisation is performed.
The resulting codebook is shown in Fig. 6. Only indices referring to the
third, fourth and
seventh spectral vectors within the codebook shown in Fig. S are significant
in this example. All
other indices reference spectral vectors that are not significant in this
example. That is, the index
array is searched for those indices that are significant. Again, when desired,
memory
optimisation of the search results is performed. Similarly, peak
identification is also easily
performed on spectral vectors within the codebook in a similar fashion. It is
advantageous that
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
the codebook of Fig. 6 uses a same index map as the codebook of Fig. 5. Since
the index map is
often much larger than the codebook, maintaining several codebooks and a
single index map
does not significantly increase memory requirements. Other methods of
processing may result in
codebooks having a smaller size, such as, a codebook merely containing the
flags corresponding
to a 10 bit codebook.
Of course, when a mathematical operation is performed on each spectral vector
in
isolation, a result can be stored in a new codebook, such as the one shown in
Fig. 6. Another
example of processing of hyper-spectral image data according to the invention
is as follows.
When performing a three-band ratio, one desires a difference between two bands
divided by the
sum of the bands. Essentially, for a three-band ratio a same weighting and
ratio calculation is not
necessary for each pair of spectral bands or channels. According to the prior
art, a calculation is
required for each spectral vector and, in the example above, 281,600 three-
band ratios are
calculated. According to the invention, a three-band ratio is calculated for
each spectral vector or
codevector within the codebook resulting in 4096 three-band ratio
calculations. As is evident to
those of skill in the art, when fewer codevectors form a codebook, the number
of calculations
decreases. With 256 codevectors, an improvement in performance is achieved for
the calculation.
Performance improvements such as these are considered significant.
According to another embodiment, the compressed data file 10 is used as a data
viewing
and filtering tool. Once those vectors that are potentially significant are
identified, those vectors
are retrieved from the original datacube D. For example, should NASA store
large volumes of
hyper-spectral data in the form of datacubes for distribution to the public,
it would be impractical
to have people downloading very large files to their computers. Using the
method described
herein, the people download codebooks and index arrays. They search for
specific spectral
vectors of interest and for those locations of interest, more accurate
spectral vectors are
downloaded across the Internet or another communication link. Communication
links are well
known in the art for both transmitting and receiving digital data. Of course,
when the codebook
data is sufficiently accurate, further downloading of data is not necessary.
26
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Further alternatively, a number of codebooks are created for a single
datacube. Users are
able to download codebooks of different size and accuracy depending on user
needs and user
system capabilities. A user interested only in infra red imaging downloads
only those spectral
ranges comprising infrared. This is straight forward as it involves a simple
transformation of
codevectors within the codebook and no modification of the index array. In yet
another
embodiment, portions of the codebook are loaded from a server as necessary and
stored within a
codebook local to a workstation. When data is queried that is not yet stored
locally, it is
requested from the server, transmitted therefrom, received locally, and stored
locally.
The method of compression according to the invention also allows for immediate
viewing
of data without decompression thereof. This is very significant when used on
systems having
minimal resources. Also, since an entire codebook and index table is not much
larger than an
image, a user is provided with much additional information using similar
resources. Of course,
some additional memory requirements exist for storing the codebook, the index
map and an
image derived therefrom over storing a single image.
As an example of resource requirements, when a data cube of 16 bits by 72
channels by
2200 lines by 128 pixels is compressed using 4096 codevectors resulting in a
memory
requirement of just over a megabyte for data storage. Since personal computers
are now
commonly provided with 16 megabytes of memory, analysis and display of
spectral data is easily
performed on a personal computer according to this invention. This is
contrasted with analysis
and display of the original 40 megabyte datacube.
As such, the use of a compression technique according to the invention
increases flexibility in
processing and displaying compressed data by obviating a need to first expand
the data.
According to another embodiment of the invention, the codevectors within a
codebook
are each provided with statistical data indicative of a confidence in those
vectors. For example, a
largest error vector associated with a vector in the codebook incorporates the
maximum distance
between a value in the codevector and an associated value in a vector that is
approximated by
27
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
that codevector; an average distance vector would measure an average error for
a band; and so
forth. This statistical information improves the confidence with which the
compressed data is
manipulated and analysed. For example, this data is useful for determining a
need to request
further data from a server such as "real" spectral data or a codebook having
higher fidelity. It also
allows analysis of result reliability to see if further analysis or reanalysis
of any portion of the
data is required.
For example, give a datacube D, whose size is N~ pixels by N, lines by Nb
spectral bands,
it is defined as:
D = IXPl P =1 ~2~..., N,, (12)
where N,, = N, x N~. is the number of total vectors in the datacube, and XP =
[xP ( 1 ), xP (2), . . . xP (Nb)]
is a spectral vector p.
A codebook C with N codevectors, which are trained from the Training Set R of
size TSs;Ze
subsampled from the datacube D, is defined as:
C = {yq~ q =1,2,...,N (13)
where yq = [yq ( 1 ), yq (2), . . . yq (N6)] is a codevector with index q, it
is the centre of gravity of
partition q. If a spectral vector XP meets
d(XP, yq) <_ d(XP, y,) for all l =1,2,..., N, (14)
where d(XP, yq) is the Euclidean distance between two vectors XP and yq , then
XP belongs to
partition q whose centre is yq . My is the number of members in the partition,
and it meets
following condition:
N
TS.vize - ~ M g ~ ( 1 5 )
v=~
~ In the codebook training module, the following measurements, which referred
to as
codevector confidence measures, are produced for the training set R. These are
measures of
each codevector's ability to span its partition. Each provides an estimate of
the accuracy of
a given encoded datacube spectrum. Of course, other confidence measures are
also possible
28
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
in accordance with the invention.
i) RMS Spectral Spanning Error eq , equal to the root mean square spanning
error of codevector yq
at each spectral band:
eq=~eq(k)~ k=1,2,...Nb qER, (15)
where
I My 2
eN~k~= -~~Yy<k~-x~~k~> > (16)
My ~=i
where My is the number of members in the partition, and it meets following
condition:
N
TS.,;:e=~My C~'ER. (17)
y=r
ii) RMS Overall Spanning Error ey-",.e,~" of codevector yq
I Nn
ey-orera!! - ~ l ey (k~J2 g E R . ( 18)
Nn k=~
iii) Maximum Spectral Spanning Error gq : The maximum spanning error (error
bound) of
codevector yq at each spectral band:
Eq-{Eq(k)~ k-1,2,...N6 qER, (19)
where
Ev~k>=maxl Yy<k~-xP~k~I ~ (2~)
~spsM,
~ In the coding module we can also compute RMS Spectral Spanning Error eP ,
RMS Overall
29
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Spanning Errorey_",,~,~," and Maximum Spectral Spanning Error gq for the
datacube D. They
are the actual errors, are transmitted to decoding module in order to provide
fidelity
information.
i) RMS Spectral Spanning Error eq , equal to the root mean square spanning
error of codevector yq
at each spectral band:
eq = {eq (k)} k =1,2, . .. Nb q E D , (21 )
where
I ~"'' z
ey~k~= -~~Yy~k~-xp~k~~ ~ (22)
My p=l
where My is the number of vectors compressed by the codevector yq , and it
meets following
condition:
N
N,.=~My C~'ED. (23)
y=l
ii) RMS Overall Spanning Error ey_",.e,~," of codevector yq
I Nn )
ey-a,~e.~u = - ~ fey ~k~~1 q E D . (24
Nn k=I
iii) Maximum Spectral Spanning Error Eq : The maximum spanning error (error
bound) of
codevector yq at each spectral band:
Eq = {Eq (k)~ k =1,2, ... N6 q E D , (25)
where
EN~k~=maxiYy<k>-xp~k>I ~ (26)
15 pS,L/i
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
Advantageously, confidence measures allow processing and analysis of a
compressed
hypercube with a clear indication of likelihood of error. When a likelihood of
error is too great
for a particular application, a higher fidelity compressed datacube, an
uncompressed datacube or
a datacube compressed using lossless compression is retrieved. This alleviates
concerns over
error and data validity which arise because of the use of lossy compression.
The same systems and methods described above may be extended to higher
dimensions.
For example, it can be applied to a three-dimensional volume composed of two-
dimensional
image slices each element of which has associated spectral information. Of
course, this is most
applicable where correlations exist between data values along dimensions of
the volume. One
example of such an application is microscopy. In this sense, hyper-spectral
data is defined within
this specification and the claims which follow to mean data that is
appropriately encoded
according to the present method - datacubes having a high correlation between
parallel vectors in
at least one dimension.
Although the exemplary embodiment is described herein with reference to three-
dimensional hyper-spectral data sets consisting of two spatial and one
spectral dimensions, it is
useful in absorption and reflection spectroscopy, in fluorometry, in energy
transfer diffractomery
(e.g. X-ray, electron, neutron) as as well as in microscopy, process control,
and energy dispersive
tomography.
Typically and as described above, three dimensions include two spatial
dimensions and
one spectral dimension. Of course, other dimensions such as time are also
possible. In effect, the
method described below is applicable to datacubes wherein there is a strong
correlation between
the vectors along one or more dimensions of the datacube. Further, in an
embodiment where
multidimensional data beyond three dimensions is compressed according to the
present
invention, codematrices are stored within a codebook in a manner analogous to
the storage of
codevectors described herein.
31
CA 02253145 1998-10-30
Doc. No 50344-1 CA Patent
For example, when a datacube has four (4) dimensions one spectral, one
temporal, and
two spatial an analysis of the datacube may determine a strong correlation
between temporal-
spectral planes. Therefore, a codematrix is used in place of a codevector. For
a datacube having
2200 lines 128 pixels 72 bands and 365 days, the amount of data within the
four-dimensional
datacube is astounding. When a correlation exists in the temporal-spectral
plane, an index map of
similar size to those described above is needed and a codebook 365 times as
large - each
codematrix is 72 by 365 data elements in size. This is a huge space savings
over the
uncompressed data. Of course, someone of skill in the art knows when such an
extension is
applicable.
In the case of fluorescence and more particularly fluorescent decay analysis,
spectral data
is acquired at a plurality of times each separated by a time interval. For
example, spectral
information is captured for a surface of a sample for each of 500 1 ms
timeslots. The resulting
four (4) dimensional datacube is helpful in analysing fluorescent decay
signatures. The present
invention is advantageous in performing the analysis. It is evident to those
of skill in the art that
the addition of another dimension to the datacube results in an exponential
growth in the size of
the original data. Compression and the ability to process the compressed data
according to the
invention is highly advantageous.
Of course, numerous other embodiments may be envisaged without departing from
the
spirit and the scope of the invention.
32