A METHOD AND AN APPARATUS FOR THE EXAMINATION OF INSTALLED SHOCK ABSORBERS (II)

METHODE ET APPAREIL POUR L'EXAMEN D'AMORTISSEURS MONTES (II)

English Abstract

In the method and the apparatus for the examination of
shock absorbers installed on a vehicle, a vibratory platform, on
which one wheel of the vehicle is stood and which may be
reciprocated with a suitable amplitude and variable frequency in
a vertical, is employed to subject the wheel to an oscillation.
The damping of the shock absorber is checked from the force
response of the running gear to the oscillations of the vibratory
platform and the relative phase function between the force exerted
by the vibratory platform and the motion of the vibratory
platform. The data signal, which represents the variations with
time of the force response at a target frequency, is split by a
tension-compression stage means into a compression stage signal,
which is characteristic for the compression stage of the shock
absorber, and a tension stage signal, which is characteristic for
the tension stage of the shock absorber. The compression stage
signal and the tension stage signal are separately supplied to
further preparing means. As a basis of assessment for the quality
of the installed shock absorber the degree of axle damping as
related to the quotient of the spring-suspended mass to the
non-spring-suspended mass is calculated. The measured values of
the degree of axle damping are related to a characteristic line of
a critical or border value degree of axle damping, which delimits
the range of non-acceptable degrees of axle damping.

Claims

THE EMBODIMENTS OF THE INVENTION IN WHICH AN EXCLUSIVE PROPERTY
OR PRIVILEGE IS CLAIMED ARE DEFINED AS FOLLOWS:
1. A method for the examination of shock absorbers installed
on a vehicle using a vibratory platform, on which one wheel of
the vehicle is stood and which is able to be reciprocated in a
vertical direction at a suitable amplitude and with a variable
frequency, an oscillating action is exerted of the wheel, the
damping of the shock absorber being derived from the force
response of the running gear to the oscillations of the vibratory
platform and the relative phase function between the force
exerted by the vibratory platform and the movement of the
vibratory platform, the data signal which represents the force
response of the shock absorber being subjected to the evaluation,
characterized in that, as a basis for assessment of the quality
of the installed shock absorber, the degree of axle damping as
related to the quotient: suspended mass divided by non-suspended
mass, is calculated, the measured values of the degree of axle
damping being related to a characteristic curve of a critical
degree of axle damping, which delimits the range of
non-acceptable degrees of axle damping.
2. The method as set forth in claim 1, characterized in that
prior to the actual evaluation the road adherence of the vehicle
being tested is examined during the measurement and in that, if
the road adherence is below a predetermined value, evaluation is
terminated and the shock absorber is classified as being
sub-standard.
3. The method as set forth in claim 1, characterized in that
the data signal is split by tension-compression stage splitting
into a compression stage signal, which is characteristic for the
-50-

compression stage of the shock absorber and a tension stage
signal, which is characteristic for the tension stage of the
shock absorber, and in that the compression stage signal and the
tension stage signal are evaluated separately as regards the
degree of axle damping.
4. The method as set forth in any one of the preceding
claims, characterized in that for extraction of the
characteristic frequency the measured amplitude and phase
spectrums are processed by interpolating the curve section of the
phase function by a polynomial.
5. The method as set forth in claim 4, characterized in that
the support points for the interpolation start at the resonant
frequency and terminate at the local maximum of the phase
function.
6. The method as set forth in claim 4, characterized in that
the frequencies f2 and f3 are subjected to a plausibility test,
the shock absorber being deemed to be good, if the n/2 frequency
f2 does not exist, and is deemed to be poor, if the n/2 frequency
f2 is larger than or equal to the resonant frequency f3.
7. The method as set forth in any one of claims 1 through 4,
characterized in that a parameter calculation is performed on the
basis of the complex frequency curve of the simple one quarter
vehicle model:
<IMG>
wherein:
m F suspended mass [kg]
-51-

m u non-suspended mass [kg]
m s static overall mass [kg]
k spring constant of the suspension spring [N/m]
k R spring constant of the tire [N/m]
d damping constant of the shock absorber [kg/s]
.omega. circular frequency of the exciting oscillation
[1/s]
and in that from such parameters the degree of axle damping
(Achs DG):
<IMG>
is found, the parameters utilized here being a result of model
iteration.
8. The method as set forth in claim 7, characterized in that
for parameter estimation of the value k R a loss function:
<IMG>
is employed, which calculates the departure of all support points
for the complex frequency curve to be estimated, wherein:
R v is the measured real fraction of the support point
v
Iv is the measured imaginary fraction of the support
point v
~v is the weight fraction of the support point v
N is the number of support points - 1.
-52-

and the loss function is differentiated after every coefficient
to be estimated and set at zero, the asymptote of the converging
form of the amplitude spectrum as plotted against the spring
constant k R of the tire at high frequencies being able to be
calculated using a modified form of the parameter estimation
method, in which of the original nine parameters to be estimated
the parameters b0 and b1 are basically zero and the parameter b2,
is the also known static mass m s so that the linear equation
system is thus reduced to six linear equations.
9. The method as set forth in claim 8, characterized in that
for such estimation a plurality, as for example 20, different
weight functions are swept, in that for each weight function the
theoretical support points are calculated and in that then the
weight function is employed with the smallest mean departure in
the support points used.
10. The method as set forth in claim 8 or in claim 9,
characterized in that after such estimation of the parameter k R
this value is compared in the k R/mS field with a target k R curve
and the measurement is not evaluated, if the estimated k R value
is outside a predetermined tolerance band.
11. The method as set forth in claim 7, characterized in that
the signal form of the frequency curve is examined and in that
measurements, which are characteristic for a disruption of road
adherence, and measurements, which have a frequency curve without
any unambiguous resonance maximum of the amplitude spectrum are
rejected.
-53-

12. The method as set forth in claim 7, characterized in that
the frequency curve, which does not have any local maximum
between the characteristic frequencies f2 and f3, is made
available for further calculation of parameters.
13. The method as set forth in claim 7, characterized in that
for parameter estimation the following calculation steps are
performed using computer algebra:
- Calculate the amplitude curve A from the complex frequency
curve F p.
- For calculation of the characteristic equation for the upper
resonant point f3 differentiate the amplitude curve A and
make A' equal to zero.
- Solve this equation in terms of the damping constant d and
the following applies:
d3 =g(.omega.3,m s, m u, k R, k).
- For calculation of the characteristic equation for the ~/2
frequency f2 calculate the real fraction of A and make A re
equal to zero.
- Solve this equation in terms of the damping constant d and
the following applies:
d2 =h(.omega.2, m S, m u, k R, k);
in both equations g and h the exciting frequencies Q and the
static weight m S are measured, the spring constant of the tire k R
is known from the parameter estimation method so that two
equations remain for d2 and d3 with two in unknowns m u and k R;
- generate the amplitude functions S2, d being replaced by d2,
and A3, d being replaced by d3, two equations with two
-54-

unknowns m u and k being obtained, which are linked for
calculation of the parameters.
14. The method as set forth in claim 7, characterized in that
owing to small influence of the spring constant k on the degree
of axle damping the spring constant k is omitted so that the
degree of axle damping is equal to:
<IMG>
the model iteration being simplified to a great extent and
consequently performed more rapidly since the solution curve for
the characteristic resonant frequency f1 is replaced by a constant
straight line at k = 100000 N/m, the non-suspended mass applying
here being calculated using the customary iteration algorithm,
this iteration algorithm leading to the solution points (m u, 10000)
with the least measured value departure and the best cover of the
damping constants of the remaining solution curves f3.
15. The method as set forth in claim 7, characterized in that
if the parameters are not able to be calculated, road adherence
is checked and if a high degree of road adherence is found, the
shock absorber is deemed to be good, whereas in the other case
evaluation is terminated and the shock absorber is deemed to be
sub-standard.
16. The method as set forth in claim 7, characterized in that
for the determination of a critical value line measurements are
made on vehicles with manipulated shock absorbers and the degrees
of axle damping of the defective shock absorbers are employed as
basic data.
-55-

17. The method as set forth in claim 16, characterized in
that the critical value line possesses a hyperbolic form with on
the one hand the minimum practical value as a pole point and on
the other hand the minimum degree of axle damping as an
asymptote.
18. The method as set forth in claim 16 or claim 17,
characterized in that the critical value line is represented by
a non-linear regression across the basic data employed, a growth
model being employed as the regression model, the growth model
having a strictly monotonous, asymptotic form, which is in
agreement with the previously made measurements
19. The method as set forth in claim 18, characterized in
that as a model the so-called saturation model is utilized, the
critical value line being able to be described by the two
parameters a and b:
<IMG>
wherein:
a is the asymptote, that is to say the minimum degree of
axle damping; and,
b is the pole point, i.e. the minimum mass ratio which is
physically possible.
20. The method as set forth in claim 14, characterized in
that in accordance with the calculation of the degree of axle
damping and its incorporation in the diagram of the degree of
axle damping to the quotient of the suspended mass to the
-56-

non-suspended mass a recommendation is made as regards the
necessity of replacement of the shock absorber.
21. The method as set forth in claim 3, characterized in that
the data signal, which represents the change with time of the
force response at a target frequency, is split by
tension-compression stage splitting into a compression stage
signal, which is characteristic for the compression stage of the
shock absorber and a tension stage signal, which is
characteristic for the tension stage of the shock absorber, and
in that the compression stage signal and the tension stage signal
are subjected to further processing.
22. The method as set forth in claim 21, characterized in
that the tension-compression stage split is performed on the
basis of a frequency split, the basic frequency being retained
and the measured data during the time ~/2 being associated with
the positive half wave of the compression stage and the measured
data of the negative half wave during the time ~/2 being
associated with the tension stage.
23. The method as set forth in claim 21, characterized in
that the tension-compression stage split is performed on the
basis of the amplitude split, the higher basic frequency of the
compression stage and the lower frequency of the tension stage
being taken into account for the calculation of the amplitude by
displacement of the narrower, positive compression stage half
wave by .delta.~ to the right, and displacement of the wider, negative
tension stage half wave by .delta.~ to the left.
-57-

24. The method as set forth in claim 22, characterized in
that the signals obtained by the frequency split are subjected to
digital filtering, preferably a Fourier transformation and more
especially a fast Fourier transformation.
25. The method as set forth in claim 23, characterized in
that the signals obtained by the frequency split are subjected to
digital filtering, preferably a Fourier transformation and more
particularly a fast Fourier transformation and the phase
displacements .delta.~ are added.
26. The method as set forth in claim 24 or claim 25,
characterized in that in the fast Fourier transformation only the
basic oscillation is filtered out.
27. The method as set forth in any one of the preceding
claims, characterized in that after such digital filtering a
quality assessment of the processed signal is carried out as to
the sine-conformity, wherein for each measured value the relative
departure from the sine-signal, which represents the ideal
filtered value, is calculated, the transverse sum of all
departures is found and those measurement points are rejected,
whose mean departure from the ideally filtered value exceeds a
predetermined value, such predetermined value preferably being
5%.
28. The method as set forth in any one of the preceding
claims, characterized in that the road adherence, i.e. the
constant of the wheel with the vibratory platform is examined and
in that in the case of a road adherence below a predetermined
value, preferably 10%, measurement is terminated.
-58-

29. The method as set forth in any one of the preceding
claims, characterized in that three complete cycles are measured,
n measured values, preferably 256 measured values, being produced
per revolution and in that several revolutions, preferably three
revolutions are measured and the results employed in forming an
average.
30. The method as set forth in any one of the preceding
claims, characterized in that the influence of the vibratory
platform on the result of measurement is compensated for by
recording a frequency curve for the vibratory platform in a
dynamic calibration run and the amplitude spectrum is
interpolated by a parabolic curve.
31. The method as set forth in any one of the preceding
claims, characterized in that the taking of measurements is only
started when, after approaching a frequency point, the frequency
fluctuations no longer exceed a predetermined tolerance level.
32. The method as set forth in any one of the preceding
claims, characterized in that frequency points, at which the
frequency fluctuations are not able to be stabilized, are
rejected.
33. The method as set forth in any one of the preceding
claims, characterized in that prior to a measuring run per se a
warm-up phase for the shock absorber takes place in order to warm
the shock absorber up to a predetermined temperature for
measurement.
-59-

34. The method as set forth in claim 33, characterized in
that during such warm-up phase the shock absorber is moved in the
environment of the upper resonant frequency in order to warm up
the damping liquid thereof.
35. The method as set forth in any one of the preceding
claims, characterized in that on recording the support points for
estimation of parameters a quality test is performed, the
departure of the actual signal from the required sinusoidal
signal being ascertained and , should the departure be
excessively large, the measured value is rejected and the next
target frequency will then be taken to be a predetermined amount,
for example 1 Hz, below the actual frequency, whereas if the
quality of the signal is satisfactory, further scanning is
performed in smaller steps, for example of 0.5 Hz.
36. The method as set forth in any one of the preceding
claims, characterized in that when the amplitude curve in the
compression stage and the tension stage direction exceeds its
maximum, the resonant range then recorded is scanned again in
small frequency steps, for example of 0.25 Hz, in order to detect
the actual resonant frequency with the required resolution.
37. The method as set forth in any one of the preceding
claims, characterized in that when the amplitude curve exceeds
its point of inflection, the resonant range then assumed is
scanned in small steps, for example of 0.25 Hz, in order to
detect the actual resonant frequency with the required
resolution.
-60-

38. The method as set forth in any one of the preceding
claims, characterized in that for recording the ~/2 frequency f2
the pitch of scanning is reduced to a small value, for example of
0.25 Hz, when a predetermined phase value, for example of 1.2
rad, is reached and in that the step pitch is reduced to a
smaller value, for example 0.1 Hz, when the phase value reaches
a larger value, for example of 1.4 rad.
39. The method as set forth in any one of the preceding
claims, characterized in that during recording the frequency
curve the following steps are performed in the order given:
- Measurement of the static weight;
- Running up to starting frequency of for example 10 Hz;
- Warming up phase of shock absorber;
- Run up of exciting vibration of the vibratory platform to
the maximum frequency of for example 35 Hz;
- Recording of support points for the estimation of parameters;
- Recording of resonant frequency f3;
- recording ~/2 frequency f2 and
- Transmission of data to evaluation system.
40. The method as set forth in any one of the preceding
claims, characterized in that for recording the frequency points
the following steps are performed in the order given;
- Run up to target frequency;
- Check to see if frequency becomes stable;
- Recording readings;
- Separation of tension from compression stage signal;
- Fourier transformation of the separated signals;
-61-

- Quality assessment of the signals;
- Check of road adherence;
- Check to see whether measurements have been recorded for a
given number of revolutions;
- Check to see whether measurements conform to the quality
standard for at least a fraction of the revolutions;
- Extraction of mean value for the measurements classified as
being good;
- Compensation of the effect of the vibratory platform.
41. The method as set forth in any one of the preceding
claims, characterized in that:
- Check to see whether the road adherence is within
predetermined tolerance limits;
- Extraction of the characteristic frequencies;
- Parameter estimation as regards the calculation of k R, the
spring constant of the tire;
- Check of air pressure in tire;
- Check of signal form of the amplitude spectrum;
- Check on whether the ~/2 phase state is reached;
Check on whether the equation f2 = f3 is fulfilled;
- Parameter calculation
- Check to see whether parameters can be calculated;
- Calculation of critical degree of axle damping;
- Assessment of degree of axle damping and issue of
recommendation concerning the need for replacement of shock
absorber.
42. An apparatus for the performance of the method for the
examination of shock absorbers installed as set forth in any one
-62-

of the preceding claims on a vehicle using a vibratory platform,
on which one wheel of the vehicle is stood and which is able to
be reciprocated in a vertical direction at a suitable amplitude
and with a variable frequency, an oscillating action is exerted
of the wheel, the damping of the shock absorber being derived
from the force response of the running gear to the oscillations
of the vibratory platform and the relative phase function between
the force exerted by the vibratory platform and the movement of
the vibratory platform, characterized by shear force sensors on
the vibratory platform and a pulse source for angularly
equidistant scanning and a means by which the data is split into
a compression stage signal and a tension stage signal, and a
means in order to supply the compression stage signal and the
tension stage signal separately to the means for further
processing of the signals.
43. The apparatus as set forth in claim 43, characterized in
that the evaluating means assesses the quality of the installed
shock absorber by reference to the quotient: suspended mass
divided by non-suspended mass, measured values of the degree of
axle damping being related to a characteristic curve of a
critical degree value of axle damping, which relationship
delimits the range of non-acceptable degrees of axle damping.
-63-

Description

CA 022~293 l998-l2-08
FIELD OF THE lNV~NllON
The present invention relates to a method and an
apparatus for the examination of shock absorbers installed on
vehicles.
BACKGROUND OF THE lNV~NLlON
Apparatus for the measurement of the efficiency of
running gear of a motor vehicle without having to remove the shock
absorber from the vehicle, have already been proposed. There are
various different methods for this purpose, as for example using
a vibratory platform, on which one wheel of the motor vehicle is
stood and which is reciprocated with a suitable amplitude and a
variable frequency in a vertical direction in order to subject the
wheel to oscillations, the reading for the force exerted by the
running gear on the vibratory platform being evaluated.
The Method of the European Shock Absorber Manufacturers'
Association (EUSAMA), the largest organization of its kind,
involves a uniform testing method for shock absorbers in the
installed state. The examination is in this case performed using
a vibratory platform, which with the aid of an eccentric drive is
caused to oscillate with a stroke of exactly 6 mm. During
examination the measuring setup is excited to run at approximately
23 Hz and freely vibrates down to 0 Hz. The respective sinusoidal
dynamic wheel load is measured by sensors and stored. prior to
producing the vibrations the static wheel load Fs is measured. The
stored, dynamic wheel loads are investigated to find their minimum
Fmin. From the data the so-called relative road adherence A is
calculated as a percentage: A = Fs/ Fmin/Fs.

CA 022~293 1998-12-08
In a real application the road adherence value is
corrected, since particularly light vehicles have only poor road
adherence figures. For evaluation the following table is employed:
100% - 60% good
59% - 40% fair
39% - 20% poor
19% - 0% insufficient.
The EUSAMA Method is widely employed but the data
provided by it depend not only on the condition of the shock
absorber but also on design features, which are characteristics of
the wheel suspension, as for example the ratio between the spring-
suspended mass and the non-spring-suspended mass, the type of
tires, the tire pressure and the type of suspension and
furthermore on the conditions of measurement, as for example the
loading of the vehicle or the temperature of the surroundings or
the operating temperature of the shock absorber. The dependence on
a large number of parameters means that in practice the value
defined by the EUSAMA Method is prevented from being
representative for the condition of the shock absorber itself.
Accordingly the EUSAMA method does not lead to any reproducible
and reliable results.
Similar problems have occurred with other known
measuring systems for shock absorbers, wherein the dependency of
the measurement on a plurality of physical parameters of the
running gear means that the measured data must be interpreted
using table or the like. This is something leading to high degree
of approximation and large ranges of error and for different types

CA 022~293 1998-12-08
of vehicle different tables are necessary, dependent on which
shock absorbers are employed.
The European patent publication 0476746 A1 discloses an
apparatus for testing running gear of a vehicle, which like the
EUSAMA Method operates with a vibratory platform means. A computer
processes the data and from such data produces a transfer function
for the wheel suspension, which is looked upon as a system with a
plurality of system elements. On the basis of a model of the
system the computer derives the values of the system elements from
the transfer function and with the calculated values of the system
elements calculates the values of at least one measurement
variable and compares such value with a stored value of the
dimensional variables. The computer assesses the wheel suspension
from such comparison and displays the result of the comparison.
Here as well suitable tables are necessary in a data base, which
must hold the values for all current types of vehicles and tires.
Furthermore the evaluation of the running gear by way of the
individual system variables is inaccurate.
The patent publication WO 96/07882 discloses an
apparatus for the examination of shock absorbers of motor
vehicles, in the case of which the wheel on a vibratory platform
is caused to vibrate and on the basis of the amplitude of
vibrations at different frequencies the results of measurement are
derived. In the case of this apparatus the resonance of the
suspension is sensed and then the frequency of the stroke and
accordingly the energy supplied is varied. The damping force of
the shock absorber is plotted against speed. In the case of this
model some important effects, as for example internal friction, as
will be described below, are not taken into account.

CA 022~293 1998-12-08
The European patent publication 0647843 A2 discloses a
system for measuring the damping coefficient of a shock absorber
mounted on a motor vehicle, as is recited in the preamble of claim
1 herein. The damping coefficient is calculated as a function of
the derivation of the frequency of the relative phase function
between the force transmitted to the vibratory platform and the
movement of the vibratory platform. In this apparatus an imperfect
vibration model is taken as a basis, the value termed the "degrees
axle damping path" only applying for the particular model employed
so that in practice there are substantial departures between the
results of this method and the actual degrees of damping of the
shock absorber being examined. In particular the effect of
external friction is not taken into account.
Methods in existence so far, in which evaluation takes
place on a basis including a vibration model, suffer from deficits
in theory. This is for instance an inappropriate dissection of the
simple vibration model into different model parts for different
characteristic frequency ranges; the inappropriate mathematical
description of the resonant frequencies. In part methods on the
basis of free undamped elastic vibration systems are utilized. The
basis is however forced and heavily damped elastic vibration
systems; the invalid simplification or omission of parts of terms
of the mathematically described model; leaving out external
friction within the simple one quarter vehicle model and
infringing against the linear force law by progressive~suspension
springs. Finally, the distortion of the appropriate sinusoidal
signal form by the different compression and tension stage
behavior is not taken into account in the known methods, or, in
other words, the measurement signals are not brought back or
compared to the sine-shaped signals upon evaluation.

CA 022~293 1998-12-08
One object of the invention is to provide a method and
an apparatus for the examination of shock absorbers mounted on
vehicles, which from the characteristic curve of the force
response using an oscillation model produces reproducible
measurement results for the quality of the shock absorber for
forced oscillations.
In order to achieve this object the method of the
invention for the examination of shock absorbers installed on a
vehicle using a vibratory platform, on which one wheel of the
vehicle is stood and which is able to be reciprocated in a
vertical direction at a suitable amplitude and with a variable
frequency, an oscillating action is exerted of the wheel, the
damping of the shock absorber being derived from the force
response of the running gear to the oscillations of the vibratory
platform and the relative phase function between the force exerted
by the vibratory platform and the movement of the vibratory
platform, the data signal which represents the force response of
the shock absorber being subjected to the evaluation, is
characterized in that, as a basis for assessment of the quality of
the installed shock absorber, the degree of axle damping as
related to the quotient: suspended mass divided by non-suspended
mass, is calculated, the measured values of the degree of axle
damping being related to a characteristic curve of a critical
degree of axle damping, which delimits the range of non-acceptable
degrees of axle damping. The assessment of the shock absorber is
performed with the classification into one of the following
quality categories: "very good", "medium" and "failed", with which
a recommendation of replacement of the installed shock absorber is
coupled. The assessment takes place in a manner dependent on the
position of the degree of axle damping found in relation to the

CA 022~293 1998-12-08
characteristic curve of the critical degree of damping and not in
a manner dependent on the individual parameters of the one quarter
running gear, i.e. of the suspension of one wheel. Since the data
signals have been processed in the above mentioned manner, it is
also possible to obtain reproducible, i. e. satisfactory results
of measurement from the evaluation of these signals.
SUMMARY OF THE lNv~NllON
In accordance with a further advantageous development of
the method of the invention calculation of parameters is
performed, as same is recited in claim 7, and from the parameters
the degree of axle damping of ascertained, the parameters utilized
here being a result of model iteration. In tests it has been shown
that with this one quarter vehicle model satisfactory results may
be obtained in the testing and classification of installed shock
absorbers. More particularly, the problematical influence of so-
called external friction is taken into account by the model
iteration.
The advantageous development of the method of the
invention as defined in claim 8 means that the amount of
computation for the evaluation of the measurements is
substantially reduced, since the number of variables to be
processed can be reduced to six.
The advantageous development of the method of the
invention as defined in claim 14 leads to a still further
reduction in computation work without any reduction in the
measurements processed.
~ ~ .

CA 022~293 1998-12-08
A further advantageous development of the method of the
invention is characterized in that after calculation of the degree
of axle damping and the plotting thereof in a graph of degree of
axle damping to the suspended/non-suspend mass quotient a
recommendation can be made as regards the need for replacement of
the shock absorber.
A further advantageous development of the method of the
invention is characterized in that the data signal, which
represents the changes in the force response with time at a target
frequency, is split up in a compression-tension stage splitting
means into a compression stage signal, which is characteristic for
the compression stage of the shock absorber, and a tension stage
signal, which is characteristic for the tension stage of the shock
absorber, and in that the compression stage signal and the tension
stage signal are separately supplied to further processing means.
This means that a reproducible basis is provided for later
evaluation of the measurements.
A further advantageous development of the method of the
invention is characterized the tension stage-compression stage
split is performed on the basis of frequency splitting, the basic
frequency being kept and the measured values during the time ~/2
of the positive half wave of the being associated with the
compression stage whereas the measured values of the negative half
wave during the time ~/2 are associated with the tension stage
A further advantageous development of the method of the
invention is characterized in that the tension-compression stage
split is performed on the basis of the amplitude split, the higher
basic frequency of the compression stage and the lower frequency

CA 022~293 1998-12-08
of the tension stage being employed for the calculation of the
amplitude by displacement of the narrower, positive compression
stage half wave by d phi to the right, and displacement of the
wider, negative tension stage half wave by d phi to the left.
A further advantageous development of the method of the
invention is characterized in that the signals obtained by the
frequency split are subjected to digital filtering, preferably a
Fourier transformation and more particularly a fast Fourier
transformation. This means that corruption of information as
possible with conventional filtering of the entire signal is
avoided and the characteristic features of the respective stage
(tension and, respectively, compression stage) are preserved.
Owing to the advantageous form of the method of the
invention as claimed in claim 26, the measured data curve is
smoothed so that the further processing is facilitated.
In an advantageous form of the method of the invention
after such digital filtering a quality assessment of the processed
signal is carried out as to the sine-conformity, wherein for each
measured value the relative departure from the sine-signal, which
represents the ideal filtered value, is calculated, the transverse
sum of all departures is found and those measurement points are
rejected, whose mean departure from the ideally filtered value
exceeds a predetermined value, such predetermined value preferably
being 5%. Thereby it can be achieved that two sine-shaped signals
are derived which are then feed to the further processing. Only by
means of the sine-shaped course of the signals the correctitude of
the calculation method with respect to the parameter calculation
and to the parameter estimation is guaranteed. Furthermore, the
... ... . ... ... .

CA 022~293 1998-12-08
measurement curve is smoothed such that the further processing is
facilitated.
According to one of the advantageous developments of the
method of the invention the effect of the vibratory platform on
the result of measurement is compensated for, because in a dynamic
calibration run the frequency response of the vibratory platform
is recorded and the amplitude spectrum is interpolated by a
parabolic curve. This means that a significant interfering factor
is cut out.
In accordance with an advantageous development of the
method in accordance with the invention prior to the actual
measuring run a warm-up phase is provided for the vibration
absorber in order to heat the shock absorber during measurement up
to a predetermined temperature and accordingly to cut out the
effect of temperature variations on the result of measurement.
In accordance with an advantageous development of the
method in accordance with the invention for recording the support
points for estimation of parameters a quality test is performed,
the departure of the actual signal from the required sinusoidal
signal is detected and, if the departure is too large, the reading
is rejected and the next frequency aimed at will then lie below
the actual frequency by a predetermined value, as for example 1
Hz, while, if the quality of the signal is sufficient, scanning is
continued in small steps of, for instance, 0.5 Hz. Accordingly the
pitch of the steps is automatically adapted to the circumstances,
something which leads to substantially improved results of
measurement.

CA 022~293 1998-12-08
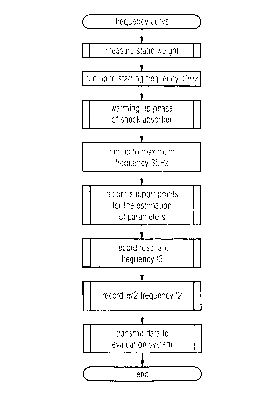
A further advantageous development of the method of the
invention is characterized in that on determining the frequency
response the following steps are performed in the order given:
- Measurement of the static weight;
- Running up to starting frequency of for example 10 Hz;
- Warming up phase of shock absorber;
- Run up of exciting vibration of the vibratory platform to the
maximum frequency of for example 35 Hz;
- Recording of support points for the estimation of parameters;
- Recording of resonant frequency f3;
- Recording ~/2 frequency f2 and
- Transmission of data to evaluation system.
A further advantageous form of the method of the
invention is characterized in that for recording the frequency
points the following steps are performed in the order indicated:
- Run up to target frequency;
- Check to see if frequency becomes stable;
- Recording readings;
- Separation of tension from compression stage signal;
20 - Digital filtering, preferably Fourier transformation, of the
separated signals;
- Quality assessment of the signals;
- Check of road adherencei
- Check to see whether measurements have been recorded for a
given number of revolutions;
- Check to see whether measurements conform to the quality
standard for at least a fraction of the revolutions;
- 10

CA 022~293 1998-12-08
- Extraction of mean value for the measurements classified as
being good;
- Compensation of the effect of the vibratory platform.
A further advantageous form of the method of the
invention is characterized in that for evaluation of the results
of measurement the following steps are performed in the order
indicated:
- Check to see whether the road adherence is within
predetermined tolerance limits;
- Extraction of the characteristic frequencies;
- Parameter estimation as regards the calculation of kR, the
spring constant of the tire;
- Check of air pressure in tire;
- Check of signal form of the amplitude spectrum;~5 - Check on whether the ~/2 phase state is reached;
Check on whether the equation f2 = f3 is fulfilled;
- Parameter calculation
- Check to see whether parameters can be calculated;
- Calculation of degree of axle damping;~0 - Assessment of degree of axle damping and issue of
recommendation concerning the need for replacement of shock
absorber.
The various different embodiments of the method of the
invention possess the following advantages: The preparation of the
measured values assesses the quality of a point of measurement,
makes it available for extraction of the mean value and separates
the upper and the lower half wave into two sinusoidal signals.
- 11 -

CA 022~293 1998-12-08
After digital filtering the corrupting effect of the vibratory
platform on the shear force sensors is compensated for.
The determination of parameters is based on mathematical
modeling of the running gear, which in its complexity can only be
solved by so-called computer algebra. The equation systems in this
case involve several hundred individual summands with complex 18th
order polynomials. This method, which is also known as parameter
calculation, is in addition combined with parameter estimation.
The assessment of the running gear is performed not by
using the isolated assessment of the model parameters, since for
each vehicle type, including its different forms of suspension,
the transmission ratios and the characteristics of the installed
shock absorbers and suspension springs must be held in the data
base. In view of the variety of possible forms such a data base
would not be practicable for real use on the customer's premises.
Here recourse is had to the EUSAMA Method, which provides a value
for road adherence which is unsatisfactory, but is not limited to
vehicle types. The so-called degree of axle damping, which is
evaluated on the basis of the ratio between suspended and
non-suspended mass, is to overcome the known disadvantages of the
road adherence value. On the basis of this assessment item a
recommendation for replacement is produced for the installed shock
absorber.
The advantages of this method are more particularly
valuable in the case of modern axle systems, as for example
employing pneumatic suspension, freely floating axles etc., in the
case of which the classical methods of assessment fail more or

CA 022~293 1998-12-08
less completely and as a rule classify such suspensions
unfavorably.
An apparatus for the performance of the method for the
examination of shock absorbers installed on a vehicle comprises a
vibratory platform, on which one wheel of the vehicle is placed,
means for causing the vibratory platform to vibrate in a vertical
direction with a suitable amplitude and variable frequency and to
cause the wheel to vibrate, the damping of the shock absorber
being derived from the force response of the running gear to the
vibrations of the vibratory platform and the relative phase
function between the force exerted by the vibratory platform and
the movement of the vibratory platform, is characterized by shear
force sensors on the vibratory platform and a pulse source for the
angularly equidistant scanning, by a means, by which the data
signal is split into a compression stage signal and a tension
stage signal and by a means in order to separately supply the
compression stage signal and the tension stage signal to the means
for the further processing of the signals.
An advantageous design of the apparatus of the invention
is characterized in that the assessment means assesses the quality
of the installed shock absorber using the degree of axle damping
as related to the quotient of the suspended mass and the
non-suspended, the readings for the degree of axle damping being
related to a characteristic curve of a critical of the degree of
axle damping, which delimits the range of non-acceptable degrees
of axle damping.
The apparatus of the invention has the advantage that
the vibrations caused by the vibratory platform are true sine-wave
- 13 -

CA 022~293 1998-12-08
vibrations as desired for being able to obtain also a sine-shaped
response of the system.
Further advantageous developments of the invention will
be seen from the remaining dependent claims.
A further understanding of the nature and advantages of
the present invention and embodiments of the invention may be
realized by reference to the remaining portions of the
specification and the drawings.
Other advantages, features and characteristics of the
present invention, as well as methods of operation and functions
of the related elements of the structure, and the combination of
parts and economies of manufacture, will become more apparent upon
consideration of the following detailed description and the
appended claims with reference to the accompanying drawings, the
latter of which is briefly described hereinbelow.
BRIEF DESCRIPTION OF THE DRAWINGS
Figure 1 of the drawings appended hereto is a flow chart
of the recording of readings.
Figure 2 of the drawings is a flow chart of the
preparation of readings.
Figures 3A and 3B of the drawings are graphs indicating
the principle of frequency splitting.
. .

CA 022~293 1998-12-08
Figures 4A and 4B of the drawings are graphs of the
principle of amplitude splitting.
Figures 5A and 5B of the drawings are flow charts of
evaluation using the method of the invention.
5Figure 6 of the drawings is a graph to indicate the
action of disruption of road adherence on the frequency curve.
Figure 7 of the drawings is a graph to indicate the
action of good shock absorber performance on the frequency curve.
Figure 8 of the drawings is a graph to indicate the
10action of poor shock absorber performance on the frequency curve.
Figure 9 of the drawings is a graph indicating the target
line kR for the pre-check of tire pressure.
Figure 10 of the drawings is a graph, which represents
the kR line of a tire (UniroyalTM 155/70 R13).
15Figure 11 of the drawings is a graph, which shows the
signal form of a satisfactory frequency curve.
Figure 12 of the drawings is a graph to show the signal
form applying for a defective shock absorber.
20Figure 13 of the drawings is a graph indicating the
signal form applying for a suspension with track jitter.
- 15 -

CA 022~293 1998-12-08
Figure 14 of the drawings shows the theoretical curve
form in the mu-k range.
Figure 15 of the drawings is a graph of the practical
curve form in the mu-k range.
Figure 16 of the drawings is a graph of the scan range
of model iteration in the mu-k range.
Figure 17 of the drawings is a graph of the pole position
and of the asymptote of the characteristic curve of the degree of
critical value damping.
Figure 18 of the drawings is a graph of the degrees of
axle damping of different compression stages.
Figure 19 of the drawings is a graph of the degrees of
axle damping of different tension stages.
Figure 20 of the drawings is a graph of dependency of the
degree of axle damping on tire pressure.
Figure 21 of the drawings is a graph of dependency of the
degree of axle damping on the loading of the vehicle.
Figure 22 of the drawings is a graph of dependency of the
degree of axle damping on the temperature of the shock absorber.
Figure 23 of the drawings is a graph of dependency of the
degree of axle damping on the tires of the vehicle.
- 16 -

CA 022~293 1998-12-08
Figure 24 of the drawings is a graph of dependency of the
degree of axle damping on changes in the non-spring-suspended mass
mU.
Figure 25 of the drawings is a graph of the direction of
displacement of the parameters on the point of assessment.
DETAILED DESCRIPTION OF A PREFERRED EMBODIMENT
The method of examination is divided up into two
principal steps, namely the recording of readings, in which
readings of data are made and processed, and the evaluation, in
which the processed data are further processed for making an
assessment as regards the quality of the running gear. The
examination means includes a vibratory platform, on which in
addition to the platform's shear force sensors a pulse source for
angularly equidistant scanning is provided.
During taking readings the static weight and the
frequency curve of the one quarter vehicle over an exciting
frequency of 35 Hz - 10 Hz range are recorded. The amplitude curve
then corresponds to the shear force sensor signal on the vibratory
platform in Newtons. The phase function corresponds to the phase
shift between the exciting oscillation of the vibratory platform
and the response oscillation of the one quarter vehicle in radians.
From the frequency curve the characteristic frequencies or,
respectively, frequency ranges are filtered out and further
processed.
In the following evaluation the three characteristic
frequency ranges are of special interest, namely the resonant

CA 022~293 1998-12-08
frequency of the non-spring-suspended mass f3 (here the amplitude
curve reaches the absolute maximum), the frequency f2 (here the
phase function is equal to exactly 90~ or, respectively, ~/2 and
the effective fraction of the amplitude curve is equal to zero at
this frequency) and the higher frequencies up to the maximum
frequency of 35 Hz. The measurement points are support points for
the parameter estimation, with which the spring constant of the
tire kR is ascertained.
The frequency-equidistant scanning of the frequency range
35 Hz to 10 Hz is only a rough approximation. For high quality and
reproducible measurements a special measurement algorithm is
provided for each characteristic frequency and, respectively, each
characteristic frequency range, the chart of such algorithm being
illustrated in Figure 1.
The amplitude curve corresponds to the changing part of
the overall signal. The unchanged part is taken into account by
digital filtering. The static weight of the one quarter vehicle is
included as mS in the calculation of parameters.
At low environment temperature the viscosity of the
damping liquid increases and consequently also the damping
dissipation of power. The increases in power may here amount to
several 100%. Consequently a warming up phase is provided for, in
which in the environment of the upper resonant frequency f3 the
damping liquid is warmed up. The initially low force response to
the vibratory platform increases on warming up and converges toward
a maximum value, whose absolute value is irrelevant. After reaching
a maximum value the measurement of the frequency curve as such is
proceeded with.
- 18 -

CA 022~293 1998-12-08
In tests made so far at 0 ~C the duration of warming up
amounted partially to substantially less than 15 seconds. At even
lower temperatures the warming up time may be assumed to be under
30 seconds.
Starting with the maximum frequency of 35 Hz the support
points for the parameter estimation are measured. At the high
frequencies so-called bounce effects are to be seen in the reading
or data signal, which substantially falsify the signal in the
tension and compression stage direction. These support points
generally have the greatest weight for parameter estimation and
must be correct. At each measurement point a quality test is hence
performed. The quality test examines the departure of the actual
signal for the required sinusoidal signal. If the departure is too
large, the reading is rejected. The next target frequency is then
1 Hz below the actual frequency. If the quality of a signal is
sufficient, scanning is further performed in 0.5 Hz steps.
For determination of the resonant frequency the following
procedure is employed. If the amplitude curve in the compression
and tension stage direction exceeds its maximum, the resonant point
f3 of the non-spring-suspended mass has been passed. This resonant
range is then scanned again in 0.25 Hz steps. The resonant
frequency is thus ascertained with a resolution of 0.25 Hz. The
algorithm also provides that in the case of suspensions with a
great change in track or shock absorbers with defective valves
several maxima may be swept successively. In all problematical
cases ultimately the actual resonant frequency is detected with the
necessary resolution.
- 19 -

CA 022~293 1998-12-08
As an alternative to the above mentioned manner of
proceeding the resonant frequency may be ascertained in such a
manner that the resonant frequency is measured in a single
frequency sweep with a resolution of 0.25 Hz. For this purpose it
is possible, if the amplitude curve exceeds its point of
inflection, for the assumed resonant range to be scanned in smaller
frequency steps, for instance in 0.25 Hz steps in the to find the
actual resonant frequency with the required resolution in one
sweep.
In the case of extremely strong damping effects the phase
function will not be able to reach the n/2 level or, in another
extreme case with very weak damping, will run through the ~/2 level
very steeply. For both cases the recording algorithm must function.
The ~/2 frequency must always be below the resonant frequency f3.
If the two frequencies were of equal size then the vibrating system
would be undamped. The phase function would rise with a falling
exciting frequency. If the phase value of 1.2 radians is reached,
the step pitch if reduced to 0.1 Hz. The resonant frequency f3 will
then be set from these support points.
During the taking of readings and preparing readings of
a single excitation frequency, in addition to the evaluation of the
spectral variations the measured force value is further processed.
Such evaluation is based of the complex frequency curves of forced,
damped, elastic oscillating systems. This implies strictly
sinusoidal oscillations. The variations with time of the data
signal is however in practice not sinusoidal. On the one hand the
elongations in the compression and tension stage direction are
quite different and on the other hand the duration in time of the
- 20 -

CA 022~293 1998-12-08
compression stage stroke is slightly shorter than the duration of
the tension stage stroke.
Figure 2 shows the taking of readings and the preparation
of data therefrom in order to achieve optimum accuracy and to
provide physically correct information for calculation.
In order to approach the next target frequency and to
stabilize same the frequency converter is provided with the
frequency value of the next scan point of the frequency spectrum.
The taking of a reading is only enabled when the target point in
time is reached and the system has become stabilized thereat. A
frequency point is deemed to be stabilized when its frequency
fluctuations no longer exceed a predetermined tolerance level. In
this respect the different frequency ranges are differently
evaluated. During run-up to the maximum frequency, attack or
transient phenomena have the most marked effects and have the worst
effects as regards the quality of the support points and
consequently for the estimation of parameters. Here longer
stabilizing times are to be preferred. In the case of low
frequencies the vehicle may come in the range of disruption of road
adherence. Here the road adherence of the suspension parts resists
acceleration due to the vibratory platform and abruptly comes to
an end as from a certain acceleration. The vehicle sags into its
suspension system. The speed of rotation controller is not capable
of dealing with this interfering factor when there are substantial
disruption effects. Frequency points, which are not able to be
stabilized, are omitted in measuring operations. The analog/digital
conversion operations are in this case caused by an interrupt
during measurement.

CA 022~293 1998-12-08
In order to be able to supply the physically correct
information for the following calculations the overall signal is
split up into two independent signal parts for the compression and
tension stage and two different split algorithms are employed.
The basic notion of such splitting is the association of
respectively half of the readings with the compression and,
respectively, tension stage signal. In such splitting there is an
exact maintenance of the exciting base frequency and the splitting
is relatively simple and rapid to implement. In this type of split
the compression stage signal is exaggerated and the tension stage
signal is minimized to an even greater extent (see Figures 3A and
3B). The various different damping power dissipations in the stages
are spread out even further. On the other hand the phase shifts
produced are not plausible. At high power dissipation simulations
on a simple one quarter vehicle model show a small phase shift and
low power dissipations show a large phase shift. In the case of
this type of stage split the phase shifts are almost identical.
The basic notion of the amplitude split is the
association of the positive half wave as a compression stage signal
and the association of the negative half wave as the tension stage
signal. This is generally the same as the association in shock
absorber tests in the non-installed state. A spread of the
compression and tension stage amplitude does not take place here
(see Figures 4A and 4B).
At the frequency of oscillation which becomes established
of the two stages the compression stage is distinctly above the
excitation frequency, whereas the tension stage is distinctly below
the excitation frequency. This is however something which can be
- 22 -

CA 022~293 1998-12-08
compensated for by phase shift, which is in agreement with the
theoretical simulation. The narrow positive compression stage half
wave must be shifted by ~ to the right ("it must have a lead") in
order to reach the~basic frequency of the exciting signa~. This is
the same as a phase shift of ~. The wide negative compression
tension stage half wave must be shifted by ~(~ to the right ("it
must have a lag") in order, to reach the basic frequency of the
exciting signal. This is the same as a phase shift of +~.
The digital filtering means that the signal of the
exciting frequency is filtered out. The digital filtering must in
this respect be adapted to the corresponding compression-tension
stage split method, the classical form of Fourier transformation
being able to be employed for frequency split, since the
compression and tension portions are exactly equal to the exciting
frequency taken as a basis. For amplitude split the higher basic
frequency of the compression stage and the lower frequency of the
tension stage must be taken in account for the calculation of the
amplitude. For this purpose the Fourier transformation of the
entire signal may be carried out and the above mentioned phase
shifts are added.
The signal curves may be considerably distorted for the
most various different reasons. Even the digital filtering for
example by the Fourier transformation will then not provide any
usable data, since the original signal differs very substantially
from the sinusoidal form. These measurement points may then not be
used for the further processing.
For assessment of quality for each measured value the
relative departure from the ideal filtered value (sine-curve) is
- 23 -

CA 022~293 1998-12-08
calculated. The transverse sum of all departures is then employed
for an evaluation. Investigations have indicated that as from a
critical value of 60% mean departure the interference, in contrast
to 4% or 5% clearly increase on a scale which cannot be tolerated.
Alternatively for assessment of quality it is possible
for the differential area of the filtered curve (sine-curve) and
the actual value curve to be added on and related to the target
area, only one division being necessary.
In the case of extremely poor running gear or,
respectively, shock absorber performance it is possible in the
frequency environment of the resonant point f3 for the vehicle to
lose contact with the vibratory platform and even to come clear of
the test bed.
In the case of road adherence of under 10% the taking of
measurements is discontinued for safety reasons. An evaluation of
the readings made so far is then no longer necessary, since the
running gear may then be classified ad hoc as being defective.
For each stored measurement point three complete cycles
are measured. If at least two cycles fulfil the quality criterion,
the qualitatively valuable measurement curve is employed to form
the mean value for the amplitude and the phase. If only one or no
cycle fulfills the quality criterion, then this frequency point is
not included in the spectrum.
The so-called vibratory platform is mounted on the shear
force sensors. If the system is excited, the oscillating mass of
the vibratory platform also has an effect on the shear force
- 24 -

CA 022~293 1998-12-08
sensors. This influence will increase in accordance with a square
law with an increase in frequency:
In the course of the measurement of the frequency
response of the vibratory platform however linear and constant
fractions were included in the amplitude. In order to minimize this
potential source of errors in a so-called 'dynamic' calibration run
the frequency response of the vibratory platform is recorded and
the amplitude spectrum is interpolated with a parabolic curve. The
three coefficients of the interpolation polynomial must here be
permanently stored. The phase shift is, but for the slight
displacement effects of the low pass filter, constant and is
employed as a zero transition reference of the vibratory platform
in later determination of phase shift.
For compensation of the vibratory platform the filtered
signal must now be corrected by the zero transition reference.
Specifically, it is 'shifted to the left', that is to say the
measured phase shift is added to the zero transition reference. Now
the phase shift is correctly determined in relation to the zero
transition reference of the vibratory platform.
The amplitude spectrum of the vibratory platform
comprises only effective fractions and no so-called dummy or
imaginary fractions. In order to eliminate the falsifying effect
of the vibratory platform this real fraction must be subtracted
from the real fraction of the measured amplitude spectrum.
From the resulting effective and imaginary fraction of
the compensated signal the actual, so-called compensated amount and
phase value of the oscillating one quarter vehicle is calculated.
- 25 -
.

CA 022~293 1998-12-08
The aim of the evaluation is a qualitative assessment of
the measured running gear. More particularly, the quality of the
installed shock absorber is to be assessed. In connection with such
statement of quality a recommendation, on which the operator of the
test bed may rely, is provided with respect to shock absorber
replacement. The following three recommendations are provided:
The shock absorber is completely in order (no replacement
required).
The reliability of the shock absorber is in the boarder
area (replacement is recommended).
The shock absorber is certainly defective (replacement
absolutely necessary).
The basis of valuation is the so-called degree of axle
damping. This degree of axle damping is then related to the
critical value degree of axle damping, which takes into account the
particular running gear properties and test conditions. In
particular, any attempts at manipulation are compensated for on the
basis of this critical value degree of axle damping. The
possibilities of manipulation are described in the following. The
critical value degree of axle damping may be defined restrictively
in a different fashion and is ultimately ascertained in a field
test after consultation with the vehicle manufacturers. The
characteristic curve of the critical value degree of axle damping
is only defined by two specific parameters. They then apply for all
types of vehicle and all test conditions.
The evaluation is based on a plurality of complex
individual steps, which are represented in the flow chart of Figure
5. One feature of the evaluation method is a plausibility test,
which comes before the calculation and evaluation of the degree of
- 26 -

CA 022~293 1998-12-08
damping. This plausibility test has the purpose of eliminating any
extreme situations of the running gear, which can possibly not be
calculated. Such incalculable, extreme running gear is not
necessarily due to bad or defective shock absorbers. Extremely good
shock absorber performances, which may possibly be enhanced by a
large fraction of external friction, offend against the one quarter
vehicle model for parameter calculation.
The characteristic frequencies for the tension and
compression stage are extracted separately for the measured
amplitude and phase spectrum. If one stage is defective, then the
shock absorber must be replaced.
The resonant frequency f3 is the same as the frequency,
at which the amplitude maximum is swept through. This extreme value
must be local and global. If for example the first value at 35 Hz
is a global maximum value wo, same is not accepted as being local
and the series of measurements is rejected as being invalid.
The following problems impair the exact ascertainment of
the ~/2 frequency. In the course of recording the spectrums
scanning takes place in frequency-equidistant steps. As a rule the
frequency point is not exactly reached, at which a compensated
phase shift of exactly ~/2 becomes established. The disruption of
road adherence, already mentioned several times, which occurs after
passage through the upper resonant frequency, will particularly
falsify the phase spectrum. Owing to disruption of road adherence
the continuously extending phase function comprises erratic values,
which may lie above the ~/2 level, although the good damping action
means that ~/2 resonance will be reached much later or even not at
all, as illustrated in Figure 6.
In the same manner certainly reaching the ~/2 level may
be prevented owing to an erratic measurement. By interpolation of
- 27 -

CA 022~293 1998-12-08
the section of the phase function using a third order polynomial
there is both an elimination of the erratic points and also an
exact calculation of the ~/2 frequency f2. The support points for
the interpolation start here at the resonant frequency and
terminate at the local maximum of the phase function. The effect
of a good shock absorber performance of the frequency curve is
illustrated in Figure 7.
The frequencies f2 and f3 may be relied upon for a
plausibility test. In this respect two extreme cases should be
dealt with before the actual parameter calculation.
If the ~/2 frequency is not present, this means that the
~/2 frequency level was not reached. The damping of the running
gear is exceptionally good. A calculation of parameters would not
be possible and is unnecessary.
If the ~/2 frequency f2 is larger than or equal to the
resonant frequency f3 then in the oscillating system without
damping the frequencies f2 and f3 are theoretically equal. If this
behavior is found during the recording of the frequency curve, then
the damping of the running gear is extremely poor. Calculation of
parameters would not be possible and is unnecessary. The effect of
poor shock absorber performance of the frequency curve is
represented in Figure 8.
The two extreme cases could be provoked by manipulation
of the tire pressure. Checking of air pressure is necessary before
the plausibility test of the characteristic frequencies.
The estimation of parameters is a method, which estimates
the parameters of a predetermined complex frequency curve on the
basis of measured support points. The complex frequency curve is
based on the simple one quarter vehicle model:

CA 022~293 1998-12-08
G bo + ib,~ - b2~ 2 _ ib3~ 3 + b4~ 4
I + ia~ a2C~ 2 - ia3(0 3 + a4~ 4
or, respectively, with the real parameters:
_ msc) 2 _ imS dk Cl~ + k ~
Fp = d ( mF + mF + ~ 2 _ imS k kR~ + k kR ~J)
wherein:
mF spring-suspended mass [kg]
mu non-spring-suspended mass [kg]
mS static overall mass [kg]
k spring constant of the suspension spring [N/m]
kR spring constant of the tire [N/m]
d damping constant of the shock absorber [kg/s]
~ circular frequency of the exciting oscillation [1/s]
The basis of the linear equation system is a loss
function V, which calculates the departure of all support points
for the complex frequency curve to be assessed:
N
V = ~v[Rv(l -a2~2 +a4~4)- Iv(alo~ -a3~3)-(bO -b2cl~2 +b4~o4)]2
v=O
+~v[Rv(a,c3-a3ct)3)+Iv(l-a2(02 +a4~4)-(b,cl)-b3cl)3)]2
wherein:
R~ is the measured real fraction of the support point
v
I~ is the measured imaginary fraction of the support
point v
~ is the weight fraction of the support point v
N is the number of support points - 1.
- 29 -

CA 022~293 1998-12-08
This loss function is differentiated after each
coefficient to be estimated and set at zero. That is to say, every
coefficient is to be so estimated that the resulting loss runs
through a minimum.
For the nine coefficients to be estimated there are
consequently nine linear equations, which are linked in a linear
equation system. The coefficients al - b5 are determined by the
solution of this linear equation system. The application of the
method is extremely complex and is hence not particularly suitable
for determination of parameters. The absolute values of the
individual parameters of the frequency curve of the simple one
quarter vehicle model differ to a great extent. This means that the
accuracy of the individual parameters suffers. The parameters bo
and b1 are always zero in the case of the frequency curve of the
simple one quarter vehicle model. The parameter estimation method
however allocates values to these parameters and deals with the
departures by means of the higher coefficients. Each support point
is weighted with the function phiV. That is to say, its influence
on the loss function is set. In this respect the it is not the
absolute amount but the ratio of the weight functions of the
support points inter se which is relevant. By appropriate
definition of the weight function the band width of the solutions
may be practically varied at will. There is no unambiguous, optimum
weight valid for all measurement curves.
The particular feature of the frequency curve for the
simple one quarter vehicle model is the convergence of the
amplitude spectrum toward the spring constant of the tire kR at
high frequencies. This asymptote may be calculated by a modified
form of the parameter estimation method. Of the originally nine
parameters to be estimated the parameters bo and b1 are basically
zero and the parameter b2 is the static mass m~, which is also
known. The linear equation system is thus reduced to six linear
- 30 -

CA 022~293 1998-12-08
equations. For estimation 20 different weight functions are swept.
For each weight function the theoretical support points are
calculated. The weight function with the minimum mean departure in
the support points employed is then used.
For verification of the estimated spring constant values
kR of the tire the frequency curves of the tire are recorded under
different amounts of bias. Three results may be derived from these
results:
The spring constant is constant over the entire frequency
range from 35 Hz to 1 Hz.
The value of the spring constant is in agreement with the
estimated value with an accuracy of 2%.
The typical kR characteristic curves of a tire are
primarily dependent on the tire pressure, the dimensions of the
tire and the bias, that is to say the weight, with which the tire
is thrust against the ground. The specific manufacturer data such
as a rubber blend, type of carcass or tread are only of secondary
significance. Furthermore the wheel employed is without any
significant influence on the spring constant kR.
The spring constant kR corresponds to the degree of
coupling between the vibratory platform and the oscillating
spring-shock absorber system of the non-spring-suspended mass mu.
If the degree of coupling too high, a large amount of oscillation
energy will be supplied to the spring-shock absorber system. The
excess energy is then interpreted as insufficient shock absorber
performance. If the degree of coupling too low, too little
oscillation energy will be supplied to the spring-shock absorber
system. The deficit of energy is then attributed to the shock
absorber performance.
- 31 -

CA 022~293 1998-12-08
As explained below, this erroneous assessment will be
satisfactorily compensated for in the case of small air pressure
departures as regards the assessment of the shock absorber, unlike
other methods with the degree of axle damping.
The spring constant kR of the tire is suitable for
examination of the tire pressure. The basis of the plausibility
test is the specification of dimensions of the tire types (for
example 225/50 R15). The rated air pressures for a certain type of
dimension vary on use of this tire on different types of vehicle
only to an insignificant extent and are then coupled at least with
the weight of the vehicle. Heavy motor vehicles imply in this case
a higher rated tire pressure than lighter vehicles (BridgestoneTM
"Ratgeber Reifen" 1992).
225/50 R16 Rated tire pressure Rated tire pressure
VA (bar) HA (bar)
Mercedes 500 3.0 3-3
Volvo 2.3 2.6
Porsche Carrera 2.0 2.5
For the tire type 225/50 R16 as indicated a minimum curve
for the minimum value of 2.0 bar (for the front axle of the Porsche
Carrera) and a maximum curve for the maximum value of 3.3 (for the
rear axle of Mercedes 500) would be stored in a data base. Both of
the curves represent the changes in the spring constant value
against biasing weight (Figure 9). The two extreme working points
are now connected by the rated kR curve. All other vehicle types,
which are fitted with these tires, then lie more or less on a rated
kR curve. For a fixed bias a change in the tire pressure has a
linear relationship to a change in the spring constant kR.
Accordingly a tolerance band of, for example, 0.5 bar may be
defined. If the estimated kR value is outside the predetermined
- 32 -

CA 022~293 1998-12-08
tolerance band, the measurement is not evaluated. An instruction
to check tire pressures is issued as well.
Figure 10 shows the results of measurement with the tire
type UniroyalTM 155/70 R15 on as tire test bed. In the case of a
test series with the Ford Escort the vehicle loading and the tire
pressure were varied. The plausibility tests did not indicate any
false assessment.
Attempts aimed at manipulating the final result by
changing the load are rendered more difficult by this plausibility
test. It is possible to see clearly whether an increased degree of
coupling is due to an excessively high tire pressure or an
extremely high load. A higher weight implies a higher bias and
accordingly a higher degree of coupling with the tire pressure
unchanged.
The actual curve of the amplitude and phase spectrum is
substantially in accord with the theoretical target or rated curve
of the simple one quarter vehicle model. It is only in the
frequency range of disruption of road adherence that the simple one
quarter vehicle model cannot be utilized. However since on reaching
the disruption of road adherence the measurement is terminated in
any case, this can be neglected. Any other departure of the
spectrum is either due to defective running gear or to an unusual
property of the running gear. The so-called signal form test is to
classify irregularities in the amplitude spectrum.
In Figure 11 a satisfactory amplitude and phase spectrum
is to be seen. At the resonant point the amplitude curve smoothly
and unambiguously runs through its maximum. The phase function
smoothly converges toward zero with increasing exciting frequency.
- 33 -

CA 022~293 1998-12-08
In Figure 12 the spectrums of a manipulated shock
absorber are represented. The resonance maximum of the amplitude
spectrum is not unambiguous. The phase spectrum is practically free
of interference in this range. This leads to a spread of the
wrongly determined characteristic frequencies f2 and f3. The
resulting degree of axle damping is then clearly above or outside
the calculable value range. This case cannot be employed for
calculation.
Owing to a camber angle some running gear sweeps through
a plurality of resonant points , in which the vehicle is subject
to powerful horizontal oscillations. Such a spectrum is illustrated
in Figure 13. In this case such so-called camber flutter could also
be interpreted as due to a defective shock absorber. The difference
between this and the amplitude curve of a mechanically defective
shock absorber is however the fact that between the characteristic
frequencies f2 and f3 no local minimum is swept through. Such
series of measurements are made available for further parameter
calculation.
The parameter calculation is based on the complex
frequency curve of the simple degree one quarter vehicle model:
F -- --mS~ --imS ~d~ ~ 3 + mu mF ~ 4
P I + i d ~ _ ( F + F + ~1 ~ -imS~ ~ +
wherein:
mF spring-suspended mass [kg]
mu non-spring-suspended mass [kg]
mS static overall mass [kg]
k spring constant of the suspension spring [N/m]
k~ spring constant of the tire [N/m]
d damping constant of the shock absorber [kg/s]
circular frequency of the exciting oscillation [1/s]
- 34 -

CA 022~293 1998-12-08
All the following calculation steps were performed using
computer algebra:
- calculate the amplitude curve A from the complex frequency
curve Fp.
- For calculation of the characteristic equation for the above
resonant point f3 differentiate the amplitude curve A and make
A' equal to zero.
- Solve this equation in terms of the damping constant d and the
following applies:
d3 =g(~3,ms,mulkRlk)-~-
- For calculation of the characteristic equation for the ~/2
frequency f2 calculate the real fraction of A and make Are
equal to zero.
- Solve this equation in terms of the damping constant d and the
following applies:
d2 =h(O2"mslmulkR~k) -
In both equations g and h the exciting frequencies omega
and the static weight mS are measured. The spring constant of the
tire kR iS determined in the parameter estimation method and is
accordingly known as well.
Two equations are now available for d2 and d3 with two
unknowns mu and kR. The same may however not be linked directly,
since the damping constant is frequency-dependent. The linking
together occurs in the amplitude curve A. Generate the amplitude
curves A2 (replace d by d2) and A3 (replace d by d3). Since the
amplitudes at both frequency points are also measured, there are
still two equations with two unknowns mI and k, which may be now
linked. It is now possible to calculate all parameters.
The calculation of the parameters is now able to be
resolved to several zero position problems as far as the fourth
- 35 -
-

CA 022~293 1998-12-08
order. If the parameters are not able to be calculated (for example
no real zero point or division by zero), a series of measurements
is to be considered, which corresponds to an extreme situation. In
such cases evaluation on the basis of the degree of axle damping
is omitted. From an extreme situation with a valid signal curve and
with characteristic frequencies present it is possible to conclude
that there is either very good or very poor running gear. For the
classification in this special case recourse is had to the ground
standing value. If this value is relatively large the running gear
is in order. If the value is on the other hand low, the running
gear must be classified as poor and replacement of the shock
absorber is recommended. If the ground standing value is not able
to be classified, an error message is issued.
Using the measurements described so far basically all
measurement series may be calculated, whose signal curves and
characteristic frequencies were satisfactory. If the above
mentioned error should be due to an unusual measuring situation,
then the original measurement values must be communicated to the
software partner for detailed investigations. The respective saving
of data is automatically performed when there is an error.
The results of the parameter calculation may not be
employed directly for an assessment of the measured running gear.
The reasons for this are the selection of the correct calculation
model, since the simple one quarter vehicle model does not
differentiate between the external friction of the suspension parts
and the internal friction of the damping liquid and the lack of
comparability of the parameters in the installed condition with
measured parameters in the dismounted condition. The dynamics of
both examination methods are extremely different. For instance,
when recording bell curves measurement is normally performed with
large strokes at relatively low exciting frequencies, whereas the
vibratory platform only implies extremely small strokes at high
- 36 -

CA 022~293 1998-12-08
frequencies at the shock absorber. If running gear is to be
assessed using the calculated parameters, then the comparison
values for this running gear must be held in a data base. In view
of the large number of types of running gear and installed shock
absorbers the production of a user friendly data base is not
possible for use in the workshop.
The aim is consequently the assessment of the complete
running gear situation, which is not tied to the type of vehicle
and takes into account attempts at manipulation or takes same into
account in assessment. The result of the assessment is to be a
recommendation to replace the installed shock absorber.
This aim is to be reached using the so-called degree of
axle damping (AchsDG):
d
2 ~I(k + kR ) mu
The parameters employed here are the result of the so-
called model iteration.
For familiar reasons the results of the parameter
calculation may not be utilized directly for the determination of
the degree of axle damping. This will be clear, when the solution
quantity is represented in an mu-k field. Theoretically all
solution curves for the different characteristic frequencies should
intersect at a single (mu,k) point, as illustrated in Figure 14.
In fact there is no unambiguous solution point (mu,k). In
practice a solution field is defined by the three solution curves,
as shown in Figure 15. As will be seen, the solution straight lines
f2 and f3 are spread apart and the solution straight line fl is
substantially above the target solution point (mI,k). With the aid

CA 022~293 1998-12-08
of computer algebra it is possible to show that principally the
influence of external friction is responsible for these shifts. The
solution range for the non-spring-suspended mass can however be
limited to a range of under 10 kg.
In the case of vehicles, which are measured with shock
absorbers of varying quality, there is a shift of the entire
solution field in the mu dimension. In the case of running gear
whose external friction is to be assumed to be large this effect
is particularly clear.
Non-spring-suspended mass Mu (kg) with different shock
absorber performances
good medium poor
BMW 740i 32.0 39.5 46.0
Ford Escort 29.0 30.5 29.5
For the calculation of the correct solution point a so-
called model iteration is swept through. Starting with the original
measured data the measured data are interactively modified in order
to eliminate the effects of the external friction. The algorithm
terminates, when all three solution straight lines intersect
precisely at one point and more particularly the fl iteration
straight line converges to the fl target solution straight line.
Model iteration is difficult to handle in this form. The
resulting parameters are to a large extent in agreement with
manufacturers' data. A problematical parameter is the spring
constant k, which in the some vehicle types is subject to a
relative variation of 50%. Model iteration may require computing
times of up to one minute. In order to be able to reliably use the
terminating model iteration, the measurement of the resonant
- 38 -

CA 022~293 1998-12-08
frequency fl of the spring-suspended mass is necessary). The amount
of time then required for measurement would then be doubled.
The resonant maximum of the resonant frequency of the
spring-suspended mass is not distinct in the case of some vehicle
types so that some search algorithms must be utilized, which find
the resonant frequency f1 on the basis of empirically determined
facts.
The work involved in determining the spring constant f
bears no relation to its influence on the final result. Neither the
damping constant d nor the degree of axle damping are significantly
influenced by the varying spring constant k or, respectively, the
absence thereof. As an example some data for the BMW 3.28 i are
relevant:
BMW 3.28i front axle right
Parameter Target value measurement measurement
measurement series 1 series 2
Non-spring-suspended
mass mu (kg) ca. 40 40.7 41.5
Suspension spring k (N/mm) 19.2 18.8 24.6
Damping coefficient d(kg/s) ? 1202 1216
Degree of
axle damping without k (%) ? 13.2 13.3
Degree of axle damping
with k (%) ? 13.0 12.9
Owing to the small influence on the degree of axle
damping and the substantial disadvantages involved in the
determination of the spring constant k the latter is omitted so
that the degree of axle damping is equal to:
- 39 -

CA 022~293 1998-12-08
2 * JkR * mu
The model iteration may be simplified to a great extent
and consequently performed more rapidly. The simplification is due
to the fact that the solution curve for the characteristic resonant
frequency fl is replaced by a constant straight line at k = 100000
N/m (Figure 16).
The non-spring-suspended mass applying here is calculated
using the customary iteration algorithm. This iteration algorithm
leads to the solution points (mu,lOOOO) with the least measured
value departure and the best cover of the damping constants of the
remaining solution curves f3.
The following statements may be made on the basis of the
degree of axle damping for an assessment of the running gear. There
is a high reproducibility in the determination of the parameters
d, kR and mu. There is no limitation t particular types of
vehicles. The larger kR the higher the fraction of the coupled
oscillation energy in the spring-shock absorber system and the
higher must the shock absorber performance be. The larger mu, the
higher must the shock absorber performance be.
For purposes of comparison vehicles with manipulated
shock absorbers were measured. The degrees of axle damping of the
defective shock absorbers were then employed as basic data for the
determination of a critical or border value line. The critical or
border value line must take into account the characteristic
properties of the running gear, which are not inherent in the
degree of axle damping.
- 40 -

CA 022~293 1998-12-08
Test measurements have indicated that the ratio between
spring-suspended to non-spring-suspended mass mF/mU represents this
decisive property. Vehicles with a large mass ratio mF/mU made do
with substantially smaller degrees of axle damping than vehicles
with relatively small mass ratios, independently of the overall
weight of the vehicle.
This fact was included in a critical or border value line
for the mass ratio in the assessment. The critical value line was
in this case to possess a hyperbolic form with on the one hand the
minimum possible mass ratio as the pole point and on the other hand
the minimum degree of axle damping as the asymptote, as shown in
Figure 17.
On the basis of the basic data non-linear regression was
employed to explicitly represent the linear boundary value line.
The regression model utilized as a basis had to be a member of the
so-called growth models. These models are characterized by a
strictly monotonous, asymptotic form, which is in agreement with
the previously made observations. The model with the best agreement
is the so-called saturation model. This model renders possible the
description of the critical value line by the two parameters a and
b (AchsDGGrenz=critical value for degree of axle damping):
a*m~
AChSDG = ~~
wherein:
a is the asymptote, that is to say the minimum degree of
axle damping.
b is the pole point, that is to say the minimum mass which
is physically possible.
- 41 -

CA 022~293 1998-12-08
In Figures 18 and 19 the degrees of axle damping of
different measured vehicle types are represented for the
compression the tension stage. All types of vehicle were measured
in this case with their rated tire pressure and unloaded weight
and, respectively, with a driver.
The basic data of the critical or border value line are
the 50% shock absorber of the BMW 3.28, the 60% shock absorber of
the Ford Escort, the minimum mass ratio of 5 and the minimum degree
of axle damping of 7%. The running gear and axle designs in an
as-new condition were all found to be poor in the EUSAMA test, as
may be seen from the following table:
Running gear EUSAMA rating (%)
BMW 3.28i HA 22
BMW 5.28T HA 25
Audi A & VA 37
Audi A6 HA 32
Passat HA 39
Golf 3 HA 35
The degrees of axle damping are on the contrary
distinctly in the range applying for satisfactory running gear.
Problematical cases are only the rear axle of the BMW 5.23T and the
front axle of the Audi A6. In these two cases the running gear the
degree of axle damping is less than for example the 50% damping of
the BMW 3.28i. However both mass ratios are substantially above
that of the BMW 3.28i and hence substantially above the critical
value line.
In order to have further measurement points below the
critical value line the rear axle of the BMW 5.28 was measured
without the shock absorber. The vehicle could however only be
measured with a tire pressure decrease of -0.5 bar and -1.0 bar,
- 42 -
. . ~ .

CA 022~293 1998-12-08
since at normal pressure the tire rose clear of the vibratory
platform.
The problem in the calculation of the parameters, in
which the non-spring-suspended mass mu fluctuates in accordance
with the quality of the installed shock absorbers, is however not
dealt with by using model iteration. However this is actually an
advantage in the case of the use of the mass value mu within the
degree of axle damping, as may be seen from the three measurement
points for the BMW 740i. Using an interface it was possible to
select between the shock absorber settings of hard, medium and
comfortable:
The poor shock absorber performance of the comfortable
setting implies a small mass ratio and displaces the degree of axle
damping to be nearer to the critical line.
The good damping performance with the hard setting
implies a large mass ratio and displaces the degree of axle damping
further away from the critical line. This effect occur to a greater
degree in the case of vehicles with a high degree of external
friction.
The rating in the running gear in separate stages and
made to apply for different vehicle type on the basis of the degree
of axle damping and including the mass ratio is a substantial
advance over the EUSAMA Method.
For maximum objectivity in rating of the test method it
is necessary additionally to compare the reactions to attempts at
manipulation with the new test method on the one hand with the
corresponding EUSAMA ratings on the other hand. The following
parameters were manipulated for this purpose:
- 43 -

CA 022~293 1998-12-08
Tire pressure - in set 0.5 bar steps from 1.0 bar under
the rated tire pressure to 1.0 above the rated tire
pressure;
Loading - all vehicle were empty, some of them
additionally with a driver and one vehicle in its
predetermined design position;
Temperature - at the start of the development phase (in
winter 1996/97) one vehicle at 0~C and at 15~C;
Tires - one vehicle with three different tire designs.
Some vehicles with a special purpose wheel clip to vary
the non-spring-suspended mass.
The illustrations mentioned only constitute the tension
stage results. The corresponding values for the compression stage
hardly differ from those of the tension stage. The critical value
lines for the tension stage are extracted from the measurement
points, which were recorded at rated tire pressure and without'a
load (at the most one driver, see Figure 19).
The values in brackets correspond to the ground standing
values at these measurement points. Same are necessary in order to
compare the reactions of the EUSAMA method with those of the new
method.
The tire pressure is one of the principal problem in the
measurement of running gear. The results of the assessment may be
manipulated to suit the particular intention. The preliminary check
of the tire pressure is to detect departures from the rated
pressure value and is the primary advantage of the new method of
testing. With the present stock of experience it is possible to
assume that departures in tire pressure of 0.5 bar may be detected
- 44 -

CA 022~293 1998-12-08
without difficulty. When further experience has been gained it may
be possible to detect a departure of 0.25 bar. Even smaller
intervals in the departure are theoretically not possible, since
the sum of the departures in the estimation of the parameters, the
preset rated value and the temperature drift constitute a natural
lower limit.
Figure 20 shows the measurement points for the rated tire
pressure and the measurement points for a pressure departure of 0.5
bar. Major variations in tire pressure are not represented, since
same are certainly filtered out by the preliminary check. The
direction of the arrow indicates the increase in tire pressure by
0.5 bar.
The following details may be derived from the above
graph. With an increase in tire pressure, the degree of damping and
the mass ratio decrease. Good running gear is more influenced by
the tire pressure than poor running gear. A change in the rating
does not occur. The influence of the tire pressure on the EUSAMA
values is on the contrary particularly great in the case of poor
running gear so that even a recommendation to replace may be
manipulated. The EUSAMA values were to some extent tripled by the
change in tire pressure. The variation in the rating points
(AchsDG,mF/mu) is certainly below 50%.
The influence of the tire pressure is not eliminated in
the result, but is made lower by a factor of 4 in comparison with
the EUSAMA method on average. Substantial departures from the rated
tire pressure can be detected. A manipulation of the recommendation
to replace on the basis of the tire pressure is not possible. In
fact poor running gear varies only around the error of propagation
as based on errors of measurement when the tire pressure is
changed.
- 45 -

CA 022~293 1998-12-08
The BMW 3.28i was measured in its design position, with
a load of ca. 230 kg and with a driver. The difference between the
empty vehicle and the vehicle with a driver was so slight that it
was not taken into account in the figure.
The following details may be gathered from Figure 21. The
degrees of axle damping were reduced by 2% owing to the load. This
is in contrast to the EUSAMA data, which increase slightly with a
load. The calculated value for the non-spring-suspended mass mu is
practically the same with and without a load. The weight of the
load means that the mass ratio is increased and the assessment
point is moved into the favorable field.
Assessment reacts to load of a vehicle with the better
classification of the running gear properties. The assessment of
this running gear situation is basically correct, but there is no
possibility of distinguishing the added load part of the mass from
the mass of the unloaded vehicle. The reaction is more significant
than with the EUSAMA method.
The manipulation of the recommendation to replace on the
basis of the loading is therefore possible in the case of running
gear in the environment of the critical value line.
The influence of the temperature of the surroundings was
investigated by making measurements at approximately 0~C and then
at the temperature of the surroundings of approximately 15~C. From
Figure 22 it will be seen that the degrees of axle damping
increases on cooling and that the mass ratio is not changed by
cooling down. The EUSAMA values remain practically unchanged.
Manipulation of the recommendation to replace on the basis of the
environmental temperature of the surroundings can consequently not
be excluded.
- 46 -

CA 022~293 l998-l2-08
With a change in tires the tire spring constant for the
vehicle and the non-spring-suspended mass will be changed. In this
connection two test series were run:
- The BMW 3 . 28i was measured with the complete sets of tires in
the design position.
- Several vehicles were measured with a special purpose wheel
clip (5.6 kg) and, respectively, a screwed-on steel plate
(14 . 3 kg) on the wheel.
The following details may be gathered from Figure 23. The
rating points (AchsDG/mF/mu) are not changed in their
classification. The slightly improved degree of axle damping which
heavy tires is compensated for by the decrease in the mass ratio.
This effect is particularly clear in the case of small
low mass ratios. The EUSAMA values decrease with an increase in the
tire spring constant kR. A change in tires mainly causes changes in
the spring constant kR and thus in the degree of coupling. The
influence on the non-spring-suspended mass is within the range of
accuracy of measurement owing to the small differences in measured
values. The influence of the spring constant kR is taken into
2 0 account in the degree of axle damping, whereas in the case of such
an increase in coupling the EUSAMA method provide poorer road
adherence data. A manipulation of the recommendation is not
possible.
The following may be seen from Figure 24. The degrees of
axle damping are, like the road adherence values, slightly reduced
by the additional weight. The additional weight is fully taken up
in the non-spring-suspended mass and in part leads to a drastic
reduction in the mass ratio.
-- 47

CA 022~293 1998-12-08
Bad running gear can be imitated by manipulation of the
non-spring-suspended mass. The EUSAMA values tend to react to
manipulation in the same manner but not to such a significant
extent. The result of this is that highly defective running gear
may still be classified as good.
By way of conclusion it is possible to say the following
on the possibilities of manipulation. The manipulation of the tire
pressure would be detected by the preliminary examination in view
of kR and m~. As compared with the EUSAMA method there is the
advantage that statement as regards the tire pressure is possible
and the sensitivity of the examination method for tire pressure is
less. Manipulation by way of the temperature of the shock absorber
is excluded by the warming up phases. To be possible manipulation
on the basis of the load would involve massive external
manipulation and may therefore also be excluded. A further point
is that the load affects the mass ratio, see the above mentioned
graph. Manipulation by way of changing the tires is not possible,
since there is a check in this respect. As compared with the EUSAMA
method there is the advantage that the influence of the changed
spring constant is removed by calculation.
Manipulation of the mass mu could make it seem that the
running gear is poorer than is the actually case, something which
would have to involve massive manipulation from the outside and can
consequently be excluded. As compared with the EUSAMA method there
is the advantage that the load is included in the mass ratio and
is therefore covered by the test method. Figure 25 shows by way of
conclusion the directions of displacement of the effective
parameters in the field of degree of axle damping to the degree of
axle damping mF/mu. Manipulations are consequently either excluded
or they have a substantial effect of the results of measurement.
- 48 -

CA 022~293 1998-12-08
It is to be understood that the above description is
intended to be illustrative and not restrictive. Many embodiments
will be apparent to those skilled in the art upon reviewing the
above description. Those skilled in the art will recognize as an
equivalent or alternative method of tire testing and combining a
tire testing machine with a wheel balancing machine. The scope of
the invention should, therefore, be determined not as reference to
the above description, but should instead be determined with
reference to the appended claims along with the full scope of
equivalence to which such claims are entitled.
- 49 -

Representative Drawing