COCHANNEL SIGNAL PROCESSING SYSTEM

SYSTEME DE TRAITEMENT DE SIGNAUX DANS LE MEME CANAL

English Abstract

A method and apparatus for processing cochannel signals received at a sensor
array (110) in a cumulant-based signal processing and separation engine to
obtain a desired set of output signals (38) or parameters. For use in a signal
recovery system, the output signals are recovered and separated versions of
the originally transmitted cochannel signals. An important feature that
distinguishes the cumulant-based system from other signal separation and
recovery systems is that it generates an estimated generalized steering vector
associated with each signal source, and representative of all received
coherent signal components attributable to the source. This feature enables
the invention to perform well in multipath conditions, by combining all
coherent multipath components from the same source. In a receiver/transmitter
system (316), the estimated generalized steering vectors associated with each
source are used to generate transmit beamformer weight vectors that permit
cochannel transmission to multiple user stations (310). The basic cumulant-
based processing and separation engine can also be used in a variety of
applications, such as high density recording, complex phase angle
equalization, receiving systems with enhanced effective dynamic range, and
signal separation in the presence of strong interference. Various embodiments
and extensions of the basic cumulant-based system are disclosed.

French Abstract

Cette invention se rapporte à un procédé et à un appareil qui servent à traiter des signaux dans le même canal reçus au niveau d'un groupement de capteurs (110) dans un moteur de traitement et de séparation de signaux à base de cumulants, afin d'obtenir un groupe désiré de signaux de sortie (38) ou de paramètres. Pour pouvoir être utilisés dans un système de récupération de signaux, des signaux de sortie en question sont des versions séparées et récupérées des signaux transmis à l'origine dans le même canal. Une caractéristique importante qui distingue le système à base de cumulants des autres systèmes de récupération et de séparation de signaux est que le système à base de cumulants génère un vecteur d'orientation généralisé estimé qui est associé à chaque source de signaux et qui est représentatif de toutes les composantes de signal cohérentes reçues attribuables à la source en question. Cette caractéristique permet au système de cette invention de bien se comporter dans des conditions multivoies, en combinant toutes les composantes multivoies cohérentes provenant de la même source. Dans un système de récepteur/émetteur (316), les vecteurs d'orientation généralisés estimés qui sont associés à chaque source sont utilisés pour générer des vecteurs de pondération conformateurs de faisceaux de transmission qui permettent la transmission dans le même canal en direction de multiples stations d'utilisateurs (310). Ce moteur de traitement et de séparation générique à base de cumulants peut également être utilisé dans une grande variété d'applications, telles que l'enregistrement haute densité, l'égalisation d'angles de phase complexes, les systèmes de réception avec plage dynamique efficace accrue, et la séparation de signaux en présence de fortes interférences. Divers modes de réalisation et diverses extensions de ce système générique à base de cumulants sont présentés.

Claims

The embodiments of the invention in which an exclusive
property or privilege is claimed are defined as follows:
1. A signal processing system for deriving at least
one output quantity of interest from received cochannel input
signals, the system comprising:
a signal receiving system, including means for generating a
set of conditioned receiver signals from received signals of
any modulation or type;
an estimated generalized steering vector (EGSV) generator,
for computing an EGSV that results in optimization of a
utility function that depends on fourth or higher even-order
statistical cumulants derived from the received signals, the
EGSV being indicative of a combination of signals received at
the signal receiving system from a signal source; and
a supplemental computation module, for deriving at least one
output quantities of interest from the conditioned receiver
signals and the EGSV.
2. A signal processing system as defined in claim 1,
wherein:
the EGSV generator uses an iterative technique to generate
the EGSV and includes means for generating successively more
accurate EGSVs based on iterative optimization of the utility
function.
3. A signal processing system as defined in claim 2,
wherein the means for generating successively more accurate
EGSVs includes:
a linear combiner, for repeatedly computing a single channel
combined signal from the conditioned receiver signals and an
EGSV;

means for supplying an initial EGSV to the linear combiner,
to produce the initial output of a single channel combined
signal;
an EGSV computation module, for computing successive values
of the EGSV from successive values of the single channel
combined signal received from the linear combiner and the
conditioned receiver signals; and
means for feeding the successive values of the EGSV back to
the linear combiner for successive iteration cycles; and
means for terminating iterative operation upon convergence of
the EGSV to a sufficiently accurate value.
4. A signal processing system as defined in claim 2,
wherein the means for generating successively more accurate
EGSVs includes:
a cross-cumulant matrix computation module, for generating a
matrix of cross-cumulants of all combinations of the
conditioned receiver signals;
a structured quadratic form computation module, for computing
successive cumulant strength functions derived from
successive EGSVs and the cross-cumulant matrix;
means for supplying an initial EGSV to the structured
quadratic form computation module, to produce the initial
output of a cumulant strength function;
an EGSV computation module, for generating successive EGSVs
from successive cumulant strength functions received from the
structured form computation module; and
means for feeding the successive values of the EGSV back to
the structured quadratic form computation module for
successive iteration cycles; and
means for terminating iterative operation upon convergence of
the EGSV to a sufficiently accurate value.

5. A signal processing system as defined in claim 1,
wherein the EGSV generator uses a direct computational
technique to generate the EGSV, and includes:
a cross-cumulant matrix computation module, for generating a
matrix of cross-cumulants of all combinations of the
conditioned receiver signals; and
an EGSV computation module for computing the EGSV directly
from the cross-cumulant matrix by solving a fourth degree
polynomial equation.
6. A signal processing system as defined in any one of
claims 1 to 5, wherein:
the means for generating the set of conditioned signals
includes an eigendecomposition module for generating an
estimate of the number of signal sources, a transformation
matrix for conditioning the receiver signals, and
an eigenstructure derived from the receiver signals; and
the EGSV generator employs signals output by the
eigendecomposition module to compute EGSVs.
7. A signal processing system as defined in any one of
claims 1 to 5, wherein:
the means for generating the set of conditioned signals
includes a covariance matrix computation module and a matrix
decomposition module, for generating a matrix; and
the system further includes a beamformer, for generating a
recovered signal from the receiver signals, the EGSV and the
matrix obtained from the matrix decomposition module.
8. A signal processing system as defined in any one of
claims 1 to 5, wherein:

the means for generating the set of conditioned signals
includes an eigendecomposition module for generating an
estimate of the number of signal sources, a transformation
matrix for conditioning the receiver signals, and an
eigenstructure derived from the receiver signals;
the EGSV generator employs signals output by the
eigendecomposition module to compute EGSVs
the system further comprises a multiple port signal recovery
unit, including means for matching current EGSVs with EGSVs
from a prior data block to impose waveform continuity from
block to block.
9. A signal processing system as defined in any one of
claims 2 to 4, wherein:
signals are processed in successive blocks of data; and
the initial of EGSVs for each new processing block are
computed by a means (FIG. 19) for combining a prior block
EGSV and a cumulant vector derived from the utility function.
10. A signal processing system as defined in claim 9,
wherein:
the means for combining takes the sum of the prior block EGSV
multiplied by a first factor, and the cumulant vector
multiplied by a second factor, wherein the first and second
factors are selected to provide an initial EGSV that
anticipates and compensates for movement of a signal source.
11. A signal processing system as defined in claim 3,
wherein:
the system functions to separate a plurality (P) of received
cochannel signals;

there is a plurality (P) of EGSV generators including P EGSV
computation modules and P linear combiners, for generating an
equal plurality (P) of EGSVs associated with P signal
sources; and
the supplemental computation module functions to recover P
separate received signals from the P generalized steering
vectors and the conditioned receiver signals.
12. A signal processing system as defined in claim 11,
wherein:
the supplemental computation module includes a recovery
beamformer weight vector computation module, for generating
from all of the EGSVs a plurality (P) of receive weight
vectors, and a plurality (P) of recovery beamformers, each
coupled to receive one of the P receive weight vectors and
the conditioned receiver signals, for generating a plurality
(P) of recovered signals.
13. A signal processing system as defined in claim 4,
wherein:
the system functions to separate a plurality (P) of received
cochannel signals;
there is a plurality (P) of EGSV generators, including P EGSV
computation modules and P structured quadratic form
computation modules, for generating an equal plurality (P) of
EGSVs associated with P signal sources; and
the supplemental computation module functions to recover P
separate received signals from the P generalized steering
vectors and the conditioned receiver signals.
14. A signal processing system as defined in claim 13,
wherein:

the supplemental computation module includes a recovery
beamformer weight vector computation module, for generating
from all of the EGSVs a plurality (P) of receive weight
vectors, and a plurality (P) of recovery beamformers, each
coupled to receive one of the P receive weight vectors and
the conditioned receiver signals, for generating a plurality
(P) of recovered signals.
15. A signal processing system as defined in claim 5,
wherein:
the system functions to separate a two received cochannel
signals;
the EGSV computation module generates two EGSVs from the
cross-cumulant matrix data; and
the supplemental computation module functions to recover two
separate received signals from the two generalized steering
vectors and the conditioned receiver signals.
16. A signal processing system as defined in claim 15,
wherein:
the supplemental computation module includes a recovery
beamformer weight vector computation module, for generating
from both of the EGSVs two receive weight vectors, and two
recovery beamformers, each coupled to receive one of the
receive weight vectors and the conditioned receiver signals,
for generating two recovered signals.
17. A signal processing system as defined in any one of
claims 1 to 5, wherein:
the system functions to derive a direction of arrival (DOA)
of a received signal;

the supplemental computation module includes a memory for
storing sensor array calibration data, and means for deriving
the DOA of a received signal from its associated generalized
steering vector and the stored sensor array manifold data.
18. A signal processing system as defined in claim 17,
wherein:
the sensor array manifold data includes a table associating
multiple DOA values with corresponding steering vectors; and
the means for deriving the DOA includes means for performing
a reverse table lookup function to obtain an approximated DOA
value from a steering vector supplied by the generalized
steering vector generator.
19. A signal processing system as defined in claim 18,
wherein:
the means for deriving the DOA further includes means for
interpolating between two DOA values to obtain a more
accurate result.
20. A signal processing system as defined in any one of
claims 1 to 5, wherein the supplemental computation module
includes:
a signal recovery module for generating received signal
beamformer weights from the conditioned receiver signals and
the EGSV; and for recovering the received signal therefrom;
and
a transmitter, for generating transmit signal beamformer
weights from the received signal beamformer weights, and for
transmitting signals containing information in a direction
determined by the transmit signal beamformer weights.

21. A signal processing system as defined in claim 12
or 14, wherein the supplemental computation module further
includes:
a transmit weight vector computation module, for generating P
transmit beamforming weight vectors from receive weight
vectors generated by the recovery beamformer weight vector
computation module; and
P linear combiners, for combining each of the P information
signals to be transmitted with its associated transmit weight
vector, to obtain a weighted transmit beam for each of the
information signals to be transmitted, and then combining
corresponding components of the weighted transmit beams, for
coupling to a transmit array.
22. A signal processing system as defined in any one of
claims 11 to 16, wherein:
the signal receiving system includes a plurality of waveguide
sensors for receiving signals transmitted onto a waveguide in
different modes, wherein the modes are subject to scrambling
in the waveguide; and
the supplemental computation module separates and recovers
the signals and mitigates the effect of mode mixing in the
waveguide.
23. A signal processing system as defined in claim 22,
wherein the waveguide is a microwave waveguide.
24. A signal processing system as defined in claim 22,
wherein the waveguide is an optical fiber.
25. A signal processing system as defined in claim 22,
wherein the waveguide is a coaxial cable.

26. A signal processing system as defined in claim 22,
wherein the waveguide includes at least one twisted pair of
conductors.
27. A signal processing system as defined in any one of
claims 11 to 16, wherein:
the signals received by the signal receiving system are in-
phase and quadrature components of a two-dimensional
communication signal, which has been subject to phase
rotation during propagation; and
the recovered signals generated automatically from the
supplemental computation module are in-phase and quadrature
components of a two-dimensional communication signal that has
been corrected for phase rotation, wherein the system
functions as a complex phase equalizer.
28. A signal processing system as defined in any one of
claims 1 to 5, wherein:
the signals received by the signal receiving system have been
subject to distortion by analog processing and analog-to-
digital conversion in a radio receiving system; and
the output quantities include a recovered signal having
significantly less distortion than the received signals,
whereby the receiving system has improved dynamic range as a
result of the use of the signal processing system.
29. A signal processing system as defined in any one of
claims 11 to 16, wherein:
the signals received by the signal receiving system include
signals from a relatively weak desired source and much
stronger signals from at least one interfering source;

wherein the recovered and separated signals include those
from the relatively weak desired source, free of
interference, and those from the stronger interfering source,
which can be discarded.
30. A method for processing cochannel signals received
at a sensor array, the method comprising the steps of:
conditioning a set of signals received at a sensor array from
multiple sources that can vary in power and location;
generating for each source an estimated generalized steering
vector (EGSV) that results in optimization of a utility
function that depends on fourth or higher even-order
statistical cumulants derived from the received signals, the
EGSV being indicative of a combination of signals received at
the sensors from a signal source; and
performing supplemental computation to derive output
quantities of interest from the conditioned receiver signals
and the EGSVs.
31. A method as defined in claim 30, wherein:
the step of generating an EGSV includes providing an initial
EGSV and then iteratively generating successive EGSVs until
an acceptable convergence is attained.
32. A method as defined in claim 31, wherein generating
an EGSV includes:
computing in a linear combiner successive values of a single
channel combined signal derived from an input EGSV and the
received signals;
supplying an initial EGSV to the linear combiner;
computing successive EGSVs from the received signals and the
successive values of the single channel combined signal;

feeding the successive EGSVs back to the linear combiner for
further iteration; and
terminating further iteration when the EGSV has
satisfactorily converged.
33. A method as defined in claim 31, wherein generating
an EGSV includes:
computing a matrix of cross-cumulants of the received
signals;
computing in a structured quadratic form computation module
successive values of a cumulant strength function derived
from an input EGSV and the cross-cumulants of the received
signals;
supplying an initial EGSV to the structured quadratic form
computation module;
computing successive EGSVs from the successive values of the
cumulant strength;
feeding the successive EGSVs back to the structured quadratic
form computation module for further iteration; and
terminating further iteration when the EGSV has
satisfactorily converged.
34. A method as defined in claim 30, wherein generating
an EGSV includes:
generating a matrix of cross-cumulants of all combinations of
the received signals; and
computing the EGSV directly from the cross-cumulants by
solving a fourth degree polynomial equation.
35. A method as defined in any one of claims 30 to 34,
wherein:

conditioning the received signals includes generating by
eigendecomposition an estimate of the number of signal
sources, a transformation matrix for conditioning the
receiver signals, and an eigenstructure derived from the
receiver signals; and
the step of generating EGSVs employs signals generated in the
foregoing step of generating by eigendecomposition.
36. A method as defined in any one of claims 30 to 34,
wherein:
conditioning the received signals includes generating a
covariance matrix and generating therefrom another matrix;
and
the method further comprises beamforming to generate a
recovered signal from the receiver signals, the EGSV and the
other matrix obtained from the covariance matrix.
37. A method as defined in any one of claims 30 to 34,
wherein:
conditioning the received signals includes generating by
eigendecomposition an estimate of the number of signal
sources, a transformation matrix for conditioning the
receiver signals, and an eigenstructure derived from the
receiver signals;
the step of generating EGSVs employs signals generated in the
foregoing step of generating by eigendecomposition
the method further comprises the step of matching current
EGSVs with EGSVs from a prior data block to impose waveform
continuity from block to block.
38. A method as defined in any one of claims 31 to 33,
wherein:

signals are processed in successive blocks of data; and
the method further comprises a step of computing an initial
EGSV for each new processing block by combining a prior block
EGSV and a cumulant vector derived from the utility function.
39. A method as defined in claim 38, wherein:
the combining step includes taking the sum of the prior block
EGSV multiplied by a first factor, and the cumulant vector
multiplied by a second factor, wherein the first and second
factors are selected to provide an initial EGSV that
anticipates and compensates for movement of a signal source.
40. A method as defined in claim 32, wherein:
the method separates a plurality (P) of received cochannel
signals;
the step of generating an EGSV is performed in a plurality
(P) of EGSV generators, including P EGSV computation modules
and P linear combiners, for generating an equal plurality (P)
of EGSVs associated with P signal sources; and
the step of performing supplemental computation includes
recovering P separate received signals from the P generalized
steering vectors and the conditioned receiver signals.
41. A method as defined in claim 40, wherein:
the step of performing supplemental computation further
includes generating, in a recovery beamformer weight vector
computation module, from all of the EGSVs a plurality (P) of
receive weight vectors, and generating a plurality (P) of
recovered signals in a plurality (P) of recovery beamformers,
each coupled to receive one of the P receive weight vectors
and the conditioned receiver signals.

42. A method as defined in claim 33, wherein:
the system functions to separate a plurality (P) of received
cochannel signals;
the step of generating EGSVs includes generating a plurality
(P) of EGSVs associated with P signal sources; and
the step of performing supplemental computation includes
recovering P separate received signals from the P generalized
steering vectors and the conditioned receiver signals.
43. A method as defined in claim 42, wherein:
the step of performing supplemental computation further
includes generating from of the EGSVs, in a recovery
beamformer weight vector computation module, a plurality (P)
of receive weight vectors, and generating a plurality (P) of
recovered signals in a plurality (P) of recovery beamformers,
each coupled to receive one of the P receive weight vectors
and the conditioned receiver signals.
44. A method as defined in claim 34, wherein:
the system functions to separate two received cochannel
signals;
the step of generating EGSVs generates two EGSVs from the
cross-cumulant matrix data; and
the step of performing supplemental computation includes
recovering two separate received signals from the two
generalized steering vectors and the conditioned receiver
signals.
45. A method as defined in claim 44, wherein:
the step of performing supplemental computation includes
generating from both of the EGSVs two weight vectors, and
generating two recovered signals in two recovery beamformers,

each coupled to receive one of the weight vectors and the
conditioned receiver signals.
46. A method as defined in any one of claims 30 to 34,
wherein:
the method functions to derive a direction of arrival (DOA)
of a received signal;
the step of performing supplemental computation module
storing sensor array manifold data in a memory, deriving the
DOA of a received signal from its associated generalized
steering vector and the stored sensor array manifold data.
47. A method as defined in claim 46, wherein:
the sensor array manifold data includes a table associating
multiple DOA values with corresponding steering vectors; and
the step of deriving the DOA includes performing a reverse
table lookup function to obtain an approximated DOA value
from a steering vector supplied by the generalized steering
vector generator.
48. A method as defined in claim 47, wherein:
the step of deriving the DOA further includes interpolating
between two DOA values to obtain a more accurate result.
49. A method as defined in any one of claims 30 to 34,
wherein the step of performing supplemental computation
includes:
generating received signal beamformer weights from the
conditioned receiver signals and the EGSV;
recovering the received signal therefrom;
generating transmit signal beamformer weights from the
received signal beamformer weights; and

transmitting signals containing information in a direction
determined by the transmit signal beamformer weights.
50. A method as defined in claim 41 or 43, wherein the
step of performing supplemental computation further includes:
generating P transmit beamforming weight vectors from receive
weight vectors generated by the recovery beamformer weight
vector computation module; and
P linear combiners, for combining each of the P information
signals to be transmitted with its associated transmit weight
vector, to obtain a weighted transmit beam for each of the
information signals to be transmitted, and then combining
corresponding components of the weighted transmit beams, for
coupling to a transmit array.
51. A method as defined in any one of claims 40 to 45,
wherein:
the method further comprises receiving signals from a
plurality of waveguide sensors positioned to detect signals
transmitted onto a waveguide in different modes, wherein the
modes are subject to scrambling in the waveguide; and
the step of performing supplemental computation includes
separating and recovering the signals, while mitigating the
effect of mode mixing in the waveguide.
52. A method as defined in claim 51, wherein the
waveguide is a microwave waveguide.
53. A method as defined in claim 51, wherein the
waveguide is an optical fiber.

54. A method as defined in claim 51, wherein the
waveguide is a coaxial cable.
55. A method as defined in claim 51, wherein the
waveguide includes at least one twisted pair of conductors.
56. A method as defined in any one of claims 40 to 45,
wherein:
the signals received by the signal receiving system are in-
phase and quadrature components of two-dimensional
communication signal, which has been subject to phase
rotation during propagation; and
the step of recovering signals automatically generating in-
phase and quadrature components of a two-dimensional
communication signal that has been corrected for phase
rotation, wherein the method functions as a complex phase
equalizer.
57. A method as defined in any one of claims 30 to 34,
wherein:
the received signals have been subject to distortion by
analog processing and analog-to-digital conversion in a radio
receiving system; and
the output quantities include a recovered signal having
significantly less distortion than the received signals,
whereby the receiving system has improved dynamic range as a
result of the use of the signal processing method.
58. A method as defined in any one of claims 40 to 45,
wherein:

the received signals include signals from a relatively weak
desired source and much stronger signals from at least one
interfering source;
wherein the step of recovering the signals includes
recovering a signal from the relatively weak desired source,
free of interference, and discarding signals from the
stronger interfering source.
59. A method for recovery and separation of multiple
cochannel signals of any modulation or type received at an
array of sensors, the method comprising the steps of:
receiving a plurality of cochannel signals from separate
signal sources at an array of sensors;
preprocessing the received signals to provide preprocessed
signals;
coupling the preprocessed signals to a plurality of signal
extraction ports, each of which is in one of two states
referred to as an active state and an inactive state;
in association with each signal extraction port in the active
state, generating an estimated steering vector and a
recovered signal corresponding to one of the signal sources,
without regard for manifold data of the sensor array;
orthogonalizing the estimated steering vectors to ensure that
each signal extraction port generates a recovered signal for
a separate signal source; and
controlling the steps of orthogonalizing and generating
recovered signals to ensure an orderly association of signal
sources with signal extraction ports.
60. A method as defined in claim 59, wherein the step
of preprocessing includes:

estimating the number of signal sources of which the signals
are being received at the sensor array; and
transforming the received signals, which have a
dimensionality based on the number sensors, to preprocessed
signals, which have a dimensionality based on the estimated
number of signal sources.
61. A method as defined in claim 60, wherein the step
of preprocessing further includes:
performing an eigendecomposition of the received signals, to
produce signal subspace and noise subspace eigenvalues and
eigenvectors, and noise subspace eigenvalues and
eigenvectors; and
computing a transformation matrix from eigenvalues and
eigenvectors, for use in the transforming step.
62. A method as defined in claim 60, wherein the step
of generating an estimated recovered signal in each active
signal recovery port includes:
computing an even-order cumulant vector of fourth or higher
order from the preprocessed signals and auxiliary signals
related to the estimated recovered signals; and
using the even-order cumulant vector to compute an estimated
recovered signal, in an iterative process that rapidly
converges on a solution for the recovered signal.
63. A method as defined in claim 61, wherein the step
of generating an estimated recovered signal includes:
initially selecting a random vector to serve as an initial
steering vector a k;
computing a weight value v k from the steering vector a k, by
using the transformation matrix computed in the preprocessing

step, wherein the weight vector has a dimensionality based on
the estimated number of sources P e and the weight value has a
dimensionality based on the number sensors in the array;
computing an estimate of the recovered signal g k(t)from the
value v k and the preprocessed signal y(t);
computing an auxiliary signal u k(t) from the value v k and the
preprocessed input signal y(t);
computing a fourth-order cumulant vector b k from the
preprocessed signals y(t) and the auxiliary signal v k;
orthogonalizing the cumulant vector b k in the orthogonalizer,
to produce an orthogonalized cumulant vector d k;
deriving an updated steering vector a k from the
orthogonalized cumulant vector d k; and
repeating the steps of computing the value v k, computing an
estimate of the recovered signal, computing an auxiliary
signal u k(t), computing a fourth-order cumulant,
orthogonalizing, and deriving an updated steering vector,
until the recovered signal converges to an acceptably
accurate solution.
64. A method as defined in claim 63, wherein the step
of generating a recovered signal further includes:
calculating a capture strength c k for the each active port.
65. A method as defined in claim 63, and further
comprising the step of:
demodulating each of the recovered signals from the signal
extraction ports.
66. A method as defined in claim 63, and further
comprising the step of:

generating direction finding data, by converting the steering
vector from each active signal extraction port to a
corresponding angular position in three-dimensional space.
67. A method as defined in claim 63, wherein the step
of computing a fourth-order cumulant vector uses as input
variables the auxiliary signal v k, two instances of the
complex conjugate of the auxiliary signal u k*(t) and the
preprocessed signals y(t).
68. A method as defined in claim 64, wherein the
controlling step includes:
detecting changes in the number of signal sources; and, if
the number of signal sources is changed;
identifying which signal extraction port was processing a
lost source; and
identifying which signal extraction port will process a new
source.
69. A receiver/transmitter system for receiving
cochannel signals simultaneously from multiple remote units
and transmitting cochannel signals to the remote units
simultaneously, the system comprising:
a signal receiving system, including means for generating
from signals received at a receive sensor array a set of
conditioned receiver signals;
a plurality of estimated generalized steering vector (EGSV)
generators, for computing for each transmitting remote unit
an EGSV that results in optimization of a utility function
that depends on fourth or higher even-order statistical
cumulants derived from the received signals, each EGSV being

indicative of a combination of signals received at the
sensors from the remote unit;
a recovery beamformer weight vector computation module, for
generating from all of the EGSVs a plurality of receive
beamforming weight vectors;
a plurality of recovery beamformers, each coupled to receive
one of the receive beamforming weight vectors and the
conditioned receiver signals, for generating a plurality of
recovered signals;
a transmit weight vector computation module, for generating
transmit beamforming weight vectors from the receive
beamforming weight vectors generated by the recovery
beamformer weight vector computation module; and
a plurality of linear combiners, for combining each
information signal to be transmitted with an associated
transmit weight vector, to obtain a weighted transmit beam
for each of the information signals to be transmitted, and
then combining corresponding components of the weighted
transmit beams, for coupling to a transmit array.
70. A receiver/transmitter system as defined in claim
69, wherein:
signals received from at least one particular remote unit are
propagated over multiple paths to the receive sensor array;
the EGSV associated with the signal received over multiple
paths is representative of a composite of all coherent
components of the signal arriving over the multiple paths,
wherein multipath components of the same signal are
automatically and dynamically combined but non-coherent
cochannel signals are separated; and
the transmit weight vector used to transmit signals back to
the particular remote unit results in transmit array

directivity pattern that achieves transmission over generally
the same multiple paths traversed by the received signals,
using a weighted combination of the multiple paths;
whereby the receiver/transmitter system achieves diversity
gain by virtue of its combination of multipath components.
71. A receiver/transmitter system as defined in claim
69, wherein the transmit weight vector computation module
includes:
means for selecting from a plurality of fixed pre-formed
transmit weight vectors, based on the receive beamforming
weight vectors.
72. A receiver/transmitter system as defined in claim
69, wherein the transmit weight vector computation module
includes:
means for generating transmit weight vectors adaptively to
reflect as accurately as possible the characteristics of the
receive beamforming weight vectors, whereby signals are
transmitted to the respective remote units with minimum
interference because a transmit weight vector associated with
a particular remote unit is selected to be practically
orthogonal to all of the estimated generalized steering
vectors associated with transmissions to and from the other
remote units.
73. A receiver/transmitter system as defined in claim
72, wherein:
the system includes receive and transmit sensor arrays that
are identical in shape but are scaled in dimension in the
same ratio as transmit and receive frequencies, respectively.

74. A method for using a receiver/transmitter system
for receiving cochannel signals simultaneously from multiple
remote units and transmitting cochannel signals to the remote
units simultaneously, the method comprising the steps of:
receiving signals from a receive sensor array;
generating from the received signals a set of conditioned
receiver signals;
computing for each transmitting remote unit an estimated
generalized steering vector that results in optimization of a
utility function that depends on fourth or higher even-order
statistical cumulants derived from the received signals, the
estimated generalized steering vector being indicative of a
combination of signals received at the sensors from the
remote unit;
generating from all of the generalized steering vectors a
plurality of receive beamforming weight vectors;
generating from the receive beamforming weight vectors and
the conditioned receiver signals a plurality of recovered
signals corresponding to the signals received from the
respective remote units;
generating transmit beamforming weight vectors from the
receive beamforming weight vectors;
combining each information signal to be transmitted with an
associated transmit weight vector, to obtain a weighted
transmit beam for each of the information signals to be
transmitted; and
combining corresponding components of the weighted transmit
beams, for coupling to a transmit array.
75. A method as defined in claim 74, wherein:
signals received from at least one particular remote unit are
propagated over multiple paths to the receive sensor array;

the estimated generalized steering vector associated with the
signal received over multiple paths is representative of a
composite of all coherent components of the signal arriving
over the multiple paths, wherein multipath components of the
same signal are automatically and dynamically combined but
non-coherent cochannel signals are separated; and
the transmit weight vector used to transmit signals back to
the particular remote unit results in transmit array
directivity pattern that achieves transmission over generally
the same multiple paths traversed by the received signals,
using a weighted combination of the multiple paths;
whereby the receiver/transmitter system achieves diversity
gain by virtue of its combination of multipath components.
76. A method defined in claim 74, wherein the step of
generating transmit beamforming weight vectors includes:
selecting from a plurality of fixed pre-formed transmit
weight vectors, based on the receive beamforming weight
vectors.
77. A method as defined in claim 74, wherein the step
of generating transmit beamforming weight vectors includes:
generating transmit weight vectors adaptively to reflect as
accurately as possible the characteristics of the receive
beamforming weight vectors, whereby signals are transmitted
to the respective remote units with minimum interference
because a transmit weight vector associated with a particular
remote unit is selected to be practically orthogonal to all
of the generalized steering vectors associated with
transmissions to and from the other remote units.

78. A method as defined in claim 77, and further
comprising:
selecting receive and transmit sensor arrays that are
identical in shape but are scaled in dimension in the same
ratio as transmit and receive frequencies.
79. A two-way communication system using cochannel
signals and diversity path multiple access (DPMA) for
transmission in both directions, the system comprising:
at least one receiver/transmitter base station for
communication with a plurality of mobile devices having
omnidirectional antennas for transmitting uplink signals at
an assigned frequency and receiving downlink signals at
another assigned frequency, wherein the receiver/transmitter
base station includes:
a receive antenna array,
a plurality of estimated generalized steering vector (EGSV)
generators, for computing for each mobile device and EGSV
that results in optimization of a utility function that
depends on fourth or higher even-order statistical cumulants
derived from the received signals, the EGSV being indicative
of a combination of uplink signals received at the receive
antenna array from the mobile device over possible multiple
paths,
receiver processing means for generating from the EGSVs a
recovered signal corresponding to each uplink signal from a
mobile device, and a receive beamforming weight vector
corresponding to the uplink signal,
a transmitter, including means for generating from each
receive beamforming weight vector a corresponding transmit
beamforming weight vector, and a modulator for modulating a

downlink transmission signal with a desired information
signal,
a transmit antenna array coupled to the transmitter and
having a similar geometrical shape as the receive antenna
array, wherein downlink transmission signals intended for a
particular mobile device are propagated along generally the
same multiple paths as the received uplink signals from the
same mobile device;
wherein coherent uplink signals received over multiple paths
from the same mobile device are automatically combined,
providing a gain enhancement effect that allows weaker
transmissions to be detected, and downlink signals
transmitted over the same multiple paths also benefit from
the gain enhancement effect and provide a stronger downlink
signal to the mobile device.
80. A two-way communication system as defined in claim
79, wherein the receiver processing means includes:
a recovery beamformer weight vector computation module, for
generating from all of the EGSVs the plurality of receive
beamforming weight vectors: and
a plurality of recovery beamformers, each coupled to receive
one of the receive beamforming weight vectors and conditioned
receiver signals, for generating the plurality of recovered
signals.
81. A two-way communication system as defined in claim
80, wherein the transmitter includes:
a transmit weight vector computation module, for generating
transmit beamforming weight vectors from the receive
beamforming weight vectors generated by the recovery
beamformer weight vector computation module; and

a plurality of linear combiners, for combining each
information signal to be transmitted with an associated
transmit weight vector, to obtain a weighted transmit beam
for each of the information signals to be transmitted, and
then combining corresponding components of the weighted
transmit beams, for coupling to the transmit antenna array.
82. A two-way communication system as defined in claim
79, wherein:
the uplink and downlink transmission frequencies are offset
from each other to avoid interference between mobile devices;
and
the transmit antenna array has dimensions scaled with respect
to those of the receive antenna array in the inverse ratio of
the uplink and downlink transmission frequencies.
83. A two-way communication system as defined in claim
81, wherein the transmit weight vector computation module
includes:
means for selecting from a plurality of fixed pre-formed
transmit weight vectors, based on the receive beamforming
weight vectors.
84. A two-way communication system as defined in claim
81, wherein the transmit weight vector computation module
includes:
means for generating transmit weight vectors adaptively to
reflect as accurately as possible the characteristics of the
receive beamforming weight vectors, whereby downlink signals
are transmitted to the respective mobile devices with minimum
interference because a transmit weight vector associated with
a particular mobile device is selected to be practically

orthogonal to all of the generalized steering vectors
associated with transmissions to and from the other mobile
devices.
85. A method of radio direction finding (DF) using a
subarray of calibrated antennas, the method comprising the
steps of:
receiving signals from multiple sources, at an antenna array
of which only a small number of antenna elements are
calibrated;
separating the signals using a cumulant recovery (CURE)
system to generate the separated signals and estimates of
their generalized steering vectors; and
processing the estimated generalized steering vectors and
signals from the calibrated antenna elements, to obtain
accurate signal directions for the multiple sources.

Description

CA 02272930 1999-OS-25
WO 98124192 PCT/US96/18867
-1-
COCHANNEL SIGNAL PROCESSING SYSTEM
BACKGROUND OF THE INVENTION
s I. Field of the Invention
This invention relates generally to signal processing systems and, more
particularly, to apparatus and methods for receiving and processing signals
that share a
common receiver frequency band at the same time, referred to as cochannel
signals.
Even two signals transmitted on slightly separated frequency bands may be
"cochannel" signals as seen by a receiver operating to receive signals on a
bandwidth
that overlaps both of the signals. In a variety of signal processing
applications, there is
a need to recover information contained in such multiple, simultaneously
received
signals. In the context of this invention, the word "recover" or "recovery"
encompasses separation of the received signals, "copying" the signals (i.e.,
retrieving
j 5 any information contained in them), and, in some applications, combining
signals
received over multiple paths from a single source. The "signals" may be
electromagnetic signals transmitted in the atmosphere or in space, acoustic
signals
transmitted through liquids or solids, or other types of signals characterized
by a time
varying parameter, such as the amplitude of a wave. In accordance with another
aspect
of the invention, signal processing includes transmission of cochannel
signals.
In the environment of the present invention, signals are received by
"sensors." A sensor is an appropriately selected transducer for converting
energy
contained in the signal to a more easily manipulated form, such as electrical
energy. In
a radio communications application, electromagnetic signals are received by
antennas
2s and converted to electrical signals for further processing. After
separation of the
signals, they may be forwarded separately to transducers of a different type,
such as
loudspeakers, for converting the separated electrical signals into audio
signals. In some
applications, the signal content may be of less importance than the directions
from
which the signals were received, and in other applications the received
signals may not
3o be amenable to conversion to audible form. Instead, each recovered signal
may contain

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96118867
-2-
information in digital form, or may contain information that is best
understood by
displaying it on a chart or electronic display device. Regardless of the
environment in
which the present invention is employed, it is characterized by multiple
signals
received by sensors simultaneously at the same or overlapping frequencies, the
need to
separate, recover, identify or combine the signals and, optionally, some type
of output
transducer to put the recovered information in a more easily discernible form.
2. Description of Related Art
Separation and recovery of signals of different frequencies is a routine
t o matter and is handled by appropriate filtering of the received signals. It
is common
knowledge that television and radio signals are transmitted on different
frequency
bands and that one may select a desired signal by tuning a receiver to a
specific
channel. Separation and recovery of multiple signals transmitted at different
frequencies and received simultaneously may be effected by similar means,
using
multiple tuned receivers in parallel. A more difficult problem, and the one
with which
the present invention is concerned, is how to separate and copy signals from
multiple
sources when the transmitted signals are at the same or overlapping
frequencies. A
single sensor, such as an antenna, is unable to distinguish between two or
more
received signals at the same frequency. However, antenna array technology
provides
2o for the separation of signals received from different directions.
Basically, and as is well
understood by antenna designers, an antenna array can be electronically
"steered" to
transmit or receive signals to or from a desired direction. Moreover, the
characteristics
of the antenna array can be selectively modified to present "nulls" in the
directions of
signals other than that of the signal of interest. A further development in
the processing
of array signals was the addition of a control system to steer the array
toward a signal
of interest. This feature is called adaptive array processing and has been
known for at
least two to three decades. See, for example, a paper by B. Widrow, P.E.
Mantey,
L.J. Griffiths and B.B. Goode, "Adaptive Antenna Systems," Proceedings of the
IEEE, vol. 55, no. 12, pp. 2143-2159, December 1967. The steering
characteristics of
3o the antenna can be rapidly switched to receive signals from multiple
directions in a

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96118867
-3-
"time-sliced" manner. At one instant the antenna array is receiving a signal
from one
source and at the next instant, from a different source in a different
direction, but
information from the multiple sources is sampled rapidly enough to provide a
complete
record of all the received signals. It will be understood that, although
steered antenna
array technology was developed principally in the communications and radar
fields, it
is also applicable to the separation of acoustic and other types of signals.
In the communications field, signals take a variety of forms. Stated most
generally, a communication signal typically includes a carrier signal at a
selected
frequency, on which is impressed or modulated an information signal. There are
a
large number of different modulation schemes, including amplitude modulation,
in
which the amplitude of the signal is varied in accordance with the value of an
information signal, while the frequency stays constant, and frequency or phase
modulation, in which the amplitude of the signal stays constant while its
frequency or
phase is varied to encode the information signal onto the carrier. Various
forms of
t 5 frequency and phase modulation are often referred to as constant modulus
modulation
methods, because the amplitude or modulus of the signal remains constant, at
least in
theory. In practice, the modulus is subject to distortion during transmission,
and
various devices, such as adaptive equalizers, are used to restore the constant-
modulus
characteristic of the signal at a receiver. The constant modulus algorithm was
2o developed for this purpose and later applied to antenna arrays in a process
called
adaptive beam forming The following references are provided by way for
further.
background on the constant modulus algorithm:
B. Agee, "The least-squares CMA: a new technique for rapid correction
of constant modulus signals," Proc. ICASSP-86, pp. 953-956, Tokyo, Japan,
April
25 1986.
R. Gooch, and J. Lundell, "The CM array, an adaptive beamformer for
constant modulus signals," Proc. ICASSP-86, pp. 2523-2526, Tokyo, Japan, April
. 1986.
J. Lundell, and B. Widrow, "Applications of the constant modulus
3o adaptive algorithm to constant and non-constant modulus signals," Proc.
Twenty-

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-4-
Second Asilomar Conference on Signals, Systems, and Computers, pp. 432-436,
Pacific
Grove, CA, November 1988.
B.G. Agee, "Blind separation and capture of communication signals
using a mufti-target constant modulus beamformer," Proc. 1989 IEEE Military
Communications Conference, pp. 340-346, Boston, MA, October 1989.
R.D. Hughes, E.H. Lawrence, and L.P. Withers, Jr., "A robust
adaptive array for multiple narrowband sources," Proc. Twenty-Sixth Asilomar
Conference on Signals, Systems, and Computers, pp. 35-39, Pacific Grove, CA,
November 1992.
1o J.J. Shynk and R.P. Gooch, "Convergence properties of the multistage
CMA adaptive beamformer," Proc. Twenty-Seventh Asilomar Conference on Signals,
Systems, and Computers, pp. 622-626, Pacific Grove, CA, November 1993.
The constant modulus algorithm works satisfactorily only for constant
modulus signals, such as frequency-modulated (FM) signals or various forms of
phase-
shift keying (PSK) in which the phase is discretely or continuously varied to
represent
an information signal, but not for amplitude-modulated (AM) signals or
modulation
schemes that employ a combination of amplitude and phase modulation. There is
a
significant class of modulation schemes used known as M-ary quadrature
amplitude
modulation (QAM), used for transmitting digital data, whereby the
instantaneous phase
2o and amplitude of the carrier signal represents a selected data state. For
example, 16-ary
QAM has sixteen distinct phase-amplitude combinations. The "signal
constellation"
diagram for such a scheme has sixteen points arranged in a square matrix and
lying on
three separate constant-modulus circles. A signal constellation diagram is a
convenient
way of depicting all the possible signal states of a digitally modulated
signal. In such a
diagram, phase is represented by angular position and modulus is represented
by
distance from an origin.
The constant modulus algorithm has been applied with limited success to
a 16-ary QAM scheme, because it can be represented as three separate constant-
modulus signal constellations. However, for higher orders of QAM the constant
3o modulus algorithm provides rapidly decreasing accuracy. For suppressed-
carrier AM,

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-5-
the constant modulus approach fails completely in trying to recover cochannel
AM
signals. If there are multiple signals, the constant modulus algorithm yields
signals
with "cross-talk," i.e. with information in the two signals being confused.
For a single
AM signal in the presence of noise, the constant-modulus algorithm yields a
relatively
noisy signal.
Because antenna arrays can be steered electronically to determine the
directions of signal sources, it was perhaps not surprising that one well
known form
signal separator available prior to the present invention used direction
finding as its
basis. The approach is referred to as DF-aided copy, where DF means direction
1o finding. This is an open-loop technique in which steering vectors that
correspond to
estimated signal source bearings are first determined; then used to extract
waveforms
of received signals. However, the direction finding phase of this approach
requires a
knowledge of the geometry and performance characteristics of the antenna
array. Then
steering vectors are fed forward to a beamformer, which nulls out the unwanted
signals
t5 and steers one or more antenna beams) toward each selected source.
Prior to the present invention, some systems for cochannel signal
separation used direction-finding (DF)-beamforming. Such systems separate
cochannel
signals by means of a mufti-source (or cochannel) super-resolution direction
fording
algorithm that determines steering vectors and directions of arrival (DOAs) of
multiple
2o simultaneously detected cochannel signal sources. An algorithm determines
beam-
forming weight vectors from the set of steering vectors of the detected
signals. The
beamforming weight vectors are then used to recover the signals. Any of
several well-
known mufti-source super-resolution DF algorithms can be used in such a
system.
Some of the better known ones are usually referred to by the acronyms MUSIC
25 (MUltiple anal Ciassiflcation), ESPRIT (Estimation of Signal Parameters via
Rotational Invariance Techniques), Weighted Subspace Fitting (WSF), and Method
of
Direction Estimation (MODE).
MUSIC was developed in 1979 simultaneously by Ralph Schmidt in the
United States and by Georges Bienvenu and Lawrence Kopp in France. The Schmidt
3o work is described in R.O. Schmidt, "Multiple emitter location and signal
parameter

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-6-
estimation," Proc. RADC Spectrum Estimation Workshop, pp. 243-258, Rome Air
Development Center, Griffiss Air Force Base, NY, October 3-5, 1979. The
Bienvenu
work is described in G. Bienvenu and L. Kopp, "Principe de la goniometrie
passive
adaptative," Proc. Colloque GRETSI, pp. 106/1-106/10, Nice, France, May 1979.
MUSIC has been extensively studied and is the standard against which other
super-
resolution DF algorithms are compared.
ESPRIT is described in many publications in the engineering signal
processing literature and is the subject of United States Patent No. 4,750,147
entitled
"Method for estimating signal source locations and signal parameters using an
array of
to sensor pairs," issued to R.H. Roy III et al. ESPRIT was developed by
Richard Roy,
III, Arogyaswami Paulraj, and Prof. Thomas Kailath at Stanford University. It
was
presented as a super-resolution algorithm for direction finding in the
following series of
publications starting in 1986:
A. Paulraj, R. Roy, and T. Kailath, "A subspace rotation approach to
signal parameter estimation," Proc. IEEE, vol. 74, no. 4, pp. 1044-1045, July
1986.
R. Roy, A. Pauiraj, and T. Kailath, "ESPRIT - A subspace rotation
approach to estimation of parameters of cisoids in noise," IEEE Trans.
Acoust.,
Speech, and Signal Processing, vol. ASSP-34, no. 5, pp. 1340-1342, October
1986.
R.H. Roy, ESPRIT - Estimation of Signal Parameters via Rotational
2o Invariance Techniques, doctoral dissertation, Stanford University,
Stanford, CA, 1987.
R. Roy and T. Kailath, "ESPRIT - Estimation of signal parameters via
rotational invariance techniques," IEEE Trans. Acoust., Speech, and Signal
Processing, vol. ASSP-37, no. 7, pp. 984-995, July 1989.
B. Ottersten, R. Roy, and T. Kailath, "Signal waveform estimation in
sensor array processing," Proc. Twenty-Third Asilomar Conference on Signals,
Systems, and Computers, pp. 787-791, Pacific Grove, CA, November 1989.
R. Roy and T. Kailath, "ESPRIT - Estimation of signal parameters via
rotational invariance techniques," Optical Engineering, vol. 29, no. 4, pp.
296-313,
April 1990.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
MUSIC and ESPRIT both require the same "narrowband array
assumption," which is further discussed below in the detailed description of
the
invention, and both are modulation independent, a feature shared by all
cochannel
signal separation and recovery techniques that are based on the DF-beamforming
method.
ESPRIT calculates two N-by-N covariance matrices, where N is the
number of antenna elements, and solves a generalized eigenvalue problem
numerically
(instead of using a calibration table search, as MUSIC does). It does this for
every
block of input samples. MUSIC calculates a single N-by-N covariance matrix,
1o performs an eigendecomposition, and searches a calibration table on every
block of
input array samples (snapshots).
MUSIC and ESPRIT have a number of shortcomings, some of which are
discussed in the following paragraphs.
ESPRIT was successfully marketed based on a single, key advantage
over MUSIC. Unlike MUSIC, ESPRIT did not require array calibration. In ESPRIT,
the array calibration requirement was eliminated, and a different requirement
on the
antenna array was substituted. The new requirement was that the array must
have a
certain geometrical property. Specifically the array must consist of two
identical sub-
arrays, one of which is offset from the other by a known displacement vector.
In
2o addition, ESPRIT makes the assumption that the phases of received signals
at one sub-
array are related to the phases at the other sub-array in an ideal theoretical
way.
Another significant disadvantage of ESPRIT is that, although it purports
not to use array calibration, it has an array manifold assumption hidden in
the
theoretical phase relation between sub-arrays. "Array manifold" is a term used
in
antenna design to refer to a multiplicity of physical antenna parameters that,
broadly
speaking, define the performance characteristics of the array.
A well known difficulty with communication systems, especially in an
urban environment, is that signals from a single source may be received over
multiple
paths that include reflections from buildings and other objects. The multiple
paths may
3o interpose different time delays, phase changes and amplitude changes on the

CA 02272930 1999-OS-25
WO 98!24192 PCT/LTS96/18867
_g_
transmitted signals, rendering reception more difficult, and transmission
uncertain.
This difficulty is referred to as the multipath problem. It is one that has
not been '
adequately addressed by signal processing systems of the prior art.
Neither MUSIC nor ESPRIT can operate in a coherent multipath
environment without major added complexity. A related problem is that, in a
signal
environment devoid of coherent multipath, no DF-beamforming method can
separate
signals from sources that are collinear with the receiving array, i.e. signal
sources that
are in line with the array and have zero angular separation. Even in a
coherent
multipath environment, DF-beamforming methods like MUSIC and ESPRIT cannot
o separate and recover cochannel signals from collinear sources.
Another difficulty with ESPRIT is that it requires two antenna sub-
arrays and is highly sensitive to mechanical positioning of the two sub-
arrays, and to
the electromagnetic matching of each antenna in one sub-array with its
counterpart in
the other sub-array. Also ESPRIT requires a 2N-channel receiver, where N is
the
number of antenna elements, and is highly sensitive to channel matching.
Another significant drawback in both MUSIC and ESPRIT is that they
fail abruptly when the number of signals detected exceeds the capacity, N,
equal to the
number of antennas in the case of MUSIC, or half the number of antennas in the
case
of ESPRIT.
2o A fundamental problem with both MUSIC and ESPRIT is that they use
open-loop feed-forward computations, in which errors in the determined
steering
vectors are uncorrected, uncorrectable, and propagate into subsequent
calculations. As
a consequence of the resultant inaccurate steering vectors, MUSIC and ESPRIT
have
poorcross-talk rejection, as measured by signal-to-interference-plus-noise
ratio (SINR)
at the signal recovery output ports.
ESPRIT is best suited to ground based systems where its antenna
requirements are best met and significant computational resources are
available.
MUSIC has simpler antenna array requirements and lends itself to a wider range
of -
platforms, but also needs significant computational resources.

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96118867
-9-
Another limitation of most signal recovery systems of the prior art is
that they rely on first-order and second-order statistical moments of the
received signal
data. A moment is simply a statistical quantity derived from the original data
by
mathematical processing at some level. An average or mean value of the several
signals
received at a given time is an example of a first-order moment. The average of
the
squares of the signal values (proportional to signal powers) is an example of
a second-
order moment. Even if one considers just one signal and a noise component,
computing
the average of the sum of the squares produces a cross-term involving the
product of
signal and noise components. Typically, engineers have managed to find a way
to
o ignore the cross-term by assuming that the signal and the noise components
are
statistically independent. At a third-order level of statistics, one has to
assume that the
signal and noise components have zero mean values in order to eliminate the
cross-
terms in the third-order moment. For the fourth-order and above, the
computations
become very complex and are not easily simplified by assumptions. In most
prior art
signal analysis systems, engineers have made the gross assumption that the
nature of all
signals is Gaussian and that there is no useful information in the higher-
order moments.
Higher-order statistics have been long recognized in other fields and there is
recent
literature suggesting their usefulness in signal recovery. Prior to this
invention,
cumulant-based solutions have been proposed to address the "blind" signal
separation
2o problem, i.e. the challenge to recover cochannel signals without knowledge
of antenna
array geometry or calibration data. See, for example, the following
references:
J.-F. Cardoso, "Source separation using higher order moments," Proc.
ICASSP-89, pp. 2109-2112, Glasgow, Scotland, May 1989.
J.-F. Cardoso, "Eigen-structure of the fourth-order cumulant tensor with
2s application to the blind source separation problem," Proc. ICASSP-90, pp.
2655-2658,
. Albuquerque, New Mexico, April 1990.
J.-F. Cardoso, "Super-symmetric decomposition of the fourth-order
- cumulant tensor: blind identification of more sources than sensors," Proc.
ICASSP-91,
pp. 3109-3112, Toronto, Canada, May 1991.

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-10-
J.-F. Cardoso, "Higher-order narrowband array processing,"
International Signal Processing Workshop on Higher Order Statistics, pp. 121--
130, -
Chamrousse-France, 3uly 10-12, 1991.
J.-F. Cardoso, "Blind beamforming for non-Gaussian sources," IEE
Proceedings Part F, vol. 140, no. 6, pp. 362--370, December 1993.
P. Comon, "Separation of stochastic processes, " Proc. Vail Workshop
on Higher-Order Spectral Analysis, pp. 174--179, Vail, Colorado, USA, June
1989.
P. Comon, "Independent component analysis," Proc. of Intl. Workshop
on Higher-Order Statistics, pp. 111-120, Chamrousse, France, 1991.
P. Comon, C. Jutten, and J. Herault, "Blind separation of sources, part
II: problems statement," Signal Processing, vol. 24, no. 1, pp. 11-20, July
1991.
E. Chaumette, P. Comon, and D. Muller, "ICA-based technique for
radiating sources estimation: application to airport surveillance," IEE
Proceedings Part
F, vol. 140, no. 6, pp. 395--401, December 1993.
t5 Z. Ding, "A new algorithm for automatic beamforming," Proc. Twenty-
Fifth Asilomar Conference on Signals, Systems, and Computers, pp. 689-693,
Pacific
Grove, CA, November 1991.
M. Gaeta and J.-L. Lacoume, "Source separation without a-priori
knowledge: the maximum likelihood solution," Proc. EUSIPCO, pp. 621-624, 1990.
2o E. Moreau, and O. Macchi, "New self adaptive algorithms for source
separation based on contrast functions," Proc. IEEE SP Workshop on Higher-
Order
Statistics, pp. 2I5-219, Lake Tahoe, USA, June 1993.
P. Ruiz, and J.L. Lacoume, "Extraction of independent sources from
correlated inputs: a solution based on cumulants," Proc. Vail Workshop on
Higher
25 Order Spectral Analysis, pp. 146--151, Vail, Colorado, USA, June 1989.
E.H. Satorius, J.J. Mulligan, Norman E. Lay, "New criteria for blind
adaptive arrays," Proc. Twenty-Seventh Asilomar Conference on Signals,
Systems, and
Computers, pp. 633-637, Pacific Grove, CA, November 1993. -

CA 02272930 1999-OS-25
WO 98124192 PCT/US96118867
-11-
L. Tong, R. Liu, V. Soon, and Y. Huang, "Indeterminacy and
' identifiability of blind identification," IEEE Trans. Circuits and Systems,
vol. 38, pp.
499-509, May 1991.
L. Tong, Y. Inouye and R. Liu, "Waveform preserving blind estimation
of multiple independent sources," IEEE Trans. Signal Processing, vol. 41, no.
7, pp.
2461--2470, July 1993.
However, all of these approaches to blind signal recovery address the
static case in which a batch of data is given to a processor, which then
determines the
steering vectors and exact waveforms. These prior approaches do not have the
ability
1o to identify new sources that appear or existing sources that are turned
off. In addition,
previously proposed algorithms require multiple levels of eigendecomposition
of array
covariance and cumulant matrices. Their convergence to reliable solutions
depends on
the initialization and utilization of the cumulant matrices that can be
derived from array
measurements. Furthermore, previous cumulant-based algorithms have convergence
problems in the case of identically modulated sources in general.
Ideally, a system for receiving and processing multiple cochannel signals
should make use of statistics of the measurements, and should not need to rely
on
knowledge of the geometry or array manifold of the sensors, i.e., the array
calibration
data. Also, the system should be able to receive and process cochannel signals
2o regardless of their modulation or signal type, e.g. it should not be
limited to constant-
modulus signals. More generally, the ideal cochannel signal processing system
should
not be limited to any modulation properties, such as baud rate or exact center
frequency. Any system that is limited by these properties has only a limited
range of
source types that can be separated, and is more suitable for interference
suppression in
situations where the desired signal properties are well known. Another
desirable
property of the ideal cochannel signal receiving and processing system is that
it should
operate in a dynamic way, identifying new signal sources that appear and
identifying
- sources that disappear. Another desirable characteristic is a very high
speed of
operation allowing received signals to be processed in real time. As will
shortly

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-12-
become apparent, the present invention meets and exceeds these ideal
characteristics
for cochannel signal processing.
SUMMARY OF THE INVENTION
The present invention resides in a system or method for processing
cochannel signals received at a sensor array and producing desired recovered
signals or
parameters as outputs. In the context of this specification, "cochannel"
signals are that
overlap in frequency, as viewed from a receiver of the signals. Even signals
that are
to transmitted in separate, but closely spaced, frequency bands may be
cochannel signals
as viewed from a receiver operating in bandwidth wide enough to overlap both
of the
signals. A key aspect of the invention is that it is capable of separating and
recovering
multiple cochannel signals very rapidly using only sensor array signals,
without
knowledge of sensor array geometry and array manifold, (e.g. array calibration
data),
~5 and without regard to the signal type or modulation. If array calibration
data are
available, the system also provides direction-of-arrival parameters for each
signal
source. The invention inherently combines coherent multipath components of a
received signal and as a result achieves improved performance in the presence
of
multipath. One embodiment of the invention also includes a transmitter, which
makes
2o use of estimated generalized steering vectors generated while separating
and recovering
received signals, in order to generate appropriate steering vectors for
transmitted
signals, to ensure that transmitted signals intended for a particular signal
source
traverse generally the same path or paths that were followed by signals
received from
the same signal source.
25 Briefly, and in general terms, the system of the invention comprises a
signal receiving system, including means for generating a set of conditioned
receiver
signals from cochannel signals of any modulation or type received at a sensor
array
from multiple sources that can vary in power and location; an estimated
generalized -
steering vector (EGSV) generator, for computing for each source an EGSV that
results
3o in optimization of a utility function that depends on fourth or higher even-
order

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-13-
statistical cumulants derived from the received signals, the EGSV being
indicative of a
combination of signals received at the sensors from a signal source; and a
supplemental
computation module, for deriving output quantities of interest from the
conditioned
receiver signals and the EGSVs.
The basic invention as described in the preceding paragraph employs
one of three basic methods for computing EGSVs: two iterative methods and one
direct
computation method. In the first iterative method, the system includes a
linear
combiner, for repeatedly computing a single channel combined signal from the
conditioned receiver signals and an EGSV; means for supplying an initial EGSV
to the
linear combiner, to produce the initial output of a single channel combined
signal; an
EGSV computation module, for computing successive values of the EGSV from
successive values of the single channel combined signal received from the
linear
combiner and the conditioned receiver signals; and means for feeding the
successive
values of the EGSV back to the linear combiner for successive iteration
cycles. Also
included is means for terminating iterative operation upon convergence of the
EGSV to
a sufficiently accurate value.
If the second iterative method is used, the system includes a cross-
cumulant matrix computation module, for generating a matrix of cross-cumulants
of all
combinations of the conditioned receiver signals; a structured quadratic form
2o computation module, for computing successive cumulant strength functions
derived
from successive EGSVs and the cross-cumulant matrix; means for supplying an
initial
EGSV to the structured quadratic form computation module, to produce the
initial
output of a cumulant strength function; an ESGV computation module, for
generating
successive EGSVs from successive cumulant strength functions received from the
structured quadratic form computation module; means for feeding the successive
values of the EGSV back to the structured quadratic form computation module
for
successive iteration cycles; and means for terminating iterative operation
upon
convergence of the EGSV to a sufficiently accurate value.
Finally, if the direct computation method is used, the system includes a
3o cross-cumulant matrix computation module, for generating a matrix of cross-
cumulants

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-14-
of all combinations of the conditioned receiver signals; and an EGSV
computation
module for computing the EGSV directly from the cross-cumulant matrix by
solving a
fourth degree polynomial equation.
Regardless which of the foregoing variants is employed, signal
processing may employ one of several different cumulant recovery (CURE)
techniques.
In a first of these techniques, the means for generating the set of
conditioned signals
includes a covariance matrix computation module, an eigendecomposition module
for
generating the eigenstructure of the covariance matrix and an estimate of the
number of
signal sources, and a transformation matrix for conditioning the receiver
signals. An
1o EGSV generator then employs signals output by the eigendecomposition module
to
compute EGSVs. This technique is referred to in this specification as the
eigenCURE
or eCURE system.
An alternate processing technique uses covariance inversion of the
received signals and is referred to as the CiCURE system. In this approach,
the means
t5 for generating the set of conditioned signals includes a covariance matrix
computation
module and a matrix decomposition module, for generating the inverse
covariance
matrix and a transformation matrix for conditioning the receiver signals. An
EGSV
generator then employs signals output by the eigendecomposition module to
compute
EGSVs. The system further includes a beamformer, for generating a recovered
signal
2o from the receiver signals by using the EGSV(s) and the matrix obtained from
the
matrix decomposition module.
Yet another processing technique is referred to as pipelined cumulant
recovery, or pipeCURE. The means for generating the set of conditioned signals
includes a covariance matrix computation module, an eigendecomposition module
for
25 generating an estimate of the number of signal sources, a transformation
matrix for
conditioning the receiver signals, and an eigenstructure derived from the
receiver
signals. Again, the EGSV generator employs signals output by the
eigendecomposition
module to compute EGSVs. Processing is on a block-by-block basis, and the
system
further comprises a multiple port signal recovery unit, including means for
matching

CA 02272930 1999-OS-25
WO 98/24192 PCT/(TS96/18867
-15-
current EGSVs with EGSVs from a prior data block to impose waveform continuity
from block to block.
Another variant that can be used in any of these processing techniques
involves the manner in which initial EGSVs are computed at the start of
processing a
new block of data. In accordance with this aspect of the invention, the
initial values of
EGSVs for each new processing block are computed by combining a prior block
EGSV
and a cumulant vector derived from the utility function used in the EGSV
generator.
More specifically, the means for combining takes the sum of the prior block
EGSV
multiplied by a first factor, and the cumulant vector multiplied by a second
factor. The
1 o first and second factors may be selected to provide an initial EGSV that
anticipates and
compensates for movement of a signal source.
In a practical embodiment of the invention, the system functions to
separate a plurality (P) of received cochannel signals. If the first iterative
method is
employed, there are multiple EGSV generators (P in number), including P EGSV
~ 5 computation modules and P linear combiners, for generating an equal
plurality (P) of
EGSVs associated with P signal sources. The supplemental computation module
functions to recover P separate received signals from the P generalized
steering vectors
and the conditioned receiver signals. More specifically, the supplemental
computation
module includes a recovery beamformer weight vector computation module, for
2o generating from all of the EGSVs a plurality {P) of receive weight vectors,
and a
plurality {P) of recovery beamformers, each coupled to receive one of the P
receive
weight vectors and the conditioned receiver signals, for generating a
plurality (P) of
recovered signals.
For recovery of multiple signals using the second iterative method, there
25 is a plurality (P) of EGSV generators, including P EGSV computation modules
and P
structured quadratic form computation modules, for generating an equal
plurality (P) of
EGSVs associated with P signal sources. Again, the supplemental computation
module
- includes a recovery beamformer weight vector computation module, for
generating
from all of the EGSVs a plurality (P) of receive weight vectors, and a
plurality (P) of

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-16-
recovery beamformers, each coupled to receive one of the P receive weight
vectors and
the conditioned receiver signals, for generating a plurality (P) of recovered
signals.
If the direct processing method is used to separate two signals, the
ESGV computation module generates two EGSVs from the cross-cumulant matrix
data;
and the supplemental computation module functions to recover two separate
received
signals from the two generalized steering vectors and the conditioned receiver
signals.
The supplemental computation module includes a recovery beamformer weight
vector
computation module, for generating from both of the EGSVs two receive weight
vectors, and two recovery beamformers, each coupled to receive one of the
receive
to weight vectors and the conditioned receiver signals, for generating two
recovered
signals .
Although the system of the invention operates in a "blind" sense,
without knowledge of the geometry or calibration data of the sensor array, it
will also
function as a direction finder if array calibration data are available. Hence,
in one
embodiment of the invention, the system functions to derive the direction of
arrival
(DOA) of a received signal; and the supplemental computation module includes a
memory for storing sensor array calibration data, and means for deriving the
DOA of a
received signal from its associated steering vector and the stored sensor
array
calibration data. More specifically, the sensor array calibration data
includes a table
2o associating multiple DOA values with corresponding steering vectors; and
the means
for deriving the DOA includes means for performing a reverse table lookup
function to
obtain an approximated DOA value from a steering vector supplied by the
generalized
steering vector generator. The means for deriving the DOA may also include
means for
interpolating between two DOA values to obtain a more accurate result.
In another important embodiment of the invention, the supplemental
computation module of the signal processing system also includes a
transmitter, for
generating transmit signal beamformer weights from the received signal
beamformer
weights, and for transmitting signals containing information in a direction
determined _
by the transmit signal beamformer weights.

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-17-
Other aspects of the invention pertain to various application of the basic
- cumulant recovery (CURE) signal processing engine described above. Some of
these
applications are summarized in the following paragraphs.
An important application of the invention is in two-way radio
communication. Because CURE processing generates an estimated generalized
steering
vector not necessarily for each received signal, but for each signal source,
the
invention provides an important benefit when used in multipath conditions.
Signals
reaching a receiving antenna array over multiple paths will be combined in the
CURE
system if the received components are coherent, and the resultant generalized
steering
to vector represents the combined effect of all the coherent multipath signals
received at
the antenna. This feature has a number of advantages. First, a radio receiving
system
using the CURE system is inherently immune to multipath problems encountered
by
conventional receivers. Second, by using generalized steering vectors, there
can be an
associated generalized null in the antenna directivity pattern, which can be
used to null
out an interfering signal having multipath structure in favor of a cochannel
signal from
another source. Third, the signal recovery method provides a diversity gain in
the
presence of multipath components, such that a stronger combined signal is
received as
compared with a system that discards all but one component. Fourth, the
generalized
steering vector concept allows multiple cochannel signals to be received and
2o transmitted in the presence of multipath effects. Fifth, cochannel signal
sources that are
collinear with the receiver sensor array can be received and separated if
there are
multipath components.
In another aspect of the invention, the CURE signal separation system
can be used to separate signals transmitted in different modes over a
"waveguide," by
which is meant any bounded propagation medium, such as a microwave waveguide,
an
optical waveguide, a coaxial cable, or even a twisted pair of conductors.
Although the
transmission modes may become mixed in the waveguide, the original signals are
- easily recovered in the CURE system.
In still another aspect of the invention, the CURE signal separation
3o system can be used to separate signals recorded on closely space tracks on
a recording

CA 02272930 2003-05-09
I8
medium. Crosstalk between the signals on adjacent tracks is eliminated by
using the
CURE system to effect recovery.
In yet another aspect of the invention, the CURE signal separation system
can be used to extend the effective dynamic range of a receiver system.
In a further aspect of the invention, the CURE signal separation system
can be used to perform a complex phase equalization function automatically,
without
knowledge of the amount of phase correction that is needed.
The CURE system may be modified to compensate for moving signal
sources, and may also be modified to handle a wideband signal separation
problem. The
1o wideband signal separator includes multiple narrowband CURE systems, means
for
decomposing a wide band of signals into multiple narrowbands for processing,
and
means for combining the narrow bands again.
Accordingly, in one aspect the invention provides a signal-processing
system for deriving at least one output quantity of interest from received
cochannel input
signals. The system comprises a signal-receiving system, including means for
generating
a set of conditioned-receiver signals from received signals of any modulation
or type. An
estimated generalized steering vector (EGSV) generator is provided for
computing an
EGSV that results in optimization of a utility function that depends on fourth
or higher
even-order statistical cumulants derived from the received signals. The EGSV
is
2o indicative of a combination of signals received at the signal-receiving
system from a
signal source. A supplemental computation module is provided for deriving at
least one
output quantity of interest from the conditioned-receiver signals and the
EGSV.
The invention also contemplates a method for processing cochannel
signals received at a sensor array. The method comprises conditioning a set of
signals
received at a sensor array from multiple sources that can vary in power and
location, and
generating for each source an estimated generalized steering vector (EGSV)
that results
in optimization of a utility function that depends on fourth or higher even-
order statistical
cumulants derived from the received signals. The EGSV is indicative of a
combination
of signals received at the sensors from a signal source. Supplemental
computation is

CA 02272930 2003-05-09
18a
performed to derive output quantities of interest from the conditioned-
receiver signals
and the EGSVs.
In another aspect, the invention also provides a method for recovery and
separation of multiple cochannel signals of any modulation or type received at
an array of
sensors. The method comprises receiving a plurality of cochannel signals from
separate
signal sources at an array of sensors, preprocessing the received signals to
provide
preprocessed signals, and coupling the preprocessed signals to a plurality of
signal-
extraction ports, each of which is in one of two states referred to as an
active state and an
inactive state. In association with each signal-extraction port in the active
state, an
estimated steering vector and a recovered signal corresponding to one of the
signal
sources are generated, without regard for manifold data of the sensor array.
The
estimated steering vectors are orthogonalized to ensure that each signal-
extraction port
generates a recovered signal for a separate signal source. The steps of
orthogonalizing
and generating recovered signals are controlled to ensure an orderly
association of signal
sources with signal-extraction ports.
Another aspect of the invention further provides a two-way
communication system using cochannel signals and diversity path multiple
access
(DPMA) for transmission in both directions. The system comprises at least one
receiver/transmitter base station for communicating with a plurality of mobile
devices
having omnidirectional antennas for transmitting uplink signals at an assigned
frequency,
and for receiving downlink signals at another assigned frequency. The
receiver/transmitter base station includes a receive antenna array, and a
plurality of
estimated generalized steering vector (EGSV) generators for computing for each
mobile
device an EGSV that results in optimization of a utility function that depends
on fourth or
higher even-order statistical cumulants derived from the received signals. The
EGSV is
indicative of a combination of uplink signals received at the receive-antenna
array from
the mobile device over possible multiple paths. Receiver processing means
generates,
from the EGSVs, a recovered signal corresponding to each uplink signal from a
mobile
device, and a receive beamforming weight vector corresponding to the uplink
signal. A
transmitter includes means for generating, from each receive beamforming
weight vector,

CA 02272930 2003-05-09
18b
a corresponding transmit beamforming weight vector, and a modulator modulates
a
downlink transmission signal with a desired information signal. A transmit-
antenna array
is coupled to the transmitter and has a similar geometrical shape as the
receive antenna
array, wherein downlink transmission signals intended for a particular mobile
device are
propagated along generally the same multiple paths as the received uplink
signals from
the same mobile device. Coherent uplink signals received over multiple paths
from the
same mobile device are automatically combined, providing a gain enhancement
effect
that allows weaker transmissions to be detected. Downlink signals transmitted
over the
same multiple paths also benefit from the gain enhancement effect and provide
a stronger
1 o downlink signal to the mobile device.
Other aspects and advantages of the invention will become apparent from
the following more detailed description, taken together with the accompanying
drawings.
BRIEF DESCRIPTION OF THE DRAWINGS
FIG. 1 is a taxonomy diagram depicting the interrelationships of the
invention's various cochannel signal processing methods.
FIG. 2A is a block diagram of the cumulant recovery (CURE) system of
the invention in general form, depicting a first iterative method.
2o FIG. 2B is a block diagram similar to FIG. 2A, but depicting a second
iterative method.
FIG. 2C is a block diagram similar to FIG. 2A, depicting a direct
computation method.
FIG. 3A is a block diagram similar to FIG. 2A, but modified to depict how
the invention functions to separate multiple received cochannel signals.
FIG. 3B is a block diagram similar to FIG. 3A, but depicting the first
iterative method.

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-19-
FIG. 3C is a block diagram similar to FIG. 3A, but depicting the direct
computation method.
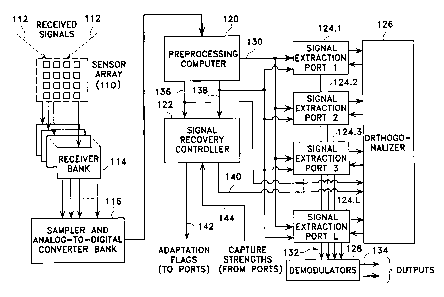
FIG. 4A, is a block diagram of a supplemental computation module for
signal recovery, shown in FIGS. 3A, 3B and 3C.
FIG. 4B is a block diagram of a supplemental computation module for
use in conjunction with the system of FIGS. 2A, 2B or 2C, to provide a
direction
fording function.
FIG. 5 is a block diagram similar to FIG. 2A, but modified to depict a
receiver/transmitter function.
1o FIG. 6 is a block diagram similar to FIG. 3A, but modified to show
input of signals from a signal "waveguide."
FIG. 7 is a block diagram showing in more detail the functions
performed in accordance with the two iterative methods for cochannel signal
separation
and .recovery.
FIG. 8A is simplified block diagram of a cochannel signal recovery
system in accordance with the present invention.
FIG. 8B is a hardware block diagram similar to FIG. 8A, of one
preferred embodiment of the invention.
FIG. 9 (comprising FIGS. 9A and 9B) is another block diagram of the
2o system of FIG. 7, with some of the subsystem functions recited in each of
the blocks.
FIG. 10 is a block diagram of the preprocessor computer of FIG. 7.
FIG. 11 (comprising FIGS. 11A and 11B) is a block diagram of a signal
extraction port in an active state.
FIG. 12 is a block diagram of the multiple port recovery unit of FIG. 9,
including multiple signal extraction ports and an orthogonalizer.
FIG. 13 (comprising FIGS. 13A, 13B and 13C) is a block diagram of
the signal recovery controller of FIG. 7.
FIG. 14 is a block diagram of a signal extraction port in the inactive
state.

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/LTS96118867
-20-
FIG. 15 is a block diagram of signal recovery system using covariance
inversion cumulant recovery (CiCURE).
FIG. 16 is a block diagram of a signal extraction port in the active state
using the CiCURE system illustrated in FIG. I5.
FIG. 17 is a block diagram of an alternate embodiment of the invention
referred to as pipeCURE.
FIG. 18 is a schematic diagram depicting a processing difficulty
associated with moving signal sources.
FIGS. 19 and 20 are vector diagrams depicting the effect of using
to a-~iCURE and uCURE updating to initialize a block of samples for eCURE
processing
in the moving source situation such as shown in FIG. 18.
FIG. 21 is a schematic diagram showing an overload condition in which
there are more signal sources that antenna elements.
FIG. 22 is a diagram of an antenna array directivity pattern for handling
t 5 the situation shown in FIG. 21.
FIG. 23 is a schematic diagram depicting multipath propagation paths
from a transmitter to a receiver array.
FIG. 24 is a schematic diagram depicting how the system of the
invention handles coherent multipath signals in the presence of interference.
2o FIG. 25 is a schematic diagram depicting how the system of the
invention handles non-coherent multipath signals in the presence of
interference.
FIG. 26 is a schematic diagram depicting how the system of the
invention handles receiving a desired signal in the presence of an
interference signal
with multipath components and a second interference source.
25 FIG. 27 is a schematic diagram depicting the invention as used in the
recovery of a received signal in the presence of a strong local transmitter.
FIG. 28 is a schematic diagram depicting the invention as used in the
recovery of a weak received signal in the presence of a strong jamming signal
located
nearby .

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-21-
FIG. 29 is a schematic diagram depicting portions of a cellular telephone
communication system of the prior art.
FIG. 30 is a schematic diagram depicting how a communication system
of the prior art separates cochannel signals.
FIG. 31 is a schematic diagram depicting how the present invention
operates in the environment of a cellular telephone communication system.
FIG. 32 is a block diagram showing major portions of a transmitter as
used in conjunction with the system of the present invention.
FIG. 33 is a block diagram showing a transmitter similar to the one in
to FIG. 32, but with more detail of some aspects of the apparatus.
FIGS. 34A and 34B are diagrams depicting operation of the invention in
recovery of dual-polarized signals.
FIG. 35 is a schematic diagram depicting the invention as used in
conjunction with an optical fiber network.
~5 FIG. 36 is a schematic diagram depicting the invention as used in copy-
aided direction finding.
FIG. 37 is a schematic diagram depicting the invention as used in
extending the dynamic range of a receiver.
FIG. 38 is a schematic diagram depicting the invention as used in disk
2o recording system.
FIG. 39 is a schematic diagram depicting the invention as used to effect
automatic phase rotation equalization of a QAM signal.
FIG. 40A is a signal constellation diagram for a QAM system with four
amplitude-phase states by way of illustration.
25 FIG. 40B is a diagram similar to FIG. 40A, showing a phase rotation of
0 as a result of propagation of the signal to the receiver.
FIG. 41 is a block diagram showing extension of the cumulant recovery
- system of the invention to cover a wide frequency band.

CA 02272930 1999-OS-25
WO 98/24192 PCT/LJS96/18867
-22-
DESCRIPTION OF THE PREFERRED EMBODIMENTS
1.0 Introduction:
Because the present invention encompasses a number of different but
related concepts and applications, and because the key signal processing
concepts of the
invention can be implemented in several different embodiments, this detailed
description is divided into sections and subsections, each of which covers a
different
specific embodiment or practical application of the invention. The following
is a table
of contents of this description of the preferred embodiments:
1.0 Introduction
2.0 Overview of the Concept of the Invention
2.1 Signal Separation Concept
2.2 Signal Separation Concept in the Multipath Environment
2.3 Direction Finding Concept
2.5 Transmitter/Receiver Concept
2.6 Concept of Separation of Signals in a "Waveguide"
3.0 Preferred Embodiment Using EigenCumulant Recovery {eCURE)
System
3.1 Overview and System Hardware
3.2 Preprocessing
3.3 Operation of an Active Signal Extraction Port
3.4 The Signal Recovery Controller
3.5 The Orthogonalizer
3.6 Operation at an Inactive Port
4.0 Alternate Embodiment Using Covariance Inversion Cumulant Recovery
(CiCURE) System
5.0 Alternate Embodiment Using Pipelined Cumulant Recovery (pipeCURE)
System
5.1 Overview of the pipeCURE Signal Separator

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-23-
5.2 Preprocessor Unit
- 5.3 Cumulant Matrix Computer
5.4 Multiple Port Signal Recovery Unit
6.0 Steering Vector Tracking Method for Situations Having Relative Motion
7.0 Alternate Embodiment Using Direct Computation
8.0 Separation Capacity and Performance When Overloaded
9.0 Performance of the Invention in the Presence of Multipath
9.1 Performance Against Coherent Multipath
9.2 Performance Against Noncoherent Multipath
to 9.3 Performance Against Mixtures of Coherent and Noncoherent
Multipath
10.0 Signal Recovery in the Presence of Strong Interfering
Signals
11.0 Diversity Path Multiple Access (DPMA) Communication
11.1 History and Prior Art of Multiple Access
Communication
11.2 A New Method of Multiple Access Communication
12.0 Application to Two-Way Wireless Communication
Systems
12.1 Transmit Beamfbrming
13.0 Application to Recovery of Multimode Signals
14.0 Application to Separation of Signals Transmitted
Over "Waveguide"
15.0 Application to Radio Direction Finding
16.0 Application to Extending the Dynamic Range of
Receiving Systems
17.0 Application to High Density Recording
18.0 Application to Complex Phase Equalization
19.0 Extension to Wideband Signal Separation
19.1 Partitioning Wideband Measurements to Narrowbands
19.2 Signal Separation in Narrowbands
19.3 Combining Narrowbands
- 20.0 Conclusion

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-24-
2.0 Overview of the Concept of the Invention:
The present invention resides in a system and method for processing
signals received by a sensor receiving system having an array of sensor
elements. The
system is capable of receiving and processing a signal from a single source,
and for
purposes of explanation the system will sometimes be described as receiving
and
processing just one signal. It will, however, shortly become clear that the
system is
capable of, and best suited for, receiving and processing signals from
multiple sources,
and that the multiple signals may utilize overlapping signal frequency bands
as viewed
at the receiver, i.e. they may be cochannel signals. As discussed above in the
to "background of the invention" section, detection and processing of
cochannel signals
presents difficulties that have not been adequately addressed by signal
processing
systems of the prior art.
One central concept that makes the various aspects of overall invention
possible is the ability to determine accurate estimates of generalized
steering vectors of
the source signals incident on a sensor array or, more generally, estimates of
the linear
combinations that represent the relative amplitudes of the source signals in
each
channel of a multichannel signal stream. The meaning of the term "generalized
steering
vector" will become better understood as this description proceeds. A
definition for
present purposes is that the generalized steering vector associated with a
particular
2o signal source represents the weighted sum of ordinary steering vectors
corresponding
to all multipath components of signals from that source. An ordinary steering
vector is
the value of the array manifold at a single angle corresponding to a source's
DOA.
Multipath components arise when a signal from a single source reaches a
receiver over
multiple propagation paths.
The invention encompasses three distinct methods for determining
estimates of the generalized steering vectors of source signals. FIG. 1
illustrates the
taxonomy and relationships among the methods. Two of the methods for
determining
the estimated generalized steering vectors (EGSVs) involve iterative
computations.
The first of these, indicated by reference numeral 10, is called the "beamform
- cross-
3o cumulant" method. In this method, an initial EGSV is iteratively updated
and

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-25-
improved by a method that involves using the initial EGSV as a complex weight
vector
- in a linear beamformer that operates on sensor signals (i.e., signal
measured at a sensor
array, to be discussed shortly with reference to other drawing figures). Cross-
cumulants are computed, specifically between the output signal from the
beamformer
used in this method and each of the beamformer's input signals.
The term "cumulant" is defined more completely in later sections of this
specification, but for purposes of this general discussion it is sufficient to
note that
cumulants are fourth-order (or higher even-order) statistical moments of the
received
signals. The cross-cumulants are formed into a vector which, upon
normalization,
1o becomes the next EGSV. This iteration cycle is repeated until convergence
is attained,
based on a predefined convergence test or on a selected number of iteration
cycles.
Upon convergence, the EGSV will have converged to the generalized steering
vector of
one of the incident source signals.
The second iterative method for obtaining EGSVs is referred to as the
t5 "C- matrix" method and is indicated at 12 in FIG. 1. In this method, a
particular
matrix of cross-cumulants among the sensor signals is calculated first, before
the
iterative process starts. There are no subsequent calculations of cumulants
within the
iterative cycle. Instead, an initial EGSV is used to calculate a structured
quadratic
form, which yields a quantity called "cumulant strength." The EGSV is adjusted
to
2o maximize the cumulant strength by means of an iterative optimization
procedure. Upon
convergence, the EGSV will have converged to the generalized steering vector
of one
of the incident source signals.
The third method of fording the EGSVs is non-iterative. It is referred to
as the "direct computation" or "analytic" method and is indicated at 14 in
FIG. 1. This
25 method can only recoverup to two incident signals, but is unrestricted as
to the number
of sensor array elements or processing channels. The method first computes the
same
matrix of cross-cumulants among the sensor signals as is used in the second
iterative
- method. However, a fourth degree polynomial equation is solved instead of
optimizing
a structured quadratic form. The solutions to the fourth degree polynomial
yield the
3o final EGSVs directly without iteration.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-26-
In addition to the three methods for generating the EGSVs of the source
signals, the present invention has three alternative basic algorithmic
structures on
which the preferred embodiments of the invention are based. FIG. 1 shows
diagrammatically that the EGSVs generated by either of the three methods (10,
12 or
14) are coupled over line 16 to a selected one of three algorithmic structures
18,
referred to as CiCURE, eCURE, and pipeCURE. As will be further explained
below,
the acronym CURE stands for cumulant recovery. The terms CiCURE, eCURE and
pipeCURE refer to specific embodiments of the invention known as covariance
inversion CURE, eigenCURE and pi~elined CURE, respectively. Each structure
to encompassed by the block 18 in FIG. I can employ any of the three methods
(i0, 12 or
14) described above for determining the source signal EGSVs.
By way of example, a subsequent section of this specification (Section
3.0) describes a preferred embodiment consisting of the eCURE algorithmic
structure
and the beamform - cross-cumulant method. Another section (Section 5.0)
details a
preferred embodiment consisting of the pipeCURE structure and the C-matrix
method.
However, all other combinations are possible and may be preferable depending
on the
specific engineering application.
The algorithmic structures (18) are described below in subsequent
descriptive sections as processing input samples in a "batch processing" mode,
meaning
2o that sampled data from the sensor signals are grouped into blocks of
samples, which
are then processed one block at a time. The block size is arbitrary and is not
W tended
to limit the scope of the present invention. For example, the block size can
be as small
as one, in which case, the batch mode reduces trivially to "sample-by-sample"
processing.
In some situations, the EGSVs of the source signals vary with time, due,
for example, to changing geometric relationships among the locations of the
sources,
the receiving sensor array, or multipath reflectors. For such situations, two
methods
are presented for determining the initial EGSVs for each block of samples.
These
methods incorporate a technique known as a-(3 tracking into the block
initialization
3o process and thereby make the acquisition, capture, separation, and recovery
of source

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-27-
signals more stable when any of the sources or the receive sensor array is
moving.
- Two block initialization methods are presented for this purpose and are
called a-
(3CURE and CURE. As indicated by block 19 in FIG. 1, these two methods are
applicable to any of the basic algorithmic structures 18.
FIG. 2A shows the system of the present invention in general form,
employing the first iterative method referred to above as the beamform - cross-
cumulant method. The system includes four principal components: a sensor
receiving
system 20, an estimated generalized steering vector (EGSV) computation module
22, a
supplemental computation module 24 and a linear combiner 26.
t o The sensor receiving system 20 includes components not shown in
FIG. 2A, but which will be discussed in more detail below, including an array
of
sensors to convert incident signals into electrical form, and some form of
signal
conditioning circuitry. In each of the embodiments and applications of the
invention,
incident signals 27 are sensed by the sensor receiving system 20 and, after
appropriate
~5 processing, the supplemental processing module 24 generates desired output
signals or
parameters as needed for a specific application of the invention. For example,
in a
signal separation application, the output signals will be the reconstructed
cochannel
signals received from separate signal sources. An important aspect and
advantage of
the invention is that the received signals may be of any modulation or type.
2o A key component of the signal processing system of the invention is the
estimated generalized steering vector (EGSV) computation module 22, which
receives
the conditioned received signals over line 28 from the sensor receiving system
20, and
computes an EGSV from the conditioned signals. The EGSV, in accordance with
the
invention, results in optimization of a utility function that depends on
fourth or higher
25 even-order statistical cumulants derived from the received signals. At this
point in the
description, cumulants have not yet been defined, but they are discussed in
Section 4Ø
For the present, it is sufficient to note that cumulants are fourth-order (or
higher even-
order) statistical moments of the received signals.
The EGSV computation module 22 functions in an iterative manner in
so cooperation with the linear combiner 26. The linear combiner 26 begins a
first iteration

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-28-
with an initial EGSV, indicated at 30, which may be an estimate or simply a
random
initial vector quantity. The linear combiner 26 then combines the received
signals on
line 28 with the initial EGSV and generates a single-channel combined signal
on line 32
to the EGSV computation module 22. The latter performs its cumulant
computation and
s generates a revised EGSV, which is fed back to the linear combiner 26 over
line 34.
The iterative process continues until the EGSV has converged to an
appropriately
accurate solution, which is output to the supplemental computation module 24
over line
36. The output on line 36 is also referred to as an estimated generalized
steering
vector, which closely approximates the actual generalized steering vector and
represents the weighted sum of ordinary steering vectors corresponding to all
multipath
components of signals from a source. Where no multipath components are
present, the
generalized steering vector reduces to an ordinary steering vector for the
source.
However, the term "generalized" steering vector is used frequently in this
specification, to convey the meaning that the steering vector generated
automatically
~ s and dynamically takes into account the possibility of receiving a signal
over multiple
paths.
The function of the supplemental computation module 24 depends on the
specific application of the invention. This module makes use of the
conditioned
received signals on line 28 and the generalized steering vector on line 36,
and
2o generates the desired output signal or parameters on output line 38.
It should be understood that the components shown in FIG. 2A, and in
particular the EGSV computation module 22 and the linear combiner 26, function
to
generate a single estimated generalized steering vector on line 36,
corresponding to a
single signal source from which signals are received at the sensor receiving
system 20.
25 In a number of applications, as will be further described, multiple linear
combiners 26
and multiple EGSV computation modules 22 will be needed to separate signals
from
multiple sources. Similarly, in most applications the supplemental computation
module
24 must also be replicated, at least in part, to generate multiple desired
output signals.
Another aspect of FIG. 2A to keep in mind is that it is an imperfect
3o attempt to depict a number of the invention's many possible forms in a
single

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-29-
conceptual diagram. The concept of the generalized steering vector is central
to all
- forms of the invention. The estimated generalized steering vector (EGSV)
provides a
means for tracking sources through time free of discontinuity. The estimated
generalized steering vector computational module, 22 in FIG. 2A, may be
partially
merged with the supplemental computation module 24 or the order of computation
modified to accommodate physical implementation. This is true in the case of a
specific
implementation of a signal recovery system, described subsequently, in which
recovered signals are generated as outputs of the supplemental computation
module 24.
An important aspect of the invention is that the EGSV computation
t o module 22, or multiple modules in some embodiments, compute estimated
generalized
steering vectors extremely rapidly, either by direct computation or by an
iterative
process that converges superexponentially. Moreover, each EGSV represents the
weighted sum of steering vectors associated with multipath components derived
from a
single signal source. As will be described in the next descriptive subsection,
multiple
EGSVs can be conveniently processed to reconstruct and separate signals from
multiple
signal sources.
As the description of the various embodiments proceeds, it will become
apparent that certain components of the invention are common to many
applications. In
terms of the components shown in FIG. 2A, the common components include the
2o EGSV computation module 22, the linear combiner 26 and signal conditioning
portions
of the sensor receiving system 20. Accordingly, in many instances it would be
advantageous to fabricate these components as a monolithic semiconductor
device or
chip, to be mounted in close association with other components in the
supplemental
computation module 24, which vary by application. Alternatively, a set of
semiconductor chips could include various embodiments of the supplemental
computation module 24, such as for signal separation, direction finding and so
forth.
FIG. 2B illustrates the form of the invention that uses the second
iterative method (12, FIG. 1), called the C-matrix method, for generating
EGSVs. It
will be observed that the figure is similar to FIG. 2A, except that there is
no linear

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96118867
-30-
combiner. Instead there is a cross-cumulant matrix computation module 40 and a
structured quadratic form computation module 42.
The cross-cumulant computation module 40 receives conditioned sensor
signals over line 28 from the sensor receiving system 20, computes the cross-
cumulants
s of all combinations of the sensor signals and stores the results in a matrix
having a
particular mathematical structure. This matrix of cross-cumulants, denoted C,
has
dimensions PZxP2, where P is the number of signal sources, and is stored for
subsequent computations. This C matrix is computed before any iterative
computations
are performed, and it will be noted that the EGSVs fed back from the EGSV
to computation module 22 over line 34 are coupled to the structured quadratic
form
computation module 42 and not to the cross-cumulant matrix computation module
40.
The structured quadratic form computation module 42 is used in an
iterative computational loop that, starting with an initial estimated
generalized steering
vector (EGSV) on line 30, produces a series of successively improved values
for the
t5 EGSV, until a termination test is satisfied. In each cycle of the iterative
loop the
module 42 receives an input EGSV and outputs a cumulant strength function (on
line
32), which is obtained by computing a structured quadratic form involving the
C
matrix and the input EGSV. The mathematical details of the computation are
described
in a later section. The cumulant strength function, so obtained, is output to
the EGSV
2o computation module 22 to update the EGSV. As in FIG. 2A, the nature of the
supplemental computation module 24 in FIG. 2B depends on the particular
application
of the invention.
The EGSV computation module 22 together with the structured
quadratic form computation module 42 are part of an iterative computational
loop that
25 produces a series of successively improved values for an EGSV of a source
signal,
starting from an initial value. The EGSV computation module 22 receives as
input a
cumulant strength value for the current value of an EGSV. Based upon this
cumulant
strength, the module 22 determines a new value for the EGSV that will cause
the value
of the cumulant strength value to increase in absolute value. This new EGSV is
output

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-31-
to the structured quadratic form computation module, where it replaces the old
EGSV,
- and the computation cycle is repeated until a termination test is satisfied.
FIG. 2C depicts the direct computation method of the invention in
conceptual form using the same basic structure as FIGS. 2A and 2B. The EGSV
computation module in this figure is referred to by numeral 22' , since it
performs its
function differently from the module 22 in FIGS. 2A and 2B. The EGSV
computation
module 22' receives as input the C matrix computed by the cross-cumulant
matrix
computation module 40. The EGSV computation module 22' computes the solutions
to
a fourth degree polynomial equation, from which the EGSVs of one or two
sources are
o directly determined. The mathematical details of the particular polynomial
equation
are described in a Section 7Ø The values of the EGSVs, so determined, are
output to
the supplemental computation module 24.
It will be understood that FIGS. 2A, 2B and 2C illustrate the processing
required to recover a single source signal from among a plurality of possible
source
signals, for purposes of explanation. We will now turn to the case of recovery
of
multiple signals.
2.1 Signal Separation Concept:
The present invention has a number of applications in the
2o communications field and, more specifically, in the separation of cochannel
signals.
FIG. 3A illustrates the concept of signal separation using the first iterative
method (10,
FIG. 1) and differs from FIG. 2A in that there are multiple linear combiners
26.1
through 26.P and multiple estimated generalized steering vector (EGSV)
computation
modules 22.1 through 22.P. The supplemental computation module 24 has been
2s replaced by a supplemental computation module 24A for signal recovery, the
details of
which will be explained with reference to FIG. 4A. The sensor receiving system
20
outputs the received signals in conditioned form on line 28, which is
connected to each
of the linear combiners 26 and EGSV computation modules 22. Signal
conditioning in
the sensor receiving system, 20, which is described subsequently, may be used
to
3o transform the received signals to P sets of signals, where P is the number
of signal

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-32-
sources being received, and to be separated. As in FIG. 2A, the EGSV
computation
modules 22 and the linear combiners 26 cooperate to produce converged values
of
estimated generalized steering vectors on output lines 28.1 through 28.P. The
supplemental computation module 24A uses these generalized steering vectors
and the
received signals on lines 28 to generate P separate recovered signals on lines
38. How
this latter step is accomplished is best understood from FIG. 4A, which will
be
discussed after consideration of FIGS. 3B and 3C.
FIG. 3B depicts a cochannel signal separation and recovery system
similar to that of FIG. 3A, but using the second iterative method (12, FIG.
1). As in
to FIG. 2B, there is a single cross-cumulant matrix computation module 40 but,
unlike the
FIG. 2B system, there are multiple (P) structured quadratic form computation
modules
42.1, 42.2 ... 42.P, each of which receives cross-cumulants from the matrix
computation module 40 and conditioned input signals from line 28. Cumulant
strength
values generated by the structured quadratic form computation modules 42 are
supplied
~ 5 to respective EGSV computation modules 22.1, 22.2 ... 22.P, which output
recomputed EGSVs for feedback over lines 34.1, 34.2 ... 34.P, respectively, to
the
structured quadratic form computation modules 42.1, 42.2 . . . 42. P, and
converged
values of the EGSVs on lines 36.1, 36.2 ... 36.P.
FIG. 3C depicts a signal separation and recovery system similar to those
20 of FIGS. 3A and 3B, but using direct computation instead of an iterative
method. This
figure is also closely similar to FIG.2C, except that the ESGV computation
module 22'
generates two EGSVs on output lines 36.1 and 36.2, and supplemental processing
is
performed in the supplemental computation module for signal recovery, which
generates two recovered signals for output on lines 38.1 and 38.2.
25 As shown in FIG. 4A, the supplemental computation recovery module
for signal recovery 24A includes a recovery beamformer weight vector
computation
module 44 and multiple recovery beamformers 46.1 through 46.P. Computation of
the
weight vectors in module 44 is made in accordance with a selected known
technique _
used in signal processing. The beamforming weight vectors for signal recovery
are
3o computed directly from the generalized steering vectors. This is done by
one of two

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-33-
methods: (1) by projecting each generalized steering vector into the
orthogonal
complement of the subspace defined by the span of the vectors of the other
sources by
matrix transformation using the Moore-Penrose pseudo-inverse matrix; or (2) by
using
the Capon beamformer, also called the Minimum Variance Distortionless Response
(MVDR) beamformer in the acoustics literature. The module 44 generates, from
the P
input estimated generalized steering vectors (EGSVs), a set of P weight
vectors w,
through wp, on lines 48.1 through 48.P. Implicit in the function performed by
the
module 44 is the orthogonalization of the output signals, such that the weight
vectors
are mutually orthogonal, i.e. each is representative of a separate signal.
Alternatively,
t o the module 44 may be implemented in the manner described in Section 3Ø
The weight vectors w, through wp are applied to the received,
conditioned signals on line 28, in the recovery beamformers 46.1 through 46.P.
This is
basically a process of linear combination, wherein each signal component is
multiplied
by a corresponding component of the weight vector and the results are added
together
I5 to produce one of the recovered signals.
As will be seen from the more detailed description of the preferred
embodiments, the functions of the linear combiners 26 (in the case of FIG.
3A), the
EGSV computation modules 22, the recovery beamformer weight vector computation
module 44 and the recovery beamformers 46 may be combined in various ways.
2o Moreover, all of these functions, together with signal conditioning
performed in the
sensor receiving system 20, may be conveniently implemented in one or more
integrated circuits.
2.2 Signal Separation Concept in the Multipath Environment:
25 As will be later described in more detail, signal separation in accordance
_ with this invention has important advantages in the context of multipath
signal
processing. Communication signals, particularly in an urban environment, often
reach
_ a receiver antenna over multiple paths, after reflection from geographical
features,
buildings and other structures. The multiple signals arrive at the antenna
with different
3o signal strengths and subject to relative time delays and other forms of
distortion.

CA 02272930 1999-OS-25
WO 98/24192 - PCTIUS96/18867
-34-
Because they arrive from different directions, such signals may be separated
in a
conventional cochannel signal separation system. However, the cochannel signal
processing system of the present invention will automatically combine the
multipath
components if they are still coherent with each other. Coherency, in this
context, is a
relative term that simply indicates the degree to which the signals are
identical.
Multiple signals are classified as coherent if they are relatively similar to
each other, as
measured by a cross-correlation function over a finite time interval.
Multipath
.components are noncoherent, and therefore not combinable, when they suffer
large
relative time delays or when a signal transmitter or receiver is in motion,
causing a
to Doppler shift in the transmitted signal that affects one path more than
another.
The key to successful processing of multipath components is that each
generalized steering vector referred to with reference to FIGS. 1, 2A-2C and
3A-3C
corresponds to the sum of all of the mutually coherent multipath components of
a
signal source incident on the sensor receiving system 20. The generalized
steering
vectors from all signal sources are then converted to a set of beamforming
weight
vectors (in recovery beamformer weight vector computation module 44), without
the
need for knowledge of array geometry or array manifold calibration data (which
relates
array steering vectors with angles of arrival for a particular array). For
many of its
applications, the invention is, therefore, completely "blind" to the array
manifold
2o calibration data and the physical parameters of the array.
2.3 Direction Finding Concept:
The invention as described with reference to FIGS. 2A-2C, 3A-3C and
4A provides for cochannel signal separation, even in a multipath environment,
without
use of specific sensor array manifold information. The array parameters, and
specifically array calibration data that relate array steering vectors with
directions of
signal arrival, are needed if one needs to know the angular directions from
which
signals are being received. FIG. 4B illustrates this concept for a single
signal source
referred to as source k. Although the concept depicted in FIG. 4B is
conventional, the
3o manner in which the present invention generates the input steering vectors
is novel. A

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-35-
generalized steering vector, referred to as a,~, is received from one of the
EGSV
- computation modules 22.k (FIG. 3A) on line 36.k and is processed in a
direction of
arrival (DOA) search module 24B, which is a specific form of the supplemental
computation module 14 (FIGS. 2A-2C). The DOA search module 14B uses stored
s array calibration data 50, which associates each possible direction of
arrival with a
steering vector. These calibration data are typically stored in a memory
device as a
lookup table. In the DOA search module 24B, a reverse table lookup is
performed to
obtain the two closest directions of arrival from the input steering vector,
as indicated
in block 52. Then a more precise angle of arrival is obtained by performing an
to interpolation between the two angle values retrieved from the calibration
data 50, as
indicated in block 54. The direction of arrival (DOA) parameter for the k'r'
signal
source is output from computation module 24B on line 38.k.
2.4 Transmitter/Receiver Concept:
15 As will be discussed further in section 12.0, an important application of
the invention is to two-way communication systems. In many communication
systems,
the allocation of transmission frequencies within a geographical area, such as
in a
predefined cell in a cellular telephone system, is often a limiting factor
that determines
the maximum number of active users that the system can handle. In accordance
with
2o this aspect of the present invention, information derived from signals
received and
separated in a receive mode of operation are used to generate signals to a
transmit
antenna array, in such a way that separate information signals can be
transmitted to
respective remote stations using the same frequency.
As already discussed, the present invention makes use of an array of
2s sensors or antennas to separate received signals of the same frequency
(cochannel
signals). In a two-way communication system of the type having multiple mobile
units,
it would be impractical, in general, to require the use of an antenna array at
each
- remote or mobile transmitterlreceiver. These remote units may be installed
in vehicles
or be hand-held devices for which the use of an antenna array is either
inconvenient or
3o simply impossible. However, in most communication systems, the
communication path

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96118867
-36-
between remote units is completed through one or more base stations operating
as a
receiver and transmitter. Since the base stations are generally larger and
more powerful
than the mobile units and are fixed in location, they may be conveniently
structured to
include antenna arrays for both receiving and transmitting. As discussed
above, a
receive array connected to the system of the invention provides for separation
of
received cochannel signals. Moreover, an important by-product of the signal
separation
process is a set of generalized steering vectors, each associated with a
separate signal
source.
As shown in FIG. 5 for a single remote transmitter/receiver station,
received signals are recovered on line 38, in the manner discussed with
reference to
FIG. 2A. In a two-way communication system, a transmitter 56 uses the
generalized
steering vector corresponding to the received signal source, obtained from the
EGSV
computation module 22, in order to generate a weight vector for application to
a
transmit antenna array (not shown). The transmitter 56 also receives, on Iine
58, an
t5 information signal to be transmitted. Typically, this will be in the form
of a digitized
voice signal, although it may be a data signal of some other type. The
transmitter 56
generates the transmit weight vector in accordance with a technique to be
described
below in Section 12.0, modifies the information signal in accordance with the
weight
vector, modulates a carrier signal with the weighted information signal
components,
2o and sends a set of signals to the transmit array, as indicated by lines 60.
The carrier
frequency, although the same for each of the transmitted cochannel signals, is
usually
selected to have a frequency different from the receive signal frequency. As
will also
be further discussed below, in the more general case of multiple received
signals and
multiple transmitted signals, the transmitter 56 generates multiple weight
vectors,
2s which are applied to the respective information signals to be transmitted,
then linearly
combined, antenna element by antenna element, and finally modulated to produce
a set
of composite antenna element signals for coupling to the transmit antenna
array.
It will be appreciated that this aspect of the invention provides a simple
but effective technique for use in a communication system base station, for
receiving
3o cochannel signals from, and transmitting cochannel signals to, multiple
remote stations

CA 02272930 1999-OS-25
WO 98!24192 - PCT/US96118867
-37-
in close proximity to a base station and to each other. Limited only by the
number of
elements in the receive and transmit arrays, the technique allows for re-use
of the same
frequencies in the multiple remote stations, with a resultant increase in
system capacity
or user density, e.g. the number of users per frequency per unit area (per
cell or sector
thereof).
2.5 Concept of Separation of Signals in a "Waveguide":
Up to this point in the description, it has been tacitly assumed that the
"incident signals" 27 shown in FIGS. 2A-2C and 3A-3C are signals transmitted
to through space, the atmosphere, the ocean or some other relatively unbounded
medium.
As will be described in more detail in descriptions of various embodiments of
the
invention, cochannel signals transmitted on a waveguide of some type may also
be
received and processed in accordance with the principles of the invention. The
term
waveguide is used in quotation marks in the heading of this descriptive
subsection
1 s because the term is not intended to be limited to a waveguide operating at
microwave
frequencies, or to an optical waveguide in the form of an optical fiber or
planar optical
waveguide. Instead, the word waveguide as used in this specification is
intended to
cover any of various types of bounded transmission media, including microwave
waveguides, optical waveguides, coaxial cables, or even twisted pairs ,of
conductors
20 operating at relatively low frequencies.
- A common attribute of these "waveguides" is that multiple signals may
be transmitted along them using the same frequency but different modes of
transmission, such as different polarization modes for microwave or optical
waveguides, or, in the case of twisted-pair conductors, different signals
being applied
25 to different wire-to-ground combinations. For various reasons, however, the
- propagation modes may become scrambled in the propagation medium and may
become difficult or impossible to separate in a receiver. As shown in FIG. 6,
a system
- in accordance with the invention can be usefully employed to separate such
signals.
Except for the sensor receiving system 20, the system of FIG. 6 is identical
with the
3o FIG. 3A system for separating received signals. The "incident signals" 27
are received

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-38-
from a signal "waveguide" 62, as defined in the preceding paragraph, and are
sensed
by "waveguide" sensors 52. In the case of a microwave or optical waveguide,
the
sensors 64 take the form of electromagnetic probes or optical sensors
appropriately
inserted into the waveguides. For twisted-pair conductors, the sensors may
include
appropriate circuitry connected to the conductors and ground. Signals from the
sensors
64 are subject to received signal conditioning, as indicated in block 66, and
are then
input to the signal separation system of the invention in the same way as
signals from
multiple elements of an antenna array. The system recovers the original
signals as
indicated on lines 38.
1o Another application of the invention is similar in some respects to the
recovery of signals from a bounded waveguide. In magnetic recording systems
using a
high density recording medium in which recording tracks are positioned very
close to
each other, there is always the potential for crosstalk between the signals on
adjacent
parallel tracks. Maintaining an acceptably low level of crosstalk imposes a
limitation on
the proximity of the tracks and the overall recording density. In this
embodiment of the
invention, a higher level of crosstalk can be tolerated because signals
retrieved from
adjacent tracks can be separated using the signal recovery system of the
invention. In
this case, the "waveguide" sensors 64 are adjacent playback sensors in a
magnetic
recording apparatus. There is no "waveguide" as such; nor are the signals
transmitted
2o through an unbounded medium. Instead they are sensed electromagnetically
from a
recording medium on a moving magnetic tape or disk.
2.6 Preview of Iterative Embodiments to be Described:
As discussed in more general terms above, there are two alternative
iterative methods that may be used in accordance with the invention in the
context of
separation and recovery of cochannel signals. Before proceeding with the
detailed -
descriptions of those methods in terms of specific embodiments, it may be
helpful to
provide a an overview of the iterative methods at a different level of
abstraction from
that of the preceding figures. FIG. 7 provides the basis for this overview.
Some of the

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-39-
technical terms used in FIG. 7 are introduced for the first time in this
specification and
- may not be completely clear until the complete description is studied.
As shown in FIG. 7, the signal separation and recovery process involves
a number of manipulations of the estimated generalized steering vectors
(EGSVs)
pertaining to the multiple signal sources. In block 70 EGSV initialization is
performed.
This is simply the selection of initial EGSV values (on line 30 in FIGS. 2A
and 2B)
from which to begin processing. It will be recalled that processing is
performed in a
batch mode in which sequential blocks of data are processed. The initial EGSVs
may
be estimates carried forward from an already processed previous block of data,
or they
to may be generated from scratch, using either random quantities or a cumulant
eigen-
decomposition algorithm.
Another function performed in block 70 is to "project" the initial
EGSVs into a P-dimensional signal space, where P is the number of signal
sources.
The antenna array provides sets of input data signals that are M-dimensional,
where M
is the number of elements in the array. Throughout the computations performed
in
accordance with the invention, there is often a design choice to be made
because the
mathematical manipulations may be performed on these M-dimensional vector
quantities, or on corresponding P-dimensional quantities, where P is the
number of
signal sources. Ultimately, the recovered signals are output as P one-
dimensional
2o signals, since there is one recovered signal per source, but signal
recovery requires
beamforming in the sensor space. The transformation from M-dimensional sensor
space
to P-dimensional signal space is called "projection," and the reverse
transformation,
from P-dimensional signal space to M-dimensional sensor space, is called
"backprojection."
Block 72 in FIG. 7 describes EGSV prioritization. This aspect of the
invention has not yet been discussed but, simply stated, prioritization is
needed to
provide a rational basis for choosing which of multiple signals should be
recovered
- first. The sensor array, having M elements, inherently limits the number of
cochannel
signals that may be recovered to M. If more than M signal sources are actively
3o transmitting, the first M signals are selected on the basis of their non-
Gaussianity, as

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-40-
determined by either of two methods: using the C-matrix or beamforming and
computing cross-cumulants. The resulting priority list of sources is passed to
a signal
separation iteration block 74, which uses one of the two iterative methods to
obtain
convergence for each EGSV in turn, starting with the highest priority source.
The steps
of the iterative procedure include updating the EGSV using either the C-matrix
or the
beamforming and cross-cumulant computations, then using a conventional
technique,
such as the Gram-Schmidt procedure, to ensure that each EGSV is orthogonal to
already-processed higher-priority EGSVs. These steps are repeated until
convergence
is achieved for each signal source.
to Block 76 of FIG. 7 describes another practical issue in signal recovery
systems that use batch processing. Each "port" from which a recovered signal
is output
in processing a block of data must be correctly associated with a recovered
signal from
the previous data block. This association is performed by comparing the EGSVs.
The
ports cannot be associated merely on their positions in the priority list
because signal
is sources may come and go from list as time passes.
Another batch processing issue is addressed in block 78 of FIG. 7. The
phase angle of an EGSV generated in processing one block of data may not
exactly
match the phase angle as determined in the next block. This processing step
applies an
EGSV phase adjustment to eliminate any discontinuity from block to block.
2o Next, in block 80 of FIG. 6, the EGSVs are "backprojected" from the
P-dimensional signal subspace to the M-dimensional sensor space and then, in
block
82, the backprojected EGSVs are used to beamform and recover the output port
signals.
This overview provides an introduction into the various embodiments
25 and forms that the invention may take. The foregoing and other aspects of
the invention
will now be discussed in more detail.
3.0 Preferred Embodiment Using eCURE:
As discussed more generally above, the present invention pertains to a
3o system and method for processing and recovering cochannel signals received
at a

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-41-
sensor array. In this descriptive section, a practical embodiment of the
cumulant
recovery (CURE) system is disclosed. Because this embodiment uses eigenvectors
and
eigenvalues in part of its computation, it is referred to as the eigenCURE
system, or
simply the eCURE system. The embodiment disclosed uses the first iterative
method
(the beamform and cross-cumulant method, first introduced at 10 in FIG. 1). It
will be
understood, however, that the eCURE system may be modified to use the C-matrix
iterative method (12, FIG. 1).
3.1 Overview And System Hardware:
to FIG. 8A shows the basic components of the eCURE system, including a
sensor array, indicated by reference numeral 110, which receives signals from
various
directions, as indicated at 112, a bank of receivers 114, and a sampler and
analog-to-
digital converter bank 116. The separate signals from the elements of the
sensor array
110 are coupled directly to the receiver bank 114, which performs conventional
filtering and frequency downconversion functions. The sensor signals are then
sampled at a high rate and converted to digital form in the sampler and analog-
to-
digital converter bank 16. At this point, the signals have been filtered,
downconverted
and digitized and processing is about to begin. It can be appreciated that,
because each
sensor in the array 110 provides a stream of digitized signals, processing may
be
2o conveniently performed in batches or blocks of data. From time to time,
reference will
be made in this description to current and previous data blocks. The block
size is
critical only in the sense that the size selected affects processing speed and
accuracy of
estimation.
The first major processing step is preprocessing the sensor data, which
is performed in a preprocessing computer 120. As will be discussed in more
detail
with reference to FIG. 10, the preprocessing computer 120 performs four
important
functions
~ It "whitens" the directional components of the signals using a technique
known as eigendecomposition, which will be discussed further below.

CA 02272930 1999-OS-25
WO 98124192 - PCT/US96/18867
-42-
~ It estimates the number of signal sources being received. P is the number of
sources and Pe is the estimated number of sources.
~ It reduces the dimensionality of the sensor data from M, the number of
sensors, to Pe, the estimated number signal sources.
~ It scales the numerical values of the signals to normalize the powers of the
sources, permitting weak signals to be separated in addition to stronger
ones.
The other major components of the cochannel signal recovery system are
a signal recovery controller 122, multiple signal extraction ports 124.1
through 124.L,
an orthogonalizer 126, and multiple demodulators 128. Preprocessed sensor
signals
are transmitted over lines 130 in parallel to each signal extraction ports
124.1. Each
port in this embodiment of the invention is implemented as a separate computer
processor. Using the iterative technique described above with reference to
FIGS. 2A
and 3A, each of the signal extraction ports 124 generates output signals
derived from a
separate source. These signals are output on lines 132 to the demodulators
128, which
produce usable output signals on lines 134. If the information contained in
the signals
is audio information, the outputs on lines 134 may be connected to separate
loudspeakers or other audio processing equipment (not shown). The function of
the
orthogonalizer 126 is to ensure that each of the ports 124 is associate with a
separate
2o signal source. The signal recovery controller 122 performs various control
functions
in conjunction with the signal extraction ports 124 and the orthogonalizer
126. The
controller 122 receives the source count estimate Pe from the preprocessing
computer
120 over line 136 and also receives eigenstructure parameters from the
preprocessing
computer over line 138. The latter are also transmitted to the signal
extraction ports
124, and the source count estimate is transmitted to the orthogonalizer 126.
The
controller 122 also sends a priority list to the orthogonalizer 126 over line
140.
Finally, the controller 122 sends adaptation flags to the signal extraction
ports 124 over
lines 142 and receives capture strength values from the signal extraction
ports over
lines 144. The specific functions of these signals will become apparent as the

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-43-
description proceeds. Basically, one function of the controller 122 is to keep
track of
signal sources as they appear and disappear and to make sure that the signal
extraction
ports 24 and the orthogonalizer 126 handle appearing and disappearing signal
sources
in an appropriate manner.
In the general terms used in FIG. 3A, the sensor receiving system 20
includes the sensor array 110, the receiving bank 114, the sampler and analog-
to-digital
converter 116 and the preprocessing computer 120. The functions performed by
the
linear combiners 26, the EGSV computation modules 22 and the supplemental
computation module for signal recovery 24A, are performed in the signal
recovery
o controller 122, the signal extraction ports 124 and the orthogonalizer 126.
Because this
practical embodiment must maintain association of signal sources to physical
output
ports, and must be able to adapt dynamically to the appearance and
disappearance of
signal sources, the architecture of the system is necessarily different from
the
conceptual architecture of FIGS. 2A, 3A and 4A. The fundamental functions
performed in the system of FIG. 8A are, however, the same as those described
with
reference to the earlier figures.
FIG. 8B is a hardware block diagram of one implementation of the
eCURE system of the present invention, as used to separate multiple signals
containing
audio information. Identical reference numbers have been used in this figure
to refer
2o to components that appear in both FIG. 8A and FIG. 8B. The preprocessor
computer
120 is implemented as a separate circuit card. It is of little significance
whether the
preprocessor computer is implemented on a single circuit card or in a stand-
alone
computer. The functions performed in both cases would be identical. Similarly,
the
controller 122 and orthogonalizer 126 are implemented in one computer on a
single
circuit card, as indicated in FIG. 8B. The signal extraction ports 124, one of
which is
shown, are implemented on separate computers on circuit cards and the
demodulators
128 are also implemented on a separate computer. All of the computers
mentioned
above may be of any appropriate type, but in a presently preferred
demonstration
embodiment, they are Intel model i860 processors. The computers are connected
to a

CA 02272930 1999-OS-25
WO 98124192 - PCT/US96/18867
-44-
high-speed crossbar switching network 150, such as Part No. ILK-4, from
Mercury
Computer Systems, Lowell, MA, 01854.
The sensors 110 may be of any appropriate type, such as Part No. 10
183-244, from TRW Inc., Sunnyvale, CA, 94088. The receivers 114 in this
embodiment include a VME synthesizer module (Part No. 1600M SYN-5, from
APCOM Inc., Gaithersburg, MD, 20878), a local oscillator module (Part No.
1600M
LOD-l, also from APCOM Inc.) and a VME RF converter module {Part No. 1600M
RFC-S, also from APCOM Inc.). The digitizer bank 116 may include an Access256
motherboard (Part No. MOB256-4) and analog input and digital output cards from
to Celerity Systems, Inc., San Jose, CA, 95117.
The receiver bank 114 tunes each sensor to the desired frequency and
downconverts any signals received. One receiver is allocated to each sensor.
The
receivers 114 enable the system to isolate a single frequency of interest and
to translate
it to a frequency where it can be more conveniently digitized and processed.
No
t5 demodulation is performed at this point. For example, one embodiment of the
invention has receivers that downconvert the received signals to a center
frequency of
225 kHz and a bandwidth of 100 kHz (specifically the 3 dB bandwidth).
The digitizer bank 116 converts the received signals to digital samples.
Only real samples, not complex samples, are generated at this stage. In the
illustrative
2o system, the digitizer bank 116 consists of a digitizer motherboard and an
input
daughtercard that samples up to eight channels simultaneously at a rate of up
to 10
megasamples per second. The samples are exported for further processing
through an
input card 151. The data processing system performs digital filtering of the
input data,
with the digital filtering card 152, and converts the real samples to complex
values
25 needed for processing, using a real-to-complex conversion card 153.
All of the processor cards mentioned above are connected to the high-
speed crossbar switching network 150. A system manager 154 in the form of a
Model
68040 CPU (Part No. CPU-40B/16-02, from Force Computers Inc., San Jose, CA,
95124) controls this demonstration system, with operator interface being
provided by a
3o workstation 56, such as a Powerlite notebook workstation (Part No. 1024-520-
32, from

CA 02272930 1999-OS-25
WO 98124192 - PCT1US96/18867
-45-
RDI Computer Corporation, San Diego, CA, 92008). In this hardware
architecture,
- the demodulated signal outputs are connected to loudspeakers 157 and a hard
disk drive
158 is provided for storage of received messages. The system manager tunes the
- receivers 116, instructs the digitizer to record samples, configures and
initiates
operation of the data processing system, and controls a peripheral interface
board (Part
No. MVME 162-63, from Motorola Computer Group, Tempe, AZ, 85282), through
which communication is had with the loudspeakers and the hard disk. It must be
understood that, because this is a demonstration system, many of these
components
would not be needed in some implementations of the invention. As noted
earlier, many
to of the components could be conveniently implemented in the form of a single
integrate-
circuit chip, or multiple chips.
FIG. 9, which is broken into two figures designated FIGS. 9A and 9B,
is a block diagram similar to FIG. 8A but showing in each block more detail of
the
functions performed by each component of the system. The functions will be
described
t5 with reference to the more detailed diagrams that follow. Another feature
shown in
FIG. 9 but not in FIG. 8A is the output of generalized steering vectors on
lines 170.
The generalized steering vectors, as discussed earlier in this specification,
are an
important product of the signal recovery process, along with the recovered
signal
outputs. The generalized steering vectors are shown as being used in a DF
search
2o processor 172, which generates signal source bearings or directions of
arrival (DOA),
output on lines 174, consistent with the description with reference to FIG.
4B.
3.2 Preprocessing:
The functions performed by the preprocessing computer 120 are shown
25 in detail in FIG. 10. The preprocessor performs a block-by-block analysis
of
"snapshots" of data from the sensor array, which has M elements. The
preprocessor
determines the eigenvectors, the number of signal sources P, and the signal
subspace of
the received array measurement data. The preprocessor also filters the
received array
data, transforming it from M-dimensional sensor space to P-dimensional signal
3o subspace. This transformation also renders the steering vectors of the
transformed

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-46-
sources orthogonal to each other, which greatly accelerates convergence on
recovered
signal solutions later in the processing, and the transformed source powers
are made
equal.
A received signal that satisfies the narrow-band assumption (to be
defined below) can be described by the following equation:
r(t) = As(t) +n(t),
where r(t) denotes the array measurements collected by M sensors, n(t) is the
measurement noise, A is the steering matrix that models the responses of the
sensors to
the directional sources, and s(t) is a time-varying signal. The sampled sensor
signals,
1o represented by a function of time r(t), are input to the preprocessing
computer until a
complete block of data has been received. While the block is being further
processed,
another block of data is input to a buffer in the computer (not shown). As
indicated at
180, each block of data is first subject to computation of an array covariance
matrix for
the current block of data. The sample covariance matrix R from N samples or
"snapshots" of data is given by:
N
R = 1 ~ r(t)rH(t) .
N ,_,
As indicated at 182, a further important step in preprocessing is
eigendecomposition,
which decomposes the covariance matrix as:
R = EAEH, EHE = IM,
2o where the diagonal matrix A=diag(~.,, ~,... ~,M) contains the eigenvalues
of R (which
are positive) in a descending order, and the columns of the matrix E consists
of the
corresponding eigenvectors. In this description, the subscript appended to the
identity
matrix I indicates its size. In the case of true statistics and with fewer
sources than
sensors (P < M), the last (M-P), eigenvalues are identical and they are equal
to the
noise variance ~,M_p+I -... =~,M=az. With sample statistics, the last (M-P)
eigenvalues
are different with a probability of one, and a statistical test has to be
performed to
determine the number of sources P.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-47-
In the presently preferred embodiment of the invention, the
preprocessing computer uses a combination of two estimates of the number of
sources,
as indicated in block 184: the estimate determined by Akaike's Information
Criteria
- (AIC) and the estimate determined by Rissanen's Minimum Description Length
principle (MDL). Specifically, the preprocessing computer averages the AIC and
MDL functions and finds the single maximizer of the average. The equations for
making this estimation are given, for example, in a dissertation by Mati Wax
submitted
to Stanford University in March 1985, and entitled "Detection and Estimation
of
Superimposed Signals," and in particular the subsection headed "Estimating the
Number of Signals," beginning on page 69 of the paper. AIC generally
overestimates
the number of sources, and MDL generally underestimates the number of sources.
By
averaging the two estimates, a good result is obtained. The averaged estimate
of the
number of sources is given as the minimizer of the cost function:
( 1 M lM-k M 1 1
Pe=a~rgmMn Nlog I M-k,~~,i~ ~a,i +2k(2M-k~l+2log(N)~ .
' k+1 i=k+1
After the number of sources is estimated, the preprocessor computer computes
estimates of the eigenvectors and eigenvalues of the signal and noise
subspaces:
M
E= ~E.~~En~~ A = Cns~aZIM-r,> a2 - 1 ~~k
M - Pe k=P +~
Ef and En are estimates of signal and noise subspace eigenvectors,
respectively, and
a " is an estimate of the noise power. The diagonal matrix AS contains the
estimates of
2o signal subspace eigenvalues. Once the subspaces are found, the preprocessor
computer
determines the transformation matrix T, as indicated in block 186, from:
T-E's(n.s -a; I)'~iz.
The transformation T is then applied to the sampled measurements r(t), as
indicated in
block 188:
y(t) = T"r(t) = T"As(t) + T"n(t) = y.s(t) + THn(t),
where ys(t) denotes the signal component in y(t). It can be proved that the
covariance
matrix of ys{t) is the identity matrix. This indicates that the steering
vectors of the

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-48-
sources after transformation to the Pe dimensional subspace are orthogonal to
each
other and the source powers are equalized.
The transformation reduces the dimensionality of the sensor
measurements from M, the number of sensors, to Pe, the estimated number of
signal
sources. The eigendecomposition performed in the preprocessing computer is a
well
known technique, sometimes referred to as spatial prewhitening, originally
developed
for use in passive sonar signal processing. It is described in more detail in
a number of
texts on signal processing. For example, see "Detection of Signals in Noise,"
by
Anthony D. Whalen, Academic Press, New York (1971), beginning at page 392. In
to spatial prewhitening, noise components at each sensor are assumed to
correlated (i.e.,
not completely random noise). The prewhitening process operates on the noise
signals
to render them uncorrelated (i.e,. "whitened"). An alternative to
eigendecomposition
is to use covariance inversion in preprocessing. In effect, the latter process
whitens
both noise and signal components of the sensor signals and it can be at least
intuitively
t5 understood that this is a less desirable approach since it renders the
signals less easy to
separate from the noise than if spatial prewhitening of the signal only were
used.
However, the present invention will still separate cochannel signals using
covariance
inversion instead of eigendecomposition as a preprocessing step. Currently,
eigendecomposition, or spatial prewhitening, is the preferred approach for
2o preprocessing.
3.3 Operation of an Active Signal Extraction Port:
A single active signal extraction port, one of the L ports 124 shown in
FIG. 8A, is shown in detail in FIG. 11, which extends over two sheets, as
FIGS. 11A
25 and 11B. L is the number of physical ports allocated for signal extraction
and is less
than M, the number of sensors. For generality, the illustrated port is
referred to as the
kth port 124.k, and signals pertaining specifically to this port are referred
to by signal
names that include the prefix k. An "active" port is one that has been
assigned
responsibility for separating a signal from the received signal data. The
functions
3o performed in an active port are critical to the invention and are
illustrated in FIG. 11.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-49-
The active signal extraction port 124.k receives as inputs over line 130
- the preprocessed sensor data y(t). As in the preprocessing computer 120
(FIG. 7), the
sensor signals are described as being processed in blocks, although it will be
understood that an alternative embodiment of the invention could be devised to
process
the signals continuously. The principal output from the port is a recovered
signal,
designated gk(t). An important intermediate output is a vector quantity called
the
normalized cumulant vector, referred to as bk. Another important output is the
generalized steering vector ak, which defines the directional location of the
signal
source.
1o To highlight the (block) iterative nature of the algorithm, the quantities
related to the mth analysis block are identified in this descriptive section
by using the
additional index m. For example, the steering vector estimate provided by the
kth port
after the mth block is processed is denoted as ak(m). The time variable t
spans from the
start of the mth block to the end of the mth block, and, with N snapshots per
block, can
t5 be expressed at t E ~(m -1)N + 1, mN~. The quantities E, A and T are
obviously
obtained by processing the mth block of data, so, for simplicity, they are not
written
with the (m) index.
It is both logical and convenient to begin describing operation of the
signal extraction port at the point in time when the port has just been made
active. No
2o accurate signal has been recovered and no cumulant vector has been computed
since the
port became active. The block number being of input data is examined, as
indicated at
200, to determine whether the current block is the first block. If so, the
steering vector
ak(0) is set to an initial random vector with a unit norm. As shown in
processing block
102, the steering vector ak(m-1) is first projected to the signal subspace by
transforming
25 it into a value vk, using the transformation T, which is input to block 202
as shown.
The steering vector projected into the signal subspace is computed as:
vk =THak(m-1).
These computed values are passed to a beamformer 204, which recovers an
auxiliary
waveform using vk as weights:

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-50-
uk(/) = vk Y(t) ~ ~~ vk ~~
The scaling by the norm of vk is performed to ensure numerical stability in
the -
cumulant computations. At convergence, the norm of vk should be unity (because
of
the preprocessing performed on the measurements). The auxiliary source
waveform is
provided to the cumulant vector computer 206, which computes sample estimates
of the
cross-cumulant vector bk, which has components defined by:
(bk )l = Cum(tlk (l), uk (t )~ uk (t)~Yr (t)) ~ 1
where (bk); denotes the ith component of bk. The asterisk indicates that the
conjugate of
the process uk(t) is used in two of the four quantities of which the cumulant
is
t o computed. The cumulant vector computer computes a fourth-order cumulant
vector of
the input signals. More specifically, the vector is the cumulant of four
quantities
derived from the input signals. An introduction to cumulants and their
properties is
provided in Section 20.4 to this specification.
After the cumulant vector bk has been computed in the cumulant vector
I5 computer 106, the capture strength ck is computed in a capture strength
computer 208.
The capture strength computer 208 determines the convergence
condition of a port by evaluating the degree of non-Gaussianity of the
auxiliary signal
uk{t), and the amount of change between bk and vk. At convergence, these two
vectors
should be pointing at the same direction. The non-Gaussianity of the auxiliary
signal
2o can be determined from the ratio of its fourth-order cumulant to its
squared power:
' cum(uk{t),uk{t),uk{t),uk{t))
~k - (E{uk(t)uk(t)~)2
Using cumulant properties, we obtain
Cllm(tlk (t), uk (t), uk (t)W k Y(t) ~ ~~ V k l l) I _ ~ V k bk ~~ ~~ V k 11
(E' luk(r)uk(t)I)2 (E~uk(t)uk(r)~)2
The denominator can be computed from the auxiliary signal uk(t). Since the
covariance
25 matrix of the signal component of y(t) is the identity matrix, the
denominator can be
ignored when the signal to noise ratios (SNRs) are high enough. The similarity
between bk and vk can be computed from the.following:

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-S1-
_ ~~~'k bk
~k IlVkll Ilbkl
The capture strength cx can be determined from ~x and r~x.. One way is to let
cx=~k.rlk~
' Alternatively, we can set cx=fix or cx=rlx.
The capture strengths cx are provided to the controller unit for priority
determination. The cross-cumulant vector is normalized by its norm and fed to
the
orthogonalizer:
(bx(tn)= bx / II bx II).
If the active ports capture different sources, their cross-cumulant vectors
should be orthogonal. To force the active ports to capture different sources,
the
t o orthogonalization unit uses the Gram-Schmidt procedure and outputs
orthogonalized
cumulant vectors (d vectors) to the ports. The steering vectors are determined
from
the orthogonalized cumulant vectors according to
ak(m)=E.s(A.r-azI~~)mdk~m)=T(ns-a2lr )ak(m)~
The steering vectors are provided to the controller unit in order to
determine the port that loses its signal in the event of a source drop-out or
to determine
which port will be activated in the case of a new signal. The steering vectors
can also
be used by an optional DF search unit to determine the source bearings.
Finally, the active port determines the signal waveform from the source
it is tracking. However, it is necessary for an active port to maintain gain
and phase
2o continuity of its recovered signal at block transitions in order to prevent
block-to-block
gain and phase modulation of the recovered signal. To accomplish this goal, we
need
to examine the properties of the algorithm in more detail. The algorithm
normalizes
the source waveforms to have unit variance and estimates the steering vectors
based on
this normalization, i.e., eCURE views the measurements as:
' 25 r(/) _ (A~sizD)(D~E.s.'iis(r)) + n(t)~
where ass is the covariance matrix of the directional sources which is
diagonal since the
sources are independent (ASS=E{s(t)sH(t)}). The diagonal matrix D contains
arbitrary
phase factors associated with the blindness of the steering vector estimation
procedure.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-52-
Even when the sources are stationary, there can be gain (due to ass) and phase
modulations (due to D) on the steering vectors estimates and waveform
estimates.
There are two different ways to determine gain and phase modulations
for each block. We can compare the steering vector estimates ak(m) and ak(m-
1),
which should be pointing to the identical direction at convergence. Suppose,
due to
power changes and arbitrary phase rotations, the following relationship holds
between
the steering vectors:
ak(m)=9kak(m-1)
where qk accounts for the gain and phase factor between the two steering
vector
1o estimates. We can estimate qk using least-squares:
qk =ak (m-1)ak~m)~Ilak~m-1)~~2
Using
ak(m) = ES (ns _ ~zI)nz dk(m)
and
i5 ak(m-1) =E~(n.s-azI)vz wk
we obtain an alternative way to compute qk:
qk -V k \ns 62I) dk(m)~(Vk (As 62I) Vk)'
In the mth block, the kth block scales the steering vector estimate by qk,
relative to the previous block. Therefore, it scales the waveform estimate at
the mth
2o block by the reciprocal of this quantity. Hence we need to multiply the
waveform
- estimate by qk (or by its estimate) in order to undo the scaling done by the
processor,
which is described as below:
gk (t) = qk (dk y(/)) _ (qkdk )H ylt) - W k ylt)
The second way to compute qk is to force the first component of the steering
vector
25 estimate to be unity. In this process, we simply let qk be the first
component of ak(m).
After qk is determined, wk will be determined using the orthogonalized
cumulant vector
dk(m) and qk.

CA 02272930 1999-OS-25
WO 98/24192 PCT/LTS96I18867
-53-
Once a source waveform is recovered, it is available for subsequent
processing as desired. It can be recorded or demodulated and listened to with
headphones or loudspeakers.
s 3.4 The Signal Recovery Controller:
Now that the basic signal extraction method has been described and
before proceeding to a description of the orthogonalizer function, it is
logical to
consider next how the signal recovery controller 122 (FIG. 8A) operates
because this
affects operation of the orthogonalizer 126 and the signal extraction ports
124. As
1o briefly discussed with reference to FIG. 9, an important function of the
controller 122
is to detect changes in the status (ON or OFF) of signal sources and to
identify lost
sources. In addition, the controller 122 maintains a priority list of ports
and a related
set of adaptation flags that indicate which ports are active.
As shown in FIG. 13, which is spread over three pages as FIGS. 13A,
t5 13B and 13C" the functions of the controller 122 include logic to detect
changes in the
number of signal sources, indicated by block 220, port allocation logic 222,
priority
list determination logic 224, and adaptation flag logic 226. The logic 220 to
detect
changes in the number of sources assumes that there is no more than one change
in the
number of sources. from one data block to the next. The logic receives the
estimated
2o number of signals Pe from preprocessing computer 120 and compares the Pe of
the
previous block with the Pe of the current block. The results of the comparison
determine the value of source change flag, referred to simply as "Flag." Flag
is set to
zero for the initial block. There are three possible outcomes of the
comparison for
subsequent blocks of data:
25 1. If current Pe = previous Pe, Flag = 0
- 2. If current Pe > previous Pe, Flag =1 (new source ON)
3. If current Pe < previous Pe, Flag =2 (source OFF)
The Flag value is transmitted over line 228 to the port allocation logic
222, which is called into operation only if Flag=2, indicating that a source
has been

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-54-
lost. The function of the port allocation logic 222 is to determine which of
the active
ports 124 was last processing signals from the source that has just been lost.
The basic
principle employed to make this determination is to identify which port has a
steering
vector with the greatest component in the current noise subspace. Each signal
that
contributes to the measurements has a steering vector that is orthogonal to
the current
noise subspace determined from the sample covariance matrix R . (In a simple
three-
dimensional space, one could think of a first signal eigenvector aligned with
the x-axis
direction and a second signal eigenvector aligned with the y-axis direction.
The signal
subspace for the two active signals includes the x-axis and y-axis directions.
The noise
1o subspace is the space defined by all remaining axes in the space. In this
case, the noise
subspace eigenvector is in the z-axis direction.)
When a signal disappears and drops out of consideration, the current
noise subspace then includes the space previously occupied by the signal. In
the three-
dimensional example, if the x-axis signal disappears, leaving only the y-axis
signal, the
t5 noise subspace is redefined to include a plane in the x and z directions.
To recognize
which signal was lost, the port allocation unit uses the steering vector
estimates from
the previous data block (indicative of the active sources before one was
lost), and
projects these vectors into the noise subspace as defined for the current data
block.
The steering vector from the previous data block that lies completely in the
current data
2o block noise subspace, or the one that has the largest component in the
noise subspace,
is determined to be the signal that was lost between the previous and current
data
blocks. Again, using the three-dimensional example, if x-axis signal
disappears and
the new noise subspace is redefined be the x-z plane, then projection of the
previous x
and y signals into the current noise subspace results in a finding that the x-
axis signal,
25 lying wholly in the current noise subspace, is the signal that was lost.
More specifically, the logic 222 obtains the steering vector estimates
from all of the ports that were active in the previous data block, and
normalizes them
(i.e., scales them have a unit norm). Steering vector estimates are obtained
for only
the first (Pe+1) ports in order of decreasing capture strength. The port
allocation

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-55-
logic is concerned with the direction of the steering vectors in space and any
_ differences in magnitude arising from different signal strengths should be
eliminated.
Then the normalized steering vectors are projected onto the current noise
subspace, as
provided from the preprocessing computer 120 in the form of noise subspace
eigenvectors En. For example, if ak(m-1) is a steering vector estimate from
the kth
port that was active in the previous block, then the port allocation logic 222
computes
the "leakage" of the steering vector of the kth port into the current noise
subspace
from:
IIE~'E~H ak~m-1)~~~ak~m-1)~) ~~
1 o The logic then declares the port that has the greatest leakage into the
noise space to be
inactive by setting its adaptation flag to zero. Also the port's capture
strength is set to
a value MIN, which is a system parameter set to some very low value, such as
0.001.
It will be recalled that the capture strength is computed in each active port
as described
earlier. However, the controller 222 can overwrite the previously computed
value
when it is determined that a port has become inactive.
For example, suppose that five ports are available for use, with three
sources present in the previous data block. Port 1 was locked onto Source 3,
Port 3
was locked onto Source 1, and Port 5 was locked onto Source 2. Assume further
that
Source 3 turned off just before the current block and that the following
capture
2o strengths were determined for the previous and current data blocks:
Previous Current
Port Previous Capture Current Capture
No. Source Strength Source Strength
No. No.
1 3 0.99 - 0.001
2 - 0.001 - 0.001
- 3 1 0.995 1 0.995
4 - 0.001 - 0.001
5 2 0.98 2 0.98

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-56-
In the previous data block, Port 2 and Port 4 were inactive and had their
capture
strengths set to 0.001. When Source 3 turned off, the port allocation logic
222
determined that Port 1 had lost its signal, using the analysis discussed
above.
Inherent in the list of capture strengths is a priority list of ports (i.e., a
list of port numbers in order of decreasing capture strength). Therefore, the
priority
list based on the previous data block is [3,1,5,2,4] and the priority list
based on the
current data block is [3,5,1,2,4]. The convention adopted is that, when ports
have
identical capture strengths, they are assigned priorities based on port
numbers. The
priority list determination logic 224 generates the priority list in this
manner, based on
1o the capture strength list transferred from the port allocation logic 222.
The priority list
is used by the adaptation flags logic 226 to generate a list or vector of
adaptation flags.
The adaptation vector contains L elements, where L is the number of physical
ports in
the system. In the example given above, the adaptation flags vector for the
previous
data block is [ 1,0,1,0,1 ] and for the current data block is [0,0,1,0,1 ] .
The adaptation
is flags vector is supplied to multiple port signal recovery unit (124, 126,
FIG. 9), and
specifically to the signal extraction ports 124. The priority list is also
supplied to the
multiple port signal recovery unit, and specifically to the orthogonalizer
126, which
will be discussed in the next descriptive section.
The purpose of the priority list is to facilitate an orderly allocation of
2o signal sources to ports, from the lowest port number to the highest.
Further, when a
signal source turns on, it is desirable that the most recently freed port be
made
available for assignment to the new signal, to provide continuity when a
source turns
off and on again without a change in the status of other sources.
If there is a new source (i.e., Flag=1), then this unit first obtains the
25 previous block steering vector estimates from the ports that are inactive
in the previous
block (Ports Pe to L in the priority list), and normalizes them to have unit
norm. It
then projects these steering vectors onto the current noise subspace. For
example, if
ak(m-1) is a steering vector estimate from a port that was inactive in the
previous block,
then the Port Allocation Unit computes the port's leakage from (here , ~ a k
(m -1) ( ~
3o denotes the norm of vector ak(m-1)):

CA 02272930 1999-OS-25
WO 98/24192 - PCT/L1S96/18867
_$7_
~~ E,~E~H ax (m -1)~~~ak (m -1)~j ~~
and declares the port which has the minimum leakage as active (sets its
adaptation flag
to one) and overwrites the port's capture strength with 2 x MIN, where MIN is
a
system parameter that is nominally set to 0.001. This is done to make the
newly
activated port be the last in the priority list. (The capture strength of a
port is
computed by the multiple port signal recovery unit described earlier in this
specification. The controller, however, can overwrite the computed value as
described
above.)
3.5 The Orthogonalizer:
As already briefly discussed, the orthogonalizer 126 functions to ensure
that each port is consistently assigned to process only one signal source,
which is to say
that each active port captures a different source. The orthogonalizer 126
receives a
normalized cumulant vector from each active port, the vector being represented
by bk
~s for the kth port. The orthogonalizer 126 outputs back to each port an
orthogonalized
cumulant vector, which is dk for the kth port. The orthogonalizer also
receives the
priority list from the signal recovery controller 122, so has knowledge of the
identities
of the active ports and their respective associated capture strengths, and
also receives
the estimated number of signals Pe, frorn the preprocessing computer 120.
2o The orthogonalizer forces the active ports to capture different sources by
orthogonalizing their cumulant vectors, which, in turn, are estimates of the
steering
vectors in the dimensionally reduced space. (It will be recalled that, in the
preprocessing computer 120, the dimensionality of the data is reduced from M,
the
number of sensor elements, to Pe, the estimated number of sources.) Ideally,
the
25 cumulant vectors for active ports should be orthogonal to each other, to
cause the ports
to capture different source signals and to prevent two ports from locking up
on the
same source signal. From the priority list and the estimated number of signals
Pe, the
orthogonalizer forms a Pe by Pe matrix Z from the active port steering vectors
bk such
that the kth column of the matrix Z is the steering vector of the port that is
the kth item

CA 02272930 1999-OS-25
WO 98124192 - PCT/US96/18867
-58-
in the priority list. The orthogonalizer uses a known procedure known as the
classical
Gram-Schmidt (CGS) algorithm to perform the orthogonalization operation. The
Gram-Schmidt algorithm is described in a number of texts on matrix
computations,
such as Matrix Computations, by Gene H. Golub and Charles F. Van Loan (The
Johns
Hopkins University Press, 1983), pp. 150-154.
As applied to the present system, the Gram-Schmidt algorithm is applied
to the matrix Z to obtain a decomposition of the type:
Z = QR,
where Q is an orthogonal matrix (Q"Q = I), and R is an upper triangular
matrix.
1o Although the Gram-Schmidt orthogonalization procedure is used because of
its
simplicity, there are alternatives that might also be used in the invention,
such as QR
decomposition and the Modified Gram-Schmidt (MGS) procedure. After the
orthogonal matrix Q is determined, its columns are shipped back to the ports
as
orthogonalized cumulant vectors dk. Specifically, the kth column of the Q
matrix is
t 5 sent back as d~ to the port that is the kth entry in the priority list.
Regardless of the
method used, the effect of the orthogonalizer is to produce a set of Pe
cumulant vectors
that are orthogonal to each other.
3.6 Operation at an Inactive Port:
2o When a port is determined to be inactive, as indicated by a zero
adaptation flag, the port performs three simple functions, as shown in FIG.
14. First,
its output signal g/t(t) is set to zero. Second, its capture strength ck is
set to a minimum
value MIN. Finally, the last steering vector ak, estimated in the port just
before it
became inactive, is stored in a memory device associated with the port, to
facilitate
25 recapture of the same signal that was lost, if it should turn on again in
the near future.
More specifically, the adaptation flag input to the inactive port is delayed
by one data
block time. Then, using the delayed adaptation flag, the port stores a
steering vector
either from two blocks earlier, if the delayed flag has a value of 1, or one
block earlier,
if the delayed flag has a value of zero.

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-59-
4.0 Alternate Embodiment Using Covariance Inversion Cure (CiCURE):
The basic cumulant recovery (CURE) system described in Section 3.0
uses eigendecomposition in preprocessing and is referred to as eigenCURE
(eCURE)
for convenience. Another variant of the CURE system uses covariance inversion
instead of eigendecomposition and is referred to as covariance-inversion CURE
(CiCURE). CiCURE is best thought of as a low-cost approximation to the high-
performance eCURE system. As such, it shares most of the same advantages over
standard CURE as the eCURE method.
1o Certain conditions must be met in order for CiCURE to mimic eCURE
and realize the same advantages. The conditions are:
~ Sensor noises must be additive Gaussian noise (eCURE assumes
independent, identically distributed, additive Gaussian noise).
~ Received signal powers must be much greater than the noise.
~ Sample covariance matrix and its inverse used by CiCURE must be accurate
enough to prevent leakage into noise subspace.
Under stationary or steady-state signal conditions, this implies a need for
a sufficiently long processing block size. Under these conditions, the
prewhitening
transformation used in CiCURE is a good approximation to that used in eCURE,
and
2o the two systems have similar performance properties. This section of the
specification
describes the components of a signal separation/recovery system that is based
on the
CiCURE algorithm.
The CiCURE signal separation/recovery system incorporates a spatial
prewhitening transformation based on the inverse of the input sample
covariance matrix
2s (this operation is performed by using an eigendecomposition in the eCURE).
The
received signal data is filtered or transformed by the prewhitening operation
in the
CiCURE, unlike eCURE. The prewhitening done in the CiCURE is implicit in the
- mathematics of the signal recovery ports, and it is only necessary to
compute a matrix
decomposition of the input sample covariance matrix. This latter operation is
done in a
3o preprocessor, whose output is made available to all of the signal recovery
ports. Key

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-60-
characteristics of the implementation described below are that the iterative
convergence
of the CURE algorithm is realized over several blocks instead of within a
single block,
and "high-priority" ports converge sooner than "low-priority" ports.
A signal recovery system based on the CiCURE method is simpler than
one based on the eCURE. There are two main architectural components to the
method:
a preprocessor unit which computes a matrix decomposition and a set of signal
recovery ports hierarchically arranged.
In addition, there can be two optional units: demodulators, to complete
the recovery of the separated signal for the purpose of recording or
listening, and a
1 o direction-finding (DF) search unit to provide copy-aided DF.
A block diagram for an overall signal recovery system based on the
CiCURE method is shown in FIG. 15. The details of the preprocessor 120' and
the
signal recovery ports (124.1, 124.2, etc.) that are unique to the CiCURE
method are
described below. All other system details are as previously described for the
eCURE
system.
The preprocessor 20' computes a matrix decomposition of the input
sample covariance matrix. It does this on a block-by-block basis by first
computing the
sample covariance matrix of the array snapshots within a processing block and
then
computing the Cholesky decomposition of the sample covariance matrix. The
Cholesky
2o decomposition is output to the signal recovery ports 124.1, 124.2, 124.3,
which use
this information to adapt their weight vectors to separate the cochannel
source signals.
The signal model for the narrowband array case is described by the
following equation:
r(t) = As(t) + n(t)
where r(t) denotes the array signals collected by M sensors.
We assume that for each block N snapshots are collected for analysis
and that there are P sources contributing to the measurements. We also assume
that the
measurement noise, n(t), is spatially white and noise power at each sensor is
identical

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-61-
but unknown and it is denoted by 6z. The preprocessor 20' first forms the
sample
' covariance matrix from the snapshots according to:
N
R = 1 ~r(t)rH(t).
N m,
After forming the sample covariance matrix, the Cholesky decomposition is
performed:
R = LL
where L is a lower triangular matrix with positive diagonal terms. L is sent
to the
signal recovery ports 124.1, 124.2, 124.3, as indicated in the drawing.
In the CiCURE structure, there is no controller unit to detect source
ON/OFF transitions as in the eCURE system. The signal recovery ports have a
1o predetermined hierarchy or priority order. The first port has highest
priority and so
on. Therefore, CiCURE is not able to compensate for dynamic changes in the
signal
environment as can the eCURE algorithm. Each port receives as input the
current
block steering vector estimates from the ports that are higher in priority,
the sensor
signal data, and the Cholesky decomposition of the sample covariance matrix
for the
is current block. Each port outputs the recovered signal and associated
steering vector
for a captured source.
FIG. 16 shows the operations of a single signal recovery port. Suppose
the higher-priority ports produce a set of steering vectors for the current
block, defined
as {a,(m), ... , ak_,(m)}. The weight vector to produce pk(t) for the current
block (the
2o mth block) is determined by modifying the MVDR weights for the kth port on
the
previous block by a computation carried out in the kth port as described next.
The first
step is to compute Gram-Schmidt orthogonalized weights (vk(m)) according to:
k-1
vk(m)=~'k(m-1)-~(ai'(m)~'k)al(m)l II aOm) IIz.
The port then uses the Gram-Schmidt orthogonalized weights (vk(m)) to
determine the
25 waveform pk(t) according to
pk (t) = vk (m)r(tO

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96J18867
-62-
Next, a vector, a~(m), of sample cross-cumulants involving this waveform is
computed
having components:
[ak(m)y =cum(Pk(t),Pk(~)~Px(t)~r~(t)), 1 <_l ~ M,
in which, [ak(m}), is the lth component of ak(m}. This vector provides an
estimate of a
source steering vector and is sent to all the ports that have lower priority
than the kth
port and the optional direction-finding unit. In addition, the MVDR weight
vector for
the kth port is determined using ak and L.
The MVDR weight vector is computed in a two-step procedure that
exploits the lower triangular structure of the Cholesky decomposition. First,
the
to temporary solution, uk is computed by solving the linear system of
equations:
Luk (m) = a k (m).
Next, the MVDR weights are computed by solving the second linear system:
LHwk(m)=uk(m)I II uk(m)II .
It is necessary to maintain phase continuity with the weights of the previous
block.
t 5 This requirement resolves the complex phase ambiguity inherent in the
blind signal
separation problem, which would otherwise cause "glitches" in the recovered
signals at
the block boundaries. Therefore, before using the weight vector wk(m) estimate
the
signal waveform, the complex phase ambiguity is resolved by computing the
scale
factor:
20 ~k(m) -wk (m)wk(m-1)/I wk (m)wk(m-1)I
and then scaling the MVDR weights according to:
~' k (m) _ ~k (m)w x (m)
This operation forces the current and previous block signal extraction weights
to have a
real inner product (i.e., no abrupt phase rotation at the block boundary).
This method
25 eliminates block-to-block phase discontinuities, leaving only a bulk phase
rotation
ambiguity that is constant over all blocks recovered by the port. This bulk
phase
rotation is unimportant to the recovery of analog AM and FM modulated signals;
however, for digital modulations, its removal is desired. Section A subsequent
section

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-63-
on phase rotation equalization presents a method for doing so. For now, we
skip over
this minor detail.
Using the modified MVDR weights, the waveform estimate is computed
according to:
gk (t) _ ~'x r(t)
The recovered waveform is available for subsequent processing, which
may consist of recording of the predetected waveform, demodulation, signal
recognition, or other operations.
The current block weights are fed into a one-block delay unit which
t o makes them available to the Gram-Schmidt orthogonalization unit as the
initial weights
for processing the next block. Key characteristics of this implementation are
that the
iterative convergence of the CURE algorithm is realized over several blocks
instead of
within a single block, and high-priority ports converge sooner than low-
priority ports.
Is 5.0 Alternate Embodiment Using Pipelined Cumulant Recovery (pipeCURE):
This section describes a variant or extension of the eigendecomposition-
based CURE (eCURE) system, which will be called the pipelined eigenCURE
(pipeCURE) system. The eigenCURE (eCURE) algorithm analyzes measurements on
a block by block basis and has dynamic capabilities to eliminate port
switching and port
2o allocation in the case of transient sources. Received signal data are
filtered or
transformed by a prewhitening operation before reaching cumulant based signal
separation processing. eCURE (described in Section 3.0) has several advantages
over
the covariance-inversion CURE (CiCURE) (described in Section 4.0), which uses
covariance-inversion instead of eigendecomposition:
2s ~ It has better signal separation performance (i.e., better crosstalk
rejection at
- port outputs).
~ It has guaranteed fast convergence, specifically a superexponential
convergence rate which is mathematically guaranteed.
~ It has improved port stability which helps minimize random port switching.

CA 02272930 1999-OS-25
WO 98124192 PCT/US96118867
-64-
~ It can operate with a much wider range of input signal strengths.
This last property is particularly useful when trying to recover a weak
signal in the presence of strong interfering signals.
The pipeCUltE system "pipelines" the eCUIZE algorithm in order to
have:
~ Simpler implementation (no feedback between operational blocks).
~ An ability to iterate more times over one block of data.
~ An option to use further eigendecompositions to improve results.
t o 5.I Overview of the pipeCURE Signal Separator:
The pipeCURE signal separator has three main components, which are
shown in FIG. 17: a preprocessor unit 120, which is basically the same as in
the
eCUIZE system, a cumulant matrix computer 240, and a multiple port signal
recovery
unit 242. In addition, there are two optional units: the demodulators 128, to
complete
the recovery of the separated signals for the purpose of recording and the
direction-
finding (DF) search unit 172 to provide copy-aided directions of arrival on
output line
174. '
5.2 Preprocessor Unit:
2o The preprocessor 120 performs a block-by-block analysis of the element
array snapshots, determining the eigenvectors, number of signal sources, and
signal
subspace of the received array measurement data. It filters the received array
data,
transforming it from the M-dimensional sensor space to the P-dimensional
signal
subspace. In so doing, the steering vectors of the transformed sources are
made
orthogonal to each other in the range of this projection, and the transformed
source
powers are made equal (at high signal-to-noise ratios). The details of the
preprocessor
operation were described in Section 3.0 in relation to the eCURE system

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-65-
5.3 Cumulant Matrix Computer:
In this section, we introduce the cumulant matrix computer, a unit that
computes the statistics as required by the iterative blind signal separation
processor.
The cumulant matrix computer computes a P2 x p2 (here we assume the number of
s sources and its estimate are identical) cumulant matrix C is defined as:
C(P~(i-1)+j,P~(k-1)+I~=cum~Y;(t),Y;(t)~Yk(t)~Yr(t)~ 1_<f,j,k,l<_P
With finite samples, this matrix can be estimated as:
N
C(P'(t-1)+ j,P~(k-1)+I)= N~Yi(t)Y;(l)Yx(lh'r(t)
1 N N
~IZ i~Y~~t~~l~t~~~Yk~tz~i~tz~
12 ~yi(tl~k~t~~~YJ~t2~~~r2~ 12 ~Yi(tt~l(tI~~YJ~t2~k~t2~
r,_1 riot N i,~1 r2.1
1 <- i, j, k, l _< P
in which the signal vector y(t) is defined as:
y(t)=TH r(t), where T °--ES(A,s -a"I) liz =US-'
5.4 Multiple Port Signal Recovery Unit:
~s The multiple port signal recovery unit 242, receives as inputs the
preprocessed array measurement y(t), the cumulant matrix C the eigenstructure
(E, A)
derived from the array measurements in the preprocessor 120 and the estimated
number
of sources (Pe) generated in the preprocessor. Using these input signals, the
multiple
port signal recovery unit derives recovered signals for output on lines 132
and steering
2o vectors for output on lines 170, in accordance with the following equations
and steps:
(a) Inputs to multiple port signal recovery unit:
~ Number of sources, P.
~ Transformation matrix T °-- E,s(A.,. -an I~ ~~2

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-66-
~ Preprocessed signals: y(t) = T H r(t)
~ Eigenstructure of the covariance matrix: ~ES,A.s,arz
~ Initial estimates of the steering vectors for sources stored as the
columns of A .
~ Cumulant matrix C:
C(P~(i-1)+j,P~(k-1)+l~=cum~y;(t),y~(t),yk(t),y;(t)) 1<-i,j,k,l<P
(b) Outputs from multiple port signal recovery unit:
~ Estimated steering vector A that will be used in the next block as a
to starting point (in place of A ).
~ Recovered signals for the analysis block , "s(t) .
t5 (c) Processing in the multiple port signal recovery unit:
1. Transformation of Steering Vectors: Project the steering matrix
estimate onto the reduced dimensional space by the transformation matrix T:
B = THA
2. Cumulant Strength Computation: Normalize the norm of each
2o column of B and store the results in V , and then compute the cumulant
strength for
each signal extracted by the weights using the matrix vector multiplication:
v", = b", / Ilb",I, where vn, (bn,) is the mth column of V (B).
~n,-I(Vnr~Vnr)NL''(vn,~Vn,)I, fOrl<_m<P.
3. Priority Determination: Reorder the columns of V and form the
25 matrix W , such that the first column of W yields the highest cumulant
strength, and
the last column of W yields the smallest cumulant strength.
Columns of V in descending cumulant strength -~ W

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-67-
4. Capture of the kth source: Starting with the kth column of W ,
proceed with the double power method followed by Gram-Schmidt
orthogonalization
with respect to higher priority columns of W , i.e., for column k:
wk (b + I) = ah+, ~ ~wk (b) ~ I,, ~N C ~wk (b) ~ wk (b)a b is the iteration
number,
where the constant ab+ 1 is chosen so that the norm of w k (b + 1) is unity
and b is the
iteration number. This operation is followed by the Gram-Schmidt
orthogonalization:
k-1
Wk (b+I) _ ~h+I ~~~'~'k(b+I)-~W~ ~(WNWk(b+1))~, SlnCe IIW~II= 1,
I=1
where the constant X36+1 is chosen so that the norm of wk (b + I) is unity. In
the last
expression, w, denotes the final weight vector with source of priority 1.
5. Capture of the remaining sources: Repeat step 4, for each column for
a predetermined K times. After iterations are complete for the kth column,
declare the
resultant vector as wk, and proceed with the remaining columns. After all
sources are
separated, form the matrix W that consists of wk's as its columns.
Converged weight vectors wk' s -~ form the columns of W .
6. Port Association: After all the power method and Gram-Schmidt
iterations are complete, we compare the angle between columns of W and the
columns
of V .
Calculate the absolute values of the elements of the matrix Z = W H V .
Take the arccosine of each component of Z.
2o To find the port number assigned to the first column of ~' in the
previous block, simply take the index of the largest element of the first row
of the
matrix Z.
For the second column of W , we proceed the same way except this time
~ we do not consider previously selected port for the first column. Using this
rule, we
reorder the columns of W , such that there is no port switching involved.
Reorder the columns of W, based on Z -> results in V .

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-68-
7. Steering Vector Adjustment: Due to the blindness of the problem,
estimated steering vectors are subject to arbitrary gain and phase
ambiguities. The
gain ambiguities are corrected by the unit amplitude constraint on the columns
of V .
However, this does not prevent phase modulations on the columns of this
matrix. To
maintain this continuity, we compute the inner product of each column of V
with the
corresponding column in V and use the resulting scalar to undo the phase
modulation,
i.e.,
En~ = angle(vn V m ), and V n~ = V n~ ~ eXp(-.J~m )
8. Backprojection: In order to use the current steering vector estimates
to for the next processing block, we need to backproject the steering vector
estimates for
the reduced dimensional space to the measurement space. This yields the
estimate of
the steering matrix and can be accomplished as:
A-f (ns-azlr)+vzV.
A will be used in the next block as A as an estimate of the steering matrix in
the first
step of the multiple port signal extraction unit.
9. Beamforming: It is important to note that beamforming for P sources
requires a matrix multiplication of two matrices: the V matrix that is P by P,
and the
reduced dimensional observation matrix y(t), which is P by N, where N is the
number
of snapshots. Usually N is larger than P and this matrix multiplication may
take a
long time because of its size. Therefore, it may be appropriate to do final
beamforming in another processor since it does not introduce any feedback.
Final
beamforming is accomplished as:
s(~) = v "y(t)
The estimated signals will be sent to the correct post processing units
because of the
orderings involved.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-69-
6.0 Steering Vector Tracking Method For Situations Having Relative Motion:
For situations in which there is relative motion of the source, receiving
array, or multipath reflectors, it is desirable to generalize the CURE
algorithms to
exploit or compensate for the motion. One rather complicated way of doing this
is to
use an extended Kalman filter to track the changes in the generalized steering
vectors
derived by the CURE algorithms. Here we present a simpler method which merely
involves using a variant of the iterative update equation used in the CURE
algorithms.
We present two such variants of the update equations, called a-~3CURE and
p.CURE,
that can be used principally to provide an improved initial weight vector for
each block
to of array samples (snapshots). These update equations can be used with any
of the
CURE algorithms discussed in previous sections (CiCURE, eCURE, pipeCURE).
Consequently a-(3CURE and p,CURE are not independent stand-alone algorithms,
but
rather are enhancements to CiCURE, eCURE, and pipeCURE that provide greater
stability and less port-switching in dynamic situations.
t5 The iterative update equations are given by:
wk+, = a wk + p vect[cum(.,.,.,.)] (a-(3CURE)
wx+ ~ _ ( 1--N~) ~'~'k + N~ vect[cum(. , . , . , . )] (p.CURE)
= wk + p, (vect[cum(.,.,.,.)] - wk] .
These iterative update equations may be compared to the standard iterative
update
2o equation presented in previous sections for CiCURE, eCURE, and pipeCURE.
wk+, = vect[cum(. , . , . , . )] . (CiCURE, eCURE, pipeCURE).
In these equations, k is a time index, and wk is the linear combiner
weight vector that converges to the generalized steering vector of one of the
input
source signals. The iteration on the index k is on individual snapshots or
block of
25 snapshots occurring through time, as opposed to multiple iterations within
a block. The
a-[i and p, update method does not preclude iteration within a block. Indeed,
within-
block iteration can be used in conjunction with block-to-block updating or
- initialization. Generally, there is no advantage to using the a-(3 or ~
update equations
for within-block iteration. Within-block iteration should be done by the
standard

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/LTS96/18867
-70-
update equation. The a-(3 and ~ update equations are best used for block-to-
block
updating, that is, to initialize a block's weight vector based on the final
converged
weight vector from the previous block.
Two equivalent forms are given for the p,CURE update equation. As is
discussed below, the first form is most convenient when the purpose is to
predict
ahead, whereas the second form is most convenient when the purpose is to
average
previous data with new data. Although a-[iCURE and p,CURE appear to involve
different update equations, the algorithms are equivalent provided there is a
renormalization of the weight vector at every iteration. Because a weight
vector
1o renormalization is always used in the iterative steps to prevent the weight
vector from
shrinking monotonically, a /3 CURE and pCURE are equivalent.
a-(3CURE and CURE updating can be used for determining the initial
EGSV(s) of a block of samples subject to eCURE or pipeCURE processing. When
used with eCURE, the block initialization can be performed in either the M-
dimensional sensor space or the P-dimensional signal subspace. FIG 19 and FIG
20
show these two cases, respectivly. The application of a-[iCURE and CURE to
CiCURE is similar to FIG 19 but is not shown.
FIG. 19 shows the relations among various vectors in one cycle of the
CURE update operating in the M dimensions of the sensor space. Five vectors
are
2o shown. wk is the current weight vector at time k and is also the current
estimate of the
generalized steering vector ak. The generalized steering vector at time k+ 1
is denoted
ak+~ ~ ak+, is the generalized steering vector of which wk+, is an
approximation. The
cumulant vector cum = vect[cum(.,.,.,.)] is represented as a vector emanating
from
the origin. The scaled difference vector ~[cum - wk] is shown as a vector
originating
at the tip of wk and extending through the tip of cum. The tip of this vector
defines
wk+ 1
For the case shown, ~. is greater than unity, and the algorithm is
anticipatory. This form of the pCURE update is useful when the purpose is to
predict

CA 02272930 1999-OS-25
WO 98124192 PCT/US96/18867
-71-
a generalized steering vector that is varying with time. It is instructive to
think of the
CURE update as an equation of motion:
New Position = Old Position + Velocity x Elapsed Time,
where New Position is identified with wk+,; Old Position is identified with
wk; Velocity
is identified with [cum - w~]; and Elapsed Time is identified with ~.
Conversely, if ~, is less than unity, the p,CURE update functions as an
averager rather than a predictor, putting weight (1-p) on the current weight
vector wk
and weight p, on cum which is an estimate of the generalized steering vector
ak+, (or its
projection bk+,). In this case, the tip of cum would lie to the right of wk+,,
and the
to scaled difference vector p,[cum - wk] would point to, but not pass through,
cum.
FIG. 20 similarly shows the vector relations for one cycle of the
pCURE update when the iteration is performed in the P dimensions of the signal
subspace. The vectors are similar to those in FIG. 19 with the key difference
being
that bk is the projection of the generalized steering vector aA into the
signal subspace,
and wk+, approximates bk+,, the projection of ak+,. At the conclusion of the
iterations,
the estimated generalized steering vector may be obtained by backprojecting
the
terminal weight vector w into the M dimensional sensor space.
a ,1i and ~, iterative updating has an advantage in the situation where
signal sources are persistent but moving (i.e., non-static geometry). CiCURE,
2o eCURE, and pipeCURE are formulated in the batch-processing mode (i.e.,
array
snapshots are processed one block of samples at a time) assuming the source
geometry
is static during a block. With these algorithms, only small changes in source
geometry
are allowed to occur from one block to the next. a ~l3 CURE and p,CURE
accommodate greater changes from block to block by providing for tracking of
the
generalized steering vectors via the a-(3 tracking method, which is well known
in the
sonar and radar engineering literature.
In summary, a-~3CURE and ~. iterative updating have tracking
capability inherently built in which can be used to improve the performance of
CiCURE, eCURE, and pipeCURE in situations in which EGSVs are changing

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-72-
dynamically. This tracking capability enables the adaptation to geometrical
changes
that occur gradually over time. Abrupt changes, like the appearance of new
signals or
disappearance of old signals, and attendant port switching are a different
problem.
Detection logic is still required to mitigate port switching caused by abrupt
changes.
7.0 Alternate Embodiment Using Direct or Analytic Computation:
Unlike the iterative methods presented in previous sections, this section
presents a method for separating signals that is non-iterative. It is, in
fact, a closed
form, analytic solution for computing the cumulant vectors and generalized
steering
to vectors without the need for iteration. Because the method is non-
iterative, the issues
of convergence and convergence rate are no longer of concern. Convergence is
both
assured and instantaneous.
In the direct method, the generalized steering vectors for a small number
of sources (two in this example) are computed directly as set forth below,
using one of
two computational methods:
Steps of Operation for Method 1:
~ Compute the covariance matrix R for M channel measurements:
N
R = 1 ~ r(t)r H (t)
N ,~,
~ Compute the eigendecomposition for R:
R = ESAsE" +6"E"E"
~ Compute the transformation matrix T:
( 2 , 1/2
T=Es\ns-6nll
~ Preprocess the measurements by the transformation matrix:
y(t) = T H r(t)
~ Compute the four by four cumulant matrix C from y(t)
C~P~(i-1)+.j,P~(k-I)+1~=cum~y;(t),y~(t),yk(t),y;(t)) 1<_i,j,k,l<_2

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-73-
~ From its definition, the C matrix can be decomposed as:
H
_ Cl1 C2l
C21 C22
in which the three matrices f C" , Cz2 , Cz, } are defined (because of
prewhitening and
circular symmetry assumption):
_ E ~~Yt (t)I4 } - 2 E ~IYI (t)I2 YI (t)Yz (l ) } _ ~I ~z
C" E{YI (t)Iz Yz (t)YI (t)} E~,YOt),2I Yz (t)1 z } -1 cz
_ E ~I YI (t )I2 YI (t)Yz (t )} E l(YI (/)Yz (t))z ~ C2 C4
Cz' z t 2 -1 E ~Y, (t)Yz (t)I Y2 (t )12 }
E ~I YI (t) IYz ( )I }
1o C E {1Y1 (t)I 2IY2 (t)I2 } -1 E ~I Yz (t)I2 YI (t )Y2 (~)} cs cs
2z - E {lyz (t)I Yz (t)YI (t)} E ~I Y2 (t )I } - 2 cs
~ Construct the fourth-order polynomial in terms of the complex variables {v,,
v2} .
_V1 _ IV112\CIVI +C2 V2/+IV212\C3V1 +CSV2/+VIV2~C2VI +C4V2~+V2Vt ~C2V1 +C3V2~
V2 (VI I2 (C2 V1 +C3V21+IV212\CSV1 +C6V2J+V1V2'C3V1 +C3V2J+V2V1 \C4V1 +CSV2/~
This requires the computation of the cumulants {c~,....c6} defined in the
above item
from the measurements.
~ Solve the polynomial for {v~, v2} . There is one trivial solution {v~ = v2 =
0} . Also
note that if the vector (v,, v2 )T is a solution, then the vector (-v2, v, )T
is also a
solution.
2o ~ Evaluate the resultant cumulant strengths from the solutions to the
polynomial:
V ~ V)H C(v~ ~ v~, V - LVI ,V2 ~H

CA 02272930 1999-OS-25
WO 98124192 PCTlUS96118867
-74-
~ Determine the solution for the polynomial that results in the highest
cumulant
strengths to estimate sources. Let this be (v,,vz)T. Then, (-v2,v,)Tis the the
second
solution.
~ For each accepted solution v, we can find the corresponding steering vector
in the
M dimensional sensor space:
~~z
a =Es~As -6,2~ v
~ Once the steering vector estimates are found as in the previous step:
I. Port association, and
2. Waveform continuity,
to can be implemented as described in Section S.0 (pipeCURE).
Steps of Operation for Method 2
~ Compute the covariance matrix R for M channel measurements:
N
R = 1 ~ r(t)rH (t)
N ,_,
~ Compute the eigendecomposition for R:
R = ESASEH +a,2EnEn
~ Compute the transformation matrix T:
2 nz
T=Es~As _6~I~
~ Preprocess the measurements by the transformation matrix:
2o y(t) = T Hr(t)
after which the measurements take the form:
y(t)=THr(t)=b,s,(t)la~ +bzsz(t)la2 +e(t)
Because of prewhitening, we have the following result for the steering vectors
for the
two sources in the two dimensional space:
b, - cos8~ ' bz - -sin8e-io ~ Ilby~ _ ~~bz~~ = 1~ Ibz by = 0.
singe cosh

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-75-
~ Construct the three by two matrix F using five of the six cumulants:
c, ~z E {I Y~ (t)/4 ~ - 2 E {I Y~ (t)/ z Yi (t)Yz (t)~
F_ ~z C3 E{IY~(t)IzYz(t)Y~(t)~ Ef~Y,(t)IzIYz(t)~z}-1
~a ~s E 1(Y1 (t)Yz (t))z ~ E ~Y~ (t)Yz (~)IYz (t)Iz ~
which can be decomposed into the following three matrices:
1 1
Y 2'' z . cos4 8 0 1 sin6 e_;ro
F - sin6 e~~ - cosA e~~ ~a, ~ cos0
cosh z sinA z 0 Y 4°z . sin' 8 1 _ cosA e_~m
sin6 e~~~ ~_ cosA e~~~ ~~,2 )z sing
cosh sin8 ' "
n
F=GDH
~ Also form the. four by four cumulant matrix C:
C~P'(t-1)+>~p'(k-1)+l~=c~~Y~Cf)~Y;~t~~Yk~~~~Y~~r~~ l~l>>>k~l <2
The symmetries involved in this matrix reduces the number of distinct
cumulants to
six. In addition, five of the six cumulants necessary are already computed
when we
formed F.
~ Compute the Singular Value Decomposition (SVD) of the matrix F:
1. If the rank of F is zero, then source separation is not possible.
2. If the rank of F is one, then the principal eigenvector can be used to
separate sources: assume e, is the principal eigenvector of F, and let its
components are defined as:
a,
e, = az ~ ~an2 +iazlz +1a31z =1
a3
Then, we can obtain the estimate of the first source, using:
H
g~(t) = a~ Y(t)
2
and the second source waveform can be estimated using:

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-76-
H
gz (t) - az y(t)
oc,
3. If the rank of F is two, then the null eigenvector can be used to
separate sources together with a solution of a quadratic equation: let x
denote
the 3 by 1 vector that is orthogonal to the columns of of F (which can be
obtained using SVD or QR decomposition of F):
xHF = 0, x = ~x,,xz,x3~
Then, due to the Vandermonde structure of the columns of G, we can obtain the
parameters ~cos0 a ~~' son0 eJ~ ~ ~ as the roots of the quadratic equation:
1o x"z=0, z=~z,,zz,z3~ -~x; +x2z+x3zz =0
Since we know the roots of the above equation should be
sine core
e'~ ,- e'~ , and we have the weight vectors to separate the sources
core sine
as:
I H I H
g' (t) sing y(t) = s, (t) l (a; cos0) + 0 ~ sz (t) + sin0 e(t)
e'~ e'~
cos0 cos0
1 H 1 H
gz (t) _ cosA y(t ) = sz (t)e-'~ I (a2 sin0 ) + 0 ~ s, (t) + rose e(t)
sin0 sin0
t 5 In addition, we can normalize the weights to conform to the structure of
the
problem:
1 1
v' ~' sin0 e~ro ' vz ~z cos0 eiro
core - sine

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96118867
_77_
in which {(3,, ~Z~ are determined to make w,~~ = w2~~ =1.
~ After the weights for signal separation are determined, then it is possible
to
compute cumulant strengths using: Iw' ~ v~H Cw' ~ v~, v = [v, , v2 ]H is one
of the
weight vectors.
~ For each solution represented byv, we can fmd the corresponding steering
vector in
the M dimensional sensor space:
vz
a=ES~AS_a"~ v
~ Once the steering vector estimates are found as in the previous step:
1. Port association, and
to 2. Waveform continuity
can be implemented as described in Section 5.0 (pipeCURE).
8.0 Separation Capacity and Performance When Overloaded:
When the number of incident signals exceeds the capacity of the system
to separate signals, one would expect system performance to degrade. Unlike
some
other cochannel signal separation methods, the present invention is able to
operate
under such overload conditions.
Cochannel signal separation systems are designed to be able to separate
and recover signals provided the number of cochannel signals incident on the
array
2o does not exceed a number that defines the separation capacity of the
system. In the
present invention, the separation capacity is equal to the number of sensors M
in the
receiving array. Consequently, a cochannel signal separation system based upon
this
method can have no more than M output ports. Of course, the number of output
ports
can be less than M. For instance, a system can have P output ports, where P <
M. In
. 25 this case the system could recover each of P signals from among M signals
incident on
the array. Each of the P signals is recovered by a different set of beamformer
weights.
Each such set or weight vector defines a sensor directivity pattern having M-1
nulls.
Next consider cochannel signals received at the receiving array
consisting of a mixture of coherent and noncoherent multipath components. A

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
_78_
complete description of how CURE algorithms behave in the presence of
multipath is
given in Section 9Ø In brief, signals with noncoherent multipath components
are
recovered on more than one output port. Each output port is associated with a
single
generalized steering vector. The system of the invention automatically creates
groups
of mutually coherent multipath arrivals and a different generalized steering
vector is
formed for each such group. Each group is treated as an independent signal and
counts
as one signal against the capacity M. The maximum number of such noncoherent
groups that can be incident on the array for which the system can perform
separation
and recovery equals the separation capacity. In the present invention, this
capacity
1 o equals the number of array elements M.
In overload situations, the cumulant optimization or iteration, which is
the basis of the invention, still converges to a generalized steering vector
of a signal or
noncoherent multipath group. Consequently, the system of the invention
determines up
to M generalized steering vectors from which beamforming weights are computed
and
which can form up to M-1 generalized nulls. However, because the number of
signals
is greater than capacity, it is not possible to recover a given signal while
simultaneously rejecting all other signals by means of generalized nulls. In
particular,
there are P-M excess signals (or G-M noncoherent groups) that leak through the
beamformers for the recovered signals. These excess signals are rejected
merely by
2o the sidelobe suppression associated with each beamformer's directivity
pattern. The
signals that are captured for recovery by the system tend to be the strongest
signals,
while the excess signals tend to be among the weakest. The excess signals
contribute
to the noise floor of the output ports. However, their contribution is minimal
because
of their low relative power and the sidelobe attenuation. Consequently, the
recovered
signals at the output ports generally have low crosstalk levels and high
signal-to
interference-plus-noise ratio (SINR).
FIGS. 21 and 22 illustrate the overload concept diagrammatically. FIG.
21 shows a basestation having a four-element antenna array, which provides
input
signals to a CURE system for separating received cochannel signals. Because
the
3o antenna array has only four elements, the system has a capacity of four
channels. The

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-79-
figure also shows five users, designated User A, User B, User C, User D and
User E,
- all attempting to transmit signals to the basestation array. FIG. 22 shows a
directivity
pattern associated with the antenna array as conditioned by the CURE system to
receive signals from User A. Because the array has only four elements, it can
present
directivity nulls in only three directions. In the example, the directivity
pattern presents
a strong lobe in the direction of User A, to receive its signals, and presents
its three
available nulls toward User B, User D and User E. User C, which produces the
weakest and most distant signal, cannot be completely nulled out. Similar
directivity
patterns will be generated for receiving signals from User B, User D and User
E. In
1o each case, the weakest signal (from User C) will not be completely nulled
out by the
directivity pattern. The system continues to operate, however, and is degraded
only in
the sense that weaker sources exceeding the system capacity cannot be
recovered and
will produce some degree of interference with the signals that are recovered.
A general conclusion is that the various embodiments of the invention
is are tolerant of separation capacity (or number-of signals) overload
conditions. In other
words, the various embodiments of the invention are "failsoft" with respect to
overload
beyond the signal separation capacities, and the ability to separate signals
degrades
gracefully as the number of signals is increased above the separation
capacity. This
property distinguishes CURE algorithms from DF-beamforming cochannel signal
copy
2o algorithms, such as MUSIC and ESPRIT , which do not function when
overloaded.
(MUSIC is an acronym for MUltiple Signal Identification and Classification,
and
ESPRIT is an acronym for Estimation of Signal Parameters via Rotational
Invariance
Techniques. For more information on these systems, see the papers cited in the
"background" section of this specification.
9.0 Performance of the Invention in the Presence of Multipath:
This section discusses the performance of the CURE systems (CiCURE,
eCURE, pipeCURE, etc.) when the signal environment includes multipath
propagation.
We confine the discussion to the phenomenon known as discrete multipath, as
opposed

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-80-
to continuous volumetric scattering, which is more complicated to describe.
However,
the statements below apply to volumetric scattering under certain conditions.
Multipath propagation occurs when a signal from a source travels by
two or more distinct paths to arrive at a receiving antenna from several
directions
simultaneously. A novel feature of the present invention is its ability to
separate
cochannel signals in a multipath signal environment.
Multipath propagation is caused by the physical processes of reflection
and refraction. A similar effect is caused by repeater jamming, wherein a
signal is
received and retransmitted at high power on the same frequency. Repeaters are
t o commonly used in radio communication to fill in shadow zones, such as
around hills or
inside tunnels, where the communication signal does not propagate naturally.
Cochannel repeaters area also used in electronic warfare (EW) systems to
"spoof" a
radar system by retransmitting a radar signal with a random delay at
sufficiently high
power to mask the actual radar return. The amount of delay is set in order to
cause a
false distance to be measured by the radar.
Naturally occurring multipath propagation can consist of a small number
of discrete specular reflections, or it can consist of a continuum of
reflections caused
by scattering from an extended object. The various multipath components
arriving at
the receiving antenna will generally be somewhat different. Differences among
the
2o various multipath components of a given source signal are (1) different
directions of
arrival (DOAs); (2) different time delays due to the different path lengths
traveled; and
(3) different Doppler shifts on each multipath component due to motion of the
transmit
antenna, receive antenna, or reflecting body.
Array-based cochannel signal separation and recovery systems
traditionally have difficulty working in a multipath environment (i.e., when
the one or
more of the arriving signals incident on the array come from several distinct
directions
simultaneously). For example, most multiple source DF-beamforming signal copy
systems generally do not work properly or well in a multipath environment, and
special
techniques such as spatial smoothing and temporal smoothing must be employed
to DF
~o on the individual multipath components of an arriving signal. The resultant
system and

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-81-
processing complexities make DF-based cochannel signal recovery systems
largely
- impractical for reception in signal environments characterized by
significant multipath
propagation. The cochannel signal separation capability of the CURE family of
systems overcomes these limitations.
To understand how the CURE system behaves in the multipath context
requires understanding the different types of multipath effects and how the
system
handles each type. In general, multipath arrivals of a source signal can be
classified as
either coherent or noncoherent depending on whether the arrivals' cross-
correlation
function computed over a finite time interval is large or small. Thus the
designation
1 o coherent or noncoherent is relative to the length of the measurement
interval. Coherent
multipath components frequently occur in situations where the scatterering
bodies are
near either the transmit or receive antennas and are geometrically fixed or
moving at
low velocities. Noncoherent multipath is caused by path delay differences and
Doppler
shift differences that are large compared to the measurement window.
The CURE algorithms recover generalized steering vectors as opposed
to ordinary steering vectors. An ordinary steering vector is the value of the
array
manifold at a single angle corresponding to a source's DOA. However in a
multipath
environment the received wavefield that the array spatially samples is
composed of
many plane waves for each source signal. Each source, therefore cannot be
2o characterized by a single DOA or steering vector. We consider how the CURE
algorithms behave under three cases:
~ Coherent multipath components,
~ Noncoherent multipath components,
~ Mixtures of coherent and noncoherent multipath components.
9.1 Performance Against Coherent Multipath:
In a coherent multipath signal environment, the CURE system finds a
single steering vector for each independent signal source. However, these
steering
vectors do not correspond to the ordinary steering vectors, which could be
innumerable
3o in the presence of many multipath scatterers. Rather, the CURE vectors are

CA 02272930 1999-OS-25
WO 98/24192 - PCT/LTS96/18867
-82-
generalized steering vectors that correspond to the sum of all the mutually
coherent
muitipath components of a signal source incident on the array. In the case of
a finite
number of discrete multipaths, the generalized steering vector depends on the
relative
power levels, phases, and ordinary steering vectors of the multipath
components.
The CURE signal recovery process is blind to the array manifold. Once
the generalized steering vectors for the cochannel sources have been obtained,
it is
unnecessary to convert them to source directions of arrival (DOAs) by using
the array
manifold, as would generally be done in a system employing direction finding
(DF).
Instead, the beamforming weight vectors for signal recovery are computed
directly
o from the generalized steering vectors. This is done by one of two methods:
(1) by
projecting each generalized steering vector into the orthogonal complement of
the
subspace defined by the span of the vectors of the other sources (by matrix
transformation using the Moore-Penrose pseudo-inverse matrix); or (2) by using
the
Capon beamformer, also called the Minimum Variance Distortionless Response
(MVDR) beamformer in the acoustics literature, to determine the recovery
weight
vectors from the generalized steering vectors. These solutions are both well
known in
the signal processing engineering literature. (See, for example, pp. 73-74 of
Hamid
Krim and Mats Viberg, "Two Decades of Array Signal Processing Research," IEEE
Signal Processing Magazine, vol. 13, no. 4, pp. 67-94, July 1996, ISSN 1053-
5888, or
2o Norman L. Owsley, "Sonar Array Processing," Chapter 3 of Array Signal
Processing,
S. Haykin (ed.), Prentice-Hall, 1985, 445 pp., ISBN 0-13-046482-l.) If the
generalized steering vectors are determined perfectly, i.e., no estimation
error, then the
former solution would provide zero crosstalk (or maximum signal-to-
interference ratio)
among the recovered signals at the beamformer output. The latter solution
would
provide recovered signals having maximum signal-to-interference-plus-noise
ratio
{SINR) .
Each output port of the CURE-based system has a beamforming weight
vector that is orthogonal or nearly orthogonal to the generalized steering
vectors of the
cochannel signals that are rejected by the output port. Each beamforming
weight
3o vector has a corresponding directivity pattern that assigns a gain and
phase to every

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-83-
possible direction of arrival. These directivity patterns can have up to N-1
nulls,
- where N is the number of array elements. The nulls can be either physical
nulls in
prescribed directions-of arrival (DOAs) or, in the case of coherent multipath,
' generalized nulls. Generalized nulls are not directional nulls but rather
are formed
s when a directivity pattern assigns gains and phases in the directions of the
coherent
multipath components of an interfering signal such that the components sum to
zero.
Generalized nulls have a major advantage over physical nulls for combating
cochannel
interference from coherent multipath because fewer degrees of freedom (i.e.,
fewer
array elements) are required to cause coherent multipath components to sum to
zero
1o than are required to directionally null each component separately.
FIG. 23 illustrates these concepts for the case of a transmission received
over a single-bounce path, designated multipath arrival A, a direct path,
designated
multipath arrival B, and a two-bounce path, designated multipath arrival C.
The three
multipath components are indicated as having steering vectors of amplitude and
angle
15 combinations A, La , Az L(3 , and A3 Ly , respectively. The CURE signal
recovery
system of the invention presents a directivity pattern that assigns a gain and
phase to
every possible direction of arrival. The gains and phases corresponding to the
three
multipath components in this example are shown as D, L~, , Dz LIZ , and D3 L~3
. The
corresponding recovered signal for the combination of multipath components is
derived
2o from signals of the form:
Y(t) _ [A,D,e'(°'+~~)+AzD2e~(P+~z)+A3D3ei(r+4~)~(t) .
Because the coherent multipath components of each output port's desired
signal are optimally phased, weighted, and combined in the recovery process,
the
CURE method realizes a diversity gain in the presence of multipath in addition
to
25 eliminating cochannel interference. The amount of the gain depends on the
number
and strengths of the distinct multipaths that are combined.

CA 02272930 1999-OS-25
WO 98124192 PCT/US96I18867
-84-
9.2 Performance Against Noncoherent Multipath:
Multipath arrivals of a source signal are not always coherent and capable
of being combined. The coherency requirement for CURE is that the multipath
components of a signal must have high cross-correlation computed over the
duration of
s a processing block or data collection interval. Multipath coherency can be
destroyed
by large path delay differences and large Doppler shift. When this happens
(i.e., when
the multipath arrivals are noncoherent), the CURE algorithms recognize and
treat the
arrivals as independent cochannel signals. The steering vector is estimated
for each
arrival, and each arrival is separately recovered and assigned to a different
output port.
to Thus, multiple recovered versions of the source signal are formed. It is
straightforward to recognize a noncoherent multipath situation because the
same signal
will be coming out of two or more output ports, each with a slightly different
time
delay or frequency offset.
FIG. 24 shows the sensor array complex directivity pattern in a situation
t5 involving receipt of two coherent multipath components of a desired signal
and a non-
coherent signal from an interference source. As indicated in the drawing, the
complex
directivity pattern includes a null presented toward the interference source,
while the
two multipath components are received and combined in the same way as
discussed
above with reference to FIG. 23.
9.3 Performance Against Mixtures of Coherent and Noncoherent Multipath:
In the general case of both coherent and noncoherent multipath, the
CURE algorithms automatically partition the multipath arrivals' into mutually
coherent
groups, and determine a generalized steering vector for each group. As in the
case of
noncoherent multipath, multiple recovered versions of the source signal are
formed.
The diversity gain is diminished relative to what would have been achieved had
the
multipath arrivals all belonged to a single coherent group. However, the loss
of
diversity gain is offset by having multiple replicas of the recovered signal
appear at the
beamformer's outputs. Moreover, a post-recovery combining gain is possible by
3o adding the signals at the output ports after correction for delay and
Doppler shift. If

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-85-
the recovered signals are to be demodulated, this post-recovery combining step
would
- precede demodulation.
FIG. 25 shows the complex directivity pattern formed by the
beamformer of the CURE system in a situation similar to that discussed above
for FIG.
24, except that the desired signal multipath components are non-coherent
instead of
coherent. The CURE system treats the three arriving signals (the non-coherent
multipath components and the interfering signal) as being from separate
sources. The
directivity pattern shown is the one that would be presented for recovery of
the
multipath component designated Arrival B. Physical nulls are presented toward
the
other arriving signals.
FIG. 26 shows a slightly different situation, in which the received
signals include a first interferon (A), a second interferon (B) having two
coherent
multipath components, and a desired signal. Interferon A is rejected by a
physical null
in the complex directivity pattern. Interferon B is rejected by a generalized
null in the
directivity pattern, such that the algebraic sum of the multipath arrivals of
the signal
from Interferon B is zero. If the Interferon B signal arrivals are
characterized by gains
and phases A~ La and AZ L~3 , and the directivity pattern at the angles of
arrival of
these components has gains and angles D, L~, and DZ L~2 , then the necessary
condition for rejection of the Interferon B signals by the generalized null
is:
2o A~D~eOa+~~).f..AzD2ei(a+mz) - 0.
I0.0 Recovering Communication Signals In The Presence Of Interfering Signals:
This section describes how the present invention is used separate and
recover signals received in the presence of other interfering signals
emanating either
from a local "friendly" source or from a deliberately operated jamming
transmitter
- located nearby. The apparatus of the invention includes an antenna array and
a
cumulant recovery (CURE) processing system, which processes signals received
through the antenna array and produces outputs at multiple ports corresponding
to the
multiple sources from which signals are received at the antenna array. The
processing

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-86-
system converges rapidly on estimates of the desired signals, without
knowledge of the
geometry of the antenna array.
Two primary problems in this area are addressed by this aspect of the
present invention. In one situation, an interfering transmitter may be
"friendly," that
is to say operated necessarily near a radio receiver, or even on the same ship
or
vehicle. Even if the transmitter is operating on a different frequency, there
is often
"spectral spatter" into the receiving band. In a related situation, the
interfering
transmitter is not "friendly" and is much more powerful than the communication
signals to be received and recovered.
1o In the first case, it might be desired to listen and receive while jamming
and transmitting simultaneously. Normally such simultaneous transmit and
receive
operations are not possible, but the friendly transmitter can be selectively
turned off to
permit reception. Prior to this invention, however, true simultaneous
operation of the
interfering transmitter and the receiver were often impossible.
In the second case, where a strong jamming signal is not under
"friendly" control, recovery of the received communication signal requires the
use of a
nulling antenna array. In the past, systems for recovering a communication
signal in
the presence of jamming required knowledge of the antenna array geometry and
did not
always provide rapid convergence on the desired signal solution.]
As shown in the drawings, the present invention pertains to systems for
recovering communication signals in the presence of interfering or jamming
signals,
whether or not on the same frequency. More specifically, as shown in FIG. 27,
a
receiving antenna 280 may be located on the same vehicle or vessel as a local
transmitter 282, and there may be a high-powered transmitter 284 located on a
nearby
friendly vessel operating at the same or a different frequency. A desired
signal is
received from another transmitter 106, located on land or on another vessel,
but is
subject to interference from the high-powered transmitter 284 and from the
local
transmitter 282. In accordance with the invention, the receiving antenna 280
is coupled
to a cumulant recovery (CURE) processing system 290, which rapidly processes
the
3o signals from the antenna array 280 and generates outputs on multiple ports,
effectively

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96118867
_87_
separating the signals received from the high-powered interfering transmitters
and the
desired received signal onto separate output channels, as indicated for ports
#1, #2 and
#3.
As shown in FIG. 28, a related situation is one in which reception at the
receiving antenna 280 is interfered with by a high-powered jamming transmitter
292,
perhaps on an enemy vessel. As in the previous case, the CURE processing
system 290
separates and recovers the desired weak signal on one output port (#2), while
the
jamming signal is isolated and may be discarded from port #l.
11.0 Diversity Path Multiple Access (DPMA) Communication:
The blind cochannel signal separation capability of the CURE algorithms
can be used to make possible a new communication channel access scheme:
Diversity
Path Multiple Access (DPMA). This technique enables the design of new
communication networks that can accommodate more users simultaneously in a
given
t 5 bandwidth allocation.
The demand for communication services has grown steadily over the
past three decades. To a limited extent this demand has been offset by
technological
improvements that have made new bandwidth available at higher frequencies up
to the
optical frequency band. Such bandwidth improvements, however, have been unable
to
2o keep pace with the growing demand for communication, and new communication
- methods became necessary. In response, communication system engineers have
developed new methods for communication, including networks, control
protocols,
channel access schemes, and modulation schemes. The principal goal of these
developments is to enable more users to use and share a communication resource
25 simultaneously without degrading the quality or creating mutual
interference.
11.1 History and Prior Art of Multiple Access Communication:
Prior to this invention, communication engineers had six channel-access
schemes at their disposal whereby multiple users in a network could share an
RF
3o communication channel in order to transmit simultaneously, more or less, to
a central

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
_88_
receiving site (e.g., cell base station or satellite). Communication engineers
would use
any of the following schemes to enable radio communication between multiple
users
and a single or multiple base stations. For a wireless network design, a
communication
engineer would pick one or more of the following methods as the basis for the
design.
~ Frequency division multiplexing/multiple access (FDM/FDMA)
~ Spatial division multiplexing/multiple access (SDM/SDMA)
~ Time division multiplexing/multiple access (TDM/TDMA)
~ Code division multiplexing/multiple access (CDM/CDMA)
~ Frequency hop multiplexinglmultiple access (FHM/FHMA)
~ Angle division multiplexing/multiple access (ADM/ADMA).
Although the terminology in this technology is still evolving, the
following distinction is often made. If two transmissions are cooperative, in
the sense
of being part of a common communication network, the term "multiple access" is
used.
If the transmissions are independent and not part of a network, the term
"multiplexing"
is commonly used. The distinction is minor and we shall largely ignore it in
this
description.
In FDMA, different transmitting users are assigned to different
frequencies. More precisely each transmitting user is assigned a different
spectral slice
that doesn't overlap with those of other users. FDMA was historically the
first
2o multiplexing/multiple access method to develop. Its origin is traced back
to the
beginning of radio, and it is the basis for radio and television broadcast
services,
whereby an individual is able to receive and select among the signals
transmitted by
many stations. In an FDMA network, the transmitting users signals are not
cochannel,
and cochannel interference is thereby avoided.
The remaining five channel access schemes enable two or more users to
be on the same frequency at the same time (i.e., user transmitted signals can
be
cochannel). The schemes mitigate or prevent mutual interference by different
means.
SDMA is the cellular concept, which originated at Bell Laboratories
(The Bell System Technical Journal, special issue on Advanced Mobile Phone
Service,
3o vol. 58, no. 1, January 1979). Users are divided geographically into cells,
seven of

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-89-
which are indicated at 300 in FIG. 29. Each cell 300 has a base station 302,
and the
- base stations are linked together via fixed land lines 304 or point to point
microwave
links. A central facility, the mobile telephone switching office (MTSO) 306,
controls
network operation and generally serves as a gateway for tying the mobile
network to
other communication services such as the public switched telephone network
(PSTN)
308. The set of base stations 302 and the MTSO 306 form the "backbone"
infrastructure of the mobile network. Each base station 302 has a finite set
of
frequencies for sending and receiving, and adjacent cells 300 have different
sets of
frequencies. Within each cell, FDMA is employed to prevent cochannel
interference.
There are only a finite number of frequency sets available, and base stations
302 that
are separated by some minimum distance use the same frequency sets. Thus, two
transmitting users, indicated at 310 that are on the same frequency are
necessarily in
different cells some distance apart. Each users signal enters the backbone
through a
different base station. The geographic distance between cells prevents
cochannel
interference.
SHMA prevents cochannel interference by prohibiting intracell
frequency reuse and allowing only intercell frequency reuse. The remaining
four
channel access schemes TDMA, CDMA, FHMA, and ADMA overcome this
restriction and enable frequency reuse among users within a cell-intracell
frequency
reuse.
In TDMA, all users transmit on the same frequency. Each transmitting
user is assigned a unique time slot in which to transmit. The average rate of
information transmission equals the peak or instantaneous rate times a duty
factor
which is the slot duration divided by the revisit interval. Although the users
are
sending at the same time, TDMA prevents cochannel interference because the
users do
not actually transmit simultaneously.
CDMA is a form of direct sequence spread spectrum in which the
various users encode their transmissions with orthogonal or nearly orthogonal
spreading sequences. All transmitting users use the same frequency. In order
to
3o receive a particular signal, a receiver must despread the signal using the
same sequence

CA 02272930 1999-OS-25
WO 98/24192 - PCT/LTS96118867
-90-
that was used to spread it at the transmitter. Because of the orthogonality
property, the
cross-correlation between any two spreading codes is near zero. For this
reason, the
user signals after reception and despreading are free of cochannel
interference. CDMA
is the basis of the IS-95 communication standard.
FHMA is used to apply frequency hop spread spectrum technology to
communication networks. A set of frequency hopping (FH) radios operate in the
same
band on the same hop frequencies and transmit to a central receiving facility
or base
station without mutual interference provided the radios use non-interfering
hop
sequences. Unlike CDMA, the required sequence property is not orthogonality or
low
1o cross-correlation, but rather a mathematical relative of the Latin Square.
FHMA can
be thought of as a dynamic form of FDMA in which the frequency assignments
change
regularly.
ADMA, which is shown in FIG. 30, uses multi-source direction finding
(DF) and beamforming technology to isolate and recover the signals from the
t 5 transmitting cochannel users in a cell. Each base station 302 is equipped
with a
receiving array connected to an N channel receiver (not shown), where N is the
number
of antennas in the receive array. The received signals are processed by a
mufti-source
DF system 312 to determine the directions or angles of arrival (DOAs) of the
signals
on a given frequency. Any mufti-source DF algorithm can be used to perform the
DF
2o function, such as MUSIC, ESPRIT, or WSF, all of which are well known in the
signal
processing engineering literature. Each user 310 is characterized by a single
unique
DOA. Beamforming weight vectors are then computed, as indicated in block 314,
from the estimated directions that enable the cochannel signals to be
recovered
(separated and copied). A transformation matrix, whose rows are the
beamforming
25 weight vectors, multiplies the array signals, and the product yields the
recovered
cochannel signals. Each row of the transformation matrix (i.e., each weight
vector)
consists of complex numbers that steer the array to one particular signal
while putting
directional nulls in the directions of the other cochannel signals. The
transmitted user
signals can be recovered free of cochannel interference provided the users are
angulariy
so dispersed such that they have distinct bearing angles measured at the
receive array.

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-91-
ADMA is described in a recent patent by Roy and Ottersten (Richard. H. Roy,
III, and
Bjorn Ottersten, Spatial Division Multiple Access Wireless Communication
Systems,
U.S. Patent No. 5,515,378, May 7, 1996), but the patent specification uses the
term
SDMA.
s
11.2 A New Method of Multiple Access Communication:
The present invention achieves a new method for channel access in
wireless communications that is distinct from the six basic methods described
above.
The new method is termed diversity path multiple access (DPMA). It overcomes
three
Io limitations of ADMA.
First, wireless channels (characterized by their angle spread, delay
spread, and Doppler spread) are dominated by multipath. The transmitting user
signals
arrive at a base station from a multiplicity of directions simultaneously.
Angle spread
arises due to multipath from local scatterers and remote scatterers. The local
scatterers
15 are near the user and near the base station. Measurements have shown that
angle
spreads for cellular channels generally lie in the range from 2 to 360
degrees.
Therefore multipath cannot be ignored, and the idea that a user's signal
arrives from a
single unique direction is demonstrably not true. The ADMA concept of a single
wave
arriving from a single direction characterized by a pair of angles for each
cochannel
2o signal source is valid in free-space communications, perhaps, but is not
valid for
wireless communication networks operating in the ultra high frequency (UHF)
band in
urban, suburban, or rural environments.
Second, most multi-source DF algorithms generally do not work
properly or well in a multipath environment. Although well-known techniques
such as
25 spatial smoothing and temporal smoothing can be used to DF on the
individual
. multipath components of an arriving signal, the resultant system/processing
complexities make such approaches impractical.
_ Third, even when multipath is absent, ADMA requires the transmitting
cochannel users DOAs to be distinct. That is, the angular separation between
users
3o cannot be zero. The users must be separated in angle from one another by
some

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-92-
minimum angle. The assignment of a frequency to several cochannel users must
take
this geometric restriction into account. This limits the utility of ADMA.
The cochannel signal separation capability of the CURE algorithms
overcomes the limitations of ADMA. CURE algorithms recover generalized
steering
vectors as opposed to ordinary steering vectors. An ordinary steering vector
is the
value of the array manifold at a single angle corresponding to a source's DOA.
However, in a multipath environment, the wavefield at the receiving array is
composed
of more than one plane wave for each source signal. Consequently, sources
cannot be
characterized unique DOAs or steering vectors.
The CURE signal recovery process is blind to the array manifold. The
CURE algorithms find, for each source, a generalized steering vector that
corresponds
to the sum of all the mutually coherent multipath components of a signal
source
incident on the array. The generalized steering vector depends on the relative
power
levels, phases, and ordinary steering vectors of the multipath components.
Formally,
each generalized steering vector is a complex weighted sum of the array
manifold
steering vectors at the multipath arrival directions. The complex weights
account for
path length and attenuation differences among the multipath arrivals. In some
cases,
the multipath structure consists of a continuum rather than a few discrete
components.
In such cases the generalized steering vector becomes an integral of the array
manifold
over all directions. The CURE system determines the generalized steering
vectors
directly from the received signals, not from the array manifold. Indeed, the
various
embodiments of the CURE system do not need the array manifold to perform
signal
separation and recovery.
Once the generalized steering vectors for the cochannel sources have
been obtained, it is unnecessary to convert them to source DOAs by using the
array
manifold, as would generally be done in a system employing DF such as ADMA.
Using CURE, the beamforming weight vectors for signal recovery are computed
directly from the generalized steering vectors. This is done by one of two
methods:
(1) projecting each generalized steering vector into the orthogonal complement
of
3o subspace or span of the vectors of the other sources; (2) using the minimum
variance

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-93-
distortionless beamformer (MVDR) equations to determine the recovery weight
vectors
- from the generalized steering vectors. These solutions are both well known
in the
signal processing engineering literature. If the generalized steering vectors
are
' determined perfectly, i.e., no estimation error, then the former solution
would provide
s zero crosstalk (i.e.; maximum signal-to-interference ratio) among the
recovered signals
at the beamformer output. The latter solution would provide recovered signals
having
maximum signal-to-interference-plus-noise ratio (SINR).
An illustration of how the invention is used in the context of a DPMA
communication system is provided in FIG. 31, which shows a single cell 300,
with a
t o basestation 302 and two users 310. One user (A) reaches the basestation
through
multipath propagation, while the other has a direct propagation path to the
basestation.
A CURE processing system 316 receives and processes the signals received by
the
basestation 302. In communicating with cochannel user A the system 316
generates a
beamformer directivity pattern that presents a physical null toward the other
user, but
t S presents a generalized steering vector that results in both multipath
components from
cochannel user A being received and combined.
A feature of the CURE systems is that the omnipresence of multipath
enables the recovery (separation and copy) of signals from sources that have
zero
angular separation from the point of view of the receiving base station array.
For
2o example, consider two sources that are collinear with the base station such
that one
source lies behind the other. Although the direction to both sources is
identical and the
ordinary steering vectors for line of sight propagation are identical, the
multipath
configurations are entirely different. Therefore, the generalized steering
vectors of the
two sources will be entirely different. This facilitates the separation and
recovery of
2s the cochannel source signals in situations where ADMA cannot work.
Because the coherent multipath components are optimally phased,
weighted, and combined in the recovery process, the CURE method realizes a
diversity
. gain in the presence of multipath. The amount of the gain depends on the
number of
distinct multipaths that are sufficiently coherent to be able to be combined.

CA 02272930 1999-OS-25
WO 98/24192 PCTlUS96/18867
-94-
Not all multipath components of a source will be coherent and capable
of being combined. The coherency requirement is that the multipath components
of a
signal must have high cross-correlation computed over the duration of a
processing
block or data collection interval. Multipath coherency can be destroyed by
large path
s delay differences and large Doppler shift. When the multipath components of
a signal
source are not all mutually coherent, the CURE algorithms automatically
partition the
multipath arrivals into coherent groupings, and determine a generalized
steering vector
for each group. When this happens, multiple recovered versions of the source
signal
are formed. The diversity gain is diminished relative to what would have been
1o achieved had the multipath arrivals all belonged to a single coherent
group. However,
the loss of diversity gain is offset by having multiple replicas of the
recovered signal
appear at the beamformer's outputs.
By using the multipath combining feature of the CURE algorithms, a
new communication network channel access method is achieved: DPMA. In DPMA,
15 the communication path that defines the link from a transmitting user to a
receiving
base station consists of a weighted combination of multipaths. The multipath
processing capability of the CURE systems provide a practical means for
implementing
a communication network employing DPMA. The CURE algorithms determine the
complex multipath-combining weights of a desired signal automatically,
dynamically,
2o and in real time, while rejecting the multipaths of cochannel other-user
signals.
It is important to note the difference between DPMA and ADMA. The
orthodox ADMA concept consists of a single wave arriving from a single
direction for
each signal source (i.e., a multipath-free environment). A direction-fording
algorithm
is employed to estimate the direction parameter associated with each arriving
cochannel
25 signal. Under this model, two signals are inseparable if their directions
of arrival are
identical (i.e., if the sources are collinear with the receive array). DPMA by
contrast
operates in a signal environment where multipath is a key feature. DPMA,
unlike
ADMA, is tolerant with regard to angular separation between sources. Even
collinear
sources having zero angular separation at the receiving array are separable
because

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-95-
different multipath structures cause the sources to have different generalized
steering
- vectors which the CURE algorithms exploit.
12.0 Application To Two-Way Mobile Wireless Communication Systems:
The CURE cochannel signal separation technology is applicable to
communication networks composed of two-way communication links in which
multiple
transmissions occur simultaneously on the same frequency. The natural
application for
CURE is to the receiving end of a communication link provided it is practical
to have
an antenna array at the receiving end. For a two-way communication link, this
would
to mean having a receiving antenna array at both ends of the /ink. In many
situations,
however, it is practical to have an array at only one end of a communication
link. For
instance, in personal mobile wireless communication networks, it is
impractical to have
an array built into the user's portable handheld units. In such situations, it
is possible,
under certain conditions, to establish and maintain isolation between
different
t5 cochannel users by putting arrays at just one end of the communication
/ink.
CURE cochannel signal separation technology can be applied to cellular
communication systems in which the earth's surface is partitioned into
localized
regions called 'cells,' as described above with reference to FIG. 29. Examples
of
cellular personal mobile wireless communication systems are the Advanced
Mobile
2o Phone stem (AMPS) and Global stem Mobile (GSM). (See The Bell System
Technical Journal, special issue on Advanced Mobile Phone Service, vol. 58,
no. 1,
January 1979.)
The CURE cochannel system has been described to this point as a
technology used at the receiving ends of communication links provided the
receiving
25 ends have mufti-element antenna arrays. In the case of cellular networks,
however,
economics dictates that arrays be put at base stations only. There are two
reasons for
this:
~ An antenna array is a large and expensive physical asset, best suited to
installation at fixed base stations where proper maintenance and repair is

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-96-
possible. Mobile units would be larger and more expensive if they were
required to have antenna arrays built in.
~ A single base station array can serve many users at once. Since each cell
has more mobile units than base stations, total system cost is lower if arrays
are employed at the base stations only.
The effect of locating arrays at base stations is to lower the initial
equipment purchase cost to the subscribers while increasing the infrastructure
cost,
which is spread over all subscribers in the form of monthly service charge.
Like the application to cellular networks, CURE cochannel signal
separation technology can be applied to satellite-based personal communication
networks in which a space-based array on a satellite forms spot beams on the
surface of
the earth that define regions similar to the cells formed with terrestrial
base stations.
All communication within a spot beam is between the mobile users and the
satellite.
Communication that bypasses the satellite, between two users in the same spot
beam, is
i5 precluded. Examples of satellite-based personal mobile wireless
communication
systems are Iridium, Odyssey, and Global Star.
There are several reasons and advantages relative to the use of CURE
cochannel signal separation technology in personal mobile wireless
communication
networks.
~ The capacity of a network to accommodate users can be increased by
employing intra-cell frequency reuse. CURE technology makes this
possible by means of diversity path multiple access (DPMA) on the reverse
links or uplinks from mobile user-to-base stations or satellite and by
transmit beamforming on the forward links or downlinks from base station
or satellite to mobile user.
~ Apart from capacity improvement, CURE provides diversity gain which,
when used with suitable power control algorithms, can enable the mobile
users to maintain reliable communication with less average transmitted
power.

CA 02272930 1999-OS-25
WO 98/24192 PCTlUS96/18867
-97-
~ CURE provides general interference immunity not only from other users in
the network but from arbitrary radiated interference, whether deliberate or
unintentional.
12.1 Transmit Beamforming:
The selectivity that enables several users to simultaneously share a
radio-frequency (RF) channel for transmission can be accomplished by
beamforming at
the transmitters instead of at the receivers. In the case of a cellular
network, it is
possible, by means of transmit beamforming, for forward link transmissions
(from base
to station to mobile user) to be sent out with directivity patterns that reach
the intended
user while preventing reception at other cochannel users. Two methods can be
used to
accomplish the requisite transmit beamforming function: switched fixed beams
and
adaptive beams. The basic principles of both approaches are known in
communication
engineering. However, proper operation depends on integration with the receive
~ 5 beamforming function provided by the CURE system. This integration is
described
below.
In the switched beam approach, a transmit antenna array and a set of
fixed pre-formed beams is available for transmission. The beams are formed by
applying signals with appropriate gains and phases to the antennas. The gains
and
2o phases can be created either by a passive beamforming matrix that is
inserted into the
signal path ahead of the antenna array. The outputs of the beamforming
matrices are
then summed in power combiners that drive each array antenna. The preferred
approach, shown in FIG. 32, eliminates the expense of RF hardware beamformers
in
favor of digital signal processing. In this method, a signal to be transmitted
to a user is
25 input on one of N multiple lines 320 to one of N sets of multipliers 322.
Each set of
multipliers has as other inputs a transmit beamformer weight vector, which is
derived
from a transmit/receive beamformer weight vector computer 324. The latter
computer
receives estimated generalized steering vectors on lines 36 from the CURE
system and
generates receive beamformer weights on lines 48 (see FIG. 4A), and transmit
3o beamformer weight vectors on lines 326.

CA 02272930 1999-OS-25
WO 98/24192 PCT/L1S96/18867
-98-
Thus, in each set of multipliers 322, a signal to be transmitted to a user
is multiplied by a transmit beamformer weight vector, which is an M-
dimensional
complex weight vector, where M is the number of antenna elements. For each of
N
users, the outputs of the multipliers 322 are summed in a plurality M of
summers 328.
That is to say, each summer 328 sums the contributions of multiple user
signals
associated with a particular antenna element. The signal to be radiated by the
i"'
antenna of M elements is the sum of N terms, each being a complex weighted
version
of the signal to a different user. An M-channel digital-to-analog converter
(DAC) 330
and linear power amplifier (LPA) 332 is used to drive each antenna. This
latter
t o method does not require expensive analog rf beamforming matrices and power
combiner hardware, since the multipliers 322 and summers 328 are digital
processing
components, as indicated by the envelope 334.
In the switched beam approach, the beamforming weight vectors are pre-
computed and stored in memory. Each weight vector can be used to create a
t 5 directional beam that puts transmitted energy in a different direction.
The set of all
such weight vectors provides a family of pencil beams that covers all
directions in the
cell. Only one such beam is selected for transmission on each of the L forward
links.
The method of selection is described below. The method mitigates, but does not
eliminate, cochannel interference because the energy of a signal
unintentionally
2o radiated to other cochannel users is suppressed to the sidelobe level of
the beam,
assuming the other users do not fall into the main lobe of the beam. For
cellular
systems that use analog frequency modulation (FM) on the forward links like
the
AMPS system in the United States, there is, in addition to sidelobe
suppression, the
signal capture effect of FM discriminators that provides additional
suppression of
25 unwanted cochannel interference.
A beam is chosen for transmission to a particular user by means of
logical rules embodied in a beam selection algorithm. The objective is to
prevent
energy from reaching the other cochannel users where it would interfere with
the
intended signals being sent to those users. Consider the following set of
assumptions,
3o reasonable for many wireless communication services that operate at UHF
frequencies:

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-99-
~ The base station has separate transmit and receive arrays.
- ~ The transmit and receive arrays are geometrically similar (i.e., have the
same shape).
~ The transmit and receive arrays have the same size-frequency products (i.e.,
the ratio of the transmit-to-receive array sizes equals the ratio of the
receive-
to-transmit frequencies).
~ The transmit and receive arrays are mounted on a common vertical mast.
~ The dominant multipath scatterers are not in the immediate vicinity of the
arrays, so that the arrays are in the farfield of reradiation from scatterers,
to and the elevation or depression angle of arrival is essentially zero at
both
arrays.
Under these assumptions, the best beam for sending energy to a given
user is the one whose beamforming vector is most nearly orthogonal to the
generalized
steering vectors of the other cochannel users (the generalized steering
vectors being
those derived from reception of the reverse link signals at the base station).
Orthogonality between two vectors is strictly defined as an inner product of
zero.
However, strict orthogonality is not generally possible. Fortunately, it is
often good
enough to pick the beam whose weight vector has the smallest inner product
with the
reverse link generalized steering vectors of the other cochannel users. This
beam will
2o radiate minimal sidelobe energy to the other users.
The beam selection criterion for using a fixed switched-beam array can
be stated precisely: Choose the beam that maximizes the ratio of the inner
product of
the beam vector with the generalized steering vector of the intended user
divided by the
sum of the inner products with the generalized steering vectors of the
unintended
cochannel users.
The method just described uses a fully adaptive array for the reverse
link receive function, as implemented by the CURE method, together with a
switched-
beam array for the forward link transmit function. The key feature of this
approach is
that antenna arrays are employed only at base stations.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96118867
-100-
A somewhat different approach would be to perform the transmit
beamforming by using the exact generalized steering vectors as are derived by
the
receive function. This method requires a transmit array that is geometrically
similar to
the receive array as described above (i.e., the transmit and receive arrays
have the
s same shape but are scaled by the ratio of the receive-to-transmit
frequencies). For
example, in the case of the AMPS analog cellular systems, the transmit and
receive
frequencies are offset by 45 MHz. Because the total system bandwidth is small
compared to the operating frequencies, the 45 MHz offset can be regarded
approximately as a 5 percent difference in scale. By using a scaled transmit
array, if a
1 o generalized steering vector obtained by CURE on receive is used for
transmit, then the
same array directivity pattern will result. Thus, lobes and nulls will be
placed at the
same angles. Nulls directed to other cochannel users on receive will also be
directed at
the same other users on transmit, thereby enabling the base station to
selectively direct
a signal at a particular desired cochannel user.
15 In a multipath environment, the desired user and other user signals will
generally be via diversity paths (i.e., the DPMA concept). In this case, the
generalized
steering vectors derived by CURE on~receive cause the receive array (and hence
the
transmit array) to have a complex directivity pattern for each user that sums
the
multipath arrivals of the desired signal with complex weights (gains and
phases) that
2o causes them to add in phase, while simultaneously summing the multipath
arrivals of
each other user cochannel signal with complex weights that causes these
signals to sum
to zero. Thus, other users are rejected by generalized nulls or orthogonality
rather
than by physical nulls at specific angles. The energy transmitted to a
particular user
will be sent in the same direction as the receive multipath components, with
the same
25 phase and gain relationships. Therefore, the signal will reach the intended
user with a
substantial signal level via the diversity path. Simultaneously, the signal
will reach the
other users via multiple paths that will sum to zero provided the mobile users
are using
a simple omnidirectional antenna for both transmit and receive.
FIG. 33 is block diagram of a transmitter for use in one form of the
3o CURE system. Some of the components of the transmitter have already been

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-101-
introduced in the discussion of FIG. 32. A transmit weight vector computation
or
- beam selection module 340 generates on lines 326 a transmit weight vector
for each
user k. the module 340 generates the transmit weight vector based on either of
the two
approaches discussed above An information signal to be transmitted to user k
is
s modulated in a modulator 342 and then multiplied by the transmit weight
vector for
user k, in a set of multipliers 328. The portion of the transmitter including
the
modulator 342 and multipliers 322 is referred to as the transmit beamformer
344. Next
the outputs of the multipliers 322 are summed in a set of M summers 328, each
summer receiving as inputs an antenna element contribution associated with
each of the
to users. Thus each summer 322 has N inputs if there are N users. The summers
328 are
collectively referred to as a signal combiner 346.
The outputs of the summers 328 are then processed in what is referred
to as the air interface 348 of the transmitter. The air interface includes a
set of complex
digital-to-analog converters (DACs), each of which produces two outputs, the
in-phase
1s and quadrature components of the complex signals. These complex signal
components
are multiplied by a carrier signal in additional pairs of multipliers More
specifically,
each complex output pair from a complex DAC 330 is multiplied by signals
proportional to cos w~t and sin w~t, respectively, where w~ is the angular
carrier
frequency. The resulting products in each pair are then added in summers 352
and
2o coupled to one of the linear power amplifiers 332, and from there the
signals are
coupled to an antenna element 110.
13.0 System For Separating And Recovering Multimode Radio Signals:
This section describes a method and apparatus for mitigating
2s polarization effects on propagated radio signals. In the case of dual-
polarized radio
transmissions, the effects of a polarization-changing propagation medium are
avoided
by separating the two received signals without regard to their polarization
states.
This invention relates generally to radio communications and, more
specifically, to problems that arise, due to natural propagation conditions,
when
3o multiple cochannel signals of practically the same frequency are received
at

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96118867
-102-
approximately the same time. Propagation conditions may cause may cause
unwanted
polarization mixing of the signals. Separating and recovering the original
signals poses
difficulties in receiver design.
A related problem is multipath propagation caused by reflections from
atmospheric layers, such as the D-layer, E-layer or F-layer. The problem
manifests
itself as frequency selective fading or phase distortion that limits the
communication
capability of high-frequency (HF) signals. As already discussed above in
Section 9.0,
the CURE system handles multipath components advantageously by combining all
coherent signals arriving over different paths as a result of reflections from
buildings in
an urban environment. Multipath propagation effects caused by atmospheric
reflections
are handled in exactly the same manner.
In some communication systems electromagnetic propagating waves are
used to carry two independent information signals on different polarizations
of the
same carrier signal. These polarizations need not be orthogonal, but do need
to be
linearly independent relative to two orthogonal "basis" polarizations, e.g.
vertical and
horizontal linear polarizations or left-hand circular and right-hand circular
polarization.
A traditional problem is that the polarization of a transmitted signal is
changed by the
propagation medium so that the signal arrives at the receiving antenna with a
different
polarization from the one in which it was transmitted. The polarization change
may be
2o due to reflection from oblique surfaces, refraction, or the phenomenon of
Faraday
rotation. Conventional receivers separate differently polarized signals
because each
receiver has knowledge of the expected polarization states. When the
polarization of
one or both signals is changed during propagation, the conventional receiver
is
incapable of properly separating the two signals.
The present invention separates the received signals without regard to
their possibly changed polarization states. If only one signal is received
with an
unknown polarization is received at a dual-polarized antenna, the invention
can extract
the signal and determine its polarization state. If two signals are sent on
orthogonal
polarizations, the signal polarizations can be random and not orthogonal at
the
3o receiving site, making reception of either signal subject to cochannel
interference from

CA 02272930 1999-OS-25
WO 98!24192 - PCT/US96/18867
-103-
the other signal. CURE processing solves the problem by separating and
recovering up
- to two independent signals arriving at the receiving array with differently
polarizations,
provided only that the polarizations are linearly independent (i.e., not
identical). The
key advantage of the invention in this application is that it is "blind" to
the polarization
states of the received signals. Prior knowledge of the polarization state is
not needed to
separate and recover the signals. In addition, the CURE approach is fast
enough to
enable the recovery of signals whose polarization is time-varying.
As shown in FIGS. 34A and 34B, one type of communication system
makes use of dual-polarized signals at the same frequency. For example,
transmitters
360A and 360B transmit uplink signals A and B to a communication satellite
362,
which retransmits the signals, with different polarization states, to a dual-
polarized
antenna 364 on the ground at a receiving site. However, an atmospheric layer
366
causes polarization mixing of the two signals, which arrive at the receiving
antenna
with scrambled polarization states. The received signals are processed by a
CURE
processing system 368, which effectively separates out the signals A and B
without
regard to their scrambled polarization states. Because of the CURE processing
system
368 is "blind" to antenna configuration, and to the polarization state of the
received
signals, separation and recovery of signals A and B can be effected even when
both
have their polarization states altered during propagation from the satellite
transmitter.
14.0 Application to Separation of Signals Transmitted Over "Waveguide":
This section describes a method and apparatus for separating and
recovering signals transmitted onto a "waveguide." As mentioned earlier, the
term
"waveguide" as used in this specification is intended to include any bounded
transmission medium, such as a waveguide operating at microwave frequencies,
an
optical fiber operating at , a coaxial cable, or even twisted-pair conductors
operating at
lower frequencies. Regardless of the waveguide medium, the signals are
received at an
array of sensor probes installed in the waveguide, and are fed to a cumulant
recovery
(CURE) system that separates and recovers the original signals without regard
to how

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-104-
the original propagation modes may have become scrambled as a result of
transmission
along the waveguide.
Waveguides and optical fibers are widely used for the transmission of
multiple independent cochannel signals simultaneously, by using a different
propagating mode for each signal. However, due to kinks, bends and surface and
refractive irregularities in the waveguide or fiber, a phenomenon called mode
conversion occurs, and the propagated energy is converted from one mode to
another
during propagation along the waveguide or optical fiber medium. Over a long
distance
of propagation, the signals tend to become scrambled across the propagating
modes.
to A well known approach to conserving bandwidth is to employ different
propagating modes for different signals of the same frequency, and to rely on
the
different propagating modes to effect separation of the signals as the
receiving end of
the waveguide or optical fiber. Unfortunately, however, mode conversion often
occurs,
especially in long waveguides or fibers, as a result of kinks, bends, and
surface and
t 5 refractive irregularities of the propagation medium. The modes become
scrambled and
separation at the receiving end becomes difficult. For optical systems, these
difficulties
are somewhat reduced by the use of expensive single-mode fiber.
FIG. 35 shows, by way of example, a computer network employing an
optical fiber 370 and having a plurality of computer workstations 372
connected to the
2o fiber by couplers 104, each of which couples a workstation to the fiber
using a
different propagation mode, but at the same optical frequency. In accordance
with the
invention, a plurality of probes 376 are also coupled to the fiber 370,
providing three
output signal lines for connection to a cumulant recovery (CURE) processing
system
378, which generates separated signals A, B and C at its signal recovery
ports.
I5.0 Application to Radio Direction Finding:
This section describes a method and apparatus for finding accurate
directions of multiple radio signal sources without the need for a fully
calibrated
antenna array. Signals from the antenna array are processed in a cumulant
recovery
(CURE) processing system to recover the signals and obtain estimated steering
vectors

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-105-
for the multiple sources. Signals from a subarray of antennas that are
calibrated are
combined with the steering vector estimates to obtain accurate directional
locations for
all of the sources. There need be only as few as two calibrated antenna
elements in the
- subarray.
This invention relates generally to direction finding (DF) systems and,
more particularly, to DF systems using arrays of radio antennas. Traditional
super-
resolution direction finding systems require an array of N+ 1 calibrated
antennas and
receiving channels to resolve N source locations (directions). Maintaining
large arrays
of antennas in calibration adds to the cost of the system. Moreover,
traditional DF
systems do not always converge rapidly on the direction solutions.
FIG. 36 shows a direction finding system in accordance with the
invention, including an array of antennas 380, only two of which are
calibrated, a
CURE processing system 382 and a copy-aided direction finding system 384.
Signals
are received from multiple sources 386 at different directional locations with
respect to
is the antenna array 380. As described in detail in the foregoing descriptive
sections, the
CURE processing system 382 separates and recovers the signals from the sources
386
and outputs the recovered signals from separate output ports, as indicated at
388. A by-
product of the signal recovery process is a set of steering vector estimates
for the
multiple sources 386.
2o Assume that the k'" port provides the steering vector estimate ak(m) from
its analysis of the m'" block of data "snapshots," and the steering vector
from the
calibration table for the bearing 8 is denoted as a(8). When an antenna array
is
"calibrated," a calibration table is generated, associating every bearing
angle with an
antenna steering vector. The dimensionality of a(8) is equal to the number of
calibrated
25 sensors, which must be greater than or equal to two. After the steering
vectors are
estimated, a search is done to estimate the directions of arrival for the
sources captured
by the ports.
The bearing 6k of the source captured by the port k is estimated by the
maximizer of the DOA spectrum:

CA 02272930 1999-OS-25
WO 98/24192 ~ PCT/US96/18867
-106-
~ ak (m)a(e)
8k = argmax
Ilak(m) II II a(e) ~~~
Some alternative methods to that just described were given by B. Agee
in "The Copy/DF Approach to Signal Specific Emitter Location," Proc. Twenty-
Fifth
Asilomar Conference on Signals, Systems, and Computers, pp. 994-999, Pacific
Grove, CA, November 1991. Agee concludes that the copy-aided DF method gives
more accurate DOA estimates than other systems, such as MUSIC (discussed at
length
in the Background of the Invention section), and that these estimates require
less
computation than does MUSIC. An additional advantage is that only two
calibrated
sensors are adequate for azimuth estimation since the search is performed
using the
to estimated steering vector for one source instead of the signal subspace. In
the case of
multipath propagation, more sources can be resolved by the copy-aided DF
approach
than by MUSIC when spatial smoothing is used.
16.0 Application to Extending the Dynamic Range of Receiving Systems:
1s This section describes a method and apparatus for extending the
effective dynamic range of a radio receiving system by removing the principle
products
of distortion through the use of a cumulant recovery processing system. A
received
signal of interest is separated from the products of distortion, which are
independent of
the signal of interest. The signal is forwarded for further processing and the
products
20 of distortion are discarded, resulting in an extended dynamic range.
The dynamic range is a measure of the useful output of a receiver in
relation to noise and other unwanted components. It is limited by the
intermodulation
and distortion products that result from analog and digital nonlinearities.
Analog
nonlinear distortion products or spurs can be generated due to signal overload
or
25 saturation of the first stage, mixer noise, and other sources. Digital
systems employ
analog-to-digital (AID) converters that produce nonlinear distortion due to
uniform
quantization noise, AID saturation, non-monotonicity of the A/D
characteristic,
sampler aperture fitter, and other physical effects. Accordingly, there has
been an
ongoing need for significant improvement in the dynamic range of a receiver
system.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-107-
FIG. 37 shows a multichannel receiver 390, receiving signals from
- sources 392 through an antenna array 393 and coupling the input signals to a
cumulant
recovery (CURE) processing system 394. The received signals, after analog
processing
- and analog-to-digital conversion, have a spectrum that includes a number of
products
s of distortion, in the form of nonlinear spurs in the spectrum, as well as
lower-level
quantization noise across the entire spectrum of interest. The effect of CURE
processing is to separate and recover (or discard) received signals. In this
case, the
CURE processing system provides an output port for the desired signal, and
generates
other outputs corresponding to the principal products of distortion, which may
be
to discarded. The resulting spectrum after CURE processing exhibits improved
effective
dynamic range, and contains only lower intensity spurs, and low level noise.
Accordingly, the invention eliminates a number of distortion products in the
receiver
output and provides a desired output signal with fewer and lesser products of
distortion.
17.0 Application to High Density Recording:
This section describes a method and apparatus for separating and
recovering data recorded on closely spaced tracks on a recording medium. An
array of
sensors senses recorded data from multiple tracks simultaneously, and a
cumulant
2o recovery processing system separates and recovers the data from each of the
multiple
tracks, without crosstalk or mutual interference. Use of the invention permits
recording
of data at much higher densities than is conventional, so that more data can
be stored
on a recording disk without increasing its physical size.
For space efficiency, magnetic recordings use multiple parallel tracks to
record information. Both rotating disks and linear tape use parallel tracks.
Tracks can
be laid down in the recording medium side-by-side on the surface and on top of
one
another at different vertical depths. On playback, a playback head attempts to
sense
individual tracks without crosstalk or interference from adjacent tracks, but
at
sufficiently high recording densities and small track sizes, crosstalk becomes
a
3o significant problem. Accordingly, designers of such systems are constantly
seeking to

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96118867
-108-
improve playback head performance and the precision with which the playback
head
can be positioned to read information from each track. The present invention
provides
for increased recording density without crosstalk or mutual interference
between
adjacent tracks.
As shown in FIG. 38, which depicts a recording disk 400 by way of
example, playback or retrieval of recorded information is effected by means of
a
multisensor array 402, which has individual sensor elements that can sense
recorded
information on more than one track simultaneously. In general, N sensors will
permit
separation of information from N adjacent tracks. In the illustrated form of
the
invention, there are three sensors in the array 402 and the array spans across
three
adjacent recording tracks. The signals from the three sensors are processed as
independent cochannel signals by a cumulant recovery (CURE) processing system
404,
which generates outputs on three ports, corresponding to the signals on the
three tracks
over which the sensor array is positioned. Depending on the design of the
system,
~5 selection from among the three outputs may be simply a matter of choosing
the
strongest signal, which should correspond to the track above which the array
is
centered, or utilizing the information in all three tracks, based on
identifying data
contained on the tracks themselves. Accordingly, the invention represents a
significant
improvement in recording and playback techniques using high-density recording
media.
18.0 Application to Complex Phase Equalization:
This section describes a method and apparatus for effecting automatic
phase rotation equalization of a quadrature amplitude modulated (QAM) signal
received
from a transmitter. Because QAM signals are subject to an unknown phase
rotation
during propagation, de-rotation or phase rotation equalization is required
before the
received signal can be QAM demodulated. In this invention, received
downconverted
QAM signals are subject to processing in a cumulant recovery (CURE) processing
system, which recovers the originally transmitted I and Q signals and
automatically
provides phase rotation equalization, without knowledge of the amount of
rotation.

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96/18867
-109-
Thus the invention provides the correct amount of phase compensation
automatically,
even as channel propagation conditions change.
This invention relates generally to communication systems and, more
particularly, to phase rotation equalization in communication systems. Many
s communication systems use a form of modulation referred to as quadrature
amplitude
modulation (QAM) for transmitting digital data. In QAM, the instantaneous
phase and
amplitude of a carrier signal represents a selected data state. For example,
16-ary
QAM has sixteen distinct phase-amplitude combinations, which may be
represented in
a "signal constellation" diagram as sixteen points arranged on a square
matrix. A
special case of QAM signals is the phase-shift keyed (PSK) signals for which
the
instantaneous phase alone represents a selected state. For example, 16-PSK has
sixteen
distinct phase selections, and can be represented as sixteen equally spaced
points on the
unit circle.
Transmission of the modulated signal causes an unknown phase rotation
15 of the signals, and phase rotation correction, or equalization, is required
at the receiver
before the QAM signals can be demodulated. The present invention provides a
convenient and automatic approach to effecting this phase rotation
equalization. FIG.
39 shows a conventional transmitter, including a QAM modulator 410 and a
transmitter
412. At the point of transmission, the signal constellation diagram is as
shown at 414,
2o with sixteen phase-modulus points arranged in a square matrix. Each point
on the
diagram represents a unique data state. At the receiver site, a receiver and
downconverter 416 generates I and Q signal components. The signal
constellation
diagram corresponding to these signals is as shown at 418. The constellation
has been
rotated and must be corrected before QAM demodulation can take place. The
receiver
25 site also has a cumulant recovery (CURE) processing system 420 installed
between the
receiver/downconverter 416 and a QAM demodulator 422. As will be further
explained, CURE processing has the effect of compensating for the phase
rotation
induced during propagation of the signal to the receiver site, as indicated by
the phase-
corrected QAM signal constellation at 424.

CA 02272930 1999-OS-25
WO 98/24192 . PCT/US96118867
-110-
The in-phase and quadrature components (I and Q) of a digital
communication signal are independent and identically distributed at the
transmitter
output, as indicated in FIG. 40Aa). If x(t) is the original communication
signal (in
analytic representation) with in-phase component xp(t) and quadrature
component xQ(t),
respectively, then xP(t) and xq(t) are statistically independent. After
transmission, the
channel distorts the transmitted signal and the receiver recovers it with gain
and phase
ambiguity (ignoring measurement noise), i.e. if y(t) is the output of the
receiver, we
have:
y(t) = G exp(j6).x(t).
to If yP(t) and y9(t) denote the in-phase and quadrature components of y(t)
respectively, then we can write:
y~ (t) cos(6 ) - sin(0 ) xP (t)
yq (t) G ~ sin(6 ) cos(6 ) xq (t) '
The gain term G is real-valued and affects only the scale of the signal
constellation, but not the constellation's shape or alignment with the I and Q
axes.
Therefore, without loss of generality, we may assume that G=1.
The effect of transmission is to rotate the entire signal constellation by
the unknown phase angle 8, as is shown in FIG. 40B. In order to demodulate the
signal
correctly, the constellation must be "de-rotated" back to its original
position prior to
demodulation. This de-rotation operation must be accomplished by complex phase
2o equalization or phase correction of the I and Q signals, which compensates
for the
distortion introduced by the communication channel and the lack of phase
reference in
the receiver downconverter's local oscillator.
The CURE method can be applied to provide a unique solution to the
problem of complex phase rotation equalization. The signal's center frequency
for
downconversion must be known accurately enough so rotation does not occur
during a
processing block. The following two paragraphs help explain how the CURE
system
effects complex phase correction:
1) yP(t) and yq(t) are not independent but are uncorrelated. The absence
of statistical independence is evident by inspection of FIG. 40B.
Uncorrelatedness is

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-111-
implied by the equation. Because the signals are uncorrelated, second-order
statistics
such as cross-correlation functions provide no information to correct for the
rotation of
the signal constellation.
2) The rotation correction problem can be considered as a blind signal
separation problem in which there are two sensor signals yP(t) and yQ(t), each
of which
is a linear combination of two independent source signals xP(t) and x9(t).
This is
precisely a problem model to which the CURE processing system can be applied.
By
applying the CURE method to the components of the analytic signal, the vector
channel
is phase equalized, the original independent I and Q signals are recovered,
and the
1 o received signal constellation is de-rotated. In addition, since yp(t) and
yq(t) are
uncorrelated, the covariance matrix used in the CURE system will be a scaled
identity
matrix, which simplifies the preprocessing required in the CURE system.
The principal advantage of using the CURE system as an equalization
technique is that the rotation angle 8 need not be known. The CURE system
~5 compensates for the angle automatically to provide independent output
signals.
Moreover, the equalization process adapts as channel conditions change.
The CURE system ca'n be used to adjust the complex phase for single-
dimensional constellations, such as pulse-amplitude modulation (PAM). In this
case,
the scenario can be considered as a two-sensor, single-source, signal
enhancement
2o problem, which can be handled by the CURE processing system.
19.0 Extension to Wideband Signal Separation:
The present invention is fundamentally a method for separating and
recovering narrowband cochannel signals illuminating a sensorarray. However,
it is
2s possible to extend the method to the separation and recovery of wideband
signals. This
is accomplished by:
1) Partitioning the wideband spectrum into multiple narrowband segments.
2) Using an array of cochannel processors to perform signal separation in each
narrowband segment.

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-112-
3) Combining the narrowband results to recover the original wideband source
waveforms .
Steps 1 and 2 are straightforward. Step 3, however, is intricate and
requires a special cumulant test to associate the ports at one frequency
segment with the
ports at adjacent frequency segments. Methods to accomplish these steps are
described
below. The overall method is capable of separating and reconstructing wideband
signals with no special constraints on the signals or their spectra other than
that the
components of the signals in each narrowband segment must be non-Gaussian. A
key
advantage of this method is that the signal spectra are not required to be gap-
free (i.e.,
to have a convex support set).
19.1 Partitioning Wideband Measurements to Narrowbands:
To apply the CURE algorithm to separate the signals, it is necessary to
decompose the sensor measurements into narrowband components. This
decomposition
step is depicted in block 430 of FIG. 41. If r(t) is the array snapshot at
time t, then let
r (t,~ denote the measurement component filtered by a bandpass filter centered
at
frequency f. The bandpass filters are designed to satisfy the expression:
I.
r(t ) _ ~ r(t, f ).
I =I~
where f < f < fu is the wideband analysis spectrum. With this analysis
approach, the
2o signal model for each band is expressed as
r (t,~ = A(~s(t,~ + n(t,~ .
The following important fact about the cross-cumulants of bandpass filtered
signals will
be exploited in order to associate the ports of different signal separation
processors
operating in different frequency bands:
CLIIlI(Sk(pfl),Sk(t,f ),SI(t~f2)~S! (!f2)) -Y4,k(Wf2) Sk.l
,
where Y4 kV i z/2) $ 0 in general, and 8k,, is the Kronecker delta function
1 if k=1
S k,1 ~ 0 otherwise

CA 02272930 1999-OS-25
WO 98/24192 PCT/US96/18867
-113-
In other words, the cross-cumulant is nonzero for different frequency
components from the same source and zero for different sources.
This property is in contrast to the cross-correlation between the
components of signals at different frequencies which, except for signals that
exhibit
s second-order cyclostationarity, is generally given by
E~Sk~t~.fi)Sr (t~.f2)~= ak (.~r)sk,rSJ,.l2
Here, we see that the components of a given signal at different
frequency bands are uncorrelated and the components of different signals are
uncorrelated.
The advantage of the cumulant property noted above is that it provides a
method (described below) for associating the narrowband parts of a wideband
signal
that is broadly applicable to all signal types regardless of whether a given
signal
exhibits 2nd-order cyclostationarity.
i s 19.2 Signal Separation in Narrowbands:
Each narrowband component (r(t,,~) is fed to a different CURE signal
separation processor 432 that separates and recovers the signals that comprise
the
narrowband component.
Let gk(t,~ be the waveform recovered by the k"' port of the CURE
2o subsystem that operates in band f processing r(t,,~. We shall show a method
of
- determining which narrowband port signals are part of a common wideband
signal, and
how to combine these port signals in order to reconstruct and recover the
wideband
signal.
2s 19.3 Combining Narrowbands:
The problem of combining the recovered narrowband signals to form
wideband signals is complicated primarily by the fact that the ports for
different bands
capture different sources. The combing step is indicated as block 434 in FIG.
41. In
general,

CA 02272930 1999-OS-25
WO 98/24192 PCTIUS96/18867
-114-
I
Sk (t) $ ~ gk (t~f )~
J=h
Consider first the case in which the wideband analysis band is broken
into two narrow bands f,,fz, and two processors, each equipped with L signal
extraction
ports to independently process the bands.
Suppose the first port of the processor operating in band f, has captured
a signal and we wish to find whether some port of a second processor assigned
to a
different band fz captures the same signal. This determination is made by the
following
test. Compute the following quantity for the active ports (indexed by ~ of the
second
processor:
E~gl(~~fl)2 ~~gl(t~f2)~z
d(f ~1~.f2~1) _ ~ cum(gOr~f )~gOt~f )~gl(t~.fz)~gr (t~.fz))
0
We associate a port of the second processor to the first port of the first
processor if both ports jointly minimize the quantity and if the minimum is
below a
threshold. The threshold is set to limit the number of false association
decisions on
average. For example, if port 3 of the second processor provides a minimum
below
threshold, then the waveforms from the two processors would be combined
according
to
Si ( t) = gOt~ fO + g3 (t~ fz )
Conversely, if the maximum is below threshold, then we let
s~(t) =gOt~.fO ,
2o In the general case, there are J signal separation processors operating in
J bands, each having active signal energy on up to L output ports. The method
of band
association in the general case is to first compute the "distance" between all
pairs of
ports by computing the pseudo-metric:
E ~Igk(ty)Iz ~E ~gl(t~fj)I2
d(i, k; j,l) ~-
cum{gk(t~.f )~gk(t~.f;)~gr(t~.fj)~8n (t~.~j)}
for l <- i, j _< J, and l 5 k, l _< L,

CA 02272930 1999-OS-25
WO 98/24192 - PCT/US96/18867
-115-
where gk(tf~ denotes the waveform from the k"' port of the processor in the
i~' band.
d (i, k; j, l) is not a true mathematical metric because it does not satisfy
two of the three
required metric properties: d (i, k; j, l) ~ 0 and the triangle inequality are
not satisfied.
Nevertheless, as a pseudo-metric, it does enable port associations to be
found.
The next step is to associate ports two at a time. This is done with a
clustering algorithm borrowed from the field of statistical pattern
recognition. An
agglomerative hierarchical clustering algorithm is used. Standard algorithms
for such
clustering are described in textbooks (e.g., Richard O. Duda and Peter E.
Hart, Pattern
Classification and Scene Analysis, John Wiley & Sons, 1973, pp. 228-237). This
type
of clustering algorithm searches through the inter-port distances to find the
two nearest
ports. If the distance is below a threshold, the ports are "merged" or
associated and all
distances to the two ports that are merged are replaced by distances to the
new
"merged" signal. This process is repeated until only distances greater than
the
threshold remain. Constraints are imposed on the clustering algorithm to
prevent the
merging of same-band ports because, if the ports are from the same processor,
they
cannot capture the same signal.
The distances between same-band ports are used to compute the
threshold that controls whether ports are sufficiently close to permit them to
be
merged. The threshold is computed by a statistical L-estimator operating on
the same-
2o band distances. The distances are sorted into ascending order, and a
particular distance
is selected based on its rank. This distance is multiplied by a constant to
obtain the
threshold. Both the rank and the constant depend on J and L and are chosen to
maintain the probability of false port association, Pte" below some small
specified level
(e.g., 0.001).
After the ports are logically merged or associated into clusters, each
cluster will correspond to exactly one wideband signal. The final step is to
recover the
waveforms of the wideband signals. This is done by adding together the output
port
signals from all the ports merged or associated to each cluster.

CA 02272930 1999-OS-25
WO 98/24192 PCT/I1S96/18867
-116-
20.0 Conclusion:
As described in detail above, the present invention provides a cochannel
signal processing and separation that has many facets. Implementation of the
basic
cumulant recovery (CURE) processing engine may take the form of any of the
proposed embodiments, including eCURE (as described in Section 3.0). CiCURE
(Section 4.0) or pipeCURE (Section 5.0), and its capabilities may be further
extended
using a,-(3CURE or p.CURE (Section 6.0), wideband processing (Section 19.0),
or
direct (non-iterative) computation (Section 7.0).
Applications of a selected form of the CURE processing engine are
o numerous, and probably not all have been described here. Of prime importance
is the
application of CURE processing to communication systems (described in Sections
8.0
through 12.0), and in particular the concept of diversity path multiple access
(DPMA,
described in Section 11.0), which not only permits operation in the presence
of
multipath propagation, but also takes advantage of multiple coherent signals
to provide
t 5 a diversity gain, and uses a generalized steering vector representative of
all the
multipath components to generate corresponding transmit weight vectors
ensuring that
each user receives intended transmissions, even in the presence of multipath
effects.
Other communication system applications include signal recovery in the
presence of
strong interfering signals (described in Section 10.0), recovery of multimode
signals
2o that have been subject to unwanted mode mixing (Section 13.0), and recovery
of signal
from a bounded waveguide of any type (Section 14.0). Other applications
include radio
direction finding (Section 15.0), extending the dynamic range of receiver
systems
(Section 1b.0), high density recording (Section 17.0), and complex phase
equalization
(Section 18.0).
25 It will be appreciated from the foregoing that the present invention
represents a significant advance in all of these diverse fields of
application. It will also
be understood that, although a number of different embodiments and
applications of the
invention have been described in detail, various modifications may be made
without
departing from the spirit and scope of the invention. Accordingly, the
invention should
3o not be limited except as by the appended claims.

Representative Drawing