Note: Descriptions are shown in the official language in which they were submitted.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
AUTO-RECOVERABLE AUTO-CERTIFIABLE CRYPTOSYSTEMS
Backctround-Field of Invention
The field of this invention is cryptography. This
invention relates to cryptosystems, and in particular to
the escrowing and recovering of cryptographic keys and data
encrypted under cryptographic keys. The escrow and recov-
ery process assures that authorized entities like
law-enforcement bodies, government bodies, users, and
organizations, can when allowed or required, read encrypted
data. The invention relates to cryptosystems implemented
in software, but is also
applicable to cryptosystems implemented in hardware.
Background-Description of Prior Art
Public Key Cryptosystems (PKC's) allow secure commu-
35 nications between two parties who have never met before.
The notion of a PKC was put forth in (W. Diffie, M.
Hellman, "New directions in cryptography", IEEE Transac-
tions on Information Theory, 22, pages 644-654, 1976).
This communication can take place over an insecure channel.
In a PKC, each user possesses a public key E and a private
key D. E is made publicly available by a key distributior.
center,.also called certification authority (CA), after the
registration authority verifies the authenticity of the
user (its identification, etc.). The registration authori-
ty is part of the certification authority. D is kept
private by the user. E is used to encrypt messages, and
only D can be used to decrypt messages. It is computation-
ally impossible to derive D from E. To use a PKC, party A
obtains party B's public key E from the key distribution
center. Party A encrypts a message with E and sends the
result to party B. B recovers the message by decrypting
with D. The key distribution center is trusted by both
parties to give correct public keys upon request. A PKC
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-2-
based based on the difficulty of computing discrete loga
rithms was published in (T. ElGamal, "A Public-Key Crypto
system and a Signature Scheme Based on Discrete
Logarithms", CRYPTO '84, pages 10-18, Springer-Verlag,
1985) .
PKC's are highly convenient in terms of use, and
permit users to conduct private communications over inse-
cure channels. They may be used to initiate symmetric key
systems like DES (Data Encryption Standard). PKC's have a
drawback, however. Criminals can use PKC's in the course
of criminal activity, since no provision is made to supply
law enforcement with the necessary decryption keys and
untappable criminal communications may result. It is
therefore desirable to permit private communications
exclusively to law abiding citizens. A general solution to
this problem is to have each user submit a representation
of his or her private key to trusted escrow authorities, or
trustees. The shares are taken out of escrow in the event
of a court authorized wire tap. Alternatively, key escrow
provides a way to recover lost private keys in an organiza-
tion, or keys of a file system.
Let us review some of the key escrow systems and show
that all require more than a PKC alone. U.S. patents
5,276,737, and 5,315,658 to Micali (1994) disclose a Fair
Public Key Cryptosystem (FPKC) (see also, S. Micali, "Fair
Public-Key Cryptosystems", CRYPTO '92, pages 113-138,
Springer-Verlag, 1992) which satisfies the needs of law
abiding citizens and law enforcement (and is based on P.
Feldman, 28th annual FOCS). Micali's prefered embodiment
discloses how to convert the Diffie-Hellman PKC, and the
RSA PKC into Fair PKC's. In the prefered embodiment of the
Fair Diffie-Hellman PKC, each user submits five shares to
five central trustees (also known as "trusted third par-
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-3-
ties") to register a public key. This solution is there-
fore not very scalable, since it requires the use of a
small number of trusted authorities, and is thus very
centralized. In the present invention, the user constructs
a key pair such that the private key is provably escrowed
automatically. Hence, no trusted third parties are needed
whatsoever. The escrowed information can be sent to one of
a multitude of decentralized certification authorities
(CA's). In Micali's scheme each trustee verifies their
respective shares. Provided the share is valid, the share
is stored in a database. Each trustee then signs the
values that were received and gives them to a key manage-
ment center. The five authorities have the burden of
securing and managing five private databases of shares. In
the present embodiment, the key information is verified by
a CA. Provided it has the correct form, the key is signed,
and placed immediately in the database of public keys.
There need only be one private database. Since only the CA
is needed to manage user keys in the current embodiment,
the least amount of communication overhead that is possible
is achieved. In the Fair PKC's, only the trustees can
verify that a key is escrowed properly. Verification is
required since without it a user can easily generate keys
which are not recoverable. In the current invention,
everyone can verify this. This is particularly useful if,
for example, a citizen suspects that a CA is failing to
insure that its keys are properly escrowed.
It has been shown that the Fair RSA PKC does not meet
certain needs of law enforcement (J. Kilian, F. Leighton,
"Fair Cryptosystems Revisited", CRYPTO '95, pages 208-221,
Springer-Verlag, 1995), since a shadow public key crypto-
system can be embedded within it. A shadow public key
system is a system that can be embedded in a key escrow
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-4-
system that permits conspiring users to conduct untappable
communications.
The flaw in the RSA FPKC lies in the fact that it is
assumed that criminals will use the same secret keys that
were provided to the escrow authorities. The shadow
cryptosystems make use of what is known in the art as
subliminal channels that exist in the public keys of the
PKC's. These channels are used to display the public keys
of the shadow PKC. The Kilian and Leighton paper discloses
how to convert PKC's into Fail-safe Key Escrow (FKE)
systems. Specifically, they disclose how to construct FKE
systems for discrete-log based PKC's like Diffie-Hellman
and DSS. In their expensive protocol, the user and the
trusted authorities engage in a protocol to generate the
user's public and private keys. In so doing, the authori-
ties are convinced that no subliminal information is
contained in the resulting public key. The user is also
convinced that the keys are escrowed properly. This system
is similar to the Fair Diffie-Hellman PKC, except for the
added overhead of this protocol. It is thus subject to the
same inefficiencies as the Fair Diffie-Hellman PKC. In the
present invention, the user chooses his or her own keys
independently. With respect to the threat of shadow PKC's,
the present invention relies on the fact that there is no
known way to inconspicuously embed a significant number of
bits within a modular exponentiation in a finite field.
Hence, the exploitation of shadow cryptosystems in
discrete-log PKC's seems remote.
De Santis et al. teach an escrow system where trust-
ees are able to open only messages in session rather than
opening the key of the party suspected of criminal activi-
ty. This refines the notion of Fair Cryptosystems. Other
technologies that teach how to open the session key of
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-5-
users rather than their permanent public key is by Walker
and Winston (TIS) and the IBM SecureWay document. These
key recovery technologies require that users be aware of
and use the keys of the set of trustees at any session
initiation. These technologies may be overburdening each
and every user since they require new protocol extensions
which are used in every communication session and further
require users to store many keys beyond what is needed for
a PKI.
A "Fraud-Detectable Alternative to Key-Escrow Propos-
als" based on ElGamal has been described in (E. Verheul, H.
van Tilborg, "Binding ElGamal: A Fraud-Detectable Alterna-
tive to Key-Escrow Proposals", Eurocrypt '97, pages 119-1-
33, Springer-Verlag, 1997). This system allows users to
send encrypted information along with a short proof that
the encrypted information can be recovered by a set of
trustees. So, this system has the advantage that it does
not depend on trusted third parties. However, this system
requires an already existing Public Key Infrastructure
(PKI). Therein lies the flaw in the Binding ElGamal ap-
proach: If the PKI is unescrowed then user A can public key
encrypt a message using user B's public key, and then send
the resulting ciphertext message using Binding ElGamal. In
this case, the proof simply serves to show that the trust-
ees can recover this ciphertext, and therefore prevents
law-enforcement from being able to monitor the communica-
tions of users suspected of criminal activity. When this
abuse is employed, fraud is not detectable. This abuse is
made possible because user B's private key is not escrowed.
Software that abuses the Binding ElGamal scheme could be
readily distributed and could severely hamper attempts at
law enforcement on a large-scale. The present invention
discloses a method of establishing an escrowed PKI, and is
hence not subject to this drawback. Like in Binding
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-6-
ElGamal, the present invention employs the general tech-
nique of non-interactive zero-knowledge proofs, though the
proofs of the present invention involve new technology. A
heuristic for how to construct such proofs was shown in (A.
Fiat, A. Shamir, "How to Prove Yourself: Practical Solu-
tions to Identification and Signature Problems", CRYPTO
'86, pages 186-194, Springer-Verlag, 1987).
An overview of key escrow schemes appears in (D.
Denning, D. Branstad, "A Taxonomy for Key Escrow Encryption
Systems," Communications of the ACM, v. 39, n. 3, 1996).
In (N. Jefferies, C. Mitchell, M. Walker, "A Proposed
Architecture for Trusted Third Party Services", Cryptogra-
phy: Policy and Algorithms, LNCS 1029, Springer, 1996) and
(R. Anderson, "The GCHQ Protocol and Its Problems", Euro-
crypt '97, pages 134-148, Springer-Verlag, 1997) a trusted
third party approach to escrow is described where the
trusted third parties of the participating users are
involved in every session key establishment stage.
All key escrow solutions heretofore known suffer from
some if not most of the following disadvantages.
(a) they require tamper-resistant implementation, or
otherwise require hardware implementation. This imposes
high implementation costs and slow establishment of use.
(b) they require use of classified or otherwise
proprietary algorithms. This may be unacceptable to users
who may be skeptical about the devices security or opera-
tion.
(c) they are implemented in software, and are there-
fore subject to alteration, resulting in improper operation
and possibly untappable communications. This is however,
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
an inherent problem of any software solution (all we can
require in this case is that if users employ the software
apparatus solely for achieving privacy then their plaintext
or keys are recoverable).
(d) they require excessive protocol interaction in
key generation and/or general use. In addition this inter-
action may be conducted with a small set of centralized
entities, thus making traffic and communication delays a
potential bottleneck. They may require users to posses the
trustees keys and use them in every session initiation, and
further require modifications to every communication
protocol.
(e) they require excessive numbers of trusted third
parties (TTP) to be involved in system operation. Spread-
ing the trust among too many parties increases the risk of
security breaches and reduces scalability.
(f) they require generation of cryptographic keys by
TTP's. A corrupt or otherwise compromised TTP may put user
security at risk by tampering or disclosing user's keys.
(g) they require the securing and management of
databases) of secret keys or secret shares on behalf of
users.
(h) they can be used to establish a shadow public key
infrastructure, thus defeating the purpose of the escrow
system altogether.
Auto-Recoverable and Auto-Certifiable Cryptosystems
Due to the above disadvantages, what is required is
a new mechanism incorporating the following advantages:
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
_g_
(a) a key escrow system that can be distributed in
source code form with no loss of security, and hence
provides a system that can be publicly scrutinized to
insure that it operates properly. Furthermore, since the
key escrow system can be available in software, it can be
implemented on a large scale, quickly, and cost-effective-
ly. This implies fast distribution of the system.
(b) in the case that a software solution is deemed
unacceptable due to the possibility of modifying of the
invention, it can be implemented directly in tamper-resis-
tant hardware. This however adversely affects the gains
from (a) (e. g., the easy distribution).
(c) the escrow system requires the least amount of
protocol interaction between the escrow authorities, CA,
I5 and user, that is theoretically possible. To register a
key, a message need only be sent to one of a multitude of
CA's. This mechanism is called a key registration based
escrow system. In comparison, in the prefered embodiment
of Fair PKC's, five messages are sent from the user to the
trustees, and then five more messages are sent to a key
management center.
(d) only one private database is required to imple-
ment the escrow system. This database need only be authen-
ticated and may be kept private to prevent a shadow PKC
from being established. User's private keys will not be
exposed if the database is exposed. This contrasts with
Fair PKC's in which several databases must be maintained
and if they are compromised, the users keys are compro-
mised. This requirement makes the new system rely only on
the CA in establishing and certifying users keys as in
usual public key systems.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
_g_
(e) the escrow system allows the user's private key
to be verified by anyone. The verification establishes
that the private key is recoverable by the escrow authori-
ties given the user's corresponding public key, the certif-
y icate, and public parameters. In comparison, in Fair
PKC's, only the trustees perform this verification. This
requirement of the new system is called universal verifi-
ability.
(f) the escrow system can be made shadow public key
resistant. Fair PKC's were shown not to be shadow public
key resistant, namely they can be abused to publish other
PKC schemes (J. Kilian, F. Leighton, "Fair Cryptosystems
Revisited", CRYPTO '95, pages 208-221).
The present invention is versatile enough so that
either (a) or (b) can be chosen (namely, a software or
hardware implementation). In each case requirements (c)
through ( f ) are met .
Summary of the Invention
In order to provide for the above and other objec-
tives and features to be described below, the present
invention introduces a new paradigm in cryptography. The
present invention provides a method to verify that a user
generated private key is contained within an encryption
under the public key of the escrow authorities without
excessive overhead. Furthermore, this verification can be
performed by anyone in possession of the escrow authorities
public key. The present invention consists of a setting up
process and three functions which process signals in
different ways. The functions are key generation, key
verification, and key recovery. In the setup process of
the prefered embodiment, the participants agree upon a set
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-10-
of initial public parameters and the authorities generate
an escrowing public key and corresponding private keys.
The initial parameters and the escrowing public key are the
public parameters of the system. The escrowing authori-
ties, Certification Authority (CA), and users of the system
all have access to the public parameters. In the key
generation process, the method generates a user's
public/private key pair, and a certificate of recoverabili-
ty which is a string of information which includes an
implicit encryption of the user's private key under the
escrowing public key. The signal information containing
the user's public key, and the certificate of recoverabili-
ty can be transmited to any entity. In the verification
process, the user transmits this signal to the verifier.
The verification process takes the input signal, processes
it, and outputs either true or false. A result of true
indicates that the user's private key is recoverable from
the certificate of recoverability by the escrow authori-
ties. A result of false indicates that the private key is
not recoverable. The invention is designed such that it is
intractable for the user to generate a public key, and
certificate of recoverability such that the key is not
escrowed and such that it passes the verification process
with a result of true. In the prefered embodiment, the
users certify their public keys with registration authority
of the certification authority (CA) who then signs their
public key after successful verification. A public key
together with a CA' s signature on a string that contains
the public key constitutes a certified public key. In more
detail, upon receiving the user's public key, and certifi-
cate of recoverability, the CA verifies that the corre-
sponding private key is recoverable. If it is, (namely,
the verification process outputs true) the public key is
certified and/or made publicly available by the CA. The
user is only required to keep his public key and to have
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-11-
access to the public key database containing public keys of
other users as in a typical PKI. In the recovery process,
the escrow authorities use the user's certificate of
recoverability, which is obtained from the CA, as an input
signal. The escrow authorities process the certificate of
recoverability, and the corresponding user's private key or
data encrypted using the corresponding public key is the
resulting output signal.
The present invention is useful in any environment
that demands the recovery of private keys, or keys en-
crypted under these keys, or information encrypted under
these keys. Such environments arise in law enforcement
nationally and internationally, in the business sector, in
secure file systems, etc. The successful escrowing of
private keys implies the successful escrowing of public key
encrypted information, and hence the present invention has
many applications.
The present invention is robust with respect to any
underlying technology since it can be implemented in both
hardware and software. When implemented in software it can
be easily scrutinized to insure that it functions as
desired and to insure that it does not compromise the
security of its users. The software implementation allows
for fast and easy dissemination of the invention, since it
can be disseminated in source code form over diskettes or
over a computer communication network. The present inven-
tion is also as communication-free as is theoretically
possible. The only communication is the act of disseminat-
ing the software itself (or the hardware device itself) and
the one-time transmission of a user's public key, certifi-
cate of recoverability, and additional information. The
signals can be processed quickly and the signals themselves
constitute a small amount of information. The invention
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-12-
does not require changes in communication protocols used in
typical unescrowed PKI's (e. g., session key establishment,
key distribution, secure message transmission, etc.). The
invention is therefore compatible with typical PKI's. The
present invention thus provides a very efficient way of
escrowing and recovering cryptographic keys.
The Drawing
The present invention will be described with refer-
ence to the accompanying figures 1-7.
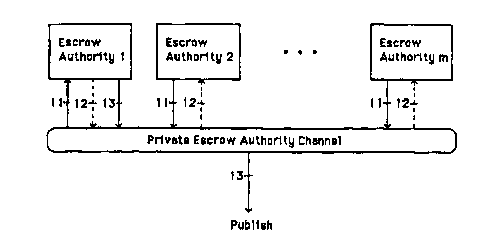
FIG. 1 is a data flow diagram of the process of
setting up the method of the invention for use with m
escrow authorities.
FIG. 2 is a flow chart of the basic steps of the
process of generating a public/private key pair and certif
icate of recoverability using the invention.
FIG. 3. is a data flow diagram of the process of
verifying the recoverability of a private key.
FIG. 4 is a data flow diagram of the process of
registering a key using the invention.
FIG. 5 is a data flow diagram of the process of
private key recovery by the escrow authorities.
FIG. 6 describes a generic public key system and its
main components and operations
FIG. 7 describes the escrowable public key system
which results by employing the present invention and its
main components and operations.
Description of the Invention: Prefered Embodiments
The following is a description of the first prefered
embodiment of the present invention. Variations on the
prefered embodiment will accompany the description of the
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-13-
prefered embodiment wherever applicable. For convenience
in the presentation, the hashing algorithm selected is SHA
(Schneier 2nd edition, pages 442-445), though any crypto-
graphic hashing algorithm will suffice in its place. In
the prefered embodiment, parameters are chosen uniformly at
random from their respective groups. Alternate embodiments
include alterations of the probability distributions from
which such values are chosen.
The system setup of the prefered embodiment shown in
FIG. 1 initiates the cryptosystem. In the prefered embodi-
ment, the participants agree upon a large prime r such that
g - 2r+1 is prime and p - 2q+1 is prime. Examples of
values for r that satisfy this relation are 5 and 11,
though they are small values. The following is a 1024 bit
value for r in hexadecimal:
fd90e33af0306c8b1a9551ba0e536023b4d2965d3aa813587ccflae
blba2da82489b8945e8899bc546dfded24c861742d2578764a9e70b
88a1fe9953469c7b5b89b1b15b1f3d775947a85e709fe97054722c7
8e31ba202379e1e16362baa4a66c6da0a58b654223fdc4844963478
441afbbfad7879864fe1d5df0a4c4b646591
An r of size 1024 bits is large enough for use in
cryptographic systems. Such values of r, q, and p are not
as easy to find as merely f finding a prime number, but doing
so is not intractable. What is needed is highly efficient
algorithms which can be implemented using, say, a multi-
precision library. Such algorithms include Karatsuba
multiplication, Montgomery reduction, addition chains, and
the Rabin-Miller probabilistic primality test (,T. Lacy, D.
Mitchell, W. Schell, "CryptoLib: Cryptography in Software,"
AT&T Bell Laboratories, cryptolib@research.att.com).
The following method can be used to find large values
for r, q, and p efficiently. Note that r mod 3 must be 2.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-14-
It can't be 0 since then r wouldn't be prime. It can be 1
since then q would be divisible by 3. Also, r mod 5 must
be 1 or 4. It can't be 0 since then r would be divisible
by 5. It can't be 2 since then q would be divisible by 5.
It can't be 3 since then p would be divisible by 5, etc.
We call this method "trial remaindering". By performing
trial remaindering, we can throw out values for r, q, and
p quickly prior to performing trial divisions and probabil-
istic primality tests. Once we perform trial remaindering
up to, say, 251, we perform trial divisions on r, q, and p.
If r, q, and p are not thrown out we then do the
Rabin-Miller primality test on r, then q, then p, then r,
then q, etc. alternating between the three. we do so using
small potential witnesses of compositeness that are fixed
in advance. If any of r, q, or p are found to be compos-
ite, we set r to be equal to r + 2 x 3 x 5 x...x 251 and
repeat starting with trial divisions and the same set of
potential witnesses. This way we need not perform trial
remaindering again, since the prior conditions on r are
assured. Once r, q, and p are found, we perform additional
primality tests using potential witnesses that are found
using a strong random number generator. If r, q, and p
pass these tests, then they are assumed to be prime and are
declared as systems parameters.
The participants agree upon, or the CA chooses, a
value g which generates the elements in the set
f1,2,3,...,p-1} and an odd value gl which generates all
values less than 2q and relatively prime to 2q. Note that
2q is a multiplicative group and has a generator. g and s
are odd in the prefered embodiment. The values r, q, p, g,
and gl are the systems initial parameters and are made
publicly available with no loss of security. They can be
chosen by the authorities themselves and/or anyone else.
Once gl and q are specified, the m authorities (m greater
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-15-
than or equal to 1) proceed to collectively compute an
escrow authority public key (Y, gl , 2q), also called the
escrowing public key, and escrow authority private keys
z_1, z_2,..., z m. To do so, authority i, where i ranges
from 1 to m, chooses a value z_i in {1,2,...,2r-1} at
random and then sets Y_i to be gl raised to this value
modulo 2q. At least one authority then receives all of the
information of the Y i's from the m-1 other escrow authori-
ties. In the prefered embodiment, authority i, where i
ranges from 2 to m, sends Y_i to authority 1. The sending
of the Y i's is depicted by step 11 in FIG. 1. Y is c~m-
puted to be the product of the Y-i's modulo 2q by at least
one of the authorities. In the prefered embodiment, Y is
computed by authority 1. Authority 1 then verifies that
(gl/Y) is a generator of all values less than 2q and
relatively prime to 2q. If it isn't then step 12 is exe-
cuted. In step 12 the other m-t authorities are told to
choose new values for z, hence the procedure is restarted
from the beginning of step 11. In the prefered embodiment,
authority 1 chooses z_1 over again also. In an alternative
embodiment, at least 1 and less than m of the authorities
generate new values for z. This process is continued as
many times as necessary until (gl/Y) is a generator of all
values less than 2q and relatively prime to 2q. Y is then
published, or otherwise made available to the users and the
CA, by one or more of the escrow authorities. This is
depicted by step 13 in FIG. 1.
FIG. 2 is-a diagram showing the process of how a
user's system generates a public/private key pair and a
certificate of recoverability. Having obtained the signal
Y that is made available to users by the escrow authori-
ties, the user system proceeds to generate an ElGamal key
(y, g, p) for the user. The signal Y may a priori have
been included in the invention. The invention proceeds by
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-16-
choosing a value k in {1,2,...,2r-1} randomly. This is
depicted by step 2004 in FIG. 2. In step 2005, the inven-
tion computes C = (gl raised to the k power) mod 2q. In
step 2006 the invention computes the user's private key x
to be ((gl/Y) rasied to the k power) mod 2q. The invention
also computes y to be (g raised to the x power) mod p.
The system then proceeds to step 2007 and computes a
certificate that can be used by any interested party to
verify that the user's private key is properly encrypted
within C. The certificate contains the value v, which is
computed by the system to be g raised to the power w mod p,
where w is ((1/Y) raised to the k power) mod 2q. The
public key parameter y can be recovered from g and v by
computing v raised to the C power mod p. The system also
processes three non-interactive zero-knowledge proofs as
they are called in the art and includes them in the certif-
icate. Let n denote the number of repetitions in each
non-interactive proof. In the prefered embodiment, n is
set to be 40. The first proof is designed so that the user
can prove that he or she knows k in C. The second proof is
d°~igned so that the user can prove that he or she knows k
in v. The last proof is designed so that the user can
prove that he or she knows k in v raised to the C power mod
p . By saying "the user knows value x" we mean that the
system has value x in its state.
In more detail, to construct the non-interactive
proofs, the system proceeds as follows. It chooses the
values e_1,1, e_1,2,..., e-l,n, e-2,1, e-2,3,...,e-2,n, and
e-3,1, e-3,2, e_3,3,..., e-3,n in (1,2,...,2r-1} randomly.
For i ranging from 1 to n, the system sets I-l,i to be gl
raised to the e-l,i power mod 2q. For i ranging from 1 to
n, the invention sets I-2,i to be v raised to the d_i power
mod p, where d-i is Y raised to the -e-2,i power modulo
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-17-
2q, For i ranging from 1 to n, the invention sets I-3,i to
be y to the t_i power mod p, where t-i is (gl/Y) raised to
the a 3,i power mod 2q. The invention then computes the
value rnd to be the SHA hash of the set formed by concate-
nating together the tuples (I-l,i, I-2,i, I_3,i) for i
ranging from 1 to n. Note that rnd is a function of all of
the I values, using a suitably strong cryptographic hash
function. In alternate embodiments, the hash function can
have an effective range of size different than 160 bits.
A greater range of the hash function allows for signifi-
cantly larger values for n. The system seLS each of the
bit-sized values b 1,1, b 1,2,..., b l,n, b 2,1, b 2,2,...,
b-2,n, b-3,1, b-3,2,..., b-3,n to be each of the corre-
sponding 3n least significant bits of rnd. There are a
multitude of ways in which an embodiment can securely
assign the bits of rnd to the values for b. The values for
b are the challenge bits, and this method of finding them
is known as the Fiat-Shamir Heuristic. The system then
proceeds to compute the responses to these challenge bits.
For i ranging from 1 to 3 and for j ranging from 1 to n,
the invention sets z-i,j to. be e-i,j + (b-i,j)k mod 2r.
Tris completes the description of step 200? ~f FIG. 2.
The system proceeds to step 2008. In step 2008, the
invention outputs the parameters C, v, y, (I_l,i, I-2,i,
I-3,i), and (z_l,i, z_2,i, z_3,i) for i ranging from 1 to
n. In an alternate embodiment the value k is output by the
invention to the user. The user then has the option to
later interactively prove that his or her private key x is
recoverable by the escrow authorities . This will be ad-
dressed in more detail later. Also, the values b can be
made a part of the certificate. This step is however, not
necessary, since the values for b can be derived frora the
values for I alone.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-18-
The description of the embodiment has thus far
explained how the system is setup for use by the CA and
authorities, and how the system is used by users (potential
receivers? to generate public/private key pairs and certif-
y icates of recoverability. These certificates are strings
showing to anyone presented with them that the key gener-
ated has the publicly specified properties. The following
describes how the invention is used by the user to prove to
a verifier that x is recoverable from C. This process is
depicted in FIG. 3. The verifier can be the CA, an escrow
authority, or anyone else who is part of the system.
The verification process of FIG. 3 is as follows. In
step 3009, the user generates a public/private key pair,
encryption of x, and a certificate using the invention as
described above. In step 3010, the user transmits a signal
containing these parameters to a verifier. In step 3011
the verifier uses this signal to verify whether or not the
user's private key is recoverable by the escrow authori-
ties. To do so, the verifier uses the user's public key,
the encryption C, the corresponding certificate, and the
escrowing public key Y.
The way in which the users signal is processed will
now be described in detail. The verifying system outputs
a 0 if the public key and/or certificate are invalid, and
a 1 otherwise. The invention may take subsequent action
and indicate to the verifier that the public key is invalid
in the event that 0 is returned. Similarly, the verifying
system may inform the verifier of a validation that passes.
To perform the verification, the verifying system
first verifies that y = v raised to the C power mod p. If
y is not equal to v raised to the C power mod p, then the
verification system returns a value of 0. The verifying
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-19-
system then verifies the three non-interactive proofs
contained within the certificate of the user. The inven-
tion computes (b-l,i, b-2,i, b-3,i) for i ranging from 1 to
n in the same way as performed during the certificate
generation process. Recall that this process was described
in regards to FIG. 2.
For the first non-interactive proof, the verifying
system checks that gl raised to the z-l,i power equals
C(I-l,i) mod 2q if b-l,i - 1, for i ranging from 1 to n.
The verifying system also checks that g1 to the z_l,i power
equals I-l,i mod 2q if b-l,i = 0, for 1 ranging from 1 to
n. If any of these equalities fails, then the verifying
system returns a value of 0. This completes the verifica-
tion of the first non-interactive proof.
For the second non-interactive proof, the verifying
system checks that g raised to the w-i power equals I_2,i
mod p if b_2,i = 1, for i ranging from 1 to n. Here w-i is
1; Y raised to the z-2, i power mod 2q. The verifying system
also checks that v to the v-i power equals I-2,i mod p if
b_2,i = ~, for i ranging from 1 to ~. Here v_i is 1/Y to
the z_2,i power mod 2q. If any of these equalities fail,
then the verifying system returns a value of 0. This
completes the verification of the second non-interactive
proof .
For the third non-interactive proof, the invention
checks that g raised to the w-i power equals I-3,i mod p if
b-3,i - 1, for i ranging from 1 to m. here w-i is (gi/Y)
raised to the z_3,i power mod 2q. The invention also
checks that y to the v-i power equals I-3,i if b-3,i = 0,
for i ranging from 1 to m. Here v_i is (gl/Y) raised to
the z_3,i power mod 2q. If any of these equalities fails,
then the verifying system returns a value 0. If all of the
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-20-
verifications pass, then the value 1 is output by the
verifying system.
In FIG. 4, the user certifies his or her public key
with the CA. In step 4012 of this process, the user gener-
ates his or her public key and certificate of recoverabili-
ty, as previously described. The user transmits this
signal to the CA. This corresponds to step 4013 of FIG. 4.
In step 4014 the CA acts as a verifier and verifies that
the user' s private key is recoverable by the escrow author-
ities. So far, steps 4012 through 4014 are identical to
steps 3009 through 3011 in the key verification process of
FIG. 3. However the CA, in addition, will make keys that
pass the verification process available to others upon
request and/or certify them. If the user's public key
fails the verification process, then either the certifica-
tion attempt i.s ignored, or alternatively the user is
notified of the failed certification attempt.
Depending on the demands of the environment in which
the invention is used, users may be required to submit
extra inform~_tion in order ~-o register a publis key and to
certify that they know the private key portion without
divulging it. Such information could be a password, social
security number, previously used private key, etc. In the
case that the CA is a trusted entity, the CA can simply
digitally sign the user's public key, and make the key
along with the CA's signature of that key available on
request. If the CA is not trusted, then the certificate
should be stored in the public file and the certificate
together with the certificate of recoverability should be
given to the escrow authorities, which in turn can insure
recoverability. This completes the description of the
public key certification process.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-21-
The last process to describe is the private key
recovery process. This process is depicted in FIG. 5. In
this process, the invention is used by the n escrow author-
ities to recover the user's private key based on C. In
this process, all m of the escrow authorities obtain C, as
depicted in step 5015 of FIG. 5. In an alternate embodi-
ment the CA transmits C and/or other parameters to one or
more of the authorities. Thus they are already in posses-
sion of C. At this point escrow authority i computes t_i
to be C raised to the z-i power mod 2q. Recall that z_i is
the private key of the ith escrow authority. This is done
for i ranging from 1 to m. Authorities 2 through m then
send their respective values for t to authority 1, as
depicted in step 5016. Authority 1 then computes Y raised
tU the k power mod 2q to be the product of the values for
t i where i ranges from 1 to m. Authority 1 then obtains
the user's private key x by computing x = (C/(Y raised to
the k power)) mod 2q. There are alternative methods in the
art for computing x so that x is represented distributively
among the authorities. These methods also allows the
authorities to decrypt messages encrypted under the public
key corresponding to x, without revealing x itself.
What has been described is an Auto-Recoverable and
Auto-Certifiable (ARC) cryptosystem. The users of such a
cryptosystem employ the public key system in a way that is
identical to a typical PKI for secure communications. This
is demonstrated schematically in FIG's 6 and 7. FIG. 6 is
a typical public key cryptosystem in a PKI environment.
The following are the steps that are followed by the users .
(1) The user first reads the CA's information and address.
(2) The user generates a public/private key pair and sends
the public key to the CA. The registration of the authori-
ty in the CA verifies the identity of the user, and pub-
lishes the public key together with the CA certificate on
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-22-
that key, identifying the user as the owner of that key.
(3) For another user to send a message to that user, the
public key is read from the CA's database and the certifi-
cate is verified. (4) Then, the message is encrypted under
new the public key and sent. FIG. 7 schematically de-
scribes the ARC cryptosystem. The additional operations
are as follows. (0) The authority generates the escrowing
public key and gives it to the CA. Steps 1 and 2 are
analogous, except that a proof is sent along with the
public key. Steps 3 and 4 are the operation of the system
and are identical. Steps 5 and 6 describe the case in
which keys are recovered from escrow. (5) The escrow
authority gets information from the CA. (6) The escrow
authority recovers the user's private key.
In an alternative to the first embodiment any large
enough subset of the authorities can recover the private
key x or messages encrypted under the public key corre-
sponding to x without revealing x itself. This is done
independently by receiving the appropriate values for t by
the other authorities. This adds robustness in the case
that some or all of the authorities cannot be completely
trusted or are otherwise unavailable. Also, the authori-
ties can require that that the certificate of recoverabili-
ty be sent along with the public key and encryption so that
the user's parameters can first be verified using the
verification process. This completes the description of
the private key recovery process.
The following are a few alternate embodiments of the
first embodiment of the present invention. An alternate
embodiment of this invention involves using an authority
public key of the form (Y, g, 2(q raised to the t power)),
where t is some integer greater than 1. We chose t to be
1 in our prefered embodiment, though other values can be
CA 02290952 1999-11-23
WO 98/54854 PCT/US98/10392
-23-
used instead and still operate based on primitive roots .
Another alternate embodiment is to use the product of two
or more large primes as part of the public parameters.
Clearly, the exact structure of the moduli used can vary
significantly without departing from the scope of the
invention. In another embodiment, the interactive versions
of the three non-interactive proofs can be used. Such an
embodiment requires that the system output k to the user
during key generation. This value k is used during the
interactive protocol, so that the verifier can be convinced
that the user' s private key is recoverable by the escrow
authorities. Note that by outputing k, however, a shadow
public key cryptosystem may result. This follows from the
fact that ((gl, C, 2q), k) is a valid ElGamal
public/private key pair mod 2q.
In yet another embodiment, the CA, or other trusted
entity, takes the further action of blinding the user's
public keys. The CA chooses a k s.t. g' - (g raised to the
k power) mod p is a generator, and sends the user (g', (y
raised to the k power) mod p). g' is the user's ElGamal
generator and y' - (y raised to the k power) mcd p is part
of the users final key (g', y', p). This prevents users
from exploiting subliminal channels in y.
In another variant the users publish their public
keys which are used for key exchanges in a Diffie-Hellman
like "key exchange". For example, the following method can
be used. Let a be user A's private key and let b be user
B's private key. Let y_a - (g to the power a) mod p be
user A's public key and let y b = (g to the power b) mod p
be user B's public key. To establish a random session key,
user B chooses a random string s. User A then sends m =
(y b to the a powers mod p to user B. User B recovers s
by computing m/(y-a to the power b) mod p. Users A and B
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-24-
derive a session key from s using a known public function
(e. g., applying to it a one-way hash function). Later,
when the session key is required to be taken out of escrow,
the trustees can use either a or b to recover s, and hence
the session key.
The following is a description of a second primary
embodiment of the present invention. The hashing algorithm
selected is SHA (Schneier 2nd edition, pages 442-445),
though any cryptographic hashing algorithm will suffice in
its place. We use the least significant bits of the hash
results for convenience, but any subset of bits is possi-
ble. In the prefered embodiment, parameters are chosen
uniformly at random from their respective groups or do-
mains. Alternate embodiments include alterations of the
probability distributions from which such values are
chosen. Such choices based on random number generators or
pseudo-random generators are available in the art.
The system setup of this alternate embodiment shown
in FIG. 1 initiates the cryptosystem. In the prefered
30 embodiment, escrow authority i for 1 <- i . m generates a
private Share D-i, and corresponding public share E-i. The
private shares D-i form the shared private key L. Escrow
authorities 2 through m send their E_i to escrow authority
1. This is depicted by step 11. Escrow authority 1 com-
bines all the public shares E_i and computes the shared
public key E. The value for E is published. by escrow
authority 1, as depicted in step 13. Each authority i
keeps D-i private. As a concrete exampls, the escrow
authorities can generate a strong prime p and a value g
which generates ~1,2,...,p-1~. Share D-i can be chosen
uniformly at random from {I,2,..,p-1}, and E-i = (g raised
to the D-i power) mod p. E is the product of all the
values E-i modulo p. Variations on joint generation of
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-25-
keys are possible, as well as an implementation with a
single escrow authority.
A process similar to FIG. 2 illustrates how a user's
system generates a public/private key pair and a certifi-
cate of recoverability. Having obtained (and verified as
much as possible) the signal E that is made available to
users by the escrow authorities, the user system proceeds
to generate an ElGamal public key (y,g,p) for the user (T.
ElGamal, "A Public-Key Cryptosystem and a Signature Scheme
Based on Discrete Logarithms", CRYPTO '84, pages 10-18,
Springer-Verlag, 1985). The user system chooses a private
key x uniformly at random from ~1,2,..,p-1~, and computes
y to be (g raised to the x power) modulo p. This key
generation process corresponds to step 2006.
The system then proceeds to step 2007 and computes a
certificate that can be used by any interested party, in
particular the CA, to verify that the user's private key x
can be recovered from the certificate of recoverability P.
Let ENC(a,s,E) denote the public key encryption of the
message a under public key E using randomness s. Here ENC
is a semantically secure probabilistic public key encryp-
tion, where the string s is used for the randomness in the
probabilistic encryption. For example, ENC can be an
ElGamal encryption, or an optimal asymmetric encryption
(Bellare-Rogaway, "Optimal Asymmetric Encryption",
Eurocrypt '94). Let DEC be the corresponding public key
decryption function which is performed in a shared fashion.
Hence, DEC(ENC(a,s,E),D_1,D_2,...,D m) - a. P is con-
structed according to the following algorithm:
1. P = ()
2. for i = 1 to M do
3. choose r i randomly from the domain
{1,2,..,p-1~
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-26-
4. choose two random strings s i,l and s i,2 for
use in ENC
5. Q-i = (g raised to the r-ipower) mod p
6. C i,l = ENC(r i, i,l, E)
s
7. C_i,2 = ENC(r_i - p-1,
x mod s-i,2,
E)
8. add (Q i, C i,l, i,2) to the end of P
C
9. val = H(P)
10. set b-1, b_2,...,b M b.ethe M least signifi-
to
cant bits of val, b-iis in f0,1}
where
11. for i=1 to M do
12. w i = r i - (b i)x
13. Z-i = ((w-i),s-i,j) where - 1 + b-i
j
14. add Z i to the end of
P
Thus, P - ((Q-1, C-1,1, C-1,2),...,(Q M, C M,1,
C M,2), Z-1,...,Z M). H is a suitable public one-way hash
function (e.g., SHA), so the b i's can be recovered from P.
The values for b are the challenge bits, and this method of
finding them and using them is analagous to the Fiat-Shamir
Heuristic. The user system outputs (y,x,P) in step 2008.
Note that the user has the option to interactively prove
that his or her private key x is recoverable by the escrow
authorities. This will be addressed in more detail later.
M is a large enough parameter of security (e. g., M=50).
The description of the embodiment has thus far
explained how the system is setup for use by the CA and
authorities, and how the system is used by users (potential
receivers) to generate public/private key pairs and certif-
icates of recoverability. These certificates are strings
showing to anyone presented with them that the private key
corresponding to the public key generated is recoverable by
the escrow authorities using P. The following describes
how the invention is used by the user to prove to a verifi-
er that x is recoverable from P. This process is depicted
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-27-
in FIG. 3. The verifier can be the CA, an escrow authori-
ty, or anyone else who knows the system parameters.
The verification process of FIG. 3 is as follows. In
step 3009, the user generates a public/private key pair,
and a certificate using the invention as described above.
In step 3010, the user transmits a signal containing these
parameters to a verifier. In step 3011 the verifier uses
this signal to verify whether or not the user's private key
is recoverable by the escrow authorities. In this process,
the verif;Ting system takes y, the corresponding certificate
P, and the escrowing public key E. The verifying system
first checks that y < p. The verifying system checks that
all of the values in P lie in the correct sets. The
verifying system also checks that the values C_i,j for all
i and j, do not contain any repetitions. The verifying
system checks that none of the Q-i for all i are repeti-
tious. If any of these verifications fail, then false is
returned. The verifying system then computes b_1,
b 2,...,b M in the same way as in the certificate genera-
tion process. For i=1 to M, the verifying system verifies
the following things:
1. ENC(w-i, s_i,j, E) - C-i,j where j - 1 + b-i
2. (Q-i/(y raised to the b-i power)) mod p = ( g
raised to the w i power) mod p
The verifying system returns true as long as all the
verifications pass and as long as both 1 and 2 above are
satisfied for 1 <= i <= M. The invention may take subse-
quent action and indicate to the verifier that the public
key is invalid in the event that false is returned. Simi-
larly, the verifying system may inform the verifier of a
validation that passes (the verifying system returns true).
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-28-
In FIG. 4, the user certifies his or her public key
with the CA. In step 4012 of this process, the user gener-
ates his or her public key and certificate of recoverabili-
ty, as previously described. The user transmits this
signal to the CA. This corresponds to step 4013 of FIG. 4.
In step 4014 the CA acts as a verifier and verifies that
the user's private key is recoverable by the escrow author-
ities.
So far, steps 4012 through 4014 are identical to
steps 3009 through 3011 in the key verification process of
FIG. 3. However the CA, in addition, will make keys that
pass the verification process available to others upon
request and/or certify them. If the user's public key
fails the verification process, then either the certifica-
tion attempt is ignored, or alternatively the user is
notified of the failed certification attempt.
Depending on the demands of the environment in which
the invention is used, users may be required to ,submit
extra information in order to register a public key and to
cArtify that they know the priv2t~ key portion without
divulging it. Such information could be a password, social
security number, previously used private key, etc. In the
case that the CA is a trusted entity, the CA can simply
digitally sign the user's public key together with the
user's name and additional information, and make the key
along with the CA's signature on this information available
on request. If the CA is not trusted (which is not the
typical assumption in PKI), then the certificate should be
stored in the public file and the certificate together with
the certificate of recoverability should be given to the
escrow authorities, who in turn can i~zsure recoverability.
This completes the description of the public key certifica-
tion process. We note that the CA keeps the certificate of
CA 02290952 1999-11-23
WO 98/54864 PCTlUS98/10392
-29-
recoverability, possibly in encrypted form under its own
key with authentication information for integrity.
The last process to describe is the private key
recovery process. This process is depicted in FIG. 5. In
this process, the invention is used by the m escrow author-
ities to recover the user's private key based on P. In
this process, all m of the escrow authorities obtain y and
P, as depicted in step 5015 of FIG. 5. In an alternate
embodiment the CA transmits y and P and/or other parameters
to one or more of the authorities. Thus they are already
in possession of y and P. At this point escrow authorities
use a subset of their shares D_1, D-2,...,D m to decipher
P to open all of the unopened C-i, j (using DEC for exam-
ple. This is accomplished by having escrow authority i
recover the ith shares of the user's private key. In this
process, escrow authority i extracts the M values for the
unopened C-i,j from P and decrypts them using D_i. The
resulting values are pooled with the values from the other
escrow authorities, as depicted in step 5016 of FIG. 5.
The pool is then used by the authorities to decrypt all of
the unopened values C_i,j from P. Thus all of the pla~n-
texts corresponding to all C-i,j are known to the escrow
authorities. There ara alternative methods in the art for
recovering the plaintext corresponding to the unopened
C_i,j, so that the unopened plaintext is represented
distributively among the authorities. The escrow authori-
ties check the plaintext of each pair C-i,l and C_i,2 for
a pair of values that when subtracted together mod p-1, are
equal to the exponent x in y = (g -raised to the x power)
mod p. Also, the quantity (g raised to the x power) mod p
can be matched against the public y to assure correctness.
Once such a pair is found, the private key of the user has
been found.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-30-
We will now describe a third primary embodiment of
this invention. In this embodiment, the users of the
system generate composite public keys. The user system
generates n and s in the same way as described in the
pending U.S. Patent 08/920,504 (by Young and Yung). Recall
that n is the product of two (preferably strong) primes p
and q, and s is a string that can be used in conjunction
with a public one-way function to derive the upper order
bits of n. Let a and d denote the public and private
exponents (e.g., for RSA), respectively. The following is
how P is constructed:
1. P = ()
2. choose a string t_0 randomly mod n
3. add t 0 to the end of P
4. for i = 1 to M do
5. choose a_i,l randomly from the set
{1, 2, - . , {p-1) (q-1) -1}
6. compute a-i,2 - d - a-i,l mod (p-1)(q-1)
7. choose two random strings s i,l and s i,2 for
use in ENC
8 . t i = H (t (i-1) )
9. v_i,l = (t_i raised to the a-i,l power) mod
n
10. v-i,2 - (t_i raised to the a-i,2 power) mod
n
11. Q-i = (t_i, v-i,l, v-i,2)
12. C-i,l = ENC(a_i,l, s-i,l, E)
13. C i,2 = ENC(a i,2, s i,2, E)
14. add {Q i, C i,l, C i,2} to the end of P
15. val = H(P)
16. set b-1, b-2,...,b M to be the M least signifi-
cant bits of val, where b-i is in {0,1~
17. for i=1 to M do
18. Z-i = (a-i,j, s-i,j) where j - 1 + b-i
19. add Z i to the end of P
20. add s to the end of P
CA 02290952 1999-11-23
WO 98/54864 PCTNS98/10392
-31-
Thus, P = (t 0, (Q 1, C 1,1, C 1,2),..., (Q M, C M,l,
C M,2), Z 1,..., Z M, s). H above can be based on SHA or
on concatenations of a few SHA applications to generate the
t_i of appropriate size. It is most likely that the t-i
will be in the set of elements less than n and relatively
prime to n.
The verifying system is a bit different than before.
The verifying system first checks that n was chosen from
the correct set of vaJ_ues. Let a denote the integer corre-
sponding to the k/2 upper order bits of n. The verifying
system makes sure that either H(s) - a or that H(s) - a+1,
as described in the pending U.S. patent 08/920,504. The
verifying system checks that all of the values in P lie in
the correct sets. For example, the verifying system checks
that the t-i fall within the range of H, and that a_i,j <
n (or some function of n) where j is 1 or 2. The verifying
system also checks that t-i = H{t-{i-1) ) for i ranging from
1 to M. The verifying system checks that elements of the
tuple Q_i for each i does not contain repetitions, and
also that the elements in the pair Z-i for all i does not
have repetitions. If any of these verifications fails,
then false i5 returned. 'rhe verifying system then computes
b-1, b-2,...,b M in the same way as in the certificate
generation process. For i ranging from 1 to M, the verify-
ing system verifies the following things:
1. ((v-i,l multiplied by v-i,2) raised to the a
power) mod n = t i
2. (t_i raised to the a-i,j power) mod n -
v-i,j,where j - 1 + b-i
The verifying system returns true as long as all the
verifications pass and as long as all both criterion are
satisfied for 1 <= i <= M.
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-32-
The escrow authorities recover the user's private key
as follows. For i ranging from 1 to M, the authorities
compute w-i to be the sum of the plaintexts corresponding
to C i,1 and C i,2. If a value w i is found such that (t i
raised to the e(w i) power) mod n equals t_i, then w-i
constitutes a valid RSA private key corresponding to e. It
is well known in the art how to factor n given such a value
w-i. Note that the RSA function is a homomorphic function
and the above embodiment is applicable to homomorphic
l0 functions similar to RSA. We remark that from the above
embodiment it is clear that this 'proof technique' for
showing that a value is recoverable by the escrow authori-
ties can be generalized to any homomorphic function.
An application of this invention is an multi-escrow
authority system where each escrow authority has its own
CAs and users. When users from two different escrow
authorities conduct secure communication the two escrow
authorities can retrieve the user's messages or keys and
exchange them through bilateral agreement. This is appli-
~a.ble to international multi-country scenarios.
Another application of key escrow systems is a secure
file system or file repository system with recoverable
keys. Such a system can be implemented based on the previ-
ous embodiments, in particular based on the preceding para-
graph. For example, user A can be the owner of the file,
user B can be the file server, and the trustees can be file
recovery agents. An example of a file could be a password,
in which case, the file recovery agents are password
recovery agents.
The above description of our first embodiment of our
cryptosystem makes novel uses of number theory in cryptog-
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-33-
raphy. It shows how to design a cryptosystem based on
three primes with direct arithmetic relations between all
them. That is r, q, and p are primes such that q = 2r+1
and p - 2q+1. The usage of three or more primes with
relations between them can produce various cryptosystems of
a similar nature to the one described above. Some of them
are described in the variation on the prefered embodiment.
Another relation can be p = 2q+1 and q = 2rs + 1 where p,
q, r, and s are all prime and r is 160 bits in length.
Another example is p = 2q+1, q = 2r+1, and r = 2s+1 where
p, q, r, and s are all prime numbers. Furthermore, another
innovative use of number theory is performing cryptographic
operations in the exponent, where the operations are, for
example, modular exponentiations. For example, the second
zero-knowledge proof in step 2007 of the first embodiment
involves proving knowledge of k in v where v is equal to g
raised to the w power mod p, where w is (Y raised tU the -k
power) mod 2q. The use of three or more domains in succes-
sive exponentiations adds flexibility and power to crypto-
systems. Applications of this fact along the lines of the
present invention, are readily available to those who are
skilled in the art.
An application of this invention is a hierarchical
public key escrow system. A hierarchical public key escrow
system is an escrow system that takes the form of a tree
data structure. The escrow authorities at the root of the
tree are able to decrypt the communications of all entities
corresponding to the nodes of the rest of the three.
Recursively, the escrow authorities at any given node i in
the tree are able to decrypt the communications of all
entities corresponding to the nodes in the rest of the
subtree for which node i is root . At any tirr~e, the leaf of
the tree can form another subtree and act as an escrow
agent(s). By ordering the size of the moduli properly, it
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-34-
is possible to have multiple escrow agents for any node of
the tree. All that is necessary is to do the commitments
of the roots starting with the smallest modulus and ending
with the largest.
Similarly, rather than a fixed tree which determines
an order, the user can decide on a subset of escrow agents
and generate its own preferred tree which is the chosen
subset of escrow agents ordered by the relative size of
their public keys in a line where the largest key is the
root. This enforces a structure of the commitment, and
assures that the subset needs to work together to recover
a key or information encrypted under the key.
Yet another application of this invention is a
certified electronic mailing system. When the users regis-
ter into the system, they register an auto-recoverable
encryption public key and a certificate of recoverability
to the CA, and they also register a signature public key.
To send a certified piece of mail, the following is done.
The sender sends a packet which includes the following: an
encryption of an e-mail key under his own auto-cert=fied
public key, the receiver's name, an encryption of the
e-mail message encrypted under the e-mail key, a header
indicating a certified e-mail message, his own certified
public key, and the CA's certificate on his certified
public key, and other information. The packet is signed
using the senders signature private key. Both the packet
and the signature on the packet are sent to the receiver.
The receiver forms a return receipt packet that cuizsists of
a fixed return receipt header, the received message (or the
hash of the received message), and additional information.
This packet is signed using the receivers private sigr~ature
key and is sent to the original sender. The original
sender verifies the signature on the return receipt packet.
CA 02290952 1999-11-23
WO 98/54864 PCT/1JS98/10392
-35-
If the signature is valid, the original sender sends the
receiver the e-mail key encrypted under the receiver's
certified public key. This message is sent along with a
signature on it using the original sender's private signing
key. The receiver verifies the signature on the encrypted
e-mail key. If the signature is valid, the receiver
decrypts the e-mail key using his private decryption key.
The receiver then encrypts the result using the original
senders certified public key. If the result matches the
ciphertext in the first packet that the original sender
sent, then the e-mail key is regarded as authentic. This
key is then used to decrypt and obtain the actual informa-
tion that the original sender sent. If the receiver is for
some reason unable to contact the original sender after the
first packet is receiv'd, the receiver sends the return
receipt and the first packet to the ascrow authorities.
The escrow authorities will recover the e-mail key, pro-
vided the packet and return receipts are authentic and
provided that the packet contains the corrects receivers
name. The escrow authorities retain the return receipt and
the packet. Provided the checks pass, the e-mail key is
sent to the receiver. This constitutes a certifie~? e-mail
system based on auto-recoverable keys and signature keys,
and where user registration is analogous to user registra-
tion in a typical public key system with a CA. Also, it is
known in the art how to employ certified e-mail systems as
above for contract signing between two parties. The above
application can be used as such.
Thus, there has been described a iiew and improved key
escrow system, its variants, and applications. It is to be
understood that the prefered embodiment is merely illustra-
tive of some of the many specific embodiments which repre-
sent applications of the principles and paradigms of the
present invention. Clearly, numerous and alternate ar-
CA 02290952 1999-11-23
WO 98/54864 PCT/US98/10392
-36-
rangements can be readily devised by those who are skilled
in the art without departing from the scope of the present
invention.