Note: Descriptions are shown in the official language in which they were submitted.
CA 02304083 2000-04-05
KAP-4398 1 00324
DESCRIPTION
METHOD FOR MEASURING THE DISTANCE TO AT LEAST ONE
TARGET
Field of the invention
The invention relates to a method for measuring
the distance to at least one target according to the
preamble of claim 1. Such methods are used in
particular in distance-measuring devices as used, for
example, in the surveying of buildings and lots.
Description of the prior art
DE-A-41 33 196 discloses a method of the
generic type in which an input signal is composed of
signals which are attributable to a plurality of
optical pulses which are reflected by a target whose
distance is to be determined and which, in order to
improve the time resolution, were each emitted with
different internal delays. From the time when said
input signal reaches its maximum, the transit time is
then derived and the distance is calculated therefrom.
This method has the disadvantage that the
determination of the distance is based in the end on an
individual measured value or at best on a small number
of measured values. If these individual or few
measured values are falsified by noise, which cannot be
ruled out, the result may likewise contain a large
error.
Although DE-A-36 20 226 discloses that the
noise of the input signal can be reduced by repeated
emission of the pulse and addition of those scanned
values of the received signal which correspond to the
same transit times, this requires a large number of
CA 02304083 2000-04-05
KAP-4398 2 00324
pulses and heTIce longer measuring times, in particular
if a high resolution is also to be achieved.
Summary of the invention
It is the object of the invention to provide a
method of the generic type in which the relationship
between the achievable accuracy and the required
effort, in particular the number of pulses required and
hence the measuring time required, is improved, and
high accuracy of the distance measurement is achieved
in particular with a small number of pulses or even
with a single pulse. This object is achieved by the
features in tl'e defining clause of claim 1.
The invention provides a method in which the
total shape of the input signal is used for the
determination of the transit time. This greatly
reduces the dependence of the result on any individual
scans falsified by noise. The distance can be
determined with great accuracy and low uncertainty of
measurement simply from the evaluation of the input
signal resulting from a single optical pulse.
Moreover, it is readily possible with the method
according to the invention to detect and to distinguish
a plurality of targets with a single measurement. This
is important especially in the case of long measuring
= 25 distances where, owing to the widening of the beam, the
latter need no longer be concentrated on a single.
target.
Brief description of the drawings
Below, the invention is explained in more
detail with reference to Figures which represent only
one embodiment.
Fig. 1 shows a block diagram of an apparatus suitable
for carrying out the method according to the
CA 02304083 2009-06-23
= KAP-4398 3 00324
invention,
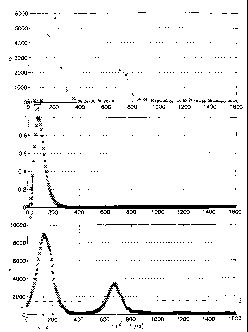
Fig. 2 shows, arranged one under the other, a received
signal, a reference function and a correlation
function formed by scalar products between the
received signal and comparison functions
produced by shifts of the reference function
based on time, in each case as a function of
time,
Fig. 3a schematically shows a setup for determining the
reference function according to a first method
and
Fig. 3b schematically shows a setup for determining the
reference function according to a second
method.
Description of the preferred embodiments
The apparatus according to Fig. 1 comprises a
calculating unit 1 which serves both for controlling
the apparatus and for evaluating the measured values.
An input unit 2 for inputting commands, for example a
keyboard, and an output unit 3 for outputting results,
etc., for example a liquid crystal display, are
connected to said calculating unit 1. A counter 4
which counts the cycles of the output signal of an
oscillator 5 is connected to the calculating unit 1 and
also transmits signals to a transmitter 6. The
oscillator 5 also controls an analogue/digital
converter 7 which is down-circuit of a receiver 8 and
is also connected to an input of the calculating unit
1.
The oscillator 5 generates an electrical signal
with a frequency of, in the example, 20 MHz, i.e. with
a period of 50 ns. After, for example, 2000 cycles in
each case, the counter 4 transmits a signal to the
CA 02304083 2000-04-05
KAP-4398 4 00324
transmitter 6, which signal causes said transmitter to
emit a short optical pulse. The pulse is reflected by
a target or by a plurality of targets which each
intersect a part of the light cone, and the reflections
are picked up by the receiver 8 and converted into an
electrical received signal e (Fig. 2, top). Owing to
the limited frequency response of the receiver and of
the electronics connected thereto, the received signal
e may be relatively greatly expanded as a function of
time. It is scanned by the A/D converter 7, which as
rIlntioned is controlled by the oscillator 5, at
intervals of a scanning increment A = 50 ns. The
corresponding values e(nA),n=0,...-,N, where N = 32 in
the example shown, are stored by the calculating unit
1. The memory address is derived in each case from the
number n which is delivered by the counter 4 and is a
measure of the time of scanning, based on the signal
which has triggered the emission of the optical pulse
by the transmitter 6.
For the evaluation in the calculating unit 1, a
reference function r (Fig. 2, center) which was
determined in a manner described in more detail further
below is used. Values of the reference function r are
used at points which follow one another with an
interval of specific reference increments. The
reference increments preferably correspond in each case
to a fixed time difference 8, for example a fraction
8=A/M of the scanning increment A, where M is an
integer >1; in the specific case described, M is 8.
The values r(i8),i=0,...,MN are permanently stored in
the calculating unit 1. Below a relatively small
carrier region, the values are equal to zero; above
CA 02304083 2009-06-23
KAP-4398
5
00324
this region, they are likewise equal to zero or
decrease exponentially so that the reference function r
can be continued beyond the interval [0, NA], in the
simplest case by setting r(i8)=0 outside said region.
Comparison functions vm,m=0,...,MN are now generated in
succession from the reference function r by producing
in each case a copy of the reference function r shifted
by a fixed time interval. The time interval is in each
case a multiple m8 of a lower case interval
corresponding here to the reference increment 8.
The
comparison functions vm can, if required, also be
modified in other ways, for example multiplied by a
suitable factor for compensating the beam expansion.
Apart from any modifications of this type, it is true
that
(1) vm(i8) = r((i-m)8).
With each comparison function vm, a similarity function
is calculated directly as a measure of the similarity
between said comparison function and the received
signal e. This is a correlation function f, which
corresponds to a scalar product between the two
functions. For those times when there is no
scanning
value of e but only one for vm, i.e. where i mod M is
#0, the value e(i8) is set =0.
The result is the
correlation function
(2) f (m8) = i=0 e (11\4,3) vm(iMo) = I e (iA) r (
iA - m6) ,i=0
for m=0,...,MN, a function shown in Fig. 2, bottom.
CA 02304083 2000-04-05
KAP-4398 6 00324
Those comparison functions which are
particularly similar to the received signal e and make
a larger contribution to said received signal are now
determined by determining those local maxima of
function f at which the value of said function exceeds
a specific threshold s which can be adjusted to the
circumstances of the measurements, in particular the
extent of expected disturbances. The corresponding
times mk.6,k=1,...,K represent approximate reception
times of reflections of the optical pulse by targets
1,...,K. In the example shown in Fig. 2, K is 2, but
larger numbers are also possible.
By interpolation with respect to.the times of
the maxima, the reception time for achieving a higher
resolution as a function of time can be determined more
accurately. In the simplest procedure, which is
suitable in particular when the maxima are relatively
far apart and the comparison functions do not overlap
or overlap only slightly - i.e. the reflections at the
various targets are not superposed or are scarcely
superposed - the individual maxima are treated
separately and the correlation function f is
interpolated in each case by an interpolation function,
and the time Tk when said interpolation function reaches
its maximum is then determined as an exact reception
time. If, for example, it is a quadratic function'
which is defined by the points ((mk-1)6, f((mk-1).5)),
(m)03, f(m1,5)) and ((mk+1)5, f((mk+1).3)), this leads to
(3) Tk=m,6+ 6 f((mk + 1)6) - f ( - 1)6)
2 2f (m.,6) - f ( (mk - 1)6) - f ( (mk +1)ö)
CA 02304083 2009-06-23
KAP-4398 7 00324
According to another procedure, the reception
times are determined more accurately by adjusting the
previously determined comparison functions \Trak, k=1, . . .K
by small time-related shifts so that they optimally
approximate to the received signal e. Using the
formulation
( 4 ) e (nA)= E akVmk(nA)
k=1
and the column vectors e=(e(nA),n=0,...,N) and
correspondingly a=(ak,k=1,...,K), the linear equation
(5) e = Va
is obtained, where Vnk=Vrak(nA)----r(nA¨mk8) , n=0 , . . .,N,
k=1,. ..,K, i.e.
vm1(0) vmk(0) _ _ r(-miS) r(-m1,6)
(6) v=
ymi(NA) vmk(NA)_ ymi(NA-mio) r (NA -
The expression can be generalized to continuous
time variables. For this purpose, starting from
reference values, the reference function r can be
supplemented to give a function which is continuous,
i.e. defined over the total interval [0, NA), and which
as far as possible is continuously differentiable,
preferably continuously differentiable at least once.
This can be done, for example, by means of quadratic
spline functions. The reference function r can be
extended beyond the stated interval by setting it equal
to zero there. Alternatively, it is also possible to
CA 02304083 2009-06-23
KAP-4398 8 00324
assume an exponential decay. The comparison functions
vm can then be replaced at the stated interval likewise
by continuous functions VT, so that the discrete
variables m are replaced by a real variable T:
(7) vT(nA) = r(nA-T).
Thus, V, too, is expanded to give a function of real
variables:
(8) V(T)nk = vTk(nA) = r(nA-Tk), n=0,...,N, k-1,...,K,
where T1,...TK together give a vector T.
Starting from the approximate initial values
Tk=mk5, it is now possible to determine exact reception
times by optimizing the approximation of e by variation
of a and T. For this purpose, the minimum point of the
mean square distance between e and V(T)a
(9) F(a,T)= 11 e-V(T)all
is determined. First, the optimization is performed
using a. F(a,T) is minimum for
(10) a=V(T)+e
_ _ _
where V(T) + is the pseudoinverse of the matrix V(T).
This matrix reproduces, vectors in the image space of
V(T) in each case on its uniquely determined original
image in the complement of the null space of V(T), whereas it
reproduces vectors in the complement of the image space
on 0 (in this context, see J. Stor: EinfUhrung in die
CA 02304083 2009-06-23
KAP-4398 9 00324
numerische Mathematik I [Introduction to Numerical
Mathematics I], Heidelberger TB 105, Springer-Verlag
1976, page 184 et seq.).
For the specific calculation V(T)+e, however, it
is not necessary to determine the matrix V(T)+. It can
be done in an efficient manner by known numerical
methods such as QR factorization by means of the Householder
Transformation (cf. for example G.H. Golub and Ch. F.
van Loan: Matrix Computations, North Oxford Academic,
London 1986, Ch. 6.1, 6.2).
(9) can now be expressed as
(11) F(T)=11e-V(T)V(T)ell.
V(T)V(T) is the projection P(T) onto the vector space
_ _
spanned by the comparison functions vn, k=1, .,K, so
that (9) corresponds to
(12) F(T)=11e-P(T)ell=11(1-P(T))ell,
i.e. the minimum of the distance between e and its
projection onto the vector space spanned by
vTk,k=1,...,K, as a function of T=(T1,...,TK), is
required.
The minimum of the nonlinear function F(T) can
be determined by known numerical methods. Examples are
the method of steepest descent or the determination of a
zero point of the gradient F by means of an iteration
of linear approximations (Newton's method). In this
context, see, for example, E. Stiefel: Einfuhrung in
die numerische Mathematik [Introduction to Numerical
Mathematics], Teubner Studienbucher Mathematik, B.G.
CA 02304083 2009-06-23
KAP-4398 10 00324
Teubner 1976, page 83 et seq. However, methods with
better convergence behaviour are preferred, as
described, for example, in the following articles: D.W.
Marquardt: An Algorithm for Least-Squares Estimation of
Nonlinear Parameters, SIAM Journal on Applied
Mathematics 11 (1963), 431-441, and K. Levenberg: A
Method for the Solution of Certain Non-Linear Problems
in Least Squares, Quarterly of Applied Mathematics 2
(1944), 164-168.
From the reception time Tk, it is now possible,
in each case by addition of a fixed term To dependent on
the determination of the zero point, to determine the
transit time Lk=To+Tk of the optical pulse and, from
this, the distance xk of the k th target in a very
simple manner according to
(13) xk=--Lk2
where c denotes the velocity of light.
With Tk,k=1,...,K, V(T) is also known, so that,
using (10), it is also possible to calculate the
coefficients ak,k=1,...,K, which weight the targets
1,...,K.
The reference function can be determined in
various ways. According to Fig. 3a, this is performed
by means of a setup comprising important parts of the
apparatus according to Fig. 1. Said setup comprises
the calculating unit 1, the counter 4 and the
oscillator 5 as well as the transmitter 6 and the
receiver 8 with the down-circuit A/D converter 7. A
time-lag element 9 is inserted between the counter 4
and the transmitter 6. A reference target 10, for
CA 02304083 2000-04-05
KAP-4398 11 00324
example a panel, is also provided and is mounted a
specific distance from the transmitter 6 and receiver
8.
After every 2000 cycles of the oscillator 5,
the counter 4 transmits a signal to the time-lag
element 9 which, after a specific delay, transmits it
onto the transmitter 6 and triggers the emission of an
optical pulse by said transmitter. The optical pulse
reflected by the reference target 10 generates at the
output of the receiver 8 a reference received signal
which is scanned. in the A/D converter 7 at time
intervals which correspond to the scanning increment A.
The reference values thus determined reach the
calculating unit 1 and are each stored there, assigned
to a specific scanning time,.
With each triggering of the transmitter 6 via
the time-lag element 9, the signal delay is changed to
the next delay value - the initial
value is T0=0 - which is reflected in corresponding
time-related shifts of the reference received signal.
Since the scanning of said received signal under
control by the oscillator 5 takes place without a
delay, this corresponds in each case - based on the
initial value - to an advance of the scanning time by
the delay value Ti. After the scanning and storage of I
signals, the reference function r is formed by =
assigning each reference value to its scanning time.
For the delay values, Ti=io,i=0-,...,I-1 may be chosen.
The reference values then follow one another at fixed
intervals which correspond to the reference increment
6. If this is not the case, the values of the
reference function r at the points corresponding to
CA 02304083 2000-04-05
KA2-4398 12 00324
integral multiples of the reference increment must be
determined by interpolation for use in (1). The
procedure essentially corresponds to that used in DE-A-
42 33 196 in the measurement of the distance of a
target. It is obvious that, instead of the signal
which triggers the emission of an optical pulse by the
transmitter 6, the same effect can be achieved by
delaying the reference received signal.
To increase the signal-to-noise ratio, it is
also possible to sum Of average the results of a
plurality of successively performed measurements in the
determination of the reference function r, similarly to
the procedure described according to DE-A-36 20 226 in
connection with the measurement of the distance of a
. target. The summing can be carried out digitally, but
it is also possible to store and to sum the measured
values in analog form, for example as electric charges,
and to convert the sum itself into digital form, as
described in a similar context in DE-A-44 40 613.
Both methods, namely the refinement of the time
resolution and the improvement of the signal-to-noise
ratio, as described above for the measurement of the
reference received signal, can incidentally also be
used in normal measurement, either individually or
together, for improving the time resolution and the
signal-to-noise ratio of the received signal e, if the-
situation that the number of required pulses is
increased as a result does not have any major
disadvantages. The apparatus according to Fig. 1
should then be supplemented appropriately.
Another possibility, shown ih Fig. 3b, for
improving the resolution of the reference received
signal as a function of time, consists in changing the
CA 02304083 2000-04-05
KAP-4398 13 00324
distance of the reference target 10. With an initial
value d, it can be measured in succession at distances
d+c-ci/2, i=0,...,I-1. This also leads to delays of the
received signal without the necessity of using the
time-lag element. However, it should be borne in mind
that the intensity of the received signal decreases
approximately proportionately to the square of the
distance of the reference target 10, owing to the beam
=
expansion.
Instead of the direct determination of the
reference values of the reference function r as
measured values or sums of measured values, however, it
is also possible to use a more complicated procedure.
For this purpose, a formulation which reduces the
amount of possible reference functions r to a vector
space of finite dimensions is postulated. Thus, it may
be assumed, for example, that the reference function r
is in the space of the quadratic spline function with a
fixed number of equidistant reference points.
Exponential decay can also be taken into account. The
reference function r is then fixed by a finite number
of real parameters.
To determine these parameters, the scanning
values of the time-shifted reference received signals
eni,n=0,...,N, i=0,...,I-1, where eni represents the
value for a delay Ti and a scanning time nA, are
approximated as exactly as possible by a superposition
of correspondingly time-shifted copies of the reference
function. For this purpose, the minimum of the mean
square distance according to the expression
N ¨1
( 1 4 )n =0 L=0
CA 02304083 2000-04-05
KAP-4398 14 00324
is found as a function of the parameters described in
the reference function r, where the wni,n=0,...,N,
i=0,...,I-1 are weighting coefficients, all of which
are set equal to 1 in the simplest case. If the delay
3 is produced by the time-lag element 9, ai can be set =1
for i=0,...,I-1. If it is produced by shifting the
reference target 10, the coefficients ai must take into
account the effect of the distance on the intensity of
the input signal. However, it is also possible to
consider the ooefficients ai likewise as variables and
to determine them from the minimizationof (14). The
delay values may be multiples of the reference
increment but may also assume other, nonequidistant
values.
List of reference symbols
1 Calculating unit
2 Input unit
3 Output unit
4 Counter
5 Oscillator
6 Transmitter
7 Analog/digital converter
8 Receiver
9 Time-lag element
10 Reference target
Received signal
Reference function
f Correlation function
A Scanning increment
6 Reference increment