Note: Descriptions are shown in the official language in which they were submitted.
CA 02310997 2000-06-08
1
A METHOD OF ENCODING A CELL BY A PRODUCT CODE, FOR A
SATELLITE APPLICATION
The field of the invention is that of encoding data.
More precisely, the present invention relates to a method
enabling data blocks to be encoded by means of a product
code using special families of row codes and column
codes. The invention applies in particular to encoding
ATM cells.
Product code encoding is a known form of encoding
that serves to encode data that is to be transmitted,
e.g. by radio. Figures 1 and 2 show the principle of
product encoding.
We consider here a block of 90 data bits to be
encoded, these bits being referenced dl to d90. The bits
are organized in an array as shown in Figure 1, the array
comprising a number k1 of rows and a number k2 of
columns, where kl = 9 and k2 - 10. Product code encoding
consists in applying a first block code (known as a row
code) to each of the k1 rows so as to obtain additional
bits referenced dli (Figure 2) corresponding to encoding
each of the kl rows. By way of example, bits dll, d12,
and d13 correspond to encoding the bits dl to d10. In
this case, n2 - 13 represents the total number of columns
after the code has been applied and n2 - k2 - 3
represents the number of additional columns due to
applying the code. Depending on the block code used,
this generates kl*(n2-k2) additional bits. These bits
are placed following the bits from which they are
derived, thus providing an array having kl rows and n2
columns.
After this first encoding operation, a second kind
of block encoding (referred to as a column encoding) is
applied to the n2 columns so as to generate (nl-kl)*n2
additional bits. Thus, in Figure.2, 20 additional bits
dci are generated by encoding the k2 columns, and 6 more
additional bits dlci are generated by encoding the (n2-
k2) columns. In this case the value of nl is equal to 11
CA 02310997 2000-06-08
2
and nl-kl = 2. By way of example, encoding the data in
the first column of the array in Figure 1 gives rise to
extra bits dcl and dc2.
A product code is defined on the basis of the
parameters (nl, kl) and (n2, k2) of the row and column
codes. The efficiency r of a product code is equal to
the product of the efficiencies of the row code and of
the column code making it up. I.e. in this case:
kl * k2
r =
nl * n2
Another characteristic of a block code is its
capacity for correction t. This depends directly on the
minimum Hamming distance dmin relating to the block code
in question.
Specifically:
t = Cdmin 1J
2
where [x] designates the integer portion of x.
In the state of the art, product codes are used in
particular for encoding ATM cells. For short cells of
this type, it is necessary to use appropriate encoding;
convolutional codes or Reed Solomon codes turn out to be
poorly adapted to encoding ATM cells and provide mediocre
performance.
French patent application FR 2 769 776 describes a
method of encoding a block of data comprising a first
zone and a second zone. The method consists in applying
a product code to the data block defined as follows:
- a first block code is applied to the first zone of
the data block;
- a second block code is applied to the second zone
of the data block; and
CA 02310997 2000-06-08
3
- a third block code is applied to the data obtained
by the first two encoding operations in a direction
perpendicular to the first two codes.
With product codes, it is common practice to apply a
row code having correction capacity t=1 and to apply a
column code having the same correction capacity t=1.
This practice has the drawback of obtaining efficiency
for the product code that is always greater than 0.5,
regardless of the code chosen. Unfortunately, with
satellite transmission, in order to obtain a good
compromise between the power that needs to be transmitted
and the bandwidth that is occupied, it is desirable for
code efficiency to come as close as possible to 0.5.
A particular object of the present invention is to
devise families of row codes and column codes which make
it possible to obtain an encoding rate that is adapted to
satellite transmission.
More precisely, one of the objects of the invention
is to determine a family of error correcting product
codes, and thus of the row codes and the column codes
making it up, such that when applied to a short cell they
imply a product code efficiency close to 0.5. To select
a code compatible with the objects of the invention, it
is necessary to satisfy the following conditions:
kl *k2 >_ Dell ( 1 )
kl*k2
r= X0.5 (2)
nl * n2
where Dell is the number of bits in the cell.
Condition (1) expresses the fact that the product
code is applied to blocks of at least cell size, with
additional bits, in particular bits referred to in this
description below as "padding" bits, and that do not
belong to the cell, optionally being added thereto in
order to pad it out to the quantity of information
required for applying the code. Preferably, it is
CA 02310997 2000-06-08
4
desirable to use codes for which the product of the
parameters k1 and k2 comes close to the value Icell~
Condition (2) determines that the product of the
efficiencies of the row code multiplied by the efficiency
of the column code must be close to 0.5 so as to provide
encoding that is suitable for satellite transmission.
Preferably, any padding bits added to make up the
quantity of information necessary for applying the code
are not transmitted. This method amounts to shortening
the product code. The decoder knows the non-transmitted
sequence that needs to be added in order to decode the
sequence of received bits correctly. Under such
circumstances, condition (2) is given by:
Icell ( 2 )
r= X0.5
nl * n2 - ( kl *k2 - Icell)
Furthermare, in order to adapt the efficiency of the
code finely, it is possible to avoid transmitting certain
redundancy bits, the number omitted being npunct~ using a
"code puncturing" method applied to the product code.
Under such circumstances, condition (2) is given by:
r = Icel1 ,:; 0 . 5 ( 2 )
n l * n2 - ( kl * k2 - Iceii) - np~ct
These objects, and others that appear below, are
achieved by a method of encoding a cell made up of bits
by means of a product code, given that the cell is
presented for coding purposes in the form of an array and
that the encoding consists specifically in:
a) applying a first binary linear block code to one
dimension of the array (rows or columns) containing the
cell; and
b) applying a second binary linear block code to the
other dimensions of the array (column or row) containing
the cell.
CA 02310997 2000-06-08
The linear block codes used satisfy the following
criterion: one of them has the capacity to correct one
error (t=1) and the other has the capacity to correct two
errors (t=2) .
5 Advantageously, the binary linear block codes
correspond to BCH codes of length n and dimension k, said
BCH codes belonging to any one of the following families:
(n, k), (n, k-1), (n+1, k), (n-s, k-s), or (n-s, k-1-s)
and (n+1-s, k-s), where k, n, and s are integers and
where s<k, define the above-mentioned criterion.
Preferably, the method of the invention consists in
interlacing the data obtained during step a) prior to
step b) .
Other characteristics and advantages of the
invention will appear on reading the following
description of a preferred implementation given by way of
non-limiting illustration, and with reference to the
accompanying drawings, in which:
- Figures 1 and 2 show the principle of product
encoding;
- Figure 3 shows an example of a product code of the
invention applied to encoding an ATM cell; and
- Figure 4 shows the efficiency characteristics of a
family of BCH codes of the invention.
Figures 1 and 2 are described above with reference
to the state of the art.
In a particular implementation of the present
invention, the row and column codes used for constructing
the product code are (n, k) BCH binary codes, their (n+1,
k) extended codes, their (n, k-1) expurgated codes, and
the (n-s, k-s), (n-s, k-1-s), and (n+1-s, k-s) shortened
codes of these codes, with k, n, and s integers, and with
s<k.
The extended codes are obtained by adding a parity
bit to each word of a BCH code having an odd minimum
Hamming distance. In other words, its generator
polynomial g(x) does not contain the factor (x+1). An
CA 02310997 2000-06-08
6
expurgated code is obtained from a BCH code having g(x)
as its generating polynomial, where g(x) does not contain
the factor (x+1). The expurgated code is obtained by the
new generator polynomial (x+1) *g (x) .
The term BCH code is used below for any of the
variants described above.
A pair of codes constituting a product code of the
invention comprises the (26,32) extended BCH code whose
correction capacity is t=1, and the (21,32) extended BCH
code whose correction capacity is t=2. The list of basic
BCH codes and of their correction capacities is given at
p. 437 of the second edition of the work entitled
"Digital communication" by John G. Proakis, published by
Mac Graw Hill.
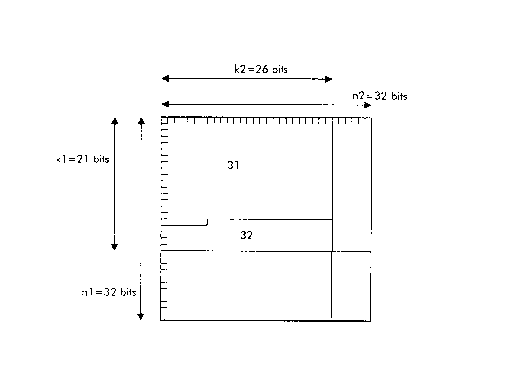
Figure 3 shows an ATM cell (31) comprising 424 bits
arranged for encoding purposes.in an array of 21 rows by
26 columns for the case where the (32,21) BCH code having
t=2 is selected as the row code and the (32,26) BCH code
having t=1 is selected as the column code. It is also
possible to envisage interchanging the row and column
codes. The method whereby the ATM cell is arranged in
the array in this case is filling the first row
sequentially from left to right, then the second, etc.,
until all of the bits of the cell have been arranged in
the array. In the present case, the first 16 rows are
filled completely with bits of the ATM cell, while the
17th cell contains the last 8 bits of the ATM cell. The
remaining locations of the array (32) can be filled by
optionally random padding bits which need not be
transmitted, which amounts to shortening the product
code. This method of arrangement has been described
because of its simplicity, however it is entirely
possible to define some other method of arrangement
providing that decoding means are available for
distinguishing bits of the ATM cell from any padding bits
or puncturing bits, and for reconstituting the ATM cell
correctly after decoding.
CA 02310997 2000-06-08
7
The efficiency of the product code based on the
(32,26) BCH row code and the (32,21) BCH column code is:
26 * 21
r = = 0.53
32 * 32
Figure 4 is made up of Figures 4a, 4b, 4c, 4d, 4e,
and 4f and shows the characteristics of pairs of codes
making up a product code. These diagram should be
considered in pairs (4a, 4b) , (4c, 4d) , (4e, 4f) where
each pair shows the results of simulations for particular
families of raw and column codes.
In the charts, the X direction represents the
shortening value for the row code, and the Y direction of
the chart represents the shortening value for the column
code. For each combination of a row code and a column
code, the direction Z1 in the charts of Figures 4a, 4c,
and 4e gives the numbers of code bits generated by the
code, while the Z2 direction of charts 4b, 4d, and 4f
gives the efficiency of the code.
For the pair (4a, 4b), the row codes and the column
codes are derived by shortening the (32,26) BCH code and
both have a correction capacity t=1. The efficiencies of
the various codes considered in this case extend over the
range about 0.55 to about 0.65.
For the pair (4c, 4d), the row codes and the column
codes are derived by shortening the (32,21) BCH code and
both have a correction capacity t=2. The efficiencies of
the various codes considered in this case extend over the
range about 0.30 to about 0.45.
For the pair (4e, 4f), the row codes are derived by
shortening the (32,26) BCH code and all have a correction
capacity t=1, while the column codes are derived by
shortening the (32,21) BCH code and all have a correction
capacity t=2. The efficiencies of the various codes
considered in this case covers the range about 0.45 to
about 0.52.
CA 02310997 2000-06-08
8
It can be seen from the various charts that for
combinations of codes in which one has correction
capacity t=1 and the other has correction capacity t=2,
i.e. charts 4e and 4f, the conditions (1) and (2) for
encoding an ATM cell for satellite transmission are
satisfied much better than for codes both having a
correction capacity t=1, charts 4a and 4b, or for codes
both having a correction capacity t=2, charts 4c and 4d.