Note: Descriptions are shown in the official language in which they were submitted.
CA 02340017 2001-02-O1
WO 00108815 1 PCT/FR99/01933
Sondage dynamique d'un canal de transmission
La présente invention concerne un procédé de sondage
d'un canal de transmission. En d'autres termes, l'invention
propose une méthode d'estimation de la réponse
impulsionnelle d'un canal de transmission.
Dans un système de transmission, notamment par ondes
radio, un émetteur émet un signal dans un canal de
transmission à destination d'un récepteur. Le signal émis
subit des fluctuations d'amplitude et de phase dans le canal
de transmission, si bien que le signal reçu par le récepteur
ne lui est pas identique. Les fluctuations du signal sont
essentiellement dues à ce que l'homme du métier appelle
l'interférence intersymbole. Cette interférence peut
provenir de la loi de modulation employée pour la
transmission ; elle est êgalement due à la propagation
multi-trajets dans le canal.
En effet, le signal reçu est généralement issu d'un
grand nombre de réflexions dans le canal, les différents
trajets empruntés par le signal émis conduisant ainsi à des
retards variés au niveau du récepteur. La rêponse
impulsionnelle du canal représente l'ensemble de ces
fluctuations, auxquelles est soumis le signal émis. I1
s'agit donc là de la caractéristique fondamentale
représentant les transmissions entre l'émetteur et le
récepteur.
La réponse impulsionnelle du canal est utilisée
notamment par un êgaliseur qui a précisément pour fonction
de corriger l'interférence intersymbole dans le récepteur.
Une méthode classique pour rêaliser une estimation de cette
réponse impulsionnelle consiste à disposer dans le signal
émis une séquence d'apprentissage formée de symboles connus.
Cette séquence est choisie en fonction de la loi de
modulation et de la dispersion temporelle du canal,
dispersion devant s'entendre ici comme le retard d'un
symbole émis empruntant le trajet le plus long du canal par
rapport à ce même symbole empruntant le trajet le plus
COPlE DE CONFiRMATiOIiI
CA 02340017 2001-02-O1
WO 00/08815 2 PCT/FR99/01933
court. La dispersion temporelle est couramment exprimée
comme un multiple de la durée qui sépare deux symboles émis
successifs, soit un nombre de "durée symbole".
Les techniques connues font l'hypothèse que la réponse
impulsionnelle d'un canal reste constante sur une durée
relativement courte. Or ce n'est pas le cas lorsque la
vitesse relative du récepteur par rapport à l'émetteur est
relativement importante. Ce n'est pas le cas non plus
lorsque les conditions de propagation entre ces deux
l0 équipements évoluent rapidement, par exemple si un objet
mobile vient temporairement obstruer l'un au moins des
trajets du canal.
La présente invention a ainsi pour objet un procédé de
sondage d'un canal de transmission qui présente des
performances sensiblement améliorées dans un environnement
mobile.
Selon l'invention, on procède au sondage d'un canal de
transmission affecté d'une dispersion temporelle d à partir
d'une séquence d'apprentissage et d'un signal de réception
correspondant à cette séquence, ceci au moyen d'une matrice
de mesure établie à partir de la séquence d'apprentissage
compte tenu de cette dispersion temporelle ; le procédé
comprend une étape pour produire la réponse impulsionnelle
dynamique de ce canal selon la technique des moindres carrés
comme la combinaison d'une réponse statique r à (d+1)
composantes et d'une dérive temporelle r' qui dépend donc du
temps.
Pour la mise en oeuvre la plus directe du procédé, le
signal de réception est défini par l'expression
s=M.r+TM.r'+n où T est une matrice temps représentant le
temps et où n représente le bruit de réception, la dérive
temporelle comportant elle aussi (d+1) composantes.
Cette méthode peut cependant nécessiter des calculs
relativement complexes, ceci d'autant plus que la dispersion
temporelle est importante.
CA 02340017 2001-02-O1
WO 00/08815 3 PCT/FR99/01933
Ainsi, selon une autre mise en oeuvre du procédé, la
réponse statique r est établie selon l'expression s=M.r+n où
n représente le bruit de réception.
De plus, selon une première variante, le procédé
comprend une ëtape pour rechercher le vecteur propre r0
associé à la plus grande valeur propre de la covariance de
la réponse statique r, la dérive temporelle r' valant le
produit d'un coefficient de dérive a0 par ce vecteur propre,
le signal de rêception étant défini par l'expression
s=M.r+aOTM.rO+n.
Avantageusement, le coefficient de dérive étant
affectë d'une variance a2, le procédé comprend une étape
pour pondërer ce coefficient par l'expression a2/(a2+Np) où
NO représente le module du bruit de réception.
On peut prévoir que le module du bruit de réception
soit êgal à la plus petite des valeurs propres de la
covariance de la réponse statique.
On peut également prévoir que le module du bruit de
réception soit obtenu par normalisation de l'énergie du
bruit instantané.
Selon une deuxième variante, le procédé comprend une
étape pour rechercher une pluralité de vecteurs propres ri
de la covariance de la réponse statique, le signal de
réception étant défini par l'expression
s = M. r + ~ aiTM. ri + n où ai est un coefficient de dêrive
i
affecté au vecteur propre ri.
Par ailleurs, l'invention prévoit aussi le cas où la
vitesse relative du récepteur par rapport à l'émetteur est
importante ; dans ce cas, le signal de réception s est
défini par l'expression s=M.r+TM.r'+1/2(T2M.r")+n où T est
une matrice temps représentant le temps et où n reprêsente
le bruit de réception.
Comme précédemment, la réponse statique est établie
selon l'expression s=M.r+n où n représente le bruit de
réception.
CA 02340017 2001-02-O1
WO 00108815 4 PCT/FR99/01933
En outre, le procédé comprend une étape pour
rechercher le vecteur propre rp associé à la plus grande
valeur propre de la covariance de la réponse statique, le
signal de réception étant défini par l'expression
s=M. r+~30TM. r0+1/2 ( (31T2M. r0 }+n où ~i0 et fil sont des
coefficients de dërive.
La présente invention apparaîtra maintenant de manière
plus détaillêe dans le cadre de la description qui suit où
sont proposés des exemples de mise en oeuvre à titre
illustratif, ceci en rêférence aux figures annexées qui
reprêsentent .
- la figure 1, un schéma de principe du procédé selon
l'invention,
- la figure 2, un schéma de principe d'une première
variante de mise en oeuvre de l'invention,
- la figure 3, un schéma de principe d'une deuxième
variante de mise en oeuvre de l'invention, et
- la figure 4, un schéma de principe d'une troisième
variante de mise en oeuvre de l'invention.
Les éléments communs à plusieurs figures sont affectés
d'une seule référence.
L'invention sera présentée dans son application au GSM
car ce système a le mérite d' être bien connu de l' homme du
métier. I1 s'agit donc là d'une présentation adoptée dans un
souci de clarté mais il ne faut y voir en aucun cas une
limitation de l'invention à ce seul système.
Ce système fait appel à des séquences d'apprentissage
TS formées de 26 symboles notés a0 à a25 prenant la valeur
+1 ou -1. Ces symboles en provenance de l'émetteur sont
connus du récepteur et l'on englobera donc sous le terme
"séquence d'apprentissage" toute séquence de bits qui sont
connus à priori de ce récepteur par quelque moyen que ce
soit.
La séquence s de symboles reçus par le rêcepteur
correspondant à la séquence d'apprentissage TS émise par
CA 02340017 2001-02-O1
WO 00/08815 5 PCT/FR99/01933
l'émetteur est formée elle aussi de 26 symboles notés sp à
s25~
En matière de rappel, les techniques d'estimation font
appel à une matrice de mesure M construite à partir de la
séquence d'apprentissage TS de longueur n. Cette matrice
comprend (n-d) lignes et (d+1) colonnes, d représentant
toujours la dispersion temporelle du canal. L'élément
figurant à la ième ligne et à la jème colonne est le (d+i-
j)ième symbole de la séquence d'apprentissage .
a4 a3 a2 al a0
a5 a4 a3 a2 a1
a6 a5 a4 a3 a2
M = agi..............
a25........... a21
La séquence d'apprentissage est choisie telle que la
matrice MtM soit inversible où l'opérateur .t représente la
transposition.
Classiquement, lorsque l'on considère que la réponse
impulsionnelle est indépendante du temps, en notant d la
dispersion temporelle du canal qui vaut 4 dans le cas du
GSM, l'estimation de cette réponse prend la forme d'un
vecteur à 5 composantes. Si l'on retient la technique des
moindres carrés, ce vecteur vaut (MtM)-1 Mt.s.
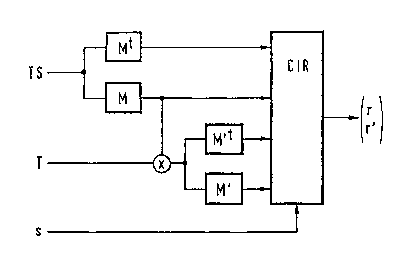
Selon l'invention, en rëférence à la figure 1, la
réponse impulsionnelle dynamique est représentée par une
combinaison d'une réponse statique r et d'une dérive
temporelle r' de sorte que le signal reçu s s'exprime au
moyen de l'équation suivante .
s = M.r + TM.r' + n (1)
où n figure le bruit additif dans le canal de transmission
et T est une matrice qui figure le temps auquel son reçus
les différents symboles, ce temps étant exprimë en durées
symbole .
CA 02340017 2001-02-O1
WO 00/08815 6 PCT/FR99/01933
-10, 5 0 0 ................ 0
0 - 9,5 0 ................ 0
0 0 - 8, 5 0 .......... 0
T = .........................................
........................ 0 9, 5 0
.................... 0 0 1 0,5
En fait, T est une matrice diagonale de dimension 22
dont l'élément qui figure à la ième ligne et à la ième
colonne représente le temps qui correspond au (d+i)ième
symbole de la séquence d'apprentissage, soit a(d+i-1)~
l'origine du temps étant arbitrairement fixée entre les
quinzième et seizième symboles.
En notant M'=TM, l'équation (1) se traduit par les
deux expressions suivantes .
Mt.s = MtM.r + MtM'.r' + Mtn
M't.s = M'tM.r + M'tM'.r' + M'tn
On peut résoudre ce système d'équations sous forme
matricielle au sens des moindres carrés .
r MtM MtM' 1 MtS
~r~~ M'tM M'tM' M'ts
La réponse impulsionnelle dynamique CIR se présente
donc comme un vecteur à lo composantes formê par les cinq
composantes de la réponse statique r et les cinq composantes
de la dérive temporelle r'. I1 s'ensuit une relative
complexité des calculs nécessaires par comparaison aux
méthodes classiques.
Afin de limiter cette complexité, selon une première
variante de l'invention, on se contente de six composantes
pour la réponse dynamique dont cinq composantes pour la
rêponse statique et une pour la dérive temporelle.
En référence à la figure 2, on commence par calculer
la réponse statique r par l'une quelconque des techniques
connues. Si l'on retient la méthode des moindres carrés,
cette réponse statique est obtenue comme suit .
r = (MtM)-1 Mt.s
CA 02340017 2001-02-O1
WO 00/08815 7 PCT/FR99/01933
On construit d'autre part une matrice de lissage L par
lissage des différentes réponses obtenues pour les séquences
d'apprentissage successivement émises, ceci afin d'obtenir
une estimation de la covariance associée à cette réponse
statique. On entend ici lissage dans un sens très général,
c'est-à-dire toute opération permettant de lisser ou de
moyenner la réponse statique.
Un premier exemple de lissage consiste à effectuer la
moyenne de la matrice rrh sur une période supposée
comprendre m séquences d'apprentissage, l'opêrateur .h
représentant la transformation hermitienne .
m
L( rrh) = 1 ~ rrh
m
Un second exemple de lissage consiste à actualiser, à
la ième séquence d'apprentissage reçue, la matrice de
lissage obtenue à la (i-1)ième séquence d'apprentissage au
moyen d'un coefficient multiplicatif ~,, ce facteur étant
généralement connu sous le nom de facteur d'oubli de lissage
et étant compris entre 0 et 1 .
Li ( rrh ) - ~,ririh + ( 1-~, ) Li-1 ( rrh )
L'initialisation peut se faire par tous moyens,
notamment au moyen de la première estimation r obtenue ou
bien par une moyenne obtenue comme ci-dessus pour un faible
nombre de séquences d'apprentissage.
On recherche alors le vecteur propre r0 associé à la
plus grande valeur propre de cette matrice L(rrh).
En notant u0 - M.rO et en reprenant les mêmes
conventions qu'auparavant, on postule que le signal reçu se
présente sous la forme suivante .
s = M.r + a0T.u0 + n (2)
La dërive temporelle correspond au terme apr0.
En notant I la matrice identité, on introduit un
opérateur de transformation A .
A = I _ M(MtM)_1Mt
L'équation (2) se traduit alors par l'expression
suivante .
CA 02340017 2001-02-O1
WO 00/08815 8 PCT/FR99/01933
A.s = apAT.up + A.n
En notant u'p - T.up, la résolution de cette équation
au sens des moindres carrés donne la valeur estimée âp du
coefficient ap
u'p A. s
ap =
u'p A. u'p
Cette estimation est non biaisëe et, en notant Np le
bruit additif ou module du bruit de réception, l'erreur
d'estimation est affectée d'une variance qui vaut .
2 N
02 _ EC ap_ ap ~ = 0
u'p A. up
Il convient donc d'estimer le bruit additif Np.
Une première solution consiste à affecter Np d'une
valeur prédéterminée qui reflète un seuil en dessous duquel
il est peu probable que le bruit additif puisse descendre.
Cette valeur pourrait étre déterminée par une mesure de
rapport signal à bruit, ou par les performances du
récepteur, ceci à titre d'exemple.
Une deuxième solution consiste à considérer que la
dernière valeur propre, (la plus faible) de la matrice de
lissage L est égale à Np.
Une troisième solution qui est sans doute la plus
performante consiste à estimer directement le bruit additif
à partir du signal reçu. En effet .
s = M.r + apT.up + n
Compte tenu du fait que les vecteurs s et n ont 22
composantes .
_ 1
Np (22) (s - M.r - apT.up)h (s - M.r - apT.up)
Le bruit additif est donc obtenu par normalisation de
l'énergie du bruit instantané.
Naturellement cette estimation du bruit additif Np
3p peut être moyennée ou lissée.
Classiquement, il est possible de diminuer la variance
du coefficient estimé ap si l'on accepte un biais, par
CA 02340017 2001-02-O1
WO 00/08815 9 PCT/FR99/01933
exemple en pondérant ce coefficient pour obtenir un
coefficient pondëré app .
02
a0P - a2 + NO a0
I1 est à noter que le coefficient pondéré app tend
vers zéro lorsque le canal de transmission est stationnaire
car la variance a2 tend elle aussi vers zéro.
En référence à la figure 3, selon une deuxième
variante de l'invention, on adopte une réponse
impulsionnelle dynamique à sept composantes dont cinq
l0 composantes pour la réponse statique et deux pour la dérive
temporelle.
Comme précédemment, on calcule la réponse statique r
par l'une quelconque des techniques connues.
On recherche alors le premier vecteur propre rp
associê à la plus grande valeur propre de la matrice de
lissage L et on recherche également le deuxième vecteur
propre rl associé à la valeur propre immédiatement
inférieure de cette matrice L.
En notant u0 - M.rO, ul - M.rl, et en reprenant les
mémes conventions qu'auparavant, on postule que le signal
reçu se présente sous la forme suivante .
s = M.r + a0T.u0 + alT.u1 + n (3)
La dérive temporelle correspond au terme apr0 + alrl.
On reprend l'opérateur de transformation A .
A = I - M(MtM)-1Mt
L'équation (3) se traduit alors par l'expression
suivante .
A.s = aOAT.uO + alAT.ul + A.n
En notant u' 0 - T . u0 et u' 1 - T . ul , la résolution de
cette équation au sens des moindres carrés donne les valeurs
estimées a0 et al des coefficients a0 et al
a0 u'~ A. u'0 u'~ A. u'1 1. u'p A. s
al u'i A. u'0 u'i A. u'1 u'i A. s
Naturellement, on peut généraliser la méthode exposêe
ci-dessus à propos des première et deuxième variantes pour
CA 02340017 2001-02-O1
WO 00/08815 10 PCT/FR99/01933
estimer la réponse impulsionnelle dynamique au moyen d'un
nombre quelconque (q+1) de vecteurs propres de la matrice de
lissage L pourvu que ce nombre (q+1) soit inférieur à la
dimension de cette matrice.
On note alors ai le coefficients affecté au vecteur
propre ui, ui - M. ri et u' i - T.ui, de sorte que le signal
reçu s'exprime de la manière suivante .
s = M. r + ~ aiT. ui + n
i
La dërive temporelle correspond ici au terme ~ airi.
i
I1 est alors nécessaire de définir une nouvelle
matrice G dont l'élément gij, qui figure à la ième ligne et
à la jième colonne, vaut u'i 1 A. u'j_1.
La solution est ainsi la suivante .
a0 u'p A. s
al u'i A. s
G_1
aq u'q A. s
Selon une troisième variante de l'invention, la
réponse impulsionnelle dynamique est représentée par une
combinaison d'une réponse statique r et d'une dérive
quadratique temporelle de sorte que le signal reçu s
s'exprime au moyen de l'équation suivante .
s = M.r + TM.r' + 1/2(T2M.r") + n
Selon cette variante qui est particulièrement bien
adaptée en cas de vitesse élevée, la rëponse impulsionnelle
dynamique se présente comme un vecteur à 15 composantes
formé par les cinq composantes de la réponse statique r et
les dix composantes de la dérive temporelle (cinq pour r' et
cinq pour r").
Afin de limiter la complexitê des calculs nêcessaires,
il est avantageux de se limiter à sept composantes pour la
réponse dynamique en conservant toujours cinq composantes
CA 02340017 2001-02-O1
WO 00/08815 11 PCT/FR99/01933
pour la réponse statique et en prenant deux composantes pour
la dêrive temporelle, une pour r' et une pour r".
En référence à la figure 4, on commence par calculer
la réponse statigue r par l'une quelconque des techniques
connues, comme auparavant.
On recherche alors le vecteur propre rp associé à la
plus grande valeur propre de la matrice de lissage L.
En reprenant les mêmes conventions que ci-dessus, on
postule que le signal reçu se présente sous la forme
suivante .
s = M.r + (30T.u0 + 1/2((31T2.u0) + n (4)
En notant u"0=1/2(T2.u0), l'équation (4) se traduit
alors par l'expression suivante .
s = M. r + j30u' 0 + (31u"0 + n
La résolution de cette équation au sens des moindres
carrés se fait de la manière suivante .
-1
(30 u'p A. u'0 u'p A. u "0 u'Ö A. s
~1 t1"p A. u'~ u"p A. u"~ u"~ A. S
L'homme du métier utilise la réponse impusionnelle
dynamique de l'invention, dans un êgaliseur par exemple, de
la même maniére que s'il s'agissait d'une réponse
impulsionnelle de l'art antérieur. I1 suffit en effet, pour
un symbole reçu à un instant rêférencé, de calculer la
réponse dynamique à cet instant précis à partir de l'une
quelconque des expressions gênérales qui figurent ci-dessus.
L'invention ne se limite pas aux exemples de
réalisations décrits ci-dessus. En particulier, il est
possible de remplacer tout moyen par un moyen équivalent.