Note: Descriptions are shown in the official language in which they were submitted.
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
SYSTEM AND METHOD FOR NONINVASIVE BLOOD ANALYTE MEASUREMENTS
TECHNICRL FIELD
The invention relates to the measurement of blood analytes. More particularly,
the
invention relates to an intelligent system for noninvasive blood analyte
prediction.
DESCR I PTI ON OF THE PR I OR H RT
The goal of noninvasive blood analyte measurement is to determine the
concentration of targeted blood analytes without penetrating the skin. Near
infrared
(NIR) spectroscopy is a promising noninvasive technology which bases
measurements on the absorbance of low energy NIR light that is transmitted
into a
subject. The light is focused onto a small area of the skin and propagates
through
subcutaneous tissue. The reflected or transmitted light that escapes and is
detected
by a spectrometer provides information about the tissue contents that it has
penetrated.
The absorbance of light at each wavelength is a function of the structural
properties
and chemical composition of the tissue. Tissue layers, each containing a
unique
heterogeneous particulate distribution, affect light absorbance through
scattering.
Chemical components, such as water, protein, fat and blood analytes, absorb
light
proportionally to their concentration through unique absorption profiles or
signatures.
The measurement of blood analyte concentrations is based on detecting the
magnitude of light attenuation caused by the absorption signature of the
targeted
analyte. The process of calibration is the development of a mathematical
transformation or model which estimates the blood analyte concentration from
the
measured tissue absorbance spectrum.
1
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
However, accurate noninvasive estimation of blood analytes is presently
limited by
the dynamic nature of the sample, the skin and living tissue of the subject.
Chemical, structural and physiological variations occur that produce dramatic
changes in the optical properties of the tissue sample.
See, for example, R. Anderson, J. Parrish, The optics of human skin, Journal
of
Investigative Dermatology, vol. 77(1 ), pp. 13-19 (1981 ); W. Cheong, S Prahl,
A.
Welch, A review of the optical properties of biological tissues, IEEE Journal
of
Quantum Electronics, vol. 26(12), pp. 2166-2185 (Dec. 1990); D. Benaron, D.
Ho,
Imaging (NIRI) and quantitation (NIBS) in tissue using time-resolved
spectrophotometry: the impact of statically and dynariiically variable optical
path
lengths, SPIE, vol. 1888, pp.l0-21 (1993); J. Conway, K. Norris, C. Bodwell, A
new
approach for the estimation of body composition: infrared interactance, The
American Journal of Clinical Nutrition, 40, pp. 1123-1140 (Dec. 1984); S.
Homma, T.
Fukunaga, A. Kagaya, Influence of adipose tissue thickness in near infrared
spectroscopic signals in the measurement of human muscle, Journal of
Biomedical
Optics, 1 (4), pp. 418-424 (Oct. 1996); A. Profio, Light transport in tissue,
Applied
Optics, vol. 28(12), pp. 2216-2222 (June 1989); and M. Van Gemert, S. Jacques,
H.
Sterenborg, W. Star, Skin optics, IEEE Transactions on Biomedical Engineering,
vol.
36(12), pp. 1146-1154 (Dec. 1989).
These variations include the following general categories:
1. Covariation of spectrally interfering species. The NIR spectral absorption
profiles
of blood analytes tend to overlap and vary simultaneously over brief time
periods.
This produces spectral interference and necessitates the measurement of
absorbance at more independently varying wavelengths than the number of
interfering species.
2. Sample heterogeneity. The tissue measurement site has multiple layers and
compartments of varied composition and scattering. The spectral absorbance
versus wavelength is related to a complex combination of the optical
properties
and composition of these tissue components. Therefore, a general
2
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
representation or model of the tissue absorbance spectrum is nonlinear and
difficult to realize on the basis of first principles.
3. State Variations. Variations in the subject's physiological state effect
the optical
properties of tissue layers and compartments over a relatively short period of
time. Such variations, for example, may be related to hydration levels,
changes
in the volume fraction of blood in the tissue, hormonal stimulation,
temperature
fluctuations and blood hemoglobin levels.
4. Structural Variations. The tissue characteristics of individuals differ as
a result of
factors that include hereditary, environmental influences, the aging process,
sex
and body composition. These differences are largely anatomical and can be
categorized as slowly varying structural properties producing diverse tissue
geometry. Consequently, the tissue of a given subject has distinct systematic
spectral absorbance features or patterns that can be related directly to
specific
characteristics such as dermal thickness, protein levels and percent body fat.
While the absorbance features are repeatable by subject, over a population of
subjects they produce confounding nonlinear spectral variation. Therefore,
differences between subjects are a significant obstacle to the noninvasive
measurement of blood analytes through NIR spectral absorbance.
In a nondispersive system, variations similar to (1 ) above are easily modeled
through
multivariate techniques, such as multiple linear regression and factor based
algorithms. Significant effort has been expended to model the scattering
properties
of tissue in diffuse reflectance although the problem outlined in (2) above
has been
largely unexplored. Variations of the type listed in (3) and (4) above causes
significant nonlinear spectral variation for which an effective solution has
not been
reported. For example, several reported methods of noninvasive glucose
measurement develop calibration models that are specific to an individual over
a
short period of time.
3
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
See, for example, K. Hazen, Glucose determination in biological matrices using
near-infrared spectroscopy, Doctoral Dissertation, University of Iowa (Aug.
1995); J.
Burmeister, In vitro model for human noninvasive blood glucose measurements,
Doctoral Dissertation, University of Iowa (Dec. 1997); and M. Robinson, R.
Eaton, D.
Haaland, G. Koepp, E. Thomas, B. Stallard, P. Robinson, Noninvasive glucose
monitoring in diabetic subjects: a preliminary evaluation, Clin. Chem, 38/9,
pp. 1618-
1622 ( 1992) .
This approach avoids modeling the differences between subjects and therefore
cannot be generalized to more individuals. However, the calibration models
have
not been tested over long time periods during which variation of type (4)
above may
require recalibration. Furthermore, the reported methods have not been shown
to be
effective over a range of type (3) above variations.
It would be desirable to provide a method and apparatus for compensating for
the
variations described above.
The invention provides a method and apparatus for compensating for covariation
of
spectrally interfering species, sample heterogeneity, state variations, and
structural
variations through an intelligent pattern recognition system that is capable
of
determining calibration models that are most appropriate for the subject at
the time
of measurement. The calibration models are developed from the spectral
absorbance of a representative population of subjects that have been
segregated
into groups. The groups or classes are defined on the basis of structural and
state
similarity, such that the variation within a class is small compared to the
variation
between classes. Classification occurs through extracted features of the
tissue
absorbance spectrum related to the current subject state and structure.
The invention provides an intelligent system for measuring blood analytes
noninvasively. The system operates on a near infrared absorbance spectrum of
in
vivo skin tissue. The hierarchical architecture employs a pattern
classification
engine to adapt the calibration to the structural properties and physiological
state of
4
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
the subject as manifested in the absorbance spectrum. A priori information
about
the primary sources of sample variability is used to establish general
categories of
subjects. The spectral interference is reduced by applying calibration schemes
specific to the various categories, resulting in improved prediction accuracy
and
parsimonious calibrations.
Two classification rules are disclosed:
~ The first rule assumes that the classes are mutually exclusive and applies
specific calibration models to the various subject categories.
~ The second rule uses fuzzy set theory to develop calibration models and
blood
analyte predictions. Therefore, each calibration sample has the opportunity to
influence more than one calibration model according to its class membership.
Similarly, the predictions from more than one calibration are combined through
defuzzification to produce the final blood analyte prediction.
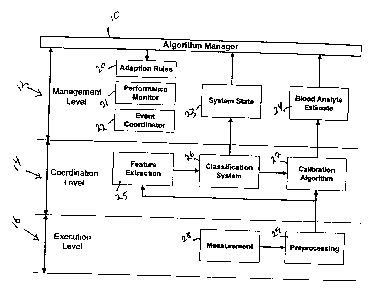
Fig. 1 is a block schematic diagram of an architecture of an intelligent
system for
noninvasive measurement of blood analytes according to the invention;
Fig. 2 is a typical noninvasive absorbance spectrum;
Fig. 3 is a block schematic diagram of a pattern classification system
according to
the invention;
Figs. 4A and 4B provide two different flow diagrams showing two embodiments of
the herein disclosed pattern classification system, where Fig. 4A shows
subject
classes that are mutually exclusive, and where Fig. 4B shows fuzzy
classification
applied to assign class membership to more than one class, both according to
the
invention;
Fig. 5 is a block schematic diagram showing a general calibration system for
mutually exclusive classes according to the invention;
Fig. 6 is a block schematic diagram showing an example of parallel calibration
models for mutually exclusive classes according to the invention;
5
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Fig. 7 is a block schematic diagram showing a general calibration system for
fuzzy
class assignments according to the invention;
Fig. 8 is a block schematic diagram showing an example of parallel calibration
models for fuzzy set assignments according to the invention;
Fig. 9 is a block schematic diagram of an intelligent measurement system
instrument
according to the invention;
Fig. 10 is a block schematic diagram of the intelligent measurement system
with
crisp classification rules according to the invention;
Fig. 11 is a flow diagram showing processing steps for preprocessing 1 and
feature
extraction 1 of Fig. 10, according to the invention;
Fig. 12 is a flow diagram showing processing steps of preprocessing 2 and
feature
extraction 2 of Fig. 10, according to the invention;
Fig. 13 is a block schematic diagram showing membership rules according to the
invention;
Fig. 14 is a block schematic diagram of an intelligent measurement system with
fuzzy classification according to the invention;
Fig. 15 is a flow diagram showing preprocessing a feature extraction processes
for
the fuzzy classification system shown in Fig. 14, according to the invention;
Fig. 16 provides a pair of graphs that plot the membership function for the
fuzzy
classification system of Fig. 14, where two features are used to determine the
degree of membership in the sex and age related sub-sets, according to the
invention;
Fig. 17 is a block schematic diagram showing fuzzy membership rules according
to
the invention; and
Fig. 18 is a block schematic diagram showing the defuzzification process
according
to the invention.
6
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
The intelligent measurement system herein disclosed provides improved NIR
noninvasive blood analyte measurement accuracy. This is accomplished by
defining
subpopulations or classes of subjects whose structure and state produce
similarly
featured NIR absorbance spectra. The classes have improved homogeneity leading
to a reduction in variation related to the optical properties and composition
of the
sample. Because the interference is reduced while the magnitude of the blood
analyte absorbance signal is unchanged, a substantial increase in signal-to-
noise
ratio is realized.
One goal of the intelligent measurement system (IMS) is to measure blood
analytes
noninvasively over a diverse population of subjects at various physiological
states.
The method is to classify subjects according to their state and structure and
apply a
combination of one or more existing calibration models to predict the blood
analytes.
The architecture of the IMS is shown in Fig. 1 and consists of a conventional
three-
layer hierarchy (see, for example, P. Antsaklis, K.Passino, ed., An
Introduction to
Intelligent and Autonomous Control, Boston: Kluwer Academic Publishers (1992))
that operates in conjunction with an algorithm manager 10. The execution layer
16
receives the tissue absorbance spectrum from an instrument 28 and performs
rudimentary preprocessing 29. The coordination layer 14 performs feature
extraction
25. A classification system 26 is used to classify the subject according to
extracted
features that represent the state and structure of a sample. Based on the
classification, the predictions from one or more existing calibration models
27 are
used to form a glucose estimate 24. The classification and blood analyte
prediction
are passed to the management level 12 and action is taken based on the
certainty of
the estimate. The management level is also responsible for coordinating 22 all
algorithmic events, monitoring the performance 21 based on the class, adapting
the
rules 20 as necessary, and maintaining information regarding system state 23.
Within the framework of Fig. 1, two different approaches to classification are
proposed. The first approach uses classes that are mutually exclusive. The
second
7
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
approach applies fuzzy set theory to form a classifier and prediction rules
which
allow membership in more than one class. The framework also allows for the
detection of outliers, the determination of samples that are significantly
different from
the existing classes, and long-term monitoring of the system performance.
Measurement and Preprocessing
The sample measurement or tissue absorbance spectrum is the vector mE ~'t" of
absorbance values pertaining to a set of N wavelengths ~.E JZ~' that span the
near
infrared (700 to 2500nm). A typical plot of m versus ~, is shown in Fig. 2.
Assuming
that variation in the target analyte is evident in a consistent absorbance
signature,
the absorbance measurement can be performed either transmissively, through
diffuse reflectance, or through alternate methods without negatively impacting
the
proposed algorithm. The number of necessary wavelengths is a function of the
cross correlation between the target analyte and the interfering species. For
rioninvasive applications with significant variation within and between
individuals, the
entire spectrum is useful.
Preprocessing 29 (Fig. 1 ) includes operations such as scaling, normalization,
smoothing, derivatives, filtering and other transformations that attenuate the
noise
and instrumental variation without affecting the signal of interest. The
preprocessed
measurement, xE 9Z~', is determined according to:
x=h(~,,m) ( 1 )
where h:~'i""2 -~JiN is the preprocessing function.
Pattern Recognition System
A set of subject groups or classes exists with members that are defined by the
similarity of specific features. Grouping of the subjects according to the
features
reduces the spectral variation related the diverse structural properties of
the subject
population and physiological states encountered. The spectral absorbance
measurements corresponding to the classes are more homogeneous than the entire
population. The magnitude of the spectral signal of the target analyte,
however,
remains unchanged. Therefore, calibration models for predicting blood analytes
that
8
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
are specific to subject classes are expected to be less complex and have an
improved level of accuracy.
The pattern recognition system is designed to classify new spectral
measurements
into the previously defined classes through structural and state similarities
as
observed in the tissue absorbance spectrum. Class membership is an indication
of
which calibration models) is(are) most likely to estimate the concentration of
the
target blood analyte accurately. Therefore, the pattern classification system
is the
essence of the proposed intelligent measurement system shown in Fig. 1.
Fig. 3 is a more detailed representation of the pattern classification system.
The
system has two general functions:
~ The extraction of features, and
~ The classification of the features according to a classification model and
decision
rule.
Feature extraction 25 is any mathematical transformation that enhances a
particular
aspect or quality of the data that is useful for interpretation. The
classification model
30 is a method for determining a set of similarity measures with the
predefined
classes. The decision rule is the assignment of class membership 32 on the
basis of
a set of measures calculated by a decision engine 31 (see, for example, R.
Duda, P.
Hart, Pattern Classification and Scene Analysis, John Wiley and Sons, New York
(1973); and J. Schurmann, Pattern Classification. A Unified View of
Statistical and
Neural Approaches, John Wiley & Sons, Inc., New York (1996)).
Within this framework, two different classification schemes are proposed. The
first
scheme, shown in Fig. 4A, provides a classification system 43 that assumes
that the
classes are mutually exclusive and forces each measurement to be assigned to a
single class 45. The scheme shown in Fig. 4B employs a fuzzy classifier 44
that is
not mutually exclusive. This allows a sample to have membership in more than
one
class simultaneously and provides a number between zero and one indicating the
degree of membership in each class 46.
9
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Feature Extraction
Feature extraction is any mathematical transformation that enhances a quality
or
aspect of the sample measurement for interpretation (see, for example, R.
Duda, P.
Hart, Pattern Classification and Scene Analysis, John Wiley and Sons, New York
(1973)). The purpose of feature extraction in Fig. 1 is to represent concisely
the
structural properties and physiological state of the tissue measurement site.
The set
of features is used to classify the subject and determine the calibration
models)
most useful for blood analyte prediction.
The features are represented in a vector, zE9~t"' that is determined from the
preprocessed measurement through:
z=_f(~,,x~ ( 2 )
where t. JZ"-~J~"' is a mapping from the measurement space to the feature
space.
Decomposing f(~) yields specific transformations, f,.(~): ~'t~'~J~"', for
determining a
specific feature. The dimension, M;, indicates whether the ith feature is a
scalar or a
vector and the aggregation of all features is the vector z. When a feature is
represented as a vector or a pattern, it exhibits a certain structure
indicative of an
underlying physical phenomenon.
The individual features are divided into two categories:
~ Abstract, and
~ Simple.
Abstract features do not necessarily have a specific interpretation related to
the
physical system. Specifically, the scores of a principal component analysis
are
useful features, although their physical interpretation is not always known.
The utility
of the principal component analysis is related to the nature of the tissue
absorbance
spectrum. The most significant variation in the tissue spectral absorbance is
not
caused by a blood analyte but is related to the state, structure, and
composition of
the measurement site. This variation is modeled by the primary principal
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
components. Therefore, the leading principal components tend to represent
variation related to the structural properties and physiological state of the
tissue
measurement site.
Simple features are derived from an a priori understanding of the sample and
can be
related directly to a physical phenomenon. Useful features that can be
calculated
from NIR spectral absorbance measurements include but are not limited to:
1. Thickness of adipose tissue (see, for example, J. Conway, K. Norris, C..
Bodwell,
A new approach for the estimation of body composition: infrared interactance,
The American Journal of Clinical Nutrition, 40, pp. 1123-1140 (Dec. 1984); and
S.
Homma, T. Fukunaga, A. Kagaya, Influence of adipose tissue thickness in near
infrared spectroscopic signals in the measurement of human muscle, Journal of
Biomedical Optics, 1 (4), pp. 418-424 (Oct. 1996)).
2. Tissue hydration (see, for example, K. Martin, Direct measurement of
moisture in
skin by NIR spectroscopy, J. Soc. Cosmet. Chem., vol. 44, pp. 249-261
(Sept./Oct. 1993)).
3. Magnitude of protein absorbance (see, for example, J. Conway, K. Norris, C.
Bodwell, A new approach for the estimation of body composition: infrared
interactance, The American Journal of Clinical Nutrition, 40, pp. 1123-1140
(Dec.
1984)).
4. Scattering properties of the tissue (see, for example, A. Profio, Light
transport in
tissue, Applied Optics, vol. 28(12), pp. 2216-2222 (June 1989); W. Cheong, S.
Prahl, A. Welch, A review of the optical properties of biological tissues,
IEEE
Journal of Quantum Electronics, vol. 26(12), pp. 2166-2185 (Dec. 1990); and R.
Anderson, J. Parrish, The optics of human skin, Journal of Investigative
Dermatology, vol. 77(1 ), pp. 13-19 (1981 )).
5. Skin thickness (see, for example, R. Anderson, J. Parrish, The optics of
human
skin, Journal of Investigative Dermatology, vol. 77(1 ), pp. 13-19 (1981 );
and M.
11
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Van Gemert, S. Jacques, H. Sterenborg, W. Star, Skin optics, IEEE Transactions
on Biomedical Engineering, vol. 36(12), pp. 1146-1154 (Dec. 1989).
6. Temperature related effects (see, for example, A. Patterson, Modeling the
thermal effects of blood flow in human skin, The South African Mechanical
Engineer, vol. 28, pp. 179-182 (May 1978)).
7. Age related effects (see, for example, W. Andrew, R. Behnke, T. Sato,
Changes
with advancing age in the cell population of human dermis, Gerontologia, vol.
10,
pp. 1-19 (1964/65); W. Montagna, K. Carlisle, Structural changes in aging
human
skin, The Journal of Investigative Dermatology, vol. 73, pp. 47-53 (1979); and
J.
Brocklehurst, Textbook of Geriatric Medicine and Gerontoloav, Churchill
Livingstone, Edinburgh and London, pp.593-623 (1973)).
8. Spectral characteristics related to sex.
9. Pathlength estimates (see, for example, R. Anderson, J. Parrish, The optics
of
human skin, Journal of Investigative Dermatology, vol. 77(1 ), pp. 13-19 (1981
);
and S. Matcher, M. Cope, D. Delpy, Use of water absorption spectrum to
quantify tissue chromophore concentration changes in near-infrared
spectroscopy, Phys. Med. Biol., vol. 38, 177-196 (1993)).
10. Volume fraction of blood in tissue (see, for example, M. Van Gemert, S.
Jacques, H. Sterenborg, W. Star, Skin optics, IEEE Transactions on Biomedical
Engineering, vol. 36(12), pp. 1146-1154 (Dec. 1989)).
11. Spectral characteristics related to environmental influences.
12. Hematocrit levels.
Spectral decomposition is employed to determine the features related to a
known
spectral absorbance pattern. Protein and fat, for example, have known
absorbance
signatures that can be used to determine their contribution to the tissue
spectral
12
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
absorbance. The measured contribution is used as a feature and represents the
underlying variable through a single value.
Features related to demographic information, such as age, are combinations of
many different effects that cannot be represented by a single absorbance
profile.
Furthermore, the relationship of demographic variables and the tissue spectral
absorbance is not deterministic. For example, dermal thickness and many other
tissue properties are statistically related to age but also vary substantially
as a result
of hereditary and environmental influences. Therefore, factor based methods
are
employed to build models capable of representing variation in the measured
absorbance related to the demographic variable. The projection of a measured
absorbance spectrum onto the model constitutes a feature that represents the
spectral variation related to the demographic variable.
The compilation of the abstract and simple features constitutes the M-
dimensional
feature space. Due to redundancy of information across the set of features,
optimum
feature selection and/or data compression is applied to enhance the robustness
of
the classifier.
Classification
Feature extraction determines the salient characteristics of measurements that
are
relevant for classification. The goal of the classification step is to
determine the
calibration models) that is/are most appropriate for the measurement. In this
step,
the subject is assigned to one of many predefined classes for which a
calibration
model has been developed and tested. Because the applied calibration model is
developed for similar tissue absorbance spectra, the blood analyte predictions
are
more accurate than those obtained from a universal calibration model.
As depicted in Fig. 3, pattern classification generally involves two steps:
~ A mapping (30), and
13
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
~ A decision engine (31 ).
The mapping measures the similarity of the features to predefined classes and
the
decision engine assigns class membership.
In the following discussion, two general methods of classification are
described. The
first method uses mutually exclusive classes and therefore assigns each
measurement to one class. The second method uses a fuzzy classification system
that allows class membership in more than one class simultaneously. Both
methods
require prior class definitions as described subsequently.
Class Definition
The development of the classification system requires a data set of exemplar
spectral measurements from a representative sampling of the population. Class
definition is the assignment of the measurements in the exploratory data set
to
classes. After class definition, the measurements and class assignments are
used
to determine the mapping from the features to class assignments.
Class definition is performed through either a supervised or an unsupervised
approach (see, for example, J. Schurmann, Pattern Classification. A Unified
View of
Statistical and Neural Approaches, John Wiley & Sons, Inc., New York (1996)).
In
the supervised case, classes are defined through known differences in the
data. The
use of a priori information in this manner is the first step in supervised
pattern
recognition which develops classification models when the class assignment is
known. For example, the majority of observed spectral variation can be modeled
by
three abstract factors which are related to several physical properties
including body
fat, tissue hydration, and skin thickness. Categorizing subjects on the basis
of these
three features produces eight different classes if each feature is assigned a
"high"
and "low" value. The drawback of this approach is that attention is not given
to
14
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
spectral similarity and the number of classes tends to increase exponentially
with the
number of features.
Unsupervised methods rely solely on the spectral measurements to explore and
develop clusters or natural groupings of the data in feature space. Such an
analysis
optimizes the within cluster homogeneity and the between cluster separation.
Clusters formed from features with physical meaning can be interpreted based
on
the known underlying phenomenon causing variation in the feature space.
However,
cluster analysis does not use a priori information and can yield inconsistent
results.
A combination of the two approaches is applied to use a priori knowledge and
exploration of the feature space for naturally occurring spectral classes.
Under this
approach, classes are first defined from the features in a supervised manner.
Each
set of features is divided into two or more regions and classes are defined by
combinations of the feature divisions. A cluster analysis is performed on the
data
and the results of the two approaches are compared. Systematically, the
clusters
are used to determine groups of classes that can be combined. After
conglomeration the number of final class definitions is significantly reduced
according to natural divisions in the data.
Subsequent to class definition a classifier is designed through supervised
pattern
recognition. A model is created based on class definitions which transforms a
measured set of features to an estimated classification. Because the ultimate
goal of
the classifier is to produce robust and accurate calibration models, an
iterative
approach must be followed in which class definitions are optimized to satisfy
the
specifications of the measurement system.
Statistical Classification
The statistical classification methods are applied to mutually exclusive
classes
whose variation can be described statistically (see, for example, J.
Schurmann,
Pattern Classification. A Unified View of Statistical and Neural Approaches,
John
Wiley & Sons, Inc., New York (1996); and J. Bezdek, S. Pal, eds., Fuzz~Models
for
Pattern Recognition, IEEE Press, Piscataway, NJ (1992)). Once class
definitions
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
have been assigned to a set of exemplary samples, the classifier is designed
by
determining an optimal mapping or transformation from the feature space to a
class
estimate which minimizes the number of misclassifications. The form of the
mapping
varies by method as does the definition of optimal. Existing methods include
linear
discriminant analysis (see, for example, R. Duda, P. Hart, Pattern
Classification and
Scene Analksis, John Wiley and Sons, New York (1973)), SIMCA (see, for
example,
S. Wold, M. Sjostrom, SIMCA: A method for analyzing chemical data in terms of
similarity and analogy, Chemometrics: Theor)/ and Application, ed. B.
Kowalski,
ACS Symposium Series, 52 (1977)), k nearest-neighbor (see, for example, R.
Duda,
P. Hart, Pattern Classification and Scene Anal~~, John Wiley and Sons, New
York
(1973)), and various forms of artificial neural networks (see, for example, S.
Haykin,
Neural Networks: A Comprehensive Foundation, Upper Saddle River, NJ, Prentice-
Hall (1994); and Y. Pao, Adaptive Pattern Recoanition and Neural Networks,
Addison-Wesley Publishing Company, Inc., Reading, MA (1989)).
The result is a function or algorithm that maps the feature to a class, c,
according to:
(3)
c= f(z)
where c is an integer on the interval [1,P ] and P is the number of classes.
The
class is used to select or adapt the calibration model as discussed below in
connection with calibration.
Fuzzy Classification
While statistically based class definitions provide a set of classes
applicable to blood
analyte estimation, the optical properties of the tissue sample resulting in
spectral
variation change over a continuum of values. Therefore, the natural variation
of
tissue thickness, hydration levels, and body fat content, among others,
results in
class overlap. Distinct class boundaries do not exist and many measurements
are
likely to fall between classes and have a statistically equal chance of
membership in
any of several classes. Therefore, hard class boundaries and mutually
exclusive
membership functions appear contrary to the nature of the target population.
A more appropriate method of class assignment is based on fuzzy set theory
(see,
for example, J. Bezdek, S. Pal, eds., Fuzzy Models for Pattern Recognition,
IEEE
16
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Press, Piscataway, NJ (1992); C. Chen, ed., Fuzzy Logic and Neural Network
Handbook, Piscataway, NJ, IEEE Press (1996); and L. Zadeh, Fuzzy Sets, Inform.
Control, vol. 8, pp. 338-353 (1965)).
Generally, membership in fuzzy sets is defined by a continuum of grades and a
set
of membership functions that map the feature space into the interval [0,1] for
each
class. The assigned membership grade represents the degree of class membership
with "1" corresponding to the highest degree. Therefore, a sample can
simultaneously be a member of more than one class.
The mapping from feature space to a vector of class memberships is given by:
Ck -Jkl Zl
where k--1,2,...P, fk(~) is the membership function of the kth class, ckE [0,1
] for all k
and the vector cE )ZP is the set of class memberships. The membership vector
provides the degree of membership in each of the predefined classes and is
passed
to the calibration algorithm.
The design of membership functions use fuzzy class definitions similar to the
methods previously described. Fuzzy cluster analysis can be applied and
several
methods, differing according to structure and optimization approach can be
used to
develop the fuzzy classifier. All methods attempt to minimize the estimation
error of
the class membership over a population of samples.
Calibration
Blood analyte prediction occurs by the application of a calibration model to
the
preprocessed measurement as depicted in Fig. 1. The proposed prediction system
involves a calibration or set of calibration models that are adaptable or
selected on
the basis of the classification step. The following discussion describes the
calibration system for the two types of classifiers.
17
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Mutually Exclusive Classes
In the general case, the designated classification is passed to a nonlinear
model
which provides a blood analyte prediction based on the subject classification
and
spectral measurement. This process, illustrated in Fig. 5, involves the
modification
of the estimation strategy for the current subject according to the structural
tissue
properties and physiological state manifested in the absorbance spectrum.
This general architecture necessitates a nonlinear calibration model 50, such
as
nonlinear partial least squares or artificial neural networks because the
mapping is
highly nonlinear. The blood analyte prediction for the preprocessed
measurement x
with classification specified by c is given by:
Y = g(c~ x) ( 5 )
where g(~) is a nonlinear calibration model which maps x and c to an estimate
of the
blood analyte concentration, y .
In the preferred realization, shown in Fig. 6, a different calibration 60 is
realized for
each class. The estimated class is used to select one of p calibration models
most
appropriate for blood analyte prediction using the current measurement. Given
that
k is the class estimate for the measurement, the blood analyte prediction is:
y = gk (x) ( 6 )
where gk(~) is the calibration model associated with the kth class.
The calibrations are developed from a set of exemplar absorbance spectra with
reference blood analyte values and pre-assigned classification definitions.
This set,
denoted the "calibration set," must have sufficient samples to completely
represent
the subject population and the range of physiological states in the subject
population. The p different calibration models are developed individually from
the
measurements assigned to each of the p classes. The models are realized using
known methods including principal component regression (see, for example, H.
Martens, T. Naes, Multivariate Calibration, New York, John Wiley and Sons
(1989)),
partial least squares regression (see, for example, P. Geladi, B. Kowalski,
Partial
18
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
least-squares regression: a tutorial, Analytica Chimica Acta, 185, pp. 1-17
(1986)),
and artificial neural networks (see, for example, S. Haykin, Neural Networks:
A
Comprehensive Foundation, Upper Saddle River, NJ, Prentice-Hall (1994)).
The various models associated with each class are evaluated on the basis of an
independent test set or cross validation and the best set of models are
incorporated
into the Intelligent Measurement System. Each class of subjects then has a
calibration model specific to it.
Fuzzy Class Membership
When fuzzy classification is employed the calibration is passed a vector of
memberships rather than a single estimated class. The vector, c, is used to
determine an adaptation of the calibration model suitable for blood analyte
prediction
or an optimal combination of several blood analyte predictions. In the general
case,
illustrated in Fig. 7, the membership vector and the preprocessed absorbance
spectrum are both used by a single calibration 70 for blood analyte
prediction. The
calculation is given by:
Y = g<~, x> ( 7 )
where g(~) is a nonlinear mapping determined through nonlinear regression,
nonlinear partial least squares or artificial neural networks. The mapping is
developed from the calibration set described previously and is generally
complex.
The preferred realization, shown in Fig. 8, has separate calibrations 80 for
each
class similar to that shown in Fig. 6. However, each calibration is generated
using all
measurements in the calibration set by exploiting the membership vector
assigned to
each measurement. In addition, the membership vector is used to determine an
optimal combination of the p blood analyte predictions from all classes
through
defuzzification 81. Therefore, during calibration development a given
measurement
of the calibration set has the opportunity to impact more than one calibration
model.
Similarly, during prediction more than one calibration model is used to
generate the
blood analyte estimate.
19
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Each of the p calibration models of Fig. 8 is developed using the entire
calibration.
However, when the kth calibration model is calculated, the calibration
measurements
are weighted by their respective membership in the kth class. As a result, the
influence of a sample on the calibration model of a particular class is a
function of its
membership in the class.
In the linear case, weighted least squares is applied to calculate regression
coefficients and, in the case of factor based methods, the covariance matrix
(see, for
example, N. Draper, H. Smith. ~alied Regression Analysis, 2"d Ed., John Wiley
and Sons, New York (1981 )).
Given a matrix of absorbance spectra XkE JZ'x"" and reference blood analyte
concentrations YE J~~ where r is the number of measurement spectra and w is
the
number wavelengths, let the membership in class k of each absorbance spectrum
be
the elements of Ck E J~~ . Then the principal components are given by:
F = XkM ( 8 )
where M is the matrix of the first n eigen vectors of P.
The weighted covariance matrix P is determined through:
P = XkVXA ( 9 )
where V is a square matrix with the elements of Ck on the diagonal.
The regression matrix, 8, is determined through:
B = ~F'~VF~~ F' VY. ( 10 )
When an iterative method is applied, such as artificial neural networks, the
membership is used to determine the frequency the samples are presented to the
learning algorithm. Alternately, an extended Kalman filter is applied with a
covariance matrix scaled according to V.
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
The purpose of defuzzification is to find an optimal combination of the p
different
blood analyte predictions, based on a measurement's membership vector that
produces accurate blood analyte predictions. Therefore, defuzzification is a
mapping
from the vector of blood analyte predictions and the vector of class
memberships to
a single analyte prediction. The defuzzifier can be denoted as transformation
such
that:
Y~ Y3 ... Yp
where d(~) is the defuzzification function, c is the class membership vector
and yk is
the blood analyte prediction of the kth calibration model. Existing methods of
defuzzification, such as the centroid or weighted average, are applied for
small
calibration sets. However, if the number of samples is sufficient, d(~) is
generated
through a constrained nonlinear model.
Algorithm Manager
The algorithm manager 10 (see Fig. 1 ) is responsible for reporting results to
the
operator, coordinating all algorithmic events, monitoring the performance
based on
the class, and adapting the rules as necessary. Both class estimates and blood
analyte predictions are reported to the algorithm manager. The classifier also
generates a measure of the certainty of class membership. If the measurement
does not fit into one of the existing classes the supervisor notifies the
operator that
the prediction is invalid. Further spectral measurements are taken to
determine if the
error is due to the instrument, measurement technique or sample. This error
detection and correction algorithm is used to determine if more classes are
necessary or if the instrument requires maintenance.
Implementation
The following discussion describes the implementation and experimental results
of
two forms of the Intelligent Measurement System for Blood Analyte Prediction
(IMS)
that were developed for the prediction of blood glucose concentration. It will
be
appreciated by those skilled in the art that other forms of the invention for
other
purposes may be developed. In the first form, a Crisp Classification System is
used
21
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
to determine one of four suitable prediction models. The second realization,
denoted
the Fuzzy Classification System, employs fuzzy membership rules to determine
the
class membership in each of six classes. The outputs of the corresponding six
prediction models are combined using a defuzzification procedure to produce a
single blood glucose prediction.
The discussion below first describes the overall instrument containing the IMS
implementations and the subsequent discussion describes the operation of the
two
implementations. The final discussion details experimental results obtained
from a
clinical study.
The two implementations are specific to the prediction of blood glucose
concentration. However, the invention is appropriate for the prediction of all
blood
analytes and other biological and other compounds that absorb in the NIR.
Instrument Description
The Intelligent Measurement System is implemented in a scanning spectrometer
which determines the NIR absorbance spectrum of the subject forearm through a
diffuse reflectance measurement. A block diagram of the integrated
instrumentation
and the IMS is shown in Figure 9 and includes the general instrument
components,
the IMS 90 and a display system (output device) 91. The instrument employs a
quartz halogen lamp 92, a monochromater 93, a subject interface module 97,
detector optics 98, and InGAs detectors 94. The detected intensity from the
subject
95 is converted to a voltage through analog electronics 94 and digitized
through a
16-bit A/D converter 96. The spectrum is passed to the IMS for processing and
results in either a glucose prediction or a message indicating an invalid
scan.
Alternately, the IMS can be employed with existing NIR spectrometers that are
commercially available, including a Perstorp Analytical NIRS 5000 spectrometer
or a
Nicolet Magna-IR 760 spectrometer.
2''
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Crisp Classification System
Overview
Figure 10 depicts an implementation of the IMS that involves subject
classification
through crisp or classical decision rules denoted IMS-CC. The objective of the
classification is to determine which of four calibration models are applied
for analyte
prediction. This decision is accomplished through feature extraction 102, 103,
classification 100, and application of a set of decision rules 104.
Prior to classification and calibration the measured noninvasive absorbance
spectrum is subjected to an outlier detection 99 through principal components
analysis (PCA). Spectra with significant deviations from the system's PCA
model
are designated as unsatisfactory and rejected. Features related to the
subjects sex
and age are extracted through factor based techniques (PCA and PLS) after
preprocessing 105, 106. The features are supplied to a set of decision rules
104 that
determine which one of four classes 107, 108, 109, 110 best represents the
absorbance spectrum of the subject, given the current state and structure of
the
tissue volume sampled during the measurement. While this implementation
depicts
four classes, the invention extends to the number of classes and features that
are
necessary for glucose prediction accuracy. Additional classes, for example,
may be
determined based on features related to hydration, skin thickness, thickness
of
adipose tissue, volume fraction of blood in tissue, blood pressure, hematocrit
levels
and others.
The absorbance spectrum is also preprocessed (Preprocessing 1 ) 105 in a
manner
suitable for calibration. Although the present implementation contains one
method of
preprocessing for all calibration models, the preferred realization supplies
separate
preprocessing methods for each calibration model. The calibration model that
is
applied to the spectrum is determined based on the classification described
above
and the model output is the glucose prediction. The implementation shown in
Figure
10 contains four calibration models associated with the four classes. However,
in
the general case an arbitrary number of calibrations are used equal to the
number of
23
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
classes needed to represent the spectral variation of individuals using the
instrument.
Detailed Description
NIR Spectral Measurement
The measured NIR spectrum m is a vector containing absorbance values evenly
distributed in the wavelength range 1100-2500 nm. In the present application
N =1400. An example measurement is depicted in Figure 1.
Outlier Detection
The detection of spectral outliers is performed through a principal components
analysis and an analysis of the residuals. First, the spectrum m is projected
onto
seven eigenvectors, contained in the matrix o, that were previously developed
through a principal components analysis (on a calibration set of exemplary
absorbance spectra) and are stored in the IMS-CC. The calculation is given by:
xpc" _ ~ mop ( 12 )
k=I
and produces the 1 by 7 vector of scores, xpco where ok is the kth column of
the
matrix o. The residual q is determined according to:
q = m - xpcooT ( 13 )
and compared to three times the standard deviation of the expected residual
(of the
a calibration set). If greater, the sample is reported by the algorithm
manager to be
an outlier.
Processing 1 and Feature Extraction 1
24
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
The first feature is the result of a classification of the subject into male
and female
categories and involves spectral preprocessing, decomposition through
principal
components analysis, and classification through linear discriminant analysis.
The
feature is not a determination of the subject's sex but rather provides a
measure of
the tissue volume sampled as compared to that of other subjects.
The process, depicted in Figure 11, receives the absorbance spectrum m from
the
outlier detection system 111. Wavelength selection 112 is applied to truncate
the
spectral range to regions with significant absorption due to fat in adipose
tissue
(1100 to 1400 nm). The spectrum is next processed through multivariate scatter
correction 113 (see P. Geladi, D. McDougall, H. Martens, Linearization and
Scatter-
Correction for Near-Infrared Reflectance Spectra of Meat, Applied
Spectroscopy,
vol. 39, pp. 491-500, 1985) through a rotation that fits it to the expected or
reference
spectrum m contained in the Intelligent System and determined from a prior set
of
examplary samples. First, the spectrum is fit via linear regression according
to:
m=a+bm+e ( 14 )
where a and b are the slope and intercept and a is the error in the fit. The
spectrum
is then corrected through:
x-~m-a~ ( 15 )
where x is the processed absorbance spectrum. The processed spectrum is
projected onto the eigenvectors, pk, that were previously developed through a
principal components analysis 114 (on a calibration set of exemplary
absorbance
spectra) and are stored in the IMS-CC. The calculation, shown in Figure 11,
produces the 1 by N vector of scores, xpc.
A discriminant function is applied to classify the subjects on the basis of
the first M
scores (M--5 is this application). The scores are rotated through a cross
product with
the discriminant , w, as depicted in Figure 11 to produce the scalar, L (115).
This
result is compared 116 to L , the center between the two classes. If L > L
then the
subject is classified as a female 118 and the feature z,=1. If not, the
spectrum is
classified as beloning to a male 117 and z,=0.
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Processing 2 and Feature Extraction 2
The second feature extraction process 103 (see Fig. 10) is represented in
Figure 12
and involves the prediction of the subject's age using a linear model
developed
through partial least squares regression (PLS). First, the wavelength range is
truncated120 to the 1100 to 1800 nm region. Next, the subject's age is
predicted
through a calibration model that is part of the IMS-CC. The model, developed
through PLS on a calibration set of exemplary samples, consists of a set of
coefficients contained in the vector vv and is applied as shown in Figure 12
to
produce the age prediction a 121. The subject is classified as "young" or
"old" by
comparing a to the mean age u=49 as detailed in Figure 12, see 122. The result
of
the classification is the calculated feature, z2, which assumes vales of zero
or one
corresponding to a classification of "old" 123 or "young" 124 respectively.
Membership Rules
The membership rules 104, shown in Figure 13, determine the appropriate
calibration model to predict the blood glucose concentration from the measured
absorbance spectrum. Based on the two features, z, and z2, four classes are
possible. The consequence of the decision it the selection of one of four
calibration
models to use to predict the blood glucose concentration denoted PLS1-4.
This classification based on spectral data and not the obvious observation of
the
subject is necessary because it is indicative of the state of the subject's
tissue. For
example, a classification of "old" indicates that the subject's spectrum
appears
similar to the spectra previously gathered from older individual's. The
results reflect
gross spectral properties that are correlated to age but not necessarily
deduced
based on the actual chronological age.
26
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Preprocessing 3
The absorbance spectrum is processed specifically for calibration through MSC
as
described above and a 31-point Savisky-Golay first derivative in the form of a
finite
impulse response filter 125 (see A. Savitzky, M. Golay, Smoothing and
Differentiation of Data by Simplified Least Squares Procedures, Anal. Chem.,
vol.
36, no. 8, pp. 1627-1639, 1964). The result is mean-centered by subtracting,
x, the
mean processed absorbance spectrum from a calibration set of exemplary samples
that is stored in the IMS-CC. Wavelength selection is performed to include the
following wavelengths: 1100-1350 nm, 1550-1750 nm and 2050-2375 nm.
Prediction Model Selection 1-2
Based on the subject's classification, one of the four calibration models is
selected
for application as depicted in the two selectors 126, 127 of Figure 10.
Calibration Models PLS1. PLS2, PLS3. PLS4
The four calibration models 107-110 each consist of a 7xN vector of
coefficients that
map x to a prediction of glucose. Each set of coefficients was developed using
samples (from a calibration set) that were classified as belonging to its
associated
class. Therefore, the models are limited to predicting glucose concentration
levels
on subjects that are classified in their respective classes.
Given the processed spectrum, x, the classification, c, and the model
coefficients w~
associated with c, the blood glucose prediction is given by:
N
?' _ ~ ~'~.kx~ ( 16 )
k=I
were w~,kis the kth element of w~..
27
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Fuzzy Classification System
Overview
While the classification system based on distinct class boundaries shown in
Figure
10 provides a set of classes applicable to blood analyte estimation, the
optical
properties of the tissue sample vary over a continuum of values. Distinct
class
boundaries do not exist and many measurements are likely to fall between
classes
and have a statistically equal chance of membership in any of several classes.
Therefore, hard class boundaries and mutually exclusive membership functions
appear contrary to the nature of the target population.
The system shown in Figure 14, denoted the IMS-FC, employs fuzzy sets to
define a
continuum of grades in each of the classes. Rather than categorizing subjects
into
distinct and independent groups, this system determines the degree of
membership
of a particular subject in each of six classes (150-155). Therefore, each
subject
shares membership in every class and each of the parallel calibration models
has
the opportunity to contribute to the prediction of the blood analyte based.
The weighted combination (based on class membership) of the prediction of all
calibration models in the system produces an apparent continuum of calibration
models. Subjects falling mid-point between two classes, for example, are
predicted
using both rather than one of the two (calibration models) and produce a
prediction
with a greater level of confidence. Similarly, the calibrations are created
through a
weighted principal components regression (WPCR) and are not exclusive to a
distinct population.
Similar to the IMS-CC, the fuzzy system (IMS-FC) classifies exclusively on the
basis
of spectral information. The measured absorbance spectrum is preprocessed for
feature extraction. The features in this implementation are continuous
(calculated)
variables related to the absorption of body fat that is manifested spectrally
and the
apparent age of the sampled tissue volume. Fuzzification occurs through a set
of
28
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
membership functions that produce five membership values associated with the
sub-
sets male, female, young, middle aged and old. These membership values are
transformed through decision rules 146 to produce the degree of class
membership
in each of six classes.
The spectrum is also preprocessed in a manner suitable for calibration and
applied
to each of the six calibration models. The results (six blood glucose
estimates) are
combined through the process of defuzzification 149 in which the degree of
class
membership is used to weight the influence of each prediction.
While the present implementation involves a specific number of features,
classes,
decision rules and calibrations models, the invention may use an arbitrary
number of
each in the configuration shown to produce a blood analyte predictions.
Further, the
invention covers the use of fuzzy classification for the purpose of blood
analyte
prediction or other analytes determinations.
Detailed Description
NIR Spectral Measurement
The measured NIR spectrum, m, 111 is a vector containing absorbance values
evenly distributed in the wavelength range 1100-2500 nm. In the present
application
N--1400 and an example measurement is depicted in Figure 1.
Outlier Detection
The detection 99 of spectral outliers is performed through a principal
components
analysis and an analysis of the residuals. First, the spectrum m is projected
onto
seven eigenvectors, contained in the matrix o that were previously developed
29
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
through a principal components analysis on a calibration set and stored in the
IMS-
FC. The calculation is given by:
xpc" _ ~ mok ( 17 )
k=I
and produces the 1 by 7 vector of scores, xpco where ok is the kth column of
the
matrix o. The residual, q, is determined according to:
q = m - xpc~oT ( 18 )
and compared to three times the standard deviation of the expected residual
determined from a calibration set. If greater, the sample is reported by the
algorithm
manager to be an outlier.
Processing 4 (140) and Feature Extraction 3 (141 ~
The first feature for the IMS-FC is related to the fat stored in adipose
tissue as
manifested through absorption bands in the 1100-1380 nm range. This feature is
extracted, as shown in Figure 15A, by performing multiplicative scatter
correction
160 (described previously) on the 1100-1380 nm range. The absorbance value
corresponding to the wavelength 1208 nm 161 is the value of the feature, z3,
associated with the measured absorbance spectrum.
Processing~143) and Feature Extraction 4 (144)
The second feature extraction, shown in Figure 15B, produces a prediction of
the
subject's age based on the measured absorbance spectrum. First, the wavelength
range is truncated to the 1100 to 1800 nm region 162. Next, the subject's age
is
predicted through a calibration model 163 that is part of the IMS-FC. The
model,
developed through PLS on a calibration set of representative samples, consists
of a
set of coefficients contained in the vector w and is applied as shown in
Figure 12 to
produce the age prediction z4.
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Fuzzy Membership Functions
The fuzzy membership functions 142, 145 are used to determine the degree of
membership of the subject in specific sub-sets that are later combined through
the
decision rules. Each membership function maps the feature input to a value
between 0 and 1 through a gaussian function. The general equation employed to
represent the membership functions is:
Y-e~az~_:) ( 19 )
where y is the degree of membership in a sub-set, z is the feature used to
determine
membership, z is the mean or center of the fuzzy sub-set and a is the standard
deviation.
In Figure 16, two broad sets are used that are denoted Membership Functions 1
(142) and Membership Functions 2 (145). Membership Functions 1 represent the
subject's sex 170 using two sub-sets (male 173 and female 174). Membership
Functions 2 uses three subsets, described below, to represent the age 171 of
the
subject. The degree of membership in each sub-set is calculated through
Equation
(15) and used through fuzzy operators and decision rules to assign class
membership.
The first set of membership functions 170, shown in Figure 16 (top), are
gaussian
functions that determine the degree of membership in the male and female sub-
sets
based on the feature related to the absorption of fat (Feature 3). The mean
and
standard deviation associated with each sub-set (and used with Equation 15)
were
determined from a large population of subjects and are listed in Table 1. As
shown
in the figure, the greater z the more likely the subject falls into the
category of
females. Conversely, lower values of z give lower membership in the category
of
females and higher in the category of males.
The second set of membership functions 171, shown in Figure 16 (bottom), are
gaussian functions that determine the degree of membership in the categories
31
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
young, middle aged and old based on the feature representing the prediction of
age
(Feature 4). The mean and standard deviation associated with each of the three
categories were determined qualitatively based on inspection of a target
population
of subjects and are listed in Table 2.
Table 1. Parameters for the Membership Functions 1 plotted
in Figure 16
Standard
Deviaion
Sub-Set Cate Mean AU AU
Females 0.6 0.03
Males 0.54 0.02
Table 2. Parameters of Membership Functions 2 plotted
in Figure 16
Standard
Mean Deviaion
Sublet Cate Years Years
Young 30 7
Middle Aged 50 10
Old 70 7
Values for the feature inputs to the membership functions that are unusually
high or
low fall outside that expected range of the sub-sets and are assigned low
membership values. This information is provided to the algorithm manager and
indicates that the subject belongs to a class for which a calibration model
has not
been constructed. For the current implementation when y<0.1 for all sub-sets
the
prediction is assigned a low confidence level.
The membership functions described have been designed for a specific
population of
subjects and cannot be generalized to all potential individuals. The
invention,
however, covers the arbitrary use of membership functions to assign a degree
of
32
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
membership in a given class to a subject for blood analyte prediction. Other
sub-
sets, for example, include the level of hydration, skin thickness, thickness
of adipose
tissue, volume fraction of blood in tissue, blood pressure, and hematocrit
levels. The
number of sub-sets per general set can also be increased arbitrarily depending
on
the necessarily level of discrimination for the accurate prediction of blood
analytes.
FuzzX Decision Rules
The output of Membership Functions 1 and Membership Functions 2 are two and
five membership values, respectively, that are associated with the sex and age
related sub-sets. The decision rules 146 are a set of operators and inferences
that
combine the membership values of the sub-sets into the class membership used
for
blood glucose prediction. The specific rules, given in Error! Reference source
not
found., are all possible combinations of the sub-sets described previously.
The rules
employ the fuzzy "and" operator which is implemented by determining the
minimum
of the two sub-set membership values comprising its antecedent.
As an example of the class membership assignment process assume that a subject
was determined to have values for features 3 and 4 of 0.55 AU and 60 years
respectively. From Figure 16, the membership values in the male and female sub-
sets are approximately 0.82 and 0.3 respectively. Similarly, the membership
values
for the young, middle aged and old sub-sets are 0, 0.6 and 0.35. From the
rules in
Figure 17 the following class membership values are calculated:
1. If Male AND Young = min(0.82, 0.0) = 0.0
2. If Male AND Middle Aged = min(0.82, 0.6) = 0.6
3. If Male AND Old = min(0.82, 0.35) = 0.35
4. If Female AND Young = min( 0.3, 0.0) = 0.0
5. If Female AND Middle Aged = min( 0.3, 0.6) = 0.3
6. If Female AND Old = min( 0.3, 0.35) = 0.3
The class membership vector, d, is given by:
33
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
d=~0.0 0.6 0.35 0.0 0.3 0.3~ ( 20 )
and is supplied to the defuzzification block for aggregation of the predicted
glucose
concentrations.
The consequent listed is the calibration model that is associated with each
class. In
the example, the second calibration model (WPCR2) 151 was created using
spectra
most similar to the measured spectrum. However, the measured spectrum also has
membership in the third, fifth, and sixth classes. The degree of membership in
the
classes is used subsequently to determine the combination of calibration
models for
blood analyte prediction.
Preprocessing 6 (147)
The absorbance spectrum is processed specifically for calibration through MSC
as
described above and a 31-point Savisky-Golay first derivative in the form of a
finite
impulse response filter (see A. Savitzky, M. Golay, Smoothing and
Differentiation of
Data by Simplified Least Squares Procedures, Anal. Chem., vol. 36, no. 8, pp.
1627-1639, 1964). The result is mean-centered by subtracting, x, the mean
processed absorbance spectrum that is stored in the IMS-FC and was determined
from a calibration set. Wavelength selection is performed to include the
following
wavelengths: 1100-1350 nm, 1550-1750 nm and 2050-2375 nm.
Calibration
The calibration process in Figure 14 involves the prediction of the blood
analyte
using all of the calibration models. Therefore, the calibration block
represents a
single input-multiple-output operation that produces six blood analyte
predictions.
The six calibration models each consist of a ixN vector of coefficients that
map x to
a prediction of the blood glucose concentration. Each set of coefficients was
developed using all samples in a population (the calibration set of exemplary
samples). However, each calibration sample was weighted using weighted
principal
components regression as described in Equations 8-10. Therefore, the models
are
associated with the six classes.
34
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Given the processed spectrum, x, and the model coefficients, w~, associated
with
class c, the blood glucose prediction for the cth model is given by:
:v
i'~ _ ~w~.kxk ( 21 )
k=I
were w~,kis the kth element of w~.
Defuzzification
Defuzzification 149 is used to aggregate the multiple predictions into one
through the
degree of class membership. Prior to defuzzifying, the vector of class
membership
values d is normalized to unit length. The defuzzification process is shown in
Figure
18 and results in a prediction that is influenced the most by the calibration
prediction
associated with the class with the high degree of class membership.
The present implementation heavily biases the prediction in favor of the
calibration
model output with the highest degree of class membership. However, other
implementations are also suggested by the invention (i.e. a simple average of
all
predictions or the average of all predictions corresponding to a membership
value
greater than a specified value).
Experimental Results
Overview
A study was performed to demonstrate the feasibility and performance of the
two
implementations (IMS-CC and IMS-FC). Diabetic subjects were scanned throughout
the study and blood draws were taken to determine reference blood glucose
concentrations. The subjects were separated at random into calibration and
test
sets to build and test the calibration models respectively. A standard (PLS)
calibration was performed for the purpose of comparison. Finally, the
performance
of the two implementations was tested and compared to the standard
calibration.
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Experiment
Diabetic subjects (266) of diverse age, sex, and ethnicity were recruited at a
local
diabetic care facility and detailed demographic information about each
participant
was recorded. Four replicate absorbance spectra were measured on each
subject's
forearm and the number of samples per participant was limited to one. Venous
blood draws, taken concurrently, were analyzed chemically via a hexakinase
enzymatic method by an independent blood laboratory to determine reference
glucose concentrations. The mean glucose concentration of the population was
120
mg/dL and the standard deviation 50 mg/dL.
The data was divided into calibration and test sets using random selection.
The
calibration set was used to construct the models necessary for classification
and
calibration in Figure 10 and Figure 14. The test set was applied to the
constructed
systems and used to evaluate for evaluation.
Results
Standard Calibration.
For the purpose of comparison, a standard PLS calibration was developed and
evaluated on the data after outlier analysis and preprocessing. The (PCA q-
residual)
outlier analysis was performed as described above and 36 samples were removed
due to unusually high residuals. The absorbance spectrum was processed through
MSC and a 31-point Savisky-Golay first derivative. The result was mean-
centered
by subtracting the mean spectrum of the calibration set from both the
calibration and
test sets.
PLS was applied to the calibration set and the number of factors (20) was
selected
by optimizing the prediction error through crossvalidation (leave-one-out).
The final
PLS calibration model was constructed using all calibration samples and 20
factors.
36
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
The calibration model was applied to both the calibration and test sets and
the
results listed in Table 3.
15
Table 3. Prediction results comparing the Intelligent Measurement
System to standard calibration methods. IMS-CC corresponds to
the system with crisp classification (Fig. 10). IMS-FC includes
fuzzy classification (Fig. 14).
Test Calibration
Set Set Results
Results
Standard Standard
Error Error
of of
Relative CorrelationRelative Correlation
Prediction Error calibration
Method of Error
(Percent)(m9~dL) Coefficient(Percent)(mg/dL) Coefficient
Prediction
PLS 262 43.9 0.48 26.2 43 0.53
IMS-CC 23.6 35.2 0.72 20.2 33.4 0.75
IMS-FC 19.7 30.5 0.8 18.4 29.5 0.82
Crisp Classification.
The outliers described in the prior section were removed and the calibration
set was
used to determine the parameters, eigenvectors and calibration models of the
structure in shown in Figure 10. This includes the eigenvectors (o) for the
outlier
analysis, the mean spectrum for MSC, the eigenvectors (p) and discriminant
function
(w) shown in Figure 11, the age calibration (w) of Figure 12, and the mean
spectrum
for MSC in Preprocessing 3 of Figure 10.
37
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
The calibration set was then classified using the membership rules of Figure
13 and
separated into four individual subsets. A calibration model was developed for
each
subset or class corresponding to calibration models P~S1-4 in Figure 10. Each
calibration model was developed through PLS and factor selection was performed
through cross validation on the calibration set.
The constructed IMS-CC was applied to the calibration and test sets and the
results
are listed in Table 3. The test set performance is seen to improve markedly
over the
base calibration indicating a performance improvement due to the system of
prediction.
Fuzzy Classification.
The outliers described in the prior sections were removed and the calibration
set was
used to determine the parameters, eigenvectors and calibration models of the
structure in shown in Figure 14. This includes the eigenvectors (o) for the
outlier
analysis, the mean spectrum for MSC in Figure 15A, the age calibration (w) of
Figure
15B and the mean spectrum for MSC in Preprocessing 3 of Figure 10. The
membership functions and all other parameters described in the Fuzzy
Classification
System Section were applied.
The calibration set was then classified using the membership functions and
rules of
Figure 16 and Figure 17 to produce a vector of class membership values for
each
sample in the calibration set. The six calibration models shown in Figure 14
were
developed using Equations 8-10 (weighted principal component regression). Each
of the six calibration models was optimized through cross validation on the
calibration set and the final model was produced using all calibration set
samples
and the optimal number of factors.
The constructed IMS-FC was applied to the calibration and test sets and the
results
are listed in Table 3. The test set performance is seen to improve markedly
over
both the base calibration and the IMS-CC system indicating a performance
improvement due to the use of a fuzzy classification system.
38
CA 02358473 2001-07-18
WO 00/42907 PCT/US00/01378
Discussion
The results in Table 3 demonstrate an improvement over the standard PLS model
in
accuracy, precision and significance. In addition, the IMS employing a fuzzy
classification system (IMS-FC) was shown to outperform the IMS that used a
crisp
system. Since the IMS-FC used six classes as opposed to the four used by IMS-
CC
the results do not provide a final judgement regarding the performance of
crisp
versus fuzzy systems. However, when the number of data points is limited and
the
dimensionality of the problem great, the number of models that can be
generated by
IMS-CC is limited since an increase in classes causes a decrease in the data
used
to perform the calibrations associated with the classes. The IMS-FC does not
share
this limitation to the same extent since all samples are used to create the
calibration
models.
Finally, while the benefit of the IMS has been demonstrated further
improvement in
the results are necessary prior to application in a product. The main areas of
necessary improvement are in the noise and stability of the instrument, the
interface
to the participant and the number of available samples for calibration.
Although the invention is described herein with reference to the preferred
embodiment, one skilled in the art will readily appreciate that other
applications may
be substituted for those set forth herein without departing from the spirit
and scope of
the present invention. Accordingly, the invention should only be limited by
the
Claims included below.
39