Note: Descriptions are shown in the official language in which they were submitted.
CA 02358857 2001-09-12
-1-
DATA COMPRESSION USING
ADAPTIVE BIT ALLOCATION AND
HYBRID LOSSLESS ENTROPY ENCODING
BACKGROUND OF THE INVENTION
s 1. Field of the Invention
This invention relates to data compression, and more particularly to data
compression
using adaptive bit allocation and hybrid lossless entropy encoding.
2. Description of Related Art
A number of methods exist for compressing data. These methods are
characterized as
either "lossy" or "lossless". Lossy compression can achieve substantial
compression
ratios by, in effect, omitting redundant or unimportant information while
still maintaining
a reasonable semblance to the original data. Since data is lost, lossy
compression is
normally used only for data, such as sound or graphics (still or motion), that
can be
perceived reasonably accurately despite the loss of information. Lossless
compression
generally results in lower compression ratios but can reconstitute the
original data in its
entirety. Thus, lossless compression is generally used for machine code, text,
and
numerical data that require perfect precision.
A number of different methods exist for performing lossy compression,
including the
well-known JPEG standard for graphics and MPEG standard for video. However, no
one
particular compression algorithm has been shown to be optimal for all data
content.
Matching an algorithm to particular data (e.g., graphics images) can achieve
higher
compression ratios. In some contexts, such as transmission of data over a
constrained
bandwidth (e.g., typical modems, LANs, or WANs), an improvement in compression
ratio by even a few percent can achieve substantial long-term savings.
CA 02358857 2001-09-12
-2-
Accordingly, a need exists for improved data compression algorithms,
particularly for
lossy compression of graphics images. The present invention provides such an
improved
lossy compression algorithm that is particularly efficient for compressing
graphics
images.
CA 02358857 2001-09-12
-3-
SUMNIARY OF THE INVENTION
The invention comprises a method and apparatus for adaptive bit allocation and
hybrid
lossless entropy encoding in a lossy compression system. The preferred
embodiment of
the compression algorithm of the present invention includes three components:
(1) a
transform stage to decorrelate image data into a baseband and multiple
subbands, (2) a
quantization stage to quantize the resulting transform coefficients, and (3) a
lossless
entropy coder stage to encode the quantized indexes. Decompression is
accomplished by
inverting the compression stages.
In the preferred embodiment, the transform stage uses a wavelet transform
algorithm.
However, other transforms may be used, such as the well-known discrete cosine
transform (DCT) algorithm. The quantization stage recursively and adaptively
estimates
the optimal quantization size for each band using an approximation between
quantization
size and quantization error. More particularly, the quantization stage
adaptively estimates
values for parameters defining an approximation between quantization size and
the
logarithm of quantization error, and recursively calculates the optimal
quantization size
for each band to achieve a desired bit rate. The baseband and subbands are
then
transformed into quantization matrices using the corresponding quantization
sizes.
The lossless entropy coder stage takes advantage of the observation that the
entropy
property of run lengths of zero index values in the subband quantization
matrices
generated by the present invention is different from the entropy property of
non-zero
indices. Accordingly, a hybrid entropy coding algorithm was developed. In
particular,
each quantization matrix is parsed so that (1) the position of each non-zero
index is
replaced by the special token "1", and (2) each non-zero index is extracted
and put in a
separate stream. This results in a simple binary mask matrix that indicates
the position of
each non-zero index in each subband, and a stream of the non-zero indices. The
binary
mask is then processed using conventional run length coding (including coding
the run
length of the "1" tokens) to generate a run length coded matrix. Since the
binary mask is
CA 02358857 2001-09-12
-4-
only bi-valued, the run lengths of"0" and "1" alternate. This pattern is
parsed into an odd
stream of run length values for "0" and an even stream of run length values
for " 1". The
result of this process is that the quantization matrix for each subband is
divided into three
streams (a non-zero stream, a "0" run length stream, and a"1" run length
stream), which
are then Huffman coded separately in conventional fashion. This hybrid entropy
coding
algorithm gives an approximately 10% percent improvement over conventional run
length
and Huffman coding for similar images. The overall compression algorithm gives
an
approximately 2-6 dB improvement in terms of peak signal-to-noise ratio (PSNR)
over
JPEG algorithms for the same images at the same bit rates.
The details of the preferred embodiment of the present invention are set forth
in the
accompanying drawings and the description below. Once the details of the
invention are
known, numerous additional innovations and changes will become obvious to one
skilled
in the art.
CA 02358857 2001-09-12
-5-
BRIEF DESCRIPTION OF THE DRAWINGS
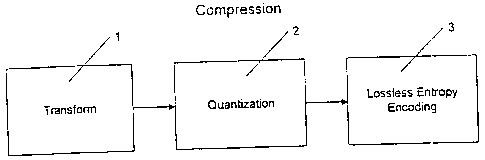
FIGURE 1 is a block diagram of the three components comprising a compression
encoder
in accordance with the present invention.
FIGURE 2 is a block diagram showing multi-level decomposition of an image.
FIGURE 3 is a diagram showing a quantization function that maps all x values
in the
interval d, to d2 to the value r,.
FIGURE 4 is a diagram showing application of a differential pulse code
modulation
algorithm to a current pixel x.
FIGURE 5 is a flow chart showing the hybrid lossless entropy coding algorithm
of the
present invention.
Like reference numbers and designations in the various drawings indicate like
elements.
CA 02358857 2001-09-12
-6-
DETAILED DESCRIPTION OF THE INVENTION
Throughout this description, the preferred embodiment and examples shown
should be
considered as exemplars, rather than as limitations on the present invention.
Overview
The preferred embodiment of the compression algorithm of the present invention
comprises three components, as shown in FIGURE 1: (1) a transform stage 1 to
decorrelate image data, (2) a quantization stage 2 to quantize the resulting
transform
coefficients, and (3) a lossless entropy coder stage 3 to encode the quantized
indexes.
Decompression is accomplished by inverting the compression stages.
In the preferred embodiment, the transform stage uses a wavelet transform
algorithm.
However, other transforms may be used, such as the well-known discrete cosine
transform (DCT) algorithm. For ease of understanding, this description will
assume that
a wavelet transform algorithm is used.
(1) Wavelet Transform
is Wavelet transforms are relatively new mathematical tools. A general wavelet
transform
can effectively decorrelate image data by decomposing an image into a number
of easily
compressible sub-images which contain high frequency (or edge) information. In
the
preferred embodiment, a wavelet transform is used in multiple levels to
decompose an
image. Each level of wavelet transform decomposes the image into four quarter-
size sub-
images, in known fashion.
For example, referring to FIGURE 2, an image 20 comprising a two-dimensional
matrix
of numbers representing pixels is decomposed in the transform stage 1 into
four quarter-
size sub-images LLO, HLO, LHO, and HHO by application of a wavelet transform.
Then,
as indicated by the dotted line, the wavelet transform is applied to the LLO
sub-image to
derive LL 1, HL 1, LH 1, and HH I sub-images, and then again is applied to the
LL 1 sub-
CA 02358857 2001-09-12
-7-
image to derive LL2, HL2, LH2, and HH2 sub-images, and then once more is
applied to
the LL2 sub-image to derive LL3, HL3, LH3, and HH3 sub-imacres.
In the example shown in FIGURE 2, the fourth level sub-image LL3 is called the
baseband image, and resembles a shrunken version of the original image 20 that
is 1/256
of the size of the original image 20. The 12 remaining sub-imaaes (referred to
as
"subband images" or just "subbands") supplement the difference between the
baseband
image and the original image 20. More particularly, the subband images
represent edge
information in the horizontal, vertical, and diagonal (labeled as HL, LH, HH)
orienta-
tions.
As a result of the preferred four level wavelet decomposition, the image 20 is
decom-
posed into one baseband image LL3 and twelve subband images (HLO-3, LHO-3, and
HHO-3). If desired, the baseband image shown can be further decomposed in a
similar
fashion several layers down, resulting in a similar pyramid structure with
additional
subbands.
is A beneficial characteristic of wavelet transform subbands is that the data
comprising each
subband is very sparse and most pixel values are very close to zero. This
characteristic
leads to improved quantization and lossless entropy encoding in accordance
with the
present invention.
In the preferred embodiment, the implementation of the wavelet transform is
achieved by
using a pair of carefully designed wavelet filters. Among the many possible
wavelet
filters, the preferred embodiment of the present invention uses Daubechies's 7
and 9
biorthogonal filters as the wavelet filters. These filters are implemented
using a
straightforward finite impulse response (FIR) implementation, in known
fashion.
CA 02358857 2001-09-12
-8-
(2) Ouantization
Quantization discards imperceptible information in baseband and subband images
to
achieve compression to meet a bit rate requirement from a user. A quantizer is
a "many
to one" function Q(x) which maps many input values into a smaller set of
output values.
s Quantizers are a staircase function characterized by a set of numbers called
decision
points d, and a set of numbers called reconstruction levels r;. An input value
x is mapped
to a reconstruction level r, if x lies the interval of (d;, d,+,). For
example, FIGURE 3 is a
diagram showing the mapping of all x values in the interval d, to d, to the
value r,. The
interval d; to d;., may not be uniform for all i.
In the preferred embodiment, since the wavelet transform does a good job of
decorrelating the image data in general, a uniform scalar quantizer is used in
the
quantization stage 2. The equation for the preferred uniform scalar
quantization is:
+q' -l,x<- q'
2
r = [O,otherwise ] ~ I )
x-q, +I,x> q'
2
where q; is the quantization size for subband i.
is In addition, since there is still a high degree of correlation among
neighboring pixals in
the baseband image, differential pulse code modulation (DPCM) is used to
predict and
quantize the baseband data further. In particular, in the preferred
embodiment, the
baseband image is scanned row by row from top to bottom and each pixel is
subjected to
the DPCM algorithm. For example, FIGURE 4 shows a current pixel x that is
predicted
using three neighboring pixels a, b, c, which have already been quantized. A
simple
prediction is used in the preferred embodiment. In particular, the prediction
residue r is
calculated by:
CA 02358857 2001-09-12
-9-
r=x-a*-b*+c* (2)
where a*, b*, c* are reconstruction (or "de-quantized") levels for a, b, c.
The prediction
residue r is then passed through a uniform scalar quantizer, such as the one
shown in
Equation (1).
Subband images represent edge information under different orientation of
different levels.
Thus, each subband will have a separate quantization size according to the
statistical
properties of such subband. The procedure for determining an optimal
quantization size
is called bit allocation. The present invention includes a novel adaptive bit
allocation
scheme described in detail below.
As a result of the preferred quantization stage, the baseband and 12 subband
images are
each processed into a quantization matrix of reconstruction levels rõ or
quantization
indices.
(3) Lossless Entropy Coding
The final compression is achieved by losslessly encoding the quantization
matrix for each
Is subband in the lossless entropy coder stage 3. The lossless entropy coder
stage 3 assigns
a variable size token to each quantization index according to the frequency
with which
that index appears; the more frequently a particular index appears, the
shorter the token
assigned to it. The preferred embodiment of the present invention uses the
well-known
Hu$man coding technique to encode the data in each subband quantization
matrix. In the
prior art, since a majority of the indices in each subband quantization matrix
are zero-
valued, conventional run length coding of each matrix would normally be
performed
before Huffinan coding. Run length coding simply replaces a sequence of like-
valued data
values with a symbol representing the data value and the number of such values
in the
sequence.
CA 02358857 2001-09-12
-10-
The output of the lossless entropy coder stage 3 is a data structure that
represents a
compressed version of the original ima~e 20. That data structure may be
transmitted
and/or stored for later reconstitution into an image that approximates the
original image
20.
s Based on extensive empirical analysis in developing the present invention,
it has been
observed that the entropy property (i.e., randomness) of run lengths of zero
index values
in the subband quantization matrices generated by the present invention is
different from
the entropy property of non-zero indices. Accordingly, a hybrid entropy coding
algorithm
was developed which gives an approximately 10% percent improvement over the
conventional run length and Huffman coding approach. This hybrid entropy
coding
algorithm is described in detail below.
Bit Allocation
Bit allocation is a process of determining the quantization size for baseband
and subband
images so that the overall quantization error approximates a minimum under the
constraint of a total bit rate set by a user. Determining such minimums is a
typical
programming problem in mathematics. One could write:
min
Rk ~ mk D k(Rk) (3 )
under the condition:
" 1 -
~ m Rk =Rtatar (4)
k
where: D,t(R,) and Rk are the distortion (quantization error) and the bit rate
for the
baseband image and each subband image, respectively; RraQ, is a selected total
bit rate;
and m,r is the down sample factor, which is defined to be the ratio of image
size to
subband size (for example, for the decomposition structure shown in FIGURE 2,
m,j.s, _
16, mLm = 256).
CA 02358857 2001-09-12
-l i-
The solution of Equation (3) can be found by a Lagrange multiplier method:
n I~(J) Rk E 1 Dk(Rk) + ~' (Rrolar - ~ 1 Rk) (5)
k= 1 nJ k k=1 mk
where J is the overall cost function, and k is the Lagrange multiplier. The
minimum of
J is achieved when the first partial derivative of J equals zero. This
condition yields:
aj aD,(IZ )
aP~ - aR, = ~ (6)
for all subbands i. To solve Equation (6), the explicit expression of Dk(Rk)
needs to be
known. However, in practice, it is hard to find the explicit expression for
Dk(Rk) "for each
subband.
It is known that the probability distribution function (PDF) of subband data
can be
approximated by a Generalized Gaussian model, for which Dk(Rk) is known. This
approach leads to allocating the bit rate in proportion to the logarithm of
the variance of
the subband data, and is widely used in various wavelet image coding schemes.
Unfortunately, carefiilly examination of this method shows that this method is
not correct
and cannot lead to optimal bit allocation. If bit rate allocation is done
simply in
is proportion to the logarithm of the variance of the subband, this implies
that, if the two
subbands have the same variance, then their curve will be the same. On the
contrary,
based on extensive empirical analysis in developing the present invention, it
has been
found that the best-fit curve is quite different for subbands with the same
variance. -
Instead of the above method, the preferred embodiment takes advantage of the
observations, made during the development of the present invention, that (1)
the
logarithm of the mean square error (MSE) of the quantization of a subband to
the
corresponding bit rate (determined by lossless coding of the quantization
indices for such
subband) can be approximated by a straight line, and (2) that such bit rate
can be
approximated from the quantization size.
CA 02358857 2001-09-12
-12-
Using a straight line model, the distortion (quantization error) to bit rate
curve for each
band can be expressed as:
D k(Rk) = e ' R,-' bk
(7)
where ak and bk are parameters representing the line and depending on subband
k. Using
Equation (7), Equation (6) becomes:
Rk=a(logQbk) (8)
ak k
Under the constraint of the total bit rate this results in:
" 1 " 1 " bk lOg (ak)
E -Rk = log(/1) E - ~ ( + ) = Rr t r (9)
k't mk k' 1 mkak k' 1 mk ak mkak
From Equation (9):
n bk l0g(ak)
Rrotar + E , +
k=1 mkak mkak
a. = exp (10)
k=i mkak
From Equation (10), the subband bit rate can be derived using Equation (8).
However,
since the goal is to find quantization size rather than bit rate, the
relationship between bit
rate and quantization size must be detennined. It is observed that the
relationship between
bit rate Rk and quantization size Qk can be approximated using following
equation:
Maxk - Mink
~s Log Q = crtRk +dk (11)
k
CA 02358857 2001-09-12
-13-
From Equation (1 1):
Maxk - Mrnk
exp (ckR,e +dk) (12)
where: Maxk, Minkare the maximum and minimum coefficients of subband k; and ck
and
d, similar to ak and bk, are constants depending on the statistical properties
of subband
k and can be estimated using simple curve fitting.
Using the above model, the bit allocation problem can be solved by estimating
ak, bcx
and dk for each subband. These estimations can be done off-line by
statistically
calculating the bit rate for each subband over a large number of sample
images. However
this may not be optimal for a particular image. Since ak, bk, ck and dk are
parameters
representing a straight line, they can easily be estimated on the fly. Suppose
n points in
the curve Dk(Rk) are known, and also Qk(Rk), i.e., (Q;, D;, R), i= 1, 2, ...
n, then:
n n
nE R log(D) -E R; E log(D)
f=t P t t=t
q n n n (13)
nrR2E R;ERJ
;=t ;=t r=t
n
E log(D) -akERS. (14)
b _ r=t r=t
k n -
tWax k Min Max Min
nE R' .log k -~Rlog k k
_ r=t O, r=t ' ~_, O;
Ck n n (15)
nF, R?
CA 02358857 2001-09-12
-14-
~ Mazk - Mink ~
[~ Log - CkL~ Ri
L 0 r-I
dk = n (16)
In the preferred embodiment, the set of Q, are set to have initial default
values covering
a reasonable range of possible quantization values. D,, the distortion (error)
of quan-
tization, is calculated using Equation (1). The bit rate, R,, is calculated by
calling the
s lossless encoder routine (described below). In the preferred embodiment, n
is empirically
set to 6. However, other values may be used for n, as desired.
Using the above approach, the following steps are performed in the preferred
embodiment
of the present invention to adaptively determine bit allocations for the
baseband and
subband images during the quantization stage 2:
(1) Estimate values for parameters defining an approximation between
quantization
size and quantization error for each subband - this is, estimate ak, bk, ck
and dk for
each subband image k, using Equations (13), (14), (15), and (16). Again, Maxk
and
Mink are the maximum and minimum coefficients of subband k, determined by
searching the coefficients. Calculate an initial set of Q. from:
Maxk-Mink
~s Q~ (17)
N
where N, = (8, 12, 15, 24, 48, 64) for the first 8 subbands, and N; 8, 10, 14,
18,
36, 50) for last 4 subbands. N; is the total number of quantization levels for
Q,.
The number of bits per index is close to Log(N,) if a lossless coding
technique is
not used. The values for Nf are empirically chosen to cover a possible range
of bit
rates for each subband.
(2) Estimate values for parameters defining an approximation between
quantization
size and quantization error for the baseband - that is, estimate ak, bk, c,F
and d,F for
the baseband image using Equations (13), (14), (15), and (16). Max and Min are
CA 02358857 2001-09-12
-15-
set to 2000 and 0, respectively, for the baseband. Mar and Min are fixed
values
for the baseband image in Equation (11) because the baseband image uses DPCM
quantization. The preferred values were empirically determined. Q, ={4, 10,
20,
40, 80, 100). The values for O, were empirically chosen to cover a reasonable
s range of Q, for the baseband image.
(3) Calculate the optimal bit rate Rk. for each of the baseband and subband
images
using Equations (8) and (10).
(4) If Rk < 0, indicating information in subband k is so small that it can be
discarded,
mark subband k and exclude it from the subband pool, and loop to step (3) and
recalculate the optimal bit rates Rk.
(5) Calculate Qk using Equation (12). The result of this process is a set of
optimal
quantization size values Qk that can be used in Equation (1) (shown there as
q).
Lossiess Entropy Coding
In the prior art, the quantization matrices would be run length code and then
Huffinan
is coded. The present invention teaches a more efficient method of coding that
gives an
approximately 10% percent improvement over the conventional run length and
Huffman
coding approach.
FIGURE 5 is a flow chart showing the hybrid lossless entropy coding algorithm
of the
present invention. Initially, each subband is represented at this stage by a
quantization
matrix 50 comprising a set of quantization indices. Each quantization matrix
50 is parsed
so that (1) the position of each non-zero index is replaced by the special
token "1", and
(2) each non-zero index is extracted and put in a separate stream. This
results in a simple
binary mask matrix 51 that indicates the position of each non-zero index in
each subband,
and a stream 52 of the non-zero indices.
Normally, such a binary mask 51 would be harder to compress than the non-zero
stream
52 because the binary mask 51 actually represents the structure information of
the
original image. However, it was observed during the development of the
invention that
CA 02358857 2001-09-12
-16-
the data in each subband is typically so sparse that the run lengths of "0"
are very long
but the run lengths of"1" are normally short. In other words, the entropy
property of run
lengths of "0" is different from the entropy property of run lengths of "I".
Thus, it was
concluded that it would be better to Huffman code the "0" run length indices
and " 1" run
length indices separately.
Accordingly, in the preferred embodiment, the binary mask 51 is processed
using
conventional run length coding (including coding the run length of the "I"
tokens) to
generate a run length coded matrix 53. It will be noted that since the binary
mask 51 is
only bi-valued, the run lengths of "0" and "I" alternate. Therefore, the run
length coded
matrix 53 has an odd-even pattern. This pattern is parsed into two run length
streams 54,
55, defining an odd stream 54 of run length values for "0" and an even stream
55 of run
length values for "1". (Of course, the designation of odd and even may be
reversed).
The result of this process is that the quantization matrix for each subband is
divided into
three streams (non-zero stream 52, "0" run length stream 54, and "1" run
length stream
Is 55), which are then Huffman coded separately in conventional fashion.
Ideally, each subband would be processed in this manner individually, since
their
statistical properties are different. However, for 12 subbands, 36 Huffrnan
streams will
be generated (further, for color images, each subband has three color space
components,
such as YLJV or RGB). This is not very efficient in terms of speed and file
size due to
additional overhead in the file format. Empirically, it was determined that
the three
subbands on each level of the wavelet transform have quite similar entropy
properties.
Accordingly, in the preferred embodiment of the present invention, the
quantization
matrices of each such set of three subbands are combined together on a row-by-
row basis
before applying the above hybrid coding scheme. (Other combinations, such as
column-
by-column, could be used as well).
CA 02358857 2001-09-12
-17-
In the preferred embodiment, conventional run length coding followed by
Huffman
codin,,, is used for the baseband because the baseband residue is not sparse
and applying
the above hybrid coding approach results in little or no gain in compression.
However,
if desired, the inventive hybrid coding algorithm could be used for the
baseband as well.
s Importantly, the hybrid coding algorithm may be used in any other context
where a
substantial difference exists in the entropy property of run lengths of "0"
compared to the
entropy property of run lengths of non-zero elements (which may be transformed
by
substitution to "1" tokens).
In the preferred embodiment, conventional run length coding plus a Huffmari
'coding
io approach is used in the lossless encoder routine for coding the baseband
and subbands
used by the quantization stage 2 to determine the bit rate associated with a
particular
quantization size Q,. This approach was selected in consideration of
computational speed
and memory limitations. However, it should be recognized that other means of
determining or estimating the bit rate could be used, such as the hybrid
approach
is described above.
Format of a Compressed Stream
In the preferred embodiment, each Huffinan coded stream for the baseband and
subbands,
as weIl as other general image information, are combined together into a
single bitstream.
In the preferred embodiment, the final bitstream is organized in the following
order to
20 achieve progressive playback (that is, decoding the baseband portion of the
bitstream for
the compressed image so as to generate a first, "grainy" image, and then
progressively
decoding each subband portion of the bitstream to successively overlay and add
, resolution to the underlying image until done):
General Image Information
25 Y Baseband
U Baseband
V Baseband
Y Subbands 1
U Subbands 1
CA 02358857 2001-09-12
-i8-
V Subbands 1
Y Subbands 2
U Subbands 2
V Subbands 2
Y Subbands 3
U Subbands 3
V Subbands 3
Y Subbands 4
U Subbands 4
V Subbands 4
General Image Information
The general image information includes information about the dimension of the
image
and color space, and comprises the following components in the preferred
embodiment:
Component Function
1 Wavelet Stream ID (0x15)
2 Color Space (0x20 for grayscale image,
0x03 for YLJV image)
3 Columns low byte
4 Columns high byte
5 Rows low byte
6 Rows high byte
Baseband Stream
Each baseband stream (i.e., one for each color) comprises a bitstream
including the
following components in the preferred embodiment:
Component Function
1 Quantization Size: 1 or 2 bytes
2 Huffman Bit Stream for baseband
CA 02358857 2001-09-12
-19-
Subbatrds Stream
Each subband stream comprises a bitstream for each color of three subbands
correspond-
ing to each level of the preferred wavelet transform, and includes the
following
components in the preferred embodiment:
s Component Function
I No. of bytes for non-zero index stream in current level
(I or 2 bytes)
2 No. of bytes for "1" run length stream in current level
(1 or 2 bytes)
3 Level information (1 byte): lowest 3 bits indicate
if the subband was discarded
4 Quantization size for LH subband if not discarded
(1 or 2 bytes)
5 Quantization size of HL subband if not discarded
(1 or 2 bytes)
6 Quantization size of HH subband if not discarded
(1 or 2 bytes)
7 Huffman stream for non-zero index
8 Huffman stream for "1" run length
9 Huffman stream for "0" run length
is Decoding
Decoding of a bitstream encoded with the present invention is straightforward,
and may
be accomplished as follows:
(1) Decode the Huffman streams;
(2) For each subband, rebuild a binary mask by interleaving and expanding the
"0"
run length streams and "1" run length streams;
(3) Rebuild the corresponding quantization matrix from the binary mask and the
non-
zero stream by sequentially substituting the non-zero values for "1" tokens
(this
may be combined with step (2));
CA 02358857 2001-09-12
-20-
(4) Apply the corresponding quantization size values to each quantization
matrix in
known fashion to generate the baseband image and subband images;
(5) Apply the inverse transform in known fashion to the baseband image and
subband
images to generate an approximation of the original image.
s The decoded images in the baseband level and each subband level from step
(5) may be
displayed before decoding the next level, thereby permitting progressive
playback.
Implementation
The invention may be implemented in hardware or software, or a combination of
both.
However, preferably, the invention is implemented in one or more computer
programs
executing on one or more programmable computers each comprising a processor, a
data
storage system (including volatile and non-volatile memory and/or storage
elements), at
least one input device, and at least one output device. Program code is
applied to input
data to perform the functions described herein and generate output
information. The
output information is applied to one or more output devices, in known fashion.
Each program is preferably implemented in a high level procedural or object
oriented
programming language to communicate with a computer system. However, the
programs
can be implemented in assembly or machine language, if desired. In any case,
the
language may be a compiled or interpreted language.
Each such computer program is preferably stored on a storage media or device
(e.g.,
ROM or magnetic diskette) readable by a general or special purpose
programmable
computer, for configuring and operating the computer when the storage media or
device
is read by the computer to perform the procedures described herein. The
inventive system
may also be considered to be implemented as a computer-readable storage
medium,
configured with a computer program, where the storage medium so configured
causes a
computer to operate in a specific and predefined manner to perform the
functions
described herein.
CA 02358857 2001-09-12
-21-
A number of embodiments of the present invention have been described.
Nevertheless,
it will be understood that various modifications may be made without departing
from the
spirit and scope of the invention. For example, while the term "matrix" has
been used to
describe an image data structure, it should not be interpreted to mean a
strict two-
dimensional data structure. Other data structures known in the art can as
easily be used
to store the relevant pixel or index information. Further, while Huffman
coding has been
referred to as the preferred method for the final lossless entropy coding
step, other
lossiess entropy coding algorithms, such as arithmetic coding, may be used.
Moreover,
while image compression has been discussed, the algorithms described herein
may be
applied to other data types. Accordingly, it is to be understood that the
invention is not
to be limited by the specific illustrated embodiment, but only by the scope
'of the
appended claims.