Note: Descriptions are shown in the official language in which they were submitted.
CA 02381937 2002-02-15
GR 99 P 2593
- 1 -
Description
Method for generating pseudorandom numbers, and a
method for electronic signature
The invention relates to a method for generating
pseudorandom numbers and a method for electronic
signature.
Random numbers are required in cryptography for
encoding or signing messages. An overview of the
development of cryptography in Germany is given in the
article entitled "Vom diplomatischen Code zur
Falltiirfunktion" ["From the diplomatic code to the
trapdoor function"] by Otto Leiberich, Spektrum der
Wissenschaft, June 1999, pages 26 to 34. This describes
a previously used worm encryption method or stream
encryption method., in the case of which a very long
character string that has no sort of internal
structure, what is termed a character worm or character
stream, is added character by character to a message,
the plaintext, that is to be encoded. If these are
letters, they are firstly converted into numbers using
the scheme a = 0, b = 1, ..., z = 25. So that no
numbers larger than 25 result, an addition modulo 26 is
carried out. In the computer age, the texts are
converted into binary numbers and zeros and ones
modular 2 are added. The receiver subtracts the
character stream - modulo 26 or 2 - from the received
secret text and therefore reobtains the clear text.
The character stream is generated with the aid of
random number generators. These were previously based
on high-frequency voltage fluctuations of specific
tubes, what are termed thyratrons, and later on
radioactive decay events.
GR 99 P 2593
CA 02381937 2002-02-15
- la -
Since, however, the character streams must in each case
be securely transmitted in parallel from the
transmitter to the receiver, a substantial throughput
of secure data transfer is required.
GR 99 P 2593
CA 02381937 2002-02-15
- 2 -
Consequently, methods for generating pseudorandom
numbers, what are termed pseudorandom number
generators, have been developed that can generate a
sequence of pseudorandom numbers of substantially any
desired length as a function of a key. In the case of
the above coding method, this has required only one key
to be transmitted secretly between the communication
partners, and this is substantially easier to handle
than transmitting a complete character stream in each
case.
For present day open networks, in particular the
Internet, methods have been developed in which two
communication partners who wish to communicate with one
another for the first time send one another encoded
messages. These methods are what are termed asymmetric
key methods which are also termed public key methods,
in the case of which the receiver publishes his key,
what is termed a public key.
One of the best known methods of this type is what is
termed the RSA method, in the case of which parts of
the key, what are termed key modules, are products of
two large prime numbers. The sender of the message
knows only the key module, that is to say the product,
and can use the latter to encode the message using a
specific mathematical function. However, knowledge of
the product is insufficient to decode the message,
however it is the two prime numbers that are required.
It is only the correct receiver, who has generated the
key, that can decode the encoded message with the aid
of these prime numbers and a corresponding inverse
function.
Given large modules, it is not possible in practice to
decompose the key module into its divisors, the two
prime numbers, with a normal computational outlay. In
"Faktorisierung grof3er Zahlen" ["Factorizing large
' GR 99 P 2593
CA 02381937 2002-02-15
- 2a -
numbers"] by Johannes Buchmann, Spektrum der
Wissenschaft, September 1996, pages 80 - 88, the
problem of decomposing large numbers into their prime
numbers is described in detail and the outlay
CA 02381937 2002-02-15
GR 99 P 2593
- 3 -
for decomposing a 129 place number is set forth. This
number was decomposed into the individual prime numbers
with the aid of 600 volunteers who made their computers
available.
A disadvantage of the RSA method is that it is too slow
for encoding messages, since ensuring a sufficiently
high level of security requires the use of very large
numbers - approximately 1000 binary or 300 decimal
spaces. Such large numbers are to be raised to the
power of others of a similar order of magnitude, and
this cannot be performed quickly enough to encode data
that are to be transmitted. The RSA method is therefore
used only for the encoded transmission of keys, which
are to be kept secret, for a conventional method which
then accomplishes the actual encoding.
Methods based on elliptic curves have been developed as
an alternative to the RSA method. Only elliptic curves
over finite fields are relevant for cryptography. These
elliptic curves over finite fields form point groups in
which an addition and a multiplication are defined that
have nothing in common with common addition and
multiplication except for the computational rules.
Multiplication on an elliptic curve over a finite field
is a one-way function, that is to say in the normal
case it is impossible by computation to carry out the
inverse - the calculation of what are termed discrete
logarithms - whereas multiplication can be executed
very simply and quickly. This fact is utilized in the
case of the cryptographic methods based on elliptic
curves by virtue of the fact that the receiver selects
a random number t for himself and uses this random
number t and a multiplication by t on the elliptic
curve to determine a curve point T. The curve point T
is published as a key, whereas the random number t is
kept secret by the receiver. A transmitter can use the
curve point T
GR 99 P 2593
CA 02381937 2002-02-15
- 4 -
to encode his message, which can then be decoded only
by the receiver, who knows the random number t on which
the curve point T is based.
Such methods based on elliptic curves require
substantially less computer power in conjunction with
the same security than does the RSA method. Such
methods can be implemented in microcomputers such as,
for example, in chip cards. Siemens AG markets a chip
card with the trade name of SLE44CR80S, in which a
signature method is implemented on the basis of
elliptic curves.
Random numbers are required, again, to generate the
keys, the public key, which the receiver publishes, and
its corresponding private key.
The invention is therefore based on the object of using
elliptic curves as a basis for creating a method for
generating pseudorandom numbers that can be executed
easily and quickly and with the aid of which it is
possible to generate a large quantity of high-quality
random numbers.
This object is achieved by means of a method having the
features of claim 1.
The invention is also based on the object of creating a
method for electronic signature on the basis of
elliptic curves, and of creating a corresponding
apparatus, which require less storage space than do
known methods and apparatuses for electronic signature
on the basis of elliptic curves, and can be implemented
on small computer systems, in particular chip cards.
GR 99 P 2593
CA 02381937 2002-02-15
4a -
The obj ect is achieved by means of a method having the
features of claim 11, and an apparatus having the
features of claim 12.
GR 99 P 2593
CA 02381937 2002-02-15
- 5 -
Advantageous refinements of the invention are specified
in the subclairns.
In the case of the method according to the invention as
claimed in claim 1 for generating pseudorandom numbers,
pairs of points are determined that lie on at least two
different elliptic curves over a finite field, and a
random number is determined as a function of in each
case one such pair of points.
Since in accordance with the invention use is made of
two different elliptic curves, and the pseudorandom
number is derived from a pair of points, the two points
of the pair lying on different elliptic curves, it is
impossible to infer the curve points from the
pseudorandom numbers determined in this way. In the
case of the use of only a single elliptic curve for
deriving pseudorandom numbers, it would be possible to
infer the curve points from the pseudorandom numbers by
calculating discrete logarithms. It would thereby be
possible for third parties to determine the computing
rule for the pseudorandom numbers and to predict the
further pseudorandom numbers. This would constitute a
substantial security risk which is avoided with the aid
of the present invention.
The method according to the invention for electronic
signature combines a signature method that is known per
se with the method according to the invention for
generating pseudorandom numbers. The same routines
and/or devices can be used both for the signature
method and for the generation of the random numbers, it
thereby being possible to save substantially on program
code and storage space. In addition, an optimization of
the EC (= elliptic curve) arithmetic has an
advantageous effect both in the case of the generation
of the pseudorandom numbers and in the case of the
GR 99 P 2593
CA 02381937 2002-02-15
- 5a -
immediate execution of the signature method. Effects of
synergy are achieved due
CA 02381937 2002-02-15
GR 99 P 2593
- 6 -
to this double use of the routines and devices on the
basis of elliptic curves.
Furthermore, the pseudorandom numbers generated in
accordance with the invention cannot be distinguished
from random numbers of a true random number generator,
and can be generated with a relatively low
computational outlay.
The invention is explained in more detail below by way
of example with the aid of the drawings in which,
schematically:
Figure 1 shows an elliptic curve over the real
numbers,
Figure 2 shows an elliptic curve over a finite field,
Figure 3 shows the addition of two points on an
elliptic curve over the real numbers,
Figure 4 shows the points on the elliptic curve
y2=x3+2x+9 over the field mod 13, which form a
cyclic group with 17 points,
Figure 5 shows the method sequence of an exemplary
embodiment of the invention in a flowchart,
Figure 6 shows the basic principle of the method
according to the invention for generating
pseudorandom numbers in a flowchart, and
Figure 7 shows the structure of a program for
executing a signature method according to the
invention.
A brief explanation will firstly be given of the
mathematical principles for computing on elliptic
GR 99 P 2593
CA 02381937 2002-02-15
- 6a -
curves. An elliptic curve E over a field K is a curve
that can be described by a cubic equation of the
following form:
GR 99 P 2593
CA 02381937 2002-02-15
_ 7 _
yz=x3+ax+b,
with a and b from K, 4a3+27bz ~ 0. Pairs (x, y) from
K x K which satisfy the equation, as well as the formal
pair (oo, Oo) are called points on the curve E over K.
An elliptic curve over the real numbers is shown in
figure 1. Note that elliptic curves are not ellipses.
Figure 2 shows an elliptic curve over a finite field.
The algebraic term field defines a "number domain" in
which it is possible to add, subtract, multiply and
divide using the formal computing rules known from the
rational numbers. There are infinite fields such as,
for example, the rational numbers, the real numbers,
the complex numbers, and finite fields. Finite fields
are, for example, the field GF(p) of the numbers mod p,
p being a prime number, or the field GF(2n) of the
binary vectors of the length n. ("GF" stands for
"Galois field", which is a synonym for "finite field").
Only elliptic curves over finite fields are relevant to
cryptography.
Figure 3 shows the addition of two points Pl, Pz on an
elliptic curve over the real numbers, the point P3 being
yielded. In this addition, the straight line connecting
the points P1 and Pz is formed and its third point of
intersection with the elliptic curve is determined.
This point of intersection is reflected at the x-axis
and yields the result P3 for the addition of P1 and Pz.
The addition of the points on elliptic curves can be
expressed by the following formulas:
x3=rz-xl-xz, Ya=r (xl-xs) -Yi, where
r= (yz-Y~) / (xz-x~) , if xl~xz,
r= (3x12+a) /2Yi. if P1=Pz
~
GR 99 P 2593
CA 02381937 2002-02-15
_ g _
xi, yi being the coordinates of the point Pi (i=1,2,3).
These formulas also hold for elliptic curves over
finite fields.
A multiplication of curve points by whole numbers k is
defined by iteration of the point addition:
k*P=P+P+...+P (k-fold sum).
This multiplication of curve points by whole numbers
can be executed easily and quickly, whereas the inverse
task of calculating what are termed discrete logarithms
can normally be solved only with an extraordinary
computational outlay. There is no algorithm with a
subexponential runtime for this. This point
multiplication therefore constitutes a one-way
function, for which reason it is used in methods with
public keys, what are termed public key methods.
The method according to the invention for generating
pseudorandom numbers is explained below with the aid of
an exemplary embodiment shown in figure 5.
A first elliptic curve E over the field GF(p) is given
by the following equation:
(y2) mod p = (x3 + 6x +
605067903441846547388214966045455206952938406771) mod p,
where p =2lso_47=
1461501637330902918203684832716283019655932542929.
p is a prime number with 160 bits.
The elliptic curve E over GF(p) has as group degree
#E (GF (p) ) - 7*q, where
q=208785948190128988314812461240940947434505754881.
Once again q is a prime number with 128 bits.
GR 99 P 2593
CA 02381937 2002-02-15
- 9 -
The group degree of an elliptic curve is the number of
the elements of the point group, that is to say the
number of the solutions of the defining equation of the
elliptic curve E over GF(p). The larger the maximum
prime divisor of the group degree, the more difficult
it is to calculate discrete logarithms. The magnitude
of the group degrees and of their maximum prime
divisors therefore constitutes a quality feature of the
method according to the invention, the group degrees
preferably being required to be at least 2100 or,
better, 2130.
A second elliptic curve E' over GF (p) is given by the
following equation:
( y2 ) mod p = ( x3 + 3 x +
168756385740498547400152923318200148712149363991) mode p.
The curve E' is isogenic relative to the curve E, that
is to say when the curve E has the form
y2=x3+ax+b,
the curve E' has the form
y2=x3+ac2x+bc3 ,
with a, b, c from GF(p), c being a quadratic nonresidue
modulo p. It holds in the present case for c that:
c= 503145425704462245322517599589013227703324936803.
Substantial advantages are offered by the use of two
isogenic curves instead of two arbitrary curves. Thus,
the degree of the elliptic curve E' over GF(p) can be
derived easily from the group degree of E since,
specifically, the sum of the two degrees is 2p+2, the
following equation being yielded as a result:
CA 02381937 2002-02-15
GR 99 P 2593
- 10 -
#E' (GF (p} ) - 2p+2 - #E (GF (p) )
In the present case, the result for the group degree of
E' is:
#E' (GF (p) ) - 2p+2 - #E (GF (p) ) - 11 * 19 * q'
where
q'= 4581509834893112596249788202965452687367789347.
q' is a prime number with the length of 152 bits.
Two points P, P' on the curves E, E' are now selected
such as, for example:
P =(27,1199480719563308855489368355308026541006624847440)
P' =(318,767790262932904318810390534329377261151321453045),
and
two starting values s, s', for example s=s'=2.
The step S1 from figure 5 is terminated by the
determination of the elliptic curves E, E', the points
P, P' and the starting values s, s'. The method
sequence now carries over to the step S2 , in which the
points P, P' are multiplied by s and s', respectively,
the result being denoted as PA and PA', respectively.
The multiplication is executed as s-fold or s'-fold
addition in accordance with the addition shown in
figure 3.
The points PA and PA' are transferred to the rule for
determining random bits (step S3). In the present case,
the x-coordinates of the two points PA and PA' are
combined with XOR and divided by c.
For isogenic elliptic curves E and E', it holds for an
arbitrary x from GF(p) that x is either the x-
coordinate of two different points on E, or else that x
is the x-coordinate of a point on E and cx is the x-
CA 02381937 2002-02-15
GR 99 P 2593
- 10a -
coordinate of a point on E' , or else that x is not the
x-coordinate of a point on E,
CA 02381937 2002-02-15
GR 99 P 2593
- 11 -
but cx is the x-coordinate of two points on E'. Thus,
when the x-coordinates on E' are divided by c every
arbitrary x occurs from GF(p) exactly 2x times as
x-coordinate. That is to say, combining an x-coordinate
on E with an x-coordinate on E' divided by c is
equivalent to combining two arbitrary, random values
between 0 and p-1. The pseudorandom bits derived
thereby therefore behave like true random bits.
From the step S2, the points PA and PA' are also
transferred to the step S4, in which the points P, P'
remain unchanged and s or s' is respectively increased
by one.
From the step S4, the method sequence transfers once
again to the step S2, in which, again, new points PA
and PA' are formed which are then transferred again to
the step S3 for calculating further random bits and to
the step S4. This method sequence can be repeated
multiply, new random bits being generated continuously.
The inventors of the present invention have used the
above-described method for generating random members to
generate 20 x one million random bits, and have
subjected these random bits to various statistical
tests. No deviations from true random bits could be
established by the tests.
It is essential to the invention that in the step S3
the random number Z is determined from the two points
PA and PA' that originate from different elliptic
curves E and E'. The combination of the two points PA
and PA' ensures that the pseudorandom numbers generated
cannot be used to determine by discrete logarithms the
points P and P' on which the calculation of the points
PA and PA' is based. It is therefore impossible to
infer from the result of S3 the method for generating
the points PA, PA'
CA 02381937 2002-02-15
GR 99 P 2593
- 12 -
with the aid of the steps S1, S2 and S4, this being
represented by the dashed line in figure 5.
The invention is not limited to the exemplary
embodiment illustrated in figure 5. It is, for example,
possible within the scope of the invention for a
different combination of the x-coordinates to be
selected in the step S3. Thus, for example, the two x-
coordinates can be combined with one another by adding
modulo p. Or, alternatively, it is the y-coordinates
that are combined. Otherwise the x-coordinates and y-
coordinates. It is also possible within the scope of
the invention, after each calculation of PA and PA',
not permanently prescribed elliptic curves E, E' with
points P, P', but new curves E*, E*' and points P*,
P*', which are used to calculate the next points PA*
and PA*'. The values s, s' can also be varied
arbitrarily per se. All that is essential to the
invention is that the values s, s' are whole numbers.
At the beginning of the method, they can be generated,
for example, with the aid of a simple random number
generator, which need not satisfy high demands. A basic
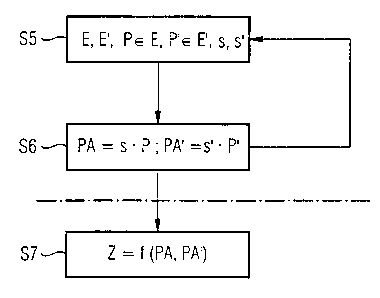
principle of the present invention is illustrated in
figure 6, the principle having a loop consisting of the
steps S5 and S6, two elliptic curves E, E' , two points
P, P' on the two curves and two starting values s, s'
being selected in the step S5. The points P, P' are
multiplied by s and s', respectively, in the step S6,
the result being PA and PA'. With each repetition of
the loop S5, S6, at least one of the pairs E, E' or P,
P' or s, s' is changed. It is also possible to change
two or three pairs using a rule to be stipulated.
With each repetition of the loop, a new pair of numbers
PA, PA' is generated and transferred to the method step
S7, in the case of which the two points PA and PA' are
respectively combined to form a pseudorandom number Z.
CA 02381937 2002-02-15
GR 99 P 2593
. - 12a -
Methods on the basis of elliptic curves use the
multiplication on elliptic curves as
GR 99 P 2593
CA 02381937 2002-02-15
- 13 -
one-way function, for which reason apparatuses for
carrying out such methods are provided with routines
and devices for arithmetics on elliptic curves. Such
methods also require random numbers in order to create
the private and public keys. By using the method
according to the invention to generate these random
numbers, it is possible, on the one hand, to generate
pseudorandom numbers that are qualitatively of high
value and, on the other hand, the program code can be
kept small since the existing routines can be used
twice. Substantial resources are saved thereby and the
security of the method is substantially enhanced at the
same time.
Figure 7 shows the architecture of a program for
executing the method according to the invention
schematically in a block diagram. The program comprises
a part P1 for carrying out the signature method, which
has recourse to a program part P2 with the aid of which
multiplications are carried out on elliptic curves over
finite fields. The program part P1 is supplied by a
further program part P3 with random numbers, the
program part P3 again having recourse to the program
part P2 for multiplication on elliptic curves.
Represented at the program part P1 is a data input
current I and a data output current O, it being
possible for the data input current to be a message to
be signed, and the data output current to be the
signature. Furthermore, the program part P1 can output
its private and public keys on the data output current
O. These functions of the program part P1 correspond to
the signature methods and devices known per se on the
basis of elliptic curves. The method according to the
invention can be used, in particular, in the case of
computing devices of low arithmetic capability such as,
for example, chip cards, since the corresponding
program code is exceptionally compact and the length of
the numbers to be processed is substantially shorter
GR 99 P 2593
CA 02381937 2002-02-15
- 13a
than in the case of an RSA method for the same security
level. However, it is also possible to market the
programs on electronically readable data media.