Note: Descriptions are shown in the official language in which they were submitted.
CA 02383764 2007-12-28
1
METHODE POUR MODELISER DES DEPLACEMENTS DE FLUIDES
DANS UN MILIEU POREUX TENANT COMPTE D'EFFETS
D'HYSTERESIS
La présente invention concerne une méthode pour modéliser des écoulements
di ou triphasiques dans un milieu poreux, en drainage et en imbibition. Elle
est basée
sur une représentation fractale du milieu poreux et sur une approche originale
pour
traiter les phénomènes liés à l'hystérésis (changement du sens de variation
des
saturations).
La méthode selon l'invention est applicable dans de nombreux domaines où
l'on veut modéliser les écoulements de fluides dans des milieux poreux, dans
le but
d'optimiser les conditions de leur déplacement en drainage et en imbibition.
Parmi les
domaines d'application, on peut citer par exemple :
a) l'exploitation d'un gisement pétrolier et nota.mrnent la production
assistée
d'hydrocarbures par injection de fluides, en utilisant par exemple des
injections
alternées de bouchons de liquide et de gaz (méthode dite WAG). Elle constitue
pour l'ingénieur de gisements, un bon outil pour étudier également les
problèmes
de productivité et d'injectivité des puits.
b) la dépollution des sols et notamment des sites industriels, par injection
dans
des couches polluées, de substances telles que des tensio-actifs;
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
2
c) le nettoyage de cakes de filtration par déplacement des substances qui y
sont
retenus ;
d) le séchage du bois ;
e) l'optimisation de réactions chimiques par déplacement par exemple de
produits
réactionnels dans une masse de catalyseur, pour augmenter les surfaces de
contact, etc.
La méthode selon l'invention est directement applicable par les ingénieurs de
réservoir pour déterminer par exemple la méthode de récupération assistée la
plus
appropriée à appliquer à un gisement souterrain d'hydrocarbures. La méthode
peut
également servir dans le cadre d'opérations de dépollution de terrains
industriels par
exemple.
Etat de la technique
1) Études expérimentales :
La détermination expérimentale des perméabilités relatives d'un milieu
poreux où se déplace un fluide polyphasique n'est pas une tâche aisée. On
simplifie
habituellement les opérations de mesure en considérant que l'une des phases
est
immobile dans un état de saturation irréductible.
Les valeurs sont acquises par exemple par une méthode expérimentale connue
dite de "steady state" pour déterminer les perméabilités relatives et qui
consiste à
laisser s'écouler un fluide triphasique avec des rapports de débit imposés
entre les
phases. Les perméabilités relatives exprimées en fonction des deux
saturations, sont
calculées en appliquant la loi de Darcy à chaque phase. Il est loin d'être
établi que les
mesures des perméabilités relatives obtenues par cette méthode soient bien
représentatives des déplacements des fluides et, de toute façon, elles sont
longues à
obtenir car à chaque changement de régime, il faut attendre qu'un régime
d'équilibre
s'établisse.
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
3
Une autre méthode connue consiste à réaliser des essais en laboratoire pour
déterminer des tableaux de mesures (tel que celui de la Fig.1) reliant les
perméabilités relatives et les saturations pour chaque couple de fluides du
mélange
triphasique. Par ajustement des courbes de production expérimentales, on
essaie
progressivement d'ajuster les perméabilités relatives triphasiques. Ces
tableaux de
données sont introduits alors dans un simulateur numérique de type Athos qui
calcule les productions de fluides. Cette méthode étant basée sur
l'acquisition
préalable de nombreuses mesures expérimentales ajustées progressivement par
calage, est longue à mettre en oeuvre.
2) Modèles de perméabilités relatives
Le modèle empirique connu dit de Stone permet, par des corrélations
empiriques, de prédire des données relatives à un écoulement triphasique à
partir de
données correspondant à un écoulement diphasique. Il est valide seulement dans
les
cas d'une forte mouillabilité à l'eau et on le considère généralement comme
faiblement prédictif.
On connaît deux types de modèles physiques pour modéliser les écoulements
triphasiques, basés sur les courbes de pression capillaire. Les courbes de
pression
capillaire sont en relation avec une saturation (par exemple celle du mercure
injecté)
et un rayon de pore, auquel s'arrête le mercure pour une pression d'injection
donnée,
déterminée par la loi de Laplace, Pinj.= 26
r
Un premier modèle de représentation des milieux poreux, est décrit par :
- Burdine, N.T.: "Relative permeability calculations from pore size
distribution
data" Trans AIME (1953) Vol. 198 ; ou par
- Corey, A.T.: "The interrelation between oil and gas relative
permeabilities", Prod
Monthly (1954) Vol.19,38.
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
4
Suivant ce modèle, le milieu poreux est représenté par un faisceau de
capillaires cylindriques avec une distribution de rayons qui sont donnés par
la courbe
de pression capillaire obtenue par injection de mercure. Les perméabilités
sont
obtenues par application de la loi de Poiseuille à l'écoulement de fluides
dans ces
capillaires.
Ce modèle est basé sur la représentation du milieu poreux comme un
assemblage de capillaires de rayons différents. La relation entre le volume et
le rayon
des pores est donnée par la valeur de la pente du pseudo-plateau. Les trois
fluides
sont censés se partager les capillaires, le fluide mouillant (l'eau) occupant
les plus
1o petits, le fluide le moins mouillant (le gaz), les plus gros, le troisième
fluide (l'huile)
une zone de pores de dimensions intermédiaires. Il n'est pas possible de
décrire les
interactions entre les fluides puisque dans un tel modèle, ils s'écoulent dans
des
chenaux séparés. Ce modèle enfin, ne peut être utile que si le pseudo-plateau
couvre
une large gamme de saturations. Suivant ce modèle, les trois phases d'un
écoulement
triphasique se déplacent dans des capillaires différents et il n'y a entre
elles aucune
interaction.
Un autre modèle physique connu de représentation d'un milieu poreux est
décrit par :
- de Gennes, P.G.: "Partial Filling of a Fractal Structure by a Wetting Fluid"
Physics of Disordered Materials 227-241, New York Plenum Pub. Corp. (1985) ;
repris par
- Lenormand, R. "Gravity Assisted Inert Gas Injection: Micromodel Experiments
and Model based on Fractal Roughness", The European Oil and Gas Conference
Altavilla Milica, Palermo, Sicily, (1990).
Suivant ce modèle, on considère que la surface interne des pores est isotrope
et à caractère fractal et peut être modélisée sous la forme d'un "bouquet" de
rainures
capillaires parallèles qui font que les pores présentent une section
transversale
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
fractale. La section transversale de chaque pore est construite suivant un
processus
itératif (Fig.l). On divise le demi-périmètre d'un cercle de rayon Ro en il
parties et en
remplaçant chacune de ces il parties par un demi-cercle ou rainure. A chaque
étape k
du processus, Nk nouvelles rainures semi-circulaires de rayon Rk et de section
totale
5 Ak sont créées.
La dimension fractale DL de la section transversale à la fin de l'étape k est
reliée au nombre d'objets Nk généré avec l'échelle donnée IK, par la relation
:
Nk ` I k DL
La dimension fractale peut être déduite d'une courbe de pression capillaire de
mercure selon la procédure suivante. Du mercure est injecté dans un milieu
poreux
avec une pression d'injection qui croît par paliers. La loi de Laplace permet
de
déduire le volume des pores connaissant le volume de mercure injecté pour une
pression d'injection donnée et l'on peut construire la courbe de pression
capillaire en
drainage reliant la pression d'injection à la quantité de mercure injectée et
la courbe
reliant la proportion du volume total occupé par les pores et la taille des
pores. Dans
le cas où l'on draine un liquide mouillant hors du milieu poreux tel que de
l'eau par
une injection de gaz, la corrélation entre la pression capillaire gaz-eau et
la saturation
de la phase mouillante est donnée par :
DL-2
P=s}y
Les résultats expérimentaux montrent aisément que les valeurs des
perméabilités relatives gaz-eau exprimées en fonction des trois saturations,
obtenues
à partir des expressions qu'en donnent les modèles connus et les modes de
répartition
des phases dans la structure des pores, sont loin des valeurs mesurées et donc
que les
modèles en cause se révèlent par trop simplistes pour représenter les
interactions
complexes qui se produisent entre les phases fluides.
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
6
Par le brevet FR 2 772 483 (US 6 021 662), on connaît une méthode de
modélisation pour optimiser de façon plus rapide et plus réaliste les
conditions de
déplacement dans un milieu poreux mouillable par un premier fluide (de l'eau
par
exemple), d'un mélange de fluides incluant ce fluide mouillant et au moins un
autre
fluide (de l'huile et éventuellement du gaz). Cette méthode fait appel à une
modélisation des pores du milieu poreux par une distribution de capillaires à
répartition fractale en considérant, dans le cas d'un mélange triphasique eau
(fluide
mouillant)-huile-gaz par exemple une stratification des constituants à
l'intérieur des
pores, avec l'eau au contact des parois, le gaz au centre et l'huile formant
une couche
intercalaire. Elle comporte une détermination expérimentale de la courbe de
variation
de la pression capillaire dans les pores en fonction de la saturation
relativement aux
phases liquides, d'où l'on déduit les valeurs de dimension fractale
correspondant à
une série de valeurs données de la saturation relativement à la phase liquide.
Elle
comporte aussi une modélisation des perméabilités relatives directement sous
forme
d'expressions analytiques dépendant des différentes valeurs de dimension
fractale
obtenues et en accord avec la répartition stratifiée des différents fluides
dans les
pores. Un simulateur de milieu poreux est utilisé à partir de ces
perméabilités
relatives pour déterminer les conditions optimales de déplacement des fluides
dans le
milieu poreux.
Le phénomène d'hystérésis fait référence aux variations des propriétés
pétrophysiques (perméabilités relatives, pression capillaire, indice de
résistivité,
etc ...) que l'on observe suivant qu'on procède à la mesure en drainage ou en
imbibition (ces modes correspondent respectivement à une augmentation et à une
diminution de saturation de la phase non-mouillante). Ce phénomène doit donc
être
pris en considération pour fournir des valeurs de perméabilités relatives
représentatives.
L'état de la technique concernant les effets d'hystérésis dans les milieux
diphasiques et triphasiques, est décrit par exemple dans les publications
suivantes :
CA 02383764 2007-12-28
7
- Land C.S. : Calculation of imbibition relative permeability for two and
three-
phase flow from rock properties , Trans AIME 1968, Vo1243, 149 ;
- Larsen J.A. , Skauge A. :" Methodology for numerical simulation with cycle-
dependent relative permeability", SPEJ, June 1998 ; et
- Carlson F.M. : Simulation of relative permeability hysteresis to the non
wetting
phase ', SPE 10157, ATCE, San Antonio Texas, 4-7 Oct 1981.
La Fig. 6 représente typiquement l'allure des courbes de perméabilités
diphasiques K,,,, résultant d'un drainage jusqu'à la saturation irréductible
en fluide
mouillant (M) puis d'une imbibition jusqu'à la saturation résiduelle en fluide
non-
mouillant (NM). L'hystérésis se manifeste à deux niveaux. A saturations égales
Sg,
on obtient des valeurs numériques différentes et le point limite final atteint
est une
inconnue qui dépend du point de rebroussement SgM à partir duquel on change de
mode de déplacement. On attribue couramment ce phénomène à la fraction de
fluide
non-mouillant piégé. A saturation égale, il n'y a donc pas la même quantité de
fluide
mobile ce qui altère les caractéristiques de l'écoulement.
Pratiquement tous les modèles prenant en compte l'hystérésis font appel à la
relation semi-empirique de Land : 1- 1= CL (1)
SSr S8i
où CL représente la constante de Land. Cette relation relie la saturation
initiale Ss; et
la saturation résiduelle Sb, en fluide non mouillant, pour évaluer les
saturations en
fluide non mouillant piégé et libre. En supposant que cette relation est
valable quelle
que soit la saturation, on l'applique pour déterminer les fractions mobiles
intermédiaires en cours de déplacement. En diphasique, l'association de cette
relation
avec des modèles de perméabilités fournit des résultats satisfaisant.
CA 02383764 2007-12-28
8
En triphasique, l'hystérésis des perméabilités relatives Krg prend une forme
particulière. Expérimentalement, on observe non seulement une hystérésis de
déplacement comme c'est le cas en diphasique (importarice du sens de variation
des
saturations) mais aussi une hystérésis de cycles puisAue les perméabilités
sont
dépendantes de l'historique des saturations. Sur la Fig. 7, les courbes de
perméabilités
relatives K,g correspondant à un premier cycle de drainage et d'imbibition
(respectivement Dl et Il) sont distinctes des courbes correspondantes (D2, I2)
d'un
deuxième cycle.
Le modèle de perméabilités relatives de Larsen et al prend en compte ces
deux formes d'hystérésis. Partant d'une approche combinant le modèle de Stone
en
parallèle avec la formule de Land et la méthode d'interpolation de Carlson,
approche
où seule l'hystérésis de déplacement est prise en compte, il faut le noter,
Larsen et al
ont introduit un facteur de réduction empirique fonction de la saturation en
eau qui
permet d'approcher la réduction de perméabilité du gaz associée à l'hystérésis
de
cycles.
Définition de la méthode selon l'invention
La méthode de modélisation selon l'invention permet d'optimiser de façon
plus rapide et plus réaliste les conditions de déplacement dans un milieu
poreux
mouillable par un premier fluide, de mélanges di ou triphasiques incluant ce
premier
fluide mouillant et au moins un deuxième fluide non mouillant. Elle offre de
ce fait
aux opérateurs, un outil plus fiable pour évaluer notamment les meilleurs
modes de
déplacement des fluides au sein du milieu poreux. en drainage et en
imbibition. Elle
est basée sur une représentation fractale du milieu poreux avec une
modélisation des
pores par une distribution de capillaires à section fractale en considérant
une
répartition stratifiée des fluides à l'intérieur des pores, le fluide
mouillant se
répartissant au contact des parois et autour du deuxième fluide (ou des deux
autres en
triphasique).
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
9
La méthode comporte en combinaison :
- la détermination expérimentale de la courbe de variation de la pression
capillaire
(Pc) dans les pores d'un échantillon de ce milieu poreux en présence d'un
fluide
mouillant et d'au moins un fluide non mouillant, (par injection de mercure
dans
un échantillon placé sous vide par exemple) ;
- la détermination à partir de cette courbe de pression capillaire, des
valeurs de la
dimension fractale correspondant à une série de valeurs données de la
saturation
relativement aux liquides ;
- la modélisation des effets d'hystérésis modifiant les saturations mobiles
des
fluides effectivement déplacés en fonction du nombre de cycles de drainage et
d'imbibition subis par l'échantillon, en faisant intervenir des constantes de
piégeage ou de dépiégeage du fluide non mouillant différentes selon que l'on
réalise une phase de drainage ou d'imbibition ;
- la modélisation des perméabilités relatives directement sous forme
d'expressions
analytiques dépendant des différentes valeurs de dimension fractale obtenues ;
et
- l'introduction des perméabilités relatives dans un simulateur du milieu
poreux et
la détermination au moyen de ce simulateur, des conditions optimales de
déplacement des fluides du mélange dans le milieu poreux.
La méthode s'applique par exemple à la détermination des déplacements de
mélanges de fluides comportant un premier fluide mouillant, un deuxième fluide
non
mouillant et un gaz, en considérant une répartition stratifiée des fluides à
l'intérieur
des pores, le fluide mouillant se répartissant au contact des parois, le gaz
occupant le
centre des pores et le deuxième fluide étant réparti sous la forme d'une
couche
annulaire au contact à la fois du gaz et du premier fluide.
La méthode peut s'appliquer notamment à la détermination par un simulateur
de gisement, des caractéristiques optimales de substances additionnées à des
CA 02383764 2007-12-28
bouchons de fluide mouillant injectés dans une formation en alternance avec
des
bouchons de gaz, dans le but de déplacer des hydrocarbures en place, ou bien
encore
celles d'un fluide injecté dans le sol pour déplacer des substances
polluantes.
La modélisation des phénomènes obtenue par la méthode présente de grands
avantages. Elle permet une meilleure adéquation avec les résultats obtenus en
laboratoire car les phénomènes physiques sont mieux pris en compte. Les
résultats du
modèle sont meilleurs de ce fait lors d'un changement d'échelle par exemple,
pour la
modélisation d'une application sur un champ d'opérations.
10 Le temps de calcul est réduit comparé à celui qui est nécessaire quand on
utilise des tables, comme avec les méthodes antérieures. La modélisation de
type
fractal réalisé est mieux à même de traiter les effets d'hystérésis rencontrés
dans
l'utilisation des procédés d'injection de type WAG.
Les résultats de la méthode sont en outre parfaitement intégrables dans de
nombreux simulateurs de réservoir : simulateurs 3D, hétérogènes,
compositionnels,
etc.
L'exploitation des résultats par les logiciels d'application est facilitée. Il
n'est
plus nécessaire de faire des interpolations risquées comme c'est la règle
quand on
opère à partir des valeurs discrètes des tableaux de résultats, pour tracer
des isoperms
par exemple.
Présentation des figures
D'autres caractéristiques et avantages de la méthode selon l'invention,
apparaîtront à la lecture de la description ci-après d'un exemple non
limitatif de
réalisation, en se référant aux dessins annexés où :
- La Fig. 1 qui illustre sous forme d'un tableau, les liens existant pour un
mélange triphasique entre les valeurs obtenues expérimentalement, de
perméabilités relatives d'un fluide et les saturations pour deux des trois
fluides;
CA 02383764 2007-12-28
11
- la Fig. 2 montre une représentation fractale d'un pore;
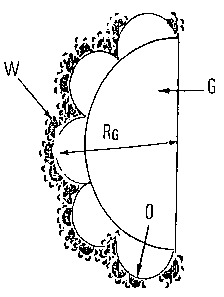
- la Fig. 3 montre de façon schématique la répartition des phases d'un
fluide triphasique dans un pore fractal avec le fluide mouillant W au
contact de la paroi, la phase gazeuse G répartie dans la plus grande
partie du volume du pore (rayon RG), l'huile O étant une couche entre le
fluide mouillant et le gaz;
- la Fig. 4 montre en fonction de la saturation en eau, la courbe de
pression capillaire d'un échantillon de grès des Vosges par exemple, dont
la pente locale S sert à déterminer la dimension fractale des pores; et
- la Fig. 5 montre en fonction du temps, les courbes de production
obtenues expérimentalement pour du gaz (G) pour de l'eau (W) et pour
de l'huile (O), comparées aux courbes équivalentes obtenues par
simulation en utilisant la méthode selon l'invention;
- les Fig. 6A, 6B montrent les effets de l'hystérésis de déplacement
affectant les perméabilités relatives du fluide mouillant et du gaz,
respectivement K,w et Kr9 ;
- la Fig. 7 montre les effets combinés de l'hystérésis de déplacement et de
cycles observés expérimentalement sur la phase gazeuse;
- la Fig. 8 montre les courbes-clés servant à la modélisation de la
constante de dépiégeage ;
- la Fig. 9 montre le résultat obtenu avec le modèle dans le cadre d'une
injection de type WAG; et
- la Fig. 10 montre la validation du modèle sur une expérience de type
WAG pour les courbes de récupération des trois phases.
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
12
Description détaillée de la méthode
La méthode selon l'invention permet de déterminer les perméabilités relatives
triphasiques de milieux poreux, en s'appuyant sur un modèle de type fractal du
milieu
poreux, en se basant sur une approche décrite par :
- Kalaydjian, F.J-M et al. : "Three Phase Flow in Water-wet Porous Media:
Determination of Gas-oil Relative Permeabilities under Various Spreading
conditions"; 68th Ann. Tech. Conf. And Exh. of the SPE, Houston, Texas, 1993.
La méthode selon l'invention comporte, comme on l'a vu une modélisation de
l'écoulement des phases avec répartition des phases à l'intérieur de la
structure
fractale de chaque pore. Dans le cas d'un écoulement d'eau et d'huile au sein
d'une
structure poreuse mouillable à l'eau, l'huile s'écoule dans le volume du pore.
Dans le
cas d'un écoulement triphasique, il y a répartition stratifiée, l'eau qui est
le fluide
mouillant, s'écoule le long des parois des pores, le gaz circule dans le
volume du pore
et l'huile s'écoule entre le gaz et l'eau. Les saturations sont calculées
comme étant la
surface relative dans une section transversale occupée par chacun des fluides.
A l'équilibre, toutes les rainures ayant un rayon supérieur à Rk qui est donné
par la loi de Laplace Pc=2 r sont occupées par le gaz, les tubes les plus
petits, par
R~_
les deux autres fluides (eau et huile). Ainsi on exprime la saturation en
fluide
mouillant comme la fraction de l'aire des tubes occupés.
En calculant la fraction de l'aire des capillaires occupée par l'eau pour tous
les
rayons entre Rk et R, on aboutit à l'expression :
R Ja-DL
Sw Ro
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
13
et comme Pc=2 R, la corrélation entre la pression capillaire et la saturation
de la
k
phase mouillante est donnée par
1
P, = Sw DL-2
où S, est la saturation de la phase mouillante.
La représentation graphique de cette corrélation dans un diagramme log-log
est une ligne droite partant du point (S, Pc) correspondant au capillaire le
plus grand
de la structure fractale avec un rayon Ro. On peut supposer que :
- le rayon Ro, le premier envahi quand le mercure est injecté (Fig.4),
correspond à
une valeur de la saturation de l'ordre de 1/r=103. Chaque segment de la courbe
de
pression capillaire est une partie d'une ligne partant de Ro (supposée la même
pour tous les différents segments), correspondant à la corrélation Pr, Sw déjà
citée. Chaque ligne a une pente donnée, on peut lui associer une dimension
linéaire fractale. Les valeurs de la pente varient de -1,5 à -3,3 comme le
montre la
Fig.4, ce qui conduit à des valeurs de la dimension linéaire fractale DL entre
1,3 et
1,7.
- chaque domaine est atteint par le mercure pour des saturations correspondant
à
l'emplacement où on trouve Ro sur chaque ligne.
La saturation des deux liquides quand le gaz est présent dans le pore, est
calculée comme expliquée plus haut pour une phase :
2-by
[~OL
SLiq. = en supposant que les deux liquides occupent les tubes dont les rayons
sont inférieurs
ou égaux à RK et le gaz, le centre de chaque pore. La saturation en huile est
l'aire
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
14
relative de la section transversale des rainures occupée par l'huile dont le
rayon est
inférieur ou égal à RK.
Modélisation de l'hystérésis
Pour procéder au calcul des perméabilités relatives, il est nécessaire de
déterminer pour chaque phase la fraction qui circule et par conséquent,
d'estimer de
façon systématique, les saturations correspondant aux fractions stagnantes.
Ceci doit
être fait pour les deux cas étudiés, par exemple le drainage de l'eau et de
l'huile par le
gaz, et l'imbibition en eau.
L'originalité de la modélisation proposée ici est de prendre en compte
l'hystérésis directement à son origine c'est-à-dire au niveau des phénomènes
de
piégeage et dépiégeage de la phase non mouillante. Sur la Fig.8, si les
courbes
pouvaient se déduire exactement par translation, cela signifierait qu'une
partie du gaz
est restée piégée au cours du drainage secondaire et ne participe pas à
l'écoulement.
En réalité, ce n'est pas le cas mais le fait qu'à saturation en gaz égale, la
perméabilité
soit plus faible au cours de D2 que pendant Il signifie que la fraction de gaz
piégé est
plus importante au cours du drainage. En d'autres termes, la non réversibilité
des
courbes de perméabilités peut s'expliquer par une non réversibilité
(hystérésis) entre
le phénomène de piégeage et celui de dépiégeage.
On conserve donc la formule de Land (équation 1) mais on introduit une
constante de dépiégeage valable pendant les phases de drainage, différente de
la
constante de Land valable pendant les phases d'imbibition. Tout revient donc à
modéliser l'évolution de la constante de dépiégeage au cours des cycles.
Les caractéristiques à prendre en compte au niveau de la formulation sont les
suivantes. On considère que CP=CL pendant toutes les phases de piégeage car on
se
trouve directement dans les conditions d'application de Land où une constante
unique suffit à décrire le phénomène. Pour S., faible en fin de drainage, CD
est proche
de C. On traduit juste ici le fait que le gaz est plus facile à dépiéger
lorsqu'il y en a
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
peu dans la carotte car on peut alors penser qu'il se trouve dans des pores de
grosse
taille facilement reconnectables lors de la réinjection. Quand Sg, augmente,
CD
devient supérieur à CL ce qui traduit un dépiégeage moins efficace.
Pour des saturations en gaz élevées, on retrouve une certaine réversibilité
5 mais il existe une fraction de gaz piégée inaccessible dans des pores de
petite taille.
On atteint donc une courbe de Krg unique basse qui correspond à un cas pseudo
diphasique où l'huile n'est plus mobile.
D' après cette représentation qui repose sur des observations expérimentales
et
des hypothèses de travail, la valeur de CD passe par un maximum puisque la
10 constante de dépiégeage est égale à CL à la fois quand Sgr est faible et
quand il est
maximum lorsque l'on décrit la courbe de basse mobilité. L'expression suivante
permet de concilier tous les aspects précédents :
1 E
- Krg - KrgSg`
CD -~- C
D KDl sr DM CL) L (2)
rg gr2
Cette formulation comporte plusieurs paramètres :
15 CDM : il prend en compte l'écart entre le piégeage et le dépiégeage ;
CL : constante de Land ;
Krgnùn : courbe de basse mobilité ;
E : paramètre de calage.
Kirg: valeur de la perméabilité relative au gaz au début de l'imbibition
précédente.
KDlrg: valeur de la perméabilité relative au gaz sur la courbe de premier
drainage
pour la saturation en gaz correspondant à K.
Quel que soit l'ordre et la nature du cycle considéré, la relation (2) et la
relation de Land (1) permettent de déterminer les saturations piégées et
mobiles par
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
16
l'intermédiaire de la formule de Land tout en prenant en compte le caractère
triphasique de l'hystérésis (déplacement et cycles) sans recours à des
facteurs de
réduction empiriques.
Sgf _ 2 SS - Sgr + (SS - Sgr )z + ~ \Sg- Sgr ) (3)
etSg=Sgt +S9f (4)
C est égal à CL ou CD suivant le mode de déplacement ;
Sgf: saturation en gaz libre ;
Sgt: saturation en gaz piégé.
Calcul des perméabilités relatives:
A) Perméabilités relatives des liquides
L'application de la loi de Poiseuille à chaque capillaire du faisceau pour la
phase qui l'occupe, permet de calculer les perméabilités relatives à l'eau et
l'huile
(Fig.5).
Des études expérimentales effectuées par ailleurs (Larsen et al) ont montré
qu'il existait une relation permettant de relier la saturation résiduelle en
huile au
cours des cycles et la fraction de gaz piégé.
Sor - (Sor ) Sgt=O -aSgt
-(SoT)sgc=o représente la saturation en huile résiduelle laissée en place dans
le
milieu avant que du gaz soit piégé.
En ne considérant que la fraction en circulation qui contribue à la
conductivité
hydraulique, les perméabilités relatives pour l'eau et l'huile s'expriment de
la manière
suivante:
CA 02383764 2002-02-27
WO 02/06794 PCT/FR01/02212
17
K,o = Kro (2Ph)[(Sz. +Sst )Q -(SN, +(1-a)Sgt +(Sor)sgt=o)a]
K,N = (SW -R(1-a)Sgt)P -SP~
R est le facteur de réduction lié au piégeage de la phase non mouillante.
Dans ces expressions, il est utile de mentionner que :
- la saturation en eau irréductible SWi est supposée stable.
- La gamme de tailles de capillaires occupée par l'huile mobile est calculée
comme
la différence entre les tailles des capillaires occupés par les deux liquides
avec la
saturation totale en liquide SL=So+Sw, et celles des capillaires saturés en
eau et en
huile stagnante.
- Kro(2ph.) représente la valeur de la perméabilité relative à l'huile
déterminée par
un test d'imbibition à l'eau et l'huile. Quand les phases eau et huile sont
seules
présentes et comme l'échantillon testé est mouillable à l'eau, l'huile
s'écoulera
dans la section du pore exactement comme le fait le gaz dans un écoulement
triphasique.
B) Perméabilité relative au gaz
Comme le gaz est une phase non mouillante, il occupe l'espace central du
pore et il s'étend vers sa périphérie au fur et à mesure que la saturation en
gaz
augmente, sans toutefois arriver au contact de la paroi solide (Fig.6). On
considère
que le gaz circule dans un seul pore dont le rayon Rg est donné par la
relation :
Rg = Ro+Rj +R2+ ... + Rk,
la perméabilité au gaz étant donnée alors par :
Krg = Krgmag (1- (SL + Sgt )" )4 (5)
CA 02383764 2007-12-28
18
avec a 2_DL DL représentant la dimension fractale linéaire du milieu poreux et
SL
étant la saturation totale en liquide égale à 1-Sg.
Le modèle de perméabilités relatives permettant de calculer K, Kro et Krg est
implanté dans un simulateur tel qu'ATHOS ou GENESYS . Cela permet de
procéder au calage d'expériences réalisées au laboratoire mais aussi
d'optimiser les
conditions à remplir pour déplacer des fluides pétroliers en place dans un
gisement,
que ce soit par injection de gaz soit par injection alternée de bouchons d'eau
et de gaz
(méthode dite WAG), en tenant compte des conditions de pression et de
température
régnant à la profondeur de production.
Validation
La méthode selon l'invention a été validée à travers plusieurs types
d'expériences :
- On a injecté du gaz dans des milieux poreux contenant de l'eau et de
l'huile, dans
des conditions très variées. On voit sur la Fig. 5 par exemple que l'on
obtient un
très bon accord entre les courbes de production des trois phases (eau, huile,
gaz)
obtenues expérimentalement et celles prédites par le simulateur de gisement
alimenté par les données obtenues en accord avec la méthode.
- On a aussi injecté alternativement du gaz et de l'eau (injection de type
WAG). La
Fig. 10 montre que l'on obtient dans ce cas aussi un accord excellent
pour les trois phases tout au long de la durée de l'expérience.