Note: Descriptions are shown in the official language in which they were submitted.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-1 -
Tamper Resistant Software Encoding
The present invention relates generally to computer software and electronic
hardware, and more specifically, to a method, apparatus and system resistant
to
tampering and reverse engineering, including a particular implementation for
the
Digital Encryption Standard (DES).
Background of the Invention
The use of computers and computer software in all of their various forms is
recognized to be very common and is growing everyday. In industrialized
nations,
hardly a business exists that does not rely on computers and software either
directly
or indirectly, in their daily operations. As well, with the expansion of
powerful
communication networks such as the Internet, the ease with which computer
software programs and data files may be accessed, exchanged, copied and
distributed is also growing daily.
In order to take advantage of these computer and communication systems
and the efficiencies that they offer, there is a need for methods of storing
and
exchanging computer software and data securely. One such method that has
demonstrated widespread use and acceptance is encryption of data using secret
cryptographic keys. Such methods are generally accepted as secure, as an
attacker
must perform an impractically large number of mathematical tests to identify
the
cryptographic key required to decode a given encrypted data file. Cracking the
Data
Encryption Standard (DES) for example, would require an average of 255
different
keys to be tested, requiring more than 1 million years of testing at a rate of
one
hundred million key tests per second. DES is a block cipher method which is
very
fast and is widely used. If the cryptographic key is kept secure, it offers
very good
security.
The number of tests required to solve triple DES and other related techniques
employing cryptographic keys varies correspondingly with the complexity of the
method.
However, present cryptographic key-based methodologies have a major
weakness in that they require the cryptographic key to be known by both the
encrypting and decrypting parties. An attacker who is able to obtain knowledge
of
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-2-
both the cryptographic key and the encrypted data is able to decode the
message.
The attacker may obtain this information in many ways, including the
following:
Intercepting data packets while in transit through the Internet. This may be
done for example, by the Internet Service Provider (ISP) for the end user, or
another party on the End User's local network. Theoretically, this may also
be done by any attacker who is able to monitor a node on the Internet which
routes the data packets, as the Internet is not a secure network.
2. Reading the cryptographic key and encrypted data file while they are stored
on the user's computer or server, which again, may easily be done by
another party on the local network. An outside attacker may also be able to
read these files by transmitting a software agent to the user's computer
programmed to search for the desired files and transmit them back to the
attacker.
If the intercepted files are not protected in some other manner, the attacker
will have immediate access to what he requires. There are methods of hiding
the
cryptographic keys and data files, but typically, the attacker need only
observe the
execution of the decryption algorithm with the target files, to obtain the
original
cryptographic key and data file.
These vulnerabilities have encouraged many attempts to hide secret
cryptographic keys in tamper-resistant, secret-hiding software. Tampering
refers to
changing computer software in a manner that is against the wishes of the
original
author. If for example, a cryptographic key is encrypted into a password file
with
which the user accesses a certain server, one would not want an attacker to
obtain
the file and modify it to: identify the cryptographic key, obtain access to
the server
himself, or modify privileges that the file may identify. However, because the
attacker has complete access to the software code he has intercepted, there is
no
way of stopping the attacker from observing its execution and making arbitrary
changes.
Attempts to hide secret cryptographic keys in software have been notably
ineffective. Therefore, a far more powerful approach to the cryptographic key-
hiding,
tamper-proofing problem is required. Because of its widespread use, it is
particularly
desirable to provide such a solution for the Data Encryption Standard (DES),
where
the software can be stored and may be executed without revealing the
cryptographic
key.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-3-
In addition to the hiding of the cryptographic key, the encrypted data file
itself
may contain information which must be secured. For example, biometric
information
may be used for identification purposes, but it is undesirable to use
biometric
information because it cannot be replaced once it is compromised. Each person
has
a finite number of biometric identifiers such as two sets of fingerprints, one
voice and
two retinas. Therefore, the use of biometric data is only practical if it can
be
implemented in a manner that eliminates risk of compromise due to
dissemination of
such non-replaceable data.
Previous Approaches Are Either Expensive or Weak
Many attempts have been made to provide secret-hiding and tamper-
resistance computer software. Hardware approaches, for example, have been
proposed in profusion.
Among hardware-based approaches, "dongles" and smart cards, which move
data and code inside a physical device, are the most common. These approaches
are costly to administrate and transport compared to software-based
approaches,
where manufacture is virtually free and transport can be electronic.
A "dongle", for example, is a special piece of plug-in hardware which
implements part of the algorithm to be protected. Hence, the software program
being protected will not work correctly unless the dongle is physically
plugged in.
Obviously, this is a high-cost approach and does not work on a standard
computer
platform. Indeed, it requires the platform to be changed to include the dongle
whenever the protected program is to be run.
Due to their structural limitations, smart cards have been far more vulnerable
to penetration of their secrets than was hoped, news media describing
incidents of
smart card penetration on a regular basis. As well, smart card methods require
an
investment in card reading hardware and the cards themselves, which can be
expensive to implement broadly.
A highly elaborate hardware-based approach which is totally inapplicable to
the installed base of personal computers is presented by Rafail Ostrovsky and
Oded
Goldreich in Comprehensive software protection system, United States Patent
No.
5,123,045. This proposal uses a physically enclosed CPU (Central Processing
Unit)
which executes code as a "black box", so that execution cannot be observed by
an
attacker. If external RAM (Random Access Memory) buffers are required, data is
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-4-
only stored in the RAM in an encrypted form. This method cannot be applied to
existing computers, is expensive, and is not mobile.
Hence, existing hardware approaches are generally inapplicable to the
installed base of personal computers, and would be, or are, costly to
administrate
and deploy. Because of these difficulties, a number of attempts have also been
made to provide a software solution to tamper-resistance and secret-hiding.
The simplest methods use special-purpose tricks to prevent unauthorized
copying of software, including start-up code examining supposedly unused parts
of
an attached hard-disk, 'fingerprinting' particular personal computer (PC)
environments, and querying hardware, operating-system-provided, or network-
provided identifiers. These methods have been defeated by attackers on a
regular
basis. As is well known, special-purpose copy programs which casually remove
copy-protection from PC software in transit are available for a fairly modest
price.
A software approach for computing with encrypted data is described by Niv
Ahituv, Yeheskel Lapid, and Seev Neumann, in Processing encrypted data,
Communications of the ACM 30(9), Sept. 1987, pp. 777-780. This method hides
the
actual value of the data from the software doing the computation. However, the
computations which are practical using this technique are quite restricted,
and as a
result, this method is not suitable for DES encryption key hiding.
Christian Collberg, Clark Thomborson, and Douglas Low, in Manufacturing
cheap, resilient, and stealthy opaque constructs, ACM SIGPLAN-SIGACT
Symposium on Principles of Programming Languages, January, 1998, provide a
method for concealing the intent of the control flow in a software program,
using
basic obfuscation methods. Obfuscation is the process of making the
organisation
of software code more confusing and hence, more difficult to modify.
The low-level structure of a software program is usually described in terms of
its data flow and control flow. Control flow, which is the subject of Collberg
et al., is
a description of how control is transferred from one location in the software
code to
another during execution, and the tests that are performed to determine those
transfers. In contrast, data flow is a description of the variables together
with the
operations performed on them.
In particular, Collburg et al. obscure the decision processes in the program,
that is, they obscure those computations on which binary or multiway
conditional
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-5-
branches determine their branch targets. Clearly, there are major deficiencies
to this
approach, including:
1. because only control flow is being addressed, domain transforms are not
used and data obfuscation is weak; and
2. there is no effort to provide tamper-resistance. In fact, Collburg et al.
do not
appear to recognize the distinction between tamper-resistance and
obfuscation, and as a result, do not provide any tamper-resistance at all.
The approach of Collburg et al. is based on the premise that obfuscation can
not offer a complete solution to tamper protection. Collburg et al. state
that: "... code
obfuscation can never completely protect an application from malicious reverse-
engineering efforts. Given enough time and determination, Bob will always be
able
to dissect Alice's application to retrieve its important algorithms and data
structures."
In Breaking abstractions and unstructuring data structures, IEEE International
Conference on Computer Languages, 1998, Christian Collberg, Clark Thomborson,
and Douglas Low provide more comprehensive proposals on obfuscation, together
with methods for obfuscation of structured and object-oriented data.
There remains a weakness, however, even in the methods proposed by
Ahituv et al. and Collberg et al. Obfuscation and tamper-resistance are
distinct
problems, and while weak obfuscation is provided by Ahituv et al. and Collberg
et al.,
they do not address tamper resistance at all. For example, consider removing
password protection from an application by changing one branch from a
conditional
one to an unconditional one. Plainly, this vulnerability cannot be eliminated
effectively by any amount of mere obfuscation. A patient attacker tracing the
code
will eventually find the "pass, friend" / "begone, foe" branch instruction.
Identifying
this branch instruction allows the attacker to circumvent a protection routine
by
simply re-coding it to a non-conditional branch. Therefore, other methods are
required to avoid such single points of failure.
Existing general-purpose commercial software obfuscators use a variety of
techniques including: removal of debugging information, changing variable
names,
introducing irreducible flow graphs, and particularly in the case of Java,
modifying
code structures to avoid stereotyped forms for source control structures.
These
methods produce superficial changes, but the information exposed by deeper
analyses employed by optimizing compilers and similar sophisticated tools is
changed very little. The data flow and control flow information exposed by
such
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-6-
analyses is either not affected at all, or is only slightly affected, by the
above
methods of obfuscation.
Irreducibilities can be handled by well-known compiler techniques.
Information present at the 'machine' code level, or equivalent, is not
obscured at all,
including the data used in computation. For example, information about DES
encryption and decryption, and probably any reasonably secure form of
encryption or
decryption, cannot be hidden effectively using techniques such as these.
An alternative approach is to encrypt the program either as a whole or in
parts, and then to decrypt the program or its components temporarily as they
are
needed. An example of such a strategy is offered by David Aucsmith and Gary
Graunke, in Tamper-resistant software: an implementation, Proceedings of the
First
International Workshop on Information Hiding, Cambridge, UK., 1996. This
method
exposes executable images of the program or its components to logic analysers
and
the like, permitting recovery of the original program either entirely, or in a
piecemeal
fashion as its components are exercised. Moreover, unless this paper's subject
problem of hiding cryptographic keys is also solved, the cryptographic key can
be
extracted from the software and used to decrypt the entire program.
The level of obfuscation obtained using the above techniques is plainly quite
weak, since the executed code, control flow and data flow analysed in graph
form, is
either isomorphic to, or nearly isomorphic to, the unprotected code. That is,
although the details of the obfuscated code are different from the original
code, the
general organisation and structure have not changed.
Attempts have also been made to hide the real code by introducing dummy
code, for example, by making every other statement a dummy statement designed
to
look much like the real code. Along with the higher overhead created, this
approach
has two fatal weaknesses:
1. It is vulnerable to data flow analysis (DFA) to discover the dummy code.
2. Even if DFA can be rendered ineffective, if x% of the code is dummy code,
then 100 - x% of the code is significant. For realistic values of x, a patient
attacker can locate which statements matter and which do not, by trial and
error.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-7-
Attempts have also been made to hide cryptographic keys by a variety of
more specific approaches, including:
1. Splitting the cryptographic key into pieces stored in different locations
in the
software code. This is ineffective as the pieces can be reassembled by
tracing execution of the code.
2. Modifying the encryption algorithm to allow use of a disguised key. This is
ineffective as human memory capacities limit the amount of disguise to a
small number of algorithmic steps.
3. Use of a disguised algorithm. Similar to point 2 above, this is ineffective
due
to the restrictions imposed by limited human memory capacities.
In addition, a variety of cryptographically weak approaches have been used
for encryption and decryption, to avoid the use of any explicit key whatever.
These
methods are vulnerable either to a cryptographic black-box attack if plain-
text can be
recognized in an automated way, or to algorithmic analysis with the aid of
debugging
tools, since the would-be encryption is then a data transformation of quite
limited
algorithmic complexity.
In general, then, the state of the art has been that programs could not be
made effectively secret-hiding and tamper-resistance. In particular,
cryptographic
keys for reasonably secure ciphers could not be securely hidden in software.
There is therefore a need for a method, apparatus and system for encryption
that is tamper-resistant, allowing secret cryptographic keys, biometric data
and
encrypted data to be transmitted and stored together, without fear that
security will
be breached.
Summary of the Invention
It is therefore an object of the invention to provide a method and system that
improves upon the problems described above.
One aspect of the invention is broadly defined as a method of increasing the
obscurity and tamper-resistance of a software program, comprising the steps
of:
randomly generating substantive yet redundant arguments; and inserting those
arguments into the data flow of the software program.
Another aspect of the invention is defined as an apparatus for increasing the
obscurity and tamper-resistance of computer software code comprising: randomly
generating substantive yet redundant arguments; and inserting those arguments
into
the data flow of the software program.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
_g_
A further aspect of the invention is defined as a computer readable memory
medium, storing computer software code executable to perform the steps of:
randomly generating substantive yet redundant arguments; and inserting those
arguments into the data flow of the software program.
An additional aspect of the invention is defined as a computer data signal
embodied in a carrier wave, the computer data signal comprising a set of
machine
executable code being executable by a computer to perform the steps of:
randomly
generating substantive yet redundant arguments; and inserting those arguments
into
the data flow of the software program.
Brief Description of the Drawings
These and other features of the invention will become more apparent from
the following description in which reference is made to the appended drawings
in
which:
Figure 1 presents a flow chart of a general algorithm for implementation of
the
invention;
Figure 2 presents an exemplary computer system in which the invention may be
embodied;
Figure 3 presents a data flow diagram of the outer structure of the DES
standard;
Figure 4 presents a data flow diagram of a single round of the DES standard;
Figure 5 presents a flow chart of the overall algorithm in a preferred
embodiment of
the invention;
Figure 6 presents a flow chart of the unrolling routine in a preferred
embodiment of
the invention;
Figure 7 presents a data flow diagram of the initial connections of one T-box
operation, in an embodiment of the invention;
Figure 8 presents a data flow diagram of T-box connections after partial
evaluation
in an embodiment of the invention;
Figure 9 presents a flow chart of a longitudinal diffusion routine in a
preferred
embodiment of the invention;
Figure 10 presents a flow chart of a lateral diffusion routine in a preferred
embodiment of the invention; and
Figure 11 presents a flow chart of network obscuring in a preferred embodiment
of
the invention.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
_g_
Description of the Invention
A method which addresses the objects outlined above, is presented as a flow
chart in Figure 1. This figure presents a method of increasing the obscurity
and
tamper-resistance of a software program by:
1. randomly generating substantive yet redundant arguments at step 10; and
2. inserting those substantive yet redundant arguments into the data flow of
the
software program at step 12.
This process obscures the valuations of the original arguments in the software
program, making it very difficult to make changes which are useful for
perturbation
analysis.
As noted above, the low-level structure of a software program is usually
described in terms of its data flow and control flow. Data flow is a
description of the
variables together with the operations performed on them. Control flow is a
description of how control jumps from place to place in the program during
execution, and the tests that are performed to determine those jumps.
The method of the invention in broad terms, is to add new redundant
arguments into the data flow of the program. The simplest example of a pair of
redundant arguments is: a first argument which increments the value of a
variable in
one operation, immediately followed by a second operation which decrements the
value of the same variable. Such a pair of operations is redundant in that
they do
not affect the outcome of the software code. This example is for illustrative
purposes
only; much more complex examples are described hereinafter.
In the method of the invention, these redundant arguments are substantive in
that they are applied to variables used in the software program, and they
actually do
alter the value of those variables. This is in contrast to "dummy code" used
in the
art, which does not actually execute and can be identified using data flow
analysis
techniques. With the method of the invention, it is quite difficult to
distinguish which
operations are from the original software code, and which have been added.
As these redundant arguments ultimately have no impact on the outcome of
the software program, they can be generated randomly. Techniques for
generating
random numbers, known in the art, can easily be applied to the generation of
random equations as explained in greater detail hereinafter.
Hence, a cryptographic key can be incorporated into a software program,
without the danger of the cryptographic key being disclosed, or the program
being
altered to do anything other than what it was originally intended to do.
Similarly,
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-10-
passwords, biometric data and other secure programs and data files can also be
securely stored, transferred and executed using the method of the invention.
As described above, cryptographic keys are often used to encrypt data flies
to prevent unwanted parties from reading or using the data files.
Unfortunately, the
cryptographic keys must also be transmitted between the communicating parties,
and are generally stored at both locations, leaving many opportunities for
discovery
by unwanted attackers.
In the invention, the cryptographic key is made secure by obscuring the data
flow of the program.
Tamper-resistance, in the sense of creating software which changes
behaviour drastically in response to small changes, was thought in the art to
be
irrelevant to secret-hiding, such as hiding a cryptographic key. Actually, it
is quite
relevant as it makes perturbation-based analysis (analysis by examination of
responses to small changes) much more difficult.
In the application of the invention to encryption using a cryptographic key,
it is
possible for an attacker to observe the execution and not obtain any useful
information. At no time during the execution does the actual key data appear.
In the preferred method described hereinafter, the new arguments are based
on multiple inputs and outputs, preferably three or more. This makes the
arguments
of the software program intimately interconnected with one another, so it is
not
possible to alter one entry without altering many outputs. This provides even
greater
tamper resistance and protection against perturbation analysis.
This method is unaffected by a data flow analysis attack, because all of the
software code, including the added redundant code, is actually executed. As
well,
the method of the invention is not vulnerable to black-box or debugging
attacks.
Being a software solution, the cost of the invention is very small and can be
transported electronically. The invention has none of the costly
administrative and
physical limitations of hardware solutions.
In terms of obfuscation, the invention is far superior to anything generally
available in a commercial obfuscator. Obfuscation may be simply defined as
making
the organisation of the software code more confusing and hence, more difficult
to
modify. Obfuscation is inherently provided by the invention, but the invention
goes
much further by providing a tamper-resistant solution. As noted above,
obfuscation
merely makes software code more confusing to analyse, while tamper-resistance
makes software code resistant to small changes, in the sense that any small
code
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-11-
change produces a massive, unpredictable behavioural change. While obfuscation
can ultimately be overcome by patient observation, tamper-resistance requires
a
great deal of analysis to overcome. The degree of complexity of tamper-
resistance
is easily scalable, so that the degree of analysis required to overcome it can
be
made impractically great.
Further, the method of the invention does not require any disguises or
personal passwords to be remembered or stored, so there is no dependence on
human memory or other human limitations.
An example of a system upon which the invention may be performed is
presented as a block diagram in Figure 2. This computer system 14 includes a
display 16, keyboard 18, computer 20 and external devices 22.
The computer 20 may contain one or more processors or microprocessors,
such as a central processing unit (CPU) 24. The CPU 24 performs arithmetic
calculations and control functions to execute software stored in an internal
memory
26, preferably random access memory (RAM) and/or read only memory (ROM), and
possibly additional memory 28. The additional memory 28 may include, for
example,
mass memory storage, hard disk drives, floppy disk drives, magnetic tape
drives,
compact disk drives, program cartridges and cartridge interfaces such as those
found in video game devices, removable memory chips such as EPROM or PROM,
or similar storage media as known in the art. This additional memory 28 may be
physically internal to the computer 20, or external as shown in Figure 2.
The computer system 14 may also include other similar means for allowing
computer programs or other instructions to be loaded. Such means can include,
for
example, a communications interface 30 which allows software and data to be
transferred between the computer system 14 and external systems. Examples of
communications interface 30 can include a modem, a network interface such as
an
Ethernet card, a serial or parallel communications port. Software and data
transferred via communications interface 30 are in the form of signals which
can be
electronic, electromagnetic, optical or other signals capable of being
received by
communications interface 30.
Input and output to and from the computer 20 is administered by the
input/output (I/O) interface 32. This I/O interface 32 administers control of
the
display 16, keyboard 18, external devices 22 and other such components of the
computer system 14.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-12-
The invention is described in these terms for convenience purposes only. It
would be clear to one skilled in the art that the invention may be applied to
other
computer or control systems 14. Such systems would include all manner of
appliances having computer or processor control including telephones, cellular
telephones, televisions, television set top units, point of sale computers,
automatic
banking machines, lap top computers, servers, personal digital assistants and
automobiles.
The invention will now be described with respect to the particular application
to the Digital Encryption Standard (DES) encryption and decryption.
High-Level View of Techniques Used for Tamper-Resistance and Obscuring
The approach of the invention to tamper-resistance, secret-hiding software is
based on the following principles. It should be recognized that while the
invention
provides inherent obscurity, which is a widely-recognized principle in
software
protection, tamper-resistance is a distinctly different focus:
1. Targeting: The approach taken is specifically directed to the operations to
be
performed and the data to be manipulated. For example, in the case of DES,
the techniques used are specially suited to the data and operations employed
in DES. It would be clear to one skilled in the art how to tailor the
techniques
disclosed herein, to other software programs.
2. Fusion: Encoded software handles the data in such a way that multiple
components are manipulated together, so that separating out individual
original (i.e., pre-encoding) data operations is difficult, and tampering with
one entity in effect modifies the behaviour of more than one entity.
3. Diffusion: Encoded data and computation distribute information among
multiple sites, so that no site alone is sufficient for understanding,
ambiguity
is increased, and tampering at individual sites is made less effective.
4. Fake robustness: Presumably, true robustness would preserve the same
computation even after some forms of tampering. The invention 'fakes' such
robustness by avoiding failure responses to data in the presence of
tampering. Instead, computation proceeds with apparent normalcy, but along
nonsensical lines. This is strongly allied to the principle of anti-
holographic
behaviour.
5. Anti-holographic behaviour: Tampering with a small part of a hologram
causes a slight reduction in resolution. The method of the invention induces
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-13-
the opposite behaviour, where the effect of any small change is to produce
large, wide-spread, cascading changes in behaviour.
6. Partial evaluation: Part of the process of hiding constant input data is to
partially evaluate the application with respect to that data. In the case of
DES
key-hiding, for example, the cryptographic key is constant and is eliminated
by partial evaluation. This principle is allied to the principle of diffusion,
where the components of the cryptographic key are then distributed to
multiple locations.
Description of DES
The Digital Encryption Standard (DES) is a block cipher, where a piece of
software to be encoded is broken down into sixty-four-bit blocks which are
operated
upon separately. DES inputs a sixty-four-bit block to be encrypted or
decrypted and
a sixty-four-bit raw key and outputs a sixty-four-bit result. Only fifty-six
bits of the
raw key are actually used: the low-order bit of each raw key 8-bit byte is
discarded,
or can be used for parity.
DES will only be described herein with sufficient detail to explain the
invention. A more detailed description of (single) DES is provided in FIPS
(Federal
Information Processing Standards in the United States) publication 46-3. A
description and an extensive discussion are also provided by Bruce Schneier,
Applied Cryptography, ISBN 0-471-11709-9, John Wiley & Sons, 1996, DES
receiving particular attention on pp. 265-294.
There are only three kinds of data operations in DES:
1. Selecting some or all bits from a bit-string and re-ordering them into a
new
bit-string, possibly with multiple appearances of certain bits. Schneier et
al.
refer to these as permutations, though this is not quite accurate since they
are not necessarily bijections. Therefore, such transformations will referred
to herein as quasi-permutations (QPMs), with the true permutations being the
special case of a OPM being a bijection.
Each QPM operation is controlled by a table which for each to-bit of the
output bit-string gives the from-bit in the input bit-string whose value it
has,
except for key-shift QPMs, which are simple rotation permutations, each of
which is described by a simple signed shift count.
2. Bit-wise exclusive or (XOR).
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-14-
3. Looking up elements in a table (LKP). In DES, before performing any
transformations, these are look-ups in sixty-four-element tables of 4-bit-
strings (each of which is called an S-box - S for "substitution"), using a 6-
bit-
string as an index. Initially, each LKP operation is controlled by one of
eight
S-box tables indicating the substitutions it is to perform.
Figure 3 presents a data flow diagram of the outer structure of DES. This
presentation is intended to emphasize the three basic kinds of operations
making up
DES, as described above. Italicized numbers adjacent to the arrows indicate
the bit-
widths of the indicated values. The outer box 34 represents the entire DES
algorithm, whether encryption or decryption. The inner structure of DES
comprises
sixteen rounds of processing 36, which are identical except for one minor
variation in
the final round and the variations in one of the internal QPM operations,
namely, the
key shift, QPMe, which is explained hereinafter. The initial permutation, QPMa
at
step 38, and the final permutation, QPMc at step 40, are true permutations,
that is,
there are no omissions and no duplicated bits. Note that QPMc at step 40 is
the
inverse of QPMa at step 38. The key transformation, QPMb at step 42, selects
fifty-
six of sixty-four bits from the raw key, and rearranges the bits.
Figure 4 presents a data flow diagram of the internal structure of one of the
sixteen DES rounds at step 36. Left In and Right In are the left and right
halves of
the data being encrypted or decrypted as it enters the round, and Left Out and
Right
Out are these halves after the processing has been performed by the rounds.
Key In
is the fifty-six-bit key as it enters the round, and Key Out is the fifty-six-
bit key as it
leaves the round. The expansion permutation, OPMd at step 46, repeats certain
bits, whereas the compression permutation, QPMf at step 48, which produces the
round sub-key as its output, omits certain bits.
The key shift, QPMe at step 44, consists of rotations of the left and right
halves of the fifty-six-bit key by an identical amount, in a direction and
with a number
of shift positions determined by the round number and by whether encryption or
decryption is being performed. LKP h 1 - h 8 at step 50 (performing S-box
substitution) are the eight S-box lookup tables performed in the round. In the
DES
standard, the indices for the LKP operations h 1 - h 8 at step 50 are each, in
effect,
preceded by yet another OPM operation, which permutes the six input bits so
that
the low-order or right-most bit becomes the bit second from the left in the
effective
index, but this OPM can be eliminated to match what has been shown above by re-
ordering the elements of the S-box tables. The P-box permutation, QPMi at step
52,
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-15-
permutes the results of LKP h 1 - h 8 at step 50, presumably to accelerate
diffusion
of information across all bits.
The XORg operation at step 54 is a simple Boolean exclusive OR on the
outputs of the QPMd at step 46 and the output from the QPMf at step 48.
Similarly,
the XORj operation at step 56 is a simple Boolean exclusive OR on the outputs
of
the Left In and the output from OPMi at step 52.
Note that all rounds are performed identically except for the previously
mentioned differences in the key shift, QPMe, and the swapping of Left Out and
Right Out, relative to what is shown in Figure 3, in the final round.
Detailed Description of Preferred Embodiments of the Invention
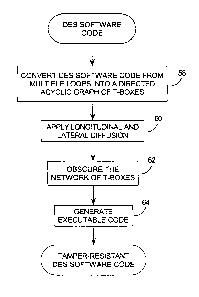
A flow chart of the preferred embodiment method of the invention is
presented in Figure 5. This flow chart provides an overview of techniques
which will
be described in greater detail with respect to Figures 6 through 10. Briefly,
these
techniques are:
1. converting the original DES software code from multiple loops to a directed
acyclic graph of T-boxes, at step 58;
2. applying lateral and longitudinal diffusion, at step 60. Lateral diffusion
is the
splitting of data flow into separate streams and diffusing data laterally
between the separate streams, while longitudinal diffusion is the additional
of
"padding" into the sequential sequence of the software program;
3. applying additional techniques to obscure the network of T-boxes, at step
62;
and
4. generating executable software code at step 64.
Due to the abundance of QPM operations, DES operations are handled by
the invention at the level of individual Boolean values in accordance with the
Targeting principle. At that level, the original QPM operations no longer
appear as
operations in the data flow; instead, they simply determine connectivity of
the LKP 50
and XOR 54, 56 operations. Note that none of the operations can terminate
abnormally, irrespective of their inputs, but changing the inputs or the
operation
changes the result, hence, the implementation of the invention is completely
fake
robust. Moreover, as with many ciphers, slight changes produce cascading, wide-
spread behavioural changes, so that the invention exhibits anti-holographic
behaviour.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-16-
Firstly, the preferred method of effecting step 58, that of converting the
original DES software code from the multiple loops to a directed acyclic graph
of T-
boxes, is presented as a flow chart in Figure 6.
Since the forty-eight bits emitted by the compression permutation, QPMf at
step 48, are entirely determined by the original key and the round number, no
information travels from the data-portion to the key-portion of the round of
DES.
Hence, when the sixteen rounds are unrolled completely, leaving a directed
acyclic
graph (DAG), that is, a loop-free network of Boolean operations, the key-
portion can
be eliminated by constant folding. Hence, the network may be partially
evaluated for
a given key. This will be described in greater detail with respect to steps 66
through
72 of Figure 6.
The unrolling of the sixteen DES rounds at step 66 can be effected by
duplicating the round network fifteen times and connecting the sixteen blocks
of
software code end-to-end. Then, the eight S-boxes can be copied fifteen times,
so
that there are separate copies of the original eight S-boxes for each round.
Since
there are sixteen rounds, this means that after copying, there are 128 S-
boxes.
Next, at step 68, the lookup tables or S-boxes of the DES can be simplified to
avoid multiple-output operations, and to facilitate optimization and other
changes.
This is done by converting the 4-output S-boxes to 1-output T-boxes, where
there is
one T-box for each output of an S-box (including each output of an S-box which
is a
copy of an original S-box). "T" stands for "tiny", since only one bit is
emitted per T-
box.
This yields sixteen rounds with thirty-two T-box tables in each round, or 512
independent T-box tables in all, each containing sixty-four Boolean elements
since
each has six Boolean inputs.
That is, the eight S-box lookup tables, LKP h 1 - h 8 at step 50, can be
replaced with thirty-two T-box lookup tables, LKP k 1 - k 32. If the bits of
the S-box
elements are regarded as columns in a Boolean or bit matrix, then each T-box
is one
column of the corresponding S-box. LKP k 1 - k 4 represent LKP h 1, with each
output representing one bit of the original h 1 output; LKP k 5 - k 8
represent LKP h
2, and so on. The T-box lookup tables in different rounds are independent of
one
another because a separate set of S-boxes were created for each round,
therefore,
the tables in one round can be modified without affecting the others.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-17-
After the above-described targeting of the operations in DES, the initial
connections surrounding one T-box operation, LKP k i , appear as shown in
Figure 7.
Forty-eight bit round keys are constant in each round as they are entirely
determined
by the round number and the original cryptographic key. Therefore, at step 70
the
forty-eight bit XOR block at the beginning of the round, shown as "XOR g" at
step 54
of Figure 4, can be eliminated.
Hence, the method is as follows:
1. Note that in Figure 7, the right operands of XOR m 1 - m 6 are constants
from the cryptographic key. Hence, the right operands can be deleted and
each XOR replaced with a Boolean identity (if the constant is false) or a
Boolean NOT operation (if it is true). Therefore, in each round, replace the
initial block of forty-eight bit-wise XORs by forty-eight unary operations,
where each unary operation is an identity operation (that is, it returns the
input unchanged) if the corresponding forty-eight-bit key bit was 0, and is a
NOT operation (that is, it returns the input's complement) if the
corresponding
forty-eight-bit key bit was 1.
This step incorporates the secret cryptographic key into the software code.
2. These identities and NOT operations can then be eliminated by connecting
the LKP inputs directly to the operations previously providing inputs to the
identities and NOTs. To do this, the contents of the LKP table must be
adjusted to allow for the effect of any inputs resulting from the elision of a
NOT operation. This is easily accomplished by re-ordering the elements of
the tables. Therefore, in each round:
a. eliminate the identity operations created above by connecting their
input directly to the destinations) of their output; and
b. eliminate the NOT operations created above by connecting their input
directly to the destinations) of their output and modifying the tables of
their destination T-boxes so that the output of the T-boxes remains
the same as it would have been if the NOTs had not been eliminated.
The operation count is then further reduced and the structure of the DES
implementation simplified at step 72 by eliminating the remaining bitwise XOR
blocks, shown as "XOR j" in Figure 4. This is done by folding the XOR shown as
XOR n in Figure 7 together with the LKP shown as LKP k i above.
In each round, replace the block of thirty-two T-boxes performing the "QPM i"
operation of Figure 4 and the block of thirty-two XORs performing the "XOR j"
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-18-
operation of Figure 4 with thirty-two new T-boxes performing both of those
operations. That means each new T-box created by this step has one extra
input;
that is, instead of six inputs, it has seven. The table is adjusted so the
combined
function of "QPM i" and "XOR j" is correctly computed.
In other words:
1. a new leftmost input is added to LKP k i and connects it to the input to
XOR
n; and then
2. XOR n is eliminated, by taking the elements of LKP k i 's table, making a
copy but with every element inverted, and concatenating that to the end of
the original table.
The result is that the new LKP (LKP k' i , say) now includes the effect of XOR
n, thereby increasing the degree of fusion in this implementation, and
yielding a
version of DES consisting of 512 seven-input T-box lookup operations,
connected
together. The connections of a typical LKP operation, after step 72, are shown
in
Figure 8. Steps 66 through 72 are referred to herein as "partial evaluation".
Information from the cryptographic key and the manipulations of the
cryptographic key has now been diffused into the T-box LKP operations,
beginning
to satisfy the principle of diffusion of computations and data. That is, the
cryptographic key does not explicitly appear in the software code. Note,
however,
that the connections of a T-box LKP from the second previous round, created by
eliding the XOR operations of XOR n (see Figure 7) reveal the identities of
the T-
box LKPs. This problem is addressed in a later transformation.
Next, the optional step of injecting identity T-boxes into the data flow may
be
performed at step 74.
Note the connectivity of the look up tables after partial evaluation, shown in
Figure 8. Six of a T-box's inputs are from T-boxes farther from the source
values
than the other; that is, six are from a more recent round and one from an
earlier
round.
In order to obscure the connectivity, the simple connection labelled from left
data in Figure 8 can be replaced with a new T-box (the "injected" T- box),
which
inputs this value and also includes a random set of six other inputs, chosen
to make
the connectivity of the injected T-box look similar to that of existing T-
boxes, that is,
injection makes the left and right side connectivity look similar. These six
other
inputs may be ignored (that is, they act as "don't care" inputs). Such T-boxes
will be
referred to herein as "identity T boxes".
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-19-
Immediately following this step, the identity T-boxes are easy to identify as
data flow analysis of the T-box table for an identity T-box reveals that only
one of the
inputs is significant. However, after further transformations are applied to
them,
other bits become significant and the identity T-boxes are harder to identify.
At this point, the original software program is now a DAG with the values of
the cryptographic key and lookup tables distributed throughout the software
code.
The techniques of longitudinal and lateral diffusion are now applied to the
partially
evaluated software code per step 60 of Figure 5.
Longitudinal diffusion injects a diffusing network before, after or between a
pair of "real" rounds. As noted above, DES is vulnerable to attacks starting
at the
beginning and the end of the computation (see Schneier et al.), so to address
this
vulnerability, the DES implementation of the invention is "padded" with
additional
code, particularly at the beginning and end. This "padding" has two very
significant
properties:
1. it is inserted into the longitudinal flow of the program in such a way that
the
programs outputs are dependent on the code. This is in contrast to "dummy
code" as known in the art, where the final outputs are not dependent on the
code. Hence it can be identified by data flow analysis (DFA) techniques; and
2. it uses cryptographic identities based on randomly chosen keys, intended to
deceive the attacker, so any information that an attacker gleans from analysis
of the pads will lead him to incorrect conclusions about the actual
cryptographic key.
The method for adding longitudinal diffusion is presented as a flow chart in
Figure 9. First, at step 76, cryptographic identities are generated,
specifically
chosen to permit their implementation by means of T-boxes. A cryptographic
identity
comprises a T-box sub graph which computes an identity by first encrypting and
then
decrypting the data, using some key not related to the DES key that is being
hidden.
Examples of cryptographic identities would be: n-round DES encryption with
some
randomly chosen key K r , followed by n-round DES decryption using K r , where
n
would typically be some even number less than sixteen. However, any DES
variant,
or indeed any sufficiently DES-like cipher whatever, can also be used, to
further
complicate the problem of identifying the S-boxes given the T-boxes. If the
cryptographic identities are DES-based, one would typically omit the initial
and final
permutations from the identities. (See Schneier et al., pp. 294-300, for
examples of
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-20-
DES variants.) Techniques for generating the various randomly chosen keys are
well known in the art.
Then, at step 78, these identities are inserted into the DES implementation,
either at the beginning, the end, or in the middle, between any pair of
unrolled
rounds. For protection against attacks beginning at the ends, it is preferred
to place
such padding before and after 1 or more initial round pairs, and before and
after 1 or
more final round pairs.
Since the pads are identities, they have no effect on the output of the
software code. At this point, they do not sound like a sensible addition as
complementary pairings of sixty-four Boolean equations would stand out during
tracing of the software. However, after further techniques have been applied,
they
no longer have the appearance of identities.
These identities, even after further processing, continue to have the property
inherent in DES-like ciphers that interfering with any individual Boolean, or
any
computation which produces such a Boolean, has a diffuse effect, altering many
bits
in future computations. Hence, this padding is not dummy code. It changes what
happens in response to tampering, thereby contributing to anti-holographic
behaviour. That is, any small change will have an increased tendency to
produce a
wide-spread, cascading effect over many output bits; even more so than in
ordinary
DES (with respect to the 'real' rounds). The specific need to protect the
beginning
and end of the computation is also addressed by the invention. Pads also
increase
the obscurity of the implementation: there is no longer just one key for an
attacker to
identify in any given hidden-key cryptographic function; there are several.
Further pads may be injected at points in the middle of the computation to
increase anti-holographic behaviour as much as one desires. At a minimum, it
is
preferred to enclose a sequence of initial round pairs (one or more) between
two
pads, and similarly for a sequence of final round pairs.
Next, lateral diffusion is performed, as presented in Figure 10. Lateral
diffusion may be described as splitting the data flow of the program into
separate
streams and then diffusing data laterally between the separate streams. A
simple
implementation will first be described which employs a two-input Boolean
function,
then improvements will be described which result in a much stronger
implementation:
At step 80, choose an existing T-box (which will be referred to as originan
and generate two new T-boxes (which will be referred to as left and right),
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-21 -
with the same dimensions as original. Note that the original T-box must not
be a final output T-box.
2. At step 82, choose a Boolean function with two inputs and one output. There
are sixteen of these, but one should not use Boolean functions for which
some input is a 'don't care'. There are six functions that must therefore be
rejected, specifically, those which output constant true, constant false, the
left input, the right input, not the left input, and not the right input. The
remaining ten Boolean functions are substantive and usable, and one of such
functions can be chosen at random for any given pair of left, right look up
tables. The function chosen for any particular left, right pair of tables will
be
identified as "func".
3. Fill the tables for left and right at step 84, proceeding as follows:
a. For each element, indexed by i in original, where i ranges from 0 to
127 inclusive (since the T-boxes have seven inputs at the start of this
transformation), choose a pair of values x, y for the left and right
elements indexed by i, respectively, such that func (x, y) has the same
value as element i of original.
b. There are often multiple choices of Boolean x, y value pairs which
achieve the desired output, so one can choose randomly among such
choices. Of course, one must be careful not to make selections that
cause the new left or right table to be identical to the original.
c. Insert the chosen x, y value pair into the outputs of the left and right
look up tables, at the same index location as the original.
4. Last, at step 86, insert the two new tables into the data flow of the
software
code so that the old index to the original table now indexes both of the new
tables. Similarly, insert the random Boolean function into the data flow of
the
program following the two new tables, so that the outputs of the two tables
are directed to the Boolean function.
This process effectively converts seven-input T-boxes into eight-input T-
boxes, randomly diffusing information from the original T-box between left and
right
T-boxes, and adding random, redundant information. This process can also be
generalized to the case of an n-input T-box LKPs, where n >_ 8. Initially, n =
8, but as
additional techniques are applied, n may take on higher values with the
splitting of
more inputs into input pairs. (Note: the T-boxes started with six inputs,
folding in the
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-22-
XOR changed it to seven, and adding one further input increases this from
seven to
eight.)
The Boolean value stored in the table of a resulting 8-input T-box look up
operation for any 8-bit input vector is determined as follows: Let A and B be
bit-
s strings with a combined length of six bits, and let u, v, and w be
individual bits. For
any element indexed by some index AuvB (variables juxtaposed in this manner
represent concatenation of their bit values) in the expanded 8-input table,
the value
stored is the same as that of the element indexed by AwB in the 7-input table
from
which it is derived, where w = func (u, v). The same logic extends to n > 8.
By working this transformation backwards from the output T-box LKP
operations to the beginning of the DES implementation graph, one can arrange
that,
in general, T-box LKP operations other than those producing the final outputs
and
the initial ones whose inputs are not from other T-box LKP operations, have
more
than seven inputs.
This transformation is quite simple, and contributes greatly to obscurity, by
diffusing information among T-box LKP operations and thereby making their
contents randomly perturbed relative to their original contents. Moreover, it
tends to
make the injected pad identities not quite identities anymore.
However, it can be made combinatorially stronger (that is, increase the
number of possible functions above ten), and at the same time address the T-
box
identification problem mentioned at the end of the section on partial
evaluation, with
the following refinement: instead of having func be a function of only two
Boolean
inputs, it can be made a function of three Boolean inputs, where one of the
inputs is
one of the inputs of original which comes from the round previous to original.
Let us
call this extra input p. Then func must be a Boolean function such that:
1. if there is a 'don't care' input, it is the p input; and
2. for each value of p, it is possible to make func return either true or
false by
modifying the other inputs.
This increases the number of choices for func from ten to 100. Then LKPs
which used to input from original input from all of: left, right, and the LKP,
or the
original input from the start of DES, which is the source of p.
Then, the uses of func (x, y) and func (u, v) above, are replaced with uses of
func (p, x, y) and func (p, u, v), respectively. Filling in the table for the
expanded
input set is a straightforward extension of the methods used above. In
addition to
increasing the combinatorial complexity of determining the contents of the
diffused
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-23-
tables in left and right, this refinement makes it much harder to identify
which T-box
LKP corresponds to which column of which S-box, since connections from two
rounds back become more frequent, and this plus a later T-box LKP input
permutation step make T-box LKP identities ambiguous.
It is important to make suitable choices for original and for the source of p.
Examination of the interconnection pattern for T-box LKP operations will show
that in
many cases one can make the identity of a T-box LKP with respect to a column
in an
S-box ambiguous, by increasing the number of inputs from two rounds previous
from
one to two or more, so that it is not clear which input from the second
previous round
came from eliding an XOR (XOR j in Figure 4) and which was added by the
diffusion
transformation. When this is combined with the obscuring transformation of
step 62,
which permutes the T-box LKP inputs, it makes identification of T-box LKPs
with
their corresponding S-box columns far more difficult, combinatorially
speaking. The
details depend on the nature of the expansion permutation (QPM d in Figure 4)
and
the P-box permutation (QPM i in Figure 4), which together determine the
connectivity among rounds.
The above approach, with or without the recommended refinement, easily
extends from producing left, right pairs of T-box LKP operations to producing
triplets
- left, middle, right- or even quadruplets or larger numbers. The number of
inputs
in non-initial T-box LKP operations can then be increased, either by producing
more
pairs, or by producing triplets or quadruplets instead of pairs, or by some
combination of these approaches. One can also vary the number of inputs among
T-box LKP operations, making the structure of the DES implementation highly
irregular.
Next, the network of T-boxes is obscured by encoding the input vectors of
non-initial T-boxes, referred to as step 62 in Figure 5. As each input vector
is
encoded, adjust the table of the T-box so its output is not affected. At this
point, the
T-box operations have 7- or 8-bit input vectors (or, optionally, larger ones).
The
encoding consists of flipping randomly chosen bits and permuting the positions
of
the vector elements as shown in the flow chart of Figure 11:
1. First, the flipping part of the encoding is performed at step 88. Inputs
are
selected for inversion randomly. This is done only where the sources of
these inputs are internal to the implementation; that is, do not flip any bits
in
the input data. When a bit is flipped, the bits of its source T-box's table
are
inverted. That is, obtaining the NOT of the output of previous outputs.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-24-
Inputs to T-boxes may come from shared sources. As a result, when two T-
boxes disagree on the encoding of inputs coming from the same other T-box,
that source T-box is no longer fully sharable (since its output must be
delivered to one client flipped and to another unflipped). As a result, this
stage increases the number of T-box LKP operations in the implementation.
2. The second part of the coding at step 90, is to randomly permute the inputs
of each T-box LKP operation. The elements of each T-box LKP table are re-
ordered to allow for the new arrangement of the inputs.
These modifications to the T-box LKP tables intermingle elements which
previously were widely separated, increasing the degree of fusion. They also
increase the obscurity, as does the presence of multiple T-boxes derived from
one
T-box, and containing different tables. Moreover, the previously described pad
rounds injected into the software code have now very definitely ceased to be
identities.
The final step is to generate executable code from the network of T-boxes
per step 64 of Figure 5.
Up to this point, a symbolic Boolean DAG has been described, which is not in
a form suitable for execution on any platform. Since the DAG consists entirely
of T-
box LKP operations, it is preferred to implement DES based on the DAG, as
follows:
Each LKP operation can be represented by a call to a utility function. For an
n-input LKP, this requires n + 1 arguments. The extra argument is a pointer to
the
table of Boolean functions to be used for that particular LKP operation. The
utility
function compresses its inputs into an index, indexes into its table to find
the result,
and returns that result.
The body of the DES function, then, consists of an initial expansion of the
sixty-four-bit input data block into sixty-four separate values, followed by a
chain of
T-box LKP routine calls, plus any needed loads and stores, implementing the
desired
Boolean DAG's connectivity, followed by a compression of the sixty-four result
Booleans into a sixty-four-bit result value, which is returned.
Optionally, one can reduce the number of arguments to each of the above
LKP routine calls by one, by taking advantage of the fact that the calls are
chained
together in a specific sequential order. Therefore, one can sequence through
the
tables used in the successive calls by having the utility routines index
through a
sequence of tables stored in just that sequential order. Thus, the tables can
be
implicit in the calls, instead of being passed as an argument in each call.
The body
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-25-
of the DES function would then begin by setting the appropriate starting state
for
iterating through these tables.
In summary, one can convert T-boxes into calls to utility routines, with
interspersed code to move outputs to inputs as follows:
1. generate T-box utility calls by topologically sorting the T-box network in
"connected to" order, and emitting code for this sorted order;
2. insert at the beginning of the software code, operations which separate the
sixty-four-bit data input into individual values for arguments to the utility
routines; and
3. insert at the end of the software code, operations which combine sixty-four
separate values into a single sixty-four bit output.
Alternative Embodiments
1. Virtual Machine Interpreter
A variation on the generation of executable code described above, which is
somewhat more compact, is to utilize an interpreter for a T-box virtual
machine (TVM) with some number (see below) of 1-bit registers. An
interpreter is a program that directly executes high-level code, as opposed to
a compiler which generates machine language for execution. A virtual
machine is a self-contained operating environment which can execute on a
computer or similar device. The Java Virtual Machine, for example, will run
the same way on any computer.
In addition to the 1-bit registers, the TVM contains a linear table of bits
and a
counter indicating how many of the bits in this linear table have been
consumed. The linear table comprises the concatenation of the tables of all
of the T-boxes in their intended execution order. Each TVM instruction
comprises a series of fields, namely:
a. bit consumption count, indicating how many bits of the linear table are
to be consumed. That is, what the size of the table is for the T-box
represented by this instruction;
b. input count, indicating how many inputs this T-box has;
c. series of input register numbers, indicating which 1-bit register
corresponds to which T-box input; and
d. output register number, indicating which 1-bit register receives the
result of the T-box lookup represented by this instruction.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-26-
The TVM's program comprises a sequence of such instructions, followed by
an instruction with a bit consumption count of 0, indicating termination of
the
program.
The number of 1-bit registers needed is the largest number of values
computed but not yet consumed at any point during execution of the
particular executable T-box ordering chosen for the graph. At start-up, a
sixty-four element prefix of the TVM's 1-bit registers are filled with the
data to
be encrypted or decrypted, and at termination, the sixty-four element prefix
contains the encrypted or decrypted result value.
2. Bit-Exploded and Bit-Tabulated Coding
Several means of data flow encoding for tamper-resistance are disclosed in
the co-pending patent application "Tamper Resistant Software Encoding",
United States Patent Application No. 09/329,117, which is incorporated
herein by reference. Two such methods disclosed in this application which
are particularly well suited to hiding Data Encryption Standard (DES) Keys
are Bit-Exploded coding and Bit-Tabulated coding.
Similar to the above, these methods begin by unrolling the DES algorithm
and introducing the tables and encryption key to each round as constants.
The sixteen 'rounds' of DES may be unrolled at the source level, or by
applying aggressive loop unrolling to unroll the rounds in the code optimizer.
The tamper resistance and obfuscation are added to this unrolled code as
follows:
a. The principle of the bit-exploded coding technique is to convert n-bit
variables into n Boolean variables. That is, each bit of the original
variable is stored in a separate and new Boolean variable.
Each such new Boolean variable may either be unchanged or inverted
by interchanging true and false. For example, this means that for a
thirty-two-bit variable, there are 232, a little over 4 billion, bit-exploded
codings to choose from. These variables and their transforms are
recorded in a "phantom parallel program", so that the inversions can
be rationalised with other equations and operations in the software.
At this point, the software code contains excessive bulk, but may be
reduced using conventional constant folding. The effect is that the
cryptographic key has now completely disappeared, but the code bulk
remains large.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-27-
b. Further encoding is now performed by bit-exploded to bit-tabular
optimization.
Bit-exploded coding may produce data flow networks having
subnetworks with the following properties: they have only a
reasonably small number of inputs; and they are acyclic; that is,
contain no loops.
When this occurs, one can replace the entire network or subnetwork
with a table lookup. This results from the fact that an m-input, n-
output Boolean function can be represented by a zero-origin table of
2"' n-bit elements. Instead of including the network in the final
encoded program, it is simply replaced with a corresponding table
lookup, in which one indexes into the table using the integer index
formed by combining the m inputs into a non-negative integer,
obtaining the n-bit result, and converting it back into individual bits.
Note that the positions of the bits in the index and the result of the
above lookup can be random, and the network can be previously
encoded using the bit-exploded coding, so the encoding chosen for
the data is not exposed.
A completely different set of look up tables has now been produced which
bears no discoverable relation to the originals and correspond only to the
encoded data. The positions of the bits, and to some extent even which part
of the computation has been assigned to which S-box, is now radically
changed. Thereby, this provides an effective means for data-coding small
tables used in table lookup operations.
The same process can be used to create a routine which performs the
corresponding decryption.
This encoding is highly suitable for code in which bitwise Boolean operations,
constant shifts or rotations, fixed bit permutations, field extractions, field
insertions, and the like are performed. Shifts, rotations, and other bit
rearrangements have no semantic equivalent in high-level code, since they
specifically involve determining which bits participate in which Boolean
operations. Hence, such changes are a significant impediment to
decompiling and reverse-engineering.
As well, variables may be transformed in a bit-wise manner using de
Morgan's laws. This encoding results in a substantial increase in the number
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-28-
of operations relative to the original program, except for operations which
can
be "factored out" because they can be done by reinterpreting which variables
represent which bits or which bits are in the representation are inverted.
Why Is It Hard to Find the Cryptographic Key?
The invention presents a new way to generate an implementation of DES
with an implicit, hidden key. It is intended for use where key-hiding is
important, but
the volume of data to be encrypted or decrypted is modest, so that a much
slower
implementation can be tolerated in order to achieve a greatly increased level
of
security. This approach injects a huge amount of random, arbitrary information
into
the structure of the hidden-key DES implementation.
At present, there are, quite simply, no widely accepted, theoretically well
founded metrics for estimating the level of security delivered by a technology
for the
production of secret-hiding, tamper-resistant software. This is a vast
unexplored
area in the theory of computational complexity.
In the absence of such metrics, the effectiveness of the invention can only be
defended on the basis of arguments. In terms of its ability to hide the
cryptographic
key, for example, the invention is highly effective for the following reasons:
1. The way S-box LKP operations are interconnected when the round loop of
DES is unrolled, determines the way the T-box LKP operations are
interconnected after converting from S-box LKPs to T-box LKP operations
and then partially evaluated with respect to the cryptographic key. The
cryptographic key has no effect on connectivity. This would allow one to
identify the T-box LKPs. However, after performing the refined version of
diffusion of information into pairs of T-box LKP tables, followed by encoding
of T-box LKP input vectors, which permutes the inputs, there is no way to
coordinate the arrangement of the T-box LKPs. While analysis of the
combinatorial complexity of T-box identification is a dauntingly difficult
undertaking, it is clear that these transformations make the problem of
identifying the effective positions of individual T-box LKP operations, as
compared to columns of the original S-boxes, a combinatorially sizable
search problem.
2. Even if one could identify all of the T-box LKPs with individual columns in
individual original S-boxes, however, one would still not know the
cryptographic key. Due to padding, an attacker must contend with multiple
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
_29_
keys and unknown boundaries between pad rounds and 'real' rounds. The
difficulty of finding the 'real' key can be increased by using more injected
pads, or pads with more rounds, or both. Due to the encoding and diffusing
of information among tables, and due the large size of the combinatorial
search for ways to coordinate the T-box LKP identities and then recombine
diffused pairs of LKPs back into single LKPs, an extremely large
combinatorial guessing problem has been created to find the cryptographic
key. This problem can be made harder to solve by increasing the number of
inputs in the T-boxes, thereby making more and more T-box tables the result
of combinatorially hidden diffused information.
Exact computation of the search problem's complexity is difficult, even if
most
T-box LKPs have only eight or nine inputs, but the combinatorial complexity of
the
guessing problem is massive, even with a small number of minimal pads
surrounding
only the initial and final round pairs of an implementation. As well, the
complexity will
vary with the particulars of the implementation.
The above method for hiding DES keys may be more useful if it is embedded
in a larger program, and control flow encoding is used in concert with data
flow
encoding in a manner of the invention. This makes the above technique highly
useful, since it is then no longer possible to extract the encryption and
decryption
routines in isolation.
Applications
1. Protection of Biometric Data
Biometric data stored in the software program could not be decrypted by
simply extracting the encryption and decryption components from the
software, because subsidiary techniques would be applied to make
separation into components an even harder problem. Moreover, one would
employ subsidiary tamper-resistant, secret-hiding methods to ensure that
comparisons of biometric data do not compromise it, even when the attacker
has full debugging access, and that the behaviour of the application
performing such operations is not modifiable in any way useful to the
attacker. Hence, the biometric information can be well protected both locally
and globally.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-30-
2. Encode 'Plain-Text' and 'Ciphertext' and Embed the DES
Implementation in a Larger Tamper-Resistance, Obscure Program
To this point, an implementation has been described in which the DES
implementation is standard. In practice, to achieve much greater protection,
the following additional methods are proposed:
Use an encoded implementation in which input and output blocks are
encrypted or decrypted from, and encrypted and decrypted to, an encoded
format with bits permuted and some bits flipped, as described in the section
on Bit-Exploded Encoding in co-pending patent application "Tamper
Resistant Software Encoding", United States Patent Application No.
09/329,117. In many contexts, one can compute with such encoded data
using the methods of co-pending patent application "Tamper Resistant
Software Encoding", United States Patent Application No. 09/329,117, and
using an encoded plain-text form makes the problem of penetrating the DES
implementation to find the cryptographic key significantly harder.
Also, deploy the product of the instant process in a larger, tamper-resistant,
information-hiding program, such as a program produced by the methods
described in co-pending patent application "Tamper Resistant Software
Encoding", United States Patent Application No. 09/329,117 and "Tamper
Resistant Software - Control Flow Encoding", United States Patent
Application No. 09/377,312. If other computations in the vicinity of the DES
implementation can be implemented similarly, this makes finding the
beginning and end of the DES implementation much harder, rendering
discovery of the cryptographic key, or information about the S-boxes, or
effective tampering with the implementation, yet more difficult.
While particular embodiments of the present invention have been shown and
described, it is clear that changes and modifications may be made to such
embodiments without departing from the true scope and spirit of the invention.
For
example, rather than using the techniques described above, alternate
techniques
could be developed which diffuse a cryptographic key, biometric or other data
throughout a software program.
There are many uses for software applications which embed and employ a
secret encryption key without making either the cryptographic key or a
substitute for
the cryptographic key available to an attacker. The method of the invention
can
generally be applied to these applications.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-31 -
The teachings herein are easily modified to apply to a different arrangement
of lookup tables, rather than the 4-output S-boxes, or to an application with
a number
of rounds, or format of the initial and final permutations. These applications
would
include, for example, the various triple DES algorithms now available. As
well, one
skilled in the art could apply these obfuscation and tamper-resistance
techniques to
any manner of other software programs.
It is understood that as de-compiling and debugging tools become more and
more powerful, the degree to which the techniques of the invention must be
applied
to ensure tamper protection, will also rise. As well, the concern for system
resources
may also be reduced over time as the cost and speed of computer execution and
memory storage capacity continue to improve.
These improvements will also increase the attacker's ability to overcome the
simpler tamper-resistance techniques included in the scope of the claims. It
is
understood, therefore, that the utility of some of the simpler encoding
techniques
that fall within the scope of the claims, may correspondingly decrease over
time.
That is, just as in the world of cryptography, increasing key-lengths become
necessary over time in order to provide a given level of protection, so in the
world of
the instant invention, increasing complexity of encoding will become necessary
to
achieve a given level of protection.
The method steps of the invention may be embodiment in sets of executable
machine code stored in a variety of formats such as object code or source
code.
Such code is described generically herein as programming code, or a computer
program for simplification. Clearly, the executable machine code may be
integrated
with the code of other programs, implemented as subroutines, by external
program
calls or by other techniques as known in the art.
The embodiments of the invention may be executed by a computer processor
or similar device programmed in the manner of method steps, or may be executed
by an electronic system which is provided with means for executing these
steps.
Similarly, an electronic memory medium may be programmed to execute such
method steps. Suitable memory media would include serial access formats such
as
magnetic tape, or random access formats such as floppy disks, hard drives,
computer diskettes, CD-Roms, bubble memory, EEPROM, Random Access Memory
(RAM), Read Only Memory (ROM) or similar computer software storage media
known in the art. Furthermore, electronic signals representing these method
steps
may also be transmitted via a communication network.
CA 02384360 2001-12-04
WO 00/77596 PCT/CA00/00677
-32-
It will be obvious to one skilled in these arts that there are many practical
embodiments of the DES implementation produced by the instant invention,
whether
in normal executable machine code, code for a virtual machine, or code for a
special
purpose interpreter. It would also be possible to directly embed the invention
in a
net-list for the production of a pure hardware implementation, that is, an
ASIC.
It would also be clear to one skilled in the art that this invention need not
be
limited to the existing scope of computers and computer systems.
Credit, debit, bank and smart cards could be encoded to apply the invention
to their respective applications. An electronic commerce system in a manner of
the
invention could for example, be applied to parking meters, vending machines,
pay
telephones, inventory control or rental cars and using magnetic strips or
electronic
circuits to store the software and passwords. Again, such implementations
would be
clear to one skilled in the art, and do not take away from the invention.