Note: Descriptions are shown in the official language in which they were submitted.
CA 02385343 2002-05-22
Introduction
Distortion product otoacoustic emissions (DPOAEs) are very low level
stimulated acoustic
responses to two pure tones presented to the ear canal. DPOAE measurement
provides
an objective non-invasive measure of peripheral auditory function and is used
for hearing
assessment. DPOAE screening is becoming a standard clinical practice to
predict potential
sensorineural hearing loss especially in newborns.
DPOAEs have been recognized for a number years. However, DPOAE measurement
is considered an active area of research because of the challenging nature of
the signal
processing task. To address. the ever-increasing demand for high performance
DPOAE
measurement methods, a number of signal processing algorithms have been
presented in
recent years. With the availability of the powerful computational tools such
as digital
signal processors (DSPs), commercial medical devices dedicated to DPOAE
measurement
are becoming available.
In this type of otoacoustic test, two pure tones with frequencies fl and f2
are presented to
the cochlea. For best results, f2 is usually chosen as l.2fr. Due to the non-
linearity of the
ear, a very low level distortion product of frequency 2 f 1 - f2 is generated
in normal ears.
The level of such a DPOAE signal is a measure of the functionality of the ear.
Estimation
of such a weak signal buried under two strong artifacts in a potentially noisy
background
is a challenging signal processing problem.
Conventionally, fast Fourier transform (FFT) is used as the main signal
processing tool to
estimate the level of the DPOAE signals. Application of FFT in this problem
has a number
of shortcomings among which long measurement time is most pronounced. Such a
long
measurement time is usually required for acquisition of more data which, when
averaged,
reduce the overall background noise effect. Unreliability of the measurements
is another
2
CA 02385343 2002-05-22
problem of FFT-based methods and is a direct effect of the sensitivity of the
FFT-based
methods to the background noise. In addition to the need to increase the
measurement
time, the tests are usually required to be conducted in low noise environments
such as
sound-proof booths.
In an attempt to devise high performance DPOAE estimation techniques, linear
adaptive
signal processing techniques have been employed. Such techniques generally
offer better
performance in terms of measurement time which may be interpreted as higher
noise
immunity of adaptive techniques compared to FFT. However, the need for sound-
proof
examination rooms is not obviated with such techniques.
This document presents a system and a method of measurement of DPOAE signals
based
on a new signal processing technique in which individual sinusoidal components
of a given
signal are extracted and their variations are adaptively tracked over time.
The present
DPOAE estimation method employs three units of core algorithms which are
described in
detail in pending Canadian patent entitled "System and Method of Extraction of
Sinusoids
of Time-varying Characteristics" filed on May 28th, 2001, by Alireza Karimi
Ziarani, serial
number: 2,349,041.
The two artifacts are first extracted by two units and are subtracted from the
input signal
to generate an input signal of which DPOAE signal has a higher relative
portion. Such a
signal is then fed to another core unit which estimates the level of DPOAE
signal. Superior
performance of the present technique in terms of noise immunity and fast
measurement
is illustrated with the aid of computer simulations.
In order to provide a brief background on the subject, a general review of the
structure
of a generic DPOAE measurement device is presented in the next section. It
will be seen
that the heart of such an apparatus is the signal processing subsystem which,
in the final
3
CA 02385343 2002-05-22
analysis, determines the performance of the overall system. Later in this
document the
structure of the present invention for the signal processing module is
presented and its
performance is demonstrated.
Structure of a Generic DPOAE Measurement Device
In this section a brief overview of the structure of a typical DPOAE detection
system is
provided. Figure 1 shows the generic block diagram of a DPOAE measurement
device.
It consists of three main modules: the data acquisition/transducers module,
the signal
processing module and the display.
Data acquisition unit is the medium between the processing unit and the probe
which
transmits and receives acoustic signals in the audio range. Components of the
compound
data acquisition/transducers module are illustrated in more detail in Figure
2. One of the
main functions of this module is to convert digital signals produced by the
signal process-
ing module to analog signals which are then conditioned and converted to audio
signals.
Conditioning of the signals in this case may or rnay not include filtering.
Conversely, the
audio signals recorded by the probe are conditioned and converted to digital
signals to be
processed by the signal processing module.
The signal processing module is the heart of the system which produces the
digital form
of- the artifacts and extracts and measures the DPOAE signal. A DSP, or if the
com-
putational/architectural demand is low even a microcontroller, can be employed
as the
hardware platform of this unit. Signal processing is embedded as the software
in such a
hardware platform. Alternatively, and provided that the complexity of the
signal process-
ing algorithms remains low, signal processing unit may be implemented solely
in hardware
using programmable logic array (PLA) or field programmable gate array (FPGA)
tech-
4
CA 02385343 2002-05-22
nology. In an ideal case, namely when the signal processing algorithm is not
excessively
complex, the hardware does not require a PC for its operation; however,
interfacing to a
PC is usually provisioned for data management.
The display unit is the interface between the device and the operator. It can
be a simple
LED/LCD and/or a small printer.
Present Technique
Figure 3 shows the main functions of the software embedded in the signal
processing
module. The software is essentially responsible for the generation of the
artifact signals
and extraction of DPOAE as well as management of input/output data. As
discussed
before, the significance of the present invention is in the introduction of a
signal processing
technique for the extraction and measurement of DPOAE signals.
The present signal processing scheme employs three core units to construct a
high perfor-
mance DPOAE extraction module. Each core unit is capable of focusing on and
extracting
a pre-specified sinusoidal component of its input signal which may contain
many other
components including noise. More importantly, they can effectively follow
variations in
the amplitude, phase (and frequency) of the extracted sinusoidal component.
Although
the underlying mathematics ensuring stability and performance of such core
units is very
complex, the structure of the core units remain extremely simple. They are
found to be
very robust with respect to variations in the internal settings as well as
external conditions
and exhibit superior performance over existing linear adaptive and FFT-based
algorithms.
The input signal is often assumed to consist of two pure sinusoids with
frequencies fl and
f2 at a very high level (usually about 60 to 70 dB) and a very low level DPOAE
2f1 - f2
CA 02385343 2002-05-22
at about -15 to 15 dB. It is polluted by a noise usually considered to be at
about -10
to 10 dB level. The noise in fact represents the totality of all undesirable
signals that
rnay be present in the environment in which the examination is being conducted
as well
as unavoidable white Gaussian noise. Because of excessive degree of pollution
(artifacts
and noise), one single core unit set to extract the DPOAE signal out of the
input exhibits
poor performance. Different arrangements were studied to construct a high
performance
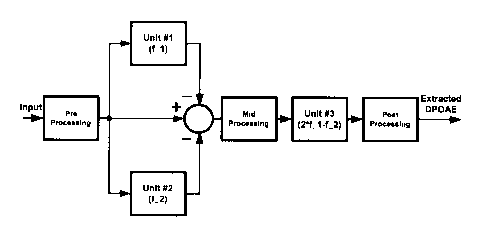
architecture. One of the most successful configurations is shown in Figure 4.
Three
core units are employed. The first two core units are set to extract the
artifacts. They
effectively do so with very small errors. The extracted artifacts are then
subtracted from
the input to produce a signal, of which DPOAE has a higher relative portion.
The third
core unit is then set to extract DPOAE.
The structure of the main embodiment of the present invention is essentially
based on the
concept of extraction of artifacts and the DPOAE as illustrated in Figure 4
and is further
illustrated in Figure 5. The stage of pre-processing consists of preliminary
normalization
and filtering. The purpose of the normalization process is to amplify the
input signal
to bring it to a certain level on the basis of which the setting of the
parameters of the
core units are adjusted. The filtering is intended to .attenuate all
components except the
DPOAE signal as much as possible to enhance the quality of the input signal.
This can
be achieved by means of a simple second order band pass filter the center
frequency of
which is set to be that of the DPOAE signal. ,
The intermediate signal out of which the two artifacts are removed may be
input to a
third core unit for the extraction of the DPOAE signal as suggested in Figure
4. Since
elimination of the two artifacts needs certain convergence time, at the very
early initial
moments a large portion of the two artifacts exist which will set the initial
operational
point of the third unit too far away from the level of the DPOAE signal. To
overcome
this, a time-gating process rnay be employed to delay the transfer of the
intermediate
6
CA 02385343 2002-05-22
signal to the third unit. This is accommodated in the mid-processing unit of
Figure 5.
The output of this unit is zero and remains zero for a short period of time
until a more
or less steady state condition for the two core units is achieved. The arid-
processing may
also include some normalization and band pass filtering just like the pre-
processing unit.
The post-processing unit consists of denormalization of the DPOAE signal and
its level
to restore the original values as well as some (low pass) filtering to further
smooth out
the estimation of the DPOAE signal and its level.
Apart from the band pass filters employed in the pre-processing and mid-
processing units
and low pass filters employed in the post-processing unit, low pass filters
may be employed
within the core units to enhance the performance of each of the three core
units.
Review of the Employed Core Units
This section reviews the structure of the core units which are the building
blocks of the
present DPOAE measurement method. Let u(t) denote a signal comprising a number
of
individual sinusoidal components and noise, expressed by
N
u(t) _ ~ Ak sin ~~ + n(t) (1)
where c~~ = cvkt + Bk is the total phase, and n(t) denotes the total noise
imposed on the
signal. The objective is to find a scheme for estimating a certain component
of such input
signal as fast and accurate as possible; a scheme which should not be
sensitive to the noise
and potential time variations of the input signal. Simplicity of the
structure, for the sake
of practical feasibility, is desirable.
7
CA 02385343 2002-05-22
Let .M be a manifold containing all pure sinusoidal signals defined as
_ ly(t' e) = Bl Srn(82t '~- e3)1 ei E (Bi,min' Bi,max~~
where B = (B1, 92, B3~T iS the matrix of parameters which belongs to the
parameter space
o = f (Br' e2' e31 T I Bi E (Bi,min' ei,max~
and T denotes matrix transposition. To extract a certain sinusoidal component
of u(t), the
solution has to be an orthogonal projection of u(t) onto the manifold Nl, or
equivalently
has to be an optirnurn B which rninirnizes a distance function d between y(t,
8) and u(t),
r.e.,
B°Pt - arg B ~ d(y(t, 8), u(t)~.
In the least squares method d is the instantaneous distance function given by
d2(t' e) _ (u(t) - y(t' e)J2 ~ e(t)2.
The error function e(t) is the totality of the components present in input
signal u(t) other
than the component of interest, plus the error incurred in the estimation
process.
The parameter matrix B is estimated by using the gradient descent method as
follows:
dte(t) I~aB (d2(t' e)~
where the positive diagonal matrix tc is the algorithm regulating constant. It
controls the
convergence rate as well as the stability of the algorithm.
Following the steps outlined above, a set of differential equations is
obtained. The gov-
erning set of equations of this algorithm can be written as
A - tore sin ~, (2)
~aeA cos ~, (3)
8
CA 02385343 2002-05-22
~3eA cos ~ + w, (4)
y(t) - A sin ~, (5)
e(t) - u(t) - y(t), (6)
in which u(t) and y(t) are the input and output signals to the core algorithm,
respectively.
State variables A, ø and w directly provide estimates of amplitude, phase and
frequency
of u(t). Parameters fir, ~t2 and ~3 are positive numbers which determine the
behavior of
the algorithm in terms of convergence speed and accuracy.
It has been shown that the dynamical system represented by the above set of
differ-
ential equations possesses a unique asymptotically stable periodic orbit which
lies in a
neighborhood of the orbit associated with the desired component of the
function u(t).
In terms of the engineering performance of the system, this indicates that the
output of
the system, y(t) = A sin ~, will approach a sinusoidal component of the input
signal u(t).
Moreover, time variations of parameters in u(t) are tolerated by the system.
If the component of interest is specified in terms of its frequency implying a
priori that
the frequency is more or less known and almost fixed (such as the case of
DPOAE signal
and artifacts), the procedure of can be a bit further simplified. For this
matter, supposing
that the frequency is more or less fixed around wo = 2~ fo, one can rewrite
the equations
as
A - p,r a sin ~,
wo -+ ~,2eA cos ~,
y(t) - A sin ~,
e(t) - u(t) - y(t).
Figure 6 shows the implementation of the algorithm in the form of composition
of simple
blocks suitable for schematic software development tools.
9
___._ -..._.. ........_.~.~.,........~_ . _.._.~.
CA 02385343 2002-05-22
Performance
Figure 7 shows the performance of the present technique in estimating the
level of the
DPOAE signals. The frequency of the DPOAE signal is 800 Hz. The two artifacts
have a level of 1 V each. Three different measurements are made for three
levels of
background noise. For each case, the level of the DPOAE signal as well as the
signal
to noise ratio (signal meaning the DPOAE signal and the noise meaning the
background
noise) is specified. A high degree of noise immunity is observed. This high
noise irrrmunity
not only obviates the need for sound-proof examination rooms, but also
provides the way
to reduce the level of the artifacts for more patient-friendly tests.