Note: Descriptions are shown in the official language in which they were submitted.
CA 02386347 2002-05-14
CANADA
HILL & SCHUMACHER
Title: ATTENTIVE PANORAMIC VISUAL SENSOR
Inventors:
James H. Elder Citizenship: Canadian
116 Grenadier Road
Toronto, Ontario
Canada, M6R 1R4
Yugian Hou
Citizenship: People's Republic of China
30 Bedle Avenue
Toronto, Ontario
Canada, M2H 1K8
Ronen Goldstein Citizenship: Canada, USA
56 Greenwin Village Road
Willowdale, Ontario
Canada, M2R 2S1
Fadi Dornaika Citizenship: Lebanon
#203-4 Assiniboine Road
Toronto, Ontario
Canada, M3J 1P3
CA 02386347 2002-05-14
ATTENTIVE PANORAMIC VISUAL SENSOR
FIELD OF THE INVENTION
The present invention relates to a panoramic visual sensor system and more
particularly the present invention provides a panoramic visual sensor system
which can
record at high and low resolutions and combine the two into a single seamless
display.
BACKGROUND OF THE INVENTION
Sensor and bandwidth constraints limit the spatial resolution and field-of-
view
(FOV) achievable in any visual system. In many applications (e.g.
surveillance,
teleconferencing), it is desirable to have both large field of view (e.g. to
survey a
panoramic area) and high resolution (e.g. to identify certain types of
activity or to
recognize faces).
Over the last ten years there has been increasing interest in the application
of
panoramic sensing to computer vision ((Danilidis & Geyer, 2000), (Hicks &
Bajcsy,
2000), (Ishiguro, Yamamoto, & Tsuji, 1992), (Nayar, 1997), (Svoboda, Pajdla, &
Hlavac,
1998), (Yagi & Kawato, 1990), (Yin & Boult, 2000)). Potential applications
include
surveillance, object tracking, and telepresence ((Haritaoglu, Harwood, &
Davis, 1998),
(Kanacle, Collins, Lipton, Burt, & L.Wixson, 1998)). Most existing panoramic
sensors are
catadioptric, i.e. the sensor is composed of a camera and a curved mirror
arranged so that
the resulting system has a single viewpoint. It has been shown ((Danilidis &
Geyer,
2000)) that the projection obtained with a catadioptric sensor with a single
viewpoint is
equivalent to the projection on a sphere followed by a perspective projection.
Catadioptric sensors allow panoramic images to be captured without any camera
motion.
However, since a single sensor is used for the entire panorama, the resolution
of such
images may be inadequate for many applications. Switching from the 14 deg FOV
of a
typical lens to the 360 deg FOV of a panoramic camera results in a 26-fold
reduction in
linear resolution. For a standard 768x494 NTSC camera, horizontal resolution
is reduced
to roughly 0.5 deg/pixel, a factor of 60 below human foveal resolution.
There has been considerable work on space-variant (foveated) sensor chips
((Ferrari, Nielsen, Questa, & Sandini, 1995), (Pardo, Dierickx, & Scheffer,
1997)).
1
CA 02386347 2002-05-14
However, since the number of photoreceptive elements on these sensors is
limited, they
do not provide a resolution or field of view advantage over traditional chips.
Moreover, it
is not clear how such sensors could be used to achieve a panoramic field of
view over
which the fovea can be rapidly deployed. A more common solution to the
FOV/resolution
tradeoff is to compose mosaics from individual overlapping high-resolution
images that
form a covering of the viewing sphere ((Irani, Anandan, & Hsu, 1995), (Kumar,
Anandan, Irani, Bergen, & Hanna, 1995), (Szelisld, 1994), (Szelisld & Shum,
1997)).
These images can be obtained by a single camera that can rotate about its
optical
centre. Such a system is useful for recording high-resolution "still life"
panoramas, but is
of limited use for dynamic scenes, since the instantaneous field of view is
typically small.
An alternative is to compose the mosaic from images simultaneously recorded by
multiple cameras with overlapping fields of view. The primary disadvantage of
this
approach is the multiplicity of hardware and independent data channels that
must be
integrated and maintained. For example, a standard 25mm lens provides a field-
of-view
of roughly 14x10 degrees. Allowing for 25% overlap between adjacent images to
support
accurate mosaicking, achieving this resolution over a hemispheric field of
view would
require roughly 260 cameras.
The human visual system has evolved a bipartite solution to the FOV/resolution
tradeoff. The field of view of the human eye is roughly 160x175 deg - nearly
hemispheric. Central vision is served by roughly five million photoreceptive
cones that
provide high resolution, chromatic sensation over a five-degree field of view,
while
roughly one hundred million rods provide relatively low-resolution achromatic
vision
over the remainder of the visual field ((Wandell, 1995)). The effective
resolution is
extended by fast gaze- shifting mechanisms and a memory system that allows a
form of
integration over multiple fixations ((Irwin & Gordon, 1998)).
Variations on this architecture are found in other species. Many insects, for
example, have panoramic visual systems ((Moller, Lambrinos, Pfeifer, & Wehner,
1998)). For example, the springing spider has four eyes that capture movement
over the
entire viewing sphere and two small field-of-view high resolution eyes used in
predation
and mating.
There have been some recent attempts to integrate high- and low-resolution
2
CA 02386347 2002-05-14
imaging in artificial sensors. In June, 1996, Hughes Electronics filed a
patent
(US5710661) Integrated panoramic and high resolution sensor optics, which
describes
an optical apparatus that monitors an entire panorama in low resolution, and
simultaneously monitors a selected portion of the panorama in high resolution.
A
drawback to this system is that both high and low resolution data are recorded
on the
same sensor, limiting both foveal and panoramic resolution.
In April, 1998, OmniView Inc. filed a patent (W09846014A1), Method and
apparatus for inserting a high resolution image into a low resolution
interactive image to
produce a realistic immersive experience. This patent describes a process of
inserting a
high resolution image into a low resolution display to produce a more
convincing virtual
reality experience. This patent was awarded in October, 1998.There are other
related
patents on the blending of high resolution and low resolution imagery in
visual displays
(e.g. US1984000576432, Filed Feb 1984, Granted Jan 1987).
Geisler and Perry (1998) have demonstrated a wavelet-based video encoding
system that progressively subsamples the video stream at image points distant
from the
viewer-defined region of interest. Recent work with saccade-contingent
displays
(Loschky & McConkie, 1999) has shown that video data viewed in the periphery
of the
human visual system can be substantially subsampled with negligible subjective
or
objective impact. While our attentive panoramic sensor is not eye-slaved,
these prior
results do suggest that attention-contingent sampling for human-in-the-loop
video is
feasible and potentially useful.
Yin and Boult (2000) have developed a multiresolution panoramic image sensor
based on stacking multiple parabolic mirrors of different sizes. Since the
entire pyramid
is sensed by a single sensor, this technique provides efficient access to very
Iow
resolution data, but does not solve the problem of obtaining and integrating
high-
resolution data with data at panoramic resolution.
Mann and Picard (1997) have investigated correlation-based methods for
computing homographies to fuse images of different resolution taken by the
same camera
at different focal lengths, but do not address the problem of fusing images
over much
greater resolution differences from different cameras in real time.
3
========== =====
CA 02386347 2002-05-14
SUMMARY OF INVENTION
The present invention provides a process for accurately combining low-
resolution
and high-resolution video streams into a single seamless display to a human
observer.
The present invention also provides a method for the smooth blending of high-
and low-resolution video boundary. In order to create an effective visual
display, it is
advantageous that the boundary between high- and low-resolution video not be
overly
distracting and irregular. The present method to reduce distractions from the
quadrilateral
boundary between low-and high-resolution video by smoothly blending the two in
an
annular region between the two. This results in a much more visually pleasing,
effective
display.
The present invention also provides a method for progressively mosaicking high
resolution imagery over a low resolution image captured by our panoramic
sensor. The
observer is continuously presented with a low-resolution panoramic image of a
remote
scene, and this image is updated with high-resolution imagery from the high-
resolution
sensor, at selected locations of interest, as they are available. These
locations may be
defmed by the observer, or automatically by an artificially intelligent
'interest operator'.
Local high resolution imagery will not be immediately replaced by low-
resolution
imagery from the panoramic sensor. Rather, we have invented a kind of
artificial
memory, that causes the high-resolution data to remain in the display even as
the high-
resolution sensor is directed toward other locations. The display duration of
foveal
images from past fixations is determined by a memory parameter. At one
extreme,
previous foveal data are immediately replaced by more recent low resolution
data from
the peripheral sensor. At the other extreme, a sequence of fixations builds up
a persistent
high resolution mosaic. In intermediate modes, foveal data from previous
fixations
gradually fade into more recent low-resolution data. Thus in this invention
there is
provided a general method for controlling the tradeoff between spatial
resolution and
temporal resolution in a remote sensing and display apparatus.
The present invention also provides methods for the static and dynamic
estimation
of homography mapping high-resolution to panoramic coordinates, allowing
accurate
fusion of data. To combine high- and low-resolution data for automatic
interpretation or
4
CA 02386347 2011-10-05
display, the data must be accurately registered. Registration is made non-
trivial by parallax due
to the displacement between the optical centres of the two sensors. To solve
this problem the
present invention provides a method to approximate the mapping between foveal
and panoramic
images by a 2D projective mapping, i.e. a homography. This is equivalent to
the assumption that
within the field-of-view of the fovea, the scene is approximately planar.
Solving for the
parameters of the projective matrix thus amounts to defining the attitude of
the local scene plane.
In general, this plane may be different in each gaze direction, and thus for a
given static scene
one can assume that the mapping between foveal and panoramic coordinates is
defined by a 2D
(pan/tilt) map of 2D projective matrices.
One possible approach to this problem is to use a manual calibration procedure
to
estimate these homographies over a lattice of pan/tilt gaze directions, and
then to interpolate over
this table of homographies to estimate an appropriate homography given
arbitrary pan/tilt
coordinates. This method is suitable for distant or static scenes.
For close-range, dynamic scenes, these homographies are functions of time, and
so
cannot be pre-computed so for close-range scenes an alternative method is
provided which gives
a mapping that is both a function of space (direction in the viewing sphere)
and time. The
method involves coarse registration using parametric templates and Pearson
correlation to
estimate translation and scaling, and staged refinement to estimate
photometric, affine
parameters and then a full homography, using Pearson correlation.
In one aspect of the invention there is provided a method for simultaneously
recording
foveal and panoramic video streams and fusing the foveal and panoramic video
streams into a
single seamless display, the foveal video stream being recorded using a high-
resolution video
sensor and the panoramic video stream being recorded using a low-resolution
video sensor, the
method comprising the steps of:
a) unwarping a panoramic video stream from said low-resolution video sensor
to
obtain an unwarped panoramic video stream, and transforming said foveal video
stream from said high-resolution video sensor and said unwarped panoramic
video
stream to common display coordinates;
b) fusing said transformed foveal video stream and said
transformed unwarped
5
CA 02386347 2002-05-14
panoramic video stream; and
c) displaying the fused video stream on a visual display means to produce a
fused
visual display.
In another aspect of the invention there is provided a method for reducing
distractions from a quadrilateral boundary between low-and high-resolution
video stream
by smoothly blending the two in an annular region between the two, the high-
resolution
video stream being recorded using a high-resolution video sensor and the low-
resolution
video stream being recorded using a low-resolution video sensor, the method
comprising
the steps of:
a) computing an annular region inscribing a quadrilateral boundary of the high-
resolution image, as projected in the coordinate frame of the panoramic
sensor; and
b) blending the high- and low-resolution video streams within this annular
region
to yield a smooth seamless display.
In another aspect of the invention there is provided a method for
progressively
mosaicking high-resolution imagery captured by a high ¨resolution video sensor
over a
low resolution image captured by a low-resolution panoramic video sensor, the
method
comprising the steps of:
a) timestamping and archiving high-resolution images from previous fixations
of
the high-resolution video sensor;
b) providing a formula defming a time decay memory parameter formula of high-
resolution images from previous fixations of the high-resolution sensor;
c) adjusting the contrast of pixels from previous fixations of the high-
resolution
sensor according to said time decay memory parameter formula;
d) combining the contrast-adjusted high-resolution pixels with cren data from
the
low-resolution panoramic sensor; and
e) adjusting the time decay memory parameter to trade off temporal and
spatial
resolution over a continuous range.
6
CA 02386347 2002-05-14
The present invention also provides a method for estimating static
homographies
mapping coordinates of a high-resolution video stream to panoramic
coordinates,
allowing accurate fusion of data for static or distanct scenes, comprising the
steps of:
a) construction of a planar calibration rig with well-defined, high-
contrast comer
features;
b) recording simultaneous low- and high-resolution video frames using a low-
resolution panoramic video sensor and a high-resolution video sensor of a
calibration rig at regular intervals over a field-of-view of the low-
resolution
panoramic sensor;
c) localizing corresponding points on the calibration rig in the high- and low-
resolution images;
d) estimating a homography for each pariltilt position of the high-resolution
video
sensor; and
e) interpolating over a resulting lattice of homographies to yield a
homography
relating high- and low-resolution coordinate frames at arbitrary pan/tilt
angles.
This invention also provides a method for estimating dynamic homographies
mapping high-resolution to panoramic coordinates, allowing accurate fusion of
data for
close-range, dynamic scenes, comprising the steps of:
a) providing a coarse registration using parametric templates over a
discrete scale
space on the high-resolution image and using Pearson correlation to estimate
translation and scaling; and
b) providing a staged refinement for estimating photometric, affme parameters
and
then a full homography, using Pearson correlation.
In another aspect of the invention there is provided an apparatus for
simultaneously
recording high- and low-resolution video streams and combining these video
streams into
a single seamless display, comprising:
a) a low-resolution panoramic video sensor for recording low-resolution video
streams;
7
CA 02386347 2002-05-14
b) a high-resolution video sensor for recording high-resolution video streams
mounted on a motorized gimballed pan/tilt platform that permits the high-
resolution sensor to be rotated about its optical centre toward any visual
direction within the panoramic field of view of the low-resolution video
sensor;
c) processing means for fusing the two video streams in real time;
d) processing means for displaying the fused video stream on a visual display
means;
e) user-interface means that allows a human user to direct the high-resolution
sensor by clicking on points of interest in the low-resolution portion of the
display; and
0 processing means for detecting motion in the low-resolution video stream and
directs the high-resolution sensor toward the moving object.
BRIEF DESCRIPTION OF THE DRAWINGS
The invention will now be described, by way of non-limiting examples only,
reference being had to the accompanying drawings, in which:
Figure 1(a) is a photograph of an attentive panoramic sensor system in
accordance
with the present invention;
Figure 1(b) shows a raw foveal image taken with the sensor system of Figure ;
Figure 1(c) shows a raw panoramic image taken with the sensor system of Figure
1;
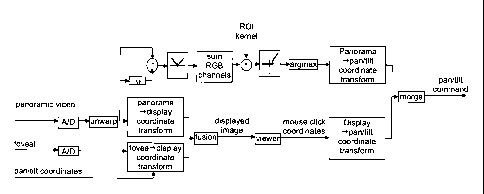
Figure 2 shows a block diagram of the attentive panoramic sensor system;
Figure 3: (a) Unwarped panoramic image. (b) Foveal/panorama fusion (c) Result
of
alpha blending with graded circular aperture.
Figures 4(a) and (b) show successive panoramic frames used for motion
computation;
Figure 4(c) shows a raw motion map;
Figure 4(d) shows a motion map after ROI convolution;
8
CA 02386347 2002-05-14
Figure 4(e) shows a motion map after thresholding;
Figure 4(f) shows resulting fixation;
Figure 5(a) shows a motion map noise distribution (no saccade);
Figure 5(b) shows a motion map noise distribution (immediately post-saccade);
Figure 6(a) shows the fixation mosaic;
Figure 6(b) shows fading fixations;
Figure 7 shows the foveal image (left) and a (roughly) corresponding region in
the
panoramic image (right) of Fig. 1(d);
Figure 8 shows the main stages of the foveal/panoramic image registration in
accordance with the present invention;
Figure 9 shows a Gaussian multi-resolution representation of the foveal image;
9(a)
Original fovea' image (640x480 pixels), 9(b), 9(c), 9(d), 9(e), and 9(f) show
the same
image at five different resolutions, subsampled by factors of: 2, 4, 8, 12,
and 16,
respectively, Figure 9(f) is only 40x30 pixels;
Figure 10 shows coarse registration using parametric template matching based
upon
two low-resolution representations f the foveal image, 10(a) shows the
original foveal
image, 10(b) and 10(c) show the reference templates associated with he two
vertical
scales 1/8 and 1/16, respectively, 10(d) shows the parametric template
associated with the
computed ertical scale (0.09Pr.,' 1/12), 10(e) shows the panoramic image
showing coarse
registration of foveal parametric template;
Figure 11 shows a process of matching based on the use of gradient maps;
Figure 12 shows feature-based registration using gradient maps;
Figure 13 shows feature-based registration by matching interest points. (a)
Original foveal image. (b) Original panorama (right half). (c) 12 interest
points are
detected in the foveal image (resolution 12:1). (d) 60 interest points are
detected in the
panoramic image. (e) fused foveal and panoramic images based on the nine
computed
matches using Pilu's technique (the matches are shown with red crosses in both
images);
Figure 14: Progressive featureless registration: (a) The coarse registration
stage (2
scales and a 2D translation), (b) affme transform, and (c) 2D projective
transform. Each
stage of the computation substantially improves the registration (see the top-
left of the
9
CA 02386347 2002-05-14
fovea);
Figure 15: Progressive featureless registration: (a) The coarse registration
stage (2
scales and a 2D translation), (b) affine transform, and (c) 2D projective
transform. Each
stage of the computation substantially improves the registration (see the top-
right of the
fovea);
Figure 16: Progressive featureless registration for a low-contrast foveal
image: (a)
The coarse registration stage (2 scales and a 2D translation), (b) affine
transform, and (c)
2D projective;
Figure 17: Featureless registration results. (a) Optimization with a purely
geometric transform. The normalized cross-correlations of the transforms are
0.79 (top)
and 0.90 (bottom). Note the misregistration of the chair and the keyboard in
(top), and the
computer screen and the mouse pad (bottom). (b) Optimization with a combined
geometric and photometric transform, the normalized cross-correlations of the
transforms
are 0.88 (top) and 0.94 (bottom);
Figure 18: Registration results using three different methods. (a) Bilinear
interpolation of four precomputed homographies. (b) Feature-matching and
robust
estimation using RANSAC. (c) Featureless method;
Figure 19: A comparison between the two registration methods: (a) Feature-
based
registration. (b) Featureless registration;
Figure 20: A comparison between the two registration methods: (a) Feature-
based
registration. (b) Featureless registration; and
Figure 21: Average transfer error as a function of image noise.
DETAILED DESCRIPTION OF THE INVENTION
In this patent there is disclosed an attentive panoramic sensor conceptually
based
upon the human foveated visual system, and we describe a framework for
automatically
combining high-resolution images with low resolution panoramas provided by an
panoramic catadioptric sensor. The peripheral component of the system consists
of a
catadioptric video sensor that provides a panoramic FOV. The foveal component
is a
video pan/tilt camera with 14x10 deg FOV. Video streams from the two sensors
are fused
at 15 fps on a standard video display. Saccades (rotations of the pan/tilt
sensor) may be
CA 02386347 2002-05-14
initiated either manually by a human observer via mouse clicks on the display,
or
automatically by a motion localization algorithm. Memory parameters govern the
tradeoff between the high spatial resolution of the foveal video stream, and
the high
temporal resolution of the panoramic stream. The system employs pre-calibrated
homographies to register foveal and panoramic video data for static or long-
range scenes,
and a more sophisticated dynamic fusion algorithm for dynamic, close-range
scenes.
Systems of this kind are useful in both autonomous and semi-autonomous
applications. Events detected in the panoramic sensor may generate saccade
commands to
allow more detailed inspection/verification at foveal resolution. In
telepresence
applications, foveal data may provide the resolution required to see facial
expressions,
read text, etc., while the panoramic data may augment the sense of presence
and
situational awareness.
1) Hardware Design
A non-limiting example of an attentive panoramic visual sensor constructed in
accordance with the present invention is shown in Figure 1(a). The panoramic
component
is a parabolic catadioptric sensor (Nayar, 1997) purchased from Cyclovision
Technologies (now Remote- Reality). The parabolic mirror stands roughly 2
metres from
the ground, facing down, and thus images the panoramic field. Panoramic images
are
captured through an orthographic lens system by a Pulnix TMC-7DSP colour CCD
camera.
The foveal component consists of a Cohu 1300 colour CCD camera with a 50mm
Fujinon lens, mounted on a Directed Perception PTU-46-17.5 pan/tilt platform.
As
loaded, the platform travels at an average speed of roughly 60 deg/sec in both
pan and tilt
directions: typical saccades complete in 150 to 1200 msec. The platform has
been
modified so that both axes of rotation coincide approximately with the optical
centre of
the lens system, so that parallax between foveal images at different pan/tilt
coordinates is
minimized.
The optical centres of the two sensors are separated by 22 cm in the vertical
direction. This means that a fixed system of coordinate transforms between the
two
sensors can be accurate only if viewing distance is large or if dynamic
variations in depth
11
______________________________________ MM.
CA 02386347 2002-05-14
are small relative to viewing distance. Since neither condition holds in our
laboratory, we
currently calibrate the system for intermediate distances and accept the
misregistrations
that occur at other depths.
Video processing, display and control are handled by a single-CPU 800 MHz
Pentium HI computer. The two colour 30 fps NTSC video streams are digitized by
a 6-
channel Data Translation DT3132 frame grabber card into two digital 640x480
video
streams. The display is driven by an NVidia 64MB GeForce2 GTS graphics card.
2) Foveal/Panoramic Fusion for Static or Distant Scenes
Coordinate Transformations
In the current prototype, we model the scene as static and piecewise planar,
and
approximate the correspondence between foveal and panoramic coordinate frames
using
a table of homographies indexed by the pan/tilt coordinates of the foveal
sensor. We
discuss our calibration procedure in the section entitled Calibration below.
The system
relies upon 4 different coordinate transformations (Figure 2):
= panorama 4 display
= fovea 4 display
= panorama 4 pan/tilt
= display 4 pan/tilt
The first two transformations map the two video streams to common display
coordinates.
The last two transformations map selected interest points from panoramic or
display
coordinates to pan/tilt coordinates used to effect a saccade.
Panorama/Display Transformation
The panorama/display coordinate transform is a fixed 3-parameter
translation/scaling, so that the observer views the scene essentially in
panoramic
coordinates. In the present con- figuration we map a 256 x 128 pixel subimage
from the
upper half of the panorama to a 1280x640 pixel window in the display.
12
CA 02386347 2002-05-14
Fovea/Display Transformation
The fovea/display transformation is composed of fovea/panorama and
panorama/display transformations. Calibration as discussed below yields a
table of
homography matrices, indexed by the pan/tilt coordinates of the foveal sensor
platform,
that are used to map foveal pixels to panoramic coordinates. Given an
arbitrary pan/tilt
index, the homography matrix is constructed by bilinearly interpolating the 8
parameters
of the homography stored at neighbouring entries. The result is then mapped to
display
coordinates using the fixed panorama/display coordinate transform. The
rectangular
foveal image is thus mapped to a general quadrilateral in the display.
Panorama/Pan/Tilt Transformation
In addition to the table of homography parameters used for the fovea/panorama
transformation, the calibration procedure yields a second table used for the
panorama/pan/tilt transformation. This table provides the pan/tilt coordinates
required for
given panoramic coordinates to map to the centre of a foveal image. Thus the
table can be
used to centre the fovea at a point of interest automatically detected in the
panorama.
Display/Pan/Tilt Transformation
The display/pan/tilt transformation is composed of a fixed translation/scaling
display/panorama transformation and the panorama/pan/tilt transformation just
described.
This transformation is used to generate saccades to points of interest
detected in the
display by the observer.
Calibration
The system may be calibrated manually, using a simple calibration rig. Since
the
sensor used in the present study was located close to a corner of the room,
the study was
done in a 90x45 deg subfield located at the top of the panorama and facing out
from the
walls. Twenty-one (21) synchronous pairs of foveal/panoramic frames were
captured
over a 7x3 regularly spaced grid in panJtilt space. The rig is positioned an
intermediate
distance from the sensor to optimize the working range of the coordinate
transformations
for the given environment. Twelve to sixteen (12-16) point pairs were manually
localized
in each foveal/panoramic image pair, and the corresponding least-squares
homography is
13
CA 02386347 2002-05-14
estimated using standard techniques. These data are used to form the
fovea/panorama
coordinate transformation, indexed by the pan/tilt coordinates of the foveal
platform.
For each image pair obtained the projection of the foveal centre is stored
into
panoramic coordinates. This allows construction of a second table, indexed by
panoramic
coordinates, that provides the pan/tilt coordinates required to centre the
fovea at a specific
panoramic location. This table is used to generate saccades from human or
machine
attention algorithms.
3) Operation
Figure 2 shows a schematic of how the foveal and panoramic video streams are
processed, combined and displayed. The panoramic video stream is first
unwarped by the
CPU using for example Cyclovision software (Nayar, 1997) to form a 1024x256
colour
video stream (Fig. 3(a)). The two video streams are then transformed into
common
display coordinates prior to fusion or blending.
The fusion algorithm is essentially to display foveal pixels where they exist,
and
panoramic pixels otherwise (Fig. 3(b)). In order to make the fusion less
jarring to the
observer, the foveal and panoramic data are blended using a set of concentric
alpha
masks, yielding a high-resolution circular fovea smoothly inset within a low-
resolution
periphery (Fig. 3(c)). All coordinate transformations and masking are done by
graphics
hardware using OpenGL. When not interrupted by saccade commands, the system
runs at
15 fps. It will be understood by those skilled in the art that the programs
referred to
herein such as for example OpenGL and Cyclovision software are non-limiting
examples
of software that may be used.
Saccades are initiated in two ways. If the observer clicks the mouse in the
display,
the location is transformed from display to pan/tilt coordinates which form
the target of
an immediate saccade. Saccades may also be initiated by a motion localization
algorithm,
which we describe below.
14
CA 02386347 2002-05-14
4) Motion Localization
Algorithm
The system may be operated to make saccades to points in the panorama where
motion is detected. A fundamental issue in motion processing is how to select
the spatial
scale of analysis. In our case, the purpose of the detection is to drive the
fovea to the
point of interest to resolve the change. Thus it is natural to match the scale
of analysis to
the FOV of the foveal sensor in panoramic coordinates. In this way, saccades
will resolve
the greatest amount of motion energy.
Successive panoramic RGB image pairs (Fig. 4(a-b)) are differenced, rectified,
and
summed to form a primitive motion map (Fig. 4(c)). This map is convolved with
a
separable square kernel that approximates the FOV of the foveal sensor in
panoramic
coordinates (50 x 50 pixels). The resulting map (Fig. 4(d)) is thresholded to
prevent the
generation of saccades due to sensor noise and vibration (Fig. 4(e)).
In order to select the appropriate threshold, an experiment was conducted in
which
motion map statistics were collected for a static scene. Thirty motion maps
yielded nearly
a million data points. We ran this experiment under two different conditions.
In the first
condition, saccades were inhibited, so that vibration in the sensor was
minimized. The
resulting distribution of motion values is shown in Fig. 5(a). In the second
condition, the
motion maps were computed immediately following a saccade, at which time it is
expected the vibration to be near its maximum (Fig. 5(b)). The noise
distribution can be
seen to depend strongly on the state of the sensor. In the present prototype
we use the first
distribution to determine the threshold (3.0) and simply inhibit motion
detection for a 2-
second period following each saccade.
The location of the maximum of the thresholded motion map determines the next
fixation (Fig. 4(f)). Since the motion computation and the video fusion
computations are
done by the same CPU, motion computation pauses the update of the display for
an
average of 400 msec. This need not occur in a true telepresence application,
in which the
attention algorithms could run on the host computer of the sensor and the
fusion
algorithms could run on the client computer of the observer.
CA 02386347 2002-05-14
5) Memory
What information the human visual system retains over a sequence of fixations
is a
subject of debate in vision science at the present time (e.g. Rensink,
O'Regan, and Clark
(1997)). There is no question, however, that humans have some forms of visual
memory
(iconic, short-term, long-term).
We have implemented a primitive sort of memory in our own artificial attentive
sensor. The display duration of foveal images from past fixations is
determined by a
memory parameter. At one extreme, previous foveal data are immediately
replaced by
more recent low resolution data from the peripheral sensor. At the other
extreme, a
sequence of fixations builds up a persistent high resolution mosaic (Fig.
6(a)). In
intermediate modes, foveal data from previous fixations gradually fade into
more recent
low-resolution data (Figure 6(b)).
6) Foveal/Panoramic Fusion for Close-Range Dynamic Scenes
In Section 2 there was described a manual calibration procedure to estimate
homographies relating foveal to panoramic coordinate systems over a lattice of
pan/tilt
gaze directions, and then to interpolate over this table of homographies to
estimate an
appropriate homography given arbitrary pan/tilt coordinates. At each pan/tilt
direction in
the lattice, calibration amounts to the selection of at least four pairs of
corresponding
scene points in panoramic and foveal images, followed by a least-squares
estimation of
the matrix parameters. A drawback with this approach is that it works well
only for
distant or static scenes. For close-range, dynamic scenes, these homographies
are
functions of time, and so cannot be pre-computed. Thus we require a method for
automatically computing a mapping that is both a function of space (direction
in the
viewing sphere) and time.
Although the problem of automatic image registration has been studied in more
conventional applications, the problem of registering panoramic and
conventional video
has not previously been addressed, and this problem presents unique challenges
due to (i)
the extreme differences in resolution between the sensors (more than 16:1
linear
resolution ratio in our application ¨ see Figure 2 for an example), (ii) the
consequent
reduction in the number of panoramic pixels within the foveal field-of-view
that may be
16
CA 02386347 2002-05-14
used for registration (less than 0.5% of the raw panoramic image), and (iii)
the resolution
inhomogeneity of panoramic images.
First, we will show how a coarse registration between the high-resolution
images
and the low-resolution panoramic images can be computed using a parametric
template
matching technique, using a discrete scale space that can accommodate the
inhomogeneity of panoramic images. Second, we develop and evaluate two
methods, one
feature-based and the other featureless, for estimating the 2D projective
transform
between the high-resolution (foveal) image and the low-resolution panoramic
images.
The featureless approach operates directly on dense image descriptors computed
in both
images.
Several factors make the automatic registration of foveal and panoramic video
streams challenging (Figures 1 and 7):
1. Many papers have been published on the problems of matching and
registration
((Brown, 1992)).However, matching and registration are resolution-dependent
processes,
and these studies generally assume roughly equivalent resolution between
sensors.
Recent studies that have addressed the problem of resolution differences
((Dufourneau &
Horaud, 2000), (Hansen & Morse, 1999)) have considered scale factors up to
only a
factor of 6. However, in our application, the linear resolution difference
between the
foveal and panoramic images is as large as 16:1. Moreover, the images
registered in
previous studies are obtained by the same conventional camera, i.e. the scale
differences
result solely by optical zooming. Thus the images to be registered are likely
to be much
more closely related than those obtained by our bipartite foveated panoramic
sensor.
2. Due to the large resolution difference between fovea and panorama, only
roughly 0.5%
of the panorama (roughly 50x30 pixels) is within the foveal field-of-view.
Thus the
information available in the panorama for registration is severely limited.
Figure 7
suggests that even the human visual system may find this problem difficult
with so little
information.
3. Unlike conventional images, the resolution of panoramic images (provided by
catadioptric sensors) varies as a function of viewing direction ((Conroy &
Moore, 1999)).
For a parabolic mirror, the resolution in the warped panorama varies as a
function of the
elevation, i.e. the vertical coordinate in the panoramic image.
17
CA 02386347 2002-05-14
The present invention solves this challenging registration problem using a
coarse-
to-fine scheme. The registration process is split into two main stages (Figure
8). In the
first stage, a coarse registration is computed using parametric template
matching between
the panoramic image and a multi-resolution representation of the foveal image.
This
provides an estimate of the translation and scale factors between the two
images.
In the second stage, this coarse registration is used to bootstrap a
refinement
process in which a full 2D projective mapping is computed. We study two
different
refinement methods. The first recovers point matches between either either
high-gradient
pixels or interest points, and then uses a robust estimation procedure (RANSAC
(Fischler
& Bolles, 1981)) to estimate the complete 2D projective transformation. The
second
method directly estimates geometric and photometric transforms between the
images by
minimizing intensity discrepancies.
The goal of coarse registration is to find the overlap region in the panoramic
image that roughly corresponds to the foveal image. The foveal and panoramic
cameras
are mounted so that the optical axis of the foveal camera and the effective
optical axis
corresponding to a local patch of the panoramic image are roughly parallel.
Thus coarse
registration can be achieved by estimating two scale factor' and a 2D
translation vector.
Once this coarse registration is estimated more elaborate methodologies can
refme it to a
full homography transform as discussed in the sections entitled Feature-based
registration
and Featureless registration discussed hereinafter.
Multi-resolution representation
Due to the difference in their resolutions, it is difficult to match the
foveal image
with the panoramic image directly. Instead we employ a discrete Gaussian
pyramid
representation ((Jolion & Rosenfeld, 1994)). The pyramid representation is
constructed
by iterating these two steps: (i) smoothing with a Gaussian kernel, and (ii)
down-
sampling by a factor of more than one. The process of smoothing is crucial to
prevent
aliasing. A 2D 7x7 Gaussian blur kernel is employed (the space constant of the
Gaussian
is roughly iJ pixels). Figure 9 shows a Gaussian pyramid representation for an
example
foveal image. While multiresolution pyramid representations for coarse-to-fine
registration have been used before (e.g, (Mann & Picard, 1997), (Szeliski,
1994), (Wu,
18
CA 02386347 2002-05-14
Kanade, Li, & Cohn, 2000)), these involve pyramids built from input images of
similar
resolution, so that corresponding levels in the pyramids are also matched in
resolution. In
our work, only one pyramid is built, and the scale factor mapping foveal to
panoramic
resolution is estimated using parametric techniques.
Parametric template matching over scale space
In the system disclosed herein, the scaling factors between foveal and
panoramic
images are roughly known. The horizontal scale factor is approximately 12:1
for the
whole warped panorama, and we use this factor in computing the subsampled
foveal
representation. The vertical scale factor, however, varies from roughly 12:1
to 16:1
within the upper two thirds of the panorama, and so a single level of the
pyramid will not
suffice. We neglect the lower third of the panoramic field of view, since in
our system it
primarily images the desk on which it stands.
The approach to this problem is to bracket the expected vertical scale with
two
pyramid levels, one at a scale lower than the expected scale, and the other at
a scale
higher than the expected scale. Translational mappings between foveal and
panoramic
images are computed for both scales using conventional template matching
techniques,
and the optimal transform (i.e., the vertical scale and the 2D translation) is
estimated
parametrically from these. In the following, the inventors first describe the
methods for
estimating the translational mapping for a fixed level of the foveal pyramid.
The
parametric technique is then used to estimate the true coarse registration.
Estimating the translational mapping
We employ featureless (correlative) techniques to estimate an approximate 2D
translation relating foveal and panoramic images. We have tested several
specific
techniques including ((Stark & Tuteur, 1979)):
1. Minimizing the Sum of Squared Difference (SSD), which is optimal assuming
the
matching images differ only by white Gaussian noise.
2. Maximizing the correlation, which is near-optimal if the matching images
differ only
by white Gaussian noise and the energy of panoramic subimages is approximately
invariant.
3. Maximizing covariance.
I The aspect ratio is not invariant due to the variation in panoramic
resolution with elevation
19
CA 02386347 2002-05-14
4. Maximizing the Pearson correlation (so-called normalized correlation).
The inventors have found the normalized correlation technique to be more
reliable
than the others, presumably because the normalization reduces error due to
photometric
differences between the two sensors. The normalized cross-correlation between
the
foveal image I,- and the panoramic image I,, at location p=(u',v', Dr is given
by:
E (u,v)(Ip(u,+u,v,+v)--fpX1f(u'v)- I )
p(P)=< I 17,1 f >= _______________________________________________________
(1)
NaPcrf
where N is the number of pixels of If , Ip is the local average over the
overlap region of
the panoramic image, oyand ap are the standard deviations associated with If
and the
panoramic image overlapped by I, . Thus by maximizing p(p) over a part of the
panoramic image Ip , we can estimate the 2D translation pr between the images:
Pr arg maxp p(p) (2)
Since the pan axis of the foveal camera is coincident with the optical axis of
the
panoramic camera, and since the optical centre of the foveal camera lies
approximately
on its rotational axes, the pan/tilt coordinates of the fovea provide
information that
constrains the probable translation between the images. To quantify these
constraints, we
determined translational correspondences for a number of scene point pairs at
different
depths and locations over a regular grid of pan/tilt gaze coordinates. Note
that given fixed
pan/tilt coordinates, the horizontal mapping is nearly invariant. The vertical
mapping
varies more, but hard constraints on the sensor system and typical room
geometry also
limits this mapping.
These constraints can be applied by pre-computing means and standard
deviations
for these distributions over a regular grid of pan/tilt locations. Given
pan/tilt coordinates
during operation, this table is bilinearly interpolated to estimate the mean
and standard
deviation of expected translational parameters. We then constrain our
panoramic search
region to lie within the 95% confidence interval determined by these
statistics, assuming
a normal model. Typical values for the horizontal and vertical standard
deviations are:
CA 02386347 2002-05-14
crh=5 pixels and crv=10 pixels. These prior constraints play a similar role to
the epipolar
constraints employed in conventional imaging systems.
Parametric template matching
Given two computed levels of the foveal pyramid bracketing the true vertical
scale factor, we use a parametric template matching method ((Tanaka, Sano,
Ohara, &
Okudaira, 2000)) to estimate the true vertical scale factor relating the
foveal and
panoramic images given the best translational mapping associated with each
reference
scale.
We proceed as follows. Let Iq and /f2be two computed levels of the foveal
pyramid at scales s1 and s2 bracketing the true vertical scale factor. Let t1
and t2be
normalized versions of If/ and 1:12 and let /pbe the panoramic image. We have:
E t, (u, v). 0
t,2(u,v) .1
(..v)
to,v). 0
(.,v)
E t22(u,
t, and t2 are the reference templates. The parametric template associated with
t1 and t2
can defined as a linear interpolation of the reference templates ((Tanaka et
al., 2000)):
t = wItl+ w2t
I Witt + W2t2
where xi 1112 E [0,1], and wi + w2 = 1. The denominator is necessary to obtain
a
normalized image. Given the reference templates t1 and t2 together with the
panoramic
image /1,, we want to determine the weights w, and w2 that optimize the
registration of
the associated parametric template t (w, + w2) with the panoramic image 4, In
other
words, we seek the w, and w, hat maximize the normalized cross-correlation of
t(w1,w2) with /p.
21
________________________________ mswwermmaiwms**msiwq......"="¨
CA 02386347 2002-05-14
By definition the normalized cross-correlation between the parametric template
and the panoramic image I,, is given by:
p(w1,w2) =< .1p,t(w1,w2)>
w1t, +wt
(Witt+ W2t21
< -FIN2 < Ip,t2>
W2t2 I
The parameters, w1 and w2, can be estimated by maximizing the above normalized
cross-
correlation over all weights wi and w2 all panoramic locations P1, p2. Since
this four-
dimensional optimization problem cannot be solved analytically, we adopt the
heuristic
of first determining the optimal pi and p2 that maximize the individual
normalized
cross-correlations pi and p2:
= max vect < >
P2 = maxvect < lp,t2>
and then optimizing the resulting parametric template over wi and w2:
P(wi w2 ) w2P2 (3)
I wit2 + w2t2 I
Since the norm of a matrix A is given by:
I Al = trace(AT A)
it follows that 11 witi w2t2 can be written as:
witi + w2t 11= NI trace((witi+ w2t2)T (wit! + w2t2))
= Vtrace(w; tiT + w22t2T t2+ww2tIT t2+w,w2t27' ti)
=11(qtrace(tirti)+14trace(t2T t2)+w,w2trace(tIT t2)+w1w2trace(t2T ti)
= wi2 + w + 2wiw2trace(02)
2
= 2 14'2 + WI W2 P12
22
CA 02386347 2002-05-14
In the above manipulations, we have used the equations: trace(t4)= 14 2 = 1,
trace(t1t2)=1t2 I 2=1 and p12=trace(tirt2) (the normalized cross-correlation
between the
two reference templates).
Therefore, Eq. (3) can be written as:
P(wi,w2) w2P2 = w c
V(v'? +2wiw2P12) (w Mw)
where c = p2) W (WI , W2)T
and M is given by:
M =
[ 1 P121
P12 1
Thus, the parameters w, can be recovered by maximizing the above normalized
cross-
correlation with a constraint:
2
W c
max= _________________________________________________ vvith Ew, =1
w (wi.mw).,2
By taking the first derivatives of the above function with respect to w and
equating to
zero we obtain:
MwvvTc = c(wT/%4w)
The above equation stipulates that the vector Mw is equal to c up to a scale,
i.e:
Mw c
2
Since w components must satisfy (E w, .1) the parameters are given by:
i-1
Mc
w = (wi w2) = y2 ________________________________________ ow- (4)
20 Thus, given the normalized cross-correlation between the two reference
templates, ., as
well as the best normalized cross-correlation between each reference template
and the
panoramic image, and., the best interpolation parameters are given by Eq.(4).
Once the interpolation parameters w are estimated, the best vertical scale
factor can be
approximated by:
23
CA 02386347 2002-05-14
S = W2S2 (5)
Figure 10 illustrates the application of this approach to coarse registration.
Two different
low resolution representations at bracketing vertical scales of sl =1/16 and
s2 = 1/8 been
constructed from the foveal image shown in Figure 9(a). Each of the scaled
foveal images
was registered using normalized cross-correlation. The estimated 2D pixel
location for
the two scaled foveal images were (792, 83) for sl and (792 68) for s2and the
corresponding normalized cross-correlations were 0.75 and 0.61 respectively.
By
applying Eq.(4) we estimated ( w1, w2) = (0.56,0.44) from which the
approximated true
vertical scale was computed by Eq. (5) (s = 0.09 1/12 ).
Once the vertical scale is estimated, a scaled, low-resolution foveal image is
computed from the original high-resolution foveal image, using the estimated
vertical
scale factor and a scale factor of 1/12 in the horizontal direction. We then
estimate the
translational parameters of the coarse registration using normalized cross-
correlation of
this resealed foveal image with the panorama. Figure 10 (e) shows the final
coarse
registration of the foveal and panoramic images.
The translation and scaling transform computed in our coarse registration
stage
can be used to initialize an estimation of the full local homography relating
foveal and
panoramic coordinates. In the following we develop and compare feature-based
and
featureless methods for estimating this homography. In both cases, we use the
foveal
parametric template estimated in the coarse registration phase.
Feature-based registration
Due to its inherent combinatorial complexity and its ill-posedness, the
matching
problem is one of the bottlenecks in computer vision and low-level image
analysis
((Moghaddam, Nastar, & Pentland, 1996)). There are two schools of thought for
solving
the matching problem. In the first, features are detected in one image and
matches are
sought in the second image. In the second, features are detected independently
in both
images and then matched up. We have developed and evaluated two matching
strategies,
one of each type. The first is based on the use of gradient maps detected in
the foveal
image /f. The second attempts to match detected interest points in both images
If and
/,.One advantage of the first strategy is that many point-to-point matches can
be obtained
24
CA 02386347 2002-05-14
even though the size of the rescaled foveal image is small, which is very
useful when
robust statistics such as M-estimators, RANdom SAmple Consensus (RANSAC), and
regression diagnostics are used.
Method 1: Matching high-gradient pixels
Feature matching
The basic idea here is to match foveal features at locations of large gradient
magnitude, estimate using the Sobel operator, with the panoramic image using a
small
search region for each foveal pixel. The restriction of matching to points of
high gradient
prevents underconstrained, featureless regions of the foveal image from being
matched.
The location of the search window is derived from the 2D location associated
with the
coarse registration ( Eq.(2)). The centre of the search window (in the
panoramic image
frame) is the sum of two 2D vectors: (i) the coarse registration, pr, and (ii)
the current
location of the pixel (in the foveal image). We use normalized cross-
correlation as a
similarity measure between each foveal feature and its associated candidates.
For each high-gradient foveal pixel, the best-matching panoramic point is
selected
from among the candidates, i.e. we select the panoramic feature having the
largest
normalized cross-correlation over the search window. If this normalized cross-
correlation
exceeds a certain threshold a match is declared (in our experiments this
threshold was set
to 0.5).
Figure 11 illustrates the basic idea. In our experiments, the size of the
search
window varied as a function of the vertical scale of the foveal image: from
7x7 pixels for
a 16:1 scale to 13x13 pixels for a 12:1 scale. The size of each local patch
(averaging
window) was 11x11 pixels.
2D projective mapping The local homographic mapping between foveal image
coordinates p=(u,v,l)T and panoramic image coordinates p' =(u',v',1)T given by
p' Hp where represents equality up to a scale factor and H
hu is a 3x3 matrix.
Thus
u'=u h12v+k3 ku+h22v+h23
v' =
h31u h32v + h33 h31u + h32v + h33
The homography H can be recovered up to a scale factor using standard linear
algebra
CA 02386347 2002-05-14
tools assuming at least four matches. To avoid numerical instability, the
image
coordinates of the matches in both images are translated and rescaled so that
the
homogeneous coordinates are close to (1,1,1)T .
Robust estimation
Robust estimation techniques provide more reliable estimation in the presence
of
outliers (mismatched features) ((Meer, Mintz, Rosenfeld, & Kim, 1990)). Here
we use
the RANSAC algorithm ((Fischler & Bolles, 1981)), which splits the set of
putative
matches into disjoint outlier and inlier subsets. The estimated homography is
that having
the largest support among putative matches. In our approach we further enhance
reliability by computing estimates over several gradient thresholds, and then
selecting the
most consistent. The entire algorithm proceeds as follows. First, the foveal
gradient
magnitude map is computed. Using a set of thresholds (10% 20% 30% of the
maximum
gradient), a set of thresholded gradient magnitude maps is computed. Next,
using the
gradient map corresponding to the lowest threshold, matches are computed using
the
process described above. Then, for each gradient threshold a homography is
computed
using RANSAC, with only the matched foveal pixels whose gradient exceeds the
threshold. Note that the matching process is performed once, at the lowest
threshold, and
only the linear computation of the homography is performed for each gradient
threshold.
From the resulting set of homographies, the selected mapping is that which
minimizes the SSD between the warped foveal image and the corresponding
panoramic
subimage. Table 1 illustrates the application of this heuristic to the foveal
image shown in
Fig. 10(d) using four different gradient maps. In this example, a gradient
threshold of
20% produces the optimal homography.
Threshold High gradient pixels Matches Inliers SSD
10% 823 264 241 11.
64 106
20% 546 173 169
11.55 106
30% 392 124 109
12.15 106
40% 282 98 91
12.08 106
Table 1: The Sum of Squared Differences evaluated with four computed
homographies.
26
CA 02386347 2002-05-14
Each one is computed with a gradient map using the RANSAC technique.
Method 2: Matching interest points
Feature extraction
We define an interest point as a locations in the image where intensity
changes
twodimensionally. Many different interest point detectors exist in the
literature. We have
chosen the Harris detector due to its reliability in terms of repeatability
and information
content ((Harris & Stephens, 1988), (Schmid & Mohr, 1998), (Schmid, Mohr, &
Bauckhage, 1998), (Zhang, Deriche, Faugeras, & Luong, 1995)). Harris ((Harris
&
Stephens, 1988))computes a matrix which is related to the auto-correlation
function of
the 2D signal. The squared first derivatives are averaged over a window. The
eigenvalues
of the resulting matrix are the principle curvatures of the auto-correlation
function. If
these two curvatures are high, an interest point is declared.
In order to compute reliable features that are adequately dispersed, we split
the
foveal image into a 10x10 square grid. For each square the best interest point
is retained.
Second, the retained features are ordered according to their quality, and only
the top 50%
are retained. Finally, the relative distances are tested in order to discard
very close
neighbours. In other words, if two features are very close, we only retain the
one of
highest quality. A similar strategy is used to detect interest points in the
corresponding
region of the panoramic image determined in the coarse registration stage.
Matching
Once the extraction step is completed in the foveal image and in the
corresponding part of the panoramic image, we are left with two sets of
features: (i) the
foveal features, and (ii) the panoramic features. The task is to put them into
correspondence. Due to its inherent combinatorial complexity, this is a hard
task,
especially when the number of features is very large. We have used Pilu's
method
which embodies the principles of similarity, proximity, and exclusion ((Pilu,
1997)). Pilu
constructs a pairing matrix whose entries encodes the similarity measure and
the
proximity measure between two arbitrary features. Then potential matches are
detected
using an enhanced version of the pairing matrix. We also apply the RANSAC
technique
to the set of matches found by Pilu's method.
27
CA 02386347 2002-05-14
Featureless registration
In this section we describe how the mapping parameters can be directly
estimated
from the images without any feature extraction. Although good results can be
obtained
from feature-based methods, they have several disadvantages:
1. There are many free parameters. There are three windows (search window,
correlation
window, smoothing window) whose sizes must be selected. The RANSAC algorithm
requires three parameters: the number of matches used in each random trial,
the total
number of random trials and a tolerance parameter for judging the consensus on
the
obtained solution. There is no general theory to guide the selection of these
parameters.
2. Point-to-point matching requires an explicit transformation of the foveal
image into a
low-resolution representation at the scale of the panorama.
3. Even if all computed matches are correct, instability associated with the
computation
of the homography may lead to severe geometrical distortion affecting the
final fusion.
This is studied by Kanatani and Ohta ((Kanatani & Ohta, 1999)).
4. Since measuring feature similarity is based on the use of correlation
windows, the
border region of the rescaled foveal image is not taken into account. For
example, if the
rescaled foveal image is 30x53 pixels (a typical size in our application) and
the
correlation window is 11 xll pixels, the border region ignored by the
correlation accounts
for roughly 46% of the foveal image.
In this section, we study a featureless registration approach that is not
subject to
these limitations. Our approach involves the direct estimation of mapping
parameters by
minimization of the discrepancy between the intensity of the two images.
Construction of
a low resolution foveal representation is not necessary since the scale can be
embedded in
the unknown transformation.
Featureless techniques have been applied to the construction of image mosaics
in
a coarse-to-fine scheme where the 2D transform is iteratively estimated from
the coarsest
level to the finest level of two pyramids ((Mann & Picard, 1997)). In this
case, the full
resolution images as well as the images associated with the two pyramid levels
(the low
resolution ones) have similar resolution. However, the application of this
approach to
images of grossly different resolutions has, to our knowledge, not been
studied.
We denote by /j(p) the intensity of the foveal pixel p=(u,v, 1)T and by /(p')
28
CA 02386347 2002-05-14
intensity of its match p' = (u',v',1)T in the panoramic image. Note that the
image /f may
be of any resolution including the original (full) resolution.
Foveal and panoramic pixels are assumed to be related by a homography p' Hp
where
H hu is a 3x3 matrix such that:
u,= hnu + hi.3 (6)
kiu h32v + h33
vi= h2u+h22v-i-h23 (7)
h31u h32v + h33
Without loss of generality, we set h33 to 1 since the homography H is defined
up to a
scale factor. Since these two pixels project from the same scene point, we
will assume
that their intensities can be related by an affme mapping ((Cox, Roy, &
Hingorani, 1995),
(Hager & Belhumeur, 1998)):
I, (Hp) = a I f (p) +
where a is the contrast gain and /3 is the brightness shift. These parameters
cannot
necessarily be precomputed, since the sensors may have dynamic gain control.
We thus
seek the photometric and geometric parameters of the transformation that
minimize
f (H , a, 13)=Iv(p)2 = E vp (Hp) ¨ aIf(p)¨ 16)2
(8)
There are ten unknowns (two photometric parameters, a and, and the eight
entries of
the homography matrix), and non-linear constraints. We use the Levenberg-
Marquardt
technique ((Fletcher, 1990), (Press, Teukolsky, Wetterling, & Flannery, 1992))
to solve
the problem. For each foveal pixel, the first derivatives of its contribution
to the error
function (8) with respect to the ten unknowns have the following form:
av al au, al av,
___________________________________________ .=( P P
ahi, aui ahu ôv ahi;
av
¨ = -1 f(u,v)
a a
av
= -1
afl
29
CA 02386347 2002-05-14
N
where (P P the spatial gradient vector associated with the panoramic image,
and
au' ay'
au'
ay'
the derivatives, ¨ and ¨ are easily derived from Eqs.(6) and (7). The
Levenberg-
ahu ij
ah
Marquardt technique uses these derivatives to iteratively update the transform
parameters
to minimize the error function.
Due to the complexity of our objective function, it is difficult to obtain a
good
solution without a good initialization. To increase the reliability of the
approach, we
estimate the transform in two stages of increasing complexity: first affine (6
parameters)
and then projective (8 parameters). For the affine stage, we use as an initial
guess the
translation and scaling parameters estimated by coarse registration. For the
projective
stage, we use the results of the affine stage as an initial guess. All other
parameters are
initially set to either zero (non-diagonal elements) or to a scale factor
(diagonal
elements).
Example Results
Feature-based registration
The feature-based registration methods described in the section entitled
Feature-
based registration were evaluated over a large number of foveal/panoramic
image pairs
for which the linear resolution difference varied from 12:1 to 16:1. In all
cases, the coarse
registration technique described in Section 8.3 was used to define the
panoramic search
window. Figure 12 shows results of the gradient-based technique (first
strategy).
Registrations are based upon between 40-250 matching points (inliers)
Figure 13 shows the results of the second strategy, i.e. the use of Harris
interest
points together with Pilu's method on the image shown in Figure 12(d). Figure
13(a)
displays the resealed fovea (the scale is 12:1 in both direction). Figure
13(b) displays a
part of the panorama. Figure 8(c) shows 12 detected foveal interest points.
Figure 8(d)
shows 60 detected panoramic interest points. Figure 13(e) shows the fusion
result based
on the nine computed matches obtained by Pilu's method (the matches are shown
in (c)
and (d) with red crosses). Qualitatively, there appears to be little
difference in
performance between the two matching techniques (see Figures 12(d) and 13(e).
_____________________________ 1.01.11.P1.1
CA 02386347 2002-05-14
Moreover, the associated CPU time is roughly the same assuming that a
reasonable
number of interest points is used.
The preliminary implementation of the feature-based registration techniques
takes
0.11 sec on average on an SGI Onyx2 machine (20 ms for the multi-resolution
representations, 20 ms for the coarse registration assuming that we have a
60x60 initial
search region based upon a pre-calibration, 70 ms for the point-to-point
matching).
Featureless registration
The featureless registration method described in the section entitled
Featureless
registration was also evaluated over a large number of foveal/panoramic image
pairs.
Figure 14 and 15 shows registration results at three stages of the
computation: ((a) coarse
registration, (b) affme, (c) projective). Each stage of computation
substantially improves
the registration.
In these studies, the 2D projective transform typically provides the best
registration. However, we find that for low-contrast foveal images the affine
transformation may prove superior. Figure 16 shows such a case. To address
such cases,
we have developed a post-hoc evaluation technique in which the normalized
cross-
correlation of both affine and projective transformations of the fovea with
the panorama
are computed, and the transformation with the largest cross-correlation is
selected. In
Figure 16, this criterion selects the affine transformation (cross-correlation
of 0.77) over
the projective (0.57). Figure 17 demonstrates the benefit of integrating a
photometric
transform (the parameters a and ) within the optimization process.
Objective confirmation of this observation may be obtained by computing the
normalized cross-correlations of the two transformations. In both cases, the
normalized
cross-correlation is greater for the transformation employing both geometric
and
photometric parameters (0.88 and 0.94) than for the purely geometric
transformation
(0.79 and 0.90). The average CPU time required for featureless registration
was 0.25
seconds including two consecutive non-linear minimizations (affine and
projective).
Feature-based registration vs. featureless registration
Figure 18 shows registration results for three different registration methods:
(a)
bilinear interpolation of four pre-computed homographies; (b) our feature-
matching
31
_____________________________ OM. ___
CA 02386347 2002-05-14
method and (c) our featureless method. While both dynamic registration methods
improve upon the static calibration, it is clear that the featureless method
provides a
superior match. The two examples shown in Figures 19 and 20 confirm this
finding.
While subjective evaluation of the fusion results is important, particularly
for
telepresence applications, objective evaluations are also important,
particularly for
automatic surveillance applications. Moreover, visual inspection of the fused
images
relies primarily upon an evaluation of the continuity of features across the
foveal
boundary: a direct comparison of foveal pixels with corresponding panoramic
pixels is
not possible, since the foveal pixels mask the panoramic pixels.
To objectively and quantitatively assess the accuracy of the two registration
methods, we used the following approach:
1. A nominal homography was invented and used to warp a foveal image to
produce a
simulation of the corresponding panoramic image.
2. Centred Gaussian noise was added to both foveal and panoramic images, and
the 2D
mapping (homography) was estimated from the noisy images using the two
registration
methods: (i) the featurebased registration method, and (ii) the featureless
registration
method.
3. At each noise level, we repeated each estimation for 100 trials, and report
the mean
pixel transfer error, defined as the Euclidean distance between the
transferred foveal
pixels (using the estimated homography) and their ground truth locations
averaged over
all the foveal pixels (640x460 pixels) and over all trials.
Figure 21 displays the average transfer error associated with the estimation
of the
homography as a function of the added Gaussian image noise. The solid curve
corresponds to the feature-based registration method, the dotted curve to the
featureless
registration method. The featureless method was found to outperform the
feature-based
method at all levels of noise.
The present invention shows that consistent and efficient registration between
high-resolution foveal images and low resolution panoramas provided by a
panoramic
video sensor can be achieved. Although image registration has been studied in
more
conventional applications, the challenging problem of registering panoramic
and
conventional video has not previously been addressed. The challenges
associated with the
32
CA 02386347 2002-05-14
extreme resolution differences, the small field-of-view of the foveal image,
and the
resolution heterogeneity of the panoramic panorama were overcome using a
coarse-to-
fme scheme. Thus, our registration process is split into two main stages.
In the first stage, a coarse registration is computed using parametric
template matching
techniques together with a multi-resolution representation of the foveal
image. Using
parametric template matching allows one to cope with the vertical resolution
heterogeneity of the panorama. The coarse registration gives a 2D transform
encompassing a rough estimation of the 2D translational mapping and the scale
factors
existing between the foveal image and the panoramic image.
In the second stage, the coarse registration is refined to a full 2D
projective
mapping. To this end two different methods have been developed and
quantitatively
evaluated. The first method attempts to recover pairs of matches using either
high-
gradient pixels or interest points, and the 2D projective mapping is then
computed using
the RANSAC technique. The second method directly estimates the 2D projective
transform and the photometric transform by minimizing intensity discrepancies.
This
featureless registration is carried out with progressive complexity using 2D
affme and 2D
projective parameters. It makes direct and complete use of all available
intensity
information, eliminating the need to identify a set of features to match, and
coping with
the physical differences affecting the two sensors (geometry,
resolution/scale,
radiometry).
It has been disclosed herein that the geometric transform is accurately
recovered
by the featureless method when both the geometric and photometric transforms
are
simultaneously estimated. Key elements of our featureless approach are (i)
increased
robustness by progressively increasing the complexity of the estimated 2D
transformation
from translation/scaling to affine and projective transformations, (ii) use of
the Pearson
(normalized) correlation for estimation of the translational mapping, and an
affme
photometric transform in estimating affine and projective transforms to
achieve
robustness to photometric differences between sensors, and (iii) parametric
template
matching for rescaling the foveal image to match the heterogeneous panoramic
scales. A
comparison between the feature-based method and the featureless method using
both real
and synthetic foveal/panoramic image pairs shows that the featureless
registration is
33
_____________________________ 10M4.4...afm 1.0WOIN
__________________________________
CA 02386347 2002-05-14
superior in accuracy.
While multi-resolution pyramid representations for coarse-to-fme registration
have been used before, previous work involves pyramids built from input images
of
similar resolution, so that corresponding levels in the pyramids are also
matched in
resolution. In our work, only one pyramid is built, and the scale factor
mapping foveal to
panoramic resolution is estimated using parametric techniques.
In coarse registration we exploit the physical constraints on our sensing
apparatus
to restrict our attention to scaling and translation parameters. This approach
can be
generalized to a foveal camera that may rotate about its optical axis by
adding a rotational
parameter in the coarse registration phase, and recovering the parameters
using a circular
projection method ((Choi & Kim, 2002)).
These results may be useful for applications in visual surveillance and
telepresence demanding both large field-of-view and high resolution at
selected points of
interest. Moreover, the developed registration methods are of general
applicability in
many fields like remote sensing and video compression. Future work may
investigate the
enhancement of the featureless registration method by combining an exhaustive
and
guided search with the gradient descent method.
The present invention discloses for the first time a panoramic visual sensor
in
which high resolution (foveal) colour video is fused in real time (17 fps as
an example)
with colour panoramic video. Saccadic behaviour is determined both by the
interest of the
observer and by autonomous attention (motion) computations. A primitive form
of
memory permits the accumulation of high resolution information over space, at
the
expense of temporal resolution.
This invention is useful in both autonomous and semi-autonomous applications.
In surveillance operations, security personnel or automatic visual
surveillance algorithms
can monitor an entire area at low resolution, and `zoom-in' on activities of
interest
without losing their global perspective of the scene or their ability to
detect other
important events. For example, the low-resolution imagery may be sufficient
for human
surveillance personnel or automatic algorithms to detect individual people.
The high-
resolution sensor then may provide the resolution required to recognize the
individuals.
In teleconferencing applications, the panoramic data may provide participants
34
CA 02386347 2002-05-14
with a sense or presence and situational awareness, while the high-resolution
data may
provide the resolution required to recognize individuals and their facial
expressions, read
text and the like. Automatic algorithms may use the low-resolution data to
localize the
participants, and to detect the main speaker to which the high-resolution
sensor is
directed.
In teleleaming applications, the remote instructor may use the panoramic
imagery
to provide a sense of the entire classroom to which s/he is teaching, while
manual or
automatic methods may be used to localize and direct the high-resolution
sensor to
students who ask questions or make comments.
As used herein, the terms "comprises" and "comprising" are to be construed as
being inclusive and open ended, and not exclusive. Specifically, when used in
this
specification including claims, the terms "comprises" and "comprising" and
variations
thereof mean the specified features, steps or components are included. These
terms are
not to be interpreted to exclude the presence of other features, steps or
components.
The foregoing description of the preferred embodiments of the invention has
been
presented to illustrate the principles of the invention and not to limit the
invention to the
particular embodiment illustrated. It is intended that the scope of the
invention be defmed
by all of the embodiments encompassed within the following claims and their
equivalents.
CA 02386347 2002-05-14
References
Brown, L. G. (1992). A survey of image registration techniques. ACM Computing
Surveys, 24(4), 325-376.
Choi, M. S., & Kim, W. Y. (2002). A novel two stage template matching method
for rotation and illumination invariance. Pattern Recognition(35), 119-129.
Conroy, T. L., & Moore, J. B. (1999). Resolution invariant surfaces for
panoramic
vision systems. Paper presented at the IEEE Conference on Computer Vision.
Cox, J., Roy, S., & Hingorani, S. L. (1995). Dynamic histogram warping of
images
pairs for constant image brightness. Paper presented at the IEEE International
Conference
on Image Processing.
Danilidis, K., & Geyer, C. (2000). Omnidirectional vision: Theory and
algorithms.
Paper presented at the IEEE International Conference on Patter Recognition.
Dufourneau, Y., & Horaud, C. S. R. (2000). Matching images with different
resolutions. Paper presented at the IEEE Conference on Computer Vision and
Pattern
Recognition.
Ferrari, F., Nielsen, J., Questa, P., & Sandini, G. (1995). Space variant
imaging.
Sensor Review, 15(2), 17-20.
Fischler, M. A., & Bolles, R. C. (1981). Random sample consensus: A paradigm
for
model fitting with applications to image analysis and automated cartography.
Communication ACM, 24(6), 381-395.
Fletcher, R. (1990). Practical Methods of Optimization. New York: Wiley.
Hager, G. D., & Belhumeur, P. N. (1998). Effecient region tracking with
parametric
models of geometry and illumination. IEEE Trans. on Pattern Analysis and
Machine
Intelligence, 20(10), 1025-1039.
Hansen, B. B., & Morse, B. S. (1999). Multiscale image registrartion using
scale
trace correlation. Paper presented at the IEEE Conference on Computer Vision
and
Pattern Recognition.
Haritaoglu, I., Harwood, D., & Davis, L. (1998). Who, when, where, what: A
real
36
CA 02386347 2002-05-14
time system for detecting and tracking people. Proceedings of the Third Face
and Gesture
Recognition Conference.
Harris, C., & Stephens, M. (1988). A combined corner and edge detector. Paper
presented at the Alvey Vision Conference.
Hicks, R. A., & Bajcsy, R. (2000). Catadioptric sensors that approximate wide-
angle perspective projections. Paper presented at the IEEE Conference on
Computer
Vision and Pattern Recognition.
Irani, M., Anandan, P., & Hsu, S. (1995). Mosaic based representations of
video
sequences and their applications. Paper presented at the IEEE International
Conference
on Computer Vision.
Irwin, D. E., & Gordon, R. D. (1998). Eye movements, attention and trans-
saccadic
memory. Visual Cognition. Visual Cognition, 5(1/2), 127-155.
Ishiguro, H., Yamamoto, M., & Tsuji, S. (1992). Omni-directional stereo. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 14(2), 257-262.
Jolion, J., & Rosenfeld, A. (1994). A Pyramid Framework For Early Vision.:
Kluwer Academic Publishers.
Kanade, T., Collins, R., Lipton, A., Burt, P., & L.Wixson. (1998). Advances in
cooperative multi-sensor video surveillance. Proceedings of DARPA Image
Understanding Workshop.
Kanatani, K., & Ohta, N. (1999). Accuracy bounds and optimal computation of
homography for image mosaicing applications. Paper presented at the IEEE
Conference
on Computer Vision.
Kumar, R, Anandan, P., Irani, M., Bergen, J., & Hanna, K. (1995).
Representations
of scenes from collections of images. ICCV Workshop on the Representation of
Visual
Scenes.
Mann, S., & Picard, R. W. (1997). Video orbits of the projective group: A
simple
approach to featureless estimation of parameters. IEEE Transactions on Image
Processing, 6(9), 1281-1295.
37
CA 02386347 2002-05-14
Meer, P., Mintz, D., Rosenfeld, A., & Kim, D. W. (1990). Robust regression
methods for computer vision: a review. International Journal of Computer
Vision, 6(1),
59-70.
Moghaddam, B., Nastar, C., & Pentland, A. (1996). A bayesian similarity metric
for
direct image matching. Paper presented at the International Conference on
Pattern
Recognition.
Moller, R., Lambrinos, D., Pfeifer, R., & Weimer, R. (1998). Wehner. Insect
strategies of visual homing in mobile robots. Paper presented at the Computer
Vision and
Mobile Robotics Workshop.
Nayar, S. (1997). Catadioptric omnidirectional camera. Paper presented at the
IEEE
Conference on Computer Vision and Pattern Recognition.
Pardo, F., Dierickx, B., & Scheffer, D. (1997). CMOS foveated image sensor:
Signal scaling and small geometry effects. IEEE Transactions on Electron
Devices,
44(10), 1731-1737.
Pilu, M. (1997). A direct method for stereo correspondence based on singular
value
decomposition. Paper presented at the IEEE Conference on Computer Vision and
Pattern
Recognition.
Press, W. H., Teukolsky, S. A., Wetterling, W. T., & Flannery, B. P. (1992).
Numerical Recipes, The Art of Scientific Computing. New York: Cambridge
University
Press.
Schmid, C., Mohr, M., & Bauckhage, C. (1998). Comparing and evaluating
interest
points. Paper presented at the IEEE International Conference on Computer
Vision.
Schmid, C., & Mohr, R. (1998). Local greyvalue invariants for image retrieval.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(5), 530-
534.
Stark, H., & Tuteur, F. B. (1979). Modern Electrical Communications. Theory
and
Systems.
Svoboda, T., Pajdla, T., & Hlavac, V. (1998). Epipolar geometry for panoramic
cameras. Paper presented at the European Conference on Computer Vision.
38
CA 02386347 2002-05-14
Szeliski, R. (1994). Image mosaicldng for tele-reality applications. Paper
presented
at the IEEE Workshop on Applications of Computer Vision.
Szelisld, R., & Shum, H. Y. (1997). Creating full view panoramic image mosaics
and texture-mapped models. SIGGRAPH'97.
Tanaka, K., Sano, M., Ohara, S., & Okudaira, M. (2000). A parametric template
method and its application to robust matching. Paper presented at the IEEE
Conference
on Computer Vision and Pattern Recognition.
Wandell, B. A. (1995). Foundations of Vision. Sinauer.
Sunderland,
Massachusetts: Sinauer.
Wu, Y., Kanade, T., Li, C. C., & Cohn, J. (2000). Image registration using
wavelet-
based motion model. International Journal of Computer Vision, 38(2).
Yagi, Y., & Kawato, S. (1990). Panoramic scene analysis with conic
projection.
Paper presented at the International Conference on Robots and Systems.
Yin, W., & Boult, T. E. (2000). Physical panoramic pyramid and noise
sensitivity in
pyramids. Paper presented at the IEEE International Conference on Computer
Vision and
Pattern Recognition.
Zhang, Z., Deriche, R., Faugeras, O., & Luong, Q.-T. (1995). A robust
technique
for matching two uncalibrated images through the recovery of the unknown
epipolar
geometry. Artificial Intelligence Journal, 78, 87-119.
39