Note: Descriptions are shown in the official language in which they were submitted.
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
GHOST ELIMINATING EQUALIZER
Technical Field of the Invention
The present invention is directed to an equal-
izer that substantially~eliminates signal ghosts of up to
and including 1000 ghosts.
Background of the Invention
Ghosts are produced in a receiver usually
because a signal arrives at the receiver through differ-
ent transmission paths. For example, in a system having
a single transmitter, the multipath transmission of a
signal may occur because of signal reflection. That is,
the receiver receives a transmitted signal and one or
more reflections of the transmitted signal. As another
example, the multipath transmission of a signal may occur
in a system having plural transmitters that transmit the
same signal to a receiver using the same carrier fre-
quency. A network which supports this type of transmis-
sion is typically referred to as a single frequency
network.
When a signal reaches a receiver through two or
more different transmission paths, an interference pat-
tern results. In the frequency domain, this interference
pattern is manifested by a variable signal amplitude
- 1 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
along the frequency axis. An interference pattern which
results when the ghost is 1000 is shown in Figure 1.
This interference pattern has amplitude nulls or near
amplitude nulls at certain frequencies. Therefore, any
information contained in the received main signal in the
neighborhood of these frequencies is likely lost because
the signal to noise ratio near these frequencies is below
a usable threshold.
A variety of systems have been devised to deal
with the problems caused by ghosts. For example, spread
spectrum systems deal very adequately with the problem of
a 1000 ghost by spreading the transmitted data over a
substantial bandwidth. Accordingly, even though a 100%
ghost means that some information may be lost in the
neighborhood of frequencies corresponding to the ampli-
tude nulls, a data element can still be recovered because
of the high probability that it was spread over frequen-
cies which do not correspond to the amplitude nulls.
Unfortunately, the data rate R associated with spread
spectrum systems is typically too low for many applica-
tions. (The data rate R is defined as the number of data
bits per Hertz of channel bandwidth.)
It is also known to use a matched filter in a
receiver in order to deal with the problem of a ghost.
- 2 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
In this approach, data is transmitted as a data vector.
The matched filter correlates the received data with
reference vectors corresponding to the possible data
vectors that can be transmitted. Correlation of the
received main signal to the reference vector correspond-
ing to the transmitted data vector produces a large peak,
and correlation of the received main signal to the other
possible reference vectors produces small peaks. Accord-
ingly, the transmitted data vector can be easily deter-
mined in the receiver. Unfortunately, the data rate R
typically associated with the use of matched filters is
still too low for many applications.
When high data rates are required, equalizers
are often used in a receiver in order to reduce ghosts of
a main signal. A classic example of a time domain equal-
izer is an FIR filter. An FIR filter convolves its
response h(t), shown generally in Figure 2, with a re-
ceived signal. The received signal contains the main
signal and the ghost of the main signal. The FIR filter
produces an output having a large peak representative of
the main signal. Ghosts of the main signal have small
components in the output of the FIR filter. However, as
shown in Figure 2, the values al, a~, a3, . . . of the
taps of an FIR filter depend on the value of a and, in
- 3 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
order to perfectly cancel a 100% ghost using an FIR
filter, the value a of the FIR filter response must
approach 1. As the value a approaches 1, the values of
the taps of the FIR filter do not asymptotically decrease
toward zero. Therefore, the FIR filter becomes infi-
nitely long if a 100% ghost is to be eliminated, making
the FIR filter impractical to eliminate a 100% ghost.
An example of a frequency domain equalizer 10
is shown in Figure 3. The frequency domain equalizer 10
includes a Fast Fourier Transform (FFT) module 12 which
performs a Fast Fourier Transform on the received signal
in order to transform the received signal to the fre-
quency domain. A multiplier I4 multiplies the frequency
domain output of the FFT module Z2 by a compensation
vector which includes a row of coefficients Az. An in-
verse FFT module 16 performs an inverse FFT on the multi-
placation results from the multiplier 14 in order to
transform the multiplication results to the time domain.
Figure 4 illustrates an exemplary set of Coef-
ficients Ai which may be used by the frequency domain
equalizer 10. The coefficients Ai are chosen so that,
when they and the FFT of the received signal are multi-
plied by the multiplier 14, the coefficients Ai cancel
the ghost in the received signal leaving only the main
4 _
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
signal. It should be noted that the coefficients Ai
should have infinite amplitudes at the frequencies where
the interference pattern has a zero amplitude. However,
the coefficients Ai cannot be made infinite as a practi-
cal matter. Accordingly, the coefficients Ai are cut off
at these frequencies, which means that information in the
received main signal is lost at the cut off frequencies
so that the output of the inverse FFT module 16 becomes
only an approximation of the transmitted data.
Moreover, it is known to use empty guard inter-
vats between the vectors employed in the frequency domain
equalizer 10 of Figure 3. The guard intervals are shown
in Figure 5 and are provided so that received vectors and
ghosts of the received vectors do not overlap because
such an overlap could otherwise cause intersymbol inter-
ference. Thus, the guard intervals should be at least as
long as the expected ghosts. It is also known to use
cyclic extensions of the vectors in order to give the
received main signal an appearance of periodicity.
Accordingly, a Fast Fourier Transform of the received
signal and a Fourier Transform of the received signal
appear identical.
The invention disclosed in U.S. Application
09/158,730 filed September 22, 1998 is directed to an
- 5 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
equalizer which overcomes one or more of the above noted
problems. According to this invention, a vector domain
equalizer 20 as shown in Figure 6 relies on vectors to
distribute the transmitted data in both time and fre-
quency so that the vectors are essentially random in the
time and frequency domains. Accordingly, in a heavily
ghosted channel, all data can be recovered with small
noise enhancement, and any enhanced noise that does exist
is near white.
The vector domain equalizer 20 includes an
inverse vector domain transform 22 and a vector domain
transform 24 which are separated by a channel 26. Ac-
cordingly, the inverse vector domain transform 22 may be
part of a transmitter, and the vector domain transform 24
may be part of a receiver. The inverse vector domain
transform 22 performs a matrix multiplication between an
input data block and a transform matrix. The input data
block may include any number of data elements arranged in
a row. These data elements may be bits, symbols, or any
other suitable data entities. The transform matrix
comprises a plurality of vectors arranged in columns, and
each vector of the transform matrix preferably has a
length commensurate with the number of data elements of
the input data block. Also, the number of vectors of the
- 6 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
transform matrix should preferably be commensurate with
the number of data elements in the input data block.
Accordingly, if there 256 data elements in the input data
block, the transform matrix should preferably have 256
vectors each having 256 elements. The output of the
inverse vector domain transform 22 is an output data
block having a number of data elements commensurate with
the number of data elements of the input data block.
Thus, if there are 256 data elements in the input data
block 32, the output data block has 256 data elements.
The vector domain transform 24 performs a
matrix multiplication between the received main signal
and a plurality of receiver vectors VR. The data trans-
mitted through the channel 26 is received, for example,
as a row vector. During matrix multiplication, the
vector domain transform 24 multiplies each component of
the received row vector by a corresponding component in a
first column of the receiver vectors VR, and sums the
multiplication results to produce a first component r1 of
a vector ri at the output of the vector domain transform
24. The vector domain transform 24 next multiplies each
component of the received row vector by a corresponding
component in a second column of the receiver vectors VR,
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
and sums the multiplication results to produce a second
component r2 of the output vector ri, and so.
Assuming no channel distortion such as may be
caused by channel interference, and assuming that the
vector domain transform 24 uses the same vectors as are
used by the inverse vector domain transform 22, the
matrix multiplication performed by the vector domain
transform 24 produces the original input data block.
However, if channel distortion exists, the actual output
data block produced by the vector domain transform 24
will not be equal to the original input data block.
Accordingly, a training session is invoked where the
vectors of the vector domain transform 24 are adjusted
according to channel distortion such that, in the pres-
ence of channel distortion, the data of the original
input data block is recovered.
The invention of U.S. Application 09/158,730
works quite well. However, the present invention pro-
duces similar results but with fewer calculations.
Summary of the Invention
In accordance with one aspect of the present
invention, an equalizer for processing blocks of data
comprises a finite filter and a post-processor. The
_ g _
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
finite filter has an output, and the finite filter is
arranged to substantially eliminate a ghost from a re-
ceived signal in order to provide a substantially ghost
free signal at the output. The post-processor is ar-
ranged to apply a window function to the output of the
finite filter. The window function has a duration sub-
stantially equal to a duration of a block of data.
In accordance with another aspect of the pres-
ent invention, an equalizer comprises a pre-processor, a
finite filter, and a post-processor. The pre-processor
applies coefficients b to a received main signal and a
ghost of the received main signal in order to modulate
the received main signal and the ghost. The finite
filter applies coefficients a to the modulated received
main signal and ghost in order to substantially eliminate
the ghost. The post-processor applies coefficients c as
a window function to the received main signal in an
output of the finite filter in order to remove the modu-
lation imposed on the received main signal by the coeffi-
cients b.
In accordance with yet another aspect of the
present invention, a method of substantially eliminating
a ghost of a received main signal containing data blocks
comprises the following steps: a) applying coefficients
- 9 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
a to the received main signal and the ghost in order to
substantially eliminate the ghost, thereby producing a
substantially ghost-free signal, wherein the coefficients
a have a duration longer than a duration of a data block;
and, b) applying coefficients c to the substantially
ghost-free signal, wherein the coefficients c form a
window function having a duration substantially equal to
the duration of a data block.
Brief Description of the Drawings
These and other features and advantages of the
present invention will become more apparent from a de-
tailed consideration of the invention when taken in
conjunction with the drawings in which:
Figure 1 shows an interference pattern which
could result when two signals in the same frequency band
are received by a receiver at substantially the same
time;
Figure 2 illustrates the response of an FIR
filter which is commonly used as a time domain equalizer
in a receiver in order to eliminate ghosts;
Figure 3 illustrates a frequency domain equal-
izer which is used in a receiver in order to eliminate
ghosts;
- 10 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
Figure 4 illustrates an exemplary set of coef-
ficients Ai that are used by the frequency domain equal-
ize of Figure 3 in order to cancel ghosts;
Figure 5 illustrates guard intervals which may
be used between transmitted vectors in systems employing
equalizers;
Figure 6 illustrates an equalizer which in-
cludes a vector domain transform pair (i.e., a vector
domain transform and an inverse vector domain transform);
Figure 7 illustrates a first embodiment of an
equalizer in accordance with the present invention;
Figure 8 illustrates a second embodiment of an
equalizer in accordance with the present invention;
Figure 9 illustrates a first embodiment of the
response of the pre-processor of the equalizers shown in
Figures 7 and 8;
Figure 10 illustrates the response of a
convolver of the equalizer shown in Figure 7;
Figure 11 illustrates the real part of the
response of a multiplier of the equalizer shown in Figure
8:
Figure 12 illustrates the imaginary part of the
response of a multiplier of the equalizer shown in Figure
8;
- 11 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
Figure 13 illustrates a first embodiment of the
response of a post-processor of the equalizers shown in
Figures 7 and 8;
Figure 14 illustrates a second embodiment of
the response of the pre-processor of the equalizers shown
in Figures 7 and 8;
Figure 15 illustrates a second embodiment of
the response of a post-processor of the equalizers shown
in Figures 7 and 8;.
Figure 16 is a time domain illustration of a
received main signal and its ghost;
Figure 17 illustrates the output of the pre-
processor response in the time domain;
Figure 18 illustrates a third embodiment of an
equalizer in accordance with the present invention;
Figure 19 illustrates a fourth embodiment of an
equalizer in accordance with the present invention;
Figure 20 illustrates the real part of the
response of a multiplier of the equalizer shown in Figure
19;
Figure 21 illustrates the imaginary part of the
response of a multiplier of the equalizer shown in Figure
19; and,
- 12 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
Figure 22 illustrates a response of a post-
processor of the equalizer shown in Figure 19.
Detailed Description
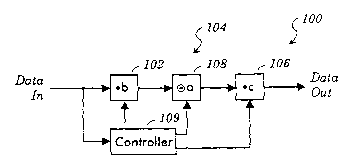
An equalizer 100 according to the present
invention is shown in Figure 7 and includes a pre-proces-
sor 102, a finite filter 104, and a post-processor 106.
The pre-processor 102 of the equalizer 100 multiplies the
signal received from the channel by coefficients b. The
signal received from the channel is designated in Figure
7 as Data In. The pre-processor 102 is a modulation
operation that modulates the received main signal and its
ghost so that the ghost is less that the received main
signal. Accordingly, the ghost is no longer a 100%
ghost.
The finite filter 104, as shown in Figure 7, is
a convolver 108. Accordingly, the multiplication results
of the pre-processor 102 are convolved in the convolver
108 with coefficients a. The convolution performed by
the convolver 108 eliminates the ghost from the multipli-
ration results of the pre-processor 102.
The post-processor 106 multiplies the convolu-
tion results from the convolver 108 by coefficients c so
- 13 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
that the output of the post-processor 106 is the data
transmitted into the channel. The data at the output of
the post-processor 106 is designated in Figure 7 as Data
Out. The post-processor 106 reverses the effects of the
modulation imposed by the pre-processor 102 and applies a
window function to the output of the convolver 108. This
window function has a duration which is substantially
equal to the duration of a Data In block.
Because the post-processor 106 applies a window
function to the output of the convolver 108 so that a
Data Out block temporally matches a corresponding Data In
block, the convolver 108 may be implemented, for example,
as an FIR filter, such as that described above in connec-
tion with Figure 2. That is, because of the window
function applied by the post-processor 106, the number of
taps of an FIR filter need not be infinite but may be
limited to a reasonable number. For example, these taps
may have a duration that is twice the duration of a Data
In block.
A controller 109 is provided to measure the
time interval, d, separating the received main signal and
its ghost. As discussed below, the interval d may be
used in shaping the coefficients b, a, and c. The con-
trolley 109 supplies the coefficients b to the pre-pro-
- 14 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
censor 102, supplies the coefficients a to the convolver
108, and supplies the coefficients c to the post-proces-
nor 106. The controller 109 also synchronizes the pre-
processor 102, the convolver 108, and the post-processor
106 to each block of data moving through the equalizer
100. Each two blocks of data may be separated by a guard
interval.
Figure 8 illustrates an equalizer 110 which is
equivalent to the equalizer 100 shown in Figure 7 and
which includes a pre-processor 112, a finite filter 114,
and a post-processor 116. The finite filter 114 includes
a Fast Fourier Transform 118, a multiplier 120, and an
inverse Fast Fourier Transform 122. Thus, whereas the
finite filter 104 operates in the time domain, the finite
filter 114 operates substantially in the frequency domain
where the multiplier 120 applies complex coefficients A
(described below) to the frequency domain output of the
Fast Fourier Transform 122.
Accordingly, the pre-processor 112 of the
equalizer 110 multiplies the signal received from the
channel by the coefficients b. Again, the pre-processor
112 is in effect a modulation operation that modulates
the received main signal and its ghost so that the ghost
is unequal to the received main signal. Accordingly, the
- 15 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
ghost is no longer a 1000 ghost. The multiplication
results of the pre-processor 112 are transformed to the
frequency domain by the Fast Fourier Transform 122, the
multiplier 120 multiplies the frequency domain multipli-
cation results from the Fast Fourier Transform 118 by the
complex coefficients A in order to eliminate the ghost
from the multiplication results of the pre-processor 112,
and the inverse Fast Fourier Transform 122 transforms the
ghost-free, frequency domain, modulated received main
signal to the time domain. The post-processor 116 multi-
plies the output from the finite filter 114 by the coef-
ficients c in order to reverse the effects of the modula-
tion imposed by the pre-processor 102 and to apply a
window function to the output of the inverse Fast Fourier
Transform 122, as described above.
A controller 124 measures the interval d,
supplies the coefficients b, A, and c to the pre-proces-
sor 112, the multiplier 120, and the post-processor 116,
respectively, and synchronizes the pre-processor 112, the
finite filter 114, and the post-processor 116 to each
block of data moving through the equalizer 110.
The coefficients b applied by the pre-proces-
sons 102 and 112 may be discrete steps as shown by way of
example in Figure 9. Each of these steps has a width
- 16 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
along the time axis equal to the interval d, which is the
time interval separating the received main signal and its
ghost. Also, the ratio of the amplitude of any one step
to the amplitude of the next previous step is a,.where a
is a constant and is preferably less than one. In the
example shown in Figure 9, a is 0.8. Moreover, the
coefficients b are applied as a block to each Data In
block and, therefore, the difference between to at the
beginning of the block of coefficients b and tb+a at the
end of the block of coefficients b is commensurate with
the length in time of a Data In block plus d, where d, as
discussed above, is the time interval separating the
received main signal and its ghost. For example, if each
Data In block has a duration of 256 samples times and d
has a duration of 32 sample times, then the difference
between to and tb is 288 sample times, as shown in Figure
9. In addition, there should be an appropriate guard
interval on each side of the block of coefficients b.
It is noted that the coefficients b modulate
both the received main signal and its ghost, so that the
amplitude of the ghost after application of the coeffi-
cients b is preferably less than the amplitude of the
received main signal. Thus, if a received main signal
130 and its ghost 132 are shown in Figure 16 as impulses
- 17 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
separated by the interval d along the time axis, the
signal 130 and its ghost 132 may have the appearance
shown in Figure 17 after application of the coefficients
b. It is also noted that the coefficients b perform a
window function in the sense that any energy received in
the intervals outside of the Data In block plus the
interval d is eliminated.
The coefficients a applied by the finite filter
104 are shown in Figure 10 by way of example. As can be
seen from Figure 10, the coefficients a are applied as in
the case of an FIR filter. Each adjacent pair of these
coefficients are separated by the interval d. Also, the
ratio of the magnitude of any one coefficient to the
magnitude of the next previous coefficient is the con-
stant a. Because a is less than one, the magnitudes of
the coefficients a asymptotically decrease toward zero.
The coefficients a preferably occupy a space in time that
is twice as long as a Data In block, For example, if a
Data In block has a duration of 256 sample times, then
the coefficients a preferably have a duration of 512
sample times. As a result of the application of the
coefficients a by the finite filter 104, the ghost in the
output from the pre-processor 102 is eliminated.
- 18 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
The coefficients A applied by the multiplier
120 are shown in Figures 11 and 12 by way of example.
Because the output of the Fast Fourier Transform 122 is
complex, the coefficients A must also be complex. Ac-
cordingly, the coefficients A have a real part shown in
Figure 11 and an imaginary part shown in Figure 12. As
can be seen from Figures 11 and 12, the coefficients A
are based upon the delay d and the ratio a. Again, the
duration of each of the real and imaginary parts of the
coefficients A is preferably twice as long as the dura-
tion of a Data In block. As a result of the application
of the coefficients A by the multiplier 120, the ghost in
the output from the pre-processor 112 is eliminated.
The coefficients c applied by the post-proces-
sors 106 and 116 may be discrete steps shown by way of
example in Figure 13. Each of these steps has the width
d along the time axis. Also, a, which is the ratio of
the amplitude of any one step to the amplitude of the
next succeeding step in the case of the coefficients c,
is preferably less than one. In the example shown in
Figure 13, a is 0.8. Moreover, the coefficients c are
applied as a block to the output of the finite filter 104
and the output of the inverse Fast Fourier Transform 120
and, therefore, the difference between to at the begin-
- 19 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
ning of the block of coefficients c and t~ at the end of
the block of coefficients c is commensurate with the
length in time of a Data In block. The difference be-
tween to and t~ is not required to include d which, as
discussed above, is the length of time separating the
received main signal and its ghost, because the ghost has
already been eliminated. For example, if a Data In block
has a duration of 256 samples times, then the difference
between to and t~ is also 256 sample times. In addition,
there should be an appropriate guard interval on each
side of the block of coefficients c. The coefficients c
reverse the modulation imposed on the received main
signal by application of the coefficients b. The coeffi-
cients c also provide a window function so that a Data
Out block at the output of the finite filters 104 and 114
has a duration which substantially matches the duration
of a Data In block. Accordingly, the number of impulses
in the response of the finite filters 104 and 114 need
not be infinite in order to eliminate a 1000 ghost, but
may instead be a practicable number.
The coefficients b and c as described above in
relation to Figures 9 and 13 generally require a priori
knowledge of d. The coefficients b and c described below
in relation to Figures 14 and 15 require no a priori
- 20 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
knowledge of d. The curve for the coefficients b as
shown by way of example in Figure 14 is such that the
ratio of the amplitude of the curve at any point x1 along
the time axis to the amplitude of the curve at a point x2
is the constant a, where x1 and x2 are separated by d,
where d may have any value, and where x2 occurs earlier
along the time axis than x1. The constant a is prefera-
bly less than one. In the example shown in Figure 14, a
is 0.8. Moreover, as before, the coefficients b are
applied as a block to a Data In block and, therefore, the
difference between to at the beginning of the curve and
tb+a at the end of the curve is commensurate with the
length in time of a Data In block plus d where d, as
discussed above, is the length of time separating the
received main signal and its ghost. In addition, there
should be an appropriate guard interval on each side of
the block of coefficients b.
The curve for the coefficients b as shown in
Figure 14 is given by the following equation:
b = k a-n, ( 1 )
where x is a point along the time axis between to and
tb+a~ a is as described above, ko is a constant such that
- 21 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
b has a desired value at the point to, and k1 is related
to d.
The curve for the coefficients c as shown by
way of example in Figure 15 is such that the ratio of the
amplitude of the curve at any point x1 along the time
axis to the amplitude of the curve at a point x2 is a,
where x1 and x2 are separated by d, where d may be any
value, and where x2 occurs later along the time axis than
x1. As shown in Figure 15, a is 0.8. As before, the
coefficients c are applied as a block to the output of
the finite filter 104 and the inverse Fast Fourier Trans-
form 120 and, therefore, the difference between to at the
beginning of the block of coefficients c and t~ at the
end of the block of coefficients c is commensurate with
the duration of a Data In block. The difference between
to and t~ is not required to include d because the ghost
has already been eliminated. In addition, there should
be an appropriate guard interval on each side of the
block of coefficients c. The coefficients c reverse the
modulation imposed on the signal by application of the
coefficients b. Also, as discussed above, the coeffi-
cients c provide a window function so that a Data Out
block at the output of the finite filters 104 and 114 has
- 22 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
a duration that substantially matches the duration of a
corresponding Data In block.
The curve for the coefficients c as shown in
Figure 15 is given by the following equation:
x
c =_ koak' (2)
where x is a point along the time axis between to and t~,
a is as described above, ko is a constant such that c has
a desired value at the point to, and k1 is related to d.
It is noted that the number of calculations
performed by the transforms shown in Figure 6 increases
in accordance with n2 as n increases, where n is the
number of data elements in a data block. It is further
noted that the number of calculations performed by a
convolver, such as the convolver 108 of Figure 7, also
increases in accordance with n2 as n increases. However,
the number of calculations performed by the finite filter
114 of Figure 8 increases in accordance with nlogn as n
increases. Thus, the calculations performed by the
equalizer 110 are considerably fewer than the calcula-
tions performed by the transforms of Figure 6.
Two embodiments of an equalizer in accordance
with the present invention have been discussed above in
- 23 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
relation to Figures 7 and 8. However, other embodiments
of an equalizer in accordance with the present invention
are possible. For example, as shown in Figure 18, a pre-
processor 150 multiplies the received main signal and its
ghost by the coefficients b. The output of the pre-
processor 150 is transformed to the frequency domain by a
Fast Fourier Transform 152, and a multiplier 154 multi-
plies the frequency domain output of the Fast Fourier
Transform 152 by the complex coefficients A such as those
shown in Figures 11 and 12. A convolver 156 convolves
the output of the multiplier 154 with the coefficients C
in order to recover the data that was transmitted through
the.channel. The coefficients C in this case must be
complex. Also, an inverse Fast Fourier Transform, which
is the complement of the Fast Fourier Transform 152, is
located in the transmitter and transforms the signals
therein to the time domain for transmission through the
channel.
Figure 19 illustrates an equalizer 160 which
includes a finite filter 162 and a post-processor 164.
The finite filter 162 includes a Fast Fourier Transform
166, a multiplier 168, and an inverse Fast Fourier Trans-
form 170. The signal received from the channel is trans-
formed to the frequency domain by the Fast Fourier Trans-
- 24 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
form 166, the multiplier 168 multiplies the frequency
domain signal from the Fast Fourier Transform 166 by
complex coefficients A in order to eliminate the ghost
from the received signal, and the inverse Fast Fourier
Transform 170 transforms the ghost-free, frequency domain
signal to the time.domain. The post-processor 172 multi-
plies the output from the finite filter 162 by the coef-
ficients c in order to apply a window function to the
output of the inverse Fast Fourier Transform 170 so that
each Data Out block at the output of the finite filter
162 has a duration that substantially matches the dura-
tion of its corresponding Data In block being processed
by the equalizer 160.
A controller 172 measures the interval d in
order to determine the coefficients A, supplies the
coefficients A and c to the multiplier 168 and the post-
processor 164, respectively, and synchronizes the finite
filter 162 and the post-processor 164 to each block of
data moving through the equalizer 160.
The coefficients A applied by the multiplier
168 are shown in Figures 20 and 21 by way of example.
Because the output of the Fast Fourier Transform 166 is
complex, the coefficients A must also be complex. Ac-
cordingly, the coefficients A have a real part shown in
- 25 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
Figure 20 and an imaginary part shown in Figure 21. As
can be seen from Figures 20 and 21, the coefficients A
are based upon the interval d and the ratio a. Again,
each of the real and imaginary parts of the coefficients
A preferably have a duration that is twice as long as the
duration of a Data In block. As a result of the applica-
tion of the coefficients A by the multiplier 168, the
ghost in the output from the pre-processor 102 is elimi-
nated.
The coefficients c applied by the post-proces-
sor 164 are shown by way of example in Figure 22. Be-
cause there is no pre-processor in the equalizer 160 that
modulates both the received main signal and the ghost,
the coefficients c are not required to undo the effects
of any modulation. Therefore, the coefficients may have
a constant non-zero value within the window from to and
t~. The coefficients c shown in Figure 22 are applied as
a block to the output of the finite filter 162 and,
therefore, the difference between to at the beginning of
the coefficients c and t~ at the end of the coefficients
c is commensurate with the duration of each Data In
block. As before, if a Data In block has a duration of
256 samples times, then the difference between to and t~
is also 256 sample times. In addition, there should be
- 26 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
an appropriate guard interval on each side of the block
of coefficients c. The coefficients c provide a window
function that limits each Data Out block at the output of
the finite filter 162 to a duration that substantially
matches the duration of its corresponding Data In block.
Accordingly, the number of impulses in the response of
the finite filter 162 need not be infinite in order to
eliminate a 100% ghost, but may instead be a practicable
number.
Certain modifications and alternatives of the
present invention have been discussed above. Other
modifications and alternatives will occur to those
practicing in the art of the present invention. For
example, because the present invention operates most
satisfactorily in the presence of ghosts and other linear
distortions, the term ghost as used herein in connection
with the present invention includes ghosts and/or other
linear distortions.
Moreover, the coefficients b have been shown
above as non-complex coefficients. However, the coeffi-
cients b may be complex, such as where the received main
signal is a QAM signal.
Accordingly, the description of the present
invention is to be construed as illustrative only and is
- 27 -
CA 02409518 2002-11-13
WO 01/89087 PCT/US00/13620
for the purpose of teaching those skilled in the art the
best mode of carrying out the invention. The details may
be varied substantially without departing from the spirit
of the invention, and the exclusive use of all modifica-
tions which are within the scope of the appended claims
is reserved.
- 28 -