SYSTEM AND METHOD FOR REGISTRATION OF CUBIC FISHEYE HEMISHPHERICAL IMAGES

SYSTEME ET PROCEDE D'ENREGISTREMENT D'IMAGES HEMISPHERIQUES EN OEUIL DE POISSON

English Abstract

Systems and methods for registering hemispheric images obtained using a
fisheye lens for panoramic viewing, relating to spatial alignment and colour
balancing of complement half-side images derived from the hemispheric images.
The systems and methods for spatial alignment determine the displacement of
the digitized recorded images using a single translation and rotation model of
distortion, which further evaluates the centre of projection, and the extent
of translation and rotation. The system and method for colour balancing
iteratively increase (or decrease) the values of pixels near the edge
(discontinuity) between the two half-sides of an image, each time taking into
consideration the average difference of pixel colour across a smaller strip of
the edge near the pixel. This invention removes the colour differential but
does not remove any detail underlying the features of the image.

French Abstract

L'invention concerne des système et des procédés d'enregistrement d'images hémisphériques obtenues au moyen d'un oeil-de-poisson destinée à un visionnement panoramique, permettant un alignement spatial et un équilibrage des couleurs de demi-images latérales complémentaires dérivées des images hémisphériques. Ces systèmes et ces procédés permettant un alignement spatial déterminent le déplacement des images enregistrées numérisées au moyen d'une translation unique et d'un modèle de rotation de distorsion, qui permet aussi d'évaluer le centre de projection, et l'étendue de la translation et de la rotation. Le système et le procédé permettant l'équilibrage des couleurs augmentent (ou diminuent) de façon itérative les valeurs de pixels à proximité (de la discontinuité) du bord entre les deux demi-images latérales d'une image, prenant à chaque fois en considération la différence moyenne de couleur de pixel à travers une bande plus petite de bord à proximité du pixel. Cette invention permet d'éliminer le différentiel de couleur, mais ne permet pas d'éliminer les détails soulignant les caractéristiques de l'image.

Claims

CLAIMS
The embodiments of the invention in which an exclusive property or privilege
is claimed are
defined as follows:
1. A method for balancing the color of an image across a discontinuity in
the image, the
discontinuity having two sides, the image having pixels comprising color
values on both
sides of the discontinuity, the method comprising iteratively adjusting the
values of each
individual pixel near the discontinuity by an adjustment amount that is a
function of the
difference of the color values across the discontinuity in a strip on the
discontinuity , the
maximum distance of pixels in the strip from the discontinuity decreasing in
each
iteration.
2. The method of claim 1 wherein the adjustment amount is based on the
differences in
color values between pairs of pixels that are adjacent to one another across
the
discontinuity.
3. The method of claim 2 wherein the adjustment amount is a weighted
average of the
differences in color values between pairs of pixels within the strip that are
adjacent to
one another across the discontinuity.
4. The method of claim 1, wherein the adjustment amount is weighted
decreasingly with
the distance of the individual pixel from the discontinuity.
5. The method of claim 1, wherein the strip has a width along the edge
equal to about
double a length, w, of the column.
6. The method of claim 5, wherein, upon each iteration, the length, w,
decreases.
7. The method of claim 6, wherein the method is repeated for a plurality of
the index, i,
along the edge.
8. The method of claim 7, wherein the plurality comprises each pair of
adjacent pixels
along the edge.
13

9. A system for balancing the color of an image across a discontinuity in
the image, the
system comprising a processor with a computer program being configured to
implement
the method of claim 1
10. The system of claim 9 wherein the adjustment amount is based on the
differences in
color values between pairs of pixels that are adjacent to one another across
the
discontinuity.
11. The method of claim 10 wherein the adjustment amount is a weighted
average of the
differences in color values between pairs of pixels within the strip that are
adjacent to
one another across the discontinuity.
12. The method of claim 9, wherein the adjustment amount is weighted
decreasingly with
the distance of the individual pixel from the discontinuity.
13. A computer readable medium having recorded thereon code for execution
by a
processor for balancing the color of an image across a discontinuity in the
image, the
code being configured to implement the method of claim 1.
14. The computer readable medium of claim 13 wherein the adjustment amount
is based on
the differences in color values between pairs of pixels that are adjacent to
one another
across the discontinuity.
15. The computer readable medium of claim 14 wherein the adjustment amount
is a
weighted average of the differences in color values between pairs of pixels
within the
strip that are adjacent to one another across the discontinuity.
16. The computer readable medium of claim 13 wherein the adjustment amount
is a
weighted average of the differences in color values between pairs of pixels
within the
strip that are adjacent to one another across the discontinuity.
17. A computer readable medium containing processor executable instructions
configured to
perform the steps of:
(A) receiving a plurality of hemispheric images in at least one
input file, a first of
said hemispheric images and a second of said hemispherical images having an
overlapping region;
14

(B) generating an intermediate image by spatially adjusting said first
hemispheric
image relative to said second hemispheric image such that a plurality of
objects within
said overlapping region of said first hemispheric image align with said
objects within said
overlapping region of said second hemispheric image;
(C) mapping each one of a plurality of surface locations of a cubic image
to a
respective one of a plurality of intermediate locations of said intermediate
image;
(D) calculating a plurality of surface pixels of said cubic image at said
surface
locations based on a plurality of intermediate pixels of said intermediate
image
proximate said intermediate locations;
(E) balancing the color difference along an edge defined between a first
hemi-cube
and a second hemi-cube of said cubic image, comprising iteratively adjusting
the values
of pixels adjacent to the edge along a strip parallel to the edge, the
adjustment taking
into consideration the difference of pixel values across a width of the strip,
the width
decreasing with each iteration; and
(F) storing said cubic image in an output file.
18. The computer readable medium according to claim 17, wherein the
balancing step
comprises the sub-steps of:
calculating the width of the strip based on an iteration value, said strip
being
oriented parallel to an edge in said cubic image, said edge being defined
where a first
given row of the first hemi-cube of said cubic image meets a second given row
of the
second hemi-cube of said cubic image and said edge is normal to a plurality of
columns
of said cubic image;
calculating a plurality of difference values across said edge, one of said
difference values for each respective one of said columns, each respective one
of said
difference values being based on a plurality of first color values of said
first hemi-cube
inside said strip and a plurality of second color values of said second hemi-
cube inside
said strip with said strip centered about said respective column;
adjusting said first color values and said second color values in each of said
columns by a weighted scheme based on both (i) said respective difference
values and
(ii) a respective distance normal from said edge; and
repeating the steps of calculating said width through adjusting said first
color
values and said second color values for each of a plurality of said iteration
values, each
successive one of said iteration values decreasing said width of said strip.

19. The computer readable medium according to claim 17, wherein step (C)
comprises the
sub-step of:
calculating a particular location (u,v) of said intermediate locations as
u=((.phi.pD/.pi.)cos(.theta.) and v=((.phi.D.pi.)sin(.theta.).
20. The computer readable medium according to claim 17, wherein step (D)
comprises the
sub-step of:
calculating a particular one of said surface pixels by interpolating at least
two of
said intermediate pixels neighboring said particular location.
21. The computer readable medium according to claim 17, wherein step (B)
comprises the
sub-step of:
aligning said hemispherical images by (i) translating a first center of
projection q1
to a second center of projection q1' and (ii) rotating said first
hemispherical image about
q1' such that a plurality of zero cross products are formed by (a) vector
q1'p1 × vector
q2p2, (b) vector q1'p3 × vector q2p4 and (c) vector q1'p5 × vector
q2p6, where ×
denotes a vector cross product.
22. The computer readable medium according to claim 17, wherein step (B)
comprises the
sub-steps of:
generating a third hemispherical image by reflecting said second hemispherical
image about an axis; and
calculating a diameter of said hemispherical images at 180 degrees field of
view
as a distance between a given one of said objects in said first hemispherical
image and
said given object in said third hemispherical image
23. The computer readable medium according to claim 17, further comprising
the step of:
automatically determining said objects as at least three points common to both
said first hemispherical image and said second hemispherical image.
24. The computer readable medium according to claim 17, wherein said
processor
executable instructions comprises a stand-alone program.
25. The computer readable medium according to claim 17, wherein said
processor
executable instructions comprises an executable module within a program.
16

26. The computer readable medium according to claim 17, wherein said output
file
comprises a Virtual Reality Modeling Language cube primitive file.
27. A computer readable medium containing processor executable instructions
configured to
perform the steps of:
(A) receiving a plurality of images in at least one input file, an edge
being
defined where a first given row of a first of said images meets a second given
row of a
second of said images and said edge is normal to a plurality of columns of
said images;
(B) calculating a width of a strip based on an iteration value, said strip
being
oriented parallel to said edge;
(C) calculating a plurality of difference values across said edge, one of
said
difference values for each respective one of said columns, each respective one
of said
difference values being based on a plurality of first color values of said
first image inside
said strip and a plurality of second color values of said second image inside
said strip
with said strip centered about said respective column;
(D) adjusting said first color values and said second color values in each
of
said columns by a weighted scheme based on both (i) said respective difference
value
and (ii) a respective distance normal from said edge;
(E) repeating the steps (B) through (D) for each of a plurality of said
iteration
values, each successive one of said iteration values decreasing said width of
said strip;
and
(F) storing said images as adjusted in an output file.
28. The computer readable medium according to claim 27, wherein step (B)
comprises the
sub-step of:
calculating said width as w=2h.
29. The computer readable medium according to claim 27, wherein step (C)
comprises the
sub-step of:
calculating said difference values as .DELTA.i=A(0,i)-B(0,i) over i=0,...,n.
30. The computer readable medium according to claim 27, wherein step (C)
comprises the
sub-step of:
17

calculating said respective difference value as a sum of a plurality of
squares of a
plurality of differences between (i) a plurality of mask values of a mask and
(ii) said first
color values and said second color values aligned with said mask.
31. The computer readable medium according to claim 27, wherein step (D)
comprises the
sub-step of:
calculating an average of said difference values in said strip as
<IMG>
32. The computer readable medium according to claim 31, wherein step (D)
further
comprises the sub-step of:
adjusting said first color values by A j,i = <IMG> and
adjusting said second color values by B j,i = <IMG> where A j,i
has a higher value than B j,i.
33. The computer readable medium according to claim 31, further comprising
the step of:
ending said repeating in response to said average of said difference value
becoming less than a threshold.
34. The computer readable medium according to claim 33, wherein said
threshold
comprises a measure of noise in a neighborhood of said edge.
35. The computer readable medium according to claim 27, wherein said
processor
executable instructions comprises a stand-alone program.
36. The computer readable medium according to claim 27, wherein said
processor
executable instructions comprises an executable module within a program.
18

Description

CA 02431214 2008-11-19
= .
SYSTEM AND METHOD FOR REGISTRATION OF
CUBIC FISHEYE HEMISHPHERICAL IMAGES
FIELD OF THE INVENTION
This invention relates to systems and methods for registering hemispheric
images for
panoramic viewing. In particular it relates to spatial alignment and colour
balancing of
images.
BACKGROUND AND GENERAL DESCRIPTION
Fisheye lens has experienced success in a number of applications involving
panoramic
or wide field-of-view applications. Such would include cinematography (US
patent
4,070,098), motionless surveillance (US patent RE036207), and image-based
virtual
reality (US patent 5,960,108).
The advantage of fisheye projection is its large field of view compared to
conventional
rectilinear film. Images of field of view up to 220 degrees and beyond may be
obtained
with a fisheye lens. It has been speculated that a field of view
infinitesimally less than
360 degrees is also obtainable, although the precise practical application of
a lens of this
type may be limited. In contrast, a conventional camera would require a
rectilinear image
recording surface of infinite dimensions for even 180 degrees of field of
view.
As long ago as 1964, formal studies have been made of the optical
characteristics of the
fisheye lens (Kenro Miyamoto, "Fish eye lens", Journal of Optical Society of
America,
54:1060-1061, 1964). In 1983, Ned Greene suggested the use of fisheye images
to
generate environmental maps (Ned Greene, "A Method for Modeling Sky for
Computer
Animation", Proc. First Intl Conf. Engineering and Computer Graphics, pp.297-
300,
1984).
In 1986, the use of perspective mapping for a fisheye image, projecting the
latter into the
sides of a rectangular box as an environmental map was introduced by Greene
(Ned
Greene, "Environmental Mapping and Other Applications of World Projections",
IEEE
Computer Graphics and Applications, November 1986, vol. 6, no. 11, pp. 21-29).
Greene
took a 180 degree fisheye image (a fisheye environmental map) and projected it
onto the
six sides of a cube for perspective viewing.
1
_
.

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
Producing high-quality panoramic imaging using Greene's approach poses a
number
of difficulties. Each hemispheric image produces four half-sides of a cube, in
addition
to a full side, which require registration with its complement from the other
hemispheric image. Registration of the half-images has two associated
problems:
spatial alignment and colour balancing.
Where the lens has a field of view greater than 180 degrees, the corresponding
half-
sides (as de-warped from the raw source image) require spatial alignment due
to
possible rotational and translational distortion. Furthermore, the image
recording
device would not necessarily capture the images precisely in the same area on
the =
recording surface. Conventional methods of aligning the sides of such images
are
essentially manual in nature; even if assisted by graphics software, the
process
requires human intervention to line up the edges of half-sides based on the
features
in the images. This is often imprecise and difficult due to the multiple
sources of
distortion. There is a need for a more automatic process which reduces human
intervention.
Chromatically, each half-side must be aligned relative to its complement. For
example, the recording device may have the same exposure times and aperture
openings for each of the two images despite the fact that the amount of light
recorded for each image differs, as where the lighting changed between the two
capture events , or alternatively, where the exposure times are different for
each
image despite equivalent lighting conditions. If aperture size is controlled
automatically, further mismatches may result. As a result the complementary
edges
of half-images have different colour intensity but generally the same detail
and level
of noise.
Existing methodology for colour balancing tend to average the colour values of
pixels
in the relevant neighbourhood of the transition. This has the desired effect
of bringing
the difference across the transition into line. However, the disadvantage
concerns the
concomitant loss of detail. As a result there is a perceptible blurring across
the region
of the transition. When the width of the overlapped region is narrow as
compared to
lighting imbalance, the transition may appear too abrupt.
SUMMARY OF THE INVENTION
This invention provides systems and methods for registering hemispheric images
obtained using a fisheye lens for panoramic viewing. In particular it relates
to spatial
2

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
alignment and colour balancing of complement half-side images derived from the
hemispheric images.
The system and method for spatial alignment determines the displacement of the
digitized recorded images using a single translation and rotation model of
distortion,
which further evaluates the centre of projection, the distance in pixel for
180 degree
in the recorded image, the extent of translation and rotation.
The system and method for colour balancing iteratively increase (or decrease)
the
values of pixels near the edge (discontinuity) between the two half-sides of
an image,
each time taking into consideration the average difference of pixel colour
across the
edge of a strip of decreasing width. This invention removes the colour
differential but
does not remOve any detail underlying the features of the image.
BRIEF DESCRIPTION OF THE DRAWINGS
Embodiments of the invention will be described by way of example and with
reference to the drawings in which:
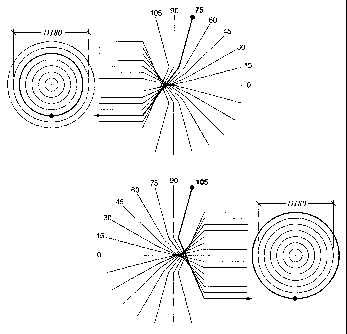
Figure 1: A diagram showing the relationship between the angle subtended by a
point and the radial position on the recorded source image.
Figure 2: A diagram showing the mapping from the hemispheric image to 5 sides
of
the cube.
Figure 3: A diagram indicating how the cartesian coordinates of a point
correspond
to its spherical coordinates.
Figure 4: A diagram of the two sides of an edge (discontinuity in colour
regimen) as
represented by two 2-dimensional arrays.
DETAILED DESCRIPTION OF THE INVENTION
The description given below assumes the use of an ideal fisheye lens, meaning
that
the lens possesses negligible if no radial distortion: the radial position
recorded in the
source image for a point imaged is proportional to the zenith angle the point
subtends
with respect to the axis of projection (see Figure 1). However, a person
knowledgeable in the art would be able to extend the invention disclosed below
to the
case where there is radial distortion. Adjustment to take into consideration
lens
characteristics are clear once the characteristics are determined.
3

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
Furthermore, the fisheye lens has a field of view greater than 180 degrees.
Overview
In the present invention, an environmental map of cube consisting of 6
canonical
views is reconstructed from two hemispherical fisheye images, as Greene had
suggested, each with field of view equal or greater than 180 degrees. Each
fisheye
image is manipulated to generate 1 complete side and 4 half-sides of a cube;
and the
half sides are then integrated to form 4 complete sides; all six sides as the
environmental map are then placed together for viewing as a complete cube
texture
map using computer graphic techniques. See Figure 2 for an overall depiction
of how
a hemispherical image may be decomposed into the various sides of a cube.
The spherical coordinates, p, 0, (1), expressed in Cartesian coordinates, x,
y, z, of a
point in space, are as follows (see Figure 3):
p = VX2 + y2
0 = tan-1(L-
x,
(i) =tan('
0 is the azimuthal angle, and 4, the zenith angle. The effect of the fisheye
lens is
such that each point is projected onto a hemisphere of diameter D, centred at
the
origin, with the projective axis being the z-axis. The point on the hemi-
sphere when
subsequently projected onto the x-y plane, corresponds to the source image
coordinate (u, v) as captured by the image recording device. As a result, the
value of
the pixel at location (u, v) of the source image is assigned as the value of
the pixel on
the environmental map that corresponds to the (x, y, z) coordinate on the
cube.
Given the above, for any point on the hemi-cube, the coordinate (u, v) in the
source
image (the environmental map) can be evaluated from 0 and (1), corresponding
to the
planar coordinates of the point of intersection of a ray extending from the
origin to the
hemi-cube with the hemi-sphere, as follows.
4

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
(1) D
u= _____________ cos(0)
v = (IL134 sin(0)
Since the lens is ideal, the radial distance from the origin of any point (u,
v) on the x-y
plane should be linear in the zenith angle (I). (Take the square root of the
squares of u
and v, which results in a linear function of 0
Given a digitized hemispheric fisheye source image formed as described above,
the
starting point is to determine the centre of projection (us, vc) on the source
image
array, and the length in image pixel, D, equal to a view of 180 degrees in
zenith
angle. In practice, the centre of projection, (i.e. the point where (I) = 0 )
is not always
the centre of the source image array. One would then determine the image array
corresponding to each of the sides by determining for each point in the
corresponding image array the (x, y, z) coordinate, compute the corresponding
(u, v)
coordinate on the source image, and estimate the value of the pixel at (u, v)
using
some sort of interpolation scheme based on the neighboring pixel values. In
the
expression for (u, v), the coordinate must be translated by the centre of
projection
(us, ye) in the source image.
At this point the images require colour balancing in order to remove visible
discrepancies in colour between any two complementary half-images along the
separating edge.
With the geometry aligned and colour balanced, the visible interface between
the
hemi-cubes disappears, resulting in a complete cube texture map comprising the
six
full-sides. The stacked face arrangement and ordering is preferably chosen to
comply
with a VRML cube primitive, for possible display on the world wide web.
Standard computer graphic techniques may be used to render the six-sided cube
centred at the origin. The viewpoint is fixed at the origin, and the view
direction along
the positive z axis. Using a pointing device such as a mouse, a viewer can
vary the
yaw and pitch of the view by rotating the cube around the Y- followed by a
rotation
about the X-axis. The faces are mapped to the cube using perspective texture
mapping, and as the user switches scenes, the texture map changes.
Preferred embodiments of this invention use one or more electronic processors
with
graphics display devices and other human interface devices. The processors may
be
5

CA 02431214 2003-06-06
WO 02/47028 PCT/CA01/01755
a native device or resident on an electronic network such as a local area
network, an
intranet, an extranet, or the Internet. The source images may be derived from
a
digital camera, such as those using CCD cells, or from digitized images of
photographs taken with a conventional camera ouffitted with a fisheye lens,
amongst
others.
Geometric Alignment
Spatial, or geometric, alignment of the two hemispheric images proceeds on the
basis that there is an overlapping annular region between the two images.
Given a
lens with a half field of view of v=105 degrees, the annulus of overlap would
be 30
degrees (two times 15 degrees on each side) if the hemispheric images were
taken
exactly 180 degrees apart. In this case, each annular region beyond the ring
denoting 180 degrees would be a mirror image of the annular region of the same
dimension in the other hemispheric image (reflected across the 180 ring).
Thus in
Figure 1 the region consisting of the two outermost concentric annuli in each
of the
mapping of the two fisheye lens is a mirror image of the another.
In practice, the camera may experience displacement from the ideal position
for
taking the reverse image after recording the initial one: rotation about each
of the 3
Cartesian axes and translational movement in the x-y plane may occur. The
model of
distortion assumed by this invention however postulates 2 types of distortion:
a
translation in the x-y plane and a rotation about the projection z-axis. The
image
recorders are assumed to be directed precisely 180 degrees apart with
coincidental
projection axes, the z-axis. The source image planes are assumed to be
coplanar,
but the image as recorded experiences a possible translational and rotational
displacement.
The approach disclosed by this invention is to align 3 points in the
overlapping region
of one hemispherical image with the same 3 points in the other image using the
above mentioned model of distortion. This method aligns the three pairs of
points
such that the zenith angle (I) from the centre of projection is the same
for,any two
pairs of points. Once aligned, the centre of projection and the distance in
pixel for
180 degrees field of view may be computed. Knowledge of these two allows the
cubic faces of the environmental map to be generated.
The following defines the notation adopted:
6
=

CA 02431214 2009-02-18
= 3 non-collinear points pl(xl, y1), pe(xe, ye), and p5(x5, y5) in the
overlapping annular
region of a hemispheric source image Ti with the centre of projection at qi
and the
complement set of points D (X 2, V ), n (x v4,, and p6(x6, y6) with its centre
of projection
,
at q2 for the reverse image12(Since T2 is the reverse image, it becomes
necessary to
reflect T2 about the vertical axis defined by the azimuthal angle 4) being 90
or 180
degrees, to yield 12'. For the purpose of simplicity though, refer henceforth
to 12' as T2;
= the angle that each source image is rotated about its axis of projection
relative to the
earth's horizon: al and a2, for T1 and T2 respectively. For the purpose of
simplicity,
assume that a2 is zero, that is to say, the second image is not rotated
relative to the
horizon;
= the true center of projection: Q;
= the diameter in pixels equivalent to 180 degrees field of view: D.
Given that the images Ti and 12 are precisely 180 degrees apart, any point pi
will form
the same azimuthal angle 0 relative to qi, the centre of projection in its own
image, as its
complement 132 would with q2. Therefore, if the two centres of projection were
the same
point Q, then the z component of the vector cross product of (pi-Q) and (p-Q)
would
equal zero since these two vectors are parallel.
The centre Q may be found assuming that displacement consists solely of a
translation
Ax and Ay, and a rotation of angle a. One embodiment of this approach assumes
that q2
is fixed as the centre Q, and determines the displacement (Ax, Ay, a) of ql,
resulting in
q1', such that the z components of the 3 vector cross products of (q11-p1) and
(q2-p2), (q11-
p3) and (q2-p4), and (q1'-p5) and (q2-p6) are all zero. (The cross products
are all zero
vectors since the initial vectors have zero z component resulting in no planar
components to the resultant cross products.)
This essentially sets up a system of 3 equations (the z components of the
cross
products) in 3 unknowns (Ax, Ay, a), which a person skilled in the art is able
to solve. For
example, the Newton-Raphson iterative method for finding roots of systems may
be
used. An initial approximation to the solution for (Ax, Ay, a) may be the
translational
difference between pi and 132, and the angle zero.
The result of this computation is the 3-tuple, (Ax, Ay, a). If p,' is the
result of translating
and rotating pi, each complementary pair of vectors (q2-p1') and (q2-p;),
where i=1, 3, and
5, and j=2, 4, and 6 respectively, are parallel, thus the lines joining each
complement
pair of p,' and p; must intersect at the same point q2 (same position
7

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
as Q and q1'). As a result, the centres of projection in each hemispheric
image
(referred to as (us, vs) for each hemispheric image earlier), Gil and q2, may
be
established.
Furthermore, it is now possible to determine D, the number of pixels equal to
180
degrees field of view, which is used for evaluating the value of coordinates
(u, v) in
the environmental map. Since the sum of the zenith angle (I) of a point in one
image
added to the zenith angle of the same point in the other hemispheric image is
180
degrees, the zenith angle 180 corresponds to the average of the radial
distance for
any two complement points. Therefore this allows D to be computed.
Given the centre of projection, (us, vs), for each hemispheric image, and the
distance
in pixel D for 180 degrees, the 6 perspective sides of the cubic environmental
map
may now be generated.
In one preferred embodiment of this invention, the user selects for display
annular
regions from both hemispheric images. Each annulus covers typically the
overlapping
region between the two source images, subtended by the zenith angles between
270-v and 90+v, where V is the half-field of view. For example, if v is 105
degrees
(i.e. the full field of view is 210 degrees), the annulus region corresponds
to the field
of view between 165 and 195 degrees. Once the two annuli of interest are
displayed,
typically at the same time, the user may then select a common point in each
annulus.
This invention also includes the variation where the user merely has to denote
the
approximate area where the second of the pair of points is located in the
second
image. The electronic processor would utilize imaging processing techniques
such as
a convolution mask to locate the precise point in the second image
corresponding to
the first point in the first image.
This invention further includes variations where automatic determination of
the 3
common points are performed without human intervention.
Although it is theoretically possible to select all three points in the same
nearby
neighbourhood, the preferred approach is to select points which are widely
spread
apart, typically in different thirds of the annular region. Therefore, display
of only a
common sector of the annuli typically occurs for the point selection process.
Displaying smaller areas permits greater spatial resolution and more precise
location
within the areas.
Once the common points are identified, the electronic processor carries out
computation of the centre of projection (us, vs) for each hemispheric image
and the
distance D in pixel for 180 degrees field of view. The environmental map of
the cubic
sides are then ready to be fully generated given these parameters and the
rotation a.
8

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
Colour Balancing
In addition to removing spatial distortions as mentioned above, two
complementary
half-images as combined typically require colour balancing due to different
prevailing
lighting conditions or imaging recorder characteristics. This invention
further
discloses methods and apparatus for colour balancing across a discontinuity
(or
edge) in an image that does not remove detail from the image as a whole.
To illustrate the method by example, let one side of the edge be represented
by a 2
dimensional array Aj,i, and the other side B1, both of dimensions m+1 rows
(indexed
0 to m) and n+1 columns (indexed 0 to n). The 0-th row of both arrays lie
adjacent to
the.edge as shown in Figure 4, with rows further away from the edge in
increasing
index of row. Although only one value for each pixel is indicated here, this
method
will work for any color model including ROB, CMY, YIQ, HSV, and HLS. These
colour
models are well known in the field of computer graphics. For example, in the
case of
an RGB colour model, there would be 3 arrays, 1Ajj, 2Ab1, and 3A;,i,
corresponding to
each of the red, green, and blue colour values; the same would apply for the B
arrays.
This invention makes use of the concept of "imbalance waves" of varying
frequency
which runs additively parallel and adjacent to the edge for a certain depth
normal to
the edge. An iterative approach is adopted whereby a different filter is
applied at
each step to the edge region. The analogy is that each filter is a low pass
filter, tuned
to a distinct "frequency" level, which eliminates imbalance waves of frequency
at that
level and greater. During each iteration, a filter of a lesser frequency is
used until a
frequency of 1 is reached.
Generally, at each iteration, a filter of level w=2h is applied, where h
decreases from
m to 0. The value w is a measure of the width of a strip on the edge, the
average
difference, in colour value across the edge on the strip, is permitted to
influence
colour values during the steps constituting the particular iteration. The
value m is
chosen such that 2m+1 is less than the width of a full side of the cube, which
will
become clear later in this discussion. Instead of powers of two, which has the
advantage of being intuitive and can enable m to decrease to the value 0
quickly as
the logarithm of w, other schemes for decreasing w will also suffice.
During an iteration, the difference at column i across the edge between any
two
adjacent A0,1 and B0,1 is evaluated as A.
9

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
A; = Ao,i- B0,1 i = 0, 1, n
In cases where there is high contrast in difference across an edge, a slightly
different
method for computing Ai is helpful to avoid "bleeding" of the high intensity
value of
the one side into the lower intensity opposite side in the balanced image.
This
approach assumes the images as slightly overlapping in the rows and slightly
offset
in columns (which is typically the case in reality), and uses both images. If
it is
assumed that there are x overlapping rows, one way of computing the value of
AI is
to use a small region across the boundary in one image and centred on A0,1 (or
B0,1,
no difference whichever is used) as a square mask (typically 3 elements by 3
elements). The region is overlaid on a series of corresponding areas in the
other
image, the other areas within a typically square domain centred on the 'A0,1
in the
other image, where 'A0,1 is the corresponding pixel for A0,1 in the original
image. Each
side of the domain has size typically twice the overlapping width (plus one).
The
sums of the squares of the differences between the values of the mask and the
underlying pixels are calculated as the mask is translated across the surface
of the
domain. One embodiment calculates 6.1 as the average of the arithmetic
difference of
the mask the underlying pixels of the image centred at the place of the
minimal sum
of squares.
If the overlap is greater than two, then the mask may be chosen be larger than
3x3,
up to the point where it may be limited in translational freedom of only one
pixel in
any of the 8 directions.
An average of the differences, 1"1, for any column i on the edge is taken for
2w+1
differences centred on i, with wraparound values for any difference with index
exceeding the bounds of the difference array.
W
r. EAk
= k="
2w+1
where k = k+(n-1), if k<0, and k = k-(n-1), if k>n, for the purpose of the
summation.
Clearly, this is just one way of calculating the average of the difference,
and the
invention is not restricted to this one way, although this results in
computational
efficiency. Other variations could weight the differences by a window
appropriate to
the type of image, e.g. a Gaussian window centred on i. Alternatively, there
may be a
threshold for discounting those differences which exceed the threshold. For
example,

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
the presence of a colour burst may be one instance where a precipitous drop in
value
across an edge should be discounted. Visually, such a measure would have
little
impact on the resultant reconstructed image.
At this point, the value of the side with the lower value is adjusted upwards
by a
variation term which is a function of the average difference across the edge.
The
adjustment used decreases with distance from the edge. A preferred embodiment
then redefines all the elements of the arrays, Ao and Bo, as follows:
= A==
'1 '1 2 w
13jj u =S + 1r; __
' 2 w
Although the above weights the average difference decreasingly with distance
on a
linear basis from the edge (w-j), this invention is not limited to this
weighting scheme.
One variation is where a faster drop-off, e.g. an inverse exponential, is
required by
the character of the image.
The way that A is calculated influences the effect of a high contrast edge.
Without
seeking out the minimum sum of square of difference, a high contrast edge will
change the value of both sides of the edge more significantly than if the
difference
where the minimum sum of square occurred was used.
Typically, the iteration ends when w reaches the value of one (filter of
frequency 1).
However, it is possible to impose a threshold beyond which no further
iterations are
carried out. One approach is based on the average difference across the edge.
Once
the average difference drops below a threshold, the iterative steps end. In
this case
the threshold may be taken relative to a measure of the noise in the
neighbourhood
of the edge.
Preferred embodiments of this invention also involve computer program products
which are recorded on a machine-readable media. Such computer program products
when loaded into an apparatus that can read and execute the instructions borne
by
the program products in order to carry out the functions of geometric
alignment or
colour balancing denoted above.
The system, methods, and products above may operate modularly or in serial.
For
example, the same system may perform both alignment and colour balancing, or
two
11
=

CA 02431214 2003-06-06
WO 02/47028
PCT/CA01/01755
separate systems operate serially on the digitized images. These may be used
in
standalone configurations or in a networked environment cooperating with many
other applications, systems, databases etc. for capturing and processing.
Environmental maps may be generated from colour balanced images.
It will be appreciated that the description above relates to the preferred
embodiments
by way of example only. Many variations on the device, method, and computer
program product for delivering the invention will be understood to those
knowledgeable in the field, and such variations are within the scope of the
invention
as described, whether or not expressly described.
12

Representative Drawing