Note: Descriptions are shown in the official language in which they were submitted.
WO 02/50513 CA 02431943 2007-12-21 PCT/FR01/04046
DISPOSITIF DE VISUALISATION BIDIMENSIONNELLE ELLIPSOMETRIQUE D UN ECHANTILLON,
PROCEDE DE VISUALISATION ET PROCEDE DE MESURE ELLIPSOMETRIQUE AVEC RESOLUTION
SPATIALE
ART ANTÉRIEUR
s La présente invention concerne un dispositif de visualisation
bidimensionnelle ellipsométrique d'un échantillon,- un procédé de
visualisation et un procédé de mesure ellipsométrique avec résolution
spatiale. Elle est particulièrement bien adaptée à une visualisation en
contraste ellipsométrique ou en contraste interférentiel.
Un échantillon recevant de la lumière et la, réfléchissant en
modifie généralement la polarisation.
Il est possible d'utiliser cette propriété pour visualiser un
échantillon ou pour le caractériser en mesurant ses paramètres
ellipsométriques généralement désignés par yr et à.
A ce sujet, on pourra, par exemple, se référer à l'ouvrage
.Azzam et Bashara publié en 1979.
Initialement,.on a cherché à exploiter l'extinction du coefficient
de Fresnel rP à l'angle de Brewster pour accéder à une mesure
ellipsométrique précise des paramètres y et à (ellipsoméirie) ou à une
ao visualisation sensible de films très minces; nôtamnient à la surface de'
l'eau (microscopie à angle de Brewster).
Par ailleurs, on a-cherché à éclairer une zone d'un échantillon
sous une incidence et un azimut uniques pour mesurer les paramètres
yf et d correspondant à cette zone.
RÉSUMÉ DE L'INVENTION
On s'intéresse dans le cadre de la présente invention à mie exploitation
simultanée des pararnètres 'Y et 0
pour un certain nombre de points d'un échantillon. définis cliacun par leurs
coordonnées x et y.
C'est ce qui est appelé une visnalisation ou nne mesure bidimensionnelle
ellipsométrique d'un
échantillon.
De plus, dans le cadre de la présente invention, on s'intéresse aux
écliantillons de petites din-iensions
observés, visualisés ou inesurés sous microscope optique en réflexion. Il peut
s'agir de microscopie
traditionnelle, de niicroscopies à contraste interférentiel différentiel ou de
microscopie à
fluorescence.
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
2
Ce type d'observations microscopiques pose des contraintes
particulières dans la mesure, d'une part, où les objectifs de
microscopes ont une ouverture numérique importante qui crée des
conditions d'observations significativement différentes des conditions
usuelles des mesures ellipsométriques, dans lesquels les faisceaux tant
d'éclairage que de mesure (ou faisceaux réfléchis) sont généralement
des faisceaux collimatés de faible ouverture et, d'autre part, où les
faisceaux d'éclairage sont le plus souvent distribués uniformément
autour de l'incidence normale, c'est-à-dire dans une ga;mme d'angles
1o d'incidence peu propice à l'ellipsométrie.
Certes, des méthodes de visualisation basées sur l'utilisation
d'un substrat antiréfléchissant ont été proposées antérieurement mais
elles sont fondées sur la réflectivité incohérente du substrat. Les
substrats proposés précédemment sont donc antiréfléchissants pour
une lumière non polarisée ou pour une lumière polarisée avec une
direction de polarisation constante par rapport au plan d'incidence, ce
qui est incompatible avec l'utilisation d'un microscope. Le principe
reposé sur la minimisation du second membre de l'équation (E4).
(DN(O,NP) 1(IrpI2+IrsI2) E4
2
où rp et rs sont les coefficients complexes de réflexion de chacune des
polarisations sur le substrat concerné qui dépendent implicitement de
x et de y, (DN(B,NP) étant le flux normalisé réfléchi pour un angle
d'incidence Of, en lumière non polarisée.
Notons que l'extinction totale ne s'obtient que pour
Irpl = irs) = 0, qui est une condition extrêmement contraignante,
puisque les valeurs des deux coefficients de Fresnel sont fixées. La
condition d'extinction totale, Irp + rsl = 0, est beaucoup plus souple
3 o- puisqu'elle se traduit seulement par une relation entre les deux
coefficients de Fresnel,
rp = -rs E6
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
3
Des substrats antiréfléchissants pour une lumière polarisée ont
aussi été proposés pour augmenter les performances des
ellipsomètres, mais l'ellipsométrie et la microscopie optique étaient
jusqu'à présent jugées inconciliables.
Le but de l'invention est donc une visualisation
bidimensionnelle ellipsométrique d'un objet de très faible épaisseur
invisible sous microscope optique dans des conditions d'observation
connues compatibles avec l'utilisation d'un microscope optique
commercial.
Zo Malgré cela, selon l'invention, il est possible à la fois de
visualiser l'objet et de mesurer son épaisseur et son indice sous
microscope.
A cette fin, l'objet d'étude est déposé sur un substrat particulier,
l'association de l'objet d'étude et du substrat formant l'ensemble
zs observé que nous appelons - l'échantillon -. Le substrat est conçu de
telle manière que l'objet d'étude, bien que très mince, suffise par sa
présence à modifier l'aspect du substrat, conduisant ainsi à la
visualisation. de l'objet.
A cette fin, le substrat est constitué d'un support recouvert d'un
2 o empilement de couches tel que, d'une part, l'épaisseur e de la dernièré
couche vérifie la condition d2/de2[Lnlrp +rsJ] = 0 et tel que, d'autre
part, le minimum de la quantité IrP +rsJ sur l'ensemble des valeurs de e
soit aussi faible que possible.
De même, la présence de l'objet suffit dans ces conditions à
25 modifier de façon mesurable sous microscope optique les paramètres
y et A du substrat, si bien que les caractéristiques optiques de l'objet
peuvent être extraites de la mesure des paramètres yJ et A de
l'échantillon.
Ainsi, le substrat est conçu de telle manière que la sensibilité
3 o des paramètres y et A de l'échantillon à une petite perturbation de ses
paramètres constitutifs soit très grande pour des angles d'incidence
faibles, donc très différents de l'angle de Brewster, tandis que les
méthodes de visualisation et de mesure proposées sont de plus
conçues de telle manière que la géométrie radiale du nmi.croscope soit
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
4
devenue compatible avec l'exploitation de ces caractéristiques
ellipsométriques.
Dans un mode de réalisation préféré, mettant en uvre un
microscope interférentiel différentiel (DIC) (grâce à un dispositif
inséré au voisinage du plan focal arrière de l'objectif, par exemple un
dispositif de Nomarski ou un dispositif de Smith), le faisceau
d'éclairage, polarisé linéairement selon l'azimut cp = 0, est décomposé
par le dispositif DIC en deux faisceaux polarisés linéairement selon
les directions cp = 45 et cp =-45 et décalés latéralement l'un par
lo rapport à l'autre d'une petite quantité Ad, les deux plans d'onde
associés à ces deux polarisations enregistrant à la réflexion sur
l'échantillon des variations de phase dues à la présence ou aux
inhomogénéités de l'objet, ces variations de phase se transformant en
variations de couleur ou d'intensité après passage au retour du
faisceau réfléchi dans le dispositif DIC, puis dans l'analyseur croisé
avec le polariseur. Dans ce mode d'observation, le contraste de l'objet
est optimisé grâce au réglage d'un compensateur inclus dans le
dispositif DIC. Ce réglage consiste à éteindre l'interférence entre les
deux faisceaux réfléchis par les régions non intéressantes de
l'échantillon en réglant leur déphasage au niveau du dispositif où elles
interfèrent, c'est-à-dire au niveau de l'analyseur, la qualité de cette
extinction conditionnant la qualité de la visualisation. La condition
mathématique de cette extinction est la même que précédemment, à
savoir rp + rs = 0. La condition de sensibilité maximale sur l'épaisseur
2s e de la derniére couche de l'empilement dans ce mode d'observation
est d2/de2[LnlrP +rsI] = 0.
Le procédé de visualisation proposé est donc globalement
optimal pour toutes les observations sous microscope entre polariseur
et analyseur croisés, y compris lorsqu'un dispositif DIC est inclus
3 o dans le microscope.
L'invention concerne donc un dispositif de visualisation
bidimensionnelle ellipsométrique d'un échantillon, comportant un
objet, placé dans un milieu incident, observé entre un analyseur et un
polariseur croisés par réflexion en lumière convergente, dans lequel
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
les paramètres ellipsométriques de l'ensemble formé par l'objet (4) et
un substrat (8) sur lequel il est placé, sont exploités.
Selon l'invention :
- le substrat comporte un support et un empilement de couches
5 et que ses propriétés ellipsométriques sont connues,
- les propriétés ellipsométriques du substrat étant telles que les
variations des paramètres ellipsométriques de l'échantillon dues à
l'objet soient visualisées avec un contraste supérieur au contraste
produit en l'absence de ce substrat.
La présente invention concern.e également les caractéristiques
qui ressortiront de la description qui va suivre et qui devront être
considérées isolément ou selon toutes leurs combinaisons
techniquement possibles :
- l'échantillon est éclairé au travers d'un objectif à grande
ouverture tel qu'un objectif de microscope,
- le microscope est un microscope à contraste interférentiel
différentiel,
- le microscope est un microscope de fluorescence,
Ce mode de réalisation est le plus efficace pour la visualisation
ou la détection d'objets de dimensions nanométriques. Il s'agit alors de
visualiser sans résoudre. Il permet en particulier la visualisation de
tous les objets filiformes isolés, c'est-à-dire distants d'une quantité
supérieure à la résolution latérale du microscope, dont la longueur est
supérieure au micron (polymères, microtubules, collagène, bactéries,
ADN, ARN, nanotubes de carbone, nanofils, etc.).
- l'épaisseur e de la couche de l'empilement en contact avec
l'objet est telle que les coefficients de réflexion complexes rp et rs du
substrat vérifient la condition d2/de2[Lnirp +rsJ] = 0,
- les propriétés optiques du substrat sont telles que la valeur
minimum prise par la quantité Irp + rsJ sur l'ensemble des valeurs de e
est aussi faible que possible,
- le dispositif comporte une source lumineuse polychromatique,
- le dispositif comporte une source lumineuse
monochromatique,
- le support est en silicium,
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
6
De manière plus générale, le support est avantageusement un
milieu absorbant, un métal ou un semi-conducteur dont la partie réelle
de l'indice optique est supérieure à 3,3.
- l'empilement est constitué d'une couche unique,
Cette couche est avantageusement minérale, constituée d'un
mélange SiO/Si02 en proportions adaptées.
- la couche est une couche de silice,
- l'épaisseur de la couche de silice est de l'ordre de 1025 A, le
milieu incident étant de l'air,
i0 - la couche est une couche de fluorure de magnésium,
- l'épaisseur de la couche de MgF2 est de l'ordre de 1055 A, le
milieu incident étant l'air,
- la couche est une couche de polymère,
- la couche est une couche de polymère, d'indice optique
approximativement égal à 1,343, le milieu incident étant de l'air,
.- la couche est une couche minérale, d'indice optique
approximativement égal à 1,74, le milieu incident étant de l'eau,
- la couche est une couche minérale, d'indice optique
approximativement égal à 1,945, le milieu incident étant une huile
2o d'indice optique 1,5,
- la couche est discontinue et formée de plots de silice et
d'indice 1,343, de même hauteur définissant l'épaisseur de la couche
et de dimensions en section très inférieures au micromètre, le milieu
incident étant de l'air,
- la couche est une couche organique ou minérale mésoporeuse
ou nanoporeuse d'indice approximativement égal à 1,343, le milieu
incident étant l'air,
- la couche est un aérogel minéral d'indice approximativement
égal à 1,343, le milieu incident étant l'air,
- le dispositif comporte un microscope comportant un
diaphragme d'ouverture en forme de fente longitudinale orientable
autour de l'axe du microscope permettant de restreindre le cône
d' éclairage à un seul plan d'incidence dans une direction choisie,
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
7
- le dispositif comporte un microscope comportant un
diaphragme d'ouverture en forme d'anneau limitant le cône
d'éclairage de l'échantillon autour d'un angle d'incidence,
- l'objet est un film mince et l'empilement comporte une couche
en biseau dont T'épaisseur varie de façon monotone dans une direction
X le long de la surface.
Ce procédé et ce dispositif de visualisation sont compatibles et
avantageusement superposables à toute technique de microscopie
optique à balayage, à toute technique optique à lumière invisible (UV
Zo ou IR), à toute technique de spectroscopie, à toute technique
d'optique non linéaire, à toute technique de diffusion ou de
diffraction, et à toutes leurs combinaisons. Ils sont en particulier
compatibles avec les techniques de fluorescence, de micro-Raman, de
microscopie confocale, de microscopie à deux photons, et à toutes
leurs combinaisons.
La mise en oeuvre de la présente invention avec la microscopie
de fluorescence est particulièrement avantageuse. En effet, la
polarisation de la lumière émise par un échantillon fluorescent est
souvent différente de la polarisation du faisceau incident. Le
marqueur fluorescent introduit donc une dépolarisation de la lumière
à laquelle le dispositif de l'invention est particulièrement sensible. De
plus, le facteur d'extinction de la lumière incidente propre au
dispositif de l'invention réduit considérablement le bruit
accompagnant le signal fluorescent.
Enfin, cette mise en oeuvre de la présente invention avec la
microscopie de fluorescence permet de reconnaître parmi des objets
fluorescents identiques ceux d'entre eux qui dépolarisent la lumière,
ce qui correspond à un environnement très particulier des molécules.
Cette mise en oeuvre est particulièrement efficace pour
l'observation de surfaces immergées dans un milieu fluorescent. Elle
est aussi très avantageuse pour la lecture du signal de fluorescence
des biopuces, incluant l'observation des cinétiques d'hybridation.
L'invention concerne aussi un procédé de mesure dans lequel :
- on découpe le dispositif de visualisation parallèlement à la
direction X en deux éléments,
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
8
- on dépose le film mince sur l'un de ces éléments,
- on place les deux éléments entre un polariseur et un analyseur
croisés sous un microscope polarisant éclairé en lumière
polychromatique, de façon à former des franges d'interférences
s colorées sur chacun des éléments,
- on mesure le décalage des franges formées respectivement
dans chacun des éléments pour en déduire les propriétés de la couche
déposée sur l'un d'eux.
L'invention concerne de plus un dispositif de visualisation d'un
lo échantillon tel que précisé plus haut, dans lequel le substrat est le
fond d'une boîte de Petri.
L'invention concerne de plus un dispositif de visualisation d'un
échantillon tel que précisé plus haut, dans lequel l'échantillon est un
multicapteur matriciel, chaque plot ou pastille de la matrice pouvant.
15 constituer la dernière couche de l'empilement. Ce multicapteur peut
être une biopuce à bactéries, à virus, à antigènes, à anticorps, à
protéines, à ADN, à ARN, ou à chromosomes, le dispositif constituant
alors un dispositif de lecture parallèle.
L'invention concerne également un procédé de mesure
2 o ellipsométrique d'un échantillon avec résolution spatiale sous
microscope polarisant formant une image de l'échantillon dans
lequel :
- l'échantillon est éclairé par un faisceau d'éclairage polarisé
linéairement au travers d'un diaphragme d'ouverture,
25 - la lumière réfléchie par l'échantillon est analysée par un
polariseur-analyseur, caractérisé par l'orientation relative ~ de sa
direction de polarisation par rapport à celle du polariseur,
- une modulation de l'intensité réfléchie est assurée par la
rotation relative de la polarisation de faisceau d'éclairage et du
3 o polariseur-analyseur.
Selon ce procédé :
- le diaphragme d'ouverture du faisceau d'éclairage est un
anneau centré sur l'axe du faisceau délimitant un seul angle
d'incidence,
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
9
- on mesure, simultanément en chaque point de l'image obtenue
de l'échantillon, le flux moyen ~M(x,y) réfléchi et son amplitude de
modulation ~m(x,y),
- on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire
simultanément en chaque point de l'échantillon deux combinaisons
des paramètres ellipsométriques y(x,y) et A(x,y) et du coefficient de
réflexion Irs1z(x,y) à partir des formules :
1Ir5I2(l + tan2y) =~M et 1 f rsl2(tanaW - 2tanycosA)
2 2
- on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire la
combinaison sin(2-y)cos des seuls paramètres ellipsométriques V(x,y)
et A(x,y) à partir de la formule :
~m -~ M(1-sln(2y)cosA)
Eventuellement, dans une étape de mesure :
- l'orientation de l'analyseur par rapport au polariseur est fixée
à une valeur différente de 7c/2 modulo 7c,
- le diaphragme d'ouverture du faisceau d'éclairagé est une
fente orientable autour de l'axe optique du microscope superposée à
un anneau délimitant un seul angle d'incidence,
- l'on mesure l'intensité du faisceau réfléchi pour au moins
deux orientations cp différentes et non redondantes de la fente,
- l'on traite ces mesures d'intensité à partir de la relation :
Irp 12 cos zCp cos 2((p -(p) + Irs 12 sin 2Cp sn12(~ - (p)
I= A? * * sin 2(p sin(2c~ - 2cp)
+ (rpr$ + rp rs )
4
- on en déduit simultanément en chaque point de l'échantillon
les valeurs des deux angles ellipsométriques y(x,y) et A(x,y) et celles
des modules des coefficients de réflexion IrPj et Irj.
Eventuellement, dans une étape complémentaire :
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
- l'analyseur est fixé dans une orientation non perpendiculaire
au polariseur, par exemple ~= 0,
- le diaphragme d'ouverture du faisceau d'éclairage est une
fente orientable autour de l'axe optique du microscope superposée à
5 un anneau délimitant un seul angle d'incidence,
- l'on mesure l'intensité réfléchie pour les deux orientations
cp=0 etcp=n/2 de la fente,
- l'on traite ces mesures d'intensité pour obtenir tany en
prenant la racine carrée de leur rapport selon les trois formules :
I= A2rp l2 cos2 pour 9 = 0 modulo n
I= A1Irsl2 sin2 pour cp =2 modulo ir
_ rP
tan yf - -
rs
Eventuellement, dans une étape de mesure :
- l'orientation de l'analyseur par rapport au polariseur est fixée
à une valeur différente de 7c/2 modulo 7c,
- une modulation de l'intensité réfléchie est assurée par la
rotation du diaphragme D autour de l'axe optique,
- l'on mesure simultanément en chaque point de l'échantillon le
flux moyen ~M(x,y) réfléchi et son amplitude de modulation ~n,(x,y),
- l'on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire les
deux angles ellipsométriques yf(x,y) et A(x,y) et les modules Irpl et irsJ
des coefficients de réflexion à partir de la relation :
IrPlZcos2(PcosZ(~-~P)+Irsl2sin2CPsina(~-9)+
I= A; * *. sin 2cp sin(2~ - 2cp)
(rprs +rrs)
4
Eventuellement, dans une étape complémentaire :
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
11
- l'orientation de l'analyseur par rapport au polariseur est fixée
à0,
- une modulation de l'intensité réfléchie est assurée par la
rotation du diaphragme D autour de l'axe optique,
- l'on mesure simultanément en chaque point de l'échantillon le
flux moyen ~M(x,y) réfléchi et son amplitude de modulation ~m(x,y),
- l'on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire les
deux angles ellipsométriques y(x,y) et A(x,y) et les modules Irpl et Irs)
des coefficients de réflexion à partir de la relation :
Irp IZ cos 2fP cos 2(~ - CP) + IrS I2 sin 29 sin 2(~ -~D) +
2 I- Aa * * sin 2cp sin(2~ - 2ep)
(rprs + rp rs )
4
L'invention concerne également un procédé de mesure
ellipsométrique d'un échantillon avec résolution spatiale sous
microscope polarisant formant une image de l'échantillon, dans
lequel :
- l'échantillon est éclairé par un faisceau d'éclairage polarisé
linéairement au travers d'un diaphragme d'ouverture,
- la lumière réfléchie par l'échantillon est analysée par un
polariseur-analyseur, caractérisé par l'orientation relative ~ de sa
direction de polarisation par rapport à celle du polariseur,
- une modulation de l'intensité réfléchie est assurée par la
rotation relative de la polarisation de faisceau d'éclairage et du
polariseur-analyseur,
Selon ce procédé :
- le diaphragme d'ouverture du faisceau d'éclairage est un
disque centré sur l'axe de ce faisceau,
- l'on mesure, simultanément en chaque point de l'image
obtenue de l'échantillon, le flux moyen ~M(x,y) réfléchi et son
3 o amplitude de modulation ~m(x,y), .
- l'on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire
simultanément en chaque point de l'échantillon deux combinaisons
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
12
des paramètres ellipsométriques effectifs yef~x,y) et Aeff(x,y) et du
coefficient de réflexion effectif Jrs ed2(x,y) à partir des formules :
2lrs I2(1 + tan2ureff ~M et 1 Irs f 2(tan2~reff - 2 tan~r cos à eff )-~m
2
- l'on traite les mesures ~M(x,y) et ~m(x,y) pour en déduire la
combinaison sin(2y)cos des seuls paramètres ellipsométriques
effectifs i~ref~X,y) et AefdX,y) à partir de la formule :
sin2ye~ cos0eff -1- ~m
~M =
L'invention concerne également un dispositif de mesure
ellipsométrique sous microscope avec résolution spatiale latérale.
Selon ce dispositif :
- il ne comporte qu'un seul polariseur situé entre le miroir
d'éclairage et l'échantillon de part ou d'autre de l'objectif,
- il comporte une fente tournante dans le plan de son
diaphragme d'ouverture, événtuellement superposée à un diaphragme
en anneau permettant d'extraire les paramètres ellipsométriques de
l'échantillon à l'aide d'au moins trois mesures pour trois orientations
différentes de la fente et de la formule :
I=A~Irs12 tan2yrcos4cp+sin4 sin2 2
cp- 2 9
tanwcosà
appliquée à ces trois mesures, dans laquelle les paramètres rs, y et
A sont éventuellement des paramètres effectifs issus de moyennes
sur tous les angles d'incidence présents
IrPI 2 cos2 cpcos2(cD -cp)+Irsl2 sin2 cpsin2(D - ep)
1 20 - 2(p)
+ r*r sin 2cp sin(
I A~ + [rpr,-
p 5 4
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
13
Selon ce dispositif :
- le polariseur et l'analyseur ont une orientation relative fixée,
- le diaphragme d'ouverture est un trou ou un anneau,
- l'image du plan focal arrière de l'objectif est formée dans le
plan focal objet de l'oculaire par une lentille de Bertrand,
- une caméra CCD est placée dans ce plan,
- la mesure de l'intensité obtenue en chaque point de la caméra
CCD est exploitée grâce à la formule générale :
rp(6,XIa cos' cpcos2(D -cp)+Irs(6,Il 2 sin2 cpsin2(0 -(p)
I(cp, ~, 8, ~}= A; * * sin 2(p sin(20 - 2cp)
+ ~rp (e~~S (e, a }+ rp ( ~ ~hs (e~ ~)] 4
afin d'obtenir directement la totalité des paramètres ellipsométriques
de l'échantillon.
Selon ce dispositif :
- une modulation de l'intensité réfléchie est obtenue par une
rotation relative de l'analyseur et du pôlariseur,
- le diaphragme d'ouverture est un trou ou un anneau,
- l'image du plan focal arrière de l'objectif est formée dans le
plan focal objet de l'oculaire par une lentille de Bertrand,
- une caméra CCD ou éventuellement tri-CCD est placée dans
ce plan,
- la mesure de l'intensité obtenue en chaque point de la caméra
CCD ou en éventuellement en chaque point et pour chaque
composante de couleur de la caméra tri-CCD est exploitée grâce à la
formule générale :
2 Irp(8;ki2 cos2 cpcos2(D -(p)+Irs(8,k~ 2 sin2 cpsinZ(D - cp)+
I(cp, ~, 6, ~,} = A; *
[rp * (6 , sin 2cp sin(2~ - 2(p)
(6, ~,}rs (6, ~,} + rp ~, }rs (6, )~
4
3 o afin d'obtenir directement la totalité des paramètres ellipsométriques
de l'échantillon.
CA 02431943 2007-12-21
WO 02/50513 PCT/FR01/04046
14
Selon ce dispositif :
- l'image du plan focal arrière de l'objectif est formée dans le
plan focal objet de l'oculaire par une lentille de Bertrand,
- une caméra CCD est placée dans ce plan,
s -1a mesure de l'intensité obtenue en chaque point de la caméra
CCD est exploitée grâce à la formule générale :
Jrp(6,X~Z cos2 cpcosZ(D -(p)+{rs(9,2,~2 5in2 cpSinZ(0-cp)
I%' 0' 8 ~,) = Aa sin 2cp si~ n(
+ [rp 20 - 2cp)
(B~hS (e~~)+=p (e~~ks(e,~?~
io afin d'obtenir directement la totalité des paramètres ellipsométriques
de l'échantillon.
La caméra est une caméra couleur tri-CCD et que la mesure de
l'intensité en chaque point est faite et exploitée pour chacune des
couleurs.
ss Avantageusement, l'objet étudié est placé sur un substrat.
L'épaisseur e de la couche de l'empilement en contact avec l'objet est
telle que les coefficients de réflexion. corrrplexes rp et rs du substrat
vérifient la condition d2lde2[Ln~p +rJ] = 0.
De préférence, 1'objet est placé sur un= substrat dont les
2o propriétés optiques sont telles que la valeur minimum prise par la
quantité (rp + rs{ sur l'ensemble des valeurs de e est aussi faible que
possible.
DESCRIPTION DES FIGURES DE L'INVENTION:
Un mode de réalisation de l'invention sera décrit plus précisénient par
référence aux dessins annexés
sur lesquejs:
25 -les figures 1 et 2 défiiiissent les paramètres de polarisation de
la lumière p et s par rapport au vecteur de propagation k et les
paramètres d'orientation en incidence et en azimut 0 et cp des rayons
dans le système optique ;
- la figure 3 représente l'échantillon par rapport à l'objectif du
30 microscope ; = .
- la figure 4 est un schéma du microscope polarisant mis en
aeuvre selon l'invention ;
- la figure 5 est une représentation schématique -du dispositif de
WO 02/50513 CA 02431943 2007-12-21 pCT/FR01/04046
mesure directe d'épaisseur selon l'invention ;
- les figures 6A et 6B sout une représentation scliématique du dispositif de
visualisation de l'un
multicapetuer mis en oeuvre dan.s certains modes de réalisation de
l'invention.
DESCRIPTION DÉTAILLÉE DE L'INVENTION
5 La description de l'invention sera faite en utilisant les notations
des figures 1 et 2, où p est le vecteur polarisation de la lumière portée
par un rayon d'angle d'incidence 0 sur l'échantillon.
Par ailleurs, on désigne par - échantillon 1 - l'ensemble agissant
sur la mesure. Cet échantillon est séparé de l'objectif 2 par un milieu '
io incident 3, il comporte, dans l'ordre en partant du milieu incident, un
objet d'étude 4 (celui que l'on cllerche à visualiser), un empilement 5
de couches dont la couche supérieure 6 est la couche en contact avec
l'échantillon, et un support 7. L'empilement de couches et le support
forment le substrat S.
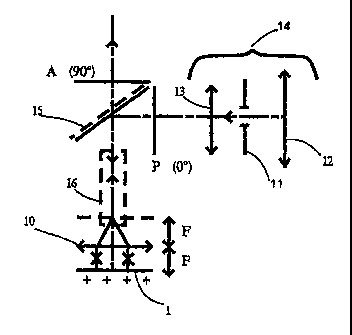
is Les figures 4A et 4B sont des représentations de dispositifs
utilisables selon l'invention ; les éléments analogues y sont
représentés avec les mêmes références numériques.
Un échantillon 1 supposé plan et isotrope est donc placé sous
un microscope optique fônctionnant en réflexion. Le microscope est
muni d'un objectif 10 et d'un éclairage de typè Kôh1er, comportant au
moins deux lentilles 12 et 13 et un diaphragme d'ouverture ou pupille
11 conjugué par la lentille 13 du plan focal arrière de l'objectif 10,
représenté par une ligne pointillée sur la figure 4A. Le polariseur P
polarise la lumière dirigée vers l'échantillon par la lame semi-
2s réfléchissante 15. La direction du polariseur P sert de référence. La
lumière renvoyée par l'objet est soumise à un analyseur A.
La figure 4B correspond à la mise en oeuvre d'un microscope à
contraste différentiel interférentiel (DIC), il comporte un élément
polarisant 16 qui est soit un biprisme de Wollaston, soit un prisme et
un compensateur de Nomarski.
Comme il est connu par ailleurs, il est également possible de
remplacer les polarisations linéaires par des polarisations circulaires.
Alors, à la place des polariseurs et analyseurs croisés, on
trouvera le miroir semi-transparent, un premier polariseur, une lame
3 s quart d'onde (X14), l'objectif, l'échantillon puis en retour à nouveau
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
16
l'objectif, la lame ~,/4, le polariseur mentionné plus haut et le miroir
semi-transparent.
Dans le cas du microscope à contraste différentiel interférentiel,
on trouvera alors le miroir semi-transparent, un polariseur, l'élément
polarisant, une lame 1/4, l'objectif, l'échantillon puis en retour à
niveau l'objectif, la lame ~,/4, l'élément polarisant, le polariseur
mentionné plus haut et le miroir semi-réfléchissant.
L'angle d'incidence d'un rayon est O. Le microscope est muni
d'un polariseur linéaire et d'un analyseur situés de part et d'autre de
lo 1'échantillon sur le trajet de la lumière. L'éclairage est épiscopique et
monochromatique. L'analyseur est tournant et fait un angle ~ avec le
polariseur. On mesure le flux réfléchi normalisé (DN comme le rapport
du flux réfléchi et d'un flux de référence. Le flux de référence est
celui qu'on obtiendrait sur le même instrument réglé de la même
maniére en l'absence de polariseur et d'analyseur avec un
hypothétique échantillon parfaitement réfléchissant. L'échantillon
parfaitement réfléchissant est défini par ses coefficients complexes de
Fresnel pour les polarisations parallèle (p) et perpendiculaire (s)
comme rp = rs = 1. Pour un angle ~ quelcônque :
cos2~
'DN (8, ~) = COS Z~(Irp 12 + lrs 12) - 4 Irp + rS 12 E 1
Dans le cas particulier où le polariseur et l'analyseur sont
croisés _7t/2), cette formule se réduit a:
Irp + rS (z
CDN 8 2 E2
Le second membre de la formule (El) est directement
interprétable. Il est constitué de deux termes :
Le premier, cos2~(IrpIz + Irs12), est le produit d'un coefficient
d'extinction et d'un coefficient de réflexion en intensité que nous
appellerons une réflectivité. Cette réflectivité peut être qualifiée de
"réflectivité moyenne incohérente" car on l'obtiendrait en ignorant les
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
17
interférences entre rp et rs, c'est-à-dire entre les composantes
réfléchies parallèle et perpendiculaire, et en moyennant sur tous les
azimuts cp possibles, c'est-à-dire sur toutes les orientations possibles
du plan d'incidence par rapport à la direction du polariseur. Réduite à
son premier terme, l'équation (El) donnerait donc la réflexion obtenue
en intervertissant l'ordre de l'échantillon et de l'analyseur sur le trajet
de la lumière, la surface ne jouant ici que le rôle d'un élément
absorbant. Ce premier terme disparaît totalement lorsque ~= 7c/2 :
entre polariseur et analyseur croisés, et en l'absence d'éléments
lô (dé)polarisants, rien ne passe.
Le second terme de l'équation (El) décrit l'interférence entre rp
et rs. Nous l'appelons "réflectivité cohérente". Il traduit la
dépolarisation du faisceau incident par la surface, qui transforme la
polarisation incidente linéaire en une polarisation elliptique. Cette
i5 ellipticité est différente pour chaque azimut, c'est-à-dire pour chaque
plan d'incidence défini par son angle cp avec la direction du polariseur,
et ce second terme décrit la réflectivité moyenne qui en résulte pour la
géométrie conique de l'éclairage. Il disparaît pour n/4, où les
contributions de tous les azimuts se compensent, et aussi pour rp =-rs.
20 Il diminue la réflectivité totale entre polariseur et analyseur parallèles
et l'augmente quand ils sont croisés.
La technique de visualisation, objet de la présente invention,
exploite directement ce second terme. Nous choisissons ~=n/2, et le
second terme de l'équation (El) reste le seul présent. L'extinction ou,
25 dans une version plus élaborée, la quasi extinction de la réflectivité
incohérente est l'un des fondements de l'invention. Ce que nous
appelons "réflectivité cohérente" peut encore s'appeler "réflectivité
ellipsométrique" puisqu'elle résulte des ellipticités (fonctiôns de
l'azimut cp) de la polarisation réfléchie.
30 Une expression équivalente à (El) est :
(Drr(e1 ~)=~(Irpl2+lr512)+co4 Irp-rs`2 E3
Cette expression permet de comparer le signal obtenu en
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
18
présence d'éléments polarisants au signal obtenu en l'absence
d'éléments polarisants, c'est-à-dire en lumière non polarisée, qui est
donné par le premier terme seul. On le notera :
CDN (e, NP) = ~ (rp (2 + Irs 12) E4
En présence des polariseurs, nous avons encore
expérimentalement acc'es à cette quantité en imposant n/4, comme
le montre l'équation E3.
Pour la visualisation du bord d'un objet d'étude 4 ayant la forme
d'un film mince posé sur la surface, nous exploitons les intensités
recueillies en observant le film et la surface nue qui sont notées IF et
Is. Elles sont proportionnelles aux flux norrnalisés correspondants.
Le contraste du bord du film est :
C=I+Is =1- 2I E5
F S 1,~. F
IS
Pour bien visualiser le film, il faut maximiser C et donc rendre
le rapport IF/Is maximal (IS -> 0, pour tendre vers un contraste de 1)
ou minimal (IF --> 0, pour tendre vers un contraste de -1). Il faut donc
éteindre soit la surface, soit le film. Ainsi, une méthode sensible
repose d'une part sur une bonne extinction, et d'autre part sur une
extinction sélective.
Notre technique conjugue deux facteurs d'extinction :
i) le polariseur et l'analyseur croisés ou presque croisés,
ii) un substrat anti-réfléchissant pour ce mode d'observation.
L'équation (E3) met en relief la nature double de notre
extinction : le polariseur et l'analyseur croisés éteignent le premier
terme du second membre, notre substrat antiréfléchissant éteint le
second. On peut donc le définir comme un substrat antiréfléchissant
pour la réflectivité cohérente. C'est le second fondement de notre
technique de visualisation.
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
19
Mais une bonne extinction ne suffit pas pour une visualisation
sensible. Il faut éteindre IF ou IS mais pas les deux en même temps.
Comme le film que nous visualisons est très mince, comme donc ses
paramètres physiques perturbent peu ceux de la surface nue, cela
signifie que l'extinction doit être critique. En d'autres termes,
l'extinction doit être perdue pour une 'toute petite modification de la
surface. Ce caractère critique de la qualité anti-réfléchissante de notre
substrat est le troisième fondement de notre technique de
visualisation.
Les performances d'une méthode de visualisation peuvent être
quantifiées par le contraste obtenu lorsque le film observé devient
extrêmement mince. Dans ce cas, IF et IS deviennent voisins et
dI = IF - Is s'apparente à un élément différentiel.
C peut alors s'écrire :
C=1dI_1 I dIAe
2 IS 2 IS de
où Ae est l'épaisseur du film qu'on peut supposer pour la circonstance
d'indice optique identique à celui de la couche supérieure, et où dI/de
2o est la dérivée de l'intensité réfléchie par le substrat nu par rapport à
l'épaisseur e de la dernière couche de l'empilement. Dans le cas où le
substrat est composé d'un support solide recouvert d'une seule couche
diélectrique, e est donc l'épaisseur de cette couche. Le fait de prendre
un indice identique pour le film et pour la dernière couche
diélectrique n'est pas obligatoire, mais il simplifie l'explication et
montre que notre méthode n'exploite pas la réflexion entre le film et
le substrat. Le film est donc considéré ici comme une simple
fluctuation d'épaisseur de la couche supérieure.
Nous définissons la sensibilité de notre technique en
3 o Angstrôms 1 comme le rapport de C sur De :
C_ 1 dLnl dLnlrp + rs I
Ae 2 de = cste + de E7
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
L'expression de rp et rs pour un - solide recouvert d'une seule
couche est classique (réf. AZZAM par exemple) :
rOl(k) + r12(k)e-2,ai E8
r(k) + 1 -2 lR1
+ rOl(k) X r12(k)e
5
avec k = soit s, soit p, selon la polarisation considérée et
avec P1= 2n le cos 81, 1'indice 1 faisant référence a la couché,
l'indice 2 au support et l'indice 0 au milieu incident.
Cette équation nous permet d'écrire :
6=r +r - 6oi+6i2(1+IIoi)e-2ia1+o;oi~i2e-4jRi E9
p S^(l + r01(P)ri2(P)e-2 j(31)(1 + r01(S)r12(s)e-2jR1
où cy;j et 11;j représentent respectivement la somme et le produit de r;j(p)
et rlj(s).
La somme 6 est une fonction périodique de l'épaisseur ôptique
N1e de période a,/2. Son module I6l présente en général deux minima
et deux maxima par période. Il en est de même pour Lni6l. La
fonction Icyl étant de plus une fonction bornée, elle reste très régulière
et sa dérivée par rapport à e n'est jamais très importante. Par contre,lâ.
fonction Lnl6l diverge lorsque I6l tend vers zéro et la sensibilité
donnée par l'équation E7 devient très importante en valeur absolue de
part et d'autre du minimum lorsque l'extinction devient totale. Le
contraste est toujours négatif à gauche d'un minimum et positif à
droite. C'est pourquoi nous désignons aussi la condition d'obtention
d'un minimum par "condition d'inversion de contraste".
En résumé, les inversions rapides de contraste correspondent
donc aux minima de lrp + 4 par rapport à e, et les inversions très
rapides de contraste sont obtenues quand ce minimum de Irp + rsJ tend
vers 0.
L'équation (E3) met en relief l'intérêt de l'utilisation d'un
microscope de fluorescence : en présence d'un signal de fluorescence,
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
21
la composante dépolarisée de cette fluorescence s'ajoute au membre
de droite de l'équation (E3) sans altérer l'extinction des deux autres
termes. Le rapport signal sur bruit est donc augmenté. Cela est aussi
transposable à un signal Raman.
L'invention concerne aussi un procédé de mesure
ellipsométrique pouvant également fonctionner sans que le recours à
un substrat particulier ne soit nécessaire :
Les angles ellipsométriques yf et A sont définis par :
rp = tan ~e' E 10
rs
Deux équations choisies arbitrairement parmi les quatre
suivantes suffisent à établir les correspondances qui seront utiles entre
réflectivités et paramètres ellipsométriques :
Irpia + Irsl2 = Irs12(1 + tan2y) El 1
Irp + rS1a = Ir512(1 + tanzy + 2 tan y cos A) E12
Irp - rs12 = IrsI2(1 + tan2yr - 2 tan y cos A) E13
rprs +rprs =2lrsIztanIF cos0 E14
La première de ces équations montre que le paramètre
ellipsométrique yf est accessible par la mesure de la réflectivité
incohérente. Chacune des trois autres montre que la détermination du
second paramètre ellipsométrique, A, nécessite de plus la mesure de
la réflectivité cohérente (ou d'une combinaison des deux
réflectivités). C'est donc en accédant au signal de réflectivité
3 o cohérente que nous pouvons déterminer y et A.
La mesure s'effectue en deux étapes :
i) La première est basée sur la rotation de l'analyseur. L'image
de l'échantillon est analysée par une caméra CCD ou tout autre
détecteur bidimensionnel. L'équation E3 montre que le signal réfléchi
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
22
oscille sinusoïdalement autour de la réflectivité incohérente avec une
amplitude Irp - rs12 et une période n sur l'angle: ~. Différentes
procédures, nécessitant au minimum deux mesures, permettent
d'obtenir deux combinaisons des trois paramètres IrsJ2, tany, et cosà,
par exemple lr5I2(l + tan2yr) et 21rs1z tanlycosà. Cela permet déjà de
déterminer la combinaison sin2yrcos0 des seuls paramètres
ellipsométriques, mais ne suffit pas pour déterminer séparément A et
y~.
ii) La seconde étape nécessite la rupture dé la symétrie radiale
lo de l'éclairage, ce qui peut s'effectuér de deux façons :
soit en modifiant physiquement la géométrie du diaphragme
d'ouverture, qui doit devenir une fente ou une croix formée de deux
fentes perpendiculaires, ou un secteur angulaire Scp (modulo n)
d'ouverture strictement inférieure à7c/4, dont le sommet est confondu
avec l'axe optique ou l'association de deux ou quatre secteurs
angulaires identiques régulièrement disposés autour de l'axe optique
du microscope, capable comme l'analyseur de tourner autour de l'axe
optique du microscope,
soit en analysant la distribution d'intensité présente dans un.
plan conjugué du diaphragme d'ouverture situé sur le trajet de la
lumière réfléchie, le microscope étant en éclairage Koehler. Le
microscope étant muni d'une caméra CCD pour recevoir l'image de
l'échantillon, cette analyse peut s'effectuer très simplement en
interposant une lentille de Bertrand entre l'objectif et la pupille de la
caméra. Il s'agit donc d'une mesure conoscopique. L'intérêt de cette
solution, facile à mettre en oeuvre, est que l'angle d'incidence et
l'azimut cp sont, dans le plan conjugué, deux paramètres
géographiquement séparables et que l'on peut donc accéder à la
totalité de la fonction (DN(8,9,2~), a, désignant la longueur d'onde de
l'éclairage. On peut ainsi ajuster la gamme des angles d'ouverture
conservés, explorer l'azimut, ou filtrer l'éclairage par des moyens
numériques. Cette solution permet aussi, en l'absence de la lentille de
Bertrand, d'effectuer la première étape de l'analyse simultanément sur
plusieurs régions d'un échantillon hétérogène, et donc de déterminer
par une mesure parallèle la quantité (sin2y cosà)(x,y). Pour une
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
23
analyse complète avec la lentille de Bertrand, il faut cependant
sélectionner une région homogène de l'échantillon par l'utilisation
d'un diaphragme de champ ou d'une géométTie confocale. Cette
solution ne permet donc pas l'analyse parallèle complète des
différents points de l'échantillon. La première solution par contre
(diaphragme à rupture de symétrie radiale), permet l'analyse parallèle
totale puisqu'on garde toujours l'image de l'échantillon sur la caméra
CCD.
L'intensité réfléchie I lorsqu'un secteur angulaire bcp très petit
zo sélectionne un azimut cp particulier sur le cône d'éclairage, fourni par
l'équivalent des équations El à E4 est maintenant :
f rp 12 cos 2(P cos a(~ -(P) + Irs 12 sin 2(P sin 2(~ - (P)
I- A`~ * *sin 2çp sin(2~ - 2(p)
+ (rprs + rp rs )
4
D'une façon générale, cette intensité est une fonction
périodique de cp de période 71 et comporte aussi des termes de période
n/2.
Si l'orientation relative de l'analyseur et du polariseur est fixe
et :
- si la fente est animée d'un mouvement de rotation uniforme
autour de l'axe optique à la fréquence co, l'intensité réfléchie par
chaque point de l'échantillon est modulée et cette modulation permet
d'extraire différentes combinaisons des quantités 1 rs 1 , W et 0
recherchés. Pour cela, plusieurs techniques peuvent étre mises en
oeuvre, notamment des techniques de type photométriques exploitant
des moyennes d'intensité dans le temps et des amplitudes d'extremum
ou des techniques de détection synchrone permettant de comparer les
amplitudes et les phases des composantes de l'intensité réfléchie à 2co
età4w ;
- si l'orientation de la fente est réglable manuellement, on peut
mesurer les intensités recueillies pôur plusieurs orientations de la
fente, deux au moins, et déduire de la formule générale ci-dessus les
valeurs de différentes combinaisons des paramètres 1 rs ~,~r et A, ce
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
24
qui permet de déterminer complètement les valeurs de ces
paramètres ;
- si l'analyseur est animé d'un mouvement de rotation uniforme
autour de l'axe optique, le signal I est modulé avec un période n (sur
et la mesure de I pour différentes valeur de cp devient plus précise ;
- si enfin l'analyseur et la fente sont tous deux animés d'une
rotation uniforme, à des fréquences différentes, la fonction I(cp, ~)
peut être entièrement reconnue et les paramètres 1 rs 1 ,y et A peuvent
être déterminés avec une très grande précision par une procédure
lo classique d'ajustement numérique à trois paramètres.
Dans le cas particulier le plus simple où l'angle ~ est fixé et où
la mesure de I est effectuée pour les deux orientations
cp = 0(modulo n) et cp =7c/2 (modulo n) de la fente, on obtient
respectivement :
04e,4P = 0) = 1/2IrpI2COS2~ et 0N(O4,9 = -x/2) = 1/21rs12COS2~
Il suffit donc de prendre la racine du rapport de ces deux
intensités pour obtenir la quantité tan y. Cettë mesure cômbinée aux
z o deux précédentes permet donc de déterminer complètement IrS12, yf, et
0, et donc aussi Irpl2.
Il faut noter que la détermination des seuls paramètres yf et A
peut s'obtenir en utilisant uniquement des rapports d'intensités
mesurées, et ne nécessite donc pas l'utilisation d'un substrat de
référence.
Un cas particulier intéressant est celui où cD=0 qui correspond à
un polariseur et un analyseur parallèles et qui peut donc se réduire à
celui d'un seul polariseur disposé entre le miroir d'éclairage et
l'objectif ou même entre l'objectif et l'échantillon. L'intensité réfléchie
3 o s'écrit dans ce cas :
a
I= A? llrp 12 cos4 cp + Irs I2 sin4 cp _ sin 2 2cp Irs I2 tan ycos A
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
Cela montre qu'avec un diaphragme tournant constitué d'une
fente, d'une croix constituée de deux fentes perpendiculaires se
croisant sur leur axe, d'un secteur angulaire dont le sommet est posé
sur l'axe optique du microscope et d'amplitude azimutale inférieure à
5 45 degrés, ou de l'association de deux ou quatre secteurs angulaires
du même type régulièrement disposés autour de l'axe optique, lequel
diaphragme est éventuellement superposé à un anneau pour délimiter
un seul angle d'incidence, il suffit d'effectuer trois mesures d'intensité
réfléchie avec trois orientations différentes et non redondantes du
1o diaphragme pour en déduire la totalité des paramètres
ellipsométriques de l'échantillon. Par exemple, dans le cas où le
diaphragme est une fente ou un secteur angulaire très petit repéré par
son orientation cp, l'intensité réfléchie en chaque point de l'image de
l'échantillon devient :
Il I(cp = 0) = A2 lrP l2 = A? Irs 1'(1 + tan 2 yJ) pour (p =0
Iz = I(cp = 2) = A? Irs Iz pour cp =7c/2
I3 = I(cp =~)= 2A? Irs 1 2 tan ycos à pour cp = 7c/4
4
Il suffit donc de calculer le rapport I1 pour en déduire tan ~r ,
a
puis le rapport I3 pour en déduire cos0 A.
2
Cet exemple illustre :
- comment la mesure de trois intensités avec trois orientations
différentes de la fente permet de déterminer la totalité des paramètres
ellipsométriques en utilisant seulement des rapports d'intensité, donc
sans calibration annexe ;
- comment une modulation de l'intensité réfléchie qui inclut ces
trois mesures mais aussi d'autres permet d'obtenir les mêmes
informations avec une précision accrue ;
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
26
- comment on peut réaliser un ellipsomètre sous microscope
optique ou sous loupe binoculaire en utilisant un seul polariseur et
une fente tournante.
Dans l'exposé de la méthode de mesure, nous avons utilisé des
équations valables pour un seul anglé d'incidence 0. Comme Irs12, yr
et A dépendent de 0, nous pouvons : soit accéder à ces quantités pour
un angle 0 unique en utilisant un diaphragme d'ouverture annulaire,
soit accéder à des quantités moyennées sur une gamme d'angles
d'incidence [Oni,,, 0m.], avec le plus souvent 0,,,;n= 0.
Les mémes formules s'appliquent à des quantités effectives,
affectées ci-dessous d'un indice eff définies à partir de moyennes
sur 0. Il convient alors de poser :
(rpfeff -~Irpl2
Irs1eff -\jrsjaa
tan y eff = Irp leff
(rs l eff
~Irs 12 tan yr cosà~e
cosAeg -
=
Irsleff oIrPleff
pour écrire l'intensité réfléchie comme :
2(r1' l eff cOs 2(P COS 2l~ -~~ + Irs I eff S~ Z~ S~ 2l~ -~)
I= Ai 2 sin 2cp sin(2~ - 2cp)
+2lrsleff tanl~Jeff COS~eff
4
La mesure de I permet donc de déterminer les quantités
effectives et, en particulier, les angles ellipsométriques yreff et Aeff, qui
peuvent être comparées à des valeurs calculées pour en déduire les
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
27
propriétés de l'objet ou de l'échantillon, comme il est pratiqué
classiquement avec les angles ellipsométriques à incidence unique.
En fait, l'intérêt de la méthode est surtout de pouvoir effectuer
des mesures ellipsométriques sous microscope afin de combiner
mesure ellipsométrique et imagerie. On doit donc considérer que la
géométrie naturelle de l'éclairage est un cône de lumière autour de la
normale. Or, les paramètres ellipsométriques varient peu pour des
incidences faibles. C'est d'ailleurs pourquoi l'ellipsométrie n'est une
techniqûe sensible qu'à des angles d'incidence élevés. La contrepartie
so dans notre procédé est que la moyenne qui s'effectue sür le cône
d'éclairage brouille peu le signal exploitable. En l'absence de substrat
optimisé, l'inconvénient de la mesure ellipsométrique sous
microscope est que sa sensibilité est mauvaise. Mais en présence des
substrats optimisés tels que nous les proposons, la sensibilité de la
mesure aux paramètres physiques de l'échantillon redevient
excellente, comparable en fait à celle des mesures traditionnelles
autour de l'angle de Brewster, alors que le signal exploité reste peu
sensible à l'angle d'incidence. Cela tient au fait qu'entre polariseur et
analyseur croisés, l'extinctiôn de la réflectivité cohérente est toujours
totale en incidence normale, si bien que seules les incidences non
nulles participent à la construction du signal que nous exploitons.
Avec les conditions d'une bonne extinction pour des incidences non
nulles, l'extinction est bonne sur l'ensemble des incidences du cône
d'éclairage.
Il est possible d'optimiser l'épaisseur de la dernière couche pour
des matériaux quelconques.
En effet, nous avons vu que la fonction I6(e)l = Irp + rsJ possède
toujours des minima plus ou moins prononcés, qui correspondent aux
conditions d'inversion de contraste. Le contraste est donc nul pour ces
valeurs particulières de e. Etant aussi périodique et continu, il atteint
un minimum à gauche de ces valeurs et un maximum à droite. Il est
donc toujours possible de choisir l'épaisseur e de façon à ce qu'un de
ces extrema soit atteint. Quelle que soit la nature du substrat, on peut
donc optimiser l'épaisseur de la couche diélectrique en calculant
Ia(e)l. Cela devient particulièrement intéressant lorsqu'on s'approche
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
28
des conditions critiques.
Les compositions critiques des substrats sont définies par
l'existence d'une solution à l'équation I6(e)l = 0. Un substrat critique
possède une épaisseur de couche proche d'une solution de cette
équation. Une solution de l'équation l6(e)j = 0 correspond
nécessairement à un minimum de l6(e)l. C'est donc une épaisseur
d'inversion du contraste. La plus petite de ces valeurs, ec, joue bien
sûr un rôle particulier. Les autres épaisseurs d'inversion de contraste
sont alors donrlées par e,,,k = ec + KN12,/2.
D'après l'équation E9, l'équation dont nous discutons est :
601 + 612(1 + Uo1)è 2'R1 + 601n12e 4'a1= 0
E15
i5 Dans le cas d'un empilement réduit à une seule couche, les
valeurs ec de e sont les solutions de l'équation E15 tirée de E9 :
(Yol + 612(1 + Uol)z + 6o1n12zz = 0 E16
Elle possède deux solutions complexes zl et z2 qui sont
fonctions des indices du milieu incident, de la couche, de l'indice
complexe du substrat, et de l'angle d'incidence 00 (ou de façon
équivalente de l'angle réfracté dans la couche, 01). Les conditions
critiques sont atteintes lorsque le module d'une de ces deux solutions
est égal à 1. Ce problème est assez simple à explorer numériquement.
Analytiquement, il est possible de développer chacun des termes
jusqu'à l'ordre 4 en 01 car chacun ne dépend que faiblement de
l'angle à proximité de la normale. On peut ainsi trouver des solutions
"à la main". En pratique, les deux milieux extrêmes sont souvent
imposés et c'est l'indice et l'épaisseur de la couche qu'il faut
déterminer. On trace donc le contraste en fonction de l'épaisseur pour
quelques indices arbitraires et on constate une variation monotone du
contraste. Il suffit donc de progresser dans la direction où les choses
s'améliorent jusqu'à ce qu'elles commencent à se dégrader. A partir
de là, on continue l'exploration autour de la meilleure valeur en
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
29
affinant les variations de l'indice. On peut aussi se servir des
nombreux résultats publiés dans la littérature pour une couche unique
en termes de yr et A. Les situations recherchées correspondent
simultanément à :
tany = 1 etA =lt E17
Les solutions que nous avons trouvées numériquement sont
assez bien approchées par la formule empirique :
N2 = N. N + 1+ N E18
f
3 3
On obtient des résultats particulièrement intéressants en
réalisant un substrat silicium recouvert d'une couche unique
répondant. aux paramètres suivants, l'éclairage étant préféré
monochromatique de longueur d'onde 1 = 540 nm et l'angle
d'ouverture du cône d'éclairage étant supposé de 30 degrés :
No N3 N2 e
1,00 (air) 3,88 - 0,02 i 1,343 1060 5.Å
1,34 (eau) 3,88 - 0,02 i 1,749 814 5 A
1,50 (huile) 3,88 - 0,02 i 1,945 750 10 Å
où N. est l'indice du milieu ambiant, N3 est l'indice du support du
substrat, N2 est l'indice de la couche et e son épaisseur.
L'épaisseur optimale e est une fonction linéaire de a, mais n'est
pas proportionnable à a,. Pour des observations dans l'air, ae = V.
aa,
Les couches d'indices 1,74 et 1,945 peuvent être fabriquées par
de nombreuses méthodes, telles que les dépôts PECVD. Les couches
d'indice 1,345 sont plus difficiles à réaliser. Elles peuvent étre
formées d'un hydrogel, d'un aérogel, d'un polymère, ou être
hétérogènes, par exemple formées de plots d'épaisseur constante et de
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
très petites dimensions. Il peut encore s'agir d'une solution dans l'eau,
de sucre, de sel, de polymère...
Une méthode de visualisation particulièrement intéressante de
l'épaisseur optique (N1 x el) d'un film très mince peut être réalisée
5 avec le substrat mis en oeuvre dans l'invention de la manière suivante
représentée sur la figure 5.
On réalise sur un support 20, un dépôt d'une couche 21
d'épaisseur variable en forme de biseau (figure 5A, figure 5B).
On découpë ensuite ce substrat 20 de façon à en obtenir deux
so éléments identiques 22, 23 (23 non représenté est alors identique à
22) (figure 5C).
On recouvre ensuite l'un de ces éléments du film 24 mince à
étudier (figure 5C).
Puis on observe alors ces deux éléments sous microscope
15 éclairés en lumière blanche avec une pupille en forme de disque,
après avoir positionné ces deux éléments l'un par rapport à l'autre,
dans leur position relative initiale, à l'aide d'un repère, d'une encoche
ou d'une cale 25.
On observe alors des franges 26, 27 en lumière blanche,
2 o respectivement sur chacun de ces éléments et leur décalage relatif 02
permet la mesure des propriétés de la couche déposée sur l'un de ces
éléments.
L'invention est particulièrement adaptée à la visualisation
d'éléments contenus dans des multicapteurs.
25 Un multicapteur chimique ou biologique (= biopuce) est
constitué d'un support 30 sur lequel sont déposées des pastilles 31
(= spots) formées chacune d'une couche différente capable de fixer
sélectivement chacune une espèce différente à reconnaître au sein
d'un mélange liquide (biopuce) ou gazeux (nez artificiel), et formant
3 o entre elles une matrice d'éléments ordonnés le long de la surface.
Chaque pastille a une surface de quelques microns carrés et souvent
une épaisseur d'ordre moléculaire.
Le multicapteur est utilisé de la façon suivante : il est mis en
contact avec le mélange que l'on veut analyser. Chaque pastille 31,
32... fixe l'espèce qu'elle sait reconnaître quand elle est présente dans
CA 02431943 2003-06-17
WO 02/50513 PCT/FR01/04046
31
le mélange. In situ ou après rinçage, on regarde alors quels plots 32 se
sont chargés et quels plots 31 sont restés vides pour connaître la
composition du mélange. Une espèce fixée crée une surépaisseur,
visualisable au niveau du plot, la position des plots 31, 32 dans la
matrice nous renseignant sur la nature de l'espèce reconnue. Cette
étape est l'étape de lecture du multicapteur.
Notre méthode de microscopie est suffisamment sensible pour
faire la différence entre un plot vide et le même plot chargé, dans
beaucoup de types de multicapteurs. Elle fournit donc une méthode de
so lecture simple, directe et parallèle pour l'ensemble des multicapteurs.
Dans un exemple préféré, nous décrivons sa mise en oeuvre sur
un type particulier de multicapteurs : les biopuces. Ils comprennent
par exemple les puces à ADN, les puces à anticorps, les puces à
bactéries, les puces à virus, les puces à chromosomes, les puces à
protéines, etc.
Dans l'exemple des puces à ADN, chaque plot est constitué
d'une couche moléculaire d'oligonucléotides identiques capables de
s'hybrider avec et seulement avec leur brin complémentaire. L'ADN
analysé est découpé en brins de longueur convenable, amplifiés par la
technique PCR, ce qui signifie que chaque brin est répliqué un grand
nombre de fois, puis mis en solution au contact de la puce. Les brins
reconnus sont fixés par les pastilles correspondantes.
Notre méthode permet de reconnaître les pastilles chargées. A
cette fin, les pastilles dont l'épaisseur est régulière et connue, sont
prises comme éléments de l'édifice multicouche, de telle sorte que
l'ensemble support + multicouche + pastille ou spot constitue un
substrat optimisé de très grande sensibilité. Dans ces conditions, la
présence de brins supplémentaires après hybridation est aisément
détectée par le changement d'intensité ou de couleur qu'elle entraîne
3 o dans l'observation de la pastille par notre procédé de visualisation. La
quantité de matière présente sur une pastille peut aussi être
quantitativement évaluée par notre procédé de mesure.