Note: Descriptions are shown in the official language in which they were submitted.
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
An ophthalmic lens
TECHNICAL FIELD OF THE INVENTION
The present invention relates to an ophthalmic lens comprising a diffractive
part.
Furthermore it relates to a method for designing said ophthalmic lenses.
BACKGROUND OF THE INVENTION
A wavefront passing the eye will be influenced by the optical parts of the eye
such
that for example chromatic aberration is provided to the wavefront. The reason
is that
the refractive indices of the materials in the optical parts of the eye differ
for different
'wavelengths. Thus light having different wavelengths will be refracted a
different
amount and they will fall on the retina at different places, i.e. different
colors can not
be focused to the same point. This is called chromatic aberration.
Recently there has been much interest in the correction of the monochromatic
aberrations of the eye. It has been revealed that when all monochromatic
aberrations
2o are corrected in the human visual system, it serves to unmask the chromatic
aberration
of the eye. Therefore, in order to optimize the optical quality of the eye, a
combination of monochromatic and chromatic aberrations needs to be corrected.
A
diffractive pattern could be configured to provide a passing wavefront with
chromatic
aberration of the opposite sign as chromatic aberration from the eye. Thus a
diffractive pattern can be used to correct for chromatic aberration introduced
to a
wavefront from the optical parts of the eye. Some background theory of
chromatic
aberration can be found in, for example Chapter 17 in "Optics of the Human
Eye"
written by David A. Atchison and George Smith. A theoretical background of the
diffractive pattern could be found in the article "Practical design of a
bifocal hologram
3o contact lens or intraocular lens", Allen L. Cohen, Applied Optics
31(19)(I992).
Ophthalmic lenses, which on at least one surface comprises a diffractive
pattern for
correcting for chromatic aberration are known from for example US 5,895,422,
US
5,117,306 and US 5895422. These lenses do, however not, compensate for other
aberrations provided by the eye surfaces. In SE 0000614-4, aspheric lenses are
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
designed to compensate for spherical aberration. In some applications these
lenses
will provide the eye with an increase in chromatic aberration. It is therefor
a need of
an ophthalmic lens for correcting refractive errors that also can correct for
monochromatic and chromatic aberrations.
DESCRIPTION OF THE INVENTION
An object of the present invention is to improve the visual quality for a
patient.
to A further object of the present invention is to provide an ophthalmic lens,
which
corrects for chromatic aberration and at least one type of monochromatic
aberration.
A further object of the present invention is to provide an ophthalmic lens,
which
corrects for both chromatic and spherical aberration.
IS
Still a further object of the invention is to correct for spherical aberration
as expressed
by the 11 ~' normalized Zernike term.
A yet further object is to provide an aspheric lens capable of correcting for
spherical
2o aberration having a diffractive part adding refractive power to the lens
and providing
compensation for chromatic aberration introduced by the optical surfaces of
the eye
and by the aspheric lens surface. In this text the term aspheric will refer to
rotationally
symmetric, asymmetric and/or irregular surfaces, i.e. all surfaces differing
from a
sphere.
These objects are achieved by an ophthalmic lens as initially described in
"technical
field of invention", which according to the invention further comprises a
refractive
part comprising at least one surface, which is configured to compensate a
passing
wavefront at least partly for at least one type of monochromatic aberration
introduced
3o by at least one of the optical parts of the eye. The diffractive part is
according to the
invention capable of compensating a passing wavefront at least partly for
chromatic
aberration introduced by at least one of the optical parts of the eye. Said
refractive and
diffractive parts together contribute to a required power of the lens. In this
text "the
optical parts of the eye" refer to the parts of the eye that contribute to the
refraction of
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
incoming light. The cornea of the eye and the natural or an implanted lens are
optical
parts of the eye. But also inhomogeneities, e.g. in the vitreous are
considered as the
optical parts of the eye. An optical element that combines both diffractive
and
refractive optics is called a hybrid element. The monochromatic aberration
could be
for example astigmatism, coma, spherical aberration, trifoil, tetrafoil or
higher
aberration terms.
Hereby an ophthalmic lens is achieved that is capable of compensating for at
least one
type of monochromatic aberration and for chromatic aberration introduced by
the
1 o optical parts of the eye to a passing wavefront.
Preferably the diffractive part also is capable of compensating a passing
wavefront at
least partly for chromatic aberration introduced by the refractive part of the
lens.
In one embodiment of the invention the monochromatic aberration corrected for
is
spherical aberration. .
The longitudinal chromatic aberration of the eye is very well understood and
has been
shown to have very similar values from subject to subject (Thibos et. al.,
"The
2o chromatic eye: a new reduced eye model of oculax chromatic aberration in
humans",
-Applied Optic, 31~; 3594-3600, (1992)). It has also been shown to be
stable~with age
(Mordi et. al., "Influence of age on chromatic aberration of the human eye",
Amer. J.
Optom. Physiol. Opt., 62, 864-869 (1985)). Hereby an ophthalmic lens to
correct for
the average chromatic aberration of the eye could be designed.
Diffractive surfaces can be characterised by their so called phase functions.
This
phase function describes the additional phase that is added to a ray when it
passes the
diffractive surface. This additional phase is dependent on the radius of the
lens where
the ray strikes the surface. For radially symmetric diffractive surfaces this
function
3o can be described using Equation 1.
~(~°) _ ~ (DFO+DFh +DF2a' +DF3i°~ +DF4a4 +...) (1)
3
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
Where r is the radial coordinate, ~, the wavelength and DFO, DFl etc. are the
coefficients of the polynomial.
The diffractive part of the lens can also introduce some spherical aberration
to a
passing wavefront. Preferably, according to the present invention, the
refractive part is
made capable to compensate a passing wavefront for the spherical aberration
introduced by the diffractive part of the lens. Hereby, the spherical
aberration could be
reduced to a minimum after the wavefront has passed the optical parts of the
eye and
said lens.
To compensate for the spherical-aber-r~:tifln,-an aspher-ical surface; with-a-
lateral height
described by Equation 2, could be introduced to the refractive part of the
lens. An
aspheric surface can be configured to counteract the spherical aberration
introduced
by the optical parts of the eye and by the diffractive part of the lens. All
the optical
parts of the eye do not necessarily have to be considered. In one embodiment
it is
sufficient to measure the spherical aberration introduced by the cornea of the
eye and
compensate for only the spherical aberration provided by the cornea and
optionally
also for the spherical aberration introduced by the diffractive part of the
lens. For
example Zernike terms could be used to describe the optical surfaces of the
eye and
2o thus also be used to configure the aspheric surface of the lens, which is
adapted to
compensate for the- spherical aberration. Table 1-shows the first 15
wormalized-
Zernike teens and the aberrations each term signifies. The spherical
aberration is the
11 th normalized Zernike term. The designing of a lens that is adapted to
compensate
for aberrations as expressed in Zernike terms is explained in further detail
in the
Swedish patent application SE 0000614-4 to which is given reference.
_1 * z
r
z = ( R ) + ADS 4 + AEr 6 (2)
1+ 1-(R)2(cc+1)~z
Where R is the radal coordinate of the lens, cc is the conic constant, and AD
and AE
are coefficients of the polynomial extension.
JO
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
i Z; (p,A) (normalizedform associated with
format) normalized polynomial
1 1 Piston
2 2pcos 8 Tilt x
3 2psine Tilt y
4 ~(2 p a _ 1) Defocus
~(p2 sin2~) Astigmatism 1S' order
(45)
6 ~(p2 cos2B) Astigmatism 1s' order
(0)
~(3p3 - 2p) sin Coma y
B
8 ~(3p3 -2p) cos ~ Coma x
~(p3 sin 38) Trifoil 30
~(p3 cos 38) Trifoil 0
11 ~(6p4 - 6pa + 1) spherical aberration
12 10 (4 p 4 - 3 p Astigmatism 2 order
2 ) cos 28 (0)
13 10 (4 p 4 - 3 p Astigmatism 2 order
z ) sin 2B (45)
... 14 . _ . 10.(P4 cos48) Tetrafoil 0 . ... , . ..
..
10(p4 sin4B) Tetrafoil 22.5
Table 1
5 The spherical aberration of the lens is influenced by the shape factor of
the lens. The
spherical aberration of a spherical refractive lens can be minimized by a
convex-plano
lens (Atchison D.A., "Optical Design of Intraocular lenses. I: On-axis
Performance",
Optometry and Vision Science, 66 (8), 492-506, (1989)). In the present
invention, the
amount of correction of spherical aberration depends on the shape factor of
the lens. It
to is also possible to use a diffractive pattern that is able to correct for
spherical
aberration as well as for chromatic aberration. This can be done by modifying
the
5
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
higher orders of the phase function of the diffractive profile (lower orders,
or terms on
r2 (Equation 1 ), describe the paraxial properties of the lens).
Other types of monochromatic aberrations can also be corrected for by aspheric
refractive surfaces. The shape of the surface becomes more complex the higher
the
order of the aberration that is corrected. To compensate for a general
aberration with
an aspherical surface, the lateral height could be described by Equation 3,
though also
other descriptions are possible.
ft
z=~z;
f=I
z; _ (asi)x~' yk
i=%2~(j+k)2+j+3k~
to Where asi are the coefficients of the polynomial.
Preferably the ophthalmic lens together with the eye provides a polychromatic
image
quality, which when expressed as MTF(50) (Modulation Transfer Function at 50
cycles per millimeter) performs at least about 40% higher than an aspheric
lens
15 compensating for the same spherical aberration as the inventive lens but
without
compensating for the chromatic aberration. A high value of the polychromatic
image
quality indicates that the amount of chromatic aberration is small and also
that the
amount of monochromatic aberrations is small.
2o The lens can correct for the spherical aberrations and the chromatic
aberrations as
defined in a model eye. Spherical aberration of the eye can run between zero
and 1.5
diopter, while chromatic aberration typically runs up to 2.5 diopters ("Optics
of the
Human Eye" written by David A. Atchison and George Smith).
25 Suitably, the diffractive part is a diffractive surface profile. Such a
diffractive surface
profile consists of a number of concentric rings. The distances between the
rings are
decreasing out from the center of the lens. The area between two rings is
called a
zone. The width of the first zone is a constant that defines the widths of all
the other
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
zones. For more background techniques see the article by Allen L. Cohen
referred to
on page 1 in this application.
In one embodiment, the profile height is equal to one design wavelength. 550
nm is
often used as the design wavelength since this is the wavelength for which the
retina
has its maximum sensitivity. When the profile height is equal to one design
wavelength the lens will have its maximum effect in its first order. The
profile height
is, in another embodiment equal to two design wavelengths and then the lens
will
have its maximum effect in its second order. See e.g. the aforementioned
article by
to Allen L. Cohen and the US patents US 5,895,422, US 5,117,306, US 5,895,422.
The
profile height could be any integer nmnber of the design wavelengths.
In one embodiment of the invention the anterior surface of the lens is an
aspheric
surface, on which a diffractive profile is superimposed. In another embodiment
of the
invention the anterior surface of the lens is an aspheric surface and the
posterior
surface of the lens is flat and has a diffractive profile. Also other
combinations are
possible. For example a diffractive profile could be provided on both the
anterior and
the posterior surface. Both the anterior and posterior surfaces could also be
aspheric.
The skilled person can readily identify alternative lens configurations which
will be
2o suitable to design the inventive chromatic and monochromatic aberration
reducing
lenses.
The objects are also achieved by a method as initially described comprising
combining a refractive part and a diffractive part of the lens such that they
together
compensate a passing wavefront at least partly for at least one type of
monochromatic
aberration and for chromatic aberration introduced by at least one of the
optical parts
of the eye, while dimensioning said refractive and diffractive parts to
provide the lens
with a required power.
3o In one embodiment the method further comprises measuring at least one type
of
monochromatic aberration provided to a wavefront from at least one of the
optical
parts of an eye and combining the refractive and diffractive parts of the lens
such that
they compensate at least partly for the measured monochromatic aberration.
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
In one embodiment of the invention the measured monochromatic aberration is
spherical aberration.
The spherical aberration of the whole eye could be measured using a wavefront
sensor. If only the cornea is considered well-known topographical measurement
methods could be used. Such topographical methods are disclosed in fox example
"Corneal wave aberration from videokeratography: accuracy and limitations of
the
procedure", Antonio Guirao and Pablo Artal, J. Opt. Soc. Am. Opt. Image Sci.
Vis.,
Jun, 17(6), 955-965, (2000). A wavefront sensor is described in US Patent No.
5,777,719 (Williams et.al.).
Suitably, the method further comprises measuring the chromatic aberration
provided
to a wavefront from at least one of the optical parts of the eye and combining
the
refractive and diffractive parts of the lens such that they together
compensate a
passing wavefront at least partly for the measured chromatic aberration
introduced by
at least one of the optical parts of the eye. The chromatic aberration of the
eye could
be measured by using vernier methods such as those similar to the methods
outlined
in Thibos et.al., "Theory and measurement of ocular chromatic aberration",
Vision
Res., 30, 33-49 (1990) and Marcos et. al, Vision Research, 39, 4309-4323,
(1999).
2o Alternative ways for measuring chromatic aberration are described in a
textbook,
"Optics of the Human Eye" by David A. Atchison and George Smith, published by
~ ° ° °
Butterworth-Heinemann, ISBN 0-7506-3775-7.
Preferably, the method further comprises measuring the refractive error of the
eye and
dimensioning the refractive and diffractive parts of the lens such that they
together
compensate at least partly for the refractive error of the eye.
With this method of designing an ophthalmic lens the chromatic aberration, the
spherical aberration and the refractive error of the eye, could all be
considered and
3o compensated for. The lens is designed with one refractive part and one
diffractive part
and they are combined, such that they together compensate a passing wavefront
for
these aberrations introduced by the optical parts of the eye.
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
The aberration corrections could all be full corrections or partial
corrections.
Furthermore all the corrections could be based on the aberrations of one or
more parts
of the eye. The corrections could also be based on either an average value of
a certain
population or on the measured values of the individual patient or on a
combination of
an average value and individual measurements. The certain population can be a
group
of people in a specific age interval or for example a group of people having
had an
eye disease or a corneal surgery. For chromatic aberration the values are
pretty much
the same for all humans so it is possible to take an average value of all
kinds of people
and correct for this chromatic aberration in the lens. Of course it is
possible to do the
same for spherical aberration but in this case it would be preferred to choose
a group
of people or even measure the spherical aberration for every individual since
the
spherical aberration will differ more from eye to eye than chromatic
aberration.
The ophthalmic lens could be configured to be a phakic or pseudophakic
intraocular
lens (IOL), a spectacle lens or a contact lens. In the examples described
below the
lenses are pseudophakic IOLs. The material used in the example lenses
described
below is a foldable silicone high refractive index material described in US
5,444,106.
Other materials are however also possible for these lenses. For example PMMA
(Poly-methylmethacrylaat) and hydrogels are suitable materials. The example
lenses
2o have a power of 20D. However, the lenses could be designed to have any
other
w ' suitable power. Also negative lenses are possible: ~ - - - ~ ~ ~ ~ - , . -
.. -. ....-- - -
A method of designing the ophthalmic lens described above comprises the steps
of:
i) selecting an eye model with a refractive aspheric ophthalmic lens of a
predetermined refractive power and a predetermined amount of at least one
monochromatic aberration;
ii) estimating the power of said eye model at different wavelengths, so as to
determine the chromatic aberration of the eye model;
iii) estimating a correction function of how the power varies with the
wavelength
3o to be an ideal compensation for said chromatic aberration of the eye model;
iv) finding a linear function of how power varies with the wavelength, which
suitably approximates said correction function;
9
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
v) calculating a provisional zone width of a diffractive profile corresponding
to
this linear function and also calculating the diffractive power of this
diffractive
profile;
vi) reducing the refractive power of the refractive ophthalmic lens by the
amount
of power calculated for the diffractive profile;
vii) estimating a new correction function of step iii), finding a new linear
function
of step iv) and calculating a new provisional zone width and a new diffractive
power for a new diffractive profile corresponding to this new linear function;
viii) adjusting the refractive power of the refractive ophthalmic lens such
that the
l0 total power of a hybrid lens, which comprises both the refractive
ophthalmic
lens and the diffractive profile and which is adapted to replace the
refractive
ophthalmic lens in the eye model, equals the predetermined power;
ix) repeating steps vii) to viii) until a suitable combination of a refractive
and a
diffractive part of the hybrid ophthalmic lens is found that both provide the
t s eye model with a predetermined power and with a suitable reduction in
chromatic aberration.
Suitably this method comprises as a last step measuring the monochromatic
aberration
of the combination of the eye and the hybrid ophthalmic lens of the method
above and
2o correcting the refractive part of the ophthalmic lens according to the
measurements
such that the monochromatic aberrationis reduced sufficiently for the
~eombination of
eye and ophthalmic lens.
One example of an eye model that can be used is the eye model of Navarro but
other
25 models are also possible. The eye model could also be an individual eye of
an
individual patient.
In one embodiment the at least one monochromatic aberration of the refractive
ophthalmic lens is spherical aberration.
There are different possibilities for the design of the lenses according to
the invention.
One possibility is to design each lens for each individual. Then the chromatic
aberration, the spherical aberration and the refractive error of the eye of
the patient are
measured and a lens is designed from these values according to the above
described
to
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
method. Another possibility is to use average values from selected categories
of
people to design lenses adapted to suit almost all the people belonging to
this
category. It would then be possible to design lenses having different powers
but
providing the same reduction of spherical and chromatic aberration to patients
within
these groups of people. The groups of people could for example be age groups
or
groups of people having had specific eye diseases or a group of people having
had a
corneal surgery. Furthermore it would be possible to provide a kit of lenses
having an
average value of chromatic aberration and a range of different values of
spherical
aberration for each power. This could be preferred since the chromatic
aberration is
to about the same in most human eyes. Hereby it would be necessary to measure
the
refractive error and the spherical aberration of each individual eye and then
choose
one Iens from this kit of lenses to comply with these measurements.
The following examples are just given as examples and are not intended to be
limiting
for the invention in any way.
BRIEF DECRIPTION OF DRAWINGS
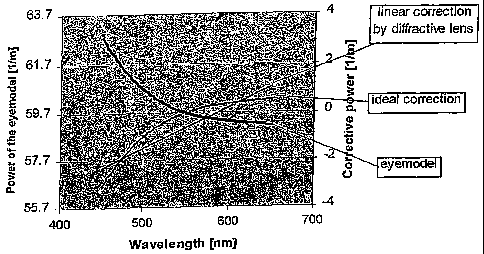
Fig. 1 shows a diagram of the relationship between refractive power and
wavelength
2o for an eyemodel and for a diffractive lens.
Fig. 2 shows the Polychromatic Modulation Transfer Function for a hybrid
refractive/diffractive lens and two other lenses.
Fig. 3 shows the light distribution between the different diffractive orders
for a
diffractive Iens with a profile height of two design wavelengths. Also shown
in this
plot is the spectral sensitivity of the eye.
Fig. 4 shows the polychromatic Modulation Transfer Function including 1st and
3ra
order for the lens of Fig. 3 and for two other non-diffractive lenses.
DETAILED DESCRIPTION OF EMBODIMENTS
11
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
Two examples are described of an intraocular lens (IOL) which corrects for
spherical
aberration and for chromatic aberration of the pseudophakic eye. Both examples
use
an aspheric lens surface for correcting the spherical aberration and a
diffractive
surface profile for correcting the chromatic aberration. The aspheric lens
surface
corrects the spherical aberration of the ocular surfaces, as well as the
spherical
aberration induced by the diffractive lens profile.
Example 2 has an extended diffractive surface profile. This type of lens is
often called
a super-zone diffractive lens and such lenses are described in: J.C. Marron et
al.,
to "Higher-Order I~inoforms", Computer and optically formed holographic
optics,
LCindrich, et al., editor, Proc. SPIE 1211, 62-66 (1990).
The configuration of the example IOLs is fully described below, based on an
eyemodel taken from the literature (Navarro et al, "Accommodation dependent
model
of the human eye with aspherics." JOSA A , 2(8), 1273-1281, (1985)) and based
on
the data of a silicone material. The optical evaluation is done by ray tracing
using the
OSLO optical design software (Lambda Research Corporation, Littleton, MA,
USA).
Example 1
,g~ckg~ouv~d theory: . . . . . . .... .. . . . ....
Both the cornea and the refractive intraocular lens (IOL) have a positive
chromatic
aberration, which means that the focal length increases with longer
wavelength. A
diffractive profile has a negative chromatic aberration. The profile consists
of a
number of rings (zones). For a diffractive lens working in the 1St diffraction
order, the
power of lens can be defined by:
p_2*~,
wz
Where P is the lens power, ~, is the design wavelength (m) and w is the Half
width
(radius) of the first zone.
3O
The chromatic aberration (CA) can be described as:
12
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
ap _ __2
CA=---
a~, w2
The diffractive lens power is linearly related to the wavelength. The relation
between
refractive lens power and wavelength, in refractive systems, is generally not
linear.
This is shown in Figure 1 where the relation between refractive power and
wavelength
for an eyemodel and for a diffractive lens is illustrated. The eyemodel has a
non-linear
relationship and the diffractive lens has a linear relationship. A curve,
representative
for an ideal correction is also shown. Therefore, a perfect correction cannot
be made
with a diffractive lens. Nevertheless, with a linear correction, the optical
performance
can be greatly improved.
to
When the eyemodel of Navarro (1985) is used, together with a 20 diopter
silicone
refractive intraocular lens instead of the natural lens, the chromatic
aberration can be
estimated by calculating the power of the eyemodel at different wavelengths. A
graph
similar to figure 1 will be the result. In order to determine how the
diffractive lens
must perform, a linear fit is made through the curve of the ideal correction.
The result
is:
P = -1.68' 107*~,+69.6
P = power [1/m]
. . . . . ~ = wavelength [m] . . . . _
2o This gives the ratio between the refractive and diffractive IOL power for a
chromatic
correction lens:
For the eyemodel with a refractive IOL:
CA=-ap =1.68~10'
aa,
So:
_ -1.68 ~ 10' ~ w = 0.345 mm ~ P~ = u~ = 9.24 diopte~°
(here, 7~ is the design wavelength of 550 rim)
Pa = IOL diffractive power
13
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
Since the diffractive IOL power is 9.24 diopter, the refractive IOL power has
to be
reduced by the same amount. Reducing the refractive IOL power will reduce the
chromatic aberration of the eyemodel also. In practice, equilibrium has to be
found
between the refractive and diffractive IOL power by an iterative design
process,
where the diffractive IOL power will end up somewhere between 0 and 9.24
diopter.
Description of the leis:
The example lens is made of silicone material. Its shape is equi-biconvex. The
anterior surface of the lens comprises an aspheric refractive lens, on which a
l0 diffractive profile is superimposed. The diffractive profile takes care of
41% (8.25D)
of the lens power, while the aspheric refractive lens does the remaining 59%
(11.75D). The width of the first zone is 0.365 mm, and there are 67 rings
needed to
fill a full 6.0 mm IOL optic. In the periphery of the lens, the diffractive
rings are 22
microns apart from each other.
The IOL is optimized for the Navarro (1985) eyemodel. The Navarro eyemodel has
an
aspheric cornea and includes dispersion for the ocular media. The surface
information
for the eye model and the lens is given in table 2. The lens designed is
dependent on
the eye model chosen. It must be noted that it is possible to design lenses
using other
2o eye models of actual physiological data from patients.
*LENS SURFACE DATA - Navarro 1985 with an TOL
Surface Radius Thickness Aperture Radius Glass Special
surface
Object -- 1.OOOOe+201.000e+14 AIR
1 7.7200 0.5500 2.833 (solved) CORNEA Asphere
2 6.5000 3.050 2.778 (solved) AQUEOUS
3 (pupil)-- -- 2.500 (solved) PUPTL
4 -- 0.900 2.500 (solved) AQUEOUS
5 20.994 1.125 2.418 (solved) SILICONEAsphere
Diffractive
6 -20.99418.157 2.298 (solved) VITREOUS
(solved)
Image -- -- 1.674e-05 (solved)--
CONIC AND POLYNOMIAL ASPHERIC DATA
Surface conic constant AD AE
14
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
1 -0.260000 -- --
-2.000000 -0.000459 -4.1000e-07
5
*DIFFRACTIVE SURFACE DATA (symmetric diffractive surface)
Surface DiffractionDesign Kinoform Kinoform DFO DF1
7~
order constructionzone depth
order
5 1 0.550 1 -- -- -0.004125
Eun
*WAVELENGTHS
11 number Wavelength Weight
(~.m)
1 0.5500 0.9950
2 0.4500 0.0380
3 0.6500 0.1070
4 0.5100 0.5030
*REFRACTIVE INDICES
SurfaceName Index Index Index Index v
a(2) A(2) A(3) A(4)
Object AIR 1.000000 1.0000001.000000 1.000000--
1 CORNEA 1.377400 1.3835001.374200 1.37932840.580645
2 AQUEOUS 1.338800 1.3451001.335600 1.34076735.663158
3 PUPIL 1.338800 1.3451001.335600 1.34076735.663158
4 AQUEOUS 1.338800 1.3451001.335600 1.34076735.663158
5 SILICONE 1.459620 1.4849501.454470 1.46568015.079396
6 VITREOUS 1.337400 1.3434001.334300 1.33928637.076923
Image IMAGE -- -- -- -- --
Table 2
Behavior of the lens:
4 discrete wavelengths were used to evaluate the eyemodel including the
refractive/diffractive IOL. The focus point is defined as the point where the
2o polychromatic MTF (Modulation Transfer Function) has it's maximum at 50
cycles/mm. The polychromatic MTF is determined by the weighed average of the 4
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
MTF's at the 4 wavelengths used. The weighting of the wavelengths was done
using
the standard luminance of the eye under photopic light conditions, which
represents
the relative sensitivity of the retina for different wavelengths.
The actual back focal length (ABFL) for the 4 different wavelengths indicates
the
presence of a chromatic difference in focus and by definition the amount of
longitudinal chromatic aberration. The calculations axe performed at a S.Omm
aperture
in order to maximize the differences.. From these figures, shown in table 3,
it can
already be concluded that the spherical aberration is virtually eliminated,
indicated by
the close to diffraction limited performance. The IOL is optimized for
chromatic
aberration, but there is still some left, as already expected theoretically.
The figures in table 4, for a corresponding aspheric refractive design,
without
chromatic correction, show that indeed at each wavelength, the spherical
aberration is
well corrected with respect to the MTF(50) for the spherical refractive IOL
and the
MTF reaches the diffraction limit. The focal points of the different
wavelengths do
not work well together, so that the polychromatic MTF is lower than that found
for
the diffractive/refractive IOL.
Spherical lenses, which are now current practice, give much lower values. The
figures
2o corresponding to these lenses are shown in table 5.
l.Z~fxactive%diffractme.
rOL
.
~, ABF~L ,'-:'-MTF~'501....Difflimxty~
~. . ~:
450 17:92 '.~ 9I 0 92''"
.
510-v-;18r 17 =0 90 0 '9Qe
550 18:16 U 90 - 0.90
'
~
65Q 1?,9~ 0 88 ' 0.8g~'
. .
,, 1g'16. 'Ø82 .:.:-090 ~
nolv . - ,, . .
[nmJ.[m~.: ,p ~ _,, [-J. ~
r, a :. ,
Table 3
A_spherzcal:refractiye
IOL
ABF'L ,.,MTF(501D'ifhmif
..,
450 ; 17:26 <,'0 92 0..~2 ,
',-. ' :
510 1798 0 90 0 91:
>.
550 ,. ~ ~ - 0 90 ,
' 90
18.22.
650. 18-:4.1 0 88 ,
0 88 '
pol'y 18:22 ~0 56 0 90,.
[.J .:v [ J:
nmJ. [mmJ .
Table 4
16
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
Spherical
refractiye
IOL
~
ABF'I;. M'TF(501 ,.'Diff.lnriif.
: ' .
4S0 .17 0 30 0:92
13
5:10 17 0 30 ' 0.:91
84
'
550. ,:18 '~ 0 31 ~ 0:90
. 06
:
~.:
65b .'-18 0 32='' 0.:88'
15.
'
~~ . :'180:21.' 0:90 : .
poly 05:..,
:
[n , ~mri1][ ].,:.-. [_y , ,
],: , :;. ,
~ m
10
Table 5
The Polychromatic Modulation Transfer Functions for these three lenses are
shown in
Fig. 2, together with the diffraction limit.
Example 2
Backg~ouhd theory:
If a lens, which has fewer rings and thus also larger distances between the
rings is
preferred, for example for manufacturing reasons, a different step height for
the
diffractive profile could be used. A diffractive lens that is on the market,
CeeOnTM
811E, Pharmacia has a 4D diffractive part, a zone width of O.Smm and 32 rings.
A 8.25D diffractive lens with the same spacings between the rings as the
existing
811 E can be achieved by doubling the step height of the rings. With a double
stepheight, the diffractive lens will have a phase jump of 2~., and therefore
give its
maximum efficiency in its 2°d order. For an 8.25D lens, the zone width
will be
0.516mm while 33 rings will be needed for a 6mm optic. The minimum distance
between the rings (periphery) is 45 microns.
The example lens is made of silicone material. Its shape is convex-piano. The
anterior
surface of the lens is aspheric. The flat posterior surface has a diffractive
profile with
a phase jump of two. The light distribution between the different diffractive
orders is
17
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
given in figure 3. From this graph we see that only order 1 to 3 are relevant
in the
visible light range. We also see that there is some bifocal behavior at 475nm,
but the
eye is very insensitive to light at this wavelength (as indicated by the eye's
spectral
sensitivity, also shown in figure 3.
Desc~iptioh of the leis:
As in example 1, the diffractive profile takes care of 4I % (8.25D) of the
lens power,
while the aspheric refractive lens does the remaining 59% (11.75D).
to The IOL is optimized for the Navarro (1985) eyemodel. The Navarro eyemodel
has an
aspheric cornea and includes dispersion for the ocular media. The surface
information
for the eye model and the lens is given in table 6.
*LENS DATA - Navarro 1985 with an IOL.
Surface Radius Thickness Aperture Radius Glass Special
surface
Object -- 1.OOOOe+201.000e+14 AIR
1 7.7200 0.5500 2.833 (solved) CORNEA Asphere
2 6.5000 3.050 2.778 (solved) AQUEOUS
3 (pupil)-- -- 2.500 (solved) PUPIL
q -- 0.900 2.500 (solved) AQUEOUS
5 10.521 1.125 2.418 (solved) SILICONE Asphere
-- -- 2.302 (solved) AQUEOUS Diffractive
*2
7 -20.99418. 256 2.302 (solved) VITREOUS
image -- -- 0.001279 (solved)--
*CONIC AND POLYNOMIAL ASPHERIC DATA
Surface Conic constant AD AE
1 -0.260000 -- --
5 -4.900000 -- --
*DIFFRACTIVE SURFACE DATA
Surface DiffractionDesign Kinoform Kinoform DFO DF1
A
order constructionzone depth
order
6 1 0.550 1 -- -- -0.002063
dun
18
CA 02441766 2003-09-22
WO 02/084381 PCT/EP02/03172
*WAVELENGTHS
11 number Wavelength Weight
(Nm)
I 0.5500 0.9950
2 0.4500 0.0380
3 0.6500 0.1070
4 0.5100 0.5030
*REFRACTIVE INDICES
Surface Name Index A(1)Index Index Index v
J~(2) A(3) J~(4)
Object AIR 1.000000 1.0000001.0000001.000000--
1 CORNEA 1.377400 1.3835001.3742001.37932840.580645
2 AQUEOUS 1.338800 1.3451001.3356001.34076735.663158
3 PUPIL 1.338800 1.3451001.3356001.34076735.663158
4 AQUEOUS 1.338800 1.3451001.3356001.34076735.663158
5 SILTCONE 1.459620 1.4849501.4544701.46568015.079396
6 AQUEOUS 1.338800 1.3451001.3356001.34076735.663158
7 VITREOUS 1.337400 1.3434001.3343001.33928637.076923
Image IMAGE -- -- -- -- --
Table 6
to Behavior of the lens:
Using the same wavelengths as in example l and ignoring the changes in
efficiency of
the diffractive lens, the polychromatic modulation at SOc/mm is 0.81 (limit =
0.90),
which is similar to the lens in example 1. If also the 1st and 3rd orders of
the
diffractive lens are included in the calculation, taking their corresponding
efficiencies
into account, the polychromatic modulation at SOchnm is 0.79.
The polychromatic MTF including 1St and 3rd order for the different lenses are
shown
in Fig. 4.
19