Note: Descriptions are shown in the official language in which they were submitted.
CA 02467466 2004-05-17
SYSTEM A~T~) NiET~I~I) FGIZ C~MPYtESSIhTG AlolD
~ECt~NSTUCTIl~(G AIJ1?IC7 FIL.ES>
Field of the Invention
This invention relates to file compression. Tn particular, this invention
relates
to a system and method for compressing and reconstructing audio files.
Background of the Invention
Compression/decompression (codec) algorithms are used to compress digital
files, including text, images, audio and video, for easier storage and faster
transmission over network connections. I~asic compression involves removing
to redundant data, leaving enough data to reco:astruct the file during
decompression with
the desired degree of accuracy, or 'tolerance.' If the original uncompressed
file has a
higher resolution than is rewired for the end use, much non-redundant data can
be
eliminated because it is unnecessary in the decompressed file; for example,
where a
high resolution image is only needed for display on a computer monitor (which
15 typically has relatively low resolution), the image file can lose a lot of
data without
sacrificing the quality of the final image.
Similarly, in the case of most audio files, some data that is not redundant
can
nevertheless be eliminated during compression because some of the frequencies
represented by the data are either not perceivable or not discernible by the
human ear.
2o The psychoacoustic characteristics of the human ear are such that ultra-
high and ultra-
law frequencies are beyond. its perceptual capabilities, and tomes that are
very close
together in pitch are often not discernible fi°om one another so the
human ear
perceives only a single tong anyway. Codecs which take advantage of this
phenomenon, including the very popular NIP3 codec, a.re known as "perceptual
audio
25 codecs." Such a codec analyzes the source audio, compares it to
psychoacoustic
models stored within the encoder, and discards data that falls outside the
models.
With the widespread use of perceptual audio codecs, the problem of high
frequency reconstruction has become of great importance. Wizen digitally
encoding an
audio signal, the high .frequency portion of the signal occupies a
disproportionately
_1_
CA 02467466 2004-05-17
large part of the encoded bit stream. To faithfully capture the high frequency
content
in the encoded signal, a very large amount of data would required to
accurately
represent the original, uncorlpressed audio signal.
~ne known method of increasing the compressibility of the encoded signal is
to take advantage of the correlation between the high and low frequency
components.
since these two components are correlated, it is possible to i~lter out the
high
frequency component at the encoder, transmit only the low f~eduency component
and
reconstruct the high frequency component at the decoder to generate an
approximation
of the original audio signal. Including additional information that describes
the
to correlation between the low and high frequency components with the
transmitted low
frequency component enables a more faithful reconstruction of the original
audio
signal.
Lossless compression in MP3 and other like compression formats uses the
l~uffman algorithm for frayne compression of signal data. These techniques
have
z s proved to be very popular, since they are able to achieve significant
compression of
the original audio signal while retaining the ability to produce a reasonably
accurate
representation of the original signal.
The allocation of the number of bits to be allottE;d to storing each interval
(e.g.
second) of sound sets a 'tolerance' level that determme:D the fidelity of the
2o decompressed audio file. Techniques that rely on this are known as "lossy"
compression techniques, b~~~ause data is lost in the compression/decompression
process and the fidelity of the reconstructed file depends upon how much data
was
lost.
The earliest examples of successful high frequency reconstruction in lossy
2s audio encoding are the MPG-Plus and Al-~~-Plus standards. Both techniques
are based
upon a patented spectral bandwidth replication technique. The problem with
this
approach is that for highly harmonic signals the high frequency content is not
always
harmonically correlated to the love frequency content. Thus, special treatment
of
harmonic signals is required. Tonality control is also missing from this
approach.
7
-
CA 02467466 2004-05-17
An alternative method is high-frequency reconstruction by linear
interpolation.
~ne example of this technique is PlusV''"~, a completely parametric approach
by VLSI
Solutions ~L3~'. This method reconstructs high frequencies using a two-part
harmonic
plus noise model. The original audio signal :is sent to an encoder. The
encoder extracts
up to the four most prominent harmonic components, identified as peaks in the
short-
time magnitude spectrum, and encodc;s their parameters" 'fhe remaining high
frequency component in the audio signal is considered to be noise. The high
frequency component is encoded by parametrization of :its amplitude envelopes
in
eight frequency bands. The encoded signal consists of only the low frequency
1o component of the original signal and the noise model parameters identified
by the
encoder. Tn order to extract a reconstructed signal from ~tl~e compressed
signal, the
decoder unpacks the parametric data and reconstructs the high frequencies by
generating the corresponding harmonic and noise components of the high
frequency
signal, without relying on the low frequency component of the audia signal.
Another approach to high frequency reconstruction has been described by Liu,
Lee, T-Isu, National Chiao T~xng University, Taiwar°x, 200 : "IIi gh
Frequency
Reconstruction by Linear L'<~trapolation", which is incorporated herein by
reference.
Liu et al. suggest using spectral replication, copying filterbanlc
coefficients to generate
a "detail spectrum" of the high frequency component of the audio signed,
followed by
2o the application of a linearly decaying amplitude envelope, with least-mean-
squares
estimation of the decay slope from the existing low frequency component.
Problems
with this approach include the absence of tonality control, non-~harmonicity
of the
restored audio, possible inadequacy of the replicated spectrum block, and the
possibly
increasing slope of the amplitude envelope.
Ultimately, however, all these techniques are limited in their ability to
compress an audio signal sin ce they do not account for l;c;mporal relations
in the audio
signal. Thus, the compressed signal inevitably retains substantial
redundancies which
must be stored in order for ire algorithm to reproduce a reasanably accurate
representation of the original uncompressed file.
-3-
CA 02467466 2004-05-17
There is accordingly a need for a compression and recoc~struction scheme that
accommodates temporal relations in an audio signal to increase compression
ratios
and improve the accuracy of reconstructed audio signals. There is a further
need for a
method of reconstruction that can be used on old archived sound files, to
reconstruct
the high frequency component of the file that had been lost due to limits in
recording
technology or storage media. existing at the ~:ime the file -vas created.
summary of the Invention
The present invention provides a system and method for the improved
compression of audio signals. The present invention also provides a system and
1 o method for the improvetnea~~ of perceptual sound quality for audio
recordings that are
missing high frequency con~:ent, for example due to limitations in the storage
medium
or where the recording was compressed by a lossy audio data compression
technique.
The method of the invention may thus be used to restore and enhance previously
archived audio recordings, where the high frequency cornpone:.~.t of the
original signal
15 has been lost due to limitations in the recording hardware or storage
media.
The compression method of the invention is capable of being fully automated
and does not require pre-inii:ialization for different types of audio data. It
is
sufficiently flexible to adjust for different sizes of spectral audio data,
permitting it to
be used with different spectral transforms. The method of the irwention is
optimized
2o for integer arithmetic, improving calculation efficiency and ex3:ending the
range of
devices that can implement the invention and the range of devices in which the
method could be applied, e.g. sound players, dictating machines, cellular
phones,
wired phones, radio receive~_°s and transmitters, the sound tracks of
television receivers
and transmitters.
25 In the present invention, context modeling is applied to all of the main
types of
audio-data: ll~odified Discrete Cosine Transform (le/IDC'f ), scalefactors,
side
information. The invention ~Nomprises applying context modeling to the data
stream
and constructed algorithmic models, and the algoritlunic optimization of a
decoder
function. The invention is based upon the use of adaptive arithmetic
compression
3o techniques involving increasing the probability of the value coded.
lVlethods of
CA 02467466 2004-05-17
context modelling are used for choosing the table of probability for
arithmetic
compression.
In the preferred embodiment tlae system and method of the invention, different
context models are applied to increase the compression ratio of spectral
information,
j quantization coefficients and other information. The spectral data is
divided into five
frequency bands (0..31, 32..sp3, 64..L27, 12~..25~, 256.._'i75), each band
corresponding
to a different frequency range, and the last ten values for each frequency
(statistics)
for each band are independently obtained. Compression of spectral data uses
the
prediction of coefficient vahzes by several preceding frames of audio data by
calculating the mean value ofthe last ten values of MDCT coe'_~cients.
Preferably context models and arithmetic compression are used for final
compression. The filtered value of the Nth MDCT coefficient is compared with
the
largest value of all MDCT coeffaci.ents in the band, to which N belongs. The
largest
value of all MDCT coefficients in the band is obtained from the first
iteration. The
ratio of those values determines the number of tables used for ~~rithmetic
compression.
The invention can be: directly applied to spectral data of' various
characteristics
and spectral bands of various frequencies. This include;> data obtained by
standard
algorithms, such as MPECT-~ Layer 3 and MPEG-4 AAC, as well as new compression
algorithms.
2o In the preferred embodiment a rough estimate of the high frequency
component is performed by .applying a mult~band distortion effect,
waveshaping, to
the low frequency content. This enables the proper harmonic structure, i.e.
overtones
of the low frequency compo:raent, to be re-created in the reconstructed high
frequency
component. Control of tonality is achieved by means of varying the number of
bands
within the multiband framework. More bands leads to less inter-modulation
distortion,
and hence greater tonality.
The use of waveshaping functions, such as Chebychev polynomials, ensures
that the number of generateu: harmonics is limited and no aliasing occurs. A
filterbank
is used that roughly shapes i:he reconstructed high frequency component
according to
_5_
CA 02467466 2004-05-17
an estimation of the most probable shape, performed us:irzg only the
information
extracted from the low frequency component v~rithout coiasidering additional
information.
To ensure accurate reconstruction of° the high frequenc;r component,
the time-
frequency amplitude envelope and degree of tonality parameters are extracted
from
the loin frequency coypone:nt.
In one aspect the present invention provides a method f~r compressing an
audio signal, comprising the steps of: a. dividing spectrai data
;corresponding to the
audio signal into a plurality of frequency bands, each ba~i~d corresponding to
a
1Q different frequency range; b. obtaining a plurality ofthe last Modified
Discrete C:'osine
Transform (MDCT) coefl~cients corresponding to the spectral data for each
frequency
for each band; and c. compressing the spectral data using a pref~iction of
coefficient
values in a plurality of frames of audio data by calculating a mean value of
the
plurality of last MDCT coeff'lcients.
15 In a further aspect the present invention provides a mef.~~od for
increasing a
compression ratio in the co~~pression of an audio signal, _: omp_rising
compressing
scalefactors using MTF'-3 method.
In a further aspect the present invention provide:9 a method of reconstructing
an audio signal from a set ol° compressed audio data corresponding to
an originai
zo audio signal, comprising the steps of: a. time-frequency decomposing the
compressed
audio data, b. estimating parameters from the audio data. comprising at least
an
amplitude envelope estimated from a modules of a first set of corresponding
filterbank coefficients and a tonality estimated from a magnitude spectrum of
a second
set of corresponding filterba~~k coefficients; and c. syntl7.esi~inghigh
frequency
25 components of the audio signal by: i) dividing the audio data into several
frequency
bands, ii) passing each frequency band through a nonlinear ~va~re-shaping
distortion
effect to generate distorted ft-equency bands, and iii) smnmir~g i:he
distorted frequency
bands to form an estimate of the high frequency comporunts.
_6_
CA 02467466 2004-05-17
brief Description of the Drawangs
In drawings which illustrate by way cf exazrzple only areferred embodiment
of the invention,
Figure 1 is a blocl~ diagram showing the IV1DCT compression scheme.
Figures 2A to 2f are plots illustrating the dependencies of the sum of signs
on
the number of the series.
Figure 3 is a flow chart showing the sign prediction method used in the
invention.
Figure ~. is a flow chart showing the method use~~~ to determine the countQ
to boundary.
Figure 5 is a flow chart showing the method of cleterznilzing the optimal LSC
value.
Figure 6 is a flow chart showing the employment; of ge3zeral statistic gained
at
the first iteration in magnitude prediction.
t5 Figure 7 is a flow chart showing the method of coding t:he general
statistic,
gained at first iteration.
figLZre 8 is a flow chart showing the implementat9zon of scalefactors in the
znventzon.
Figure 9 is a flow chart showing the dispersion calculation.
20 figure 10 is a flow chart showing thc~ low frequency fihtering by means of
a
recursive filter.
Detailed Description of the l:nvention
Some components ot.'the present invention are b~~sed upon an extension of
known algorithms of arithmetic compression techniques.. for e~:ample as
described in
25 the following US patents, al:l of which are incorporated I:zerein by
reference:
_7_
CA 02467466 2004-05-17
4,122,440 Langdon, Jr.; Glenn George (San Josc, CA.); lssanen; J~rnaa
J~bannen (San Jose, CA), Method and means for arithmetic; string coding,
t~et~aber
24, 197;
4,286,256 L.angdon, Jr.; Glen . (~>an Jose, CA); I~ISSanen; J~rana J. (Los
CJatos, CA), Method and means for arithmetic coding utilizing a reduced number
of
operations, August 25, 191;
4,295,125 Langd~n9 Jr.; Glen G. (San Jose, CA), Me~lzod and means for
pipeline decoding of the high to low order pairwise combined digits of a
decodable set
of relatively shifted finite number of strings, ct~ber 1:~, 191;
4,463,342 I,angdon, Jr.; Gleb G. (San :rose, CA); l~.ass,anen; J~rma J. (Los
~atos, CA), Method and means fog- carry-over control ire she high order to low
order
pairwise combining of digits of a decodable set of relatively shifted finite
number
strings, July 31, 194;
4,467,317 L.angdon, Jr.; glen . (San Jose, C~.); I~issanen; Ja~r~raa .1. (Los
CIatOS, CA), Nigh-speed arid metic compression coding using concurrent value
a,~pdating, August 21, 194;
4,633,490 G~ertzel; Gerald (VYhite flai.ns, hi Y); lZitchell; Japan L.
(C3ssining, I~TY), Symmetrical optipr~ized adaptive data
compression/transfer/decom:~ression system, December 30, 196;
4,652,8561VI~l~ia~ddin; I~ottappram IVI. A. (S~m Jose, CA); l~issanen;
J~rrna J. (Los Gatos, CA), lVlultiplication-free mufti-alphabet arithmetic
code,
March 24, 197;
4,792,954 Arps; Donald 1B. ( san Jose, CA); I~arnin; E,hud 11~. (I~iriat-
Motzkin, IL), Concurrent detection of errors in arithmetic data compression
coding,
2s December 20, 19~~;
_g_
CA 02467466 2004-05-17
4,891,643 Mitchell; Joan L. (Jssining,1VT'~'); Pa~nneb~:er; illian~ 13.
(Carmel, N~'), Arithmetic coding data compression/de-<~c~mpression by
selectively
employed, diverse arithmetic coding encoders and decoders, January 2, 1990;
4,901,363 'Toyol~a~.a; I~azuharu (~'amato, JP), System for compressing bi-
level data, Febrraary I~,19~90;
4,905,29? L,angdon; Jr.; Glen G. (San Jose, CA;%%; Mitchell; Joan L.
(~ssining, NY); Pennebal~er; William 13. (Carmel, N'~); T~issanen; Jor~a J.
(Los
C7atos, CA), Arithmetic coding encoder and decoder system, ~'f~bruary 27,
1990;
4,933,883 Pennebaher; Williapn ~. (Carmel, N~); Mitchell; Joan L.
70 (C~ssining, NY), probability adaptation for arithmetic coders, Jone 12,
1990;
4,935,882 Pennebah;er; William ~. (Carmel, N~'); lVIitehell; Joan L.
(C3ssining, N~'), Probability adaptation for arithmetic coders, June 19, 1990;
5,045,852 Mitchell; Joan L. (Cssini.ng, N~); Po~nnebaker; William .
(Carmel, N"~'); Rissanen; Jorra~a J. (Los C3atos, CA), I)ynarnic: model
selection
~ 5 during data compression, September ~, 199I;
5,099,440 Pennebal~er; Williaan . (Carmel, N~'); Mitchell; Joan L.
(~ssining, NY), Probability adaptation for arithmetic coders, lWare24, 1992;
5,142,283 Chevion; Dan S. (I~aifa, i'.L); I~arnin; Ehud( ~. (Kiryat l~otzkin,
IL); Walaeh; Eu~eniusz (I~iryat 1'~lotzkin, 1L), Arithmetic corrlpression
coding using
2o interpolation for ambiguous symbols, ~-luust 25, 1992;
5,210,53 Furlan; Gtilbert (San Jose, CA), Date. c;o~npression/coding method
and device for implementing said method, May I I, 199:x;
5,414,423 3~ennebal~er; ~'illia~ D. (Carmel, N~~), Stabilization of
probability estimates by conditioning on prior decisions of a given context,
May 9,
2s 1995;
_~-
CA 02467466 2004-05-17
5,~46,0~0 L~n~do, J~°.; glen . (Aptos, CA); ;~~ndi, Ah~ci (Cupertino,
CA), Order-preserving, fast-decoding arithmetic coding a rithmc;tic coding and
compression method and ap.;~aratus, August 13, 196.
The present inventioc~ also m~.kes usf° of data context modeling
methods that
have recently been developed, the best known application of context modeling
being
the Context Arithmetic Based Adaptive Coding (CABAL) algorithm; as implemented
in the MPECa-4 A~IC standard, which is incorporated herein by reference.
~~~nitions
For purposes of this description the hollowing de:ilnitions are provided:
to ''Sign" is the sign of Modified Discrete Cosine ~Cransform (~J1DCT)
coefficient.
"Magnitude" is the magnitude of MDCT coefficient.
"count0" is the region of zero MDCT coefficients (coded by storing only the
boundary of this region).
"count0 boundary" is the left boundary of the count0. It is equG.l to the last
nonzero
IS MDCT coefficient position plus one.
"Delta-coding" is storing flee difference between a current valu~° and
the .previous one.
A standard implementation has redundancy, concerned 'r~ith doubling the range
of the
value to be coded. E.g. ifthe value to be coded has the r,~~~.lge (a...b), the
difference
between the value to be cod~:d and ,.he value previously coded has the range
(a-b...b-
2o a), which is twice as wide.
"Arithmetic compression'' is the method of coding based on dividing the
unitary
interval into sections, which length is proportional to the; probability of
the value to be
coded.
''Accumulated frequency of ~he value'' is a number which indicates how maiay
times
z5 the value was previously meted.
- 10-
CA 02467466 2004-05-17
':Recursive filter" is a filter based on summation of previous values weighted
by
exponentially decreasing coefficients. To avoid a large amount of summations
and
multiplications, the recursive filter calculates the current filter value
using the linear
combination of the previous filter result and the current value to be f
ltered.
"Scalefactor" is the value needed to rascals the 1VIDCT coefficients. The
resealing is
implemented by the following equations for short and long blocks,
respectively:
-(blolxal _gaixx-210-8",subbloak_gcun~ _ ,,kale ac uxultr lier~scale actor r
MDCT - ~es~caled = .sign * O!IDKT ~ * 2 4 ' * 2 ( f _ ~ r _. )
~-(~lalxaf -gain-210) _ .E-ccrle ixc mxxlti lien".wale actor l+ ire la " retab
MDCT _ re,scaled = s ign * ~rIDCT ~ * 24 * 2 ( t _ ~ t _ I t ~ n
is the normalizing multiplier for MDCT data.
"Band" is the group of frequency values in one or several frames (for example
with
indices: 0..3I, 32..63, 64..127, 12..255, 256..575.
"Series'' is the set of valuc;s in different frequencies, but in one frame.
"Columns'' is the set of values in one frequency but in different frames.
"ESC-symbol" is the value chosen so that all values larger than it are
assLimed to have
approximately identical probability.
''ESC-sequence" is the sequence of ESC-symbol and the difference between the
current value and ESC-symbol.
''ESC-sequence coding'' is the method of coding values with small probability,
which
consists of coding the ESC-symbol and the difference between the value to be
coded
2o and the ESC-symbol.
"Table" is the table of probabilities of the value to be coded. The
probability table can
be changed during the coding process. The more symbols that were coded using
the
table, the larger is the probability of this value.
"Statistics" is the last values stored in a buivfer.
-li-
CA 02467466 2004-05-17
"The MTF-3" (Move To Front 3 last values) is a method. of coding by v,~hicl~
the last
three different values coded are remembered and placed in stacl~, then coded
with the
probability of the location vv~ere they are stored plus th~:i.r own
probability, while all
other values are coded with their own probabilities.
''Aggressiveness" is the parameter that shows the frequency of table
resealing.
"Symbol" is the value to be ;;oded, e.g. sealefactor, MI~~T coefficient etc.
">3inary code" is a code whi~rh consists of 0 and 1. 'This code needs N bits
for
encoding 2~N different values. The value can be calcul~.ted as: ~rxlue = ~ r~;
2' .
"IJnary code" - is a code, which consists of N symbols "'1" anct one symbol
"0" in the
end (if the value isn't the largest; for the largest value the last "'0" isn't
necessary).
This code needs from 1 to I~ bits for encodi~lg N different valwus. 'The value
can be
calculated as Yaiue = ~~z; .
"e" is the base of natural logarithm, e=2.718281828.
Entropy Compressio~a
In the preferred embodiment the entropy comprfasion stage of the invention
comprises the following coYnponents:
1. MDCT data compression:
a. T he method scheme;
b. The method description;
c. Sign prediction algorithm;
d. count0 boundary;
e. Magnitude prediction algorithm;
f. ESC-sequence employment;
_ 12-
CA 02467466 2004-05-17
g. First iteration employment.
2. Scalefactors usage and compression.
M.DCT Data ~'cheme
Input data have a corrlplicated structure and consist of fzve parts. The first
type
of data is the MDCT coeff dents. l~IL~CT coefficients have the following
format:
~Ialues in the range of-820;'...207 are grouped into series of ~7G values
each. The
number of series containing these values is limited with ~2-bit arithmetic
usage. The
algorithm works by the series, that is the coding of each series is started
only after all
previous series are coded. each series is divided into 5 bands as shown in
Table l,
1o each "band" is a subset of data within the series. The di~rision into bands
does not
depend upon the values, but depends only upon the place of thc~ symbol in the
series.
For example, the first band starts at tl3e zero position and ends at the 31 st
position,
composed of a group of values dependent upon their series position. The series
in
each band are shown in Table 1.
Table l
Band number First position in Last position in band
band ~
0 ~ 0 31
i
1 ~ 32 63
i
2 b4 12'7
i
_
128 25:>
4 J 256 ~ 57:~
The algorithm separately treats magnitudes and signs of values, because there
is no correlation between tlleTrl. EnGOdlng the Sign "~" G(3rreS~iOndS $o "+"
and "~"
corresponds to ''-". If the magnitude is equal to 0, the sign is not written
to output
stream.
_13_
CA 02467466 2004-05-17
if (l~TI7CT<0) then Magnitude=-MDCT else Magnitude=MDCT
If (MI7CT<0) then Sign=1 else Sign=0
NIDCT Comp~er~ion Met~oc~
The algorithm is based on any suitable arithmetic compression procedure.
Input data for this procedure are the following: the number of possible values
for the
symbol to be compressed, the table of appearance frequencies (a probability
table
analogue) and the sum frequency (total weight of the table). Tho table is
generated
during the compression process as described below. The: arodinl; (compression)
of the
data is thus reduced to the optimum table fitting for each magnitude or sign
to be
1 o compressed, by implementation of aritlunetic;al compression. The optimal
table is
taken in dependence of the, filtered MI)CT Coefficient to the maximal MI7CT
coefficient in the band ratio.
The table refresh x:rea~uency is controlled by the "aggres,siveness"
parameter.
'~~Jhen the sum of all accumulated frequencies in the table exceeds the
aggressiveness
1 s parameter, the entire table is'. divided by 2 (re,scaled). The
''aggressiveness" parameter
is constant and is fitted for better compression.
The procedure implementing the arie:hmetic compression calculates the left and
the right ranges for the range coder, to be used for further com~~ression. It
can be
e,alled by the following string:
20 ~ncodeONEint(int a, int ~Cnt, int step, int Size, int totfreq)
in which:
int a = the value to be encoded;
int ~'Cnt = the table of accumulated frequencies pointer:,
int step = the value, which is added to the appearance frequency of the symbol
after
2s coding;
int Size = the table size;
-14-
CA 02467466 2004-05-17
int totfreq = the whole frequency of the table equal to the sum of all its
elements and
the size of the table.
The table is pre-initialized bvy the information gainod at the first
iteration, and then the
appearance frequency of the symbol to be compressed is. increased oath time
when the
appropriate symbol is coded.
During the coding process the procedure uses a table of accumulated
frequencies which differs fr~~m the original table by increasing each
accumulated
frequency by 1. This increment is implemented to avoid the possibility of a
zero
probability for a symbol.
l0 There is a restriction for tho mochanism of suboptimu rn table fitting. The
algorithm must be reproducible while decocting. The original series is
transformed
into the serios of magnitudes and signs by the rule described alcove. Tables
during the
initialization process are filled (~ to 11 itoms per band) by Gau;Ssian
distribution
according to the formula: ~3~.~~ = f~~X~ -- 2~-- , where
G~, ~' are defined parameters and .f~ is normalization coefficient. Such a
distribution
approximates accumulation by the file distribution tables, described below
(different
bands for each f le of IVIDCT data).
Sign P~ec~iction Algor~ith~
Considering the values signs distribution for different columns of 1V1DCT
data,
Figures 2A to 2F illustrato the dependencies of the sum. of signs ("+''_ +l,
''-"- -1 to
the sure) on the numbex of oho series (designated "row number" in Figuros lA
to 2F)
for 576 columns. Each plot corresponds to a real melody.
The independent behaviour of the first sign colaxmn is clear in these plots.
For
most melodies the first sign column generally has the same value for all
series, so this
2s sign column is coded separately fi°om the other columns using the
compression
algorithm.
-15-
CA 02467466 2004-05-17
lather sign columns behave chaotically. There is ~. slight: dependence of the
signs in these columns on the sequence of previous sign: in the sara~e column.
The
table number for sign compression depends upon the sequence of previous signs,
as
shown in Table 2 and Figure 3.
s 'fable 2
Sequence of signs in column Numerical equivalence Tabie Number
+ + + + + I OflOflfl I fl
++++- I flflOfll I 1
+++-+ I flflfllfl I 2
+++-- I flflflll I ~
++-++ I flfll0fl I 4
--_-- I 11111 i ~1
"co~ent0" b~undary
The position where the last non-zero MDC'T-coefficient is located plus one, is
the "count0 boundary''. The magnitude distribution through the series has a
tendency
to include high values at the start of the series and to decrease to Iow
values at the end
of the series. Therefore, it i<.5 more efficient to point to the location of
the Past non-zero
element than to automatically include the last data poinia of a series in the
compression, since they may all be zero. The eountfl bocrndary is coded as the
difference between the current count0 boundary and the countfl boundary in
previous
t 5 series.
Because of the Delta-coding used for count0 boundary compression it is often
more efficient to shift the eount0 boundary artificially 1:o the right for
some numbers
-l~-
CA 02467466 2004-05-17
and to compress all zeros between the last non-zero MDCT coefficient and the
artificially shifted count0 boundar~T. I-lowever, storing the precise last non-
zero vah~e
position can eliminate the asymmetry of such an approach. also, coding the
last non-
zero value with a smaller table can eliminate the redundancy of" this
approach. The last
non-zero value cannot be equal to zero, so the zero value probability must be
zero.
This approach allows the compression ratio to be increased.
Magnitude P~edic~ion Method
The prediction algoritlun uses the filtered value of the previous MDCT-
coefficient in the same colmnn {Fi.ltexed_va:~ue). The f ltering is carried
out by the
to low-frequency recursive filter. The table with which the number will be
coded is
selected depending on the ~omparisor~ of the Filtered value with the largest
value in
the band (MaxBand). The concordance coefficients
I~= Filtered value /Maxl3afad are fixed for each band. The current coefficient
distribution is illustrated in Table ~.
1s Table 3
Band\Table0 1 2 3 4 5 6 7 ~ 9 10
i
'
Band 0 0 0.01C.03 , 0.1 0.2 0.3 0.6 1.0 2.0 ......
0.06 f
j
Band 1 0 0.050.1 0.2, 0.3 0.5 0.'7I.0 3.0 5.0 ......
Band 2 0 0.05~?.l 0.2 0.3 0.5 0.~ 3.0 5.0 ......
~ ~
1..0
Band 3 0 0.010.03 0.06 0.1 0.2 0.3 1.0 ......-
0.6
The standard recursive alter is used to carry out the low fivequency
Iiltering.
Coefficients of the recursive alter are selected to decrease the value meted 7
frames
previously in a times-
2o Filtered value[t--dt~ = Filtered-value[t~ * 6fi' + Last vatue[t]~~ 1/7
-17_
CA 02467466 2004-05-17
When using integer values, to reduce the rounding error the Last value is
multiplied
by 10:
Filtered value[t+dt] _ (Filtered value[t] * 6 + Last value[t]* 10)/7;
The maximal values in each band are calculated dL~ring i.he firs: iteration.
To code a "high amplitude'' frame it is desirable to use the previous value in
the same frame. It is filtered by means of a lo~~ frequency recursive filter:
Filtered value[f+ df] _ (Filtered value[f] * 4 + Last value[f]* 10)/5;
and the filtered value is con spared with the faltered valLre of the: MDCT
coefficient
from the previous frame. It can be compared not only with the filtered value,
bud with
the filtered value plus the s~~iaare root of dispersion. The; dispersion is
calculated by
the following equation:
Dis,~ersion = < value~2 > - <value>~2,
where <...> - is a low frequency filtering (by means of the recursive filter).
Value sq = Value~2;
15 Filtered value sq=Filtered- value sq*e~(-2f)+Value_sq*(1- a"(-2f));
Filtered value=Filtered va)~ue*e~(-f~+Value*(1-a~(-f))
Dispersion=Filtered value sq-(Filtered'value~2)
After the comparison, in different cases different sots of tables are picked
out.
The recursive filtering is shown in Figure 10 and the dispersion calculation
is shown
2o in Figure 9.
To improve the compression ratio, the mixing of tables can be implemented. If
the
ratio of the filtered MDCT coefficient to the maximal MDCT coefi~cient is not
exactly the value from table 3, a linear combination of two tables can be used
for
_ 1~
CA 02467466 2004-05-17
encoding. The coefficients of the linear combination are ~,alculated as a
simple linear
approximation:
'W1=(Filtered_MDCT-Left_boundary);(Right boundary-i.eft boundary)
"~2=(Right boundary-Filtered MDC T )/(Right boundary-Left boundary)
Mixed table--Left table"VV2+Right table*'~11
(~Uhere Left boundary<Filtered_MDCT<Right boundary)
To increase compression rafio for binary da~~a (where the data c;an be 0 or I)
a simple
limitation of the largest and the lowest probability of 1 and 0 can be
implemented. To
reduce the MDCT coefficie='t encoding to the binary data encoding, each MDCT
coefficient can be converted to binary or unary code. In fact, it is valuable
to
implement unary code for some small values (for example, for vahaes 0..15).
For some
larger values it's preferable to use binary code (for example, for values
16..527). It is
preferable to compress the largest values with the equiprobablfv table (for
example, for
values 528..8207).
I S ESC-Sequence Usage
Sometimes it is necessary to encode a large value with the table, even though
there is a small probability of this value occurring. In such cases it can be
more
efficient to use the ESC-sequence and to write the enccned ESC-value and the
difference between that value and the ESC-value to the output: stream. The ESC-
value
2o is fitted dynamically for ea h table from the ratio
Price{ESC) + Price{Walue-ESC) < lPrice(4~'alue)
This inequality corresponds to the discontinuous variety of ESC-values. Thus,
the
selection of the optimal ESC-value is not a single-value problem. The optimal
ESC-
value is located between tb.e smallest ESC-value that sai~is~'°zes this
inequality and the
biggest ESC-value that does riot satisfy this inequality.. The optimal ESC-
value
calculation process is shown in Figure 5.
-19-
CA 02467466 2004-05-17
When using the arithmetic cedar to code the data, high values have a low
probability of occurring {they were in previous data only once, or there are
no such
values at all). This Iow probability can be inadvertently reduced to zero due
to
truncation error. To prevent this error, and to compress such values more
effectively,
ESC-coding is used. Namely, one of the possible values is taken as the ESC-
symbol
and alI values after it and th6~ ESC-symbol essentially arc: coded with the
same
probability. In this algorithm the probability of these values are added and
are said to
be the probability of the ESC-symbol. When a data point has a value that is
greater
than or equal to the ESC-symbol, the ESC-symbol is coded with the probability
of the
to ESC-symbol and the difference of the value and the ESC-symbol (zero
included) is
coded by the equiprobable table.{The coding with equiprobable table is a
particular
case of arithmetic compression, which uses a probability table in which all
probabilities are equal) The selection of the ESC-symbol is carried out by
minimizing
the integral of function f{x)~log{p(x)), where p(x) is the probability to be
coded with,
and f(x) is tl~e estimated probability, i.e. the smoothed probability,
collected through
the process of coding. The smoothing is an ordinary calculation of the mean
value of
the probabilities of the five nearest values. however, when the highest and
non-
possible values are known with high precision, ESC-coding is not necessary.
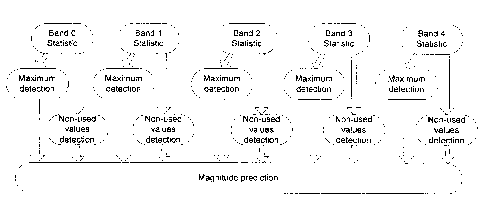
The Fist I~e~°ation E~cplc~yaner~t
2o The first iteration is used for general statistic collection. This
statistic is used
for initialization of tables before the second iteration, for maxrnnum
detection in each
band, and for detection ofrcon-used values. The general statistic is collected
for each
band separately (0..31, 32..63, 64..127, 128..255, 256..575), as shown in
Figure 6. The
general statistic can be changed during the coding. When the ~~alue is coded,
the
corresponding number in tlm general statistic (with the same ~~alue and in the
same
band) is decreased by 1.
The general statistic is stored in a compressed lzle. It contains numbers,
which
indicates how many times ;,ach value appeared in each band. The number of
series is
known, so the sum of all n:~ambers for each band can be calculated as the
product of
3o the series number to the band width (bands have the following width: first -
32,
-20-
CA 02467466 2004-05-17
second - 32, third - 64, forth -128, fifth - 320). As the number of MDCT-lines
is
known, the last zero-values in the file do not need to bE: stored. The 8206th
value is
not stored even if it is not zero, because it can be reconstructed correctly
as the
difference between the sung of all values (vuhich is known and the sum of all
values
except the 8206th (which were stored before). The table is compressed by
arithmetic
compression with four different tables for each byte of 32-bit words of
statistic.
When decoding it is necessary to reconstruct the last zeros and the 8206th
value. When storing such a statistic some redundancy is introduced i.n the
output file.
To eliminate the redundancy unused values are excluded from the table when
coding
I o the absolute values of the NIDCT coefficients.
Scale, factors Usage and Compt~ession
There is a redundancy of scalefactor, in that when the scaiefactor is known
not
all MDCT coeff dents are possible. For example, when the scalefactor is not
the
smallest, all MDCT coefficients in the band of this scalefactor cannot be
small
because in such a case the scalefactor would have to be smaller. So when the
last
value of the MDCT coefficient is coded the low values from the table can be
discarded when all previoL~s values were small. For low bit rates the
scalefactor
precision is artificially reduced to achieve higher compression. The context
model
uses not only time correlation but also frequency correlation. Preferably the
MTF-3
2o method is applied in the temporal domain to increase the compression rate
of
scalefactors.
Frequency ~2ec~nstruction
Frequency construction comprises the following components:
1. Analysis of the input signal
2. Synthesis of high frequencies
3. Analysis of generated high frequencies
4. Extrapolation of parameters
-21 -
CA 02467466 2004-05-17
Analysis of the Input Sig~aal
The f'zrst stage of the reconstruction of the audio file according to the
method
of the invention is the analysis of the sound file to be improved, or of the
input audio
stream, passed from the decoder. The analysis comprises two stages: time-
frequency
decampositions and parameter estimation.
There are two types of time-frequency decompositions that are performed
during the analysis stag. 'fhe furst type is the oversampled windowed Fast
Fourier
Transform (FFT) filterbanlc, which is time-frequency aligned with the
filterbank used
in the reconstruction phase: the size of the window is small enough (around 5
to 10
1 o ms) to provide a sufficient time resolution. This filterbank is used for
the estimation of
the time-frequency amplitude envelope (described below). The second filterbank
is a
simple windowed FFT with a longer time window. This filterbanlc provides line
frequency resolution for the tonality estimation (described below).
The parameters estimated from the input audio are the time-frequency
15 amplitude envelope and the degree of tonality. The amplitude envelope is a
odulus
of the corresponding filterbank coefficients, obtained from the first
filterbank. The
tonality is estimated from the magnitude spectrum of zv second falterbanlc.
Several
tonality estimates are currently elaborated. The estimator that is preferred
for use in
the invention calculates the ratio of the maximal spect~°al magnitude
value over the
2o specified frequency range to the total energy in the specified frequency
range. The
higher this ratio, the higl-ser the degree of tonality is. The frequency range
used for
estimation of the tonality is [F/2, F], where F is the cut-off frequency of
the given
audio file or of the input audio stream. The magnitude spectrL~m undergoes a
"whitening" modification before calculation of the tonality. The purpose of
the
25 whitening modification is to increase the robustness of the estimator in
case of a low
degree of tonality. The ~lhitening modification comprises multiplication of
the
spectral magnitude array by sqrt(f), where f is the frequency. This operation
converts
the pink noise spectrum into a white noise spectrum and lowers the tonality
degree for
the naturally non-tonal pink noise.
CA 02467466 2004-05-17
The output of the analysis block provides the estimates of amplitude envelope
and tonality, comprising a 2D tine-frequency array of amplitudes and 1l~ array
of
tonality variations in time.
Synthesis of High Freq~ce~zcies
The synthesis of high frequencies comprises the following srteps:
1. The input audio is split into several frequency bands by means of a
crossover.
If the cut-off frequency is denoted as F and the desired. nLn~nber of bands is
2N+1, then
the crossover bands are assigned with the following frequencies: [F~'2-dF/2,
F/2+dF/2], [F/2, F/2+dF'~, [F/2+3dF/2, F/2+SdF/2], ..., [F-dF/2, F-~-dF/2,].
The
to crossover comprises band-pass F1R filters designed using a windowed sync
method.
The size of the window is around 10 ms. 'The window used is preferably Kaiser
(beta
= 9). The filtered full-rate signals comprise outputs of the crossover.
2. Each of the output crossover output signals is passed throug:n a nonlinear
wave-shaping distortion effect. The distortion effect is provided by the
following
formula: y(t) = F(x(t)), where F is the non-linear transiPormation. The
simplest form of
F (not used in the invention) is a simple clipping, i.e. F=x(t) when abs(x(t))
<= A, and
F=~-/-A where A is sons arbitrar~T threshold amplitude. This distortion
generates an
infinite row of harmonics of the input signal, which is undesirable for
digital audio
processing because higher harmonics may be aliased about tl°~e Nyqaaist
frequency and
2o generate undesirable intermodulation distortion. To prevent this
distortion, the
invention preferably employs a special kind of distortion function in the form
of
Chebychev polynomials, which allows control over the exact number of generated
harmonics. For the present invention the second-order polynomial is suitable,
so y(t) _
F(x(t)) = x(t)~2 is a useful formula. It generates the second harmonic of the
input
~5 signals.
j. The resulting distorted bands are summed up to form the .first estimate of
the
reconstructed high freqL~encies in [F, 2F] frequency range. The
intermodulation
distortion products are out of the [F, 2F] range, so they can be filtered out
by simply
excluding all frequencies above ~F.
_ '73 _
CA 02467466 2004-05-17
~~nalysis ~f ~eaae~°ated ~i~la Fr~g~ce~~ie,s
The generated high frequencies are analy;~cd ire. the same way as the analysis
of
the input audio signal (step l, above. Since these two steps of analysis are
identical,
they can be combined into one analysis step. At the output of this analysis
step the
estimates of amplitude envelope and tonality of the ge;t~erated high
f=rcquencies are
obtained.
~xt~c~polataon ~f Paramet~a~,s
The parameters detected from step 1 are extrapolated into the domain of high
frequencies. The following extrapolation methods are preferred:
1o For extrapolation of the amplitude envelope, detect the slope of the
amplitude
envelope in the frequency range ~F/2, ..., F ]. The calculation is done as
follows.
1. Spectral whitening ~nodif~cation, multiplication of magnitudes by sqrt(f)
for
each tTequency point.
n+.nr ~
~Xz
1
f=~'=''v
2. Detection of the slope over a wide frequency range: ~1 =
Xa
t
l =~' -~ .fir
t 5 where K is the number of lilterbanh frequency bins between F/2 and F, and
i~T is the
number of bins used for energy averaging. 1-Iere it is assumed to be l~/4
z
r:_+:v x
1 ...4 __x?
1 1-,~~ ~'~~ 1
3. Detection of a slope over a narrower frequency range: ~Sz =
,; __
4
~~ X1
1=/;-N
4
- '~ 4 -
CA 02467466 2004-05-17
4. The final slope is calculated vas S = '~l + S'
2
5. The slope is linearly extrapolated in the decibel domain to the higher
frequencies.
6. The resulting slope is smoothed in time using a recursive low-pass filter:
Xsmoothed[t][f] = aX[t][fj + (1-~) Xsmoothed[t-1][f].
For extrapolation ofthc tonality a simple zero-order extrapolation is used.
The
tonality of the reconstructed high-frequency signal should be equal ~:o the
tonality of
the [F/2, F] band.
fldjustment ~f I~igher F~equea~cies
I laving obtaincd the estimated parameters of tl;e, reconstructed high
frequency
component, the Final step is to adjust the estimated parameters to approximate
the
actual parameters.
The first adjustment to be undertaken is the tonality adjustment. There are
two
methods for adjustment of tonality. The first is to adjust the number of bands
used in
the crossover in step 2. T he second method is a direct adjustment in the
domain of
filterbank coefficients. ~t is performed by means of ampliucation of peaks in
a
spectrum. Two possibilities exist for this: either each coefncient is scaled
proportionally to its energy, or only peaks in a spectrvrrz are located and
arnpiified.
2o 'f'he peaks are located using the X[f ~]<X[~ l ]<=X[f]>=X(f+i ]>X[f+2]
criterion for
magnitudes of adjacent iilterbank frequency bins.
The second adjustment is the adjustment of the amplitude envelope. This
adjustment is performed in the domain of ~ilterbank cocfficients. The
difference
between the extrapolated envelope end the real estimated envelope is
calculated and
then smoothed in frequency by means of a ~-piss simple zero-phase low-pass
recursive filter: Xsmoothed[f] _ ~X[f] + (l-[3) Xsmoothed[f 1] and
Xsmoothed[f] _
(3X[fj + (1-[~) Xsmoothed[f+1]. Then the smoothed correction amplitude
envelope is
CA 02467466 2004-05-17
applied to filterbank coefficients, i.e. the filterbank coefficients are
multiplied by the
magnitude correction coeff dents.
Mixing with the input audie3
The resulting reconstructed high-frequency signal, that contains no energy
below f', is mixed with the input audio to form the final output signal of the
algorithm.
The pracess of mixing is just addition of two signals in time domain.
Optionally, the
amplitude coefficient A can be applied to the reconstructed high frequency
signal in
order to alter its amplitude accordin ; to user demand.
carious embodiments of the present invention having beard thus described in
1o detail by way of example, it will be apparent to those skilled in the art
that variations
and modifications may be made without departing from the invention. The
invention
includes all such variations and modifications as fall within the scope of the
appended
claims.
-~6-