Note: Descriptions are shown in the official language in which they were submitted.
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
METHODS FOR IMPROVING UNPREDICTABILITY OF OUTPUT OF PSEUDO-RANDOM NUMBER
GENERATORS
TECHNICAL FIELD
The present invention relates to aspects of improving unpredictability of
pseudo-random
numbers which originate from numerical computations in mathematical systems
comprising
at least one function, in particular a non-linear function. The mathematical
system may be a
non-linear system of differential equations which exhibits chaotic behavior.
The invention is
useful in encryption and decryption in, e.g., electronic devices.
BACKGROUND OF THE INVENTION
Cryptography is a generally used term covering science and technology
concerned with
transforming data, such transforming of data being performed with the aim of
allowing for
storing and transmitting of the data while preventing unauthorized access to
the data. By
means of cryptography, the data are made non-comprehensible for any other
person but the
intended recipient or recipients of the data. Accordingly, cryptography plays
an increasingly
more important role in the protection of intellectual property, including
copyright protection,
as the technological advancements require safe transmission and storage of
huge amounts of
data.
In an encryption and decryption algorithm, the specific transformation of data
is dependent
on an input to the algorithm, a so-called key. In case the sender and the
recipient of the data
have an appropriate set of keys, the sender and the recipient are able to
correctly encrypt
and decrypt the data while any third person who may gain access to the
encrypted data is
not able to view a properly decrypted version of the encrypted data, as she or
he is not in
possession of an appropriate key,
Usually, a set of data to be encrypted is referred to as "plaintext" or
"original data", whereas
the encrypted version of the set of data is referred to as "ciphertext" or
"encrypted data".
Two types of symmetric cryptographic algorithms are the so-called "block
cipher" and the so-
called "stream cipher", Both types of algorithms use symmetric keys, i.e. the
keys used for
encryption and decryption are equal or trivially related. A block cipher is a
cryptographic
algorithm which splits an original set of data into a plurality of blocks of a
given size, e.g. 64
bits per block. Mathematical and logical operations are performed on each
block, whereby the
original amount of data is usually transformed into blocks of pseudo-random
data. In case
decryption is initiated with the correct decryption key, the original data can
be re-called by
reversing the mathematical and logical operations used for encryption.
In a (synchronous) stream cipher, a pseudo-random number generator generates,
based on
a key, a sequence of pseudo-random numbers, the sequence being referred to as
a
keystream. The keystream is mixed, by arithmetic and/or logical operations,
with a plurality
of sub-sets of the original set of data, the sum of sub-sets of data defining
the original data
to be encrypted. The result of the mixing is the encrypted data. The set of
encrypted data
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
2
may be decrypted by repeating the procedure in such a way that the pseudo-
random
sequence is extracted from the encrypted data, so as to arrive at the
original, decrypted
data.
The plaintext is often mixed with the keystream by use of a logical operator,
most often by
the so-called XOR operator, also referred to as the "exclusive or" operator,
which is
symbolized by the ~ symbol. XOR generates a one-bit result from two one-bit
arguments. All
possible combinations are:
0~0=0
0~1=1
1~0=1
1~1=0
Utilization of the XOR operator on a plaintext and a pseudo-random keystream
yields a
ciphertext. During decryption, an identical keystream is generated, and the
XOR operator is
now utilized on the keystream and the ciphertext, resulting in the original
plaintext. The
identical keystream can only be generated by using the key on which the
keystream for
encryption was initially based.
Further, so-called public key systems have been developed, such systems being
characterized by a pair of asymmetric keys, i.e. a public key and a private
key, the two keys
being different. In such systems, the public key is usually used for
encryption, and the
private key is usually used for decryption. The private and the public key
correspond to each
other in a certain manner. The key which is used for encryption cannot be used
for
decryption, and vice versa. Thus, the public key may be published without
violating safety in
respect of accessibility of the original data. Accordingly, when transmitting
encrypted data via
a computer communications network, the recipient of the data first generates a
set of keys,
including a public and a private key. The public key, for example, is then
provided to the
sender of the data, whereas the private key is stored at a secure location.
The sender of the
data utilizes the public key For encrypting the original data, and the
encrypted data are then
transferred to the recipient. When the recipient receives the encrypted data,
the private key,
which corresponds to the public key previously utilized for encryption, is
provided to the
decryption system which processes the encrypted data so as to arrive at the
original
decrypted data. Public key systems are primarily used for transmitting keys
which are utilized
in, e.g., block or stream ciphers, which in turn perform encryption and
decryption of the
data.
The methods of the present invention are applicable to cryptographic methods
and
cryptographic systems, in particular but not exclusively to stream cipher
algorithms, block
cipher algorithms, Hash functions, and MAC (Message Authentication Code)
functions. Such
methods, functions and algorithms may include pseudo-random number generators
which are
capable of generating pseudo-random numbers in a reproducible way, i.e. in a
way that
results in the same numbers being generated in two different cycles when the
same key is
used as an input for the pseudo-random number generator in the two cycles.
In pseudo-random number generators, numerical solutions of chaotic systems,
i.e. systems
of non-linear differential equations or mappings exhibiting chaotic behavior,
have been
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
3
proposed. The term "chaotic" may in a strict mathematical sense only be used
in the context
of a continuous system. However, the present text also refers to discrete or
finite systems
having at least one positive Lyapunov exponent as being "chaotic".
A chaotic system normally governs at least one state variable X, the numerical
solution
method of such a system normally comprising performing iteration or
integration steps. In a
chaotic system, the solution X~ at a given instant is dependent on the initial
condition Xo to
such an extent that a small deviation in Xo will result in a huge deviation in
the solution X~,
the system often being referred to as exhibiting sensitivity on initial
conditions. Thus, in order
for the pseudo-random number generator, i.e, the algorithm numerically solving
the chaotic
system, to give a reproducible stream of pseudo-random numbers, the exact
initial condition
Xo must be known. Thus, in cryptographic algorithms relying on chaotic
systems, the initial
condition Xo used in the numerical solution of the chaotic system is derived
from the key
entered by a user of the cryptographic system, thereby allowing the same
stream of pseudo-
random numbers to be generated for e.g. encryption and decryption of data.
Lyapunov exponents measure the rates of divergence or convergence of two
neighboring
trajectories, i.e. solution curves, and can be used to determine the stability
of various types
of solutions, i.e. determine whether the solution is for example periodic or
chaotic. A
Lyapunov exponent provides such a measure from a comparison between a
reference orbit
and a displaced orbit. Iterates of the initial condition xo are denoted the
reference orbit, and
the displaced orbit is given by iterates of the initial condition xo + yo,
where yo is a vector of
infinitely small length denoting the initial displacement. The initial
orientation of the initial
displacement is given by uo = yo /1 Yol. Using this notation, the Lyapunov
exponent, h(xo, yo).
is defined as
h(~o,uo)=~If1'111n~YnI~IyoO
n->w n
where y" is the deviation of the displaced orbit from the reference orbit,
given by the n'th
iterate of xo. For systems whose dimension is larger than one, there is a set
or spectrum of
Lyapunov exponents, each one characterizing orbital divergence or convergence
in a
particular direction. Thus, if the system has N degrees of freedom, it will
have N Lyapunov
exponents which, however, are not necessarily distinct. In all practical
situations, a positive
Lyapunov exponent indicates chaos. The type of irregular behavior referred to
as hyperchaos
is characterized by two or more positive Lyapunov exponents. Numerical
calculation of
Lyapunov exponents may be performed according to the suggested method in T.S.
Parker
and L.O. Chua: Practical Numerical Algorithms for Chaotic Systems, pp. 73-81.
Even more irregular systems than hyperchaotic systems exhibit so-called
turbulence, which
refers to the type of behaviour exhibited by a system having a continuous
spectrum of
positive Lyapunov exponents. Turbulence may be modeled by partial differential
equations,
for example the well-known Navier-Stokes equations.
A large number of prior art documents are concerned with solving chaotic
systems, in
particular to be used in cryptographic algorithms, also including stream
cipher algorithms
relying on chaotic systems, some of which are briefly mentioned below as a
general
introduction to the background art.
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
4
US 5,007,087 assigned to Loral Aerospace Corp, discloses a method and an
apparatus for
generating random numbers using chaos. The patent describes solving chaotic
systems for
generating random number sequences and mentions its possible use in
cryptography, in
particular in the field of key generation and management. The document
mentions that
repeatability of the number sequence should be avoided.
US 5,048,086 assigned to Hughes Aircraft Company is related to an encryption
system based
on chaos theory. The system uses the logistic equation x"+1=~,x"(1-xn), which
is a mapping
exhibiting chaos for certain values of P. In the computations, floating-point
operations are
used.
PCT Application WO 98/36523 assigned to Apple Computer, Inc. discloses a
method of using
a chaotic system to generate a public key and an adjustable back door from a
private key.
The need for establishing rules of precision during computations on a chaotic
system is
mentioned. The document states, as an example, that a specified floating point
or fixed point
precision can be identified along with specific standards for round-off.
PCT Application WO 02/47272 assigned to the assignee of the present
application discloses
various aspects of cryptography, including the use of so-called fixed-point
numbers.
PCT application WO 01/50676 assigned to Honeywell Inc. discloses a non-linear
cryptographic
isolator for converting a so-called vulnerable keystream into a so-called
protected keystream.
The non-linear filter cryptographic isolator includes a multiplier for
performing a multiplication
function on the vulnerable keystream to provide a lower partial product array
and an upper
partial product array, and a simple unbiased operation for combining the lower
partial
product array and the upper partial product array to provide the protected
keystream.
"Numerical Methods and Software" by D. Kahaner, C. Moler and S. Nash (Prentice-
Hall
International Editions, 1989) contains a general introduction to (pseudo-
)random number
generation. The book mentions the following criteria for judging the quality
of (pseudo-
)random number generators:
a) High quality: the generator should pass all the statistical tests and have
an extremely long
period,
b) Efficiency: execution should be rapid and storage requirements minimal.
c) Repeatability: Specifying the same starting conditions will generate the
same sequence.
The user should be able to restart the generator at any time, but explicit
initialization is not
necessary. A slight change in the starting procedure will result in a
different random
sequence.
d) Machine independence and portability: The algorithm should work on
different kinds of
computers; in particular, no operation should cause the program to stop. The
same sequence
of random numbers should be produced on different computers by initializing
the generator in
exactly the same way.
e) Simplicity: The algorithm should be easy to implement and use.
The book further states that no generator can be successful in satisfying all
of these criteria.
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
It is further known to use fixed-point variables in numerical computations,
for example in
Intel Mandelbrot computations. Intel (cf. MMXT"' Technology Application Notes,
"Implementing Fractals with MMXT"' Technology", publicly accessible on
htto~//cedar intel.com/cgi-
5 bin~/ids dlllcontentlcontent_,jsp7cntKe~r-Legacywirtm MANDEL
10491&cntTvpe=IDS EDITORIAL&c
atCode=0 on 6 June 2003) has explained how a Mandelbrot set (the set being
derivable from a
non-linear system) may be computed in a fast manner using MMX technology (an
add-on to
Intel's processors which speeds up certain computations). This is done using
fixed-point
computations.
The Mandelbrot set is computed by means of the below mapping:
Zn+1 - Zn
Intel utilizes a constant decimal separator position in their computations. A
so-called 5.11 is
utilized, i.e. a 16 bit number is utilized wherein the decimal separator is
placed after the 5'th
bit, °5'° referring to 5 bits after the decimal separator, "11"
referring to 11 bits after the
decimal separator.
SUMMARY OF THE INVENTION
Pseudo-random numbers generators as those used in cryptography should, while
allowing for
reproducibility of a sequence of pseudo-random numbers, generally be as
unpredictable as
possible. In other words, an internal state of a mathematical system
underlying the generator
should contain as little information as possible concerning other internal
states of the
mathematical system. For example, the information that a particular value
°X," was contained
in state variable "X" at iteration No. i should not in a predictable manner
lead to another
value "X~" which was contained in the variable "X" at another iteration,
iteration No. j. When
an iterative mathematical system is expressed in discrete terms, problems with
small periods
can arise in the sense that a certain degree of predictability may arise if or
when the
mathematical system becomes periodic. In a cryptographic system this is a
serious problem
since it will have the effect that data will be encrypted repeating the same
block of pseudo-
random data which comprises security.
The present invention provides four aspects, preferred embodiments of which
improve
security by improving unpredictability:
1. Variation of a parameter of a mathematical system exhibiting a positive
Lyapunov
exponent (claims 1-17)
2. Manipulation of at least one of the most significant bits of a number
resulting from a
multiplication operation (claims 18-43 and 55), the "g-function"
3. Combining of the quotient and the remainder of a number resulting from a
division
operation (claim 44).
4. Updating of counter values by means of a carry value (claims 45-55).
With the additional aim of improving speed in computations, the present
invention provides,
in a further independent aspect:
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
6
5. Concurrent encryption and identification value generation (claims 56-61).
The above aspects of the invention will be discussed in sections 1-5 below.
Disclosure and
discussions which apply to all aspects of the invention are included in
sections A-L below.
VARIATION OF A PARAMETER OF A MATHEMATICAL SYSTEM EXHIBITING A POSITIVE
LYAPUNOV EXPONENT
A first aspect of the present invention provides a method for repeatedly
performing
computations in a mathematical system which exhibits a positive Lyapunov
exponent,
comprising varying at least one parameter of the mathematical system after a
certain
number of computations. The parameter, which may, e.g., be a counter, may vary
independently of the mathematical system and may cause the mathematical system
to
produce output periods which are longer than if the parameter would not have
been varied,
or it may cause the mathematical system to exhibit periodic behaviour with
periods which are
so long that, in any practical application, the mathematical system will not
repeat itself. The
parameter may be repeatedly varied throughout computations in the mathematical
system.
In connection with a system with a positive Lyapunov exponent, i.e. a system
exhibiting so-
called chaotic behaviour, there exists the further challenge that rounding-off
of floating-point
numbers is not necessarily performed consistently on two different processors,
in which case
- due to the positive Lyapunov exponent - a sequence of pseudo-random numbers
generated
on a first processor may not be reproducible on a second processor. Usually on
a computer,
real numbers are represented by floating point type numbers. A floating-point
number is
defined as a number consisting of a mantissa and an exponent, e.g. 31415 ~ 10-
4, where
"31415" is the mantissa and "-4" is the exponent. When a computer is
performing a
calculation on a floating-point variable, it recalculates the exponent to
match the result. The
name "floating-point" refers to the fact that the decimal separator is moving
at calculations,
caused by the varying exponent. However, floating point arithmetic is defined
differently on
various processor architectures causing different handling of precision and
rounding off. The
present inventors have realised that, instead of floating-point numbers, fixed-
point numbers
can be used. Thus, in embodiments of the methods of the invention,
computations such as
iterations in the mathematical system, which usually comprises at least one
function and is
expressed in discrete terms, are performed by means of at least one fixed-
point number. All
computations may be performed as fixed-point or integer computations. A fixed-
point
number is represented as an integer type number on a computer, where a virtual
decimal
point or separator (also referred to as an imaginary decimal separator) is
introduced
"manually", i.e. by the programmer, to separate the integer part and the
fractional part of
the real number. Hence, calculations on fixed-point numbers are performed by
simple integer
operations, which are identical on all processors in the sense that the same
computation,
performed on two different processors, yields identical results on the two
processors, except
for possible different representations of negative numbers. Such possible
different
representations may occur as a consequence of some processors utilizing ones
complement
and other processors utilizing twos complement. Furthermore, these operations
are also
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
7
usually faster than the corresponding floating point operations. The use of
fixed-point
variables is further discussed in section B below.
The mathematical system may comprise at least one non-linear map or at least
one non
linear equation, or a set of non-linear maps or a set of non-linear equations,
as discussed
further below, cf. in particular section C.
The counter referred to above may be increased at each iteration in the
mathematical
system, in which case a maximum value may be defined for the counter. The
method may
thus comprise resetting the counter to a minimum value once the counter has
reached said
maximum value, whereby the counter varies with a certain period. However, this
does not
necessarily mean that the mathematical system also varies with a period.
Resetting the
counter avoids overflow in the system.
In order to further improve unpredictability, multiple parameters may be
employed. Some of
such multiple parameters may be dynamic, i.e. varying, whereas others may be
static, i.e.
constant. A constant parameter may for example be generated from a seed value
provided to
the mathematical system, such as an encryption key. The variation of a first
one of the
parameters, such as of a counter, may be dependent from the variation of a
second one of
said counters in such a way that the period of the first counter is different
from the period of
the second counter. The variation of each individual one of the counters may
be dependent
from the variation of at least another one of said counters so as to obtain a
period of the
counters which is longer than the period which would have existed if each
individual counter
would not have been dependent from the variation of another counter. The one
or more
counters may be increased linearly or by any other function.
The computations performed by the first aspect of the invention may be used
for generating
pseudo-random numbers, which may be used in any kind of cryptography and/or
identification value generation.
2 MANIPULATION OF AT LEAST ONE OF THE MOST SIGNIFICANT BITS OF A NUMBER
RESULTING FROM A MULTIPLICATION OPERATION, ~~G-FUNCTION"
In a second aspect, the invention provides a method for manipulating a first
set of data in a
cryptographic system, the first set of data comprising a first and a second
number of a first
and a second bit size A and B, respectively, the method comprising:
- multiplying the first and the second number to obtain a third number of a
third bit size
A+B, the third number consisting of P most significant and Q least significant
bits,
wherein A+B=P+Q, and wherein Q is equal to the largest of the first bit size A
and the
second bit size B, Q=max(A,B),
- manipulating the third number to obtain a fourth number which is a function
of at least
one of the P most significant bits of the third number,
- using the fourth number for deriving an output of the cryptographic system.
More specifically, the fourth number may be used for generating or updating a
pseudo-
random number as the output of the cryptographic system.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
8
It has been found that a general multiplication function has good
cryptographic properties.
These properties are good mixing, i.e. most input bits affect all output bits,
and poor linear
approximations. Furthermore, the multiplication has the property that the
number of bits of
the output is the same as the total number of bits in the inputs, i.e. if a
number of bit-size A
is multiplied with a number of bit size B then the output is of bit size A+B.
This larger bit size
enables further manipulation of the output, such that the final output is of a
bit size smaller
than A+B, for instance A or B. Thereby improved cryptographic properties for
the
manipulated multiplication function may be achieved, i.e. all input bits
affect all output bits,
and all linear approximations are very poor.
The first and second number may have different bit sizes, for example 8 and 16
bit. However,
for practical reasons it may be desirable that the first and second numbers
are of the same
bit size. For example, each of the first and second number may be a 32-bit
number, in which
case the third number is a 64-bit number, consisting of 32 most significant
and 32 least
significant bits. The fourth number may then, for example, consist of the 32
most significant
bits of the 64-bit number. The first set of data may consist of a single
number, such as a
number assigned to a variable, and the first number may thus equal the second
number, so
that the step of multiplying comprises squaring the first number. Such
squaring may be
advantageous as compared to other multiplication functions implying the
multiplication of two
different numbers, as it requires handling of a single variable only. Further,
the squaring of a
number of a certain bit size A results in a number, referred to above as the
third number, of
bit size 2~A. Thus, by applying a manipulation to the third number to obtain
the fourth
number of another bit size, such as bit size A, further complexity is added to
cryptographic
systems incorporating the method of the second aspect of the invention. The
squaring is
further advantageous, as it - when performed on small processors, such as 8-
or 16-bit
processors - requires fewer operations than multiplying two different numbers
whereby
computational resources may be saved. For example, multiplication of two
different 32-bit
numbers requires sixteen 8-bit multiplications, whereas the squaring of a 32-
bit number only
requires ten 8-bit multiplications. Also, by applying the method in a
cryptographic system, a
keystream of a satisfactory quality (with respect to unpredictability) may be
directly
generated as a pseudo-random output by means of simple operations, such as by
XOR
operations. Further, in a cryptographic system, the squaring function does not
normally
result in a certain result more often than it results in other results.
However, the
multiplication of two different numbers may results in the result zero every
time one of the
two numbers being multiplied has the value zero. In other words, the squaring
function may
have a reduced bias towards a certain result, in particular towards zero, as
compared to
other multiplication functions. Such bias towards zero may leak information
concerning an
input to the multiplication, as it reveals that one of the two inputs to the
multiplication
operation most likely was zero.
45
The fourth number may itself represent a pseudo-random number which is used as
the
output of the cryptographic system. Alternatively, the fourth number may be
used as an
input for further computations, such as iterations in a mathematical system,
following which
a pseudo-random number or other output of the cryptographic system is derived.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
9
In a cryptographic system one or more state variables may be iterated in a
mathematical
system. A counter or variable may be added to each or some of the state
variables in each or
some of the iterative steps, as described further below. The step of
multiplying may comprise
identical operations in each iterative step, or it may, alternatively,
comprise different
operations. For example, in a first iterative step, the step of multiplying
may comprise
squaring a variable x, whereas in one or more subsequent iterative steps, the
step of
multiplying may comprise multiplying variable x with another variable y.
In the case of at least two state variables being iterated, a value assigned
to each of the
IO state variables may be updated as a function of at feast one value of the
same and/or
another state variable, for example according to the general formula
x;+~=f(x,,y~), subscript i
denoting the i'th iteration, x and y denoting the state variables.
The step of manipulating preferably comprises using as well most significant
bits of the third
15 number as least significant bits. The manipulating may comprise a logical
or arithmetic
operation. One logical operation which is easily applied is the XOR function
which may, e.g.,
be applied on a number of most significant bits and an equal number of least
significant bits.
The XORing may be performed bitswise, in which case each bit of the most
significant bits
may be XORed with a bit of the least significant bits. The XOR operation may
thus be
20 performed N times, resulting in a result of bit size N . The step of
manipulating may be
performed by applying an operation to bits of two or more different numbers.
For example, in
a cryptographic system in which several numbers xl...x" are being generated
based on
iterations of one or more state variables, the step of manipulating may
comprise XORing bits
of one number xm with bits of another number xP, one or both of xm and xP
representing the
25 third number.
Likewise, an arithmetic operation may be performed bitwise.
In a cryptographic system, the first and second number may be derived from a
set of data to
30 be encrypted or decrypted, in which case the fourth number may be used to
generate an
encrypted or decrypted representation of the second set of data, such as
plaintext or
ciphertext, for example in a block cipher algorithm or in an algorithm for
determining an
identification value for identifying a set of data.
35 The method according to the second aspect of the invention may also be
applied for
generating an identification value for identifying a second set of data. In
that case, at least
one of the first and second number is derived from the second set of data, so
that the fourth
number is used for generating an identification value identifying the second
set of data. The
term "identification value" may be a hash value or a cryptographic check-sum
which
40 identifies the set of data, cf. for example Applied Cryptography by Bruce
Schneier, Second
Edition, John Wiley & Sons, L996. In case a cryptographic key is used as a
seed value for the
computations, the hash function is usually referred to as a MAC function
(Message
Authentication Code).
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
In any application of the method, at least one of the first and second number
may be derived
from a cryptographic key, i.e. an input value for an algorithm of the
cryptographic system
which is used for initializing iterations.
5 In the method of the second aspect of the invention, the first number may
equal the second
number, in which case the step of multiplying comprises squaring the first
number.
In a mathematical system, in which a state variable is iterated, the state
variable may be
updated as a function of the fourth number, or as a function of a permutation
of the fourth
10 number, such permutation comprising, e.g., bitwise rotation of the bits of
the fourth number.
With the aim of providing a good mixing and making each output bit of the
cryptographic
system dependent from as many input bits as possible, the step of multiplying
may be
performed multiple times, each multiplication being performed on a number
which represents
or is a function of one of a plurality of state variables, the step of
multiplying thereby
resulting in a plurality of third numbers. Thus, also the step of manipulating
may result in an
array comprising a plurality of fourth numbers, whereby at least one state
variable may
updated as a function of at least two of the fourth numbers.
At least one of the first and second number may be a state value X; to which
there is added a
variable parameter value, such as a counter C;. The step of multiplying may
thus comprise
squaring (X;+C;), X; denoting a state variable or an array of state variables,
and C; denoting
the counter or an array of counters. The at least one parameter may be
repeatedly varied at
predetermined intervals in the computations. A counter C; may be added to the
fourth
number or to a number which is a function of the fourth number to result in an
updated state
variable X;+1.
The step of multiplying may comprise a plurality of multiplication functions
resulting in a
plurality of numbers of bit size A+B, whereby the step of manipulating may
comprise
combining at least one of the bits of a first one of the plurality of numbers
with at least one
of the bits of a second one of the plurality of numbers. The plurality of
multiplication
functions may comprise at least one squaring operation, whereby the step of
manipulating
may comprise combining at least one of the P most significant bits of a first
one of the
plurality of numbers with at least one of the Q least significant bits of a
second one of the
plurality of numbers.
The step of multiplying is usually performed in a mathematical system in which
at least one
state variable is being iterated, most often in a system in which two or more
state variables
are being iterated. In each computational sequence, values assigned to each of
the at least
two state variables may be updated as a function of at least one value of the
same and/or
another state variable.
In a cryptographic application, at least one of the first and second number
may be derived
from a set of data to be encrypted or decrypted, whereby the fourth number may
be used for
generating an encrypted or decrypted representation of the set of data.
Likewise, the fourth
number may be used for generating an identification value identifying the set
of data.
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
11
At least one of the first and second number may be derived from a
cryptographic key.
The method of the second aspect of the invention may advantageously be applied
in a
system/method, wherein an identification value for identifying a set of data
is determined,
and wherein a set of data is concurrently encrypted/decrypted, e.g., by means
of a pseudo-
random number generator in which numerical computations are performed in a
mathematical
system, cf. the below discussion of the fifth aspect of the invention.
3 COMBINING OF THE QUOTIENT AND THE REMAINDER OF A NUMBER RESULTING
FROM A DIVISION OPERATION
In a third aspect, the invention provides method for manipulating a first set
of data in a
cryptographic system, the first set of data comprising a first and a second
number, the
method comprising:
- dividing the first number by the second number to obtain a quotient and a
remainder,
- combining, by means of a mathematical operation, the quotient and the
remainder to
obtain a resulting number,
- using the resulting number for deriving an output of the cryptographic
system.
Such manipulating may be applied in the method according to the second aspect
of the
invention. The step of combining may comprise any manipulating discussed above
in
connection with the method according to the second aspect of the invention,
for example a
logical operation, such as an XOR operation, or an arithmetic operation. The
output of the
cryptographic system may be any output discussed above in connection with the
second
aspect of the invention.
The method of the third aspect of the invention results in an improved mixing
of numbers in
a cryptographic system, in particular in a pseudo-random number generator. The
method is
useful in connection with any cryptographic system, including those described
herein.
4 UPDATING OF COUNTER VALUES BY MEANS OF A CARRY VALUE
With the aim of providing a method for ensuring very long periods of a
sequence of numbers
in a cryptographic system, and thus with the aim of improving unpredictability
and security,
there is provided as a fourth aspect of the invention a method for generating
a periodic
sequence of numbers in a cryptographic system in which computational steps are
repeatedly
performed, the method comprising updating, in each computational step i, an
array of
counters, the counters being updated by a logical and/or by an arithmetic
function, whereby,
at each computational step, a carry value is added to each counter in the
array, and wherein
the carry value added to the first counter in the array, co, is obtained from
at least one of:
- a selected computation of a value of the array of counters,
- a value which is a function of a counter value at a previous computational
step.
In other words, the method comprises updating, in each computational step i,
an array C; of
counters c;,;, the counters being updated as:
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
12
c°,.+1=c°,~+a°+d; mod N°.
c;,;+1=c~,,+aj+b;_i,;+1 mod N~ for j>0,
where:
c;,;+1 is a value assigned to position j of array C at step i+1, j=O...n-1, n
denoting a
dimension of the array C, i.e. the number of elements in the array,
c~,, is a value assigned to position j of array C at step i, j=O...n-1,
a; is a value, typically a constant, assigned to position j of an array A,
j=O...n-1,
for j>0: b;_l,;+1 is a carry value resulting from the computation of c~_l,;+1,
N; is a constant, j=O...n-1,
for i=0: d;=d° is an initial value,
for i>0 d; is a carry value obtained from a selected computation of a value of
the array of
counters C; and/or a function of C;.
It should be understood that the carry values may be zero.
As demonstrated below, a mathematical proof is established showing that the
period of the
counter system is very long. Thus, in a pseudo-random number generator
employing the
above counter system and generating a keystream, huge amounts of data may be
encrypted
without the keystream becoming periodic by repeating itself. Thereby,
unpredictability and
security is improved.
It should be understood that the sequences of numbers generated by the method
according
to the fourth aspect of the invention preferably has a period which is so long
that the
sequence of numbers generated, in most practical applications, does not become
periodic,
i.e. that any sequence of numbers generated is not repeated.
The array of counters C; will below be referred to as a "counter with carry
feedback", in
contradiction to an ordinary counter of the form c;+1=c;+a mod N. In order to
explain the
effect of a counter with carry feedback, an ordinary counter will first be
discussed:
Consider a system defined by:
c;+1 = c; + a mod N,
where c; is the value of the counter at step i (the array C; containing a
single element, c;), c;+1
is the value of the counter at step i+1, a is a constant number and N is a
large number
usually defined by a register size of an electronic processor which performs
the computations,
i.e. N=23z for a 32-bit processor.
In the case where a=1, c is constantly incremented by 1 until it reaches the
value N-1, and in
the following iteration c restarts from zero. In such a system, the period of
c is equal to N.
The single bits in the number have, however, different periods. The least
significant bit, c~°~,
is successively added the value 1, and will thereby repeatedly obtain the
values 0 and 1, i.e.
have a period of 2. For every second incrementation this will give rise to a
carry being added
to the next bit in the register, c~l~, which thereby will have a period of 4.
For bits at position j,
.the period will be given by 2'+1.
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
13
Such a system suffers from the disadvantage that all bits, except the most
significant, have
periods smaller than the total period N. Another disadvantage is that the
dynamic behaviour
of the bits is rather predictable. For instance, the value of the least
significant bit changes at
every iteration. Thereby, even though the value at a given iteration is not
known, the value
will be the opposite in the following iteration. Also, the value of the most
significant bit will
change only when half of the period N has passed. This means that the value of
the most
significant bit is constant for a long time, resulting in poor non-
predictability characteristics
which are crucial in cryptographic systems.
As indicated above, the counter with carry feedback, in a single-dimensional
system, may be
defined by:
c;+~=c;+a+d; mod N,
d;+1=lifc;+a+d;>N,
d;+1=Oifc;+a+d;~N,
where c, is the value of the counter at step i, c;+1 is the value of the
counter at step i+1, a is a
constant number, d; is the value of the feedback carry at step i, and N is a
large number
usually equal 2 to the power of the register size of the processor on which
computations are
being performed.
Again consider the case where a=1, starting with co=0, the behaviour is
similar to the
ordinary counter until c; + a + b; becomes larger than or equal to N, then
b;+1 is put equal to
1, and in the subsequent iterations added to the value of the counter. Thereby
the period 2
behaviour at the least significant bit is interrupted, thereby making it less
predictable than in
the case of an ordinary counter. This furthermore means that the least
significant and the
rest of the bits all will have periodic behaviour equal to that of c. This
period is N-1.
The period of the counter system with carry feedback can be proven as follows.
The above recurrence relation is equivalent to the following linear
congruential generator:
Z;+1=Z; + A mod (N-1),
which has a period length of N-1, when A has been chosen such that gcd(A,N-
1)=1, i.e. the
greatest common divisor of A and N-1 is one, cf. B. Schneier: Applied
Cryptography, John
Wiley & Sons, Inc. (1996).
To show that Z is equivalent to C, we consider an initial value Co=Zo for
Zo>A. The recurrence
relation for C; can be defined in terms of Z;:
C; = Z; if (Z;_1 + A)< N-1 and Z;_l~ 0, A denoting a concatenated value
a~_l...ao, cf, below,
C; = N-1 if (Z;_1 + A)=N-1
C; = Z;-1 if (Z;_i + A) > N-1 or Z;_1=0
Therefore, C; will attain the same set of numbers as Z;, though in a different
order, except
that C; will attain the value N-1 but not the value A. Thus, the period of the
recurrence
relation, C, is the same as for the linear congruential generator, Z.
To sum up, the purpose of the counter system is to generate a sequence of
numbers with a
given long period, wherein each binary value at each bit-position have the
same period as
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
14
the complete system. Additionally, the least significant bit is, due to the
carry feedback,
influenced by all other bits, which is not the case when no feedback is
applied.
The application of the long periodic sequence is to ensure that the internal
state of the
stream cipher has a large period.
When the constant incrementation value A is chosen appropriately, it can
furthermore be
achieved that the values at each bit position in C have relatively high
frequencies, i.e.
changes often. Thereby, in a situation where the values of the counter bits
are secret, for
instance when they are applied as part of the input to a stream cipher with an
internal state,
the exploitation of any relation between the output of the stream cipher and
the values of the
bits, is additionally complicated since the values of the bits change
relatively often.
The value A may be appropriately chosen by ensuring that the product of
(No*NZ*...*N"_i)-1 and a concatenated value of the values a; are mutually
prime. The
concatenated value of the values a; is determined as a single sequence of bits
a~_la"_z...ao, cf.
the below example.
An example of appropriate chosen constants, when performing computations with
32-bit
registers (i.e. N=23z), are:
ao = Ox4D34D34D
al = OxD34D34D3
az = Ox34D34D34
a3 = Ox4D34D34D
a4 = OxD34D34D3
as = Ox34D34D34
as = Ox4D34D34D
a~ = OxD34D34D3
where Ox indicates that the numbers are represented as hexadecimal numbers.
The
connection to the single counter system with carry feedback, is easily
obtained by
concatenating all constants and concatenating all counter elements, and
thereby performing
the calculations on these 256-bit numbers, i.e. with modulus 256. In the above
example, the
concatenated value of A is a,a6a5a4a3aZalao=
OxD34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D34D.
Another example of appropriate chosen constants, when performing computations
with 8-bit
registers, are:
ao = Ox2C
al = OxCB
as = OxB2
a3 = Ox2C
a4 = OxCB
as = OxB2
a6 = Ox2C
a7 = OxCB
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
where Ox indicates that the numbers are represented as hexadecimal numbers.
The
connection to the single counter system with carry feedback is easily obtained
by
concatenating all constants and concatenating all counter elements, and
thereby performing
the calculations on these 64-bit numbers, i.e. with modulus 26a.
5
The counter system with carry feedback as discussed above may be applied for
using the
counter values as a periodic input for a cryptographic function, e.g.:
- Using the counter values as input to a stream cipher or pseudo-random-number-
generator with an internal state.
10 - Using the counter values as part of the input in a computation of an
identification value.
In one embodiment, an internal state of a cryptographic system is updated as a
function of
the counter values, e.g, by adding a counter value to an internal state. Such
update may be
performed before the computation of a next-state value or subsequent to the
computation of
15 a next-state value. An output function may then be applied to the current
or the next internal
state in order to generate a pseudo-random output, often referred to as a
"keystream".
The following pseudo code illustrates a preferred embodiment of the
computation of multiple
counters, the pseudo code illustrating a single iteration of the counter:
25
// Save old counter values
for i=0 to 2
c old[i] = c[i]
end for
// Increase counters
c[0] _ (c[0] + a[0] + d) mod 232
if c[0] < c old[0] then
b[0]=1
else
b[0]=0
end if
c[1] _ (c[1] + a[1] + b[0]) mod 232
if c[1] < c old[1] then
b[1]=1
else
b[1]=0
end if
c[2] _ (c[2] + a[2] + b[1]) mod 232
a.f c[2] < c old[2] then
d=1
else
d=o
end if
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
16
The following pseudo code illustrates a preferred embodiment of the
computation of a single
counter:
// Save old counter value
a old = c
// Increase counter
c = (c + a + d) mod 23z
i.f c < c old then
d=1
else
d=0
end if
In the above pseudo-codes, it is presumed that all values of a are smaller
than 232-1.
As will be understood from the above discussion, the size of the arrays C and
A may be 1, i.e.
n=1, so that:
- the array C contains a single value co,;,
the array A contains a single value ao,
the counter co,; being updated as co,;+1=co,;+ao+d; mod No.
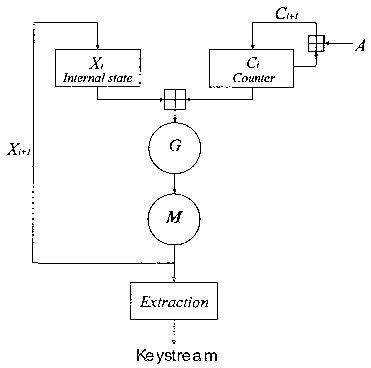
As further described below in connection with Fig. 4, for i>0, d; may be a
carry value
resulting from the computation of C"_1,;, i.e. the latest carry value computed
at a preceding
iterative step.
In case the array C only contains a single element c, the number c may be
successively
incremented by the constant value a, and the value of the carry register d. If
c becomes
larger than a value N, N is subtracted from the number, i.e. modulus N, and
the value in the
carry register is set to 1. If the number is less than N, the value in the
carry register is set to
0. This procedure can formalistically be described as:
c;+1=c;+a+d;
if c;+1 >= N then d;+~ = 1 else d;+1 = 0
if c;+1 >= N then c;+1 = c,+1-N
In case the array C contains a plurality of elements or numbers C=(co, cl,
c2,..., c~_1), such
numbers may successively be incremented by a set of constant values A=(ao, al,
a2,... d"_1)
and values of a set of carry registers (bo, bl, b2,... b"_1), bn_1=d. If any
of the numbers become
larger than a value N, N is subtracted from the number in question, i.e.
modulus N, and the
value in the corresponding carry register is set to 1. The carry register
involved in the
addition is the carry arising from the neighbour number, such that the set of
numbers are
coupled by the carry registers to form a chain. The first number is added with
the carry
register from the last number in the previous incrementation. This procedure
can
formalistically be described as:
co,~+1 = co,~ + ao + d;.
if Co,;+1 >= N then bo,;+i = 1 else bo,;+1 = 0.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
17
if co,;+1 >= N then co,;+1 = co,;+~ - N.
The rest of the numbers are determined by:
c~,i+~ = c;,~ + a; + b~_l,;+1.
if cj,;+1 >= N then b;,;+1 = 1 else b~,;+1 = 0, for j<n-1.
if Cn_i,i+1 >= N then d,+1 = 1 else d,+~ = 0.
if c~,;+1 >= N then c~,t+i = c~,~+i - N.
The above procedure is graphically illustrated in Fig. 4.
Alternatively, d; may be a carry value determined in the same iteration, that
is: firstly a
constant is added to the first counter, the carry from this operation and a
constant are then
added to the next counter in the chain and so forth. This procedure is
continued until and
including the last counter in the chain, the carry from this last addition is
then added to the
first counter, and if a carry occurs it is added to the next counter and so
on. The procedure is
illustrated in the following pseudo-code:
20
// Save old counter values
for i=0 to 2
c old[i] = c[i]
end for
// Increase counters
c[0] _ (c[0] + a[0]) mod 23z
a.f c[0] < c old[0] then
b[0]=1
else
b[0]=0
end if
c[1] _ (c[1] + a[1] + b[0]) mod p3z
if c[1] < c old[1] then
b[1]=1
else
b[1]=0
end if
c[2] _ (c[2] + a[2] + b[1] ) mod 23z
if c[2] < c old[2] then
d=1
else
d=0
end if
// Add final carry
c[0] _ (c[0] + d) mod 23z
if c[0] < c old[0] then
b[0]=1
else
b[0]=0
end if
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
18
c[1] _ (c[1] + b[0]) mod 232
if c[1] < c old[1] then
b[1]=1
else
b[1]=0
end if
c[2] _ (c[2] + b[1]) mod 23~
In the above pseudo-code, it is presumed that all values of a are smaller than
23Z-1.
The computational steps which are performed in the cryptographic system
usually comprise
an iterative procedure in which an array of state variables, X, is repeatedly
iterated so that at
least one value assigned to a position in the array of state variable X at
computational step
i+1 is a function of:
- at least one value assigned to a position in the array of state variables X
at computational
step i, and
- at least one value assigned to a position of the array of counters C at
computational step
For example, X;+1 may be computed according to the general formula X;+1=f(X;,
C;), such as
X;+1=f(X;+C;). It should be understood that the array X may contain one or
more state
variables.
The method of the second aspect of the invention may advantageously be applied
in a
system/method, wherein an identification value for identifying a set of data
is determined,
and wherein a set of data is concurrently encrypted/decrypted, e.g., by means
of a pseudo-
random number generator in which numerical computations are performed in a
mathematical
system, cf. the below discussion of the fifth aspect of the invention.
Combination of carr)r-updating of counters and "a-function"
In a further aspect, the invention provides a method for generating an output
in a
cryptographic system, the method combining the general concepts underlying the
second and
the fourth aspects of the invention. Thus, according to the sixth aspect of
the invention,
computational sequences may performed as an iterative procedure wherein an
array of state
variables, X, is repeatedly iterated so that at least one value assigned to a
position in the
array of state variables X at iteration step i+1 is a function of:
- at least one value assigned to a position in the array of state variables X
at iteration i,
and
- at least one value assigned to a position of an array of counters C at
iteration i,
the array of counters being updated in each iteration as:
co,~+i=co,~+ao+d; mod No,
c~,;+1=c~,;+a;+b;_l,;+1 mod N; for j>0,
where:
c;,,+1 is a value assigned to position j of array C at step i+1, j=O...n-i, n
denoting a
dimension of the array C,
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
19
c;,, is a value assigned to position j of array C at step i, j=O...n-1,
a; is a value assigned to position j of an array A, j=O...n-1,
for j>0: b;_l,,+1 is a carry value resulting from the computation of c;_i,,+1.
N; is a constant, j=O...n-1,
for i=0: d;=do is an initial value,
for i>0 d, is a carry value obtained from a selected computation of a value of
the array of
counters C; and/or a function of C;,
each iteration comprising:
- multiplying a first number of a first bit size A and a second number of a
second bit size B
to obtain a third number of a third bit size A+B, at least one of the first
and second
number being equal to or a function of at least one value assigned to a
position of the
array of state variables X at iteration i, the third number consisting of P
most significant
and Q least significant bits, wherein A+B=P+Q, and wherein Q is equal to the
largest of
the first bit size A and the second bit size B, Q=max(A,B),
- manipulating the third number to obtain a fourth number which is a function
of at least
one of the P most significant bits of the third number,
using the fourth number for deriving the output of the cryptographic system
and/or for
assigning new values to positions of the array of state variables X.
The above method combines the qualities of the methods according to the second
and fourth
aspects of the invention, i.e. good mixing of bits and long counter periods,
with the overall
aim of improving unpredictability.
It should be understood that any feature and functionality described above in
connection with
the second and fourth aspects of the invention may be applied in the method of
the present
aspect of the invention.
The present aspect of the invention will be further discussed below in
connection with Figs. 1-
5.
5 CONCURRENT ENCRYPTION AND IDENTIFICATION VALUE GENERATION
In a further aspect, the invention provides a method of determining an
identification value for
identifying a set of data and for concurrently encrypting and/or decrypting
the set of data.
The method preferably comprises performing numerical computations in a
mathematical
system exhibiting a positive Lyapunov exponent, the method further comprising
at least one
of the following steps:
- repeatedly performing mathematical computations as iterations in the
mathematical
system, whereby various parts of the set of data or modifications thereof may
be used as
input to the computations,
- following each computation or a certain number of computations:
- extracting a resulting number from the computations, the resulting number
representing at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
- optionally determining an updated value for the identification value based
on the
resulting number, whereby various parts of the set of data or modifications
thereof
may be used as input in the step of determining,
- encrypting and/or decrypting a certain portion of the set of data based on
the
5 resulting number,
whereby as many iterations are performed as required for encrypting and/or
decrypting the
entire set of data.
The use of one or more fixed-point variables may confer advantages related to
reproducibility
10 and computational speed, cf. section B below. By performing
encryption/decryption and
identification value generation concurrently, computational resources may be
saved.
Encryption and/or decryption and determining the identification value may be
performed in
the same process or in distinct processes, i.e. for example in such a way that
the entire set of
15 data is processed in order to obtain an intermediate result which is then
used as an input for
further computations which yield the identification value and the encrypted
and/or decrypted
version of the set of data.
The method may comprise:
20 - expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as a fixed-point
number,
- performing said computations in such a way that the computations include the
at least
one variable expressed as a fixed-point number, fixed-point variables and
numbers being
discussed further above in connection with the first aspect of the invention
and in section
B below.
The identification value may be further modified following encryption and/or
decryption of the
entire set of data.
Encryption/decryption and determination of the identification value can take
place at the
same time or in parallel. The identification value can be a hash value, a
check-sum or a MAC
(Message Authentication Code), see the above description. In some cases, the
calculation of
identification value and the encryption process takes place sequentially.
However, it can also
be done in one working process or instance, in parallel or at the same time.
This may be
done in order to reduce the number of computations and/or to be able to
process a sequence
of data as it becomes available or is given to an algorithm which embodies the
mathematical
system, or to increase ease-of-use. The identification value can be calculated
with or without
a key.
The identification value may be related to a specific message, i.e. the
message must be used
as input to the algorithm. Instead of first encrypting the message and then
running through
the entire message again to calculate the identification value, the two
methods may be
combined, i.e. in each iteration of the mathematical system, a pseudo-random
number may
be extracted and combined with the message in order to encrypt/decrypt, after
which the
identification value may be updated. After each iteration this intermediate
identification value
may be stored.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
21
In the method according to the present aspect of the invention, a mathematical
system may
be defined, the mathematical system exhibiting a positive Lyapunov exponent.
The method
may comprise the following steps:
1. Defining a key/seed value.
2. Performing computations on the mathematical system, and/or
3. Performing computations on the mathematical system and the message.
4. Extracting a pseudo-random number.
5. Calculating a new intermediate identification value.
6. Continuing step 2-5 until the entire message has been used in the
computations
performed on the mathematical system and the message.
7. Calculating the final identification value based on the intermediate
identification value.
In an alternative embodiment, the method may comprise the following steps:
1. Defining a key/seed value.
2. Performing computations on the mathematical system and the message.
3. Extracting a pseudo-random number.
4. Continuing step 2-3 until the entire message has been used in the
computations
performed on the mathematical system and the message.
5. Determining the final identification value from variables in the
mathematical system.
In the method, the
- message may be plaintext or ciphertext,
- message may be used as input to some or all of the calculations,
- the pseudo-random number may be used to encrypt/decrypt the message by means
of
logical and/or artithmetical operations,
- at least one variable is expressed in fixed-point format.
In case of a block cipher, no pseudo-random numbers are generated, in which
case step 3
above is substituted by the step of manipulating a block or part of message in
order to
encrypt and/or decrypt it.
In one embodiment, the calculation of the identification value is dependent on
a key.
In a mathematical system exhibiting a positive Lyapunov exponent computations
may be
performed using fixed-point arithmetic, whereby a cryptographic key (as
described for a
stream cipher) is used as an initialization value. This key, or part thereof,
is also used to
initialize the identification value.
4-0 The determination of the identification value and encryption of a set of
data, message, or
plaintext, is then performed by
1. Iterating the mathematical system one step.
2. Extracting a number of n pseudo-random bits from the system.
3. Selecting the next n bits of the data, message, or plaintext.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
22
4. Using a function, FN, to obtain a new value for the identification value,
given the
extracted bits, the selected bits of the data, message or plaintext and the
old value of the
identification value.
5. Applying the logical XOR function on the n pseudo-random bits and the
selected n bits
thereby encryption the selected n bits of the data, message or plaintext..
6. Steps 1 through 5 are repeated until all bits are encrypted.
7. The system may be iterated further to extract more pseudo-random bits.
8. Further computations may be performed on the identification value to obtain
a final
identification value.
The generated identification value can be combined with the encrypted message,
and the
result can e.g. be transmitted over the Internet to a receiver.
When decrypting and recalculating the identification value, the algorithm is
initialized in same
manner as for encryption. Then the following steps are performed:
1. Iterating the mathematical system one step.
2. Extracting n pseudo-random bits from the mathematical system.
3. Selecting the next n bits of the encrypted data/message.
4. Applying the logical XOR function on the encrypted bits to decrypt these.
5. Using a function, FH, to obtain a new value for the identification value,
given the
extracted bits, the bits to be decrypted and the old value of the
identification value.
6. Repeating steps 1 through 5 until all bits are decrypted.
7. The system may be iterated further to extract more pseudo-random bits.
Further computations may be performed on the identification value to obtain a
final
identification value.
End of Section 5.
It should be understood that the present invention also extends to any
apparatus and to any
computer program for carrying out all the methods of the invention, including
electronic
devices incorporating digital signal processors. The invention also extends to
data derived
from any method and/or computer program of the present invention and any
signal
containing such data do also fafl within the scope of the appended claims. It
should further be
understood that any feature, method step, or functionality described below in
connection with
the further aspects of the invention discussed below may be combined with the
method of
the first aspect of the invention.
Further features and functions which may be employed in the various aspects of
the
invention, and definitions applicable to the aspects of the present invention,
are discussed
below. The below considerations apply, where appropriate, to all
aspects/methods of the
present invention.
A GENERAL DEFINITIONS AND CONSIDERATIONS
Where in the present context, the term "pseudo-random number" is used, this
should be
understood as a random number which may be generated in a reproducible and/or
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
23
deterministic way, i.e. in a way that results in the same pseudo-random number
being
generated in two different executions of a pseudo-random number generating
algorithm
when the same key or seed value is used as an input for the pseudo-random
number
generating algorithm in the two executions.
In general, a mathematical system may comprise a system which expresses
certain relations
between variables. For example, such relations may be constituted by
mathematical
operations, including discrete operations, such as binary and/or logical
operations. Thus,
mathematical operations may comprise multiplication, division, addition,
subtraction,
involution, AND, OR, XOR, NOT, shift operations, modulus (mod), truncation
and/or rounding
off.
Numerical computations may involve computations in which numbers are
manipulated by
mathematical operations.
A counter is herein defined as a variable which may serve as a parameter in a
mathematical
system. The counter is continuously iterated and updated by means of a
mathematical
function. Such a function may, e.g., be a simple addition, c;+1=c;+a, where
c;+1 represents the
counter value at iteration step i+1, c; represents the counter value at
iteration step i, and a a
number added to c;. The function may alternatively be more sophisticated and
include linear
and/or non-linear operations and/or logical operations. Preferably, the
counter varies
independently of the mathematical system in which the counter is used as a
parameter.
In the present context, the term "data carrier" or "computer readable data
carrier" should be
understood as any device or media capable of storing data which is accessible
by a computer
or a computer system. Thus, a computer readable data carrier may, e.g.,
comprise a
memory, such as RAM, ROM, EPROM, or EEPROM, a CompactFlash Card, a MemoryStick
Card, a floppy or a hard disk drive, a Compact Disc (CD), a DVD, a data tape,
or a DAT tape.
Signals comprising data derived from the methods of the present invention and
data used in
such methods may be transmitted via communications lines, such as electrical
or optical
wires or wireless communication means using radio or optical transmission.
Examples are the
Internet, LANs (Local Area Networks), MANS (Metropolitan Are Networks), WANs
(Wide Area
Networks), telephone lines, leased lines, private lines, and cable or
satellite television
networks.
In the present context, the term "electronic device" should be understood as
any device
capable of processing data by means of electronic or optical impulses.
Examples of applicable
electronic devices to the methods of the present invention are: a processor,
such as a CPU, a
microcontroller, or a DSP (Digital Signal Processor), a computer or any other
device
incorporating a processor or another electronic circuit for performing
mathematical
computations, including a personal computer, a mainframe computer, portable
devices,
smartcards, chips specifically designed for certain purposes, e.g.,
encryption. Further
examples of electronic devices are: a microchip adapted or designed to perform
computations
and/or operations, and a chip which performs binary operations.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
24
Processors are usually categorized by: (a) the size of data that is operated
on (b) the
instruction size and (c) the memory model. These characteristics may have
different sizes,
normally between 4 and 128 bit (e.g. 15, 16, 32, 64 bit) and not limited to
powers of two.
In the present context, the term "processor" covers any type of processor,
including but not
limited to:
- "Microcontroller", also called "embedded processor". The term
"microcontroller" and
"embedded processor" usually refers to a small processor (usually built with
fewer
transistors than big processors and with limited power consumption). Examples
of
microcontroller architectures are:
- Z80
- 8051 (e.g. produced by Intel)
- CPU8 / 6800 (e.g. 68HC05 68HC08 and 68HC11 e.g. produced by Motorola)
- CPU32 / 68k (e.g. 68000 Dragonball produced by Motorola)
- Other processors which are typically used in different kinds of computer and
control
systems, examples of architectures being:
- Alpha 2lxxx (e.g. 21164, 21264, 21364)
- AMD x86-64 (e.g. Sledgehammer)
- ARM (e.g. ARM10, StrongARM)
- CPU32 / 68k (e.g. 68000, 68030, 68040 e.g. produced by Motorola)
- IA32 (e.g. the x86 family produced by Intel (e.g. i486, Pentium), AMD (e.g.
K6, K7),
and Cyrix)
- IA64 (e.g. Itanium produced by HP/Intel)
- MIPS (e.g. 84000, 810000 produced by SGI)
- PA-RISC (e.g. 8000, produced by HP)
- PowerPC (e.g. G3, G4, produced by IBM/Motorola)
- SPARC (e.g. UItraSPARC II, UItraSPARC III, produced by SUN)
- DSPs. Examples are:
- DSP56300 (produced by Motorola)
- MSC8100 (produced by Motorola)
- TI TMS320C6711 (produced by Texas Instruments).
In the present context, the term "register" should be understood as any memory
space
containing data, such as a number, the memory space being for example a CPU
register,
RAM, memory in an electronic circuit, or any data carrier, such as a hard
disk, a floppy disk,
a Compact Disc (CD), a DVD, a data tape, or a DAT tape.
It should be understood that the present invention also relates to, in
independent aspects,
data derived from the methods of the present invention. It should also be
understood that
where the present invention relates to methods, it also relates to, in
independent aspects,
computer programs being adapted to perform such methods, data carriers or
memory means
loaded with such computer programs, and/or computer systems for carrying out
the
methods.
Any and all computational operations involved in the methods of the present
invention may
be carried out on or by means of an electronic device.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
In one aspect, which constitutes an independent aspect of the present
invention, a method of
performing numerical computations in a mathematical system comprising at least
one
function, the method comprising the steps of:
5 - expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as a fixed-point
number,
- performing said computations in such a way that the computations include the
at least
one variable expressed as a fixed-point number,
- obtaining, from said computations, a resulting number, the resulting number
representing
10 at least one of:
- a. at least a part of a solution to the mathematical system, and
- b. a number usable in further computations involved in the numerical
solution of the
mathematical system,
the method further comprising:
15 - extracting a set of data which represents at least one of:
- i. a subset of digits of the resulting number, and
- ii. a subset of digits of a number derived from the resulting number.
A subset of a number may be regarded as a part of that number, such as some,
but not
20 necessarily all digits or bits of the number. For example, the 8 least
significant bits of a 16-bit
number may be regarded as a subset of the 16-bit number.
The term "extracting" covers, but is not limited to: outputting the number or
subset in
question, for example as a keystream or a part of a keystream or as any other
final or
25 intermediate result of a computational process; storing the number or
subset in question in a
register, for example in order to allow for further use thereof, such as for
further
computations, on the subset.
By extracting a subset of digits of a number instead of extracting the entire
number, random
properties are improved in case the method is used in a pseudo-random number
generator,
for example for encryption and/or decryption purposes. Moreover, as only a
subset is
extracted, less information concerning the internal state of the mathematical
system is
contained in the extracted set of data which enhances the security of an
encryption/decryption system incorporating the method.
Though the mathematical system may comprise a continuous system, for example a
system
of differential equations, it may also or alternatively comprise a system
which is originally
defined in discrete terms, for example in the case of a map. The at least one
function of the
mathematical system may be non-linear, as discussed in more detail in section
C below.
Usually, the subset of digits comprises k bits of an m-bit number, k<_m, for
example
extracting 8 bits of a 32-bit number. The number from which the subset is
extracted and/or
the extracted set of data may be expressed as one or more binary number, octal
number,
decimal numbers, hexadecimal number, etc. The k bits may be the least
significant bits of
the number, or it may be k bits selected from predetermined or random
positions within the
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
26
number from which the bits are extracted. For example, from a 64-bit number,
bits Nos. 42,
47, 53, 55, 56, 57, 61, and 63 may be extracted, or bits Nos. 47-54.
In the methods of the present invention, one or more computations may be
performed as
floating-point operations. The step of expressing at least one variable of the
mathematical
system as a fixed-point number may thus comprise converting a floating-point
type number
to an integer type number, optionally performing a certain manipulation on the
integer
number, for example truncating it, and converting the integer number back to a
floating-
point type number.
The methods of the invention may be applied for encryption and decryption,
modulation of
radio waves, synchronization of chaos in picture and sound signals so as to
reduce noise,
data compression, in control systems, watermarking, steganography, e.g. for
storing a
document in the least significant bits of a sound file, so as to hide the
document in digital
transmission.
Many SIM-cards and smart cards exhibit weaknesses to power analysis attacks,
which
exploits the fact that the power consumption is directly related to the
arithmetic functions
performed by the processor. To avoid this, a program for executing one of the
methods
described herein may randomly execute some operations which only function is
to disrupt the
systematic power consumption. The pseudo-random number generator may be used
to
determine the operations to be performed.
The pseudo-random number generator can be used to generate keys for other
encryption
algorithms, i.e. asymmetric or public-key algorithms. For example, it could be
used to
generate pseudo-random numbers used to calculate at least one prime number. In
this way it
is possible to generate the public and private key pair used in the RSA
algorithm.
In the present context, the term "resulting number" should be understood as
any number
occurring in the computations. More than one resulting number may be obtained.
The
resulting number may, as stated above, be a part of the solution to the
mathematical system
and/or an intermediate result, i.e. a number assigned to any variable or
parameter of the
mathematical system or to any other variable or parameter used in the
computations. In an
implementation of a mathematical method, the resulting number or a part
thereof may be
extracted, for example as a pseudo-random number for use in an
encryption/decryption
system. Alternatively, one or more mathematical and/or logical operations may
be performed
on the resulting number or on a plurality of resulting numbers, so as to
obtain a further
number which is extracted. All or only selected bits in a binary
representation of the resulting
number may be extracted. It should be understood that a number generated from
selected
bits of a number occurring in the computations may be referred to as the
resulting number.
Thus, the term "resulting number" also covers any part of a number occurring
in the
computations.
The methods of the invention are, as discussed above, useful in cryptography,
for example in
the following implementations: a symmetric encryption algorithm, a public key
(or
asymmetric key) algorithm, a secure or cryptographic Hash function, or a
Message
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
27
Authentication Code (MAC). These algorithms may, for example, be used in
accomplishing
one or more of the following tasks:
- Ensuring confidentiality of digital data, so as to protect data from
unauthorized access.
- Ensuring integrity of digital data, so as to ensure that information is
accurate or has not
been tampered with.
- Authorization, e.g. to allow permission to perform certain tasks or
operations.
- Authentication, such as user authentication, so as to verify the identity of
another party,
or data origin authentication, so as to verify the origin of the data.
- Nonrepudiation, to provide proof of participation in an electronic
transaction, for example
to prevent that a first person A sends a message to a second person B and
subsequently
denies that the message has been sent. Digital signatures are used for this
purpose. The
generation of a digital signature may incorporate the use of a public key
algorithm and a
hash function.
The methods of the invention are also applicable to a so-called Hash function.
A Hash
function provides a kind of digital fingerprint wherein a small amount of data
serves to
identify other data, usually a set of data which is considerably larger than
the aforementioned
small amount of data. Hash functions are usually public functions wherein no
secret keys are
involved. Hash functions can also provide a measure of authentication and
integrity. They are
often essential for digital signature algorithms and for protecting passwords,
as a Hash value
of a password may be used for password control instead of the password itself,
whereby only
the hash value and not the password itself needs to be transmitted, e.g. via a
communications network.
A Hash function employing a secret key as an input is often referred to as a
MAC algorithm or
a "keyed Hash function". MAC algorithms are used to ensure authentication and
data
integrity. They ensure that a particular message came from the person or
entity from whom
it purports to have come from (authentication), and that the message was not
altered in
transit (integrity). They are used in the IPsec protocols (cf. RFC 2401
available on
http://www.rfc-editor.org on 6 June 2003), for example to ensure that IP
packets have not
been modified between when they are sent and when they reach their final
destination. They
are also used in all sorts of interbank transfer protocols.
As discussed above, the methods of the invention may be implemented in a Hash
or a MAC
algorithm. A Hash or a MAC algorithm calculates a checksum of an amount of
data of an
arbitrary length, and gives the checksum as a result. The process should be
irreversible (one-
way), and a small change of an input value should result in a significantly
different output.
Accordingly, the sensitivity to data input should be high. Whereas a Hash
function does not
use a key as a seed value, a MAC algorithm uses such a key which represents or
determines
a seed value for the algorithm, whereby the result depends on the key. Instead
of a key, the
Hash function relies on a constant value, for example certain bits from the
number ~.
Alternatively, a part of the data to which the Hash function is applied may be
used as a seed
value.
A Hash/MAC algorithm may be implemented as follows:
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
28
- A mathematical system in the form of a logistic map is used in the
algorithm, the logistic
map having the form: X~+1=~xn(1-xn), wherein I~ is a parameter. Other chaotic
systems
may be employed, such as the Lorenz system which is discussed in detail
hereinafter.
- As the result of the algorithm should depend on the message m for which the
checksum
is to be calculated, the message is incorporated in the system as a component
thereof.
For example, a kind of coupling between the message and the dynamic variable,
x, may
be performed as follows: xn+1°~xn(1-xn)+~(Xwm").
- The parameters h and E and the initial value xo may be predetermined and/or
derived
from the message. In the case of a MAC algorithm, the parameters ~ and E and
the initial
value xo may, completely or partially, be determined by the secrete key.
- The system is iterated until the end of the message is reached. The last
calculated value
of x or part thereof, such as the least significant digits, is denoted, for
example, the Hash
value, the MAC or the checksum. Alternatively, a number of additional
iterations may be
performed prior to extracting the resulting number. Instead of or in addition
to extracting
the last calculated value of x, certain bits which have been ignored in the
computations
may be extracted as the Hash value.
- The way of introducing the message, m, into the dynamical system can be
varied. As an
example, a part of the message may be used to influence the x-variable in each
iteration.
Such influence may, e.g., be achieved by XORing certain bits of the message
into the
least significant digits of x.
For further details concerning Hash/MAC functions, reference is made to
Applied
Cryptography by Bruce Schneier, Second Edition, John Wiley & Sons, 1996.
One possible field of use of the method of the methods of the invention is
public-key
encryption, also referred to as asymmetric algorithms. The key used for
decryption is
different from the key used for encryption. For example, a key-generation
function generates
a pair of keys, one key for encryption and one key for decryption. One of the
keys is private,
and the other is public. The latter may for example be sent in an unencrypted
version via the
Internet. The encryption key may constitute or contain parameters and/or
initial conditions
for a chaotic system. A plaintext is used to modulate the chaotic system which
is irreversible
unless initiated by the private key. For decryption, a mathematical system is
used which has
dynamics which are inverse to the dynamics of the system used for encryption.
B FIXED-POINT VARIABLES
Fixed-point variables are mentioned in section 1 above and will now be further
discussed,
starting from a brief discussion of certain disadvantages related to floating
point variables
which arise in connection with certain cryptographic methods.
The utilization of floating point variables in the numerical solution of
mathematical systems
may create non-predictable truncation and/or rounding errors. In case of the
mathematical
system to be solved being non-linear, and in particular in case of the system
being chaotic,
the accuracy of the solution at all integration steps is of paramount
importance, as a small
deviation at one step may confer huge deviations at subsequent steps. If the
truncation
and/or rounding errors are created consistently in the same manner in any and
all
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
29
computations, two solutions based on the same initial conditions are
identical, and
accordingly the computations are reproducible. However, in most cases
truncation and/or
rounding errors of floating point numbers are not entirely controlled by
software but also by
hardware on which the software is running. Accordingly, truncation and/or
rounding errors
are hardware dependent, and consequently truncations and/or roundings may be
performed
differently in two different hardware processors. For most computations this
is without
importance, as the truncations and roundings create inaccuracies of an order
of magnitude
which is far below the required accuracy of the computations. But in the
solution of, e.g.,
chaotic systems, a small deviation in the way truncations are performed may
confer huge
deviations in the solution at later computational steps.
Therefore, with the aim of being able to control, by software, truncation or
rounding errors
created by hardware, the present inventors have proposed the use of fixed-
point variables.
In general, a fixed-point number type is denoted c~(a.[3) where a is the
number of bits used
to hold the integer part, and (3 the number of bits to hold the fractional
part. The values of a
and a, and thus the position of the decimal point, are usually predetermined
and stationary.
The fixed-point number can be either unsigned or signed, in which case ~ is
denoted U or S
respectively. In the latter case, a bit is needed to hold the sign, thus a+~+1
bits are needed
to hold S(a.(3).The range of U(a.(3) is [0;2"-2-R], and the range of S(a.[3)
is [-2";2"-2-a]. The
resolution of the fixed-point numbers is thereby 2-R.
The position of the decimal separator in a fixed-point number is a weighting
between digits in
the integer part and digits in the fraction part of the number. To achieve the
best result of a
calculation, it is usually desired to include as many digits after the decimal
separator as
possible, to obtain the highest resolution. However, it may also be important
to assign
enough bits to the integer part to ensure that no overflow will occur.
Overflow is loading or
calculating a value into a register that is unable to hold a number as big as
the value loaded
or calculated. Overflow results in deletion of the most significant bits
(digits) and possible
sign change.
In the various aspects of the present invention, the position of the decimal
separator may be
assigned at design time. To choose the right position, the possible range of
the number, for
which the position is to be chosen, is preferably analyzed. The most positive
and most
negative possible values are determined, and the highest absolute value of the
two is
inserted into the following formula:
a = ceil(logz(abs(Maxval)))
to determine the value of a.
The position of the decimal point may vary between different fixed-point
variables. However,
addition and subtraction operations require input numbers with similar
positions. Hence, it is
sometimes necessary to shift the position of the decimal point. Right shift by
n bits
corresponds to a conversion from c~(a.a) to c~(a+n.R-n). Left shift by n bits
will convert e~(a.~)
to ~(a-n.(3+n).Conversion of unsigned numbers is done by logical shift
operations, whereas
arithmetical shifts are used for signed numbers.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
The mathematical operations addition, subtraction, multiplication and division
on fixed-point
numbers are carried out as plain integer operations. The addition and
subtraction operations
may result in a number of size ~(a+1.R) because of the carry. However, the
result is
normally truncated to give a number with the same format as the input.
5
Multiplication and division do not require arguments with similar positions of
the decimal
separators. However, prior to division, the numerator is expanded as it must
have twice the
length of the denominator and the result. The results will have a format of:
S(a.~3)~S(c.d) _
S(a+c+1.(3+d) and S(a+c+1.(3+d) / S(a.[3) = S(c.d). For unsigned
multiplication and division
10 S(a+c+1.(3+d) is replaced by U(a+c.~i+d). Exceeding digits in the
multiplication compared to
the predetermined result format are cut off to match the target register size.
A fixed-point number may be handled by representing the integer part of the
fixed point
number in one register, and representing the fractional part in another
register.
Further information on fixed-point calculations can be found in "Fixed-Point
Arithmetic: An
Introduction" by R. Yates (The text can be found at
http://personal.mia.bellsouth.net/lig/y/a/yatesc/fp.pdf on 6 June 2003).
In the present context, a fixed-point variable is defined as an integer type
number with an
imaginary decimal separator, an integer being defined as a number without
digits after the
decimal separator. Accordingly, real numbers are represented by inserting the
imaginary
decimal separator (or decimal point) at some fixed predetermined position
within an integer,
for example four digits from the left. The position might be changed as a
consequence of a
mathematical operation on the number. The position may also be forced to be
changed by
use of a logical operation.
As it occurs from the above discussion, fixed-point numbers are integers, on
which a virtual
decimal separator is imposed. The number consists of a so-called "integer
part", referring to
the bits before the decimal separator, and a "fraction part" referring to the
bits after the
decimal separator. In the present context, bits are also referred to as digits
and vice versa.
In a computer program comprising fixed-point number computations or in an
electronic
circuit or device for performing fixed-point computations, means may be
provided for
determining a suitable location of the decimal separator. Thus, the program,
circuit or device
may, during computations, detect possible overflow and, in the case of a
possible overflow
being detected, change the number of bits on either side of the decimal
separator, i.e. the
location of the decimal separator in a register which stores the variable or
variables in
question. This change may be performed by moving the decimal separator one or
more
positions to the left or to the right. Preferably as many bits as possible are
used to the right
of the decimal separator in order to minimize the number of possible unused
bits in the
register and thereby to obtain an optimal accuracy in the computations. By
changing the
position of the decimal separator, though some computational speed may be lost
due to the
requirement for additional operations for detecting possible overflow, the
accuracy of the
computations is optimized while the risk of overflow is eliminated or reduced,
without a
designer or programmer of an application incorporating the computer program,
circuit or
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
31
device needing to make considerations concerning accuracy and overflow in a
design or
programming phase. Alternatively, or additionally, a test program may be
provided which
determines when or where in the computations overFlow will occur or is likely
to occur, so
that a programmer or designer of the program may fix the position of the
decimal separator
in one or more variables such that no overflow occurs, whereby, in the final
implementation,
no determination of possible overflow is needed. However, the determination of
possible
overflow may also be incorporated in the final implementation as an additional
safeguarding
feature. Further, the programmer or designer may choose to implement changing
of the
decimal separator at fixed, predetermined stages in the computations.
As discussed above, a real number may be expressed by means of one or more
fixed-point
numbers. Likewise, a complex number, c=a+ib, where i~=-1, may be expressed by
means of
one or more fixed-point numbers, e.g. by expressing the real part a and/or the
imaginary
part b as a fixed-point number. In case only one of the real and imaginary
parts is expressed
as a fixed-point number, the other one may be expressed by means of any other
type of
number, such as a floating-point or an integer number.
In the methods according to the invention, the computations involving the
variable expressed
as a fixed-point number may possibly include computations on other types of
variables,
including one or more variables expressed as other kinds of numbers, such as
floating point
numbers and integer numbers.
The use of fixed-point numbers has the advantage over floating-point numbers
that rounding
and/or truncations errors occurring in fixed-point number computations are
identically
defined on all processors. By use of fixed-point variables, decimal numbers
may be expressed
as integer type numbers where an imaginary decimal separator is placed in the
number. In
cases where floating-point variables are used, truncation/rounding errors are
not performed
identically on different types of processors.
As a consequence of truncation/rounding errors being controllable or
predictable, numerical
computations in mathematical systems which are sensible to truncation/rounding
errors may
be performed in a reproducible manner. Thus, for example, non-linear systems,
in particular
chaotic systems, may be numerically solved in a reproducible manner. This
opens up for
utilizing chaotic systems in pseudo-random number generators, such as in
encryption/decryption algorithms, without the need for feed-back or correction
algorithms or
registers in order to prevent inaccuracies, or without the need for
synchronization techniques
ensuring identical solution of the systems in encryption as in decryption.
This in turn
contributes to the computations, the pseudo-random number generation and/or
the
encryption/decryption algorithm being fast as compared to algorithms involving
such feed-
back or correction algorithms or synchronization techniques. Further, there is
no need for
transmission of synchronization data with the encrypted data, such
synchronization data
often amounting to a size comparable to the size of the encrypted data, which
may be a
major problem due to, e.g., lack of bandwidth when transmitting data via the
Internet.
Further, transmission of such data compromises the security of the system. The
computations are also performed faster than computations in methods involving
a floating-
point variable for the variable in question, as in computations involving
fixed-point numbers
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
32
the hardware processor performs computations as integer number computations,
computations on integer number being generally faster than computations on
floating-point
numbers.
C APPLICABLE MATHEMATICAL SYSTEMS AND COMPUTER IMPLEMENTATION THEREOF,
IN PARTICULAR WITH A VIEW TO CRYPTOGRAPHIC APPLICATIONS
In the methods described herein, the mathematical system may be a discrete or
a continuous
system. Various types of mathematical systems are discussed below.
The computations may involve at least a first and a second fixed-point number,
each fixed-
point number having a decimal separator, wherein the decimal separator of the
first fixed-
point number is positioned at a position different from the position of the
decimal separator
of the second fixed-point number. The decimal separator of the first and
second fixed-point
number may be positioned at selected positions.
The resulting number may be expressed as a variable selected from the group
consisting of:
an integer number,
a floating point number, and
a fixed-point number.
In general, the mathematical system may comprise one or more differential
equations, or
one or more discrete maps or mappings. In the case of differential equations,
the
mathematical system may comprise one or more ordinary differential equations
and/or one
or more partial differential equations. In the case discrete mappings, the
mathematical
system may comprise one or more area-preserving maps and/or one or more non
area-
preserving maps. At least one function of the mathematical system may be non-
linear.
The method is also applicable to other types of functions or equations,
including integral
equations. The at least one non-linear differential equation or mapping may
exhibit chaotic
behavior, i.e. it may have at least one positive Lyapunov exponent, in which
case the method
may comprise computing a Lyapunov exponent at least once during the
mathematical
computations. In case of a mathematical system exhibiting chaotic behavior,
the method may
advantageously be applied in a pseudo-random number generating method, such as
in an
encryption/decryption method. At least one Lyapunov exponent may be computed
at least
once during the mathematical computations in order to determine whether the
mathematical
system exhibits chaotic behavior. If this is not the case, e.g. if the
computed Lyapunov
exponent is not positive, the computations may be interrupted and resumed from
other initial
values and/or other parameters.
The at least non-linear differential equation or mapping preferably governs at
least one state
variable, X, which may be a function of at least one independent variable, t.
More specifically, the mathematical system may comprise one or more of the
following
systems:
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
33
- continuous differential equations, including:
- partial differential equations, such as the Navier-Stokes equations,
- ordinary differential equations, including:
- autonomous systems, such as dissipative flows, including the Lorenz system,
coupled Lorenz systems, the Rossler system, coupled Rossler systems, hyper
chaotic Rossler system, the Ueda system, simplest quadratic dissipative
chaotic
flow, simplest piecewise linear dissipative chaotic flow
- Hamiltonian systems, including the N body problem from celestial mechanics,
for
N>_3,
- Non-autonomous systems, including forced systems, such as the forced
Duffing's
equation, forced negative resistance oscillator, forced Brusselator, forced
damped
pendulum equation, coupled pendulums, forced double-well oscillator, forced
Van
de Pol oscillator,
- delay differential equations, including delay logistic equation, population
models,
- Discrete mappings, including
- area preserving as well as non area-preserving maps, including
- maps which are piecewise linear in any dimension, such as a tent map, an
asymmetric tent map, 2x modulo 1 map, and also the Anosov map, the
generalized Baker's map, the Lozi map, as well as higher order generalizations
and/or couplings of piecewise linear maps
- polynomial maps (quadratic or higher), including a logistic map, the Henon
map,
higher order generalizations and/or couplings of polynomial map, e.g. N
coupled
logistic maps, N coupled Henon maps,
- Trigonometric maps, including a Sine circle map, a Sine map, the Chirikov
standard map, the Sinai map, the standard map, and Higher order
generalizations
and/or couplings of trigonometric maps,
- other maps, including the Bernoulli shift, a decimal shift, the Horseshoe
map, the
Ikeda map, a pastry map, a model of a digital filter, a construction of the
Henon
type map in two dimensions from an arbitrary map in one dimension, the
DeVogelaere map,
- Cellular automata,
- Neural networks.
The Rossler system referred to above has the form:
_dx _--y_z
dt
ay =x+ay
dt
dz =b+z(x-c)
at
wherein typical parameter values are: a = b = 0.2, c = 5.7. The Rossler system
is described
in more detail in O.E. Rossler, Phys. Lett. 57A, 397-398 (1976).
The Henon map referred to above has the form:
z
Cxn+y = C1 + yn - axn
yn+1J bxn
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
34
wherein typical parameter values are: a = 1.4, b = 0.3. For more details, see
M. Henon,
Commun. Math. Phys. 50, 69-77 (1976).
A logistic map of the form x".,.1=wxn(1-xn) may be employed. The Anosov map,
often referred
to as the cat map having the form:
xn+1l _ 1 11 xn1 mod 1
CYn+n Ci 2JCynJ
may also be used.
The map is composed of two steps; i) a linear matrix multiplication, ii) a non-
linear modulo
operation, which forces the iterates to remain within the unit square. It is
possible to
generalize the Anosov maps to an arbitrary number of variables. Furthermore,
the matrix
may have arbitrary coefficient only limited by the requirement of being area-
preserving and
having at least one positive Lyapunov exponent for the system. These exponents
can be
calculated analytically for such systems. For more details, reference is made
to A.J.
Lichtenberg and M.A. Lieberman, Regular and Chaotic Dynamics, Springer 1992
(p.305).
Systems of arbitrarily high dimension may be constructed by coupling systems
of lower
dimensions, referred to as subsystems. The subsystems can be identical or
different. They
can e.g. be different by using different parameters in the various subsystems,
and/or they
may be different by employing different equations. The coupling can be a
function of one or
more of the state variables in the individual subsystems. Several types of
coupling exist,
including local and global coupling.
Local coupling implies that the individual subsystems are affected through a
coupling by
some but not all the subsystems in the entire system. Examples of local
couplings are
unidirectional and bi-directional coupling, which implies that the coupling is
a function of one
and two subsystems, respectively. By use of these types, map lattices can by
constructed. An
example of such a system with a local unidirectional copuling is the following
N-dimensional
system :
x~ ~ OxO+EixN~
xZ ~ fz~xzO'~zxu
xN ~' .fN ~xrr ~+ ErrxN-n
where f1"N are mathematical functions and s1"N are coupling constants. The
mathematical
functions and coupling constants may be different for each subsystem.
A usual choice of local coupling can be the diffusive coupling, referring to a
type of coupling
proportional to the difference between two subsystems. This can be defined as:
X ~ f(X)+ s(X - Y),
where ~C and Y are two subsystems of at least dimension one and s is a matrix
of coupling
constants.
The term global coupling refers to situations where all subsystems are coupled
to each other,
sometimes termed an all-to-all coupling. This can, for instance, be achieved
by letting the
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
5
coupling be a function of the mean field, i.e. the average of all the
subsystems. This is
defined by:
N
X-~f(X)+el~X"
N i=1
where X is a subsystem of at least dimension one and ~ is a coupling constant.
Furthermore, the coupling function can be any linear or non-linear function of
the
subsystems.
An example of a local bi-directional coupling is given in the following
equation:
x; -~ f(x;~+ E~x;_1- (1 + y~x; + Yx~+1~ ~ E ~1~ M~ .
Another type of local coupling is the unidirectional local coupling, where a
given state is
coupled to one of its neighbouring states. This can for example be defined as:
x; ~ f(x; ) + Eg(x;_1 ~, i E ~1, M
where g is either a linear or non-linear function. For the linear case, the
system is simply
defined by:
x; -~ f(x, ~ + Ex;_l, i E ~1, M
Furthermore global coupling can be applied, i.e. each individual system is
coupled to all other
systems. This could be done in the following way:
X; -~ f(x;~+Eg(xl,xa,X3...XM),I E ~1,M~
where g is a function of all states in the system and g can be a linear or
nonlinear function.
Furthermore g can be a linear or nonlinear function of a subset of the M
states.
Further, a map lattice which is a type of coupled maps may be employed. In the
example
below, x, denotes a variable on a lattice (represented by an N-dimensional
array of points),
the lattice being a iD array with M points. Each point on the lattice is
updated according to
the function on the right hand side of the arrow, where the function f may for
example be the
logistic map. As is seen, neighbouring points on the lattice couple linearly,
where the linear
coupling is adjusted by the parameters y and E. Boundary conditions refer to
the way lattice
elements 1 and M are treated.
x; --> f(x; ) + E~x;_i - (1 + ~y~X, + ~yx,+1 ~ i E ~1~ M~ .
Finally, certain simple 3D flow equations may be employed, the systems consist
normally of
fewer terms than the Lorenz and Rossler systems. That is, either five terms
and two
nonlinearities or six terms and one nonlinearity. In comparison the Lorenz and
Rossler
systems each consist of seven terms, cf. J C SprottLPhys Rev. E 50 8647-8650
11994).
Appropriate systems are given in the below list:
dx/dt = y, dy/dt = -X + yz, dz/dt = 1 - yz
dx/dt = yz, dy/dt = x - y, dz/dt = 1 - xy
dX/dt = yz, dy/dt = X - y, dz/dt = 1 - x~
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
36
dx/dt = -y, dy/dt = x + z, dz/dt = xz + 3y2
dx/dt = yz, dy/dt = x2 - y, dz/dt = 1 - 4x
dx/dt = y + z, dy/dt = -x + 0.5y, dz/dt = xa - z
dx/dt = 0.4x + z, dy/dt = xz - y, dz/dt = -x + y
dx/dt = -y + za, dy/dt = x + 0.5y, dz/dt = x - z
dx/dt = -0.2y, dy/dt = x + z, dz/dt = x + yz - z
dx/dt = 2z, dy/dt = -2y + z, dz/dt = -x + y + yz
dx/dt=xy-z,dy/dt=x-y,dz/dt=x+0.3z
dx/dt = y + 3.9z, dy/dt = 0.9x2 - y, dz/dt = 1 - x
dx/dt = -z, dy/dt = -xz - y, dz/dt = 1.7 + 1.7x + y
dx/dt = -2y, dy/dt = x + zZ, dz/dt = 1 + y - 2x
dx/dt = y, dy/dt = x - z, dz/dt = x + xz + 2.7y
dx/dt = 2.7y + z, dy/dt = -x + y2, dz/dt = x + y
dx/dt = -z, dy/dt = x - y, dz/dt = 3.1x + ya + 0.5z
dx/dt = 0.9 - y, dy/dt = 0.4 + z, dz/dt = xy - z
dx/dt = -x - 4y, dy/dt = x + zz, dz/dt = 1 + x
25
A further mathematical system is described below with reference to Fig. 28,
cf. the below
description of the drawings.
The Lorenz system comprises the following differential equations:
_dx _
dt a(y - x),
dy =rx-y-xz,
dt
dz = xy - bz,
at
wherein X=(x, y, z) are state variables, t is the independent variable, and a,
r and b are
parameters.
In case the following conditions are fulfilled:
(a-b-1)>0 , r>1, r>a~s+b+1~, a,r,b>0,
the stationary points of the Lorenz system are not stable, in which case the
Lorenz system is
likely to exhibit chaotic behavior. The parameters may be constant or
variable, variable
parameters contributing, e.g., to the results of the computations being more
unpredictable
which may be useful in a pseudo-random number generating method or in an
encryption/decryption method.
In the case of a non-linear mapping, the computations may comprise numerically
iterating
the non-linear function, the iteration being based on an initial condition Xo
of the state
variable X.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
37
The step of performing computations may comprise numerically integrating the
non-linear
differential equations by repeatedly computing a solution X~+1 based on one or
more previous
solutions Xm, m<_n+1, and a step length, oT~, of the independent variable, t.
Preferably, at
least one initial condition, Xo, of the state variable, X, and an initial step
length, ~To, are
provided. The step length may be given before the computations are initiated,
or it may be
computed as the computations proceed. For example, the initial step length,
4To, may be
computed from the initial condition Xn.
The step length may vary between equations in a system. It may for example
differ from one
equation to another. The step length vector 0T is used to represent the step
length for each
equation in the system. The DT vector has the same dimension as the system.
In a discretized formulation of the Lorenz system, the solution X"+~ may be
computed using
the step length OT=(otX,~, oty,n, ~tz,~) as follows:
xn+1 - Xn + \a\yn - xn~~' OtX,n
yn+1 - yn + ~Xn~r - Zn ~ - yn l ' ~ty.n
Zn+1 - Zn + \xnyn - bZn) ~ L~tZ,ni
wherein:
4tx," is the step length used in the computation of x~+1.
vty," is the step length used in the computation of y"+1.
OtZ," is the step length used in the computation of z"+1.
As mentioned above, the step length 4T may be constant or may vary throughout
the
computations. For example, in each or in some of the integration steps, at
least one of the
elements (otX,", oty,~, ~t~,n) of the step length DT may be a function of one
or more numbers
involved in or derived from the computations. Also, in each integration step,
at least one of
the elements (ot,~,", Oty,~, Ot~,~) of the step length OT may be a function of
at least one
solution, Xm, which is a current or previous solution to the mathematical
system. In each or
some of the integration steps, at least one of the elements (Otx,", ~tY,~,
~t~,~) of the step
length oT is a function of at least one step length, OTm, which is a current
or previous
integration step. The varying step length oT may be used in any numerical
solution of
differential equations, and accordingly -there is disclosed a method of
numerically solving
differential equations using a variable step length. In a pseudo-random number
generating
method, such as in an encryption/decryption method, the variable step length
may contribute
to improving the security of the system, i.e. to make the resulting keystream
more
unpredictable.
In a pseudo-random number generating method, the initial condition Xo and/or
the initial step
length OTo may be calculated from or represent a seed value. In an
encryption/decryption
method, at least a part of the initial condition Xo and/or at least a part of
the initial step
length oTo may be calculated from or represent an encryption key. Also, at
least a part of at
least some of the parameters of the mathematical system may be calculated from
or
represent a seed value or an encryption key. The key may be a public or a
private key.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
38
The extracted set of data may comprise a pseudo-random number which may be
used for
encryption. A plurality of numbers resulting from the computations may be
extracted. The
step of extracting may comprise extracting one or more numbers derived from a
number, k,
of bits of the resulting number, such as the k least significant bits from the
resulting number
or numbers, which contributes to the unpredictability of the derived number.
The k bits
extracted may for example be derived by applying a modulus or a logical "and"
function to
the resulting number or numbers. As an alternative to extracting the k least
significant bits,
the step of extracting may comprise extracting k bits at predetermined or
variable positions
in the resulting number. The number k may be an integer value selected from in
the range
between 8 and 128, such as 16-64, such as 24-32. In case a plurality of
numbers are
extracted, the extracted numbers may be derived by means of different values
of k, which
further contributes to the unpredictability of the derived number. The
extracted number or
numbers may be manipulated by means of arithmetic and/or logical operations,
so as to
obtain a combined set of data. One or more of the extracted numbers and/or the
combined
set of data may be combined with original data in an arithmetic and/or logical
operation, so
as to encrypt the original data. Similarly, one or more of the extracted
numbers and/or the
combined set of data may be combined with encrypted data in a arithmetic
and/or logical
operation, so as to decrypt the encrypted data and obtain the original data.
The arithmetic
and/or logical operation may comprise an XOR operation, multiplication or
addition. For
example, the arithmetic and/or logical operation may comprise addition of the
original data
and the combined set of data for encryption, and subtraction of the combined
set of data
from the encrypted data for decryption. Alternatively, the arithmetic and/or
logical operation
comprises subtraction of the combined set of data from the original data for
encryption, and
addition of the combined set of data and the encrypted data for decryption. It
may be
necessary to apply a modulus function when subtracting or adding numbers. In
case the
extracted set of data comprises data derived from a plurality of numbers, one
set of bits, for
example the k least significant bits may be extracted from one number, whereas
other bits,
for example the 47th - 54th bit in a 64-bit number, may be extracted from the
other number.
In a block-cipher encryption/decryption system, the computations may involve
data
representing a block of plaintext, so that the plaintext and a key is entered
into, e.g., an
encryption system which gives the ciphertext as an output. The extracted set
of data may be
used to define at least one operation on a block of plaintext in the block-
cipher encryption
and decryption system. The methods described herein may be applied in a block-
cipher
algorithm, wherein a block of plaintext is divided into two sub-blocks, and
one sub-block is
used to influence the other, for example where a modified version of a first
block (or a part
thereof) is used to influence the other (or a part thereof), e.g., by an XOR
function. Such an
algorithm is generally referred to as a Feistel Network, cf. Applied
Cryptography by Bruce
Schneier, Second Edition, John Wiley & Sons, 1996. In such case the first sub-
block or the
modified version thereof may be transformed by a Hash function relying on the
method, the
Hash function being given a cryptographic key as an input. In each round, a
new
cryptographic key may be given as input to the Hash function. Alternatively,
the same
cryptographic key may be given to the Hash function in all rounds. As a
further alternative,
the cryptographic key may vary from block to block, for example by giving the
same
cryptographic key as an input in all rounds for each block, or by giving
different cryptographic
keys as inputs for each block and for each round.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
39
The extracted data may be used as a decryption or an encryption key. In a
system, wherein
computations are performed in two mathematical systems, the extracted set of
data from
one of the systems may be used to generate keys or used as keys for the other
system. The
extracted data may also be used in generation of data representing a digital
signature,
and/or in watermarking of digital data.
In the methods described herein, the electronic device may comprise an
electronic processing
unit having a register width, whereby the method may comprising the steps of:
- expressing at least one integer number of a bit width larger than said
register width as at
least two sub-numbers each having a bit width which is at most equal to said
register
width,
- performing at least one of said computations as a sub-computation on each of
the sub-
numbers so as to arrive at at least two partial results, expressed as integer
numbers of a
bit width smaller which is at most equal to the register width of the
processing unit,
- concatenating the partial results to yield a representation of a result of
said at least one
computation.
Analogously, computations on numbers of a width smaller than the register
width of the
processor may also be performed, whereby an operation, for example a logical
AND, may be
performed, so that the upper half of, e.g., a 64-bit register is not used for
computations on
32-bit numbers. In order to maintain the sign of the number in question, the
most significant
bit of, e.g., the 32-bit number may be copied into the upper 32 bits of the 64-
bit register.
The integer numbers usually comprise or represent the fixed-point number or
numbers used
in the computations. A fixed-point number expressed in terms of an integer
type number
may represent a real number.
D DETECTION OF PERIODIC BEHAVIOR
A method of detecting periodic behavior in the solution of a mathematical
system comprising
at least one non-linear function governing at least one state variable with
respect to at least
one independent variable, comprises:
- expressing the mathematical system in discrete terms,
- performing computations so as to obtain resulting numbers, the resulting
numbers
3representing at least parts of solutions to the mathematical system,
- storing selected solutions in an array, A, in a memory of the electronic
device, the array
being adapted to store a finite number, n+1, of solutions,
- determining whether at least one of:
- a current solution, and
q.p - a particular one of said solutions stored in the array
is substantially identical to another solution stored in the array. It should
be understood that
this method constitutes an independent aspect of the present invention.
The steps of performing computations, storing selected solutions, and
determining may be
performed continuously during the computations, i.e, repetitively during the
computations,
such as in each computational step, such as in connection with each iteration.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
If a current solution or a particular one of the solutions stored in the array
is substantially
identical to one or more other solutions stored in the array the solution of
the mathematical
system is likely to show periodic behavior. In case one of the methods
described herein is
used in a pseudo-random number generating method, in particular if it is used
in an
5 encryption/decryption method, such periodic behavior is undesirable, as it
negatively
influences the unpredictability of the generated pseudo-random numbers or the
keystream.
By applying the above method, periodic behavior may be detected.
The step of determining whether a current solution or a particular one of the
solutions stored
10 in the array is substantially identical to one or more other solutions
stored in the array
preferably comprises determining whether the solutions are completely
identical. When
solving a mathematical system expressing an array of state variables X, the
step of
determining may comprise determining whether only some of the entries of X are
substantially identical.
In order to save computational time and/or memory, only selected solutions may
be stored in
the memory.
In the method, each entry in the array may contain a solution having an age
which is
growing by array level, A;, 0<_i<-n, and the method may comprise:
- at the step of storing selected solutions in the array: storing a current
solution at the 0'th
level, Ao, in the array, A, thereby overwriting an old value stored at the
0'th level in the
array, A,
- if a 0'th predetermined criterion is fulfilled: transferring the old value
to the 1'st level in
the array, A, before the 0'th level is overwritten by the current solution,
and
for the 1st level and each further level i in the array:
- if an i'th predetermined criterion for level i is fulfilled: transferring
the old value stored at
the i'th level to the i+1'st level in the array, A, before the i'th level is
overwritten by the
value transferred from the i-1'st level,
if the n'th level is to be updated: discarding the old value previously stored
at the n'th level.
For each level, i, in the array, the number of times an old value stored at
the i'th level has
been overwritten by a new value without the old value being transferred to the
i+1'st level
may be counted, the i'th predetermined criterion being fulfilled if the old
value has not been
transferred for a predetermined number of times. The predetermined number of
times may
be the same for all levels of the array, A, or it may vary between the levels.
The
predetermined number of times for the i'th level of the array, A, may for
example be
dependent on one or more values stored in the array, such as when there occurs
a change of
sign in one or more of the values.
The step of
determining whether a current solution or a particular one of said solutions
stored in
the array is substantially identical to one or more other solutions stored in
the array
may only be performed when a test criterion is fulfilled. For example, the
test criterion may
be fulfilled when the sign of at least one state variable changes from + to -,
or from - to +,
or both. The test criterion may also be fulfilled when there occurs a change
of sign of at least
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
41
one derivative of at least one state variable with respect to at least one
independent variable,
in which case the method further comprises computing the derivative.
In the method, a test value may be computed from the at least one state
variable and/or
from the derivative, the test criterion being based on the test value. The
test criterion may
for example be fulfilled when there occurs a change of sign in the test value
or in a derivative
of the test value, or predetermined values may be provided.
E PSEUDO-NUMBER GENERATION AND ENCRYPTION/DECRYPTION
A method of generating a pseudo-random number, comprises:
I) expressing a mathematical system in discrete terms,
II) defining a seed value representing at least an initial condition for the
mathematical
system,
III) expressing at least one variable of the mathematical system as a fixed-
point number,
IV) performing computations including the at least one variable expressed as a
fixed-point
number and obtaining, from said computations, a resulting number, the
resulting number
representing at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
V) extracting, as the pseudo-random number, a number derived from at least one
number
which has occurred during the computations. This method constitutes an
independent aspect
of the present invention.
The seed value may be a user-defined value, such as an encryption/decryption
key in case
the method is applied in an encryption/decryption method.
The pseudo-random number may be extracted as a number derived from the k
digits of the
one or more numbers which have occurred during the computations, e.g. the k
least
significant bits or k selected bit from the one or more numbers.
The method may comprise repeating steps IV) and V) until a given amount of
pseudo-
random numbers has been generated.
40
A given amount of pseudo-random numbers may be generated and stored in a
memory of
the electronic device as a spare seed value, which may, e.g., be used if
periodic behavior is
detected by the above method or by another method. The given amount of pseudo-
random
numbers may be stored internally in an algorithm.
The method may further comprise a method for detecting periodic behavior as
discussed
above. In that case the method for generating a pseudo-random number may
comprise, if
the step of:
determining whether a current solution or a particular one of said solutions
stored in
the array is substantially identical to one or more other solutions stored in
the array
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
42
reveals that the current solution or the particular solution is identical to
one or more other
solutions,
interrupt the pseudo-random-number generation, i.e. interrupting repetition of
steps IV) and
V),
use the spare seed value as the seed value in the step II),
resume the pseudo-random-number generation, i.e. resuming repetition of steps
IV) and V).
Thus, for example, in an encryption/decryption method, a spare
encryption/decryption key
may be used if periodic behavior is detected.
Prior to the step of resuming the pseudo-random number generation, a given
amount of
pseudo-random numbers may be generated and stored, in a memory of the
electronic device,
as a new spare seed value. Each level in the array, A, is preferably reset
prior to step IV),
when steps IV) and V) are initiated with a new seed value at step II).
A method of encrypting a set of original data into a set of encrypted data,
comprises the
steps of:
A) generating a pseudo-random number by performing the steps of:
I) expressing a mathematical system in discrete terms,
II) defining an encryption key representing at least an initial condition for
the
mathematical system,
III) expressing at least one variable of the mathematical system as a fixed-
point
number,
IV) performing computations including the at least one variable expressed as a
fixed-
point number and obtaining, from the computations, a resulting number, the
resulting
number representing at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
V) extracting, as the pseudo-random number, a number derived from at least one
number which has occurred during the computations,
B) manipulating the original data and the pseudo-random number by means of at
least one
of:
i. an arithmetic operation, and
ii. a logical operation,
so as to obtain a combined set of data, the combined set of data being the
encrypted data.
Prior to step A), a sub-set of the original data may be separated from the set
of data, and
step B) may be performed on the sub-set of data. This step may be repeated
until a plurality
of sub-sets which in common constitute the entire set of original data have
been encrypted.
The pseudo-random number may be extracted as a number derived from the k bits
of the
one or more numbers which have occurred during the computations, e.g. the k
least
significant bits or k selected bits.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
43
Steps IV) and V) may be repeated until a given amount of pseudo-random numbers
has been
generated.
A given amount of pseudo-random numbers may be generated and stored in a
memory of
the electronic device as a spare encryption key. For example, a number
resulting from or
occurring in at least one integration or iteration step of the computations
may be stored as a
spare encryption key. The spare encryption key may, e.g., be used if
encryption is
interrupted due to the occurrence of periodic behavior in the solution to the
mathematical
system. In case no output of the spare encryption key is needed, it may be
stored internally
in an encryption algorithm. When the method is used for decryption, the spare
key is a
decryption key.
As it appears from the above, the method may comprise a method for detecting
periodic
behavior, in which case the method for encrypting may comprise, if the step of
determining whether a current solution or a particular one of said solutions
stored in
the array is substantially identical to one or more other solutions stored in
the array
reveals that the current solution or the particular solution is identical to
one or more other
solutions,
interrupt the pseudo-random number generation, i,e. interrupting repetition of
steps IV) and
V),
use the spare encryption key as the encryption key in step II),
resume the pseudo-random number generation, i.e. resuming repetition of steps
IV) and V).
Prior to the step of resuming the pseudo-random number generation, a given
amount of
pseudo-random numbers may be generated and stored in a memory of the
electronic device
as a new spare encryption key.
Preferably, each level in the array, A, is reset prior to step IV), when steps
IV) and V) are
initiated with a new seed value at step II).
A method of decrypting a set of encrypted data which has been encrypted by the
method
discussed above, comprises the. steps of:
a) performing step A) as defined above in connection with the encryption
method, so as to
extract the same pseudo-random number as extracted in step V) of the
encryption method,
b) manipulating the encrypted data and the pseudo-random number by means of
arithmetic
and/or logical operations, so as to obtain the original, i.e. decrypted,
version of the data.
Prior to step a), a sub-set of the encrypted data may be separated from the
set of encrypted
data, and in case the sub-set of data has been encrypted by the above
encryption method,
the method of decrypting may comprise performing steps a) and b) on the sub-
set of data.
This step may be repeated until a plurality of sub-sets which in common
constitute the entire
set of encrypted data have been decrypted.
Any of the steps of the encryption method may be applied in an identical
manner when
decrypting the encrypted data as during the previous sequence of encrypting
the original
data.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
44
F PROCESSING IN A PLURALITY OF INSTANCES IN PARALLEL
A method of generating a pseudo-random number, comprises, in one instance:
I) expressing a mathematical system in discrete terms,
II) defining a seed value representing at least an initial condition for the
mathematical
system,
III) expressing at least one variable of the mathematical system as a fixed-
point number,
IV) performing computations including the at least one variable expressed as a
fixed-point
number and obtaining a resulting number, the resulting number representing at
least one of:
a. a part of a solution to the mathematical system, and
b, a number usable in further computations involved in the numerical solution
of the
mathematical system,
V) extracting, as the pseudo-random number, a number derived from at least one
number
which has occurred during the computations,
performing steps I) - V) in a plurality of instances in parallel. This method
constitutes an
independent aspect of the present invention.
Computations in the two or more instances may be performed either at the same
time, or
successively. Thus, the computations in the two or more instances may be
performed by
executing instructions which process a plurality of computations at the same
time, or by
executing instructions which only process a single computation at a time.
Thus, pseudo-random number generation in a plurality of instances in parallel
may, in some
cases, be faster than if the steps are performed in one instance only, in
particular if the
hardware on which the method is executed supports parallel processing.
Further, by coupling
the two or more instances, a larger key length in encryption may be applied
than if only one
instance were used. For example, one part of an encryption key may be used for
a first
instance, and another part of the encryption key may be used for a second
instance.
Mathematical systems of arbitrarily high dimension may be constructed by
coupling systems
of lower dimension, referred to as subsystems. For example, N logistic maps
can be coupled,
yielding an N-dimensional system. The coupling mechanism can be engineered by
including
either linear or non-linear coupling functions in the N different maps
corresponding to the N
different variables. The coupling function in the map governing one variable
may or may not
depend on all other variables. Alternatively, the coupling can be carried out
by substituting
one of the N variables into one or more of the N-1 remaining maps.
Two or more logistic maps may be coupled through linear coupling terms. In the
example
shown below, the parameters El and Ez in front of the coupling terms control
the strength of
the coupling, i.e. the degree of impact that each one of the two logistic maps
has on the
other one.
Cxn+11 _ Ca,lxn(j. - xn)-I- El\yn - xn/\1
yn+1 a'2yn~~' ynl+ E2\xn - ynl
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
Numbers or data may be transmitted between the plurality of instances at least
while
performing step IV) for each of the instances. The same applies to step V).
The method may comprise combining, by use of arithmetic and/or logical
operations, a
5 plurality of pseudo-random numbers extracted at step V) in each of the
instances into a
common pseudo-random number.
Parameter and/or variable values, or parts thereof, may be exchanged between
the two
instances. Thus, for example x"+1 of one instance and x"+1 of another instance
may be
10 exchanged after each iteration step, or x~+1 of one instance may be
exchanged with y"+1 of
another instance. Likewise, the step length ot~ may be exchanged between the
two
instances. The exchange of variable or parameter values may also be achieved
by performing
logical and/or arithmetic operations on a value of a first instance before
using that value for
modifying a value of a second instance.
G USING A CRYPTOGRAPHIC ICEY AS AN INPUT TO A MATHEMATICAL SYSTEM
A method of performing numerical computations in a mathematical system
comprising at
least one function, may comprises the steps of:
- expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as a fixed-point
number,
- performing said computations in such a way that the computations include the
at least
one variable expressed as a fixed-point number,
- obtaining, from said computations, a resulting number, the resulting number
representing
at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
the step of performing computations comprising:
- repeatedly computing a solution X"+1 based on at least one previous
solutions Xm, m<-n+1,
whereby the step of performing computations is initiated based on at least one
initial
condition, Xo, of the state variable, X,
the method further comprising:
- providing a cryptographic key as an input to said computations, whereby the
cryptographic key is used in generation of the initial condition Xo. This
method constitutes
an independent aspect of the present invention.
It should be understood, that, in the present context, the term "previous
solutions" also
covers the current solution, X"+1.
The cryptographic key may further be used for initializing parameters of the
mathematical
system.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
46
H GENERATION OF AN IDENTIFICATION VALUE FOR IDENTIFYING OR PROVING THE
IDENTITY OF A SET OF DATA
A method of determining an identification value for identifying a set of data,
comprises
performing numerical computations in a mathematical system comprising at least
one
function, the method comprising the steps of:
- expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as a fixed-point
number,
- performing said computations in such a way that the computations include the
at least
one variable expressed as a fixed-point number,
- obtaining, from said computations, a resulting number, the resulting number
representing
at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
whereby a representation of at least part of the set of data is used in said
computations, the
method further comprising:
- extracting, as said identification value, at least a part of said resulting
number. This
method constitutes an independent aspect of the present invention.
Thus, the above method may be regarded a Hash function or Hash algorithm which
have
been discussed in detail above. The identification value may be constituted by
a number of
extracted numbers which have been extracted at different computational stages
in the
numerical computations. Extraction may occur at each computational step or at
each iteration
step, or it may occur only at selected computational stages.
The term "identification value" may be a hash value or a cryptographic check-
sum which
identifies the set of data, cf. for example Applied Cryptography by Bruce
Schneier, Second
Edition, John Wiley & Sons, 1996. In case a cryptographic key is used as a
seed value for the
computations, the hash function is usually referred to as a MAC function
(Message
Authentication Code).
The mathematical system may comprise a differential equation, such as a
partial differential
equation or an ordinary differential equation, or a discrete mapping, such as
an area-
preserving map or a non area-preserving map. The mathematical system may
comprise at
least one non-linear mapping function governing at least one state variable X.
A non-linear mapping function may for example comprise a logistic map of the
form
xn+~=~xn(1'xn), wherein A is a parameter, x~+1 is the value of state variable
x at the (n+1)'th
stage in the computations, and x~ is the value of state variable x at the n'th
stage in the
computations.
The logistic map may be modified into the form x"+1=J~xn(1-xn)+E(x"-m~),
wherein A and E are
parameters, x~+1 is the value of state variable x at the (n+1)'th stage in the
computations, x"
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
47
is the value of state variable x at the n'th stage in the computations, and m"
contains a
representation of an n'th portion of the set of data.
A cryptographic key may be used for at least partially determining at least
one of the
following: ~, c and an initial value xo of state variable x.
The mathematical system may comprise a set of non-linear mapping functions,
such as:
- an Anosov map of the form:
CXn+il _ Ci ilCXn1 mod 1, Or
yn+1 1 ~J yn
- a Henon map of the form:
Cxn+11 = Ci -I- yn - aXn~ ~ .
yn+1 bxn
The mathematical system may comprise at least one non-linear differential
equation and/or a
set of non-linear differential equations.
Preferably, the mathematical system has at least one positive Lyapunov
exponent, whereby a
certain degree of irregular or chaotic behavior is achieved, whereby
randomness properties of
the system and security are enhanced.
At least one Lyapunov exponent may be computed at least once during the
mathematical
computations in order to determine whether the mathematical system exhibits
chaotic
behavior. If this is not the case, e.g. if the computed Lyapunov exponent is
not positive, the
computations may be interrupted and resumed from other initial values and/or
other
parameters.
The at least non-linear differential equation preferably governs at least one
state variable, X,
which is a function of at least one independent variable, t. The set of non-
linear differential
equations may for example comprise a Lorenz system.
I HANDLING OF OVERFLOW, DELIBERATE GENERATION OF OVERFLOW
A method of performing numerical computations in a mathematical system
comprising at
least one function, comprises the steps of:
- expressing the mathematical system in discrete terms,
- restricting the range of at least a selected variable of said function, the
range being
sufficiently narrow so as to exclude values which the selected variable, by
virtue of said
function, would assume if not restricted by said range,
- performing computations so as to obtain a resulting number, the resulting
number
representing at least one of:
a. a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system,
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
48
- when the computations result in a value for the selected variable which is
beyond the
range, assigning a value within the range to the selected variable. This
method
constitutes an independent aspect of the present invention.
For example, if the upper bits of the value, which is beyond the range, are
truncated, the
step of assigning a value within the range may be seen as a modulus function.
The steps of
the method may thus provide deliberate overflow, e.g. in order to enhance
randomness
properties of an encryption/decryption system and/or in order to make it more
difficult to
derive information about internal states of the mathematical system from
encrypted data.
15
The above method may thus be a part of a pseudo-random number generating
method
which, e.g., generates pseudo-random numbers for use in at least one of
encryption and
decryption. The mathematical system preferably has at least one positive
Lyapunov
exponent.
IC HANDLING OF IMAGINARY OR VIRTUAL DECIMAL SEPARATOR
A further method of performing numerical computations in a mathematical system
comprising at least one function, comprises:
- expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as an integer
number,
- placing an imaginary decimal separator in said integer number, whereby the
integer
number represents a real number,
- performing computations including the at least one variable expressed as an
integer
number so as to obtain a resulting number, the resulting number being
expressed as an
integer number,
- positioning the imaginary decimal separator in the resulting number at a
predetermined
position by performing at least one of the steps of:
- correcting the position of the imaginary decimal separator in the integer
number, and
- placing an imaginary separator in the resulting number.
This method constitutes an independent aspect of the present invention.
The resulting number is usually a fixed-point number having a fixed position
of the decimal
separator. Alternatively, the position of the decimal separator in the
resulting number may be
corrected after the computation has been completed. A third possibility is to
correct the
position of the decimal separator before and after performing the computation.
This may be
relevant if not all positions to the left of the decimal separator in the
resulting number are
used, and it is desired to maintain a relatively higher resolution in the
computations than the
resolution of the resulting number. For example, the resulting number is
desired to have a
S(10.21) format. Thus, the addition of, say, two S(7.24) format numbers may be
performed
in a S(8.23) format which then is converted to the S(10.21) format resulting
number.
Thereby, the carry from the second and third least significant bits in the
arguments may
influence the result.
Finally, for some computations no correction of the position of any decimal
separator may be
required or needed.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
49
The correction of the position of a decimal separator are usually performed by
means of shift
operations.
In a most general form, a method of performing numerical computations in a
mathematical
system comprising at least one function, comprises the steps of:
- expressing the mathematical system in discrete terms,
- expressing at least one variable of the mathematical system as a fixed-point
number,
- performing said computations in such a way that the computations include the
at least
one variable expressed as a fixed-point number,
- obtaining, from said computations, a resulting number, the resulting number
representing
at least one of:
a. at least a part of a solution to the mathematical system, and
b. a number usable in further computations involved in the numerical solution
of the
mathematical system.
L SUBSTITUTE COMPUTATIONS REQUIRING NO POSITIONING OF AN IMAGINARY
DECIMAL SEPARATOR
There is further disclosed, as an independent aspect of the present invention,
a circuit for
performing numerical computations in a non-linear mathematical system
comprising at least
one function, the circuit being designed or programmed so that the
mathematical system, in
the circuit or in the computer program code, is represented in modified terms
in such a way
that at least a selected one of the numerical computations involves an integer
operation,
whereby said selected numerical computation in a non-modified representation
of the
mathematical system would require one or more floating point operations or
controlling the
positioning of a decimal separator in one or more fixed-point numbers, the
circuit being
designed or programmed so that said selected computation is substituted by at
least one
substitute computation on one or more integer numbers, whereby the
mathematical system,
in the circuit or in the computer program code, is represented in such a way
that the at least
one substitute computation requires no positioning of an imaginary decimal
separator.
The mathematical system may exhibit chaotic behavior.
Thus, for example, the computations:
xn+1=xn'E'yn and
yn+1=xn'E' Zyn
may be performed by first computing xn+1. Then, the expression for yn+~ may be
computed
as:
yn+1=xn+1'E'yn
whereby the computational step of multiplying yn by 2 may be omitted.
Thus, by performing the substitute computations, computational time may be
saved.
Likewise, there is disclosed a method of, in an electronic circuit, performing
numerical
computations in a non-linear mathematical system comprising at least one
function, the
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
method comprising, in the circuit or in a computer program segment according
to which the
circuit operates, the steps of:
- representing the mathematical system in modified terms in such a way that at
least a
selected one of the numerical computations involves an integer operation,
whereby said
5 selected numerical computation in a non-modified representation of the
mathematical
system would require one or more floating point operations or controlling the
positioning
of a decimal separator in one or more fixed-point numbers,
- substituting said selected computation by at least one substitute
computation on one or
more integer numbers, whereby the mathematical system, in the circuit or in
the
10 computer program code, is represented in such a way that the at least one
substitute
computation requires no positioning of an imaginary decimal separator,
performing said substitute computation.
BRIEF DESCRIPTION OF THE DRAWINGS
20
The above methods will now be further described with reference to the
drawings, in which:
Fig. 1 is an illustration of a cryptographic method employing a squaring
function of a state
variable x,
Fig. 2 is an illustration of a next-state function including a counter
increment,
Fig. 3 is an illustration of the system of Fig. 1 with coupling,
Fig. 4 is an illustration of a system with counter incrementation,
Fig. 5 is an illustration of an encryption/decryption process,
Fig. 6 is an illustration of a sequence for encrypting, transmitting and
decrypting electronic
data,
Fig. 7 is an illustration of an encryption sequence in a block cipher system,
Fig. 8 is an illustration of an encryption sequence in a stream cipher system,
Fig. 9 is an illustration of the key elements in an encryption/decryption
algorithm,
Fig. 10 is a plot of a numerical solution to a Lorenz system,
Fig. 11 is an illustration of key extension by padding,
Fig. 12 illustrates a possible method of simultaneously computing two or more
instances of
identical or different chaotic systems,
Fig. 13 illustrates the principle of performing a check for periodic
solutions,
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
51
Fig. 14 shows a mathematical system with a periodic solution,
Fig. 15 illustrates transport between levels in the coordinate cache which
stores previously
calculated coordinates,
Figs. 16-18 illustrate various criteria for the detection of periodic
solutions,
Fig. 19 contains an illustration of a method for multiplication of 16-bit
numbers on an 8-bit
processor,
Figs. 20-27 are flow charts showing the operation of one embodiment of an
encryption
method,
Fig. 28 is an illustration of a mathematical system which may be employed in
the methods of
the present invention.
DETAILED DESCRIPTION OF THE DRAWINGS
Figs. 1-5 illustrate various aspects and embodiments of the methods of the
invention. As
discussed above, stream ciphers produce a stream of pseudo-random bits
specified by a key.
This stream of bits is referred to as the keystream, and encryption is
performed by bitwise
XOR'ing a plaintext with the keystream to obtain the ciphertext. The resulting
ciphertext is
decrypted by reproducing the same keystream specified by the same key and
XOR'ing the
ciphertext with this keystream to obtain the plaintext.
In order to generate a keystream, an embodiment of a Pseudo Random Number
Generator
(PRNG) may be built upon 512 internal bits divided between eight 32-bit state
variables and
eight corresponding 32-bit counter variables, which are incremented and added
to the state
variables at each iteration. The PRNG works by iterating a system of eight
coupled equations
based on a non-linear function and extracting 128 bits from the eight state
variables after
each iteration.
The algorithm is initialized by expanding the 128-bit key into 512 bits which
are used to
setup both the eight state variables and the eight counter values. The system,
defined by the
next-state function shown in Fig. 1, is then iterated four times in order to
diminish correlation
between the state variables and the key. Finally, the counter values are
modified by XOR'ing
them with the state variables in order to obtain the initial counter value.
A function, in the following referred to as the "g-function" may be employed,
the g-function
squaring a 32-bit number resulting in a 64-bit number, from which the upper 32-
bits and the
lower 32-bits are XOR'ed, cf. Fig. 1.
The g-function is used in the system of eight coupled equations, the system
being iterated
once in order to generate a new state from which 128-bits of random data are
extracted.
Before each iteration the counter values are incremented according to the
counter system
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
52
described below, and then the new state values are calculated by iterating the
following
system, cf. also Fig. 2 illustration a system with counter incrementation:
~~+1 =M x G(X, + C;
Where X~ _ (xo>;,xl>i,...,x~>;), with x~>; being the value of state j at
iteration i,
C; =(co>;,cl>;,...,c~>,), where c~>; is the value of counter j at iteration
i,G(X) being the g-
function evaluated on X, i.e. G(~Y) ~g(xo>;),g(xl>;),...,g(x~>;))and M being a
coupling
matrix defined by:
1 0 0 0 0 0 k16k16
k8 1 0 0 0 0 0 1
k16 k161 0 0 0 0 0
0 1 k8 1 0 0 0 0
M
0 0 k16 k161 0 0 0
0 0 0 1 k8 1 0 0
0 0 0 0 k16 k16
0 0 0 0 0 1 k8 1
where k8 and k16 imply that the coupling includes permutations of the 32-bits,
i.e. for a
permutation k, the expression kx g(x;) implies that some or all bits in the
number g(xl)
are mixed. k8 indicates that the permutation in question is a 8-bit left
rotation, and k16
likewise indicates a 16-bit left rotation. Fig. 3 illustrates such a coupled
system.
The dynamics of the counter is defined by C;+1 =A+C; . If a carry occurs, it
is saved and
added at next iteration step. A ~ao,al,...,a~) may for example be a 256 bit
constant
integer partitioned into eight 32-bit integers. Fig. 4 illustrates the counter
incrementation.
After each iteration step, 128 bits of keystream are extracted by XOR'ing
different state
variables. For example, the upper 16 bits and the lower 16-bits from two
different state
variables may be XOR'ed creating a total of eight 16 bit combinations
resulting in 128-bits of
random data. The keystream is XOR'ed with the plaintext/ciphertext to
encrypt/decrypt. Fig.
5 illustrates such an encryption/decryption process.
Many practical applications of pseudo-random number generators require the use
of a so-
called Initialization Vector (IV). For instance, when large amounts of data
are
encrypted/decrypted it is necessary to start from one end of the data and
continue through
all the data. If only a part of the data is to be decrypted, which is towards
the end of the
data, it is necessary to iterate the appropriate number of times from the
beginning of the
data to arrive at the output corresponding to the data to be decrypted, which
requires a
number of computations which are of no direct use and which are time-
consuming. This
problem can be solved by use of an IV. An IV is also useful in a Virtual
Private Network
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
53
(VPN). In such a network, the data may be divided into packages, and a unique
IV is
transmitted along with each package, whereby each package can be decrypted
individually,
even if other packages are lost. The data to be encrypted/decrypted is divided
into sections,
and each section is associated with a unique IV. The cipher is firstly setup
by use of the key,
and thereafter the internal state of the mathematical system is changed in an
unpredictably
way, as function of the IV. These changes may be performed on counters, on the
state values
or on both. The output of the cipher is then a function of both the key and
the IV, and
thereby a given section or package can be encrypted/decrypted, without
iterating multiple
times.
In one example of a method employing an IV, a master state of the mathematical
system is
created by a usual setup procedure, and subsequently a counter state is
manipulated as
follows: the 64-bit IV is expanded to 256-bits and XOR'ed on the counter
values, and the
system is then iterated a number of times to make all bits in the state
dependent on all bits
in the IV.
The algorithm discussed above is further elaborated in M. Boesgaard, M.
Vesterager, T.
Pedersen, J. Christiansen and O. Scavenius: Rabbit: A New High-Performance
Stream Cipher,
Proceedings of Fast Software Encryption (FSE) 2003, Springer, Berlin, (2003).
Fig. 6 is a general illustration of a sequence for encrypting, transmitting
and decrypting
digital data. Fig. 7 is an illustration of an encryption sequence in a block
cipher system, and
Fig. 8 is an illustration of an encryption sequence in a stream cipher system,
block cipher and
stream cipher systems being discussed in the above discussion of the
background of the
invention.
A method and algorithm for encrypting/decrypting data will now be described.
The algorithm
is applicable for most purposes in data encryption/decryption. However, the
nature of the
algorithm favours encryption of data streams or other continuous data, such as
large files,
live or pre-recorded audio/video, copyrighted material (e.g. computer games or
other
software) and data for storage (e.g. backup and/or transportation).
Furthermore, the speed
of the algorithm makes it particularly suitable for these purposes. Because of
the calculation
method, the algorithm is also useable on very small processors.
The algorithm relies on a Pseudo-Random Sequence Stream Cipher system (PRSSC).
PSSRC
systems are characterized by a pseudo-random number generator (the content of
the outer
boxes on Fig. 9), which generates a sequence of data, which is pseudo-random,
based on a
binary key. This sequence, the so-called keystream, cf. Fig. 9, is used for
the encryption and
decryption. The keystream is unique for each possible key.
Applying the logical XOR-function (stated in the figure by the ~-symbol) on
the plaintext and
an equal amount of keystream encrypts the plaintext. The output of the XOR-
function is the
ciphertext. Applying the same approach once more on the ciphertext decrypts it
into
plaintext. The decryption will only reveal the encrypted plaintext if the key
used for the
decryption is fully identical to the key used for the encryption.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
54
The integrity of the encrypted data is lying in the key capable of decrypting
the ciphertext.
Therefore it must be difficult to guess the key. To ensure this, the basic
design of the
algorithm is using a key of at least 128 bit. A key-size of 128 bit gives
approximately
3.4~103$ different keys.
The algorithm uses a system, which exhibits chaotic behaviour, such as a
Lorenz system,
which consists of the following three ordinary differential equations:
d =o-V'_x)
dY
=rx-y-xz
dt
_dz = xy - bz
dt
where ~', r, b are parameters, and x, y, z are state variables.
Fig. 10 shows a plot of a numerical solution to a Lorenz system.
The following parameter criteria should be satisfied for chaos to occur in the
system:
(a-b-1)>0 , r>1, r>a~6+b+ij, a,r,b>0
Even then, not all solutions will be chaotic. In the parameter space, there
will be so called
periodic windows, referring to combinations of parameters, which give rise to
periodic
solutions. Before implementing the system, analysis of the parameter-space
will be
performed using calculation of a Lyapunov exponent. Generally, a positive
Lyapunov
exponent indicates that the solution to the mathematical system is chaotic,
cf. Edward Ott,
Chaos in Dynamicai Systems, Cambridge University Press 1993.
The parameters are typically determined from a seed value, such as an
encryption key or a
part of an encryption key. Preferably, algorithms embodying the method of the
present
invention are designed so that only parameter values within predefined
intervals are made
possible, whereby it is ensured that the probability of the system having a
positive Lyapunov
exponent is high. Accordingly, the mathematical system will have a high
probability of
exhibiting chaotic behavior. The Lyapunov exponent may additionally or
alternatively be
determined at the beginning or during the mathematical computations, so as to
be able to
detect non-chaotic behavior of the solution to the mathematical system.
The mathematical system could as well be another continuous system (such as
the Rossler
system) or a discrete map (such as the Henon map).
The integration is performed using a numerical integration routine. Provided
an initial
condition and an integration step length, the numerical integration routine
calculates the
solution at discrete mesh points, e.g. by using the Euler method or a Runge-
Kutta method.
Using the Euler method to express the Lorenz equations in discrete terms, the
solution can
be computed from the following equations
xn+1 - xn ~ y~Yn - xn))' ~tx
yn+1 = yn + ~xn~r - Zn~ - yn)' ~tY
Zn+1 = Zn + ~xnYn - bZn) ~ Otz
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
The calculations are performed using fixed-point numbers which are described
below.
During numerical integration of a system of differential equations, the
continuous non-
dependent variables (such as time t or space s) are discretized. This process
refers to
5 replacing the continuous interval (a;bJ with a set of discrete points.In
such a system,
DT=(otX, 4ty, OtZ) is usually referred to as the step length of the
integration or the integration
step.
Fig. 12 illustrates a possible method of simultaneously computing two or more
instances of
10 the same system or different systems, such as chaotic systems. The method
confers higher
computational speed and improved security, and a larger key may be used.
Preferably there
should be some kind of communication or coupling between the two systems, like
for
example exchange of step length, such as exchange of Ot,~, qty, and/or ~t~.
15 The internal variables are in the basic design 32 bits wide each, but any
variable width could
be used. When using the Lorenz system, there are 6 internal variables (3 state
variables and
3 parameters). Thus, 192 bits (in the basic design) are used to represent an
internal state of
the generator given by a set of the internal variables. The padding of the 128
bits key up to
192 bits should be done in such a way as to avoid illegal values, i.e. to
ensure that all
20 variables contain allowed values, and as to avoid that bits from the key
are ignored. The
padding may include inserting predetermined values of zeros and ones or
repetitions of bits
from the key. Fig. 11 contains an illustration of key extension by padding.
The integration may be performed with variable time steps, which e.g. can be
calculated from
25 any one of the state variables. In the basic design, the step length dt
varies in each
integration step. This variation is coupled to the state variable X.
The keystream is extracted from some of the data related to the state
variables. This may be
done by extracting the 8 least significant bits from the y variable or by
collecting some of the
30 data wiped out in the calculations; e.g. from one or more of the
multiplications performed in
the calculation of one step.
Usually, calculations on a chaotic system are performed on computers using
floating-point
variables. However, this method introduces problems. One problem is that the
use of
35 floating-point variables may cause generation of different keystreams on
different computers
even if the same key is used, because of the slight differences in the
implementation of
floating-points on different computer systems.
Therefore fixed-point variables are used. The fixed-point variable is based on
the integer data
40 type; which is implemented identically on various computer systems. To
express numbers,
such as real numbers, digits after the decimal point are needed, the decimal
point being
artificially located somewhere else than at the end of the number (e.g. 12.345
instead of
12345).
45 To ensure proper operation of the algorithm, some tests should preferably
be performed.
Some of these tests are performed at run-time, and others are performed at
design-time.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
56
As a part of the initialization process, an amount of keystream equal to the
complete data
content of the state variables (e.g. 192 bits) or equal to the amount of a
complete key (e.g.
128 bits) are generated using the algorithm and saved, in case the key has to
be reloaded
due to detection of periodic solutions or stationary points. In that case, the
saved sequence is
loaded as a new key, and the initialization, including extraction of extra
key, is redone.
Do to the finite representation of numbers on a computer, any numerical
solution will be
periodic. However, some keys may result in keystreams having a rather small
period.
This is undesirable as it may compromise the security of the system. Therefore
the there is
propsed an algorithm for detecting such periodic solutions. This algorithm
watches the sign of
a variable or the slope of a variable. When using the Lorenz system, the check
is performed
on x. When the sign changes from minus to plus (or plus to minus or just
alters) the position
check is performed (the position check can also be performed after all
iterations). The
position check compares the complete set of state variables with buffered sets
from earlier. If
a complete match is found, a periodic solution is detected.
Stationary points of a dynamical system are sets of state variables which
remain unchanged
during iteration. Such stationary points may be detected by comparing the
current set of
state variables with the last set, or by checking if the slopes of all of the
variables are zero or
by checking if both the current slope of one variable and its previous slope
are zero.
Chaotic systems may, for one reason or another, enter into periodic solutions.
This has to be
detected and corrected in order not to compromise the security of the system.
If the solution
of the system becomes periodic, encryption may preferably be stopped, as the
extracted
number from the solution of the mathematical system will also be periodic and
hence not
pseudo-random. The test for periodic solutions includes comparing coordinates
of the solution
with previously calculated coordinates. If a complete match is found, the
system has entered
a periodic solution.
To reduce the amount of memory required to store previously calculated
coordinates, and to
reduce the processing time required to test the coordinates, only selected
coordinates are
stored in the coordinate cache. To reduce the processor time required to test
for periodic
solutions, the test is only performed when the coordinates meet certain
criteria. Fig. 13
illustrates the principle of performing a check for periodic solutions.
Fig. 14 shows a mathematical system with a period solution, more specifically
a two-
dimensional non-linear system with a periodic solution. The system is
deterministic meaning
that the solution is completely specified by its initial conditions. In
theory, the solution will be
continuous, thereby consisting of infinite many points. When solving the
system numerically,
the time-interval is discretized, and the solution is calculated at these
points. The numerical
solution to a mathematical system is simply a sequence of coordinate sets. If
we consider a
two-dimensional system, then the solution is specified at a number of points
(x,y), illustrated
by dots on the curve in Fig. 14. The deterministic nature of the system
implies that if the
solution ever hits a point, which it has visited previously, the solution is
periodic and will keep
being periodic, This property is employed in the present test.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
57
In order to test for periodic solutions during numerical integration, we have
to compare the
present calculated coordinate set with the previous values. In order to do
this, the coordinate
sets are stored as they are calculated. This storage works like a queue and is
referred to as
the coordinate cache. A calculated coordinate set is compared to every
coordinate set in the
coordinate cache. If a complete match (all values in the two coordinate sets
are equal) is
found, the system is in a periodic state. If the test is passed without a
complete match, no
periodic behavior is detected, and the calculations may continue. Before the
calculations
continue, the tested coordinate is added to the cache, for further
comparisons.
It will require too much memory and processor time to keep all calculated
coordinate sets of
the system in the cache. Hence, only selected coordinates are stored, as
illustrated in Fig. 15.
The cache consists of a number of levels, each containing a coordinate of age
growing by
level. After each test or after a number of tests, the tested coordinate is
inserted at level 0.
Every second time (or any other time) a coordinate is inserted into level 0,
the old value is
inserted into level 1 before it is overwritten. The method for inserting
coordinates at the
other levels is similar; every second time a value is inserted at any level,
the old value is
transported to the next level before it is overwritten at the current level.
This method results in a coordinate cache containing coordinates with an
exponentially
growing age. Level 0 stores coordinates with an age of 1 or 2 (the prior
checked coordinate
or the one before the prior checked coordinate), level 1 stores coordinates
with an age of 3 -
6 (3 at the test after the coordinate has been inserted, and then growing to 6
before the next
coordinate is inserted), level 2 stores coordinates with an age of 7 - 14, and
so on.
The pseudo program code in Example I shows how the cache may be implemented.
Because the age of the levels is varying, a periodic solution may not be found
immediately. A
periodic solution having a period length of 11 tests will be detected at level
2 of the cache,
because the age of the data at level 2 is between 7 and 14. However, the test
will not detect
the periodic solution before the coordinate is exactly 11 tests old. Therefore
up to 12 tests
may be performed before the periodic behavior is detected. In this case, it
means that the
system may pass through up to 12/11 period before it is detected.
A possible expansion to the algorithm described above is a varying
TransportAge, cf. the
pseudo code program in Example I. If some coordinates can be identified as
more likely to
take part of a periodic solution then others, the InsertCoordinate procedure,
cf. the pseudo
code program in Example I, may recognize them, and use a reduced value of
TransportAge
for those. This will favor the critical coordinates in the cache, and make the
data in cache
become younger if many critical coordinates are stored. The younger age of
data in the cache
makes a periodical solution detectable after less iteration within the
periodic solution.
The test may be performed after each iteration. That means every time we have
calculated a
new coordinate set of the solution. However, to save processor resources, the
test should
instead be performed at a periodic interval. I order to make the test work;
the test must be
performed when the solutions is at a recognizable position.One way to make
sure the test is
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
58
10
performed at the same position each time is to find a recognizable point in
the graphical plot
of the solution. To do so, the system has to be analyzed for its
characteristic behavior, and a
criterion has to be chosen. For the above shown non-linear system, the
examples of criteria
illustrated in Figs. 16-18 are useable.
First possible criterion, as illustrated in Fig. 16 is change of sign of x
from minus to plus. That
is, when the sign of x changes from minus to plus, the test is performed. The
second criterion
is change of sign of dx from plus to minus, as illustrated in Fig. 17. The
third criterion is
change of dy from plus to minus, as illustrated in Fig. 18.
When choosing the criterion, two considerations have to be made. First of all,
all possible
periodic solutions shall be able to fulfil the criterion. Secondly, to reduce
processor load, the
criterion with fewest tests should be selected.
At design time some extra tests can be performed on the systems and the chosen
parameter
spaces, to ensure the efficiency, stability and correctness of the system.
These tests may
include calculations of Lyapunov exponents, using Gram-Schmidt
orthogonalization, as well
as statistical analysis of the keystream.
EXAMPLE I
The following pseudo code program shows an example of a program for encrypting
and
decrypting data which encrypts one byte at a time. The program works in
accordance with
the flow charts of Figs. 20-27. The program works with 32-bit registers. Fig.
20 illustrates a
method which encrypts a file containing data. Figs. 21-27 correspond to those
functions
shown in the pseudo-code below which relate to check for periodic solution and
to a stream-
cipher using the Lorenz system.
Pseudo-code for fixed-point library
FIoatToFixedPoint: Converts a floating-point number, X, into a fixed-point
number. The result
of the function has the format S(a.b) or U(a.b)
fixedpoint FloatToFixedPoint(float X)
40
return X*2b; // b is the number of bits after the decimal
// separator in the fixed-point
// representation of the result
FixedPointToFloat: Converts a fixed-point number, X, having the format S(a.b)
or U(a.b), into
a floating-point number.
float FixedPointToFloat(fixedpoint X)
(
return X*2-b; // b i.s the number of bits after the decimal
// separator in the fixed-point
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
59
)
// representation of x
ConvertFixedPoint: Converts an input fixed-point number, X, having the format
S(a.b) or
U(a.b), into the requested format, S(c.d) or U(c.d). The result is signed if
the argument, X, is
signed, and vise versa.
fixedpoint ConvertFixedPoint(fixedpoint X)
I
return X*2d-b; // b is the number of bits after the decimal
// separator in the fixed-point
// representation of X. d is the number of
// bits after the decimal separator in the
// fixed-point representaiton of the result
)
Addition and subtraction of fixed-point numbers in the same format are
performed using
ordinary integer addition and subtraction functions.
MuIFixedPoint: Multiply two fixed-point numbers, X and Y. X has the format
S(a.b) or U(a.b)
and Y has the format S(c.d) or U(c.d). The resulting fixed-point number, has
the format
S(e.f) or U(e.f). The result as well as X and Y must all be either signed or
unsigned values
and stored in 32-bit registers. "»" is the arithmetic shift right for signed
multiplication and
30
logical shift right for unsigned multiplication.
fixedpoint MulFixedPoint(fixedpoint X, fixedpoint Y)
fixedpoint64 Temp; // A 64-bit register to hold the intermediate
// result
Temp = X*Y; // Tyro 32-bit values X and Y are multiplied
// into the 64-bit intermediate result
return Temp » b+d-f; // b and d are the number of bits after the
// decimal separator in the fixed-point
// representation of X and Y respectively.
// f is the number of bits after the decimal
// separator in the fixed-point
// representation of the result.
// The conversion of the value of a 64-bit
// register into a 32-bit register is
// performed by ignoring the 32 most
// significant bits and copying
// the 32 least significant bit into the
// destination register.
Pseudo-code for check for periodic solution
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
Global constants in the sub-system for checking for periodic solutions. The
code is able to
detect periods when the number of inflexions is lesser than
TransportAge~a~neoePtn-~ (Note that
there can only be half as many inflexions as iterations.)
5 const int CacheDepth = 32;
const int TransportAge = 2;
const int SpareSeedLength = 16;
The sub-system for checking for periodic solutions has a number of global
variables e.g. to
10 store the cache of old coordinates and the spare key to be loaded if a
periodic solutions is
found.
fixedpoint xCache[CacheDepth];
fixedpoint yCache[CacheDepth];
15 fixedpoint zCache[CacheDepth];
int CoordinateAge[CacheDepth];
25
char SpareSeed[SpareSeedZength];
fixedpoint xOld, xOldOld;
SetupCoordinateCheck: Set up the sub-system for checking for periodic
solutions. All
positions of the coordinate cache is reset to (x, y, z) _ (0, 0, 0), since (0,
0, 0) is a
stationary point for the Lorenz system, and therefore is a coordinate value
indicating that a
reload of the key is needed.
void SetupCoordinateCheck()
int i;
// Clear coordinate cache
for (i=0; i<CacheDepth; i++)
xCache[i] = 0;
yCache[i] = 0;
zCache[i] = 0;
CoordinateAge[i] = 1;
)
xOld = 0; // Variables for detecting when to check are
xOldOld = 0; // reset
// Prepare spare seed
for (i=0; i<SpareSeedLength ;i++)
SpareSeed[i] = 0;
// Generate the spare key
Crypt(SpareSeed, SpareSeed+SpareSeedLength-1);
]
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
61
InsertCoordinate: Inserts a coordinate at a certain level of the coordinate
cache if the age of
the previous values stored at that level has passed a certain threshold value.
Before the old
coordinate at that certain level is overwritten, is it inserted at the next
level.
void InsertCoordinate(fixedpoint x, fixedpoint y, fixedpoint z, int Level)
// Transfer current coordinate at this level
// ("Level") to next level ("Level"+1), if
// its age is equal to "TransportAge", unless
// this level is the highest level possible.
if ((CoordinateAge[Level] >= TransportAge) && (Level+1 < CacheDepth))
InsertCoordinate(xCache[Level], yCache[Level], zCache[Level], Level+1);
CoordinateAge[Level] = 0;
)
)
xCache[Level] = x; // Insert the new coordinate
yCache[Level] = y;
zCache[Level] = z;
// Increase the age counter for this level
CoordinateAge[Level]++;
CheckCoordinate: Checks if the x variable solution curve has an inflexion, for
which the sign
of the slope of the curve changes from positive to negative. If not, the
function exits.
Otherwise the function checks if an equal coordinate is stored in the
coordinate cache. If a
match is found, the function loads the spare key into the algorithm. Finally,
the coordinate is
inserted into the coordinate cache.
void CheckCoordinate(fixedpoint x, fixedpoint y, fixedpoint z)
f
1nt 1;
// If inflexion, where the slope of
// x curve changes from positive to
// negative ...
if ((x <= xOld) && (xOldOld <= xOld))
f
// Check all stored coordinates ...
for (i=O;i.<CacheDepth;i++)
f
// If match is found ...
if ((xCache[i] _= x) && (yCache[i] _= y) && (zCache[i.] _= z))
// Period is found! - Load spare key
// and reinitialize
Init128(SpareSeed);
break;
)
)
SUBSTITUTE SHEET
CA 02488514 2004-12-03
)
WO 03/104969 PCT/DK03/00375
62
// Insert the coordinate into the
// coordinate cache
InsertCoordinate(x, y, z, 0);
/J Store the x value for future comparison
xOldOld = xOld;
xOld = x;
)
Pseudo-code for stream-cipher using the Lorenz system
In this context, the modulus function, MOD, which takes an argument, q,
returns a positive
values in the range [O;q[.
The 6-variable in the Lorenz equations has been renamed to °s".
The format of the fixed-point variables are defined according to Table I.
Table I:
VariableFixed-point format
r S(7.24)
b S(7.24)
s S(7.24)
x S(7.24)
y s(~.24)
S(7.24)
The format of the temporary fixed-point variables used in the Crypt function
are defined
according to Table II.
Table II:
VariableFixed-point format
tx S(15.16)
ty S(15.16)
tz S(15.16)
dt S(12.19)
Allowed values for parameters, r, b, and s, and allowed starting conditions
for coordinates, x,
y, and z are listed in Table III:
Table III:
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
VariableAllowed value
r [1;5[
b [b+10;b+18[
s [4~b+0.5~s+12.5;4~b+0.5~s+20.5[
xa [-32;32[
Yo [-32; 32[
zo [-32; 32 [
63
Crypt: Encryption, decryption and PRNG function. Arguments are PData (pointer
to the first
byte to encrypt/decrypt) and PEnd (pointer to the last byte to
encrypt/decrypt). If the
function is intended to generate pseudo-random numbers, the function should be
given an
amount of data to encrypt (e.g. zeroes) of the same size as the requested
pseudo-random
data.
void Crypt(char* PData, char* PEnd)
I
fixedpoint dt;
While (PData <= PEnd)
// Calculation of the time step
dt = 10 * 2-11 + x MOD 2-11;
tx = s*(y-x); // Calculation of the next state
ty = x*(r-z)-y;
tz = x*y-b*z;
x = x + tx*dt;
y = y + ty*dt;
z = z + tz*dt;
// Cheek and insert the coordinate
InsertCoordinate(x, y, z, 0);
// Extract and encrypt
*PData = *PData XOR ((y*224 XOR y*216) MOD 28);
PData = PData + 1; // Increase the pointer to data to encrypt
)
)
MaskParameters: To ensure that the initial state and the parameters are valid
after loading
an expanded key or a pseudo-random sequence, the state and parameters has to
be
modified using this function. The correction is performed according to the
restrictions defined
in to ble III.
void MaskParameters()
x = x*0.25;
y = y*0.25;
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
64
z = z*0.25;
b = (b MOD 4) + 1;
s = (s MOD 8) + 10 + b;
r = (r MOD 8) + 12.5 + 2*b + 0.5*s;
)
Init192: Load a 192-bit seed (pointed to by the PSeed pointer) into the state
of the system.
void Init192(char* PSeed)
{
x = *PSeed; // Copy the seed into the state
y = *(PSeed+4);
z = *(PSeed+8);
r = *(PSeed+12);
b = * (PSeed+16) ;
s = *(PSeed+20);
MaskParameters(); // Correct the state to make it valid
)
Init128: Load a 128-bit seed (or key) (pointed to by the PSeed pointer) into
the state of the
system performing the key setup procedure.
void Init128(char* PSeed)
{
char Seed192[24]; // Allocate 24 bytes of memory
int i;
x = *PSeed; // The seed is expanded into the state
y = * (PSeed+3) ;
z = * (PSeed+6) ;
r = *(PSeed+8);
b = *(PSeed+10);
s = *(PSeed+12);
MaskParameters(); // Make state valid
// Iterate 16 rounds before extraction
Crypt(Seed192, Seed192+15);
for (i=O;a.<24;i++) // Reset the data in Seed to zeroes
Seed192[i] = 0;
// Generate 24 bytes of pseudo-random data
Crypt(Seed192, Seed192+23);
Init192(Seed192); // hoad the pseudo-random data into the state
// Iterate 16 rounds before using the
// algorithm
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
Crypt(Seed192, Seed192+15);
// Initiate the coordinate check algorithm
5 )
SetupCoordinateCheck()~
The statistical properties of the output of the system, i.e. the keystream,
may be tested
according to the NIST (National Institute of Standards and Technology) Test
Suite, cf. 'A
statistical test suite for random and pseudo-random number generators for
cryptographic
10 applications', NIST Special Publication 800-22. See also
http://csrc.nist.gov/rng/rng2.html.
The NIST Test Suite comprises sixteen different tests, which are briefly
summarized below.
The tests may for example be performed on a program similar to the above
pseudo-code for
a stream cipher using the Lorenz system.
15 The tests deliver a number of almost non-overlapping definitions of
randomness. The simpler
definitions are included below, whereas those definitions which require more
complicated
concepts from the theory of probability are referred to by the phrase "what
can be
calculated/is expected for a truly random sequence". The above NIST
publications contain the
appropriate definitions and references to works on the theory of probability.
25
Frequency monobit test: This test determines the proportion.of zeroes and ones
for the entire
keystream sequence. For a truly random keystream sequence, the number of ones
is
expected to be about the same as the number of zeros. During the test, it is
investigated
whether this property holds for the keystream sequence in question.
Frequency block test: In this test, the keystream sequence is divided into M-
bit blocks. In a
truly random keystream sequence, the number of ones in each block is
approximately M/2. If
this also characterizes the tested keystream sequence, the test is regarded as
successful.
Runs test: A run within the keystream sequence is defined as a sub-sequence of
identical
bits. The test checks for runs of different lengths, where a run of length k
is constituted by k
identical bits bounded by bits of a value opposite to the bits in the run. The
occurrence of
runs of different lengths is compared to what is expected for a truly random
sequence.
Longest run of zeroes: In this test, the sequence is divided into blocks of M
bits each, and the
longest run of ones within each block is found. The distribution of the
lengths of runs for the
blocks is compared to the distribution for blocks in a random sequence. An
irregularity in the
expected length of the longest run of ones indicates that there is also an
irregularity in the
expected length of the longest run of zeroes.
45
Binary matrix rank test: In this test, fixed length sub-sequences of the
keystream sequence
are used to form a number of matrices by colllecting M~Q bit seggments into M
by Q matrices.
By calculating the rank of these matrices, the test checks for linear
dependence among the
sub-sequences.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
66
Discrete Fourier transform test: By applying the discrete Fourier transform,
this test checks
for periodic characteristics of the keystream sequence. The height of the
resulting frequency
components are compared to a threshold defined from a truly random sequence.
Non-overlapping template matching test: When performing this test, a number of
non-
periodic m-bit patterns are defined, and the occurrences of the particular
patterns are
counted.
Overlapping template matching test: This test is very similar to the non-
overlapping template
matching test, the only differences being the structure of the pattern of m
bits, and the way
the search for the pattern is performed. The pattern of m bits is now a
sequence of m ones.
Maurer's universal statistical test: This test calculates the distance between
matching
patterns in the keystream sequence. By doing so, a measure of the
compressibility of the
keystream sequence is obtained. A significantly compressible keystream
sequence is
considered to be non-random.
Lempel-Ziv compression test: In this test, the number of cumulatively distinct
patterns is
calculated, thus providing a measure of the compressibility of the keystream
sequence. The
result is compared to a random sequence, which has a characteristic number of
distinct
patterns.
30
40
Linear complexity test: This test calculates the length of a linear feedback
shift register in
order to determine whether or not the sequence is complex enough to be
considered random.
Serial test: This test calculates the frequency of all possible overlapping m-
bit patterns across
the entire sequence. For a truly random keystream sequence, all of the 2m
possible m-bit
patterns occur with the same probability. The deviation from this probability
is calculated for
the keystream sequence in question.
Approximate entropy test: This test has the same focus as the serial test, but
with the added
feature that the frequencies of m- and (m+1)-bit patterns are calculated. The
results
obtained for the patterns of different length are compared and used to
characterize the
sequence as either random or non-random.
Cumulative sums test: In this test, the sequence is used to define a random
walk with ones
and zeroes corresponding to +1 and -1, respectively. It is determined whether
the
amplitudes of the cumulative sums of the partial keystream sequences are too
large or too
small relative to what is expected for a truly random keystream sequence.
Random excursions test: In this test, the sequence is similarly to the
cumulative sums test
transferred into a random walk. The number of visits to certain states (values
the cumulative
sum can hold), which the random walk potentially passes through, is used to
characterize the
sequence as either random or non-random. The considered states are -4, -3, -2,
-1, 1, 2, 3,
4.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
67
Random excursions variant test: Almost identical to the random excursions
test. Eighteen
states are used in this test.
For each test, a P-value, P"ai. is calculated, which provides a quantitative
comparison of the
actual sequence and an assumed truly random sequence. The definitions of the P-
values
depend on the actual test (see the NIST documentation). Values of P"a, > a
indicate
randomness, where a is a value in the interval 0.001 <_ a <_ 0.01, the exact
value of a being
defined for each test. Otherwise, non-randomness is declared.
The NIST Test Suite defines, for each test, the proportion of samples, whose P-
value should
pass the criterion P"ai > a. In all of the above tests, except the Random
excursions test, the
proportion of samples whose respective P-values, P"ai. pass the appropriate
criteria should be
at least 0.972766. For the Random excursions test, the proportion given by
NIST is at least
0.967813.
20
In preferred embodiments of the method, the following proportions are
preferably achieved,
as an average of at least 104 samples obtained by use of randomly chosen keys:
at least
0.975, such as at least 0.98, such as at least 0.985, such as at least 0.99,
such as at least
0.995, such as at least 0.998.
Possible input parameters to the NIST Test Suite are given in Table IV below
in the notation
used in the documentation accompanying the NIST Test Suite.
TABLE IV:
Name of test Input
Frequency block test m = 100
Longest run test M = 10000
Non-overlapping templates m = 9
matching test
Overlapping templates matchingm = 9
test
Maurer's universal test L = 7, Q =
1280
Serial test m = 5
Approximate entropy test m = 5
EXAMPLE II
- Table V shows the speed of encryption provided by a method as generally
disclosed
herein, cf. Figs. 1-5, as well as speeds of encryption of various known
encryption
methods. The speed of encryption provided by the methods of the present
invention was
measured in respect of an algorithm as described in M. Boesgaard, M.
Vesterager, T.
Pedersen, J. Christiansen and O. Scavenius: Rabbit: A New High-Performance
Stream Cipher,
Proceedings of Fast Software Encryption (FSE) 2003, Springer, Berlin, (2003).
The algorithm
was implemented in assembly language using MMXT"' instructions.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
68
From the measurements, the speed was calculated to be equivalent to an
encryption/decryption speed of 947 Mbit/sec on a 450 MHz Pentium III
processor.
Table V:
Name Year Type Key Block Speed Speed Memory
of size size [clocks/[Mbit/s]Requirements
intro- [bit] [bit] byte] for tables
duction etc.
[bytes]
AES/Rijndael1998 block 128-256128-25614.83 243 >256-4096
Blowfish 1994 block 32-448 64 18z 200 <5K
Present stream 128 - 3.7 947 60
Method
DES 1975 block 56 64 45~ 80 >256
IDEA 1992 block 128 64 50~ 72 >12
Panama 1998 stream 256 - 6.71 537 >1092
RC4 1987 stream 32-2048- 7z 514 >256
SNOW 2000 stream 128-256- 6.54 554 1024
SOBER-t32 2000 stream 128 - 214 171 ?
Speed is estimated from different sources. The superscripts in the "Speed
[clocks/byte]"
column of Table V refers to the below source references:
1. Crypto++ 4.0 Benchmarks, www.eskimo.com/Nweidai/benchmarks.html,
MS C++ (Intel Celeron 850MHz), available on 6 June 2003.
2. Bruce Schneier et al.: Fast Software Encryption: Designing Encryption
Algorithms for
Optimal Software Speed on the Intel Pentium Processor.
3. Kazumaro Aoki et al.: Fast Implementation of AES Candidates (128 bit keys,
128 bit
blocks, Pentium II).
4. Performance of Optimized Implementations of the NESSIE Primitives (version
2.0),
http://www.cosic.esat.kuleuven.ac.be/nessie/ available on 6 June 2003 (Pentium
III numbers
are used).
In general, speed and memory can'be traded for many of the implementations,
e.g. by using
lookup tables which require more memory but may save processing time.
End of Example II
When performing computations on numbers expressed as binary numbers, for
example when
adding or multiplying two numbers, it may be possible to omit parts of the
computations
involved in addition or multiplication, if bits of a number resulting from the
addition or
multiplication may be omitted or disregarded. Thus, if the least significant
bits of the
resulting number are not necessary or if the most significant bits of the
resulting number
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
69
may be disregarded (which may be the case in a pseudo-random number generator,
where
what is needed is not the true result of the computations but merely a pseudo-
random
number), the least and/or most significant bits of the resulting number need
not be
computed.
Thus, a method for performing mathematical operations on integer numbers of a
certain bit
width which is larger than the register width of the processing unit on which
the
computations are performed is disclosed. Mathematical operations or
computations on fixed-
point numbers are performed as integer operations, whereby the integer numbers
are
expressed as binary numbers. The binary representation of integer numbers
requires a
certain register width, e.g. 32 bit. When performing mathematical operations,
such as
addition or multiplication, by means of a processing unit having a register
width which is
smaller than the width required for representation of the binary numbers, e.g.
8 bit, the
binary numbers may be split into a plurality of binary sub-numbers, each
represented by a
width equal to or smaller than the register width of the processing unit.
Thus, two 32 bit
numbers may be split into two sets of four 8 bit sub-numbers, and
multiplication or addition
may be performed on the 8 bit sub-numbers by means of an 8 bit processing
unit. For
example, addition of a number
A = 11011001101101010110101010110111 and a number
B = 10000111011110111111010101001001
to achieve a result R=A+B may be performed by performing the following steps:
1. Each of the numbers A and B is split into four sub-numbers, A1, A2, A3, A4,
and B1, B2,
B3, and B4. A1 represents the 8 most significant bits of the number A, and A4
represents
the 8 least significant bits of the number A, etc. Thus, in the example shown
above, the
sub-numbers are:
A1=11011001
A2=10110101
A3=01101010
A4=10110111
B1=10000111
B2=01111011
B3=11110101
B4=01001001
2. The least significant sub-numbers, A4 and B4 are then added: R4=A4+B4. Any
carry
resulting from the addition of A4 and B4, C4, is stored.
3. The second least significant sub-numbers, A3 and B3, and the carry from
step 2 above,
C4, are then added: R3=A3+B3+C4. Any carry resulting from this addition, C3,
is stored.
4. Addition of A2 and B2 in a way analogous to step 3, to achieve R2 and C2.
5. Addition of A1 and B1 in a way analogous to steps 3 and 4 to achieve R1.
Any carry
resulting from this addition, C1, is regarded as overflow and is not taken
into
consideration.
6. The number resulting from the addition of A and B is stored as four sub-
numbers, Ri, R2,
R3 and R4, and/or represented by a 32 bit wide string built from the sub-
numbers R1,
R2, R3, and R4.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
In case not all bits in a number resulting from a multiplication operation are
to be used in
further computations, and/or in case not all bits are significant for the
further computations
and may be disregarded, processing time in connection with multiplication
operations on a
processing unit having a register width smaller than the bit width of the
numbers to be
5 multiplied may be reduced by performing only partial multiplication as
explained below. For
example, multiplication of two 16 bit numbers, D and E, wherein
D = 1101100110110101 and
E = 0110101010110111
on an 8 bit processing unit to achieve a 32 bit number, F, may be performed by
the following
10 steps:
1. Each of the numbers D and E are split into two sub-numbers, D1, D2, and E1,
E2. D1
represents the 8 most significant bits of D, D2 represents the 8 least
significant bits of D,
etc. Thus, in the example shown above, the sub-numbers are:
D1=11011001
15 D2=10110101
E1=01101010
E2=10110111
2. D1 is multiplied with E1 to achieve a 16 bit number expressed as two 8 bit
numbers, G1
and G2.
20 3. D1 is multiplied with E2 to achieve a 16 bit number expressed as two 8
bit numbers, H1
and H2.
4. D2 is multiplied with E1 to achieve a 16 bit number expressed as two 8 bit
numbers, I1
and I2.
5. D2 is multiplied with E2 to achieve a 16 bit number expressed as two 8 bit
numbers, J1
25 and J2.
6. The resulting 32 bit number F is expressed as four 8 bit numbers, F1, F2,
F3, and F4,
wherein:
F4=J 2
F3=H2+I2+J1
30 F2=G2+H1+I1+[any carry resulting from the calculation of F3]
F1=G1+[any carry resulting from the calculation of F2],
as illustrated in Fig. 19 wherein MS denotes "most significant 8 bit" and LS
denotes "least
significant 8 bit".
Processing time may be saved by disregarding F4, i.e. the least significant
bits of the number
35 resulting from the multiplication, and by disregarding J1 in the addition
which leads to F3.
Thus, the multiplication of D2 with E2 at step 5 may be omitted, whereby less
mathematical
operations are performed, which leads to saving of processing time. This
omission has an
impact on the computational result which, however, may be acceptable if the
omission is
performed consistently throughout the computations in, e.g. a pseudo-random
number
40 generator, e.g. in an encryption/decryption algorithm, and if it is
performed both in
decryption and encryption. It should usually be ensured that properties of the
mathematical
system, e.g. chaotic behavior, which are of importance in the context in
question, e.g.
encryption/decryption, are maintained in spite of the impact which the
omission of one or
more computational steps has on the computations.
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
71
There is further provided a method of performing multiplication operations on
a first binary
number and a second binary number. The method comprises summing a number of
intermediate results, whereby the sum of the intermediate results is equal to
the product of
the two numbers. Each intermediate result is achieved as the product of one
single bit (1 or
0) of the first number and the entire second number, a, whereby the product
and thus the
intermediate number may be determined by a simple "if...then" algorithm and/or
a logical
AND operation, as the product of 1 ~ a = a, and as the product of 0 ~ a = 0.
Subsequent to computing the intermediate number, the intermediate number is
shifted a
number of positions to the left, the number of positions corresponding to the
position of the
bit of the first number from which that particular intermediate number is
calculated.
Alternatively, either the second number or the particular bit of the first
number is switched to
the left. Accordingly, the step of multiplying one bit of a first one of the
two numbers is
repeated for each bit of the first number. For example the product of a first
number, 0110,
and a second number 1010 is computed as follows: the least significant bit of
the first
number, 0, is multiplied with the second number 1010 to obtain a first
intermediate number,
0000. Then, the second least significant bit of the first number, 1, is
multiplied with the
second number and shifted one position to the left to obtain a second
intermediate number,
10100. Then, the third least significant bit of the first number, 1, is
multiplied with the
second number and shifted two positions to the left to obtain a third
intermediate number,
101000. Finally, the most significant bit of the first number, 0, is
multiplied with the second
number and shifted three positions to the left to obtain a fourth intermediate
number,
0000000. The resulting number is obtained as a sum of the four intermediate
numbers, as
illustrated below, the underlinings indicating which bits are being multiplied
in the individual
steps:
0110 1010 -~ 0000 (first intermediate
number)
0110 1010 -~ 10100 (second intermediate
number)
0110 1010 ~ 101000 (third intermediate
number)
0_110 1010 0000000(fourth intermediate
-+ number)
Result: 0111100 (sum of intermediate numbers)
Fig. 28 illustrates a further mathematical system which may be employed in the
methods of
the present invention. A set of five coupled subsystems is provided, wherein
the subsystems
are one-dimensional maps. Three of the maps contain static parameters and two
of the maps
are influenced by a counter. The system configuration is illustrated in Fig.
28.
The iteration scheme of
the system is defined
by the following equations:
xo,~+~ _ ~(xo,i + po ) mod 1
mod 1~ + 2xo,i + kx4,1
xl,i+1 = ((xl,i + co,i mod 1
) mod 1~ + 2X1,, + kxo,i
xz,i+1 = ((xz,i + pl ) mod 1
mod 1~ + 2xz,; + kxl,l
x3,1+1 - \(x3,1 + Cl,i mod 1
) mod 1~ + 2x3,1 + kxz,i
x4,i+1 - ((x4,i + p2 ) mod 1
mod 1~ + 2x4,1 + kx3,1
SUBSTITUTE SHEET
CA 02488514 2004-12-03
WO 03/104969 PCT/DK03/00375
72
where x",; is the state variable of system n at iteration i, po,p1 and pz are
static parameters,
co,; and cl,; are counters. The coupling is unidirectional with coupling
strength k. Values in the
interval (0;1[ may be assigned to the parameters po,P1 and p2. The counters
co,; and cl,;, cycle
through the interval [0;1[ by increments which are a fraction of 1. The
increments of co,;and
cl,; need not be identical. The counters may be incremented independently of
each other. In
another embodiment, a first one of the counters is only incremented when a
second one of
the counters reaches a certain value. A first one of the counters may be
incremented in each
iteration, whereas a second one of the counters may be incremented only when
the first one
reaches its maximum. Alternatively, both counters may be incremented in each
iteration, or
they may be incremented in an alternating way, so that the first counter is
incremented in
every second iteration and the second counter is incremented in those
iterations where the
first counter is not incremented.
SUBSTITUTE SHEET