Note: Descriptions are shown in the official language in which they were submitted.
CA 02488871 2004-11-26
SYSTEM, METHOD AND COMPUTER PROGRAM FOR OPTIMIZATION
IN DIGITAL SUBSCRIBER LINES FOR MULTI-USER SPECTRUM
BALANCING
Background
Numerous digital communication networks and related systems (or "digital
communication systems") are known that include copper wiring. The copper
wiring
typically consists of twisted pairs (also known as "loops" or "lines"). Such
digital
communication systems include, for example, DSL, but also ISDN, HDSL, ADSL,
VDSL, and Local Area Networks such as Ethernet. These systems commonly include
a transceiver of some type (such as a modem) that connects a computer (such as
a
personal computer) to the digital communication system. The transceiver
generally
also incorporates copper wiring.
The copper wiring (such as in telephone lines) is often bundled to provide
service to
one user, or to permit service to multiple users over the copper wiring.
Communication over the digital communication system in such situations,
however, is
often negatively affected by well known factors such as "crosstalk", which
refers to
interference caused by the electromagnetic coupling between neighbouring pairs
of
copper wire. Crosstalk affects the signal carried across the copper wire pair.
Another problem with the current multiple user digital communication systems
is
power control. In a typical interference limited digital communication system,
each
user's performance depends not only on its power allocation, but also on the
power
location of all other users.
Also, demand for higher data rates is increasing, and digital communication
systems
are moving toward higher frequency bands, where the crosstalk problem is more
pronounced. Accordingly, spectral compatibility and power control are
important
issues in the design and deployment of such digital communication systems. In
particular, power allocation in this context requires not only for the total
amount of
power allocated for each user to be optimized, but also the power allocation
for each
user in each frequency to be optimized. This is particularly the case, in VDSL
CA 02488871 2004-11-26
2
systems where interference from a transmitter that is closer to the central
office can
overwhelm the signal at a transmitter that is farther from the central office,
when
communication is attempted with the central office from the farther
transmitter.
Numerous prior art solutions have been devised for addressing the aforesaid
problems. One category of such solutions involves the control of physical
layer
signals by a single service provider (whether central or by means of
distributed
control linked to the single service provider) for the purpose of coordination
of
transmitted signals in manner that favours optimal service over the digital
communication system.
United States Patent Application No. 2003/0086514 A1, assigned to The Board of
Trustees of the Leland Stanford Junior University ('514) discloses a dynamic
spectral
control method commonly known as the iterative water-filling process.
Specifically
I 5 'S 14 describes a method whereby a central office collects information
regarding the
line, signal, and interference characteristics for each of a plurality of
communication
lines; a model is created for such line, signal and interference
characteristics; signals
between transmitters and receivers are synchronized; and signals are processed
using
the model to remove interference from such signals. A particular method and
related
algorithms for enabling the foregoing are also described in '514.
One of the disadvantages of the '514 solution is that the particular methods
described
for controlling the interference affecting signals in a digital communication
system is
that the data transmission rates that are provided by the solution described
in '514 are
less than optimal.
Another prior art solution generally known as "optimal spectrum balancing" is
described in a prior publication "Optimal Multiuser Spectrum Management for
Digital
Subscriber Lines", authored by R. Cendrillon, M. Moonen, J. Verliden, T.
Bostoen,
and W. Yu, published in the Proceedings of the 2004 IEEE International
Conference
on Communications, 20-24 June 2004. The particular methods described in this
publication for achieving spectrum balancing are relatively difficult to
implement in a
digital communication system environment because such methods are difficult to
deploy in a computationally efficient way.
CA 02488871 2004-11-26
3
What is required therefore is a system, method and computer program for
spectrum
balancing in an interference-affected digital communication system that
provides
improved data transmission rates and is computationally efficient to deploy,
especially in multi-user digital communication system environments.
Summary of the Invention
The present invention relates to a method, and a system and computer program
for
deploying the method, for dynamically optimizing digital communication systems
such as a DSL system. In an embodiment of the present invention, the
optimization
method enables the efficient maximization of the joint transmission rates of
multiple
DSL lines in a DSL bundle subject to a total power constraint for each line.
A method for optimal spectrum balancing is provided that consists of iterative
per-
tone optimization, whereby each user iteratively optimizes a joint objective
function
by operation of Lagrange multipliers. Specifically, a g function
(particularized
below) is iteratively evaluated by approximation.
Also, a method for dynamically optimizing a digital communication system (such
as a
DSL system) is provided, the method including the steps of (1) applying a dual
optimization method (i.e, that updates the dual variables) for mufti-user
orthogonal
frequency-division multiplex systems, such as the particular subgradient
method
described below, and (2) applying the iterative method of the present
invention that
involves the evaluation of a function g (particularized below) by
approximation.
It should be understood that other dual optimization methods can be used in
(1) such
as an ellipsoid method or an analytic centering cutting plane method.
The maximization problem (in the course of optimization) can take various
forms,
including but not limited to the formulation in equations (12) and (21)
described
below. The optimization method described in this invention can be realized in
a
computationally efficient way.
CA 02488871 2004-11-26
The update in accordance with (1) can be done on all dual variables at the
same time,
or the update can be done on a subset of variables at a time. In the
subgradient
method, described in one particular embodiment of the present invention, the
subgradient update equation (10) described below may be used with a wide range
of
step sizes. In one implementation of the update equation, the step size s' in
step l is
chosen to be equal to an arbitrary constant divided by a number equal to l
raised to kth
power, where k can take values such as'/z, 1, 2 or other values.
Exact evaluation of g in (2) above is generally computationally prohibitive.
One
particular method for approximate evaluation is described below under the
heading
"Iterative and Near-Optimal Spectrum Management". This method is iterative and
it
enables g to be evaluated approximately with a lower complexity as compared to
an
exact evaluation.
In another embodiment of the present invention, the optimization.methods of
the
present invention enable the optimal usage of the frequency spectrum among the
upstream and downstream transmissions of multiple DSL lines in the same
bundle. A
detailed description of this aspect of the invention can be found below under
the
heading "Optimal Frequency Planning".
ZO
In yet another embodiment of the present invention, the optimization method of
the
present invention enables the optimal usage of mufti-user crosstalk
cancellation units.
A detailed description of the related methods is provided below under the
heading
"Partial Crosstalk Cancellation in Vector DSL".
Brief Description of the Drawings
The present invention can be readily understood by the following detailed
drawings:
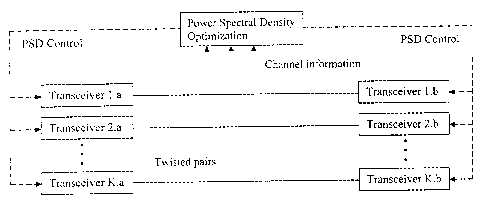
Fig. 1 is a schematic diagram of a set of twisted pair telephone lines
controlled by a
power spectral density optimization unit.
Fig. 2 is a graphical depiction of the power spectral density control method.
This
provisional patent covers methods to evaluate dual function g (~,,, ~,2, ...,
~,K), such as
CA 02488871 2004-11-26
the iterative method described, and methods to update dual variables (~,,,
~.2, ..., ~.K)
such as the subgradient method described herein.
Fig. 3 illustrates time-sharing property implies zero duality gap.
Fig. 4 illustrates rate region for the two-user ADSL lines.
Fig. 5 illustrates topology of the two-user ADSL lines.
Fig. 6 illustrates loop topology for two downstream ADSL users.
Fig. 7 illustrates rate region for two downstream ADSL users.
Fig. 8 illustrates OBS (left) and IOSB (right) power spectral densities for
two
distributive ADSL users at equal rate. Power spectral densities for both CO-
based
(top) and RT-based (down) lines are plotted.
Fig. 9 illustrates loop topology for 10-User VDSL.
Fig. 10 illustrates rate region for upstream for 10-User VDSL.
Fig. 11 illustrates loop topology for 5-User VDSL.
Fig. 12 illustrates rate region for 5-User full duplex VDSL.
Fig. 13 illustrates downstream (top) and upstream (bottom) power spectral
densities
for 5-user full duplex VDSL at equal rate. The power spectra depend on the
ordering
in iteration in IOSB. Downstream-upstream order is on the left, and the
upstream-
downstream order is on the right.
Fig. 14 illustrates power spectral densities for 10-user full duplex VDSL at
maximum
minimal rate.
CA 02488871 2004-11-26
In an orthogonal frequency-division multiplex (OFDA~I) system, the frequency
domain is partitioned
into a large number of tones. Data transmission takes place in each tone
independently. The overall
system throughput is the sum of individual rates in each frequency tone. The
design constraints
are typically linear but coupled across all the tones. The design problem
involves the optimization
of the overall performance subject to design constraints. For example, the
optimal bit and power
allocation problem is often formulated as follows. Let H(n), P(n) and N(n)
denote the channel
frequency response, the transmit power spectral density and the noise power
spectral density at tone
n, respectively. The optimization problem is:
N P{r)Hz(n.)
maximize ~ log Cl + N(n) ~ (1)
n=1
N
subject to ~ P(n) < P
n=1
P(n) > 0.
The above problem has a well-known solution called "water-filling" . Efficient
solution exists in this
case because the objective function is concave in the optimizing variable
P(n).
However, not all optimization objectives are concave. The multiuser bit and
power allocation is
such an example. In this case, several OFDM transmitters interfere with each
other, and the sum
rate rnaxirnization problem becomes:
x ~' Pk(n)H~~(n)
rnax ~ ah ~ log 1 +
k=i n-r N(n) + ~~~k H~~(n)P~(n)
N
s.t. ~ P,~(n) < Pk ~ = 1, . . . , h' (2)
P,~(~z) > 0, k; = 1. . . . K
where H~,~(n) is the channel transfer function from system j to system ~: in
tone n, Pk(r) is the power
allocation for user k; in tone n, each user has a separate power constraint.
Because the objective
function is not concave in Pk(~a), the optimization problem is difficult to
solve. Previous approaches
(e.b. itc;rative water-filling) us<-a Io;uristics to c'lerivc: suboptimal
solutions.
In a prior work. an exact. "Opt.imal Spectrum Balancing" algorithm to solve
this problem was
proposed by Cendrillon. et, al. Tl-ie basically idea is as follows. Forrn the
Lagnangian of the optimization
CA 02488871 2004-11-26
problem (2):
x N Pk(n)Hkk(n)
max aK ~ ~ log 1 + N(rt) + ~~~k H ~(n)P~ (n)
K N
+ ~ ~,~ (Px - ~ Pk(n)1
k=I \ n=I /
s.t. I'k(-n,) > 0, k: = 1. . . . , K.
Solve the Lagrangian for each set of positive and fixed (.~I; ~ ~ ~ , ~K).
Then, the solution to the
original pr oblenl may be found by an exhaustive search over the a-space. ,>,k
is increased or decreased
depending on whether ~n I Pk(rr,) is greater or less than Pk. When the process
converges, either
ak = 0 or ~n I Pk(n) = Pk for each k. In this case, the Lagrangian objective
is identical to the
original objective, thus solving tile original problem.
This Lagrangian approach works because of the following. First, for a fixed
ak, the objective
decouples into N independent problems corresponding to the N frequency tones.
Thus, solving the
dual problem requires a much lower computational complexity as compared to the
original problem.
Second, .~k represents the price of power for user k. A higher price leads to
a lower power usage.
Thus, as a function of .~k, the optirTlal ~~ r Pk(n) is monotonic in ~k. An
exhaustive search over the
~-space can then be perforn ued using bisection on each .~k. This is
essentially an exhaustive search
over all power usages. It leads to tine global optimum regardless of whether
the original problem is
convex. However, with K users, K loops of bisections are involved, one for
each ak. Therefore, the
cornputat,ional complexity of optimal spectrum balancing, a,ltlnough linear in
N, is exponential in I~C.
~'l%llerl the rmmber of users is large, the complexity becomes prohibitive.
Tllis invention eliminates the exponential complexity in Lagrangian search,
and generalizes the
algoritl-un for other optimization problems in rnultiuser OFDA1 system design.
Toward this end, we
show that true optimal spectrum balancing algorithm belongs to a class of dual
optimization methods.
Contrary to genes al non-convex problems, the duality gap for rnultiuser OFDM
optimization always
tends to zero as the number of frequency tones goes to infinit~~ regardless of
whether the optimization
problem is convex. This approach leads to more efficient ~-search methods.
Further, we show that
the general tl-leory is applicable to many other areas of OFDM systerrl
design. Optirrlal frequency
planning a.nd optimal cornplexit.v a,lloca,t,ion in vectored digital
subscriber line systems are some
of these examples. In true second part of this invention, we further reduce
the complexity of the
CA 02488871 2004-11-26
q
optimization method by near-optimal methods for spectrum balancing.
I. Dual Optirrrization Methods
A. Duality Gap
Consider an optimization problem in which both the constraints and the
objective function consist
of a large number of individual functions. corresponding to the N frequency
tones:
N
maximize ~ f~(xn) (4)
~.=r
N
subject to ~ hn(xn) < P,
n=r
where fn(~) is a scalar function which is not necessarily concave, and h~(~)
is a vector-valued function
that is not necessarily~ convex. P is a vector of constraints. Also, there may
be other (possibly integer)
constraints irxrplicit in the problem. The idea of the dual method is to solve
(4) via its Lagrangian:
N N
L(:L~, ~) _ ~.ln(~r~) -E- ~T ' P - ~ I~,n(a;n)
~.=1 n=r
where .~ is a vector, and "~'' denotes vector dot product. Note that the
Lagrangian decouples into
a set of N smaller problems, so optimizing the Lagrangian is much easier than
solving' (4). Define
the dual objective g(~) as the solution to the following:
g(a) = max L(x.~, .~) (6)
~n
The dual optimization problem is:
minimize g(~) ( r )
subject to .~ > 0.
When fn(x~) is concave and h.,~(x~) is convex, standard convex optimization
results guarantee that
tire primal problerrr (4) acrd the dual problem (7) have the same solution.
When convexity does not
bold, the dual problerrr provides a solution wlniclr is an upper bound to tire
solution of (4). Tlue
upper bound is not always tight, and the di$~erence is called the "duality
gap''.
In multiuser OFDI\~I design, convexity often does not. hold. However, it is
usually the case that.
the following ''tune-sharing" proper ty is satisfied:
CA 02488871 2004-11-26
Definition 1: An optimization problem of the form (4) satisfies the time-
sharing property if the
following holds: Let xn and y~ be optimal solutions to the problem with P = P~
and P = Py,
respectively. Then, for any 0 < v < 1, there exists a set of zn such that ~n
h~,(z~) < vP~+(1-v)Py,
and ~ f~.(zn) ~ v ~ fn(xn) + (1 - v) ~ fn(yn)~
This property is clearly satisfied if time-division multiplexing may be
implemented. (Throughout the
document, the channels are assumed to be time invariant.) The frequency tones
can then be assigned
to x~ for v percentage of the time and y~ for (1 - v) percentage of the time.
In practical OFDM
systems in which channel conditions in adjacent tomes are similar and there
are a large number
of frequency tones. the time-sharing property can be satisfied with frequency-
sharing. This is true
because time-sharing can be approximately implemented by interleaving x~ and
y~ in the frequency
dorrrain. As N --> oo, frequency-sharing is equivalent to time-sharing.
Note that the concavity of fn(x~) and the convexity of h~(x,~) and all other
constraints imply
time-sharing but not vice versa. Time-sharing is alwa.~~s satisfied regardless
of convexity as long as
N is sufficiently large and f,~ ~ ~ ~ fn.,.~ are sufficiently similar for
small values of k (and likewise for
Icn - ~ ~ )a.~+~.) This is the case in almost all OFDM systems as the
subchannel width in OFDM systems
is chosen so that. tine channel response in adjacent subchannels are
approximately the same.
The main result of this section is that the tune-sharing property implies that
the duality gap is
zero. Specifically, if an optimization problem satisfies the time-sharing
property, then it ha,s zero
duality gap, i.e. the primal problem (4) and the dual problem (7) have the
same solution.
The proof of tloe above result is previously known if (4) is convex. Fig. 3
illustrates the proof when
convexity does not hold but time-sharing does. The first diagram illustrates a
function that satisfies
the tune-sharing property. The solid line plots the optimal (~ Iz~ (xn), ~
f.~(xn)) as the constraint P
varies. The intersection of the curve with the vertical axis where ~ hn(x~) =
P is the optimal value
of the primal objective. Clearly larger P leads to higher objective value, so
the curve is increasing.
More importantly, the curve is concave because of the time-sharing property.
Now, consider a fixed
tangent, line with slope ~. By the definition of L(~, x~,), the intersection
of the tangent line with
the vertical axis is precisely g(.~). This allows the minimization of tlne
dual problerrr to be visualized
easily. As a varies, g(.1) achieves a minimum at. exactly the rnaxirrmrn value
of the primal objective.
Thus, the duality gap is zero. (The second diagram illustrates a case where
time-sharing property
does not 1-~old. In this case, the minimum g(~) is strictly larger tluan the
maximum ~ fn(x~).)
CA 02488871 2004-11-26
~1
~ f,c~.~) 5lape=a
. a~
gca) ,,
.:, I. = s,
P ~ h~aT;,)
P
~ h" ~x;~)
Fig. 3. Time-sharing property implies zero duality gap.
The main consequence of the above result is that as long as the time-sharing
property is satisfied,
even a non-convex optimization problem can be solved by solving its dual. The
dual problem is
typically much easier to solve because it usually lies in a lower dimension.
~rther, g(a) is convex
regardless of the concavity of f~(x~). (This is because L(x~, ~) is linear in
~ for each fixed xn, and g(~)
is the maximum of linear functions and is therefore convex.) Tlnus, any
gradient-based algorithm
is guaranteed to converge. Note tluat the optimization of g(~) requires an
efficient evaluation of
g(.~). This usually involves an exhaustive search over the primal variables.
However, as g(a) is
unconstrained and it decouples into N independent sub-problems, such an
exhaustive search is much
more manageable.
B. Dual ll.~Ietluods
The optimal spectrum balancing algorithm solves L(xn, a) exhaustively for all
possible values of a.
The multiuser spectrum optimization problem (2) consists of K constraints, and
successive bisection
on each component of a would yield the primal optimum. The main innovation of
this invention is
that we can take advantage of the duality relation and solve the dual
objective g(.~) instead. By
using am cHicicnt search of ~, the computational efficiency of the optimal
spectrum balancing can
be improved drastically.
The main difficulty in deriving an efficient direction for ~ is that g(~) is
not necessarily
CA 02488871 2004-11-26
differentiable. Thus, it does not always have a gradient. Nevertheless, it is
possible to find a search
direction based on what is called a subgradient. A vector d is a subgradient
of g(~) at ~ if for alt a'
Subgradient is a generalization of gradient for (possibly) non-differentiable
functions. Intuitively, d
is a subgradient if the linear function with slope d passing through (.~,
g(.~)) lies entirely below g(~).
For g(.1) defined in (6), the following choice of d
N
d=p-~hn(xn)
".=r
satisfies the subgradient condition (8). The subgradient search suggests that
~ should be increased
if ~,~ 1 h.~(xn) > P and decreased otherwise. Here, ~ represents a price for
power. Price should
increase if the constraint is violated. In fact, ~ updates can be done
systematically. The following
update rule
~t+r - ~t _ St p _ ~ ~"~(x~,) (10)
is guaranteed to converge to the optimal .~ as long as st is chosen to be
sufficiently small. Here,
st is a scalar. In one implementation of the update equation, the step size st
may be chosen to be
equal to an arbitrary constant divided by a number equal to l raised to kth
power, where k can take
values such as 0.5, 1, 2 or other values. Or, st may be chosen to be a.
sufficiently small constant.
The above update is called the subgradient method.
The search of optimal ~ can also be dOlle uslllg ellipsoid method, where the
search for the a is
done using an ellipsoidal search. The search of optimal a can also be done
using analytic center
cutting plane method, or a combination of above methods.
By the result described previously, the minimum g(~) is also equal to the
maximum ~ ,/',~(xn).
Thus, the solution to the dual problem immediately yields the optimal solution
to the original
problem.
The crucial difference between the update equation (10) a,nd that suggested by
Cendrillon is that
( 10) updates all components of ~ at the same time. Instead of doing bisection
on each component
individually, the subgradient method collectively finds a suitable direction
for all components of ~
at once. This eliminates the exponential complexity in ~-search.
CA 02488871 2004-11-26
t3
However, note that the evaluation of g(~) is still exponential in K. This is
probably inevitable if an
exact solution to the non-convex optimization problerrr is desired. For
practical problems, however,
sub-optimal rrrethods in evaluating g(a) often exist.
II. Applications
A. Multiuser Spectrum Management
VVe now return to the rrrultiuser optimal spectrum management problem. In
digital subscriber line
applications, electromagnetic coupling induces crosstalk between adjacent
lines. The goal of optimal
spectrum management. is to find a set of power allocations (Pr(n), ~ ~ ~ ,
PK(n)) so that a target
rate-tuple is satisfied. There is generally a trade-off between the achievable
data rates of different
users. Such a trade-off can be represented in a rate region defined as the set
of all achievable rates
(Rr, ~ ~ ~ , Rx). When the channel transfer function is a slow varying
function of n, the spectrum
optimization problem satisfies the time-sharing property.
In this section, we formulate a novel optimization problem that characterizes
the boundary of the
rate region. The objective is the nraxirnization of a base rate R subject to a
fixed ratio between Rk and
R. for each k, = 1, ~ ~ ~ , K. More, specifically, we rnay insist that Rr : RZ
: - ~ - : RK = ,fir : ,~2 : - : ~jx,
where
Pk (n) Hkk(n)
Rk _ ~ log 1 + N(n) + ~~~k H ~(n)P~(n) ' (11)
Then, the maximization problem becomes
ma,x R (12)
s.t. Rk > RkR
N
~'k(~-) < Pk, k = l, . . . , K
n=r
pk(n) >_ 0, ~; = 1. . . . h-
Here, the variables ~jk directly represent the ratios of service rates among
the diff~ererrt users.
The dual function for (12) can be written as follows:
9(wr, ~ . . , ~K~ ~1. . . . , ,~K) - max (13)
P," R
h x N
R+~~k(Rk-~kR)+~~k Pk-~pk(~Z)
k=1 k=r n=r
CA 02488871 2004-11-26
s
v- a - ~ -6 OSM - FWI Lagranpien Search
8 v d OSM - Reducs0 Compexiry Search
q B- Itaralive Waler-Fix
\ \G
G
N 0.
D
o b .
y b
1 2 3 4 5 8 7 8 5
User t ADSI Downsueam Rats (MDps)
Fig. 9. Rate region for the two-user ADSL lines
I OK feet
CO RT
7K feet
I OK feet
Fig. 5. Topology of the two-user ADSL lines
Collecting terms, we see that the maxirr>ization involves a term (1 -
~Wk,3k)R. Since R is a free
variable to be optimized, the maximization leads to R = oo if (1 - ~ wk~ik) >
0 and R = 0 if
(1 - ~ wk~3k) < 0. Thus, non-trivial solution exists only if (I - ~ wk,Qk) =
0.
It. is now straightforward to apply the technique developed in the previous
section to derive a
subgradient search for the minimization of g(wl, ~ - ~ , wx, ~1. - ~ ~ , ax).
The idea is the following. First,
solve the maximization problem ( 13) for a fixed set of (wl, - - - , wK. y . -
- - , .fix) with ( 1-~ wk,Qk) = 0.
This is done using exhaustive search in each tone separately and it yields a
set of power allocation
Pk(~n.) and achievable rates R.k. The maximum R can be found as R = mink
Rk/,Cjk. The subgradient
method can now be used to update wk and .~k:
wok ] - [wk - Sk (Rk - ~kR~,+ (14)
N +
t~ ~' - ~ pk(n)
n=7
'dote that the new wk may no longer satisfy ~ wk~k = 1. Renormalization is
needed to project wk.
CA 02488871 2004-11-26
back to the proper subspace
~~+i
~c+i - W k . (16)
~k ~~~ la~
As long as s~ and t~ is suf~cicntly small. the subgradient algorithm is
guaranteed to converge. This
sub-gradient algorithm improves the computational complexity of the optimal
spectrum balancing
algorithm described by Cendrillon. No bisection is needed. The number of times
that g(wk, J~~) is
evaluated is polynomial in K.
Note that the evaluation of g(wk, ~,~), if done exhaustively, still has a
complexity exponential in K.
However, for the spectrum optimization problem, experimental results suggest
that lower complexity
search algorithms often work well. Fig. 4 shows the rate region for a two-user
ADSL system with
a configuration shown in Fig. 5. Both the full implementation of optimal
spectrum balancing and
a reduced complexity gradient search are shown. Their performances are very
similar, and both
outperform iterative water-filling significantly.
B. Optimal Frequency Planning
The optimal spectrum balancing algorithm is 'applicable to many other areas of
OFDM system
design. For example, in a wireless multiuser OFDI\~Z system, different users
are often allocated to
different sets of tones. The optimal power and bit allocation problem is
essentially the spectrum
management problem (12) with an additional constraint that only one user
occupies each tone:
Pk(n)P~(n) = 0 tlk ~ 7
Previous solutions to tluis problem rely on a relaxation of the non-convex
constraint. As Theorem
1 in Section II slows. this problem can instead be efficiently solved in the
dual domain. The same
subgradient, updates as in the previous section apply here. The constraint,
P~(n)P~(n) = 0 for all k~
and .j is incorporated in tlue evaluation of the dual function. Theorem 1
guarantees that. the dual
solution is identical to the primal solution.
In fact. the complexity of this problem is strictly sub-exponential. The
evaluation of the dual
g(~,~~,, ~k) involves an exhaustive search in It possible power allocations.
Its complexity is therefore
linear in li .
CA 02488871 2004-11-26
C. Partial Crosstalk Cancellation in Vector DSL
Future digital subscriber line applications are expected to implement
crosstalk cancellation and
precoding to further improve the data rates in twisted-pair transmission.
Multiple transmitters and
multiple receivers at the central office can be regarded as a single entity.
Crosstalk cancellation can
be done in a similar way as echo cancellation.
A typical DSL bundle consists of 50 to 100 twisted pairs. Cancelling all
crosstalk involves 50 x 50
to 100 x 100 matrix processing, which is beyond the computational complexity
constraints of current
digital signal processors. On the other hand, in a 50-pair DSL bundle each
twisted-pair has only
a limited number of nearest neighbours. Thus, we expect that the cancellation
of only a few pairs
would achieve most of the benefits. Furthermore, crosstalk is frequency
dependent. The crosstalk
level is low in low frequency bands, so cancellation in these frequency bands
has limited utility. On
the other hand, in very high frequency bands, the data rates are already
small. Thus, data rate
improvement due to crosstalk cancellation is most noticeable in the mid-
frequency range.
Given a complexity constraint, how to choose the best combination of lines and
tones in which
to implement crosstalk cancellation is an interesting problem. This problem
was previously solved
by greedy algorithms. However, the greedy solution assumes a fixed transmit
spectrum level. In this
section, w~e formulate a more realistic problem that jointly performs
line/tone selection and spectrum
optimization.
The basic setup is the same as the optimization problem (12) except the
evaluation of Rk now
takes the following form:
R,~ _ ~ log 1 + N(7i) + ~i~k G.ik(n)1'~(n) . (17)
where G~~(n) = Hkj(n) except where crosstalk cancellation takes place, in
which case G~~(n) = 0.
The total number of places where G,~~ (n) = 0 represents the number of
crosstalk cancellation units
that can be implemented. Tluis number is typically constrained by an
implementation limit. More
formally,
~r
1{Hkj('~»G'kj(~.)1 C C (18)
n=1 k~7
where 1{1 is an indicator function and C is a constant representing the
complexity constraint over
all tones and all users.
CA 02488871 2004-11-26
Clearly (17) rrray be solved using the dual formulation. The complexity
constraint is the same as
the power constraints. As long as exhaustive search within each tone can be
done with manageable
complexity, the optimization over tire N tones only adds a polynomial factor.
III. Brief Summary of the First Part of the Invention
The main result in the first part of the invention is that many optimization
problems in OFDM
design can be decoupled in a tone-by-tone basis via the dual method. It is
shown that the time-sharing
property is always satisfied when the number of tones is large, and when the
time-sharing property
is satisfied, the duality gap becomes zero r egar Bless of whether the
original problem is convex. This
observation leads to efficient dual optimization techniques such as the
subgradient method. As long
as the evaluation of the dual objective for each tone may be done with
manageable complexity, the
entire problem may be solved efficiently. This principle is applicable to a
wide range of OFDM design
problems. Multiuser spectrurrr optimization, frequency planning and line/tone
selection in reduced
complexity crosstalk cancellation are some of these examples. In the second
part of this invention,
methods for evaluating the dual objective is described in more detail.
IV. Low Complexity Spectrum Balancing AMethods
In a digital subscr fiber line system, rnult.iple copper pairs are bundled
together. The electromagnetic
coupling b~aval<-x:n t1 : coppc;r pairs eaizsc.s crosstallc interference,
whicIu leas long been idr~utified as tlm
primary source of line impairment in DSL deployments. Current DSL systems use
a static spectrum
management (SSM) approach where a fixed transmit power spectral density is
applied for each line
regardless of the loop topology or user service requirements. The performance
projection under SSM
is based on tire levels of worst-case crosstalk interference.
Future generation of DSL services are envisioned to utilize d5-namic spectrum
management (DSM).
DSM gives each line an ability to adapt to its loop environment and service
requirements, and it leas
the potential to drastically improve the achievable r a,tes and ser vice r
anges of current DSL systems.
The crosstalk problem is the most severe when the channel transfer functions
are heavily
unbalanced. This is the situation in downstream ADSL systems where a remote
optical network unit.
(ONL:) is deployed (ONLT is usually located much closer to the customer
premise modems served
from the central office) and in upstream VDSL systems where some of the
upstream transmitters may
CA 02488871 2004-11-26
be much closer to the central office than others. Power back-off methods are
traditionally applied in
these cases.
Digital Multi-tone (DMT) is the modulation format used in almost all digital
subscriber line
standards. In a DMT system, the frequency spectrum is divided into many
parallel subchannels.
Different amount of power and different number of bits can be assigned in each
subchannel. This
gives DSL applications great flexibility in performing spectrum optimization.
In particular, spectral
shaping may be done in a tone-by-tone basis for each line individually.
However, precisely also
because of this flexibility, the number of variables in a spectrum
optimization problem is the product
of the number of users If and the cumber of frequency tones N. Further, the
objective function
in the spectrum optimization problem is non-convex. Thus, a brute-force search-
based optimization
has a computational complexity that is exponential in KN, which is
intractable.
Iterative water-filling is one of the first low-complexity spectrum
optimization techniques that. takes
advantage of the ability for DSL modems to perform spectral shaping. In the
iterative water-filling
algorithm, each user iterativeiy maximizes its own achievable rate by
performing a single-user water-
filling with the crosstalk interference from all other users treated as noise.
The single-user water-filling
process is a convex optimization process and has a complexity of O(N log(N)).
Thus, each iteration
of the iterative water-filling process has an O(KN log(N)) complexity.
However, the iterative water-
filling process does not seek to find the global optimum for the entire
binder. Instead, each user
participates in a non-cooperative game, and the convergence point of the
iterative water-filling
process corresponds to a competitive equilibrium. Although not optimum; the
iterative water-filling
algorithm has been shown to significantly outperform static spectrum
management schemes. Further,
iterative water-filling can be implemented distributively.
Recently. Cendrillon proposed an optimal spectrum balancing (OSB) algorithm
which finds the
true global optimal solution to the spectrum optin uization problem. The OSB
algorithm transforms
the spectrum optimization problem into the dual domain by forming the
Lagrangian dual of the
primal optimization. As pointed out earlier, the class of spectrum
optimization problems for digital
subscriber lines has the special property that the primal and the dual
optimization problems yield
the carne solution even when the primal problem is non-convex. As the dual
problem has a much
lower dimension; the computational complexity of solving the dual problem is
much lower. It. can
be shown that the OSB algorithm has a computational complexity that is linear
in the number of
CA 02488871 2004-11-26
frequency tones N. The optimal spectrum balancing algorithm can provide a
significant performance
improvement as compared to iterative water-filling.
However, the computational complexity of the optimal spectrum balancing (OSB)
algorithm,
although linear in N, is still exponential in the number of users h'.
Implementation experience
shows that the complexity of the OSB algorithm becomes unmanageable when the
number of users
in the binder is larger than two.
The main objective of this part of the document is to describe an appropriate
middle ground
between iterative water-filling and optimal spectrum balancing. The goal is to
take advantage of
both the dual formulation of the optimal spectrum balancing algorithm and the
competitive (thus
low-complexity) nature of iterative water-filling. Toward this end, this
document proposes an iterative
spectrum balancing technique that achieves almost all the gain of optimal
spectrum balancing while
having a computational complexity that is comparable to iterative water-
filling.
The computational methods proposed here has a wider irnplicatio~ beyond that
of DSL
applications. The optimal power and bit loading problem for wireless
orthogonal frequency-division
multiplex (OFDM) systems leas been extensively studied in the past. A low-
complexity near-optimal
solution to this class of long-standing problems can lead to many other
applications.
V. System Model
The achievable data rates in a K-user DMT-based DSL system are computed as
follows:
N
Rk = T ~ b~ (19)
n=1
where k is the user's index, n is the tone's index, N is the total number of
frequency tones, T is
the symbol period. bk denotes the achievable bit rate for user k in tone n,
and it is computed as
n
b~ = Iog2 1 -I- . ~ Sk n n (20)
~k + ~i~k ai,k'~i
where Sk is the transmit power for user k in tone n, Qk is the normalized
channel noise for user k
in tone n, and ai k is the normalized crosstalk transfer function from the ith
user to the kth user
in tone n. Channel noise and crosstalk transfer function are normalized by T/
~Hk ~z, where r is the
SNR gap for the system and ~ Hk ~2 is the kth user's direct channel transfer
function in tone n..
The spectrum optimization problem in a multiuser DSL system is formulated as
the maximization
CA 02488871 2004-11-26
of a weighted sum rate of all participating users subject to power constraints
K
max ~ wkRk s.t. Pk < Pk dk (2I)
Si ,...,SK -
k=1
where Pk is the kth user's power constraint. The weights wk > 0 are chosen so
that ~~ 1 wk = 1.
The total power used by user k is computed as
N
Pk = Of ~5,~. (22)
~,=i
Here ~ f is the frequency width of the DMT tones. The weights {w1, w2, . . . ,
wK~ are the priority
put on the users.
In a two-user system, (21) reduces to
rnax mRl + (1 - m)R2 s.t. Pk < Pk b'k: (23)
si~S2
By varying w between 0 and 1, an achievable rate region can be generated.
VI. Optimal Spectrum Balancing
The main idea of the optimal spectrum balancing (OSB) is to solve the
constrained optimization
problem (21) in the dual domain. Instead of an exhaustive search over all
possible bit allocations and
over all frequency tones, the optimal spectrum balancing algorithm fixes dual
variables (.~I, ~ ~ ~ , ax),
corresponding to each of the K power constraints, and forms the dual objective
function:
9(~i, ~ . . ~ ~K)
K K
- max ~ mkRk - ~ ak(Pk - Pk)
{s; ,...,sxln ~ km k=~
m N K nr
- max ~ wk~b~ -~~k ~Sk -Pk
{Si ,...,Sj~}~ i k-1 ~=1 k=1 n-1
N K K
- ~ max ~ (u~kb;~ - ~kS~ ) '+ ~ akPk~ (24)
n n
n-1 S~ ,...,Sly k_1 k=1
Note that the evaluation of g(~1, ~ ~ ~ ; ~K) is now decoupled in a tone-by-
tone basis. Therefore, if B is
the maxirrmrn number of bits that can be loaded in each tone, the evaluation
of g(~1, ~ ~ ~ . aK) requires
O(.NBK) operations. Although still exponential in K, this is nevertheless a
significant computational
saving as compared to the O(BI''f~) operations needed for an exhaustive search
over all frequency
CA 02488871 2004-11-26
a~
tones.
In the first part of this invention, we showed that even when the original
problem (21) is a non-
convex optirrrization problem, the dual objective is always convex. Further,
the minimal value of
9(~r, ~ ~ ~ , ax) over all positive a's is equal to the optimal solution of
(21):
x
min g(~r, . . . ~,K) = rrrax ~ wkRk. (25)
~1,... ,aK s; ,...,sK
k=1
This crucial observation enables a subgradient search method to be implemented
for the spectrum
optimization problem. In particular, the number of subgradient steps needed to
reach a global optimal
solution is a polynomial function of the number of dimensions, which is K.
The above statement is rrreaningful, however, only if the function g(al, ~ ~ ~
,.1K) can be evaluated
efficiently. Unfortunately, as seen in (24), the evaluation of g(~r, ~ ~ ~ ,
fix) is exponential in K.
Therefore, the evaluation of g(~r, ~ ~ ~ , aK) is the computational bottleneck
of the optimal spectrum
balancing algorithm. Computational experience shows that optirrral spectrum
balancing algorithm is
impractical when the nurrrber of users is larger than two.
VII. Iterative Near-Optimal Spectrum Management
The main innova.t.ion of this part of the invention is an efficient algorithm
that enables g(ar, ~ ~ ~ , fix)
to be approximately evaluated with a complexity that is linear in li . Recall
that the evaluation of
9(~r, ~ ~ ~ , fix) involves the tone-by-tone optimization of the following
function:
K
maxn ~ (wkb~ - ~kS~ ) ~ max h(S~ , . . . SK) (26)
s; ,...,sK k_r s; ,...,sK
Our main idea is that the optimization of h(Si ; ~ ~ ~ , SK) may be done in an
iterative water-filling
fashion via coordinate descent. For each fixed set of (~1, ~ ~ ~ , .fix), our
proposed approach first finds
the optirrral S~ while keeping S2 . ~ ~ ~ ; SK fixed, then optimizes S2
keeping all other S~ fixed, then
S3 . ~ - ~ . S'~ , tluen S~ , S2 . ~ ~ ~ , and so on. Such an iterative
process is guaranteed to converge because
each iteration strictly increases the objective function. The convergence
point is guaranteed to be
at Ieast a local maximum for h(S~ , ~ ~ ~ , Sk ).
This new aL~proach differs from iterative water-filling im the following two
kev aspects. First..
unlike the iterative water-filling algorithm where each user maximizes its own
rate in each step
of the iteration, the above algorithm optimizes an objective function drat
includes the joint rates
CA 02488871 2004-11-26
a~
of all users. Thus, the new algorithm has the potential to reach the social
optimum. Second, the
power constraint in the iterative water-filling process is handled in an ad-
hoc basis, while the new
algorithm proposed here dualizes the power constraint in an optimal fashion.
The correct values
of the dual variables are then used in a sub-gradient search. We called this
approach the Iterative
OSB (IOSB) algorithm. The performance of the IOSB algorithm is near-optimal as
compared to the
optimal spectrum balancing method.
The computational complexity of this new iterative approach is significantly
Lower than that of
optimal spectrum balancing (OSB) algorithm proposed in. In the evaluation of
h(Si , ~ ~ ~ , S~ ), each
iteration has a computational complexity that is linear in K. Let Ti be the
number of iterations
needed in the evaluation of each h(Si , ~ ~ ~ , Sk ). Let T2 be the number of
subgradient updates
needed in the optimal spectrum balancing algorithm. The total computational
complexity of IOSB
is O(TiT2BNK). Computational experience suggests that Tl and T2 are not strong
functions of N
and K. The overall complexity is therefore approximately linear in K. This is
significant as K may
be large in realistic DSL deployment scenarios. Table I summarizes the
computational complexity
comparison. (Here, T3 is the number of iterations needed in iterative water-
filling.)
Algorithm Computational Complexity
Exhaustive Search O(B )
Optimal Spectrum Balancing_
O(T1NB )
Iterative OSB O(T1T2BNK)
Iterative ~'~~ater-FillingO(T3KN log(N))
TABLE I
Computational Complexity Analysis
VIII. Performance Evaluation
This section shows drat the proposed iterative algorithm has a near-optimal
performance as
compared to optimal spectrum balancing. This is verified with extensive
simulation. In the following
simulation, all DSL lines are 26-AWG twisted pairs with a background noise
level of -140dBm/Hz.
Users are assumed to be symbol synchronized so that the sidelobe interference
is not in effect. Also.
no spectral masks are enforced.
CA 02488871 2004-11-26
12k feet
3k feel
Optical FILer
RT
CO
13k feet
Fig. 6. Loop Topology for Two Downstream ADSL Users
A. 2-User ADSL Downstream
The first set of simulations examines a 2-user ADSL downstream distributive
environment with both
users having a loop length of 12k feet and with a crosstalk distance of 3k
feet. No other disturbers
are assumed to exist in the binder. The loop topology is shown in Fig. 6. Such
a distributive
environment is expected to benefit significantly from dynamic spectrum
management because of
its highly unbalanced crosstalk channels. The power constraint for each user
is set to 20.4dBm as
defined in the ADSL standard. For fair comparisons, the number of iterations
and initial ~ settings
are identical for OSB and IOSB in simulations.
Fig. 7 shows the achievable rate regions of OSB, IOSB, iterative water-filling
and static spectrum
management algorithms. As can be seen in the figure. the rate regions for OSB
and IOSB are almost
identical to each other. Both outperform iterative water-filling
significantly. Interestingly, although
the a.clrievable rates of OSB and IOSB are identical, the optimal spectra
obtained from the two
algorithms can be different. Fig. 8 shows the downstream spectra obtained from
the two algorithms.
The frequency band belowr 38UkHz is shared by both direct channels for
downstream transrrrission,
and all tones that are beyond this range are occupied by a single user only.
The frequency division
multiplex (FDM) is optimal because of the strong far-end crosstalk (FEXT)
generated by the RT
modem. The main difference between the spectra of OSB and IOSB is in the FDM
region. Both power
spectral densities (PSDs) essentially achieve the same rates because many
equivalent permutations
of frequency tones in the FDM regions are possible.
B. 10-user VDSL Upstream
The next set of simulations examines a 10-user VDSL upstream environment with
two loop lengths:
five; linc;s are at 2kft acrd the other five are at 4lcft. All twisted pairs
are connected to tire same
Central Office (CO) as shown in Fig. 9. The 998 frequency ba.ndplan is used in
the simulation with
the upstream bands at 3.75MHz to 5.2>\MHz and 8.2MHz to l2MHz. The power
constraint on each
CA 02488871 2004-11-26
a~
osa
P
I ~r
IOSB
-!
.~,~,r IWF
T .
.
SSM
1
1
1
1
1
a
1 .
1
1
Z 1 ..
.
O i
1
1
1
1
~ z a a s
s
GO User Downstream
Rele (MOps)
Fig. 7. Rate Region
for Two Downstream
ADSL Users
.,~ _"
I_ c ~..,I t_ Cou.~
P
.m ~ -p° I
a az o.v o.e , a ~~ o o.l a3 oe , is t..
.,aw~,nwer .wwtwu~
.b
- onu u..:
i- ow, i
.b _b
a ..1
a 03 0A Pe , t3 a o 0.1 O~ i ,3 a
w~weYIMW I t.ywq.nwlYl
Fig. 8. OS$ (left) and IOSB (right) power spectral densities for two
distributive ADSL users at equal rate. Power spectral
densities for both CO-based (top) and RT-based (down) lines are plotted.
co
141an
Fig. 9. Loop Topology for IO-User VDSL
line is Il.5dBm. Again, as shown in Fig. 10. the rate region achieved by IOSB
algorithm is almost
identical to that achieved by OSB.
CA 02488871 2004-11-26
per
v ,s
. ...
a
a i2
x
8
y
0 0.5 7 1.5 2 2.5 3 J.5 4 4.5
4k /eel Users UpSUeam Rare (MCpa)
Fig. 10. Rate Region for Upstream for 10-User VDSL
C. 5-user VDSL F1r11 Duplex
The current VDSL standard uses a fixed frequency bandplan (i.e. 998) to
separate upstream and
downstream. This is not optimal because no overlapping of upstream and
downstream transmissions
is allowed. In this set of simulations, we explore the achievable rate-region
and the optimal power
allocations with overlap spectra for full duplex transmission in a VDSL
environment. The simulation
setup consists of 5 users with the same Loop length (3k feet long) in the same
binder. As the loop
characteristics for the five users are identical, this is essentially a two-
user scenario between upstream
and downstream. Perfect echo cancellation is assumed. The near-end crosstalk
(NEXT) is modelled
in addition to the far-end crosstadk (FEXT). The downstream transmission has a
power constraint
of 11.5dBm, and the upstream transmission has a power constraint of 14.5dBm,
in accordance to
VDSL standard.
Fig. 12 shows the achievable rate regions obtained from the OSB and IOSB
algorithms, As can
be seen, the performance of IOSB is very close to that of OSB, although IOSB
is clearly a sub-
optimal algorithm. Furthermore, it observed that the solution provided by IOSB
is not unique.
The non-uniqueness of this algorithm is exposed by choosing a different order
of users during the
iteration procedure in IOSB. IOSB gives slightly different rate regions for
different iteration orders.
Interestingly, no particular order has a rate region that is completely
superior to the rate regions
of all other orders. In addition, as seen in PSD plots ordering affects the
power spectral densities
as well. Fig. 13 shows the PSD pairs corresponding to the downstream-upstream
ordering and the
CA 02488871 2004-11-26
3k feet
CU Users' Terminals
Fig. 11. Loop Topology for 5-User VDSL
~ iOSB
~ iOSB
v~
E 25 ~7~
~'
~ 20 ~.
N
15 , ~ "
\W
\.\ a
\.\
0
0 5 10 15 20 25 30 35 40 4;
VDSL DownsW am Rate (Mbps)
Fig. 12. Rate region for 5-User Full Duplex VDSL
Algorithm Downstream Upstream
Rate Rate
IOSB (Down-Up)23.87Mbps 23.67Mbps
IOSB (Up-Down)23.93Mbps 23.87Mbps
OSB 29.71\Mbps 29.7A~Ibps
TABLE II
Mlaximum Equal Rate for 5-User Full Duplex VDSL
upstrearrr-downstream ordering. As can be seen, a narrow low frequency
spectrum is always shared
by both directions. In tire high frequency range, frequency-division duplex
(FDD) separates the
upstream and the downstream. FDD is optimal in the high frequency range
because of the strong
NEXT interference. Interestingly, if the downstream-upstream ordering is used
in IOSB, the resulting
frequency division follows an Up-Down-Up pattern. The situation is completely
reversed when the
upst.rearn-downstream ordering is used. Tyre upstream-downstream ordering
produces a FDD solution
that. follows Dowrr-Up-Down pattern.
CA 02488871 2004-11-26
a~-
_ oe
,
a
o ~ .,m
,bu i m . i i "~~ n . i i i
- o x . . rs ,. a n a x . a rs a n a
w.w.~.r,~i ~.a.~wn~r
~.m.a
,-w. of i-w. vm,
b p
.m ~ .,m
a x ~~ ~ a ,x a ,a ,a o x . a rs ,e ,e ,e
..a.~w,rem...~"vra,
Fig. 13. Downstream (top) and upstream (bottom) power spectral densities for 5-
user full duplex VDSL at equal rate. The power
spectra depend on the ordering in iteration in IOSB. Downstream-upstream order
is on the left, and the upstream-downstream
order is on the right.
D. 10-user VDSL Full-Duplex
In this final set of simulations, we explore the full duplex transmission of a
10-user VDSL scenario
with the same topology as in Fig. 9, but allowing overlapping spectra. Perfect
echo cancellation is
again assumed. The OSB algorithm is not computationally practical in this
case.
Table III compares the performance of the proposed IOSB algorithm with that of
iterative water-
filling (IWF). Iterative water-filling is able to support a minimal data rate
of 12.2A~Ibps, while IOSB
is able to achieve at least 15.2Mbps. A minimum gain of at least 2.8Mbps is
possible.
The power spectral densities obtained from the IOSB algorithm are shown in
Fig. 14. Interestingly,
a shall low frequency band is shared by all four transmitters with full duplex
operation. In the
middle frequency band, frequency-division mutiplex (FDD) separates upstream
and downstream
transmissions of the 2kft and 4kft users. The high frequency band is used
exclusively by the 2kft
lines. Again, frequency division duplex (FDD) is used there. This type of
optimal spectrum usage
is non-obvious and is channel and user data rates dependent.
'I~ansmitter IOSB IWF
4k ft Downstream15.2Mbps12.2Mbps
4k ft Upstream15.2Mbps12.4Mbps
2k ft Downstream21.8Mbps12.7Mbps
2k ft Upstream25.2Mbps12.5Mbps
TABLE III
INaximum Aiinimum Rate for 10-User Full Duplex VDSL
CA 02488871 2004-11-26
a$
-2p
-40 - -
4k
tt
Users
Downslnam
.
_-g0
~o-g0
~(700
p720
6740
0 8 10
2 g 12
4 14
-20 Fr
ra
-4p- - -
2k
tt
Users
DownshHm
B
_gp
-BO
rt00
ft720
f~tao
0 s t0
2 a t2
a to
1
a ~
-40 -
-60 4k
0
users
U
slrsam
~
-80
700
720
laO
D g 10
2 8 12
4 14
f, Fr
-20 wnc -
-40 M 2k
- tt
Users
U
Uwm
D g 10
2 B t2
4 to
Frpwncy
(MHy
Fig. 14. Power spectral densities for 10-user full duplex VDSL at maximum
minimal rate
IX. Summary of the Second Part of the Invention
The second part of the invention comprises of low-complexity and near-optimal
spectrum balancing
algorithm for digital subscriber line applications. As compared to previous
optimal spectrum
balancing methods, the new algorithm offers a significant complexity
reduction. The complexity
is reduced from an exponential complexity in the number of users to a linear
complexity. The rrrain
idea of tl-le algorithm is an iterative evaluation of the Lagrangian function
in the optimization step.
Simulation results show that the performance of the new algorithm is very
close to that of the
optimal algorithm. The proposed iterative algorithm is a. significant step
forward in making optimal
spear unr balancing practical.
The proposed iterative algorithm has a wider implication beyond that of
digital subscriber lines.
The proposed algorithm can be easily applied to the adaptive bit, power and
subcarrier allocation
problems for wireless applications whenever multiuser orthogonal frequency
division multiplex
(OFDM) is used.