Note: Descriptions are shown in the official language in which they were submitted.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
METHODS, TILES AND BOARDS FOR
PLAYING GAMES THAT SCHEMATIZE
COMPETITIVE YET NON-COMBATIVE
ECOLOGICAL PROCESSES, INCLUDING
MULTI-GENERATION GAMES OF STRATEGY
AND TERRITORY OCCUPATION PLAYED WITH
PROGRESSIVELY SIZED TILES
ON GEOMETRIC GRIDS
COPT'RIGHT NOTICE
A portion of the disclosure of this patent document contains material which is
subject to
copyright protection. The copyright owner has no objection to the facsimile
reproduction by
anyone of the patent document or the patent disclosure, as it appears in the
Patent and
Trademark Office patent file or records, but otherwise reserves all copyright
rights whatsoever.
In particular, the graphics, designs and layouts of game elements, names, and
rules of play for
the various embodiments disclosed herein, including 2"0" are, in addition to
any patent rights,
also covered by copyright and/or trademark. Permission to copy those materials
is solely limited
to their use in conjunction with the lawful distribution of this patent
document and all other
rights, including their publication and use as or with games, are xeserved.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
2
BACKGROUND OF THE INVENTION
FIELD OF THE INVENTION
Generally, the .instant invention relates to strategy board games that
schematize
competitive, yet non-combative, ecological or biological processes, including
a preferred
embodiment which comprises a mufti-generation game of strategy and territory
occupation, played
with tokens on a gridded board. Here generation means a level or phase of play
where a
particular set or sets of tokens are utilized.
DESCRIPTION OF RELATED ART
The instant invention has been made in the general realm of games; however, it
is a game
of strategy, as opposed to games such as sports (e.g., baseball, basketball,
football ar tennis)
video action games or games of skill (e.g., Doona or Pacnaan) physical games
(e.g., jacks or
Twister) or role playing games (e.g., Pokenion or Dungeons and Dragons).
Further, it is a board game, as opposed to other strategy games such as those
utilizing
cards (e.g., Gin., Poker or Mille Bornes) or tiles. (e.g., Mah .long). Note
that as used in
conjunction with Mala Jong, the word "tiles" refers to solid pieces with
symbols that are
comparable to playing cards. However, as used in conjunction with this
application, the word
"tiles" is generally synonymous with game pieces, markers or tokens, such as
those used in chess,
checkers, etc.
More particularly, the instant invention is a board game of territory
occupation, as opposed
to theme games (e.g., Monopoly or Careers) or games of position and
rearranging pieces (e.g.,
checkers, chess or backgammon).
However, unlike games such as Risk, or other tactic ~ strategy war simulation
games, the
instant invention is generally played on a geometric grid and, thus, has most
in common with
games such as 'go' and Othello (Reversi).
There are also some similarities with the game Cathedral, in as much as that
game does
use pieces of several shapes; however, that game only has a single generation,
and the pieces are
not used in the same way as with the instant invention.
Unlike 'go', in which stones are placed at grid intersections, with the
instant invention,
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
3
tiles are placed within the grid's squares (or, whatever grid units are used).
(Note, it is possible
to construct versions of the instant invention, where the game pieces are
played at intersections,
which are the equivalent or 'dual' - in the sense of graph theory - of the
embodiments
described herein. However, for clarity, these variations will not be further
described herein.)
Further, unlike any game currently known to inventor, with the instant
invention, pieces
(also called tiles, tokens or markers) at different generations of play are of
different sizes and/or
configurations - generally, progressively larger - and are replaced by each
other. That is, the
tiles are geometrically distinct and successively played, as opposed to
different types of pieces
in other games which are generally played during the same phase of the game,
Different pieces
in games like chess have completely distinct functions, and are not replaced
by larger pieces; nor
is 'kinging' a checker like the use of alternative tiles in the instant
invention. Even with those
games that do use pieces of different sizes or values, the pieces are not used
as in the instant
invention. For example, in Risk - in order to save space on the board and the
number of pieces
needed to play - 10 small cube-like pieces representing 1 army each can be
replaced by a single
loaf like piece, approximately twice the volume, representing 10 armies.
Similarly, in Monopoly,
after purchasing four houses on a property, you can trade them (and additional
cash) in for one
slightly larger hotel piece. These represent different amounts of military
strength or monetary
value, not geometric territory and, as will be seen, the configuration and use
of distinct types of
tiles in the instant invention is quite different.
The intended practitioner of the present invention is someone who is skilled
in designing,
implementing, building, creating, printing or publishing board games; or,
programming computer
versions of such board games. That is, one skilled in the art required to
practice the instant
invention is capable of one or more of the following: design, graphics
production, printing,
publishing and/or construction of game boards, pieces and/or packaging; or,
programming
computer simulations of such games.
The details of accomplishing such standard tasks are well known and within the
ken of
those skilled in those arts; are not (in and of themselves, except where
noted) within the scope
of the instant invention; and, if mentioned at all, will be referred to but
not described in detail
in the instant disclosure.
Rather, what will be disclosed are novel configurations of boards and pieces,
and move
algorithms or rules of play.
In summary, the disclosure of the instant invention will focus on what is new
and novel
and will not repeat the details of what is known in the art.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
4
BRIEF SUMMARY OF INVENTION
As stated, the instant invention has most in common with the extant games 'go'
and its
simplified cousin Othello (itself a commercial version of the classic
Reversi). However, those
games, as well as chess and many other games, are metaphors for, or schematics
of, war; and,
play is combative, with opponents attacking or capturing each other's pieces
or positions.
In contrast, games based upon the instant invention are competitive, yet not
combative.
The mechanism for success, generally (a few specific embodiments aside), is
not battle with, or
decimation of, the enemy but, rather, fitness (expressed as strategy and
tactics of taking, releasing
and re-takilig space) to expand into unoccupied areas better, or faster, or
more stably, than the
competition.
Further, the basic idea of a main class of embodiments is to provide a
'schematic version
of what happens as single-celled organisms, over multiple generations, become
larger and more
complex, and compete with each other for biological niches 'and resources
(SPACE).
Briefly, in a preferred embodiment of a version of the game called 2"0 - short
for
BINARY (base ,~) EVOLUTION - a three (or more) generation (or phase, or level)
game of strategy
and territory occupation is played on a 7x7 (or larger, for more than three
generations) grid of
squares. During a first generation, players (usually two but, optionally,
more) alternate placing
1x1 unit-square game pieces (of a different color for each player) into
unoccupied spaces on the
grid, until substantially all territory is occupied; in the two-player game,
one space is left open.
During the second generation, order of play is reversed. The pieces put into
play are now
larger - 2x1 - and are placed on any two adjacent unoccupied squares, either
horizontally or
vertically. Each player, in turn: a) removes one lxl piece of their own color;
b) places as many
laxger 2x1 pieces as possible of their own color into adjacent pairs of
unoccupied spaces; and,
c) removes a smaller 1x1 piece of their own color. Players alternate these
three-step moves until
no more smaller pieces are on the board.
During the third generation, order of play is again reversed. The pieces put
into play are
now larger still - 2x2 - and are placed on any 2x2 cell of adjacent unoccupied
squares. Each
player, in turn: a) removes one 2x1 piece of their own color; b) places as
many larger 2x2 pieces
as possible of their own color into unoccupied 2x2 cells; and, c) removes a
smaller 2x1 piece of
their own color. Players alternate these three-step moves until no more
smaller pieces are on the
board. In the embodiment just described, at most nine 2x2 pieces can be fit on
the board (usually,
it is nine, but some placements of pieces can lower this amount) and, thus,
with two players a
tie, while possible, is rare.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
Optionally, additional generations are played with progressively larger tiles
alternating
between the 'brick' and square configurations.
After the final generation, the player with the. most pieces/terntory wins.
Figure 16 depicts a more general flow diagram of the preceding algorithm,
comprising
a functional specification from which to program the algorithmic control
portion of a computer
simulation of the game. Methods for creating other portions. of such a
program, for example
display of graphic representations and GUI implementation, are well developed
and well known
to those skilled in the programming arts.
BRIEF DESCRIPTION OF DRAWINGS
Figure 1 depicts a 7x7 square grid board suitable for playing some embodiments
of the
instant invention.
Figure 2 depicts seven progressively sized pieces suitable for playing some
embodiments
of the instant invention and, in particular, 2~0.
Figure 3 depicts additional size-3 pieces suitable for playing additional
embodiments of
the instant invention.
Figure 4 depicts additional size-4 pieces suitable for playing additional
embodiments of
the instant invention.
Figure S depicts additional preferred 45° angled pieces suitable for
playing additional
embodiments of the instant invention.
Figure 6 depicts additional 'oddity' 45° angled pieces.
Figure 7 depicts use of additional preferred 45° angled pieces.
Figure 8 depicts board layouts with markings suitable for playing additional
embodiments
of the instant invention.
Figure 9 depicts marked tiles and grid squares suitable for playing additional
embodiments
of the instant invention.
Figure 10 depicts two-colored pieces, and alternatively shaped pieces,
suitable for playing
additional embodiments of the instant invention.
Figure 11 depicts a board on which the first three generations of the basic
game 2"o are
played by placing markers at the center, edges and corners of the grid's unit-
squares. Such
markings permit playing with (nearly) uniformly sized tokens.
Figure 12 depicts how the scheme of Figure 11 can be generalized to a fourth
generation
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
6
in three dimensions; and to.four and one dimensions as well.
Figure 13 depicts a board with irregular and discontinuous areas suitable for
playing
additional embodiments of the instant invention.
Figure 14 depicts a board inscribed with square grids of three resolutions.
Figure 15 depicts board and tiles with examples of 'colonies'.
Figure 16 depicts a flow diagram of the moves for the first and subsequent
generations
for the basic preferred embodiment of the instant invention.
Figure 17 depicts an additional tile set with "L" units.
Figure 18 depicts a board with grid units composed of equilateral triangles.
Figure 19 depicts tiles suitable for playing on the board of Figure 18. ,
Figure 20 depicts a grid with two types of unit squares.
Figure 21 depicts tiles suitable for playing on the board of Figure 20.
Figure 22 depicts grids comprising multiple shapes, and appropriate game
tiles.
Figure 23 depicts a three-dimensional board and pieces for an alternative
embodiment.
Figure 24 depicts a more general three-dimensional board and pieces.
Figure 25 depicts a device to randomize player order.
Figure 26 depicts a single set of elements to construct both board and tiles.
DETAILED DESCRIPTION OF PREFERRED EMBODIMENTS
WITH REFERENCE TO THE DRAWINGS
J3ASIC GAME: The instant invention, generally, relates to strategy board games
that schematize
competitive, yet non-combative, ecological or biological (or even societal or
cultural, including
economic or political) processes, including but not limited to, a preferred
embodiment comprising
a mufti-generation game of strategy and territory occupation, played on a
grid. During a first
generation, players alternate placing game pieces, generally one grid unit in
size, into unoccupied
spaces on the grid, until substantially all territory is occupied. During
successive generations
progressively larger game pieces are used and players alternate moves
consisting of: a) removing
a smaller piece of one owns color; b) placing as many larger pieces as
possible of one owns
color; and, c) removing a smaller piece of one owns color. Players alternate
these three-step
moves until no more smaller pieces are on the board. After each generation: a)
the order of play.
is reversed (1608, 1631); and, b) the pieces that were put down in the
previous generation
become the 'small' pieces to be picked up in the upcoming generation, and
still larger pieces are
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
7
selected to be the ones to be put down (1631 ). After the final generation,
the player with the most
pieces on the board, or territory, wins.
STRATEGIC STRUCTURE: A key element of this preferred embodiment that enhances
'playability',
is the structure of the three-part move. In an alternative embodiment, in
generation two and
beyond, the game is played by picking up a small piece and then, if possible,
putting down a
large piece. Since the default opening of generation two (with two players) is
one space open,
the first player will pick up an adjacent small piece, thereby create a 2x1
hole, and then take it.
There will then be no open space. The second player will pick up one small
piece and have no
space to place a large piece. This set of circumstances will repeat, almost
always, and the first
player will obtain virtually all territory in generation two. Therefore (at
least on the average) two
small pieces must be removed for each turn permitting a large piece to be
placed.
The previously disclosed three-part move will be referred to as "up down up"
("UDU").
Two alternatives are: both removals precede the placement ("UUD"); or, both
follow ("DUU").
Although any of the three will work, UDU is preferable because it provides a
good balance
between offense and defense, while UUD is primarily offensive and DUU is
primarily defensive.
That is, a removal prior to placement is offensive in that the player attempts
to open a (best) hole
for themselves to occupy; and, a removal subsequent to a placement is
defensive in that the
player attempts to avoid providing any similar (or, at least, only to provide
the strategically
worst) opportunity for their opponent(s). With UDU each move comprises both
elements.
Further, with ULTD many moves will comprise picking up two adj acent pieces of
one's
own color and immediately filling the vacated space. The players do not fully
interact
strategically until a relatively few scattered small pieces remain.
Additionally, if a situation
develops where a player has no alternative but to pick up two non-adjacent
pieces, because there
are no two adjacent pieces of their own color, then it is highly likely that
the opponent will be
able to pick up two of their own pieces, one next to each just vacated, and
take two larger pieces
of territory. The first player is then in the same position on the next turn.
This is an unstable
situation that will then to lead to lopsided and, thus, unsatisfying games.
Similarly, with DUU many moves will comprise picking up two pieces from within
occupied territory so that no holes develop that are large enough for the
opponents) to occupy
with a large piece. It is only after the board becomes 'swiss cheese' that the
players fully interact
strategically, and that large enough holes are open to take territory with
large pieces. Again, at
that point, the game tends to become unstable and cascade in favor of a first
player, when their
opponent is forced to vacate pieces that connect individual holes into a large
size area. The first
player fills that area and, likely, can also create a situation where they can
(more) safely perform
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
8
their removals. The opponent, then, is often put in the same bad position
repeatedly.
Thus, , UUD and DUU each, in their own way, provide games that tend to spiral
out of
control for one player or the other; and, the winning strategy is based on
factors that are often
tiny andlor hard to comprehend (a'la the butterfly effect of chaos theory)
and; most likely, not
intended on the part of the winner. Such games may be exciting. However, this
inventor believes
that games which are stable and balanced, and are won by carefully considered
strategy and
astutely executed tactics, are ultimately much more satisfying. That is, this
is especially so as one
gains understanding (for example, the strategic significance of edges,
corners, arid 'safe' positions
where a tile of one's own color is surrounded left, right, top. and bottom by
one's own color or
'edges), develops skill and sees their game improve. Further, such well-
balanced games exercise
logical thinking, attention, visualization, planning and imagination.
Providing these experiences
as an absorbing and open-ended challenge (especially in a face-to-face
physical format) provides
,educational and social benefits to children too often exposed to solitary
electronic pastimes.
.Recently, chess has been offered to some students as a way to develop
cognitive skills and self
esteem. However, chess is .a fairly complex game with a substantial learning
curve; and, in some
circles, it has a bit of an 'egghead' taint. 2"o has neither of these
problems, and has been tested
with children as young as six, who are able to play and comprehend the rules
and basic strategy
of the game by the second game they play. Finally, it is suggested that the
"competitive, yet non-
combative" paradigm of games employing the instant invention, provides an
ethically distinct, and
arguably preferable, model for children to emulate, when compared to the
schematic "war" that
characterizes games such as chess, checkers, 'go', Othello, Stratego,
Battleships, Risk, etc.
~ther optional variations on these strategic structures are practiced, to take
into account
other playing sequences of tiles, or for other reasons. For example, if (201)
tiles are used in
generation one and (302) tiles in generation two, an UUDU or UDUU structure
will balance the
1:3 area ratio of these two tiles. Similarly, if (201), (203) and (205) square
tiles are used in the
first three generations, structures with 4 Us and 1D, for example UUDUU, will
balance the 1:4
area ratio between successive square tiles. In general any structure of the
form Xuydzu with
removals on both sides of a potential placement will exhibit the balance
between offense and
defense described above. Each of the three phases, but especially the D phase
may, optionally,
consist of 0, 1, N, 'as many as possible', etc., in different circumstances,
and are either
specifically required, or at the player's option. Additionally, .move
structures such as UWD and
DUUU can also be used, but are less preferred because they do not balance well
offense and
defense in a single move. However, for some embodiments, such structures, are
necessary.
Longer sequences are also optional, for example UDUDU..., where each D is of a
single
piece only (generally, a player may place as many pieces as possible during a
single D phase)
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
9
so long as the alternation can be maintained; i.e., until there are no more
spaces opened by an
U phase that permit a larger piece to be placed in a D phase.
In the D phase, generally, as many pieces as possible may be placed if
the.player desires.
However, under some circumstances or in some embodiments: the number is
restricted to only
one piece; the player is required to place as many as possible; or, the player
may at his discretion
place fewer than that maximum possible, even refraining from placing any.
In addition, there are optional relaxations of the strict requirement that a
first generation
of tiles is completely replaced by a second generation of tiles before a third
generation of tiles
comes into play. For example, during generation two of the basic game, it is
possible (although,
more likely toward the end of a generation) that a hole will develop that is
big enough to place
two adjacent (202) tiles in a 2x2 open area and, with this variation, it is
permitted to place a
(203) instead, even though it is still generation two. Optionally, if a (203)
tile is being placed in
generation two, the comparable U phases) removal must be a (202) tile, or two
(201 ) tiles.
ALTERNATIVE LAST MOVE TO GENERATION ONE: With two, three, four or six players,
the last
move of of the first generation (phase or level o~f play) of 2"0 leaves open a
single empty grid
space on the board. Particularly with two players, the second player (who now
opens generation
two) may be perceived to have too great an advantage (as will be explained,
below).
Tn the standard game of two players, player one goes first in generation one
and
generation three, ,and second in generation two.
1. Generally, going first in generation one is arguably a (slight) advantage
in that the
first player is the first to have an opportunity to grab a corner, for
example, and
the second player may feel (if not actually be) at a disadvantage - constantly
on
the defensive.
2. Going first in generation three may, actually, often be a disadvantage.
Since there
is no compelentary 2x1 space intentionally left open at the end of generation
two,
player one (who, again, goes first in generation.three) may need to remove two
small pieces without being able to put down a laxge piece. This can give
player
two a lot of opportunities early on in generation three.
The above two elements can be thought to approximately balance out; however,
in
generation two, player two starts and will almost certainly be able to take
the only open grid
space by removing a lxl tile next to it, and placing a 1x2 brick tile in the
larger space opened
up. Player two then, by removal of another 1x1 tile, opens another grid space,
but it is of their
own choice. And that choice may make it impossible for player one to make a
good move; they
may be forced to remove two 1x1 tiles without being able to play a 1x2 brick
tile. If player one
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
has not prepared adequately, by arranging two 'safe haven' configurations,
then player two will
again have at least one good move. From this point, the game will likely
proceed fairly evenly
with players of similar skill (mostly depending upon consolidation of position
and 'safe haven'
configurations). However, player two may well be up by a critical piece or
two.
A'slight modification to the end of generation one is suggested as an
alternative that will
tend to lessen the imbalance described above.
In the standard game, in the last move of generation one, player two takes one
of the last
two open grid spaces, leaving one space open.
In the alternative last move of generation one, with two grid spaces open
player two,
instead, removes one 1xl tile (presumably next to one of the two open grid
spaces), and (most
likely) places a 2x1 brick tile. Then, because player two did riot get to
place their 24''" tile; they
,do not pick up a 1x1 tile to end this move.
Play proceeds normally from that point on, with player one having a single
open grid
space to work with.
Alternatively - especially for seven players, where there are no open spots at
the end of
the first phase of play - for at least a first round in generation two have
moves proceed LTCTD
so that moves can generally be made. However, as that will still not guarantee
open spaces,
another alternative for the first one or few rounds) is to utilize UUDIJ moves
that will both,
generally, permit moves and leave at least one grid space open. ***
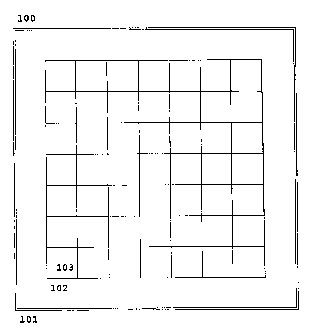
COMPONENTS FOR BASIC GAME: Figure 1 shows a board (100) suitable for playing
the particular
preferred embodiment, comprising three generations and played on a 7x7 grid of
squares, as
described in the sections entitled BRIEF SU1~~ARY OF INVENTION and BASIC GAME,
above.
A decorative edge, or the physical border of the playing board, is indicated
by the double line
(101). The edge of the active playing area is depicted by the single line
(102). One of 49 unit-
squares is designated as (103). Playing tiles are to be placed within the
boundaries of the grid's
squares.
Figure 2 shows game pieces, or tiles, suitable for playing the version of the
game
described thus far. A 1x1 tile is shown at (201), a 2xl tile is shown at
(202), and a 2x2 tile is
shown at (203). The double lines (20~) show the tile outlines; the single
lines (209) are drawn
to show the number of unit-squares involved and, although such lines might,
optionally, be drawn
on the tiles, are not meant to show physical divisions or other features of
the tiles.
Figure 16 depicts a general flow diagram of the algorithm for the basic game,
played by
any number of players, and played for any number of generations. It comprises
a functional
specification from which to program the algorithmic control portion of a
computer simulation of
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
11
the game. Methods for creating other portions of such a program, for example
display of graphic
representations and GUI implementation, are well developed, and well known to
those skilled in
the programming arts. The flow diagram, in concert with the instant
specification, is essentially
self explanatory; but, several comments, following, will elucidate.
The loop of elements (1601) through (1606) comprise the first generation,
ellipsis (1603)
indicates steps for~additional players between 1 and N, if N > 2; (1607)
results in branching to
a later generation(s), first passing through element (1608) which reverses
order of play; looped
passes through elements (1609) through (1628) comprise a later generation,
ellipsis (1619-1621)
indicates steps for additional players between First) and L(ast), if N > 2;
(1629) through (1633)
determine whether to perform an additional generation, or not (1634); and,.
(1635-1636) are
performed after play is over.
When it is decided (1630) that an additional generation is to be played: a)
the order of
play is reversed (1608, 1631); and, b) the pieces that were put down in the
previous generation
become the 'small' pieces to be picked up in the upcoming generation, and
still larger pieces are
selected to be the ones to be put down (1631). In generation one the players
are described as 1
through N. In later generations they are referred to as First) and Last)
because the order of play
is reversed in alternate generations.
BOARD SIZE AND SHAPE: In the preferred embodiment described thus far, with
three generations
played on a 7x7 grid, three types of pieces (201-203) are used. However, two
additional
generations are, optionally, played with 2x4 tiles (204) and 4x4 tiles (205)
resulting in only a
single 4x4 tile fitting on the board at the last move. However, such play 'to
the bitter end' would
be anticlimactic, and too dependent upon who was going first in the last two
generations, and it
is recommended that play end when nine square tiles can be fit onto the board.
With the three-
generation preferred embodiment described, a 7x7 grid was chosen because this
was the
maximum size grid that fit this criteria. With a 5x5 board only four 2x2 tiles
would fit. With a
6x6 board nine tiles would fit, but there would be no 'wiggle room'; that is,
labeling both rows
and columns from 0 through 6 with the upper-left corner labeled (0,0), if any
tiles were not put
with their upper-left corner on a square with both X and Y being even, fewer
than nine tiles
would fit. Put another way: nine 2x2 tiles cover 36 squares; and, a 6x6 board
is exactly 36
squares. On the other hand, a 7x7 board permits some of the 2x2 tiles to be
offset by one grid
square, in X and/or Y, and yet still have nine tiles fit on the board. (Note
that with some offsets
in the placement of 2x2 tiles, fewer than 9 will fit on the board, with 4 as a
minimum.) If an 8x8
board is used, than up to 16 2x2 tiles can be fit on the board. Thus, in this
case, the only number
that is greater than 6 and less than 8 is 7; so a 7x7 grid is used.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
12
Using the same criteria, if it is desired to increase the number of
generations to 5 - using
tiles of size ~xl (201), 2x1 (202), 2x2 (203), 4x2 (204) and 4x4 (205) - then
the size of a
square grid would need to be more than 12x12 (where there is no 'wiggle room')
and less than
16x16 which would permit 16 4x4 tiles to fit. Thus, acceptable values are 13,
14 or 15. Two
resulting elements trade off as the size of the board is increased. With a
13x13 board only 168
moves need to be made during the first generation, but a minimum of 'wiggle
room' is available.
With a 15x15 board 224 moves need to be made during the first generation, but
there is a
maximum of 'wiggle room' permitting more variation in moves and strategy. With
a 14x14 board
these two elements are both intermediate; however, with an even number of
squares, when
playing with the most usual number of players - two - either 0 or 2 spaces
will be left open
after the first generation; thus, odd-numbered boards are not necessary, but
preferred.
On the other hand, if dual (or more) resolutions are to be inscribed on a
single board, such
,as is shown in Figure 14, then the 7x7 board leads to 14x14 and 28x28 higher
resolutions as unit
squares are halved and quartered, in each direction.
Similarly, for a game of 7 generations, the board size would need to be
greater than 24x24
(if at least a single row and column of 'wiggle room' were made available,
exactly 24x24 if no
'wiggle room' were made available) and less than 32x32 (or up to 16 8x8 tiles
would fit). Again,
a 25x25 board would make for the fastest game; and 31x31 board would make for
the most
flexible placement of tiles and, thus, the most complex strategy and tactics.
Even larger boards are, optionally, used and, with the embodiment using
generations
alternating between tiles that are squares and those that are 2:1 ratio
'bricks' on a square board,
the following algorithm holds. For N = 1, 2, 3, etc.: the number of
generations = (Nx2)+1; the
minimum tile is lxl and the maximum tile is a square of 2N on a side. In order
to have nine tiles
in the last generation, the minimum sized board (permitting at least some
'wiggle room') is
(3x2N)+1 on a side, and the maximum sized board is (2N+Z)-1 on a side.
However, for physical
board games, grids much beyond 25x25 may not be practical; for example, 'go'
is typically
played on (the intersections of) a 19x19 grid, and is a long game of one
generation only.
Nevertheless, with a computer-mediated version of 2"0, or of other variations
on or
embodiments of the instant invention, larger board sizes are practical. Played
over a network, in
particular, . many players may conveniently collaborate on a large game; or,
long games with
players making moves asynchronously are also practicable. Also, on a large
computer-mediated
board, several games may go on simultaneously, where pieces from other games
block by taking
up space, but do not otherwise interact. For example, in one embodiment,
several games, each
going on in its own area of a very large board, are generally disjoint, but
overlap somewhat with
other games at the edges of areas. Such abutting games are played
synchronously or
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
13
asynchronously. Also, a board on a computer screen may be zoomed into, or out
of, permitting
larger board sizes to be conveniently viewed. Further, it is possible to have
the computer fill in
some or all of the tiles in the initial generation, at random or with some
pattern, in order to speed
along the game. Similarly one or more generations are, optionally, skipped (or
the computer fills
in from a later generation). However, if two generations are skipped, this is
just equivalent to
starting with a 2x2 square as the first generation; or, starting with a board
of (roughly) N/2 x N/2.
Figure 14 shows how a single board is inscribed with three (as shown, or even
more) grids
of different resolutions, so that play with several sizes of unit tiles may be
played on the same
board. In practice, different colors of lines are, optionally, used; and,
lines which overlap may
be inscribed with adjacent lines of all colors present. However, in Figure 14,
which shows only
the upper-left comer of a board, grids of the largest size, or lowest
resolution, are shown as thick
lines; lines of the intermediate resolution are shown as medium lines; and,
lines of the smallest
size, or highest resolution, are shown as thin lines.. Only the lowest
resolution line is shown where
they overlap. A game of three generations would utilize the largest squares; a
game of five
generations would utilize the intermediate squares; and, a game of seven
generations would utilize
the small squares.
An example of an alternative embodiment playable, for example, on a board with
both
7x7 and 14x14 resolutions is as follows. The basic three generations are
played with tiles suitable
for the 7x7 grid. However, it is permitted to place the tiles on the lines of
the 14x14 grid. Thus,
it is possible to place the unit square 1x1 tiles on half unit line
increments. Therefore, by placing
a tile one half unit from an edge, 1.5 units are blocked or controlled; and,
by placing a tile one
half unit out in both directions from a corner, 2.25 units are blocked or
controlled. Similarly,
being able to place tiles on half unit increments opens additional strategic
and tactical techniques
throughout the entire game. Another way to think of this particular example is
as a game of five
generations played on a 14x14 grid, but started at the third generation.
Further, as will be shown later, the units on the grid need not be squares
(e.g., see Figure
8, diagrams (801) ~ (802), and Figures 12 and 18), or even uniform (e.g., see
Figure 8, diagrams
(801) & (802), and Figure 20). However, even with a square grid, the board
need not conform
to the NxN sizes described above. The board is alternatively an NxM rectangle;
or, optionally,
is not even rectangular, regular, convex or even contiguous. While there may
be certain
advantages of strategic comprehensibility when using a square board as
described above, and in
using the same size or type of board at all times, the instant invention, as
generally described in
its various embodiments, can be played on an arbitrarily sized and shaped
board. For example,
Figure 13 shows a playing field (1300) which comprises: two discontiguous
sections (1301 &
1302); and a 'hole' (1303); as well as concave (1304) and convex (1302)
sections. Further,
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
14
neither the tiles need be rectangular (e.g., see Figures 3, 4, 5, 6, 17, 19,
21 and 22) nor the grids
square (e.g., see Figure 8, diagrams (801) & (802), and Figures 12, 18 and
22).
NUMBER OF PLAYERS: Returning now to the 7x7 board, the number of players will
be discussed.
With the standard default of two players, in~the first generation each player
puts down 24 1x1
tiles so that 48 squares are covered, leaving one square open tp begin the
second generation. With
three players, each puts down 16 1x1 tiles so that, again, 48 squares are
covered and one is left
open for generation two. With four player, each places 12 tiles and, again, 48
squares are covered
and one is left open at the end of generation one. Similarly for 6 players
each placing 8 tiles and
8 players each placing 6 tiles. With the 7x7 board, even more than eight
players is possible, but
more than about six are probably not very practical, strategically.
With 7 players, the board is full at the end of generation one, each player
having placed
7 lxl tiles. Thus, when generation two is started the first player in
generation two (who was the
last player in generation one) will have to pick up two 1x1 tiles without
being able to put any
down. Alternatives to avoid this are: each player only places 6 tiles, leaving
7 spaces open to
begin generation two; or, each player picks up one piece before generation two
starts, which is
mathematically equivalent, but not strategically, because the first tile
picked up may not be the
same as the last one put down (or the one left open) by any particular player.
Similarly, with five
players, each would place nine tiles, leaving three squares open for
generation two.
For other board sizes, and numbers of players, similar situations develop. In
general, the
algorithm for generation one is that N players alternate placing 1x1 tiles,
until there are N or
fewer open squares. However; there are optional variations on this rule, and
these and other such
variations are within the scope of the instant invention. For example, in a
game where several
open squares are present between the first and second generations, the number
of larger pieces
put down is limited to one for each player, during the first round (or two, or
more) of turns for
that generation. Alternatively, if there are several spaces open, all but one
are filled with null
pieces (e.g., of a color not used by any player, or specially marked as in
(901)). These are placed:
by players tatting turns before, after, or anytime during play of the first
generation; by some
published rule (e.g., symmetrically equivalent, any corner for 1, any 2
diagonal corners for 2, any
3 corners for 3, all corners for four); or, by chance (e.g., by throwing two
special dice with more
than 6 sides displaying (columns) 1-7 and (rows) A-G, as. per Figure 15). The
pieces are: left
throughout the second generation only and then removed before generation
three; left throughout
the game as 'dead zones'; picked up algorithmically during generation two
(e.g., a null is
removed with every fifth regular unit tile picked up); any one picked up as
the first, second or
on both removes, by players until null pieces are gone; any one picked up by a
player as an open
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
strategic option at any time instead of, or in addition to, a piece of their
own color; etc.
Tournament structures of any kind are practiced to score multiple games,
particularly for
multiple players. Scoring over multiple games optionally counts or
accumulates: number of games
won; total area or number of pieces; highest scores; or, other ranking method.
Timing is
optionally made an element. Total game time, or the time of individual moves
is optionally
limited, or scoring optionally takes time expended into account.
Any known or custom tournament structure and rules are optionally applied. For
example,
with three players, games of only two players are used and a 'round .robin'
tournament is
performed with three games consisting of A vs B, B vs C, and C vs A. The
player with the best
accumulated score wins; or, the best two players then go head-to-head in one
game or a series.
Such a series, between several or even just two players, is decided based
upon: winning N out
of M games (e.g., 2 out of 3); total score after N games; play as many games
as necessary until
one (or more) player reaches a score of N, at which time play is ended
immediately or the current
game is completed before scoring; or, otherwise.
When playing with several people, in one variation, play starts with all
playing together,
and proceeds to eliminate players until only two are left to play a final game
or series. One or
more worst scorer is eliminated at each round; and, how many are eliminated
depends; optionally,
upon the particular scores. For example, consider four players A, B, C ~ D and
a final round
with nine tiles. A number of example scores and possible outcomes follow:
~ A=1 B=2 C=2 D=4: D wins, or drop A only.
~ A=1 B=1 C=3 D=4: D wins, or drop both A and B.
~ A=0 B=1 C=3 D=4: D wins, or drop A, or drop both A and B.
~ A=0 B=1 C=3 D=3: Drop A, or drop both A and B.
~ A=1 B=1 C=3 D=3: C and D play run-off game or series.
In most games of strategy, there is a real or perceived strategic advantage
(or
disadvantage) to going first. Thus, the standard embodiment of the instant
invention reverses
order of play at each generation, and reverses starting order in the first
generation in alternate
games. However, when playing with more than two people, the situation is not
symmetrical
because there will be one or more players 'in the middle' who never go first
or last. Further, with
two players, A follows B, and B follows A. However, with three players, for
example, A follows
B, B follows C, and C follows A, again strategically asymmetrical. While
knowledge of the
strengths and weaknesses of who precedes and follows a player can be used to
strategic
advantage, it nevertheless may be desired to eliminate or, at least, randomize
such relationships
after each game or generation, or even as often as after each round of moves.
This is
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
16
accomplished by rolling dice or cutting cards for rank, or any other standard
selection mechanism
but, in particular, iwo example embodiments follow.
There are six ways three players may be ordered, 24 ways for four players, 120
ways for
five players, and so on. A single standard die shows six sides; two such
distinguishable (e.g., one
red and one blue) dice provide 36 combinations; two distinguishable 12-sided
dice provide 144
combinations, etc. A simple printed table is provided to convert dice outcomes
to player order
so that player order may be quickly enough established so as to be practicable
to perform even
for each move. For rolls beyond the range needed, table entries will repeat
some entries or
specify, 'roll again' 'reverse last order' 'use last order' or some other
instruction. For three
players the table data constitutes:
~ for a die roll of 1, player order is A B C;
~ for a die roll of 2, player order is A C B;
~ for a die roll of 3, player order is B C A;
~ for a die roll of 4, player order is B A C;
~ for a die roll of 5, player order is C A B; and, .
~ for a die roll of 6, player order is C B A.
For more than four (and certainly beyond five) players, such a print table is,
perhaps, too
cumbersome. In that case, a device similar to an electronic calculator is
provided into which the
number of player is initially entered. Than at each move a randomize button is
hit and a random
player sequence is displayed. Such a function is trivially included in a
computer-mediated
embodiment. However, for physical embodiments, an inexpensive alternative to
the electronic
calculator is shown in Figure 25.
A number of uniform small balls or beads (2501-2500 typically of plastic, are
provided
and are distinguishable by their color, a number or letter, or some other
marking. Enough are
supplied for the maximum number of players and are sealed within the supplied
container (2500),
or the container is supplied with a hatch (2510), or a removable cap on tube
end (2530), into
which the appropriate beads are loaded. If the device is sealed and contains
more beads than
needed, each player selects a color, letter, etc. and any not selected are
ignored when reading a
player sequence. One end of the container is preferably bulbous (2515); but of
any shape with
sufficiently large volume, and preferably opaque. The other end tapers or
funnels (2520) into, or
just ends in, a tube (2525) that is transparent, closed at the other end
(2530) and of sufficient
diameter to accommodate a single bead without friction, but narrow enough to
prevent two beads
from being positioned laterally to each other. Thus, the container is held
with the tube up and the
beads fall into the bulb; the bulb is shaken, randomizing the beads; the
container is then turned
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
17
and held with the tube downward; the beads accumulate in the tube in an
ordered column; and,
the beads are read, from the top or bottom, to determine player order.
Further, this device
performs other functions with appropriate sets of beads.
TILE CONSTRUCTION: With the basic 7x7 board, three generations, and two
players, for each
color: 24 1 x 1 tiles (24 units in area) are required, always; : 24 1 x2 tiles
(48 units in area) are
required at an absolute maximum, although this is a highly unlikely,
strategically lopsided
situation in the middle game (12 are the average, but not sufficient, and 1S
each would probably
cover well more than.95% of situations, but what do you do in those few other
situations?); and,
9,2x2 tiles (36 units in area) are required at a maximum, but a shutout is a
much more likely
possibility in the end game. Thus, for each color, 57 pieces, totaling 108
units in area are
required. If one color, pieces can comprise inexpensive reversible tokens like
wooden checkers
or plastic tiddlywinks; or, they may be more expensive weighted pieces with a
felted bottom, like
pieces supplied with deluxe versions of other games.
An elegant alternative is to produce dual-sided pieces,' as are used with the
game Qthello.
These are one color (nominally black) on one side and a second color
(nominally white) on the
other. They are turned one side up, or the other, depending upon which player
places them in
play. In addition to elegance, an advantage is that only 24 1x2 pieces are
needed in total, not 24
for each color; and, similarly only 9 2x2 pieces. If the pieces are painted
with two different
colors, or imprinted with two symbols, the material (but not necessarily the
manufacturing) cost
is cut in half for the middle and larger pieces. However, if a standard black
piece and a standard
white piece are sandwiched, then the cost of sandwiching is added to the
materials cost. Further,
for the 1x1 tiles, only 24 of each single color are needed. If these are
sandwiched, then only 24
dual-sided 1x1 pieces result, and 24 more are needed, doubling materials. So,
an alternative is
to have 24 single-sided (a geometric misnomer) 1x1 pieces of each color, and
dual-sided pieces
for the larger sizes. Dual-sided pieces are painted, stained, coated or
printed; or, different colors
of material (wood, plastic, metal, foam or otherwise) may be sandwiched; etc.
If a single layer,
or sandwiched materials, or a middle layer between a sandwich, is magnetic or
metallic, and the
playing board is complementary, then pieces adhere to the board and a 'travel'
style game is
produced.
Additionally, if pieces of a third color are added, and'these are definitely
designated as
the third color (or dual-sided third/fourth color), then only 16 lxl's are
needed; but, to cover all
possibilities, 24 lx2's and 9 2x2's are still needed. Similarly, the
designated fourth color requires
only 12 lxl's. However, limiting color choice for primary colors may not be
worth the corner
cutting; and, providing full complements of all colors is preferred to
maximize customer
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
18
satisfaction.
On a computer screen, the tiles will, generally, be the same size as the grid
elements they
are placed upon. However, with a physical game, it is necessary to be able to
place and remove
tiles from the board without disturbing the other tiles on the board. Thus,
the tiles will, generally,
be somewhat smaller than the territory they are meant to occupy. For example,
if the unit grid
is a 1x1 square, the unit tile would be a 3/4x3/4 square, leaving 1/4 unit
between tiles for fingers
to grasp the tiles. However, for later generations and larger tiles, the ratio
will need to be
adjusted. At the fifth generation, tiles are 4x4 unit squares. If the 3/4
factor were applied, this
would result in a 3x3 unit tile that could be exactly fit into a 3x3 space,
when a 4x4 space is
what is required strategically. Therefore, rather than making tiles a uniform
size that is 3/4 of the
linear distance of the space they are to occupy, leaving a uniform (or, just
slightly progressively
larger) border around the tile will produce tiles that are both handlable and
unambiguously fill
the required space. For example, the 4x4 unit tile would be produced as 3--
1/2x3-1/2 units.
Another alternative that will help with distinguishing, and physical handling
of, the tiles
is to make them of different heights. For example, for a three generation game
the 1x1 tiles are
made 1 unit high, creating a lxlxl cube; the 2xl rectangles are made 1/2 unit
high, making a
fairly standard 'brick' shape; .and the 2x2 squares are made 1/4 unit high,
making a shape similar
to ceramic wall tiles.
Further, if the pieces are made thicker, e.g., as lxlxl unit cubes, then up to
six different
colors (one on each side), for six different players, are presented. For the
lxlx2 'bricks' only
four long sides are available (the piece is not useful for the game, as
described thus far, if stood
on either of the two lxl ends) so four colors for four players is a practical
limit. Thus, two sides
of the unit cube are available for markings such as 'dead zones' (901).
Similarly, a large 2x2x2 .
cube can be painted for four players on four of its six sides. Of course
'painted' is meant loosely,
and such pieces are, optionally, constructed of different colored plastic
(such as the Instant
Ircsaraity cubes), or other materials, or by other methods.
Creating a tool for plastic injection molding is expensive, so limiting the
number of molds
is desired. Figure 26 shows how a small set of molded pieces are used to
construct both pieces
and boards. Element (2610) shows a piece that has interlocking jigsaw puzzle-
like protrusions at
top and left, and indentations at bottom and right. Alternatively (2615) shows
a tile with tongue
at top and left, and groove at bottom and right. Either may be used (in one
color for each player)
alone for a unit square tile (201), interlocked in a 2x1 or 1x2 tile
configuration (202), interlocked
in a 2x2 tile configuration (203), etc.; or, (in a different color) in a 7x7
board configuration
(100).
Alternatively element (2620), shown from top and side, is a tile that is
grooved on all
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
19
edges, and element (2625), shown from top and end, is a double-tongued 'grout
strip' that has
a visible divider (2626) that is optionally of zero width, and which is cut
into appropriate lengths.
The tongue and grove are, optionally, keystoned (exaggerated as shown) so
that, once snapped
in place, they will not slip apart. Assuming just two players, these pieces
are fabricated in gray
for the board (with (2625) optionally contrasting), and black and white for
the players. The board
is made up of 49 gray tiles (2620); six horizontal strips of (2625) that, in
length, are seven times
the width of (2620) plus six times the width of (2626); and, 42 (6 each for 7
rows) vertical
spacers of (2625) that are each the length of the width of (2620). A single
(2620] is comparable
to (2, O1); two (2620) tiles with a short spacer connecting them are
comparable to a (202); ete. For
the tiles, the tiles and grout are matching for each player; or, the
contrasting grout may be used
to enhance visibility between adjacent larger tiles of the same color, which
have internal~but no
bordering grout strips. Additionally, an optional protrusion or knob (2621 ) ~
on one side of each
piece will serve as a handle to assist in placing and removing tiles and, when
formed upside down,
one, of many feet on the board. Alternately, if not turned upside down, and
optional indentation
(2622) is present, their combination will ensure proper registration of the
tiles as placed on the
board. Lastly single-tongued (2631) and notched (2632) frame strips, such
as~(2630), not drawn
to the same scale, are supplied to finish the board. Fabrication cost and
shipping space may be
saved by supplying the game in pieces to be assembled by the user.
ADDITIONAL TILES COMPOSED OF GRID UNITS: Thus far, with the embodiment called
2VO:
playing pieces start as a single grid unit (a square in the basic game) in the
first generation;
double in one dimension to a 2xl unit cell in the second generation; and,
double in the other
dimension to a 2x2 unit cell, returning to a larger version of the original
configuration, in the
third generation; and so on. At each generation after the first, the larger
piece is twice the area
of the smaller and, thus, the three-part move - remove a small piece, add a
(usually one,
strategic or tactical advantage aside) larger piece, and remove a second small
piece - yields
neither a net gain or loss of territory.
In an alternative embodiment, pieces grow linearly, by one unit at each
generation, instead
of doubling in size. (Such an embodiment can be titled 1 "o" or L"o' in
keeping with the
typographical convention of the 2"a name, or LINEAR 2"0°.) Thus, when
two small pieces are
removed and one larger piece deposited, territory is changed by (N+1)-2N; or,
N-1 additional grid
units are left open. Once such 'holes' accumulate, it is very likely a player
will be able to deposit
more than one larger piece on a given move. Alternatively, a move structure of
UD or DU results
in (N+1)-N; or, an ifZCrease by one unit of occupied territory on the average.
Thus, players will
not be able to place a larger piece in every move.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
With the linear growth embodiment the first two generations are still played
with pieces
(201) and (202) respectively. However, in generation three, while pieces (202)
are picked up,
pieces of size-3 are put down. There are two possible configurations of size-3
and these are
shown as (301 ) and (302) in Figure 3. Since the occupiable space on the basic
board comprises,
nominally, 48 squares it is possible to place, at most, 16 size-3 pieces on
the board. This is an
average of 8 each for two players assuming equal strategic performance. Thus,
it must be decided
how many of each of the two possible configurations to supply and how they are
to be played.
For example, if dual-sided pieces are supplied with one player's color on each
side, eight of each
configuration will be enough to cover the board, and (since (301) and (302)
are symmetrical)
each player may choose the configuration they desire until pieces of one type
run out for both
players. Alternatively, each player may get 8 of each configuration in their
own color and, on the
average, have enough of either (301) or (302) but, only in toto, have enough
of (301) and (302)
taken together, under the most extreme circumstances, to fill all but' one
square of the board. In
still another option, 16 dual-sided pieces of each configuration will permit
each player to choose
either (301) or (302), at each turn, without the possibility of running out of
either.
Similarly, at generation four, (301) and/or (302) are picked up, and pieces
comprising four
grid units are put down. Figure 4 shows the six (401-406) possible
configurations (in addition
to 203) of size-4 with square grid units. Note that two pairs of pieces, (402
& 403) and (405 &
406), are mirror reflections of each other. If pieces are of a single color,
and sufficiently uniform
on both sides as to be reversible (such as checkers), then only one type of
piece for each pair
need be manufactured and is used reversibly. However, if the pieces have a
bottom (e.g., lined
with felt, such as with some chess pieces) or are dual-sided with two colors
(such as with
Othello) the pieces of both polarities will need to be manufactured. In
particular, with dual-sided
pieces, a black (402) is a white (403) and vise versa; and, similarly with
(405) and (406). Again,
these are supplied according to any of several alternative plans: sufficient
number of each
configuration in each color are provided to completely cover the boaxd; or,
two of each
configuration are supplied to each player totalling 56 squares in toto, more
than 48; or, some
larger number of (203) and just one or two each of (401-406); and, if pieces
are reversible and
of a single color than 'each' may include both (402) and (403) or just one
reversible type, and
similarly for (405) and (406); etc.
Other game variations and embodiments include, without limitation, any
combination of
rules and/or pieces for the geometric growth (e.g., doubling) or linear growth
embodiments. For
example, the first two generations are played as per the rules of 2VO. The
third generation is as
well, going to pieces of four units in axes, not three, except that some
combination of standard
pieces (203) and other pieces (401-406) are used instead of just the (203)
pieces.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
21
Other game embodiments include, for example, using (201), (202) and (203)
tiles, as well
as the tiles of Figures 3 and 4, to play a 'continuous' game, as opposed to a
game with distinct
generations. Complements of tiles other than just described are, optionally,
used. However, the
rules and strategy are critically dependent on, and adjusted depending upon,
which tiles are
chosen and how many of each are available. In one .such embodiment there are
two phases of
play.
During a first phase the empty board is filled. On each move: a player places
a (201) of
their own color in an empty square; or, a player removes any tile of their own
color of size-N
and places a tile of size-N+1 in the same space plus any one ,adjacent square.
(To generalize, the
first type of move may be considered as a tile of size-0 being removed and
replaced with a size-1
tile.) This continues until all space is covered.
During a second 'attrition' or 'consolidation' phase, during each move, a
player removes
~a (201) of their own color and places one, or more, larger tile, if possible.
This continues until
there are no (201) tiles left. Optionally, during this phase, during a move,
any tile next to open
space may be removed and replaced by a larger (or, at least not a smaller)
tile. Play continues
until no more such moves are possible, or until each player is happy with
their position.
Scoring options include: area occupied for each player is simply counted;
(201) tiles do
not count; only the largest pieces count; larger pieces count
disproportionately, for example, tiles
score as N-1 each or NZ each; etc.
ADDITIONAL 45° ANGLED TILES: A further alternative to the game tiles
akeady described are
those constructed out of unit squares and half squares (in this case, right
isosceles triangles) used
in combination. Figure 5 shows a grouping of tiles that are used as
substitutions for, or in
combination with, those of Figure 2 and/or Figures 3 and 4. Tiles (501-503)
each comprise one
unit square in area, but span two half grid units; they are comparable to
piece (201). Pieces (501)
and (503) are mirror images of each other and the manufacturing and supply
principles discussed
earlier regarding reversible and dual-sided pieces apply here as well. (The
same also applies to
(504) and (508), for which only one of two mirror images are shown.) Each of
these three pieces
may be turned by multiples of 90° (but not 45° as the tile side
lengths would not then coincide
with sides and diagonals of the grid squares, even though the angles would
align) for placement
on the standard square grid. These pieces are, perhaps, more interesting when
used in conjunction
with (201) tiles in generation one and, particularly, when at least some
rectangular (202) pieces
are used in generation two. Pieces (501-503) contribute to, or block, more
than one grid unit; but,
they do not entirely vacate either of those spaces upon removal. For example,
in configuration
(701) of Figure 7, five (501) tiles are laid in a horizontal sequence (A, B,
C, D and E). Even if
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
22
any two internal (B, C and D) adjacent (SO1) tiles are removed, vacating two
unit squares in area,
a {202) piece cannot be put down in generation two. However, a (504) tile, if
available, can be
placed in such a circumstance. Similarly, if (B) and (D) are removed, then no
two unit area piece
can be placed; but, when (C) is removed, (202), (505) or {504) (but not its
mirror image) can be
put in the space so vacated.
Tiles comparable to the two unit (202) tiles are asymmetrical (504) (and its
mirror image,
not shown) as well as symmetrical tiles (505-507). Each can, again, be rotated
by multiples of
90°, some with no effect. Tiles (508), its mirror image (not shown),
and (509) are all 4 units in
area, are similar in shape to, but larger than, {501), {503) and (502)
respectively, and are
comparable to (203) and its relation to (201). The aiternating enlarging
progression, comparable
to that of the (2xx) tiles, can continue indefinitely (within reason) with the
(Sxx) tiles as well.
What are called the asymmetrical tiles (501), (504) and (508) (and their
mirror images) are
skewed (to the right, or left, on top) versions of (201), (202) and (203)
respectively.
Embodiments of the instant invention are, optionally, played with the Figure 2
tiles, the
Figure 5 tiles, or any combination at each generation; and can be played in
any combination with
Figure 3 and/or Figure 4 tiles {or other tiles explicitly described or
depicted herein, or otherwise)
as well. Again, some embodiments provide effectively unlimited numbers of
tiles (e.g., for each
of two colors, 24 each of (201), (SO1), (502) and (503)) permitting choice
without restriction for
each player. Alternatively, for example, a set of 24 tiles may be composed of
six of each type;
or, eight each of types (201), a reversible (501/503), and (502); or, 12 of
(201), and an additional
12 equally divided between the two or three other shapes. In an intermediate
approach, more than
24 unit area tiles are provided in total, but not 24 of each; for example, 24
of (201) and 8 each
of the two or three other shapes, providing some but not maximal flexibility
of which shapes to
play. And so on. Similar options for mixing tiles are applicable to the number
of tiles provided
of the two and four unit area sizes.
Additional tiles are possible and optionally supplied to be used instead of,
or in addition
to, any of those disclosed herein. These optionally incorporate elements
embodying: other shapes;
other angles; partial or half cells of rectangles, or other shapes, instead of
triangles; protrusions
and/or indentations that are complementary, interlocking or otherwise; are
symrmetrical or
asymmetrical, uniform or non-uniform; blank or colored or marked in a number
of ways; etc.
Further, some or all tiles are supplied in limited quantities {for any
particular type, or any
combination, or in.toto) so that, optionally, the entire board cannot be
covered by a single player,
some combination of players, or all player together, during some phases) of
play.
It is suggested that for pieces with 45° sections, the foregoing are
the most strategically
comprehensible and, thus, more interesting. However, in the interests of
thoroughness, Figure 6
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
23
shows two additional symmetrical one unit area tiles (601 & 602) each composed
of two triangles
connected at vertices. (These are most practical in computer-mediated
embodiments, because such
vertex connections are physically fragile.) The other tiles on this page (603-
608) are symmetrical
(606 & 608) and asymmetrical (i.e., requiring mirror image versions or
reversing) tiles of two
unit areas. Some of these (particularly 606 and 608) are more likely to be
strategically
comprehensible and useful when optionally provided in an,embodirrient.
Figure 7 shows several combinations (701), (702) and (704) of one unit area
pieces; and
one combination (703) of two unit area pieces. It should be noted that skewed
pieces of the same
mirror polarity are abutted linearly (701); and that pieces o;f opposite skews
(703) are used to
'turn the corner'. Configuration (704) shows an example of how skewed,
triangular ,and square
pieces, each one unit in area, are combined to tile the grid of squares
without leaving gaps.
Some elements of Figure 9 (depicted in single-lined boxes) show markings that
are,
optionally, inscribed within the squares of the grid. These alter the grid to
comprise, at least in
part, right isosceles triangles as well as squares; and axe used to restrict
which pieces are
permitted to be placed on areas of the grid. The four inscriptions are: empty
(917), slash (918),
backslash (919) and X (920). These are, optionally, interpreted in either an
enabling or disabling
fashion.
With the enabling interpretation: only tiles or tile sections that comprise
full squares can
be placed in, or atop, an empty square (917); tile sections that proceed from
lower-left to upper-
right may be placed in either slash (918) or X (920) inscribed squares; and,
tile sections that
proceed from lower-right to upper-left may be placed in either backslash (919)
or X (920)
inscribed squares. Square sections can be placed anywhere, as the square grid
lines enable them.
With the disabling interpretation, a tile may not 'cut' an inscribed line.
Thus, with the
disabling interpretation: tile sections that proceed from lower-left to upper-
right are prohibited
from being placed in either backslash (9.19) or X (920) inscribed squares;
tile sections that
proceed from lower-right to upper-left are prohibited from being placed in
either slash (918) or
X (920) inscribed squares; square tile sections can be placed upon any square
(in one sub-
variation) or only upon empty (917) squares (in a second sub-variation).
(Such embodiments which include angled tiles can be titled 45"0" or A"o" in
keeping with
convention of the 2~0 name, or ANGLED 2"0".)
MARKINGS ON BOARDS: Two schematic examples of how the markings (917-920) are
applied to
a grid, to control how angled pieces may be placed, are shown in layouts (801)
and (802) of
Figure 8. In (802) the grid comprises right isosceles triangles, one quarter
unit square in axes,
with their bases orthogonal to the sides of the square, as well as squares; in
(801) right isosceles
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
24
triangles, one half unit square in area, with their bases diagonal to the
sides of the square, are
added as well.
Markings are also placed directly on the board for additional purposes. In
computer-
mediated versions, this is more flexible because the markings are not
permanent. Diagram (810)
of Figure 8 shows several alternative markings on a 7x7 board, but these are
only exemplary and
any type of marking is used to incorporate additional game features into
various embodiments
of the instant invention. Elements (811) and (812) each show an 'X' indicating
a dead zone. The
position of (812) is as far out from the corner as possible without permitting
a 2x2 tile to be
placed behind it. Two such tiles placed in diagonally opposite corners would
reduce the maximum
number of possible tiles at the end of the game from 9 to 7; and, that number
works well
regarding the avoidance of ties. If (811) is the lone dead spot then eight 2x2
tiles are possible and
ties, with the most usual number of players (i.e., 2) are likely.
The other example markings shown are used in scoring at the end generation.
Tiles or unit
squares are counted at the end, in order to arrive at a final score to
determine the winner.
Element (813) indicates 'times 2' and will multiply the value of the tile (its
area, or if tiles have
marked values, like Scrabble tiles) or the entire tile or terntory count, if a
player manages to
cover this square at the end of the game. Similarly (814) and (815) 'add 4' or
'subtract 8' points,
respectively, from the final score of the player who occupies those squares.
Since, optionally, as
many tiles as possible must be placed, it is possible to intentionally lose
space, to advantage, if
it will cost an opponent a net loss in their score. Lastly, for the 3D boards
depicted in Figures
23 and 24, each level is, optionally, assigned a different value for scoring
purposes.
ALTERNATIVE FIRST GENERATIONS: A number of the embodiments described,
particularly those
following with regard to marked tiles, work only, or better, with the first
generation, using unit
tiles. A use of these embodiments is to add variety to the first generation,
and to have the game
proceed from there, to later generations, as usual. (Alternatively, the same
variations are applied,
as appropriate, to any of the second or later generations as well.) Other
alternative first
generations used in this way include any game algorithm, now known or later
developed, that will
assign units of two or more colors to the spaces of the game board. Random
placement of tiles
will add an interesting element to the game. For example, a random-number
generator is used in
a computer-mediated embodiment. Or, grid spaces are specified by repeatedly
throwing two
special dice, with more than 6 sides, displaying numbers and letters
representing coordinates of
columns 1-7 and rows A-G, as shown in Figure 15. Twelve-sided dice are
available and, if
used, the other five faces are blank, or have options such as 'player's
choice', 'roll again', 'same
as other die', etc. In standard embodimants, strategy in the first generation
is reflected throughout
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
the game; with a random first generation, that strategic ability is removed,
and the skills needed
for the second and subsequent generations are contemplated in isolation. Also,
this can serve as
an 'equalizer' by taking the mufti-level strategic impact of the first
feneration play out of the
hands of experienced players. Alternatively, embodiments of the invention,
which comprise those
disclosed'variations suitable for alternative first generation play are,
optionally, played as a first
and only generation, and pieces or territory are tallied at the end of that
generation.
MARKED TILES: Figure 9 shows various marking that are, optionally, inscribed
upon, or otherwise
affixed to, tiles (depicted in double-lined boxes). Only unit square tiles are
shown and, generally,
these are placed down in generation one. However, markings are, optionally,
made on any tiles
as desired, and are played in any generation as appropriate. further, these
are examples; other
,marking are optionally used for similar or other purposes to incorporate
other gaming elements
into various embodiments of the instant invention. '
Through the marking of an X (901) on tiles, or the use of tiles of a different
color than
any player is using, a 'dead zone' is indicated. As discussed, above, some
dead zones rnay be
temporary, being removed during play. Generally, however, one or more dead
zone pieces are
placed: prior to play according to some rule or diagram; as a requirement or
by the players at
their choice (if and/or where) before or during generation one play; with, or
in lieu of, a standard
move; or, otherwise. With a 7x7 board, if more than a few dead pieces are
placed (say up to five
or six at a,practical maximum) the number of 2x2 tiles placable in generation
three will possibly
be severely reduced. Alternatively some dead pieces may be placed or others
removed during
generation two or three play. However placed or removed, a dead zone prevents
any player's
pieces from being placed and, usually, is permanent for the game. Thus,
depending on how many
and where placed, even a few single square dead zones may prevent 2x2 (or
larger) pieces from
being placed on the boaxd. Such may be used to advantage by a player, for
example as follows.
Consider that during generation one Black has three out of four in a corner.
If White takes the
fourth, it is still likely that Black will be able to eventually get a black
2x2 tile in the corner at
generation three. However, if White plays an optional one of a limited number
of permanent dead
zone unit tiles as the fourth in that corner, then neither player will be able
to get their 2x2 tile
there in generation three. Given that it is unlikely White will occupy the
corner in the end game,
it is to White's advantage to play such a spoiler tile.
Lead zones may also be 'provisional'. For example, dead zone pieces may be
colored like
other tiles and also have an X on them. Each player will then get one or more
X tiles of their
own color and, optionally be required or permitted to, place them in
generation one. These
colored X tiles are dead zones for the other player(s); but, they are 'free
space' for the player
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
26
who placed them, able to be removed, and the vacated space moved into, at any
convenient time.
Other alternatives include placing one or more 'provisional' dead zone piece
for your opponent,
instead of, or in addition to, one, or more, for yourself.
Elements (902-908) depict a set of tile markings used to enclose a colony
that, once
consolidated, becomes the territory of the player completing it. Two basic
ways for playing such
tiles are described, following, but other variations are within the scope of
the invention. In a first
main embodiment such tiles are provided for both (all) players in their own
colors. Then, when
a player creates a properly enclosed and filled colony (or, just an enclosing
border, with optional
automatic fill-in of the enclosed empty space), the colony is complete and the
player may proceed
to start another colony. In this main embodiment, colonies are, generally,
limited to tiles of a
single color. An option permits colors to be mixed until a colony is complete,
but this may be
confusing and, is similar to the second main embodiment which is clearer.
Another option permits
removal of opponents' pieces within the completed enclosure as is done in
'go'. Another option
permits more than one simultaneous colony to be worked on by a particular
player. In a second
main embodiment, only one set of such tiles is supplied (in a neutral color,
say white with black
dots, and with players using tiles with true hues, say red and blue) and all
players use them to
grow one (or more) colonies. Once a colony i's completed, the player who
completed it replaces
all black and white tiles in the colony with colored tiles of their own. Other
options include the
various contiguous placement alternatives as described elsewhere in this
application.
In any event, the primary algorithm for using this set of tile markings tb
enclose colonies
is as follows. A set of tiles is enclosed when all external sides: 1. have a
dot; 2. abut an edge of
the board; 3. abut an edge of another tile that has a dot on it; or, 4. abut a
colored tile that has
been converted to a particular player's consolidated terntory. Several
examples follow in diagram
(1500) of Figure 15.
In section (1501): tile AS is of type (904); tiles A6 and A7 are either empty
or, filled
with type (908) as shown or, equivalently, with unmarked type (902, 201),
depending upon the
requirements of whether the consolidated area just needs to be bordered or
filled; tiles BS and
B6 axe of type (903); and, tile B7 is a tile that has already been
consolidated and converted to
a standard colored player's tile (201). Tiles A5, A6, A7 and B6 comprise the
surrounded area just
completed and which is, optionally converted and consolidated, or just left as
is in favor of
starting a new colony. Tile AS has its own dots below and to the left, a board
edge above, and
an internal colony edge on its right; tile A6 has a board edge above, and
internal colony edges
on the other three sides; Tile A7 has board edges above and right, an internal
colony edge on the
left, and abuts a previously consolidated tile below; and, tile B6 has the dot
of tile BS to the left,
its own dot below, in internal colony edge above, and abuts the previously
consolidated tile on
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
27
the right. Tile BS is not part of the consolidated area in that, while it
contributes to the border
with its dot, it is not entirely within that border; it is vulnerable or open
on its left and below.
Now, if tile BS had instead been a (904) turned with its dots down and to the
left, it would
(potentially) have been included in the consolidated colony. Rcasons this was
not done include:
the (903)'tile may have been placed early before the plan to consolidate the
colony was formed;
placed by another player in an attempt to block formation of the colony;
another (904) may not
have been available due to tile type scarcity; a strategic decision not to
include tile BS in the
colony may have been made; or, this action would have put the lower dot in AS
within the
colony and, in one optional rule about colony formation, internal dots are not
permitted.
In configuration (1502), at C2: a (903) placed with its dot down would
complete a colony
consisting of the one cell D2; but, if the (903) is placed with ids dot up,
cells C1, C2 and C3 join
,D2 in the colony; if a (906) is placed with its open side up, the colony
consist of Cl, D2 and C3,
but not C2 itself which is open at the top; if a (907) is placed there, it
will make he colony of
C1, ~C2, C3 and D2, or be disallowed because of the three internal dots thus
created, depending
upon which optional rule is applied. Alternatively, at B2: plalcing a (906)
with dots up, left and
right completes a colony of five cells (B2 and the previous four) unless C2
requires filling with
a (902) or (980) first; and, placing a (905) with dots left and right sets the
stage for a colony of
six cells by extending to A2 with a (906) with dots up, left and right. And so
on.
Configuration (1503) is complete and tiles D6, E6 and E7 are ready to be
consolidated.
A (908) tile is, optionally, used to create a single-cell stand-alone colony;
or, these are
optionally used in place of (902) to depict internal cells of a colony.
Similarly (907) is,
optionally, considered a single-cell stand-alone colony. It may also be used
to connect up to four
partially completed colonies at once. In such a circumstance, so,long as all
four dots are used to
complete lobes of the colony, even if and of the four dots of the (907) become
internal at that
move, it is, optionally, permitted (with a conceptual opening in the middle of
the tile between
the four dots making them external). Thus, along row G (1504), four single
tiles are shown that
each, in at least some alternatives, comprise one-celled colonies. As just
explained, the (908) at
G1 and (907) at G3 are, optionally, considered stand-alone colonies. The (906)
at GS has three
sides dotted and, against an edge, is completed; the (904) at G7 has two sides
dotted and, against
a corner, is completed.
In general, particularly if internal dots are not permitted, laying down
border dots has two
conflicting effects: the border protects the enclosed cells; but, it also
limits the growth of the
colony.
Markings (909) and (910) are the symbols for "male" and "female" respectively.
Any two
symbols could be used, but these are particularly 'biological'. Alternatively,
different shapes of
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
28
tiles are used, for example (1009) and (1010) shown in Figure 10. Each player
is given 12 of
each to place in generation one. These may be placed: without restriction; all
the males first; all
the females first; alternating; or, otherwise. As two pieces must be removed
during a move in
generation two (or later), for any particular move one tile removed must be
male and the other
female., The order required may be male first, female first, alternating,
player's option, or
otherwise. ~r, on any move both must be either male or female, and this may be
at player's
option, or alternating. Larger tiles are, optionally, also supplied in
marlced, or rounded and .
rectangular, form, and played similarly.
Markings (911) and (912) show a "1" and "2" respectively, but these are
examples. In one
embodiment all 24 tiles are marked uniquely from 1 to 24. In another
embodiment there are
several sets with numbers; for example, four each of 1, 2, 3, 4, 5 and 6; etc.
In any case, the
pieces must be picked up, during generation two, in order: 1, 2, 3 ... 24 in
the first case; and, all
the 1's before any 2, and so on, in the other cases. In an optional further
restriction, the pieces
must also be placed in the same order during generation one. The first of
these restrictions makes
the playing of generation two (but not three) determined, to at least some
degree, at the end of
generation one. However, the mechanical nature of generation two is offset by
the additional
attention to strategy that must be applied during the play of generation one.
Marking (913) shows an "A" but this is an example. Each player may be given 12
each
of A and B; 8 each of A, B and C; 6 each of A, B, C and D; 12 of A, 6 of B, 3
each of C and
D; etc. More than 24 pieces may also be given; for example, 12 each of A, B,
C, D, E and F,
etc. Grouping symbols, other than letters, may also be used. A set of lettered
pieces must be
placed on the board contiguously. That is, once a first "A" piece (of a given
color separately, or
for all players together) is placed on the board, a subsequent "A" piece can
only be played in an
open grid location that is also adjacent (just the four orthogonal positions
or, optionally, any of
the eight orthogonal and diagonal positions) to some other "A" piece. In a
further optional
restriction, the new piece must be adjacent to the last such piece played.
'Colonies' or 'cultures'
of cells are, thus, built up. Options for continued play include: at any time
a new letter may be
played without the adjacency requirement, starting a new colony; a new colony
may only be
started when a (all) players) runs) out of tiles of a given letter, and/or if
a colony is 'boxed in'
with no more adjacent open space; the remainder of tiles from a boxed in
colony are then not
used or, alternatively, (if there are not sufficient total tiles) they may be
used to start a separate
colony; if two, or more, lettered colonies (e.g., "A" and "B") touch (again,
options for just
orthogonal, or both orthogonal and diagonal), then they combine and a tile of
any involved letter
may be played adjacent to another tile of any involved letter. Again, options
include that a
particular letter of a particular color is distinct; or colonies may include
tiles of all colors with
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
29
a particular letter: Also, larger pieces may have the same markings and
similar placement
restrictions; and/or, have the additional restriction that they may only
replace smaller tiles of the
same letter.
Another example, using lettered (or similarly marked in groups) tiles,
embodying a process
that is more societal or cultural (specifically economic or political) than
biological or ecological,
follows. This ispecific example employs: a 13x13 board; three generations
utilizing tiles (201), '
(203) and (205); equal numbers of tiles marked with letters A, B, C ~ D; and,
four players; but,
this type of process is also practiced in games with other elements and
options. In particular, the
rules defining the complementary groupings optionally increase in complexity
(in concert with,
or instead of, the geometric size or complexity of the tiles themselves) from
generation to
generation.
In generation one, each of four players has ten each of IA, B, C and D tiles,
as well as two
,N wild (201 ) tiles of their own color. These are placed as normally during
generation one,
leaving one open space. In generation two, each player must pick up four
tiles, comprising a
complementary grouping or 'deal', that consists of one each of A, B, C and D,
where an N may
substitute for one of the other lettered tiles. Optionally, these tiles must'
also consist of all the
player's own color; all of any one player's color; one each of each player's
color; some other
fixed or variable rule. After such a pick up of four tiles the player places
one or more (203) tiles,
if possible, which are similarly lettered and colored (where the move is,
optionally, structured as
UUDW, DUWtJ or otherwise, instead of UUUCTD). At most 36 (203) tiles are
placed, so it is
recommended that each player have sufficient tiles of each letter and,
optionally, a few N's as
well. Generation three proceeds quite similarly to generation two except that
the (205) tiles are
colored, but need not be lettered. Alternately, the (205) tiles are also
lettered, and only
complementary groups of four count at scoring time.
Marking (914) is an example of a schematic 'biomarking' (a single celled
organism with
cilia) and may be either decorative or functional. Purely decorative markings
will progress in
complexity of organism depicted, or other pattern, as the size of the tiles
progress; and are,
optionally, different for each player. As an example of functional markings:
some tiles (say half)
are marked as cocci and the others as amoebas. Amoebas may be played singly as
with the
standard game; but, cocci can only be placed in a contiguous culture or
colony, as with any of
the options for the lettered groups described, above.
Marking (915) shows a clock. This is probably only playable on a computer
display with
the clock counting down; but, may also be implemented using the 24 numbered
tiles on a
physical board. In either case, the organisms represented by the tiles have a
limited life that starts
when they are placed down. Thus, although a player is not forced to pick up
tiles in the order
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
they were placed, he must pick them up fairly soon (say, within one or two
moves of their
assigned order) or they will 'die' at the end of that turn and vacate the
board giving additional
empty space for the opponents) to occupy. As an aid to tracking which tiles
will die, a counter
(such as beads or pegs used in pool or cribbage, or a mechanical 'clicker' for
head counting, or
an electronic timer's Icd display) will indicate which numbered tile (plus any
with lower
numbers) is in danger. The count is incremented at each move, or at each round
of moves, or
after a timed period. Alternatively, a rack for removed tiles has a number
printed next to each
tile position so, as tiles are removed, moves are counted, and the adjacent
number represents
which numbered tile is in danger at the current move. If the first slot is
labeled "1", then no
flexibility is permitted. However, if the first N are blank, and the N+first
is labeled "1", then
there is some flexibility when removing tiles, and other tiles may be
strategically favored for N
moves. Placing the number labels on a movable slide permits the degree of
delay/flexibility to
be adjusted; and, providing separate slides for each player permits the delay
to be used as a
handicapping mechanism.
In an embodiment similar to the colony groupings described with the grouping
letters,
players must put down unmarked tiles in contiguous groupings and: may start a
new colony at
will; only after a colony reaches a certain minimum size; or, is forced to at
maximum a size;
and/or if a colony is 'boxed in' (perhaps with a missed turn as a penalty for
poor strategy). With
any of those alternative embodiments, the arrow tiles (916) are optionally
used as follows. A
further restriction is optionally applied that says, "not only must the new
piece be adjacent to the
colony, but to the last piece played." In that case, the arrow on the previous
piece played is
pointed to the next open square (if not boxed in) which is chosen, as a way of
reserving it so no
other opponent will take it. They may however, take 'next over' spaces to
force a block in, etc.
If this 'add on to last piece and reserve the space' rule is at the players'
option, pointing the
arrow 'back the way you came' indicates that the next move will be
discontiguous (but, otherwise
secret) and no next space is reserved. Alternatively, just a circle,. or a
face, or some other symbol
(not shown) is used at the head of such a growing path, to memorialize the
last tile added, which
is now the position to be extended from. Then when the next move is made, the
head marker is
moved into the new space, and a blank tile put in its place.
MUTATIONS ON A THEME: The principle of evolution as manifested in many
embodiments of the
instant invention is that, in concert with growth and succession, what happens
early on enables
what happens in the middle game and that, in turn, determines what happens in
the end game.
This may be conceived of and enacted upon: as a simple gestalt visualization
geared toward
'clumping' smaller pieces into sufficiently large masses that they will
persist until the end; or,
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
31
as a set of analytically strategic configuratiors implemented at each level
that are intended to
affect similarly particular configurations at each later level, with the goal
of maneuvering your
opponent into attrition; or, any number of other ways. However, these have in
common that two
(or more) players are competing, and that the players' actions ire
deterministic of the outcome.
What follows are a number of optional or alternative embodiments where a
player's own
actions are not entirely deterministic of the disposition of the tiles he
places or removes. Rather,
other players' actions, or random forces~comparable to 'mutation', interfere
with a player's game
plan in unpredictable ways. These uncertainties must be taken into account
when playing, even
i~,they cannot be predicted precisely. The examples below, generally, will
assume two players,
black and white, on a 7x7 board, playing three generations, using (201), (202)
and (203)' tiles,
respectively; but, are applicable to other embodiments as well.
In the most straightforward variation, player one plays white in generation
one, black in
generation two, and white again in generation three; and, vice versa for
player two. Thus, at
generation two, each player will attempt to 'trash' the strategic advantage of
the set of pieces they
are removing, and create as little strategic advantage for the pieces they axe
putting down.
Consequently, at generation one, the goal is changed, from setting up a
position that is maximally
advantageous if managed correctly, to setting up a position that is maximally
robust if mis-
managed with extreme prejudice. Similarly, at generation two, the goal is
changed to placing
pieces in a way that they cannot be managed at all well. Optionally, the
switching is done only
at one generation or the other; and, for longer games, switching occurs at any
combination of
generations.
A variation on the above is for player one to place white pieces at generation
one; and,
to remove white pieces but place black pieces at generation two; and, vice
versa for player two.
A similar arrangement, between generation two and three, etc., can optionally
be performed
instead of, or in addition to, the one just described.
Another slightly different variation on the above is for player one to place
white pieces
at generation one; and, to remove black pieces but place white pieces at
generation two; and, vice
versa for player two. A similar arrangement, between generation two and three,
etc., can
optionally be performed instead of, or in addition to, the one just described.
These elements of these variations can be assembled in other combinations in
the various
generations as well.
The classes of embodiments just described are 'all or nothing' at each
generation.
Alternatively, in generation one, instead of giving 'white' 24 white pieces
and 'black' 24 black
pieces, each player rnay be given 12 of each, or same other combination such
as 20 of your own
and 4 of your opponent's pieces to place. Various optional rules will specify
how much choice
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
32
each player has to place the two types of pieces: your opponents first, last,
alternating with your
own, at your discretion, etc. At later generations, such partial ownership of
tiles will be more
confusing, and harder to manage, because it is not pre-determined how many
tiles each player
will be placing. Consequently, next will be described special sets of tiles
that will enhance and
enable such embodiments.
Figure 10 depicts alternative rectangular tiles, each with a border area
(1001, 1003, 1005
& 1007) and central area (1002, 1004, 1006 & 1008) of different colors. Two
tiles, (100I/I002)
and (1003/1004), are both of unit size but two different color schemes, which
are shown by the
four different patterns. More than two color schemes are supplied as needed,
for additional
players or other embodiments. For larger tiles, only the first color scheme is
depicted but both
(or more) are supplied. Further, the particular shape of the border and
central areas are
exemplary, other shapes or symbols (such as are used in Figure 9) are used for
the same purposes
in alternative embodiments.
These tiles are put down according to the color of the border, and picked up
according
to the color of the central area. Now, it is possible to use black and white
for both color sets;
however, for black/black and white/white tiles will look solid and black/white
and white/black
tiles will visibly exhibit two areas. If this is confusing, two sets of colors
are assigned to each
player: for example, the first player plays white and blue and the second
player plays black and
red. The unit tiles (1001/1002) and (1003/1004) are then colored black (1001)
and white (1003)
in the border area and red or blue (depending) in either of the central areas
(1002 & 1004). Thus,
there are now four types of unit tiles: black/red, black/blue, white/red and
white/blue. The first
player puts down all the white tiles in generation one, and picks up all the
blue tiles in generation
two; the second player puts down alI the black tiles in generation one, and
picks up all the red
tiles in generation two. The four color combinations may be supplied in equal
numbers of 12
each; then each player in generation one will play 12 tiles for themselves and
12 for their
opponent, when it is considered who will play those tiles in generation two.
Alternatively, any
ratio can be embodied, e.g., 20 of your own and 4 of your opponent, etc. The
two types of unit
tiles may be placed in generation one: in any order as desired by player, one
per turn; alternating
on odd and even turns; one of each at each turn; etc.
Similarly, with three, four or more players. However, in that case there are
probably not
enough colors for each player to have two. For example, if there were four
colors black, white,
red and blue, each player would get 12 tiles in generation one. Of the 12
tiles for the black player
all 12 would have black border areas, and 3 of each central area would be
black, white, red and
blue; thus, three of black's tiles would be black/black and appear solid. A
thin white border
between the border and central areas would fix this anomaly. Similarly for the
other three players.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
33
Alternatively, for black, four of each would have central areas in red, white
and blue. In that
case, in the first generation, each player plays four pieces for each opponent
and none for
themselves. Other ratios and variations are also within the scope of the
instant invention.
Returning, now, to the embodiment with two players and four colors, the next
sized 2x1
pieces (1005/1006), comparable to (202), would be colored red or blue in the
border area and
black or white in the central area. Thus, in a move where two 1 x 1 tiles with
blue central areas
are picked up, one 2x1 tile with a blue outer area is put down; and, it will
have either a black
or white central area. Since in the second generation it is not guaranteed
that each player will be
placing exactly 12 tiles, some other mechanism is needed for distributing
among 'your' tiles and
'their' tiles. One such mechmism is to alternate, or do one out of 3 or 4 for
your opponent, etc.;
or, each player may place only their own or only their opponent's pieces in
generation two; or
the border area colors of the tiles) vacating is deterministic of whose piece
is placed. In the third
(and finally, for this example) generation the 2x1 tiles are picked up by then
inner colors and
single colored 2x2 pieces, of white for player one and black for player two,
are placed.
Alternatively, these tiles may be used like (909) and (910). The outer area
determines the
player (white or black) the inner area determines the gender (red or blue) at
all generations.
Players, at each generation have equal numbers of each gender, and the
placement and pick up
rules are any of those discussed earlier. More than two inner colors are used
for similar purposes.
For example, foux color 'genders' are put down and/or picked up, in groups, or
cyclic order on
moves alternating in cycles of four.
Shapes, several colors, and symbols can be combined on any of the tiles to
create other
variations for additional embodiments.
An embodiment employing both different colors and different shapes (or related
sets of
colors, or markings) permits complete or partial (depending on whether scoring
is individual or
by team) cooperative team play as follows.
Two teams of two players each will be described, but this embodiment is
optionally
practiced with more teams (basic colors) and/or more members per team
(distinguished by
additional shades, shapes or markings on tiles, for example).
The members of a team will share a basic color (e.g. redish or bluish) but
have distinct
shades (e.g., for three each: brick red, pink and orange vs. royal blue, sky
blue and green); or,
will have identical colors but two (or more) distinct shapes (e.g., 1x1
circles, 2x1 ovals and 2x2
circles vs. 1x1 squares, 2x1 rectangles and 2x2 squares).
In this example, player 1 is red round, player~2 is blue round, player 3 is
red square, and
player 4 is blue square.
play progresses as usual for four players. However, for generations two and
three (and
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
34
beyond) players may optionally, or are required to, adhere to rules for
removing pieces which
include, without limitation, for example:
~ pick up two of their own pieces;
~ pick up two of their partners pieces;
~ pick up two o~ the same, either theirs or their partner's;
~ pick up one of each, partner's first;
~ pick up one of each, partner's last; or,
~ pick up one of each, in either order.
The choice is alternatively fixed and determined before play begins, entirely
at players' option,
based on the roll of a die or other random choice device, or otherwise.
Generally, like with bridge, communication between partners as to strategy is
forbidden
or, at least, sub rosa; but, open verbal cooperation and planning is
optionally permitted.
Scoring is done on a team basis (complete team play) or per player
(cooperative but still
competitive partial team play).
Thus far, it is the other players) who are interfering, or cooperating, with a
particular
player's strategy. Next will be described how random elements, more akin to
'mutations', are
incorporated into the instant invention. It is practical, with computer-
mediated versions, to apply
these features as entirely random events that may happen at any time to any
tile, and the use of
random number generators to select the tile involved, and the probabilistic
distribution of events
that happen, are well known and within the ken of those skilled in
programming, in general, and
in programming games of chance in particular. Therefore, what follows, is an
example of how
to implement such elements as components of a physical board game.
If a 'mutation' is to be applied to any tile, it is selected by the use of the
1-7 and A-G
dice, as described above, to select a grid position, or by use of one or more
dice to specify a
number or symbol that is imprinted on the tile. Alternatively, mutations are
limited to one or a
few tiles which have a special symbol (e.g., a red dot) and an optional
sequence designation (e.g.,
the numbers l, 2, 3 or 4) to distinguish them. Then, at an appropriate time,
the appropriate player
rolls a special die. For example, between generations one and two, each player
rolls the special
die in alternating fashion four times each, for the four red-dotted and
numbered tiles each player
placed. The die, for example, is a twelve-sided kind, with: six sides
indicating nothing happens,
and the tile is replaced by a standard blank tile of the same color; three
sides indicating that the
tile 'mutates' and is replaced by a plain tile of the other player's (the
player to the right, if more
than two players) color; two sides indicating that the tile 'dies' and the
grid space is vacated; and,
the final side indicating that the tile becomes a 'bio-hazard' and is replaced
by a dead zone tile.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
Generation two then proceeds.
Such 'mutations' are optionally applied at later generations as well; and,
occur between
generations, as described, or at any time.
PROGRESSIVE PLAY WITH UNIFORM TOKENS: Although not ideal, special markings on
the board
permit 2"o to be played with readily-available or inexpensive tokens of two
colors (although
shades of those colors, or additional colors will help prevent confusion) but
with uniform or near
uniform (again to help avoid confusion) size. These may consist of
tiddlywinks, checkers, coins
(p,ennies and dimes), 'go' stones, or any other available tokens.
Figure 11 shows that each grid unit square has a small square inscribed at its
center, one
of which is designated (1101). In generation one, tokens are, placed here. For
generation two,
tokens on the central squares are removed and, for any two empty squares that
are adjacent
horizontally (1102) or vertically (1103), a token is placed on the small 2x1
rectangle crossing
their common edge, indicating that both those squares are occupied and may not
be occupied via
any of their remaining three edges. For generation three, the tokens over the
rectangles are
removed and, for any 2x2 cell of squares that are unoccupied, a token is
placed on the larger
square (1104) that is at the grid intersection common to the four, and
indicates that all four are
occupied. Thus, the size, shape, and placement of the symbols (1101-1104) they
occupy indicates
the use of tokens that are uniform in size, rather than embodying the use
information into the
shape and ,size of the tokens themselves.
Since the tokens are of uniform size, to prevent confusion, as an option, for
example,
black and white are used in generations one and three, and red and blue are
used in generation
two. ~r, dark, medium and light shades of each color are used progressively.
Alternatively, if
available, small, medium and large (but not in the correct shape and size
relationship, such as
small medium and large 'go' stones) tokens of the same two colors are used for
the same
purpose.
Alternatively, the markings of Figure 11 are constructed as indentations or
holes in the
board and each tile has an appropriate complementary peg in its bottom (with
an optional similar
peg on its top serving as a handle). This guarantees that the tiles are placed
properly during play,
no matter what their size.
GENERALIZATION TO THREE DIMENSIONS AND BEYOND (AND BEHIND): The three-
dimensional
and four-dimensional embodiments that result from the following theoretical
discussion are likely
to only be practicable to implement in a computer-mediated version, where
internal elements of
the playing volume are displayed translucently, transparently, or removed
transiently, to see
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
36
internal structure; and where it is easy to vary the orientation of the
playing volume.
The previous section disclosed, and depicted in Figure 11, that the basic game
as
described:
~ is played in two dimensions, on a grid of squares;
~ alternates two types of tiles (squares and flat 'bricks' or 2x1 rectangles)
and then returns
to larger squares (2x2) as the tiles grow;
~ the intermediate rectangular tile configuration can be oriented in two
orthogonal
directions, while the square tile configuration that starts and ends the
sequence is
orientable in only one way;
~ comprises three generations as the tiles return to the first configuration
(but larger);
~ the tiles comprise size 1, 2 and 4 units of area as generations progress;
and,
~ the three generations are played on the: one center, four edges, and four
corners of the
grid squares.
Figure 12 depicts a generalisation where the game:
~ is played in three dimensions, in a grid of cubes;
~ alternates three types of tiles (cubes (lxlxl), bricks (1x2x1), and
flattened cubes (2x1x2))
and then returns to larger cubes (2x2x2) as the tiles' grow;
~ the two tile configurations intermediate to the cubes can each be oriented
in three
orthogonal directions, while the cubic tile configuration that starts and ends
the sequence
is orientable in only one way;
~ comprises four generations as the tiles return to the f rst configuration
(but larger); .
~ the tiles comprise size 1, 2, 4 and 8 units of volume as generations
progress; and,
~ the four generations are played on the: one center, six faces, twelve edges,
and eight
corners of the grid cubes. .
In Figure 12, element (1201) shows how, in the first generation, an occupied
cube would
be depicted in a computer display by placing a solid or luminous small cube
within the partially
or entirely transparent grid cube. Note that each cube is occupied, or not,
independent of any
adjacent cube, and the unit is orientable in only one way.
Element (1202) shows how, in the second generation, an adjacent pair of cubes
is marked
as occupied by placing a small similar shape spanning the face the two cubes
share in common.
Note that: (playing volume edge effects aside) any given cube can participate
in any of six such
pairings, one via each face, but only one at a time. Further note that the
2x1x2 rectangular solid
so made can be oriented in any of three orthogonal orientations.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
37
Element (1203) shows how, in the third generation, four adjacent cubes in a
2x2 matrix
form a 2x1x2 rectangular solid, which is marked as occupied by placing a small
similar shape
spanning the edge that the four cubes share in common. Note that: (playing
volume edge effects
aside) any given cube can participate in any of twelve such pairings, one via
each edge, but only
one at a time. Further note that the 2x1x2 rectangular solid so made can be
oriented in any of
three orthogonal orientations.
Finally, element (1204) shows how, in the fourth generation, eight adjacent
cubes in a
2x2x2 matrix form a 2x2x2 cube, which is marked as occupied by placing a
smaller (but larger
than the first internal) cube spanning the corner that the eight,cubes share
in common. Note that:
(playing volume edge effects aside) any given cube can participate in any of
eight such pairings,
one via each corner, but only one at a time. Further note that the 2x2x2 cube
so made is
orientable in only one way.
This pattern and play algoritlun can be generalized to four dimensions (with
the fourth
dimension being conceptualized as temporal or hyper-spatial) or more. It may
also be applied to
other grids; for example, the equilateral triangles in two dimensions of
Figure 1 g, can be
generalized to tetrahedxons in three dimensions, etc.
The scheme of 2D squares and 3D cubes is generalizable to N dimensions as
follows:
Let D equal the number of dimensions. C(M,N) is the combination function,
being 'the
number of ways M objects can be taken N at a time'; or,~(M!)/(N! (M-N)!),
where ! is the
factorial function. The results of C(M,N) are conveniently arranged in
Pascal's triangle where the
row, counting from the top, starting at 0, is M; and, the entries in a row,
counting from the left,
are 0 through N. For the object that, in two dimensions is a square and, in
three dimensions is
a cube, the following tables are developed.
D=1 ITEM N=0 N=1
Tll C(D,N) 1 1
T12 2" 1 2
T13 PRODUCT 1 2
TABLE I
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
38
D=2 ITEM ~ N=0 N=I N=2
T2I C(D,N) 1 2 1
T22 2" 1 2 4
T23 ~ PRODUCT 1 4 4
TABLE II
D=3 ITEM N=0 N=1 N=2 N=3
T31 C(D,N) 1 3 3 1
T32 2" 1 2 4 8
T33 PRODUCT 1 6 12 8
TABLE III
D=4 ITEM N=0 N=1 N=2 N=3 N=4
T41 C(D,N) 1 4 6 4 I
T42 2" 1 2 4 8 16
T43 PRODUCT 1 8 24 32 16
TABLE IV
Each of the four tables has the same structure. The upper-left corner states
the number of
dimensions, D. Then, labels aside, there are columns for N=0 through N=I?. The
entries in rows
TD1, TD2 and TD3 are the combinatorial function, C(D,N), ZN and the product of
those two
terms, respectively.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
39
For the one-dimensional case, D=1, TABLE I (for example, see Figure 12,
diagram
(1206)):
~ the entries in row T13 are 1 and 2; and, these correspond to the 1 center
and 2 ends of
the unit line segment.
~ the entries in row Tl 1 are 1 and 1; and, these correspond to the possible
orientations for
the unit line segment, and the doubled line segment;as the segments progress.
For the two-dimensional case, D=2, TABLE II (for example, see Figure 11):
~ the entries in row T23 are 1, 4 and 4; and, these correspond to the 1
center, 4 sides and
4 corners of the unit square.
~ the entries in row T21 are 1, 2 and l; and, these correspond to the possible
orientations
for the square, 'brick', and large square as the tile types cycle.
For the three-dimensional case, D=3, TABLE III (for example, see Figure 12,
diagrams
(1201-1204)):
~ the entries in row T33 are 1, 6, 12 and 8; and, these correspond to the 1
center, 6 faces,
12 edges and 8 corners of the unit cube.
~ the entries in row T31 are 1, 3, 3 and 1; and, these correspond to the
possible orientations
for the cube, 'brick', 'flat tile' and Large cube as the solid tile types
cycle.
For the four-dimensional case, D=4, TABLE IV:
~ the entries in row T43 are l, 8, 24, 32 and 16; and, these correspond to the
1 center, 8
faces, 24 edges, 32 corners and 16 hyper-corners of the unit hyper-cube.
~ the entries in row T41 are 1, 4, 6, 4 and I; and, these correspond to the
possible
orientations for the five hyper-tiles as they double and cycle back to hyper-
cube.
As far as practicable embodiments: a 7x7x7x7 hyper-cube is displayed as seven
separate,
but ordered, 7x7x7 cubes in a computer-mediated navigable display. See Figure
I2, diagram
(1205). Further, a one-dimensional version of the game can be played, simply,
as expected: on
a board of 1xN array of squares (where values for N could comprise any number,
but 13, 15, 17,
19, 21 and 23 are reasonable.) Two (or more) players alternate placing lxl
units (1212 & 1214)
in generation one. In each subsequent generation: order of play is reversed;
the length of the 1xN
tiles are doubled; the previous tiles are removed and the larger tiles (1211 &
1213) deposited in
the IJDU method, growing an occupied area (e.g., from 1214), by a factor of
two, to the left (L)
or right (R), or placed anywhere there is room. The player with the most tiles
at the end wins.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
See Figure 12, diagram (1210) which is not fully populated with tiles, only
showing one single
and one double tile for each of two colors.
In 2~0, the unit 1x1 square tile is doubled in one dimension leading to a 2x1
'brick', and
then doubled in the other dimension returning to a 2x2 square shape. This
characteristic trait, that
the alternate generation tiles (at least) are self similar at increasing
scale, is shared by several
two-dimensional embodiments, and is also a characteristic associated with
"fractals". Some
specific tile pairs (which are extensible onward) that exhibit this
characteristic are: (201) & (203);
(202) & (204); (SO1) & (508); (502) & (509); (1701) & (1710); (1901) & (1903);
(1902) &
(1904); etc. In three dimensions, the self similarity is, generally, exhibited
every third generation;
and, in four dimensions, every fourth generation.
ADDITIONAL EXAMPLE EMBODIMENTS NOT BASED SOLELY ON THE UNIT SQUARE: The game
is
generalizable in other ways as well. For example, in Figure 17 are shown a set
of tiles that are
used to play an additional embodiment exhibiting binary geometric growth, or
doubling. Although
this embodiment is playable on the same type of square unit grid, the base
tile unit here (1701
or 302) is an "L", shown in a double line, made of three unit squares shown in
single lines that
would not necessarily be drawn on the tiles. Like the squares in (201) and
(203) appearing at four
times the area in odd alternating generations, the "L" also appears in odd
alternating generations
at four times the area. Tile (1710) shows the third generation "L" tile with,
again, the single lines
shown for illustration only. In the intervening even generations, tiles of
intermediate area
(comparable to (202) for example) are used, the most straightforward
embodiment of which is
(1704). However, tiles (1702) through (1709) show a number (not necessarily
exhaustive) of tiles
of the correct area ratio, and any combination of these in any number are
supplied as desired.
Figure 18 shows an alternative board (1800) that uses equilateral triangles,
e.g., (1801),
in lieu of squares. Again, any number of players (within reason) can play;
but, this board
configuration is particularly inviting of three players. The triangular board
can also be of any
reasonable size; and, the number of grid units is the square of the number of
triangles on the
edge. Board (1800), for example, has 7, triangles on each edge and has 49
units total, like the 7x7
square board. A board with an edge length of 8 would have 64 units; with an
edge length of 9,
81 units; with an edge length of 10, 100 units; etc.
Figure 19 shows tiles suitable for playing on a board such as is shown in
Figure 18. Tiles
are shown in solid lines, and the grid units shown in dashed lines for
illustration only. Tile (1901)
corresponds to the grid unit to be used in generation one, comparable to the
square (201) tile.
Tiles (1902), (1903), (1904) and (1905) correspond to (202), (203), (204) and
(205) respectively;
and, the same alternating shape, doubling in area, relationship in the
triangles and rhombuses can
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
41
go on indefinitely, just as with the squares and 'bricks'.
With the board of length 7 and area 49, only about 9 (1003) tiles will fit at
generation
three, or one (1905) tile will fit at generation five. With the three
generation version, this will
easily result in a three-way tie, but is unlikely to for two player. The board
of length 8 and area
64 will hold, at a maximum, 16 (1903) tiles or 4 (1905) tiles, better numbers
for three players.
An alternative set of tiles, roughly comparable to the linear growth
embodiment, comprises
tiles (1901), (1902), (1906), (1903 and/or 1907) and (1908) of areas 1, 2, 3,
4 and 6 grid units,
respectively, on successive generations. With the 49 triangle board, six
(1907) tiles would fit at
generation five; with the 81 triangle board, 10 would fit. ,For triangular has
well as other)
embodiments of the instant invention, all of the myriad variations of board
size and shape, tile
size and shape, tile supply, markings on the board and tiles, adjacency and
timing rules, etc., that
have been described with square embodiments, are practiced as options.
An additional way to extend the biological or evolutionary metaphor is ~' for
the tiles - in
addition to, or in lieu of, growing and/or becoming more complex in shape - to
exhibit some
form of 'behavior' as the 'organism' evolves. An example follows, as shown in
Figures 20 and
21.
Figure 20 shows a pattern, with two types of unit squares, that is instructive
for playing
another embodiment of the instant invention; however, it is also an option to
play this
embodiment without the darkened type of squares and no restrictions on the
placement of the
third generation tiles. The pattern has two mirror-image configurations (2001)
and (2002); and,
a board is, optionally, inscribed with areas of each. The pattern of (2001) is
shown, enlarged, in
(2003). Note that, edges aside, each 2x2 cell of white squares is surrounded
by four black
squares; and, each black square is surrounded by four 2x2 cells of white
squares.
This embodiment is, optionally, played with tiles (201) and (202) in
generations one and
two as usual. However, in generation three, the tiles shown in Figure 21 are
used instead of (203)
tiles. The tiles are f ve unit squares in area and comprise a 2x2 white cell
and an attached black
square. Shown at (2101), (2102), (2103) and (2104) are such a tile, polarized
suitably for the
pattern shown in (2001), in four orientations at 90° rotations. Mirror
image tiles axe optionally
supplied, but are not shown. Tiles are supplied only in one orientation, or in
both; both players
are supplied with the same orientation, each with only one, or each with both.
If the board is
unmarked the (210x) tiles are placed without restriction; if the board is
marked with (2001)
and/or (2002) patterns, tile placement is restricted to correspond with the
pattern; or, alternatively,
if the board is marked, tile placement is unrestricted, but only the tiles
that correspond to the
pattern will "spin". The embodiment where tiles "spin" is more practical with
computer-mediated
display.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
42
With the "spinning" tile embodiments, a 2x2 cell of white squares and the four
surrounding black squares must be empty in order to place the body of a (210x)
tile because, at _
each move (a move comprising one player's turn, or both players' turns) the
tile will rotate 90°.
However, optionally, so long as, the tile can be placed on a move, the
additional surrounding
black squares are vacated only as they are needed during the next few moves.
Direction of tile
spin is: uniform for all tiles; dependant on the tile (e.g., by color,
'gender', or polarity); player's
choice; assigned by the computer; or, determined by some random mechanism such
as the roll
of a die; etc. Spin speed is, optionally, also variable to values other than
90° per move.
Particularly if computer-mediated, these elements are, optionally, varied
dynamically.
In (2105) two pairs of tiles are shown. On the left (2106), if both (2107) on
top and
(2108) on bottom are turning counterclockwise their black appendages will
collide at (2109) on
the next 90° rotation (or the third rotation in the clockwise
direction). However, if (2108) spins
at half the speed of (2107) they will not collide. On the other hand, on the
right (2110) the top
tile (2111) has its black tooth in the overlapping square (2113) and, so, it
will be vacating that
spot as the tooth of the bottom tile (2112) moves into the conflicting square,
and collision is
avoided.
If a tile hits an obstacle (any type of tile present) there are several
alternatives: the tile
may knock off what it hits and/or itself be knocked off the board; the
'junior' (or, alternatively,
'senior' in size, or time on the board) party may be eliminated; the tile may
simply stop spinning
permanently, or until the blockage is removed; etc.
Spinning tiles, optionally, have some scoring or other advantage. It may be as
simple as
spinning tiles are worth extra points; or, tiles that 'mesh' with other tiles
of their own player's
color gain in value, while 'meshing' with other player's tiles reduce value.
Further, the advantage
is, optionally, that at the end of the game a pattern of spinning gears is
established. If a player
is able to place a marker on one of the teeth of one of the (or only one of
his own) gears, it is
transported and deposited, to be picked up by the tooth of some other gear,
and so on. A goal
(for example, being able to transport the marker from one edge of the board to
the opposite
edge), if established, creates a winning strategy (for the first to achieve
it), or scores additional
points.
Figure 22 depicts two repeating grids composed of more than one shape. These
axe
illustrative, non-limiting examples only; and, embodiments of the invention
axe implemented by
use of, or combined with, any other pattern or algorithm (decorative or
mathematical, uniform
or non-uniform, periodic or non-periodic, etc.) that tiles the plane, or fills
space of three or more
dimensions. Grid (2201) is composed of semi-regular octagons and squares; grid
(2202) is
composed of the same semi-regular octagons and rhombuses twice the area of the
squares. Dotted
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
43
lines show how a grid of unit squares is, optionally, overlaid on either grid.
Also shown is a set
of tiles, any combination of which (optionally, in combination with other
tiles described herein
such as (202), etc.) is used to play embodiments of the instant invention on
grids (2201) and/or
(2202), comprising: a right isosceles triangle (2203) one half unit in area;
the unit square (2204),
the same as (201); a rhombus (2205) two units in area, the same as (506); a
trapezoid (2206) two
units in area, the same as (505); a 3x1 bar (2207), three units in area, the
same as (301); a cross
(2208), five units in area; and, the semi-regular octagon (2209), seven units
in area.
Figure 23 shows a straightforward physical (or computer-mediated) embodiment
of the
instant invention played in three dimensions. This is a non-limiting example
only. Board (2300)
is a 'wedding cake' structure comprising: a 7x7 grid of unit squares; onto
which has been
centered a 5x5 grid of unit cubes; onto which has been centered a 3x3 grid of
unit cubes; onto
which has been centered a single unit cube. This comprises a mound, of 35 unit
cubes in volume,
onto which an additional 112 units of volume ' are to be stacked to complete a
7x7x3 unit
rectangular solid. No parts of a tile may exceed this boundary; and, each
generation is over when
no more tiles in play can be added. '
The solid 'tiles' used are: a unit cube (2301) at generation one, a 2x I
'brick' at generation
two; and, an "L" of three units in generation three.
In the first generation, unit tiles (2301) are added according to the
following rule: a tile
may be placed atop an empty square face of the board (except the central
tier), or atop a face of
another tile of the same color.
In the second generation (2301) tiles are removed and (2302) tiles are placed
in the UDU
(or other) method already described; however, it is not required to place
every (or any) tiles on
a particular turn. This is important because, in generations two and three,
the structure already
made is in the process of being dismantled from smaller tiles and re-built
from larger tiles. On
any given turn, it may be desired (or not) to do more dismantling and 'hit
bottom' before
building up. If this is not done, smaller tiles axe trapped below larger
tiles; and, this may or may
not be desired strategically. The rule for placing the larger tile is that, in
whatever orientation it
is placed: it may not exceed the edges of the 7x7x3 space; it, optionally,
must be entirely
supported, with no overhangs; and, optionally, each of its bottom squares must
rest on squaxes
of board, or top squares of tiles of its own color.
The third generation follows the same basic rules except that if a single unit
tile was
trapped and now exposed it (or two of them) are, optionally, removed in lieu
of a brick on either
'up' phase of a move.
The bricks (2302) are laid flat, or stood on end. The L's (2303) are laid flat
and 'wrapped
around' a corner; are laid on their back with a foot in the air; or, are even
stood on a foot, with
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
44
an optional requirement that the overhang is supported by the board or another
tile of the same
color.
The winner is, optionally: the player with the most volume; or, the player
with the most
squares among the 48 units of the top surface (excluding the central tier) of
the 7x7x3 rectangular
solid.
Figure 24 shows non-limiting examples of more general shapes of a three-
dimensional
board and tiles, that are representative of those used in alternative
embodiments of the instant
invention.
Additionally, any three-dimensional board is, optionally, played with a single
layer of
solid tiles, or flat tiles. Additional rules optionally determine how
different levels or 'geographic
features' of the terrain are to be played (e.g., lower levels before higher
levels) and scored (e.g.,
extra points for higher altitudes).
BOARI? WRAP-AROUND: Lastly, particularly when embodied as a computer-mediated
game, the
instant invention optionally employs exotic rules for board wrap-around.
Normally, at the edge
of a board, pieces are not permitted to hang over the edges, and certain
strategic factors come
into play at edges and corners. However, through the use of computer-mediated
displays,
situations that are physically impossible are implemented.
The first, most straightforward, is board wrap-around in either of the two
directions. In
that case, a piece that partially 'hangs off' the right side of the board (not
normally permitted)
shows up (to that same partial extent) on the left side of the board, and vice
versa. The technique
is optionally applied horizontally (left and right), vertically (top and
bottom) or both. This
mathematically creates a cylinder in one direction or a torus in both.
The cylinder is, optionally, projected on an annular board with a circular
hole in the
middle around which is the top of the cylinder; the bottom is at the outer
edge of the annulus.
This requires different sized tiles, as the circumference of the rows
increases; however, if the
game is implemented on a computer, the size of the tiles is easily adjusted
accordingly. Spirals
and sunflower-like patterns are also, optionally, applied to such boards.
In a somewhat more exotic 'twist' as the board is wrapped-around in either
direction a
half twist (as in a MoebiuS Strip) is applied and, thus, a game piece that
hangs off the top (for
example) not only re-appears at the bottom of the board, but on the back as
well. Further,
because of the twist, the order of rows (or columns) is reversed. Because the
computer is not
restricted to the physical geometry of the twist, the move to the back and the
reversal of rows
can be implemented separately or together. A different mode is optionally
applied to each
direction, or each edge.
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
Further, other 'impossible' options for continuity can be mathematically
implemented, and
displayed, by the computer. Just two more examples are disclosed, but the
inclusion of any such
exotic variation is intended to be within the scope of the instant invention.
First, 90° continuity
is implemented by connecting (for example) the right edge to the top of the
board. Finally,
instead of the reversal of rows (columns) in the Moebius option, a 'spiral'
option connects, for
example, the right of each row to the left of the next lower row, and the
right of the bottom row
to the left of the top.
A last embodiment that is impractical, if not quite impossible, to implement
without the
use ,of a computer-mediated display involves continuity of ,tiles, rather than
the board. In this
,embodiment, tiles at a particular phase are placed, and groups of adjacent,
tiles 'merge' into a
continuous area. Then, during a subsequent phase, sub-sets of such an area,
within boundaries of
permitted configurations, are removed from the area, without regard for the
boundaries of the tiles
that were placed to create the area. '
INTELLECTUAL PRQPERTY
The graphics and layouts of boards, graphics and configuration of pieces,
algorithms and
rules of play, steps described and/or depicted in any flow diagram, and other
elements disclosed
herein, are exemplary. A number of alternatives for each element have been
disclosed, as have
specific choices of alternatives comprising some specific preferred
embodiments. To whatever
degree these alternatives are not in conflict, any and all of the alternatives
for any element are
practiced, in any combination, with any and all of the alternatives for other
elements, in order
to create alternative preferred embodiments of the instant invention.
Furthermore, certain steps
or other elements may be arranged differently, combined, separated, modified
or eliminated
entirely, without deviating from the intended scope of the invention.
Further, these elements can be combined with elements of other games, now in
existence
or later developed, without deviating from the intended scope of the
invention. Additionally, any
method of manufacture, publishing or distribution of physical game boards and
pieces used to
play such games, now known or later developed, is intended to be within the
scope of the instant
invention. Similarly, any method of designing, displaying, distributing or
programming computer-
mediated versions of the instant invention (including but not limited to,
artificial intelligence to
produce a version where a computer plays a human, stereographic display, or
versions where
several players communicate over a network) now known or later developed, is
intended to be
CA 02514520 2005-07-27
WO 03/063979 PCT/US03/02316
46
within the scope of the instant invention.
The contents of the disclosure of this patent document, and the accompanying
figures, is
copyright to the inventor. The copyright owner has no~objection to the
facsimile reproduction of
the patent document or the patent disclosure, as it appears as issued by the
Patent and Trademark
Office, to the extent permitted by law. Written permission of the copyright
holder must be
obtained for any other use. Copyright holder otherwise reserves all copyright
rights whatsoever,
including the right to excerpt, compile or otherwise alter or adapt, or make
any other use of, this
information.
Further, the names 2va, 1 vo, Lvo, LINEAR Zvo, 45vo, Avo, ATIGLED 2vo, other
names
used herein, the numeral and subscripted text namizig convention, and any
other trademarkable
elements are trademarked to the inventor.
In any event, any publication of or about any of the infornzation contained
herein must
contain appropriate patent, trademark and copyright notices.
It will thus be seen that the objects set forth above, among those made
apparent from the
preceding description, are efficiently attained and certain changes may be
made in carrying out
the above method and in the construction set forth. Accordingly, it is
intended that all matter
contained in the above description or shown in the accompanying figures shall
be interpreted as
illustrative and not in a limiting sense.
Now that the invention has been described, what is claimed as new and desired
to be
secured by Letters Patent is: