Note: Descriptions are shown in the official language in which they were submitted.
DEMANDES OU BREVETS VOLUMINEUX
LA PRESENTE PARTIE DE CETTE DEMANDE OU CE BREVETS
COMPREND PLUS D'UN TOME.
CECI EST LE TOME DE _2
NOTE: Pour les tomes additionels, veillez contacter le Bureau Canadien des
Brevets.
JUMBO APPLICATIONS / PATENTS
THIS SECTION OF THE APPLICATION / PATENT CONTAINS MORE
THAN ONE VOLUME.
THIS IS VOLUME 1 OF 2
NOTE: For additional volumes please contact the Canadian Patent Office.
CA 02564047 2006-11-06
YU139 PCT 1
PRINTING CARTRIDGE HAVING SENSORS FOR
COLLECTIVE IDENTIFICATION OF MEDIA AND/OR MEDIA
COLORANT AND METHOD THEREOF
FIELD OF THE INVENTION
The present invention relates to the field of printer technology and discloses
a printing cartridge for use
in an image printer or the like. In particular, the present invention
discloses a printing cartridge which
incorporates capacitance sensor identification.
BACKGROUND OF THE INVENTION
Recently, digital printing technology has been proposed as a suitable
replacement for traditional camera
and photographic film techniques. The traditional film and photographic
techniques rely upon a film roll having
a number of pre-formatted negatives which are drawn past a lensing system and
onto which is imaged a negative
of a image taken by the lensing system. Upon the completion of a film roll,
the film is rewound into its container
and forwarded to a processing shop for processing and development of the
negatives so as to produce a
corresponding positive set of photos.
Unfortunately, such a system has a number of significant drawbacks. Firstly,
the chemicals utilized are
obviously very sensitive to light and any light impinging upon the film roll
will lead to exposure of the film.
They are therefore required to operate in a light sensitive environment where
the light imaging is totally
controlled. This results in onerous engineering requirements leading to
increased expense. Further, film
processing techniques require the utilizing of a "negative" and its subsequent
processing onto a "positive" film
paper through the utilization of processing chemicals and complex silver
halide processing etc. This is generally
unduly cumbersome, complex and expensive. Further, such a system through its
popularity has lead to the
standardization on certain size film formats and generally minimal flexibility
is possible with the aforementioned
techniques.
Recently, all digital cameras have been introduced. These camera devices
normally utilize a charge
coupled device (CCD) or other form of photosensor connected to a processing
chip which in turn is connected to
and controls a media storage device which can take the form of a detachable
magnetic card. In this type of
device, the image is captured by the CCD and stored on the magnetic storage
device. At some later time, the
image or images which have been captured are down loaded to a computer device
and printed out for viewing.
The digital camera has the disadvantage that access to images is non-immediate
and the further post processing
step of loading onto a computer system is required, the further post
processing often being a hindrance to ready
and expedient use.
Therefore, there remains a general need for an improved form of camera picture
image production
apparatus which is convenient, simple and effective in operation. Further,
there also remains a need for a simple
form of portable, immediate print media on which images can be effectively
reproduced.
In the parent application, there is disclosed the use of an authentication
chip to provide information in
connection with the print media and the media colorant that is supplied with
the cartridge.
The Applicant has identified that it would be highly desirable to provide a
means whereby information
concerning one or both of the media and the media colorant could be supplied
together with the cartridge. The
CA 02564047 2006-11-06
YU139 PCT 2
reason for this is that such information could be used, in a suitable form, by
a processor of such a device to
enhance operation of a printing mechanism. It will be appreciated that
printing mechanisms need to operate
differently with different types of media and media colorant. It follows that
it would be useful to supply
information concerning media and media colorant to a controller of the
printing mechanism so that operation of
the printing mechanism could be automatically adjusted to suit the particular
media and media colorant.
With suitable encryption techniques, this could be used to inhibit after-
market refilling. As is well
known in the field of printing technology, such after-market refilling has
become a cause for substantial concern
in the printing industry.
In European patent number EP 0779 497, which claims priority from US
application no 08/573,100,
incorporated herein by reference, there is disclosed a fingerprint acquisition
sensor. The sensor is described as an
apparatus for detecting topological variations on an object such as a finger.
The apparatus includes an array of
sensing elements disposed on a substrate which each have a parasitic
capacitance. An insulating material that
covers the sensing elements defines a receiving surface. When a finger is
placed on the receiving surface, the
capacitance of the sensors changes. A fingerprint comprises ridges and
valleys. It will be appreciated that when
the finger is positioned on the surface, the ridges create a greater change in
capacitance than the valleys. Thus,
data representing the fingerprint can be generated using suitable algorithmic
electronic circuits. The fingerprint
sensor is in the form of a ceramic metal oxide semiconductor (CMOS) device.
US Patent no. 6,049,620 also claims priority from US patent application no
08/573,100. This patent
discloses a fingerprint-sensing device comprising a planar array of closely
spaced capacitive sense elements. The
sense elements serve to measure a capacitance between the finger and a single
electrode in each sense element.
In this patent, each electrode or capacitor plate is charged and then a known
current source is used to remove an
amount of charge from each plate to measure the capacitance. The measured
capacitance varies as a function of a
distance between the fmger surface and the capacitor plate. Thus, the distance
between the finger surface and
each capacitor plate can be determined. The distance measurements are used to
produce a representation of a
pattern of ridges on the fmger surface.
Applicant has identified a manner in which this form of technology can be
applied to achieve a means
whereby printing cartridges can be provided with suitable identification data.
SUMMARY OF THE INVENTION
According to a first aspect of the invention, there is provided a printing
cartridge that comprises
a housing; and
an actuating formation that is positioned on the housing and is capable of
actuating a number of
capacitive sensors in an array of such sensors, the actuating formation being
configured to represent data
relating to at least one of a serial number of the cartridge, a media and a
media colorant, so that the capacitive
sensors, when actuated, together generate a signal carrying such data.
According to a second aspect of the invention, there is provided a method of
determining a media
colorant of a printing cartridge, the method comprising the step of actuating
a number of capacitive sensors within
an array of such sensors with an actuating formation positioned on the
printing cartridge, the actuating formation
representing data relating to a media colorant in the cartridge, so that the
capacitive sensors, when actuated,
generate a signal carrying data relating to the media colorant.
CA 02564047 2006-11-06
YU139 PCT 3
According to a third aspect of the invention, there is provided a printing
cartridge that comprises
a housing;
a media colorant supply arrangement positioned within the housing and
containing a supply of media
colorant; and
an actuating formation positioned on the housing and being capable of
actuating a number of capacitive
sensors in an array of such sensors, the actuating formation being configured
to represent data relating to the
media colorant so that a signal generated by the capacitive sensors, when
actuated, carries said data relating to the
media colorant.
According to a fourth aspect of the invention, there is provided a method of
determining media of a
printing cartridge, the method comprising the step of actuating a number of
capacitive sensors in an array of such
sensors with an actuating formation positioned on the printing cartridge, the
actuating formation representing data
relating to a media in the cartridge, so that the capacitive sensors, when
actuated, generate a signal carrying data
relating to the media.
According to a fifth aspect of the invention, there is provided a printing
cartridge that comprises
a housing;
a media supply arrangement positioned within the housing and containing a
supply of media; and
an actuating formation positioned on the housing and being capable of
actuating a number of capacitive
sensors in an array of such sensors, the actuating formation being configured
to represent data relating to the
media so that a signal generated by the capacitive sensors, when actuated,
carries said data relating to the media.
According to a sixth aspect of the invention, there is provided a method of
determining media and media
colorant of a printing cartridge, the method comprising the step of actuating
a number of capacitive sensors in an
array of such sensors with an actuating formation positioned on the printing
cartridge, the actuating formation
representing data relating to the media and the media colorant in the
cartridge, so that the capacitive sensors, when
actuated, generate a signal carrying data relating to the media and the media
colorant.
According to a seventh aspect of the invention, there is provided a printing
cartridge that comprises
a housing;
media and media colorant supply arrangements positioned within the housing and
containing a supply of
media and a supply of media colorant, respectively; and
an actuating formation positioned on the housing and being capable of
actuating a number of capacitive
sensors in an array of such sensors, the actuating formation being configured
to represent data relating to the
media and the media colorant so that a signal generated by the capacitive
sensors, when actuated, carries said data
relating to the media and the media colorant.
According to an eighth aspect of the invention, there is provided a printing
device which comprises
a body, a printing cartridge being engageable with the body, the printing
cartridge having a housing,
a media colorant supply arrangement positioned within the housing and
containing a supply of media
colorant, an actuator formation being positioned on the housing and
representing data relating to the media
colorant;
a processor positioned in the body to control operation of a media colorant
feed mechanism and a
printing mechanism; and
CA 02564047 2006-11-06
YU139 PCT 4
an array of capacitive sensors positioned in the body and being configured so
that predetermined
combinations of capacitive sensors in the sensor array, when actuated,
generate signals carrying data related
to the media colorant, such predetermined combinations of capacitive sensors
in the sensor array being
actuable by the actuator formation positioned on the housing of the printing
cartridge when the printing
cartridge is engaged with the body so that the array of capacitive sensors
generates a signal carrying said data
relating to the media colorant of the printing cartridge.
According to a ninth aspect of the invention, there is provided a printing
device which comprises
a body, a printing cartridge being engageable with the body, the printing
cartridge having a housing,
a media supply arrangement positioned within the housing and containing a
supply of media, an actuating
formation being positioned on the housing and representing data relating to
the media;
a processor positioned in the body to control operation of a media feed
mechanism and a printing
mechanism; and
an array of capacitive sensors positioned in the body and being configured so
that predetermined
combinations of capacitive sensors in the sensor array, when actuated,
generate signals carrying data related
to the media, such predetermined combinations of capacitive sensors in the
sensor array being actuable by the
actuator formation positioned on the housing of the printing cartridge when
the printing cartridge is engaged
with the body so that the array of capacitive sensors generates a signal
carrying said data relating to the media
of the printing cartridge.
According to a tenth aspect of the invention, there is provided a printing
device which comprises
a body, a printing cartridge being engageable with the body, the printing
cartridge having a housing,
media colorant and media supply arrangements positioned within the housing and
containing a supply of
media and media colorant, an actuating formation being positioned on the
housing and representing data
relating to the media colorant and the media;
a processor positioned in the body to control operation of media colorant and
media feed
mechanisms and a printing mechanism; and
an array of capacitive sensors positioned in the body and being configured so
that predetermined
combinations of capacitive sensors in the sensor array, when actuated,
generate signals carrying data related
to the media and the media colorant, such predetermined combinations of
capacitive sensors in the sensor
array being actuable by the actuator formation positioned on the housing of
the printing cartridge when the
printing cartridge is engaged with the body so that the array of capacitive
sensors generates a signal carrying
said data relating to the media and the media colorant.
The invention is now described, by way of example, with reference to the
accompanying drawings.
The specific nature of the following description should not be construed as
limiting in any way the broad
nature of this summary.
BRIEF DESCRIPTION OF THE DRAWINGS
Notwithstanding any other forms that may fall within the scope of the present
invention, preferred forms
of the invention will now be described, by way of example only, with reference
to the accompanying drawings in
which:
Fig. I illustrates an Artcam device constructed in accordance with the
preferred embodiment;
CA 02564047 2006-11-06
YU139 PCT 5
Fig. 2 is a schematic block diagram of the main Artcam electronic components;
Fig 2A is a schematic block diagram of the main Artcam components, including
an array of capacitive sensors for
actuation by an actuating formation on a printing cartridge;
Fig. 3 is a schematic block diagram of the Artcam Central Processor;
Fig. 3(a) illustrates the VLIW Vector Processor in more detail;
Fig. 3A is a schematic block diagram of the Artcam Central Processor
incorporating an interface for the array of
capacitive sensors;
Fig. 4 illustrates the Processing Unit in more detail;
Fig. 5 illustrates the ALU 188 in more detail;
Fig. 6 illustrates the In block in more detail;
Fig. 7 illustrates the Out block in more detail;
Fig. 8 illustrates the Registers block in more detail;
Fig. 9 illustrates the Crossbarl in more detail;
Fig. 10 illustrates the Crossbar2 in more detail;
Fig. 11 illustrates the read process block in more detail;
Fig. 12 illustrates the read process block in more detail;
Fig. 13 illustrates the barrel shifter block in more detail;
Fig. 14 illustrates the adder/logic block in more detail;
Fig. 15 illustrates the multiply block in more detail;
Fig. 16 illustrates the 1/0 address generator block in more detail;
Fig. 17 illustrates a pixel storage format;
Fig. 18 illustrates a sequential read iterator process;
Fig. 19 illustrates a box read iterator process;
Fig. 20 illustrates a box write iterator process;
Fig. 21 illustrates the vertical strip read/write iterator process;
Fig. 22 illustrates the vertical strip read/write iterator process;
Fig. 23 illustrates the generate sequential process;
Fig. 24 illustrates the generate sequential process;
Fig. 25 illustrates the generate vertical strip process;
Fig. 26 illustrates the generate vertical strip process;
Fig. 27 illustrates a pixel data configuration;
Fig. 28 illustrates a pixel processing process;
Fig. 29 illustrates a schematic block diagram of the display controller;
Fig. 30 illustrates the CCD image organization;
Fig. 31 illustrates the storage format for a logical image;
Fig. 32 illustrates the internal image memory storage format;
Fig. 33 illustrates the image pyramid storage format;
Fig. 34 illustrates a time line of the process of sampling an Artcard;
Fig. 35 illustrates the super sampling process;
Fig. 36 illustrates the process of reading a rotated Artcard;
CA 02564047 2006-11-06
YU139 PCT 6
Fig. 37 illustrates a flow chart of the steps necessary to decode an Artcard;
Fig. 38 illustrates an enlargement of the left hand corner of a single
Artcard;
Fig. 39 illustrates a single target for detection;
Fig. 40 illustrates the method utilised to detect targets;
Fig. 41 illustrates the method of calculating the distance between two
targets;
Fig. 42 illustrates the process of centroid drift;
Fig. 43 shows one form of centroid lookup table;
Fig. 44 illustrates the centroid updating process;
Fig. 45 illustrates a delta processing lookup table utilised in the preferred
embodiment;
Fig. 46 illustrates the process of unscrambling Artcard data;
Fig. 47 illustrates a magnified view of a series of dots;
Fig. 48 illustrates the data surface of a dot card;
Fig. 49 illustrates schematically the layout of a single datablock;
Fig. 50 illustrates a single datablock;
Fig. 51 and Fig. 52 illustrate magnified views of portions of the datablock of
Fig. 50;
Fig. 53 illustrates a single target structure;
Fig. 54 illustrates the target structure of a datablock;
Fig. 55 illustrates the positional relationship of targets relative to border
clocking regions of a data region;
Fig. 56 illustrates the orientation columns of a datablock;
Fig. 57 illustrates the array of dots of a datablock;
Fig. 58 illustrates schematically the structure of data for Reed-Solomon
encoding;
Fig. 59 illustrates an example Reed-Solomon encoding;
Fig. 60 illustrates the Reed-Solomon encoding process;
Fig. 61 illustrates the layout of encoded data within a datablock;
Fig. 62 illustrates the sampling process in sampling an alternative Artcard;
Fig. 63 illustrates, in exaggerated form, an example of sampling a rotated
alternative Artcard;
Fig. 64 illustrates the scanning process;
Fig. 65 illustrates the likely scanning distribution of the scanning process;
Fig. 66 illustrates the relationship between probability of symbol errors and
Reed-Solomon block errors;
Fig. 67 illustrates a flow chart of the decoding process;
Fig. 68 illustrates a process utilization diagram of the decoding process;
Fig. 69 illustrates the dataflow steps in decoding;
Fig. 70 illustrates the reading process in more detail;
Fig. 71 illustrates the process of detection of the start of an alternative
Artcard in more detail;
Fig. 72 illustrates the extraction of bit data process in more detail;
Fig. 73 illustrates the segmentation process utilized in the decoding process;
Fig. 74 illustrates the decoding process of fording targets in more detail;
Fig. 75 illustrates the data structures utilized in locating targets;
Fig. 76 illustrates the Lancos 3 function structure;
Fig. 77 illustrates an enlarged portion of a datablock illustrating the
clockmark and border region;
CA 02564047 2010-02-22
YU139 PCT 7
Fig. 78 illustrates the processing steps in decoding a bit image;
Fig. 79 illustrates the dataflow steps in decoding a bit image;
Fig. 80 illustrates the descrambling process of the preferred embodiment;
Fig. 81 illustrates one form of implementation of the convolver;
Fig. 82 illustrates a convolution process;
Fig. 83 illustrates the compositing process;
Fig. 84 illustrates the regular compositing process in more detail;
Fig. 85 illustrates the process of warping using a warp map;
Fig. 86 illustrates the warping bi-linear interpolation process;
Fig. 87 illustrates the process of span calculation;
Fig. 88 illustrates the basic span calculation process;
Fig. 89 illustrates one form of detail implementation of the span calculation
process;
Fig. 90 illustrates the process of reading image pyramid levels;
Fig. 91 illustrates using the pyramid table for bilinear interpolation;
Fig. 92 illustrates the histogram collection process;
Fig. 93 illustrates the color transform process;
Fig. 94 illustrates the color conversion process;
Fig. 95 illustrates the color space conversion process in more detail;
Fig. 96 illustrates the process of calculating an input coordinate;
Fig. 97 illustrates the process of compositing with feedback;
Fig. 98 illustrates the generalized scaling process;
Fig. 99 illustrates the scale in X scaling process;
Fig. 100 illustrates the scale in Y scaling process;
Fig. 101 illustrates the tessellation process;
Fig. 102 illustrates the sub-pixel translation process;
Fig. 103 illustrates the compositing process;
Fig. 104 illustrates the process of compositing with feedback;
Fig. 105 illustrates the process of tiling with color from the input image;
Fig. 106 illustrates the process of tiling with feedback;
Fig. 107 illustrates the process of tiling with texture replacement;
Fig. 108 illustrates the process of tiling with color from the input image;
Fig. 109 illustrates the process of applying a texture without feedback;
Fig. 110 illustrates the process of applying a texture with feedback;
Fig. 111 illustrates the process of rotation of CCD pixels;
Fig. 112 illustrates the process of interpolation of Green subpixels;
Fig. 113 illustrates the process of interpolation of Blue subpixels;
Fig. 114 illustrates the process of interpolation of Red subpixels;
Fig. 115 illustrates the process of CCD pixel interpolation with 0 degree
rotation for odd pixel lines;
Fig. 116 illustrates the process of CCD pixel interpolation with 0 degree
rotation for even pixel lines;
CA 02564047 2006-11-06
YU139 PCT 8
Fig. 117 illustrates the process of color conversion to Lab color space;
Fig. 118 illustrates the process of calculation of I NX;
Fig. 119 illustrates the implementation of the calculation of 1NX in more
detail;
Fig. 120 illustrates the process of Normal calculation with a bump map;
Fig. 121 illustrates the process of illumination calculation with a bump map;
Fig. 122 illustrates the process of illumination calculation with a bump map
in more detail;
Fig. 123 illustrates the process of calculation of L using a directional
light;
Fig. 124 illustrates the process of calculation of L using a Omni lights and
spotlights;
Fig. 125 illustrates one form of implementation of calculation of L using a
Omni lights and spotlights;
Fig. 126 illustrates the process of calculating the N.L dot product;
Fig. 127 illustrates the process of calculating the N.L dot product in more
detail;
Fig. 128 illustrates the process of calculating the R.V dot product;
Fig. 129 illustrates the process of calculating the R.V dot product in more
detail;
Fig. 130 illustrates the attenuation calculation inputs and outputs;
Fig. 131 illustrates an actual implementation of attenuation calculation;
Fig. 132 illustrates an graph of the cone factor;
Fig. 133 illustrates the process of penumbra calculation;
Fig. 134 illustrates the angles utilised in penumbra calculation;
Fig. 135 illustrates the inputs and outputs to penumbra calculation;
Fig. 136 illustrates an actual implementation of penumbra calculation;
Fig. 137 illustrates the inputs and outputs to ambient calculation;
Fig. 138 illustrates an actual implementation of ambient calculation;
Fig. 139 illustrates an actual implementation of diffuse calculation;
Fig. 140 illustrates the inputs and outputs to a diffuse calculation;
Fig. 141 illustrates an actual implementation of a diffuse calculation;
Fig. 142 illustrates the inputs and outputs to a specular calculation;
Fig. 143 illustrates an actual implementation of a specular calculation;
Fig. 144 illustrates the inputs and outputs to a specular calculation;
Fig. 145 illustrates an actual implementation of a specular calculation;
Fig. 146 illustrates an actual implementation of an ambient only calculation;
Fig. 147 illustrates the process overview of light calculation;
Fig. 148 illustrates an example illumination calculation for a single infinite
light source;
Fig. 149 illustrates an example illumination calculation for an Omni light
source without a bump map;
Fig. 150 illustrates an example illumination calculation for an Omni light
source with a bump map;
Fig. 151 illustrates an example illumination calculation for a Spotlight light
source without a bump map;
Fig. 152 illustrates the process of applying a single Spotlight onto an image
with an associated bump-map;
Fig. 153 illustrates the logical layout of a single printhead;
Fig. 154 illustrates the structure of the printhead interface;
Fig. 155 illustrates the process of rotation of a Lab image;
Fig. 156 illustrates the format of a pixel of the printed image;
CA 02564047 2006-11-06
YU139 PCT 9
Fig. 157 illustrates the dithering process;
Fig. 158 illustrates the process of generating an 8 bit dot output;
Fig. 159 illustrates a perspective view of the card reader;
Fig. 160 illustrates an exploded perspective of a card reader;
Fig. 161 illustrates a close up view of the Artcard reader;
Fig. 162 illustrates a perspective view of the print roll and print head;
Fig. 163 illustrates a first exploded perspective view of the print roll;
Fig. 164 illustrates a second exploded perspective view of the print roll;
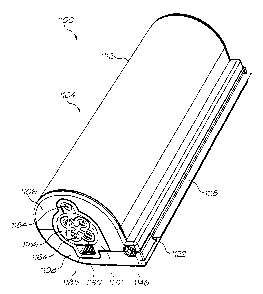
Fig. 164A illustrates a three dimensional view of another embodiment of the
print roll and print head in the form
of a printing cartridge also in accordance with the invention;
Fig. 164B illustrates a three dimensional, sectional view of the print
cartridge of Fig. 164A;
Fig. 164C shows a three dimensional, exploded view of the print cartridge of
Fig. 164A;
Fig 164D shows a three dimensional, exploded view of an ink cartridge forming
part of the print cartridge of Fig
164A;
Fig. 164E shows a three dimensional view of an air filter of the print
cartridge of Fig. 164A;
Fig. 164F illustrates a three dimensional view of a further embodiment of a
print cartridge incorporating an
actuating formation in combination with an array of capacitive sensors of an
Artcam device;
Fig. 164G illustrates a detailed view of part of the actuating formation of
the print cartridge of Fig 164F;
Fig. 164H illustrates a schematic side view of an array of capacitive sensors
of the Artcam device;
Figure 1641 illustrates a high level circuit used to determine capacitance
generated when the actuating formation
of the print cartridge actuates the array of capacitive sensors;
Figure 164J illustrates a simple diagram indicating operation of the pressure
sensor array and a lookup algorithm
carried by a processor of the Artcam device;
Fig. 165 illustrates the print roll authentication chip;
Fig. 166 illustrates an enlarged view of the print roll authentication chip;
Fig. 167 illustrates a single authentication chip data protocol;
Fig. 168 illustrates a dual authentication chip data protocol;
Fig. 169 illustrates a first presence only protocol;
Fig. 170 illustrates a second presence only protocol;
Fig. 171 illustrates a third data protocol;
Fig. 172 illustrates a fourth data protocol;
Fig. 173 is a schematic block diagram of a maximal period LFSR;
Fig. 174 is a schematic block diagram of a clock limiting filter;
Fig. 175 is a schematic block diagram of the tamper detection lines;
Fig. 176 illustrates an oversized nMOS transistor;
Fig. 177 illustrates the taking of multiple XORs from the Tamper Detect Line
Fig. 178 illustrates how the Tamper Lines cover the noise generator circuitry;
Fig. 179 illustrates the normal form of FET implementation;
Fig. 180 illustrates the modified form of FET implementation of the preferred
embodiment;
Fig. 181 illustrates a schematic block diagram of the authentication chip;
CA 02564047 2006-11-06
YU139 PCT 10
Fig. 182 illustrates an example memory map;
Fig. 183 illustrates an example of the constants memory map;
Fig. 184 illustrates an example of the RAM memory map;
Fig. 185 illustrates an example of the Flash memory variables memory map;
Fig. 186 illustrates an example of the Flash memory program memory map;
Fig. 187 shows the data flow and relationship between components of the State
Machine;
Fig. 188 shows the data flow and relationship between components of the FO
Unit.
Fig. 189 illustrates a schematic block diagram of the Arithmetic Logic Unit;
Fig. 190 illustrates a schematic block diagram of the RPL unit;
Fig. 191 illustrates a schematic block diagram of the ROR block of the ALU;
Fig. 192 is a block diagram of the Program Counter Unit;
Fig. 193 is a block diagram of the Memory Unit;
Fig. 194 shows a schematic block diagram for the Address Generator Unit;
Fig. 195 shows a schematic block diagram for the JSIGEN Unit;
Fig. 196 shows a schematic block diagram for the JSRGEN Unit.
Fig. 197 shows a schematic block diagram for the DBRGEN Unit;
Fig. 198 shows a schematic block diagram for the LDKGEN Unit;
Fig. 199 shows a schematic block diagram for the RPLGEN Unit;
Fig. 200 shows a schematic block diagram for the VARGEN Unit.
Fig. 201 shows a schematic block diagram for the CLRGEN Unit.
Fig. 202 shows a schematic block diagram for the BITGEN Unit.
Fig. 203 sets out the information stored on the print roll authentication
chip;
Fig. 204 illustrates the data stored within the Artcam authorization chip;
Fig. 205 illustrates the process of print head pulse characterization;
Fig. 206 is an exploded perspective, in section, of the print head ink supply
mechanism;
Fig. 207 is a bottom perspective of the ink head supply unit;
Fig. 208 is a bottom side sectional view of the ink head supply unit;
Fig. 209 is a top perspective of the ink head supply unit;
Fig. 210 is a top side sectional view of the ink head supply unit;
Fig. 211 illustrates a perspective view of a small portion of the print head;
Fig. 212 illustrates is an exploded perspective of the print head unit;
Fig. 213 illustrates a top side perspective view of the internal portions of
an Artcam camera, showing the parts
flattened out;
Fig. 214 illustrates a bottom side perspective view of the internal portions
of an Artcam camera, showing the parts
flattened out;
Fig. 215 illustrates a first top side perspective view of the internal
portions of an Artcam camera, showing the
parts as encased in an Artcam;
Fig. 216 illustrates a second top side perspective view of the internal
portions of an Artcam camera, showing the
parts as encased in an Artcam;
Fig. 217 illustrates a second top side perspective view of the internal
portions of an Artcam camera, showing the
CA 02564047 2006-11-06
YU139 PCT 11
parts as encased in an Artcam;
Fig. 218 illustrates the backing portion of a postcard print roll;
Fig. 219 illustrates the corresponding front image on the postcard print roll
after printing out images;
Fig. 220 illustrates a form of print roll ready for purchase by a consumer;
Fig. 221 illustrates a layout of the software/hardware modules of the overall
Artcam application;
Fig. 222 illustrates a layout of the software/hardware modules of the Camera
Manager;
Fig. 223 illustrates a layout of the software/hardware modules of the Image
Processing Manager;
Fig. 224 illustrates a layout of the software/hardware modules of the Printer
Manager;
Fig. 225 illustrates a layout of the software/hardware modules of the Image
Processing Manager;
Fig. 226 illustrates a layout of the software/hardware modules of the File
Manager;
Fig. 227 illustrates a perspective view, partly in section, of an alternative
form of printroll;
Fig. 228 is a left side exploded perspective view of the print roll of Fig.
227;
Fig. 229 is a right side exploded perspective view of a single printroll;
Fig. 230 is an exploded perspective view, partly in section, of the core
portion of the printroll; and
Fig. 231 is a second exploded perspective view of the core portion of the
printroll.
DESCRIPTION OF PREFERRED AND OTHER EMBODIMENTS
The digital image processing camera system constructed in accordance with the
preferred embodiment is
as illustrated in Fig. 1. The camera unit I includes means for the insertion
of an integral print roll (not shown).
The camera unit 1 can include an area image sensor 2 which sensors an image 3
for captured by the camera.
Optionally, the second area image sensor can be provided to also image the
scene 3 and to optionally provide for
the production of stereographic output effects.
The camera 1 can include an optional color display 5 for the display of the
image being sensed by the
sensor 2. When a simple image is being displayed on the display 5, the button
6 can be depressed resulting in the
printed image 8 being output by the camera unit 1. A series of cards, herein
after known as "Artcards" 9 contain,
on one surface encoded information and on the other surface, contain an image
distorted by the particular effect
produced by the Artcard 9. The Artcard 9 is inserted in an Artcard reader 10
in the side of camera 1 and, upon
insertion, results in output image 8 being distorted in the same manner as the
distortion appearing on the
surface of Artcard 9. Hence, by means of this simple user interface a user
wishing to produce a particular effect
can insert one of many Artcards 9 into the Artcard reader 10 and utilize
button 19 to take a picture of the image 3
resulting in a corresponding distorted output image 8.
The camera unit 1 can also include a number of other control button 13, 14 in
addition to a simple LCD
output display 15 for the display of informative information including the
number of printouts left on the internal
print roll on the camera unit. Additionally, different output formats can be
controlled by CHP switch 17.
Turning now to Fig. 2, there is illustrated a schematic view of the internal
hardware of the camera unit 1.
The internal hardware is based around an Artcam central processor unit (ACP)
31.
Artcam Central Processor 31
The Artcam central processor 31 provides many functions which form the `heart'
of the system. The
ACP 31 is preferably implemented as a complex, high speed, CMOS system on-a-
chip. Utilising standard cell
design with some full custom regions is recommended. Fabrication on a 0.25
micron CMOS process will provide
CA 02564047 2006-11-06
YU139 PCT 12
the density and speed required, along with a reasonably small die area.
The functions provided by the ACP 31 include:
1. Control and digitization of the area image sensor 2. A 3D stereoscopic
version of the ACP
requires two area image sensor interfaces with a second optional image sensor
4 being provided for stereoscopic
effects.
2. Area image sensor compensation, reformatting, and image enhancement.
3. Memory interface and management to a memory store 33.
4. Interface, control, and analog to digital conversion of an Artcard reader
linear image sensor 34
which is provided for the reading of data from the Artcards 9.
5. Extraction of the raw Artcard data from the digitized and encoded Artcard
image.
6. Reed-Solomon error detection and correction of the Artcard encoded data.
The encoded surface
of the Artcard 9 includes information on how to process an image to produce
the effects displayed on the image
distorted surface of the Artcard 9. This information is in the form of a
script, hereinafter known as a "Vark
script". The Vark script is utilised by an interpreter running within the ACP
31 to produce the desired effect.
7. Interpretation of the Vark script on the Artcard 9.
8. Performing image processing operations as specified by the Vark script.
9. Controlling various motors for the paper transport 36, zoom lens 38,
autofocus 39 and Artcard
driver 37.
10. Controlling a guillotine actuator 40 for the operation of a guillotine 41
for the cutting of
photographs 8 from print roll 42.
11. Half-toning of the image data for printing.
12. Providing the print data to a print-head 44 at the appropriate times.
13. Controlling the print head 44.
14. Controlling the ink pressure feed to print-head 44.
15. Controlling optional flash unit 56.
16. Reading and acting on various sensors in the camera, including camera
orientation sensor 46,
autofocus 47 and Artcard insertion sensor 49.
17. Reading and acting on the user interface buttons 6, 13, 14.
18. Controlling the status display 15.
19. Providing viewfinder and preview images to the color display 5.
20. Control of the system power consumption, including the ACP power
consumption via power
management circuit 51 .
21. Providing external communications 52 to general purpose computers (using
part USB).
22. Reading and storing information in a printing roll authentication chip 53.
23. Reading and storing information in a camera authentication chip 54.
24. Communicating with an optional mini-keyboard 57 for text modification.
Quartz crystal 58
A quartz crystal 58 is used as a frequency reference for the system clock. As
the system clock is very
high, the ACP 31 includes a phase locked loop clock circuit to increase the
frequency derived from the crystal 58.
Image Sensing
CA 02564047 2006-11-06
YU139 PCT 13
Area image sensor 2
The area image sensor 2 converts an image through its lens into an electrical
signal. It can either be a
charge coupled device (CCD) or an active pixel sensor (APS)CMOS image sector.
At present, available CCD's
normally have a higher image quality, however, there is currently much
development occurring in CMOS
imagers. CMOS imagers are eventually expected to be substantially cheaper than
CCD's have smaller pixel
areas, and be able to incorporate drive circuitry and signal processing. They
can also be made in CMOS fabs,
which are transitioning to 12" wafers. CCD's are usually built in 6" wafer
fabs, and economics may not allow a
conversion to 12" fabs. Therefore, the difference in fabrication cost between
CCD's and CMOS imagers is likely
to increase, progressively favoring CMOS imagers. However, at present, a CCD
is probably the best option.
The Artcam unit will produce suitable results with a 1,500 x 1,000 area image
sensor. However, smaller
sensors, such as 750 x 500, will be adequate for many markets. The Artcam is
less sensitive to image sensor
resolution than are conventional digital cameras. This is because many of the
styles contained on Artcards 9
process the image in such a way as to obscure the lack of resolution. For
example, if the image is distorted to
simulate the effect of being converted to an impressionistic painting, low
source image resolution can be used with
minimal effect. Further examples for which low resolution input images will
typically not be noticed include
image warps which produce high distorted images, multiple miniature copies of
the of the image (eg. passport
photos), textural processing such as bump mapping for a base relief metal
look, and photo-compositing into
structured scenes.
This tolerance of low resolution image sensors may be a significant factor in
reducing the manufacturing
cost of an Artcam unit 1 camera. An Artcam with a low cost 750 x 500 image
sensor will often produce superior
results to a conventional digital camera with a much more expensive 1,500 x
1,000 image sensor.
Optional stereoscopic 3D image sensor 4
The 3D versions of the Artcam unit 1 have an additional image sensor 4, for
stereoscopic operation. This
image sensor is identical to the main image sensor. The circuitry to drive the
optional image sensor may be
included as a standard part of the ACP chip 31 to reduce incremental design
cost. Alternatively, a separate 3D
Artcam ACP can be designed. This option will reduce the manufacturing cost of
a mainstream single sensor
Artcam.
Print roll authentication chip 53
A small chip 53 is included in each print roll 42. This chip replaced the
functions of the bar code, optical
sensor and wheel, and ISO/ASA sensor on other forms of camera film units such
as Advanced Photo Systems film
cartridges.
The authentication chip also provides other features:
1. The storage of data rather than that which is mechanically and optically
sensed from APS rolls
2. A remaining media length indication, accurate to high resolution.
3. Authentication Information to prevent inferior clone print roll copies.
The authentication chip 53 contains 1024 bits of Flash memory, of which 128
bits is an authentication
key, and 512 bits is the authentication information. Also included is an
encryption circuit to ensure that the
authentication key cannot be accessed directly.
Print-head 44
The Artcam unit I can utilize any color print technology which is small
enough, low enough power, fast
CA 02564047 2006-11-06
YU139PCT 14
enough, high enough quality, and low enough cost, and is compatible with the
print roll. Relevant printheads will
be specifically discussed hereinafter.
The specifications of the ink jet head are:
Image type Bi-level, dithered
Color CMY Process Color
Resolution 1600 dpi
Print head length 'Page-width' (I 00mm)
Print speed 2 seconds per photo
Optional ink pressure Controller (not shown)
The function of the ink pressure controller depends upon the type of ink jet
print head 44 incorporated in
the Artcam. For some types of ink jet, the use of an ink pressure controller
can be eliminated, as the ink pressure
is simply atmospheric pressure. Other types of print head require a regulated
positive ink pressure. In this case,
the in pressure controller consists of a pump and pressure transducer.
Other print heads may require an ultrasonic transducer to cause regular
oscillations in the ink pressure,
typically at frequencies around 100KHz. In the case, the ACP 31 controls the
frequency phase and amplitude of
these oscillations.
Pager transport motor 36
The paper transport motor 36 moves the paper from within the print roll 42
past the print head at a
relatively constant rate. The motor 36 is a miniature motor geared down to an
appropriate speed to drive rollers
which move the paper. A high quality motor and mechanical gears are required
to achieve high image quality, as
mechanical nimble or other vibrations will affect the printed dot row spacing.
Paper transport motor driver 60
The motor driver 60 is a small circuit which amplifies the digital motor
control signals from the APC 31
to levels suitable for driving the motor 36.
Paper pull sensor
A paper pull sensor 50 detects a user's attempt to pull a photo from the
camera unit during the printing
process. The APC 31 reads this sensor 50, and activates the guillotine 41 if
the condition occurs. The paper pull
sensor 50 is incorporated to make the camera more `foolproof in operation.
Were the user to pull the paper out
forcefully during printing, the print mechanism 44 or print roll 42 may (in
extreme cases) be damaged. Since it is
acceptable to pull out the `pod' from a Polaroid type camera before it is
fully ejected, the public has been `trained'
to do this. Therefore, they are unlikely to heed printed instructions not to
pull the paper.
The Artcam preferably restarts the photo print process after the guillotine 41
has cut the paper after pull
sensing.
The pull sensor can be implemented as a strain gauge sensor, or as an optical
sensor detecting a small
plastic flag which is deflected by the torque that occurs on the paper drive
rollers when the paper is pulled. The
latter implementation is recommendation for low cost.
Paper guillotine actuator 40
The paper guillotine actuator 40 is a small actuator which causes the
guillotine 41 to cut the paper either
at the end of a photograph, or when the paper pull sensor 50 is activated.
CA 02564047 2006-11-06
YU139 PCT 15
The guillotine actuator 40 is a small circuit which amplifies a guillotine
control signal from the APC tot
the level required by the actuator 41.
Artcard 9
The Artcard 9 is a program storage medium for the Artcam unit. As noted
previously, the programs are
in the form of Vark scripts. Vark is a powerful image processing language
especially developed for the Artcam
unit. Each Artcard 9 contains one Vark script, and thereby defines one image
processing style.
Preferably, the VARK language is highly image processing specific. By being
highly image processing
specific, the amount of storage required to store the details on the card are
substantially reduced. Further, the ease
with which new programs can be created, including enhanced effects, is also
substantially increased. Preferably,
the language includes facilities for handling many image processing functions
including image warping via a warp
map, convolution, color lookup tables, posterizing an image, adding noise to
an image, image enhancement filters,
painting algorithms, brush jittering and manipulation edge detection filters,
tiling, illumination via light sources,
bump maps, text, face detection and object detection attributes, fonts,
including three dimensional fonts, and
arbitrary complexity pre-rendered icons. Further details of the operation of
the Vark language interpreter are
contained hereinafter.
Hence, by utilizing the language constructs as defined by the created
language, new affects on arbitrary
images can be created and constructed for inexpensive storage on Artcard and
subsequent distribution to camera
owners. Further, on one surface of the card can be provided an example
illustrating the effect that a particular
VARK script, stored on the other surface of the card, will have on an
arbitrary captured image.
By utilizing such a system, camera technology can be distributed without a
great fear of obsolescence in
that, provided a VARK interpreter is incorporated in the camera device, a
device independent scenario is provided
whereby the underlying technology can be completely varied over time. Further,
the VARK scripts can be
updated as new filters are created and distributed in an inexpensive manner,
such as via simple cards for card
reading.
The Artcard 9 is a piece of thin white plastic with the same format as a
credit card (86mm long by 54mm
wide). The Artcard is printed on both sides using a high resolution ink jet
printer. The inkjet printer technology is
assumed to be the same as that used in the Artcam, with 1600 dpi (63dpmm)
resolution. A major feature of the
Artcard 9 is low manufacturing cost. Artcards can be manufactured at high
speeds as a wide web of plastic film.
The plastic web is coated on both sides with a hydrophilic dye fixing layer.
The web is printed simultaneously on
both sides using a `pagewidth' color ink jet printer. The web is then cut and
punched into individual cards. On
one face of the card is printed a human readable representation of the effect
the Artcard 9 will have on the sensed
image. This can be simply a standard image which has been processed using the
Vark script stored on the back
face of the card.
On the back face of the card is printed an array of dots which can be decoded
into the Vark script that
defines the image processing sequence. The print area is 80mm x 50mm, giving a
total of 15,876,000 dots. This
array of dots could represent at least 1.89 Mbytes of data. To achieve high
reliability, extensive error detection
and correction is incorporated in the array of dots. This allows a substantial
portion of the card to be defaced,
worn, creased, or dirty with no effect on data integrity. The data coding used
is Reed-Solomon coding, with half
of the data devoted to error correction. This allows the storage of 967 Kbytes
of error corrected data on each
Artcard 9.
CA 02564047 2006-11-06
YU139 PCT 16
Linear image sensor 34
The Artcard linear sensor 34 converts the aforementioned Artcard data image to
electrical signals. As
with the area image sensor 2, 4, the linear image sensor can be fabricated
using either CCD or APS CMOS
technology. The active length of the image sensor 34 is 50mm, equal to the
width of the data array on the Artcard
9. To satisfy Nyquist's sampling theorem, the resolution of the linear image
sensor 34 must be at least twice the
highest spatial frequency of the Artcard optical image reaching the image
sensor. In practice, data detection is
easier if the image sensor resolution is substantially above this. A
resolution of 4800 dpi (189 dpmm) is chosen,
giving a total of 9,450 pixels. This resolution requires a pixel sensor pitch
of 5.31Am. This can readily be achieved
by using four staggered rows of 20 m pixel sensors.
The linear image sensor is mounted in a special package which includes a LED
65 to illuminate the
Artcard 9 via a light-pipe (not shown).
The Artcard reader light-pipe can be a molded light-pipe which has several
function:
1. It diffuses the light from the LED over the width of the card using total
internal reflection facets.
2. It focuses the light onto a 16 m wide strip of the Artcard 9 using an
integrated cylindrical lens.
3. It focuses light reflected from the Artcard onto the linear image sensor
pixels using a molded
array of microlenses.
The operation of the Artcard reader is explained further hereinafter.
Artcard reader motor 37
The Artcard reader motor propels the Artcard past the linear image sensor 34
at a relatively constant rate.
As it may not be cost effective to include extreme precision mechanical
components in the Artcard reader, the
motor 37 is a standard miniature motor geared down to an appropriate speed to
drive a pair of rollers which move
the Artcard 9. The speed variations, rumble, and other vibrations will affect
the raw image data as circuitry within
the APC 31 includes extensive compensation for these effects to reliably read
the Artcard data.
The motor 37 is driven in reverse when the Artcard is to be ejected.
Artcard motor driver 61
The Artcard motor driver 61 is a small circuit which amplifies the digital
motor control signals from the
APC 31 to levels suitable for driving the motor 37.
Card Insertion sensor 49
The card insertion sensor 49 is an optical sensor which detects the presence
of a card as it is being
inserted in the card reader 34. Upon a signal from this sensor 49, the APC 31
initiates the card reading process,
including the activation of the Artcard reader motor 37.
Card eject button 16
A card eject button 16 (Fig. 1) is used by the user to eject the current
Artcard, so that another Artcard can
be inserted. The APC 31 detects the pressing of the button, and reverses the
Artcard reader motor 37 to eject the
card.
Card status indicator 66
A card status indicator 66 is provided to signal the user as to the status of
the Artcard reading process.
This can be a standard bi-color (red/green) LED. When the card is successfully
read, and data integrity has been
verified, the LED lights up green continually. If the card is faulty, then the
LED lights up red.
If the camera is powered from a 1.5 V instead of 3V battery, then the power
supply voltage is less than
CA 02564047 2006-11-06
YU139 PCT 17
the forward voltage drop of the greed LED, and the LED will not light. In this
case, red LEDs can be used, or the
LED can be powered from a voltage pump which also powers other circuits in the
Artcam which require higher
voltage.
64 Mbit DRAM 33
To perform the wide variety of image processing effects, the camera utilizes 8
Mbytes of memory 33.
This can be provided by a single 64 Mbit memory chip. Of course, with changing
memory technology increased
Dram storage sizes may be substituted.
High speed access to the memory chip is required. This can be achieved by
using a Rambus DRAM
(burst access rate of 500 Mbytes per second) or chips using the new open
standards such as double data rate
(DDR) SDRAM or Synclink DRAM.
Camera authentication chin
The camera authentication chip 54 is identical to the print roll
authentication chip 53, except that it has
different information stored in it. The camera authentication chip 54 has
three main purposes:
1. To provide a secure means of comparing authentication codes with the print
roll authentication
chip;
2. To provide storage for manufacturing information, such as the serial number
of the camera;
3. To provide a small amount of non-volatile memory for storage of user
information.
Displays
The Artcam includes an optional color display 5 and small status display 15.
Lowest cost consumer
cameras may include a color image display, such as a small TFT LCD 5 similar
to those found on some digital
cameras and camcorders. The color display 5 is a major cost element of these
versions of Artcam, and the display
5 plus back light are a major power consumption drain.
Status display 15
The status display 15 is a small passive segment based LCD, similar to those
currently provided on silver
halide and digital cameras. Its main function is to show the number of prints
remaining in the print roll 42 and
icons for various standard camera features, such as flash and battery status.
Color display 5
The color display 5 is a full motion image display which operates as a
viewfinder, as a verification of the
image to be printed, and as a user interface display. The cost of the display
5 is approximately proportional to its
area, so large displays (say 4" diagonal) unit will be restricted to expensive
versions of the Artcam unit. Smaller
displays, such as color camcorder viewfinder TFT's at around 1", may be
effective for mid-range Artcams.
Zoom lens (not shown)
The Artcam can include a zoom lens. This can be a standard electronically
controlled zoom lens,
identical to one which would be used on a standard electronic camera, and
similar to pocket camera zoom lenses.
A referred version of the Artcam unit may include standard interchangeable
35mm SLR lenses.
Autofocus motor 39
The autofocus motor 39 changes the focus of the zoom lens. The motor is a
miniature motor geared
down to an appropriate speed to drive the autofocus mechanism.
Autofocus motor driver 63
The autofocus motor driver 63 is a small circuit which amplifies the digital
motor control signals from
CA 02564047 2006-11-06
YU139 PCT 18
the APC 31 to levels suitable for driving the motor 39.
Zoom motor 38
The zoom motor 38 moves the zoom front lenses in and out. The motor is a
miniature motor geared
down to an appropriate speed to drive the zoom mechanism.
Zoom motor driver 62
The zoom motor driver 62 is a small circuit which amplifies the digital motor
control signals from the
APC 31 to levels suitable for driving the motor.
Communications
The ACP 31 contains a universal serial bus (USB) interface 52 for
communication with personal
computers. Not all Artcam models are intended to include the USB connector.
However, the silicon area required
for a USB circuit 52 is small, so the interface can be included in the
standard ACP.
Optional Keyboard 57
The Artcam unit may include an optional miniature keyboard 57 for customizing
text specified by the
Artcard. Any text appearing in an Artcard image may be editable, even if it is
in a complex metallic 3D font. The
miniature keyboard includes a single line alphanumeric LCD to display the
original text and edited text. The
keyboard may be a standard accessory.
The ACP 31 contains a serial communications circuit for transferring data to
and from the miniature
keyboard.
Power Supply
The Artcam unit uses a battery 48. Depending upon the Artcam options, this is
either a 3V Lithium cell,
1.5 V AA alkaline cells, or other battery arrangement.
Power Management Unit 51
Power consumption is an important design constraint in the Artcam. It is
desirable that either standard
camera batteries (such as 3V lithium batters) or standard AA or AAA alkaline
cells can be used. While the
electronic complexity of the Artcam unit is dramatically higher than 35mm
photographic cameras, the power
consumption need not be commensurately higher. Power in the Artcam can be
carefully managed with all unit
being turned off when not in use.
The most significant current drains are the ACP 31, the area image sensors
2,4, the printer 44 various
motors, the flash unit 56, and the optional color display 5 dealing with each
part separately:
1. ACP: If fabricated using 0.25 m CMOS, and running on 1.5V, the ACP power
consumption
can be quite low. Clocks to various parts of the ACP chip can be quite low.
Clocks to various parts of the ACP
chip can be turned off when not in use, virtually eliminating standby current
consumption. The ACP will only
fully used for approximately 4 seconds for each photograph printed.
2. Area image sensor: power is only supplied to the area image sensor when the
user has their
finger on the button.
3. The printer power is only supplied to the printer when actually printing.
This is for around 2
seconds for each photograph. Even so, suitably lower power consumption
printing should be used.
4. The motors required in the Artcam are all low power miniature motors, and
are typically only
activated for a few seconds per photo.
5. The flash unit 45 is only used for some photographs. Its power consumption
can readily be
CA 02564047 2006-11-06
YU139 PCT 19
provided by a 3V lithium battery for a reasonably battery life.
6. The optional color display 5 is a major current drain for two reasons: it
must be on for the whole
time that the camera is in use, and a backlight will be required if a liquid
crystal display is used. Cameras which
incorporate a color display will require a larger battery to achieve
acceptable batter life.
Flash unit 56
The flash unit 56 can be a standard miniature electronic flash for consumer
cameras.
Overview of the ACP 31
Fig. 3 illustrates the Artcam Central Processor (ACP) 31 in more detail. The
Artcam Central Processor
provides all of the processing power for Artcam. It is designed for a 0.25
micron CMOS process, with
approximately 1.5 million transistors and an area of around 50 mm2. The ACP 31
is a complex design, but
design effort can be reduced by the use of datapath compilation techniques,
macrocells, and IP cores. The
ACP 31 contains:
A RISC CPU core 72
A 4 way parallel VLIW Vector Processor 74
A Direct RAMbus interface 81
A CMOS image sensor interface 83
A CMOS linear image sensor interface 88
A USB serial interface 52
An infrared keyboard interface 55
A numeric LCD interface 84, and
A color TFT LCD interface 88
A 4Mbyte Flash memory 70 for program storage 70
The RISC CPU, Direct RAMbus interface 81, CMOS sensor interface 83 and USB
serial interface 52 can be
vendor supplied cores. The ACP 31 is intended to run at a clock speed of 200
MHz on 3V externally and 1.5V
internally to minimize power consumption. The CPU core needs only to run at
100 MHz. The following two
block diagrams give two views of the ACP 31:
A view of the ACP 31 in isolation
An example Artcam showing a high-level view of the ACP 31 connected to the
rest of the Artcam hardware.
Image Access
As stated previously, the DRAM Interface 81 is responsible for interfacing
between other client portions
of the ACP chip and the RAMBUS DRAM. In effect, each module within the DRAM
Interface is an address
generator.
There are three logical types of images manipulated by the ACP. They are:
-CCD Image, which is the Input Image captured from the CCD.
-Internal Image format - the Image format utilised internally by the Artcam
device.
Print Image - the Output Image format printed by the Artcam
These images are typically different in color space, resolution, and the
output & input color spaces which
can vary from camera to camera. For example, a CCD image on a low-end camera
may be a different resolution,
or have different color characteristics from that used in a high-end camera.
However all internal image formats are
CA 02564047 2006-11-06
YU 139 PCT 20
the same format in terms of color space across all cameras.
In addition, the three image types can vary with respect to which direction is
`up'. The physical
orientation of the camera causes the notion of a portrait or landscape image,
and this must be maintained
throughout processing. For this reason, the internal image is always oriented
correctly, and rotation is performed
on images obtained from the CCD and during the print operation.
CPU Core (CPU) 72
The ACP 31 incorporates a 32 bit RISC CPU 72 to run the Vark image processing
language interpreter and to
perform Artcam's general operating system duties. A wide variety of CPU cores
are suitable: it can be any
processor core with sufficient processing power to perform the required core
calculations and control
functions fast enough to met consumer expectations. Examples of suitable cores
are: MIPS R4000 core from
LSI Logic, StrongARM core. There is no need to maintain instruction set
continuity between different Artcam
models. Artcard compatibility is maintained irrespective of future processor
advances and changes, because
the Vark interpreter is simply re-compiled for each new instruction set. The
ACP 31 architecture is therefore
also free to evolve. Different ACP 31 chip designs may be fabricated by
different manufacturers, without
requiring to license or port the CPU core. This device independence avoids the
chip vendor lock-in such as
has occurred in the PC market with Intel. The CPU operates at 100 MHz, with a
single cycle time of l Ons. It
must be fast enough to run the Vark interpreter, although the VLIW Vector
Processor 74 is responsible for
most of the time-critical operations.
PROGRAM CACHE 72
Although the program code is stored in on-chip Flash memory 70, it is unlikely
that well packed Flash
memory 70 will be able to operate at the l Ons cycle time required by the CPU.
Consequently a small cache is
required for good performance. 16 cache lines of 32 bytes each are sufficient,
for a total of 512 bytes. The
program cache 72 is defined in the chapter entitled Program cache 72.
DATA CACHE 76
A small data cache 76 is required for good performance. This requirement is
mostly due to the use of a
RAMbus DRAM, which can provide high-speed data in bursts, but is inefficient
for single byte accesses. The
CPU has access to a memory caching system that allows flexible manipulation of
CPU data cache 76 sizes. A
minimum of 16 cache lines (512 bytes) is recommended for good performance.
CPU MEMORY MODEL
An Artcam's CPU memory model consists of a 32MB area. It consists of 8MB of
physical RDRAM off-chip
in the base model of Artcam, with provision for up to 16MB of off-chip memory.
There is a 4MB Flash
memory 70 on the ACP 31 for program storage, and finally a 4MB address space
mapped to the various
registers and controls of the ACP 31. The memory map then, for an Artcam is as
follows:
Contents Size
Base Artcam DRAM 8 MB
Extended DRAM 8 MB
Program memory (on ACP 31 in Flash memory 70) 4 MB
Reserved for extension of program memory 4 MB
CA 02564047 2006-11-06
YU139 PCT 21
ACP 31 registers and memory-mapped I/O 4 MB
Reserved 4 MB
TOTAL 32 MB
A straightforward way of decoding addresses is to use address bits 23-24:
If bit 24 is clear, the address is in the lower 16-MB range, and hence can be
satisfied from
DRAM and the Data cache 76. In most cases the DRAM will only be 8 MB, but 16
MB is
allocated to cater for a higher memory model Artcams.
If bit 24 is set, and bit 23 is clear, then the address represents the Flash
memory 70 4Mbyte
range and is satisfied by the Program cache 72.
If bit 24 = 1 and bit 23 = 1, the address is translated into an access over
the low speed bus to the
requested component in the AC by the CPU Memory Decoder 68.
Flash memory 70
The ACP 31 contains a 4Mbyte Flash memory 70 for storing the Artcam program.
It is envisaged that Flash
memory 70 will have denser packing coefficients than masked ROM, and allows
for greater flexibility for
testing camera program code. The downside of the Flash memory 70 is the access
time, which is unlikely to
be fast enough for the 100 MHz operating speed (1 Ons cycle time) of the CPU.
A fast Program Instruction
cache 77 therefore acts as the interface between the CPU and the slower Flash
memory 70.
Program cache 72
A small cache is required for good CPU performance. This requirement is due to
the slow speed Flash
memory 70 which stores the Program code. 16 cache lines of 32 bytes each are
sufficient, for a total of 512
bytes. The Program cache 72 is a read only cache. The data used by CPU
programs comes through the CPU
Memory Decoder 68 and if the address is in DRAM, through the general Data
cache 76. The separation
allows the CPU to operate independently of the VLIW Vector Processor 74. If
the data requirements are low
for a given process, it can consequently operate completely out of cache.
Finally, the Program cache 72 can be read as data by the CPU rather than
purely as program instructions. This
allows tables, microcode for the VLIW etc to be loaded from the Flash memory
70. Addresses with bit 24 set
and bit 23 clear are satisfied from the Program cache 72.
CPU Memory Decoder 68
The CPU Memory Decoder 68 is a simple decoder for satisfying CPU data
accesses. The Decoder translates
data addresses into internal ACP register accesses over the internal low speed
bus, and therefore allows for
memory mapped I/O of ACP registers. The CPU Memory Decoder 68 only interprets
addresses that have bit
24 set and bit 23 clear. There is no caching in the CPU Memory Decoder 68.
DRAM interface 81
The DRAM used by the Artcam is a single channel 64Mbit (8MB) RAMbus RDRAM
operating at 1.6GB/sec.
RDRAM accesses are by a single channel (16-bit data path) controller. The
RDRAM also has several useful
operating modes for low power operation. Although the Rambus specification
describes a system with
random 32 byte transfers as capable of achieving a greater than 95%
efficiency, this is not true if only part of
the 32 bytes are used. Two reads followed by two writes to the same device
yields over 86% efficiency. The
primary latency is required for bus turn-around going from a Write to a Read,
and since there is a Delayed
CA 02564047 2006-11-06
YU139 PCT 22
Write mechanism, efficiency can be further improved. With regards to writes,
Write Masks allow specific
subsets of bytes to be written to. These write masks would be set via internal
cache "dirty bits". The upshot
of the Rambus Direct RDRAM is a throughput of>1GB/sec is easily achievable,
and with multiple reads for
every write (most processes) combined with intelligent algorithms making good
use of 32 byte transfer
knowledge, transfer rates of >1.3 GB/sec are expected. Every l Ons, 16 bytes
can be transferred to or from the
core.
DRAM ORGANIZATION
The DRAM organization for a base model (8MB RDRAM) Artcam is as follows:
Contents Size
Program scratch RAM 0.50 MB
Artcard data 1.00 MB
Photo Image, captured from CMOS Sensor 0.50 MB
Print Image (compressed) 2.25 MB
1 Channel of expanded Photo Image 1.50 MB
1 Image Pyramid of single channel 1.00 MB
Intermediate Image Processing 1.25 MB
TOTAL 8 MB
Notes:
Uncompressed, the Print Image requires 4.5MB (1.5MB per channel). To
accommodate other objects in the
8MB model, the Print Image needs to be compressed. If the chrominance channels
are compressed by 4:1
they require only 0.375MB each).
The memory model described here assumes a single 8 MB RDRAM. Other models of
the Artcam may have
more memory, and thus not require compression of the Print Image. In addition,
with more memory a
larger part of the final image can be worked on at once, potentially giving a
speed improvement.
Note that ejecting or inserting an Artcard invalidates the 5.5MB area holding
the Print Image, 1 channel of
expanded photo image, and the image pyramid. This space may be safely used by
the Artcard Interface
for decoding the Artcard data.
Data cache 76
The ACP 31 contains a dedicated CPU instruction cache 77 and a general data
cache 76. The Data cache 76
handles all DRAM requests (reads and writes of data) from the CPU, the VLIW
Vector Processor 74, and the
Display Controller 88. These requests may have very different profiles in
terms of memory usage and
algorithmic timing requirements. For example, a VLIW process may be processing
an image in linear
memory, and lookup a value in a table for each value in the image. There is
little need to cache much of the
image, but it may be desirable to cache the entire lookup table so that no
real memory access is required.
Because of these differing requirements, the Data cache 76 allows for an
intelligent definition of caching.
CA 02564047 2006-11-06
YU139 PCT 23
Although the Rambus DRAM interface 81 is capable of very high-speed memory
access (an average
throughput of 32 bytes in 25ns), it is not efficient dealing with single byte
requests. In order to reduce
effective memory latency, the ACP 31 contains 128 cache lines. Each cache line
is 32 bytes wide. Thus the
total amount of data cache 76 is 4096 bytes (4KB). The 128 cache lines are
configured into 16
programmable-sized groups. Each of the 16 groups must be a contiguous set of
cache lines. The CPU is
responsible for determining how many cache lines to allocate to each group.
Within each group cache lines
are filled according to a simple Least Recently Used algorithm. In terms of
CPU data requests, the Data cache
76 handles memory access requests that have address bit 24 clear. If bit 24 is
clear, the address is in the lower
16 MB range, and hence can be satisfied from DRAM and the Data cache 76. In
most cases the DRAM will
only be 8 MB, but 16 MB is allocated to cater for a higher memory model
Artcam. If bit 24 is set, the address
is ignored by the Data cache 76.
All CPU data requests are satisfied from Cache Group 0. A minimum of 16 cache
lines is recommended for
good CPU performance, although the CPU can assign any number of cache lines
(except none) to Cache
Group 0. The remaining Cache Groups (1 to 15) are allocated according to the
current requirements. This
could mean allocation to a VLIW Vector Processor 74 program or the Display
Controller 88. For example, a
256 byte lookup table required to be permanently available would require 8
cache lines. Writing out a
sequential image would only require 2-4 cache lines (depending on the size of
record being generated and
whether write requests are being Write Delayed for a significant number of
cycles). Associated with each
cache line byte is a dirty bit, used for creating a Write Mask when writing
memory to DRAM. Associated
with each cache line is another dirty bit, which indicates whether any of the
cache line bytes has been written
to (and therefore the cache line must be written back to DRAM before it can be
reused). Note that it is
possible for two different Cache Groups to be accessing the same address in
memory and to get out of sync.
The VLIW program writer is responsible to ensure that this is not an issue. It
could be perfectly reasonable,
for example, to have a Cache Group responsible for reading an image, and
another Cache Group responsible
for writing the changed image back to memory again. If the images are read or
written sequentially there may
be advantages in allocating cache lines in this manner. A total of 8 buses 182
connect the VLIW Vector
Processor 74 to the Data cache 76. Each bus is connected to an I/O Address
Generator. (There are 2 I/O
Address Generators 189, 190 per Processing Unit 178, and there are 4
Processing Units in the VLIW Vector
Processor 74. The total number of buses is therefore 8.)
In any given cycle, in addition to a single 32 bit (4 byte) access to the
CPU's cache group (Group 0), 4
simultaneous accesses of 16 bits (2 bytes) to remaining cache groups are
permitted on the 8 VLIW Vector
Processor 74 buses. The Data cache 76 is responsible for fairly processing the
requests. On a given cycle, no
more than 1 request to a specific Cache Group will be processed. Given that
there are 8 Address Generators
189, 190 in the VLIW Vector Processor 74, each one of these has the potential
to refer to an individual Cache
Group. However it is possible and occasionally reasonable for 2 or more
Address Generators 189, 190 to
access the same Cache Group. The CPU is responsible for ensuring that the
Cache Groups have been
allocated the correct number of cache lines, and that the various Address
Generators 189, 190 in the VLIW
Vector Processor 74 reference the specific Cache Groups correctly.
The Data cache 76 as described allows for the Display Controller 88 and VLIW
Vector Processor 74 to be
active simultaneously. If the operation of these two components were deemed to
never occur simultaneously,
CA 02564047 2006-11-06
YU139 PCT 24
a total 9 Cache Groups would suffice. The CPU would use Cache Group 0, and the
VLIW Vector Processor
74 and the Display Controller 88 would share the remaining 8 Cache Groups,
requiring only 3 bits (rather
than 4) to define which Cache Group would satisfy a particular request.
JTAG Interface 85
A standard JTAG (Joint Test Action Group) Interface is included in the ACP 31
for testing purposes. Due to
the complexity of the chip, a variety of testing techniques are required,
including BIST (Built In Self Test)
and functional block isolation. An overhead of 10% in chip area is assumed for
overall chip testing circuitry.
The test circuitry is beyond the scope of this document.
Serial Interfaces
USB SERIAL PORT INTERFACE 52
This is a standard USB serial port, which is connected to the internal chip
low speed bus, thereby allowing the
CPU to control it.
KEYBOARD INTERFACE 65
This is a standard low-speed serial port, which is connected to the internal
chip low speed bus, thereby
allowing the CPU to control it. It is designed to be optionally connected to a
keyboard to allow simple data
input to customize prints.
AUTHENTICATION CHIP SERIAL INTERFACES 64
These are 2 standard low-speed serial ports, which are connected to the
internal chip low speed bus, thereby
allowing the CPU to control them. The reason for having 2 ports is to connect
to both the on-camera
Authentication chip, and to the print-roll Authentication chip using separate
lines. Only using 1 line may
make it possible for a clone print-roll manufacturer to design a chip which,
instead of generating an
authentication code, tricks the camera into using the code generated by the
authentication chip in the camera.
Parallel Interface 67
The parallel interface connects the ACP 31 to individual static electrical
signals. The CPU is able to control
each of these connections as memory-mapped I/O via the low speed bus The
following table is a list of
connections to the parallel interface:
Connection Direction Pins
-Paper transport stepper motor out 4
Artcard stepper motor Out 4
Zoom stepper motor Out 4
Guillotine motor Out 1
Flash trigger Out 1
Status LCD segment drivers Out 7
Status LCD common drivers Out 4
Artcard illumination LED Out 1
Artcard status LED (red/green) In 2
Artcard sensor In 1
Paper pull sensor In 1
Orientation sensor In 2
Buttons In 4
CA 02564047 2006-11-06
YU139 PCT 25
TOTAL 136
VLIW Input and Output FIFOs 78, 79
The VLIW Input and Output FIFOs are 8 bit wide FIFOs used for communicating
between processes and the
VLIW Vector Processor 74. Both FIFOs are under the control of the VLIW Vector
Processor 74, but can be
cleared and queried (e.g. for status) etc by the CPU.
VLIW INPUT FIFO 78
A client writes 8-bit data to the VLIW Input FIFO 78 in order to have the data
processed by the VLIW Vector
Processor 74. Clients include the Image Sensor Interface, Artcard Interface,
and CPU. Each of these processes
is able to offload processing by simply writing the data to the FIFO, and
letting the VLIW Vector Processor
74 do all the hard work. An example of the use of a client's use of the VLIW
Input FIFO 78 is the Image
Sensor Interface (ISI 83). The ISI 83 takes data from the Image Sensor and
writes it to the FIFO. A VLIW
process takes it from the FIFO, transforming it into the correct image data
format, and writing it out to
DRAM. The ISI 83 becomes much simpler as a result.
VLIW OUTPUT FIFO 79
The VLIW Vector Processor 74 writes 8-bit data to the VLIW Output FIFO 79
where clients can read it.
Clients include the Print Head Interface and the CPU. Both of these clients is
able to offload processing by
simply reading the already processed data from the FIFO, and letting the VLIW
Vector Processor 74 do all
the hard work. The CPU can also be interrupted whenever data is placed into
the VLIW Output FIFO 79,
allowing it to only process the data as it becomes available rather than
polling the FIFO continuously. An
example of the use of a client's use of the VLIW Output FIFO 79 is the Print
Head Interface (PHI 62). A
VLIW process takes an image, rotates it to the correct orientation, color
converts it, and dithers the resulting
image according to the print head requirements. The PHI 62 reads the dithered
formatted 8-bit data from the
VLIW Output FIFO 79 and simply passes it on to the Print Head external to the
ACP 31. The PHI 62
becomes much simpler as a result.
VLIW Vector Processor 74
To achieve the high processing requirements of Artcam, the ACP 31 contains a
VLIW (Very Long Instruction
Word) Vector Processor. The VLIW processor is a set of 4 identical Processing
Units (PU e.g 178) working
in parallel, connected by a crossbar switch 183. Each PU e.g 178 can perform
four 8-bit multiplications, eight
8-bit additions, three 32-bit additions, I/O processing, and various logical
operations in each cycle. The PUs
e.g 178 are microcoded, and each has two Address Generators 189, 190 to allow
full use of available cycles
for data processing. The four PUs e.g 178 are normally synchronized to provide
a tightly interacting VLIW
processor. Clocking at 200 MHz, the VLIW Vector Processor 74 runs at 12 Gops
(12 billion operations per
second). Instructions are tuned for image processing functions such as
warping, artistic brushing, complex
synthetic illumination, color transforms, image filtering, and compositing.
These are accelerated by two
orders of magnitude over desktop computers.
As shown in more detail in Fig. 3(a), the VLIW Vector Processor 74 is 4 PUs
e.g 178 connected by a crossbar
switch 183 such that each PU e.g 178 provides two inputs to, and takes two
outputs from, the crossbar switch
CA 02564047 2006-11-06
YU139 PCT 26
183. Two common registers form a control and synchronization mechanism for the
PUs e.g 178. 8 Cache
buses 182 allow connectivity to DRAM via the Data cache 76, with 2 buses going
to each PU e.g 178 (1 bus
per I/O Address Generator).
Each PU e.g 178 consists of an ALU 188 (containing a number of registers &
some arithmetic logic for
processing data), some microcode RAM 196, and connections to the outside world
(including other ALUs). A
local PU state machine runs in microcode and is the means by which the PU e.g
178 is controlled. Each PU
e.g 178 contains two I/O Address Generators 189, 190 controlling data flow
between DRAM (via the Data
cache 76) and the ALU 188 (via Input FIFO and Output FIFO). The address
generator is able to read and
write data (specifically images in a variety of formats) as well as tables and
simulated FIFOs in DRAM. The
formats are customizable under software control, but are not microcoded. Data
taken from the Data cache 76
is transferred to the ALU 188 via the 16-bit wide Input FIFO. Output data is
written to the 16-bit wide Output
FIFO and from there to the Data cache 76. Finally, all PUs e.g 178 share a
single 8-bit wide VLIW Input
FIFO 78 and a single 8-bit wide VLIW Output FIFO 79. The low speed data bus
connection allows the CPU
to read and write registers in the PU e.g 178, update microcode, as well as
the common registers shared by all
PUs e.g 178 in the VLIW Vector Processor 74. Turning now to Fig. 4, a closer
detail of the internals of a
single PU e.g 178 can be seen, with components and control signals detailed in
subsequent hereinafter:
MICROCODE
Each PU e.g 178 contains a microcode RAM 196 to hold the program for that
particular PU e.g 178. Rather
than have the microcode in ROM, the microcode is in RAM, with the CPU
responsible for loading it up. For
the same space on chip, this tradeoff reduces the maximum size of any one
function to the size of the RAM,
but allows an unlimited number of functions to be written in microcode.
Functions implemented using
microcode include Vark acceleration, Artcard reading, and Printing. The VLIW
Vector Processor 74 scheme
has several advantages for the case of the ACP 31:
Hardware design complexity is reduced
Hardware risk is reduced due to reduction in complexity
Hardware design time does not depend on all Vark functionality being
implemented in
dedicated silicon
Space on chip is reduced overall (due to large number of processes able to be
implemented as
microcode)
Functionality can be added to Vark (via microcode) with no impact on hardware
design time
Size and Content
The CPU loaded microcode RAM 196 for controlling each PU e.g 178 is 128 words,
with each word being 96
bits wide. A summary of the microcode size for control of various units of the
PU e.g 178 is listed in the
following table:
Process Block Size (bits)
Status Output 3
Branching (microcode control) 11
In 8
Out 6
CA 02564047 2006-11-06
YU139 PCT 27
Registers 7
Read 10
Write 6
Barrel Shifter 12
Adder/Logical 14
Multiply/Interpolate 19
TOTAL 96
With 128 instruction words, the total microcode RAM 196 per PU e.g 178 is
12,288 bits, or 1.5KB exactly.
Since the VLIW Vector Processor 74 consists of 4 identical PUs e.g 178 this
equates to 6,144 bytes, exactly
6KB. Some of the bits in a microcode word are directly used as control bits,
while others are decoded. See
the various unit descriptions that detail the interpretation of each of the
bits of the microcode word.
Synchronization Between PUs e.g 178
Each PU e.g 178 contains a 4 bit Synchronization Register 197. It is a mask
used to determine which PUs e.g
178 work together, and has one bit set for each of the corresponding PUs e.g
178 that are functioning as a
single process. For example, if all of the PUs e.g 178 were functioning as a
single process, each of the 4
Synchronization Register 197s would have all 4 bits set. If there were two
asynchronous processes of 2 PUs
e.g 178 each, two of the PUs e.g 178 would have 2 bits set in their
Synchronization Register 197s
(corresponding to themselves), and the other two would have the other 2 bits
set in their Synchronization
Register 197s (corresponding to themselves).
The Synchronization Register 197 is used in two basic ways:
Stopping and starting a given process in synchrony
Suspending execution within a process
Stopping and Starting Processes
The CPU is responsible for loading the microcode RAM 196 and loading the
execution address for the first
instruction (usually 0). When the CPU starts executing microcode, it begins at
the specified address.
Execution of microcode only occurs when all the bits of the Synchronization
Register 197 are also set in the
Common Synchronization Register 197. The CPU therefore sets up all the PUs e.g
178 and then starts or
stops processes with a single write to the Common Synchronization Register
197.
This synchronization scheme allows multiple processes to be running
asynchronously on the PUs e.g 178,
being stopped and started as processes rather than one PU e.g 178 at a time.
Suspending Execution within a Process
In a given cycle, a PU e.g 178 may need to read from or write to a FIFO (based
on the opcode of the current
microcode instruction). If the FIFO is empty on a read request, or full on a
write request, the FIFO request
cannot be completed. The PU e.g 178 will therefore assert its SuspendProcess
control signal 198. The
SuspendProcess signals from all PUs e.g 178 are fed back to all the PUs e.g
178. The Synchronization
Register 197 is ANDed with the 4 SuspendProcess bits, and if the result is non-
zero, none of the PU e.g 178's
register WriteEnables or FIFO strobes will be set. Consequently none of the
PUs e.g 178 that form the same
CA 02564047 2006-11-06
YU139 PCT 28
process group as the PU e.g 178 that was unable to complete its task will have
their registers or FIFOs
updated during that cycle. This simple technique keeps a given process group
in synchronization. Each
subsequent cycle the PU e.g 178's state machine will attempt to re-execute the
microcode instruction at the
same address, and will continue to do so until successful. Of course the
Common Synchronization Register
197 can be written to by the CPU to stop the entire process if necessary. This
synchronization scheme allows
any combinations of PUs e.g 178 to work together, each group only affecting
its co-workers with regards to
suspension due to data not being ready for reading or writing.
Control and Branching
During each cycle, each of the four basic input and calculation units within a
PU e.g 178's ALU 188 (Read,
Adder/Logic, Multiply/Interpolate, and Barrel Shifter) produces two status
bits: a Zero flag and a Negative
flag indicating whether the result of the operation during that cycle was 0 or
negative. Each cycle one of those
4 status bits is chosen by microcode instructions to be output from the PU e.g
178. The 4 status bits (1 per PU
e.g 178's ALU 188) are combined into a 4 bit Common Status Register 200.
During the next cycle, each PU
e.g 178's microcode program can select one of the bits from the Common Status
Register 200, and branch to
another microcode address dependant on the value of the status bit.
Status bit
Each PU e.g 178's ALU 188 contains a number of input and calculation units.
Each unit produces 2 status bits
- a negative flag and a zero flag. One of these status bits is output from the
PU e.g 178 when a particular unit
asserts the value on the 1-bit tri-state status bit bus. The single status bit
is output from the PU e.g 178, and
then combined with the other PU e.g 178 status bits to update the Common
Status Register 200. The
microcode for determining the output status bit takes the following form:
# Bits Description
2 Select unit whose status bit is to be output
00 = Adder unit
01 = Multiply/Logic unit
10 = Barrel Shift unit
11 = Reader unit
1 0 = Zero flag
1 = Negative flag
3 TOTAL
Within the ALU 188, the 2-bit Select Processor Block value is decoded into
four 1-bit enable bits, with a
different enable bit sent to each processor unit block. The status select bit
(choosing Zero or Negative) is
passed into all units to determine which bit is to be output onto the status
bit bus.
Branching Within Microcode
Each PU e.g 178 contains a 7 bit Program Counter (PC) that holds the current
microcode address being
executed. Normal program execution is linear, moving from address N in one
cycle to address N+1 in the next
cycle. Every cycle however, a microcode program has the ability to branch to a
different location, or to test a
status bit from the Common Status Register 200 and branch. The microcode for
determining the next
execution address takes the following form:
CA 02564047 2006-11-06
YU139 PCT 29
# Bits Description
2 00 = NOP (PC = PC+1)
01 = Branch always
= Branch if status bit clear
11 = Branch if status bit set
2 Select status bit from status word
7 Address to branch to (absolute address, 00-7F)
11 TOTAL
ALU 188
Fig. 5 illustrates the ALU 188 in more detail. Inside the ALU 188 are a number
of specialized processing
blocks, controlled by a microcode program. The specialized processing blocks
include:
5 Read Block 202, for accepting data from the input FIFOs
Write Block 203, for sending data out via the output FIFOs
Adder/Logical block 204, for addition & subtraction, comparisons and logical
operations
Multiply/Interpolate block 205, for multiple types of interpolations and
multiply/accumulates
Barrel Shift block 206, for shifting data as required
10 In block 207, for accepting data from the external crossbar switch 183
Out block 208, for sending data to the external crossbar switch 183
Registers block 215, for holding data in temporary storage
Four specialized 32 bit registers hold the results of the 4 main processing
blocks:
M register 209 holds the result of the Multiply/Interpolate block
L register 209 holds the result of the Adder/Logic block
S register 209 holds the result of the Barrel Shifter block
R register 209 holds the result of the Read Block 202
In addition there are two internal crossbar switches 213m 214 for data
transport. The various process blocks
are further expanded in the following sections, together with the microcode
definitions that pertain to each
block. Note that the microcode is decoded within a block to provide the
control signals to the various units
within.
Data Transfers Between PUs e.g 178
Each PU e.g 178 is able to exchange data via the external crossbar. A PU e.g
178 takes two inputs and outputs
two values to the external crossbar. In this way two operands for processing
can be obtained in a single cycle,
but cannot be actually used in an operation until the following cycle.
In 207
This block is illustrated in Fig. 6 and contains two registers, In, and In2
that accept data from the external
crossbar. The registers can be loaded each cycle, or can remain unchanged. The
selection bits for choosing
from among the 8 inputs are output to the external crossbar switch 183. The
microcode takes the following
form:
# Bits Description
I 0 = NOP
CA 02564047 2006-11-06
YU139 PCT 30
1 = Load In, from crossbar
3 Select Input 1 from external crossbar
1 0 = NOP
1 = Load In2 from crossbar
3 Select Input 2 from external crossbar
8 TOTAL
Out 208
Complementing In is Out 208. The Out block is illustrated in more detail in
Fig. 7. Out contains two registers,
Out, and Out2, both of which are output to the external crossbar each cycle
for use by other PUs e.g 178. The
Write unit is also able to write one of Out, or Out2 to one of the output
FIFOs attached to the ALU 188.
Finally, both registers are available as inputs to Crossbarl 213, which
therefore makes the register values
available as inputs to other units within the ALU 188. Each cycle either of
the two registers can be updated
according to microcode selection. The data loaded into the specified register
can be one of Do - D3 (selected
from Crossbarl 213) one of M, L, S, and R (selected from Crossbar2 214), one
of 2 programmable constants,
or the fixed values 0 or 1. The microcode for Out takes the following form:
# Bits Description
1 0 = NOP
1 = Load Register
1 Select Register to load Out, or Out2
4 Select input [Inl,In2,OUtl,OUt2,Do,D1,D2,D3,M,L,S,R,K1,K2,0,11
6 TOTAL
Local Registers and Data Transfers within ALU 188
As noted previously, the ALU 188 contains four specialized 32-bit registers to
hold the results of the 4 main
processing blocks:
M register 209 holds the result of the Multiply/Interpolate block
L register 209 holds the result of the Adder/Logic block
S register 209 holds the result of the Barrel Shifter block
R register 209 holds the result of the Read Block 202
The CPU has direct access to these registers, and other units can select them
as inputs via Crossbar2 214.
Sometimes it is necessary to delay an operation for one or more cycles. The
Registers block contains four 32-
bit registers Do - D3 to hold temporary variables during processing. Each
cycle one of the registers can be
updated, while all the registers are output for other units to use via
Crossbarl 213 (which also includes In,,
In2, Out, and Out2). The CPU has direct access to these registers. The data
loaded into the specified register
can be one of Do - D3 (selected from Crossbar 1213) one of M, L, S, and R
(selected from Crossbar2 214),
one of 2 programmable constants, or the fixed values 0 or 1. The Registers
block 215 is illustrated in more
detail in Fig. 8. The microcode for Registers takes the following form:
# Bits Description
I 0 = NOP
1 = Load Register
2 Select Register to load [Do - D3]
CA 02564047 2006-11-06
YU139 PCT 31
4 Select input [Ini,ln2,OUtl,OUt2,Do,D1,D2,D3,M,L,S,R,K1,K2,0,1]
7 TOTAL
Crossbar] 213
Crossbarl 213 is illustrated in more detail in Fig. 9. Crossbarl 213 is used
to select from inputs In,, In2, Out,,
Out2i Do-D3. 7 outputs are generated from Crossbar1 213: 3 to the
Multiply/Interpolate Unit, 2 to the Adder
Unit, 1 to the Registers unit and 1 to the Out unit. The control signals for
Crossbarl 213 come from the
various units that use the Crossbar inputs. There is no specific microcode
that is separate for Crossbarl 213.
Crossbar2 214
Crossbar2 214 is illustrated in more detail in Fig. 10.Crossbar2 214 is used
to select from the general ALU
188 registers M, L, S and R. 6 outputs are generated from Crossbar1 213: 2 to
the Multiply/Interpolate Unit, 2
to the Adder Unit, 1 to the Registers unit and 1 to the Out unit. The control
signals for Crossbar2 214 come
from the various units that use the Crossbar inputs. There is no specific
microcode that is separate for
Crossbar2 214.
Data Transfers Between PUs e.g 178 and DRAM or External Processes
Returning to Fig. 4, PUs e.g 178 share data with each other directly via the
external crossbar. They also
transfer data to and from external processes as well as DRAM. Each PU e.g 178
has 2 I/O Address Generators
189, 190 for transferring data to and from DRAM. A PU e.g 178 can send data to
DRAM via an I/O Address
Generator's Output FIFO e.g. 186, or accept data from DRAM via an I/O Address
Generator's Input FIFO
187. These FIFOs are local to the PU e.g 178. There is also a mechanism for
transferring data to and from
external processes in the form of a common VLIW Input FIFO 78 and a common
VLIW Output FIFO 79,
shared between all ALUs. The VLIW Input and Output FIFOs are only 8 bits wide,
and are used for printing,
Artcard reading, transferring data to the CPU etc. The local Input and Output
FIFOs are 16 bits wide.
Read
The Read process block 202 of Fig. 5 is responsible for updating the ALU 188's
R register 209, which
represents the external input data to a VLIW microcoded process. Each cycle
the Read Unit is able to read
from either the common VLIW Input FIFO 78 (8 bits) or one of two local Input
FIFOs (16 bits). A 32-bit
value is generated, and then all or part of that data is transferred to the R
register 209. The process can be seen
in Fig. 11. The microcode for Read is described in the following table. Note
that the interpretations of some
bit patterns are deliberately chosen to aid decoding.
# Bits Description
2 00 = NOP
01 = Read from VLIW Input FIFO 78
10 = Read from Local FIFO 1
11 = Read from Local FIFO 2
1 How many significant bits
0 = 8 bits (pad with 0 or sign extend)
1 = 16 bits (only valid for Local FIFO reads)
1 0 = Treat data as unsigned (pad with 0)
1 = Treat data as signed (sign extend when reading from FIFO)r
2 How much to shift data left by:
00 = 0 bits (no change)
CA 02564047 2006-11-06
YU139 PCT 32
01 = 8 bits
10= 16 bits
11 = 24 bits
4 Which bytes of R to update (hi to lo order byte)
Each of the 4 bits represents 1 byte WriteEnable on R
TOTAL
Write
The Write process block is able to write to either the common VLIW Output FIFO
79 or one of the two local
Output FIFOs each cycle. Note that since only 1 FIFO is written to in a given
cycle, only one 16-bit value is
5 output to all FIFOs, with the low 8 bits going to the VLIW Output FIFO 79.
The microcode controls which of
the FIFOs gates in the value. The process of data selection can be seen in
more detail in Fig. 12. The source
values Out, and Out2 come from the Out block. They are simply two registers.
The microcode for Write takes
the following form:
# Bits Description
2 00 = NOP
01 = Write VLIW Output FIFO 79
10 = Write local Output FIFO 1
11 = Write local Output FIFO 2
1 Select Output Value Out, or Out2
3 Select part of Output Value to write (32 bits = 4 bytes ABCD)
000 = OD
001 = OD
010 = OB
011 =OA
100 = CD
101 = BC
110 =AB
111 =0
6 TOTAL
10 Computational Blocks
Each ALU 188 has two computational process blocks, namely an Adder/Logic
process block 204, and a
Multiply/Interpolate process block 205. In addition there is a Barrel Shifter
block to provide help to these
computational blocks. Registers from the Registers block 215 can be used for
temporary storage during
pipelined operations.
Barrel Shifter
The Barrel Shifter process block 206 is shown in more detail in Fig. 13 and
takes its input from the output of
Adder/Logic or Multiply/Interpolate process blocks or the previous cycle's
results from those blocks (ALU
registers L and M). The 32 bits selected are barrel shifted an arbitrary
number of bits in either direction (with
sign extension as necessary), and output to the ALU 188's S register 209. The
microcode for the Barrel Shift
process block is described in the following table. Note that the
interpretations of some bit patterns are
deliberately chosen to aid decoding.
# Bits Description
CA 02564047 2006-11-06
YU139 PCT 33
3 000 = NOP
001 = Shift Left (unsigned)
010 = Reserved
011 = Shift Left (signed)
100 = Shift right (unsigned, no rounding)
101 = Shift right (unsigned, with rounding)
110 = Shift right (signed, no rounding)
111 = Shift right (signed, with rounding)
2 Select Input to barrel shift:
00 = Multiply/Interpolate result
01 =M
= Adder/Logic result
11 =L
5 # bits to shift
1 Ceiling of 55
1 Floor of 0 (signed data)
12 TOTAL
Adder/Logic 204
The Adder/Logic process block is shown in more detail in Fig. 14 and is
designed for simple 32-bit
addition/subtraction, comparisons, and logical operations. In a single cycle a
single addition, comparison, or
5 logical operation can be performed, with the result stored in the ALU 188's
L register 209. There are two
primary operands, A and B, which are selected from either of the two crossbars
or from the 4 constant
registers. One crossbar selection allows the results of the previous cycle's
arithmetic operation to be used
while the second provides access to operands previously calculated by this or
another ALU 188. The CPU is
the only unit that has write access to the four constants (K1-K4). In cases
where an operation such as (A+B) x
10 4 is desired, the direct output from the adder can be used as input to the
Barrel Shifter, and can thus be shifted
left 2 places without needing to be latched into the L register 209 first. The
output from the adder can also be
made available to the multiply unit for a multiply-accumulate operation. The
microcode for the Adder/Logic
process block is described in the following table. The interpretations of some
bit patterns are deliberately
chosen to aid decoding. Microcode bit interpretation for Adder/Logic unit
# Bits Description
4 0000 = A+B (carry in = 0)
0001 = A+B (carry in = carry out of previous operation)
0010 = A+B+1 (carry in = 1)
0011 = A+l (increments A)
0100 = A-B-1 (carryin = 0)
0101 = A-B (carry in = carry out of previous operation)
0110 = A-B (carry in = 1)
0111 =A-1 (decrements A)
1000 = NOP
1001 = ABS(A-B)
CA 02564047 2006-11-06
YU139 PCT 34
1010 = M1N(A, B)
1011 = MAX(A, B)
1100 = A AND B (both A & B can be inverted, see below)
1101 = A OR B (both A & B can be inverted, see below)
1110 = A XOR B (both A & B can be inverted, see below)
1111 = A (A can be inverted, see below)
1 If logical operation:
0 = A=A
I = A=NOT(A)
If Adder operation:
0 = A is unsigned
1 = A is si ned
1 If logical operation:
0=B=B
I = B=NOT(B)
If Adder operation
0 = B is unsigned
1 = B is signed
4 Select A Ini,In2,Outi,Out2,Do,D,,D2,D3,M,L,S,R,K1,K2,K3,K4
4 Select B Ini,Inz,Outl,Out2,Do,D1 ,D2iD3,M,L,S,R,KI,K2,K3,K4]
14 TOTAL
Multiply/Interpolate 205
The Multiply/Interpolate process block is shown in more detail in Fig. 15 and
is a set of four 8 x 8 interpolator
units that are capable of performing four individual 8 x 8 interpolates per
cycle, or can be combined to
perform a single 16 x 16 multiply. This gives the possibility to perform up to
4 linear interpolations, a single
bi-linear interpolation, or half of a tri-linear interpolation in a single
cycle. The result of the interpolations or
multiplication is stored in the ALU 188's M register 209. There are two
primary operands, A and B, which
are selected from any of the general registers in the ALU 188 or from four
programmable constants internal to
the Multiply/Interpolate process block. Each interpolator block functions as a
simple 8 bit interpolator [result
= A + (B-A)f] or as a simple 8 x 8 multiply [result = A * B]. When the
operation is interpolation, A and B are
treated as four 8 bit numbers A0 thru A3 (A0 is the low order byte), and Bo
thru B3. Agen, Bgen, and Fgen are
responsible for ordering the inputs to the Interpolate units so that they
match the operation being performed.
For example, to perform bilinear interpolation, each of the 4 values must be
multiplied by a different factor &
the result summed, while a 16 x 16 bit multiplication requires the factors to
be 0. The microcode for the
Adder/Logic process block is described in the following table. Note that the
interpretations of some bit
patterns are deliberately chosen to aid decoding.
# Bits Description
4 0000=(Ato*B10)+V
0001=(A0*B0)+(Al *B1)+V
0010 = (Aio * B,,) - V
0011=V A,0*B10
CA 02564047 2006-11-06
YU139 PCT 35
0100 = Interpolate A0,B0 by to
0101 = Interpolate A0,B0 by fo, A1,131 by f,
0110 = Interpolate A0,B0 by fo, A1,131 by fl, A2,132 by f2
0111 = Interpolate A0,B0 by fo, A 1,131 by fl, A2,132 by f2, A3,133 by f3
1000 = Interpolate 16 bits stage 1 [M = A 1 o * f, o]
1001 = Interpolate 16 bits stage 2 [M = M + (A,o * f10)]
1010 = Tri-linear interpolate A by f stage 1 [M=Aofo+A,f,+A2f2+A3f3]
1011 = Tri-linear interpolate A by f stage 2 [M=M+Aofo+A,f,+Azfz+A3f3]
1100 = Bi-linear interpolate A by f stage 1 [M=Aofo+A,f,]
1101 = Bi-linear interpolate A by f stage 2 [M=M+Aofo+A,f,]
1110 = Bi-linear interpolate A by f complete [M=Aofo+A,f,+Azfz+A3f3]
1111 =NOP
4 Select A In1 ,In2,Out1 ,Out2,Do,D1,D2,D3iM,L,S,R,K1,K2,K3JK4]
4 Select B In,,In2,Out,,Out2,Do,D,,D2,D3,M,L,S,R,K,,K2,K3,K4
If
Mult:
4 Select V In1 ,In2,Out1 ,Out2iDo,D1 ,D2,D3,K1 ,K2,K3iK4,Adder result,M,0,1
1 Treat A as signed
1 Treat B as signed
1 Treat V as signed
If
Interp:
4 Select basis for f In1 ,In2,Out1 ,Out2,Do,D1 ,D2iD3,K1 ,K2,K3,K4,X,X,X,X]
1 Select interpolation f generation from P, or P2
P. is interpreted as # fractional bits in f
If P,,=0, f is range 0..255 representing 0..1
2 Reserved
19 TOTAL
The same 4 bits are used for the selection of V and f, although the last 4
options for V don't generally make
sense as f values. Interpolating with a factor of 1 or 0 is pointless, and the
previous multiplication or current
result is unlikely to be a meaningful value for f.
I/O ADDRESS GENERATORS 189, 190
The I/O Address Generators are shown in more detail in Fig. 16. A VLIW process
does not access DRAM
directly. Access is via 2 I/O Address Generators 189, 190, each with its own
Input and Output FIFO. A PU
e.g 178 reads data from one of two local Input FIFOs, and writes data to one
of two local Output FIFOs. Each
I/O Address Generator is responsible for reading data from DRAM and placing it
into its Input FIFO, where it
can be read by the PU e.g 178, and is responsible for taking the data from its
Output FIFO (placed there by
the PU e.g 178) and writing it to DRAM. The I/O Address Generator is a state
machine responsible for
generating addresses and control for data retrieval and storage in DRAM via
the Data cache 76. It is
customizable under CPU software control, but cannot be microcoded. The address
generator produces
addresses in two broad categories:
CA 02564047 2006-11-06
YU139 PCT 36
Image Iterators, used to iterate (reading, writing or both) through pixels of
an image in a variety
of ways
Table I/O, used to randomly access pixels in images, data in tables, and to
simulate FIFOs in
DRAM
Each of the I/O Address Generators 189, 190 has its own bus connection to the
Data cache 76, making 2 bus
connections per PU e.g 178, and a total of 8 buses over the entire VLIW Vector
Processor 74. The Data cache
76 is able to service 4 of the maximum 8 requests from the 4 PUs e.g 178 each
cycle. The Input and Output
FIFOs are 8 entry deep 16-bit wide FIFOs. The various types of address
generation (Image Iterators and Table
I/O) are described in the subsequent sections.
Re isg ters
The I/O Address Generator has a set of registers for that are used to control
address generation. The
addressing mode also determines how the data is formatted and sent into the
local Input FIFO, and how data
is interpreted from the local Output FIFO. The CPU is able to access the
registers of the I/O Address
Generator via the low speed bus. The first set of registers define the
housekeeping parameters for the I/O
Generator:
Register Name # bits Description
Reset 0 A write to this register halts any operations, and writes Os to all
the data
registers of the I/O Generator. The input and output FIFOs are not
cleared.
Go 0 A write to this register restarts the counters according to the current
setup. For example, if the I/O Generator is a Read Iterator, and the
Iterator is currently halfway through the image, a write to Go will cause
the reading to begin at the start of the image again. While the I/O
Generator is performing, the Active bit of the Status register will be set.
Halt 0 A write to this register stops any current activity and clears the
Active
bit of the Status register. If the Active bit is already cleared, writing to
this register has no effect.
Continue 0 A write to this register continues the I/O Generator from the
current
setup. Counters are not reset, and FIFOs are not cleared. A write to this
register while the I/O Generator is active has no effect.
ClearFIFOsOnGo 1 0 = Don't clear FIFOs on a write to the Go bit.
1 = Do clear FIFOs on a write to the Go bit.
Status 8 Status flags
The Status register has the following values
Register Name # bits Description
Active 1 0 = Currently inactive
1 = Currently active
Reserved 7 -
Caching
Several registers are used to control the caching mechanism, specifying which
cache group to use for inputs,
outputs etc. See the section on the Data cache 76 for more information about
cache groups.
CA 02564047 2006-11-06
YU139PCT 37
Register Name # bits Description
CacheGroup 1 4 Defines cache group to read data from
CacheGroup2 4 Defines which cache group to write data to, and in the case of
the ImagePyramidLookup I/O mode, defines the cache to use
for reading the Level Information Table.
Image Iterators = Sequential Automatic Access to pixels
The primary image pixel access method for software and hardware algorithms is
via Image Iterators. Image
iterators perform all of the addressing and access to the caches of the pixels
within an image channel and read,
write or read & write pixels for their client. Read Iterators read pixels in a
specific order for their clients, and
Write Iterators write pixels in a specific order for their clients. Clients of
Iterators read pixels from the local
Input FIFO or write pixels via the local Output FIFO.
Read Image Iterators read through an image in a specific order, placing the
pixel data into the local Input
FIFO. Every time a client reads a pixel from the Input FIFO, the Read Iterator
places the next pixel from the
image (via the Data cache 76) into the FIFO.
Write Image Iterators write pixels in a specific order to write out the entire
image. Clients write pixels to the
Output FIFO that is in turn read by the Write Image Iterator and written to
DRAM via the Data cache 76.
Typically a VLIW process will have its input tied to a Read Iterator, and
output tied to a corresponding Write
Iterator. From the PU e.g 178 microcode program's perspective, the FIFO is the
effective interface to DRAM.
The actual method of carrying out the storage (apart from the logical ordering
of the data) is not of concern.
Although the FIFO is perceived to be effectively unlimited in length, in
practice the FIFO is of limited length,
and there can be delays storing and retrieving data, especially if several
memory accesses are competing. A
variety of Image Iterators exist to cope with the most common addressing
requirements of image processing
algorithms. In most cases there is a corresponding Write Iterator for each
Read Iterator. The different Iterators
are listed in the following table:
Read Iterators Write Iterators
Sequential Read Sequential Write
Box Read -
Vertical Strip Read Vertical Strip Write
The 4 bit Address Mode Register is used to determine the Iterator type:
Bit # Address Mode
3 0 = This addressing mode is an Iterator
2 to 0 Iterator Mode
001 = Sequential Iterator
010 = Box [read only]
100 = Vertical Strip
remaining bit patterns are reserved
The Access Specific registers are used as follows:
I Register Name LocalName Description
CA 02564047 2006-11-06
YU139 PCT 38
AccessS ecific, Flags Flags used for reading and writing
AccessSpecific2 XBoxSize Determines the size in X of Box Read. Valid values
are
3, 5, and 7.
AccessSpecific3 YBoxSize Determines the size in Y of Box Read. Valid values
are
3, 5, and 7.
AccessSpecific4 BoxOffset Offset between one pixel center and the next during
a
Box Read only.
Usual value is 1, but other useful values include 2, 4, 8...
See Box Read for more details.
The Flags register (AccessSpecificI) contains a number of flags used to
determine factors affecting the
reading and writing of data. The Flags register has the following composition:
Label #bits Description
ReadEnable 1 Read data from DRAM
WriteEnable 1 Write data to DRAM [not valid for Box mode]
PassX 1 Pass X (pixel) ordinate back to Input FIFO
PassY 1 Pass Y (row) ordinate back to Input FIFO
Loop 1 0 = Do not loop through data
1 = Loop through data
Reserved 11 Must be 0
Notes on ReadEnable and WriteEnable:
When ReadEnable is set, the I/O Address Generator acts as a Read Iterator, and
therefore reads
the image in a particular order, placing the pixels into the Input FIFO.
When WriteEnable is set, the I/O Address Generator acts as a Write Iterator,
and therefore
writes the image in a particular order, taking the pixels from the Output
FIFO.
When both ReadEnable and WriteEnable are set, the I/O Address Generator acts
as a Read
Iterator and as a Write Iterator, reading pixels into the Input FIFO, and
writing pixels from
the Output FIFO. Pixels are only written after they have been read - i.e. the
Write Iterator
will never go faster than the Read Iterator. Whenever this mode is used, care
should be
taken to ensure balance between in and out processing by the VLIW microcode.
Note that
separate cache groups can be specified on reads and writes by loading
different values in
CacheGroupl and CacheGroup2.
Notes on PassX and PassY:
If PassX and PassY are both set, the Y ordinate is placed into the Input FIFO
before the X
ordinate.
PassX and PassY are only intended to be set when the ReadEnable bit is clear.
Instead of
passing the ordinates to the address generator, the ordinates are placed
directly into the
Input FIFO. The ordinates advance as they are removed from the FIFO.
If WriteEnable bit is set, the VLIW program must ensure that it balances reads
of ordinates
from the Input FIFO with writes to the Output FIFO, as writes will only occur
up to the
ordinates (see note on ReadEnable and WriteEnable above).
CA 02564047 2006-11-06
YU139 PCT 39
Notes on Loop:
If the Loop bit is set, reads will recommence at [StartPixel, StartRow] once
it has reached
[EndPixel, EndRow]. This is ideal for processing a structure such a
convolution kernel or a
dither cell matrix, where the data must be read repeatedly.
Looping with ReadEnable and WriteEnable set can be useful in an environment
keeping a
single line history, but only where it is useful to have reading occur before
writing. For a
FIFO effect (where writing occurs before reading in a length constrained
fashion), use an
appropriate Table I/O addressing mode instead of an Image Iterator.
Looping with only WriteEnable set creates a written window of the last N
pixels. This can be
used with an asynchronous process that reads the data from the window. The
Artcard
Reading algorithm makes use of this mode.
Sequential Read and Write Iterators
Fig. 17 illustrates the pixel data format. The simplest Image Iterators are
the Sequential Read Iterator and
corresponding Sequential Write Iterator. The Sequential Read Iterator presents
the pixels from a channel one
line at a time from top to bottom, and within a line, pixels are presented
left to right. The padding bytes are
not presented to the client. It is most useful for algorithms that must
perform some process on each pixel from
an image but don't care about the order of the pixels being processed, or want
the data specifically in this
order. Complementing the Sequential Read Iterator is the Sequential Write
Iterator. Clients write pixels to the
Output FIFO. A Sequential Write Iterator subsequently writes out a valid image
using appropriate caching
and appropriate padding bytes. Each Sequential Iterator requires access to 2
cache lines. When reading, while
32 pixels are presented from one cache line, the other cache line can be
loaded from memory. When writing,
while 32 pixels are being filled up in one cache line, the other can be being
written to memory.
A process that performs an operation on each pixel of an image independently
would typically use a
Sequential Read Iterator to obtain pixels, and a Sequential Write Iterator to
write the new pixel values to their
corresponding locations within the destination image. Such a process is shown
in Fig. 18.
In most cases, the source and destination images are different, and are
represented by 2 I/O Address
Generators 189, 190. However it can be valid to have the source image and
destination image to be the same,
since a given input pixel is not read more than once. In that case, then the
same Iterator can be used for both
input and output, with both the ReadEnable and WriteEnable registers set
appropriately. For maximum
efficiency, 2 different cache groups should be used - one for reading and the
other for writing. If data is
being created by a VLIW process to be written via a Sequential Write Iterator,
the PassX and PassY flags can
be used to generate coordinates that are then passed down the Input FIFO. The
VLIW process can use these
coordinates and create the output data appropriately.
Box Read Iterator
The Box Read Iterator is used to present pixels in an order most useful for
performing operations such as
general-purpose filters and convolve. The Iterator presents pixel values in a
square box around the
sequentially read pixels. The box is limited to being 1, 3, 5, or 7 pixels
wide in X and Y (set XBoxSize and
YBoxSize- they must be the same value or 1 in one dimension and 3, 5, or 7 in
the other). The process is
shown in Fig. 19:
CA 02564047 2006-11-06
YU139PCT 40
BoxOffset: This special purpose register is used to determine a sub-sampling
in terms of which input pixels
will be used as the center of the box. The usual value is 1, which means that
each pixel is used as the center of
the box. The value "2" would be useful in scaling an image down by 4:1 as in
the case of building an image
pyramid. Using pixel addresses from the previous diagram, the box would be
centered on pixel 0, then 2, 8,
and 10. The Box Read Iterator requires access to a maximum of 14 (2 x 7) cache
lines. While pixels are
presented from one set of 7 lines, the other cache lines can be loaded from
memory.
Box Write Iterator
There is no corresponding Box Write Iterator, since the duplication of pixels
is only required on input. A
process that uses the Box Read Iterator for input would most likely use the
Sequential Write Iterator for
output since they are in sync. A good example is the convolver, where N input
pixels are read to calculate 1
output pixel. The process flow is as illustrated in Fig. 20. The source and
destination images should not
occupy the same memory when using a Box Read Iterator, as subsequent lines of
an image require the
original (not newly calculated) values.
Vertical-Strip Read and Write Iterators
In some instances it is necessary to write an image in output pixel order, but
there is no knowledge about the
direction of coherence in input pixels in relation to output pixels. An
example of this is rotation. If an image is
rotated 90 degrees, and we process the output pixels horizontally, there is a
complete loss of cache coherence.
On the other hand, if we process the output image one cache line's width of
pixels at a time and then advance
to the next line (rather than advance to the next cache-line's worth of pixels
on the same line), we will gain
cache coherence for our input image pixels. It can also be the case that there
is known `block' coherence in
the input pixels (such as color coherence), in which case the read governs the
processing order, and the write,
to be synchronized, must follow the same pixel order.
The order of pixels presented as input (Vertical-Strip Read), or expected for
output (Vertical-Strip Write) is
the same. The order is pixels 0 to 31 from line 0, then pixels 0 to 31 of line
1 etc for all lines of the image,
then pixels 32 to 63 of line 0, pixels 32 to 63 of line 1 etc. In the final
vertical strip there may not be exactly
32 pixels wide. In this case only the actual pixels in the image are presented
or expected as input. This process
is illustrated in Fig. 21.
process that requires only a Vertical-Strip Write Iterator will typically have
a way of mapping input pixel
coordinates given an output pixel coordinate. It would access the input image
pixels according to this
mapping, and coherence is determined by having sufficient cache lines on the
`random-access' reader for the
input image. The coordinates will typically be generated by setting the PassX
and PassY flags on the
VerticalStripWrite Iterator, as shown in the process overview illustrated in
Fig. 22.
It is not meaningful to pair a Write Iterator with a Sequential Read Iterator
or a Box read Iterator, but a
Vertical-Strip Write Iterator does give significant improvements in
performance when there is a non trivial
mapping between input and output coordinates.
It can be meaningful to pair a Vertical Strip Read Iterator and Vertical Strip
Write Iterator. In this case it is
possible to assign both to a single ALU 188 if input and output images are the
same. If coordinates are
required, a further Iterator must be used with PassX and PassY flags set. The
Vertical Strip Read/Write
Iterator presents pixels to the Input FIFO, and accepts output pixels from the
Output FIFO. Appropriate
CA 02564047 2006-11-06
YU139 PCT 41
padding bytes will be inserted on the write. Input and output require a
minimum of 2 cache lines each for
good performance.
Table I/O Addressing Modes
It is often necessary to lookup values in a table (such as an image). Table
I/O addressing modes provide this
functionality, requiring the client to place the index/es into the Output
FIFO. The I/O Address Generator then
processes the index/es, looks up the data appropriately, and returns the
looked-up values in the Input FIFO for
subsequent processing by the VLIW client.
1D, 2D and 3D tables are supported, with particular modes targeted at
interpolation. To reduce complexity on
the VLIW client side, the index values are treated as fixed-point numbers,
with AccessSpecific registers
defining the fixed point and therefore which bits should be treated as the
integer portion of the index. Data
formats are restricted forms of the general Image Characteristics in that the
PixelOffset register is ignored, the
data is assumed to be contiguous within a row, and can only be 8 or 16 bits (1
or 2 bytes) per data element.
The 4 bit Address Mode Register is used to determine the I/O type:
Bit # Address Mode
3 1 = This addressing mode is Table I/O
2 to 0 000 = 1D Direct Lookup
001 = 1D Interpolate (linear)
010 = DRAM FIFO
011 = Reserved
100 = 2D Interpolate (bi-linear)
101 = Reserved
110 = 3D Interpolate (tri-linear)
111 = Image Pyramid Lookup
The access specific registers are:
Register Name LocalName #bits Description
AccessSpecifici Flags 8 General flags for reading and writing.
See below for more information.
AccessS ecific2 FractX 8 Number of fractional bits in X index
AccessS ecific3 FractY 8 Number of fractional bits in Y index
AccessSpecific4 FractZ 8 Number of fractional bits in Z index
(low 8 bits / next 12 or 24 ZOffset 12 or See below
bits)) 24
FractX, FractY, and FractZ are used to generate addresses based on indexes,
and interpret the format of the
index in terms of significant bits and integer/fractional components. The
various parameters are only defined
as required by the number of dimensions in the table being indexed. A 1D table
only needs FractX, a 2D table
requires FractX and FractY. Each Fract value consists of the number of
fractional bits in the corresponding
index. For example, an X index may be in the format 5:3. This would indicate 5
bits of integer, and 3 bits of
fraction. FractX would therefore be set to 3. A simple 1D lookup could have
the format 8:0, i.e. no fractional
component at all. FractX would therefore be 0. ZOffset is only required for 3D
lookup and takes on two
different interpretations. It is described more fully in the 3D-table lookup
section. The Flags register
CA 02564047 2006-11-06
YU139 PCT 42
(AccessSpecificI) contains a number of flags used to determine factors
affecting the reading (and in one case,
writing) of data. The Flags register has the following composition:
Label #bits Description
ReadEnable 1 Read data from DRAM
WriteEnable 1 Write data to DRAM [only valid for 1D direct lookup]
DataSize 1 0 = 8 bit data
1 = 16 bit data
Reserved 5 Must be 0
With the exception of the 1D Direct Lookup and DRAM FIFO, all Table I/O modes
only support reading, and
not writing. Therefore the ReadEnable bit will be set and the WriteEnable bit
will be clear for all I/O modes
other than these two modes. The 1D Direct Lookup supports 3 modes:
Read only, where the ReadEnable bit is set and the WriteEnable bit is clear
Write only, where the ReadEnable bit is clear and the WriteEnable bit is clear
Read-Modify-Write, where both ReadEnable and the WriteEnable bits are set
The different modes are described in the 1D Direct Lookup section below. The
DRAM FIFO mode supports
only 1 mode:
Write-Read mode, where both ReadEnable and the WriteEnable bits are set
This mode is described in the DRAM FIFO section below. The DataSize flag
determines whether the size of
each data elements of the table is 8 or 16 bits. Only the two data sizes are
supported. 32 bit elements can be
created in either of 2 ways depending on the requirements of the process:
Reading from 2 16-bit tables simultaneously and combining the result. This is
convenient if
timing is an issue, but has the disadvantage of consuming 2 I/O Address
Generators 189,
190, and each 32-bit element is not readable by the CPU as a 32-bit entity.
Reading from a 16-bit table twice and combining the result. This is convenient
since only 1
lookup is used, although different indexes must be generated and passed into
the lookup.
I Dimensional Structures
Direct Lookup
A direct lookup is a simple indexing into a 1 dimensional lookup table.
Clients can choose between 3 access
modes by setting appropriate bits in the Flags register:
Read only
Write only
Read-Modify-Write
Read Only
A client passes the fixed-point index X into the Output FIFO, and the 8 or 16-
bit value at Table[Int(X)] is
returned in the Input FIFO. The fractional component of the index is
completely ignored. If the index is out of
bounds, the DuplicateEdge flag determines whether the edge pixel or
ConstantPixel is returned. The address
generation is straightforward:
If DataSize indicates 8 bits, X is barrel-shifted right FractX bits, and the
result is added to the
table's base address ImageStart.
CA 02564047 2006-11-06
YU139 PCT 43
If DataSize indicates 16 bits, X is barrel-shifted right FractX bits, and the
result shifted left 1 bit
(bitO becomes 0) is added to the table's base address ImageStart.
The 8 or 16-bit data value at the resultant address is placed into the Input
FIFO. Address generation takes 1
cycle, and transferring the requested data from the cache to the Output FIFO
also takes 1 cycle (assuming a
cache hit). For example, assume we are looking up values in a 256-entry table,
where each entry is 16 bits,
and the index is a 12 bit fixed-point format of 8:4. FractX should be 4, and
DataSize 1. When an index is
passed to the lookup, we shift right 4 bits, then add the result shifted left
1 bit to ImageStart.
Write Only
A client passes the fixed-point index X into the Output FIFO followed by the 8
or 16-bit value that is to be
written to the specified location in the table. A complete transfer takes a
minimum of 2 cycles. 1 cycle for
address generation, and 1 cycle to transfer the data from the FIFO to DRAM.
There can be an arbitrary
number of cycles between a VLIW process placing the index into the FIFO and
placing the value to be written
into the FIFO. Address generation occurs in the same way as Read Only mode,
but instead of the data being
read from the address, the data from the Output FIFO is written to the
address. If the address is outside the
table range, the data is removed from the FIFO but not written to DRAM.
Read-Modify-Write
A client passes the fixed-point index X into the Output FIFO, and the 8 or 16-
bit value at Table[Int(X)] is
returned in the Input FIFO. The next value placed into the Output FIFO is then
written to Table[Int(X)],
replacing the value that had been returned earlier. The general processing
loop then, is that a process reads
from a location, modifies the value, and writes it back. The overall time is 4
cycles:
Generate address from index
Return value from table
Modify value in some way
Write it back to the table
There is no specific read/write mode where a client passes in a flag saying
"read from X" or "write to V.
Clients can simulate a "read from X" by writing the original value, and a
"write to X" by simply ignoring the
returned value. However such use of the mode is not encouraged since each
action consumes a minimum of 3
cycles (the modify is not required) and 2 data accesses instead of 1 access as
provided by the specific Read
and Write modes.
Interpolate table
This is the same as a Direct Lookup in Read mode except that two values are
returned for a given fixed-point
index X instead of one. The values returned are Table[Int(X)], and
Table[Int(X)+l]. If either index is out of
bounds the DuplicateEdge flag determines whether the edge pixel or
ConstantPixel is returned. Address
generation is the same as Direct Lookup, with the exception that the second
address is simply Address 1+ 1 or
2 depending on 8 or 16 bit data. Transferring the requested data to the Output
FIFO takes 2 cycles (assuming
a cache hit), although two 8-bit values may actually be returned from the
cache to the Address Generator in a
single 16-bit fetch.
DRAM FIFO
A special case of a read/write 1D table is a DRAM FIFO. It is often necessary
to have a simulated FIFO of a
given length using DRAM and associated caches. With a DRAM FIFO, clients do
not index explicitly into the
CA 02564047 2006-11-06
YU139 PCT 44
table, but write to the Output FIFO as if it was one end of a FIFO and read
from the Input FIFO as if it was
the other end of the same logical FIFO. 2 counters keep track of input and
output positions in the simulated
FIFO, and cache to DRAM as needed. Clients need to set both ReadEnable and
WriteEnable bits in the Flags
register.
An example use of a DRAM FIFO is keeping a single line history of some value.
The initial history is written
before processing begins. As the general process goes through a line, the
previous line's value is retrieved
from the FIFO, and this line's value is placed into the FIFO (this line will
be the previous line when we
process the next line). So long as input and outputs match each other on
average, the Output FIFO should
always be full. Consequently there is effectively no access delay for this
kind of FIFO (unless the total FIFO
length is very small - say 3 or 4 bytes, but that would defeat the purpose of
the FIFO).
2 Dimensional Tables
Direct Lookup
A 2 dimensional direct lookup is not supported. Since all cases of 2D lookups
are expected to be accessed for
bi-linear interpolation, a special bi-linear lookup has been implemented.
Bi-Linear lookup
This kind of lookup is necessary for bi-linear interpolation of data from a 2D
table. Given fixed-point X and
Y coordinates (placed into the Output FIFO in the order Y, X), 4 values are
returned after lookup. The values
(in order) are:
Table[Int(X), Int(Y)]
Table[Int(X)+1, Int(Y)]
Table[Int(X), Int(Y)+1]
Table[Int(X)+1, Int(Y)+1]
The order of values returned gives the best cache coherence. If the data is 8-
bit, 2 values are returned each
cycle over 2 cycles with the low order byte being the first data element. If
the data is 16-bit, the 4 values are
returned in 4 cycles, 1 entry per cycle. Address generation takes 2 cycles.
The first cycle has the index (Y)
barrel-shifted right FractY bits being multiplied by RowOffset, with the
result added to ImageStart. The
second cycle shifts the X index right by FractX bits, and then either the
result (in the case of 8 bit data) or the
result shifted left 1 bit (in the case of 16 bit data) is added to the result
from the first cycle. This gives us
address Adr = address of Table[Int(X), Int(Y)]:
Adr = ImageStart
+ ShiftRight(Y, FractY)* RowOffset)
+ ShiftRight(X, FractX)
We keep a copy of Adr in AdrOld for use fetching subsequent entries.
If the data is 8 bits, the timing is 2 cycles of address generation, followed
by 2 cycles of data
being returned (2 table entries per cycle).
If the data is 16 bits, the timing is 2 cycles of address generation, followed
by 4 cycles of data
being returned (1 entry per cycle)
The following 2 tables show the method of address calculation for 8 and 16 bit
data sizes:
CA 02564047 2006-11-06
YU139 PCT 45
Cycle Calculation while fetching 2 x 8-bit data entries from Adr
1 Adr = Adr + RowOffset
2 < re aring next lookup>
Cycle Calculation while fetching 1 x 16-bit data entry from Adr
1 Adr=Adr+2
2 Adr = AdrOld + RowOffset
3 Adr=Adr+2
4 <Preparing next lookup>
In both cases, the first cycle of address generation can overlap the insertion
of the X index into the FIFO, so
the effective timing can be as low as 1 cycle for address generation, and 4
cycles of return data. If the
generation of indexes is 2 steps ahead of the results, then there is no
effective address generation time, and the
data is simply produced at the appropriate rate (2 or 4 cycles per set).
3 Dimensional Lookup
Direct Lookup
Since all cases of 2D lookups are expected to be accessed for tri-linear
interpolation, two special tri-linear
lookups have been implemented. The first is a straightforward lookup table,
while the second is for to -linear
interpolation from an Image Pyramid.
Tri-linear lookup
This type of lookup is useful for 3D tables of data, such as color conversion
tables. The standard image
parameters define a single XY plane of the data - i.e. each plane consists of
ImageHeight rows, each row
containing RowOffset bytes. In most circumstances, assuming contiguous planes,
one XY plane will be
ImageHeight x RowOffset bytes after another. Rather than assume or calculate
this offset, the software via the
CPU must provide it in the form of a 12-bit ZOffset register. In this form of
lookup, given 3 fixed-point
indexes in the order Z, Y, X, 8 values are returned in order from the lookup
table:
Table[Int(X), Int(Y), Int(Z)]
Table[Int(X)+1, Int(Y), Int(Z)]
Table[Int(X), Int(Y)+1, Int(Z)]
Table[Int(X)+1, Int(Y)+1, Int(Z)]
Table[Int(X), Int(Y), Int(Z)+l]
Table[Int(X)+1, Int(Y), Int(Z)+l]
Table[Int(X), Int(Y)+1, Int(Z)+1]
Table[Int(X)+1, Int(Y)+1, Int(Z)+1]
The order of values returned gives the best cache coherence. If the data is 8-
bit, 2 values are returned each
cycle over 4 cycles with the low order byte being the first data element. If
the data is 16-bit, the 4 values are
returned in 8 cycles, 1 entry per cycle. Address generation takes 3 cycles.
The first cycle has the index (Z)
barrel-shifted right FractZ bits being multiplied by the 12-bit ZOffset and
added to ImageStart. The second
cycle has the index (Y) barrel-shifted right FractY bits being multiplied by
RowOffset, with the result added
to the result of the previous cycle. The second cycle shifts the X index right
by FractX bits, and then either the
CA 02564047 2006-11-06
YU139 PCT 46
result (in the case of 8 bit data) or the result shifted left 1 bit (in the
case of 16 bit data) is added to the result
from the second cycle. This gives us address Adr = address of Table[Int(X),
Int(Y), Int(Z)]:
Adr = ImageStart
+ (ShiftRight(Z, FractZ) * ZOffset)
+ (ShiftRight(Y, FractY)* RowOffset)
+ ShiftRight(X, FractX)
We keep a copy of Adr in AdrOld for use fetching subsequent entries.
If the data is 8 bits, the timing is 2 cycles of address generation, followed
by 2 cycles of data
being returned (2 table entries per cycle).
If the data is 16 bits, the timing is 2 cycles of address generation, followed
by 4 cycles of data
being returned (1 entry per cycle)
The following 2 tables show the method of address calculation for 8 and 16 bit
data sizes:
Cycle Calculation while fetching 2 x 8-bit data entries from Adr
1 Adr = Adr + RowOffset
2 Adr = AdrOld + ZOffset
3 Adr = Adr + RowOffset
4 < re arin next lookup
Cycle Calculation while fetching 1 x 16-bit data entries from Adr
1 Adr=Adr+2
2 Adr = AdrOld + RowOffset
3 Adr = Adr + 2
4 Adr, AdrOld =AdrOld + Zoffset
5 Adr=Adr+2
6 Adr = AdrOld + RowOffset
7 Adr=Adr+2
8 < re arin next lookup
In both cases, the cycles of address generation can overlap the insertion of
the indexes into the FIFO, so the
effective timing for a single one-off lookup can be as low as 1 cycle for
address generation, and 4 cycles of
return data. If the generation of indexes is 2 steps ahead of the results,
then there is no effective address
generation time, and the data is simply produced at the appropriate rate (4 or
8 cycles per set).
Image Pyramid Lookup
During brushing, tiling, and warping it is necessary to compute the average
color of a particular area in an
image. Rather than calculate the value for each area given, these functions
make use of an image pyramid.
The description and construction of an image pyramid is detailed in the
section on Internal Image Formats in
the DRAM interface 81 chapter of this document. This section is concerned with
a method of addressing
given pixels in the pyramid in terms of 3 fixed-point indexes ordered: level
(Z), Y, and X. Note that Image
Pyramid lookup assumes 8 bit data entries, so the DataSize flag is completely
ignored. After specification of
Z, Y, and X, the following 8 pixels are returned via the Input FIFO:
CA 02564047 2006-11-06
YU139 PCT 47
The pixel at [Int(X), Int(Y)], level Int(Z)
The pixel at [Int(X)+l, Int(Y)], level Int(Z)
The pixel at [Int(X), Int(Y)+1], level Int(Z)
The pixel at [Int(X)+1, Int(Y)+1], level Int(Z)
The pixel at [Int(X), Int(Y)], level Int(Z)+l
The pixel at [Int(X)+1, Int(Y)], level Int(Z)+1
The pixel at [Int(X), Int(Y)+1], level Int(Z)+1
The pixel at [Int(X)+1, Int(Y)+1], level Int(Z)+l
The 8 pixels are returned as 4 x 16 bit entries, with X and X+1 entries
combined hi/lo. For example, if the
scaled (X, Y) coordinate was (10.4, 12.7) the first 4 pixels returned would
be: (10, 12), (11, 12), (10, 13) and
(11, 13). When a coordinate is outside the valid range, clients have the
choice of edge pixel duplication or
returning of a constant color value via the DuplicateEdgePixels and
ConstantPixel registers (only the low 8
bits are used). When the Image Pyramid has been constructed, there is a simple
mapping from level 0
coordinates to level Z coordinates. The method is simply to shift the X or Y
coordinate right by Z bits. This
must be done in addition to the number of bits already shifted to retrieve the
integer portion of the coordinate
(i.e. shifting right FractX and FractY bits for X and Y ordinates
respectively). To find the ImageStart and
RowOffset value for a given level of the image pyramid, the 24-bit ZOffset
register is used as a pointer to a
Level Information Table. The table is an array of records, each representing a
given level of the pyramid,
ordered by level number. Each record consists of a 16-bit offset ZOffset from
Image Start to that level of the
pyramid (64-byte aligned address as lower 6 bits of the offset are not
present), and a 12 bit ZRowOffset for
that level. Element 0 of the table would contain a ZOffset of 0, and a
ZRowOffset equal to the general register
RowOffset, as it simply points to the full sized image. The ZOffset value at
element N of the table should be
added to ImageStart to yield the effective ImageStart of level N of the image
pyramid. The RowOffset value
in element N of the table contains the RowOffset value for level N. The
software running on the CPU must set
up the table appropriately before using this addressing mode. The actual
address generation is outlined here
in a cycle by cycle description:
Cycle Read ter Address Other Operations
0 - - ZAdr = ShiftRight(Z, FractZ) + ZOffset
Zlnt = ShiftRi ht Z, FractZ)
1 ZOffset Zadr ZAdr += 2
YInt = ShiftRight(Y, FractY)
2 ZRowOffset ZAdr ZAdr += 2
YInt = ShiftRight(YInt, ZInt)
Adr = ZOffset + Image Start
3 ZOffset ZAdr ZAdr += 2
Adr += ZrowOffset * YInt
Xlnt = ShiftRight(X, FractX)
4 ZAdr ZAdr Adr += ShiftRight(XInt, ZInt)
ZOffset += ShiftRi ht(XInt, 1)
5 FIFO Adr Adr += ZrowOffset
ZOffset += ImageStart
6 FIFO Adr Adr = (ZAdr * ShiftRight(Yint, 1)) + ZOffset
CA 02564047 2006-11-06
YU139PCT 48
7 FIFO Adr Adr += Zadr
8 FIFO Adr < Cycle 0 for next retrieval>
The address generation as described can be achieved using a single Barrel
Shifter, 2 adders, and a single
16x16 multiply/add unit yielding 24 bits. Although some cycles have 2 shifts,
they are either the same shift
value (i.e. the output of the Barrel Shifter is used two times) or the shift
is 1 bit, and can be hard wired. The
following internal registers are required: ZAdr, Adr, ZInt, YInt, XInt,
ZRowOffset, and ZlmageStart. The _Int
registers only need to be 8 bits maximum, while the others can be up to 24
bits. Since this access method
only reads from, and does not write to image pyramids, the CacheGroup2 is used
to lookup the Image
Pyramid Address Table (via ZAdr). CacheGroupl is used for lookups to the image
pyramid itself (via Adr).
The address table is around 22 entries (depending on original image size),
each of 4 bytes. Therefore 3 or 4
cache lines should be allocated to CacheGroup2, while as many cache lines as
possible should be allocated to
CacheGroupl. The timing is 8 cycles for returning a set of data, assuming that
Cycle 8 and Cycle 0 overlap in
operation - i.e. the next request's Cycle 0 occurs during Cycle 8. This is
acceptable since Cycle 0 has no
memory access, and Cycle 8 has no specific operations.
GENERATION OF COORDINATES USING VLIW VECTOR PROCESSOR 74
Some functions that are linked to Write Iterators require the X and/or Y
coordinates of the current pixel being
processed in part of the processing pipeline. Particular processing may also
need to take place at the end of
each row, or column being processed. In most cases, the PassX and PassY flags
should be sufficient to
completely generate all coordinates. However, if there are special
requirements, the following functions can
be used. The calculation can be spread over a number of ALUs, for a single
cycle generation, or be in a single
ALU 188 for a multi-cycle generation.
Generate Sequential [X, Y]
When a process is processing pixels in sequential order according to the
Sequential Read Iterator (or
generating pixels and writing them out to a Sequential Write Iterator), the
following process can be used to
generate X, Y coordinates instead of PassX/PassY flags as shown in Fig. 23.
The coordinate generator counts up to ImageWidth in the X ordinate, and once
per ImageWidth pixels
increments the Y ordinate. The actual process is illustrated in Fig. 24, where
the following constants are set by
software:
Constant Value
K, ImageWidth
K2 Ima eHei ht (optional)
The following registers are used to hold temporary variables:
Variable Value
Reg, X starts at 0 each line)
Re 92 Y (starts at 0)
The requirements are summarized as follows:
Requirements I I *+ + I R I K LU Iterators
CA 02564047 2006-11-06
YU139 PCT 49
General 0 3/4 2 1/2 0 0
TOTAL 0 3/4 2 1/2 0 0
Generate Vertical Strip [X, Yl
When a process is processing pixels in order to write them to a Vertical Strip
Write Iterator, and for some
reason cannot use the PassX/PassY flags, the process as illustrated in Fig. 25
can be used to generate X, Y
coordinates. The coordinate generator simply counts up to Image Width in the X
ordinate, and once per
ImageWidth pixels increments the Y ordinate. The actual process is illustrated
in Fig. 26, where the
following constants are set by software:
Constant Value
K, 32
K2 Image Width
K3 ImageHeight
The following registers are used to hold temporary variables:
Variable Value
Reg, StartX (starts at 0, and is incremented by 32 once per vertical strip)
Re 92 X
Reg3 EndX (starts at 32 and is incremented by 32 to a maximum of Image Width)
once
per vertical strip)
Rea Y
The requirements are summarized as follows:
Requirements *+ + R K LU Iterators
General 0 4 4 3 0 0
TOTAL 0 4 4 3 0 0
The calculations that occur once per vertical strip (2 additions, one of which
has an associated MIN) are not
included in the general timing statistics because they are not really part of
the per pixel timing. However they
do need to be taken into account for the programming of the microcode for the
particular function.
Image Sensor Interface (ISI 83)
The Image Sensor Interface (ISI 83) takes data from the CMOS Image Sensor and
makes it available for
storage in DRAM. The image sensor has an aspect ratio of 3:2, with a typical
resolution of 750 x 500 samples,
yielding 375K (8 bits per pixel). Each 2x2 pixel block has the configuration
as shown in Fig. 27. The ISI 83
is a state machine that sends control information to the Image Sensor,
including frame sync pulses and pixel
clock pulses in order to read the image. Pixels are read from the image sensor
and placed into the VLIW Input
FIFO 78. The VLIW is then able to process and/or store the pixels. This is
illustrated further in Fig. 28. The
ISI 83 is used in conjunction with a VLIW program that stores the sensed Photo
Image in DRAM. Processing
occurs in 2 steps:
A small VLIW program reads the pixels from the FIFO and writes them to DRAM
via a
Sequential Write Iterator.
CA 02564047 2006-11-06
YU139 PCT 50
The Photo Image in DRAM is rotated 90, 180 or 270 degrees according to the
orientation of the
camera when the photo was taken.
If the rotation is 0 degrees, then step 1 merely writes the Photo Image out to
the final Photo Image location
and step 2 is not performed. If the rotation is other than 0 degrees, the
image is written out to a temporary area
(for example into the Print Image memory area), and then rotated during step 2
into the final Photo Image
location. Step 1 is very simple microcode, taking data from the VLIW Input
FIFO 78 and writing it to a
Sequential Write Iterator. Step 2's rotation is accomplished by using the
accelerated Vark Affine Transform
function. The processing is performed in 2 steps in order to reduce design
complexity and to re-use the Vark
affine transform rotate logic already required for images. This is acceptable
since both steps are completed in
approximately 0.03 seconds, a time imperceptible to the operator of the
Artcam. Even so, the read process is
sensor speed bound, taking 0.02 seconds to read the full frame, and
approximately 0.01 seconds to rotate the
image.
The orientation is important for converting between the sensed Photo Image and
the internal format image,
since the relative positioning of R, G, and B pixels changes with
orientation.. The processed image may also
have to be rotated during the Print process in order to be in the correct
orientation for printing. The 3D model
of the Artcam has 2 image sensors, with their inputs multiplexed to a single
ISI 83 (different microcode, but
same ACP 31). Since each sensor is a frame store, both images can be taken
simultaneously, and then
transferred to memory one at a time.
Display Controller 88
When the "Take" button on an Artcam is half depressed, the TFT will display
the current image from the
image sensor (converted via a simple VLIW process). Once the Take button is
fully depressed, the Taken
Image is displayed. When the user presses the Print button and image
processing begins, the TFT is turned
off. Once the image has been printed the TFT is turned on again. The Display
Controller 88 is used in those
Artcam models that incorporate a flat panel display. An example display is a
TFT LCD of resolution 240 x
160 pixels. The structure of the Display Controller 88 isl illustrated in Fig.
29. The Display Controller 88
State Machine contains registers that control the timing of the Sync
Generation, where the display image is to
be taken from (in DRAM via the Data cache 76 via a specific Cache Group), and
whether the TFT should be
active or not (via TFT Enable) at the moment. The CPU can write to these
registers via the low speed bus.
Displaying a 240 x 160 pixel image on an RGB TFT requires 3 components per
pixel. The image taken from
DRAM is displayed via 3 DACs, one for each of the R, G, and B output signals.
At an image refresh rate of
30 frames per second (60 fields per second) the Display Controller 88 requires
data transfer rates of.
240 x 160 x 3 x 30 = 3.5MB per second
This data rate is low compared to the rest of the system. However it is high
enough to cause VLIW programs
to slow down during the intensive image processing. The general principles of
TFT operation should reflect
this.
Image Data Formats
As stated previously, the DRAM Interface 81 is responsible for interfacing
between other client portions
of the ACP chip and the RAMBUS DRAM. In effect, each module within the DRAM
Interface is an address
generator.
CA 02564047 2006-11-06
YU139 PCT 51
There are three logical types of images manipulated by the ACP. They are:
-CCD Image, which is the Input Image captured from the CCD.
-Internal Image format - the Image format utilised internally by the Artcam
device.
Print Image - the Output Image format printed by the Artcam
These images are typically different in color space, resolution, and the
output & input color spaces which
can vary from camera to camera. For example, a CCD image on a low-end camera
may be a different resolution,
or have different color characteristics from that used in a high-end camera.
However all internal image formats are
the same format in terms of color space across all cameras.
In addition, the three image types can vary with respect to which direction is
`up'. The physical
orientation of the camera causes the notion of a portrait or landscape image,
and this must be maintained
throughout processing. For this reason, the internal image is always oriented
correctly, and rotation is performed
on images obtained from the CCD and during the print operation.
CCD Image Organization
Although many different CCD image sensors could be utilised, it will be
assumed that the CCD itself is a
750 x 500 image sensor, yielding 375,000 bytes (8 bits per pixel). Each 2x2
pixel block having the configuration
as depicted in Fig. 30.
A CCD Image as stored in DRAM has consecutive pixels with a given line
contiguous in memory. Each
line is stored one after the other. The image sensor Interface 83 is
responsible for taking data from the CCD and
storing it in the DRAM correctly oriented. Thus a CCD image with rotation 0
degrees has its first line G, R, G, R,
G, R... and its second line as B, G, B, G, B, G.... If the CCD image should be
portrait, rotated 90 degrees, the
first line will be R, G, R, G, R, G and the second line G, B, G, B, G,
B...etc.
Pixels are stored in an interleaved fashion since all color components are
required in order to convert to
the internal image format.
It should be noted that the ACP 31 makes no assumptions about the CCD pixel
format, since the actual
CCDs for imaging may vary from Artcam to Artcarn, and over time. All
processing that takes place via the
hardware is controlled by major microcode in an attempt to extend the
usefulness of the ACP 31.
Internal Image Organization
Internal images typically consist of a number of channels. Vark images can
include, but are not limited
to:
Lab
Laba
LabA
aA
L
L, a and b correspond to components of the Lab color space, a is a matte
channel (used for compositing),
and A is a bump-map channel (used during brushing, tiling and illuminating).
The VLIW processor 74 requires images to be organized in a planar
configuration. Thus a Lab image
would be stored as 3 separate blocks of memory:
one block for the L channel,
CA 02564047 2006-11-06
YU139 PCT 52
one block for the a channel, and
one block for the b channel
Within each channel block, pixels are stored contiguously for a given row
(plus some optional padding
bytes), and rows are stored one after the other.
Turning to Fig. 31 there is illustrated an example form of storage of a
logical image 100. The logical
image 100 is stored in a planar fashion having L 101, a 102 and b 103 color
components stored one after another.
Alternatively, the logical image 100 can be stored in a compressed format
having an uncompressed L component
101 and compressed A and B components 105, 106.
Turning to Fig. 32, the pixels of for line n 110 are stored together before
the pixels of for line and n + 1
(111). With the image being stored in contiguous memory within a single
channel.
In the 8MB-memory model, the final Print Image after all processing is
finished, needs to be compressed
in the chrominance channels. Compression of chrominance channels can be 4:1,
causing an overall compression
of 12:6, or 2:1.
Other than the final Print Image, images in the Artcam are typically not
compressed. Because of memory
constraints, software may choose to compress the final Print Image in the
chrominance channels by scaling each
of these channels by 2:1. If this has been done, the PRINT Vark function call
utilised to print an image must be
told to treat the specified chrominance channels as compressed. The PRINT
function is the only function that
knows how to deal with compressed chrominance, and even so, it only deals with
a fixed 2:1 compression ratio.
Although it is possible to compress an image and then operate on the
compressed image to create the
final print image, it is not recommended due to a loss in resolution. In
addition, an image should only be
compressed once - as the final stage before printout. While one compression is
virtually undetectable, multiple
compressions may cause substantial image degradation.
Clip image Organization
Clip images stored on Artcards have no explicit support by the ACP 31.
Software is responsible for
taking any images from the current Artcard and organizing the data into a form
known by the ACP. If images are
stored compressed on an Artcard, software is responsible for decompressing
them, as there is no specific hardware
support for decompression of Artcard images.
Image Pyramid Organization
During brushing, tiling, and warping processes utilised to manipulate an image
it is often necessary to
compute the average color of a particular area in an image. Rather than
calculate the value for each area given,
these functions make use of an image pyramid. As illustrated in Fig. 33, an
image pyramid is effectively a multi-
resolutionpixel- map. The original image 115 is a 1:1 representation. Low-pass
filtering and sub-sampling by 2:1
in each dimension produces an image '/4 the original size 116. This process
continues until the entire image is
represented by a single pixel. An image pyramid is constructed from an
original internal format image, and
consumes 1/3 of the size taken up by the original image (1/4 + 1/16 + 1/64 +
...). For an original image of 1500 x
1000 the corresponding image pyramid is approximately '/2MB. An image pyramid
is constructed by a specific
Vark function, and is used as a parameter to other Vark functions.
Print Image Organization
The entire processed image is required at the same time in order to print it.
However the Print Image
output can comprise a CMY dithered image and is only a transient image format,
used within the Print Image
CA 02564047 2006-11-06
YU139 PCT 53
functionality. However, it should be noted that color conversion will need to
take place from the internal color
space to the print color space. In addition, color conversion can be tuned to
be different for different print rolls in
the camera with different ink characteristics e.g. Sepia output can be
accomplished by using a specific sepia
toning Artcard, or by using a sepia tone print-roll (so all Artcards will work
in sepia tone).
Color Spaces
As noted previously there are 3 color spaces used in the Artcam, corresponding
to the different image
types.
The ACP has no direct knowledge of specific color spaces. Instead, it relies
on client color space
conversion tables to convert between CCD, internal, and printer color spaces:
CCD:RGB
Intemal:Lab
Printer:CMY
Removing the color space conversion from the ACP 31 allows:
-Different CCDs to be used in different cameras
-Different inks (in different print rolls over time) to be used in the same
camera
-Separation of CCD selection from ACP design path
-A well defined internal color space for accurate color processing
Artcard Interface 87
The Artcard Interface (AI) takes data from the linear image Sensor while an
Artcard is passing under it, and
makes that data available for storage in DRAM. The image sensor produces
11,000 8-bit samples per
scanline, sampling the Artcard at 4800 dpi. The Al is a state machine that
sends control information to the
linear sensor, including LineSync pulses and PixelClock pulses in order to
read the image. Pixels are read
from the linear sensor and placed into the VLIW Input FIFO 78. The VLIW is
then able to process and/or
store the pixels. The Al has only a few registers:
Register Name Description
NumPixels The number of pixels in a sensor line (approx 11,000)
Status The Print Head Interface's Status Register
PixelsRemaining The number of bytes remaining in the current line
Actions
Reset A write to this register resets the Al, stops any scanning, and loads
all
registers with 0.
Scan A write to this register with a non-zero value sets the Scanning bit of
the
Status register, and causes the Artcard Interface Scan cycle to start.
A write to this register with 0 stops the scanning process and clears the
Scanning bit in the Status register.
The Scan cycle causes the Al to transfer NumPixels bytes from the sensor
to the VLIW Input FIFO 78, producing the PixelClock signals
appropriately. Upon completion of NumPixels bytes, a LineSync pulse is
given and the Scan cycle restarts.
The PixelsRemaining register holds the number of pixels remaining to be
CA 02564047 2006-11-06
YU139 PCT 54
I I read on the current scanline.
Note that the CPU should clear the VLIW Input FIFO 78 before initiating a
Scan. The Status register has bit
interpretations as follows:
Bit Name Bits Description
Scanning 1 If set, the Al is currently scanning, with the number of pixels
remaining to be transferred from the current line recorded in
PixelsRemaining.
If clear, the Al is not currently scanning, so is not transferring pixels
to the VLIW Input FIFO 78.
Artcard Interface (AI) 87
The Artcard Interface (AI) 87 is responsible for taking an Artcard image from
the Artcard Reader 34 ,
and decoding it into the original data (usually a Vark script). Specifically,
the Al 87 accepts signals from the
Artcard scanner linear CCD 34, detects the bit pattern printed on the card,
and converts the bit pattern into the
original data, correcting read errors.
With no Artcard 9 inserted, the image printed from an Artcam is simply the
sensed Photo Image cleaned
up by any standard image processing routines. The Artcard 9 is the means by
which users are able to modify a
photo before printing it out. By the simple task of inserting a specific
Artcard 9 into an Artcam, a user is able to
define complex image processing to be performed on the Photo Image.
With no Artcard inserted the Photo Image is processed in a standard way to
create the Print Image. When a single
Artcard 9 is inserted into the Artcam, that Artcard's effect is applied to the
Photo Image to generate the Print
Image.
When the Artcard 9 is removed (ejected), the printed image reverts to the
Photo Image processed in a standard
way. When the user presses the button to eject an Artcard, an event is placed
in the event queue maintained by the
operating system running on the Artcam Central Processor 31. When the event is
processed (for example after the
current Print has occurred), the following things occur:
If the current Artcard is valid, then the Print Image is marked as invalid and
a `Process Standard' event is
placed in the event queue. When the event is eventually processed it will
perform the standard image processing
operations on the Photo Image to produce the Print Image.
The motor is started to eject the Artcard and a time-specific `Stop-Motor'
Event is added to the event queue.
Inserting an Artcard
When a user inserts an Artcard 9, the Artcard Sensor 49 detects it notifying
the ACP72. This results in
the software inserting an `Artcard Inserted' event into the event queue. When
the event is processed several things
occur:
The current Artcard is marked as invalid (as opposed to `none').
The Print Image is marked as invalid.
The Artcard motor 37 is started up to load the Artcard
The Artcard Interface 87 is instructed to read the Artcard
The Artcard Interface 87 accepts signals from the Artcard scanner linear CCD
34, detects the bit pattern
CA 02564047 2006-11-06
YU139 PCT 55
printed on the card, and corrects errors in the detected bit pattern,
producing a valid Artcard data block in DRAM.
Reading Data from the Artcard CCD - General Considerations
As illustrated in Fig. 34, the Data Card reading process has 4 phases operated
while the pixel data is read
from the card. The phases are as follows:
Phase 1. Detect data area on Artcard
Phase 2. Detect bit pattern from Artcard based on CCD pixels, and write as
bytes.
Phase 3. Descramble and XOR the byte-pattern
Phase 4. Decode data (Reed-Solomon decode)
As illustrated in Fig. 35, the Artcard 9 must be sampled at least at double
the printed resolution to satisfy
Nyquist's Theorem. In practice it is better to sample at a higher rate than
this. Preferably, the pixels are sampled
230 at 3 times the resolution of a printed dot in each dimension, requiring 9
pixels to define a single dot. Thus if
the resolution of the Artcard 9 is 1600 dpi, and the resolution of the sensor
34 is 4800 dpi, then using a 50mm
CCD image sensor results in 9450 pixels per column. Therefore if we require
2MB of dot data (at 9 pixels per dot)
then this requires 2MB*8*9/9450 = 15,978 columns = approximately 16,000
columns. Of course if a dot is not
exactly aligned with the sampling CCD the worst and most likely case is that a
dot will be sensed over a 16 pixel
area (4x4) 231.
An Artcard 9 may be slightly warped due to heat damage, slightly rotated (up
to, say 1 degree) due to
differences in insertion into an Artcard reader, and can have slight
differences in true data rate due to fluctuations
in the speed of the reader motor 37. These changes will cause columns of data
from the card not to be read as
corresponding columns of pixel data. As illustrated in Fig. 36, a 1 degree
rotation in the Artcard 9 can cause the
pixels from a column on the card to be read as pixels across 166 columns:
Finally, the Artcard 9 should be read in a reasonable amount of time with
respect to the human operator.
The data on the Artcard covers most of the Artcard surface, so timing concerns
can be limited to the Artcard data
itself. A reading time of 1.5 seconds is adequate for Artcard reading.
The Artcard should be loaded in 1.5 seconds. Therefore all 16,000 columns of
pixel data must be read
from the CCD 34 in 1.5 second, i.e. 10,667 columns per second. Therefore the
time available to read one column
is 1/10667 seconds, or 93,747ns. Pixel data can be written to the DRAM one
column at a time, completely
independently from any processes that are reading the pixel data.
The time to write one column of data (9450/2 bytes since the reading can be 4
bits per pixel giving 2 x 4
bit pixels per byte) to DRAM is reduced by using 8 cache lines. If 4 lines
were written out at one time, the 4 banks
can be written to independently, and thus overlap latency reduced. Thus the
4725 bytes can be written in 11,840ns
(4725/128 * 320ns). Thus the time taken to write a given column's data to DRAM
uses just under 13% of the
available bandwidth.
Decoding an Artcard
A simple look at the data sizes shows the impossibility of fitting the process
into the 8MB of memory 33
if the entire Artcard pixel data (140 MB if each bit is read as a 3x3 array)
as read by the linear CCD 34 is kept. For
this reason, the reading of the linear CCD, decoding of the bitmap, and the un-
bitmap process should take place in
real- time (while the Artcard 9 is traveling past the linear CCD 34), and
these processes must effectively work
without having entire data stores available.
When an Artcard 9 is inserted, the old stored Print Image and any expanded
Photo Image becomes
CA 02564047 2006-11-06
YU139 PCT 56
invalid. The new Artcard 9 can contain directions for creating a new image
based on the currently captured Photo
Image. The old Print Image is invalid, and the area holding expanded Photo
Image data and image pyramid is
invalid, leaving more than 5MB that can be used as scratch memory during the
read process. Strictly speaking, the
1MB area where the Artcard raw data is to be written can also be used as
scratch data during the Artcard read
process as long as by the time the final Reed-Solomon decode is to occur, that
1MB area is free again. The reading
process described here does not make use of the extra 1 MB area (except as a
final destination for the data).
It should also be noted that the unscrambling process requires two sets of 2MB
areas of memory since
unscrambling cannot occur in place. Fortunately the 5MB scratch area contains
enough space for this process.
Turning now to Fig. 37, there is shown a flowchart 220 of the steps necessary
to decode the Artcard data.
These steps include reading in the Artcard 221, decoding the read data to
produce corresponding encoded XORed
scrambled bitmap data 223. Next a checkerboard XOR is applied to the data to
produces encoded scrambled data
224. This data is then unscrambled 227 to produce data 225 before this data is
subjected to Reed-Solomon
decoding to produce the original raw data 226. Alternatively, unscrambling and
XOR process can take place
together, not requiring a separate pass of the data. Each of the above steps
is discussed in further detail
hereinafter. As noted previously with reference to Fig. 37, the Artcard
Interface, therefore, has 4 phases, the first
2 of which are time-critical, and must take place while pixel data is being
read from the CCD:
Phase 1. Detect data area on Artcard
Phase 2. Detect bit pattern from Artcard based on CCD pixels, and write as
bytes.
Phase 3. Descramble and XOR the byte-pattern
Phase 4. Decode data (Reed-Solomon decode)
The four phases are described in more detail as follows:
Phase 1. As the Artcard 9 moves past the CCD 34 the Al must detect the start
of the data area by robustly
detecting special targets on the Artcard to the left of the data area. If
these cannot be detected, the card is marked
as invalid. The detection must occur in real-time, while the Artcard 9 is
moving past the CCD 34.
If necessary, rotation invariance can be provided. In this case, the targets
are repeated on the right side of
the Artcard, but relative to the bottom right corner instead of the top
corner. In this way the targets end up in the
correct orientation if the card is inserted the "wrong" way. Phase 3 below can
be altered to detect the orientation of
the data, and account for the potential rotation.
Phase 2. Once the data area has been determined, the main read process begins,
placing pixel data from
the CCD into an `Artcard data window', detecting bits from this window,
assembling the detected bits into bytes,
and constructing a byte-image in DRAM. This must all be done while the Artcard
is moving past the CCD.
Phase 3. Once all the pixels have been read from the Artcard data area, the
Artcard motor 37 can be
stopped, and the byte image descrambled and XORed. Although not requiring real-
time performance, the process
should be fast enough not to annoy the human operator. The process must take 2
MB of scrambled bit-image and
write the unscrambled/XORed bit-image to a separate 2MB image.
Phase 4. The final phase in the Artcard read process is the Reed-Solomon
decoding process, where the
2MB bit-image is decoded into a 1MB valid Artcard data area. Again, while not
requiring real-time performance
it is still necessary to decode quickly with regard to the human operator. If
the decode process is valid, the card is
marked as valid. If the decode failed, any duplicates of data in the bit-image
are attempted to be decoded, a
process that is repeated until success or until there are no more duplicate
images of the data in the bit image.
CA 02564047 2006-11-06
YU139 PCT 57
The four phase process described requires 4.5 MB of DRAM. 2MB is reserved for
Phase 2 output, and
0.5MB is reserved for scratch data during phases 1 and 2. The remaining 2MB of
space can hold over 440
columns at 4725 byes per column. In practice, the pixel data being read is a
few columns ahead of the phase 1
algorithm, and in the worst case, about 180 columns behind phase 2,
comfortably inside the 440 column limit.
A description of the actual operation of each phase will now be provided in
greater detail.
Phase 1 - Detect data area on Artcard
This phase is concerned with robustly detecting the left-hand side of the data
area on the Artcard 9.
Accurate detection of the data area is achieved by accurate detection of
special targets printed on the left side of
the card. These targets are especially designed to be easy to detect even if
rotated up to 1 degree.
Turning to Fig. 38, there is shown an enlargement of the left hand side of an
Artcard 9. The side of the
card is divided into 16 bands, 239 with a target eg. 241 located at the center
of each band. The bands are logical in
that there is no line drawn to separate bands. Turning to Fig. 39, there is
shown a single target 241. The target
241, is a printed black square containing a single white dot. The idea is to
detect firstly as many targets 241 as
possible, and then to join at least 8 of the detected white-dot locations into
a single logical straight line. If this can
be done, the start of the data area 243 is a fixed distance from this logical
line. If it cannot be done, then the card
is rejected as invalid.
As shown in Fig. 38, the height of the card 9 is 3150 dots. A target (TargetO)
241 is placed a fixed
distance of 24 dots away from the top left corner 244 of the data area so that
it falls well within the first of 16
equal sized regions 239 of 192 dots (576 pixels) with no target in the final
pixel region of the card. The target 241
must be big enough to be easy to detect, yet be small enough not to go outside
the height of the region if the card
is rotated 1 degree. A suitable size for the target is a 31 x 31 dot (93 x 93
sensed pixels) black square 241 with the
white dot 242.
At the worst rotation of 1 degree, a 1 column shift occurs every 57 pixels.
Therefore in a 590 pixel sized
band, we cannot place any part of our symbol in the top or bottom 12 pixels or
so of the band or they could be
detected in the wrong band at CCD read time if the card is worst case rotated.
Therefore, if the black part of the rectangle is 57 pixels high (19 dots) we
can be sure that at least 9.5
black pixels will be read in the same column by the CCD (worst case is half
the pixels are in one column and half
in the next). To be sure of reading at least 10 black dots in the same column,
we must have a height of 20 dots. To
give room for erroneous detection on the edge of the start of the black dots,
we increase the number of dots to 31,
giving us 15 on either side of the white dot at the target's local coordinate
(15, 15). 31 dots is 91 pixels, which at
most suffers a 3 pixel shift in column, easily within the 576 pixel band.
Thus each target is a block of 31 x 31 dots (93 x 93 pixels) each with the
composition:
15 columns of 31 black dots each (45 pixel width columns of 93 pixels).
1 column of 15 black dots (45 pixels) followed by 1 white dot (3 pixels) and
then a further 15 black dots
(45 pixels)
15 columns of 31 black dots each (45 pixel width columns of 93 pixels)
Detect targets
Targets are detected by reading columns of pixels, one column at a time rather
than by detecting dots. It
is necessary to look within a given band for a number of columns consisting of
large numbers of contiguous black
pixels to build up the left side of a target. Next, it is expected to see a
white region in the center of further black
CA 02564047 2006-11-06
YU139PCT 58
columns, and finally the black columns to the left of the target center.
Eight cache lines are required for good cache performance on the reading of
the pixels. Each logical read
fills 4 cache lines via 4 sub-reads while the other 4 cache-lines are being
used. This effectively uses up 13% of the
available DRAM bandwidth.
As illustrated in Fig. 40, the detection mechanism FIFO for detecting the
targets uses a filter 245, run-
length encoder 246, and a FIFO 247 that requires special wiring of the top 3
elements (S 1, S2, and S3) for random
access.
The columns of input pixels are processed one at a time until either all the
targets are found, or until a
specified number of columns have been processed. To process a column, the
pixels are read from DRAM, passed
through a filter 245 to detect a 0 or 1, and then run length encoded 246. The
bit value and the number of
contiguous bits of the same value are placed in FIFO 247. Each entry of the
FIFO 249 is in 8 bits, 7 bits 250 to
hold the run-length, and 1 bit 249 to hold the value of the bit detected.
The run-length encoder 246 only encodes contiguous pixels within a 576 pixel
(192 dot) region.
The top 3 elements in the FIFO 247 can be accessed 252 in any random order.
The run lengths (in pixels)
of these entries are filtered into 3 values: short, medium, and long in
accordance with the following table:
Short Used to detect white dot. RunLength < 16
Medium Used to detect runs of black above or below the 16<= RunLength < 48
white dot in the center of the target.
Long Used to detect run lengths of black to the left and RunLength >= 48
right of the center dot in the target.
Looking at the top three entries in the FIFO 247 there are 3 specific cases of
interest:
Case 1 Si = white long We have detected a black column of the target to
S2 = black long the left of or to the right of the white center dot.
S3 = white medium/long
Case 2 Si = white long If we've been processing a series of columns of
S2 = black medium Case Is, then we have probably detected the
S3 = white short white dot in this column. We know that the next
Previous 8 columns were Case 1 entry will be black (or it would have been
included in the white S3 entry), but the number of
black pixels is in question. Need to verify by
checking after the next FIFO advance (see Case
3).
Case 3 Prev = Case 2 We have detected part of the white dot. We
S3 = black med expect around 3 of these, and then some more
columns of Case 1.
Preferably, the following information per region band is kept:
TargetDetected 1 bit
BlackDetectCount 4 bits
WhiteDetectCount 3 bits
PrevColumnStartPixel 15 bits
CA 02564047 2006-11-06
YU139 PCT 59
TargetColumn ordinate 16 bits (15:1)
TargetRow ordinate 16 bits (15:1
TOTAL 7 b es (rounded to 8 bytes for easy addressing)
Given a total of 7 bytes. It makes address generation easier if the total is
assumed to be 8 bytes. Thus 16
entries requires 16 * 8 = 128 bytes, which fits in 4 cache lines. The address
range should be inside the scratch
0.5MB DRAM area since other phases make use of the remaining 4MB data area.
When beginning to process a given pixel column, the register value
S2StartPixel 254 is reset to 0. As
entries in the FIFO advance from S2 to S1, they are also added 255 to the
existing S2StartPixel value, giving the
exact pixel position of the run currently defined in S2. Looking at each of
the 3 cases of interest in the FIFO,
S2StartPixel can be used to determine the start of the black area of a target
(Cases 1 and 2), and also the start of
the white dot in the center of the target (Case 3). An algorithm for
processing columns can be as follows:
1 TargetDetected[0-15]:= 0
BlackDetectCount[0-15] 0
WhiteDetectCount[0-15] := 0
TargetRow[0-15] := 0
TargetColumn[0-15] := 0
PrevColStartPixel[0-15] := 0
CurrentColumn := 0
2 Do ProcessColunm
3 CurrentColunui++
4 If (CurrentColunm <= LastValidColumn)
Goto 2
The steps involved in the processing a column (Process Column) are as follows:
1 S2StartPixel := 0
FIFO := 0
B1ackDetectCount = 0
WhiteDetectCount := 0
ThisColumnDetected := FALSE
PrevCaseWasCase2 := FALSE
2 If (! TargetDetected[Target]) & (! ColumnDetected[Target])
ProcessCases
Endlf
3 PrevCaseWasCase2 := Case=2
4 Advance FIFO
The processing for each of the 3 (Process Cases) cases is as follows:
Case 1:
BlackDetectCount[target] < 8 A := ABS(S2StartPixel -
PrevColStartPixel[Target])
OR If (0<=A< 2)
WhiteDetectCount[Target] = 0 BlackDetectCountTar et ++ (max value =8)
CA 02564047 2006-11-06
YU139 PCT 60
Else
BlackDetectCount[Target] 1
WhiteDetectCount[Target] := 0
Endlf
PrevColStartPixel[Target] := S2StartPixel
ColumnDetected[Target] := TRUE
BitDetected = 1
BlackDetectCount[target] >= 8 PrevColStartPixel[Target] := S2StartPixel
WhiteDetectCount[Target] != 0 ColumnDetected[Target] := TRUE
BitDetected = 1
TargetDetected[Target] := TRUE
TargetColumn[Target] := CurrentColumn - 8
(WhiteDetectCount[Tar et /2)
Case 2:
No special processing is recorded except for setting the `PrevCaseWasCase2'
flag for identifying Case 3
(see Step 3 of processing a column described above)
Case 3:
PrevCaseWasCase2 = TRUE If (WhiteDetectCount[Target] < 2)
BlackDetectCount[Target] >= 8 TargetRow[Target] = S2StartPixel +
(S2RunLengh/2)
WhiteDetectCount=l Endlf
A := ABS(S2StartPixel - PrevColStartPixel[Target])
If (0<=A< 2)
WhiteDetectCount[Target]++
Else
WhiteDetectCount[Target] := 1
Endlf
PrevColStartPixel[Target] := S2StartPixel
ThisColumnDetected := TRUE
BitDetected = 0
At the end of processing a given column, a comparison is made of the current
column to the maximum
number of columns for target detection. If the number of columns allowed has
been exceeded, then it is necessary
to check how many targets have been found. If fewer than 8 have been found,
the card is considered invalid.
Process targets
After the targets have been detected, they should be processed. All the
targets may be available or merely
some of them. Some targets may also have been erroneously detected.
This phase of processing is to determine a mathematical line that passes
through the center of as many
targets as possible. The more targets that the line passes through, the more
confident the target position has been
found. The limit is set to be 8 targets. If a line passes through at least 8
targets, then it is taken to be the right one.
It is all right to take a brute-force but straightforward approach since there
is the time to do so (see
below), and lowering complexity makes testing easier. It is necessary to
determine the line between targets 0 and I
(if both targets are considered valid) and then determine how many targets
fall on this line. Then we determine the
line between targets 0 and 2, and repeat the process. Eventually we do the
same for the line between targets 1 and
CA 02564047 2006-11-06
YU139 PCT 61
2, 1 and 3 etc. and finally for the line between targets 14 and 15. Assuming
all the targets have been found, we
need to perform 15+14+13+ ...= 90 sets of calculations (with each set of
calculations requiring 16 tests = 1440
actual calculations), and choose the line which has the maximum number of
targets found along the line. The
algorithm for target location can be as follows:
TargetA := 0
MaxFound := 0
BestLine := 0
While (TargetA < 15)
If (TargetA is Valid)
TargetB:= TargetA + 1
While (TargetB<= 15)
If (TargetB is valid)
CurrentLine := line between TargetA and TargetB
TargetC := 0;
While (TargetC <= 15)
If (TargetC valid AND TargetC on line AB)
TargetsHit++
Endlf
If (TargetsHit > MaxFound)
MaxFound := TargetsHit
BestLine := CurrentLine
Endlf
TargetC++
EndWhile
Endlf
TargetB ++
EndWhile
Endif
TargetA++
EndWhile
If (MaxFound < 8)
Card is Invalid
Else
Store expected centroids for rows based on BestLine
Endlf
As illustrated in Fig. 34, in the algorithm above, to determine a CurrentLine
260 from Target A 261 and
target B, it is necessary to calculate Arow (264) & Acolumn (263) between
targets 261, 262, and the location of
Target A. It is then possible to move from Target 0 to Target 1 etc. by adding
Arow and Acolunm. The found (if
actually found) location of target N can be compared to the calculated
expected position of Target N on the line,
CA 02564047 2006-11-06
YU139 PCT 62
and if it falls within the tolerance, then Target N is determined to be on the
line.
To calculate Arow & Acolumn:
Arow = (roWTargetA - row TargetB)/(B-A)
Acolumn = (COlumnTargetA - cOlmmnTargetB)/(B-A)
Then we calculate the position of Target:
row = rowTargetA - (A * Arow)
column = columnTargetA - (A * Acolumn )
And compare (row, column) against the actual rowTargeto and columnTargem. To
move from one expected
target to the next (e.g. from TargetO to Targetl), we simply add Arow and
Acolumn to row and column
respectively. To check if each target is on the line, we must calculate the
expected position of TargetO, and then
perform one add and one comparison for each target ordinate.
At the end of comparing all 16 targets against a maximum of 90 lines, the
result is the best line through
the valid targets. If that line passes through at least 8 targets (i.e.
MaxFound >= 8), it can be said that enough
targets have been found to form a line, and thus the card can be processed. If
the best line passes through fewer
than 8, then the card is considered invalid.
The resulting algorithm takes 180 divides to calculate Arow and Acolumn, 180
multiply/adds to calculate
targetO position, and then 2880 adds/comparisons. The time we have to perform
this processing is the time taken
to read 36 columns of pixel data = 3,374,892ns. Not even accounting for the
fact that an add takes less time than a
divide, it is necessary to perform 3240 mathematical operations in
3,374,892ns. That gives approximately 1040ns
per operation, or 104 cycles. The CPU can therefore safely perform the entire
processing of targets, reducing
complexity of design.
Update centroids based on data edge border and clockmarks
Step 0: Locate the data area
From Target 0 (241 of Fig. 38) it is a predetermined fixed distance in rows
and columns to the
top left border 244 of the data area, and then a further 1 dot column to the
vertical clock marks 276. So we use
TargetA, Arow and Acolumn found in the previous stage (Arow and Acolumn refer
to distances between targets)
to calculate the centroid or expected location for Target as described
previously.
Since the fixed pixel offset from Target to the data area is related to the
distance between targets (192
dots between targets, and 24 dots between Target and the data area 243),
simply add Arow/8 to TargetO's
centroid column coordinate (aspect ratio of dots is 1:1). Thus the top co-
ordinate can be defined as:
(columnpoCOI,,,,,,,Top = columnTargero + (Arow/8)
(rOWDotColmtmTop = rOwTargetO + (Acolumn /8)
Next Arow and Acolumn are updated to give the number of pixels between dots in
a single column
(instead of between targets) by dividing them by the number of dots between
targets:
Arow = Arow/192
Acolumn =Acolumn/192
We also set the currentColumn register (see Phase 2) to be -1 so that after
step 2, when phase 2 begins,
the currentColumn register will increment from -1 to 0.
Step 1: Write out the initial centroid deltas (A) and bit history
CA 02564047 2006-11-06
YU139 PCT 63
This simply involves writing setup information required for Phase 2.
This can be achieved by writing Os to all the Arow and Acolumn entries for
each row, and a bit history.
The bit history is actually an expected bit history since it is known that to
the left of the clock mark column 276 is
a border column 277, and before that, a white area. The bit history therefore
is 011, 010, 011, 010 etc.
Step 2: Update the centroids based on actual pixels read.
The bit history is set up in Step I according to the expected clock marks and
data border. The actual
centroids for each dot row can now be more accurately set (they were initially
0) by comparing the expected data
against the actual pixel values. The centroid updating mechanism is achieved
by simply performing step 3 of
Phase 2.
Phase 2 - Detect bit pattern from Artcard based on pixels read, and write as
bytes.
Since a dot from the Artcard 9 requires a minimum of 9 sensed pixels over 3
columns to be represented,
there is little point in performing dot detection calculations every sensed
pixel column. It is better to average the
time required for processing over the average dot occurrence, and thus make
the most of the available processing
time. This allows processing of a column of dots from an Artcard 9 in the time
it takes to read 3 columns of data
from the Artcard. Although the most likely case is that it takes 4 columns to
represent a dot, the 4`I' column will be
the last column of one dot and the first column of a next dot. Processing
should therefore be limited to only 3
columns.
As the pixels from the CCD are written to the DRAM in 13% of the time
available, 83% of the time is
available for processing of 1 column of dots i.e. 83% of (93,747*3) = 83% of
281,24 Ins = 233,430ns.
In the available time, it is necessary to detect 3150 dots, and write their
bit values into the raw data area
of memory. The processing therefore requires the following steps:
For each column of dots on the Artcard:
Step 0: Advance to the next dot column
Step 1: Detect the top and bottom of an Artcard dot column (check clock marks)
Step 2: Process the dot column, detecting bits and storing them appropriately
Step 3: Update the centroids
Since we are processing the Artcard's logical dot columns, and these may shift
over 165 pixels, the worst
case is that we cannot process the first column until at least 165 columns
have been read into DRAM. Phase 2
would therefore finish the same amount of time after the read process had
terminated. The worst case time is: 165
* 93,747ns = 15,468,25 5ns or 0.015 seconds.
Step 0: Advance to the next dot column
In order to advance to the next column of dots we add Arow and Acolumn to the
dotColumnTop to give
us the centroid of the dot at the top of the column. The first time we do
this, we are currently at the clock marks
column 276 to the left of the bit image data area, and so we advance to the
first column of data. Since Arow and
Acolumn refer to distance between dots within a column, to move between dot
columns it is necessary to add
Arow to columndotcolunmTop and Acolumn to rowdotColumnTop=
To keep track of what column number is being processed, the column number is
recorded in a register
called CurrentColumn. Every time the sensor advances to the next dot column it
is necessary to increment the
CurrentColumn register. The first time it is incremented, it is incremented
from-1 to 0 (see Step 0 Phase 1). The
CA 02564047 2006-11-06
YU139 PCT 64
CurrentColumn register determines when to terminate the read process (when
reaching maxColumns), and also is
used to advance the DataOut Pointer to the next column of byte information
once all 8 bits have been written to
the byte (once every 8 dot columns). The lower 3 bits determine what bit we're
up to within the current byte. It
will be the same bit being written for the whole column.
Step 1: Detect the top and bottom of an Artcard dot column.
In order to process a dot column from an Artcard, it is necessary to detect
the top and bottom of a
column. The column should form a straight line between the top and bottom of
the column (except for local
warping etc.). Initially dotColumnTop points to the clock mark column 276. We
simply toggle the expected
value, write it out into the bit history, and move on to step 2, whose first
task will be to add the Arow and Acolumn
values to dotColumnTop to arrive at the first data dot of the column.
Step 2: Process an Artcard's dot column
Given the centroids of the top and bottom of a column in pixel coordinates the
column should form a
straight line between them, with possible minor variances due to warping etc.
Assuming the processing is to start at the top of a column (at the top
centroid coordinate) and move down
to the bottom of the column, subsequent expected dot centroids are given as:
rowiex1= row + Arow
columnnext = column + Acolumn
This gives us the address of the expected centroid for the next dot of the
column. However to account for
local warping and error we add another Arow and Acolumn based on the last time
we found the dot in a given
row. In this way we can account for small drifts that accumulate into a
maximum drift of some percentage from
the straight line joining the top of the column to the bottom.
We therefore keep 2 values for each row, but store them in separate tables
since the row history is used in
step 3 of this phase.
* Arow and Acolumn (2 @ 4 bits each = 1 byte)
* row history (3 bits per row, 2 rows are stored per byte)
For each row we need to read a Arow and Acolumn to determine the change to the
centroid. The read
process takes 5% of the bandwidth and 2 cache lines:
76*(3150/32) + 2*3150 = 13,824ns = 5% of bandwidth
Once the centroid has been determined, the pixels around the centroid need to
be examined to detect the
status of the dot and hence the value of the bit. In the worst case a dot
covers a 4x4 pixel area. However, thanks to
the fact that we are sampling at 3 times the resolution of the dot, the number
of pixels required to detect the status
of the dot and hence the bit value is much less than this. We only require
access to 3 columns of pixel columns at
any one time.
In the worst case of pixel drift due to a 1% rotation, centroids will shift 1
column every 57 pixel rows, but
since a dot is 3 pixels in diameter, a given column will be valid for 171
pixel rows (3*57). As a byte contains 2
pixels, the number of bytes valid in each buffered read (4 cache lines) will
be a worst case of 86 (out of 128 read).
Once the bit has been detected it must be written out to DRAM. We store the
bits from 8 columns as a set
of contiguous bytes to minimize DRAM delay. Since all the bits from a given
dot column will correspond to the
next bit position in a data byte, we can read the old value for the byte,
shift and OR in the new bit, and write the
CA 02564047 2006-11-06
YU139 PCT 65
byte back. The read / shift&OR / write process requires 2 cache lines.
We need to read and write the bit history for the given row as we update it.
We only require 3 bits of
history per row, allowing the storage of 2 rows of history in a single byte.
The read / shift&OR / write process
requires 2 cache lines.
The total bandwidth required for the bit detection and storage is summarised
in the following table:
Read centroid 0 5%
Read 3 columns of pixel data 19%
Read/Write detected bits into byte buffer 10%
Read/Write bit history 5%
TOTAL 39%
Detecting a dot
The process of detecting the value of a dot (and hence the value of a bit)
given a centroid is accomplished
by examining 3 pixel values and getting the result from a lookup table. The
process is fairly simple and is
illustrated in Fig. 42. A dot 290 has a radius of about 1.5 pixels. Therefore
the pixel 291 that holds the centroid,
regardless of the actual position of the centroid within that pixel, should be
100% of the dot's value. If the centroid
is exactly in the center of the pixel 291, then the pixels above 292 & below
293 the centroid's pixel, as well as the
pixels to the left 294 & right 295 of the centroid's pixel will contain a
majority of the dot's value. The further a
centroid is away from the exact center of the pixel 295, the more likely that
more than the center pixel will have
100% coverage by the dot.
Although Fig. 42 only shows centroids differing to the left and below the
center, the same relationship
obviously holds for centroids above and to the right of center. center. In
Case 1, the centroid is exactly in the
center of the middle pixel 295. The center pixel 295 is completely covered by
the dot, and the pixels above,
below, left, and right are also well covered by the dot. In Case 2, the
centroid is to the left of the center of the
middle pixel 291. The center pixel is still completely covered by the dot, and
the pixel 294 to the left of the center
is now completely covered by the dot. The pixels above 292 and below 293 are
still well covered. In Case 3, the
centroid is below the center of the middle pixel 291. The center pixel 291 is
still completely covered by the dot
291, and the pixel below center is now completely covered by the dot. The
pixels left 294 and right 295 of center
are still well covered. In Case 4, the centroid is left and below the center
of the middle pixel. The center pixel
291 is still completely covered by the dot, and both the pixel to the left of
center 294 and the pixel below center
293 are completely covered by the dot.
The algorithm for updating the centroid uses the distance of the centroid from
the center of the middle
pixel 291 in order to select 3 representative pixels and thus decide the value
of the dot:
Pixel 1: the pixel containing the centroid
Pixel 2: the pixel to the left of Pixel 1 if the centroid's X coordinate
(column value) is <'/2, otherwise the
pixel to the right of Pixel 1.
Pixel 3: the pixel above pixel I if the centroid's Y coordinate (row value) is
< '/2, otherwise the pixel
below Pixel 1.
As shown in Fig. 43, the value of each pixel is output to a pre-calculated
lookup table 301. The 3 pixels
CA 02564047 2006-11-06
YU139 PCT 66
are fed into a 12-bit lookup table, which outputs a single bit indicating the
value of the dot - on or off. The lookup
table 301 is constructed at chip definition time, and can be compiled into
about 500 gates. The lookup table can be
a simple threshold table, with the exception that the center pixel (Pixel 1)
is weighted more heavily.
Step 3: Update the centroid As for each row in the column
The idea of the As processing is to use the previous bit history to generate a
`perfect' dot at the expected
centroid location for each row in a current column. The actual pixels (from
the CCD) are compared with the
expected `perfect' pixels. If the two match, then the actual centroid location
must be exactly in the expected
position, so the centroid As must be valid and not need updating. Otherwise a
process of changing the centroid As
needs to occur in order to best fit the expected centroid location to the
actual data. The new centroid As will be
used for processing the dot in the next column.
Updating the centroid As is done as a subsequent process from Step 2 for the
following reasons:
to reduce complexity in design, so that it can be performed as Step 2 of Phase
1 there is enough
bandwidth remaining to allow it to allow reuse of DRAM buffers, and
to ensure that all the data required for centroid updating is available at the
start of the process without special
pipelining.
The centroid A are processed as Acolumn Arow respectively to reduce
complexity.
Although a given dot is 3 pixels in diameter, it is likely to occur in a 4x4
pixel area. However the edge of
one dot will as a result be in the same pixel as the edge of the next dot. For
this reason, centroid updating requires
more than simply the information about a given single dot.
Fig. 44 shows a single dot 310 from the previous column with a given centroid
311. In this example, the
dot 310 extend A over 4 pixel columns 312-315 and in fact, part of the
previous dot column's dot (coordinate =
(Prevcolumn, Current Row)) has entered the current column for the dot on the
current row. If the dot in the current
row and column was white, we would expect the rightmost pixel column 314 from
the previous dot column to be
a low value, since there is only the dot information from the previous
column's dot (the current column's dot is
white). From this we can see that the higher the pixel value is in this pixel
column 315, the more the centroid
should be to the right Of course, if the dot to the right was also black, we
cannot adjust the centroid as we cannot
get information sub-pixel. The same can be said for the dots to the left,
above and below the dot at dot coordinates
(PrevColumn, CurrentRow).
From this we can say that a maximum of 5 pixel columns and rows are required.
It is possible to simplify
the situation by taking the cases of row and column centroid As separately,
treating them as the same problem,
only rotated 90 degrees.
Taking the horizontal case first, it is necessary to change the column
centroid As if the expected pixels
don't match the detected pixels. From the bit history, the value of the bits
found for the Current Row in the current
dot column, the previous dot column, and the (previous-1)th dot column are
known. The expected centroid
location is also known. Using these two pieces of information, it is possible
to generate a 20 bit expected bit
pattern should the read be `perfect'. The 20 bit bit-pattern represents the
expected A values for each of the 5 pixels
across the horizontal dimension. The first nibble would represent the
rightmost pixel of the leftmost dot. The next
3 nibbles represent the 3 pixels across the center of the dot 310 from the
previous column, and the last nibble
would be the leftmost pixel 317 of the rightmost dot (from the current
column).
CA 02564047 2006-11-06
YU139 PCT 67
If the expected centroid is in the center of the pixel, we would expect a 20
bit pattern based on the
following table:
Bit history Expected pixels
000 00000
001 OOOOD
010 ODFDO
011 ODFDD
100 D0000
101 D000D
110 DDFDO
111 DDFDD
The pixels to the left and right of the center dot are either 0 or D depending
on whether the bit was a 0 or
1 respectively. The center three pixels are either 000 or DFD depending on
whether the bit was a 0 or 1
respectively. These values are based on the physical area taken by a dot for a
given pixel. Depending on the
distance of the centroid from the exact center of the pixel, we would expect
data shifted slightly, which really only
affects the pixels either side of the center pixel. Since there are 16
possibilities, it is possible to divide the distance
from the center by 16 and use that amount to shift the expected pixels.
Once the 20 bit 5 pixel expected value has been determined it can be compared
against the actual pixels
read. This can proceed by subtracting the expected pixels from the actual
pixels read on a pixel by pixel basis, and
finally adding the differences together to obtain a distance from the expected
A values.
Fig. 45 illustrates one form of implementation of the above algorithm which
includes a look up table 320
which receives the bit history 322 and central fractional component 323 and
outputs 324 the corresponding 20 bit
number which is subtracted 321 from the central pixel input 326 to produce a
pixel difference 327.
This process is carried out for the expected centroid and once for a shift of
the centroid left and right by 1
amount in Acolumn. The centroid with the smallest difference from the actual
pixels is considered to be the
`winner' and the Acolumn updated accordingly (which hopefully is `no change').
As a result, a Acolumn cannot
change by more than 1 each dot column.
The process is repeated for the vertical pixels, and Arow is consequentially
updated.
There is a large amount of scope here for parallelism. Depending on the rate
of the clock chosen for the
ACP unit 31 these units can be placed in series (and thus the testing of 3
different A could occur in consecutive
clock cycles), or in parallel where all 3 can be tested simultaneously. If the
clock rate is fast enough, there is less
need for parallelism.
Bandwidth utilization
It is necessary to read the old A of the As, and to write them out again. This
takes 10% of the bandwidth:
2 * (76(3150/32) + 2*3150) = 27,648ns = 10% of bandwidth
It is necessary to read the bit history for the given row as we update its As.
Each byte contains 2 row's
bit histories, thus taking 2.5% of the bandwidth:
76((315012)/32) + 2*(3150/2) = 4,085ns = 2.5% of bandwidth
In the worst case of pixel drift due to a I% rotation, centroids will shift 1
column every 57 pixel rows, but
CA 02564047 2006-11-06
YU139 PCT 68
since a dot is 3 pixels in diameter, a given pixel column will be valid for
171 pixel rows (3 *57). As a byte contains
2 pixels, the number of bytes valid in cached reads will be a worst case of 86
(out of 128 read). The worst case
timing for 5 columns is therefore 31 % bandwidth.
*(((9450/(128 * 2)) * 320) * 128/86) = 88, 112ns = 31 % of bandwidth.
5 The total bandwidth required for the updating the centroid A is summarised
in the following table:
Read/Write centroid A 10%
Read bit history 2.5%
Read 5 columns of pixel data 31%
TOTAL 43.5%
Memory usage for Phase 2:
The 2MB bit-image DRAM area is read from and written to during Phase 2
processing. The 2MB pixel-
data DRAM area is read.
The 0.5MB scratch DRAM area is used for storing row data, namely:
Centroid array 24bits (16:8) * 2 * 3150 = 18,900 byes
Bit History array 3 bits * 3150 entries (2 per byte) = 1575 bytes
Phase 3 -Unscramble and XOR the raw data
Returning to Fig. 37, the next step in decoding is to unscramble and XOR the
raw data. The 2MB byte
image, as taken from the Artcard, is in a scrambled XORed form. It must be
unscrambled and re-XORed to
retrieve the bit image necessary for the Reed Solomon decoder in phase 4.
Turning to Fig. 46, the unscrambling process 330 takes a 2MB scrambled byte
image 331 and writes an
unscrambled 2MB image 332. The process cannot reasonably be performed in-
place, so 2 sets of 2MB areas are
utilised. The scrambled data 331 is in symbol block order arranged in a 16x16
array, with symbol block 0 (334)
having all the symbol 0's from all the code words in random order. Symbol
block 1 has all the symbol l's from all
the code words in random order etc. Since there are only 255 symbols, the 256'
symbol block is currently unused.
A linear feedback shift register is used to determine the relationship between
the position within a symbol
block eg. 334 and what code word eg. 355 it came from. This works as long as
the same seed is used when
generating the original Artcard images. The XOR of bytes from alternative
source lines with OxAA and 0x55
respectively is effectively free (in time) since the bottleneck of time is
waiting for the DRAM to be ready to
read/write to non-sequential addresses.
The timing of the unscrambling XOR process is effectively 2MB of random byte-
reads, and 2MB of
random byte-writes i.e. 2 * (2MB * 76ns + 2MB * 2ns) = 327,155,712ns or
approximately 0.33 seconds. This
timing assumes no caching.
Phase 4 - Reed Solomon decode
This phase is a loop, iterating through copies of the data in the bit image,
passing them to the Reed-
Solomon decode module until either a successful decode is made or until there
are no more copies to attempt
decode from.
CA 02564047 2006-11-06
YU139 PCT 69
The Reed-Solomon decoder used can be the VLIW processor, suitably programmed
or, alternatively, a
separate hardwired core such as LSI Logic's L64712. The L64712 has a
throughput of 50Mbits per second
(around 6.25MB per second), so the time may be bound by the speed of the Reed-
Solomon decoder rather than
the 2MB read and 1 MB write memory access time (500MB/sec for sequential
accesses). The time taken in the
worst case is thus 2/6.25s = approximately 0.32 seconds.
Phase 5 Running the Vark script
The overall time taken to read the Artcard 9 and decode it is therefore
approximately 2.15 seconds. The
apparent delay to the user is actually only 0.65 seconds (the total of Phases
3 and 4), since the Artcard stops
moving after 1.5 seconds.
Once the Artcard is loaded, the Artvark script must be interpreted, Rather
than run the script
immediately, the script is only run upon the pressing of the `Print' button 13
(Fig. 1). The taken to run the script
will vary depending on the complexity of the script, and must be taken into
account for the perceived delay
between pressing the print button and the actual print button and the actual
printing.
Alternative Artcard Fomat
Of course, other artcard formats are possible. There will now be described one
such alternative artcard format
with a number of preferable feature. Described hereinafter will be the
alternative Artcard data format, a
mechanism for mapping user data onto dots on an alternative Artcard, and a
fast alternative Artcard reading
algorithm for use in embedded systems where resources are scarce.
Alternative Artcard Overview
The Alternative Artcards can be used in both embedded and PC type
applications, providing a user-
friendly interface to large amounts of data or configuration information.
While the back side of an alternative Artcard has the same visual appearance
regardless of the application
(since it stores the data), the front of an alternative Artcard can be
application dependent. It must make sense to the
user in the context of the application.
Alternative Artcard technology can also be independent of the printing
resolution. The notion of storing
data as dots on a card simply means that if it is possible put more dots in
the same space (by increasing
resolution), then those dots can represent more data. The preferred embodiment
assumes utilisation of 1600 dpi
printing on a 86 mm x 55 mm card as the sample Artcard, but it is simple to
determine alternative equivalent
layouts and data sizes for other card sizes and/or other print resolutions.
Regardless of the print resolution, the
reading technique remain the same. After all decoding and other overhead has
been taken into account, alternative
Artcards are capable of storing up to 1 Megabyte of data at print resolutions
up to 1600 dpi. Alternative Artcards
can store megabytes of data at print resolutions greater than 1600 dpi. The
following two tables summarize the
effective alternative Artcard data storage capacity for certain print
resolutions:
Format of an alternative Artcard
The structure of data on the alternative Artcard is therefore specifically
designed to aid the recovery of
data. This section describes the format of the data (back) side of an
alternative Artcard.
Dots
The dots on the data side of an alternative Artcard can be monochrome. For
example, black dots printed
CA 02564047 2006-11-06
YU139 PCT 70
on a white background at a predetermined desired print resolution.
Consequently a "black dot" is physically
different from a "white dot". Fig. 47 illustrates various examples of
magnified views of black and white dots.
The monochromatic scheme of black dots on a white background is preferably
chosen to maximize dynamic
range in blurry reading environments. Although the black dots are printed at a
particular pitch (eg. 1600
dpi), the dots themselves are slightly larger in order to create continuous
lines when dots are printed contiguously.
In the example images of Fig. 47, the dots are not as merged as they may be in
reality as a result of bleeding.
There would be more smoothing out of the black indentations. Although the
alternative Artcard system described
in the preferred embodiment allows for flexibly different dot sizes, exact dot
sizes and ink/printing behaviour for a
particular printing technology should be studied in more detail in order to
obtain best results.
In describing this artcard embodiment, the term dot refers to a physical
printed dot (ink, thermal, electro-
photographic, silver-halide etc) on an alternative Artcard. When an
alternative Artcard reader scans an alternative
Artcard, the dots must be sampled at least double the printed resolution to
satisfy Nyquist's Theorem. The term
pixel refers to a sample value from an alternative Artcard reader device. For
example, when 1600 dpi dots are
scanned at 4800 dpi there are 3 pixels in each dimension of a dot, or 9 pixels
per dot. The sampling process will
be further explained hereinafter.
Turning to Fig. 48, there is shown the data surface 1101 a sample of
alternative Artcard. Each alternative
Artcard consists of an "active" region 1102 surrounded by a white border
region 1103. The white border 1103
contains no data information, but can be used by an alternative Artcard reader
to calibrate white levels. The active
region is an array of data blocks eg. 1104, with each data block separated
from the next by a gap of 8 white dots
eg. 1106. Depending on the print resolution, the number of data blocks on an
alternative Artcard will vary. On a
1600 dpi alternative Artcard, the array can be 8 x 8. Each data block 1104 has
dimensions of 627 x 394 dots.
With an inter-block gap 1106 of 8 white dots, the active area of an
alternative Artcard is therefore 5072 x 3208
dots (8.lmm x 5.lmm at 1600 dpi).
Data blocks
Turning now to Fig. 49, there is shown a single data block 1107. The active
region of an alternative
Artcard consists of an array of identically structured data blocks 1107. Each
of the data blocks has the following
structure: a data region 1108 surrounded by clock-marks 1109, borders 1110,
and targets 1111. The data region
holds the encoded data proper, while the clock-marks, borders and targets are
present specifically to help locate
the data region and ensure accurate recovery of data from within the region.
Each data block 1107 has dimensions of 627 x 394 dots. Of this, the central
area of 595 x 384 dots is the
data region 1108. The surrounding dots are used to hold the clock-marks,
borders, and targets.
Borders and Clockmarks
Fig. 50 illustrates a data block with Fig. 51 and Fig. 52 illustrating
magnified edge portions thereof. As
illustrated in Fig. 51 and Fig. 52, there are two 5 dot high border and
clockmark regions 1170, 1177 in each data
block: one above and one below the data region. For example, The top 5 dot
high region consists of an outer
black dot border line 1112 (which stretches the length of the data block), a
white dot separator line 1113 (to ensure
the border line is independent), and a 3 dot high set of clock marks 1114. The
clock marks alternate between a
white and black row, starting with a black clock mark at the 8th column from
either end of the data block. There is
no separation between clockmark dots and dots in the data region.
The clock marks are symmetric in that if the alternative Artcard is inserted
rotated 180 degrees, the same
CA 02564047 2006-11-06
YU139 PCT 71
relative border/clockmark regions will be encountered. The border 1112, 1113
is intended for use by an alternative
Artcard reader to keep vertical tracking as data is read from the data region.
The clockmarks 1114 are intended to
keep horizontal tracking as data is read from the data region. The separation
between the border and clockmarks
by a white line of dots is desirable as a result of blurring occurring during
reading. The border thus becomes a
black line with white on either side, making for a good frequency response on
reading. The clockmarks alternating
between white and black have a similar result, except in the horizontal rather
than the vertical dimension. Any
alternative Artcard reader must locate the clockmarks and border if it intends
to use them for tracking. The next
section deals with targets, which are designed to point the way to the
clockmarks, border and data.
Targets in the Target region
As shown in Fig. 54, there are two 15-dot wide target regions 1116, 1117 in
each data block: one to the
left and one to the right of the data region. The target regions are separated
from the data region by a single
column of dots used for orientation. The purpose of the Target Regions 1116,
1117 is to point the way to the
clockmarks, border and data regions. Each Target Region contains 6 targets eg.
1118 that are designed to be easy
to find by an alternative Artcard reader. Turning now to Fig. 53 there is
shown the structure of a single target
1120. Each target 1120 is a 15 x 15 dot black square with a center structure
1121 and a run-length encoded target
number 1122. The center structure 1121 is a simple white cross, and the target
number component 1122 is simply
two columns of white dots, each being 2 dots long for each part of the target
number. Thus target number 1's
target id 1122 is 2 dots long, target number 2's target id 1122 is 4 dots wide
etc.
As shown in Fig. 54, the targets are arranged so that they are rotation
invariant with regards to card
insertion. This means that the left targets and right targets are the same,
except rotated 180 degrees. In the left
Target Region 1116, the targets are arranged such that targets 1 to 6 are
located top to bottom respectively. In the
right Target Region, the targets are arranged so that target numbers 1 to 6
are located bottom to top. The target
number id is always in the half closest to the data region. The magnified view
portions of Fig. 54 reveals clearly
the how the right targets are simply the same as the left targets, except
rotated 180 degrees.
As shown in Fig. 55, the targets 1124, 1125 are specifically placed within the
Target Region with centers
55 dots apart. In addition, there is a distance of 55 dots from the center of
target 1 (1124) to the first clockmark dot
1126 in the upper clockmark region, and a distance of 55 dots from the center
of the target to the first clockmark
dot in the lower clockmark region (not shown). The first black clockmark in
both regions begins directly in line
with the target center (the 8th dot position is the center of the 15 dot-wide
target).
The simplified schematic illustrations of Fig. 55 illustrates the distances
between target centers as well as
the distance from Target 1 (1124) to the first dot of the first black
clockmark (1126) in the upper
border/clockmark region. Since there is a distance of 55 dots to the
clockmarks from both the upper and lower
targets, and both sides of the alternative Artcard are symmetrical (rotated
through 180 degrees), the card can be
read left-to-right or right-to-left. Regardless of reading direction, the
orientation does need to be determined in
order to extract the data from the data region.
Orientation columns
As illustrated in Fig. 56, there are two I dot wide Orientation Columns 1127,
1128 in each data block:
one directly to the left and one directly to the right of the data region. The
Orientation Columns are present to give
orientation information to an alternative Artcard reader: On the left side of
the data region (to the right of the Left
Targets) is a single column of white dots 1127. On the right side of the data
region (to the left of the Right
CA 02564047 2006-11-06
YU139 PCT 72
Targets) is a single column of black dots 1128. Since the targets are rotation
invariant, these two columns of dots
allow an alternative Artcard reader to determine the orientation of the
alternative Artcard - has the card been
inserted the right way, or back to front. From the alternative Artcard
reader's point of view, assuming no
degradation to the dots, there are two possibilities:
* If the column of dots to the left of the data region is white, and the
column to the right of the
data region is black, then the reader will know that the card has been
inserted the same way as it was written.
* If the column of dots to the left of the data region is black, and the
column to the right of the
data region is white, then the reader will know that the card has been
inserted backwards, and the data region is
appropriately rotated. The reader must take appropriate action to correctly
recover the information from the
alternative Artcard.
Data Region
As shown in Fig. 57, the data region of a data block consists of 595 columns
of 384 dots each, for a total
of 228,480 dots. These dots must be interpreted and decoded to yield the
original data. Each dot represents a
single bit, so the 228,480 dots represent 228,480 bits, or 28,560 bytes. The
interpretation of each dot can be as
follows:
Black 1
White 0
The actual interpretation of the bits derived from the dots, however, requires
understanding of the
mapping from the original data to the dots in the data regions of the
alternative Artcard.
Mapping original data to data region dots
There will now be described the process of taking an original data file of
maximum size 910,082 bytes
and mapping it to the dots in the data regions of the 64 data blocks on a 1600
dpi alternative Artcard. An
alternative Artcard reader would reverse the process in order to extract the
original data from the dots on an
alternative Artcard. At f i r s t glance it seems trivial to map data onto
dots: binary data is comprised of 1 s and Os, so
it would be possible to simply write black and white dots onto the card. This
scheme however, does not allow for
the fact that ink can fade, parts of a card may be damaged with dirt, grime,
or even scratches. Without error-
detection encoding, there is no way to detect if the data retrieved from the
card is correct. And without redundancy
encoding, there is no way to correct the detected errors. The aim of the
mapping process then, is to make the data
recovery highly robust, and also give the alternative Artcard reader the
ability to know it read the data correctly.
There are three basic steps involved in mapping an original data file to data
region dots:
* Redundancy encode the original data
* Shuffle the encoded data in a deterministic way to reduce the effect of
localized alternative
Artcard damage
* Write out the shuffled, encoded data as dots to the data blocks on the
alternative Artcard
Each of these steps is examined in detail in the following sections.
Redundancy encode using Reed-Solomon encoding
The mapping of data to alternative Artcard dots relies heavily on the method
of redundancy encoding
employed. Reed-Solomon encoding is preferably chosen for its ability to deal
with burst errors and effectively
detect and correct errors using a minimum of redundancy. Reed Solomon encoding
is adequately discussed in the
standard texts such as Wicker, S., and Bhargava, V., 1994, Reed-Solomon Codes
and their Applications, IEEE
CA 02564047 2006-11-06
YU139 PCT 73
Press. Rorabaugh, C, 1996, Error Coding Cookbook, McGraw-Hill. Lyppens, H.,
1997, Reed-Solomon Error
Correction, Dr. Dobb's Journal, January 1997 (Volume 22, Issue 1).
A variety of different parameters for Reed-Solomon encoding can be used,
including different symbol
sizes and different levels of redundancy. Preferably, the following encoding
parameters are used:
* m=8
* t=64
Having m=8 means that the symbol size is 8 bits (1 byte). It also means that
each Reed-Solomon encoded
block size n is 255 bytes (28 - 1 symbols). In order to allow correction of up
to t symbols, 2t symbols in the final
block size must be taken up with redundancy symbols. Having t=64 means that 64
bytes (symbols) can be
corrected per block if they are in error. Each 255 byte block therefore has
128 (2 x 64) redundancy bytes, and the
remaining 127 bytes (k=127) are used to hold original data. Thus:
* n = 255
* k= 127
The practical result is that 127 bytes of original data are encoded to become
a 255-byte block of Reed-
Solomon encoded data. The encoded 255-byte blocks are stored on the
alternative Artcard and later decoded back
to the original 127 bytes again by the alternative Artcard reader. The 384
dots in a single column of a data block's
data region can hold 48 bytes (384/8). 595 of these columns can hold 28,560
bytes. This amounts to 112 Reed-
Solomon blocks (each block having 255 bytes). The 64 data blocks of a complete
alternative Artcard can hold a
total of 7168 Reed-Solomon blocks (1,827,840 bytes, at 255 bytes per Reed-
Solomon block). Two of the 7,168
Reed-Solomon blocks are reserved for control information, but the remaining
7166 are used to store data. Since
each Reed-Solomon block holds 127 bytes of actual data, the total amount of
data that can be stored on an
alternative Artcard is 910,082 bytes (7166 x 127). If the original data is
less than this amount, the data can be
encoded to fit an exact number of Reed-Solomon blocks, and then the encoded
blocks can be replicated until all
7,166 are used. Fig. 58 illustrates the overall form of encoding utilised.
Each of the 2 Control blocks 1132, 1133 contain the same encoded information
required for decoding the
remaining 7,166 Reed-Solomon blocks:
The number of Reed-Solomon blocks in a full message (16 bits stored 1o/hi),
and
The number of data bytes in the last Reed-Solomon block of the message (8
bits)
These two numbers are repeated 32 times (consuming. 96 bytes) with the
remaining 31 bytes reserved
and set to 0. Each control block is then Reed-Solomon encoded, turning the 127
bytes of control information into
255 bytes of Reed-Solomon encoded data.
The Control Block is stored twice to give greater chance of it surviving. In
addition, the repetition of the
data within the Control Block has particular significance when using Reed-
Solomon encoding. In an uncorrupted
Reed-Solomon encoded block, the first 127 bytes of data are exactly the
original data, and can be looked at in an
attempt to recover the original message if the Control Block fails decoding
(more than 64 symbols are corrupted).
Thus, if a Control Block fails decoding, it is possible to examine sets of 3
bytes in an effort to determine the most
likely values for the 2 decoding parameters. It is not guaranteed to be
recoverable, but it has a better chance
through redundancy. Say the last 159 bytes of the Control Block are destroyed,
and the first 96 bytes are perfectly
ok. Looking at the first 96 bytes will show a repeating set of numbers. These
numbers can be sensibly used to
decode the remainder of the message in the remaining 7,166 Reed-Solomon
blocks.
CA 02564047 2006-11-06
YU139 PCT 74
By way of example, assume a data file containing exactly 9,967 bytes of data.
The number of Reed-
Solomon blocks required is 79. The first 78 Reed-Solomon blocks are completely
utilized, consuming 9,906 bytes
(78 x 127). The 79th block has only 61 bytes of data (with the remaining 66
bytes all Os).
The alternative Artcard would consist of 7,168 Reed-Solomon blocks. The first
2 blocks would be
Control Blocks, the next 79 would be the encoded data, the next 79 would be a
duplicate of the encoded data, the
next 79 would be another duplicate of the encoded data, and so on. After
storing the 79 Reed-Solomon blocks 90
times, the remaining 56 Reed-Solomon blocks would be another duplicate of the
first 56 blocks from the 79
blocks of encoded data (the final 23 blocks of encoded data would not be
stored again as there is not enough room
on the alternative Artcard). A hex representation of the 127 bytes in each
Control Block data before being Reed-
Solomon encoded would be as illustrated in Fig. 59.
Scramble the Encoded Data
Assuming all the encoded blocks have been stored contiguously in memory, a
maximum 1,827,840 bytes
of data can be stored on the alternative Artcard (2 Control Blocks and 7,166
information blocks, totalling 7,168
Reed-Solomon encoded blocks). Preferably, the data is not directly stored onto
the alternative Artcard at this
stage however, or all 255 bytes of one Reed-Solomon block will be physically
together on the card. Any dirt,
grime, or stain that causes physical damage to the card has the potential of
damaging more than 64 bytes in a
single Reed-Solomon block, which would make that block unrecoverable. If there
are no duplicates of that Reed-
Solomon block, then the entire alternative Artcard cannot be decoded.
The solution is to take advantage of the fact that there are a large number of
bytes on the alternative
Artcard, and that the alternative Artcard has a reasonable physical size. The
data can therefore be scrambled to
ensure that symbols from a single Reed-Solomon block are not in close
proximity to one another. Of course
pathological cases of card degradation can cause Reed-Solomon blocks to be
unrecoverable, but on average, the
scrambling of data makes the card much more robust. The scrambling scheme
chosen is simple and is illustrated
schematically in Fig 14. All the Byte Os from each Reed-Solomon block are
placed together 1136, then all the
Byte 1 s etc. There will therefore be 7,168 byte 0's, then 7,168 Byte l's etc.
Each data block on the alternative
Artcard can store 28,560 bytes. Consequently there are approximately 4 bytes
from each Reed-Solomon block in
each of the 64 data blocks on the alternative Artcard.
Under this scrambling scheme, complete damage to 16 entire data blocks on the
alternative Artcard will
result in 64 symbol errors per Reed-Solomon block. This means that if there is
no other damage to the alternative
Artcard, the entire data is completely recoverable, even if there is no data
duplication.
Write the scrambled encoded data to the alternative Artcard
Once the original data has been Reed-Solomon encoded, duplicated, and
scrambled, there are 1,827,840
bytes of data to be stored on the alternative Artcard. Each of the 64 data
blocks on the alternative Artcard stores
28,560 bytes.
The data is simply written out to the alternative Artcard data blocks so that
the first data block contains
the first 28,560 bytes of the scrambled data, the second data block contains
the next 28,560 bytes etc.
As illustrated in Fig. 61, within a data block, the data is written out column-
wise left to right. Thus the
left-most column within a data block contains the first 48 bytes of the 28,560
bytes of scrambled data, and the last
column contains the last 48 bytes of the 28,560 bytes of scrambled data.
Within a column, bytes are written out
top to bottom, one bit at a time, starting from bit 7 and finishing with bit
0. If the bit is set (1), a black dot is placed
CA 02564047 2006-11-06
YU139 PCT 75
on the alternative Artcard, if the bit is clear (0), no dot is placed, leaving
it the white background color of the card.
For example, a set of 1,827,840 bytes of data can be created by scrambling
7,168 Reed-Solomon
encoded blocks to be stored onto an alternative Artcard. The first 28,560
bytes of data are written to the first data
block. The first 48 bytes of the first 28,560 bytes are written to the first
column of the data block, the next 48 bytes
to the next column and so on. Suppose the first two bytes of the 28,560 bytes
are hex D3 5F. Those first two bytes
will be stored in column 0 of the data block. Bit 7 of byte 0 will be stored
first, then bit 6 and so on. Then Bit 7 of
byte 1 will be stored through to bit 0 of byte 1. Since each "1" is stored as
a black dot, and each "0" as a white dot,
these two bytes will be represented on the alternative Artcard as the
following set of dots:
* D3 (1101 0011) becomes: black, black, white, black, white, white, black,
black
* 5F (0101 1111) becomes: white, black, white, black, black, black, black,
black
Decoding an alternative Artcard
This section deals with extracting the original data from an alternative
Artcard in an accurate and robust
manner. Specifically, it assumes the alternative Artcard format as described
in the previous chapter, and describes
a method of extracting the original pre-encoded data from the alternative
Artcard.
There are a number of general considerations that are part of the assumptions
for decoding an alternative
Artcard.
User
The purpose of an alternative Artcard is to store data for use in different
applications. A user inserts an
alternative Artcard into an alternative Artcard reader, and expects the data
to be loaded in a "reasonable time".
From the user's perspective, a motor transport moves the alternative Artcard
into an alternative Artcard reader.
This is not perceived as a problematic delay, since the alternative Artcard is
in motion. Any time after the
alternative Artcard has stopped is perceived as a delay, and should be
minimized in any alternative Artcard
reading scheme. Ideally, the entire alternative Artcard would be read while in
motion, and thus there would be no
perceived delay after the card had stopped moving.
For the purpose of the preferred embodiment, a reasonable time for an
alternative Artcard to be
physically loaded is defined to be 1.5 seconds. There should be a minimization
of time for additional decoding
after the alternative Artcard has stopped moving. Since the Active region of
an alternative Artcard covers most of
the alternative Artcard surface we can limit our timing concerns to that
region.
Sampling Dots
The dots on an alternative Artcard must be sampled by a CCD reader or the like
at least at double the
printed resolution to satisfy Nyquist's Theorem. In practice it is better to
sample at a higher rate than this. In the
alternative Artcard reader environment, dots are preferably sampled at 3 times
their printed resolution in each
dimension, requiring 9 pixels to define a single dot. If the resolution of the
alternative Artcard dots is 1600 dpi, the
alternative Artcard reader's image sensor must scan pixels at 4800 dpi. Of
course if a dot is not exactly aligned
with the sampling sensor, the worst and most likely case as illustrated in
Fig. 62, is that a dot will be sensed over a
4x4 pixel area.
Each sampled pixel is 1 byte (8 bits). The lowest 2 bits of each pixel can
contain significant noise.
Decoding algorithms must therefore be noise tolerant.
Alignment/Rotation
It is extremely unlikely that a user will insert an alternative Artcard into
an alternative Artcard reader
CA 02564047 2006-11-06
YU139 PCT 76
perfectly aligned with no rotation. Certain physical constraints at a reader
entrance and motor transport grips will
help ensure that once inserted, an alternative Artcard will stay at the
original angle of insertion relative to the
CCD. Preferably this angle of rotation, as illustrated in Fig. 63 is a maximum
of 1 degree. There can be some
slight aberrations in angle due to jitter and motor rumble during the reading
process, but these are assumed to
essentially stay within the 1-degree limit.
The physical dimensions of an alternative Artcard are 86mm x 55mm. A 1 degree
rotation adds 1.5mm
to the effective height of the card as 86mm passes under the CCD (86 sin 1 ),
which will affect the required CCD
length.
The effect of a 1 degree rotation on alternative Artcard reading is that a
single scanline from the CCD
will include a number of different columns of dots from the alternative
Artcard. This is illustrated in an
exaggerated form in Fig. 63 which shows the drift of dots across the columns
of pixels. Although exaggerated in
this diagram, the actual drift will be a maximum 1 pixel column shift every 57
pixels.
When an alternative Artcard is not rotated, a single column of dots can be
read over 3 pixel scanlines.
The more an alternative Artcard is rotated, the greater the local effect. The
more dots being read, the longer the
rotation effect is applied. As either of these factors increase, the larger
the number of pixel scanlines that are
needed to be read to yield a given set of dots from a single column on an
alternative Artcard. The following table
shows how many pixel scanlines are required for a single column of dots in a
particular alternative Artcard
structure.
Region Height 0 rotation 10 rotation
Active region 3208 dots 3 pixel columns 168 pixel columns
Data block 394 dots 3 pixel columns 21 pixel columns
To read an entire alternative Artcard, we need to read 87 mm (86mm + 1mm due
to 1 rotation). At 4800
dpi this implies 16,252 pixel columns.
CCD (or other Linear Image Sensor) Length
The length of the CCD itself must accommodate:
- the physical height of the alternative Artcard (55 mm),
vertical slop on physical alternative Artcard insertion (I mm)
insertion rotation of up to 1 degree (86 sin 1 = 1.5mm)
These factors combine to form a total length of 57.5mm.
When the alternative Artcard Image sensor CCD in an alternative Artcard reader
scans at 4800 dpi, a
single scanline is 10,866 pixels. For simplicity, this figure has been rounded
up to 11,000 pixels. The Active
Region of an alternative Artcard has a height of 3208 dots, which implies
9,624 pixels. A Data Region has a
height of 384 dots, which implies 1,152 pixels.
DRAM Size
The amount of memory required for alternative Artcard reading and decoding is
ideally minimized. The
typical placement of an alternative Artcard reader is an embedded system where
memory resources are precious.
This is made more problematic by the effects of rotation. As described above,
the more an alternative Artcard is
rotated, the more scanlines are required to effectively recover original dots.
CA 02564047 2006-11-06
YU139 PCT 77
There is a trade-off between algorithmic complexity, user perceived delays,
robustness, and memory
usage. One of the simplest reader algorithms would be to simply scan the whole
alternative Artcard, and then to
process the whole data without real-time constraints. Not only would this
require huge reserves of memory, it
would take longer than a reader algorithm that occurred concurrently with the
alternative Artcard reading process.
The actual amount of memory required for reading and decoding an alternative
Artcard is twice the
amount of space required to hold the encoded data, together with a small
amount of scratch space (1-2 KB). For
the 1600 dpi alternative Artcard, this implies a 4 MB memory requirement. The
actual usage of the memory is
detailed in the following algorithm description.
Transfer rate
DRAM bandwidth assumptions need to be made for timing considerations and to a
certain extent affect
algorithmic design, especially since alternative Artcard readers are typically
part of an embedded system.
A standard Rambus Direct RDRAM architecture is assumed, as defined in Rambus
Inc, Oct 1997, Direct
Rambus Technology Disclosure, with a peak data transfer rate of 1.6GB/sec.
Assuming 75% efficiency (easily
achieved), we have an average of 1.2GB/sec data transfer rate. The average
time to access a block of 16 bytes is
therefore 12ns.
Dirty Data
Physically damaged alternative Artcards can be inserted into a reader.
Alternative Artcards may be
scratched, or be stained with grime or dirt. A alternative Artcard reader
can't assume to read everything perfectly.
The effect of dirty data is made worse by blurring, as the dirty data affects
the surrounding clean dots.
Blurry Environment
There are two ways that blurring is introduced into the alternative Artcard
reading environment:
* Natural blurring due to nature of the CCD's distance from the alternative
Artcard.
* Warping of alternative Artcard
Natural blurring of an alternative Artcard image occurs when there is overlap
of sensed data from the
CCD. Blurring can be useful, as the overlap ensures there are no high
frequencies in the sensed data, and that there
is no data missed by the CCD. However if the area covered by a CCD pixel is
too large, there will be too much
blurring and the sampling required to recover the data will not be met. Fig.
64 is a schematic illustration of the
overlapping of sensed data.
Another form of blurring occurs when an alternative Artcard is slightly warped
due to heat damage.
When the warping is in the vertical dimension, the distance between the
alternative Artcard and the CCD will not
be constant, and the level of blurring will vary across those areas.
Black and white dots were chosen for alternative Artcards to give the best
dynamic range in blurry
reading environments. Blurring can cause problems in attempting to determine
whether a given dot is black or
white.
As the blurring increases, the more a given dot is influenced by the
surrounding dots. Consequently the
dynamic range for a particular dot decreases. Consider a white dot and a black
dot, each surrounded by all
possible sets of dots. The 9 dots are blurred, and the center dot sampled.
Fig. 65 shows the distribution of
resultant center dot values for black and white dots.
The diagram is intended to be a representative blurring. The curve 1140 from 0
to around 180 shows the
range of black dots. The curve 1141 from 75 to 250 shows the range of white
dots. However the greater the
CA 02564047 2006-11-06
YU139 PCT 78
blurring, the more the two curves shift towards the center of the range and
therefore the greater the intersection
area, which means the more difficult it is to determine whether a given dot is
black or white. A pixel value at the
center point of intersection is ambiguous - the dot is equally likely to be a
black or a white.
As the blurring increases, the likelihood of a read bit error increases.
Fortunately, the Reed-Solomon
decoding algorithm can cope with these gracefully up to t symbol errors. Fig.
65 is a graph of number predicted
number of alternative Artcard Reed-Solomon blocks that cannot be recovered
given a particular symbol error rate.
Notice how the Reed-Solomon decoding scheme performs well and then
substantially degrades. If there is no
Reed-Solomon block duplication, then only 1 block needs to be in error for the
data to be unrecoverable. Of
course, with block duplication the chance of an alternative Artcard decoding
increases.
Fig. 66 only illustrates the symbol (byte) errors corresponding to the number
of Reed-Solomon blocks in
error. There is a trade-off between the amount of blurring that can be coped
with, compared to the amount of
damage that has been done to a card. Since all error detection and correction
is performed by a Reed-Solomon
decoder, there is a finite number of errors per Reed-Solomon data block that
can be coped with. The more errors
introduced through blurring, the fewer the number of errors that can be coped
with due to alternative Artcard
damage.
Overview of alternative Artcard Decoding
As noted previously, when the user inserts an alternative Artcard into an
alternative Artcard reading unit,
a motor transport ideally carries the alternative Artcard past a monochrome
linear CCD image sensor. The card is
sampled in each dimension at three times the printed resolution. Alternative
Artcard reading hardware and
software compensate for rotation up to 1 degree, jitter and vibration due to
the motor transport, and blurring due to
variations in alternative Artcard to CCD distance. A digital bit image of the
data is extracted from the sampled
image by a complex method described here. Reed-Solomon decoding corrects
arbitrarily distributed data
corruption of up to 25% of the raw data on the alternative Artcard.
Approximately 1 MB of corrected data is
extracted from a 1600 dpi card.
The steps involved in decoding are so as indicated in Fig. 67.
The decoding process requires the following steps:
* Scan 1144 the alternative Artcard at three times printed resolution (eg scan
1600 dpi alternative
Artcard at 4800 dpi)
* Extract 1145 the data bitmap from the scanned dots on the card.
* Reverse 1146 the bitmap if the alternative Artcard was inserted backwards.
* Unscramble 1147 the encoded data
* Reed-Solomon 1148 decode the data from the bitmap
Algorithmic Overview
Phase 1- Real time bit image extraction
A simple comparison between the available memory (4 MB) and the memory
required to hold all the
scanned pixels for a 1600 dpi alternative Artcard (172.5 MB) shows that unless
the card is read multiple times (not
a realistic option), the extraction of the bitmap from the pixel data must be
done on the fly, in real time, while the
alternative Artcard is moving past the CCD. Two tasks must be accomplished in
this phase:
* Scan the alternative Artcard at 4800 dpi
* Extract the data bitmap from the scanned dots on the card
CA 02564047 2006-11-06
YU139 PCT 79
The rotation and unscrambling of the bit image cannot occur until the whole
bit image has been
extracted. It is therefore necessary to assign a memory region to hold the
extracted bit image. The bit image fits
easily within 2MB, leaving 2MB for use in the extraction process.
Rather than extracting the bit image while looking only at the current
scanline of pixels from the CCD, it
is possible to allocate a buffer to act as a window onto the alternative
Artcard, storing the last N scanlines read.
Memory requirements do not allow the entire alternative Artcard to be stored
this way (172.5MB would be
required), but allocating 2MB to store 190 pixel columns (each scanline takes
less than 11,000 bytes) makes the
bit image extraction process simpler.
The 4MB memory is therefore used as follows:
* 2 MB for the extracted bit image
* -2 MB for the scanned pixels
* 1.5 KB for Phase 1 scratch data (as required by algorithm)
The time taken for Phase 1 is 1.5 seconds, since this is the time taken for
the alternative Artcard to travel
past the CCD and physically load.
Phase 2 - Data extraction from bit image
Once the bit image has been extracted, it must be unscrambled and potentially
rotated 180 . It must then
be decoded. Phase 2 has no real-time requirements, in that the alternative
Artcard has stopped moving, and we are
only concerned with the user's perception of elapsed time. Phase 2 therefore
involves the remaining tasks of
decoding an alternative Artcard:
* Re-organize the bit image, reversing it if the alternative Artcard was
inserted backwards
* Unscramble the encoded data
* Reed-Solomon decode the data from the bit image
The input to Phase 2 is the 2MB bit image buffer. Unscrambling and rotating
cannot be performed in
situ, so a second 2MB buffer is required. The 2MB buffer used to hold scanned
pixels in Phase 1 is no longer
required and can be used to store the rotated unscrambled data.
The Reed-Solomon decoding task takes the unscrambled bit image and decodes it
to 910,082 bytes. The
decoding can be performed in situ, or to a specified location elsewhere. The
decoding process does not require any
additional memory buffers.
The 4MB memory is therefore used as follows:
* 2 MB for the extracted bit image (from Phase 1)
* -2 MB for the unscrambled, potentially rotated bit image
* < 1KB for Phase 2 scratch data (as required by algorithm)
The time taken for Phase 2 is hardware dependent and is bound by the time
taken for Reed-Solomon
decoding. Using a dedicated core such as LSI Logic's L64712, or an equivalent
CPU/DSP combination, it is
estimated that Phase 2 would take 0.32 seconds.
Phase 1 - Extract Bit Image
This is the real-time phase of the algorithm, and is concerned with extracting
the bit image from the
alternative Artcard as scanned by the CCD.
As shown in Fig. 68 Phase 1 can be divided into 2 asynchronous process
streams. The first of these
streams is simply the real-time reader of alternative Artcard pixels from the
CCD, writing the pixels to DRAM.
CA 02564047 2006-11-06
YU139 PCT 80
The second stream involves looking at the pixels, and extracting the bits. The
second process stream is itself
divided into 2 processes. The first process is a global process, concerned
with locating the start of the alternative
Artcard. The second process is the bit image extraction proper.
Fig. 69 illustrates the data flow from a data/process perspective.
Timing
For an entire 1600 dpi alternative Artcard, it is necessary to read a maximum
of 16,252 pixel-columns.
Given a total time of 1.5 seconds for the whole alternative Artcard, this
implies a maximum time of 92,296ns per
pixel column during the course of the various processes.
Process 1 - Read pixels from CCD
The CCD scans the alternative Artcard at 4800 dpi, and generates 11,000 1-byte
pixel samples per
column. This process simply takes the data from the CCD and writes it to DRAM,
completely independently of
any other process that is reading the pixel data from DRAM. Fig. 70
illustrates the steps involved.
The pixels are written contiguously to a 2MB buffer that can hold 190 full
columns of pixels. The buffer
always holds the 190 columns most recently read. Consequently, any process
that wants to read the pixel data
(such as Processes 2 and 3) must firstly know where to look for a given
column, and secondly, be fast enough to
ensure that the data required is actually in the buffer.
Process 1 makes the current scanline number (CurrentScanLine) available to
other processes so they can
ensure they are not attempting to access pixels from scanlines that have not
been read yet.
The time taken to write out a single column of data (11,000 bytes) to DRAM is:
11,000/16 * 12 = 8,256ns
Process 1 therefore uses just under 9% of the available DRAM bandwidth
(8256/92296).
Process 2 - Detect start of alternative Artcard
This process is concerned with locating the Active Area on a scanned
alternative Artcard. The input to
this stage is the pixel data from DRAM (placed there by Process 1). The output
is a set of bounds for the first 8
data blocks on the alternative Artcard, required as input to Process 3. A high
level overview of the process can be
seen in Fig. 71.
An alternative Artcard can have vertical slop of 1mm upon insertion. With a
rotation of 1 degree there is
further vertical slop of 1.5mm (86 sin 1 ). Consequently there is a total
vertical slop of 2.5mm. At 1600dpi, this
equates to a slop of approximately 160 dots. Since a single data block is only
394 dots high, the slop is just under
half a data block. To get a better estimate of where the data blocks are
located the alternative Artcard itself needs
to be detected.
Process 2 therefore consists of two parts:
* Locate the start of the alternative Artcard, and if found,
* Calculate the bounds of the first 8 data blocks based on the start of the
alternative Artcard.
Locate the Start of the alternative Artcard
The scanned pixels outside the alternative Artcard area are black (the surface
can be black plastic or
some other non-reflective surface). The border of the alternative Artcard area
is white. If we process the pixel
columns one by one, and filter the pixels to either black or white, the
transition point from black to white will
mark the start of the alternative Artcard. The highest level process is as
follows:
CA 02564047 2006-11-06
YU139 PCT 81
for (Column; Column < MAX COLUMN; Column++)
{
Pixel = ProcessColumn(Column)
if (Pixel)
return (Pixel, Column) II success!
}
return failure // no alternative Artcard found
The ProcessColumn function is simple. Pixels from two areas of the scanned
column are passed through
a threshold filter to determine if they are black or white. It is possible to
then wait for a certain number of white
pixels and announce the start of the alternative Artcard once the given number
has been detected. The logic of
processing a pixel column is shown in the following pseudocode. 0 is returned
if the alternative Artcard has not
been detected during the column. Otherwise the pixel number of the detected
location is returned.
// Try upper region first
count = 0
for (i=0; i<UPPER REGION BOUND; i++)
{
if (GetPixel(column, i) < THRESHOLD)
{
count = 0 pixel is black
}
else
{
count++ pixel is white
if (count > WHITE-ALTERNATIVE ARTCARD)
return i
}
}
// Try lower region next. Process pixels in reverse
count = 0
for (i=MAX PIXEL BOUND; i>LOWER REGION BOUND; i--)
{
if (GetPixel(column, i) < THRESHOLD)
{
count = 0 pixel is black
}
else
{
CA 02564047 2006-11-06
YU139 PCT 82
count++ // pixel is white
if (count > WHITE-ALTERNATIVE ARTCARD)
return i
}
}
//Not in upper bound or in lower bound. Return failure
return 0
Calculate Data Block Bounds
At this stage, the alternative Artcard has been detected. Depending on the
rotation of the alternative
Artcard, either the top of the alternative Artcard has been detected or the
lower part of the alternative Artcard has
been detected. The second step of Process 2 determines which was detected and
sets the data block bounds for
Phase 3 appropriately.
A look at Phase 3 reveals that it works on data block segment bounds: each
data block has a StartPixel
and an EndPixel to determine where to look for targets in order to locate the
data block's data region.
If the pixel value is in the upper half of the card, it is possible to simply
use that as the first StartPixel
bounds. If the pixel value is in the lower half of the card, it is possible to
move back so that the pixel value is the
last segment's EndPixel bounds. We step forwards or backwards by the
alternative Artcard data size, and thus set
up each segment with appropriate bounds. We are now ready to begin extracting
data from the alternative Artcard.
// Adjust to become first pixel if is lower pixel
if (pixel > LOWER-REGION-BOUND)
{
pixel = 6 * 1152
if (pixel < 0)
pixel = 0
}
for (i=0; i<6; i++)
{
endPixel = pixel + 1152
segment[i].MaxPixel = MAX-PIXEL-BOUND
segment[i].SetBounds(pixel, endPixel)
pixel = endPixel
}
The MaxPixel value is defined in Process 3, and the SetBounds function simply
sets StartPixel and
EndPixel clipping with respect to 0 and MaxPixel.
Process 3 - Extract bit data from pixels
CA 02564047 2006-11-06
YU139 PCT 83
This is the heart of the alternative Artcard Reader algorithm. This process is
concerned with extracting
the bit data from the CCD pixel data. The process essentially creates a bit-
image from the pixel data, based on
scratch information created by Process 2, and maintained by Process 3. A high
level overview of the process can
be seen in Fig. 72.
Rather than simply read an alternative Artcard's pixel column and determine
what pixels belong to what
data block, Process 3 works the other way around. It knows where to look for
the pixels of a given data block. It
does this by dividing a logical alternative Artcard into 8 segments, each
containing 8 data blocks as shown in Fig.
73.
The segments as shown match the logical alternative Artcard. Physically, the
alternative Artcard is likely
to be rotated by some amount. The segments remain locked to the logical
alternative Artcard structure, and hence
are rotation-independent. A given segment can have one of two states:
* LookingForTargets: where the exact data block position for this segment has
not yet been
determined. Targets are being located by scanning pixel column data in the
bounds indicated by the segment
bounds. Once the data block has been located via the targets, and bounds set
for black & white, the state changes
to ExtractingBitlmage.
* ExtractingBitlmage: where the data block has been accurately located, and
bit data is being
extracted one dot column at a time and written to the alternative Artcard bit
image. The following of data block
clockmarks gives accurate dot recovery regardless of rotation, and thus the
segment bounds are ignored. Once the
entire data block has been extracted, new segment bounds are calculated for
the next data block based on the
current position. The state changes to LookingForTargets.
The process is complete when all 64 data blocks have been extracted, 8 from
each region.
Each data block consists of 595 columns of data, each with 48 bytes.
Preferably, the 2 orientation
columns for the data block are each extracted at 48 bytes each, giving a total
of 28,656 bytes extracted per data
block. For simplicity, it is possible to divide the 2MB of memory into 64 x
32k chunks. The nth data block for a
given segment is stored at the location:
StartBuffer + (256k * n)
Data Structure for Segments
Each of the 8 segments has an associated data structure. The data structure
defining each segment is
stored in the scratch data area. The structure can be as set out in the
following table:
DataName Comment
CurrentState Defines the current state of the segment. Can be one of:
LookingForTargets
ExtractingBitlmage
Initial value is Lookin ForTar ets
Used during Lookin ForTar ets.
StartPixel Upper pixel bound of segment. Initially set by Process 2.
EndPixel Lower pixel bound of segment. Initially set by Process 2
MaxPixel The maximum pixel number for any scanline.
It is set to the same value for each segment: 10,866.
CurrentColumn Pixel column we're up to while looking for targets.
CA 02564047 2006-11-06
YU139 PCT 84
FinalColumn Defines the last pixel column to look in for targets.
LocatedTar ets Points to a list of located Targets.
PossibleTargets Points to a set of pointers to Target structures that
represent currently
investigated pixel shapes that may be targets
AvailableTargets Points to a set of pointers to Target structures that are
currently unused.
TargetsFound The number of Targets found so far in this data block.
PossibleTargetCount The number of elements in the PossibleTargets list
AvailabletargetCount The number of elements in the AvailableTargets list
Used during Extra ctin Bitlma e:
Bitlmage The start of the Bit Image data area in DRAM where to store the next
data block:
Segment 1 = X, Segment 2 = X+32k etc
Advances by 256k each time the state changes from
Extractin Bitlma eData to Looking ForTargets
CurrentByte Offset within Bitlma e where to store next extracted byte
CurrentDotColumn Holds current clockmark/dot column number.
Set to -8 when transitioning from state LookingForTarget to
Extractin Bitlma e.
UpperClock Coordinate (column/ pixel) of current upper clockmark/border
LowerClock Coordinate (column/pixel) of current lower clockmark/border
CurrentDot The center of the current data dot for the current dot column.
Initially set
to the center of the first (topmost) dot of the data column.
DataDelta What to add (column/pixel) to CurrentDot to advance to the center of
the
next dot.
BlackMax Pixel value above which a dot is definitely white
WhiteMin Pixel value below which a dot is definitely black
MidRange The pixel value that has equal likelihood of coming from black or
white.
When all smarts have not determined the dot, this value is used to
determine it. Pixels below this value are black, and above it are white.
High Level of Process 3
Process 3 simply iterates through each of the segments, performing a single
line of processing depending
on the segment's current state. The pseudocode is straightforward:
blockCount = 0
while (blockCount < 64)
for (i=0; i<8; i++)
{
finishedBlock = segment[i].ProcessState()
if (finishedBlock)
blockCount++
}
Process 3 must be halted by an external controlling process if it has not
terminated after a specified
amount of time. This will only be the case if the data cannot be extracted. A
simple mechanism is to start a
countdown after Process 1 has finished reading the alternative Artcard. If
Process 3 has not finished by that time,
CA 02564047 2006-11-06
YU139 PCT 85
the data from the alternative Artcard cannot be recovered.
CurrentState = LookingForTargets
Targets are detected by reading columns of pixels, one pixel-column at a time
rather than by detecting
dots within a given band of pixels (between StartPixel and EndPixel) certain
patterns of pixels are detected. The
pixel columns are processed one at a time until either all the targets are
found, or until a specified number of
columns have been processed. At that time the targets can be processed and the
data area located via clockmarks.
The state is changed to ExtractingBitImage to signify that the data is now to
be extracted. If enough valid targets
are not located, then the data block is ignored, skipping to a column
definitely within the missed data block, and
then beginning again the process of looking for the targets in the next data
block. This can be seen in the
following pseudocode:
fmishedBlock = FALSE
if(CurrentColumn < Process 1.CurrentScanLine)
{
ProcessPixelColumn()
CurrentColumn++
}
if ((TargetsFound == 6) 11 (CurrentColumn > LastColumn))
{
if (TargetsFound >= 2)
ProcessTargets()
if (TargetsFound >= 2)
{
BuildClockmarkEstimates()
SetBlackAndWhiteBounds()
CurrentState = ExtractingBitlmage
CurrentDotColumn = -8
}
else
{
data block cannot be recovered. Look for
// next instead. Must adjust pixel bounds to
// take account of possible 1 degree rotation.
fmishedBlock = TRUE
SetBounds(StartPixel-12, EndPixel+12)
Bitlmage += 256KB
CurrentByte = 0
LastColumn += 1024
TargetsFound = 0
}
CA 02564047 2006-11-06
YU139 PCT 86
}
return finishedBlock
ProcessPixelColumn
Each pixel column is processed within the specified bounds (between StartPixel
and EndPixel) to search
for certain patterns of pixels which will identify the targets. The structure
of a single target (target number 2) is as
previously shown in Fig. 54:
From a pixel point of view, a target can be identified by:
* Left black region, which is a number of pixel columns consisting of large
numbers of
contiguous black pixels to build up the first part of the target.
* Target center, which is a white region in the center of further black
columns
* Second black region, which is the 2 black dot columns after the target
center
* Target number, which is a black-surrounded white region that defines the
target number by its
length
* Third black region, which is the 2 black columns after the target number
An overview of the required process is as shown in Fig. 74.
Since identification only relies on black or white pixels, the pixels 1150
from each column are passed
through a filter 1151 to detect black or white, and then run length encoded
1152. The run-lengths are then passed
to a state machine 1153 that has access to the last 3 run lengths and the 4th
last color. Based on these values,
possible targets pass through each of the identification stages.
The GatherMin&Max process 1155 simply keeps the minimum & maximum pixel values
encountered
during the processing of the segment. These are used once the targets have
been located to set BlackMax,
WhiteMin, and MidRange values.
Each segment keeps a set of target structures in its search for targets. While
the target structures
themselves don't move around in memory, several segment variables point to
lists of pointers to these target
structures. The three pointer lists are repeated here:
LocatedTargets Points to a set of Target structures that represent located
targets.
PossibleTargets Points to a set of pointers to Target structures that
represent currently
investigated pixel shapes that may be targets.
AvailableTargets Points to a set of pointers to Target structures that are
currently unused.
There are counters associated with each of these list pointers: TargetsFound,
PossibleTargetCount, and
AvailableTargetCount respectively.
Before the alternative Artcard is loaded, TargetsFound and PossibleTargetCount
are set to 0, and
AvailableTargetCount is set to 28 (the maximum number of target structures
possible to have under investigation
since the minimum size of a target border is 40 pixels, and the data area is
approximately 1152 pixels). An
example of the target pointer layout is as illustrated in Fig. 75.
As potential new targets are found, they are taken from the AvailableTargets
list 1157, the target data
structure is updated, and the pointer to the structure is added to the
PossibleTargets list 1158. When a target is
completely verified, it is added to the LocatedTargets list 1159. If a
possible target is found not to be a target after
all, it is placed back onto the AvailableTargets list 1157. Consequently there
are always 28 target pointers in
CA 02564047 2006-11-06
YU139 PCT 87
circulation at any time, moving between the lists.
The Target data structure 1160 can have the following form:
DataName Comment
CurrentState The current state of the target search
DetectCount Counts how long a target has been in a given state
StartPixel Where does the target start? All the lines of pixels in this target
should
start within a tolerance of this pixel value.
TargetNumber Which target number is this (according to what was read)
Column Best estimate of the target's center column ordinate
Pixel Best estimate of the target's center pixel ordinate
The ProcessPixelColumn function within the find targets module 1162 (Fig. 74)
then, goes through all
the run lengths one by one, comparing the runs against existing possible
targets (via StartPixel), or creating new
possible targets if a potential target is found where none was previously
known. In all cases, the comparison is
only made if SO.color is white and S L color is black.
The pseudocode for the ProcessPixelColumn set out hereinafter. When the first
target is positively
identified, the last column to be checked for targets can be determined as
being within a maximum distance from
it. For 1 rotation, the maximum distance is 18 pixel columns.
pixel = StartPixel
t=0
target=PossibleTarget[t]
while ((pixel < EndPixel) && (TargetsFound < 6))
{
if ((SO.Color = white) && (S 1.Color = black))
{
do
{
keepTrying = FALSE
if
(
(target != NULL)
&&
(target->AddToTarget(Column, pixel, S1, S2, S3))
{
if (target->CurrentState = IsATarget)
{
Remove target from PossibleTargets List
Add target to LocatedTargets List
CA 02564047 2006-11-06
YU139 PCT 88
TargetsFound++
if (TargetsFound = 1)
FinalColumn = Column + MAX-TARGET-DELTA)
else if (target->CurrentState = NotATarget)
{
Remove target from PossibleTargets List
Add target to AvailableTargets List
keepTrying = TRUE
}
else
{
t++ advance to next target
}
target = PossibleTarget[t]
}
else
{
tmp = AvailableTargets[0]
if (tmp->AddToTarget(Column,pixel,S1,S2,S3)
{
Remove tmp from AvailableTargets list
Add tmp to PossibleTargets list
t++ target t has been shifted right
}
}
} while (keepTrying)
}
pixel += Si.RunLength
Advance SO/Sl/S2/S3
}
AddToTarget is a function within the find targets module that determines
whether it is possible or not to
add the specific run to the given target:
* If the run is within the tolerance of target's starting position, the run is
directly related to the
current target, and can therefore be applied to it.
* If the run starts before the target, we assume that the existing target is
still ok, but not relevant to
the run. The target is therefore left unchanged, and a return value of FALSE
tells the caller that the run was not
applied. The caller can subsequently check the run to see if it starts a whole
new target of its own.
* If the run starts after the target, we assume the target is no longer a
possible target. The state is
changed to be NotATarget, and a return value of TRUE is returned.
CA 02564047 2006-11-06
YU139 PCT 89
If the run is to be applied to the target, a specific action is performed
based on the current state and set of
runs in Si, S2, and S3. The AddToTarget pseudocode is as follows:
MAX TARGET DELTA = 1
if (CurrentState != NothingKnown)
{
if (pixel > Star(Pixel) // run starts after target
{
diff = pixel - StartPixel
if (diff> MAX-TARGET-DELTA)
{
CurrentState = NotATarget
return TRUE
}
}
else
{
diff = StartPixel - pixel
if (diff> MAX-TARGET-DELTA)
return FALSE
}
}
runType = DetermineRunType(S I, S2, S3)
EvaluateState(runType)
StartPixel = currentPixel
return TRUE
Types of pixel runs are identified in DetermineRunType is as follows:
Types of Pixel Runs
Type How identified (Si is always black)
TargetBorder S 1 = 40 < RunLength < 50
S2 = white run
TargetCenter S I = 15 < RunLength < 26
S2 = white run with [RunLength < 12]
S3 = black run with [15 < RunLen th < 26
TargetNumber S2 = white run with [RunLength <= 40]
The EvaluateState procedure takes action depending on the current state and
the run type.
The actions are shown as follows in tabular form:
CA 02564047 2006-11-06
YU139 PCT 90
CurrentState Type of Pixel Run Action
NothingKnown TargetBorder DetectCount = 1
CurrentState = LeftOfCenter
LeftOfCenter TargetBorder DetectCount++
if (DetectCount > 24)
CurrentState = NotATarget
TargetCenter DetectCount = 1
CurrentState = InCenter
Column = currentColumn
Pixel = currentPixel + S1.RunLen th
CurrentState = NotATarget
InCenter TargetCenter DetectCount++
tmp = currentPixel + S i.RunLength
if (tmp < Pixel)
Pixel = tmp
if (DetectCount > 13)
CurrentState = NotATar et
TargetBorder DetectCount = 1
CurrentState = RightOfCenter
CurrentState = NotATarget
RightOfCenter TargetBorder DetectCount++
if (DetectCount >= 12)
CurrentState = NotATarget
TargetNumber DetectCount = I
CurrentState = InTargetNumber
TargetNumber = (S2.RunLength+ 2)/6
CurrentState = NotATarget
InTargetNumber TargetNumber tmp = (S2.RunLength+ 2)/6
if (tmp > TargetNumber)
TargetNumber = tmp
DetectCount++
if (DetectCount >= 12)
CurrentState = NotATarget
TargetBorder if (DetectCount >= 3)
CurrentState = IsATarget
else
CurrentState = NotATarget
CurrentState = NotATarget
IsATarget or - -
NotATarget
Processing Targets
he located targets (in the LocatedTargets list) are stored in the order they
were located. Depending on
alternative Artcard rotation these targets will be in ascending pixel order or
descending pixel order. In addition,
the target numbers recovered from the targets may be in error. We may have
also have recovered a false target.
Before the clockmark estimates can be obtained, the targets need to be
processed to ensure that invalid targets are
discarded, and valid targets have target numbers fixed if in error (e.g. a
damaged target number due to dirt). Two
CA 02564047 2006-11-06
YU139 PCT 91
main steps are involved:
* Sort targets into ascending pixel order
* Locate and fix erroneous target numbers
The first step is simple. The nature of the target retrieval means that the
data should already be sorted in
either ascending pixel or descending pixel. A simple swap sort ensures that if
the 6 targets are already sorted
correctly a maximum of 14 comparisons is made with no swaps. If the data is
not sorted, 14 comparisons are
made, with 3 swaps. The following pseudocode shows the sorting process:
for (i = 0; i < TargetsFound-1; i++)
{
oldTarget = LocatedTargets[i]
bestPixel = oldTarget->Pixel
best = i
j = i+1
while (j<TargetsFound)
{
if (LocatedTargets[j]-> Pixel < bestPixel)
best =j
j++
}
if (best != i) // move only if necessary
LocatedTargets[i] = LocatedTargets[best]
LocatedTargets[best] = oldTarget
}
}
Locating and fixing erroneous target numbers is only slightly more complex.
One by one, each of the N
targets found is assumed to be correct. The other targets are compared to this
"correct" target and the number of
targets that require change should target N be correct is counted. If the
number of changes is 0, then all the targets
must already be correct. Otherwise the target that requires the fewest changes
to the others is used as the base for
change. A change is registered if a given target's target number and pixel
position do not correlate when compared
to the "correct" target's pixel position and target number. The change may
mean updating a target's target
number, or it may mean elimination of the target. It is possible to assume
that ascending targets have pixels in
ascending order (since they have already been sorted).
kPixelFactor =1/(55 * 3)
bestTarget = 0
bestChanges = TargetsFound + 1
for (i 0; i< TotalTargetsFound; i++)
CA 02564047 2006-11-06
YU139 PCT 92
{
numberOfChanges = 0;
fromPixel = (LocatedTargets[i])->Pixel
fromTargetNumber = LocatedTargets[i].TargetNumber
for (j=1; j< TotalTargetsFound; j++)
{
toPixel = LocatedTargets[j]->Pixel
deltaPixel = toPixel - fromPixel
if (deltaPixel >= 0)
deltaPixel += PIXELS-BETWEEN-TARGET-CENTRES/2
else
deltaPixel -= PIXELS-BETWEEN-TARGET-CENTRES/2
targetNumber =deltaPixel * kPixelFactor
targetNumber += fromTargetNumber
if
(targetNumber < 1) I I(targetNumber > 6)
11
(targetNumber != LocatedTargets[j]-> TargetNumber)
)
numberOfChanges++
}
if (numberOfChanges < bestChanges)
{
bestTarget = i
bestChanges = numberOfChanges
}
if (bestChanges < 2)
break;
}
In most cases this function will terminate with bestChanges = 0, which means
no changes are required.
Otherwise the changes need to be applied. The functionality of applying the
changes is identical to counting the
changes (in the pseudocode above) until the comparison with targetNumber. The
change application is:
if ((targetNumber < I)II(targetNumber > TARGETS-PER-BLOCK))
{
LocatedTargets[j] = NULL
TargetsFound--
CA 02564047 2006-11-06
YU139 PCT 93
}
else
{
LocatedTargets[j]-> TargetNumber = targetNumber
}
At the end of the change loop, the LocatedTargets list needs to be compacted
and all NULL targets
removed.
At the end of this procedure, there may be fewer targets. Whatever targets
remain may now be used (at
least 2 targets are required) to locate the clockmarks and the data region.
Building Clockmark Estimates from Targets
As shown previously in Fig. 55, the upper region's first clockmark dot 1126 is
55 dots away from the
center of the first target 1124 (which is the same as the distance between
target centers). The center of the
clockmark dots is a further 1 dot away, and the black border line 1123 is a
further 4 dots away from the first
clockmark dot. The lower region's first clockmark dot is exactly 7 targets-
distance away (7 x 55 dots) from the
upper region's first clockmark dot 1126.
It cannot be assumed that Targets 1 and 6 have been located, so it is
necessary to use the upper-most and
lower-most targets, and use the target numbers to determine which targets are
being used. It is necessary at least 2
targets at this point. In addition, the target centers are only estimates of
the actual target centers. It is to locate the
target center more accurately. The center of a target is white, surrounded by
black. We therefore want to fmd the
local maximum in both pixel & column dimensions. This involves reconstructing
the continuous image since the
maximum is unlikely to be aligned exactly on an integer boundary (our
estimate).
Before the continuous image can be constructed around the target's center, it
is necessary to create a
better estimate of the 2 target centers. The existing target centers actually
are the top left coordinate of the
bounding box of the target center. It is a simple process to go through each
of the pixels for the area defining the
center of the target, and find the pixel with the highest value. There may be
more than one pixel with the same
maximum pixel value, but the estimate of the center value only requires one
pixel.
The pseudocode is straightforward, and is performed for each of the 2 targets:
CENTER WIDTH = CENTER HEIGHT = 12
maxPixel = 0x00
for (i=0; i<CENTER WIDTH; i++)
for (jam; j<CENTER HEIGHT; j++)
{
p = GetPixel(column+i, pixel+j)
if (p > maxPixel)
f
maxPixel = p
centerColumn = column + i
centerPixel = pixel + j
CA 02564047 2006-11-06
YU139 PCT 94
}
}
Target.Colunm = centerColumn
Target.Pixel = centerPixel
At the end of this process the target center coordinates point to the whitest
pixel of the target, which
should be within one pixel of the actual center. The process of building a
more accurate position for the target
center involves reconstructing the continuous signal for 7 scanline slices of
the target, 3 to either side of the
estimated target center. The 7 maximum values found (one for each of these
pixel dimension slices) are then used
to reconstruct a continuous signal in the column dimension and thus to locate
the maximum value in that
dimension.
Given estimates column and pixel, determine a
betterColumn and betterPixel as the center of
/1 the target
for (y=O; y<7; y++)
{
for (x-0; x<7; x++)
samples[x] = GetPixel(column-3+y, pixel-3+x)
FindMax(samples, pos, maxVal)
reSamples[y] = maxVal
if (y == 3)
betterPixel = pos + pixel
}
FindMax(reSamples, pos, maxVal)
betterColumn = pos + column
FindMax is a function that reconstructs the original 1 dimensional signal
based sample points and returns
the position of the maximum as well as the maximum value found. The method of
signal
reconstruction/resampling used is the Lanczos3 windowed sinc function as shown
in Fig. 76.
The Lanczos3 windowed sinc function takes 7 (pixel) samples from the dimension
being reconstructed,
centered around the estimated position X, i.e. at X-3, X-2, X- 1, X, X+ 1,
X+2, X+3. We reconstruct points from X-
1 to X+1, each at an interval of 0.1, and determine which point is the
maximum. The position that is the
maximum value becomes the new center. Due to the nature of the kernel, only 6
entries are required in the
convolution kernel for points between X and X+1. We use 6 points for X-1 to X,
and 6 points for X to X+1,
requiring 7 points overall in order to get pixel values from X-1 to X+1 since
some of the pixels required are the
same.
Given accurate estimates for the upper-most target from and lower-most target
to, it is possible to
calculate the position of the first clockmark dot for the upper and lower
regions as follows:
CA 02564047 2006-11-06
YU139 PCT 95
TARGETS-PER-BLOCK = 6
numTargetsDiff = to.TargetNum - from.TargetNum
deltaPixel = (to.Pixel - from.Pixel) / numTargetsDiff
deltaColumn = (to.Column - from.Column) / numTargetsDiff
UpperClock.pixel = fromPixel - (fromTargetNum*deltaPixel)
UpperClock.column = from.Column-(from.TargetNum*deltaColunm)
11 Given the first dot of the upper clockmark, the
// first dot of the lower clockmark is straightforward.
LowerClock.pixel = UpperClock.pixel +
((TARGETS-PER BLOCK+ 1) * deltaPixel)
LowerClock.column = UpperClock.column +
((TARGETS-PER BLOCK+1) * deltaColumn)
This gets us to the first clockmark dot. It is necessary move the column
position a further 1 dot away
from the data area to reach the center of the clockmark. It is necessary to
also move the pixel position a further 4
dots away to reach the center of the border line. The pseudocode values for
deltaColumn and deltaPixel are based
on a 55 dot distance (the distance between targets), so these deltas must be
scaled by 1/55 and 4/55 respectively
before being applied to the clockmark coordinates. This is represented as:
kDeltaDotFactor = 1/DOTS BETWEEN TARGET CENTRES
deltaColumn *= kDeltaDotFactor
deltaPixel *= 4 * kDeltaDotFactor
UpperClock.pixel = deltaPixel
UpperClock.column = deltaColumn
LowerClock.pixel += deltaPixel
LowerClock.column += deltaColumn
UpperClock and LowerClock are now valid clockmark estimates for the first
clockmarks directly in line
with the centers of the targets.
Setting Black and White Pixel/Dot Ranges
Before the data can be extracted from the data area, the pixel ranges for
black and white dots needs to be
ascertained. The minimum and maximum pixels encountered during the search for
targets were stored in
WhiteMin and BlackMax respectively, but these do not represent valid values
for these variables with respect to
data extraction. They are merely used for storage convenience. The following
pseudocode shows the method of
obtaining good values for WhiteMin and BlackMax based on the min & max pixels
encountered:
MinPixel = WhiteMin
MaxPixel = BlackMax
MidRange = (MinPixel + MaxPixel) / 2
CA 02564047 2006-11-06
YU139 PCT 96
WhiteMin = MaxPixel - 105
BlackMax = MinPixel + 84
CurrentState = ExtractingBitlmage
The ExtractingBitlmage state is one where the data block has already been
accurately located via the
targets, and bit data is currently being extracted one dot column at a time
and written to the alternative Artcard bit
image. The following of data block clockmarks/borders gives accurate dot
recovery regardless of rotation, and
thus the segment bounds are ignored. Once the entire data block has been
extracted (597 columns of 48 bytes
each; 595 columns of data + 2 orientation columns), new segment bounds are
calculated for the next data block
based on the current position. The state is changed to LookingForTargets.
Processing a given dot column involves two tasks:
* The first task is to locate the specific dot column of data via the
clockmarks.
* The second task is to run down the dot column gathering the bit values, one
bit per dot.
These two tasks can only be undertaken if the data for the column has been
read off the alternative
Artcard and transferred to DRAM. This can be determined by checking what
scanline Process 1 is up to, and
comparing it to the clockmark columns. If the dot data is in DRAM we can
update the clockmarks and then
extract the data from the column before advancing the clockmarks to the
estimated value for the next dot column.
The process overview is given in the following pseudocode, with specific
functions explained hereinafter:
finishedBlock = FALSE
if((UpperClock.column < Process 1.CurrentScanLine)
&&
(LowerClock.column < Process 1.CurrentScanLine))
{
DetermineAccurateClockMarks()
DetermineDatalnfo()
if (CurrentDotColumn >= 0)
ExtractDataFromColumn()
AdvanceClockMarks()
if (CurrentDotColumn == FINAL COLUMN)
{
finishedBlock = TRUE
currentState = LookingForTargets
SetBounds(UpperClock.pixel, LowerClock.pixel)
BitImage += 256KB
CurrentByte = 0
TargetsFound = 0
}
}
return finishedBlock
CA 02564047 2006-11-06
YU139 PCT 97
Locating the dot column
A given dot column needs to be located before the dots can be read and the
data extracted. This is
accomplished by following the clockmarks/borderline along the upper and lower
boundaries of the data block. A
software equivalent of a phase-locked-loop is used to ensure that even if the
clockmarks have been damaged, good
estimations of clockmark positions will be made. Fig. 77 illustrates an
example data block's top left which corner
reveals that there are clockmarks 3 dots high 1166 extending out to the target
area, a white row, and then a black
border line.
Initially, an estimation of the center of the first black clockmark position
is provided (based on the target
positions). We use the black border 1168 to achieve an accurate vertical
position (pixel), and the clockmark eg.
1166 to get an accurate horizontal position (column). These are reflected in
the UpperClock and LowerClock
positions.
The clockmark estimate is taken and by looking at the pixel data in its
vicinity, the continuous signal is
reconstructed and the exact center is determined. Since we have broken out the
two dimensions into a clockmark
and border, this is a simple one-dimensional process that needs to be
performed twice. However, this is only done
every second dot column, when there is a black clockmark to register against.
For the white clockmarks we simply
use the estimate and leave it at that. Alternatively, we could update the
pixel coordinate based on the border each
dot column (since it is always present). In practice it is sufficient to
update both ordinates every other column
(with the black clockmarks) since the resolution being worked at is so fine.
The process therefore becomes:
Turn the estimates of the clockmarks into accurate
positions only when there is a black clockmark
// (ie every 2nd dot column, starting from -8)
if (BitO(CurrentDotColumn) = 0) // even column
{
DetermineAccurateUpperpotCenter()
DeterniineAccurateLowerpotCenter()
}
If there is a deviation by more than a given tolerance
(MAX_CLOCKMARK_DEVIATION), the found
signal is ignored and only deviation from the estimate by the maximum
tolerance is allowed. In this respect the
functionality is similar to that of a phase-locked loop. Thus
DetermineAccurateUpperpotCenter is implemented
via the following pseudocode:
// Use the estimated pixel position of
the border to determine where to look for
a more accurate clockmark center. The clockmark
// is 3 dots high so even if the estimated position
!/ of the border is wrong, it won't affect the
// fixing of the clockmark position.
CA 02564047 2006-11-06
YU139PCT 98
MAX CLOCKMARK DEVIATION = 0.5
diff = GetAccurateColumn(UpperClock.column,
UpperClock.pixel+(3*PIXELS PER DOT))
diff -= UpperClock.colunm
if (diff > MAX CLOCKMARK DEVIATION)
duff = MAX CLOCKMARK DEVIATION
else
if (diff < -MAX CLOCKMARK DEVIATION)
diff = -MAX CLOCKMARK DEVIATION
UpperClock.column += diff
Use the newly obtained clockmark center to
determine a more accurate border position.
diff = GetAccuratePixel(UpperClock.column, UpperClock.pixel)
diff -= UpperClock.pixel
if (diff> MAX_CLOCKMARK DEVIATION)
diff= MAX CLOCKMARK DEVIATION
else
if (diff < -MAX_CLOCKMARK_DEVIATION)
diff=-MAX CLOCKMARK DEVIATION
UpperClock.pixel += diff
DetermineAccurateLowerpotCenter is the same, except that the direction from
the border to the
clockmark is in the negative direction (-3 dots rather than +3 dots).
GetAccuratePixel and GetAccurateColumn are functions that determine an
accurate dot center given a
coordinate, but only from the perspective of a single dimension. Determining
accurate dot centers is a process of
signal reconstruction and then finding the location where the minimum signal
value is found (this is different to
locating a target center, which is locating the maximum value of the signal
since the target center is white, not
black). The method chosen for signal reconstruction/resampling for this
application is the Lanczos3 windowed
sinc function as previously discussed with reference to Fig. 76.
It may be that the clockmark or border has been damaged in some way - perhaps
it has been scratched. If
the new center value retrieved by the resampling differs from the estimate by
more than a tolerance amount, the
center value is only moved by the maximum tolerance. If it is an invalid
position, it should be close enough to use
for data retrieval, and future clockmarks will resynchronize the position.
Determining the center of the first data dot and the deltas to subsequent dots
Once an accurate UpperClock and LowerClock position has been determined, it is
possible to calculate
the center of the first data dot (CurrentDot), and the delta amounts to be
added to that center position in order to
advance to subsequent dots in the column (DataDelta).
The first thing to do is calculate the deltas for the dot column. This is
achieved simply by subtracting the
UpperClock from the LowerClock, and then dividing by the number of dots
between the two points. It is possible
CA 02564047 2006-11-06
YU139 PCT 99
to actually multiply by the inverse of the number of dots since it is constant
for an alternative Artcard, and
multiplying is faster. It is possible to use different constants for obtaining
the deltas in pixel and column
dimensions. The delta in pixels is the distance between the two borders, while
the delta in columns is between the
centers of the two clockmarks. Thus the function DetermineDatalnfo is two
parts. The first is given by the
pseudocode:
kDeltaColumnFactor = 1 / (DOTS PER DATA COLUMN + 2 + 2 - 1)
kDeltaPixelFactor =1 / (DOTS-PER-DATA-COLUMN + 5 + 5 - 1)
delta = LowerClock.column - UpperClock.column
DataDelta.column = delta * kDeltaColumnFactor
delta = LowerClock.pixel - UpperClock.pixel
DataDelta.pixel = delta * kDeltaPixelFactor
It is now possible to determine the center of the first data dot of the
column. There is a distance of 2 dots
from the center of the clockmark to the center of the first data dot, and 5
dots from the center of the border to the
center of the first data dot. Thus the second part of the function is given by
the pseudocode:
CurrentDot.column = UpperClock.column + (2*DataDelta.column)
CurrentDot.pixel = UpperClock.pixel + (5*DataDelta.pixel)
Running down a dot column
Since the dot column has been located from the phase-locked loop tracking the
clockmarks, all that
remains is to sample the dot column at the center of each dot down that
column. The variable CurrentDot points
is determined to the center of the first dot of the current column. We can get
to the next dot of the column by
simply adding DataDelta (2 additions: 1 for the column ordinate, the other for
the pixel ordinate). A sample of the
dot at the given coordinate (bi-linear interpolation) is taken, and a pixel
value representing the center of the dot is
determined. The pixel value is then used to determine the bit value for that
dot. However it is possible to use the
pixel value in context with the center value for the two surrounding dots on
the same dot line to make a better bit
judgement.
We can be assured that all the pixels for the dots in the dot column being
extracted are currently loaded in
DRAM, for if the two ends of the line (clockmarks) are in DRAM, then the dots
between those two clockmarks
must also be in DRAM. Additionally, the data block height is short enough
(only 384 dots high) to ensure that
simple deltas are enough to traverse the length of the line. One of the
reasons the card is divided into 8 data blocks
high is that we cannot make the same rigid guarantee across the entire height
of the card that we can about a single
data block.
The high level process of extracting a single line of data (48 bytes) can be
seen in the following
pseudocode. The dataBuffer pointer increments as each byte is stored, ensuring
that consecutive bytes and
columns of data are stored consecutively.
CA 02564047 2006-11-06
YU139 PCT 100
bitCount = 8
curr = 0x00 // definitely black
next = GetPixel(CurrentDot)
for (i=0; i < DOTS-PER-DATA-COLUMN; i++)
{
CurrentDot += DataDelta
prey = curr
curr = next
next = GetPixel(CurrentDot)
bit = DetermineCenterpot(prev, curr, next)
byte = (byte << 1) 1 bit
bitCount--
if (bitCount = 0)
{
*(Bitlmage I CurrentByte) = byte
CurrentByte++
bitCount = 8
}
}
The GetPixel function takes a dot coordinate (fixed point) and samples 4 CCD
pixels to arrive at a center
pixel value via bilinear interpolation.
The DetermineCenterpot function takes the pixel values representing the dot
centers to either side of the
dot whose bit value is being determined, and attempts to intelligently guess
the value of that center dot's bit value.
From the generalized blurring curve of Fig. 64 there are three common cases to
consider:
* The dot's center pixel value is lower than WhiteMin, and is therefore
definitely a black dot. The
bit value is therefore definitely 1.
* The dot's center pixel value is higher than BlackMax, and is therefore
definitely a white dot.
The bit value is therefore definitely 0.
* The dot's center pixel value is somewhere between BlackMax and WhiteMin. The
dot may be
black, and it may be white. The value for the bit is therefore in question. A
number of schemes can be devised to
make a reasonable guess as to the value of the bit. These schemes must balance
complexity against accuracy, and
also take into account the fact that in some cases, there is no guaranteed
solution. In those cases where we make a
wrong bit decision, the bit's Reed-Solomon symbol will be in error, and must
be corrected by the Reed-Solomon
decoding stage in Phase 2.
The scheme used to determine a dot's value if the pixel value is between
BlackMax and WhiteMin is not
too complex, but gives good results. It uses the pixel values of the dot
centers to the left and right of the dot in
question, using their values to help determine a more likely value for the
center dot:
* If the two dots to either side are on the white side of MidRange (an average
dot value), then we
can guess that if the center dot were white, it would likely be a "definite"
white. The fact that it is in the not-sure
CA 02564047 2006-11-06
YU139 PCT 101
region would indicate that the dot was black, and had been affected by the
surrounding white dots to make the
value less sure. The dot value is therefore assumed to be black, and hence the
bit value is 1.
* If the two dots to either side are on the black side of MidRange, then we
can guess that if the
center dot were black, it would likely be a "definite" black. The fact that it
is in the not-sure region would indicate
that the dot was white, and had been affected by the surrounding black dots to
make the value less sure. The dot
value is therefore assumed to be white, and hence the bit value is 0.
* If one dot is on the black side of MidRange, and the other dot is on the
white side of MidRange,
we simply use the center dot value to decide. If the center dot is on the
black side of MidRange, we choose black
(bit value 1). Otherwise we choose white (bit value 0).
The logic is represented by the following:
if (pixel < WhiteMin) definitely black
bit = 0x01
else
if (pixel > BlackMax) definitely white
bit = 0x00
else
if ((prev > MidRange) && (next> MidRange)) //prob black
bit = 0x01
else
if ((prey < MidRange) && (next < MidRange)) //prob white
bit = 0x00
else
if (pixel < MidRange)
bit = 0x01
else
bit = 0x00
From this one can see that using surrounding pixel values can give a good
indication of the value of the
center dot's state. The scheme described here only uses the dots from the same
row, but using a single dot line
history (the previous dot line) would also be straightforward as would be
alternative arrangements.
Updating clockmarks for the next column
Once the center of the first data dot for the column has been determined, the
clockmark values are no
longer needed. They are conveniently updated in readiness for the next column
after the data has been retrieved
for the column. Since the clockmark direction is perpendicular to the
traversal of dots down the dot column, it is
possible to use the pixel delta to update the column, and subtract the column
delta to update the pixel for both
clocks:
UpperClock.column += DataDelta.pixel
LowerClock.column += DataDelta.pixel
CA 02564047 2006-11-06
YU139 PCT 102
UpperClock.pixel = DataDelta.column
LowerClock.pixel = DataDelta.column
These are now the estimates for the next dot column.
Timing
The timing requirement will be met as long as DRAM utilization does not exceed
100%, and the addition
of parallel algorithm timing multiplied by the algorithm DRAM utilization does
not exceed 100%. DRAM
utilization is specified relative to Process 1, which writes each pixel once
in a consecutive manner, consuming 9%
of the DRAM bandwidth.
The timing as described in this section, shows that the DRAM is easily able to
cope with the demands of
the alternative Artcard Reader algorithm. The timing bottleneck will therefore
be the implementation of the
algorithm in terms of logic speed, not DRAM access. The algorithms have been
designed however, with simple
architectures in mind, requiring a minimum number of logical operations for
every memory cycle. From this point
of view, as long as the implementation state machine or equivalent CPU/DSP
architecture is able to perform as
described in the following sub-sections, the target speed will be met.
Locating the targets
Targets are located by reading pixels within the bounds of a pixel column.
Each pixel is read once at
most. Assuming a run-length encoder that operates fast enough, the bounds on
the location of targets is memory
access. The accesses will therefore be no worse than the timing for Process 1,
which means a 9% utilization of the
DRAM bandwidth.
The total utilization of DRAM during target location (including Process 1) is
therefore 18%, meaning that
the target locator will always be catching up to the alternative Artcard image
sensor pixel reader.
Processing the targets
The timing for sorting and checking the target numbers is trivial. The finding
of better estimates for each
of the two target centers involves 12 sets of 12 pixel reads, taking a total
of 144 reads. However the fixing of
accurate target centers is not trivial, requiring 2 sets of evaluations.
Adjusting each target center requires 8 sets of
20 different 6-entry convolution kernels. Thus this totals 8 x 20 x 6 multiply-
accumulates = 960. In addition, there
are 7 sets of 7 pixels to be retrieved, requiring 49 memory accesses. The
total number per target is therefore 144 +
960 + 49 = 1153, which is approximately the same number of pixels in a column
of pixels (1152). Thus each
target evaluation consumes the time taken by otherwise processing a row of
pixels. For two targets we effectively
consume the time for 2 columns of pixels.
A target is positively identified on the first pixel column after the target
number. Since there are 2 dot
columns before the orientation column, there are 6 pixel columns. The Target
Location process effectively uses up
the first of the pixel columns, but the remaining 5 pixel columns are not
processed at all. Therefore the data area
can be located in 2/5 of the time available without impinging on any other
process time.
The remaining 3/5 of the time available is ample for the trivial task of
assigning the ranges for black and
white pixels, a task that may take a couple of machine cycles at most.
Extracting data
There are two parts to consider in terms of timing:
* Getting accurate clockmarks and border values
CA 02564047 2006-11-06
YU139 PCT 103
* Extracting dot values
Clockmarks and border values are only gathered every second dot column.
However each time a
clockmark estimate is updated to become more accurate, 20 different 6-entry
convolution kernels must be
evaluated. On average there are 2 of these per dot column (there are 4 every 2
dot-columns). Updating the pixel
ordinate based on the border only requires 7 pixels from the same pixel
scanline. Updating the column ordinate
however, requires 7 pixels from different columns, hence different scanlines.
Assuming worst case scenario of a
cache miss for each scanline entry and 2 cache misses for the pixels in the
same scanline, this totals 8 cache
misses.
Extracting the dot information involves only 4 pixel reads per dot (rather
than the average 9 that define
the dot). Considering the data area of 1152 pixels (384 dots), at best this
will save 72 cache reads by only reading
4 pixel dots instead of 9. The worst case is a rotation of 1 which is a
single pixel translation every 57 pixels,
which gives only slightly worse savings.
It can then be safely said that, at worst, we will be reading fewer cache
lines less than that consumed by
the pixels in the data area. The accesses will therefore be no worse than the
timing for Process 1, which implies a
9% utilization of the DRAM bandwidth.
The total utilization of DRAM during data extraction (including Processl) is
therefore 18%, meaning
that the data extractor will always be catching up to the alternative Artcard
image sensor pixel reader. This has
implications for the Process Targets process in that the processing of targets
can be performed by a relatively
inefficient method if necessary, yet still catch up quickly during the
extracting data process.
Phase 2 - Decode Bit Image
Phase 2 is the non-real-time phase of alternative Artcard data recovery
algorithm. At the start of Phase 2
a bit image has been extracted from the alternative Artcard. It represents the
bits read from the data regions of the
alternative Artcard. Some of the bits will be in error, and perhaps the entire
data is rotated 180 because the
alternative Artcard was rotated when inserted. Phase 2 is concerned with
reliably extracting the original data from
this encoded bit image. There are basically 3 steps to be carried out as
illustrated in Fig. 79:
* Reorganize the bit image, reversing it if the alternative Artcard was
inserted backwards
* Unscramble the encoded data
* Reed-Solomon decode the data from the bit image
Each of the 3 steps is defined as a separate process, and performed
consecutively, since the output of one
is required as the input to the next. It is straightforward to combine the
first two steps into a single process, but for
the purposes of clarity, they are treated separately here.
From a data/process perspective, Phase 2 has the structure as illustrated in
Fig. 80.
The timing of Processes 1 and 2 are likely to be negligible, consuming less
than 1/1000" of a second
between them. Process 3 (Reed Solomon decode) consumes approximately 0.32
seconds, making this the total
time required for Phase 2.
Reorganize the bit image, reversing it if necessary
The bit map in DRAM now represents the retrieved data from the alternative
Artcard. However the bit image is
not contiguous. It is broken into 64 32k chunks, one chunk for each data
block. Each 32k chunk contains only
28,656 useful bytes:
48 bytes from the leftmost Orientation Column
CA 02564047 2006-11-06
YU139 PCT 104
28560 bytes from the data region proper
48 bytes from the rightmost Orientation Column
4112 unused bytes
The 2MB buffer used for pixel data (stored by Process 1 of Phase 1) can be
used to hold the reorganized
bit image, since pixel data is not required during Phase 2. At the end of the
reorganization, a correctly oriented
contiguous bit image will be in the 2MB pixel buffer, ready for Reed-Solomon
decoding.
If the card is correctly oriented, the leftmost Orientation Column will be
white and the rightmost
Orientation Column will be black. If the card has been rotated 180 , then the
leftmost Orientation Column will be
black and the rightmost Orientation Column will be white.
A simple method of determining whether the card is correctly oriented or not,
is to go through each data
block, checking the first and last 48 bytes of data until a block is found
with an overwhelming ratio of black to
white bits. The following pseudocode demonstrates this, returning TRUE if the
card is correctly oriented, and
FALSE if it is not:
totalCountL = 0
totalCountR = 0
for (i=0; i<64; i++)
{
blackCountL = 0
blackCountR = 0
currBuff = dataBuffer
for (j-0; j<48; j++)
{
blackCountL += CountBits(*currBuff)
currBuff++
}
currBuff+= 28560
for (j=0; j<48; j++)
{
blackCountR += CountBits(*currBuff)
currBuff++
}
dataBuffer += 32k
if (blackCountR > (blackCountL * 4))
return TRUE
if (blackCountL > (blackCountR * 4))
return FALSE
totalCountL += blackCountL
totalCountR += blackCountR
}
CA 02564047 2006-11-06
YU139 PCT 105
return (totalCountR > totalCountL)
The data must now be reorganized, based on whether the card was oriented
correctly or not. The simplest
case is that the card is correctly oriented. In this case the data only needs
to be moved around a little to remove the
orientation columns and to make the entire data contiguous. This is achieved
very simply in situ, as described by
the following pseudocode:
DATA-BYTES-PER-DATA-BLOCK = 28560
to = dataBuffer
from = dataBuffer + 48) left orientation column
for (i=0; i<64; i++)
{
BlockMove(fron-4 to, DATA-BYTES-PER-DATA BLOCK)
from += 32k
to += DATA-BYTES-PER-DATA-BLOCK
}
The other case is that the data actually needs to be reversed. The algorithm
to reverse the data is quite
simple, but for simplicity, requires a 256-byte table Reverse where the value
of Reverse[N] is a bit-reversed N.
DATA-BYTES-PER-DATA-BLOCK = 28560
to = outBuffer
for (i=0; i<64; i++)
{
from = dataBuffer + (i * 32k)
from += 48 skip orientation column
from += DATA-BYTES-PER-DATA-BLOCK - I // end of block
for (j=0; j < DATA-BYTES-PER-DATA-BLOCK; j++)
{
*to++ = Reverse[*from]
from--
}
}
The timing for either process is negligible, consuming less than 1/1000" of a
second:
* 2MB contiguous reads (2048/16 x 12ns =1,536ns)
* 2MB effectively contiguous byte writes (2048/16 x 12ns = 1,536ns)
Unscramble the encoded image
The bit image is now 1,827,840 contiguous, correctly oriented, but scrambled
bytes. The bytes must be
unscrambled to create the 7,168 Reed-Solomon blocks, each 255 bytes long. The
unscrambling process is quite
CA 02564047 2006-11-06
YU139 PCT 106
straightforward, but requires a separate output buffer since the unscrambling
cannot be performed in situ. Fig. 80
illustrates the unscrambling process conducted memory
The following pseudocode defines how to perform the unscrambling process:
groupSize = 255
numBytes = 1827840;
inBuffer = scrambledBuffer;
outBuffer = unscrambledBuffer;
for (i=0; i<groupSize; i++)
for (j=i; j<numBytes; j+=groupSize)
outBuffer[j] = *inBuffer++
The timing for this process is negligible, consuming less than 1/1000' of a
second:
* 2MB contiguous reads (2048/16 x 12ns = 1,536ns)
* 2MB non-contiguous byte writes (2048 x 12ns = 24,576ns)
At the end of this process the unscrambled data is ready for Reed-Solomon
decoding.
Reed Solomon decode
The final part of reading an alternative Artcard is the Reed-Solomon decode
process, where
approximately 2MB of unscrambled data is decoded into approximately 1MB of
valid alternative Artcard data.
The algorithm performs the decoding one Reed-Solomon block at a time, and can
(if desired) be
performed in situ, since the encoded block is larger than the decoded block,
and the redundancy bytes are stored
after the data bytes.
The first 2 Reed-Solomon blocks are control blocks, containing information
about the size of the data to
be extracted from the bit image. This meta-information must be decoded first,
and the resultant information used
to decode the data proper. The decoding of the data proper is simply a case of
decoding the data blocks one at a
time. Duplicate data blocks can be used if a particular block fails to decode.
The highest level of the Reed-Solomon decode is set out in pseudocode:
Constants for Reed Solomon decode
sourceBlockLength = 255;
destBlockLength = 127;
numControlBlocks = 2;
// Decode the control information
if (! GetControlData(source, destBlocks, lastBlock))
return error
destBytes = ((destBlocks-1) * destBlockLength) + lastBlock
offsetToNextDuplicate = destBlocks * sourceBlockLength
CA 02564047 2006-11-06
YU139 PCT 107
// Skip the control blocks and position at data
source += numControlBlocks * sourceBlockLength
// Decode each of the data blocks, trying
II duplicates as necessary
blocksInError = 0;
for (i=0; i<destBlocks; i++)
{
found = DecodeBlock(source, dest);
if (! found)
{
duplicate = source + offsetToNextDuplicate
while ((! found) && (duplicate<sourceEnd))
{
found = DecodeBlock(duplicate, dest)
duplicate += offsetToNextDuplicate
}
}
if (! found)
blocksInError++
source += sourceBlockLength
dest += destBlockLength
}
return destBytes and blocksInError
DecodeBlock is a standard Reed Solomon block decoder using m=8 and t=64.
The GetControlData function is straightforward as long as there are no
decoding errors. The function
simply calls DecodeBlock to decode one control block at a time until
successful. The control parameters can then
be extracted from the first 3 bytes of the decoded data (destBlocks is stored
in the bytes 0 and 1, and lastBlock is
stored in byte 2). If there are decoding errors the function must traverse the
32 sets of 3 bytes and decide which is
the most likely set value to be correct. One simple method is to find 2
consecutive equal copies of the 3 bytes, and
to declare those values the correct ones. An alternative method is to count
occurrences of the different sets of 3
bytes, and announce the most common occurrence to be the correct one.
The time taken to Reed-Solomon decode depends on the implementation. While it
is possible to use a
dedicated core to perform the Reed-Solomon decoding process (such as LSI
Logic's L64712), it is preferable to
select a CPU/DSP combination that can be more generally used throughout the
embedded system (usually to do
something with the decoded data) depending on the application. Of course
decoding time must be fast enough
with the CPU/DSP combination.
The L64712 has a throughput of 50Mbits per second (around 6.25MB per second),
so the time is bound
CA 02564047 2006-11-06
YU139 PCT 108
by the speed of the Reed-Solomon decoder rather than the maximum 2MB read and
1 MB write memory access
time. The time taken in the worst case (all 2MB requires decoding) is thus
2/6.25s = approximately 0.32 seconds.
Of course, many further refinements are possible including the following:
The blurrier the reading environment, the more a given dot is influenced by
the surrounding dots. The
current reading algorithm of the preferred embodiment has the ability to use
the surrounding dots in the same
column in order to make a better decision about a dot's value. Since the
previous column's dots have already been
decoded, a previous column dot history could be useful in determining the
value of those dots whose pixel values
are in the not-sure range.
A different possibility with regard to the initial stage is to remove it
entirely, make the initial bounds of
the data blocks larger than necessary and place greater intelligence into the
ProcessingTargets functions. This may
reduce overall complexity. Care must be taken to maintain data block
independence.
Further the control block mechanism can be made more robust:
* The control block could be the first and last blocks rather than make them
contiguous (as is the
case now). This may give greater protection against certain pathological
damage scenarios.
* The second refinement is to place an additional level of redundancy/error
detection into the
control block structure to be used if the Reed-Solomon decode step fails.
Something as simple as parity might
improve the likelihood of control information if the Reed-Solomon stage fails.
Phase 5 Running the Vark script
The overall time taken to read the Artcard 9 and decode it is therefore
approximately 2.15 seconds. The
apparent delay to the user is actually only 0.65 seconds (the total of Phases
3 and 4), since the Artcard stops
moving after 1.5 seconds.
Once the Artcard is loaded, the Artvark script must be interpreted, Rather
than run the script
immediately, the script is only run upon the pressing of the `Print' button 13
(Fig. 1). The taken to run the script
will vary depending on the complexity of the script, and must be taken into
account for the perceived delay
between pressing the print button and the actual print button and the actual
printing.
As noted previously, the VLIW processor 74 is a digital processing system that
accelerates
computationally expensive Vark functions. The balance of functions performed
in software by the CPU core 72,
and in hardware by the VLIW processor 74 will be implementation dependent. The
goal of the VLIW processor
74 is to assist all Artcard styles to execute in a time that does not seem too
slow to the user. As CPUs become
faster and more powerful, the number of functions requiring hardware
acceleration becomes less and less. The
VLIW processor has a microcoded ALU sub-system that allows general hardware
speed up of the following time-
critical functions.
1) Image access mechanisms for general software processing
2) Image convolver.
3) Data driven image warper
4) Image scaling
5) Image tessellation
6) Affine transform
7) Image compositor
CA 02564047 2006-11-06
YU139 PCT 109
8) Color space transform
9) Histogram collector
10) Illumination of the Image
11) Brush stamper
12) Histogram collector
13) CCD image to internal image conversion
14) Construction of image pyramids (used by warper & for brushing)
The following table summarizes the time taken for each Vark operation if
implemented in the ALU
model. The method of implementing the function using the ALU model is
described hereinafter.
Operation Speed of Operation 1500 * 1000 image
1 channel 3 channels
Image composite 1 cycle per output pixel 0.015s 0.045 s
Image convolve k/3 cycles per output
pixel
(k = kernel size)
3x3 convolve 0.045 s 0.135 s
5x5 convolve 0.125 s 0.375 s
7x7 convolve 0.245 s 0.735 s
Image warp 8 cycles per pixel 0.120 s 0.360 s
Histogram collect 2 cycles per pixel 0.030 s 0.090 s
Image Tessellate 1/3 cycle per pixel 0.005 s 0.015s
Image sub-pixel Translate 1 cycle per output pixel
- -
Color lookup replace '/2 c cle per pixel 0.008 s 0.023
Color space transform 8 cycles per pixel 0.120s 0.360s
Convert CCD image to 4 cycles per output pixel 0.06 s 0.18 s
internal image (including
color convert & scale)
Construct image pyramid 1 cycle per input pixel 0.015 s 0.045 s
Scale Maximum of: 0.015s 0.045 s (minimum)
2 cycles per input pixel (minimum)
2 cycles per output pixel
2 cycles per output pixel
(scaled in X only)
Affine transform 2 cycles per output pixel 0.03 s 0.09 s
Brush rotate/translate and ?
composite
Tile Image 4-8 cycles per output 0.015 s to 0.030 s 0.060 s to 0.120 s to for
pixel 4 channels (Lab,
texture)
Illuminate image Cycles per pixel
Ambient only '/2 0.008 s 0.023 s
Directional light 1 0.015s 0.045 s
Directional (bm) 6 0.09 s 0.27 s
Omni light 6 0.09 s 0.27 s
Omni (bm) 9 0.137s 0.41 s
Spotlight 9 0.137s 0.41 s
Spotlight (bm) 12 0.18 s 0.54 s
(bm) = bumpmap
CA 02564047 2006-11-06
YU139 PCT 110
For example, to convert a CCD image, collect histogram & perform lookup-color
replacement (for image
enhancement) takes: 9+2+0.5 cycles per pixel, or 11.5 cycles. For a 1500 x
1000 image that is 172,500,000, or
approximately 0.2 seconds per component, or 0.6 seconds for all 3 components.
Add a simple warp, and the total
comes to 0.6 + 0.36, almost 1 second.
Image Convolver
A convolve is a weighted average around a center pixel. The average may be a
simple sum, a sum of
absolute values, the absolute value of a sum, or sums truncated at 0.
The image convolver is a general-purpose convolver, allowing a variety of
functions to be implemented
by varying the values within a variable-sized coefficient kernel. The kernel
sizes supported are 3x3, 5x5 and 7x7
only.
Turning now to Fig. 82, there is illustrated 340 an example of the convolution
process. The pixel
component values fed into the convolver process 341 come from a Box Read
Iterator 342. The Iterator 342
provides the image data row by row, and within each row, pixel by pixel. The
output from the convolver 341 is
sent to a Sequential Write Iterator 344, which stores the resultant image in a
valid image format.
A Coefficient Kernel 346 is a lookup table in DRAM. The kernel is arranged
with coefficients in the
same order as the Box Read Iterator 342. Each coefficient entry is 8 bits. A
simple Sequential Read Iterator can be
used to index into the kernel 346 and thus provide the coefficients. It
simulates an image with ImageWidth equal
to the kernel size, and a Loop option is set so that the kernel would
continuously be provided.
One form of implementation of the convolve process on an ALU unit is as
illustrated in Fig. 81.The
following constants are set by software:
Constant Value
K, Kernel size (9, 25, or 49)
The control logic is used to count down the number of multiply/adds per pixel.
When the count
(accumulated in Latch2) reaches 0, the control signal generated is used to
write out the current convolve value
(from Latch,) and to reset the count. In this way, one control logic block can
be used for a number of parallel
convolve streams.
Each cycle the multiply ALU can perform one multiply/add to incorporate the
appropriate part of a pixel.
The number of cycles taken to sum up all the values is therefore the number of
entries in the kernel. Since this is
compute bound, it is appropriate to divide the image into multiple sections
and process them in parallel on
different ALU units.
On a 7x7 kernel, the time taken for each pixel is 49 cycles, or 490ns. Since
each cache line holds 32
pixels, the time available for memory access is 12,740ns. ((32-7+1) x 490ns).
The time taken to read 7 cache lines
and write 1 is worse case 1,120ns (8*140ns, all accesses to same DRAM bank).
Consequently it is possible to
process up to 10 pixels in parallel given unlimited resources. Given a limited
number of ALUs it is possible to do
at best 4 in parallel. The time taken to therefore perform the convolution
using a 7x7 kernel is 0.18375 seconds
(1500*1000 * 490ns / 4 = 183,750,000ns).
On a 5x5 kernel, the time taken for each pixel is 25 cycles, or 250ns. Since
each cache line holds 32
pixels, the time available for memory access is 7,000ns. ((32-5+1) x 250ns).
The time taken to read 5 cache lines
CA 02564047 2006-11-06
YU139 PCT 111
and write 1 is worse case 840ns (6 * 140ns, all accesses to same DRAM bank).
Consequently it is possible to
process up to 7 pixels in parallel given unlimited resources. Given a limited
number of ALUs it is possible to do at
best 4. The time taken to therefore perform the convolution using a 5x5 kernel
is 0.09375 seconds (1500*1000
250ns / 4 = 93,750,000ns).
On a 3x3 kernel, the time taken for each pixel is 9 cycles, or 90ns. Since
each cache line holds 32 pixels,
the time available for memory access is 2,700ns. ((32-3+1) x 90ns). The time
taken to read 3 cache lines and write
1 is worse case 560ns (4 * 140ns, all accesses to same DRAM bank).
Consequently it is possible to process up to
4 pixels in parallel given unlimited resources. Given a limited number of ALUs
and Read/Write Iterators it is
possible to do at best 4. The time taken to therefore perform the convolution
using a 3x3 kernel is 0.03375
seconds (1500*1000 * 90ns / 4 = 33,750,000ns).
Consequently each output pixel takes kemelsize/3 cycles to compute. The actual
timings are summarised in the
following table:
Kernel size Time taken to Time to process Time to Process
calculate output pixel 1 channel at 1500x1000 3 channels at
1500x1000
3x3 (9) 3 cycles 0.045 seconds 0.135 seconds
5x5 (25) 8 1/3 cycles 0.125 seconds 0.375 seconds
7x7 (49) 16 1/3 cycles 0.245 seconds 0.735 seconds
Image Compositor
Compositing is to add a foreground image to a background image using a matte
or a channel to govern
the appropriate proportions of background and foreground in the final image.
Two styles of compositing are
preferably supported, regular compositing and associated compositing. The
rules for the two styles are:
Regular composite: new Value = Foreground + (Background - Foreground) a
Associated composite: new value = Foreground + (1- a) Background
The difference then, is that with associated compositing, the foreground has
been pre-multiplied with the
matte, while in regular compositing it has not. An example of the compositing
process is as illustrated in Fig. 83.
The alpha channel has values from 0 to 255 corresponding to the range 0 to 1.
Regular Composite
A regular composite is implemented as:
Foreground + (Background - Foreground) * a/ 255
The division by X/255 is approximated by 257X/65536. An implementation of the
compositing process
is shown in more detail in Fig. 84, where the following constant is set by
software:
Constant Value
K, 257
Since 4 Iterators are required, the composite process takes 1 cycle per pixel,
with a utilization of only half
of the ALUs. The composite process is only run on a single channel. To
composite a 3-channel image with
another, the compositor must be run 3 times, once for each channel.
The time taken to composite a full size single channel is 0.015s (1500 * 1000
* 1 * lOns), or 0.045s to
composite all 3 channels.
CA 02564047 2006-11-06
YU139 PCT 112
To approximate a divide by 255 it is possible to multiply by 257 and then
divide by 65536. It can also be
achieved by a single add (256 * x + x) and ignoring (except for rounding
purposes) the final 16 bits of the result.
As shown in Fig. 42, the compositor process requires 3 Sequential Read
Iterators 351-353 and 1
Sequential Write Iterator 355, and is implemented as microcode using a Adder
ALU in conjunction with a
multiplier ALU. Composite time is I cycle (iOns) per-pixel. Different
microcode is required for associated and
regular compositing, although the average time per pixel composite is the
same.
The composite process is only run on a single channel. To composite one 3-
channel image with another,
the compositor must be run 3 times, once for each channel. As the a channel is
the same for each composite, it
must be read each time. However it should be noted that to transfer (read or
write) 4 x 32 byte cache-lines in the
best case takes 320ns. The pipeline gives an average of 1 cycle per pixel
composite, taking 32 cycles or 320ns (at
100MHz) to composite the 32 pixels, so the a channel is effectively read for
free. An entire channel can therefore
be composited in:
1500/32 * 1000 * 320ns = 15,040,000ns = 0.015seconds.
The time taken to composite a full size 3 channel image is therefore 0.045
seconds.
Construct Image P, ramid
Several functions, such as warping, tiling and brushing, require the average
value of a given area of
pixels. Rather than calculate the value for each area given, these functions
preferably make use of an image
pyramid. As illustrated previously in Fig. 33, an image pyramid 360 is
effectively a multi-resolution pixelmap.
The original image is a 1:1 representation. Sub-sampling by 2:1 in each
dimension produces an image 1/4 the
original size. This process continues until the entire image is represented by
a single pixel.
An image pyramid is constructed from an original image, and consumes 1/3 of
the size taken up by the
original image (1/4 + 1/16 + 1/64 + ...). For an original image of 1500 x 1000
the corresponding image pyramid is
approximately'/2 MB
The image pyramid can be constructed via a 3x3 convolve performed on 1 in 4
input image pixels
advancing the center of the convolve kernel by 2 pixels each dimension. A 3x3
convolve results in higher
accuracy than simply averaging 4 pixels, and has the added advantage that
coordinates on different pyramid levels
differ only by shifting 1 bit per level.
The construction of an entire pyramid relies on a software loop that calls the
pyramid level construction
function once for each level of the pyramid.
The timing to produce 1 level of the pyramid is 9/4 * 1/4 of the resolution of
the input image since we are
generating an image 1/4 of the size of the original. Thus for a 1500 x 1000
image:
Timing to produce level I of pyramid = 9/4 * 750 * 500 = 843, 750 cycles
Timing to produce level 2 of pyramid = 9/4 * 375 * 250 = 210, 938 cycles
Timing to produce level 3 of pyramid = 9/4 * 188 * 125 = 52, 735 cycles
Etc.
The total time is 3/4 cycle per original image pixel (image pyramid is 1/3 of
original image size, and each
pixel takes 9/4 cycles to be calculated, i.e. 1/3 * 9/4 = 3/4). In the case of
a 1500 x 1000 image is 1,125,000 cycles
(at 100MHz), or 0.011 seconds. This timing is for a single color channel, 3
color channels require 0.034 seconds
processing time.
General Data Driven Image Warpeer
CA 02564047 2006-11-06
YU139 PCT 113
The ACP 31 is able to carry out image warping manipulations of the input
image. The principles of
image warping are well-known in theory. One thorough text book reference on
the process of warping is "Digital
Image Warping" by George Wolberg published in 1990 by the IEEE Computer
Society Press, Los Alamitos,
California. The warping process utilizes a warp map which forms part of the
data fed in via Artcard 9. The warp
map can be arbitrarily dimensioned in accordance with requirements and
provides information of a mapping of
input pixels to output pixels. Unfortunately, the utilization of arbitrarily
sized warp maps presents a number of
problems which must be solved by the image warper.
Turning to Fig. 85, a warp map 365, having dimensions AxB comprises array
values of a certain
magnitude (for example 8 bit values from 0 - 255) which set out the coordinate
of a theoretical input image which
maps to the corresponding "theoretical" output image having the same array
coordinate indices. Unfortunately,
any output image eg. 366 will have its own dimensions CxD which may further be
totally different from an input
image which may have its own dimensions ExF. Hence, it is necessary to
facilitate the remapping of the warp
map 365 so that it can be utilised for output image 366 to determine, for each
output pixel, the corresponding area
or region of the input image 367 from which the output pixel color data is to
be constructed. For each output pixel
in output image 366 it is necessary to first determine a corresponding warp
map value from warp map 365. This
may include the need to bilinearly interpolate the surrounding warp map values
when an output image pixel maps
to a fractional position within warp map table 365. The result of this process
will give the location of an input
image pixel in a "theoretical" image which will be dimensioned by the size of
each data value within the warp
map 365. These values must be re-scaled so as to map the theoretical image to
the corresponding actual input
image 367.
In order to determine the actual value and output image pixel should take so
as to avoid aliasing effects,
adjacent output image pixels should be examined to determine a region of input
image pixels 367 which will
contribute to the final output image pixel value. In this respect, the image
pyramid is utilised as will become more
apparent hereinafter.
The image warper performs several tasks in order to warp an image.
Scale the warp map to match the output image size.
Determine the span of the region of input image pixels represented in each
output pixel.
Calculate the final output pixel value via tri-linear interpolation from the
input image pyramid
Scale warp map
As noted previously, in a data driven warp, there is the need for a warp map
that describes, for each
output pixel, the center of a corresponding input image map. Instead of having
a single warp map as previously
described, containing interleaved x and y value information, it is possible to
treat the X and Y coordinates as
separate channels.
Consequently, preferably there are two warp maps: an X warp map showing the
warping of X
coordinates, and a Y warp map, showing the warping of the Y coordinates. As
noted previously, the warp map
365 can have a different spatial resolution than the image they being scaled
(for example a 32 x 32 warp-map 365
may adequately describe a warp for a 1500 x 1000 image 366). In addition, the
warp maps can be represented by 8
or 16 bit values that correspond to the size of the image being warped.
There are several steps involved in producing points in the input image space
from a given warp map:
1. Determining the corresponding position in the warp map for the output pixel
CA 02564047 2006-11-06
YU139 PCT 114
2. Fetch the values from the warp map for the next step (this can require
scaling in the
resolution domain if the warp map is only 8 bit values)
3. Bi-linear interpolation of the warp map to determine the actual value
4. Scaling the value to correspond to the input image domain
The first step can be accomplished by multiplying the current X/Y coordinate
in the output image by a
scale factor (which can be different in X & Y). For example, if the output
image was 1500 x 1000, and the warp
map was 150 x 100, we scale both X & Y by 1/10.
Fetching the values from the warp map requires access to 2 Lookup tables. One
Lookup table indexes
into the X warp-map, and the other indexes into the Y warp-map. The lookup
table either reads 8 or 16 bit entries
from the lookup table, but always returns 16 bit values (clearing the high 8
bits if the original values are only 8
bits).
The next step in the pipeline is to bi-linearly interpolate the looked-up warp
map values.
Finally the result from the bi-linear interpolation is scaled to place it in
the same domain as the image to
be warped. Thus, if the warp map range was 0-255, we scale X by 1500/255, and
Y by 1000/255.
The interpolation process is as illustrated in Fig. 86 with the following
constants set by software:
Constant Value
K, Xscale (scales 0-Ima eWidth to 0-Wa ma Width
KZ Yscale (scales 0-Ima eHei ht to 0-Wa ma Hei ht)
K3 XrangeScale (scales warpmap range (eg 0-255) to 0-ImageWidth)
K4 YrangeScale (scales warpmap range (eg 0-255) to 0-Ima eHei ht)
The following lookup table is used:
Lookup Size Details
LUI and WarpmapWidth x Warpmap lookup.
LU2 WarpmapHeight Given [X,Y] the 4 entries required for bi-linear
interpolation
are returned. Even if entries are only 8 bit, they are returned
as 16 bit (high 8 bits 0).
Transfer time is 4 entries at 2 bytes per entry.
Total time is 8 cycles as 2 lookups are used.
Span calculation
The points from the warp map 365 locate centers of pixel regions in the input
image 367. The distance
between input image pixels of adjacent output image pixels will indicate the
size of the regions, and this distance
can be approximated via a span calculation.
Turning to Fig. 87, for a given current point in the warp map P1, the previous
point on the same line is
called P0, and the previous line's point at the same position is called P2. We
determine the absolute distance in X
& Y between P 1 and P0, and between P 1 and P2. The maximum distance in X or Y
becomes the span which will
be a square approximation of the actual shape.
Preferably, the points are processed in a vertical strip output order, PO is
the previous point on the same
line within a strip, and when P1 is the first point on line within a strip,
then PO refers to the last point in the
previous strip's corresponding line. P2 is the previous line's point in the
same strip, so it can be kept in a 32-entry
history buffer. The basic of the calculate span process are as illustrated in
Fig. 88 with the details of the process as
CA 02564047 2006-11-06
YU139 PCT 115
illustrated in Fig. 89.
The following DRAM FIFO is used:
Lookup Size Details
FIFO1 8 Image Width bytes. P2 history/lookup (both X & Y in same FIFO)
[ImageWidth x 2 entries at PI is put into the FIFO and taken out again at the
same
32 bits per entry] pixel on the following row as P2.
Transfer time is 4 cycles
(2 x 32 bits, with 1 cycle per 16 bits)
Since a 32 bit precision span history is kept, in the case of a 1500 pixel
wide image being warped 12,000
bytes temporary storage is required.
Calculation of the span 364 uses 2 Adder ALUs (1 for span calculation, 1 for
looping and counting for PO
and P2 histories) takes 7 cycles as follows:
Cycle Action
1 A = AB S(P I, - P2X)
Store P I. in P2X history
2 B = ABS(PI, - POX)
Store Pl. in PO, history
3 A = MAX(A, B)
4 B =ABS(P1y-P2,,)
Store P 1 in P2 history
5 A = MAX(A, B)
6 B = ABS(P 1,, - PO,,)
Store P I in PO history
7 A = MAX(A, B)
The history buffers 365, 366 are cached DRAM. The `Previous Line' (for P2
history) buffer 366 is 32
entries of span-precision. The `Previous Point' (for PO history). Buffer 365
requires I register that is used most of
the time (for calculation of points 1 to 31 of a line in a strip), and a DRAM
buffered set of history values to be
used in the calculation of point 0 in a strip's line.
32 bit precision in span history requires 4 cache lines to hold P2 history,
and 2 for PO history. P0's
history is only written and read out once every 8 lines of 32 pixels to a
temporary storage space of
(ImageHeight*4) bytes. Thus a 1500 pixel high image being warped requires 6000
bytes temporary storage, and a
total of 6 cache lines.
Tri-linear interpolation
Having determined the center and span of the area from the input image to be
averaged, the final part of
the warp process is to determine the value of the output pixel. Since a single
output pixel could theoretically be
represented by the entire input image, it is potentially too time-consuming to
actually read and average the specific
area of the input image contributing to the output pixel. Instead, it is
possible to approximate the pixel value by
using an image pyramid of the input image.
If the span is 1 or less, it is necessary only to read the original image's
pixels around the given
coordinate, and perform bi-linear interpolation. If the span is greater than
1, we must read two appropriate levels
CA 02564047 2006-11-06
YU139 PCT 116
of the image pyramid and perform tri-linear interpolation. Performing linear
interpolation between two levels of
the image pyramid is not strictly correct, but gives acceptable results (it
errs on the side of blurring the resultant
image).
Turning to Fig. 90, generally speaking, for a given span `s', it is necessary
to read image pyramid levels
given by Inns (370) and ln2s+l (371). Ln2s is simply decoding the highest set
bit of s. We must bi-linear interpolate
to determine the value for the pixel value on each of the two levels 370,371
of the pyramid, and then interpolate
between levels.
As shown in Fig. 91, it is necessary to first interpolate in X and Y for each
pyramid level before
interpolating between the pyramid levels to obtain a final output value 373.
The image pyramid address mode issued to generate addresses for pixel
coordinates at (x, y) on pyramid
level s & s+l. Each level of the image pyramid contains pixels sequential in
x. Hence, reads in x are likely to be
cache hits.
Reasonable cache coherence can be obtained as local regions in the output
image are typically locally
coherent in the input image (perhaps at a different scale however, but
coherent within the scale). Since it is not
possible to know the relationship between the input and output images, we
ensure that output pixels are written in
a vertical strip (via a Vertical-Strip Iterator) in order to best make use of
cache coherence.
Tri-linear interpolation can be completed in as few as 2 cycles on average
using 4 multiply ALUs and all
4 adder ALUs as a pipeline and assuming no memory access required. But since
all the interpolation values are
derived from the image pyramids, interpolation speed is completely dependent
on cache coherence (not to
mention the other units are busy doing warp-map scaling and span
calculations). As many cache lines as possible
should therefore be available to the image-pyramid reading. The best speed
will be 8 cycles, using 2 Multiply
ALUs.
The output pixels are written out to the DRAM via a Vertical-Strip Write
Iterator that uses 2 cache lines.
The speed is therefore limited to a minimum of 8 cycles per output pixel. If
the scaling of the warp map requires
8 or fewer cycles, then the overall speed will be unchanged. Otherwise the
throughput is the time taken to scale
the warp map. In most cases the warp map will be scaled up to match the size
of the photo.
Assuming a warp map that requires 8 or fewer cycles per pixel to scale, the
time taken to convert a single
color component of image is therefore 0.12s (1500 * 1000 * 8 cycles * l Ons
per cycle).
Histogram Collector
The histogram collector is a microcode program that takes an image channel as
input, and produces a
histogram as output. Each of a channel's pixels has a value in the range 0-
255. Consequently there are 256 entries
in the histogram table, each entry 32 bits - large enough to contain a count
of an entire 1500x1000 image.
As shown in Fig. 92, since the histogram represents a summary of the entire
image, a Sequential Read
Iterator 378 is sufficient for the input. The histogram itself can be
completely cached, requiring 32 cache lines
(1K).
The microcode has two passes: an initialization pass which sets all the counts
to zero, and then a "count"
stage that increments the appropriate counter for each pixel read from the
image. The first stage requires the
Address Unit and a single Adder ALU, with the address of the histogram table
377 for initialising.
Relative Microcode Address Unit Adder Unit 1
CA 02564047 2006-11-06
YU139 PCT 117
Address A = Base address of histogram
0 Write 0 to Outl =A
A + (Adderl.Outl << 2) A = A - 1
BNZ 0
1 Rest of processing Rest of processing
The second stage processes the actual pixels from the image, and uses 4 Adder
ALUs:
Adder l Adder 2 Adder 3 Adder 4 Address Unit
1 A=0 A=-1
2 Outl =A A = Adderl.Outl A = A = A + 1 Outl = Read 4 bytes
BZ A = pixel Z = pixel - Adr.Outl from: (A +
2 Adderl.Outl (Adderl.Outl << 2))
3 Outl = A Outl = A Outl = A Write Adder4.Out1 to:
A = (A + (Adder 2.Out << 2)
Adder3.Out 1
4 Write Adder4.Outl to:
(A + (Adder 2.Out << 2)
Flush caches
The Zero flag from Adder2 cycle 2 is used to stay at microcode address 2 for
as long as the input pixel is
the same. When it changes, the new count is written out in microcode address
3, and processing resumes at
microcode address 2. Microcode address 4 is used at the end, when there are no
more pixels to be read.
Stage I takes 256 cycles, or 2560ns. Stage 2 varies according to the values of
the pixels. The worst case
time for lookup table replacement is 2 cycles per image pixel if every pixel
is not the same as its neighbor. The
time taken for a single color lookup is 0.03s (1500 x 1000 x 2 cycle per pixel
x IOns per cycle = 30,000,000ns).
The time taken for 3 color components is 3 times this amount, or 0.09s.
Color Transform
Color transformation is achieved in two main ways:
Lookup table replacement
Color space conversion
Lookup Table Replacement
As illustrated in Fig. 86, one of the simplest ways to transform the color of
a pixel is to encode an
arbitrarily complex transform function into a lookup table 380. The component
color value of the pixel is used to
lookup 381 the new component value of the pixel. For each pixel read from a
Sequential Read Iterator, its new
value is read from the New Color Table 380, and written to a Sequential Write
Iterator 383. The input image can
be processed simultaneously in two halves to make effective use of memory
bandwidth. The following lookup
table is used:
Lookup Size Details
LU, 256 entries Replacement[X]
8 bits per entry Table indexed by the 8 highest significant bits of X.
Resultant 8 bits treated as fixed point 0:8
The total process requires 2 Sequential Read Iterators and 2 Sequential Write
iterators. The 2 New Color
CA 02564047 2006-11-06
YU139 PCT 118
Tables require 8 cache lines each to hold the 256 bytes (256 entries of I
byte).
The average time for lookup table replacement is therefore '/2 cycle per image
pixel. The time taken for a
single color lookup is 0.0075s (1500 x 1000 x '/2 cycle per pixel x l Ons per
cycle = 7,500,000ns). The time taken
for 3 color components is 3 times this amount, or 0.0225s. Each color
component has to be processed one after the
other under control of software.
Color Space Conversion
Color Space conversion is only required when moving between color spaces. The
CCD images are
captured in RGB color space, and printing occurs in CMY color space, while
clients of the ACP 31 likely process
images in the Lab color space. All of the input color space channels are
typically required as input to determine
each output channel's component value. Thus the logical process is as
illustrated 385 in Fig. 94.
Simply, conversion between Lab, RGB, and CMY is fairly straightforward.
However the individual color
profile of a particular device can vary considerably. Consequently, to allow
future CCDs, inks, and printers, the
ACP 31 performs color space conversion by means of tri-linear interpolation
from color space conversion lookup
tables.
Color coherence tends to be area based rather than line based. To aid cache
coherence during tri-linear
interpolation lookups, it is best to process an image in vertical strips. Thus
the read 386-388 and write 389
iterators would be Vertical-Strip Iterators.
Tri-linear color space conversion
For each output color component, a single 3D table mapping the input color
space to the output color
component is required. For example, to convert CCD images from RGB to Lab, 3
tables calibrated to the physical
characteristics of the CCD are required:
RGB->L
RGB->a
RGB->b
To convert from Lab to CMY, 3 tables calibrated to the physical
characteristics of the ink/printer are
required:
Lab->C
Lab->M
Lab->Y
The 8-bit input color components are treated as fixed-point numbers (3:5) in
order to index into the
conversion tables. The 3 bits of integer give the index, and the 5 bits of
fraction are used for interpolation. Since 3
bits gives 8 values, 3 dimensions gives 512 entries (8 x 8 x 8). The size of
each entry is 1 byte, requiring 512 bytes
per table.
The Convert Color Space process can therefore be implemented as shown in Fig.
95 and the following
lookup table is used:
Lookup Size Details
LU, 8 x 8 x 8 entries Convert[X, Y, Z]
512 entries Table indexed by the 3 highest bits of X, Y, and Z.
8 bits per entry 8 entries returned from Tri-linear index address unit
Resultant 8 bits treated as fixed point 8:0
Transfer time is 8 entries at 1 byte per entry
CA 02564047 2006-11-06
YU139 PCT 119
Tri-linear interpolation returns interpolation between 8 values. Each 8 bit
value takes 1 cycle to be
returned from the lookup, for a total of 8 cycles. The tri-linear
interpolation also takes 8 cycles when 2 Multiply
ALUs are used per cycle. General tri-linear interpolation information is given
in the ALU section of this
document. The 512 bytes for the lookup table fits in 16 cache lines.
The time taken to convert a single color component of image is therefore
0.105s (1500 * 1000 * 7 cycles
* lOns per cycle). To convert 3 components takes 0.415s. Fortunately, the
color space conversion for printout
takes place on the fly during printout itself, so is not a perceived delay.
If color components are converted separately, they must not overwrite their
input color space
components since all color components from the input color space are required
for converting each component.
Since only I multiply unit is used to perform the interpolation, it is
alternatively possible to do the entire
Lab->CMY conversion as a single pass. This would require 3 Vertical-Strip Read
Iterators, 3 Vertical-Strip Write
Iterators, and access to 3 conversion tables simultaneously. In that case, it
is possible to write back onto the input
image and thus use no extra memory. However, access to 3 conversion tables
equals 1/3 of the caching for each,
that could lead to high latency for the overall process.
Affine Transform
Prior to compositing an image with a photo, it may be necessary to rotate,
scale and translate it. If the
image is only being translated, it can be faster to use a direct sub-pixel
translation function. However, rotation,
scale-up and translation can all be incorporated into a single affine
transform.
A general affine transform can be included as an accelerated function. Affime
transforms are limited to
2D, and if scaling down, input images should be pre-scaled via the Scale
function. Having a general affine
transform function allows an output image to be constructed one block at a
time, and can reduce the time taken to
perform a number of transformations on an image since all can be applied at
the same time.
A transformation matrix needs to be supplied by the client - the matrix should
be the inverse matrix of
the transformation desired i.e. applying the matrix to the output pixel
coordinate will give the input coordinate.
A 2D matrix is usually represented as a 3 x 3 array:
a b 0
c d 0
e f 1
Since the 3`d column is always[0, 0, 1] clients do not need to specify it.
Clients instead specify a, b, c, d,
e, and f.
Given a coordinate in the output image (x, y) whose top left pixel coordinate
is given as (0, 0), the input
coordinate is specified by: (ax + cy + e, bx + dy + f). Once the input
coordinate is determined, the input image is
sampled to arrive at the pixel value. Bi-linear interpolation of input image
pixels is used to determine the value of
the pixel at the calculated coordinate. Since affme transforms preserve
parallel lines, images are processed in
output vertical strips of 32 pixels wide for best average input image cache
coherence.
Three Multiply ALUs are required to perform the bi-linear interpolation in 2
cycles. Multiply ALUs 1
and 2 do linear interpolation in X for lines Y and Y+1 respectively, and
Multiply ALU 3 does linear interpolation
in Y between the values output by Multiply ALUs 1 and 2.
As we move to the right across an output line in X, 2 Adder ALUs calculate the
actual input image
CA 02564047 2006-11-06
YU139 PCT 120
coordinates by adding `a' to the current X value, and `b' to the current Y
value respectively. When we advance to
the next line (either the next line in a vertical strip after processing a
maximum of 32 pixels, or to the first line in a
new vertical strip) we update X and Y to pre-calculated start coordinate
values constants for the given block
The process for calculating an input coordinate is given in Fig. 96 where the
following constants are set
by software:
Calculate Pixel
Once we have the input image coordinates, the input image must be sampled. A
lookup table is used to
return the values at the specified coordinates in readiness for bilinear
interpolation. The basic process is as
indicated in Fig. 97 and the following lookup table is used:
Lookup Size Details
LU, Image Bilinear Image lookup [X, Y]
width by Table indexed by the integer part of X and Y.
Image 4 entries returned from Bilinear index address unit, 2 per cycle.
height Each 8 bit entry treated as fixed point 8:0
8 bits per Transfer time is 2 cycles (2 16 bit entries in FIFO hold the 4 8
bit entries)
entry
The affine transform requires all 4 Multiply Units and all 4 Adder ALUs, and
with good cache coherence
can perform an affine transform with an average of 2 cycles per output pixel.
This timing assumes good cache
coherence, which is true for non-skewed images. Worst case timings are
severely skewed images, which
meaningful Vark scripts are unlikely to contain.
The time taken to transform a 128 x 128 image is therefore 0.00033 seconds
(32,768 cycles). If this is a
clip image with 4 channels (including a channel), the total time taken is
0.00131 seconds (131,072 cycles).
A Vertical-Strip Write Iterator is required to output the pixels. No Read
Iterator is required. However,
since the affme transform accelerator is bound by time taken to access input
image pixels, as many cache lines as
possible should be allocated to the read of pixels from the input image. At
least 32 should be available, and
preferably 64 or more.
Scales
Scaling is essentially a re-sampling of an image. Scale up of an image can be
performed using the Affine
Transform function. Generalized scaling of an image, including scale down, is
performed by the hardware
accelerated Scale function. Scaling is performed independently in X and Y, so
different scale factors can be used
in each dimension.
The generalized scale unit must match the Affine Transform scale function in
terms of registration. The
generalized scaling process is as illustrated in Fig. 98. The scale in X is
accomplished by Fant's re-sampling
algorithm as illustrated in Fig. 99.
Where the following constants are set by software:
Constant Value
K, Number of input pixels that contribute to an output pixel in X
Kz _l/K,
The following registers are used to hold temporary variables:
Variable Value
CA 02564047 2006-11-06
YU139 PCT 121
Latch, Amount of input pixel remaining unused (starts at I and decrements)
Latch2 Amount of input pixels remaining to contribute to current output pixel
(starts at K,
and decrements)
Latch3 Next pixel (in X)
Latch4 Current pixel
Latch5 Accumulator for output pixel (unsealed)
Latch6 Pixel Scaled in X (output)
The Scale in Y process is illustrated in Fig. 100 and is also accomplished by
a slightly altered version of Fant's re-
sampling algorithm to account for processing in order of X pixels.
Where the following constants are set by software:
Constant Value
K, Number of input pixels that contribute to an output pixel in Y
K2 1 /K,
The following registers are used to hold temporary variables:
Variable Value
Latch, Amount of input pixel remaining unused (starts at 1 and decrements)
Latch2 Amount of input pixels remaining to contribute to current output pixel
(starts at K,
and decrements)
Latch3 Next pixel (in Y)
Latch4 Current pixel
Latch5 Pixel Scaled in Y (output)
The following DRAM FIFOs are used:
Lookup Size Details
FIFO1 ImageWidthoUT entries 1 row of image pixels already scaled in X
8 bits per entry I cycle transfer time
FIFO2 ImageWidthoUT entries 1 row of image pixels already scaled in X
16 bits per entry 2 cycles transfer time (1 byte per cycle)
Tessellate Image
Tessellation of an image is a form of tiling. It involves copying a specially
designed "tile" multiple times
horizontally and vertically into a second (usually larger) image space. When
tessellated, the small tile forms a
seamless picture. One example of this is a small tile of a section of a brick
wall. It is designed so that when
tessellated, it forms a full brick wall. Note that there is no scaling or sub-
pixel translation involved in tessellation.
The most cache-coherent way to perform tessellation is to output the image
sequentially line by line, and
to repeat the same line of the input image for the duration of the line. When
we finish the line, the input image
must also advance to the next line (and repeat it multiple times across the
output line).
An overview of the tessellation function is illustrated 390 in Fig. 101. The
Sequential Read Iterator 392
is set up to continuously read a single line of the input tile (StartLine
would be 0 and EndLine would be 1). Each
input pixel is written to all 3 of the Write Iterators 393-395. A counter 397
in an Adder ALU counts down the
number of pixels in an output line, terminating the sequence at the end of the
line.
At the end of processing a line, a small software routine updates the
Sequential Read Iterator's StartLine
CA 02564047 2006-11-06
YU139 PCT 122
and EndLine registers before restarting the microcode and the Sequential Read
Iterator (which clears the FIFO and
repeats line 2 of the tile). The Write Iterators 393-395 are not updated, and
simply keep on writing out to their
respective parts of the output image. The net effect is that the tile has one
line repeated across an output line, and
then the tile is repeated vertically too.
This process does not fully use the memory bandwidth since we get good cache
coherence in the input
image, but it does allow the tessellation to function with tiles of any size.
The process uses 1 Adder ALU. If the 3
Write Iterators 393-395 each write to 1/3 of the image (breaking the image on
tile sized boundaries), then the
entire tessellation process takes place at an average speed of 1/3 cycle per
output image pixel. For an image of
1500 x 1000, this equates to .005 seconds (5,000,000ns).
Sub-pixel Translator
Before compositing an image with a background, it may be necessary to
translate it by a sub-pixel
amount in both X and Y. Sub-pixel transforms can increase an image's size by 1
pixel in each dimension. The
value of the region outside the image can be client determined, such as a
constant value (e.g. black), or edge pixel
replication. Typically it will be better to use black.
The sub-pixel translation process is as illustrated in Fig. 102. Sub-pixel
translation in a given dimension
is defined by:
Pixelo,,, = Pixel;, * (1-Translation) + Pixel;n_I * Translation
It can also be represented as a form of interpolation:
Pixeloõ, = Pixel;n-1 + (Pixel; - Pixel;,,_,)* Translation
Implementation of a single (on average) cycle interpolation engine using a
single Multiply ALU and a
single Adder ALU in conjunction is straightforward. Sub-pixel translation in
both X & Y requires 2 interpolation
engines.
In order to sub-pixel translate in Y, 2 Sequential Read Iterators 400, 401 are
required (one is reading a
line ahead of the other from the same image), and a single Sequential Write
Iterator 403 is required.
The first interpolation engine (interpolation in Y) accepts pairs of data from
2 streams, and linearly
interpolates between them. The second interpolation engine (interpolation in
X) accepts its data as a single 1
dimensional stream and linearly interpolates between values. Both engines
interpolate in 1 cycle on average.
Each interpolation engine 405, 406 is capable of performing the sub-pixel
translation in 1 cycle per
output pixel on average. The overall time is therefore 1 cycle per output
pixel, with requirements of 2 Multiply
ALUs and 2 Adder ALUs.
The time taken to output 32 pixels from the sub-pixel translate function is on
average 320ns (32 cycles).
This is enough time for 4 full cache-line accesses to DRAM, so the use of 3
Sequential Iterators is well within
timing limits.
The total time taken to sub-pixel translate an image is therefore 1 cycle per
pixel of the output image. A
typical image to be sub-pixel translated is a tile of size 128 * 128. The
output image size is 129 * 129. The process
takes 129 * 129 * IOns = 166,41Ons.
The Image Tiler function also makes use of the sub-pixel translation
algorithm, but does not require the
writing out of the sub-pixel-translated data, but rather processes it further.
Image Tiler
The high level algorithm for tiling an image is carried out in software. Once
the placement of the tile has
CA 02564047 2006-11-06
YU139 PCT 123
been determined, the appropriate colored tile must be composited. The actual
compositing of each tile onto an
image is carried out in hardware via the microcoded ALUs. Compositing a tile
involves both a texture application
and a color application to a background image. In some cases it is desirable
to compare the actual amount of
texture added to the background in relation to the intended amount of texture,
and use this to scale the color being
applied. In these cases the texture must be applied first.
Since color application functionality and texture application functionality
are somewhat independent,
they are separated into sub-functions.
The number of cycles per 4-channel tile composite for the different texture
styles and coloring styles is
summarised in the following table:
Constant Pixel
color color
Replace texture 4 4.75
25% background + tile texture 4 4.75
Average height algorithm 5 5.75
Avera e height algorithm with feedback 5.75 6.5
Tile Coloring and Compositing
A tile is set to have either a constant color (for the whole tile), or takes
each pixel value from an input
image. Both of these cases may also have feedback from a texturing stage to
scale the opacity (similar to thinning
paint).
The steps for the 4 cases can be summarised as:
- Sub-pixel translate the tile's opacity values,
- Optionally scale the tile's opacity (if feedback from texture application is
enabled).
- Determine the color of the pixel (constant or from an image map).
- Composite the pixel onto the background image.
Each of the 4 cases is treated separately, in order to minimize the time taken
to perform the function. The
summary of time per color compositing style for a single color channel is
described in the following table:
Tiling color style No feedback from Feedback from
texture (cycles per texture
ixel (cycles per pixel)
Tile has constant color per pixel 1 2
Tile has per pixel color from input image 1.25 2
Constant color
In this case, the tile has a constant color, determined by software. While the
ACP 31 is placing down one
tile, the software can be determining the placement and coloring of the next
tile.
The color of the tile can be determined by bi-linear interpolation into a
scaled version of the image being
tiled. The scaled version of the image can be created and stored in place of
the image pyramid, and needs only to
be performed once per entire tile operation. If the tile size is 128 x 128,
then the image can be scaled down by
128:1 in each dimension.
CA 02564047 2006-11-06
YU139 PCT 124
Without feedback
When there is no feedback from the texturing of a tile, the tile is simply
placed at the specified
coordinates. The tile color is used for each pixel's color, and the opacity
for the composite comes from the tile's
sub-pixel translated opacity channel. In this case color channels and the
texture channel can be processed
completely independently between tiling passes.
The overview of the process is illustrated in Fig. 103. Sub-pixel translation
410 of a tile can be
accomplished using 2 Multiply ALUs and 2 Adder ALUs in an average time of 1
cycle per output pixel. The
output from the sub-pixel translation is the mask to be used in compositing
411 the constant tile color 412 with the
background image from background sequential Read Iterator.
Compositing can be performed using 1 Multiply ALU and 1 Adder ALU in an
average time of 1 cycle
per composite. Requirements are therefore 3 Multiply ALUs and 3 Adder ALUs. 4
Sequential Iterators 413-416
are required, taking 320ns to read or write their contents. With an average
number of cycles of 1 per pixel to sub-
pixel translate and composite, there is sufficient time to read and write the
buffers.
With feedback
When there is feedback from the texturing of a tile, the tile is placed at the
specified coordinates. The tile
color is used for each pixel's color, and the opacity for the composite comes
from the tile's sub-pixel translated
opacity channel scaled by the feedback parameter. Thus the texture values must
be calculated before the color
value is applied.
The overview of the process is illustrated in Fig. 97. Sub-pixel translation
of a tile can be accomplished
using 2 Multiply ALUs and 2 Adder ALUs in an average time of 1 cycle per
output pixel. The output from the
sub-pixel translation is the mask to be scaled according to the feedback read
from the Feedback Sequential Read
Iterator 420. The feedback is passed it to a Scaler (1 Multiply ALU) 421.
Compositing 422 can be performed using 1 Multiply ALU and 1 Adder ALU in an
average time of 1
cycle per composite. Requirements are therefore 4 Multiply ALUs and all 4
Adder ALUs. Although the entire
process can be accomplished in 1 cycle on average, the bottleneck is the
memory access, since 5 Sequential
Iterators are required. With sufficient buffering, the average time is 1.25
cycles per pixel.
Color from Input Image
One way of coloring pixels in a tile is to take the color from pixels in an
input image. Again, there are
two possibilities for compositing: with and without feedback from the
texturing.
Without feedback
In this case, the tile color simply comes from the relative pixel in the input
image. The opacity for
compositing comes from the tile's opacity channel sub-pixel shifted.
The overview of the process is illustrated in Fig. 105. Sub-pixel translation
425 of a tile can be
accomplished using 2 Multiply ALUs and 2 Adder ALUs in an average time of 1
cycle per output pixel. The
output from the sub-pixel translation is the mask to be used in compositing
426 the tile's pixel color (read from the
input image 428 ) with the background image 429.
Compositing 426 can be performed using 1 Multiply ALU and 1 Adder ALU in an
average time of 1
cycle per composite. Requirements are therefore 3 Multiply ALUs and 3 Adder
ALUs. Although the entire
process can be accomplished in 1 cycle on average, the bottleneck is the
memory access, since 5 Sequential
Iterators are required. With sufficient buffering, the average time is 1.25
cycles per pixel.
CA 02564047 2006-11-06
YU139 PCT 125
With feedback
In this case, the tile color still comes from the relative pixel in the input
image, but the opacity for
compositing is affected by the relative amount of texture height actually
applied during the texturing pass. This
process is as illustrated in Fig. 106.
Sub-pixel translation 431 of a tile can be accomplished using 2 Multiply ALUs
and 2 Adder ALUs in an
average time of 1 cycle per output pixel. The output from the sub-pixel
translation is the mask to be scaled 431
according to the feedback read from the Feedback Sequential Read Iterator 432.
The feedback is passed to a
Scaler (1 Multiply ALU) 431.
Compositing 434 can be performed using 1 Multiply ALU and 1 Adder ALU in an
average time of 1
cycle per composite.
Requirements are therefore all 4 Multiply ALUs and 3 Adder ALUs. Although the
entire process can be
accomplished in 1 cycle on average, the bottleneck is the memory access, since
6 Sequential Iterators are required.
With sufficient buffering, the average time is 1.5 cycles per pixel.
Tile Texturing
Each tile has a surface texture defined by its texture channel. The texture
must be sub-pixel translated and
then applied to the output image. There are 3 styles of texture compositing:
Replace texture
25% background + tile's texture
Average height algorithm
In addition, the Average height algorithm can save feedback parameters for
color compositing.
The time taken per texture compositing style is summarised in the following
table:
Tiling color style Cycles per pixel Cycles per pixel
(no feedback from (feedback from
texture) texture)
Replace texture 1 -
25% background + tile texture value 1 -
Average height algorithm 2 2
Replace texture
In this instance, the texture from the tile replaces the texture channel of
the image, as illustrated in Fig.
107. Sub-pixel translation 436 of a tile's texture can be accomplished using 2
Multiply ALUs and 2 Adder ALUs
in an average time of 1 cycle per output pixel. The output from this sub-pixel
translation is fed directly to the
Sequential Write Iterator 437.
The time taken for replace texture compositing is 1 cycle per pixel. There is
no feedback, since 100% of
the texture value is always applied to the background. There is therefore no
requirement for processing the
channels in any particular order.
25% Background + Tile's Texture
In this instance, the texture from the tile is added to 25% of the existing
texture value. The new value
must be greater than or equal to the original value. In addition, the new
texture value must be clipped at 255 since
the texture channel is only 8 bits. The process utilised is illustrated in
Fig. 108.
CA 02564047 2006-11-06
YU139 PCT 126
Sub-pixel translation 440 of a tile's texture can be accomplished using 2
Multiply ALUs and 2 Adder
ALUs in an average time of 1 cycle per output pixel. The output from this sub-
pixel translation 440 is fed to an
adder 441 where it is added to '/4 442 of the background texture value. Min
and Max functions 444 are provided
by the 2 adders not used for sub-pixel translation and the output written to a
Sequential Write Iterator 445.
The time taken for this style of texture compositing is 1 cycle per pixel.
There is no feedback, since
100% of the texture value is considered to have been applied to the background
(even if clipping at 255 occurred).
There is therefore no requirement for processing the channels in any
particular order.
Average height al org ithm
In this texture application algorithm, the average height under the tile is
computed, and each pixel's
height is compared to the average height. If the pixel's height is less than
the average, the stroke height is added to
the background height. If the pixel's height is greater than or equal to the
average, then the stroke height is added
to the average height. Thus background peaks thin the stroke. The height is
constrained to increase by a minimum
amount to prevent the background from thinning the stroke application to 0
(the minimum amount can be 0
however). The height is also clipped at 255 due to the 8-bit resolution of the
texture channel.
There can be feedback of the difference in texture applied versus the expected
amount applied. The
feedback amount can be used as a scale factor in the application of the tile's
color.
In both cases, the average texture is provided by software, calculated by
performing a bi-level
interpolation on a scaled version of the texture map. Software determines the
next tile's average texture height
while the current tile is being applied. Software must also provide the
minimum thickness for addition, which is
typically constant for the entire tiling process.
Without feedback
With no feedback, the texture is simply applied to the background texture, as
shown in Fig. 109.
4 Sequential Iterators are required, which means that if the process can be
pipelined for 1 cycle, the
memory is fast enough to keep up.
Sub-pixel translation 450 of a tile's texture can be accomplished using 2
Multiply ALUs and 2 Adder
ALUs in an average time of 1 cycle per output pixel. Each Min & Max function
451,452 requires a separate
Adder ALU in order to complete the entire operation in 1 cycle. Since 2 are
already used by the sub-pixel
translation of the texture, there are not enough remaining for a 1 cycle
average time.
The average time for processing 1 pixel's texture is therefore 2 cycles. Note
that there is no feedback, and
hence the color channel order of compositing is irrelevant.
With feedback
This is conceptually the same as the case without feedback, except that in
addition to the standard
processing of the texture application algorithm, it is necessary to also
record the proportion of the texture actually
applied. The proportion can be used as a scale factor for subsequent
compositing of the tile's color onto the
background image. A flow diagram is illustrated in Fig. 110 and the following
lookup table is used:
Lookup Size Details
LUi 256 entries 1/N
16 bits per entry Table indexed by N (range 0-255)
Resultant 16 bits treated as fixed point 0:16
Each of the 256 entries in the software provided 1/N table 460 is 16 bits,
thus requiring 16 cache lines to
CA 02564047 2006-11-06
YU139 PCT 127
hold continuously.
Sub-pixel translation 461 of a tile's texture can be accomplished using 2
Multiply ALUs and 2 Adder
ALUs in an average time of I cycle per output pixel. Each Min 462 & Max 463
function requires a separate
Adder ALU in order to complete the entire operation in 1 cycle. Since 2 are
already used by the sub-pixel
translation of the texture, there are not enough remaining for a 1 cycle
average time.
The average time for processing 1 pixel's texture is therefore 2 cycles.
Sufficient space must be allocated
for the feedback data area (a tile sized image channel). The texture must be
applied before the tile's color is
applied, since the feedback is used in scaling the tile's opacity.
CCD Image Interpolator
Images obtained from the CCD via the ISI 83 (Fig. 3) are 750 x 500 pixels.
When the image is captured
via the ISI, the orientation of the camera is used to rotate the pixels by 0,
90, 180, or 270 degrees so that the top of
the image corresponds to `up'. Since every pixel only has an R, G, or B color
component (rather than all 3), the
fact that these have been rotated must be taken into account when interpreting
the pixel values. Depending on the
orientation of the camera, each 2x2 pixel block has one of the configurations
illustrated in Fig. 111:
Several processes need to be performed on the CCD captured image in order to
transform it into a useful
form for processing:
Up-interpolation of low-sample rate color components in CCD image
(interpreting correct
orientation of pixels)
Color conversion from RGB to the internal color space
- Scaling of the internal space image from 750 x 500 to 1500 x 1000.
Writing out the image in a planar format
The entire channel of an image is required to be available at the same time in
order to allow warping. In a
low memory model (8MB), there is only enough space to hold a single channel at
full resolution as a temporary
object. Thus the color conversion is to a single color channel. The limiting
factor on the process is the color
conversion, as it involves tri-linear interpolation from RGB to the internal
color space, a process that takes
0.026ns per channel (750 x 500 x 7 cycles per pixel x l Ons per cycle =
26,250,000ns).
It is important to perform the color conversion before scaling of the internal
color space image as this
reduces the number of pixels scaled (and hence the overall process time) by a
factor of 4.
The requirements for all of the transformations may not fit in the ALU scheme.
The transformations are
therefore broken into two phases:
Phase 1: Up-interpolation of low-sample rate color components in CCD image
(interpreting correct
orientation of pixels)
Color conversion from RGB to the internal color space
Writing out the image in a planar format
Phase 2: Scaling of the internal space image from 750 x 500 to 1500 x 1000
Separating out the scale function implies that the small color converted image
must be in memory at the
same time as the large one. The output from Phase 1 (0.5 MB) can be safely
written to the memory area usually
kept for the image pyramid (1 MB). The output from Phase 2 can be the general
expanded CCD image.
Separation of the scaling also allows the scaling to be accomplished by the
Affine Transform, and also allows for
a different CCD resolution that may not be a simple 1:2 expansion.
CA 02564047 2006-11-06
YU139 PCT 128
Phase 1: Up-interpolation of low-sample rate color components.
Each of the 3 color components (R, G, and B) needs to be up interpolated in
order for color conversion to
take place for a given pixel. We have 7 cycles to perform the interpolation
per pixel since the color conversion
takes 7 cycles.
Interpolation of G is straightforward and is illustrated in Fig. 112.
Depending on orientation, the actual
pixel value G alternates between odd pixels on odd lines & even pixels on even
lines, and odd pixels on even lines
& even pixels on odd lines. In both cases, linear interpolation is all that is
required. Interpolation of R and B
components as illustrated in Fig. 113 and Fig. 113, is more complicated, since
in the horizontal and vertical
directions, as can be seen from the diagrams, access to 3 rows of pixels
simultaneously is required, so 3 Sequential
Read Iterators are required, each one offset by a single row. In addition, we
have access to the previous pixel on
the same row via a latch for each row.
Each pixel therefore contains one component from the CCD, and the other 2 up-
interpolated. When one
component is being bi-linearly interpolated, the other is being linearly
interpolated. Since the interpolation factor
is a constant 0.5, interpolation can be calculated by an add and a shift 1 bit
right (in 1 cycle), and bi-linear
interpolation of factor 0.5 can be calculated by 3 adds and a shift 2 bits
right (3 cycles). The total number of cycles
required is therefore 4, using a single multiply ALU.
Fig. 115 illustrates the case for rotation 0 even line even pixel (EL, EP),
and odd line odd pixel (OL, OP)
and Fig. 116 illustrates the case for rotation 0 even line odd pixel (EL, OP),
and odd line even pixel (OL, EP).
The other rotations are simply different forms of these two expressions.
Color conversion
Color space conversion from RGB to Lab is achieved using the same method as
that described in the
general Color Space Convert function, a process that takes 8 cycles per pixel.
Phase 1 processing can be
described with reference to Fig. 117.
The up-interpolate of the RGB takes 4 cycles (1 Multiply ALU), but the
conversion of the color space
takes 8 cycles per pixel (2 Multiply ALUs) due to the lookup transfer time.
Phase 2
Scaling the image
This phase is concerned with up-interpolating the image from the CCD
resolution (750 x 500) to the
working photo resolution (1500 x 1000). Scaling is accomplished by running the
Affine transform with a scale of
1:2. The timing of a general affine transform is 2 cycles per output pixel,
which in this case means an elapsed
scaling time of 0.03 seconds.
Illuminate Image
Once an image has been processed, it can be illuminated by one or more light
sources. Light sources can be:
1. Directional - is infinitely distant so it casts parallel light in a single
direction
2. Omni - casts unfocused lights in all directions.
3. Spot - casts a focused beam of light at a specific target point. There is a
cone and penumbra associated
with a spotlight.
The scene may also have an associated bump-map to cause reflection angles to
vary. Ambient light is
also optionally present in an illuminated scene.
In the process of accelerated illumination, we are concerned with illuminating
one image channel by a
CA 02564047 2006-11-06
YU139 PCT 129
single light source. Multiple light sources can be applied to a single image
channel as multiple passes one pass per
light source. Multiple channels can be processed one at a time with or without
a bump-map.
The normal surface vector (N) at a pixel is computed from the bump-map if
present. The default normal
vector, in the absence of a bump-map, is perpendicular to the image plane i.e.
N = [0, 0, 1].
The viewing vector V is always perpendicular to the image plane i.e. V = [0,
0, 1].
For a directional light source, the light source vector (L) from a pixel to
the light source is constant across
the entire image, so is computed once for the entire image. For an omni light
source (at a finite distance), the light
source vector is computed independently for each pixel.
A pixel's reflection of ambient light is computed according to: lakaOd
A~~pixel's diffuse and specular reflection of a light source is computed
according to the Phong model:
fattlp[Od(`SL) + kO,(R=V)"]
When the light source is at infinity, the light source intensity is constant
across the image.
Each light source has three contributions per pixel
Ambient Contribution
Diffuse contribution
Specular contribution
The light source can be defined using the following variables:
dL Distance from light source
fatt Attenuation with distancefatt = 1 / dLz
R Normalised reflection vector [R = 2N .L - L]
Ia Ambient light intensity
I Diffuse light coefficient
ka Ambient reflection coefficient
kd Diffuse reflection coefficient
ks Secular reflection coefficient
k,c Secular color coefficient
L Normalised light source vector
N Normalised surface normal vector
n Secular exponent
Od Object's diffuse color (i.e. image pixel color)
OS Object's specular color (k,cOd + (1 - k,c)I )
V Normalised viewing vector [V = [0, 0, 1]]
The same reflection coefficients (ka, k5, kd) are used for each color
component.
A given pixel's value will be equal to the ambient contribution plus the sum
of each light's diffuse and
specular contribution.
Sub-Processes of Illumination Calculation
In order to calculate diffuse and specular contributions, a variety of other
calculations are required. These
are calculations of:
1 /'iX
N
CA 02564047 2006-11-06
YU139 PCT 130
L
N=L
R=V
fatt
f~p
Sub-processes are also defined for calculating the contributions of:
ambient
diffuse
specular
The sub-processes can then be used to calculate the overall illumination of a
light source. Since there are
only 4 multiply ALUs, the microcode for a particular type of light source can
have sub-processes intermingled
appropriately for performance.
Calculation of l/JX
The Vark lighting model uses vectors. In many cases it is important to
calculate the inverse of the length
of the vector for normalization purposes. Calculating the inverse of the
length requires the calculation of
1 /SquareRoot[X].
Logically, the process can be represented as a process with inputs and outputs
as shown in Fig. 118.
Referring to Fig. 119, the calculation can be made via a lookup of the
estimation, followed by a single iteration of
the following function:
V.+, V.(3 - XVõ )
The number of iterations depends on the accuracy required. In this case only
16 bits of precision are
required. The table can therefore have 8 bits of precision, and only a single
iteration is necessary. The following
constant is set by software:
Constant Value
K1 3
The following lookup table is used:
Lookup Size Details
LU, 256 entries 1/SquareRoot[X]
8 bits per entry Table indexed by the 8 highest significant bits of X.
Resultant 8 bits treated as fixed point 0:8
Calculation of N
N is the surface normal vector. When there is no bump-map, N is constant. When
a bump-map is present,
N must be calculated for each pixel.
No bump-map
When there is no bump-map, there is a fixed normal N that has the following
properties:
N=[XN,YN,ZN]=[0,0, 1]
JIN11 =1
1/1INII = 1
normalized N = N
CA 02564047 2006-11-06
YU 139 PCT 131
These properties can be used instead of specifically calculating the normal
vector and 1/IINII and thus
optimize other calculations.
With bump-map
As illustrated in Fig. 120, when a bump-map is present, N is calculated by
comparing bump-map values
in X and Y dimensions. Fig. 120 shows the calculation of N for pixel P 1 in
terms of the pixels in the same row
and column, but not including the value at P 1 itself. The calculation of N is
made resolution independent by
multiplying by a scale factor (same scale factor in X & Y). This process can
be represented as a process having
inputs and outputs (ZN is always 1) as illustrated in Fig. 121.
As ZN is always 1. Consequently XN and YN are not normalized yet (since ZN =
1). Normalization of N is
delayed until after calculation of N.L so that there is only 1 multiply by
1/IINII instead of 3.
An actual process for calculating N is illustrated in Fig. 122.
The following constant is set by software:
Constant Value
K, ScaleFactor (to make N resolution independent)
Calculation of L
Directional lights
When a light source is infinitely distant, it has an effective constant light
vector L. L is normalized and
calculated by software such that:
L = [XL, YL, ZL]
IILII = 1
1/IILII =1
These properties can be used instead of specifically calculating the L and
1/IILII and thus optimize other
calculations. This process is as illustrated in Fig. 123.
Omni lights and Spotlights
When the light source is not infinitely distant, L is the vector from the
current point P to the light source PL. Since
P = [Xp, Yp, 0], L is given by:
L = [XL, YL, ZL]
XL = XP - XPL
YL=YP-YPL
ZL = -ZPL
We normalize XL, YL and ZL by multiplying each by 1/IILII= The calculation of
1/IILII (for later use in normalizing)
is accomplished by calculating
V = XL2 + YL2 + ZL2
and then calculating V_"2
In this case, the calculation of L can be represented as a process with the
inputs and outputs as indicated
in Fig. 124.
Xp and Yp are the coordinates of the pixel whose illumination is being
calculated. Zp is always 0.
The actual process for calculating L can be as set out in Fig. 125.
CA 02564047 2006-11-06
YU139 PCT 132
Where the following constants are set by software:
Constant Value
K 1 XPL
K2 YPL
K3 ZPL2 (as Zp is 0)
K4 -ZPL
Calculation of N.L
Calculating the dot product of vectors N and L is defined as:
XNXL+YNYL+ZNZL
No bump-map
When there is no bump-map N is a constant [0, 0, 1]. N.L therefore reduces to
ZL.
With bump-map
When there is a bump-map, we must calculate the dot product directly. Rather
than take in normalized N
components, we normalize after taking the dot product of a non-normalized N to
a normalized L. L is either
normalized by software (if it is constant), or by the Calculate L process.
This process is as illustrated in Fig. 126.
Note that ZN is not required as input since it is defined to be 1. However
1/IINI is required instead, in
order to normalize the result. One actual process for calculating N.L is as
illustrated in Fig. 127.
Calculation of R=V
R=V is required as input to specular contribution calculations. Since V = [0,
0, 1], only the Z components
are required. R=V therefore reduces to:
R=V = 2ZN(N=L) - ZL
In addition, since the un-normalized ZN = 1, normalized ZN = 1/TINA
No bump--map
The simplest implementation is when N is constant (i.e. no bump-map). Since N
and V are constant, N.L
and R=V can be simplified:
V =[0,0,l]
N =[0,0,l]
L = [XL, YL, ZLI
N.L = ZL
R=V = 2ZN(N.L) - ZL
= 2ZL - ZL
= ZL
When L is constant (Directional light source), a normalized ZL can be supplied
by software in the form of
a constant whenever R=V is required. When L varies (Omni lights and
Spotlights), normalized ZL must be
calculated on the fly. It is obtained as output from the Calculate L process.
With bump-map
When N is not constant, the process of calculating R=V is simply an
implementation of the generalized
formula:
R=V = 2ZN(N.L) - ZL
CA 02564047 2006-11-06
YU139 PCT 133
The inputs and outputs are as shown in Fig. 128 with the an actual
implementation as shown in Fig. 129.
Calculation of Attenuation Factor
Directional lights
When a light source is infinitely distant, the intensity of the light does not
vary across the image. The
attenuation factor fatt is therefore 1. This constant can be used to optimize
illumination calculations for infinitely
distant light sources.
Omni lights and Spotlights
When a light source is not infinitely distant, the intensity of the light can
vary according to the following
formula:
fatt = fo + f,/d + f2/d2
Appropriate settings of coefficients fo, f,, and f2 allow light intensity to
be attenuated by a constant,
linearly with distance, or by the square of the distance.
Since d = IILIh the calculation of fatt can be represented as a process with
the following inputs and outputs
as illustrated in Fig. 130.
The actual process for calculating fatt can be defined in Fig. 131.
Where the following constants are set by software:
Constant Value
K, F2
K2 f,
K3 Fo
Calculation of Cone and Penumbra Factor
Directional lights and Omni lights
These two light sources are not focused, and therefore have no cone or
penumbra. The cone-penumbra
scaling factor ff is therefore 1. This constant can be used to optimize
illumination calculations for Directional and
Omni light sources.
Spotlights
A spotlight focuses on a particular target point (PT). The intensity of the
Spotlight varies according to
whether the particular point of the image is in the cone, in the penumbra, or
outside the cone/penumbra region.
Turning now to Fig. 132, there is illustrated a graph of f p with respect to
the penumbra position. Inside
the cone 470, f, is 1, outside 471 the penumbra fp is 0. From the edge of the
cone through to the end of the
penumbra, the light intensity varies according to a cubic function 472.
The various vectors for penumbra 475 and cone 476 calculation are as
illustrated in Fig. 133 and Fig.
134.
Looking at the surface of the image in I dimension as shown in Fig. 134, 3
angles A, B, and C are
defined. A is the angle between the target point 479, the light source 478,
and the end of the cone 480. C is the
angle between the target point 479, light source 478, and the end of the
penumbra 481. Both are fixed for a given
light source. B is the angle between the target point 479, the light source
478, and the position being calculated
482, and therefore changes with every point being calculated on the image.
CA 02564047 2006-11-06
YUI39 PCT 134
We normalize the range A to C to be 0 to 1, and find the distance that B is
along that angle range by the
formula:
(B-A)/(C-A)
The range is forced to be in the range 0 to I by truncation, and this value
used as a lookup for the cubic
approximation of fcp.
The calculation of fan can therefore be represented as a process with the
inputs and outputs as illustrated
in Fig. 135 with an actual process for calculating fcp is as shown in Fig. 136
where the following constants are set
by software:
Constant Value
K 1 XLT
K2 YLT
K3 ZLT
K4 A
K5 1/(C-A). MAXNUM if no penumbral
The following lookup tables are used:
Lookup Size Details
LU, 64 entries Arcos(X)
16 bits per entry Units are same as for constants K5 and K6
Table indexed by highest 6 bits
Result by linear interpolation of 2 entries
Timing is 2 * 8 bits * 2 entries = 4 cycles
LU2 64 entries Light Response function fcp
16 bits per entry F(1) = 0, F(0) = 1, others are according to cubic
Table indexed by 6 bits (1:5)
Result by linear interpolation of 2 entries
Timing is 2 * 8 bits = 4 cycles
Calculation of Ambient Contribution
Regardless of the number of lights being applied to an image, the ambient
light contribution is performed
once for each pixel, and does not depend on the bump-map.
The ambient calculation process can be represented as a process with the
inputs and outputs as illustrated
in Fig. 131. The implementation of the process requires multiplying each pixel
from the input image (0d) by a
constant value (Iaka), as shown in Fig. 138 where the following constant is
set by software:
Constant Value
K, laka
Calculation of Diffuse Contribution
Each light that is applied to a surface produces a diffuse illumination. The
diffuse illumination is given
by the formula:
diffuse = kdOd(N.L )
There are 2 different implementations to consider:
CA 02564047 2006-11-06
YU139 PCT 135
Implementation 1 - constant N and L
When N and L are both constant (Directional light and no bump-map):
N.L =ZL
Therefore:
diffuse = kdOdZL
Since Od is the only variable, the actual process for calculating the diffuse
contribution is as illustrated in
Fig. 139 where the following constant is set by software:
Constant Value
K, kd N.L = kdZL
Implementation 2 - non-constant N & L
When either N or L are non-constant (either a bump-map or illumination from an
Omni light or a
Spotlight), the diffuse calculation is performed directly according to the
formula:
diffuse = kdOd(N.L )
The diffuse calculation process can be represented as a process with the
inputs as illustrated in Fig. 140.
N.L can either be calculated using the Calculate N.L Process, or is provided
as a constant. An actual process for
calculating the diffuse contribution is as shown in Fig. 141 where the
following constants are set by software:
Constant Value
K. kd
Calculation of Specular Contribution
Each light that is applied to a surface produces a specular illumination. The
specular illumination is given
by the formula:
specular = kO,(R=V)
where OS = kSCOd + (1-k,c)IP
There are two implementations of the Calculate Specular process.
Implementation 1- constant N and L
The first implementation is when both N and L are constant (Directional light
and no bump-map). Since
N, L and V are constant, N.L and R=V are also constant:
V=[0,0, 1]
N=[0,0, 1]
L=[XL,YL,ZLI
N.L = ZL
R=V = 2ZN(N.L) - ZL
=2ZL-ZL
= ZL
The specular calculation can thus be reduced to:
specular = kO, ZL
= k$ZL (k.Od + (1-ksc)1 )
CA 02564047 2006-11-06
YU139 PCT 136
= kSkSCZL"Od + (1-ksC)I,ksZL"
Since only Od is a variable in the specular calculation, the calculation of
the specular contribution can
therefore be represented as a process with the inputs and outputs as indicated
in Fig. 142 and an actual process for
calculating the specular contribution is illustrated in Fig. 143 where the
following constants are set by software:
Constant Value
K, kskS,:ZL"
KZ 1-kSC)I kSZL"
Implementation 2 - non constant N and L
This implementation is when either N or L are not constant (either a bump-map
or illumination from an
Omni light or a Spotlight). This implies that R=V must be supplied, and hence
R=V" must also be calculated.
The specular calculation process can be represented as a process with the
inputs and outputs as shown in
Fig. 144. Fig. 145 shows an actual process for calculating the specular
contribution where the following constants
are set by software:
Constant Value
K, ks
K2 ksc
K3 (1-ksc)I
The following lookup table is used:
Lookup Size Details
LU, 32 entries X"
16 bits per Table indexed by 5 highest bits of integer R=V
entry Result by linear interpolation of 2 entries using fraction of R.V.
Interpolation by 2 Multiplies.
The time taken to retrieve the data from the lookup is 2 * 8 bits * 2
entries = 4 cycles.
When ambient light is the only illumination
If the ambient contribution is the only light source, the process is very
straightforward since it is not
necessary to add the ambient light to anything with the overall process being
as illustrated in Fig. 146.
We can divide the image vertically into 2 sections, and process each half
simultaneously by duplicating
the ambient light logic (thus using a total of 2 Multiply ALUs and 4
Sequential Iterators). The timing is therefore
'/2 cycle per pixel for ambient light application.
The typical illumination case is a scene lit by one or more lights. In these
cases, because ambient light
calculation is so cheap, the ambient calculation is included with the
processing of each light source. The first light
to be processed should have the correct Iaka setting, and subsequent lights
should have an Iaka value of 0 (to
prevent multiple ambient contributions).
If the ambient light is processed as a separate pass (and not the first pass),
it is necessary to add the
ambient light to the current calculated value (requiring a read and write to
the same address). The process
overview is shown in Fig. 147.
The process uses 3 Image Iterators, 1 Multiply ALU, and takes 1 cycle per
pixel on average.
CA 02564047 2006-11-06
YU139 PCT 137
Infinite W ht Source
In the case of the infinite light source, we have a constant light source
intensity across the image. Thus
both L and fatt are constant.
No Bump Map
When there is no bump-map, there is a constant normal vector N [0, 0, 1]. The
complexity of the
illumination is greatly reduced by the constants of N, L, and fatt. The
process of applying a single Directional light
with no bump-map is as illustrated in Fig. 147 where the following constant is
set by software:
Constant Value
K, I
For a single infinite light source we want to perform the logical operations
as shown in Fig. 148 where K,
through K4 are constants with the following values:
Constant Value
K, Kd sL = Kd Lz
K2 ksc
K3 K,(NsH " = K, Hz2
K4 I
The process can be simplified since K2, K3, and K4 are constants. Since the
complexity is essentially in
the calculation of the specular and diffuse contributions (using 3 of the
Multiply ALUs), it is possible to safely add
an ambient calculation as the 4d' Multiply ALU. The first infinite light
source being processed can have the true
ambient light parameter Iaka, and all subsequent infinite lights can set Iaka
to be 0. The ambient light calculation
becomes effectively free.
If the infinite light source is the first light being applied, there is no
need to include the existing
contributions made by other light sources and the situation is as illustrated
in Fig. 149 where the constants have
the following values:
Constant Value
K, kd(LsN = kdLz
K4 I
K5 (1- ks(NsH)tt)I = 1 - kHztt)I
K6 k,cks NsH n I = k5Ck,Hz I
K7 Iaka
If the infinite light source is not the first light being applied, the
existing contribution made by previously
processed lights must be included (the same constants apply) and the situation
is as illustrated in Fig. 148.
In the first case 2 Sequential Iterators 490, 491 are required, and in the
second case, 3 Sequential Iterators
490, 491, 492 (the extra Iterator is required to read the previous light
contributions). In both cases, the application
of an infinite light source with no bump map takes 1 cycle per pixel,
including optional application of the ambient
light.
With Bump Map
When there is a bump-map, the normal vector N must be calculated per pixel and
applied to the constant
light source vector L. 1/IINJJ is also used to calculate R=V, which is
required as input to the Calculate Specular 2
CA 02564047 2006-11-06
YU139 PCT 138
process. The following constants are set by software:
Constant Value
K, XL,
KZ YL,
K3 Z,,
K4 I
Bump-map Sequential Read Iterator 490 is responsible for reading the current
line of the bump-map. It
provides the input for determining the slope in X. Bump-map Sequential Read
Iterators 491, 492 and are
responsible for reading the line above and below the current line. They
provide the input for determining the slope
in Y.
Omni Lights
In the case of the Omni light source, the lighting vector L and attenuation
factor fan change for each pixel
across an image. Therefore both L and faõ must be calculated for each pixel.
No Bump May
When there is no bump-map, there is a constant normal vector N [0, 0, 1].
Although L must be calculated
for each pixel, both N.L and R=V are simplified to ZL. When there is no bump-
map, the application of an Omni
light can be calculated as shown in Fig. 149 where the following constants are
set by software:
Constant Value
K, X,
K2 Y,
K3 I
The algorithm optionally includes the contributions from previous light
sources, and also includes an
ambient light calculation. Ambient light needs only to be included once. For
all other light passes, the appropriate
constant in the Calculate Ambient process should be set to 0.
The algorithm as shown requires a total of 19 multiply/accumulates. The times
taken for the lookups are
1 cycle during the calculation of L, and 4 cycles during the specular
contribution. The processing time of 5 cycles
is therefore the best that can be accomplished. The time taken is increased to
6 cycles in case it is not possible to
optimally microcode the ALUs for the function. The speed for applying an Omni
light onto an image with no
associated bump-map is 6 cycles per pixel.
With Bump-map
When an Omni light is applied to an image with an associated a bump-map,
calculation of N, L, N.L and R=V are
all necessary. The process of applying an Omni light onto an image with an
associated bump-map is as indicated
in Fig. 150 where the following constants are set by software:
Constant Value
K, X,
K2 Yp
K3 I
The algorithm optionally includes the contributions from previous light
sources, and also includes an
CA 02564047 2006-11-06
YU139 PCT 139
ambient light calculation. Ambient light needs only to be included once. For
all other light passes, the appropriate
constant in the Calculate Ambient process should be set to 0.
The algorithm as shown requires a total of 32 multiply/accumulates. The times
taken for the lookups are
1 cycle each during the calculation of both L and N, and 4 cycles for the
specular contribution. However the
lookup required for N and L are both the same (thus 2 LUs implement the 3
LUs). The processing time of 8 cycles
is adequate. The time taken is extended to 9 cycles in case it is not possible
to optimally microcode the ALUs for
the function. The speed for applying an Omni light onto an image with an
associated bump-map is 9 cycles per
pixel.
Spotlights
Spotlights are similar to Omni lights except that the attenuation factor fatt
is modified by a cone/penumbra
factor f p that effectively focuses the light around a target.
No bump-map
When there is no bump-map, there is a constant normal vector N [0, 0, 1].
Although L must be calculated
for each pixel, both N.L and R=V are simplified to ZL. Fig. 151 illustrates
the application of a Spotlight to an
image where the following constants are set by software:
Constant Value
K, X,
KZ Yp
K3 I
The algorithm optionally includes the contributions from previous light
sources, and also includes an
ambient light calculation. Ambient light needs only to be included once. For
all other light passes, the appropriate
constant in the Calculate Ambient process should be set to 0.
The algorithm as shown requires a total of 30 multiply/accumulates. The times
taken for the lookups are
1 cycle during the calculation of L, 4 cycles for the specular contribution,
and 2 sets of 4 cycle lookups in the
cone/penumbra calculation.
With bump-map
When a Spotlight is applied to an image with an associated a bump-map,
calculation of N, L, N.L and
R=V are all necessary. The process of applying a single Spotlight onto an
image with associated bump-map is
illustrated in Fig. 152 where the following constants are set by software:
The algorithm optionally includes the contributions from previous light
sources, and also includes an
ambient light calculation. Ambient light needs only to be included once. For
all other light passes, the appropriate
constant in the Calculate Ambient process should be set to 0. The algorithm as
shown requires a total of 41
multiply/accumulates.
Print Head 44
Fig. 153 illustrates the logical layout of a single print Head which logically
consists of 8 segments, each
printing bi-level cyan, magenta, and yellow onto a portion of the page.
Loading a segment for printing
CA 02564047 2006-11-06
YU139 PCT 140
Before anything can be printed, each of the 8 segments in the Print Head must
be loaded with 6 rows of
data corresponding to the following relative rows in the final output image:
Row 0 = Line N, Yellow, even dots 0, 2, 4, 6, 8, ...
Row 1 = Line N+8, Yellow, odd dots 1, 3, 5, 7, ...
Row 2 = Line N+10, Magenta, even dots 0, 2, 4, 6, 8, ...
Row 3 = Line N+18, Magenta, odd dots 1, 3, 5, 7, ...
Row 4 = Line N+20, Cyan, even dots 0, 2, 4, 6, 8, .. .
Row 5 = Line N+28, Cyan, odd dots 1, 3, 5, 7, ...
Each of the segments prints dots over different parts of the page. Each
segment prints 750 dots of one
color, 375 even dots on one row, and 375 odd dots on another. The 8 segments
have dots corresponding to
positions:
Segment First dot Last dot
0 0 749
1 750 1499
2 1500 2249
3 2250 2999
4 3000 3749
5 3750 4499
6 4500 5249
7 5250 5999
Each dot is represented in the Print Head segment by a single bit. The data
must be loaded 1 bit at a time
by placing the data on the segment's BitValue pin, and clocked in to a shift
register in the segment according to a
BitClock. Since the data is loaded into a shift register, the order of loading
bits must be correct. Data can be
clocked in to the Print Head at a maximum rate of 10 MHz.
Once all the bits have been loaded, they must be transferred in parallel to
the Print Head output buffer,
ready for printing. The transfer is accomplished by a single pulse on the
segment's ParallelXferClock pin.
Controlling the Print
In order to conserve power, not all the dots of the Print Head have to be
printed simultaneously. A set of
control lines enables the printing of specific dots. An external controller,
such as the ACP, can change the number
of dots printed at once, as well as the duration of the print pulse in
accordance with speed and/or power
requirements.
Each segment has 5 NozzleSelect lines, which are decoded to select 32 sets of
nozzles per row. Since
each row has 375 nozzles, each set contains 12 nozzles. There are also 2
BankEnable lines, one for each of the
odd and even rows of color. Finally, each segment has 3 ColorEnable lines, one
for each of C, M, and Y colors. A
pulse on one of the ColorEnable lines causes the specified nozzles of the
color's specified rows to be printed. A
pulse is typically about 2' 1 s in duration.
If all the segments are controlled by the same set of NozzleSelect, BankEnable
and ColorEnable lines
(wired externally to the print head), the following is true:
If both odd and even banks print simultaneously (both BankEnable bits are
set), 24 nozzles fire
simultaneously per segment, 192 nozzles in all, consuming 5.7 Watts.
CA 02564047 2006-11-06
YU139 PCT 141
If odd and even banks print independently, only 12 nozzles fire simultaneously
per segment, 96 in all,
consuming 2.85 Watts.
Print Head Interface 62
The Print Head Interface 62 connects the ACP to the Print Head, providing both
data and appropriate
signals to the external Print Head. The Print Head Interface 62 works in
conjunction with both a VLIW processor
74 and a software algorithm running on the CPU in order to print a photo in
approximately 2 seconds.
An overview of the inputs and outputs to the Print Head Interface is shown in
Fig. 154. The Address and
Data Buses are used by the CPU to address the various registers in the Print
Head Interface. A single BitClock
output line connects to all 8 segments on the print head. The 8 DataBits lines
lead one to each segment, and are
clocked in to the 8 segments on the print head simultaneously (on a BitClock
pulse). For example, dot 0 is
transferred to segmento, dot 750 is transferred to segment,, dot 1500 to
segment2 etc. simultaneously.
The VLIW Output FIFO contains the dithered bi-level C, M, and Y 6000 x 9000
resolution print image
in the correct order for output to the 8 DataBits. The ParallelXferClock is
connected to each of the 8 segments on
the print head, so that on a single pulse, all segments transfer their bits at
the same time. Finally, the NozzleSelect,
BankEnable and ColorEnable lines are connected to each of the 8 segments,
allowing the Print Head Interface to
control the duration of the C, M, and Y drop pulses as well as how many drops
are printed with each pulse.
Registers in the Print Head Interface allow the specification of pulse
durations between 0 and 6 s, with a typical
duration of 2 s.
Printing an Image
There are 2 phases that must occur before an image is in the hand of the
Artcam user:
1. Preparation of the image to be printed
2. Printing the prepared image
Preparation of an image only needs to be performed once. Printing the image
can be performed as many
times as desired.
Prepare the Image
Preparing an image for printing involves:
1. Convert the Photo Image into a Print Image
2. Rotation of the Print Image (internal color space) to align the output for
the orientation of the
printer
3. Up-interpolation of compressed channels (if necessary)
4. Color conversion from the internal color space to the CMY color space
appropriate to the
specific printer and ink
At the end of image preparation, a 4.5MB correctly oriented 1000 x 1500 CMY
image is ready to be
printed.
Convert Photo Image to Print Image
The conversion of a Photo Image into a Print Image requires the execution of a
Vark script to perform
image processing. The script is either a default image enhancement script or a
Vark script taken from the currently
inserted Artcard. The Vark script is executed via the CPU, accelerated by
functions performed by the VLIW
Vector Processor.
Rotate the Print Image
CA 02564047 2006-11-06
YU 139 PCT 142
The image in memory is originally oriented to be top upwards. This allows for
straightforward Vark
processing. Before the image is printed, it must be aligned with the print
roll's orientation. The re-alignment only
needs to be done once. Subsequent Prints of a Print Image will already have
been rotated appropriately.
The transformation to be applied is simply the inverse of that applied during
capture from the CCD when
the user pressed the "Image Capture" button on the Artcam. If the original
rotation was 0, then no transformation
needs to take place. If the original rotation was +90 degrees, then the
rotation before printing needs to be -90
degrees (same as 270 degrees). The method used to apply the rotation is the
Vark accelerated Affme Transform
function. The Affine Transform engine can be called to rotate each color
channel independently. Note that the
color channels cannot be rotated in place. Instead, they can make use of the
space previously used for the
expanded single channel (1.5MB).
Fig. 155 shows an example of rotation of a Lab image where the a and b
channels are compressed 4:1.
The L channel is rotated into the space no longer required (the single channel
area), then the a channel can be
rotated into the space left vacant by L, and finally the b channel can be
rotated. The total time to rotate the 3
channels is 0.09 seconds. It is an acceptable period of time to elapse before
the first print image. Subsequent prints
do not incur this overhead.
Up Interpolate and color convert
The Lab image must be converted to CMY before printing. Different processing
occurs depending on
whether the a and b channels of the Lab image is compressed. If the Lab image
is compressed, the a and b
channels must be decompressed before the color conversion occurs. If the Lab
image is not compressed, the color
conversion is the only necessary step. The Lab image must be up interpolated
(if the a and b channels are
compressed) and converted into a CMY image. A single VLIW process combining
scale and color transform can
be used.
The method used to perform the color conversion is the Vark accelerated Color
Convert function. The
Affine Transform engine can be called to rotate each color channel
independently. The color channels cannot be
rotated in place. Instead, they can make use of the space previously used for
the expanded single channel
(1.5MB).
Print the Image
Printing an image is concerned with taking a correctly oriented 1000 x 1500
CMY image, and generating
data and signals to be sent to the external Print Head. The process involves
the CPU working in conjunction with a
VLIW process and the Print Head Interface.
The resolution of the image in the Artcam is 1000 x 1500. The printed image
has a resolution of 6000 x
9000 dots, which makes for a very straightforward relationship: 1 pixel = 6 x
6 = 36 dots. As shown in Fig. 156
since each dot is 16.6 m, the 6 x 6 dot square is 100 m square. Since each of
the dots is bi-level, the output must
be dithered.
The image should be printed in approximately 2 seconds. For 9000 rows of dots
this implies a time of
222 .ts time between printing each row. The Print Head Interface must generate
the 6000 dots in this time, an
average of 37ns per dot. However, each dot comprises 3 colors, so the Print
Head Interface must generate each
color component in approximately 12ns, or 1 clock cycle of the ACP (1 Ons at
100 MHz). One VLIW process is
responsible for calculating the next line of 6000 dots to be printed. The odd
and even C, M, and Y dots are
generated by dithering input from 6 different 1000 x 1500 CMY image lines. The
second VLIW process is
CA 02564047 2006-11-06
YU139 PCT 143
responsible for taking the previously calculated line of 6000 dots, and
correctly generating the 8 bits of data for the
8 segments to be transferred by the Print Head Interface to the Print Head in
a single transfer.
A CPU process updates registers in the fist VLIW process 3 times per print
line (once per color
component = 27000 times in 2 secondsO, and in the 2nd VLIW process once every
print line (9000 times in 2
seconds). The CPU works one line ahead of the VLIW process in order to do
this.
Finally, the Print Head Interface takes the 8 bit data from the VLIW Output
FIFO, and outputs it
unchanged to the Print Head, producing the BitClock signals appropriately.
Once all the data has been transferred
a ParallelXferClock signal is generated to load the data for the next print
line. In conjunction with transferring the
data to the Print Head, a separate timer is generating the signals for the
different print cycles of the Print Head
using the NozzleSelect, ColorEnable, and BankEnable lines a specified by Print
Head Interface internal registers.
The CPU also controls the various motors and guillotine via the parallel
interface during the print
process.
Generate C, M, and Y Dots
The input to this process is a 1000 x 1500 CMY image correctly oriented for
printing. The image is not
compressed in any way. As illustrated in Fig. 157, a VLIW microcode program
takes the CMY image, and
generates the C, M, and Y pixels required by the Print Head Interface to be
dithered.
The process is run 3 times, once for each of the 3 color components. The
process consists of 2 sub-
processes run in parallel - one for producing even dots, and the other for
producing odd dots. Each sub-process
takes one pixel from the input image, and produces 3 output dots (since one
pixel = 6 output dots, and each sub-
process is concerned with either even or odd dots). Thus one output dot is
generated each cycle, but an input pixel
is only read once every 3 cycles.
The original dither cell is a 64 x 64 cell, with each entry 8 bits. This
original cell is divided into an odd
cell and an even cell, so that each is still 64 high, but only 32 entries
wide. The even dither cell contains original
dither cell pixels 0, 2, 4 etc., while the odd contains original dither cell
pixels 1, 3, 5 etc. Since a dither cell repeats
across a line, a single 32 byte line of each of the 2 dither cells is required
during an entire line, and can therefore
be completely cached. The odd and even lines of a single process line are
staggered 8 dot lines apart, so it is
convenient to rotate the odd dither cell's lines by 8 lines. Therefore the
same offset into both odd and even dither
cells can be used. Consequently the even dither cell's line corresponds to the
even entries of line L in the original
dither cell, and the even dither cell's line corresponds to the odd entries of
line L+8 in the original dither cell.
The process is run 3 times, once for each of the color components. The CPU
software routine must
ensure that the Sequential Read Iterators for odd and even lines are pointing
to the correct image lines
corresponding to the print heads. For example, to produce one set of 18,000
dots (3 sets of 6000 dots):
= Yellow even dot line = 0, therefore input Yellow image line = 0/6 = 0
= Yellow odd dot line = 8, therefore input Yellow image line = 8/6 = 1
= Magenta even line = 10, therefore input Magenta image line = 10/6 = 1
= Magenta odd line = 18, therefore input Magenta image line = 18/6 = 3
= Cyan even line = 20, therefore input Cyan image line = 20/6 = 3
= Cyan odd line = 28, therefore input Cyan image line = 28/6 = 4
Subsequent sets of input image lines are:
CA 02564047 2006-11-06
YU139 PCT 144
= Y=[0, 1], M=[1, 3], C=[3, 4]
= Y=[0, 1], M=[1, 3], C=[3, 4]
= Y=[0, 1], M=[2, 3], C=[3, 5]
= Y=[0, 1], M=[2, 3], C=[3, 5]
= Y=[0, 2], M=[2, 3], C=[4, 5]
The dither cell data however, does not need to be updated for each color
component. The dither cell for
the 3 colors becomes the same, but offset by 2 dot lines for each component.
The Dithered Output is written to a Sequential Write Iterator, with odd and
even dithered dots written to
2 separate outputs. The same two Write Iterators are used for all 3 color
components, so that they are contiguous
within the break-up of odd and even dots.
While one set of dots is being generated for a print line, the previously
generated set of dots is being
merged by a second VLIW process as described in the next section.
Generate Merged 8 bit Dot Output
This process, as illustrated in Fig. 158, takes a single line of dithered dots
and generates the 8 bit data
stream for output to the Print Head Interface via the VLIW Output FIFO. The
process requires the entire line to
have been prepared, since it requires semi-random access to most of the
dithered line at once. The following
constant is set by software:
Constant Value
K, 375
The Sequential Read Iterators point to the line of previously generated dots,
with the Iterator registers set
up to limit access to a single color component. The distance between
subsequent pixels is 375, and the distance
between one line and the next is given to be 1 byte. Consequently 8 entries
are read for each "line". A single
"line" corresponds to the 8 bits to be loaded on the print head. The total
number of "lines" in the image is set to be
375. With at least 8 cache lines assigned to the Sequential Read Iterator,
complete cache coherence is maintained.
Instead of counting the 8 bits, 8 Microcode steps count implicitly.
The generation process first reads all the entries from the even dots,
combining 8 entries into a single
byte which is then output to the VLIW Output FIFO. Once all 3000 even dots
have been read, the 3000 odd dots
are read and processed. A software routine must update the address of the dots
in the odd and even Sequential
Read Iterators once per color component, which equates to 3 times per line.
The two VLIW processes require all
8 ALUs and the VLIW Output FIFO. As long as the CPU is able to update the
registers as described in the two
processes, the VLIW processor can generate the dithered image dots fast enough
to keep up with the printer.
Data Card Reader
Fig. 159, there is illustrated on form of card reader 500 which allows for the
insertion of Artcards 9 for
reading. Fig. 158 shows an exploded perspective of the reader of Fig. 159.
Cardreader is interconnected to a
computer system and includes a CCD reading mechanism 35. The cardreader
includes pinch rollers 506, 507 for
pinching an inserted Artcard 9. One of the roller e.g. 506 is driven by an
Artcard motor 37 for the advancement of
the card 9 between the two rollers 506 and 507 at a uniformed speed. The
Artcard 9 is passed over a series of
LED lights 512 which are encased within a clear plastic mould 514 having a
semi circular cross section. The
cross section focuses the light from the LEDs eg 512 onto the surface of the
card 9 as it passes by the LEDs 512.
CA 02564047 2006-11-06
YU139 PCT 145
From the surface it is reflected to a high resolution linear CCD 34 which is
constructed to a resolution of
approximately 480 dpi. The surface of the Artcard 9 is encoded to the level of
approximately 1600 dpi hence, the
linear CCD 34 supersamples the Artcard surface with an approximately three
times multiplier. The Artcard 9 is
further driven at a speed such that the linear CCD 34 is able to supersample
in the direction of Artcard movement
at a rate of approximately 4800 readings per inch. The scanned Artcard CCD
data is forwarded from the Artcard
reader to ACP 31 for processing. A sensor 49, which can comprise a light
sensor acts to detect of the presence of
the card 13.
The CCD reader includes a bottom substrate 516, a top substrate 514 which
comprises a transparent
molded plastic. In between the two substrates is inserted the linear CCD array
34 which comprises a thin long
linear CCD array constructed by means of semi-conductor manufacturing
processes.
Turning to Fig. 160, there is illustrated a side perspective view, partly in
section, of an example
construction of the CCD reader unit. The series of LEDs eg. 512 are operated
to emit light when a card 9 is
passing across the surface of the CCD reader 34. The emitted light is
transmitted through a portion of the top
substrate 523. The substrate includes a portion eg. 529 having a curved
circumference so as to focus light emitted
from LED 512 to a point eg. 532 on the surface of the card 9. The focused
light is reflected from the point 532
towards the CCD array 34. A series of microlenses eg. 534, shown in
exaggerated form, are formed on the
surface of the top substrate 523. The microlenses 523 act to focus light
received across the surface to the focused
down to a point 536 which corresponds to point on the surface of the CCD
reader 34 for sensing of light falling on
the light sensing portion of the CCD array 34.
A number of refinements of the above arrangement are possible. For example,
the sensing devices on the
linear CCD 34 may be staggered. The corresponding microlenses 34 can also be
correspondingly formed as to
focus light into a staggered series of spots so as to correspond to the
staggered CCD sensors.
To assist reading, the data surface area of the Artcard 9 is modulated with a
checkerboard pattern as
previously discussed with reference to Fig. 38. Other forms of high frequency
modulation may be possible
however.
It will be evident that an Artcard printer can be provided as for the printing
out of data on storage
Artcard. Hence, the Artcard system can be utilized as a general form of
information distribution outside of the
Artcam device. An Artcard printer can prints out Artcards on high quality
print surfaces and multiple Artcards
can be printed on same sheets and later separated. On a second surface of the
Artcard 9 can be printed information
relating to the files etc. stored on the Artcard 9 for subsequent storage.
Hence, the Artcard system allows for a simplified form of storage which is
suitable for use in place of
other forms of storage such as CD ROMs, magnetic disks etc. The Artcards 9 can
also be mass produced and
thereby produced in a substantially inexpensive form for redistribution.
Print Rolls
Turning to Fig. 162, there is illustrated the print roll 42 and print-head
portions of the Artcam. The paper/film 611
is fed in a continuous "web-like" process to a printing mechanism 15 which
includes further pinch rollers 616 -
619 and a print head 44
The pinch roller 613 is connected to a drive mechanism (not shown) and upon
rotation of the print roller
613, "paper" in the form of film 611 is forced through the printing mechanism
615 and out of the picture output
slot 6. A rotary guillotine mechanism (not shown) is utilised to cut the roll
of paper 611 at required photo sizes.
CA 02564047 2006-11-06
YU139 PCT 146
It is therefore evident that the printer roll 42 is responsible for supplying
"paper" 611 to the print
mechanism 615 for printing of photographically imaged pictures.
In Fig. 163, there is shown an exploded perspective of the print roll 42. The
printer roll 42 includes
output printer paper 611 which is output under the operation of pinching
rollers 612, 613.
Referring now to Fig. 164, there is illustrated a more fully exploded
perspective view, of the print roll 42
of Fig. 163 without the "paper" film roll. The print roll 42 includes three
main parts comprising ink reservoir
section 620, paper roll sections 622, 623 and outer casing sections 626, 627.
Turning first to the ink reservoir section 620, which includes the ink
reservoir or ink supply sections 633.
The ink for printing is contained within three bladder type containers 630 -
632. The printer roll 42 is assumed to
provide full color output inks. Hence, a first ink reservoir or bladder
container 630 contains cyan colored ink. A
second reservoir 631 contains magenta colored ink and a third reservoir 632
contains yellow ink. Each of the
reservoirs 630 - 632, although having different volumetric dimensions, are
designed to have substantially the same
volumetric size.
The ink reservoir sections 621, 633, in addition to cover 624 can be made of
plastic sections and are
designed to be mated together by means of heat sealing, ultra violet
radiation, etc. Each of the equally sized ink
reservoirs 630 - 632 is connected to a corresponding ink channel 639 - 641 for
allowing the flow of ink from the
reservoir 630 - 632 to a corresponding ink output port 635 - 637. The ink
reservoir 632 having ink channel 641,
and output port 637, the ink reservoir 631 having ink channel 640 and output
port 636, and the ink reservoir 630
having ink channel 639 and output port 637.
In operation, the ink reservoirs 630 - 632 can be filled with corresponding
ink and the section 633 joined
to the section 621. The ink reservoir sections 630 - 632, being collapsible
bladders, allow for ink to traverse ink
channels 639 - 641 and therefore be in fluid communication with the ink output
ports 635 - 637. Further, if
required, an air inlet port can also be provided to allow the pressure
associated with ink channel reservoirs 630 -
632 to be maintained as required.
The cap 624 can be joined to the ink reservoir section 620 so as to form a
pressurized cavity, accessible
by the air pressure inlet port.
The ink reservoir sections 621, 633 and 624 are designed to be connected
together as an integral unit and
to be inserted inside printer roll sections 622, 623. The printer roll
sections 622, 623 are designed to mate together
by means of a snap fit by means of male portions 645 - 647 mating with
corresponding female portions (not
shown). Similarly, female portions 654 - 656 are designed to mate with
corresponding male portions 660 - 662.
The paper roll sections 622, 623 are therefore designed to be snapped
together. One end of the film within the role
is pinched between the two sections 622, 623 when they are joined together.
The print film can then be rolled on
the print roll sections 622, 625 as required.
As noted previously, the ink reservoir sections 620, 621, 633, 624 are
designed to be inserted inside the
paper roll sections 622, 623. The printer roll sections 622, 623 are able to
be rotatable around stationery ink
reservoir sections 621, 633 and 624 to dispense film on demand.
The outer casing sections 626 and 627 are further designed to be coupled
around the print roller sections
622, 623. In addition to each end of pinch rollers eg 612, 613 is designed to
clip in to a corresponding cavity eg
670 in cover 626, 627 with roller 613 being driven externally (not shown) to
feed the print film and out of the print
roll.
CA 02564047 2006-11-06
YU139 PCT 147
Finally, a cavity 677 can be provided in the ink reservoir sections 620, 621
for the insertion and gluing of
an silicon chip integrated circuit type device 53 for the storage of
information associated with the print roll 42.
As shown in Fig. 155 and Fig. 164, the print roll 42 is designed to be
inserted into the Artcam camera
device so as to couple with a coupling unit 680 which includes connector pads
681 for providing a connection
with the silicon chip 53. Further, the connector 680 includes end connectors
of four connecting with ink supply
ports 635 - 637. The ink supply ports are in turn to connect to ink supply
lines eg 682 which are in turn
interconnected to printheads supply ports eg. 687 for the flow of ink to print-
head 44 in accordance with
requirements.
The "media" 611 utilised to form the roll can comprise many different
materials on which it is designed
to print suitable images. For example, opaque rollable plastic material maybe
utilized, transparencies may be
used by using transparent plastic sheets, metallic printing can take place via
utilization of a metallic sheet film.
Further, fabrics could be utilised within the printer roll 42 for printing
images on fabric, although care must be
taken that only fabrics having a suitable stiffness or suitable backing
material are utilised.
When the print media is plastic, it can be coated with a layer, which fixes
and absorbs the ink. Further,
several types of print media may be used, for example, opaque white matte,
opaque white gloss, transparent film,
frosted transparent film, lenticular array film for stereoscopic 3D prints,
metallized film, film with the embossed
optical variable devices such as gratings or holograms, media which is pre-
printed on the reverse side, and media
which includes a magnetic recording layer. When utilizing a metallic foil, the
metallic foil can have a polymer
base, coated with a thin (several micron) evaporated layer of aluminum or
other metal and then coated with a clear
protective layer adapted to receive the ink via the ink printer mechanism.
In use the print roll 42 is obviously designed to be inserted inside a camera
device so as to provide ink
and paper for the printing of images on demand. The ink output ports 635 - 637
meet with corresponding ports
within the camera device and the pinch rollers 672, 673 are operated to allow
the supply of paper to the camera
device under the control of the camera device.
As illustrated in Fig. 164, a mounted silicon chip 53 is inserted in one end
of the print roll 42. In Fig. 165
the authentication chip 53 is shown in more detail and includes four
communications leads 680 - 683 for
communicating details from the chip 53 to the corresponding camera to which it
is inserted.
Turning to Fig. 165, the chip can be separately created by means of encasing a
small integrated circuit
687 in epoxy and running bonding leads eg. 688 to the external communications
leads 680 - 683. The integrated
chip 687 being approximately 400 microns square with a 100 micron scribe
boundary. Subsequently, the chip can
be glued to an appropriate surface of the cavity of the print roll 42. In Fig.
166, there is illustrated the integrated
circuit 687 interconnected to bonding pads 681, 682 in an exploded view of the
arrangement of Fig. 165.
In Fig.'s 164A to 164E of the drawings, reference numeral 1100 generally
designates a print cartridge
1100. The print cartridge 1100 includes an ink cartridge 1102, in accordance
with the invention.
The print cartridge 1100 includes a housing 1104. As illustrated more clearly
in Figure 2 of the
drawings, the housing 1104 is defined by an upper molding 1106 and a lower
molding 1108. The moldings
1106 and 1108 clip together by means of clips 1110. The housing 1104 is
covered by a label 1112 which
provides an attractive appearance to the cartridge 1100. The label 1112 also
carries information to enable a
user to use the cartridge 1100.
CA 02564047 2006-11-06
YU139 PCT 148
The housing 1104 defines a chamber 1114 in which the ink cartridge 1102 is
received. The ink
cartridge 1102 is fixedly supported in the chamber 1114 of the housing 1104.
A supply of print media 1116 comprising a roll 1126 of film/media 1118 wound
about a former 1120
is received in the chamber 1114 of the housing 1104. The former 1120 is
slidably received over the ink
cartridge 1102 and is rotatable relative thereto.
As illustrated in Figure 164B of the drawings, when the upper molding 1106 and
lower molding
1108 are clipped together, an exit slot 1122 is defined through which a tongue
of the paper 1118 is ejected.
The cartridge 1100 includes a roller assembly 1124 which serves to de-curl the
paper 1118 as it is fed
from the roll 1126 and also to drive the paper 1118 through the slot 1122. The
roller assembly 1124 includes
a drive roller 1128 and two driven rollers 1130. The driven rollers 1130 are
rotatably supported in ribs 1132
which stand proud of a floor 1134 of the lower molding 1108 of the housing
1104. The rollers 1130, together
with the drive roller 1128, provide positive traction to the paper 1118 to
control its speed and position as it is
ejected from the housing 1104. The rollers 1130 are injection moldings of a
suitable synthetic plastics
material such as polystyrene. In this regard also, the upper molding 1106 and
the lower molding 1108 are
injection moldings of suitable synthetic plastics material, such as
polystyrene.
The drive roller 1128 includes a drive shaft 1136 which is held rotatably
captive between mating
recesses 1138 and 1140 defined in a side wall of each of the upper molding
1106 and the lower molding 1108,
respectively, of the housing 1104. An opposed end 1142 of the drive roller
1128 is held rotatably in suitable
formations (not shown) in the upper molding 1106 and the lower molding 1108 of
the housing 1104.
The drive roller 1128 is a two shot injection molding comprising the shaft
1136 which is of a high
impact polystyrene and on which are molded a bearing means in the form of
elastomeric or rubber roller
portions 1144. These portions 1144 positively engage the paper 1118 and
inhibit slippage of the paper 1118
as the paper 1118 is fed from the cartridge 1100.
The end of the roller 1128 projecting from the housing 1104 has an engaging
formation in the form
of a cruciform arrangement 1146 (Figure 164A) which mates with a geared drive
interface (not shown) of a
printhead assembly of a device, such as a camera, in which the print cartridge
1100 is installed. This
arrangement ensures that the speed at which the paper 1118 is fed to the
printhead is synchronised with
printing by the printhead to ensure accurate registration of ink on the paper
1118.
The ink cartridge 1102 includes a container 1148 which is in the form of a
right circular cylindrical
extrusion. The container 1148 is extruded from a suitable synthetic plastics
material such as polystyrene.
In a preferred embodiment of the invention, the printhead with which the print
cartridge 1100 is
used, is a multi-colored printhead. Accordingly, the container 1148 is divided
into a plurality of, more
particularly, four compartments or reservoirs 1150. Each reservoir 1150 houses
a different color or type of
ink. In one embodiment, the inks contained in the reservoirs 1150 are cyan,
magenta, yellow and black inks.
In another embodiment of the invention, three different colored inks, being
cyan, magenta and yellow inks,
are accommodated in three of the reservoirs 1150 while a fourth reservoir 1150
houses an ink which is visible
in the infra-red light spectrum only.
CA 02564047 2006-11-06
YU139 PCT 149
As shown more clearly in Figures 164C and 164D of the drawings, one end of the
container 1148 is
closed off by an end cap 1152. The end cap 1152 has a plurality of openings
1154 defined in it. An opening
1154 is associated with each reservoir 1150 so that atmospheric pressure is
maintained in the reservoir 1150 at
that end of the container 1148 having the end cap 1152.
A seal arrangement 1156 is received in the container 1148 at the end having
the end cap 1152. The
seal arrangement 1156 comprises a quadrant shaped pellet 1158 of gelatinous
material slidably received in
each reservoir 1150. The gelatinous material of the pellet 1158 is a compound
made of a thermoplastic rubber
and a hydrocarbon. The hydrocarbon is a white mineral oil. The thermoplastic
rubber is a copolymer which
imparts sufficient rigidity to the mineral oil so that the pellet 1158 retains
its form at normal operating
temperatures while permitting sliding of the pellet 1158 within its associated
reservoir 1150. A suitable
thermoplastic rubber is that sold under the registered trademark of "Kraton"
by the Shell Chemical Company.
The copolymer is present in the compound in an amount sufficient to impart a
gel-like consistency to each
pellet 1158. Typically, the copolymer, depending on the type used, would be
present in an amount of
approximately three percent to twenty percent by mass.
In use, the compound is heated so that it becomes fluid. Once each reservoir
1150 has been charged
with its particular type of ink, the compound, in a molten state, is poured
into each reservoir 1150 where the
compound is allowed to set to form the pellet 1158. Atmospheric pressure
behind the pellets 1158, that is, at
that end of the pellet 1158 facing the end cap 1152 ensures that, as ink is
withdrawn from the reservoir 1150,
the pellets 1158, which are self-lubricating, slide towards an opposed end of
the container 1148. The pellets
1158 stop ink emptying out of the container when inverted, inhibit
contamination of the ink in the reservoir
1150 and also inhibit drying out of the ink in the reservoir 1150. The pellets
1158 are hydrophobic further to
inhibit leakage of ink from the reservoirs 1150.
The opposed end of the container 1148 is closed off by an ink collar molding
1160. Baffles 1162
carried on the molding 1160 receive an elastomeric seal molding 1164. The
elastomeric seal molding 1164,
which is hydrophobic, has sealing curtains 1166 defined therein. Each sealing
curtain 1166 has a slit 1168 so
that a mating pin (not shown) from the printhead assembly is insertable
through the slits 1168 into fluid
communication with the reservoirs 1150 of the container 1148. Hollow bosses
1170 project from an opposed
side of the ink collar molding 1160. Each boss 1170 is shaped to fit snugly in
its associated reservoir 1150 for
locating the ink collar molding on the end of the container 1148.
Reverting again to Figure 164C of the drawings, the ink collar molding 1160 is
retained in place by
means of a carrier or fascia molding 1172. The fascia molding 1172 has a four
leaf clover shaped window
1174 defined therein through which the elastomeric seal molding 1164 is
accessible. The fascia molding
1174 is held captive between the upper molding 1106 and the lower molding 1108
of the housing 1104. The
fascia molding 1174 and webs 1176 and 1178 extending from an interior surface
of the upper molding 1106
and the lower molding 1108 respectively, of the housing 1104 define a
compartment 1180. An air filter 1182
is received in the compartment 1180 and is retained in place by the end
molding 1174. The air filter 1182
cooperates with the printhead assembly. Air is blown across a nozzle guard of
a printhead assembly to effect
CA 02564047 2006-11-06
YU139 PCT 150
cleaning of the nozzle guard. This air is filtered by being drawn through the
air filter 1182 by means of a pin
(not shown) which is received in an inlet opening 1184 in the fascia molding
1172.
The air filter 1182 is shown in greater detail in Figure 164E of the drawings.
The air filter 1182
comprises a filter medium 1192. The filter medium 1192 is synthetic fiber
based and is arranged in a fluted
form to increase the surface area available for filtering purposes. Instead of
a paper based filter medium 1192
other fibrous batts could also be used.
The filter medium 1192 is received in a canister 1194. The canister 1194
includes a base molding
1196 and a lid 1198. To be accommodated in the compartment 1180 of the housing
1104, the canister 1194 is
part-annular or horse shoe shaped. Thus, the canister 1194 has a pair of
opposed ends 1200. An air inlet
opening 1202 is defined in each end 1200.
An air outlet opening 1204 is defined in the lid 1198. The air outlet opening
1204, initially, is closed
off by a film or membrane 1206. When the filter 1182 is mounted in position in
the compartment 1180, the
air outlet opening 1204 is in register with the opening 1184 in the fascia
molding 1172. The pin from the
printhead assembly pierces the film 1206 then draws air from the atmosphere
through the air filter 1182 prior
to the air being blown over the nozzle guard and the printhead of the
printhead assembly.
The base molding 1194 includes locating formations 1208 and 1210 for locating
the filter medium
1192 in position in the canister 1194. The locating formations 1208 are in the
form of a plurality of pins 1212
while the locating formations 1210 are in the form of ribs which engage ends
1214 of the filter medium 1192.
Once the filter medium 1192 has been placed in position in the base mold 1196,
the lid 1198 is
secured to the base molding 1196 by ultrasonic welding or similar means to
seal the lid 1198 to the base
molding 1196.
When the print cartridge 1100 has been assembled, a membrane or film 1186 is
applied to an outer
end of the fascia molding 1172 to close off the window 1174. This membrane or
film 1186 is pierced or
ruptured by the pins, for use. The film 1186 inhibits the ingress of detritus
into the ink reservoirs 1150.
An authentication means in the form of an authentication chip 1188 is received
in an opening 1190 in
the fascia molding 1172. The authentication chip 1188 is interrogated by the
printhead assembly 1188 to
ensure that the print cartridge 1100 is compatible and compliant with the
printhead assembly of the device.
In Fig. 164F, reference numeral 1230 generally indicates a further embodiment
of a printing
cartridge, in accordance with the invention. With reference to the preceding
drawings, like reference numerals
refer to like parts, unless otherwise specified.
This embodiment of the printing cartridge and the Artcam device uses
capacitive sensor technology
to provide the ACP 31 with data relating to the contents of the printing
cartridge 1230. In particular, this
embodiment uses an array 1232 of capacitive sensors 1234 (Fig 164H) together
with an actuating formation
1234 on the printing cartridge 1230.
As is known, it is possible to represent data two dimensionally with a matrix
of dots that are read by
a sensor. It follows that data can be represented by a formation that acts on
a combination of capacitive
CA 02564047 2006-11-06
YU139 PCT 151
sensors in an array of such sensors to generate a unique signal that carries
the data to the ACP 31. As set out
in the preamble, such sensors have been the subject of fingerprint acquisition
and recordal technology. One
particular reason for their popularity in this field is that they are of low
cost and are relatively robust because
of their solid state nature. It will be appreciated that in such technology,
each sensor is constrained to be
smaller that an individual ridge or valley of a fingerprint. It follows that
an array of sensors used with such
technology incorporates a high number of sensors. This is made possible with
integrated circuit fabrication
techniques. Thus, it is possible to achieve the representation of a
substantial amount of data with such an
array.
There have been substantial developments in the field of micromolding. Such
molding has
been developed to an extent where it is possible to injection mold components
having dimensions as small as
3 micrometers. It follows that it is possible to injection mold an actuating
formation that is capable of discrete
operation on individual capacitive sensors.
It follows that such an actuating formation can be used to represent data in a
similar manner as does
an array of dots in a two dimensional code. Further, using fingerprint sensing
technology, it is possible to
achieve an array of capacitive sensors which incorporate predetermined
combinations of capacitive sensors
which correspond to possible shapes of actuating formation that represent
data. This data is then effectively
read as the capacitive sensors corresponding to a particular shape of
actuating formation are actuated by that
actuating formation.
The high number of possible capacitive sensors and the fact that the
projections are micromolded
allows a significant amount of data to be represented by the actuating
formation.
For two parallel conducting plates of a capacitive sensor, separated by an
insulating material, the
capacitance between the plates is given by C = eAld, where C is capacitance, A
is the area of the plates, d is
the distance between the plates and e is a constant depending on the material
between the plates.
It follows that the measured capacitance is inversely proportional to the
distance between the two
plates. In fingerprint technology, one of the plates is defined by human skin
that forms the fingerprint. Thus,
the measured capacitance varies with finger topography. In particular, the
capacitance of a capacitor formed
between a capacitor plate and a valley of a finger surface is less than the
capacitance of a capacitor formed
between a capacitor plate and a ridge of a finger surface. Still further,
regions intermediate the ridges and the
valleys will generate capacitances between the limits defined by the valleys
and the ridges. It follows that with
suitable electronic circuitry, this can be used to generate an image of the
fingerprint.
The cartridge 1230 includes a housing 1231 that contains a supply of media and
ink. The actuating
formation 1232 is positioned on an end 1236 of the housing 1231. The actuating
formation 1234 is of a
conductive material such as a metallized or conductive plastic. The actuating
formation 1234 is the product of
a micromolding process and defines an array 1240 of projections 1238, shown in
detail in Fig. 164G. The end
1236 is that end which is inserted into the Artcam device when the printing
cartridge 1230 is loaded.
The array 1232 of capacitive sensors is positioned in the Artcam device so
that, when the printing
cartridge 1230 is inserted into the Artcam device, the array 1240 bears
against the array 1232.
CA 02564047 2006-11-06
YU139 PCT 152
The array 1232 is in the form of a ceramic metal oxide semiconductor (CMOS)
device. In particular,
the array 1232 includes a wafer substrate 1242. A plurality of capacitive
sensors 1244 is positioned on the
wafer substrate (Fig 164H). Each sensor 1244 is embedded in a layer 1246 of
dielectric material positioned on
the wafer substrate 1242 and defining a contact surface 1248 for the
projections 1238. Each sensor 1244
includes a capacitor plate 1250 that is spaced from the contact surface 1248,
the capacitor plates 1250 being
coplanar.
The array 1232 is positioned so that when the end 1236 of the cartridge 1230
is inserted into the
Artcam device, each micromolded projection 1240 corresponds with a respective
capacitive sensor 1244 to
define a capacitor 1252 indicated schematically in a circuit 1254 of Fig.
1641. Each capacitive sensor 1244 is
connected to such a circuit 1254.
The circuit 1254 includes a voltage source 1256 and a switch 1258, which are
used to bring its
respective capacitor plate 1250 to a predetermined potential. The switch 1258
is then used to disconnect the
capacitor plate 1250 from the voltage source 1256 and to connect the capacitor
plate 1250 to a current source
1260.
It will be appreciated that a capacitance at a sensor 1244 that corresponds to
a particular projection
1238 is substantially higher than a capacitance at a sensor 1244 that does not
correspond to a particular
projection. This distinction in capacitances across the array 1232 is used to
generate a signal carrying the data
represented by the actuating formation 1234. It will be appreciated that by
using suitable electronic algorithms
applied to the capacitances across the array 1232 there is achieved a two
dimensional array of high and low
capacitance values. This two dimensional array thus represents the data
relating to the media and the ink of
the printing cartridge 1230.
The ACP 31 incorporates a capacitive sensor array interface 1264 to interpret
the signals received
from the array 1232 of capacitive sensors 1244 into a form that is readable by
the ACP 31,
The data represented by the actuating formation 1234 can relate to a number of
characteristics of the
media and ink. For example, the data can relate to:
(a) Serial numbers identifying the media and the ink;
(b) A length of the media in the cartridge 1230;
(c) A type of the media in the cartridge 1230;
(d) Physical characteristics of the ink such as surface tension and viscosity;
(e) Optical characteristics of the ink, such as optical density of red, green
and blue components;
(f) A preferred ink drop volume to suit the media type.
It will be appreciated that other forms of data can also be represented by the
actuating formation
1234.
The data carried by a signal generated by the array 1232 can incorporate
script that is readable by the
ACP 31, once decoded. The script can be in the form of instructions to which
the ACP 31 is responsive. The
CA 02564047 2006-11-06
YU139 PCT 153
instructions can relate to the operation of the printhead 44 to suit the
characteristics of the media and the ink
within the cartridge 1230.
In some cases, the amount of data that can be carried by the array 1232 of
projections 1236 is
limited. It follows that the CPU core 72 can be configured to hold data lookup
tables in a memory.
An example of such a lookup table is indicated by reference numeral 1262 in
Fig. 164J. As can be
seen, the table 1262 represents the above types of data. The memory contains a
plurality of different values
for each of the data types listed in the data lookup table 1262 as a, ...a.,
bi...b,,, ci...c,,, di...d,,, eI...e., f,...ff,
g,...g,,, respectively. Each of these values is predetermined to correspond
with possible values relating to
media and ink corresponding to those found in the range of inks and media
types which could be found in the
cartridge 1230.
Each of the possible values is represented by a code indicated by x1, x2, xõ
in the lookup table 1262.
The codes are not divided into different data types and each code is therefore
unique to its particular
associated value in the lookup table 1262.
The data represented by the actuating formation 1234 can define a number of
codes xi, x;, Xk, X1, x,,,,
x,,, xo representing a value of each of the data types. An algorithm is used
to look up the data relating to the
actual value represented by these codes. It will thus be appreciated that the
necessity for the actuating
formation 1234 to represent a substantial amount of information is obviated.
Authentication Chip
Authentication Chips 53
The authentication chip 53 of the preferred embodiment is responsible for
ensuring that only correctly
manufactured print rolls are utilized in the camera system. The authentication
chip 53 utilizes technologies that are
generally valuable when utilized with any consumables and are not restricted
to print roll system. Manufacturers
of other systems that require consumables (such as a laser printer that
requires toner cartridges) have struggled
with the problem of authenticating consumables, to varying levels of success.
Most have resorted to specialized
packaging. However this does not stop home refill operations or clone
manufacture. The prevention of copying is
important to prevent poorly manufactured substitute consumables from damaging
the base system. For example,
poorly filtered ink may clog print nozzles in an ink jet printer, causing the
consumer to blame the system
manufacturer and not admit the use of non-authorized consumables.
To solve the authentication problem, the Authentication chip 53 contains an
authentication code and circuit
specially designed to prevent copying. The chip is manufactured using the
standard Flash memory
manufacturing process, and is low cost enough to be included in consumables
such as ink and toner
cartridges. Once programmed, the Authentication chips as described here are
compliant with the NSA export
guidelines. Authentication is an extremely large and constantly growing field.
Here we are concerned with
authenticating consumables only.
Symbolic Nomenclature
CA 02564047 2006-11-06
YU139 PCT 154
The following symbolic nomenclature is used throughout the discussion of this
embodiment:
Symbolic Nomenclature Description
F[X] Function F, taking a single parameter X
F[X, Y] Function F, taking two parameters, X and Y
X Y X concatenated with Y
X A Y Bitwise X AND Y
X v Y Bitwise X OR Y (inclusive-OR)
XO+Y Bitwise X XOR Y (exclusive-OR)
-X Bitwise NOT X (complement)
X F Y X is assigned the value Y
X - {Y, Z The domain of assignment inputs to X is Y and Z.
X=Y Xis equal toY
X#Y X is not equal to Y
~X Decrement X by 1 (floor 0)
I X Increment X by 1 (with wrapping based on register length)
Erase X Erase Flash memory register X
SetBits[X, Y] Set the bits of the Flash memory register X based on Y
Z +- ShiftRight[X, Y] Shift register X right one bit position, taking input
bit from Y and
placing the output bit in Z
BASIC TERMS
A message, denoted by M, is plaintext. The process of transforming M into
cyphertext C, where the substance
of M is hidden, is called encryption. The process of transforming C back into
M is called decryption.
Referring to the encryption function as E, and the decryption function as D,
we have the following identities:
E[M] = C
D[C] = M
Therefore the following identity is true:
D[E[M]] = M
SYMMETRIC CRYPTOGRAPHY
A symmetric encryption algorithm is one where:
the encryption function E relies on key Ki,
the decryption function D relies on key K2,
K2 can be derived from K,, and
K, can be derived from K2.
In most symmetric algorithms, K, usually equals K2. However, even if K, does
not equal K2, given that one
key can be derived from the other, a single key K can suffice for the
mathematical definition. Thus:
EK[M] = C
DK[C] = M
An enormous variety of symmetric algorithms exist, from the textbooks of
ancient history through to
sophisticated modern algorithms. Many of these are insecure, in that modern
cryptanalysis techniques can
successfully attack the algorithm to the extent that K can be derived. The
security of the particular symmetric
algorithm is normally a function of two things: the strength of the algorithm
and the length of the key. The
following algorithms include suitable aspects for utilization in the
authentication chip.
CA 02564047 2006-11-06
YU139 PCT 155
DES
Blowfish
RC5
IDEA
DES
DES (Data Encryption Standard) is a US and international standard, where the
same key is used to encrypt
and decrypt. The key length is 56 bits. It has been implemented in hardware
and software, although the
original design was for hardware only. The original algorithm used in DES is
described in US patent
3,962,539. A variant of DES, called triple-DES is more secure, but requires 3
keys: K1, K2, and K3.The keys
are used in the following manner:
EK3[DK2[EKI[M77
J]] = C
DK3[EK2[DKJ [C]]J = M
The main advantage of triple-DES is that existing DES implementations can be
used to give more security
than single key DES. Specifically, triple-DES gives protection of equivalent
key length of 112 bits. Triple-
DES does not give the equivalent protection of a 168-bit key (3 x 56) as one
might naively expect.
Equipment that performs triple-DES decoding and/or encoding cannot be exported
from the United States.
Blowfish
Blowfish, is a symmetric block cipher first presented by Schneier in 1994. It
takes a variable length key, from
32 bits to 448 bits. In addition, it is much faster than DES. The Blowfish
algorithm consists of two parts: a
key-expansion part and a data-encryption part. Key expansion converts a key of
at most 448 bits into several
subkey arrays totaling 4168 bytes. Data encryption occurs via a 16-round
Feistel network. All operations are
XORs and additions on 32-bit words, with four index array lookups per round.
It should be noted that
decryption is the same as encryption except that the subkey arrays are used in
the reverse order. Complexity
of implementation is therefore reduced compared to other algorithms that do
not have such symmetry.
RC5
Designed by Ron Rivest in 1995, RC5 has a variable block size, key size, and
number of rounds. Typically,
however, it uses a 64-bit block size and a 128-bit key. The RC5 algorithm
consists of two parts: a key-
expansion part and a data-encryption part. Key expansion converts a key into
2r+2 subkeys (where r = the
number of rounds), each subkey being w bits. For a 64-bit blocksize with 16
rounds (w=32, r=16), the subkey
arrays total 136 bytes. Data encryption uses addition mod 2"" , XOR and
bitwise rotation.
IDEA
Developed in 1990 by Lai and Massey, the first incarnation of the IDEA cipher
was called PES. After
differential cryptanalysis was discovered by Biham and Shamir in 1991, the
algorithm was strengthened, with
the result being published in 1992 as IDEA. IDEA uses 128 bit-keys to operate
on 64-bit plaintext blocks.
The same algorithm is used for encryption and decryption. It is generally
regarded to be the most secure block
algorithm available today. It is described in US Patent No.5,214,703, issued
in 1993.
ASYMMETRIC CRYPTOGRAPHY
As alternative an asymmetric algorithm could be used. An asymmetric encryption
algorithm is one where:
the encryption function E relies on key KI,
the decryption function D relies on key K2,
CA 02564047 2006-11-06
YU139 PCT 156
K2 cannot be derived from K, in a reasonable amount of time, and
K, cannot be derived from K2 in a reasonable amount of time.
Thus:
EKI[M] = C
DK2[C] = M
These algorithms are also called public-key because one key K, can be made
public. Thus anyone can encrypt
a message (using K,), but only the person with the corresponding decryption
key (K2) can decrypt and thus
read the message. In most cases, the following identity also holds:
EK2[M] = C
DK,[C] =M
This identity is very important because it implies that anyone with the public
key K, can see M and know that
it came from the owner of K2. No-one else could have generated C because to do
so would imply knowledge
of K2. The property of not being able to derive K, from K2 and vice versa in a
reasonable time is of course
clouded by the concept of reasonable time. What has been demonstrated time
after time, is that a calculation
that was thought to require a long time has been made possible by the
introduction of faster computers, new
algorithms etc. The security of asymmetric algorithms is based on the
difficulty of one of two problems:
factoring large numbers (more specifically large numbers that are the product
of two large primes), and the
difficulty of calculating discrete logarithms in a finite field. Factoring
large numbers is conjectured to be a
hard problem given today's understanding of mathematics. The problem however,
is that factoring is getting
easier much faster than anticipated. Ron Rivest in 1977 said that factoring a
125-digit number would take 40
quadrillion years. In 1994 a 129-digit number was factored. According to
Schneier, you need a 1024-bit
number to get the level of security today that you got from a 512-bit number
in the 1980's. If the key is to last
for some years then 1024 bits may not even be enough. Rivest revised his key
length estimates in 1990: he
suggests 1628 bits for high security lasting until 2005, and 1884 bits for
high security lasting until 2015. By
contrast, Schneier suggests 2048 bits are required in order to protect against
corporations and governments
until 2015.
A number of public key cryptographic algorithms exist. Most are impractical to
implement, and many
generate a very large C for a given M or require enormous keys. Still others,
while secure, are far too slow to
be practical for several years. Because of this, many public-key systems are
hybrid - a public key mechanism
is used to transmit a symmetric session key, and then the session key is used
for the actual messages. All of
the algorithms have a problem in terms of key selection. A random number is
simply not secure enough. The
two large primes p and q must be chosen carefully - there are certain weak
combinations that can be factored
more easily (some of the weak keys can be tested for). But nonetheless, key
selection is not a simple matter of
randomly selecting 1024 bits for example. Consequently the key selection
process must also be secure.
Of the practical algorithms in use under public scrutiny, the following may be
suitable for utilization:
RSA
DSA
ElGamal
CA 02564047 2006-11-06
YU139 PCT 157
RSA
The RSA cryptosystem, named after Rivest, Shamir, and Adleman, is the most
widely used public-key
cryptosystem, and is a de facto standard in much of the world. The security of
RSA is conjectured to depend
on the difficulty of factoring large numbers that are the product of two
primes (p and q). There are a number
of restrictions on the generation of p and q. They should both be large, with
a similar number of bits, yet not
be close to one another (otherwise pq ~pq). In addition, many authors have
suggested that p and q should be
strong primes. The RSA algorithm patent was issued in 1983 (US patent number
4,405,829).
DSA
DSA (Digital Signature Standard) is an algorithm designed as part of the
Digital Signature Standard (DSS). As
defined, it cannot be used for generalized encryption. In addition, compared
to RSA, DSA is 10 to 40 times slower
for signature verification. DSA explicitly uses the SHA-1 hashing algorithm
(see definition in
One-way Functions below). DSA key generation relies on finding two primes p
and q such that q divides p-1.
According to Schneier, a 1024-bit p value is required for long term DSA
security. However the DSA standard
does not permit values of p larger than 1024 bits (p must also be a multiple
of 64 bits). The US Government owns
the DSA algorithm and has at least one relevant patent (US patent 5,231,688
granted in 1993).
ElGamal
The ElGamal scheme is used for both encryption and digital signatures. The
security is based on the difficulty
of calculating discrete logarithms in a finite field. Key selection involves
the selection of a prime p, and two
random numbers g and x such that both g and x are less than p. Then calculate
y = gx mod p. The public key
is y, g, and p. The private key is x.
CRYPTOGRAPHIC CHALLENGE-RESPONSE PROTOCOLS AND ZERO KNOWLEDGE PROOFS
The general principle of a challenge-response protocol is to provide identity
authentication adapted to a
camera system. The simplest form of challenge-response takes the form of a
secret password. A asks B for the
secret password, and if B responds with the correct password, A declares B
authentic. There are three main
problems with this kind of simplistic protocol. Firstly, once B has given out
the password, any observer C will
know what the password is. Secondly, A must know the password in order to
verify it. Thirdly, if C
impersonates A, then B will give the password to C (thinking C was A), thus
compromising B. Using a
copyright text (such as a haiku) is a weaker alternative as we are assuming
that anyone is able to copy the
password (for example in a country where intellectual property is not
respected). The idea of cryptographic
challenge-response protocols is that one entity (the claimant) proves its
identity to another (the verifier) by
demonstrating knowledge of a secret known to be associated with that entity,
without revealing the secret
itself to the verifier during the protocol. In the generalized case of
cryptographic challenge-response
protocols, with some schemes the verifier knows the secret, while in others
the secret is not even known by
the verifier. Since the discussion of this embodiment specifically concerns
Authentication, the actual
cryptographic challenge-response protocols used for authentication are
detailed in the appropriate sections.
However the concept of Zero Knowledge Proofs will be discussed here. The Zero
Knowledge Proof protocol,
first described by Feige, Fiat and Shamir is extensively used in Smart Cards
for the purpose of authentication.
The protocol's effectiveness is based on the assumption that it is
computationally infeasible to compute
square roots modulo a large composite integer with unknown factorization. This
is provably equivalent to the
CA 02564047 2006-11-06
YU139 PCT 158
assumption that factoring large integers is difficult. It should be noted that
there is no need for the claimant to
have significant computing power. Smart cards implement this kind of
authentication using only a few
modular multiplications. The Zero Knowledge Proof protocol is described in US
Patent 4,748,668.
ONE-WAY FUNCTIONS
A one-way function F operates on an input X, and returns F[X] such that X
cannot be determined from F[X].
When there is no restriction on the format of X, and F[X] contains fewer bits
than X, then collisions must
exist. A collision is defined as two different X input values producing the
same F[X] value - i.e. Xi and X2
exist such that X11 X2 yet F[X1] = F[X21. When X contains more bits than F[X],
the input must be
compressed in some way to create the output. In many cases, X is broken into
blocks of a particular size, and
compressed over a number of rounds, with the output of one round being the
input to the next. The output of
the hash function is the last output once X has been consumed. A pseudo-
collision of the compression
function CF is defined as two different initial values V1 and V2 and two
inputs XI and X2 (possibly identical)
are given such that CF(V1, X1) = CF(V2, X2). Note that the existence of a
pseudo-collision does not mean that
it is easy to compute an X2 for a given X1.
We are only interested in one-way functions that are fast to compute. In
addition, we are only interested in
deterministic one-way functions that are repeatable in different
implementations. Consider an example F
where F[X] is the time between calls to F. For a given F[X] X cannot be
determined because X is not even
used by F. However the output from F will be different for different
implementations. This kind of F is
therefore not of interest.
In the scope of the discussion of the implementation of the authentication
chip of this embodiment, we are
interested in the following forms of one-way functions:
Encryption using an unknown key
Random number sequences
Hash Functions
Message Authentication Codes
Encryption Using an Unknown Key
When a message is encrypted using an unknown key K, the encryption function E
is effectively one-way.
Without the key, it is computationally infeasible to obtain M from EK[M]
without K. An encryption function
is only one-way for as long as the key remains hidden. An encryption algorithm
does not create collisions,
since E creates EK[M] such that it is possible to reconstruct M using function
D. Consequently F[X] contains
at least as many bits as X (no information is lost) if the one-way function F
is E. Symmetric encryption
algorithms (see above) have the advantage over Asymmetric algorithms for
producing one-way functions
based on encryption for the following reasons:
The key for a given strength encryption algorithm is shorter for a symmetric
algorithm than an
asymmetric algorithm
Symmetric algorithms are faster to compute and require less software/silicon
CA 02564047 2006-11-06
YU139 PCT 159
The selection of a good key depends on the encryption algorithm chosen.
Certain keys are not strong for
particular encryption algorithms, so any key needs to be tested for strength.
The more tests that need to be
performed for key selection, the less likely the key will remain hidden.
Random Number Sequences
Consider a random number sequence R0, R,, ..., R1, Ri+i. We define the one-way
function F such that F[X]
returns the Xt' random number in the random sequence. However we must ensure
that F[X] is repeatable for a
given X on different implementations. The random number sequence therefore
cannot be truly random.
Instead, it must be pseudo-random, with the generator making use of a specific
seed.
There are a large number of issues concerned with defining good random number
generators. Knuth,
describes what makes a generator "good" (including statistical tests), and the
general problems associated
with constructing them. The majority of random number generators produce the
ith random number from the
i-1'h state - the only way to determine the i`h number is to iterate from the
0th number to the ith. If i is large, it
may not be practical to wait for i iterations. However there is a type of
random number generator that does
allow random access. Blum, Blum and Shub define the ideal generator as
follows:"... we would like a
pseudo-random sequence generator to quickly produce, from short seeds, long
sequences (of bits) that appear
in every way to be generated by successive flips of a fair coin". They defined
the x2 mod n generator, more
commonly referred to as the BBS generator. They showed that given certain
assumptions upon which modern
cryptography relies, a BBS generator passes extremely stringent statistical
tests.
The BBS generator relies on selecting n which is a Blum integer (n = pq where
p and q are large prime
numbers, p # q, p mod 4 = 3, and q mod 4 = 3). The initial state of the
generator is given by x0 where xo = x2
mod n, and x is a random integer relatively prime to n. The i`h pseudo-random
bit is the least significant bit of
xi where xi = xi_12 mod n. As an extra property, knowledge of p and q allows a
direct calculation of the i`h
number in the sequence as follows: x; = xo'" mod n, where y = 2' mod ((p-l)(q-
1))
Without knowledge of p and q, the generator must iterate (the security of
calculation relies on the difficulty of
factoring large numbers). When first defined, the primary problem with the BBS
generator was the amount of
work required for a single output bit. The algorithm was considered too slow
for most applications. However
the advent of Montgomery reduction arithmetic has given rise to more practical
implementations. In addition,
Vazirani and Vazirani have shown that depending on the size of n, more bits
can safely be taken from x;
without compromising the security of the generator. Assuming we only take 1
bit per xi, N bits (and hence N
iterations of the bit generator function) are needed in order to generate an N-
bit random number. To the
outside observer, given a particular set of bits, there is no way to determine
the next bit other than a 50/50
probability. If the x, p and q are hidden, they act as a key, and it is
computationally unfeasible to take an
output bit stream and compute x, p, and q. It is also computationally
unfeasible to determine the value of i
used to generate a given set of pseudo-random bits. This last feature makes
the generator one-way. Different
values of i can produce identical bit sequences of a given length (e.g. 32
bits of random bits). Even if x, p and
q are known, for a given F[i], i can only be derived as a set of
possibilities, not as a certain value (of course if
the domain of i is known, then the set of possibilities is reduced further).
However, there are problems in
selecting a good p and q, and a good seed x. In particular, Ritter describes a
problem in selecting x. The nature
of the problem is that a BBS generator does not create a single cycle of known
length. Instead, it creates
CA 02564047 2006-11-06
YU139 PCT 160
cycles of various lengths, including degenerate (zero-length) cycles. Thus a
BBS generator cannot be
initialized with a random state - it might be on a short cycle.
Hash Functions
Special one-way functions, known as Hash functions map arbitrary length
messages to fixed-length hash
values. Hash functions are referred to as H[M]. Since the input is arbitrary
length, a hash function has a
compression component in order to produce a fixed length output. Hash
functions also have an obfuscation
component in order to make it difficult to find collisions and to determine
information about M from H[M].
Because collisions do exist, most applications require that the hash algorithm
is preimage resistant, in that for
a given X, it is difficult to find X2 such that H[XI] = H[X2]. In addition,
most applications also require the
hash algorithm to be collision resistant (i.e. it should be hard to find two
messages X, and X2 such that H[XI]
= H[X2]). It is an open problem whether a collision-resistant hash function,
in the idealist sense, can exist at
all. The primary application for hash functions is in the reduction of an
input message into a digital
"fingerprint" before the application of a digital signature algorithm. One
problem of collisions with digital
signatures can be seen in the following example.
A has a long message M, that says "I owe B $10". A signs H[MI] using his
private
key. B, being greedy, then searches for a collision message M2 where H[M2] =
H[M,]
but where M2 is favorable to B, for example "I owe B $lmillion". Clearly it is
in A's
interest to ensure that it is difficult to find such an M2.
Examples of collision resistant one-way hash functions are SHA-1, MD5 and
RIPEMD-160, all derived from
MD4.
MD4
Ron Rivest introduced MD4 in 1990. It is mentioned here because all other one-
way hash functions are
derived in some way from MD4. MD4 is now considered completely broken in that
collisions can be
calculated instead of searched for. In the example above, B could trivially
generate a substitute message M2
with the same hash value as the original message Mt.
MD5
Ron Rivest introduced MD5 in 1991 as a more secure MD4. Like MD4, MD5 produces
a 128-bit hash value.
Dobbertin describes the status of MD5 after recent attacks. He describes how
pseudo-collisions have been
found in MD5, indicating a weakness in the compression function, and more
recently, collisions have been
found. This means that MD5 should not be used for compression in digital
signature schemes where the
existence of collisions may have dire consequences. However MD5 can still be
used as a one-way function. In
addition, the HMAC-MD5 construct is not affected by these recent attacks.
SHA-1
SHA-1 is very similar to MD5, but has a 160-bit hash value (MD5 only has 128
bits of hash value). SHA-1
was designed and introduced by the NIST and NSA for use in the Digital
Signature Standard (DSS). The
original published description was called SHA, but very soon afterwards, was
revised to become SHA- 1,
supposedly to correct a security flaw in SHA (although the NSA has not
released the mathematical reasoning
behind the change). There are no known cryptographic attacks against SHA-1. It
is also more resistant to
brute-force attacks than MD4 or MD5 simply because of the longer hash result.
The US Government owns
CA 02564047 2006-11-06
YU139 PCT 161
the SHA-1 and DSA algorithms (a digital signature authentication algorithm
defined as part of DSS) and has
at least one relevant patent (US patent 5,231,688 granted in 1993).
RIPEMD-160
RIPEMD- 160 is a hash function derived from its predecessor RIPEMD (developed
for the European
Community's RIPE project in 1992). As its name suggests, RIPEMD- 160 produces
a 160-bit hash result.
Tuned for software implementations on 32-bit architectures, RIPEMD- 160 is
intended to provide a high level
of security for 10 years or more. Although there have been no successful
attacks on RIPEMD- 160, it is
comparatively new and has not been extensively cryptanalyzed. The original
RIPEMD algorithm was
specifically designed to resist known cryptographic attacks on MD4. The recent
attacks on MD5 showed
similar weaknesses in the RIPEMD 128-bit hash function. Although the attacks
showed only theoretical
weaknesses, Dobbertin, Preneel and Bosselaers further strengthened RIPEMD into
a new algorithm
RIPEMD-160.
Message Authentication Codes
The problem of message authentication can be summed up as follows:
How can A be sure that a message supposedly from B is in fact from B?
Message authentication is different from entity authentication. With entity
authentication, one entity (the
claimant) proves its identity to another (the verifier). With message
authentication, we are concerned with
making sure that a given message is from who we think it is from i.e. it has
not been tampered en route from
the source to its destination. A one-way hash function is not sufficient
protection for a message. Hash
functions such as MD5 rely on generating a hash value that is representative
of the original input, and the
original input cannot be derived from the hash value. A simple attack by E,
who is in-between A and B, is to
intercept the message from B, and substitute his own. Even if A also sends a
hash of the original message, E
can simply substitute the hash of his new message. Using a one-way hash
function alone, A has no way of
knowing that B's message has been changed. One solution to the problem of
message authentication is the
Message Authentication Code, or MAC. When B sends message M, it also sends
MAC[M] so that the
receiver will know that M is actually from B. For this to be possible, only B
must be able to produce a MAC
of M, and in addition, A should be able to verify M against MAC[M]. Notice
that this is different from
encryption of M - MACs are useful when M does not have to be secret. The
simplest method of constructing
a MAC from a hash function is to encrypt the hash value with a symmetric
algorithm:
Hash the input message H[M]
Encrypt the hash EK[H[M]]
This is more secure than first encrypting the message and then hashing the
encrypted message. Any
symmetric or asymmetric cryptographic function can be used. However, there are
advantages to using a key-
dependant one-way hash function instead of techniques that use encryption
(such as that shown above):
Speed, because one-way hash functions in general work much faster than
encryption;
Message size, because EK[H[M]] is at least the same size as M, while H[M] is a
fixed size (usually
considerably smaller than M);
Hardware/software requirements - keyed one-way hash functions are typically
far less complexity than their
encryption-based counterparts; and
One-way hash function implementations are not considered to be encryption or
decryption devices and
CA 02564047 2006-11-06
YU139 PCT 162
therefore are not subject to US export controls.
It should be noted that hash functions were never originally designed to
contain a key or to support message
authentication. As a result, some ad hoc methods of using hash functions to
perform message authentication,
including various functions that concatenate messages with secret prefixes,
suffixes, or both have been
proposed. Most of these ad hoc methods have been successfully attacked by
sophisticated means. Additional
MACs have been suggested based on XOR schemes and Toeplitz matricies
(including the special case of
LFSR-based constructions).
HMA C
The HMAC construction in particular is gaining acceptance as a solution for
Internet message authentication
security protocols. The HMAC construction acts as a wrapper, using the
underlying hash function in a black-
box way. Replacement of the hash function is straightforward if desired due to
security or performance
reasons. However, the major advantage of the HMAC construct is that it can be
proven secure provided the
underlying hash function has some reasonable cryptographic strengths - that
is, HMAC's strengths are
directly connected to the strength of the hash function. Since the HMAC
construct is a wrapper, any iterative
hash function can be used in an HMAC. Examples include HMAC-MD5, HMAC-SHAT,
HMAC-
RIPEMD 160 etc. Given the following definitions:
H = the hash function (e.g. MD5 or SHA-1)
n = number of bits output from H (e.g. 160 for SHA-1, 128 bits for MD5)
M = the data to which the MAC function is to be applied
K = the secret key shared by the two parties
ipad = 0x36 repeated 64 times
opad = Ox5C repeated 64 times
The HMAC algorithm is as follows:
Extend K to 64 bytes by appending OxOO bytes to the end of K
XOR the 64 byte string created in (1) with ipad
Append data stream M to the 64 byte string created in (2)
Apply H to the stream generated in (3)
XOR the 64 byte string created in (1) with opad
Append the H result from (4) to the 64 byte string resulting from (5)
Apply H to the output of (6) and output the result
Thus:
HMAC[M] = H[(K+Oopad) I H[(KO+ipad)IM]]
The recommended key length is at least n bits, although it should not be
longer than 64 bytes (the length of
the hashing block). A key longer than n bits does not add to the security of
the function. HMAC optionally
allows truncation of the final output e.g. truncation to 128 bits from 160
bits. The HMAC designers' Request
for Comments was issued in 1997, one year after the algorithm was first
introduced. The designers claimed
that the strongest known attack against HMAC is based on the frequency of
collisions for the hash function H
and is totally impractical for minimally reasonable hash functions. More
recently, HMAC protocols with
replay prevention components have been defined in order to prevent the capture
and replay of any M,
HMAC[M] combination within a given time period.
CA 02564047 2006-11-06
YU139 PCT 163
RANDOM NUMBERS AND TIME VARYING MESSAGES
The use of a random number generator as a one-way function has already been
examined. However, random
number generator theory is very much intertwined with cryptography, security,
and authentication. There are
a large number of issues concerned with defining good random number
generators. Knuth, describes what
makes a generator good (including statistical tests), and the general problems
associated with constructing
them. One of the uses for random numbers is to ensure that messages vary over
time. Consider a system
where A encrypts commands and sends them to B. If the encryption algorithm
produces the same output for a
given input, an attacker could simply record the messages and play them back
to fool B. There is no need for
the attacker to crack the encryption mechanism other than to know which
message to play to B (while
pretending to be A). Consequently messages often include a random number and a
time stamp to ensure that
the message (and hence its encrypted counterpart) varies each time. Random
number generators are also
often used to generate keys. It is therefore best to say at the moment, that
all generators are insecure for this
purpose. For example, the Berlekamp-Massey algorithm, is a classic attack on
an LFSR random number
generator. If the LFSR is of length n, then only 2n bits of the sequence
suffice to determine the LFSR,
compromising the key generator. If, however, the only role of the random
number generator is to make sure
that messages vary over time, the security of the generator and seed is not as
important as it is for session key
generation. If however, the random number seed generator is compromised, and
an attacker is able to
calculate future "random" numbers, it can leave some protocols open to attack.
Any new protocol should be
examined with respect to this situation. The actual type of random number
generator required will depend
upon the implementation and the purposes for which the generator is used.
Generators include Blum, Blum,
and Shub, stream ciphers such as RC4 by Ron Rivest, hash functions such as SHA-
1 and RIPEMD- 160, and
traditional generators such LFSRs (Linear Feedback Shift Registers) and their
more recent counterpart FCSRs
(Feedback with Carry Shift Registers).
ATTACKS
This section describes the various types of attacks that can be undertaken to
break an authentication
cryptosystem such as the authentication chip. The attacks are grouped into
physical and logical attacks.
Physical attacks describe methods for breaking a physical implementation of a
cryptosystem (for example,
breaking open a chip to retrieve the key), while logical attacks involve
attacks on the cryptosystem that are
implementation independent. Logical types of attack work on the protocols or
algorithms, and attempt to do
one of three things:
Bypass the authentication process altogether
Obtain the secret key by force or deduction, so that any question can be
answered
Find enough about the nature of the authenticating questions and answers in
order to, without the key, give
the right answer to each question.
The attack styles and the forms they take are detailed below. Regardless of
the algorithms and protocol used
by a security chip, the circuitry of the authentication part of the chip can
come under physical attack. Physical
attack comes in four main ways, although the form of the attack can vary:
Bypassing the Authentication Chip altogether
Physical examination of chip while in operation (destructive and non-
destructive)
Physical decomposition of chip
CA 02564047 2006-11-06
YU139 PCT 164
Physical alteration of chip
The attack styles and the forms they take are detailed below. This section
does not suggest solutions to these
attacks. It merely describes each attack type. The examination is restricted
to the context of an Authentication
chip 53 (as opposed to some other kind of system, such as Internet
authentication) attached to some System.
Logical Attacks
These attacks are those which do not depend on the physical implementation of
the cryptosystem. They work
against the protocols and the security of the algorithms and random number
generators.
Ciphertext only attack
This is where an attacker has one or more encrypted messages, all encrypted
using the same algorithm. The
aim of the attacker is to obtain the plaintext messages from the encrypted
messages. Ideally, the key can be
recovered so that all messages in the future can also be recovered.
Known plaintexi attack
This is where an attacker has both the plaintext and the encrypted form of the
plaintext. In the case of an
Authentication Chip, a known-plaintext attack is one where the attacker can
see the data flow between the
System and the Authentication Chip. The inputs and outputs are observed (not
chosen by the attacker), and
can be analyzed for weaknesses (such as birthday attacks or by a search for
differentially interesting
input/output pairs). A known plaintext attack is a weaker type of attack than
the chosen plaintext attack, since
the attacker can only observe the data flow. A known plaintext attack can be
carried out by connecting a logic
analyzer to the connection between the System and the Authentication Chip.
Chosen plaintext attacks
A chosen plaintext attack describes one where a cryptanalyst has the ability
to send any chosen message to the
cryptosystem, and observe the response. If the cryptanalyst knows the
algorithm, there may be a relationship
between inputs and outputs that can be exploited by feeding a specific output
to the input of another function.
On a system using an embedded Authentication Chip, it is generally very
difficult to prevent chosen plaintext
attacks since the cryptanalyst can logically pretend he/she is the System, and
thus send any chosen bit-pattern
streams to the Authentication Chip.
Adaptive Chosen plaintext attacks
This type of attack is similar to the chosen plaintext attacks except that the
attacker has the added ability to
modify subsequent chosen plaintexts based upon the results of previous
experiments. This is certainly the case
with any System / Authentication Chip scenario described when utilized for
consumables such as
photocopiers and toner cartridges, especially since both Systems and
Consumables are made available to the
public.
Brute force attack
A guaranteed way to break any key-based cryptosystem algorithm is simply to
try every key. Eventually the
right one will be found. This is known as a Brute Force Attack. However, the
more key possibilities there are,
the more keys must be tried, and hence the longer it takes (on average) to
find the right one. If there are N
keys, it will take a maximum of N tries. If the key is N bits long, it will
take a maximum of 2N tries, with a
50% chance of finding the key after only half the attempts (2N-1). The longer
N becomes, the longer it will
take to find the key, and hence the more secure the key is. Of course, an
attack may guess the key on the first
try, but this is more unlikely the longer the key is. Consider a key length of
56 bits. In the worst case, all 256
CA 02564047 2006-11-06
YU139 PCT 165
tests (7.2 x 1016 tests) must be made to find the key. In 1977, Diffie and
Hellman described a specialized
machine for cracking DES, consisting of one million processors, each capable
of running one million tests per
second. Such a machine would take 20 hours to break any DES code. Consider a
key length of 128 bits. In
the worst case, all 2128 tests (3.4 x 1038 tests) must be made to find the
key. This would take ten billion years
on an array of a trillion processors each running 1 billion tests per second.
With a long enough key length, a
Brute Force Attack takes too long to be worth the attacker's efforts.
Guessing attack
This type of attack is where an attacker attempts to simply "guess" the key.
As an attack it is identical to the
Brute force attack, where the odds of success depend on the length of the key.
Quantum Computer attack
To break an n-bit key, a quantum computer (NMR, Optical, or Caged Atom)
containing
n qubits embedded in an appropriate algorithm must be built. The quantum
computer effectively exists in 2"
simultaneous coherent states. The trick is to extract the right coherent state
without causing any decoherence.
To date this has been achieved with a 2 qubit system (which exists in 4
coherent states). It is thought possible
to extend this to 6 qubits (with 64 simultaneous coherent states) within a few
years.
Unfortunately, every additional qubit halves the relative strength of the
signal representing the key. This
rapidly becomes a serious impediment to key retrieval, especially with the
long keys used in cryptographically
secure systems. As a result, attacks on a cryptographically secure key (e.g.
160 bits) using a Quantum
Computer are likely not to be feasible and it is extremely unlikely that
quantum computers will have achieved
more than 50 or so qubits within the commercial lifetime of the Authentication
Chips. Even using a 50 qubit
quantum computer, 2110 tests are required to crack a 160 bit key.
Purposeful Error Attack
With certain algorithms, attackers can gather valuable information from the
results of a bad input. This can
range from the error message text to the time taken for the error to be
generated. A simple example is that of
a userid/password scheme. If the error message usually says "Bad userid", then
when an attacker gets a
message saying "Bad password" instead, then they know that the userid is
correct. If the message always says
"Bad userid/password" then much less information is given to the attacker. A
more complex example is that
of the recent published method of cracking encryption codes from secure web
sites. The attack involves
sending particular messages to a server and observing the error message
responses. The responses give
enough information to learn the keys - even the lack of a response gives some
information. An example of
algorithmic time can be seen with an algorithm that returns an error as soon
as an erroneous bit is detected in
the input message. Depending on hardware implementation, it may be a simple
method for the attacker to
time the response and alter each bit one by one depending on the time taken
for the error response, and thus
obtain the key. Certainly in a chip implementation the time taken can be
observed with far greater accuracy
than over the Internet.
Birthday attack
This attack is named after the famous "birthday paradox" (which is not
actually a paradox at all). The odds of
one person sharing a birthday with another, is 1 in 365 (not counting leap
years). Therefore there must be 183
people in a room for the odds to be more than 50% that one of them shares your
birthday. However, there
only needs to be 23 people in a room for there to be more than a 50% chance
that any two share a birthday.
CA 02564047 2006-11-06
YU139 PCT 166
This is because 23 people yields 253 different pairs. Birthday attacks are
common attacks against hashing
algorithms, especially those algorithms that combine hashing with digital
signatures. If a message has been
generated and already signed, an attacker must search for a collision message
that hashes to the same value
(analogous to finding one person who shares your birthday). However, if the
attacker can generate the
message, the Birthday Attack comes into play. The attacker searches for two
messages that share the same
hash value (analogous to any two people sharing a birthday), only one message
is acceptable to the person
signing it, and the other is beneficial for the attacker. Once the person has
signed the original message the
attacker simply claims now that the person signed the alternative message -
mathematically there is no way to
tell which message was the original, since they both hash to the same value.
Assuming a Brute Force Attack
is the only way to determine a match, the weakening of an n-bit key by the
birthday attack is 2x,12. A key
length of 128 bits that is susceptible to the birthday attack has an effective
length of only 64 bits.
Chaining attack
These are attacks made against the chaining nature of hash functions. They
focus on the compression function
of a hash function. The idea is based on the fact that a hash function
generally takes arbitrary length input and
produces a constant length output by processing the input n bits at a time.
The output from one block is used
as the chaining variable set into the next block. Rather than finding a
collision against an entire input, the idea
is that given an input chaining variable set, to find a substitute block that
will result in the same output
chaining variables as the proper message. The number of choices for a
particular block is based on the length
of the block. If the chaining variable is c bits, the hashing function behaves
like a random mapping, and the
block length is b bits, the number of such b-bit blocks is approximately 2b /
2c. The challenge for finding a
substitution block is that such blocks are a sparse subset of all possible
blocks. For SHA-1, the number of
512 bit blocks is approximately 2512/21e0, or 2352. The chance of finding a
block by brute force search is about
1 in 21eo
Substitution with a complete lookup table
If the number of potential messages sent to the chip is small, then there is
no need for a clone manufacturer to
crack the key. Instead, the clone manufacturer could incorporate a ROM in
their chip that had a record of all
of the responses from a genuine chip to the codes sent by the system. The
larger the key, and the larger the
response, the more space is required for such a lookup table.
Substitution with a sparse lookup table
If the messages sent to the chip are somehow predictable, rather than
effectively random, then the clone
manufacturer need not provide a complete lookup table. For example:
If the message is simply a serial number, the clone manufacturer need simply
provide a lookup table that
contains values for past and predicted future serial numbers. There are
unlikely to be more than 109 of
these.
If the test code is simply the date, then the clone manufacturer can produce a
lookup table using the date as
the address.
If the test code is a pseudo-random number using either the serial number or
the date as a seed, then the clone
manufacturer just needs to crack the pseudo-random number generator in the
System. This is probably
not difficult, as they have access to the object code of the System. The clone
manufacturer would then
produce a content addressable memory (or other sparse array lookup) using
these codes to access stored
CA 02564047 2006-11-06
YU139 PCT 167
authentication codes.
Differential cryptanalysis
Differential cryptanalysis describes an attack where pairs of input streams
are generated with known
differences, and the differences in the encoded streams are analyzed. Existing
differential attacks are heavily
dependent on the structure of S boxes, as used in DES and other similar
algorithms. Although other
algorithms such as HMAC-SHAT have no S boxes, an attacker can undertake a
differential-like attack by
undertaking statistical analysis of:
Minimal-difference inputs, and their corresponding outputs
Minimal-difference outputs, and their corresponding inputs
Most algorithms were strengthened against differential cryptanalysis once the
process was described. This is
covered in the specific sections devoted to each cryptographic algorithm.
However some recent algorithms
developed in secret have been broken because the developers had not considered
certain styles of differential
attacks and did not subject their algorithms to public scrutiny.
Message substitution attacks
In certain protocols, a man-in-the-middle can substitute part or all of a
message. This is where a real
Authentication Chip is plugged into a reusable clone chip within the
consumable. The clone chip intercepts all
messages between the System and the Authentication Chip, and can perform a
number of substitution attacks.
Consider a message containing a header followed by content. An attacker may
not be able to generate a valid
header, but may be able to substitute their own content, especially if the
valid response is something along the
lines of "Yes, I received your message". Even if the return message is "Yes, I
received the following message
... ", the attacker may be able to substitute the original message before
sending the acknowledgement back to
the original sender. Message Authentication Codes were developed to combat
most message substitution
attacks.
Reverse engineering the key generator
If a pseudo-random number generator is used to generate keys, there is the
potential for a clone manufacture
to obtain the generator program or to deduce the random seed used. This was
the way in which the Netscape
security program was initially broken.
Bypassing authentication altogether
It may be that there are problems in the authentication protocols that can
allow a bypass of the authentication
process altogether. With these kinds of attacks the key is completely
irrelevant, and the attacker has no need
to recover it or deduce it. Consider an example of a system that Authenticates
at power-up, but does not
authenticate at any other time. A reusable consumable with a clone
Authentication Chip may make use of a
real Authentication Chip. The clone authentication chip 53 uses the real chip
for the authentication call, and
then simulates the real Authentication Chip's state data after that. Another
example of bypassing
authentication is if the System authenticates only after the consumable has
been used. A clone Authentication
Chip can accomplish a simple authentication bypass by simulating a loss of
connection after the use of the
consumable but before the authentication protocol has completed (or even
started). One infamous attack
known as the "Kentucky Fried Chip" hack involved replacing a microcontroller
chip for a satellite TV system.
When a subscriber stopped paying the subscription fee, the system would send
out a "disable" message.
CA 02564047 2006-11-06
YU139 PCT 168
However the new microcontroller would simply detect this message and not pass
it on to the consumer's
satellite TV system.
Garrote/bribe attack
If people know the key, there is the possibility that they could tell someone
else. The telling may be due to
coercion (bribe, garrote etc), revenge (e.g. a disgruntled employee), or
simply for principle. These attacks are
usually cheaper and easier than other efforts at deducing the key. As an
example, a number of people claiming
to be involved with the development of the Divx standard have recently
(May/June 1998) been making noises
on a variety of DVD newsgroups to the effect they would like to help develop
Divx specific cracking devices
- out of principle.
Physical Attacks
The following attacks assume implementation of an authentication mechanism in
a silicon chip that the
attacker has physical access to. The first attack, Reading ROM, describes an
attack when keys are stored in
ROM, while the remaining attacks assume that a secret key is stored in Flash
memory.
Reading ROM
If a key is stored in ROM it can be read directly. A ROM can thus be safely
used to hold a public key (for use
in asymmetric cryptography), but not to hold a private key. In symmetric
cryptography, a ROM is completely
insecure. Using a copyright text (such as a haiku) as the key is not
sufficient, because we are assuming that
the cloning of the chip is occurring in a country where intellectual property
is not respected.
Reverse engineering of chip
Reverse engineering of the chip is where an attacker opens the chip and
analyzes the circuitry. Once the
circuitry has been analyzed the inner workings of the chip's algorithm can be
recovered. Lucent
Technologies have developed an active method known as TOBIC (Two photon OBIC,
where OBIC stands for
Optical Beam Induced Current), to image circuits. Developed primarily for
static RAM analysis, the process
involves removing any back materials, polishing the back surface to a mirror
finish, and then focusing light on
the surface. The excitation wavelength is specifically chosen not to induce a
current in the IC. A Kerckhoffs
in the nineteenth century made a fundamental assumption about cryptanalysis:
if the algorithm's inner
workings are the sole secret of the scheme, the scheme is as good as broken.
He stipulated that the secrecy
must reside entirely in the key. As a result, the best way to protect against
reverse engineering of the chip is to
make the inner workings irrelevant.
Usurping the authentication process
It must be assumed that any clone manufacturer has access to both the System
and consumable designs. If the
same channel is used for communication between the System and a trusted System
Authentication Chip, and a
non-trusted consumable Authentication Chip, it may be possible for the non-
trusted chip to interrogate a
trusted Authentication Chip in order to obtain the "correct answer". If this
is so, a clone manufacturer would
not have to determine the key. They would only have to trick the System into
using the responses from the
System Authentication Chip. The alternative method of usurping the
authentication process follows the same
method as the logical attack "Bypassing the Authentication Process", involving
simulated loss of contact with
the System whenever authentication processes take place, simulating power-down
etc.
CA 02564047 2006-11-06
YU139 PCT 169
Modification of System
This kind of attack is where the System itself is modified to accept clone
consumables. The attack may be a
change of System ROM, a rewiring of the consumable, or, taken to the extreme
case, a completely clone
System. This kind of attack requires each individual System to be modified,
and would most likely require the
owner's consent. There would usually have to be a clear advantage for the
consumer to undertake such a
modification, since it would typically void warranty and would most likely be
costly. An example of such a
modification with a clear advantage to the consumer is a software patch to
change fixed-region DVD players
into region-free DVD players.
Direct viewing of chip operation by conventional probing
If chip operation could be directly viewed using an STM or an electron beam,
the keys could be recorded as
they are read from the internal non-volatile memory and loaded into work
registers. These forms of
conventional probing require direct access to the top or front sides of the IC
while it is powered.
Direct viewing of the non-volatile memory
If the chip were sliced so that the floating gates of the Flash memory were
exposed, without discharging them,
then the key could probably be viewed directly using an STM or SKM (Scanning
Kelvin Microscope).
However, slicing the chip to this level without discharging the gates is
probably impossible. Using wet
etching, plasma etching, ion milling (focused ion beam etching), or chemical
mechanical polishing will
almost certainly discharge the small charges present on the floating gates.
Viewing the light bursts caused by state changes
Whenever a gate changes state, a small amount of infrared energy is emitted.
Since silicon is transparent to
infrared, these changes can be observed by looking at the circuitry from the
underside of a chip. While the
emission process is weak, it is bright enough to be detected by highly
sensitive equipment developed for use
in astronomy. The technique, developed by IBM, is called PICA (Picosecond
Imaging Circuit Analyzer). If
the state of a register is known at time t, then watching that register change
over time will reveal the exact
value at time t+n, and if the data is part of the key, then that part is
compromised.
Monitoring EMI
Whenever electronic circuitry operates, faint electromagnetic signals are
given off. Relatively inexpensive
equipment (a few thousand dollars) can monitor these signals. This could give
enough information to allow an
attacker to deduce the keys.
Viewing Idd fluctuations
Even if keys cannot be viewed, there is a fluctuation in current whenever
registers change state. If there is a
high enough signal to noise ratio, an attacker can monitor the difference in
Idd that may occur when
programming over either a high or a low bit. The change in Idd can reveal
information about the key. Attacks
such as these have already been used to break smart cards.
Differential Fault Analysis
This attack assumes introduction of a bit error by ionization, microwave
radiation, or environmental stress. In
most cases such an error is more likely to adversely affect the Chip (eg cause
the program code to crash)
rather than cause beneficial changes which would reveal the key. Targeted
faults such as ROM overwrite, gate
destruction etc are far more likely to produce useful results.
CA 02564047 2006-11-06
YU139 PCT 170
Clock glitch attacks
Chips are typically designed to properly operate within a certain clock speed
range. Some attackers attempt to
introduce faults in logic by running the chip at extremely high clock speeds
or introduce a clock glitch at a
particular time for a particular duration. The idea is to create race
conditions where the circuitry does not
function properly. An example could be an AND gate that (because of race
conditions) gates through Input,
all the time instead of the AND of Input, and Input2. If an attacker knows the
internal structure of the chip,
they can attempt to introduce race conditions at the correct moment in the
algorithm execution, thereby
revealing information about the key (or in the worst case, the key itself).
Power supply attacks
Instead of creating a glitch in the clock signal, attackers can also produce
glitches in the power supply where
the power is increased or decreased to be outside the working operating
voltage range. The net effect is the
same as a clock glitch - introduction of error in the execution of a
particular instruction. The idea is to stop
the CPU from XORing the key, or from shifting the data one bit-position etc.
Specific instructions are
targeted so that information about the key is revealed.
Overwriting ROM
Single bits in a ROM can be overwritten using a laser cutter microscope, to
either 1 or 0 depending on the
sense of the logic. With a given opcode/operand set, it may be a simple matter
for an attacker to change a
conditional jump to a non-conditional jump, or perhaps change the destination
of a register transfer. If the
target instruction is chosen carefully, it may result in the key being
revealed.
Modifying EEPROM/Flash
EEPROM/Flash attacks are similar to ROM attacks except that the laser cutter
microscope technique can be
used to both set and reset individual bits. This gives much greater scope in
terms of modification of
algorithms.
Gate Destruction
Anderson and Kuhn described the rump session of the 1997 workshop on Fast
Software Encryption, where
Biham and Shamir presented an attack on DES. The attack was to use a laser
cutter to destroy an individual
gate in the hardware implementation of a known block cipher (DES). The net
effect of the attack was to force
a particular bit of a register to be "stuck". Biham and Shamir described the
effect of forcing a particular
register to be affected in this way - the least significant bit of the output
from the round function is set to 0.
Comparing the 6 least significant bits of the left half and the right half can
recover several bits of the key.
Damaging a number of chips in this way can reveal enough information about the
key to make complete key
recovery easy. An encryption chip modified in this way will have the property
that encryption and decryption
will no longer be inverses.
Overwrite Attacks
Instead of trying to read the Flash memory, an attacker may simply set a
single bit by use of a laser cutter
microscope. Although the attacker doesn't know the previous value, they know
the new value. If the chip still
works, the bit's original state must be the same as the new state. If the chip
doesn't work any longer, the bit's
original state must be the logical NOT of the current state. An attacker can
perform this attack on each bit of
the key and obtain the n-bit key using at most n chips (if the new bit matched
the old bit, a new chip is not
required for determining the next bit).
CA 02564047 2006-11-06
YU139 PCT 171
Test Circuitry Attack
Most chips contain test circuitry specifically designed to check for
manufacturing defects. This includes BIST
(Built In Self Test) and scan paths. Quite often the scan paths and test
circuitry includes access and readout
mechanisms for all the embedded latches. In some cases the test circuitry
could potentially be used to give
information about the contents of particular registers. Test circuitry is
often disabled once the chip has passed
all manufacturing tests, in some cases by blowing a specific connection within
the chip. A determined
attacker, however, can reconnect the test circuitry and hence enable it.
Memory Remanence
Values remain in RAM long after the power has been removed, although they do
not remain long enough to
be considered non-volatile. An attacker can remove power once sensitive
information has been moved into
RAM (for example working registers), and then attempt to read the value from
RAM. This attack is most
useful against security systems that have regular RAM chips. A classic example
is where a security system
was designed with an automatic power-shut-off that is triggered when the
computer case is opened. The
attacker was able to simply open the case, remove the RAM chips, and retrieve
the key because of memory
remanence.
Chip Theft Attack
If there are a number of stages in the lifetime of an Authentication Chip,
each of these stages must be
examined in terms of ramifications for security should chips be stolen. For
example, if information is
programmed into the chip in stages, theft of a chip between stages may allow
an attacker to have access to key
information or reduced efforts for attack. Similarly, if a chip is stolen
directly after manufacture but before
programming, does it give an attacker any logical or physical advantage?
Requirements
Existing solutions to the problem of authenticating consumables have typically
relied on physical patents on
packaging. However this does not stop home refill operations or clone
manufacture in countries with weak
industrial property protection. Consequently a much higher level of protection
is required. The authentication
mechanism is therefore built into an Authentication chip 53 that allows a
system to authenticate a consumable
securely and easily. Limiting ourselves to the system authenticating
consumables (we don't consider the
consumable authenticating the system), two levels of protection can be
considered:
Presence Only Authentication
This is where only the presence of an Authentication Chip is tested. The
Authentication Chip can be reused in
another consumable without being reprogrammed.
Consumable Lifetime Authentication
This is where not only is the presence of the Authentication Chip tested for,
but also the Authentication chip
53 must only last the lifetime of the consumable. For the chip to be reused it
must be completely erased and
reprogrammed. The two levels of protection address different requirements. We
are primarily concerned with
Consumable Lifetime Authentication in order to prevent cloned versions of high
volume consumables. In this
case, each chip should hold secure state information about the consumable
being authenticated. It should be
noted that a Consumable Lifetime Authentication Chip could be used in any
situation requiring a Presence
Only Authentication Chip. The requirements for authentication, data storage
integrity and manufacture
should be considered separately. The following sections summarize requirements
of each.
CA 02564047 2006-11-06
YU139 PCT 172
AUTHENTICATION
The authentication requirements for both Presence Only Authentication and
Consumable Lifetime
Authentication are restricted to case of a system authenticating a consumable.
For Presence Only
Authentication, we must be assured that an Authentication Chip is physically
present. For Consumable
Lifetime Authentication we also need to be assured that state data actually
came from the Authentication
Chip, and that it has not been altered en route. These issues cannot be
separated - data that has been altered
has a new source, and if the source cannot be determined, the question of
alteration cannot be settled. It is not
enough to provide an authentication method that is secret, relying on a home-
brew security method that has
not been scrutinized by security experts. The primary requirement therefore is
to provide authentication by
means that have withstood the scrutiny of experts. The authentication scheme
used by the Authentication
chip 53 should be resistant to defeat by logical means. Logical types of
attack are extensive, and attempt to do
one of three things:
Bypass the authentication process altogether
Obtain the secret key by force or deduction, so that any question can be
answered
Find enough about the nature of the authenticating questions and answers in
order to, without the key, give
the right answer to each question.
DATA STORAGE INTEGRITY
Although Authentication protocols take care of ensuring data integrity in
communicated messages, data
storage integrity is also required. Two kinds of data must be stored within
the Authentication Chip:
Authentication data, such as secret keys
Consumable state data, such as serial numbers, and media remaining etc.
The access requirements of these two data types differ greatly. The
Authentication chip 53 therefore requires
a storage/access control mechanism that allows for the integrity requirements
of each type.
Authentication Data
Authentication data must remain confidential. It needs to be stored in the
chip during a
manufacturing/programming stage of the chip's life, but from then on must not
be permitted to leave the chip. It
must be resistant to being read from non-volatile memory. The authentication
scheme is responsible for ensuring
the key cannot be obtained by deduction, and the manufacturing process is
responsible for ensuring that the key
cannot be obtained by physical means. The size of the authentication data
memory area must be large enough to
hold the necessary keys and secret information as mandated by the
authentication protocols.
Consumable State Data
Each Authentication chip 53 needs to be able to also store 256 bits (32 bytes)
of consumable state data.
Consumable state data can be divided into the following types. Depending on
the application, there will be
different numbers of each of these types of data items. A maximum number of 32
bits for a single data item is
to be considered.
Read Only
ReadWrite
Decrement Only
CA 02564047 2006-11-06
YU139 PCT 173
Read Only data needs to be stored in the chip during a
manufacturing/programming stage of the chip's life,
but from then on should not be allowed to change. Examples of Read Only data
items are consumable batch
numbers and serial numbers.
ReadWrite data is changeable state information, for example, the last time the
particular consumable was
used. ReadWrite data items can be read and written an unlimited number of
times during the lifetime of the
consumable. They can be used to store any state information about the
consumable. The only requirement for
this data is that it needs to be kept in non-volatile memory. Since an
attacker can obtain access to a system
(which can write to ReadWrite data), any attacker can potentially change data
fields of this type. This data
type should not be used for secret information, and must be considered
insecure.
Decrement Only data is used to count down the availability of consumable
resources. A photocopier's toner
cartridge, for example, may store the amount of toner remaining as a Decrement
Only data item. An ink
cartridge for a color printer may store the amount of each ink color as a
Decrement Only data item, requiring
3 (one for each of Cyan, Magenta, and Yellow), or even as many as 5 or 6
Decrement Only data items. The
requirement for this kind of data item is that once programmed with an initial
value at the
manufacturing/programming stage, it can only reduce in value. Once it reaches
the minimum value, it cannot
decrement any further. The Decrement Only data item is only required by
Consumable Lifetime
Authentication.
MANUFACTURE
The Authentication chip 53 ideally must have a low manufacturing cost in order
to be included as the
authentication mechanism for low cost consumables. The Authentication chip 53
should use a standard
manufacturing process, such as Flash. This is necessary to:
Allow a great range of manufacturing location options
Use well-defined and well-behaved technology
Reduce cost
Regardless of the authentication scheme used, the circuitry of the
authentication part of the chip must be
resistant to physical attack. Physical attack comes in four main ways,
although the form of the attack can vary:
Bypassing the Authentication Chip altogether
Physical examination of chip while in operation (destructive and non-
destructive)
Physical decomposition of chip
Physical alteration of chip
Ideally, the chip should be exportable from the U.S., so it should not be
possible to use an Authentication chip
53 as a secure encryption device. This is low priority requirement since there
are many companies in other
countries able to manufacture the Authentication chips. In any case, the
export restrictions from the U.S. may
change.
AUTHENTICATION
Existing solutions to the problem of authenticating consumables have typically
relied on physical patents on
packaging. However this does not stop home refill operations or clone
manufacture in countries with weak
industrial property protection. Consequently a much higher level of protection
is required. It is not enough to
provide an authentication method that is secret, relying on a home-brew
security method that has not been
scrutinized by security experts. Security systems such as Netscape's original
proprietary system and the GSM
CA 02564047 2006-11-06
YU139 PCT 174
Fraud Prevention Network used by cellular phones are examples where design
secrecy caused the
vulnerability of the security. Both security systems were broken by
conventional means that would have been
detected if the companies had followed an open design process. The solution is
to provide authentication by
means that have withstood the scrutiny of experts. A number of protocols that
can be used for consumables
authentication. We only use security methods that are publicly described,
using known behaviors in this new
way. For all protocols, the security of the scheme relies on a secret key, not
a secret algorithm. All the
protocols rely on a time-variant challenge (i.e. the challenge is different
each time), where the response
depends on the challenge and the secret. The challenge involves a random
number so that any observer will
not be able to gather useful information about a subsequent identification.
Two protocols are presented for
each of Presence Only Authentication and Consumable Lifetime Authentication.
Although the protocols differ
in the number of Authentication Chips required for the authentication process,
in all cases the System
authenticates the consumable. Certain protocols will work with either one or
two chips, while other protocols
only work with two chips. Whether one chip or two Authentication Chips are
used the System is still
responsible for making the authentication decision.
Single Chip Authentication
When only one Authentication chip 53 is used for the authentication protocol,
a single chip (referred to as
ChipA) is responsible for proving to a system (referred to as System) that it
is authentic. At the start of the
protocol, System is unsure of ChipA's authenticity. System undertakes a
challenge-response protocol with
ChipA, and thus determines ChipA's authenticity. In all protocols the
authenticity of the consumable is
directly based on the authenticity of the chip, i.e. if ChipA is considered
authentic, then the consumable is
considered authentic. The data flow can be seen in Fig. 167. In single chip
authentication protocols, System
can be software, hardware or a combination of both. It is important to note
that System is considered insecure
- it can be easily reverse engineered by an attacker, either by examining the
ROM or by examining circuitry.
System is not specially engineered to be secure in itself.
Double Chip Authentication
In other protocols, two Authentication Chips are required as shown in Fig.
168. A single chip (referred to as
ChipA) is responsible for proving to a system (referred to as System) that it
is authentic. As part of the
authentication process, System makes use of a trusted Authentication Chip
(referred to as ChipT). In double
chip authentication protocols, System can be software, hardware or a
combination of both. However ChipT
must be a physical Authentication Chip. In some protocols ChipT and ChipA have
the same internal structure,
while in others ChipT and ChipA have different internal structures.
PRESENCE ONLY AUTHENTICATION (INSECURE STATE DATA)
For this level of consumable authentication we are only concerned about
validating the presence of the
Authentication chip 53. Although the Authentication Chip can contain state
information, the transmission of
that state information would not be considered secure. Two protocols are
presented. Protocol 1 requires 2
Authentication Chips, while Protocol 2 can be implemented using either 1 or 2
Authentication Chips.
Protocol 1
Protocol 1 is a double chip protocol (two Authentication Chips are required).
Each Authentication Chip
contains the following values:
K Key for FK[X]. Must be secret.
CA 02564047 2006-11-06
YU139 PCT 175
R Current random number. Does not have to be secret, but must be seeded with a
different initial value for
each chip instance. Changes with each invocation of the Random function.
Each Authentication Chip contains the following logical functions:
Random[] Returns R, and advances R to next in sequence.
F[X] Returns FK[X], the result of applying a one-way function F to X based
upon the secret key K.
The protocol is as follows:
System requests Random[] from ChipT;
ChipT returns R to System;
System requests F[R] from both ChipT and ChipA;
ChipT returns FKT[R] to System;
ChipA returns FKT[R] to System;
System compares FKT[R] with FKT[R]. If they are equal, then ChipA is
considered valid. If not, then ChipA is
considered invalid.
The data flow can be seen in Fig. 169. The System does not have to comprehend
FK[R] messages. It must
merely check that the responses from ChipA and ChipT are the same. The System
therefore does not require
the key. The security of Protocol I lies in two places:
The security of F[X]. Only Authentication chips contain the secret key, so
anything that can produce an F[X]
from an X that matches the F[X] generated by a trusted Authentication chip 53
(ChipT) must be
authentic.
The domain of R generated by all Authentication chips must be large and non-
deterministic. If the domain of
R generated by all Authentication chips is small, then there is no need for a
clone manufacturer to crack
the key. Instead, the clone manufacturer could incorporate a ROM in their chip
that had a record of all of
the responses from a genuine chip to the codes sent by the system. The Random
function does not
strictly have to be in the Authentication Chip, since System can potentially
generate the same random
number sequence. However it simplifies the design of System and ensures the
security of the random
number generator will be the same for all implementations that use the
Authentication Chip, reducing
possible error in system implementation.
Protocol 1 has several advantages:
K is not revealed during the authentication process
Given X, a clone chip cannot generate FK[X] without K or access to a real
Authentication Chip.
System is easy to design, especially in low cost systems such as ink jet
printers, as no encryption or
decryption is required by System itself.
A wide range of keyed one-way functions exists, including symmetric
cryptography, random number
sequences, and message authentication codes.
One-way functions require fewer gates and are easier to verify than asymmetric
algorithms).
Secure key size for a keyed one-way function does not have to be as large as
for an asymmetric (public key)
algorithm. A minimum of 128 bits can provide appropriate security if F[X] is a
symmetric cryptographic
function.
However there are problems with this protocol:
It is susceptible to chosen text attack. An attacker can plug the chip into
their own system, generate chosen
CA 02564047 2006-11-06
YU139 PCT 176
Rs, and observe the output. In order to find the key, an attacker can also
search for an R that will
generate a specific F[M] since multiple Authentication chips can be tested in
parallel.
Depending on the one-way function chosen, key generation can be complicated.
The method of selecting a
good key depends on the algorithm being used. Certain keys are weak for a
given algorithm.
The choice of the keyed one-way functions itself is non-trivial. Some require
licensing due to patent
protection.
A man-in-the middle could take action on a plaintext message M before passing
it on to ChipA - it would be
preferable if the man-in-the-middle did not see M until after ChipA had seen
it. It would be even more
preferable if a man-in-the-middle didn't see M at all.
If F is symmetric encryption, because of the key size needed for adequate
security, the chips could not be exported
from the USA since they could be used as strong encryption devices.
If Protocol 1 is implemented with F as an asymmetric encryption algorithm,
there is no advantage over the
symmetric case - the keys needs to be longer and the encryption algorithm is
more expensive in silicon.
Protocol 1 must be implemented with 2 Authentication Chips in order to keep
the key secure. This means that
each System requires an Authentication Chip and each consumable requires an
Authentication Chip.
Protocol 2
In some cases, System may contain a large amount of processing power.
Alternatively, for instances of
systems that are manufactured in large quantities, integration of ChipT into
System may be desirable. Use of
an asymmetrical encryption algorithm allows the ChipT portion of System to be
insecure. Protocol 2
therefore, uses asymmetric cryptography. For this protocol, each chip contains
the following values:
K Key for EK[X] and DK[X]. Must be secret in ChipA. Does not have to be secret
in ChipT.
R Current random number. Does not have to be secret, but must be seeded with a
different initial value for
each chip instance. Changes with each invocation of the Random function.
The following functions are defined:
E[X] ChipT only. Returns EK[X] where E is asymmetric encrypt function E.
D[X] ChipA only. Returns DK[X1 where D is asymmetric decrypt function D.
Random[] ChipT only. Returns R I EK[R], where R is random number based on seed
S. Advances R to next
in random number sequence.
The public key KT is in ChipT, while the secret key KA is in ChipA. Having KT
in ChipT has the advantage
that ChipT can be implemented in software or hardware (with the proviso that
the seed for R is different for
each chip or system). Protocol 2 therefore can be implemented as a Single Chip
Protocol or as a Double Chip
Protocol. The protocol for authentication is as follows:
System calls ChipT's Random function;
ChipT returns R I EKT[R] to System;
System calls ChipA's D function, passing in EKT[R];
ChipA returns R, obtained by DKA[EKT[R]];
System compares R from ChipA to the original R generated by ChipT. If they are
equal, then ChipA is
considered valid. If not, ChipA is invalid.
The data flow can be seen in Fig. 170. Protocol 2 has the following
advantages:
KA (the secret key) is not revealed during the authentication process
CA 02564047 2006-11-06
YU139 PCT 177
Given EKT[X], a clone chip cannot generate X without KA or access to a real
ChipA.
Since KT # KA, ChipT can be implemented completely in software or in insecure
hardware or as part of
System. Only ChipA (in the consumable) is required to be a secure
Authentication Chip.
If ChipT is a physical chip, System is easy to design.
There are a number of well-documented and cryptanalyzed asymmetric algorithms
to chose from for
implementation, including patent-free and license-free solutions.
However, Protocol 2 has a number of its own problems:
For satisfactory security, each key needs to be 2048 bits (compared to minimum
128 bits for symmetric
cryptography in Protocol 1). The associated intermediate memory used by the
encryption and decryption
algorithms is correspondingly larger.
Key generation is non-trivial. Random numbers are not good keys.
If ChipT is implemented as a core, there may be difficulties in linking it
into a given System ASIC.
If ChipT is implemented as software, not only is the implementation of System
open to programming error
and non-rigorous testing, but the integrity of the compiler and mathematics
primitives must be rigorously
checked for each implementation of System. This is more complicated and costly
than simply using a
well-tested chip.
Although many symmetric algorithms are specifically strengthened to be
resistant to differential cryptanalysis
(which is based on chosen text attacks), the private key KA is susceptible to
a chosen text attack
If ChipA and ChipT are instances of the same Authentication Chip, each chip
must contain both asymmetric
encrypt and decrypt functionality. Consequently each chip is larger, more
complex, and more expensive
than the chip required for Protocol 1.
If the Authentication Chip is broken into 2 chips to save cost and reduce
complexity of design/test, two chips
still need to be manufactured, reducing the economies of scale. This is offset
by the relative numbers of
systems to consumables, but must still be taken into account.
Protocol 2 Authentication Chips could not be exported from the USA, since they
would be considered strong
encryption devices.
Even if the process of choosing a key for Protocol 2 was straightforward,
Protocol 2 is impractical at the
present time due to the high cost of silicon implementation (both key size and
functional implementation).
Therefore Protocol I is the protocol of choice for Presence Only
Authentication.
Clone Consumable using Real Authentication Chip
Protocols 1 and 2 only check that ChipA is a real Authentication Chip. They do
not check to see if the
consumable itself is valid. The fundamental assumption for authentication is
that if ChipA is valid, the
consumable is valid. It is therefore possible for a clone manufacturer to
insert a real Authentication Chip into
a clone consumable. There are two cases to consider:
In cases where state data is not written to the Authentication Chip, the chip
is completely reusable. Clone
manufacturers could therefore recycle a valid consumable into a clone
consumable. This may be made
more difficult by melding the Authentication Chip into the consumable's
physical packaging, but it
would not stop refill operators.
In cases where state data is written to the Authentication Chip, the chip may
be new, partially used up, or
completely used up. However this does not stop a clone manufacturer from using
the Piggyback attack,
CA 02564047 2006-11-06
YU139 PCT 178
where the clone manufacturer builds a chip that has a real Authentication Chip
as a piggyback. The
Attacker's chip (ChipE) is therefore a man-in-the-middle. At power up, ChipE
reads all the memory state
values from the real Authentication chip 53 into its own memory. ChipE then
examines requests from
System, and takes different actions depending on the request. Authentication
requests can be passed
directly to the real Authentication chip 53, while read/write requests can be
simulated by a memory that
resembles real Authentication Chip behavior. In this way the Authentication
chip 53 will always appear
fresh at power-up. ChipE can do this because the data access is not
authenticated.
In order to fool System into thinking its data accesses were successful, ChipE
still requires a real
Authentication Chip, and in the second case, a clone chip is required in
addition to a real Authentication Chip.
Consequently Protocols 1 and 2 can be useful in situations where it is not
cost effective for a clone
manufacturer to embed a real Authentication chip 53 into the consumable. If
the consumable cannot be
recycled or refilled easily, it may be protection enough to use Protocols 1 or
2. For a clone operation to be
successful each clone consumable must include a valid Authentication Chip. The
chips would have to be
stolen en masse, or taken from old consumables. The quantity of these
reclaimed chips (as well as the effort in
reclaiming them) should not be enough to base a business on, so the added
protection of secure data transfer
(see Protocols 3 and 4) may not be useful.
Longevity of Key
A general problem of these two protocols is that once the authentication key
is chosen, it cannot easily be
changed. In some instances a key-compromise is not a problem, while for others
a key compromise is
disastrous. For example, in a car/car-key System/Consumable scenario, the
customer has only one set of
car/car-keys. Each car has a different authentication key. Consequently the
loss of a car-key only
compromises the individual car. If the owner considers this a problem, they
must get a new lock on the car by
replacing the System chip inside the car's electronics. The owner's keys must
be reprogrammed/replaced to
work with the new car System Authentication Chip. By contrast, a compromise of
a key for a high volume
consumable market (for example ink cartridges in printers) would allow a clone
ink cartridge manufacturer to
make their own Authentication Chips. The only solution for existing systems is
to update the System
Authentication Chips, which is a costly and logistically difficult exercise.
In any case, consumers' Systems
already work - they have no incentive to hobble their existing equipment.
CONSUMABLE LIFETIME AUTHENTICATION
In this level of consumable authentication we are concerned with validating
the existence of the
Authentication Chip, as well as ensuring that the Authentication Chip lasts
only as long as the consumable. In
addition to validating that an Authentication Chip is present, writes and
reads of the Authentication Chip's
memory space must be authenticated as well. In this section we assume that the
Authentication Chip's data
storage integrity is secure - certain parts of memory are Read Only, others
are Read/Write, while others are
Decrement Only (see the chapter entitled Data Storage Integrity for more
information). Two protocols are
presented. Protocol 3 requires 2 Authentication Chips, while Protocol 4 can be
implemented using either 1 or
2 Authentication Chips.
Protocol 3
This protocol is a double chip protocol (two Authentication Chips are
required). For this protocol, each
Authentication Chip contains the following values:
CA 02564047 2006-11-06
YU139 PCT 179
K, Key for calculating FKI[X]. Must be secret.
K2 Key for calculating FK2[X]. Must be secret.
R Current random number. Does not have to be secret, but must be seeded with a
different initial value for
each chip instance. Changes with each successful authentication as defined by
the Test function.
M Memory vector of Authentication chip 53. Part of this space should be
different for each chip (does not
have to be a random number).
Each Authentication Chip contains the following logical functions:
F[X] Internal function only. Returns FK[XI, the result of applying a one-way
function F to X based
upon either key K1 or key K2
Random[] Returns R (FK,[R].
Test[X, Y] Returns land advances Rif FK2[R I X] = Y. Otherwise returns 0. The
time taken to return 0 must
be identical for all bad inputs.
Read[X, Y] Returns M I FK2[X I M] if FKI [X] = Y. Otherwise returns 0. The
time taken to return 0 must be
identical for all bad inputs.
Write[X] Writes X over those parts of M that can legitimately be written over.
To authenticate ChipA and read ChipA's memory M:
System calls ChipT's Random function;
ChipT produces R I FK[R] and returns these to System;
System calls ChipA's Read function, passing in R, FK[R];
ChipA returns M and FK[R I M];
System calls ChipT's Test function, passing in M and FK[R I M];
System checks response from ChipT. If the response is 1, then ChipA is
considered authentic. If 0, ChipA is
considered invalid.
To authenticate a write of Mi1ew to ChipA's memory M:
System calls ChipA's Write function, passing in Mnew;
The authentication procedure for a Read is carried out;
If ChipA is authentic and Mõew = M, the write succeeded. Otherwise it failed.
The data flow for read authentication is shown in Fig. 171. The first thing to
note about Protocol 3 is that
FK[X] cannot be called directly. Instead FK[X] is called indirectly by Random,
Test and Read:
Random[] calls FKI[X] X is not chosen by the caller. It is chosen by the
Random function. An attacker must
perform a brute force search using multiple calls to Random, Read, and Test to
obtain a desired X,
FKI[X] pair.
Test[X,Y] calls FK2[R I X] Does not return result directly, but compares the
result to Y and then returns
1 or 0. Any attempt to deduce K2 by calling Test multiple times trying
different values of FK2[R I X] for a
given X is reduced to a brute force search where R cannot even be chosen by
the attacker.
Read[X, Y] calls FKI[X] X and FK,[X] must be supplied by caller, so the caller
must already know the
X, FK1 [X] pair. Since the call returns 0 if
Y :i& FKI[X], a caller can use the Read function for a brute force attack on
K1.
Read[X, Y] calls FK2[X I M], X is supplied by caller, however X can only be
those values already given
out by the Random function (since X and Y are validated via K1). Thus a chosen
text attack must first
CA 02564047 2006-11-06
YU139 PCT 180
collect pairs from Random (effectively a brute force attack). In addition,
only part of M can be used in a
chosen text attack since some of M is constant (read-only) and the decrement-
only part of M can only be
used once per consumable. In the next consumable the read-only part of M will
be different.
Having FK[X] being called indirectly prevents chosen text attacks on the
Authentication Chip. Since an
attacker can only obtain a chosen R, FKI[R] pair by calling Random, Read, and
Test multiple times until the
desired R appears, a brute force attack on K, is required in order to perform
a limited chosen text attack on
K2. Any attempt at a chosen text attack on K2 would be limited since the text
cannot be completely chosen:
parts of M are read-only, yet different for each Authentication Chip. The
second thing to note is that two keys
are used. Given the small size of M, two different keys K, and K2 are used in
order to ensure there is no
correlation between F[R] and F[RIM]. K, is therefore used to help protect K2
against differential attacks. It is
not enough to use a single longer key since M is only 256 bits, and only part
of M changes during the lifetime
of the consumable. Otherwise it is potentially possible that an attacker via
some as-yet undiscovered
technique, could determine the effect of the limited changes in M to
particular bit combinations in R and thus
calculate FKZ[X I M] based on FKI [X]. As an added precaution, the Random and
Test functions in ChipA
should be disabled so that in order to generate R, FK[R] pairs, an attacker
must use instances of ChipT, each of
which is more expensive than ChipA (since a system must be obtained for each
ChipT). Similarly, there
should be a minimum delay between calls to Random, Read and Test so that an
attacker cannot call these
functions at high speed. Thus each chip can only give a specific number of X,
FK[X] pairs away in a certain
time period. The only specific timing requirement of Protocol 3 is that the
return value of 0 (indicating a bad
input) must be produced in the same amount of time regardless of where the
error is in the input. Attackers
can therefore not learn anything about what was bad about the input value.
This is true for both RD and TST
functions.
Another thing to note about Protocol 3 is that Reading data from ChipA also
requires authentication of
ChipA. The System can be sure that the contents of memory (M) is what ChipA
claims it to be if FK2[R I M] is
returned correctly. A clone chip may pretend that M is a certain value (for
example it may pretend that the
consumable is full), but it cannot return FK2[R I M] for any R passed in by
System. Thus the effective
signature FK2[R I M] assures System that not only did an authentic ChipA send
M, but also that M was not
altered in between ChipA and System. Finally, the Write function as defined
does not authenticate the Write.
To authenticate a write, the System must perform a Read after each Write.
There are some basic advantages
with Protocol 3:
K, and K2 are not revealed during the authentication process
Given X, a clone chip cannot generate FK2[X I M] without the key or access to
a real Authentication Chip.
System is easy to design, especially in low cost systems such as ink jet
printers, as no encryption or
decryption is required by System itself.
A wide range of key based one-way functions exists, including symmetric
cryptography, random number
sequences, and message authentication codes.
Keyed one-way functions require fewer gates and are easier to verify than
asymmetric algorithms).
Secure key size for a keyed one-way function does not have to be as large as
for an asymmetric (public key)
algorithm A minimum of 128 bits can provide appropriate security if F[X] is a
symmetric cryptographic
function.
CA 02564047 2006-11-06
YU139 PCT 181
Consequently, with Protocol 3, the only way to authenticate ChipA is to read
the contents of ChipA's
memory. The security of this protocol depends on the underlying FK[X] scheme
and the domain of R over the
set of all Systems. Although FK[X] can be any keyed one-way function, there is
no advantage to implement it
as asymmetric encryption. The keys need to be longer and the encryption
algorithm is more expensive in
silicon. This leads to a second protocol for use with asymmetric algorithms -
Protocol 4. Protocol 3 must be
implemented with 2 Authentication Chips in order to keep the keys secure. This
means that each System
requires an Authentication Chip and each consumable requires an Authentication
Chip
Protocol 4
In some cases, System may contain a large amount of processing power.
Alternatively, for instances of
systems that are manufactured in large quantities, integration of ChipT into
System may be desirable. Use of
an asymmetrical encryption algorithm can allow the ChipT portion of System to
be insecure. Protocol 4
therefore, uses asymmetric cryptography. For this protocol, each chip contains
the following values:
K Key for EK[X] and DK[X]. Must be secret in ChipA. Does not have to be secret
in ChipT.
R Current random number. Does not have to be secret, but must be seeded with a
different initial value for
each chip instance. Changes with each successful authentication as defined by
the Test function.
M Memory vector of Authentication chip 53. Part of this space should be
different for each chip, (does not
have to be a random number).
There is no point in verifying anything in the Read function, since anyone can
encrypt using a public key.
Consequently the following functions are defined:
E[X] Internal function only. Returns EK[X] where E is asymmetric encrypt
function E.
D[X] Internal function only. Returns DK[X] where D is asymmetric decrypt
function D.
Random[] ChipT only. Returns EK[R].
Test[X, Y] Returns 1 and advances R if DK[R I X] = Y. Otherwise returns 0. The
time taken to return 0
must be identical for all bad inputs.
Read[X] Returns M I EK[R I M] where R = DK[X] (does not test input).
Write[X] Writes X over those parts of M that can legitimately be written over.
The public key KT is in ChipT, while the secret key KA is in ChipA. Having KT
in ChipT has the advantage
that ChipT can be implemented in software or hardware (with the proviso that R
is seeded with a different
random number for each system). To authenticate ChipA and read ChipA's memory
M:
System calls ChipT's Random function;
ChipT produces ad returns EKT[R] to System;
System calls ChipA's Read function, passing in EKT[R];
ChipA returns M I EKA[R I M], first obtaining R by DKA[EKT[R]];
System calls ChipT's Test function, passing in M and EKA[R I M];
ChipT calculates DKT[EKA[R I M]] and compares it to R I M.
System checks response from ChipT. If the response is 1, then ChipA is
considered authentic. If 0, ChipA is
considered invalid.
To authenticate a write of Mnew to ChipA's memory M:
System calls ChipA's Write function, passing in Mnew;
The authentication procedure for a Read is carried out;
CA 02564047 2006-11-06
YU139 PCT 182
If ChipA is authentic and M1e,N = M, the write succeeded. Otherwise it failed.
The data flow for read authentication is shown in Fig. 172. Only a valid ChipA
would know the value of R,
since R is not passed into the Authenticate function (it is passed in as an
encrypted value). R must be obtained
by decrypting E[R], which can only be done using the secret key KA. Once
obtained, R must be appended to
M and then the result re-encoded. ChipT can then verify that the decoded form
of EKA[R I M] = R I M and
hence ChipA is valid. Since KT # KA, EKT[R] # EKA[R]. Protocol 4 has the
following advantages:
KA (the secret key) is not revealed during the authentication process
Given EKT[X], a clone chip cannot generate X without KA or access to a real
ChipA.
Since KT # KA, ChipT can be implemented completely in software or in insecure
hardware or as part of
System Only ChipA is required to be a secure Authentication Chip.
Since ChipT and ChipA contain different keys, intense testing of ChipT will
reveal nothing about KA.
If ChipT is a physical chip, System is easy to design.
There are a number of well-documented and cryptanalyzed asymmetric algorithms
to chose from for
implementation, including patent-free and license-free solutions.
Even if System could be rewired so that ChipA requests were directed to ChipT,
ChipT could never answer
for ChipA since KT # KA. The attack would have to be directed at the System
ROM itself to bypass the
Authentication protocol.
However, Protocol 4 has a number of disadvantages:
All Authentication Chips need to contain both asymmetric encrypt and decrypt
functionality. Consequently
each chip is larger, more complex, and more expensive than the chip required
for Protocol 3.
For satisfactory security, each key needs to be 2048 bits (compared to a
minimum of 128 bits for symmetric
cryptography in Protocol 1). The associated intermediate memory used by the
encryption and decryption
algorithms is correspondingly larger.
Key generation is non-trivial. Random numbers are not good keys.
If ChipT is implemented as a core, there may be difficulties in linking it
into a given System ASIC.
If ChipT is implemented as software, not only is the implementation of System
open to programming error
and non-rigorous testing, but the integrity of the compiler and mathematics
primitives must be rigorously
checked for each implementation of System This is more complicated and costly
than simply using a
well-tested chip.
Although many symmetric algorithms are specifically strengthened to be
resistant to differential cryptanalysis
(which is based on chosen text attacks), the private key KA is susceptible to
a chosen text attack
Protocol 4 Authentication Chips could not be exported from the USA, since they
would be considered strong
encryption devices.
As with Protocol 3, the only specific timing requirement of Protocol 4 is that
the return value of 0 (indicating
a bad input) must be produced in the same amount of time regardless of where
the error is in the input.
Attackers can therefore not learn anything about what was bad about the input
value. This is true for both RD
and TST functions.
Variation on call to TST
If there are two Authentication Chips used, it is theoretically possible for a
clone manufacturer to replace the
System Authentication Chip with one that returns 1 (success) for each call to
TST. The System can test for
CA 02564047 2006-11-06
YU139 PCT 183
this by calling TST a number of times - N times with a wrong hash value, and
expect the result to be 0. The
final time that TST is called, the true returned value from ChipA is passed,
and the return value is trusted. The
question then arises of how many times to call TST. The number of calls must
be random, so that a clone chip
manufacturer cannot know the number ahead of time. If System has a clock, bits
from the clock can be used
to determine how many false calls to TST should be made. Otherwise the
returned value from ChipA can be
used. In the latter case, an attacker could still rewire the System to permit
a clone ChipT to view the returned
value from ChipA, and thus know which hash value is the correct one. The worst
case of course, is that the
System can be completely replaced by a clone System that does not require
authenticated consumables - this
is the limit case of rewiring and changing the System. For this reason, the
variation on calls to TST is
optional, depending on the System, the Consumable, and how likely
modifications are to be made. Adding
such logic to System (for example in the case of a small desktop printer) may
be considered not worthwhile,
as the System is made more complicated. By contrast, adding such logic to a
camera may be considered
worthwhile.
Clone Consumable using Real Authentication Chip
It is important to decrement the amount of consumable remaining before use
that consumable portion. If the
consumable is used first, a clone consumable could fake a loss of contact
during a write to the special known
address and then appear as a fresh new consumable. It is important to note
that this attack still requires a real
Authentication Chip in each consumable.
Longevity of Key
A general problem of these two protocols is that once the authentication keys
are chosen, it cannot easily be
changed. In some instances a key-compromise is not a problem, while for others
a key compromise is
disastrous.
CHOOSING A PROTOCOL
Even if the choice of keys for Protocols 2 and 4 was straightforward, both
protocols are impractical at the
present time due to the high cost of silicon implementation (both due to key
size and functional
implementation). Therefore Protocols 1 and 3 are the two protocols of choice.
However, Protocols 1 and 3
contain much of the same components:
both require read and write access;
both require implementation of a keyed one-way function; and
both require random number generation functionality.
Protocol 3 requires an additional key (K2), as well as some minimal state
machine changes:
a state machine alteration to enable FKI[XI to be called during Random;
a Test function which calls FK2[X]
a state machine alteration to the Read function to call FKI[X] and FK2[X]
Protocol 3 only requires minimal changes over Protocol 1. It is more secure
and can be used in all places
where Presence Only Authentication is required (Protocol 1). It is therefore
the protocol of choice. Given that
Protocols 1 and 3 both make use of keyed one-way functions, the choice of one-
way function is examined in
more detail here. The following table outlines the attributes of the
applicable choices. The attributes are
worded so that the attribute is seen as an advantage.
CA 02564047 2006-11-06
YU139 PCT 184
U Q
GJ _
a' `r' d W
w Q x ~
3 ,, w d d d
H W ~ Q ~ x ~ x
Free of patents = = = = = =
Random key generation = = =
Can be exported from the USA = = = =
Fast = = = =
Preferred Key Size (bits) for use in 168 128 128 128 512 128 160 160
this application
Block size (bits) 64 64 64 64 256 512 512 512
Cryptanalysis Attack-Free
= = = = =
(apart from weak keys)
Output size given input size N >_N >_N >_N >_N 128 128 160 160
Low storage requirements = = = =
Low silicon complexity = = = =
NSA designed = =
An examination of the table shows that the choice is effectively between the 3
HMAC constructs and the
Random Sequence. The problem of key size and key generation eliminates the
Random Sequence. Given that
a number of attacks have already been carried out on MD5 and since the hash
result is only 128 bits, HMAC-
MD5 is also eliminated. The choice is therefore between HMAC-SHA1 and HMAC-
RIPEMD160. RIPEMD-
160 is relatively new, and has not been as extensively cryptanalyzed as SHA 1.
However, SHA-1 was
designed by the NSA, so this may be seen by some as a negative attribute.
Given that there is not much between the two, SHA-1 will be used for the HMAC
construct.
CHOOSING A RANDOM NUMBER GENERATOR
Each of the protocols described (1-4) requires a random number generator. The
generator must be "good" in the
sense that the random numbers generated over the life of all Systems cannot be
predicted. If the random numbers
were the same for each System, an attacker could easily record the correct
responses from a real Authentication
Chip, and place the responses into a ROM lookup for a clone chip. With such an
attack there is no need to obtain
Kt or K2. Therefore the random numbers from each System must be different
enough to be unpredictable, or non-
deterministic. As such, the initial value for R (the random seed) should be
programmed with a physically
generated random number gathered from a physically random phenomenon, one
where there is no information
about whether a particular bit will be 1 or 0. The seed for R must NOT be
generated with a computer-run random
number generator. Otherwise the generator algorithm and seed may be
compromised enabling an attacker to
generate and therefore know the set of all R values in all Systems.
CA 02564047 2006-11-06
YU139 PCT 185
Having a different R seed in each Authentication Chip means that the first R
will be both random and
unpredictable across all chips. The question therefore arises of how to
generate subsequent R values in each
chip.
The base case is not to change Rat all. Consequently R and FKI[R] will be the
same for each call to Random[]. If
they are the same, then FKI[R] can be a constant rather than calculated. An
attacker could then use a single valid
Authentication Chip to generate a valid lookup table, and then use that lookup
table in a clone chip programmed
especially for that System. A constant R is not secure.
The simplest conceptual method of changing R is to increment it by 1. Since R
is random to begin with, the values
across differing systems are still likely to be random. However given an
initial R, all subsequent R values can be
determined directly (there is no need to iterate 10,000 times - R will take on
values from Ro to R0+ 10000). An
incrementing R is immune to the earlier attack on a constant R. Since R is
always different, there is no way to
construct a lookup table for the particular System without wasting as many
real Authentication Chips as the clone
chip will replace.
Rather than increment using an adder, another way of changing R is to
implement it as an LFSR (Linear Feedback
Shift Register). This has the advantage of less silicon than an adder, but the
advantage of an attacker not being
able to directly determine the range of R for a particular System, since an
LFSR value-domain is determined by
sequential access. To determine which values an given initial R will generate,
an attacker must iterate through the
possibilities and enumerate them. The advantages of a changing R are also
evident in the LFSR solution. Since R
is always different, there is no way to construct a lookup table for the
particular System without using-up as many
real Authentication Chips as the clone chip will replace (and only for that
System). There is therefore no
advantage in having a more complex function to change R. Regardless of the
function, it will always be possible
for an attacker to iterate through the lifetime set of values in a simulation.
The primary security lies in the initial
randomness of R. Using an LFSR to change R (apart from using less silicon than
an adder) simply has the
advantage of not being restricted to a consecutive numeric range (i.e. knowing
R, RN cannot be directly calculated;
an attacker must iterate through the LFSR N times).
The Random number generator within the Authentication Chip is therefore an
LFSR with 160 bits. Tap
selection of the 160 bits for a maximal-period LFSR (i.e. the LFSR will cycle
through all 2160-1 states, 0 is
not a valid state) yields bits 159, 4, 2, and 1, as shown in Fig. 173. The
LFSR is sparse, in that not many bits
are used for feedback (only 4 out of 160 bits are used). This is a problem for
cryptographic applications, but
not for this application of non-sequential number generation. The 160-bit seed
value for R can be any random
number except 0, since an LFSR filled with Os will produce a never-ending
stream of Os. Since the LFSR
described is a maximal period LFSR, all 160 bits can be used directly as R.
There is no need to construct a
number sequentially from output bits of b0. After each successful call to TST,
the random number (R) must
be advanced by XORing bits 1, 2, 4, and 159, and shifting the result into the
high order bit. The new R and
corresponding FKLLR] can be retrieved on the next call to Random.
HOLDING OUT AGAINST LOGICAL ATTACKS
Protocol 3 is the authentication scheme used by the Authentication Chip. As
such, it should be resistant to
defeat by logical means. While the effect of various types of attacks on
Protocol 3 have been mentioned in
discussion, this section details each type of attack in turn with reference to
Protocol 3.
CA 02564047 2006-11-06
YU139 PCT 186
Brute Force attack
A Brute Force attack is guaranteed to break Protocol 3. However the length of
the key means that the time for
an attacker to perform a brute force attack is too long to be worth the
effort. An attacker only needs to break
K2 to build a clone Authentication Chip. K, is merely present to strengthen K2
against other forms of attack. A
Brute Force Attack on K2 must therefore break a 160-bit key. An attack against
K2 requires a maximum of
2160 attempts, with a 50% chance of finding the key after only 2159 attempts.
Assuming an array of a trillion
processors, each running one million tests per second, 2159 (7.3 x 1047) tests
takes 2.3 x 1023 years, which is
longer than the lifetime of the universe. There are only 100 million personal
computers in the world. Even if
these were all connected in an attack (e.g. via the Internet), this number is
still 10,000 times smaller than the
trillion-processor attack described. Further, if the manufacture of one
trillion processors becomes a possibility
in the age of nanocomputers, the time taken to obtain the key is longer than
the lifetime of the universe.
Guessing the key attac
It is theoretically possible that an attacker can simply "guess the key". In
fact, given enough time, and trying
every possible number, an attacker will obtain the key. This is identical to
the Brute Force attack described
above, where 2159 attempts must be made before a 50% chance of success is
obtained. The chances of
someone simply guessing the key on the first try is 2160. For comparison, the
chance of someone winning the
top prize in a U.S. state lottery and being killed by lightning in the same
day is only 1 in 261. The chance of
someone guessing the Authentication Chip key on the first go is 1 in 2160,
which is comparative to two people
choosing exactly the same atoms from a choice of all the atoms in the Earth
i.e. extremely unlikely.
Quantum Computer attack
To break K2, a quantum computer containing 160 qubits embedded in an
appropriate algorithm must be built.
An attack against a 160-bit key is not feasible. An outside estimate of the
possibility of quantum computers is
that 50 qubits may be achievable within 50 years. Even using a 50 qubit
quantum computer, 2110 tests are
required to crack a 160 bit key. Assuming an array of 1 billion 50 qubit
quantum computers, each able to try
250 keys in 1 microsecond (beyond the current wildest estimates) finding the
key would take an average of 18
billion years.
Cyphertext Only attack
An attacker can launch a Cyphertext Only attack on K, by calling monitoring
calls to RND and RD, and on
K2 by monitoring calls to RD and TST. However, given that all these calls also
reveal the plaintext as well as
the hashed form of the plaintext, the attack would be transformed into a
stronger form of attack - a Known
Plaintext attack.
Known Plaintext attack
It is easy to connect a logic analyzer to the connection between the System
and the Authentication Chip, and
thereby monitor the flow of data. This flow of data results in known plaintext
and the hashed form of the
plaintext, which can therefore be used to launch a Known Plaintext attack
against both K, and K2. To launch
an attack against K,, multiple calls to RND and TST must be made (with the
call to TST being successful, and
therefore requiring a call to RD on a valid chip). This is straightforward,
requiring the attacker to have both a
System Authentication Chip and a Consumable Authentication Chip. For each K,
X, HK I [X] pair revealed, a
K2 Y, HK2[Y] pair is also revealed. The attacker must collect these pairs for
further analysis. The question
arises of how many pairs must be collected for a meaningful attack to be
launched with this data. An example
CA 02564047 2006-11-06
YU139 PCT 187
of an attack that requires collection of data for statistical analysis is
Differential Cryptanalysis. However,
there are no known attacks against SHA-1 or HMAC-SHA1, so there is no use for
the collected data at this
time.
Chosen Plaintext attacks
Given that the cryptanalyst has the ability to modify subsequent chosen
plaintexts based upon the results of
previous experiments, K2 is open to a partial form of the Adaptive Chosen
Plaintext attack, which is certainly
a stronger form of attack than a simple Chosen Plaintext attack. A chosen
plaintext attack is not possible
against K1, since there is no way for a caller to modify R, which used as
input to the RND function (the only
function to provide the result of hashing with K1). Clearing R also has the
effect of clearing the keys, so is not
useful, and the SSI command calls CLR before storing the new R-value.
Adaptive Chosen plaintext attacks
This kind of attack is not possible against K1, since K, is not susceptible to
chosen plaintext attacks. However,
a partial form of this attack is possible against K2, especially since both
System and consumables are typically
available to the attacker (the System may not be available to the attacker in
some instances, such as a specific
car). The HMAC construct provides security against all forms of chosen
plaintext attacks. This is primarily
because the HMAC construct has 2 secret input variables (the result of the
original hash, and the secret key).
Thus finding collisions in the hash function itself when the input variable is
secret is even harder than finding
collisions in the plain hash function. This is because the former requires
direct access to SHA-1 (not permitted
in Protocol 3) in order to generate pairs of input/output from SHA- 1. The
only values that can be collected by
an attacker are HMAC[R] and HMAC[R I M]. These are not attacks against the SHA-
1 hash function itself,
and reduce the attack to a Differential Cryptanalysis attack, examining
statistical differences between
collected data. Given that there is no Differential Cryptanalysis attack known
against SHA-1 or HMAC,
Protocol 3 is resistant to the Adaptive Chosen Plaintext attacks.
Purposeful Error Attack
An attacker can only launch a Purposeful Error Attack on the TST and RD
functions, since these are the only
functions that validate input against the keys. With both the TST and RD
functions, a 0 value is produced if
an error is found in the input - no further information is given. In addition,
the time taken to produce the 0
result is independent of the input, giving the attacker no information about
which bit(s) were wrong. A
Purposeful Error Attack is therefore fruitless.
Chaining attack
Any form of chaining attack assumes that the message to be hashed is over
several blocks, or the input
variables can somehow be set. The HMAC-SHA1 algorithm used by Protocol 3 only
ever hashes a single
512-bit block at a time. Consequently chaining attacks are not possible
against Protocol 3.
Birthday attack
The strongest attack known against HMAC is the birthday attack, based on the
frequency of collisions for the
hash function. However this is totally impractical for minimally reasonable
hash functions such as SHA- 1.
And the birthday attack is only possible when the attacker has control over
the message that is signed.
Protocol 3 uses hashing as a form of digital signature. The System sends a
number that must be incorporated
into the response from a valid Authentication Chip. Since the Authentication
Chip must respond with H[R 1
M], but has no control over the input value R, the birthday attack is not
possible. This is because the message
CA 02564047 2006-11-06
YU139 PCT 188
has effectively already been generated and signed. An attacker must instead
search for a collision message
that hashes to the same value (analogous to finding one person who shares your
birthday). The clone chip
must therefore attempt to find a new value R2 such that the hash of R2 and a
chosen M2 yields the same hash
value as H[R I M]. However the System Authentication Chip does not reveal the
correct hash value (the TST
function only returns 1 or 0 depending on whether the hash value is correct).
Therefore the only way of
finding out the correct hash value (in order to find a collision) is to
interrogate a real Authentication Chip. But
to find the correct value means to update M, and since the decrement-only
parts of M are one-way, and the
read-only parts of M cannot be changed, a clone consumable would have to
update a real consumable before
attempting to find a collision. The alternative is a Brute Force attack search
on the TST function to find a
success (requiring each clone consumable to have access to a System
consumable). A Brute Force Search, as
described above, takes longer than the lifetime of the universe, in this case,
per authentication. Due to the fact
that a timely gathering of a hash value implies a real consumable must be
decremented, there is no point for a
clone consumable to launch this kind of attack.
Substitution with a complete lookup table
The random number seed in each System is 160 bits. The worst case situation
for an Authentication Chip is
that no state data is changed. Consequently there is a constant value returned
as M. However a clone chip
must still return FK2[R I M], which is a 160 bit value. Assuming a 160-bit
lookup of a 160-bit result, this
requires 7.3 x 1048 bytes, or 6.6 x 1036 terabytes, certainly more space than
is feasible for the near future. This
of course does not even take into account the method of collecting the values
for the ROM. A complete
lookup table is therefore completely impossible.
Substitution with a sparse lookup table
A sparse lookup table is only feasible if the messages sent to the
Authentication Chip are somehow
predictable, rather than effectively random. The random number R is seeded
with an unknown random
number, gathered from a naturally random event. There is no possibility for a
clone manufacturer to know
what the possible range of R is for all Systems, since each bit has a 50%
chance of being a 1 or a 0. Since the
range of R in all systems is unknown, it is not possible to build a sparse
lookup table that can be used in all
systems. The general sparse lookup table is therefore not a possible attack.
However, it is possible for a clone
manufacturer to know what the range of R is for a given System. This can be
accomplished by loading a
LFSR with the current result from a call to a specific System Authentication
Chip's RND function, and
iterating some number of times into the future. If this is done, a special ROM
can be built which will only
contain the responses for that particular range of R, i.e. a ROM specifically
for the consumables of that
particular System. But the attacker still needs to place correct information
in the ROM. The attacker will
therefore need to find a valid Authentication Chip and call it for each of the
values in R.
Suppose the clone Authentication Chip reports a full consumable, and then
allows a single use before
simulating loss of connection and insertion of a new full consumable. The
clone consumable would therefore
need to contain responses for authentication of a full consumable and
authentication of a partially used
consumable. The worst case ROM contains entries for full and partially used
consumables for R over the
lifetime of System. However, a valid Authentication Chip must be used to
generate the information, and be
partially used in the process. If a given System only produces about n R-
values, the sparse lookup-ROM
CA 02564047 2006-11-06
YU139 PCT 189
required is IOn bytes multiplied by the number of different values for M. The
time taken to build the ROM
depends on the amount of time enforced between calls to RD.
After all this, the clone manufacturer must rely on the consumer returning for
a refill, since the cost of
building the ROM in the first place consumes a single consumable. The clone
manufacturer's business in such
a situation is consequently in the refills. The time and cost then, depends on
the size of R and the number of
different values for M that must be incorporated in the lookup. In addition, a
custom clone consumable ROM
must be built to match each and every System, and a different valid
Authentication Chip must be used for
each System (in order to provide the full and partially used data). The use of
an Authentication Chip in a
System must therefore be examined to determine whether or not this kind of
attack is worthwhile for a clone
manufacturer. As an example, of a camera system that has about 10,000 prints
in its lifetime. Assume it has a
single Decrement Only value (number of prints remaining), and a delay of 1
second between calls to RD. In
such a system, the sparse table will take about 3 hours to build, and consumes
1 OOK. Remember that the
construction of the ROM requires the consumption of a valid Authentication
Chip, so any money charged
must be worth more than a single consumable and the clone consumable combined.
Thus it is not cost
effective to perform this function for a single consumable (unless the clone
consumable somehow contained
the equivalent of multiple authentic consumables). If a clone manufacturer is
going to go to the trouble of
building a custom ROM for each owner of a System, an easier approach would be
to update System to
completely ignore the Authentication Chip.
Consequently, this attack is possible as a per-System attack, and a decision
must be made about the chance of
this occurring for a given System/Consumable combination. The chance will
depend on the cost of the
consumable and Authentication Chips, the longevity of the consumable, the
profit margin on the consumable,
the time taken to generate the ROM, the size of the resultant ROM, and whether
customers will come back to
the clone manufacturer for refills that use the same clone chip etc.
Differential cryptanalysis
Existing differential attacks are heavily dependent on the structure of S
boxes, as used in DES and other
similar algorithms. Although other algorithms such as HMAC-SHAT used in
Protocol 3 have no S boxes, an
attacker can undertake a differential-like attack by undertaking statistical
analysis of:
Minimal-difference inputs, and their corresponding outputs
Minimal-difference outputs, and their corresponding inputs
To launch an attack of this nature, sets of input/output pairs must be
collected. The collection from Protocol 3
can be via Known Plaintext, or from a Partially Adaptive Chosen Plaintext
attack. Obviously the latter, being
chosen, will be more useful. Hashing algorithms in general are designed to be
resistant to differential
analysis. SHA-1 in particular has been specifically strengthened, especially
by the 80 word expansion so that
minimal differences in input produce will still produce outputs that vary in a
larger number of bit positions
(compared to 128 bit hash functions). In addition, the information collected
is not a direct SHA-1 input/output
set, due to the nature of the HMAC algorithm. The HMAC algorithm hashes a
known value with an unknown
value (the key), and the result of this hash is then rehashed with a separate
unknown value. Since the attacker
does not know the secret value, nor the result of the first hash, the inputs
and outputs from SHA- 1 are not
known, making any differential attack extremely difficult. The following is a
more detailed discussion of
minimally different inputs and outputs from the Authentication Chip.
CA 02564047 2006-11-06
YU139 PCT 190
Minimal Difference Inputs
This is where an attacker takes a set of X, FK[X] values where the X values
are minimally different, and
examines the statistical differences between the outputs FK[X]. The attack
relies on X values that only differ
by a minimal number of bits. The question then arises as to how to obtain
minimally different X values in
order to compare the FK[X] values.
K,:With K,, the attacker needs to statistically examine minimally different X,
FK,[X] pairs. However the
attacker cannot choose any X value and obtain a related FKI [X] value. Since
X, FKI [X] pairs can only be
generated by calling the RND function on a System Authentication Chip, the
attacker must call RND multiple
times, recording each observed pair in a table. A search must then be made
through the observed values for
enough minimally different X values to undertake a statistical analysis of the
FK, [X] values.
K2:With K2, the attacker needs to statistically examine minimally different X,
FKZ[X] pairs. The only way of
generating X, FKZLX] pairs is via the RD function, which produces FK2[X] for a
given Y, FKI[Y] pair, where X
= Y I M. This means that Y and the changeable part of M can be chosen to a
limited extent by an attacker. The
amount of choice must therefore be limited as much as possible.
The first way of limiting an attacker's choice is to limit Y, since RD
requires an input of the format Y, FK, [Y].
Although a valid pair can be readily obtained from the RND function, it is a
pair of RND's choosing. An
attacker can only provide their own Y if they have obtained the appropriate
pair from RND, or if they know
K1. Obtaining the appropriate pair from RND requires a Brute Force search.
Knowing K, is only logically
possible by performing cryptanalysis on pairs obtained from the RND function -
effectively a known text
attack. Although RND can only be called so many times per second, K, is common
across System chips.
Therefore known pairs can be generated in parallel.
The second way to limit an attacker's choice is to limit M, or at least the
attacker's ability to choose M. The
limiting of M is done by making some parts of M Read Only, yet different for
each Authentication Chip, and
other parts of M Decrement Only. The Read Only parts of M should ideally be
different for each
Authentication Chip, so could be information such as serial numbers, batch
numbers, or random numbers. The
Decrement Only parts of M mean that for an attacker to try a different M, they
can only decrement those parts
of M so many times - after the Decrement Only parts of M have been reduced to
0 those parts cannot be
changed again. Obtaining a new Authentication chip 53 provides a new M, but
the Read Only portions will be
different from the previous Authentication Chip's Read Only portions, thus
reducing an attacker's ability to
choose M even further. Consequently an attacker can only gain a limited number
of chances at choosing
values for Y and M.
Minimal Difference Outputs
This is where an attacker takes a set of X, FK[X] values where the FK[X]
values are minimally different, and
examines the statistical differences between the X values. The attack relies
on FK[X] values that only differ by
a minimal number of bits. For both K, and K2, there is no way for an attacker
to generate an X value for a
given FK[X]. To do so would violate the fact that F is a one-way function.
Consequently the only way for an
attacker to mount an attack of this nature is to record all observed X, FK[X]
pairs in a table. A search must
then be made through the observed values for enough minimally different FK[X]
values to undertake a
statistical analysis of the X values. Given that this requires more work than
a minimally different input attack
(which is extremely limited due to the restriction on M and the choice of R),
this attack is not fruitful.
CA 02564047 2006-11-06
YU139 PCT 191
Message substitution attacks
In order for this kind of attack to be carried out, a clone consumable must
contain a real Authentication chip
53, but one that is effectively reusable since it never gets decremented. The
clone Authentication Chip would
intercept messages, and substitute its own. However this attack does not give
success to the attacker. A clone
Authentication Chip may choose not to pass on a WR command to the real
Authentication Chip. However the
subsequent RD command must return the correct response (as if the WR had
succeeded). To return the correct
response, the hash value must be known for the specific R and M. As described
in the Birthday Attack
section, an attacker can only determine the hash value by actually updating M
in a real Chip, which the
attacker does not want to do. Even changing the R sent by System does not help
since the System
Authentication Chip must match the R during a subsequent TST. A Message
substitution attack would
therefore be unsuccessful. This is only true if System updates the amount of
consumable remaining before it
is used.
Reverse en ing eering the keygenerator
If a pseudo-random number generator is used to generate keys, there is the
potential for a clone manufacture
to obtain the generator program or to deduce the random seed used. This was
the way in which the Netscape
security program was initially broken.
Bypassing authentication alto eg ther
Protocol 3 requires the System to update the consumable state data before the
consumable is used, and follow
every write by a read (to authenticate the write). Thus each use of the
consumable requires an authentication.
If the System adheres to these two simple rules, a clone manufacturer will
have to simulate authentication via
a method above (such as sparse ROM lookup).
Reuse of Authentication Chips
As described above, Protocol 3 requires the System to update the consumable
state data before the
consumable is used, and follow every write by a read (to authenticate the
write). Thus each use of the
consumable requires an authentication. If a consumable has been used up, then
its Authentication Chip will
have had the appropriate state-data values decremented to 0. The chip can
therefore not be used in another
consumable. Note that this only holds true for Authentication Chips that hold
Decrement-Only data items. If
there is no state data decremented with each usage, there is nothing stopping
the reuse of the chip. This is the
basic difference between Presence-Only Authentication and Consumable Lifetime
Authentication. Protocol 3
allows both. The bottom line is that if a consumable has Decrement Only data
items that are used by the
System, the Authentication Chip cannot be reused without being completely
reprogrammed by a valid
Programming Station that has knowledge of the secret key.
Management decision to omit authentication to save costs
Although not strictly an external attack, a decision to omit authentication in
future Systems in order to save
costs will have widely varying effects on different markets. In the case of
high volume consumables, it is
essential to remember that it is very difficult to introduce authentication
after the market has started, as
systems requiring authenticated consumables will not work with older
consumables still in circulation.
Likewise, it is impractical to discontinue authentication at any stage, as
older Systems will not work with the
new, unauthenticated, consumables. In he second case, older Systems can be
individually altered by replacing
the System Authentication Chip by a simple chip that has the same programming
interface, but whose TST
CA 02564047 2006-11-06
YU139 PCT 192
function always succeeds. Of course the System may be programmed to test for
an always-succeeding TST
function, and shut down. In the case of a specialized pairing, such as a
car/car-keys, or door/door-key, or
some other similar situation, the omission of authentication in future systems
is trivial and non-repercussive.
This is because the consumer is sold the entire set of System and Consumable
Authentication Chips at the one
time.
Garrote/bribe attack
This form of attack is only successful in one of two circumstances:
K,, K2, and R are already recorded by the chip-programmer, or
the attacker can coerce future values of K,, K2, and R to be recorded.
If humans or computer systems external to the Programming Station do not know
the keys, there is no amount
of force or bribery that can reveal them. The level of security against this
kind of attack is ultimately a
decision for the System/Consumable owner, to be made according to the desired
level of service. For
example, a car company may wish to keep a record of all keys manufactured, so
that a person can request a
new key to be made for their car. However this allows the potential compromise
of the entire key database,
allowing an attacker to make keys for any of the manufacturer's existing cars.
It does not allow an attacker to
make keys for any new cars. Of course, the key database itself may also be
encrypted with a further key that
requires a certain number of people to combine their key portions together for
access. If no record is kept of
which key is used in a particular car, there is no way to make additional keys
should one become lost. Thus an
owner will have to replace his car's Authentication Chip and all his car-keys.
This is not necessarily a bad
situation. By contrast, in a consumable such as a printer ink cartridge, the
one key combination is used for all
Systems and all consumables. Certainly if no backup of the keys is kept, there
is no human with knowledge of
the key, and therefore no attack is possible. However, a no-backup situation
is not desirable for a consumable
such as ink cartridges, since if the key is lost no more consumables can be
made. The manufacturer should
therefore keep a backup of the key information in several parts, where a
certain number of people must
together combine their portions to reveal the full key information. This may
be required if case the chip
programming station needs to be reloaded. In any case, none of these attacks
are against Protocol 3 itself,
since no humans are involved in the authentication process. Instead, it is an
attack against the programming
stage of the chips.
HMAC-SHA I
The mechanism for authentication is the HMAC-SHA1 algorithm, acting on one of:
HMAC-SHA1 (R, K,), or
HMAC-SHA 1 (R I M, K2)
We will now examine the HMAC-SHA1 algorithm in greater detail than covered so
far, and describes an
optimization of the algorithm that requires fewer memory resources than the
original definition.
HMAC
The HMAC algorithm proceeds, given the following definitions:
H = the hash function (e.g. MD5 or SHA-1)
n = number of bits output from H (e.g. 160 for SHA-1, 128 bits for MD5)
M = the data to which the MAC function is to be applied
K = the secret key shared by the two parties
CA 02564047 2006-11-06
YU139 PCT 193
ipad= 0x36 repeated 64 times
opad = Ox5C repeated 64 times
The HMAC algorithm is as follows:
Extend K to 64 bytes by appending 0x00 bytes to the end of K
XOR the 64 byte string created in (1) with ipad
Append data stream M to the 64 byte string created in (2)
Apply H to the stream generated in (3)
XOR the 64 byte string created in (1) with opad
Append the H result from (4) to the 64 byte string resulting from (5)
Apply H to the output of (6) and output the result
Thus:
HMAC[M] = H[(KOopad) I H[(KOipad)IM]]
HMAC-SHA1 algorithm is simply HMAC with H = SHA-1.
SHA-1
The SHAT hashing algorithm is defined in the algorithm as summarized here.
Nine 32-bit constants are defined. There are 5 constants used to initialize
the chaining variables, and there are
4 additive constants.
Initial Chaining Values Additive Constants
h, 0x67452301 , 0x5A827999
h2 OxEFCDAB89 2 0x6ED9EBA1
h3 Ox98BADCFE 3 Ox8FIBBCDC
h4 0x10325476 4 OxCA62C1D6
h5 0xC3D2E1F0
Non-optimized SHA-1 requires a total of 2912 bits of data storage:
Five 32-bit chaining variables are defined: H,, H2, H3, H4 and H5.
Five 32-bit working variables are defined: A, B, C, D, and E.
One 32-bit temporary variable is defined: t.
Eighty 32-bit temporary registers are defined: Xo-79=
The following functions are defined for SHA- 1:
Symbolic Nomenclature Description
+ Addition modulo 232
XOY Result of rotating X left through Y bit positions
f(X, Y, Z) (X A Y) v (.X A Z)
CA 02564047 2006-11-06
YU139 PCT 194
g(X, Y, Z) (X A Y) V (X A Z) V (Y A Z)
h(X,Y,Z) X(DYOZ
The hashing algorithm consists of firstly padding the input message to be a
multiple of 512 bits and
initializing the chaining variables H1_5 with h1_5. The padded message is then
processed in 512-bit chunks,
with the output hash value being the final 160-bit value given by the
concatenation of the chaining variables:
H1 I H2 I H3 I H4 I H5. The steps of the SHA-1 algorithm are now examined in
greater detail.
Step 1. Preprocessing
The first step of SHA-1 is to pad the input message to be a multiple of 512
bits as follows and to initialize the
chaining variables.
Steps to follow to preprocess the input essage
Pad the input message Append a 1 bit to the message
Append 0 bits such that the length of the padded message is
64-bits short of a multiple of 512 bits.
Append a 64-bit value containing the length in bits of the
original input message. Store the length as most significant bit
through to least significant bit.
Initialize the chaining variables H1 <- hl, H2 <- h2, H3 <- h3, H4 h4, H5 - h5
Step 2. Processing
The padded input message can now be processed. We process the message in 512-
bit blocks. Each 512-bit
block is in the form of 16 x 32-bit words, referred to as InputWordo-15=
Steps to follow for each 512 bit block In utWordo-1s
Copy the 512 input bits into Xo-15 For j=0 to 15
X = In utWord
Expand Xo-15 into X16.79 For j=16 to 79
X) <- ((X1.3 O+ Xj_8 (D X1 14 (D X'-16) 0 1)
Initialize working variables A F H1i B <- H2, C <- H3, D <- H4, E - H5
Round l For j=0 to 19
t <- ((A05) + f(B, C, D) + E + X; + y1)
E<- D,D-C,C<-(B030),B<- A,A--t
Round 2 For j = 20 to 39
t<- ((A05)+h(B,C,D)+E+X;+y2)
E<-D,D-C,C<-(B030),B<-A,A ---t
Round 3 For j = 40 to 59
t- ((A(55)+g(B,C,D)+E+X;+y3)
E<-D,D<-C,C<-(B030),B4-A,A-t
Round 4 For j = 60 to 79
t- ((A05)+h(B,C,D)+E+X,+y4)
E<- D,D4-C,C<-(B030),B-A,A-t
Update chaining variables H1 <- H1 + A, H2 H2 + B,
H3-H3+C,H4<-H4+D,
H5-H5+E
CA 02564047 2006-11-06
YU139 PCT 195
Step 3. Completion
After all the 512-bit blocks of the padded input message have been processed,
the output hash value is the
final 160-bit value given by: HI I H2 I H3 I H4 I H5-
Optimization for Hardware Implementation
The SHA-1 Step 2 procedure is not optimized for hardware. In particular, the
80 temporary 32-bit registers
use up valuable silicon on a hardware implementation. This section describes
an optimization to the SHA-1
algorithm that only uses 16 temporary registers. The reduction in silicon is
from 2560 bits down to 512 bits, a
saving of over 2000 bits. It may not be important in some applications, but in
the Authentication Chip storage
space must be reduced where possible. The optimization is based on the fact
that although the original 16-
word message block is expanded into an 80-word message block, the 80 words are
not updated during the
algorithm. In addition, the words rely on the previous 16 words only, and
hence the expanded words can be
calculated on-the-fly during processing, as long as we keep 16 words for the
backward references. We require
rotating counters to keep track of which register we are up to using, but the
effect is to save a large amount of
storage. Rather than index X by a single value j, we use a 5 bit counter to
count through the iterations. This
can be achieved by initializing a 5-bit register with either 16 or 20, and
decrementing it until it reaches 0. In
order to update the 16 temporary variables as if they were 80, we require 4
indexes, each a 4-bit register. All 4
indexes increment (with wraparound) during the course of the algorithm.
Steps to follow for each 512 bit block In utWordo_15
Initialize working variables A F HI, B - H2, C <- H3, D F- H4, E H5
NI <- 13,N2<-8,N3<-2,N4<- 0
Round 0 Do 16 times:
Copy the 512 input bits into Xo_ XN4 = InputWordN4
15 IINI, ( IIN2, fIN3]o tional fN4
Round 1A Do 16 times:
t - ((A05) + f(B, C, D) + E + XN4 + Y1)
[INI, 1)N2, fN3]optional fIN4
E <- D, D <- C, C <- (Bi30),B-A,A4-t
Round lB Do 4 times:
XN4 <- ((XNI $ XN2 XN3 @ XN4) CS 1)
t-((A05)+f(B, C, D) + E + XN4 + Y1)
IN1, fN2, fN3i fN4
E<-D,D<-C,C<-(BO30),B<-A,A<- t
Round 2 Do 20 times:
XN4 - ((XNI XN2 (@ XN3 (@ XN4) 0 1)
t <- ((A05) + h(B, C, D) + E + XN4 + Y2)
fN1i fN2, fN3i fN4
E<-D,D-C,C<-(B030),B-A,A<- t
Round 3 Do 20 times:
XN4 - ((XNI (@ XN2 (D XN3 @ XN4) 0 1)
t F- ((A05) + g(B, C, D) + E + XN4 + Y3)
IN1, fN2i fIN3, fN4
E<-D,D<- C,C<- (B030),B-A,A-t
Round 4 Do 20 times:
CA 02564047 2006-11-06
YU139 PCT 196
XN4 - ((XNI Q XN2 XN3 (D XN4) 0 1)
t 4- ((A05) + h(B, C, D) + E + XN4 + y4)
fN,, f1N2i f1N3, fN4
E<- D,DE-C,C-(B030),B4-A,A4-t
Update chaining variables H, 4- H, + A, H2 4- H2 + B,
H3 H3 + C, H4 4- H4 + D,
H54-H5+E
The incrementing of N1, N2, and N3 during Rounds 0 and IA is optional. A
software implementation would
not increment them, since it takes time, and at the end of the 16 times
through the loop, all 4 counters will be
their original values. Designers of hardware may wish to increment all 4
counters together to save on control
logic. Round 0 can be completely omitted if the caller loads the 512 bits of
X0-15=
HMAC-SHA 1
In the Authentication Chip implementation, the HMAC-SHA1 unit only ever
performs hashing on two types
of inputs: on R using K, and on R I M using K2. Since the inputs are two
constant lengths, rather than have
HMAC and SHA-1 as separate entities on chip, they can be combined and the
hardware optimized. The
padding of messages in SHA-1 Step 1 (a 1 bit, a string of 0 bits, and the
length of the message) is necessary to
ensure that different messages will not look the same after padding. Since we
only deal with 2 types of
messages, our padding can be constant Os. In addition, the optimized version
of the SHA-1 algorithm is used,
where only 16 32-bit words are used for temporary storage. These 16 registers
are loaded directly by the
optimized HMAC-SHAT hardware. The Nine 32-bit constants h1_5 and y1_4 are
still required, although the fact
that they are constants is an advantage for hardware implementation. Hardware
optimized HMAC-SHA-1
requires a total of 1024 bits of data storage:
Five 32-bit chaining variables are defined: HI, H2, H3, H4 and H5.
Five 32-bit working variables are defined: A, B, C, D, and E.
Five 32-bit variables for temporary storage and final result: Buffl 601_5
One 32 bit temporary variable is defined: t.
Sixteen 32-bit temporary registers are defined: XO-15=
The following two sections describe the steps for the two types of calls to
HMAC-SHA 1.
H_lll
In the case of producing the keyed hash of R using K1i the original input
message R is a constant length of
160 bits. We can therefore take advantage of this fact during processing.
Rather than load X0.15 during the first
part of the SHA-1 algorithm, we load X0-15 directly, and thereby omit Round 0
of the optimized Process Block
(Step 2) of SHA-1. The pseudocode takes on the following steps:
Step Description Action
1 Process K i ad X04 4- K, O+ 0x363636...
2 X5.15 E- 0x363636...
3 H1-5 F h1-5
4 Process Block
CA 02564047 2006-11-06
YU139 PCT 197
Process R X0.4 - R
6 X5-15 <- 0
7 Process Block
8 Buff1601.5 - H1-5
9 Process K O opad X0-4 - K1 +O Ox5C5C5C...
X5-15 <- Ox5C5C5C...
11 H1-5 <- h1-5
12 Process Block
13 Process previous H[x] X0.4 - Result
14 X5-15 0
Process Block
16 Get results Buff1601-5 <- H1-5
H[RLM,K,1
In the case of producing the keyed hash of R I M using K2, the original input
message is a constant length of
416 (256+160) bits. We can therefore take advantage of this fact during
processing. Rather than load XO-15
5 during the first part of the SHA-1 algorithm, we load
X0.15 directly, and thereby omit Round 0 of the optimized Process Block (Step
2) of SHA-1. The pseudocode
takes on the following steps:
Step Description Action
1 Process K O+ ipad X0.4 - K2 O+ 0x363636...
2 X5-15 - 0x363636...
3 H1_5 <- 111.5
4 Process Block
5 Process R I M X0-4 <- R
6 X5-124-M
7 X13-15 -0
8 Process Block
9 Tem <- H1-5
10 Process K O o pad X0.4 K2 O Ox5C5C5C...
11 X5.15 - Ox5C5C5C...
12 H1_5 <- h1-5
13 Process Block
14 Process previous H[x] X0.4 -Temp
15 X5-15<-0
16 Process Block
17 Get results Result <- H1-5
CA 02564047 2006-11-06
YU139 PCT 198
DATA STORAGE INTEGRITY
Each Authentication Chip contains some non-volatile memory in order to hold
the variables required by
Authentication Protocol 3. The following non-volatile variables are defined:
Variable Name Size (in bits) Description
M[0..15] 256 16 words (each 16 bits) containing state data such as
serial numbers, media remaining etc.
K, 160 Key used to transform R during authentication.
K2 160 Key used to transform M during authentication.
R 160 Current random number
AccessMode 0..15 32 The 16 sets of 2-bit AccessMode values for M n .
MinTicks 32 The minimum number of clock ticks between calls to
key-based functions
SlWritten 1 If set, the secret key information (K1, K2, and R) has
been written to the chip. If clear, the secret information
has not been written yet.
IsTrusted 1 If set, the RND and TST functions can be called, but
RD and WR functions cannot be called.
If clear, the RND and TST functions cannot be called,
but RD and WR functions can be called.
Total bits 802
Note that if these variables are in Flash memory, it is not a simple matter to
write a new value to replace the
old. The memory must be erased first, and then the appropriate bits set. This
has an effect on the algorithms
used to change Flash memory based variables. For example, Flash memory cannot
easily be used as shift
registers. To update a Flash memory variable by a general operation, it is
necessary to follow these steps:
Read the entire N bit value into a general purpose register;
Perform the operation on the general purpose register;
Erase the Flash memory corresponding to the variable; and
Set the bits of the Flash memory location based on the bits set in the general-
purpose register.
A RESET of the Authentication Chip has no effect on these non-volatile
variables.
M AND ACCESSMODE
Variables M[0] through M[ 15] are used to hold consumable state data, such as
serial numbers, batch numbers,
and amount of consumable remaining. Each M[n] register is 16 bits, making the
entire M vector 256 bits (32
bytes). Clients cannot read from or written to individual M[n] variables.
Instead, the entire vector, referred to
as M, is read or written in a single logical access. M can be read using the
RD (read) command, and written
to via the WR (write) command. The commands only succeed if K, and K2 are both
defined (SlWritten = 1)
and the Authentication Chip is a consumable non-trusted chip (IsTrusted = 0).
Although M may contain a
number of different data types, they differ only in their write permissions.
Each data type can always be read.
Once in client memory, the 256 bits can be interpreted in any way chosen by
the client. The entire 256 bits of
CA 02564047 2006-11-06
YU139 PCT 199
M are read at one time instead of in smaller amounts for reasons of security,
as described in the chapter
entitled Authentication. The different write permissions are outlined in the
following table:
Data Type Access Note
Read Only Can never be written to
ReadWrite Can always be written to
Decrement Only Can only be written to if the new value is less than the old
value. Decrement
Only values are typically 16-bit or 32-bit values, but can be any multiple of
16 bits.
To accomplish the protection required for writing, a 2-bit access mode value
is defined for each M[n]. The
following table defines the interpretation of the 2-bit access mode bit-
pattern:
Bits Op Interpretation Action taken during Write command
00 RW ReadWrite The new 16-bit value is always written to M [n .
01 MSR Decrement Only The new 16-bit value is only written to M[n] if it is
(Most Significant less than the value currently in M[n]. This is used for
Region) access to the Most Significant 16 bits of a Decrement
Only number.
NMSR Decrement Only The new 16-bit value is only written to M[n] if
(Not the Most M[n+1] can also be written. The NMSR access mode
Significant Region) allows multiple precision values of 32 bits and more
(multiples of 16 bits) to decrement.
11 RO Read Only The new 16-bit value is ignored.
M[n] is left unchanged.
The 16 sets of access mode bits for the 16 M[n] registers are gathered
together in a single 32-bit AccessMode
10 register. The 32 bits of the AccessMode register correspond to M[n] with n
as follows:
MSB LSB
114 113 12 11 11019 8 7 6 5 4 3 2 1 0
Each 2-bit value is stored in hi/lo format. Consequently, if M[0-5] were
access mode MSR, with M[6-15]
15 access mode RO, the 32-bit AccessMode register would be:
11-11-11-11-11-11-11-11-11-11-01-01-01-01-01-01
During execution of a WR (write) command, AccessMode[n] is examined for each
M[n], and a decision made
as to whether the new M[n] value will replace the old. The AccessMode register
is set using the
Authentication Chip's SAM (Set Access Mode) command. Note that the Decrement
Only comparison is
unsigned, so any Decrement Only values that require negative ranges must be
shifted into a positive range.
For example, a consumable with a Decrement Only data item range of -50 to 50
must have the range shifted
to be 0 to 100. The System must then interpret the range 0 to 100 as being -50
to 50. Note that most instances
of Decrement Only ranges are N to 0, so there is no range shift required. For
Decrement Only data items,
CA 02564047 2006-11-06
YU139 PCT 200
arrange the data in order from most significant to least significant 16-bit
quantities from M[n] onward. The
access mode for the most significant 16 bits (stored in M[n]) should be set to
MSR. The remaining registers
(M[n+l], M[n+2] etc) should have their access modes set to NMSR. If
erroneously set to NMSR, with no
associated MSR region, each NMSR region will be considered independently
instead of being a multi-
precision comparison.
K,
K, is the 160-bit secret key used to transform R during the authentication
protocol. K, is programmed along
with K2 and R with the SSI (Set Secret Information) command. Since K, must be
kept secret, clients cannot
directly read K,. The commands that make use of K, are RND and RD. RND returns
a pair R, FKI[R] where
R is a random number, while RD requires an X, FKI[X] pair as input. K, is used
in the keyed one-way hash
function HMAC-SHA1. As such it should be programmed with a physically
generated random number,
gathered from a physically random phenomenon. K, must NOT be generated with a
computer-run random
number generator. The security of the Authentication chips depends on K,, K2
and R being generated in a way
that is not deterministic. For example, to set K,, a person can toss a fair
coin 160 times, recording heads as 1,
and tails as 0. K, is automatically cleared to 0 upon execution of a CLR
command. It can only be
programmed to a non-zero value by the SSI command.
K2
K2 is the 160-bit secret key used to transform M I R during the authentication
protocol. K2 is programmed
along with K, and R with the SSI (Set Secret Information) command. Since K2
must be kept secret, clients
cannot directly read K2. The commands that make use of K2 are RD and TST. RD
returns a pair M, FK2[M
X] where X was passed in as one of the parameters to the RD function. TST
requires an M, FK2[M I R] pair as
input, where R was obtained from the Authentication Chip's RND function. K2 is
used in the keyed one-way
hash function HMAC-SHA1. As such it should be programmed with a physically
generated random number,
gathered from a physically random phenomenon. K2 must NOT be generated with a
computer-run random
number generator. The security of the Authentication chips depends on K,, K2
and R being generated in a way
that is not deterministic. For example, to set K2, a person can toss a fair
coin 160 times, recording heads as 1,
and tails as 0. K2 is automatically cleared to 0 upon execution of a CLR
command. It can only be
programmed to a non-zero value by the SSI command.
R AND ISTRUSTED
R is a 160-bit random number seed that is programmed along with K, and K2 with
the SSI (Set Secret
Information) command. R does not have to be kept secret, since it is given
freely to callers via the RND
command. However R must be changed only by the Authentication Chip, and not
set to any chosen value by a
caller. R is used during the TST command to ensure that the R from the
previous call to RND was used to
generate the FK2[M I R] value in the non-trusted Authentication Chip (ChipA).
Both RND and TST are only
used in trusted Authentication Chips (ChipT).
IsTrusted is a 1-bit flag register that determines whether or not the
Authentication Chip is a trusted chip
(ChipT):
If the IsTrusted bit is set, the chip is considered to be a trusted chip, and
hence clients can call RND and TST
functions (but not RD or WR).
If the IsTrusted bit is clear, the chip is not considered to be trusted.
Therefore RND and TST functions cannot
CA 02564047 2006-11-06
YU139 PCT 201
be called (but RD and WR functions can be called instead). System never needs
to call RND or TST on
the consumable (since a clone chip would simply return 1 to a function such as
TST, and a constant
value for RND).
The IsTrusted bit has the added advantage of reducing the number of available
R, FKI [R] pairs obtainable by
an attacker, yet still maintain the integrity of the Authentication protocol.
To obtain valid R, FKI[R] pairs, an
attacker requires a System Authentication Chip, which is more expensive and
less readily available than the
consumables. Both R and the IsTrusted bit are cleared to 0 by the CLR command.
They are both written to by
the issuing of the SSI command. The IsTrusted bit can only set by storing a
non-zero seed value in R via the
SSI command (R must be non-zero to be a valid LFSR state, so this is quite
reasonable). R is changed via a
160-bit maximal period LFSR with taps on bits 1, 2, 4, and 159, and is changed
only by a successful call to
TST (where 1 is returned).
Authentication Chips destined to be trusted Chips used in Systems (ChipT)
should have their IsTrusted bit set
during programming, and Authentication Chips used in Consumables (ChipA)
should have their IsTrusted bit
kept clear (by storing 0 in R via the SSI command during programming). There
is no command to read or
write the IsTrusted bit directly. The security of the Authentication Chip does
not only rely upon the
randomness of K, and K2 and the strength of the HMAC-SHA1 algorithm. To
prevent an attacker from
building a sparse lookup table, the security of the Authentication Chip also
depends on the range of R over the
lifetime of all Systems. What this means is that an attacker must not be able
to deduce what values of R there
are in produced and future Systems. As such R should be programmed with a
physically generated random
number, gathered from a physically random phenomenon. R must NOT be generated
with a computer-run
random number generator. The generation of R must not be deterministic. For
example, to generate an R for
use in a trusted System chip, a person can toss a fair coin 160 times,
recording heads as 1, and tails as 0. 0 is
the only non-valid initial value for a trusted R is 0 (or the IsTrusted bit
will not be set).
SIWRITTEN
The SlWritten (Secret Information Written) 1-bit register holds the status of
the secret information stored
within the Authentication Chip. The secret information is K1, K2 and R. A
client cannot directly access the
SlWritten bit. Instead, it is cleared via the CLR command (which also clears
Kt, K2 and R). When the
Authentication Chip is programmed with secret keys and random number seed
using the SSI command
(regardless of the value written), the SlWritten bit is set automatically.
Although R is strictly not secret, it
must be written together with Ki and K2 to ensure that an attacker cannot
generate their own random number
seed in order to obtain chosen R, FKI[R] pairs. The SlWritten status bit is
used by all functions that access K,,
K2, or R. If the SlWritten bit is clear, then calls to RD, WR, RND, and TST
are interpreted as calls to CLR.
MINTICKS
There are two mechanisms for preventing an attacker from generating multiple
calls to TST and RD functions
in a short period of time. The first is a clock limiting hardware component
that prevents the internal clock
from operating at a speed more than a particular maximum (e.g. 10 MHz). The
second mechanism is the 32-
bit MinTicks register, which is used to specify the minimum number of clock
ticks that must elapse between
calls to key-based functions. The MinTicks variable is cleared to 0 via the
CLR command. Bits can then be
set via the SMT (Set MinTicks) command. The input parameter to SMT contains
the bit pattern that
CA 02564047 2006-11-06
YU139 PCT 202
represents which bits of MinTicks are to be set. The practical effect is that
an attacker can only increase the
value in MinTicks (since the SMT function only sets bits). In addition, there
is no function provided to allow
a caller to read the current value of this register. The value of MinTicks
depends on the operating clock speed
and the notion of what constitutes a reasonable time between key-based
function calls (application specific).
The duration of a single tick depends on the operating clock speed. This is
the maximum of the input clock
speed and the Authentication Chip's clock-limiting hardware. For example, the
Authentication Chip's clock-
limiting hardware may be set at 10 MHz (it is not changeable), but the input
clock is 1 MHz. In this case, the
value of 1 tick is based on 1 MHz, not 10 MHz. If the input clock was 20 MHz
instead of 1 MHz, the value of
I tick is based on 10 MHz (since the clock speed is limited to 10 MHz).
Once the duration of a tick is known, the MinTicks value can to be set. The
value for MinTicks is the
minimum number of ticks required to pass between calls to the key-based RD and
TST functions. The value is
a real-time number, and divided by the length of an operating tick. Suppose
the input clock speed matches the
maximum clock speed of 10 MHz. If we want a minimum of 1 second between calls
to key based functions,
the value for MinTicks is set to 10,000,000. Consider an attacker attempting
to collect X, FKI[X] pairs by
calling RND, RD and TST multiple times. If the MinTicks value is set such that
the amount of time between
calls to TST is 1 second, then each pair requires 1 second to generate. To
generate 225 pairs (only requiring
1.25 GB of storage), an attacker requires more than 1 year. An attack
requiring 264 pairs would require 5.84 x
l0" years using a single chip, or 584 years if 1 billion chips were used,
making such an attack completely
impractical in terms of time (not to mention the storage requirements!).
With regards to K1, it should be noted that the MinTicks variable only slows
down an attacker and causes the
attack to cost more since it does not stop an attacker using multiple System
chips in parallel. However
MinTicks does make an attack on K2 more difficult, since each consumable has a
different M (part of M is
random read-only data). In order to launch a differential attack, minimally
different inputs are required, and
this can only be achieved with a single consumable (containing an effectively
constant part of M). Minimally
different inputs require the attacker to use a single chip, and MinTicks
causes the use of a single chip to be
slowed down. If it takes a year just to get the data to start searching for
values to begin a differential attack
this increases the cost of attack and reduces the effective market time of a
clone consumable.
AUTHENTICATION CHIP COMMANDS
The System communicates with the Authentication Chips via a simple operation
command set. This section
details the actual commands and parameters necessary for implementation of
Protocol 3. The Authentication
Chip is defined here as communicating to System via a serial interface as a
minimum implementation. It is a
trivial matter to define an equivalent chip that operates over a wider
interface (such as 8, 16 or 32 bits). Each
command is defined by 3-bit opcode. The interpretation of the opcode can
depend on the current value of the
IsTrusted bit and the current value of the IsWritten bit. The following
operations are defined:
Op T W Mn Input Output Description
000 - - CLR - - Clear
001 0 0 SSI 160, 160, 160 - Set Secret Information
010 0 1 RD 160, 160 [256, 160 Read M securely
010 1 1 RND - 160, 160] Random
CA 02564047 2006-11-06
YU139 PCT 203
011 0 1 WR [256] - Write M
011 1 1 TST [256, 160] [1] Test
100 0 1 SAM [32] [32] Set Access Mode
101 - 1 GIT - [1] Get Is Trusted
110 - 1 SMT [32] - Set MinTicks
Op = Opcode, T = IsTrusted value, W = IsWritten value,
Mn = Mnemonic, [n] = number of bits required for parameter
Any command not defined in this table is interpreted as NOP (No Operation).
Examples include opcodes 110
and 111 (regardless of IsTrusted or IsWritten values), and any opcode other
than SSI when IsWritten = 0.
Note that the opcodes for RD and RND are the same, as are the opcodes for WR
and TST. The actual
command run upon receipt of the opcode will depend on the current value of the
IsTrusted bit (as long as
IsWritten is 1). Where the IsTrusted bit is clear, RD and WR functions will be
called. Where the IsTrusted bit
is set, RND and TST functions will be called. The two sets of commands are
mutually exclusive between
trusted and non-trusted Authentication Chips, and the same opcodes enforces
this relationship. Each of the
commands is examined in detail in the subsequent sections. Note that some
algorithms are specifically
designed because Flash memory is assumed for the implementation of non-
volatile variables.
CLR Clear
Input None
Output None
Changes All
The CLR (Clear) Command is designed to completely erase the contents of all
Authentication Chip memory.
This includes all keys and secret information, access mode bits, and state
data. After the execution of the CLR
command, an Authentication Chip will be in a programmable state, just as if it
had been freshly manufactured.
It can be reprogrammed with a new key and reused. A CLR command consists of
simply the CLR command
opcode. Since the Authentication Chip is serial, this must be transferred one
bit at a time. The bit order is LSB
to MSB for each command component. A CLR command is therefore sent as bits 0-2
of the CLR opcode. A
total of 3 bits are transferred. The CLR command can be called directly at any
time. The order of erasure is
important. SlWritten must be cleared first, to disable further calls to key
access functions (such as RND, TST,
RD and WR). If the AccessMode bits are cleared before SlWritten, an attacker
could remove power at some
point after they have been cleared, and manipulate M, thereby have a better
chance of retrieving the secret
information with a partial chosen text attack. The CLR command is implemented
with the following steps:
Ste Action
1 Erase SlWritten
Erase IsTrusted
Erase K,
Erase K2
Erase R
CA 02564047 2006-11-06
YU139 PCT 204
Erase M
2 Erase AccessMode
Erase MinTicks
Once the chip has been cleared it is ready for reprogramming and reuse. A
blank chip is of no use to an
attacker, since although they can create any value for M (M can be read from
and written to), key-based
functions will not provide any information as K, and K2 will be incorrect. It
is not necessary to consume any
input parameter bits if CLR is called for any opcode other than CLR. An
attacker will simply have to RESET
the chip. The reason for calling CLR is to ensure that all secret information
has been destroyed, making the
chip useless to an attacker.
SSI - SET SECRET INFORMATION
Input: K,, K2, R = [160 bits, 160 bits, 160 bits]
Output: None
Changes: K1, K2, R, SlWritten, IsTrusted
The SSI (Set Secret Information) command is used to load the K1, K2 and R
variables, and to set SlWritten
and IsTrusted flags for later calls to RND, TST, RD and WR commands. An SSI
command consists of the SSI
command opcode followed by the secret information to be stored in the K,, K2
and R registers. Since the
Authentication Chip is serial, this must be transferred one bit at a time. The
bit order is LSB to MSB for each
command component. An SSI command is therefore sent as: bits 0-2 of the SSI
opcode, followed by bits 0-
159 of the new value for K,, bits 0-159 of the new value for K2, and finally
bits 0-159 of the seed value for R.
A total of 483 bits are transferred. The K,, K2, R, SlWritten, and IsTrusted
registers are all cleared to 0 with a
CLR command. They can only be set using the SSI command.
The SSI command uses the flag SlWritten to store the fact that data has been
loaded into K1, K2, and R. If the
SlWritten and IsTrusted flags are clear (this is the case after a CLR
instruction), then K1, K2 and R are loaded
with the new values. If either flag is set, an attempted call to SSI results
in a CLR command being executed,
since only an attacker or an erroneous client would attempt to change keys or
the random seed without calling
CLR first. The SSI command also sets the IsTrusted flag depending on the value
for R. If R = 0, then the chip
is considered untrustworthy, and therefore IsTrusted remains at 0. If R # 0,
then the chip is considered
trustworthy, and therefore IsTrusted is set to 1. Note that the setting of the
IsTrusted bit only occurs during the
SSI command. If an Authentication Chip is to be reused, the CLR command must
be called first. The keys
can then be safely reprogrammed with an SSI command, and fresh state
information loaded into M using the
SAM and WR commands. The SSI command is implemented with the following steps:
Step Action
1 CLR
2 Ki +- Read 160 bits from client
3 K2 - Read 160 bits from client
4 R F- Read 160 bits from client
5 IF(R#0)
CA 02564047 2006-11-06
YU139 PCT 205
IsTrusted F- 1
6 SlWritten F- 1
RD - READ
Input: X, FK1[X] _ [160 bits, 160 bits]
Output: M, FK2[X I M] = [256 bits, 160 bits]
Changes: R
The RD (Read) command is used to securely read the entire 256 bits of state
data (M) from a non-trusted
Authentication Chip. Only a valid Authentication Chip will respond correctly
to the RD request. The output
bits from the RD command can be fed as the input bits to the TST command on a
trusted Authentication Chip
for verification, with the first 256 bits (M) stored for later use if (as we
hope) TST returns 1. Since the
Authentication Chip is serial, the command and input parameters must be
transferred one bit at a time. The bit
order is LSB to MSB for each command component. A RD command is therefore:
bits 0-2 of the RD opcode,
followed by bits 0-159 of X, and bits 0-159 of FKI[X]. 323 bits are
transferred in total. X and FKI[X] are
obtained by calling the trusted Authentication Chip's RND command. The 320
bits output by the trusted
chip's RND command can therefore be fed directly into the non-trusted chip's
RD command, with no need for
these bits to be stored by System. The RD command can only be used when the
following conditions have
been met:
SlWritten = 1 indicating that K1, K2 and R have been set up via the SSI
command; and
IsTrusted = 0 indicating the chip is not trusted since it is not permitted to
generate random number sequences;
In addition, calls to RD must wait for the MinTicksRemaining register to reach
0. Once it has done so, the
register is reloaded with MinTicks to ensure that a minimum time will elapse
between calls to RD. Once
MinTicksRemaining has been reloaded with MinTicks, the RD command verifies
that the input parameters
are valid. This is accomplished by internally generating FKI[X] for the input
X, and then comparing the result
against the input FKI[X]. This generation and comparison must take the same
amount of time regardless of
whether the input parameters are correct or not. If the times are not the
same, an attacker can gain information
about which bits of FK 1 [X] are incorrect. The only way for the input
parameters to be invalid is an erroneous
System (passing the wrong bits), a case of the wrong consumable in the wrong
System, a bad trusted chip
(generating bad pairs), or an attack on the Authentication Chip. A constant
value of 0 is returned when the
input parameters are wrong. The time taken for 0 to be returned must be the
same for all bad inputs so that
attackers can learn nothing about what was invalid. Once the input parameters
have been verified the output
values are calculated. The 256 bit content of M are transferred in the
following order: bits 0-15 of M[0], bits
0-15 of M[1], through to bits 0-15 of M[15]. FKZLX I M] is calculated and
output as bits 0-159. The R register
is used to store the X value during the validation of the X, FKI[X] pair. This
is because RND and RD are
mutually exclusive. The RD command is implemented with the following steps:
Step Action
1 IF (MinTicksRemaining * 0
CA 02564047 2006-11-06
YU139 PCT 206
GOTO 1
2 MinTicksRemaining - MinTicks
3 R F- Read 160 bits from client
4 Hash - Calculate FKI[R]
OK - (Hash = next 160 bits from client)
Note that this operation must take constant time so an attacker cannot
determine
how much of their guess is correct.
6 IF (OK)
Output 256 bits of M to client
ELSE
Output 256 bits of 0 to client
7 Hash +- Calculate FKZ R M]
8 IF (OK)
Output 160 bits of Hash to client
ELSE
Output 160 bits of 0 to client
RND - RANDOM
Input: None
5 Output: R, FKI [R] 160 bits, 160 bits]
Changes: None
The RND (Random) command is used by a client to obtain a valid R, FKI[R] pair
for use in a subsequent
authentication via the RD and TST commands. Since there are no input
parameters, an RND command is
therefore simply bits 0-2 of the RND opcode. The RND command can only be used
when the following
conditions have been met:
SlWritten = 1 indicating K, and R have been set up via the SSI command;
IsTrusted = 1 indicating the chip is permitted to generate random number
sequences;
RND returns both R and FKL[R] to the caller. The 288-bit output of the RND
command can be fed straight
into the non-trusted chip's RD command as the input parameters. There is no
need for the client to store them
at all, since they are not required again. However the TST command will only
succeed if the random number
passed into the RD command was obtained first from the RND command. If a
caller only calls RND multiple
times, the same R, FKI[R] pair will be returned each time. R will only advance
to the next random number in
the sequence after a successful call to TST. See TST for more information. The
RND command is
implemented with the following steps:
Step Action
1 Output 160 bits of R to client
2 Hash - Calculate FKi R
3 Output 160 bits of Hash to client
CA 02564047 2006-11-06
YU139PCT 207
TST - TEST
Input: X, FK2[R I X] = [256 bits, 160 bits]
Output: 1 or 0 = [1 bit]
Changes: M, R and MinTicksRemaining (or all registers if attack detected)
The TST (Test) command is used to authenticate a read of M from a non-trusted
Authentication Chip. The
TST (Test) command consists of the TST command opcode followed by input
parameters: X and FK2[R I X].
Since the Authentication Chip is serial, this must be transferred one bit at a
time. The bit order is LSB to MSB
for each command component. A TST command is therefore: bits 0-2 of the TST
opcode, followed by bits 0-
255 of M, bits 0-159 of FKZLR I M]. 419 bits are transferred in total. Since
the last 416 input bits are obtained
as the output bits from a RD command to a non-trusted Authentication Chip, the
entire data does not even
have to be stored by the client. Instead, the bits can be passed directly to
the trusted Authentication Chip's
TST command. Only the 256 bits of M should be kept from a RD command. The TST
command can only be
used when the following conditions have been met:
SIWritten = 1 indicating K2 and R have been set up via the SSI command;
IsTrusted = 1 indicating the chip is permitted to generate random number
sequences;
In addition, calls to TST must wait for the MinTicksRemaining register to
reach 0. Once it has done so, the
register is reloaded with MinTicks to ensure that a minimum time will elapse
between calls to TST. TST
causes the internal M value to be replaced by the input M value. FK2[M I R] is
then calculated, and compared
against the 160 bit input hash value. A single output bit is produced: 1 if
they are the same, and 0 if they are
different. The use of the internal M value is to save space on chip, and is
the reason why RD and TST are
mutually exclusive commands. If the output bit is 1, R is updated to be the
next random number in the
sequence. This forces the caller to use a new random number each time RD and
TST are called. The resultant
output bit is not output until the entire input string has been compared, so
that the time to evaluate the
comparison in the TST function is always the same. Thus no attacker can
compare execution times or number
of bits processed before an output is given.
The next random number is generated from R using a 160-bit maximal period LFSR
(tap selections on bits
159, 4, 2, and 1). The initial 160-bit value for R is set up via the SSI
command, and can be any random
number except 0 (an LFSR filled with Os will produce a never-ending stream of
Os). R is transformed by
XORing bits 1, 2, 4, and 159 together, and shifting all 160 bits right 1 bit
using the XOR result as the input bit
to b159. The new R will be returned on the next call to RND. Note that the
time taken for 0 to be returned from
TST must be the same for all bad inputs so that attackers can learn nothing
about what was invalid about the
input.
The TST command is implemented with the following steps:
Step Action
1 IF (MinTicksRemaining # 0
GOTO 1
2 MinTicksRemaining - MinTicks
CA 02564047 2006-11-06
YU139 PCT 208
3 M 4- Read 256 bits from client
4 IF (R = 0)
GOTO CLR
Hash <- Calculate FK2[R I M]
6 OK - (Hash = next 160 bits from client)
Note that this operation must take constant time so an attacker cannot
determine how
much of their guess is correct.
7 IF (OK)
Temp E- R
Erase R
Advance TEMP via LFSR
R<-TEMP
8 Output 1 bit of OK to client
Note that we can't simply advance R directly in Step 7 since R is Flash
memory, and must be erased in order
for any set bit to become 0. If power is removed from the Authentication Chip
during Step 7 after erasing the
old value of R, but before the new value for R has been written, then R will
be erased but not reprogrammed.
5 We therefore have the situation of IsTrusted=1, yet R=O, a situation only
possible due to an attacker. Step 4
detects this event, and takes action if the attack is detected. This problem
can be avoided by having a second
160-bit Flash register for R and a Validity Bit, toggled after the new value
has been loaded. It has not been
included in this implementation for reasons of space, but if chip space allows
it, an extra 160-bit Flash register
would be useful for this purpose.
WR - WRITE
Input: Mn,, _ [256 bits]
Output: None
Changes: M
A WR (Write) command is used to update the writeable parts of M containing
Authentication Chip state data.
The WR command by itself is not secure. It must be followed by an
authenticated read of M (via a RD
command) to ensure that the change was made as specified. The WR command is
called by passing the WR
command opcode followed by the new 256 bits of data to be written to M. Since
the Authentication Chip is
serial, the new value for M must be transferred one bit at a time. The bit
order is LSB to MSB for each
command component. A WR command is therefore: bits 0-2 of the WR opcode,
followed by bits 0-15 of
M[0], bits 0-15 of M[l], through to bits 0-15 of M[15]. 259 bits are
transferred in total. The WR command
can only be used when SlWritten = 1, indicating that K1, K2 and R have been
set up via the SSI command (if
SlWritten is 0, then K1, K2 and R have not been setup yet, and the CLR command
is called instead). The
ability to write to a specific M[n] is governed by the corresponding Access
Mode bits as stored in the
AccessMode register. The AccessMode bits can be set using the SAM command.
When writing the new
value to M[n] the fact that M[n] is Flash memory must be taken into account.
All the bits of M[n] must be
erased, and then the appropriate bits set. Since these two steps occur on
different cycles, it leaves the
possibility of attack open. An attacker can remove power after erasure, but
before programming with the new
value. However, there is no advantage to an attacker in doing this:
CA 02564047 2006-11-06
YU139 PCT 209
A Read/Write M[n] changed to 0 by this means is of no advantage since the
attacker could have written any
value using the WR command anyway.
A Read Only M[n] changed to 0 by this means allows an additional known text
pair (where the M[n] is 0
instead of the original value). For future use M[n] values, they are already
0, so no information is given.
A Decrement Only M[n] changed to 0 simply speeds up the time in which the
consumable is used up. It does
not give any new information to an attacker that using the consumable would
give.
The WR command is implemented with the following steps:
Step Action
1 DecEncountered <- 0
EqEncountered - 0
n<-15
2 Temp <- Read 16 bits from client
3 AM = AccessMode[-n
Compare to the previous value
5 LT <- (Temp < M[-n]) [comparison is unsigned]
EQ <- (Temp = M[-n])
6 WEF-(AM=RW)v
((AM = MSR) A LT) v
((AM =NMSR A (DecEncountered v LT))
7 DecEncountered #- ((AM = MSR) A LT) v
((AM = NMSR) A DecEncountered) v
((AM = NMSR) A EqEncountered A LT)
EqEncountered - ((AM = MSR) A EQ) v
AM = NMSR) A EgEncountered A EQ)
Advance to the next Access Mode set
and write the new M[-n] if
applicable
8 IF (WE)
Erase M[-n]
M -n Temp
un
11 IF (n # 0)
GOTO 2
SAM - SET ACCESSMODE
Input: AccessModetew = [32 bits]
Output: AccessMode = [32 bits]
Changes: AccessMode
The SAM (Set Access Mode) command is used to set the 32 bits of the AccessMode
register, and is only
available for use in consumable Authentication Chips (where the IsTrusted flag
= 0). The SAM command is
called by passing the SAM command opcode followed by a 32-bit value that is
used to set bits in the
AccessMode register. Since the Authentication Chip is serial, the data must be
transferred one bit at a time.
CA 02564047 2006-11-06
YU139 PCT 210
The bit order is LSB to MSB for each command component. A SAM command is
therefore: bits 0-2 of the
SAM opcode, followed by bits 0-31 of bits to be set in AccessMode. 35 bits are
transferred in total. The
AccessMode register is only cleared to 0 upon execution of a CLR command.
Since an access mode of 00
indicates an access mode of RW (read/write), not setting any AccessMode bits
after a CLR means that all of
M can be read from and written to. The SAM command only sets bits in the
AccessMode register.
Consequently a client can change the access mode bits for M[n] from RW to RO
(read only) by setting the
appropriate bits in a 32-bit word, and calling SAM with that 32-bit value as
the input parameter. This allows
the programming of the access mode bits at different times, perhaps at
different stages of the manufacturing
process. For example, the read only random data can be written to during the
initial key programming stage,
while allowing a second programming stage for items such as consumable serial
numbers.
Since the SAM command only sets bits, the effect is to allow the access mode
bits corresponding to M[n] to
progress from RW to either MSR, NMSR, or RO. It should be noted that an access
mode of MSR can be
changed to RO, but this would not help an attacker, since the authentication
of M after a write to a doctored
Authentication Chip would detect that the write was not successful and hence
abort the operation. The setting
of bits corresponds to the way that Flash memory works best. The only way to
clear bits in the AccessMode
register, for example to change a Decrement Only M[n] to be Read/Write, is to
use the CLR command. The
CLR command not only erases (clears) the AccessMode register, but also clears
the keys and all of M. Thus
the AccessMode[n] bits corresponding to M[n] can only usefully be changed once
between CLR commands.
The SAM command returns the new value of the AccessMode register (after the
appropriate bits have been
set due to the input parameter). By calling SAM with an input parameter of 0,
AccessMode will not be
changed, and therefore the current value of AccessMode will be returned to the
caller.
The SAM command is implemented with the following steps:
Step Action
1 Temp f- Read 32 bits from client
2 SetBits(AccessMode, Temp)
3 Output 32 bits of AccessMode to client
GIT - GET Is TRUSTED
Input: None
Output: IsTrusted = [I bit]
Changes: None
The GIT (Get Is Trusted) command is used to read the current value of the
IsTrusted bit on the Authentication
Chip. If the bit returned is 1, the Authentication Chip is a trusted System
Authentication Chip. If the bit
returned is 0, the Authentication Chip is a consumable Authentication Chip. A
GIT command consists of
simply the GIT command opcode. Since the Authentication Chip is serial, this
must be transferred one bit at a
time. The bit order is LSB to MSB for each command component. A GIT command is
therefore sent as bits 0-
2 of the GIT opcode. A total of 3 bits are transferred. The GIT command is
implemented with the following
steps:
CA 02564047 2006-11-06
YU139 PCT 211
Step Action
1 Output IsTrusted bit to client
SMT - SET MINTIcics
Input: MinTicks1e,,, _ [32 bits]
Output: None
Changes: MinTicks
The SMT (Set MinTicks) command is used to set bits in the MinTicks register
and hence define the minimum
number of ticks that must pass in between calls to TST and RD. The SMT command
is called by passing the
SMT command opcode followed by a 32-bit value that is used to set bits in the
MinTicks register. Since the
Authentication Chip is serial, the data must be transferred one bit at a time.
The bit order is LSB to MSB for
each command component. An SMT command is therefore: bits 0-2 of the SMT
opcode, followed by bits 0-
31 of bits to be set in MinTicks. 35 bits are transferred in total. The
MinTicks register is only cleared to 0
upon execution of a CLR command. A value of 0 indicates that no ticks need to
pass between calls to key-
based functions. The functions may therefore be called as frequently as the
clock speed limiting hardware
allows the chip to run.
Since the SMT command only sets bits, the effect is to allow a client to set a
value, and only increase the time
delay if further calls are made. Setting a bit that is already set has no
effect, and setting a bit that is clear only
serves to slow the chip down further. The setting of bits corresponds to the
way that Flash memory works
best. The only way to clear bits in the MinTicks register, for example to
change a value of 10 ticks to a value
of 4 ticks, is to use the CLR command. However the CLR command clears the
MinTicks register to 0 as well
as clearing all keys and M. It is therefore useless for an attacker. Thus the
MinTicks register can only usefully
be changed once between CLR commands.
The SMT command is implemented with the following steps:
Step Action
1 Temp (- Read 32 bits from client
2 SetBits(MinTicks, Temp)
PROGRAMMING AUTHENTICATION CHIPS
Authentication Chips must be programmed with logically secure information in a
physically secure
environment. Consequently the programming procedures cover both logical and
physical security. Logical
security is the process of ensuring that KI, K2, R, and the random M[n] values
are generated by a physically
random process, and not by a computer. It is also the process of ensuring that
the order in which parts of the
chip are programmed is the most logically secure. Physical security is the
process of ensuring that the
programming station is physically secure, so that K, and K2 remain secret,
both during the key generation
stage and during the lifetime of the storage of the keys. In addition, the
programming station must be resistant
CA 02564047 2006-11-06
YU139 PCT 212
to physical attempts to obtain or destroy the keys. The Authentication Chip
has its own security mechanisms
for ensuring that K, and K2 are kept secret, but the Programming Station must
also keep K, and K2 safe.
OVERVIEW
After manufacture, an Authentication Chip must be programmed before it can be
used. In all chips values for
K, and K2 must be established. If the chip is destined to be a System
Authentication Chip, the initial value for
R must be determined. If the chip is destined to be a consumable
Authentication Chip, R must be set to 0, and
initial values for M and AccessMode must be set up. The following stages are
therefore identified:
Determine Interaction between Systems and Consumables
Determine Keys for Systems and Consumables
Determine MinTicks for Systems and Consumables
Program Keys, Random Seed, MinTicks and Unused M
Program State Data and Access Modes
Once the consumable or system is no longer required, the attached
Authentication Chip can be reused. This is
easily accomplished by reprogrammed the chip starting at Stage 4 again. Each
of the stages is examined in
the subsequent sections.
STAGE 0: MANUFACTURE
The manufacture of Authentication Chips does not require any special security.
There is no secret information
programmed into the chips at manufacturing stage. The algorithms and chip
process is not special. Standard
Flash processes are used. A theft of Authentication Chips between the chip
manufacturer and programming
station would only provide the clone manufacturer with blank chips. This
merely compromises the sale of
Authentication chips, not anything authenticated by Authentication Chips.
Since the programming station is
the only mechanism with consumable and system product keys, a clone
manufacturer would not be able to
program the chips with the correct key. Clone manufacturers would be able to
program the blank chips for
their own systems and consumables, but it would be difficult to place these
items on the market without
detection. In addition, a single theft would be difficult to base a business
around.
STAGE 1: DETERMINE INTERACTION BETWEEN SYSTEMS AND CONSUMABLES
The decision of what is a System and what is a Consumable needs to be
determined before any Authentication
Chips can be programmed. A decision needs to be made about which Consumables
can be used in which
Systems, since all connected Systems and Consumables must share the same key
information. They also need
to share state-data usage mechanisms even if some of the interpretations of
that data have not yet been
determined. A simple example is that of a car and car-keys. The car itself is
the System, and the car-keys are
the consumables. There are several car-keys for each car, each containing the
same key information as the
specific car. However each car (System) would contain a different key (shared
by its car-keys), since we don't
want car-keys from one car working in another. Another example is that of a
photocopier that requires a
particular toner cartridge. In simple terms the photocopier is the System, and
the toner cartridge is the
consumable. However the decision must be made as to what compatibility there
is to be between cartridges
and photocopiers. The decision has historically been made in terms of the
physical packaging of the toner
cartridge: certain cartridges will or won't fit in a new model photocopier
based on the design decisions for
CA 02564047 2006-11-06
YU139 PCT 213
that copier. When Authentication Chips are used, the components that must work
together must share the
same key information.
In addition, each type of consumable requires a different way of dividing M
(the state data). Although the way
in which M is used will vary from application to application, the method of
allocating M[n] and
AccessMode[n] will be the same:
Define the consumable state data for specific use
Set some M[n] registers aside for future use (if required). Set these to be 0
and Read Only. The value can be
tested for in Systems to maintain compatibility.
Set the remaining M[n] registers (at least one, but it does not have to be
M[15]) to be Read Only, with the
contents of each M[n] completely random. This is to make it more difficult for
a clone manufacturer to
attack the authentication keys.
The following examples show ways in which the state data may be organized.
Example 1
Suppose we have a car with associated car-keys. A 16-bit key number is more
than enough to uniquely
identify each car-key for a given car. The 256 bits of M could be divided up
as follows:
M[n] Access Description
0 RO Key number (16 bits)
1-4 RO Car engine number (64 bits)
5-8 RO For future expansion = 0 (64 bits)
8-15 RO Random bit data (128 bits)
If the car manufacturer keeps all logical keys for all cars, it is a trivial
matter to manufacture a new physical
car-key for a given car should one be lost. The new car-key would contain a
new Key Number in M[0], but
have the same K, and K2 as the car's Authentication Chip. Car Systems could
allow specific key numbers to
be invalidated (for example if a key is lost). Such a system might require Key
0 (the master key) to be inserted
first, then all valid keys, then Key 0 again. Only those valid keys would now
work with the car. In the worst
case, for example if all car-keys are lost, then a new set of logical keys
could be generated for the car and its
associated physical car-keys if desired. The Car engine number would be used
to tie the key to the particular
car. Future use data may include such things as rental information, such as
driver/renter details.
Example 2
Suppose we have a photocopier image unit which should be replaced every
100,000 copies. 32 bits are
required to store the number of pages remaining. The 256 bits of M could be
divided up as follows:
M[n] Access Description
0 RO Serial number (16 bits)
1 RO Batch number (16 bits)
2 MSR Page Count Remaining (32 bits, hi/lo)
3 NMSR
4-7 RO For future expansion = 0 (64 bits)
8-15 RO Random bit data (128 bits)
CA 02564047 2006-11-06
YU139PCT 214
If a lower quality image unit is made that must be replaced after only 10,000
copies, the 32-bit page count can
still be used for compatibility with existing photocopiers. This allows
several consumable types to be used
with the same system.
Example 3
Consider a Polaroid camera consumable containing 25 photos. A 16-bit countdown
is all that is required to
store the number of photos remaining. The 256 bits of M could be divided up as
follows:
M[n] Access Description
0 RO Serial number (16 bits)
1 RO Batch number 16 bits)
2 MSR Photos Remaining (16 bits)
3-6 RO For future expansion = 0 (64 bits)
7-15 RO Random bit data (144 bits)
The Photos Remaining value at M[2] allows a number of consumable types to be
built for use with the same
camera System. For example, a new consumable with 36 photos is trivial to
program. Suppose 2 years after
the introduction of the camera, a new type of camera was introduced. It is
able to use the old consumable, but
also can process a new film type. M[3] can be used to define Film Type. Old
film types would be 0, and the
new film types would be some new value. New Systems can take advantage of
this. Original systems would
detect a non-zero value at M[3] and realize incompatibility with new film
types. New Systems would
understand the value of M[3] and so react appropriately. To maintain
compatibility with the old consumable,
the new consumable and System needs to have the same key information as the
old one. To make a clean
break with a new System and its own special consumables, a new key set would
be required.
Example 4
Consider a printer consumable containing 3 inks: cyan, magenta, and yellow.
Each ink amount can be
decremented separately. The 256 bits of M could be divided up as follows:
M[n] Access Description
0 RO Serial number (16 bits)
I RO Batch number (16 bits)
2 MSR Cyan Remaining (32 bits, hi/lo)
3 NMSR
4 MSR Magenta Remaining (32 bits, hi/lo)
5 NMSR
6 MSR Yellow Remaining (32 bits, hi/lo)
7 NMSR
8-11 RO For future expansion = 0 (64 bits)
12-15 RO Random bit data (64 bits)
CA 02564047 2006-11-06
YU139 PCT 215
STAGE 2: DETERMINE KEYS FOR SYSTEMS AND CONSUMABLES
Once the decision has been made as to which Systems and consumables are to
share the same keys, those keys
must be defined. The values for K, and K2 must therefore be determined. In
most cases, K, and K2 will be
generated once for all time. All Systems and consumables that have to work
together (both now and in the
future) need to have the same K, and K2 values. K, and K2 must therefore be
kept secret since the entire
security mechanism for the System/Consumable combination is made void if the
keys are compromised. If the
keys are compromised, the damage depends on the number of systems and
consumables, and the ease to
which they can be reprogrammed with new non-compromised keys: In the case of a
photocopier with toner
cartridges, the worst case is that a clone manufacturer could then manufacture
their own Authentication Chips
(or worse, buy them), program the chips with the known keys, and then insert
them into their own
consumables. In the case of a car with car-keys, each car has a different set
of keys. This leads to two
possible general scenarios. The first is that after the car and car-keys are
programmed with the keys, K, and
K2 are deleted so no record of their values are kept, meaning that there is no
way to compromise K, and K2.
However no more car-keys can be made for that car without reprogramming the
car's Authentication Chip.
The second scenario is that the car manufacturer keeps K, and K2i and new keys
can be made for the car. A
compromise of K, and K2 means that someone could make a car-key specifically
for a particular car.
The keys and random data used in the Authentication Chips must therefore be
generated by a means that is
non-deterministic (a completely computer generated pseudo-random number cannot
be used because it is
deterministic - knowledge of the generator's seed gives all future numbers).
K, and K2 should be generated
by a physically random process, and not by a computer. However, random bit
generators based on natural
sources of randomness are subject to influence by external factors and also to
malfunction. It is imperative
that such devices be tested periodically for statistical randomness.
A simple yet useful source of random numbers is the Lavarand system from
SGI. This generator uses a
digital camera to photograph six lava lamps every few minutes. Lava lamps
contain chaotic turbulent systems.
The resultant digital images are fed into an SHA-1 implementation that
produces a 7-way hash, resulting in a
160-bit value from every 7th bye from the digitized image. These 7 sets of 160
bits total 140 bytes. The 140
byte value is fed into a BBS generator to position the start of the output
bitstream. The output 160 bits from
the BBS would be the key or the Authentication chip 53.
An extreme example of a non-deterministic random process is someone flipping a
coin 160 times for K, and
160 times for K2 in a clean room. With each head or tail, a 1 or 0 is entered
on a panel of a Key Programmer
Device. The process must be undertaken with several observers (for
verification) in silence (someone may
have a hidden microphone). The point to be made is that secure data entry and
storage is not as simple as it
sounds. The physical security of the Key Programmer Device and accompanying
Programming Station
requires an entire document of its own. Once keys K, and K2 have been
determined, they must be kept for as
long as Authentication Chips need to be made that use the key. In the first
car/car-key scenario K, and K2 are
destroyed after a single System chip and a few consumable chips have been
programmed. In the case of the
photocopier / toner cartridge, K, and K2 must be retained for as long as the
toner-cartridges are being made
for the photocopiers. The keys must be kept securely.
CA 02564047 2006-11-06
YU139 PCT 216
STAGE 3: DETERMINE MINTICKS FOR SYSTEMS AND CONSUMABLES
The value of MinTicks depends on the operating clock speed of the
Authentication Chip (System specific)
and the notion of what constitutes a reasonable time between RD or TST
function calls (application specific).
The duration of a single tick depends on the operating clock speed. This is
the maximum of the input clock
speed and the Authentication Chip's clock-limiting hardware. For example, the
Authentication Chip's clock-
limiting hardware may be set at 10 MHz (it is not changeable), but the input
clock is 1 MHz. In this case, the
value of 1 tick is based on 1 MHz, not 10 MHz. If the input clock was 20 MHz
instead of 1 MHz, the value of
1 tick is based on 10 MHz (since the clock speed is limited to 10 MHz). Once
the duration of a tick is known,
the MinTicks value can be set. The value for MinTicks is the minimum number of
ticks required to pass
between calls to RD or RND key-based functions. Suppose the input clock speed
matches the maximum
clock speed of 10 MHz. If we want a minimum of 1 second between calls to TST,
the value for MinTicks is
set to 10,000,000. Even a value such as 2 seconds might be a completely
reasonable value for a System such
as a printer (one authentication per page, and one page produced every 2 or 3
seconds).
STAGE 4: PROGRAM KEYS, RANDOM SEED, MINTICKS AND UNUSED M
Authentication Chips are in an unknown state after manufacture. Alternatively,
they have already been used in
one consumable, and must be reprogrammed for use in another. Each
Authentication Chip must be cleared
and programmed with new keys and new state data. Clearing and subsequent
programming of Authentication
Chips must take place in a secure Programming Station environment.
Programming a Trusted System Authentication Chip
If the chip is to be a trusted System chip, a seed value for R must be
generated. It must be a random number
derived from a physically random process, and must not be 0. The following
tasks must be undertaken, in the
following order, and in a secure programming environment:
RESET the chip
CLR[]
Load R (160 bit register) with physically random data
SSI[K1, K2, R]
SMT[MinTickss, ,õ]
The Authentication Chip is now ready for insertion into a System. It has been
completely programmed. If the
System Authentication Chips are stolen at this point, a clone manufacturer
could use them to generate R,
FKI[R] pairs in order to launch a known text attack on K1, or to use for
launching a partially chosen-text attack
on K2. This is no different to the purchase of a number of Systems, each
containing a trusted Authentication
Chip. The security relies on the strength of the Authentication protocols and
the randomness of K, and K2.
Programming a Non-Trusted Consumable Authentication Chip
If the chip is to be a non-trusted Consumable Authentication Chip, the
programming is slightly different to
that of the trusted System Authentication Chip. Firstly, the seed value for R
must be 0. It must have additional
programming for M and the AccessMode values. The future use M[n] must be
programmed with 0, and the
random M[n] must be programmed with random data. The following tasks must be
undertaken, in the
following order, and in a secure programming environment:
RESET the chip
CA 02564047 2006-11-06
YU139 PCT 217
CLR[]
Load R (160 bit register) with 0
SSI[K1, K2, R]
Load X (256 bit register) with 0
Set bits in X corresponding to appropriate M[n] with physically random data
WR[X]
Load Y (32 bit register) with 0
Set bits in Y corresponding to appropriate M[n] with Read Only Access Modes
SAM[Y]
SMT[MinTiCksconsui bye]
The non-trusted consumable chip is now ready to be programmed with the general
state data. If the
Authentication Chips are stolen at this point, an attacker could perform a
limited chosen text attack. In the
best situation, parts of M are Read Only (0 and random data), with the
remainder of M completely chosen by
an attacker (via the WR command). A number of RD calls by an attacker obtains
FK2[MjR] for a limited M. In
the worst situation, M can be completely chosen by an attacker (since all 256
bits are used for state data). In
both cases however, the attacker cannot choose any value for R since it is
supplied by calls to RND from a
System Authentication Chip. The only way to obtain a chosen R is by a Brute
Force attack. It should be noted
that if Stages 4 and 5 are carried out on the same Programming Station (the
preferred and ideal situation),
Authentication Chips cannot be removed in between the stages. Hence there is
no possibility of the
Authentication Chips being stolen at this point. The decision to program the
Authentication Chips at one or
two times depends on the requirements of the System/Consumable manufacturer.
STAGE 5: PROGRAM STATE DATA AND ACCESS MODES
This stage is only required for consumable Authentication Chips, since M and
AccessMode registers cannot
be altered on System Authentication Chips. The future use and random values of
M[n] have already been
programmed in Stage 4. The remaining state data values need to be programmed
and the associated Access
Mode values need to be set. Bear in mind that the speed of this stage will be
limited by the value stored in the
MinTicks register. This stage is separated from Stage 4 on account of the
differences either in physical
location or in time between where/when Stage 4 is performed, and where/when
Stage 5 is performed. Ideally,
Stages 4 and 5 are performed at the same time in the same Programming Station.
Stage 4 produces valid
Authentication Chips, but does not load them with initial state values (other
than 0). This is to allow the
programming of the chips to coincide with production line runs of consumables.
Although Stage 5 can be run
multiple times, each time setting a different state data value and Access Mode
value, it is more likely to be run
a single time, setting all the remaining state data values and setting all the
remaining Access Mode values. For
example, a production line can be set up where the batch number and serial
number of the Authentication
Chip is produced according to the physical consumable being produced. This is
much harder to match if the
state data is loaded at a physically different factory.
The Stage 5 process involves first checking to ensure the chip is a valid
consumable chip, which includes a
RD to gather the data from the Authentication Chip, followed by a WR of the
initial data values, and then a
SAM to permanently set the new data values. The steps are outlined here:
CA 02564047 2006-11-06
YU139 PCT 218
IsTrusted = GIT[]
If (IsTrusted), exit with error (wrong kind of chip!)
Call RND on a valid System chip to get a valid input pair
Call RD on chip to be programmed, passing in valid input pair
Load X (256 bit register) with results from a RD of Authentication Chip
Call TST on valid System chip to ensure X and consumable chip are valid
If (TST returns 0), exit with error (wrong consumable chip for system)
Set bits of X to initial state values
WR[X]
Load Y (32 bit register) with 0
Set bits of Y corresponding to Access Modes for new state values
SAM[Y]
Of course the validation (Steps 1 to 7) does not have to occur if Stage 4 and
5 follow on from one another on
the same Programming Station. But it should occur in all other situations
where Stage 5 is run as a separate
programming process from Stage 4. If these Authentication Chips are now
stolen, they are already
programmed for use in a particular consumable. An attacker could place the
stolen chips into a clone
consumable. Such a theft would limit the number of cloned products to the
number of chips stolen. A single
theft should not create a supply constant enough to provide clone
manufacturers with a cost-effective
business. The alternative use for the chips is to save the attacker from
purchasing the same number of
consumables, each with an Authentication Chip, in order to launch a partially
chosen text attack or brute force
attack. There is no special security breach of the keys if such an attack were
to occur.
MANUFACTURE
The circuitry of the Authentication Chip must be resistant to physical attack.
A summary of manufacturing
implementation guidelines is presented, followed by specification of the
chip's physical defenses (ordered by
attack).
GUIDELINES FOR MANUFACTURING
The following are general guidelines for implementation of an Authentication
Chip in terms of manufacture:
Standard process
Minimum size (if possible)
Clock Filter
Noise Generator
Tamper Prevention and Detection circuitry
Protected memory with tamper detection
Boot circuitry for loading program code
Special implementation of FETs for key data paths
Data connections in polysilicon layers where possible
OverUnderPower Detection Unit
No test circuitry
CA 02564047 2006-11-06
YU139 PCT 219
Standard Process
The Authentication Chip should be implemented with a standard manufacturing
process (such as Flash). This
is necessary to:
Allow a great range of manufacturing location options
Take advantage of well-defined and well-known technology
Reduce cost
Note that the standard process still allows physical protection mechanisms.
Minimum size
The Authentication chip 53 must have a low manufacturing cost in order to be
included as the authentication
mechanism for low cost consumables. It is therefore desirable to keep the chip
size as low as reasonably
possible. Each Authentication Chip requires 802 bits of non-volatile memory.
In addition, the storage
required for optimized HMAC-SHAT is 1024 bits. The remainder of the chip
(state machine, processor, CPU
or whatever is chosen to implement Protocol 3) must be kept to a minimum in
order that the number of
transistors is minimized and thus the cost per chip is minimized. The circuit
areas that process the secret key
information or could reveal information about the key should also be minimized
(see Non-Flashing CMOS
below for special data paths).
Clock Filter
The Authentication Chip circuitry is designed to operate within a specific
clock speed range. Since the user
directly supplies the clock signal, it is possible for an attacker to attempt
to introduce race-conditions in the
circuitry at specific times during processing. An example of this is where a
high clock speed (higher than the
circuitry is designed for) may prevent an XOR from working properly, and of
the two inputs, the first may
always be returned. These styles of transient fault attacks can be very
efficient at recovering secret key
information. The lesson to be learned from this is that the input clock signal
cannot be trusted. Since the input
clock signal cannot be trusted, it must be limited to operate up to a maximum
frequency. This can be achieved
a number of ways. One way to filter the clock signal is to use an edge detect
unit passing the edge on to a
delay, which in turn enables the input clock signal to pass through. Fig. 174
shows clock signal flow within
the Clock Filter. The delay should be set so that the maximum clock speed is a
particular frequency (e.g.
about 4 MHz). Note that this delay is not programmable - it is fixed. The
filtered clock signal would be
further divided internally as required.
Noise Generator
Each Authentication Chip should contain a noise generator that generates
continuous circuit noise. The noise
will interfere with other electromagnetic emissions from the chip's regular
activities and add noise to the Idd
signal. Placement of the noise generator is not an issue on an Authentication
Chip due to the length of the
emission wavelengths. The noise generator is used to generate electronic
noise, multiple state changes each
clock cycle, and as a source of pseudo-random bits for the Tamper Prevention
and Detection circuitry. A
simple implementation of a noise generator is a 64-bit LFSR seeded with a non-
zero number. The clock used
for the noise generator should be running at the maximum clock rate for the
chip in order to generate as much
noise as possible.
CA 02564047 2006-11-06
YU139 PCT 220
Tamper Prevention and Detection circuitry
A set of circuits is required to test for and prevent physical attacks on the
Authentication Chip. However what
is actually detected as an attack may not be an intentional physical attack.
It is therefore important to
distinguish between these two types of attacks in an Authentication Chip:
where you can be certain that a physical attack has occurred.
where you cannot be certain that a physical attack has occurred.
The two types of detection differ in what is performed as a result of the
detection. In the first case, where the
circuitry can be certain that a true physical attack has occurred, erasure of
Flash memory key information is a
sensible action. In the second case, where the circuitry cannot be sure if an
attack has occurred, there is still
certainly something wrong. Action must be taken, but the action should not be
the erasure of secret key
information. A suitable action to take in the second case is a chip RESET. If
what was detected was an attack
that has permanently damaged the chip, the same conditions will occur next
time and the chip will RESET
again. If, on the other hand, what was detected was part of the normal
operating environment of the chip, a
RESET will not harm the key.
A good example of an event that circuitry cannot have knowledge about, is a
power glitch. The glitch may be
an intentional attack, attempting to reveal information about the key. It may,
however, be the result of a faulty
connection, or simply the start of a power-down sequence. It is therefore best
to only RESET the chip, and not
erase the key. If the chip was powering down, nothing is lost. If the System
is faulty, repeated RESETs will
cause the consumer to get the System repaired. In both cases the consumable is
still intact.A good example of
an event that circuitry can have knowledge about, is the cutting of a data
line within the chip. If this attack is
somehow detected, it could only be a result of a faulty chip (manufacturing
defect) or an attack. In either case,
the erasure of the secret information is a sensible step to take.
Consequently each Authentication Chip should have 2 Tamper Detection Lines as
illustrated in Fig. - one for
definite attacks, and one for possible attacks. Connected to these Tamper
Detection Lines would be a number
of Tamper Detection test units, each testing for different forms of tampering.
In addition, we want to ensure
that the Tamper Detection Lines and Circuits themselves cannot also be
tampered with.
At one end of the Tamper Detection Line is a source of pseudo-random bits
(clocking at high speed compared
to the general operating circuitry). The Noise Generator circuit described
above is an adequate source. The
generated bits pass through two different paths - one carries the original
data, and the other carries the inverse
of the data. The wires carrying these bits are in the layer above the general
chip circuitry (for example, the
memory, the key manipulation circuitry etc). The wires must also cover the
random bit generator. The bits are
recombined at a number of places via an XOR gate. If the bits are different
(they should be), a I is output, and
used by the particular unit (for example, each output bit from a memory read
should be ANDed with this bit
value). The lines finally come together at the Flash memory Erase circuit,
where a complete erasure is
triggered by a 0 from the XOR. Attached to the line is a number of triggers,
each detecting a physical attack
on the chip. Each trigger has an oversize nMOS transistor attached to GND. The
Tamper Detection Line
physically goes through this nMOS transistor. If the test fails, the trigger
causes the Tamper Detect Line to
become 0. The XOR test will therefore fail on either this clock cycle or the
next one (on average), thus
RESETing or erasing the chip. Fig. 175 illustrates the basic principle of a
Tamper Detection Line in terms of
tests and the XOR connected to either the Erase or RESET circuitry.
CA 02564047 2006-11-06
YU139 PCT 221
The Tamper Detection Line must go through the drain of an output transistor
for each test, as illustrated by the
oversize nMOS transistor layout of Fig. 176. :It is not possible to break the
Tamper Detect Line since this
would stop the flow of I s and Os from the random source. The XOR tests would
therefore fail. As the Tamper
Detect Line physically passes through each test, it is not possible to
eliminate any particular test without
breaking the Tamper Detect Line. It is important that the XORs take values
from a variety of places along the
Tamper Detect Lines in order to reduce the chances of an attack. Fig. 177
illustrates the taking of multiple
XORs from the Tamper Detect Line to be used in the different parts of the
chip. Each of these XORs can be
considered to be generating a ChipOK bit that can be used within each unit or
sub-unit.
A sample usage would be to have an OK bit in each unit that is ANDed with a
given ChipOK bit each cycle.
The OK bit is loaded with 1 on a RESET. If OK is 0, that unit will fail until
the next RESET. If the Tamper
Detect Line is functioning correctly, the chip will either RESET or erase all
key information. If the RESET or
erase circuitry has been destroyed, then this unit will not function, thus
thwarting an attacker. The destination
of the RESET and Erase line and associated circuitry is very context
sensitive. It needs to be protected in
much the same way as the individual tamper tests. There is no point generating
a RESET pulse if the attacker
can simply cut the wire leading to the RESET circuitry. The actual
implementation will depend very much on
what is to be cleared at RESET, and how those items are cleared. Finally, Fig.
178 shows how the Tamper
Lines cover the noise generator circuitry of the chip. The generator and NOT
gate are on one level, while the
Tamper Detect Lines run on a level above the generator.
Protected memory with tamper detection
It is not enough to simply store secret information or program code in Flash
memory. The Flash memory and
RAM must be protected from an attacker who would attempt to modify (or set) a
particular bit of program
code or key information. The mechanism used must conform to being used in the
Tamper Detection Circuitry
(described above). The first part of the solution is to ensure that the Tamper
Detection Line passes directly
above each Flash or RAM bit. This ensures that an attacker cannot probe the
contents of Flash or RAM. A
breach of the covering wire is a break in the Tamper Detection Line. The
breach causes the Erase signal to be
set, thus deleting any contents of the memory. The high frequency noise on the
Tamper Detection Line also
obscures passive observation.
The second part of the solution for Flash is to use multi-level data storage,
but only to use a subset of those
multiple levels for valid bit representations. Normally, when multi-level
Flash storage is used, a single
floating gate holds more than one bit. For example, a 4-voltage-state
transistor can represent two bits.
Assuming a minimum and maximum voltage representing 00 and 11 respectively,
the two middle voltages
represent 01 and 10. In the Authentication Chip, we can use the two middle
voltages to represent a single bit,
and consider the two extremes to be invalid states. If an attacker attempts to
force the state of a bit one way or
the other by closing or cutting the gate's circuit, an invalid voltage (and
hence invalid state) results.
The second part of the solution for RAM is to use a parity bit. The data part
of the register can be checked
against the parity bit (which will not match after an attack). The bits coming
from Flash and RAM can
therefore be validated by a number of test units (one per bit) connected to
the common Tamper Detection
Line. The Tamper Detection circuitry would be the first circuitry the data
passes through (thus stopping an
attacker from cutting the data lines).
CA 02564047 2006-11-06
YU139 PCT 222
Boot circuitry for loading program code
Program code should be kept in multi-level Flash instead of ROM, since ROM is
subject to being altered in a
non-testable way. A boot mechanism is therefore required to load the program
code into Flash memory (Flash
memory is in an indeterminate state after manufacture). The boot circuitry
must not be in ROM - a small
state-machine would suffice. Otherwise the boot code could be modified in an
undetectable way. The boot
circuitry must erase all Flash memory, check to ensure the erasure worked, and
then load the program code.
Flash memory must be erased before loading the program code. Otherwise an
attacker could put the chip into
the boot state, and then load program code that simply extracted the existing
keys. The state machine must
also check to ensure that all Flash memory has been cleared (to ensure that an
attacker has not cut the Erase
line) before loading the new program code. The loading of program code must be
undertaken by the secure
Programming Station before secret information (such as keys) can be loaded.
Special implementation of FETs for key data paths
The normal situation for FET implementation for the case of a CMOS Inverter
(which involves a pMOS
transistor combined with an nMOS transistor) is shown in Fig. 179. During the
transition, there is a small
period of time where both the nMOS transistor and the pMOS transistor have an
intermediate resistance. The
resultant power-ground short circuit causes a temporary increase in the
current, and in fact accounts for the
majority of current consumed by a CMOS device. A small amount of infrared
light is emitted during the short
circuit, and can be viewed through the silicon substrate (silicon is
transparent to infrared light). A small
amount of light is also emitted during the charging and discharging of the
transistor gate capacitance and
transmission line capacitance.
For circuitry that manipulates secret key information, such information must
be kept hidden. An alternative
non-flashing CMOS implementation should therefore be used for all data paths
that manipulate the key or a
partially calculated value that is based on the key. The use of two non-
overlapping clocks 4 1 and +2 can
provide a non-flashing mechanism. +1 is connected to a second gate of all nMOS
transistors, and +2 is
connected to a second gate of all pMOS transistors. The transition can only
take place in combination with the
clock. Since +1 and +2 are non-overlapping, the pMOS and nMOS transistors will
not have a simultaneous
intermediate resistance. The setup is shown in Fig. 180.
Finally, regular CMOS inverters can be positioned near critical non-Flashing
CMOS components. These
inverters should take their input signal from the Tamper Detection Line above.
Since the Tamper Detection
Line operates multiple times faster than the regular operating circuitry, the
net effect will be a high rate of
light-bursts next to each non-Flashing CMOS component. Since a bright light
overwhelms observation of a
nearby faint light, an observer will not be able to detect what switching
operations are occurring in the chip
proper. These regular CMOS inverters will also effectively increase the amount
of circuit noise, reducing the
SNR and obscuring useful EMI.
There are a number of side effects due to the use of non-Flashing CMOS:
The effective speed of the chip is reduced by twice the rise time of the clock
per clock cycle. This is not a
problem for an Authentication Chip.
The amount of current drawn by the non-Flashing CMOS is reduced (since the
short circuits do not occur).
However, this is offset by the use of regular CMOS inverters.
Routing of the clocks increases chip area, especially since multiple versions
of +1 and +2 are required to cater
CA 02564047 2006-11-06
YU139 PCT 223
for different levels of propagation. The estimation of chip area is double
that of a regular
implementation.
Design of the non-Flashing areas of the Authentication Chip are slightly more
complex than to do the same
with a with a regular CMOS design. In particular, standard cell components
cannot be used, making
these areas full custom. This is not a problem for something as small as an
Authentication Chip,
particularly when the entire chip does not have to be protected in this
manner.
Connections in polysilicon layers where possible
Wherever possible, the connections along which the key or secret data flows,
should be made in the
polysilicon layers. Where necessary, they can be in metal 1, but must never be
in the top metal layer
(containing the Tamper Detection Lines).
OverUnderPower Detection Unit
Each Authentication Chip requires an OverUnderPower Detection Unit to prevent
Power Supply Attacks. An
OverUnderPower Detection Unit detects power glitches and tests the power level
against a Voltage Reference
to ensure it is within a certain tolerance. The Unit contains a single Voltage
Reference and two comparators.
The OverUnderPower Detection Unit would be connected into the RESET Tamper
Detection Line, thus
causing a RESET when triggered. A side effect of the OverUnderPower Detection
Unit is that as the voltage
drops during a power-down, a RESET is triggered, thus erasing any work
registers.
No Test Circuitry
Test hardware on an Authentication Chip could very easily introduce
vulnerabilities. As a result, the
Authentication Chip should not contain any BIST or scan paths. The
Authentication Chip must therefore be
testable with external test vectors. This should be possible since the
Authentication Chip is not complex.
Reading ROM
This attack depends on the key being stored in an addressable ROM. Since each
Authentication Chip stores its
authentication keys in internal Flash memory and not in an addressable ROM,
this attack is irrelevant.
Reverse En ing eering the Chip
Reverse engineering a chip is only useful when the security of authentication
lies in the algorithm alone.
However our Authentication Chips rely on a secret key, and not in the secrecy
of the algorithm. Our
authentication algorithm is, by contrast, public, and in any case, an attacker
of a high volume consumable is
assumed to have been able to obtain detailed plans of the internals of the
chip. In light of these factors,
reverse engineering the chip itself, as opposed to the stored data, poses no
threat.
Usurping the Authentication Process
There are several forms this attack can take, each with varying degrees of
success. In all cases, it is assumed
that a clone manufacturer will have access to both the System and the
consumable designs. An attacker may
attempt to build a chip that tricks the System into returning a valid code
instead of generating an
authentication code. This attack is not possible for two reasons. The first
reason is that System Authentication
chips and Consumable Authentication Chips, although physically identical, are
programmed differently. In
particular, the RD opcode and the RND opcode are the same, as are the WR and
TST opcodes. A System
authentication Chip cannot perform a RD command since every call is
interpreted as a call to RND instead.
The second reason this attack would fail is that separate serial data lines
are provided from the System to the
System and Consumable Authentication Chips. Consequently neither chip can see
what is being transmitted to
CA 02564047 2006-11-06
YU139 PCT 224
or received from the other. If the attacker builds a clone chip that ignores
WR commands (which decrement
the consumable remaining), Protocol 3 ensures that the subsequent RD will
detect that the WR did not occur.
The System will therefore not go ahead with the use of the consumable, thus
thwarting the attacker. The same
is true if an attacker simulates loss of contact before authentication - since
the authentication does not take
place, the use of the consumable doesn't occur. An attacker is therefore
limited to modifying each System in
order for clone consumables to be accepted
Modification of System
The simplest method of modification is to replace the System's Authentication
Chip with one that simply
reports success for each call to TST. This can be thwarted by System calling
TST several times for each
authentication, with the first few times providing false values, and expecting
a fail from TST. The final call to
TST would be expected to succeed. The number of false calls to TST could be
determined by some part of the
returned result from RD or from the system clock. Unfortunately an attacker
could simply rewire System so
that the new System clone authentication chip 53 can monitor the returned
result from the consumable chip or
clock. The clone System Authentication Chip would only return success when
that monitored value is
presented to its TST function. Clone consumables could then return any value
as the hash result for RD, as the
clone System chip would declare that value valid. There is therefore no point
for the System to call the
System Authentication Chip multiple times, since a rewiring attack will only
work for the System that has
been rewired, and not for all Systems. A similar form of attack on a System is
a replacement of the System
ROM. The ROM program code can be altered so that the Authentication never
occurs. There is nothing that
can be done about this, since the System remains in the hands of a consumer.
Of course this would void any
warranty, but the consumer may consider the alteration worthwhile if the clone
consumable were extremely
cheap and more readily available than the original item.
The System/consumable manufacturer must therefore determine how likely an
attack of this nature is. Such a
study must include given the pricing structure of Systems and Consumables,
frequency of System service,
advantage to the consumer of having a physical modification performed, and
where consumers would go to
get the modification performed. The limit case of modifying a system is for a
clone manufacturer to provide
a completely clone System which takes clone consumables. This may be simple
competition or violation of
patents. Either way, it is beyond the scope of the Authentication Chip and
depends on the technology or
service being cloned.
Direct viewing of chip operation by conventional probing
In order to view the chip operation, the chip must be operating. However, the
Tamper Prevention and
Detection circuitry covers those sections of the chip that process or hold the
key. It is not possible to view
those sections through the Tamper Prevention lines. An attacker cannot simply
slice the chip past the
Tamper Prevention layer, for this will break the Tamper Detection Lines and
cause an erasure of all keys at
power-up. Simply destroying the erasure circuitry is not sufficient, since the
multiple ChipOK bits (now all 0)
feeding into multiple units within the Authentication Chip will cause the
chip's regular operating circuitry to
stop functioning. To set up the chip for an attack, then, requires the
attacker to delete the Tamper Detection
lines, stop the Erasure of Flash memory, and somehow rewire the components
that relied on the ChipOK
lines. Even if all this could be done, the act of slicing the chip to this
level will most likely destroy the charge
patterns in the non-volatile memory that holds the keys, making the process
fruitless.
CA 02564047 2006-11-06
YU139 PCT 225
Direct viewing of the non-volatile memory
If the Authentication Chip were sliced so that the floating gates of the Flash
memory were exposed, without
discharging them, then the keys could probably be viewed directly using an STM
or SKM. However, slicing
the chip to this level without discharging the gates is probably impossible.
Using wet etching, plasma etching,
ion milling, or chemical mechanical polishing will almost certainly discharge
the small charges present on the
floating gates. This is true of regular Flash memory, but even more so of
multi-level Flash memory.
Viewing the light bursts caused by state changes
All sections of circuitry that manipulate secret key information are
implemented in the non-Flashing CMOS
described above. This prevents the emission of the majority of light bursts.
Regular CMOS inverters placed in
close proximity to the non-Flashing CMOS will hide any faint emissions caused
by capacitor charge and
discharge. The inverters are connected to the Tamper Detection circuitry, so
they change state many times (at
the high clock rate) for each non-Flashing CMOS state change.
Monitoring EMI
The Noise Generator described above will cause circuit noise. The noise will
interfere with other
electromagnetic emissions from the chip's regular activities and thus obscure
any meaningful reading of
internal data transfers.
Viewing Ida fluctuations
The solution against this kind of attack is to decrease the SNR in the Idd
signal. This is accomplished by
increasing the amount of circuit noise and decreasing the amount of signal.
The Noise Generator circuit
(which also acts as a defense against EMI attacks) will also cause enough
state changes each cycle to obscure
any meaningful information in the Idd signal. In addition, the special Non-
Flashing CMOS implementation of
the key-carrying data paths of the chip prevents current from flowing when
state changes occur. This has the
benefit of reducing the amount of signal.
Differential Fault Analysis
Differential fault bit errors are introduced in a non-targeted fashion by
ionization, microwave radiation, and
environmental stress. The most likely effect of an attack of this nature is a
change in Flash memory (causing
an invalid state) or RAM (bad parity). Invalid states and bad parity are
detected by the Tamper Detection
Circuitry, and cause an erasure of the key. Since the Tamper Detection Lines
cover the key manipulation
circuitry, any error introduced in the key manipulation circuitry will be
mirrored by an error in a Tamper
Detection Line. If the Tamper Detection Line is affected, the chip will either
continually RESET or simply
erase the key upon a power-up, rendering the attack fruitless. Rather than
relying on a non-targeted attack and
hoping that "just the right part of the chip is affected in just the right
way", an attacker is better off trying to
introduce a targeted fault (such as overwrite attacks, gate destruction etc).
For information on these targeted
fault attacks, see the relevant sections below.
Clock Glitch Attacks
The Clock Filter (described above) eliminates the possibility of clock glitch
attacks.
Power Supply Attacks
The OverUnderPower Detection Unit (described above) eliminates the possibility
of power supply attacks.
CA 02564047 2006-11-06
YU139 PCT 226
Overwriting ROM
Authentication Chips store Program code, keys and secret information in Flash
memory, and not in ROM.
This attack is therefore not possible.
Modifying EEPROM/Flash
Authentication Chips store Program code, keys and secret information in Flash
memory. However, Flash
memory is covered by two Tamper Prevention and Detection Lines. If either of
these lines is broken (in the
process of destroying a gate) the attack will be detected on power-up, and the
chip will either RESET
(continually) or erase the keys from Flash memory. However, even if the
attacker is able to somehow access
the bits of Flash and destroy or short out the gate holding a particular bit,
this will force the bit to have no
charge or a full charge. These are both invalid states for the Authentication
Chip's usage of the multi-level
Flash memory (only the two middle states are valid). When that data value is
transferred from Flash, detection
circuitry will cause the Erasure Tamper Detection Line to be triggered -
thereby erasing the remainder of
Flash memory and RESETing the chip. A Modify EEPROM/Flash Attack is therefore
fruitless.
Gate Destruction Attacks
Gate Destruction Attacks rely on the ability of an attacker to modify a single
gate to cause the chip to reveal
information during operation. However any circuitry that manipulates secret
information is covered by one of
the two Tamper Prevention and Detection lines. If either of these lines is
broken (in the process of destroying
a gate) the attack will be detected on power-up, and the chip will either
RESET (continually) or erase the keys
from Flash memory. To launch this kind of attack, an attacker must first
reverse-engineer the chip to
determine which gate(s) should be targeted. Once the location of the target
gates has been determined, the
attacker must break the covering Tamper Detection line, stop the Erasure of
Flash memory, and somehow
rewire the components that rely on the ChipOK lines. Rewiring the circuitry
cannot be done without slicing
the chip, and even if it could be done, the act of slicing the chip to this
level will most likely destroy the
charge patterns in the non-volatile memory that holds the keys, making the
process fruitless.
Overwrite Attacks
An Overwrite Attack relies on being able to set individual bits of the key
without knowing the previous value.
It relies on probing the chip, as in the Conventional Probing Attack and
destroying gates as in the Gate
Destruction Attack. Both of these attacks (as explained in their respective
sections), will not succeed due to
the use of the Tamper Prevention and Detection Circuitry and ChipOK lines.
However, even if the attacker is
able to somehow access the bits of Flash and destroy or short out the gate
holding a particular bit, this will
force the bit to have no charge or a full charge. These are both invalid
states for the Authentication Chip's
usage of the multi-level Flash memory (only the two middle states are valid).
When that data value is
transferred from Flash detection circuitry will cause the Erasure Tamper
Detection Line to be triggered -
thereby erasing the remainder of Flash memory and RESETing the chip. In the
same way, a parity check on
tampered values read from RAM will cause the Erasure Tamper Detection Line to
be triggered. An Overwrite
Attack is therefore fruitless.
Memory Remanence Attack
Any working registers or RAM within the Authentication Chip may be holding
part of the authentication keys
when power is removed. The working registers and RAM would continue to hold
the information for some
time after the removal of power. If the chip were sliced so that the gates of
the registers/RAM were exposed,
CA 02564047 2006-11-06
YU139 PCT 227
without discharging them, then the data could probably be viewed directly
using an STM. The first defense
can be found above, in the description of defense against Power Glitch
Attacks. When power is removed, all
registers and RAM are cleared, just as the RESET condition causes a clearing
of memory. The chances then,
are less for this attack to succeed than for a reading of the Flash memory.
RAM charges (by nature) are more
easily lost than Flash memory. The slicing of the chip to reveal the RAM will
certainly cause the charges to
be lost (if they haven't been lost simply due to the memory not being
refreshed and the time taken to perform
the slicing). This attack is therefore fruitless.
Chip Theft Attack
There are distinct phases in the lifetime of an Authentication Chip. Chips can
be stolen when at any of these
stages:
After manufacture, but before programming of key
After programming of key, but before programming of state data
After programming of state data, but before insertion into the consumable or
system
After insertion into the system or consumable
A theft in between the chip manufacturer and programming station would only
provide the clone
manufacturer with blank chips. This merely compromises the sale of
Authentication chips, not anything
authenticated by the Authentication chips. Since the programming station is
the only mechanism with
consumable and system product keys, a clone manufacturer would not be able to
program the chips with the
correct key. Clone manufacturers would be able to program the blank chips for
their own Systems and
Consumables, but it would be difficult to place these items on the market
without detection. The second form
of theft can only happen in a situation where an Authentication Chip passes
through two or more distinct
programming phases. This is possible, but unlikely. In any case, the worst
situation is where no state data has
been programmed, so all of M is read/write. If this were the case, an attacker
could attempt to launch an
Adaptive Chosen Text Attack on the chip. The HMAC-SHA1 algorithm is resistant
to such attacks. The third
form of theft would have to take place in between the programming station and
the installation factory. The
Authentication chips would already be programmed for use in a particular
system or for use in a particular
consumable. The only use these chips have to a thief is to place them into a
clone System or clone
Consumable. Clone systems are irrelevant - a cloned System would not even
require an authentication chip
53. For clone Consumables, such a theft would limit the number of cloned
products to the number of chips
stolen. A single theft should not create a supply constant enough to provide
clone manufacturers with a cost-
effective business.The final form of theft is where the System or Consumable
itself is stolen. When the theft
occurs at the manufacturer, physical security protocols must be enhanced. If
the theft occurs anywhere else, it
is a matter of concern only for the owner of the item and the police or
insurance company. The security
mechanisms that the Authentication Chip uses assume that the consumables and
systems are in the hands of
the public. Consequently, having them stolen makes no difference to the
security of the keys.
Authentication Chip Design
CA 02564047 2006-11-06
YU139 PCT 228
The Authentication Chip has a physical and a logical external interface. The
physical interface defines how
the Authentication Chip can be connected to a physical System, and the logical
interface determines how that
System can communicate with the Authentication Chip.
PHYSICAL INTERFACE
The Authentication Chip is a small 4-pin CMOS package (actual internal size is
approximately 0.30 mm2
using 0.25 m Flash process). The 4 pins are GND, CLK, Power, and Data. Power
is a nominal voltage. If
the voltage deviates from this by more than a fixed amount, the chip will
RESET. The recommended clock
speed is 4-10 MHz. Internal circuitry filters the clock signal to ensure that
a safe maximum clock speed is not
exceeded. Data is transmitted and received one bit at a time along the serial
data line. The chip performs a
RESET upon power-up, power-down. In addition, tamper detection and prevention
circuitry in the chip will
cause the chip to either RESET or erase Flash memory (depending on the attack
detected) if an attack is
detected. A special Programming Mode is enabled by holding the CLK voltage at
a particular level. This is
defined further in the next section.
LOGICAL INTERFACE
The Authentication Chip has two operating modes - a Normal Mode and a
Programming Mode. The two
modes are required because the operating program code is stored in Flash
memory instead of ROM (for
security reasons). The Programming mode is used for testing purposes after
manufacture and to load up the
operating program code, while the normal mode is used for all subsequent usage
of the chip.
PROGRAMMING MODE
The Programming Mode is enabled by holding a specific voltage on the CLK line
for a given amount of time.
When the chip enters Programming Mode, all Flash memory is erased (including
all secret key information
and any program code). The Authentication Chip then validates the erasure. If
the erasure was successful, the
Authentication Chip receives 384 bytes of data corresponding to the new
program code. The bytes are
transferred in order byteo to byte383. The bits are transferred from bito to
bit7. Once all 384 bytes of program
code have been loaded, the Authentication Chip hangs. If the erasure was not
successful, the Authentication
Chip will hang without loading any data into the Flash memory. After the chip
has been programmed, it can
be restarted. When the chip is RESET with a normal voltage on the CLK line,
Normal Mode is entered.
NORMAL MODE
Whenever the Authentication Chip is not in Programming Mode, it is in Normal
Mode. When the
Authentication Chip starts up in Normal Mode (for example a power-up RESET),
it executes the program
currently stored in the program code region of Flash memory. The program code
implements a
communication mechanism between the System and Authentication Chip, accepting
commands and data from
the System and producing output values. Since the Authentication Chip
communicates serially, bits are
transferred one at a time.The System communicates with the Authentication
Chips via a simple operation
command set. Each command is defined by 3-bit opcode. The interpretation of
the opcode depends on the
current value of the IsTrusted bit and the IsWritten bit.
The following operations are defined:
Op T W Mn Input Output Description
000 - - CLR - - Clear
001 0 0 SSI 160, 160, 160] - Set Secret Information
CA 02564047 2006-11-06
YU139 PCT 229
010 0 1 RD 160,160 [256, 160] Read M securely
010 1 1 RND - [160, 160] Random
011 0 1 WR [256] - Write M
011 1 1 TST [256, 160] [1] Test
100 0 1 SAM [32] [32] Set Access Mode
101 - 1 GIT - [1] Get Is Trusted
110 - 1 SMT [32] - Set MinTicks
Op = Opcode, T = IsTrusted value, W = IsWritten value,
Mn = Mnemonic, [n] = number of bits required for parameter
Any command not defined in this table is interpreted as NOP (No operation).
Examples include opcodes 110
and 111 (regardless of IsTrusted or IsWritten values), and any opcode other
than SSI when IsWritten = 0.
Note that the opcodes for RD and RND are the same, as are the opcodes for WR
and TST. The actual
command run upon receipt of the opcode will depend on the current value of the
IsTrusted bit (as long as
Is Written is 1). Where the IsTrusted bit is clear, RD and WR functions will
be called. Where the IsTrusted bit
is set, RND and TST functions will be called. The two sets of commands are
mutually exclusive between
trusted and non-trusted Authentication Chips. In order to execute a command on
an Authentication Chip, a
client (such as System) sends the command opcode followed by the required
input parameters for that opcode.
The opcode is sent least significant bit through to most significant bit. For
example, to send the SSI command,
the bits 1, 0, and 0 would be sent in that order. Each input parameter is sent
in the same way, least significant
bit first through to most significant bit last. Return values are read in the
same way - least significant bit first
and most significant bit last. The client must know how many bits to retrieve.
In some cases, the output bits from one chip's command can be fed directly as
the input bits to another chip's
command. An example of this is the RND and RD commands. The output bits from a
call to RND on a trusted
Authentication Chip do not have to be kept by System. Instead, System can
transfer the output bits directly to
the input of the non-trusted Authentication Chip's RD command. The description
of each command points out
where this is so. Each of the commands is examined in detail in the subsequent
sections. Note that some
algorithms are specifically designed because the permanent registers are kept
in Flash memory.
Re isg ters
The memory within the Authentication Chip contains some non-volatile memory to
store the variables
required by the Authentication Protocol. The following non-volatile (Flash)
variables are defined:
Variable Name Size Description
(in bits)
M[0..15] 256 16 words (each 16 bits) containing state data such as
serial numbers, media remaining etc.
Kl 160 Key used to transform R during authentication.
K2 160 Key used to transform M during authentication.
R 160 Current random number
AccessMode 0..15 32 The 16 sets of 2-bit AccessMode values for M [n].
MinTicks 32 The minimum number of clock ticks between calls to key-
CA 02564047 2006-11-06
YU139 PCT 230
based functions
SlWritten 1 If set, the secret key information (K1, K2, and R) has been
written to the chip. If clear, the secret information has not
been written yet.
IsTrusted 1 If set, the RND and TST functions can be called, but RD
and WR functions cannot be called.
If clear, the RND and TST functions cannot be called, but
RD and WR functions can be called.
Total bits 802
ARCHITECTURE OVERVIEW
This section chapter provides the high-level definition of a purpose-built CPU
capable of implementing the
functionality required of an Authentication Chip. Note that this CPU is not a
general purpose CPU. It is
tailor-made for implementing the Authentication logic. The authentication
commands that a user of an
Authentication Chip sees, such as WRITE, TST, RND etc are all implemented as
small programs written in
the CPU instruction set. The CPU contains a 32-bit Accumulator (which is used
in most operations), and a
number of registers. The CPU operates on 8-bit instructions specifically
tailored to implementing
authentication logic. Each 8-bit instruction typically consists of a 4-bit
opcode, and a 4-bit operand.
OPERATING SPEED
An internal Clock Frequency Limiter Unit prevents the chip from operating at
speeds any faster than a
predetermined frequency. The frequency is built into the chip during
manufacture, and cannot be changed.
The frequency is recommended to be about 4-10 MHz.
COMPOSITION AND BLOCK DIAGRAM
The Authentication Chip contains the following components:
Unit Name CMOS Type Description
Clock Frequency Normal Ensures the operating frequency of the Authentication
Limiter Chip does not exceed a specific maximum frequency.
OverUnderPower Normal Ensures that the power supply remains in a valid
Detection Unit operating range.
Programming Mode Normal Allows users to enter Programming Mode.
Detection Unit
Noise Generator Normal For generating Idd noise and for use in the Tamper
Prevention and Detection circuitry.
for controlling the two operating modes of the chip
(Programming Mode and Normal Mode). This
State Machine Normal includes generating the two operating cycles of the
CPU, stalling during long command operations, and
storing the op-code and operand during operating
cycles.
I/O Unit Normal Responsible for communicating serially with the
outside world.
ALU Non-flashing Contains the 32-bit accumulator as well as the general
mathematical and logical operators.
MinTicks Unit Normal (99%), Responsible for a programmable minimum delay (via
a
Non-flashing (1%) countdown) between certain key-based operations.
CA 02564047 2006-11-06
YU139 PCT 231
Address Generator Normal (99%), Generates direct, indirect, and indexed
addresses as
Unit Non-flashing (1%) required by specific operands.
Program Counter Unit Normal Includes the 9 bit PC (program counter), as well
as
logic for branching and subroutine control
Addressed by 9 bits of address. It contains an 8-bit
wide program Flash memory, and 32-bit wide Flash
Memory Unit Non-flashing memory, RAM, and look-up tables. Also contains
Programming Mode circuitry to enable loading of
program code.
Fig. 181 illustrates a schematic block diagram of the Authentication Chip. The
tamper prevention and
Detection Circuitry is not shown: The Noise Generator, OverUnderPower
Detection Unit, and
ProgrammingMode Detection Unit are connected to the Tamper Prevention and
Detection Circuitry and not to
the remaining units.
MEMORY MAP
Fig. 182 illustrates an example memory map. Although the Authentication Chip
does not have external
memory, it does have internal memory. The internal memory is addressed by 9
bits, and is either 32-bits wide
or 8-bits wide (depending on address). The 32-bit wide memory is used to hold
the non-volatile data, the
variables used for HMAC-SHAT, and constants. The 8-bit wide memory is used to
hold the program and the
various jump tables used by the program. The address breakup (including
reserved memory ranges) is
designed to optimize address generation and decoding.
Constants
Fig. 183 illustrates an example of the constants memory map. The Constants
region consists of 32-bit
constants. These are the simple constants (such as 32-bits of all 0 and 32-
bits of all 1), the constants used by
the HMAC algorithm, and the constants y0_3 and h0_4 required for use in the
SHA-1 algorithm. None of these
values are affected by a RESET. The only opcode that makes use of constants is
LDK. In this case, the
operands and the memory placement are closely linked, in order to minimize the
address generation and
decoding.
RAM
Fig. 184 illustrates an example of the RAM memory map. The RAM region consists
of the 32 parity-checked
32-bit registers required for the general functioning of the Authentication
Chip, but only during the operation
of the chip. RAM is volatile memory, which means that once power is removed,
the values are lost. Note that
in actual fact, memory retains its value for some period of time after power-
down (due to memory remnance),
but cannot be considered to be available upon power-up. This has issues for
security that are addressed in
other sections of this document. RAM contains the variables used for the HMAC-
SHAT algorithm, namely:
A-E, the temporary variable T, space for the 160-bit working hash value H,
space for temporary storage of a
hash result (required by HMAC) B 160, and the space for the 512 bits of
expanded hashing memory X. All
RAM values are cleared to 0 upon a RESET, although any program code should not
take this for granted.
Opcodes that make use of RAM addresses are LD, ST, ADD, LOG, XOR, and RPL. In
all cases, the operands
and the memory placement are closely linked, in order to minimize the address
generation and decoding
(multiword variables are stored most significant word first).
CA 02564047 2006-11-06
YU139 PCT 232
Flash Memory - Variables
Fig. 185 illustrates an example of the Flash memory variables memory map. The
Flash memory region
contains the non-volatile information in the Authentication Chip. Flash memory
retains its value after power
is removed, and can be expected to be unchanged when the power is next turned
on. The non-volatile
information kept in multi-state Flash memory includes the two 160-bit keys (K1
and K2), the current random
number value (R), the state data (M), the MinTicks value (MT), the AccessMode
value (AM), and the
IsWritten (ISW) and IsTrusted (IST) flags.Flash values are unchanged by a
RESET, but are cleared (to 0)
upon entering Programming Mode. Operations that make use of Flash addresses
are LD, ST, ADD, RPL,
ROR, CLR, and SET. In all cases, the operands and the memory placement are
closely linked, in order to
minimize the address generation and decoding. Multiword variables K1, K2, and
M are stored most
significant word first due to addressing requirements. The addressing scheme
used is a base address offset by
an index that starts at N and ends at 0. Thus MN is the first word accessed,
and Mo is the last 32-bit word
accessed in loop processing. Multiword variable R is stored least significant
word first for ease of LFSR
generation using the same indexing scheme.
Flash Memory - Program
Fig. 186 illustrates an example of the Flash memory program memory map. The
second multi-state Flash
memory region is 384 x 8-bits. The region contains the address tables for the
JSR, JSI and TBR instructions,
the offsets for the DBR commands, constants and the program itself. The Flash
memory is unaffected by a
RESET, but is cleared (to 0) upon entering Programming Mode. Once Programming
Mode has been entered,
the 8-bit Flash memory can be loaded with a new set of 384 bytes. Once this
has been done, the chip can be
RESET and the normal chip operations can occur.
REGISTERS
A number of registers are defined in the Authentication Chip. They are used
for temporary storage during
function execution. Some are used for arithmetic functions, others are used
for counting and indexing, and
others are used for serial I/O. These registers do not need to be kept in non-
volatile (Flash) memory. They
can be read or written without the need for an erase cycle (unlike Flash
memory). Temporary storage registers
that contain secret information still need to be protected from physical
attack by Tamper Prevention and
Detection circuitry and parity checks.
All registers are cleared to 0 on a RESET. However, program code should not
assume any particular state, and
set up register values appropriately. Note that these registers do not include
the various OK bits defined for
the Tamper Prevention and Detection circuitry. The OK bits are scattered
throughout the various units and are
set to 1 upon a RESET.
Cycle
The 1-bit Cycle value determines whether the CPU is in a Fetch cycle (0) or an
Execute cycle (1). Cycle is
actually derived from a 1-bit register that holds the previous Cycle value.
Cycle is not directly accessible
from the instruction set. It is an internal register only.
Program Counter
A 6-level deep 9-bit Program Counter Array (PCA) is defined. It is indexed by
a 3-bit Stack Pointer (SP). The
current Program Counter (PC), containing the address of the currently
executing instruction, is effectively
CA 02564047 2006-11-06
YU139 PCT 233
PCA[SP]. In addition, a 9-bit Adr register is defined, containing the resolved
address of the current memory
reference (for indexed or indirect memory accesses). The PCA, SP, and Adr
registers are not directly
accessible from the instruction set. They are internal registers only
CMD
The 8-bit CMD register is used to hold the currently executing command. While
the CMD register is not
directly accessible from the instruction set, and is an internal register
only.
Accumulator and Z flag
The Accumulator is a 32-bit general-purpose register. It is used as one of the
inputs to all arithmetic
operations, and is the register used for transferring information between
memory registers. The Z register is a
1-bit flag, and is updated each time the Accumulator is written to. The Z
register contains the zero-ness of the
Accumulator. Z = 1 if the last value written to the Accumulator was 0, and 0
if the last value written was non-
0. Both the Accumulator and Z registers are directly accessible from the
instruction set.
Counters
A number of special purpose counters/index registers are defined:
Name Register Bits Description
Size
Cl 1 x 3 3 Counter used to index arrays:
AE, B 160, M, H, y, and h.
C2 1 x 5 5 General purpose counter
N14 4x4 16 Used to index array X
All these counter registers are directly accessible from the instruction set.
Special instructions exist to load
them with specific values, and other instructions exist to decrement or
increment them, or to branch
depending on the whether or not the specific counter is zero. There are also 2
special flags (not registers)
associated with Cl and C2, and these flags hold the zero-ness of Cl or C2. The
flags are used for loop
control, and are listed here, for although they are not registers, they can be
tested like registers.
Name Description
CIZ I = Cl is current zero, 0 =C1 is currently non-zero.
C2Z 1 = C2 is current zero, 0 =C2 is currently non-zero.
Flags
A number of 1-bit flags, corresponding to CPU operating modes, are defined:
Name Bits Description
WE 1 WriteEnable for X register array:
0 = Writes to X registers become no-ops
1 = Writes to X registers are carried out
K2MX 1 0 = KI is accessed during K references. Reads from M are interpreted as
reads
of o
CA 02564047 2006-11-06
YU139 PCT 234
1 = K2 is accessed during K references. Reads from M succeed.
All these 1-bit flags are directly accessible from the instruction set.
Special instructions exist to set and clear these
flags. Registers used for Write Integrity
Name Bits Description
EE I Corresponds to the EqEncountered variable in the WR command pseudocode.
Used during the writing of multi-precision data values to determine whether
all
more significant components have been equal to their previous values.
DE 1 Corresponds to the DecEncountered variable in the WR command pseudocode.
Used during the writing of multi-precision data values to determine whether a
more significant components has been decremented already.
Registers used for I/O
Four 1-bit registers are defined for communication between the client (System)
and the Authentication Chip.
These registers are InBit, InBitValid, OutBit, and OutBitValid. InBit and
InBitValid provide the means for
clients to pass commands and data to the Authentication Chip. OutBit and
OutBitValid provide the means for
clients to get information from the Authentication Chip. A client sends
commands and parameter bits to the
Authentication Chip one bit at a time. Since the Authentication Chip is a
slave device, from the
Authentication Chip's point of view:
Reads from InBit will hang while InBitValid is clear. InBitValid will remain
clear until the client has written
the next input bit to InBit. Reading InBit clears the InBitValid bit to allow
the next InBit to be read from
the client. A client cannot write a bit to the Authentication Chip unless the
InBitValid bit is clear.
Writes to OutBit will hang while OutBitValid is set. OutBitValid will remain
set until the client has read the
bit from OutBit. Writing OutBit sets the OutBitValid bit to allow the next
OutBit to be read by the client.
A client cannot read a bit from the Authentication Chip unless the OutBitValid
bit is set.
Registers Used for Timing Access
A single 32-bit register is defined for use as a timer. The MTR
(MinTicksRemaining) register decrements
every time an instruction is executed. Once the MTR register gets to 0, it
stays at zero. Associated with MTR
is a 1-bit flag MTRZ, which contains the zero-ness of the MTR register. If
MTRZ is 1, then the MTR register
is zero. If MTRZ is 0, then the MTR register is not zero yet. MTR always
starts off at the MinTicks value
(after a RESET or a specific key-accessing function), and eventually
decrements to 0. While MTR can be set
and MTRZ tested by specific instructions, the value of MTR cannot be directly
read by any instruction.
Register Summary
The following table summarizes all temporary registers (ordered by register
name). It lists register names, size
(in bits), as well as where the specified register can be found.
Register Name Bits Parity Where Found
Acc 32 1 Arithmetic Logic Unit
Adr 9 1 Address Generator Unit
AMT 32 Arithmetic Logic Unit
CA 02564047 2006-11-06
YU139 PCT 235
Cl. 3 1 Address Generator Unit
C2 5 1 Address Generator Unit
CMD 8 1 State Machine
Cycle (Old = prey 1 State Machine
Cycle)
DE 1 Arithmetic Logic Unit
EE 1 Arithmetic Logic Unit
InBit 1 Input Output Unit
InBitValid 1 Input Output Unit
K2MX 1 Address Generator Unit
MTR 32 1 MinTicks Unit
MTRZ 1 MinTicks Unit
N[ 1-4 16 4 Address Generator Unit
OutBit 1 Input Output Unit
OutBitValid 1 Input Output Unit
PCA 54 6 Program Counter Unit
RTMP 1 Arithmetic Logic Unit
SP 3 1 Program Counter Unit
WE 1 Memory Unit
Z I Arithmetic Logic Unit
Total bits 206 17
INSTRUCTION SET
The CPU operates on 8-bit instructions specifically tailored to implementing
authentication logic. The
majority of 8-bit instruction consists of a 4-bit opcode, and a 4-bit operand.
The high-order 4 bits contains the
opcode, and the low-order 4 bits contains the operand.
Opcodes and Operands (Summary)
The opcodes are summarized in the following table:
Opcode Mnemonic Simple Description
0000 TBR Test and branch.
0001 DBR Decrement and branch
001 JSR Jump subroutine via table
01000 RTS Return from subroutine
01001 JSI Jump subroutine indirect
0101 SC Set counter
0110 CLR Clear specific flash registers
0111 SET Set bits in specific flash register
1000 ADD Add a 32 bit value to the Accumulator
1001 LOG Logical operation (AND, and OR)
1010 XOR Exclusive-OR Accumulator with some value
1011 LD Load Accumulator from specified location
1100 ROR Rotate Accumulator right
1101 RPL Replace bits
1110 LDK Load Accumulator with a constant
1111 ST Store Accumulator in specified location
CA 02564047 2006-11-06
YU139 PCT 236
The following table is a summary of which operands can be used with which
opcodes. The table is ordered
alphabetically by opcode mnemonic. The binary value for each operand can be
found in the subsequent tables.
code Valid Operand
ADD {A, B, C, D, E, T, MT, AM,
AE C1 , B160 C1 , H C1 , M C1 , K [CI], R[Cl], X[N4]}
CLR WE, K2MX, M C1 , Grou 1, Grou 2
DBR (Cl, CC2 ),Offset into DBR Table
JSI
JSR Offset into Table 1
LD {A, B, C, D, E, T, MT, AM,
AEC1,B160C1,HC1,MC1,KC1,RC1,XN4
LDK 0x0000..., 0x3636..., Ox5C5C..., OxFFFF, h[Cl], [Cl]}
LOG (AND, OR), A, B, C, D, E, T, MT, AM)
ROR InBit, OutBit, LFSR, RLFSR, IST, ISW, MTRZ, 1, 2, 27, 31
RPL Init, MHI, MLO
RTS
Sc C1, C2 , Offset into counter list
SET WE, K2MX, Nx, MTR, IST, ISW
ST {A, B, C, D, E, T, MT, AM,
AEC1 ,B160C1,HC1,MC1,KC1 ,RC1 ,XN4]}
TBR 0, 11, Offset into Table 1
XOR {A, B, C, D, E, T, MT, AM, X[NI], X[N2], X[N3], X[N4
The following operand table shows the interpretation of the 4-bit operands
where all. 4 bits are used for direct
interpretation.
Operand DDT XOR ROR LDK RPL SET CLR
0000 E E InBit Ox00... Init WE WE
0001 D D OutBit 0x36... - K2MX K2MX
0010 C C RB Ox5C... - Nx -
0011 B B XRB OxFF... - - -
0100 A A IST C1 - IST -
0101 T T ISW - - ISW -
0110 MT MT MTRZ - - MTR -
0111 AM AM 1 - - - -
1000 AE[C1] - hC1 - - -
1001 B160[CI] - 2 - - - -
1010 HC1 - 27 - - - -
1011 - - - - - - -
1100 R[C1] X[NI] 31 - - - R
1101 K[C1] X[N2] - - - - Group 1
1110 MC1 X[N3] - - MLO - MC1
1 111 X[N4] X[N4] - - MHI - Group2
CA 02564047 2006-11-06
YU139PCT 237
The following instructions make a selection based upon the highest bit of the
operand:
Operand3 Which Counter? Which operation? Which Value?
(DBR, SC) (LOG) (TBR)
0 C l AND Zero
1 C2 OR Non-zero
The lowest 3 bits of the operand are either offsets (DBR, TBR), values from a
special table (SC) or as in the
case of LOG, they select the second input for the logical operation. The
interpretation matches the
interpretation for the ADD, LD, and ST opcodes:
Operand2-0 LOG Input2 SC Value
000 E 2
001 D 3
010 C 4
011 B 7
100 A 10
101 T 15
110 MT 19
111 AM 31
ADD - Add To Accumulator
Mnemonic: ADD
Opcode: 1000
Usage: ADD Value
The ADD instruction adds the specified operand to the Accumulator via modulo
232 addition. The operand is
one of A, B, C, D, E, T, AM, MT, AE[CI], H[Cl], B160[C1], R[C1], K[C1], M[C1],
or X[N4]. The Z flag is
also set during this operation, depending on whether the value loaded is zero
or not.
CLR - Clear Bits
Mnemonic: CLR
Opcode: 0110
Usage: CLR Flag/Register
The CLR instruction causes the specified internal flag or Flash memory
registers to be cleared. In the case of
Flash memory, although the CLR instruction takes some time the next
instruction is stalled until the erasure of
Flash memory has finished. The registers that can be cleared are WE and K2MX.
The Flash memory that can
be cleared are: R, M[C1], Group 1, and Group2. Group 1 is the IST and ISW
flags. If these are cleared, then the
only valid high level command is the SSI instruction. Group2 is the MT, AM, K1
and K2 registers. R is
CA 02564047 2006-11-06
YU139 PCT 238
erased separately since it must be updated after each call to TST. M is also
erased via an index mechanism to
allow individual parts of M to be updated. There is also a corresponding SET
instruction.
DBR - Decrement and Branch
Mnemonic: DBR
Opcode: 0001
Usage: DBR Counter, Offset
This instruction provides the mechanism for building simple loops. The high
hit of the operand selects
between testing Cl or C2 (the two counters). If the specified counter is non-
zero, then the counter is
decremented and the value at the given offset (sign extended) is added to the
PC. If the specified counter is
zero, it is decremented and processing continues at PC+1. The 8-entry offset
table is stored at address 0 1100
0000 (the 64th entry of the program memory). The 8 bits of offset are treated
as a signed number. Thus OxFF
is treated as -1, and Ox01 is treated as +1. Typically the value will be
negative for use in loops.
JSI - Jump Subroutine Indirect
Mnemonic: JSI
Opcode: 01001
Usage: JSI (Ace)
The JSI instruction allows the jumping to a subroutine dependant on the value
currently in the Accumulator.
The instruction pushes the current PC onto the stack, and loads the PC with a
new value. The upper 8 bits of
the new PC are loaded from Jump Table 2 (offset given by the lower 5 bits of
the Accumulator), and the
lowest bit of the PC is cleared to 0. Thus all subroutines must start at even
addresses. The stack provides for
6 levels of execution (5 subroutines deep). It is the responsibility of the
programmer to ensure that this depth
is not exceeded or the return value will be overwritten (since the stack
wraps).
JSR - Jump Subroutine
Mnemonic: JSR
Opcode: 001
Usage: JSR Offset
The JSR instruction provides for the most common usage of the subroutine
construct. The instruction pushes
the current PC onto the stack, and loads the PC with a new value. The upper 8
bits of the new PC value comes
from Address Table 1, with the offset into the table provided by the 5-bit
operand (32 possible addresses).
The lowest bit of the new PC is cleared to 0. Thus all subroutines must start
at even addresses. The stack
provides for 6 levels of execution (5 subroutines deep). It is the
responsibility of the programmer to ensure
that this depth is not exceeded or the return value will be overwritten (since
the stack wraps).
LD - Load Accumulator
Mnemonic: LD
Opcode: 1011
Usage: LD Value
CA 02564047 2006-11-06
YU139 PCT 239
The LD instruction loads the Accumulator from the specified operand. The
operand is one of A, B, C, D, E, T,
AM, MT, AE[Cl], H[CI], B160[CI], R[C1], K[C1], M[C1], or X[N4]. The Z flag is
also set during this
operation, depending on whether the value loaded is zero or not.
LDK - Load Constant
Mnemonic: LDK
Opcode: 1110
Usage: LDK Constant
The LDK instruction loads the Accumulator with the specified constant. The
constants are those 32-bit values
required for HMAC-SHA1 and all Os and all Is as most useful for general
purpose processing. Consequently
they are a choice of:
0x00000000
0x36363636
Ox5C5C5C5C
OxFFFFFFFF
or from the h and y constant tables, indexed by C 1. The h and y constant
tables hold the 32-bit tabular
constants required for HMAC-SHAI. The Z flag is also set during this
operation, depending on whether the
constant loaded is zero or not.
LOG - Logical Operation
Mnemonic: LOG
Opcode: 1001
Usage: LOG Operation Value
The LOG instruction performs 32-bit bitwise logical operations on the
Accumulator and a specified value.
The two operations supported by the LOG instruction are AND and OR. Bitwise
NOT and XOR operations
are supported by the XOR instruction. The 32-bit value to be ANDed or ORed
with the accumulator is one of
the following: A, B, C, D, E, T, MT and AM. The Z flag is also set during this
operation, depending on
whether resultant 32-bit value (loaded into the Accumulator) is zero or not.
ROR - Rotate Right
Mnemonic: ROR
Opcode: 1100
Usage: ROR Value
The ROR instruction provides a way of rotating the Accumulator right a set
number of bits. The bit coming in
at the top of the Accumulator (to become bit 31) can either come from the
previous bit 0 of the Accumulator,
or from an external 1-bit flag (such as a flag, or the serial input
connection). The bit rotated out can also be
output from the serial connection, or combined with an external flag. The
allowed operands are: InBit, OutBit,
LFSR, RLFSR, IST, ISW, MTRZ, 1, 2, 27, and 31. The Z flag is also set during
this operation, depending on
whether resultant 32-bit value (loaded into the Accumulator) is zero or not.
In its simplest form, the operand
for the ROR instruction is one of 1, 2, 27, 31, indicating how many bit
positions the Accumulator should be
CA 02564047 2006-11-06
YU139 PCT 240
rotated. For these operands, there is no external input or output - the bits
of the Accumulator are merely
rotated right. With operands IST, ISW, and MTRZ, the appropriate flag is
transferred to the highest bit of the
Accumulator. The remainder of the Accumulator is shifted right one bit
position (bit31 becomes bit 30 etc),
with lowest bit of the Accumulator shifted out. With operand InBit, the next
serial input bit is transferred to
the highest bit of the Accumulator. The InBitValid bit is then cleared. If
there is no input bit available from
the client yet, execution is suspended until there is one. The remainder of
the Accumulator is shifted right one
bit position (bit31 becomes bit 30 etc), with lowest bit of the Accumulator
shifted out.
With operand OutBit, the Accumulator is shifted right one bit position. The
bit shifted out from bit 0 is stored
in the OutBit flag and the OutBitValid flag is set. It is therefore ready for
a client to read. If the OutBitValid
flag is already set, execution of the instruction stalls until the OutBit bit
has been read by the client (and the
OutBitValid flag cleared). The new bit shifted in to bit 31 should be
considered garbage (actually the value
currently in the InBit register). Finally, the RB and XRB operands allow the
implementation of LFSRs and
multiple precision shift registers. With RB, the bit shifted out (formally bit
0) is written to the RTMP register.
The register currently in the RTMP register becomes the new bit 31 of the
Accumulator. Performing multiple
ROR RB commands over several 32-bit values implements a multiple precision
rotate/shift right. The XRB
operates in the same way as RB, in that the current value in the RTMP register
becomes the new bit 31 of the
Accumulator. However with the XRB instruction, the bit formally known as bit 0
does not simply replace
RTMP (as in the RB instruction). Instead, it is XORed with RTMP, and the
result stored in RTMP. This
allows the implementation of long LFSRs, as required by the Authentication
protocol.
RPL - Replace Bits
Mnemonic: RPL
Opcode: 1101
Usage: ROR Value
The RPL instruction is designed for implementing the high level WRITE command
in the Authentication
Chip. The instruction is designed to replace the upper 16 bits of the
Accumulator by the value that will
eventually be written to the M array (dependant on the Access Mode value). The
instruction takes 3
operands: Init, MHI, and MLO. The Init operand sets all internal flags and
prepares the RPL unit within the
ALU for subsequent processing. The Accumulator is transferred to an internal
AccessMode register. The
Accumulator should have been loaded from the AM Flash memory location before
the call to RPL Init in the
case of implementing the WRITE command, or with 0 in the case of implementing
the TST command. The
Accumulator is left unchanged. The MHI and MLO operands refer to whether the
upper or lower 16 bits of
M[C1] will be used in the comparison against the (always) upper 16 bits of the
Accumulator. Each MHI and
MLO instruction executed uses the subsequent 2 bits from the initialized
AccessMode value. The first
execution of MHI or MLO uses the lowest 2 bits, the next uses the second two
bits etc.
RTS - Return From Subroutine
Mnemonic: RTS
Opcode: 01000
Usage: RTS
CA 02564047 2006-11-06
YU139 PCT 241
The RTS instruction causes execution to resume at the instruction after the
most recently executed JSR or JSI
instruction. Hence the term: returning from the subroutine. In actuality, the
instruction pulls the saved PC
from the stack, adds 1, and resumes execution at the resultant address.
Although 6 levels of execution are
provided for (5 subroutines), it is the responsibility of the programmer to
balance each JSR and JSI instruction
with an RTS. An RTS executed with no previous JSR will cause execution to
begin at whatever address
happens to be pulled from the stack.
SC - Set Counter
Mnemonic: SC
Opcode: 0101
Usage: SC Counter Value
The SC instruction is used to load a counter with a particular value. The
operand determines which of
counters Cl and C2 is to be loaded. The Value to be loaded is one of 2, 3, 4,
7, 10, 15, 19, and 31. The
counter values are used for looping and indexing. Both Cl and C2 can be used
for looping constructs (when
combined with the DBR instruction), while only Cl can be used for indexing 32-
bit parts of multi-precision
variables.
SET - Set Bits
Mnemonic: SET
Opcode: 0111
Usage: SET Flag/Register
The SET instruction allows the setting of particular flags or flash memory.
There is also a corresponding CLR
instruction. The WE and K2MX operands each set the specified flag for later
processing. The IST and ISW
operands each set the appropriate bit in Flash memory, while the MTR operand
transfers the current value in
the Accumulator into the MTR register. The SET Nx command loads N1 - N4 with
the following constants:
Index Constant Loaded Initial X referred to
NI 2 X13
N2 7 X[8]
N3 13 X[21
N4 15 X[0]
Note that each initial X[Nn] referred to matches the optimized SHA-1 algorithm
initial states for indexes Ni -
N4. When each index value N. decrements, the effective X[N] increments. This
is because the X words are
stored in memory with most significant word first.
ST - Store Accumulator
Mnemonic: ST
Opcode: 1111
Usage: ST Location
CA 02564047 2006-11-06
YU139 PCT 242
The ST instruction is stores the current value of the Accumulator in the
specified location. The location is one
of A, B, C, D, E, T, AM, MT, AE[C1], H[C1], B160[C1], R[C1], K[C1], M[C1], or
X[N4]. The X[N4]
operand has the side effect of advancing the N4 index. After the store has
taken place, N4 will be pointing to
the next element in the X array. N4 decrements by 1, but since the X array is
ordered from high to low, to
decrement the index advances to the next element in the array. If the
destination is in Flash memory, the
effect of the ST instruction is to set the bits in the Flash memory
corresponding to the bits in the Accumulator.
To ensure a store of the exact value from the Accumulator, be sure to use the
CLR instruction to erase the
appropriate memory location first.
TBR - Test and Branch
Mnemonic: TBR
Opcode: 0000
Usage: TBR Value Index
The Test and Branch instruction tests whether the Accumulator is zero or non-
zero, and then branches to the
given address if the Accumulator's current state matches that being tested
for. If the Z flag matches the TRB
test, replace the PC by 9 bit value where bitO = 0 and upper 8 bits come from
MU. Otherwise increment
current PC by 1. The Value operand is either 0 or 1. A 0 indicates the test is
for the Accumulator to be zero.
A I indicates the test is for the Accumulator to be non-zero. The Index
operand indicates where execution is
to jump to should the test succeed. The remaining 3 bits of operand index into
the lowest 8 entries of Jump
Table 1. The upper 8 bits are taken from the table, and the lowest bit (bit 0)
is cleared to 0. CMD is cleared to
0 upon a RESET. 0 is translated as TBR 0, which means branch to the address
stored in address offset 0 if the
Accumulator = 0. Since the Accumulator and Z flag are also cleared to 0 on a
RESET, the test will be true, so
the net effect is a jump to the address stored in the 0th entry in the jump
table.
XOR - Exclusive OR
Mnemonic: XOR
Opcode: 1010
Usage: XOR Value
The XOR instruction performs a 32-bit bitwise XOR with the Accumulator, and
stores the result in the
Accumulator. The operand is one of A, B, C, D, E, T, AM, MT, X[N1], X[N2],
X[N3], or X[N4]. The Z flag
is also set during this operation, depending on the result (i.e. what value is
loaded into the Accumulator). A
bitwise NOT operation can be performed by XORing the Accumulator with
OxFFFFFFFF (via the LDK
instruction). The X[N] operands have a side effect of advancing the
appropriate index to the next value (after
the operation). After the XOR has taken place, the index will be pointing to
the next element in the X array.
N4 is also advanced by the ST X[N4] instruction. The index decrements by 1,
but since the X array is ordered
from high to low, to decrement the index advances to the next element in the
array.
PROGRAMMINGMODE DETECTION UNIT
The ProgrammingMode Detection Unit monitors the input clock voltage. If the
clock voltage is a particular
value the Erase Tamper Detection Line is triggered to erase all keys, program
code, secret information etc and
CA 02564047 2006-11-06
YU139 PCT 243
enter Program Mode. The ProgrammingMode Detection Unit can be implemented with
regular CMOS, since
the key does not pass through this unit. It does not have to be implemented
with non-flashing CMOS. There
is no particular need to cover the ProgrammingMode Detection Unit by the
Tamper Detection Lines, since an
attacker can always place the chip in ProgrammingMode via the CLK input. The
use of the Erase Tamper
Detection Line as the signal for entering Programming Mode means that if an
attacker wants to use
Programming Mode as part of an attack, the Erase Tamper Detection Lines must
be active and functional.
This makes an attack on the Authentication Chip far more difficult.
NOISE GENERATOR
The Noise Generator can be implemented with regular CMOS, since the key does
not pass through this unit. It
does not have to be implemented with non-flashing CMOS. However, the Noise
Generator must be protected
by both Tamper Detection and Prevention lines so that if an attacker attempts
to tamper with the unit, the chip
will either RESET or erase all secret information. In addition, the bits in
the LFSR must be validated to ensure
they have not been tampered with (i.e. a parity check). If the parity check
fails, the Erase Tamper Detection
Line is triggered. Finally, all 64 bits of the Noise Generator are ORed into a
single bit. If this bit is 0, the
Erase Tamper Detection Line is triggered. This is because 0 is an invalid
state for an LFSR. There is no point
in using an OK bit setup since the Noise Generator bits are only used by the
Tamper Detection and Prevention
circuitry.
STATE MACHINE
The State Machine is responsible for generating the two operating cycles of
the CPU, stalling during long
command operations, and storing the op-code and operand during operating
cycles. The State Machine can be
implemented with regular CMOS, since the key does not pass through this unit.
It does not have to be
implemented with non-flashing CMOS. However, the opcode/operand latch needs to
be parity-checked. The
logic and registers contained in the State Machine must be covered by both
Tamper Detection Lines. This is
to ensure that the instructions to be executed are not changed by an attacker.
The Authentication Chip does not require the high speeds and throughput of a
general purpose CPU. It must
operate fast enough to perform the authentication protocols, but not faster.
Rather than have specialized
circuitry for optimizing branch control or executing opcodes while fetching
the next one (and all the
complexity associated with that), the state machine adopts a simplistic view
of the world. This helps to
minimize design time as well as reducing the possibility of error in
implementation.
The general operation of the state machine is to generate sets of cycles:
Cycle 0. Fetch cycle. This is where the opcode is fetched from the program
memory, and the effective
address from the fetched opcode is generated.
Cycle 1: Execute cycle. This is where the operand is (potentially) looked up
via the generated effective
address (from Cycle 0) and the operation itself is executed.
Under normal conditions, the state machine generates cycles: 0, 1, 0, 1, 0, 1,
0, 1 ... However, in some cases.
the state machine stalls, generating Cycle 0 each clock tick until the stall
condition finishes. Stall conditions
include waiting for erase cycles of Flash memory, waiting for clients to read
or write serial information, or an
invalid opcode (due to tampering). If the Flash memory is currently being
erased, the next instruction cannot
CA 02564047 2006-11-06
YU139 PCT 244
execute until the Flash memory has finished being erased. This is determined
by the Wait signal coming from
the Memory Unit. If Wait = 1, the State Machine must only generate Cycle Os.
There are also two cases for
stalling due to serial I/O operations:
The opcode is ROR OutBit, and OutBitValid already = 1. This means that the
current operation requires
outputting a bit to the client, but the client hasn't read the last bit yet.
The operation is ROR InBit, and InBitValid = 0. This means that the current
operation requires reading a bit
from the client, but the client hasn't supplied the bit yet.
In both these cases, the state machine must stall until the stalling condition
has finished. The next "cycle"
therefore depends on the old or previous cycle, and the current values of CMD,
Wait, OutBitValid, and
InBitValid. Wait comes from the MU, and OutBitValid and InBitValid come from
the I/O Unit. When Cycle
is 0, the 8-bit op-code is fetched from the memory unit and placed in the 8-
bit CMD register. The write enable
for the CMD register is therefore -Cycle. There are two outputs from this
unit: Cycle and CMD. Both of
these values are passed into all the other processing units within the
Authentication Chip. The 1-bit Cycle
value lets each unit know whether a fetch or execute cycle is taking place,
while the 8-bit CMD value allows
each unit to take appropriate action for commands related to the specific
unit.
Fig. 187 shows the data flow and relationship between components of the State
Machine where:
Logic,: Wait OR
-(Old OR ((CMD=ROR) & ((CMD=InBit AND -InBitValid) OR
(CMD=OutBit AND OutBitValid))))
Old and CMD are both cleared to 0 upon a RESET. This results in the first
cycle being 1, which causes the 0
CMD to be executed. 0 is translated as TBR 0, which means branch to the
address stored in address offset 0 if
the Accumulator = 0. Since the Accumulator is also cleared to 0 on a RESET,
the test will be true, so the net
effect is a jump to the address stored in the 0th entry in the jump table. The
two VAL units are designed to
validate the data that passes through them. Each contains an OK bit connected
to both Tamper Prevention and
Detection Lines. The OK bit is set to I on RESET, and ORed with the ChipOK
values from both Tamper
Detection Lines each cycle. The OK bit is ANDed with each data bit that passes
through the unit. In the case
of VAL,, the effective Cycle will always be 0 if the chip has been tampered
with. Thus no program code will
execute since there will never be a Cycle 1. There is no need to check if Old
has been tampered with, for if an
attacker freezes the Old state, the chip will not execute any further
instructions. In the case of VAL2, the
effective 8-bit CMD value will always be 0 if the chip has been tampered with,
which is the TBR 0
instruction. This will stop execution of any program code. VAL2 also performs
a parity check on the bits from
CMD to ensure that CMD has not been tampered with. If the parity check fails,
the Erase Tamper Detection
Line is triggered.
I/O UNIT
The 1/0 Unit is responsible for communicating serially with the outside world.
The Authentication Chip acts
as a slave serial device, accepting serial data from a client, processing the
command, and sending the resultant
CA 02564047 2006-11-06
YU139 PCT 245
data to the client serially. The I/O Unit can be implemented with regular
CMOS, since the key does not pass
through this unit. It does not have to be implemented with non-flashing CMOS.
In addition, none of the
latches need to be parity checked since there is no advantage for an attacker
to destroy or modify them. The
I/O Unit outputs Os and inputs Os if either of the Tamper Detection Lines is
broken. This will only come into
effect if an attacker has disabled the RESET and/or erase circuitry, since
breaking either Tamper Detection
Lines should result in a RESET or the erasure of all Flash memory
The InBit, InBitValid, OutBit, and OutBitValid I bit registers are used for
communication between the client
(System) and the Authentication Chip. InBit and InBitValid provide the means
for clients to pass commands
and data to the Authentication Chip. OutBit and OutBitValid provide the means
for clients to get information
from the Authentication Chip. When the chip is RESET, InBitValid and
OutBitValid are both cleared. A client
sends commands and parameter bits to the Authentication Chip one bit at a
time. From the Authentication
Chip's point of view:
Reads from InBit will hang while InBitValid is clear. InBitValid will remain
clear until the client has written
the next input bit to InBit. Reading InBit clears the InBitValid bit to allow
the next InBit to be read from
the client. A client cannot write a bit to the Authentication Chip unless the
InBitValid bit is clear.
Writes to OutBit will hang while OutBitValid is set. OutBitValid will remain
set until the client has read the
bit from OutBit. Writing OutBit sets the OutBitValid bit to allow the next
OutBit to be read by the client.
A client cannot read a bit from the Authentication Chip unless the OutBitValid
bit is set.
The actual stalling of commands is taken care of by the State Machine, but the
various communication
registers and the communication circuitry is found in the I/O Unit.
Fig. 188 shows the data flow and relationship between components of the I/O
Unit where:
Logic,: Cycle AND (CMD = ROR OutBit)
The Serial I/O unit contains the circuitry for communicating externally with
the external world via the Data
pin. The InBitUsed control signal must be set by whichever unit consumes the
InBit during a given clock
cycle (which can be any state of Cycle). The two VAL units are validation
units connected to the Tamper
Prevention and Detection circuitry, each with an OK bit. The OK bit is set to
1 on RESET, and ORed with the
ChipOK values from both Tamper Detection Lines each cycle. The OK bit is ANDed
with each data bit that
passes through the unit.
In the case of VAL,, the effective bit output from the chip will always be 0
if the chip has been tampered
with. Thus no useful output can be generated by an attacker. In the case of
VAL2, the effective bit input to the
chip will always be 0 if the chip has been tampered with. Thus no useful input
can be chosen by an attacker.
There is no need to verify the registers in the I/O Unit since an attacker
does not gain anything by destroying
or modifying them.
ALU
Fig. 189 illustrates a schematic block diagram of the Arithmetic Logic Unit.
The Arithmetic Logic Unit
(ALU) contains a 32-bit Acc (Accumulator) register as well as the circuitry
for simple arithmetic and logical
operations. The ALU and all sub-units must be implemented with non-flashing
CMOS since the key passes
CA 02564047 2006-11-06
YU139 PCT 246
through it. In addition, the Accumulator must be parity-checked. The logic and
registers contained in the
ALU must be covered by both Tamper Detection Lines. This is to ensure that
keys and intermediate
calculation values cannot be changed by an attacker. A 1-bit Z register
contains the state of zero-ness of the
Accumulator. Both the Z and Accumulator registers are cleared to 0 upon a
RESET. The Z register is updated
whenever the Accumulator is updated, and the Accumulator is updated for any of
the commands: LD, LDK,
LOG, XOR, ROR, RPL, and ADD. Each arithmetic and logical block operates on two
32-bit inputs: the
current value of the Accumulator, and the current 32-bit output of the MU.
Where:
I Logic,: Cycle AND CMD7 AND (CMD6_4 * ST)
Since the WriteEnables of Acc and Z takes CMD7 and Cycle into account (due to
Logic,), these two bits are
not required by the multiplexor MX, in order to select the output. The output
selection for MX, only requires
bits 6-3 of CMD and is therefore simpler as a result.
Output CMD1-3
ADD ADD
AND LOG AND
OR LOG OR
MX, XOR XOR
RPL RPL
ROR ROR
From MU LD or LDK
The two VAL units are validation units connected to the Tamper Prevention and
Detection circuitry, each
with an OK bit. The OK bit is set to 1 on RESET, and ORed with the ChipOK
values from both Tamper
Detection Lines each cycle. The OK bit is ANDed with each data bit that passes
through the unit. In the case
of VAL,, the effective bit output from the Accumulator will always be 0 if the
chip has been tampered with.
This prevents an attacker from processing anything involving the Accumulator.
VAL, also performs a parity
check on the Accumulator, setting the Erase Tamper Detection Line if the check
fails. In the case of VAL,,
the effective Z status of the Accumulator will always be true if the chip has
been tampered with. Thus no
looping constructs can be created by an attacker. The remaining function
blocks in the ALU are described as
follows. All must be implemented in non-flashing CMOS.
Block Description
OR Takes the 32-bit output from the multiplexor MX,, ORs all 32 bits together
to get 1 bit.
ADD Outputs the result of the addition of its two inputs, modulo 232.
AND Outputs the 32-bit result of a parallel bitwise AND of its two 32-bit
inputs.
OR Outputs the 32-bit result of a parallel bitwise OR of its two 32-bit
inputs.
XOR Outputs the 32-bit result of a parallel bitwise XOR of its two 32-bit
inputs.
RPL Examined in further detail below.
ROR Examined in further detail below.
CA 02564047 2006-11-06
YU139 PCT 247
RPL
Fig. 190 illustrates a schematic block diagram of the RPL unit. The RPL unit
is a component within the ALU.
It is designed to implement the RPLCMP functionality of the Authentication
Chip. The RPLCMP command
is specifically designed for use in secure writing to Flash memory M, based
upon the values in AccessMode.
The RPL unit contains a 32-bit shift register called AMT (AccessModeTemp),
which shifts right two bits each
shift pulse, and two 1-bit registers called EE and DE, directly based upon the
WR pseudocode's
EqEncountered and DecEncountered flags. All registers are cleared to 0 upon a
RESET. AMT is loaded with
the 32 bit AM value (via the Accumulator) with a RPL INIT command, and EE and
DE are set according to
the general write algorithm via calls to RPL MHI and RPL MLO. The EQ and LT
blocks have functionality
exactly as documented in the WR command pseudocode. The EQ block outputs 1 if
the 2 16-bit inputs are
bit-identical and 0 if they are not. The LT block outputs 1 if the upper 16-
bit input from the Accumulator is
less than the 16-bit value selected from the MU via MX2. The comparison is
unsigned. The bit patterns for the
operands are specifically chosen to make the combinatorial logic simpler. The
bit patterns for the operands are
listed again here since we will make use of the patterns:
-Operand CMD,-,
Init 0000
MLO 1110
MHI 1111
The MHI and MLO have the hi bit set to easily differentiate them from the Init
bit pattern, and the lowest bit
can be used to differentiate between MHI and MLO. The EE and DE flags must be
updated each time the
RPL command is issued. For the Init stage, we need to setup the two values
with 0, and for MHI and MLO,
we need to update the values of EE and DE appropriately. The WriteEnable for
EE and DE is therefore:
Logic,: Cycle AND (CMD74 = RPL)
With the 32 bit AMT register, we want to load the register with the contents
of AM (read from the MU) upon
an RPL Init command, and to shift the AMT register right two bit positions for
the RPL MLO and RPL MHI
commands. This can be simply tested for with the highest bit of the RPL
operand (CMD3). The WriteEnable
and ShiftEnable for the AMT register is therefore:
Lo ice Logic, AND CMD3
Lo ic3 Logic, AND CMD3
The output from Logic3 is also useful as input to multiplexor MX1, since it
can be used to gate through either
the current 2 access mode bits or 00 (which results in a reset of the DE and
EE registers since it represents the
access mode RW). Consequently MXI is:
CA 02564047 2006-11-06
YU139 PCT 248
Output LO ic3
MX, AMT output 0
00 1
The RPL logic only replaces the upper 16 bits of the Accumulator. The lower 16
bits pass through untouched.
However, of the 32 bits from the MU (corresponding to one of M[0-15]), only
the upper or lower 16 bits are
used. Thus MX2 tests CMDo to distinguish between MHI and MLO.
Output CMD,
MXZ Lower 16 bits 0
Upper 16 bits I
The logic for updating the DE and EE registers matches the pseudocode of the
WR command. Note that an
input of an AccessMode value of 00 (=RW which occurs during an RPL INIT)
causes both DE and EE to be
loaded with 0 (the correct initialization value). EE is loaded with the result
from Logic4i and DE is loaded
with the result fromLogic5.
Logic4 (((AccessMode=MSR) AND EQ) OR
((AccessMode=NMSR) AND EE AND EQ))
Logics (((AccessMode=MSR) AND LT) OR
((AccessMode=NMSR) AND DE) OR
AccessMode=NMSR AND EQ AND LT))
The upper 16 bits of the Accumulator must be replaced with the value that is
to be written to M. Consequently
Logic6 matches the WE flag from the WR command pseudocode.
Logic6 ((AccessMode=RW) OR
((AccessMode=MSR) AND LT) OR
((AccessMode=NMSR) AND (DE OR LT)))
The output from Logic6 is used directly to drive the selection between the
original 16 bits from the
Accumulator and the value from M[0-15] via multiplexor MX3. If the 16 bits
from the Accumulator are
selected (leaving the Accumulator unchanged), this signifies that the
Accumulator value can be written to
M[n]. If the 16-bit value from M is selected (changing the upper 16 bits of
the Accumulator), this signifies
that the 16-bit value in M will be unchanged. MX3 therefore takes the
following form:
Lo ic6
output
MX3 16 bits from MU 0
16 bits from Acc 1
There is no point parity checking AMT as an attacker is better off forcing the
input to MX3 to be 0 (thereby
enabling an attacker to write any value to M). However, if an attacker is
going to go to the trouble of laser-
DEMANDES OU BREVETS VOLUMINEUX
LA PRESENTE PARTIE DE CETTE DEMANDE OU CE BREVETS
COMPREND PLUS D'UN TOME.
CECI EST LE TOME 1 DE 2
NOTE: Pour les tomes additionels, veillez contacter le Bureau Canadien des
Brevets.
JUMBO APPLICATIONS / PATENTS
THIS SECTION OF THE APPLICATION / PATENT CONTAINS MORE
THAN ONE VOLUME.
THIS IS VOLUME 1 OF 2
NOTE: For additional volumes please contact the Canadian Patent Office.