Note: Descriptions are shown in the official language in which they were submitted.
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
A METHOD, AN INSTALLATION, AND A COMPUTER PROGRAM FOR
ESTIMATING THE INITIAL SIZE OF A POPULATION OF NUCLEIC
ACIDS, IN PARTICULAR BY PCR
The present invention 'elates to estimating the
initial size of a population of interest in a sample
subjected to a succession of amplification reactions.
BACKGROUND OF THE INVENTION
The present invention finds a particularly
advantageous, but non-limiting, application in
determining an initial quantity of nucleic acids in a
sample subjected to a polymerase chain reaction (PCR) in
real time. A technique of this type, known as 'PCR
quantification", is used in particular for evaluating the
number of copies of pathogenic agents (e.g. of the human
immunodeficiency virus (HIV)) in a sample of body fluids
taken from a patient, typically in the context of a
medical checkup.
Reference is made to Figure 1 for a brief
description of the diagrammatic appearance of a real time
PCR amplification curve with PCR cycle index, numbers
plotted along the abscissa and, in the example shown,
with quantities of fluorescence emitted (in arbitrary
units) as measured for each PCR cycle plotted up the
ordinate. For each PCR cycle, it should b.e understood
that the sample is subjected to temperature variations
enabling DNA polymerase to amplify nucleic acids and
enabling the corresponding PCR products to be detected by
fluorescent molecules. By plotting the measured
fluorescence Fn as a function of PCR cycle number n,
-30 variation is obtained of the type shown in Figure 1, and
comprises at least:
= a first portion BN where fluorescence measurements
coincide substantially with the background noise of the
apparatus for measuring fluorescence;
a second portion EXP in which the measured
quantities of fluorescence increase in substantially
exponential manner;
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
2
a third portion LIN in which the increase in the
measured quantities of fluorescence is significantly
attenuated and behaves overall in substantially linear
manner; and
a fourth portion PLA in which fluorescence
measurements reach a plateau stage.
It should be observed that for the initial PCR
cycles (first and second portions), the population of
interest increases in substantially exponential manner,
whereas for the following cycles (third and fourth
portions), other phenomena come into competition with
growth in the population of interest, so that said growth
is then damped up to the plateau stage PLA.
The document "Mathematics of quantitative kinetic
PCR and the application of standard curves" by
R.G. Rutledge and C. Cote, published in Nucleic Acids
Research, 2003, Vol. 31, No. 16, discloses a method of
estimating the unknown initial quantity of nucleic acids
in a sample of interest by means of PCR. That method
consists in using a plurality of samples having known
initial quantities of nucleic acids, referred to as
"standards", in order to determine by interpolation the
initial quantity of nucleic acids present in the sample
of interest.
In general, the greater the initial quantity of
nucleic acids in a sample, the sooner a detectable
quantity of PCR product is obtained, i.e. the sooner a
detectable quantity of emitted fluorescence is obtained.
With reference to Figure 2, relating to the prior art, it
will be understood that the initial population in the
standard Stl is greater than that in __the .standard St2_
which is greater than that in the standard St3, etc.,
since the cycle Ctl for the standard Stl occurs before
the corresponding cycle Ct2 for the standard St2, which
occurs before the cycle Ct3 for the standard St3, etc.
Thus, such a CT cycle, corresponding to the cycle at
which the fluorescence measurements reach a fluorescence
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
3
threshold- THR (as shown in Figure 2), sets at an
arbitrary level (typically below the background noise),
and acts as a parameter representative of the initial
size NO of a population of nucleic acids subjected to the
PCR cycles. Use has been made of this observation in the
above-cited prior art to establish a relationship of the
kind shown in Figure 3 between cycle numbers Ctl, Ct2,
Ct3, Ct4 for a plurality of standards having known
initial populations, and their initial populations N01,
N02, No3, No4. Thus, by plotting the cycles Ctl, Ct2, Ct3,
Ct4, etc. up the ordinates and the logarithm of the
initial population sizes No', N02, No3, No4 along the
abscissa, a regression slope REG is obtained. On this
regression slope PEG, the cycle Ctint detected for the
sample of interest is plotted (dashed-line arrow Fl). By
interpolation on the regression slope REG (dashed-line
arrow F2), the initial population size NOint is then
determined for the sample of interest.
Although that method is in widespread use, it
nevertheless presents some drawbacks.
Firstly, it requires the use of a plurality of
standard samples having respective known initial
populations.
Secondly, the method depends on the judgment of the
user, since the fluorescence threshold value, as selected
by the user, has a direct influence on the values of the
Ct cycles in the amplification curves, and consequently
on the estimated values for the initial population size
in the sample of interest. The threshold value also has
an impact on the accuracy of the result, since accuracy
is generally better if the threshold is selected to lie
in the exponential growth stage EXP of the amplification
curve. Nevertheless, in practice, it is difficult for
the user to know whether the fluorescence threshold level
THR that has been set does indeed correspond to the
exponential stage of the curves, and does so for all of
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
4
the samples (the standard samples and the sample of
interest).
Finally, the method assumes without any verification
that the population has the same amplification yield in
the sample of interest and in all of the stands rd
samples. Thus, if the sample of interest contains PCR
inhibitors, as is typically the case, then its result
will be falsely lowered.
It should thus be understood that the prior E art
technique depends on the fluorescence threshold THR as
defined by the user. The value selected has an influence
on the values of the Ct cycles and consequently on
determining the initial quantity in the sample of
interest. That is one of the reasons why a large amoLant
of work has recently been undertaken to automate Ct cycle
detection and make it reliable.
OBJECTS AND SUMMARY OF THE INVENTION
The present invention seeks to improve the situation
by proposing an approach that is completely different.
Firstly, the invention provides a method, the method
being implemented by computer means for quantifying in
absolute and/or relative manner an initial population of
nucleic acids in a sample of interest. The sample is
subjected to a succession of applications of a reaction
for amplifying the population of interest. In v~ ry
general manner, this amplification may be undertaken by
implementing successive PCR cycles, however any otl-i.er
amplification technique could also be used. Above al1,
it should be understood that the amplification needs
merely to be defined by a reaction yield, as described
below. During these successive amplification operations,
experimental measurements are taken that a re
representative of a current population size, at least in
the sample of interest. It will be understood that ne
or more measurements can be taken after or during each
amplification reaction without loss of generality.
CA 02589129 2012-01-19
Ire ~, nL entIy :r arxcid d irnitioon ooi_ t:ri<
inven is , Lil- rrotr_cci in the r,i:=_arning 0f t h e i nventicjl
ccmpri..so- the following steps:
a) pr o v _dino a model of Che Yield 0- trig=
5 amplification ` act:i on as a function of the successionn CJJ
a [tpl-J. f cation s, saj d model comprising:
a substantially constant s Lage for a fir's
por tion of the applications of the amplification
reaction; and
= a non-1-onsta .t stage for a second portion co:f
the applicat:i ens o the amps' i ..cation reaction;
t? e first and second portions being United by a
changeover re-g- J,_-)n in which yield changes over between thie,
constant and non-constant stages, said region having are
amplification index corresponding substantially to thÃa
changeover;
b) usincr the yield model to express a relationship
involving at least the changeover index and a parameter
representative of the initial population size in th
sarnple of inter'e at;
c) determining at least the changeover index by
comparison with the experimental_ measurements; and, in 3-
o u)-,}segque t or irr nad.iately following step d) c educinc;
population size in the sample of
interest.
STATEMENT OF INVENTION
According to one aspect of the present invention,
there is provided a computer-implemented method to
quantify an initial population of nucleic acids in a
sample of interest subjected to a succession of
applications of a population amplification reaction, the
method comprising:
a) performing by means of an apparatus experimental
measurements representative of a current size of the
population of the sample of interest;
CA 02589129 2012-01-19
5a
b) providing a model of the yield of the
amplification reaction as a function of the succession of
amplifications, said model comprising:
= a substantially constant stage for a first
portion of the applications of the amplification reaction;
and
= a non-constant stage for a second portion of
the applications of the amplification reaction;
the first and second portions being united by a
changeover region in which yield changes over between the
constant and non-constant stages, said changeover region
having an amplification index corresponding substantially
to a changeover index CEEP;
c) determining a relationship between the changeover
index CEEP and a parameter No representative of an initial
population size in the sample of interest, from the
following formula:
N.+1 = NO X (1 + EO) CEEP X function (CEEP, n+1)
where Nn+1 is a parameter representative of the
population size at the current amplification index, E0 is
the value of the yield at the first constant portion of
the yield model, the term function (CEEP, n+1) is a
particular function characterizing the second non-constant
portion of the yield model and that depends at least on
the changeover index CEEP and on the current amplification
index n+l, and (CEEP - 1) is the last index of the
amplification reaction during which the yield is still
constant;
d) determining an experimental variation of the yield
and a changeover index value from the experimental
measurements performed by said apparatus; and
e) determining the initial population size in the
sample of interest from the changeover index value by
means of the relationship between the changeover index and
CA 02589129 2012-01-19
5b
said parameter representative of the initial population
size.
According to another aspect of the present invention,
there is provided a system for implementing the method
described herein, the system comprising:
. a sample support for supporting at least the sample
of interest;
. a first apparatus for applying said succession of
amplification reactions, at least to the population of
interest in the sample of interest;
a second apparatus for taking measurements
representative of the current size of the population of
interest; and
= computer means suitable for receiving measurement
signals from the second apparatus and implementing the
method described herein.
According to still another aspect of the present
invention, there is provided a computer program product
comprising a computer readable memory storing computer
executable instructions thereon that when executed by a
computer perform the method steps described herein.
I ;:E -DE', SCR7 ?`IGIN) OF THE DRAWINGS
other advantages and characteristics of the
i rr-,rent 1on appear o : ending the following detailed
description of an i 1 ezmieri aLion given below by way of
example with reference to the -accompanying figures, in
which:
= E'igur_e I relat~.os to the prior art and represents
a t is 7 on in the quantity cf f l11 fluorescence as a
f1.u,nct:: on of the number of PCR cycles, as described a.'ove;
1gure 2 relates h ? S i r arr,: and is
reprcnenrat.ive of the increasing suan_tities of
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
6
fluorescence that are emitted as a function of the number
of PCR cycles, as described above;
= Figure 3 represents an interpolation method for
determining the initial quantity of the population of
interest in the sample of interest using a method known
in the prior art, and described above;
Figure 4A is a diagram showing variation in the
above-described experimental measurements as a function
of the succession of amplifications applied to the sample
of interest;
= Figure 4B is a diagram showing variation in the
yield of the amplification reaction, obtained from
experimental measurements, as a function of the
succession of amplifications applied to the sample of
interest;
= Figure 5 plots a regression relationship between
the yield changeover indices that occur at the changeover
between the constant stage and the non-constant stage,
and the logarithms of the initial populations for
standard samples and for the sample of interest,, for use
in a first implementation;
= Figure 6A shows typical variation in the measured
quantity of fluorescence after it has been adjusted by
taking account of background noise specific to the
measurements, and plotted as a function of the number n
of PCR reaction cycles;
Figure 6B shows the variation in the effectiveness
of the PCR shown in Figure 6A as a function of the number
n of cycles;
Figure 7 compares the experimental variation in
emitted fluorescence as shown in Figure _ 6A ___wit_h the
results obtained by applying the emitted fluorescence
model obtained by including an effectiveness model in a
second implementation;
= Figure 8 is a comparison between the variation in
the effectiveness of Figure 6B and the application of an
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
7
effectiveness model deduced from the emitted fluorescence
model of Figure 7;
= Figure 9 is a flow chart outlining the main steps
in the method in a proposed implementation of the present
invention; and
= Figure 10 is a diagram of an installation for
quantifying the initial population of a sample of
interest.
MORE DETAILED DESCRIPTION
Reference is made to Figures 4A and 4B for briefly
describing a few principles of the invention illustrating
the characteristics of the above method.
Firstly, it should be understood that Figure 4A
plots a succession of experimental measurements Fn
representative of the current size of a population of
interest which is being subjected progressively to a
succession of amplification reactions, each reaction
being indexed by an index number n. In the non-limiting
example described herein, this succession of reactions
corresponds to a succession of PCR cycles. In this non-
limiting example, the experimental measurements Fn
correspond to measured quantities of fluorescence on each
PCR cycle. Thus, in a quantification method which
combines the PCR reaction and the fluorescence emitted by
the sample of interest, fluorescent reagents are
introduced into the sample so that the fluorescence that
is emitted during a PCR cycle is proportional to the size
of the nucleic acid population in the sample. Indeed, it
can be preferable to perform a plurality of measurements
or no measurements at all for certain PCR cycles.
Furthermore, more generally, the__measurement_method may
make use of techniques other than fluorescence, even if
fluorescence is the method that is often used for
quantifying by PCR. Finally, it should be understood
that other amplification techniques could be implemented
in the context of the present invention, providing it is
possible to track variation in the yield of the reaction
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
8
corresponding to the amplification. Since the example
described below relates preferentially to PCP cycles,
reference is made to the "effectiveness of the PCR""
written En for each PCR cycle of index n, in order to
refer to the yield of the amplification reaction.
As mentioned above with reference to Figure 1,
Figure 4A mainly comprises two regions in which:
= during the initial PCR cycles (portion EXP), the
population increases substantially exponentially; whereas
during the following cycles (the LIN and PLA
portions), other phenomena come into competition with
growth of the population of interest, so the growth
becomes damped.
The following two assumptions are made:
= the yield of the reaction Eõ is relatively constant
during the initial cycles over the portion EXP; and
= after some number of cycles have been performed,
the yield En of the reaction starts to decrease over the
portions LIN and PLA.
This decrease in yield may have a variety of
explanations, in particular a degradation and/or a lack
of PCR reagents (DNA polymerase, dNTPs, primers, etc.)
and/or inhibition by the products that are made
themselves.
It is assumed herein that the yield is initially
constant and that it subsequently decreases.
Nevertheless, it should be understood that the invention
applies more generally to the context of yield:
= that is initially constant, which corresponds to a
normal situation for growth by amplification; and
= that is subsequently not 'con-stant _(decreases -or
increases) which corresponds to a situation that is
substantially abnormal.
In the context of reactions for amplifying the
quantity of nucleic acids, it has been found that the
yield often changes over from a constant stage to a non-
constant stage. In the meaning of the invention,
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
9
advantage is taken of this observation to deduce
therefrom the initial quantity of nucleic acids, as
described below in detail. Initially, it is merely
stated that the yield can also change over from a non-
constant stage during early cycles to a subsequent
constant stage. The present invention is equally
applicable to such a circumstance. In general, it should
therefore be understood that in the meaning of the
invention, a changeover of yield between a constant stage
and a non-constant stage is detected.
The objective is to find the initial size of the
population that has been subjected to amplification.
With reference to Figure 4, it will be understood that
the measurement F0 representative of this initial
population size, which coincides in practice with the
measurement background noise BN, cannot be used on its
own for determining directly the initial population size.
In the prior art, attempts have been made to quantify
this initial population size by making use of the
exponential stage, i.e. a stage that occurs typically on
exiting background noise. A threshold cycle Ct is then
determined (corresponding to point PA for "prior art") in
Figure 4A. As mentioned above, in this region
measurements are often affected by noise and it is
difficult to determine accurately a threshold cycle Ct
representative of exiting background noise.
In a completely different approach, the present
invention instead makes use of nearly all of the points
of the amplification curve in order to determine
accurately a region CHO where the yield changes over
between a constant staige and .a_ _ non-cons_t ant _ stage,
typically in present circumstances between the
exponential stage EXP and the linear stage LIN. It will
be understood that measurements are logically less
affected by noise in this region CHO than in the
background noise exit region since the region CHO occurs
during later cycles. Furthermore, particularly because
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
of the mathematical properties associated with yield, it
is shown below that, most advantageously, the number of
standards that need to be used for quantifying the
initial size of the population of interest is smaller
5 than the number of standards used in prior art
quantification.
The relationship for associating the changeover
region CHO with the initial size of the population of
interest is briefly described below. The yield of an
10 amplification reaction is given by:
Nn+1 = Nn + En x Nn
in which:
= Nn is the size of the population of interest after
an amplification of index n in a succession of
amplifications;
Nn+1 is the size of the population of interest
after a following amplification, of index n+1, in the
above-mentioned succession of amplifications; and
En is the yield of the amplification reaction of
index n in the above-mentioned succession of
amplifications.
Reformulating this relationship as a recurrence
relationship, we obtain:
Nn+1 = (1 + En) (1 + En-1) (1 + En-2) ... (1 + Eo) No
where No is the initial size of the population of
interest. So long as the yield Eõ is constant, it will be
understood that the above relationship can be written
more simply as follows:
Nn+1 = No x (1 + Eo) n+1
where the index n+1 has not yet reached the changeover
region CHO. While the yield is constant --during the
initial cycles, the following applies:
En = En-1 = En-2 = ... = Eo
where E0 is the value of the yield during the constant
stage. Nevertheless, when the index n+l moves into the
changeover region CHO, the relationship becomes:
Nn+1 = No X (1 + EO)CEEp x function(CEEP, n+l)
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
11
where:
= (CEEP - 1) is the last index of the amplification
reaction during which the yield is still constant (it
will thus be understood that the index CEEP itself
represents the changeover index proper between the
exponential stage and the linear stage); and
the term function(CEEP, n-+1) is a particular
function characterizing the non-constant stage of the
yield and that depends at least on the changeover index
CEEP and on the current amplification index n+l.
It can thus be seen how it is possible to associate
the changeover index CEEP and the initial size No of the
population of interest. At this stage it can be
understood that steps a) and b) of the above-defined
method have already been implemented.
A first implementation consists in determining the
changeover index CEEP experimentally and in correlating it
with the initial size by regression by using a plurality
of standard samples that are subjected to the same
amplification treatment as the sample of interest. Under
such circumstances, it will be understood that steps b)
and c) of the above-defined method are merely
interchanged since initially the changeover index CEEP
(step c)) is determined experimentally, and subsequently
the relationship between the index CEEP and the initial
size No (step b)) is determined in order to end up with
the initial size N. (step d))
Before describing all of these steps in detail in
the meaning of the first implementation, a method is
described for determining the index CEEP on the basis of
-experimental-.-measurements.- _ __In_- -part __culrar-,---it will be--
understood that this method of determining the index CEEP
experimentally can be applied to another implementation
that is different from the above-mentioned first
implementation.
Returning to the relationship between the
effectiveness En of a given cycle n and the current size
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
12
of the population of interest in the same cycle N,, and in
a subsequent cycle Nn+1, the effectiveness of the
amplification can be expressed as follows:
En = (Nn+1/Nn) - 1
In certain circumstances, in particular when there
is no need to take account of background noise BN in the
measurements, it is possible to a first approximation to
assume that the measurements are substantially
proportional to the current size of the population of
interest. Nevertheless, in practice, account will more
often be taken of measurement drift, with corrected
experimental measurements F'n being determined on the
basis of direct measurements F. as shown in Figure 4A.
A prior step of processing the experimental
measurements Fn is preferably applied, this step
consisting in subtracting the background noise BN and
subsequently in introducing compensation to take account
of a non-zero measurement s representative of the initial
population size. In the example shown in Figure 4A, the
variation in the background noise BN as a function of the
index n can be represented by a linear function since
tests have shown that a linear model is satisfactory for
fluorescence measurements in PCR. Nevertheless, in
certain circumstances it may be preferable to use an
exponentially-varying model. In any event, a model is
applied that complies best with variation in the
background noise BN as given typically by the initial
measurement points. Thereafter, the selected model for
variation in background noise BN is subtracted from all
of the experimental measurement values F. By applying
this step, _it will be understood that the theoretical __
fluorescence measurement F0 is reduced to a measurement
value of zero, corresponding to an initial population
size No of zero, which is not representative of physical
reality. Consequently, it is advantageous to apply
compensation for this correction as follows:
F' n Fn - BN + s
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
13
where:
= the term F'n corresponds to a corrected measurement
for a current index n;
= the term Fn corresponds to the raw experimental
measurement at said current index n;
= the term BN corresponds to the value for the
background noise as modeled for the current index n; and
= 8 is the corresponding compensation term which is
assumed to be constant in the example being described and
which directly represents the initial population size N0.
Although these steps of correcting for background
noise are very advantageous in determining the changeover
index C55, they may also be applied to any determination
and quantification of the initial population size No
whenever background noise is likely to falsify
measurement of said population size No. In this respect,
these steps may constitute the subject matter of separate
protection, where appropriate.
The corrected measurements F'n as obtained in this
way are advantageously proportional to the: current
population sizes Nn in the samples of interest, such that
the yield En can now be expressed directly as a function
of measurement values (corrected as described above), by
the following relationship:
En (F'1/F') 1
Thus, from the experimental measurements Fn of
Figure 4A, corrected measurements F'n are obtained from
which there is subsequently determined the variation in
the effectiveness En as a function of the succession of
indices n, as shown in Figure 4B.
In short, the experimental measurements are
expressed in the form of an experimental variation in the
effectiveness En of the kind shown in Figure 4B as a
function of the succession of amplifications n. This
provides an experimentally-determined variation for the
yield comprising:
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
14
a} perceptibly noisy first region for low
amplification indices n (specifically prior to the cycle
CG in the example of Figure 4B) ; and
followed by a second region exhibiting less noise
for higher amplification indices (at least after the
changeover region CHO).
At least in the most usual circumstance of
amplification by PCR and measurement by fluorescence, the
non-constant stage of yield is decreasing and corresponds
to said second region presenting little noise (as shown
in Figure 4B). Specifically for the purpose of
eliminating measurement points that run the risk of
falsifying results when selecting a model to apply to the
variation in yield:
a crude value Eo is estimated for the constant
yield stage; and
= particularly when searching for the changeover
index CEEP, at least some of the measurements in the less
noisy second region are ignored for which the estimated
yield is less than a threshold value, e.g. corresponding
to some fraction of the constant stage E0.
These points NEG (Figure 4) that are eliminated are
typically those that correspond to very high
amplification indices n and that might no longer satisfy
the model for effectiveness which is selected
substantially around the changeover region CHO. By way
of example, in order to eliminate them, an average is
evaluated for the constant stage of yield Eo, typically
for the initial indices n. Thereafter, a threshold value
is selected that corresponds to a fraction of the average
found for the constant stage E0, e.g. 10%. Thereafter,
starting from the highest indices n, all measurement
points NEG of measured yield lower than or equal to said
threshold value are eliminated. This step, which is most
advantageous for detecting the index CEEP, can
nevertheless be applied to any determination based on
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
yield En, and may constitute the subject matter of
separate protection, where appropriate.
When yield presents a non-constant stage in which
yield is decreasing and which follows a constant stage,
5 as shown in Figure 4B, the changeover region CHO is
identified by working in the direction of decreasing
index numbers n, starting from the less noisy second
region, and by detecting a coarse index CG for which the
yield passes a predetermined value. Thus, with reference
10 to Figure 4B, going in the direction of decreasing index
numbers n so as to rise towards the changeover region
CHO, the yield associated with each index number is
evaluated. For the first measurement point of yield that
is significantly greater than the above-mentioned
15 predetermined value, it is considered that the above-
mentioned coarse index CG has been detected a nd
corresponds to the index of the measurement point.
As described below in a subsequent implementation,
it is possible for each measurement point to model the
variation in its yield as though said set point itself
corresponds to the changeover index CEEP. In th at
implementation, if the constant yield stage E0 is
estimated, and if the estimated value exceeds the above-
mentioned predetermined value, then the point is
considered as corresponding to the coarse index CG.
In general, a maximum yield has a value of 1 so it
is possible to select the above-mentioned predetermined
value as being equal to 1. Nevertheless, this can be
varied, and, for example, provision can be made to set
the predetermined value as corresponding to the me an
yield Eo as evaluated over the initial reaction cycles.
Thereafter, the estimate of the value of the
,p in the changeover region is
amplification index C.,
refined, which value may advantageously be a fraction, by
working in the direction of increasing amplification
index numbers, starting from the coarse index CG, and by
detecting an amplification index for which the yield is
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
16
approximately equal to the above-mentioned predetermined
value. Thus, referring again to Figure 4B, in order to
refine the search for the changeover index CEEp after the
coarse index CG has been determined, a search is made
downwards starting from the coarse index CG and going in
the direction of increasing index number n, in steps of a
size smaller than one whole index, and the abscissa value
is determined, e.g. by interpolation, at which the
predetermined value is crossed. Typically, so long as
the constant stage value remains greater than 1, the
search is continued in the direction of increasing number
n, and the index (CEEP - 1) preceding the changeover is
determined as soon as the constant value Eo is equal to or
very close to 1. That is why it is appropriate to select
a search step size corresponding to a fraction of the
index, for example 10% of one cycle n.
In the above-mentioned first implementation, a
plurality of standard samples are provided having
respective known initial population sizes, and the
succession of amplifications is applied thereto under
substantially the same conditions as for the sample of
interest. Their respective changeover indices are
determined in accordance with above-described steps a),
b), and c). In step d):
a dependency relationship is established between
the initial population sizes of the standard samples Nost
and their indices CEEpst; and
= after determining the index CEEp for the sample of
interest, the initial size of the population of interest
No is determined by interpolation on that dependency
relationship._
Thus, with reference to Figure 5, a dependency
relationship can be established between the changeover
cycles CEEP1, CEEP2 of the standards and their initial
concentrations N01, No2 (actually the logarithms thereof),
e.g. by regression. By measuring the changeover index
CEEpint for the sample of interest and by plotting its
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
17
value on the regression slope of Figure 5, the initial
concentration No'-nt in the sample of interest is obtained
by interpolation.
This first implementation is thus quite similar to
that of the prior art described with reference to
Figure 3. Nevertheless, it should not be forgotten that
the changeover index CEEP on which this first
implementation relies does not correspond in any way to
the threshold cycle Ct of the prior art.
In an approach that is significantly different from
this first implementation:
in step b), use is made of the yield model to
express variation that is parameterized as a function of
the succession of amplifications, said variation ma king
use of at least one parameter representing the change over
index CEEP; and
in step c), at least said parameter representing
the changeover index CEEP is determined by comparison with
the experimental measurements.
In a second implementation, this parameter ized
variation is representative of the current population
size N. in the sample of interest.
Typically, this parameterized variation can be drawn
from an expression of the type given above:
Nn+1 = No X (1 + Eo) CEEP X function (CEEP, n+1)
Thus, in addition to a parameter representing the
changeover index CEEP, this variation makes use of a
parameter representative of the initial population size No
in the sample of interest.
Thereafter, in steps c) and d) of this second
implementation,- _ these -two -parameters _CEEP and . No -are- determined
substantially together.
Previously, in step a), it is necessary to determine
a model for the above-mentioned function function (CEEP,
n+1).
Usually, for PCR quantification, a model is selected
for the non-constant stage of the yield corresponding to
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
18
a decreasing exponential having a decrease parameter 13
which is described in greater detail below. This
decrease parameter (3 is then determined in step c), at
least with the changeover index CEEP, by comparison with
the experimental measurements.
Thus, in this second implementation, once the yield
model En has been selected, it is applied to the general
expression for the current population size Nn given by the
above relationship. This provides a model for variation
in the current population size Nn.
Nevertheless, unless the experimental measurements
give the value for the current population size Nn directly
(which is rarely true in practice at present), it is
appropriate subsequently to model the experimental
measurements Fn themselves, taking account of the
subtracted background noise and the subsequent
compensation 8 as described above.
Thus, in a presently preferred implementation, the
above-mentioned parameterized variation:
is representative of experimental measurements;
and
includes a parameter corresponding to a
measurement value FO representative of the initial
population size.
Thereafter, the measured value of the initial
population size FO is determined by comparing said
parameterized variation Fn with the experimental
measurements.
In order to perform this comparison, it is possible,
for example, to adjust the parameters Fo, Ep, CEEP and the
decrease parameter 1 in the model of the measurements Fn
by using statistical correlations (typically the least
squares method) applied to the raw experimental
measurements. An example implementation is described in
detail below.
Initially, variation is obtained for the measured
and adjusted quantity of fluorescence as a function of
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
19
the number of PCR cycles that have been applied, as shown
for example in Figure 6A. This figure shows the
amplification curve for a sample of interest containing
nucleic acids, in this case a fragment of DNA having an
initial quantity of 100,000 copies, marked by the
SYBRGREEN intercalant during the PCR reaction which is
performed on the I-Cycler IQ apparatus from the supplier
BI-RAD .
In the example described, it will be understood that
the amplification reaction is a PCR reaction in real
time. The experimental measurement represents quantities
of emitted fluorescence.
The fluorescence of cycle n after adjustment for
background noise, as described above, is written Fn below.
The theoretical initial fluorescence before the first
cycle is written F0. The effectiveness of the PCR in
cycle n is written En. The total number of cycles
performed during the PCR reaction is written N.
By assumption, the fluorescence measured on each
cycle n of the PCR reaction cycle is defined by:
Fn+1 Fn(1+En) for all n e {0, 1, 2,...,N-1} (1)
with 0 S En S 1.
The effectiveness of the reaction on each cycle n is
calculated as follows:
En-Nn+l - 1 N Fn+1 - 1 for all n e {0,1,2,...,N-1} (2)
Nn F.
It should be observed that equation (1) is assumed
to be true for n=0. Nevertheless, by definition, the
initial fluorescence FO is unknown. It is therefore not
possible to calculate the effectiveness on the first
-30 -cycle Eo- -directly for- formula (2)
Figure 6B shows the effectiveness of the PCR
reaction as approximated by formula (2) and on the basis
of the adjusted variation in fluorescence of Figure 6A,
as a function of cycle number n.
The following assumptions are preferably made:
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
the effectiveness of the reaction is relatively
constant during the initial cycles; and
after a certain number of cycles have been
performed, the effectiveness of the reaction decreases.
5 Figure 6B confirms the second assumption since it
can be seen that effectiveness decreases as from cycle
n=17. However, the measured effectivenesses in cycles 1
to 16 are very noisy, which makes it difficult to verify
the first assumption graphically.
10 Nevertheless, it is preferable to assume that
variation in effectiveness obeys a model of the type
including:
a first stage that is constant between the first
PCR cycle and the cycle (C,,,-1) preceding the changeover
15 cycle written CEEp; and
a second stage in which it decreases for cycles of
numbers greater than or equal to cycle (CEEp-l).
The cycle (CEEp-1) thus represents the last cycle
(which may be a fraction) for which effectiveness
20 continues to be constant.
It is then proposed to model the effectiveness of
the reaction as follows:
1EQ for 0 - n <_ (CEEp -1)
En eYp(-P(n-Ceee+1) (3)
(1+Eo) - 1 for (CEP. -1) _< n S (N-1)
where Ep and (3 are real parameters which are estimated
using the amplification curve of Figure 6A, or using the
effectiveness curve of Figure 6B in a manner described
below.
In a variant, some other selection may be preferred,
e.g. from the models Fl to F3 given below, particularly
^30 depending _ on he type --Of nucleic- acid- that " is- -to be-
quantified.
Fl: En = exp (-(3 (n-CEEp+1)) -1
F2: En = exp (-p (n-CEEp+l) a) -1
F3: En = a - exp(-}1(n-CfEp+1)a)-l
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
G1
Preferably, several sets of parameters are estimated
in step c) for several candidate changeover cycles CEEP'
and the minimum candidate cycle is selected for which the
associated parameters maximize the statistical
correlations that can be undertaken in step c), for each
changeover cycle CEEP'
As mentioned above, expression (1) may also be
written in the form:
n-1
Fn = Fo fl(1+Ek) for n E {l,2,...,N} (4)
k=0
Thus, by introducing the expression (3) for
effectiveness into formula (4), a new model is obtained
having four parameters (Fo, Eo, 13, CEEP) for the adjusted
emitted fluorescence Fn:
1F0(1+E0) for 1 5 n C CEEP
Fn = 1-exp (-R (n-CEEP)) (5)
CeeP+
exp (R)-1
L F0(1+E0) for CEEP S n <_ N
The initial size No of the population of interest,
the effectiveness Eo of the reaction of n=0, the parameter
(3, and the changeover cycle CEEP are evaluated
repetitively for several cycle values in the vicinity of
the changeover region CHO in order to find a statistical
correlation maximum that is achieved for a minimum cycle
value that is equal to the changeover cycle CEEP'
In this second implementation, it is preferred to
model variation in the measured and adjusted quantities
of fluorescence as a function of cycle number on the
basis of the models or variation in effectiveness, and
-subsequently-- to- carry out -- t-he----cor-r-el-ati-ons ---directly on-
the measured and adjusted quantities of fluorescence.
It should be observed that by adjusting the measured
emitted fluorescence for background noise, an artificial
adjustment is also made on the initial fluorescence F0.
Thus, estimating the parameters of the effectiveness
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
2 2
model on the basis of effectiveness measurements that are
deduced from adjusted fluorescence measurements
constitutes an additional source of error and it might be
preferable to proceed in two stages as described below
for the third implementation.
Nevertheless, the second implementation as described
is simpler and adapts well to PCR quantification using
fluorescence measurements. It is based on the real
measurements of fluorescence F'n which correspond to the
fluorescence measurements adjusted for drift in
background noise together with compensation s on said
measurements. Once the background noise has been
subtracted, we have a relationship of the following type:
F'n = Fn + E
where s is a quantity that may or may not depend on cycle
number n. It is preferably selected to be constant.
Under such circumstances, the measured and
adjusted" effectiveness also written E'n on cycle n is
defined by:
En =F n+1 - 1 = n+1 + s - 1 for all n e (7)
F 'n Fn + s
The model of above relationship (5) thus becomes:
F0(1+E,)n for1<_n <CEEP
Fn = 1-exp i-p ,(n-CEEB) (8)
C + exp (pl)-1
Fo(1+Eo) eee for CEEP :-< n < N
Under such circumstances, the effectiveness values
E'n are approximated experimentally from the measurements
so as to be able to set a minimum acceptable
effectiveness _ threshold- _d-uring- the - - stage of-- decreasing
effectiveness. A threshold cycle is thus determined
beyond which the adjusted fluorescence measurements are
not used for the purposes of the model (points NEG in
Figure 4B). Typically, the threshold cycle corresponds
to the first cycle in the stage of decreasing
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
23
effectiveness at which effectiveness drops below some
minimum acceptable effectiveness threshold (e.g. O.lE0).
More generally, the value of the effectiveness
threshold preferably lies in the range 0 to 0.5, and PCR
having an effectiveness value below said threshold is
potentially biased by uncontrolled inhibition phenomena.
In the example shown in Figure 7, the threshold
value for effectiveness was set at 0.02 (i.e. 2% of E0).
The threshold cycle CS corresponded to cycle n=36.
Figure 7 shows the adjusted measurements of emitted
fluorescence. It can be seen that there is satisfactory
correlation with the model (continuous line) for those
experimental measurements (marked with an "o") up to
cycle n=36. Figure 8 also shows good correlation with
experimental measurements for predictive effectiveness as
obtained from Figure 7 using the model based on measured
and adjusted fluorescence.
The main steps of this implementation can be
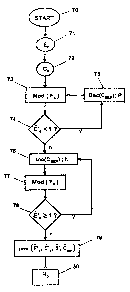
summarized as follows, with reference to Figure 9.
In a start step 70, the measured values for
quantities of fluorescence have been obtained and
adjusted relative to background noise as a function of
cycle number n, as shown in Figure 6A.
In step 71, an approximation for effectiveness of
the reaction in cycle n is calculated using above formula
(2) for each of the cycles n = 1, 2, ..., (N-i)
In step 72, the minimum cycle CS is determined for
which the following two conditions are satisfied:
the cycle CS lies in the stage of decreasing
effectiveness; and
the effectiveness of the threshold cycle is less--
than the threshold effectiveness value ES (e.g. ES =
0.1E0) :
ECS <_ Es
It is already possible to eliminate the points NEG
for which effectiveness is less than E5.
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
24
In step 73, a model is formed for the curve of
adjusted emitted fluorescence which effectiveness is
decreasing over the cycle range CEEP = (CS - 5) to Cs1
using expression (8) in which it is assumed that
compensation s is given by 8 = F'0:
/ 1-exp (-f3 (n-C,
CEEP * ee ) )
Fn = F'(1+E'o ) exp(f31-1 - F'
Thereafter, test 74 on the value E'o estimated for
the value E'o and the decrementation in step 75 of the
value for the changeover cycle CEEP seeks to find the
looked-for value of CEEP using a step size P (which may be
equal to 1), and in repeating step 73 so long as the
value of B'o is less than 1.
Thereafter, when the estimated effectiveness value
exceeds the value 1 (arrow n on exiting the test 74), the
value of the index CEEP is incremented by a step of size h
(which may be a fraction smaller than unity) in step 76
and in step 77 fluorescence Fn is modeled in the same
manner as in step 73. So long as the estimated
effectiveness E'o is greater than or equal to 1 in step
78, steps 76 to 78 are repeated. When the estimated
effectiveness takes a value of less than 1, the estimated
parameters ( F'o , E'o , P'0 rOEEP) are conserved in an end step
79.
In this step, a value F'0 has finally been obtained
that alone is representative of the initial population
size No in the sample of interest. It is then possible to
use at least one standard sample having a known
population size Nost so as to determine in step 80 the
initial population size No in the sample of interest.
For this purpose, a measured value of an initial
population size Fost in a standard sample of known initial
population Nost is obtained. Thereafter, the value of the
initial population size No in the sample of interest is
obtained by deriving a proportionality relationship
between the measurement for the standard sample and its
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
known initial population size, and applying that
relationship to the measurement F'o to obtain the actual
initial population size No.
In other words, in step 80 of Figure 9, it is
5 possible to determine the value N. of the initial
population size in the sample of interest by applying a
simple proportionality relationship of the type:
No = F'o (Nost / Post
implying that the initial population size in the standard
10 Nast and the ratio of the corrected fluorescences as
compensated and estimated by adjusting the fluorescence
model apply both to the sample of interest and to the
standard sample.
It will thus be understood that a single standard
15 ought to be sufficient for determining the initial size
of the population of interest in the sample of interest,
which is an advantage provided by the invention.
Nevertheless, in a variant, and where necessary,
provision could also be made to obtain respective
20 measured values for initial population sizes F'ost in a
plurality of standard samples having known initial
population sizes Nost. Thereafter, a dependency
relationship is established between the initial
population sizes Nost of the standard samples and the
25 respective measured values for their initial population
sizes F'ost= Thereafter, after finding the measured value
for the initial population size of the sample of interest
F'o, the actual initial population size No of interest is
determined by interpolation using the dependency
relationship. It will be understood that this dependency
,relationship- may -also- -typical-ly- -be-- -a- regress-ion of- the
type shown in Figure 5, but having the initial
fluorescence values F'ost and F'o of the standards and of
the sample of interest plotted up the ordinate (or the
values of their respective logarithms) instead of
plotting values for the changeover index CEEP.
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
26
Once use is made of one or more standards, provision
can be made for one or more standard samples having
respective known initial population sizes Nost to which
the succession of amplification reactions is applied
under substantially the same conditions as for the sample
of interest. Thereafter, the measured values F'o5t for
their initial population sizes are determined by making
comparisons of the parameterized variations with the
experimental measurements, as for the sample of interest.
In other words, the same calculations are naturally
applied concerning the measured and adjusted quantities
of fluorescence both on the standard(s) and on the sample
of interest. The quantity of fluorescence F',,t before the
first cycle is estimated for the standard(s) using the
same method as is used for determining F'o for the sample
of interest, as described above.
A third implementation, corresponding to a variant
of the above-described second implementation consists
overall in adjusting the model for the effectiveness En
relative to the experimental measurements, , and in
subsequently injecting said adjusted effectiveness model
into the model for the current population size Nn, or into
the model for the measurement F. This third
implementation can be summarized as follows.
The parameterized variation constructed in step b)
is representative of yield, and in step c), experimental
variation of the yield is determined on the basis of-
experimental measurements in order to compare the
parameterized variations with the experimental variation.
Thereafter, in order to obtain a parameter representative
of the initial population size N 0 the following steps are
performed in step d):
dl) determining a second parameterized variation
representative of the current population size Nn in the
sample of interest, making use at least of the parameter
representing the changeover index CEEP, and a parameter
representative of the initial population size No;
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
27
d2) 'applying, to said second variation, a
parameterized value for the changeover index CEEP as
determined in step c); and
d3) adjusting at least the parameter representative
of the initial population size No by direct comparison of=
the second variation with the experimental measurements.
Advantageously the following are performed:
= in step d2), applying a coarse value for thz
changeover index CEEP in the same manner as described for-
detecting it with reference to above Figure 4B; and
= in step d3), subsequently refining the index value
together with adjusting the parameter representative of
the initial population size No.
Finally, it should be understood that the presently
preferred second implementation of Figures 7 and 8
differs from this third implementation by the fact that
no attempt is made to perform correlations on
effectiveness, but use is made merely of the mathematical
model for effectiveness variation in order to model and
refine the estimate of the correct and compensated
fluorescence.
Naturally, the present invention is not limited to
the embodiments described above by way of example, and it
extends to other variants.
Thus, it will be understood that the present
invention can also apply to relative quantification, in
particular by PCR. In this application, as well as
amplifying the population of interest, a reference
population is also amplified either simultaneously in the
same medium, or separately. Measurements are taken as
follows:
experimental measurements representative of the
size of the population of interest; and
= experimental measurements representative of the
reference population size.
The method can then continue by applying steps a),
b) , and c) to the reference population while step d)
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
28
consists merely in determining a ratio between the
respective initial sizes of the population of interest
and of the reference population.
Relative quantification can be used for analyzing
the expression of a gene of interest during the
development of an organism. In order to correct in
particular for variations in quantity and in quality
between samples taken from the organism at different
times, in addition to analyzing the target gene of
interest, a reference gene is also analyzed that is knojan
for having a level of expression that remains stable
during development.
A final step then consists in comparing the ratios
Notarget
Noref
between the various samples that have been taken.
In order to achieve the desired results, two
strategies are possible.
The prior art strategy is based on detecting the
threshold cycle Ct and it normally takes place as
follows. For each sample taken at different instants t O,
t1, t2, ..., tn, the ratio
N Otarget
Noref
is determined, making use of at least one standard (i.
a standard for which Notarget and Noref are known), which
amounts to performing two successive absolute
quantifications followed by calculating a ratio.
Another strategy that is particularly advantageous
in the context of the invention consists in determinirig
for each sample taken at different instants t0, t1, t2,
..., to the ratio:
Notarget
N Oref sample
Notarget
Noref sample to
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
29
directly by using the following formula:
NOtarget ( FOtarget)sample
NOref sample FOtarget)sample-t0
NOtarget ( Foref)sample
N Oref sample_t0 ( FOref)sample_tO
In this second implementation, which in the end
makes use only of the parameter FO, in combination with
the technique of the invention, no standard sample is
needed, which is particularly advantageous.
Reference is now made to Figure 10 which shows an
installation for implementing the method of the
invention. It comprises a support SUPP in this case
comprising a well containing the sample of interest ECH
and a well containing a standard sample referenced St,
for example. The support SUPP is enclosed in an
enclosure ENC, e.g. fitted with heater means (not shown)
for applying a PCR reaction to the standard and to the
sample of interest.
In the example described, provision is preferably
made to take measurements of the quantities of
fluorescence emitted on each cycle, both by the standard
St and by the sample of interest ECH. To this end, a
selected reagent is inserted into the wells and the
samples are illuminated by a lamp (e.g. a halogen-
tungsten lamp) in order to measure the respective
quantities of fluorescence coming from the sample of
interest and from the standard sample on each PCR cycle
that is applied. In addition, an apparatus for detecting
fluorescence comprises, for example, an objective lens 11
for collecting the light coming from the fluorescence,
and photon counting means 10, e.g. a charge-coupled
device (CCD) camera, and/or photomultipliers, in order to
measure the fluorescence emitted on each PCR cycle from
the sample of interest and from the standard. Thus, the
fluorescence emitted by each well is advantageously
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
focused by the lens' 11 and then is preferably detected by
a CCD camera 10 connected to an acquisition card 21, e.g.
of the Personal Computer Memory Card International
Association (PCMCIA) type provided in a central unit 20
5 of a computer.
The computer is then connected to the above-
mentioned measuring means 10 to receive therefrom signals
that are representative of the measured quantities of
fluorescence detected on each PCR cycle, and to process
10 these signals in order to determine an initial size for
the population of interest prior to the first cycle, by
implementing the method of the invention.
Typically, the processor unit comprises the
following:
15 an acquisition card 21 connected to the
measurement means 10;
= working memory 25 (e.g. of the random access
memory (RAM) type) for temporary storage and processing
of the above-mentioned signals;
20 permanent memory 24 for storing the computer
program product in the meaning of the invention and for
storing the data that has been processed and that is
ready for use, e.g. in subsequent diagnosis;
= where appropriate, a reader 22 of a memory medium
25 such as a CD-ROM, for example, which may initially carry
the computer program product;
optionally a communications interface 26 for
communicating with a local or remote site (conne(--tion
28), e.g. for transmitting the processed data so as to
30 enable a diagnosis to be made remotely concerning a
patient;
= a graphics interface 27 typically connected to a
display screen 30; and
a processor 23 for managing the. interact ions
between these various items of equipment.
CA 02589129 2007-05-23
WO 2006/048337 PCT/EP2005/013021
31
The computer may also have input members such as a
keyboard 41 and/or a mouse 42 connected to the centra l
unit 20.
Nevertheless, it should be understood that in tine
meaning of the invention the installation comprisEas
overall:
a sample support SUPP, at least for the sample o f
interest;
= a first apparatus ENC for applying said successic n
of amplification reactions at least to the population f
interest in the sample of interest;
a second apparatus 10 for taking measurements
representative of the current size of the population o f
interest; and
computer means 20 suitable for receivirng
measurement signals from the second apparatus 10 and fo r
implementing all or some of the steps of the method cDf
the invention.
For this purpose, a computer program product can ]De
used for controlling the computer means. The program may
be stored in a memory of the processor unit 20 or on a
removable memory medium (CD-ROM etc.) and suitable fc>r
co-operating with the reader of the processor unit. T1ie
computer program in the meaning of the invention then
contains instructions for implementing all or some of the
steps of the method of the invention. For example, the
algorithm of the program may be represented by a flow
chart equivalent to the diagram of Figure 9.