Note: Descriptions are shown in the official language in which they were submitted.
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
1
Optimisation d'une réaction chimique
dans un réacteur ouvert du type à plaques
La présente invention concerne un procédé d'optimisation d'une
réaction chimique dans un réacteur ouvert du type à plaques constitué d'un
empilement de plaques délimitant entre elles au moins un bloc comprenant
une chambre de réaction et deux chambres latérales de circulation d'un
fluide utilitaire d'échange de chaleur.
On cherche actuellement à optimiser le déroulement et à améliorer
le rendement des réactions chimiques en général, qui sont réalisées le plus
souvent dans des réacteurs du type batch , c'est à dire des réacteurs à
fonctionnement discontinu, comprenant des cuves dans lesquelles on
dépose et on mélange des quantités déterminées de réactifs que l'on
soumet ensuite à des conditions optimales d'environnement (pression,
température, pH, etc.) pour favoriser les réactions.
Un inconvénient majeur de ces réacteurs est la difficulté d'évacuer la
chaleur produite par une réaction, ce qui limite les possibilités de contrôle
et d'optimisation de la réaction.
La présente invention a notamment pour but d'apporter une solution
simple et efficace au côntrôle et à l'optimisation des réactions chimiques
grâce à l'optimisation d'un réacteur du type ouvert qui ne présente pas les
inconvénients précités des réacteurs discontinus ou réacteurs du type
batch .
Elle propose à cet effet un procédé d'optimisation d'une réaction
chimique dans un réacteur, caractérisé en ce qu'il consiste à:
- utiliser un réacteur ouvert constitué d'un empilement de plaques délimitant
entre elles au moins un bloc comprenant une chambre de réaction formée
entre deux chambres latérales d'échange thermique à circulation de fluide
utilitaire d'échange de chaleur, des moyens d'alimentation de la chambre
de réaction par un débit continu d'un ou de plusieurs réactifs et des moyens
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
2
d'alimentation des deux chambres latérales par un débit continu de fluide
utilitaire ;
- établir un modèle dynamique du réacteur pour une réaction donnée, à
partir d'une modélisation de la chambre de réaction et des échanges
thermiques entre cette chambre de réaction et les chambres latérales à
circulation de fluide utilitaire, ce modèle dynamique comprenant des
équations de bilans de matière et d'énergie et de contraintes ;
- appliquer un outil logiciel d'intégration à ce modèle dynamique pour
résoudre les équations précitées ;
- déterminer et optimiser un ensemble de paramètres dimensionnels et/ou
fonctionnels du réacteur à partir d'évaluations des objectifs à atteindre, des
contraintes à respecter, et des données variables du réacteur et/ou de la
réaction ;
- construire un réacteur à plaques du type précité conforme audit ensemble
optimisé de paramètres ; et
- faire des mesures de paramètres physiques tels que la température et la
pression lors de la mise en oeuvre de ladite réaction dans le réacteur
construit, pour valider son fonctionnement.
L'utilisation d'un réacteur continu ou ouvert comprenant une
superposition de plaques délimitant au moins une chambre de réaction
entre deux chambres de circulation de fluide utilitaire, permet de résoudre
les problèmes de dissipation de chaleur constatés dans les réacteurs
discontinus ou fermés du type batch , par une sélection appropriée des
températures et débits du ou des fluides utilitaires, qui circulent de part et
d'autre de la chambre de réaction, et également par la sélection des sens
de passage de ces fluides (à co-courant, à contre-courant ou à courants
croisés) par rapport au sens de passage du fluide réactionnel dans la
chambre de réaction.
Cela permet aussi d'optimiser le dimensionnement ou la
configuration optimale du réacteur ainsi que le fonctionnement ou les
conditions opératoires optimales du réacteur, en fournissant des
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
3
paramètres de contrôle de la réaction chimique, et de décrire avec
précision la distribution de la température dans le réacteur.
La détermination précise de la loi de variation de la température
dans ce réacteur, qui constitue la différence essentielle entre l'invention et
les procédés connus d'optimisation des réactions dans des réacteurs
discontinus, est rendue possible par la modélisation dynamique du réacteur
pour la réaction étudiée, et par l'optimisation d'un ensemble de paramètres
dimensionnels et/ou fonctionnels du réacteur en fonction des objectifs à
atteindre et des contraintes à respecter.
Un réacteur à plaques du type précité est ensuite construit
conformément à l'ensemble de paramètres dimensionnels et/ou
fonctionnels préalablement optimisé, la réaction chimique est mise en
oruvre dans ce réacteur et des mesures expérimentales de paramètres
physiques sont faites pour vérifier l'optimisation de la réaction chimique.
Le procédé selon l'invention peut également consister, après la
construction du réacteur, à :
- établir un nouveau modèle dynamique de réacteur à partir du réacteur
construit ;
- appliquer l'outil logiciel d'intégration à ce nouveau modèle dynamique
pour résoudre les équations précitées ;
- optimiser à nouveau ledit ensemble de paramètres dimensionnels et /ou
fonctionnels du réacteur ; et
- modifier si nécessaire ledit réacteur construit, conformément au nouvel
ensemble optimisé de paramètres.
Le modèle dynamique du réacteur comprend des équations de bilan
de matière et d'énergie et des équations de contraintes, qui sont
caractéristiques du réacteur et de la réaction chimique.
Selon une autre caractéristique de l'invention, la modélisation de la
chambre de réaction comprend une décomposition de cette chambre en
cellules élémentaires successives contenant chacune un milieu fluide
parfaitement agité. Les chambres de circulation de fluide utilitaire sont de
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
4
même modélisées par décomposition en cellules élémentaires dont le
nombre est égal au nombre de cellules élémentaires de la chambre de
réaction.
La modélisation des échanges thermiques tient également compte
du sens de passage du fluide dans chaque cellule élémentaire de la
chambre de réaction par rapport au sens de passage (à co-courant, à
contre-courant ou à courants croisés) du ou des fluides utilitaires dans les
cellules élémentaires correspondantes des chambres latérales situées de
part et d'autre de cette cellule élémentaire de la chambre de réaction. Elle
comprend également des équations de bilan thermique relatives au fluide
réactionnel, aux plaques délimitant les chambres latérales d'échange
thermique, et aux fluides utilitaires circulant dans les chambres latérales,
et
des équations de bilan de matière du milieu réactionnel et des fluides
utilitaires dans les cellules élémentaires des différentes chambres.
Chaque chambre de réaction est reliée à des zones d'entrée et des
zones de sortie qui sont associées à une cellule élémentaire de la chambre
de réaction et qui sont par exemple des éléments de liaison entre les
moyens d'alimentation en réactifs et un point d'alimentation d'une chambre
de réaction, et des éléments de liaison entre un point de sortie d'une
chambre de réaction et des moyens de collecte du produit de la réaction.
Dans le cas où deux chambres de réaction sont reliées entre elles en série,
l'élément de sortie de la première chambre est confondu avec l'élément
d'entrée de la seconde chambre.
Le modèle dynamique du réacteur comprend avantageusement un
modèle des zones d'entrée et de sortie du réacteur, des zones d'entrée et
de sortie de chaque chambre de réaction et des zones de transition entre
les différents blocs du réacteur.
Le modèle dynamique offre en outre la possibilité d'un point
d'alimentation par cellule élémentaire de la chambre de réaction.
L'outil logiciel d'intégration, appliqué au système d'équations du
modèle dynamique du réacteur, permet de résoudre ces équations et de
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
simuler le comportement du réacteur appelé état du réacteur pour la
réaction chimique étudiée.
La détermination et l'optimisation des paramètres dimensionnels du
réacteur sont obtenues, pour des objectifs et des contraintes donnés, par
5 ajustement de caractéristiques variables du réacteur comprenant le nombre
de points d'alimentation dans la chambre de réaction, les sens de passage
des fluides utilitaires par rapport au milieu réactionnel, la nature et la
distribution des fluides utilitaires, le volume total de la chambre de
réaction
et/ou les volumes des chambres latérales à circulation de fluide utilitaire,
et
la détermination et l'optimisation des paramètres fonctionnels du réacteur
sont obtenues, pour des objectifs et des contraintes donnés, par
ajustement de données variables de réaction ou de paramètres opératoires
comprenant les températures, les pressions, les compositions et/ou les
débits du milieu réactionnel et du ou des fluides utilitaires.
Le procédé consiste par exemple à ajuster les débits d'alimentation
d'un ou de plusieurs réactifs dans différentes cellules élémentaires afin
d'obtenir un meilleur rendement de la réaction, et à définir des valeurs
limites des paramètres opératoires satisfaisant à des contraintes de
sécurité et/ou environnementales.
Dans le cas d'une réaction chimique en milieu homogène, le modèle
dynamique du réacteur comprend un modèle dynamique de la chambre de
réaction formé à partir d'équations de bilan de matière, de bilan
enthalpique, de bilan de pression et de contraintes de volume. Ces
équations permettent de définir l'état et les évolutions du milieu fluide dans
chaque cellule élémentaire.
Pour cela, on considère que dans les cellules élémentaires à
contenu parfaitement agité de la chambre de réaction, les grandeurs
caractéristiques (température, pression, débit, composition, etc.), les
propriétés physiques (masse volumique, viscosité, etc.) et les phénomènes
physico-chimiques (réaction, transfert de matière, etc.) sont homogènes
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
6
dans chaque cellule et les propriétés physiques des fluides utilitaires sont
homogènes et constantes pour une température donnée.
Dans le cas d'une réaction chimique en milieu diphasique (liquide-
liquide ou liquide-gaz), où le milieu réactionnel est un mélange d'une phase
continue et d'une phase dispersée, et dans le cas où le milieu réactionnel
est un mélange de deux liquides miscibles, l'état et l'évolution du milieu
réactionnel sont définis dans chaque cellule élémentaire à partir
d'équations d'estimation de la masse volumique, de la chaleur spécifique,
de la conductivité thermique et de la viscosité du milieu réactionnel, et
d'équations de bilan de matière, de bilan enthalpique, de bilan de pression
et de contraintes de volume.
On considère que dans les cellules élémentaires à contenu
parfaitement agité de la chambre de réaction, les grandeurs
caractéristiques (température, pression, débit, composition, etc.), les
propriétés physiques (masse volumique, viscosité, etc.) et les phénomènes
physico-chimiques (réaction, transfert de matière, etc.) sont homogènes
dans chaque cellule, les températures et les pressions des phases sont
identiques, on assimile le milieu réactionnel à un milieu pseudo-homogène
et les propriétés physiques des deux phases sont déterminées par des lois
d'association permettant de relier les propriétés physiques du milieu aux
propriétés de chacune des phases ainsi qu'à leurs proportions, la
répartition des phases étant supposée homogène dans chaque cellule
élémentaire.
On peut en outre appliquer au mélange de phases des règles
d'équilibre entre les deux phases en fonction de la dimension des
gouttelettes de la phase dispersée, des propriétés thermodynamiques des
phases en présence, et/ou des conditions d'écoulement.
Le diamètre de Sauter permet de déterminer la dimension des
gouttelettes de la phase dispersée. L'évolution de la taille des gouttelettes
de la phase dispersée peut en outre être suivie dans les différentes cellules
élémentaires de la chambre de réaction.
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
7
D'autres modélisations peuvent venir compléter et préciser le
modèle dynamique du réacteur, telles que :
- une modélisation du comportement hydrodynamique du réacteur faite à
partir d'études expérimentales de distribution de temps de séjour des
fluides dans les différentes parties du réacteur, et permettant de définir le
nombre de cellules élémentaires à contenu parfaitement agité ;
- une modélisation de la réaction à partir d'équations de vitesse de la
réaction, de taux de production de constituants de la réaction et de
génération de chaleur, dans chaque cellule élémentaire de la ou des
chambres de réaction ;
- une modélisation du transfert de matière, dans une réaction en milieu
diphasique, entre les deux phases du milieu réactionnel, à partir de
propriétés physiques du milieu diphasique et de la taille des gouttelettes de
la phase dispersée ;
- une modélisation du transfert thermique à partir de définitions des
coefficients de transfert thermique entre les plaques délimitant les
chambres latérales et les fluides circulant dans la chambre de réaction et
dans les chambres latérales, et d'estimations des coefficients de film du
fluide.réactionnel et du fluide utilitaire ; et
- une modélisation des pertes de charge du fluide réactionnel dans le
réacteur, faite à partir de mesures expérimentales.
Le procédé peut comprendre également une estimation des
propriétés physiques des composants du réacteur et des fluides
réactionnels et utilitaires.
Le procédé selon l'invention présente l'avantage de prédire le
comportement d'un réacteur à plaques pour des conditions opératoires
données, et permet également de définir le dimensionnement ou la
configuration optimale et le fonctionnement ou les conditions opératoires
optimales du réacteur pour une réaction ou un ensemble de réactions
donné. Ce procédé permet aussi de décrire les évolutions de ce
comportement au cours du temps, la représentation de cette évolution
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
8
offrant de nombreuses possibilités en termes de contrôle optimal du
réacteur, d'études de sécurité et de gestion des périodes transitoires non
productives.
D'autres avantages et caractéristiques de l'invention apparaîtront à
la lecture de la description suivante faite à titre d'exemple non limitatif et
en
référence aux dessins annexés dans lesquels :
- la figure 1 est une vue schématique en perspective éclatée d'un réacteur
ouvert du type à plaques utilisé dans le procédé selon l'invention ;
- la figure 2 est une vue schématique de la chambre de réaction du
réacteur de la figure 1, décomposée en cellules élémentaires ;
- la figure 3 est une vue schématique d'une cellule élémentaire de la
chambre de réaction de la figure 2;
- la figure 4 est une vue schématique d'une cellule élémentaire de réaction
associée à deux cellules élémentaires de circulation de fluide utilitaire ;
- les figures 5a, 5b et 5c sont des diagrammes illustrant les principales
étapes du procédé d'optimisation selon l'invention ;
- les figures 6 et 7 sont des graphes représentant l'influence de la
concentration et du débit des réactifs, et du débit de fluide utilitaire sur
la
température et le rendement de la réaction d'oxydation du thiosulfate de
sodium ;
- les figures 8 à 10 sont des graphes représentant l'influence du nombre et
de la disposition des points d'alimentation des réactifs sur la température
de la réaction d'hydrolyse de l'anhydride acétique ;
- les figures 11 et 12 sont des graphes représentant l'influence du débit
d'alimentation des réactifs en plusieurs points d'alimentation sur la
température et le rendement de la réaction de production du néopentyl
glycol.
On se réfère d'abord à la figure 1 qui représente schématiquement
un réacteur ouvert ou continu comprenant un empilement de plaques 20,
21, 22, 23 qui délimitent entre elles des chambres parallèles. Les plaques
21 et 22, appelées plaques de transition, délimitent entre elles une
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
9
chambre de réaction 24 comprenant un point 25a d'alimentation d'un réactif
et un ou plusieurs points 25b d'alimentation d'un autre ou de plusieurs
autres réactifs, et un point 26 de sortie *du ou des produits de la réaction.
Les plaques 20 et 23 sont des plaques adiabatiques et délimitent avec les
plaques 21, 22 une chambre latérale gauche 27 et une chambre latérale
droite 28 de circulation de fluide utilitaire d'échange de chaleur, chaque
chambre latérale 27, 28 comprenant une entrée 29 et une sortie 30 de
fluide utilitaire.
Le fluide utilitaire qui circule dans la chambre latérale gauche 27
peut être identique ou différent de celui qui circule dans la chambre latérale
droite 28, le fluide utilitaire couramment utilisé étant l'eau ou l'éthylène
glycol.
L'empilement des plaques 20, 21, 22, 23 forme un bloc de réaction
que les plaques 20 et 23 permettent d'isoler thermiquement de
l'environnement extérieur ou d'un ou de plusieurs autres blocs de réaction
montés en série avec celui-ci.
Les chambres 24, 27, 28 sont généralement équipées de moyens
déterminant les trajets de passage des fluides à l'intérieur de ces
chambres. La chambre de réaction 24 comprend par exemple des inserts
en chicane qui imposent au milieu réactionnel une circulation en zigzag à
l'intérieur de la chambre de réaction 24, comme cela est représenté aux
figures 1 et 2.
Les chambres 24, 27, 28 sont alimentées en continu par des moyens
appropriés non représentés.
Dans des conditions optimales de fonctionnement, le coefficient de
transfert thermique global d'un réacteur à plaques peut varier entre 2000 et
5000 W.m-2.K-1. Le contrôle de la température dans la chambre de réaction
24 est réalisé par exemple par une sélection appropriée de la température
et/ou du débit du ou des fluides utilitaires qui circulent de part et d'autre
de
la chambre de réaction 24, de la composition, de la température et/ou du
débit du milieu réactionnel dans la chambre de réaction, et/ou par le sens
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
de passage de fluide utilitaire dans chaque chambre latérale par rapport à
celui du milieu réactionnel dans la chambre de réaction. Un fluide utilitaire
circule à co-courant s'il circule dans les deux chambres latérales 27, 28
dans le même sens que le milieu réactionnel dans la chambre de réaction
5 24, à contre-courant s'il circule dans le sens inverse, et à courants
croisés
s'il circule dans une chambre latérale dans le même sens que le milieu
réactionnel et dans le sens inverse dans l'autre chambre latérale, comme
représenté en figure 1. Dans cet exemple, le milieu réactionnel et les
fluides utilitaires se croisent en raison de la circulation horizontale en
10 zigzag du milieu réactionnel et de la circulation verticale de fluide
utilitaire,
mais toute autre configuration de circulation peut être adoptée telle qu'une
configuration en parallèle.
Une caractéristique essentielle du procédé selon l'invention consiste
à établir un modèle dynamique de ce réacteur pour une réaction donnée.
La modélisation comprend une décomposition de la chambre de
réaction en cellules élémentaires parfaitement agitées, au moyen d'études
expérimentales de distribution de temps de séjour permettant une analyse
de l'écoulement avec la mise en évidence de volumes morts et de
passages préférentiels, et une caractérisation du mélange dans la chambre
de réaction 24.
L'analyse de la distribution de temps de séjour expérimentale permet
de la caractériser en termes de temps de séjour moyen (t ) et de variance
(62). A partir de ces caractéristiques, il est possible d'estimer le nombre de
cellules élémentaires représentatif du degré de mélange et de
l'hydrodynamique du réacteur réel. Ce nombre est calculé par exemple au
moyen de la formule suivante :
-2
N= t Z
6
En pratique, ce nombre dépend notamment du débit d'alimentation
de la chambre de réaction 24 et de la viscosité du milieu réactionnel. Le
nombre de cellules élémentaires dans le cas d'un réacteur à plaques
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
11
comprenant trois blocs de réaction est par exemple de 70 pour un milieu
réactionnel composé uniquement d'eau alimentée à un débit de 25 L.h-', de
100 pour de l'eau alimentée à 50 L.h"', de 130 pour de l'eau alimentée à 80
L.h"1 et de 25 pour un milieu réactionnel composé d'éthylène glycol
alimenté à un débit de 50 L.h"1.
Dans l'exemple des figures 1 et 2, les cellules élémentaires de la
chambre de réaction sont au nombre de 12. Ces 12 cellules sont
numérotées de 1 à 12 suivant la circulation horizontale en zig-zag du milieu
réactionnel dans la chambre de réaction 24, depuis le ou les points
d'alimentation 25a, 25b jusqu'au point de sortie 26 de cette chambre 24.
Cette circulation est imposée par les inserts précités présents dans la
chambre de réaction 24.
Les 12 cellules forment 4 rangées de 3 cellules. Un réactif est
introduit dans la chambre de réaction 24 depuis le point d'alimentation 25a
dans la cellule 1. Le milieu réactionnel passe horizontalement de la cellule
1 à la cellule 2, puis à la 3, il sort de la cellule 3 et pénètre dans la
cellule 4
située verticalement sous elle, puis passe horizontalement dans les cellules
5 et 6. Le milieu réactionnel sort de la cellule 6 et pénètre dans la cellule
7
située verticalement sous elle, puis passe horizontalement dans les cellules
8 et 9. Enfin, le milieu réactionnel sort de la cellule 9 et pénètre dans la
cellule 10 située verticalement sous elle, puis passe horizontalement dans
les cellules 11 et 12 pour sortir de la chambre de réaction 24 par le point
26. D'autres points d'alimentation 25b d'un ou de plusieurs autres réactifs
peuvent en outre être prévus sur la première cellule ou d'autres cellules
élémentaires que la première.
En variante, le milieu réactionnel peut circuler dans la chambre de
réaction 24 en parallèle par rapport au fluide utilitaire circulant dans les
chambres latérales 27, 28.
De même, les chambres latérales 27 et 28 sont décomposées en
cellules élémentaires de circulation de fluide utilitaire, afin que chaque
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
12
cellule élémentaire de réaction soit située entre deux cellules élémentaires
de circulation dé fluide utilitaire.
En figure 1, les chambres latérales gauche 27 et droite 28
comprennent respectivement des séries A, B, C, D, E, F, G, H, I, J, K, L et
A', B', C', D', E', F, G', H', I', J', K', L' de cellules élémentaires de
circulation
de fluide utilitaire. L'ordre alphabétique des lettres des cellules tient
compte
de l'ordre croissant des chiffres des cellules élémentaires de réaction, et
non pas de la circulation de fluide utilitaire qui est de haut en bas dans la
chambre de gauche 27 et de bas en haut dans la chambre de droite 28.
La décomposition de la chambre de réaction 24 en cellules
élémentaires permet de déterminer pour le milieu réactionnel circulant dans
chaque cellule élémentaire de réaction, l'influence thermique du fluide
utilitaire circulant dans les deux cellules élémentaires latérales
correspondantes, à travers les deux plaques 21, 22 de transition délimitant
la chambre de réaction 24. De la chaleur est par exemple échangée entre
la cellule élémentaire E de circulation de fluide utilitaire et la cellule
élémentaire de réaction 5 à travers la plaque 21 et entre la cellule
élémentaire E' de circulation de fluide utilitaire et la cellule élémentaire
de
réaction 5 à travers la plaque 22.
Dans l'exemple de réalisation représenté en figure 1, les
caractéristiques thermiques de la cellule 5 sont déterminées par celles de
la cellule située juste avant elle dans le sens de circulation du milieu
réactionnel, c'est-à-dire la cellule 4. De la même façon, les caractéristiques
thermiques des cellules E et E' sont déterminées respectivement par celles
des cellules B et H', situées avant E et E' dans le sens de circulation du
fluide utilitaire.
Les cellules élémentaires de réaction sont considérées comme des
réacteurs agités continus, ce qui permet de généraliser les équations
caractéristiques et de bilan du réacteur et de la réaction chimique du
modèle mathématique à un nombre d'équations qui est fonction du nombre
de cellules élémentaires de réaction, et qui a pour expression :
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
13
n = [nombre de cellules] * (nombre d'équations par cellule)
Le nombre d'équations du modèle mathématique est également
fonction du nombre de zones d'utilité dans les chambres de circulation de
fluide utilitaire. On entend par zone d'utilité, une partie de chambre de
circulation de fluide utilitaire qui comprend ses propres points
d'alimentation
et de sortie de fluide utilitaire. Une chambre de circulation de fluide
utilitaire
qui comprend trois zones d'utilité présente donc trois points d'alimentation
et trois points de sortie de fluide utilitaire. Le nombre d'équations du
modèle
mathématique a alors pour expression :
n=[nombNe de cellatles] *(nombre d'équations par cellule) +
(nombre d'équations par zone) *[noinbre de zones d'utilité]
En fonction du modèle considéré, milieu homogène ou milieu
diphasique, ce nombre d'équations n'est pas le même, le nombre total
d'équations du modèle étant défini à partir des équations suivantes :
- Modèle homogène :
n - [(ncelll block + 3) x nblock + 1] X(16 + ncons )+ 3 x nzone / block x
nblock - Modèle diphasique
n - [(ncll / blok + 3) x nblock + 1] X(21 + 2 x ncons ) + 3%< nzone/ block
xnblock dans lesquels nC015 est le nombre de constituants de la réaction
chimique,
nbio,k le nombre de blocs de réaction, nZoõeibiock le nombre de zones
d'utilité
par bloc de réaction et nCeu/biock le nombre de cellules élémentaires par bloc
de réaction.
Pour une réaction chimique en milieu homogène ou monophasique,
les équations caractéristiques sont par exemple :
- pour chaque cellule élémentaire de la chambre de réaction :
un bilan de matière global, des bilans de matière partiels, un bilan
enthalpique, un bilan de pression, un modèle de volume, un modèle
d'enthalpie molaire, une contrainte de volume, un modèle de volume
molaire, un bilan thermique de l'environnement thermique, des bilans
thermiques des plaques de transition, des bilans thermiques des fluides
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
14
utilitaires, des bilans thermiques des plaques adiabatiques et des bilans de
matière des fluides utilitaires ;
- pour chaque zone d'utilité de circulation de fluide utilitaire :
des contraintes de température des fluides utilitaires et une contrainte de
débit de fluides utilitaires.
Pour une réaction chimique en milieu diphasique ou hétérogène, les
équations caractéristiques sont par exemple :
- pour chaque cellule élémentaire de la chambre de réaction :
des bilans de matière globaux de la phase continue et de la phase
dispersée, des bilans de matière partiels de la phase continue et de la
phase dispersée, un bilan enthalpique, un bilan de pression, des modèles
de volume de la phase continue et de la phase dispersée, des modèles
d'enthalpie molaire de la phase continue et de la phase dispersée, des
modèles de volume molaire de la phase continue et de la phase dispersée,
des contraintes de volume de la phase dispersée et de la phase continue,
un bilan thermique de l'environnement thermique, des bilans thermiques
des plaques de transition, des bilans thermiques des fluides utilitaires, des
bilans thermiques des plaques adiabatiques et des bilans de matières des
fluides utilitaires ;
- pour chaque zone d'utilité de circulation de fluide utilitaire :
des contraintes de température des fluides utilitaires et une contrainte de
débit des fluides utilitaires.
Le modèle dynamique du réacteur selon l'invention est établi à partir
d'un modèle dynamique de la chambre de réaction et d'un modèle
dynamique des échanges thermiques, chaque modèle dynamique
comprenant des équations rapportées à une cellule élémentaire de réaction
5, schématiquement représentée en figure 3 par un rectangle.
Les flèches 32 et 33 représentent respectivement le sens de
circulation du milieu réactionnel dans la cellule élémentaire 5 de la chambre
de réaction 24, et du fluide utilitaire dans les cellules latérales
élémentaires
E et E' des chambres latérales 27, 28, le sens de passage du fluide
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
utilitaire dans les deux chambres 27, 28 étant dans cet exemple à co-
courant par rapport à la circulation du milieu réactionnel dans la chambre
de réaction 24, contrairement à la figure 1.
On définit par les indices p et u respectivement le milieu réactionnel
5 et le fluide utilitaire. Fp représente le débit molaire du milieu
réactionnel
dans une cellule élémentaire en mol.s"1, Tp et Tu respectivement la
température du milieu réactionnel et de fluide utilitaire dans leur cellule
élémentaire en K, Hp l'enthalpie molaire du milieu réactionnel dans une
cellule élémentaire en J.mol-1, Vp le volume d'une cellule élémentaire de
10 réaction en m3, up le nombre de moles dans le milieu réactionnel dans une
cellule élémentaire et x la fraction molaire d'un réactif ou d'un constituant
(i)
dans une cellule élémentaire, les exposants k-1 et k indiquant le numéro de
la cellule élémentaire de réaction (1 à 12 pour l'exemple de réalisation de la
chambre de réaction 24 des figures 1 et 2) ou la lettre de la cellule
15 élémentaire de circulation de fluide utilitaire (A à L et A' à L' pour les
chambres gauche 27 et droite 28 de la figure 1).
Si on considère que dans les cellules élémentaires à contenu
parfaitement agité de la chambre de réaction 24, la réaction chimique est
réalisée dans un milieu homogène monophasique liquide dans lequel on
peut appliquer la loi d'Arrhenius, le modèle dynamique de la chambre de
réaction comprend par exemple les équations suivantes :
- équation de bilan de masse ou de matière global du milieu réactionnel
dans une cellule élémentaire (en mol.s-1)
k
G~Zfp = Ff'k +Fk-1 -Fk +,ànk XVk
dt P P P P p
E
avec An p=, Anp,% , Ann,l at,.i yj et rj = k~ exp( R~ k)~ (Cp,i
~ ~
- équation de bilan de masse ou de matière partiel des constituants (i) du
milieu réactionnel dans une cellule élémentaire (en moi.s 1)
d(Zfp X xpi) - fk fk k 1 k 1 k k k k
-F~ xp~ +Fp-xP_; -Fpxp;+AnpXV~
dt
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
16
- équation de bilan de pression du milieu réactionnel dans une cellule
élémentaire (en Pa) :
Pk = Pk-1 - Apk .
P P P
- équation de modèle de volume du milieu réactionnel dans une cellule
élémentaire (en m) :
Vk -mVk =0 avec ï72V =Zlk XVn~I'k
P P P P P
- équation d'enthalpie molaire du milieu réactionnel dans une cellule
élémentaire (en J.mol-') :
Hp -mHp =0
- contrainte de volume ou équation de débit molaire du milieu réactionnel
dans une cellule élémentaire (en m3 ou moi.s'1) :
Fp = 0 pendant la phase de remplissage de toutes les cellules
Vi cell
élémentaires de réaction puis u p- Vn~l k= 0 ~ Vp = Vicell une fois les
P
cellules remplies ;
dans lesquelles Ff est le débit d'alimentation en mol.s"1, An représente la
vitesse de production en mol.m-3.s 1 , a le coefficient stoechiométrique, r la
vitesse de réaction en mol.m-3.s"1 , k le facteur pré-exponentiel, Ea
l'énergie
d'activation en J.moi-1, R la constante des gaz parfaits, C la concentration
d'un réactif en mol.m-3, xf la fraction molaire dans le débit d'alimentation,
V
le volume en m3, mV et mH le modèle de volume et le modèle d'enthalpie
en m3 et en J.mol"1, respectivement, Vml le volume molaire en m3.mol-1,
l'exposant cell désigne la cellule physique, l'exposant P l'ordre de réaction,
l'indice j le numéro de la réaction, l'indice i le constituant considéré, t le
temps en s, T la température en K, P la pression, et AP la perte de charge
en Pa qui est définie par l'équation suivante :
Ap -4fL 1P vz
dl, 2
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
17
dans laquelle le facteur de frottement ou de Fanning f est donné par
f= 5.0464 Re-0.1321 pour un écoulement laminaire (nombre de Reynolds Re
< 2200) du milieu réactionnel dans la cellule élémentaire de réaction ou
f= 2.17347 Re-0.12316 pour un écoulement turbulent (Re > 2200) ;
L étant la longueur du parcours du milieu réactionnel dans la chambre de
réaction 24 en m, p la densité du milieu réactionnel en kg.m"3, v la vitesse
du milieu réactionnel en m.s"1 et dh le diamètre hydraulique équivalent d'une
cellule élémentaire de réaction en m.
Si on considère que le réacteur à plaques est constitué d'une
succession de réacteurs agités continus et que les propriétés physiques du
fluide utilitaire sont constantes et homogènes pour une température
donnée, le modèle dynamique de fluide utilitaire comprend par exemple les
équations suivantes :
- équation de continuité de débit de fluide utilitaire (en m3.s 1) :
F=lõ = F atr: ;
- équation de continuité de température de fluide utilitaire (en K) :
nc
Y, T,t
Tol,t = r_õc-nc,=+l
u 1'lCY'
dans lesquelles les exposants in et out désignent respectivement l'entrée et
la sortie de la chambre de circulation de fluide utilitaire, ncr désigne le
nombre de cellule par rangée de cellules dans la chambre de circulation de
fluide utilitaire (en figure 1, ncr est égal à trois pour les chambres 27 et
28),
et nc désigne la dernière cellule dans la chambre de circulation de fluide
utilitaire (en figure 1, dans la chambre 27, nc désigne L, nc-1 désigne K et
nc-2 désigne J, et dans la chambre 28, nc désigne A', nc-1 désigne B' et
nc-2 désigne C').
Le modèle dynamique comprend également un modèle de
comportement du ou des réactifs dans l'élément de liaison 34 (figure 2)
entre les moyens d'alimentation des réactifs et le point d'alimentation 25a
sur la cellule 1, et un modèle de comportement du milieu réactionnel dans
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
18
l'élément de liaison 35 entre le point de sortie 26 sur la cellule 12 et les
moyens de collecte des produits de la réaction ou un point d'alimentation
ou d'entrée sur une cellule d'une deuxième chambre de réaction non
représentée (deuxième bloc de réaction). La prise en compte des éléments
de liaison 34, 35 dans la modélisation dynamique du réacteur à plaques est
importante car le volume cumulé de ces éléments n'est pas négligeable par
rapport au volume de la chambre de réaction 24, et peut avoir une
influence sur le rendement de la réaction chimique. Par ailleurs, dans ces
éléments de liaison, les échanges thermiques sont limités avec les fluides
utilitaires.
Plusieurs éléments du réacteur à plaques participent aux échanges
thermiques, tels que les plaques de transition 21, 22, les chambres de
circulation de fluide utilitaire 27, 28, les plaques adiabatiques 20, 23 et
l'environnement thermique du milieu réactionnel (présence d'inserts dans la
chambre de réaction 24).
Le modèle des échanges thermiques du milieu réactionnel dans les
cellules élémentaires de réaction comprend des équations caractéristiques
rapportées à une cellule élémentaire de réaction 5 schématiquement
représentée en figure 4 par un rectangle qui est délimitée par les deux
plaques 21 et 22, et deux cellules E, E' latérales de circulation de fluide
utilitaire délimitées respectivement par les plaques 20, 21 et 22, 23 en
figure 1. Les flèches 32 et 33 représentent respectivement le sens de
circulation du milieu réactionnel dans la cellule élémentaire 5 de la chambre
de réaction 24 et de fluide utilitaire dans les cellules latérales
élémentaires
E, E' des chambres latérales 27, 28, le sens de passage de fluide utilitaire
dans les deux chambres 27, 28 étant à co-courant par rapport à la
circulation du milieu réactionnel dans la chambre de réaction 24,
contrairement à la figure 1.
La température de fluide utilitaire dans une cellule élémentaire
latérale dépend de celle de la cellule élémentaire latérale précédente dans
le sens d'écoulement de fluide utilitaire et également de la présence de
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
19
zones d'utilité dans le bloc de réaction. On peut ainsi représenter toutes les
configurations thermiques envisageables pour les différents sens de
passage de fluide utilitaire par rapport au milieu réactionnel.
On définit par les indices uL et uR, les fluides utilitaires
respectivement dans la chambre gauche 27 et dans la chambre droite 28,
les autres désignations et représentations étant les mêmes que
précédemment décrites.
Si on considère que les propriétés physiques des plaques de
transition et adiabatiques et du fluide utilitaire sont constantes pour une
cellule élémentaire à une température donnée et que la température de
chaque plaque est calculée au milieu de la paroi, le modèle des échanges
thermiques du milieu réactionnel comprend par exemple les équations
suivantes :
- équation de bilan énergétique du milieu réactionnel dans une cellule
élémentaire de réaction (en J.s-1) :
d(Uk px HP k)
k-1 k 1 k k k k k k k k k k k k
=Fp Hp- -F
dt pHp +OqP xVp +hpuLAp(Tu~ Tp )+IZpuRAp(TR -Tp )
k
avec hk = 1 hk = 1 Ak = Acell x ~p
P,=Q e k ' P' tix ek P Vicell
1 puL 1 1 puR 1
k7+ k + k) ( k)+~] k + k7)
i'luL ~ puL h p /ZuR /~, p:[R /Z p
et Oq p(OHrj x ~k
J.
- équation de bilan thermique de fluide utilitaire dans la cellule latérale de
la
chambre gauche 27 (en J.s-1, la même équation est utilisée pour la cellule
latérale de la chambre droite 28) :
k
pkLV~Cp ~ ~ =F~pkLCp ~(TL-' -T~)+ht~PAn(Tn -Ti) ;
- équation de bilan thermique de la plaque 21 disposée entre une cellule
élémentaire de réaction et la cellule latérale de la chambre gauche 27 (en
J.s"1, la même équation est utilisée pour la plaque 22 disposée entre une
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
cellule élémentaire de réaction et la cellule latérale de la chambre droite
28) :
k
pk Vk C1Uk dTpu' = hk Ak ~T k-T k~-I- hk Acell ~Tk -Tk ~
Puc P='L Put dt Puc,P P P Pi~t Pi~t,ut ut Put
t[L uL k 1 '
avec hpuL,P k 1 et hpk
2 put 1 / E puL 1
~ k + k~ l k + k)
2% puL h p 2 pua huL
5 dans lesquelles Fp et FU représentent respectivement le débit volumique du
milieu réactionnel en mol.s'1 et de fluide utilitaire en m3.s-1 , e
l'épaisseur
des plaques 21, 22 délimitant la chambre de réaction 24 en m, a, la
conductivité thermique en J.s"l.m"l.K-', h le coefficient de transfert
thermique en J.s"l.m'2.K-1, T la température en K, Cp la chaleur spécifique
10 du milieu en J.kg-l.K-1, p la masse volumique du milieu en kg.m-3, Aq la
chaleur générée par les réactions en J.m-3.s-1, OHr la chaleur molaire de
réaction en J.mol-1, A l'aire d'échange thermique en m2, et les indices PUL et
PUR désignent respectivement la plaque 21 entre la chambre de réaction 24
et la chambre gauche 27 et la plaque 22 entre la chambre de réaction 24 et
15 la chambre droite 28.
Le modèle précité des échanges thermiques est complété pour
inclure l'inertie thermique du réacteur à plaques. Le modèle d'inertie
thermique permet de tenir compte de la structure et de la composition des
différents éléments du réacteur à plaques. Il comprend par exemple les
20 équations suivantes, qui diffèrent des équations précédentes en ce qu'elles
prennent en compte l'environnement thermique des différents fluides :
- équation de bilan énergétique de l'environnement du milieu réactionnel
dans une cellule élémentaire de réaction (en J.s 1) :
d(llp X Hp)
=Fp'kH~'k+Fp-1H~-1--FpHp+AL~pXVpi-I1Y.P tflp(TpuL-Tp)
L~t
k kP k k) k( k k)
+'hP,YuRApITp,,R -Tp +hp~ePAp TcP -Tp
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
21
- équation de bilan thermique de l'environnement de fluide utilitaire dans la
cellule latérale de la chambre gauche 27 (en J.s"1, la même équation est
utilisée pour la cellule latérale de la chambre droite 28)
k
PkLVLCp L d~'L =FiPuLCP ~(Ti-' -TL)
+hk Aceu Tk -Tk +hk Acen 7-k -Z,k
p1IL,uL ( ptty aL ) uteteõy ~ te,ry !L )
- équation de bilan thermique de l'environnement du milieu réactionnel
dans une cellule élémentaire de réaction (en J.s 1)
k
k k k dTrea _ k k k k
PreP Vrep CPre, dt hP,reP Ap (Tp -T,ep
- équation de bilan thermique de l'environnement de la plaque adiabatique
20 de la chambre gauche 27 (en J.s'1, la même équation est utilisée pour la
plaque adiabatique 23 de la chambre droite 28) :
k
dTte
P eõy Vi~,y C!~ eõy dt y h' Lk ,reõy Ap k (Ti Tte y)
dans lesquelles les coefficients de transfert thermique ont pour
expression (en J.m-2.K-'.s"1):
/I k 1 k_ 1 k 1 k 1
P,PIry e P,Ptra 5 hp1eP eP,+eP e ylp,ry,fry = epvy,}ry et /Zuy1ey
1 +
1+ 1+ 1+~try,teõy
l2P ~P,P+ry r'P ~P.reP htry ~ Pxy,rry hay ~ry,teõy
dans lesquelles les indices tep et teu désignent respectivement
l'environnement thermique du milieu réactionnel et du fluide utilitaire, et Hf
l'enthalpie molaire du débit d'alimentation en J.mol"1.
Les échanges thermiques entre le milieu réactionnel et les fluides
utilitaires ont été pris en compte séparément pour chaque plaque de
transition 21, 22, afin d'inclure l'inertie thermique due à ces plaques (par
exemple en acier inoxydable) dans le modèle dynamique.
L'équation de bilan thermique de l'environnement du milieu
réactionnel dans la cellule élémentaire de réaction, qui dépend de la
température de l'environnement thermique du milieu réactionnel, a permis
de prendre en compte l'inertie thermique due à la structure de la chambre
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
22
de réaction 24 et aux inserts (par exemple en polyétheréthercétone)
présents dans cette chambre. Pour une cellule élémentaire donnée, la
surface de transfert thermique et la masse de cet environnement thermique
sont calculées à partir des caractéristiques géométriques des inserts et de
la structure de la chambre de réaction 24.
Les équations de bilan thermique de l'environnement des fluides
utilitaires dans les cellules élémentaires des chambres latérales gauche 27
et droite 28, qui dépendent de la température de l'environnement thermique
des fluides utilitaires, ont permis de prendre en compte l'inertie thermique
due aux plaques adiabatiques 20 et 23 (par exemple en acier inoxydable)
dans le modèle dynamique. Les caractéristiques de l'environnement
thermique (surface de transfert thermique, masse) sont calculées à partir
des caractéristiques géométriques de ces plaques adiabatiques.
Pour une réaction chimique réalisée en milieu diphasique, le modèle
dynamique du réacteur comprend toutes les équations caractéristiques et
de bilan (énergétique, thermique, de masse, etc.) précitées établies pour
chaque phase, la phase continue étant liquide et la phase dispersée étant
liquide ou gaz. Les modèles dynamiques du milieu réactionnel dans la
chambre de réaction 24, des fluides utilitaires dans les chambres latérales
27, 28, de comportement du milieu réactionnel dans les éléments d'entrée
34 et de sortie 35 de la ou des chambres de réaction 24, des pertes de
charge, des échanges thermique du milieu réactionnel dans les cellules
élémentaires 1 à 12 et de l'inertie thermique du réacteur, sont adaptés pour
l'établissement du modèle dynamique d'un réacteur ouvert du type à
plaques pour une réaction en milieu diphasique donnée.
Pour cela, les températures et les pressions dans chacune des
phases sont considérées comme identiques et on assimile le milieu
réactionnel à un milieu pseudo-homogène dont les propriétés physiques du
milieu diphasique correspondant sont déterminées par des lois
d'association qui relient les propriétés physiques du milieu diphasique aux
propriétés de chacune des phases ainsi qu'à leurs proportions respectives,
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
23
la répartition des phases étant supposée homogène dans chaque cellule
élémentaire. Des exemples de lois d'association sont présentés ci-
dessous :
- estimation de la masse volumique du milieu diphasique
1 nrM; X 1 .
p m Pr
- estimation de la chaleur spécifique du milieu diphasique
Cla = 1 Yln;M1Cpl
m
- estimation de la conductivité thermique du milieu diphasique
1
m
- estimation de la viscosité du milieu diphasique
fu 1/3 = 1 1 1/3
niM~,ur m
dans lesquelles n; représente le nombre de mole de la phase en mol, M; la
masse molaire de la phase en kg.moi-1, m la masse totale du milieu
diphasique en kg, i l'indice de la phase continue ou dispersée, 1 la
conductivité thermique du milieu en J.m-1.s 1.K"1 et la viscosité du milieu
en Pa.s.
La précision du modèle dynamique du réacteur pour une réaction en
milieu diphasique est basée sur la stabilité du milieu réactionnel et donc de
l'équilibre entre les deux phases. Les règles d'équilibre utilisées dans le
modèle mathématique sont fonction de la dimension des gouttelettes de la
phase dispersée dans la phase continue. La dimension des gouttelettes et
leur distribution sont déterminées au moyen d'un outil logiciel d'évaluation
de la population des gouttelettes.
L'outil logiciel d'évaluation de la population permet de prédire
l'évolution au cours du temps d'une distribution de tailles de gouttelettes
initiale et donc par conséquent du diamètre de Sauter dans les différentes
cellules élémentaires de réaction de la chambre 24 du réacteur à plaques.
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
24
Cette évolution dépend des vitesses d'apparition et de disparition des
gouttelettes, qui sont directement liés aux phénomènes de coalescence et
de rupture. Les phénomènes de coalescence et de rupture sont introduits
dans le programme à partir de corrélations faisant appel aux propriétés
physiques et de transport du milieu diphasique.
La modélisation du transfert de matière repose sur l'hypothèse que
la phase dispersée se présente sous la forme de gouttelettes sphériques
dont le diamètre moyen est le diamètre de Sauter. Le transfert de matière
entre les deux phases est modélisé à partir de la théorie du double film de
Whitman.
Dans le modèle dynamique du procédé d'optimisation selon
l'invention, les caractéristiques de transfert de masse sont calculées pour
chaque cellule élémentaire de réaction. Grâce à des corrélations de
transfert de masse, toutes les caractéristiques de transfert de masse
(coefficient de transfert de masse, surface interfaciale, solubilité) sont
reliées aux propriétés physiques d'un milieu diphasique liquide-liquide et au
diamètre de Sauter. En conséquence, pour un milieu diphasique liquide-
liquide donnée, une représentation précise du comportement du réacteur à
plaques nécessite seulement une estimation correcte du diamètre de
Sauter pour chaque cellule élémentaire de la chambre de réaction.
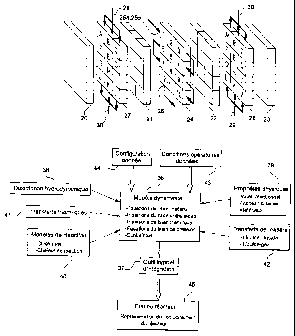
On se réfère désormais à la figure 5a qui est un diagramme illustrant
les étapes essentielles du procédé d'optimisation selon l'invention, dans
laquelle le modèle dynamique 36 du réacteur à plaques comprend une
pluralité d'équations caractéristiques et de bilan du réacteur telles que
décrites précédemment.
Un outil logiciel d'intégration 37 est utilisé pour simuler le
comportement du réacteur à plaques à partir du modèle dynamique du
réacteur pour une réaction donnée. Cet outil permet de résoudre les
systèmes mixtes d'équations algébriques et différentielles du modèle
dynamique, par couplage avec une base de données qui comprend la
description hydrodynamique du réacteur 38, les propriétés physiques 39 du
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
milieu réactionnel, du ou des fluides utilitaires et des matériaux des
composants du réacteur (inserts, plaques,...), les modèles cinétiques et de
chaleur de réaction de la réaction chimique 40, les transferts thermiques 41
entre les différents fluides, et les transferts de matière 42 liquide-liquide
ou
5 liquide-gaz pour les réactions en milieu diphasique.
De nombreux paramètres ou entrées qui interviennent dans les
différents modèles sont nécessaires à l'outil pour l'intégration du modèle
dynamique. Ces paramètres comprennent les conditions opératoires 43 de
la réaction tels que le nombre de réactions, le nombre de réactifs, la nature
10 des réactifs, leur débit, leur température, leur pression, leur durée
d'alimentation, les caractéristiques des réactions, les coefficients
stoechiométriques, les ordres réactionnels, le facteur préexponentiel des
constantes de vitesse, les énergies d'activation, et les débits et les
températures des fluides utilitaires, un descriptif d'une configuration de
15 base 44 du réacteur comprenant par exemple le nombre de cellules
élémentaires par bloc de réaction, le nombre de cellules élémentaires par
rangées, le nombre de blocs de réaction, le nombre de zones d'utilité par
bloc de réaction, les dimensions du réacteur à plaques, la température du
milieu extérieur, les aires d'échange thermique, le nombre de plaques, leur
20 épaisseur, leur masse volumique, leur capacité calorifique, leur
conductivité
thermique, les dimensions des inserts, leur masse volumique, leur capacité
calorifique, et la nature des fluides utilitaires, et d'autres paramètres
d'intégration tels que les tolérances sur les erreurs absolues ou le temps
final de l'intégration.
25 L'homme du métier connaît ce genre d'outil et de base de données.
La base de donnée est par exemple Bipphy . L'outil logiciel d'intégration
est par exemple DISCo, capable de résoudre des modèles dynamiques
avec plus de 5000 équations caractéristiques et de bilan avec une grande
rapidité et précision.
DISCo (Do Integrate by Software Components) est un outil
d'intégration de systèmes d'équations algébro-différentielles basé sur la
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
26
méthode de Gear de différentiation rétrograde selon un schéma de
prédicteur-correcteur. Cet outil présente de nombreux avantages tels qu'un
traitement global du système, sans discrimination entre équations ou
variables, la possibilité d'intégrer au système de base des équations et
donc des variables supplémentaires, offrant ainsi une grande flexibilité au
modèle mathématique, des procédures automatiques de détection des
évènements et de calcul de conditions initiales cohérentes, particulièrement
utiles dans la recherche et la gestion d'évènements (procédure de
démarrage, dynamiques) et la possibilité d'un traitement du système par
matrice creuse, ce qui conduit à une réduction importante du temps de
calcul.
L'outil logiciel d'intégration 37 permet de simuler le comportement du
réacteur chimique appelé état du réacteur 45 pour une réaction
chimique donnée. Cette simulation permet par exemple de prévoir le
rendement de la réaction chimique, l'évolution de la température au cours
de la réaction, etc.
En figure 5b, l'opérateur cherche d'abord à définir un
dimensionnement ou une configuration optimale du réacteur 46. Pour cela,
il détermine ou évalue le ou les objectif(s) 47 à atteindre tels que
l'amélioration de la productivité (rendement de la réaction), le respect de
l'environnement (quantité de rejets faibles), ou un coût réduit, les
contraintes 48 à respecter qui peuvent concerner la sécurité par exemple
avec une température maximale du milieu réactionnel à ne pas dépasser,
la productivité ou la rentabilité avec des quantités maximales ou minimales
de réactifs prédéterminées, ou l'environnement avec une limitation des
rejets toxiques ou néfastes ou difficilement recyclables ou biodégradables,
et les caractéristiques variables 49 de structure du réacteur .
Ces caractéristiques variables 49 comprennent par exemple le
nombre de blocs de réaction, le nombre de zones d'utilité par bloc, le
nombre et la position des points d'alimentation, les dimensions des
chambres de réaction, le sens de passage à co-couran't, contre courant ou
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
27
courants croisés des fluides utilitaires par rapport à la circulation du
milieu
réactionnel dans la chambre de réaction, et le nombre, la nature et la
géométrie des inserts dans la chambre de réaction.
En variante, l'objectif à atteindre peut être une fonction
mathématique comprenant plusieurs critères quantitatifs. A titre d'exemple,
la fonction objectif d'une ligne de production peut être définie par rapport à
un critère de productivité et un critère environnemental, par l'équation
suivante :
f=qp.kp-qx.kX
dans laquelle qp est la quantité de produit recherché de la réaction, kp le
coût unitaire de ce produit, qx la quantité de produit non valorisable de la
réaction, et kx le coût de traitement ou d'élimination de ce produit.
L'opérateur peut également définir des variations acceptables de ces
objectifs et de ces contraintes, c'est-à-dire des marges autorisées.
Le procédé selon l'invention permet d'optimiser le dimensionnement
ou la configuration optimale 46 du réacteur à partir de l'état du réacteur 45
précédemment défini, des conditions opératoires 43 précitées et de ces
objectifs 47, contraintes 48 et variables 49. L'optimisation est obtenue par
une pluralité de simulations 50 successives qui permettent d'atteindre le
plus possible d'objectifs ou de fonctions objectifs en respectant les
contraintes, voire les marges autorisées des objectifs et des contraintes, et
en agissant sur toutes les caractéristiques variables de structure du
réacteur à plaques.
L'optimisation du dimensionnement du réacteur est réalisée au
moyen d'un second outil logiciel 51 tel par exemple que SQP (Successive
Quadratic Programming) qui permet de définir les paramètres du
dimensionnement ou de la configuration optimale 46 du réacteur pour une
réaction donnée.
En figure 5c, l'opérateur cherche ensuite à déterminer les conditions
opératoires optimales 52 pour optimiser le fonctionnement du réacteur pour
la réaction donnée. Le ou les objectif(s) 47 à atteindre et les contraintes 48
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
28
à respecter restent les mêmes que lors de l'optimisation du
dimensionnement du réacteur. Seules les variables changent, celles-ci
étant des données variables de réaction 53 qui comprennent par exemple
le débit, la température, la pression et la composition des différents
réactifs,
l'ordre d'alimentation de ces réactifs dans la chambre de réaction 24, et le
débit et la température des fluides utilitaires.
Le procédé selon l'invention permet d'optimiser le fonctionnement du
réacteur en déterminant les conditions opératoires optimales du réacteur
pour une réaction donnée, à partir du dimensionnement ou de la
configuration optimale du réacteur précédemment défini, des conditions
opératoires précitées et des objectifs, contraintes et variables précités.
L'optimisation est obtenue par une pluralité de simulations 50 successives
qui permettent d'atteindre le plus possible d'objectifs ou de fonctions
objectifs précitées en respectant les contraintes, voire les marges
autorisées des objectifs et des contraintes, et en agissant sur toutes les
données variables de réaction.
L'optimisation du fonctionnement du réacteur est également réalisée
au moyen de l'outii logiciel 51 précité. Les conditions opératoires optimales
permettent par exemple de réaliser des études comparatives en termes de
contrôle du réacteur, et de sécurité et de sensibilité de la réaction
chimique.
Des exemples d'optimisation du comportement d'un réacteur à
plaques pour un dimensionnement donné et pour une réaction donnée sont
illustrés en figures 6 à 12.
Les figures 6 et 7 sont des graphes du suivi de la réaction
d'oxydation du thiosulfate de sodium. L'axe 149 des abscisses représente
le volume de la chambre de réaction en litre. L'axe 150 des ordonnés à
gauche représente la température en degré Celsius et l'axe 151 des
ordonnés à droite représente le rendement de la, réaction sur une échelle
de 1.
La courbe 152 est l'évolution du rendement de la réaction
d'oxydation, les courbe 153, 154 et 155 sont respectivement l'évolution de
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
29
la température du milieu réactionnel, des fluides utilitaires et des plaques
délimitant la chambre de réaction.
L'oxydation du thiosulfate de sodium est réalisée par du peroxyde
d'hydrogène selon la réaction ci-dessous, les produits de la réaction étant
du trithionate de sodium, du sulfate de sodium et de l'eau.
2 NaZSzO3 + 4H202 -> NaZS3O6 + Na2SO 4 + 4H20
La réaction est très exothermique et réalisée en milieu homogène
liquide dans un réacteur à plaques comprenant trois blocs de réaction. Les
études expérimentales précitées de distribution de temps de séjour
permettent d'assimiler le réacteur à plaques à une succession de 91
cellules élémentaires, le réacteur comprenant trois blocs de réaction en
parallèle formés de 27 cellules élémentaires chacun, et séparés les uns
des autres par un élément de transition formé de 10 cellules élémentaires.
Le nombre d'équations dans le modèle dynamique du réacteur pour. cette
réaction est de 1920.
En figure 6, le milieu réactionnel est peu concentré en réactifs, le
thiosulfate de sodium est injecté à 40 L.h'1 avec une concentration de 0,62
mol.L-1, le peroxyde d'hydrogène à 10 L.h-1 avec une concentration de 1,28
mol.L-1, et les fluides utilitaires sont de l'eau à 14 C alimentée à un débit
de
1,8 m3.h'1 dans le premier bloc de réaction et de 0,9 m3.h-1 dans les deux
autres blocs de réactions.
L'opérateur fixe un unique objectif, l'amélioration du rendement de la
réaction d'oxydation, une donnée variable de réaction qui est les débits des
fluides utilitaires, et une contrainte de température du milieu réactionnel
qui
doit rester inférieure à 100 C.
En figure 7, le milieu réactionnel est plus concentré en réactif, le
thiosulfate de sodium est injecté à 40 L.h"1 avec une concentration de 0,75
mol.L"1, le peroxyde d'hydrogène à 10 L.h"1 avec une concentration de 1,59
mol.L"1, et les fluides utilitaires sont de l'eau à 14 C alimentée à un débit
de
2,3 m3.h-1 dans le premier bloc de réaction et de 1,2 m3.h"1 dans les deux
autres blocs de réactions.
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
Le procédé selon l'invention permet d'optimiser le réacteur à plaques
pour la réaction d'oxydation du thiosulfate de sodium en agissant sur des
données variables de réaction qui sont les débits des fluides utilitaires.
La réaction d'oxydation du thiosulfate de sodium est ensuite mise en
5 oruvre dans un réacteur à plaques construit pour fonctionner avec les
débits optimisés des fluides utilitaires, et des mesures de paramètres
physiques tels que la température et la pression sont réalisées lors de cette
mise en ceuvre pour valider le fonctionnement du réacteur.
En figures 6 et 7, les points en forme de losange 156 sont des
10 mesures expérimentales du rendement de la réaction, les points en forme
de carré 157 et de triangle 158 sont respectivement des mesures
expérimentales de la température du milieu réactionnel et des fluides
utilitaires.
Les résultats expérimentaux sont proches des courbes
15 correspondantes, ce qui permet de valider la simulation de cette réaction
chimique dans le réacteur à plaques et donc la précision du modèle
dynamique.
La simulation permet d'autre part de localiser précisément le pic de
température 158 en figure 7 (à plus de 90 C), qui n'apparaît pas dans les
20 mesures expérimentales à cause du petit nombre de capteurs et leur
disposition, la température maximale mesurée étant inférieure à 60 C.
Les figures 8 à 10 sont des graphes du suivi de la réaction
d'hydrolyse de l'anhydride acétique. L'axe 159 des abscisses représente le
numéro de la cellule élémentaire de réaction. Dans cet exemple de
25 réalisation, le réacteur à plaques comprend 30 cellules élémentaires
séparées en trois blocs de réaction, le passage d'une chambre de réaction
d'un bloc à la suivante étant schématiquement représenté par les lignes
verticales en pointillés 160. L'axe 161 des ordonnées représente la
température en degré Celsius. Les courbes 162, 163 et 164 sont
30 respectivement l'évolution de la température du milieu réactionnel, des
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
31
fluides utilitaires et des plaques de transition délimitant la chambre de
réaction.
L'hydrolyse de l'anhydride acétique produit de l'acide acétique selon
la réaction ci-dessous.
CH3-CO-O-CO-CH3 + H20 -~ 2 CH3-CO-OH
L'opérateur fixe un objectif de productivité maximale, une contrainte
de température du milieu réactionnel qui doit rester inférieure à 80 C, et
des caractéristiques variables de structure du réacteur qui sont le nombre
et la disposition des points d'alimentation des réactifs pour l'optimisation
du
dimensionnement du réacteur.
En figure 8, l'anhydride acétique a été entièrement injecté dans la
cellule 1 de la chambre de réaction, à une température de 30 C et un débit
de 40 L.h-1. L'eau a aussi été injectée dans la cellule 1 à une température
de 30 C et un débit de 10 L.h"1. Les fluides utilitaires ont une température
de 15 C et un débit de 10800 L.h'1 car la réaction est très exothermique.
On voit que les valeurs choisies des variables d'optimisation ne permettent
pas de respecter la contrainte de température.
En figure 9, l'anhydride acétique a été entièrement injecté dans la
cellule 1 de la chambre de réaction, à une température de 30 C et un débit
de 40 L.h"1. L'eau a été injectée dans la cellule 1(première cellule du
premier bloc), à une température de 30 C et un débit de 5 L.h"1, et dans la
cellule 11 (première cellule du deuxième bloc de réaction), à une
température de 30 C et un débit de 5 L.h"'. Les fluides utilitaires ont une
température de 15 C et un débit de 10800 L.h'1.
L'eau a donc été introduite dans la chambre de réaction en deux fois
et en deux points d'alimentation différents. Cela permet de diminuer un peu
la température maximale du milieu réactionnel qui passe de 138 C en
figure 8 à 104 C en figure 9. Le nombre et la disposition des points
d'alimentation des réactifs du réacteur ne sont toutefois pas corrects
puisque la contrainte de température n'est toujours pas respectée.
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
32
En figure 10, l'anhydride acétique a été entièrement injecté dans la
cellule 1 de la chambre de réaction, à une température de 30 C et un débit
de 40 L.h-1. L'eau a été injectée dans la cellule 1, à une température de
30 C et un débit de 3,33 L.h-', dans la cellule 11, à une température de
30 C et un débit de 3, 33 L.h"1, et dans la cellule 21 (première cellule du
troisième bloc), à une température de 30 C et un débit de 3,33 L.h"1. Les
fluides utilitaires ont une température de 15 C et un débit de 10800 L.h-1.
L'eau a ici été introduite dans la chambre de réaction en trois fois et
en trois points d'alimentation différents. Cela permet de diminuer la
température maximale du milieu réactionnel en dessous de la contrainte de
80 C. Le procédé d'optimisation a permis d'identifier un dimensionnement
approprié répondant à l'objectif de productivité et respectant la contrainte
de température.
Les figures 11 et 12 sont des graphes du suivi de la réaction de
production du néopentyl glycol. L'axe 165 des abscisses représente le
volume de la chambre de réaction en litre. Dans cet exemple de réalisation,
la chambre de réaction comprend 40 cellules élémentaires séparées en
quatre blocs de 10 cellules élémentaires ayant chacune un volume de
0,035L environ. L'axe 166 des ordonnés à gauche représente la
température en degré Celsius et l'axe 167 des ordonnés à droite
représente le rendement de la réaction en pourcentage.
La courbe 168 est l'évolution du rendement de la réaction, les
courbe 169, 170 et 171 sont respectivement l'évolution de la température
du milieu réactionnel, des fluides utilitaires et des plaques délimitant la
chambre de réaction.
L'équation de production du néopentyl glycol est la suivante :
2 (Forfnaldéhyde) + (2-tnéthyl propanal) + (hydroxyde de sodiuna) --~
(néopentyl glycol) + (fornaate de sodiuna)
Aux figures 11 et 12, les lignes verticales en pointillés 172 et 173
représentent respectivement les points d'alimentation de l'hydroxyde de
sodium et du 2-méthyl propanal. L'hydroxyde de sodium est donc introduit
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
33
en une seule fois lorsque le volume de la chambre de réaction est proche
de 0,05L, ce qui correspond à la deuxième cellule de la chambre de
réaction (0,035L par cellule élémentaire), et le 2-méthyl propanal est
introduit en trois fois, dans la troisième cellule, la quinzième cellule et la
vingt-huitième cellule.
En figure 11, la réaction étant exothermique, les fluides utilitaires ont
une température de 50 C et un débit de 1,5 m3.h"1. Les réactifs sont
injectés à une température de 18 C, et le 2-méthyl propanal a une
concentration de 2 mol.kg-1 pour un débit total de 9,14 L.h-1 (trois
injections
à des débits identiques de 3,05 L.h-1 environ). Le taux de conversion atteint
est de 89,4% et la température maximale du milieu réactionnel au cours de
la réaction est 66,6 C.
L'opérateur fixe un objectif d'augmentation du rendement de la
réaction de production du néopentyl glycol, des données variables
d'optimisation du fonctionnement de la réaction qui sont les débits
d'alimentation du 2-méthyl propanal pour chaque point d'alimentation, et
une contrainte à respecter qui est une température limite du milieu
réactionnel à ne pas dépasser, qui est de 65 C.
Le résultat est représenté en figure 12, où les fluides utilitaires ont
une température de 50 C et un débit de 1,5 m3.h-1, les réactifs sont
alimentés à une température de 18 C, et le 2-méthyl propanal a une
concentration de 2 mol.kg'1 pour un débit total de 9,14 L.h"1. Les trois
injections de 2-méthyl propanal ont des débits différents : de 5,91 L.h-1 pour
la première alimentation en cellule 3, de 2,73 L.h-1 pour la deuxième
alimentation en cellule 11 et de 0,50 L.h-1 pour la troisième alimentation en
cellule 21. Le taux de conversion atteint est de 95,6% et la température
maximale du milieu réactionnel au cours de la réaction atteint 65 C et
respecte la contrainte fixée.
Le procédé d'optimisation a donc permis d'atteindre un objectif de
rendement d'une réaction et de respecter une contrainte de température en
CA 02594822 2007-07-13
WO 2006/075085 PCT/FR2006/000049
34
agissant sur des données variables de réaction qui sont les débits
d'alimentation d'un réactif en plusieurs points de la chambre de réaction.