Note: Descriptions are shown in the official language in which they were submitted.
CA 02639649 2008-09-19
Cryptography Method and System
FIELD OF INVENTION
[0001 ] The present invention relates to a method and system for protecting
electronic data and
communications.
BACKGROUND OF THE INVENTION
[0002] Electronic devices such as personal computers, servers, cellular
telephones, portable
digital assistants (PDAs), portable email devices, portable electronic storage
devices and the
like are becoming pervasive in modem society, both in business and in private
environments.
Along with the growth of such devices has been the growth of applications that
communicate
and store private, proprietary and otherwise valuable content, information and
property. To
name just a few of such applications: credit card numbers are routinely
transmitted over the
Intern.et to effect online purchases, individuals pay their bills and
manipulate their bank
accounts using online banking services, song and video rights are bought and
sold over
wireless networks, and corporations offer remote access to their internal
networks. In all of
these cases and in numerous others, it is important that communications,
access and storage of
data be secure. A truly effective data protection system is not currently
available.
[0003] One of the most commonly used encryption systems today is AES (advanced
encryption standard). Block-cipher algorithms such as DES, triple DES (or
3DES) and AES
all rely on computing difficulty to provide protection. Theoretically, none of
these
technologies can withstand a brute force attack, where the attacker simply
tries all possible
key values until he is successful (a brute force attack can also be combined
with a dictionary
attack, or other systems for reducing the number of possible tests to
perform). There are also
other more efficient attacks, such as the cache-timing attack on AES, for
example.
[0004] The disadvantages of AES are:
= it is a non-linear method which leads to the worst case, that a brute force
attack can
break the AES encryption;
= it needs periodical key refreshing to reduce the risk of being cracked.
However, each
-1-
CA 02639649 2008-09-19
process of exchanging keys presents an attacker with an opportunity to crack
the system;
= the large S-box table lookups using input-dependent indices make it
vulnerable to
cache-timing attacks which are much faster than a brute force attack. This
probably is the
biggest disadvantage of the AES. To avoid this, one could implement AES using
"Hide
Timing" which takes the worst-case constant time (each operation as slow as
memory access),
but the trade-off is very slow performance;
= it needs more than 10 rounds for encryption/decryption (slow and consumes
value
system resources); and
= the performance for decryption is worse than that for encryption.
[0005] AES also tries to solve the "key reuse" problem known in the art, in
two ways. Firstly,
because longer keys are harder to break, they enlarge the key length (128
bits, 192 bits and
256 bits). And secondly, additional processing rounds are performed, adding to
the
complexity: for a 128 bit key they use 10 rounds; a 192 bit key, 12 rounds; a
256 bit key, 14
rounds. However, these techniques increase the demand on the system resources
and simply
increase the amount of testing that must be done under a brute force attack,
by an incremental
degree.
[0006] Thus, while AES provides limited security that is useful in certain
applications (for
example, where side-channel attacks such as cache-timing attacks, as well as
brute force
attacks, cannot be applied), it does not provide acceptable overall encryption
security where
such attacks are possible.
[0007] Claude E. Shannon, a mathematician and historic leader in information
theory, has
proven that a "one-time-pad" would be the only way to offer theoretically
"perfect" secrecy.
Shannon proposed that perfect secrecy could be provided under these
conditions:
= there must be equally likely key distribution; and
= the encryption algorithm must be a 1-to-1 mapping from message to cipher by
a
unique key.
-2-
CA 02639649 2008-09-19
[0008] However, Shannon's theoretical system has such serious drawbacks that
it has never
been practically implemented. For example:
= perfectly random one-time pad keys are very difficult to provide;
= with such a system it would be necessary to communicate the one-time pad
keys ahead
of time between the parties. It is very difficult to achieve 100% secure
exchange of such keys
(even quantum key distribution cannot provide perfect key distribution without
using classical
authentication);
= key re-use allows a "running key" attack to be successful. A running key
attack is one
in which the key can be eliminated because the key XOR'd with itself yields
zero. Thus, the
encryption just becomes an English character XOR'd with some other English
character;
= there is no provision for message integrity checks, making the system
vulnerable to
"man-in-the-middle" attacks.
[0009] Because of these drawbacks, there is no practical use for the one-time-
pad system.
[0010] There is therefore a need for an alternative method of and system for
protecting
electronic data and communications.
SUMMARY OF THE INVENTION
[0011] It is an object of the invention to provide an improved method and
system for
protecting electronic data and communications.
[0012] This disclosure describes a new technology which can provide
theoretical perfect
secrecy system which can stand for brute force attack with key reusability.
[0013] In one embodiment of the invention there is provided a method of
encryption
comprising the steps of: producing a set of encryption keys, the encryption
keys defining a
multidimensional key space; generating an expanded set of encryption keys by
manipulating
the set of encryption keys using a set of equations where order of operations
must be
maintained; and encrypting data using the expanded set of encryption keys.
-3-
CA 02639649 2008-09-19
[0014] In another embodiment of the invention there is provided a method of
protection for a
long-biased message, comprising the steps of: adding a run-time IV (initial
vector) to the front
of the message; padding anything for the last block to make it as long as
other blocks; adding
an MAC block at the end of the padded message, using a shared secret of (block
length - 2)
bytes, the last two bytes holding the length of the whole message without
padding; performing
message block chaining (MBC) starting from first message block, the block
right after the IV,
the i-th message block mi being chained with the (i-l)-th chained message
block m'i-1 by using
an operation which is not exchangeable with the right-most operation of the
selected key
operator: m'i = mi op m';-l (op denotes the chaining operation); encrypting;
decrypting; and
performing MAC verification.
[0015] In an additional embodiment of the invention there is provided an
encryption system
comprising: a computing device including a visual display, a user interface,
read-only memory
and random-access memory; a plurality of servers; and a network for
interconnecting the
computing device with the plurality of servers. The plurality of servers is
operable to:
produce a set of encryption keys; generate an expanded set of encryption keys
using a set of
equations where order of operations must be maintained; encrypt data using the
expanded set
of encryption; and transmit the encrypted data to the computing device.
[0016] In a further embodiment of the invention there is provided an
encryption system
comprising: first and second computing devices including a visual display, a
user interface,
read-only memory and random-access memory; and a communication network for
interconnecting the first and second computing devices. One of the first and
second
computing devices is operable to: produce a set of encryption keys; generate
an expanded set
of encryption keys using a set of equations where order of operations must be
maintained;
encrypt data using the expanded set of encryption; and transmit the encrypted
data to the
second one of the first and second computing devices.
[0017] Other systems, methods, features and advantages of the invention will
be, or will
become, apparent to one with skill in the art upon examination of the
following figures and
detailed description. It is intended that all such additional systems,
methods, features and
-4-
CA 02639649 2008-09-19
advantages be included within this description, be within the scope of the
invention, and be
protected by the following claims.
BRIEF DESCRIPTION OF THE DRAWINGS
[0018] These and other features of the invention will become more apparent
from the
following description in which reference is made to the appended drawings
wherein:
Figure 1 presents a block diagram setting out the characteristics of the
various forms of
cryptographic protection;
Figure 2 presents a graphic representation of an exemplary two-dimensional key
operator
space (KOS) in an embodiment of the invention;
Figure 3 presents a block diagram showing the mapping of a message onto a
cipher, in an
embodiment of the invention;
Figure 4 presents a data structure diagram of an exemplary one-way
authentication process, in
an embodiment of the invention;
Figure 5 presents a process flow diagram of an exemplary one-way
authentication process, in
an embodiment of the invention;
Figure 6 presents a data structure diagram of an exemplary message encryption
process, in an
embodiment of the invention;
Figure 7 presents a table setting out the complexity of a brute force attack
on an exemplary
cipher in each selected try of a 2-dimensional key operator;
Figure 8 presents a flow chart of a method of generating an ID-based key, in
an embodiment
of the invention;
Figure 9 presents a process flow diagram of an ID-base key agreement process
in a client-
server environment, in an embodiment of the invention; and
-5-
CA 02639649 2008-09-19
Figure 10 presents a process flow diagram of an ID-base key agreement process
in a client-
server-client environment, in an embodiment of the invention.
DETAILED DESCRIPTION
[0019] One or more currently preferred embodiments have been described by way
of example.
It will be apparent to persons skilled in the art that a number of variations
and modifications
can be made without departing from the scope of the invention as defined in
the claims.
[0020] As a matter of overview, the field of cryptographic systems 110 may be
divided into
two groups as shown in the block diagram of Figure 1: theoretically perfect
systems 115
(Perfect Secrecy, or PS), and systems which are difficult to break 120.
"Difficult" systems
120 are divided into symmetric systems 125 such as RC4, DES and AES 130; and
asymmetric
systems 135 such as RSA and DH (Diffie-Hellman) 140. Symmetric systems 125 use
a single
key for both encryption and decryption, so two parties necessarily must be
informed of the
same key. The communication of the single key to both parties, as well as the
internal storage
and repeated use of the key, becomes a significant point of vulnerability.
Asymmetric systems
135 rely on a pair of keys, a public key being used for encryption and a
private key being used
for decryption. Asymmetric systems 135 are vulnerable to man-in-the-middle and
brute force
attacks (for example) without identity verification.
[0021] Theoretically perfect systems number only two: the system described
herein 145, and
the impractical but theoretically perfect "one-time-pad" 150 where each pad is
only used a
single time 155. In contrast, the system of the invention provides a "life
time pad" 160, in that
the pad (key) may be re-used without fear of being cracked.
SHANNON'S INFORMATION ENTROPY
[0022] In his 1948 paper "A Mathematical Theory of Communication", Claude E.
Shannon
introduced the concept of "entropy" - a measure of the uncertainty associated
with a random
variable. For example, if the probability of finding a bit string with length
n is p, then the
average entropy is defined as:
H = -Y-; pi logap;
-6-
CA 02639649 2008-09-19
[0023] The amount of entropy that may be contained in an n-bit message "M" may
be defined
as follows:
H(M) = -j; p;(M) logZp;(M)
[0024] Thus, message entropy is maximized where:
p;(M)=2-",i=0, 1,...,2"-1
H(M) = n bits if all n-bit messages are equally probable
[0025] Of course, in general, this is not the case. That is, all n-bit
messages are generally not
equally probable, so H(M) <_ n bits.
[0026] The amount of entropy that may be contained in an encryption key "K"
may be defined
as follows:
H(K) = -j; p;(K) log2p;(K)
[0027] Thus, key entropy is maximized where:
p;(K) = 2- , i = 0, 1, ..., 2 -1
H(K) = n bits if key is uniformly distributed.
[0028] And again, in general, H(K) is not equal to n-bits, but rather H(K) < n-
bits if key
distribution is not equally likely.
[0029] To achieve theoretically perfect secrecy, one must have H(K) > H(M).
H(K) = n is the
maximum entropy for an n-bit key system and can only be realized if truly
random key
generation can be achieved. There is a limit to what we can obtain with a
given uncertainty in
the key - Shannon stated "the amount of uncertainty we can introduce into the
solution cannot
be greater than the key (a simple bit string, based on classical sense)
uncertainty". This is true
in a one-dimensional system. In order to achieve higher than n-bit entropy for
a key system
with a key length of n-bits, the system of the invention applies a key system
with more than
one-dimension.
-7-
CA 02639649 2008-09-19
[0030] In the classical view of an encryption key system there are two primary
premises.
Firstly, that the key is only related to a pure bit string: a one-dimensional
variable with
discrete state values. And secondly, that the encryption algorithm is a
transformation by
applying a key on a message with some operation such as XOR. Except for the
theoretical
one-time-pad, previously known encryption systems cannot withstand a brute
force attack of
exhausting all possible key states (values).
BASIC DEFINITIONS
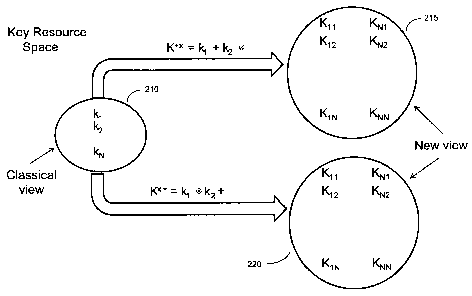
1. Key Resource Space
[0031 ] In a classical encryption system with an n-bit key, the Key Resource
Space (KRS, see
FIGURE 2) consists of all possible pure n-bit strings. That is, the space is
defmed as a one-
dimensional variable with 2" discrete values. In such a space, the total
number of possible
keys (or states) will be 2", and the probability of a random key being
discovered, 2-". All
possible numbers form a cyclic group which can be generated by a generator, g.
2. One-dimensional Key Operator
[0032] We define a new concept of a "key operator" which is simply defined as
a key (an n-
bit integer) with an associated arithmetic operation:
Key addition operator: k+
Key subtraction operator: k", it is not independent k- = 1+(~k+)
Key XOR operator: k "
[0033] In operation, an n-bit key operator can operate on an n-bit message
integer m, where:
k+m=k+m
k-m=k-m=(1+(-k))+m
k" m = k m, 0 is a bit-wise XOR operation
Note that:
"+" is a 1-bit addition operator with 1< n , where:
1= 8: byte addition
-8-
CA 02639649 2008-09-19
1 = 16: short integer addition
1= 32: long integer addition, and so on
if 1< n, the + operation should be understood as a concatenation of
corresponding sub-
additions. Also, the addition should be understood as addition with a modulus
by 2I.
3. 2-dimensional Key Operator
[0034] Thus, a 2-dimensional key operator associated with two random variables
kl and k2,
can be defined as follows:
K+" = kl+kZX = ki + k2 which is applied to an n-bit message integer m as K+X
m
kl+(k2 (9 m)
K"+ = klx kz+ = ki k2 + which is applied to an n-bit message integer m as
K"+ m
=k1 0 (k2+m)
States of 2-dimensional key operator:
a. states(K+X) = states(k) * states(k') = (2 ) *(2 )
b. state values: all possible pairs (kl, k2), kl, k2 = 0, 1, ..., 2n-1
[0035] As noted above, it is important to define key operators for which the
order of
operations must be preserved; otherwise it may be possible to reduce the
dimensions of the
key operators. For example, K++ = kl+ k2+ and K"X = k," k2" are not suitable 2-
dimensional
operators as they can be reduced to 1-dimension:
K++m =kl+(k2+m)
= (ki + k2 ) + m
= k3+ m, which is 1-dimensional, and
K"m =kl 0 (k2 0 m)
=(k, (9 k2) m
= k4" m , which is 1-dimensional
[0036] It is possible to define more 2-dimensional key operators by
introducing more
operations such as 2-bit, 4-bit, 8-bit, etc., additions. Then for a given pair
(kl, k2), one will
-9-
CA 02639649 2008-09-19
have many more 2-D key operators. In this document, we will use 2-D key
operators K+" and
K'+ as examples.
4. Multidimensional Key Operator
[0037] Following the same progression, one can define 3 or higher dimensional
key operators
associated with three or more random variables such as:
K+"+ = k,+ k2" k3+ : 3-dimensional
K"+" = kl" k2+k3X : 3-dimensional
K+++ = k1+ k2+ k3+ : 1-dimensional
K""" = kl" k2" k3" : 1-dimensional
K++" = kl+ k2+ k3X : 2-dimensional
KX"+ = kl" k2" k3+ : 2-dimensional
[0038] From the above, higher dimensional key systems can be easily
constructed by
concatenating one-dimensional keys in such a way that two neighboring key
operators are not
exchangeable.
5. KEY OPERATOR SPACES
[0039] A "key operator space" (KOS) is the whole set of key operators with the
same ordered
operation(s) defined. There are number of 1-dimensional key operator spaces
which may be
defined:
= k+ space: total2 operators. Once they operate on an n-bit message integer
m, they all
do additions with m;
= k- space: this is not an independent space, it is overlapped with the k+
space because
they are just mutually reverse operations; and
= k" space: total 2' operators. Once they operate on an n-bit message integer
m, they all
do XORs with m.
-10-
CA 02639649 2008-09-19
[0040] There are number of 2-dimensional key operator spaces, for example:
= K+X space: all key operators defined as kl+k2", kl, k2 = 0, .., 2" -1
= K"+ space: all key operators defined as kl"k2+, kl, k2 = 0, .., 2"-1
[0041] A112-dimensional key operator space consists of 22n key operators,
while in a 3-
dimensional space, such as K+"+ space, there are a total of (2 ")3 key
operators.
[0042] The above are just examples for the concept of key operators and key
operator spaces.
One can easily define any other key operators and their key operator spaces.
[0043] Figure 2 presents a graphic representation of an exemplary two-
dimensional key
operator space of the invention, contrasting it to the classical 1-dimensional
key space. The
classical 1-dimensional key space 210 provides a space of kl, k2 ... kN; a
total of N=2" keys.
[0044] In contrast, the two-dimensional key space of the invention, K+x space
215 or K"+
space 220, for example, will have 22" key operators.
6. ENTROPY OF KEY OPERATOR
[0045] Based on Shannon's definition, for an equally likely key operator
system, the entropy
of a 1-dimensional key operator will be H(k) = - Y-; p; log2 p; and H(k") = -
Y-; p; log2 p;, where
p; is the key k;'s probability. For a true random key, p; = 2-". Thus, H(k) =
H(kx) = n bits.
[0046] For a 2-dimensional key operator system:
H(K+")Y_IPIlog2P, ,Pi=Pi pi, i,j=0, 1,2,...,2n-1
Y-ii pi pi 1092 (Pi pJ)
Y-ij pi Pj (1og2 pi + 1092 pJ)
Y-ij pi Pj 1092 pi -Y-ij pi pj 1092 Pj
(Lpj ) Ji pi 1092 pi -(Y-i pi ) Y-i Pi 1092 pi
= H(kx) + H(k)
= 2 H(k)
-t1-
CA 02639649 2008-09-19
[0047] For a true random key distribution, H(K+") = 2n bits. This doubles the
entropy of the
one-dimensional key operator but the key operator in each dimension is still
an n-bit string.
Thus, it is clear that an m-dimensional key operator system will have entropy
of H(K'-D) = m
n bits if each dimension of a key operator is uniformly distributed .
[0048] It should be clear that key length is different from its entropy
length. The former refers
to its physical bit length and the later refers to its entropy, the
uncertainty of a random
variable, in bits. For example, in a uniformly distributed 1-dimensional
system, both lengths
are equal. But in a 2-dimensional space, the entropy length is twice the
physical length.
Therefore, in cryptography we should refer to entropy length for uncertainty
not the physical
length.
[0049] In summary, the dimension of a key system becomes the entropy holder.
Each
dimension can hold maximum entropy of n bits for an n-bit long key. So an m-
dimensional
key operator system can store mn bits entropy.
THEOREM OF PERFECT SECRECY
[0050] The invention may be considered in the context of Shannon's concept of
perfect
secrecy. Shannon defined:
1) a priori probability p(m): the probability of knowing the message m before
interception;
2) posteriori probability p(m ( c): the probability of knowing the message m
based on
interception of cipher text c; and
3) p(c): the probability of obtaining cryptogram (cipher text) c from any
cause.
[0051] Perfectness of encryption requires that p(m I c) = p(m). That is, the
interception of
cipher text does not provide the attacker with any useful information to gain
extra knowledge
of the message, other than just guessing the message.
[0052] Referring to the block diagram of Figure 3, given a message space that
is n-bits long
310, there are a total of 2" possible messages in the message space. In an
abstract key system
-12-
CA 02639649 2008-09-19
315 with a space dimension (total possible abstract keys) not less than N = 2
, each key can
operate on each n-bit message and produce an n-bit cipher text 320.
[0053] Suppose the message space consists of all n-bit messages. Then the
total possible
messages are N = 2 . Accordingly, the cipher space also has N cipher texts.
[0054] Theorem of perfectness: For a uniformly distributed abstract key system
with
dimension >= N, perfect secrecy can be achieved iff for any pair of message-
cipher (m, c), the
total conditional probabilities of abstract keys meet:
Y-k(MM p(k) = 1/ 2
Where p(k) is the probability of finding the abstract key k. The sum over k
takes all possible
abstract keys under the condition that the keys can transform m into c.
PROOF OF PERFECT SECRECY
[0055] Bayes Theorem reads that:
(m c)
P(m l c) = p(m)p(k)
p(c)
(m c)
p(m)p(k)
~km C)P(m,)P(k)
[0056] The sum over k takes all possible abstract keys which can transform
m/m' into c. The
sum over m' takes all possible messages.
[0057] If a uniformly distributed abstract key system with the number of
possible abstract
keys >= N always satisfies Y-k("'' ) p(k) = 1/ 2" for all possible (m, c)
pairs, then:
-13-
CA 02639649 2008-09-19
(m,c)
p(m)p(k)
p(m l c) = k
(m',C)
I p(m')p(k)
M. k
(m,c)
p(m) I p(k)
k
(m',c)
p(m') Y p(k)
m' k
p(m) 2n
Ep(m,) 1
M. 2
= p(m)
[0058] Since p (m I c) = p (m), the encryption is perfect. That is, the
probability finding the
message given the intercepted cipher text is the same as the probability of
finding the message
just by guessing it. Knowing the cipher text does not provide any additional
useful
information to gain extra knowledge to find the message.
UNCERTAINTY LAW
[0059] It is possible to achieve both perfect secrecy and key reusability iff:
1) the abstract key system satisfies the theorem of perfectness; and
2) action on a message applied by an abstract key can be considered as a
transformation.
All key transformations from an abstract key system meet the uncertainty
relationship
ksi k ~ m - ks, ksi m^ 0, i7~ j from the key system,
where m is any message from the message space, "s" denotes an abstract key
system, and ^
should be interpreted as "not always equal to".
[0060] The uncertainty relationship in the above indicates that two different
key
transformations on the same message in one order may be different from the
other order. The
difference between these two different transformations cannot be determined
without knowing
the message. That is the reason why it is called uncertainty law.
-14-
CA 02639649 2008-09-19
The uncertainty law provides the opportunity for the reusability of an
abstract key.
PERFECT SECRECY OF MULTI-DIMENSIONAL KEY SYSTEM
[0061 ] Any multidimensional key system introduced in this invention
automatically satisfies
the condition of perfectness. For a uniformly distributed t-dimensional key
operator space:
1) there are 2t" key operators, t=1, 2, ...
2) probability of finding a key operator K is p(K) = 2-t"
3) for a given message m, all these 2`" key operators are automatically
(mathematically)
grouped into N=2 groups. Each group contains 2(t-1) key operators; and
4) there exists one group within which each key operator can transform the
given m into
the given c, hence
Y-k("'> ) p(k) = 2(t-1) p(k) = 2(" ) 2-m - 1/ 2" for all possible (m, c)
pairs.
[0062] Thus, the multidimensional cryptography described herein provides
theoretically
perfect secrecy.
KEY REUSABILITY
[0063] Key reusability is also addressed by this system. In a t-dimensional
key system, the
total key operators in a key operator group is Nk = 2(t-1) . If t=1, Nk = 1,
there is just one key
operator in each group. That is so-called 1-to-1 mapping: one message is
mapped to one
cipher text by a unique key. No key operators in a 1-dimensional KOS satisfy
the uncertainty
law, for example:
a. k1+k2+m-k2+kl+m=kl+k2+m-(k2+kl+m)=0
b. kl"k2Xm-k2"kl"m=kl k2 m-(kZ kl (&m)=k3 m-k3 m=0,
so it is vulnerable to a so-called running key attack (i.e. the key can be
eliminated from cipher
texts yielding an encryption with the message itself). Hence, no key operator
in a 1-D system
can be reused. This is the restriction that occurs in the well-known one-time-
pad system.
-15-
CA 02639649 2008-09-19
[0064] However, in the case of the invention with t> 1, all key operators from
the same KOS
meet the uncertainty law, that is, the order of two different key operators
operating on the
same message is critical for the result. So a running key attack against the
system of the
invention would not be useful. Therefore, a key operator from a
multidimensional key system
can be reused, being governed by the uncertainty law presented in the above.
SINGLE-BLOCK ENCRYPTION AND DECRYPTION
[0065] For single block encryption and decryption, given one n-bit block
message, encryption
would proceed as follows.
A suitable encryption key operator in a 2-dimensional key system would be, for
example:
K+x=k,+k2
ii. Encryption of a message m, into a cipher C, would therefore proceed as
follows (note
that the operation order is from right to left):
K+Xm=k,+kz m=C
iii. Decryption would follow in the inverse of the encryption. That is, with
key operator:
(K+x )-' = k2 ( - kl+), decryption proceeds:
(K+X)-I C = k2 (-ki+C)
= k2 {-kl+[kl+(kZ(D m)]}
= k2 (k2 m)
(k2 (D k2) (9 m
=m
It can be seen from the decryption m = k2 (- ki + C) that the decryption
performance looks
like the same as the encryption one.
-16-
CA 02639649 2008-09-19
AVOIDING A BRUTE FORCE ATTACK
[0066] A brute force attack is mainly used to find a reused key, once the
potential message is
resolved, by exhausting all possible keys with a known algorithm on an
intercepted cipher text
c.
[0067] With the system of the invention, one given cipher text c can form N
(m, c)-pairs with
all possible plaintexts from the message space. Each (m, c) pair is connected
by a unique set
of N = 2" key operators in a 2-dimensional system, so there are N key
operators capable of
decrypting the cipher into the same message. By exhausting all N2 key
operators, the
adversary will find all possible messages in the message space with the same
possibility N-'.
But the adversary will not know which the correct message for the intercepted
cipher text is.
Therefore, the key operator is undetermined.
[0068] Thus, the algorithm is immune to such a brute force attack.
IS THE SYSTEM PERFECT NOW?
[0069] The system is theoretically perfect ifjust one block message or message
consists of
random bytes. It is not perfect if the message is highly biased and has
multiple blocks, but
there are ways to mitigate the information that these flaws can introduce. For
example, as
described hereinafter, one can "randomize" a long and biased message or
perform other pre-
encryption modifications to the message.
AUTHENTICATION
[0070] The discussion of authentication that follows assumes that the server
and client share
kl and k2 ahead of time, using 2-dimensional key system as an example. Then we
can
construct at least the four following key operators in a 2-dimensional key
space:
Ko=kl+k2
K1=k2+ki
K2 = k, 0 k2 +
K3 = k2 k, +
-17-
CA 02639649 2008-09-19
[0071 ] In one-way authentication the server typically authenticates the
client. This could be
done as follows, referring to the data structure diagram of Figure 4 and the
process flow
diagram of Figure 5.
[0072] There are three messages used for authentication: Auth-Req
(authentication request)
410, Auth-Rep (authentication reply) 415 and Auth-Ack (authentication
acknowledge) 510.
In general, both sides can issue any of these messages depending on the actual
situation. If
just one-way client-server authentication is being performed, the server sends
the Auth-Req
410 to the client first, which can avoid hostile flooding Auth-Req from
attacker(s).
[0073] Firstly, the server 515 generates a random byte string maõth with a
multiple of blocks
ml, m2 ... mP, 420. In general, there is no restriction on the length of the
random byte string.
This appears as the "RT secret" ("runtime random message") 520 in the Figures.
The server
515 then encrypts these blocks as follows:
= co=Komo,
= c;=K;-m;,i'=mi_1%4,andi= 1,2,3, ....;
= constructing an authentication request "Auth-Req" 410, caõth =<co I cl ~...
~ cp > 425
and sending it to the client 525;
= The client 525 decrypts caõth to get maõth using the inverse process;
= The client 525 applies (both sides agreed) some key scheduling algorithm 530
such as
KSA in RC4, used as an example here, to generate a set of state tables m'aõth
535 (if the
maõth is longer than 256 bytes); chop m'auth into n-bit blocks {m';};
= And the client 525 then encrypts m'aõth : c; = K;- m'; , i' = m'; % 4. The
client 525 sends
the new cipher text back to the server 515 as authentication response "Auth-
Rep"
message 415.
[0074] The server 515 decrypts the Auth-Rep message 415 to determine m'aõth
and then
compares the state tables generated from mauth with the m'aõth. If both are
the same, then the
client 525 is authenticated and the server 515 sends an Auth-Ack message 510
with an
authentication result set to 0, indicating it is successful. If the two are
different, the client 525
-18-
CA 02639649 2008-09-19
has failed the authentication test. The server 515 then sends an Auth-Ack
message 510 with
the authentication result set to 1, indicating that the authentication is a
failure. After
successful authentication, both sides share a run-time secret. This secret can
be used during
the whole session.
[0075] Two-way authentication is performed in the same manner, except that the
server 515
and client 525 mutually authenticate each other in successive phases.
LONG MESSAGE ENCRYPTION AND DECRYPTION -
SOLUTION 1: RANDOMIZE ENCRYPTION ORDER
[0076] When a long message is encrypted the intrinsic logics between
successive message
blocks reveals information to the attacker and help him/her to narrow the
scope of potential
key operators. Randomizing the order of the message block to be encrypted is
one way to
resolve this kind of problem.
[0077] With the system described herein, one could use the encryption sequence
index table
to control the order of the message blocks to be encrypted. The index table
can be generated
using shared secrets such as secrets shared during authentication phase.
[0078] Message block chaining will change the readability of the blocks. It is
impossible to
eliminate the chaining effect without know the shared secret. Based on the
index control
table indxCtr[i], index i is the encryption order index and indxCtrl[i] is
corresponding to
message block index bi. The message block chaining in this case must chain
block b; with
block b;-I by using an operation that is not exchangeable with block b;-I.
After the chaining is
performed, the chained message blocks are a concatenation like this M' =<m'o I
m'l I m'2 I==== I
m'p>, so the internal logics that a human understands are effectively
eliminated.
-19-
CA 02639649 2008-09-19
LONG MESSAGE ENCRYPTION AND DECRYPTION -
SOLUTION 2-"RANDOMIZE" MESSAGE AND "RANDOMIZE" SELECTION OF KEY
OPERATORS
[0079] For a long and biased message, the strong internal logics between
message blocks may
potentially leak key operator information when a brute force attack is
applied. This problem
can be addressed by randomizing the message before encrypting it, and
randomizing the
selection of key operators. Figure 6 presents a data structure diagram which
mirrors the
following process:
[0080] To begin with, we generate a pseudo-random initial vector (IV) 610,
which is used for
both message integrity checks, and to help randomize the message blocks. This
IV block 610
is added to the front end of the message ml, m2 , ... mp 615.
[0081] We also add a block for a message integrity check, also called message
access code
(MAC) 620 at the end of the message 615.
[0082] This MAC 620 could be constructed as follows, for example. Of course,
it can also be
designed in other formats without losing its generality:
I secret (block size - 2) 1 msg length ( 2 bytes)
[0083] That is, the MAC 620 is constructed from the shared secret with length
of the block
size - 2 bytes, followed by the last 2 bytes which carry the message length.
[0084] We then use a new message block chaining process (MBC) to remove the
intrinsic
logic between blocks. Starting from mi and progressing through the message
610, at the i-th
block, the (i-1)-th chained message block is combined with the i-th block by
using a different
operation from the most right operation in the key operator applied to the
block:
= if the K+" operator is used for the i-th block m;, the chaining operation at
the i-th
chaining block will be "+". Then the chained message will be: m;' = m;_,' +
mi, and mo' = mo =
IV, where m;' is the i-th chained block; and
-20-
CA 02639649 2008-09-19
= if K'+ operator is used, the chaining operation at the i-th chaining block
will be " ".
Then the chained message 625 will be: m;' = m;_l' m;, and ma' = mo = IV.
[0085] The message block chaining (MBC) technique, together with the initial
vector (IV),
can effectively randomize messages. Even given two same messages, after MBC,
they
become different due to the run-time generated IV.
[0086] The MBC technique introduced here is equivalent to increasing one-
dimension k= m;-
1' of the key operator. That means, a one-dimensional key operator together
with this MBC
produces an effect of a two-dimensional key operator.
[0087] The second part of this process is to randomize the run-time selection
of the
encryption key operators. For a given pair of keys (kl, k2), in a 2-
dimensional key operator
system, there have at least 4 different key operators:
Ko=kl+k2 0
K1=kZ+ki
K2=k1 0 k2+
K3 = k2 k, +
[0088] It is possible during run-time to choose a key operator from these four
choices. This
technique further introduces uncertainty into the solution for a long message.
This technique
also uses a shared secret between communication peers such as:
= a password;
= a run-time shared secret during the authentication;
= a key generated from an ID-based key generation; or
= any other known technique for shared secrets.
[0089] RC4 key scheduling algorithm (KSA) is used to produce a state table
called
ctrTable[256] by inputting the shared secret(s).
-21-
CA 02639649 2008-09-19
[0090] For the example here, at block i, the selected key operator should be
at an index
keylndex = ctrTable[i mod 2561 mod 4. If keylndex = 0, the selected key
operator will be Ko
and keylndex = 2, thus the selected key operator should be K2, and so on.
[0091] For IV encryption, the key operator is always determined by
ctrTable[0]. All other
blocks can optionally combine IV with the block index to select a ctrTable
element. For
example, keylndex = ctrlTable[ (IV + i) mod 256] mod 4. In such a way, the
adversary must
try all operators for each block and for each selected key pair (kl, k2)
during a brute force
attack. This leads to exponential complexity for each try in the brute force
attack.
[0092] By increasing the number of potential key operators at a given
dimension of a key
operator, the complexity of each step in a brute force attack is exponentially
increased. Each
step in the brute force attack is equivalent to a new brute force attack.
[0093] Because the control table is independent from the message, the cipher
text, or the keys,
and given the uncertainty introduced in IV, there is no definite way to make a
decision as to
which key operator is used for a specific message block. In order to apply a
brute force attack
on the long and biased message encryption, the adversary must either
successfully guess the
shared secret, or for each key pair, apply all possible key operators (for the
example here, 4
operators) for each message block. This is an exponential problem. For each
selected (kl, k2),
the following shows the complexity of possible decrypted message blocks:
IV: 4
Block 1: 4z,
Block 2: 43
Block 50: 451
[0094] This run-time determining encryption key operator method can generally
apply to any
dimensional key operator space, including a one-dimensional key operator space
in which we
will select key operator from two key operators k+ and k'.
-22-
CA 02639649 2008-09-19
[0095] To reiterate, the encryption process consists of three basic steps.
[0096] In step 1, we chop the message into blocks with n bits for each block.
The last block
can be randomly padded.
[0097] In step 2, we pick a pseudo-random number as an initial vector (IV),
the same n-bits in
length as the message blocks.
[0098] In step 3 we perform the encryption, beginning by computing the
ctrTable (which
actually can be pre-computed and used for the whole session) using a shared
secret such as
password, secret shared during authentication, etc. For IV encryption, for
example, we use the
control table to select a key operator, where (ctrlTable[0] mod 4) to select
key operator: Ko,
Kl, K2, K3. With encryption we would have, for example:
ctrlTable[ 0] mod 4 = 0: Ko iv = k, + (k2 iv) = co
ctrlTable[ 0] mod 4= 1: Kl iv = k2 +(kl (9 iv) = co
ctrlTable[ 0] mod 4= 2: K2 iv = k, (9 ( k2 + iv) = co
ctrlTable[ 0] mod 4 =3: K3 iv = k2 (D ( kl + iv) = co
[0099] We then construct the MAC, as noted above, with the structure and
organization:
(block size - 2 bytes shared secret plus 2 bytes holding the message length).
[00100] We then perform the message block encryption, defining a mask (mask =
iv &
Oxff) and using { ctrlTable[ (mask + i) mod 256] mod 4} to select the key
operator for i-th
block from Ko, KI, K2, K3.
[00101 ] Encryption for the i-th block, with i starting from 1 to the last
block (MAC), is
then performed as follows, yielding the cipher text co, c1, c2, ... cP, cMAc
630 of Figure 6:
(ctrlTable[(mask+i) mod 256] mod 4) = 0:
))MBC(message block chain):mi' = m;-1' + mi, mo' = mo = iv
Ciphertextc; : Komi'=k1 +(k2 m;')=c;
(ctrlTable[(mask + i) mod 256] mod 4) = 1:
MBC(message block chain): m;' = m;_1' + m;, mo' = mo = iv
- 23 -
CA 02639649 2008-09-19
Ciphertextc;: Klm;'=k2+(k, m;')=ci
(ctrlTable[(mask + i) mod 256] mod 4) = 2:
MBC: m;'=m;-1' m;, mo'=mo=iv
cipher text c; ; K2 m;'= k, (kz + m;' )= c;
(ctrlTable[(mask + i) mod 256] mod 4) = 3:
MBC:m;'=mi-1' m;, mo'=mo=iv
>>cipher text c; :K3 m;'= k2 (kl + m;' )= c;
LONG MESSAGE ENCRYPTION AND DECRYPTION -
SOLUTION 2 - MESSAGE DECRYPTION
[00102] Message decryption for solution 2 is performed in a complementary
manner.
Specifically, we begin by computing the ctrTable using a shared secret such as
password,
secrets shared during authentication, and the like, based on pre-agreement
between the
communication peers.
[00103] We then decrypt the initial vector (IV), using ( ctrlTable[ 0] mod 4)
to select
the key operator from Ko, Kl, K2, K3. For the four cases of the mod 4 output:
= 0: Ko' co:
iv: iv = (co - k, ) k2
= 1: KI-' co:
iv: iv = (co - k2 ) ki
=2: K2'co:
iv: iv = (co (9 ki ) - k2
= 3: K3"' co
iv: iv = (co k2 ) - k,
[00104] We then decrypt the message block, again, in a manner that is
complementary
to the encryption process for block i, with i starting from 1 to the last
block (MAC):
mask = iv & OxFF
(ctrlTable[(mask +i) mod 256] mod 4) = 0: Ko-' c;
-24-
CA 02639649 2008-09-19
m;' : m;' = (c; - kl) k2
m;: m;=m;' -mi_1',mo'=iv
(ctrlTable[(mask +i) mod 256] mod 4) = 1: K1-' c;
m;':m;'=(c;-k2) kl
m;: m;=m;' -m;-i',mO'=iv
(ctrlTable[(mask +i) mod 256] mod 4) = 2: KZ-' c;
m;':m;'=(c; kl)-k2
mi: m; = m;' m;-I' , mo' = iv
(ctrlTable[(mask +i) mod 256] mod 4) = 3: K3-1 ci
mi':m;'=(c; (D k2)-k,
m;: m; = m;' m;_I' , mo' = iv
[00105] The MAC Check is then performed as follows: take the first (block size
-2)
bytes of the last block (MAC) and compare it with the shared secret (block
size - 2) bytes. If
they are the same, extract the message length from the last 2 bytes of MAC
block, and return
the decrypted message with the length. If they are different, update the error
log and discard
the message.
[00106] Because the MAC is the last block, the message block chaining contains
all
information starting from IV. If any piece of cipher text is modified during
its journey, the
MAC check will fail.
BRUTE FORCE ATTACK - ILLUSTRATION ON EACH SELECTED KEY PAIR
[00107] Figure 7 presents a table setting out the complexity of a brute force
attack on
an exemplary cipher.
[00108] Given a set of cipher text blocks: co , cl , c2 , C3...Cp, Cmac 710
the attacker's
desire is to decode the cipher text co, cl , c2 , c3 ,.. ., c32 710 into iv,
ml, m2, m3, ..., mp, MAC
and then discover the keys. If the attacker knows (or guesses right) what the
dimension of the
key operators is, he will know how many key operators are used for a given
encryption
/decryption. In the simplest case this will be a key pair (kl, k2). In such a
case there will be at
- 25 -
CA 02639649 2008-09-19
least 4 key operators 720 to consider for each block of cipher text co cl c2
c3...c32 710 as
shown in Figure 7.
[00109] Because message block chaining (MBC) was performed, as described in
the
above solution 2 (see row 725 of Figure 7): co --+4 IVs
Each IV: cl -+4 ml', so co --+42 ml'->42 ml
Each ml', C2 --*4 m2' , so Co --). 43 m2'-->43 m2
Each m2', c3 --+4 m3' , SO c0 --+44 m3'-44 m3
............................
Each m31', C31 -44 m32', SO Cp --+433 m32'-+433 m32
[00110] Thus, the resolution of the message block (see row 730 of Figure 7)
will be 42
for ml, 43 for m2, 44 for m3, ... 433 for m32. In other words, the attacker
will have to resolve 4
possible messages for the first block, 42 for the second, 43 for the third,
and up to 433 for the
last in the example here (433 = 266 z 7 x 1019), which is more than another
brute force for 64-
bit key operators (see row 735 of Figure 7). More specifically, each step of
the brute force
attack during its exhausting of potential key operators will be a new brute
force attack. By
using this technique, we can successfully stop the attacker from gaining
advantages from the
intrinsic logic between message blocks for his brute force attack. Therefore,
the attacker is
forced to apply a brute force attack to each individual block. As shown above,
it has been
proven that the invention can withstand a brute force attack for any one
block.
[00111] By defining more operations, even for a given key pair (kl, k2), we
can
introduce more than four 2-dimensional key operators, the complexity
exponentially
increases. For the example listed here, the complexity at block 32 is
equivalent to a 64-bit
brute force attack in a 2-dimensional key system.
POTENTIAL OPERATIONS
[00112] Some of the potential operations that could be used to implement this
system
include the following:
-26-
CA 02639649 2008-09-19
0 1 bit addition, -+ XOR
+Z: 2 bit addition
+4 4-bit addition
+8 8-bit addition --* byte addition
+16 : 16-bit addition -> short addition
+32 32-bit addition ~ long addition
+64 : 64-bit addition -~ long long addition
[00113] All these operations are un-exchangeable with each other. For 2-
dimensional
KOS, it is possible to form up to 84 different key operators. For each step in
a brute force
attack of such a system, the complexity at the m-th cipher text block would be
84m+1 In
general, the shorter a message, the fewer blocks and more operators it needs
for effective
protection.
KEY LENGTH CONSIDERATION
[00114] The proposed technology is scalable to key length, for example, one
could
choose 64-bits, 128-bits, 192-bits, 256-bits, etc. Shorter key lengths lead to
more blocks for a
given length message. The more blocks increases the complexity of a brute
force attack.
[00115] Overall, a 64-bit key length should be a good practical choice for
most
applications. A 64-bit key length will show better procession performance on
most existing
systems. The actual size of the key can be decided based on the CPU
performance. For a 32-
bit CPU, a 32-bit key may perform better than a 64-bit key or longer. And for
a 64-bit CPU, it
may be better to use a 64-bit key.
[00116] This invention can be also used to provide perfect secure key
distribution for
existing cryptographic standards such as AES. This way makes the one-time pad
possible for
existing systems.
-27-
CA 02639649 2008-09-19
ID-BASED KEY AGREEMENT
[00117] A key-agreement protocol is a protocol for generating a key(s), where
the two
parties communicating, both influence the outcome. To be effective, the
process of generating
the key should not reveal the key to any eavesdropping party. As well, the
process should not
allow an eavesdropper or attacker to influence the key choice.
[00118] An identity-based key agreement protocol is simply a key agreement
protocol
in which the IDs of the user include some unique information about the user's
identity (public
and private). The shared key could, for example, be based on a user's email
address, secret,
password, passphrase or keyword. The identity-based key agreement protocol of
the invention
is described with respect to Figures 8 - 10.
[00119] A given n-bit key space will have a space equivalent to integers 0-+ 2
-1.
Thus, the total number of states in the key space will be 2 . These states
form an additive
cyclic group. In group theory, an additive cyclic group is a group that can be
generated by a
single element, in the sense that the group has an element g (called a
"generator" of the group)
such that, when written additively, every element of the group is a multiple
of g.
[00120] The trivial generator for this n-bit additive cyclic group is "1",
where x[i] = x[i-
1] +1, x[0] = 0. Thus, all numbers in the key space can be generated by this
generator 1. Of
course, the numbers generated in this way are not random at all.
[00121] The total number of generators in the special cyclic group (N = 2 )
will be
cp(N=2") where phi is the Euler cp function. Over all possible distinct prime
number p:
~p(N = 2" )== Nfl (1-1 / p)
PIN
[00122] N here is a special cyclic group with only one prime number "2".
Substituting
p = 2 into the above equation yields:
-28-
CA 02639649 2008-09-19
~p(N = 2" )= Nfl (1-1 / 2)
P) N
= N/2
= 2"-1
[00123] That is, there are 2 "1 generators in this key space (cyclic group).
All of these
generators can fully generate entire numbers in the group, with equal
probability.
[00124] So what are these generators? An even number can only generate even
numbers:
g= 2: x[i] = x[i-1] + g--), all even numbers in the group.
[00125] Any odd number in the group can be a group generator which generates
the
entire group with equal probability for each number. There are a total of 2 -1
odd numbers, so
there are 2 -' generators and they are all odd numbers.
RANDOM NUMBER GENERATION
[00126] We need to find a generator, a secret seed g, that generates random
numbers for
us. Given an n-bit integer m, we can construct a generator g = (2 * m + 1) mod
(2 ) to make
sure it is an odd number.
[00127] Pseudo random numbers can then be generated from:
X[i] _(X[i-1] + g) mod (2 ) , where X[0] = 0, i = 1, 2,..., (2 -1)
[00128] Are the numbers generated by this process truly random? No, they are
not:
= X[1] = g: the first pseudo random number reveals the secret generator g;
= X[i] - X[i-1] = g: the difference between two neighboring generated numbers
also
reveals the secret generator; and
= Because g is an odd number, the sequence will alternate between even and odd
numbers (see the formula above; for example, if g= 3, the sequence will be 3,
6, 9,
etc.). That is, even and odd numbers will appear one after another, following
either
-29-
CA 02639649 2008-09-19
the pattern: e o e o e o e o (even, odd, even, odd, etc.) or o e o e o e o e
(odd, even,
odd, even, etc.).
[00129] So we need to solve three problems. Firstly, in order to avoid X[1] =
g, we
need a secret seed for X[0] = s. Thus: X[i] = (X[i-1] + g) mod (2') , X[0] =
s, i = 1, 2,..., (2 -
1). Secondly, in order to avoid X[i] - X[i-1 I] g, we need a mask to break the
relation. For
example, we could use a secret seed for mask x. Thus:
X' [i] = X[i] x -> X' [i] - X' g
[00130] But this mask will not change the even / odd pattern (o e o e...). In
order to
avoid the even / odd pattern, we need the third element - a key buffer.
[00131] We define the key buffer as K[size], where size = 32 is enough. With
this, we
create an index table: indx[size], using an algorithm similar to an RC4 key
setup algorithm
(described herein below). Then for the i-th generated random number X'[i] will
be stored in
K[indx[i]] = X' [i].
[00132] Thus, we can obtain output keys in sequence with good randomness with:
K[ i
], i = 0, 1, 2, ..., size-1
[00133] In summary, there are three seeds as inputs: Generator g, Starting
point s and
Mask x, as well as a key buffer.
[00134] We can use the following algorithm to generate an index table
indx[size] for
random number generation:
*indx: index table
size: the size in bytes of index table
secret: input secret
tLen: the length of the secret
void indx_setup(unsigned char *indx, int size, unsigned char *secret, int
tLen)
{
-30-
CA 02639649 2008-09-19
inti,j,k,a;
unsigned char *m;
m = indx;
for( i= 0; i< size; i++ )
m[i] = (unsigned char) i;
j=k0;
for( i 0; i < size; i++, k++ )
{
if( k>= tLen ) k= 0;
a = m[i];
j = ((j + a + secret [k] ) & OxFF) % size;
m[i] = m[j];
m[j] = (unsigned char) a;
}
}
[00135] Our goal is to generate pseudo random numbers with equally likely
distribution
by giving the above three seeds: generator g, starting number s and the mask
x. In general, the
communication peers do not share these seeds in advance. Instead, they usually
share a
password such as a user trying to login to his/her banking account with
his/her account
number and password. The password can be considered as a shared secret.
However, a
password is low entropy secret and cannot be used as a cryptographic key. The
invention
turns the shared low entropy secret into secret seeds: generator g, starting
number s, and mask
x by using a key scheduling algorithm such as in RC4.
[00136] The key (a secret) in RC4 KSA, could be any character string with
length up
to 256. The total entropy of the RC4 KSA state table is: Log2 (256! * (256)2)
;Z 1700 bits,
which is a very high level of entropy. Therefore, our strategy is to put the
low entropy shared
secret into a high entropy basket RC4 state table and then produce the secret
seeds: g, s, x.
-31-
CA 02639649 2008-09-19
[00137] This table can be used as raw materials for the initialization of key
generation:
= Seed ko = X[0]
= Generator g
= Mask x
[00138] Using this process and suitable seeds, we can generate random keys
from our
ID-based key agreement protocol, as shown in Figures 8 & 9. From Figure 9,
there are two
messages Sess-Req 910 (session request, request to start a new session) and
Sess-Rep 915
(session reply). A user client sends Sess-Req 910 to start a new session. Sess-
Req message
910 will contain client ID 920 (not the secret ID 930 such as password, it may
be the pseudo
ID or a public ID which will map to shared ID such as account number) and a
run-time
variable as a public salt 925 (see step 810 of Figure 8). This salt 925 is
used to ensure that
the state table generated is different every time. At step 815 of Figure 8,
the salt 925 can be
XORED with the shared secret 930 and the resultant will be used as the input
secret (key) in
the RC4 KSA. The output from RC4 KSA is the state table 820 S-table[256]. The
S-table
820 provides the raw materials for the three secrets: g, s = ko, and x at step
825.
[00139] We then generate the keys at step 830 performing the steps of:
1. Finding ko, g and x from the S-table 820
We start by chopping the S-table[256] 820 into blocks with each block n-bit
long. The
number of blocks is N = 256 * 8/ n. We store the blocks into tmp[N], which is
considered as
an n-bit integer array. Pseudo code to produce the seeds g, ko, and x, is
shown in step 825 and
is as follows:
k0=0;g=0;
for(i=0; i<N; i+=2)
{
k0 ^= tmp[i]; kO +=tmp[i+l];
g += tmp[i]; g ^= tmp[i+l];
-32-
CA 02639649 2008-09-19
}
x=k0^g;
g += 1;
2. set the size of the key buffer: K[32] keys
3. Setting up the indx[32] with kO as the secret in indx_setup() procedure
4. Generating keys
tK = kO
For (i =0; i<32; i++)
{
tK += g;
K[indx[i]] = tK x
}
5. Returning K[32]
[00140] Both communication peers perform the same procedure as described in
the
above to eventually share the array K[32]. Hereafter, both sides should be
considered as "pre-
shared secret keys". The key agreement process continues with respect to two
cases: the
client-server model, and the client-server-client model, both of which are
described below,
with respect to Figures 9 and 10 respectively.
ID-BASED KEY AGREEMENT - FLOW CHART: CLIENT-SERVER MODEL
[00141] Figure 9 presents a flow chart of a Client-Server based model for
performing
the ID-based key agreement protocol. A "Client-Server" software model is a
distributed
system where both the client and server are required to have complementary
processing
software. Typically, a client software process will initiate a communication
session with the
server, while the server waits for requests from any client.
[00142] In this case "Bob" 935, the Client, is attempting to establish a
secure
connection with "Alice" 940, the Server. Bob 935 determines identification
data (public ID
such as user name, etc, which will map to a secret ID such as password on both
sides) and a
-33-
CA 02639649 2008-09-19
public salt, and issues a Session Request message 910 to Alice 940, including
both the
identification data and public salt.
[00143] Upon receipt of this session request, Alice 940 verifies the ID,
locates the
client, associates the salt with the client, and issues a complementary
Session Reply 915 back
to Bob 935, including the identification data and the public salt. In the
Session Reply message
915, she can indicate whether the session can be started based on whether the
client is legal
user, or the policy is allowed to start it. A field in the reply message,
RESULT, is used to
carry the indication. RESULT set to 0 means OK and to 1 means FAILED.
[00144] With the transfer of this information, Alice 940 and Bob 935 can both
start the
RC4 KSA procedure by using the secret ID XORed with the public salt as the
input key in the
RC4 KSA algorithm and then getting their synchronized RC4 State Tables 820 at
steps 815,
820, 825, 830, generating keys as described above with respect to Figure 8
(i.e. Key Gen:
K[32]). Both Alice 940 and Bob 935 share a set of keys (32 n-bit keys in the
K[32] array). A
complementary authentication phase 945, by using ki = K[0] and k2 = K[1] as
their pre-shared
keys, is then executed as described above with respect to Figure 5.
ID-BASED KEY AGREEMENT - FLOW CHART: CLIENT-SERVER-CLIENT MODEL
[00145] Figure 10 presents a state diagram of how secure communication is
established
in a Client-Server-Client model. A "Client-Server-Client" model is a
distributed system
where two clients wish to interact, using a trusted Server as an intermediary
or to provide
functionality used by the two Clients. All three parties are required to have
interoperable
processing software.
[00146] In this case "Alice" 940 is attempting to establish a secure
connection with
"Bob" 935 through the server 1010 (in general, the server 1010 should be
common for both
Alice 940 and Bob 935, otherwise, there needs to be another secure connection
between their
servers). For example, if Alice 940 wants to establish a secure communication
with Bob 935:
1. Alice 940 initiates a Sess-Req 1015 with the server 1010, sending a Sess-
Req message
to the server 1010 with her public ID and salt, also the public ID of Bob 935.
-34-
CA 02639649 2008-09-19
2. The server 1010 extracts the public ID of Bob 935 and initiates a Sess-Req
1020 with
Bob 935, sending a Sess-Req message to Bob 935 with a new salt, also the
public ID
of Alice 940.
3. After receiving the Sess-Req message from the server 1010, Bob 935 issues a
Sess-
Rep message to the server 1010 to indicate whether he is willing to
communicate with
Alice 940 by setting RESULT to OK or FAILED.
4. If Bob 935 is not willing to talk, the server 1010 sends a Sess-Rep message
to Alice
940 with RESULT setting to FAILED and then the session is stopped.
5. If Bob 935 is willing to talk, the server 1010 sends a Sess-Rep message to
Alice 940
with RESULT set to OK.
6. Now both Alice-server and Bob-server start the client-server model key
agreement to
verify identities of Alice 940 and Bob 935 separately via the Auth-Req/Rep/Ack
protocol 1025, 1030.
7. After completion of client-server model, Alice 940 and the server 1010
share KA[32]
and Bob 935 and the server 1010 share KB[32]:
a. Alice 940 and the server 1010 both take kal = KA[0] and ka2 = KA[1] as
their shared
keys 1035. Therefore, they share four key operators: KAO = ka, + ka2 , KA1=
ka2 +
kal , KA2 = kai ka2 +, KA3 = ka2 kal +
b. Bob 935 and the server 1010 both take kb1= KB[0] and kb2 = KB[1] as their
shared
keys 1040. Therefore, they share four key operators: KBO = kbl + kb2 , KB1=
kb2 +
kbi , K132 = kbi kb2 +, KB3 = kb2 0 kbi +
8. The server 1010 utilizes any available cryptographic random number
generator 1045
(software or hardware, making sure equally likely distribution) to generate
two n-bit
keys called kl and k2 1050
9. The server 1010 distributes kI and k2 to Alice 940 and Bob 935, based on
the multi-
dimensional cryptographic technique of the invention, by using message Key-EX
(key
exchange) 1055, 1060:
a. To Alice 940:
i. Select key operator: KA; ,i = KA[2] mod 4
-35-
CA 02639649 2008-09-19
ii. Key-EX = < KA; kl I KA; k2 I KAj kl I KAj k2) >, j=(i + 2) mod 4
b. To Bob 935:
i. Select key operator: KB; ,i = KB[2] mod 4
ii. Key-EX = < KB; kl I KB; k2 I KBj kl I KAj k2) >, j=(i + 2) mod 4
10. After receiving Key-EX 1055, 1060 from the server 1010, both Alice 940 and
Bob 935
decrypt it. Both of them should discover that the first and third blocks
reveal the key
kl and the 2"d and fourth block reveal k2. If they find that k, from the first
block is
different from the third block or k2 from the 2 nd block is different from the
fourth
block, they should send Key-ACK message 1065, 1070 with RESULT set to FAILED
to the server 1010 and discard kl and k2. If anyone NACKs (FAILED) the key
exchanged, the server 1010 should retransmit the Key-EX message 1065, 1070 to
him/her.
11. After successfully sharing kl and k2 on both communication peers 1075,
1080, the key
array KA[32] and KB[32] can be deleted from memory on both sides
ADVANTAGES
[00147] The system and method described herein are fast and theoretically
proven to
provide perfect secrecy. Except for the theoretically possible one-time-pad
(OTP), existing
security technologies are not proven to be perfectly secure. They all rely on
computational
difficulties for protection. For example, AES (advanced encryption standard)
is built for the
reason that an established shared key (usually through D-H protocol) can be
reused for a
period (key refresh period).
[00148] It is very straightforward to implement this solution. It can be
easily
implemented by pure software or just as easily in hardware / firmware. The key
bit length is
scalable. Existing encryption systems just attempt to increase the difficulty
and complexity of
breaking them (then a key can be used for longer time), however, the
multidimensional key
system described herein cannot be broken, even if a key is continuously used.
The system and
method described herein has all of the advantages of AES, plus:
-36-
CA 02639649 2008-09-19
1) it is a first time theoretically proven to be perfect secure technology
with reusable key
by using the so-called multi-dimensional key:
a) pre-shared keys or ID-based key agreement with unique, equally likely key
generation;
b) the uncertainty law -> key re-usable;
2) it is faster than AES. In general, the proposed system (using a 2-
dimensional key) only
requires CPU processing equivalent to 3-4 rounds (in 2-dimensional case) of an
AES process:
a) it needs just one addition and one XOR operation for encryption;
b) on the receiving side, it just needs one subtraction and one XOR operation;
c) roughly one operation here equals one round in AES; and
d) it also overcomes the slow decryption in AES. In the proposed solution,
encryption
and decryption have the same speed;
e) there is no big static table, such as S-box in AES, existing in the
multidimensional
cryptography, so the so-called side-channel attacks in AES can be effectively
avoid.
3) the key length is scalable. Because it is theoretically perfect, it is not
necessary to gain
better security by increasing key length. Even a 64-bit key is good enough;
4) There is no need to exchange keys during communications although the
invention can
be used for secure key distribution; and
5) there is no worry about the security of communications, regardless of what
the
network infrastructure is between communication peers.
APPLICATIONS
[00149] The proposed new encryption technology can be directly applied to a
variety of
applications such as:
1) Highly secure communications between two or multiple remote locations. This
kind
of communications includes governments, military, defense, etc. For these
communications,
the pre-shared key(s) have been provided when the secret relationship is first
established. Due
to lack of secure key distribution technology, periodically refreshing keys
reduces the security
of communications. They require a new technology which can theoretically prove
that it is
perfect during the course of long time communications;
-37-
CA 02639649 2008-09-19
2) Financial institutions. They need secure communications between their
branches,
offices for financial transactions, customer accounts, daily updates, etc. In
this kind of
communications, they usually follow a client-server model. Their server and
client machines
usually have pre-shared keys. The proposed technology can directly apply to
them. There are
only very minor changes to the existing applications.
3) The proposed technology can be provided to all virtual private networks
(VPNs).
Most VPN networks use device authentication with tunneling between peers. The
system and
method described herein can provide perfect security between two remote VPN
communications;
4) With the proposed ID-based key agreement, the key sharing between
communication
parties can be automatically established by providing a public "salt" plus a
shared secret such
as password, secret question-and-answer, etc.
a) Secure email service: this is a client-server communication. The client
user generally
has a user name and a password. The Usemame is the public ID and can be used
to identify
the user and the password can be used for ID-based key agreement protocol to
establish initial
key sharing for encryption of email sent by the client. The email will be
decrypted at the
server side and store in the email server. Once the email receiver tries to
download the email,
the receiver and the email server will establish the same procedure as in the
sender. The
server will encrypt the email by the newly shared keys (kl and k2, for
example) and the
receiver will decrypt it.
b) Online banking service: this is a client-server model too. An account
holder and
his/her bank share account ID, personal info, and a user password. After the
user enters his ID
and password, and before sending this information to the server, both sides
must start a ID-
based key agreement session to share keys (kl and k2, for example). The keys
can be used to
encrypt and decrypt data during the session.
c) Secure wireless communication such as WLAN, Wi-Fi, WiMAX to provide secure
communications between the end user device and the corresponding base station;
and
d) Wireless sensor network: the system and method described herein is also
effective for
wireless sensor networks. For this kind of wireless network, the communication
needs a high
-38-
CA 02639649 2008-09-19
security level and also less processing power. This invention meets all
requirements for
wireless sensor networks.
OPTIONS AND ALTERNATIVES
[00150] Additional options include the following:
1) Different multi-dimensional key construction: 2-dimensional keys are used
in the
examples above to make the idea much easier to be understood. Any number of
dimensions
may be used; and
2) Initial key establishment: A new ID-based key agreement scheme is described
herein.
This scheme can be used or modified. Alternatively, one could propose a
different initial key
agreement protocol. Any shared secret or key sharing agreement could be used
based on the
fact highly acceptable security is guaranteed.
CONCLUSIONS
[00151] The present invention has been described with regard to one or more
embodiments. However, it will be apparent to persons skilled in the art that a
number of
variations and modifications can be made without departing from the scope of
the invention as
defined in the claims.
[00152] The method steps of the invention may be embodied in sets of
executable
machine code stored in a variety of formats such as object code or source
code. Such code
may be described generally as programming code, software, or a computer
program for
simplification. Clearly, the executable machine code or portions of the code
may be
integrated with the code of other programs, implemented as subroutines, plug-
ins, add-ons,
software agents, by external program calls, in firmware or by other techniques
as known in the
art.
[00153] The embodiments of the invention may be executed by a computer
processor or
similar device programmed in the manner of method steps, or may be executed by
an
electronic system which is provided with means for executing these steps.
Similarly, an
-39-
CA 02639649 2008-09-19
electronic memory medium such as computer diskettes, hard drives, thumb
drives, CD-Roms,
Random Access Memory (RAM), Read Only Memory (ROM) or similar computer
software
storage media known in the art, may be programmed to execute such method
steps. As well,
electronic signals representing these method steps may also be transmitted via
a
communication network.
[00154] All citations are hereby incorporated by reference.
-40-