Note: Descriptions are shown in the official language in which they were submitted.
CA 02640641 2008-09-16
PUBLIC KEY CRYPTOGRAPHY UTILIZING ELLIPTIC CURVES
FIELD OF THE INVENTION
The present invention relates to public key
cryptography.
The increasing use and sophistication of data
transmission in such fields as telecommunications,
networking, cellular communication, wireless
communications, "smart card" applications, audio-visual
and video communications has led to an increasing need
for systems that permit data encryption, authentication
and verification.
It is well known that data can be encrypted by
utilizing a pair of keys, one of which is public and one
of which is private. The keys are mathematically related
such that data encrypted with the public key may only be
decrypted with the private key and conversely, data
encrypted with the private key can only be decrypted with
the public key. In this way, the public key of a
recipient may be made available so that data intended for
that recipient may be encrypted with the public key and
only decrypted by the recipient's private key, or
conversely, encrypted data sent can be verified as
authentic when decrypted with the sender's public key.
CA 02640641 2008-09-16
2
The most well known and accepted public key
cryptosystems are those based on integer factorization
and discrete logarithms in finite groups. In particular,
the RSA system for modulus n = p=q where p and q
are primes, the Diffie-Hellman key exchange and the
ElGamal protocol in Zp, (p a prime) have been implemented
worldwide.
The RSA encryption scheme, where two primes p and q
are multiplied to provide a modulus n, is based on the
integer factorization problem. The public key e and
private key d are related such that their product e=d
equals 1 (mod ~) where ~= (p-1) (q-1). A message M is
encrypted by exponentiating it with the private key e to
the modulus n, [ C = M e (mod n) ] and decrypted by
exponentiating with the public key mod n [M = Cd (mod n) ].
This technique requires the transmission of the modulus n
and the public key and the security of the system is
based on the difficulty of factoring a large number that
has no relatively small factors. Accordingly both p and
q must be relatively large primes.
One disadvantage of this system is that p and q must
be relatively large (at least 512 bits) to attain an
adequate level of security. With the RSA protocol this
results in a 1024 bit modulus and a 512 bit public key
CA 02640641 2008-09-16
3
which require significant bandwidth and storage
capabilities. For this reason researchers have looked
for public key schemes which reduce the size of the
public key. Moreover, recent advances in analytical
techniques and associated algorithms have rendered the
RSA encryption scheme potentially vulnerable and
accordingly raised concerns about the security of such
schemes. This implies that larger primes, and therefore a
larger modulus, need to be employed in order to maintain
an acceptable level of security. This in turn increases
the bandwidth and storage requirements for the
implementation of such a scheme.
Since the introduction of the concept of public key
cryptography by Diffie and Hellman in 1976, the potential
for the use of the discrete logarithm problem in public
key cryptosystems has been recognized. In 1985, ElGamal
described an explicit methodology for using this problem
to implement a fully functional public key cryptosystem,
including digital signatures. This methodology has been
refined and incorporated with various protocols to meet a
variety of applications, and one of its extensions forms
the basis for a proposed U.S. digital signature standard
(DSS). Although the discrete logarithm problem, as first
employed by Diffie and Hellman in their public key
exchange algorithm, referred explicitly to the problem of
finding logarithms with respect to a primitive element in
the multiplicative group of the field of integers modulo
CA 02640641 2008-09-16
4
a prime p, this idea can be extended to arbitrary groups
(with the difficulty of the problem apparently varying
with the representation of the group).
The discrete logarithm problem assumes that G is a
finite group, and a and b are elements of G. Then the
discrete logarithm problem for G is to determine a value
x (when it exists) such that a" = b. The value for x is
called a logarithm of b to the base of a, and is denoted
by logab .
The difficulty of determining this quantity depends
on the representation of G. For example, if the abstract
cyclic group of order m is represented in the form of the
integers modulo m, then the solution to the discrete
logarithm problem reduces to the extended Euclidean
algorithm, which is relatively easy to solve. However,
the problem ismade much more difficult if m+1 is a
prime, and the group is represented in the form of the
multiplicative group of the finite field Fm+l. This is
because the computations must be performed according to
the special calculations required for operating in finite
fields.
It is also known that by using computations in a
finite field whose members lie on an elliptic curve, that
is by defining a group structure G on the solutions of
CA 02640641 2008-09-16
y2+xy=x3+axZ+b over a finite field, the problem is again
made much more difficult because of the attributes of
elliptic curves. Therefore, it is possible to attain an
increased level of security for a given size of key.
5 Alternatively a reduced key may be used to maintain a
required degree of security.
The inherent security provided by the use of
elliptic curves is derived from the characteristic that
an addition of two points on the curve can be defined as
a further point that itself lies on the curve. Likewise
the result of the addition of a point to itself will
result in another point on the curve. Therefore, by
selecting a starting point on the curve and multiplying
it by an integer, a new point is obtained that lies on
the curve. This means that where P = (x,y) is a point on
an elliptic curve over a finite field [E(Fqn)], with x
and y each represented by a vector of n elements then,
for any other point R E< P>(the subgroup generated by
P), dP = R. To attack such a scheme, the task is to
determine an efficient method to find an integer d,
0 s d s( order of P) - 1 such that dP = R. To break such a
scheme, the best algorithms known to date have running
times no better than 0(~fp-), where p is the largest prime
dividing the order of the curve (the number of points on
the curve).
CA 02640641 2008-09-16
6
Thus, in a cryptographic system where the integer d
remains secret, the difficulty of determining d can be
exploited.
An ElGamal protocol of key exchange based on
elliptic curves takes advantage of this characteristic in
its definition of private and public keys. Such an
ElGamal protocol operates as follows:
1. In order to set up the protocol, where a message is
to be sent from A to B, an elliptic curve must be
selected and a point P = (x, y) , known as the
generating point, must be selected.
Encryption
2. The receiver, B, then picks a random integer d as
his private key. He then computes dP, which is
another point on the curve, which becomes his public
key that is made available to the sender and the
public. Although the sender knows the value dP, due
to the characteristic of elliptic curves noted
above, he has great difficulty determining the
private key d.
3. The sender A, chooses another random integer k,the
session seed, and computes another point on the
curve, kP which serves as a public session key.
CA 02640641 2008-09-16
7
This also exploits the characteristic of elliptic
curves mentioned above.
4. The sender, A, then retrieves the public key dP of
receiver B and computes kdP, another point on the
curve, which serves as the shared encryption key for
that session.
5. The sender, A, then encrypts the message M with the
encryption key to obtain the ciphertext C.
6. The sender then sends the public session key kP and
the ciphertext C to the receiver B.
Decryption
7. The receiver, B, determines the encryption key kdP
by multiplying his private key d by kP.
8. The receiver, B, can then retrieve the message M by
decrypting the ciphertext C with the encryption key
kdP.
During the entire exchange, the private key d and the
seed key k remain secret so that even if an interloper
intercepts the session key kP he cannot derive the
encryption key kdP from B's public key dP.
CA 02640641 2008-09-16
8
Elliptic curve cryptosystems can thus be implemented
employing public and private keys and using the ElGamal
protocol.
The elliptic curve cryptography method has a number
of benefits. First, each person can define his own
el'liptic curve for encryption and decryption, which gives
rise to increased security. If the private key security
is compromised, the elliptic curve can be easily
redefined and new public and private keys can be
generated to return to a secure system. In addition, to
decrypt data encoded with the method, only the parameters
for the elliptic curve and the session key need be
transmitted.
One of the drawbacks of other public key systems is
the large bandwidth and storage requirements for the
public keys. The implementation of a public key system
using elliptic curves reduces the bandwidth and storage
requirements of the public key system because the
parameters can be stored in fewer bits. Until now,
however, such a scheme was considered impractical due to
the computational difficulties involved and the
requirement for high speed calculations. The computation
of kP, dP and kdP used in a key exchange protocol
require complex calculations due to the mathematics
involved in adding points in elliptic curve fields.
CA 02640641 2008-09-16
9
Computations on an elliptic curve are performed
according to a well known set of relationships. If K
defines any field, then an equation of the form
y2 + alxy + a3y = x3 + aZx2 + a4x + a6 , where each of the
coefficients az lie in K, defines an elliptic curve over
K. If E is the set of points on this curve, then an
abelian group can be defined on the set E U{01 , where 0
is a special element not occurring in E. 0 acts as the
zero element of the group. If P = (x, y) , then -P = (x, -y)
in the case of an odd characteristic, and for two points
P and Q on the curve where Q# P, the sum P+ Q is the
third point on the curve where the line joining P and Q
again meets the curve. If P = Q, then the tangent line
is used. As in any abelian group, we use the notation nP
to denote P added to itself n times if n is positive,
and -P added to itself I nI times if n is negative, and
OP=0.
If Fq is a finite field, then elliptic curves over Fq
can be divided into two classes, namely supersingular and
non-supersingular curves. If Fq is of characteristic 2,
i.e. q=2M , then the classes are defined as follows.
i) The set of all solutions to the equation
y2 + ay = x3 + bx + c where a, b, c E Fq , ai4- 0, together with
CA 02640641 2008-09-16
a special point called the point at infinity 0 is a
supersingular curve over Fq.
ii) The set of all solutions to the equation
5 y2 + xy = x3 + ax2 + b where a,b E Fq , b~0 , together with a
special point called the point at infinity 0 is a
nonsupersingular curve over Fq.
By defining an appropriate addition on these points,
10 we obtain an additive abelian group. The addition of two
points P(x1, yl) and Q(x2, y2) for the supersingular
elliptic curve E with y2 + ay = x3 + bx + c is given by the
following:-
If P = (x1,y1) E E; then define
-P =(xl, yl + a) , P+ 0= 0+ P= P for all P E E.
If Q = (x2, y2) E E and Q~-P, then the point
representing the sum of P + Q, is denoted (x3, y3) , where
z
xl x2 (P~Q)
X3 = (y~1 2 )
or
Ixi b2
x3 = P
2 (
a
= Q)
CA 02640641 2008-09-16
11
and
y3 = yl y2 ( xl x3 ) yl a (P # Q)
XX2)
or
y3 = {(xeb)(e) 1 a yl a ( P = Q )
The addition of two points P(xl,yl) and Q(x2,y2) for
the nonsupersingular elliptic curve y2 + xy = x3 + ax2 + b
is given by the following:-
If P (xl, yl) E E then define -P =(xl, yl + xl) . For all
PEE, 0 + P = P + 0 = P. If Q= (xz,y2) E E and Q:0 -P,
then P + Q is a point (x3,y3) , where
x 3 = yl y2)2 y1 y2 x1 x2 a( P o Q)
( X X
or
X3 Xi ~ ( P= Q)
lt Xl
CA 02640641 2008-09-16
12
and
y3 = y( xl x3 ) (1) X3 (1) yl (P
# 9)
(x., 2)
or
y3 = Xl (Xl Xi f X3 X3 (P - Q~
Accordingly it can be seen that computing the sum of
two points on E requires several multiplications,
additions, and inverses in the underlying field Fq. In
turn, each of these operations requires a sequence of
elementary bit operations
When implementing an ElGamal or Diffie-Hellman
scheme with elliptic curves, one is required to compute
kp =p+ p+,,, + p (P added k times) where k is a
positive integer and P E E. This requires the
computation of (x3,y3) to be computed k-i times. Even if
alternative techniques such as "double and add" are
utilised, it is still necessary to compute the addition
of two points several times, each of which requires
multiplications, additions and inverses in the underlying
finite field. For large values of k which are typically
necessary in cryptographic applications, this has
previously been considered impractical for data
communication.
CA 02640641 2008-09-16
13
It is an object of the present invention to provide
a method of encryption utilizing elliptic curves that
facilitates the computation of additions of points while
providing an adequate level of security in an efficient
and effective manner.
The applicants have developed a method using a
modified version of the Diffie-Hellman and ElGamal
protocols defined in the group associated with the points
on an elliptic curve over a finite field. The method
involves formulating the elliptic curve calculations so
as to make elliptic curve cryptography efficient,
practical and viable, and preferably employs the use of
finite field processor such as the Computational Method
and Apparatus for Finite Field Multiplication as
disclosed in U.S. Patent 4,745,568. The preferred method
exploits the strengths of such a processor with its
computational abilities in finite fields. The inventive
method structures the elliptic curve calculations as
finite field multiplication and exponentiation over the
field r2m . In the preferred method, a normal basis
representation of the finite field is selected and the
calculations which can readily be performed on a finite
field processor.
The inventors have recognized that the computations
necessary to implement the elliptic curve calculations
CA 02640641 2008-09-16
14
can be performed efficiently where a finite field of
characteristic 2 is chosen.
When computing in a field of characteristic 2,
i.e. -kZm , squaring is a linear operation, i.e. (A+B)2 is
A 2 + B2. By adapting appropriate representations, the
computation of the squared terms required in the addition
of two points is greatly simplified. In particular, if a
normal basis representation is chosen, squaring can be
achieved through a cyclic shift of the binary vector
representing the field element to be squared.
Moreover, computing inverses in I-zm can be
implemented with simple shift and XOR operations by
selection of an appropriate representation. In some
implementations, the computation of an inverse can be
arranged to utilize multiple squaring operations and
thereby improve the efficiency of the computation.
When such computations are performed using a normal
basis representation of the finite field, the inventors
have also recognized that the elliptic curve calculations
are further simplified with the computations presented in
this form, the applicants have realized that specialized
semiconductor devices can be fabricated to perform the
calculations. With the calculations presented in such a
form, additions in the field FZm can be efficiently
CA 02640641 2008-09-16
performed in one clock cycle utilizing a simple XOR
operation.
Multiplications can be performed very efficiently in
5 only n clock cycles where n is the number of bits being
multiplied. Furthermore, squaring can be efficiently
performed in 1 clock cycle as a cyclic shift of the bit
register. Finally, inverses can easily be computed,
requiring approximately log2n multiplications rather than
10 the approximately 2n multiplications required in other
arithmetic systems.
The inventors have also recognized that the
bandwidth and storage requirements of a cryptographic
15 system utilizing elliptic curves can be significantly
reduced where for any point P(x,y) on the curve, only the x
coordinate and one bit of the y coordinate need be stored
and transmitted, since the one bit will indicate which of
the two possible solutions is the second coordinate.
The inventors have also recognized when using the
ElGamal protocol that messages need not be points on the
curve if the protocol is modified such that the message M
is considered as a pair of field elements M1M2 and each is
operated on by the coordinates (x,y) of the session
encryption key kdP in a predetermined manner to produce
new field elements CICZ that represent the ciphertext C.
CA 02640641 2008-09-16
16
The receiver can then extract the message M=(m1,m2) by
applying the inverse transformation of the predetermined
manner. Although this may require an inverse operation
in the field, they may be performed efficiently in the
field F2,55 , and in particular when operating with the
processor noted above.
To assist in the appreciation of the implementation
of the present invention , it is believed that a review
of the underlying principles of finite field operations
is appropriate. The finite field F2 is the number system
in which the only elements are the binary numbers 0 and 1
and in which the rules of addition and multiplication are
the following:
0+ 0= 1+ 1= 0
0+ 1= 1+ 0= 1
0 x 0= 1 x 0= 0 x 1= 0
1 x 1 = 1
These rules are commonly called modulo-2 arithmetic. All
additions specified in logic expressions or by adders in
this application are performed modulo-2 as an XOR
operation. Furthermore, multiplication is implemented
with logical AND gates.
CA 02640641 2008-09-16
17
The finite field F2., where m is an integer greater
than 1, is the number system in which there are 2m
elements and in which the rules of addition and
multiplication correspond to arithmetic modulo an
irreducible polynomial of degree m with coefficients in
F2. Although in an abstract sense there is for each m
only one field. FZm, the complexity of the logic required
to perform operations in F2m depends strongly on the
particular way in which the field elements are
represented. These operations may be performed using
processors implemented in either hardware or software
with dedicated hardware processors generally considered
faster.
The conventional approach to operations performed in F2m
is described in such papers as T. Bartee and D.
Schneider, "Computation with Finite Fields", Information
and Control, Vol. 6, pp. 79-98, 1963. In this
conventional approach, one first chooses a polynomial
P(X) of degree m which is irreducible over F2m, that is,
P(X) has binary coefficients but cannot be factored into
a product of polynomials with binary coefficients each of
whose degree is less than m. An element A in F2,, is then
defined to be a root of P(X), that is, to satisfy P(A)=0.
The fact that P(X) is irreducible guarantees that the m
CA 02640641 2008-09-16
18
elements A = 1, A, A2, A"r-1 of F2m are linearly
independent over FZ.
For the purposes of illustration, the example of F23
will be used with the choice of P(X) = X3 + X + 1 for the
irreducible polynomial of degree 3. The next step is to
define A as an element of F23 such that A3 + A + 1 = 0.
The following assignment of unit vectors is then made:
A = 1 = [1, 0, 0]
A' = [0, 1, 0]
A2 = [0,0,1]
An arbitrary element B of F23 is now represented by
the binary vector [b2, b, ,b ] with the meaning that
B = [b2, bl, b ] = b2A 2 + b1A + b .
If we represent a second element C = [c2, c1, c ] , it
follows that B + C = [b2 c2 , bi cl, bo co] .
Thus, in the conventional approach, addition in F23
is easily performed by logic that merely forms the
modulo-2 sum of the two vectors representing the elements
to be summed component-by-component. Multiplication is,
however, considerably more complex to implement.
CA 02640641 2008-09-16
19
Continuing the example, from the irreducible
polynomial it can be seen that A3 = A + 1 and A4 = A2 + A
where use has been made of the fact that -1 = +1 in F(2).
In hardware, multiplication can be simplified by taking
advantage of the special feature of a finite field FZ-
that there always exists a so-called normal basis for the
finite field. That is, one can always find a field
element N such that N,N2, N4 ... N2m-1 are a basis for F2..
Every field element B can be uniquely written as
B = bm-,N2m-1 + . . . + b2N4 + b1Nz + boN = [bm-i , . . . , b2, bl, bo ]
where bo, bl, b2, ... bm-1 are binary digits.
For example, in the finite field FZ,, if we let
N= [111,01
Element Field Normal Basis Representation Normal basis
Vector
[0, 0, 0] - 1010,01
1110,01 N2 + N4 [1, 1, 1]
[0, 1, 0] N+N2 + N4 1011,11
[0, 0, 1] N+ N2 [1, 0, 1]
[1, 1, 0] N [1, 0, 0]
[1, 0, 1] N+N4 1011,01
[011,11 N 1111,01
1111,11 N2 1010,11
CA 02640641 2008-09-16
Then, if B = [bm_,_, ..., b2, bl, bo] and
C = [cm_l, ., c2, cl, cO] - are any two elements of FZm in
normal basis representation, then the product
D = B x C = [dm_1, . . . , dz, dl, do] has the property
5 that the same logic circuitry which when
applied to the components or binary digits of the vectors
representing B and C produces dm-1 will sequentially
produce the remaining components d,n_Z, ..., d2, dl, do of the
product when applied to the components of the successive
10 shifts of the vectors representing B and C.
As illustrated in U.S. Patent 4,745,568 for
Computational Method and Apparatus for Finite Field
Multiplication, multiplication may be implemented by
15 storing bit vectors B and C in respective shift registers
and establishing connections to respective accumulating
cells such that a grouped term of each of the expressions dl
is generated in respective ones of m accumulating cells.
By rotating the bit vectors B and C in the shift
20 registers and by rotating the contents of the
accumulating cells, each grouped term of a respective
binary digit di is accumulated in successive cells. Thus
all of the binary digits of the product vector are
generated simultaneously in the accumulating cells after
one complete rotation of the bit vectors B and C.
CA 02640641 2008-09-16
21
One attribute of operating such a processor is that
in the field F2m, is that squaring is a linear operation
in the sense that for every pair of elements B and C in
FZ., (B + C) 2 = B2 + C2. It is the case for every element B
of F2. that B2M = B.
In particular in a normal basis representation,
squaring an element involves a cyclic shift of the
vectors representation of the element, i.e. if
B = [bm-1, . . . , bZ, bl, bol then B2 = [bm-2 . . . , b2, bl, bo, bm-11
Thus when using the processor exemplified above,
squaring may be achieved in one cycle. Moreover, this
general characteristic of F2m, where squaring is a linear
operation, may be exploited in other implementations,
such as software, where a normal basis representation is
not used.
. As noted above, the inventors have taken advantage
of the efficiency of the mathematical operations in F2.
in the implementation of an elliptic curve encryption
scheme. The applicants have developed a method of
formulating the elliptic curve calculations so as to make
elliptic curve cryptography efficient, practical and
viable. The preferred method employs the use of a finite
field processor such as the Computational Method and
CA 02640641 2008-09-16
22
Apparatus for Finite Field Multiplication as disclosed in
U.S. Patent 4,745,568. The method couples the attractive
cryptographic characteristics of elliptic curves with the
strengths of the field processor through its
computational abilities in finite field F2m. The
inventive method structures the elliptic curve
calculations as operations, such as multiplication and
exponentiation, over the field where F2., which can
readily be calculated on a finite field processor.
An embodiment of the invention will now be described
by way of example only with reference to the accompanying
drawings in which:-
Figure 1 is a diagram of the transmission of an
encrypted message from one location to another,
Figure 2 is a diagram of an encryption module used
with the communication system of Figure 1,
Figure 3 is a diagram of a finite field processor
used in the encryption and decryption module of Figure 2.
Figure 4 is a flow chart showing movement of the
elements through the processor of Figure 3 in computing
an inverse function.
CA 02640641 2008-09-16
23
Figure 5 is a flow chart showing movement of
elements through the processor of Figure 3 to compute the
addition of two points.
An embodiment of the invention will first be
described utilising an E1Gamal key exchange protocol and
a Galois field FZz55 to explain the underlying principles.
Further refinements will then be described.
System Components
Referring therefore to Figure 1, a message M is to
be transferred from a transmitter 10 to a receiver 12
through a communication channel 14. Each of the
transmitters 10 and receiver 12 has an
encryption/decryption module 16 associated therewith to
implement a key exchange protocol and an
encryption/decryption algorithm.
The module 16 is shown schematically in Figure 2 and
includes an arithmetic unit 20 to perform the
computations in the key exchange and generation. A
private key register 22 contains a private key, d,
generated as a 155 bit data string from a random number
generator 24, and used to generate a public key stored in
a public key register 26. A base point register 28
contains the coordinates of a base point P that lies in
the elliptic curve selected with each coordinate (x, y),
CA 02640641 2008-09-16
24
represented as a 155 bit data string. Each of the data
strings is a vector of binary digits with each digit
being the coefficient of an element of the finite field
in the normal basis representation of the coordinate.
The elliptic curve selected will have the general
form yZ + xy = x3 + axZ + b and the parameters of that
curve, namely the coefficients a and b are stored in a
parameter register 30. The contents of registers 22, 24,
26, 28, 30 may be transferred to the arithmetic unit 20
under control of a CPU 32 as required.'
The contents of the public key register 26 are also
available to the communication channel 14 upon a suitable
request being received. In the simplest implementation,
each encryption module 16 in a common security zone will
operate with the same curve and base point so that the
contents of registers 28 and 30 need not be accessible.
If further sophistication is required, however, each
module 16 may select its own curve and base point in
which case the contents of registers 28, 30 have to be
accessible to the channel 14.
The module 16 also contains an integer register 34
that receives an integer k, the session seed, from the
generator 24 for use in encryption and key exchange. The
module 16 has a random access memory (RAM) 36 that is
CA 02640641 2008-09-16
used as a temporary store as required during
computations.
The encryption of the message M with an -gjicryption
5 key kdP derived from the public key dP and session seed
integer k is performed in an encryption unit 40 which
implements a selected encryption algorithm. A simple yet
effective algorithm is provided by an XOR function which
XOR's the message m with the 310 bits of the encryption
10 key kdP. Alternative implementations such as the DES
encryption algorithm could of course be used.
An alternative encryption protocol treats the
message m as pairs of coordinates ml,mZ, each of 155 bit
15 lengths in the case of FZi55, and XOR's the message ml, m2
with the coordinates of the session key kdP to provide a
pair of bit strings (ml xo) (mZ yo) . For further
security a pair of field elements zlz2 are also formed
from the coordinates (xoyo) of kdP.
In one embodiment, the elements zlz2 are formed from
the concatenation of part of xo with part of yo, for
example, z, = xo111Yoz and zZ = xo211Yo1
where xo, is the first half of the bit string of xo
xM is the second half of the bit string of xo
Yoi is the first half of the bit string of yo
y02 is the second half of the bit string of yo
CA 02640641 2008-09-16
26
The first elements zl and z2 when treated as field
elements are then multiplied with respective bit strings
(ml (D xo) and (m2 (D yo) to provide bit strings cl c2 of
ciphertext c.
i. e. cl = zi (ml xo)
c2 = z2 (m2 Yo)
In a preferred implementation of the encryption
protocol, a function of xo is used in place of yo in the
above embodiment. For example the function xo is
used as the second 155 bit string so that
c1=z1 lm,_(Dxo )
c2=z2 (m2(Bx0 )
and
z1=x01 11xo32
3
ZZ=XOZXO1
where xol is the first half of xo
x02 is the second half of xo
This protocol is also applicable to implementation
of elliptic curve encryption in a field other than F2.,
for example Z. or in general FPm.
Where ZP is used it may be necessary to adjust the
values of xo and yo or xo to avoid overfow in the
CA 02640641 2008-09-16
27
multiplication with z, and z2. Conventionally this may be
done by setting the most significant bit xo and FP- or Yo
to zero.
Key generation, exchange and encryQtion
In order for the transmitter 10 to send the message
M to the receiver 12, the receivers public key is
retrieved by the transmitter 10. The public key is
obtained by the receiver 12 computing the product of the
secret key d and base point P in the arithmetic unit 20
as will be described more fully below. The product dP
represents a point on the selected curve and serves as
the public key. The public key dP is stored as two 155
bit data strings in the public key register 26.
Upon retrieval of the public key dP by the
transmitter 10, it is stored in the RAM 36. It will be
appreciated that even though the base point P is known
and publicly available, the attributes of the elliptic
curve inhibit the extraction of the secret key d.
The transmitter 10 uses the arithmetic unit 20 to
compute the product of the session seed k and the public
key dP and stores the result, kdP, in the RAM 36 for use
in the encryption algorithm. The result kdP is a further
point on the selected curve, again represented by two 155
CA 02640641 2008-09-16
28
bit data strings or vectors, and serves as an encryption
key.
The transmitter 10 also computes the product of the
session seed k with the base point P to provide a new
point kP, the session public key, which is stored in the
RAM 36.
The transmitter 10 has now the public key dP of the
receiver 12, a session public key kP and an encryption
key kdP and may use these to send an encrypted message.
The transmitter 10 encrypts the message M with the
encryption key kdP in the encryption unit 40 implementing
the selected encryption protocols discussed above to
provide an encrypted message C. The ciphertext C is
transmitted together with the value kP to the encryption
module 16 associated with receiver 12.
The receiver 12 utilises the session public key kP
with its private key d to compute the encryption key kdP
in the arithmetic unit 20 and then decrypt the ciphertext
C in the encryption unit 40 to retrieve the message M.
During this exchange, the secret key d and the
session seed k remain secret and secure. Although P, kP
and dP are known, the encryption key kdP cannot be
computed due to the difficulty in obtaining either d or
k.
CA 02640641 2008-09-16
29
The efficacy of the encryption depends upon the
efficient computation of thevalues kP, dP and kdP by the
arithmetic unit 20. Each computation requires the
repetitive addition of two points on the curve which in
turn requires the computation of squares and inverses in
FZ- .
operation of the Arithmetic Unit
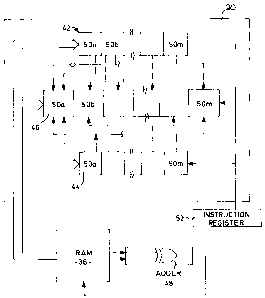
The operation of the arithmetic unit 20 is shown
schematically in Figure 3. The unit 20 includes a
multiplier 48 having a pair of cyclic shift registers 42,
44 and an accumulating register 46. Each of the
registers 42, 44, 46 contain M cells 50a, 50b...50m, in
this example 155, to receive the m elements of a normal
basis representation of one of the coordinates of e.g. x,
of P. As fully explained in U.S. Patent No. 4,745,568,
the cells 50 of registers 42, 44 are connected to the
corresponding cells 50 of accumulating register 46 such a
way that a respective grouped term is generated in each
cell of register 46. The registers 42,44,46 are also
directly interconnected in a bit wise fashion to allow
fast transfers of data between the registers.
The movement of data through the registers is
controlled by a control register 52 that can execute the
instruction set shown in the table below:
CA 02640641 2008-09-16
TABLE 1
INSTRUCTION SET
Operation Size Clock Cycles
5
Field Multiplication 155 bit blocks 156
MULT
10 Calculation of Inverse 24 multiplications approx. 3800
INVERSE
I/O 5-32 bit transfers per 10
10 clock cycles
WRITE(A,B or C)
read/write to registers 2 clock cycles
READ(A,B or C) per transfer
Elementary Register 155 bit parallel
operation
(idle)
NOP
Rotate (A,B or C)
Copy
(A(--B)
(A-C)
(A<-B)
(BE-C)
SWAP (AHB)
CLEAR (A,B or C)
SET (A,B or C)
ADD (A B)
ACCUMULATE
The unit 20 includes an adder 54 to receive data
from the registers 42,44,46 and RAM 36. The adder 54 is
an XOR function and its output is a data stream that may
be stored in RAM 36 or one of the registers 42, 44.
Although shown as a serial device, it will be appreciated
that it may be implemented as a parallel device to
CA 02640641 2008-09-16
31
improve computing time. Similarly the registers 42,44,46
may be parallel loaded. Each of the registers 42,44,46,
is a 155 bit register and is addressed by a 32 bit data
bus to allow 32 bit data transfer in 2 clock cycles and
the entire loading in 5 operations.
The subroutines used in the computation will now be
described.
a) Multiplication
The cyclic shift of the elements through the
registers 42, 44 m times with a corresponding shift of
the accumulating register 46 accumulates successive group
terms in respective accumulating cells and a complete
rotation of the elements in the registers 42, 44,
produces the elements of the product in the accumulating
register 46.
b) Squaring
By operating in F2A and adopting a normal basis
representation of the field elements, the multiplier 48
may also provide the square of a number by cyclically
shifting the elements one cell along the registers 42.
After a one cell shift, the elements in the register
represent the square of the number. In general, a number
CA 02640641 2008-09-16
32
may be raised to the power 2g by cyclically shifting g
times through a register.
c) Inversion
Computation of the inverse of a number can be
performed efficiently with the multiplier 48 by
implementing an algorithm which utilises multiple
squaring operations. The inverse X-1 is
represented as Xz"-z or X2 (2M-1-1) .
If m-1 is considered as the product of two factors
g,h then X-1 may be written as X2 (29h-1) or
2 h-1 where /3 = X2.
The exponent 2gh-1 is equivalent to
h-1
(29-1) E 2ig
t=o
g-1
The term 2g-1 may be written as F, 2i
j=0
2is
z3 ~^ ! ~h-1
~i(=o
R V `I
so that X'1 =
CA 02640641 2008-09-16
33
y-1
2i f21+2+2Z+23..... 29-1
and
is denoted y
This term may be computed on multiplier 48 as shown
in Figure 4 by initially loading registers 42, with the
value X. This is shifted 1 cell to represent 0 (i.e. X2)
and the result loaded into both registers 42, 44.
Register 44 is then shifted to provide 02 and the
registers 42, 44 multiplied to provide (32+1 in the
accumulating register 46. The multiplication is obtained
with one motion, i.e. a m bit cyclic shift, of each of
the registers 42, 44, 46.
The accumulated term '-+2 is transferred to
register 44 and register 42, which contains (,i2 is shifted
one place to provide 04. The registers 42, 44 are
multiplied to provide (31+2+4
This procedure is repeated g-2 times to obtain y.
As will be described below, y can be exponentiated in a
similar manner to obtain
A-1
F, 219
1''=0
i.e x'
CA 02640641 2008-09-16
34
,Y 1+29+2Z9+23g...... 2(h-t)9
This term can be expressed as
As noted above, 7 can be exponentiated to the 2g by
shifting the normal basis representation g times in the
register 42, or 44.
Accordingly, the registers 42, 44 are each loaded
with the value y and the register 42 shifted g times to
provide y 29 . The registers 42, 44 are multiplied
to provide y. y29 or y1+2 in the accumulating
register 46. This value is transferred to the register
44 and the register 42 shifted g times to provide
Y 2ZQ
=
The multiplication will then provide y1+29+2Zg
Repetition of this procedure (h-1)g-1 times produces the
inverse of X in the accumulating register 46.
From the above it will be seen that squaring,
multiplying, and inverting can be effectively performed
utilising the finite field multiplier 48.
CA 02640641 2008-09-16
Addition of point P to itself (P + P) using the
subroutines
To compute the value of dP for generation of the
5 public key, the arithmetic unit 20 associated with the
receiver 12 initially computes the addition of P + P. As
noted in the introduction, for a nonsupersingular curve
the new point Q has coordinates (X3,Y3) where
X3 =Xi e '
X1
_
10 Y3-X1 ( X1 X ) X3~X3
1
To compute X3, the following steps may be implemented
as shown in Figure 5.
15 The m bits representing X1 are loaded into register
42 from base point register 28 and shifted one cell to
the right to provide Xi . This value is stored in
RAM 36 and the inverse of Xi computed as described
above.
20 The value of X12 is loaded into register 44
and the parameter b extracted from the parameter register
30 and loaded into register 42. The product bx12 is
CA 02640641 2008-09-16
36
computed in the accumulating register 46 by rotating the
bit vectors and the resultant value XOR'd in adder 52
with value of Xi stored in RAM 36 to provide the
normal basis representation of X3. The result may be
stored in RAM 36.
A similar procedure can be followed to generate Y3 by
first inverting Xõ multiplying the result by Y, and
XORing with X1 in the adder 52. This is then multiplied
by X3 stored in RAM 36 and the result XOR'd with the value
of X3 and Xi to produce Y3.
The resultant value of (X3, Y3) represents the sum of
P + P and is a new point Q on the curve. This could then
be added to P to produce a new point Q'. This process
could be repeated d-2 times to generate dP.
The addition of P + Q requires the computation of
(X3, Y3) where
a e
x3 = (-V1 yZ)Z y1 Yz x1 x2
X X
and y3 = l~ (xl X3) X3 yl
( i 2)
This would be repeated d-2 times with a new value
for Q at each iteration to compute dP.
CA 02640641 2008-09-16
37
Whilst in principal this is possible with the
arithmetic unit 20, in practice the large numbers used
make such a procedure infeasible. A more elegant
approach is available using the binary representation of
the integer d.
Computation of dP from 2P
To avoid adding dissimilar points P and Q, the
binary representation of d is used with a doubling method
to reduce the number of additions and the complexity of
the additions.
The integer d can be expressed as
d= ~Xi2i,XiE(0,1) and dP =EJ1,i(22P) i.e.
i=0 i=0
a'm2-mP+a'm-12m-1P. . . ,X323P+a.222P+'X 12P+IoP
The values of X are the binary representation of d.
Having computed 2P, the value obtained may be added
to itself, as described above at Figure 5 to obtain 22P,
which in turn can be added itself to provide 23P etc.
This is repeated until 2`P is obtained.
CA 02640641 2008-09-16
38
At each iteration, the value of 21P is retained in
RAM 36 for use in subsequent additions to obtain dp.
The arithmetic unit 20 performs a further set of
additions for dissimilar points for those terms where ~
is 1 to provide the resultant value of the point (x3,y3)
representing dP.
If for example k=5, this can be computed as 22P + P
or 2P + 2P + P or Q+ Q + P. Therefore the result can be
obtained in 3 additions; 2P = Q takes 1 addition, 2P + 2P
= Q + Q= R takes 1 and R + P takes 1 addition. At most
t doublings and t subsequent additions are required
depending on how many X are 1.
Performance of Arithmetic units 20
For computations in a Galois field F22.55
it has been found that computing the inverse takes
approximately 3800 clock cycles.
The doubling of a point, i.e. the addition of point
to itself, takes in the order of 4500 clock cycles and
for a practical implementation of a private key, the
computation of the public key dP may be computed in the
order of 1.5 x 105 clock cycles. With a clock rate
typically in the order of 40 mHz, the computation of dP
will take in the order of 3 x 10"2 seconds. This
CA 02640641 2008-09-16
39
throughput can be enhanced by bounding the seed key k
with a Hamming weight of, for example, 20 and thereby
limit the number of additions of dissimilar points.
Computation of session public key kP and encryption
key kdP
The session public key kP can similarly be computed
with the arithmetic unit 20 of transmitter 10 using the
base point P from register 28. Likewise, because the
public key dP is represented as a point,(x3,y3), the
encryption key kdP can be computed in similar fashion.
Each of these operations will take a similar time
and can be completed prior to the transmission.
The recipient 12 is similarly required to compute
dkP as he received the ciphertext C which again will take
in the order of 3 x 10'2 seconds, well within the time
expected for a practical implementation of an encryption
unit.
The public key dP, and the session key kP are each
represented as a 310 bit data string and as such require
a significantly reduced bandwidth for transmission. At
the same time, the attributes of elliptic curves provides
a secure encryption strategy with a practical
CA 02640641 2008-09-16
implementation due to the efficacy of the arithmetic unit
20.
Curve selection
5
a) The selection of the field F m
The above example has utilised a field of 2155 and a
non-supersingular curve. The value 155 was chosen in
10 part because an optimal normal basis exists in F21sS
over F2. However, a main consideration is the security
and efficiency of the encryption system. The value 155
is large enough to be secure but small enough for
efficient operation. A consideration of conventional
15 attacks that might be used to break the ciphertext
suggests that with elliptic curves over FZm , a
value of m of about 130 provides a very secure system.
Using one thousand devices in parallel, the time taken to
find one logarithm is about 1.5 x 1011 seconds or at least
20 1500 years using the best known method and the field
F2155 . Other techniques produce longer run times.
b) Supersingular v. Nonsupersingular Curves
25 A comparison of attacks on data encrypted using
elliptic curves suggests that non-supersingular curves
are more robust than supersingular curves. For a field
CA 02640641 2008-09-16
41
Fqk , an attack based on the method suggested by
Menezes! Okamoto and Vanstone in an article entitled
"Reducing elliptic curve logarithms to logarithms in
finite field" published in the Proceeding 22 Annual ACM
Symposium Theory Computing 1991, pp. 80-89, (The MOV
attack) shows that for small values of k, the attack
becomes subexponential. Most supersingular curves have
small values of k associated with them. In general
however, non-supersingular curves have large values of k
and provided k>log2q then the MOV attack becomes less
efficient than more conventional general attacks.
The use of a supersingular curve is attractive since
the doubling of a point (i.e. the case where P = Q) does
not require any real time inversions in the underlying
field. For a supersingular curve, the coordinates of 2P
4 2 2
are x3 = xl b and y3 = xl b~ (xl (D xj ) yl a.
a2 a
Since a is a constant, a"' and a"2 is fixed for a given
curve and can be precomputed. The values of xi
and xi can be computed with a single and double
cyclic shift respectively on the multiplier 48. However,
the subsequent addition of dissimilar points to provide
the value of dP still requires the computation of an
CA 02640641 2008-09-16
42
lZ
inverse as Xs =( Yl ~ YzX! xi 0 xz and
i zJJ
y3 = Y1 Yzl ( xl x3 ) yl a
( xxz l
Accordingly, although supersingular curves lead to
efficient implementations, there is a relatively small
set of supersingular curves from which to choose,
particularly if the encryption is to be robust. For a
supersingular curve where m is odd, there are 3 classes
of curve that can be considered further, namely
yZ+y = x3
y 2 + y = x3+x
yz+y = x3+x+1
However, a consideration of these curves for the
case where m= 155 shows that none provide the necessary
robustness from attack.
Enhanced security for supersingular curves can be
obtained by employing quadratic extensions of the
underlying field. In fact, in Fq where q = 2310 , i.e. a
quadratic extension of 1"2155 , amongst the
supersingular curves, there are four which under the MOV
attack require computation of discrete logs in r293o
These curves provide the requisite high security and also
CA 02640641 2008-09-16
43
exhibit a high throughput. Similarly, in other
extensions of subfields of r2:,55 (e.g. 1231 )
other curves exist that exhibit the requisite robustness.
However, their use increases the digits that define a
point and hence the bandwidth when they are transmitted.
By contrast, the number of nonsupersingular curves
of Fq,q = 21ss, is 2(2iss - 1) . By selecting q = 2 i.e. a
field t2M , the value of a in the representation of the
curve, y2 + xy = x3 + ax2 + b, can be chosen to be either 1
or 0 without loss of generality. This large choice of
curves permits large numbers of curves over this field to
be found for which the order of a curve is divisible by a
large prime factor. In general, determining the order of
an arbitrary nonsupersingular curve over Fq is not trivial
and one approach is explained further in a paper entitled
"Counting Points'on Elliptic Curves" by Menezes, Vanstone
and Zuccherato, Mathematics of Computation 1992.
In general however, the selection of suitable curves
is well known in the art, as exemplified in "Application
of Finite Fields", chapters 7 and 8, by Menezes, Blake et
al, Kluwer Academic Publishers (ISBN 0-7923-9282-5).
Because of the large numbers of such curves that meet the
requirements, the use of nonsupersingular curves is
preferred despite the added computations.
CA 02640641 2008-09-16
44
An alternative approach that reduces the number of
inversions when using nonsupersingular curves is to
employ homogeneous coordinates. A point P is defined by
the coordinates (x, y, z,) and Q by the point (x2, y2, xZ)
The point (0 , 1 , 0) represents the identity 0 in
E.
To derive the addition formulas for the elliptic
curve with this representation, we take points
P = (x1, y1, z1) and Q = (xz, y2, z2) , normalize each to
(xl/zl, yl/zl, 1) ,(x'~/zz, y2/z2, 1) , and apply the previous
addition formulas. If
P= (x1,Y1, zl) , Q= (x2,Y2, z2) , P, Q00, and P;1 -Q then
P+ Q= (x3, y3, z3) where if P# Q, then
X3 = AD
y3 = CD +A 2 (Bx1 + Ay1)
Z3 = A3z1Z2
where A = xZzl + xlz2 , B = y2Z1 + yiz2 , C A + B and
D A2 (A + azlzz) + z1z2BC.
In the case of P = Q, then
X3 = AB
y3 = xiA + B( xi + yl z1 + A)
z3 = A3
CA 02640641 2008-09-16
where A= xlz,, and B= bzi + xi =
It will be noted that the computation of x3 y3 and z3
does not require any inversion. However, to derive the
5 coordinates x3,y3 in a nonhomogeneous representation,
it is necessary to normalize the representation so that
X3 - X3 Y3 - Y3
Z3 Z3
This operation requires an inversion that utilizes
10 the procedure noted above. However, only one inversion
operation is required for the computation of dP.
Using homogeneous coordinates, it is still possible
to compute dP using the version of the double and add
15 method described above. The computing action of
P + Q , P# Q, requires 13 field multiplications, and 2P
requires 7 multiplications.
Alternative Key Transfer
In the example above, the coordinates of the keys kP
kdP are each transferred as two 155 bit field elements
for F23-55 . To reduce the bandwidth further it is
possible to transmit only one of the co-ordinates and
compute the other coordinate at the receiver. An
CA 02640641 2008-09-16
46
identifier, for example a single bit of the correct value
of the other coordinate, may also be transmitted. This
permits the possibilities for the second coordinate to be
computed by the recipient and the correct one identified
from the identifier.
Referring therefore to Figure 1, the transmitter 10
initially retrieves as the public key dP of the receiver
12, a bit string representing the coordinate xo and a
single bit of the coordinate yo.
The transmitter 10 has the parameters of the curve
in register 30 and therefore may use the coordinate xo and
the curve parameters to obtain possible values of the
other coordinate yo from the arithmetic unit 20.
For a curve of the f orm y2 + xy = x3 + ax2 + b and a
coordinate xo, then the possible values y1,y2 for yo are
the roots of the quadratic y2 + xoy = xo3 + axo + b.
By solving for y, in the arithmetic unit 20 two
possible roots will be obtained and comparison with the
transmitted bit of information will indicate which of the
values is the appropriate value of y.
The two possible values of the second coordinate
(yo) differ by xo, i.e. yl = Y2+xo.
CA 02640641 2008-09-16
47
Since the two values of yo differ by xo, then y, and
y2 will always differ iahere a"1" occurs in the
representation of xo. Accordingly the additional bit
transmitted is selected from one of those positions and
examination of the corresponding bit of values of yo, will
indicate which of the two roots is the appropriate value.
The receiver 10 thus can generate the coordinates of
the public key dP'even though only 156 bits are
retrieved.
Similar efficiencies may be realized in transmitting
the session key kP to the receiver 12 as the transmitter
10 need only forward one coordinate, xo and the selected
identifying bit of yo. The receiver 12 may then
reconstruct the possible values of yo and select the
appropriate one.
In the field r2m it is not possible to solve for y
using the quadratic formula as 2a = 0. Accordingly,
other techniques need to be utilised and the arithmetic
unit 20 is particularly adapted to perform this
efficiently.
In general provided xo is not zero, if y = xoz then
xp2z2 + xO2z = x3p + ax, 2 + b.
CA 02640641 2008-09-16
48
This may be written as z2 + z = xo + a + 2 = c.
xo
i.e. zZ + z= c.
If m is odd then either z C+C4+C16 2m-'
....+....+c
C20+C2Z+C24+ . . . +C2g+C2m-l
or z= 1+C2 o+===+c2`1 to provide two possible
values for yo.
A similar solution exists for the case where m is
even that also utilises terms of the form c2g
This is particularly suitable for use with a normal
basis representation in FZm .
As noted above, raising a field element in F2m to a
power g can be achieved by a g fold cyclic shift where
the field element is represented as a normal basis.
Accordingly, each value of z can be computed by
shifting and adding and the values of yo obtained. The
correct one of the values is determined by the additional
bit transmitted.
The use of a normal basis representation in Fz.
therefore simplifies the protocol used to recover the
coordinate yo.
CA 02640641 2008-09-16
49
If P=(xo yo) is a point on the elliptic curve E : y2
+ xy = x3 + ax2 + b defined over a f ield 'F'2m , then yo is
defined to be 0 if xo = 0; if xo ;;6 0 then go is defined to
be the least significant bit of the field element yo = xo 1=
The x-coordinate xo of P and the bit yo are
transmitted between the transmitter 10 and receiver 12.
Then the y coordinate yo can be recovered as follows.
1. If xo = 0 then yo is obtained by cyclically
shifting the vector representation of the field
element. b that is stored in parameter register
30 one position to the left. That is, if
b=bm-Zbm-2 . . . blbo
then Yo bm-2 , . ' b1bo-bm-1
2. If xo ;z4- 0 then do the following:
2.1 Compute the field element c = xo + a + bxo2
in F2m.
2.2 Let the vector representation of c be
C = cm-1 Cm-2. . . CIco=
2.3 Construct a field element z zm_lzm_2= ==zlzo
by setting
zo = Yor
zl = co zo,
z2 = cl zl,
Zm-2 = Cm-3 ~) Zm-3 i
CA 02640641 2008-09-16
Z._i = Cm_2 Z._2-
2.4 Finally, compute yo = xo = z.
It will be noted that the computation of xo' can be
5 readily computed in the arithmetic unit 20 as described
above and that the computation of yo can be obtained from
the multiplier 48.
In the above examples, the identification of the
10 appropriate value of yo has been obtained by transmission
of a single bit and a comparison of the values of the
roots obtained. However, other indicators may be used to
identify the appropriate one of the values and the
operation is not restricted to encryption with elliptic
15 curves in the field GF ( 2 `) . For example, if the field is
selected as ZP p 3(mod 4) then the Legendre symbol
associated with the appropriate value could be
transmitted to designate the appropriate value.
Alternatively, the set of elements in Zp could be
20 subdivided into a pair of subsets with the property that
if y is in one subset, then -y is in the other, provided
y;v-'0. An arbitrary value can then be assigned to
respective subsets and transmitted with the coordinate xo
to indicate in which subset the appropriate value of yo is
25 located. Accordingly, the appropriate value of yo can be
determined. Conveniently, it is possible to take an
appropriate representation in which the subsets are
CA 02640641 2008-09-16
51
arranged as intervals to facilitate the identification of
the appropriate value of yo.
These techniques are particularly suitable for
encryption utilizing elliptic curves but may also be used
with any algebraic curves and have applications in other
fields such as error correcting coding where coordinates
of points on curves have to be transferred.
It will be seen therefore that by utilising an
elliptic curve lying in the finite field GFZm and
utilising a normal basis representation, the computations
necessary for encryption with elliptic curves may be
efficiently performed. Such operations may be
implemented in either software or hardware and the
structuring of the computations makes the use of a finite
field multiplier implemented in hardware particularly
efficient.