Note: Descriptions are shown in the official language in which they were submitted.
CA 02739778 2011-05-10
-1-
METHOD AND SYSTEM FOR PERFORMING COMPLEX SAMPLING OF
SIGNALS BY USING TWO OR MORE SAMPLING CHANNELS AND FOR
CALCULATING TIME DELAYS BETWEEN THESE CHANNELS
Field of the Invention
The present invention relates to digital signal processing. More particularly,
the present
invention relates to a method and system for performing complex sampling of
signals by
using two or more sampling channels (second-order sampling or higher) and
calculating
corresponding time delays between the two or more sampling channels.
Definitions, Acronyms and Abbreviations
Throughout this specification, the following definitions are employed:
Signal Sampling: is the process of converting a signal (e.g., that
continuously varies in
time or space) into a numeric sequence (e.g., having discrete values in time
or space). It
should be noted that a sampler is, generally, a system/device or operation(s)
that enables
extracting (producing) one or more samples from a signal. A theoretical ideal
sampler
produces samples equivalent to the instantaneous value of the continuous
signal at one or
more desired points in time or space.
Complex Sampling: is a sampling, in which an input signal is sampled, for
example, by
two samplers (sampling channels) that are shifted by ninety degrees, each
relative to
another. The output signal of the above sampling is a complex signal.
Complex Signal: is a signal consisting of real and imaginary parts. For
example, if a
complex signal is denoted X(t), then X (t) = xrea, (t) + i . ximaginary (t) ,
wherein i = . It
should be noted that in actual physical systems, signals x,,,,,, (t) and
ximaginary (t) are both
real, but are called the "real" and "imaginary" parts. The multiplier i is
used to help define
an operation(s) between different signals.
CA 02739778 2011-05-10
-2-
FFT: is an acronym for Fast Fourier Transform, which is an efficient algorithm
to
compute Discrete Fourier Transform (DFT) and its inverse. There are many
distinct FFT
algorithms in the art, involving a wide range of mathematic calculations, from
simple
complex-number arithmetic to group theory and number theory. Generally, the
output of
the Fast Fourier Transform is called the FFT spectrum.
FFT Bin: is a single frequency component of the FFT spectrum.
Background of the Invention
The subject matter of signal sampling is widely known in the prior art.
Generally, it
relates to digital signal processing and has high relevance in a variety of
fields, such as
communication, electronics, medicine, electro-optics, and many others. For
example, in
radio communication, sampling a signal and obtaining sufficient signal
attenuation, while
demodulating the desired signal from radio frequencies as close as possible to
the
baseband, is one of the main tasks. According to the commonly known Nyquist-
Shannon
sampling theorem, which is well known in the field of information theory, and
in
particular, in the field of digital signal processing and telecommunications,
an analog
signal that has been sampled can be fully reconstructed from the samples if
the sampling
frequency Fs exceeds 2B samples per second (2B is a Nyquist rate that is the
minimum
sampling rate required to avoid aliasing), where B is the bandwidth of the
original signal,
i.e. Fs>2B or F&12>B (half of the sampling rate is larger than the signal
bandwidth).
However, the above theorem is valid when the signal frequency range does not
contain
whole multiples or half-multiples of the sampling rate (sampling frequency).
It should be noted that signals that are used in many applications are, in
many cases, band
limited to a predefined frequency interval, and thus these signals are called
bandpass
signals. A uniform sampling theorem for bandpass signal is known from the
prior art, and
its analysis is usually based on the time frequency equivalence. Thus, for
example, A. W.
Kohlenberg proposed the second order sampling for a bandpass signal (in the
article titled
"Exact interpolation of band-limited functions", published in the journal of
Applied
Physics, in 1953, issue 24(12), pages 1432-1436), which is considered to be
the simplest
CA 02739778 2011-05-10
-3-
case of non-uniform sampling where two uniform sampling sequences are
interleaved.
Second order sampling allows the theoretical minimal sampling rate of two-
times
bandwidth, in the form of an average rate, to be applied independent of the
band position.
In second order sampling, when the delay z between two or more samplers is
properly
predefined, the signal can be fully reconstructed (e.g., by performing signal
interpolation)
even when the signal frequency range contains whole multiples or half-
multiples of the
sampling frequency.
Fig. IA schematically illustrates a conventional interpolation system 100 of
second order
sampling, according to the prior art. In Fig. IA, the input signal X(t) (t is
a time
parameter) passes through two Analog-to-Digital (A/D) converters 105' and 105"
with a
predefined time delay r between them. Then, the converted signals Xj(l) and
X2(l) are
inputted into interpolation filters 110' and 110", respectively, for
performing signal
interpolation, which includes digital to analog conversion. After that, the
resulting
interpolated signals are summed together, giving rise to the output signal
Y(1), and in turn
Y(t).
It should be noted that second order sampling and its limitations are well-
known in the
prior art, and this issue is discussed in the literature. For example, R.G.
Vaughan et al., in
the article titled "The Theory of Bandpass Sampling" published in the "IEEE
Transactions on Signal Processing" journal (volume 39, number 2, pp. 1973-
1984,
September 1991), discusses sampling of bandpass signals with respect to band
position,
noise considerations, and parameter sensitivity, presenting acceptable and
unacceptable
sample rates with specific discussion of the practical rates which are non-
minimum.
According to Vaughan et al., the construction of a bandpass signal from second-
order
samples depends on sampling factors and the relative delay between the uniform
sampling streams. For another example, M. Valkama et al., in the article
titled "A Novel
Image Rejection Architecture for Quadrature Radio Receivers" published in the
"IEEE
Transactions on Circuits and Systems" journal (volume 51, number 2, pp. 61-68,
February 2004), presents a novel structure for obtaining an image-free
baseband
observation of the received bandpass signal by utilizing I/Q
(Inphase/Quadrature) signal
CA 02739778 2011-05-10
-4-
processing. The phase difference between I and Q branches is approximated by a
relative
time delay of one quarter of the carrier cycle. Also, Valkama et al. presents
and analyzes
an analog delay processing based model, and then determines the obtainable
image
rejection of the delay processing. In addition, Valkama et al. in another
article titled
"Second-Order Sampling of Wideband Signals", published in the "IEEE
International
Symposium on Circuits and Systems" journal (volume 2, pp. 801-804, May 2001),
discusses and analyzes the second-order sampling based digital demodulation
technique.
According to Valkama et al., the modest image rejection of the basic second-
order
sampling scheme is improved to provide sufficient demodulation performance
also for
wideband receivers. Further, for example, H. Yong et al. in the article titled
"Second-
Order Based Fast Recovery of Bandpass Signals", published in the
"International
Conference on Signal Processing Proceedings" journal (volume 1, pp. 7-10,
1998),
discusses fast recovery and frequency-differencing of real bandpass signals
based on
second-order sampling. According to H. Yong et al., by using second-order
sampling, the
sampling rate can be lowered to the bandwidth. Although the spectrum of the
two
interleaved sampling streams are aliasing, it is possible to reconstruct the
original or
frequency-differencing bandpass signal.
Further, it should be noted that the conventional complex signal processing is
also used in
processing schemes where an input signal is bandpass in its origin, and is to
be processed
in a lowpass form. This normally requires two-channel processing in quadrature
channels
to remove an ambiguity as to whether a signal is higher or lower than the
bandpass center
frequency. The complex signal processing can be extended to the digital signal
processing field, and the processed signal can be first mixed to zero-center
frequency in
two quadrature channels, then filtered to remove the high frequency mixing
products, and
after that digitized by a number of A/D (Analog-to-Digital) converters.
According to the prior art, Fig. 113 schematically illustrates a conventional
complex
sampling system 160, in which an input signal is sampled in two sampling
channels 150'
and 150", while shifting the phase by ninety degrees. At the output of such a
system, a
complex signal is obtained, said signal having a real part Re{X(l)} and an
imaginary part
CA 02739778 2011-05-10
-5-
Im{X(l)}, wherein parameter l represents a series of discrete values. Filters
151, 152' and
152" are used to filter the undesired frequency range (in a time domain) of
input signals
X(t), X,'(t) and X2'(t), respectively.
US 5,099,194 discloses an approach to extending the frequency range uses non-
uniform
sampling to gain the advantages of a high sampling rate with only a modest
increase in
the number of samples. Two sets of uniform samples with slightly different
sampling
frequency are used. Each set of samples is Fourier transformed independently
and the
frequency of the lowest aliases determined. It is shown that knowledge of
these two alias
frequencies permits unambiguous determination of the signal frequency over a
range far
exceeding the Nyquist frequency, except at a discrete set of points.
US 5,099,243 presents a technique for extending the frequency range which
employs in-
phase and quadrature components of the signal coupled with non-uniform
sampling to
gain the advantages of a high sampling rate with only a small increase in the
number of
samples. By shifting the phase of the local oscillator by 90 degrees, a
quadrature IF signal
can be generated. Both in-phase and quadrature components are sampled and the
samples
are combined to form a complex signal. When this signal is transformed, only
one alias is
obtained per periodic repetition and the effective Nyquist frequency is
doubled. Two sets
of complex samples are then used with the slightly different sampling
frequency. Each set
is independently Fourier transformed and the frequency of the lowest aliases
permits
unambiguous determination of the signal frequency over a range far exceeding
the
Nyquist frequency.
US 5,109,188 teaches a technique for extending the frequency range which
employs a
power divider having two outputs, one output being supplied to a first Analog-
to-Digital
(A/D) converter, and the other output being supplied via a delay device to a
second A/D
converter. A processor receives the outputs of the two A/D converters. In
operation, the
input signal is subjected to a known delay and both original and delayed
signals are
sampled simultaneously. Both sampled signals are Fourier transformed and the
phase and
amplitudes calculated. The phase difference between the original and delayed
signals is
CA 02739778 2011-05-10
-6-
also calculated, and an approximation to the true frequency for each peak
observed in the
amplitude spectrum is estimated.
Based on the above observations, there is a continuous need in the art to
provide a
method and system configured to perform complex sampling of signals by using
two or
more sampling channels (second-order sampling or higher) and enabling
operating with a
signal bandwidth that can be equal to the sampling frequency (or to higher
multiples of
the sampling frequency). In addition, there is a need in the art to provide a
method and
system for performing signal processing by using second order (or higher
order)
sampling, in a frequency domain, without considering whether the signal
frequency range
contains whole multiples or half-multiples of the sampling frequency. Further,
there is a
continuous need in the prior art to enable calculating corresponding time
delays between
the two or more sampling channels in a relatively accurate manner.
Summary of the Invention
The present invention relates to a method and system for performing complex
sampling
of signals by using two or more sampling channels (second-order sampling or
higher) and
calculating corresponding time delays between the two or more sampling
channels.
A system is configured to perform a complex sampling of a signal in a
frequency-domain
by means of a predefined-order sampling, said system comprising:
a) a sampling channel comprising:
a.l. at least one analog-to-digital converter configured to convert an
analog signal to a corresponding substantially non-delayed digital
signal; and
a.2. at least one frequency-domain discrete transformation unit for
transforming said digital signal to a plurality of corresponding
frequency-domain substantially non-delayed discrete components;
b) one or more additional sampling channels enabling to perform a
predefined-order sampling, the predefined-order depending on a number
CA 02739778 2011-05-10
-7-
of said one or more additional sampling channels, each additional
sampling channel comprising:
b.l. at least one delay unit configured to delay an analog signal by a
predefined value, giving rise to a delayed analog signal;
b.2. at least one analog-to-digital converter configured to convert said
delayed analog signal to a corresponding delayed digital signal;
b.3. at least one frequency-domain discrete transformation unit for
transforming said delayed digital signal to a plurality of frequency-
domain delayed discrete components;
b.4. at least one data unit configured to provided one or more
corresponding coefficients for each frequency-domain delayed
discrete component; and
b.5. at least one multiplication unit configured to multiply said one or
more corresponding coefficients with said each corresponding
frequency-domain delayed discrete component, giving rise to the
multiplied frequency-domain delayed discrete components; and
c) at least one summation unit for summing said multiplied frequency-
domain delayed discrete components with the corresponding frequency-
domain substantially non-delayed discrete components, giving rise to an
output frequency-domain complex signal.
According to an embodiment of the present invention, the one or more
coefficients are at
least one of the following:
a) phase coefficients; and
b) gain coefficients.
According to an embodiment of the present invention, the frequency-domain
transformation is a Fourier transform.
According to another embodiment of the present invention, the Fourier
transform is the
FFT (Fast Fourier Transform).
CA 02739778 2011-05-10
-8-
According to still another embodiment of the present invention, an inverse
frequency-
domain transformation is applied on the output frequency-domain complex signal
for
obtaining an output time-domain complex signal.
According to still another embodiment of the present invention, the inverse
frequency-
domain transformation is the IFFT (Inverse FFT).
According to a further embodiment of the present invention, the system further
comprises
a processing unit configured to calculate a time delay between two or more
sampling
channels.
According to still a further embodiment of the present invention, the output
frequency-
domain complex signal has a predefined frequency spectrum that comprises one
or more
predefined frequencies, which are whole multiples and/or half-multiples of a
sampling
frequency, according to which the analog signal is sampled.
According to another embodiment of the present invention, a system is
configured to
perform a complex sampling of a signal in a frequency-domain, said system
comprising:
a) a non-delayed sampling channel module configured to provide a
plurality of frequency-domain substantially non-delayed discrete
signal components; and
b) one or more additional sampling channel modules, each additional
sampling channel module comprising at least one delay unit and at
least one coefficient unit for enabling providing a plurality of
frequency-domain delayed discrete components, said plurality of
frequency-domain delayed discrete components being adapted to a
specific frequency band, wherein said system is further configured to
combine the delayed discrete components with the corresponding
substantially non-delayed discrete components, for generating an
output frequency-domain complex signal.
CA 02739778 2011-05-10
-9-
According to another embodiment of the present invention, the coefficient unit
provides
coefficients for the specific frequency band.
According to still another embodiment of the present invention, a system is
configured to
perform a complex sampling of a signal in a time-domain by means of a
predefined-order
sampling, said system comprising:
a) a sampling channel comprising:
a.l. at least one analog-to-digital converter configured to convert an
analog signal to a corresponding time-domain substantially non-
delayed digital signal;
b) one or more additional sampling channels enabling to perform a
predefined-order sampling, the predefined-order depending on a number
of said one or more additional sampling channels, each additional
sampling channel comprising:
b.l. at least one delay unit configured to delay an analog signal by a
predefined value, giving rise to a delayed analog signal;
b.2. at least one analog-to-digital converter configured to convert said
delayed analog signal to a corresponding delayed digital signal;
and
b.3. at least one complex digital filter to be applied to said delayed
digital signal for generating complex samples of said delayed
digital signal, giving rise to a complex time-domain delayed digital
signal; and
c) at least one summation unit for combining the real portion of said complex
time-domain delayed digital signal with said time-domain substantially
non-delayed digital signal, giving rise to a combined digital signal, and
thereby giving a rise to an output time-domain complex signal, the real
portion of which is said combined digital signal and the imaginary portion
of which is the imaginary portion of said complex time-domain delayed
digital signal.
CA 02739778 2011-05-10
-10-
According to still another embodiment of the present invention, the digital
filter is a FIR
(Finite Impulse Response) filter.
According to a further embodiment of the present invention, a system is
configured to
perform a complex sampling of a signal in a time-domain, said system
comprising:
a) a non-delayed sampling channel module configured to provide a time-domain
substantially non-delayed digital signal; and
b) one or more additional sampling channel modules, each additional sampling
channel module comprising at least one delay unit and at least one complex
digital filter unit for enabling providing a complex time-domain delayed
digital
signal, wherein the real portion of said complex time-domain delayed digital
signal is further combined with said time-domain substantially non-delayed
digital signal, giving rise to a combined digital signal, and thereby giving a
rise
to an output time-domain complex signal, the real portion of which is said
combined digital signal and the imaginary portion of which is the imaginary
portion of said complex time-domain delayed digital signal.
According to an embodiment of the present invention, a method of performing
complex
sampling of a signal in a frequency-domain by means of a predefined-order
sampling,
said method comprising:
a) providing a sampling channel configured to:
a. 1. convert an analog signal to a corresponding substantially non-
delayed digital signal; and
a.2. transform said digital signal to a plurality of corresponding
frequency-domain substantially non-delayed discrete components;
b) providing one or more additional sampling channels enabling to perform a
predefined-order sampling, the predefined-order depending on a number
of said one or more additional sampling channels, each additional
sampling channel configured to:
CA 02739778 2011-05-10
-11-
b. 1. delay an analog signal by a predefined value, giving rise to a
delayed analog signal;
b.2. convert said delayed analog signal to a corresponding delayed
digital signal;
b.3. transform said delayed digital signal to a plurality of frequency-
domain delayed discrete components;
b.4. provide one or more corresponding coefficients for each frequency-
domain delayed discrete component; and
b.5. multiply said one or more corresponding coefficients with said each
corresponding frequency-domain delayed discrete component,
giving rise to the multiplied frequency-domain delayed discrete
components; and
c) combining said multiplied frequency-domain delayed discrete components
with the corresponding frequency-domain substantially non-delayed
discrete components, giving rise to an output frequency-domain complex
signal.
According to another embodiment of the present invention, a method of
performing a
complex sampling of a signal in a frequency-domain, said method comprising:
a) generating a plurality of frequency-domain substantially non-delayed
discrete signal components;
b) generating a plurality of frequency-domain delayed discrete components,
said plurality of frequency-domain delayed discrete components being
adapted to a specific frequency band by means of one or more
corresponding coefficients; and
c) combining the delayed discrete components with the corresponding
substantially non-delayed discrete components, for generating an output
frequency-domain complex signal.
CA 02739778 2011-05-10
-12-
According to still another embodiment of the present invention, a method of
performing
complex sampling of a signal in a time-domain by means of a predefined-order
sampling,
said method comprising:
a) providing a sampling channel for converting an analog signal to a
corresponding time-domain substantially non-delayed digital signal;
b) providing one or more additional sampling channels enabling to perform a
predefined-order sampling, the predefined-order depending on a number
of said one or more additional sampling channels, each additional
sampling channel configured to:
b.l. delay an analog signal by a predefined value, giving rise to a
delayed analog signal;
b.2. convert said delayed analog signal to a corresponding delayed
digital signal; and
b.3. generate complex samples of said delayed digital signal, giving rise
to a complex time-domain delayed digital signal; and
c) combining the real portion of said complex time-domain delayed digital
signal with said time-domain substantially non-delayed digital signal,
giving rise to a combined digital signal, and thereby giving a rise to an
output time-domain complex signal, the real portion of which is said
combined digital signal and the imaginary portion of which is the
imaginary portion of said complex time-domain delayed digital signal.
According to still another embodiment of the present invention, the method
further
comprises generating the complex time-domain delayed digital signal by using a
digital
filter.
According to a further embodiment of the present invention, a method of
performing a
complex sampling of a signal in a time-domain, said method comprising:
a) generating a time-domain substantially non-delayed digital signal;
b) generating a complex time-domain delayed digital signal; and
CA 02739778 2011-05-10
- 13-
c) combining the real portion of said complex time-domain delayed digital
signal with said time-domain substantially non-delayed digital signal,
giving rise to a combined digital signal, and thereby giving a rise to an
output time-domain complex signal, the real portion of which is said
combined digital signal and the imaginary portion of which is the
imaginary portion of said complex time-domain delayed digital signal.
According to an embodiment of the present invention, a method of calculating a
time
delay between two or more sampling channels in a signal processing system,
said method
comprising:
a) providing a first sampling channel for enabling sampling of a substantially
non-delayed signal; and
b) providing one or more additional sampling channels, each sampling channel
providing a predefined delay r to said signal, giving rise to a delayed
signal, and then enabling sampling of said delayed signal, wherein said
predefined delay r is calculated by using the relationship between said
delay r and the phase difference Lq$ of said delayed signal.
According to another embodiment of the present invention, the method further
comprises
defining the relationship between the time delay r and the phase difference
iq' by
means of at least one of the following:
a) 2=r=f =r=A01+2=7r=N;and
b) 2=ir.(f,+Af)=r=0q2+2='r.(N+M),
wherein A is a phase difference of a first delayed signal having a first
predefined
frequency f , A02 is a phase difference of a second delayed signal having a
second
predefined frequency f2, Of is a difference between said second and first
predefined
frequencies, thereby f2 = f, + df , and M and N are predefined integers.
According to still another embodiment of the present invention, the method
further
comprises determining the bound of integer Mby using the following
relationship:
CA 02739778 2011-05-10
-14-
M `r.Af_ A02 -o01
2,r
According to still another embodiment of the present invention, the method
further
comprises determining the approximation of the integer M by considering that
0<0q1 <2,r and 0<AO2 <2'z.
According to still another embodiment of the present invention, the method
further
comprises determining the approximation of the integer M by considering that
4f is
predefined.
According to a further embodiment of the present invention, the method further
comprises measuring frequency differences Af12 and Of 3 between the first
predefined
frequency f , the second predefined frequency f2 and a third predefined
frequency f3,
giving rise to frequency differences 4f12 = f2 - f and Af 3 = f3 - J I .
According to still a further embodiment of the present invention, the method
further
comprises calculating the time delay r approximation by using the one or more
of the
following:
a) r=A02-d01+Ml and
2T=Of12 Oft
b) 003-A01 +M2
IT = Of 3 Aft 3
wherein 003 is a phase difference of a third delayed signal having a third
predefined frequency f3 , and MI and M2 are integers.
According to still a further embodiment of the present invention, the method
further
comprises using the calculated time delay r approximation for determining a
value of the
integer M.
CA 02739778 2011-05-10
-15-
According to still a further embodiment of the present invention, the method
further
comprises determining a value of the integer N by using the determined value
of the
integer M.
According to still a further embodiment of the present invention, the method
further
comprises calculating the time delay r by using both determined values of the
integers M
and N.
Brief Description of the Drawings
In order to understand the invention and to see how it may be carried out in
practice,
various embodiments will now be described, by way of non-limiting examples
only, with
reference to the accompanying drawings, in which:
- Fig. 1A schematically illustrates a conventional interpolation system of
second order
sampling, according to the prior art;
- Fig. 1 B schematically illustrates a conventional complex sampling system,
in which
an input signal is sampled in two sampling channels, while shifting the phase
by
ninety degrees, according to the prior art;
- Fig. 2 is a schematic illustration of complex sampling in a frequency domain
by
performing second-order sampling, according to an embodiment of the present
invention;
- Fig. 3 is a schematic illustration of a complex sampling system, performing
sampling
in a time domain, according to another embodiment of the present invention;
and
- Fig. 4 is a schematic illustration of a system for complex sampling by
performing
sampling of 2M-order, according to still another embodiment of the present
invention.
CA 02739778 2011-05-10
-16-
It will be appreciated that for simplicity and clarity of illustration,
elements shown in the
figures have not necessarily been drawn to scale. For example, the dimensions
of some of
the elements may be exaggerated relative to other elements for clarity.
Further, where
considered appropriate, reference numerals may be repeated among the figures
to indicate
corresponding or analogous elements.
Detailed Description of the Embodiments
Unless specifically stated otherwise, as apparent from the following
teachings, it is noted
that throughout the specification utilizing terms such as "processing",
"computing",
"calculating", "determining", or the like, refer to the action and/or
processes of a
computer (machine) that manipulate and/or transform data into other data, said
data
represented as physical, e.g. such as electronic, quantities. The term
"computer" should
be expansively construed to cover any kind of electronic device with data
processing
capabilities, comprising, by the way of non-limiting examples, personal
computers,
servers, computing systems/units, communication devices, processors (e.g.,
digital signal
processors (DSPs), microcontrollers, field programmable gate arrays (FPGAs),
application specific integrated circuits (ASICs), etc.), and any other
electronic computing
devices. Also it should be noted that operations in accordance with the
teachings herein
may be performed by a computer that is specially constructed for the desired
purposes or
by a general purpose computer that is specially configured for the desired
purpose by
means of a computer program stored in a computer readable storage medium.
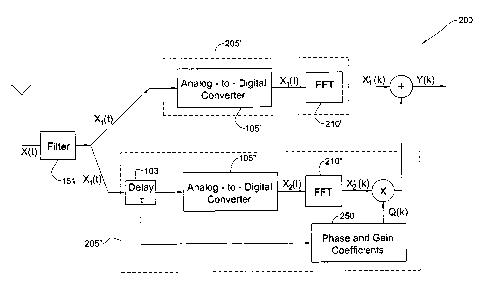
Fig. 2 is a schematic illustration 200 of complex sampling in a frequency
domain by
performing second-order sampling, according to an embodiment of the present
invention.
According to this embodiment, input signal X(t) is first filtered by means of
filter 151 in
order to remove the undesired frequency range (in a time domain). Then, the
filtered
signal XI(t) is sampled by means of two sampling channels (systems/modules)
205' and
205", having a predefined time delay r between them, and then is converted to
corresponding digital signals by means of conventional A/D converters 105' and
105",
giving rise to XI(l) and X2(7) signals respectively. After that, digital
signals X1(1) and X2(7)
are processed and converted to a frequency domain by means of the FFT (Fast
Fourier
CA 02739778 2011-05-10
-17-
Transform), which is a conventional technique for performing a discrete
Fourier
transform. As a result, discrete signals Xj'(k) and X2'(k) are obtained,
wherein k is an
index. It should be noted that the frequency band of input analog signal X(t)
is known (the
frequency bandwidth is equal to the sampling frequency Fs), and therefore the
phase
difference of each frequency component of the delayed signal X2'(k), which is
provided
via delayed sampling channel 205", can be calculated. According to an
embodiment of
the present invention, the frequency spectrum of delayed signal X2'(k) is
multiplied by a
corresponding set of predefined phase and gain coefficients Q(k) 250, each
having a gain
and phase (e.g., Q(k) = gk - exp(i = A(Pk) , wherein k is an index). Then, the
spectrum of
delayed signal X2(k) is summed (combined) with the spectrum of signal Xj'(k),
giving
rise to (generating) signal Y(k) that has a spectrum being equivalent to the
spectrum of a
complex signal, which can be also obtained by means of conventional complex
sampling.
According to an embodiment of the present invention, the desired time delay r
may be
different for different frequency bands. Further, the time delay r may be
obtained either
by providing time delay component/unit 103 (in which the time delay r can be
predefined) or by performing a phase difference (e.g., a phase shift) of a
sampling
frequency, leading to a desired time delay of a signal. It should be noted
that one or more
phase and gain coefficients Q(k) 250 are used for (are applied to) each
frequency
component of signal X2'(k). These phase and gain coefficients Q(k), provided
within the
corresponding coefficients data unit 250, can be predefined, for example,
empirically by
substantially accurate measuring of the above time delay r. It should be noted
that even in
a case when time delay r is a frequency-dependent component, the corresponding
phase
and gain coefficients Q(k) can be still calculated and predefined thereof.
According to an embodiment of the present invention, the phase and gain
coefficients are
pre-calculated during the calibration process of system 200, and then are
stored within the
memory means (not shown), while there is a need for a coefficient for each
frequency
component of signal X2'(k), after applying the FFT transform. Further, for
calculating the
corresponding phase difference Arp(k), there is a need to provide a signal of
a predefined
frequency, and then calculate the corresponding phase difference Orp(k)
between the
CA 02739778 2011-05-10
-18-
delayed and reference signals X2'(k) and Xj'(k), respectively. In addition, it
should be
noted that the power ratio between two channels (the non-delayed channel 205'
and
delayed channel 205") is calculated and corresponding gain coefficients gk (k
is an
index) are determined and stored within memory means (not shown) for later
usage. This
can be achieved in several ways, according to various embodiments of the
present
invention. According to one embodiment of the present invention, substantially
all
frequencies that correspond to the FFT frequency component to be calculated
are
provided, and then a phase difference for each such component is calculated.
If it is
supposed, for example, that the frequency range is (FS, 2F5) and the FFT
length is N, then
the set of frequencies f (k) that correspond to the FFT frequency components
are:
f(k)=FS+ =FS, for k=0,...,N-1 (1)
For each of the above N frequencies, the phase difference 0OP between the
sampling
channels 205' and 205" is calculated.
According to another embodiment of the present invention, a number of
frequencies are
provided in intervals that are greater than the FFT bin (bin is defined as
F'/N, wherein N
represents a number of FFT frequency components), and then the phase
difference for
each provided frequency is calculated by performing interpolation for each FFT
frequency component. Thus, for example, if the frequency range is (F5, 2F5)
and N/16
frequencies are provided, then the set of frequencies that correspond to the
FFT
frequency components are:
f(m)=Fs+1 . Fs, for m=0,...,N/16-1 (2)
According to this embodiment, for each of the above N/16 frequencies, the
phase
difference A(p between the sampling channels 205' and 205" is calculated.
After that, the
phase differences for each frequency component is calculated by performing
interpolation
CA 02739778 2011-05-10
-19-
of the corresponding phase difference Aco for each FFT frequency component of
signal
X2'(k):
Ocp(k;16m <_ k < 16m + 15) = 0q$(m) + k - 16m 16 (0O(m + 1) - 0q$(m)) (3)
According to a further embodiment of the present invention, a relatively small
number of
frequencies are provided in non-uniform frequency intervals, and then the
phase
differences A(p(m) between these frequencies are determined. After that, the
time delay r
is calculated by using the above-determined phase differences Acp(m) by means
of a
novel method for calculating time delays between sampling channels (such as
channels
205' and 205"), according to an embodiment of the present invention. The phase
differences A (m) for each FFT frequency component can be calculated by using
the
following equation:
A(p = mod(22r - f . r)2g (4)
wherein f is a frequency, and mod02ir is a "modulo" mathematical operator.
In general, when a real signal (having frequency J) is received, and the FFT
(having
length N) of said signal is calculated, then the resulting signal will appear
at the
frequency spectrum as a frequency component of the FFT bin k (generally, a FFT
bin is a
single frequency of the FFT, to which each frequency component contributes):
f = FS =(n+ N (5)
wherein f is a signal frequency; Fs is a sampling frequency; N is the FFT
length; n is an
integer; and k is a FFT bin number. Also, an additional (for example,
undesired)
frequency component appears in the FFT bin (N-k), due to the symmetry of the
conventional FFT. It should be noted that the phase difference Op,,,-, of the
above
CA 02739778 2011-05-10
-20-
undesired frequency component has an opposite sign compared to the phase
difference
Acok of the desired frequency component that appears in the FFT bin k.
According to an embodiment of the present invention, in order to cancel the
above
undesired frequency component appearing in the FFT bin (N-k), the frequency
components can be summed (combined) by using the following equation:
Y(k) = Xl (k) - gN-k = exp(i - ASoN-k) . X 2 (k) (6)
wherein AcoN-k is a predefined phase difference of the frequency component
that
contributes to bin N-k; gN-k is a gain coefficient calculated for that
frequency
component; X, (k) and X2 (k) are corresponding frequency components of non-
delayed
and delayed signals, respectively; and Y(k) represents frequency components at
the
output of system 200. As a result, the frequency spectrum of the output signal
Y(k) is
equivalent to the frequency spectrum of the conventional complex sampling.
It should be noted that according to an embodiment of the present invention,
when a
complex sampling is required in a time domain, then an inverse frequency-
domain
transformation, such as the Inverse Fourier transform (IFFT), can be performed
on the
frequency spectrum obtained by implementing system 200.
According to an embodiment of the present invention, time delays (time
differences)
between sampling channels (such as channels 205' and 205" (Fig. 2)) can be
calculated in
a relatively accurate manner (for example, by means of a processing
unit/system), as
described below in detail. According to this embodiment, the corresponding
time delay r
can be calculated by using the following relationship between the time delay
'r and phase
difference AO:
2.7r. fi =z=A01 +2=2r.N (7)
and
CA 02739778 2011-05-10
-21 -
2=,r=(.f,+Of)=T=0b2+2=,r=(N+M) (8)
wherein AO, is a phase difference of a signal having frequency fl; A02 is a
phase
difference of a signal having frequency f2, while f2 = f, + of ; and M and N
are
integers. It should be noted that the above two equations have three
variables: time delay
T, integer M and integer N.
For the bound range of values of time delay r, the bound for integer M can be
determined
by using the following equation, which is a result of subtracting equation (8)
from
equation (7):
M ='r = Of - 022 01 (9)
In such a way, the first approximation of integer M can be determined,
considering that
0 < AO1 < 27c and 0 < A02 < 27r, and considering that Of is known.
Further, by measuring frequency differences 4f12 and Of13 between three
predefined
frequencies fi, f2 and f3, such that Af12 = f2 - f, and Af13 = f3 - f1, the
corresponding
time delay r can be calculated by dividing the above equation (9) by said
frequency
differences 4f12 and Of 3 , respectively:
A02-A01+M, (10)
27r = 4f12 Lif12 and
T=A03-A01+M{~'2 (11)
27r = Of13 QJ 13
CA 02739778 2011-05-10
-22-
wherein M1 and M2 are bounded integers. Then, as a result, the following
equation is
obtained:
A02 - {A'01 + Ml 003 -D01 + M2 (12)
2Tr . df12 4112 2yr . 4f13 LJ 13
Thus, considering that M1 and M2 are bounded integers, and also phase
differences 0O1,
A02, 003 and frequency differences tf12 , 1 f13 are all known, then the first
approximation of time delay r can be determined. This time delay approximation
can be
inserted in equation (9) for obtaining a value of M in a relatively accurate
manner,
considering that M is a bounded integer. Then, after determining the value of
M, the value
of N can be also determined by inserting the determined value of M into
equations (7)
and (8). As a result, both bounded integers M and N are determined, and the
time delay r
is calculated in a relatively accurate manner by using the same equations (7)
and (8).
It should be noted that according to an embodiment of the present invention,
the range of
time delays r can be selected in the following way. It is supposed, for
example, that the
frequencies are within the range of [Fsrart, Fstart+BWJ, wherein Fstart is a
starting
frequency, and BW is a bandwidth, while Fs >_ BW (Fs is a sampling frequency).
The
gain (in dB (Decibels)) for the desired frequency component (of the FFT) can
be
presented by the following equation:
101og10 2 sinOCPk -I- OCp,~_k )2]
2
(13)
wherein dcpk is the phase difference of the frequency component that appears
in the FFT
bin k, when the frequency is f = Cn + N I = FS ; and D((N-k is the phase
difference of the
frequency component that appears in the FFT bin N-k, when the frequency is
CA 02739778 2011-05-10
-23-
f = Cn + k FS . If nF, Fs arr > (n -1) FS , then the phase difference Oq7k is
presented by:
D(pk = 22r(n + ) F, = r (14)
wherein n is an integer, and r is a time delay, which can be, for example, in
the range
determined by the following equation:
>Fs r> 1
6=(2n+1) 6=(2n-1) (15)
It should be noted that selecting the delay r within the above range ensures
that in
addition to removing the undesired frequency component (FFT bin (N-k)) of the
frequency spectrum, the power of the desired frequency component (FFT bin k)
will not
be decreased more than 3dB (Decibels), as shown in the equation below:
m z
l o logo 2 sin A~Pk 2 Y'N-k > -3 dB (16)
wherein Ocpk and API-k are phase differences in bins k and (N-k),
respectively. In
addition, it should be noted that any other constraints can be considered,
such as ensuring
that the power of the desired frequency component will not be decreased, for
example,
more than 2dB (instead of 3dB), and the like.
Fig. 3 is a schematic illustration of a complex sampling system 300,
performing sampling
in a time domain, according to another embodiment of the present invention.
According
to this embodiment of the present invention, signal X2(l) passes through a
digital FIR
(Finite Impulse Response) filter unit 310. This filter is a complex filter and
at its output,
CA 02739778 2011-05-10
-24-
complex signal samples are obtained. The real part of the signal samples after
FIR filter
310 is added to signal X1(1) that is outputted from A/D converter 105', giving
rise to
Re{Y(s)} signal, which is a real part of the signal, to which the complex
sampling is
applied. On the other hand, in the delayed sampling channel 305", the
imaginary part of
the signal samples, after passing via the FIR filter 310, is the imaginary
part (Im{Y(s)}) of
the signal, to which the complex sampling is applied.
According to an embodiment of the present invention, the FIR filter
coefficients h(p)
can be obtained by applying an inverse Fast Fourier transform (IFFT) on phase
and gain
coefficients Q(k) 250 (Fig. 2):
I N-1 k .
ph(p) _ -E 9k = exp(i = A(Pk) - exp(21r . i ) (17)
N k_o N
wherein gk and Dcok are a gain and phase difference, respectively, of the
corresponding
signal passing via delayed sampling channel 305"; k and p are indices; i is ;
and N is
a number of frequency components. It should be noted that each phase and gain
coefficient Q(k) can be equal to gk = exp(i = A(ok) , which is indicated
within the above
expression of h(p).
Fig. 4 is a schematic illustration of a system 400 for complex sampling by
performing
sampling of the 2M-order sampling (the predefined-order sampling), according
to still
another embodiment of the present invention. According to this embodiment, if
providing
2M sampling channels (two or more sampling channels) with predefined delays
r, , r2 , ..., r, between them, then operating with signal bandwidth B W = M =
F,
becomes possible, wherein F,s is a sampling frequency. This can be compared to
system
200 (Fig. 2), for which signal bandwidth BW is less or equal to the sampling
frequency: BW <_ F,.
CA 02739778 2011-05-10
-25-
It is supposed, for example, that sampling channels 205', 205", etc. are
represented by
index n, while n E [1, 2M]. The output frequency bands (Band 1, Band 2, etc.)
are
represented by index m, while in E [1, M]. In addition, each FFT bin is
numbered by
index k. The FFT of a signal is calculated in each sampling channel and is
represented as
Xn (k), the output frequency spectrum is represented as Ym (k), and phase and
gain
coefficients 250' are shown as Q, (k) . Thus, according to an embodiment of
the present
invention, the output frequency signal Y. (k) can be calculated by using the
following
equation, in which each at least one phase and gain coefficient Qõ", (k) is
multiplied with
its corresponding signal X,, (k) :
2M
Ym(k)=ZjQm(k)-Xn(k) (18)
n=1
It can be further supposed, for example, that input frequency F belongs to
Band M if
F E [F,põ + (m -1)F, , Fs,nõ + m = Fr ], wherein FS,Qõ is a starting frequency
that is defined
manually or automatically according to the need of a user of system 400; and
FS is a
sampling frequency, while m E [1, M] . Also, the frequency appears in the FFT
bin, if one
of the following two equations takes place:
round mod(F, F) = N = k or round mod(F, F) . N = (N - k) (19)
F,) FS F,) FS
wherein k and (N-k) are corresponding FFT bins; N is the FFT length; and
mod(.) is a
"modulo" mathematical operator.
The phase difference Ocpõ (k) of each corresponding frequency component
depends on
frequency Fm (k) (of FFT bin k in Band m (m E [1, M] )) and on the sampling
channel
delay r1 , r2 , ..., zn , as shown in the following equation:
CA 02739778 2011-05-10
-26-
A(p,,(k)=21r =F'(k)=zn (20)
It should be noted that the frequency spectrum of a signal Xn (k) passing via
each
corresponding sampling channel (such as sampling channels 205', 205", etc.) is
composed
of frequencies received from all bands (such as Band 1, Band 2, etc.). Thus,
signals from
2M possible frequency sources are provided to the corresponding bin k of the
FFT, as
presented in the following equation.
M
Xõ(k)=I[X(F"'(k))=e`4m~"k) +X`(Ft(N-k))=e-i-AVR(N-k)J (21)
M=1
As a result, the corresponding matrices of signals X,, (k) can be presented as
follows:
X1(k) e'-Agq (k) e-'-Afi (N-k) ... e-bA9,1 (N-k) X (F' (k))
X2(k) e~oro4(k) X`(F1(N-k))
(22)
X2M -1 (k) e o~~M-1(k) X(FM(k))
X 2M (k) eJ'o 'hi (k) e i=4p2M (N-k) ... e-!=OW2(N-k) X * (F"' (N - k))
wherein k and (N-k) are corresponding FFT bins; and N is the FFT length. If it
is
supposed, for example, that P(k) matrix is defined as follows:
e i-Aci (k) a-i=/Aci (N-k) ... e ' (N-k)
e i-owz (k) .
P(k) (23)
ei-e,p4M-i(k)
e i Apl (k) e i=e92M (N-k) e i'A(pM (N-k)
CA 02739778 2011-05-10
-27-
then, by further considering that the desired frequency spectrum at the output
is
2M
Ym( (k)_X(F"'(k))) EQ. Xn(k) (i.e., the output signal Ym(k) is adapted to a
n=1
specific frequency band/spectrum), the corresponding phase and gain
coefficients Q,; (k)
can be calculated by inverting the matrix P(k) and obtaining:
1 0 -.= 0 0
Qm (k) _ = P-' (k) (24)
0 0 === 1 0
Thus, for example, if M=2, the phase and gain coefficients Qõ, (k) are equal
to:
Q. "(k) - 0 0 10 0 P 1(k) (25)
For another example, if M=3, then the phase and gain coefficients Q,,; (k) are
equal to:
1 0 0 0 0 0
Qõ", (k) = 0 0 1 0 0 0- P-' (k) (26)
0 0 0 0 1 0
According to an embodiment of the present invention, the constraint for
selecting time
delay values in this case can be such that P(k) matrix is not singular, which
means that
the determinant of said P(k) matrix does not become equal to zero or almost
equal to
zero (i.e., there are no two or more substantially equal time delays r, for
example).
While some embodiments of the invention have been described by way of
illustration, it
will be apparent that the invention can be put into practice with many
modifications,
variations and adaptations, and with the use of numerous equivalents or
alternative
solutions that are within the scope of persons skilled in the art, without
departing from the
spirit of the invention or exceeding the scope of the claims.