Note: Descriptions are shown in the official language in which they were submitted.
CA 02774131 2012-04-11
METER ELECTRONICS AND METHODS FOR VERIFICATION
DIAGNOSTICS FORA FLOW METER
This application is a divisional application of co-pending application Serial
No. 2,622,976, filed September 19, 2005.
Background of the Invention
1. Field of the Invention
The present invention relates to a meter electronics and methods for
verification diagnostics for a flow meter.
2. Statement of the Problem
Vibrating conduit sensors, such as Coriolis mass flow meters or vibrating tube
densitometers, typically operate by detecting motion of a vibrating conduit
that
contains a flowing material. Properties associated with the material in the
conduit,
such as mass flow, density and the like, can be determined by processing
measurement signals received from motion transducers associated with the
conduit.
The vibration modes of the vibrating material-filled system generally are
affected by
the combined mass, stiffness, and damping characteristics of the containing
conduit
and the material contained therein.
A conduit of a vibratory flow meter can include one or more flow tubes. A
flow tube is forced to vibrate at a resonant frequency, where the resonant
frequency
of the tube is proportional to the density of the fluid in the flow tube.
Sensors located
on the inlet and outlet sections of the tube measure the relative vibration
between the
ends of the tube. During flow, the vibrating tube and the flowing mass couple
together due to Coriolis forces, causing a phase shift in the vibration
between the
ends of the tube. The phase shift is directly proportional to the mass flow.
A typical Coriolis mass flow meter includes one or more conduits that are
connected inline in a pipeline or other transport system and convey material,
e.g.,
fluids, slurries and the like, in the system. Each conduit may be viewed as
having a
set of natural vibration modes including, for example, simple bending,
torsional,
radial, and coupled modes. In a typical Coriolis mass flow measurement
application,
a conduit is excited in one or more vibration modes as a material flows
through the
1
CA 02774131 2012-04-11
conduit, and motion of the conduit is measured at points spaced along the
conduit.
Excitation is typically provided by an actuator, e.g., an electromechanical
device,
such as a voice coil-type driver, that perturbs the conduit in a periodic
fashion. Mass
flow rate may be determined by measuring time delay or phase differences
between
motions at the transducer locations. Two such transducers (or pickoff sensors)
are
typically employed in order to measure a vibrational response of the flow
conduit or
conduits, and are typically located at positions upstream and downstream of
the
actuator. The two pickoff sensors are connected to electronic instrumentation
by
cabling. The instrumentation receives signals from the two pickoff sensors and
processes the signals in order to derive a mass flow rate measurement.
The phase difference between the two sensor signals is related to the mass
flow rate of the material flowing through the flow tube or flow tubes. The
mass flow
rate of the material is proportional to the time delay between the two sensor
signals,
and the mass flow rate can therefore be determined by multiplying the time
delay by
a Flow Calibration Factor (FCF), where the time delay comprises a phase
difference
divided by frequency. The FCF reflects the material properties and cross-
sectional
properties of the flow tube. In the prior art, the FCF is determined by a
calibration
process prior to installation of the flow meter into a pipeline or other
conduit. In the
calibration process, a fluid is passed through the flow tube at a given flow
rate and
the proportion between the phase difference and the flow rate is calculated.
One advantage of a Coriolis flow meter is that the accuracy of the measured
mass flow rate is not affected by wear of moving components in the flow meter.
The
flow rate is determined by multiplying the phase difference between two points
of the
flow tube and the flow calibration factor. The only input is the sinusoidal
signals
from the sensors, indicating the oscillation of two points on the flow tube.
The phase
difference is calculated from these sinusoidal signals. There are no moving
components in the vibrating flow tube. Therefore, the measurement of the phase
difference and the flow calibration factor are not affected by wear of moving
components in the flow meter.
The FCF can be related to a stiffness characteristic of the meter assembly. If
the stiffness characteristic of the meter assembly changes, then the FCF will
also
change. Changes therefore will affect the accuracy of the flow measurements
2
CA 02774131 2012-04-11
generated by the flow meter. Changes in the material and cross-sectional
properties
of a flow tube can be caused by erosion or corrosion, for example.
Consequently, it
is highly desirable to be able to detect and/or quantify any changes to the
stiffness of
the meter assembly in order to maintain a high level of accuracy in the flow
meter.
Summary of the Solution
Meter electronics for a flow meter is provided according to an embodiment of
the invention. The meter electronics comprises an interface for receiving a
vibrational response from the flow meter and a processing system in
communication
with the interface. The vibrational response comprises a response to a
vibration of
the flow meter at a substantially resonant frequency. The processing system is
configured to receive the vibrational response from the interface, determine a
frequency (0)) of the vibrational response, determine a response voltage (V)
and a
drive current (I) of the vibrational response, measure a decay characteristic
(~) of the
flow meter, and determine the stiffness parameter (K) from the frequency
((00), the
response voltage (V), the drive current (I), and the decay characteristic (c).
A method for determining a stiffness parameter (K) of a flow meter is
provided according to an embodiment of the invention. The method comprises
receiving a vibrational response from the flow meter. The vibrational response
comprises a response to a vibration of the flow meter at a substantially
resonant
frequency. The method further comprises determining a frequency ((oo) of the
vibrational response, determining a response voltage (V) and a drive current
(I) of the
vibrational response, and measuring a decay characteristic (t) of the flow
meter. The
method further comprises determining the stiffness parameter (K) from the
frequency
(w0), the response voltage (V), the drive current (I), and the decay
characteristic (Q.
A method for determining a stiffness change (AK) in a flow meter is provided
according to an embodiment of the invention. The method comprises receiving a
vibrational response from the flow meter. The vibrational response comprises a
response to a vibration of the flow meter at a substantially resonant
frequency. The
method further comprises determining a frequency ((oo) of the vibrational
response,
determining a response voltage (V) and a drive current (I) of the vibrational
response,
and measuring a decay characteristic (~) of the flow meter. The method further
comprises determining the stiffness parameter (K) from the frequency ((oo),
the
3
CA 02774131 2012-04-11
response voltage (V), the drive current (I), and the decay characteristic (c).
The
method further comprises receiving a second vibrational response from the flow
meter at a second time t2, generating a second stiffness characteristic (K2)
from the
second vibrational response, comparing the second stiffness characteristic
(K2) to the
stiffness parameter (K), and detecting the stiffness change (AK) if the second
stiffness characteristic (K2) differs from the stiffness parameter (K) by more
than a
predetermined tolerance.
Meter electronics for a flow meter is provided according to an embodiment of
the invention. The meter electronics comprises an interface for receiving
three or
more vibrational responses from the flow meter. The three or more vibrational
responses include a substantially fundamental frequency response and two or
more
non-fundamental frequency responses. The meter electronics further comprises a
processing system in communication with the interface and configured to
receive the
three or more vibrational responses from the interface, generate a pole-
residue
frequency response function from the three or more vibrational responses, and
determine at least a stiffness parameter (K) from the pole-residue frequency
response
function.
A method for determining a stiffness parameter (K) of a flow meter is
provided according to an embodiment of the invention. The method comprises
receiving three or more vibrational responses. The three or more vibrational
responses include a substantially fundamental frequency response and two or
more
non-fundamental frequency responses. The method further comprises generating a
pole-residue frequency response function from the three or more vibrational
responses and determining at least a stiffness parameter (K) from the pole-
residue
frequency response function.
A method for determining a stiffness parameter (K) of a flow meter is
provided according to an embodiment of the invention. The method comprises
receiving three or more vibrational responses. The three or more vibrational
responses include a substantially fundamental frequency response and two or
more
non-fundamental frequency responses. The method further comprises generating a
pole-residue frequency response function from the three or more vibrational
responses and determining at least a stiffness parameter (K) from the pole-
residue
4
CA 02774131 2012-04-11
frequency response function. The method further comprises receiving a second
set of
three or more vibrational responses from the flow meter at a second time t2,
generating a second stiffness characteristic (K2) from the second set of three
or more
vibrational responses, comparing the second stiffness characteristic (K2) to
the
stiffness parameter (K), and detecting the stiffness change (AK) if the second
stiffness characteristic (K2) differs from the stiffness parameter (K) by more
than a
predetermined tolerance.
Aspects of the Invention
In one aspect of the meter electronics, measuring the decay characteristic (~)
further comprises allowing the vibrational response of the flow meter to decay
down
to a predetermined vibrational target.
In another aspect of the meter electronics, the processing system is further
configured to measure the decay characteristic Q by removing the excitation of
the
flow meter and allowing the vibrational response of the flow meter to decay
down to
a predetermined vibrational target while measuring the decay characteristic.
In another aspect of the meter electronics, the stiffness parameter (K)
comprises K = (I*BLpo*BLDR*(0o) / 2~V.
In one aspect of the method, measuring the decay characteristic Q further
comprises allowing the vibrational response of the flow meter to decay down to
a
predetermined vibrational target.
In another aspect of the method, measuring the decay characteristic (Q further
comprises removing the excitation of the flow meter and allowing the
vibrational
response of the flow meter to decay down to a predetermined vibrational target
while
measuring the decay characteristic.
In yet another aspect of the method, the stiffness parameter (K) comprising K
(I*BLpo*BLDR*0)0) / 2~V.
In yet another aspect of the method, generating the second stiffness
characteristic (K2) from the second vibrational response comprises generating
the
second stiffness characteristic (K2) from a second frequency, a second
response
voltage, a second drive current, and a second damping characteristic.
5
CA 02774131 2012-04-11
In yet another aspect of the method, the method further comprises detecting
the stiffness change (AK) if the second stiffness characteristic (K2) differs
from the
stiffness parameter (K) by more than a predetermined stiffness tolerance.
In yet another aspect of the method, the method further comprises quantifying
the stiffness change (AK) from the comparing of K and K2.
In one embodiment of the meter electronics, the processing system is further
configured to determine a damping parameter (C) from the pole-residue
frequency
response function.
In another embodiment of the meter electronics, the processing system is
further configured to determine a mass parameter (M) from the pole-residue
frequency response function.
In yet another embodiment of the meter electronics, the processing system is
further configured to compute a pole (X), a left residue (RL), and a right
residue (RR)
from the pole-residue frequency response function.
In yet another embodiment of the meter electronics, the three or more
vibrational responses comprise at least one tone above the fundamental
frequency
response and at least one tone below the fundamental frequency response.
In yet another embodiment of the meter electronics, the three or more
vibrational responses comprise at least two tones above the fundamental
frequency
response and at least two tones below the fundamental frequency response.
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a first order pole-residue frequency
response
function.
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a first order pole-residue frequency
response
function that comprises H(o)) = R/(jcw-2) + R /0 (o- A).
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a first order pole-residue frequency
response
function that comprises H(w) = R/(jc)-??) + R /0 (o- A) and wherein the
stiffness
parameter (K), the damping parameter (C), and the mass parameter (M) are
determined according to the equations M=1/2jRcod, K = (COõ )2M, and C = 2(wõM.
6
CA 02774131 2012-04-11
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a second order pole-residue frequency
response function.
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a second order pole-residue frequency
response function that comprises H (w) = X (w) _ j
F(co) -Mw2 + jCwo+K
In yet another embodiment of the meter electronics, the pole-residue
frequency response function comprises a second order pole-residue frequency
response function that comprises H (w) = X (CO) = jw and wherein
F(w) -Mw' + jCco+K
the stiffness parameter (K) is determined according to K = ((wõ )20Im[ II
((O)])/((wn)2-
w2)I IH (w)12), the mass parameter (M) is determined according to M = K/(wõ
)2, and the
damping parameter (C) is determined according to C = Re[ IH (w)]/I H ((0) 12.
In one embodiment of the method, the determining comprises further
determining a damping parameter (C) from the pole-residue frequency response
function.
In another embodiment of the method, the determining comprises further
determining a mass parameter (M) from the pole-residue frequency response
function.
In yet another embodiment of the method, the determining further comprises
computing a pole (X), a left residue (RL), and a right residue (RR) from the
pole-
residue frequency response function.
In yet another embodiment of the method, the three or more vibrational
responses comprise at least one tone above the fundamental frequency response
and
at least one tone below the fundamental frequency response.
In yet another embodiment of the method, the three or more vibrational
responses comprise at least two tones above the fundamental frequency response
and
at least two tones below the fundamental frequency response.
In yet another embodiment of the method, the pole-residue frequency
response function comprises a first order pole-residue frequency response
function.
7
CA 02774131 2012-04-11
In yet another embodiment of the method, the pole-residue frequency
response function comprises a first order pole-residue frequency response
function
comprising H((o) = R/(j(o-X) + R /0 o)- A).
In yet another embodiment of the method, the pole-residue frequency
response function comprises a first order pole-residue frequency response
function
comprising H(w) = R/(jw-?) + R /0 (o- A) and wherein the stiffness parameter
(K), the
damping parameter (C), and the mass parameter (M) are determined according to
the
equations M=1/2jRwd, K = ((On)2M, and C = 2cwõM.
In yet another embodiment of the method, the pole-residue frequency
response function comprises a second order pole-residue frequency response
function.
In yet another embodiment of the method, the pole-residue frequency
response function comprises a second order pole-residue frequency response
function
X(co) H (w) = _ ~`'
F(w) -Mw2 + jCw+K
In yet another embodiment of the method, the pole-residue frequency
response function comprises a second order pole-residue frequency response
function
that comprises H ((o) = X (O)) = j CO and wherein the stiffness
F(w) -Mw2 + jCw+K
parameter (K) is determined according to K = ((wõ )2wIm[ II ((O)])/(((Oõ )2-
(02)j H (w)j2),
the mass parameter (M) is determined according to M = K/(wn)2, and the damping
parameter (C) is determined according to C = Re[ H ((o)]/I II ((0)12.
In yet another embodiment of the method, the method further comprises
detecting the stiffness change (AK) if the second stiffness characteristic
(K2) differs
from the stiffness parameter (K) by more than a predetermined stiffness
tolerance.
In yet another embodiment of the method, the method further comprises
quantifying the stiffness change (AK) from the comparing of K and K2.
Description of the Drawings
The same reference number represents the same element on all drawings.
FIG. 1 shows a flow meter comprising a meter assembly and meter
electronics.
8
CA 02774131 2012-04-11
FIG. 2 shows meter electronics according to an embodiment of the invention.
FIG. 3 is a flowchart of a method for determining a stiffness parameter (K) of
a flow meter according to an embodiment of the invention.
FIG. 4 is a flowchart of a method for determining a stiffness change (AK) in a
flow meter according to an embodiment of the invention.
FIG. 5 shows the meter electronics according to another embodiment of the
invention.
FIG. 6 is a flowchart of a method for determining a stiffness parameter (K) of
a flow meter according to an embodiment of the invention.
FIG. 7 shows an implementation of the pole (X) and residue (R) solutions
according to an embodiment of the invention.
FIG. 8 is a block diagram showing the calculation of the M, C, and K system
parameters according to an embodiment of the invention.
FIG. 9 shows an overall FRF-based stiffness estimation system according to
an embodiment of the invention.
FIG. 10 is a flowchart of a method for determining a stiffness parameter (K)
of a flow meter according to an embodiment of the invention.
FIG. 11 shows the implementation of the M, C, and K solutions for the second
order pole-residue response from equations (29) according to an embodiment of
the
invention.
FIG. 12 shows the overall FRF-based stiffness estimation system according to
an embodiment of the invention.
Detailed Description of the Invention
FIGS. 1-12 and the following description depict specific examples to teach
those skilled in the art how to make and use the best mode of the invention.
For the
purpose of teaching inventive principles, some conventional aspects have been
simplified or omitted. Those skilled in the art will appreciate variations
from these
examples that fall within the scope of the invention. Those skilled in the art
will
appreciate that the features described below can be combined in various ways
to form
multiple variations of the invention. As a result, the invention is not
limited to the
specific examples described below, but only by the claims and their
equivalents.
9
CA 02774131 2012-04-11
FIG. 1 shows a flow meter 5 comprising a meter assembly 10 and meter
electronics 20. Meter assembly 10 responds to mass flow rate and density of a
process material. Meter electronics 20 is connected to meter assembly 10 via
leads
100 to provide density, mass flow rate, and temperature information over path
26, as
well as other information not relevant to the present invention. A Coriolis
flow meter
structure is described although it is apparent to those skilled in the art
that the present
invention could be practiced as a vibrating tube densitometer without the
additional
measurement capability provided by a Coriolis mass flow meter.
Meter assembly 10 includes a pair of manifolds 150 and 150', flanges 103 and
103' having flange necks 110 and 110', a pair of parallel flow tubes 130 and
130',
drive mechanism 180, temperature sensor 190, and a pair of velocity sensors
170L
and 170R. Flow tubes 130 and 130' have two essentially straight inlet legs 131
and
131' and outlet legs 134 and 134' which converge towards each other at flow
tube
mounting blocks 120 and 120'. Flow tubes 130 and 130' bend at two symmetrical
locations along their length and are essentially parallel throughout their
length. Brace
bars 140 and 140' serve to define the axis W and W' about which each flow tube
oscillates.
The side legs 131, 131' and 134, 134' of flow tubes 130 and 130' are fixedly
attached to flow tube mounting blocks 120 and 120' and these blocks, in turn,
are
fixedly attached to manifolds 150 and 150'. This provides a continuous closed
material path through Coriolis meter assembly 10.
When flanges 103 and 103', having holes 102 and 102' are connected, via inlet
end 104 and outlet end 104' into a process line (not shown) which carries the
process
material that is being measured, material enters end 104 of the meter through
an
orifice 101 in flange 103 is conducted through manifold 150 to flow tube
mounting
block 120 having a surface 121. Within manifold 150 the material is divided
and
routed through flow tubes 130 and 130'. Upon exiting flow tubes 130 and 130',
the
process material is recombined in a single stream within manifold 150' and is
thereafter routed to exit end 104' connected by flange 103' having bolt holes
102' to
the process line (not shown).
Flow tubes 130 and 130' are selected and appropriately mounted to the flow
tube mounting blocks 120 and 120' so as to have substantially the same mass
CA 02774131 2012-04-11
distribution, moments of inertia and Young's modulus about bending axes W--W
and
W'--W', respectively. These bending axes go through brace bars 140 and 140'.
Inasmuch as the Young's modulus of the flow tubes change with temperature, and
this change affects the calculation of flow and density, resistive temperature
detector
(RTD) 190 is mounted to flow tube 130', to continuously measure the
temperature of
the flow tube. The temperature of the flow tube and hence the voltage
appearing
across the RTD for a given current passing therethrough is governed by the
temperature of the material passing through the flow tube. The temperature
dependent voltage appearing across the RTD is used in a well known method by
meter electronics 20 to compensate for the change in elastic modulus of flow
tubes
130 and 130' due to any changes in flow tube temperature. The RTD is connected
to
meter electronics 20 by lead 195.
Both flow tubes 130 and 130' are driven by driver 180 in opposite directions
about their respective bending axes W and W' and at what is termed the first
out-of-
phase bending mode of the flow meter. This drive mechanism 180 may comprise
any
one of many well known arrangements, such as a magnet mounted to flow tube
130'
and an opposing coil mounted to flow tube 130 and through which an alternating
current is passed for vibrating both flow tubes. A suitable drive signal is
applied by
meter electronics 20, via lead 185, to drive mechanism 180.
Meter electronics 20 receives the RTD temperature signal on lead 195, and the
left and right velocity signals appearing on leads 165L and 165R,
respectively. Meter
electronics 20 produces the drive signal appearing on lead 185 to drive
element 180
and vibrate tubes 130 and 130'. Meter electronics 20 processes the left and
right
velocity signals and the RTD signal to compute the mass flow rate and the
density of
the material passing through meter assembly 10. This information, along with
other
information, is applied by meter electronics 20 over path 26 to utilization
means 29.
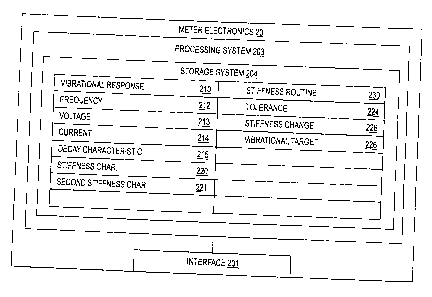
FIG. 2 shows the meter electronics 20 according to an embodiment of the
invention. The meter electronics 20 can include an interface 201 and a
processing
system 203. The meter electronics 20 receives a vibrational response 210, such
as
from the meter assembly 10, for example. The meter electronics 20 processes
the
vibrational response 210 in order to obtain flow characteristics of the flow
material
flowing through the meter assembly 10. In addition, in the meter electronics
20
11
CA 02774131 2012-04-11
according to the invention, the vibrational response 210 is also processed in
order to
determine a stiffness parameter (K) of the meter assembly 10. Furthermore, the
meter electronics 20 can process two or more such vibrational responses, over
time,
in order to detect a stiffness change (OK) in the meter assembly 10. The
stiffness
determination can be made under flow or no-flow conditions. A no-flow
determination may offer the benefit of a reduced noise level in the resulting
vibrational response.
As previously discussed, the Flow Calibration Factor (FCF) reflects the
material properties and cross-sectional properties of the flow tube. A mass
flow rate
of flow material flowing through the flow meter is determined by multiplying a
measured time delay (or phase difference/frequency) by the FCF. The FCF can be
related to a stiffness characteristic of the meter assembly. If the stiffness
characteristic of the meter assembly changes, then the FCF will also change.
Changes in the stiffness of the flow meter therefore will affect the accuracy
of the
flow measurements generated by the flow meter.
The invention is significant because it enables the meter electronics 20 to
perform a stiffness determination in the field, without performing an actual
flow
calibration test. It enables a stiffness determination without a calibration
test stand or
other special equipment or special fluids. This is desirable because
performing a
flow calibration in the field is expensive, difficult, and time-consuming.
However, a
better and easier calibration check is desirable because the stiffness of the
meter
assembly 10 can change over time, in use. Such changes can be due to factors
such
as erosion of a flow tube, corrosion of a flow tube, and damage to the meter
assembly
10, for example.
The invention can be illustrated with a mathematical model. The vibrational
response of a flow meter can be represented by an open loop, second order
drive
model, comprising:
Mc+Cx+Kx= f (1)
where f is the force applied to the system, M is a mass of the system, C is a
damping
characteristic, and K is a stiffness characteristic of the system. The term K
comprises
K = M((00)2 and the term C comprises C = M2~wo, where ( comprises a decay
12
CA 02774131 2012-04-11
characteristic, and o: = 27tfo where fo is the natural/resonant frequency of
the meter
assembly 10 in Hertz. In addition, x is the physical displacement distance of
the
vibration, z is the velocity of the flowtube displacement, and z is the
acceleration.
This is commonly referred to as the MCK model. This formula can be rearranged
into the form:
M[s2 +2Lw0s+wo]x= f (2)
Equation (2) can be further manipulated into a transfer function form. In the
transfer function form, a term of displacement over force is used, comprising:
x S
(3)
f M[s2 +2,"w0s+w0 ]
Well-know magnetic equations can be used to simplify equation (3). Two
applicable equations are:
V = BLPO (4)
and
f = BLDR *1 (5)
The sensor voltage VEMF of equation (4) (at a pick-off sensor 170L or 170R) is
equal to the pick-off sensitivity factor BLpo multiplied by the pick-off
velocity of
motion .z . The pick-off sensitivity factor BLpo is generally known or
measured for
each pick-off sensor. The force (f) generated by the driver 180 of equation
(5) is
equal to the driver sensitivity factor BLDR multiplied by the drive current
(I) supplied
to the driver 180. The driver sensitivity factor BLDR of the driver 180 is
generally
known or measured. The factors BLpo and BLDR are both a function of
temperature,
and can be corrected by a temperature measurement.
By substituting the magnetic equations (4) and (5) into the transfer function
of
equation (3), the result is:
V = BLPO * BLDR * S (6)
I M[s2 +2L"w0s+wo ]
If the meter assembly 10 is driven open loop on resonance, i.e., at a
resonant/natural frequency wo (where (oo=27tfo), then equation (6) can be
rewritten as:
V BLPO * BLDR * w0 (7)
I W 2jMwo ]
13
CA 02774131 2012-04-11
By substituting for stiffness, equation (7) is simplified to:
V 1 BLPD * BLDR * coo
J (8)
wa 2~K
Here, the stiffness parameter (K) can be isolated in order to obtain:
K = I* BLPO * BLDR * a)0 O
9
2
As a consequence, by measuring/quantifying the decay characteristic (c),
along with the drive voltage (V) and drive current (I), the stiffness
parameter (K) can
be determined. The response voltage (V) from the pick-offs can be determined
from
the vibrational response, along with the drive current (I). The process of
determining
the stiffness parameter (K) is discussed in more detail in conjunction with
FIG. 3,
below.
In use, the stiffness parameter (K) can be tracked over time. For example,
statistical techniques can be used to determine any changes over time (i.e., a
stiffness
change (AK)). A statistical change in the stiffness parameter (K) can indicate
that the
FCF for the particular flow meter has changed.
The invention provides a stiffness parameter (K) that does not rely on stored
or recalled calibration density values. This is in contrast to the prior art,
where a
known flow material is used in a factory calibration operation to obtain a
density
standard that can be used for all future calibration operations. The invention
provides
a stiffness parameter (K) that is obtained solely from vibrational responses
of the
flow meter. The invention provides a stiffness detection/calibration process
without
the need for a factory calibration process.
The interface 201 receives the vibrational response 210 from one of the
velocity sensors 170L and 170R via the leads 100 of FIG. 1. The interface 201
can
perform any necessary or desired signal conditioning, such as any manner of
formatting, amplification, buffering, etc. Alternatively, some or all of the
signal
conditioning can be performed in the processing system 203. In addition, the
interface 201 can enable communications between the meter electronics 20 and
external devices. The interface 201 can be capable of any manner of
electronic,
optical, or wireless communication.
14
CA 02774131 2012-04-11
The interface 201 in one embodiment is coupled with a digitizer (not shown),
wherein the sensor signal comprises an analog sensor signal. The digitizer
samples
and digitizes an analog vibrational response and produces the digital
vibrational
response 210.
The processing system 203 conducts operations of the meter electronics 20
and processes flow measurements from the flow meter assembly 10. The
processing
system 203 executes one or more processing routines and thereby processes the
flow
measurements in order to produce one or more flow characteristics.
The processing system 203 can comprise a general purpose computer, a
microprocessing system, a logic circuit, or some other general purpose or
customized
processing device. The processing system 203 can be distributed among multiple
processing devices. The processing system 203 can include any manner of
integral or
independent electronic storage medium, such as the storage system 204.
The storage system 204 can store flow meter parameters and data, software
routines, constant values, and variable values. In one embodiment, the storage
system 204 includes routines that are executed by the processing system 203,
such as
a stiffness routine 230 that determines the stiffness parameter (K) of the
flow meter 5.
The stiffness routine 230 in one embodiment can configure the processing
system 203 to receive a vibrational response from the flow meter, with the
vibrational
response comprising a response to a vibration of the flow meter at a
substantially
resonant frequency, determine a frequency (wo) of the vibrational response,
determine
a response voltage (V) and a drive current (I) of the vibrational response,
measure a
decay characteristic (~) of the flow meter, and determine the stiffness
parameter (K)
from the frequency (coo), the response voltage (V), the drive current (I), and
the decay
characteristic (t) (see FIG. 3 and the accompanying discussion).
The stiffness routine 230 in one embodiment can configure the processing
system 203 to receive the vibrational response, determine the frequency,
determine
the response voltage (V) and the drive current (I), measure the decay
characteristic
(c), and determine the stiffness parameter (K). The stiffness routine 230 in
this
embodiment further configures the processing system 203 to receive a second
vibrational response from the flow meter at a second time t2, repeat the
determining
and measuring steps for the second vibrational response in order to generate a
second
CA 02774131 2012-04-11
stiffness characteristic (K2), compare the second stiffness characteristic
(K2) to the
stiffness parameter (K), and detect the stiffness change (AK) if the second
stiffness
characteristic (K2) differs from the stiffness parameter (K) by more than a
tolerance
224 (see FIG. 4 and the accompanying discussion).
In one embodiment, the storage system 204 stores variables used to operate
the flow meter 5. The storage system 204 in one embodiment stores variables
such as
the vibrational response 210, which can be received from the velocity/pickoff
sensors
170L and 170R, for example.
In one embodiment, the storage system 204 stores constants, coefficients, and
working variables. For example, the storage system 204 can store a determined
stiffness characteristic 220 and a second stiffness characteristic 221 that is
generated
at a later point in time. The storage system 204 can store working values such
as a
frequency 212 of the vibrational response 210, a voltage 213 of the
vibrational
response 210, and a drive current 214 of the vibrational response 210. The
storage
system 204 can further store a vibrational target 226 and a measured decay
characteristic 215 of the flow meter 5. In addition, the storage system 204
can store
constants, thresholds, or ranges, such as the tolerance 224. Moreover, the
storage
system 204 can store data accumulated over a period of time, such as the
stiffness
change 228.
FIG. 3 is a flowchart 300 of a method for determining a stiffness parameter
(K) of a flow meter according to an embodiment of the invention. In step 301,
a
vibrational response is received from the flow meter. The vibrational response
is a
response of the flow meter to a vibration at a substantially resonant
frequency. The
vibration can be continuous or intermittent. A flow material can be flowing
through
the meter assembly 10 or can be static.
In step 302, a frequency of the vibrational response is determined. The
frequency o)o can be determined from the vibrational response by any method,
process, or hardware.
In step 303, the voltage (V or VEMF) of the vibrational response is
determined,
along with the drive current (I). The voltage and drive current can be
obtained from
an unprocessed or a conditioned vibrational response.
16
CA 02774131 2012-04-11
In step 304, a damping characteristic of the flow meter is measured. The
damping characteristic can be measured by allowing the vibrational response of
the
flow meter to decay down to a vibrational target while measuring the decay
characteristic. This decaying action can be performed in several ways. The
drive
signal amplitude can be reduced, the driver 180 can actually perform braking
of the
meter assembly 10 (in appropriate flow meters), or the driver 180 can be
merely
unpowered until the target is reached. In one embodiment, the vibrational
target
comprises a reduced level in a drive setpoint. For example, if the drive
setpoint is
currently at 3.4 mV/Hz, then for the damping measurement the drive setpoint
can be
reduced to a lower value, such as 2.5 mV/Hz, for example. In this manner, the
meter
electronics 20 can let the meter assembly 10 simply coast until the
vibrational
response substantially matches this new drive target.
In step 305, the stiffness parameter (K) is determined from the frequency, the
voltage, the drive current, and the decay characteristic (c). The stiffness
parameter
(K) can be determined according to equation (9), above. In addition to
determining
and tracking the stiffness (K), the method can also determine and track a
damping
parameter (C) and a mass parameter (M).
The method 300 can be iteratively, periodically, or randomly performed. The
method 300 can be performed at predetermined landmarks, such as at a
predetermined hours of operation, upon a change in flow material, etc.
FIG. 4 is a flowchart 400 of a method for determining a stiffness change (AK)
in a flow meter according to an embodiment of the invention. In step 401, a
vibrational response is received from the flow meter, as previously discussed.
In step 402, a frequency of the vibrational response is determined, as
previously discussed.
In step 403, the voltage and drive current of the vibrational response are
determined, as previously discussed.
In step 404, the decay characteristic Q of the flow meter is measured, as
previously discussed.
In step 405, the stiffness parameter (K) is determined from the frequency, the
voltage, the drive current, and the decay characteristic (c), as previously
discussed.
17
CA 02774131 2012-04-11
In step 406, a second vibrational response is received at a second time
instance t2. The second vibrational response is generated from a vibration of
the
meter assembly 10 at time t2.
In step 407, a second stiffness characteristic K2 is generated from the second
vibrational response. The second stiffness characteristic K2 can be generated
using
steps 401 through 405, for example.
In step 408, the second stiffness characteristic K2 is compared to the
stiffness
parameter (K). The comparison comprises a comparison of stiffness
characteristics
that are obtained at different times in order to detect a stiffness change
(AK).
In step 409, any stiffness change (AK) between K2 and K is determined. The
stiffness change determination can employ any manner of statistical or
mathematical
method for determining a significant change in stiffness. The stiffness change
(AK)
can be stored for future use and/or can be transmitted to a remote location.
In
addition, the stiffness change (AK) can trigger an alarm condition in the
meter
electronics 20. The stiffness change (AK) in one embodiment is first compared
to the
tolerance 224. If the stiffness change (AK) exceeds the tolerance 224, then an
error
condition is determined. In addition to determining and tracking the stiffness
(K), the
method can also determine and track a damping parameter (C) and a mass
parameter
(M).
The method 400 can be iteratively, periodically, or randomly performed. The
method 400 can be performed at predetermined landmarks, such as at a
predetermined hours of operation, upon a change in flow material, etc.
FIG. 5 shows the meter electronics 20 according to another embodiment of the
invention. The meter electronics 20 in this embodiment can include the
interface
201, the processing system 203, and the storage system 204, as previously
discussed.
The meter electronics 20 receives three or more vibrational responses 505,
such as
from the meter assembly 10, for example. The meter electronics 20 processes
the
three or more vibrational responses 505 in order to obtain flow
characteristics of the
flow material flowing through the meter assembly 10. In addition, the three or
more
vibrational responses 505 are also processed in order to determine a stiffness
parameter (K) of the meter assembly 10. The meter electronics 20 can further
determine a damping parameter (C) and a mass parameter (M) from the three or
more
18
CA 02774131 2012-04-11
vibrational responses 505. These meter assembly parameters can be used to
detect
changes in the meter assembly 10, as previously discussed.
The storage system 204 can store processing routines, such as the stiffness
routine 506. The storage system 204 can store received data, such as the
vibrational
responses 505. The storage system 204 can store pre-programmed or user-entered
values, such as the stiffness tolerance 516, the damping tolerance 517, and
the mass
tolerance 518. The storage system 204 can store working values, such as the
pole (k)
508 and the residue (R) 509. The storage system 204 can store determined final
values, such as the stiffness (K) 510, the damping (C) 511, and the mass (M)
512.
The storage system 204 can store comparison values generated and operated on
over
periods of time, such as a second stiffness (K2) 520, a second damping (C2)
521, a
second mass (M2) 522, a stiffness change (AK) 530, a damping change (AC) 531,
and
a mass change (AM) 532. The stiffness change (AK) 530 can comprise a change in
the stiffness parameter (K) of the meter assembly 10 as measured over time.
The
stiffness change (AK) 530 can be used to detect and determine physical changes
to
the meter assembly 10 over time, such as corrosion and erosion effects. In
addition,
the mass parameter (M) 512 of the meter assembly 10 can be measured and
tracked
over time and stored in a mass change (AM) 532 and a damping parameter (C) 511
can be measured over time and stored in a damping change (AC) 531. The mass
change (AM) 532 can indicate the presence of build-up of flow materials in the
meter
assembly 10 and the damping change (AC) 531 can indicate changes in a flow
tube,
including material degradation, erosion and corrosion, cracking, etc.
In operation, the meter electronics 20 receives three or more vibrational
responses 505 and processes the vibrational responses 505 using the stiffness
routine
506. In one embodiment, the three or more vibrational responses 505 comprise
five
vibrational responses 505, as will be discussed below. The meter electronics
20
determines the pole (?.) 508 and the residue (R) 509 from the vibrational
responses
505. The pole (2) 508 and residue (R) 509 can comprise a first order pole and
residue
or can comprise a second order pole and residue. The meter electronics 20
determines the stiffness parameter (K) 510, the damping parameter (C) 511, and
the
mass parameter (M) 512 from the pole (a,) 508 and the residue (R) 509. The
meter
electronics 20 can further determine a second stiffness (K2) 520, can
determine a
19
CA 02774131 2012-04-11
stiffness change (AK) 530 from the stiffness parameter (K) 510 and the second
stiffness (K2) 520, and can compare the stiffness change (AK) 530 to a
stiffness
tolerance 516. If the stiffness change (AK) 530 exceeds the stiffness
tolerance 516,
the meter electronics 20 can initiate any manner of error recordation and/or
error
processing routine. Likewise, the meter electronics 20 can further track the
damping
and mass parameters over time and can determine and record a second damping
(C2)
521 and a second mass (M2), and a resulting damping change (AC) 531 and mass
change (AM) 532. The damping change (AC) 531 and the mass change (AM) 532
can likewise be compared to a damping tolerance 517 and a mass tolerance 518.
The invention can be illustrated with a mathematical model. The vibrational
response of a flow meter can be represented by an open loop, second order
drive
model, comprising:
MY+Cx+Kx= f(t) (10)
where f is the force applied to the system, M is a mass parameter of the
system, C is a
damping parameter, and K is a stiffness parameter. The term K comprises K =
M((oo)2 and the term C comprises C = M2~w0, where o)o = 2nfo and fo is the
resonant
frequency of the meter assembly 10 in Hertz. The term ( comprises a decay
characteristic measurement obtained from the vibrational response, as
previously
discussed. In addition, x is the physical displacement distance of the
vibration, .z is
the velocity of the flowtube displacement, and x is the acceleration. This is
commonly referred to as the MCK model. This formula can be rearranged into the
form:
(ms 2 + cs + k)X (s) = F(s) + (ms + c)x(0) + mi(0) (11)
Equation (11) can be further manipulated into a transfer function form, while
ignoring the initial conditions. The result is:
1
H(s) _output X(s)_ In (12)
input F(s) s2 + cs + k
m m
Further manipulation can transform equation (12) into a first order pole-
residue frequency response function form, comprising:
CA 02774131 2012-04-11
H(co) = R + R (13)
Gw-A) (Jw-A)
where ? is the pole, R is the residue, the term (j) comprises the square root
of -
1, and w is the circular excitation frequency (in radians per second).
The system parameters comprising the natural/resonant frequency ((On), the
damped natural frequency ((Od), and the decay characteristic (~) are defined
by the
pole.
0)_i =JAI (14)
co,, = imag(2) (15)
= real(,) (16)
ton
The stiffness parameter (K), the damping parameter (C), and the mass
parameter (M) of the system can be derived from the pole and residue.
M _ 1 (17)
2 jRcod
K=OJ M (18)
C = 2cw,M (19)
Consequently, the stiffness parameter (K), the mass parameter (M), and the
damping parameter (C) can be calculated based on a good estimate of the pole
(k)
and the residue (R).
The pole and residue are estimated from the measured frequency response
functions. The pole (X) and the residue (R) can be estimated using some manner
of
direct or iterative computational method.
The response near the drive frequency is composed of primarily the first term
of equation (13), with the complex conjugate term contributing only a small,
nearly
constant "residual" part of the response. As a result, equation (13) can be
simplified
to:
H(co) = R (20)
GO) -A)
In equation (20), the H(w) term is the measured frequency response function
(FRF), obtained from the three or more vibrational responses. In this
derivation, H is
21
CA 02774131 2012-04-11
composed of a displacement output divided by a force input. However, with the
voice coil pickoffs typical of a Coriolis flow meter, the measured FRF (i.e.,
a
H term) is in terms of velocity divided by force. Therefore, equation (20) can
be
transformed into the form:
H(w) = H(w) = jw = jwR (21)
(Jw-A)
Equation (21) can be further rearranged into a form that is easily solvable
for
the pole (A,) and the residue (R).
Hjw-H2 = jwR
H=R+ H A (22)
Jw
1 H R =H
jw A
Equation (22) forms an over-determined system of equations. Equation (22)
can be computationally solved in order to determine the pole (k) and the
residue (R)
from the velocity/force FRF (R). The terms H, R, and ? are complex.
In one embodiment, the forcing frequency w is 5 tones. The 5 tones in this
embodiment comprise the drive frequency and 2 tones above the drive frequency
and
2 tones below. The tones can be separated from the fundamental frequency by as
little as 0.5-2 Hz. However, the forcing frequency co can comprise more tones
or
fewer tones, such as a drive frequency and 1 tone above and below. However, 5
tones strikes a good compromise between accuracy of the result and the
processing
time needed to obtain the result.
Note that in the preferred FRF measurement, two FRFs are measured for a
particular drive frequency and vibrational response. One FRF measurement is
obtained from the driver to the right pickoff (RPO) and one FRF measurement is
obtained from the driver to the left pickoff (LPO). This approach is called
single
input, multiple output (SIMO). In a distinguishing new feature of this
invention, a
SIMO technique is used to better estimate the pole (?) and the residue (R).
Previously, the two FRFs were used separately to give two separate pole (X)
and
residue (R) estimates. Recognizing that the two FRFs share a common pole (X)
but
22
CA 02774131 2012-04-11
separate residues (RL) and (RR), the two measurements can be combined
advantageously to result in a more robust pole and residue determination.
HLPO R L
1 0 JCO
RR = II (23)
0 1 HRPO 2
JO)
Equation (23) can be solved in any number of ways. In one embodiment, the
equation is solved through a recursive least squares approach. In another
embodiment, the equation is solved through a pseudo-inverse technique. In yet
another embodiment, because all of the measurements are available
simultaneously, a
standard Q-R decomposition technique can be used. The Q-R decomposition
technique is discussed in Modern Control Theory, William Brogan, copyright
1991,
Prentice Hall, pp. 222-224, 168-172.
In use, the stiffness parameter (K), along with the damping parameter (C) and
the mass parameter (M), can be tracked over time. For example, statistical
techniques can be used to determine any changes in the stiffness parameter (K)
over
time (i.e., a stiffness change (AK)). A statistical change in the stiffness
parameter (K)
can indicate that the FCF for the particular flow meter has changed.
The invention provides a stiffness parameter (K) that does not rely on stored
or recalled calibration density values. This is in contrast to the prior art,
where a
known flow material is used in a factory calibration operation to obtain a
density
standard that can be used for all future calibration operations. The invention
provides
a stiffness parameter (K) that is obtained solely from vibrational responses
of the
flow meter. The invention provides a stiffness detection/calibration process
without
the need for a factory calibration process.
FIG. 6 is a flowchart 600 of a method for determining a stiffness parameter
(K) of a flow meter according to an embodiment of the invention. In step 601,
three
or more vibrational responses are received. The three or more vibrational
responses
can be received from the flow meter. The three or more vibrational responses
can
include a substantially fundamental frequency response and two or more
non-fundamental frequency responses. In one embodiment, one tone above the
fundamental frequency response is received and one tone below the fundamental
23
CA 02774131 2012-04-11
frequency response is received. In another embodiment, two or more tones above
the
fundamental frequency response are received and two ore more tones below the
fundamental frequency response are received.
In one embodiment, the tones are substantially equidistantly spaced above and
below the fundamental frequency response. Alternatively, the tones are not
equidistantly spaced.
In step 602, a first order pole-residue frequency response is generated from
the three or more vibrational responses. The first order pole-residue
frequency
response takes the form given in equation (23).
In step 603, the mass parameter (M) is determined from the first order
pole-residue frequency response. The mass parameter (M) is determined by
determining the first order pole (?,) and the first order residue (R) of the
vibrational
responses. Then, the natural frequency c),,, the damped natural frequency cod,
and the
decay characteristic (~) are determined from the first order pole (?,) and
residue (R).
Subsequently, the damped natural frequency (nd, the residue (R), and the
imaginary
term (j) are plugged into equation (17) in order to obtain the mass parameter
(M).
In step 604, the stiffness parameter (K) is determined from the solution of
equation (18). The solution employs the natural frequency coõ and the
determined
mass parameter (M) from step 603 are plugged into equation (18) in order to
obtain
the stiffness parameter (K).
In step 605, the damping parameter (C) is determined from the solution of
equation (19). The solution employs the decay characteristic (c), the natural
frequency (O,,, and the determined mass parameter (M).
FIG. 7 shows an implementation of the pole (7.) and residue (R) solutions
according to an embodiment of the invention. The implementation follows
equation
(23). The FRF inputs are at the left of the diagram. These FRF inputs are the
five
frequencies at which FRF coefficients are calculated in this embodiment (four
test
signal frequencies and the drive frequency). The FRF_L and FRFR inputs are the
driver-pickoff complex FRF coefficients calculated at those frequencies,
corresponding to ALPO and IIRPO in equation (23). The FRF coefficients are
passed
into the B input of the QR solver block 701. The A matrix for the QR solver
block
24
CA 02774131 2012-04-11
701 is formed from the FRF coefficients divided by jcw on a term-by-term basis
and
comprises columns of l's and 0's to conform with equation (23). The matrix is
reshaped into the proper [10x3] complex dimensions and passed into the A input
of
the QR solver block 701. The x vector output of the QR solver block 701
comprises
the left and right residues RL and RR and the pole X. These outputs are passed
out of
the QR block 701 for processing in order to generate the system parameters.
FIG. 8 is a block diagram showing the calculation of the M, C, and K system
parameters according to an embodiment of the invention. The implementation
determines the M, C, and K system parameters from the pole and residue
estimates
per equations (14-16) and equations (17-19). The residues are purely imaginary
for a
real normal modal model. However, there will always be some real part due to
noise
in the measurement data and due to model-fitting numerical precision issues.
Therefore, the absolute value of the residue is used, which has a similar
effect as
dividing by j per equation (17). The mass and stiffness are calculated using
the pole
and residue per equations (17-18). Note that there is a "Left" and "Right"
mass and
stiffness, i.e., the mass and stiffness calculated from the FRFs of the
LPO/Driver and
the RPO/Driver. The mass and stiffness estimates may differ from right to left
due to
asymmetries in the coils and magnets and in the structure itself. Changes in
the
differences or the difference ratios indicate a non-uniform change in mass or
stiffness
and can be exploited to give additional diagnostic information about changes
to the
FCF or the integrity of the flow meter.
Two other outputs from the system parameter calculations are the damping
coefficient, zeta or ~, and the natural frequency co,,. This embodiment gives
a more
over-determined or better estimated set of global parameters.
The estimate of (o,, makes a good quality check for the closed loop drive
system. If the drive is indeed operating at resonance, the drive frequency
should
agree to within a few milliHertz to the natural frequency estimate. If the
difference in
more than a few milliHertz, a warning flag can be set, indicating that the
drive system
is not operating properly or that the current stiffness estimate is suspect.
FIG. 9 shows an overall FRF-based stiffness estimation system according to
an embodiment of the invention. There are seven distinct inputs to the
stiffness
CA 02774131 2012-04-11
estimation subsystem, indicated by pentagons that are signal sources (five on
the top
left, and two on the far right). The "RawDrive" and "RawPOs" inputs are the
raw
readings of the pickoff voltages and the drive current. These signals are
down-sampled to 2 kHz by decimation, for example, and are then fed into the
FRF
coefficient estimation subsystem. The "CmdmA" input is the commanded current
that is taken from the output of a corresponding digital drive system. The
"StiffnessEnable" estimate is a logical input, allowing the digital drive
system to
control when the FCF validation algorithm is active. The "freq" input is the
drive
frequency, as estimated by the digital drive system. It is input to the test
signal
generator subsystem and the stiffness calculation subsystem.
The FRF Stiffness calculation block 902 outputs the system parameter
estimates M & K Lft and Rt as well as Zeta and FreqEst. These are the primary
diagnostic outputs used in FCF validation. The figure also shows a freq diff
Warn
block 903 and a freq diff Error block 904 that implement the drive quality
check
discussed above by comparing the drive frequency to the estimated natural
frequency.
Measuring the FRF would normally require a current measurement,
necessitating an additional analog-to-digital (AID) converter. However, this
embodiment uses a calibrated commanded current, obviating the need for an
additional AID converter. The CL Input Select block 906 and the CL Output
Correction block 907 implement the calibration algorithm. The calibration
process
uses the "Test Signal FRF" block 901 to calculate the frequency response
function of
the actual (RawDrive) current to the commanded current (CmdmA) at one state of
the
controlling logic. During the FCF validation logic state, the FRF between the
raw
POs and the commanded current is calculated and corrected by the raw to
commanded current FRF coefficients to give the FRFs used for further
processing.
The FRF stiffness estimation algorithm outputs the "TestSignal" output at the
center left of the diagram of the figure. This test signal output contains
excitation at
the four test frequencies that are added to the drive command immediately
before
output. These test signals are added to the digital drive signal when FCF
validation is
enabled.
The logic is such that when the FCF validation is off, the digital drive
signal
passes right through a switch or other device, where it is upsampled from its
base rate
26
CA 02774131 2012-04-11
(typically 4 kHz) by the interpolation filter to the appropriate output rate,
typically 8
kHz. When FCF validation is enabled, the test signals, upsampled from 2 to 4
kHz,
are added to the digital drive signal. The drive signal then consists of the
closed loop
drive frequency signal and the 4 test tones, all of which then go through the
upsample
filter.
The FCF validation procedure is desirably transparent to the drive system. In
one embodiment, the test signals are removed from the pickoffs to ensure a
good
frequency and amplitude estimate for the closed loop drive. This is done with
a set of
notch filters tuned to the exact frequencies of the test signals.
In another embodiment, the pole-residue approach can employ a second-order
pole-residue frequency response function in order to achieve a better result.
A second
order pole-residue approach provides a truer fit to the real data than a first
order
pole-residue approach. The trade-off is a greater numerical complexity and
increased
processing time.
The MCK embodiment of the stiffness estimation begins with a simple second
order system model, as shown in equation (24), below. Since the pickoffs on
the flow
meter measure velocity, not position, the equation is differentiated and then
evaluated
at a particular frequency w.
H(s) = X (s) =
F(s) Ms2+Cs+K
X (s) = s (s) = F(s) Ms2 +Cs+K (24)
H(w) = X (w) = Jw
F(w) -Mw2 + jCw+K
Since the goal is to solve for M, C, and K from measurements of drive current
(or force) and pickoff voltage (or velocity), it is convenient to rewrite
equation (24)
to isolate the unknowns. This produces equation (25).
(25)
K-Mw2 +jCw = Hw (CO)
At this point the equation may be separated into real and imaginary parts.
27
CA 02774131 2012-04-11
K-Mw2 =Re Jw
H (w) (26)
Cw=Im Jw
II -(CO)
Expanding out H (w) , equation (26) can be rewritten as:
wIm{H(w)}
K-Mw2 =
H(w)I2 (27)
wRe{H(w)}
Cw= IH(w)IZ
The second equation is now a simple, algebraic solution. In order to further
simplify the first part of the equation, the measured resonant drive frequency
is
employed. Since co, = K/M , it may be found that:
wIm{H(w)}
(0,2
K wn _w2 - wIm{II(w)} 28
w`2 IH(w)IZ ( )
C02
K=(( ll
\w, -w2/I H(w)I2
so long as co # wõ . Backing out M from this solution for K, the three
solutions for M,
C, and K are given in equation (29).
wnwIm{II(w)}
K= }}
(wõ -w21I H(w)12
M = K (29)
wn
Re{H(w)}
IH(w)Iz
Note that given the resonant frequency co, a driver-pickoff FRF at one
particular frequency w, is sufficient to solve the equations and determine the
28
CA 02774131 2012-04-11
parameters M, C, and K. This is particularly useful; when FRFs are taken at
multiple
frequencies the least-squares fit to the data is simply the average of the
individual
estimates of each coefficient. This is a good deal simpler than the pseudo
inverse that
typically would have to be performed. Note, though, that the restriction that
co # co,, precludes the use of the resonant drive FRF in the solution for K or
M. This is
not particularly surprising since the height of a peak at a resonance is
determined
solely by the damping. One potential shortcoming of this approach, though, is
that
the parameters estimated from left and right pickoff data are necessarily
independent
of each other. This is in contrast to the pole-residue method, where some
benefit is
gained by restricting the left and right pickoffs to estimate the same pole,
despite
their differences in amplitude.
FIG. 10 is a flowchart 1000 of a method for determining a stiffness parameter
(K) of a flow meter according to an embodiment of the invention. In step 1001,
three
or more vibrational responses are received, as previously discussed.
In step 1002, a second order pole-residue frequency response is generated
from the three or more vibrational responses. The second order pole-residue
frequency response takes the form given in equation (24).
In step 1003, the stiffness parameter (K) is determined from the solution of
equation (29). The solution employs the natural frequency w,,, the one or more
frequency tones w, the imaginary portion of the FRF (i.e., an imaginary
component of
H (co)), and an amplitude of the FRF (i.e., the absolute value of H (w)).
In step 1004, the mass parameter (M) is determined from the second order
pole-residue frequency response. The mass parameter (M) is determined from the
solution of equation (29) and is obtained using the stiffness parameter (K)
and the
natural frequency w,,.
In step 1005, the damping parameter (C) is determined from the second order
pole-residue frequency response. The damping parameter (C) is determined from
the
solution of equation (29) and is obtained using the one or more frequency
tones co,
the real portion of the FRF (i.e., a real component of H (w)), and an
amplitude of the
FRF (i.e., the absolute value of H (w)).
29
CA 02774131 2012-04-11
FIG. 11 shows the implementation of the M, C, and K solutions for the second
order pole-residue response from equations (29) according to an embodiment of
the
invention. The inputs appear as oval input ports at the left of the diagram.
These are
the measured drive frequency o)-drive, which is used in equations (29) as co,
the five
frequencies at which FRF coefficients have been calculated (four test signal
frequencies and the drive frequency, represented by o)-test), and the driver-
pickoff
complex FRF coefficients calculated at those frequencies (H or Hdot). The
drive
frequency FRF is discarded by the selector blocks, since it cannot be used in
the M
and K solutions as described earlier. The K solution is computed as
wIm1H(w)1
K = (30)
1-w/2 2
which is an equivalent form of the solution given in equations (29). The
solution for
C is the same form as the derived solution in equations (29), and M is
directly
computed from the solution for K. Note the averaging operation that is applied
to
each coefficient estimate. This averaging results in solutions that are least-
squares
fits to the input data. Finally, given the M, C, and K estimates, the decay
characteristic (~ or zeta) is computed as:
CCO
Kt (31)
~ 2
The decay characteristic (~') is considered a more useful parameter than the
damping parameter C. Therefore, the mass M, stiffness K, and decay
characteristic
(~ )are the outputs of the measurement.
FIG. 12 shows the overall FRF-based stiffness estimation system according to
an embodiment of the invention. There are six distinct inputs to the system,
indicated
by pentagons that are signal sources (three on the upper left and three on the
lower
right). The "RawDrive" and "RawPOs" inputs are the raw readings from the
pickoffs
and the drive current. These are down sampled to 2 kHz by the Decimator block
1201 and then fed into the FRF coefficient estimation subsystem. The
"DriveDemod" input is a sine and cosine signal at the drive frequency that is
taken
from a digital drive system. These signals are combined with sinusoids
generated at
CA 02774131 2012-04-11
the test frequencies and fed into the FRF coefficient estimation subsystem as
bases
for demodulation. The "StiffnessEnable" estimate is a logical input, allowing
the
digital drive system to control when the stiffness estimation algorithm is
active. The
"freq" input is the drive frequency, as estimated by the digital drive system.
It is
input to the test signal generation block 1204 and the stiffness calculation
block 1206.
The "Temp" input is the temperature read from the flow meter that is inputted
into
the temperature correction block 1207. The FRF stiffness estimation algorithm
outputs the system parameter estimates, as well as the "TestSignal" output at
the far
left side of the diagram. This test signal output contains excitation at the
four test
frequencies that are to be added to the driver command.
These inputs and outputs form the bulk of the interface to the digital drive.
The test signals are added to the drive command immediately before output to a
driver device. In order to make this FCF validation procedure transparent to
the drive
system, it is necessary to remove the test signals from the pickoffs. This is
done in
one embodiment with a set of notch filters tuned to the exact frequencies of
the test
signals.
The Test Signal FRF block 1208 of FIG. 11 performs demodulations. The
pickoff and drive signals are demodulated at each of five input frequencies,
the four
generated test signal frequencies, and the drive frequency. After doing the
complex
demodulation using the sine and cosine bases, the real and imaginary
components of
each signal are decimated down to a lower frequency and low pass filtered to
0.4 Hz.
It is necessary that these signals be uncontaminated in this region, as any
spectral
component within 0.4 Hz of the test signal will not be suppressed and will
appear in
the output. The complex coefficients for the pickoffs and drive current at
each
frequency are then used to estimate the FRF at that frequency. The power
spectra are
averaged over a number of samples, and the lower-rate FRF estimate is output.
The meter electronics and methods according to the invention can be
employed according to any of the embodiments in order to provide several
advantages, if desired. The invention provides a stiffness parameter (K) that
is
substantially related to a flowtube stiffness of the flow meter. The invention
provides
a stiffness parameter (K) that does not rely on stored or recalled calibration
values for
generation. The invention provides a stiffness parameter (K) that is obtained
solely
31
CA 02774131 2012-04-11
from a vibrational response of the flow meter. Likewise, the invention
provides a
mass parameter (M) and a damping parameter (C) from the vibrational response.
The invention provides a stiffness detection/calibration process without the
need for a factory calibration process. The invention can perform a
stiffness/FCF
calibration process in the field. The invention can perform a stiffness/FCF
calibration process at any time. The invention can perform a stiffness/FCF
calibration process without the need for a calibration test rig and/or known
flow
materials. The invention can perform stiffness/FCF calibration processes that
determine changes in stiffness of the flow meter over time.
32