Note: Descriptions are shown in the official language in which they were submitted.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
1
Procédé et dispositif d'analyse d'images hyper-spectrales
La présente invention concerne l'analyse d'images et plus
particulièrement la classification statistique des pixels d'une image.
Elle concerne plus particulièrement la classification statistique des
pixels d'une image en vue de la détection de lésions cutanées, telles
que l'acné, le mélasma et la rosacée.
Les matériaux et éléments chimiques réagissent plus ou moins
différemment lors de l'exposition à un rayonnement d'une longueur
d'onde donnée. En balayant la gamme des rayonnements, il est
possible de différencier des matériaux intervenant dans la composition
d'un objet de par leur différence d'interaction. Ce principe peut être
généralisé à un paysage, ou à une partie d'un objet.
L'ensemble des images issues de la photographie d'une même
scène à des longueurs d'onde différentes est appelé image hyper-
spectrale ou cube hyper-spectral.
Une image hyper-spectrale est constituée d'un ensemble
d'images dont chaque pixel est caractéristique de l'intensité de
l'interaction de la scène observée avec le rayonnement. En connaissant
les profils d'interaction des matériaux avec différents rayonnements, il
est possible de déterminer les matériaux présents. Le terme matériau
doit être compris dans un sens large, visant aussi bien les matières
solides, liquides et gazeuses, et aussi bien les éléments chimiques purs
que les assemblages complexes en molécules ou macromolécules.
L'acquisition d'images hyper-spectrales peut être réalisée selon
plusieurs méthodes.
La méthode d'acquisition d'images hyper-spectrales dite de
scan spectral consiste à utiliser un capteur de type CCD, pour réaliser
des images spatiales, et à appliquer des filtres différents devant le
capteur afin de sélectionner une longueur d'onde pour chaque image.
Différentes technologies de filtres permettent de répondre aux besoins
de tels imageurs. On peut par exemple citer les filtres à cristaux
liquides qui isolent une longueur d'onde par stimulation électrique des
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
2
cristaux, ou les filtres acousto-optique qui sélectionnent une longueur
d'onde en déformant un prisme grâce à une différence de potentiel
électrique (effet de piézo-électricité). Ces deux filtres présentent
l'avantage de ne pas avoir de parties mobiles qui sont souvent source
de fragilité en optique.
La méthode d'acquisition d'images hyper-spectrales dite de
scan spatial vise à acquérir ou imager simultanément toutes les
longueurs d'ondes du spectre sur un capteur de type CCD. Pour
réaliser la décomposition du spectre, un prisme est placé devant le
capteur. Ensuite, pour constituer le cube hyperspectral complet, on
réalise un balayage spatial ligne par ligne.
La méthode d'acquisition d'images hyper-spectrales dite de
scan temporel consiste à réaliser une mesure d'interférence, puis de
reconstituer le spectre en faisant une transformée de Fourrier rapide
(acronyme anglais : FFT) sur la mesure d'interférence. L'interférence
est réalisée grâce à un système de type Michelson, qui fait interférer
un rayon avec lui-même décalé temporellement.
La dernière méthode d'acquisition d'images hyper-spectrales
vise à combiner le scan spectral et le scan spatial. Ainsi, le capteur
CCD est partitionné sous forme de blocs. Chaque bloc traite donc la
même région de l'espace mais avec des longueurs d'ondes différentes.
Puis, un balayage spectral et spatial permet de constituer une image
hyper-spectrale complète.
Plusieurs méthodes existent pour analyser et classer des images
hyper-spectrales ainsi obtenues, en particulier pour la détection des
lésions ou maladies d'un tissu humain.
Le document WO 99 44010 décrit une méthode et un dispositif
d'imagerie hyper-spectrale pour la caractérisation d'un tissu de la
peau. Il s'agit, dans ce document, de détecter un mélanome. Cette
méthode est une méthode de caractérisation de l'état d'une région
d'intérêt de la peau, dans laquelle l'absorption et la diffusion de la
lumière dans différentes zones de fréquence sont fonction de l'état de
la peau. Cette méthode comprend la génération d'une image numérique
de la peau incluant la région d'intérêt dans au moins trois bandes
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
3
spectrales. Cette méthode met en oeuvre une classification et une
caractérisation de lésions. Elle comprend une étape de segmentation
servant à réaliser une discrimination entre les lésions et le tissu
normal en fonction de l'absorption différente des lésions en fonction
de la longueur d'onde, et une identification des lésions par analyse de
paramètres tels que la texture, la symétrie, ou le contour. Enfin, la
classification proprement dite est réalisée à partir d'un paramètre de
classification L.
Le document US 5,782,770 décrit un appareil de diagnostic de
tissus cancéreux et une méthode de diagnostic comprenant la
génération d'une image hyper-spectrale d'un échantillon de tissu et la
comparaison de cette image hyper-spectrale à une image de référence
afin de diagnostiquer un cancer sans introduire d'agents spécifiques
facilitant l'interaction avec les sources lumineuses.
Le document WO 2008 103918 décrit l'utilisation de la
spectrométrie d'imagerie pour la détection d'un cancer de la peau. Il
propose un système d'imagerie hyper-spectrale permettant d'acquérir
rapidement des images à haute résolution en évitant le recalage
d'images, les problèmes de distorsion d'images ou le déplacement des
composants mécaniques. Il comprend une source de lumière multi-
spectrale qui illumine la zone de la peau à diagnostiquer, un capteur
d'images, un système optique recevant la lumière de la zone de peau et
élaborant sur un capteur d'image une cartographie de la lumière
délimitant les différentes régions, et un prisme de dispersion
positionné entre le capteur d'image et le système optique afin de
projeter le spectre des régions distinctes sur le capteur d'image. Un
processeur d'image reçoit le spectre et l'analyse afin d'identifier des
anomalies cancéreuses.
Le document WO 02/057426 décrit un appareil de génération
d'une carte histologique bidimensionnelle à partir d'un cube de
données hyper-spectrales tridimensionnelles représentant l'image
scannée de col de l'utérus d'une patiente. Il comprend un processeur
d'entrée normalisant les signaux spectraux fluorescents collectés du
cube de données hyper-spectrales et extrayant les pixels des signaux
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
4
spectraux indiquant la classification des tissus cervicaux. Il comprend
également un dispositif de classification qui fait correspondre une
catégorie de tissu à chaque pixel et un processeur d'image en lien avec
le dispositif de classification qui génère une image bidimensionnelle
du col de l'utérus à partir des pixels incluant des régions codées à
l'aide de code couleurs représentant les classifications des tissus du
col de l'utérus.
Le document US 2006/0247514 décrit un instrument médical et
une méthode de détection et d'évaluation d'un cancer à l'aide
d'images hyper-spectrales. L'instrument médical comprend notamment
un première étage optique illuminant le tissu, un séparateur spectral,
un ou plusieurs polarisateurs, un détecteur d'image, un processeur de
diagnostic et une interface de contrôle de filtre. La méthode peut être
utilisée sans contact, à l'aide d'une caméra, et permet d'obtenir des
informations en temps réel. Elle comporte notamment un prétraitement
de l'information hyper-spectrale, la construction d'une image visuelle,
la définition d'une région d'intérêt du tissu, la conversion des
intensités des images hyper-spectrales en unités de densité optique, et
la décomposition d'un spectre pour chaque pixel dans plusieurs
composantes indépendantes.
Le document US 2003/0030801 décrit une méthode permettant
l'obtention d'une ou plusieurs images d'un échantillon inconnu en
éclairant l'échantillon cible avec une distribution spectrale de
référence pondérée pour chaque image. La méthode analyse la ou les
images résultantes et identifie les caractéristiques cibles. La fonction
spectrale pondérée ainsi générée peut être obtenue à partir d'un
échantillon d'images de référence et peut par exemple être déterminée
par une analyse de sa composante principale, par poursuite de
projection ou par analyse de composantes indépendantes ACI. La
méthode est utilisable pour l'analyse d'échantillons de tissus
biologiques.
Ces documents traitent les images hyper-spectrales soit comme
des collections d'images à traiter individuellement, soit en réalisant
une coupe du cube hyper-spectral afin d'obtenir un spectre pour
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
chaque pixel, le spectre étant alors comparé à une base de référence.
L'homme du métier perçoit clairement les déficiences de ces méthodes
tant sur le plan méthodologique que sur le plan de la vitesse de
traitement.
5 Par ailleurs, on peut citer les méthodes basées sur le système
de représentation CIEL*a*b, et les méthodes d'analyse spectrale,
notamment les méthodes fondées sur la mesure de réflectance, et celles
fondées sur l'analyse du spectre d'absorption. Cependant ces méthodes
ne sont pas adaptées aux images hyper-spectrales et à la quantité de
données les caractérisant.
Il a donc été constaté que la combinaison d'une poursuite de
projection et d'une séparation à vaste marge permettait d'obtenir une
analyse fiable d'images hyper-spectrales dans un temps de calcul
suffisamment court pour être industriellement exploitable.
Selon l'état de la technique, lorsque l'on utilise la poursuite de
projection, le partitionnement des données est réalisé à pas constant.
Ainsi, pour un cube hyper-spectral, on choisit la taille du sous-espace
dans lequel on souhaite projeter les données spectrales puis, on
découpe le cube de telle sorte qu'il y ait le même nombre de bandes
dans chaque groupe.
Cette technique présente l'inconvénient de réaliser un
découpage arbitraire, qui ne suit donc pas les propriétés physiques du
spectre. Dans son manuscrit de thèse (G. Rellier. Analyse de texture
dans l'espace hyper-spectral par des méthodes probabilistes. Thèse de
Doctorat, Université de Nice Sophia Antipolis, Novembre 2002.), G.
Rellier propose un découpage à pas variable. Ainsi, on choisit toujours
le nombre de groupes de bandes, mais cette fois-ci, les bornes des
groupes sont choisies à pas variables de manière à minimiser la
variance interne à chaque groupe.
Dans la même publication, il est proposé un algorithme itératif
qui, à partir d'un découpage à pas constant, minimise la fonction Is
pour chacun des groupes. Cette méthode permet de réaliser un
partitionnement suivant les propriétés physiques du spectre, mais reste
le choix du nombre de groupes, fixé par l'utilisateur.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
6
Cette méthode n'est pas adaptée aux cas où les images à traiter
sont d'une grande diversité, aux cas où il est difficile de fixer le
nombre de groupes K, ou aux cas où l'utilisateur n'est pas en mesure
de choisir le nombre de groupes.
Il existe donc un besoin pour une méthode capable de fournir
une analyse fiable d'images hyper-spectrales dans un temps de calcul
suffisamment court, et capable de réduire automatiquement une image
hyper-spectrale en images hyper-spectrales réduites avant le
classement.
L'objet de la présente demande de brevet est un procédé
d'analyse d'images hyper-spectrales.
Un autre objet de la présente demande de brevet est un
dispositif d'analyse d'images hyper-spectrales.
Un autre objet de la présente demande de brevet est
l'application du dispositif d'analyse à l'analyse de lésions cutanées.
Le dispositif d'analyse d'une image hyper-spectrale comprend
au moins un capteur apte à produire une série d'images dans au moins
deux longueurs d'ondes, un moyen de calcul apte à classer les pixels
d'une image selon une relation de classement à deux états, l'image
étant reçue d'un capteur et un moyen d'affichage apte à afficher au
moins une image résultante du traitement des données reçues du moyen
de calcul.
Le moyen de calcul comprend un moyen de détermination de
pixels d'apprentissage liés à la relation de classement à deux états
recevant des données d'un capteur, un moyen de calcul d'une poursuite
de projection recevant des données du moyen de détermination de
pixels d'apprentissage et étant apte à procéder à un découpage
automatique du spectre de l'image hyper-spectrale, et un moyen de
réalisation d'une séparation à vaste marge recevant des données du
moyen de calcul d'une poursuite de projection, le moyen de calcul
étant apte à produire des données relatives à au moins une image
améliorée dans laquelle sont distinguables les pixels obtenus à l'issue
de la séparation à vaste marge en fonction de leur classement selon la
relation de classement à deux états.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
7
Le dispositif d'analyse peut comprendre une cartographie de
pixels classés reliée au moyen de détermination de pixels
d'apprentissage.
Le moyen de calcul d'une poursuite de projection peut
comprendre un premier moyen de découpage, un deuxième moyen de
découpage et un moyen de recherche de vecteurs de projection.
Le moyen de calcul d'une poursuite de projection peut
comprendre un moyen de découpage à nombre de bandes constant et un
moyen de recherche de vecteurs de projection.
Le moyen de calcul d'une poursuite de projection peut
comprendre un moyen de déplacement des bornes de chaque groupe
issu du moyen de découpage à nombre de bandes constant, le moyen de
déplacement étant apte à minimiser la variance interne de chaque
groupe.
Le moyen de calcul d'une poursuite de projection peut
comprendre un moyen de découpage à détermination automatique du
nombre de bandes en fonction de seuils prédéterminés et un moyen de
recherche de vecteurs de projection.
Le moyen de détermination de pixels d'apprentissage peut être
apte à déterminer les pixels d'apprentissage comme les pixels les plus
proches des seuils.
Le moyen de réalisation d'une séparation à vaste marge peut
comprendre un moyen de détermination d'un hyperplan, et un moyen
de classement des pixels en fonction de leur distance à l'hyperplan.
Le moyen de calcul peut être apte à produire une image
affichable par le moyen d'affichage en fonction de l'image hyper-
spectrale reçue d'un capteur et des données reçues du moyen de
réalisation d'une séparation à vaste marge.
Selon un autre aspect, on définit un procédé d'analyse d'une
image hyper-spectrale, provenant d'au moins un capteur apte à
produire une série d'images dans au moins deux longueurs d'ondes,
comprenant une étape d'acquisition d'une image hyper-spectrale par
un capteur, une étape de calcul du classement des pixels d'une image
hyper-spectrale reçue d'un capteur selon une relation de classement à
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
8
deux états, l'affichage d'au moins une image améliorée résultante du
traitement des données de l'étape d'acquisition d'une image hyper-
spectrale et des données de l'étape de calcul du classement des pixels
d'une image hyper-spectrale.
L'étape de calcul comprend une étape de détermination de
pixels d'apprentissage liés à la relation de classement à deux états, une
étape de calcul d'une poursuite de projection de l'image hyper-
spectrale comprenant les pixels d'apprentissage, comprenant un
découpage automatique du spectre de ladite image hyper-spectrale, et
une étape de séparation à vaste marge, l'étape de calcul étant apte à
produire au moins une image améliorée dans laquelle sont
distinguables les pixels obtenus à l'issue de la séparation à vaste
marge en fonction de leur classement selon la relation de classement à
deux états.
L'étape de détermination de pixels d'apprentissage peut
comprendre la détermination de pixels d'apprentissage en fonction de
données d'une cartographie, l'étape de détermination de pixels
d'apprentissage comprenant en outre l'introduction desdits pixels
d'apprentissage dans l'image hyper-spectrale reçue d'un capteur.
L'étape de calcul d'une poursuite de projection peut
comprendre une première étape de découpage portant sur les données
issues de l'étape de détermination de pixels d'apprentissage et une
étape de recherche de vecteurs de projection.
L'étape de calcul d'une poursuite de projection peut
comprendre une deuxième étape de découpage si la distance entre deux
images issues de la première étape de découpage est supérieure à un
premier seuil ou si la valeur maximale de la distance entre deux
images issues de la première étape de découpage est supérieure à un
deuxième seuil.
L'étape de calcul d'une poursuite de projection peut
comprendre un découpage à nombre de bandes constant.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
9
On peut déplacer les bornes de chaque groupe issu du
découpage à nombre de bandes constant afin de minimiser la variance
interne de chaque groupe.
L'étape de calcul d'une poursuite de projection peut
comprendre un découpage à détermination automatique du nombre de
bandes en fonction de seuils prédéterminés.
L'étape de détermination de pixels d'apprentissage peut
comprendre une détermination des pixels d'apprentissage comme les
pixels les plus proches des seuils.
L'étape de séparation à vaste marge peut comprendre une étape
de détermination d'un hyperplan, et une étape de classement des pixels
en fonction de leur distance à l'hyperplan, l'étape de détermination
d'un hyperplan portant sur les données issues de l'étape de calcul de
poursuite de projection.
Selon un autre aspect, le dispositif d'analyse est appliqué à la
détection de lésions cutanées d'un être humain, l'hyperplan étant
déterminé en fonction de pixels d'apprentissage issus de clichés
préalablement analysés.
D'autres buts, caractéristiques et avantages apparaîtront à la
lecture de la description suivante donnée uniquement en tant
qu'exemple non limitatif et faite en référence en référence aux figures
annexées sur lesquelles :
-la figure 1 illustre le dispositif d'analyse d'images hyper-
spectrales ,
-la figure 2 illustre le procédé d'analyse d'images hyper-
spectrales ; et
-la figure 3 illustre les bandes d'absorption de l'hémoglobine
et de la mélanine pour des longueurs d'onde entre 300 nm et 1000 nm.
Comme indiqué précédemment, il existe plusieurs façons
d'obtenir une image hyper-spectrale. Toutefois, quelle que soit la
méthode d'acquisition, il n'est pas possible de réaliser un classement
directement sur l'image hyper-spectrale telle qu'acquise.
On rappelle à l'occasion qu'un cube hyper-spectral est un
ensemble d'images réalisées chacune à une longueur d'onde donnée.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
Chaque image est à deux dimensions, les images étant empilées selon
une troisième direction en fonction de la variation de la longueur
d'onde leur correspondant. De part la structure tridimensionnelle
obtenue, on appelle l'ensemble un cube hyper-spectral. L'appellation
5 image hyper-spectrale peut également être employée pour désigner la
même entité.
Un cube hyper-spectral contient une quantité importante de
données. Cependant, dans de tels cubes, on retrouve de grands espaces
vides en terme d'information et des sous-espaces contenant beaucoup
10 d'information. La projection des données dans un espace de dimension
inférieure permet donc de regrouper l'information utile dans un espace
réduit en n'engendrant que très peu de perte d'information. Cette
réduction est alors importante pour la classification.
On rappelle que le but de la classification est de déterminer
parmi l'ensemble des pixels composant l'image hyper-spectrale, ceux
qui répondent favorablement ou défavorablement à une relation de
classement à deux états. Il est ainsi possible de déterminer les parties
d'une scène présentant une caractéristique ou une substance.
La première étape est d'intégrer des pixels d'apprentissage
dans l'image hyper-spectrale. En effet, pour réaliser une classification,
on utilise une méthode dite supervisée. Ainsi, pour classer l'ensemble
de l'image, cette méthode supervisée consiste à utiliser un certain
nombre de pixels que l'on associe à une classe. Ce sont les pixels
d'apprentissage. Puis, un séparateur de classe est calculé sur ces
pixels, pour ensuite classer l'ensemble de l'image.
Les pixels d'apprentissage sont en très petit nombre, comparé à
la quantité d'information que contient une image hyper-spectrale.
Ainsi, si l'on fait une classification directement sur le cube de données
hyper-spectrales avec un petit nombre de pixels d'apprentissage, le
résultat de la classification a de fortes chances d'être mauvais,
conformément au phénomène de Hughes. On a donc intérêt à réduire la
dimension de l'image hyper-spectrale analysée.
Un pixel d'apprentissage correspond à un pixel dont le
classement est déjà connu. A ce titre, le pixel d'apprentissage reçoit
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
11
une classe y,=l ou y,=-l qui servira lors de la séparation à vaste marge
à déterminer le plan hyper-spectral.
En d'autres termes, si on cherche à déterminer si une partie
d'une image est relative à l'eau, le critère de classement sera eau ,
une distribution sera caractéristique des zones sans eau , une autre
distribution sera caractéristique des zones avec eau , toutes les
zones de l'image étant dans une ou dans l'autre de ces distributions.
Afin d'initialiser la méthode de classement, il sera nécessaire de
présenter une distribution de pixels d'apprentissage caractéristique
d'une zone avec eau , et une distribution de pixels d'apprentissage
caractéristique d'une zone sans eau . Le procédé sera alors ensuite
capable de traiter tous les autres pixels de l'image hyper-spectrale afin
de trouver les zones avec ou sans eau . Il est également possible
d'extrapoler l'apprentissage réalisé pour une image hyper spectrale à
d'autres images hyper-spectrales présentant des similitudes.
Les pixels de l'image hyper-spectrale appartiennent à l'une des
deux distributions possibles. Une reçoit la classe y,=l et l'autre reçoit
la classe y,=-1, selon que leur classement répond positivement ou non
au critère de classement à deux états choisie pour l'analyse.
La poursuite de projection présentée ici vise donc une
réduction du cube hyper-spectral permettant de garder un maximum
d'informations induites par le spectre pour ensuite appliquer une
classification adaptée au contexte par séparateur à vaste marge (SVM).
La poursuite de projection vise à produire une image hyper-
spectrale réduite comprenant des vecteurs de projection partitionnant
le spectre de l'image hyper-spectrale. Plusieurs méthodes de
partitionnement peuvent être employées. Cependant, dans tous les cas
il s'agit d'optimiser la distance entre les pixels d'apprentissage. Pour
cela il est nécessaire de pouvoir déterminer une distance statistique.
L'indice I permet de déterminer cette distance statistique entre deux
distributions de points. L'indice I choisi est l'indice de Kullback-
Leibler
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
12
I=DI 2(91-92Y '(E1+E2(91-laz)+tr(Eii=Ez+Ezi=Ei-21d) (Eq. 1)
Avec i et z, les moyennes des deux distributions, E1 et E2 les
matrices de covariance des deux distributions et E12 = Y-1 2 Y,2 tr(M)
correspondant à la trace de la matrice M, MT correspondant à la
matrice M transposée et Id la matrice identité.
La méthode de poursuite de projection comprend un
partitionnement du spectre en groupes, suivie de la détermination d'un
vecteur de projection au sein de chaque groupe et la projection des
vecteurs du groupe sur le vecteur de projection correspondant.
Le partitionnement du spectre est réalisé par une technique de
découpage automatique, grâce à une fonction Fi qui mesure la distance
I entre bandes consécutives. Par analyse de cette fonction Fi, on va
rechercher les discontinuités du spectre au sens de l'indice de
projection I, et ainsi, choisir ces points de discontinuité comme
frontières des différents groupes.
La fonction Fi est une fonction discrète, qui, pour chaque
indice k allant de 1 à Nb-1, avec Nb le nombre de bandes du spectre,
prend la valeur de la distance entre deux bandes consécutives. Les
discontinuités du spectre vont donc apparaître comme étant les maxima
locaux de cette fonction Fi.
Fr (k) = I(image(k), image (k + 1)) (E q. 2)
Avec I la distance, ou l'indice, entre deux images.
Une première étape du découpage du spectre est de rechercher
les maxima locaux significatifs, c'est-à-dire ceux supérieurs à un
certain seuil. Ce seuil est alors égal à un pourcentage de la valeur
moyenne de la fonction Fi. Ce premier découpage permet, ainsi, de
créer un nouveau groupe à chaque discontinuité du spectre.
Cependant, l'analyse des maxima locaux est insuffisante pour
faire un découpage du spectre à la fois fin et fiable, le but de la
seconde étape est d'analyser les groupes issus du premier découpage.
On va donc s'intéresser aux groupes contenant un nombre de bandes
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
13
trop élevé de manière à, soit les découper en plusieurs groupes, soit
les garder tels qu'ils sont.
Un exemple de la nécessité de cette deuxième étape est illustré
par l'exemple d'une image hyper-spectrale contenant un pas
d'échantillonnage spectral fin. A cause de ce pas d'échantillonnage,
les propriétés physiques entre les bandes vont évoluer lentement. Par
conséquent, la fonction Fi va avoir tendance à être inférieure au seuil
du premier découpage sur un grand nombre de bandes consécutives.
Des bandes contenant des propriétés physiques différentes risquent
donc de se retrouver dans un même groupe. Il est alors nécessaire de
redécouper les groupes définis à l'issue de la première étape. Par
contre, dans le cas d'un pas d'échantillonnage plus important, il n'est
pas nécessaire d'avoir recourt à un tel redécoupage. La manière de
découper les groupes est connue en soi par l'homme du métier.
Faire le choix de redécouper ou non un groupe a plusieurs
intérêts. Le but initial est de récupérer de l'information non
sélectionnée par le premier découpage, en ajoutant une dimension à
l'espace de projection chaque fois que l'on scinde un groupe en deux.
Cependant, on peut faire le choix de ne pas découper certains
groupes en deux, de manière à ne pas privilégier de l'information
d'une zone par rapport à une autre, et de ne pas avoir un découpage
qui contient trop de groupes.
Afin de contrôler le deuxième découpage, on définit un
deuxième seuil en dessus duquel on procédera à un deuxième
découpage.
Selon le comportement de la fonction Fi, le découpage est
réalisé différemment.
Si la fonction Fi est monotone et présente un point où la
courbure est maximale sur l'intervalle considéré, alors le découpage
intervient au point de courbure maximale de l'intervalle, si
I(image(a),image(b))> seuill .
Si la fonction Fi est monotone et linéaire sur l'intervalle
considéré, alors le découpage intervient au milieu de l'intervalle, si
I(image(a),image(b))> seuill .
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
14
Si la fonction Fi n'est pas monotone et ne présente pas de
maximum local sur l'intervalle considéré, alors le découpage
intervient au milieu de l'intervalle, si I(image(a),image(b))> seuill .
Si la fonction Fi n'est pas monotone et présente un maximum
local sur l'intervalle considéré, et si max(I(image(a),image(b)))> seuil2,
[a,b]
alors le découpage intervient au niveau de ce maximum local.
On définit seuill = moy(Fj) * C avec C généralement égal à deux.
On définit seuil2 = seuill * C'avec C' généralement égal à deux
tiers.
Le premier et le deuxième découpages permettent d'obtenir une
partition du spectre en groupe contenant chacun plusieurs images de
l'image hyper-spectrale.
La recherche des vecteurs de projection permet de calculer les
vecteurs de projection à partir d'un découpage de l'espace initial en
sous groupes. Pour rechercher des vecteurs de projection, on procède à
une initialisation arbitraire des vecteurs de projection VkO. Pour cela,
au sein de chaque groupe k, on choisit pour vecteur de projection VkO
le vecteur correspondant au maximum local du groupe.
On calcule ensuite le vecteur VI qui minimise un indice de
projection I en maintenant les autres vecteurs constants. Ainsi VI est
calculé en maximisant l'indice de projection. On fait ensuite de même
pour les K-1 autres vecteurs. Il en résulte donc un ensemble de
vecteurs Vkl avec O<k<K.
On réitère le processus décrit précédemment, jusqu'à ce que les
nouveaux vecteurs calculés n'évoluent plus au delà d'un seuil
préalablement fixé.
Un vecteur de projection est homogène à une image d'une
longueur d'onde donnée comprise dans l'image hyper-spectrale.
A l'issue du procédé de recherche des vecteurs de projection,
chaque vecteur de projection peut être exprimé comme étant égal à la
combinaison linéaire des images comprises dans l'image hyper-
spectrale adjacentes au vecteur de projection considéré.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
L'ensemble des vecteurs de projection forme l'image hyper-
spectrale réduite.
On propose d'utiliser un séparateur à vaste marge (SVM) pour
classer les pixels de l'image hyper-spectrale réduite. Comme illustré
5 précédemment, on va chercher au sein d'une image les parties vérifiant
un critère de classement et les parties ne vérifiant pas ce même critère
de classement. Une image hyper-spectrale réduite correspond à un
espace à K dimensions.
Une image hyper-spectrale réduite est ainsi assimilable à un
10 nuage de points dans un espace à K dimensions. On va appliquer à ce
nuage de points la méthode de classification par SVM qui consiste à
séparer un nuage de points en deux classes. Pour ce faire, on recherche
un hyperplan qui sépare l'espace du nuage de points en deux. Les
points se trouvant d'un cote de l'hyperplan sont associés à une classe
15 et ceux se trouvant de l'autre coté sont associés à l'autre classe.
La méthode de SVM se décompose donc en deux étapes. La
première étape, l'apprentissage, consiste à déterminer l'équation de
l'hyperplan séparateur. Ce calcul nécessite d'avoir un certain nombre
de pixels d'apprentissage dont la classe (y,) est connue. La seconde
étape est l'association à chaque pixel de l'image d'une classe suivant
sa position par rapport à l'hyperplan calculé lors de la première étape.
La condition pour une bonne classification est donc de trouver
l'hyperplan optimal, de manière à séparer au mieux les deux nuages de
points. Pour ce faire, on cherche à optimiser la marge entre
l'hyperplan séparateur et les points des deux nuages d'apprentissage.
Ainsi, si la marge à maximiser est notée IllI2 , alors l'équation
ffi
de l'hyperplan séparateur s'écrit c).x + b = 0, c) et b étant les
inconnues à déterminer. Finalement, en introduisant une classe (y,=+l
et y,=-1), la recherche de l'hyperplan séparateur se résume ainsi à
v z w.x+b>+1 si y, =+1
minimiser tel que (Eq. 3)
2 w x+ b<---1 si y, =-1
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
16
Le problème d'optimisation de l'hyperplan tel que présenté par
l'équation (Eq. 3) n'est pas implantable en tant que tel. En
introduisant les polynômes de Lagrange, on obtient le problème dual:
maxW(~022i . 2i =xi =x;+',i (Il q. 4)
N
avec Lk, = yi =0,X ?O, Vie [1,n]
Z=1
Avec N le nombre de pixels d'apprentissage. L'équation (Eq. 4)
représente un problème d'optimisation quadratique non spécifique aux
SVM, et donc bien connu des mathématiciens. Il existe divers
algorithmes permettant d'effectuer cette optimisation.
S'il n'existe pas d'hyperplan linéaire entre deux classes de
pixels, ce qui est souvent le cas lorsque l'on traite des données réelles,
on plonge le nuage de point dans un espace de dimension supérieure
grâce à une fonction c. Dans ce nouvel espace, il devient alors
possible de déterminer un hyperplan séparateur. La fonction c
introduite est une fonction très complexe. Mais si l'on revient à
l'équation d'optimisation dans l'espace dual, alors, on ne calcule pas
C mais le produit scalaire de c en deux points différents:
maxW1 2i2; . (P (xi )=(P (x;+(Eq. 5)
N
avec LX -Yi =0,Xi>O, Vie [1,n]
Z=1
Ce produit scalaire est appelé fonction noyau et noté
K(x,, x1)_ (J(x,) (D(x1)) . Dans la littérature, il existe de nombreuses
fonctions noyaux. Pour notre application, nous utiliserons un noyau
gaussien, qui est très utilisé en pratique, et donne de bons résultats
2
K(xi,xi) =exp zi - zj - 2 (Il q. 6)
2.6
6 apparaît alors comme un paramètre de réglage.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
17
Lors du calcul de l'hyperplan séparateur, pour chaque pixel
d'apprentissage, on calcule un coefficient a, (cf. (Eq. 5)). Pour la
majeure partie des pixels d'apprentissage, ce coefficient a, est nul. Les
pixels d'apprentissage pour lesquels a, est non nul sont nommés
vecteurs support, car ce sont ces pixels qui définissent l'hyperplan
séparateur:
N
0) =~~~y~`~(x~) (Il q. 7)
Z=~
Lorsque l'algorithme parcourt l'ensemble des pixels
d'apprentissage pour calculer le a,, correspondant à chaque x;, le
paramètre 6 du noyau gaussien, qui correspond à la largeur du noyau
gaussien, permet de déterminer la taille du voisinage du pixel x;
considéré, pris en compte pour le calcul du a,, correspondant.
L'inconnue b de l'hyperplan est en suite déterminée en
résolvant:
Ai [yi -(w+b)-1]=0 (Eq. 8)
Lorsque l'hyperplan est déterminé, il reste à classer l'ensemble
de l'image en fonction de la position de chaque pixel vis-à-vis de
l'hyperplan séparateur. Pour ce faire, on utilise une fonction de
décision:
N
f(x)=w x+b=~~Z yl ~(xl) te(x)+b (Il q. 9)
Z=~
Cette relation permet de déterminer la classe y, associée à
chaque pixel en fonction de sa distance à l'hyperplan. Les pixels sont
alors considérés classés.
Comme les pixels de l'image hyper-spectrale réduite ne
correspondent plus aux pixels de l'image hyper-spectrale produite par
le capteur, on ne peut pas aisément reconstituer une image affichable.
Cependant, les coordonnées spatiales de chaque pixel de l'image
hyper-spectrale réduite correspondent toujours aux coordonnées de
l'image hyper-spectrale produite par le capteur. Il est alors possible de
transposer la classification des pixels de l'image hyper-spectrale
réduite à l'image hyper-spectrale produite par le capteur.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
18
L'image améliorée présentée à l'utilisateur est alors générée en
intégrant des parties du spectre afin de déterminer une image
affichable informatiquement, par exemple en déterminant des
coordonnées RVB. Si le capteur fonctionne au moins en partie dans le
spectre visible, il est possible d'intégrer des longueurs d'ondes
discrètes afin de déterminer de façon fidèle les composantes R, V et B,
et permettant d'avoir une image proche d'une photographie.
Si le capteur fonctionne en dehors du spectre visible, ou dans
une fraction du spectre visible, il est possible de déterminer des
composantes R, V et B qui permettront d'obtenir une image en fausses
couleurs.
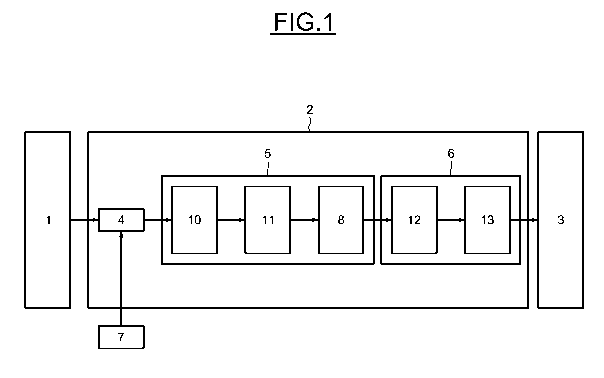
La figure 1 présente les principaux éléments d'un dispositif
d'analyse d'une image hyper-spectrale. On peut voir un capteur 1
hyper-spectral, un moyen de calcul 2 et un dispositif d'affichage 3.
Le moyen de calcul 2 comprend un moyen de détermination 4
de pixels d'apprentissage relié en entrée à un capteur hyper-spectral et
relié en sortie à un moyen de calcul 5 d'une poursuite de projection.
Le moyen de calcul 5 d'une poursuite de projection est relié en
sortie à un moyen de réalisation 6 d'une séparation à vaste marge relié
à son tour en sortie au dispositif d'affichage 3. Par ailleurs, le moyen
de détermination 4 de pixels d'apprentissage est relié en entrée à une
cartographie 7 de pixels classés.
Le moyen de réalisation 6 d'une séparation à vaste marge
comprend un moyen de détermination 12 d'un hyperplan, et un moyen
de classement 13 des pixels en fonction de leur distance à l'hyperplan.
Le moyen de détermination 12 d'un hyperplan est relié en entrée à
l'entrée du moyen de réalisation 6 d'une séparation à vaste marge et en
sortie au moyen de classement 13 des pixels. Le moyen de classement
13 des pixels est relié en sortie à la sortie du moyen de réalisation 6
d'une séparation à vaste marge.
Le moyen de calcul 5 d'une poursuite de projection comprend
un premier moyen 10 de découpage, relié lui-même à un
deuxième moyen 11 de découpage et un moyen de recherche 8 de
vecteurs de projection.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
19
Lors de son fonctionnement, le dispositif d'analyse produit des
images hyper-spectrales grâce au capteur 1. On notera que par capteur
1, on entend un capteur hyper-spectral unique, une collection de
capteurs mono-spectraux, ou une combinaison de capteurs multi-
spectraux. Les images hyper-spectrales sont reçues par le moyen de
détermination 4 de pixels d'apprentissage qui insère dans chacune
quelques pixels d'apprentissage en fonction d'une cartographie 7 de
pixels classés. Pour ces pixels d'apprentissage, l'information de
classement est remplie par la valeur présente dans la cartographie. Les
pixels de l'image hyper-spectrale qui ne sont pas des pixels
d'apprentissage n'ont à ce stade pas d'information relative au
classement.
Par cartographie 7 de pixels classés, on entend un ensemble
d'images de forme similaire à une image comprise dans une image
hyper-spectrale, et dans laquelle tout ou partie des pixels est classée
dans une ou l'autre de deux distributions répondant à une relation de
classement à deux états.
Les images hyper-spectrales munies de pixels d'apprentissage
sont ensuite traitées par le moyen de calcul 5 d'une poursuite de
projection.
Le premier moyen 10 de découpage et le deuxième moyen 11 de
découpage compris dans le moyen de calcul 5 d'une poursuite de
projection vont découper l'image hyper-spectrale selon la direction
relative au spectre afin de former des ensembles d'images réduites
comprenant chacune une partie du spectre. Pour cela, le premier moyen
10 de découpage applique l'équation (Eq. 2). Le deuxième moyen 11
de découpage réalise un nouveau découpage des données reçues du
premier moyen 10 de découpage selon les règles précédemment
décrites en relation avec les valeurs seuill et seuil2, sinon le deuxième
moyen 11 de découpage est inactif.
Le moyen de recherche 8 de vecteurs de projection compris
dans le moyen de calcul 5 d'une poursuite de projection, initialise
arbitrairement l'ensemble des vecteurs de projection en fonction des
données reçues du premier moyen 10 de découpage et/ou du deuxième
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
moyen 11 de découpage, puis détermine les coordonnées d'un vecteur
de projection qui minimise la distance I entre ledit vecteur de
projection et les autres vecteurs de projection en appliquant l'équation
(Eq. 1). Le même calcul est effectué pour les autres vecteurs de
5 projection. On réitère les étapes de calcul précédentes jusqu'à ce que
les coordonnées de chaque vecteur n'évoluent plus au delà d'un seuil
prédéterminé. L'image hyper-spectrale réduite est alors formée des
vecteurs de projection.
L'image hyper-spectrale réduite est ensuite traitée par le
10 moyen de détermination 12 d'un hyperplan, puis par le moyen de
classement 13 des pixels en fonction de leur distance à l'hyperplan.
Le moyen de détermination 12 d'un hyperplan applique les
équations (Eq. 4) à (Eq. 8) afin de déterminer les coordonnées de
l'hyperplan.
15 Le moyen de classement 13 des pixels en fonction de leur
distance à l'hyperplan applique l'équation (Eq. 9). Suivant la distance
à l'hyperplan, les pixels sont classés, et reçoivent la classe y,=-l ou
y,=+1. En d'autres termes, les pixels sont classés selon une relation de
classement à deux états, généralement la présence ou l'absence d'un
20 composé ou d'une propriété.
Les données comportant les coordonnées (x ; y) et la classe des
pixels sont ensuite traitées par le moyen d'affichage 3 qui est alors
apte à distinguer les pixels selon leur classe, par exemple en fausses
couleurs, ou en délimitant le contour délimitant les zones comprenant
les pixels portant l'une ou l'autre des classes.
Dans le cas d'une application dermatologique, les capteurs 1
hyper-spectraux sont caractéristiques de la gamme de fréquence visible
et infrarouge. De plus, la relation de classement à deux états peut être
relative à la présence de lésions cutanées d'un type donné, la
cartographie 7 de pixels classés est alors relative à ces dites lésions.
Selon le mode de réalisation, la cartographie 7 est constituée de pixels
d'images hyper-spectrales de peau de patient analysées par des
dermatologues afin de déterminer les zones lésées. La cartographie 7
peut comprendre uniquement des pixels de l'image hyper-spectrale
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
21
classée ou des pixels d'autres images hyper-spectrales classées ou une
combinaisons des deux. L'image améliorée produite correspond à
l'image du patient en superposition de laquelle se trouvent affichées
les zones lésées.
La figure 2 illustre le procédé d'analyse et comprend une étape
d'acquisition 14 d'images hyper-spectrales, suivie d'une étape de
détermination 15 de pixels d'apprentissage, suivie d'une étape de
poursuite 16 de projection, une étape de réalisation 17 d'une
séparation à vaste marge et une étape d'affichage 18.
L'étape de détermination 16 de vecteurs de projection
comprend des étapes successives de premier découpage 20, de
deuxième découpage 21 et de détermination 19 de vecteurs de
projection.
L'étape de réalisation 17 d'une séparation à vaste marge
comprend les sous-étapes successives de détermination 22 d'un
hyperplan, et de classement 23 des pixels en fonction de leur distance
à l'hyperplan.
Un autre exemple de classification d'image hyper spectrale
concerne l'analyse spectrale de la peau.
L'analyse spectrale de la peau est importante pour les
dermatologues pour évaluer les quantités de chromophores de façon à
quantifier les maladies. Les images multispectrales et hyperspectrales
permettent la prise en compte à la fois des propriétés spectrales et des
informations spatiales d'une zone malade. Dans la littérature, il est
proposé dans plusieurs méthodes d'analyse de la peau, de sélectionner
des régions d'intérêts du spectre. La maladie est ensuite quantifiée en
fonction d'un petit nombre de bandes du spectre. On rappelle
également que la différence entre images multispectrales et images
hyperspectrales réside uniquement dans le nombre d'acquisitions
réalisées à des longueurs d'ondes différentes. Il est généralement
accepté qu'un cube de données comprenant plus de 15 à 20
acquisitions constitue une image hyperspectrale. A contrario, un cube
de données comprenant moins de 15 à 20 acquisitions constitue une
image multispectrale.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
22
Sur la figure 3, on peut voir que les bandes q et la bande de
Soret d'absorption de l'hémoglobine présentent des maxima dans une
zone comprise entre 600 nm et 1000 nm dans laquelle la mélanine
présente une absorbance assez linéaire. L'idée principale de ces
méthodes est d'évaluer la quantité d'hémoglobine grâce à des données
multispectrales en compensant l'influence de la mélanine dans
l'absorption des bandes q, par une bande située autour de 700nm dans
laquelle l'absorption de l'hémoglobine est faible comparée à
l'absorption de la mélanine. Cette compensation est illustrée par
l'équation suivante :
Ihaemoglobin = -log(Iq-band/1700) (Eq. 10)
dans laquelle Ihaemoglobin est l'image obtenue représentant
principalement l'influence de l'hémoglobine, 1q-band est l'image prise
au niveau de l'une des deux bandes q et 1700 est l'image prise à une
longueur d'onde de 700nm.
Pour extraire une cartographie représentative de la mélanine,
une méthode a été proposée par G.N. Stamatas, B.Z. Zmudzka, N.
Kollias, and J. Z. Beer, dans Non-invasive measurements of skin
pigmentation in situ. , Pigment cell res, vol. 17, pp.618-626,2004, qui
consiste à modéliser la réponse de la mélanine comme une réponse
linéaire entre 600 nm et 700nm.
Am=aX+b, (Eq. 11)
avec
Am : l'absorbance de la mélanine
k : la longueur d'onde
a et b : des coefficients linéaires.
Dans la présente approche fondée sur des techniques
d'apprentissage, la réduction de données est utilisée afin d'éviter le
phénomène de Hughes. La combinaison d'une réduction de données et
d'une classification par SVM est connue pour donner de bons résultats.
Dans le cadre de l'analyse de données multi-dimensionnelles
dont les variations sont liées à la physique, on utilise la poursuite de
projection pour la réduction de données. La poursuite de projection va
être employée afin de fusionner les données en K groupes. Les K
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
23
groupes obtenus pour initialiser la poursuite de projection peuvent
contenir un nombre de bandes différent. La poursuite de projection va
ensuite projeter chaque groupe sur un vecteur unique pour obtenir une
image en niveau de gris par groupe. Ceci est réalisé en maximisant un
indice I entre les groupes projetés.
Etant donné qu'une classification entre peau saine et malade
est recherchée, on maximise cet indice I entre classes dans les groupes
projetés, tel que suggéré dans les travaux de L.O. Jimenez and D.A
Landgrebe, "Hyperspectral data analysis and supervised feature
reduction via projection pursuit," IEEE Trans. on Geoscience and
Remote Sensing, vol. 37, pp. 2653-2667, 1999.
La distance de Kullback-Leibler est généralement utilisée
comme indice pour les poursuites de projection. Si i et j représentent
les classes à discriminer, la distance de Kullback-Leibler entre les
classes i et j peut être écrite de la façon suivante :
Dkb(i,j)= Hkb(i,j) Hkb(J,i) (Eq. 12)
avec
Hkb(i,j)=J f,(x)=lnf'(x)dx (Eq. 13)
f- (x)
et avec f; et f; les distributions des deux classes.
Pour des distributions gaussiennes, l'indice I et la distance de
Kullback-Leibler peuvent être écrits de la façon suivante:
)T )..
2 (Eq.14)
+tr(E~1 =E +E7' E; -2Id)
avec et E représentant respectivement la valeur moyenne et la
matrice de covariance de chaque classe.
De cette façon, l'indice I permet de mesurer les variations
entre deux bandes ou deux groupes. Comme on peut le constater,
l'expression de l'indice I est une généralisation de l'équation 1
précédente.
Le but de la réduction de données est de réunir les informations
redondantes des bandes. Le spectre est découpé en fonction des
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
24
variations d'absorption de la peau. Les façons de découper peuvent
différer selon le mode de réalisation. Outre le mode de partitionnement
décrit en relation avec le premier mode de réalisation, on peut citer un
partitionnement non constant ou un partitionnement constant suivi
d'un déplacement des bornes de chaque groupe permettant de
minimiser la variance interne 62
i de chaque groupe. La variance
interne au sein d'un groupe est caractérisée par l'équation suivante
1 K-1 1 K-1 2
ci(k)--LI2(Zk~Zk+J -LI(Zk'Zi,+1) (Eq. 15)
K k=o K k=o
avec Zk la borne supérieure du k-ième groupe.
Ainsi, en utilisant la poursuite de projection pour la réduction
des données et le séparateur à vaste marge (SVM) pour la
classification, on peut utiliser différentes initialisations pour classer
les données.
Une première initialisation est K, le nombre désiré de groupes
d'information redondante des bandes spectrales. Une seconde
initialisation correspond au jeu de pixels d'apprentissage pour le SVM.
Etant donné que les images de peau présentent des
caractéristiques différentes d'une personne à une autre et que les
caractères de la maladie peuvent être répartis sur le spectre, il est
nécessaire de définir deux initialisations pour chaque image.
De façon à supprimer la contrainte relative au nombre de
groupes K, le spectre est partitionné en utilisant une fonction Fi.
FI(k)=I(k-l,k) avec k=2,...,Nb (Eq. 16)
avec k l'indice de la bande considérée et Nb le nombre total de
bandes du spectre.
Analyser la fonction Fi permet de déterminer où apparaissent
les changements d'absorption des bandes spectrales. Les bornes de
groupes sont choisies lors du partitionnement du spectre pour
correspondre aux plus hauts maxima locaux de la fonction Fi. Si la
variation de l'indice I le long du spectre est considérée comme étant
gaussienne, on peut utiliser la valeur moyenne et l'écart type de la
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
distribution pour déterminer les maxima locaux de F1 les plus
significatifs.
Ainsi, les bornes des K groupes spectraux sont les bandes
correspondant aux maxima de F1 jusqu'au seuil T1 et des minima de F1
5 jusqu'au seuil T2 :
Tl =pFF +tXCF T2 =N1F, -tXCF (Eq. 17)
dans lequel ~tF et 6F sont respectivement la valeur moyenne et
l'écart type de F1 et t est un paramètre.
Le paramètre t est choisi une fois pour traiter tout l'ensemble
10 de données. Il est préférable de choisir un tel paramètre plutôt que de
choisir le nombre de groupes car cela permet d'avoir des nombres de
groupes différents d'une image à l'autre ce qui peut se révéler utile
dans le cas d'images ayant des variations spectrales différentes.
Cette méthode de partitionnement peut être appliquée avec
15 n'importe quel indice, comme la corrélation ou la distance de
Kullback-Leibler.
Introduire un indice spatial dans cette méthode d'analyse
spectrale permet d'initialiser le SVM. En fait, seuiller l'indice
spatial que l'on notera Is, déterminé entre des bandes adjacentes,
20 permet de créer des images cartographiant les changements spatiaux
d'une bande à l'autre.
Dans cette application, les zones d'hyperpigmentation de la
peau ne présentent pas de motif spécifique. C'est pourquoi, dans
certains modes de réalisation, un gradient spatial tel que l'indice Is,
25 est déterminé sur une zone spatiale carrée 3 x 3 dénotée v. Pour
extraire l'information spatiale portée par chaque bande spectrale, on
utilise un indice spatial Is défini par l'équation suivante :
Is(k-1,k)= 1 L S(i, j,k)-S(i, j,k-1) (Eq. 18)
N 1jcv
dans lequel N dénote le nombre de pixels dans la zone v, x est
l'indice de la bande étudiée ou du groupe projeté et V(i, j)Ev . S est
l'intensité du pixel situé à la position spatiale (i,j) et dans la bande
spectrale k. v est une zone adjacente au pixel (i,j) de 3 x 3 pixels.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
26
En fait, l'indice IS est, pour chaque zone spatiale de 3 x 3
pixels, la valeur moyenne de la différence entre deux bandes. Un seuil
sur l'indice IS permet d'obtenir une image binaire qui représente les
variations spatiales entre deux bandes consécutives. Ainsi, une image
binaire contient une valeur 1 aux coordonnées d'un pixel si l'intensité
du pixel a changé de façon significative lors du passage de la bande k-
1 à la bande k. L'image binaire contient une valeur 0 dans le cas
contraire. Le seuil sur l'indice spatial Is représente ainsi un paramètre
permettant de définir le niveau de changement des valeurs de Is qui est
considéré comme significatif. On choisit ensuite parmi les images
binaires obtenues celle qui est la plus pertinente afin de réaliser
l'apprentissage du SVM. L'image binaire choisie peut être celle
donnant le maximum global de la fonction Fis ou une image d'une
zone d'intérêt du spectre. Afin d'optimiser le temps de calcul, il est
préférable de choisir seulement une partie d'une image binaire pour
réaliser l'apprentissage du SVM.
Cet indice spatial peut aussi être utilisé pour partitionner le
spectre. On définit la fonction Fis sous la forme suivante :
FI,(k)=A(Is(k-1,k)) avec k=2,...,Nb (Eq. 19)
et dans laquelle A est l'aire que représentent les pixels pour
lesquels un changement a été détecté.
Pour chaque image binaire obtenue à partir de Is(k-l,k) par
seuillage, la fonction Fis en k calcule un nombre réel qui est l'aire de
la zone où des changements ont été détectés. Ainsi, la fonction Fis et
la fonction Fi avec un indice non spatial tel que la distance de
Kullback-Leibler (Eq. 12) sont homogènes. La méthode d'analyse de Fi
décrite précédemment permet alors à nouveau d'obtenir les bornes des
groupes spectraux.
Finalement, l'analyse du spectre avec la fonction Fi et un
indice spatial Is permet une double initialisation pour obtenir un
schéma de classification automatique. Pour résumer, le schéma de
classification automatique est le suivant :
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
27
1. analyse spectrale pour partitionner les données en groupes
pour la poursuite de projection et extraction d'un ensemble
d'apprentissage pour le SVM
2. poursuite de projection pour réduire les données et
3. Classification par SVM.
En d'autres termes, la méthode d'analyse comprend une analyse
automatique du spectre de façon que les informations redondantes
soient réduites et de façon que les formes des zones d'intérêt soient
globalement extraites. En utilisant les zones d'intérêt obtenues pour
l'apprentissage d'un SVM appliqué au cube de données réduit par
poursuite de projection, on obtient une classification précise de
l'hyperpigmentation de la peau. Le présent exemple est décrit en
relation avec l'hyperpigmentation de la peau, cependant il n'échappera
pas à l'homme du métier que l'hyperpigmentation de la peau
n'intervient dans le procédé décrit que par une variation de couleur
et/ou de contraste. Ce procédé est donc applicable sans modification à
d'autres pathologies cutanées générant un contraste.
Dans ce cas, un indice sans a priori est utilisé pour l'analyse
spectrale, les zones d'hyperpigmentation ne présentant pas de motif
particulier. Dans les cas où les zones d'intérêt présentent un motif
particulier, un indice spatial comprenant une forme prédéterminée peut
être utilisé. Cela est le cas par exemple, pour la détection des
vaisseaux sanguins, l'indice spatial comprenant alors une forme de
ligne.
Le temps de calcul de cette méthode d'analyse spectrale est
proportionnel au nombre de bandes spectrales. Néanmoins, comme
l'indice spatial Is permet d'estimer les changements dans des
voisinages spatiaux locaux, l'algorithme correspondant à la méthode
est facilement parallélisable.
L'enseignement d'une méthode de classement d'images
multispectrales est applicable à des images hyperspectrales. En effet,
étant donné que l'image hyper-spectrale ne se différencie de l'image
multi-spectrale que par le nombre de bandes, les espaces entre les
bandes spectrales sont plus petits. Les changements d'une bande à
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
28
l'autre sont donc également plus petits. Une méthode d'analyse
spectrale d'images hyper-spectrales comporte une détection de
changements plus sensible. Il est également possible d'améliorer la
sensibilité de détection en procédant à l'intégration de plusieurs
images Is lors du traitement d'images hyper-spectrales. Une telle
intégration permet de fusionner les changements spectraux dans le
groupe choisi pour l'apprentissage du SVM.
Un autre mode de réalisation comprend le traitement de
données multispectrales, dont les variations sont reliées à des
phénomènes physiques. Selon une approche similaire à celle divulguée
ci-dessus, le traitement de données multispectrales est applicable au
traitement de données hyperspectrales, les images multispectrales et
les images hyperspectrales se différenciant seulement par le nombre
d'images acquises à des longueurs d'ondes différentes.
La poursuite de projection peut être utilisée pour réaliser la
réduction de données. On rappelle que, selon un mode de réalisation,
les algorithmes de poursuite de projection fusionnent les données en K
groupes comprenant un nombre égal de bandes, chaque groupe étant
ensuite projeté sur un vecteur unique en maximisant l'indice I entre les
groupes projetés. K est alors un paramètre.
Habituellement, le nombre de groupes souhaités K pour le
partitionnement du spectre est fixé manuellement après une analyse de
la problématique de classification. On peut partitionner les données en
fonction des variations d'absorption du spectre. Après une
initialisation avec K groupes comprenant chacun le même nombre de
bandes, les bornes de chaque groupe sont réestimées de façon itérative
afin de minimiser la variance interne de chaque groupe. De façon à
retirer la contrainte sur le nombre de groupes K, le spectre est
partitionné en utilisant la fonction Fi. La méthode d'analyse de spectre
est utilisée pour balayer les longueurs d'onde du spectre avec un
indice I, tel que la variance interne ou la distance de Kullback-Leibler
(Eq. 1). La méthode permet ainsi de déduire les parties intéressantes
du spectre des variations de l'indice I.
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
29
Une zone du spectre comprenant des variations est détectée
lorsque Fj(k) dépasse le seuil Ti ou passe en dessous du seuil T2. Les
seuils Ti et T2 sont similaires aux seuils seuill et seuil2
précédemment définis. En d'autres termes, le partitionnement du
spectre est déduit de l'analyse de la fonction Fi. Les extrema locaux de
la fonction Fi jusqu'aux seuils Ti et T2 deviennent les bornes des
groupes. Ainsi, un paramètre t définissant Ti et T2 (Eq. 17) peut être
préféré au paramètre K pour le partitionnement du spectre.
Les inventeurs ont découvert qu'il était possible d'obtenir un
partitionnement du spectre sans fixer un nombre K car les bandes
d'intérêt du spectre peuvent être modifiées en fonction de la maladie.
L'analyse spectrale avec un indice statistique ne permet pas d'obtenir
un jeu d'apprentissage pour la classification.
Un indice spatial Is pour chaque voisinage de voxel peut
présenter une cartographie spatiale de variations spectrales. Dans la
présente méthode, les tissus présentant une hyperpigmentation ne
présentent pas de texture particulière. Il apparaît ainsi que la détection
est basée sur la détection d'une variation de contraste indépendante de
la cause qui en est à l'origine.
Le gradient spectral Is et la fonction Fis ont été précédemment
définis (Eq. 18 et Eq. 19).
Fis est une fonction tridimensionnelle. Pour chaque paire de
bandes, la fonction Fis permet de déterminer une cartographie spatiale
de variations spectrales. Comme on peut le voir d'après l'expression
de la fonction Fis, la fonction A est appliquée à la fonction Fi. La
fonction A quantifie les zones de changement de pixels, de façon
similaire à la fonction illustrée par l'équation 19 relative au mode de
réalisation précédent.
Une méthode permettant d'extraire un jeu de pixels
d'apprentissage depuis la fonction Fis va maintenant être décrite.
La méthode comprend une poursuite de projection pour la
réduction de données. Généralement, pour déterminer un sous-espace
de projection par poursuite de projection, un indice I est maximisé sur
l'ensemble des groupes projetés. Dans l'application visée, on attend
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
une classification des tissus sains ou pathologiques. On détermine la
maximisation de l'indice I entre les classes projetées. La distance de
Kullback-Leibler est conventionnellement utilisée comme indice I de
poursuite de projection. La distance de Kullback-Leibler peut être
5 exprimée sous la forme précédemment décrite (Eq. 1).
On initialise la poursuite de projection avec le partitionnement
du spectre obtenu par analyse spectrale, puis on détermine le sous-
espace de projection en maximisant la distance de Kullback-Leibler
entre les deux classes définies par le jeu d'apprentissage.
10 Le jeu d'apprentissage du SVM est extrait de l'analyse
spectrale. Comme défini précédemment, le SVM est un algorithme
supervisé de classification, notamment de classification à deux
classes. Grâce à un jeu d'apprentissage définissant les deux classes, un
séparateur de classes optimal est déterminé. Chaque point de données
15 est alors classé en fonction de sa distance avec le séparateur.
On propose d'utiliser l'analyse spectrale obtenue avec l'indice
I pour obtenir le jeu d'apprentissage le SVM. Comme décrit plus haut,
l'analyse spectrale avec un indice spatial permet d'obtenir une
cartographie spatiale des changements spectraux entre deux bandes
20 consécutives. Pour l'apprentissage du SVM, on choisit une de ces
cartographies spatiales obtenues par Fj(k) avec un indice spatial. La
cartographie choisie peut être celle révélant le plus de changements
sur tout le spectre, par exemple celle contenant les extrema globaux de
la fonction Fis sur une partie d'intérêt ou sur l'ensemble du spectre.
25 Une fois la cartographie spatiale Fis(k) choisie, les N plus
proches pixels des seuils Ti ou T2 sont extraits pour apprentissage de
le SVM. Sur les N pixels d'apprentissage, la moitié est choisie sous le
seuil et l'autre moitié au dessus du seuil.
La méthode décrite ci-dessus a été appliquée à des images
30 multi-spectrales comprenant 18 bandes de 405 nm à 970 nm avec un
pas moyen de 25 nm. Ces images sont d'une taille d'environ 900 x
1200 pixels. Pour partitionner le spectre, la fonction d'analyse
spectrale F a été employée en conjonction avec l'indice spatial Is. Sur
les 18 bandes du cube de données concernant à la fois des tissus de
CA 02778682 2012-04-23
WO 2011/051382 PCT/EP2010/066341
31
peau sains et des tissus de peau hyperpigmentés, l'analyse spectrale a
donné un nombre K égal à 5.
Dans cet exemple de classification d'images de peau atteinte
d'hyperpigmentation, l'ensemble d'apprentissage extrait comprend les
50 plus proches pixels du seuil T2.
Indépendamment de l'exemple présenté ci-dessus, la méthode
décrite peut être appliquée à des données hyperspectrales, c'est-à-dire
à des données comprenant beaucoup plus de bandes spectrales.
La méthode d'analyse spectrale présentée ici est adaptée à
l'analyse d'images multispectrales parce que le pas entre bandes
spectrales est suffisant pour mesurer des variations significatives de la
fonction Fi. Pour adapter cette méthode au traitement d'images
hyperspectrales, il est nécessaire d'introduire un paramètre n dans la
fonction Fi de façon à mesurer les variations non pas entre des bandes
consécutives mais entre deux bandes avec un décalage n. La fonction
Fi devient alors :
Fr =Is(k-n,k) (Il q. 20)
avec k=n+1,...,Nb
Le paramètre n peut être adapté manuellement ou
automatiquement en fonction notamment du nombre de bandes
considéré.