Note: Descriptions are shown in the official language in which they were submitted.
CA 02917806 2016-01-08
1
DATA PROCESSING DEVICE AND DATA PROCESSING METHOD
Technical Field
[0001]
The present technology relates to a data processing device and a data
processing method, and more particularly, a data processing device and a data
processing method, which are capable of securing excellent communication
quality in
data transmission using an LDPC code, for example.
Background Art
[0002]
Some of the information disclosed in this specification and the drawings was
provided by Samsung Electronics Co., Ltd. (hereinafter referred to as
Samsung), LG
Electronics Inc., NERC, and CRC/ETRI (indicated in the drawings).
[0003]
A low density parity check (LDPC) code has a high error correction
capability, and in recent years, the LDPC code has widely been employed in
transmission schemes of digital broadcasting such as Digital Video
Broadcasting
(DVB)-S.2, DVB-T.2, and DVB-C.2 of Europe and the like, or Advanced Television
Systems Committee (ATSC) 3.0 of the USA and the like (for example, see Non-
Patent
Literature 1).
[0004]
From a recent study, it is known that performance near a Shannon limit is
obtained from the LDPC code when a code length increases, similar to a turbo
code.
Because the LDPC code has a property that a shortest distance is proportional
to the
code length, the LDPC code has advantages of a block error probability
characteristic
being superior and a so-called error floor phenomenon observed in a decoding
characteristic of the turbo code being rarely generated, as characteristics
thereof.
Citation List
Non-Patent Literature
[0005]
Non-Patent Literature 1: DVB-S.2: ETSI EN 302 307 V1.2.1 (2009-08)
CA 02917806 2016-01-08
2
Summary of Invention
Technical Problem
[0006]
In data transmission using the LDPC code, for example, the LDPC code is
converted into a symbol of an orthogonal modulation (digital modulation) such
as
Quadrature Phase Shift Keying (QPSK), and the symbol is mapped to a signal
point
of the orthogonal modulation and transmitted.
[0007]
The data transmission using the LDPC code has spread worldwide, and there
is a demand to secure excellent communication (transmission) quality.
[0008]
The present technology was made in light of the foregoing, and it is desirable
to secure excellent communication quality in data transmission using the LDPC
code.
Solution to Problem
[0009]
A first data processing device/method according to the present technology is
a data processing device/method including: an encoding unit/step configured to
perform LDPC encoding based on a parity check matrix of an LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 10/15; a group-wise
interleaving
unit/step configured to perform group-wise interleave of interleaving the LDPC
code
in units of bit groups of 360 bits; and a mapping unit/step configured to map
the
LDPC code to any of 256 signal points decided in a modulation scheme in units
of 8
bits. In the group-wise interleave, when an (i+1)-th bit group from a head of
the
LDPC code is indicated by a bit group i, a sequence of bit groups 0 to 44 of
the LDPC
code of 16200 bits is interleaved into a sequence of bit groups
17, 2, 30, 12, 7, 25, 27, 3, 15, 14, 4, 26, 34, 31, 13, 22, 0, 39, 23, 24, 21,
6, 38,
5, 19, 42, 11, 32, 28, 40, 20, 18, 36, 9,41, 10, 33, 37, 1, 16, 8, 43, 29, 35,
and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
CA 02917806 2016-01-08
3
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
352 747 894 1437 1688 1807 1883 2119 2159 3321 3400 3543 3588 3770
3821 4384 4470 4884 5012 5036 5084 5101 5271 5281 5353
505 915 1156 1269 1518 1650 2153 2256 2344 2465 2509 2867 2875 3007
3254 3519 3687 4331 4439 4532 4940 5011 5076 5113 5367
268 346 650 919 1260 4389 4653 4721 4838 5054 5157 5162 5275 5362
220 236 828 1590 1792 3259 3647 4276 4281 4325 4963 4974 5003 5037
381 737 1099 1409 2364 2955 3228 3341 3473 3985 4257 4730 5173 5242
88 771 1640 1737 1803 2408 2575 2974 3167 3464 3780 4501 4901 5047
749 1502 2201 3189
2873 3245 3427
2158 2605 3165
1 3438 3606
10 3019 5221
371 2901 2923
9 3935 4683
1937 3502 3735
507 3128 4994
25 3854 4550
1178 4737 5366
2 223 5304
1146 5175 5197
1816 2313 3649
740 1951 3844
1320 3703 4791
1754 2905 4058
7 917 5277
3048 3954 5396
4804 4824 5105
2812 3895 5226
0 5318 5358
1483 2324 4826
CA 02917806 2016-01-08
4
2266 4752 5387.
[0010]
In the first data processing device/method according to the present
technology, LDPC encoding is performed based on a parity check matrix of an
LDPC
code in which a code length N is 16200 bits and an encoding rate r is 10/15.
Group-
wise interleave of interleaving the LDPC code in units of bit groups of 360
bits is
performed. The LDPC code is mapped to any of 256 signal points decided in a
modulation scheme in units of 8 bits. In the group-wise interleave, when an
(i+1)-th
bit group from a head of the LDPC code is indicated by a bit group i, a
sequence of bit
groups 0 to 44 of the LDPC code of 16200 bits is interleaved into a sequence
of bit
groups
17, 2, 30, 12, 7, 25, 27, 3, 15, 14, 4, 26, 34, 31, 13, 22, 0, 39, 23, 24, 21,
6, 38,
5, 19, 42, 11, 32, 28, 40, 20, 18, 36, 9, 41, 10, 33, 37, 1, 16, 8, 43, 29,
35, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
352 747 894 1437 1688 1807 1883 2119 2159 3321 3400 3543 3588 3770
3821 4384 4470 4884 5012 5036 5084 5101 5271 5281 5353
505 915 1156 1269 1518 1650 2153 2256 2344 2465 2509 2867 2875 3007
3254 3519 3687 4331 4439 4532 4940 5011 5076 5113 5367
268 346 650 919 1260 4389 4653 4721 4838 5054 5157 5162 5275 5362
220 236 828 1590 1792 3259 3647 4276 4281 4325 4963 4974 5003 5037
381 737 1099 1409 2364 2955 3228 3341 3473 3985 4257 4730 5173 5242
88 771 1640 1737 1803 2408 2575 2974 3167 3464 3780 4501 4901 5047
749 1502 2201 3189
2873 3245 3427
2158 2605 3165
1 3438 3606
10 3019 5221
371 2901 2923
CA 02917806 2016-01-08
9 3935 4683
1937 3502 3735
507 3128 4994
25 3854 4550
5 1178 4737 5366
2 223 5304
1146 5175 5197
1816 2313 3649
740 1951 3844
1320 3703 4791
1754 2905 4058
7 917 5277
3048 3954 5396
4804 4824 5105
2812 3895 5226
0 5318 5358
1483 2324 4826
2266 4752 5387.
[0011]
A second data processing device/method according to the present technology
is a data processing device/method including: a group-wise deinterleaving
unit/step
configured to restore a sequence of an LDPC code that has undergone group-wise
interleave and has been obtained from data transmitted from a transmitting
device to
an original sequence, the transmitting device including an encoding unit
configured to
perform LDPC encoding based on a parity check matrix of the LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 10/15, a group-wise
interleaving
unit configured to perform the group-wise interleave of interleaving the LDPC
code in
units of bit groups of 360 bits, and a mapping unit configured to map the LDPC
code
to any of 256 signal points decided in a modulation scheme in units of 8 bits.
In the
group-wise interleave, when an (i+1)-th bit group from a head of the LDPC code
is
indicated by a bit group i, a sequence of bit groups 0 to 44 of the LDPC code
of 16200
bits is interleaved into a sequence of bit groups
17, 2, 30, 12, 7, 25, 27, 3, 15, 14, 4, 26, 34, 31, 13, 22, 0, 39, 23, 24, 21,
6, 38,
CA 02917806 2016-01-08
6
5, 19, 42, 11, 32, 28, 40, 20, 18, 36, 9, 41, 10, 33, 37, 1, 16, 8, 43, 29,
35, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
352 747 894 1437 1688 1807 1883 2119 2159 3321 3400 3543 3588 3770
3821 4384 4470 4884 5012 5036 5084 5101 5271 5281 5353
505 915 1156 1269 1518 1650 2153 2256 2344 2465 2509 2867 2875 3007
3254 3519 3687 4331 4439 4532 4940 5011 5076 5113 5367
268 346 650 919 1260 4389 4653 4721 4838 5054 5157 5162 5275 5362
220 236 828 1590 1792 3259 3647 4276 4281 4325 4963 4974 5003 5037
381 737 1099 1409 2364 2955 3228 3341 3473 3985 4257 4730 5173 5242
88 771 1640 1737 1803 2408 2575 2974 3167 3464 3780 4501 4901 5047
749 1502 2201 3189
2873 3245 3427
2158 2605 3165
1 3438 3606
10 3019 5221
371 2901 2923
9 3935 4683
1937 3502 3735
507 3128 4994
25 3854 4550
1178 4737 5366
2 223 5304
1146 5175 5197
1816 2313 3649
740 1951 3844
1320 3703 4791
1754 2905 4058
7 917 5277
CA 02917806 2016-01-08
7
3048 3954 5396
4804 4824 5105
2812 3895 5226
0 5318 5358
1483 2324 4826
2266 4752 5387.
[0012]
In the second data processing device/method according to the present
technology, a sequence of an LDPC code that has undergone group-wise
interleave
and has been obtained from data transmitted from a transmitting device is
restored to
an original sequence, the transmitting device including an encoding unit
configured to
perform LDPC encoding based on a parity check matrix of the LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 10/15, a group-wise
interleaving
unit configured to perform the group-wise interleave of interleaving the LDPC
code in
units of bit groups of 360 bits, and a mapping unit configured to map the LDPC
code
to any of 256 signal points decided in a modulation scheme in units of 8 bits.
In the
group-wise interleave, when an (i+1)-th bit group from a head of the LDPC code
is
indicated by a bit group i, a sequence of bit groups 0 to 44 of the LDPC code
of 16200
bits is interleaved into a sequence of bit groups
17, 2, 30, 12, 7, 25, 27, 3, 15, 14, 4, 26, 34, 31, 13, 22, 0, 39, 23, 24, 21,
6, 38,
5, 19, 42, 11, 32, 28, 40, 20, 18, 36, 9, 41, 10, 33, 37, 1, 16, 8, 43, 29,
35, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
352 747 894 1437 1688 1807 1883 2119 2159 3321 3400 3543 3588 3770
3821 4384 4470 4884 5012 5036 5084 5101 5271 5281 5353
505 915 1156 1269 1518 1650 2153 2256 2344 2465 2509 2867 2875 3007
3254 3519 3687 4331 4439 4532 4940 5011 5076 5113 5367
268 346 650 919 1260 4389 4653 4721 4838 5054 5157 5162 5275 5362
220 236 828 1590 1792 3259 3647 4276 4281 4325 4963 4974 5003 5037
CA 02917806 2016-01-08
8
381 737 1099 1409 2364 2955 3228 3341 3473 3985 4257 4730 5173 5242
88 771 1640 1737 1803 2408 2575 2974 3167 3464 3780 4501 4901 5047
749 1502 2201 3189
2873 3245 3427
2158 2605 3165
1 3438 3606
3019 5221
371 2901 2923
9 3935 4683
10 1937 3502 3735
507 3128 4994
25 3854 4550
1178 4737 5366
2 223 5304
1146 5175 5197
1816 2313 3649
740 1951 3844
1320 3703 4791
1754 2905 4058
7 917 5277
3048 3954 5396
4804 4824 5105
2812 3895 5226
0 5318 5358
1483 2324 4826
2266 4752 5387.
[0013]
A third data processing device/method according to the present technology is
a data processing device/method including: an encoding unit/step configured to
perform LDPC encoding based on a parity check matrix of an LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 12/15; a group-wise
interleaving
unit/step configured to perform group-wise interleave of interleaving the LDPC
code
in units of bit groups of 360 bits; and a mapping unit/step configured to map
the
CA 02917806 2016-01-08
9
LDPC code to any of 256 signal points decided in a modulation scheme in units
of 8
bits. In the group-wise interleave, when an (i+1)-th bit group from a head of
the
LDPC code is indicated by a bit group i, a sequence of bit groups 0 to 44 of
the LDPC
code of 16200 bits is interleaved into a sequence of bit groups
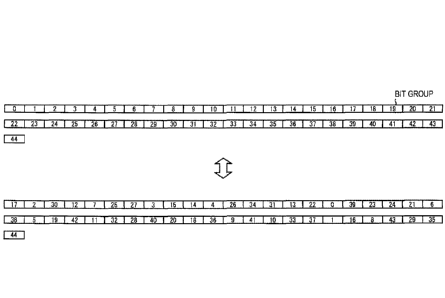
28, 21, 10, 15, 8, 22, 26, 2, 14, 1, 27, 3, 39, 20, 34, 25, 12, 6, 7, 40, 30,
29, 38,
16, 43, 33, 4, 35, 9, 32, 5, 36, 0, 41, 37, 18, 17, 13, 24, 42, 31, 23, 19,
11, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
3 394 1014 1214 1361 1477 1534 1660 1856 2745 2987 2991 3124 3155
59 136 528 781 803 928 1293 1489 1944 2041 2200 2613 2690 2847
155 245 311 621 1114 1269 1281 1783 1995 2047 2672 2803 2885 3014
79 870 974 1326 1449 1531 2077 2317 2467 2627 2811 3083 3101 3132
4 582 660 902 1048 1482 1697 1744 1928 2628 2699 2728 3045 3104
175 395 429 1027 1061 1068 1154 1168 1175 2147 2359 2376 2613 2682
1388 2241 3118 3148
143 506 2067 3148
1594 2217 2705
398 988 2551
1149 2588 2654
678 2844 3115
1508 1547 1954
1199 1267 1710
2589 3163 3207
1 2583 2974
2766 2897 3166
929 1823 2742
1113 3007 3239
1753 2478 3127
0 509 1811
CA 02917806 2016-01-08
1672 2646 2984
965 1462 3230
3 1077 2917
1183 1316 1662
5 968 1593 3239
64 1996 2226
1442 2058 3181
513 973 1058
1263 3185 3229
10 681 1394 3017
419 2853 3217
3 2404 3175
2417 2792 2854
1879 2940 3235
647 1704 3060.
[0014]
In the third data processing device/method according to the present
technology, LDPC encoding is performed based on a parity check matrix of an
LDPC
code in which a code length N is 16200 bits and an encoding rate r is 12/15.
Group-
wise interleave of interleaving the LDPC code in units of bit groups of 360
bits is
performed. The LDPC code is mapped to any of 256 signal points decided in a
modulation scheme in units of 8 bits. In the group-wise interleave, when an
(i+1)-th
bit group from a head of the LDPC code is indicated by a bit group i, a
sequence of bit
groups 0 to 44 of the LDPC code of 16200 bits is interleaved into a sequence
of bit
groups
28, 21, 10, 15, 8, 22, 26, 2, 14, 1, 27, 3, 39, 20, 34, 25, 12, 6, 7, 40, 30,
29, 38,
16, 43, 33, 4, 35, 9, 32, 5, 36, 0, 41, 37, 18, 17, 13, 24, 42, 31, 23, 19,
11, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
CA 02917806 2016-01-08
ii
3 394 1014 1214 1361 1477 1534 1660 1856 2745 2987 2991 3124 3155
59 136 528 781 803 928 1293 1489 1944 2041 2200 2613 2690 2847
155 245 311 621 1114 1269 1281 1783 1995 2047 2672 2803 2885 3014
79 870 974 1326 1449 1531 2077 2317 2467 2627 2811 3083 3101 3132
4 582 660 902 1048 1482 1697 1744 1928 2628 2699 2728 3045 3104
175 395 429 1027 1061 1068 1154 1168 1175 2147 2359 2376 2613 2682
1388 2241 3118 3148
143 506 2067 3148
1594 2217 2705
398 988 2551
1149 2588 2654
678 2844 3115
1508 1547 1954
1199 1267 1710
2589 3163 3207
1 2583 2974
2766 2897 3166
929 1823 2742
1113 3007 3239
1753 2478 3127
0 509 1811
1672 2646 2984
965 1462 3230
3 1077 2917
1183 1316 1662
968 1593 3239
64 1996 2226
1442 2058 3181
513 973 1058
1263 3185 3229
681 1394 3017
419 2853 3217
3 2404 3175
CA 02917806 2016-01-08
12
2417 2792 2854
1879 2940 3235
647 1704 3060.
[0015]
A fourth data processing device/method according to the present technology
is a data processing device/method including: a group-wise deinterleaving
unit/step
configured to restore a sequence of an LDPC code that has undergone group-wise
interleave and has been obtained from data transmitted from a transmitting
device to
an original sequence, the transmitting device including an encoding unit
configured to
perform LDPC encoding based on a parity check matrix of the LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 12/15, a group-wise
interleaving
unit configured to perform the group-wise interleave of interleaving the LDPC
code in
units of bit groups of 360 bits, and a mapping unit configured to map the LDPC
code
to any of 256 signal points decided in a modulation scheme in units of 8 bits.
In the
group-wise interleave, when an (i+1)-th bit group from a head of the LDPC code
is
indicated by a bit group i, a sequence of bit groups 0 to 44 of the LDPC code
of 16200
bits is interleaved into a sequence of bit groups
28, 21, 10, 15, 8, 22, 26, 2, 14, 1, 27, 3, 39, 20, 34, 25, 12, 6, 7, 40, 30,
29, 38,
16, 43, 33, 4, 35, 9, 32, 5, 36, 0, 41, 37, 18, 17, 13, 24, 42, 31, 23, 19,
11, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
3 394 1014 1214 1361 1477 1534 1660 1856 2745 2987 2991 3124 3155
59 136 528 781 803 928 1293 1489 1944 2041 2200 2613 2690 2847
155 245 311 621 1114 1269 1281 1783 1995 2047 2672 2803 2885 3014
79 870 974 1326 1449 1531 2077 2317 2467 2627 2811 3083 3101 3132
4 582 660 902 1048 1482 1697 1744 1928 2628 2699 2728 3045 3104
175 395 429 1027 1061 1068 1154 1168 1175 2147 2359 2376 2613 2682
1388 2241 3118 3148
143 506 2067 3148
CA 02917806 2016-01-08
13
1594 2217 2705
398 988 2551
1149 2588 2654
678 2844 3115
1508 1547 1954
1199 1267 1710
2589 3163 3207
1 2583 2974
2766 2897 3166
929 1823 2742
1113 3007 3239
1753 2478 3127
0 509 1811
1672 2646 2984
965 1462 3230
3 1077 2917
1183 1316 1662
968 1593 3239
64 1996 2226
1442 2058 3181
513 973 1058
1263 3185 3229
681 1394 3017
419 2853 3217
3 2404 3175
2417 2792 2854
1879 2940 3235
647 1704 3060.
[0016]
In the fourth data processing device/method according to the present
technology, a sequence of an LDPC code that has undergone group-wise
interleave
and has been obtained from data transmitted from a transmitting device is
restored to
an original sequence, the transmitting device including an encoding unit
configured to
CA 02917806 2016-01-08
14
perform LDPC encoding based on a parity check matrix of the LDPC code in which
a
code length N is 16200 bits and an encoding rate r is 12/15, a group-wise
interleaving
unit configured to perform the group-wise interleave of interleaving the LDPC
code in
units of bit groups of 360 bits, and a mapping unit configured to map the LDPC
code
to any of 256 signal points decided in a modulation scheme in units of 8 bits.
In the
group-wise interleave, when an (i+1)-th bit group from a head of the LDPC code
is
indicated by a bit group i, a sequence of bit groups 0 to 44 of the LDPC code
of 16200
bits is interleaved into a sequence of bit groups
28, 21, 10, 15, 8, 22, 26, 2, 14, 1, 27, 3, 39, 20, 34, 25, 12, 6, 7, 40, 30,
29, 38,
16, 43, 33, 4, 35, 9, 32, 5, 36, 0, 41, 37, 18, 17, 13, 24, 42, 31, 23, 19,
11, and 44.
The LDPC code includes an information bit and a parity bit. The parity check
matrix includes an information matrix portion corresponding to the information
bit
and a parity matrix portion corresponding to the parity bit. The information
matrix
portion is represented by a parity check matrix initial value table. The
parity check
matrix initial value table is a table in which a position of a 1 element of
the
information matrix portion is indicated for every 360 columns, and includes
3 394 1014 1214 1361 1477 1534 1660 1856 2745 2987 2991 3124 3155
59 136 528 781 803 928 1293 1489 1944 2041 2200 2613 2690 2847
155 245 311 621 1114 1269 1281 1783 1995 2047 2672 2803 2885 3014
79 870 974 1326 1449 1531 2077 2317 2467 2627 2811 3083 3101 3132
4 582 660 902 1048 1482 1697 1744 1928 2628 2699 2728 3045 3104
175 395 429 1027 1061 1068 1154 1168 1175 2147 2359 2376 2613 2682
1388 2241 3118 3148
143 506 2067 3148
1594 2217 2705
398 988 2551
1149 2588 2654
678 2844 3115
1508 1547 1954
1199 1267 1710
2589 3163 3207
1 2583 2974
2766 2897 3166
CA 02917806 2016-01-08
929 1823 2742
1113 3007 3239
1753 2478 3127
0 509 1811
5 1672 2646 2984
965 1462 3230
3 1077 2917
1183 1316 1662
968 1593 3239
10 64 1996 2226
1442 2058 3181
513 973 1058
1263 3185 3229
681 1394 3017
15 419 2853 3217
3 2404 3175
2417 2792 2854
1879 2940 3235
647 1704 3060.
[0017]
The data processing device may be an independent device and may be an
internal block constituting one device.
Advantageous Effects of Invention
[0018]
According to the present technology, it is possible to secure excellent
communication quality in data transmission using the LDPC code.
[0019]
The effects described herein are not necessarily limited and may include any
effect described in the present disclosure.
Brief Description of Drawings
[0020]
CA 02917806 2016-01-08
16
[FIG 1] FIG I is an illustration of a parity check matrix H of an LDPC code.
[FIG. 2] FIG. 2 is a flowchart illustrating a decoding sequence of an LDPC
code.
[FIG 3] FIG. 3 is an illustration of an example of a parity check matrix of an
LDPC
code.
[FIG 4] FIG 4 is an illustration of an example of a Tanner graph of a parity
check
matrix.
[FIG 5] FIG. 5 is an illustration of an example of a variable node.
[FIG. 6] FIG. 6 is an illustration of an example of a check node.
[FIG 7] FIG 7 is an illustration of a configuration example of an embodiment
of a
transmission system to which the present invention is applied.
[FIG 8] FIG. 8 is a block diagram illustrating a configuration example of a
transmitting device 11.
[FIG. 9] FIG 9 is a block diagram illustrating a configuration example of a
bit
interleaver 116.
[FIG 10] FIG. 10 is an illustration of an example of a parity check matrix.
[FIG 11] FIG. 11 is an illustration of an example of a parity matrix.
[FIG 12] FIG 12 is an illustration of the parity check matrix of the LDPC code
that is
defined in the standard of the DVB-T.2.
[FIG 13] FIG 13 is an illustration of the parity check matrix of the LDPC code
that is
defined in the standard of the DVB-T.2.
[FIG 14] FIG 14 is an illustration of an example of a Tanner graph for
decoding of an
LDPC code.
[FIG 15] FIG 15 is an illustration of an example of a parity matrix H'
becoming a
staircase structure and a Tanner graph corresponding to the parity matrix HT.
[FIG 16] FIG. 16 is an illustration of an example of a parity matrix HT of a
parity
check matrix H corresponding to an LDPC code after parity interleave.
[FIG 17] FIG. 17 is a flowchart illustrating an example of a process performed
by a
bit interleaver 116 and a mapper 117.
[FIG 18] FIG 18 is a block diagram illustrating a configuration example of an
LDPC
encoder 115.
[FIG 19] FIG 19 is a flowchart illustrating processing of an example of an
LDPC
encoder 115.
[FIG 20] FIG 20 is an illustration of an example of a parity check matrix
initial value
CA 02917806 2016-01-08
17
table in which an encoding rate is 1/4 and a code length is 16200.
[FIG. 211 FIG. 21 is an illustration of a method of calculating a parity check
matrix H
from a parity check matrix initial value table.
[FIG 22] FIG. 22 is an illustration of a structure of a parity check matrix.
[FIG 23] FIG. 23 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 24] FIG 24 is an illustration of an A matrix generated from a parity
check
matrix initial value table.
[FIG 25] FIG. 25 is an illustration of parity interleave of a B matrix.
[FIG. 26] FIG 26 is an illustration of a C matrix generated from a parity
check matrix
initial value table.
[FIG. 27] FIG. 27 is an illustration of parity interleave of a D matrix.
[FIG. 28] FIG 28 is an illustration of a parity check matrix obtained by
performing a
column permutation serving as parity deinterleave for restoring parity
interleave to an
original state on a parity check matrix.
[FIG 29] FIG. 29 is an illustration of a transformed parity check matrix
obtained by
performing a row permutation on a parity check matrix.
[FIG 30] FIG 30 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 31] FIG. 31 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 32] FIG. 32 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 33] FIG. 33 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 34] FIG. 34 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 35] FIG 35 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 36] FIG 36 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 37] FIG 37 is an illustration of an example of the parity check matrix
initial
value table.
CA 02917806 2016-01-08
18
[FIG. 38] FIG 38 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 39] FIG 39 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 40] FIG 40 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 41] FIG. 41 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 42] FIG. 42 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 43] FIG. 43 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 44] FIG. 44 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 45] FIG 45 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 46] FIG 46 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 47] FIG. 47 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 48] FIG 48 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 49] FIG 49 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 50] FIG. 50 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 51] FIG. 51 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 52] FIG 52 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 53] FIG 53 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 54] FIG. 54 is an illustration of an example of the parity check matrix
initial
CA 02917806 2016-01-08
19
value table.
[FIG. 55] FIG 55 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 56] FIG. 56 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 57] FIG. 57 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 58] FIG. 58 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 59] FIG. 59 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 60] FIG. 60 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 61] FIG 61 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 62] FIG 62 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 63] FIG. 63 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 64] FIG. 64 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 65] FIG 65 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 66] FIG 66 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 67] FIG 67 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 68] FIG 68 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 69] FIG 69 is an illustration of an example of the parity check matrix
initial
value table.
[FIG. 70] FIG. 70 is an illustration of an example of the parity check matrix
initial
value table.
CA 02917806 2016-01-08
[FIG 71] FIG 71 is an illustration of an example of the parity check matrix
initial
value table.
[FIG 72] FIG 72 is an illustration of an example of the parity check matrix
initial
value table.
5 [FIG. 73] FIG. 73 is an illustration of an example of a tanner graph of
an ensemble of
a degree sequence in which a column weight is 3, and a row weight is 6.
[FIG. 74] FIG. 74 is an illustration of an example of a tanner graph of an
ensemble of
a multi-edge type.
[FIG. 75] FIG. 75 is an illustration of a parity check matrix.
10 [FIG 76] FIG. 76 is an illustration of a parity check matrix.
[FIG 77] FIG 77 is an illustration of a parity check matrix.
[FIG 78] FIG 78 is an illustration of a parity check matrix.
[FIG 79] FIG. 79 is an illustration of a parity check matrix.
[FIG 80] FIG. 80 is an illustration of a parity check matrix.
15 [FIG 81] FIG 81 is an illustration of a parity check matrix.
[FIG 82] FIG. 82 is an illustration of a parity check matrix.
[FIG 83] FIG. 83 is an illustration of an example of a constellation when a
modulation
scheme is 16QAM.
[FIG. 84] FIG. 84 is an illustration of an example of a constellation when a
modulation
20 scheme is 64QAM.
[FIG. 85] FIG 85 is an illustration of an example of a constellation when a
modulation
scheme is 256QAM.
[FIG 86] FIG. 86 is an illustration of an example of a constellation when a
modulation
scheme is 1024QAM.
[FIG 87] FIG. 87 is an illustration of an example of a constellation when a
modulation
scheme is 4096QAM.
[FIG 88] FIG 88 is an illustration of an example of a constellation when a
modulation
scheme is 4096QAM.
[FIG 89] FIG 89 is an illustration of an example of coordinates of a signal
point of a
UC when a modulation scheme is QPSK.
[FIG 90] FIG 90 is an illustration of an example of coordinates of a signal
point of a
2D NUC when a modulation scheme is 16QAM.
[FIG 91] FIG 91 is an illustration of an example of coordinates of a signal
point of a
CA 02917806 2016-01-08
21
2D NUC when a modulation scheme is 64QAM.
[FIG. 92] FIG 92 is an illustration of an example of coordinates of a signal
point of a
2D NUC when a modulation scheme is 256QAM.
[FIG. 93] FIG 93 is an illustration of an example of coordinates of a signal
point of a
2D NUC when a modulation scheme is 256QAM.
[FIG. 94] FIG. 94 is an illustration of an example of coordinates of a signal
point of a
1D NUC when a modulation scheme is 1024QAM.
[FIG. 95] FIG. 95 is an illustration of relations of a symbol y of 1024QAM
with a real
part Re (zq) and an imaginary part Im (zq) of a complex number serving as
coordinates
of a signal point zq of a 1D NUC corresponding to the symbol y.
[FIG 96] FIG 96 is an illustration of an example of coordinates of a signal
point of a
11) NUC when a modulation scheme is 4096QAM.
[FIG. 97] FIG. 97 is an illustration of relations of a symbol y of 4096QAM
with a real
part Re (zq) and an imaginary part Im (zq) of a complex number serving as
coordinates
of a signal point zq of a 1D NUC corresponding to the symbol y.
[FIG. 98] FIG 98 is an illustration of another example of a constellation when
a
modulation scheme is 16QAM.
[FIG 99] FIG 99 is an illustration of another example of a constellation when
a
modulation scheme is 64QAM.
[FIG 100] FIG 100 is an illustration of another example of a constellation
when a
modulation scheme is 256QAM.
[FIG 101] FIG 101 is an illustration of another example of coordinates of a
signal
point of a 2D NUC when a modulation scheme is 16QAM.
[FIG 102] FIG 102 is an illustration of another example of coordinates of a
signal
point of a 2D NUC when a modulation scheme is 64QAM.
[FIG 103] FIG 103 is an illustration of another example of coordinates of a
signal
point of a 2D NUC when a modulation scheme is 256QAM.
[FIG. 104] FIG 104 is an illustration of another example of coordinates of a
signal
point of a 2D NUC when a modulation scheme is 256QAM.
[FIG 105] FIG. 105 is a block diagram illustrating a configuration example of
a block
interleaver 25.
[FIG 106] FIG. 106 is an illustration of an example of the number C of columns
of
parts 1 and 2 and part column lengths R1 and R2 for a combination of a code
length N
CA 02917806 2016-01-08
22
and a modulation scheme.
[FIG 107] FIG 107 is an illustration of block interleave performed by a block
interleaver 25.
[FIG. 108] FIG 108 is an illustration of group-wise interleave performed by a
group-
wise interleaver 24.
[FIG 109] FIG. 109 is an illustration of a 1st example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 110] FIG 110 is an illustration of a 2nd example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 111] FIG. 111 is an illustration of a 3rd example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 112] FIG 112 is an illustration of a 4th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 113] FIG. 113 is an illustration of a 5th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 114] FIG 114 is an illustration of a 6th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 115] FIG. 115 is an illustration of a 7th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 116] FIG. 116 is an illustration of an 8th example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG. 117] FIG. 117 is an illustration of a 9th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 118] FIG. 118 is an illustration of a 10th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 119] FIG. 119 is an illustration of an 11th example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG. 120] FIG 120 is an illustration of a 12th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 121] FIG. 121 is an illustration of a 13th example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG. 122] FIG 122 is an illustration of a 14th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
CA 02917806 2016-01-08
23
[FIG 123] FIG. 123 is an illustration of a 15th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 124] FIG. 124 is an illustration of a 16th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 125] FIG 125 is an illustration of a 17th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 126] FIG. 126 is an illustration of an 18th example of a GW pattern for
an
LDPC code in which a code length N is 64k bits.
[FIG 127] FIG. 127 is an illustration of a 19th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 128] FIG. 128 is an illustration of a 20th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 129] FIG 129 is an illustration of a 21st example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 130] FIG. 130 is an illustration of a 22nd example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG. 131] FIG. 131 is an illustration of a 23rd example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG 132] FIG 132 is an illustration of a 24th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 133] FIG. 133 is an illustration of a 25th example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG 134] FIG 134 is an illustration of a 26th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG. 135] FIG 135 is an illustration of a 27th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 136] FIG 136 is an illustration of a 28th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 137] FIG 137 is an illustration of a 29th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 138] FIG 138 is an illustration of a 30th example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 139] FIG 139 is an illustration of a 31st example of a GW pattern for an
LDPC
CA 02917806 2016-01-08
24
code in which a code length N is 64k bits.
[FIG. 140] FIG. 140 is an illustration of a 32nd example of a GW pattern for
an LDPC
code in which a code length N is 64k bits.
[FIG 141] FIG. 141 is an illustration of a 33rd example of a GW pattern for an
LDPC
code in which a code length N is 64k bits.
[FIG 142] FIG 142 is an illustration of a 1st example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG. 143] FIG 143 is an illustration of a 2nd example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 144] FIG. 144 is an illustration of a 3rd example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG. 145] FIG 145 is an illustration of a 4th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 146] FIG 146 is an illustration of a 5th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 147] FIG. 147 is an illustration of a 6th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG. 148] FIG. 148 is an illustration of a 7th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 149] FIG. 149 is an illustration of an 8th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 150] FIG. 150 is an illustration of a 9th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 151] FIG 151 is an illustration of a 10th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG. 152] FIG. 152 is an illustration of an 1 1 th example of a GW pattern
for an
LDPC code in which a code length N is 16k bits.
[FIG. 153] FIG 153 is an illustration of a 12th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 154] FIG 154 is an illustration of a 13th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
[FIG 155] FIG. 155 is an illustration of a 14th example of a GW pattern for an
LDPC
code in which a code length N is 16k bits.
CA 02917806 2016-01-08
[FIG. 156] FIG. 156 is an illustration of a 15th example of a GW pattern for
an LDPC
code in which a code length N is 16k bits.
[FIG. 157] FIG. 157 is an illustration of a 16th example of a GW pattern for
an LDPC
code in which a code length N is 16k bits.
5 [FIG 158] FIG. 158 is an illustration of a simulation result of a
simulation of
measuring an error rate.
[FIG. 159] FIG. 159 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 160] FIG. 160 is an illustration of a simulation result of a simulation
of
10 measuring an error rate.
[FIG 161] FIG. 161 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 162] FIG 162 is an illustration of a simulation result of a simulation of
measuring an error rate.
15 [FIG 163] FIG 163 is an illustration of a simulation result of a
simulation of
measuring an error rate.
[FIG 164] FIG 164 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 165] FIG. 165 is an illustration of a simulation result of a simulation
of
20 measuring an error rate.
[FIG. 166] FIG. 166 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 167] FIG 167 is an illustration of a simulation result of a simulation of
measuring an error rate.
25 [FIG 168] FIG. 168 is an illustration of a simulation result of a
simulation of
measuring an error rate.
[FIG 169] FIG. 169 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 170] FIG 170 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 171] FIG 171 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 172] FIG 172 is an illustration of a simulation result of a simulation of
CA 02917806 2016-01-08
26
measuring an error rate.
[FIG 1731 FIG 173 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 174] FIG 174 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 175] FIG. 175 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 176] FIG 176 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 177] FIG 177 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 178] FIG. 178 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 179] FIG 179 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 180] FIG 180 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 181] FIG. 181 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 182] FIG 182 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 183] FIG 183 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 184] FIG 184 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 185] FIG. 185 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 186] FIG. 186 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 187] FIG 187 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 188] FIG 188 is an illustration of a simulation result of a simulation of
measuring an error rate.
CA 02917806 2016-01-08
27
[FIG. 189] FIG. 189 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 190] FIG 190 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 191] FIG. 191 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 192] FIG. 192 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 193] FIG 193 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 194] FIG 194 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 195] FIG. 195 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 196] FIG. 196 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 197] FIG. 197 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 198] FIG 198 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 199] FIG 199 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 200] FIG 200 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG 201] FIG 201 is an illustration of a simulation result of a simulation of
measuring an error rate.
[FIG. 202] FIG 202 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 203] FIG. 203 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 204] FIG. 204 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG 205] FIG 205 is an illustration of a simulation result of a simulation of
CA 02917806 2016-01-08
28
measuring an error rate.
[FIG. 206] FIG 206 is an illustration of a simulation result of a simulation
of
measuring an error rate.
[FIG. 207] FIG. 207 is a block diagram illustrating a configuration example of
a
receiving device 12.
[FIG. 208] FIG. 208 is a block diagram illustrating a configuration example of
a bit
deinterleaver 165.
[FIG 209] FIG. 209 is a flowchart illustrating an example of a process
performed by a
demapper 164, a bit deinterleaver 165, and an LDPC decoder 166.
[FIG. 210] FIG 210 is an illustration of an example of a parity check matrix
of an
LDPC code.
[FIG 211] FIG 211 is an illustration of an example of a matrix (a transformed
parity
check matrix) obtained by performing a row permutation and a column
permutation
on a parity check matrix.
[FIG 212] FIG. 212 is an illustration of an example of a transformed parity
check
matrix divided into 5x5 units.
[FIG. 213] FIG. 213 is a block diagram illustrating a configuration example of
a
decoding device that collectively performs P node operations.
[FIG 214] FIG. 214 is a block diagram illustrating a configuration example of
an
LDPC decoder 166.
[FIG 2151 FIG 215 is a block diagram illustrating a configuration example of a
block
deinterleaver 54.
[FIG 216] FIG 216 is a block diagram illustrating another configuration
example of a
bit deinterleaver 165.
[FIG. 217] FIG. 217 is a block diagram illustrating a first configuration
example of a
reception system that can be applied to the receiving device 12.
[FIG 218] FIG 218 is a block diagram illustrating a second configuration
example of
a reception system that can be applied to the receiving device 12.
[FIG. 219] FIG 219 is a block diagram illustrating a third configuration
example of a
reception system that can be applied to the receiving device 12.
[FIG 220] FIG 220 is a block diagram illustrating a configuration example of
an
embodiment of a computer to which the present technology is applied.
CA 02917806 2016-01-08
29
Description of Embodiments
[0021]
Hereinafter, exemplary embodiments of the present technology will be
described, but before the description of the exemplary embodiments of the
present
technology, an LDPC code will be described.
[0022]
<LDPC code>
[0023]
The LDPC code is a linear code and it is not necessary for the LDPC code to
be a binary code. However, in this case, it is assumed that the LDPC code is
the
binary code.
[0024]
A maximum characteristic of the LDPC code is that a parity check matrix
defining the LDPC code is sparse. In this case, the sparse matrix is a matrix
in
which the number of "1" of elements of the matrix is very small (a matrix in
which
most elements are 0).
[0025]
FIG. 1 is an illustration of an example of a parity check matrix H of the
LDPC code.
[0026]
In the parity check matrix H of FIG 1, a weight of each column (the column
weight) (the number of "1") becomes "3" and a weight of each row (the row
weight)
becomes "6".
[0027]
In encoding using the LDPC code (LDPC encoding), for example, a
generation matrix G is generated on the basis of the parity check matrix H and
the
generation matrix G is multiplied by binary information bits, so that a code
word
(LDPC code) is generated.
[0028]
Specifically, an encoding device that performs the LDPC encoding first
calculates the generation matrix G in which an expression GHT = 0 is realized,
between a transposed matrix HT of the parity check matrix H and the generation
CA 02917806 2016-01-08
matrix G. In this case, when the generation matrix G is aK xN matrix, the
encoding
device multiplies the generation matrix G with a bit string (vector u) of
information
bits including K bits and generates a code word c (= uG) including N bits. The
code
word (LDPC code) that is generated by the encoding device is received at a
reception
5 side through a predetermined communication path.
[0029]
The LDPC code can be decoded by an algorithm called probabilistic
decoding suggested by Gallager, that is, a message passing algorithm using
belief
propagation on a so-called Tanner graph, including a variable node (also
referred to as
10 a message node) and a check node. Hereinafter, the variable node and the
check
node are appropriately referred to as nodes simply.
[0030]
FIG. 2 is a flowchart illustrating a decoding sequence of an LDPC code.
[0031]
15 Hereinafter, a real value (a reception LLR) that is obtained by
representing
the likelihood of "0" of a value of an i-th code bit of the LDPC code (one
code word)
received by the reception side by a log likelihood ratio is appropriately
referred to as a
reception value uo,. In addition, a message output from the check node is
referred to
as uj and a message output from the variable node is referred to as v,.
20 [0032]
First, in decoding of the LDPC code, as illustrated in FIG 2, in step Si!, the
LDPC code is received, the message (check node message) uj is initialized to
"0", and
a variable k taking an integer as a counter of repetition processing is
initialized to "0",
and the processing proceeds to step S12. In step S12, the message (variable
node
25 message) v, is calculated by performing an operation (variable node
operation)
represented by an expression (1), on the basis of the reception value uo,
obtained by
receiving the LDPC code, and the message uj is calculated by performing an
operation
(check node operation) represented by an expression (2), on the basis of the
message
vl.
30 [0033]
[Math. 1]
CA 02917806 2016-01-08
31
Vi=1-10i
=1 === (1)
[0034]
[Math. 2]
LI elycl
tanh tanh
i =1 === (2)
[0035]
Here, d, and dc in an expression (1) and expression (2) are respectively
parameters which can be arbitrarily selected and illustrates the number of "1"
in the
longitudinal direction (column) and transverse direction (row) of the parity
check
matrix H. For example, in the case of an LDPC code ((3, 6) LDPC code) with
respect to the parity check matrix H with a column weight of 3 and a row
weight of 6
as illustrated in FIG 1, dv=3 and dc=6 are established.
[0036]
In the variable node operation of the expression (1) and the check node
operation of the expression (2), because a message input from an edge (line
coupling
the variable node and the check node) for outputting the message is not an
operation
target, an operation range becomes 1 to dõ ¨ 1 or 1 to (lc ¨ 1. The check node
operation of the expression (2) is performed actually by previously making a
table of
a function R (vi, v2) represented by an expression (3) defined by one output
with
respect to two inputs vi and v2 and using the table consecutively
(recursively), as
represented by an expression (4).
[0037]
[Math. 3]
x=2tanh-1 (tanh (v1/2) tanh (v2/2) I =R (vi, v2) = (3)
[0038]
[Math. 4]
=R (v , R (v2, R (v3, ="R (vd0-2, Vc10-1)))) === (4)
[0039]
In step S12, the variable k is incremented by "1" and the processing proceeds
to step S13. In step S13, it is determined whether the variable k is more than
the
predetermined repetition decoding number of times C. When it is determined in
step
CA 02917806 2016-01-08
32
S13 that the variable k is not more than C, the processing returns to step S12
and the
same processing is repeated hereinafter.
[0040]
When it is determined in step S13 that the variable k is more than C, the
processing proceeds to step S14, the message vi that corresponds to a decoding
result
to be finally output is calculated by performing an operation represented by
an
expression (5) and is output, and the decoding processing of the LDPC code
ends.
[0041]
[Math. 5]
d,
Vi=1.10i
J1 = (5)
[0042]
In this case, the operation of the expression (5) is performed using messages
uj from all edges connected to the variable node, different from the variable
node
operation of the expression (1).
[0043]
FIG. 3 illustrates an example of the parity check matrix H of the (3, 6) LDPC
code (an encoding rate of 1/2 and a code length of 12).
[0044]
In the parity check matrix H of FIG. 3, a weight of a column is set to 3 and a
weight of a row is set to 6, similar to FIG I.
[0045]
FIG 4 illustrates a Tanner graph of the parity check matrix H of FIG 3.
[0046]
In FIG. 4, the check node is represented by "+"(plus) and the variable node is
represented by ""(equal). The check node and the variable node correspond to
the
row and the column of the parity check matrix H. A line that couples the check
node
and the variable node is the edge and corresponds to "1" of elements of the
parity
check matrix.
[0047]
That is, when an element of a j-th row and an i-th column of the parity check
matrix is 1, in FIG 4, an i-th variable node (node of"") from the upper side
and a j-
th check node (node of "+") from the upper side are connected by the edge. The
CA 02917806 2016-01-08
33
edge shows that a code bit corresponding to the variable node has a
restriction
condition corresponding to the check node.
[0048]
In a sum product algorithm that is a decoding method of the LDPC code, the
variable node operation and the check node operation are repetitively
performed.
[0049]
FIG. 5 illustrates the variable node operation that is performed by the
variable node.
[0050]
In the variable node, the message v, that corresponds to the edge for
calculation is calculated by the variable node operation of the expression (1)
using
messages III and u2 from the remaining edges connected to the variable node
and the
reception value uo,. The messages that correspond to the other edges are also
calculated by the same method.
[0051]
FIG 6 illustrates the check node operation that is performed by the check
node.
[0052]
In this case, the check node operation of the expression (2) can be rewritten
by an expression (6) using a relation of an expression a x b = exp{ln(lal) +
in(1131)} x
sign(a) x sign(b). However, sign(x) is 1 in the case of x? 0 and is -1 in the
case of x
<0.
[0053]
[Math. 6]
d0-1
ui----2tanh-1 TT tanh \-2
d
dc--1
=2tanh-1 exp{.I In( tanh )1x Tr sign
tanh(¨vi ))
2
_
( d0--1 I I )\ µ} c10-1
exp ¨1r V' 0 tanh xli sign (vi)
2 i=1
1.1 / = = =
(6)
CA 02917806 2016-01-08
34
[0054]
In x > 0, if a function 4i(x) is defined as an expression 4)(x) =
ln(tanh(x/2)), an
expression 4)-I(x) = 2tanh-1(e-x) is realized. For this reason, the expression
(6) can be
changed to an expression (7).
[0055]
[Math. 7]
(do-1 do-1
Uj=0-1 (IVi I)) x TT sign(vi)
\i_1 i=1
=== (7)
[0056]
In the check node, the check node operation of the expression (2) is
performed according to the expression (7).
[0057]
That is, in the check node, as illustrated in FIG. 6, the message uj that
corresponds to the edge for calculation is calculated by the check node
operation of
the expression (7) using messages vi, V2, V3, va, and vs from the remaining
edges
connected to the check node. The messages that correspond to the other edges
are
also calculated by the same method.
[0058]
The function 14)(x) of the expression (7) can be represented as 4)(x) =
ln((ex+1)/(ex-1)) and 4)(x) = 4)-I(x) is satisfied in x> 0. When the functions
.1)(x) and
4)-1(x) are mounted to hardware, the functions 4)(x) and 4)-1(x) may be
mounted using
an LUT (Look Up Table). However, both the functions 4)(x) and 4)-1(x) become
the
same LUT.
[0059]
<Configuration example of transmission system to which present disclosure is
applied>
[0060]
FIG 7 illustrates a configuration example of an embodiment of a
transmission system (a system means a logical gathering of a plurality of
devices and
a device of each configuration may be arranged or may not be arranged in the
same
casing) to which the present invention is applied.
[0061]
CA 02917806 2016-01-08
In FIG. 7, the transmission system includes a transmitting device 11 and a
receiving device 12.
[0062]
For example, the transmitting device 11 transmits (broadcasts) (transfers) a
5 program of television broadcasting, and so on. That is, for example, the
transmitting
device 11 encodes target data that is a transmission target such as image data
and
audio data as a program into LDPC codes, and, for example, transmits them
through a
communication path 13 such as a satellite circuit, a ground wave and a cable
(wire
circuit).
10 [0063]
The receiving device 12 receives the LDPC code transmitted from the
transmitting device 11 through the communication path 13, decodes the LDPC
code to
obtain the target data, and outputs the target data.
[0064]
15 In this case, it is known that the LDPC code used by the transmission
system
of FIG 7 shows the very high capability in an AWGN (Additive White Gaussian
Noise) communication path.
[0065]
Meanwhile, in the communication path 13, burst error or erasure may be
20 generated. Especially in the case where the communication path 13 is the
ground
wave, for example, in an OFDM (Orthogonal Frequency Division Multiplexing)
system, power of a specific symbol may become 0 (erasure) according to delay
of an
echo (paths other than a main path), under a multi-path environment in which
D/U
(Desired to Undesired Ratio) is 0 dB (power of Undesired = echo is equal to
power of
25 Desired = main path).
[0066]
In the flutter (communication path in which delay is 0 and an echo having a
Doppler frequency is added), when D/U is 0 dB, entire power of an OFDM symbol
at
a specific time may become 0 (erasure) by the Doppler frequency.
30 [0067]
In addition, the burst error may be generated due to a situation of a wiring
line from a receiving unit (not illustrated in the drawings) of the side of
the receiving
device 12 such as an antenna receiving a signal from the transmitting device
11 to the
CA 02917806 2016-01-08
36
receiving device 12 or instability of a power supply of the receiving device
12.
[0068]
Meanwhile, in decoding of the LDPC code, in the variable node
corresponding to the column of the parity check matrix H and the code bit of
the
LDPC code, as illustrated in FIG 5, the variable node operation of the
expression (1)
with the addition of (the reception value u0i of) the code bit of the LDPC
code is
performed. For this reason, if error is generated in the code bits used for
the variable
node operation, precision of the calculated message is deteriorated.
[0069]
In the decoding of the LDPC code, in the check node, the check node
operation of the expression (7) is performed using the message calculated by
the
variable node connected to the check node. For this reason, if the number of
check
nodes in which error (including erasure) is generated simultaneously in (the
code bits
of the LDPC codes corresponding to) the plurality of connected variable nodes
increases, decoding performance is deteriorated.
[0070]
That is, if the two or more variable nodes of the variable nodes connected to
the check node become simultaneously erasure, the check node returns a message
in
which the probability of a value being 0 and the probability of a value being
1 are
equal to each other, to all the variable nodes. In this case, the check node
that
returns the message of the equal probabilities does not contribute to one
decoding
processing (one set of the variable node operation and the check node
operation). As
a result, it is necessary to increase the repetition number of times of the
decoding
processing, the decoding performance is deteriorated, and consumption power of
the
receiving device 12 that performs decoding of the LDPC code increases.
[0071]
Therefore, in the transmission system of FIG. 7, tolerance against the burst
error or the erasure can be improved while performance in the AWGN
communication
path (AWGN channel) is maintained.
[0072]
<Configuration example of transmitting device 11>
[0073]
FIG 8 is a block diagram illustrating a configuration example of the
CA 02917806 2016-01-08
37
transmitting device 11 of FIG. 7.
[0074]
In the transmitting device 11, one or more input streams corresponding to
target data are supplied to a mode adaptation/multiplexer 111.
[0075]
The mode adaptation/multiplexer 111 performs mode selection and processes
such as multiplexing of one or more input streams supplied thereto, as needed,
and
supplies data obtained as a result to a padder 112.
[0076]
The padder 112 performs necessary zero padding (insertion of Null) with
respect to the data supplied from the mode adaptation/multiplexer 111 and
supplies
data obtained as a result to a BB scrambler 113.
[0077]
The BB scrambler 113 performs base-band scrambling (BB scrambling) with
respect to the data supplied from the padder 112 and supplies data obtained as
a result
to a BCH encoder 114.
[0078]
The BCH encoder 114 performs BCH encoding with respect to the data
supplied from the BB scrambler 113 and supplies data obtained as a result as
LDPC
target data to be an LDPC encoding target to an LDPC encoder 115.
[0079]
The LDPC encoder 115 performs LDPC encoding according to a parity
check matrix or the like in which a parity matrix to be a portion
corresponding to a
parity bit of an LDPC code becomes a staircase (dual diagonal) structure with
respect
to the LDPC target data supplied from the BCH encoder 114, for example, and
outputs an LDPC code in which the LDPC target data is information bits.
[0080]
That is, the LDPC encoder 115 performs the LDPC encoding to encode the
LDPC target data with an LDPC such as the LDPC code (corresponding to the
parity
check matrix) defined in the predetermined standard of the DVB-S.2, the DVB-
T.2,
the DVB-C.2 or the like, and the LDPC code (corresponding to the parity check
matrix) or the like that is to be employed in ATSC 3.0, and outputs the LDPC
code
obtained as a result.
CA 02917806 2016-01-08
38
[0081]
The LDPC code defined in the standard of the DVB-T.2 and the LDPC code
that is to be employed in ATSC 3.0 are an IRA (Irregular Repeat Accumulate)
code
and a parity matrix of the parity check matrix of the LDPC code becomes a
staircase
structure. The parity matrix and the staircase structure will be described
later. The
IRA code is described in "Irregular Repeat-Accumulate Codes", H. Jin, A.
Khandekar,
and R. J. McEliece, in Proceedings of 2nd International Symposium on Turbo
codes
and Related Topics, pp. 1-8, Sept. 2000, for example.
[0082]
The LDPC code that is output by the LDPC encoder 115 is supplied to the bit
interleaver 116.
[0083]
The bit interleaver 116 performs bit interleave to be described later with
respect to the LDPC code supplied from the LDPC encoder 115 and supplies the
LDPC code after the bit interleave to an mapper 117.
[0084]
The mapper 117 maps the LDPC code supplied from the bit interleaver 116
to a signal point representing one symbol of orthogonal modulation in a unit
(symbol
unit) of code bits of one or more bits of the LDPC code and performs the
orthogonal
modulation (multilevel modulation).
[0085]
That is, the mapper 117 performs maps the LDPC code supplied from the bit
interleaver 116 to a signal point determined by a modulation scheme performing
the
orthogonal modulation of the LDPC code, on an IQ plane (IQ constellation)
defined
by an I axis representing an I component of the same phase as a carrier and a
Q axis
representing a Q component orthogonal to the carrier, and performs the
orthogonal
modulation.
[0086]
When the number of signal points decided in the modulation scheme of the
orthogonal modulation performed by the mapper 117 is 2m, m-bit code bits of
the
LDPC code are used as a symbol (one symbol), and the mapper 117 maps the LDPC
code supplied from the bit interleaver 116 to a signal point indicating a
symbol among
the 2m signal points in units of symbols.
CA 02917806 2016-01-08
39
[0087]
Here, examples of the modulation scheme of the orthogonal modulation
performed by the mapper 117 include a modulation scheme specified in a
standard
such as DVB-T.2, a modulation scheme that is scheduled to be employed in ATSC
3.0,
and other modulation schemes, that is, includes Binary Phase Shift Keying
(BPSK),
Quadrature Phase Shift Keying (QPSK), 8 Phase-Shift Keying (8PSK), 16
Amplitude
Phase-Shift Keying (APSK), 32APSK, 16 Quadrature Amplitude Modulation (QAM),
16QAM, 64QAM, 256QAM, 1024QAM, 4096QAM, and 4 Pulse Amplitude
Modulation (PAM). A modulation scheme by which the orthogonal modulation is
performed in the mapper 117 is set in advance, for example, according to an
operation
of an operator of the transmitting device 11.
[0088]
The data (a mapping result of mapping the symbol to the signal point)
obtained by the process of the mapper 117 is supplied to a time interleaver
118.
[0089]
The time interleaver 118 performs time interleave (interleave in a time
direction) in a unit of symbol with respect to the data supplied from the
mapper 117
and supplies data obtained as a result to an single input single
output/multiple input
single output encoder (SISO/MISO encoder) 119.
[0090]
The SISO/MISO encoder 119 performs spatiotemporal encoding with respect
to the data supplied from the time interleaver 118 and supplies the data to
the
frequency interleaver 120.
[0091]
The frequency interleaver 120 performs frequency interleave (interleave in a
frequency direction) in a unit of symbol with respect to the data supplied
from the
SISO/MISO encoder 119 and supplies the data to a frame builder/resource
allocation
unit 131.
[0092]
On the other hand, for example, control data (signalling) for transfer control
such as BB signaling (Base Band Signalling) (BB Header) is supplied to the BCH
encoder 121.
[0093]
CA 02917806 2016-01-08
The BCH encoder 121 performs the BCH encoding with respect to the
signaling supplied thereto and supplies data obtained as a result to an LDPC
encoder
122, similar to the BCH encoder 114.
[0094]
5 The LDPC
encoder 122 sets the data supplied from the BCH encoder 121 as
LDPC target data, performs the LDPC encoding with respect to the data, and
supplies
an LDPC code obtained as a result to a mapper 123, similar to the LDPC encoder
115.
[0095]
The mapper 123 maps the LDPC code supplied from the LDPC encoder 122
10 to a signal
point representing one symbol of orthogonal modulation in a unit (symbol
unit) of code bits of one or more bits of the LDPC code, performs the
orthogonal
modulation, and supplies data obtained as a result to the frequency
interleaver 124,
similar to the mapper 117.
[0096]
15 The frequency
interleaver 124 performs the frequency interleave in a unit of
symbol with respect to the data supplied from the mapper 123 and supplies the
data to
the frame builder/resource allocation unit 131, similar to the frequency
interleaver 120.
[0097]
The frame builder/resource allocation unit 131 inserts symbols of pilots into
20 necessary
positions of the data (symbols) supplied from the frequency interleavers
120 and 124, configures a frame (for example, a physical layer (PL) frame, a
T2
frame, a C2 frame, and so on) including symbols of a predetermined number from
data (symbols) obtained as a result, and supplies the frame to an OFDM
generating
unit 132.
25 [0098]
The OFDM generating unit 132 generates an OFDM signal corresponding to
the frame from the frame supplied from the frame builder/resource allocation
unit 131
and transmits the OFDM signal through the communication path 13 (FIG 7).
[0099]
30 Here, for
example, the transmitting device 11 can be configured without
including part of the blocks illustrated in FIG 8 such as the time interleaver
118, the
SISO/MISO encoder 119, the frequency interleaver 120 and the frequency
interleaver
124.
CA 02917806 2016-01-08
41
[0100]
<Configuration example of bit interleaver 116>
[0101]
FIG. 9 illustrates a configuration example of the bit interleaver 116 of FIG.
8.
[0102]
The bit interleaver 116 has a function of interleaving data, and includes a
parity interleaver 23, a group-wise interleaver 24, and a block interleaver
25.
[0103]
The parity interleaver 23 performs parity interleave for interleaving the
parity
bits of the LDPC code supplied from the LDPC encoder 115 into positions of
other
parity bits and supplies the LDPC code after the parity interleave to the
group-wise
interleaver 24.
[0104]
The group-wise interleaver 24 performs the group-wise interleave with
respect to the LDPC code supplied from the parity interleaver 23 and supplies
the
LDPC code after the group-wise interleave to the block interleaver 25.
[0105]
Here, in the group-wise interleave, 360 bits of one segment are used as a bit
group, where the LDPC code of one code is divided into segments in units of
360 bits
equal to the unit size P which will be described later, and the LDPC code
supplied
from the parity interleaver 23 is interleaved in units of bit groups, starting
from the
head.
[0106]
When the group-wise interleave is performed, the error rate can be improved
to be better than when the group-wise interleave is not performed, and as a
result, it is
possible to secure the excellent communication quality in the data
transmission.
[0107]
The block interleaver 25 performs block interleave for demultiplexing the
LDPC code supplied from the group-wise interleaver 24, converts, for example,
the
LDPC code corresponding to one code into an m-bit symbol serving as a unit of
mapping, and supplies the m-bit symbol to the mapper 117 (FIG 8).
[0108]
Here, in the block interleave, for example, the LDPC code corresponding to
CA 02917806 2016-01-08
42
one code is converted into the m-bit symbol such that the LDPC code supplied
from
the group-wise interleaver 24 is written in a storage region in which columns
serving
as a storage region storing a predetermined number of bits in a column
(vertical)
direction are arranged in a row (horizontal) direction by the number m of bits
of the
symbol in the column direction and read from the storage region in the row
direction.
[0109]
<Parity check matrix H of the LDPC code>
[0110]
Next, FIG. 10 illustrates an example of the parity check matrix H that is used
for LDPC encoding by the LDPC encoder 115 of FIG. 8.
[0111]
The parity check matrix H becomes an LDGM (Low-Density Generation
Matrix) structure and can be represented by an expression H = [HAIHT] (a
matrix in
which elements of the information matrix HA are set to left elements and
elements of
the parity matrix HT are set to right elements), using an information matrix
HA of a
portion corresponding to information bits among the code bits of the LDPC code
and
a parity matrix HT corresponding to the parity bits.
[0112]
In this case, a bit number of the information bits among the code bits of one
code of LDPC code (one code word) and a bit number of the parity bits are
referred to
as an information length K and a parity length M, respectively, and a bit
number of
the code bits of one code (one code word) of LDPC code is referred to as a
code
length N (= K + M).
[0113]
The information length K and the parity length M of the LDPC code having
the certain code length N are determined by an encoding rate. The parity check
matrix H becomes a matrix in which row x column is M x N (a matrix of M x N).
The information matrix HA becomes a matrix of M x K and the parity matrix HT
becomes a matrix of M x M.
[0114]
FIG. 11 is an illustration of an example of the parity matrix HT of the parity
check matrix H used for LDPC encoding in the LDPC encoder 115 of FIG 8.
[0115]
CA 02917806 2016-01-08
43
The parity matrix HT of the parity check matrix H used for LDPC encoding
in the LDPC encoder 115 is identical to, for example, the parity matrix HT of
the
parity check matrix H of the LDPC code specified in a standard such as DVB-
T.2.
[0116]
The parity matrix HT of the parity check matrix H of the LDPC code that is
defined in the standard of the DVB-T.2 or the like becomes a staircase
structure
matrix (lower bidiagonal matrix) in which elements of 1 are arranged in a
staircase
shape, as illustrated in FIG. 11. The row weight of the parity matrix HT
becomes 1
with respect to the first row and becomes 2 with respect to the remaining
rows. The
column weight becomes 1 with respect to the final column and becomes 2 with
respect to the remaining columns.
[0117]
As described above, the LDPC code of the parity check matrix H in which
the parity matrix HT becomes the staircase structure can be easily generated
using the
parity check matrix H.
[0118]
That is, the LDPC code (one code word) is represented by a row vector c and
a column vector obtained by transposing the row vector is represented by CT.
In
addition, a portion of information bits of the row vector c to be the LDPC
code is
represented by a row vector A and a portion of the parity bits is represented
by a row
vector T.
[0119]
The row vector c can be represented by an expression c = [AIT] (a row vector
in which elements of the row vector A are set to left elements and elements of
the row
vector T are set to right elements), using the row vector A corresponding to
the
information bits and the row vector T corresponding to the parity bits.
[0120]
In the parity check matrix H and the row vector c = [AIT] corresponding to
the LDPC code, it is necessary to satisfy an expression He = 0. The row vector
T
that corresponds to the parity bits constituting the row vector c = [AIT]
satisfying the
expression HcT = 0 can be sequentially calculated by setting elements of each
row to 0,
sequentially (in order) from elements of a first row of the column vector HcT
in the
expression HO' = 0, when the parity matrix HT of the parity check matrix H =
[HAIN
CA 02917806 2016-01-08
44
becomes the staircase structure illustrated in FIG. 11.
[0121]
FIG. 12 is an illustration of the parity check matrix H of the LDPC code that
is defined in the standard of the DVB-T.2 or the like.
[0122]
The column weight becomes X with respect KX columns from a first column
of the parity check matrix H of the LDPC code defined in the standard of the
DVB-
T.2 or the like, becomes 3 with respect to the following K3 columns, becomes 2
with
respect to the following (M-1) columns, and becomes 1 with respect to a final
column.
[0123]
In this case, KX + K3 + M ¨ 1 + 1 is equal to the code length N.
[0124]
FIG. 13 is an illustration of column numbers KX, K3, and M and a column
weight X, with respect to each encoding rate r of the LDPC code defined in the
standard of the DVB-T.2 or the like.
[0125]
In the standard of the DVB-T.2 or the like, LDPC codes that have code
lengths N of 64800 bits and 16200 bits are defined.
[0126]
With respect to the LDPC code having the code length N of 64800 bits, 11
encoding rates (nominal rates) of 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6,
8/9, and
9/10 are defined. With respect to the LDPC code having the code length N of
16200
bits, 10 encoding rates of 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, and
8/9 are defined.
[0127]
Hereinafter, the code length N of the 64800 bits is referred to as 64 kbits
and
the code length N of the 16200 is referred to as 16 kbits.
[0128]
With respect to the LDPC code, an error rate tends to be lower in a code bit
corresponding to a column of which a column weight of the parity check matrix
H is
large.
[0129]
In the parity check matrix H that is illustrated in FIGS. 12 and 13 and is
defined in the standard of the DVB-T.2 or the like, a column weight of a
column of a
CA 02917806 2016-01-08
head side (left side) tends to be large. Therefore, with respect to the LDPC
code
corresponding to the parity check matrix H, a code bit of a head side tends to
be
robust to error (there is tolerance against the error) and a code bit of an
ending side
tends to be weak for the error.
5 [0130]
<Parity interleave>
[0131]
Next, the parity interleave by the parity interleaver 23 of FIG. 9 will be
described with reference to FIGS. 14 to 16.
10 [0132]
FIG. 24 illustrates an example of (a part of) a Tanner graph of the parity
check matrix of the LDPC code.
[0133]
As illustrated in FIG. 14, if a plurality of, for example, two variable nodes
15 among (the code bits corresponding to) the variable nodes connected to
the check
node simultaneously become the error such as the erasure, the check node
returns a
message in which the probability of a value being 0 and the probability of a
value
being 1 are equal to each other, to all the variable nodes connected to the
check node.
For this reason, if the plurality of variable nodes connected to the same
check node
20 simultaneously become the erasure, decoding performance is deteriorated.
[0134]
Meanwhile, the LDPC code that is output by the LDPC encoder 115 of FIG.
8 is an IRA code, same as the LDPC code that is defined in the standard of the
DVB-
T.2 or the like, and the parity matrix HT of the parity check matrix H becomes
a
25 staircase structure, as illustrated in FIG. 11.
[0135]
FIG. 15 illustrates the parity matrix HT becoming the staircase structure as
illustrated in FIG 11, and an example of a Tanner graph corresponding to the
parity
matrix HT.
30 [0136]
That is, A of FIG 15 illustrates an example of the parity matrix HT becoming
the staircase structure and B of FIG 15 illustrates the Tanner graph
corresponding to
the parity matrix HT of A of FIG 15.
CA 02917806 2016-01-08
46
[0137]
In the parity matrix HT with a staircase structure, elements of 1 are adjacent
in each row (excluding the first row). Therefore, in the Tanner graph of the
parity
matrix HT, two adjacent variable nodes corresponding to a column of two
adjacent
elements in which the value of the parity matrix HT is 1 are connected with
the same
check node.
[0138]
Therefore, when parity bits corresponding to two above-mentioned adjacent
variable nodes become errors at the same time by burst error and erasure, and
so on,
the check node connected with two variable nodes (variable nodes to find a
message
by the use of parity bits) corresponding to those two parity bits that became
errors
returns message that the probability with a value of 0 and the probability
with a value
of 1 are equal probability, to the variable nodes connected with the check
node, and
therefore the performance of decoding is deteriorated. Further, when the burst
length (bit number of parity bits that continuously become errors) becomes
large, the
number of check nodes that return the message of equal probability increases
and the
performance of decoding is further deteriorated.
[0139]
Therefore, the parity interleaver 23 (FIG. 9) performs the parity interleave
for
interleaving the parity bits of the LDPC code from the LDPC encoder 115 into
positions of other parity bits, to prevent the decoding performance from being
deteriorated.
[0140]
FIG 16 is an illustration of the parity matrix HT of the parity check matrix I-
1
corresponding to the LDPC code that has undergone the parity interleave
performed
by the parity interleaver 23 of FIG 9.
[0141]
Here, the information matrix HA of the parity check matrix H corresponding
to the LDPC code output by the LDPC encoder 115 has a cyclic structure,
similarly to
the information matrix of the parity check matrix H corresponding to the LDPC
code
specified in a standard such as DVB-T.2.
[0142]
The cyclic structure refers to a structure in which a certain column matches
CA 02917806 2016-01-08
47
one obtained by cyclically shifting another column, and includes, for example,
a
structure in which a position of 1 of each row of P columns becomes a position
obtained by cyclically shifting a first column of the P columns in the column
direction
by a predetermined value such as a value that is proportional to a value q
obtained by
dividing a parity length M for every P columns. Hereinafter, the P columns in
the
cyclic structure are referred to appropriately as a unit size.
[0143]
As an LDPC code defined in a standard such as DVB-T.2, as described in
FIG 12 and FIG. 13, there are two kinds of LDPC codes whose code length N is
64800 bits and 16200 bits, and, for both of those two kinds of LDPC codes, the
unit
size P is defined as 360 which is one of divisors excluding 1 and M among the
divisors of the parity length M.
[0144]
The parity length M becomes a value other than primes represented by an
expression M=q x P=q x 360, using a value q different according to the
encoding
rate. Therefore, similar to the unit size P, the value q is one other than 1
and M
among the divisors of the parity length M and is obtained by dividing the
parity length
M by the unit size P (the product of P and q to be the divisors of the parity
length M
becomes the parity length M).
[0145]
As described above, when information length is assumed to be K, an integer
equal to or greater than 0 and less than P is assumed to be x and an integer
equal to or
greater than 0 and less than q is assumed to be y, the parity interleaver 23
interleaves
the K+qx+y+1 -th code bit among code bits of an LDPC code of N bits to the
position
of the K+Py+x+1-th code bit as parity interleave.
[0146]
Since both of the K+qx+y+1 -th code bit and the K+Py+x+1-th code bit are
code bits after the K+1-th one, they are parity bits, and therefore the
positions of the
parity bits of the LDPC code are moved according to the parity interleave.
[0147]
According to the parity interleave, (the parity bits corresponding to) the
variable nodes connected to the same check node are separated by the unit size
P, that
is, 360 bits in this case. For this reason, when the burst length is less than
360 bits,
CA 02917806 2016-01-08
48
the plurality of variable nodes connected to the same check node can be
prevented
from simultaneously becoming the error. As a result, tolerance against the
burst
error can be improved.
[0148]
The LDPC code after the interleave for interleaving the (K + qx + y + 1)-th
code bit into the position of the (K + Py + x + 1)-th code bit is matched with
an LDPC
code of a parity check matrix (hereinafter, referred to as a transformed
parity check
matrix) obtained by performing column replacement for replacing the (K + qx +
y+
1)-th column of the original parity check matrix H with the (K + Py + x + 1)-
th
column.
[0149]
In the parity matrix of the transformed parity check matrix, as illustrated in
FIG 16, a pseudo cyclic structure that uses the P columns (in FIG 16, 360
columns)
as a unit appears.
[0150]
Here, the pseudo cyclic structure is a structure in which the remaining
portion excluding a part has the cyclic structure.
[0151]
The transformed parity check matrix obtained by performing the column
permutation corresponding to the parity interleave on the parity check matrix
of the
LDPC code specified in the standard such as DVB-T.2 has the pseudo cyclic
structure
rather than the (perfect) cyclic structure since it is one 1 element short (it
is a 0
element) in a portion (a shift matrix which will be described later) of a
360x360
matrix of a right top corner portion of the transformed parity check matrix.
[0152]
The transformed parity check matrix for the parity check matrix of the LDPC
code output by the LDPC encoder 115 has the pseudo cyclic structure, for
example,
similarly to the transformed parity check matrix for the parity check matrix
of the
LDPC code specified in the standard such as DVB-T.2.
[0153]
The transformed parity check matrix of FIG 16 becomes a matrix that is
obtained by performing the column replacement corresponding to the parity
interleave
and replacement (row replacement) of a row to configure the transformed parity
check
CA 02917806 2016-01-08
49
matrix with a constitutive matrix to be described later, with respect to the
original
parity check matrix H.
[0154]
FIG 17 is a flowchart illustrating processing executed by the LDPC encoder
115, the bit interleaver 116, and the mapper 117 of FIG. 8.
[0155]
The LDPC encoder 115 awaits supply of the LDPC target data from the BCH
encoder 114. In step S101, the LDPC encoder 115 encodes the LDPC target data
with the LDPC code and supplies the LDPC code to the bit interleaver 116. The
processing proceeds to step S102.
[0156]
In step S102, the bit interleaver 116 performs the bit interleave on the LDPC
code supplied from the LDPC encoder 115, and supplies the symbol obtained by
the
bit interleave to the mapper 117, and the process proceeds to step S103.
[0157]
That is, in step S102, in the bit interleaver 116 (FIG. 9), the parity
interleaver
23 performs parity interleave with respect to the LDPC code supplied from the
LDPC
encoder 115 and supplies the LDPC code after the parity interleave to the
group-wise
interleaver 24.
[0158]
The group-wise interleaver 24 performs the group-wise interleave on the
LDPC code supplied from the parity interleaver 23, and supplies the resulting
LDPC
code to the block interleaver 25.
[0159]
The block interleaver 25 performs the block interleave on the LDPC code
that has undergone the group-wise interleave performed by the group-wise
interleaver
24, and supplies the m-bit symbol obtained as a result to the mapper 117.
[0160]
In step S103, the mapper 117 maps the symbol supplied from the block
interleaver 25 to any of the 2m signal points decided in the modulation scheme
of the
orthogonal modulation performed by the mapper 117, performs the orthogonal
modulation, and supplies data obtained as a result to the time interleaver
118.
[0161]
CA 02917806 2016-01-08
As described above, by performing the parity interleave and the group-wise
interleave, it is possible to improve the error rate when transmission is
performed
using a plurality of code bits of the LDPC code as one symbol.
[0162]
5 Here, in FIG.
9, for the sake of convenience of description, the parity
interleaver 23 serving as the block performing the parity interleave and the
group-
wise interleaver 24 serving as the block performing the group-wise interleave
are
configured individually, but the parity interleaver 23 and the group-wise
interleaver
24 may be configured integrally.
10 [0163]
That is, both the parity interleave and the group-wise interleave can be
performed by writing and reading of the code bits with respect to the memory
and can
be represented by a matrix to convert an address (write address) to perform
writing of
the code bits into an address (read address) to perform reading of the code
bits.
15 [0164]
Therefore, if a matrix obtained by multiplying a matrix representing the
parity interleave and a matrix representing the group-wise interleave is
calculated, the
code bits are converted by the matrixes, the parity interleave is performed,
and a
group-wise interleave result of the LDPC code after the parity interleave can
be
20 obtained.
[0165]
In addition to the parity interleaver 23 and the group-wise interleaver 24,
the
block interleaver 25 can be integrally configured.
[0166]
25 That is, the
block interleave executed by the block interleaver 25 can be
represented by the matrix to convert the write address of the memory storing
the
LDPC code into the read address.
[0167]
Therefore, if a matrix obtained by multiplying the matrix representing the
30 parity
interleave, the matrix representing the group-wise interleave, and the matrix
representing the block interleave is calculated, the parity interleave, the
group-wise
interleave, and the block interleave can be collectively executed by the
matrixes.
[0168]
CA 02917806 2016-01-08
51
<Configuration example of LDPC encoder 115>
[0169]
FIG. 18 is a block diagram illustrating a configuration example of the LDPC
encoder 115 of FIG. 8.
[0170]
The LDPC encoder 122 of FIG. 8 is also configured in the same manner.
[0171]
As described in FIGS. 12 and 13, in the standard of the DVB-T.2 or the like,
the LDPC codes that have the two code lengths N of 64800 bits and 16200 bits
are
defined.
[0172]
With respect to the LDPC code having the code length N of 64800 bits, 11
encoding rates of 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 8/9, and 9/10
are defined.
With respect to the LDPC code having the code length N of 16200 bits, 10
encoding
rates of 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, and 8/9 are defined
(FIGS. 12 and 13).
[0173]
For example, the LDPC encoder 115 can perform encoding (error correction
encoding) using the LDPC code of each encoding rate having the code length N
of
64800 bits or 16200 bits, according to the parity check matrix H prepared for
each
code length N and each encoding rate.
[0174]
The LDPC encoder 115 includes an encoding processing unit 601 and a
storage unit 602.
[0175]
The encoding processing unit 601 includes an encoding rate setting unit 611,
an initial value table reading unit 612, a parity check matrix generating unit
613, an
information bit reading unit 614, an encoding parity operation unit 615, an a
control
unit 616. The encoding processing unit 601 performs the LDPC encoding of LDPC
target data supplied to the LDPC encoder 115 and supplies an LDPC code
obtained as
a result to the bit interleaver 116 (FIG 8).
[0176]
That is, the encoding rate setting unit 611 sets the code length N and the
encoding rate of the LDPC code, according to an operation of an operator.
CA 02917806 2016-01-08
52
[0177]
The initial value table reading unit 612 reads a parity check matrix initial
value table to be described later, which corresponds to the code length N and
the
encoding rate set by the encoding rate setting unit 611, from the storage unit
602.
[0178]
The parity check matrix generating unit 613 generates a parity check matrix
H by arranging elements of 1 of an information matrix HA corresponding to an
information length K (= information length N ¨ parity length M) according to
the
code length N and the encoding rate set by the encoding rate setting unit 611
in the
column direction with a period of 360 columns (unit size P), on the basis of
the parity
check matrix initial value table read by the initial value table reading unit
612, and
stores the parity check matrix H in the storage unit 602.
[0179]
The information bit reading unit 614 reads (extracts) information bits
corresponding to the information length K, from the LDPC target data supplied
to the
LDPC encoder 115.
[0180]
The encoding parity operation unit 615 reads the parity check matrix H
generated by the parity check matrix generating unit 613 from the storage unit
602,
and generates a code word (LDPC code) by calculating parity bits for the
information
bits read by the information bit reading unit 614 on the basis of a
predetermined
expression using the parity check matrix H.
[0181]
The control unit 616 controls each block constituting the encoding
processing unit 601.
[0182]
In the storage unit 602, a plurality of parity check matrix initial value
tables
that correspond to the plurality of encoding rates illustrated in FIGS. 12 and
13, with
respect to the code lengths N such as the 64800 bits and 16200 bits, are
stored. In
addition, the storage unit 602 temporarily stores data that is necessary for
processing
of the encoding processing unit 601.
[0183]
FIG 19 is a flowchart illustrating an example of processing of the LDPC
CA 02917806 2016-01-08
53
encoder 115 of FIG. 18.
[0184]
In step S201, the encoding rate setting unit 611 determines (sets) the code
length N and the encoding rate r to perform the LDPC encoding.
[0185]
In step S202, the initial value table reading unit 612 reads the previously
determined parity check matrix initial value table corresponding to the code
length N
and the encoding rate r determined by the encoding rate setting unit 611, from
the
storage unit 602.
[0186]
In step S203, the parity check matrix generating unit 613 calculates
(generates) the parity check matrix H of the LDPC code of the code length N
and the
encoding rate r determined by the encoding rate setting unit 611, using the
parity
check matrix initial value table read from the storage unit 602 by the initial
value
table reading unit 612, supplies the parity check matrix to the storage unit
602, and
stores the parity check matrix in the storage unit.
[0187]
In step S204, the information bit reading unit 614 reads the information bits
of the information length K (= N x r) corresponding to the code length N and
the
encoding rate r determined by the encoding rate setting unit 611, from the
LDPC
target data supplied to the LDPC encoder 115, reads the parity check matrix H
calculated by the parity check matrix generating unit 613 from the storage
unit 602,
and supplies the information bits and the parity check matrix to the encoding
parity
operation unit 615.
[0188]
In step S205, the encoding parity operation unit 615 sequentially operates
parity bits of a code word c that satisfies an expression (8) using the
information bits
and the parity check matrix H that have been read from the information bit
reading
unit 614.
[0189]
HcT = 0 = = = (8)
[0190]
In the expression (8), c represents a row vector as the code word (LDPC
CA 02917806 2016-01-08
54
code) and cT represents transposition of the row vector c.
[0191]
As described above, when a portion of the information bits of the row vector
c as the LDPC code (one code word) is represented by a row vector A and a
portion of
the parity bits is represented by a row vector T, the row vector c can be
represented by
an expression c = [A/T], using the row vector A as the information bits and
the row
vector T as the parity bits.
[0192]
In the parity check matrix H and the row vector c = [AIT] corresponding to
the LDPC code, it is necessary to satisfy an expression HO. = 0. The row
vector T
that corresponds to the parity bits constituting the row vector c = [AIT]
satisfying the
expression HcT = 0 can be sequentially calculated by setting elements of each
row to 0,
sequentially from elements of a first row of the column vector HcT in the
expression
HcT = 0, when the parity matrix HT of the parity check matrix H = [HAIHT]
becomes
the staircase structure illustrated in FIG 11.
[0193]
If the encoding parity operation unit 615 calculates the parity bits T with
respect to the information bits A from the information bit reading unit 614,
the
encoding parity operation unit 615 outputs the code word c = [A/T] represented
by the
information bits A and the parity bits T as an LDPC encoding result of the
information
bits A.
[0194]
Then, in step S206, the control unit 616 determines whether the LDPC
encoding ends. When it is determined in step S206 that the LDPC encoding does
not end, that is, when there is LDPC target data to perform the LDPC encoding,
the
processing returns to step S201 (or step S204). Hereinafter, the processing of
steps
S201 (or step S204) to S206 is repeated.
[0195]
When it is determined in step S206 that the LDPC encoding ends, that is,
there is no LDPC target data to perform the LDPC encoding, the LDPC encoder
115
ends the processing.
[0196]
As described above, the parity check matrix initial value table corresponding
CA 02917806 2016-01-08
to each code length N and each encoding rate r is prepared and the LDPC
encoder 115
performs the LDPC encoding of the predetermined code length N and the
predetermined encoding rate r, using the parity check matrix H generated from
the
parity check matrix initial value table corresponding to the predetermined
code length
5 N and the predetermined encoding rate r.
[0197]
<Example of the parity check matrix initial value table>
[0198]
The parity check matrix initial value table is a table that represents
positions
10 of elements of 1 of the information matrix HA (FIG. 10) of the parity
check matrix H
corresponding to the information length K according to the code length N and
the
encoding rate r of the LDPC code (LDPC code defined by the parity check matrix
H)
for every 360 columns (unit size P) and is previously made for each parity
check
matrix H of each code length N and each encoding rate r.
15 [0199]
That is, the parity check matrix initial value table represents at least
positions
of elements of! of the information matrix HA for every 360 columns (unit size
P).
[0200]
Examples of the parity check matrix H include a parity check matrix in
20 which the (whole) parity matrix HT has the staircase structure, which is
specified in
DVB-T.2 or the like and a parity check matrix in which a part of the parity
matrix HT
has the staircase structure, and the remaining portion is a diagonal matrix (a
unit
matrix), which is proposed by CRC/ETRI.
[0201]
25 Hereinafter, an expression scheme of a parity check matrix initial value
table
indicating the parity check matrix in which the parity matrix HT has the
staircase
structure, which is specified in DVB-T.2 or the like, is referred to as a DVB
scheme,
and an expression scheme of a parity check matrix initial value table
indicating the
parity check matrix proposed by CRC/ETRI is referred to as an ETRI scheme.
30 [0202]
FIG. 20 is an illustration of an example of the parity check matrix initial
value table in the DVB method.
[0203]
CA 02917806 2016-01-08
56
That is, FIG 20 illustrates a parity check matrix initial value table with
respect to the parity check matrix H that is defined in the standard of the
DVB-T.2
and has the code length N of 16200 bits and the encoding rate (an encoding
rate of
notation of the DVB-T.2) r of 1/4.
[0204]
The parity check matrix generating unit 613 (FIG 18) calculates the parity
check matrix H using the parity check matrix initial value table in the DVB
method,
as follows.
[0205]
FIG. 21 is an illustration of a method of calculating a parity check matrix H
from a parity check matrix initial value table in the DVB method.
[0206]
That I, FIG 21 illustrates a parity check matrix initial value table with
respect to the parity check matrix H that is defined in the standard of the
DVB-T.2
and has the code length N of 16200 bits and the encoding rate r of 2/3.
[0207]
The parity check matrix initial value table in the DVB method is the table
that represents the positions of the elements of 1 of the whole information
matrix HA
corresponding to the information length K according to the code length N and
the
encoding rate r of the LDPC code for every 360 columns (unit size P). In the i-
th
row thereof, row numbers (row numbers when a row number of a first row of the
parity check matrix H is set to 0) of elements of 1 of a (1 + 360 x (i ¨ 1)-th
column of
the parity check matrix H are arranged by a number of column weights of the (1
+ 360
x (i ¨ 1)-th column.
[0208]
Here, since the parity matrix HT (FIG 10) corresponding to the parity length
M in the parity check matrix H of the DVB scheme is fixed to the staircase
structure
illustrated in FIG. 15, it is possible to obtain the parity check matrix H if
it is possible
to obtain the information matrix HA (FIG 10) corresponding to the information
length
K through the parity check matrix initial value table.
[0209]
A row number k + 1 of the parity check matrix initial value table in the DVB
method is different according to the information length K.
CA 02917806 2016-01-08
57
[0210]
A relation of an expression (9) is realized between the information length K
and the row number k + 1 of the parity check matrix initial value table.
[0211]
K = (k + 1) x 360 = = = (9)
[0212]
In this case, 360 of the expression (9) is the unit size P described in FIG.
16.
[0213]
In the parity check matrix initial value table of FIG 21, 13 numerical values
are arranged from the first row to the third row and 3 numerical values are
arranged
from the fourth row to the (k + 1)-th row (in FIG 21, the 30th row).
[0214]
Therefore, the column weights of the parity check matrix H that are
calculated from the parity check matrix initial value table of FIG. 21 are 13
from the
first column to the (1+ 360 x (3 - 1) - 1)-th column and are 3 from the (1+
360 x (3 -1))-th column to the K-th column.
[0215]
The first row of the parity check matrix initial value table of FIG 21
becomes 0, 2084, 1613, 1548, 1286, 1460, 3196, 4297, 2481, 3369, 3451, 4620,
and
2622, which shows that elements of rows having row numbers of 0, 2084, 1613,
1548,
1286, 1460, 3196, 4297, 2481, 3369, 3451, 4620, and 2622 are 1 (and the other
elements are 0), in the first column of the parity check matrix H.
[0216]
The second row of the parity check matrix initial value table of FIG. 21
becomes 1, 122, 1516, 3448, 2880, 1407, 1847, 3799, 3529, 373, 971, 4358, and
3108,
which shows that elements of rows having row numbers of 1, 122, 1516, 3448,
2880,
1407, 1847, 3799, 3529, 373, 971, 4358, and 3108 are 1, in the 361 (= 1 + 360
x (2 -1))-th column of the parity check matrix H.
[0217]
As described above, the parity check matrix initial value table represents
positions of elements of 1 of the information matrix HA of the parity check
matrix H
for every 360 columns.
[0218]
CA 02917806 2016-01-08
58
The columns other than the (1 + 360 x (i ¨ 1))-th column of the parity check
matrix H, that is, the individual columns from the (2 + 360 x (i ¨ 1))-th
column to the
(360 x i)-th column are arranged by cyclically shifting elements of 1 of the
(1 + 360 x
(i ¨ 1))-th column determined by the parity check matrix initial value table
periodically in a downward direction (downward direction of the columns)
according
to the parity length M.
[0219]
That is, the (2 + 360 x (i ¨ 1))-th column is obtained by cyclically shifting
(1
+ 360 x (i ¨ 1))-th column in the downward direction by M/360 (= q) and the
next (3
+ 360 x (i ¨ 1))-th column is obtained by cyclically shifting (1 + 360 x (i ¨
1))-th
column in the downward direction by 2 x M/360 (= 2 x q) (obtained by
cyclically
shifting (2 + 360 x (i ¨ 1))-th column in the downward direction by M/360 (=
q)).
[0220]
If a numerical value of a j-th column (j-th column from the left side) of an i-
th row (i-th row from the upper side) of the parity check matrix initial value
table is
represented as hi j and a row number of the j-th element of 1 of the w-th
column of the
parity check matrix H is represented as Hw_j, the row number 1-1,,,j of the
element of 1
of the w-th column to be a column other than the (1 + 360 x (i ¨ 1))-th column
of the
parity check matrix H can be calculated by an expression (10).
[0221]
= mod{h, + mod((w-1),P) x q,M) = = = (10)
[0222]
In this case, mod(x, y) means a remainder that is obtained by dividing x by y.
[0223]
In addition, P is a unit size described above. In the present embodiment, for
example, same as the standard of the DVB-S.2, the DVB-T.2, and the DVB-C.2, P
is
360. In addition, q is a value M/360 that is obtained by dividing the parity
length M
by the unit size P (= 360).
[0224]
The parity check matrix generating unit 613 (FIG 18) specifies the row
numbers of the elements of 1 of the (1 + 360 x (i ¨ 1))-th column of the
parity check
matrix H by the parity check matrix initial value table.
[0225]
CA 02917806 2016-01-08
59
The parity check matrix generating unit 613 (FIG 18) calculates the row
number of the
element of 1 of the w-th column to be the column other than the (1
+ 360 x (i - 1))-th column of the parity check matrix H, according to the
expression
(10), and generates the parity check matrix H in which the element of the
obtained
row number is set to 1.
[0226]
FIG. 22 is an illustration of a structure of the parity check matrix of the
ETRI
scheme.
[0227]
The parity check matrix of the ETRI scheme is configured with an A matrix,
a B matrix, a C matrix, a D matrix, and a Z matrix.
[0228]
The A matrix is a gxK upper left matrix of the parity check matrix expressed
by a predetermined value g and the information length K of the LDPC code (=
the
code length Nxthe encoding rate r).
[0229]
The B matrix is a gxg matrix having the staircase structure adjacent to the
right of the A matrix.
[0230]
The C matrix is an (N¨K¨g)x(K+g) matrix adjacently below the A matrix
and the B matrix.
[023 1 ]
The D matrix is an (N¨K¨g)x(N¨K¨g) unit matrix adjacent to the right of
the C matrix.
[0232]
The Z matrix is a gx(N¨K¨g) zero matrix (zero matrix) adjacent to the right
of the B matrix.
[0233]
In the parity check matrix of the ETRI scheme configured with the A to D
matrices and the Z matrix, the A matrix and a portion of the C matrix
configure an
information matrix, and the B matrix, the remaining portion of the C matrix,
the D
matrix, and the Z matrix configure a parity matrix.
[0234]
CA 02917806 2016-01-08
Further, since the B matrix is the matrix having the staircase structure, and
the D matrix is the unit matrix, a portion (a portion of the B matrix) of the
parity
matrix of the parity check matrix of the ETRI scheme has the staircase
structure, and
the remaining portion (the portion of the D matrix) is the diagonal matrix
(the unit
5 matrix).
[0235]
Similarly to the information matrix of the parity check matrix of the DVB
scheme, the A matrix and the C matrix have the cyclic structure for every 360
columns (the unit size P), and the parity check matrix initial value table of
the ETRI
10 scheme indicates positions of 1 elements of the A matrix and the C
matrix in units of
360 columns.
[0236]
Here, as described above, since the A matrix, and a portion of the C matrix
configure the information matrix, it can be said that the parity check matrix
initial
15 value table of the ETRI scheme that indicates positions of 1 elements of
the A matrix
and the C matrix in units of 360 columns indicates at least positions of 1
elements of
the information matrix in units of 360 columns.
[0237]
FIG. 23 is an illustration of an example of the parity check matrix initial
20 value table of the ETRI scheme.
[0238]
In other words, FIG 23 illustrates an example of a parity check matrix initial
value table for a parity check matrix in which the code length N is 50 bits,
and the
encoding rate r is 1/2.
25 [0239]
The parity check matrix initial value table of the ETRI scheme is a table in
which positions of 1 elements of the A matrix and the C matrix are indicated
for each
unit size P, and row numbers (row numbers when a row number of a first row of
the
parity check matrix is 0) of 1 elements of a (1+Px(i-1))-th column of the
parity check
30 matrix that correspond in number to the column weight of the (1+Px(i-1))-
th column
are arranged in an i-th row.
[0240]
Here, in order to simplify the description, the unit size P is assumed to be,
for
CA 02917806 2016-01-08
61
example, 5.
[0241]
Further, parameters for the parity check matrix of the ETRI scheme include g
= MI, M2, Qi, and Q2.
[0242]
g = MI is a parameter for deciding the size of the B matrix and has a value
that is a multiple of the unit size R The performance of the LDPC code is
changed
by adjusting g = MI, and g = Mi is adjusted to a predetermined value when the
parity
check matrix is decided. Here, 15, which is three times the unit size P (= 5),
is
assumed to be employed as g = Mi.
[0243]
M2 has a value M¨Mi obtained by subtracting MI from the parity length M.
[0244]
Here, since the information length K is Nxr = 50x 1/2 = 25, and the parity
length M is N¨K = 50-25 = 25, M2 is M¨M1 = 25-15 = 10.
[0245]
Qi is obtained from the formula Qi = Mi/P, and indicates the number of
shifts (the number of rows) of the cyclic shift in the A matrix.
[0246]
In other words, in each column other than the (1+Px(i-1))-th column of the
A matrix of the parity check matrix of the ETRI scheme, that is, in each of a
(2+Px(i-1))-th column to a (Pxi)-th column, 1 elements of a (1+360x(i-1))-th
column decided by the parity check matrix initial value table have
periodically been
cyclically shifted downward (downward in the column) and arranged, and Qi
indicates the number of shifts the cyclic shift in the A matrix.
[0247]
Q2 is obtained from the formula Q2 = M2/P, and indicates the number of
shifts (the number of rows) of the cyclic shift in the C matrix.
[0248]
In other words, in each column other than the (1+Px(i-1))-th column of the
C matrix of the parity check matrix of the ETRI scheme, that is, in each of a
(2+Px(i-1))-th column to a (Pxi)-th column, 1 elements of a (1+360x(i-1))-th
column decided by the parity check matrix initial value table have
periodically been
CA 02917806 2016-01-08
62
cyclically shifted downward (downward in the column) and arranged, and Q2
indicates the number of shifts the cyclic shift in the C matrix.
[0249]
Here, Qi is Mi/P = 15/5 = 3, and Q2 is M2/P = 10/5 = 2.
[0250]
In the parity check matrix initial value table of FIG. 23, 3 numerical values
are arranged in 1st and 2nd rows, and one numerical value is arranged in 3rd
to 5th
rows, and according to a sequence of the numerical values, the column weight
of the
parity check matrix obtained from the parity check matrix initial value table
of FIG
23 is 3 in the 1st column to a (1+5x(2-1)-1)-th column and 1 in a (1+5x(2-1))-
th
column to a 5th column.
[0251]
In other words, 2, 6, and 18 are arranged in the 1st row of the parity check
matrix initial value table of FIG 23, which indicates that elements of rows
having the
row numbers of 2, 6, and 18 are 1 (and the other elements are 0) in the 1st
column of
the parity check matrix.
[0252]
Here, in this case, the A matrix is a 15x25 (gxK) matrix, the C matrix is a
10x40 ((N¨K¨g)x(K+g)) matrix, rows having the row numbers of 0 to 14 in the
parity check matrix are rows of the A matrix, and rows having the row numbers
of 15
to 24 in the parity check matrix are rows of the C matrix.
[0253]
Thus, among the rows having the row numbers of 2, 6, and 18 (hereinafter
referred to as rows #2, #6, and #18), the rows #2 and #6 are the rows of the A
matrix,
and the row #18 is the row of the C matrix.
[0254]
2, 10, and 19 are arranged in the 2nd row of the parity check matrix initial
value table of FIG. 23, which indicates that elements of the rows #2, #10, and
#19 are
1 in a 6 (= 1+5x(2-1))-th column of the parity check matrix.
[0255]
Here, in the 6 (= 1+5x(2-1))-th column of the parity check matrix, among
the rows #2, #10, and #19, the rows #2 and #10 are the rows of the A matrix,
and the
row #19 is the row of the C matrix.
CA 02917806 2016-01-08
63
[0256]
22 is arranged in the 3rd row of the parity check matrix initial value table
of
FIG 23, which indicates that an element of the row #22 is 1 in an 11 (= 1+5x(3-
1))-th
column of the parity check matrix.
[0257]
Here, in the 11 (= 1+5x(3-1))-th column of the parity check matrix, the row
#22 is the row of the C matrix.
[0258]
Similarly, 19 in the 4th column of the parity check matrix initial value table
of FIG. 23 indicates that an element of the row #19 is 1 in a 16 (= 1+5x(4-1))-
th
column of the parity check matrix, and 15 in the 5th row of the parity check
matrix
initial value table of FIG 23 indicates that an element of the row #15 is 1 in
a
21( = 1+5 x(5-1))-st column of the parity check matrix.
[0259]
As described above, the parity check matrix initial value table indicates the
positions of the 1 elements of the A matrix and the C matrix of the parity
check matrix
for each unit size P (= 5 columns).
[0260]
In each column other than a (1+5x(i-1))-th column of the A matrix and the C
matrix of the parity check matrix, that is, in each of a (2+5x(i-1))-th column
to a
(5 xo-th column, the 1 elements of the (1+5x(i-1))-th column decided by the
parity
check matrix initial value table have periodically been cyclically shifted
downward
(downward in the column) and arranged according to the parameters Qi and Q2.
[0261]
In other words, for example, in the (2+5x(i-1))-th column of the A matrix,
the (1+5 x(i-1))-th column has been cyclically shifted downward by Qi (= 3),
and in a
(3+5 x(i-1))-th column, the (1+5x(i-1))-th column has been cyclically shifted
downward by 2 x()1 2x3) (the
(2+5x(i-1))-th column has been cyclically shifted
downward by Q1).
[0262]
Further, for example, in the (2+5 x (i-1))-th column of the C matrix, the
(1+5x(i-1))-th column has been cyclically shifted downward by Q2 (= 2), and in
a
(3+5x(i-1))-th column, the (1+5x(i-1))-th column has been cyclically shifted
CA 02917806 2016-01-08
64
downward by 2xQ2 2x2) (the
(2+5x(i-1))-th column has been cyclically shifted
downward by Q2).
[0263]
FIG. 24 is an illustration of the A matrix generated from the parity check
matrix initial value table of FIG 23.
[0264]
In the A matrix of FIG 24, according to the 1st row of the parity check
matrix initial value table of FIG 23, elements of rows #2 and #6 of a 1 (= 1+5
x(1-1))-
st column are 1.
[0265]
Further, in each of a 2 (= 2+5x(1-1))-nd column to a 5 (= 5+5x(1-1))-th
column, an immediately previous column has been cyclically shifted downward by
Qi
=3.
[0266]
Further, in the A matrix of FIG 24, according to the 2nd row of the parity
check matrix initial value table of FIG 23, elements of rows #2 and #10 of a 6
(-
1+5 x(2-1))-th column are 1.
[0267]
Further, in each of a 7 (= 2+5x(2-1))-th column to a 10 (= 5+5x(2-1))-th
column, an immediately previous column has been cyclically shifted downward by
Qi
=3.
[0268]
FIG. 25 is an illustration of the parity interleave of the B matrix.
[0269]
The parity check matrix generating unit 613 (FIG. 18) generates the A matrix
using the parity check matrix initial value table, and arranges the B matrix
having the
staircase structure at the right of the A matrix. Further, the parity check
matrix
generating unit 613 regards the B matrix as the parity matrix, and performs
the parity
interleave so that the adjacent 1 elements of the B matrix having the
staircase
structure are away from each other in the row direction by the unit size P =
5.
[0270]
FIG. 25 illustrates the A matrix and the B matrix after the B matrix has
undergone the parity interleave.
CA 02917806 2016-01-08
[0271]
FIG. 26 is an illustration of the C matrix generated from the parity check
matrix initial value table of FIG 23.
[0272]
5 In the C
matrix of FIG. 26, according to the 1st row of the parity check
matrix initial value table of FIG. 23, element of a row #18 of a 1 (= 1+5x(1-
1))-st
column of the parity check matrix is 1.
[0273]
Further, each of a 2 (= 2+5x(1-1))-nd column to a 5 (= 5+5x(1-1))-th
10 column is one
in which an immediately previous column has been cyclically shifted
downward by Q2 = 2.
[0274]
Further, in the C matrix of FIG. 26, according to the 2nd to 5th columns of
the parity check matrix initial value table of FIG. 23, elements of a row #19
of a 6 (=
15 1+5 x(2-1))-
th column of the parity check matrix, a row #22 of an 11 (= 1+5 x(3-1))-
th column, a row #19 of a 16 (= 1+5x(4-1))-th column, and a row #15 of a 21 (-
1+5 x (5-1))-th column are 1.
[0275]
Further, in each of the 7 (= 2+5 x(2-1))-th column to the 10 (= 5+5x(2-1))-th
20 column, each
of a 12 (= 2+5 x(3-1))-th column to a 15 (= 5+5 x(3-1))-th column, each
of a 17 (= 2+5 x(4-1))-th column to a 20 (= 5+5x(4-1))-th column, and each of
a 22
(= 2+5x(5-1))-nd column to a 25 (= 5+5 x(5-1))-th column, an immediately
previous
column has been cyclically shifted downward by Q2 = 2.
[0276]
25 The parity
check matrix generating unit 613 (FIG. 18) generates the C matrix
using the parity check matrix initial value table, and arranges the C matrix
below the
A matrix and the B matrix (that has undergone the parity interleave).
[0277]
Further, the parity check matrix generating unit 613 arranges the Z matrix at
30 the right of
the B matrix, arranges the D matrix at the right of the C matrix, and
generates the parity check matrix illustrated in FIG 26.
[0278]
FIG 27 is an illustration of the parity interleave of the D matrix.
CA 02917806 2016-01-08
66
[0279]
After generating the parity check matrix of FIG 26, the parity check matrix
generating unit 613 regards the D matrix as the parity matrix, and performs
the parity
interleave (only for the D matrix) so that the I elements of the odd-numbered
rows
and the next even-numbered rows of the D matrix of the unit matrix are away
from
each other in the row direction by the unit size P (= 5).
[0280]
FIG. 27 illustrates the parity check matrix after the parity interleave of the
D
matrix is performed on the parity check matrix of FIG. 26.
[0281]
(The encoding parity operation unit 615 (FIG. 18) of) The LDPC encoder 115
performs LDPC encoding (generation of the LDPC code), for example, using the
parity check matrix of FIG 27.
[0282]
Here, the LDPC code generated using the parity check matrix of FIG. 27 is
the LDPC code that has undergone the parity interleave, and thus it is
unnecessary to
perform the parity interleave on the LDPC code generated using the parity
check
matrix of FIG 27 in the parity interleaver 23 (FIG 9).
[0283]
FIG. 28 is an illustration of the parity check matrix obtained by performing
the column permutation serving as the parity deinterleave for restoring the
parity
interleave to an original state on the B matrix, the portion of the C matrix
(the portion
of the C matrix arranged below the B matrix), and the D matrix of the parity
check
matrix of FIG 27.
[0284]
The LDPC encoder 115 can perform LDPC encoding (generation of the
LDPC code) using the parity check matrix of FIG. 28.
[0285]
When the LDPC encoding is performed using the parity check matrix of FIG.
28, the LDPC code that does not undergo the parity interleave is obtained
according
to the LDPC encoding. Thus, when the LDPC encoding is performed using the
parity check matrix of FIG. 28, the parity interleaver 23 (FIG. 9) performs
the parity
interleave.
CA 02917806 2016-01-08
67
[0286]
FIG. 29 is an illustration of the transformed parity check matrix obtained by
performing the row permutation on the parity check matrix of FIG 27.
[0287]
As will be described later, the transformed parity check matrix is a matrix
represented by a combination of a PxP unit matrix, a quasi unit matrix
obtained by
setting one or more is of the unit matrix to zero (0), a shift matrix obtained
by
cyclically shifting the unit matrix or the quasi unit matrix, a sum matrix
serving as a
sum of two or more matrices of the unit matrix, the quasi unit matrix, and the
shifted
matrix, and a PxP zero matrix.
[0288]
As the transformed parity check matrix is used for decoding of the LDPC
code, an architecture of performing P check node operations and P variable
node
operations at the same time can be employed for decoding the LDPC code as will
be
described later.
[0289]
<New LDPC code>
[0290]
Incidentally, a terrestrial digital television broadcasting standard called
ATSC
3.0 is currently pending.
[0291]
In this regard, a novel LDPC code which can be used in ATSC 3.0 and other
data transmission (hereinafter referred to as a new LDPC code) will be
described.
[0292]
For example, the LDPC code of the DVB scheme or the LDPC code of the
ETRI scheme having the unit size P of 360, similarly to DVB-T.2 or the like,
and
corresponding to the parity check matrix having the cyclic structure can be
employed
as the new LDPC code.
[0293]
The LDPC encoder 115 (FIGS. 8 and 18) can perform LDPC encoding for
generating a new LDPC code using the parity check matrix obtained from the
parity
check matrix initial value table of the new LDPC code in which the code length
N is
16 kbits or 64 kbits, and the encoding rate r is any of 5/15, 6,15, 7/15,
8/15, 9/15,
CA 02917806 2016-01-08
68
10/15, 11/15,12/15, and 13/15.
[0294]
In this case, the storage unit 602 of the LDPC encoder 115 (FIG. 8) stores the
parity check matrix initial value of the new LDPC code.
[0295]
FIG. 30 is an illustration of an example of a parity check matrix initial
value
table of the DVB scheme for a parity check matrix of a new LDPC code in which
the
code length N is 16 kbits, and the encoding rate r is 8/15 (hereinafter, also
referred to
as Sony symbol (16k, 8/15)), proposed by the applicant of the present
application.
[0296]
FIG. 31 is an illustration of an example of a parity check matrix initial
value
table of the DVB scheme for a parity check matrix of a new LDPC code in which
the
code length N is 16 kbits, and the encoding rate r is 10/15 (hereinafter, also
referred to
as Sony symbol (16k, 10/15)), proposed by the applicant of the present
application.
[0297]
FIG. 32 is an illustration of an example of a parity check matrix initial
value
table of the DVB scheme for a parity check matrix of a new LDPC code in which
the
code length N is 16 kbits, and the encoding rate r is 12/15 (hereinafter, also
referred to
as Sony symbol (16k, 12/15)), proposed by the applicant of the present
application.
[0298]
FIGS. 33, 34, and 35 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 7/15
(hereinafter,
also referred to as Sony symbol (64k, 7/15)), proposed by the applicant of the
present
application.
[0299]
FIG. 34 is an illustration subsequent to FIG 33, and FIG 35 is an illustration
subsequent to FIG 34.
[0300]
FIGS. 36, 37, and 38 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 9/15
(hereinafter,
also referred to as Sony symbol (64k, 9/15)), proposed by the applicant of the
present
CA 02917806 2016-01-08
69
application.
[0301]
FIG. 37 is an illustration subsequent to FIG. 36, and FIG 38 is an
illustration
subsequent to FIG. 37.
[0302]
FIGS. 39, 40, 41, and 42 are illustrations of an example of a parity check
matrix initial value table of the DVB scheme for a parity check matrix of a
new LDPC
code in which the code length N is 64 kbits, and the encoding rate r is 11/15
(hereinafter, also referred to as Sony symbol (64k, 11/15)), proposed by the
applicant
of the present application.
[0303]
FIG. 40 is an illustration subsequent to FIG 39, and FIG 41 is an illustration
subsequent to FIG. 40.
[0304]
FIGS. 43, 44, 45, and 46 are illustrations of an example of a parity check
matrix initial value table of the DVB scheme for a parity check matrix of a
new LDPC
code in which the code length N is 64 kbits, and the encoding rate r is 13/15
(hereinafter, also referred to as Sony symbol (64k, 13/15)), proposed by the
applicant
of the present application.
[0305]
FIG. 44 is an illustration subsequent to FIG 43, and FIG 45 is an illustration
subsequent to FIG. 44.
[0306]
FIGS. 47 and 48 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 6/15
(hereinafter,
also referred to as Samsung symbol (64k, 6/15)), proposed by Samsung.
[0307]
FIG. 48 is an illustration subsequent to FIG. 47.
[0308]
FIGS. 49, 50, and 51 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 8/15
(hereinafter,
CA 02917806 2016-01-08
also referred to as Samsung symbol (64k, 8/15)), proposed by Samsung.
[0309]
FIG. 50 is an illustration subsequent to FIG 49, and FIG. 51 is an
illustration
subsequent to FIG. 50.
5 [0310]
FIGS. 52, 53, and 54 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 12/15
(hereinafter,
also referred to as Samsung symbol (64k, 12/15)), proposed by Samsung.
10 [0311]
FIG. 53 is an illustration subsequent to FIG 52, and FIG 54 is an illustration
subsequent to FIG. 53.
[0312]
FIG. 55 is an illustration of an example of a parity check matrix initial
value
15 table of the DVB scheme for a parity check matrix of a new LDPC code in
which the
code length N is 16 kbits, and the encoding rate r is 6/15 (hereinafter, also
referred to
as LGE symbol (16k, 6/15)), proposed by LG Electronics Inc..
[0313]
FIG. 56 is an illustration of an example of a parity check matrix initial
value
20 table of the DVB scheme for a parity check matrix of a new LDPC code in
which the
code length N is 16 kbits, and the encoding rate r is 7/15 (hereinafter, also
referred to
as LGE symbol (16k, 7/15)), proposed by LG Electronics Inc..
[0314]
FIG. 57 is an illustration of an example of a parity check matrix initial
value
25 table of the DVB scheme for a parity check matrix of a new LDPC code in
which the
code length N is 16 kbits, and the encoding rate r is 9/15 (hereinafter, also
referred to
as LGE symbol (16k, 9/15)), proposed by LG Electronics Inc..
[0315]
FIG. 58 is an illustration of an example of a parity check matrix initial
value
30 table of the DVB scheme for a parity check matrix of a new LDPC code in
which the
code length N is 16 kbits, and the encoding rate r is 11/15 (hereinafter, also
referred to
as LGE symbol (16k, 11/15)), proposed by LG Electronics Inc..
[0316]
CA 02917806 2016-01-08
71
FIG. 59 is an illustration of an example of a parity check matrix initial
value
table of the DVB scheme for a parity check matrix of a new LDPC code in which
the
code length N is 16 kbits, and the encoding rate r is 13/15 (hereinafter, also
referred to
as LGE symbol (16k, 13/15)), proposed by LG Electronics Inc..
[0317]
FIGS. 60, 61, and 62 are an illustrations of an example of a parity check
matrix initial value table of the DVB scheme for a parity check matrix of a
new LDPC
code in which the code length N is 64 kbits, and the encoding rate r is 10/15
(hereinafter, also referred to as LGE symbol (64k, 10/15)), proposed by LG
Electronics Inc..
[0318]
FIG. 61 is an illustration subsequent to FIG 60, and FIG 62 is an illustration
subsequent to FIG. 61.
[0319]
FIGS. 63, 64, and 65 are illustrations of an example of a parity check matrix
initial value table of the DVB scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 9/15
(hereinafter,
also referred to as NERC symbol (64k, 9/15)), proposed by NERC.
[0320]
FIG. 64 is an illustration subsequent to FIG. 63, and FIG 65 is an
illustration
subsequent to FIG. 64.
[0321]
FIG. 66 is an illustration of an example of a parity check matrix initial
value
table of the ETRI scheme for a parity check matrix of a new LDPC code in which
the
code length N is 16 kbits, and the encoding rate r is 5/15 (hereinafter, also
referred to
as ETRI symbol (16k, 5/15)), proposed by CRC/ETRI.
[0322]
FIGS. 67 and 68 are illustrations of an example of a parity check matrix
initial value table of the ETRI scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 5/15
(hereinafter,
also referred to as ETRI symbol (64k, 5/15)), proposed by CRC/ETRI.
[0323]
FIG 68 is an illustration subsequent to FIG. 67.
CA 02917806 2016-01-08
72
[0324]
FIGS. 69 and 70 are illustrations of an example of a parity check matrix
initial value table of the ETRI scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 6/15
(hereinafter,
also referred to as ETRI symbol (64k, 6/15)), proposed by CRC/ETRI.
[0325]
FIG. 70 is an illustration subsequent to FIG 69.
[0326]
FIGS. 71 and 72 are illustrations of an example of a parity check matrix
initial value table of the ETRI scheme for a parity check matrix of a new LDPC
code
in which the code length N is 64 kbits, and the encoding rate r is 7/15
(hereinafter,
also referred to as ETRI symbol (64k, 7/15)), proposed by CRC/ETRI.
[0327]
FIG. 72 is an illustration subsequent to FIG 71.
[0328]
Among the new LDPC codes, the Sony symbol is an LDPC code having
particularly excellent performance.
[0329]
Here, the LDPC code of good performance is an LDPC code obtained from
an appropriate parity check matrix H.
[0330]
The appropriate parity check matrix H is, for example, a parity check matrix
that satisfies a predetermined condition to make BER (and FER) smaller when an
LDPC code obtained from the parity check matrix H is transmitted at low Es/No
or
Eb/No (signal-to-noise power ratio per bit).
[0331]
For example, the appropriate parity check matrix H can be found by
performing simulation to measure BER when LDPC codes obtained from various
parity check matrices that satisfy a predetermined condition are transmitted
at low
Es/No.
[0332]
As a predetermined condition to be satisfied by the appropriate parity check
matrix 1-1, for example, an analysis result obtained by a code performance
analysis
CA 02917806 2016-01-08
73
method called density evolution (Density Evolution) is excellent, and a loop
of
elements of 1 does not exist, which is called cycle 4, and so on.
[0333]
Here, in the information matrix HA, it is known that the decoding
performance of LDPC code is deteriorated when elements of 1 are dense like
cycle 4,
and therefore it is requested that cycle 4 does not exist, as a predetermined
condition
to be satisfied by the appropriate parity check matrix H.
[0334]
Here, the predetermined condition to be satisfied by the appropriate parity
check matrix H can be arbitrarily determined from the viewpoint of the
improvement
in the decoding performance of LDPC code and the facilitation (simplification)
of
decoding processing of LDPC code, and so on.
[0335]
FIG 73 and FIG 74 are diagrams to describe the density evolution that can
obtain an analytical result as a predetermined condition to be satisfied by
the
appropriate parity check matrix H.
[0336]
The density evolution is a code analysis method that calculates the
expectation value of the error probability of the entire LDPC code (ensemble)
with a
code length N of 00 characterized by a degree sequence described later.
[0337]
For example, when the dispersion value of noise is gradually increased from
0 on the AWGN channel, the expectation value of the error probability of a
certain
ensemble is 0 first, but, when the dispersion value of noise becomes equal to
or
greater than a certain threshold, it is not 0.
[0338]
According to the density evolution, by comparison of the threshold of the
dispersion value of noise (which may also be called a performance threshold)
in
which the expectation value of the error probability is not 0, it is possible
to decide
the quality of ensemble performance (appropriateness of the parity check
matrix).
[0339]
Here, as for a specific LDPC code, when an ensemble to which the LDPC
code belongs is decided and density evolution is performed for the ensemble,
rough
CA 02917806 2016-01-08
74
performance of the LDPC code can be expected.
[0340]
Therefore, if an ensemble of good performance is found, an LDPC code of
good performance can be found from LDPC codes belonging to the ensemble.
[0341]
Here, the above-mentioned degree sequence shows at what percentage a
variable node or check node having the weight of each value exists with
respect to the
code length N of an LDPC code.
[0342]
For example, a regular (3,6) LDPC code with an encoding rate of 1/2 belongs
to an ensemble characterized by a degree sequence in which the weight (column
weight) of all variable nodes is 3 and the weight (row weight) of all check
nodes is 6.
[0343]
FIG. 73 illustrates a Tanner graph of such an ensemble.
[0344]
In the Tanner graph of FIG. 73, there are variable nodes shown by circles
(sign 0) in the diagram only by N pieces equal to the code length N, and there
are
check nodes shown by quadrangles (sign o) only by N/2 pieces equal to a
multiplication value multiplying encoding rate 1/2 by the code length N.
[0345]
Three branches (edge) equal to the column weight are connected with each
variable node, and therefore there are totally 3N branches connected with N
variable
nodes.
[0346]
Moreover, six branches (edge) equal to the row weight are connected with
each check node, and therefore there are totally 3N branches connected with
N/2
check nodes.
[0347]
In addition, there is one interleaver in the Tanner graph in FIG. 73.
[0348]
The interleaver randomly rearranges 3N branches connected with N variable
nodes and connects each rearranged branch with any of 3N branches connected
with
N/2 check nodes.
CA 02917806 2016-01-08
[0349]
There are (3N)! (= (3N)x (3N-1)x xl) rearrangement patterns to rearrange
3N branches connected with N variable nodes in the interleaver. Therefore, an
ensemble characterized by the degree sequence in which the weight of all
variable
5 nodes is 3 and the weight of all check nodes is 6, becomes aggregation of
(3N)!
LDPC codes.
[0350]
In simulation to find an LDPC code of good performance (appropriate parity
check matrix), an ensemble of a multi-edge type is used in the density
evolution.
10 [0351]
In the multi edge type, an interleaver through which the branches connected
with the variable nodes and the branches connected with the check nodes pass,
is
divided into plural (multi edge), and, by this means, the ensemble is
characterized
more strictly.
15 [0352]
FIG. 74 illustrates an example of a Tanner graph of an ensemble of the multi-
edge type.
[0353]
In the Tanner graph of FIG. 74, there are two interleavers of the first
20 interleaver and the second interleaver.
[0354]
Moreover, in the Tanner graph chart of FIG. 74, vi variable nodes with one
branch connected with the first interleaver and no branch connected with the
second
interleaver exist, v2 variable nodes with one branch connected with the first
25 interleaver and two branches connected with the second interleaver
exist, and v3
variable nodes with no branch connected with the first interleaver and two
branches
connected with the second interleaver exist, respectively.
[0355]
Furthermore, in the Tanner graph chart of FIG. 74, el check nodes with two
30 branches connected with the first interleaver and no branch connected
with the second
interleaver exist, c2 check nodes with two branches connected with the first
interleaver and two branches connected with the second interleaver exist, and
c3
check nodes with no branch connected with the first interleaver and three
branches
CA 02917806 2016-01-08
76
connected with the second interleaver exist, respectively.
[0356]
Here, for example, the density evolution and the mounting thereof are
described in "On the Design of Low-Density Parity-Check Codes within 0.0045 dB
of
the Shannon Limit", S.Y.Chung, G.D.Forney, T.J.Richardson, R.Urbanke, IEEE
Communications Leggers, VOL.5, NO.2, Feb 2001.
[0357]
In simulation to find (a parity check matrix initial value table of) a Sony
code,
by the density evaluation of the multi-edge type, an ensemble in which a
performance
threshold that is Eb/No (signal-to-noise power ratio per bit) with
deteriorating
(decreasing) BER is equal to or less than a predetermined value is found, and
an
LDPC code that decreases BER in a case using one or more orthogonal
modulations
such as QPSK is selected from LDPC codes belonging to the ensemble as an LDPC
code of good performance.
[0358]
The parity check matrix initial value table of the Sony code is found from the
above-mentioned simulation.
[0359]
Thus, according to the Sony symbol obtained from the parity check matrix
initial value table, it is possible to secure the excellent communication
quality in the
data transmission.
[0360]
FIG 75 is an illustration of parity check matrices H (hereinafter, also
referred
to as "parity check matrices H of Sony symbols (16k, 8/15), (16k, 10/15), and
(16k,
12/15)") obtained from the parity check matrix initial value table of the Sony
symbols
(16k, 8/15), (16k, 10/15), and (16k, 12/15).
[0361]
Every minimum cycle length of the parity check matrices H of the Sony
symbols (16k, 8/15), (16k, 10/15), and (16k, 12/15) has a value exceeding
cycle 4,
and thus there is no cycle 4 (a loop of I elements in which a loop length is
4). Here,
the minimum cycle length (girth) is a minimum value of a length (a loop
length) of a
loop configured with 1 elements in the parity check matrix H.
[0362]
CA 02917806 2016-01-08
77
A performance threshold value of the Sony symbol (16k, 8/15) is set to
0.805765, a performance threshold value of the Sony symbol (16k, 10/15) is set
to
2.471011, and a performance threshold value of the Sony symbol (16k, 12/15) is
set to
4.269922.
[0363]
The column weight is set to X1 for KX1 columns of the parity check
matrices H of the Sony symbols (16k, 8/15), (16k, 10/15), and (16k, 12/15)
starting
from the 1st column, the column weight is set to X2 for KX2 columns subsequent
thereto, the column weight is set to Y1 for KY1 columns subsequent thereto,
the
column weight is set to Y2 for KY2 columns subsequent thereto, the column
weight is
set to 2 for M-1 columns subsequent thereto, and the column weight is set to 1
for the
last column.
[0364]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
16200 bits) of the Sony symbols (16k, 8/15), (16k, 10/15), and (16k, 12/15).
[0365]
In the parity check matrices H of the Sony symbols (16k, 8/15), (16k, 10/15),
and (16k, 12/15), the numbers KX1, KX2, KY1, KY2, and M of columns and column
weights XI, X2, Yl, and Y2 are set as illustrated in FIG. 75.
[0366]
In the parity check matrices H of the Sony symbols (16k, 8/15), (16k, 10/15),
and (16k, 12/15), similarly to the parity check matrix described above with
reference
to FIGS. 12 and 13, columns closer to the head side (the left side) have
higher column
weights, and thus a code bit at the head of the Sony symbol tends to be robust
to error
(have error tolerance).
[0367]
According to the simulation conducted by the applicant of the present
application, an excellent BERNER is obtained for the Sony symbols (16k, 8/15),
(16k,
10/15), and (16k, 12/15), and thus it is possible to secure the excellent
communication
quality in the data transmission using the Sony symbols (16k, 8/15), (16k,
10/15), and
(16k, 12/15).
[0368]
FIG. 76 is an illustration of parity check matrices H of the Sony symbols
CA 02917806 2016-01-08
78
(64k, 7/15), (64k, 9/15), (64k, 11/15), and (64k, 13/15).
[0369]
Every minimum cycle length of the parity check matrices H of the Sony
symbols (64k, 7/15), (64k, 9/15), (64k, 11/15), and (64k, 13/15) has a value
exceeding
a cycle 4, and thus there is no cycle 4.
[0370]
A performance threshold value of the Sony symbol (64k, 7/15) is set to
-0.093751, a performance threshold value of the Sony symbol (64k, 9/15) is set
to
1.658523, a performance threshold value of the Sony symbol (64k, 11/15) is set
to
3.351930, and a performance threshold value of the Sony symbol (64k, 13/15) is
set
to 5.301749.
[0371]
The column weight is set to X1 for KX1 columns of the parity check
matrices H of the Sony symbols (64k, 7/15), (64k, 9/15), (64k, 11/15), and
(64k,
13/15) starting from the 1st column, the column weight is set to X2 for KX2
columns
subsequent thereto, the column weight is set to Y1 for KY1 columns subsequent
thereto, the column weight is set to Y2 for KY2 columns subsequent thereto,
the
column weight is set to 2 for M-1 columns subsequent thereto, and the column
weight is set to 1 for the last column.
[0372]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
64800 bits) of the Sony symbols (64k, 7/15), (64k, 9/15), (64k, 11/15), and
(64k,
13/15).
[0373]
In the parity check matrices H of the Sony symbols (64k, 7/15), (64k, 9/15),
(64k, 11/15), and (64k, 13/15), the numbers KX1, KX2, KY1, KY2, and M of
columns and column weights Xl, X2, Yl, and Y2 are set as illustrated in FIG.
76.
[0374]
In the parity check matrices H of the Sony symbols (64k, 7/15), (64k, 9/15),
(64k, 11/15), and (64k, 13/15), similarly to the parity check matrix described
above
with reference to FIGS. 12 and 13, columns closer to the head side (the left
side) have
higher column weights, and thus a code bit at the head of the Sony symbol
tends to be
robust to error (have error tolerance).
CA 02917806 2016-01-08
79
[0375]
According to the simulation conducted by the applicant of the present
application, an excellent BER/FER is obtained for the Sony symbols (64k,
7/15), (64k,
9/15), (64k, 11/15), and (64k, 13/15), and thus it is possible to secure the
excellent
communication quality in the data transmission using the Sony symbols (64k,
7/15),
(64k, 9/15), (64k, 11/15), and (64k, 13/15).
[0376]
FIG. 77 is an illustration of parity check matrices H of Samsung symbols
(64k, 6/15), (64k, 8/15), and (64k, 12/15).
[0377]
The column weight is set to X1 for KX1 columns of the parity check
matrices H of the Samsung symbols (64k, 6/15), (64k, 8/15), and (64k, 12/15)
starting
from the 1st column, the column weight is set to X2 for KX2 columns subsequent
thereto, the column weight is set to Y1 for KY1 columns subsequent thereto,
the
column weight is set to Y2 for KY2 columns subsequent thereto, the column
weight is
set to 2 for M-1 columns subsequent thereto, and the column weight is set to 1
for the
last column.
[0378]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
64800 bits) of the Samsung symbols (64k, 6/15), (64k, 8/15), and (64k, 12/15).
[0379]
In the parity check matrices H of the Samsung symbols (64k, 6/15), (64k,
8/15), and (64k, 12/15), the numbers KX1, KX2, KY1, KY2, and M of columns and
column weights Xl, X2, Yl, and Y2 are set as illustrated in FIG. 77.
[0380]
FIG 78 is an illustration of parity check matrices H of the LGE symbols (16k,
6/15), (16k, 7/15), (16k, 9/15), (16k, 11/15), and (16k, 13/15).
[0381]
The column weight is set to X1 for KX1 columns of the parity check
matrices H of the LGE symbols (16k, 6/15), (16k, 7/15), (16k, 9/15), (16k,
11/15),
and (16k, 13/15) starting from the 1st column, the column weight is set to X2
for KX2
columns subsequent thereto, the column weight is set to Y1 for KY1 columns
subsequent thereto, the column weight is set to Y2 for KY2 columns subsequent
CA 02917806 2016-01-08
thereto, the column weight is set to 2 for M-1 columns subsequent thereto, and
the
column weight is set to 1 for the last column.
[0382]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
5 16200 bits) of the LGE symbols (16k, 6/15), (16k, 7/15), (16k, 9/15),
(16k, 11/15),
and (16k, 13/15).
[0383]
In the parity check matrices H of the LGE symbols (16k, 6/15), (16k, 7/15),
(16k, 9/15), (16k, 11/15), and (16k, 13/15), the numbers KX1, KX2, KY1, KY2,
and
10 M of columns and column weights Xl, X2, Yl, and Y2 are set as
illustrated in FIG 78.
[0384]
FIG 79 is an illustration of parity check matrices H of the LGE symbols (64k,
10/15).
[0385]
15 The column weight is set to X1 for KX1 columns of the parity check
matrices H of the LGE symbols (64k, 10/15) starting from the 1st column, the
column
weight is set to X2 for KX2 columns subsequent thereto, the column weight is
set to
Y1 for KY1 columns subsequent thereto, the column weight is set to Y2 for KY2
columns subsequent thereto, the column weight is set to 2 for M-1 columns
20 subsequent thereto, and the column weight is set to 1 for the last
column.
[0386]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
64800 bits) of the LGE symbols (64k, 10/15).
[0387]
25 In the parity check matrices H of the LGE symbols (64k, 10/15), the
numbers
KX1, KX2, KY1, KY2, and M of columns and column weights X 1, X2, Y 1, and Y2
are set as illustrated in FIG 79.
[0388]
FIG 80 is an illustration of parity check matrices H of the NERC symbols
30 (64k, 9/15).
[0389]
The column weight is set to X1 for KX1 columns of the parity check
matrices H of the NERC symbols (64k, 9/15) starting from the 1st column, the
CA 02917806 2016-01-08
81
column weight is set to X2 for KX2 columns subsequent thereto, the column
weight is
set to Y1 for KY1 columns subsequent thereto, the column weight is set to Y2
for
KY2 columns subsequent thereto, the column weight is set to 2 for M-1 columns
subsequent thereto, and the column weight is set to 1 for the last column.
[0390]
Here, KX1+KX2+KY1+KY2+M-1+1 is equal to the code length N (=
64800 bits) of the NERC symbols (64k, 9/15).
[0391]
In the parity check matrices H of the NERC symbols (64k, 9/15), the
numbers KX1, KX2, KY1, KY2, and M of columns and column weights X 1 , X2, Y 1
,
and Y2 are set as illustrated in FIG 80.
[0392]
FIG. 81 is an illustration of a parity check matrix H of an ETRI symbol (16k,
5/15).
[0393]
For the parity check matrix H of the ETRI symbol (16k, 5/15), the parameter
g = MI is 720.
[0394]
Further, for the ETRI symbol (16k, 5/15), since the code length N is 16200
and the encoding rate r is 5/15, the information length K = Nxr is 16200x5/15
= 5400
and the parity length M = N¨K is 16200-5400 = 10800.
[0395]
Further, the parameter M2 = M¨M1 = N¨K¨g is 10800-720 = 10080.
[0396]
Thus, the parameter Qi = Mi/P is 720/360 = 2, and the parameter Q2 = M2/P
is 10080/360 = 28.
[0397]
FIG 82 is an illustration of parity check matrices H of ETRI symbols of (64k,
5/15), (64k, 6/15), and (64k, 7/15).
[0398]
For the parity check matrices H of the ETRI symbols of (64k, 5/15), (64k,
6/15), and (64k, 7/15), the parameters g = Ml, M2, Q1, and Q2 are set as
illustrated in
FIG 82.
CA 02917806 2016-01-08
82
[0399]
<Constellation>
[0400]
FIGS. 83 to 104 are illustrations of examples of constellation types employed
in the transmission system of FIG. 7.
[0401]
In the transmission system of FIG 7, for example, a constellation used in
MODCOD can be set to MODCOD serving as a combination of a modulation scheme
and an LDPC code.
[0402]
In other words, in the transmission system of FIG 7, for example, the LDPC
codes can be classified into 9 types of LDPC codes in which the encoding rate
r is
5/15, 6/15, 7/15, 8/15, 9/15, 10/15, 11/15, 12,15, and 13/15 according to the
encoding
rate r (regardless of the code length N), and a combination of the 9 types of
LDPC
codes (each of the LDPC codes in which the encoding rate r is 5/15, 6/15,
7/15, 8/15,
9/15, 10/15, 11/15, 12,15, and 13/15) and each modulation scheme can be
employed
as MODCOD.
[0403]
Further, in the transmission system of FIG 7, one or more of constellations
can be set to MODCOD of 1 using the modulation scheme of MODCOD.
[0404]
The constellations include uniform constellations (UCs) in which an
arrangement of signal points is uniform, and non uniform constellations (NUCs)
in
which an arrangement of signal points is not uniform.
[0405]
Examples of NUCs include a constellation called a 1-dimensional M2-QAM
non-uniform constellation (1D NUC) and a constellation called a 2-dimensional
QQAM non-uniform constellation (2D NUC).
[0406]
Commonly, the 1D NUC is better in the BER than the UC, and the 2D NUC
is better in the BER than the 1D NUC.
[0407]
A constellation in which the modulation scheme is QPSK is the UC. For
CA 02917806 2016-01-08
83
example, the 2D NUC can be employed as the constellation in which the
modulation
scheme is 16QAM, 64QAM, 256QAM, or the like, and for example, the 1D NUC can
be employed as the constellation in which the modulation scheme is 1024QAM,
4096QAM, or the like.
[0408]
Hereinafter, a constellation of an NUC used in MODCOD in which the
modulation scheme is a modulation scheme in which an m-bit symbol is mapped to
any of 2' signal points, and an encoding rate of an LDPC is r is also referred
to as
NUC 2" r.
_ _
[0409]
For example, "NUC_16_6/15" indicates a constellation of an NUC used in
MODCOD in which the modulation scheme is 16QAM (or the modulation scheme in
which a symbol is mapped to any of 16 signal points), and the encoding rate r
of the
LDPC code is 6/15.
[0410]
In the transmission system of FIG 7, when the modulation scheme is QPSK,
the same constellation is used for each encoding rate r of the LDPC code.
[0411]
Further, in the transmission system of FIG. 7, when the modulation scheme is
16QAM, 64QAM, or 256QAM, a different constellation of a 2D NUC is used
according to each encoding rate r of the LDPC code.
[0412]
Further, in the transmission system of FIG 7, when the modulation scheme is
1024QAM or 4096QAM, a different constellation of a 1D NUC is used according to
each encoding rate r of the LDPC code.
[0413]
Thus, as described above, when the LDPC codes are classified into the 9
types of LDPC codes of r = 5/15, 6/15, 7/15, 8/15, 9/15, 10/15, 11/15, 12,15,
13/15
according to the encoding rate r, one type of constellation is prepared for
QPSK, 9
types of constellations of a 2D NUC are prepared for each of 16QAM, 64QAM, and
256QAM, and 9 types of constellations of a 1D NUC are prepared for each of
1024QAM and 4096QAM.
[0414]
CA 02917806 2016-01-08
84
FIG 83 is an illustration of an example of a constellation of a 2D NUC for
each of 9 types of encoding rates r (= 5/15, 6/15, 7/15, 8/15, 9/15, 10/15,
11/15, 12,15,
and 13/15) of LDPC codes when the modulation scheme is 16QAM.
[0415]
FIG. 84 is an illustration of an example of a constellation of a 2D NUC for
each of 9 types of encoding rates r (= 5/15, 6/15, 7/15, 8/15, 9/15, 10/15,
11/15, 12,15,
and 13/15) of LDPC codes when the modulation scheme is 64QAM.
[0416]
FIG. 85 is an illustration of an example of a constellation of a 2D NUC for
each of 9 types of encoding rates r (= 5/15, 6/15, 7/15, 8/15, 9/15, 10/15,
11/15, 12,15,
and 13/15) of LDPC codes when the modulation scheme is 256QAM.
[0417]
FIG. 86 is an illustration of an example of a constellation of a 1D NUC for
each of 9 types of encoding rates r (= 5/15, 6/15, 7/15, 8/15, 9/15, 10/15,
11/15, 12,15,
and 13/15) of LDPC codes when the modulation scheme is 1024QAM.
[0418]
FIG. 87 and FIG 88 are illustrations of examples of a constellation of a ID
NUC for each of 9 types of encoding rates r (= 5/15, 6/15, 7/15, 8/15, 9/15,
10/15,
11/15, 12,15, and 13/15) of LDPC codes when the modulation scheme is 4096QAM.
[0419]
In FIGS. 83 to 88, a horizontal axis and a vertical axis are an I axis and a Q
axis, and Re{xi} and Im{xi} indicate a real part and an imaginary part of a
signal
point xi serving as coordinates of the signal point xi.
[0420]
In FIGS. 83 to 88, a numerical value written after "for CR" indicates the
encoding rate r of the LDPC code.
[0421]
FIG. 89 is an illustration of an example of coordinates of a signal point of a
UC that is used in common to 9 types of encoding rates r (= 5/15, 6/15, 7/15,
8/15,
9/15, 10/15, 11/15, 12,15, and 13/15) of LDPC codes when the modulation scheme
is
QPSK.
[0422]
In FIG 89, "Input cell word y" indicates a 2-bit symbol that is mapped to a
CA 02917806 2016-01-08
UC of QPSK, and "Constellation point zq" indicates coordinates a signal point
zq.
An index q of the signal point zq indicates a discrete time (a time interval
between a
certain symbol and a next symbol) of a symbol.
[0423]
5 In FIG. 89,
coordinates of the signal point zq are indicated in the form of a
complex number, in which i indicates an imaginary unit (A-1)).
[0424]
FIG. 90 is an illustration of an example of coordinates of the signal point of
the 2D NUC of FIG. 83 used for the 9 types of encoding rates r (= 5/15, 6/15,
7/15,
10 8/15, 9/15,
10/15, 11/15, 12,15, and 13/15) of the LDPC codes when the modulation
scheme is 16QAM.
[0425]
FIG 91 is an illustration of an example of coordinates of the signal point of
the 2D NUC of FIG 84 used for the 9 types of encoding rates r (= 5/15, 6/15,
7/15,
15 8/15, 9/15,
10/15, 11/15, 12,15, and 13/15) of the LDPC codes when the modulation
scheme is 64QAM.
[0426]
FIGS. 92 and 93 are illustrations of an example of coordinates of the signal
point of the 2D NUC of FIG. 85 used for the 9 types of encoding rates r (=
5/15, 6/15,
20 7/15, 8/15,
9/15, 10/15, 11/15, 12,15, and 13/15) of the LDPC codes when the
modulation scheme is 256QAM.
[0427]
In FIGS. 90 to 93, NUC_2m_r indicates coordinates of a signal point of a 2D
NUC used when the modulation scheme is 2mQAM, and the encoding rate of the
25 LDPC code is r.
[0428]
In FIGS. 90 to 93, similarly to FIG 89, coordinates of the signal point zq are
indicated in the form of a complex number, in which i indicates an imaginary
unit.
[0429]
30 In FIGS. 90
to 93, w#k indicates coordinates of a signal point of a first
quadrant of the constellation.
[0430]
In the 2D NUC, a signal point of a second quadrant of the constellation is
CA 02917806 2016-01-08
86
arranged at a position to which the signal point of the first quadrant has
moved
symmetrically to the Q axis, and a signal point of a third quadrant of the
constellation
is arranged at a position to which the signal point of the first quadrant has
moved
symmetrically to an origin. Further, a signal point of a fourth quadrant of
the
constellation is arranged at a position to which the signal point of the first
quadrant
has moved symmetrically to the I axis.
[0431]
Here, when the modulation scheme is 2mQAM, m bits are used as one
symbol, and one symbol is mapped to a signal point corresponding to the
symbol.
[0432]
The m-bit symbol is expressed by, for example, an integer value of 0 to 2m-1,
but if b = 2m/4 is assumed, symbols y(0), y(1), ..., and y(2m-1) expressed by
the
integer value of 0 to 2m-1 can be classified into four symbols y(0) to y(b-1),
y(b) to
y(2b-1), y(2b) to y(3b-1), and y(3b) to y(4b-1).
[0433]
In FIGS. 90 to 93, a suffix k of w#k has an integer value within a range of 0
to b-1, and w#k indicates coordinates of a signal point corresponding to the
symbol
y(k) within the range of the symbols y(0) to y(b-1).
[0434]
Further, coordinates of a signal point corresponding to the symbol y(k+b)
within the range of the symbols y(b) to y(2b-1) are indicated by ¨conj(w#k),
and
coordinates of a signal point corresponding to the symbol y(k+2b) within the
range of
the symbols y(2b) to y(3b-1) are indicated by conj(w#k). Further, coordinates
of a
signal point corresponding to the symbol y(k+3b) within the range of the
symbols
y(3b) to y(4b-1) are indicated by ¨w#k.
[0435]
Here, conj(w#k) indicates a complex conjugate of w#k.
[0436]
For example, when the modulation scheme is 16QAM, the symbols y(0),
y(1), ..., and y(15) of m = 4 bits are classified into four symbols y(0) to
y(3), y(4) to
y(7), y(8) to y(11), and y(12) to y(15) if b = 24/4 = 4.
[0437]
Among the symbols y(0) to y(15), for example, the symbol y(12) is the
CA 02917806 2016-01-08
87
symbol y(k+3b) = y(0+3 x4) within the symbols y(3b) to y(4b-1), and k is zero
(0),
and thus the coordinates of the signal point corresponding to the symbol y(12)
are
¨w#k = ¨w0.
[0438]
Now, for example, if the encoding rate r of the LDPC code is 9/15, according
to FIG 90, when the modulation scheme is 16QAM, and the encoding rate r is
9/15,
w0 of (NUC_16_9/15) is 0.4967+1.1932i, and thus the coordinates ¨w0 of the
signal
point corresponding to the symbol y(12) are ¨(0.4967+1.1932i).
[0439]
FIG 94 is an illustration of an example of the coordinates of the signal point
of the 1D NUC of FIG. 86 used for the 9 types of encoding rates r (= 5/15,
6/15, 7/15,
8/15, 9/15, 10/15, 11/15, 12,15, and 13/15) of the LDPC codes when the
modulation
scheme is 1024QAM.
[0440]
In FIG. 94, a column of NUC_lk r indicates a value of u#k indicating the
coordinates of the signal point of the 1D NUC used when the modulation scheme
is
1024QAM, and the encoding rate of the LDPC code is r.
[0441]
u#k indicates the real part Re(zq) and the imaginary part Im(zq) of the
complex number serving as the coordinates of the signal point zq of the ID
NUC.
[0442]
FIG. 95 is an illustration of a relation between the symbol y of 1024QAM
and u#k serving as each of the real part Re(zq) and the imaginary part Im(zq)
of the
complex number indicating the coordinates of the signal point zq of the ID NUC
corresponding to the symbol y.
[0443]
Now, the 10-bit symbol y of 1024QAM is assumed to be indicated by yo,q,
yi,q, y2,q, y3,q, ya,q, y5,q, y6,q, y7,q, y8,q, and y9,q from the first bit
(the most significant
bit).
[0444]
A of FIG 95 illustrates a correspondence relation between 5 odd-numbered
bits yo,q, y2,q, y4,q, 316,q, Y8,q of the symbol y and u#k indicating the real
part Re(zq) (of
the coordinates) of the signal point zq corresponding to the symbol y.
CA 02917806 2016-01-08
88
[0445]
B of FIG 95 is a correspondence relation between 5 even-numbered bits yi,q,
y3,q, y5,q, y7,q, and y9,q of the symbol y and u#k indicating the imaginary
part Im(zq) (of
the coordinates) of the signal point zq corresponding to the symbol y.
[0446]
For example, when the 10-bit symbol y = (yo,q, yi,q, y2,q, y3,q, y4,q, y5,q,
y6,q,
y7,q, y8,q, y9,q) of 1024QAM is (0, 0, 1, 0, 0, 1, 1, 1, 0, 0), the 5 odd-
numbered bits (yo,q,
y2,q, ya,q, y6,q, y8,q) are (0, 1, 0, 1, 0), and the 5 even-numbered bits
(yi,q, Y3,q, y5,q, y7,q,
and y9,q) are (0, 0, 1, 1, 0).
[0447]
In A of FIG 95, the 5 odd-numbered bits (0, 1, 0, 1, 0) are associated with
u3,
and thus the real part Re(zq) of the signal point zq corresponding to the
symbol y = (0,
0, 1, 0, 0, 1, 1, 1, 0, 0) is u3.
[0448]
In B of FIG 95, the 5 even-numbered bits (0, 0, 1, 1, 0) are associated with
u11, and thus the imaginary part Im(zq) of the signal point zq corresponding
to the
symbol y = (0, 0, 1, 0, 0, 1, 1, 1, 0, 0) is u 1 1.
[0449]
Meanwhile, for example, if the encoding rate r of the LDPC code is 7/15,
according to FIG 94, for the 1D NUC (NUC_lk_7/15) used when the modulation
scheme is 1024QAM and the encoding rate r of the LDPC code is 7/15, u3 is
1.1963,
and u 11 is 6.9391.
[0450]
Thus, the real part Re(zq) of the signal point zq corresponding to the symbol
y
= (0, 0, 1, 0, 0, 1, 1, 1, 0, 0) is u3 (= 1.1963), and Im(zq) is ul 1 (=
6.9391). As a
result, the coordinates of the signal point zq corresponding to the symbol y =
(0, 0, 1,
0, 0, 1, 1, 1, 0, 0) are indicated by 1.1963+6.9391i.
[0451]
FIG. 96 is an illustration of an example of the coordinates of the signal
point
of the 1D NUC of FIGS. 87 and 88 used for the 9 types of encoding rates r (=
5/15,
6/15, 7/15, 8/15, 9/15, 10/15, 11/15, 12,15, and 13/15) of the LDPC codes when
the
modulation scheme is 4096QAM.
[0452]
CA 02917806 2016-01-08
89
In FIG. 96, each column indicates a value of u#k indicating the coordinates
of the signal point of the 1D NUC used when the modulation scheme is 4096QAM
and the encoding rates r of the LDPC codes are 5/15, 6/15, 7/15, 8/15, 9/15,
10/15,
11/15, 12,15, and 13/15.
[0453]
u#k indicates the real part Re(zq) and the imaginary part Im(zq) of the
complex number serving as the coordinates of the signal point zq of the 1D
NUC.
[0454]
FIG. 97 is an illustration of a relation between the symbol y of 4096QAM
and u#k serving as each of the real part Re(zq) and the imaginary part Im(zq)
of the
complex number indicating the coordinates of the signal point zq of the 1D NUC
corresponding to the symbol y.
[0455]
A method of obtaining the coordinates of the signal point of the 1D NUC of
4096QAM using FIGS. 96 and 97 is the same as the method of obtaining the
coordinates of the signal point of the 1D NUC of 1024QAM using FIGS. 94 and
95,
and thus a description thereof is omitted.
[0456]
FIG. 98 is an illustration of another example of the constellation of the 2D
NUC for each of the 9 types of encoding rates r of the LDPC codes when the
modulation scheme is 16QAM.
[0457]
FIG. 99 is an illustration of another example of the constellation of the 2D
NUC for each of the 9 types of encoding rates r of the LDPC codes when the
modulation scheme is 64QAM.
[0458]
FIG 100 is an illustration of another example of the constellation of the 2D
NUC for each of the 9 types of encoding rates r of the LDPC codes when the
modulation scheme is 256QAM.
[0459]
In FIGS. 98 to 100, similarly to FIGS. 83 to 88, a horizontal axis and a
vertical axis are the I axis and the Q axis, and Re{xi} and Im {xi} indicate
the real part
and the imaginary part of the signal point xi serving as the coordinates of
the signal
CA 02917806 2016-01-08
point xi. Further, in FIGS. 98 to 100, a numerical value written after "for
CR"
indicates the encoding rate r of the LDPC code.
[0460]
FIG. 101 is an illustration of another example of the coordinates of the
signal
5 point of the 2D NUC of FIG 98 used for each of the 9 types of encoding
rates r of the
LDPC codes when the modulation scheme is 16QAM.
[0461]
FIG 102 is an illustration of another example of the coordinates of the signal
point of the 2D NUC of FIG 99 used for each of the 9 types of encoding rates r
of the
10 LDPC codes when the modulation scheme is 64QAM.
[0462]
FIGS. 103 and 104 are illustrations of another example of the coordinates of
the signal point of the 2D NUC of FIG 100 used for each of the 9 types of
encoding
rates r of the LDPC codes when the modulation scheme is 256QAM.
15 [0463]
In FIGS. 101 to 104, NUC_2m_r indicates the coordinates of the signal point
of the 2D NUC used when the modulation scheme is 2mQAM, and the encoding rate
of the LDPC code is r, similarly to FIGS. 90 to 93.
[0464]
20 The signal points of the 1D NUC are arranged in a grid form on a
straight
line parallel to the I axis or a straight line parallel to the Q axis.
However, an
interval between the signal points is not constant. Further, when the signal
point (the
mapped data) is transmitted, average power of the signal points on the
constellation is
normalized. The normalization is performed by multiplying each signal point zq
on
A __
25 the constellation by a reciprocal 1/(4Pave) of a square root l_ Pave a a
root mean square
value Pave when a root mean square value of an absolute value for (coordinates
of) all
signal points on the constellation is indicated by Pave.
[0465]
According to the constellations described above with reference to FIGS. 83
30 to 104, it is confirmed that the excellent error rate is obtained.
[0466]
<Block interleaver 25>
[0467]
CA 02917806 2016-01-08
91
FIG. 105 is a block diagram illustrating a configuration example of the block
interleaver 25 of FIG 9.
[0468]
The block interleaver 25 includes a storage region called a part 1 and a
storage region called a part 2.
[0469]
Each of the parts 1 and 2 is configured such that a number C of columns
equal in number to the number m of bits of the symbol and serving as storage
regions
that store one bit in the row (horizontal) direction and store a predetermined
number
of bits in the column (vertical) direction are arranged.
[0470]
If the number of bits (hereinafter, also referred to as a part column length)
that are stored in the column direction by the column of the part 1 is
indicated by RI,
and the part column length of the column of the part 2 is indicated by R2,
(R1+R2)xC
is equal to the code length N (64800 bits or 16200 bits in the present
embodiment) of
the LDPC code of the block interleave target.
[0471]
Further, the part column length R1 is equal to a multiple of 360 bits serving
as the unit size P, and the part column length R2 is equal to a remainder when
a sum
(hereinafter, also referred to as a column length) R1+R2 of the part column
length R1
of the part 1 and the part column length R2 of the part 2 is divided by 360
bits serving
as the unit size P.
[0472]
Here, the column length R 1+R2 is equal to a value obtained by dividing the
code length N of the LDPC code of the block interleave target by the number m
of
bits of the symbol.
[0473]
For example, when 16QAM is employed as the modulation scheme for the
LDPC code in which the code length N is 16200 bits, the number m of bits of
the
symbol is 4 bits, and thus the column length R 1+R2 is 4050 (= 16200/4) bits.
[0474]
Further, since the remainder when the column length R1+R2 = 4050 is
divided by 360 bits serving as the unit size P is 90, the part column length
R2 of the
CA 02917806 2016-01-08
92
part 2 is 90 bits.
[0475]
Further, the part column length R1 of the part 1 is R1+R2¨R2 = 4050-90 =
3960 bits.
[0476]
FIG 106 is an illustration of the number C of columns of the parts 1 and 2
and the part column lengths (the number of rows) R1 and R2 for a combination
of the
code length N and the modulation scheme.
[0477]
FIG. 106 illustrates the number C of columns of the parts 1 and 2 and the part
column lengths R1 and R2 for combinations of the LDPC code in which the code
length N is 16200 bits and the LDPC code in which the code length N is 64800
bits
and the modulation schemes of QPSK, 16QAM, 64QAM, 256QAM, 1024QAM, and
4096QAM.
[0478]
FIG 107 is an illustration of the block interleave performed by the block
interleaver 25 of FIG 105.
[0479]
The block interleaver 25 performs the block interleave by writing the LDPC
code in the parts 1 and 2 and reading the LDPC code from the parts 1 and 2.
[0480]
In other words, in the block interleave, writing of the code bits of the LDPC
code of one code word downward (in the column direction) in the column of the
part
1 is performed from the column at the left side to the column at the right
side as
illustrated in A of FIG. 107.
[0481]
Then, when the writing of the code bits is completed to the bottom of the
rightmost column (a C-th column) of the columns of the part 1, writing of the
remaining code bits downward (in the column direction) in the column of the
part 2 is
performed from the column at the left side to the column at the right side.
[0482]
Thereafter, when the writing of the code bits is completed to the bottom of
the rightmost column (the C-th column) of the columns of the part 2, the code
bits are
CA 02917806 2016-01-08
93
read from the 1st rows of all the C columns of the part 1 in the row direction
in units
of C =m bits.
[0483]
Then, the reading of the code bits from all the C columns of the part 1 is
sequentially performed toward a row therebelow, and when the reading is
completed
up to an R 1-th row serving as the last row, the code bits are read from the
1st rows of
all the C columns of the part 2 in the row direction in units of C = m bits.
[0484]
The reading of the code bits from all the C columns of the part 2 is
sequentially performed toward a row therebelow and the reading is performed up
to
an R2 row serving as the last row.
[0485]
As a result, the code bits read from the parts 1 and 2 in units of m bits are
supplied to the mapper 117 (FIG. 8) as the symbol.
[0486]
<Group-wise interleave>
[0487]
FIG. 108 is an illustration of the group-wise interleave performed by the
group-wise interleaver 24 of FIG 9.
[0488]
In the group-wise interleave, 360 bits of one segment are used as the bit
group, where the LDPC code of one code word is divided into segments in units
of
360 bits equal to the unit size P, and the LDPC code of one code word is
interleaved
according to a predetermined pattern (hereinafter, also referred to as a GW
pattern),
starting from the head.
[0489]
Here, when the LDPC code of one code word is segmented into the bit
groups, an (i+1)-th bit group from the head is also referred to as a bit group
i.
[0490]
When the unit size P is 360, for example, the LDPC code in which the code
length N is 1800 bits is segmented into bit groups 0, 1, 2, 3, and 4, that is,
5 (=
1800/360) bit groups. Further, for example, the LDPC code in which the code
length
N is 16200 bits is segmented into bit groups 0, 1, ..., and 44, that is, 45 (=
16200/360)
CA 02917806 2016-01-08
94
bit groups, and the LDPC code in which the code length N is 64800 bits is
segmented
into bit groups 0, 1, ..., and 179, that is, 180 (= 64800/360) bit groups.
[0491]
Hereinafter, the GW pattern is assumed to be indicated by a sequence of
numbers indicating a bit group. For example, for the LDPC code in which the
code
length N is 1800 bits, for example, the GW pattern 4, 2, 0, 3, 1 indicates
that a
sequence of bit groups 0, 1, 2, 3, and 4 is interleaved (rearranged) into a
sequence of
bit groups 4, 2, 0, 3, and 1.
[0492]
The GW pattern can be set at least for each code length N of the LDPC code.
[0493]
<Example of GW pattern for LDPC code of 64 kbits>
[0494]
FIG 109 is an illustration of a 1st example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0495]
According to the GW pattern of FIG 109, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
39, 47, 96, 176, 33, 75, 165, 38, 27, 58, 90, 76, 17, 46, 10, 91, 133, 69,
171,
32, 117, 78, 13, 146, 101, 36, 0, 138, 25, 77, 122, 49, 14, 125, 140, 93, 130,
2, 104,
102, 128, 4, 111, 151, 84, 167, 35, 127, 156, 55, 82, 85, 66, 114, 8, 147,
115, 113, 5,
31, 100, 106, 48, 52, 67, 107, 18, 126, 112, 50, 9, 143, 28, 160, 71, 79, 43,
98, 86, 94,
64, 3, 166, 105, 103, 118, 63, 51, 139, 172, 141, 175, 56, 74, 95, 29, 45,
129, 120, 168,
92, 150, 7, 162, 153, 137, 108, 159, 157, 173, 23, 89, 132, 57, 37, 70, 134,
40, 21, 149,
80, 1, 121, 59, 110, 142, 152, 15, 154, 145, 12, 170, 54, 155, 99, 22, 123,
72, 177, 131,
116, 44, 158, 73, 11, 65, 164, 119, 174, 34, 83, 53, 24, 42, 60, 26, 161, 68,
178, 41,
148, 109, 87, 144, 135, 20, 62, 81, 169, 124, 6, 19, 30, 163, 61, 179, 136,
97, 16, and
88.
[0496]
FIG. 110 is an illustration of a 2nd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0497]
According to the GW pattern of FIG 110, a sequence of bit groups 0 to 179
CA 02917806 2016-01-08
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
6, 14, 1, 127, 161, 177, 75, 123, 62, 103, 17, 18, 167, 88, 27, 34, 8, 110,
7,78,94, 44, 45, 166, 149, 61, 163, 145, 155, 157, 82, 130, 70, 92, 151, 139,
160, 133,
26, 2, 79, 15, 95, 122, 126, 178, 101, 24, 138, 146, 179, 30, 86, 58, 11, 121,
159, 49,
5 84, 132, 117,
119, 50, 52, 4, 51, 48, 74, 114, 59, 40, 131, 33, 89, 66, 136, 72, 16, 134,
37, 164, 77, 99, 173, 20, 158, 156, 90, 41, 176, 81, 42, 60, 109, 22, 150,
105, 120, 12,
64, 56, 68, 111,21, 148, 53, 169, 97, 108, 35, 140, 91, 115, 152, 36, 106,
154, 0, 25,
54, 63, 172, 80, 168, 142, 118, 162, 135, 73, 83, 153, 141, 9,28, 55, 31, 112,
107, 85,
100, 175, 23, 57, 47, 38, 170, 137, 76, 147, 93, 19, 98, 124, 39, 87, 174,
144, 46, 10,
10 129, 69, 71,
125, 96, 116, 171, 128, 65, 102, 5, 43, 143, 104, 13, 67, 29, 3, 113, 32,
and 165.
[0498]
FIG 111 is an illustration of a 3rd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
15 [0499]
According to the GW pattern of FIG. 111, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
103, 116, 158, 0, 27, 73, 140, 30, 148, 36, 153, 154, 10, 174, 122, 178, 6,
106,
162, 59, 142, 112, 7, 74, 11, 51, 49, 72, 31, 65, 156, 95, 171, 105, 173, 168,
1, 155,
20 125, 82, 86,
161, 57, 165, 54, 26, 121, 25, 157, 93, 22, 34, 33, 39, 19, 46, 150, 141, 12,
9, 79, 118, 24, 17, 85, 117, 67, 58, 129, 160, 89, 61, 146, 77, 130, 102, 101,
137, 94,
69, 14, 133, 60, 149, 136, 16, 108, 41, 90, 28, 144, 13, 175, 114, 2, 18, 63,
68, 21, 109,
53, 123, 75, 81, 143, 169, 42, 119, 138, 104, 4, 131, 145, 8, 5, 76, 15, 88,
177, 124, 45,
97, 64, 100, 37, 132, 38, 44, 107, 35, 43, 80, 50, 91, 152, 78, 166, 55, 115,
170, 159,
25 147, 167, 87,
83, 29, 96, 172, 48, 98, 62, 139, 70, 164, 84, 47, 151, 134, 126, 113, 179,
110, 111, 128, 32, 52, 66, 40, 135, 176, 99, 127, 163,3, 120, 71, 56, 92, 23,
and 20.
[0500]
FIG. 112 is an illustration of a 4th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
30 [0501]
According to the GW pattern of FIG 112, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
139, 106, 125, 81, 88, 104, 3, 66, 60, 65, 2, 95, 155, 24, 151, 5, 51, 53, 29,
75,
CA 02917806 2016-01-08
96
52, 85, 8, 22, 98, 93, 168, 15, 86, 126, 173, 100, 130, 176, 20, 10, 87, 92,
175, 36, 143,
110, 67, 146, 149, 127, 133, 42, 84, 64, 78, 1, 48, 159, 79, 138, 46, 112,
164, 31, 152,
57, 144, 69, 27, 136, 122, 170, 132, 171, 129, 115, 107, 134, 89, 157, 113,
119, 135,
45, 148, 83, 114, 71, 128, 161, 140, 26, 13, 59, 38, 35, 96, 28, 0, 80, 174,
137, 49, 16,
101, 74, 179, 91, 44, 55, 169, 131, 163, 123, 145, 162, 108, 178, 12, 77, 167,
21, 154,
82, 54, 90, 177, 17, 41, 39, 7, 102, 156, 62, 109, 14, 37, 23, 153, 6, 147,
50, 47, 63, 18,
70, 68, 124, 72, 33, 158, 32, 118, 99, 105, 94, 25, 121, 166, 120, 160, 141,
165, 111,
19, 150, 97, 76, 73, 142, 117,4, 172, 58, 11, 30, 9, 103, 40, 61, 43, 34, 56,
and 116.
[0502]
FIG 113 is an illustration of a 5th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0503]
According to the GW pattern of FIG. 113, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
72, 59, 65, 61, 80, 2, 66, 23, 69, 101, 19, 16, 53, 109, 74, 106, 113, 56, 97,
30,
164, 15, 25, 20, 117, 76, 50, 82, 178, 13, 169, 36, 107, 40, 122, 138, 42, 96,
27, 163,
46, 64, 124, 57, 87, 120, 168, 166, 39, 177, 22, 67, 134, 9, 102, 28, 148, 91,
83, 88,
167, 32, 99, 140, 60, 152, 1, 123, 29, 154, 26, 70, 149, 171, 12, 6, 55, 100,
62, 86, 114,
174, 132, 139, 7, 45, 103, 130, 31, 49, 151, 119, 79, 41, 118, 126, 3, 179,
110, 111, 51,
93, 145, 73, 133, 54, 104, 161, 37, 129, 63, 38, 95, 159, 89, 112, 115, 136,
33, 68, 17,
35, 137, 173, 143, 78, 77, 141, 150, 58, 158, 125, 156, 24, 105, 98, 43, 84,
92, 128,
165, 153, 108, 0, 121, 170, 131, 144, 47, 157, 11, 155, 176, 48, 135, 4, 116,
146, 127,
52, 162, 142, 8, 5, 34, 85, 90, 44, 172, 94, 160, 175, 75, 71, 18, 147, 10,
21, 14, and
81.
[0504]
FIG. 114 is an illustration of a 6th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0505]
According to the GW pattern of FIG 114, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
8, 27, 7, 70, 75, 84, 50, 131, 146, 99, 96, 141, 155, 157, 82, 57, 120, 38,
137,
13, 83, 23, 40, 9, 56, 171, 124, 172, 39, 142, 20, 128, 133, 2, 89, 153, 103,
112, 129,
151, 162, 106, 14, 62, 107, 110, 73, 71, 177, 154, 80, 176, 24, 91, 32, 173,
25, 16, 17,
CA 02917806 2016-01-08
97
159, 21, 92, 6, 67, 81, 37, 15, 136, 100, 64, 102, 163, 168, 18, 78, 76, 45,
140, 123,
118, 58, 122, 11, 19, 86, 98, 119, 111, 26, 138, 125, 74, 97, 63, 10, 152,
161, 175, 87,
52, 60, 22, 79, 104, 30, 158, 54, 145, 49, 34, 166, 109, 179, 174, 93, 41,
116, 48, 3, 29,
134, 167, 105, 132, 114, 169, 147, 144, 77, 61, 170, 90, 178, 0, 43, 149, 130,
117, 47,
44, 36, 115, 88, 101, 148, 69, 46, 94, 143, 164, 139, 126, 160, 156, 33, 113,
65, 121,
53, 42, 66, 165, 85, 127, 135, 5, 55, 150, 72, 35, 31, 51, 4, 1, 68, 12, 28,
95, 59, and
108.
[0506]
FIG. 115 is an illustration of a 7th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0507]
According to the GW pattern of FIG. 115, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40,
42,
44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80,
82, 84, 86, 88,
90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120,
122, 124,
126, 128, 130, 132, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 154,
156, 158,
160, 162, 164, 166, 168, 170, 172, 174, 176, 178, 1, 3, 5, 7, 9, 11, 13, 15,
17, 19, 21,
23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59,
61, 63, 65, 67,
69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 105,
107, 109,
111, 113, 115, 117, 119, 121, 123, 125, 127, 129, 131, 133, 135, 137, 139,
141, 143,
145, 147, 149, 151, 153, 155, 157, 159, 161, 163, 165, 167, 169, 171, 173,
175, 177,
and 179.
[0508]
FIG 116 is an illustration of an 8th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0509]
According to the GW pattern of FIG 116, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
11, 5, 8, 18, 1, 25, 32, 31, 19, 21, 50, 102, 65, 85, 45, 86, 98, 104, 64, 78,
72,
53, 103, 79, 93, 41, 82, 108, 112, 116, 120, 124, 128, 132, 136, 140, 144,
148, 152,
156, 160, 164, 168, 172, 176, 4, 12, 15, 3, 10, 20, 26, 34, 23, 33, 68, 63,
69, 92, 44, 90,
75, 56, 100, 47, 106, 42, 39, 97, 99, 89, 52, 109, 113, 117, 121, 125, 129,
133, 137,
CA 02917806 2016-01-08
98
141, 145, 149, 153, 157, 161, 165, 169, 173, 177, 6, 16, 14, 7, 13, 36, 28,
29, 37, 73,
70, 54, 76, 91, 66, 80, 88, 51, 96, 81, 95, 38, 57, 105, 107, 59, 61, 110,
114, 118, 122,
126, 130, 134, 138, 142, 146, 150, 154, 158, 162, 166, 170, 174, 178, 0, 9,
17, 2, 27,
30, 24, 22, 35, 77, 74, 46, 94, 62, 87, 83, 101, 49, 43, 84, 48, 60, 67, 71,
58, 40, 55,
111, 115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163, 167,
171, 175,
and 179.
[0510]
FIG. 117 is an illustration of a 9th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0511]
According to the GW pattern of FIG 117, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
9, 18, 15, 13, 35, 26, 28, 99, 40, 68, 85, 58, 63, 104, 50, 52, 94, 69, 108,
114,
120, 126, 132, 138, 144, 150, 156, 162, 168, 174, 8, 16, 17, 24, 37, 23, 22,
103, 64, 43,
47, 56, 92, 59, 70, 42, 106, 60, 109, 115, 121, 127, 133, 139, 145, 151, 157,
163, 169,
175,4, 1, 10, 19, 30, 31, 89, 86, 77, 81, 51, 79, 83, 48, 45, 62, 67, 65, 110,
116, 122,
128, 134, 140, 146, 152, 158, 164, 170, 176, 6, 2, 0, 25, 20, 34, 98, 105, 82,
96, 90,
107, 53, 74, 73, 93, 55, 102, 111, 117, 123, 129, 135, 141, 147, 153, 159,
165, 171,
177, 14, 7, 3, 27, 21, 33, 44, 97, 38, 75, 72, 41, 84, 80, 100, 87, 76, 57,
112, 118, 124,
130, 136, 142, 148, 154, 160, 166, 172, 178, 5, 11, 12, 32, 29, 36, 88, 71,
78, 95, 49,
54, 61, 66, 46, 39, 101, 91, 113, 119, 125, 131, 137, 143, 149, 155, 161, 167,
173, and
179.
[0512]
FIG. 118 is an illustration of a 10th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0513]
According to the GW pattern of FIG 118, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
0, 14, 19, 21, 2, 11,22, 9, 8, 7, 16, 3, 26, 24, 27, 80, 100, 121, 107, 31,
36, 42,
46, 49, 75, 93, 127, 95, 119, 73, 61, 63, 117, 89, 99, 129, 52, 111, 124, 48,
122, 82,
106, 91, 92, 71, 103, 102, 81, 113, 101, 97, 33, 115, 59, 112, 90, 51, 126,
85, 123, 40,
83, 53, 69, 70, 132, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 154,
156, 158,
160, 162, 164, 166, 168, 170, 172, 174, 176, 178, 4, 5, 10, 12, 20, 6, 18, 13,
17, 15, 1,
CA 02917806 2016-01-08
99
29, 28, 23, 25, 67, 116, 66, 104, 44, 50, 47, 84, 76, 65, 130, 56, 128, 77,
39, 94, 87,
120, 62, 88, 74, 35, 110, 131, 98, 60, 37, 45, 78, 125, 41, 34, 118, 38, 72,
108, 58, 43,
109, 57, 105, 68, 86, 79, 96, 32, 114, 64, 55, 30, 54, 133, 135, 137, 139,
141, 143, 145,
147, 149, 151, 153, 155, 157, 159, 161, 163, 165, 167, 169, 171, 173, 175,
177, and
179.
[0514]
FIG. 119 is an illustration of an 11th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0515]
According to the GW pattern of FIG. 119, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
21, 11, 12, 9,0, 6, 24, 25, 85, 103, 118, 122, 71, 101, 41, 93, 55, 73, 100,
40,
106, 119, 45, 80, 128, 68, 129, 61, 124, 36, 126, 117, 114, 132, 136, 140,
144, 148,
152, 156, 160, 164, 168, 172, 176, 20, 18, 10, 13, 16, 8, 26, 27, 54, 111, 52,
44, 87,
113, 115, 58, 116, 49, 77, 95, 86, 30, 78, 81, 56, 125, 53, 89, 94, 50, 123,
65, 83, 133,
137, 141, 145, 149, 153, 157, 161, 165, 169, 173, 177, 2, 17, 1, 4, 7, 15, 29,
82, 32,
102, 76, 121, 92, 130, 127, 62, 107, 38, 46, 43, 110, 75, 104, 70, 91, 69, 96,
120, 42,
34, 79, 35, 105, 134, 138, 142, 146, 150, 154, 158, 162, 166, 170, 174, 178,
19, 5, 3,
14, 22, 28, 23, 109, 51, 108, 131, 33, 84, 88, 64, 63, 59, 57, 97, 98, 48, 31,
99, 37, 72,
39, 74, 66, 60, 67, 47, 112, 90, 135, 139, 143, 147, 151, 155, 159, 163, 167,
171, 175,
and 179.
[0516]
FIG 120 is an illustration of a 12th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0517]
According to the GW pattern of FIG. 120, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
12, 15, 2, 16, 27, 50, 35, 74, 38, 70, 108, 32, 112, 54, 30, 122, 72, 116, 36,
90,
49, 85, 132, 138, 144, 150, 156, 162, 168, 174,0, 14, 9, 5, 23, 66, 68, 52,
96, 117, 84,
128, 100, 63, 60, 127, 81, 99, 53, 55, 103, 95, 133, 139, 145, 151, 157, 163,
169, 175,
10, 22, 13, 11,28, 104, 37, 57, 115, 46, 65, 129, 107, 75, 119, 110, 31, 43,
97, 78, 125,
58, 134, 140, 146, 152, 158, 164, 170, 176, 4, 19, 6, 8, 24, 44, 101, 94, 118,
130, 69,
71, 83, 34, 86, 124, 48, 106, 89, 40, 102, 91, 135, 141, 147, 153, 159, 165,
171, 177, 3,
CA 02917806 2016-01-08
100
20, 7, 17, 25, 87, 41, 120, 47, 80, 59, 62, 88, 45, 56, 131, 61, 126, 113, 92,
51, 98, 136,
142, 148, 154, 160, 166, 172, 178, 21, 18, 1, 26, 29, 39, 73, 121, 105, 77,
42, 114, 93,
82, 111, 109, 67, 79, 123, 64, 76, 33, 137, 143, 149, 155, 161, 167, 173, and
179.
[0518]
FIG. 121 is an illustration of a 13th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0519]
According to the GW pattern of FIG. 121, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40,
42,
44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80,
82, 84, 86, 88,
90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120,
122, 124,
126, 128, 130, 132, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 154,
156, 158,
160, 162, 164, 166, 168, 170, 172, 174, 176, 178, 1, 3, 5, 7, 9, 11, 13, 15,
17, 19, 21,
23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59,
61, 63, 65, 67,
69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 105,
107, 109,
111, 113, 115, 117, 119, 121, 123, 125, 127, 129, 131, 133, 135, 137, 139,
141, 143,
145, 147, 149, 151, 153, 155, 157, 159, 161, 163, 165, 167, 169, 171, 173,
175, 177,
and 179.
[0520]
FIG. 122 is an illustration of a 14th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0521]
According to the GW pattern of FIG. 122, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76,
80, 84,
88, 92, 96, 100, 104, 108, 112, 116, 120, 124, 128, 132, 136, 140, 144, 148,
152, 156,
160, 164, 168, 172, 176, 1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53,
57, 61, 65,
69, 73, 77, 81, 85, 89, 93, 97, 101, 105, 109, 113, 117, 121, 125, 129, 133,
137, 141,
145, 149, 153, 157, 161, 165, 169, 173, 177, 2, 6, 10, 14, 18, 22, 26, 30, 34,
38, 42, 46,
50, 54, 58, 62, 66, 70, 74, 78, 82, 86, 90, 94, 98, 102, 106, 110, 114, 118,
122, 126,
130, 134, 138, 142, 146, 150, 154, 158, 162, 166, 170, 174, 178, 3, 7, 11, 15,
19, 23,
27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99,
103, 107, 111,
CA 02917806 2016-01-08
101
115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163, 167, 171,
175, and
179.
[0522]
FIG. 123 is an illustration of a 15th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0523]
According to the GW pattern of FIG. 123, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
8, 112, 92, 165, 12, 55, 5, 126, 87, 70, 69, 94, 103, 78, 137, 148, 9, 60, 13,
7,
178, 79, 43, 136, 34, 68, 118, 152, 49, 15, 99, 61, 66, 28, 109, 125, 33, 167,
81, 93, 97,
26, 35, 30, 153, 131, 122, 71, 107, 130, 76, 4, 95, 42, 58, 134, 0, 89, 75,
40, 129, 31,
80, 101, 52, 16, 142, 44, 138, 46, 116, 27, 82, 88, 143, 128, 72, 29, 83, 117,
172, 14,
51, 159, 48, 160, 100, 1, 102, 90, 22, 3, 114, 19, 108, 113, 39, 73, 111, 155,
106, 105,
91, 150, 54, 25, 135, 139, 147, 36, 56, 123, 6, 67, 104, 96, 157, 10, 62, 164,
86, 74,
133, 120, 174, 53, 140, 156, 171, 149, 127, 85, 59, 124, 84, 11, 21, 132, 41,
145, 158,
32, 17, 23, 50, 169, 170, 38, 18, 151, 24, 166, 175, 2, 47, 57, 98, 20, 177,
161, 154,
176, 163, 37, 110, 168, 141, 64, 65, 173, 162, 121, 45, 77, 115, 179, 63, 119,
146, and
144.
[0524]
FIG. 124 is an illustration of a 16th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0525]
According to the GW pattern of FIG. 124 a sequence of bit groups 0 to 179 of
the LDPC code of 64 kbits is interleaved into a sequence of bit groups
103, 138, 168, 82, 116, 45, 178, 28, 160, 2, 129, 148, 150, 23, 54, 106, 24,
78,
49, 87, 145, 179, 26, 112, 119, 12, 18, 174, 21, 48, 134, 137, 102, 147, 152,
72, 68, 3,
22, 169, 30, 64, 108, 142, 131, 13, 113, 115, 121, 37, 133, 136, 101, 59, 73,
161, 38,
164, 43, 167, 42, 144, 41, 85, 91, 58, 128, 154, 172, 57, 75, 17, 157, 19, 4,
86, 15, 25,
35, 9, 105, 123, 14, 34, 56, 111, 60, 90, 74, 149, 146, 62, 163, 31, 16, 141,
88, 6, 155,
130, 89, 107, 135, 79, 8, 10, 124, 171, 114, 162, 33, 66, 126, 71, 44, 158,
51, 84, 165,
173, 120, 7, 11, 170, 176, 1, 156, 96, 175, 153, 36, 47, 110, 63, 132, 29, 95,
143, 98,
70, 20, 122, 53, 100, 93, 140, 109, 139, 76, 151, 52, 61, 46, 125, 94, 50, 67,
81, 69, 65,
40, 127, 77, 32, 39, 27, 99, 97, 159, 166, 80, 117, 55, 92, 118, 0, 5, 83,
177, and 104.
CA 02917806 2016-01-08
102
[0526]
FIG. 125 is an illustration of a 17th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0527]
According to the GW pattern of FIG. 125, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
104, 120, 47, 136, 116, 109, 22, 20, 117, 61, 52, 108, 86, 99, 76, 90, 37, 58,
36, 138, 95, 130, 177, 93, 56, 33, 24, 82, 0, 67, 83, 46, 79, 70, 154, 18, 75,
43, 49, 63,
162, 16, 167, 80, 125, 1, 123, 107, 9,45, 53, 15, 38, 23, 57, 141,4, 178, 165,
113, 21,
105, 11, 124, 126, 77, 146, 29, 131, 27, 176, 40, 74, 91, 140, 64, 73, 44,
129, 157, 172,
51, 10, 128, 119, 163, 103, 28, 85, 156, 78, 6, 8, 173, 160, 106, 31, 54, 122,
25, 139,
68, 150, 164, 87, 135, 97, 166, 42, 169, 161, 137, 26, 39, 133, 5, 94, 69, 2,
30, 171,
149, 115, 96, 145, 101, 92, 143, 12, 88, 81, 71, 19, 147, 50, 152, 159, 155,
151, 174,
60, 32, 3, 142, 72, 14, 170, 112, 65, 89, 175, 158, 17, 114, 62, 144, 13, 98,
66, 59, 7,
118, 48, 153, 100, 134, 84, 111, 132, 127, 41, 168, 110, 102, 34, 121, 179,
148, 55,
and 35.
[0528]
FIG. 126 is an illustration of a 18th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0529]
According to the GW pattern of FIG 126, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
37, 98, 160, 63, 18, 6, 94, 136, 8, 50, 0, 75, 65, 32, 107, 60, 108, 17, 21,
156,
157, 5, 73, 66, 38, 177, 162, 130, 171, 76, 57, 126, 103, 62, 120, 134, 154,
101, 143,
29, 13, 149, 16, 33, 55, 56, 159, 128, 23, 146, 153, 141, 169, 49, 46, 152,
89, 155, 111,
127, 48, 14, 93, 41, 7, 78, 135, 69, 123, 179, 36, 87, 27, 58, 88, 170, 125,
110, 15, 97,
178, 90, 121, 173, 30, 102, 10, 80, 104, 166, 64, 4, 147, 1, 52, 45, 148, 68,
158, 31,
140, 100, 85, 115, 151, 70, 39, 82, 122, 79, 12, 91, 133, 132, 22, 163, 47,
19, 119, 144,
35, 25, 42, 83, 92, 26, 72, 138, 54, 124, 24, 74, 118, 117, 168, 71, 109, 112,
106, 176,
175, 44, 145, 11,9, 161, 96, 77, 174, 137, 34, 84,2, 164, 129, 43, 150, 61,
53, 20, 165,
113, 142, 116, 95, 3, 28, 40, 81, 99, 139, 114, 59, 67, 172, 131, 105, 167,
51, and 86.
[0530]
FIG. 127 is an illustration of a 19th example of the GW pattern for an LDPC
CA 02917806 2016-01-08
103
code in which the code length N is 64 kbits.
[0531]
According to the GW pattern of FIG 127, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
58, 70, 23, 32, 26, 63, 55, 48, 35, 41, 53, 20, 38, 51, 61, 65, 44, 29, 7, 2,
113,
68, 96, 104, 106, 89, 27, 0, 119, 21, 4, 49, 46, 100, 13, 36, 57, 98, 102, 9,
42, 39, 33,
62, 22, 95, 101, 15, 91, 25, 93, 132, 69, 87, 47, 59, 67, 124, 17, 11, 31, 43,
40, 37, 85,
50, 97, 140, 45, 92, 56, 30, 34, 60, 107, 24, 52, 94, 64, 5, 71, 90, 66, 103,
88, 86, 84,
19, 169, 159, 147, 126, 28, 130, 14, 162, 144, 166, 108, 153, 115, 135, 120,
122, 112,
139, 151, 156, 16, 172, 164, 123, 99, 54, 136, 81, 105, 128, 116, 150, 155,
76, 18, 142,
170, 175, 83, 146, 78, 109, 73, 131, 127, 82, 167, 77, 110, 79, 137, 152, 3,
173, 148,
72, 158, 117, 1, 6, 12, 8, 161, 74, 143, 133, 168, 171, 134, 163, 138, 121,
141, 160,
111, 10, 149, 80, 75, 165, 157, 174, 129, 145, 114, 125, 154, 118, 176, 177,
178, and
179.
[0532]
FIG. 128 is an illustration of a 20th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0533]
According to the GW pattern of FIG. 128, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
40, 159, 100, 14, 88, 75, 53, 24, 157, 84, 23, 77, 140, 145, 32, 28, 112, 39,
76,
50, 93, 27, 107, 25, 152, 101, 127, 5, 129, 71, 9, 21, 96, 73, 35, 106, 158,
49, 136, 30,
137, 115, 139, 48, 167, 85, 74, 72, 7, 110, 161, 41, 170, 147, 82, 128, 149,
33, 8, 120,
47, 68, 58, 67, 87, 155, 11, 18, 103, 151, 29, 36, 83, 135, 79, 150, 97, 54,
70, 138, 156,
31, 121, 34, 20, 130, 61, 57, 2, 166, 117, 15, 6, 165, 118, 98, 116, 131, 109,
62, 126,
175, 22, 111, 164, 16, 133, 102, 55, 105, 64, 177, 78, 37, 162, 124, 119, 19,
4, 69, 132,
65, 123, 160, 17, 52, 38, 1, 80, 90, 42, 81, 104, 13, 144, 51, 114, 3, 43,
146, 163, 59,
45, 89, 122, 169, 44, 94, 86, 99, 66, 171, 173, 0, 141, 148, 176, 26, 143,
178, 60, 153,
142, 91, 179, 12, 168, 113, 95, 174, 56, 134, 92, 46, 108, 125, 10, 172, 154,
and 63.
[0534]
FIG. 129 is an illustration of a 21st example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0535]
CA 02917806 2016-01-08
104
According to the GW pattern of FIG. 129, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
143, 57, 67, 26, 134, 112, 136, 103, 13, 94, 16, 116, 169, 95, 98, 6, 174,
173,
102, 15, 114, 39, 127, 78, 18, 123, 121, 4, 89, 115, 24, 108, 74, 63, 175, 82,
48, 20,
104, 92, 27, 3, 33, 106, 62, 148, 154, 25, 129, 69, 178, 156, 87, 83, 100,
122, 70, 93,
50, 140, 43, 125, 166, 41, 128, 85, 157, 49, 86, 66, 79, 130, 133, 171, 21,
165, 126, 51,
153, 38, 142, 109, 10, 65, 23, 91, 90, 73, 61, 42, 47, 131, 77, 9, 58, 96,
101, 37, 7, 159,
44,2, 170, 160, 162, 0, 137, 31, 45, 110, 144, 88, 8, 11, 40, 81, 168, 135,
56, 151, 107,
105, 32, 120, 132, 1, 84, 161, 179, 72, 176, 71, 145, 139, 75, 141, 97, 17,
149, 124, 80,
60, 36, 52, 164, 53, 158, 113, 34, 76, 5, 111, 155, 138, 19, 35, 167, 172, 14,
147, 55,
152, 59, 64, 54, 117, 146, 118, 119, 150, 29, 163, 68, 99, 46, 177, 28, 22,
30, and 12.
[0536]
FIG. 130 is an illustration of a 22nd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0537]
According to the GW pattern of FIG. 130, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
116, 47, 155, 89, 109, 137, 103, 60, 114, 14, 148, 100, 28, 132, 129, 105,
154,
7, 167, 140, 160, 30, 57, 32, 81, 3, 86, 45, 69, 147, 125, 52, 20, 22, 156,
168, 17, 5, 93,
53, 61, 149, 56, 62, 112, 48, 11, 21, 166, 73, 158, 104, 79, 128, 135, 126,
63, 26, 44,
97, 13, 151, 123, 41, 118, 35, 131, 8, 90, 58, 134, 6, 78, 130, 82, 106, 99,
178, 102, 29,
108, 120, 107, 139, 23, 85, 36, 172, 174, 138, 95, 145, 170, 122, 50, 19, 91,
67, 101,
92, 179, 27, 94, 66, 171, 39, 68, 9, 59, 146, 15, 31, 38, 49, 37, 64, 77, 152,
144, 72,
165, 163, 24, 1, 2, 111, 80, 124, 43, 136, 127, 153, 75, 42, 113, 18, 164,
133, 142, 98,
96, 4, 51, 150, 46, 121, 76, 10, 25, 176, 34, 110, 115, 143, 173, 169, 40, 65,
157, 175,
70, 33, 141, 71, 119, 16, 162, 177, 12, 84, 87, 117,0, 88, 161, 55, 54, 83,
74, and 159.
[0538]
FIG. 131 is an illustration of a 23rd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0539]
According to the GW pattern of FIG. 131, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
62, 17, 10, 25, 174, 13, 159, 14, 108, 0, 42, 57, 78, 67, 41, 132, 110, 87,
77,
CA 02917806 2016-01-08
105
27, 88, 56, 8, 161, 7, 164, 171, 44, 75, 176, 145, 165, 157, 34, 142, 98, 103,
52, 11, 82,
141, 116, 15, 158, 139, 120, 36, 61, 20, 112, 144, 53, 128, 24, 96, 122, 114,
104, 150,
50, 51, 80, 109, 33, 5, 95, 59, 16, 134, 105, 111, 21, 40, 146, 18, 133, 60,
23, 160, 106,
32, 79, 55, 6, 1, 154, 117, 19, 152, 167, 166, 30, 35, 100, 74, 131, 99, 156,
39, 76, 86,
43, 178, 155, 179, 177, 136, 175, 81, 64, 124, 153, 84, 163, 135, 115, 125,
47, 45, 143,
72, 48, 172, 97, 85, 107, 126, 91, 129, 137, 83, 118, 54, 2, 9, 58, 169, 73,
123, 4, 92,
168, 162, 94, 138, 119, 22, 31, 63, 89, 90, 69, 49, 173, 28, 127, 26, 29, 101,
170, 93,
140, 147, 149, 148, 66, 65, 121, 12, 71, 37, 70, 102, 46, 38, 68, 130, 3, 113,
and 151.
[0540]
FIG. 132 is an illustration of a 24th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0541]
According to the GW pattern of FIG 132, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
168, 18, 46, 131, 88, 90, 11, 89, 111, 174, 172, 38, 78, 153, 9, 80, 53, 27,
44,
79, 35, 83, 171, 51, 37, 99, 95, 119, 117, 127, 112, 166, 28, 123, 33, 160,
29, 6, 135,
10, 66, 69, 74, 92, 15, 109, 106, 178, 65, 141, 0, 3, 154, 156, 164, 7,45,
115, 122, 148,
110, 24, 121, 126, 23, 175, 21, 113, 58, 43, 26, 143, 56, 142, 39, 147, 30,
25, 101, 145,
136, 19, 4, 48, 158, 118, 133, 49, 20, 102, 14, 151, 5, 2, 72, 103, 75, 60,
84, 34, 157,
169, 31, 161, 81, 70, 85, 159, 132, 41, 152, 179, 98, 144, 36, 16, 87, 40, 91,
1, 130,
108, 139, 94, 97, 8, 104, 13, 150, 137, 47, 73, 62, 12, 50, 61, 105, 100, 86,
146, 165,
22, 17, 57, 167, 59, 96, 120, 155, 77, 162, 55, 68, 140, 134, 82, 76, 125, 32,
176, 138,
173, 177, 163, 107, 170, 71, 129, 63, 93, 42, 52, 116, 149, 54, 128, 124, 114,
67, and
64.
[0542]
FIG. 133 is an illustration of a 25th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0543]
According to the GW pattern of FIG 133, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
18, 150, 165, 42, 81, 48, 63, 45, 93, 152, 25, 16, 174, 29, 47, 83, 8, 60, 30,
66,
11, 113, 44, 148, 4, 155, 59, 33, 134, 99, 32, 176, 109, 72, 36, 111, 106, 73,
170, 126,
64, 88, 20, 17, 172, 154, 120, 121, 139, 77, 98, 43, 105, 133, 19, 41, 78, 15,
7, 145, 94,
CA 02917806 2016-01-08
106
136, 131, 163, 65, 31, 96, 79, 119, 143, 10, 95, 9, 146, 14, 118, 162, 37, 97,
49, 22, 51,
127, 6, 71, 132, 87, 21, 39, 38, 54, 115, 159, 161, 84, 108, 13, 102, 135,
103, 156, 67,
173, 76, 75, 164, 52, 142, 69, 130, 56, 153, 74, 166, 158, 124, 141, 58, 116,
85, 175,
169, 168, 147, 35, 62, 5, 123, 100, 90, 122, 101, 149, 112, 140, 86, 68, 89,
125, 27,
177, 160, 0, 80, 55, 151, 53, 2, 70, 167, 114, 129, 179, 138, 1, 92, 26, 50,
28, 110, 61,
82, 91, 117, 107, 178, 34, 157, 137, 128, 40, 24, 57, 3, 171, 46, 104, 12,
144, and 23.
[0544]
FIG 134 is an illustration of a 26th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0545]
According to the GW pattern of FIG 134, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
18, 8, 166, 117, 4, 111, 142, 148, 176, 91, 120, 144, 99, 124, 20, 25, 31, 78,
36, 72, 2, 98, 93, 74, 174, 52, 152, 62, 88, 75, 23, 97, 147, 15, 71, 1, 127,
138, 81, 83,
68, 94, 112, 119, 121, 89, 163, 85, 86, 28, 17, 64, 14, 44, 158, 159, 150, 32,
128, 70,
90, 29, 30, 63, 100, 65, 129, 140, 177, 46, 84, 92, 10, 33, 58, 7, 96, 151,
171, 40, 76, 6,
3, 37, 104, 57, 135, 103, 141, 107, 116, 160, 41, 153, 175, 55, 130, 118, 131,
42, 27,
133, 95, 179, 34, 21, 87, 106, 105, 108, 79, 134, 113, 26, 164, 114, 73, 102,
77, 22,
110, 161, 43, 122, 123, 82, 5, 48, 139, 60, 49, 154, 115, 146, 67, 69, 137,
109, 143, 24,
101, 45, 16, 12, 19, 178, 80, 51, 47, 149, 50, 172, 170, 169, 61, 9, 39, 136,
59, 38, 54,
156, 126, 125, 145, 0, 13, 155, 132, 162, 11, 157, 66, 165, 173, 56, 168, 167,
53, and
35.
[0546]
FIG. 135 is an illustration of a 27th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0547]
According to the GW pattern of FIG. 135, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
77, 50, 109, 128, 153, 12, 48, 17, 147, 55, 173, 172, 135, 121, 99, 162, 52,
40,
129, 168, 103, 87, 134, 105, 179, 10, 131, 151, 3,26, 100, 15, 123, 88, 18,
91, 54, 160,
49, 1, 76, 80, 74, 31, 47, 58, 161, 9, 16, 34, 41, 21, 177, 11, 63, 6, 39,
165, 169, 125,
114, 57, 37, 67, 93, 96, 73, 106, 83, 166, 24, 51, 142, 65, 43, 64, 53, 72,
156, 81, 4,
155, 33, 163, 56, 150, 70, 167, 107, 112, 144, 149, 36, 32, 35, 59, 101, 29,
127, 138,
CA 02917806 2016-01-08
107
176, 90, 141, 92, 170, 102, 119, 25, 75, 14, 0, 68, 20, 97, 110, 28, 89, 118,
154, 126, 2,
22, 124, 85, 175, 78, 46, 152, 23, 86, 27, 79, 130, 66, 45, 113, 111, 62, 61,
7, 30, 133,
108, 171, 143, 60, 178, 5, 122, 44, 38, 148, 157, 84, 42, 139, 145, 8, 104,
115, 71, 137,
132, 146, 164, 98, 13, 117, 174, 158, 95, 116, 140, 94, 136, 120, 82, 69, 159,
and 19.
[0548]
FIG. 136 is an illustration of a 28th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0549]
According to the GW pattern of FIG. 136, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
51, 47, 53, 43, 55, 59, 49, 33, 35, 31, 24, 37, 0, 2, 45, 41, 39, 57, 42, 44,
52,
40, 23, 30, 32, 34, 54, 56, 46, 50, 122, 48, 1, 36, 38, 58, 77, 3, 65, 81, 67,
147, 83, 69,
26, 75, 85, 73, 79, 145, 71, 63, 5, 61, 70, 78, 68, 62, 66, 6, 64, 149, 60,
82, 80, 4, 76,
84, 72, 154, 86, 74, 89, 128, 137, 91, 141, 93, 101, 7, 87, 9, 103, 99, 95,
11, 13, 143,
97, 133, 136, 12, 100, 94, 14, 88, 142, 96, 92, 8, 152, 10, 139, 102, 104,
132, 90, 98,
114, 112, 146, 123, 110, 15, 125, 150, 120, 153, 29, 106, 134, 27, 127, 108,
130, 116,
28, 107, 126, 25, 131, 124, 129, 151, 121, 105, 111, 115, 135, 148, 109, 117,
158, 113,
170, 119, 162, 178, 155, 176, 18, 20, 164, 157, 160, 22, 140, 16, 168, 166,
172, 174,
175, 179, 118, 138, 156, 19, 169, 167, 163, 173, 161, 177, 165, 144, 171, 17,
21, and
159.
[0550]
FIG. 137 is an illustration of a 29th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0551]
According to the GW pattern of FIG. 137, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
49, 2, 57, 47, 31, 35, 24, 39, 59, 0, 45, 41, 55, 53, 51, 37, 33, 43, 56, 38,
48,
32, 50, 23, 34, 54, 1, 36, 44, 52, 40, 58, 122, 46, 42, 30, 3, 75, 73, 65,
145, 71, 79, 67,
69, 83, 85, 147, 63, 81, 77, 61, 5, 26, 62, 64, 74, 70, 82, 149, 76, 4, 78,
84, 80, 86, 66,
68, 72, 6, 60, 154, 103, 95, 101, 143, 9, 89, 141, 128, 97, 137, 133, 7, 13,
99, 91, 93,
87, 11, 136, 90, 88, 94, 10, 8, 14, 96, 104, 92, 132, 142, 100, 98, 12, 102,
152, 139,
150, 106, 146, 130, 27, 108, 153, 112, 114, 29, 110, 134, 116, 15, 127, 125,
123, 120,
148, 151, 113, 126, 124, 135, 129, 109, 25, 28, 158, 117, 105, 115, 111, 131,
107, 121,
CA 02917806 2016-01-08
108
18, 170, 164, 20, 140, 160, 166, 162, 119, 155, 168, 178, 22, 174, 172, 176,
16, 157,
159, 171, 161, 118, 17, 163, 21, 165, 19, 179, 177, 167, 138, 173, 156, 144,
169, and
175.
[0552]
FIG 138 is an illustration of a 30th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0553]
According to the GW pattern of FIG. 138, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
71, 38, 98, 159, 1, 32, 28, 177, 125, 102, 83, 17, 121, 151, 66, 92, 140, 6,
165,
23, 75, 91, 87, 108, 163, 50, 77, 39, 110, 128, 73, 148, 14, 5, 68, 37, 53,
93, 149, 26,
166, 48, 79, 10, 122, 150, 103, 178, 119, 101, 61, 34, 8, 86, 36, 138, 146,
72, 179, 143,
147, 89, 4, 107, 33, 144, 141, 40, 100, 29, 118, 63, 46, 20, 153, 90, 152,
124, 7, 30, 31,
43, 78, 120, 85, 25, 52, 47, 64, 81, 175, 94, 115, 15, 112, 99, 13, 21, 42,
169, 76, 19,
168, 16, 27, 162, 167, 164, 97, 82, 44, 106, 12, 109, 132, 145, 161, 174, 95,
0, 105,
134, 173, 84, 9, 65, 88, 54, 67, 116, 154, 80, 22, 172, 60, 111, 133, 56, 170,
104, 131,
123, 24, 49, 113, 136, 55, 3, 157, 156, 35, 58, 45, 155, 70, 59, 57, 171, 176,
74, 117,
18, 127, 114, 11, 69, 158, 129, 139, 62, 135, 96, 142, 41, 130, 160, 2, 126,
51, and
137.
[0554]
FIG. 139 is an illustration of a 31th example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0555]
According to the GW pattern of FIG. 139, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
66, 61, 150, 157, 63, 42, 78, 44, 23, 154, 133, 101, 82, 26, 84, 123, 89, 31,
45,
102, 36, 134, 83, 117, 170, 27, 73, 137, 25, 32, 62, 91, 4, 20, 144, 145, 21,
74, 113,
148, 24, 135, 5, 19, 2, 34, 43, 168, 14, 64, 142, 115, 87, 38, 147, 39, 51,
152, 56, 86,
122, 76, 57, 129, 172, 6, 126, 10, 97, 85, 164, 3, 80, 90, 79, 124, 138, 120,
17, 103, 99,
116, 46, 98, 162, 151, 143, 11, 175, 160, 96, 132, 81, 171, 94, 65, 118, 161,
125, 178,
95, 112, 88, 174, 13, 35, 1, 167, 0, 128, 12, 58, 29, 169, 67, 28, 119, 166,
60, 55, 54,
130, 92, 146, 177, 149, 111, 9, 173, 179, 176, 75, 77, 114, 48, 159, 8, 141,
107, 139,
52, 100, 136, 105, 127, 47, 18, 69, 109, 16, 121, 59, 163, 165, 108, 106, 70,
22, 93, 41,
CA 02917806 2016-01-08
109
33, 110, 53, 140, 153, 158, 50, 15, 37, 72, 156, 7, 131, 49, 71, 68, 104, 30,
40, 155.
[0556]
FIG. 140 is an illustration of a 32nd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0557]
According to the GW pattern of FIG 140, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
75, 83, 11, 24, 86, 104, 156, 76, 37, 173, 127, 61, 43, 139, 106, 69, 49, 2,
128,
140, 68, 14, 100, 8, 36, 73, 148, 65, 16, 47, 177, 6, 132, 45, 5, 30, 13, 22,
29, 27, 101,
150, 23, 90, 41, 93, 89, 92, 135, 4, 71, 87, 44, 124, 26, 64, 1, 129, 157,
130, 107, 18,
91, 118, 3, 82, 144, 113, 121, 54, 84, 97, 122, 120, 7, 154, 56, 134, 57, 161,
33, 116,
28, 96, 72, 172, 12, 115, 38, 164, 32, 167, 145, 17, 88, 39, 151, 80, 0, 136,
169, 142,
74, 147, 126, 166, 163, 40, 110, 171, 50, 160, 131, 70, 175, 103, 125, 77,
162, 31, 85,
66, 67, 52, 108, 159, 133, 42, 153, 21, 51, 119, 123, 98, 35, 48, 111, 149,
25, 58, 60,
158, 102, 59, 117, 20, 141, 143, 46, 53, 155, 15, 165, 152, 112, 176, 105,
178, 99, 174,
168, 114, 179, 78, 10, 19, 62, 63, 170, 138, 34, 109, 9, 146, 95, 94, 55, 137,
81, and
79.
[0558]
FIG. 141 is an illustration of a 33rd example of the GW pattern for an LDPC
code in which the code length N is 64 kbits.
[0559]
According to the GW pattern of FIG. 141, a sequence of bit groups 0 to 179
of the LDPC code of 64 kbits is interleaved into a sequence of bit groups
98, 159, 59, 125, 163, 89, 26, 4, 102, 70, 92, 36, 37, 142, 176, 95, 71, 19,
87,
45, 81, 47, 65, 170, 103, 48, 67, 61, 64, 35, 76, 80, 140, 77, 10, 167, 178,
155, 120,
156, 151, 12, 58, 5, 83, 137, 41, 109, 2, 66, 133, 62, 135, 28, 93, 128, 86,
57, 153, 161,
110, 52, 147, 141, 31, 79, 32, 88, 160, 84, 150,6, 100, 73, 126, 164, 17, 42,
101, 7, 55,
105, 91, 22, 130, 154, 1, 82, 14, 0, 9, 21, 50, 165, 72, 138, 175, 106, 108,
3, 169, 30,
157, 54, 18, 20, 44, 34, 134, 107, 56, 53, 15, 162, 38, 166, 24, 33, 60, 85,
145, 115, 43,
39, 40, 124, 149, 144, 132, 96, 11, 146, 90, 129, 119, 111, 171, 8, 152, 121,
173, 131,
49, 27, 118, 16, 148, 68, 177, 94, 179, 13, 114, 75, 51, 117, 25, 46, 136,
143, 139, 113,
127, 174, 74, 29, 122, 158, 69, 97, 78, 63, 99, 112, 104, 116, 172, 168, 23,
and 123.
[0560]
CA 02917806 2016-01-08
110
The 1st to 33rd examples of the GW pattern for the LDPC code in which the
code length N is 64 kbits can be applied to any combination of the LDPC code
in
which the code length N is 64 kbits with an arbitrary encoding rate r and
modulation
scheme (constellation).
[0561]
However, when the GW pattern to be applied to the group-wise interleave is
set for each combination of the code length N of the LDPC code, the encoding
rate r
of the LDPC code, and the modulation scheme (constellation), the error rate of
each
combination can be further improved.
[0562]
When the GW pattern of FIG. 109 is applied to, for example, the combination
of the ETRI symbol (64k, 5/15) and QPSK of FIG 89, a particularly excellent
error
rate can be achieved.
[0563]
When the GW pattern of FIG 110 is applied to, for example, the combination
of the ETRI symbol (64k, 5/15) and 16QAM of FIG 90, a particularly excellent
error
rate can be achieved.
[0564]
When the GW pattern of FIG 111 is applied to, for example, the combination
of the ETRI symbol (64k, 5/15) and 64QAM of FIG. 91, a particularly excellent
error
rate can be achieved.
[0565]
When the GW pattern of FIG 112 is applied to, for example, the combination
of the Sony symbol (64k, 7/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0566]
When the GW pattern of FIG 113 is applied to, for example, the combination
of the Sony symbol (64k, 7/15) and 16QAM of FIG 90, a particularly excellent
error
rate can be achieved.
[0567]
When the GW pattern of FIG 114 is applied to, for example, the combination
of the Sony symbol (64k, 7/15) and 64QAM of FIG 91, a particularly excellent
error
rate can be achieved.
CA 02917806 2016-01-08
111
[0568]
When the GW pattern of FIG 115 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0569]
When the GW pattern of FIG 116 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and 16QAM of FIG. 90, a particularly excellent
error
rate can be achieved.
[0570]
When the GW pattern of FIG 117 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and 64QAM of FIG 91, a particularly excellent
error
rate can be achieved.
[0571]
When the GW pattern of FIG 118 is applied to, for example, the combination
of the Sony symbol (64k, 11/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0572]
When the GW pattern of FIG 119 is applied to, for example, the combination
of the Sony symbol (64k, 11/15) and 16QAM of FIG 90, a particularly excellent
error
rate can be achieved.
[0573]
When the GW pattern of FIG. 120 is applied to, for example, the combination
of the Sony symbol (64k, 11/15) and 64QAM of FIG. 91, a particularly excellent
error
rate can be achieved.
[0574]
When the GW pattern of FIG 121 is applied to, for example, the combination
of the Sony symbol (64k, 13/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0575]
When the GW pattern of FIG 122 is applied to, for example, the combination
of the Sony symbol (64k, 13/15) and 16QAM of FIG. 90, a particularly excellent
error
rate can be achieved.
[0576]
CA 02917806 2016-01-08
112
When the GW pattern of FIG 123 is applied to, for example, the combination
of the Sony symbol (64k, 13/15) and 64QAM of FIG. 91, a particularly excellent
error
rate can be achieved.
[0577]
When the GW pattern of FIG 124 is applied to, for example, the combination
of the ETRI symbol (64k, 5/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0578]
When the GW pattern of FIG 125 is applied to, for example, the combination
of the ETRI symbol (64k, 7/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0579]
When the GW pattern of FIG. 126 is applied to, for example, the combination
of the Sony symbol (64k, 7/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0580]
When the GW pattern of FIG. 127 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0581]
When the GW pattern of FIG. 128 is applied to, for example, the combination
of the NERC symbol (64k, 9/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0582]
When the GW pattern of FIG 129 is applied to, for example, the combination
of the Sony symbol (64k, 11/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0583]
When the GW pattern of FIG 130 is applied to, for example, the combination
of the Sony symbol (64k, 13/15) and 256QAM of FIGS. 92 and 93, a particularly
excellent error rate can be achieved.
[0584]
When the GW pattern of FIG. 131 is applied to, for example, the combination
CA 02917806 2016-01-08
113
of the ETRI symbol (64k, 5/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0585]
When the GW pattern of FIG. 132 is applied to, for example, the combination
of the ETRI symbol (64k, 7/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0586]
When the GW pattern of FIG 133 is applied to, for example, the combination
of the Sony symbol (64k, 7/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0587]
When the GW pattern of FIG. 134 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0588]
When the GW pattern of FIG 135 is applied to, for example, the combination
of the NERC symbol (64k, 9/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0589]
When the GW pattern of FIG 136 is applied to, for example, the combination
of the Sony symbol (64k, 11/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0590]
When the GW pattern of FIG. 137 is applied to, for example, the combination
of the Sony symbol (64k, 13/15) and 1024QAM of FIGS. 94 and 95, a particularly
excellent error rate can be achieved.
[0591]
When the GW pattern of FIG. 138 is applied to, for example, the combination
of the Samsung symbol (64k, 6/15) and 4096QAM of FIGS. 96 and 97, a
particularly
excellent error rate can be achieved.
[0592]
When the GW pattern of FIG 139 is applied to, for example, the combination
of the ETRI symbol (64k, 7/15) and 4096QAM of FIGS. 96 and 97, a particularly
CA 02917806 2016-01-08
114
excellent error rate can be achieved.
[0593]
When the GW pattern of FIG. 140 is applied to, for example, the combination
of the Samsung symbol (64k, 8/15) and 4096QAM of FIGS. 96 and 97, a
particularly
excellent error rate can be achieved.
[0594]
When the GW pattern of FIG 141 is applied to, for example, the combination
of the Sony symbol (64k, 9/15) and 4096QAM of FIGS. 96 and 97, a particularly
excellent error rate can be achieved.
[0595]
<Example of GW pattern for LDPC code of 16k bits>
[0596]
FIG. 142 is an illustration of a 1st example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0597]
According to the GW pattern of FIG 142, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
21, 41, 15, 29, 0, 23, 16, 12, 38, 43, 2, 3, 4, 20, 31, 27, 5, 33, 28, 30, 36,
8,40,
13, 6, 9, 18, 24, 7, 39, 10, 17, 37, 1, 19, 22, 25, 26, 14, 32, 34, 11, 35,
42, and 44.
[0598]
FIG. 143 is an illustration of a 2nd example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0599]
According to the GW pattern of FIG 143, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
1, 3, 2, 8, 5, 23, 13, 12, 18, 19, 17, 20, 24, 26, 28, 30, 32, 34, 36, 38, 40,
42, 0,
4, 6, 7, 21, 16, 10, 15,9, 11,22, 14, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43,
and 44.
[0600]
FIG. 144 is an illustration of a 3rd example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0601]
According to the GW pattern of FIG 144, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
CA 02917806 2016-01-08
115
1, 4, 5, 6, 24, 21, 18, 7, 17, 12, 8, 20, 23, 29, 28, 30, 32, 34, 36, 38, 40,
42, 0,
2, 3, 14, 22, 13, 10, 25, 9, 27, 19, 16, 15, 26, 11, 31, 33, 35, 37, 39, 41,
43, and 44.
[0602]
FIG. 145 is an illustration of a 4th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0603]
According to the GW pattern of FIG 145, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
3, 0, 4, 7, 18, 9, 19, 27, 32, 10, 12, 24, 8, 35, 30, 17, 22, 20, 36, 38, 40,
42, 2,
5, 1,6, 14, 15, 23, 16, 11, 21, 26, 13, 29, 33, 31, 28, 25, 34, 37, 39, 41,
43, and 44.
[0604]
FIG. 146 is an illustration of a 5th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0605]
According to the GW pattern of FIG 146, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
37, 0,41, 19, 43, 8, 38, 3,29, 13, 22, 6, 4, 2, 9, 26, 39, 15, 12, 10, 33, 17,
20,
16, 21, 44, 42, 27, 7, 11, 30, 34, 24, 1, 23, 35, 36, 25, 31, 18, 28, 32, 40,
5, and 14.
[0606]
FIG. 147 is an illustration of a 6th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0607]
According to the GW pattern of FIG 147, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
6, 28, 17,4, 3, 38, 13, 41, 44, 43, 7,40, 19, 2, 23, 16, 37, 15, 30, 20, 11,
8, 1,
27, 32, 34, 33, 39, 5, 9, 10, 18, 0, 31, 29, 26, 14, 21, 42, 22, 12, 24, 35,
25, and 36.
[0608]
FIG 148 is an illustration of a 7th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0609]
According to the GW pattern of FIG 148, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
27, 11, 20, 1, 7, 5,29, 35,9, 10, 34, 18, 25, 28, 6, 13, 17, 0,23, 16, 41, 15,
19,
CA 02917806 2016-01-08
116
44, 24, 37, 4, 31, 8,32, 14, 42, 12, 2, 40, 30, 36, 39, 43, 21, 3, 22, 26, 33,
and 38.
[0610]
FIG. 149 is an illustration of an 8th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0611]
According to the GW pattern of FIG 149, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
3, 6, 7, 27, 2, 23, 10, 30, 22, 28, 24, 20, 37, 21, 4, 14, 11, 42, 16, 9, 15,
26, 33,
40, 5, 8, 44, 34, 18, 0, 32, 29, 19, 41, 38, 17, 25, 43, 35, 36, 13, 39, 12,
1, and 31.
[0612]
FIG. 150 is an illustration of a 9th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0613]
According to the GW pattern of FIG 150, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
31, 38, 7,9, 13, 21, 39, 12, 10, 1,43, 15, 30, 0, 14, 3, 42, 34, 40, 24, 28,
35, 8,
11, 23, 4, 20, 17, 41, 19, 5, 37, 22, 32, 18, 2, 26, 44, 25, 33, 36, 27, 16,6,
and 29.
[0614]
FIG 151 is an illustration of a 10th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0615]
According to the GW pattern of FIG 151, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
36, 6, 2, 20, 43, 17, 33, 22, 23, 25, 13, 0, 10, 7, 21, 1, 19, 26, 8, 14, 31,
35, 16,
5, 29, 40, 11, 9, 4, 34, 15, 42, 32, 28, 18, 37, 30, 39, 24, 41, 3, 38, 27,
12, and 44.
[0616]
FIG. 152 is an illustration of a 11th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0617]
According to the GW pattern of FIG 152, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
14, 22, 18, 11, 28, 26, 2, 38, 10, 0, 5, 12, 24, 17, 29, 16, 39, 13, 23, 8,
25, 43,
34, 33, 27, 15, 7, 1,9, 35, 40, 32, 30, 20, 36, 31, 21, 41, 44, 3, 42, 6, 19,
37, and 4.
CA 02917806 2016-01-08
117
[0618]
FIG. 153 is an illustration of a 12th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0619]
According to the GW pattern of FIG 153, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
17, 11, 14, 7,31, 10, 2, 26, 0, 32, 29, 22, 33, 12, 20, 28, 27, 39, 37, 15, 4,
5, 8,
13, 38, 18, 23, 34, 24, 6, 1, 9, 16, 44, 21, 3, 36, 30, 40, 35, 43, 42, 25,
19, and 41.
[0620]
FIG. 154 is an illustration of a 13th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0621]
According to the GW pattern of FIG 154, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
1, 27, 17, 30, 11, 15, 9, 7, 5, 6, 32, 33, 2, 14, 3, 39, 18, 12, 29, 13, 41,
31, 4,
43, 35, 34, 40, 10, 19, 44, 8, 26, 21, 16, 28, 0, 23, 38, 25, 36, 22, 37, 42,
24, and 20.
[0622]
FIG. 155 is an illustration of a 14th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0623]
According to the GW pattern of FIG 155, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
41, 2, 12, 6, 33, 1, 13, 11, 26, 10, 39, 43, 36, 23, 42, 7, 44, 20, 8, 38, 18,
22,
24, 40, 4, 28, 29, 19, 14, 5, 9, 0, 30, 25, 35, 37, 27, 32, 31, 34, 21, 3, 15,
17, and 16,
[0624]
FIG. 156 is an illustration of a 15th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0625]
According to the GW pattern of FIG 156, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
17, 2, 30, 12, 7, 25, 27, 3, 15, 14, 4, 26, 34, 31, 13, 22, 0, 39, 23, 24, 21,
6, 38,
5, 19, 42, 11, 32, 28, 40, 20, 18, 36, 9, 41, 10, 33, 37, 1, 16, 8, 43, 29,
35, and 44.
[0626]
CA 02917806 2016-01-08
118
FIG. 157 is an illustration of a 16th example of a GW pattern for an LDPC
code in which a code length N is 16k bits.
[0627]
According to the GW pattern of FIG 157, a sequence of bit groups 0 to 44 of
the LDPC code of 16 kbits is interleaved into a sequence of bit groups
28, 21, 10, 15, 8, 22, 26, 2, 14, 1, 27, 3, 39, 20, 34, 25, 12, 6, 7, 40, 30,
29, 38,
16, 43, 33,4, 35, 9, 32, 5, 36, 0,41, 37, 18, 17, 13, 24, 42, 31, 23, 19, 11,
and 44.
[0628]
The 1st to 16th examples of the GW pattern for the LDPC code in which the
code length N is 16 kbits can be applied to any combination of the LDPC code
in
which the code length N is 16 kbits with an arbitrary encoding rate r and
modulation
scheme (constellation).
[0629]
However, when the GW pattern to be applied to the group-wise interleave is
set for each combination of the code length N of the LDPC code, the encoding
rate r
of the LDPC code, and the modulation scheme (constellation), the error rate of
each
combination can be further improved.
[0630]
When the GW pattern of FIG. 142 is applied to, for example, the combination
of the LGE symbol (16k, 6/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0631]
When the GW pattern of FIG. 143 is applied to, for example, the combination
of the Sony symbol (16k, 8/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0632]
When the GW pattern of FIG 144 is applied to, for example, the combination
of the Sony symbol (16k, 10/15) and QPSK of FIG. 89, a particularly excellent
error
rate can be achieved.
[0633]
When the GW pattern of FIG 145 is applied to, for example, the combination
of the Sony symbol (16k, 12/15) and QPSK of FIG 89, a particularly excellent
error
rate can be achieved.
CA 02917806 2016-01-08
119
[0634]
When the GW pattern of FIG. 146 is applied to, for example, the combination
of the LGE symbol (16k, 6/15) and 16QAM of FIG. 101, a particularly excellent
error
rate can be achieved.
[0635]
When the GW pattern of FIG. 147 is applied to, for example, the combination
of the Sony symbol (16k, 8/15) and 16QAM of FIG. 101, a particularly excellent
error
rate can be achieved.
[0636]
When the GW pattern of FIG 148 is applied to, for example, the combination
of the Sony symbol (16k, 10/15) and 16QAM of FIG. 101, a particularly
excellent
error rate can be achieved.
[0637]
When the GW pattern of FIG 149 is applied to, for example, the combination
of the Sony symbol (16k, 12/15) and 16QAM of FIG. 101, a particularly
excellent
error rate can be achieved.
[0638]
When the GW pattern of FIG 150 is applied to, for example, the combination
of the LGE symbol (16k, 6/15) and 64QAM of FIG 102, a particularly excellent
error
rate can be achieved.
[0639]
When the GW pattern of FIG 151 is applied to, for example, the combination
of the Sony symbol (16k, 8/15) and 64QAM of FIG. 102 a particularly excellent
error
rate can be achieved.
[0640]
When the GW pattern of FIG. 152 is applied to, for example, the combination
of the Sony symbol (16k, 10/15) and 64QAM of FIG 102 a particularly excellent
error rate can be achieved.
[0641]
When the GW pattern of FIG 153 is applied to, for example, the combination
of the Sony symbol (16k, 12/15) and 64QAM of FIG. 102 a particularly excellent
error rate can be achieved.
[0642]
CA 02917806 2016-01-08
120
When the GW pattern of FIG 154 is applied to, for example, the combination
of the LGE symbol (16k, 6/15) and 256QAM of FIGS. 103 and 104 a particularly
excellent error rate can be achieved.
[0643]
When the GW pattern of FIG 155 is applied to, for example, the combination
of the Sony symbol (16k, 8/15) and 256QAM of FIGS. 103 and 104 a particularly
excellent error rate can be achieved.
[0644]
When the GW pattern of FIG. 156 is applied to, for example, the combination
of the Sony symbol (16k, 10/15) and 256QAM of FIGS. 103 and 104 a particularly
excellent error rate can be achieved.
[0645]
When the GW pattern of FIG. 157 is applied to, for example, the combination
of the Sony symbol (16k, 12/15) and 256QAM of FIGS. 103 and 104 a particularly
excellent error rate can be achieved.
[0646]
<Simulation result>
[0647]
FIG. 158 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 109 is
applied to a combination of the ETRI symbol (64k, 5/15) and QPSK of FIG. 89.
[0648]
FIG. 159 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 110 is
applied to a combination of the ETRI symbol (64k, 5/15) and 16QAM of FIG. 90.
[0649]
FIG. 160 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 111 is
applied
to a combination of the ETRI symbol (64k, 5/15) and 64QAM of FIG 91.
[0650]
FIG. 161 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 112 is
applied to a combination of the Sony symbol (64k, 7/15) and QPSK of FIG 89.
CA 02917806 2016-01-08
121
[0651]
FIG. 162 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 113 is
applied to a combination of the Sony symbol (64k, 7/15) and 16QAM of FIG 90.
[0652]
FIG. 163 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 114 is
applied to a combination of the Sony symbol (64k, 7/15) and 64QAM of FIG 91.
[0653]
FIG. 164 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 115 is
applied to a combination of the Sony symbol (64k, 9/15) and QPSK of FIG. 89.
[0654]
FIG. 165 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 116 is
applied to a combination of the Sony symbol (64k, 9/15) and 16QAM of FIG 90.
[0655]
FIG. 166 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 117 is
applied to a combination of the Sony symbol (64k, 9/15) and 64QAM of FIG 91.
[0656]
FIG 167 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 118 is
applied to a combination of the Sony symbol (64k, 11/15) and QPSK of FIG 89.
[0657]
FIG 168 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 119 is
applied to a combination of the Sony symbol (64k, 11/15) and 16QAM of FIG. 90.
[0658]
FIG. 169 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 120 is
applied to a combination of the Sony symbol (64k, 11/15) and 64QAM of FIG 91.
[0659]
CA 02917806 2016-01-08
122
FIG. 170 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 121 is
applied to a combination of the Sony symbol (64k, 13/15) and QPSK of FIG 89.
[0660]
FIG. 171 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 122 is
applied to a combination of the Sony symbol (64k, 13/15) and 16QAM of FIG 90.
[0661]
FIG. 172 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 123 is
applied to a combination of the Sony symbol (64k, 13/15) and 64QAM of FIG 91.
[0662]
FIG 173 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 124 is
applied to a combination of the ETRI symbol (64k, 5/15) and 256QAM of FIGS. 92
and 93.
[0663]
FIG. 174 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 125 is
applied to a combination of the ETRI symbol (64k, 7/15) and 256QAM of FIGS. 92
and 93.
[0664]
FIG. 175 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 126 is
applied to a combination of the Sony symbol (64k, 7/15) and 256QAM of FIGS. 92
and 93.
[0665]
FIG. 176 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 127 is
applied to a combination of the Sony symbol (64k, 9/15) and 256QAM of FIGS. 92
and 93.
[0666]
FIG. 177 is an illustration of a BER/FER curve indicating a simulation result
CA 02917806 2016-01-08
123
of a simulation of measuring the error rate when the GW pattern of FIG 128 is
applied to a combination of the NERC symbol (64k, 9/15) and 256QAM of FIGS. 92
and 93.
[0667]
FIG. 178 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 129 is
applied to a combination of the Sony symbol (64k, 9/15) and 256QAM of FIGS. 92
and 93.
[0668]
FIG. 179 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 130 is
applied to a combination of the Sony symbol (64k, 13/15) and 256QAM of FIGS.
92
and 93.
[0669]
FIG. 180 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 131 is
applied to a combination of the ETRI symbol (64k, 5/15) and 1024QAM of FIGS.
94
and 95.
[0670]
FIG. 181 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 132 is
applied to a combination of the ETRI symbol (64k, 7/15) and 1024QAM of FIGS.
94
and 95.
[0671]
FIG. 182 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 133 is
applied to a combination of the Sony symbol (64k, 7/15) and 1024QAM of FIGS.
94
and 95.
[0672]
FIG 183 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 134 is
applied to a combination of the Sony symbol (64k, 9/15) and 1024QAM of FIGS.
94
and 95.
CA 02917806 2016-01-08
124
[0673]
FIG 184 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 135 is
applied to a combination of the NERC symbol (64k, 9/15) and 1024QAM of FIGS.
94
and 95.
[0674]
FIG 185 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 136 is
applied to a combination of the Sony symbol (64k, 11/15) and 1024QAM of FIGS.
94
and 95.
[0675]
FIG. 186 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 137 is
applied to a combination of the Sony symbol (64k, 13/15) and 1024QAM of FIGS.
94
and 95.
[0676]
FIG. 187 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 138 is
applied to a combination of the Samsung symbol (64k, 6/15) and 4096QAM of
FIGS.
96 and 97.
[0677]
FIG. 188 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 139 is
applied to a combination of the ETRI symbol (64k, 7/15) and 4096QAM of FIGS.
96
and 97.
[0678]
FIG. 189 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 140 is
applied to a combination of the Samsung symbol (64k, 8/15) and 4096QAM of
FIGS.
96 and 97.
[0679]
FIG. 190 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 141 is
CA 02917806 2016-01-08
125
applied to a combination of the Sony symbol (64k, 9/15) and 4096QAM of FIGS.
96
and 97.
[0680]
FIG. 191 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 142 is
applied to a combination of the LGE symbol (16k, 6/15) and QPSK of FIG. 89.
[0681]
FIG. 192 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 143 is
applied to a combination of the Sony symbol (16k, 8/15) and QPSK of FIG 89.
[0682]
FIG. 193 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 144 is
applied to a combination of the Sony symbol (16k, 10/15) and QPSK of FIG. 89.
[0683]
FIG. 194 is an illustration of a BERNER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 145 is
applied to a combination of the Sony symbol (16k, 12/15) and QPSK of FIG. 89.
[0684]
FIG. 195 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 146 is
applied to a combination of the LGE symbol (16k, 6/15) and 16QAM of FIG. 101.
[0685]
FIG. 196 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 147 is
applied to a combination of the Sony symbol (16k, 8/15) and 16QAM of FIG 101.
[0686]
FIG. 197 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 148 is
applied to a combination of the Sony symbol (16k, 10/15) and 16QAM of FIG 101.
[0687]
FIG. 198 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 149 is
CA 02917806 2016-01-08
126
applied to a combination of the Sony symbol (16k, 12/15) and 16QAM of FIG.
101.
[0688]
FIG. 199 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 150 is
applied to a combination of the LGE symbol (16k, 6/15) and 64QAM of FIG 102.
[0689]
FIG 200 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 151 is
applied to a combination of the Sony symbol (16k, 8/15) and 64QAM of FIG. 102.
[0690]
FIG. 201 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 152 is
applied to a combination of the Sony symbol (16k, 10/15) and 64QAM of FIG.
102.
[0691]
FIG. 202 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 153 is
applied to a combination of the Sony symbol (16k, 12/15) and 64QAM of FIG 102.
[0692]
FIG. 203 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 154 is
applied to a combination of the LGE symbol (16k, 6/15) and 256QAM of FIGS. 103
and 104.
[0693]
FIG. 204 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 155 is
applied to a combination of the Sony symbol (16k, 8/15) and 256QAM of FIGS.
103
and 104.
[0694]
FIG 205 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG 156 is
applied to a combination of the Sony symbol (16k, 10/15) and 256QAM of FIGS.
103
and 104.
[0695]
CA 02917806 2016-01-08
127
FIG. 206 is an illustration of a BER/FER curve indicating a simulation result
of a simulation of measuring the error rate when the GW pattern of FIG. 157 is
applied to a combination of the Sony symbol (16k, 12/15) and 256QAM of FIGS.
103
and 104.
[0696]
FIGS. 158 to 206 illustrate BER/FER curves when an AWGN channel is
employed as the communication path 13 (FIG 7) (the upper drawings) and BER/FER
curves when a Rayleigh (fading) channel is employed as the communication path
13
(FIG. 7) (the lower drawings).
[0697]
In FIGS. 158 to 206, "w bil" indicates a BER/FER curve when the parity
interleave, the group-wise interleave, and the block-wise interleave are
performed,
and "w/o bil" indicates a BER/FER curve when the parity interleave, the group-
wise
interleave, and the block-wise interleave are not performed.
[0698]
As can be seen from FIGS. 158 to 206, when the parity interleave, the group-
wise interleave, and the block-wise interleave are performed, it is possible
to improve
the BER/FER and achieve the excellent the error rate compared to when they are
not
performed.
[0699]
Further, it is possible to apply the GW patterns of FIGS. 109 to 157 to the
constellation in which the signal point arrangements illustrated in FIGS. 83
to 104
have been moved symmetrically to the I axis or the Q axis, the constellation
in which
the signal point arrangements illustrated in FIGS. 83 to 104 have been moved
symmetrically to the origin, the constellation in which the signal point
arrangements
illustrated in FIGS. 83 to 104 have been rotated at an arbitrary angle
centering on the
origin, and the like in addition to the constellation of QPSK, 16QAM, 64QAM,
256QAM, 1024QAM, and 4096QAM of the signal point arrangements illustrated in
FIGS. 83 to 104, and it is possible to obtain the same effects as when the GW
patterns
of FIGS. 109 to 157 are applied to the constellation of QPSK, 16QAM, 64QAM,
256QAM, 1024QAM, and 4096QAM of the signal point arrangements illustrated in
FIGS. 83 to 104.
[0700]
CA 02917806 2016-01-08
128
Further, it is possible to apply the GW pattern of FIGS. 109 to 157 to the
constellation in which the most significant bit (MSB) and the least
significant bit
(LSB) of the symbol to be associated with (allocated to) the signal point are
interchanged in the signal point arrangements illustrated in FIGS. 83 to 104
in
addition to the constellation of QPSK, 16QAM, 64QAM, 256QAM, 1024QAM, and
4096QAM of the signal point arrangements illustrated in FIGS. 83 to 104, and
it is
possible to obtain the same effects as when the GW patterns of FIGS. 109 to
157 are
applied to the constellation of QPSK, 16QAM, 64QAM, 256QAM, 1024QAM, and
4096QAM of the signal point arrangements illustrated in FIGS. 83 to 104 as
well.
[0701]
<Configuration example of receiving device 12>
[0702]
FIG. 207 is a block diagram illustrating a configuration example of the
receiving device 12 of FIG 7.
[0703]
An OFDM operating unit 151 receives an OFDM signal from the
transmitting device 11 (FIG 7) and executes signal processing of the OFDM
signal.
Data that is obtained by executing the signal processing by the OFDM operating
unit
151 is supplied to a frame managing unit 152.
[0704]
The frame managing unit 152 executes processing (frame interpretation) of a
frame configured by the data supplied from the OFDM operating unit 151 and
supplies a signal of target data obtained as a result and a signal of
signaling to
frequency deinterleavers 161 and 153.
[0705]
The frequency deinterleaver 153 performs frequency deinterleave in a unit of
symbol, with respect to the data supplied from the frame managing unit 152,
and
supplies the symbol to a demapper 154.
[0706]
The demapper 154 performs demapping (signal point arrangement decoding)
and orthogonal demodulation on the data (the data on the constellation)
supplied from
the frequency deinterleaver 153 based on the arrangement (constellation) of
the signal
points decided according to the orthogonal modulation performed at the
transmitting
CA 02917806 2016-01-08
129
device 11 side, and supplies the data ((the likelihood of) the LDPC code)
obtained as
a result to the LDPC decoder 155.
[0707]
The LDPC decoder 155 performs LDPC decoding of the LDPC code
supplied from the demapper 154 and supplies LDPC target data (in this case, a
BCH
code) obtained as a result to a BCH decoder 156.
[0708]
The BCH decoder 156 performs BCH decoding of the LDPC target data
supplied from the LDPC decoder 155 and outputs control data (signaling)
obtained as
a result.
[0709]
Meanwhile, the frequency deinterleaver 161 performs frequency deinterleave
in a unit of symbol, with respect to the data supplied from the frame managing
unit
152, and supplies the symbol to a SISO/MISO decoder 162.
[0710]
The SISO/MISO decoder 162 performs spatiotemporal decoding of the data
supplied from the frequency deinterleaver 161 and supplies the data to a time
deinterleaver 163.
[0711]
The time deinterleaver 163 performs time deinterleave in a unit of symbol,
with respect to the data supplied from the SISO/MISO decoder 162, and supplies
the
data to a demapper 164.
[0712]
The demapper 164 performs demapping (signal point arrangement decoding)
and orthogonal demodulation on the data (the data on the constellation)
supplied from
the time deinterleaver 163 based on the arrangement (constellation) of the
signal
points decided according to the orthogonal modulation performed at the
transmitting
device 11 side, and supplies the data obtained as a result to a bit
deinterleaver 165.
[0713]
The bit deinterleaver 165 perform the bit deinterleave on the data supplied
from the demapper 164, and supplies (the likelihood of) the LDPC code serving
as the
data that has undergone the bit deinterleave to an LDPC decoder 166.
[0714]
CA 02917806 2016-01-08
130
The LDPC decoder 166 performs LDPC decoding of the LDPC code
supplied from the bit deinterleaver 165 and supplies LDPC target data (in this
case, a
BCH code) obtained as a result to a BCH decoder 167.
[0715]
The BCH decoder 167 performs BCH decoding of the LDPC target data
supplied from the LDPC decoder 155 and supplies data obtained as a result to a
BB
descrambler 168.
[0716]
The BB descrambler 168 executes BB descramble with respect to the data
supplied from the BCH decoder 167 and supplies data obtained as a result to a
null
deletion unit 169.
[0717]
The null deletion unit 169 deletes null inserted by the padder 112 of FIG. 8,
from the data supplied from the BB descrambler 168, and supplies the data to a
demultiplexer 170.
[0718]
The demultiplexer 170 individually separates one or more streams (target
data) multiplexed with the data supplied from the null deletion unit 169,
performs
necessary processing to output the streams as output streams.
[0719]
Here, the receiving device 12 can be configured without including part of the
blocks illustrated in FIG 207. That is, for example, in a case where the
transmitting
device 11 (FIG 8) is configured without including the time interleaver 118,
the
SISO/MISO encoder 119, the frequency interleaver 120 and the frequency
interleaver
124, the receiving device 12 can be configured without including the time
deinterleaver 163, the SISO/MISO decoder 162, the frequency deinterleaver 161
and
the frequency deinterleaver 153 which are blocks respectively corresponding to
the
time interleaver 118, the SISO/MISO encoder 119, the frequency interleaver 120
and
the frequency interleaver 124 of the transmitting device 11.
[0720]
<Configuration Example of Bit Deinterleaver 165>
[0721]
FIG. 208 is a block diagram illustrating a configuration example of the bit
CA 02917806 2016-01-08
131
deinterleaver 165 of FIG. 207.
[0722]
The bit deinterleaver 165 is configured with a block deinterleaver 54 and a
group-wise deinterleaver 55, and performs the (bit) deinterleave of the symbol
bits of
the symbol serving as the data supplied from the demapper 164 (FIG. 207).
[0723]
In other words, the block deinterleaver 54 performs the block deinterleave
(the inverse process of the block interleave) corresponding to the block
interleave
performed by the block interleaver 25 of FIG 9, that is, the block
deinterleave of
restoring the positions of (the likelihood of) of the code bits of the LDPC
code
rearranged by the block interleave to the original positions on the symbol
bits of the
symbol supplied from the demapper 164, and supplies the LDPC code obtained as
a
result to the group-wise deinterleaver 55.
[0724]
The group-wise deinterleaver 55 performs the group-wise deinterleave (the
inverse process of the group-wise interleave) corresponding to the group-wise
interleave performed by the group-wise interleaver 24 of FIG 9, that is, the
group-
wise deinterleave of restoring the original sequence by rearranging the code
bits of the
LDPC code whose sequence has been changed in units of bit groups by the group-
wise interleave described above, for example, with reference to FIG 108 in
units of
bit groups on the LDPC code supplied from the block deinterleaver 54
[0725]
Here, when the LDPC code supplied from the demapper 164 to the bit
deinterleaver 165 has undergone the parity interleave, the group-wise
interleave, and
the block interleave, the bit deinterleaver 165 can perform all of the parity
deinterleave (the inverse process of the parity interleave, that is, the
parity
deinterleave of restoring the code bits of the LDPC code whose sequence has
been
changed by the parity interleave to the original sequence) corresponding to
the parity
interleave, the block deinterleave corresponding to the block interleave, and
the
group-wise deinterleave corresponding to the group-wise interleave.
[0726]
However, the bit deinterleaver 165 of FIG 208 is provided with the block
deinterleaver 54 that performs the block deinterleave corresponding to the
block
CA 02917806 2016-01-08
132
interleave and the group-wise deinterleaver 55 that performs the group-wise
deinterleave corresponding to the group-wise interleave, but no block that
performs
the parity deinterleave corresponding to the parity interleave is provided,
and thus the
parity deinterleave is not performed.
[0727]
Thus, the LDPC code that has undergone the block deinterleave and group-
wise deinterleave but has not undergone the parity deinterleave is supplied
from (the
group-wise deinterleaver 55 of) the bit deinterleaver 165 to the LDPC decoder
166.
[0728]
The LDPC decoder 166 performs LDPC decoding of the LDPC code
supplied from the bit deinterleaver 165 using the transformed parity check
matrix
obtained by performing at least the column permutation corresponding to the
parity
interleave on the parity check matrix I-I of the DVB scheme used for the LDPC
encoding by the LDPC encoder 115 of FIG. 8 (or the transformed parity check
matrix
(FIG. 29) obtained by performing the row permutation on the parity check
matrix of
the ETRI scheme (FIG. 27)), and outputs data obtained as a result as a
decoding result
of LDPC target data.
[0729]
FIG. 209 is a flowchart illustrating a process performed by the demapper 164,
the bit deinterleaver 165, and the LDPC decoder 166 of FIG. 208.
[0730]
In step S111, the demapper 164 performs demapping and orthogonal
demodulation on the data (the data on the constellation mapped to the signal
points)
supplied from the time deinterleaver 163, and supplies the resulting data to
the bit
deinterleaver 165, and the process proceeds to step S112.
[0731]
In step S112, the bit deinterleaver 165 performs the deinterleave (the bit
deinterleave) on the data supplied from the demapper 164, and the process
proceeds to
step S113.
[0732]
In other words, in step S112, in the bit deinterleaver 165, the block
deinterleaver 54 performs the block deinterleave on the data (symbol) supplied
from
the demapper 164, and supplies the code bits of the LDPC code obtained as a
result to
CA 02917806 2016-01-08
133
the group-wise deinterleaver 55.
[0733]
The group-wise deinterleaver 55 performs the group-wise deinterleave on the
LDPC code supplied from the block deinterleaver 54, and supplies (the
likelihood of)
the LDPC code obtained as a result to the LDPC decoder 166.
[0734]
In step S113, the LDPC decoder 166 performs LDPC decoding of the LDPC
code supplied from the group-wise deinterleaver 55 using the parity check
matrix H
used for the LDPC encoding by the LDPC encoder 115 of FIG. 8, that is, using
the
transformed parity check matrix obtained from the parity check matrix H, for
example,
and outputs the data obtained as a result to the BCH decoder 167 as a decoding
result
of the LDPC target data.
[0735]
In FIG 208, similarly to the example of FIG. 9, for the sake of convenience
of description, the block deinterleaver 54 that performs the block
deinterleave and the
group-wise deinterleaver 55 that performs the group-wise deinterleave are
configured
individually, but the block deinterleaver 54 and the group-wise deinterleaver
55 may
be configured integrally.
[0736]
<LDPC decoding>
[0737]
The LDPC decoding performed by the LDPC decoder 166 of FIG 207 will
be described.
[0738]
As described above, the LDPC decoder 166 of FIG 207 performs the LDPC
decoding of the LDPC code that is supplied from the bit deinterleaver 165 and
has
undergone the block deinterleave and the group-wise deinterleave but has not
undergone the parity deinterleave using the transformed parity check matrix
obtained
by performing at least the column permutation corresponding to the parity
interleave
on the parity check matrix H of the DVB scheme used for the LDPC encoding by
the
LDPC encoder 115 of FIG 8 (or the transformed parity check matrix (FIG 29)
obtained by performing the row permutation on the parity check matrix of the
ETRI
scheme (FIG 27)).
CA 02917806 2016-01-08
134
[0739]
In this case, LDPC decoding that can suppress an operation frequency at a
sufficiently realizable range while suppressing a circuit scale, by performing
the
LDPC decoding using the transformed parity check matrix, is previously
suggested
(for example, refer to JP 4224777B).
[0740]
Therefore, first, the previously suggested LDPC decoding using the
transformed parity check matrix will be described with reference to FIGS. 210
to 213.
[0741]
FIG 210 illustrates an example of a parity check matrix H of an LDPC code
in which a code length N is 90 and an encoding rate is 2/3.
[0742]
In FIG 210 (and FIGS. 211 and 212 to be described later), 0 is represented
by a period (.).
[0743]
In the parity check matrix H of FIG 210, the parity matrix becomes a
staircase structure.
[0744]
FIG. 211 illustrates a parity check matrix H' that is obtained by executing
row
replacement of an expression (11) and column replacement of an expression (12)
with
respect to the parity check matrix H of FIG 210.
[0745]
Row Replacement: (6s + t + 1)-th row ¨> (5t + s + 1)-th row = = = (11)
[0746]
Column Replacement: (6x + y + 61)-th column ¨> (5y + x + 61)-th column
= = = (12)
[0747]
In the expressions (11) and (12), s, t, x, and y are integers in ranges of 0 s
<
5, 0 < t < 6, 0 < x <5, and 0 < t < 6, respectively.
[0748]
According to the row replacement of the expression (11), replacement is
performed such that the 1st, 7th, 13rd, 19th, and 25th rows having remainders
of 1
when being divided by 6 are replaced with the 1st, 2nd, 3rd, 4th, and 5th
rows, and the
CA 02917806 2016-01-08
135
2nd, 8th, 14th, 20th, and 26th rows having remainders of 2 when being divided
by 6
are replaced with the 6th, 7th, 8th, 9th, and 10th rows, respectively.
[0749]
According to the column replacement of the expression (12), replacement is
performed such that the 61st, 67th, 73rd, 79th, and 85th columns having
remainders
of 1 when being divided by 6 are replaced with the 61st, 62nd, 63rd, 64th, and
65th
columns, respectively, and the 62nd, 68th, 74th, 80th, and 86th columns having
remainders of 2 when being divided by 6 are replaced with the 66th, 67th,
68th, 69th,
and 70th columns, respectively, with respect to the 61st and following columns
(parity
matrix).
[0750]
In this way, a matrix that is obtained by performing the replacements of the
rows and the columns with respect to the parity check matrix H of FIG. 210 is
a parity
check matrix H' of FIG 211.
[0751]
In this case, even when the row replacement of the parity check matrix H is
performed, the sequence of the code bits of the LDPC code is not influenced.
[0752]
The column replacement of the expression (12) corresponds to parity
interleave to interleave the (K + qx+ y+ 1)-th code bit into the position of
the (K + Py
+ x + 1)-th code bit, when the information length K is 60, the unit size P is
5, and the
divisor q (= M/P) of the parity length M (in this case, 30) is 6.
[0753]
Therefore, the parity check matrix H' in FIG 211 is a transformed parity
check matrix obtained by performing at least column replacement that replaces
the
K+qx+y+1 -th column of the parity check matrix H in FIG. 210 (which may be
arbitrarily called an original parity check matrix below) with the K+Py+x+1-th
column.
[0754]
If the parity check matrix H' of FIG 211 is multiplied with a result obtained
by performing the same replacement as the expression (12) with respect to the
LDPC
code of the parity check matrix H of FIG 210, a zero vector is output. That
is, if a
row vector obtained by performing the column replacement of the expression
(12)
CA 02917806 2016-01-08
136
with respect to a row vector c as the LDPC code (one code word) of the
original
parity check matrix FI is represented as c', HcT becomes the zero vector from
the
property of the parity check matrix. Therefore, H'c'T naturally becomes the
zero
vector.
[0755]
Thereby, the transformed parity check matrix H' of FIG. 211 becomes a parity
check matrix of an LDPC code c' that is obtained by performing the column
replacement of the expression (12) with respect to the LDPC code c of the
original
parity check matrix H.
[0756]
Therefore, the column replacement of the expression (12) is performed with
respect to the LDPC code of the original parity check matrix H, the LDPC code
c'
after the column replacement is decoded (LDPC decoding) using the transformed
parity check matrix H' of FIG. 211, reverse replacement of the column
replacement of
the expression (12) is performed with respect to a decoding result, and the
same
decoding result as the case in which the LDPC code of the original parity
check
matrix H is decoded using the parity check matrix H can be obtained.
[0757]
FIG. 212 illustrates the transformed parity check matrix H' of FIG 211 with
being spaced in units of 5 x 5 matrixes.
[0758]
In FIG 212, the transformed parity check matrix H' is represented by a
combination of a 5 x 5 (= p x p) unit matrix that is a unit size P, a matrix
(hereinafter,
appropriately referred to as a quasi unit matrix) obtained by setting one or
more 1 of
the unit matrix to zero, a matrix (hereinafter, appropriately referred to as a
shifted
matrix) obtained by cyclically shifting the unit matrix or the quasi unit
matrix, a sum
(hereinafter, appropriately referred to as a sum matrix) of two or more
matrixes of the
unit matrix, the quasi unit matrix, and the shifted matrix, and a 5 x 5 zero
matrix.
[0759]
The transformed parity check matrix H' of FIG. 212 can be configured using
the 5 x 5 unit matrix, the quasi unit matrix, the shifted matrix, the sum
matrix, and the
zero matrix. Therefore, the 5 x 5 matrixes (the unit matrix, the quasi unit
matrix, the
shifted matrix, the sum matrix, and the zero matrix) that constitute the
transformed
CA 02917806 2016-01-08
137
parity check matrix H' are appropriately referred to as constitutive matrixes
hereinafter.
[0760]
When the LDPC code represented by the parity check matrix represented by
the P x P constitutive matrixes is decoded, an architecture in which P check
node
operations and variable node operations are simultaneously performed can be
used.
[0761]
FIG. 213 is a block diagram illustrating a configuration example of a
decoding device that performs the decoding.
[0762]
That is, FIG 213 illustrates the configuration example of the decoding device
that performs decoding of the LDPC code, using the transformed parity check
matrix
H' of FIG 210 obtained by performing at least the column replacement of the
expression (12) with respect to the original parity check matrix H of FIG 212.
[0763]
The decoding device of FIG 213 includes a branch data storing memory 300
that includes 6 FIFOs 3001 to 3006, a selector 301 that selects the FIFOs 3001
to 3006,
a check node calculating unit 302, two cyclic shift circuits 303 and 308, a
branch data
storing memory 304 that includes 18 FIFOs 3041 to 30418, a selector 305 that
selects
the FIFOs 3041 to 30418, a reception data memory 306 that stores reception
data, a
variable node calculating unit 307, a decoding word calculating unit 309, a
reception
data rearranging unit 310, and a decoded data rearranging unit 311.
[0764]
First, a method of storing data in the branch data storing memories 300 and
304 will be described.
[0765]
The branch data storing memory 300 includes the 6 FIFOs 3001 to 3006 that
correspond to a number obtained by dividing a row number 30 of the transformed
parity check matrix H' of FIG. 212 by a row number 5 of the constitutive
matrix (the
unit size P). The FIFO 300y (y = 1, 2, = = and 6) includes a plurality of
steps of
storage regions. In the storage region of each step, messages corresponding to
five
branches to be a row number and a column number of the constitutive matrix
(the unit
size P) can be simultaneously read or written. The number of steps of the
storage
CA 02917806 2016-01-08
138
regions of the FIFO 300y becomes 9 to be a maximum number of the number
(Hamming weight) of 1 of a row direction of the transformed parity check
matrix of
FIG 212.
[0766]
In the FIFO 3001, data (messages vi from variable nodes) corresponding to
positions of 1 in the first to fifth rows of the transformed parity check
matrix H' of
FIG. 212 is stored in a form filling each row in a transverse direction (a
form in which
0 is ignored). That is, if a j-th row and an i-th column are represented as
(j, i), data
corresponding to positions of 1 of a 5 x 5 unit matrix of (1, 1) to (5, 5) of
the
transformed parity check matrix H' is stored in the storage region of the
first step of
the FIFO 3001. In the storage region of the second step, data corresponding to
positions of 1 of a shifted matrix (shifted matrix obtained by cyclically
shifting the 5
x 5 unit matrix to the right side by 3) of (1, 21) to (5, 25) of the
transformed parity
check matrix H' is stored. Similar to the above case, in the storage regions
of the
third to eighth steps, data is stored in association with the transformed
parity check
matrix H'. In the storage region of the ninth step, data corresponding to
positions of
1 of a shifted matrix (shifted matrix obtained by replacing 1 of the first row
of the 5 x
5 unit matrix with 0 and cyclically shifting the unit matrix to the left side
by 1) of (1,
86) to (5, 90) of the transformed parity check matrix H' is stored.
[0767]
In the FIFO 3002, data corresponding to positions of 1 in the sixth to tenth
rows of the transformed parity check matrix H' of FIG 212 is stored. That is,
in the
storage region of the first step of the FIFO 3002, data corresponding to
positions of 1
of the first shifted matrix constituting a sum matrix (sum matrix to be a sum
of the
first shifted matrix obtained by cyclically shifting the 5 x 5 unit matrix to
the right
side by 1 and the second shifted matrix obtained by cyclically shifting the 5
x 5 unit
matrix to the right side by 2) of (6, 1) to (10, 5) of the transformed parity
check matrix
H' is stored. In addition, in the storage region of the second step, data
corresponding
to positions of 1 of the second shifted matrix constituting the sum matrix of
(6, 1) to
(10, 5) of the transformed parity check matrix H' is stored.
[0768]
That is, with respect to a constitutive matrix of which the weight is two or
more, when the constitutive matrix is represented by a sum of multiple parts
of aPx P
CA 02917806 2016-01-08
139
unit matrix of which the weight is 1, a quasi unit matrix in which one or more
elements of 1 in the unit matrix become 0, or a shifted matrix obtained by
cyclically
shifting the unit matrix or the quasi unit matrix, data (messages
corresponding to
branches belonging to the unit matrix, the quasi unit matrix, or the shifted
matrix)
corresponding to the positions of 1 in the unit matrix of the weight of 1, the
quasi unit
matrix, or the shifted matrix is stored at the same address (the same FIFO
among the
FIFOs 3001 to 3006).
[0769]
Subsequently, in the storage regions of the third to ninth steps, data is
stored
in association with the transformed parity check matrix H', similar to the
above case.
[0770]
In the FIFOs 3003 to 3006, data is stored in association with the transformed
parity check matrix H', similar to the above case.
[0771]
The branch data storing memory 304 includes 18 FIFOs 3041 to 30418 that
correspond to a number obtained by dividing a column number 90 of the
transformed
parity check matrix H' by 5 to be a column number of a constitutive matrix
(the unit
size P). The FIFO 304,, (x = 1, 2, = = =, and 18) includes a plurality of
steps of storage
regions. In the storage region of each step, messages corresponding to five
branches
corresponding to a row number and a column number of the constitutive matrix
(the
unit size P) can be simultaneously read or written.
[0772]
In the FIFO 3041, data (messages uj from check nodes) corresponding to
positions of 1 in the first to fifth columns of the transformed parity check
matrix H' of
FIG 212 is stored in a form filling each column in a longitudinal direction (a
form in
which 0 is ignored). That is, if a j-th row and an i-th column are represented
as (j, i),
data corresponding to positions of 1 of a 5 x 5 unit matrix of (1, 1) to (5,
5) of the
transformed parity check matrix H' is stored in the storage region of the
first step of
the FIFO 3041. In the storage region of the second step, data corresponding to
positions of 1 of the first shifted matrix constituting a sum matrix (sum
matrix to be a
sum of the first shifted matrix obtained by cyclically shifting the 5 x 5 unit
matrix to
the right side by 1 and the second shifted matrix obtained by cyclically
shifting the 5
x 5 unit matrix to the right side by 2) of (6, 1) to (10, 5) of the
transformed parity
CA 02917806 2016-01-08
140
check matrix H' is stored. In addition, in the storage region of the third
step, data
corresponding to positions of 1 of the second shifted matrix constituting the
sum
matrix of (6, 1) to (10, 5) of the transformed parity check matrix H' is
stored.
[0773]
That is, with respect to a constitutive matrix of which the weight is two or
more, when the constitutive matrix is represented by a sum of multiple parts
of aPxP
unit matrix of which the weight is 1, a quasi unit matrix in which one or more
elements of 1 in the unit matrix become 0, or a shifted matrix obtained by
cyclically
shifting the unit matrix or the quasi unit matrix, data (messages
corresponding to
branches belonging to the unit matrix, the quasi unit matrix, or the shifted
matrix)
corresponding to the positions of 1 in the unit matrix of the weight of 1, the
quasi unit
matrix, or the shifted matrix is stored at the same address (the same FIFO
among the
FIFOs 3041 to 30418).
[0774]
Subsequently, in the storage regions of the fourth and fifth steps, data is
stored in association with the transformed parity check matrix H', similar to
the above
case. The number of steps of the storage regions of the FIFO 3041 becomes 5 to
be a
maximum number of the number (Hamming weight) of 1 of a row direction in the
first to fifth columns of the transformed parity check matrix H'.
[0775]
In the FIFOs 3042 and 3043, data is stored in association with the transformed
parity check matrix H', similar to the above case, and each length (the number
of
steps) is 5. In the FIFOs 3044 to 30412, data is stored in association with
the
transformed parity check matrix H', similar to the above case, and each length
is 3.
In the FIFOs 30413 to 30418, data is stored in association with the
transformed parity
check matrix H', similar to the above case, and each length is 2.
[0776]
Next, an operation of the decoding device of FIG 213 will be described.
[0777]
The branch data storing memory 300 includes the 6 FIFOs 3001 to 3006.
According to information (matrix data) D312 on which row of the transformed
parity
check matrix H' in FIG 212 five messages D311 supplied from a cyclic shift
circuit
308 of a previous step belongs to, the FIFO storing data is selected from the
FIFOs
CA 02917806 2016-01-08
141
3001 to 3006 and the five messages D311 are collectively stored sequentially
in the
selected FIFO. When the data is read, the branch data storing memory 300
sequentially reads the five messages D3001 from the FIFO 3001 and supplies the
messages to the selector 301 of a next step. After reading of the messages
from the
FIFO 3001 ends, the branch data storing memory 300 reads the messages
sequentially
from the FIFOs 3002 to 3006 and supplies the messages to the selector 301.
[0778]
The selector 301 selects the five messages from the FIFO from which data is
currently read, among the FIFOs 3001 to 3006, according to a select signal
D301, and
supplies the selected messages as messages D302 to the check node calculating
unit
302.
[0779]
The check node calculating unit 302 includes five check node calculators
3021 to 3025. The check node calculating unit 302 performs a check node
operation
according to the expression (7), using the messages D302 (D3021 to D3025)
(messages vi of the expression 7) supplied through the selector 301, and
supplies five
messages D303 (D3031 to D3035) (messages uj of the expression (7)) obtained as
a
result of the check node operation to a cyclic shift circuit 303.
[0780]
The cyclic shift circuit 303 cyclically shifts the five messages D3031 to
D3035 calculated by the check node calculating unit 302, on the basis of
information
(matrix data) D305 on how many the unit matrixes (or the quasi unit matrix)
becoming the origin in the transformed parity check matrix H' are cyclically
shifted to
obtain the corresponding branches, and supplies a result as messages D304 to
the
branch data storing memory 304.
[0781]
The branch data storing memory 304 includes the eighteen FIFOs 3041 to
30418. According to information D305 on which row of the transformed parity
check matrix H' five messages D304 supplied from a cyclic shift circuit 303 of
a
previous step belongs to, the FIFO storing data is selected from the FIFOs
3041 to
30418 and the five messages D304 are collectively stored sequentially in the
selected
FIFO. When the data is read, the branch data storing memory 304 sequentially
reads
the five messages D3041 from the FIFO 3041 and supplies the messages to the
selector
CA 02917806 2016-01-08
142
305 of a next step. After reading of the messages from the FIFO 3041 ends, the
branch data storing memory 304 reads the messages sequentially from the FIFOs
3042
to 30418 and supplies the messages to the selector 305.
[0782]
The selector 305 selects the five messages from the FIFO from which data is
currently read, among the FIFOs 3041 to 30418, according to a select signal
D307, and
supplies the selected messages as messages D308 to the variable node
calculating unit
307 and the decoding word calculating unit 309.
[0783]
Meanwhile, the reception data rearranging unit 310 rearranges the LDPC
code D313, that is corresponding to the parity check matrix H in FIG 210,
received
through the communication path 13 by performing the column replacement of the
expression (12) and supplies the LDPC code as reception data D314 to the
reception
data memory 306. The reception data memory 306 calculates a reception LLR (Log
Likelihood Ratio) from the reception data D314 supplied from the reception
data
rearranging unit 310, stores the reception LLR, collects five reception LLRs,
and
supplies the reception LLRs as reception values D309 to the variable node
calculating
unit 307 and the decoding word calculating unit 309.
[0784]
The variable node calculating unit 307 includes five variable node calculators
3071 to 3075. The variable node calculating unit 307 performs the variable
node
operation according to the expression (1), using the messages D308 (D3081 to
D3085)
(messages U of the expression (1)) supplied through the selector 305 and the
five
reception values D309 (reception values uo, of the expression (1)) supplied
from the
reception data memory 306, and supplies messages D310 (D3101 to D3105)
(message
v, of the expression (1)) obtained as an operation result to the cyclic shift
circuit 308.
[0785]
The cyclic shift circuit 308 cyclically shifts the messages D3101 to D3105
calculated by the variable node calculating unit 307, on the basis of
information on
how many the unit matrixes (or the quasi unit matrix) becoming the origin in
the
transformed parity check matrix H' are cyclically shifted to obtain the
corresponding
branches, and supplies a result as messages D311 to the branch data storing
memory
300.
CA 02917806 2016-01-08
143
[0786]
By circulating the above operation in one cycle, decoding (variable node
operation and check node operation) of the LDPC code can be performed once.
After decoding the LDPC code by the predetermined number of times, the
decoding
device of FIG. 213 calculates a final decoding result and outputs the final
decoding
result, in the decoding word calculating unit 309 and the decoded data
rearranging
unit 311.
[0787]
That is, the decoding word calculating unit 309 includes five decoding word
calculators 3091 to 3095. The decoding word calculating unit 309 calculates a
decoding result (decoding word) on the basis of the expression (5), as a final
step of
multiple decoding, using the five messages D308 (D3081 to D3085) (messages uj
of
the expression) output by the selector 305 and the five reception values D309
(reception values uo, of the expression (5)) supplied from the reception data
memory
306, and supplies decoded data D315 obtained as a result to the decoded data
rearranging unit 311.
[0788]
The decoded data rearranging unit 311 performs the reverse replacement of
the column replacement of the expression (12) with respect to the decoded data
D315
supplied from the decoding word calculating unit 309, rearranges the order
thereof,
and outputs the decoded data as a final decoding result D316.
[0789]
As mentioned above, by performing one or both of row replacement and
column replacement on the parity check matrix (original parity check matrix)
and
converting it into a parity check matrix (transformed parity check matrix)
that can be
shown by the combination of a pxp unit matrix, a quasi unit matrix in which
one or
more elements of 1 thereof become 0, a shifted matrix that cyclically shifts
the unit
matrix or the quasi unit matrix, a sum matrix that is the sum of two or more
of the unit
matrix, the quasi unit matrix and the shifted matrix, and a pxp 0 matrix, that
is, the
combination of constitutive matrixes, as for LDPC code decoding, it becomes
possible to adopt architecture that simultaneously performs check node
calculation
and variable node calculation by P which is the number less than the row
number and
column number of the parity check matrix. In the case of adopting the
architecture
CA 02917806 2016-01-08
144
that simultaneously performs node calculation (check node calculation and
variable
node calculation) by P which is the number less than the row number and column
number of the parity check matrix, as compared with a case where the node
calculation is simultaneously performed by the number equal to the row number
and
column number of the parity check matrix, it is possible to suppress the
operation
frequency within a feasible range and perform many items of iterative
decoding.
[0790]
The LDPC decoder 166 that constitutes the receiving device 12 of FIG. 207
performs the LDPC decoding by simultaneously performing P check node
operations
and variable node operations, similar to the decoding device of FIG. 213.
[0791]
That is, for the simplification of explanation, if the parity check matrix of
the
LDPC code output by the LDPC encoder 115 constituting the transmitting device
11
of FIG 8 is regarded as the parity check matrix H illustrated in FIG. 210 in
which the
parity matrix becomes a staircase structure, in the parity interleaver 23 of
the
transmitting device 11, the parity interleave to interleave the (K + qx + y +
1)-th code
bit into the position of the (K + Py + x + 1)-th code bit is performed in a
state in
which the information K is set to 60, the unit size P is set to 5, and the
divisor q (=
M/P) of the parity length M is set to 6.
[0792]
Because the parity interleave corresponds to the column replacement of the
expression (12) as described above, it is not necessary to perform the column
replacement of the expression (12) in the LDPC decoder 166.
[0793]
For this reason, in the receiving device 12 of FIG 207, as described above,
the LDPC code in which the parity deinterleave is not performed, that is, the
LDPC
code in a state in which the column replacement of the expression (12) is
performed is
supplied from the group-wise deinterleaver 55 to the LDPC decoder 166. In the
LDPC decoder 166, the same processing as the decoding device of FIG 213,
except
that the column replacement of the expression (12) is not performed, is
executed.
[0794]
That is, FIG. 214 illustrates a configuration example of the LDPC decoder
166 of FIG. 207.
CA 02917806 2016-01-08
145
[0795]
In FIG 214, the LDPC decoder 166 has the same configuration as the
decoding device of FIG. 213, except that the reception data rearranging unit
310 of
FIG. 213 is not provided, and executes the same processing as the decoding
device of
FIG. 213, except that the column replacement of the expression (12) is not
performed.
Therefore, explanation of the LDPC decoder is omitted.
[0796]
As described above, because the LDPC decoder 166 can be configured
without providing the reception data rearranging unit 310, a scale can be
decreased as
compared with the decoding device of FIG 213.
[0797]
In FIGS. 210 to 214, for the simplification of explanation, the code length N
of the LDPC code is set to 90, the information length K is set to 60, the unit
size (the
row number and the column number of the constitutive matrix) P is set to 5,
and the
divisor q (= M/P) of the parity length M is set to 6. However, the code length
N, the
information length K, the unit size P, and the divisor q (= M/P) are not
limited to the
above values.
[0798]
That is, in the transmitting device 11 of FIG 8, the LDPC encoder 115
outputs the LDPC code in which the code length N is set to 64800 or 16200, the
information length K is set to N ¨ Pq (= N ¨ M), the unit size P is set to
360, and the
divisor q is set to M/P. However, the LDPC decoder 166 of FIG 214 can be
applied
to the case in which P check node operation and variable node operations are
simultaneously performed with respect to the LDPC code and the LDPC decoding
is
performed.
[0799]
Further, when the parity portion of the decoding result is unnecessary, and
only the information bits of the decoding result are output after the decoding
of the
LDPC code by the LDPC decoder 166, the LDPC decoder 166 may be configured
without the decoded data rearranging unit 311.
[0800]
<Configuration example of block deinterleaver 54>
[0801]
CA 02917806 2016-01-08
146
FIG. 215 is a block diagram illustrating a configuration example of the block
deinterleaver 54 of FIG. 208.
[0802]
The block deinterleaver 54 has a similar configuration to the block
interleaver 25 described above with reference to FIG 105.
[0803]
Thus, the block deinterleaver 54 includes the storage region called the part 1
and the storage region called the part 2, and each of the parts 1 and 2 is
configured
such that a number C of columns equal in number to the number m of bits of the
symbol and serving as storage regions that store one bit in the row
(horizontal)
direction and store a predetermined number of bits in the column (vertical)
direction
are arranged.
[0804]
The block deinterleaver 54 performs the block deinterleave by writing the
LDPC code in the parts 1 and 2 and reading the LDPC code from the parts 1 and
2.
[0805]
However, in the block deinterleave, the writing of the LDPC code (serving as
the symbol) is performed in the order in which the LDPC code is read by the
block
interleaver 25 of FIG 105.
[0806]
Further, in the block deinterleave, the reading of the LDPC code is
performed in the order in which the LDPC code is written by the block
interleaver 25
of FIG. 105.
[0807]
In other words, in the block interleave performed by the block interleaver 25
of FIG 105, the LDPC code is written in the parts 1 and 2 in the column
direction and
read from the parts 1 and 2 in the row direction, but in the block
deinterleave
performed by the block deinterleaver 54 of FIG 215, the LDPC code is written
in the
parts 1 and 2 in the row direction and read from the parts 1 and 2 in the
column
direction.
[0808]
<Other configuration example of bit deinterleaver 165>
[0809]
CA 02917806 2016-01-08
147
FIG. 216 is a block diagram illustrating another configuration example of the
bit deinterleaver 165 of FIG 217.
[0810]
In the drawings, portions that correspond to the case of FIG. 208 are denoted
with the same reference numerals and explanation thereof is appropriately
omitted
hereinafter.
[0811]
That is, the bit deinterleaver 165 of FIG 216 has the same configuration as
the case of FIG. 208, except that a parity deinterleaver 1011 is newly
provided.
[0812]
Referring to FIG. 216, the bit deinterleaver 165 is configured with a block
deinterleaver 54, a group-wise deinterleaver 55, and a parity deinterleaver
1011, and
performs the bit deinterleave on the code bits of the LDPC code supplied from
the
demapper 164.
[0813]
In other words, the block deinterleaver 54 performs the block deinterleave
(the inverse process of the block interleave) corresponding to the block
interleave
performed by the block interleaver 25 of the transmitting device 11, that is,
the block
deinterleave of restoring the positions of the code bits rearranged by the
block
interleave to the original positions on the LDPC code supplied from the
demapper 164,
and supplies the LDPC code obtained as a result to the group-wise
deinterleaver 55.
[0814]
The group-wise deinterleaver 55 performs the group-wise deinterleave
corresponding to the group-wise interleave serving as the rearrangement
process
performed by the group-wise interleaver 24 of the transmitting device 11 on
the
LDPC code supplied from the block deinterleaver 54.
[0815]
The LDPC code that is obtained as a result of the group-wise deinterleave is
supplied from the group-wise deinterleaver 55 to the parity deinterleaver
1011.
[0816]
The parity deinterleaver 1011 performs the parity deinterleave (reverse
processing of the parity interleave) corresponding to the parity interleave
performed
by the parity interleaver 23 of the transmitting device 11, that is, the
parity
CA 02917806 2016-01-08
148
deinterleave to restore the sequence of the code bits of the LDPC code of
which a
sequence is changed by the parity interleave to the original sequence, with
respect to
the code bits after the group-wise deinterleave in the group-wise
deinterleaver 55.
[0817]
The LDPC code that is obtained as a result of the parity deinterleave is
supplied from the parity deinterleaver 1011 to the LDPC decoder 166.
[0818]
Therefore, in the bit deinterleaver 165 of FIG 216, the LDPC code in which
the block deinterleave, the group-wise deinterleave, and the parity
deinterleave are
performed, that is, the LDPC code that is obtained by the LDPC encoding
according
to the parity check matrix H is supplied to the LDPC decoder 166.
[0819]
The LDPC decoder 166 performs the LDPC decoding of the LDPC code
supplied from the bit deinterleaver 165 using the parity check matrix H used
for the
LDPC encoding by the LDPC encoder 115 of the transmitting device 11. In other
words, the LDPC decoder 166 performs the LDPC decoding of the LDPC code
supplied from the bit deinterleaver 165 using the parity check matrix H (of
the DVB
scheme) used for the LDPC encoding by the LDPC encoder 115 of the transmitting
device 11 or the transformed parity check matrix obtained by performing at
least the
column permutation corresponding to the parity interleave on the parity check
matrix
H (for the ETRI scheme, the parity check matrix (FIG. 28) obtained by
performing the
column permutation on the parity check matrix (FIG 27) used for the LDPC
encoding
or the transformed parity check matrix (FIG 29) obtained by performing the row
permutation on the parity check matrix (FIG. 27) used for the LDPC encoding).
[0820]
In FIG 216, the LDPC code that is obtained by the LDPC encoding
according to the parity check matrix H is supplied from (the parity
deinterleaver 1011
of) the bit deinterleaver 165 to the LDPC decoder 166. For this reason, when
the
LDPC decoding of the LDPC code is performed using the parity check matrix H
(of
the DVB method) itself used by the LDPC encoder 115 of the transmitting device
11
to perform the LDPC encoding (for the ETRI scheme, the parity check matrix
(FIG.
28) obtained by performing the column permutation on the parity check matrix
(FIG
27) used for the LDPC encoding), the LDPC decoder 166 can be configured by a
CA 02917806 2016-01-08
149
decoding device performing the LDPC decoding according to a full serial
decoding
method to sequentially perform operations of messages (a check node message
and a
variable node message) for each node or a decoding device performing the LDPC
decoding according to a full parallel decoding method to simultaneously (in
parallel)
perform operations of messages for all nodes.
[0821]
In the LDPC decoder 166, when the LDPC decoding of the LDPC code is
performed using the transformed parity check matrix obtained by performing at
least
the column replacement corresponding to the parity interleave with respect to
the
parity check matrix H (of the DVB method) used by the LDPC encoder 115 of the
transmitting device 11 to perform the LDPC encoding (for the ETRI scheme, the
transformed parity check matrix (FIG 29) obtained by performing the row
permutation on the parity check matrix (FIG. 27) used for the LDPC encoding),
the
LDPC decoder 166 can be configured by a decoding device (FIG. 213) that is a
decoding device of an architecture simultaneously performing P (or divisor of
P other
than 1) check node operations and variable node operations and has the
reception data
rearranging unit 310 to perform the same column replacement as the column
replacement (parity interleave) to obtain the transformed parity check matrix
with
respect to the LDPC code and rearrange the code bits of the LDPC code.
[0822]
In FIG. 216, for the sake of convenience of description, the block
deinterleaver 54 that performs the block deinterleave, the group-wise
deinterleaver 55
that performs the group-wise deinterleave, and the parity deinterleaver 1011
that
performs the parity deinterleave are configured individually, but two or more
of the
block deinterleaver 54, the group-wise deinterleaver 55, and the parity
deinterleaver
1011 may be configured integrally, similarly to the parity interleaver 23, the
group-
wise interleaver 24, and the block interleaver 25 of the transmitting device
11.
[0823]
<Configuration Example of Reception System>
[0824]
FIG. 217 is a block diagram illustrating a first configuration example of a
reception system that can be applied to the receiving device 12.
[0825]
CA 02917806 2016-01-08
150
In FIG 217, the reception system includes an acquiring unit 1101, a
transmission path decoding processing unit 1102, and an information source
decoding
processing unit 1103.
[0826]
The acquiring unit 1101 acquires a signal including an LDPC code obtained
by performing at least LDPC encoding with respect to LDPC target data such as
image data or sound data of a program, through a transmission path
(communication
path) not illustrated in the drawings, such as terrestrial digital
broadcasting, satellite
digital broadcasting, a CATV network, the Internet, or other networks, and
supplies
the signal to the transmission path decoding processing unit 1102.
[0827]
In this case, when the signal acquired by the acquiring unit 1101 is broadcast
from a broadcasting station through a ground wave, a satellite wave, or a CATV
(Cable Television) network, the acquiring unit 1101 is configured using a
tuner and an
STB (Set Top Box). When the signal acquired by the acquiring unit 1101 is
transmitted from a web server by multicasting like an IPTV (Internet Protocol
Television), the acquiring unit 1101 is configured using a network I/F
(Interface) such
as an NIC (Network Interface Card).
[0828]
The transmission path decoding processing unit 1102 corresponds to the
receiving device 12. The transmission path decoding processing unit 1102
executes
transmission path decoding processing including at least processing for
correcting
error generated in a transmission path, with respect to the signal acquired by
the
acquiring unit 1101 through the transmission path, and supplies a signal
obtained as a
result to the information source decoding processing unit 1103.
[0829]
That is, the signal that is acquired by the acquiring unit 1101 through the
transmission path is a signal that is obtained by performing at least error
correction
encoding to correct the error generated in the transmission path. The
transmission
path decoding processing unit 1102 executes transmission path decoding
processing
such as error correction processing, with respect to the signal.
[0830]
As the error correction encoding, for example, LDPC encoding or BCH
CA 02917806 2016-01-08
151
encoding exists. In this case, as the error correction encoding, at least the
LDPC
encoding is performed.
[0831]
The transmission path decoding processing includes demodulation of a
modulation signal.
[0832]
The information source decoding processing unit 1103 executes information
source decoding processing including at least processing for extending
compressed
information to original information, with respect to the signal on which the
transmission path decoding processing is executed.
[0833]
That is, compression encoding that compresses information may be
performed with respect to the signal acquired by the acquiring unit 1101
through the
transmission path to decrease a data amount of an image or a sound
corresponding to
information. In this case, the information source decoding processing unit
1103
executes the information source decoding processing such as the processing
(extension processing) for extending the compressed information to the
original
information, with respect to the signal on which the transmission path
decoding
processing is executed.
[0834]
When the compression encoding is not performed with respect to the signal
acquired by the acquiring unit 1101 through the transmission path, the
processing for
extending the compressed information to the original information is not
executed in
the information source decoding processing unit 1103.
[0835]
In this case, as the extension processing, for example, MPEG decoding exists.
In the transmission path decoding processing, in addition to the extension
processing,
descramble may be included.
[0836]
In the reception system that is configured as described above, in the
acquiring unit 1101, a signal in which the compression encoding such as the
MPEG
encoding and the error correction encoding such as the LDPC encoding are
performed
with respect to data such as an image or a sound is acquired through the
transmission
CA 02917806 2016-01-08
152
path and is supplied to the transmission path decoding processing unit 1102.
[0837]
In the transmission path decoding processing unit 1102, the same processing
as the receiving device 12 executes as the transmission path decoding
processing with
respect to the signal supplied from the acquiring unit 1101 and a signal
obtained as a
result is supplied to the information source decoding processing unit 1103.
[0838]
In the information source decoding processing unit 1103, the information
source decoding processing such as the MPEG decoding is executed with respect
to
the signal supplied from the transmission path decoding processing unit 1102
and an
image or a sound obtained as a result is output.
[0839]
The reception system of FIG 217 described above can be applied to a
television tuner to receive television broadcasting corresponding to digital
broadcasting.
[0840]
Each of the acquiring unit 1101, the transmission path decoding processing
unit 1102, and the information source decoding processing unit 1103 can be
configured as one independent device (hardware (IC (Integrated Circuit) and
the like)
or software module).
[0841]
With respect to the acquiring unit 1101, the transmission path decoding
processing unit 1102, and the information source decoding processing unit
1103, each
of a set of the acquiring unit 1101 and the transmission path decoding
processing unit
1102, a set of the transmission path decoding processing unit 1102 and the
information source decoding processing unit 1103, and a set of the acquiring
unit
1101, the transmission path decoding processing unit 1102, and the information
source decoding processing unit 1103 can be configured as one independent
device.
[0842]
FIG. 218 is a block diagram illustrating a second configuration example of
the reception system that can be applied to the receiving device 12.
[0843]
In the drawings, portions that correspond to the case of FIG. 217 are denoted
CA 02917806 2016-01-08
153
with the same reference numerals and explanation thereof is appropriately
omitted
hereinafter.
[0844]
The reception system of FIG 218 is common to the case of FIG. 217 in that
the acquiring unit 1101, the transmission path decoding processing unit 1102,
and the
information source decoding processing unit 1103 are provided and is different
from
the case of FIG. 217 in that an output unit 1111 is newly provided.
[0845]
The output unit 1111 is a display device to display an image or a speaker to
output a sound and outputs an image or a sound corresponding to a signal
output from
the information source decoding processing unit 1103. That is, the output unit
1111
displays the image or outputs the sound.
[0846]
The reception system of FIG 218 described above can be applied to a TV
(television receiver) receiving television broadcasting corresponding to
digital
broadcasting or a radio receiver receiving radio broadcasting.
[0847]
When the compression encoding is not performed with respect to the signal
acquired in the acquiring unit 1101, the signal that is output by the
transmission path
decoding processing unit 1102 is supplied to the output unit 1111.
[0848]
FIG 219 is a block diagram illustrating a third configuration example of the
reception system that can be applied to the receiving device 12.
[0849]
In the drawings, portions that correspond to the case of FIG. 217 are denoted
with the same reference numerals and explanation thereof is appropriately
omitted
hereinafter.
[0850]
The reception system of FIG 219 is common to the case of FIG 217 in that
the acquiring unit 1101 and the transmission path decoding processing unit
1102 are
provided.
[0851]
However, the reception system of FIG 219 is different from the case of FIG.
CA 02917806 2016-01-08
154
217 in that the information source decoding processing unit 1103 is not
provided and
a recording unit 1121 is newly provided.
[0852]
The recording unit 1121 records (stores) a signal (for example, TS packets of
TS of MPEG) output by the transmission path decoding processing unit 1102 on
recording (storage) media such as an optical disk, a hard disk (magnetic
disk), and a
flash memory.
[0853]
The reception system of FIG. 219 described above can be applied to a
recorder that records television broadcasting.
[0854]
In FIG 219, the reception system is configured by providing the information
source decoding processing unit 1103 and can record the signal obtained by
executing
the information source decoding processing by the information source decoding
processing unit 1103, that is, the image or the sound obtained by decoding, by
the
recording unit 1121.
[0855]
<Embodiment of Computer>
[0856]
Next, the series of processing described above can be executed by hardware
or can be executed by software. In the case in which the series of processing
is
executed by the software, a program configuring the software is installed in a
general-
purpose computer.
[0857]
Therefore, FIG 220 illustrates a configuration example of an embodiment of
the computer in which a program executing the series of processing is
installed.
[0858]
The program can be previously recorded on a hard disk 705 and a ROM 703
corresponding to recording media embedded in the computer.
[0859]
Alternatively, the program can be temporarily or permanently stored
(recorded) on removable recording media 711 such as a flexible disk, a CD-ROM
(Compact Disc Read Only Memory), an MO (Magneto Optical) disk, a DVD (Digital
CA 02917806 2016-01-08
155
Versatile Disc), a magnetic disk, and a semiconductor memory. The removable
recording media 711 can be provided as so-called package software.
[0860]
The program is installed from the removable recording media 711 to the
computer. In addition, the program can be transmitted from a download site to
the
computer by wireless through an artificial satellite for digital satellite
broadcasting or
can be transmitted to the computer by wire through a network such as a LAN
(Local
Area Network) or the Internet. The computer can receive the program
transmitted as
described above by a communication unit 708 and install the program in the
embedded hard disk 705.
[0861]
The computer includes a CPU (Central Processing Unit) 702 embedded
therein. An input/output interface 710 is connected to the CPU 702 through a
bus
701. If a user operates an input unit 707 configured using a keyboard, a
mouse, and
a microphone and a command is input through the input/output interface 710,
the
CPU 702 executes the program stored in the ROM (Read Only Memory) 703,
according to the command. Alternatively, the CPU 702 loads the program stored
in
the hard disk 705, the program transmitted from a satellite or a network,
received by
the communication unit 708, and installed in the hard disk 705, or the program
read
from the removable recording media 711 mounted to a drive 709 and installed in
the
hard disk 705 to the RAM (Random Access Memory) 704 and executes the program.
Thereby, the CPU 702 executes the processing according to the flowcharts
described
above or the processing executed by the configurations of the block diagrams
described above. In addition, the CPU 702 outputs the processing result from
the
output unit 706 configured using an LCD (Liquid Crystal Display) or a speaker,
transmits the processing result from the communication unit 708, and records
the
processing result on the hard disk 705, through the input/output interface
710,
according to necessity.
[0862]
In the present specification, it is not necessary to process the processing
steps
describing the program for causing the computer to execute the various
processing in
time series according to the order described as the flowcharts and processing
executed
in parallel or individually (for example, parallel processing or processing
using an
CA 02917806 2016-01-08
156
object) is also included.
[0863]
The program may be processed by one computer or may be processed by a
plurality of computers in a distributed manner. The program may be transmitted
to a
remote computer and may be executed.
[0864]
An embodiment of the disclosure is not limited to the embodiments
described above, and various changes and modifications may be made without
departing from the scope of the disclosure.
[0865]
That is, for example, (the parity check matrix initial value table of) the
above-described new LDPC code can be used even if the communication path 13
(FIG
7) is any of a satellite circuit, a ground wave, a cable (wire circuit) and
others. In
addition, the new LDPC code can also be used for data transmission other than
digital
broadcasting.
[0866]
The GW patterns can be applied to a code other than the new LDPC code.
Further, the modulation scheme to which the GW patterns are applied is not
limited to
QPSK, 16QAM, 64QAM, 256QAM, 1024QAM, and 4096QAM.
[0867]
The effects described in this specification are merely examples and not
limited, and any other effect may be obtained.
Reference Signs List
[0868]
11 transmitting device
12 receiving device
23 parity interleaver
24 group-wise interleaver
25 block interleaver
54 block deinterleaver
55 group-wise deinterleaver
111 mode adaptation/multiplexer
CA 02917806 2016-01-08
157
112 padder
113 BB scrambler
114 BCH encoder
115 LDPC encoder
116 bit interleaver
117 mapper
118 time interleaver
119 SISO/MISO encoder
120 frequency interleaver
121 BCH encoder
122 LDPC encoder
123 mapper
124 frequency interleaver
131 frame builder/resource allocation unit
132 OFDM generating unit
151 OFDM operating unit
152 frame managing unit
153 frequency deinterleaver
154 demapper
155 LDPC decoder
156 BCH decoder
161 frequency deinterleaver
162 SISO/MISO decoder
163 time deinterleaver
164 demapper
165 bit deinterleaver
166 LDPC decoder
167 BCH decoder
168 BB descrambler
169 null deletion unit
170 demultiplexer
300 branch data storing memory
301 selector
CA 02917806 2016-01-08
158
302 check node calculating unit
303 cyclic shift circuit
304 branch data storing memory
305 selector
306 reception data memory
307 variable node calculating unit
308 cyclic shift circuit
309 decoding word calculating unit
310 reception data rearranging unit
311 decoded data rearranging unit
601 encoding processing unit
602 storage unit
611 encoding rate setting unit
612 initial value table reading unit
613 parity check matrix generating unit
614 information bit reading unit
615 encoding parity operation unit
616 control unit
701 bus
702 CPU
703 ROM
704 RAM
705 hard disk
706 output unit
707 input unit
708 communication unit
709 drive
710 input/output interface
711 removable recording media
1001 reverse interchanging unit
1002 memory
1011 parity deinterleaver
1101 acquiring unit
CA 02917806 2016-01-08
159
1101 transmission path decoding processing unit
1103 information source decoding processing unit
1111 output unit
1121 recording unit