TRANSMITTING APPARATUS AND INTERLEAVING METHOD THEREOF

APPAREIL D'EMISSION ET SON PROCEDE D'ENTRELACEMENT

English Abstract

A transmitting apparatus is provided. The transmitting apparatus includes: an encoder configured to generate a low-density parity check (LDPC) codeword by LDPC encoding based on a parity check matrix; an interleaver configured to interleave the LDPC codeword; and a modulator configured to map the interleaved LDPC codeword onto a modulation symbol, wherein the modulator is further configured to map a bit included in a predetermined bit group from among a plurality of bit groups constituting the LDPC codeword onto a predetermined bit of the modulation symbol.

French Abstract

L'invention concerne un appareil d'émission. L'appareil d'émission comprend: un codeur configuré pour générer un mot de code avec vérification de parité à basse densité (LDPC) par codage LDPC basé sur une matrice de vérification de parité; un entrelaceur configuré pour entrelacer le mot de code LDPC; et un modulateur configuré pour faire correspondre le mot de code LDPC entrelacé à un symbole de modulation, le modulateur étant en outre configuré pour faire correspondre un bit compris dans un groupe prédéterminé bits parmi une pluralité de groupes de bits constituant le mot de code LDPC à un bit prédéterminé du symbole de modulation.

Claims

89
[CLAIMS]
1. A transmitting apparatus comprising:
an encoder configured to encode input bits to generate parity bits based on a
low density
parity check (LDPC) code according to a code rate of 6/15 and a code length of
64800;
an interleaver configured to interleave the parity bits, split a codeword into
a plurality of
bit groups, and interleave the plurality of bit groups to provide an
interleaved codeword, wherein
the codeword comprising the input bits and the interleaved parity bits; and
a mapper configured to map bits of the interleaved codeword onto constellation
points for
16-quadrature amplitude modulation(QAM),
wherein the plurality of bit groups are interleaved based on a following
equation:
Y j = X .pi.(j) for (0.ltoreq.j< N group)
where X j is a j th bit group among the plurality of bit groups, Y j is a j th
bit group among the
interleaved plurality of bit groups, N group is a total number of the
plurality of bit groups, and .pi.(j)
denotes a permutation order for the interleaving of the plurality of bit
groups, and
wherein the .pi.(j) is defined as follows:
<IMG>

90
2. The transmitting apparatus of claim 1, wherein each of the plurality of bit
groups
comprises 360 bits.

Description

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
1
[DESCRIPTION]
[Invention Title]
TRANSMITTING APPARATUS AND INTERLEAVING METHOD THEREOF
[Technical Field]
Apparatuses and methods consistent with exemplary embodiments relate to a
transmitting
apparatus and an interleaving method thereof, and more particularly, to a
transmitting apparatus
which processes and transmits data, and an interleaving method thereof.
[Background Art]
In the 21st century information-oriented society, broadcasting communication
services are
moving into the era of digitalization, multi-channel, wideband, and high
quality. In particular, as
high quality digital televisions, portable multimedia players and portable
broadcasting equipment
are increasingly used in recent years, there is an increasing demand for
methods for supporting
various receiving methods of digital broadcasting services.
In order to meet such demand, standard groups are establishing various
standards and are
providing a variety of services to satisfy users' needs. Therefore, there is a
need for a method for
providing improved services to users with high decoding and receiving
performance.
[Disclosure]
[Technical Problem]
Exemplary embodiments of the inventive concept may overcome the above
disadvantages
and other disadvantages not described above. However, it is understood that
the exemplary
embodiment are not required to overcome the disadvantages described above, and
may not
overcome any of the problems described above.
The exemplary embodiments provide a transmitting apparatus which can map a bit
included
in a predetermined bit group from among a plurality of bit groups of a low
density parity check
(LDPC) codeword onto a predetermined bit of a modulation symbol, and transmit
the bit, and an
interleaving method thereof.
[Technical Solution]
According =to an aspect of an exemplary embodiment, there is provided a
transmitting
apparatus incluidng: an encoder configured to generate an LDPC codeword by
LDPC encoding

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
2
based on a parity check matrix; an interleaver configured to interleave the
LDPC codeword; and
a modulator configured to map the interleaved LDPC codeword onto a modulation
symbol,
wherein the modulator is further configured to map a bit included in a
predetermined bit group
from among a plurality of bit groups constituting the LDPC codeword onto a
predetermined bit
of the modulation symbol.
Each of the plurality of bit groups may be formed of M number of bits. M may
be a common
divisor of NUN and &ape and may be determined to satisfy Q1dpc=(1\11dpc-
K1dpc)/M. In this case,
Qidpc may be a cyclic shift parameter value regarding columns in a column
group of an
information word submatrix of the parity check matrix, Nidpc may be a length
of the LDPC
codeword, and Kidp, may be a length of information word bits of the LDPC
codeword.
The interleaver may include: a parity interleaver configured to interleave
parity bits of the
LDPC codeword; a group interleaver configured to divide the parity-interleaved
LDPC
codeword by the plurality of bit groups and rearrange an order of the
plurality of bit groups in bit
group wise; and a block interleaver configured to interleave the plurality of
bit groups the order
of which is rearranged.
The group interleaver may be configured to rearrange the order of the
plurality of bit groups
in bit group wise by using the following equation:
=X)(0 j < Nrour )
where Xj is a jth bit group before the plurality of bit groups are
interleaved, Yj is a jth bit group
after the plurality of bit groups are interleaved, Ngroup is a total number of
the plurality of bit
groups, and N(j) is a parameter indicating an interleaving order.
Here, it(j) may be determined based on at least one of a length of the LDPC
codeword, a
modulation method, and a code rate.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 6/15, n(j) may be defined as in table 11.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 10/15, n(j) may be defined as in table 14.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 12/15, Ic(j) may be defined as in table 15.
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 6/15, n(j) may be defined as in table 17.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
3
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 8/15, 7r(j) may be defined as in table 18.
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 12/15, 7r(j) may be defined as in table 21.
The block interleaver may be configured to interleave by writing the plurality
of bit groups in
each of a plurality of columns in bit group wise in a column direction, and
reading each row of
the plurality of columns in which the plurality of bit groups are written in
bit group wise in a row
direction.
The block interleaver may be configured to serially write, in the plurality of
columns, at least
some bit groups which are writable in the plurality of columns in bit group
wise from among the
plurality of bit groups, and then divide and write the other bit groups in an
area which remains
after the at least some bit groups are written in the plurality of columns in
bit group wise.
According to an aspect of another exemplary embodiment, there is provided an
interleaving
method of a transmitting apparatus, including: generating an LDPC codeword by
LDPC
encoding based on a parity check matrix; interleaving the LDPC codeword; and
mapping the
interleaved LDPC codeword onto a modulation symbol, wherein the mapping
comprises
mapping a bit included in a predetermined bit group from among a plurality of
bit groups
constituting the LDPC codeword onto a predetermined bit of the modulation
symbol.
Each of the plurality of bit groups may be formed of M number of bits, and M
may be a
common divisor of Nidpc and Kid and may be determined to satisfy Qmpc=(Nbipc-
Kidpc)/M. In this
case, Qidpc may be a cyclic shift parameter value regarding columns in a
column group of an
information word submatrix of the parity check matrix, Nidp, may be a length
of the LDPC
codeword, and Kid may be a length of information word bits of the LDPC
codeword.
The interleaving may include: interleaving parity bits of the LDPC codeword;
dividing the
parity-interleaved LDPC codeword by the plurality of bit groups and
rearranging an order of the
plurality of bit groups in bit group wise; and interleaving the plurality of
bit groups the order of
which is rearranged.
The rearranging in bit group wise may include rearranging the order of the
plurality of bit
groups in bit group wise by using the following equation:
171 =X( J)(0 j < N
group
where Xj is a jth bit group before the plurality of bit groups are
interleaved, Yi is a ith bit group

4
after the plurality of bit groups are interleaved, Ngroup is a total number of
the plurality of bit
groups, and ir(j) is a parameter indicating an interleaving order.
Here, 7r(j) may be determined based on at least one of a length of the LDPC
codeword, a
modulation method, and a code rate.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 6/15, 7r(j) may be defined as in table 11.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 10/15, m(j) may be defined as in table 14.
When the LDPC codeword has a length of 64800, the modulation method is 16-QAM,
and
the code rate is 12/15, 7r(j) may be defined as in table 15.
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 6/15, m(j) may be defined as in table 17.
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 8/15, it(j) may be defined as in table 18.
When the LDPC codeword has a length of 64800, the modulation method is 64-QAM,
and
the code rate is 12/15, rr(j) may be defined as in table 21.
The interleaving the plurality of bit groups may include interleaving by
writing the plurality
of bit groups in each of a plurality of columns in bit group wise in a column
direction, and
reading each row of the plurality of columns in which the plurality of bit
groups are written in bit
group wise in a row direction.
The interleaving the plurality of bit groups may include serially writing, in
the plurality of
columns, at least some bit groups which are writable in the plurality of
columns in bit group wise
from among the plurality of bit groups, and then dividing and writing the
other bit groups in an
area which remains after the at least some bit groups are written in the
plurality of columns in bit
group wise.
According to an embodiment, there is provided a transmitting apparatus
comprising: an
encoder configured to encode input bits to generate parity bits based on a low
density parity
check (LDPC) code according to a code rate of 6/15 and a code length of 64800;
an interleaver
configured to interleave the parity bits, split a codeword into a plurality of
bit groups, and
interleave the plurality of bit groups to provide an interleaved codeword,
wherein the codeword
comprising the input bits and the interleaved parity bits; and a mapper
configured to map bits of
the interleaved codeword onto constellation points for 16-quadrature amplitude
CA 2940011 2017-07-27

4a
modulation(QAM), wherein the plurality of bit groups are interleaved based on
a following
Y = X,r0) for =th
equation: (0 j < Ng'""P) , where Xj is a 3 bit group among the
plurality of bit
groups, Yj is a =th bit group among the interleaved plurality of bit groups,
Ngroup is a total number
of the plurality of bit groups, and n(j) denotes a permutation order for the
interleaving of the
plurality of bit groups, and wherein the z(j) is defined as follows:
Order of interleaving
n(j) (0 j <180)
2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22
23 24 25 26 27 28 29 30 31 32 33 34
35 36 37 38 39 40 41 42 43 44 45
Code Rate 46 47 48 49 50 51 52 53 54 55 56
57 58 59 60 0) 62 61 64 65 66 07 66
69 70 71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90 91
92 93 94 95 96 97 98 99 100 101 102
103 104 105 106 107 108 109 110 III 112 113
114
115 116 117 118 119 120 121 122 123 124
125 126 127 128 129 130 131 132 133 134 135
136 137
138 139 140 141 142 143 144 145 146 147
148 149 150 151 152 153 154 155 156 157 158
159 160
161 162 161 164 165 160 167 168 169 170
171 172 171 174 175 176 177 178 179
55 146 83 52 62 176 100 68 53 56 81 97 79 113 163 61 58 69 133 108 66 71 86
144 57 67 116 59 70 156 172 65 149 155
82 138 136 141 III 90 170 90 140 64 159 15
14 37 54 44 63 43 18 47 7 25 34 29
30 26 39 16 41 45 36 0 23 32 28
27 38 48 33 22 49 51 60 46 21 4 3 20 13 50 35 24 40 17 42 0 112 93
6/15 7r(i)
127 101 94 115 105 31 19 177 74 10 145
162 102 120 126 95 73 152 129 174 125 72 128
78 171 8 142 178 154 85 107 75 12 9
151 77 117 109 80 106 134 98 I 122 173 161
150 110 175 166 131 119 103 139 148 157
114 147 87 158 121 164 104 89 179 123 118 99
88
II 92 165 84 168 124 169 2 130 167 153
137 143 91 100 5 76 132 135
[Advantageous Effects]
According to various exemplary embodiments, improved decoding and receiving
performance can be provided.
[Description of Drawings]
The above and/or other aspects will be more apparent by describing in detail
exemplary
embodiments, with reference to the accompanying drawings, in which:
CA 2940011 2017-07-27

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
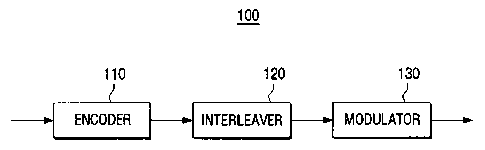
FIG. 1 is a block diagram to illustrate a configuration of a transmitting
apparatus, according
to an exemplary embodiment;
FIGs. 2 to 4 are views to illustrate a configuration of a parity check matrix,
according to
exemplary embodiments;
FIG. 5 is a block diagram to illustrate a configuration of an interleaver,
according to an
exemplary embodiment;
FIGs. 6 to 8 are views to illustrate an interleaving method, according to
exemplary
embodiments;
FIGs. 9 to 14 are views to illustrate an interleaving method of a block
interleaver, according
to exemplary embodiments;
FIG. 15 is a view to illustrate an operation of a demultiplexer, according to
an exemplary
embodiment;
FIGs. 16 and 17 are views to illustrate a method for designing an interleaving
pattern,
according to exemplary embodiments;
FIG. 18 is a block diagram to illustrate a configuration of a receiving
apparatus according to
an exemplary embodiment;
FIG. 19 is a block diagram to illustrate a configuration of a deinterleaver,
according to an
exemplary embodiment;
FIG. 20 is a view to illustrate a deinterleaving method of a block
deinterleaver, according to
an exemplary embodiment; and
FIG. 21 is a flowchart to illustrate an interleaving method, according to an
exemplary
embodiment.
[Mode for Invention]
Hereinafter, various exemplary embodiments will be described in greater detail
with reference
to the accompanying drawings.
In the following description, same reference numerals are used for the same
elements when
they are depicted in different drawings. The matters defined in the
description, such as detailed
construction and elements, are provided to assist in a comprehensive
understanding of the
exemplary embodiments. Thus, it is apparent that the exemplary embodiments can
be carried out
without those specifically defined matters. Also, functions or elements known
in the related art
are not described in detail since they would obscure the exemplary embodiments
with

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
6
unnecessary detail.
FIG. 1 is a block diagram to illustrate a configuration of a transmitting
apparatus according to
an exemplary embodiment. Referring to FIG. 1, the transmitting apparatus 100
includes an
encoder 110, an interleaver 120, and a modulator 130 (or a constellation
mapper).
The encoder 110 generates a low density parity check (LDPC) codeword by
performing
LDPC encoding based on a parity check matrix. To achieve this, the encoder 110
may include an
LDPC encoder (not shown) to perform the LDPC encoding.
Specifically, the encoder 110 LDPC-encodes information word(or information)
bits to
generate the LDPC codeword which is formed of information word bits and parity
bits (that is,
LDPC parity bits). Here, bits input to the encoder 110 may be used as the
information word bits.
Also, since an LDPC code is a systematic code, the information word bits may
be included in the
LDPC codeword as they are.
The LDPC codeword is formed of the information word bits and the parity bits.
For example,
the LDPC codeword is formed of Nidp, number of bits, and includes Ickipc
number of information
word bits and Nparity=N1dpc-K1dpc number of parity bits.
In this case, the encoder 110 may generate the LDPC codeword by performing the
LDPC
encoding based on the parity check matrix. That is, since the LDPC encoding is
a process for
generating an LDPC codeword to satisfy II- CT=0, the encoder 110 may use the
parity check
matrix when performing the LDPC encoding. Herein, H is a parity check matrix
and C is an
LDPC codeword.
For the LDPC encoding, the transmitting apparatus 100 may include a memory and
may pre-
store parity check matrices of various formats.
For example, the transmitting apparatus 100 may pre-store parity check
matrices which are
defined in Digital Video Broadcasting-Cable version 2 (DVB-C2), Digital Video
Broadcasting-
Satellite-Second Generation (DVB-S2), Digital Video Broadcasting-Second
Generation
Terrestrial (DVB-T2), etc., or may pre-store parity check matrices which are
defined in the North
America digital broadcasting standard system Advanced Television System
Committee (ATSC)
3.0 standards, which are currently being established. However, this is merely
an example and the
transmitting apparatus 100 may pre-store parity check matrices of other
formats in addition to
these parity check matrices.
Hereinafter, a parity check matrix according to various exemplary embodiments
will be

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
7
explained in detail with reference to the drawings. In the parity check
matrix, elements other than
elements having 1 have 0.
For example, the parity check matrix according to an exemplary embodiment may
have a
configuration of FIG. 2.
Referring to FIG. 2, a parity check matrix 200 is formed of an information
word submatrix(or
an information submatrix) 210 corresponding to information word bits, and a
parity submatrix
220 corresponding to parity bits.
The information word submatrix 210 includes Kkipc number of columns and the
parity
submatrix 220 includes Nparity=Nidpc-Kidpc number of columns. The number of
rows of the parity
check matrix 200 is identical to the number of columns of the parity submatrix
220, Nparity=N1d13c"
Kldpc=
In addition, in the parity check matrix 200, NIdpc is a length of an LDPC
codeword, Kldpc is a
length of information word bits, and Nparity=Nidpc-Kidpc is a length of parity
bits. The length of the
LDPC codeword, the information word bits, and the parity bits mean the number
of bits included
in each of the LDPC codeword, the information word bits, and the parity bits.
Hereinafter, the configuration of the information word submatrix 210 and the
parity
submatrix 220 will be explained in detail.
The information word submatrix 210 includes Kid number of columns (that is,
0th column to
(lcdpc-1)th column), and follows the following rules:
First, M number of columns from among Kid number of columns of the information
word
submatrix 210 belong to the same group, and Kid number of columns is divided
into Kkipc/M
number of column groups. In each column group, a column is cyclic-shifted from
an
immediately previous column by Qldpc. That is, Qicipc may be a cyclic shift
parameter value
regarding columns in a column group of the information word submatrix 210 of
the parity check
matrix 200.
Herein, M is an interval at which a pattern of a column group, which includes
a plurality of
columns, is repeated in the information word submatrix 210 (e.g., M=360), and
Qicipc is a size by
which one column is cyclic-shifted from an immediately previous column in a
same column
group in the information word submatrix 210. Also, M is a common divisor of
I=1Idp, and Kid and
is determined to satisfy Qtapc=(Ntapc-Kidpc)/M. Here, M and Qmpc are integers
and Kidpc/M is also
an integer. M and Qtdp, may have various values according to a length of the
LDPC codeword

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
8
and a code rate (CR)(or, coding rate).
For example, when M=360 and the length of the LDPC codeword, Nidpc, is 64800,
Qidpc may
be defined as in table 1 presented below, and, when M=360 and the length
I=Tidpc of the LDPC
codeword is 16200, Qmp, may be defined as in table 2 presented below.
[Table 1]
Code Rate Nidpc M Qldpc
5/15 64800 360 120
6/15 64800 360 108
7/15 64800 360 96
8/15 64800 360 84
9/15 64800 360 72
10/15 64800 360 60
11/15 64800 360 48
12/15 64800 360 36
13/15 64800 360 24
[Table 2]
Code Rate NIdoc M Qldpc
5/15 16200 360 30
6/15 16200 360 27
7/15 16200 360 24
8/15 16200 360 21
9/15 16200 360 18
10/15 16200 360 15
11/15 16200 360 12
12/15 16200 360 9
13/15 16200 360 6
Second, when the degree of the 0th column of the ith column group (i=0, 1,
..., Kidpc/M-1) is D,
(herein, the degree is the number of value 1 existing in each column and all
columns belonging
to the same column group have the same degree), and a position (or an index)
of each row where
1 exists in the 0th column of the ith column group is RP0),R,(1c)õ- = =,Ri(Do'-
') , an index Ri(kj) of a row
where kth 1 is located in the jth column in the ith column group is determined
by following
Equation 1:
kkj) =k4()1_1) + a/pc mod(NidPc ¨K )
idPc ... (1),
where k=0, 1,2, ...D1-1; i=0, 1, ..., K1dpc/M-1; and j=1, 2, ..., M-1.
Equation 1 can be expressed as following Equation 2:

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
9
IC ¨irko)
+ jmodM)x adpc} mod(Nktp, ¨ Kidpc) . . . (2),
where k=0, 1,2, ...Di-1; 1=0, 1, ..., K1dpe/M-1; and j=1, 2, ..., M-1. Since
j=1, 2, ..., M-1, (j
mod M) of Equation 2 may be regarded as j.
In the above equations, Ri(ki) is an index of a row where le 1 is located in
the ith column in the
-th
column group, NIdpc is a length of an LDPC codeword, Kidpc is a length of
information word
bits, Di is a degree of columns belonging to the ith column group, M is the
number of columns
belonging to a single column group, and Qldpc is a size by which each column
in the column
group is cyclic-shifted.
As a result, referring to these equations, when only Ri(,k0) is known, the
index Ri(kj) of the row
where the kth 1 is located in the jth column in the ith column group can be
known. Therefore,
when the index value of the row where the kth 1 is located in the 0th column
of each column
group is stored, a position of column and row where 1 is located in the parity
check matrix 200
having the configuration of FIG. 2 (that is, in the information word submatrix
210 of the parity
check matrix 200) can be known.
According to the above-described rules, all of the columns belonging to the
ith column group
have the same degree Di. Accordingly, the LDPC codeword which stores
information on the
parity check matrix according to the above-described rules may be briefly
expressed as follows.
For example, when Nidpc is 30, Kldpc is 15, and Qicipc is 3, position
information of the row
where 1 is located in the Oth column of the three column groups may be
expressed by a sequence
of Equations 3 and may be referred to as "weight-1 position sequence".
R1( =1, R20) = 2, R1(30) = 8,R1(40) = 10,
1:41)0 ¨0, M.2?) ¨9, R = 13,
= = 14.
(3),
where Ri(kj) is an index of a row where kth 1 is located in the ith column in
the ith column group.
The weight-1 position sequence like Equation 3 which expresses an index of a
row where 1 is
located in the Oth column of each column group may be briefly expressed as in
Table 3 presented
below:
[Table 3]

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
1 2810
0 9 13
. 014
Table 3 shows positions of elements having value 1 in the parity check matrix,
and the ith
weight-1 position sequence is expressed by indexes of rows where 1 is located
in the Oth column
belonging to the ith column group.
The information word submatrix 210 of the parity check matrix according to an
exemplary
embodiment may be defined as in Tables 4 to 8 presented below, based on the
above descriptions.
Specifically, Tables 4 to 8 show indexes of rows where 1 is located in the 0th
column of the ith
column group of the information word submatrix 210. That is, the information
word submatrix
210 is formed of a plurality of column groups each including M number of
columns, and
positions of 1 in the Oth column of each of the plurality of column groups may
be defined by
Tables 4 to 8.
Herein, the indexes of the rows where 1 is located in the 0th column of the
ith column group
mean "addresses of parity bit accumulators". The "addresses of parity bit
accumulators" have the
same meaning as defined in the DVB-C2/S2/T2 standards or the ATSC 3.0
standards which are
currently being established, and thus, a detailed explanation thereof is
omitted.
For example, when the length Nicipc of the LDPC codeword is 64800, the code
rate is 6/15,
and M is 360, the indexes of the rows where 1 is located in the Oth column of
the ith column group
of the information word submatrix 210 are as shown in Table 4 presented below:
[Table 4]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
11
i Index Of row where 1 is lacatecii cotiiiim Of ifililth,Tafuom group.
_ . õ
0 1606 3402 4961 6951 7132 11516 12300 12482 12592 13342 13764 14123 21576
23946 24533 25376 25667 26636 31799 34193
35462 36153 36740 37035 37152 37468 37658
1 4621 5007 5910 5732 9757 11.508 13099 15513 26335 18052 19512 21319
2366325628.27208 31333 32219 33003 33239 33447
36200 36473 36938 37201 37283 37495 38642
2 16 1094 2020 3080 4194 5098 5631 6877 7889 8237 9304 10067 21017 11366
13136 13354 15379 18934 20199 24522 26172
28666 30336 3271426390 37015 37162
- - .
3 700 897 1708 6017 6490 7372 7825 9546 10398 16605 18561 18745 21625 22137
23693 24340 24966 25015 26995 28586 28895
,296137 3'3638 3452034358 37056 38297
4 159 201D 2573 3617 4452 4958 5556 5832 6481 8227 9924 10835 14954 15594
16623 18065 19249 22394 22677 23408 23731
24076 24776 27007 28222 30343 38371
3118 3545 4768 4992 5227 6732 8170 9397 10522 11508 15536 20218 21921 28599
29445 29758 29968 31014 32027 33685
34378 35867 36323 36729 3687638335 18623
6 1264 4254 6936 9165 9486 9950 10861 11653 1.3697 13961 15164 15665 18444
19470 20313 21189 24371 26431 26999 28086
28251 29261 31991 34015 35850 36129 37186
7 = 111 1307 1628 2041. 1524 5353 7988 8191 16122 11905 12919 14127 15515
15711. 17061 19024 21195 12902 8727 24401
24608 25111 2522827338 35398 37794 38196
3 961 3085 7174 7948 13355 13607 14971 18189 18339 286E6 13875 19142 20615
21136 21309 21758 23366 24745 25849 25982
27583 30006 31118, 3210636460 i6sea 37920
9 2690 3549 4273 4808 5707 6021 6509 7456 8240 10044 12262 12660 13085
14750 15680 16049 21587 23097 25.303 26343
28693 34393 34860 35490 36021 37737 38296
955 4323 51.45 6835 8123 9730 11840 12216 19134 20313 23056 24148 24830 25268
26617 26801 28557 29753 30745 31450
31973 32839 33025 33296 35710 37366 37509
11 264 605 4181 4483 5156 7238 8863 10939 11251 12964 16254 17511 20017
22395 22818 23261 23422 24064 26329 27723
- 28186 30434 31956 33971 34372 36764 38123
12 520 2562 2794 3528 3860 4402 5676 6963 8555 9018 9783 11933 16336 17193
17320 19035 20606 23579 23769 24123 24966
27866 32457 34011 34499 36620 37526 _
13 10106 10637 10906 34242
14 1856 15100 19378 21348
, 943 11191 2780629411
_
16 4575 6359 13629 19383
. õ.
17 4476 4953 18782 24313
18 5441. 6381 21840 35943
19 9538 976312543 30120
.9587 W626 11047 25700
! 21 4088 15298 28768 35047
22 2332 6363 8782 26863 .
23 - 4625 4933 28293 30289
24 3541 491818257 31746

CA 02940011 2016-08-17
WO 2015/126194 PC T/KR20 15/00 1695
12
25 1221 25233 25757 34892
26 8150 15677 27934 30021
27 850225015 33043 38070
28 7374 10207 16189 35811
29 611 18480 20064 38251
30 25416 27352 36089 38469
31 1667 17614 25839 32776
32 4118 12481 21912 32945
33 5573 13222 23519 31271
34 18.271 26251 27182 30587
35 14690 26430 26799 34355
36 13688 16040 20716 34558
37 2740 14957 23436 32540
38 3491 14365 14581 36858
39 4295 6238 25203 27854
40 1732 12816 17344 25025
41 19182 21552 23742 27872
42 6502 13641 17509 34713
43 12246 12372 15745 27452
44 1589 21$28 30621 34003
45 12328 20525 30551 31432
46 3415 22555 23427 35395
47 632 5209 25958 31085
48 6193650 19648 37778
49 9528 13581 26965 38447
50 2147 26249 26968 28776
51 1569818209 30683
52 1132 1988834111
53 4508 25513 38874
54 475 1729 34100
55 7348 32277 38587
56 182 16473 33082
57 3855 9678 21265
58 444710151 27618
59 6335 14371 38711
60 704 9595 28858
61 41669757 30546
62 1993 19361 30732
63 756 20300 29138
64 3821 24075 31813
65 4611 12326 32291
66 7628 21515 34995
67 1246 13294 30068
68 6466 33233 35855
69 14484 23274 38150
70 21269 36411 37450
71 23179 26195 37653
In another example, when the length Nidp, of the LDPC codeword is 64800, the
code rate is
8/15, and M is 360, the indexes of the rows where 1 is located in the Oth
column of the ith column
group of the information word submatrix 210 are as shown in Table 5 presented
below:
[Table 5]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
13
Index of row where 1 is located in the 0th column of the ith column group
= 0 2768 3039 4059 58566245 7013 8157 9341 9302 10470 11521 12083 16610
13361 20321 24601 27420 23206.29788
1 2739 8244 8891 9157 1262412973 15534 16622 1819 18402 18760 19654 20220
20543 22306 25540 27478 27678 28053
2 1727 22686246 7815 9010 9556 1013410472 1138 14599 15719 16204 17342
1766618850 22053 25575 25360 29207
3 28 1346 3721 5565 70199240 12355 1310914800 16040 16839 1736917631 19357
19473 19391 20381 23911 29683
4 869 2450 4386 53166160 7107 10362 11132 11271 13149 163971653Z 17113
1989422043 22784 27383 23615 28804.
508 4292 5831 85591004410412 11283 14810 15888 17243 17538 19903 20528 22090
22652 27235 27384 28208 28485
6 389 2248 5$40 6043 7000 9054 11075 1176012217 12565 13587 1540$ 19422
19528 21493 25142 27777 28566 28702
.7 1015 2002 5764 6777 93469629 11039 11153 12690 13068 13990 1,6841. 17702
20021. 24106 26300 29332 30081 30196
8 ' 1430 30843467 4401 4798 5187 7851 11368 12323 14325 14546 16360 17158
13010 21333 25612 2655626906 27005
9 6925 8876 12392 14529 15253 15437 19226 19950 20321 23021 23651 24393
24653 26668 27205 28269 28529 29041 29292
2547 3404 3538 4666 5126 5463 7695 8799 14732 15072 15881 1741018971
196091971.7 22150 24941 27908 29018
11 -! $S8 171-81 2311 5511 72189107.10454 12252 13662 1571.415894
17025_18671 243_04 25316 25556 28439 28977 29212
12 1047 1494 1713 4645 5030 6811 7868 8146 10611 1.5767'1782 18191.
22614.23021. 23763 25478: 26491,29088' 29757
13 I 59 1781 1900 38144121 8044.39069175 11156 14841 15789 160-33 16755
17292 IWO 19310 22505 29567 29850
14 1 1957 3057 4399 9476 10171 10769 11335 11569 15002 19501 20621 22642.
234$2 24360 23109 252902823 28505 29122
I 2395 3070 3437 4764 4905 6670 9244 11845 13352 13573 1397$ 14600 15871 17996
19672 20079 20579 25327 27956
16 612 1528 2004 4244 45994926 5843 7684 10122 10443 12267 14363 13413
19058 22985 24257 26202 26596 27899
17 I 1361 2195 4146 6703 7153 7533 9138 9996 14862 15359 16076 18925 21401
21573 22503 24146 24247 27778 29312
18 I 5229 6235 7134 7655 9139 13527 15408 1.6058 16705 18320 19909 20901
22238 22437 2365425131 2755028247 29903 .
19 I 6972035 4887 5275 6909 9166 11805 15338 16381 18403 20425 20688 21547
24590 25171 26726 28848 29224 29412
I 5379 17129 22659 23062
21 11814 14759 22329 22936
22 I 2423 2811 10296 12727
23 I 8460 1526916769 17290
24 I 14191 14608 29536 30187
I 7103 10069 201,11 22850
, 26 4285 15413 26448 29069
27 548 2137 9189 10928
28 4581 7077 23382 23949
: 29 3942 17248 19486 27922
ao 8668 10230 16922 26678
= 31 6158 9980 13788 28198
= 32 12422 16076 24206 29887
! 33 8778 10649 18747 22111
= 34. 21029 22677 27150 28980. .
7918 15423 27672 27803
36 5927 18086 23525
37 3397 15058 30224
as 24016 25880 26268
39 10964775 7912
3259 17301 20802
41 129 8396 15132
42 17825 28119 28676
= 43 2343 8382 28840
44 3907 18374.26939
= 45 1132 1.290 $786
=
46 1481 4710 28846
47 2185 3705 26834
48 5496 15681 21854
49. 12697 13407 22178
12788 21227 22894',
51 629 2854 6232,
52. 2289 18227 27458
= 53 7593 21935 230011
54.- 3836 7081, 12282
7925 18440 23135
56 497 6342 9717
57 11199 22046 30067
58 12572 28045 28990
59 1240 2023 10933
. 60 195642062925186

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
14
61 6442 13303 26813
62 4765 10572 16180
63 552 19301 24286
64 6782 18480 21383
65 11267 12288 15756
66 771 5652 15531
67 16131 20047 25649
68 _13227 33035 24450
69 4839 13467 27488
70 2852 1677 22993
71 2504 28116 29524
72 12.518 17374 24267
73. 1222 11859 27922
74 - 9660 1726615261
75 232 11296 2997S
76 - 9750 11165 16295
77 48949505 23622
78 10861 11980 14110
79 2128 15883 22636
SO 6374 17343 21%9
81 10866 13202 22517 -
82 11159 16111 2160S
83 3719 16787 22100
84 1756 2020 23901
8$ 20913 29473 30103
86 2729 15091 26976
87 4410 8317 12963
88 5395 24564 28235
89 3859 17909 23051
90 5733 26005 29797
91 1935 3492 29773
92 11903 21380 29914
93 6091 1046929997
94 2895 893015594
95 1827 10028 20070
In another example, when the length Num of the LDPC codeword is 64800, the
code rate is
10/15, and M is 360, the indexes of rows where 1 exists in the 0th column of
the ith column group
of the information word submatrix 210 are defined as shown in Table 6 below.
[Table 6]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
Index of row where I is located in the 0th column of the ith column group
O 979 142341664509 6341 825810334 10348 3409814514 17091 17333 17653
x7sag17990
.j. 2559 4025'5344 5510 9167 9728 11112 1485917104 17721 18900 1379129079
19597 19840
2 1243 6894 7950 1053912042 13233 23938 14752 1644916727 17023 18297 18196
19400 21577
5 5272 3574 041 6722 9191 10807 10957 11511 140361558018651 17007 17509
1941519845
4 1554598 10201 10975 1108611296 12713 15564 1597816395 1794218164 18451
13612 20617
5 11281999 3926 4069 5558 69856-337 833610693 12450 1545816223 16370 17508
18634
^ 24082929 3630 4357 5851 73298536 8695 10603 11003 14304 14937 15767 18402
21502
/ 199 3066 644638498973 9536 10452 118-57 13675 15913 16717 1733419801
2011521579
a M2 870 209525855517 4196 6767 7311 73651.3046 16-35415576 2054921424
21587
9 935 1591 5248 3509 3706 3)547617452767864 90331361815675 154453.83ss
18843
10 975 377440133 sals 6166 7218 76339657,20203 1052'14740 1732018126 19544
20209
1.1 1795 2005 21441418 61489051 64169 9728.10575 16/921-1111 13171 179i3
20491 21099
1.2 197 3151824 2325 2640 2E68 5070 5597 7016 8109 9935 12608 16142 17912
39625
13 1298 1896 1039 4303 4690 8787 12241 13600 14679 1549245502 1711517913
19456 20197
14 1.19 3485-15041 6624 93.311404 66969.059 9246-115.7014336198g 189411-
92te 215as
15 228 1999 1967 229930/1 5074 447595758,99341024410697116911230221418.
16 13301579 1739 2.234 3701 386557136677 7263 112721214512765 17121 20011
21436
17 3031658 2501 492557785985 96351014010820 11779 118491205815650 20426
20527
18 698 2434 5071 311940544125 56635949 6928 7086 8034 12173
'15280174519392'
r, 19 2321613 3040 49017435 5135 91173139 10131 11321 17947 17435 15153 18556
19929
10 1/372/ 6254 5509 78808139 1043712252 13929 140$S'14149130$2 15694
152641119115
21 482 915 1548 1637 6687 5336 10163 1176911970 15524 13995 17335 18787
19210 15340
22 = 1291 2500 4209 4312 3099-9194 1001413ms 23256 13972 11409 /An 3 15214
23584 20998
1761-4779 7444 7740 8129 93418931 9116 9207 1000310678 13959 17673 19194 20990
24 30603522 5361 54926333 93428792 11025 11211 11549 1191413937 15442 15541-
19707
25 1322 2349 2970 5632 6349 75778782911392679376 12042 12943 16680 16970
21321
. 25 6785 11950214.55
27 12131567219550
22_ 5976 1193=1 20395,
29 2818 9397 13317
276556-21202
= 11, 5230=11459 119997
32 5809 15779 20574,
33 2520 17835 18533'
1015 9542 9931,
õ 35 3728 5337 12142'
, , 25106666 9166
37 12892,15307 20911
38 10736 12394 16539
' = 19 1075 2497 12563
4921S411182D6-
41.
ssss 15547 16839.
, ¨42 8384 1933819266
43 429 10421 17266
44 4880 10431 12208'
291011895 12642'
46 7366 18362 18772
'47 '4541 7905 14994
, 48 4564 6714 7378
49 4639 3651 18871*
,,.50_ 1578718948 20246

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
16
.52 nqi. lion 14640
62 1559293615831
.55 1737 6519 101$1
.54 1039415107171073
55 1.8287i045 12974
56 nos 1605817903
57 . t1139 15717 17764
5&231t23 14516
59 . I 11039 20390.20924
1_551 1163'17411
, N?.46 9557 6552
62 , I 2E90 1093G 14756
i 9011 ii124 21517
64 :1529.12955.15102
65 I 419.6750173.5.
16 I 67841201216421
67 12811 1379415303
63 12538 1537117675
59 5067 14511 19501
70 ;' 1244 5177 6015
71 16897 -11319 19913
72 L47E739/%2264
75 34568931120Th
74 r-15342 11271.20952
-75 I 51.19 159.52 13711
II 7031 7626.11031
77 12O071617
72 4170 10569 14835
'79 3539 7111 16S75
_ . . .
10 46E1212891 1.5792
11 4.884 7959 1435 ,
12 809 5441 11111
! 22l04747311
14 6563 1121 12631
õ .õ
I .5795 1,0821 11514
.16 15939 18316 11941
= 17 1786 8057 21566
As 2212 13259-16432
139 46253U8W900.
16 I 4510 640416754
Si 145241275121.226
.12 I ,5989 11111 '12441
93 8182 10719 1.6350
94 653Ã1765113100
95 I 17765 19795 20116
= 96. 228311907 17567
-11 = I. 654014121.15175
19 I 1177 120,35 14901
19 , 1136 6458 11311
- 101 1 5949-91A8.12809
.õ
-101 17825681 12441
102 1710 134.6 112.44
103, i 7384.1213111989

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
17
104 1461'1139S 20999
05 1943 1045133.5k17
ids 5005815510E135
fat 17750 SS B29331513
to& 47258041,10112
31337:162645 VMS
III 14349 Va61,_17513
111 12694E11 4774
2522 10813 1,6157
%FM Ni4tAti
ti4'7114412S 1E75.3:
5165 8153 153161
Ils 160 R045 15525
U? 14112 13724167913
, _
113 4291 ,7(1,42 181741
Lisr 594519$79 20721
In another example, when the length Nidp, of the LDPC codeword is 64800, the
code rate is
10/15, and M is 360, the indexes of rows where 1 exists in the 0th column of
the lth column group
of the information word submatrix 210 are defined as shown in Table 7 below.
[Table 7]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
18
i Index of row where 1 is located in the 0th column of the ith column group
0 316 1271 3692 9495 12147 12849 14928 16671 16938 17864 19108 20502 21097
21115
1 2341 2559 2643 2816 2865 5137 5331 7000 7523 8023 10439 10797 13208 15041
2 5556 6858 7677 10162 10207 11349 12321 12398 14787 15743 15859 15952 19313
20879
3 349 573 910 2702 3654 6214 9246 9353 10638 11772 14447 14953 16620 19888
4 204 1390 2887 3835 6230 6533 7443 7876 9299 10291 10896 13960 18287 20086
541 2429 2838 7144 8523 8637 10490 10585 11074 12074 15762 16812 17900 18548
6 733 1659 3838 5323 5805 7882 9429 10682 13697 16909 18846 19587 19592 20904
7 1134 2136 4631 4653 4718 5197 10410 11666 14996 15305 16048 17417 18960
20303
8 734 1001 1283 4959 10016 10176 10973 11578 12051 15550 15915 19022 19430
20121
9 745 4057 5855 9885 10594 10989 13156 13219 13351 13631 13685 14577 17713
20386
968 1446 2130 2502 3092 3787 5323 8104 8418 9998 11681 13972 17747 17929
11 3020 3857 5275 5786 6319 8608 11943 14062 17144 17752 18001 18453 19311
21414
12 709 747 1038 2181 5320 8292 10584 10859 13964 15009 15177 16953 20675 21509
13 1663 3247 5003 5760 7186 7360 10346 14211.14717 14792 15155 16128 17355
17970
14 516 578 1914 6147 9419 11148 11434 13289 13325 13332 19106 19257 20962
21556
5009 5632 6531 9430 9886 10621 11765.13969 16178 16413 18110 18249 20616 20759
16 457 2686 3318 4608 5620 5858 6480 7430 9602 12691 14664 18777 20152
20848
17 33 2877 5334 6851 7907 8654 10688 15401 16123 17942 17969 18747 18931
20224
18 87 897 7636 8663 11425 12288 12672 14199 16435 17615 17950 18953 19667
20281
19 1042 1832 2545 2719 2947 3672 3700 6249 6398 6833 11114 14283 17694
20477
326 488 2662 2880 3009 5357 6587 8882 11604 14374 18781 19051 19057 20508
21 854 1294 2436 2852 4903 6466 7761 9072 9564 10321 13638 15658 16946
19119
22 194 899 1711 2408 2786 5391 7108 8079 8716 11453 17303 19484 20989 21389
2.3 1631 3121 3994 5005 7810 8850 10315 10589 13407 17162 18624 18758 19311
20301
24 736 2424 4792.5600 6370 10061 16053 16775 18600
1254 8163 8876,9.157 12141 14587 16545 17,1,75.18191
26 388 6641 8974 10607 10716 14477 16825 17191 18400
27 5578 6082 6824 7360 7745 8655 11402 1166512428
28 3603 8729 13463 14698 15210 19112 19550 20727 21052
29 48 1732 3805 5158 15442 16909 19854 21071 21579
11707 14014 21531
31 1542 4133 4925
32 10083 13505 21198
33 14300 15765 16752
34 778 1237 11215
1325 3199 14534
36 2007 14510 20599
37 1996 5881 16429
38 5111 15018 15980
39 4989 10681 12810
3763 10715 16515
41 2259 10080 15642
42 9032 11319 21305
43 3915 15213 20884
44 11150 15022 20201
1147 6749 19625
46 12139 12939 18870
47 3840 4634 10244
48 1018 1023.1 17720
49 2708 13056 13393
5781 11588,18888

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
19
51 1345 2036 5252
52 5908 8143 15141
53 1804 13693 18640
54 10433 13965 16950
55. 9568 10122 15945
56 547 6722 14015
57 321 12844 14095
58 263210513 14936
59 6369 11995 20321
60 9920 19136 21529
61 1990 2726 10183
62 5763 12118 15467
63 503 10006 19564
64 9839 11942 19472
65 11205 13552 15389
66 8841 13797 19697
67 124 6053 18224
68 6477 14406 21146
69 1224 8027 16011
70 3046 4422 17717
71 739 12308 17760
72 4014 4130 7835
73 2266 5652 11981
74 2711 7970 18317
75 2196 15229 17217
76 8636 13302 16764
77 5612 15010 16657
78 615 1249 4639
79 3821 12073 18506
80 1066 16522 21536
81 11307 18363 19740
82 3240 8560 10391
83 3124 11424 20779
84 1604 8861 17394
85 2083 7400 8093
86 3218 7454 9155
87 9855 15998 20533
88 316 2850 20652
89: 5583 9768 10333
90 7147 7713 18339
91 12607 17428 21418
92 14216 16954 18164
= 93 8477 15970 18488
94 1632 8032 9751
95 4573 9080 13507
96 11747 12441 13876
97 1183 15605 16675
98 4408 10264 17109
99 5495 7882 12150
100 1010 3763 5065
101 9828 18054 21599
102 6342 7353 15358
103 6362 9462 19999

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
104 7184 13693 17622
105 4343 4654 10995
106 7099 8466 18520
107 11505 14395 15138
108 6779 16691 18726
109 7146 12644 20196
110 5865 16728 19634
111 4657 8714 21246
112 4580 5279 18750
113 3767 6620 18905
114 9209 13093 17575
115 12486 15875 19791
116 8046 14636 17491
117 2120 4643 13206
118 6186 9675 12601
119 784 5770 21585
In another example, when the length Nidpc of the LDPC codeword is 64800, the
code rate is
12/15, and M is 360, the indexes of rows where 1 exists in the 0 column of the
ith column group
of the information word submatrix 210 are defined as shown in Table 8 below.
[Table 8]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
21
i I Index of row where 1 is located in the 0th column of the 'ith column
group
. _
0 5341472 1521 1357.3338 3358'3723 4185 5126 5889 7737 8632 8940 9725
1 2.21 445 590 3779 3835 6929 7743 8280 8448 8451 9367 10042 11242:12917
2 44524837 49005029 6449 6587 6751 3684 9935 11681 11811 11885 12089,12909,
3 2418 1018 3647 4210 4471 7447 7502 9490 10067 1/092 1/139 /1255 12203.
12383
4 2591 2947 3349:3406.44174519 5176 6672 8498 8863 9201 11294 11375 12134
27 /01 197 290 871-1727 3911 5411 6676 601 9350'10310'10798'12439
6 1765 1897 2923 3584 3901 4048 6963 7054 7132 9165 10184 10324 11278 12669
7 2193 1740 4808 5217 5660 6375 6787 8219 8466 9037 10353 10581 11118 /2762.
.8 731594 2146 2715 3501 3572 3639 3725 6959 7287 8406 10120 18507 10691.
9 240 732 1215 2165 2738 2830 3439 3881 4197 4991.6429 7061 9756 10451
3;0 831 1568 2828.3424 4319 4516 4639 6018 9702 10203 10417 11240 11518
12458:
11 2024 2970 3048 3838 36754152 3234 5779 5926 5426 9945 10373 1178711837
22 10491215 1651 2325 3493 4353 5750 6483 762.3 8782 9735 9503 11744 11937
13 1193 2060 2289 2964 3478 4992 4758 6709 7162 8231 8126 11140 11908'12243-
14 9732220 2439'3338 3850 4559 65675745 9656 970810162 10542 10711 22639
2403 2938 3117.3247 3711 5993 5844 5932 7801 10152 10226 11498 12162 12941
15 3782 2229.2275 2533 3582 3951 5275 5774 7930 9824 10920 11035 12340 22440
17 285 384 1580 2230;3464 3873.555* 86568942 5006 10175 11425.11745 12536
18 155 354 1090 1330 2002 2236, 3539 3705 4922 5958'5575 8554 9972 12760
19 303 876 2059 2142 5244 5330 6644 7576 861.4 9598 /0410 10718 11033 12957
3449 3617-4408 4502 4727 6i82 3335 3928 9372 9544 10237 10747 11455 12747
21 811 2555 2820 8677 8974 963211069'11548 11839 12107 12411 12695 12812
12890
22 97241/3 4943 5385 6449 7339 7477 8379 9177 9359 10074 11709 12552 12331
23 842 973 1541 2262-2905 5276 6758 7099 7894 8128 8325 8663 8875 10050
24 .474791 958 3902 4924 4965 5085 5908 5109 5325 7931 9038 9401 15568
13574461 4658 5911 6037 7127,7318 8678 8924 9000 5473 96402 10446 12692
26 1394.7571 12881
27 13931447 7972:
ZS 633 1257 10597'
29 4843 5102 11055
3294 8015 10513
31 1108 10374 10546'
32 5353 7024 10111
33 33983574 8569
34 7719 9475 20503:
2997 9418.9561.
35 5777 6510 11229'
37 19665214 9899
18 640885327
39 836 9248 9612-
481 7229 7543;
, 7865 8289 9804
42 2915 11093 11900
43 __________________ 6180 7096 9481

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
22
44 1431 6786 8924
45 748 5757 8525
46 3312 4475 7204
47 1852 8.958 11020
48 191S2903 4006
49 6776 10886 12531
50, 2594 9958 12742
,159 2062 12079
52 651 3281 3762
53 5201 5798 6413
54 3882 6062 12047
55 4133 6775 9657
56 228 6874 11183
57 7433 20723 10864
sa W35 8673 12734
1 59 28.4448.21 11:779
60 3908 7103 12804
61 60112 9704 11060
62 5864 6856 7681
63 3652 5869 7605
64 2646 2657 4462
65 2423 4203 6111
66 244 1855 4651.
67 11062173 6371
s 391 16/7 10126
69 "25Q925910603
70 3435 4614 5924
71 1742 6045 9529
72 7667 8.875 11451
73 4023 6108 6911
74¨ 802110184 11656
75 - 572610951:12348
75 32t8 6362 736a
77 1.1137 53581
78 181 2424 8537
79 3256 7508 10044
40. 1980 2219 4569
81 2468 5639 10329
82 "2803 3314 12808
83 6578 9642 11533
84 329 4535 7921-
85 59329 5575
86 1057 5709 6867
87 ,1175 47'44 12219
48 109 2518 6756
39 '2206 166,26 11151
90 5132 10696 10749
91 6260 7641 8233
92 2993 3094 1124

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
23
93 3398 6406 11494
94 6574 10448 12160
95 Mot 10755 12780
9e 1028 7958 10825
97 I am 8602 10793
90 392 3398 11417
99 6639 9291 12571
100 1067 7919 8994
104. 1064 2848 12753
102-I 6076 8656 12690
ia3 5504 6/9310171
_
104 I 1951 7156 7356
105 4389 4780 7839
106 52164804 9141
107 1238 3648 10464
103 2587 5624 12557
109 5960 590311961
110 1134 2570 3297
11/ 10041 11383 12157
112 1.263 9585 12912
113 37447898 10646
114 45 9074 10315
115 1.051 6188 10038
116 2242 8394 12712
117 3598 9025 12651
128 2295 3.540 5610
/19 1914 4378 12423
120 1766 3635 12759
124, 5177 9586 11143
in 943 3590 11649
123 4864 6905 10454
134 5852 6042 10421
125 I 60358235 12549
1261 2070 7171 8563
127 718 12234 12716
128 512 1055711951
129 3629 6485 7040
130 2880 8865 11466
131 4490 10220 11796
132 5440 8829 9103
133 5262 7543 12411
134 516 1779 10540
135 251.5 5843 9202
136 4684 5994 10586
137 573 2270 3324
138 7870 831.7 10322
139 6856 7638 12909
140 1583 7669 10781
141 *1419085 12555
142 3903 9185 9992
143, 4457,11398 12904
In the above-described examples, the length of the LDPC codeword is 64800 and
the code
rate is 6/15, 8/15, 10/15, and 12/15. However, this is merely an example and
the position of 1 in

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
24
the information word submatrix 210 may be defined variously when the length of
the LDPC
codeword is 16200 or the code rate has different values.
According to an exemplary embodiment, even when the order of numbers in a
sequence
corresponding to the ith column group of the parity check matrix 200 as shown
in the above-
described Tables 4 to 8 is changed, the changed parity check matrix is a
parity check matrix used
for the same code. Therefore, a case in which the order of numbers in the
sequence
corresponding to the ith column group in Tables 4 to 8 is changed is covered
by the inventive
concept.
According to an exemplary embodiment, even when the arrangement order of
sequences
corresponding to each column group is changed in Tables 4 to 8, cycle
characteristics on a graph
of a code and algebraic characteristics such as degree distribution are not
changed. Therefore, a
case in which the arrangement order of the sequences shown in Tables 4 to 8 is
changed is also
covered by the inventive concept.
In addition, even when a multiple of Qidpc is equally added to all sequences
corresponding to a
certain column group in Tables 4 to 8, the cycle characteristics on the graph
of the code or the
algebraic characteristics such as degree distribution are not changed.
Therefore, a result of
equally adding a multiple of Qmpc to the sequences shown in Tables 4 to 8 is
also covered by the
inventive concept. However, it should be noted that, when the resulting value
obtained by adding
the multiple of Qmpc to a given sequence is greater than or equal to (Nidpc-
Kidp,), a value obtained
by applying a modulo operation for (Nidpc-Kkipc.) to the resulting value
should be applied instead.
Once positions of the rows where 1 exists in the Oth column of the ith column
group of the
information word submatrix 210 are defined as shown in Tables 4 to 8,
positions of rows where 1
exists in another column of each column group may be defined since the
positions of the rows
where 1 exists in the 0th column are cyclic-shifted by Qmpc in the next
column.
For example, in the case of Table 4, in the Oth column of the 0th column group
of the
information word submatrix 210, 1 exists in the 1606th row, 3402nd row, 4961st
row.....
In this case, since Okipc=(Nidpc-K1dp,)/M464800-25920)/360.108, the indexes of
the rows
where 1 is located in the 1st column of the 0th column group may be
1714(.1606+108),
3510(.3402+108), 5069(=4961+108),..., and the indexes of the rows where 1 is
located in the
2nd column of the Oth column group may be 1822(=1714+108), 3618(.3510+108),
5177(=5069+108),....

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
In the above-described method, the indexes of the rows where 1 is located in
all rows of each
column group may be defined.
The parity submatrix 220 of the parity check matrix 200 shown in FIG. 2 may be
defined as
follows:
The parity submatrix 220 includes Nidpc-Kidpc number of columns (that is,
Kidpcth column to
(Nipdc-1)th column), and has a dual diagonal or staircase configuration.
Accordingly, the degree of
columns except the last column (that is, (Nidpc-1)th column) from among the
columns included in
the parity submatrix 220 is 2, and the degree of the last column is 1.
As a result, the information word submatrix 210 of the parity check matrix 200
may be
defined by Tables 4 to 8, and the parity submatrix 220 of the parity check
matrix 200 may have
a dual diagonal configuration.
When the columns and rows of the parity check matrix 200 shown in FIG. 2 are
permutated
based on Equation 4 and Equation 5, the parity check matrix shown in FIG. 2
may be changed to
a parity check matrix 300 shown in FIG. 3.
adpc =i+ = j+i (0 i<M,0 j < Qupc)... (4)
Kidpcadpc = k + 1 up, + M = 1 + k (0 k < M ,0 1 < Vdpc) . . . (5)
The method for permutating based on Equation 4 and Equation 5 will be
explained below.
Since row permutation and column permutation apply the same principle, the row
permutation
will be explained by the way of an example.
In the case of the row permutation, regarding the Xth row, i and j satisfying
X = ,dp,x i + fare calculated and the Xth row is permutated by assigning
the calculated i and j to
Mx j+i. For example, regarding the 7th row, i and j satisfying 7 = 2 x i + j
are 3 and 1,
respectively. Therefore, the 7th row is permutated to the 13th row (10 x 1+3
=13 ).
When the row permutation and the column permutation are performed in the above-
described
method, the parity check matrix of FIG. 2 may be converted into the parity
check matrix of FIG.
3.
Referring to FIG. 3, the parity check matrix 300 is divided into a plurality
of partial blocks,
and a quasi-cyclic matrix of M x M corresponds to each partial block.
Accordingly, the parity check matrix 300 having the configuration of FIG. 3 is
formed of
matrix units of M x M. That is, the submatrices of M x M are arranged in the
plurality of partial

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
26
blocks, constituting the parity check matrix 300.
Since the parity check matrix 300 is formed of the quasi-cyclic matrices of
MxM, M
number of columns may be referred to as a column block and M number of rows
may be referred
to as a row block. Accordingly, the parity check matrix 300 having the
configuration of FIG. 3 is
formed of Nqc_cohnim=Nidpc/M number of column blocks and Nqc_row=Nparity/M
number of row
blocks.
Hereinafter, the submatrix of M x M will be explained.
First, the (Nqc_columrr1)th column block of the 0th row block has a form shown
in Equation 6
presented below:
0 0 ... 0 0
10...00
A = 0 1 ... 00
0 0 ... 1 0
- ... (6)
As described above, A 330 is an MxM matrix, values of the 0th row and the (M-
1)th column
are all "0", and, regarding 0< k(M-2), the (i+1)th row of the ith column is
"1" and the other
values are "0".
Second, regarding 0<i<(NIapc-Kidp,)/M-1 in the parity submatrix 320, the ith
row block of the
(Kidpc/M+i)th column block is configured by a unit matrix MM 340. In addition,
regarding
0<i<(Nkipc-K1dpc)/M-2, the (i+1)th row block of the (Kidpc/M+i)th column block
is configured by a
unit matrix fm.m 340.
Third, a block 350 constituting the information word submatrix 310 may have a
cyclic-shifted
format of a cyclic matrix P. Pau , or an added format of the cyclic-shifted
matrix P"u of the
cyclic matrix P (or an overlapping format).
For example, a format in which the cyclic matrix P is cyclic-shifted to the
right by 1 may be
expressed by Equation 7 presented below:
0 1 0 0
001...0
P=
000...1
1 0 0 0
- = = = (7)

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
27
The cyclic matrix P is a square matrix having an M xM size and is a matrix in
which a
weight of each of M number of rows is 1 and a weight of each of M number of
columns is 1.
When aii is 0, the cyclic matrix P, that is, P indicates a unit matrix /m.m ,
and when is co, 13 is
a zero matrix.
A submatrix existing where the ith row block and the ith column block
intersect in the parity
check matrix 300 of FIG. 3 may be Pau . Accordingly, i and j indicate the
number of row blocks
and the number of column blocks in the partial blocks corresponding to the
information word.
Accordingly, in the parity check matrix 300, the total number of columns is
Nidpc=M X Nqc_column,
and the total number of rows is Nparity=M Nqe_row= That is, the parity check
matrix 300 is formed
of Nqc_coiumn number of "column blocks" and Nqc_row number of "row blocks".
Hereinafter, a method for performing LDPC encoding based on the parity check
matrix 200
as shown in FIG. 2 will be explained. An LDPC encoding process when the parity
check matrix
200 is defined as shown in Table 4 by way of an example will be explained for
the convenience
of explanation.
First, when information word bits having a length of Kidpc are [io, ir, i2, =
licap,_ib and parity
bits having a length of Nid are
[po, pi, p2,.= = pc-Kidpc põ1], the LDPC encoding is performed
by the following process.
Step 1) Parity bits are initialized as '0'. That is, po= pi= P2'= = ==PN4,-
K1=0.
Step 2) The Oth information word bit io is accumulated in a parity bit having
the address of the
parity bit defined in the first row (that is, the row of i=0) of table 4 as
the index of the parity bit.
This may be expressed by Equation 8 presented below:

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
28
P1606 = P16060 0 P24533= P24533 0 0
P3402 = P34020 0 P25376= P253760 0
P4961 = P49610 0 P25667= P25667 010
P6751 = P6751 0 0 P26836= P26836 0 0
P7132 = P71320 0 P31799 = P31799 'O
P11516 = P11516 OI 0 P34173 = P34173 0 0
P12300= P12300 0 0 P35462= P35462 0 0
P12482= P12482 Oi 0 P36153 = P361530 0
P12592= P12592iIO P36740 = P36740 0 0
P13342= P13342 0 0 P37085¨ P37085 I0
P13764= P13764 cI 0 P37152 = P37152 0 0
P14123 = P1412301 0 P37468 = P37468 0 0
P21576= P6 i0 P37658 = P37553 I0
ID23946 = P23946 0 0
...(8)
Herein, io is a 0th information word bit, n is an ith parity bit, and is a
binary operation.
According to the binary operation, 1 8 1 equals 0, 110 0 equals 1, 0 e 1
equals 1, 0 0 0 equals 0.
Step 3) The other 359 information word bits in, (m=1, 2, ..., 359) are
accumulated in the
parity bit. The other information word bits may belong to the same column
group as that of io. In
this case, the address of the parity bit may be determined based on Equation 9
presented below:
(x + (m mod 360) x Qmpc) mo d (Nmp, ¨ Kidp, ) . . . (9)
Herein, x is an address of a parity bit accumulator corresponding to the
information word bit
and Qtdpc is a size by which each column is cyclic-shifted in the information
word submatrix,
and may be 108 in the case of table 4. In addition, since m=1, 2, ..., 359, (m
mod 360) in
Equation 9 may be regarded as m.
As a result, information word bits in, (m=1,2,..., 359) are accumulated in the
parity bits
having the address of the parity bit calculated based on Equation 9 as the
index. For example, an
operation as shown in Equation 10 presented below may be performed for the
information word
bit

CA 02940011 2016-08-17
WO 2015/126194 PCT/ICR2015/001695
29
P1714 = P17140 i 1 P24641= P24641
P3510 = P351o0i 1 P25484= P25484 0 i 1
P5069 = P50690 i 1 P25775= P25775
P6859 = P6859@ i 1 P26944= P26944
P7240 = P72400 i 1 P31907= P31907 0 i 1
P11624= P11624 CDI 1 P34281= P34281
P12408= P12408 (D i 1 P35570= P35570 0 i 1
P12590= P12590 CD i 1 P36261= P36261 (Di 1
P12700= P12700 0 i 1 P36848= P36848 i 1
P13450= P13450 0 i 1 P37193= P37193 0 i 1
P13872= P13872 ei 1 P37260= P37260 01 1
P14231= P14231 ei 1 P37576= P37576 0i 1
P21684 = P21684 i 1 P37766= P37766 ei 1
P24054 = P24054 CD i 1
...(10)
Herein, i1 is a 1st information word bit, pi is an ith parity bit, and is a
binary operation.
According to the binary operation, 1 1 equals 0, 1 C) 0 equals 1, 0 1 equals
1, 0 0 0 equals 0.
Step 4) The 360th information word bits i360 is accumulated in a parity bit
having the address
of the parity bit defined in the 2nd row (that is, the row of i=1) of table 4
as the index of the parity
bit.
Step 5) The other 359 information word bits belonging to the same group as
that of the
information word bit i360 are accumulated in the parity bit. In this case, the
address of the parity
bit may be determined based on Equation 9. However, in this case, x is the
address of the parity
bit accumulator corresponding to the information word bit i360.
Step 6) Steps 4 and 5 described above are repeated for all of the column
groups of table 4.
Step 7) As a result, a parity bit pi is calculated based on Equation 11
presented below. In this
case, i is initialized as 1.
Pr = p, p,_,i =1,2,..., Nidp, ¨ Kidp, ¨1 ... (11)
In Equation 11, pi is an ith parity bit, Nidpc is a length of an LDPC
codeword, Kid is a length
of an information word of the LDPC codeword, and is a binary operation.
As a result, the encoder 110 may calculate the parity bits according to the
above-described

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
method.
In another example, a parity check matrix according to an exemplary embodiment
may have a
configuration as shown in FIG. 4.
Referring to FIG. 4, the parity check matrix 400 may be formed of 5 matrices
A, B, C, Z, and
D. Hereinafter, the configuration of each matrix will be explained to explain
the configuration of
the parity check matrix 400.
First, Ml, M2, Ql, and 02, which are parameter values related to the parity
check matrix 400
as shown in FIG. 4, may be defined as shown in table 9 presented below
according to the length
and the code rate of the LDPC codeword.
[Table 9]
sizc$
Rate Length
2
2520 12600 7 35
1/15 16200
64800 1080 59400 3 165
2/15 16200 3240 10800 9 30
64800 1800 54360 5 151
3/15 16200 1080 11.880 3 33
64800 1800 50040 5 139
4/15 16200 1080 10800 3 30
64800 1800 45720 5 127
16200 720 10080= 2 28
5/15 64800 1440 41760 4 116
16200 1080 8640 3 24
6/15 64800 1080 31800 3 105
The matrix A is formed of K number of columns and g number of rows, and the
matrix C is
formed of K+g number of columns and N-K-g number of rows. Herein, K is a
length of
information word bits, and N is a length of the LDPC codeword.
Indexes of rows where 1 is located in the 0th column of the ith column group
in the matrix A
and the matrix C may be defined based on table 10 according to the length and
the code rate of
the LDPC codeword. In this case, an interval at which a pattern of a column is
repeated in each
of the matrix A and the matrix C, that is, the number of columns belonging to
the same group,
may be 360.
For example, when the length N of the LDPC codeword is 64800 and the code rate
is 6/15,
the indexes of rows where 1 is located in the 0th column of the ith column
group in the matrix A
and the matrix C are defined as shown in table 10 presented below:
[Table 10]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
31
I Index of row where 1 is located in the Oth column of the ith column group
. _
0 71276856 6867. 12354 17373..18159 26420 2/460. 28477
1 257 322 672.2533 5316 5578 9037 10231 13845 36497
'2 233 765 904 1,366 3875 13145 15409 18620 23910'30825-
.3 100 224 405 127761386114787 16781 23886 29099 31419
.4 23496.891 2512 12589 14074 19392-.20339 2765828684:
. 5 473712 759 1215 4574 3838:12551 i38144242: 32728
511567 fi15 11823 1710617900 19338 22315, 24396 26448
' 7 45733 836 1923 372717458 2.5746 33805 35995 36557
8 17487 575 26703122514518009 n99131673:36624
3 72751773 1937,1732421512 3066630334 31016 31143
257345594 1404119141 2491426864 28809 32pss 34753.
. 11 39 241 491 265D 3570 17433 17785718988-12235 30742
-12 , 198299 655 5737 8504 10917'16092 19387 2075537690:
13 351 916 926 1815121708- 2321530321 33578 34052 37949
14 54 332 373'2010 3332562316301 34337.354513-7851
139257.10681103020289 29694123732 32640 35.131 35434
-16 457885 36821154956 5422 5949 1757026673 32.387
'17 13:7570 619 5005 6039 7979 14429 16650 25443 32789
r 28 46 282 287 10258,18313,20258 27185 27494 22423 33266
= 23 445486.1058 1861997611234 20354 23635 33826.35330
,. 20 134300 93112518 14544 17715,19623 21111 33868 34570
21 5265 516 /02020270 23231 31041 31965 32224 35189
22 174290 714 6740 14673 17642 26286 27382 3344734879
= 23 332 675 1033 183112004 15439 20765 31721 3422518863
.24 527551832 326763118317 lona 13466 12427 25377
431780.10211112 2173 767513059 17793 20570 20771
" 26 ' 3-39536 1013 5725 6916 2084614487 21156 28123 32614
27 456 830, 19787311 1180112362 12705 27402 28367 34032
21 222538 919 55958022 530214098 23445 25127 29022.
29 .31 393 7/130217758 11367 22276 227612823230394
_ 30 .234257 1345 1307 2908 6337:26530 28142 34129'35997:
.31 3146 978 9912997812567 17843 24194 34827 35206
= 32 39959 967 302710147 14657 18859 28075 2821436325:.
33. 275477 823 .113-76-18073'-28997'3052111661 3194132116
.34 185.580 966 1173a 12013 12750 13358 19372.32534.35504
760891 1046 11150 20358 21531.29930 3101433050,34840
36 360389 1057 5316 5958 14186 164041244534021 35722
37 305344 579 5224667410305 18753 2558330535:35341
55 103 171 101587141174112144 19470. 20955 2/495 27377
. 59 118 832 894 3883 14273 14497 22505 28129.28715 31246,
. 215411.7505886 25612 28556 3222312704 35901 36130'
. 41 229489 10671385E587 20565 23431 2810230147 32859'
42 28/664. 980 815.8 8531 2167623787 26708 2,8798 34490:'
-43 89552 847 6656:9889 23949 26225170101123.6 35823
44 66142 445 3339.5513 7077 14944-1546419186 259,ga
605875 93116512 17659158017 18220.3343235738 37382-
' 45 346423 aos 566376688783 3928 19724 2403527835
I 47 '45460 10553512 73:89 7549.29215 2.2180 2522135437
. 48 187531124157a 450113581 19683 21750.3033.1. 31480..
.=49' .257689352856 8187 905211850 299413321734253
= 50 349624 71.6165/ 6333 64358974106491593217378
=

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
32
51 ' 336 410 871. 3582 9830 10835 13892 1302T192(33 36659
52 176849 107g 17302 19379 27964 28164 26720 32557 35495
53- 23489010759431 9605 9700 10113 11332 12679 24268
54 516 638 733 6851 19871'22740 25791 30152 32659 35568'
55 253 830 8742086 168E5 22952 23765 25389 3465537293
56 94 954 99&2003'3359 6870 7321 29856 31373 34868
- -
57 79 350 933 4353 6252 11932 12053 21631 24552 24376
-56- '246547 7784035 10391 10656 13194 32335 32360 34179
59 149 339 435 6971 83558715 11577 22376 28684 31249
_60. 36 149 220 6936 18408 19192 19288 23055 28411 35312
61 273 633 1042 6327 10011 1E041 21704 29097 30791 31425
62 46 138 722 2701 10964 13002 19430 2662528458 2E965,
63 12101)9 1040 1990 2930 5302 21215 22625023011 29288
64 123 241 819 2245 31998415 21133 26785 2722636838
65' 45 476 1075 7393 1514120414 31244 33336 35004 3E391
66 432578 6571343 10466 11314 11507 23314 27720 34465
67 248 291 555 1971 3939 8992 18000 19998 23932 34652
68 68594 837 22457472 7873 11073 12E63 20937 35591
59' 7Z49492030 4350,&23 9737 19705 13902 3E039
70 21 314 979 2311 2632 4109 19527 2192 D 31413 34277
71 197 253 304 1249 4315 10021 14353 20559 27099 30525
--
72 9802 16164 17499 22373 22403 22704 26742 29908-
73 9064 10904 123135 14057 16155 26000 32613 34536
74 5178 6319 10239 19343 25628 30577 31110 32291
In the above-described example, the length of the LDPC codeword is 64800 and
the code rate
6/15. However, this is merely an example and the indexes of rows where 1 is
located in the 06
column of the ith column group in the matrix A and the matrix C may be defined
variously when
the length of the LDPC codeword is 16200 or the code rate has different
values.
Hereinafter, positions of rows where 1 exists in the matrix A and the matrix C
will be
explained with reference to table 10 by way of an example.
Since the length N of the LDPC codeword is 64800 and the code rate is 6/15 in
table 10,
M1=1080, M2=37800, Qi=3, and Q2=105 in the parity check matrix 400 defined by
table 10 with
reference to table 9.
Herein, Qi is a size by which columns of the same column group are cyclic-
shifted in the
matrix A, and Q2 is a size by which columns of the same column group are
cyclic-shifted in the
matrix C.
In addition, Qi=Mi/L, 02=M2/1,, Mi=g, and M2=N-K-g, and L is an interval at
which a
pattern of a column is repeated in the matrix A and the matrix C, and for
example, may be 360.
The index of the row where 1 is located in the matrix A and the matrix C may
be determined
based on the M1 value.
For example, since M1=1080 in the case of table 10, the positions of the rows
where 1 exists

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
33
in the Oth column of the ith column group in the matrix A may be determined
based on values
smaller than 1080 from among the index values of table 10, and the positions
of the rows where
1 exists in the Oth column of the ith column group in the matrix C may be
determined based on
values greater than or equal to 1080 from among the index values of table 10.
Specifically, in table 10, the sequence corresponding to the Oth column group
is "71, 276, 856,
6867, 12964, 17373, 18159, 26420, 28460, 28477". Accordingly, in the case of
the Oth column of
the 0th column group of the matrix A, 1 may be located in the 71st row, 276th
row, and 856th row,
and, in the case of the 0th column of the Oth column group of the matrix C, 1
may be located in
the 6867th row, 12964th row, 173731d row, 18159th row, 26420th row, 28460th
row, and 28477th
row.
Once positions of 1 in the Oth column of each column group of the matrix A are
defined,
positions of rows where 1 exists in another column of each column group may be
defined by
cyclic-shifting from the previous column by Qi. Once positions of 1 in the 0th
column of each
column group of the matrix C are defined, position of rows where 1 exists in
another column of
each column group may be defined by cyclic-shifting from the previous column
by Q2.
In the above-described example, in the case of the 0th column of the Oth
column group of the
matrix A, 1 exists in the 71st row, 276th row, and 856th row. In this case,
since Q1=3, the indexes
of rows where 1 exists in the 18t column of the Oth column group are
74(=71+3), 279(.276+3),
and 859(=856+3), and the index of rows where 1 exists in the 2nd column of the
0th column group
are 77(=74+3), 282 (=279+3), and 862(=859+3).
In the case of the 0th column of the 0th column group of the matrix C, 1
exists in the 6867th
row, 12964th row, 17373`d row, 18159th row, 26420th row, 28460th row, and
28477th row. In this
case, since Q2=105, the index of rows where 1 exists in the 1st column of the
Oth column group
are 6972(=6867+105), 13069(=12964+105), 17478(=17373+105), 18264(=18159+105),
26525(=26420+105), 28565(=28460+105), 28582(=28477+105), and the indexes of
rows where
1 exists in the 2nd column of the 0th column group are 7077(=6972+105),
13174(.13069+105),
17583(.17478+105), 18369(=18264+105), 26630(.26525+105), 28670(.28565+105),
28687(=28582+105).
In this method, the positions of rows where 1 exists in all column groups of
the matrix A and
the matrix C are defined.
The matrix B may have a dual diagonal configuration, the matrix D may have a
diagonal

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
34
configuration (that is, the matrix D is an identity matrix), and the matrix Z
may be a zero matrix.
As a result, the parity check matrix 400 shown in FIG. 4 may be defined by the
matrices A, B,
C, D, and Z having the above-described configurations.
Hereinafter, a method for performing LDPC encoding based on the parity check
matrix 400
shown in FIG. 4 will be explained. An LDPC encoding process when the parity
check matrix 400
is defined as shown in Table 10 by way of an example will be explained for the
convenience of
explanation.
For example, when an information word block S=(so, sl, SK_i)
is LDPC-encoded, an
LDPC codeword A = (
0===,Aw_i) = (sõ.91,...,Sõ_1,po,p1,...,Pmi,,,,,2_1) including a parity bit
P = (Po,191,¨,Pm1+m 2-1) may be generated.
Mi and M2 indicate the size of the matrix B having the dual diagonal
configuration and the
size of the matrix C having the diagonal configuration, respectively, and
Mi=g, M2=N-K-g.
A process of calculating a parity bit is as follows. In the following
explanation, the parity
check matrix 400 is defined as shown in table 10 by way of an example, for the
convenience of
explanation.
Step 1) X and p are initialized as Xj=s; (i=0,1,..., K-1), p3=0 (j=0,1,...,
Mi+M2-1).
Step 2) The 0th information word bit X0 is accumulated in the address of the
parity bit defined
in the first row (that is, the row of i=0) of table 10. This may be expressed
by Equation 12
presented below:
P71 = P710 k 0 P17373= P17373 0 X 0
P276= P276 ex.0 P18159= P18159 OK 0
P856= P856 0 X 0 P25420 = P26420 .0
P6867 = P68670 X 0 P28460 = P28460 0 X 0
P12964= P 12964 OX0 P28477 = P28477 0 X 0
...(12)
Step 3) Regarding the next L-1 number of information word bits Ain (m=1, 2,
..., L-1), Xin is
accumulated in the parity bit address calculated based on Equation 13
presented below:
(x + m x ) mod Mi (if x <
M +{(,' ¨ M 1+ mx Q2) modM2} (if fr )...(13)
Herein, x is an address of a parity bit accumulator corresponding to the 0th
information word
bit ko.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
In addition, Q1=M1/L and Q2=M2/L. In addition, since the length N of the LDPC
codeword is
64800 and the code rate is 6/15 in table 10, M1=1080, M2=37800, Q1=3, Q2=105,
and L=360
with reference to table 9.
Accordingly, an operation as shown in Equation 14 presented below may be
performed for
the 1St information word bit Xi:
P74= P74 X1 P17478 = P17478 OA- 1
P279= P2790 A-1 P18264 P18264 0 k 1
P859= P85910 A- 1 P26525= P26525 0 A- 1
P6972 = P69720 A- 1 P28565= P28565 A- 1
P13069 = P130690 A- 1 P28582= P285820 A-1
...(14)
Step 4) Since the same address of the parity bit as in the second row (that is
the row of i=1) of
table 10 is given to the Lth information word bit XL, in a similar method to
the above-described
method, the address of the parity bit regarding the next L-1 number of
information word bits A.,õ
(m=L+1, L+2, 2L-1)
is calculated based on Equation 13. In this case, x is the address of the
parity bit accumulator corresponding to the information word bit XL, and may
be obtained based
on the second row of table 10.
Step 5) The above-described processes are repeated for L number of new
information word
bits of each group by considering new rows of table 10 as the address of the
parity bit
accumulator.
Step 6) After the above-described processes are repeated for the codeword bits
Ao to kx-i,
values regarding Equation 15 presented below are calculated in sequence from
i=1:
Step 7) Parity bits kic to
corresponding to the matrix B having the dual diagonal
configuration are calculated based on Equation 16 presented below:
2K4-Lxt+s = PQixS+t (0 s <L,0 t <Q1) ...(16)
Step 8) The address of the parity bit accumulator regarding L number of new
codeword bits
XIC to Alc+mi_i of each group is calculated based on table 10 and Equation 13.
Step 9) After the codeword bits kic to are
calculated, parity bits 2,c+mi to .1./c,mi+m,_1
corresponding to the matrix C having the diagonal configuration are calculated
based on

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
36
Equation 17 presented below:
K+Mi q,xt+s = P (0 S <L,0 t <Q2) ...(17)
As a result, the parity bits may be calculated in the above-described method.
Referring back to FIG. 1, the encoder 110 may perform the LDPC encoding by
using various
code rates such as 3/15, 4/15, 5/15, 6/15, 7/15, 8/15, 9/15, 10/15, 11/15,
12/15, 13/15, etc. In
addition, the encoder 110 may generate an LDPC codeword having various lengths
such as
16200, 64800, etc., based on the length of the information word bits and the
code rate.
In this case, the encoder 110 may perform the LDPC encoding by using the
parity check
matrix, and the parity check matrix is configured as shown in FIGS. 2 to 4.
In addition, the encoder 110 may perform Bose, Chaudhuri, Hocquenghem (BCH)
encoding
as well as LDPC encoding. To achieve this, the encoder 110 may further include
a BCH encoder
(not shown) to perform BCH encoding.
In this case, the encoder 110 may perform encoding in an order of BCH encoding
and LDPC
encoding. Specifically, the encoder 110 may add BCH parity bits to input bits
by performing
BCH encoding and LDPC-encodes the information word bits including the input
bits and the
BCH parity bits, thereby generating the LDPC codeword.
The interleaver 120 interleaves the LDPC codeword. That is, the interleaver
120 receives the
LDPC codeword from the encoder 110, and interleaves the LDPC codeword based on
various
interleaving rules.
In particular, the interleaver 120 may interleave the LDPC codeword such that
a bit included
in a predetermined bit group from among a plurality of bit groups constituting
the LDPC
codeword (that is, a plurality of groups or a plurality of blocks) is mapped
onto a predetermined
bit of a modulation symbol. Accordingly, the modulator 130 may map a bit
included in a
predetermined group from among the plurality of groups of the LDPC codeword
onto a
predetermined bit of the modulation symbol.
To achieve this, as shown in FIG. 5, the interleaver 120 may include a parity
interleaver 121,
a group interleaver (or a group-wise interleaver 122), a group twist
interleaver 123 and a block
interleaver 124.
The parity interleaver 121 interleaves the parity bits constituting the LDPC
codeword.
Specifically, when the LDPC codeword is generated based on the parity check
matrix 200
having the configuration of FIG. 2, the parity interleaver 121 may interleave
only the parity bits

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
37
of the LDPC codeword by using Equations 18 presented below:
14, = C, for 0<i<Kkipc, and
= cicia +0,õ .s.õ for 0.s<M, 05A<Qmpc = = = (18),
where M is an interval at which a pattern of a column group is repeated in the
information word submatrix 210,
that is, the number of columns included in a column group (for example,
M=360), and Qldp, is a size by which each
column is cyclic-shifted in the information word submatrix 210. That is, the
parity interleaver 121 performs parity
interleaving with respect to the LDPC codeword c=(co, C),/,,,_1), and
outputs U=(uo, tiNwpc_i).
The LDPC codeword parity-interleaved in the above-described method may be
configured
such that a predetermined number of continuous bits of the LDPC codeword have
similar
decoding characteristics (cycle distribution, a degree of a column, etc.).
For example, the LDPC codeword may have the same characteristics on the basis
of M
number of continuous bits. Herein, M is an interval at which a pattern of a
column group is
repeated in the information word submatrix 210 and, for example, may be 360.
Specifically, a product of the LDPC codeword bits and the parity check matrix
should be "0".
This means that a sum of products of the ith LDPC codeword bit, ci(i=0, 1,
..., N1dix-1) and the ith
column of the parity check matrix should be a "0" vector. Accordingly, the ith
LDPC codeword
bit may be regarded as corresponding to the ith column of the parity check
matrix.
In the case of the parity check matrix 200 of FIG. 2, M number of columns in
the information
word submatrix 210 belong to the same group and the information word submatrix
210 has the
same characteristics on the basis of a column group (for example, the columns
belonging to the
same column group have the same degree distribution and the same cycle
characteristic).
In this case, since M number of continuous bits in the information word bits
correspond to the
same column group of the information word submatrix 210, the information word
bits may be
formed of M number of continuous bits having the same codeword
characteristics. When the
parity bits of the LDPC codeword are interleaved by the parity interleaver
121, the parity bits of
the LDPC codeword may be formed of M number of continuous bits having the same
codeword
characteristics.
However, regarding the LDPC codeword encoded based on the parity check matrix
300 of
FIG. 3 and the parity check matrix 400 of FIG. 4, parity interleaving may not
be performed. In
this case, the parity interleaver 121 may be omitted.
The group interleaver 122 may divide the parity-interleaved LDPC codeword into
a plurality

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
38
of bit groups and rearrange the order of the plurality of bit groups in bit
group wise (or bit group
unit). That is, the group interleaver 122 may interleave the plurality of bit
groups in bit group
wise.
To achieve this, the group interleaver 122 divides the parity-interleaved LDPC
codeword into
a plurality of bit groups by using Equation 19 or Equation 20 presented below.
X.I ={uk 1 j=[¨k ],0 k < Ndpc } for j < Ngroup
360 l
... (19)
Xi = 1E441360 x j k < 360 x ( j +1),0 k < N hipci for j < N grõup . . . (20)
where Ng,õõp is the total number of bit groups, N is the jth bit group, and uk
is the kth LDPC codeword bit input to
the group interleaver 122. In addition, ¨k is the largest integer below k/360.
[
360
Since 360 in these equations indicates an example of the interval M at which
the pattern of a
column group is repeated in the information word submatrix, 360 in these
equations can be
changed to M.
The LDPC codeword which is divided into the plurality of bit groups may be as
shown in FIG.
6.
Referring to FIG. 6, the LDPC codeword is divided into the plurality of bit
groups and each
bit group is formed of M number of continuous bits. When M is 360, each of the
plurality of bit
groups may be formed of 360 bits. Accordingly, the bit groups may be formed of
bits
corresponding to the column groups of the parity check matrix.
Specifically, since the LDPC codeword is divided by M number of continuous
bits, Kidpc
number of information word bits are divided into (Kkipc/M) number of bit
groups and Nmpc-Kidpc
number of parity bits are divided into (I\lidpc-Kwpc)/M number of bit groups.
Accordingly, the
LDPC codeword may be divided into (Islidpc/M) number of bit groups in total.
For example, when M=360 and the length Nidpc of the LDPC codeword is 16200,
the number
of groups Ngroups constituting the LDPC codeword is 45(.16200/360), and, when
M=360 and the
length Nidpc of the LDPC codeword is 64800, the number of bit groups Ngroup
constituting the
LDPC codeword is 180(=64800/360).
As described above, the group interleaver 122 divides the LDPC codeword such
that M
number of continuous bits are included in a same group since the LDPC codeword
has the same
codeword characteristics on the basis of M number of continuous bits.
Accordingly, when the

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
39
LDPC codeword is grouped by M number of continuous bits, the bits having the
same codeword
characteristics belong to the same group.
In the above-described example, the number of bits constituting each bit group
is M. However,
this is merely an example and the number of bits constituting each bit group
is variable.
For example, the number of bits constituting each bit group may be an aliquot
part of M. That
is, the number of bits constituting each bit group may be an aliquot part of
the number of
columns constituting a column group of the information word submatrix of the
parity check
matrix. In this case, each bit group may be formed of aliquot part of M number
of bits. For
example, when the number of columns constituting a column group of the
information word
submatrix is 360, that is, M=360, the group interleaver 122 may divide the
LDPC codeword into
a plurality of bit groups such that the number of bits constituting each bit
group is one of the
aliquot parts of 360.
In the following explanation, the number of bits constituting a bit group is M
by way of an
example, for the convenience of explanation.
Thereafter, the group interleaver 122 interleaves the LDPC codeword in bit
group wise.
Specifically, the group interleaver 122 may group the LDPC codeword into the
plurality of bit
groups and rearrange the plurality of bit groups in bit group wise. That is,
the group interleaver
122 changes positions of the plurality of bit groups constituting the LDPC
codeword and
rearranges the order of the plurality of bit groups constituting the LDPC
codeword in bit group
wise.
Herein, the group interleaver 122 may rearrange the order of the plurality of
bit groups in bit
group wise such that bit groups including bits mapped onto the same modulation
symbol from
among the plurality of bit groups are spaced apart from one another at
predetermined intervals.
In this case, the group interleaver 122 may rearrange the order of the
plurality of bit groups in
bit group wise by considering at least one of the number of rows and columns
of the block
interleaver 124, the number of bit groups of the LDPC codeword, and the number
of bits
included in each bit group, such that bit groups including bits mapped onto
the same modulation
symbol are spaced apart from one another at predetermined intervals.
To achieve this, the group interleaver 122 may rearrange the order of the
plurality of groups
in bit group wise by using Equation 21 presented below:
Y., = X,(j)(0 j<N )
gr uP (21),

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
where x.; is the ith bit group before group interleaving, and Yj is the ith
bit group after group
interleaving. In addition, 7r(j) is a parameter indicating an interleaving
order and is determined by
at least one of a length of an LDPC codeword, a modulation method, and a code
rate. That is,
n(j) denotes a permutation order for group wise interleaving.
Accordingly, X,,o) is a n(j)th bit group before group interleaving, and
Equation 21 means that
the pre-interleaving n(j)th bit group is interleaved into the jth bit group.
According to an exemplary embodiment, an example of n(j) may be defined as in
Tables 11
to 22 presented below.
In this case, n(j) is defined according to a length of an LPDC codeword and a
code rate, and a
parity check matrix is also defined according to a length of an LDPC codeword
and a code rate.
Accordingly, when LDPC encoding is performed based on a specific parity check
matrix
according to a length of an LDPC codeword and a code rate, the LDPC codeword
may be
interleaved in bit group wise based on n(j) satisfying the corresponding
length of the LDPC
codeword and code rate.
For example, when the encoder 110 performs LDPC encoding at a code rate of
6/15 to
generate an LDPC codeword of a length of 64800, the group interleaver 122 may
perform
interleaving by using n(j) which is defined according to the length of the
LDPC codeword of
16200 and the code rate of 6/15 in tables 11 to 22 presented below.
For example, when the length of the LDPC codeword is 64800, the code rate is
6/15, and the
modulation method(or modulation format) is 16-Quadrature Amplitude Modulation
(QAM), t(j)
may be defined as in table 11 presented below. In particular, table 11 may be
applied when
LDPC encoding is performed based on the parity check matrix defined by table
4.
[Table 11]
Order of bit groups to be block
interleaved
rc(j) (0 j <180)
j-th
1 1 1 1 1 1 1 1
1 1 2 2 2
Li of 0 I 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
group_ 23 2 2 2 2 2 2 3 3 3 3 3 3 3
3 3 3 4 4 4 4 4 4
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
wise
4 4 4 5 5 5 5 5 5 5 5 5 5 6 6 6
6 6 6 6 6 6
46
interleaver 7 8 9 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9 9
output 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
9 9 9 9 9 9 9 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1
92
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
41
11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 I 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
1 8 5 6 1 1 6 5 5 8 9 7 1 1
6 5 6 1 1 6 7 8
46 3 2 2 76 60 8 3 6 1 7 9 13 63 1 8 9 33 08 6 1 6
14 5 6 1 5 7 1 1 6 1 1 8 1 1 1 1
9 1 9 1 6 1 1
4 7 7 16 9 0 56 72 5 49 55 2 38 36 41 11 6 70 0 40 4 59 5
7L6)-th 3 14 5 4 6 4 1 4 2 3 2 3 2 3
1 4 4 3 0 2 3 2
7
7 4 4 3 3 8 7 5 4 9 0 6 9 6
1 5 6 3 2 8
block of
3 4 3 2 4 5 6 4 2 2 1 5 3
2 4 1 4 1 9
27 4 3
group- 8 8 3 2 9 1 0 6 1 0 3 0 5 4 0 7 2 6
12 3
wise 12 1 9 1 1 3 1 1 7 1 1 1 1 1
1 9 7 1 1 1 1 7 1
7 01 4 15 05 1 9 77 4 0 45 62 02 20 26 5 3 52 29 74 25 2 28
interleaver
1 1 1 1 8 1 7 1 1 7 1 1 8
1 1 9 1 1 1
78 8 9 1
input 71 42 78 54 5 07 5 2 51 7 17
09 0 06 34 8 22 73 61
15 1 1 1 1 1 1 1 1 1 1 1 8 1 1 -
1 1 8 1 1- 1 9 8
0 10 75 66 31 19 03 39 48 57 14 47 7 58 21 64 04 9 79 23 18 9 8
9 1 8 1 1 1 1 1 1 1 1 9 1
7 1 1
11 2 5
2 65 4 68 24 69 30 67 53 37 43 1 00
6 32 35
In the case of Table 11, Equation 21 may be expressed as YO=X70)=X55,
Yi=Xx(1)=X146,
Y2=X(2)=X-83, = = =, Y178=X7(l78)=X132, and Yi79=X7(l79)=X135. Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 551h
bit group to the 0th bit group, the 146th bit group to the 1st bit group, the
83rd bit group to the 2nd
bit group, ..., the 132nd bit group to the 1781h bit group, and the 135th bit
group to the 179th bit
group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 8/15,
and the modulation method is 16-QAM, n(j) may be defined as in table 12
presented below. In
particular, table 12 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 5.
[Table 12]
j-th Order of bit groups to be block
interleaved
block of n(j) (0 <j < 180)
group- 1 2 3 4 5 6 7 8 9 1 1 1 1
1 1 1 1 1 1 2 2 2
0 1 2 3 4 5 6 7
8 9 0 1 2
wise
2 2 2 2 2 2 3 3 3 3 3 3 3 3
3 3 4 4 4 4 4 4
23
interleaver 4 5 6 7 8 9 0 1 2 3 4 5 6
7 8 9 0 1 2 3 4 5
4 4 4 5 5 5 5 5 5 5 5 5 5 6
6 6 6 6 6 6 6 6
output 46
7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
42
7 7 7 7 7 7 7 7 7 7 8 8 8 8
8 8 8 8 8 8 9 9
69
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
6 7 8 9 0 1
9 9 9 9 9 9 9 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
92
3 4 5 6 7 8 9 GO 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 - 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 - 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 -
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
5 1 7 1 8 1 7 1 4 4 1 1 6 1
9 8 1 1 8 6 5 8
58
5 11 3 50 7 10 1 72 5 1 13 15 9 20 5 8 78 23 0 6 3 2
11 3 8 9 8 7 7 8 6 6 4 7 1 7 8 1
4 9 3 7 4 6 5
8 8 9 9 5 9 5 3 8 3 0 7 17 0 1 12 3 4 7 2 6 7 1
ic(j)-th 92 1 6 6 2 2 2 2 6 5 7 5 4
6 7 8 3 9 4 4 9 2 2
7 5 0 5 9 3 8 1 9 4 7 9 2 8 6 0
3 2 4 0 2 6
block of
________________________________________________________________________
2 9 4 1 5 5 2 3 4 3 2 5 1 3
7 2 3 5 8 1 1
33 0
group- 4 1 7 0 2 0 0 1 8 9 7 4 5
2 6 1 6 6 4 8 69
Wise 1 1 3 1 1 1 1 1 1 1 1 1
1 1 1 1
7 5 8 3 4 1 6
1 36 5 65 06 59 38 9 28 68 66
44 49 79 41 3
interleaver
_____________________________________________________________________
1 9 3 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1
2 9
input 0 42 6 4 61 70 34 56 2 54 74 45 46 4 24 6 02 33 76 32 35
11 1 1 1 1 1 1 1 9 1 1 1 1 1 1 6
1 1 1 1 1 1 9
6 30 77 60 29 08 25 47 7 48 62 73 63 22 04 4 43 67 03 40 58 39 8
10 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
5 26 09 19 01 21 07 31 52 64 75 51 27 14 37 57 53 71 55
In the case of Table 12, Equation 21 may be expressed as Y0=X70)=X58,
Yi=Xn0)=X55,
Y2=X7,(2)=Xiii, = = =, Y178=Xx(178)=X171, and Yr9=Xic(179)=X155. Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 58th
bit group to the 0th bit group, the 55th bit group to the 1st bit group, the
111111 bit group to the 2nd
bit group, ..., the 171st bit group to the 178th bit group, and the 1551h bit
group to the 179th bit
group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 10/15,
and the modulation method is 16-QAM, n(j) may be defined as in table 13
presented below. In
particular, table 13 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 6.
[Table 13]
j-th Order of bit groups to be block
interleaved
block of it(j) (0 <j < 180)
1I I 1 1 1 1 1 1 1
1 1 1 2 2 2
group- 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7
8 9 1 2

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
43
wise 23 2 2 2 2 2 2 3 3 3 3 3 3 3
3 3 3 4 4 4 4 4 4
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
interleaver
_____________________________________________________________________
4 4 4 5 5 5 5 5 5 5 5 5 5 6
6 6 6 6 6 6 6 6
46
output 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8
8 8 8 8 8 8 9 9
69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
9 9 9 9 9 9 9 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
92
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1- 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
5 8 1 2 1 9 6 4 5 1 9 1 2 4
2 3 8 6-- 8 7
74 1
8
3 4 09 8 03 9 5 1 0 2 5 15 9 8 5 5 9 2 0 1
7 8 5 1 4 4 4 3 4 9 1 9 - 8
1 4 9 1 3 9 1 5 1
34
7 1 8 13 4 9 5 3 0 1 7 4 2 6 6 3 04 6 2 11 7 16
7[0)-th 10 8 3 7 3 8 7 6 5 7 1 4 1 8
1 9 1 3 6 2 6 1 6
7 6 8 2 1 3 6 1 4 3 02 2 08 5 10 7 4 0 0 7 6 18 9
block of
56
1 1 3 3 7 1 1 5 4 1 1 1 5
3 9 8 1 6 1
4 7
5
group- 05 19 9 2 0 01 14 2 7 5 17 3 5 7 6 8 12 8 06
wise 16 7 1 5 2 6 1 7 1 6 2 2 1 9
2 1 7 2 9 2 1
3
9
0 8 8 9 3 4 9 9 34 3 4 0 56 0 0 5 1 8 6
28
interleaver
_____________________________________________________________________
14 1 1 1 1 1 1 1 1 2 8 1 1 1
1 4 5 6 1 1 1
6 0
input 7 1 61 62 23 38 73 77 00 2 7 37 32 69 58 3 1 7 68 43 31
14 1 1 1 1 1 1 - 1 1 1 1 1 1 1
1 1 1 1 1 1 1 - 1 1-
6 44 39 76 64 55 75 70 25 71 52 54 57 27 24 29 42 35 72 51 53 22 66
16 1 1 1 1 1 1 1 1 1 1 1 1 1
/ 1 1 1 1
5 49 36 45 30 20 50 67 26 78 40 33 21 74 41 48 79 59 63
In the case of Table 13, Equation 21 may be expressed as Y0=X70)=X74,
Yi=Xki)=X53,
Y2=Xx(2)=X84, Yi78=X/(l78)=X159, and Yi79=Xn(i79)=X163. Accordingly, the
group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 74th
bit group to the 0th bit group, the 53rd bit group to the 18t bit group, the
841h bit group to the 2" bit
group, ..., the 159th bit group to the 178th bit group, and the 163rd bit
group to the 179th bit group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 10/15,
and the modulation method is 16-QAM, it(j) may be defined as in table 14
presented below. In
particular, table 14 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 7.
[Table 14]
j-th Order of bit groups to be block
interleaved
block of rc(j) (0 j <180)

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
44
1 1 1 1 1 1 1 1
1 1 2 2 2
group- 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7
8 9 0 1 2
wise
2 2 2 2 2 2 3 3 3 3 3 3 3 3
3 3 4 4 4 4 4 4
23
interleaver 4 5 6 7 8 9 0 1 2 3 4 5 6
7 8 9 0 1 2 3 4 5
4 4 4 5 5 - 5 5 5 5 5 5 5 5 6
6 6 6 6 6 6 6 6
output 46
7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8
8 8 8 8 8 8 9 9
69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
9 9 9 9 9 9 9 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
92
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 - 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
7 5 1 2 2 1 3 1 2 1 7 5 8 1
9 6 9 8 4 8 5 4
68
1 4 9 5 1 02 2 05 9 6 9 3 2 07 1 7 4 5 8 3 8 2
2 7 3 2 9 6 1 1 1 1 8 4 1 9
7 4 8 1 6 4 6
57 9
8 6 1 6 6 5 19 14 09
25 1 3 03 3 0 6 9 12 1 5 6
Tta)-111 38 7 1 5 8 1 1 7 7 6 4 9 3
9 5 6 4 2 8 7 9
4 3
7 15 6 7 13 00 5 2 0 7 2 6 8 9 4 0 6
3 5
block of
3 8 1 3 3 6 5 8 4 9 1 2 6 6 7 6
1 1 1 1
8 0
group- 4 4 4 11 5 0 4 5 0 0 7 01
9 3 4 2 18 10 59 8
wise 3 50 1 5 1 1 1 8 1 1 1 1 1 1
1 1 3 1 1 9 3 1
7
3
75 1 31 06 34 8 40 17 32 47 53 16 61 0 9 26 36 0 7 74
interleaver
1 1 1 5 9 1 1 7 1 1 1 1 1
1 1 1 1 1 1 2 4
41 5
input 58
20 2 2 9 46 44 8 55 28 65 41 79 50 57 71 43 08 70 2 9
2 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
11
7 60 78 33 42 21 68 73 23 3 5 54 27 39 51 63 72 38 76 45 29 62
1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1
2
1
2 77 37 49 67 4 69 24 48 64 30 7 56 22 3 66
35 4
In the case of Table 14, Equation 21 may be expressed as Yo=¨Xls(0)=X683
Y1=Xx(1)=X713
Y2=Xit(2)=X54, = = = Yi78=Xn(178)=X135, and Yr9=X,(l79)=X2.4. Accordingly, the
group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 68th
- =
bit group to the 01h bit group, the 71st bit group to the 1st bit group, the
54th bit group to the 2nd bit
group, ..., the 135th bit group to the 1781h bit group, and the 24th bit group
to the 179th bit group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 12/15,
and the modulation method is 16-QAM, Ir(j) may be defined as in table 15
presented below. In
particular, table 15 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 8.
[Table 15]

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
Order of bit groups to be block interleaved
rc(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 - 2 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of 4 4 4 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6
46
group-
7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9 9
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1' 1 1 1
1 1 1 1 1 1 1
5 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
12 3 3 1 7 3 6 1 3 1 1 6 2 8 1 1
8 7 7 8 1 4 3
0 2 8 13 1 1 5 09 6 06 34 6 9 6 36 08 3 0 9 1 05 8 0
12 1 4 9 7 6 7 5 9 8 4 6 5 1 1 1
8 7 1 8 1 5
3
5 07 4 9 5 4 8 1 5 8 9 0 4 22 40 37 9 4 29 2 64 9
it(j)-th 9 9 4 7 2 1 8 1 2 9 7 1 1
5 9 1 1 9 6
67 2 9 8
2 8 2 7 8 21 7 8 1 3 2 42 12 0 0 39 4 7 3
block of
1 1 5 2 1 3 9 4 6 8 1 1 1 1 5 1
1 9 6 1 3
5
group- 04 24 2 0 18 4
4 1 8 0 10 2 33 31 3 16 23 6 1 11 3
wise 17 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 4 1 1 3 1
3 65 75 66 69 74 59 48 58 55 45 78 26 00 54 56 79 57 6 49 71 7 53
interleaver
16 1 1 1 1 1 1 7 1 1 1 1 1 1 1 1
1 1 1 1 4 2 1
input 3 52 46 77 03 60 47 6 72 44 50 32 76 68 67 62 70 38 51 61 0 6 30
11 1 1 1 8 5 6 1 4 2 1 6 1 1 1
1 2 9 7 3
0 7 4
9 14 17 15 4 7 2 3 7 4 0 9 9 27 7 6 7 1 3 5
10 1 5 2 2 1 5 4 5 1 4 1 1 1 2
1 3
1 6
2 5 5 3 5 1 6 5 8 28 3 35 43 41 2 01 9
In the case of Table 15, Equation 21 may be expressed as YO=X*0)=Xi2o,
Yt=Xx(I)=X32,
Y2=3Q2)=X38, = = =, Y178;---X7(l78)=Xtot, and Yr9=-X2r(179)=X39. Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 120th
bit group to the 0111 bit group, the 32'd bit group to the 15t bit group, the
38th bit group to the 2nd
bit group, ..., the 101st bit group to the 178th bit group, and the 391h bit
group to the 179th bit
group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 6/15,
and the modulation method is 16-QAM, n(j) may be defined as in table 16
presented below. In
particular, table 16 may be applied when LDPC encoding is performed based on
the parity check

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
46
matrix defined by table 10.
[Table 16]
Order of bit groups to be block
interleaved
it(j) (0 5 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of 4 4 4 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6
46
group- 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9 9
wise 69
0 I 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 111
111 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
_
16 1 1 1 8 1 1 1 9 1 1 1 1 7 1 1
1 1 1 7 1 1 9
3 60 38 43 5 08 28 21 1 47 40 42 31 9 09 26 11 62 44 5 10 18 7
1 1 1 9 1 8 1 1 1 1 1 1 1 1 1 1
1 1 1 9 1 2
81
68 57 67 0 03 0 50 25 05 29 46 41 52 64 30 14 23 34 07 6 73 0
rc(j)-th 6 1 6 8 1 4 1 1 6 6 8 3 1
6 8 1 2 5 5 5 6
44 5
4 9 13 5 16 1 3 6 4 9 0 9 8
35 5 5 4 8 1
block of
5 5 1 1 1 2 5 3 2 4 6 1 4 5 3 2
1 2 1 4
3
group- 33 7 9 6 8 55 1 6 6 9 8 2 54 3 1 4
7 2 4 7 2
wise 14 3 2 2 1 3 611 3 5 911 2 7
1 4 1 8 1
1 9
5 8 8 12 1 0 79 3 0 0 5 4 5
6 1 32 0 04 9 06
interleaver
1 4 1 1 4 2 4 1 6 5 9 1 1
1 1 2 1 1 1 1
= 46 4 7
input 66 7 61 74 9 3 1 39 8 2 9 49 15 01 27 2 58
69 53 22
11 1 9 1 8 1 1 6 9 1 7 7 7 7 8 7
1 3 3 3 1 8 1
7 59 3 00 2 51 71 7 4 36 2 3 4 0 6 6 37 5 7 2 77 7 70
17 7 1 1 1 5 1 1 1 6 8 1 9 7 1 1
1 1 9
8 7 75 20 65 3 72 33 76 5 3 24 2 8 19 02 56 48 8
In the case of Table 16, Equation 21 may be expressed as Y0=X70)=X163,
Yi=X/K0=Xi6o,
Y2=Xik2)=X138, = = = , Yi78=X7(l78)=X148, and Yi79=X,1(l79)=X98. Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 163"I
bit group to the 0th bit group, the 160th bit group to the 1st bit group, the
138th bit group to the 2nd
bit group, ..., the 148th bit group to the 1781h bit group, and the 98th bit
group to the 179th bit
group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 6/15,

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
47
and the modulation method is 64-QAM, it(j) may be defined as in table 17
presented below. In
particular, table 17 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 4.
[Table 17]
Order of bit groups to be block
interleaved
rc(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3
4 4 - 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of 4 4 4 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6
46
group- 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8- 8 9 9
wise 69
0 1 2 3 4 5 6 7 8 9 (1 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
1 3 3 2 4 3 3 1 4 4 2 3 4 1 1
1 1 2 4 5
29 9 1
7 8 7 7 3 1 5 6 6 4 3
4 5 4 8 56 9 2 0 0
5 4 2 4 6 4 5 6 6 5 6 6 6 5 1 6
1 5 7 4 2
24
5
6 9 6 2 9 7 9 1 6 2 4 5 7 4 70 8 32 1 0 1 1
rc(j)-th 16 1 5 6 5 6 5 1 7 5 1 6 3
2 7 3 3 7 8 8 1
7 3
0 3 5 2 3 3 8
67 1 7 51 0 6 5 4 9 2 2 5 6 07
block of
11 4 8 1 1 2 7 1 7 7 1 1 1 1
2 1 9 1 3 1 1 1
group- 3 8 8 229 37 0 3 66 5 7 42 74 5 49 8 45 2 69 0 33 63 19
wise 82 0 1 1 1 1 1 1 9 1 1 8 1 1
1 1 1 1 9 1 9 9 1
76 52 34 39 48 64 9 73 04 3 06 12 35 53
28 44 8 71 4 7 43
interleaver
11 1 1 8 7 1 1 1 9 1 9 1 1 1
1 1 1 1 1 1 8 1
input 0 18 27 4 9 08 26 31 3 11 1 425 62 57 58 09 40 23 54 50 0 1
1 9 8 1 8 1 1 1 1 1 1 1 7 1 1
1 1 1 1 1
12 8 6
46 6 1 65 9 38 05 41 03
00 61 72 8 01 15 79 47 16 36 22
3 1 1 1 1 9 1 1 1 1 7 1 1 1 1 9
1 1
87
3 30 24 75 20 0 02 0 14 59 6 77 78 21 68 5 17 55
In the case of Table 17, Equation 21 may be expressed as Yo.--X,0)=X2.9,
Yi=X*1)=X17,
Y2=Xx(2)=X3s, = = =, Yi78=X7(l78)=Xir, and Yi79=X7(J79)=X155. Accordingly, the
group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 29th
bit group to the 0th bit group, the 17th bit group to the 1st bit group, the
38th bit group to the 2nd bit
th th
group, ..., the 117th bit group to the 178 bit group, and the 155th bit group
to the 179 bit group.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
48
In another example, when the length of the LDPC codeword is 64800, the code
rate is 8/15,
and the modulation method is 64-QAM, 7r(j) may be defined as in table 18
presented below. In
particular, table 18 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 5.
[Table 18]
Order of bit groups to be block
interleaved
TE(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 - 2 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of
4 4 4 5 5 5 5 5 5 5 5 5 5 6 6 6
6 6 6 6 6 6
46
group-
7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 - 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9- 9
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 2.3 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
7 5 4 8 9 4 8 6 4 8 3 5 6 3 5 5
9 6 8 7 7 4
86
1 1 8 9 4 6 1 7 9 0 7 5 1 6
7 2 2 0 2 6 2 4
9 6 5 9 4 7 5 5 4 8 7 6 4 5 8 9
3 6 1
42 4 8
6
1 2 0 0 0 8 3 8 7 5 (1 9 3 4
4 3 8 4 8
7C(J)-th 9 6 5 8 7 1 8 7 6 8 7 1 1
1 3 2 1 3 3 1 1
77 3
5 6 9 3 3 7 7
5 5 8 9 4 51 17 2 2 23 0 3 62 44
block of
1 1 1 1 2 3 2 1 1 1 1 2 1 1 1 1
1 3 1 3 1 2
9
group-
21 08 39 42 4 4 0 57 59 38 43 9 40 63 50 75 14 1 2 5 45 8
wise 2 1 9 1 1 1 1 2 2 1 1 4 1
2 1 .. 1 .. 5 .. 1 .. 1 .. 1
27 5
1
6 6 8 02 03 33 61 1 5 07 53 5 56 3 25 41 6 66
70 19
interleaver
1 4 7 1 1 1 1 9 1 1 1 1 1 1 1
1 1 1 1 1
68 2 0
input 34 1 4 79 29 69 01 9 09 27 68 76
1 22 10 13 46 32 65 9
3 1 1 1 1 1 1 1 1 1 6 1 1 1 1
1 1 1 1 1 1
13 7
9
64 06 72 54 49 0 73 31 67 3 47 55 00 71 58 60 5 78 48 52
1 1 9 1 1 1 1 1 1 1 1 1 1 9 1 1
1 1
4 24 77 7 30 18 37 11 26 20 05 15 36 12 6 35 16 74 28
In the case of Table 18, Equation 21 may be expressed as Y0=- -3(70)=X86,
Y1=X7,(1)=X71,
Y2=X*2)=X51, = = = 5 Y178=Xx(178)=X174, and Yi79=Xx(179)=X128- Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 861h
bit group to the Oth bit group, the 7181 bit group to the 1st bit group, the
51st bit group to the 2nd bit

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
49
group, ..., the 174th bit group to the 178th bit group, and the 128th bit
group to the 179th bit group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 10/15,
and the modulation method is 64-QAM, ir(j) may be defined as in table 19
presented below. In
particular, table 19 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 6.
[Table 19]
Order of bit groups to be block
interleaved
n(j) (0 5 j < 180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3
3 3 4 4 4 4 4 4-
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of -
4 4 4 5 5 5 5 5 5 5 5 5 5 6
6 6 6 6 6 6 6 6-
46
group- 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8
8 8 8 8 8 8 9 9-
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 - 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 - 1 - 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
-
3 2 5 3 7 1 1 8 7 4 7 1 5 5
4 1 4 4 9 3 4 1
73
6 1 3 7 8 02 19 2 5 0 7 04 9 8 1 8 6 5 3 0 9 14
9 6 3 1 1 9 1 2 3 2 7 8 1
6 5 5 9 1 5 5 8
79 1
7 6 3 15 12 9 07 6 9 3 0 9 16 2 5 0 6 08 7 1 6
7t(1)-th 8 5 6 7 1 8 1 6 1 1 6 4 - 1
8 3- 1 2 1 9 9
28 8
6
8 2 9 4 13 4 09 5 01 11 1 4 05 3 5 30 7 06 0 2
block of
_________________________________________________________________________
8 3 3 8 6 1 6 1 7 9 3 1 4
4 6 7 6 9 6 1 1
54 group- 7 7 8 1 5 3 17 7 10 2 4 2 18 7 8 8 6 0 1 4
7 42
wise 15 2 1 4 5
4 1 1
5 1 3 1 2 1 2 1 1
1 4 9 1 1 9
6 4 2 2 6 70 72
6 4 52 9 1 0 36 58 34 3 8 41 60 5
interleaver
1 8 1 7 1 1 1 1 1 2 1 1 1 1
1 1 1 1 1 1 1
0 9
input 54 1 69 1 71 62 39 75 29 5 67
31 23 65 40 24 78 0 4 45 64
1 1 1 1 2 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
3 2
5 43 73 76 2 61 53
9 51 50 74 44 57 63 22 47 32 37 28 59 55
12 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 8 1 1
7 38 03 00 20 46 68 66 48 3 25 77 33 26 21 79 0 49 35
In the case of Table 19, Equation 21 may be expressed as Yo.X7,0)=X73,
Yi.Xõ(1)=X36,
Y2=X2(2)=X2i, = = =, Y178=Xx(178)=X149, and Yi79=X7(l79)=X135. Accordingly,
the group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 73rd

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
bit group to the Of" bit group, the 361h bit group to the 181 bit group, the
21st bit group to the 2nd bit
group, ..., the 149th bit group to the 1781h bit group, and the 135th bit
group to the 179th bit group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 10/15,
and the modulation method is 64-QAM, ir(j) may be defined as in table 20
presented below. In
particular, table 20 may be applied when LDPC encoding is performed 'based on
the parity
check matrix defined by table 7.
[Table 20]
Order of bit groups to be block
interleaved
n(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of 4 4 4 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6
46
group-
7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9 9
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
5 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
11 1 4 1 3 8 3 8 3 8 1 8 4 1 1 5
7 7 9 1 5 1 9
3 15 7 11 5 4 4 3 1 8 09 6 6 77 03 7 7 3 5 50 2 07 8
6 5 5 4 7 1 7 2 3 9 4 7 7 6 9 5
1 2 1 5 1
43 6
6 5 6 9 2 18 8 7 9 7 0
5 9 8 3 9 19 0 0 1 08
7t(j)-th 1 6 1 3 1 5 1 3 9 7 9 1 8
9 1 6 1 1 4 1
65 1 7
14 9 16
0 01 0 4 8 9 1 6 28 2 2 66 0 78 17 5 57
block of
1 6 3 9 8 5 1 5 9 1 1 6 1 1 7 6
1 1 1 8 2 1
group- 4829 7 7 4 9 3 00 4 1 73 69 3 49 04 0 1 02 10 24 0 9 8
2 3 2 5 6 3 6 4 2 8 2 1 8 7 1 2
1 4 8 7
wise 19 0 5
4 6 2 8 2 3 4 2 8 6 12 5
4 3 1 05 4 7 6
interleaver
10 2 8 9 1 1 1 1 1 1 1 1 2 1 1 1
1 1 1 1 1
3 9
input 6 5 1 0 1 68 21 53 40 52 35
74 3 39 2 6 46 64 42 5 47
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
2 4
61 20 33 55 23 58 67 54 48 37 60 45 59
7 26 43 51 62 56 72 71
13 4 1 1 1 3 1 1 1 1 1 1 1 1 1 1
1 1 1
1 1 79 32 36 2 75 63 65 41 38 22 27 25 44 70 34 30 76
=.!Atto.-
In the case of Table 20, Equation 21 may be expressed as 110=X70)=X113,
Yi=Xx(1)=X115,
Y2=Xn(2)=X47, = = Y178=Xx(178)=X130, and Y179=Xir(I79)=X176. Accordingly, the
group interleaver

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
51
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 113th
bit group to the 0th bit group, the 115th bit group to the 1st bit group, the
47th bit group to the 2nd
bit group, ..., the 130th bit group to the 178th bit group, and the 176th bit
group to the 179th bit
group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 12/15,
and the modulation method is 64-QAM, Ir(j) may be defined as in table 21
presented below. In
particular, table 21 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 8.
[Table 21]
Order of bit groups to be block
interleaved
n(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4
j-th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of 4 4 4 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6
46
group- 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8
8 8 8 8 9 9
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
11 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 311 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
16 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
9 9 4 5 4 3 7 1 1 8 6 1 7 3 3 9
5 7 1 1 7 6
83
3 4 7 5 0 8 7 10 24 7 1 02 6 3 5 2 9 4 1 38 2 7
1 9 1 1 4 5 9 5 1 1 1 8 1 2 1 7
6 1 6 1
37 0 9
0 5 39 31 4 7 7 3 42 36 43 6 00 1 5 5 2 9 5 29
n(j)-th 10 7 2 6 7 2 1 8 9 1 1 1 2 4
1 5 9 2 1 4 9 4
8
1 9 2 8 3 3 8 1 8 12 28 03 5 3 26 4 0 8 09 6 1 1
block of
8 2 1 1 5 1 7 2 1 9 5 1 6 6 8
3 1 1 6 4 6 1 8 3
group-
13 34 2 05 8 7 35 6 6 40 4 6 9 4 20 08 3 5 9 21 8 9
1 1 1 1 3 4 5 7 1 5 8 8 8 1 1 1
3 2 4 5 3 1
wise 29
33 06 17 27 2 2 8 1 18 1 4 5 0 04 32 11 0 6 8 0 1 41
interleaver
11 1 1 7 1 1 1 1 3 1 1 1 1 1
1 9 1 1 2 1 1 1 1
input 6 23 14 0 07 78 45 73 6 44 30 76 71 75 25 9 62 59 0 64 15 69 72
16 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 4 1
4
6
5 61 51 19 22 52 57 37 48 53 70 54 66 3 50 6
67 74 63 9 68
14 1 1 1 1 1 1- 1 6- 2 1 1 1
1 5 7 3 2
7 46 49 56 79 2 60 77 0 4 56 55 7

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
52
In the case of Table 21, Equation 21 may be expressed as Y0=X70)=X83,
Y1=Xrr(1)=X939
Y2=Xn(2)=X94, = = =, Y178=XE(178)--=X2, and Yi79=X179)=X14. Accordingly, the
group interleaver 122
may rearrange the order of the plurality of bit groups in bit group wise by
changing the 83r1 pit
r
group to the 0th bit group, the 93' bit group to the lst bit group, the 94"
bit group to the 2' bit
=
group, the 2" bit group to the 178di bit group, and the 14th bit group to
the 179th bit group.
In another example, when the length of the LDPC codeword is 64800, the code
rate is 6/15,
and the modulation method is 64-QAM, Ic(j) may be defined as in table 22
presented below. In
particular, table 22 may be applied when LDPC encoding is performed based on
the parity check
matrix defined by table 10.
[Table 22]
Order of bit groups to be block
interleaved
Tt(j) (0 j <180)
1 1 1 1 1 1 1 1
1 1 2 2 2
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 0 1 2
2 2 2 2 2 2 3 3 3 3 3 3 3 3
3 3 4 4 4 4 4 4
j -th 23
4 5 6 7 8 9 0 1 2 3 4 5 6 7
8 9 0 1 2 3 4 5
block of - 4 4 4 5 5 5 5 5 5 5 5 5
5 6 6 6 6 6 6 6 6 6
46
group- 7 8 9 0 1 2 3 4 5 6 7 8 9 0
1 2 3 4 5 6 7 8
7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8 9- 9-
wise 69
0 1 2 3 4 5 6 7 8 9 0 1 2 3
4 5 6 7 8 9 0 1
interleaver 9 9 9 9 9 9 9 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
92
output
3 4 5 6 7 8 9 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14
_
11 1 1 1 1 1 1 1 1 1- 1 1 1 1 1 1
1 1 1 1 1 1 1
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1- 1- 1 1 1 1
8 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
- 16 1 - 1 1 1 1 1 1 1 1 1 1 1
1 - 1 1 1 1 1
1 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
17 1 1 1 8 3 I 8 8 3 1 1 9 1 8 1
1 1 1 1 1 4
4
5 77 73 25 9 7 65 5 2 4 7 62 2 61 8 37 49 15 13 72 23 3
7 1 9 1 2 1 1 5 - 5 2 2 1 1 1 5 1
8 1 2 5 1
8
2 6 43 8 39 0 50 3 2 0 5 4 53 33 22 5 0 3 8 7 1 5
74.1)-th
1 1 8 1 5 1 2 4 6 1 5 2 1
5 1 2 1 1 6 1
46 7 1
block of 64 55 1 02 3 1 1 7 1 26 7 6
48 6 71 2 66 01 7 19
17 1 1 9 8 9 6 1 9 6 1 3 1 1 8 1
1 5 6 6 9
group- 8 5 3
21 18 6 0 9 8 67 0 2 47 6 40 03 7 57 76 9 6
4 1
wise 7 1 7 1 4 3 3 2 1 4 6 4 1
3 1 4 1 1 5 1 1
29 0
interleaver 1 07 7 11 2 5 8 3 GO 5 9 0 29 3 63 9 12 45 4 05 17
10 9 7 1 1 1 6 3 1 - 2 7 9 7 - 1 8
5- 1 9 1 1 1 4
inut
4 9 2 9 06 0 9 04 8 2
3 7 5 54 4 8 44 5 36 6 70 4
15 7 6 4 1 1 4 1 1 8 1 1 7 1 1
1 6 1 1 9 3
9 6
1 0 3 8 28 14 1 74 16 6 41 09 8 27 42 59 5 30 24 3
0
11 3 1 1 1 1 1 1 7 1 1 1 1 1 1 1
1 3 7

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
53
lo 12 I 60 1 35 32 34 I 4 I 46 I 4 I 20 1 58 138
179 69 56 I 31 I 68 1 1 I 2 17-1--
In the case of Table 22, Equation 21 may be expressed as Y0=X70)=X175,
Y1=Xx(j)=X177,
Y2=XX(2)=X1731 = = = Y178=XTE(178)=X31, and Y179=Xn(179)=X72- Accordingly, the
group interleaver
122 may rearrange the order of the plurality of bit groups in bit group wise
by changing the 175th
bit group to the 0th bit group, the 177th bit group to the 1st bit group, the
173rd bit group to the fd
bit group, ..., the 31st bit group to the 178111 bit group, and the 72nd bit
group to the 179111 bit group.
In the above-described examples, the length of the LDPC codeword is 64800 and
the code
rate is 6/15, 8/15, 10/15, and 12/15. However, this is merely an example and
the interleaving
pattern may be defined variously when the length of the LDPC codeword is 16200
or the code
rate has different values.
As described above, the group interleaver 122 may rearrange the order of the
plurality of bit
groups in bit group wise by using Equation 21 and Tables 11 to 22.
"j-th block of Group-wise Interleaver output" in tables 11 to 22 indicates the
j-th bit group
output from the group interleaver 122 after interleaving, and "n(j)-th block
of Group-wise
Interleaver input" indicates the 7r(j)-th bit group input to the group
interleaver 122.
In addition, since the order of the bit groups constituting the LDPC codeword
is rearranged by
the group interleaver 122 in bit group wise, and then the bit groups are block-
interleaved by the
block interleaver 124, which will be described below, "Order of bit groups to
be block
interleaved" is set forth in Tables 11 to 22 in relation to n(j).
The LDPC codeword which is group-interleaved in the above-described method is
illustrated
in FIG. 7. Comparing the LDPC codeword of FIG. 7 and the LDPC codeword of FIG.
6 before
group interleaving, it can be seen that the order of the plurality of bit
groups constituting the
LDPC codeword is rearranged.
That is, as shown in FIGs. 6 and 7, the groups of the LDPC codeword are
arranged in order of
bit group )Co, bit group Xi, ..., bit group XNgr00p-1 before being group-
interleaved, and are
arranged in an order of bit group Yo, bit group Yi, ..., bit group Y
- Ngroup-1 after being group-
interleaved. In this case, the order of arranging the bit groups by the group
interleaving may be
determined based on Tables 11 to 22.
The group twist interleaver 123 interleaves bits in a same group. That is, the
group twist
interleaver 123 may rearrange the order of the bits in the same bit group by
changing the order of

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
54
the bits in the same bit group.
In this case, the group twist interleaver 123 may rearrange the order of the
bits in the same bit
group by cyclic-shifting a predetermined number of bits from among the bits in
the same bit
group.
For example, as shown in FIG. 8, the group twist interleaver 123 may cyclic-
shift bits
included in the bit group Y1 to the right by 1 bit. In this case, the bits
located in the 0th position,
the 1st position, the 2hd position, ..., the 358th position, and the 359th
position in the bit group Y1
as shown in FIG. 8 are cyclic-shifted to the right by 1 bit. As a result, the
bit located in the 359th
position before being cyclic-shifted is located in the front of the bit group
Yi and the bits located
in the 0th position, the 1st position, the 2nd position, ..., the 358th
position before being cyclic-
shifted are shifted to the right serially by 1 bit and located.
In addition, the group twist interleaver 123 may rearrange the order of bits
in each bit group
by cyclic-shifting a different number of bits in each bit group.
For example, the group twist interleaver 123 may cyclic-shift the bits
included in the bit
group Y1 to the right by 1 bit, and may cyclic-shift the bits included in the
bit group Y2 to the
right by 3 bits.
However, the above-described group twist interleaver 123 may be omitted
according to
circumstances.
In addition, the group twist interleaver 123 is placed after the group
interleaver 122 in the
above-described example. However, this is merely an example. That is, the
group twist
interleaver 123 changes only the order of bits in a certain bit group and does
not change the order
of the bit groups. Therefore, the group twist interleaver 123 may be placed
before the group
interleaver 122.
The block interleaver 124 interleaves the plurality of bit groups the order of
which has been
rearranged. Specifically, the block interleaver 124 may interleave the
plurality of bit groups the
order of which has been rearranged by the group interleaver 122 in bit group
wise (or bits group
unit). The block interleaver 124 is formed of a plurality of columns each
including a plurality of
rows and may interleave by dividing the plurality of rearranged bit groups
based on a
modulation order determined according to a modulation method.
In this case, the block interleaver 124 may interleave the plurality of bit
groups the order of
which has been rearranged by the group interleaver 122 in bit group wise.
Specifically, the block

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
interleaver 124 may interleave by dividing the plurality of rearranged bit
groups according to a
modulation order by using a first part and a second part.
Specifically, the block interleaver 124 interleaves by dividing each of the
plurality of columns
into a first part and a second part, writing the plurality of bit groups in
the plurality of columns of
the first part serially in bit group wise, dividing the bits of the other bit
groups into groups (or
sub bit groups) each including a predetermined number of bits based on the
number of columns,
and writing the sub bit groups in the plurality of columns of the second part
serially.
Herein, the number of bit groups which are interleaved in bit group wise may
be determined
by at least one of the number of rows and columns constituting the block
interleaver 124, the
number of bit groups and the number of bits included in each bit group. In
other words, the block
interleaver 124 may determine the bit groups which are to be interleaved in
bit group wise
considering at least one of the number of rows and columns constituting the
block interleaver
124, the number of bit groups and the number of bits included in each bit
group, interleave the
corresponding bit groups in bit group wise, and divide bits of the other bit
groups into sub bit
groups and interleave the sub bit groups. For example, the block interleaver
124 may interleave
at least part of the plurality of bit groups in bit group wise using the first
part, and divide bits of
the other bit groups into sub bit groups and interleave the sub bit groups
using the second part.
Meanwhile, interleaving bit groups in bit group wise means that the bits
included in the same
bit group are written in the same column. In other words, the block
interleaver 124, in case of bit
groups which are interleaved in bit group wise, may not divide the bits
included in the same bit
groups and write the bits in the same column, and in case of bit groups which
are not interleaved
in bit group wise, may divide the bits in the bit groups and write the bits in
different columns.
Accordingly, the number of rows constituting the first part is a multiple of
the number of bits
included in one bit group (for example, 360), and the number of rows
constituting the second
part may be less than the number of bits included in one bit group.
In addition, in all bit groups interleaved by the first part, the bits
included in the same bit
group are written and interleaved in the same column of the first part, and in
at least one group
interleaved by the second part, the bits are divided and written in at least
two columns of the
second part.
The specific interleaving method will be described later.
Meanwhile, the group twist interleaver 123 changes only the order of bits in
the bit group and

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
56
does not change the order of bit groups by interleaving. Accordingly, the
order of the bit groups
to be block-interleaved by the block interleaver 124, that is, the order of
the bit groups to be
input to the block interleaver 124, may be determined by the group interleaver
122. Specifically,
the order of the bit groups to be block-interleaved by the block interleaver
124 may be
determined by 7r(j) defined in Tables 11 to 22.
As described above, the block interleaver 124 may interleave the plurality of
bit groups the
order of which has been rearranged in bit group wise by using the plurality of
columns each
including the plurality of rows.
In this case, the block interleaver 124 may interleave the LDPC codeword by
dividing the
plurality of columns into at least two parts. For example, the block
interleaver 124 may divide
each of the plurality of columns into the first part and the second part and
interleave the plurality
of bit groups constituting the LDPC codeword.
In this case, the block interleaver 124 may divide each of the plurality of
columns into N
number of parts (N is an integer greater than or equal to 2) according to
whether the number of
bit groups constituting the LDPC codeword is an integer multiple of the number
of columns
constituting the block interleaver 124, and may perform interleaving.
When the number of bit groups constituting the LDPC codeword is an integer
multiple of the
number of columns constituting the block interleaver 124, the block
interleaver 124 may
interleave the plurality of bit groups constituting the LDPC codeword in bit
group wise without
dividing each of the plurality of columns into parts.
Specifically, the block interleaver 124 may interleave by writing the
plurality of bit groups of
the LDPC codeword on each of the columns in bit group wise in a column
direction, and reading
each row of the plurality of columns in which the plurality of bit groups are
written in bit group
wise in a row direction.
In this case, the block interleaver 124 may interleave by writing bits
included in a
predetermined number of bit groups, which corresponds to a quotient obtained
by dividing the
number of bit groups of the LDPC codeword by the number of columns of the
block interleaver
124, on each of the plurality of columns serially in a column direction, and
reading each row of
the plurality of columns in which the bits are written in a row direction.
Hereinafter, the group located in the jth position after being interleaved by
the group
interleaver 122 will be referred to as group Y.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
57
For example, it is assumed that the block interleaver 124 is formed of C
number of columns
each including R1 number of rows. In addition, it is assumed that the LDPC
codeword is formed
of Nom, number of bit groups and the number of bit groups Ngroup is a multiple
of C.
In this case, when the quotient obtained by dividing Ngroup number of bit
groups constituting
the LDPC codeword by C number of columns constituting the block interleaver
124 is A
(=NgrOUp/C) (A is an integer greater than 0), the block interleaver 124 may
interleave by writing A
(=Ngroup/C) number of bit groups on each column serially in a column direction
and reading bits
written on each column in a row direction.
For example, as shown in FIG. 9, the block interleaver 124 writes bits
included in bit group
Yo, bit group bit group YA_-1 in the 1st column from the 1st row to the
Rith row, writes bits
included in bit group YA, bit group YA+1, , bit group Y2A4 in the 2nd column
from the 1st row
to the Rig' row, ..., and writes bits included in bit group YCA-A, bit group
YCA-A+1, , bit group
YcA-1 in the column C from the 1st row to the RP row. The block interleaver
124 may read the
bits written in each row of the plurality of columns in a row direction.
Accordingly, the block interleaver 124 interleaves all bit groups constituting
the LDPC
codeword in bit group wise.
However, when the number of bit groups of the LDPC codeword is not an integer
multiple of
the number of columns of the block interleaver 124, the block interleaver 124
may divide each
column into 2 parts and interleave a part of the plurality of bit groups of
the LDPC codeword in
bit group wise, and divide bits of the other bit groups into sub bit groups
and interleave the sub
bit groups. In this case, the bits included in the other bit groups, that is,
the bits included in the
number of groups which correspond to the remainder when the number of bit
groups constituting
the LDPC codeword is divided by the number of columns are not interleaved in
bit group wise,
but interleaved by being divided according to the number of columns.
Specifically, the block interleaver 124 may interleave the LDPC codeword by
dividing each
of the plurality of columns into two parts.
In this case, the block interleaver 124 may divide the plurality of columns
into the first part
and the second part based on at least one of the number of columns of the
block interleaver 124,
the number of bit groups of the LDPC codeword, and the number of bits of bit
groups.
Here, each of the plurality of bit groups may be formed of 360 bits. In
addition, the number of
bit groups of the LDPC codeword is determined based on the length of the LDPC
codeword and

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
58
the number of bits included in the bit group. For example, when an LDPC
codeword in the
length of 16200 is divided such that each bit group has 360 bits, the LDPC
codeword is divided
into 45 bit groups. Alternatively, when an LDPC codeword in the length of
64800 is divided
such that each bit group has 360 bits, the LDPC codeword may be divided into
180 bit groups.
Further, the number of columns constituting the block interleaver 124 may be
determined
according to a modulation method. This will be explained in detail below.
Accordingly, the number of rows constituting each of the first part and the
second part may
be determined based on the number of columns constituting the block
interleaver 124, the
number of bit groups constituting the LDPC codeword, and the number of bits
constituting each
of the plurality of bit groups.
Specifically, in each of the plurality of columns, the first part may be
formed of as many rows
as the number of bits included in at least one bit group which can be written
in each column in
bit group wise from among the plurality of bit groups of the LDPC codeword,
according to the
number of columns constituting the block interleaver 124, the number of bit
groups constituting
the LDPC codeword, and the number of bits constituting each bit group.
In each of the plurality of columns, the second part may be formed of rows
excluding as many
rows as the number of bits included in at least some bit groups which can be
written in each of
the plurality of columns in bit group wise. Specifically, the number rows of
the second part may
be the same value as a quotient when the number of bits included in all bit
groups excluding bit
groups corresponding to the first part is divided by the number of columns
constituting the block
interleaver 124. In other words, the number of rows of the second part may be
the same value as
a quotient when the number of bits included in the remaining bit groups which
are not written in
the first part from among bit groups constituting the LDPC codeword is divided
by the number
of columns.
That is, the block interleaver 124 may divide each of the plurality of columns
into the first
part including as many rows as the number of bits included in bit groups which
can be written in
each column in bit group wise, and the second part including the other rows.
Accordingly, the first part may be formed of as many rows as the number of
bits included in
bit groups, that is, as many rows as an integer multiple of M. However, since
the number of
codeword bits constituting each bit group may be an aliquot part of M as
described above, the
first part may be formed of as many rows as an integer multiple of the number
of bits

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
59
constituting each bit group.
In this case, the block interleaver 124 may interleave by writing and reading
the LDPC
codeword in the first part and the second part in the same method.
Specifically, the block interleaver 124 may interleave by writing the LDPC
codeword in the
plurality of columns constituting each of the first part and the second part
in a column direction,
and reading the plurality of columns constituting the first part and the
second part in which the
LDPC codeword is written in a row direction.
That is, the block interleaver 124 may interleave by writing the bits included
in at least some
bit groups which can be written in each of the plurality of columns in bit
group wise in each of
the plurality of columns of the first part serially, dividing the bits
included in the other bit groups
except the at least some bit groups and writing in each of the plurality of
columns of the second
part in a column direction, and reading the bits written in each of the
plurality of columns
constituting each of the first part and the second part in a row direction.
In this case, the block interleaver 124 may interleave by dividing the other
bit groups except
the at least some bit groups from among the plurality of bit groups based on
the number of
columns constituting the block interleaver 124.
Specifically, the block interleaver 124 may interleave by dividing the bits
included in the
other bit groups by the number of a plurality of columns, writing each of the
divided bits in each
of a plurality of columns constituting the second part in a column direction,
and reading the
plurality of columns constituting the second part, where the divided bits are
written, in a row
direction.
That is, the block interleaver 124 may divide the bits included in the other
bit groups except
the bit groups written in the first part from among the plurality of bit
groups of the LDPC
codeword, that is, the bits in the number of bit groups which correspond to
the remainder when
the number of bit groups constituting the LDPC codeword is divided by the
number of columns,
by the number of columns, and may write the divided bits in each column of the
second part
serially in a column direction.
For example, it is assumed that the block interleaver 124 is formed of C
number of columns
each including R1 number of rows. In addition, it is assumed that the LDPC
codeword is formed
of Ngroup number of bit groups, the number of bit groups Ngroup is not a
multiple of C, and
Ax C +1= Ngroup (A is an integer greater than 0). In other words, it is
assumed that when the

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
number of bit groups constituting the LDPC codeword is divided by the number
of columns, the
quotient is A and the remainder is 1.
In this case, as shown in FIGs 10 and 11, the block interleaver 124 may divide
each column
into a first part including R1 number of rows and a second part including R2
number of rows. In
this case, R1 may correspond to the number of bits included in bit groups
which can be written in
each column in bit group wise, and R2 may be R1 subtracted from the number of
rows of each
column.
That is, in the above-described example, the number of bit groups which can be
written in
each column in bit group wise is A, and the first part of each column may be
formed of as many
rows as the number of bits included in A number of bit groups, that is, may be
formed of as
many rows as Ax M number.
In this case, the block interleaver 124 writes the bits included in the bit
groups which can be
written in each column in bit group wise, that is, A number of bit groups, in
the first part of each
column in the column direction.
That is, as shown in FIGs. 10 and 11, the block interleaver 124 writes the
bits included in
each of bit group Yo, bit group Yi, ..., group Y,k_i in the 1St to Rith rows
of the first part of the 1st
column, writes bits included in each of bit group YA, bit group YA4-1, = = bit
group Y2A-1 in the 1st
to Rith rows of the first part of the 2nd column, ..., writes bits included in
each of bit group YCA-A5
bit group YcA_A+1, ..., bit group YcA4 in the 1st to Rith rows of the first
part of the column C.
As described above, the block interleaver 124 writes the bits included in the
bit groups which
can be written in each column in bit group wise in the first part of each
column.
In other words, in the above exemplary embodiment, the bits included in each
of bit group
(Yo), bit group (Y1),..., bit group (YA_i) may not be divided and all of the
bits may be written in
the first column, the bits included in each of bit group (YA), bit group
(YA+1),..., bit group (Y2A-1)
may not be divided and all of the bits may be written in the second columnõõ
and the bits
included in each of bit group (YcA.A), bit group (YcA-A+1),... , group (YcA4)
may not be divided
and all of the bits may be written in the C column. As such, all bit groups
interleaved by the first
part are written in the same column of the first part.
Thereafter, the block interleaver 124 divides bits included in the other bit
groups except the
bit groups written in the first part of each column from among the plurality
of bit groups, and
writes the bits in the second part of each column in the column direction. In
this case, the block

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
61
interleaver 124 divides the bits included in the other bit groups except the
bit groups written in
the first part of each column by the number of columns, so that the same
number of bits are
written in the second part of each column, and writes the divided bits in the
second part of each
column in the column direction.
In the above-described example, since A x C +1 =N group 7 when the bit groups
constituting the
LDPC codeword are written in the first part serially, the last bit group
YNgroup_i of the LDPC
codeword is not written in the first part and remains. Accordingly, the block
interleaver 124
divides the bits included in the bit group YNgroup-i into C number of sub bit
groups as shown in
FIG. 10, and writes the divided bits (that is, the bits corresponding to the
quotient when the bits
included in the last group (YNgroup-i) are divided by C) in the second part of
each column serially.
The bits divided based on the number of columns may be referred to as sub bit
groups. In this
case, each of the sub bit groups may be written in each column of the second
part. That is, the
bits included in the bit groups may be divided and may form the sub bit
groups.
That is, the block interleaver 124 writes the bits in the 1" to R2th rows of
the second part of the
1" column, writes the bits in the 1" to R2th rows of the second part of the
2"1 column, ..., and
writes the bits in the 1" to R2th rows of the second part of the column C. In
this case, the block
interleaver 124 may write the bits in the second part of each column in the
column direction as
shown in FIG. 10.
That is, in the second part, the bits constituting the bit group may not be
written in the same
column and may be written in the plurality of columns. In other words, in the
above example, the
last bit group (YNgroup-1) is formed of M number of bits and thus, the bits
included in the last bit
group (YNgroup_i) may be divided by M/C and written in each column. That is,
the bits included
in the last bit group (Y
, - Ngroup-1) are divided by M/C, forming M/C number of sub bit groups, and
each of the sub bit groups may be written in each column of the second part.
Accordingly, in at least one bit group which is interleaved by the second
part, the bits
included in the at least one bit group are divided and written in at least two
columns constituting
the second part.
In the above-described example, the block interleaver 124 writes the bits in
the second part in
the column direction. However, this is merely an example. That is, the block
interleaver 124 may
write the bits in the plurality of columns of the second part in the row
direction. In this case, the
block interleaver 124 may write the bits in the first part in the same method
as described above.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
62
Specifically, referring to FIG. 11, the block interleaver 124 writes the bits
from the 1st row of
the second part in the 1st column to the 1st row of the second part in the
column C, writes the bits
from the 2n1 row of the second part in the 1st column to the 2nd row of the
second part in the
column C, ..., etc., and writes the bits from the RP row of the second part in
the 1St column to
the R2th row of the second part in the column C.
On the other hand, the block interleaver 124 reads the bits written in each
row of each part
serially in the row direction. That is, as shown in FIGs. 10 and 11, the block
interleaver 124
reads the bits written in each row of the first part of the plurality of
columns serially in the row
direction, and reads the bits written in each row of the second part of the
plurality of columns
serially in the row direction.
Accordingly, the block interleaver 124 may interleave a part of the plurality
of bit groups
constituting the LDPC codeword in bit group wise, and divide and interleave
some of the
remaining bit groups. That is, the block interleaver 124 may interleave by
writing the LDPC
codeword constituting a predetermined number of bit groups from among the
plurality of bit
groups in the plurality of columns of the first part in bit group wise,
dividing the bits of the other
bit groups and writing the bits in each of the columns of the second part, and
reading the
plurality of columns of the first and second parts in the row direction.
As described above, the block interleaver 124 may interleave the plurality of
bit groups in the
methods described above with reference to FIGs. 9 to 11.
In particular, in the case of FIG. 10, the bits included in the bit group
which does not belong
to the first part are written in the second part in the column direction and
read in the row
direction. In view of this, the order of the bits included in the bit group
which does not belong to
the first part is rearranged. Since the bits included in the bit group which
does not belong to the
first part are interleaved as described above, bit rrror rate (BER)/frame
error rate (FER)
performance can be improved in comparison with a case in which such bits are
not interleaved.
However, the bit group which does not belong to the first part may not be
interleaved as
shown in FIG. 11. That is, since the block interleaver 124 writes and reads
the bits included in
the group which does not belong to the first part in and from the second part
in the row direction,
the order of the bits included in the group which does not belong to the first
part is not changed
and the bits are output to the modulator 130 serially. In this case, the bits
included in the group
which does not belong to the first part may be output serially and mapped onto
a modulation

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
63
symbol.
In FIGs. 10 and 11, the last single bit group of the plurality of bit groups
is written in the
second part. However, this is merely an example. The number of bit groups
written in the second
part may vary according to the total number of bit groups of the LDPC
codeword, the number of
columns and rows, the number of transmission antennas, etc.
The block interleaver 124 may have a configuration as shown in tables 23 and
24 presented
below:
[Table 23]
Nom= 64800
QM< 16 QAM 64 QAM 256 QAM 1024 QAM 4096 QAM"
2 4 6 8 10 12
Ai 32400 16200 10800 7920 6480 5400
A2 0 0 0 180 0 0
[Table 24]
16200
____________________ QPSF 16 QAM 64 QAM 256 QAM 1024 QAM 4096 QAM
C 2 4 6 8 10 12
R 7920 3960 2520 1800 1440 1080
1t2 180 90 180 225 180 270
Herein, C (or NO is the number of columns of the block interleaver 124, R1 is
the number of
rows constituting the first part in each column, and R2 is the number of rows
constituting the
second part in each column.
Referring to Tables 23 and 24, the number of columns has the same value as a
modulation
order according to a modulation method, and each of a plurality of columns is
formed of rows
corresponding to the number of bits constituting the LDPC codeword divided by
the number of a
plurality of columns.
For example, when the length Nidp, of the LDPC codeword is 64800 and the
modulation
method is 16-QAM, the block interleaver 124 is formed of 4 columns as the
modulation order is
4 in the case of 16-QAM, and each column is formed of rows as many as
R1+R2=16200(=64800/4). In another example, when the length Nidpe of the LDPC
codeword is
64800 and the modulation method is 64-QAM, the block interleaver 124 is formed
of 6 columns
as the modulation order is 6 in the case of 64-QAM, and each column is formed
of rows as many
as R1+R2=10800(=64800/6).

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
64
Meanwhile, referring to Tables 23 and 24, when the number of bit groups
constituting an
LDPC codeword is an integer multiple of the number of columns, the block
interleaver 124
interleaves without dividing each column. Therefore, R1 corresponds to the
number of rows
constituting each column, and R2 is 0. In addition, when the number of bit
groups constituting an
LDPC codeword is not an integer multiple of the number of columns, the block
interleaver 124
interleaves the groups by dividing each column into the first part formed of
R1 number of rows,
and the second part formed of R2 number of rows.
When the number of columns of the block interleaver 124 is equal to the number
of bits
constituting a modulation symbol, bits included in a same bit group are mapped
onto a single bit
of each modulation symbol as shown in Tables 23 and 24.
For example, when N1dpc=64800 and the modulation method is 16-QAM, the block
interleaver
124 may be formed of four (4) columns each including 16200 rows. In this case,
the bits
included in each of the plurality of bit groups are written in the four (4)
columns and the bits
written in the same row in each column are output serially. In this case,
since four (4) bits
constitute a single modulation symbol in the modulation method of 16-QAM, bits
included in the
same bit group, that is, bits output from a single column, may be mapped onto
a single bit of
each modulation symbol. For example, bits included in a bit group written in
the 1st column may
be mapped onto the first bit of each modulation symbol.
In another example, when N1dpc=64800 and the modulation method is 64-QAM, the
block
interleaver 124 may be formed of six (6) columns each including 10800 rows. In
this case, the
bits included in each of the plurality of bit groups are written in the six
(6) columns and the bits
written in the same row in each column are output serially. In this case,
since six (6) bits
constitute a single modulation symbol in the modulation method of 64-QAM, bits
included in the
same bit group, that is, bits output from a single column, may be mapped onto
a single bit of
each modulation symbol. For example, bits included in a bit group written in
the 1st column may
be mapped onto the first bit of each modulation symbol.
Referring to Tables 23 and 24, the total number of rows of the block
interleaver 124, that is,
R1+R2, is Nidpc/C.
In addition, the number of rows of the first part, R1, is an integer multiple
of the number of
bits included in each group, M (e.g., M=360), and maybe expressed as LATgroup
I C i> M and the
number of rows of the second part, R2, may be Nmpc,/C-Ri. Herein, [N group icj
is the largest

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
integer below Ngroup/C. Since R1 is an integer multiple of the number of bits
included in each
group, M, bits may be written in R1 in bit groups wise.
In addition, when the number of bit groups of the LDPC codeword is not a
multiple of the
number of columns, it can be seen from Tables 23 and 24 that the block
interleaver 124
interleaves by dividing each column into two parts.
Specifically, the length of the LDPC codeword divided by the number of columns
is the total
number of rows included in the each column. In this case, when the number of
bit groups of the
LDPC codeword is a multiple of the number of columns, each column is not
divided into two
parts. However, when the number of bit groups of the LDPC codeword is not a
multiple of the
number of columns, each column is divided into two parts.
For example, it is assumed that the number of columns of the block interleaver
124 is
identical to the number of bits constituting a modulation symbol, and an LDPC
codeword is
formed of 64800 bits as shown in Table 28. In this case, each bit group of the
LDPC codeword is
formed of 360 bits, and the LDPC codeword is formed of 64800/360(=180) bit
groups.
When the modulation method is 16-QAM, the block interleaver 124 may be formed
of four
(4) columns and each column may have 64800/4(=16200) rows.
In this case, since the number of bit groups of the LDPC codeword divided by
the number of
columns is 180/4(=45), bits can be written in each column in bit group wise
without dividing
each column into two parts. That is, bits included in 45 bit groups which is
the quotient when the
number of bit groups constituting the LDPC codeword is divided by the number
of columns, that
is, 45x360(=16200) bits can be written in each column.
However, when the modulation method is 256-QAM, the block interleaver 124 may
be
formed of eight (8) columns and each column may have 64800/8(=8100) rows.
In this case, since the number of bit groups of the LDPC codeword divided by
the number of
columns is 180/8=22.5, the number of bit groups constituting the LDPC codeword
is not an
integer multiple of the number of columns. Accordingly, the block interleaver
124 divides each
of the eight (8) columns into two parts to perform interleaving in bit group
wise.
In this case, since the bits should be written in the first part of each
column in bit group wise,
the number of bit groups which can be written in the first part of each column
in bit group wise is
22, which is the quotient when the number of bit groups constituting the LDPC
codeword is
divided by the number of columns, and accordingly, the first part of each
column has

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
66
22x360(=7920) rows. Accordingly, 7920 bits included in 22 bit groups may be
written in the
first part of each column.
The second part of each column has rows which are the rows of the first part
subtracted from
the total rows of each column. Accordingly, the second part of each column
includes 8100-
7920(.180) rows.
In this case, the bits included in the other bit groups which have not been
written in the first
part are divided and written in the second part of each column.
Specifically, since 22x8(=176) bit groups are written in the first part, the
number of bit
groups to be written in the second part is 180-176 (=4) (for example, bit
group Y1765 bit group
Y177, bit group Y178, and bit group Y179 from among bit group Yo, bit group
Yi, bit group Y2, = = =,
bit group Y178, and bit group Y179 constituting the LDPC codeword).
Accordingly, the block interleaver 124 may write the four (4) bit groups which
have not been
written in the first part and remains from among the groups constituting the
LDPC codeword in
the second part of each column serially.
That is, the block interleaver 124 may write 180 bits of the 360 bits included
in the bit group
Y176 in the 1st row to the 180th row of the second part of the 1st column in
the column direction,
and may write the other 180 bits in the 1st row to the 180th row of the second
part of the 2nd
column in the column direction. In addition, the block interleaver 124 may
write 180 bits of the
360 bits included in the bit group Y177 in the 18t row to the 180th row of the
second part of the 31d
column in the column direction, and may write the other 180 bits in the rt row
to the 180th row
of the second part of the 4th column in the column direction. In addition, the
block interleaver
124 may write 180 bits of the 360 bits included in the bit group Y178 in the
1st row to the 180th
row of the second part of the 5th column in the column direction, and may
write the other 180
bits in the 1st row to the 180th row of the second part of the 6th column in
the column direction. In
addition, the block interleaver 124 may write 180 bits of the 360 bits
included in the bit group
Y179 in the 1st row to the 180th row of the second part of the 7th column in
the column direction,
and may write the other 180 bits in the 1st row to the 180th row of the second
part of the 8th
column in the column direction.
Accordingly, the bits included in the bit group which has not been written in
the first part and
remains are not written in the same column in the second part and may be
divided and written in
the plurality of columns.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
67
Hereinafter, the block interleaver 124 of FIG. 5 according to an exemplary
embodiment will
be explained in detail with reference to FIG. 12.
In a group-interleaved LDPC codeword (vo, v1, ..., _,),
Irj is continuously arranged like
V={Yo, Yt, = = = YN -1.} =
W.2gP
The LDPC codeword after group interleaving may be interleaved by the block
interleaver 124
as shown in FIG. 12. In this case, the block interleaver 124 divide a
plurality of columns into the
first part(Part 1) and the second part(Part 2) based on the number of columns
of the block
interleaver 124 and the number of bits of bit groups. In this case, in the
first part, the bits
constituting the bit groups may be written in the same column, and in the
second part, the bits
constituting the bit groups may be written in a plurality of columns(i.e. the
bits constituting the
bit groups may be written in at least two columns).
Specifically, input bits vi are written serially from the first part to the
second part column
wise, and then read out serially from the first part to the second part row
wise. That is, the data
bits v, are written serially into the block interleaver column-wise starting
in the first aprt and
continuing column-wise finishing in the second part, and then read out
serially row-wise from
the first part and then row-wise from the second part. Accordingly, the bit
included in the same
bit group in the first part may be mapped onto a single bit of each modulation
symbol.
In this case, the number of columns and the number of rows of the first part
and the second
part of the block interleaver 124 vary according to a modulation format and a
length of the
LDPC codeword as in Table 25 presented below. That is, the first part and the
second part block
interleaving configurations for each modulation format and code length are
specified in Table 25
presented below. Herein, the number of columns of the block interleaver 124
may be equal to the
number of bits constituting a modulation symbol. In addition, a sum of the
number of rows of the
first part, N11 and the number of rows of the second part, Nr2, is equal to
Nidpc/Nc (herein, Nc is
Ogroup /Nd x 360
the number of columns). In addition, since Nri(= )is a
multiple of 360, a multiple
of bit groups may be written in the first part.
[Table 25]

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
68
Rows in Part 1 No Rows in Part 2 Nr2
Modulation Columns Nc
Roc =64800 Nidpc =16200 Nicipc = 64800 Nidpc =16200
QPSK 32400 7920 0 180 2
16-QAM 16200 3960 0 90 4
64-QAM 10800 2520 0 180 6
256-QAM 7920 1800 180 225 8
1024-QAM 6480 1440 0 180 10
4096-QAM 5400 1080 0 270 12
Hereinafter, an operation of the block interleaver 124 will be explained in
detail.
Specifically, as shown in FIG. 12, the input bit v, (0 i <N, xN,i) is written
in r, row of q
i
column of the first part of the block interleaver 124. Herein, q and r, are c,
= - and r,=(i
N
_ rl
mod MO, respectively.
In addition, the input bit v, (Ncx111,ii <Nwpc) is written in r, row of q
column of the
second part of the block interleaver 124. Herein, q and r, satisfy c, = [(It -
Nc x Nri)] and
Nr2
r, = N, +{(i-NcxNõdmodN,2}, respectively.
An output bit qi(0.j<N1dpc) is read from q column of ri row. Herein, ri and q
satisfy
J
r' = [ ---. and c3=6 mod NO, respectively.
N,
For example, when the length Nidpe of an LDPC codeword is 64800 and the
modulation
method is 256-QAM, the order of bits output from the block interleaver 124 may
be
(qopqi,q2,===04633579(163358,C163359,C1633601C163361,= = =,q64799)=
(VO,V7920)V15840)===0747519,V55439,V63359,V63360,V635401===3V64799)= Herein,
the indexes of the right side of
the foregoing equation may be specifically expressed for the eight (8) columns
as 0, 7920, 15840,
23760, 31680, 39600, 47520, 55440, 1, 7921, 15841, 23761, 31681, 39601, 47521,
55441, ... ,
7919, 15839, 23759, 31679, 39599, 47519, 55439, 63359, 63360, 63540, 63720,
63900, 64080,
64260, 64440, 64620, ... , 63539, 63719, 63899, 64079, 64259, 64439, 64619,
64799.
Hereinafter, the interleaving operation of the block interleaver 124 will be
explained in detail.
The block interleaver 124 may interleave by writing a plurality of bit groups
in each column
in bit group wise in a column direction, and reading each row of the plurality
of columns in

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
69
which the plurality of bit groups are written in bit group wise in a row
direction.
In this case, the number of columns constituting the block interleaver 124 may
vary according
to a modulation method, and the number of rows may be the length of the LDPC
codeword/the
number of columns.
For example, when the modulation method is 16-QAM, the block interleaver 124
may be
formed of 4 columns. In this case, when the length Nicipc of the LDPC codeword
is 16200, the
number of rows is 16200 (.64800/4). In another example, when the modulation
method is 64-
QAM, the block interleaver 124 may be formed of 6 columns. In this case, when
the length Nicipc
of the LDPC codeword is 64800, the number of rows is 10800 (.64800/6).
Hereinafter, the method for interleaving the plurality of bit groups in bit
group wise by the
block interleaver 124 will be explained in detail.
When the number of bit groups constituting the LDPC codeword is an integer
multiple of the
number of columns, the block interleaver 124 may interleave by writing the bit
groups as many
as the number of bit groups divided by the number of columns in each column
serially in bit
group wise.
For example, when the modulation method is 16-QAM and the length Niapc of the
LDPC
codeword is 64800, the block interleaver 124 may be formed of four (4) columns
each including
16200 rows. In this case, since the LDPC codeword is divided into
(64800/360=180) number of
bit groups when the length I=11dpc of the LDPC codeword is 64800, the number
of bit groups
(=180) of the LDPC codeword may be an integer multiple of the number of
columns (=4) when
the modulation method is 16-QAM. That is, no remainder is generated when the
number of bit
groups of the LDPC codeword is divided by the number of columns.
In this case, as shown in FIG. 13, the block interleaver 124 writes the bits
included in each of
the bit group Yo, bit group ...., bit group Y44 in the 1st row to 16200th
row of the first column,
writes the bits included in each of the bit group Y45, the bit group Y46, . .
. , the bit group Y89 in the
1st row to 162001h row of the second column, writes the bits included in each
of the bit group Y90,
the bit group Y91,..., the bit group Y134 in the 1st row to 16200th row of the
third column, and
writes the bits included in each of the bit group Y135, the bit group
Y136,..., the bit group Y179 in
the 1st row to 16200th row of the fourth column. In addition, the block
interleaver 124 may read
the bits written in each row of the two columns serially in the row direction.
In another, when the modulation method is 64-QAM and the length Nidp, of the
LDPC

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
codeword is 64800, the block interleaver 124 may be formed of six (6) columns
each including
10800 rows. In this case, since the LDPC codeword is divided into
(64800/360=180) number of
bit groups when the length Nidp, of the LDPC codeword is 64800, the number of
bit groups
(.180) of the LDPC codeword may be an integer multiple of the number of
columns (=4) when
the modulation method is 64-QAM. That is, no remainder is generated when the
number of bit
groups of the LDPC codeword is divided by the number of columns.
In this case, as shown in FIG. 14, the block interleaver 124 writes the bits
included in each of
the bit group Yo, bit group bit
group Y29 in the 1st row to 108001h row of the first column,
writes the bits included in each of the bit group Y30, the bit group the
bit group Y59 in the
1st row to 10800th row of the second column, writes the bits included in each
of the bit group Y60,
the bit group the
bit group Y89 in the 1st row to 10800th row of the third column, writes
the bits included in each of the bit group Y90, the bit group Y91,..., the bit
group Y119 in the 1st
row to 10800th row of the fourth column, writes the bits included in each of
the bit group Y1201
the bit group Y121,..., the bit group Y149 in the 1st row to 10800th row of
the fifth column, and
writes the bits included in each of the bit group Y150, the bit group
Y151,..., the bit group Y179 in
the I.st row to 10800th row of the sixth column.. In addition, the block
interleaver 124 may read
the bits written in each row of the two columns serially in the row direction.
As described above, when the number of bit groups constituting the LDPC
codeword is an
integer multiple of the number of columns of the block interleaver 124, the
block interleaver 124
may interleave the plurality of bit groups in bit group wise, and accordingly,
the bits belonging to
the same bit group may be written in the same column.
As described above, the block interleaver 124 may interleave the plurality of
bit groups of the
LDPC codeword in the method described above with reference to FIGs. 13 and 14.
The modulator 130 maps the interleaved LDPC codeword onto a modulation symbol.
Specifically, the modulator 130 may demultiplex the interleaved LDPC codeword,
modulate the
demultiplexed LDPC codeword, and map the LDPC codeword onto a constellation.
In this case, the modulator 130 may generate a modulation symbol using the
bits included in
each of a plurality of bit groups.
In other words, as described above, the bits included in different bit groups
are written in each
column of the block interleaver 124, and the block interleaver 124 reads the
bits written in each
column in the row direction. In this case, the modulator 130 generates a
modulation symbol by

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
71
mapping the bits read in each column onto each bit of the modulation symbol.
Accordingly, each
bit of the modulation symbol belongs to a different bit group.
For example, it is assumed that the modulation symbol consists of C number of
bits. In this
case, the bits which are read from each row of C number of columns of the
block interleaver 124
may be mapped onto each bit of the modulation symbol and thus, each bit of the
modulation
symbol consisting of C number of bits belong to C number of different bit
groups.
Hereinbelow, the above feature will be described in greater detail.
First, the modulator 130 demultiplexes the interleaved LDPC codeword. To
achieve this, the
modulator 130 may include a demultiplexer (not shown) to demultiplex the
interleaved LDPC
codeword.
The demultiplexer (not shown) demultiplexes the interleaved LDPC codeword.
Specifically,
the demultiplexer (not shown) performs serial-to-parallel conversion with
respect to the
interleaved LDPC codeword, and demultiplexes the interleaved LDPC codeword
into a cell
having a predetermined number of bits (or a data cell).
For example, as shown in FIG. 15, the demultiplexer (not shown) receives the
LDPC
codeword Q=(q0, qi, q2, ...) output from the interleaver 120, outputs the
received LDPC
codeword bits to a plurality of substreams serially, converts the input LDPC
codeword bits into
cells, and outputs the cells.
In this case, the bits having the same index in each of the plurality of
substreams may
constitute the same cell. Accordingly, the cells may be configured like (yo,o,
yi,o, y1moD-
1,0=(q0, qi, chmoD-1), (yo,i, yi,i, = = =, yilmoD-1,1)=( %mop, q040D+1, = = =,
q2õm0D-1), . = ===
Herein, the number of substreams, Nsubstreams9 may be equal to the number of
bits constituting
a modulation symbol, ImoD. Accordingly, the number of bits constituting each
cell may be equal
to the number of bits constituting a modulation symbol (that is, a
modulationorder).
For example, when the modulation method is 16-QAM, the number of bits
constituting the
modulation symbol, 11/9,40D, is 4 and thus the number of substreams,
Nsubstreams, is 4, and the cells
may be configured like (y0,0, Y1,09 Y2,09 Y3,0)=(:109 qi, (42, q3), (yo,i,
yi,i, y2,1, y3,1)---(q4,q5, q6,q7), (Y0,29
Y1,29 Y2,29 y3,2)=(q8, q9, q10, qii), = = = =
In another example, when the modulation method is 64-QAM, the number of bits
constituting
the modulation symbol, imoD, is 6 and thus the number of substreams, Nsubstr.,
is 6, and the
cells may be configured like (yo,o, Y1,09 Y2,09 Y3,09 Y4,09 Y5,0)4C109 qi, q2,
q3, q4, q5), (yo,i, yi,i, Y2,19 Y3,19

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
72
Y4,1, Y5,1)=(q6,C177 q8,1:19, q10,c111), (Y0,2, Y1,25 Y2,25 Y3,25 Y4,25
Y5,2)=(q123 q13, q14, q15, q16, q17)/ = = ' =
The modulator 130 may map the demultiplexed LDPC codeword onto modulation
symbols.
Specifically, the modulator 130 may modulate bits (that is, cells) output from
the
demultiplexer (not shown) in various modulation methods such as Quadrature
Phase Shift
Keying (QPSK), 16-QAM, 64-QAM, 256-QAM, 1024-QAM, 4096-QAM, etc. For example,
when the modulation method is QPSK, 16-QAM, 64-QAM, 256-QAM, 1024-QAM, and
4096-
QAM, the number of bits constituting the modulation symbol, iimoD (that is,
the modulation
order), may be 2, 4, 6, 8, 10 and 12, respectively.
In this case, since each cell output from the demultiplexer (not shown) is
formed of as many
bits as the number of bits constituting the modulation symbol, the modulator
130 may generate
the modulation symbol by mapping each cell output from the demultiplexer (not
shown) onto a
constellation point serially. Herein, the modulation symbol corresponds to a
constellation point
on the constellation.
However, the above-described demultiplexer (not shown) may be omitted
according to
circumstances. In this case, the modulator 130 may generate modulation symbols
by grouping a
predetermined number of bits from interleaved bits serially and mapping the
predetermined
number of bits onto constellation points. In this case, the modulator 130 may
generate the
modulation symbols by mapping rimoD number of bits onto the constellation
points serially
according to a modulation method.
The modulator 130 may modulate by mapping cells output from the demultiplexer
(not
shown) onto constellation points in a non-uniform constellation (NUC) method.
In the non-uniform constellation method, once a constellation point of the
first quadrant is
defined, constellation points in the other three quadrants may be determined
as follows. For
example, when a set of constellation points defined for the first quadrant is
X, the set becomes ¨
conj(X) in the case of the second quadrant, becomes conj(X) in the case of the
third quadrant,
and becomes ¨(X) in the case of the fourth quadrant.
That is, once the first quadrant is defined, the other quadrants may be
expressed as follows:
1 Quarter (first quadrant)=X
2 Quarter (second quadrant)=-conj(X)
3 Quarter (third quadrant)=conj(X)
4 Quarter (fourth quadrant)=-X
Specifically, when the non-uniform M-QAM is used, M number of constellation
points may

CA 02 940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
73
be defined as z=lzo, z1, zm_11. In this case, when the constellation points
existing in the first
quadrant are defined as {xo, xi, x2, ..., xm/44}, z may be defined as follows:
from zo to zmi41=from xo to Xm/4
from Zh4/4 to zam/4-1=-conj(from xo to xm/4)
from Z2x4g to z3xM/4-1=COnKfrOM x0 to XM/4)
from zwot to Z4xM/4-1=-(from xo to xm/4)
Accordingly, the modulator 130 may map the bits [yo, ..., y.4] output from the
demultiplexer
(not shown) onto constellation points in the non-uniform constellation method
by mapping the
output bits onto ZL having an index of L = (y1 x 2m1). An example of the
constellation
i=0
defined according to the non-uniform constellation method may be expressed as
in tables 26 to
30 presented below when the code rate is 5/15, 7/15, 9/15, 11/15, 13/15:
[Table 26]
Input data cell y Constellation point z,
(00) (1+10/4T
(01) (1 -11)/4T
(10) (-1+10/4r
(11) (-1-14/.1F
[Table 27]
xi Olaf* aiitis 015 33115 3331/3 fk0/15 wits Invis
rnvis
no
0.4330+3.26531 i21um.sozai 0,4813+3,25751 3,41509+1.20071 02173+041031
11,3031+045471 0.2995+4.29591 05517+035111
61
0.16614A5301 0.3014+1.21021 OM-75+001M 1.2007+0.49091' 1316711+0.25711
0.0917+0.20001 0.954114.2936X 0.3531+3.33611
x2
1.7002+3.51131 0.0100.211241 1.2000A0511 3.207640-30031, 34333423031
0.2121+040301 0-230+34301 0-3007401324
x3
(0.5115.1.23921 0.2621=11,05171 3455,01.211611 3,305.30.L31731 1,2083+05E011
11,29050.21271 64500+3.53401 0,3301+0,33571
[Table 28]
Lx/Shape I 13164.003 4041,,,V13 assjen 9/I5 R64_10/15
...F464.73/.15 _It#1..1745 5103..1388
! (6õ0367.1.00331, 0.3351+110arsu 14827.0,29201 , 413347411.51451
1A363+012761 0.3317Ø66701 1.0154,10,33941 04.100+0.74731
xx. I1.6023041-4,3671 0.8777Ø65041 1.Z46010.114111 6.1681Ø68421 imscosetaa
111318081,3241, 0.7308Ø4623k 0.1349+0.33314
x2 ! 06r13+3.43311 0.1.11.10170iti L3213Ø23./At , tai4110.2701,
10 .03+3,2219i1 0.10Ziotosmth, .4.004+0 0 42,0 .1051 0.-70+3t
xXs 1,06611.41.87031 ' 0.230+0,3003i
cifxse0.3702o =0,3330Ø37004 110484.1.3.81401C 011804.1,13,721,õ
0.72,4340150,41- 012300.160W
I 0,2202+342101 0Ø100,3$151
3.2120+13017$ 34177+0,0101 , 02531=1465611 .0,5332+13.4.9301' Loontemoto
0A85+0,0174
' I 0,1019033161 0,65770.2.0841' ...,t41041,2301
dt3142+0,17561, 0.821091õ22731 0.67230.1335P. 376720407N
30430.3019ii
,
in6 111.3049+0460011 03071.017111 V.Z170.1,03131
9.70404017361'. 0.200394,084911. 3,35370,14011, 1A2.110,20 01.
V56070.13611
02003.17346+612061 6.576140,67601 0-3771.-0.11481 -0.6774080-
71i 0.3040Ø32041 01111,3510.17631 83994Ø13004
0.7018,1120191 0.0800Ø69726 0.3040,41114731, .2363941.811441 0.411.9Ø1177i
0.6034.089221 01962Ø40701 0.7260-4.1120111
' 0.93.33Ø72181 0.2353.1.01401 &'c*1I4t101L cuoaaamm 0369802316.
I 3.2.1.30r.L9zat 0.4181,-0,92,031 3_0483.D949Si
K10. I 0,.734188.26531, 03430.1.26191 41,8365=01.11731 ,
8199+1.74101 0.7441.43-13831- 0.9394.1177141 01407.013361
01968.1.77331
611 00454Ø30691 0.2603.1.48344 8.4013690.36661
11.310otA6311 0,5n4Pxx4x3er 0.5{41.145,051, qAzas+gu an!
0.550741,479,11
I 0007018,34791 ' 0.690f8,000041' ' 0-1470/000464 8,6604=0604651
0,1105+016701 11,007+043731 01200+0,79070 090010.51,40x
' 435, ! 02171+326751 1.01170,23501 $,1091+0.30031
14102+0.2101 315120.025V ' 9.9739049501 0.4197*072061 1.3100,502V
44, 1 0,2090.3.27311 1.2621104070 0:317140.313011
1.210+0.04161 .. 0,13160.7x381 .. 1.2210+0.6701 .. 0.13$241.01.01 ..
041,76+0.17161
810 0,71161.823901 _ 1,63941Ø193.21 11...300040.01161
1.41191340.29731, 0,37.174,0.07001 1.38644A 73231 0.2261441.30141.
1.44124019440
[Table 29]

CA 02940011 2016-08-17
WO 2015/126194
PCT/KR2015/001695
74
x/Shape NUC_64 005 NM 64 7/15 NUL 64 Elvis MX 9/15 INUIL64 10/15 KUC 60 11/15
NUL 64_12/11.5 101,1C_64
x0 13.4387+1.60231
0.335240.60281 , 1,41827Ø252011 0.3547+0.61491 143884.28781 03317+0.6970
108544.53941 .. 0.8624 + 1.17151
xl 14023443871
0.20774.65841 1.25634.84111 0.15814.68421 11150.081331 0.1386403241
0.7353+046231 1.1184 Ø84621
4 08753+1.0888
01711.030281 111211+0.21741 015674.27491 10385+012191 0.1323Ø44371
10474+016951 0.2113 . 1.38431
x3 108814.87531
0355640,30351 0.87984.57021 0.1336.037001 0.8494+0.61451 0.1015413721
0.724340.15041 07535+0.77071
x4 0.2202+0.92381
0602840.33451 0.29204148271 0617740.40301 02932+146561 05682Ø4500
10693+0.94091 .. 1.1796 Ø16611
x5 , 023194.781.81
0.6577Ø20841 õ 0.8410+1.25631 0.7262Ø17561 0.8230+1.22781 0.67394.14351
0.7092+0.80731 1.0995+0.19921
16 0.30494.84.541
0.302140.17111 0.2174+1.02111 03568+0.17561 0.2069441.06491 0.3597+0.34011
1.42614.22161 08101 0.14921
x7 0.255340.75401
0.302840.15561 ' 0.5702+0.87981 0.3771+0,13361 0,5677.0 29711 0_3660+0.12041
04106+1.1783i .. 07482 . 044771
0.78/8+01019i 0.55564.89221 0.304040.147 0.5639.4.88641
0.4119441.11771 0.600440.89221 01392+0.40781 0.1524 + 0.9943i
//9 0.9238Ø2200
0.235241,01906 0.302840.16911 0.1980+1.02771 0.399840.25161 0.21204122531
0,4262+0.42051 01482 + 0.68771
10 1175404.26531
0.945041.26191 0.6855Ø18711 0.8199.1.23151 _0.74424.15591 0.9594+107241
0.1,4074.13361 0,4692 . 1.08531
41 0.84544.30491
0292241.48941 0.612640.35631 0.2854+14691/ 0se54so.43291 03829*1.3995
0.4265Ø13881 04492 + 0.73531
x12 01675.024791
0.8929+055491 014754.31310 016564.60581 01166+0.16781 11843940-56751
0.13884.7135,71 0.1579+0.13191
x13 02479+0.26751
1.019(74.23591 0.16914030291 1.038240.21411 015824033151 0.97594.19593
0.4197+0.72061 0.14634 0.40251
x14 0.2890+02701i
1.2626+0,84571 0.187140.68551 1.23624084191 0.1355414081 122394067601
01682.1.03161 04163+0.14071
0.2701+0.28901 1.48944.29221 03553+0.61251 1.1663s0.29733 0.372144.621301
135534013231 0.77874139141 04411 49.42611
[Table 30]

CA 02 940011 2 016 -08-17
WO 2015/126194 PCT/KR2015/001695
x /Shape 06/15 67/15 101/15 89/15 1110/15 011/15
612/15 013/15
0.6800+1.69261 1.2905+1.3099 1.080441.37881 1.323141.15061
1.609140.15481 0.310540.33821 1.101441.16701 0.355640.34971
41 0.391181.36451 1.0504Ø95771 1.048740.98621
0.9851+1.23111 1554940.46051 0.43424.33601 0.855741/4211
0.35794.49451
82 0.2191+1.7524i 1.532940.89351 1.6464+0.74281
1.14394.89741 1.3226Ø12901 0.314940.48291 1.295740.80391
0.5049Ø35711
83 0.2274+14208i 1.15774.81161 1.324540.94141
0.9343+0.92711 1.2772033291 0.4400Ø48071 1.08810.89561
0.505610.50631
x4 0.8678.1.24871 1.78814.2509 0.7198+1.24271
1.53984.79621 1.2753+102421 0.181140.13751 0.579541.21101
0.212340.34971
45 0.727581.16671 1.4275+0.14001 0.810641.0049
0.90924.55991 1.4434+0.75401 0.06334.34041 0.6637+1.4219
0.211640.49001
xe 0.8747+1.04701 1.4784Ø52011 0.559541.03171
1.222240.65741 1.04910.84761 0.181840.48511 0.693041.00821
0.07134.34891
47 0.7930+1.04061 1.3408+0.43461 0.611840.97221
0.957940.63731 1.186140.62531 0.063340.48151 0.884940.96471
0.06904.49601
0209840.97681 0.7837+0.58671 1.676840.20021 0.7748+1.58671
0.932640.09701 0.30844.19711 1.2063+0.51151 0.352740.20861
.9 0.2241+1.04541 0025040.64551 0999740.68441
0.6876+1.24891 0.8962+0.28041 0.43564.19931 1.005940,49521
0.34974.07131
810 0.185E10.98781 0.825640.56011 1.421240.47691
059924.92081 1.104440.11021 0.309840.05761 1.417140.59011
0.496040.21231
.11 0.190181.06591 0.87774.61101 1.147940.63121
0.679640.9740 1.0648+031671 0.434240.06911 1.046640.69351
0.49744.06961
.12 0.5547+0.83121 1.0080+0.18431 0.6079Ø6569
0.58364.58791 0.73250.60711 0.1775+0.19851 0.66394.62861
0.208640.2079
413 17547940.86511 1.0759+0.17211 0.72844.69571
0.69154.57691 0.82604.45591 0.06404.19781 0.8353Ø58511
0.209440.06901
.14 0.6073+0.81821 1.0056+0.27581 0.5724,0.70311
0.58584.70581 0.3744.10.71531 0.1775+0.06761 0.687940.80221
0.067640.20791
x15 0.595540.84201 1.06624.29641 0.630240.72591
0.6568+0.67931 0.988240.53001 006474.06691 0.863440.76221
0.069840.0689
.16 1.407040.17901 0.8334+1.55541 0.1457+1.40101
1.6118+0.14971 0.1646+1.64071 0.7455.034111 0.1213+1.43661
0.35864.79591
817 1.7227+0/9001 00165+1.10921 0.186641.73461
0.951140.11401 0.4867+1.57431 0,581140.3399 0.1077.1.20981
0.357140.63921
818 1.324640.25621 0.6092+1.27291 0.117441.10351
1.297040.12341 0.1363+1.3579 0.755640.46691 0.065140.98011
0.50344.8270
819 1.36354.36541 0.6728.1.14561 01095.1.01321
1.0266Ø1195 0.4023+130261 0.5862+0.47561 0.200941.01151
0.5063+0.66001
520 1.370341.28341 0.3061+1.74691 0.4357.1.36361
1.53314.44961 1.0542+1.25841 0.95564.32801 0.3764+1.42641
0.214610.78621
821 1.610140.84031 0.1327+1.40561 0.5853+1.68201
0.93284.35861 0.7875.1.44501 1.176740.30911 0.3237+1.2139
0.21094.63401
.22 1.161440.79091 0.3522+1.34141 0.343941.06891
1.27964.38941 0.8687+1.04071 0.967340.47201 0.520540.98141
0.07134.80931
.23 1.224140.73671 0.2273+1.30811 0.323440.99621
1.01880.34471 0.6502.1.19511 1.2051+0.51351 0.361541.01631
0.069840.64671
624 0376340.18631 0,5007Ø80981 0109240.61741
0594040.10591 0.098240.97451 0736740.20151 0.071540.65961
0.279944.08621
825 0.945249.20571 0.5528+1183471 0.107440.63071
012154.11901 0.28420.93441 0.581140.20151 0.211640.65971
0.2806+1.27551
x26 1.0100Ø21821 0.484340.84861 0.110940.69961
0,5863Ø1139 0.1142+1.14481 0.7316+0.06591 0.072940.8130
0.432840.99041
.27 0.979540.24171 0.530440.87591 0.107640.73451
0.6909+0.11661 0.3385+1.09731 0.57824.06691 0.215840.82461
0.45510.18121
.28 032414048561 0.171540.91471 0.329110.62641
0.5843+0.36041 0.6062Ø74651 0.906240.19711 0.503640.64671
0.23090.94141
.29 0023240.48371 0.15400.9519 0312640.63731 0.69704.35921
0.460740.85381 1.28294.11851 0.352640.65721 01077+1.38911
.30 0.879940.53911 0.19644.94381 0.3392+0.69991
0S808+0.3250 0.72634.87641 0.91564.07351 0.518540.80861
0.077240.98521
831 0.87960.53561 0.17884.98321 0.3202+0.72821 00678432901
0.5450+1.00671 1101103.07351 0.35934.82451 0.0802.1.17531
x32 0.137640.33421 0.375240.16671 0.965240.10661
0.14060.61821 0.265540.07461 0.3244+0.80441 12545401010I
0.8301Ø37271
.33 0.138340.32921 0.3734Ø16671 0.9075+0.16661
0.1272.129841 0.266440.07591 0.4589+0.82181 1.06764.09561
0.825640.52561
439 0.136340.33221 0375840.1661/ 0.972440.11711
0.1211+09640 0.4571+0.08521 032074.6415/ 1.4792Ø11671
0.6593,036681
135 0.137040.32731 0.374640.16491 0.918640.17521
0.1220+1.03931 0.451640.1060 0,45090.63711 0.398140.08821
0,6623+0.51821
x36 0.165540.32651 0.4013Ø12301 0.63420.13721
0.11244061011 0.255940.17901 0.192040.81961 0.55180.06901
1.01864.36491
x37 0.16564.32271 0.4001+0.12301 0.6550Ø14951
0.117740.60411 0.2586+0.17721 00633+0.81671 0.6903+005521
1.0001452421
x38 0.163440.32461 0.403740.12301 0.629010.13931
0.1136+0.74551 0.35920.28111 013114.63711 0.5740+019871
1.185740.27251
.39 0.163640.32081 0.401940.1219 0.6494+015041
0.118540.7169 0.372840.26541 0.06404064151 0.73740.15641
1.39290.34081
x40 0.177940.68411 0.60254.39341 1312740.12401
0.4324+1.56791 0.770640.09221 03331+1.06691 1.237840.30491
0.80114.22271
.41 0.1828+0.68451 0.59464.39281 0.9572+0.43441
0.39134+1.28251 0.7407+0.22601 04655+1.00871 1.0518+0.30321
0.79814.0739
442 0174540.68281 0.611640.38791 1.2403+0.26311
0.3766+0.95341 0.618040.09271 034334128651 1.458440.35111
06459+0.21981
.43 0.179340.68291 0.60194.38371 1.0254Ø41301
113568.1.03011 0.601940.1650 0.5004+1.50621 0.910740.26031
0.643040.07131
.44 0.354740.60091 0.7377+0.1610 0.6096+0.42141
0.36670.59951 0.600740.49801 0.1971.1.00511 0.632/Ø47291
0.96814.22051
145 0.359340.60111 0.72984.15821 0.6773Ø42841
0.332840.59601 0.66730.39231 0.0735+1.02981 0.7880+0.43921
0.961540.07351
x46 0.357640.59901 0.727440.17821 0.5995+0.41021
0.35874.71941 0.478640.39351 01498+1.50181 0.60450.32741
1.33274.10391
.47 0.362440.59941 0.716544117461 0.653140.4100
0.3373+0.69641 0.517640.33911 0.086541.25531 0.76294.29651
1.135940.08091
x48 0.26974014431 0.150940.24251 0.125040.11531
0.106540.11461 0.0757+0.10031 0.781140.80801 0.059640.07391
0.838240.87091
.49 0.070440.14331 0,15034.24001 0.125240.11581
0.114540.11081 0.075340.10041 0.6/6740.81531 0.176740.0730
0.814540.69341
.50 0.264403.14421 0.15154.24371 0.124540.11521
0.105340.12741 0.077740.47881 0.76364.62551 0.061240.21981
0.664540.84861
.51 0.2650+014321 0150340.24251 0.1247+0.11561
0.11340.12361 0.086740.47541 0,60004.6320 0.181540.21921
0.6600Ø67861
152 0.276340.16381 0.1285Ø2389 0.376840.12441
0.111140.38211 0.102340.22431 0.989880.76801 0.42184007151
1.16120.69491
x53 3.276840.16261 0,12794.24191 0.3707+0.12371
01186+038671 0.101040.22421 1.58550.14981 0.297840.07251
0.978540.69421
x54 0.271540.16301 0.12794.24311 0.377940.12601
0.10804.34311 0.195040.39191 0.947640.6179 0.4337+0.21151
1369840.62591
.55 0.271940.16181 0.12794.24061 0.37170.12521
0.117740.34591 0.188140.39691 1.462540.40151 0.305740.21671
1.2111341.48411
456 0.648840.16961 0.339440.57641 0.116140.36931
03644+0.10801 0.093040.81221 0.8276+1.02251 0.066780.51241
07989+104981
.57 0.646240.17061 0.33644.57221 0.115740.36451
0.3262+0.11041 0.2215+0.78401 0.631341.03641 0.2008+0.50951
0.4395+1.42031
x58 0.64564.17451 033284.575E11 0.11760.34691
0.3681+0.11131 0.093740.65141 0.88154128651 0.062540.36581
0.6118+1.02461
859 0.643140.17531 0.3303+0.56981 0.1171+0.34241
0.3289+0.11961 0.1540+0.63661 0.6342+1.27051 0.189940.35421
0.6303+1.24211
x60 0.585440.31861 0.1491+0.63161 0.3530Ø38991
0.366540.37581 0.481040.6300 1.0422+0.95931 0081840.49461
1,055040.89241
x61 0586240.31671 01461Ø62501 0.3422+0.38081
0.3310+0.3799 0.385640.70371 1.27494.85381 0.338040.50501
0.861241.28001
.62 0.5864032751 0.15094.62801 0.3614+0.37551
0.36790.33531 0.3527+0.52301 11556+1.18471 0.457140.34991
1.269640.89691
x63 0.587340.32541 0.147340.62251 0.3509Ø36561
0333610.34021 0.310040.55591 1.4771+067421 0.321640.35991
1.0342.1.11811
Table 26 indicates non-uniform QPSK, table 27 indicates non-uniform 16-QAM,
Tables 28

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
76
and 29 indicate non-uniform 64-QAM, and table 30 indicates non-uniform 256-
QAM.
Referring to these tables, the constellation point of the first quadrant may
be defined with
reference to tables 26 to 30, and the constellation points in the other three
quadrants may be
defined in the above-described method.
However, this is merely an example and the modulator 130 may map the output
bits outputted
from the demultiplexer (not shown) onto the constellation points in various
methods.
The interleaving is performed in the above-described method for the following
reasons.
Specifically, when the LDPC codeword bits are mapped onto the modulation
symbol, the bits
may have different reliability (that is, receiving performance or receiving
probability) according
to where the bits are mapped onto in the modulation symbol. The LDPC codeword
bits may have
different codeword characteristics according to the configuration of a parity
check matrix. That is,
the LDPC codeword bits may have different codeword characteristics according
to the number of
1 existing in the column of the parity check matrix, that is, the column
degree.
Accordingly, the interleaver 120 may interleave to map the LDPC codeword bits
having a
specific codeword characteristic onto specific bits in the modulation symbol
by considering both
the codeword characteristics of the LDPC codeword bits and the reliability of
the bits
constituting the modulation symbol.
For example, when the LDPC codeword formed of bit groups X0 to X179 is group-
interleaved
based on Equation 21 and Table 11, the group interleaver 122 may output the
bit groups in the
order of X55, X146, X83, - = ., X132, X135.
In this case, when the modulation method is 16-QAM, the number of columns of
the block
interleaver 124 is four (4) and each column may be formed of 16200 rows.
Accordingly, from among the 180 groups constituting the LDPC codeword, 45 bit
groups
(X55, X146, X83, X52, )(62, X176, X160, X68, X53, X56, X81, X97, X79, X113,
X163, X61, X58, X69, X133,
X108, X66, X71, X86, X144, X57, X67, X116, X59, X70, X156, X172, X65, X149,
X155, X82, X138, X136, X141,
Xi I 1, X96, X170, X90, X140, X64, X159) may be inputted to the first column
of the block interleaver
124, 45 bit groups (X15, X14, X37, X54, X44, X63, X43, X18, X47, X7, X25, X34,
X29, X30, X26, X39,
X16, X41, X45, X36, X0, X23, X32, X28, X27, X38, X48, X33, X22, X49, X51, X60,
X46, X21, X4, X3, X20,
X13, X50, X35, X24, X40, X17, X42, X6) may be inputted to the second column of
the block
interleaver 124, 45 bit groups (X112, X93, X127, X101, X94, X115, X105, X31,
X19, X177, X74, X10, X145,
X162, X102, X120, X126, X95, X73, X152, X129, X174, X125, X72, X128, X78,
X171, X8, X142, X178, X154,

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
77
X85, X107, X75, X12, X9, X151, X77, X117, X109, X80, X106, X134, X98, Xi) may
be inputted to the third
column of the block interleaver 124, and 45 bit groups (X122, X173, X161,
X150, X110, X175, X166,
X131, X119, X103, X139, X148, X157, X114, X147, X87, X158, X121, X164, X104,
X895 X179, X123, X118, X99,
)(88, X11, X92, X165, X84, X168, X124, X169, X2, X130, X167, X153, X137, X143,
X91, X100, X5, X76, X132,
X135) may be inputted to the fourth column of the block interleaver 124.
In addition, the block interleaver 124 may output the bits inputted to the 1st
row to the last
row of each column serially, and the bits outputted from the block interleaver
124 may be
inputted to the modulator 130 serially. In this case, the demultiplexer (not
shown) may be
omitted or the bits may be outputted serially without changing the order of
bits inputted to the
demultiplexer (not shown). Accordingly, the bits included in each of the bit
groups X55, X15, X112,
and X122 may constitute the modulation symbol.
When the modulation method is 64-QAM, the number of columns of the block
interleaver
124 is six (6) and each column may be formed of 10800 rows.
Accordingly, from among the 180 groups constituting the LDPC codeword, 30 bit
groups
(X55, X146, X83, X52, X62, X176, X160, X68, X53, X56, X81/ X97, X79, X113,
X163, X61, X58, X69, X133,
X108, X66, X71, X86, X144, X57, X67, X116, X59, X70, X156) may be inputted to
the first column of the
block interleaver 124, 30 bit groups (X172, X65, X149, X155, X82, X138, X136,
X141, X111, X96, X170,
X90, X140, X64, X1595 X15, X14, X37, X54, X44, X63, X435 X18, X47, X7, X25,
X34, X29, X30, X26) may
be inputted to the second column of the block interleaver 124, 30 bit groups
(X39, X16, X41, X45,
X36, X0, X23, X325 X28, X27, X38, X48, X33, X22, X49, X51, X60, X46, X21, X4,
X3, X20, X13, X50, X35,
X24, X40, X17, X42, X6) may be inputted to the third column of the block
interleaver 124, 30 bit
groups (X112, X93, X127, X101, X94, X115, X105/ X31, X19, X177, X74, X10,
X145, X162, X1025 X120, X126,
X95, X73, X152, X129, X174, X125, X72, X128, X78, X171, X8, X142, X178) may be
inputted to the fourth
column of the block interleaver 124, 30 bit groups (X154, Xs5, X107, X75, X12,
X9, X151, X77, X117,
X109, X80, X106, X134, X98, X1, X122, X173, X161, X150, X110, X175, X166,
X131, X119, X103, X139, X148,
X157, X114, X147) may be inputted to the fifth column of the block interleaver
124, and 30 bit
groups (X87, X158, X121, X164, X104, X89, X179, X123, X118, X99, X88, X11,
X92, X165, )(84, X168, X124,
X169, X2, X130, X167, X153, X137, X143, X91, X100, X5, X76, X132, X135) may be
inputted to the sixth
column of the block interleaver 124.
In addition, the block interleaver 124 may output the bits inputted to the
1.8' row to the last
row of each column serially, and the bits outputted from the block interleaver
124 may be

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
78
inputted to the modulator 130 serially. In this case, the demultiplexer (not
shown) may be
omitted or the bits may be outputted serially without changing the order of
bits inputted to the
demultiplexer (not shown). Accordingly, the bits included in each of the bit
groups X55, X172, X39,
X112, X154 ,and X87 may constitute the modulation symbol.
As described above, since a specific bit is mapped onto a specific bit in a
modulation symbol
through interleaving, a receiver side can achieve high receiving performance
and high decoding
performance.
That is, when LDPC codeword bits of high decoding performance are mapped onto
high
reliability bits from among bits of each modulation symbol, the receiver side
may show high
decoding performance, but there is a problem that the LDPC codeword bits of
the high decoding
performance may not be received. In addition, when the LDPC codeword bits of
high decoding
performance are mapped onto low reliability bits from among the bits of the
modulation symbol,
initial receiving performance is excellent, and thus, overall performance is
also excellent.
However, when many bits showing poor decoding performance are received, error
propagation
may occur.
Accordingly, when LDPC codeword bits are mapped onto modulation symbols, an
LDPC
codeword bit having a specific codeword characteristic is mapped onto a
specific bit of a
modulation symbol by considering both codeword characteristics of the LDPC
codeword bits
and reliability of the bits of the modulation symbol, and is transmitted to
the receiver side.
Accordingly, the receiver side can achieve high receiving performance and
decoding
performance.
Hereinafter, a method for determining n(j), which is a parameter used for
group interleaving,
according to various exemplary embodiments, will be explained.
According to an exemplary embodiment, when the length of the LDPC codeword is
64800,
the size of the bit group is determined to be 360 and thus 180 bit groups
exist. In addition, there
may be 180! possible interleaving patterns (Herein, factorial means A!=Ax(A-1)
x ...x2x1)
regarding an integer A.
In this case, since a reliability level between the bits constituting a
modulation symbol may be
the same according to a modulationorder, many number of interleaving patterns
may be regarded
as the same interleaving operation when theoretical performance is considered.
For example,
when an MSB bit of the X-axis (or rear part-axis) and an MSB bit the Y-axis(or
imaginary part-

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
79
axis) of a certain modulation symbol have the same theoretical reliability,
the same theoretical
performance can be achieved regardless of the way how specific bits are
interleaved to be
mapped onto the two MSB bits.
However, such a theoretical prediction may become incorrect as a real channel
environment is
established. For example, in the case of the QPSK modulation method, two bits
of a symbol in a
part of a symmetric channel like an additive white Gaussian noise (AWGN)
channel theoretically
have the same reliability. Therefore, there should be no difference in the
performance
theoretically when any interleaving method is used. However, in a real channel
environment, the
performance may be different depending on the interleaving method. In the case
of a well-known
Rayleigh channel which is not a real channel, the performance of QPSK greatly
depends on the
interleaving method and thus the performance can be predicted somewhat only by
the reliability
between bits of a symbol according to a modulation method. However, there
should be a limit to
predicting the performance.
In addition, since code performance by interleaving may be greatly changed
according to a
channel which evaluates performance, channels should be always considered to
drive an
interleaving pattern. For example, a good interleaving pattern in the AWGN
channel may be not
good in the Rayleigh channel. If a channel environment where a given system is
used is closer to
the Rayleigh channel, an interleaving pattern which is better in the Rayleigh
channel than in the
AWGN channel may be selected.
As such, not only a specific channel environment but also various channel
environments
considered in a system should be considered in order to derive a good
interleaving pattern. In
addition, since there is a limit to predicting real performance only by
theoretical performance
prediction, the performance should be evaluated by directly conducting
computation experiments
and then the interleaving pattern should be finally determined.
However, since there are so many number of possible interleaving patterns to
be applied (for
example, 180!), reducing the number of interleaving patterns used to predict
and test
performance is an important factor in designing a high performance
interleaver.
Therefore, the interleaver is designed through the following steps according
to an exemplary
embodiment.
1) Channels C1, C2, ... Ck to be considered by a system are determined.
2) A certain interleaver pattern is generated.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
3) A theoretical performance value is predicted by applying the interleaver
generated in step
2) to each of the channels determined in step 1). There are various methods
for predicting a
theoretical performance value, but a well-known noise threshold determining
method like density
evolution analysis is used according to an exemplary embodiment. The noise
threshold recited
herein refers to a value that can be expressed by a minimum necessary signal-
to-noise ratio
(SNR) capable of error-free transmission on the assumption that a cycle-free
characteristic is
satisfied when the length of a code is infinite and the code is expressed by
the Tanner graph. The
density evolution analysis may be implemented in various ways, but is not the
subject matter of
the inventive concept and thus a detailed description thereof is omitted.
4) When noise thresholds for the channels are expressed as THIN, TH2[i],
THk[i] for the
i-th generated interleaver, a final determination threshold value may be
defined as follows:
TH[i]=WixTHi [i]+W2xTH2N+ +WkxTHk[i],
where Wi +W2+ +Wk=1,Wi,W2, = = . , Wk>0
Here, W19 W25 = = = Wk are adjusted according to importance of the channels.
That is, W1 W2,
===) Wk are adjusted to a larger value in a more important channel and W1, W2,
= = Wk are
adjusted to a smaller value in a less important channel (for example, if the
weight values of
AWGN and Rayleigh channels are W1 and W2, respectively, WI may be set to 0.25
and W2 may
be set to 0.75 when one of the channels is determined to be more important.).
5) B number of interleaver patterns are selected in an ascending order of
TH[i] values from
among the tested interleaver patterns and are directly tested by conducting
performance
computation experiments. An PER level for the test is determined as 10^ ¨3
(for example,
B=100).
6) D number of best interleaver patterns are selected from among the B number
of interleaver
patterns tested in step 5) (for example, D=5).
In general, an interleaver pattern which has a great SNR gain in the area of
FER=10^ ¨3 may
be selected as a good performance interleaver in step of 5). However,
according to an exemplary
embodiment, as shown in FIG. 16, performance of FER required in the system
based on the
result of real computation experiments for the area of FER=10A ¨3 may be
predicted through
extrapolation, and then an interleaver pattern having good performance in
comparison with the
expected performance in the FER required in the system may be determined as a
good
interleaver pattern. According to an exemplary embodiment, the extrapolation
based on a linear

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
81
function may be applied. However, various extrapolation methods may be
applied. FIG. 16
illustrates an example of performance extrapolation predicted by the result of
computation
experiments.
7) The D number of interleaver patterns selected in step 6) are tested by
conducting
performance computation experiments in each channel. Herein, the FER level for
testing is
selected as FER required in the system (for example, FER=10" ¨6 )
8) When an error floor is not observed after the computation experiments, an
interleaving
pattern having the greatest SNR gain is determined as a final interleaving
pattern.
FIG. 17 is a view schematically showing a process of determining B number of
interleaver
patterns in the steps 2), 3), 4), and 5) of the above-described method for
determining the
interleaving pattern in the case of AWGN and Rayleigh channels for example.
Referring to FIG. 17, necessary variables i, j, and etc. are initialized in
operation S1701, and a
noise threshold for the AWGN channel TH1[i] and a noise threshold for the
Rayleigh channel
TH2[i] are calculated in operation S1702. Then, a final determination noise
threshold TH[i]
defined in step 4) is calculated in operation S1703, and is compared with a
previously calculated
final determination noise threshold TH[i-1] in operation S1704. When the final
determination
noise threshold TH[i] is smaller than the previously calculated final
determination noise
threshold TH[i-1], TH_S[i] is replaced with the TH[i] and is sotred in
operation S1706. Next, i, j
values increase by 1 in operation S1707 and this process is repeated until the
i value exceeds A
which is pre-defined in operation S1708. In this case, A is the total number
of interleaver
patterns to be tested in steps 2), 3), 4), and 5) and A is typically
determined to be greater than or
equal to 10000. When all operations described above are completed, interleaver
patterns
corresponding to TH_S[0], TH_S[1], TH_S[B-1] which are stored in a
descending order of
final noise thresholds values in operation S1709.
The transmitting apparatus 100 may transmit the signal mapped onto the
constellation to a
receiving apparatus (for example, 1200 of FIG. 18). For example, the
transmitting apparatus 100
may map the signal mapped onto the constellation onto an Orthogonal Frequency
Division
Multiplexing (OFDM) frame using OFDM, and may transmit the signal to the
receiving
apparatus 1200 through an allocated channel.
FIG. 18 is a block diagram to illustrate a configuration of a receiving
apparatus according to
an exemplary embodiment. Referring to FIG. 18, the receiving apparatus 1200
includes a

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
82
demodulator 1210, a multiplexer 1220, a deinterleaver 1230 and a decoder 1240.
The demodulator 1210 receives and demodulates a signal transmitted from the
transmitting
apparatus 100. Specifically, the demodulator 1210 generates a value
corresponding to an LDPC
codeword by demodulating the received signal, and outputs the value to the
multiplexer 1220. In
this case, the demodulator 1210 may use a demodulation method corresponding to
a modulation
method used in the transmitting apparatus 100. To do so, the transmitting
apparatus 100 may
transmit information regarding the modulation method to the receiving
apparatus 1200, or the
transmitting apparatus 100 may perform modulation using a pre-defined
modulation method
between the transmitting apparatus 100 and the receiving apparatus 1200.
The value corresponding to the LDPC codeword may be expressed as a channel
value for the
received signal. There are various methods for determining the channel value,
and for example, a
method for determining a Log Likelihood Ratio (LLR) value may be the method
for determining
the channel value.
The LLR value is a log value for a ratio of the probability that a bit
transmitted from the
transmitting apparatus 100 is 0 and the probability that the bit is 1. In
addition, the LLR value
may be a bit value which is determined by a hard decision, or may be a
representative value
which is determined according to a section to which the probability that the
bit transmitted from
the transmitting apparatus 100 is 0 or 1 belongs.
The multiplexer 1220 multiplexes the output value of the demodulator 1210 and
outputs the
value to the deinterleaver 1230.
Specifically, the multiplexer 1220 is an element corresponding to a
demultiplexer (not shown)
provided in the transmitting apparatus 100, and performs an operation
corresponding to the
demultiplexer (not shown). That is, the multiplexer 1220 performs an inverse
operation of the
operation of the demultiplexer (not shown), and performs cell-to-bit
conversion with respect to
the output value of the demodulator 1210 and outputs the LLR value in the unit
of bit. However,
when the demultiplexer (not shown) is omitted from the transmitting apparatus
100, the
multiplexer 1220 may be omitted from the receiving apparatus 1200.
The information regarding whether the demultiplexing operation is performed or
not may be
provided by the transmitting apparatus 100, or may be pre-defined between the
transmitting
apparatus 100 and the receiving apparatus 1200.
The deinterleaver 1230 deinterleaves the output value of the multiplexer 1220
and outputs the

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
83
values to the decoder 1240.
Specifically, the deinterleaver 1230 is an element corresponding to the
interleaver 120 of the
transmitting apparatus 100 and performs an operation corresponding to the
interleaver 120. That
is, the deinterleaver 1230 deinterleaves the LLR value by performing the
interleaving operation
of the interleaver 120 inversely.
To do so, the deinterleaver 1230 may include a block deinterleaver 1231, a
group twist
deinterleaver 1232, a group deinterleaver 1233, and a parity deinterleaver
1234 as shown in FIG.
18.
The block deinterleaver 1231 deinterleaves the output of the multiplexer 1220
and outputs the
value to the group twist deinterleaver 1232.
Specifically, the block deinterleaver 1231 is an element corresponding to the
block interleaver
124 provided in the transmitting apparatus 100 and performs the interleaving
operation of the
block interleaver 124 inversely.
That is, the block deinterleaver 1231 deinterleaves by writing the LLR value
output from the
multiplexer 1220 in each row in the row direction and reading each column of
the plurality of
rows in which the LLR value is written in the column direction by using at
least one row formed
of the plurality of columns.
In this case, when the block interleaver 124 interleaves by dividing the
column into two parts,
the block deinterleaver 1231 may deinterleave by dividing the row into two
parts.
In addition, when the block interleaver 124 writes and reads in and from the
bit group that
does not belong to the first part in the row direction, the block
deinterleaver 1231 may
deinterleave by writing and reading values corresponding to the group that
does not belong to the
first part in the row direction.
Hereinafter, the block deinterleaver 1231 will be explained with reference to
FIG. 20.
However, this is merely an example and the block deinterleaver 1231 may be
implemented in
other methods.
An input LLR vi (0<i<Nkipc) is written in a ri row and a ci column of the
block deinterleaver
[ i
1231. Herein, ci=(i mod NO and r, =
Nc
On the other hand, an output LLR qi(0<i<I=I0x No) is read from a ci column and
a ri row of the

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
84
i
first part of the block deinterleaver 1231. Herein, c, = ¨ , ri.(i mod Nri).
[
Nrl
In addition, an output LLR qi(Nc x Nri<i<Nidpc) is read from a c, column and a
ri row of the
second part. Herein, c, = [ (i ¨ Ncx NTH, ri=Nri+{(i-Ncx Nri) mode Nr2}.
Nr2
The group twist deinterleaver 1232 deinterleaves the output value of the block
deinterleaver
1231 and outputs the value to the group deinterleaver 1233.
Specifically, the group twist deinterleaver 1232 is an element corresponding
to the group
twist interleaver 123 provided in the transmitting apparatus 100, and may
perform the
interleaving operation of the group twist interleaver 123 inversely.
That is, the group twist deinterleaver 1232 may rearrange the LLR values of
the same bit
group by changing the order of the LLR values existing in the same bit group.
When the group
twist operation is not performed in the transmitting apparatus 100, the group
twist deinterleaver
1232 may be omitted.
The group deinterleaver 1233 (or the group-wise deinterleaver) deinterleaves
the output value
of the group twist deinterleaver 1232 and outputs the value to the parity
deinterleaver 1234.
Specifically, the group deinterleaver 1233 is an element corresponding to the
group
interleaver 122 provided in the transmitting apparatus 100 and may perform the
interleaving
operation of the group interleaver 122 inversely.
That is, the group deinterleaver 1233 may rearrange the order of the plurality
of bit groups in
bit group wise. In this case, the group deinterleaver 1233 may rearrange the
order of the plurality
of bit groups in bit group wise by applying the interleaving method of Tables
11 to 22 inversely
according to a length of the LDPC codeword, a modulation method and a code
rate.
The parity deinterleaver 1234 performs parity deinterleaving with respect to
the output value
of the group deinterleaver 1233 and outputs the value to the decoder 1240.
Specifically, the parity deinterleaver 1234 is an element corresponding to the
parity
interleaver 121 provided in the transmitting apparatus 100 and may perform the
interleaving
operation of the parity interleaver 121 inversely. That is, the parity
deinterleaver 1234 may
deinterleave the LLR values corresponding to the parity bits from among the
LLR values output
from the group deinterleaver 1233. In this case, the parity deinterleaver 1234
may deinterleave
the LLR value corresponding to the parity bits inversely to the parity
interleaving method of

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
Equation 18.
However, the parity deinterleaver 1234 may be omitted depending on the
decoding method
and embodiment of the decoder 1240.
Although the deinterleaver 1230 of FIG. 18 includes three (3) or four (4)
elements as shown
in FIG. 19, operations of the elements may be performed by a single element.
For example, when
bits each of which belongs to each of bit groups Xa, Xb, X, Xd constitute a
single modulation
symbol, the deinterleaver 1230 may deinterleave these bits to locations
corresponding to their bit
groups based on the received single modulation symbol.
For example, when the code rate is 6/15 and the modulation method is 16-QAM,
the group
deinterleaver 1233 may perform deinterleaving based on table 11.
In this case, bits each of which belongs to each of bit groups X55, X15, X112,
X122 may
constitute a single modulation symbol. Since one bit in each of the bit groups
X55, X15, X112, X122
constitutes a single modulation symbol, the deinterleaver 1230 may map bits
onto decoding
initial values corresponding to the bit groups X55, X15, X112, X122 based on
the received single
modulation symbol.
The decoder 1240 may perform LDPC decoding by using the output value of the
deinterleaver 1230. To achieve this, the decoder 1240 may include an LDPC
decoder (not
shown) to perform the LDPC decoding.
Specifically, the decoder 1240 is an element corresponding to the encoder 110
of the
transmitting apparatus 100 and may correct an error by performing the LDPC
decoding by using
the LLR value output from the deinterleaver 1230.
For example, the decoder 1240 may perform the LDPC decoding in an iterative
decoding
method based on a sum-product algorithm. The sum-product algorithm is one
example of a
message passing algorithm, and the message passing algorithm refers to an
algorithm which
exchanges messages (e.g., LLR value) through an edge on a bipartite graph,
calculates an output
message from messages input to variable nodes or check nodes, and updates.
The decoder 1240 may use a parity check matrix when performing the LDPC
decoding. In
this case, the parity check matrix used in the decoding may have the same
configuration as that
of the parity check matrix used in the encoding of the encoder 110, and this
has been described
above with reference to FIGs. 2 to 4.
In addition, information on the parity check matrix and information on the
code rate, etc.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
86
which are used in the LDPC decoding may be pre-stored in the receiving
apparatus 1200 or may
be provided by the transmitting apparatus 100.
FIG. 21 is a flowchart to illustrate an interleaving method of a transmitting
apparatus
according to an exemplary embodiment.
First, an LDPC codeword is generated by LDPC encoding based on a parity check
matrix
(S1410), and the LDPC codeword is interleaved (S1420).
Then, the interleaved LDPC codeword is mapped onto a modulation symbol
(S1430). In this
case, a bit included in a predetermined bit group from among a plurality of
bit groups
constituting the LDPC codeword may be mapped onto a predetermined bit in the
modulation
symbol.
Each of the plurality of bit groups may be formed of M number of bits, and M
may be a
common divisor of Nidpc and Kidpc and may be determined to satisfy
Qldpc=(Nldpc-Kldpc)/M.
Herein, Qapc is a cyclic shift parameter value regarding columns in a column
group of an
information word submatrix of the parity check matrix, Nidpc is a length of
the LDPC codeword,
and Kid is a length of information word bits of the LDPC codeword.
Operation S1420 may include interleaving parity bits of the LDPC codeword,
dividing the
parity-interleaved LDPC codeword by the plurality of bit groups and
rearranging the order of the
plurality of bit groups in bit group wise, and interleaving the plurality of
bit groups the order of
which is rearranged.
The order of the plurality of bit groups may be rearranged in bit group wise
based on the
above-described Equation 21 presented above.
As described above, t(j) in Equation 21 may be determined based on at least
one of a length
of the LDPC codeword, a modulation method, and a code rate.
For example, when the LDPC codeword has a length of 64800, the modulation
method is 16-
QAM, and the code rate is 6/15, n(j) may be defined as in table 11.
In addition, when the LDPC codeword has a length of 64800, the modulation
method is 16-
QAM, and the code rate is 10/15, n(j) may be defined as in table 14.
In addition, when the LDPC codeword has a length of 64800, the modulation
method is 16-
QAM, and the code rate is 12/15, z(j) may be defined as in table 15.
In addition, when the LDPC codeword has a length of 64800, the modulation
method is 64-
QAM, and the code rate is 6/15, n(j) may be defined as in table 17.

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
87
In addition, when the LDPC codeword has a length of 64800, the modulation
method is 64-
QAM, and the code rate is 8/15, n(j) may be defined as in table 18.
In addition, when the LDPC codeword has a length of 64800, the modulation
method is 64-
QAM, and the code rate is 12/15, m(j) may be defined as in table 21.
The interleaving the plurality of bit groups may include: writing the
plurality of bit groups in
each of a plurality of columns in bit group wise in a column direction, and
reading each row of
the plurality of columns in which the plurality of bit groups are written in
bit group wise in a row
direction.
In addition, the interleaving the plurality of bit groups may include:
serially write, in the
plurality of columns, at least some bit group which is writable in the
plurality of columns in bit
group wise from among the plurality of bit groups, and then dividing and
writing the other bit
groups in an area which remains after the at least some bit group is written
in the plurality of
columns in bit group wise.
A non-transitory computer readable medium, which stores a program for
performing the
interleaving methods according to various exemplary embodiments in sequence,
may be
provided.
The non-transitory computer readable medium refers to a medium that stores
data semi-
permanently rather than storing data for a very short time, such as a
register, a cache, and a
memory, and is readable by an apparatus. Specifically, the above-described
various applications
or programs may be stored in a non-transitory computer readable medium such as
a compact disc
(CD), a digital versatile disk (DVD), a hard disk, a Blu-ray disk, a universal
serial bus (USB), a
memory card, and a read only memory (ROM), and may be provided.
At least one of the components, elements or units represented by a block as
illustrated in
FIGs. 1, 5, 15, 18 and 19 may be embodied as various numbers of hardware,
software and/or
firmware structures that execute respective functions described above,
according to an exemplary
embodiment. For example, at least one of these components, elements or units
may use a direct
circuit structure, such as a memory, processing, logic, a look-up table, etc.
that may execute the
respective functions through controls of one or more microprocessors or other
control
apparatuses. Also, at least one of these components, elements or units may be
specifically
embodied by a module, a program, or a part of code, which contains one or more
executable
instructions for performing specified logic functions. Also, at least one of
these components,

CA 02940011 2016-08-17
WO 2015/126194 PCT/KR2015/001695
88
elements or units may further include a processor such as a central processing
unit (CPU) that
performs the respective functions, a microprocessor, or the like. Further,
although a bus is not
illustrated in the above block diagrams, communication between the components,
elements or
units may be performed through the bus. Functional aspects of the above
exemplary
embodiments may be implemented in algorithms that execute on one or more
processors.
Furthermore, the components, elements or units represented by a block or
processing steps may
employ any number of related art techniques for electronics configuration,
signal processing
and/or control, data processing and the like.
The foregoing exemplary embodiments and advantages are merely exemplary and
are not to
be construed as limiting the present inventive concept. The exemplary
embodiments can be
readily applied to other types of apparatuses. Also, the description of the
exemplary
embodiments is intended to be illustrative, and not to limit the scope of the
inventive concept,
and many alternatives, modifications, and variations will be apparent to those
skilled in the art.

Representative Drawing