Note: Descriptions are shown in the official language in which they were submitted.
HIGH DYNAMIC RANGE COLOR CONVERSION CORRECTION
[0001] BACKGROUND OF THE INVENTION
Field of the Invention
[0002] Embodiments of the present invention relate generally to audiovisual
processing
and, more particularly, to high dynamic range (HDR) color conversion
correction.
Description of the Related Art
1.0 [0003] High Dynamic Range (HDR) imaging is a technique that enables a
wider range of
luminance values to be represented than is typically possible via conventional
imaging
techniques. In particular, conventional imaging equipment is capable of
capturing and
reproducing only a limited luminance range, commonly resulting in a loss of
detail in the
luminance ranges associated with shadows and/or highlights. By contrast, HDR
techniques are capable of capturing and representing a luminance range that is
closer to
the range perceived by the human visual system. Consequently, HDR techniques
are
expected to significantly improve the visual quality of many types of
multimedia content.
[0004] In order to represent the luminance values associated with HDR content
(e.g.,
luminance values of approximately 0 to 10,000 cd/m2) using moderate bit depths
(e.g., 10
to 12 bits per sample), various standards apply a highly nonlinear transfer
function to the
HDR content. Bit depth generally refers to the number of bits used to
represent one
image component sample (e.g. a luma or chroma value). More specifically,
because the
human visual system is more sensitive to differences in luminance values when
the
luminance values are low, a nonlinear transfer function is commonly applied to
linear
color values (e.g., RGB values) associated with HDR
1
CA 3004769 2019-08-01
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
content in order to allocate a greater number of values to the lower end of
the
luminance range. Allocating more values to the lower end of the luminance
range
allows quantization to be achieved at moderate bit depths without any
perceptible
artifacts from the perspective of the viewer.
[0005] After a nonlinear transfer function is applied to HDR content, the
resulting
nonlinear values are converted to a desired color space and further processed
so that
the HDR content can be transmitted and broadcast more efficiently. Those
additional
processing operations typically include chroma subsampling and video
compression,
each of which are performed to reduce the bitrate of the HDR content. For
example,
with respect to the HDR10 specification recently adopted by the Digital
Entertainment
Content Ecosystems (DECE), a ST.2084 nonlinear transfer function is applied to
linear RGB values. The nonlinear R'G'B' values are then converted into the
BT.2020
color space, and the resulting Y'CbCr 4:4:4 values are subsampled to generate
Y'CbCr 4:2:0 values. The Y'CbCr 4:2:0 values are then compressed via High
Efficiency Video Coding (HEVC) Main10 encoding to generate a compressed video
stream.
[0006] One drawback of conventional HDR conversion processes is that, when
color
values (e.g., Y'CbCr 4:4:4 values) associated with HDR content are subsampled,
the
chroma values are subsampled by a process similar to averaging, for example by
applying a low-pass filter and subsequently decimating samples (e.g., to
generate
Y'CbCr 4:2:2 values or Y'CbCr 4:2:0 values), but the luma values are not. When
the
HDR content is reconstructed, the averaged chrome values are upsam pled and
then
combined with the original luma values. Thus, because the chroma values were
modified in the first instance, when an inverse of the nonlinear transfer
function is
applied to the upsam pled values, the reconstructed color values may be
significantly
different than the color values present in the original HDR content. These
types of
differences are most noticeable with color values that fall within regions of
the
nonlinear opto-electrical transfer function that have a steep slope (e.g.,
color
components with low luminance values), since, in these regions, small
variations in
the value of a color component can have a significant impact on Y', Cb, and Cr
values.
[00071 For example, if one color component has a value close to zero, while
other
color components have higher values ¨ which is commonly the case for colors
that
2
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
are close to color gamut boundaries ¨ then the low intensity color component
value
would have disproportionally high contribution to the resulting Y'CbCr 4:4:4
signal.
That is, small variations in this low intensity color component value would
result in
significantly different values for the Y', Cb, and Cr components, despite the
corresponding linear RGB values being similar. Consequently, when Y'CbCr 4:2:0
color values are later upsampled to Y'CbCr 4:4:4 color values and the inverse
nonlinear transfer function is applied, changes in the Cb and/or Cr values due
to
subsam piing may cause saturated colors to be reconstructed to significantly
different
values, producing artifacts in the final image.
[0008] One solution to the above problem is to iterate over different luma
values to
select a luma value that, when reconstructed (e.g., by upsampling Y'CbCr 4:2:0
color
values to Y'CbCr 4:4:4 color values) results in a linear luminance that is
closest to the
linear luminance of the original signal. However, in order to select a luma
value for a
10-bit signal, for example, this particular approach would require ten
iterations to be
performed for each luma sample. Because a single iteration requires an inverse
nonlinear transfer function to be calculated and an inverse color transform to
be
applied, these types of conventional techniques can be very slow, even when
the
electro-optical transfer function is implemented as a look-up table.
[0009] As the foregoing illustrates, improved techniques for converting and
correcting
high dynamic range (HDR) color values would be useful.
SUMMARY OF THE INVENTION
polo] One embodiment of the present invention sets forth a method for
correcting
color values. The method includes downsampling first color space values to
generate
downsampled color space values and upsampling the downsampled color space
values to generate second color space values. The method further includes
modifying at least one component value included in the downsampled color space
values based on a first component value included in the first color space
values, a
second component value included in the second color space values, and an
approximation of a nonlinear transfer function
[0011] Further embodiments provide, among other things, a non-transitory
computer-
readable medium and a computing device configured to implement the method set
forth above.
3
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
[0012] At least one advantage of the disclosed techniques is that the
resulting
reconstructed HDR images are more accurate relative to the original HDR images
than images generated via conventional chroma downsampling. Additionally, the
complexity of the disclosed techniques is significantly lower than that of the
conventional approaches, enabling an optimal component value (e.g., a luma
value)
to be determined in real-time via a single iteration.
BRIEF DESCRIPTION OF THE DRAWINGS
[0013] So that the manner in which the above recited features of the present
invention
can be understood in detail, a more particular description of the invention,
briefly
summarized above, may be had by reference to embodiments, some of which are
illustrated in the appended drawings. It is to be noted, however, that the
appended
drawings illustrate only typical embodiments of this invention and are
therefore not to
be considered limiting of its scope, for the invention may admit to other
equally
effective embodiments.
[0014] Figure 1 is a conceptual illustration of a computing device configured
to
implement one or more aspects of the present invention;
[0015] Figure 2 illustrates a nonlinear opto-electrical transfer function
(OETF) that can
be implemented to convert linear light/color values to nonlinear light/color
values,
according to various embodiments of the present invention;
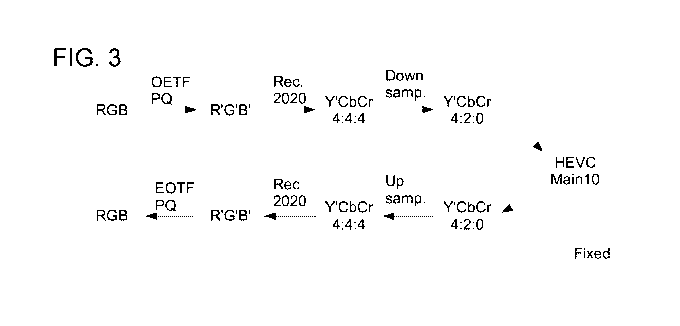
[0016] Figure 3 illustrates a process for converting, compressing, and
reconstructing
high dynamic range (HDR) content, according to various embodiments of the
present
invention;
[0017] Figures 4A and 5A are original HDR images, Figures 4B and 5B are images
processed according to conventional techniques, and Figures 4C and 5C are
images
processed according to one or more embodiments of the present invention; and
[0018] Figure 6 illustrates a flow diagram of method steps for performing HDR
color
conversion correction on an image, according to various embodiments of the
present
invention.
4
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
DETAILED DESCRIPTION
[0019] In the following description, numerous specific details are set forth
to provide a
more thorough understanding of the embodiments of the present invention.
However,
it will be apparent to one of skill in the art that the embodiments of the
present
invention may be practiced without one or more of these specific details.
[0020] Figure 1 is a conceptual illustration of a computing device 100
configured to
implement one or more aspects of the present invention. As shown, the color
conversion system includes a computing device 100. The computing device 100
includes a processor 102, input/output (I/O) devices 104, and a memory 110.
The
memory 110 includes a color conversion application 112 configured to interact
with a
database 114.
[00211 The processor 102 may be any technically feasible form of processing
device
configured to process data and execute program code. The processor 102 could
be,
for example, and without limitation, a central processing unit (CPU), a
graphics
processing unit (GPU), an application-specific integrated circuit (ASIC), a
digital signal
processor (DSP), a field-programmable gate array (FPGA), and so forth.
[0022] Memory 110 may include a memory module or a collection of memory
modules. The color conversion application 112 within memory 110 is executed by
the
processor 102 to implement the overall functionality of the color conversion
system .
For example, and without limitation, multimedia content (e.g., images, video,
etc.)
received by the color conversion system may be processed by the color
conversion
application 112 to apply linear and/or nonlinear transfer functions to the
multimedia
content, to convert the multimedia content between one or more color spaces,
to
perform downsampling, subsampling, upsampling, etc. on the multimedia content,
and/or to apply one or more compression algorithms to the multimedia content.
Database 114 within memory 110 may store images, video, algorithms,
parameters,
lookup tables, and/or other types of data associated with transfer functions,
color
spaces, lossy and/or lossless codecs, etc.
[0023] I/O devices 104 may include input devices, output devices, and devices
capable of both receiving input and providing output. For example, and without
limitation, I/O devices 104 could include wired and/or wireless communication
devices
that send data to and/or receive data from a camera, a display screen, a media
5
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
player, a storage device, speakers, a microphone, a networking device and/or
another computing device.
[0024] Generally, computing device 100 is configured to coordinate the overall
operation of the color conversion system. In other embodiments, the computing
device 100 may be coupled to, but separate from other components of the color
conversion system. However, the embodiments disclosed herein contemplate any
technically feasible system configured to implement the functionality of the
color
conversion system.
[0025] Figure 2 illustrates a nonlinear opto-electrical transfer function
(OETF) that can
be implemented to convert linear light/color values to nonlinear light/color
values,
according to various embodiments of the present invention. As shown, the slope
of
the transfer function is steep in the low-luminance range and shallow in the
high
luminance range, since the human visual system is more sensitive to
differences in
luminance values when the luminance values are low. As a result, the nonlinear
transfer function allocates more codewords and uses smaller quantization steps
in the
low luminance range, reducing the likelihood that quantization will produce
visible
artifacts in an image. Although the techniques disclosed herein are described
in
conjunction with the OETF shown in Figure 2, in various embodiments, any other
type
of nonlinear transfer function having any shape may be implemented to convert
and
reconstruct linear color values.
[0026] Figure 3 illustrates a process for converting, compressing, and
reconstructing
HDR content, according to various embodiments of the present invention. As
shown,
a nonlinear transfer function is applied to the linear RGB values to generate
nonlinear
R'G'B' values. The nonlinear R'G'B' values are then converted to a desired
color
space, and the resulting color values are processed so that the HDR content
can be
transmitted and broadcast more efficiently.
[0027] For example, in some embodiments, nonlinear R'G'B values are generated
by
applying the OETF perceptual quantizer (PO) to each linear light R, G, and B
component separately. Then, the nonlinear R'G'B' values are converted to the
non-
constant luminance BT.2020 color space according to Equation 1, shown below.
Next. further processing may be performed on the Y'CbCr 4:4:4 color values,
for
example, to reduce the bitrate for ease of transmission.
6
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
Y' = 0.2627 R' + 0.6780 G' + 0.0593 B';
Cb = (B' ¨ Y') / 1.8814; Cr = (R' ¨ Y') / 1.4746; (1)
[0028] In some embodiments, after the color values are converted to a
particular color
space, the color values are further processed via subsampling, such as chroma
subsampling. When subsampling color values, luma and/or chrome information is
averaged over adjacent pixels in order to reduce the bitrate of the processed
images.
Typically, the chrome components of the image are subsam pled while retaining
the
original resolution of the luma components, since the human visual system is
able to
detect differences in luminance more readily than differences in color.
Accordingly,
as shown in Figure 3, color values specified in a Y'CbCr 4:4:4 format may be
subsam pled to generate Y'CbCr 4:2:2 values or Y'CbCr 4:2:0 values. The
resulting
color values are then optionally compressed via a codec, such as HEVC, H.264,
etc.
[0029] As noted above, one drawback of these conventional HDR conversion
processes is that reconstructing the subsampled color values can produce
artifacts.
Notably, although applying an inverse of the color space transform and an
inverse of
.. the nonlinear transform function (e.g., an EOTF PQ) to the Y'CbCr 4:4:4
color values
would result in reconstructed color values that are substantially the same as
the
original linear RGB signal, when subsampling is applied to the Y'CbCr 4:4:4
color
values, the chroma values are effectively averaged. Consequently, when these
downsampled chroma values are upsampled back to Y'CbCr 4:4:4 color values and
the inverse of the nonlinear transfer function is applied to the upsampled
values, the
reconstructed color values may be significantly different than the color
values present
in the original linear RGB signal. Such artifacts are particularly noticeable
in
saturated colors, when one or more or color components (e.g. R, G, and/or B)
have
values close to zero, where small variations in a particular component value
(e.g., R,
G, or B) can result in significantly different Y', Cb, and Cr component
values, despite
each of the linear light RGB values being similar. An example of such
artifacts are
shown in Figures 4B and 5B, each of which includes detail that was not present
in the
original images, shown in Figures 4A and 5A.
[0030] Accordingly, in various embodiments, in order to reduce the occurrence
and/or
visibility of artifacts, the color conversion application 112 adjusts one or
more of the
downsampled component values such that the values, when upsampled and
reconstructed, produce color values that are similar to the color values
present in the
7
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
original HDR content. More specifically, the color conversion application 112
downsamples chroma values. In some embodiments, the color conversion
application 112 can obtain downsampled chroma directly from Y'CbCr 4:4:4 color
values, as shown in Figure 3. Alternatively, the color conversion application
112 may
downsample the linear RGB color values directly and then apply the OETF PQ and
color transform to the down-sampled values.
[0031] After obtaining the downsam pled chroma, the color conversion
application 112
upsamples the chroma by applying a selected upsampling filter. The color
conversion
application 112 then modifies one or more of the Y, Cb, and Cr values such
that
reconstructing these values to a linear RGB signal produces color values
similar to
the color values present in the original linear RGB signal. For reference, an
example
of an EOTF P0 that may be used to reconstruct linear RGB values from nonlinear
R'G'B' values is shown below in Equation 2.
I c +c2
PQ TF(L)= ________________________ ; = 0.1593017578125,
1 + c
\ 3 ( 2 )
=78.84375, e.,= 0.8359375, e 2 =18.8515625, c3 =18.6875.
[0032] In some embodiments, the color conversion application 112 modifies the
Y',
Cb, and Cr values by estimating each of the Y', Cb, and Cr values
simultaneously. In
other embodiments, in order to obtain a faster estimation, the value of Y' may
be
obtained while keeping the values of Cb and Cr constant. This latter approach
may
be beneficial because the filter used to upsample the chroma components is not
defined by a standard and, thus, may vary across different hardware and
software
platforms. Moreover, depending on which upsampling filter is used, modifying a
chroma sample may also change the upsam pled chroma values at neighboring
locations.
[0033] Accordingly, in various embodiments, the color conversion application
112
determines a value of the luma component rx, y) by finding new Y', Cb, and Cr
component values which correspond to RGBneõv(x,y) values that are
substantially
similar to the original RG13,õg(x, y) values. In this notation, x and y are
horizontal and
vertical positions of the sample, respectively.
8
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
Example 1 ¨ First Cost Function
[0034] In some embodiments, the distance (D) between RGBnew(x,y) and RGBorg(x,
y)
could be measured as the Euclidean norm (e.g., the squared error for each
component):
D = (Rnew(x,Y) ¨ Rorg(x,Y))2 + (Gnew(x,Y) ¨ Gorg(x,Y))2 + (Bnew(x,Y) ¨
Borg(x,y))2 (3)
[0035] Omitting sample coordinates for simpler notation, the cost function is
as
follows:
D = (Rnew ¨ Rorg)2 + (Gnew ¨ Gorg)2 + (Bnew ¨ Borg )2 (4)
[00361 In a more general case. we can also weight the importance of each color
component R, G and B with a weighting factor wx, where X corresponds to a
color
component, wR, wG, and wB. Then, our cost function would take a form of
Equation 5
or Equation 6, where f is the EOTF function, such as the ST.2084 EOTF PQ.:
o = wR (Rnew¨ Rorg)2 + NAIG (Gnevv ¨ Gorg)2 + WB (Bnew ¨ Borg)2 (5)
D = wR (f(R'new) ¨ f (R'org))2 wc (f (G'new)¨ f (Gorg))2 + we (f (13'new) ¨ f
(aorg))2 (6)
[0037] The values R', G' and B' can be obtained from the original Y'CbCr
values by
applying an inverse color transform, which depends on the color space
associated
with the Y'CbCr values. For example, an inverse color transform for Y'CbCr
values
within the BT.709 and BT.2020 color spaces has the following form:
R' a1,1 a1,2 a1,3 Y '
G' = a2,1 a2,2 az, Cb (7)
) a aõ aõ Cr )
[0038] Attempting to minimize the cost function D for an EOTF with a complex
expression, such as ST.2084, requires significant processing resources.
Consequently, the EOTF may be approximated using a truncated Taylor series
(e.g.,
the first, second, or third degree polynomials), enabling the cost function D
to be
minimized via a closed form solution. Two examples of closed form solutions
for
minimizing the cost function D shown in Equations 3-6 are described below in
conjunctions with Equations 8-17. Notably, although the techniques described
below
implement RGB values, color spaces other than RGB can also be used.
9
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
Linear Approximation of EOTF (First Cost Function)
[0039] In order to obtain a closed form, one-step solution for estimating a
better luma
component Y'(x, y) that corresponds to RGB,,õõ(x,y) values that are
substantially
similar to the original RGBõg(x, y) values, the EOTF f (X) could be
approximated with
a first degree polynomial, where the f' (X1) is the value of the derivative of
the f (X')
with respect to X at point Xi.:
f (Xi + A) = f (X i) + f ' (Xi) A (8)
[0040] Then, by substituting the EOTF approximation of Equation 8 into
Equation 6,
the cost function could be approximated as:
D = wR (f I (IR org) AR)2 wG (f I (G lag) AG)2 wB (f (B forg) AB)
2
(9)
[0041] Next, AR in Equation 9 is substituted with (a11 Y'5 + eR) ¨ based on
the
inverse color transform ¨ and similar substitutions are made for AG and AB.
The cost
function D is then differentiated with respect to Y to find a closed form
solution for the
local minimum. This closed form solution for the value of Y' can be obtained
as
follows. First, we calculate eR, eG, and eB based on the new chroma values,
the
original chroma values, and the inverse color transform parameters:
eR = ¨Ylorg ati + (Cbnew ¨ Cborg) at2 + (Crnew ¨ Crorg) at3 ,
eG = ¨Yerg a2,1 + (Cbnew ¨ Cborg) a2,2 + (Crnew Crorg) a2,3 ,
eB = ¨Yorg a3,1 + (Cbnew ¨ Cborg) a3,2 + (Crnew Crorg) a3,3, (10)
[0042] The value of Y' is then equal to:
v ,r(Ro' õ)2 G.f eGar2,1+14, õRA,' ,g)2 e
Y: (11)
wRfr(g,,,)2,11- wGf(G)2a;,1-1- BI(B,r ,g)2 a32,1
[0043] When ai,i = a2,1 = a3,1 = 1, as in BT.709 and BT.2020, the expression
simplifies
to:
wRf(R02e,+m, g)2 eG+11,,f'(B' e,
07 (12)
wRf(Rõ'õ )2+1vGf(G0',)2+ wBr(B )2
[0044] Further, if all of the weights are set equal to 1, then Y' can be found
as follows:
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
_ . or
fi(R1g )2e + f(G0',.g)2 ec + .r(Bocg)2 eB
R
AROrg)2 +AGocg)2 +./(Borg)2 (13)
[0045] In some embodiments, values of the EOTF derivative squared f' (X)2 can
be
pre-computed and stored in a look-up table. In particular, for a video with
bit depth of
10, a look-up table with 1024 entries could be used when the fixed point
processing of
10 bits is used. In case of a higher fixed point or floating point precision,
more table
entries could be used to improve accuracy.
Second Degree Approximation of EOTF (First Cost Function)
[0046] Alternatively, the EOTF could be approximated using a second degree
polynomial, as shown in Equation 14:
f (Xi + A) = f (X i) + f ' (Xi) A + f "(Xi) A2! 2 (14)
[0047] The resulting approximation is closer to the real EOTF than a linear
approximation. However, finding local minima of the cost function D requires
finding
roots of a cubic equation, which involves more complexity and processing
resources
as compared to the linear approximation discussed above.
.. [0048] With respect to the second degree approximation, the derivations may
be
performed in a similar manner to the linear approximation and are omitted for
brevity.
The solution, assuming a1,1 = a2,1 = a3,1 = 1, is as follows:
eR = ¨ Yorg + (Cbnew ¨ Cborg) a1,2 (Crnew ¨ Crorg) a1,3,
eG = ¨ Y'org + (Cbnew ¨ Cborg) a2,2 + (Crnew ¨
Crorg) _ a 2,3 ,
eB = ¨ Yorg + (Cbnew ¨ Cborg) a3,2 (Crnew Crorg) a3,3 (15)
[0049] Then:
T3,x = f" (X)2,
T2,x = 3 f ' (X) f" (X) + 3 f" (X)2 ex,
Ttx = 2 f 1(X)2 + 6 f '(X) f" (X) ex + 3 f' (x)2 (ex)2
1-0,x = 2 f 1(X)2 ex + 3 f ' (X) f" (X) (ex)2 + f' (X)2 (ex)3, (16)
[0050] where X stands for R, G, and B. and f '(X) stands for the first
derivative f'
(R0), f ' (G'org), or f '(Bag), and f" (X) stands for the second derivative f'
(R'0,0), f"
11
CA 03004769 2018-05-08
WO 2017/083426
PCT/1JS2016/061190
(Giorg), or f' (Biorg). The derivatives are taken with respect to the
corresponding non-
linear color component.
[0051] In order to minimize the cost function D, the cubic equation below is
solved
with respect to )(new:
(WR T3R WG T3,0 WB T3,B) (Ynew)3 (WR T2,R WG T2.G WB T2,B) (Ynew)2
(WR T1.R WG T1,G WB T1,B) Ynew (WR TO,R + WG TOG + WB To,B) -= 0 (17)
[0052] The cubic equation has either one or three real roots. In the case of
three real
roots, the minimum is achieved in either the root having the largest value or
the
smallest value, due to the fact that the cost function D is quadratic with a
positive
coefficient at the fourth degree term. The values of the cost function D are
then
calculated for both roots, and the root resulting in a smaller value is chosen
as Ynew.
[0053] If Equation 3 has only one real root, then the real part of the two
complex roots
may still be considered as a possible solution. Specifically, because an
approximation of an EOTF is used, small changes in values of the equation
terms can
result in Equation 17 having only one real root instead of three real roots.
However,
in some cases, when two real roots ¨ one of which would result in the cost
function
minimum ¨ become two complex roots, the real part of the pair of complex roots
represents a better approximation of the solution than the value of the
remaining real
root.
Example 2 ¨ Second Cost Function
[0054] In some embodiments, the distance (D) could be measured as a sum of
weighted differences between individual R, G, and B components of RGBnew(x,y)
and
RGBorg(x, y). In such embodiments, the difference between the two values could
be
calculated according to Equation 18, where wiR, WG, and WB are the weights
corresponding to each color component and R, G, and B.
D = wR(Rnew(x,y) ¨ Rordx,y)) + \NG (Gnew(x,y)¨ Gorg(x,Y)) + WB (Bnew(x,y) ¨
Bordx,y))
(18)
[0055] Then, after omitting pixel coordinates for a simpler notation, the cost
function is
defined by Equation 19 or Equation 20, where f(X) is the EOTF function:
12
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
D = wR ( Rnew¨ Rorg) WG (Gnow Gorg) WB (Bnew ¨ Borg) (19)
D = wR ( f (RI new) ¨ f (R' org)) + wG (GI new) f (G' org)) + we (f (131 new)
¨ f (B' org)) (20)
[0056] As noted above, the transfer function domain values R, G', and B can
then be
obtained from Y'CbCr by applying an inverse color transform, such as the
BT.709 and
BT 2020 transform:
( ( \
R' a1,1 a1,2 a1,3 Y'
G' = a a22 a73 Cb (21)
B' Cr
,
a3,1 a3,2 a3,3
[0057] In various embodiments, the absolute value of the cost function D
(i.e., IDI)
shown in Equations 18-20 may be minimized in order to minimize the difference
between RGI3new(x,y) and RGBorg(x,y). However, minimizing the absolute value
of D
is a non-trivial task, since the absolute value function is not differentiable
at 0.
Accordingly, in some embodiments, the function D2 is instead minimized, since
IDI
and D2 reach the minimum at the same point, and the function D2 is
differentiable on
the entire range of real numbers R. Therefore, the optimization is instead
performed
for function D1:
D1 = (wR ( f (R1 new) ¨ f (R'org)) + wG (f (G' new) ¨ f (G' org)) + wB (f
(anew) ¨ f (B'org)))2 (22)
[0058] Next, the EOTF is approximated with a truncated Taylor series in order
to find
a closed form solution to minimizing the cost function D1.
Linear Approximation of EOTF (Second Cost Function)
[0059] Substituting (8) into (22), the cost function can be approximated as
follows:
D = (wR f ' (Riorg) AR + wG f ' (Giorg) AG + we f (B'org) AB)2 (23)
[0060] Then, AR in Equation 23 is substituted with (ati rnew eR) and similar
substitutions are made for AG and AB. The cost function D is then
differentiated with
respect to Y' to find a closed form solution for the local minimum. To find a
closed
form solution for the value of Y', we first calculate eR, eG, and eB according
to
Equation 10. The value of Y' is equal to:
13
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
wRif(Ro'Oeir w ofrde w Hf(Bioõ)e
Ynfew (24)
w,f'(Rocdat, Gf'(Go' rg)a2,1+11; Br (B'rg)a,,
[0061] When a1,1 = a2,1 = a3,1 = 1, as in BT.709 and BT.2020, the expression
simplifies
to:
_ ___________________________________________________
r(R01 = ' g)eõ+w G f (Go'
rg)eG +1, r B.f (B ocg)e,
ynciv (25)
11;Rf(Rocg)-FWG./(Gocg)-EWBf(Bocg)
.. [0062] In some embodiments, values of the EOTF derivative f' (X) can be pre-
computed and stored in a look-up table (e.g., stable having 1024 entries for
video
with a bit depth of 10 when the fixed point processing of 10 bits is used). In
case of a
higher fixed point or floating point precision, more table entries could be
used to
improve accuracy.
[0063]
Second Degree Approximation of EOTF (Second Cost Function)
[0064] Alternatively, the EOTF could be approximated using a second degree
polynomial, as shown in Equation 14. Then, the solution, assuming ati = a2,1 =
a31 =
1, is as follows:
eR = ¨ Yorg + (Cbnew ¨ Cborg) al 2 + (Crnew ¨ Crorg) ato ,
eG = ¨ Yorg + (Cbnew ¨ Cborg) a2,2 (Crnew Crorg) a2,3
eB = ¨ Yorg + (Cbnew ¨ Cborg) a3,2 (Crnew Crorg) a3,3 (26)
[0065] Then:
a = wR f (R'org) + WG f (G'org) + WB f (B'org),
c= eR wR f (Rim) + eG wG f (gorg) + eB f (EYorg),
rn2 = wB f" (R'org) + wG f" (G'org) + wB f" (B'org)
n71 = a + eR wR f"(R'org) + eG wG f "(gorg) + eB wB "(B'org)
mo = 2c + (eR)2 wR f "(R'org) + (eG)2 wG f "(gorg) + (eB)2 wB f "(gorg),
(27)
14
CA 03004769 2018-05-08
WO 2017/083426
PCT/1JS2016/061190
[0066] where X stands for R, G, and B, and f '(X) stands for the first
derivative f'
(R'org), f ' (G'õg), or f ' (B'org), and f" (X) stands for the second
derivative f' (R'org), f"
(G'org), or
f" (B10,9).
[0067] In order to minimize the cost function D, the cubic equation below is
solved
with respect to )(new:
(m2)2 (Ynew)3 3m2m1 (Ynew)2 (2(m1)2 + m2 mo) Ynew (mo no) = 0
(28)
[0068] As discussed above, the cubic equation has either one or three real
roots. If
three real roots are determined, then the minimum is achieved in either the
root
having the largest value or the smallest value. The values of cost function D
are then
calculated for both real roots, and the real root resulting in a smaller value
is chosen
as Y'nõ. In case Equation 28 has only one real root, the real part of the
remaining
complex roots may be considered as a solution.
[00691 In other embodiments, any of the techniques described above can be
implemented with other types of transfer functions, including ST.2084 or
BT.1886.
Additionally, the techniques described above can be applied to other color
spaces,
such as BT.709 and BT.2020. Further, in some embodiments, the derivative of an
EOTF can be obtained either by differentiating the EOTF or by numerically
approximating the EOTF, for example, using the definition of a derivative
(e.g.,
dividing a change in the value of the EOTF by a change in the EOTF argument).
An
average or a weighted average of two or more of EOTF could also be implemented
in
the closed form solutions ¨ instead of a single EOTF ¨ in order to optimize
the
approach for compatibility with several transfer functions. In such
embodiments, the
derivatives of the EOTFs could be replaced with an average or a weighted
average
(e.g., a weighted sum) of the derivatives of the EOTFs.
[0070] The techniques described herein could also use higher order polynomials
to
approximate an EOTF. In addition, in some embodiments, the cost function D
could
be minimized with respect to several values (e.g., Y', Cb, and Cr), such as
several
values that correspond to neighboring pixels. In such embodiments, partial
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
derivatives could be taken with respect to each Y', Cb, and Cr component to
find the
optimal values of Y', Cb, and Cr.
[0071] In various embodiments, the weights wR, wG, and wB could be chosen
based
on the desired precision or importance of each color component. For example,
the
.. weights could be set equal to 1. In some embodiments, the weights wR, wG,
and we
are chosen on a picture basis or a sequence basis. The weights wR, wG and we
could
also be set adaptively on a sample/pixel basis, for example, based on the
original R,
G, and B values for each sample (e.g., based on an inverse relationship with
the
intensity of R, G, and B for each sample) or based on some other algorithm. In
other
embodiments, the weights could be set based on the contribution of each color
component to the luminance. For example, the weights could be set equal to the
contributions of the R, G, and B, components, respectively, to the Y component
of the
XYZ color space. In the case of BT.709, weights of 0.212639, 0.715169, and
0.072192 could be assigned to wR, wG, and we, respectively. In the case of
BT.2020,
.. weights of 0.262700, 0.677998, and 0.059302 could be assigned to wR, wG,
and we,
respectively.
[0072] Figure 6 illustrates a flow diagram of method steps for performing HDR
color
conversion correction on an image, according to various embodiments of the
present
invention. Although the method steps are described in conjunction with the
systems
of Figures 1-3, persons skilled in the art will understand that any system
configured to
perform the method steps, in any order, falls within the scope of the present
invention.
[0073] As shown in Figure 6, a method 600 begins at step 610, where the color
conversion application 112 converts one or more linear RGB values to
R'G'B'org(x,y)
values based on a nonlinear transfer function (e.g., an OETF PQ). Next, at
step 620,
the color conversion application 112 converts the R'G'B'õg(x,y) values to
Y'CbCrorg
4:4:4 values based on transform parameters associated with a target colored
space.
The color conversion application 112 then subsamples the Y'CbCrorg 4:4:4
values to
generate YCbCrnew 4:2:2 values or Y'CbCrnew 4:2:0 values.
[0074] At step 640, the color conversion application 112 upsamples the Y'CbCr
4:2:2
values or the Y'CbCrorg 4:2:0 values to generate Y'CbCrnõ 4:4:4 values. Then,
at
step 650, the color conversion application 112 calculates a luma value
Y'new(x,y)
based on a closed form equation derived from an approximation of an EOTF. In
16
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
various embodiments, the color conversion application 112 could calculate the
luma
value Y'new(x,y) based on any of Equations 11-13, 17, 24, 25, and/or 28. For
example, the color conversion application 112 could calculate Y'new(x,y) based
on the
R'G'B'org(x,y) values, the Y'CbCrorg(x,y) values, the Y'CbCrnew(x,y) values,
one or more
color space transform parameters, and/or an approximation of a nonlinear
transfer
function, in accordance with one or more of Equations 11-13, 17, 24, 25,
and/or 28.
[0075] Then, at step 660, the color conversion application 112 assigns
Y'new(x,y) to
the corresponding pixel (x,y). At step 670, the color conversion application
112
determines whether Y'õw should be determined for one or more additional
pixels. If
additional pixels are to be processed, then the method 600 returns to step
650, where
the color conversion application 112 calculate one or more additional luma
values
Ynew, for example, based on the R'G'B'org values, the Y'CbCrorg values, the
Y'CbCrnew
values, one or more color space transform parameters, and/or an approximation
of a
nonlinear transfer function. The method 600 then terminates.
[0076] Although the method 600 is described with respect to specific types of
color
values, color space parameters, transfer functions, and approximations, the
color
conversion application 112 may use any type of color values, color space
parameters,
transfer functions, and approximations to modify Y', Cb, and/or Cr values.
Experimental Results and Computational Complexity
[00771 As discussed above, the complexity of the linear approximation approach
is
significantly lower than that of the conventional luma micro-grading approach.
The
techniques described herein use a closed form solution to find the value of
Yin a
single iteration. By contrast, the conventional micro-grading approach
requires 10
iterations for a 10-bit video, including the last two boxes in the chain in
Figure 2 ¨
obtaining the R'G'B' values, applying the EOTF, and calculating the linear
light
luminance. Therefore, the proposed linear approximation approach has a good
complexity versus quality trade-off that makes this approach well suited for
real-time
systems.
[0078] The algorithms described above were compared to conventional techniques
that implement a luma micro-grading algorithm. Each of the algorithms was run
on
sequences FireEater (shown in Figures 4A-4C), Market (shown in Figures 5A-5C),
and Tibul in a BT.709 container. Each sequence was 1920x1080p with a peak
17
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
luminance of 4000 cd/m2. In each simulation, [-2 16 54 -4]/64 and [-4 36 36 -
4]/64
filters were used for vertical and horizontal upsampling, respectively. Other
upsampling and downsampling filters could alternatively be used in the
algorithm.
[0079] Figures 4A-4C and 5A-5C demonstrate the effect of the linear
approximation
.. algorithm, with weights wR, wG, and wB equal to the coefficients of the
contribution of
the R, G, and B components, respectively, to the Y component of the XYZ color
space. In the case of BT.709, the weights could be 0.212639, 0.715169, and
0.072192 for wR, wG, and wB, respectively. In the case of BT.2020, the weights
could
be 0.262700, 0.677998, and 0.059302 for wR, wG, and \Art, respectively.
[0080] As shown in Figures 4C and 5C, the image resulting from the closed form
solution based on a linear approximation of the EOTF is more accurate relative
to the
original image than the image generated via conventional chroma downsampling.
[0081] Objective results are provided in Tables 1-4 below. The values in the
Tables
1-4 represent PSNR in the linear light domain and tPSNR. tPSNR involves
.. transforming the RGB color space to the XYZ color space, averaging the
output of
two transfer functions, PQ (ST.2084) and Philips, and then calculating PSNR in
X, Y,
and Z components.
[0082] As observed from the results in Tables 1-4, the average PSNR is
increased by
more than 1.75dB compared to conventional chroma downsampling. Additionally, a
.. 3.65dB improvement is seen in tPSNR when implementing a linear
approximation of
EOTF. As compared to the slower, conventional luma micro-grading approach, the
various embodiments disclosed herein yield a 0.07dB lower average PSNR when
implementing a linear approximation of the EOTF and a 0.01dB higher average
PSNR
for the second degree polynomial approximation of the EOTF. The tPSNR metric
is
.. 0.17dB lower than the conventional luma micro-grading approach, on average.
In
addition, the second degree approximation method results in a slightly better
PSNR
and tPSNR measures than the linear approximation.
[0083] Notably, each of the techniques disclosed herein significantly improve
the
subjective quality of the tested videos, removing perceptual artifacts.
Another
.. observation is that the techniques disclosed herein produce smoother luma
than the
18
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
conventional chroma downsampling, likely resulting in gains in subsequent
compression of the resulting video.
Table 1. Direct downsampling of chroma components
PSNR- PSNR- tPSNR- tPSNR- tPSNR-
Sequence R G PSNR-B PSNR X Y Z
tPSNR-XYZ
FireEater 50.80 71.20 67.45 63.15 54.48 57.13 54.76
55.30
Market 46.35 58.59 48.98 51.31 47.22 49.31 44.59
46.61
Tibul 62.51 82.75 81.61 75.62 50.26 52.21 59.73
52.56
Total 53.22 70.85 66.01 63.36 50.65 52.88 53.03
51.49
Table 2. Results of conventional luma micro-grading
PSNR- PSNR- tPSNR- tPSNR- tPSNR-
Sequence R G PSNR-B PSNR X Y Z
tPSNR-XYZ
FireEater 57.92 68.95 66.79 64.55 64.34 70.91 53.20
57.58
Market 48.29 59.87 49.81 52.66 55.43 69.38 45.69
50.00
Tibul 71.36 82.69 80.94 78.33 62.43 66.94 54.45
58.33
Total 59.19 70.50 65.85 65.18 60.73 69.08 51.11
55.31
Table 3. Second cost function D and linear approximation of EOTF
PSNR- PSNR- tPSNR- tPSNR- tPSNR-
Sequence R G PSNR-B PSNR X Y Z
tPSNR-XYZ
FireEater 56.69 69.86 66.96 64.50 63.89 70.22 53.23
57.56
Market 48.17 59.71 49.71 52.53 55.37 63.93 45.59
49.87
Tibul 71.05 82.87 80.96 78.29 62.18 65.83 54.13
57.99
Total 58.64 70.81 65.88 65.11 60.48 66.66 50.98
55.14
Table 4. Second cost function D and second degree approximation of EOTF
PSNR- PSNR- tPSNR- tPSNR- tPSNR-
Sequence R G PSNR-B PSNR X Y Z
tPSNR-XYZ
FireEater 58.05 68.71 66.74 64.50 64.31 70.33 53.17
57.54
Market 48.30 59.93 49.85 52.69 55.16 64.78 45.66
49.92
19
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
Tibul 71.39 82.67 80.94 78.33 62.55 66.74 54.39
58.29
Total 59.24 70.44 65.84 65.17 60.67 67.28 51.07
55.25
[0084] In sum, a color conversion application downsamples chroma values and
then
upsamples the chroma values by applying an upsampling filter. The color
conversion
application then modifies one or more of the downsampled Y'CbCr values such
that
the reconstruction of these values to a linear RGB signal produces values
similar to
those of the original linear RGB signal. In various embodiments, the color
conversion
application calculates an optimal value of Y', while keeping the values of Cb
and Cr
constant, by evaluating a closed form solution that is based on an
approximation of a
nonlinear transfer function.
[0085] At least one advantage of the disclosed techniques is that resulting
reconstructed HDR images are more accurate relative to the original HDR images
than images generated via conventional chroma downsampling. Additionally, the
complexity of the disclosed techniques is significantly lower than that of the
conventional approaches, enabling an optimal component value (e.g., a luma
value)
to be determined in real-time via a single iteration.
[0086] 1. In some embodiments, a non-transitory computer-readable storage
medium
includes instructions that, when executed by a processor, cause the processor
to
perform the steps of: downsampling first color space values to generate
downsampled color space values; upsampling the downsampled color space values
to generate second color space values; and modifying at least one component
value
included in the downsampled color space values based on a first component
value
included in the first color space values, a second component value included in
the
second color space values, and an approximation of a nonlinear transfer
function.
[0087] 2. The non-transitory computer-readable storage medium of clause 1,
wherein
the at least one component value comprises at least one luma value.
[00881 3. The non-transitory computer-readable storage medium of any of
clauses 1-
2, wherein the approximation of the nonlinear transfer function comprises at
least one
of a linear approximation of an electro-optical transfer function (EOTF) and a
second
order approximation of the EOTF.
CA 03004769 2018-05-08
WO 2017/083426 PCT/1JS2016/061190
[0089] 4. The non-transitory computer-readable storage medium of any of
clauses 1-
3, wherein the first color space values are generated based on linear color
values and
the nonlinear transfer function.
[0090] 5. The non-transitory computer-readable storage medium of any of
clauses 1-
4, further comprising calculating a first difference between the second
component
value included in the second color space values and the first component value
included in the first color space values, wherein the at least one component
value is
modified based on the first difference.
[0091] 6. The non-transitory computer-readable storage medium of any of
clauses 1-
5, wherein the first component value, the second component value, a third
component
value included in the first color space values, and a fourth component value
included
in the second color space values comprise chroma values, and wherein the at
least
one component value is modified based on the chroma values and a luma value
included in the first color space values.
[0092] 7. The non-transitory computer-readable storage medium of any of
clauses 1-
6, wherein the first color space values and the second color space values
comprise
4:4:4 Y'CbCr values, and the downsampled color space values comprise at least
one
of 4:2:2 Y'CbCr values and 4:2:0 Y'CbCr values.
[0093] 8. The non-transitory computer-readable storage medium of any of
clauses 1-
7, wherein the at least one component value is modified based on a lookup
table
associated with the approximation of the nonlinear transfer function.
[0094] 9. The non-transitory computer-readable storage medium of any of
clauses 1-
8, wherein the at least one component value is modified based on nonlinear
color
space component values and color space transform parameters, and wherein the
first
color space values are generated by applying the color space transform
parameters
to the nonlinear color space component values.
[0095] 10. The non-transitory computer-readable storage medium of any of
clauses 1-
9, wherein the at least one component value is modified based on at least one
of a
first weighting applied to a red color value, a second weighting applied to a
green
color value, and a third weighting applied to a blue color value.
21
CA 03004769 2018-05-08
WO 2017/083426 PCT/1JS2016/061190
[0096] 11. The non-transitory computer-readable storage medium of any of
clauses 1-
10, wherein the first weighting corresponds to a red contribution to a
nonlinear color
space luma, the second weighting corresponds to a green contribution to the
nonlinear color space luma, and the third weighting corresponds to a blue
contribution
value associated with the nonlinear color space luma.
[0097] 12. The non-transitory computer-readable storage medium of any of
clauses I-
ll, wherein the first weighting corresponds to a red contribution to a linear
color
space luminance, the second weighting corresponds to a green contribution to
the
linear color space luminance, and the third weighting corresponds to a blue
contribution to the linear color space luminance.
[0098] 13. In some embodiments, a method comprises: downsampling first color
space values to generate downsampled color space values; upsampling the
downsampled color space values to generate second color space values; and
modifying at least one component value included in the downsampled color space
values based on an approximation of a nonlinear transfer function.
[0099] 14. The method of clause 13, wherein the at least one component value
is
modified based on a first component value included in the first color space
values and
a second component value included in the second color space values, and the at
least one component value comprises at least one luma value.
[00100115. The method of any of clauses 13-14, further comprising calculating
a first
difference between the second component value included in the second color
space
values and the first component value included in the first color space values,
wherein
the at least one component value is modified based on the first difference.
[00101] 16. The method of any of clauses 13-15, wherein the first component
value, the
second component value, a third component value included in the first color
space
values, and a fourth component value included in the second color space values
comprise chronna values, and wherein the at least one component value is
modified
based on the chroma values and a luma value included in the first color space
values.
[00102] 17. The method of any of clauses 13-16, wherein the first color space
values
and the second color space values comprise 4:4:4 Y'CbCr values, and the
22
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
downsampled color space values comprise at least one of 4:2:2 Y'CbCr values
and
4:2:0 Y'CbCr values.
[00103] 18. The method of any of clauses 13-17, wherein the approximation of
the
nonlinear transfer function comprises at least one of a linear approximation
of an
electro-optical transfer function (EOTF) and a second order approximation of
the
EOTF.
[00104] 19. The method of any of clauses 13-18, wherein the first color space
values
are generated based on linear color values and the nonlinear transfer
function.
[00105120. The method of any of clauses 13-19, wherein the at least one
component
value is modified based on a lookup table associated with the approximation of
the
nonlinear transfer function.
[00106121. A computing device, comprises: a memory storing a color correction
application; and a processor that is coupled to the memory and, when executing
the
color correction application, is configured to: downsample first color space
values to
generate downsam pled color space values; upsample the downsampled color space
values to generate second color space values; and modify at least one luma
value
included in the downsampled color space values based on a first chroma value
included in the first color space values, a second chroma value included in
the second
color space values, and an approximation of a nonlinear transfer function.
[00107] The descriptions of the various embodiments have been presented for
purposes of illustration, but are not intended to be exhaustive or limited to
the
embodiments disclosed. Many modifications and variations will be apparent to
those
of ordinary skill in the art without departing from the scope and spirit of
the described
embodiments.
[00108]Aspects of the present embodiments may be embodied as a system, method
or computer program product. Accordingly, aspects of the present disclosure
may
take the form of an entirely hardware embodiment, an entirely software
embodiment
(including firmware, resident software, micro-code, etc.) or an embodiment
combining
software and hardware aspects that may all generally be referred to herein as
a
"module" or "system.' Furthermore, aspects of the present disclosure may take
the
23
CA 03004769 2018-05-08
WO 2017/083426 PCT/US2016/061190
form of a computer program product embodied in one or more computer readable
medium(s) having computer readable program code embodied thereon.
[001 09] Any combination of one or more computer readable medium(s) may be
utilized.
The computer readable medium may be a computer readable signal medium or a
computer readable storage medium. A computer readable storage medium may be,
for example, but not limited to, an electronic, magnetic, optical,
electromagnetic,
infrared, or semiconductor system, apparatus, or device, or any suitable
combination
of the foregoing. More specific examples (a non-exhaustive list) of the
computer
readable storage medium would include the following: an electrical connection
having
one or more wires, a portable computer diskette, a hard disk, a random access
memory (RAM), a read-only memory (ROM), an erasable programmable read-only
memory (EPROM or Flash memory), an optical fiber, a portable compact disc read-
only memory (CD-ROM), an optical storage device, a magnetic storage device, or
any
suitable combination of the foregoing. In the context of this document, a
computer
readable storage medium may be any tangible medium that can contain, or store
a
program for use by or in connection with an instruction execution system,
apparatus,
or device.
[0011D]Aspects of the present disclosure are described above with reference to
flowchart illustrations and/or block diagrams of methods, apparatus (systems)
and
.. computer program products according to embodiments of the disclosure. It
will be
understood that each block of the flowchart illustrations and/or block
diagrams, and
combinations of blocks in the flowchart illustrations and/or block diagrams,
can be
implemented by computer program instructions. These computer program
instructions may be provided to a processor of a general purpose computer,
special
purpose computer, or other programmable data processing apparatus to produce a
machine, such that the instructions, which execute via the processor of the
computer
or other programmable data processing apparatus, enable the implementation of
the
functions/acts specified in the flowchart and/or block diagram block or
blocks. Such
processors may be, without limitation, general purpose processors, special-
purpose
processors, application-specific processors, or field-programmable processors
or gate
arrays.
[001111The flowchart and block diagrams in the figures illustrate the
architecture,
functionality, and operation of possible implementations of systems, methods
and
24
CA 03004769 2018-05-08
WO 2017/083426
PCT/US2016/061190
computer program products according to various embodiments of the present
disclosure. In this regard, each block in the flowchart or block diagrams may
represent a module, segment, or portion of code, which comprises one or more
executable instructions for implementing the specified logical function(s). It
should
also be noted that, in some alternative implementations, the functions noted
in the
block may occur out of the order noted in the figures. For example, two blocks
shown
in succession may, in fact, be executed substantially concurrently, or the
blocks may
sometimes be executed in the reverse order, depending upon the functionality
involved. It will also be noted that each block of the block diagrams and/or
flowchart
illustration, and combinations of blocks in the block diagrams and/or
flowchart
illustration, can be implemented by special purpose hardware-based systems
that
perform the specified functions or acts, or combinations of special purpose
hardware
and computer instructions.
[001 1 2] While the preceding is directed to embodiments of the present
disclosure,
other and further embodiments of the disclosure may be devised without
departing
from the basic scope thereof, and the scope thereof is determined by the
claims that
follow.