SEQUENTIAL FULLY IMPLICIT WELL MODEL WITH TRIDIAGONAL MATRIX STRUCTURE FOR RESERVOIR SIMULATION

MODELE DE PUITS SEQUENTIEL ENTIEREMENT IMPLICITE AVEC STRUCTURE DE MATRICE TRIDIAGONALE POUR SIMULATION DE RESERVOIR

English Abstract

A subsurface hydrocarbon reservoir with a horizontal well or multiple vertical wells is simulated by sequential solution of reservoir and well equations to simulate fluid flow inside the reservoir and well production rates. Sequential solution of reservoir and well equations treats wells as specified bottom hole pressure wells. This avoids solving large matrices resulting from the simultaneous solution of the reservoir and well equations which can be computationally very expensive for large number of unknowns and require special sparse matrix solvers. Such sequential solution involves regular reservoir system solvers complemented by small matrices for the numerical solution of the well bottom hole pressures. The solution is performed on tridiagonal matrices for the adjacent reservoir cells to the well cells at the perforated well intervals; and a vector of the unknown reservoir potentials for the adjacent reservoir cells.

French Abstract

Cette invention concerne la simulation d'un réservoir souterrain d'hydrocarbures avec un puits horizontal ou de multiples puits verticaux par résolution séquentielle d'équations de réservoir et de puits pour simuler l'écoulement de fluide à l'intérieur du réservoir et les taux de production de puits. La résolution séquentielle d'équations de réservoir et de puits traite les puits comme des puits à pression de fond spécifique. Ceci permet d'éviter la résolution de grandes matrices résultant de la résolution simultanée des équations de réservoir et de puits, qui peut être informatiquement très coûteuse pour grand nombre d'inconnues et nécessiter des résolveurs spéciaux par matrice creuse. Une telle résolution séquentielle met en uvre des résolveurs normaux de système de réservoir complétés par de petites matrices pour la résolution numérique des pressions de fond de trou. La résolution est effectuée sur des matrices tridiagonales pour les cellules de réservoir adjacentes aux intervalles de puits perforés ; et un vecteur des potentiels de réservoir inconnus pour les cellules de réservoir adjacentes.

Claims

CLAIMS
1. A computer implemented method of forming a model of determined well
production
rate of component fluids from a plurality of wells in a subsurface reservoir
and of determined
layer completion rates of perforated well intervals in the wells, from
measured total well
production, with a coupled well reservoir model during reservoir simulation of
well
production at a time step during life of the subsurface reservoir, the coupled
well reservoir
model being organized into a reservoir grid subdivided into a plurality of
reservoir cells at the
perforated well intervals, the perforated well intervals in the reservoir
being located at a
plurality of formation layers, the formation layers having unknown well
potentials and fluid
completion rates for component fluids at the time step, and the formation
layers comprising
vertical fluid flow layers having vertical fluid flow therefrom and flow
barrier layers with no
vertical fluid flow therefrom, the formation layers further having a
permeability, thickness
and a layer potential, the coupled well reservoir model further having a
plurality of well cells
at locations of the wells in formation layers of the reservoir, the computer
implemented
method determining layer completion rates for the component fluids from the
formation
layers of the wells and well production rates of the component fluids from the
wells, the
computer implemented method comprising the steps of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
vertical
flow layers in the matrix the data of the vertical fluid flow layers of
vertical fluid flow layers
having vertical fluid flow therebetween and being located between flow barrier
layers in the
reservoir model;
(c) determining a bottomhole pressure for the wells;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
well as a
bottomhole, pressure specified well having the determined bottomhole pressure,
the coupled
reservoir well model being in the form of a matrix:
-47-

<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A RW is a diagonal
matrix of the
productivity indexes of the formation layers adjacent the perforated well
intervals; A WR is a
diagonal matrix of the productivity indexes from wells to the formation layers
of the
reservoir; A WW is a matrix of the productivity indexes of the wells; .PHI. R
is a matrix of
unknown reservoir potentials for the cells around the wells; .PHI. W is a
matrix of unknown well
potentials in the wellbores of the wells; b R is a matrix of reservoir data
constants for the
reservoir cells around the wells; and b w is a matrix of the well data
constants for the wells;
(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
(f) solving the coupled reservoir well model for the productivity
indexes of the
well cells at the perforated well intervals of the reservoir at the time step;
(g) determining layer completion rates for the component fluids of the
vertical
fluid flow layers and the flow barrier layers of the well based on the
determined productivity
indexes of the reservoir and well cells at the perforated well intervals of
the reservoir at the
time step;
(h) determining total well production rate for the well from the determined
layer
completion rates for the component fluids of the vertical fluid flow layers
and the flow barrier
layers of the well at the time step ; and
(i) forming a record of the determined layer completion rates for the
component
fluids of the vertical fluid flow layers and the flow barrier layers of the
well and the
determined total well production rate for the well at the time step.
2. The computer implemented method of Claim 1, wherein the tridiagonal
matrix of the
reservoir cells comprises a diagonal representing the transmissivities of the
cells of the
reservoir.
3. The computer implemented method of Claim 1, wherein the steps of solving
the
coupled well reservoir model comprise applying a full matrix solver.
-48-

4. The computer implemented method of Claim 3, further including the steps
of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances; and
if the tolerances are satisfied at the time step, and for each time step
during life of the
subsurface reservoir, proceeding to the step of forming a record; and
if the tolerances are not satisfied at the time step, returning to step (a)
and repeating
steps (b) through (h) for another iteration of processing at the time step.
5. The computer implemented method of Claim 3, further including the steps
of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances; and
if the specified tolerances are satisfied at the time step, but not for each
time step
during life of the reservoir, incrementing the simulator time step; and
returning to step (a) and repeating steps (b) through (h) for another
iteration of
processing at the incremented simulator time step.
6. The computer implemented method of Claim 1, wherein the step of solving
the
coupled well reservoir model comprises the step of solving for fluid flows
based on the
permeability, thickness and layer potentials of the formation layers.
7. The computer implemented method of Claim 1, wherein the plurality of
wells
comprise a plurality of vertical wells.
8. A data processing system forming a model of determined well production
rate of
component fluids from a plurality of well in a subsurface reservoir and of
determined layer
completion rates of perforated well intervals in the wells, from measured
total well
production, with a coupled well reservoir model during reservoir simulation of
well
production at a time step during life of the subsurface reservoir, the coupled
well reservoir
model being organized into a reservoir grid subdivided into a plurality of
reservoir cells at the
perforated well intervals, the perforated well intervals in the reservoir
being located at a
plurality of formation layers, the formation layers having unknown well
potentials and fluid
completion rates for component fluids at the time step, and the formation
layers comprising
vertical fluid flow layers having vertical fluid flow therefrom and flow
barrier layers with no
vertical fluid flow therefrom, the formation layers further having a
permeability, thickness
and a layer potential, the coupled well reservoir model further having a
plurality of well cells
-49-

at locations of the wells in formation layers of the reservoir, the data
processing system
determining layer completion rates for the component fluids from the formation
layers of the
wells and well production rates of the component fluids from the wells, and
comprising:
a processor performing the steps of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
vertical
flow layers in the matrix the data of the vertical fluid flow layers of
vertical fluid flow layers
having vertical fluid flow therebetween and being located between flow barrier
layers in the
reservoir model;
(c) determining a bottomhole pressure for the wells;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
well as a
bottomhole, pressure specified well having the determined bottomhole pressure,
the coupled
reservoir well model being in the form of a matrix::
<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A RW is a diagonal
matrix of the
productivity indexes of the formation layers adjacent the perforated well
intervals; A WR is a
diagonal matrix of the productivity indexes from wells to the formation layers
of the
reservoir; A WW is a matrix of the productivity indexes of the wells; .PHI. R
is a matrix of
unknown reservoir potentials for the cells around the wells; .PHI. w is a
matrix of unknown well
potentials in the wellbores of the wells; b R is a matrix of reservoir data
constants for the
reservoir cells around the wells; and b w is a matrix of the well data
constants for the wells;
(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
-50-

solving the coupled reservoir well model for the productivity indexes of the
well cells at the perforated well intervals of the reservoir at the time step;
(8) determining layer completion rates for the component fluids of the
vertical
fluid flow layers and the flow barrier layers of the well based on the
determined productivity
indexes of the reservoir and well cells at the perforated well intervals of
the reservoir at the
time step;
(h) determining total well production rate for the well from the
determined layer
completion rates for the component fluids of the vertical fluid flow layers
and the flow barrier
layers of the well at the time step ; and
a memory performing the step of forming a record of the determined layer
completion
rates for the component fluids of the vertical fluid flow layers and the flow
barrier layers of
the well and the determined total well production rate for the well at the
time step.
9. The data processing system of Claim 8, wherein the tridiagonal matrix of
the reservoir
cells comprises a diagonal representing the transmissivities of the cells of
the reservoir.
10. The data processing system of Claim 8, wherein the processor in solving
the coupled
well reservoir model performs the step of applying a full matrix solver.
11. The data processing system of Claim 10, further including the processor
performing
the steps of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances; and
if the tolerances are satisfied at the time step, and for each time step
during life of the
subsurface reservoir, causing the memory to perform the step of forming a
record; and
if the tolerances are not satisfied at the time step, returning to step (a)
and repeating
steps (b) through (h) for another iteration of processing at the time step.
12. The data processing system of Claim 10, further including the processor
performing
the steps of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances; and
if the specified tolerances are satisfied at the time step, but not for each
time step
during life of the reservoir, incrementing the simulator time step; and
-51-

returning to step (a) and repeating steps (b) through (h) for another
iteration of
processing at the incremented simulator time step.
13. The data processing system of Claim 8, wherein the processor in solving
the coupled
well reservoir model performs the step of solving for fluid flows based on the
permeability,
thickness and layer potentials of the formation layers.
14. The data processing system of Claim 8, wherein the plurality of wells
comprise a
plurality of vertical wells.
15. A data storage device having stored in a non-transitory computer
readable medium
computer operable instructions for causing a data processor to form a model of
determined
well production rate of component fluids from a plurality of well in a
subsurface reservoir
and of determined layer completion rates of perforated well intervals in the
wells, from
measured total well production, with a coupled well reservoir model during
reservoir
simulation of well production at a time step during life of the subsurface
reservoir, the
coupled well reservoir model being organized into a reservoir grid subdivided
into a plurality
of reservoir cells at the perforated well intervals, the perforated well
intervals in the reservoir
being located at a plurality of formation layers, the formation layers having
unknown well
potentials and fluid completion rates for component fluids at the time step,
and the formation
layers comprising vertical fluid flow layers having vertical fluid flow
therefrom and flow
barrier layers with no vertical fluid flow therefrom, the formation layers
further having a
permeability, thickness and a layer potential, the coupled well reservoir
model further having
a plurality of well cells at locations of the wells in formation layers of the
reservoir, the stored
computer operable instructions causing the data processor to determine layer
completion rates
for the component fluids from the formation layers of the wells and well
production rates of
the component fluids from the wells by performing the steps of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
vertical
flow layers in the matrix the data of the vertical fluid flow layers of
vertical fluid flow layers
having vertical fluid flow therebetween and being located between flow barrier
layers in the
reservoir model;
-52-

(c) determining a bottomhole pressure for the wells;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
well as a
bottomhole, pressure specified well having the determined bottomhole pressure,
the coupled
reservoir well model being in the form of a matrix:
<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A RW is a diagonal
matrix of the
productivity indexes of the formation layers adjacent the perforated well
intervals; A WR is a
diagonal matrix of the productivity indexes from wells to the formation layers
of the
reservoir; A WW is a matrix of the productivity indexes of the wells; .PHI. R
is a matrix of
unknown reservoir potentials for the cells around the wells; .PHI. W is a
matrix of unknown well
potentials in the wellbores of the wells; b R is a matrix of reservoir data
constants for the
reservoir cells around the wells; and b W is a matrix of the well data
constants for the wells;
(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
(f) solving the coupled reservoir well model for the productivity indexes
of the
well cells at the perforated well intervals of the reservoir at the time step;
(g) determining layer completion rates for the component fluids of the
vertical
fluid flow layers and the flow barrier layers of the well based on the
determined productivity
indexes of the reservoir and well cells at the perforated well intervals of
the reservoir at the
time step;
(h) determining total well production rate for the well from the determined
layer
completion rates for the component fluids of the vertical fluid flow layers
and the flow barrier
layers of the well at the time step ; and
(i) forming a record of the determined layer completion rates for the
component
fluids of the vertical fluid flow layers and the flow barrier layers of the
well and the
determined total well production rate for the well at the time step.
-53-

16. The data storage device of Claim 15, wherein the instructions for
causing the
processor to perform the steps of solving the coupled well reservoir model
comprise
instructions for applying a full matrix solver.
17. The data storage device of Claim 15, wherein the instructions further
include
instructions causing the processor to perform the steps of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances;
if the tolerances are satisfied at the time step, and for each time step
during life of the
reservoir, proceeding to the step of forming a record; and
if the tolerances are not satisfied at the time step, returning to step (a)
and repeating
steps (b) through (h) for another iteration of processing. at the time step.
18. The data storage device of Claim 15, wherein the instructions further
include
instructions causing the processor to perform the steps of:
reducing residuals from the step of applying a full matrix solver against
specified
tolerances; and
if the specified tolerances are satisfied at the time step, but not for each
time step
during life of the reservoir, incrementing the simulator time step; and
returning to step (a) and repeating steps (b) through (h) for another
iteration of
processing at the incremented simulator time step.
20. The data storage device of Claim 15, wherein the instructions for
causing the
processor to perform the step of solving the coupled well reservoir model
comprise
instructions for solving for fluid flows based on the permeability, thickness
and layer
potentials of the formation layers.
21. The data storage device of Claim 15, wherein the plurality of wells
comprise a
plurality of vertical wells.
22. A computer implemented method of forming a model of determined well
production
rate of component fluids from a horizontal well in a subsurface reservoir and
of determined
layer completion rates of perforated well intervals in the horizontal well,
from measured total
well production, with a coupled well reservoir model during reservoir
simulation of well
-54-

production at a time step during life of the subsurface reservoir, the coupled
well reservoir
model being organized into a reservoir grid subdivided into a plurality of
reservoir cells at the
perforated well intervals, the perforated well intervals in the reservoir
being located at a
plurality of formation layers, the formation layers having unknown well
potentials and fluid
completion rates for component fluids at the time step, and the formation
layers comprising
horizontal fluid flow layers having horizontal fluid flow therefrom and flow
barrier layers
with no horizontal fluid flow therefrom, the formation layers further having a
permeability,
thickness and a layer potential, the coupled well reservoir model further
having a plurality of
well cells at locations of the horizontal well in formation layers of the
reservoir, the computer
implemented method determining layer completion rates for the component fluids
from the
formation layers of the horizontal well and well production rates of the
component fluids
from the horizontal well, the computer implemented method comprising the steps
of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
horizontal flow layers in the matrix the data of the horizontal fluid flow
layers of horizontal
fluid flow layers having horizontal fluid flow therebetween and being located
between flow
barrier layers in the reservoir model;
(c) determining a bottomhole pressure for the horizontal well;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
horizontal
well as a bottomhole, pressure specified well having the determined bottomhole
pressure, the
coupled reservoir well model being in the form of a matrix:
<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A WR is a vector
of the productivity
indexes of the formation layers adjacent the perforated well intervals; A WR
is a vector of the
productivity indexes from well to the formation layers of the reservoir; A WW
is a linear scalar
-55-

of the productivity indexes of the horizontal well; .PHI. R is a vector of
unknown reservoir
potentials for the cells around the horizontal well; .PHI. W is a vector of
unknown well potentials
in the wellbore; b R is a vector of reservoir data constants for the reservoir
cells around the
horizontal well; and b W is a vector of the well data constants for the
horizontal well;
(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
(f) solving the coupled reservoir well model for the productivity indexes
of the
well cells at the perforated well intervals of the reservoir at the time step;
(g) determining layer completion rates for the component fluids of the
horizontal
fluid flow layers and the flow barrier layers of the horizontal well based on
the determined
productivity indexes of the reservoir and well cells at the perforated well
intervals of the
reservoir at the time step;
(h) determining total well production rate for the horizontal well from the
determined layer completion rates for the component fluids of the horizontal
fluid flow layers
and the flow barrier layers of the horizontal well at the time step ; and
(i) forming a record of the determined layer completion rates for the
component
fluids of the horizontal fluid flow layers and the flow barrier layers of the
horizontal well and
the determined total well production rate for the horizontal well at the time
step.
23. A data processing system forming a model of determined well production
rate of
component fluids from a horizontal well in a subsurface reservoir and of
determined layer
completion rates of perforated well intervals in the horizontal well, from
measured total well
production, with a coupled well reservoir model during reservoir simulation of
well
production at a time step during life of the subsurface reservoir, the coupled
well reservoir
model being organized into a reservoir grid subdivided into a plurality of
reservoir cells at the
perforated well intervals, the perforated well intervals in the reservoir
being located at a
plurality of formation layers, the formation layers having unknown well
potentials and fluid
completion rates for component fluids at the time step, and the formation
layers comprising
horizontal fluid flow layers having horizontal fluid flow therefrom and flow
barrier layers
with no horizontal fluid flow therefrom, the formation layers further having a
permeability,
thickness and a layer potential, the coupled well reservoir model further
having a plurality of
-56-

well cells at locations of the horizontal well in formation layers of the
reservoir, the data
processing system determining layer completion rates for the component fluids
from the
formation layers of the horizontal well and well production rates of the
component fluids
from the horizontal well, and comprising:
a processor performing the steps of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
horizontal flow layers in the matrix the data of the horizontal fluid flow
layers of horizontal
fluid flow layers having horizontal fluid flow therebetween and being located
between flow
barrier layers in the reservoir model;
(c) determining a bottomhole pressure for the horizontal well;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
horizontal
well as a bottomhole, pressure specified well having the determined bottomhole
pressure, the
coupled reservoir well model being in the form of a matrix:
<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A WR is a vector
of the productivity
indexes of the formation layers adjacent the perforated well intervals; A WW
is a vector of the
productivity indexes from well to the formation layers of the reservoir; A WW
is a linear scalar
of the productivity indexes of the horizontal well; .PHI. R is a vector of
unknown reservoir
potentials for the cells around the horizontal well; .PHI. W is a vector of
unknown well potentials
in the wellbore; b R is a vector of reservoir data constants for the reservoir
cells around the
horizontal well; and b W is a vector of the well data constants for the
horizontal well;
-57-

(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
(f) solving the coupled reservoir well model for the productivity indexes
of the
well cells at the perforated well intervals of the reservoir at the time step;
(g) determining layer completion rates for the component fluids of the
horizontal
fluid flow layers and the flow barrier layers of the horizontal well based on
the determined
productivity indexes of the reservoir and well cells at the perforated well
intervals of the
reservoir at the time step;
(h) determining total well production rate for the horizontal well from the
determined layer completion rates for the component fluids of the horizontal
fluid flow layers
and the flow barrier layers of the horizontal well at the time step ; and
a memory forming a record of the determined layer completion rates for the
component fluids
of the horizontal fluid flow layers and the flow barrier layers of the
horizontal well and the
determined total well production rate for the horizontal well at the time
step.
24. A data storage device having stored in a non-transitory computer
readable medium
computer operable instructions for causing a data processor to form a model of
determined
well production rate of component fluids from a horizontal well in a
subsurface reservoir and
of determined layer completion rates of perforated well intervals in the
horizontal well, from
measured total well production, with a coupled well reservoir model during
reservoir
simulation of well production at a time step during life of the subsurface
reservoir, the
coupled well reservoir model being organized into a reservoir grid subdivided
into a plurality
of reservoir cells at the perforated well intervals, the perforated well
intervals in the reservoir
being located at a plurality of formation layers, the formation layers having
unknown well
potentials and fluid completion rates for component fluids at the time step,
and the formation
layers comprising horizontal fluid flow layers having horizontal fluid flow
therefrom and
flow barrier layers with no horizontal fluid flow therefrom, the formation
layers further
having a permeability, thickness and a layer potential, the coupled well
reservoir model
further having a plurality of well cells at locations of the horizontal well
in formation layers
of the reservoir, the stored computer operable instructions causing the data
processor to
determine layer completion rates for the component fluids from the formation
layers of the
-58-

horizontal well and well production rates of the component fluids from the
horizontal well by
performing the steps of:
(a) forming a full computation matrix reservoir model of reservoir data of
cells of
the model, including the reservoir data for the reservoir cells at the
perforated well intervals,
the reservoir data including the permeability, thickness and a potential for
the formation
layers;
(b) forming a reduced well model system matrix by assembling as single
horizontal flow layers in the matrix the data of the horizontal fluid flow
layers of horizontal
fluid flow layers having horizontal fluid flow therebetween and being located
between flow
barrier layers in the reservoir model;
(c) determining a bottomhole pressure for the horizontal well;
(d) forming a coupled reservoir well model comprising the full computation
matrix reservoir model and the reduced well model system matrix, treating the
horizontal
well as a bottomhole, pressure specified well having the determined bottomhole
pressure, the
coupled reservoir well model being in the form of a matrix:
<IMG>
wherein A RR is a tridiagonal matrix of the reservoir data, A RW is a vector
of the productivity
indexes of the formation layers adjacent the perforated well intervals; A WR
is a vector of the
productivity indexes from well to the formation layers of the reservoir; A WW
is a linear scalar
of the productivity indexes of the horizontal well; .PHI. R is a vector of
unknown reservoir
potentials for the cells around the horizontal well; .PHI. W is a vector of
unknown well potentials
in the wellbore; b R is a vector of reservoir data constants for the reservoir
cells around the
horizontal well; and b W is a vector of the well data constants for the
horizontal well;
(e) solving the coupled reservoir well model for the fluid flows in the
reservoir
cells of the formation layers and the productivities and potentials of the
reservoir cells at the
time step for each of the formation layers;
(f) solving the coupled reservoir well model for the productivity indexes
of the
well cells at the perforated well intervals of the reservoir at the time step;
-59-

(g) determining layer completion rates for the component fluids of the
horizontal
fluid flow layers and the flow barrier layers of the horizontal well based on
the determined
productivity indexes of the reservoir and well cells at the perforated well
intervals of the
reservoir at the time step;
(h) determining total well production rate for the horizontal well from the
determined layer completion rates for the component fluids of the horizontal
fluid flow layers
and the flow barrier layers of the horizontal well at the time step ; and
(i) forming a record of the determined layer completion rates for the
component
fluids of the horizontal fluid flow layers and the flow barrier layers of the
horizontal well and
the determined total well production rate for the horizontal well at the time
step.
-60-

Description

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
PCT PATENT APPLICATION
SEQUENTIAL FULLY IMPLICIT WELL MODEL WITH TRIDIAGONAL
MATRIX STRUCTURE FOR RESERVOIR SIMULATION
Inventor: Ali H. DOGRU
[0001] Cross-Reference to Related Applications: The present application is a
continuation
in part of, and claims priority to, Applicant's co-pending, commonly owned U.
S. Patent
Application No. 14/040,930, filed September 30, 2013, and to U. S. Patent
Application No.
13/023,728, filed February 9, 2011, now U. S. Patent No. 9,164,191, issued
October 20,
2015.
[0002] The present application is also related to commonly owned U. S. Patent
Application
No. 15/061,572, filed of even date herewith, entitled "Sequential Fully
Implicit Well Model
with Tridiagonal Matrix Structure for Reservoir Simulation," (Attorney Docket
No.
004159.005477) and having the same inventor as the present application.
BACKGROUND OF THE INVENTION
1. Field of the Invention
[0003] The present invention relates to computerized simulation of hydrocarbon
reservoirs in
the earth, and in particular to simulation of flow profiles along wells in a
reservoir.
2. Description of the Related Art
[0004] Well models have played an important role in numerical reservoir
simulation. Well
models have been used to calculate oil, water and gas production rates from
wells in an oil
and gas reservoirs. If the well production rate is known, they are used to
calculate the flow
profile along the perforated interval of the well. With the increasing
capabilities for
measuring flow rates along the perforated intervals of a well, a proper
numerical well model
-1-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
is necessary to compute the correct flow profile to match the measurements in
a reservoir
simulator.
[0005] It is well known that simple well models such as explicit or semi
implicit models
could be adequate if all reservoir layers communicated vertically for any
vertical wells in a
reservoir simulator. For these models, well production rate is allocated to
the perforations in
proportion to the layer productivity indices (or total mobility). Therefore,
the calculations are
simple and computationally inexpensive. The structure of the resulting
coefficient matrix for
the reservoir unknowns remains unchanged. Specifically, the coefficient matrix
maintains a
regular sparse structure. Therefore, any such sparse matrix solver could be
used to solve the
linear system for the grid block pressures and saturations for every time step
for the entire
reservoir simulation model.
[0006] However, for highly heterogeneous reservoirs with some vertically non-
communicating layers, the above-mentioned well models cannot produce the
correct physical
solution. Instead, they produce incorrect flow profiles and in some occasions
cause simulator
convergence problems.
[0007] With the increasing sophistication of reservoir models, the number of
vertical layers
has come to be in the order of hundreds to represent reservoir heterogeneity.
Fully implicit,
fully coupled well models with simultaneous solution of reservoir and well
equations have
been necessary to correctly simulate the flow profiles along the well and also
necessary for
the numerical stability of the reservoir simulation. In order to solve the
fully coupled system,
generally well equations are eliminated first. This creates an unstructured
coefficient matrix
for the reservoir unknowns to be solved. Solutions of this type of matrices
require
specialized solvers with specialized preconditioners. For wells with many
completions and
many wells in a simulation model, this method has become computationally
expensive in
terms of processor time.
-2-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
SUMMARY OF THE INVENTION
[0008] Briefly, the present provides a new and improved computer implemented
method of
solving well equations together with reservoir equations in a reservoir
simulation model
having formation layers having vertical fluid flow and flow barrier layers
with no vertical
fluid flow. The computer implemented method forms a reduced well model system
for
horizontal as well as multiple vertical wells in a reservoir simulation model
by assembling as
a single flow layer the flow layers having flow between the flow barriers in
the reservoir
model in the vicinity of the wells only. For a production rate specified well,
the method then
solves the reduced well model system by matrix computation (using a direct
sparse matrix
solver) for the bottom hole pressure of the well and reservoir unknowns for
the grid blocks
where well is going through (reduced well model system). This method is
repeated for the
well or wells in a reservoir simulator. Next, the method then solves the full
reservoir
simulation model by treating each well as having the determined bottom hole
pressure, and
based on a steady state volume balance relationship of the layer completion
rates, formation
pressures and transmissibilities to determine completion rates for the layers
of the well or
wells for the full reservoir model, and determine total rate for the well from
the determined
completion rates for the layers of the well or wells. The method then forms a
record of the
determined completion rates for the layers and the determined total rate for
the well or wells.
The simulator calculates the pressure distribution of multi-phase flow fluid
saturations
distribution in the reservoir by using the calculated perforation rates and
the reservoir data
assigned to the simulator grid blocks. The simulator is thus able to calculate
pressure and
saturation distribution within the reservoir with given production and
injection rates at the
wells at a given time.
[0009] The present invention provides a new and improved data processing
system for
forming a well model for horizontal as well as multiple vertical wells by
reservoir simulation
of a subsurface reservoir from a reservoir model having formation layers
having fluid flow
and flow barrier layers with no fluid flow. The data processing system
includes a processor
which performs the steps of solving by matrix computation the reduced well
model system
model for the bottom hole pressure of the well or wells and reservoir unknowns
around the
well or wells and solving the full reservoir model by treating the well(s) as
having the
determined bottom hole pressure, and based on a steady state volume balance
relationship of
the layer completion rates, formation pressures and transmissibilities to
determine
completion rates for the layers of the well(s) for the full reservoir model.
The processor also
-3-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
determines total rate for the well(s) from the determined completion rates for
the layers of the
well(s). The data processing system also includes a memory forming a record
the determined
completion rates for the layers and the determined total rate or rates.
[0010] The present invention further provides a new and improved data storage
device
having stored in a computer readable medium computer operable instructions for
causing a
data processor in forming a well model for horizontal as well as multiple
vertical wells by
reservoir simulation of a subsurface reservoir from a reservoir model having
formation layers
having fluid flow and flow barrier layers with no fluid flow to perform steps
of solving by
matrix computation the reduced well model system model for the bottom hole
pressure of the
well or wells and reservoir unknowns and solving the full reservoir model by
treating the
well(s) as having the determined bottom hole pressureõ and based on a steady
state volume
balance relationship of the layer completion rates, formation pressures and
transmissibilities
to determine completion rates for the layers of the well(s) for the full
reservoir model. The
instructions stored in the data storage device also include instructions
causing the data
processor to determine the total rate for the well(s) from the determined
completion rates for
the layers of the well or wells, and form a record the determined completion
rates for the
layers and the determined total rate for the well(s).
-4-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
BRIEF DESCRIPTION OF THE DRAWINGS
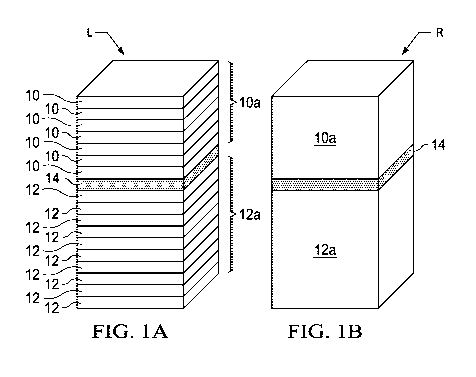
[0011] Figures 1A and 1B are schematic diagrams for a well model in a
reservoir simulator
of multiple subsurface formation layers above and below a flow barrier in a
reservoir being
formed into single layers according to the present invention.
[0012] Figures 2A and 2B are schematic diagrams for a well model in a
reservoir simulator
of multiple subsurface formation layers above and below several vertically
spaced flow
barriers in a reservoir being formed into single layers according to the
present invention.
[0013] Figure 3 is a schematic diagram of a well model for simulation based on
an explicit
model methodology illustrated in radial geometry.
[0014] Figure 4 is a schematic diagram of a well model for simulation based on
a fully
implicit, fully coupled model methodology.
[0015] Figure 5 is a schematic diagram of a well model for reservoir
simulation with a
comparison of flow profiles obtained from the models of Figures 3 and 4.
[0016] Figure 6 is a schematic diagram of a finite difference grid system for
the well models
of Figures 3 and 4.
[0017] Figure 7A and 7B are schematic diagrams illustrating the well model
reservoir layers
for an unmodified conventional well layer model and a well layer model
according to the
present invention, respectively.
[0018] Figures 8A and 8B are schematic diagrams of flow profiles illustrating
comparisons
between the models of Figures 7A and 7B, respectively.
[0019] Figure 9 is a schematic diagram of a well layer model having two
fracture layers in
radial coordinates.
[0020] Figure 10 is a functional block diagram or flow chart of data
processing steps for a
method and system for a fully implicit fully coupled well model with
simultaneous numerical
solution for reservoir simulation.
[0021] Figure 11 is a functional block diagram or flow chart of data
processing steps for a
method and system for a sequential fully implicit well model for reservoir
simulation
according to the present invention.
-5-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[0022] Figure 12 is a schematic diagram of a linear system of equations with a
tridiagonal
coefficient matrix for an explicit well model for a one dimensional reservoir
simulator with a
vertical well
[0023] Figure 13 is a schematic diagram of a linear system of equations with a
tridiagonal
coefficient matrix for a fully implicit well model for a one dimensional
reservoir simulator
with a vertical well
[0024] Figure 14 is a schematic diagram of a linear system of equations with a
tridiagonal
coefficient matrix for a constant bottom hole pressure well model for a one
dimensional
reservoir simulator with a vertical well for processing according to the
present invention.
[0025] Figure 15 is a functional block diagram or flow chart of steps
illustrating the
analytical methodology for reservoir simulation according to the present
invention.
[0026] Figure 16 is a schematic diagram of a computer network for a sequential
fully implicit
well model for reservoir simulation according to the present invention.
[0027] Figure 17 is a schematic diagram of a tridiagonal coefficient matrix.
[0028] Figure 18 is a schematic diagram of a linear system of equations with a
tridiagonal
coefficient matrix.
[0029] Figure 19 is a schematic diagram of a finite difference grid system for
a horizontal
well model oriented in a y-axis direction according to the present invention.
[0030] Figures 20A and 20B are schematic diagrams of horizontal well models in
a reservoir
simulator of multiple subsurface formation layers in the area of a flow
barrier in a reservoir,
before and after being formed into a reduced horizontal well model according
to the present
invention.
[0031] Figure 20C is a schematic diagram of a linear system of equations for
the reduced
horizontal well model of Figure 20B.
[0032] Figure 21 and 22 are functional block diagrams or flow charts of data
processing steps
for a method and system for a reduced horizontal well model according to the
present
invention.
[0033] Figure 23 is a schematic diagram of a finite difference grid system for
a reservoir
model with multiple wells according to the present invention.
-6-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[0034] Figures 24A and 24B are schematic diagrams illustrating notations for
grid
nomenclature in the multiple well reservoir model of Figures 19 and 23.
[0035] Figures 25A, 25B, 25C and 25D are schematic diagrams illustrating grid
numbering
for a three-dimensional reservoir model.
[0036] Figure 26 is a functional block diagram or flow chart of data
processing steps for a
method and system for a modification of the block diagram of Figure 11 for
multiple wells in
a reservoir with a fully implicit fully coupled well model with simultaneous
numerical
solution for reservoir simulation.
[0037] Figure 27 is a schematic diagram of a linear system of equations for a
simplified two
well, three-dimensional reservoir model.
-7-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENTS
[0038] By way of introduction, the present invention provides a sequential
fully implicit well
model for reservoir simulation. Reservoir simulation is a mathematical
modeling science for
reservoir engineering. The fluid flow inside the oil or gas reservoir (porous
media) is
described by a set of partial differential equations. These equations describe
the pressure
(energy) distribution, oil, water and gas velocity distribution, fractional
volumes (saturations)
of oil, water, gas at any point in reservoir at any time during the life of
the reservoir which
produces oil, gas and water. Fluid flow inside the reservoir is described by
tracing the
movement of the component of the mixture. Amounts of components such as
methane,
ethane, CO2, nitrogen, H2S and water are expressed either in mass unit or
moles.
[0039] Since these equations and associated thermodynamic and physical laws
describing the
fluid flow are complicated, they can only be solved on digital computers to
obtain pressure
distribution, velocity distribution and fluid saturation or the amount of
component mass or
mole distribution within the reservoir at any time at any point. This only can
be done by
solving these equations numerically, not analytically. Numerical solution
requires that the
reservoir be subdivided into computational elements (cells or grid blocks) in
the area and
vertical direction (x, y, z ¨ three dimensional spaces) and time is sub-
divided into intervals of
days or months. For each element, the unknowns (pressure, velocity, volume
fractions, etc.)
are determined by solving the complicated mathematical equations.
[0040] In fact, a reservoir simulator model can be considered the collection
of rectangular
prisms (like bricks in the walls of a building). The changes in the pressure
and velocity fields
take place due to oil, water and gas production at the wells distributed
within the reservoir.
Simulation is carried out over time (t). Generally, the production or
injection rate of each
well is known during the production history of a reservoir. However, since the
wells go
through several reservoir layers (elements), the contribution of each
reservoir element (well
perforation) to the production is calculated by different methods. This
invention deals with
the calculation of how much each well perforation contributes to the total
well production.
Since these calculations can be expensive and very important boundary
conditions for the
simulator, the proposed method suggests a practical method to calculate
correctly the flow
profiles along a well trajectory. As will be described, it can be shown that
some other
methods used will result in incorrect flow profiles which cause problems in
obtaining the
correct numerical solution and can be very expensive computationally.
-8-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
Nomenclature
Ax, Ay, Az= Grid dimension in x, y and z directions
kx, ky, k = permeability in x, y and z directions
p = pressure
p = Fluid (oil) density
g = gravitational constant
z = vertical depth from a datum depth
r, = Peaceman's radius = 0.2 Ax
r, = wellbore radius
Tx, Ty, T = Rock Transmissibility in the x, y and z directions
[0041] The equations describing a general reservoir simulation model and
indicating the well
terms which are of interest in connection with the present invention are set
forth below in
Equation (1):
np np np np
Atn
A x1T p Act. +A, IT p J Act. +A, IT p Act. q =
x J Y Y z z IJ At
1=1 1=1 1=1 J=1 (1)
i=1,..n,..
where Ax is the difference operator in the x direction, Tx, Ty, T, are the
rock transmissibilities
in the x, y and z directions as defined in Equation below), j stands for the
number of fluid
phases, np is the total number of fluid phases, usually 3 (oil, water and
gas), / is the
summation term, xi is the density of component i in the fluid phase j, 2j is
the mobility of the
phase j (Equation 6), is the
fluid potential (datum corrected pressure) of fluid phase j,
similarly Ay is the difference operator in y direction, and A, is the
difference operator in z
direction of the reservoir, qj, is the well term (source or sink) for the
component i for grid
block (cell) k, At is the difference operator in time domain, ni is the total
number of moles for
component i, and n, is the total number of components in the fluid
system(methane, ethane,
propane, CO2, etc.).
[0042] Equation (1) is a set of coupled nonlinear partial differential
equations describing the
fluid flow in the reservoir. In the above set of equations ni represents the
ith component of
the fluids. ne is the total number of components of the hydrocarbons and water
flowing in the
-9-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
reservoir. Here a component means such as methane, ethane, propane, CO2, H2S,
water, etc.
The number of components depends on the hydrocarbon water system available for
the
reservoir of interest. Typically, the number of components can change from 3
to 10.
Equation (1) combines the continuity equations and momentum equations.
[0043] In Equation (1) qjwk is the well perforation rate at location xõ, y, Zk
for component i
and k is the grid block (cell) number. Again, the calculation of this term
from the specified
production rates at the well head is the subject of the present invention.
[0044] In addition to the differential equations in Equation (1), pore volume
constraint at any
point (element) in the reservoir must be satisfied:
14(P (x, y, z))= EnP -Nj (2)
where Vp is the grid block pore volume, P (x, y, z) is the fluid pressure at
point x, y, z, Aij is
the total number of moles in fluid phase j, pi is the density of fluid phase
j.
[0045] There are nc+ 1 equations in Equations (1) and (2), and nc+ 1 unknowns.
These
equations are solved simultaneously with thermodynamics phase constraints for
each
component i by Equation (3):
(niv; n2, ...nc, P, T) = fiL(niL; n2, ...nc, P, T) (3)
where f, is the component fugacity , superscript V stands for the vapor phase,
L stands for the
liquid phase, n, is the total number of moles of component i, P is the
pressure and T
represents the temperature.
[0046] In the fluid system in a reservoir typically there are three fluid
phases: oil phase, gas
phase and water phase. Each fluid phase may contain different amounts of
components
described above based on the reservoir pressure and temperature. The fluid
phases are
described by the symbol j. The symbol j has the maximum value 3 (oil, water
and gas
phases). The symbol np is the maximum number of phases (sometimes it could be
1 (oil); 2
(oil and gas or oil and water); or 3 (oil, water and gas)). The number of
phases np varies
based on reservoir pressure (P) and temperature (T). The symbol ni is the
number of moles
of component i in the fluid system. The symbol n, is the maximum number of
components
in the fluid system. The number of phases and fraction of each component in
each phase
no as well as the phase density pj and pi,j are determined from Equation (3).
In Equation
(3), V stands for the vapor (gas) phase and L stands for liquid phase (oil or
water).
-10-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[0047] Total number of moles in a fluid phase j is defined by:
= Eni-c 1 ni,J (4)
[0048] Total component moles are defined by Equation (5).
v,np
Li=i (5)
[0049] Phase mobility in Equation (1), the relation between the phases,
definition of fluid
potential and differentiation symbols are defined in Equations (6) through
(9).
= krj /pi (6)
[0050] In Equation (6), the numerator defines the phase relative permeability
and the
denominator is the phase viscosity.
[0051] The capillary pressure between the phases are defined by Equation (7)
with respect to
the phase pressures:
P (s , s .,) = P1 ¨ P
C(7)
[0052] The fluid potential for phase j is defined by:
(13 = P. ¨ gp .z
J (8)
[0053] Discrete differentiation operators in the x, y, and z directions are
defined by:
6 6 6 6
(9)
aX Y5 zSz St
where A defines the discrete difference symbol and U is any variable.
[0054] Equations (1), together with the constraints and definitions in
Equations (3) through
(9), are written for every grid block (cell) in a reservoir simulator using
control volume finite
difference method (some of the grid blocks may include wells). Resulting
equations are
solved simultaneously. This is done to find the distribution of n, (x, y, x,
and t), P (x, y, z,
and t) for the given well production rates qr for each well from which the
component rates in
Equation (1) are calculated according to the present invention using the new
well model
formulation. In order to solve Equations (1) and (2), reservoir boundaries in
(x, y, z) space,
rock property distribution K (x, y, z), rock porosity distribution and fluid
properties and
saturation dependent data is entered into simulation.
-11-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[0055] According to the present invention and as will be described below, a
reduced well
model system is formed which yields the same determination of a calculated
bottom hole
pressure as complex, computationally time consuming prior fully coupled well
models.
[0056] According to the present invention, it has been determined that for the
grid blocks
where the well trajectory is going through where a number of formation layers
communicate
vertically, the communicating layers can be combined for processing into a
single layer, as
indicated schematically in Figures 1 and 2 for the well model. This is done by
identifying the
vertical flow barriers in the reservoir for the well cells, and combining the
layers above and
below the various flow barriers of the well cells. Therefore, the full well
model system is
reduced to a smaller dimensional well model system with many fewer layers for
incorporation into a well model for processing.
[0057] As shown in Figure 1, a well model L represents in simplified schematic
form a
complex subsurface reservoir grid blocks (cells) where the well is going
through which is
composed of seven individual formation layers 10, each of which is in flow
communication
vertically with adjacent layers 10. The model L includes another group of ten
formation
layers around the well 12, each of which is in flow communication vertically
with adjacent
layers 12. The groups of formation layers 10 and 12 in flow communication with
other
similar adjacent layers in model L are separated as indicated in Figure 1 by a
fluid
impermeable barrier layer 14 which is a barrier to vertical fluid flow.
[0058] According to the present invention, the well model L is reduced for
processing
purposes to a reduced or simplified well model R (Figure 1A) by lumping
together or
combining, for the purposes of determining potential 0 and completion rates,
the layers 10 of
the well model L above the flow barrier 14 into a composite layer 10a in the
reduced model
R. Similarly, the layers 12 of the well model L below the flow barrier 14 are
combined into a
composite layer 12a in the reduced well model R.
[0059] Similarly, as indicated by Figure 2, a reservoir model L-1 is composed
of five upper
individual formation layers 20, each of which is in flow communication
vertically with
adjacent layers 20. The model L-1 includes another group of seven formation
layers 22, each
of which is in flow communication vertically with adjacent layers 22. The
groups of
formation layers 20 and 22 in flow communication with other similar adjacent
layers in
model L-1 are separated as indicated in Figure 2 by a fluid impermeable
barrier layer 24
which is a barrier to vertical fluid flow. Another group of nine formation
layers 25 in flow
-12-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
communication with each other are separated from the layers 22 below a fluid
barrier layer
26 which is a vertical fluid flow barrier as indicated in the model L-1. A
final lower group of
ten formation layers 27 in flow communication with each other are located
below a fluid flow
barrier layer 28 in the model L-1.
[0060] According to the present invention, the well model L-1 is reduced for
processing
purposes to a reduced or simplified model R-1 (Figure 2A) by lumping together
or
combining, for the purposes of determining well layer potential 0 and
completion rates, the
layers 20 of the model L-1 above the flow barrier 24 into a composite layer
20a in the
reduced model R. Similarly, other layers 22, 25, and 27 of the model L-1 below
flow barriers
24, 26 and 28 are combined into composite layers 22a, 25a, and 27a in the
reduced model R-
1.
[0061] The reduced well model systems or well models according to the present
invention
are solved for the reservoir unknowns and the well bottom hole pressure. Next,
the wells in
the full reservoir simulation model system are treated as specified bottom
hole well pressure
and solved implicitly for the reservoir unknowns. The diagonal elements of the
coefficient
matrix and the right hand side vector for the reservoir model are the only
components which
are modified in processing according to the present invention, and these are
only slightly
modified. A regular sparse solver technique or methodology is then used to
solve for the
reservoir unknowns. The perforation rates are computed by using the reservoir
unknowns
(pressures and saturations). These rates are then summed up to calculate the
total well rate.
The error between the determined total well rate according to the present
invention and the
input well rate will diminish with the simulator's non-linear Newton
iterations for every time
step.
[0062] The flow rates calculated according to the present invention also
converge with the
flow rates calculated by the fully coupled simultaneous solution for the
entire reservoir
simulation model including many wells. Because the present invention requires
solving a
small well system model, the computational cost is less. It has been found
that the
methodology of the present invention converges if the reduced well system is
constructed
properly, by using upscaling properly when combining communicating layers.
[0063] It is well known that simple vertical well models such as explicit or
semi-implicit
models have been generally adequate if all reservoir layers communicate
vertically. As
shown in Figure 3, an explicit well model E is composed of a number Nz of
reservoir layers
-13-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
30 in vertical flow communication, each layer having a permeability k (here i
represents
the layer number, not a component) and a thickness Azi and a perforation layer
rate q,
defined as indicated in Figure 3. The total production rate qT for the
explicit model E is then
the sum of the individual production rates q, for the Nz layers of the
explicit model as
indicated in Equation (3) in the same Figure.
[0064] For explicit models, the well production rate is allocated to the
perforations in
proportion to the layer productivity indices (or total mobility). Therefore,
the calculations are
simple. The resulting coefficient matrix for the unknowns remains unchanged,
i.e., maintains
a regular sparse structure, as shown in matrix format in Figure 12. Therefore,
any sparse
matrix solver can be used to solve the linear system for the grid block
pressures and
saturations for every time step.
Well Models
[0065] The methodology of several vertical well models of a reservoir
simulator is presented
based also for simplicity on a simple fluid system in the form of flow of a
slightly
compressible single phase oil flow inside the reservoir. However, it should be
understood
that the present invention general in applicability to reservoirs, and can be
used for any
number of wells and fluid phases in a regular reservoir simulation model.
[0066] Figure 6 illustrates the finite difference grid G used in this
description for a vertical
well model. As seen, a well is located at the center of the central cell in
vertical directions.
The models set forth below also contemplate that the well is completed in the
vertical Nz
directions, and the potentials in the adjacent cells:
CI3BW/ CDBE CI) B N CI) BS
are constants and known from the simulation run (previous time step or
iteration value). Here
subscript B refers to "Boundary", W indicates west neighbor, E stands for East
neighbor, and
N and S stand for north and south respectively. Again describes the fluid
potential (datum
corrected pressure).
[0067] As can be seen in Figure 6, the well is penetrating a number of
reservoir layers in the
vertical direction represented by the index /, for i =1, 2, 3... Nz, with Nz
is being the total
number of vertical layers in the reservoir model. For each layer i, there are
four neighboring
-14-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
cells at the same areal plane (x, y). These neighboring cells are in the East -
West (x
direction) and North - South (y direction).
[0068] The potential j of the East, West, North and South neighbors are known
from the
simulator time step calculations, and those potentials are set in that they
are assumed not to
change over the simulator time step. The vertical potential variations at the
well location are
then considered, but neighbor potentials which can vary in the vertical
direction but are
assumed to be known.
[0069] The steady state volume balance equation for the cell (i) in Figure 6
is as follows:
¨ (I),)+ TEi(
.43BE Tvi(OBN Tsi(OBs
Tup (CD i ¨ CD i) ((Di, ¨ cDoi )¨ qi =0. (10)
[0070] In Equation (10), T represents the transmissibility between the cells.
The subscripts
W, E, N, and S denote west, east, south and north directions, and (i)
represent the cell index.
[0071] The transmissibilities between cells for three directions are defined
by Equation (11)
below:
AyiAzi
Twi = k x ,i-11 2 (11)
.5(AXi_1 Ax)
A A
yi zi
= k ,
x,E+7 o.soxi+i +Axi)
AxiAzi
T = k 1I 2
0.5(Ayi + Ayi)
Ts,1 = k . 1 AxiAzi
Y,E+7 0.5(AYi+1 +AY i)
AxiAyi
T Up,i = k z,i-112
0.5(AZ Az)
AxiAyi
T = k
Down z,i+11 2 ,i
0.5(Az1 + Az)
[0072] In the above Equations (11), Axi is the grid block size (cell size) in
the x direction for
the grid block(cell) number i. Similarly, Ayi is the grid block size (cell
size) in the y direction
-15-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
for the grid block(cell) number I, and Az, is the grid block size (cell size)
or grid layer
thickness in the z direction for the grid block(cell) number i. ki_1/2 is the
vertical
permeability at the interface of the cells i and i-/. Similarly, ki+//2 is the
vertical
permeability at the interface of the cells i and i+/. As seen in Figure 6, the
cell i is at the
center, i + 1/2 interface between the cell i and i + 1. For convenience the
subscript j is
dropped while expressing East - West flow. Similarly (i, j - 1) is the north
neighbor of the
central cell (i, j). Therefore, the notation (i, j - 1/2) is the interface
between the central cell
and north neighbor in the y direction.
[0073] The same notation is carried out for the south neighbor: (i, j + 1/2)
denotes the
interface between the central cell (i, j) and south neighbor (i, j+1), in the
y direction. For
convenience in the above equations, subscript i is dropped while expressing y
(or j) direction.
As is evident, transmissibilities in Equation (11) are defined in a similar
manner.
[0074] In Figure 14, the diagonal terms are
defined by Equation (17a) below, and the
transmissibilities between cells for three directions are as defined in
Equations 11, as set forth
above.
[0075] The term -6 in the Figure 14 (right hand side) are expressed by
Equation (17b) in the
text. It is extracted here as follows:
= ¨ (P/Pw + Tw,i (Dnw + Tw,i (DBE + Tw,i (DBN + Tw,i OBS)
where i = 1, 2, ...Nz, with Nz again being the total number of grids in the
vertical directions,
the number of vertical layers. In this extraction of Equation (17b), PI, the
layer productivity
index is defined by Equation (17) and the OB potential terms are the known
boundary
potentials at boundaries of the neighbor cells to the west, east, north and
south of the central
cell. As is conventional, the terms, cell and grid block are used
interchangeably.
[0076] Conventional well models can be generally classified in three groups:
(a) the Explicit
Well Model; (b) the Bottom Hole Pressure Specified Well Model; and the Fully
Implicit Well
Model (Aziz K, Settari A, Petroleum Reservoir Simulation, Applied Science
Publishers Ltd,
London 1979). For a better understanding of the present invention, a brief
review of each
well model is presented.
Explicit Well Model
[0077] For an explicit well model, the source term qi in Equation (10) is
defined according to
Equation (12) by:
-16-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
k Az
a = _____
1=Nz qT
(12)
k Azi
where qi is the production rate for cell (grid block) i where the well is
going through and
perforated.
[0078] Substituting Equation (12) into Equation (10) for cell i results in
TUpi (13 i-1 + T + TDown ,1 i+1 = bi
.(13
c
(13)
where
T = ¨(T . +T . +T +T +T +T .)
Up,1 clomp WI Et NI SI (14a)
and
kxiAzi
=-:' __________________ qT ¨(TwNw +TEiCDBE +TNiC1313N +TSPBS) (14b)
/kxjAzi
[0079] Writing Equation (13) for all the cells i = 1, Nz around the well for
the well cells only
results in a linear system of equations with a tridiagonal coefficient matrix
of the type
illustrated in Figure 12, which can be written in matrix vector notation as
below:
A =b
RR R R (15)
[0080] In Equation (15), ARR is a (Nz x Nz) tridiagonal matrix, and OR and bR
are (Nz x 1)
vectors. Equation (15) is solved by computer processing for the reservoir
unknown potentials
OR grid blocks where well is going through by a tridiagonal linear system
solver such as the
Thomas algorithm.
Tridiagonal Matrices and Systems
[0081] Tridiagonal Matrices are the matrices with only three diagonals in the
middle, with
real or complex number as the entries in the diagonals. These diagonals are
called "lower
diagonal", "central diagonal" and "upper diagonal". The remaining elements or
entries of a
tridiagonal matrix are zeros. For example, Figure 17 illustrates a tridiagonal
matrix A of 8x8
-17-

CA 03015833 2018-08-24
WO 2017/151844 PCT/US2017/020327
matrix dimensions (or order n=8 ). In the Figure 17, elements of A ; the ith
element of A,
namely al, a2, a3, ai, i = 1, 8, represents the lower diagonal; b1, b2, b3,
bi, the central
diagonal; and c1, c2, c3, ci, the upper diagonal elements.
[0082] An example tridiagonal system of equations is illustrated in Figure 18.
Solution of a
linear system of equations with a Tridiagonal Matrix such as defined above and
shown in
Figure 18 is easily solved by Gaussian elimination. An example of a solution
of equations in
this manner is contained at:
https://en.wikipedia.org/wild/Tridiagonal_matrix_algorithm.
[0083] Thus the solution for xi as shown below and in Figure 18 performed by
solving the
matrix relationships of Equations (16a) through (16e) as follows:
,......., lit
4 (4
4
' 141 ¨ esitt-i (16a)
; ¨ Ae t abci÷ X IQ n (16b)
da
4 . 4 1
b,,......m.
_______________________ ., ., I .... 2, ap ,3 Q4 ZI IL
= ¨1 (16c)
Zs = 41 (16d)
,r
(16e)
Bottomhole Pressure Specified Well Model
[0084] (1) is the uniform potential along the wellbore open to production
using
conventional techniques according to techniques explained in the literature,
such as the
textbooks by Muskat "Physical Principles of Oil Production", McGraw-Hill Book
Co. (1949)
and "The Flow of Homogeneous Fluids Through Porous Media", McGraw-Hill Book
Co.
(1937). For the purposes of modeling in the present context, the friction
pressure drop along
the well is considered negligible. Assuming that (:13 ,,,, is known (or
specified), the oil rate
from the perforation is calculated by Equation (17) as follows:
-18-

CA 03015833 2018-08-24
WO 2017/151844 PCT/US2017/020327
qi=Pli ((1) ¨(1)w)
211-kõ,jAzi (17)
___________________________ (0i ¨Ow)
ln(ro,i /c)
where PI is the layer productivity index, c13w is the specified bottom hole
potential( datum
corrected pressure), <Di is the reservoir grid block pressure where well is
going through for
grid block(cell) i, ro,i is called Peaceman's well block radius for grid block
i defined as
0.2Ax , c is the radius of the well.
[0085] The variables in Equation (17) are explained in the Nomenclature
section above.
Substituting Equation (17) into Equation (10) and collecting the terms for the
cell i, for cell i
the following result occurs:
TUpiC13 i-1 T .c1) + TDown ,i(131 i+1W = b (18)
c ,
[0086] Let
T ci = ¨(Tumi + TdOWfl Twi T Ei +TNi + +Tsi + PIE)
(18a)
b = ¨ (PI jct. w + Twict. Bw T Ei 443 BE TNi (13 BN TSic') BS)
(18b)
[0087] Equation (18) when written for all the grid blocks i = 1, Nz results in
a matrix system
illustrated in Figure 14. The matrix of Figure 14 for the bottom hole pressure
specified well
model can be seen to be similar to the matrix of Figure 12, and in a
comparable manner
Equation (18) is similar to Equation (13). The bottom hole pressure specified
well model can
be easily solved by matrix computer processing with a tridiagonal equation
solver
methodology.
Fully Implicit Well Model
[0088] Total production rate qT for a well according to a fully implicit well
model is specified
according to Equation (19).
i=vz
=0.0
i=i (19)
-19-

CA 03015833 2018-08-24
WO 2017/151844 PCT/US2017/020327
[0089] The individual completion rate qi is calculated by Equation (17). For
the implicit well
model, the wellbore potential 0, is assumed constant throughout the well but
it is unknown.
[0090] Substituting Equation (19) into Equation (10) and collecting the terms
for the cell i for
cell (i) arrives at the following expression:
T cl) + T cl) + TDown ,icI) i+1W P1 ic13 w
= b (20)
Upi i ¨1 C i
[0091] Let
=¨(Tumi +Tdown,i +Twi + TEi +TNi+131i)
(20A)
b = - (Twi (13 Bw BE TNiC1) BN TSiC1) BS) (20B)
[0092] Writing Equation (20) for all cells yields a linear system of equations
with the form
illustrated in Figure 13 upper diagonal solid line represents Tuo as defined
by Equation (11),
and the lower diagonal solid line describes the elements called TDown,i
described in Equation
(11). The central term Tu,) is defined by Equation (20A) and right hand side
bi is defined by
Equation (20B).
[0093] The linear system of the matrix (Equation 20) of Figure 13 can be
represented in
vector matrix notation as below:
ARR ARW CI) b R
A wR A w w 4:13 =
_ _ w _
_ w _ (21)
[0094] In Equation (21), ARR is a (Nz x Nz) tridiagonal matrix, A Rw is a (Nz
x 1) vector
(reservoir PI' s), AwR is a (1 x Nz) vector ( PI' s) and A is (1x1) scalar.
For this example:
Aww = PINZ
i=1
[0095] Writing in algebraic form:
A RR CI) + A Rw W = b R
(22)
A wRR + A ci =b
W w (23)
-20-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[0096] Solving for 0, from Eq 22 results in:
CI) = (b ¨ A 0 )
wR R (24)
[0097] Substituting into Equations (21)
A 0 + A (A-1. (b ¨ A 0 )) = b
RR R Rw wR R (25)
[0098] Collecting the terms in Equation (25) produces:
(A ¨A 'A A A) =b ¨A A 'b.
RR ww wR RW R R Rw ww w (26)
[0099] The coefficient matrix (ARR - 1A,R ARõ
) of Equation (26) is an (Nz x Nz) full
matrix.
[00100] The resulting coefficient matrix can be defined as follows:
A = ARR Aww-1 AvvRARw
(27)
and
-1
b = bR - AR,vA,v,v
bW
[00101] Then Equation (26) can be written as:
AR _/2R (28)
[00102] The matrix of Equation (28) can be solved by a direct solver by
Gaussian
elimination or any other suitable conventional solver for the full matrices.
[00103] If in the implicit well model the number of layers Nz is large, and
wells are fully
completed in all the layers, then the solution of Equation (28) becomes
expensive in
computation time. For this reason and also if many wells are involved,
generally Equation
(28) is solved by iterative methods. An example of this is described in "A
Fully-Implicit
Fully-Coupled Well Model for Parallel Mega-Cell Reservoir Simulation", SPE
Technical
Symposium of Saudi Arabia Section, 14-16 May 2005.
[00104] A flow chart I (Figure 10) indicates the basic computer processing
sequence of
fully implicit, fully coupled well model simultaneous solution for the type of
matrix
-21-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
illustrated in Figure 13. During a step 100, simulation begins by reading the
reservoir and
production data. Reservoir data includes reservoir geometric information-its
size, extent
(length) in x, y, and z directions, reservoir properties such as permeability
distribution,
porosity distribution, thickness of layers, relative permeability data,
capillary pressure data,
fluid property data such as fluid density tables, formation volume factor
tables, viscosity
tables, location of wells, location of well perforations within the reservoir.
[00105] Production data includes oil, water, and gas production rate measured
or specified
for the wells defined in the previous step. Production data also includes
minimum
bottomhole pressure for each well.
[00106] In many instances, only oil production rates and water production
rates are input if
the gas production data is not available. If no water is produced in the
field, only oil
production rates are read as input.
[00107] During step 102 the time step is incremented by one, and an iteration
counter of the
number of non-linear iterations performed during the present time step is set
to zero. During
step 104, a Jacobian matrix of reservoir data is formed. In step 106, the
resultant linear
system of Equation (19) is then solved by iterative methods using sparse
preconditioners
(Yousef Saad, Iterative Methods for Sparse Linear Systems, Society of
Industrial & Applied
Mathematics (SIAM) Publication, 2003).
[00108] During step 108, a convergence step is performed to determine whether
the non-
linear iterations have converged. The individual residuals of the equations
resulting from
step 106 are checked against user-specified tolerances. If these tolerances
are satisfied, the
non-linear iteration loop is exited, the solution output is written to file
for the current time
step and processing returns to step 102 for the time step to be advanced, and
processing for
the incremented time step then proceeds as indicated. If the user-specified
tolerances are
determined not satisfied during step 108, processing according to the non-
linear iteration loop
returns to step 104 and continues. If the number on non-linear iterations
becomes too large, a
decision may be made to reduce the time step size and go back to step 102.
[00109] However, based on the strength of the preconditioning, this method can
also be
very expensive in computation time, since there is no exact way of
representing the full
matrix in Equation (19). For difficult problems, with extreme heterogeneity
and small layer
thicknesses, the iterative method may not converge.
-22-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00110] Additionally, for highly heterogeneous reservoirs with some vertically
non-
communicating layers, the above described well models do not produce the
correct physical
solution. Instead, they can produce incorrect flow profiles, and in some
occasions they can
cause simulator convergence problems.
The Present Invention
[00111] Explicit and fully implicit models can produce totally different flow
profiles in
case of some vertical flow barriers. This is displayed in Figure 5. As shown
in Figure 5, a
reservoir model V is composed of an upper layer 50 of relatively low
permeability, and with
vertical flow, located above an isolated high permeability layer 52 with no
vertical flow
communication with adjacent layers. The flow barrier layer 52 is located in
the reservoir V
above a layer 54 of medium permeability and having vertical flow
communication. As can
be seen in Figure 5, the production rates qT for the well model V are the same
for both
implicit and explicit well modeling methods.
[00112] However, the production rates ql, q2, and q3 of layers 50, 52 and 54
differ
significantly. The production rate q2 for the layer 52 is the major
contribution to the total
production rate qT as shown by curve 56 for the explicit model. On the
contrary, for the
implicit model as shown by curve 58, production rate q2 for the layer 52 is
markedly less.
[00113] In the fully implicit well model, the production rate for the layer 2
is significantly
less due to the fact that this method takes into account internal reservoir
heterogeneity (all the
reservoir properties throughout the reservoir) and heterogeneity around the
well blocks in
addition to the perforation index (or layer 2 property alone as is used by the
explicit method
as the only data to assign the rate fraction to this perforation). For
example, the fully implicit
well method sees that there is no fluid supplied into layer 2 from layer 1 and
layer 3 due to
the impermeable barrier between layer 2 and layer 1 and 3. Therefore, once
some fluid is
produced from well model layer 2, the pressure of layer 2 should go down and
this layer
should not supply at a high rate into the well, although the layer has very
high permeability.
[00114] On the other hand, the explicit method assigns the rate for layer 2
based on the
permeability of this layer alone without considering the layer connection to
the above and
below layers. Based on this, the explicit method will assign a very high rate
for this layer and
will keep it for the next simulation time step. In later simulation time
steps, this will cause
instability in the production rates, i.e., the simulator will reduce the time
step size and will
take a very long time to complete the simulation. It is unsatisfactory for
reservoir simulation
-23-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
to have models provide divergent results for the same input data based on the
modeling
technique selected for use.
[00115] According to the present invention, a more comprehensive well model is
provided.
The well model according to the present invention is called a coupled
reservoir well model.
The associated numerical solution is referred to fully implicit, fully coupled
and simultaneous
solution. A fully implicit fully coupled reservoir well model produces correct
flow profile
along the perforated well interval, as will be described. As shown in Figure 4
a reservoir
model 0 is composed of a number z of i individual layers 1 through Nz, each
with a
permeability and a
thickness Az, and a potential 01), defined as indicated in Figure 4, and
upper and lower layers 40 of relatively low permeability, and with vertical
flow, located
above and below, respectively, an isolated high permeability layer 42 with no
vertical flow
communication with adjacent layers. As can be seen in Figure 4, the production
rates q, for
layer i of the model 0 is an indicated by the expression set forth in Figure
4.
[00116] The fully implicit coupled reservoir well model V of Figure 5 is
presented in
Equation (20) above and is also presented here in matrix format for further
description:
- ARR ARw PR b
(21)
AwR 47,õ
Pw
[00117] The present invention is based on the fact that the bottom hole
pressure of a
layered reservoir with a vertical well is the same as a system according to
the present
invention. The system according to the present invention is formed by
identifying flow
barriers and lumping together or combining for processing purposes the
reservoir layers
around the well which are communicating in the vertical direction. Care should
be taken
according to the present invention in the formation of the reduced system. The
reduced
system must be formed correctly, or otherwise errors in the reduced system
construction can
increase the total number of nonlinear Newton iterations.
[00118] The system according to the present invention is solved for the bottom
hole
pressure. The solution is carried out by treating the well as specified bottom
hole pressure
well. The procedure is fully implicit; however, it is not a simultaneous
solution. Instead, the
solution is sequential. The method of the present invention is convergent
since it is part of
the global Newton iteration of the simulator. Therefore, if the model
according to the present
-24-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
invention is constructed correctly, any possible error in rate calculations
will be small and
will diminish with the simulator Newtonian iterations.
[00119] A flow chart F (Figure 11) illustrates the basic computer processing
sequence
according to the present invention and the computational methodology taking
place during a
typical embodiment of a sequential fully implicit well model for reservoir
simulation with the
present invention.
[00120] During a step 200, simulation begins by reading the reservoir and
production data.
Reservoir and production data read in during step 200 are of the types
discussed above. The
reservoir simulator is also initialized during step 200, setting the
simulation day and the time
step to zero. During step 202 the time step is incremented by one, and an
iteration counter of
the number of non-linear iterations performed during the present time step is
set to zero.
[00121] During step 204, a Jacobian matrix of reservoir data is formed. In
step 206, a
reduced system like that defined by the model R described above is formed
according to the
present invention and the matrix solved for bottom hole potential Ow in the
manner described
above. During step 208, the modified linear system matrix A is solved
according to the
present invention in the manner set forth above.
[00122] Figure 15 illustrates the methodology of forming the reduced well
model system
matrix R and solving for bottom hole potential 01:0, according to steps 204
and 206 of Figure
11. As indicated at step 210, vertical flow barriers in the original well
model system are
identified. This can be done based on well log data or by specification by a
reservoir analyst
from data in the original reservoir model.
[00123] After steps 210, a reduced well model system model is then formed by
the data
processing system D during a step 212. Those layers in the well model which
are located
between flow barrier layers and have vertical flow are combined together for
analytical
model purposes.
[00124] Next, during step 214, the resulting reduced well model system is
solved by
computer processing for bottom hole potential Ow and reservoir unknowns using
the
techniques discussed of Equations (17), (17a) and (17b). Step 216 then solves
with the data
processing system D the full well model system structural matrix of Equation
(27) using a
direct solver or other suitable technique described above. Completion rates q,
and total well
-25-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
flow rate qT are then determined with the data processing system D based on
the results of
step 216.
[00125] Referring again to Figure 11, during step 220, a convergence step is
performed to
determine whether the non-linear iterations have converged. The individual
residuals of the
equations resulting from step 216 are checked against user-specified
tolerances. If these
tolerances are satisfied, the non-linear iteration loop is exited, the
solution output is written to
file for the current time step and processing returns to step 202 for the time
step to be
advanced, and processing for the incremented time step the proceeds as
indicated. If the
user-specified tolerances are determined not satisfied during step 208,
processing according
to the non-linear iteration loop returns to step 204 and continues. If the
number on non-linear
iterations becomes too large, a decision may be made to adjust the model.
Horizontal Wells
[00126] Figure 19 displays a horizontal well 300 oriented in y direction
located in a three
dimensional reservoir model H. The model H of Figure 19 is like Figure 6, a
finite difference
grid, but of horizontal well 300. The well 300 is located in the center of a
central cell in each
of a succession of subsurface formation segments 304 in the y-direction
extending in vertical
plans or in the z-direction. Figures 24A and 24B illustrate notations for grid
cells in the
horizontal wall model H of figure 19. As seen in Figure 19, the well 300 is
completed in the
horizontal or y-direction through Ny cells, and the potentials in the adjacent
cells:
BE, (I)B Down, (I)B w
are constants and known from the simulation run (previous time step or
iteration value). The
subscript B refers to boundary, Up indicates above neighbor, E indicates east
neighbor, down
indicates below neighbor, and W indicates west neighbor, with (I) again
describing the fluid
potential or datum corrected pressure. In Figure 19, the well 300 extends
horizontally along a
longitudinal axis through each of a succession of grid blocks 302 in the y
direction. If a
known total well rate, (IT is input into a reservoir simulator, the reservoir
simulator calculates
for each time step the potential values (I) for each grid block 302 shown in
Figure 19.
[00127] As will be set forth, the present invention improves computer
performance as a
reservoir simulator in forming measures of perforation rate qi for the layers
which adds up
to known total rate qT
-26-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00128] Similar to Equation (16), perforation rate q, for each grid block can
be expressed
as:
q,=P1,(43,-(13,,,) (29)
[00129] In Equation (29), the productivity index is governed by
22-1- k Ay
PI = ZY (30)
I r)
Ny
= 11=1 ql
k = \lk k
zy z y
k
... 4.. I\,
'
k.
r 028 ________________________________________
0., k =
),.
s-
k.
(31)
[00130] The above expression of reservoir parameters and their physical
relationships is
according to Chen and Zhang, "Well Flow Models for Various Numerical Methods".
International Journal of Numerical Analysis and Modeling, Vol 6, No 3, pages
378-388.
[00131] Figures 21 and 22 collectively represent a flow chart G which
illustrates the basic
computer processing sequence according to the present invention and the
computational
methodology taking place during a typical embodiment of a sequential fully
implicit well
model for horizontal well models, such as shown in Figure 19 for reservoir
simulation with
the present invention. During a step 400, simulation begins by initializing
the reservoir
model H in the data processing system D and reading the reservoir and
production data. The
reservoir and production data read in during step 400 are of the types
discussed above for
vertical well models in connection with the flow chart F and step 200 (Figure
11).
[00132] During step 400 an estimate of cell potentials Ok is formed for the k
cells of the
horizontal well model H. As indicated schematically in Figure 19, k =
nx*ny*nz. During
step 402, an estimate of well bore potential is formed according to Equation
(32) as set forth
below:
-27-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
PI (13
cl) = PI q t
(32)
PI
where (Di in Equation (32) is calculated from the initial potential
distribution determined in
step 400.
[00133] During step 404, perforation rates qi are determined for each cell /
according to
the relationship expressed in Equation (29) above. In step 406, the reservoir
simulator is
initialized and the simulator iteration countery set to zero. The simulation
time step t is also
initialized to zero for an initial iteration. The iteration counter and the
time step counter are
thereafter incremented, as will be set forth below, before performing step 406
during
subsequent iterations. The grid block potential for the initial time step is
determined during
step 406 by solving a three dimensional potential equation with the reservoir
simulator
according to Equation (1) for a single phase oil flow. During step 408
boundary potentials
are determined around each perforation OBw, B,Up, (I) BE, (1) B,Down for each
perforation (i),
for i=1,2, Ny and stored in memory of the data processing system D.
[00134] Step 410 is then performed to form a reduced well model H-1 (Figure
20B) by
lumping the grid blocks 302 with no flow barriers among them as shown at 306
in Figure
20A. For performing step 410, horizontal flow barriers such as shown at 303 in
the original
horizontal well model system H are identified. This can be done based on well
log data or by
specification by a reservoir analyst from data in the original reservoir
model. The reduced
well model system model forming during step 410 results in those layers 302 in
the well
model H which are located between flow barrier grid blocks or layers 303 and
have
horizontal flow between them being combined together for analytical model
purposes.
[00135] As can be seen in the example of Figures 20A and 20B, the horizontal
well model
H of Figure 20A with two groups of four grid blocks 302 on opposite sides of a
flow barrier
grid block 303 is transformed to reduced well model H-1 as a result of step
410, the reduced
well model H-1 having two grid blocks 308, one on each side of flow barrier
block 303.
[00136] The reduced well model equations for the reduced well model system H-1
in
Figure 20B thus as shown in Figure 20C becomes:
-28-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
(T TEl P/1
cl
Tw2 Tc2 TE2 P12 4:1)2 0
= (18)
0 Tw3 Tc3 1313 4:133 0
\PI1 PI2 PI3 ¨ 'T) 4:13147) \qt)
where NT = 13 PI .
¨1
[00137] Then, during step 410 (Figure 22) the reduced well model is solved for
ail, &12,
J)3, and (I) w, where 45 represents the grid block potential of the reduced
horizontal well
model H-1.
[00138] During step 412, the horizontal well model is converted to a fixed
flowing bottom
hole potential well using (I) w. Step 414 involves solving the three diagonal
matrix system of
Figure 20C for the reduced horizontal well model H-1 shown in Figure 20B to
determine the
potentials for each grid 302 shown in Figure 19.
[00139] Referring again to Figure 22, during step 416, a convergence step is
performed to
determine whether the non-linear iterations have converged. The individual
residuals of the
equations resulting from step 414 are checked against user-specified
tolerances. If these
tolerances are satisfied, the non-linear iteration loop is exited, the
solution output is written to
file and stored in memory of the data processing system D for the current time
step and
processing returns to step 418 for the time step t to be advanced, and
processing for the
incremented time step the proceeds to step 406 as indicated . If the user-
specified tolerances
are determined not satisfied during step 416, processing according to the non-
linear iteration
loop returns to step 406 and continues. If the number on non-linear iterations
becomes too
large, a decision may be made to adjust the model.
Multiple Vertical Wells
[00140] A 3 dimensional reservoir model M is shown in Figure 23 with multiple
vertical
wells 500, each with assumed single phase, slightly compressible oil flow. The
model M is
organized according to the nomenclature in the notations schematically
illustrated in Figures
25A, 25B, 25C and 25D.
[00141] The model M of Figure 23 is, like Figures 6 and, a finite difference
grid, but of a
number of vertical wells 500. The wells 500 are each located in the center of
a central cell in
-29-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
each of a succession of subsurface formation segments 504 in the z-direction
extending in
horizontally or in the y- and z-directions.
[00142] As in Figure 6, each well 500 is completed in the vertical or z-
direction through Nz
cells, and the potentials in the adjacent cells:
OBN, OBE,OBs,OBw
are constants and known from the simulation run (previous time step or
iteration value). As
in Figure 6, the subscript B refers to boundary, N indicates above neighbor, E
indicates east
neighbor, down indicates below neighbor, and W indicates west neighbor, with 0
again
describing the fluid potential or datum corrected pressure.
[00143] Each well 500 extends vertically along a longitudinal axis through
each of a
succession of grid blocks 502 in the z direction, and at certain formation
layers at various
depths each well 500 is intersected by completions 506. Figures 25A through
25D illustrate
schematically the numbering notations in the model M for wells 50 designated
Well 1 and
Well 2 in Figure 23.
[00144] If a known total well rate, qT, for each well 500 is provided as an
input parameter
into a reservoir simulator, the reservoir simulator calculates for each time
step the potential
values 0 for each grid block 502 shown in Figure 23.
[00145] For a generalized case of 3-dimensional vertical reservoir model M,
the number of
the wells is represented by nw, and the total well rates for each well 500 are
given and
denoted by q7(1), 1 = 1, nw are known from production data and provided as
input parameters
into the reservoir simulator.
[00146] Figure 26 represent a flow chart for processing according to the
present invention
where multiple vertical wells are present, as is the case in the model M of
Figure 23. Thus
for the 3-dimensional vertical reservoir model M, in step 602, the reservoir
simulator is
initialized and reservoir and production are read from memory for processing.
This is done in
a comparable manner to step 200 if Figure 11. Simulation processing continues
in 602 shown
in Figure 26, where an estimate of the well bore potential 0w (1),1 = 1, 2,
... nw is formed
for each well according to Equation (32), with the productivity index PI being
determined
according to the measures expressed in Equation (17). During step 604, the
perforation rates
qi (0,1 = 1, ...nw are computed for each well, based on the estimates of well
bore
potentials resulting from step 602.
-30-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00147] Step 606 involves forming of reduced well models for each well 1 = 1,
2, ... nw
for the 3-dimensional multiple well model M. The reservoir simulation is
performed by
combining or merging adjacent well cells 502 of the formation layers which
have fluid
communication between each other and are also located between flow barrier
layers which
have no flow through them. This is done in a manner for layers of a 3-
dimensional in a
manner such as that shown schematically in Figures 1A and 1B for layers
adjacent a single
vertical low well, and in Figures 20A and 20B for layers adjacent horizontal
flow wells.
[00148] In step 608, reduced well matrices are formed for each well based on
the reduced
well models form step 606, in a comparable manner to the reduced well matrix
of Figure 20C
for the horizontal well model H of Figure 19.
[00149] Then, in step 610, bottom hole potential Ow (I), 1 = 1, 2, ... nw is
determined for
each well by solving the reduced well matrices resulting from step 608. In
step 612, the
diagonal To and right hand side bi term of the main matrix for each well is
modified
according to the relationships according to Equations 18, 18A and 18B above.
Figure 27 is
an example schematic diagram of a reduced well matrix of a linear system of
equations for a
simplified two well, three-dimensional reservoir model, or 3 x 3 x 2 reservoir
model using the
numbering system explained in Figures 24A and 24B and Figures 25A through 25D.
[00150] During step 614, a total matrix, such as the example of Figure 27, is
formed for all
the grid blocks 502 for the unknowns of the model M. Processing then after
step 614 of
Figure 26 proceeds to convergence testing in the manner of step 416 of Figure
27 and
iteration and time step incrementing with return to step 602 for further
processing iterations
for the total system including each of the n, wells.
Data Processing System
[00151] As illustrated in Figure 16, a data processing system D according to
the present
invention includes a computer 240 having a processor 242 and memory 244
coupled to the
processor 242 to store operating instructions, control information and
database records
therein. The computer 240 may, if desired, be a portable digital processor,
such as a personal
computer in the form of a laptop computer, notebook computer or other suitable
programmed
or programmable digital data processing apparatus, such as a desktop computer.
It should
also be understood that the computer 240 may be a multi-core processor with
nodes such as
those from Intel Corporation or Advanced Micro Devices (AMD), or a mainframe
computer
-31-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
of any conventional type of suitable processing capacity such as those
available from
International Business Machines (IBM) of Armonk, N.Y. or other source.
[00152] The computer 240 has a user interface 246 and an output display 248
for
displaying output data or records of processing of well logging data
measurements performed
according to the present invention to obtain measurements and form models of
determined
well production of formation layers in a well or wells of subsurface
formations. The output
display 48 includes components such as a printer and an output display screen
capable of
providing printed output information or visible displays in the form of
graphs, data sheets,
graphical images, data plots and the like as output records or images.
[00153] The user interface 246 of computer 240 also includes a suitable user
input device
or input/output control unit 250 to provide a user access to control or access
information and
database records and operate the computer 240. Data processing system D
further includes a
database 252 stored in computer memory, which may be internal memory 244, or
an external,
networked, or non-networked memory as indicated at 254 in an associated
database server
256.
[00154] The data processing system D includes program code 260 stored in non-
transitory
memories 244 of the computer 240. The program code 260, according to the
present
invention is in the form of computer operable instructions causing the data
processor 242 to
form a sequential fully implicit well model for reservoir simulation according
to the present
invention in the manner that has been set forth.
[00155] It should be noted that program code 260 may be in the form of
microcode,
programs, routines, or symbolic computer operable languages that provide a
specific set of
ordered operations that control the functioning of the data processing system
D and direct its
operation. The instructions of program code 260 may be stored in memory 244 of
the
computer 240, or on computer diskette, magnetic tape, conventional hard disk
drive,
electronic read-only memory, optical storage device, or other appropriate data
storage device
having a computer usable non-transitory medium stored thereon. Program code
260 may also
be contained on a data storage device such as server 64 as a non-transitory
computer readable
medium, as shown.
[00156] Two illustrative example model problems are presented below: a seven
layer
homogeneous reservoir with one fracture flow barrier (Figure 7); and a twenty-
two layer
heterogeneous reservoir with two fracture flow barriers (Figure 9).
-32-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
Seven Layer Homogeneous Well Model
[00157] Figure 7A illustrates the seven reservoir layers and properties for
the original
model 70 and reduced model 71. As seen, it was assumed that reservoir has
seven layers.
Layer thickness of each layer 72 with vertical flow is 10 ft. A layer 73 which
represents a
fracture with no vertical flow is present which is 1 ft. thick. It was further
assumed that the
layer 73 does not communicate with the layers 72 above and below. It was
assumed that
there is a vertical well in the middle, as indicated by an arrow. Initial
reservoir potential
(datum corrected pressure) is 3,000 psi for the model of Figure 7A. Each layer
72 was
assumed to have 10md areal permeability kx and ky and lmd vertical
permeability kz.
[00158] Table 1 summarizes the reservoir and grid properties for the model 70.
The grid
size in the area direction (square grid) was assumed to be 840 ft. Oil
viscosity was set to 1 cp
and Oil Formation Volume factor was assumed to be 1. Well Total Oil Production
rate was
set to 1,000B/D. A Layer Productivity Index PI for each layer completion was
calculated by
Peaceman's method, as described, and is also shown in Table 1.
Table 1: Problem 1 - Reservoir Properties
Layer Thickness, ft Kx=Ky, md Kõ md Layer, PI
b/d/psi
1 10. 10. 1 0.12
2 10. 10. 1 0.12
3 1 10,000 1.e-9 12.14
4 10 10 1 0.12
10 10 1 0.12
6 10 10 1 0.12
7 10 10 1 0.12
Fully Implicit Fully Coupled Simultaneous Solution
[00159] The coefficient matrix for the solution of reservoir pressures and the
bottom hole
pressure is formed in a similar manner explained above with regard to
Equations (18-19) and
as shown in Figure 13. It can be seen that there are only 8 unknowns (7
potentials or datum
-33-

CA 03015833 2018-08-24
WO 2017/151844 PCT/US2017/020327
corrected pressures) and the one bottom hole potential), and that the
coefficient matrix is non-
sparse. The linear system of equations can be solved by a direct method, such
as Gaussian
Elimination, for the unknown reservoir (layer) potentials (13, , i = 1,7 and
the other unknown
Results
[00160] Table 2 summarizes the calculated layer potentials, wellbore potential
and layer
(completion) flow rates for the model 70 of Figure 7A.
Table 2¨ Exact Solution of the Original Problem
Layer Potential, psi Bottom hole (Wellbore) Rate/d
Potential, psi
1 2630.61 1257.36 166.67
2 2630.61 1257.36 166.67
3 1257.37 1257.36 0.0
4 2630.61 1257.36 166.67
2630.61 1257.36 166.67
6 2630.61 1257.36 166.67
7 2630.61 1257.36
[00161] From the computed results we see that computed bottom hole potential
= 1257.36 psi.
Formation of the Problem According to The Present Invention
[00162] According to the reservoir data in Table 1 and as shown in Figure 7A,
there is only
one layer 73 which does not communicate vertically with the other layers.
Therefore, as
shown in Figure 7B, the layers 72 above the fracture layer 73 are combined
into a single layer
according to form the reduced well model in accordance with the present
invention.
Similarly layers 72 below layer 73 are combined into a single layer. The
reduced model now
can be seen to have only three layers. The total number of the unknowns is 4
as opposed to 8
as in the full model.
-34-

CA 03015833 2018-08-24
WO 2017/151844 PCT/US2017/020327
[00163] Table 3 summarizes the properties of reduced well model 71 formed
according to
processing with the present invention.
Table 3 - Reduced Well Model
Layer Thickness, ft Kx=Ky, md Kõ md PI, b/d/psi
1 20 10 1 0.24
2 1 10,000 0 12.14
3 40 10 1 0.40
[00164] The linear system of equations (Equation 20) for the reduced system
still has an
unstructured coefficient matrix, but with a 50% less number of unknowns. In
actual
reservoirs, with hundreds of layers and only a few flow barriers, the well
model size
reduction according to the present invention would be drastic, for example, a
reduced well
model system model according to the present invention could be 1 percent of
size of the full
system. The reduced system is solved by a direct solver for the layer
potentials and the
bottom hole potential. Table 4 presents the results.
Table 4 - Results of the Reduced System
Layer Potential, psi Bottom hole (Wellbore)
Potential, psi
1 2630.61 1257.36
2 1257.37 1257.36
3 2630.61 1257.36
[00165] It can be seen that computed bottom hole potential:
0,7=1257.36 psi
is exactly the same as the 0,7 calculated for the full model.
-35-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00166] The determined well potential is the only information needed for the
next step.
The well is next treated as a specified bottom hole pressure (potential)
model. Computer
processing according to the procedure described with the matrix of Figure 14
and Equations
(16 and 18) are followed to calculate the flow profile (layer rates) and the
total well rate. In
Figure 14, upper diagonal solid line of the matrix represents Tup,, as defined
by Equation (11),
and the lower diagonal solid line of the matrix describes the elements called
T
- Down,i as also
defined by Equation (2). The central term Tc,i is defined by Equation (17a)
and the right
hand side hi defined by Equation (17b).
[00167] The results are summarized in Table 5. It is to be noted that total
calculated well
rate is exactly the same as input value of 1,000b/d.
Table 5 - Results for the Total System with the Present Invention
Layer Potential, psi Rate/d
1 2630.61 166.67
2 2630.61 166.67
3 1257.37 0.0
4 2630.61 166.67
2630.61 166.67
6 2630.61 166.67
7 2630.61 166.67
Total 1,000.
[00168] Results presented in Table 5 are the same as in Table 1 for the fully
implicit well
model. Difference or error between well rates for the calculated and input
well is zero for
this case and there no need for an extra iteration. This is because of the
fact that the reservoir
was homogeneous and no upscaling errors were made while forming the reduced
system.
Matrix diagonal elements and right hand side are the same as in Figure 14,
i.e., lower
diagonal solid line represents Tuip,, defined by Equation (11), upper diagonal
solid line
describes the elements called TDow" described above. The central term Tc,,
defined by
Equation (17a) and right hand side bi defined by Equation (17b).
-36-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00169] The terms PI appear on Equation (17) are the perforation productivity
indexes for a
square grid is defined by:
Az,
PI =2,71-kx,
1n(0.2Ax / rw)
where r, is the well bore radius.
Comparison with the Explicit Well Model
[00170] In several reservoir simulators, semi implicit well models or explicit
well models
are used. If the formulation of the well model is semi-implicit but it
collapses to explicit in
the pressure variable, this formulation collapses to explicit well models. The
explicit well
model is for this problem obtained by following the computer processing
procedures for the
matrix of Figure 12 and Equations (12-14). In Figure 12, the terms TD0 Tumi
which
appear on the diagonal elements are defined by Equation (11), and Tc,õ bl are
defined by
Equation (14a) and Equation (14b). Figure 8A illustrates the seven reservoir
layers and
properties for an implicit well model 80 and Figure 8B an explicit well model
81, of like
structure to the model of Figures 7A and 7B. As seen it was assumed that
reservoir has seven
layers. Layers 82 each have a potential 0 of 2630 psi. A layer 83 which
represents a fracture
and was further assumed that does not communicate with the layers 72 above and
below has a
potential 0 of 1257 psi. It was assumed that there is a vertical well in the
middle, as
indicated by an arrow. Figure 8A and 8B compare the results of Implicit and
Explicit
Models. Computed perforation (layer) rates are summarized in Table 6.
Table 6 - Comparison of Perforation (Layer) Rates for Different Well Models
Layer Exact Solution New Method Explicit Method
/Perforation (Fully Implicit Fully Coupled Rate, b/d Rate,
b/d
Simultaneous Solution ), Rate
b/d
1 166.67 166.67 9.43
2 166.67 166.67 9.73
3 0.0 0.0 943.40
4 166.67 166.67 9.43
-37-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
166.67 166.67 9.43
6 166.67 166.67 9.43
7 166.67 166.67 9.43
[00171] As can be seen, the model 81 according to the explicit method is
inaccurate; it
totally miscalculates the perforation rate. The explicit model method assigns
practically all
the well production from the thin fracture layer 83 as indicated in Figure 8B
since this layer
has the highest productivity index.
[00172] The implicit methods (whether the computationally intensive fully
implicit model
or the reduced model according to the present invention) do not make such an
assignment and
instead determine that the layer 83 is not getting fluid support from the
layers 82 above and
below. The only fluid support a fracture layer of this type shown at 83 when
present in an
actual reservoir can get is from its planar neighboring cells. However, since
the fracture layer
is a very thin layer, transmissibility in these directions is by nature small.
Therefore, the
fracture layer cannot supply fluid at the rates simulated by the explicit
model.
[00173] In fact, conventional implicit well models show that during the
transient time the
fracture layers support most of the well production as do the explicit
methods. However, the
layer pressure in layer 83 quickly declines and assumes the value of the
uniform wellbore
potential (constant bottom hole pressure). After the pressure declines, it
reaches steady state,
and the well production rate is in fact made by the contribution from the
layers 82 above and
below the vertical flow barrier 83.
Twenty-two Layer Heterogeneous Reservoir Model
[00174] A model grid system 90 includes twenty two layers as shown in Figure
9. The
location of high permeability fracture layers 6 and 12 as counted moving
downward through
the layer and indicated schematically at 91 and 92. There are five layers 93,
numbered 1
through 5 above layer 91, each with vertical flow. There are also five layers
94 in the model
90 with vertical flow between the flow barrier layers 91 and 92, and ten
layers 95 with
vertical flow located below the flow barrier layer 92. Reservoir data for the
model 90 is
shown in Table 7.
Table 7-Reservoir Data for 22 Layer Problem
-38-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
Layer Thickness, ft Permeability, mD Vertical Permeability,
(Kõ=Ky) Kõ mD
1 10 2 2
2 10 5 1
3 10 3 3
4 10 10 5
10 5 4
6 1 1,000. 1.e-9
7 10 6 6
8 10 3 3
9 10 9 6
10 12 2
11 10 5 5
12 1 1,000. 1.e-9
13 10 7.5 3.5
14 10 7.5 3.5
10 7.5 3.5
16 10 7.5 3.5
17 10 7.5 3.5
18 10 9.2 1.2
19 10 9.2 1.2
10 9.2 1.2
21 10 9.2 1.2
22 10 9.2 1.2
Areal neighboring cell permeabilities = 20 mD
-39-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
Total Well Production Rate = 2,500 B/D
Well Completed in all layers.
Results:
Fully Implicit Fully Coupled Simultaneous Solution
Calculated bottom hole potential 0 = 1421.247 psi
-40-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
Table 8 - Potential Distribution, psi
Layer
1 1421.25 2901.32
2 1421.25 2900.82
3 1421.25 2900.38
4 1421.25 2900.38
1421.25 2900.38
6 1421.25 1421.25
7 1421.25 2864.43
8 1421.25 2864.37
9 1421.25 2864.10
1421.25 2863.88
11 1421.25 2864.03
12 1421.25 1421.25
13 1421.25 2841.62
14 1421.25 2841.58
1421.25 2841.48
16 1421.25 2841.33
17 1421.25 2841.13
18 1421.25 2840.65
19 1421.25 2840.08
1421.25 2839.65
21 1421.25 2839.37
22 1421.25 2839.24
-41-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
[00175] The model 90 was then subjected to the explicit model techniques of
the type
described above and flow data determined. A comparison of flow rate
distribution for fully
implicit and explicit processing of the reservoir model 90 using techniques
previously
described is set forth in Table 9.
Table 9 - Comparison of Flow Rates for Fully Implicit Fully Coupled
and Explicit Well Methods
Layer Implicit Explicit
1 35.93 14.56
2 89.78 36.39
3 53.85 21.83
4 179.48 72.78
89.74 36.39
6 0.00 727.80
7 105.09 43.67
8 52.54 21.83
9 157.60 65.50
210.10 87.34
11 87.55 36.39
12 0.00 727.80
13 129.29 54.59
14 129.28 54.59
129.28 54.59
16 129.26 54.59
17 129.24 54.59
18 158.49 66.96
-42-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
19 158.42 66.96
20 158.37 66.96
21 158.34 66.96
22 158.33 66.96
Reduced Model Construction
[00176] Since there are only two vertical flow barriers layers 91 and 92,
layers 93 above
layer 91 in Figure 9 can be combined into one layer; layers 94 below layer 91
into one layer,
and layers 95 below layer 92 into another single layer. Therefore the total
number of layers
according to the present invention is 5. The properties of the reduced model
are as follows:
Table 10 - Reduced Well Model Properties
Layer Thickness, ft Kõ mD Kõ mD PI, PI Fraction
b/d/psi
1 50 5 2.19 0.3 0.07
2 1 1000 0 1.21 0.29
3 50 7 3.66 0.42 0.10
4 1 1000 0 1.21 0.29
100 8.35 1.79 1.01 0.24
Calculated Bottom hole Potential
= 1421.34 psi
[00177] The reduced model in accordance with the present invention the
proceeds to
determine bottom hole potential Ow . The results of the reduced model with
five layers are
set forth below in Table 11.
Table 11 - Potential Distribution
Layer Pot wf Pot
1 1421.34 2900.53
-43-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
2 1421.34 1421.35
3 1421.34 2864.16
4 1421.34 1421.35
1421.34 2740.61
[00178] Using the bottom hole Potential Ow calculated from the reduced model
and
computing potentials using specified bottom hole pressure 0 for the full
model, completion
layer rates are calculated according to Equation (17). The results are
indicated below in
Table 12.
Table 12 - Calculated Well Layer Rates
Layer New Method Fully Coupled Method
1 35.92 35.93
2 89.78 89.78
3 53.85 53.48
4 179.47 179.47
5 89.73 89.73
6 0.00 0.00
7 105.09 105.09
8 52.54 52.54
9 157.59 157.60
210.09 210.10
11 87.55 87.55
12 0.00 0.00
13 129.28 129.29
14 129.28 129.28
129.27 129.28
-44-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
16 129.25 129.26
17 129.24 129.24
18 158.48 158.49
19 158.41 158.42
20 158.37 158.37
21 158.33 158.34
22 158.32 158.33
Newly calculated qt = 2499.84 b/d
Error = 2,500. - 2499.8488
=0.15 b/d
[00179] Error in the total rate and computed bottom hole pressure vanishes
with the
simulator's non-linear Newton iterations. The present invention obtains a
reduced model
with a production rate acceptably accurate in comparison to the results
obtained by the fully
implicit, fully coupled processing techniques of the prior art, but with a
substantial reduction
in model complexity and computer processing time.
[00180] The present invention, as has been described above, does not require a
special
linear solver for the solution of the coupled reservoir and well equations. In
contrast, the
coefficient matrix for the previously used coupled reservoir and well
equations does not have
regular sparse structure. Therefore, the conventional types of coupled
reservoir and well
equations require special solvers which can be expensive and can also face
convergence
problems.
[00181] It can be seen that, as described above, the present invention does
not require any
special solver for the solution of coupled reservoir and well equations. The
same solver used
for reservoir equations is utilized. The only modification made to the
coefficient matrix is in
the diagonal terms.
[00182] The present invention solves reservoir simulation problems where the
vertical
wells have many completions, which is a common occurrence in reservoirs. In
recent
-45-

CA 03015833 2018-08-24
WO 2017/151844
PCT/US2017/020327
simulation studies wells with more than 100 vertical layers (completions) are
very common.
The fully coupled fully implicit well model with simultaneous solution is very
expensive for
these cases. The present invention can save significant amounts of computer
time.
[00183] The present invention is very useful for wells having hundreds of
perforations
completed in highly heterogeneous reservoirs. The present invention reduces
the large, time
consuming problem of well modeling simulation in reservoirs with large numbers
of layers
(completions) problem to a small problem by recognizing and advantageously
using the
physical principles involved. With the present invention, it has been found
that vertically
communicating layers can be lumped into a single layer. The reduced model so
formed
preserves the same bottom hole pressure as the original full model. Once the
reduced model
is solved for the bottom hole pressure, the wells in the large system are then
treated as
specified bottom hole pressure and solved easily by a conventional linear
solver. Thus, the
present invention eliminates the need for writing or acquiring unstructured
linear solvers for
many wells with hundreds of completions, which would be expensive.
[00184] The invention has been sufficiently described so that a person with
average
knowledge in the matter may reproduce and obtain the results mentioned in the
invention
herein Nonetheless, any skilled person in the field of technique, subject of
the invention
herein, may carry out modifications not described in the request herein, to
apply these
modifications to a determined structure, or in the manufacturing process of
the same, requires
the claimed matter in the following claims; such structures shall be covered
within the scope
of the invention.
[00185] It should be noted and understood that there can be improvements and
modifications made of the present invention described in detail above without
departing from
the spirit or scope of the invention as set forth in the accompanying claims.
-46-

Representative Drawing