Note: Descriptions are shown in the official language in which they were submitted.
SEED KEY EXPANSION METHOD AND ITS USES
TECHNICAL FIELD
[0001] The present invention relates to cryptography. More
specifically, the present invention relates to a
cryptographic system based on an internal entropy of a
seed key.
BACKGROUND
[0002] The rise of the information age has led to countless
advantages in our daily lives. We can now communicate
with people on the other side of the world as well as
shop, bank, and conduct business without leaving the
comfort of our homes. One backbone of this information
age is encryption. Without encryption, all of our
digital activities would be open to everyone who can
intercept our digital communications.
[0003] Practically all digital communications in today's world
is encrypted in one form or another. Such encryption
typically comes at a cost in computational power --
generally speaking, the more secure an encryption scheme
is, the more computational power is required.
[0004] One possible issue with current cryptographic or
encryption schemes is that the creation of keys based on
one or more seed keys may result in degenerated keys
(e.g. keys having all ones or all zeroes). There is
therefore a need for systems, methods, and devices that
provides suitably secure encryption while not requiring
- 1 -
,
CA 3025502 2018-11-27
inordinate amounts of computing resources and which does
not result in degenerate (and thereby insecure) keys.
SUMMARY
[0005] The present invention provides systems and methods for
generating encryption schemes from seed keys. A seed
key is expanded into multiple expanded keys using a base
primitive scheme. The first x bits of a seed key are
used to determine a count number. In determining this
count number, these first x bits of the seed key are
rotated from the front of the seed key to the back of
the seed key. A pointer is then moved down the seed key
a number of places corresponding to the count number. A
specific bit pointed to by the pointer is then extracted
and deleted from the seed key and placed in the expanded
key. After the deletion, the bit pointed to by the
pointer is considered the front of the seed key and the
process repeats until all the bits have been extracted,
deleted, and placed in the expanded key. In addition,
these count numbers are used to determine the specific
bits to be removed from the plain text block and
inserted into the cipher text block.
[0006] In a first aspect, the present invention provides a
method for producing a binary expansion key from a
binary seed key, the method comprising:
a) storing said seed key in an ordered sequential
data structure;
b) pointing a pointer at a front of said data
structure;
- 2 -
CA 3025502 2018-11-27
c) reading a first a bits of said seed key from said
front of said seed key to determine a count number,
a being a natural number;
d) shifting the first a bits from said front to a
back of said data structure;
e)moving said pointer cn positions along said data
structure, cn being equal to said count number;
f) moving said pointer another position along said
data structure;
g) extracting a bit pointed to by said pointer and
placing said bit into an expansion key;
h) removing a bit extracted in step g) from said
data structure and to thereby move said pointer one
more position in said data structure;
i) defining a bit pointed to by said pointer as said
front of said data structure;
j) repeating steps c) - i) until all bits in said
data structure have been extracted from said seed
key and placed into said expansion key;
wherein when executing step e), a count to said on
positions begins said count from 0.
[0007] In a second aspect, the present invention provides a
method for transforming a binary plain text block into a
binary cipher text block by utilizing the count numbers
generated by expanding a binary seed key into a binary
expansion key, the method comprising:
- 3 -
CA 3025502 2018-11-27
a) determining a count number based on a subset of
bits from said binary seed key;
b) using said count number determined in step a) to
determine a specific bit bl to be extracted from
said binary seed key;
c) also using said count number determined in step
a) to determine a specific bit b2 to be extracted
from said binary plain text block;
d) extracting and removing said specific bit bl from
said binary seed key;
e) extracting and removing said specific bit b2 from
said binary plain text block;
f) placing said specific bit bl into said binary
expansion key;
g) placing said specific bit b2 into said binary
cipher text block;
h) repeating steps a) - g) until all bits in said
binary plain text block have been removed and placed
into said binary cipher text block.
[0008] In a third aspect, the present invention provides
computer readable media having encoded thereon computer
readable and computer executable code which, when
executed, implements a method for expanding a binary
seed key into a binary expansion key, the method
comprising:
- 4 -
CA 3025502 2018-11-27
a) determining a count number based on a subset of
bits from said seed key;
b) using said count number determined in step a) to
determine a specific bit to be extracted from said
seed key;
c) extracting and removing said specific bit from
said seed key;
d) placing said specific bit into said expansion
key;
e) repeating steps a) - d) until all bits in said
seed key have been removed and placed in said
expansion key.
BRIEF DESCRIPTION OF THE DRAWINGS
[0009] The embodiments of the present invention will now be
described by reference to the following figures, in
which identical reference numerals in different figures
indicate identical elements and in which:
FIGURE 1 is a diagram illustrating an example of a Seed
Key and how each bit in a Seed Key of a bits is
accessible using a b bit combination;
FIGURES 2A-2H are tables and diagrams illustrating an
example implementation of the EKEA method according to
one aspect of the invention;
FIGURE 3 is a block diagram illustrating a system for
implementing the EKEA method;
- 5 -
CA 3025502 2018-11-27
FIGURE 4 is a block diagram of a black box
implementation of the system illustrated in Figure 3 and
details the inputs and outputs of such a black box
implementation;
FIGURE 5 is a block diagram of a system for implementing
the encryption/decryption method detailed in this
document;
FIGURE 6 is a block diagram of a system for implementing
the hashing method detailed in this document; and
FIGURE 7 is a block diagram of a system using the EKEA
method black box in Figure 6 and a block box
implementing the hashing method implemented in Figure 6.
FIGURE 8 is a block diagram of a system using the EKEA
method black box in Figure 3 and X0Ring the initial CN
output from the current cycle with the ON of the
previous cycle to determine the final ON of the current
cycle.
DETAILED DESCRIPTION
[0010] The present invention encompasses a number of
cryptographic methods forming the Entropic Encryption
Suite (EES). The first is a key expansion method that is
used to expand a symmetric key to generate additional
keys (pseudo-randomly). The second method is a hash
algorithm which generates a digest from the input
message. The third method is a block encryption
algorithm which takes a plaintext message and encrypts
it to generate a ciphertext message. This third method
also allows for the generation of the plaintext from the
- 6 -
CA 3025502 2018-11-27
ciphertext. The fourth method is key scheduler which
generates a key sequence. The cryptographic strength of
all four algorithmic methods is underpinned by the
selection and use of a strong seed-key. The use of a
weak seed-key could lead to the early compromise of the
information that these methods are designed to protect.
[0011] The first of the methods expands a seed key into an
expansion key. This method is referred to in this
document as the Entropic Key Expansion Algorithm (EKEA)
method and this method forms the foundation for the
other algorithmic methods. It should be clear that,
while the examples provided below uses keys and variable
values that are exponents of or multiples of 2, other
keys and values may also be used.
[0012] To explain the EKEA method, it should be noted that
every bit in a key having a bits can be mapped (and
accessed) from any combination of bits having b bits
where 2b = a. Thus, as an example, a key with 8 bits can
be accessed using any combination of 3 bits since 23 = 8.
For this example, a - 8 and b = 3. The advantage of
this is that any progression beyond the end of the key
is modulo to the beginning of the key. For simplicity,
one can designate the first bit in any key or block as
the zeroeth (0th) bit (i.e., not the first bit).
Accordingly, a key having a bits would have 0 to a-1
individual bits.
[0013] As an example of the above, a key with size of one (1)
byte (i.e. equal to eight (8) bits) can have all of its
bits accessed by a three (3) bit combination. As noted
above, 23=8 with b=3 and a=8. If a Seed Key (SK) of size
- 7 -
CA 3025502 2018-11-27
of 1 byte is set to 01110001, then a three-bit
combination of 100 (i.e. having a decimal value of four
4) would access the 5th bit (see Figure 1).
[0014] The EKEA method is a novel primitive that utilizes the
entropy contained within a Seed Key itself to randomly
generate an Expansion Key (EK). The EKEA method
processes the Seed Key through the following
subprocesses to result in the Expansion Key:
- Entropic Count Generation
- Left Cycle Shifting
- Random Bit Reading
[0015] Entropic Count Generation (ECG) The Count Number (CN) is
a number that is randomly generated by sampling a bit
stream of length b from the Seed Key. Starting from the
beginning of the Seed Key (SK), the first b bits are
left-shifted (LS) out of the Seed Key and read to
determine the CN between 0 and a-1. Once read, the bits
are left-shifted back to the end of the Seed Key. An
iteration of two left-shifts (one from the front and one
into the back) form the process of Left Cycle Shifting
(LCS) and is formalized in equation la below.
CN(SK) = decirnalfEmb =0 concat[LC Sni(S K)]} (1a)
[0016] Left Cycle Shifting (LCS) With the random number of the
Count Number, a series of Left Cycle Shifts are
performed equal to the Count Number. The counting always
starts with zero (0) and increments up to the Count
Number. Note that a CN equal to zero (0) means that no
- 8 -
CA 3025502 2018-11-27
cycle shifting is performed for that iteration. This
process is described mathematically as follows:
LCScw(sio(SK) =Eic_No(sio
LCS(SK) (lb)
[0017] Random Bit Reading (RBR) Once the Count Number has been
reached, one additional left shift is performed to
arrive at the bit to be extracted and added to the
Expansion Key. This bit is read from the Seed Key and a
copy of it added to the Expansion Key. The Expansion Key
bits are populated in order such that the first
iteration of the EKEA populates the 0th bit of the
Expansion Key, the second iteration of the EKEA
populates the 1st bit of the Expansion Key and so on.
The bit extracted from the Seed Key is then removed from
the Seed Key. This process is described mathematically
as follows:
EKBit = LS1n(Bitc0py[LS0ut(LCSmsio(SK))11 (1c)
[0018] The Expansion Key is generated by iterating the
subprocesses noted above a-1 times. Thus the EKEA method
to generate the Expansion Key can thus be expressed
mathematically as:
EK = Ena:10- concat LSn-in tBitcopy [L,Sn (SKn))1} (1d)
-out (LCScN(sKu)
[0019] It should be clear that the process cannot be reversed
and, as such, the Seed Key cannot be reformed or derived
from the Expansion Key. The EKEA method is
unidirectional in generating the Expansion Key as it can
only be forward generated from the Seed Key itself.
Depending on the values used, this technique allows
- 9 -
CA 3025502 2018-11-27
access to the full key space. Preferably, the value of
a is set by the plaintext block size which, preferably,
is a multiple of 2.
[0020] It should be clear that the EKEA method avoids pattern
repetition and key strength decay by removing the
sampled bit from the Seed Key. As the Seed Key shrinks,
the Count Number can also be set to shrink. Because of
this, the Key Size (KS) shrinks as well. The Expansion
Key generation process is thus captured in equations 2a-
2c:
EK = Ena =0 concat LSõ(CScN(sKn(SKTI)) (2a)
where
)
CN (SK) = decimalfKS(SKn
Ein=0 concat[LCSin(SKA) (2b)
and
KS(SK) = integer[log2(SKn)] (2c)
[0021] One variation of the EKEA method fixes the Key Size to a
fixed size b which simplifies the Count Number (CN)
algorithm to equation la. This avoids the need to
calculate the Key Size for each iteration of bit
expansion but at the cost of significantly more
shifting.
[0022] The EKEA method can be summarized as in the following
steps:
a) take the first n bits of a seed key and use these n
bits to determine a count number (CN)
- 10 -
CA 3025502 2018-11-27
b) cycle shift the n bits from the front of the seed key
to the rear of the seed key
c) from the start of the resulting key after the cycle
shift, traverse CN positions down the resulting key,
with the counting beginning at 0 and not at 1
d) traverse one extra position down the resulting key
e) at the bit position pointed to, extract and remove
the bit at this resulting position from the key and
place this extracted bit in the first available bit
position in the expansion key
f) since a bit has been removed, the seed key has shrunk
by one bit and the position pointed to after extraction
is now the front of the seed key
g) repeat steps a) to f) until no bits are left in the
seed key.
[0023] The "front" or start of the seed key can be tracked by
way of a pointer that always points at the bit that is
at the "front" of the seed key. To traverse a seed key,
the pointer merely has to be moved so that it is
pointing to a different bit position in the seed key.
Thus, for a left shift cycling, the pointer merely moves
to the right in the bit positions while moving to the
left in the bit positions would implement a right shift
cycling.
[0024] The results of the above EKEA method can be seen with
reference to Figures 2A-2H. Figures 2A-2H illustrate
one example of an implementation of the EKEA method with
- 11 -
CA 3025502 2018-11-27
each step being represented by a figure. For this
example, the Seed Key is given as 01110001. Also for
this example, a = 8 and b = 3. For this example, b = n
= 3. Thus, the first 3 bits of the Seed Key are read.
These bits correspond to a value of 3 and, as such, the
Count Number (CN) = 3. The first n bits are thus read
from the front of the Seed Key and rotated/cycle shifted
to the back of the Seed Key (see right side of Fig. 2A)
[0025] As can be seen from the right side of Fig. 2A, after the
first n bits have been cycled to the back of the Seed
Key, a traversal of CN = 3 positions is executed with
the count beginning at O. Thus, from the right side of
Fig. 2A, since the 0th, 1st, and 2nd bits of the seed
key were cycled to the rear of the seed key, the count
begins at the 3rd bit of the seed key (for easy
reference, see the "bit number" index in Fig. 2A).
Designating this 3rd bit as count 0, a traversal of the
seed key proceeds with the 4th bit being count 1, the
5th bit being count 2, and the 6th bit being count 3.
[0026] Once a count of 3 has been reached, an extra position is
traversed to the 7th bit. This 7th bit is then
extracted (i.e. removed) from the seed key and placed in
the first available bit position in the expansion key
(i.e. bit position 0 in the expansion key). Because of
this removal of the 7th bit, the next bit (i.e. the 0th
bit) in the seed key is pointed to. This bit is thus
the new start of the resulting seed key.
[0027] After extraction of the 7th bit, the process begins anew
in Fig. 2B. It should be clear that the left side of
Fig. 2B is simply a redrawing of the remaining bits of
- 12 -
CA 3025502 2018-11-27
the left side of Fig. 2A. The beginning of this seed
key is thus the 0th bit and the first n bits (with n =
3) being read to determine the count number. These n
bits are then cycle shifted to the rear of the seed key
in the right side of Fig. 2B. Once the cycle shifting
has been accomplished, the traversal of the seed key
using the count number begins.
[0028] For this iteration of the process, since CN=3 again,
then the right side of Fig. 2B shows that traversal
process results in the 0th bit as being the bit to be
extracted and placed in the expansion key. Once
extraction has been accomplished, the beginning of the
seed key is thus at the 1st bit (see right side of Fig.
2B and the "bit number" index on the right side of Fig.
2B for clarity).
[0029] To assist in understanding Figures 2A-2H, a marker or
pointer to the start of "front" of the Seed Key is
provided in the figures. This pointer is shown in the
right side of Fig. 2A at the top of the table with a
small rectangle and the number 0 inside to denote that
this is the 0th iteration of the EKEA method. In Figure
2B, the left side shows that the pointer indicates the
last bit position pointed after the 0th iteration. The
right side of Fig. 2B shows that the pointer is now
pointing at a different bit position after the 1st
iteration of the EKEA method.
[0030] For Fig. 20, the next iteration begins, again, with
reading the first n bits of the seed key to yield a
count number of 7. Once the count number has been
determined, these first n bits are cycle shifted to the
- 13 -
CA 3025502 2018-11-27
rear of the seed key and the traversal of the bits using
the count number result proceeds.
[0031] The traversal of the bit positions in the right side of
Fig. 20 shows that the count begins at the 4th bit being
designated count 0. The 5th bit is thus designated as
count 1 and so on. It should be clear that the count
number traversal of the bit positions wraps around the
seed key such that the 4th bit is both count 0 and count
6 while the 5th bit is both count 1 and count 7. Since
the 5th bit is count 7, then the 6th bit is the bit to
be extracted and placed in the next bit slot in the
expansion key. This is shown in Fig. 20. The beginning
of the seed key is thus designated to be, after the bit
extraction, the 1st bit (again, see the right side of
Fig. 20 and the "bit number" index).
[0032] The process proceeds through Figures 2D, 2E, and 2F as
described above. It should, however, be clear that, for
Figure 2G, this iteration has a count number of 0.
Thus, for a count number of 0, the first n bits are
still cycle shifted to the rear of the remaining seed
key. Of course, if there are less than n bits left in
the seed key, these bits are still cycle shifted to the
rear of the seed key. Thus, for Fig. 20, the 4th bit
and the 5th bit are the only bits left to determine the
count number. Once these are cycle shifted to the rear
of the seed key, their sequence is reversed (see the bit
number index for the resulting seed key at the right
side of Fig. 2G). Since the count number is 0,
traversal does not occur for the count number. The 4th
bit is then extracted from the right side of Figure 20.
- 14 -
CA 3025502 2018-11-27
[0033] For Fig. 2H, the last bit is extracted. It should be
clear that, for the iteration in Fig. 2H, all the steps
of the process are still executed and that this
execution results in the last bit being extracted and
placed in the expansion key.
[0034] The result from the example is an expanded key (EK) that
has a value 10011100. This expanded key has been
randomly generated from the Seed Key. In effect,
randomly selecting randomly generated bits (from a
stream of bits) generates a new random stream of bits
(and thus a new random number). Clearly, the Seed Key
can be selected from a subset of any bitstream.
[0035] It should be noted that, for the example, b = n = 3.
Since there were eight bits in the seed key (i.e. a =
8), and since 2' = a, then the example easily works out
with n = 3. However, it should be clear that for seed
keys which have a bits where a is not a multiple of 2
(i.e. not even) or a is not a direct power of 2, n can
be any number. One drawback to using a seed key whose
number of bits (i.e. a) is not a power of 2 is that not
all of the key space can be directly accessed. However,
if a is a power of 2 (i.e. 2b = a), using b = n
simplifies matters and allows access to the complete key
space for that seed key. For clarity, n is the number
of bits in the seed key that is used to calculate the
count number and the number of bits that are cycle
shifted to the rear of the seed key at every iteration
of the EKEA method.
[0036] One of the disadvantages of the above method as detailed
in the example is that the key space is limited to those
- 15 -
CA 3025502 2018-11-27
keys with the same quantity of Os and is as the seed
key. This key space represents a significantly smaller
key space (in the generation of the Expansion Key) than
the size of the Seed Key. That being said, one of the
advantages of the EKEA method is that the expanded key
will not degrade to a weak key (e.g. an expanded key
that are all Os).
[0037] While the above EKEA process works, variants are also
possible which may help in expanding the usefulness of
the process.
[0038] In one variant, the Expanded Key could be modified by
performing an XOR operation between the Expanded Key and
the Seed Key. This allows access to the full key space.
For this variant, the process is adjusted by performing
an XOR operation between the Shifted Seed Key (SSK) and
the Final Expansion Key (FEK). Both the SSK and the FEK
are, of course, functions of the Seed Key (SK) and the
Expansion Key (EK). These variables are used to generate
the Next Key (NK) per equation 3a:
NK = SSK e FEK (3a)
[0039] In equation 3a, the SSK is a function of the Seed Key
and the Expanded Key (which is also a function of the
Seed Key). The FEK is solely a function of the SK. To
generate the SSK, a count number is drawn from the
Expanded Key and used to LCS the SK. The FEK is
generated after the Count Number is drawn/calculated
from the Expanded Key. Thus, to arrive at the FEK, the
first n bits of the Expanded Key are read and this
provides the Count Number. These n bits are then cycle
- 16 -
CA 3025502 2018-11-27
shifted to the rear of the Expanded Key. After the
cycle shifting, the resulting key is the Final Expanded
Key. The count number from the Expanded Key is then
used as the number of bits from the Seed Key that are
cycle shifted to the rear of the Seed Key. The
resulting key is the Shifted Seed Key. Mathematically,
these operations can be expressed as:
FEK = LCSocN(Elq (EK)
(3b)
SSK = LCS oCN (EK) (SK) (3c)
In these equations, CN(EK) is given by equation la
above. Once the NK has been generated, this NK is then
used as the Seed Key and the EKEA method is applied to
this Seed Key to generate the new Expanded Key.
[0040] While the XOR operation variant grants full access to
the key space, this method of key expansion can also
result in key strength decay. Key space access and key
strength decay can be addressed by expanding the key
size to be significantly larger than the plaintext block
that it will protect.
[0041] In this case, the key size could be made several bits
(A) larger to a multiple (c) of 2 times the bit size pt
of the plaintext block (i.e. the plaintext block is of
length pt bits). The Key Size (or the number of bits in
the Seed Key) is then expressed as KS = 2c(pt+A), and d =
10g2[2c(pt+A)] = c + b, which represent the bits that
must be withdrawn (cycled) to almost access the full key
space (minus the LI bits). The first Key Expansion can be
obtained by applying the EKEA method to an SK of size
- 17 -
CA 3025502 2018-11-27
2c(a+.6). For clarity, the variable b is derived from the
above equation where a key can be defined as having a
bits from any combination of bits having b bits where 2b
= a.
[0042] As we will see, the Expansion Key can be split at least
once to generate the two or more encryption/decryption
keys. Note that this method will generate two or more
keys, where each key, having a bits, has full access to
the key space. These keys are balanced between the set
of keys (i.e. decreases in is in one key is balanced by
increases in is in one of the sister keys). Coupling the
keys maintains key strength but at the cost of increased
key size and at least double the encryption cycles. The
EKEA process then becomes:
EK= Een=0 concat LS,,(CSCN(SKn)51(n)) (4a)
where e = 2c(a + A) - 1 and
CN(SK,) = decimal {Enid =0 concat [LCS,,(SKT)D (4b)
where d = c + b and from which one or more Transmission
Keys (TKs) are generated. The Transmission Keys are
determined by:
TKe = EPa
q=(p-1)a concat LSq(EK,) (4c)
where e = 2c and r = pa-q.
[0043] In one implementation, the Seed Key is loaded into a
Dynamic Key Shift Register that performs the shifts on
the relevant key stored within. The Dynamic Key Shift
Register can take the form of a physical hardware
- 18 -
CA 3025502 2018-11-27
register or it can take the form of a software data
structure (e.g. a linked list or a suitably configured
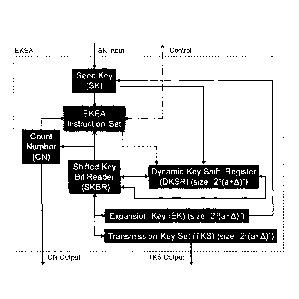
software array) for storing bits in a key with each bit
occupying a dedicated data slot. This allows for bit
shifting and traversing the various bit positions as
required by the EKEA method. Such an implementation is
illustrated in Figure 3 where each block is either a
data structure for storing a variable (e.g. Count
Number) or a data structure for both storing and
manipulating a key or variable (e.g. Dynamic Key Shift
Register). Note that the EKEA Instruction Set is
illustrated in Figure 3 for clarity to illustrate which
variables are used by or adjusted by the EKEA method. As
should be clear, each data structure represented in
Figure 3 can be replaced by a physical hardware device
that performs that same function as the software data
structure.
[0044] It should be clear that the Dynamic Key Shift Registers
(DKSR) and the Shifted Key Bit Reader (SKBR) in Figure 3
can perform both Left Shifts and Right Shifts. It
should also be noted that the implementation in Figure 3
illustrates another possible variant for the EKEA
method. As will be explained below, the cycle shifting
for the EKEA method can be performed as a left shift or
as a right shift. Depending on the Seed Key, using the
EKEA method with all cycle shifts being left shifts to
produce an EK will produce a different Expansion Keys
than an implementation where all cycle shifts are right
shifts. As will be shown below, having a single SK to
produce two EKs (one produced using left shift cycle
- 19 -
CA 3025502 2018-11-27
shifts and one produced using right shift cycle shifts)
can result in paired Transmission Keys.
[0045] For the implementation in Figure 3, the Seed Key is
initially loaded into the Dynamic Key Shift Register
(DKSR). The first bit of the DKSR is left-shifted into
the Shifted Bit Reader and determines the direction of
expansion to generate the EK (where 0 = Left-Shifting
and 1 = Right-Shifting). Once the EK is generated, the
SK is reloaded in the DKSR and sequenced in the opposite
direction that was used to generate the EK -- this
produces the Transmission Key Set (TKs). As such the EK
and the TKs are isolated from each other by the opposite
(and irreversible) directions of expansion. The TKs can
be exported or the generated Count Numbers (along with
the Control signals) can be used directly for
encryption/decryption. If exported, the TKs can be
spliced to produce TKs of size (a+A) where a is the
number of bits in the Seed Key.
[0046] Once generated, the Expansion Key can be used to replace
the original Seed Key and the cycle recommences to
generate the next Expansion Key and Transmission Keys.
[0047] It should be clear that once the Seed Key has been used
in the EKEA method, knowledge of either the SK or the EK
is no longer needed as only the TKs can be read. As will
be explained below, the EKEA method can be used in an
encryption/decryption method and in a hash method. For
these two methods, the CN and Control signals are used
to sequence the methods. For such implementations, it
is possible to reverse engineer knowledge of the
Transmission Keys through the CN.
- 20 -
CA 3025502 2018-11-27
[0048] The block diagram in Figure 3 is simplified to a black
box in Figure 4. The EKEA method can be used in an
encryption/decryption method as well as in a hashing
method. In the explanations of these methods below, the
EKEA method is simplified into a block.
[0049] Depending on how the EKEA method is used and depending
on the configuration of the encryption/decryption
methods used, variants of the above are possible. As an
example of such variants, the Transmission Key sizes
could be any size larger than the plaintext block size
and could vary in length between the TKs themselves
(i.e. each TK could have a different key length). For
such a variant, the length of the Transmission Keys
could vary randomly between key sets and would be
determined through the entropy of the Seed Key.
[0050] As noted above, EKEA method may be implemented through
software or hardware. With software, the DKSR can be
developed with any suitable data structure such as a
linked list. In terms of dedicated hardware, the DKSR
can be built with suitably sequentially linked J-K or D
flip-flops, or with Programmable Logic Arrays (PLAs).
[0051] The EKEA method can be used to encrypt blocks of
plaintext (PT). As noted above, the size of the
plaintext block is preferably of the same size or
smaller than that of the Transmission Keys (TKs).
[0052] To establish a secure transmission session, the Seed-Key
(SK) must be shared between the transmitter and the
receiver. The EKEA method is then used to expand the SK
to generate the individual set of symmetric Transmission
- 21 -
CA 3025502 2018-11-27
Keys (TKs). A unique set of TKs is used for each block
that is transmitted. The Seed-Key or Expansion Keys are
never used to encrypt a block as only the expanded TKs
are used. It should be clear that, when the EKEA method
is used to generate the Transmission Keys, the
parameters used by the transmitter and receiver for the
EKEA method are the same.
[0053] For encryption, the EKEA method is used to generate a
new set of TKs to encrypt each block of plaintext. While
the EKEA method generates the next key it also uses the
Count Number (see equation 2b or 4b) to transform the
plaintext into ciphertext. The EKEA based encryption
method thus generates a one-to-one map between the
plaintext set and the ciphertext and this map changes
with each transmission. While similar to a one-time pad
(in that each TK is used only once for a transmission),
the key space is restricted to that of the TK. For each
TK used, the sequencing direction (forward or reverse)
of each TK is established by reading the first bit of
the TK with a first bit value of 0 denoting a left-shift
sequencing while a first bit value of 1 denotes right-
shift sequencing.
[0054] In the case where two TKs are used, if the first bit of
the first TK is read as "0", then left-shift sequencing
of the first TK occurs. To generate each bit of the
ciphertext (CT) from the plaintext (PT), the following
equation denotes the operation:
CTx-z, = LSAIiagcwoxco (PTm) ] (5a)
- 22 -
CA 3025502 2018-11-27
[0055] For equation 5a, it should be clear that x-n denotes an
index to the ciphertext's block number and bit position
being encoded with x denoting the block number and n
denoting the bit position of the bit being encoded.
Thus, CT0_5 denotes the bit at bit position 5 in block
number 0 of the ciphertext. For further clarity, m = a-
n and denotes m as the size of plaintext (PT,n) or the
Transmission Key (TX0 being used in the encryption. It
should be clear that both the full plaintext and the
full TK have a bits. Thus, as an example, if both the
plaintext and the TK have a size of 10 bits (i.e. a =
10) and we wish to encrypt bit 3 of the ciphertext (i.e.
n = 3), then m = 10 - 3 = 7. This means that, for the
example, a 7 bit subset of the plaintext and of the TK
are used to encrypt the ciphertext.
[0056] The count number is thus determined based on a subset of
the Transmission Key and the actual bit used in the
ciphertext is selected from a subset of the plaintext.
[0057] The full ciphertext block for block number x is thus
generated with:
CT, = concat CT,, (5b)
where, as in equation 5a, x-n denotes an index and not
an operation
[0058] If the first bit of the second TK yields a 1, then
right-shift sequencing occurs where each bit at position
n of the ciphertext is derived from the PT through
C27,2 = RS, 0403= mcE0 (Crx-n) ] (5c)
- 23 -
CA 3025502 2018-11-27
[0059] In equation 5c, x-m again denotes an index with x being
the block number and m having the same definition as for
equation 5a. Thus, to encrypt bit n, the result of the
previous encryption is used by taking the encrypted
block and using its bits with a right shift to arrive at
the final encrypted bit. It should be clear that RS is
a Right Shift out of the back of DTSR and RCS is a Right
Cycle Shift consisting of an RS out of the back followed
by an RS into the front of the DTSR.
[0060] The full CT Block is generated with:
CT= unicat CT, (5d)
[0061] It should be clear that, if 2 TKs are used, then there
are four possibilities for the first bits of the 2 TKs:
00, 01, 10, 11. The example provided is for the case
where the first bits of the 2 TKs equals 01. For
completeness, if the first bits of the 2 TKs equal 00,
then the PT is encrypted with a LS sequencing of the
first TK and a LS sequencing of the second TK. If the
first 2 bits of the 2 TKs equal 10, then the PT is
encrypted with a RS sequencing of the first TK and a LS
sequencing of the second TK. If the first two bits of
the 2 TKs equal 11, then the PT is encrypted with a RS
sequencing with the first TK and a RS sequencing with
the second TK.
[0062] It should be noted that, for a more reliable
transmission (i.e. to increase availability), the Block
Number (BN) may need to be included as a plaintext
number to ensure that the Key Expansion remains
synchronized between the transmitter (encryption) and
- 24 -
CA 3025502 2018-11-27
receiver (decryption). If, however, this is deemed to be
unacceptable, then the BN may be included in the
plaintext block and encrypted.
[0063] For decryption, the receiver also uses the EKEA method
to generate the TK to decrypt the CT that it has
received from the transmitter. The decryption method
reverses the encryption process by acting on each
individual bit of the ciphertext block. It accomplishes
this by first generating the Count Numbers (CNs) and
then storing these in the Count Number Stack (CNS). The
CNs are then popped out of the stack one at a time to
determine the decrypted location for the previously
encrypted bit.
[0064] The decryption process assumes that the receiver has the
TKs used in the encryption of the ciphertext and that
the receiver and the transmitter have agreed as to which
Transmission Key is to be considered as the first or the
second Transmission Key. If two TKs were used in the
encryption of the ciphertext, then the first read bit of
the TKs generates the sequencing directions that are
opposite to that of encryption. In this case, the
sequencing directions are established by reading the
first bit of the TKs. If the first bit is a 1, then
left-shift sequencing is used while if the first bit is
a 0, then right-shift sequencing is used. Starting with
the second TK (if the first bit is a 1), each bit of the
PT block is generated with:
PTy, = LS. [LCSawm (=I) ] (6a)
- 25 -
CA 3025502 2018-11-27
[0065] As with equation 5a, the subscript y-n indicates an
index with y denoting the ciphertext block number (which
runs in reverse order to the x block number used in
encryption) and n denoting the bit position in that
block of the bit being decrypted. For further clarity,
m = a-(n-1) with n denoting the bit position of the bit
being decrypted and m denotes the CN reference number in
the CNS. It should also be clear that m denotes the bit
position of the bit being accessed in the ciphertext.
As with equation 5a, it should be clear that both the
full plaintext and the full TK have a bits.
[0066] To generate the full plaintext block for block number y,
the following is used:
PTy = Ena:10- concat (6b)
[0067] For the first TK (if the first bit is a 0), each bit of
the PT block is generated with right-shift sequencing
where each bit of the PT is derived from the CT using
PTõ = RSõ ERCSasis. (PTy...)] (6c)
[0068] For equation 6c, m=a-(n-1) and denotes the CN reference
number in the CNS as well as the CT bit number that is
being inserted into the PT block. The full PT Block is
generated with
PT= InconcatPTi (6d)
[0069] As an implementation note, it should be clear that, for
both the encryption and decryption methods above, the
Count Number [CN(TKm)] is being executed at the same
time within the EKEA method to generate the next TK.
- 26 -
CA 3025502 2018-11-27
This causes the Count Number to decrease in bits for
every iteration. It should be clear that the Count
Number decreases based on equations 2b and 2c above. As
can be seen, what results is a logarithmic calculation
to determine b based on the remaining PT/CT bits (i.e. m
that is always smaller than a).
[0070] It should also be clear that, if the last PT block of a
message is only partly filled, that PT block can be
filled with pseudo random bits prior to being converted
into CT block.
[0071] For an implementation of the encryption/decryption
methods, a block diagram of a system is illustrated in
Figure 5. As can be seen, an EBEDA instruction set
block for the encryption/decryption instructions/control
mechanism is used along with a suitable EKEA method
block.
[0072] As we can see from Figure 5, the Count Number Stack
exists strictly for decryption. This occurs because of
the unidirectional nature of the EKEA method. It should
thus be clear that decryption requires that all the
count numbers need to be determined prior to reversing
the encryption process.
[0073] The EKEA method can also be used to generate hashes or
hash digests from digital messages. For such a use, the
input message can be of any size. The size of the digest
message can also be set to any size. The hash algorithm
relies on a shared symmetric key rather than on a series
of known transformations (e.g. such as MD5, SHA-1,
- 27 -
CA 3025502 2018-11-27
etc...). Depending on the use of the hash algorithm, the
shared symmetric key can be private or public. The key
must be private if the hash digest is used for
authentication but it can be public if the hash digest
is being used to assess the integrity of the original
message. In the case of a public key (for message
integrity), the key would be included with the digest.
[0074] The digest employs the encryption technique of the
encryption/decryption method noted above with the
additional step that each encrypted (CT) block (known as
the Block Hash Digest) is used in an XOR operation with
the previous CT block (known as the Cumulative Hash
Digest) to produce the final Hash Digest. Equation 7a is
used to generate the Block Hash Digest (BHD):
BHDx = Ena=, concat CT,_õ (7a)
where x = 1 ... number of blocks.
[0075] The Cumulative Hash Digest (CHD) is generated by
performing an XOR operation between the previous CHD and
the BHD (see equation 7b).
CRE)õ = CHEZ,1 XOR BRA, (7b)
[0076] For equation 7b, each bit of CHDO is initialized with a
zero (0). The Hash Digest (HD) is thus generated with
equation 7c:
HD = Exnumiber of blocksCHD,_i XOR BHD, (7c)
[0077] It should be clear that the hash digest has a size of a
bits.
- 28 -
CA 3025502 2018-11-27
[0078] To implement the hashing method noted above, a system
such as that illustrated in Figure 6 may be used. As
can be seen, the system in Figure 6 is similar to the
system shown in Figure 5. However, the system in Figure
7 does not have a Count Number Stack and has an XOR
function for performing an XOR operation between the CHD
and the BHD.
[0079] In this implementation, each Block Hash Digest is
sequentially X0Red with the Cumulative Hash Digest.
After the final XOR operation with the last Block Hash
Digest, the Cumulative Hash Digest is then outputted as
the final Hash Digest.
[0080] The EKEA method can also be used to generate a key
scheduler. The underlying principle of this is
accomplished by X0Ring the initial Count Number (of the
existing cycle) with the Count Number of the previous
cycle, thus producing a final Count Number for the
existing cycle (see Figure 8). This final Count Number
is fed back to the EKEA to determine the sequenced bit
to be withdrawn in that cycle.
[0081] As a variant of the EKEA method, the feature illustrated
in Figure 8 can be used to introduce additional entropy
in the system. Such additional entropy can disrupt
symmetries within keys as such symmetries can cause
weaknesses or degenerations in key strength. For each
key expansion cycle, two (2) bits are sequentially X0Red
and this operation determines which branch will be
followed for the expansion. From Figure 8, it should be
clear that the 2 bits to be X0Red with each other are
from the Seed Key and that these bits determine the
- 29 -
CA 3025502 2018-11-27
direction of shifting. The four options of such a
branch selector feature, and the branch selected, are as
follows:
- 00 : LS EKEA
- 01 : RS EKEA
- 10 : LS (d bits)
- 11 : RS (d bits)
[0082] For a LS or RS branch (i.e. the 2 bits from the SK are
either 10 or 11), d bits from the current CN and from
the previous ON are X0Red with each other, and that
number of left or right shifts are executed and the
result is fed into the EKEA as the ON. If, however, the
2 bits from the SK are 00 or 01, then the shifting
performed by the EKEA method is either left shifting or
right shifting as noted above.
[0083] The result is a key scheduler that randomly moves
throughout the Key Space generating a pseudo-random
sequence of keys. The EKS Block Diagram (Figure 8) shows
that the first two bits of the branch selector feature
are initialized with the SK (as is the CN). The final-
current ON is determined by X0Ring the initial-current
ON with the previous ON.
[0084] It should be clear that the various EKEA method
components may be used for other cryptographic uses. As
an example, the Transmission Keys may be used to
generate the so-called "salt" for other well-known hash
algorithms (e.g. SHA). For such a use, the Transmission
- 30 -
CA 3025502 2018-11-27
Keys would need to be spliced to the quantity (in bits)
of "salt" needed by these algorithms.
[0085] It should be clear that the various methods described
above have many uses. They can be implemented to
encode/encrypt an incoming bitstream to result in an
encoded bitstream. The encoded bitstream can then be
transmitted to a receiver and, at the receiver end, the
incoming bitstream can be decoded to result in a decoded
bitstream.
[0086] It should also be clear that the methods outlined above
can be implemented using a general purpose computing
device or they could be implemented using a dedicated
computing device such as an ASIC (application specific
integrated circuit). Similarly, the methods can be
implemented as one or more software modules that are
called by specific programs as necessary.
[0087] The embodiments of the invention may be executed by a
computer processor or similar device programmed in the
manner of method steps, or may be executed by an
electronic system which is provided with means for
executing these steps. Similarly, an electronic memory
means such as computer diskettes, CD-ROMs, Random Access
Memory (RAM), Read Only Memory (ROM) or similar computer
software storage media known in the art, may be
programmed to execute such method steps. As well,
electronic signals representing these method steps may
also be transmitted via a communication network.
[0088] Embodiments of the invention may be implemented in any
conventional computer programming language. For example,
- 31 -
CA 3025502 2018-11-27
preferred embodiments may be implemented in a procedural
programming language (e.g."C") or an object-oriented
language (e.g."C++", "java", "PHP", "PYTHON" or "C#").
Alternative embodiments of the invention may be
implemented as pre-programmed hardware elements, other
related components, or as a combination of hardware and
software components.
[0089] Embodiments can be implemented as a computer program
product for use with a computer system. Such
implementations may include a series of computer
instructions fixed either on a tangible medium, such as
a computer readable medium (e.g., a diskette, CD-ROM,
ROM, or fixed disk) or transmittable to a computer
system, via a modem or other interface device, such as a
communications adapter connected to a network over a
medium. The medium may be either a tangible medium
(e.g., optical or electrical communications lines) or a
medium implemented with wireless techniques (e.g.,
microwave, infrared or other transmission techniques).
The series of computer instructions embodies all or part
of the functionality previously described herein. Those
skilled in the art should appreciate that such computer
instructions can be written in a number of programming
languages for use with many computer architectures or
operating systems. Furthermore, such instructions may be
stored in any memory device, such as semiconductor,
magnetic, optical or other memory devices, and may be
transmitted using any communications technology, such as
optical, infrared, microwave, or other transmission
technologies. It is expected that such a computer
program product may be distributed as a removable medium
- 32 -
CA 3025502 2018-11-27
with accompanying printed or electronic documentation
(e.g., shrink-wrapped software), preloaded with a
computer system (e.g., on system ROM or fixed disk), or
distributed from a server over a network (e.g., the
Internet or World Wide Web). Of course, some embodiments
of the invention may be implemented as a combination of
both software (e.g., a computer program product) and
hardware. Still other embodiments of the invention may
be implemented as entirely hardware, or entirely
software (e.g., a computer program product).
[0090] A person understanding this invention may now conceive
of alternative structures and embodiments or variations
of the above all of which are intended to fall within
the scope of the invention as defined in the claims that
follow.
- 33 -
CA 3025502 2018-11-27