Note: Descriptions are shown in the official language in which they were submitted.
~ ~ ~ Q ~
Method of generating a correction function for an
1 elimination of phase and amplitude errors of a
compressed signal
BACXGROUND OF THE INV~TION
1. Field of the Invention
The invention relates to a method of generating a
correction function for an elimination of phase and
amplitude errors of a compressed signal, a reference
function Hi(t) of an ideal filter being generated and a r~ef~ce function
hf(t) being generated in accordance with the optimum
filter theory.
SUMMARY OF THE INVENTION
The invention has as its object the extension of the
concept of the ideal filter so that phase and amplitude
errors can be eliminated with an already compressed
signal ff(t) after a pulse compression in accordance
with the theory of the optimum filter has already been
carried out.
as
The invention therefore provides a method of generating
a correction function for an elimination of phase and
amplitude errors of a compressed signal, in which for
generating a reference function (hi(t)) an error-free
frequency-modulated signal (so(t)), a signal (Sf(t))
containing phase and amplitude errors, a reference
signal (ho(t)) corresponding to a conjugate complex
time-inverted function of the error-free signal (sf(t))
and a reference signal (hf(t)) corresponding to the
conjugate complex time-inverted input signal (Sf(t))
are each fourier-transformed to respective signals (SO,
Sf, Ho and Hf) in FFT units (6.2, 6.5), then in each
B
2 2110218
.
case two of the signals (Sf, Hf; SO' Ho) are multiplied
1 together and the reciprocal value of the signal (Ff)
arising from the first multiplication is multiplied by
the output signal (Fo) arising in the second
multiplication and thereupon said signal (Fo/Ff) is
multiplied by the fourier-transformed signal (Hf), and
the signal (Hi) thus obtained is subjected to an
inverse transformation for generating the reference
function (hi(t)) in the time domain, and furthermore a
reference function (hf(t)) is generated by the optimum
filter theory, wherein
the reciprocal value (1/Hf) of the one fourier-
transformed signal (Hf) is multiplied by the other
fourier-transformed signal (Hi),
the signal (Hi/Hf) obtained by the multiplication is
subjected to an inverse fourier transformation in the
time domain in a following IFFT unit (6.7) for
generating the correction function (hCorr(t))~ and
a signal (ff(t)) containing phase and amplitude errors
and the correction function (hCorr(t)) are convoluted
in the time or frequency domain for generating an
error-free signal ~fo(t))~
A requirement for carrying out the method according to
the invention is however that the amount ( I + Q ) of
the compressed signal ff(t~ is not formed so that said
signal ff(t) is present as complex function. With the
aid of the reference function hi(t) of the ideal filter
a correction function hCorr(t) is then calculated which
is convoluted with a compressed signal ff(t). The
result of such a convolution is an error-free pulse
response fo(t) because the phase and amplitude errors
of the functions ff(t) are eli~inated by the calculated
functi~n hCorr(t)-
According to a modified further development of the
method of generating a correction function for the
elimination of phase and amplitude errors of the
2110218
-
compressed signals, the phase and amplitude errors may
1 be removed from the actual compressed signal ff(t) if a
pronounced point target response is present in the
compressed signal ff(t). The selected pronounced point
target response is then employed to determine the
function hCorr(t)~ In this case the replica Sf(t) of
the transmitted pulse is not required. The advantage
of such a configuration of an ideal filter resides in
that the information of the phase and amplitude errors
can be taken from the compressed signal ff(t) and that
the processing can be carried out in accordance with
the concept of the ideal filter dir~ctly with the
compressed signal or the corresponding image data.
BRIEF DESCRIPTION OF THE DRAWINGS
The invention will be explained in more detail
hereinafter with reference to preferred embodiments and
with the aid of the attached drawings, wherein:
Fig. 1 shows in the form of a block diagram an
apparatus for carrying out a pulse
compression in the time domain using the
method according to P 41 17 849.1-35 for
obtaining an ideal pulse response in spite of
an erroneous frequency-modulated input
signal;
Fig. 2 shows in the form of a block diagram an
apparatus for generating an ideal pulse
response, a pulse compression being carried
out in the processing in the frequency
domain;
Fig. 3 shows in the form of a block diagram an
apparatus for generating a reference function
hi(t);
4 Z ~ ~2~
Fig. 4 shows in the form of a block diagram a
1 further apparatus for generating a reference
function hi(t);
Fig. 5 shows in the form of a further block diagram
an apparatus for carrying out a pulse
compression using the concept of an ideal
filter according to the invention, a
correction of phase and amplitude errors of a
compressed signal ff(t) being carried out by
convolution with a correction function
- hcorr(t);
Fig. 6 is a block diagram of an embodiment for
performing the method of generating the
correction function hCorr(t) for eliminating
phase and amplitude errors of the compressed
signal ff(t) and
Fig. 7 is a further block diagram of an embodiment
for implementing the method of generating the
correction function hCorr(t) for eliminating
phase and amplitude errors of the compressed
signal ff(t).
DESCRIPTION OF THE PREFERRED EMBODIMENTS
When using the method, acting as a sort of ideal
filter, for generating a reference function hi(t)
as will be described below, a sin(x)/x function can
be obtained independently of the phase and amplitude
errors present in the received signal. A received
signal Sf(t) containing phase and amplitude errors is
convoluted in Fig. 1 in a convolution unit 1 with the
aid of a reference function hi(t), as will be described
below. In Fig. 1 a pulse response fo(t) obtained by
the convolution then has the form of a sin(x)/x
~~~
"- 2 ~I lo21~
function if no amplitude weighting is additionally
1 carried out for suppressing sidelobes.
In Fig. 2 implementation of a me~od of performing a
pulse comp~ession is illustrated, the pulse compression
being shown in the frequency domain by means of a
reference function generated according to P 41 17
849.1-35. ~ received signal Sf(t) and the reference
function hi(t), the determination of which will be
explained in detail below with the aid of Fig. 3 or 4,
are each-fourier-transformed by FFT units 2.1 and 2.3
respectively, the spectra Sf and Hi thereby being
obtained. The two spectra Sf and Hi are multiplied
together in a multiplying unit 2.2 and then subjected
to an inverse fourier transformation (IFFT) by an IFFT
unit 2.4 and thereby transformed to the time domain.
The pulse response fo(t) present at the output of the
IFFT unit 2.4 then has the form of a sin(x)/x function.
The reference function hi(t) m~st then be determined by
performing a pulse compression. In Fig. 3, in the form
of a block diagram an embodiment is illustrated for
determining the reference function hi(t) with the aid
of a fast fourier transformation (F~T). By FFT units
3.1 to 3.4 the signals applied Sf(t), so(t), hf(t) and
ho(t~ are fourier-transformed to the frequency domain.
The two signals so(t) and sf(t) here relate to the
backscattering of only a single point target. The
signal Sf(t) therefore corresponds to the replica of
the transmitted pulse and is measured directly on
reception whilst the signal so(t) can be determined
from parameters such as the modulation rate and
duration of the frequency modulation, contains no phase
and amplitude errors and exhibits a linear frequency
modulation. The reference functions hf(t) and ho(t)
are determined from conjugate complex functions of the
signal Sf(t) and the signal so(t) respectively.
B
6 211021~
1 As can be seen from Fig. 3, signals Ff and Fo are
obtained by multiplying the spectra Sf and Hf and SO
and Ho in multiplying unitS3.5 and 3.6. The signal Ff
thus corresponds to the fourier-transformed pulse
response ff(t) whilst the signal Fo corresponds to the
fourier-transformed pulse response fo(t)~
A reciprocal value l/Ff of the signal Ff formed in a
unit 3.7 is multiplied by the signal Fo in a further
multiplying member 3.8 so that the signal Fo/Ff is
obtained which plays the part of a correction signal.
Phase and amplitude errors in the pulse compression can
be eliminated by means of this correction signal. In a
further multiplying member 3.9 the correction signal
Fo/Ff is multiplied by the fourier-transformed signal
Hf.
For pulse compression in the frequency domain the
signal Hi can be multiplied by the signal Sf in the
multiplying unit 2. If a pulse compression is to be
carried out in the time domain as well, the signal Hi
is fourier-transformed by an IFFT unit 3.10, thereby
obtaining the reference function hi(t).
A further generation of the reference function hi(t) of
the ideal filter is illustrated in Fig. 4. The signal
Sf(t) here corresponds to the replica of the
transmitted signal and thus contains all the phase and
amplitude errors which have occurred on transmission
and reception. The signal ho(t) corresponds to the
error-free reference function so(t) with a linear
frequency modulation. Signals Ho and Sf are generated
from the signals ho(t) and Sf(t) by the FFT units 4.1
and 4.2. The signal Ho is then supplied to an
intensity-forming unit 4.3, thereby obtaining the
signal Ho
7 211~13
-
A reciprocal value l/Ff of the signal Sf formed in a
1 unit 4.4 is multiplied by the signal Ho in a
further multiplying member 4.5, thereby obtaining a
fourier-transformed reference function Hi of the ideal
filter. An inverse fourier transformation may then be
carried out by an IFFT unit 4.~ ~o that at the output
of the IFFT unit 4.6 the reference function hi(t) of
the ideal filter is obtained for pulse compression in
the time domain.
~ith the aid of the block diagram in ~ig. 5 a pulse
compression will be described corresponding to the
theory of the optim~m filter. This pulse compression
is carried out by means of a convolution unit 5.1, the
input signal Sf(t) applied and the reference function
hf(t) of the optimum filter applied, as well as the
compressed output signal ff(t) of the convolution unit
5.1, each containing phase and amplitude errors. If
the phase and amplitude e~rors of the input signal
Sf(t) are known, a correction function hçorr(t) can be
determined by means of which these errors can be
eliminated in accordance with ~he concept of the ideal
filter. An error-free pulse response fo(t) càn then be
obtained by a further convolution unit 5.2 in which the
signal ff(t) applied is convoluted with the correction
functiOn hCorr(t)-
The following relationship can be derived from a
comparison of Figs. 1 and 5:
hi(t) = hf(t) ~) hkorr( ) '
8 2 110218
where ~ is the convolution operator. It can be
1 seen from the above equation that the reference
function hi(t) of the ideal filter contains two terms.
The first term hf(t) ensures the compression of the
reception signal Sf(t) in accordance with the theory of
the optimum filter and the second term is hCorr(t)~ ah
additional correction term by which phase and amplitude
errors are eliminated.
Hereinafter, with reference to Figs. 6 and 7 two
embodiments will be described for implementing the
method of generating the correction functions hCorr(t).
In a generating unit 6.1 the reference function hf(t)
of the optimum filter is generated, the reference
function hf(t) being determined from the conjugate
complex and time-inverted replica Sf(t~ of the
transmitted signal. The reference function hi(t~ of
the ideal filter is generated as described above with
the aid of the block diagrams of Figs. 3 or 4 and in
Fig. 6 is combined i~ a generating unit 6.4. The
signals hf(t) and hi(t) are fourier-transformed by FFT
units 6.2 and 6.5 so that the spectra Hf and Hi are
obtained at the output of said FFT units. In a unit
6.3 forming a reciprocal value the reciprocal value
l/Hf of the fourier-transformed signal Hf is formed.
The reciprocal value 1/Hf is multiplied in a further
multiplying unit 6.6 by the output spectrum Hi of the
FFT unit 6.5 and consequently at the output of the
multiplying unit 6.6 the signal Hi/Hf = HCorr is
present which is inversely fourier-transformed by an
IFFT unit 6.7 to give the correction signal hCorr(t)~
If a convolution operation is carried out in the time
domain by means of a time correlation by ~he
convolution unit 5.2, the signal hCorr(t) is taken from
the output of the IFFT unit 6.7 and supplied to said
convolution unit 5.2, the phase and amplitude errors
9 211021~
then thereby being eliminated. If the convolution
1 operation by the convolution unit 5.2 is carried out in
the frequency domain, the signal hCorr is taken from
the output of the mutiplying member 6.6 fo~ a spectral
multiplication by the fourier-tranformed signal of the
compressed erroneous signal ff(t) at the output of the
convolution uni~ 5.5. After spectral multiplication of
the signal hCorr by Ff an IFFT operation is carried
out, the error-free pulse response fQ(t) then once
again being obtained.
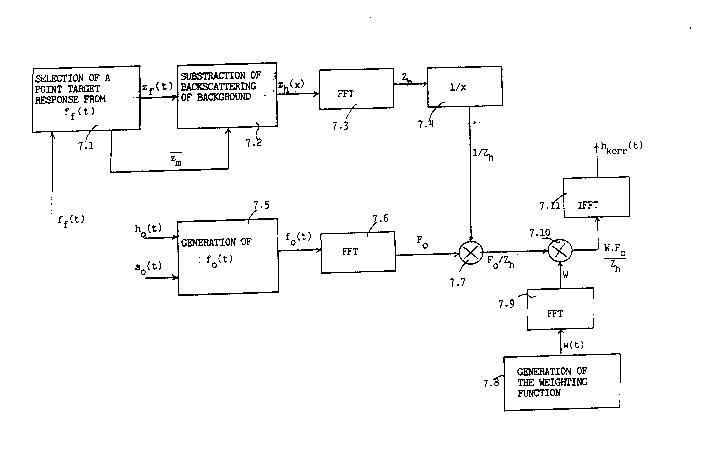
It may happen in some cases that the replica sf(t) of
the transmitted signal is not available. With the aid
of Fig. 7 a method will therefore be described with
which the correction function hCorr is determined from
a selected point target response Zf(t) of the erroneous
compressed signal ff(t). The selected point target
response must have a pronounced backscattering to
ensure that the backscattering of the background can be
neglected compared with the backscattering of the point
target response. If this condition is not fulfilled
the phase and amplitude errors cannot be taken from the
selected point target response. Experience ~ith
practical data have shown that the peak value of the
selected point target response must be at least 25 dB
above the mean value of the background backscattering
to enable the influence of the background to be
neglected.
Selection of the point target response may be carried
out automatically by a simple search method by checking
the 25 dB suppression of the background in the vicinity
of pronounced ~oint target responses. Such a search
method is carried out in a unit 7.1 in Fig. 7, thus
giving at the output thereof a selected point target
response Zf(t~ and the mean background backscattering
Zm In a su~traction unit 7.2 the calculated mean
background back~c~ring Zm is subtracted from the
lO 211021~
-
backscattering of the selected point target response
1 Zf(t) so that at the output thereof the signal Zh(t) is
available (Zh = Zf ~ Zm) This subtraction gives a
more exact determination of the actual pulse response
with phase and amplitude errors.
The signal Zh(t) is fourier-transformed to the
frequency domain by an FFT unit 7.3 and the reciprocal
value l/Zh is formed by a reciprocal-forming unit 7.4.
The error-free pulse response fo(t) required for
determining the correction function hCorr(t) is
generated by convolution of the error-free replica
so(t) of the transmitted signal sf(t) in the unit 7.5.
The nominal parameters of the frequency modulation of
the transmitted signal Sf(t) are employed to determine
so(t) whilst the reference functions ho(t) are
determined from the conjugate complex and time-inverted
function of the replica fo~t)~ The pulse response
fo(t) is fourier-transformed to the frequency domain by
an FFT unit 7.6 so that the signal Fo is available at
the output of the FFT unit 7.6. ~he signal Fo/Zh
playing the part of the fourier transformation of the
correction function hCorr(t~ is then present at the
output of a multiplying member 7.7 in which the signal
Fo is multiplied by the reciprocal value 1/Zh
The point target response Zf(t) having a limited number
of points was used to generate the signal Fo/Zh at the
output of the multiplying member 7.7. Due to the
limited number of points irregularities occur with
regard to the selected data set Zftt) and lead in the
signal Fo/zh to interference components with higher
frequency components. To reduce these irregularities a
weighting function w(t) is generated ih a unit 7.8, for
example in the form of a Hamming weighting, the point
number of the weighting function w(t) being the same as
that of the FFT operation in the FFT units 7.3, 7.6 and
7.9. By the FFT unit 7.9 the weighting function w(t)
11 211021~
,_
is fourier-transformed to the weighting function W
1 which is available at the output of the FFT unit 7.9.
In a multiplying member 7.1 the product of the
weighting function W and the signal Fo/Zh is formed so
that at the output thereof the actual fourier
transformation hCorr = W . Fo/Zh of the correction
signal is formed. By a further IFFT unit 7.11 the
correction signal hCorr(t) is generated in the time
domain. For eliminating the phase and amplitude errors
the correction signal hCorr(t) is applied to the
convolution unit 5.2.