Note: Descriptions are shown in the official language in which they were submitted.
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
STRESS STEERING STRUCTURE
Background Of The Invention
= This invention relates in general to structures
such as load bearing structures and more particularly to
structures that provide an enhanced trade-off between the
stress that can be safely carried in relation to the amount
of material required for the structure.
This enhanced strength to weight ratio is the
goal of a large number of designs including many of those
proposed and constructed by Richard Buckminster Fuller.
In most contexts where load bearing structures
are employed and especially in bridges and beams, in arches
and trusses, failure occurs because of a failure in
tension rather than in compression. Although the loads
imposed primarily induce compressive stress in the
material, that stress is resolved within the material by
vectors which introduce tension. For example, a bridge
subject to load on its upper surface will tend to deflect
in such a fashion as to introduce a tension along its lower
surface. Failure will occur because of a failure in
tension.
To compensate for this effect, rods or fibers
which are particularly strong in tension can be
incorporated. Multiple ply and laminated materials having
varied fiber orientation in different layers are frequently
employed to resist tension. In some materials and in
particular with ceramics, careful attention is paid to
1
CA 02203371 1997-04-22
WO 96/15332 PCTIUS95/13151
minimize grain boundaries where failure tends to appear.
Attention has been paid to developing materials
which have great tensile strength for use in load bearing
structures in such a way as to employ the tensile strength 5 of these
materials so that loads applied to the structure
will be resolved, at least in part, by the tension created
in these tension members. Such an approach is outlined in
the Buckminster Fuller U. S. Patent No. 3,354,591 issued in
1967. A more recent improvement on that structure is set
forth in U. S. Patent No. 4,207,715 issued in 1980. This
combination of tension and compression members is also
disclosed in the structure shown in U. S. Patent No.
4,711,062 issued in 1987.
As a general rule, most cost effective materials
of load bearing structures are far stronger in compression
than in tension. This is true of concrete, steel and
aluminum, for example. The design of structures using such
materials is widespread because of availability and
reasonable cost.
Accordingly, it is a major object of this
invention to provide a structure which has an improved
stress resolution performance using a material having
greater compression strength than tensile strength.
It is a related purpose of this invention to
provide an improved load bearing structure whose critical
failure point will be a function of its strength in
compression, rather than its strength in tension. 2
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
It is a further related purpose of this invention
to provide a load bearing structure which for a
predetermined failure point will require less material than
is currently required by known structures.
3
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Brief Description
This invention involves a unitary substance
having a uniformly spaced set of predetermined voids. The
voids are so spaced that stress is resolved within the 5 structure in a way
that minimizes the creation of tensile
stress.
These voids are deployed in a particular fashion,
uniformly throughout the structure, so that stress, which
cannot be transmitted through the voids, is resolved around
the voids in a fashion that minimizes the creation of
tensile stress.
For present purposes, consider this unitary
structure as if it were composed of a closely packed set of
rhombic dodecahedra (RD). A set of equal dimension rhombic
dodecahedra can be packed so as to completely fill the
space involved without any voids. Such a packing is what
is meant by referring to the set as a closely packed set.
Six of the vertices of the RDs are four edge vertices and
eight of the vertices are three edge vertices. If one now
truncates each of the six four edge vertices at
approximately the mid-point of the edges, one then obtains
a truncated rhombic dodecahedron (hereinafter TRD) which is
the basic solid unit for purposes of analysis of this
invention.
In one embodiment, the voids in the load bearing .
structures are the voids left by such a truncation of the
four edge vertices of the closely packed solid RDs.
4
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Obviously, the size of these hypothetical RDs can
vary appreciably. It is important that there be a large
number of hypothetical RDs so that there are a large number
of voids. The voids left by the truncated four edge
vertices will be uniformly spaced throughout the structure.
In order to visualize the above, it has to be
kept in mind that in a closely packed set of RDs, not only
are there no voids but adjacent RDs have coincident four
edge vertices and coincident three edge vertices. Thus a
truncation of the four edge vertices of closely packed RDs
cre4te. a void in the form of a cube.
Essentially, these cubic voids prevent the
resolutions of stress along the "imaginary" adjacent edges
of the RDs and require resolutions of stress through zones
which involve the "faces" of the adjacent RDs. The result
is that stress is resolved in a fashion that minimizes the
generation of tension.
Definitions
Rhombic Dodecahedron (RD).
The rhombic dodecahedron, like the cube, is a
space filling structure. That is, a set of identical
rhombic dodecahedra (RDs) can be stacked so as to
completely fill the space they encompass without any voids.
The RD has twelve rhombic surfaces; that is, all four.edges
of the rhombus are equal. It has twelve surfaces and
fourteen vertices. Six of the vertices are formed by four
5
CA 02203371 1997-04-22
WO 96/15332 PCTIUS95/13151
edges and eight of the vertices are formed by three edges.
One can consider a unitary substance to be composed of a
set of any arbitrarily sized, identical, closely packed,
rhombic dodecahedra. One can conceptually impose such a =
set on a unitary substance.
Truncated Rhombic Dodecahedron (TRD).
This is the term applied herein to the RD on
which the six four edge vertices of a space filling set of
conceptual RDs are truncated. Truncating each of the six
four edge vertices of each RD at approximately the mid
point of"the edge and removing the truncated portions from
the substance provides one-sixth of a cubic void. The six
voids at each point result in a set of cubic voids. These
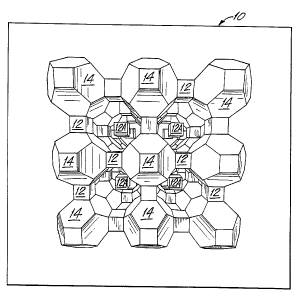
are the cubic voids 12 shown in FIGs. 1 and 2.
The truncation is preferably at the point on the
edge of the RD which provides a TRD in which all edges are
equal. FIGs. 4 and 5 illustrate two views of a TRD. The
TRD has twelve hexagonal faces and six square faces. The
ideal TRD has forty-eiqht equal edctes.. All vertices are
three edge vertices.
In the FIG. 1 structure described herein, one out
of four of the conceptually imposed TRDs are removed to
form the TRD voids 14.
6
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Matrix.
As used herein, the term "matrix of points"
refers to a set of points arranged in a three dimensional
fashion. The set of points are a three dimensional matrix
of points. It is useful herein to refer to the matrix of
points because of the relation of the voids to the points.
Both the voids 12 and the voids 14, are centered on these
matrix points.
It has to be kept in mind that the matrix of
points on which the cubic voids 12 are centered is a
different matrix than the matrix of points on which the TRD
voids 14 are centered. The matrices of points are not
orthogonal matrices. In an given matrix, the distance
between adjacent points is identical. The magnitude of
that distance can vary greatly.
A f irst matrix is def ined by the set of points
that constitute the four edge vertices of a set of closely
packed, space filling RDs.
A second matrix is defined by the set of points
that constitute the center points of the same set of
closely packed, space filling RDs.
7
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Size Of RD And TRD.
The RDs and TRDs referred to herein are not
specified in size. That is because a uriitary substance can
be mathematically divided into a closely packed set of
congruent RDs of any size. It is only important that the
size of the geometric RD be small enough so that a large
number, preferably hundreds, fit within the structure
constructed.
8
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Brief Description Of The Figures
FIG. 1 is a geometric perspective view of a
segment of the optimum void structure of a load bearing
substance of this invention. FIG. 1 shows members 12 of a
f irst set of voids as cubic voids and members 14 of a
second set of voids as truncated rhombic dodecahedra (TRD).
In reviewing FIG. 1, it helps to keep in mind that each TRD
void 14 has six square surfaces. Thus each TRD void is in
communication with six cubic voids. In addition, a certain
number of the cubic voids such as the voids 12A are not in
communication with any other void. in this FIG. 1
embodiment. All of the volume of the substance, except for
the voids shown, is filled with material of the substance
involved.
FIG. 2 is a geometric perspective representation
of a segment of a second embodiment of this invention in
which only the cubic voids 12 are retained and the
truncated rhombic dodecahedra voids 14 are omitted.
Accordingly, the space taken by the TRD voids 14 in FIG. 1
420 are filled in FIG. 2 with the material of the structure.
FIG. 3 is a perspective view showing a segment of
a preform that could be used to create the FIG. 2
structure. FIG. 3 shows only a single race of preform
elements 16. The actual preform, like the actual
structure, would have a three dimensional set of elements
16 to establish a three dimensional set: of voids 12 in the
structure.
9
CA 02203371 1997-04-22
WO 96/15332 PCTIUS95/13151
FIGs. 4 and 5 are perspective views of the
truncated rhombic dodecahedra which constitute the elements
of the second set of voids; such as the voids 14 shown in
FIG. 1.
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Description Of The Preferred Embodiments
The load bearing structure of this invention is
an appropriate substance 10, such as concrete, which is
preferably substantially unitary and which contains a
particular set of voids. It is found that this particular
set of voids causes such steering and i-esolution of induced
stress on the load bearing structure as to minimize the
development of tension in the substance involved. Thus a
material such as concrete which is strong.in compression
and weak in tension will withstand applied loads until it
fails in compression.
Some of the reasons why this desirable resolution
of forces occurs are discussed under the heading "Some
Theory Of Operation". At this point, the discussion herein
is for the purpose of teaching how to construct the
inventive structure.
It may help in visualizing the relationship
between the voids generated by this invention by
considering the rhombic dodecahedron (RD) as set forth in
the Definitions and then consider the truncated RD (TRD) as
set forth in the Definitions.
The hypothetical set of space filling RDs provide
a first matrix of points defined by the four edge vertices
of that set of RDs. The set of RDs with each four edge
' 25 vertex truncated provide a set of imaginary TRDs with
actual cubic voids. This is the set of voids 12
represented by FIG. 2 and the preform of FIG. 3.
The optimum arrangement is believed to be one in
11
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
which the hypothetical edges of the TRDs will be equal to
one another. This means that 46.41 percent of the edge
length extending from the four edge vertex is the point at
which truncation occurs. However, as long as there is a
meaningful void at these four edge vertices, the nature of
the stress resolution will tend to minimize the development
of tension.
It then turns out that one in four of these
hypothetical TRDs can be made as a void in order to create
the structure represented by FIG. 1.
This means that the structure shown in FIG. 1 has
four cubic voids 12 for each TRD void 14. This structure
provides the maximum reduction in the development of
tension. It does so with a minimum amount of material
required for the unitary substance.
One modification of the optimum arrangement shown
in FIG. 1 immediately commends itself and, from a practical
point of view, provides one of the preferred embodiments.
That is a modification that omits those cubic voids 12A
which are not in communication with the rest of the void
structure. This eliminates one out of every four cubic
voids 12. It is expected to have only a minimal impact on
the advantageous resolution of stress yet it would make the
construction of a preform much easier.
The FIG. 1 arrangement of voids with the omission
of the "floating" cubic voids 12A can be considered the
negative of a segment of a preform that could be used for
making a preferred embodiment.
12
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
The critical voids for guiding and resolving the
stress in the optimum fashion to reduce developing tension
in the material are the cubic voids 12. Thus the FIG. 2
embodiment is a further preferred embodiment. FIG. 2 is
the FIG. 1 arrangement with the TRD voids 14 eliminated.
That is, the TRD voids 14 are filled in with the material
of the structure. The FIG. 2 embodiment provides
essentially as optimum a resolution of forces as does the
FIG. 1 embodiment. However, it does so with a less
efficient use of material.
FIG. 3 illustrates a segment of a preform that
can be used to fabricate or mold the FIG. 2 embodiment.
Each cubic element 16 of the preform could be made of a
non-structural material that will not transmit force and
thus perform as if the void were air. The material of the
elements 16 can either be left in place in the structure,
as long as the material is less stiff than is the load
bearing material of the structure, or the elements 16 can
be volatilized after molding. It should be understood
herein that the term void means a zone through which forces
are not transmitted.
It should be noted that FIG. 1 leaves the
impression that deployment of the cubic voids 12 are in
some sort of orthogonal matrix and that the deployment of
the TRD voids 14 are also in some sort of orthogonal
matrix. That is an incorrect impression. It is an
inevitable consequence of illustrating these three
dimensional structures in two dimensional projection. What
13
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
has to be kept in mind is that the center point of each
cubic void is equally spaced from the center points of the
twelve cubic voids which surround any one cubic void. This
relationship applies to any cubic void that may be selected
throughout the structure.
Similarly, the center point of each TRD void 14
is spaced an equal distance from the center points of the
six TRD voids 14 that surround it. This relationship is
maintained throughout the structure.
Although an optimum design will place an
appropriately sized void at each matrix point, it should be
appreciated that to provide the appropriate resolution of
forces there must be a large number of voids 12 at matrix
points. The larger the number of matrix points encompassed
by voids 12, the better will the structures of this
invention operate. As long as there are a large number of
voids, the fact that some of the matrix points are not
encompassed by a void will only cause minor degradation in
the performance of the structures involved.
There is a continuum from an optimum performance
down to a lesser performance which is a function of how
many of the parameters of the optimum design are not fully
met. Those parameters include; (a) a void 12 at each
matrix point; (b) the size of the void 12, wherein the
optimum is a cube as defined herein; (c) the orientation of
the cubic voids and (d) the inclusion of the TRD set of
voids 14.
14
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
The cubic void 12 is of particular interest
because there appears to be some optimization of the
resolution of stress if the set of cubic voids are oriented
so that one of the corner to corner axes of each void 12 is
substantially perpendicular to the load bearing surface of
the structure involved. It is not clear how important it
is from a practical engineering point of view that this
orientation be sought. Experimentation with different
materials and marginal design should indicate how much
additional performance advantage will be obtained from such
orientation.
The Octetruss.
The octetruss taught by Buckminster Fuller, as
exemplified in his Patent No. 2,986,241 issued May 30,
1961, is a particular truss design in which an applied
force will resolve in a more favorable fashion than in
prior known structures. As a consequence, the framework
defined by an octetruss provides strength greater than
would be expected based on certain presumed resolutions of
forces. Although the analogy may not be complete,
Applicant believes that to some extent, the solid unitary
structure taught herein is one that can be analogized to an
octetruss in which the openings have been filled in except
for certain critical zones; namely the voids 12 of this
invention. These voids 12 assure that the transmission of
stress will provide an enhanced resolution that reduces the
development of tension in the structure. One reason the
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
analogy to the octetruss is limited is that the Fuller
design uses additional bars to obtain stability. The
stability of the design of this invention arises from the
fact that is a solid material 10 having only the voids 12,
14 deployed as explained herein. But to facilitate
thinking about some aspects of this invention, one can
consider it to be similar to an octetruss with very thick
bars.
Mixed Structures.
The stress steering structure of this
invention, which is a unitary substance 10 having the set
of voids described above, may be employed as a portion of
an overall construction or as a portion of a load bearing
structure. For example, the middle third of a beam might
be composed of the FIG. 1 or FIG. 2 structure thereby
greatly enhancing the functioning of the beam.
As another example, a beam, or other
structure, might be laminated out of a number of different
materials one or more of which are the structure of this
invention, thereby providing an enhanced laminated product
without necessarily incorporating the structure of this
invention throughout the entire product:.
The structure of this invention provides the
capability of creating an entire load bearing structure in
accordance with the teachings of this invention or the
capability of incorporating structural sub-units created in
16
CA 02203371 1997-04-22
WO 96/15332 PCTIUS95/13151
accordance with the teaching of this invention. The zones
of failure resulting in the highest concentration of
tension might be zones which are best replaced with the
structures of this invention.
Void Volume.
In an optimal design such as that shown in FIG.
1, approximately five (5.0) percent of the volume of the
structure is constituted by the cubic set of voids 12.
Further, in FIG. 1, 23.75 percent of the volume of the
structure is constituted by the second set of voids 14;
that is, one out of four of the TRDs are voids.
Accordingly, in the FIG. 1 structure, 28.75 percent of the
volume is voids. These void volume percentages for an
optimal design hold regardless of the predetermined
distance between matrix points.
One in four of the cubic voids 12 are floating
voids 12A. If the floating voids 12A are eliminated, the
percentage of the total volume that is constituted by cubic
voids is 3.75 percent and the percentage of the entire
structure that is constituted by voids 12 and 14 is 27.5
percent.
In the second embodiment, shown in FIG. 2, the
cubic voids optimally constitute five percent of the
material out of which the structure of this invention is
made. From a theoretical point of view, where the cubic
void is created so that all edges of the hypothetical TRD
17 -
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
have exactly the same length, the volume of these cubic
voids is 4.99815 percent.
As a practical matter, appreciable variation can
be had in the size and even in the shape of these voids
with relatively little degradation in the optimum
performance of structures built in accordance with the
teaching of this invention. That is, a substantial
variation in the size and shape of these voids can be
accommodated with only a minor reduction in the ability of
the, material to avoid developing tensile stress.
In general terms, any significant void around the
points which constitutes the center of the cubic voids 12
of FIGs. 1 and 2 will serve to prevent stress from being
transmitted through those points and will serve to guide
the stress in a fashion that minimizes generation of
tensile stress. Experimentation is required to show how
fast the drop off of performance will be as the size and
shape of these voids is changed. The precise selection of
void size and shape can be a function of the strength
required for the particular application.
In addition, some of the cubic voids 12 can be
omitted without serious degradation of performance. It is
contemplated that in one preferred practical embodiment,
approximately one-fourth of the cubic voids will be
eliminated; namely the floating voids 12A of the FIG. 1
embodiment. As long as there are a substantial number of
18
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
these voids 12 properly positioned at the matrix points,
the stress resolution as taught by this invention will be
achieved. The number of voids that can be omitted will be
a function of the requirements of particular applications.
What is important is that a sufficiently large number of
voids be in existence which are surrounded by other voids
such that there are at least twelve surrounding voids
equally spaced from the void under consideration. These
overlapping subsets of thirteen voids 12 are what provide
the stress resolution functioning of this invention. As
long as there are a substantial number of these overlapping
thirteen member subsets, the development of tensile stress
will be minimized.
Applicant believes that if the voids are all
precisely located to encompass each matrix point and are
equal in size, then the size of the voids may be
substantially reduced from the optimum size indicated in
this disclosure. Applicant believes that a set of voids,
each one of which is one-fifth the volume of the optimum
void size will provide a meaningful and useful embodiment
of this invention. Applicant believes that the appropriate
placement of the voids and the number of the voids is more
important than the size of the voids.
19
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Void Fill.
It is important that the voids not transmit
force. As used herein, the term void means a three
dimensional zone through which stress is substantially not
transmitted. The void can be filled with air or any
relatively soft material. What is a relatively soft
material is a function of the substance out of which the
load bearing structure is made. Essentially, as long as
the material in the void is substantially less stiff than
is the material of the load bearing structure, it will not
transmit substantial stress and the void will perform an
appropriate function of causing the stress to be properly
steered in accordance with this invention. More
particularly, if the slope of the initial linear portion of
a stress versus strain curve of the material in the void is
substantially less than the slope of the comparable portion
of the stress versus strain curve of the material out of
which the structure is made, then the void will operate as
a void in accordance with the requirements of this
invention. The preform of FIG. 3 can be made of a material
which is much less stiff than is the material of the
structure.
Some Theory Of Operation.
The above description of the invention suggests
certain aspects of why and how the invention operates. It
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
might aid in comprehension of this invention to state what
the applicant believes to be some of the reasons why this
invention works as it does.
Essentially, what is involved through the use of
the voids is a structuring of the mass so as to steer
stress generated in the structure when a load is applied to
the structure. The voids 12 prevent stress from going
through the first matrix of points. That first matrix of
points are the four edge vertices of a closely packed set
of RDs. The stress is channelled along the zone of the
mass and tends to be transmitted through the faces of these
geometrically defined RDs and thus, in part, through the
second set of matrix points.
Such transmission eventually results in a
steering of stress that provides an ultimate resolution of
stress in terms of compressive stress within the material
rather than tensile stress.
In broad general terms, it is believed that the
resolution of stress is constrained to follow paths
analogous to the paths that stress follows in a closely
packed set of spheres. A closely packed set of spheres is
a set of equal diameter spheres in which each sphere is
surrounded by twelve other spheres. In such an
arrangement, the spheres can only transmit compressive
forces through their contact points. Of course, the sphere
would fly apart if a force were applied to the set of
spheres. Thus conceptually one has to think of the set of
spheres as bounded by a barrier that prevents them flying
21
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
apart. Under those conditions, all stress is transmitted
within the barrier through the contact point of the spheres
as stress in compression. Applicant believes that the
arrangement of voids 12 at the first set of points which
define the first matrix, creates bridges through the
material which steers stress in an analogous fashion to a
closely packed set of spheres.
It might be noted that a closely packed set of
spheres contains a set of tetrahedral gaps and octahedral
gaps. The number of gaps are three times the number of
spheres. Two out of three of the gaps are tetrahedral gaps
and one out of three is a octahedral gap. The cubic voids
12 of this invention have the same geometric positional
relationship to one another as do the octahedral gaps in a
closely packed set of spheres. Thus the hypothetical set
of RDs can be considered to be a replacement for comparable
spheres in which the tetrahedral gaps have been filled in
and in which the octahedral gaps have been made into cubic
voids as taught by this invention. The steering and
resolution of stress through the material pathways in the
structure of this invention is one that has some similarity
to the manner in which stress is steered through the
contact points in a closely packed set of spheres. Stress
cannot be transmitted through the voids 12 (or the
octahedral gaps of the spheres) and thus is transmitted
along paths in which the stress is resolved by means of
compression rather than tension.
22
CA 02203371 1997-04-22
WO 96/15332 PCT/US95/13151
Applicant believes that the above provides a
partial explanation of what happens and at least give some
indication of the type of stress resolution involved in the
structure of this invention.
23