Note: Descriptions are shown in the official language in which they were submitted.
CA 02220107 2006-05-05
CONSTRUCTION OF A MULTICARRIER SIGNAL
1. Field of Invention
1.1 General field
The field of the invention is that of the transmission or broadcasting of
digital
data, or of analog and sampled data, designed to be received in particular by
mobile
receivers. More specifically, the invention relates to signals produced by
means of
new forms of modulation as well as the corresponding techniques of modulation
and
demodulation.
For many years now, it has been sought to build modulation schemes adapted
to highly non-stationary channels, such as channels for transmission towards
mobile
receivers. In such channels, the signal sent out is affected by phenomena of
fading and
multiple paths. The work carried out by the CCETT within the framework of the
European project EUREKA 147 (DAB: Digital Audio Broadcasting) has shown the
value, for this type of channel, of multicarrier modulation (MCM) and
especially of
OFDM (Orthogonal Frequency Division Multiplexing).
OFDM has been chosen within the framework of this European project as the
basis of the DAB standard. This technique can also be envisaged as a
modulation
technique for the broadcasting of television programs. However, it has been
observed
that there are a certain number of limitations (specified hereinafter) in
dealing with
the problem of modulation encoded with high spectral efficiency such as the
modulation required for digital television applications.
1.2 Possible applications
The invention can be applied in many fields, especially when high spectral
efficiency is desired and when the channel is highly non-stationary.
A first category of applications relates to terrestrial digital radio-
broadcasting,
whether of images, sound and/or data. In particular, the invention can be
applied to
synchronous broadcasting which intrinsically generates long-term multiple
paths. It
can also advantageously be applied to broadcasting toward mobile receivers.
CA 02220107 2006-05-05
2
Another category of applications relates to digital radiocommunications. The
invention can be applied especially in systems of digital communications at
high bit
rates with mobile receivers, in the framework for example of the UMTS (RACE
project). It can also be envisaged for high bit rate local radio networks (of
the
HIPERLAN type).
A third category of applications is that of underwater transmission. The
transmission channel in underwater acoustics is highly disturbed because of
the low
speed of transmission of acoustic waves in water. This leads to a major spread
of the
multiple paths and of the Doppler spectrum. The techniques of multicarrier
modulation, and especially the techniques that are an object of the present
invention,
are therefore well suited to this field.
2. Prior Art
2.1 Theoretical observations on the representation of the sib
Before presenting the signals according to the invention, a description is
given
here below of the known signals. This description is based on a general
approach to
multicarrier signals defined by the inventors. This approach is novel per se.
This
general approach has indeed no equivalent in the prior art and is no way
obvious to
those skilled in the art. It must therefore be considered to be a part of the
invention
and not as forming part of the prior art.
The signals of interest are real signals (an electrical magnitude for
example),
that have finite energy and are a function of time. The signals may therefore
be
represented by real functions of LZ(R). Furthermore, these signals are limited
band w
f _ W ~ Wl
signals and their spectrum is contained in c 2 ~ c + 2 , f~ being the "carrier
frequency" of the signal. It is therefore possible, in an equivalent manner,
to represent
a real signal a(t) by its complex envelope s(t) with:
s(t) - e-2i~ fit F,A~a~(t) (1)
where FA designates the analytical filter.
CA 02220107 2006-05-05
3
The signal s(t) belongs to a vector subspace (characterized by the band
limitation to ~ ~ ) of the space of the complex functions of a real variable
with a
summable square Lz(R). This vector space can be defined in two different ways,
depending on whether the construction is done on the field of the complex
values or
on the field of the real values. With each of these spaces, it is possible to
associate a
scalar product that takes values in C or in R to build a Hilbertian space. H
designates
the Hilbertian space built on the field of the complex values and HR
designates the
Hilbertian space built on the field of the real values.
The corresponding scalar values are written as follows:
~x y> = Jx(t)yi (t)dt in the case of H (2)
R
and
~x y~R = ~e Jx(t)y~ (t)dt in the case of HR (3)
R
The associated standards are obviously identical in both cases:
yz
(4)
ilxll = j x(t)Iz dt
R
2.2 General principles of the OFDM
The general principles of the OFDM are presented for example in the French
patent FR-86 09622 filed on 2 July 1986. The basic idea of the technique is
that of
transmitting encoded signals as coefficients of elementary waveforms that are
confined as far as possible in,the time-frequency plane and for which the
transmission
channel may be considered to be locally stationary. The channel then appears
to be a
simple multiplier channel characterized by the distribution of the modulus of
the
coefficients which follows a law of Rice or of Rayleigh.
CA 02220107 2006-05-05
4
Protection is then provided against fading phenomena by means of a code.
This code can be used in soft decision mode in association with time and
frequency
interleaving that ensures that the signals playing a part in the minimum
meshing of the
code are affected, to the utmost possible extent, by independent fading
phenomena.
This technique of encoding with interleaving in the time-frequency plane is
known as COFDM. It is described for example in the document [23] (see Appendix
1
(to simplify the reading, most of the prior art references are listed in
Appendix I . This
Appendix as well as Appendices 2 and 3 must of course be considered to be
integral
parts of the present description)).
There are two types of known OFDM modulation. The terms applied in the
literature are often ambiguous. Here we introduce new appellations that are
more
precise while recalling their correspondence with the exiting literature. We
shall use
the generic name OFDM followed by a suffix specifying the type of modulation
within this group.
2.3 OFDM/QAM
2.3.1 Theoretical principles
A first category of modulation is considered to be a multiplex of QAM
(Quadrature Amplitude Modulation) modulated carriers or possibly QPSK
(Quadrature Phase Shift Keying) modulated carriers in the particular case of
binary
data elements. Hereinafter, this system shall be called OFDM/QAM. The carriers
are
all synchronized and the carrier frequencies are spaced out in reverse to the
symbol
time. Although the spectra of these carriers overlap, the synchronization of
the system
makes it possible to ensure orthogonality between the symbols sent out by the
different carriers.
The references [1] to [7] give a good idea of the literature available on this
subject.
For greater simplicity in the writing, and according to the novel approach of
the invention, the signals will be represented by their complex envelope
described
CA 02220107 2006-05-05
here above. Under these conditions, the general equation of an OFDM/QAM signal
is
written as follows:
S(t) dam nxm n(t) (5)
m,n 7 7
The coefficients am," take complex values representing the data sent. The
functions xm,"(t) are translated into the time-frequency space of one and the
same
prototype function x(t):
1 if It < z0 / 2
x(t) = zo (6)
0 elsewhere
xm'n(tl = ea(z~mvor+~~x(t _ nZo) With voio =1 (~>
cp being any phase that can be arbitrarily set at 0. The function x(t) is
centered, namely
its first order moments are zero, giving:
jtlx(t)2dt= Jf X(.f)2df =~ (g)
X(f) designating the Fourier transform of x(t).
Under these conditions, it is observed that:
J t xm,n (t)I 2 dt = n zo
JJ l xm,n (~~ z dJ m v0 (9)
The barycenters of the basic functions therefore form a lattice of the time-
frequency plane generated by the vectors (i0, 0) and (0, vo), as shown in FIG.
1. This
lattice has a density of one, namely voio = 1. Reference may be made to the
article [9]
for a more detailed discussion on this subject.
The prototype function x(t) has the special characteristic wherein the
functions
{Xm ~} are mutually orthogonal and more specifically constitute a Hilbertian
base of
LZ(R), giving:
CA 02220107 2006-05-05
6
/, 1 if (m,n) _ (m',n')
\Xm,lll Xm..ll. ~ _
0 if not
(lo)
Projecting a signal on this basis is equivalent simply to breaking down the
signal into sequences with a duration of zo and representing each of these
sequences
by the corresponding Fourier series development. This type of breakdown is a
first
step towards a localization both in time and in frequency as opposed to the
standard
Fourier analysis which provides for perfect frequency localization with a
total loss of
temporal information.
Unfortunately, while the temporal localization is excellent, the frequency
localization is far less efficient owing to the slow decreasing function of
X(f). The
Balian-Low-Coifman-Semmes theorem (see [9], p. 976) furthermore shows that if
X
designates the Fourier transform of x, then tx(t) and fX(f) cannot
simultaneously be
summable squares.
2.3.2 The OFDM/OAM with euard interval
Generally, the tolerance of an OFDM modulation with respect to multiple
paths and Doppler spreading can be characterized by a parameter that
comprehensively measures the variation of the level of intersymbol
interference (II)
as a function of a temporal or frequency shift. The justification of this
concept is
given in Appendix 2. This tolerance parameter is called ~ and is defined by
the
relationship:
~=1/4~Ot~ f (11)
With:
Ot2 Jlx(t) Zdt = Jt2 x(t) Zdt (12)
0 X 2 2 X Zd (13)
By virtue of Heisenberg's inequality, ~ cannot exceed unity.
CA 02220107 2006-05-05
Given the Balian-Low-Coifman-Semmes theorem referred to here above, the
parameter ~ is equal to 0 for the OFDM/QAM. This is a major defect of the
OFDM/QAM modulation as described here above. This is characterized in practice
by
high sensitivity to temporal errors and consequently multiple paths.
This defect can be circumvented by the use of a guard interval described for
example in [5]. This is a device consisting in extending the rectangular
window of the
prototype function. The density of the lattice of base symbols is then
strictly smaller
than unity.
This technique is possible because an infinity of translated versions of the
initial symbol is found within a symbol extended by a guard interval. Of
course, this
works only because the prototype function is a rectangular window. In this
sense, the
OFDM/QAM with a guard interval is a unique and singular point.
OFDM/QAM modulation with guard interval is the basis of the DAB system.
This guard interval makes it possible to limit inter-symbol interference at
the cost of a
loss of performance since a part of the information transmitted is not really
used by
the receiver but is used only to absorb the multiple paths.
Thus, in the case of the DAB system, where the guard interval represents
25°/o
of the useful symbol, the loss is 1 dB. Furthermore, there is an additional
loss due to
the fact that to obtain a given comprehensive spectral efficiency, it is
necessary to
compensate for the loss due to the guard interval by a greater efficiency of
the code
used.
This loss is marginal in the case of the DAB system because the spectral
efficiency is low. On the contrary, if it is sought to obtain an overall
spectral
efficiency of 4 bits/Hz, it is necessary to use a 5 bit/Hz code giving,
according to the
Shannon theorem, a loss of the order of 3 dB. The total loss is therefore in
this case
about 4 dB.
CA 02220107 2006-05-05
2.3.3 Other OFDM/OAM systems
It is possible to conceive of other systems of the OFDM/QAM type.
Unfortunately, no filtered QAM modulation, namely one using a conventional
half
Nyquist (or more specifically "Nyquist square root") type of shaping verifies
the
requisite constraints of orthogonality. The known prototype functions
verifying the
requisite criteria of orthogonality are:
~ the rectangular window;
~ the cardinal sine.
These two examples are trivial and appear to be dual with respect to each
other
by the Fourier transform. The case of the rectangular window corresponds to
the
OFDM/QAM without guard interval. The case of the cardinal sine corresponds to
a
standard frequency multiplex (namely one where the carriers have disjoint
spectra)
with a 0% roll-off which is an asymptotic case that is difficult to achieve in
practice.
In each of these cases, it is observed that the prototype function is
perfectly
limited either in time or in frequency but has a poor decay (in 1/t or 1/f) in
the dual
domain.
The Balian-Low-Coifman-Semmes theorem furthermore leaves little hope that
there might exist satisfactory solutions. As indicated here above, this
theorem shows
that tx(t) and fX(f) cannot simultaneously have a summable square. There can
therefore be no hope of finding a function x(t) such that x(t) and X(f)
decrease
simultaneously with an exponent smaller than -3/2.
This furthermore does not rule out the possible existence of functions that
are
satisfactory from the viewpoint of an engineer. However, a recent article [10J
dealing
with this subject shows another exemplary prototype function having the
requisite
properties. The shape of the prototype function proposed in this article is
very far
from what may be hoped for in terms of temporal concentration. It is therefore
probable that there is no satisfactory OFDM/QAM type solution.
CA 02220107 2006-05-05
9
In conclusion, the OFDM/QAM approach corresponding to the use of a lattice
with a density 1 and complex coefficients am," can be put into practice only
in the case
of a rectangular temporal window and in the case of the use of a guard
interval. Those
skilled in the art seeking other modulations will therefore have to turn
towards the
techniques described here below under the designation of OFDM/OQAM.
2.4 OFDM/OOAM
A second category of modulations uses a multiplex of OQAM (Offset
Quadrature Amplitude Modulation) modulated carriers. Hereinafter, this system
shall
be called OFDM/OQAM. The carriers are all synchronized and the carrier
frequencies
are spaced out by half of the reverse of the symbol time. Although the spectra
of these
carriers overlap, the synchronization of the system and the choices of the
phases of
the carriers can be used to guarantee the orthogonality between the symbols
put out by
the different carriers. The references [11-18] give a clear picture of the
literature
available on this subject.
For greater simplicity in the writing, the signals are represented in their
analytical form. Under these conditions, the general equation of an OFDM/OQAM
signal be written as follows:
s(t) - ~ am,nxm,n (t) (14)
m,n
The coefficients a",," assume real values representing the data elements
transmitted. The functions xm," (t) are translated in the time-frequency space
of one
and the same prototype function x(t):
~(znmvat+rp)
xm," (t) = a x(t - n zo ) if m + n is even
xm n(t) =.l ef(2nmv~t+So)x(t-nzo) if m+n is odd (15)
with vo.io =1/2,
cp being any phase that can be arbitrarily set at 0.
The barycenters of the basic functions therefore form a lattice of the time-
frequency plane generated by the vectors (io, 0) and (0, vo), as shown in FIG.
2.
CA 02220107 2006-05-05
This lattice has a density 2. The functions xm,"(t) are mutually orthogonal
with
respect to the scalar product in R. In the known approaches, the prototype
function is
limited in frequency in such a way that the spectrum of each carrier overlaps
only that
of the adjacent carriers. In practice, the prototype functions considered are
even-order
functions (real or possibly complex) verifying the following relationship:
X(f)=0 if fl>_>o
X(f)IZ +IX(f -v)2 =1 / v if0<_f <_ o
( 16)
A possible choice for x(t) is the pulse response of half Nyquist filter with
I00% roll-off, namely:
cos ~ f to if I f I 5 v° (17)
0
0 elsewhere
When x(t) and its Fourier transform are observed, it is noted that X(f) has a
bounded support and that x(t) decreases in f2, i.e. this is a result
substantially better
than the theoretical limit resulting from the Balian-Low-Coifman-Semmes
theorem.
The elementary waveforms are better localized in the time-frequency plane than
in the
case of the OFDM/QAM, which gives this modulation a better behavior in the
presence of multiple paths and of Doppler phenomena. As above, it is possible
to
define the parameter ~ measuring the tolerance of the modulation to the delay
and to
the Doppler phenomenon. This parameter ~ is equal to 0.865.
3. Drawbacks of the prior art s, s
These known systems have many drawbacks and limits, especially in very
disturbed channels and when high efficiency is required.
3. I OFDM/QAM
The main problem of the OFDM/QAM system is that it imperatively requires
the use of a guard interval. As indicated here above, this gives rise to a
substantial loss
of efficiency when high spectral efficiency values are aimed at.
CA 02220107 2006-05-05
11
Furthermore, the signals sent out are poorly concentrated in the frequency
domain, which also limits the performance characteristics in the highly non-
stationary
channels. In particular, this spread makes it difficult to use equalizers.
3.2 OFDM/OQAM
Conversely, the frequency performance characteristics of the OFDM/OQAM
are rather satisfactory and the problem of the loss related to the guard
interval does
not arise. By contrast, the pulse response of the prototype function has a
relatively
slow temporal decrease, namely a decrease in 1/x2.
This implies two types of difficulties. First of all, it is difficult to
truncate the
waveform in a short interval of time. This implies complex processing in the
receiver.
Furthermore, this also implies possible systems of equalization.
In other words, the efficiency of the OFDM/OQAM techniques is greater than
that of the OFDM/QAM techniques, but these techniques prove to be more
complicated to implement and therefore costly, especially in receivers.
4. Presentation of the invention
4.1 Goals of the invention
It is an aim of the invention in particular to overcome these different
drawbacks and limitations of the prior art.
Thus, an aim of the invention is to provide a digital signal designed to be
transmitted or broadcast to receivers, that can be used to obtain better
performance
characteristics in non-stationary channels and especially in highly non-
stationary
channels.
The invention is also aimed at providing a signal of this kind that can be
used
to obtain high spectral efficiency.
Another aim of the invention is to provide a signal of this kind that avoids
the
drawbacks of the OFDM/QAM approach related to the guard interval while at the
CA 02220107 2006-05-05
12
same time preserving a temporal response of the prototype function that is as
concentrated as possible, in particular so as to simplify the processing at
the receiver.
The invention is also aimed at providing a signal of this kind enabling the
making of receivers with limited complexity and cost, especially as regards
demodulation and equalization.
An additional goal of the invention is to provide transmitters, receivers,
methods of transmission or broadcasting, methods of reception and methods for
the
construction, namely the definition, of a modulation corresponding to such a
signal.
4.2 Main characteristics of the invention
These aims as well as others that shall appear hereinafter are achieved
according to the invention by a multicarrier signal designed to be transmitted
to
digital receivers, especially in a non-stationary transmission channel,
corresponding to
the frequency multiplexing of several elementary carriers each corresponding
to a
series of symbols, two consecutive symbols being separated by a symbol time
io, a
signal in which firstly the spacing vo between two neighboring carriers is
equal to half
of the reverse of the symbol time io, and in which secondly each carrier
undergoes an
operation of filtering for the shaping of its spectrum having a bandwidth
strictly
greater than twice said spacing between carriers vo. This spectrum is chosen
so that
each symbol element is concentrated as far as possible both in the temporal
field and
the frequency field.
In particular, a signal of this kind may correspond to the following equation:
S'(t) -~am,n.xm,n (tl
m,n
where:
a,n,n is a real coefficient representing the signal source chosen in a
predetermined alphabet of modulation;
~ m is an integer representing the frequency dimension;
CA 02220107 2006-05-05
13
~ n is an integer representing the temporal dimension;
~ t represents time;
~ xm,n(t) is a basic function translated into the time-frequency space of one
and
the same even-order prototype function x(t) taking real or complex values,
namely:
xm'n(t) - +Zm+nef(z~rm vy+yo)x(t - nZ~ ) WltI1 V~Z~ =1 ~ 2
where cp is an arbitrary phase parameter,
~ the Fourier transform X(f) of the function x(t) having a support extending
beyond the interval [-vo, vo],
~ and where said basic functions {xm,"} are mutually orthogonal, the real part
of
the scalar product of two different basic functions being zero.
The symbol "t" indicates that xm,~(t) may, without distinction, take a
negative
sign or a positive sign. It does not of course mean that xm,n(t) takes both
values.
Thus, the invention is based on a system of modulation that uses prototype
functions that are as concentrated as possible in the time-frequency plane.
The value
of this approach is that of having available a modulation producing a signal
that
avoids the drawbacks of the OFDM/QAM related to the guard interval while at
the
same time preserving a temporal response of the prototype function that is as
concentrated as possible so as to simplify the processing at the receiver.
In other words, an object of the invention relates to novel systems of
modulation built, like the OFDM/OQAM modulation, on an orthogonal lattice with
a
density 2 without the prototype function thereby in any way being a function
with a
frequency-bounded support. Among the types of modulation proposed, there are
either modulations using prototype functions with time-bounded supports or
prototype
functions that are not bounded either in time or in frequency but on the
contrary have
CA 02220107 2006-05-05
14
properties of fast decrease both in time and in frequency and an almost
optimum
concentration in the time-frequency plane.
Signals of this kind are in no way obvious to those skilled in the art, in
view of
the prior art. As indicated here above, there are basically two modes of
construction of
OFDM Type modulations.
The first known mode of construction uses a lattice with a density 1. This
first
approach uses a base for the breaking down of the signals where every signal
is
subdivided into intervals, each interval being then broken down in the form of
a
Fourier series. This is the OFDM/QAM approach. The literature gives few
examples
of alternative approaches built on the same lattice, and the results obtained
are of little
practical interest [10].
Furthermore, the OFDM/QAM technique is the only one that can benefit from
the method of the guard interval. The OFDM/QAM approach is therefore a
singular
feature that permits no extension.
The second known mode of construction (OFDM/OQAM) uses a lattice with
the density 2. The orthogonality between symbols centered on one and the same
frequency or on adjacent frequencies is ensured by a shaping of the half
Nyquist
signals and by an appropriate choice of the phase of the signal. Finally, the
orthogonality beyond the adj acent frequencies is ensured by the fact that the
frequency bands do not overlap.
Consequently, it is not obviously easy to build new modulations that do not
verify this property.
All the variants of the invention described here below have the advantage of
using a prototype function either limited in the temporal domain or having a
fast
decrease so that the function can be easily truncated.
CA 02220107 2006-05-05
According to a first variant, said prototype function x(t) is an even-order
function that is zero outside the interval [-io,io], and verifies the
relationship:
x(t) = 0 if Itl >_ zo
ix(t)IZ + Ix(t - zo )I2 =1 / zo if 0 <_ t _< zo
Advantageously, said prototype function x(t) is defined by:
1
cos ~ct/2zo if ItI <_ zo
x(t) - zo
0 elsewhere
In the first case (hereinafter called OFDM/MSK), the performance
characteristics in terms of resistance to the Doppler phenomenon and to the
multiple
paths are equivalent to the OFDM/OQAM modulation, and the making of the
receiver
is simplified.
According to a second variant of the invention, said prototype function x(t)
is
characterized by the equation:
x(t) = Y(t)
z
zo ~ Y(t - kzo
k
the function y(t) being defined by its Fourier transform Y(f):
G(f)
Y(f ) _
vo~~G(.f -kvo)2
k
where G(f) is a normalized Gaussian function of the type: G( f ) _ (2a)'~4 e-
"afZ
a being a strictly positive real parameter and k varying from -oo to +oo .
Advantageously, the parameter a is equal to unity. The corresponding
modulation is hereinafter called OFDM/IOTA. In this case, the corresponding
prototype function referenced 5 is identical to the Fourier transform.
CA 02220107 2006-05-05
16
The making of the receiver is simpler than in the case of the OFDM/OQAM,
although slightly more complex than in the previous case, but the performance
characteristics are substantially higher.
The invention also relates to a method for the transmission of a digital
signal
especially in a non-stationary transmission channel, comprising the following
steps:
~ the channel encoding of a digital signal to be transmitted, delivering real
digital coefficients am,n chosen out of a predetermined alphabet;
~ the construction of a signal s(t) meeting the equation defined here above;
~ the transmission of a signal, having said signal s(t) as its complex
envelope, to
at least one receiver.
Advantageously, a method of this kind furthermore comprises a step of
frequency and/or time interleaving applied to the binary elements forming said
digital
signal to be transmitted or to the digital coefficients am,n.
This makes it possible to provide for optimal performance characteristics in
the non-stationary channels.
The invention also relates to the transmitters of a signal of this kind.
The invention also relates to a method for the reception of a signal as
described here above, comprising the following steps:
~ the reception of a signal having, as its complex envelope, a signal r(t)
corresponding to the signal s(t) at transmission;
~ the estimation of the response of the transmission channel comprising an
estimation of the phase response Am," and of the amplitude response pm,~;
~ the demodulation of said signal r(t) comprising the following steps:
~ the multiplication of said signal r(t) by the prototype function x(t);
CA 02220107 2006-05-05
17
~ the abasing of the filtered waveform modulo 2io;
~ the application of a Fourier transform (FFT);
~ the correction of the phase 6m," induced by the transmission channel;
~ the correction of the phase corresponding to the term lm+°;
~ the selection of the real part of the coefficient obtained a",,n
corresponding to
the coefficient am," transmitted weighted by the amplitude response pm," of
the
transmission channel.
Preferably, this reception method comprises a step for the frequency and/or
time de-interleaving of said real digital coefficients am,n and, possibly, of
the
corresponding values pm,~ of the amplitude response of the channel, said de-
interleaving being the reverse of an interleaving implemented at transmission
and/or a
step of weighted-decision decoding that is adapted to the channel encoding
implemented at transmission.
The invention also relates to the corresponding receivers.
Finally, the invention also relates to a preferred method for the construction
of
a prototype function x(t) for a signal as described here above comprising the
following steps:
~ the selection of a normalized Gaussian function G(f) of the type:
G(~ _ (2a)va e-~arz ;
~ the determining of said prototype function x(t) such that:
y(t)
x(t) _
Z
z° ~ I y(t - kzo )I
k
~ the function y(t) being defined by its Fourier transform Y(f):
CA 02220107 2006-05-05
18
G
vo~ G~.f - kvo)Iz
k
This method makes it possible in particular to define the prototype function
5, described here above.
5. Descr~tion of~articular embodiments of the invention
5.1. List of Figures
FIG. 1 illustrates a lattice with a density 1, corresponding to the one
implemented in the case of the known OFDM/QAM modulation;
FIG. 2 illustrates a lattice with a density 2, corresponding to the one
implemented in the case of the known OFDM/OQAM modulation, and in the case of
the invention;
FIGS. 3A to 3D, 4C to 4D, 5A to SD, 6A to 6D and 7A to 7D respectively
show the known OFDM/QAM modulation (3), OFDM/QAM modulation with guard
interval (4), OFDM/OQAM modulation (5) and the types of modulation used in the
invention namely OFDM/MSK modulation (6) and OFDM/IOTA modulation (7),
according to the following aspects:
~ A: the prototype function x(t);
~ B: the linear Fourier transform of the prototype function;
~ C: the modulus of the linear ambiguity function (as defined in Appendix 2);
~ D: the intersymbol function (as defined in Appendix 2);
FIG. 7E shows the decrease of the signal OFDM/IOTA in logarithmic scale;
FIG. 8 shows the ambiguity function of a Gaussian function;
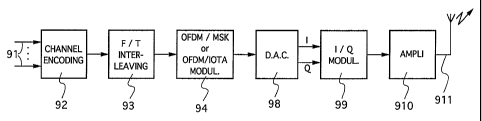
FIG. 9 is a block diagram of a transmitter (and of a corresponding
transmission method) that can be used according to the invention;
FIG. 10 is a block diagram of a receiver (and to the corresponding reception
method) that can be used according to the invention;
FIG. 11 gives a more precise view of the method of the modulation
implemented in the receiver of FIG. 10.
CA 02220107 2006-05-05
19
5.2. Main theories of the si , als according to the invention
All the basic signals of the OFDM/OQAM defined in (15) can be rewritten in
the following form:
'xm,n(t)=+im+ne2ismvotx(t-nTp) wlth VETO =1/2 (1g)
The barycenters of the basic functions therefore form a lattice of the time-
frequency plane generated by the vectors (~0,0) and (O,vo) (see FIG. 2). This
lattice has
a density of 2, namely voio = 1/2. As indicated in [16], these functions
constitute a
Hilbertian basis of HR. In order to simplify the writing, we shall hereinafter
omit the
sign reversals.
In general, it is sought to have conditions on x(t) so that the group {Xm,n}
constitutes a Hilbertian basis of HR. It is laid down that x(t) should be an
even-order
function. The scalar product of xm," and of x",~,"~ can be written a follows:
C.xm n Ixm',n' ~ - ~.e f Z (m m')+(n n')e2iA(m-m')vot x(t - n Zo ~x * (t - n~
T~ ?Cl~~ (19)
R
namely, by assuming t'=t-(n+n) rd2 and z'o=(n-n) ro:
Cxm'n ~xm'n~ ~ R
=~e~Ji(m-m')+(n-n')e2itr(m-m')(n+n')vorol2e2in(m-m')vot'x(t'-
Z,~~2)x*(t'+z'o2~dt,~ (20)
_ ~.e~l(m m')+(n-n')i(m-m')(n+n') j even function + i odd function,
The o'rthogonality is therefore obtained if the coefficient of the integral is
a
pure imaginary number. The analysis of this coefficient shows that it is
enough for
this purpose for m-m' or for n-n' to be an odd number.
The lattice can therefore be split up into four sub-lattices, as can be seen
in
FIG. 2 ({m even number, n even number}, {m even number, n odd number}, {m odd
number n even number}, {m odd number, n odd number}) which are mutually
orthogonal (any function of one of the sub-lattices is orthogonal to any
function of
another sub-lattice). A sufficient condition in order that {xm,n} may
constitute a
Hilbertian basis is therefore that:
xm,nl xm',n'> = 0 d m - m' even, 'd n - n' even, (m, n) ~ (m', n' ) (21)
R
CA 02220107 2006-05-05
It is therefore enough to find an even-parity function x(t) such that the
functions of the type:
xZ,n 2n (t) = e4"""va 'x(t - 2n za ) (22)
are mutually orthogonal with respect to the scalar product in R. Furthermore,
if such
is the case, these functions are also orthogonal with respect to the scalar
product in C,
for reasons of symmetry similar to those referred to here above. Another way
of
expressing this condition is to use the function of ambiguity of x [19]:
Ax(z, v) = f x(t + z l 2)x * (t - z l 2)e-z""''dt (23)
It is then enough to find an even order function x(t) such that:
Ax (2nzo,2mvo) = 0 ,d(m,n) ~ (0,0) (24)
If the problem thus raised is compared to that of finding a Hilbertian basis
with respect to the scalar product in C, the constraints of orthogonality are
substantially lower since the lattice concerned is half as dense. Indeed, the
basic
functions are centered on the points of the lattice ~2m vo,2nzo } , namely a
lattice with
a density of 1/2. The reasons for the inapplicability of the Balian-Low-
Coifman-
Semmes theorem therefore can be seen here in an intuitively evident manner.
In the case of the OFDM/OQAM approach, the orthogonality of the functions
x2m,2n(t) with respect to one another is obtained by two constraints of
different natures.
Indeed, if m ~ m', Cxz~2n ~xzm,z"~ > is zero because these functions have
disjoint
spectra. Furthermore, ~xz~zn ~ xz~,zn~ > is zero because X(f) has a half
Nyquist type
shaping.
As can be seen in the abundant literature already referred to, those skilled
in
the art consider it imperative to verify these two constraints. In particular,
they are of
the view that the prototype function must be one with a frequency-bounded
support.
CA 02220107 2006-05-05
21
5.3. General principles of the invention
The invention is based on a wholly novel approach to the multicarrier signals
of the OFDM/OQAM type. According to this novel approach orthogonality is
obtained no longer by respect for the two constraints mentioned here above but
by a
specific definition of the prototype functions.
In other words, an object of the invention is new signals based on systems of
modulation built like the OFDM/OQAM modulation on an orthogonal lattice with a
density of 2 without this implying that the prototype function is in any way
one with a
frequency-bounded support.
The principle used is that of building orthogonal lattices with a density 1/2
and
then deducing therefrom lattices with a density of 2 by a judicious choice of
the
phases of the signals.
Very many signals may be constructed according to the technique of the
invention. Two non-restricted examples of such signals are given here below,
respectively called OFDM/MSK and OFDM/IOTA. A particular method for building
such signals is also given by way of a non-exhaustive example in Appendix 3.
This
method of course forms part of the invention and has been put in an appendix
only to
simplify the reading of the present description.
5.4. OFDM/MSK modulation
Here we consider a new modulation built according to the same generic
equation as the OFDM/OQAM modulation (equations 14 and 15), but using a
different prototype function. It shall be called OFDM/MSK because each carrier
is
MSK modulated [20]. The prototype function is written as follows:
I cos ~t/zo if Itl <_ zo
(25)
x(t) - zo
0 elsewhere
In fact, it is observed on an a posteriori basis that this modulation can be
considered as being dual with respect to the OFDM/OQAM because it corresponds
to
CA 02220107 2006-05-05
22
an exchange of the time and frequency axes. The essential value of this
modulation
with respect to the OFDM/OQAM is that the prototype function is strictly
limited in
time. This particularly simplifies the implementation of the receiver since
the number
of coefficients of the input filter is considerably reduced. Furthermore, the
performance characteristics in the presence of multiple paths are unchanged,
the
parameter ~ being identical.
5.5. The IOTA modulation
The OFDM/IOTA modulation on the contrary results from a totally novel and
original approach to the field of signal processing that we have named the
IOTA
(Isotropic Orthogonal Transform Algorithm) transform, described in Appendix 3.
5.5.1. Equation of the signal
Here we shall consider a new modulation built according to the same generic
equation as the OFDM/OQAM modulation (equations 14 and 15), but on the basis
of
a different prototype function. It shall be named OFDM/IOTA owing to the
choice of
the prototype function. The prototype function is written as follows:
'x~t) - 2 va 1 z ~~t l To ~) (26)
s designing the function IOTA defined in Appendix 3.
It will be noted that the building method given in Appendix 3 can be used to
obtain an infinity of solutions, the function IOTA constituting a remarkable
solution.
The basic functions of the OFDM/IOTA modulation are therefore written as
follows:
~m,n(t) - 2114 n2 e2immvot~( ~ _ n) / ~) with vozo =1 / 2 (27)
'''l o
The transmitted signal can therefore be written as follows:
s(t) _ ~ am n..Sm n (t) (2g)
m,n
with:
am,n _ ~Jie Js(t) sm,n(t)dt (29)
CA 02220107 2006-05-05
23
5.5.2. Comments on the figures and advantages related to raid decrease
In order to highlight the advantages of the invention in a visual manner, the
following are presented for each modulation discussed here above:
~ A: the prototype function x(t);
~ B: the linear Fourier transform linearly of the prototype function;
~ C: the modulus of the linear ambiguity function (as described in Appendix
2);
~ D: the intersymbol function (as defined in Appendix 2).
The views shown of the ambiguity function (figures referenced C) enable the
judgment of the confinement of the prototype function in the time-frequency
plane.
The views shown of the intersymbol function (figures referenced D) enable an
appreciation of the sensitivity of a modulation to delay and to the Doppler
phenomenon. The phase errors are not considered since all the modulations are
equivalent in this respect.
FIGS. 3A to 3D relate to the known case of the conventional OFDM/QAM
modulation. The main defect of this modulation is not, as might be suggested
by the
frequency response of the prototype function, the slow decrease of the level
of the
minor lobes.
Indeed, the sensitivity of the OFDM to the frequency errors is only slightly
greater than that of the other types of considered. By contrast, the II has a
different set
of statistical values expressed by a horizontal closing of the eye equivalent
to that of a
modulation with a zero roll-off. There therefore exist traces, which are
admittedly
improbable but could create systematic errors when there is no coding. This
detail is
an unesthetic one but is of no real consequence in the presence of coding. By
contrast,
this slow decrease means that the II energy is distributed over a large number
of
neighboring symbols, which makes any attempt at equalization difficult.
CA 02220107 2006-05-05
24
Paradoxically, the real problem comes from the sudden truncation of the
temporal response which corresponds to an ambiguity function that is
triangular along
this axis. This gives an intersymbol function with very high sensitivity to
the temporal
errors: the slope is vertical and the parameter ~ is therefore zero. This is
what warrants
the use of a guard interval.
FIGS. 4C and 4D relate to the OFDM/QAM modulation with a guard interval
(the prototype function and Fourier transform are identical to those of the
OFDM/QAM illustrated in FIGS. 3A and 3C. The use of a guard interval creates a
flat
zone at a level of the ambiguity function. In fact, the term that ought to be
used in this
case is rather that of "cross-ambiguity". Obviously, this flat part is found
at the
intersymbol function, giving immunity to temporal errors. The figures show the
case
of a guard interval 0.25 i0.
At the level of the frequency errors, the properties are the same as those of
the
standard OFDM.
The cost of the guard interval is acceptable when the field of interest
concerns
modulations with low spectral efficiency. On the contrary, it becomes
prohibitive if it
is sought to have high spectral efficiency: let us take for example a guard
interval
equal to a quarter of the useful symbol. Under these conditions, in order to
have a net
efficiency of 4 bits/s/Hz, it is necessary to have a system of modulation and
encoding
with a rough efficiency of 5 bits/s/Hz, giving a loss of 3 dB with respect to
Shannon's
limit capacity. And moreover, to this loss it is necessary to add an
additional loss of 1
dB due to the power that is "unnecessarily" transmitted in the guard interval.
In all
therefore, it is 4 dB that are lost with respect to the optimum.
FIGS. 5A to SD present the case of the OFDM/OQAM.
The temporal response of the OFDM/OQAM has a better shape than that of
the OFDM/QAM. Nevertheless, the temporal decrease will be only in 1/t2. The
ambiguity function is cancelled out on a lattice with a density I/2. The
sensitivity to
CA 02220107 2006-05-05
frequency errors is greater than that to temporal errors. The parameter ~ is
equal to
0.8765.
FIGS. 6A to 6D relate to the first embodiment of the invention corresponding
to the OFDM/MSK modulation. It is ascertained that it has properties strictly
identical
to those of the OQAM in reversing the temporal and frequency scales. The
parameter
~ is unchanged.
Finally, FIGS. 7A to 7D present the OFDM/IOTA modulation. This
modulation has a fast decrease (in the mathematical sense of the term) in time
and in
frequency, thus enabling equalization with the greatest possible efficiency.
It furthermore has perfect symmetry with respect to these two axes. Its
intersymbol function is almost ideal. In general, its behavior approaches that
of a
Gaussian function. The parameter ~ is equal to 0.9769.
The ambiguity function of the function 5 (FIG. 7C) can be compared with
that of a Gaussian function as illustrated in FIG. 8. The general shape of
these two
functions is very similar at the peak. On the contrary it is different at the
base.
FIG. 7E gives a view in a logarithmic scale of the decrease in time of the
IOTA signal. It can be seen that the amplitude of the signal decreases
linearly in
logarithmic scale (in time and frequency of course since the two aspects are
identical),
namely exponentially in terms of linear scale. This property therefore makes
it
possible, in a practical embodiment, to truncate the waveform and thus limit
the
complexity of the receiver.
5.6. Principle of a transmitter
FIG. 9 shows a simplified block diagram of a transmitter of a signal according
to the invention. The method of transmission is deduced therefrom directly.
A binary source with a high bit rate (typically some tens of megabits/s) is
considered. The term binary source is understood to mean a series of data
elements
CA 02220107 2006-05-05
26
corresponding to one or more sampled, digital or analog source signals 91 of
all types
(sounds, images, data). These binary data elements are subjected to a binary-
to-binary
channel encoding 92 adapted to fading channels. It is possible for example to
use a
trellis coded modulation possibly concatenated with a Reed-Solomon code. More
specifically, if a spectral efficiency of 4 bits/Hz is desired, it is possible
to use a code
with an efficiency of 2/3 associated with an 8AM modulation taking eight
amplitude
levels.
Then, according to the principle explained in the patent FR-88 15216, these
encoded data elements are distributed (93) in the time-frequency space so as
to
provide the necessary diversity and decorrelate the Rayleigh fading that
affects the
symbols transmitted.
More generally, a first binary-to-binary encoding, a time and frequency
interlacing and a mapping operation are carried out. It is clear that the
interlacing may
be done without distinction before or after the mapping depending on the needs
and
the codes used.
At the end of this encoding operation, there are real symbols to be
transmitted
am,". The principle of the making of the OFDM/MSK or OFDM/IOTA modulator 94
is similar to that of an OFDM/OQAM transmitter. Only the prototype waveform
differs. Reference may be made to [15] for a detailed description of the
modulation
system. To build the signal to be transmitted, the symbols of the same order n
are
grouped together, and the following is computed:
.S(t) ~Clm,n.xm,n (t) ~ ~ Clm,nlm+ne2i~rmvatx(t - ylZ~ ) (3~)
m,n n m
This operation may advantageously be done digitally by a fast Fourier
transform (FFT) relating to all the symbols of the same order n, followed by a
multiplication of the resultant waveform by the prototype function IOTA and
finally
by an addition of the symbols of different ranks (summation according to the
index n).
CA 02220107 2006-05-05
27
The complex signal thus generated is then converted into analog form 98 and
then transposed to the final frequency by a two-channel quadrature modulator
99 (I &
Q modulator) and finally amplified 910 before being transmitted 911.
5.7. Principle of a receiver
FIG. 10 gives a schematic illustration of a receiver of a signal according to
the
invention (as well as the corresponding reception method).
The OFDM/MSK or OFDM/IOTA receiver is substantially similar to the one
adapted to the OFDM/OQAM modulation. The input stages are conventional. The
signal is preamplified 101 and then converted into intermediate frequency 102
in
order to obtain the channel f Itering 103. The intermediate frequency-signal
is then
converted into baseband at 105 on two channels in quadrature. In addition, the
automatic gain correction (AGC) functions 104 are performed. These AGC
functions
control the preamplification 101.
Another solution consists in transposing the intermediate frequency signal to
a
low carrier frequency so as to sample the signal on a single channel, the
complex
representation being then obtained by digital filtering. Alternately, the RF
signal may
be transposed directly into baseband (direct conversion), the channel
filtering being
then done on each of the two channels I & Q. In every case, it is possible to
return to a
discrete representation of the signal of the complex envelope corresponding to
the
received signal.
In order to provide a detailed description of the digital processing in
baseband,
we shall consider a multicarrier type modulation characterized by the equation
of the
complex envelope of the transmitted signal:
s(t) _ ~ Qm.~xm,"(t) (31)
m,n
Let us take a transmission channel characterized by its variable transfer
function T(ft) (see Appendix 2). The complex envelope of the received signal
r(t) is
written as follows:
CA 02220107 2006-05-05
28
r(t) = js(f )T (f ~ t)e2;~~, d f (32)
The demodulator estimates (106) the transfer function T(ft) by conventional
means which for example may use a reference lattice of explicit carriers
according to
the patent FR-90 01491. To demodulate the signal proper (107), the channel is
likened
locally to a multiplier channel characterized by an amplitude and a phase
corresponding to the value of T(ft) for the instant and the frequency
considered. To
estimate am,"(t), the received signal is therefore identified with the signal:
r (t) = JS( f )T(m vo, nzo )ez"'f 'df = T(m vo, nzo )s(t) (33)
It shall be supposed that:
T(m vo,nzo) = pm,ne'8~,.~ (34)
The demodulator therefore performs the following processing operation:
n = ~e ~~(t)e-iBm.~ x *m n ~t)dt (35)
In the case of a stationary channel with a transfer function pe'e, the
following
is found obviously:
Clm,n - Pam,n (36)
In practice, the processing 107 is performed in digital form according to the
method shown in FIG. 11. The receiver works similarly to an OFDM/OQAM receiver
[13-16]. It performs the following processing operations:
~ multiplication 111 of said received signal r(t) by its prototype function
x(t)
112;
«aliasing» 113 of the filtered waveform modulo 2io ;
~ application 114 of a Fourier transform (FFT);
~ correction 115 of the phase 0m," as a function of the estimation of the
channel
116, comprising for example an estimation pm," of the amplitude response and
an estimation 0m,n of the phase response of the transmission channel;
CA 02220107 2006-05-05
29
~ correction 117 of the phase corresponding to the term lm+", the data
elements
being alternately in phase and in quadrature;
~ the selection 118 of the real part of the coefficient obtained a",,"
corresponding
to the transmitted coefficient Cln,,n weighted by the amplitude response p~,,~
of
the transmission channel.
This algorithm therefore enables the comprehensive computation of all the
coefficients of a given index n. The magnitude of the corresponding complexity
is
approximately twice that of the algorithm used for the OFDM/QAM.
The coefficients thus obtained are then de-interlaced 108, symmetrically with
the interlacing implemented at transmission, and then decoded 109
advantageously
according to a soft decision decoding technique implementing for example an
algorithm of the Viterbi algorithm type. If the channel decoding takes account
of the
estimation of the response of the amplitude of the channel pm,n, the
corresponding
values are also de-interlaced 110. Furthermore, the de-interlacing is of
course
performed before or after the mapping depending on the point in time when the
interlacing has been carried out at transmission.
CA 02220107 2006-05-05
APPENDIX 1: REFERENCES
[1] M. L. Doeltz, E. T. Heald and D.L. Martin, "Binary data transmission
techniques for linear systems" Proceedings of the IRE, pp. 656-661, May 1957.
[2] R. R. Mosier, "A data transmission system using pulse phase modulation"
IRE Conv. Rec. Ist Nat'1 Conv Military Electronics (Washington, D.C., Jun. 17-
19,
1957) pp. 233-238.
[3] G. A. Franco and G. Lachs, "An orthogonal coding technique for
communications" 1961 IRE Internat'1 Conv. Rec., vol. 9, pp. 126-133.
[4] H. F. Harmuth, "On the transmission of information by orthogonal time
functions" AIEE Trans. (Communications and Electronics) vol. 79, pp. 248-255,
July
1960.
[5] S. B. Weinstein and Paul M. Ebert, "Data transmission by frequency-
division multiplexing using the discrete Fourier transform" IEEE Trans.
Commun.,
vol. COM-19, pp. 628-634, October 1971.
[6] L. J. Cimini, "Analysis and simulation of a digital mobile channel using
orthogonal frequency division multiplexing," IEEE Trans. Commun., vol. COM-33,
pp. 665-675, July 1985.
[7] E. F. Casas and C. Leung, "OFDM for data communication over mobile
radio FM channels--Part I: Analysis and experimental results" IEEE Trans.
Commun.,
vol. 39, pp. 783-793, May 1991.
[8] E. F. Casas and C. Leung, "OFDM for data communication over mobile
radio FM channels--Part II: Performance improvement"IEEE Trans. Commun., vol.
40, pp. 680-683, April 1992.
[9] I. Daubechies, "The wavelet transform, time-frequency localization and
signal analysis" IEEE Trans. Inform. Theory, vol. IT-36, pp. 961-1005,
September
1990.
[10] H. E. Jensen, T. Hoholdt, and J. Justesen, "Double series representation
of
bounded signals" IEEE Tranr. Inform. Theory, vol. IT-34, pp. 613-624, July
1988.
[11] R. W. Chang, "Synthesis of band-limited orthogonal signals for multi-
CA 02220107 2006-05-05
31
channel data transmission" Bell Syst. Tech. J., vol. 45,.pp. 1775-1796,
December
1966.
[12] B. R. Saltzberg, "Performance of an efficient parallel data transmission
system" IEEE Trans. Commun. Technol., vol. COM-15, pp. 805-811, December
1967.
(13] R. W. Chang, "A theoretical study of performance of an orthogonal
multiplexing data transmission scheme" IEEE Trans. Commun. Technol., vol. COM-
16, pp. 529-540, August 1968.
[14] B. Hirosaki, "An analysis of automatic equalizers for orthogonally
multiplexed QAM systems" IEEE Trans. Commun., vol. COM-28, pp. 73-83, January
1980.
[15] B. Hirosaki, "An orthogonally multiplexed QAM system using the
discrete Fourier transform" IEEE Trans. Commun., vol. COM-29, pp. 982-989,
July.
1981.
(16] B. Hirosaki, "A maximum likelihood receiver for an orthogonally
multiplexed QAM system" IEEE Journal on Selected Areas in Commun., vol. SAC-
22, pp. 757-764, September 1984.
[17] B. Hirosaki, S. Hasegawa, and A. Sabato, "Advanced group-band modem
using orthogonally multiplexed QAM technique" IEEE Trans. Commun., vol. COM-
34, pp. 587-592, June. 1986.
[18] John A. C. Bingham, "Multicarrier modulation for data transmission: An
idea whose time has come" IEEE Communications Magazine, pp. 5-14,. May 1990.
[19] P. M. Woodward, "Probability and information theory with application to
radar" Pergamon Press, London 1953.
[20] F. Amoroso and J. A. Kivett, "Simplified MSK signalling technique"
IEEE Trans. Commun., vol. COM-25, pp. 433-441, April 1977.
[21] P. A. Bello, "Characterization of randomly time-variant linear channels"
IEEE Trans. Commun. Systems, pp. 360-393, December 1964.
[22] P. M. Woodward, "Probability and information theory with application to
radar" Pergamon Press, London 1953.
[23] M. Alard and R. Lassalle, "Principes de modulation et de codage canal en
radiodiffusion numerique vers les mobiles" Revue de 1'U.E.R, No. 224, August
1987,
pp. 168-190.
CA 02220107 2006-05-05
32
APPENDIX 2
1. Modelling of the channel
1.1. General model
A dispersive channel may be considered to be a linear system having a pulse
response that is variable in time. There are two ways of defining this pulse
response.
This approach will be based broadly on the conventions proposed in [21J:
~ the pulse response at input or input delay spread function g(t,i) defined
by:
r(t) = Js(t - z)g(t, z)dz
where s(t) and r(t) respectively represent the signals transmitted and
received,
~ the pulse response at output or output delay spread function h(t,i) defined
by:
~(t) = js(t - t)h(t - t, z)dz
We evidently have h(t, z) = g(t+i,i) h(t,i) represents the pulse response of
the
channel at the instant t. These conventions being established, it is possible
to define
the following characteristic functions:
the delay-Doppler spread function U(i,v) is characterized by:
g(t~z)= jU(z,v)e~z~~rdv
with r(t) = f f U(z, v)s(t - z)e'z"~'d vd z
the Doppler-delay spread function V(v,i) is characterized by:
h(t~ z) - w(v~ z)e-azn~rdv
with r(t)= jJV(v,z)s(t-z)e'2~"~'-'~dvdz
Or quite simply:
v(v' ~) - erz~rvrv(T~ v)
the time-variant transfer function T(ft) is characterized by:
CA 02220107 2006-05-05
33
T (f ~ t) = f g(t~ z)e-' z~fzdz
with r(t) = JS( f )T( f, t)e'z"f 'df
The same equation as in the case of a stationary channel is therefore got
again,
the difference being simply that the transfer function becomes variable in
time. This
transfer function T(ft) is the 2D Fourier transform of U(i,v), namely:
T(f,t)= JfU(z,v)e-'z"Ife'z"°'dzdv
In any case, it is assumed that U(i,v) has a bounded support. This means that
the transfer function T(ft) can be represented by a lattice of discrete values
by virtue
of the sampling theorem.
1.2. The static delay-Doppler model
The delay-Doppler model is defined by the equation:
r(t) = J f U(z, v)s(t - z)e'z"~'dzd v
This equation shows the channel as a sum of elementary channels
characterized by an amplitude, a phase, a temporal offset and a frequency
offset. It is
therefore legitimate to take an interest in the behavior of the various
existing
modulations of this type of channel, which shall be named the static delay-
Doppler
model.
The equation of the channel is written then in the following simplified form:
r(t) = Ae'BS(t - z)e'z"'"
2. Performance characteristics of the OFDM in the non-stationary channels
2.I . General case
Let us consider an OFDM multicarrier modulation of any type (OFDM/QAM,
OFDM/OQAM or OFDM/IOTA) characterized by the generic equation:
s\t) _ ~ akxk \t)
keE
CA 02220107 2006-05-05
34
ak being real variables, E being a 2D lattice with a density 2 in the time-
frequency
space, the functions xk(t) being translated functions in time and in frequency
of one
and the same prototype function x(t) and constituting a Hilbertian basis of
Lz(R).
xk(t)=e~~kx(t-zk)ezr~~kr ~kEE
It will be noted that no hypothesis is made on the structure of the lattice E.
In
the particular case of the OFDM/QAM, this lattice can be divided into two co-
localized sub-lattices with phases in quadrature.
The demodulation operation can be written as follows:
an = ~ie[e-'~ Jr(t)x;, (t)dt,
~ being a phase estimated by the demodulator and r(t) being the complex
envelope of
the signal received. It is therefore possible to write:
an = ~e[e-'~ J[ f ~U(z, v)s(t - z)e'Z""'d zd v~x;, (t)dt,
_ ~ie~e-'~ J JU(z, v)[ Js(t - z)e'2""'x;, (t)dt]a'zd v,
Now:
Js(t- z)erz~~txn (t)dt = ~ak Jxk (t - z)g'z~~'xn (t)dt
k
=~a eowk-woe2»~~+~k-~">c=+rk+~~>A z -z -z v -v -v
k x( n k ~ n k )
k
It is deduced therefrom that:
Cln =~ak~e[e-'~e~ok-W~> ~~e2hrcv+vk-v.. )(r+rk+r,>>U(z v)Ax(zn -Zk -z~vn -vk -
v)dZdV]
Jk
The optimum value of ~ is the one that maximizes the coefficient an, giving:
~ = Arg JJe2r"~~U(z, v)Ax(-z,-v)dzdv
Although they are general, the above equations can hardly be exploited.
However they show that the useful signal and the intersymbol appear as
integrations
of the ambiguity function weighted by the delay-Doppler spread function.
CA 02220107 2006-05-05
2.2. Case of the static channel
If we look at a static delay-Doppler type of channel, characterized by a phase
A, a delay T and an offset v (the amplitude A will be normalized at 1), the
demodulation will be done similarly by introducing a phase parameter ~ into
the
estimator. The result of this operation is written as follows:
a" _ ~e~ f r(t)x;, (t)e '~dt,= ~ie[e'B ~ Js(t - z)e2"rvtxn (t)dt]
_ ~ak5~e~~e'(B-m)xk (t - Z)g2invt xn (t)dt,= ~ak~8[~e'(~-B)g-2i>rv(t+r)xn (t +
Z)xk (t)dt]
kLeEr J keE
_ ~akCk , Wlth Ck = ~8[~e'(~ B)g 2i~rv(t+z)xn (t + Z)xk (t)dt]
keE
The demodulated signal is therefore finally written as:
an - Cnan + ~ Ckak
keE,k*n
The second term represents the intersymbol interference (II). If the data
elements ak are considered to be independent random variables with a variance
6z, the
variance I of the II is written as follows:
I - ~ ckZ~z
keE,k*n
Now, the coefficients ck are the coefficients of the breakdown of the function
e~(~-e)e-Zr>rv(t+r)x~ (t + Z) , with a norm equal to unity, on the Hilbertian
basis of the
functions xk(t). We therefore have:
ck2 =1 and I = (1 - Cn2~ ~z
kEE
In other words, the variance of the received signal is constant and is
distributed between the "useful" signal c"a" and II, having a variance I = ( 1-
c"z)az,
The computation of the coefficient cn gives:
Cn = ~e~~ei(ø-B)e-2i>rv(t+r)xn (t + Z)xn (t)dt,=
~vr) re-2invtxn(t+Z~2)xn(t-Zl2)dt]=~2[2'(~-B-nvz)AXn(2'v)1
CA 02220107 2006-05-05
36
Now, the ambiguity function of x" is written as:
Axrt (,~'v ) _ a 2i~r(v "t-z av )Ax (~~ ~ V )
Finally, it is possible to write:
c = ate et(~-B-~,.~)ezrn~,."r-rn~)A z v
n ~ x( ~ )~
It will be assumed that the demodulation phase ~ is written in the form
~oPt+0 ~, where Copt is the demodulation phase that minimizes the II, i.e.
maximizes
c", giving:
~op~ =B+~vi+2~(i"v-v"i)
Then, the variance of the II can be written simply as follows:
I = (1 - (Jie~Ax(z,v)e~o~ ~z)6z
When the prototype function is an even order function (which corresponds to
the case of the method of construction of the Hilbertian bases described in
the main
part of this document), the ambiguity function is real and we therefore have:
I = (1- AX (z, v ) cos z 4 ~)) o-z
This result is quite remarkable since it shows that the sensitivity to the
delay
and to the Doppler phenomenon of any multicarrier modulation depends only on
the
ambiguity function of its prototype function. Hereinafter, the term
"intersymbol
function" (used loosely to designate the intersymbol interference function),
will be
used to designate the function Is(i,v)= 1- Axz (z, v) in general),
representing the
mean quadratic value of the intersymbol normalized by the mean quadratic value
of
the data elements in the case of an estimation of optimal phase.
CA 02220107 2006-05-05
37
3. Comparative analysis of the different types of OFDM
3.1. Theoretical limits
The description here below shall deal with the properties of the intersymbol
function. It is observed that the sensitivity of a multicarrier modulation is
directly
related to the behavior of the ambiguity function of the corresponding
prototype
function in the vicinity of (0, 0). The problem raised is quite similar to the
problems
of uncertainty encountered in the field of radar and reference may be made to
the
abundant literature on the subject (see for example [22]). Without any loss of
generality, it is possible to choose a function x(t), by an appropriate
temporal and
frequency translation in such a way that its first order moments are zero,
namely:
Jtx(t)zdt= Jf X(f)Zdf =0
Under these conditions, it is easy to verify that the partial derivatives of
the
first order cancel each other out:
av (z'v) -2iTC Je-Z"'~'tx(t+zl2)x'(t-zl2)dt~
wx (0,0) _ -2l~ Jt Ix(t)IZ dt = 0
a~ (z,v)=-2iTC fe-2"'ft f X(f +v/2)X'(f -vl2)df ~
~~ (0,0) _ -2i~z f f X(f ) z df = 0
It is possible to characterize the behavior of the ambiguity function around
(0,0) on the basis of the second order partial derivatives:
2
ozov(z'v)--i~ Jte-2'~~'(x'(t+zl2)x'(t-zl2)-x(t+zl2)x''(t-zl2))dt
2
azav(0,0)=2~t Jt sm~x'(t)x'(t)~a't
It will be assumed that
a ZA
X (o~o) _ ~X
a~av
CA 02220107 2006-05-05
38
z
a AX (z, v) _ -4~2 ~e-Z'~"'t2 x(t + z / 2)x' (t - z l2)dt ~
av
2
a AX (o,0)=-4~z ft2lx(t)~Zdt=-4~Zot2
a~
Z
~'4X (z, v)=-4~cz fe-Z"'fr fzX(f+vl2)X'(f+vl2)df
2
~ZX (0,0)=-4~2 JfzIX(f)Izdf =-4~Z4fz
Let us consider the Taylor-Young development of the ambiguity function in
(0, 0):
AX(dz,dv) =1-2~ (4tzdv2 +4f Zdz2)+,crluz'z+o(dvz +dzz)
A deduction is made therefrom of the Taylor-Young development of the
variance of the intersymbol:
I = (1 - (~e[Ax (T ,V)~2 COSZ 0~)6 2
that is:
I(dz, dv,d~) _ ~z~4~z(4tZdvz + 4f2dz2)-2~.rdvdz+ d~z +o(dv2 +dz2 + d~2)~
It is deduced therefrom that the intersymbol function Is accepts, at the
outset, a
tangential cone with the following equation:
z=~4~Z(OtZv2 +~fZz2)-2~vz
The intersection of this cone with the plane z = 1 (maximum intersymbol)
demarcates a surface with an elliptic contour whose area ~ may be considered
as a
measure of the sensitivity to the delay and to the Doppler phenomenon. When ~X
is
zero, this ellipse has the temporal and frequency axes as its axes of symmetry
and
extends from ~1/2~ 0 f along the temporal axis and ~1/2~ 0 t along the
frequency
axis. We therefore have:
~=1/4~ 0 t ~ f
CA 02220107 2006-05-05
39
In view of Heisenberg's inequality, ~ cannot exceed unity. This result is
generalized when pX is different from 0. Let us consider the function y(t)
obtained by
multiplying the function x(t) by a wobbulation:
y(t) = a"~'Z x(t) ~ y' (t) = a"'~'2 (x' (t) + 2i~z/3t x(t) )
It is therefore possible to write:
,uy = ~A'' (0,0) = 2~z jt sm~y'(t)y'(t)~dt
azav
= 2~c Jt sm[x'(t)x' (t),dt + 42/.3 JtZI x(t)I Zdt =,ux + 4~Z~Ot2
It is therefore always possible to cancel pY by choosing (3 appropriately.
Now,
the operation of multiplication by a wobbulation achieves a simple change of
axes of
the associated ambiguity function with preservation of the areas. It is
deduced
therefrom that the parameter ~ is always between 0 and 1.
This result is extremely important since it enables the comparison of the
performance characteristics of all the MCMs in the dispersive channels on the
basis of
a single parameter. It can be seen therefore that these performance
characteristics
depend only on the concentration of the associated prototype function. The
optimum
is achieved virtually by the Gaussian function but this optimum is
inaccessible since
the Gaussian functions do not enable the construction of a Hilbertian basis.
CA 02220107 2006-05-05
APPENDIX 3
1. Introduction
This appendix gives a method of construction of prototype functions verifying
the requisite criteria of orthogonality. The method can be used to obtain an
infinity of
functions, among them a particular solution (called an IOTA function)
possessing the
particular feature of being identical to its Fourier transform.
2. AmbigLy function
This chapter recalls the main properties of the ambiguity function and
describes various operators acting on this function.
2.1 Reminders concerning the ambi uity function
2.1.1 Definitions
Let us take a function x(t) and its Fourier transform X(f). With this
function, it
is possible to associate its temporal and frequency products respectively
defined by
yx (t, z) = x(t + z l 2)x' (t - z l 2)
rx(f,v)=X(f + vl2)X'(f - v/2)
The Wigner-Ville transform and the ambiguity function of x are then given by:
Wx (t~ .f ) = JYx (t~ z)e-zr~fTdz = JrX (.~~ v)ez'n~~dv
Ax(z~ v) = JYx(t~ z)e-Z'~,.rdt = Jrx(.f~ v)e2'~fTdf
2.1.2. Properties of s,~ry of the ambi uity function
Let us take a function x(t). The notations x and X will be applied
respectively
to the functions defined as follows:
x- (t) = x(-t)
x (t) = x' (-t)
We then have the relationships:
AX (z, v)= ~e-2"'"'x(t+zl2)x*(t-zl2)dt= fe-Z"'~'x(-t-zl2)x*(-t+zl2)dt
CA 02220107 2006-05-05
41
that is, assuming that u=-t:
AX (z, v)= Je2"'""x(-a+zl2)x*(-u-zl2)du=
!ez'~""x(u - zl2)x*(u + z l2)du = Ax' (z, v)
It is concluded therefrom in particular that if a function x is an even order
value, namely that x=x , then its ambiguity function is real. Furthermore, the
following relationship will be noted:
AX. (z, v)= Je-2"~"'x'(u+zl2)x(u-zl2)du=Ax(-z, v)
By combining these two relationships, we get:
AX(z, v) = Ax(z,-v)
2 1 3 Ambiguity function and Fourier transform
It is possible to rewrite the definition of the ambiguity function as follows:
Ax (z~ v) = Jrx (.~~ v)ez'n~ ~d f = JYx (.f ~ v)e2'n frd f = AX (v~_z)
or again: A X (i, v) = A x (-v, i)
2 1 4 Ambig_uiiy function and time-freduency translation
Let us consider a translated function of any prototype function x(t), namely:
x = e~~e2r~"ktx(t _ zk)
k
The associated ambiguity function is written as follows:
Axk (z~ v) _ (e-zr~"reek ezr~"k~r+riz>x(t _ zk + z l2)e-'~k e-z'~"kit-riz>x*
(t _ zk _ z l2)dt =
je-z"'"'ez"'"k'x(t-zk +zl2)x*(t-zk -zl2)dt
that is, assuming that u=t-iK
Axt (z, v) = ez~"~"k~-"rk > [e-z»~~x(u + z l2)x* (u - z l2)du = ez'n("ks-vrk
)Ax (~~ v)
2 2 Ortho~onalit~and ambiguit~function
2.2.1 General case
We consider two translated functions of one and the same function x(t),
namely:
- el~ke2i~vktx~t _,z k)
x
CA 02220107 2006-05-05
42
xk~ = ei~Px' e2i~vx,tx~t ~ Zk
The scalar product of these two functions can be written as follows:
/xx I xx.\ =elc~k-~k~> ~e2t~wk-~k,>tx(t-zx~x*(t-zx,~dt
that is, assuming that a = t-(ik +ik')/2:
/xk~xk~-e~(~k-~Ok')e2in(vk-vk.xrk+rk,) re2in(vk-vk,)ux(a+(Tk~-Zk)l2)xs(u-(Zk'-
Zk)l2)du=
\e~(~t-~k')e2iR(Vk-Vk~)(Tk+Tk~)A ~ . -Tr JV . -v
x( k k~ k k)
3 Hilbertian bases on the ortho~~onal lattices
3 1. General principles of construction
We consider a set of functions {xm,"} defined by:
xm'n(t)=ei(m+n)sl2e2ismvotx(t-YITQ) wltllV~T~=1/2
A search is made for the conditions on x(t) so that the set {Xm,"} is a
Hilbertian
basis of HR. It is laid down that x(t) is an even function whose ambiguity
function AX
is therefore real.
The scalar product in R of xm," and of x",~,n~ can be written as:
xm,n 'xm',n'/R = ~2L2r(m+n-m-n')nl2ein(m-niXn+d)~otoAx((~ _n)~0~(m~ m)v0)~
_ ~BL2i((m-m')+(n->f~(m-m')(~+rl»nlZ)AX((n~_n)~o~(m~-m)Vp),
The following relationship of congruence modulo 2 will be noted:
(m-m ~+(n-n ~+(m-m ~(~+n ~ = 1-(m-m'+1 )(n-n'+1 )
Consequently, if (m, fit) ~ (m ; n ~ modulo 2, the scalar product is zero. The
lattice {Xm,n} can therefore be broken up into four sub-lattices characterized
by: {m
even, n even}, {m even, n odd}, {m odd n even}, {m odd, n odd}. The
orthogonality
between functions belonging to different sub-lattices is therefore automatic
and does
not depend on the properties of the prototype function, since this function is
an even
value.
CA 02220107 2006-05-05
43
What remains to be done then is to ensure that the functions of one and the
same sub-lattice are mutually orthogonal. It is enough for this purpose that
the
ambiguity function Ax should verify:
AX(2nio,2mvol=0 b' (m,n)~(0,0)
It can be seen therefore that the problem of the construction of the
Hilbertian
bases of HR on the orthogonal lattice With a density 2 amounts to that of the
construction of an even prototype function whose ambiguity function is
cancelled out
on a lattice of the density 1/2.
3.2. Methods of ortho~onalization
3.2.1. Temporal orthogonalization
Definition:
Let us take a function x(t) with a Fourier transform X(f). The designation Ot
is
given to the temporal orthogonalization operator which associates a function
y(t) with
x(t), this function y(t) being defined by its Fourier transform Y(f):
X(f)
Y(f ) _
vo~ I X (f - kvo)Iz
k
By construction, we have:
vv ~ ~Y(.f - m vv ) Z = vv ~ ry (f - m vv ,0) =1
m m
namely by reverse Fourier transform:
~(z - 2nzo)JAy(z,0) = 8(z)
n
or again:
Ay (2nzo,0) = 0 'dn ~ 0 and Ay(0,0) =1
The orthogonalization is therefore really done on the temporal axis. It is
furthermore noted that this operator normalizes y.
CA 02220107 2006-05-05
44
Let x be a Gaussian function and y = Otx. Let us consider the expression:
hy(f,2mvo)=Y(f +mvo)Y*(f -mvo)= X(f +mvo)X*(f -mvo)
vo~~X(f -kvo)I2
k
Since X is a Gaussian function, it is possible to write:
X(f +mvo)X*(f -mvo)=cm X(f)2
where cm is a constant. It is deduced therefrom that:
r,,(f,2mva) = GmI-'y(.f~0)
By reverse Fourier transform we get:
Ay( z,2m vo ) = c", Ay ( z,0)
Consequently:
b'm, ~l n ~ 0 Ay (2n zo ,2m vo ) = 0
The temporal orthogonalization operator Ot therefore orthogonalizes the entire
lattice except for the frequency axis.
Theorem 1
Let x be a Gaussian function and y=Otx, then:
'dm, bn ~ 0 Ay (2n zo ,2m vo ) = 0
3.2.2. Frequenc,~gonalization
Definition
Let us take a function x(t). Of is the designation given to the frequency
orthogonalization operator which associates a function y(t) with x(t),
function y(t)
being defined by:
y(t) = x(t)
zo ~ x(t - kzo ) 2
k
Y
CA 02220107 2006-05-05
By construction, we have:
zo~ (y(t - nzo)IZ - zo~ yy(t - nzo,0) =1
n n
gluing, by Fourier transform:
~~ b(v - 2mvo}~~4y(O,v) = ~(v) with vozo =1 / 2
m
or again:
Ay(0,2mvo)=0 dm~0 and Ay(0,0)=1
The orthogonalization is therefore really done on the frequency axis. It is
furthermore noted that this operator normalizes y.
Let x be a Gaussian function and z = O fy, with y = Otx. Let us consider the
expression:
y(t + nzo }y~ (t - nzo }
y= (t,2nzo ) = z(t + nzo }z (t - nzo ) _
2
zo ~ ~y(t - kza }~
x
It is therefore possible to write:
yZ(t,2nzo) = yy(t,2nzo)~(t)
where P(t) is a periodic fimction vvi~h a period io that accepts a development
in
atnxvor
Fourier series ofthe type ~ ake
By Fourier transform, we obtain:
Ar(2nzo,v) _ ~axAy(2nzo,v-2kvo)
x
Where:
~lm,'dn ~ d, Ay(2n~to,2mvo) = 0 ~
drn,dn ~ 0, Az(2nza,2mvo) = 0
Furthermore by construction,
dnt .= 0, Ar(0, 2mvo) = 0
CA 02220107 2006-05-05
46
We finally have:
b'(rtt,n) ~ (0,p} , AZ(2rzzo,2mvo) = 0
Thus, the ambiguity function of z gets cancelled out outside (0;0) for all the
multiples of 2io and 2vo, giving a lattice with a density 1/2.
Theorem 2
Let x be a Gaussian function and z = OtOfx, then:
d(m, n} ~ (0, 0), ~(2n2o, 2mvo ) = 0
3.3. The orthogonalization operator O
In view of the above, it can clearly be seen that there is a time-frequency
scale
that symmetrizes the writing of the equations: it is enough for this purpose
to choose
io = vo = 1 / ~ . The scales will therefore be renormalized accordingly
without
harming the general character of the demonstrations.
3.3.1. Definition
The designation O is applied to the orthogonalization operator which
associates, with a function x, the function y defined by:
2~ r a x(u)
Y(u) = x(u - k ! ~) 2
~4 t
k
Furthermore, the Fourier transform operator will subsequently be designated
by F.
3.3.2. Idempoterice of the operator O
Let z=Oy and y = Ox. It is possible to write:
2i r a ~(u} - 2i r a y(u} = Y(u)
~~ytu - k l ~)I2
2i t 4 x(u _ k /.~)
t ~ ~Ix(u - (k + k' } / ~)lz
k'
CA 02220107 2006-05-05
47
We therefore have OOx = Ox which shows the idempotence of the operator
O. In the same way, the dual operator F-lOF is also idempotent, since
F-iOFF-lOF = F-IOOF = F'lOF.
3.3.3. Lemma 1
Let P be a periodic function with a period 1 / ~ and D a distribution having
the form:
D(u) _ ~ akb(u - k~)
k
Let x be any function:
(D ~ (P x)~(u) _ ~ a*P(u - k~) x(u - k~) _
*
P(u)~ ak x(u k~) - ~~' (D * x)~(u)
k
Lemma 1
Let P be a periodic function with a period 1 / ~ and D a distribution having
the form:
D(u) - ~ ak8(u _ k~) .
x
Let x be any function. We have:
D*(~) _ ~'CD * x)
Lemma 2
Let us take the function yQ defined by:
ya = D * xa with xa = (2x)1'4 e-"~"z , and D being a distribution having the
form
D(u) _ ~ ak &(u - k~)
It is therefore possible to write:
Ya(u) _ ~,a*xa(u-k~) .
x
Let us consider the sure:
2 1
~'Ya~u ~~~ ~~ak~ak~~xa~u-~~-k'~~xa~u-~~-k"~~':
CA 02220107 2006-05-05
48
Or again by application of the result given in appendix (~ 4):
_~ra(k~_k ) 2
~lya(u-kl~)IZ=~~ak~ak»e ~2'xa(u-(k+k'+k")l~)'
k k k~,k~
and then by reorganizing the indices and redefining k as k+k'+k":
a(u-kl~ _ ~ ~axak"e 'g'~x k°)Zlxa(u-kl~~z
k k x,x°
It is therefore possible to write:
with
the form:
~~Ya (u -1t l ~~2 = c~~xa(u _. k/ ~~Z
k k
C ' ~Cl'k~Clk"8-~ra(k'-k,~)?
k,k'
The coefficient c can easily be estimated by rewriting the above relationship
in
~Y~Q (u - k / ~~ 4) = c~,Y~Q (u " k l ~, a)
k k
Giving, by Fourier transform:
2 ~ s(v-k~) ,Q (0, v) = c~ ~ 8(v-k~) AsQ (0, v)
k x
In particular, it is possible therefrom to deduce:
2 A~Q ~~~)
We therefore have finally:
~~~'a(u-kl~))Z ~~xa(u-kl~~Z
k _ t
Lemma 2
Let us take the function yQ defined by ya = D * xQ, with xa = (2a)'~4 e-"avZ ,
and D being a distribution having the form
D(u) =_ ~ ak S(u - k~).
k
It is possible to write:
CA 02220107 2006-05-05
49
~~ya(u-kl~)~2 ~~xa(u-k/~)Iz
t _ k
I(Xa ~~z
3.3.5. Commutative nature of the operators O and F-~OF
VJe shall now show that the operators O and F-~OF switch over when they are
applied to a Gaussian function. Let xa = (2a)'~4 e-"au~ .
Then Fxa = xll~
and Ox~ = Paxa
P~ being defined by the relationship:
2c!4
PQ (u) -
~Lxa(u-kl.~)~Z
and its Fourier transform Da by:
Da(u) _ ~ as>x8(u _ k~)
k
Let ya = F-lOFxa and z~ = Oy~,. It is possible to write:
Ya = F IOFxQ = F'lOxl ! a = ~1 \ P I axI I a ~ = Di ! a '~ x~
and Zt ! a ya ~u)
Za(u) ~
k!~)p
k
Since x« and ya having a norm equal to unity, it is possible to write, by
applying lemma 2:
2114ya(u) ~ =Paya-Pa~Dtla~'Xa)
~~xa(u _ k/.~)~
fk
In the same way, the following is defined:
w1 la -FOXa =F(PaXa)=Da'kXlla
It is possible to write:
ZI ! 41y1 ! a(u)
QW~Ja~u) -
,~,l~l'VIIa~ZI-k/~)~Z
k
CA 02220107 2006-05-05
Since xl/a and was have a norm equal to unity, we have, in application of the
lemma 2: 2' /'~ W a _
lla~ ) _ 1
OWI/a~u)- 2 -PlaWila-PIa~Da'kxlla~
~,Ixt/aU-k/~)~
Giving, by reverse Fourier transform:
F-IOFOxa F-iOwna Dt/a*(I'a xa)
Now, by application of the lemma 1:
D1/a*(paxa)-Pa(~1/a*xa)
If is deduced therefrom that:
OF'IOFxa F'IOFOxa
Theorem 3
For any Gaussian function x, the operators O and F-IOF switch over, giving:
OF lOFx = F ~OFOx
Corollary 1
Let za = OF-lOFxa, with xa = (2a)1/4 e-"a"Z , then Fza = zl/a-
Demonstration:
Fza FF-IOFOx a OF-10x a OF-lOF xl~a = Zya
Noteworthy particular case
Fzl = zi
This particular function gives perfect symmetry to the time and frequency axes
and therefore constitutes the prototype function of the IOTA transform
(Isotropic
Orthogonal Transform Algorithm). This particular function s will be noted.
Corollary 2
Let x be a Gaussian function and z = OF-IOFx, then Oz = z.
Demonstration:
CA 02220107 2006-05-05
d
OZ = OOF'IOFx = OF'IOFx = Z
Corollary 3
Let x be a Gaussian function and z=OF-lOF'x, then F-IOFz = z.
Demonstration:
F-IOFz=F-IOFF-lOFOx=F-IOOFOx=F-IOFOx=z
3.3.6. Ambiguity function of the functions z«
Let us consider the theorem 2, with the normalization io=vo=1 / ~ . Then:
O f = O and Ot = F'lOF
Consequently, the theorem 2 can be rewritten:
Theorem 4
Let x be a Gaussian function and z = F-IOFOx, then:
=fl
4. Appendix
Let us take a normalized Gaussian function x~ defined by:
xa (u) _ (2a)vae-nave
The product xa(u-a)xa(u-b) can therefore be ~~ritten:
x(u- a)x(u - b) = 2a a ~«~~u-a)~+(u-6)2
Now we have the identity:
2 2
(u_a)z+~u_b)z=2 (u-a+b~ +~a2b~
/,2
Finally, it is possible to write:
x(u-a)x(u-b)-e_"a~~-6~=iz x(u_ a+b ) 2
C2)