Note: Descriptions are shown in the official language in which they were submitted.
CA 02277252 1999-07-09
Semi-Blind Multi-User Detectors for CDMA
Anders Hrast-Madsen
FIELD OF THE INVENTION
This invention relates to mufti-user detection in CDMA, spread spectrum, mufti-
user
communications.
BACKGROUND OF THE INVENTION
Mufti-user detection is a method to improve detection performance and capacity
of multiple access
spread spectrum (or CDMA) systems. Mufti-user detection was introduced by
Verdu in [ 1 ], where
1o the optimal mufti-user detector was derived. The optimal detector has an
exponential complexity in
the number of users, and less complex (linear) mufti-user detectors were
therefore derived in an
number of papers, in particular the decorrelating detector [2] and the minimum
mean square error
(MMSE) detector [3]. For a review of mufti-user detection and further
references, see, e.g., [4]. All
references in square brackets are listed at the end of the background section
of this disclosure.
~s The early works on mufti-user detection assumed that the codes of all users
were known at
the receiver, and made a simultaneous detection of all users (therefrom the
name mufti-user detection
or joint detection). If the detection for example is at the base station of a
mobile communication
system, this seems realistic, as the base station needs to perform detection
for all users. On the other
hand, it is unrealistic that a mobile station should know the codes of all
other users in a cell, and
2o therefore it is desirable to consider mufti-user detectors that need to
know only the code of the
desired user, blind mufti-user detection. The blind MMSE detector was
introduced in a number of
papers [6,7], and recently it was also shown that the decorrelating detector
can be implemented
blindly [13,14].
Although a base station knows all codes of the users within a cell, it
typically will not know
25 the codes of interfering users from surrounding cells. Even if a base
stations could obtain this
knowledge from surrounding base stations, it would be a waste of resources if
it were to also
perform detection for these users just to cancel interference (including
synchronization etc.). This is a
serious problem to mufti-user detection, since typically 1/3 of the
interference could be from other
cells, intercell interference [8,9]. Thus, also at the base station blind
detectors could be relevant. On
1
CA 02277252 1999-07-09
the other hand, blind detectors do not use neither the fact that the codes of
in-cell users are known at
the base station, nor that these other users also have to be detected.
REFERENCES
[1] Verdil, S.: "Minimum Probability of Error for Asynchronous Gaussian
Multiple-Access
Channel," IEEE Trans. Info. Theo., Vol. IT-32, No. 1, pp. 85-96, Jan. 1986.
[2] Lupas, R. and Verdu, S.: "Linear Multi-User Detectors for Synchronous Code-
Division
Multiple-Access Channels," IEEE Trans. Info. Theory, vol. 35, no. l, pp. 123-
36, Jan. 1989.
[3] Xie, Z. Short, R. T. and Rushforth, C. K.: "A Family of Suboptimum
Detectors for Coherent
Multi-User Communications," IEEE J. on Selected Areas in Commun., vol. 8, no.
4, pp. 683-
to 690, May 1990.
[4] Shimon, M.: "Multi-User Detection for DS-CDMA Communications," IEEE Comm.
Mag., pp.
124-136, Oct. 1996.
[S] Madhow, U. and Honig, M.L.: "MMSE Interference Suppression for Direct-
Sequence Spread-
Spectrum CDMA," IEEE Trans. Comm., Vol. 42, No. 12, pp. 3188-3188, Dec. 1994.
[6] Honig, M., Madhow, U. and Verdu, S: "Blind Adaptive Multiuser Detection,"
IEEE Trans.
Info. Theo., Vol. 41, no.4, pp. 944-960, July 1995.
[7] Tsatsanis, M.K.: "Inverse Filtering Criteria for CDMA Systems," IEEE
Trans. on. Signal
Processing, vol. 45, no. 1, pp. 102-112, January 1997.
[8] Duel-Hallen, A., Holtzman, J. and Zvonar, Z.: "Multiuser Detection for
CDMA Systems," IEEE
2o Personal Communications, pp. 46-57, April 1995.
[9] Viterbi, A.J.:"The Orthogonal-Random Wave form Dichotomy for Digital
Mobile
Communications," IEEE Personal Communications, pp. 18-24, First Quarter 1994.
[ 10] Poor, H. V. and Verdu, S.: "Probability of Error in MMSE Multi-user
Detection," IEEE Trans.
Info. Theo., Vol. 43, no. 3, pp. 858-881, May 1997.
[11] Hest-Madsen, A. and Cho, K.S.: "MMSE/PIC Multi-User Detection for DS/CDMA
Systems
with Inter- and Intra-Cell Interference," accepted for publication in IEEE
Trans.
Communications.
[12] Anton-Haro, C. and Fonollosa, J.R.: "Interference Cancellation for UMTS
using Adaptive
Antennas," ACTS '97 (Aalborg, Denmark), pp. 320-325.
2
CA 02277252 1999-07-09
[ 13] Wang, X. and Poor, H. V.: "Blind Equalization and Multiuser Detection in
Dispersive CDMA
Channels," IEEE Trans. Communications, Vol. 46, No. 1, pp. 91-103, January
1998.
[ 14] Wang, X. and Poor, H. V.: "Blind multiuser detection: A subspace
approach," IEEE Trans.
Inform. Theory, to be published.
[15] Sharf, L.L.: "Statistical Signal Processing - Detection, Estimation and
Time Series Analysis,"
Addison-Wesley (New York), 1991.
( 16] P. Comon, and G.H. Golub, "Tracking a few extreme singular values and
vectors in signal
processing," Proc. IEEE, 78(8), 1327-1343, Aug. 1990.
[17] R.A. Iltis and L. Mailaender: "Multiuser Detection of Quasisynchronous
CDMA Signals Using
to Linear Decorrelators," IEEE Trans. Comm., Vol. 44, No. 11, pp. 1561-1571,
November 1996.
[18] H. Ge: "The LMMSE Estimate-Based Multiuser Detector: Performance Analyses
and Adaptive
Implementation," ICASSP'97 (Munich, Germany, April 1998).
[19] Schodorf, J.B. and Williams, D.B.: "A Constrained Optimization Approach
to Multiuser
Detection," IEEE Trans. Sig. Pro., Vol. 45, No. 1, pp. 258 -262, January 1997.
is [20] Schodorf, J.B. and Williams, D.B.: "Array Processing Techniques for
Multiuser Detection,"
IEEE Trans. Comm., Vol. 45, No. 11, pp. 1375 -1378, November 1997.
[21 ] Host-Madsen, A.: "Semi-Blind Decorrelating Multi-User Detectors for
CDMA: Subspace
Methods," presented at IEEE PIMRC '98, Boston, Sept. 1998.
2o SUMMARY OF THE INVENTION
This invention provides multi-user detectors that can cancel interference from
both known
and unknown users, while utilizing the information about known users and the
fact that detection has
to be done for all known users. A blind mufti-user detector basically in some
way has to estimate the
codes of interfering users, and by using the known codes the estimation
accuracy can be improved.
25 On the other hand, since several users have to be detected jointly, it is
also advantageous,
considering computational complexity, if some of the processing can be common
to all users. In this
patent document we propose detectors that satisfy these two criteria.
We call this class of detectors semi-blind mufti-user detectors. We use the
term semi-blind to
mean that the detector has partial information: some, but not all, users'
codes are known, as opposed
3o to blind detector of [6], which knows only the code of the desired user.
3
CA 02277252 1999-07-09
In the preferred embodiment, we consider linear detectors, i.e., the
decorrelating and the
MMSE detector. For non-linear approaches see [11] and [12]. We use the
subspace approach of
Wang and Poor [14]. We consider synchronous systems because of their
conceptual simplicity.
However, although the theoretical development and the simulations assume that
all users are
synchronous, the formulas developed can be applied without change to systems
where the unknown
users are not synchronous. The results can therefore be directly applied to
systems where the known
users are synchronous, e.g., the downlink in a cellular system, and the up-
link in some systems. With
some additional development, the results can also be applied to a quasi-
synchronous CDMA system
[17], where the users within a cell are (almost) synchronous, but the
interference from other cells is
1o asynchronous.
BRIEF DESCRIPTION OF THE FIGURES
There will now be described preferred embodiments of the invention in which
like reference
characters denote like elements, for purposes of illustration only, and
without intending to limit the
scope of the invention, and in which:
Fig. 1 is a schematic of a conventional detector for use in multi-user
detection;
Fig. 2 is a schematic of a conventional detector for use in non-blind multi-
user detection;
Fig. 3 is a schematic of a conventional detector for use in blind multi-user
detection;
Fig. 4 is a schematic showing a semi-blind multi-user detector according to
the invention;
2o Fig. 5 is a schematic showing a prior art system model for synchronous
CDMA;
Fig. 6 illustrates how a received signal contains interference from other
users, which may be
detected according to the conventional linear detector and general linear
detector provided on the
left hand side of the figure;
Fig. 7 illustrates operation of a conventional decorrelating detector,
according to the
equations shown on the left hand side;
Fig. 8 is a schematic showing a semi-blind decorrelating detector according to
the invention;
Figs. 9A-9D show simulation results for:
A) detector convergence with 7 known users and 4 unknown users (the curve
marked 1 is for
the algorithms calculated using ( 17) and the one marked 2 for the algorithm (
16));
3o B) simulation results of detector convergence for 7 known and 10 unknown
users;
4
CA 02277252 1999-07-09
C) simulation results of detector convergence for 7 known and 10 unknown
users, with
subspace dimension set to 4; and
D) bit error rate versus SNR for 7 known and 4 unknown users, for which, in
each detector,
the lower curve is the median and the upper curve is the 90 percentile.
DETAILED DESCRIPTION OF PREFERRED EMBODIMENTS
In this patent document, "comprising" means "including". In addition, a
reference to an
element by the indefinite article "a" does not exclude the possibility that
more than one of the
element is present. Immaterial modifications may be made to the invention
described here without
departing from the essence of the invention.
I. AN IMPLEMENTATION OF THE INVENTION
The principles of operation of the invention are illustrated primarily by
mathematical
equations and algorithms. These equations and algorithms are implemented in a
computer, whether
general purpose or designed for the purpose, to yield the practical
implementation of multi-user
detection. The apparatus used is illustrated with block diagrams accompanied
by the equations since
these fully define the apparatus. The design of the apparatus, apart from
being configured to carry
out the invention, is conventional. Upon programming in accordance with the
algorithms and
equations set out in this patent document, the apparatus becomes a novel
apparatus. For the purpose
of describing the invention, the general configuration of the apparatus will
first be described,
2o followed by the algorithms and equations implemented by the invention.
Referring to Fig. l, a conventional detector is shown in which a received
signal r(t) is applied
to a matched filter bank 10, and the resultant applied to a multi-user
detector 12. The matched filter
bank 10 is achieved by correlation of the received signal with the codes sI{t)
using conventional
correlators 14, followed by integration over the symbol length in integrators
16, and sampling at the
symbol interval at sampler 18. The multi-user detector 12 is carried out by k
decision sub-systems
20. Fig. 2 shows the same matched filter bank 10 followed by the multi-user
detector 12, which
accomplish cancellation of intracell interference. Referring to Fig. 3, a
conventional blind multi-user
detector is shown which uses plural conventional adaptive ICs to detect the
received signal and
cancel both intracell and intercell interference.
5
CA 02277252 1999-07-09
Referring to Fig. 4, a semi-blind mufti-user detector 24 is shown which uses
an adaptive IC
26 followed by a matched filter 28 and non-blind mufti-user detector 30. Some
but not all codes of
users are known. This system cancels both intracell and intercell interference
using all information
available to the user. Only one adaptive IC is used that is common to all
users, which assists in
reducing complexity of the system.
Referring to Fig. 5, a conventional system model is shown in which the
received signal is
processed in the chip matched filter 10, sampled at the chip rate at 14 and
then provided to serial to
parallel buffer 32.
Referring to Fig. 6, a conventional received vector rl is formed as the
desired signal plus
1o interference. The detector works by finding the projection of rl on s2. In
Fig. 7, a similar principle is
shown for the decorrelating detector, except that the projection on wl is
found.
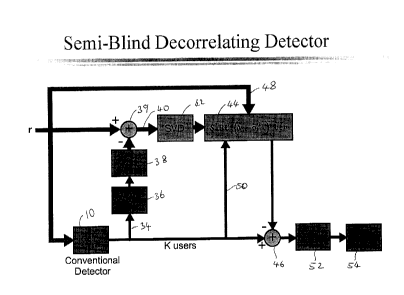
The complete semi-blind decorrelating detector is shown in Fig. 8. Fig. 8
essentially is a
practical implementation of equation 13 described in the following. Received
signal r, which includes
the signal from known and unknown users received at a single cell site, is
processed along two paths.
The lower path forms a conventional non-blind conventional correlating mufti-
user detector as
shown in Fig. 2. On the upper path a blind mufti-user detector calculates the
interference due to
unknown, outside, users, which is then subtracted from the output from the
conventional detector 10
to generate a signal from which intracell and intercell interference has been
removed.
In the lower path, a matched filter 10 (Fig. 1 ) is first applied to the
received signal r. The
output from the matched filter 10 is provided along path 34 where (STS)-1 at
36 followed by S at 38
is applied to the signal. This effectively projects the received data on the
subspace orthonormal to the
subspace of the known users, which isolates the signal from users inside the
cell (the known users).
The signal from users inside the cell is then subtracted from the received
signal r at 39 to yield a
signal that only contains the signal from outside users. The signal from
outside users is then
processed along the upper path 40 to find the interference from the outside
users by first applying
singular value decomposition 42 to the signal. SVD 42 is followed by the
equation shown at 44,
which projects the output from the subtractor 39 onto a basis for the subspace
defined by the codes
of the mobile users whose codes are unknown. This produces the interference
from the outside users,
justification for which is shown in the proof of Theorem 2 given at the end of
this description.
3o Equation 44 uses both the received signal r provided along path 48 and the
output from the matched
6
CA 02277252 1999-07-09
filter 10 along path 50. The interference from outside users is then provided
to subtractor 46, which
subtracts the interference from outside users from the output from the matched
filter 10. (STS)'' is
then applied at 52 to the signal to complete the detector. A decision (sgn
function) is made at 54
which generates the transmitted bits +1 or -1 for each of the K users, thus
completing the detector.
The details of operation of the system elements will now be described.
7
CA 02277252 1999-07-09
IL SYSTEM MODEL
Consider a synchronous spread spectrum communications system with the users
transmitting through an additive white l:raussian
noise channel. The user population consists of K users with known codes, and K
users with unknown codes. As we consider
synchronous systems, it is su~cient to consider a single symbol interval
[O,T], where the received signal can be written as
K K _ _
~t ) _ ~ bkAksk (~)'f ~ bkAk sk (t ) +n(r)~ E [a. T l
kal k=1
where sk is the normalized code waveform of the k'th known user with support
in [O,T], sk the waveform of the k'th unknown user,
bk,6k are the transmitted bits (tl), Ak,Ak the amplitudes and n white Gaussian
noise. We assume that the codes are given by chip
coda, sx(t) _ ~ctyr(t-iT IM), where ct a {-1,+1} and yr is the chip waveform,
and similarly for the unknown users. A
suffcient statistic for the received signal is therefore the output of a chip
rate sampled chip matched 5lter, and we can write this
statistic on vector form as
x K _ __
r = ~bkAkak +~bkAk sk +n = SAb +SAb +n
k=1 k=1
where S = [sl,ai,...,:K1S =~, ii,...,sx]. The correlation matrix of r is given
by
R=E[rrr]=SAzSr +SAZSr +azI
We will assume that all codes, of both known a~ unknown users, are linearly
independent, so that ~S S~ has full rank.
As mentioned in the iatroduaron, the system model can still be used if the
unknown users are asynchronous. In that case,
different bits within the interval [O,TJ from the same user are considered as
different 'virtual' users, and K is now the number of
'virtual' unknown users, which can be between one and two times the actual
number of unknown users.
I>tZ DETECTOR STRUCTURES
A general liar detector for user i is given by
b, = sgn(w; r~
For jointly detection of all users, the detector can be written
b - sgn~W r r~
8
CA 02277252 1999-07-09
where W = ~w ~ w Z ~ ~ ~ w x ~ . As argued in [10], any interesting detector
must have w; a range~S SD, since any component of
w, outside this subspace will only increase noise without reducing
interference.
A. The decorrelating detector
Prior to developing the semi-blind detector we will discuss general
decorrelating detectors in a geometrical framework useful to
understanding the decorrelating detector. A decorrelating detector for user i
satisfies
w; s;=1
w; sk =O,k ~i (1)
w; sk = O,k =1,...,K
These conditions imply that the decorrelating detector cancels the
interference from other users completely,
wrr=Atb; +wi n
The conditions (1) oondidons together with w, a range~S SD determine w,
uniquely, since ~S Sl has full rank. We can also write
w, as w, = M,s, . Although w, is unique, clearly M, need not be unique, and in
the following we will discuss some different natural
choices of M,. A practical solution for M, is a solution M that does not
depend on i, since then wTr=s; MTr and MTr can be
calculated common to all users. Especially if M is low-rank, or if it has to
be estimated, as is the case when some user codes are
unknown, this can yield an efficient solution.
To understand how the deoorrelating estimator can be estimated, we will at
first analyze the case when all codes are known,
i.e., K = 0 . Without loss of generality we can consider detection for user 1.
There are two natural approaches to the decorrelating
detector: the projection approach and the orthogonalization approach. In the
projection approach the received vector r is projected on
the subspace orthogonal to the codes of the other users, whereby their
interference has been removed, followed by a projection on the
subspace spanned by user 1. An explicit solution can be derived as follows.
Let
S~ =[s2s3..sK] (2)
and lei
i
P~ = SySi Sy Si (3)
be the projection unto the subspace spanned by S,, with Pi = I - Pl the
projection unto the orthogonal subspace. Then we can write
the decorrelating detector as
9
CA 02277252 1999-07-09
1
T 1
R'~ = s~ P~ s~ P~ si
The factor s; P~ s, is simply a normalizing factor, and can be omitted if we
consider BPSK, where we are only interested in the sign
of the output. It is easy to see that the conditions (I) are satisfied. The
disadvantage of this solution is that P; is specific to user 1,
and each user will therefore use a different projection.
We will therefore consider the orthogonalization approach. The problem with
the traditional matched filter solution is that
the vectors st,si,...,sx are not orthogonal. However, since sl,sZ,...,sK are
linearly independent, there exists some inner product in
Ru with respect to which al,s2,...,sx are orthonormal. Specifically, there
exists some (positive semi definite) matrix W a R"f ""'f so
that sT Ws~ = 8;,~ . Since s,, sZ,...,sx are not a basis of R"~ the matrix W
is not unique, but two solutions are
W =S~STsr2ST (4)
and
Ww = SA~ASTSA~2 ASr ,
which gives
w, = Ws, (5)
or
rl
y = si Wwsi Wwsi .
The conditions (1) are satisfied (seen most easily be noticing that ST WS = I
, and that scaling of vectors do not influence
orthogonality). This solution is in fact equivalent to the "traditional"
decorrelating detector [2] , since S r W r = ~S r Sr ~ S r r . The
solution fiuiher has the advantage that W is independent of the user
oonsider~ed and that it is a low rank matrix, which makes the
transformation efficient to calculate.
To estimate W (or rather W,~ we can make use of the following. The eigenvalue
decomposition of R can be written as [14]
r
R ~ITs LT"~ 0' Q I jjT
CA 02277252 1999-07-09
where Ua is an orthonormal basis of the signal subspace spanned by S and U" is
a basis for the noise subspace orthogonal to Ua. The
diagonal matrix Aa contains the K largest eigenvalues of R, while ~ is the
minimum eigenvalue. We then have, by examining the
proofs in [14]
Proposition 1
Ww = Ua(Aa -QZI) I Us
Thus, as R can be estimated from the received data only, Ww can be estimated
by EVD, and the orthogonalizing decorrelating
detector can be implemented blindly [14].
B. The MMSE detector
The minimum mean square error (MMSE) detector is defined as the detector that
minimizes the mean square error (MSE):
we _ ~~~(~i -wTr
Equivalently, the solution is given as the vector that satisfies
Elr{b; -w~ r~=0
which results in the equation
Rw; = A;s;
Thus, we can write
b, = sgn(s T R-t r~
(~ (8)
b=s~~rR tr~
Notice that this detector can be implemented blindly by replacing R by a time-
averaged estimate [18]. Using the eigenvalue
decomposition (6), this can also be written as
j!i =Sgn(S; UaAs1 Ua r!
1 (9)
b =s~~T UaAalUa rl
which is the idea of the subspace method in [14].
Now suppose that w, is constrained to lie in some subspace ?l, let u,,
u2,...,um be an orthonormal basis of ?l, and let
U = ~u, u2 ~ ~ ~ u,"~. We can then write w; = Uci for some vector c;.
Inserting this to (7) gives
11
CA 02277252 1999-07-09
e; =~~UrRUrtUr9a (10)
if P is the projection onto ?t we can also find w; as
ct = AOP~~tPsr
where t denotes pseudo-inverse (which is needed here, since PRP does not have
full rank).
IV. SEMI-BLIND DETECTORS
A. Semi-blind decorrelating detectors
In our first approach to semifilind decorrelating detectors, we use a mixed
projection/orthogonalization approach, as described in
section IILA The idea is to first project the received data r on the subspace
orthogonal to span(St ) , with S, given by (2). Thereby
all interference from the larown users has been removed. The orthogonalization
approach is then used in span(S t ) 1. The
calailarions can be done as follows. Let P, be defined by (3), and define S, =
P; .C"S. st ~, A, _ ~A A, ~ and
(. r
Wt =StAytSt StAtr AtSt
We can write the eigenvalue decomposition of Rt = P~ RPi as
As 0 0 UJ
R, _ ~U, U" Uo 0 ~zI 0 U"
0 0 0 Uo
Here U, is an orthonormal basis of the signal subspace, which in this case is
spanned by CS s, ~, while U" is the noise subspace. The
matrix Uo is an orthonormal basis of the space spanned by St. Furthermore, Aa
= diag(.tt , ~li,...,~.K+t ) with .i; > 0-2 . Similarly to
the blind deoorrelating detector we now have that
Wt =U.~.=-~ZIx+trtU= (I1)
We can then state the semi-blind deoorrelating detector as
Theorem l: The deoorrelating detector is given by
1
wt = r Wtst (l2)
si Wtsi
12
CA 02277252 1999-07-09
In our setting, S; is unknown. Equation (11), however, outlines a method for
estimating W,, and the method can therefore be
implemented without knowledge of the unknown users' codes.
The problem of the above method is that W, is specific to user 1. It can be
used with advantage in the case where some
users' codes are known, but still only one user's data is of interest, as for
example in a mobile station. However, if several users are
to be detected simultaneously, an SVD/subspace tracking has to be done for
each user, and the method is ine~cient.
We will therefore develop a method that requires only one SVD common to all
users. This method will be based on the
orthogonalization approach. Fiat, define the projection on span(S) ,
P =s~Tsr~sT
with Pl = I - P . The eigenvalue decomposition of P 1 RP 1 , is then given by
At 0 0 Ua
P1RP1 =[Us U" Uo 0 QZI 0 U"
0 0 0 Uo
where As = diag(.i,,,.iz,...,.iK ) with ~.; > a'2 , and Uo has K rows.
The idea in the semi-blind detector is first to apply the projection P1 to the
received data. Thereby the signal from known
all users have been eliminated. The subspace of the unknown users, projected
to span(S)1, is then found. This is span~U, ~. The last
step is to combine this subspace with the code of each user through some
algebraic manipulations. For details, see the proof of
Theorem 2.
We can now state the semi-blind decorrelating detector as follows
Theorem 2: The decorrelating detector is given by
b=sg~~.STSrIST~I-RIJf~AJ -v2Ir~Ua JrJ (13)
Proof see Appendix A.
Notice that all quantities in the theorem can be estimated with knowledge of
only the known users' codes. Notice also that
although R appears explicitly, R itself does not have to be estimated. Define
T(n) = ST R(n)Us (n)
13
CA 02277252 1999-07-09
where R(n) etc. denote the estimated quantities over n samples. Then we can
rewrite (13) as
b(n)=s~~TS~ tI ST -T(~)(Ar(n)-~~I,Us (n))r~, (14)
The quantity T(n) can be calculated as follows,
T(n)=Sr 1 L.rlrt Us(n)
n f=I
_l ~ 1
~, ~Srrt ~U; (n)ri)T ~ (IS)
~=t
~~Trr~'i Us (n)
n .-_t
The implementation using the formula on the second line only roquires KK
multiplications per bit, instead of the MZ multiplications
to calculate R On the other hand this formula is not directly suitable for
recursive implementation, since Us (n) has to be applied to
all previous samples. The formula on the third line requires KM
multiplicadons, and can be implemented recursively as long as S is
time-invariant.
B. Hybrid Semi-Blind Detectors
We will in this section consider detectors that are combinations of the
decorrelating detector and the MMSE detector. Specifically,
we will study detectors that are decornelating among the known users and MMSE
with respect to the unknown users. We will call
this class of detectors hybrid semi-blind detectors. The idea is similar to
ideas used in array processing: to direct nulls in the
direction of known interferers, and find the MMSE solution for the remaining
interference, and has in this ~ntext also been studied
for mufti-user detection [19,20].
As for the decorrelating detector, we will give two solutions for the hybrid
detector: one that makes a subspace calculation
for each user, and one that makes a common subspace calculation. For the
former case we get the following Theorem 3. The notation
is the same as for Theorem 1.
Theorem 3: The hybrid semi-blind detector is given by
wl = s; UsAfIUsSt UfAsIUss~ (16)
14
CA 02277252 1999-07-09
where Us and A~ is given from the eigenvalue decomposition of Ri = P~ RP~l
Aj 0 0 Us
R, _ ~Ua U" Uo 0 ~2I 0 U
0 0 0 Ua
where As =diag(.i,,.'tz,...,~.K+~) with ~,; >a~2
This detector is similar to the detector of [19], but is here stated in a
subspace context.
For the case of common subspace tracking we get, with the same notation as for
Theorem 2
Tfreorem 4: The hybrid semi-blind detector is given by
b =sg~~SrSr~ST(I-RU,As~U; )rJ (17)
Proof-. see Appendix B.
We notice that the hybrid semi-blind detector (17) is very similar to the semi-
blind decorrelating detector (13). The only
difference is that As -6~I is replaced by A, . As for (17), R itself does not
have to be estimated, as the quantities needed can be
calculated using (15).
In general, the MMSE detector has superior performance to the decorrelating
detector [10], and it would therefore be
natural to study pure MMSE semi-blind detectors. However, the hybrid approach
has a number of advantages. For the known users,
the decorrelating detector does not need a~ estimated information, whereas the
MMSE solution requires estimates and tracking of
user powers. On the other hand, the deoornelating detector for the unknown
users requires a noise estimate and is therefore rather
dependent on an accurate estimate of the number of users, while the MMSE
detector does not have these shortcomings. Finally, the
semi-blind hybrid detector has a compact, simple expression (17), while it
seems impossible to derive the true MMSE detector by the
methods used here.
One way to make ( 17) closer to a true MMSE solution, is to replace it with
the following expression
b=sgnC(STS+QZA-ZrIST(I-RUtAs~Us)r~ (18)
The argument for (18) is heuristic. We first find the MMSE solution in the
subspace spanned by the known users, ignoring all
interference from unknown users. For each user, we then find the MMSE solution
in the subspace spanned by this solution and iJ s .
CA 02277252 1999-07-09
This solution can avoid the amplification of noise that ~uld happen in ( 17),
but it is not an NIIviSE solution and does not satisfy any
orthogonality or IvFvISE conditions.
V. SUBSPACE TRACKIrIG
A large number of different subspace tracking methods exist, with varying
convergence speed and complexity, and most of them can
be applied to the current problem, but with some modifications. To illustrate
the principles we have chosen to use the F2 algorithm
( 16], summarized in Tabte 1. We use a standard exponential window with
It(n) _ .ZR(n -1) +r"r~
Table I: The F2 algorithm [16] for tracking a d-dimensional subspace.
Let the data vecxors be v~, v2,...
U(0) arbitrary m x d matrix, U(0)T U(0) = I
E(0) = I.
For n = 1,2,3,...
Define W(n)_~U(n-1)E(n-1) v"~
Compute the m x d and d x d matrices, U(n), E(n)
from the SVD:
~U(n) u~~~n) ~~Y(n)T = W (n)
For the semi-blind algorithms (16) and (12) the input to the F2 algorithm for
user 1 are the vectors
1
V n = Pl rn
The subspace dimension is d = K +1. The matrix U,(n) is directly the output
U(n) of the F2 algorithm, while Ad(n) = E(n)2 .
For the semi-blind detectors (17) and (13), the input to the F2 algorithm is
Vn =Plrn
and the subspace dimension is d = K . Again, the subspace information can be
obtained directly from the output of the F2 algorithm
with the matrix Us(n) equal to U(n) and Aj(n) = E(n)Z . However, also T(n)
(equation (15)) has to be calculated to implement the
algorithms. As stated below equation (15) this formula on the second line is
not suitable for recursive implementation. We will here
give some approximate formula for a recursive implementation, that can also be
used when S is time-varying.
16
CA 02277252 1999-07-09
With the weighting factor included, T(n) can be rewritten as
T(n)=~~° ~(Srrr~Us(~)ryr (19)
The level of approximation used in evaluating (19) should correspond to the
level of approximation used in the specific subspace
tracking algorithm used, so that there is an agreement in convergence speed
and complexity between the subspace tracking
algorithm and the update formula for T(n). Thus, a general update formula
cannot be given, and we will look at two examples. The
first possibility is to replace U~(n) with i1,(i) inside the summation in
(19), to get
T(n) ~ ~ ~~f ~rrt ~Us (l)rt \r
r= J~
~., r
=~,T(n_1)+Prrn'lUi (n)r~J
This approximation is essentially the same as the key approximation used in
deriving PASTd, and gives good performance with this
algorithm. However, for a fast converging algorithm such as F2, we lave found
this does not result in good convergence. Another
approximation is
T(n) ~ ~.T(n-1)Us (n-1)Us(n)+Srr"(i1; (n)r"~r (20)
The justification of this approximation is geometrical. The quantity Us (n -
i)Tr (n -1) represents the orthogonal projection of
R(n-I~Sr onto the subspace spanned by Ua(n-1). To find the projection of R(n-
1)Sr onto the subspace spanned by Us(n) we
should reproject R(n -1)Sr . Instead we project the previous projection. If
the subspace does not change too much from n to n+l, the
approximation is only slight. Notice also that this approximation is similar
to the key approximation in deriving F2 (equation (27) in
[16])
The calculation of Us (n -1)Us (n) is complex in itself. Fortunately, this can
be obtained as an intermediate result in the FZ
algorithm. Notice that since ~U(n) u~ ~U(n) u~= I (Table i), we have
C~n) O~YrC~n_1) 0~_~
0 a ~
~F(n_1) U~_
_ ~U(n) u~ W(n
0
_ ~~U(n)r U(n -1) ~~
17
CA 02277252 1999-07-09
where ~ indicates elements with values irrelevant to the result. Thus, LTs (n-
1)IJs(n) can be found from the upper Left K x K
matrix of the above matrix. The total multiplication count for this approach
is KK z + 2K , which compares well with the
multiplication count of 3MK Z +MK for the F2 algorithm itself. However, if K
is large, the formula in the second line of equation
( 15) has less complexity.
VL SIMULATION STUDIES
We consider a system with K--7 users with known codes, all with the same
power, and a variable number K of users with unknown
codes. The users are assigned purely random codes of length M=31, and the SNR
is 20 dB. An ensemble of 50 different random code
assignments is generated, and the median signal to inference and noise ratio
(SINK) is calculated over all code choices and users, in
total an ensemble of 350. The SINK for a user is calculated using a moving
average filter of length 20.
In all cases we consider 8 different detectors:
single user The oom~entional single user detector. This is the lower bound on
performance of any mufti-user detector.
Full The hypothetical non-blind MMSE mufti-user detector that knows all codes.
This is the upper bound of
performance for any linear mufti-user detector.
non-blind The nonfilind MMSE detector that uses only the known codes and
ignores the interference from the unknown
users.
Direct The blind MMSE detector calculated using direct inversion of the
correlation matrix (equation (8)).
Blind The blind MMSE detector calculated using (9) and using SVD for subspace
calculation.
Semi-blind SVD The semi-blind detector calculated using (17) and using SVD for
subspace calculation.
Semi-blind 2 The stmt-blind detector calculated using (16) and using SVD for
subspace calculation.
Semi-blind F2 The semi-blind detector calculated using (17) and using the F2
algorithm for subspace calculation with T(n)
calculated using (20).
Decorrelating detectors are not considered, since they in general have an
inferior performance and are sensitive to
estimation errors. Performance of the dacorrelating detectors can be seen in
[21]. For the F2 algorithm, it was initialized with an
18
CA 02277252 1999-07-09
ordinary SVD over the first 50 samples, i.e., U(0) and E(0) in Table 1 was
initialized from the SVD over the first 50 samples.
Without this initialization, the F2 algorithm diverged in the beginning, until
it would start converging.
QA
Figure'l4shows the convergence with K = 4 unknown users, all of the same power
as the known users. It can be seen that
the semi-blind detector has a performance gain over the blind detector
starting at 4 dB and decreasing to 2 dB. As the number of bits
increase both detectors should converge towards the full MMSE, and the
performance gain go towards zem. It also seen that the
performance of the semi-blind detector is better than the non-blind MMSE
already after 50 bits, whereas the blind detector requires
100 bits.
The performance of the semi-blind algorithm using F2 is almost
indistinguishable from the performance using SVD, and is
therefore di~eult to see in the figures. The performance of the semi-blind
algorithm using (16) is slightly worse than the one using
(17). From other simulations we have made, this seems to be a general
behavior. Since (17) has much less complexity than (16) for
simultaneous detection, ( 17) must be prefered.
19
CA 02277252 1999-07-09
The performance gain of course depends on many factors: SNR, user powers, the
codes used, and the number of users.
Figure shows the performance when the number of unknown users is increased to
K =10 users. Of these, 4 have the same power
as the known users, while the 6 others have power -6dB. As expected, the
performance gain of the semi-blind detector over the blind
is less than for Figure~~ Basically, when the number of unknown users is high,
the information on known users does help relatively
less. However, the gain is still around 2dB.
It can also be seen that the performance of both blind and semi-blind
detectors is worse than the non-blind detector in the
beginning. In this case, the semi-blind detector has a further advantage to
the blind detector: the non-blind part can be used alone
until the blind part has converged. This cannot be done for the blind
detector. An even better way is to replace (14) with the
following formula
b(n)=s~~TSr~(sT -X(n)T(n)Aa'(n)Uf (n))rnJ
where OSx(n)sl is a weighting function with x(Or-0 and x(aor 1. The optimal
(or even a good) way of choosing x(n) is a subject for
further study. However, some preliminary tests show that this gives a superior
performance in the beginning.
CA 02277252 1999-07-09
_ K
The previous results were under the assumption that K was known or estimated
without errors. In Figure'B the same data
g
is used as for Figure, i.e., K =10 , but the value of K used for the
estimators is set to 4, i.e., equal to the number of high power
users. Remarkably, the performance of both the blind and the semi-blind
algorithms improve, at least for a small number of bits, and
in addition, the gain of the semi-blind algorithm is increased, now again
ranging between 2 and 4 dB. Two conclusions can be
drawn
1. The estimators, both blind and semi-blind, are relatively insensitive to
estimation errors on K .
2. The performance is better if only the largest eigem~alues are used in the
subspace algorithms, rather than the full interference
subspace.
Item 2 is in particular important. This can be interpreted so that it pays off
to track only a few high power unknown users.
In a cellular system, this means that it is advantageous to track only the out-
of-cell users on the boundary of the cell considered,
while the interference from other users inside neighboring cells are
considered background noise because of path loss. This means
that the number of users (or, rather, eigenmodes) that need to be tracked in
the semi-blind algorithms can be quite low, and low-
complexity subspace tracking algorithms such as PASTd could be employed,
resulting in a very low complexity system.
This conclusion is only true for a small number of bits. As the number of bits
go towards infinity, the blind and semi-blind
algorithm with the correct value of K should converge towards the full MMSE
detector, which is not true if the estimated value of
21
CA 02277252 1999-07-09
K is too small. Thus, in a dynamic environment, the best value of K depends
not only on the number of users and their power, but
also on the time scale for change in the environment.
In order to find the performance in terms of bit error rate (BER) versus SNR a
difi'erent simulation scenario was used. Three
detectors were considered: the non-blind MMSE detector, the blind MMSE
detector, and the semi-blind hybrid detector implemented
using (17), with the latter two implemented using SVD for a fixed block size
of 200. The data was generated in the following way:
the number of known users was K--7, and the number of unknown users K = 4 . An
ensemble of 20 different code matrices was
generated. For each code matrix, 100 different ensembles of 10,000 bits were
generated. For each ensemble of 10,000 bits, the
detectors were estimated over the 200 first bits, and the BER was calculated
over all 10,000 bits, and averaged over the 100 different
ensembles (i.e., the total number of bits were 1,000,000). Thus, for each SNR
value, 20 code matrices x 7 users = 140 ensembles
9D
were available. For these, the median and 90-percentile (i.e., the 14'~ worst)
BER were calculated, shown in Figure ~. This gives a
reasonable impression of performance, but does not completely reveal the
performance of the detectors. By plotting each of the 140
ensembles and observing them manually, we made the following observations for
high SNR (> 10 dB)
~ The semi-blind detector always had a lower BER than the blind detector
~ The blind detector was in most cases better than the non-blind detector. In
some cases, the non-blind detector was somewhat
better (up to 1 dB).
22
CA 02277252 1999-07-09
~ The semi-blind detector was almost always better than the non-blind
detector. In a few cases the non-blind detector was better,
but then only insignificantly (0.1-0.2 dB).
qD
~ In some cases the non-blind detector had a very poor performance (which is
reflected in the 90-percentile in Figure ~). The
reason must be that there is an unknown user with a code very close to a known
user. Thus, even a few high power out-of-cell
users can corrupt the performance of a non-blind multi-user detector in a
cellular system.
The last observation is reason enough that the non-blind detector should not
be used when there is inter~ell interference. Since out-
of-cell users cannot be controlled the same way that in-cell users can, this
last case could happen, and as the worst~case performance
essentially determines the quality of service, this would not be acceptable.
VIL CONCLUSION
In this paper we have developed a class of new multi-user detectors, called
semi-blind linear detectors. They are distinguished by the
fact that they can cancel interference from both known and unknown users, like
blind detectors, while simultaneously using the
knowledge of known users. Simulations have shown that the semi~lind detectors
have notably better performance than both the pure
blind detectors and the non-blind detectors, and furthermore they have a
considerably lower computational complexity.
Our simulations have also shown that the interference from even a few out-of-
cell users can totally corrupt the performance
of a non-blind multi-user detector. This problem can e~ciently be handled by
the semi-blind detector.
23
CA 02277252 1999-07-09
APPENDIX A: PROOF OF THEOREM 2
We will approach the proof constructively. Denote in the following by w, the
weight vector for the decorrelating detector for user 1,
and let v, be defined by
vt =Wat.W =Sr'rSl 2Sr
(see also (5), and the discussion), and consider the subspace V = spanQUs vt
D. Notice that U J S = 0 and Ul vt = 0 by the
definition of U~ . We must have w, a ~, sinoe~ is orthogonal to all
interference by the other known users. Thus,
wt = Lil. vt Ft
for some vector ct. As in the proof of proposition 1 of [14], we now see that
we can write
Ct =argmincr UT J(SAZSr +SAZSr~Ut vl~
c V1
__ T D UsSAZSrvt
argmmc Cv; SA2SrU, vi ~SA2Sr +SAZSr~'t~
c
511bjeCttO wj S~ =1, With
D=As _o.2lx
Now notice that
Pt ~ Ua Rvt = U; ~.SAZSr +SAZSr +Q2Iwt
= Us SAZSry
and
v~ Rvt = vi AZSr +SAZSr +QZI}y
=v~ AZST +SAZSr}vt +QZV;
Thus,
D
c, =argmincT T vrRvP' QZVz
CPt t t t
Following the proof of [ 14J proposition 1, we then find that
wt = 1 Mvi
v~ Mvt
24
CA 02277252 1999-07-09
with
M=~U v D P~ ~ iJf
s 1 T vTRv -~2v2
Here we apply a matrix inversion theorem (see, e.g., (15], sedion 2.9) to get
Or 0
M ~UJ v~ CD ' OJ
1 D ~P~Pi D 1 -D ~P~ Us
vi Rv~ -pi D-~P~ -~ZVi -(D 'Py 1 vi
To calculate Mvl notice that since Ul v~ = 0 in fad only the last row of the
matrix inside { } is needed, which yields
Mv, =~U, v~ v~ -D- p~
v~ Rvl -p~ D Cpl -o~ZV~ ~ 11
2 _
- '_ wt -UdD ~Py
vi Rv~ 'Pi D 1P~ -~ZVi
Thus,
wi r =xv; (I-RUsD 'Us
for some positive constant ~ Combining the solutions for the different users,
we obtain (13).
APPENDIX B: PROOF OF THEOREM 4
The proof follows the proof of theorem 2 closely. Thus, at first we see that
we can write
wl _ LUs vu
For some vector c,. By (10) we now have, except for a scaling constant
-i
c~ - T R U, vl r y
_ ~U~ ~ ( 1 ~U=
v~ v .~,
_ r _ -' r
wi = ~U~ y CUT JRLUr vy CUr ~s~
v, v,
Similarly to the proof of theorem 2, we see that
s R[U v ]= As P~
v s ~ PT vi Rv~
We can now follow the same steps as the proof of theorem 2 with D replaced by
As and v; Rv, -~ZV; replaced by v; Rv, ,
arriving at ( 17).