Note: Descriptions are shown in the official language in which they were submitted.
CA 02360656 2001-10-31
1
REAL-TIME IMAGE RECONSTRUCTION FOR
COMPUTED TOMOGRAPHY SYSTEMS
BACKGROUND OF THE INVENTION
1. Field of the invention:
The present invention relates to a method and apparatus for conducting
matrix pseudo-inverse tomographic reconstruction, in particular but not
exclusively in real-time.
2. Brief description of the current technology:
Tomography refers to the cross-sectional imaging of an object from either
transmission, emission or reflection data collected from many different
directions.
Tomographic imaging deals with reconstructing an image from such data,
commonly called projections. From a purely mathematical standpoint, a
projection at a given angle is the integral of the image in the direction
specified
by that angle. The solution to the problem of reconstructing a function from
its
projections dates back to Radon in 1917, hence the denomination inverse-Radon
transform. However, it was only in the early 1970's, with the invention of the
X-
ray computed tomographic (CT) scanner and the development of reconstruction
algorithms, that tomographic imaging came into widespread use. Tomographic
methods now find applications in a vast number of fields, including radio
astronomy, seismology, nondestructive analyses, electron microscopy, and
above all medical imaging. In fact, most of the powerful new medical imaging
modalities that have been introduced during the last three decades, such as X-
CA 02360656 2001-10-31
2
ray CT, Single Photon Emission Computed Tomography (SPELT), Positron
Emission Tomography (PET), Magnetic Resonance Imaging (MRI) and 3D
(three-dimensional) ultrasound (US), were the result of the application of
tomographic principles.
A. Review of current tomo4raphic reconstruction algorithms
Many tomographic reconstruction algorithms are disclosed in the art and
a comprehensive description of these can be found in the literature. There are
two main classes of tomographic reconstruction methods currently in use today:
analytical reconstruction algorithms, which aim at solving the inverse-Radon
transform, and iterative algorithms, which attempt to reach a solution by
successive estimation of the underlying image and improvement of image
estimates at every iteration.
A.1 Filtered Back Pro~iection
The most common tomographic reconstruction method nowadays is the
filtered back projection (FBP) algorithm, which makes use of the projection-
slice
theorem, see generally A.C. Kak & M. Slaney, Principles of Computerized
Tomographic Imaging, IEEE Press, New York, 1988. The algorithm generally
proceeds by first transferring each measured projection into Fourier space,
filtering with an appropriate filter in frequency space, transferring the
result back
into the projection space and then back projecting the result onto the image
grid:
z =Back-Project{F~'~c(f)xF,~b'~~ (1)
where b' is a j-th projection vector (j=1,...,A), A is a total number of
projection
angles, F, is a 1-D Fourier transform, F;' is a 1-D inverse Fourier transform,
CA 02360656 2001-10-31
3
c(f~ is a 1-D filter function in the Fourier space, commonly referred to as a
"ramp" filter in the simplest noise-free case, and x = ~xk : k =1,..., M} is
the
image that has to be found, M being the total number of image pixels (or
voxels).
The filtering step, which is commonly pertormed as a multiplication with the
ramp
filter in Fourrier space, can also be carried out as a convolution of the
projection
vector in the spatial domain with a filter kernel that is the inverse Fourier
transform of the ramp filter.
The FBP algorithm produces an image that is a linear combination of the
projection data. It can be efficiently implemented in general purpose
computers,
its memory requirements are modest and the computation is rather fast. It is
the
reconstruction method of choice for virtually all X-ray CT and most emission
tomography (SPELT, PET) systems currently in operation. Since the FBP
algorithm is linear, it can be reduced to event-by-event reconstruction based
on
the principle of superposition, by deriving a filter function representing the
contribution of an individual event to the image. However, its widespread
popularity stems more from historical reasons of computational simplicity than
any widely accepted advantage in image quality. In fact, there are several
problems with this algorithm:
- data must be assumed to be uniformly distributed on projections (which is
generally not the case with the cylindrical scanner geometry), or must be
rebinned with equal spacing to accommodate the convolution operation
(commonly performed in Fourier space);
- models for the detector response must be space invariant and can only be
incorporated into the algorithm as a deconvolution with the attendant noise
amplification;
- the ideal ramp filter amplifies high-frequency noise in the projection, and
it
must often be apodized with a window function to reduce noise in the
CA 02360656 2001-10-31
4
reconstructed image;
- even though the intensity is known to be non-negative, the algorithm yields
negative values, particularly if the data are noisy;
- streak artifacts are present; and
- event-by-event reconstruction involves some elaborate computation to align,
rotate and scale the single event filters before summation to the image
matrix.
A.2 Algebraic Reconstruction
In the art there are known other tomographic image reconstruction
methods called algebraic reconstruction techniques. They aim at solving the
system of linear equations:
Pl lxl + P12x2 '~' ... + plMxM = b1
P21x1 +P22x2 +...+ p2MxM = b2 (2)
PNlx1 + PN2x2 +... + pNMxM = bN
where bt : i =1,..., N are the measured projections (sinogram),
x = {xk : k =1,..., M~ is the image that has to be found, N and M are the
total
number of tubes-of response and image pixels (or voxels), respectively.
These methods are usually iterative in nature and preferably (though not
always) converge to the minimum norm least-squares solution as the iteration
number goes to infinity, see in particular X.-L. Xu, J.-S. Liow & S.C.
Strother,
"Iterative algebraic reconstruction algorithms for emission computed
CA 02360656 2001-10-31
tomography: A unified framework and its application to positron emission
tomography", Med. Phys., vol. 20(6), pp. 1675-1684, 1993. Some of the
drawbacks of the iterative algebraic methods are:
5 - they are very computer intensive and have large memory requirements;
- given the inherently iterative nature of the algorithms, real-time
reconstruction
is virtually not implementable;
- the need to optimize the iteration number and the order in which projections
are being utilized in the reconstruction;
- the non-linearity of the solution due to the iterative nature of
reconstruction
algorithm, which results in complex quantitative dependence of the image
estimate on input data; and
- the complete measured projection data set is required before starting
reconstruction.
A.3 Statistical Reconstruction
Statistical image reconstruction methods were introduced in an attempt
to overcome some of the drawbacks of the previous methods, in particular
taking
account of the stochastic nature of the measured data in emission tomography
and the physical modeling of the detection process. In general, statistical
iterative reconstruction methods yield images with a greatly superior visual
quality when compared to FBP reconstructed images, especially in the case of
low projection statistics. The absence of negative values and proper modeling
of the detector response helps to avoid several of the artifacts present in
FBP
images. Unfortunately, the superior image quality does not necessarily
translate
into better quantitation accuracy. The use of statistical reconstruction
methods
CA 02360656 2001-10-31
6
also raises other practical problems that still hamper their utilization
outside the
research environment. In addition to most of the drawbacks that are common
with iterative algebraic methods, statistical methods also give rise to the
following problems:
- in the case of unconstrained iterative estimation, the need to optimize the
number of iterations: If the number of iterations is too low, the spatial
resolution is sub-optimal; if the number of iterations is too high, the
spatial
resolution is artificially enhanced at the expense of unacceptable noise
amplification;
- in the case of so called Bayesian approach the necessity to optimize an
extra
parameter, called prior, that controls noise or image smoothness (see E.
Levitan & G.T. Herman, "A maximum a posteriors probability expectation
maximization algorithm for image reconstruction in emission tomography",
IEEE Trans. Med. Imag., vol. 6, no. 3, pp. 185-192, 1987); and
- the non-linearity of the solution due to the iterative nature of the
reconstruction algorithm, which results in a complex quantitative dependence
of the image estimate on input data.
SUMMARY OF THE INVENTION
In an attempt to overcome the above discussed drawbacks of the prior
art, there is provided, according to the present invention, a method for
reconstructing an image, formed of an array of pixels (or voxels), from a
series
of measured individual tomographic projection data, comprising creating a
system matrix defining vectors relating the measured individual projection
data
to the pixels (or voxels) of the image, associating one of the vectors of the
CA 02360656 2001-10-31
7
system matrix to each measured individual projection data and, for each
measured individual projection data of the series, updating the image by
adding
to a previous image estimate the vector of the system matrix associated to the
measured individual projection data.
According to preferred embodiments of the image recontructing method:
- the image reconstructing method comprises conducting the vector
associating and the image updating in real-time while the individual
projection
data are measured;
- creating a system matrix comprises factoring a system matrix defining
vectors relating the measured individual projection data to the pixels of the
image, and inverting the factored system matrix;
- the factored system matrix presents the form P=UWVT , and inverting the
system matrix comprises pseudo-inverting the factored system matrix of the
form P=UWVT to obtain a pseudo-inverse system matrix of the form
P+=VIiV+UT where U and V are orthogonal matrices, W is a diagonal matrix
containing singular values, W'' is the inverted diagonal matrix hV, and T
denotes transpose of matrices V and U;
- the image reconstructing method comprises truncating the pseudo-inverse
system matrix to remove small singular values;
- the image reconstructing method comprises modifying a singular value
spectrum to reduce the effect of inversion of very small singular values,
wherein modifying the singular value spectrum comprises replacing the
singular values in the diagonal matrix W''' by a function of these singular
values;
- the measured individual projection data comprise events detected through
tubes-of-response of a tomographic scanner, the system matrix comprises
CA 02360656 2001-10-31
a number of columns equal to the number of tubes-of-response and a
number of rows equal to the number of pixels of the image, the columns of
the system matrix define respective vector-columns relating the events
detected through the tubes-of response to the pixels of the image, each tube-
s of response is associated to a respective vector-column of the system
matrix, associating one of the vectors of the system matrix to each measured
individual projection data comprises associating each detected event to the
vector-column of the system matrix associated to the tube-of response
through which the event has been detected, and updating the image
comprises, for each detected event, adding to the previous image estimate
the vector-column of the system matrix associated to the tube-of response
through which the event has been detected;
- the image reconstructing method comprises, prior to adding to the previous
image estimate the vector-column, scaling that vector-column with a
correction factor; and
- the image reconstructing method comprises obtaining the previous image
estimate by adding together all vectors of the system matrix associated to all
measured individual projection data prior to measurement of the individual
projection data under consideration.
The present invention also relates to an apparatus for reconstructing an
image, formed of an array of pixels, from a series of measured individual
tomographic projection data and a system matrix defining vectors relating the
measured individual projection data to the pixels of the image. This image
reconstructing apparatus comprises means for associating one of the vectors of
the system matrix to each measured individual projection data, and means for
updating the image for each measured individual projection data of the series.
The latter updating means comprises an adder for adding to a previous image
estimate the vector of the system matrix associated to the measured individual
projection data.
CA 02360656 2001-10-31
9
Advantageously, this image reconstructing apparatus includes means for
operating the associating means and the updating means in real time while the
individual projection data of the series are measured.
Still further in accordance with the present invention, there is provided an
apparatus for reconstructing an image, formed of an array of pixels, from a
series of measured individual tomographic projection data and a system matrix
defining vectors relating the measured individual projection data to the
pixels of
the image. This image reconstructing apparatus comprises a generator of a
projection data index in response to each measured individual projection data,
a memory unit storing the system matrix and comprising an address input
supplied with the projection data index from the generator and a data output
delivering a vector of the system matrix corresponding to the projection data
index and, for updating the image for each individual projection data, an
adder
for adding to a previous image estimate the vector of the system matrix
delivered
on the data output of the memory unit.
According to preferred embodiments of the image reconstructing
apparatus:
- the image recontructing apparatus comprises means for operating the
generator, memory unit and adder in real time while the individual projection
data are measured;
- the system matrix is a pseudo-inverse system matrix of the form
P+=VW+UT, which results from a peuso inversion of a system matrix having
the form P=UWVT, where U and V are orthogonal matrices and W is a
diagonal matrix containing singular values, W+ is the inverted diagonal matrix
W, and T denotes transpose of matrices V and U;
CA 02360656 2001-10-31
- the image reconstructing apparatus comprises means for truncating the
pseudo-inverse system matrix to remove small singular values;
- the image reconstructing apparatus comprises means for modifying a
singular value spectrum to reduce the effect of inversion of very small
5 singular values, wherein the means for modifying the singular value spectrum
comprises means for replacing the singular values of the diagonal matrix INS
by a function of these singular values;
- the measured individual projection data comprise events detected through
tubes-of-response of a tomographic scanner, the memory unit comprises a
10 number of columns of memory locations equal to the number of tubes-of
response and a number of rows of memory locations equal to the number of
pixels of the image, the columns of the memory unit store respective vector-
columns relating the events detected through the tubes-of response to the
pixels of the image, each tube-of-response is associated to a respective
column of the memory unit, and the adder has a first input receiving the
previous image estimate and a second input receiving the vector-column
stored in the column of the memory unit associated to the tube-of response
through which the event has been detected;
- the image reconstructing apparatus further comprises a multiplier which,
prior
to adding to the previous image estimate the vector-column, multiplies this
vector-column with a correction factor; and
- the image reconstructing apparatus comprises means for obtaining the
previous image estimate by adding together all vectors of the system matrix
associated to all measured individual projection data prior to measurement
of the individual projection data under consideration.
The method of the invention presents, amongst others, the following
advantages:
CA 02360656 2001-10-31
11
- it allows real-time reconstruction of projection data;
- it allows event-by-event updating of a tomographically
reconstructed image;
- it allows individual projection data to be reconstructed
independently to update an existing image;
- it allows real-time updating and display of an image;
- it allows to monitor tomographic data acquisition in real-time;
- it avoids data rebinning into projection vectors, since the exact
geometry of the measuring instrument can be utilized; and
- it may avoid storage of measured projection data (either in list
mode, histogram or rebinned sinogram) if further processing of
the measured projection data is unnecessary.
The foregoing and other objects, advantages and features of the present
invention will become more apparent upon reading of the following non
restrictive
description of a preferred embodiment thereof, given as illustrative example
only
with reference to the accompanying drawings.
BRIEF DESCRIPTION OF THE DRAWINGS
In the appended drawings:
CA 02360656 2001-10-31
12
Figure 1 a is a schematic diagram of the detection unit of a PET scanner;
Figure 1 b is a schematic diagram of the detection unit of a PET scanner
showing, for a fan-beam response, tubes-of response between one detector
paired with a plurality of other detectors;
Figure 1c is a schematic diagram of the detection unit of a PET scanner
showing, for linear sampling, parallel tubes-of-response between pairs of
detectors in a detector array;
Figure 2a is a schematic diagram of a phantom used for generating test
images in a PET sanner;
Figure 2b is an illustration of the various steps involved in a real-time
tomographic image reconstruction using the matrix pseudo-inverse method;
Figure 3 is a schematic diagram of a dedicated hardware for performing
real-time tomographic image reconstruction based on the matrix pseudo-inverse
method;
Figure 4 is a singular value spectrum of the system matrix for an animal
PET scanner and a 64x64 pixel image;
Figure 5 is a first sequence of phantom images demonstrating the use of
real-time TSVD reconstruction; and
Figure 6 is a second sequence of phantom images demonstrating the use
of real time TSVD reconstruction with projections acquired at eight (8)
consecutive angles.
CA 02360656 2001-10-31
13
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENT
An approach that was disclosed some time ago (see Y.S. Shim & Z.H.
Cho, "SVD pseudoinversion image reconstruction", IEEE Trans. ASSP, vo1.29,
no.4, pp.904-909, 1981), but has not yet gained popularity for tomographic
reconstruction is the matrix pseudo-inverse method, whereby the system matrix
relating the tomographic image grid (pixels) to the measured projections must
be pseudo-inverted. Its use has been suggested in situations where only a
limited number of projections are required. To provide complete number of
projections, which is necessary in any practical application of tomographic
medical imaging, its use has been hindered by the computational burden
resulting from the size of the matrix and ill-conditioning of the system
matrix
which has to be accounted for in a manner preferably independent of the image
being reconstructed. Matrix pseudo-inversion can be performed based on
singular value decomposition (SVD) of the system matrix with some
regularization to diminish the effect of small singular values. Its
application to the
tomographic reconstruction problem is described below.
Matrix Pseudo-Inverse Tomograahic Reconstruction
The image reconstruction problem in tomography can be written in the
matrix form
Px = b (3)
where
CA 02360656 2001-10-31
14
N
P = p J : i =1,..., N; ~ p~~ =1, j =1,..., M (4)
t=i
is the system matrix, b = {b~ : i =1,..., N~ is a vector-column of measured
projections (sinogram), x = {xk : k =1,...,M} is a vector-column (image) that
has
to be found, and N and M are the total number of tubes-of response and image
pixels (or voxels), respectively. As known to those of ordinary skill in the
art, the
matrix P may be obtained in PET for a given scanner geometry with the
approach described in V.V. Selivanov, Y. Picard, J. Cadorette, S. Rodrigue &
R.
Lecomte, "Detector response models for statistical iterative image
reconstruction
in high resolution PET", IEEE Trans. Nucl. Sci., vol. 47, No. 3, pp. 1168-
1175,
2000.
Any matrix P can be factored into
P = UWV T (5)
where U = {ul~ : i =1,..., N; j =1,..., M and V = {v;~ : i, j =1,..., M are
orthogonal
matrices, W = f ,ulf : i, j =1,..., M; ~Z~ = 0 if i ~ j is a diagonal matrix
containing
singular values ,u1 ---- ,u11, i =1,..., M . T denotes matrix transpose.
Factored matrix
representation (5) is referred to as Singular Value Decomposition (SVD). An
algorithm to compute a matrix SVD is disclosed in W. H. Press & B. P.
Flannery,
S. A. Teukolsky, W. T. Vetterling, "Numerical recipes in C: The art of
scientific
computing", Cambridge University Press, 1988, pp. 60-72.
In the case where measured data are noisy and/or Equation (3) is
overdetermined/underdetermined, and the exact solution of Equation (3) does
CA 02360656 2001-10-31
not exist, one may find a minimum norm least-squares solution of Equation (3)
using
z = P+b (6)
5
where
P+ = VW +UT (7)
10 is the pseudo-inverse of P. tN+ is the pseudo-inverse diagonal matrix hV.
Singular values are usually presented as a non-increasing sequence called
singular value spectrum. Some singular values can be very small (or in some
cases equal to zero if the matrix is singular).
15 The condition number
max,u;
c = ' (8)
min ~1
t
of the system matrix can be very high (even infinity for a singular matrix).
Thus,
the inverse problem of tomographic image reconstruction is ill-conditioned and
any solution attempting to exploit the pseudo-inverse of matrix P (7) will be
very
sensitive to noise.
One way of regularizing the solution is to truncate the singular value
spectrum at some index T and remove small singular values ,u;, i =T +1,...,M
from the solution expansion, leaving
CA 02360656 2001-10-31
16
T _1 N
x = zk : zk = ~vktf~~ ~u~tbJ ~ k =1,...,M (9)
t=t >=1
which is referred to as the truncated SVD (TSVD) solution.
Another regularization approach would be to modify the singular value
spectrum in order to diminish the effect of the inversion of very small
singular
values (and zeros if any):
M N
z = zk : xk = ~ vk; f (,tt; y u;,b~; k =1,..., M (10)
i_t
where f (,u~ ~ is a function of the singular value. Such a solution is
referred to as
the modified SVD (MSVD) solution. An example of the MSVD can be found in
R. Lecomte, J. M.F. Smith, "Generalized matrix inverse reconstruction for
SPECT using a uveighted singular value spectrum", IEEE Trans. Nucl. Sci., vol.
43, no. 3, pp. 2008-2017, 1996.
Real-Time Reconstruction
Rearranging the summation order in Equation (9) we get:
CA 02360656 2001-10-31
17
xk = ~ E vk~W lu~tb~ _ ~ ~vkr~t lu~~ b~; k=1,...,M (11)
f=Ij=1 ~=1 i=~
Let P+ be the "truncated pseudo-inverse":
_ T
p+ - Pk~ ~ Pk~ _ ~vkil~i ~u~t~ k =1,...,M; j =1,...,N (12)
t=t
Then the TSDV solution in the matrix form is:
z = P+b (13)
Let b(t) be a sinogram containing a total of t counts:
N
b(t) = b~ (t) --__ b; : i =1,..., N; ~ b1 = t ( 14)
c=i
and x(t) _ ~xk (t~ : k =1,..., M is the respective solution given for b(t) by
Equation
(13). Let Ob(S) _ {O b; : i =1,...,N such that
0, i =1,..., s -1
Obl-~-= l,i=s (15)
O,i=s+1,...,N
and
CA 02360656 2001-10-31
18
b(s) (t~ --- b(t -1~+ 0 b(S) (16)
In other words, b(S)(t~= {b~s)(t): i =1,...,N is a sinogram, which differs
from
b(t-1~ by only one count, the count being located in a bin with index s:
bZ(t-1~, i =1,...,s-1
b~s)(t)= b1 (t-1~+l,i=s (17)
b; (t-l~,i=s+1,...,N
Assuming that x~s~(r) stands for the image estimate obtained using input
data b~'~(t~, then the solution given by
z(S)(t~= P+b(S)(t) (18)
may be found as follows. Given that the sinogram b~s~(t~ differs from b(t-1~
by
only one (1 ) count, we have:
N s-1
xx(t~- ~pkjbjs~~(t~- ~pkjbj(t-1)+ pksfbs(t-1)+lJ
j=1 l=1
N _ N (19)
+ ~Pkjbj(t-1~=~Pkb;(t-l~+P~~ k=1~...,M
j=s+1 j=1
Thus, the new image estimate is the sum of the previous image estimate and
one column (vector-column) of matrix P+
x(S)(t)= ~xks)(t): xks)(t)= xk(t-1~+ per, k =1,...,M (20)
CA 02360656 2001-10-31
19
The natural starting point for the described image reconstruction is the
blank image x(0~= ~xk (0~: k =1,..., M; xk (0~= 0 , using Equation (20)
subsequently to obtain a current image estimate in real-time based on the
previous image and the column of P+ defined by the sinogram bin index where
the last event was registered.
The MSVD solution can be obtained in real time as well using Equation
(20) and the modified pseudo-inverse matrix P+, given in this case by:
_ M
- hkj ~ Pkj = ~ vki.~(f~i ~ ji ~ k =1,..., M; j =1,..., N (21 )
i=1
where ~ is a function of other than ~ _ ~' ~' t ~ T
f (,u; ,u; ( f (~; , which was used
0, f > T
for deriving the TSVD).
The proposed approach is general and can be applied with any number of
projection bins and image pixels (or voxels), for 2D as well as for 3D-
reconstruction geometry, with scanners collecting complete or incomplete sets
of projections, for non-singular or singular system matrices. The proposed
approach is not limited to PET, but can also be applied with any tomographic
imaging system, such as SPECT, CT, etc., as long as a system matrix P relating
the image pixels to the measured projection data can be obtained and inverted.
In the following preferred embodiment a PET scanner having 2D reconstruction
geometry is disclosed.
CA 02360656 2001-10-31
Referring now to Figure 1a, a radioisotope which decays by positron (~i+)
emission is injected into (or inhaled by) a patient (not shown). The spatial
and
temporal distribution of the radioisotope within the patient will then depend
on
the manner in which the organ or tissue being scanned manages the
5 radioisotope both biochemically and physiologically. Once within the
patient, the
positrons escape from the radioisotope and travel a short distance, colliding
with
electrons of nearby atoms. The collision of a positron and electron results in
an
annihilation reaction 2 whereby the mass of the positron and electron are
converted into a pair of coincident 511 keV photons 4 which are emitted at
180°
10 to one another (note that a very small portion of the annihilation
reactions result
in the emission of three (3) annihilation photons but these are statistically
unimportant). The annihilation photons easily escape the patient's body and
can
be recorded by detectors 6 arranged in a circular array, or any other
convenient
geometry, around the patient.
The detectors 6 which are used in a PET scanner such as the one
generally designated by the reference 1 in Figure 1 a, typically consist of
scintillation crystals 8 of bismuth germanate (BGO) which convert the gamma
rays into light photons. The light photons are converted in the detectors 6
(for
example, photomultiplier tubes or avalanche photodiodes) into electrical
signals
10 which can then be transferred to the PET scanner's processing subsystem
12. The detectors 6 are typically arranged in rings such as14, generally with
a
number of rings such as 14 distributed along an axis 16 making up the PET
scanner.
As stated above, the coincident rays 4 are emitted simultaneously and at
180° to one another and, therefore, by detecting the occurrence of
simultaneous
(i.e. within 5-15 nanoseconds typically) reception of coincident rays 4 at two
different detectors 6 (known as a coincident event), the annihilation
reaction, and
CA 02360656 2001-10-31
21
therefore the radioisotope, can be localised within the patient along a line
drawn
between the two detectors 6 having sensed the two coincident rays 4.
As higher concentrations of a positron emitting radioisotope give rise to a
larger number of annihilation reactions 2 and therefore coincident events, the
processing subsystem 12 can process the coincident events and reconstruct an
image of the concentration and location of the radioisotope within the
patient.
Referring now to Figure 2a, the process of real-time tomographic image
reconstruction in its preferred PET embodiment will be further described. To
model the effects of a positron emitting substance injected into a patient
while
at the same time providing an image which is easily recognizable, a
cylindrical
phantom 18 is used. The phantom 18 is preferably constructed of Lucite~
(plexiglass material) or an equivalent material with a series of holes 20 of
different diameters for accepting a positron emitting substance 22, for
example
18F-fluorodeoxyglucose (FDG). The phantom 18 is placed within the PET
scanner (not shown) for recording coincident annihilation photon emissions. At
time TO the positron emitting substance 22 emits positrons which collide with
electrons of nearby atoms (neither shown) resulting in an annihilation
reaction,
the generation of two (2) annihilation photons 24180° apart from each
other and
the detection of a new coincident event 26 by a pair of detectors 6.
Referring back to Figure 1a, as stated above, the BGO detectors 6 of the
PET scanner 1 are typically arranged in rings 14. The region within the center
of the PET scanner 1 between a given pair of detectors 6 is defined as a tube-
of
response 28. Given the large number of detectors 6 and the multiple rings of
detectors 14, tubes-of-response 28 are typically defined (and therefore
coincident events recorded) for only a portion of the pairs of detector 6.
CA 02360656 2001-10-31
22
Referring now to Figure 1 b, for example, in a PET scanner comprising
rings 14 each of 256 detectors 6, 32 tubes-of response 28 are defined between
each given detector and 32 opposing detectors. In the preferred embodiment,
the PET scanner would therefore comprise 256 X 32, i.e. 8192 tubes-of-
response 28.
Referring now to Figure 1c, in general, the detectors 6 at the ends of the
tubes-of response 28 will be selected such that groups of tubes-of response
run
in parallel to one another, and such that tubes-of-response of different
groups
are not parallel. In the present example there would be 256 groups of 32
parallel
tubes-of-response, with the angles between the tubes-of-response in
consecutive, adjacent groups being 360/256 degrees.
Referring now to Figure 2b in addition to Figures 1 a, 1 b and 1 c, a pseudo
inverse matrix P+ 30 is disclosed wherein each tube-of response 28
corresponds to a column 32 of the pseudo inverse matrix P+ 30. For an image
of 64 X 64 = 4096 pixels, column 32 comprises 64 X 64 = 4096 elements 34
respectively relating a coincident event that has occurred in the associated
tube-
of-response to the 4096 pixels of the image. Therefore, the pseudo inverse
matrix P+ 30 for a given ring 14 of detectors 6 in the preferred embodiment
consists of 8192 columns and 4096 rows. The number of pixels may be safely
reduced for a given image grid by not taking into account the pixels at the
corners of the square image grid during the computation of the system matrix;
see V.V. Selivanov, Y. Picard, J. Cadorette, S. Rodrigue & R. Lecomte,
"Detector response models for statistical iterative image reconstruction in
high
resolution PET", IEEE Trans. Nucl. Sci., vol. 47, No. 3, pp. 1168-1175, 2000.
CA 02360656 2001-10-31
23
The index of the tube-of-response 28 of the coincident event 26 detected
at time TO has a one to one correspondence with a column 32 of the pseudo
inverse matrix P+ 30. The image prior to TO 36 is used as basis for the first
updated image 38 which is derived by adding the image prior to TO 36 to the
column 32 of the pseudo inverse matrix P+ 30 corresponding to the coincident
event 26.
A second coincident event 40 is detected at time T1. The index of the tube-
of response 42 of the second coincident event 40 detected at time T1 has a one
to one correspondence with a second column 44 of the pseudo inverse matrix
P+ 30. The updated image 38 is used as basis for the second updated image
46 which is derived by adding the updated image 38 to the second column 44
of the pseudo inverse matrix P+ 30 corresponding to the second coincident
event 40.
Continuing in a similar fashion, a third coincident event 48 is detected at
time T2. The index of the tube-of response 50 of this third coincident event
48
detected at time T2 has a one to one correspondence with a third column 52 of
the pseudo inverse matrix P+ 30. The second updated image 46 is used as
basis for the third updated image 54 which is derived by adding the second
updated image 46 to the third column 52 of the pseudo inverse matrix P+ 30
corresponding to the third coincident event 48.
Corrections of ~nro~iection data
In order to provide the most accurate rendition of the tomographic image,
it is appropriate to take into account physical factors and factors related to
particular instruments that affect the measurement of the projection data
during
CA 02360656 2001-10-31
24
image reconstruction. Factors including the spatially variant system response
and the model of the emission and detection processes can be taken into
account when generating the system matrix. Other factors related to the
specific
instrument being used as well as the subject under study, such as the
normalization of detector efficiency or correction for signal attenuation in
tissue
(e.g., photon attenuation in the case of emission tomography), can be included
by multiplying the elements of regularized pseudo-inverse matrix P+ by
appropriate factors, either before reconstruction or on the fly during
reconstruction. The updating Equation (20) will change slightly in the case of
correction on the fly:
x(S)(t)=~Cks)(t): xks)(t)=xk~t-1~+FS x per, k=1,...,M (22)
where FS is the correction factor assigned to the tube-of response s.
Similarly, random coincidence events in PET could be accounted for by
subtracting one column of matrix P+ from the previous image estimate:
x(S)(t)- t"kS)ltl: xks)(t)=xk~t-1~-p,~, k=1....,M (23)
or, instead, by skipping the next column addition given by Equation (20) when
the next coincident event is registered. In the case of correction on the fly,
Equation (23) would be replaced by:
x(S)~t~=~xks)(t~: xks)(t)=xk~t-1)-FS x per, k=1,...,M (24)
CA 02360656 2001-10-31
Hardware implementation
The reconstruction of tomographic images using the above method can
be implemented as a sum of two vectors representing the previous image
5 estimate and the current update from a new measured event or additional
single
(or individual) projection data. Additionally, it may be necessary to adjust
the
value of the current vector by multiplying it by a correction factor prior to
addition
to the previous image estimate. As discussed above, the correction factor
serves
to take into account any physical irregularities or irregularities in
instrumentation.
Preferably, data processing is performed in an environment supporting
floating point arithmetic to satisfy requirements as to precision, although in
some
special cases integer, or fixed point, arithmetic may be used. One major
consideration which inevitably arises when attempting to carry out
calculations
in a fixed point environment is scaling. Scaling is necessary to maintain
accuracy
when a high resolution is required for signals having a wide dynamic range.
Additionally, there is the possibility of value overflow due to the limited
number
of bits used for the integer representation. Due to this, quantization from
regions-
of-interest in the reconstructed image is preferably carried out using
floating
point arithmetic to avoid overflow and ensure the required precision.
Real-time reconstruction subjects the processing of data to the additional
constraint that the time necessary to reconstruct the image must be less than
the
average time between successive events. This includes the time necessary for
retrieving the column of matrix P+ defined by the bin index of the current
coincident event, multiplying the column by a correction factor if necessary,
adding the M elements of the column to the previous image estimate and finally
storing the updated image.
Depending on the manner in which projection data is being generated by
CA 02360656 2001-10-31
26
the tomographic scanner, data may be acquired in one of two different ways,
sequentially or randomly.
In the sequential acquisition mode, the measuring instrument sequentially
supplies projection data which is measured only once in each projection bin. X-
ray CT scanners and ultrasound probes are examples of tomographic scanners
which fall into this category. In these cases the average time between events
is
determined by the scanning speed of the instrument, and is typically in the
millisecond range or more. Data processing in these cases may be performed
using a general-purpose computer.
In the random acquisition mode events are registered randomly in all
available projection bins. SPECT and PET scanners, which operate in counting
mode, are examples of tomographic scanners which fall into this category.
Assuming a peak event rate of one million counts per second, the processing of
data would have to be terminated in less than one microsecond. For a
relatively
small 2D image (e.g., 64x64 pixels, M=4096), the requisite computational speed
can merely be reached with current general-purpose computer technology by
clever implementation of the algorithm. Additionally, the system matrix P+,
having dimensions N x M, must also be loaded into main memory for fast
access. Although extending the reconstruction to larger image sizes or 3D
imaging geometry makes such implementation impractical with the current
computer technology, this should become feasible in the foreseeable future
given the constant increase in both memory capacity and processing speed.
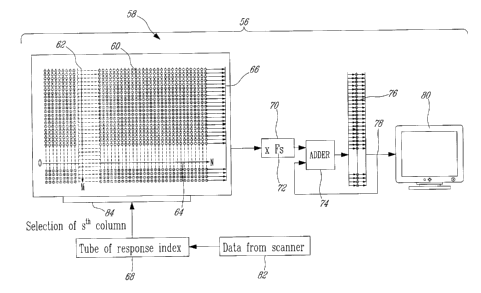
Referring now to Figure 3, a schematic diagram of a preferred image
processing subsystem 56 in accordance with the present invention is disclosed.
The image processing subsystem 56 may implement a high level of parallel
processing and storage capacity necessary to efficiently perform the data
processing required by the real-time reconstruction of tomographic images
CA 02360656 2001-10-31
27
based on the matrix pseudo-inverse method. The image processing subsystem
56 can be implemented using general purpose high-performance processors,
Digital Signal Processors (DSP), programmable logic devices (e.g., Field
Programmable Gate Arrays or FPGA) or application specific integrated circuits
(ASIC) by persons of ordinary skill in the art.
In the preferred embodiment of Figure 3, a memory unit 58 of the image
processing subsystem 56 is provided for storing the above mentioned pseudo
inverse matrix P+ 30. This memory unit 58 comprises a large number of sixty-
four (64) bit memory locations 60 arranged in an array of 8192 columns 62 and
4096 rows 64. As indicated in the foregoing description, each of the 8192
tubes-
of response such as 28 in Figures 1 a, 1 b and 1 c of the PET scanner (not
shown)
is associated to a respective one of the 8192 columns of the memory unit 58.
Each column 62 comprises 4096 memory locations 60 to relate a coincident
event that has occurred in the associated tube-of response to the 4096 pixels
(or
voxels) of the image. In operation, an index 68 associated to a tube-of-
response
in which a coincident event has occurred is supplied as data 82 from a PET
scanner (not shown). This index 68 is placed in an address register 84 which
causes the image data from the column 62 corresponding to the tube-of-
response index 68 to be placed on a data bus 66 for transfer to an optional
multiplying unit 70. The image data received in the multiplying unit 70 via
the
data bus 66 is multiplied by a factor 72 (see correction factor Fs of Equation
(23)) prior to its transfer to an adder 74. In the adder 74 the image data
received
from the multiplying unit 70 is used to update the image in an image buffer
76.
The contents of the image buffer 76 are made available via a display unit bus
78
to a display unit 80.
Results
A series of PET scans were performed on a high-resolution animal
CA 02360656 2001-10-31
28
tomograph. The PET scanner consisted of 2 rings of 256 BGO crystals
individually coupled to avalanche photodiodes. Referring now to Figure 4, the
singular value spectrum of the system matrix P for the above PET scanner and
an image of 64x64 pixels in 2D is shown. In this case, the matrix condition
number c is equal to 4441.5.
Sequences of images demonstrating the use of real time TSVD
reconstruction are presented in both Figure 5 and Figure 6. Data was acquired
using a phantom of 110 mm diameter fabricated from Lucite~. Holes having
diameters of 2, 3.4, 6.7, 9.7, 13, 15.8, 20.3, 22.7 mm and located on a
circumference at a distance of 28 mm from the center were machined in the
phantom. Each hole was then filled with 18F-fluorodeoxyglucose, placed inside
the PET scanner and the image of the acquired events reconstructed.
Referring to Figure 5, proceeding from left to right and from top to bottom
each successive image is reconstructed from approximately 23800 additional
counts (i.e. coincident events) in comparison to the number of counts used to
reconstruct the previous image estimate. In Figure 5 the coincident events
were
detected randomly at all angles by a ring of detectors.
Referring now to Figure 6 an image reconstructed from the same data as
that used in Figure 5 is disclosed. However, instead of proceeding
sequentially
in time the images are rendered using all the coincident data recorded by a
detector bank, i.e. a subset of detectors, each detector in a given detector
bank
being selected such that pairs of detectors within the bank define parallel,
or
almost parallel, tubes-of-response. Proceeding from left to right and top to
bottom, each successive image is reconstructed from approximately 29,750
additional counts (i.e. coincident events) in comparison to the number of
counts
used to reconstruct the previous image estimate, with the counts used in each
successive image being detected by a eight (8) new detector banks as described
above. The selection of detector banks is such that the angle of the
coincident
CA 02360656 2001-10-31
29
events rotated around the phantom, which allows data from a progressively
increasing number of incidence angles to be included in the image
reconstruction. At the outset of image reconstruction, therefore, only one or
a
few angles along one direction are available which gives rise to streaking
artifacts appearing across the reconstructed image along the direction of
incidence. Referring to the initial series of reconstructed images in Figure
6,
these artifacts are quite visible. As the image reconstruction progresses with
data recorded from successive detector banks being added image detail is
increased. In order to achieve good results, projection angles through 180
degrees are generally required.
In both Figures 5 and 6, less than 1/3 of the singular value spectrum was
used. An approach for singular value spectrum truncation based on spatial
resolution analysis may be found in V. Selivanov & R. Lecomte, "Fast PET
image reconstruction based on SVD decomposition of the system matrix", ",
IEEE Trans. Nucl. Sci., vol. 48, no. 3, pp. 761-767, 2001.
Discussion of application in medical imac~in4
The SVD of the system matrix, apart from precise numerical diagnostics
of the tomographic reconstruction ill-conditioning with a given detection
system
geometry, provides a linear and very fast reconstruction means. It should be
pointed out that there are other means of obtaining the inverse system matrix,
for example, through direct analytical inversion of the Radon transform for
individual projection data. The image of the filtered backprojected data,
which
represents the contribution of an individual event to the FBP reconstructed
image, can be used as the corresponding column of the inverse system matrix,
and the set of images of filtered backprojected data for all projections
define the
inverse system matrix.
CA 02360656 2001-10-31
Singular value spectrum truncation allows separation of the signal and
noise at the reconstruction step. Index T, as discussed above, determines the
trade-off between noise and resolution. Truncation of the singular spectrum is
not the only way of solution regularization. Spectrum modification without
5 truncation may be an appropriate regularizing approach in some situations.
It is
possible as well that in some special situations, when the system matrix
corresponding to a particular tomographic system is sufFciently well
conditioned,
no SVD pseudo-inversion is necessary and direct matrix inversion will be
feasible.
TSVD reconstruction however has some drawbacks: negative values in
the image estimate, streak artifacts with low-count images if the index T is
lower
than a certain threshold value or noise artifacts if T is higher than the
threshold
value. But these features (except for the noise artifacts with high T, which
is
analogous to the artifact developing with high iteration numbers when
unconstrained iterative image estimation is performed) are also common to FBP
image reconstruction, the most popular method used in medical practice today.
Regardless of its drawbacks, TSVD (as well as MSVD) displays some
very attractive benefits:
1 ) A spatially variant system response and model of the signal emission and
detection processes can be easily included into image reconstruction
through the system matrix;
2) Data rebinning is unnecessary since the geometry of a given system is
utilized;
3) The resolution in reconstructed images may be adjusted, based on the
spatial resolution analysis in reconstructed images, by varying the
truncation index T (or modifying the singular value spectrum in the MSVD
CA 02360656 2001-10-31
31
case);
4) Noise amplification may be controlled by varying the truncation index T
(or modifying the singular value spectrum in the MSVD case);
5) Image reconstruction can be performed in real time, on an event-by-event
or projection-by-projection basis, allowing for instant visualization of the
radioactivity distribution while the subject is being scanned; and
6) Since the measured projection data can be reconstructed "on the fly" as
soon as acquired by the scanner, storage of the measured data or
intermediary calculation results, except for the image estimate being
updated, is unnecessary, thus allowing for optimal compression of the
tomographic data.
Although the present invention has been described hereinabove by way
of a preferred embodiment thereof, this embodiment can be modified at will,
within the scope of the present invention, without departing from the spirit
and
nature of the subject of the present invention. Moreover, the application of
the
present invention is not limited to medical imaging only, but has possible
applications in other imaging techniques utilizing tomographic principles and
image reconstruction from projections.